专题检测卷二(选择) 答案及解析

合集下载

人教版2018-2019学年度高二生物选修三专题2 细胞工程检测试卷(含答案详解)

人教版2018-2019学年度高二生物选修3专题2检测卷一、选择题1.若获得脱毒苗，一般选取植物体的哪一部分组织()A．叶 B．花粉 C．根 D．茎尖2.从母羊甲的体细胞中取出细胞核，注入到母羊乙的去核卵细胞中，融合后的细胞经卵裂形成早期胚胎，再植入到另一只母羊丙的子宫内，出生小羊的大多数性状() A．像甲 B．像乙 C．像丙 D．难以预测3.下列有关植物细胞与组织培养的叙述中，错误的是()A．花药、胚等不能作为组织培养的材料B．植物细胞具有全能性C．外植体是指用于培养的植物组织或器官D．外植体可诱导出愈伤组织4.玉米是一种重要的农作物，为了提高玉米的产量，科学家在玉米育种中和栽培中作了大量的研究。

如图是关于玉米培养的过程，据图判断下列说法中错误的是()A．从繁殖原理上分析，A→D属于无性生殖B．植株D和G中的染色体组数不同C．E→G不能体现细胞的全能性D．E→F过程中获得的植株一般没有直接的使用价值(即应用于大田生产)5.利用细胞工程方法，以SARS病毒核衣壳蛋白为抗原制备出单克隆抗体。

下列相关叙述正确的是()A．用纯化的核衣壳蛋白反复注射到小鼠体内，产生的血清抗体为单克隆抗体B．体外培养单个B淋巴细胞可以获得大量针对SARS病毒的单克隆抗体C．将等量B淋巴细胞和骨髄瘤细胞混合，经PEG诱导融合后的细胞均为杂交瘤细胞D．利用该单克隆抗体与SARS病毒核衣壳蛋白特异性结合的方法可诊断出病毒感染者6.下列细胞全能性最高的是()A．玉米的卵细胞 B．哺乳动物的精子C．绿色开花植物的受精卵 D．裸子植物的叶肉细胞7.下列动物细胞中，恢复其全能性相对较容易的是()A．神经细胞 B．骨细胞 C．囊胚期细胞 D．肝细胞8.超氧化物歧化酶(SOD)是一种源于生命体的活性物质，在生活实践中有非常重要的应用价值。

下图为人工培育含SOD植物新品种的过程，相关叙述正确的是()A．①过程中最常用的方法是采用显微注射技术将SOD基因导入植物细胞B．②、③分别表示脱分化、再分化过程，均无需严格的无菌操作就可以完成C．SOD催化O2形成H2O2的机制是为该反应提供活化能－D．该育种方式利用了细胞工程和基因工程，能体现细胞的全能性9.关于植物组织培养技术的叙述正确的是()A．用于培养的材料不一定需要离体B．植物可通过光合作用合成有机物，培养基中不需加入含碳有机物C．愈伤组织可制造成人工种子D．脱分化和再分化都需要培养基中生长素和细胞分裂素刺激、诱导10.以下描述正确的一组是()①植物组织培养是指离体的植物器官或细胞培养成愈伤组织②从免疫学的应用来看，给儿童服用小儿麻痹糖丸属于免疫预防③动物细胞工程常用的技术手段中，最基础的是动物细胞培养④动物细胞融合技术的最重要的用途是培养具双亲优良性状的经济动物A．①②④ B．②③ C．③④ D．①④11.下图示“番茄—马铃薯”杂种植株的培育过程，其中①～⑤表示过程，字母表示细胞、组织或植株。

七年级数学上册期中检测试卷2(含答案解析)

七年级数学上册期中检测试卷2（含答案解析）一、选择题（每小题2分，共16分，请把正确答案填入下面对应表格中）1．下列各数中，绝对值最大的数是( )A．﹣3 B．﹣2 C．0 D．12．下列各式中不是整式的是( )A．3x B．C．D．x﹣3y3．下列各组数中，互为相反数的是( )A．﹣（﹣2）与2 B．（﹣2）2与4 C．|﹣2|与2 D．﹣22与44．若﹣3x2m y3与2x4y n是同类项，则|m﹣n|的值是( )A．0 B．1 C．7 D．﹣15．如图，数轴上的A、B、C三点所表示的数分别为a、b、c，AB=BC，如果|a|＞|c|＞|b|，那么该数轴的原点O的位置应该在( )A．点A的左边B．点A与点B之间C．点B与点C之间D．点C的右边6．下列根据等式基本性质变形正确的是( )A．由﹣x=y，得x=2y B．由3x﹣2=2x+2，得x=4C．由2x﹣3=3x，得x=3 D．由3x﹣5=7，得3x=7﹣57．如图，是李明同学在求阴影部分的面积时，列出的4个式子，其中错误的是( )A．ab+（c﹣a）a B．ac+（b﹣a）a C．ab+ac﹣a2D．bc+ac﹣a28．一个长方形的周长为26cm，这个长方形的长减少1cm，宽增加2cm，就可成为一个正方形，设长方形的长为xcm，则可列方程( )A．x﹣1=（26﹣x）+2 B．x﹣1=（13﹣x）+2 C．x+1=（26﹣x）﹣2 D．x+1=（13﹣x）﹣2二、填空题（每小题2分，共16分）9．在一条东西走向的跑道上，设向东的方向为正方形，如果小芳向东走了8m，记作“+8m”，那么她向西走了10m，应该记作__________．10．对单项式“0.8a”可以解释为：一件商品原价为a元，若按原价的8折出售，这件商品现在的售价是0.8a 元，请你对“0.8a”再赋予一个含义：__________．11．2015年初，一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞越，将300000用科学记数法表示为__________．12．已知x2+3x+5的值是7，则式子x2+3x﹣2的值为__________．13．若关于x的方程（2a+1）x2+5x b﹣2﹣7=0是一元一次方程，则方程ax+b=0的解是__________．14．若多项式2x3﹣8x2+x﹣1与多项式3x3+2mx2﹣5x+3相加后不含二次项，则m的值为__________．15．李明与王伟在玩游戏，游戏的规则是=ad﹣bc，李明计算，根据规则=3×1﹣2×5=3﹣10=﹣7，现在轮到王伟计算，请你帮忙算一算，其结果是__________．16．《庄子．天下篇》中写道：“一尺之棰，日取其半，万世不竭”意思是：一根一尺的木棍，如果每天截取它的一半，永远也取不完，如图．由图易得：=__________．三、解答题（17题10分，18、19题各6分，共22分）17．（1）计算：（﹣4）2×[（﹣）+（﹣）]（2）计算：﹣22﹣（1﹣0.5）××[2﹣（﹣4）2]．18．化简，求值．已知：（a+2）2+|b﹣3|=0，求（ab2﹣3）+（7a2b﹣2）+2（ab2+1）﹣2a2b的值．19．解方程：=3x﹣．四、解答题（每小题8分，共24分）20．有8筐白菜，以每筐25千克为标准，超过的千克数记作正数，不足的千克数记作负数，称后的记录如下：回答下列问题：（1）这8筐白菜中最接近标准重量的这筐白菜重__________千克；（2）与标准重量比较，8筐白菜总计超过或不足多少千克？（3）若白菜每千克售价2.6元，则出售这8筐白菜可卖多少元？21．已知多项式+2xy2﹣4x3+1是六次四项式，单项式26x2n y5+m的次数与该多项式的次数相同，求（﹣m）3+2n的值．22．关于x的方程x﹣2m=﹣3x+4与2﹣m=x的解互为相反数．求m的值．五、23．小华在课外书中看到这样一道题：计算：（）+（）．她发现，这个算式反映的是前后两部分的和，而这两部分之间存在着某种关系，利用这种关系，她顺利地解答了这道题（1）前后两部分之间存在着什么关系？（2）先计算哪部分比较简便？并请计算比较简便的那部分．（3）利用（1）中的关系，直接写出另一部分的结果．（4）根据以上分析，求出原式的结果．六、列方程解应用题24．假期里，某学校组织部分学生参加社会实践活动，分乘大、小两辆车去农业科技园区体验生活，早晨6点钟出发，计划2小时到达；（1）若大车速度为80km/h，正好可以在规定时间到达，而小车速度为100km/h，如果两车同时到达，那么小车可以晚出发多少分钟？（2）若小车每小时能比大车多行30千米，且大车在规定时间到达，小车要提前30分钟到达，求大、小车速度．（3）若小车与大车同时以相同速度出发，但走了20分钟以后，发现有物品遗忘，小车准备返回取物品，若小车仍想与大车同时在规定时间到达，应提速到原来的多少倍？2015-2016学年辽宁省鞍山市台安县七年级（上）期中数学试卷一、选择题（每小题2分，共16分，请把正确答案填入下面对应表格中）1．下列各数中，绝对值最大的数是( )A．﹣3 B．﹣2 C．0 D．1【考点】绝对值；有理数大小比较．【分析】根据绝对值是实数轴上的点到原点的距离，可得答案．【解答】解：|﹣3|＞|﹣2|＞|1|＞|0|，故选：A．【点评】本题考查了绝对值，绝对值是实数轴上的点到原点的距离．2．下列各式中不是整式的是( )A．3x B．C．D．x﹣3y【考点】整式．【分析】根据单项式与多项式统称为整式，根据整式及相关的定义解答即可．【解答】解：A、3x是单项式，是整式，故A不符合题意；B、既不是单项式，又不是多项式，不是整式，故B符合题意；C、是单项式，是整式，故C不符合题意；D、x﹣3y是多项式，是整式，故D不符合题意．故选：B．【点评】本题主要考查整式的相关的定义，解决此题的关键是熟记整式的相关定义．3．下列各组数中，互为相反数的是( )A．﹣（﹣2）与2 B．（﹣2）2与4 C．|﹣2|与2 D．﹣22与4【考点】相反数；有理数的乘方．【分析】利用化简符号法则，绝对值的性质，有理数的乘方，以及只有符号不同的两个数叫做互为相反数对各选项分析判断后利用排除法求解．【解答】解：A、﹣（﹣2）=2，不是互为相反数，故本选项错误；B、（﹣2）2=4，不是互为相反数，故本选项错误；C、|﹣2|=2，不是互为相反数，故本选项错误；D、﹣22=﹣4，﹣4与4互为相反数，故本选项正确．故选D．【点评】本题考查了相反数的定义，绝对值的性质，有理数的乘方，是基础题，熟记概念是解题的关键．4．若﹣3x2m y3与2x4y n是同类项，则|m﹣n|的值是( )A．0 B．1 C．7 D．﹣1【考点】同类项．【分析】根据同类项的定义得出2m=4，n=3，求出后代入，即可得出答案．【解答】解：∵﹣3x2m y3与2x4y n是同类项，∴2m=4，n=3，∴m=2，∴|m﹣n|=|2﹣3|=1，故选B．【点评】本题考查了同类项的定义的应用，注意：所含字母相同，并且相同字母的指数也分别相等的项，是同类项．5．如图，数轴上的A、B、C三点所表示的数分别为a、b、c，AB=BC，如果|a|＞|c|＞|b|，那么该数轴的原点O的位置应该在( )A．点A的左边B．点A与点B之间C．点B与点C之间D．点C的右边【考点】实数与数轴．【分析】根据绝对值是数轴上表示数的点到原点的距离，分别判断出点A、B、C到原点的距离的大小，从而得到原点的位置，即可得解．【解答】解：∵|a|＞|c|＞|b|，∴点A到原点的距离最大，点C其次，点B最小，又∵AB=BC，∴原点O的位置是在点B、C之间且靠近点B的地方．故选C．【点评】本题考查了实数与数轴，理解绝对值的定义是解题的关键．6．下列根据等式基本性质变形正确的是( )A．由﹣x=y，得x=2y B．由3x﹣2=2x+2，得x=4C．由2x﹣3=3x，得x=3 D．由3x﹣5=7，得3x=7﹣5【考点】等式的性质．【分析】根据等式的性质1，等式的两边都加或减同一个整式，结果不变，根据等式的性质2，等式的两边都乘或除以同一个不为零的整式，结果不变，可得答案．【解答】解：A、等是左边乘以﹣﹣3，右边乘以3，故A错误；B、等式的两边都加（2﹣2x），得x=4，故B正确；C、等式的两边都减2x，得x=﹣﹣3，故C错误；D、等式的两边都加5，得3x=7+5，故D错误；故选：B．【点评】本题考查了等式的性质，利用了等式的性质1，等式的性质2．7．如图，是李明同学在求阴影部分的面积时，列出的4个式子，其中错误的是( )A．ab+（c﹣a）a B．ac+（b﹣a）a C．ab+ac﹣a2D．bc+ac﹣a2【考点】列代数式．【专题】计算题；整式．【分析】根据图形表示出阴影部分面积，化简得到结果，即可作出判断．【解答】解：根据题意得：阴影部分面积S=ab+a（c﹣a）=ac+a（b﹣a）=ab+ac﹣a2．故选D．【点评】此题考查了列代数式，正确表示出阴影部分面积是解本题的关键．8．一个长方形的周长为26cm，这个长方形的长减少1cm，宽增加2cm，就可成为一个正方形，设长方形的长为xcm，则可列方程( )A．x﹣1=（26﹣x）+2 B．x﹣1=（13﹣x）+2 C．x+1=（26﹣x）﹣2 D．x+1=（13﹣x）﹣2【考点】由实际问题抽象出一元一次方程．【专题】几何图形问题．【分析】首先理解题意找出题中存在的等量关系：长方形的长﹣1cm=长方形的宽+2cm，根据此列方程即可．【解答】解：设长方形的长为xcm，则宽是（13﹣x）cm，根据等量关系：长方形的长﹣1cm=长方形的宽+2cm，列出方程得：x﹣1=（13﹣x）+2，故选B．【点评】列方程解应用题的关键是找出题目中的相等关系，有的题目所含的等量关系比较隐藏，要注意仔细审题，耐心寻找．二、填空题（每小题2分，共16分）9．在一条东西走向的跑道上，设向东的方向为正方形，如果小芳向东走了8m，记作“+8m”，那么她向西走了10m，应该记作﹣10m．【考点】正数和负数．【分析】首先审清题意，明确“正”和“负”所表示的意义；在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．【解答】解：正”和“负”相对，所以向东是正，则向西就是负，因而向西运动10m应记作﹣10m．故答案为：﹣10m．【点评】此题考查了正数和负数，解题关键是理解“正”和“负”的相对性，确定一对具有相反意义的量．10．对单项式“0.8a”可以解释为：一件商品原价为a元，若按原价的8折出售，这件商品现在的售价是0.8a 元，请你对“0.8a”再赋予一个含义：练习本每本0.8元，小明买了a本，共付款0.8a元（答案不唯一）．【考点】代数式．【专题】开放型．【分析】根据生活实际作答即可．【解答】解：答案不唯一，例如：练习本每本0.8元，小明买了a本，共付款0.8a元．【点评】本题考查了代数式的意义，此类问题应结合实际，根据代数式的特点解答．11．2015年初，一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞越，将300000用科学记数法表示为3×105．【考点】科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：将300000用科学记数法表示为：3×105．故答案为：3×105．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．12．已知x2+3x+5的值是7，则式子x2+3x﹣2的值为0．【考点】代数式求值．【分析】首先根据已知列出方程x2+3x+5=7，通过移项推出x2+3x=2，通过代入式子即可推出结果为0．【解答】解：∵x2+3x+5=7，∴x2+3x=2，∴x2+3x﹣2=2﹣2=0．故答案为0．【点评】本题主要考查代数式的求值，关键在于根据已知推出x2+3x=2．13．若关于x的方程（2a+1）x2+5x b﹣2﹣7=0是一元一次方程，则方程ax+b=0的解是x=6．【考点】一元一次方程的定义．【分析】根据一元一次方程的定义可知2a+1=0，b﹣2=1，从而得到a、b的值，然后将a、b的值代入方程ax+b=0求解即可．【解答】解：∵关于x的方程（2a+1）x2+5x b﹣2﹣7=0是一元一次方程，∴2a+1=0，b﹣2=1．解得：a=﹣，b=3．将a=﹣，b=3代入ax+b=0得：﹣x+3=0．解得x=6．故答案为：x=6．【点评】本题主要考查的是一元一次方程的定义，由一元一次方程的定义得到2a+1=0，b﹣2=1是解题的关键．14．若多项式2x3﹣8x2+x﹣1与多项式3x3+2mx2﹣5x+3相加后不含二次项，则m的值为4．【考点】整式的加减．【分析】先把两式相加，合并同类项得5x3﹣8x2+2mx2﹣4x+2，不含二次项，即2m﹣8=0，即可得m的值．【解答】解：据题意两多项式相加得：5x3﹣8x2+2mx2﹣4x+2，∵相加后结果不含二次项，∴当2m﹣8=0时不含二次项，即m=4．【点评】本题主要考查整式的加法运算，涉及到二次项的定义知识点．15．李明与王伟在玩游戏，游戏的规则是=ad﹣bc，李明计算，根据规则=3×1﹣2×5=3﹣10=﹣7，现在轮到王伟计算，请你帮忙算一算，其结果是8．【考点】有理数的混合运算．【专题】计算题；新定义．【分析】原式利用已知的新定义计算即可得到结果．【解答】解：根据题意得：原式=2×（﹣5）﹣3×（﹣6）=﹣10+18=8．故答案为：8．【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．16．《庄子．天下篇》中写道：“一尺之棰，日取其半，万世不竭”意思是：一根一尺的木棍，如果每天截取它的一半，永远也取不完，如图．由图易得：=1﹣．【考点】规律型：图形的变化类．【专题】规律型．【分析】由图可知第一次剩下，截取1﹣；第二次剩下，共截取1﹣；…由此得出第n次剩下，共截取1﹣，得出答案即可．【解答】解：=1﹣故答案为：1﹣．【点评】此题考查图形的变化规律，找出与数据之间的联系，得出规律解决问题．三、解答题（17题10分，18、19题各6分，共22分）17．（1）计算：（﹣4）2×[（﹣）+（﹣）]（2）计算：﹣22﹣（1﹣0.5）××[2﹣（﹣4）2]．【考点】有理数的混合运算．【专题】计算题．【分析】（1）原式先计算乘方运算，再利用乘法分配律计算即可；（2）原式先计算乘方运算，再计算乘法运算，最后算加减运算即可．【解答】解：（1）原式=16×（﹣﹣）=﹣12﹣10=﹣22；（2）原式=﹣4﹣××（﹣14）=﹣4+=﹣1．【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．18．化简，求值．已知：（a+2）2+|b﹣3|=0，求（ab2﹣3）+（7a2b﹣2）+2（ab2+1）﹣2a2b的值．【考点】整式的加减—化简求值．【专题】计算题．【分析】原式去括号合并得到最简结果，利用非负数的性质求出a与b的值，代入计算即可求出值．【解答】解：原式=ab2﹣1+7a2b﹣2+2ab2+2﹣2a2b=ab2+5a2b﹣1，∵（a+2）2+|b﹣3|=0，∴a+2=0，b﹣3=0，即a=﹣2，b=3，则原式=﹣42+60﹣1=17．【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．19．解方程：=3x﹣．【考点】解一元一次方程．【专题】计算题；一次方程（组）及应用．【分析】方程去分母，去括号，移项合并，把x系数化为1，即可求出解．【解答】解：去分母得2（2x﹣1）﹣2×6=18x﹣3（x+4），去括号得4x﹣2﹣12=18x﹣3x﹣12，移项得4x﹣18x+3x=2+12﹣12，合并同类项得﹣11x=2，系数化成1得x=﹣．【点评】此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．四、解答题（每小题8分，共24分）20．有8筐白菜，以每筐25千克为标准，超过的千克数记作正数，不足的千克数记作负数，称后的记录如下：回答下列问题：（1）这8筐白菜中最接近标准重量的这筐白菜重﹣0.5千克；（2）与标准重量比较，8筐白菜总计超过或不足多少千克？（3）若白菜每千克售价2.6元，则出售这8筐白菜可卖多少元？【考点】正数和负数．【分析】（1）根据绝对值的意义，绝对值越小越接近标准，可得答案；（2）根据有理数的加法运算，可得答案；（3）根据单价乘以数量等于总价，可得答案．【解答】解：（1）∵|﹣3|＞|﹣2.5|＞|﹣2|=|2|＞|1.5|＞|1|＞|﹣0.5|，∴﹣0.5的最接近标准．故答案为：﹣0.5千克；（2）由题意，得1.5+（﹣3）+2+（﹣0.5）+1+（﹣2）+（﹣2）+（﹣2.5）=﹣5.5（千克）．答：与标准重量比较，8筐白菜总计不足5.5千克；（3）由题意，得（25×8﹣5.5）×2.6=194.5×2.6=505.7（元）．答：出售这8筐白菜可卖505.7元．【点评】本题考查了正数和负数，利用了绝对值的意义，有理数的加法运算．21．已知多项式+2xy2﹣4x3+1是六次四项式，单项式26x2n y5+m的次数与该多项式的次数相同，求（﹣m）3+2n的值．【考点】多项式；单项式．【分析】利用多项式与单项式的次数与系数的确定方法得出关于m与n的等式进而得出答案．【解答】解：由于多项式是六次四项式，所以m+1+2=6，解得：m=3，单项式26x2n y5﹣m应为26x2n y2，由题意可知：2n+2=6，解得：n=2，所以（﹣m）3+2n=（﹣3）3+2×2=﹣23．【点评】此题主要考查了多项式与单项式的次数，正确得出m，n的值是解题关键．22．关于x的方程x﹣2m=﹣3x+4与2﹣m=x的解互为相反数．求m的值．【考点】一元一次方程的解．【专题】计算题．【分析】将m看做已知数分别表示出两方程的解，根据互为相反数两数之和为0列出关于m的方程，求出方程的解即可得到m的值．【解答】解：x﹣2m=﹣3x+4，移项合并得：4x=2m+4，解得：x=m+1，根据题意得：m+1+2﹣m=0，解得：m=6．【点评】此题考查了一元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．五、23．小华在课外书中看到这样一道题：计算：（）+（）．她发现，这个算式反映的是前后两部分的和，而这两部分之间存在着某种关系，利用这种关系，她顺利地解答了这道题（1）前后两部分之间存在着什么关系？（2）先计算哪部分比较简便？并请计算比较简便的那部分．（3）利用（1）中的关系，直接写出另一部分的结果．（4）根据以上分析，求出原式的结果．【考点】有理数的除法．【分析】（1）根据倒数的定义可知：（）与（）互为倒数；（2）利用乘法的分配律可求得（）的值；（3）根据倒数的定义求解即可；（4）最后利用加法法则求解即可．【解答】解：（1）前后两部分互为倒数；（2）先计算后一部分比较方便．（）=（）×36=9+3﹣14﹣1=﹣3；（3）因为前后两部分互为倒数，所以（）=﹣；（4）根据以上分析，可知原式==﹣3．【点评】本题主要考查的是有理数的乘除运算，发现（）与（）互为倒数是解题的关键．六、列方程解应用题24．假期里，某学校组织部分学生参加社会实践活动，分乘大、小两辆车去农业科技园区体验生活，早晨6点钟出发，计划2小时到达；（1）若大车速度为80km/h，正好可以在规定时间到达，而小车速度为100km/h，如果两车同时到达，那么小车可以晚出发多少分钟？（2）若小车每小时能比大车多行30千米，且大车在规定时间到达，小车要提前30分钟到达，求大、小车速度．（3）若小车与大车同时以相同速度出发，但走了20分钟以后，发现有物品遗忘，小车准备返回取物品，若小车仍想与大车同时在规定时间到达，应提速到原来的多少倍？【考点】一元一次方程的应用．【专题】应用题．【分析】（1）计算出小车需要的时间，然后可得出可以晚出发的时间；（2）设大车速度为每小时x千米，则小车速度为每小时（x+30）千米，根据小车要提前30分钟到达，可得出方程，解出即可．（3）设原速度为a，小车提速到原来的m倍，根据仍按时到达可得出方程，解出即可．【解答】解：（1）总路程=80×2=160km，小车需要的时间为：=1.6（小时），故小车可以晚出发0.4小时，即24分钟，（2）设大车速度为每小时x千米，则2x=1.5（x+30），解得x=90，即大车速度为每小时90千米，小车速度为每小时120千米．（3）设原速度为a，小车提速到原来的m倍，根据题意得：a+2a=（2﹣）ma，解得：m=1.4，答：应提速到原来的1.4倍．【点评】本题考查了一元一次方程的应用，属于行程问题，解答本题的关键是仔细审题，找到等量关系，利用方程思想解答．。

专题02第二单元测试题卷及答案解析在线练习-2022-2023年部编人教版九年级初三语文中考总复习历

专题02第二单元测试题卷及答案解析在线练习-2022-2023年部编人教版九年级初三语文中考总复习历史上册同步单元AB卷-全国选择题“一提到希腊这个名字，在有教养的欧洲人心中……自然会引起一种家园之感。

”黑格尔之所以这样说，主要是因为古代希腊A.是欧洲文明B.法学系统完整C.神话影响广D.哲学成就突出【答案】A【解析】黑格尔的言论意在强调古希腊文明对后世欧洲的影响深远，所以黑格尔之所以这样说，是因为希腊文明可以看做欧洲文明的源头，古代希腊就是欧洲文明，故选A；法学系统完整的是古罗马，排除B；CD项无法体现出希腊文明的深远影响，排除。

故选A。

选择题如表所示内容体现了古代希腊城邦的特点是城邦面积（平方千米）人口（万）雅典2500 约30 斯巴达8400 约40 A.等级森严B.小国寡民C.自给自足D.军事独裁【答案】B【解析】考查点：古希腊城邦。

解题思路：雅典和斯巴达是古希腊诸多城邦中最有影响力的两个城邦。

分析图表可知，这两个城邦都是面积狭小，人口较少。

根据所学知识可知，希腊城邦一般是以一个城市或市镇为中心，把周围的农村联合起来，组成一个小国。

希腊城邦的突出特点是小国寡民。

B正确；雅典施行奴隶制民主，A错误；希腊是典型的海洋文明，商品经济发展。

自给自足是小农经济的特点，C错误；雅典不是独裁政治，且材料没有涉及到政治。

因此D错误。

综上故选B。

选择题英国浪漫主义诗人雪莱说：“我们全都是希腊人，我们的法律、我们的文学、我们的宗教，根源皆在希腊。

”该观点认为（）A.英国照抄了古希腊的文化B.古代希腊文明影响了西方文明的发展C.古代希腊人统治了世界D.近代西方的文化缺乏创新性【答案】B【解析】“根源皆在希腊”可以看出雪莱强调希腊文明对西方文明影响深远。

英国浪漫主义诗人雪莱这句话很显然是强调希腊文明对西方文明影响深远，所以B项符合题意；ACD三项都背离了原意，排除。

故选B。

选择题希腊雅典城邦的“民众法庭审判官由公民抓签选出，任期只有一年，每个公民一生中只能担任两次审判官的职务。

人教版初中八年级下册数学第十八章单元检测卷(2)(附答案解析)

第十八章卷（2）一、选择题1．如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）A．当AB=BC时，它是菱形B．当AC⊥BD时，它是菱形C．当∠ABC=90°时，它是矩形D．当AC=BD时，它是正方形2．下列命题中正确的是（）A．对角线互相平分的四边形是菱形B．对角线互相平分且相等的四边形是菱C．对角线互相垂直的四边形是菱形D．对角线互相垂直平分的四边形是菱形3．如图，某花木场有一块等腰梯形ABCD的空地，其各边的中点分别是E、F、G、H，测得对角线AC=10m，现想利用篱笆围成四边形EFGH场地，则需篱笆得总长度是（）A．40 m B．30 m C．20 m D．10 m4．在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC=10，BD=6，则该梯形的面积是（）A．30 B．15 C．D．605．如图，已知矩形ABCD中，R、P分别是DC、BC上的点，E、F分别是AP、RP 的中点，当P在BC上从B向C移动而R不动时，那么下列结论成立的是（）A．线段EF的长逐渐增大B．线段EF的长逐渐减小C．线段EF的长不改变D．线段EF的长不能确定6．已知一个直角梯形，一腰长为6，这腰与一底所成的角为30°，那么另一腰的长是（）A．1.5 B．3 C．6 D．97．如图所示，将一张正方形纸片对折两次，然后在上面打3个洞，则纸片展开后是（）A．B．C．D．8．用两个全等的直角三角形拼下列图形：①矩形；②菱形；③正方形；④平行四边形；⑤等腰三角形；⑥等腰梯形．其中一定能拼成的图形是（）A．①②③B．①④⑤C．①②⑤D．②⑤⑥二、填空题9．如图，在平行四边形ABCD中，DB=DC，∠C=70°，AE⊥BD于E，则∠DAE=度．10．如图，点E、F在▱ABCD的对角线BD上，要使四边形AECF是平行四边形，还需添加一个条件．（只需写出一个结论，不必考虑所有情况）．11．如图所示，工人师傅做铝合金窗框分下面三个步骤进行：(1)先截出两对符合规格的铝合金窗料（如图①所示），使AB=CD，EF=GH．(2)摆放成如图②的四边形，则这时窗框的形状是，根据的数学道理是．(3)将直尺紧靠窗框的一个角（如图③），调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图④，说明窗框合格，这时窗框是，根据的数学道理是．12．如图，菱形ABCD中，AC=2，BD=5，P是AC上一动点（P不与A、C重合），PE∥BC交AB于E，PF∥CD交AD于F，则图中阴影部分（即多边形BCPFEB）的面积为．13．如图所示，菱形ABCD中，对角线AC，BD相交于点O，若再补充一个条件能使菱形ABCD成为正方形，则这个条件是．（只填一个条件即可，答案不唯一）14．等腰梯形两底之差为12cm，高为6cm，则其锐角底角为度．15．若矩形的对角线长为8cm，两条对角线的一个交角为60°，则该矩形的面积为cm2．三、解答题16．已知：如图，在梯形ABCD中，AD∥BC，CD=10cm，∠B=45度，∠C=30度，AD=5cm．求：(1)AB的长；(2)梯形ABCD的面积．17．如图，在菱形ABCD中，∠A与∠B的度数比为1：2，周长是48cm．求：(1)两条对角线的长度；(2)菱形的面积．18．如图，在平行四边形ABCD中，E、F是AC上的两点，且AE=CF．求证：DE=BF．19．如图，在梯形ABCD中，AD∥BC，AB∥DE，AF∥DC，E、F两点在边BC上，且四边形AEFD是平行四边形．(1)AD与BC有何等量关系，请说明理由；(2)当AB=DC时，求证：平行四边形AEFD是矩形．20．如图，△ABC中，AC的垂直平分线MN交AB于点D，交AC于点O，CE∥AB交MN于E，连接AE、CD．请判断四边形ADCE的形状，说明理由．答案1．如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）A．当AB=BC时，它是菱形B．当AC⊥BD时，它是菱形C．当∠ABC=90°时，它是矩形D．当AC=BD时，它是正方形【考点】正方形的判定；平行四边形的性质；菱形的判定；矩形的判定．【专题】选择题．【分析】根据邻边相等的平行四边形是菱形；根据所给条件可以证出邻边相等；根据有一个角是直角的平行四边形是矩形；根据对角线相等的平行四边形是矩形．【解答】解：A、根据邻边相等的平行四边形是菱形可知：四边形ABCD是平行四边形，当AB=BC时，它是菱形，故A选项正确；B、∵四边形ABCD是平行四边形，∴BO=OD，∵AC⊥BD，∴AB2=BO2+AO2，AD2=DO2+AO2，∴AB=AD，∴四边形ABCD是菱形，故B选项正确；C、有一个角是直角的平行四边形是矩形，故C选项正确；D、根据对角线相等的平行四边形是矩形可知当AC=BD时，它是矩形，不是正方形，故D选项错误；综上所述，符合题意是D选项；故选D．【点评】此题主要考查学生对正方形的判定、平行四边形的性质、菱形的判定和矩形的判定的理解和掌握，此题涉及到的知识点较多，学生答题时容易出错．2．下列命题中正确的是（）A．对角线互相平分的四边形是菱形B．对角线互相平分且相等的四边形是菱C．对角线互相垂直的四边形是菱形D．对角线互相垂直平分的四边形是菱形【考点】菱形的判定．【专题】选择题．【分析】对角线互相垂直平分的四边形是菱形．【解答】解：根据菱形的判定，知对角线互相垂直平分的四边形是菱形，A、B、C错误，D正确．故选D．【点评】本题考查菱形的判定方法．3．如图，某花木场有一块等腰梯形ABCD的空地，其各边的中点分别是E、F、G、H，测得对角线AC=10m，现想利用篱笆围成四边形EFGH场地，则需篱笆得总长度是（）A．40 m B．30 m C．20 m D．10 m【考点】三角形中位线定理．【专题】选择题．【分析】据等腰梯形的性质和三角形的中位线定理有EF=GH=AC，EH=GF=BD，可知四边形EFGH的周长=4EF=2AC，进而可得出四边形EFGH的周长，即需篱笆得总长．【解答】解：如图，连接BD，∵E、F、G、H是等腰梯形ABCD各边中点，∴EF=GH=AC，EH=GF=BD，∵等腰梯形ABCD，∴BD=AC，∴四边形EFGH的周长=4EF=2AC=20m．故选C．【点评】此题主要考查了等腰梯形的性质和三角形中位线定理，得出四边形EFGH的周长与AC 的关系是解题的关键，难度一般．4．在梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD ，且AC=10，BD=6，则该梯形的面积是（） A ．30 B ．15 C ．D ．60【考点】根据边的关系判定平行四边形．【专题】选择题．【分析】根据对角线互相垂直的四边形的面积公式，得该梯形的面积是10×6÷2=30．【解答】解：如图，作DE ∥AC 交BC 延长线于E∵AD ∥BC∴四边形ADEC 为平行四边形 ∴CE=AD ，∠CDE=∠DCA ∵AC ⊥BD ， ∴AC ⊥DE ，∴△BDE 为直角三角形， ∴S 梯ABCD =S △EBD ，∴S 梯ABCD =DE•BD=AC•BD=10×6÷2=30，故选A ．【点评】根据三角形的面积公式可以导出：对角线互相垂直的四边形的面积等于两条对角线乘积的一半．5．如图，已知矩形ABCD 中，R 、P 分别是DC 、BC 上的点，E 、F 分别是AP 、RP 的中点，当P 在BC 上从B 向C 移动而R 不动时，那么下列结论成立的是（）A．线段EF的长逐渐增大B．线段EF的长逐渐减小C．线段EF的长不改变D．线段EF的长不能确定【考点】三角形中位线定理．【专题】选择题．【分析】因为R不动，所以AR不变．根据中位线定理，EF不变．【解答】解：连接AR．因为E、F分别是AP、RP的中点，则EF为△APR的中位线，所以EF=AR，为定值．所以线段EF的长不改变．故选C．【点评】本题考查了三角形的中位线定理，只要三角形的边AR不变，则对应的中位线的长度就不变．6．已知一个直角梯形，一腰长为6，这腰与一底所成的角为30°，那么另一腰的长是（）A．1.5 B．3 C．6 D．9【考点】根据边的关系判定平行四边形．【专题】选择题．【分析】作梯形的另一高，则得一个矩形和一个30°的直角三角形，根据直角三角形中，30°所对的直角边是斜边的一半，得另一腰是已知腰的，即是3．【解答】解：作DE⊥BC，∵AD∥BC，∴四边形ABED为平行四边形，∴AB=DE，又∠C=30°，∴DE=DC=3．故选B．【点评】注意：直角梯形中常见的辅助线即作另一高．熟练运用30°的直角三角形的性质．7．如图所示，将一张正方形纸片对折两次，然后在上面打3个洞，则纸片展开后是（）A．B．C．D．【考点】正方形的性质．【专题】选择题．【分析】结合空间思维，分析折叠的过程及打孔的位置，易知展开的形状．【解答】解：当正方形纸片两次沿对角线对折成为一直角三角形时，在平行于斜边的位置上打3个洞，则直角顶点处完好，即原正方形中间无损，且有12个洞．故选D．【点评】本题主要考查学生抽象思维能力，错误的主要原因是空间观念以及转化的能力不强，缺乏逻辑推理能力，需要在平时生活中多加培养．8．用两个全等的直角三角形拼下列图形：①矩形；②菱形；③正方形；④平行四边形；⑤等腰三角形；⑥等腰梯形．其中一定能拼成的图形是（）A．①②③B．①④⑤C．①②⑤D．②⑤⑥【考点】菱形的判定；等腰三角形的判定；平行四边形的判定；矩形的判定；正方形的判定；等腰梯形的判定．【专题】选择题．【分析】根据菱形、正方形、梯形、矩形、平行四边形、等腰三角形的性质判断．【解答】解：由于菱形和正方形中都四边相等的特点，而直角三角形中不一定有两边相等，故两个全等的直角三角形不能拼成菱形和正方形；由于等腰梯形有两边不等，故也不能．矩形，平行四边形，等腰三角形可以拼成．如图：故选B．【点评】本题考查了三角形的拼接图形的特点．以及特殊四边形的性质．9．如图，在平行四边形ABCD中，DB=DC，∠C=70°，AE⊥BD于E，则∠DAE=度．【考点】平行四边形的性质．【专题】填空题．【分析】由DB=DC，∠C=70°可以得到∠DBC=∠C=70°，又由AD∥BC推出∠ADB=∠DBC=∠C=70°，而∠AED=90°，由此可以求出∠DAE．【解答】解：∵DB=DC，∠C=70°，∴∠DBC=∠C=70°，∵AD∥BC，AE⊥BD，∴∠ADB=∠DBC=∠C=70°，∠AED=90°，∴∠DAE=90﹣70=20°．故答案为：20°．【点评】主要考查了平行四边形的基本性质，并利用性质解题．平行四边形基本性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线互相平分．10．如图，点E、F在▱ABCD的对角线BD上，要使四边形AECF是平行四边形，还需添加一个条件．（只需写出一个结论，不必考虑所有情况）．【考点】平行四边形的判定与性质．【专题】填空题．【分析】使四边形AECF也是平行四边形，则要证四边形的两组对边相等，或两组对边分别平行，可添加条件DF=BE．【解答】解：需要添加的条件可以是：DF=BE．理由如下：∵四边形ABCD是平行四边形，∴AD∥BC，BC=AD，∴∠CBE=∠ADF，在△ADF与△BCE中，，∴△ADF≌△BCE（SAS），∴CE=AF，同理，△ABE≌△CDF，∴CF=AE，∴四边形AECF是平行四边形．【点评】此题主要考查了平行四边形的判定以及矩形的判定方法，此题属于开放题熟练掌握各判定定理是解题的关键．11．如图所示，工人师傅做铝合金窗框分下面三个步骤进行：(1)先截出两对符合规格的铝合金窗料（如图①所示），使AB=CD，EF=GH．(2)摆放成如图②的四边形，则这时窗框的形状是，根据的数学道理是．(3)将直尺紧靠窗框的一个角（如图③），调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图④，说明窗框合格，这时窗框是，根据的数学道理是．【考点】平行四边形的判定；矩形的判定．【专题】填空题．【分析】此题主要考查平行四边形，矩形的判定问题，掌握其判定定理，即可作答．【解答】解：平行四边形；两组对边分别相等的四边形是平行四边形；矩形；由一个角是直角的平行四边形是矩形．【点评】熟练掌握平行四边形及矩形的判定．12．如图，菱形ABCD中，AC=2，BD=5，P是AC上一动点（P不与A、C重合），PE∥BC交AB于E，PF∥CD交AD于F，则图中阴影部分（即多边形BCPFEB）的面积为．【考点】菱形的性质．【专题】填空题．【分析】根据菱形性质得出AC⊥BD，求出△ABC的面积，求出△AEF的面积和△PEF的面积相等，得出阴影部分的面积等于三角形ABC的面积，即可得出答案．【解答】解：∵四边形ABCD是菱形，∴AC⊥BD，BO=OD=BD=2.5，∴△ABC的面积是×AC×BO=2.5，∵AD∥BC，AB∥DC，又∵PE∥BC，PF∥CD，∴PF∥AB，PE∥AD，∴四边形AEPF是平行四边形，∴△AEF的面积和△PEF的面积相等，∴阴影部分的面积等于△ABC的面积是2.5．故答案为：2.5．【点评】本题考查了菱形的性质，三角形的面积，平行四边形的性质和判定等知识点的应用．13．如图所示，菱形ABCD中，对角线AC，BD相交于点O，若再补充一个条件能使菱形ABCD成为正方形，则这个条件是．（只填一个条件即可，答案不唯一）【考点】正方形的判定；菱形的性质．【专题】填空题．【分析】根据菱形的性质及正方形的判定来添加合适的条件．【解答】解：要使菱形成为正方形，只要菱形满足以下条件之一即可，(1)有一个内角是直角(2)对角线相等．即∠BAD=90°或AC=BD．故答案为：∠BAD=90°或AC=BD．【点评】本题比较容易，考查特殊四边形的判定．14．等腰梯形两底之差为12cm，高为6cm，则其锐角底角为度．【考点】根据边的关系判定平行四边形．【专题】填空题．【分析】先作图，过点D作DE∥AB，四边形ABED是平行四边形，根据题意得CE=12cm，△CDE是等腰三角形，从而得出DF=CF=6cm，则锐角底角为45°．【解答】解：过点D作DE∥AB，∵AD∥BC，∴四边形ABED是平行四边形，∴AB=DE，∵AB=CD，∴DE=CD，∴△CDE是等腰三角形，又DF⊥CE，∴EF=CF=CE=（BC﹣AD）=6cm，∵高DF=6cm，∴DF=CF=6cm，而∠DFC=90°，∴∠DCF=45°．【点评】本题考查了梯形中辅助线的作法：平移一腰得出两底之差，还考查了等腰三角形的性质．15．若矩形的对角线长为8cm，两条对角线的一个交角为60°，则该矩形的面积为cm2．【考点】矩形的性质．【专题】填空题．【分析】根据矩形的性质，画出图形求解．【解答】解：∵ABCD为矩形∴OA=OC=OB=OD∵一个角是60°∴BC=OB=cm∴根据勾股定理==∴面积=BC•CD=4×=cm2．故答案为．【点评】本题考查的知识点有：矩形的性质、勾股定理．16．已知：如图，在梯形ABCD中，AD∥BC，CD=10cm，∠B=45度，∠C=30度，AD=5cm．求：(1)AB的长；(2)梯形ABCD的面积．【考点】矩形的判定定理2．【专题】解答题．【分析】(1)过点D作DE⊥BC于E，根据30°角所对的直角边等于斜边的一半可得DE=CD，再判断△ABH是等腰直角三角形，然后根据等腰直角三角形斜边等于直角边的倍解答；(2)先判定四边形AHED是矩形，根据矩形对边相等求出HE=AD，再求出BC的长，然后根据梯形的面积公式列式进行计算即可得解．【解答】解：(1)如图，过点D作DE⊥BC于E，∵∠C=30°，CD=10cm，∴DE=CD=×10=5cm，过A作AH⊥BC于H，则AH=DE=5cm，∵∠B=45°，∴△ABH是等腰直角三角形，∴AB=AH=5cm；(2)∵AH、DE都是梯形的高线，∴四边形AHED是矩形，∴HE=AD=5cm，又∵BH=AH=5cm，CE===5cm，∴BC=BH+HE+CE=5+5+5=（10+5）cm，∴梯形ABCD的面积=（5+10+5）×5=（+）cm．【点评】本题考查了梯形的性质，直角三角形30°角所对的直角边等于斜边的一半的性质，等腰直角三角形的判定与性质，勾股定理的应用，熟记性质并作出辅助线是解题的关键．17．如图，在菱形ABCD中，∠A与∠B的度数比为1：2，周长是48cm．求：(1)两条对角线的长度；(2)菱形的面积．【考点】菱形的性质．【专题】解答题．【分析】在菱形ABCD中，∠A与∠B互补，即∠A+∠B=180°，因为∠A与∠B的度数比为1：2，就可求出∠A=60°，∠B=120°，根据菱形的性质得到∠BDA=120°×=60°，则△ABD是正三角形，所以BD=AB=48×=12cm，根据勾股定理得到AC的值；然后根据菱形的面积公式求解．【解答】解：(1)连接BD，∵∠A与∠B互补，即∠A+∠B=180°，∠A与∠B的度数比为1：2，∴∠A=60°，∠B=120°．∴∠BDA=120°×=60°．∴△ABD是正三角形．∴BD=AB=48×=12cm．AC=2×=12cm．∴BD=12cm，AC=12cm．(2)S菱形ABCD=×两条对角线的乘积=×12×12=72cm2【点评】本题考查的是菱形的面积求法及菱形性质的综合．18．如图，在平行四边形ABCD中，E、F是AC上的两点，且AE=CF．求证：DE=BF．【考点】平行四边形的性质．【专题】解答题．【分析】由平行四边形的性质得AD=CB，∠DAE=∠BCF，再由已知条件，可得△ADE≌△CBF，进而得出结论．【解答】证明：在平行四边形ABCD中，则AD=CB，∠DAE=∠BCF，又AE=CF，∴△ADE≌△CBF（SAS），∴DE=BF．【点评】本题主要考查平行四边形的性质及全等三角形的判定问题，应熟练掌握．19．如图，在梯形ABCD中，AD∥BC，AB∥DE，AF∥DC，E、F两点在边BC上，且四边形AEFD是平行四边形．(1)AD与BC有何等量关系，请说明理由；(2)当AB=DC时，求证：平行四边形AEFD是矩形．【考点】平行四边形的性质；矩形的判定．【专题】解答题．【分析】(1)由题中所给平行线，不难得出四边形ABED和四边形AFCD都是平行四边形，而四边形AEFD也是平行四边形，三个平行四边形都共有一条边AD，所以可得出AD=BC的结论．(2)根据矩形的判定和定义，对角线相等的平行四边形是矩形．只要证明AF=DE 即可得出结论．【解答】(1)解：AD=BC．理由如下：∵AD∥BC，AB∥DE，AF∥DC，∴四边形ABED和四边形AFCD都是平行四边形．∴AD=BE，AD=FC，又∵四边形AEFD是平行四边形，∴AD=EF．∴AD=BE=EF=FC．∴AD=BC．(2)证明：∵四边形ABED和四边形AFCD都是平行四边形，∴DE=AB，AF=DC．∵AB=DC，∴DE=AF．又∵四边形AEFD是平行四边形，∴平行四边形AEFD是矩形．【点评】本题考查了梯形、平行四边形的性质和矩形的判定，是一道集众多四边形于一体的小综合题，难度中等稍偏上的考题．有的学生往往因为基础知识不扎实，做到一半就做不下去了，建议老师平时教学中，重视一题多变，适当地变式联系，可以触类旁通．20．如图，△ABC中，AC的垂直平分线MN交AB于点D，交AC于点O，CE∥AB交MN于E，连接AE、CD．请判断四边形ADCE的形状，说明理由．【考点】菱形的判定；线段垂直平分线的性质．【专题】解答题．【分析】根据中垂线的性质中垂线上的点线段两个端点的距离相等可得出AE=CE，AD=CD，OA=OC∠AOD=∠EOC=90°，再结合CE∥AB，可证得△ADO≌△CEO，从而根据由一组对边平行且相等知，四边形ADCE是平行四边形，结合OD=OE，OA=OC，∠AOD=90°可证得为菱形．【解答】四边形ADCE是菱形．证明：∵MN是AC的垂直平分线，∴AE=CE，AD=CD，OA=OC，∠AOD=∠EOC=90°，∵CE∥AB，∴∠DAO=∠ECO，∴△ADO≌△CEO．（ASA）∴AD=CE，OD=OE，∵OD=OE，OA=OC，∴四边形ADCE是平行四边形又∵∠AOD=90°，∴▱ADCE是菱形．【点评】本题考查了菱形的判定及线段垂直平分线的性质，利用了：中垂线的性质；全等三角形的判定和性质；平行四边形和菱形的判定．。

新人教版八年级(上)期末数学检测卷2——数学人教版8年级册期中期末试卷及答案(73份)

20××-20××学年新人教版八年级（上）期末数学检测卷2一、选择题（每小题3分，共24分）1．（3分）下列图案中不是轴对称图形的是（）A．B．C．D．2．（3分）下列运算结果正确的是（）A．a3•a4=a12B．（a2）3=a6C．（3a）3=3a3D．a（a+1）=a2+13．（3分）下列说法中：①三条线段组成的图形叫做三角形；②三角形的角平分线是射线；③三角形的三条高所在的直线相交于一点，这一点不在三角形的内部，就在三角形的外部；④三角形的三条中线相交于一点，且这点一定在三角形的内部．其中正确的有（）A．4个B．3个C．2个D．1个4．（3分）下列说法不正确的是（）A．在锐角三角形中，最大的锐角x的取值范围是60°≤x＜90°B．在△ABC中，锐角的个数最多C．在△ABC中三个内角α：β：γ=1：3：5，这个三角形是直角三角形D．一个三角形中至多有一个角是锐角5．（3分）下列条件中，能判定△ABC≌△DEF的是（）A．A B=DE，BC=EF，∠A=∠D B．∠A=∠D，∠C=∠F，AC=EFC．∠B=∠E，∠A=∠D，AC=EF D．∠B=∠E，∠A=∠D，AB=DE6．（3分）下列分解因式正确的是（）A．m3﹣m=m（m﹣1）（m+1）B．x2﹣x﹣6=x（x﹣1）﹣6 C．2a2+ab+a=a（2a+b）D．x2﹣y2=（x﹣y）2 7．（3分）对于分式，当x=﹣时，下列说法中：①分式值一定为0；②分式一定有意义；③当a=﹣时，分式无意义．其中正确的个数有（）A．3个B．2个C．1个D．0个8．（3分）（20××•齐齐哈尔）如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B 与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE、EF．下列结论：①tan∠ADB=2；②图中有4对全等三角形；③若将△DEF沿EF折叠，则点D不一定落在AC上；④BD=BF；⑤S四边形DFOE=S△AOF，上述结论中正确的个数是（）A．1个B．2个C．3个D．4个二、填空题（每小题3分，共24分）9．（3分）（20××•鞍山一模）已知等腰三角形的一个内角为40°，则这个等腰三角形的顶角为_________．10．（3分）化简：（a2b）﹣2（a﹣1b﹣2）﹣3=_________．11．（3分）（20××•青羊区一模）如图，△ABC中，AB=AC，∠A=30°，DE垂直平分AC，则∠BCD的度数为_________．12．（3分）如图，在△ABC中，AB=AC，∠B=30°，AB的垂直平分线EF交AB于点E，交BC于点F，EF=2，则BC的长为_________．13．（3分）如果（a+b）2=19，a2+b2=14，则（a﹣b）2=_________．14．（3分）如图，在△ABC中，AB=a，AC=b，∠BAC=150°，则S△ABC=_________．15．（3分）（20××•海门市二模）如图，在△ABC中，AD为BC边上的中线．已知AC=5，AD=4，则AB的取值范围是_________．16．（3分）（20××•襄阳）关于x的分式方程的解为正数，则m的取值范围是_________．三、解答题（其中17，18题各9分，19，21，22，24，26题各10分，20题12分，23题8分，25题14分，共102分）17．（9分）已知2x+y=4，求代数式[（x+y）2﹣（x﹣y）2﹣2y（x﹣y）]÷4y的值．18．（9分）（1）计算：÷（a﹣）．（2）解方程：+=．19．（10分）（20××•德州）有公路l1同侧、l2异侧的两个城镇A，B，如下图．电信部门要修建一座信号发射塔，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条公路l1，l2的距离也必须相等，发射塔C应修建在什么位置？请用尺规作图找出所有符合条件的点，注明点C的位置．（保留作图痕迹，不要求写出画法）20．（12分）如图，在△ABC中，AB=AC，点D、E、F分别在边AB、BC、AC上，且BD=CE，∠DEF=∠B．图中是否存在和△BDE全等的三角形？说明理由．21．（10分）（20××•河北）甲、乙两人准备整理一批新到的实验器材．若甲单独整理需要40分钟完工：若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工．（1）问乙单独整理多少分钟完工？（2）若乙因工作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？22．（10分）（20××•日照）如图，已知点D为等腰直角△ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA．（1）求证：DE平分∠BDC；（2）若点M在DE上，且DC=DM，求证：ME=BD．23．（8分）某种产品的原料降价，因而厂家决定对产品进行降价．现有两种方案：方案1：第一次降价p%，第二次降价q%．方案2：第一、二次降价均为%．其中p，q是不相等且使此情境有意义的正数，两种方案哪种降价最多？24．（10分）一块原边长分别为a，b（a＞1，b＞1）的长方形，一边增加1，另一边减少1．（1）当a=b时，变化后的面积是增加还是减少？（2）当a＞b时，有两种方案，第一种方案如图1，第二种方案如图2．请你比较这两种方案，确定哪一种方案变化后的面积比较大．25．（14分）（20××•黑河）如图1，在正方形ABCD中，点M、N分别在AD、CD上，若∠MBN=45°，易证MN=AM+CN （1）如图2，在梯形ABCD中，BC∥AD，AB=BC=CD，点M、N分别在AD、CD上，若∠MBN=∠ABC，试探究线段MN、AM、CN有怎样的数量关系？请写出猜想，并给予证明．（2）如图3，在四边形ABCD中，AB=BC，∠ABC+∠ADC=180°，点M、N分别在DA、CD的延长线上，若∠MBN=∠ABC，试探究线段MN、AM、CN又有怎样的数量关系？请直接写出猜想，不需证明．26．（10分）在△ABC中，∠A=90°，点D在线段BC上，∠EDB=∠C，BE⊥DE，垂足为点E，DE与AB相交于点F．当AB=AC时（如图所示）．（1）∠EBF=_________．（2）探究线段BE与FD的数量关系，并加以证明．20××-20××学年新人教版八年级（上）期末数学检测卷2参考答案与试题解析一、选择题（每小题3分，共24分）1．（3分）下列图案中不是轴对称图形的是（）A．B．C．D．考点：轴对称图形．分析：根据轴对称图形的概念对各选项分析判断后利用排除法求解．解答：解：A、是轴对称图形，故本选项错误；B、是轴对称图形，故本选项错误；C、不是轴对称图形，故本选项正确；D、是轴对称图形，故本选项错误．故选C．点评：本题考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．2．（3分）下列运算结果正确的是（）A．a3•a4=a12B．（a2）3=a6C．（3a）3=3a3D．a（a+1）=a2+1考点：单项式乘多项式；同底数幂的乘法；幂的乘方与积的乘方．分析：同底数幂的乘法、幂的乘方、积的乘方，单项式乘多项式的法则分别进行计算即可．解答：解：A、a3•a4=a7，故本选项错误；B、（a2）3=a6，故本选项正确；C、（3a）3=27a3，故本选项错误；D、a（a+1）=a2+a，故本选项错误；故选B．点评：此题考查了同底数幂的乘法、幂的乘方、积的乘方，单项式乘多项式，熟练掌握运算法则是解题的关键，计算时要注意符号的处理．3．（3分）下列说法中：①三条线段组成的图形叫做三角形；②三角形的角平分线是射线；③三角形的三条高所在的直线相交于一点，这一点不在三角形的内部，就在三角形的外部；④三角形的三条中线相交于一点，且这点一定在三角形的内部．其中正确的有（）A．4个B．3个C．2个D．1个考点：三角形的角平分线、中线和高．分析：根据三角形的定义，三角形的角平分线、高线、中线对各选项分析判断后利用排除法求解．解答：解：①应为三条线段首尾顺次相接组成的图形叫做三角形，故本小题错误；②三角形的角平分线是线段，故本小题错误；③三角形的三条高所在的直线相交于一点，这一点不在三角形的内部，就在三角形的外部，也有可能是直角三角形的直角顶点，故本小题错误；④三角形的三条中线相交于一点，且这点一定在三角形的内部正确，综上所述，正确的有④共1个．故选D．点评：本题考查了三角形的定义，以及三角形的角平分线、高线、中线，是基础题，需熟记．4．（3分）下列说法不正确的是（）A．在锐角三角形中，最大的锐角x的取值范围是60°≤x＜90°B．在△ABC中，锐角的个数最多C．在△ABC中三个内角α：β：γ=1：3：5，这个三角形是直角三角形D．一个三角形中至多有一个角是锐角考点：三角形内角和定理．分析：根据三角形内角和定理可以进行判断．解答：解：A、正确；B、在△ABC中，至少有2个锐角，故正确；C、在△ABC中三个内角α：β：γ=1：3：5，则α+β＜γ，γ是钝角，因而是钝角三角形．故错误；D、一个三角形中至多有两个角是锐角，故错误．故选C．点评：本题考查了三角形内角和定理，一个三角形中至多有两个角是锐角，最多有一个直角或一个钝角．5．（3分）下列条件中，能判定△ABC≌△DEF的是（）A．A B=DE，BC=EF，∠A=∠D B．∠A=∠D，∠C=∠F，AC=EFC．∠B=∠E，∠A=∠D，AC=EF D．∠B=∠E，∠A=∠D，AB=DE考点：全等三角形的判定．分析：全等三角形的判定定理有SAS，ASA，AAS，SSS，看看已知是否符合条件，即可得出答案．解答：解：A、根据AB=DE，BC=EF和∠A=∠D不能判定两三角形全等，故本选项错误；B、根据∠A=∠D，∠C=∠F，AC=DF才能得出两三角形全等，故本选项错误；C、根据∠B=∠E，∠A=∠D，AC=DF才能得出两三角形全等，故本选项错误；D、∵在△ABC和△DEF中，∴△ABC≌△DEF（ASA），故本选项正确；故选D．点评：本题考查了全等三角形的判定定理，注意：①全等三角形的判定定理有SAS，ASA，AAS，SSS，②应对应相等，符合条件才能得出两三角形全等．6．（3分）下列分解因式正确的是（）A．m3﹣m=m（m﹣1）（m+1）B．x2﹣x﹣6=x（x﹣1）﹣6 C．2a2+ab+a=a（2a+b）D．x2﹣y2=（x﹣y）2考点：提公因式法与公式法的综合运用．分析：根据提公因式法和公式法分别分解因式，从而可判断求解．解答：解：A、m3﹣m=m（m2﹣1）=m（m﹣1）（m+1），故此选项正确；B、x2﹣x﹣6=（x﹣3）（x+2），故此选项错误；C、2a2+ab+a=a（2a+b+1），故此选项错误；D、x2﹣y2=（x﹣y）（x+y），故此选项错误；故选：A．点评：本题主要考查提公因式法与公式法分解因式综合运用，能熟练地运用提公因式法分解因式是解此题的关键．7．（3分）对于分式，当x=﹣时，下列说法中：①分式值一定为0；②分式一定有意义；③当a=﹣时，分式无意义．其中正确的个数有（）A．3个B．2个C．1个D．0个考点：分式的值为零的条件；分式有意义的条件．分析：分式有意义：分母不等于零；分式无意义：分式等于零；分式的值等于零：分子等于零，且分母不等于零．解答：解：当x=﹣时，分子2x+a=0，当x=时，分母3x﹣1=0，当﹣=，即a=﹣时，分母3x﹣1=0．综上所述，正确的说法是③．故选C．点评：本题考查了分式有意义的条件、分式的值为零的条件．若分式的值为零，需同时具备两个条件：（1）分子为0；（2）分母不为0．这两个条件缺一不可．8．（3分）（20××•齐齐哈尔）如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B 与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE、EF．下列结论：①tan∠ADB=2；②图中有4对全等三角形；③若将△DEF沿EF折叠，则点D不一定落在AC上；④BD=BF；⑤S四边形DFOE=S△AOF，上述结论中正确的个数是（）A．1个B．2个C．3个D．4个考点：翻折变换（折叠问题）；全等三角形的判定与性质；锐角三角函数的定义．专题：几何综合题；压轴题．分析：根据折叠的知识，锐角正切值的定义，全等三角形的判定，面积的计算判断所给选项是否正确即可．解答：解：①由折叠可得BD=DE，而DC＞DE，∴DC＞BD，∴tan∠ADB≠2，故①错误；②图中的全等三角形有△ABF≌△AEF，△ABD≌△AED，△FBD≌△FED，（由折叠可知）∵OB⊥AC，∴∠AOB=∠COB=90°，在Rt△AOB和Rt△COB中，，∴Rt△AOB≌Rt△COB（HL），则全等三角形共有4对，故②正确；③∵AB=CB，BO⊥AC，把△ABC折叠，∴∠ABO=∠CBO=45°，∠FBD=∠DEF，∴∠AEF=∠DEF=45°，∴将△DEF沿EF折叠，可得点D一定在AC上，故③错误；④∵OB⊥AC，且AB=CB，∴BO为∠ABC的平分线，即∠ABO=∠OBC=45°，由折叠可知，AD是∠BAC的平分线，即∠BAF=22.5°，又∵∠BFD为三角形ABF的外角，∴∠BFD=∠ABO+∠BAF=67.5°，易得∠BDF=180°﹣45°﹣67.5°=67.5°，∴∠BFD=∠BDF，∴BD=BF，故④正确；⑤连接CF，∵△AOF和△COF等底同高，∴S△AOF=S△COF，∵∠AEF=∠ACD=45°，∴EF∥CD，∴S△EFD=S△EFC，∴S四边形DFOE=S△COF，∴S四边形DFOE=S△AOF，故⑤正确；正确的有3个，故选C．点评：综合考查了有折叠得到的相关问题；注意由对称也可得到一对三角形全等；用到的知识点为：三角形的中线把三角形分成面积相等的2部分；两条平行线间的距离相等．二、填空题（每小题3分，共24分）9．（3分）（20××•鞍山一模）已知等腰三角形的一个内角为40°，则这个等腰三角形的顶角为40°或100°．考点：等腰三角形的性质；三角形内角和定理．专题：计算题；分类讨论．分析：首先知有两种情况（顶角是40°和底角是40°时），由等边对等角求出底角的度数，用三角形的内角和定理即可求出顶角的度数．解答：解：△ABC，AB=AC．有两种情况：（1）顶角∠A=40°，（2）当底角是40°时，∵AB=AC，∴∠B=∠C=40°，∵∠A+∠B+∠C=180°，∴∠A=180°﹣40°﹣40°=100°，∴这个等腰三角形的顶角为40°和100°．故答案为：40°或100°．点评：本题考查了等腰三角形的性质和三角形的内角和定理的理解和掌握，能对有的问题正确地进行分类讨论．10．（3分）化简：（a2b）﹣2（a﹣1b﹣2）﹣3=．考点：负整数指数幂．分析：根据负整数指数幂的运算法则进行计算即可．解答：解：原式=•a3b6=．故答案为：．点评：本题考查的是负整数指数幂，熟知负整数指数幂等于该数正整数指数幂的倒数是解答此题的关键．11．（3分）（20××•青羊区一模）如图，△ABC中，AB=AC，∠A=30°，DE垂直平分AC，则∠BCD的度数为45°．考点：线段垂直平分线的性质．专题：计算题．分析：首先利用线段垂直平分线的性质推出∠DAC=∠DCA，根据等腰三角形的性质可求出∠ABC=∠ACB，易求∠BCD的度数．解答：解：∵AB=AC，∠A=30°（已知）∴∠ABC=∠ACB==75°∵DE垂直平分AC，∴AD=CD；∴∠A=∠ACD=30°，∴∠BCD=∠ACB﹣∠ACD，∴∠BCD=45°；故答案为：45°．点评：本题主要考查了线段垂直平分线的性质以及等腰三角形的性质，难度一般．12．（3分）如图，在△ABC中，AB=AC，∠B=30°，AB的垂直平分线EF交AB于点E，交BC于点F，EF=2，则BC的长为12．考点：线段垂直平分线的性质；等腰三角形的性质；含30度角的直角三角形．专题：计算题．分析：连接AF，根据等腰三角形性质求出∠C=∠B=30°，根据线段垂直平分线求出AF=BF=2EF=4，求出CF=2AF=8，即可求出答案．解答：解：连接AF，∵AC=AB，∴∠C=∠B=30°，∵EF是AB的垂直平分线，∴AF=BF，∴∠B=∠FAB=30°，∴∠CFA=30°+30°=60°，∴∠CAF=180°﹣∠C﹣∠CFA=90°，∵EF⊥AB，EF=2，∴AF=BF=2EF=4，∵∠C=30°，∠CAF=90°，∴CF=2AF=8，∴BC=CF+BF=8+4=12，故答案为：12．点评：本题考查了等腰三角形性质，线段垂直平分线性质，含30度角的直角三角形性质等知识点的应用，关键是求出CF和BF的长，题目比较典型，难度不大13．（3分）如果（a+b）2=19，a2+b2=14，则（a﹣b）2=9．考点：完全平方公式．专题：计算题．分析：先根据完全平方公式得到a2+2ab+b2=19，则2ab=5，再根据完全平方公式得（a﹣b）2=a2﹣2ab+b2，把a2+b2=14，2ab=5代入计算即可．解答：解：∵（a+b）2=19，即a2+2ab+b2=19，而a2+b2=14，∴14+2ab=19，∴2ab=5，∴（a﹣b）2=a2﹣2ab+b2=14﹣5=9．故答案为9．点评：本题考查了完全平方公式：a2±2ab+b2=（a±b）2，也考查了代数式的变形能力以及整体思想的运用．14．（3分）如图，在△ABC中，AB=a，AC=b，∠BAC=150°，则S△ABC=ab．考点：含30度角的直角三角形．分析：作CD⊥AB于点D，在直角三角形ACD中利用直角三角形的性质定理求得CD的长，然后根据三角形的面积公式即可求解．解答：解：作CD⊥AB于点D．∵在直角三角形ACD中，∠CAD=180°﹣∠BAC=30°，∴CD=AC=b，则S△ABC=AB•CD=a•b=ab．故答案是：ab．点评：本题考查了直角三角形的性质：30度的锐角所对的直角边等于斜边的一半，正确作出辅助线是关键．15．（3分）（20××•海门市二模）如图，在△ABC中，AD为BC边上的中线．已知AC=5，AD=4，则AB的取值范围是3＜AB＜13．考点：三角形三边关系；全等三角形的判定与性质．分析：延长AD到E，使DE=AD，连接CE，利用“边角边”证明△ABD和△ECD全等，再根据全等三角形对应边相等可得CE=AB，然后根据三角形的任意两边之和大于第三边，两边之差小于第三边解答．解答：解：延长AD到E，使DE=AD，连接CE，则AE=2AD=2×4=8，∵AD是BC边上的中线，∴BD=CD，∵在△ABD和△ECD中，，∴△ABD≌△ECD（SAS），∴CE=AB，又∵AC=5，∴5+8=13，8﹣5=3，∴3＜CE＜13，即AB的取值范围是：3＜AB＜13．故答案为：3＜AB＜13．点评：本题考查了全等三角形的判定与性质，“遇中线加倍延”作辅助线构造出全等三角形是解题的关键．16．（3分）（20××•襄阳）关于x的分式方程的解为正数，则m的取值范围是m＞2且m≠3．考点：分式方程的解．专题：计算题；压轴题．分析：方程两边同乘以x﹣1，化为整数方程，求得x，再列不等式得出m的取值范围．解答：解：方程两边同乘以x﹣1，得，m﹣3=x﹣1，解得x=m﹣2，∵分式方程的解为正数，∴x=m﹣2＞0且x﹣1≠0，即m﹣2＞0且m﹣2﹣1≠0，∴m＞2且m≠3，故答案为m＞2且m≠3．点评：本题考查了分式方程的解，要注意分式的分母不为0的条件，此题是一道易错题，有点难度．三、解答题（其中17，18题各9分，19，21，22，24，26题各10分，20题12分，23题8分，25题14分，共102分）17．（9分）已知2x+y=4，求代数式[（x+y）2﹣（x﹣y）2﹣2y（x﹣y）]÷4y的值．考点：整式的混合运算—化简求值．分析：先根据整式混合运算的法则把原式进行化简，再把2x+y=4代入进行计算即可．解答：解：原式=[x2+y2+2xy﹣x2﹣y2+2xy﹣2xy+y2]÷4y=（2xy+y2）÷4y=（2x+y）=×4=1．点评：本题考查的是整式的混合运算，熟知整式混合运算的法则是解答此题的关键．18．（9分）（1）计算：÷（a﹣）．（2）解方程：+=．考点：解分式方程；分式的混合运算．专题：计算题．分析：（1）原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算，约分即可得到结果；（2）方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．解答：解：（1）原式=•=；（2）去分母得：2（3x﹣1）+3x=1，去括号得：6x﹣2+3x=1，解得：x=，经检验x=是增根，原分式方程无解．点评：此题考查了解分式方程，以及分式的混合运算，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．19．（10分）（20××•德州）有公路l1同侧、l2异侧的两个城镇A，B，如下图．电信部门要修建一座信号发射塔，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条公路l1，l2的距离也必须相等，发射塔C应修建在什么位置？请用尺规作图找出所有符合条件的点，注明点C的位置．（保留作图痕迹，不要求写出画法）考点：作图—应用与设计作图．分析：根据题意知道，点C应满足两个条件，一是在线段AB的垂直平分线上；二是在两条公路夹角的平分线上，所以点C应是它们的交点．（1）作两条公路夹角的平分线OD或OE；（2）作线段AB的垂直平分线FG；则射线OD，OE与直线FG的交点C1，C2就是所求的位置．解答：解：作图如下：C1，C2就是所求的位置．注：本题学生能正确得出一个点的位置得（6分），得出两个点的位置得（8分）．点评：此题考查了作图﹣应用与设计作图，本题的关键是：①对角平分线、线段垂直平分线作法的运用，②对题意的正确理解．20．（12分）如图，在△ABC中，AB=AC，点D、E、F分别在边AB、BC、AC上，且BD=CE，∠DEF=∠B．图中是否存在和△BDE全等的三角形？说明理由．考点：全等三角形的判定；等腰三角形的性质．分析：根据已知得出∠BDE=∠CEF，再得出∠B=∠C，利用角边角得出三角形全等．解答：解：△CEF≌△BDE．（1分）理由如下：∵∠DEF=∠B，∠DEC=∠B+∠BDE=∠DEF+∠CEF，（已知）（三角形外角的性质）（等量代换），∴∠BDE=∠CEF．（等式的性质）（3分），在△ABC中，∵AB=AC，（已知），∴∠B=∠C．（等边对等角）（4分）在△CEF和△BDE中，，（5分）∴△CEF≌△BDE．（角边角）（6分）点评：此题主要考查了三角形的全等判定，根据题意得出∠BDE=∠CEF是解决问题的关键．21．（10分）（20××•河北）甲、乙两人准备整理一批新到的实验器材．若甲单独整理需要40分钟完工：若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工．（1）问乙单独整理多少分钟完工？（2）若乙因工作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？考点：分式方程的应用；一元一次不等式的应用．专题：应用题．分析：（1）将总的工作量看作单位1，根据本工作分两段时间完成列出分式方程解之即可；（2）设甲整理y分钟完工，根据整理时间不超过30分钟，列出一次不等式解之即可．解答：解：（1）设乙单独整理x分钟完工，根据题意得：，解得x=80，经检验x=80是原分式方程的解．答：乙单独整理80分钟完工．（2）设甲整理y分钟完工，根据题意，得，解得：y≥25，答：甲至少整理25分钟完工．点评：分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．此题等量关系比较多，主要用到公式：工作总量=工作效率×工作时间．22．（10分）（20××•日照）如图，已知点D为等腰直角△ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA．（1）求证：DE平分∠BDC；（2）若点M在DE上，且DC=DM，求证：ME=BD．考点：全等三角形的判定与性质；等边三角形的判定与性质；等腰直角三角形．专题：证明题；压轴题．分析：（1）根据等腰直角△ABC，求出CD是边AB的垂直平分线，求出CD平分∠ACB，根据三角形的外角性质求出∠BDE=∠CDE=60°即可．（2）连接MC，可得△MDC是等边三角形，可求证∠EMC=∠ADC．再证明△ADC≌△EMC即可．解答：证明：（1）∵△ABC是等腰直角三角形，∴∠BAC=∠ABC=45°，∵∠CAD=∠CBD=15°，∴∠BAD=∠ABD=45°﹣15°=30°，∴BD=AD，∴D在AB的垂直平分线上，∵AC=BC，∴C也在AB的垂直平分线上，即直线CD是AB的垂直平分线，∴∠ACD=∠BCD=45°，∴∠CDE=15°+45°=60°，∴∠BDE=∠DBA+∠BAD=60°；∴∠CDE=∠BDE，即DE平分∠BDC．（2）如图，连接MC．∵DC=DM，且∠MDC=60°，∴△MDC是等边三角形，即CM=CD．∠DMC=∠MDC=60°，∵∠ADC+∠MDC=180°，∠DMC+∠EMC=180°，∴∠EMC=∠ADC．又∵CE=CA，∴∠DAC=∠CEM．在△ADC与△EMC中，，∴△ADC≌△EMC（AAS），∴ME=AD=BD．点评：此题主要考查等腰直角三角形，全等三角形的判定与性质，等边三角形的判定与性质的等知识点，难易程度适中，是一道很典型的题目．23．（8分）某种产品的原料降价，因而厂家决定对产品进行降价．现有两种方案：方案1：第一次降价p%，第二次降价q%．方案2：第一、二次降价均为%．其中p，q是不相等且使此情境有意义的正数，两种方案哪种降价最多？考点：整式的混合运算．专题：应用题．分析：设该产品原价为a元，根据题意列出两种方案的价格，利用作差法比较大小即可．解答：解：设该产品的原价是a元，根据题意得：方案1的价格为：a（1﹣p%）（1﹣q%），方案2的价格为：a（1﹣%）2，则a（1﹣p%）（1﹣q%）﹣a（1﹣%）2=﹣（q%﹣p%）2，∵p≠q，∴﹣（q%﹣p%）2＜0，则方案1降价多．点评：此题考查了整式的混合运算，弄清题意是解本题的关键．24．（10分）一块原边长分别为a，b（a＞1，b＞1）的长方形，一边增加1，另一边减少1．（1）当a=b时，变化后的面积是增加还是减少？（2）当a＞b时，有两种方案，第一种方案如图1，第二种方案如图2．请你比较这两种方案，确定哪一种方案变化后的面积比较大．考点：整式的混合运算．分析：（1）根据题意得出算式，求出两式的差，再判断即可；（2）求出两种方案的算式，求出两式的差，再判断即可．解答：解：（1）设原来长方形的面积是S1，变化后的长方形的面积是S2，根据题意得：S=ab，S2=（a+1）（b﹣1）=ab+b﹣a﹣1，∴S2﹣S1=ab+b﹣a﹣1﹣ab=b﹣a﹣1，∵a=b，∴b﹣a﹣1=﹣1＜0，∴S2＜S1，∴变化后面积减小了．（2）方案1，S1=（a+1）（b﹣1）=ab﹣a+b﹣1，方案2，S2=（a﹣1）（b+1）=ab+a﹣b﹣1，∴S1﹣S2=﹣2a+2b=﹣2（a﹣b），∵a＞b，∴S1﹣S2＜0，∴方案2变化后面积大．点评：本题考查了整式的混合运算的应用，关键是能根据题意列出算式．25．（14分）（20××•黑河）如图1，在正方形ABCD中，点M、N分别在AD、CD上，若∠MBN=45°，易证MN=AM+CN（1）如图2，在梯形ABCD中，BC∥AD，AB=BC=CD，点M、N分别在AD、CD上，若∠MBN=∠ABC，试探究线段MN、AM、CN有怎样的数量关系？请写出猜想，并给予证明．（2）如图3，在四边形ABCD中，AB=BC，∠ABC+∠ADC=180°，点M、N分别在DA、CD的延长线上，若∠MBN=∠ABC，试探究线段MN、AM、CN又有怎样的数量关系？请直接写出猜想，不需证明．考点：旋转的性质；全等三角形的判定与性质；正方形的性质；梯形．专题：几何综合题．分析：（1）先判定梯形ABCD是等腰梯形，根据等腰梯形的性质可得∠A+∠BCD=180°，再把△ABM绕点B顺时针旋转90°，点A与点C重合，点M到达点M′，根据旋转变换的性质，△ABM和△CBM′全等，根据全等三角形对应边相等可得AM=CM′，BM=BM′，根据全等三角形对应角相等可得∠A=∠BCM′，∠ABM=∠M′BC，然后证明M′、C、N三点共线，再利用“边角边”证明△BMN和△BM′N全等，然后根据全等三角形对应边相等即可得证；（2）在∠CBN内部作∠CBM′=∠ABM交CN于点M′，然后证明∠C=∠BAM，再利用“角边角”证明△ABM 和△CBM′全等，根据全等三角形对应边相等可得AM=CM′，BM=BM′，再证明∠MBN=∠M′BN，利用“边角边”证明△MBN和△M′BN全等，根据全等三角形对应边相等可得MN=M′N，从而得到MN=CN﹣AM．解答：解：（1）MN=AM+CN．理由如下：如图，∵BC∥AD，AB=BC=CD，∴梯形ABCD是等腰梯形，∴∠A+∠BCD=180°，把△ABM绕点B顺时针旋转90°到△CBM′，则△ABM≌△CBM′，∴AM=CM′，BM=BM′，∠A=∠BCM′，∠ABM=∠M′BC，∴∠BCM′+∠BCD=180°，∴点M′、C、N三点共线，∵∠MBN=∠ABC，∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC﹣∠MBN=∠ABC，∴∠MBN=∠M′BN，在△BMN和△BM′N中，∵，∴△BMN≌△BM′N（SAS），∴MN=M′N，又∵M′N=CM′+CN=AM+CN，∴MN=AM+CN；（2）MN=CN﹣AM．理由如下：如图，作∠CBM′=∠ABM交CN于点M′，∵∠ABC+∠ADC=180°，∴∠BAD+∠C=360°﹣180°=180°，又∵∠BAD+∠BAM=180°，∴∠C=∠BAM，在△ABM和△CBM′中，，∴△ABM≌△CBM′（ASA），∴AM=CM′，BM=BM′，∵∠MBN=∠ABC，∴∠M′BN=∠ABC﹣（∠ABN+∠CBM′）=∠ABC﹣（∠ABN+∠ABM）=∠ABC﹣∠MBN=∠ABC，∴∠MBN=∠M′BN，在△MBN和△M′BN中，∵，∴△MBN≌△M′BN（SAS），∴MN=M′N，∵M′N=CN﹣CM′=CN﹣AM，∴MN=CN﹣AM．点评：本题考查了旋转的性质，全等三角形的判定与性质，等腰梯形的两底角互补，利用旋转变换作辅助线，构造出全等三角形，把MN、AM、CN通过等量转化到两个全等三角形的对应边是解题的关键，本题灵活性较强，对同学们的能力要求较高．26．（10分）在△ABC中，∠A=90°，点D在线段BC上，∠EDB=∠C，BE⊥DE，垂足为点E，DE与AB相交于点F．当AB=AC时（如图所示）．（1）∠EBF=22.5°．（2）探究线段BE与FD的数量关系，并加以证明．考点：全等三角形的判定与性质．专题：计算题．分析：（1）作DH⊥AB于H，根据等腰直角三角形的性质得∠ABC=∠C=45°，则∠EDB=∠C=22.5°，所以∠EBD=90°﹣22.5°=67.5°，然后根据∠EBF=∠EBD﹣∠ABC进行计算；（2）BE与DH的延长线交于G点，由DH∥AC得到∠BDH=45°，则△HBD为等腰直角三角形，于是HB=HD，由∠EBF=22.5°得到DE平分∠BDG，根据等腰三角形性质得BE=GE，即BE=BG，然后根据“AAS”证明△BGH≌△DFH，则BG=DF，所以BE=FD．解答：解：（1）作DH⊥AB于H，如图，∵∠A=90°，AB=AC，∴∠ABC=∠C=45°，∴∠EDB=∠C=22.5°，∵BE⊥DE，∴∠E=90°，∴∠EBD=90°﹣22.5°=67.5°，∴∠EBF=∠EBD﹣∠ABC=22.5°．（2）BE=FD．理由如下：BE与DH的延长线交于G点，如图，∵DH∥AC，∴∠BDH=∠C=45°，∴△HBD为等腰直角三角形∴HB=HD，而∠EBF=22.5°，∵∠EDB=∠C=22.5°，∴DE平分∠BDG，而DE⊥BG，∴BE=GE，即BE=BG，∵∠DFH+∠FDH=∠G+∠FDH=90°，∴∠DFH=∠G，∵∠GBH=90°﹣∠G，∠FDH=90°﹣∠G，∴∠GBH=∠FDH在△BGH和△DFH中，，∴△BGH≌△DFH（AAS），∴BG=DF，∴BE=FD．故答案为22.5°．点评：本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；全等三角形的对应边相等．也考查了等腰直角三角形的性质．第20页，共20页。

期末检测卷02(解析版) -2020-2021学年八年级数学上册期末综合复习专题提优训练(人教版)

2020-2021学年八年级数学上册期末综合复习专题提优训练（人教版）期末检测卷02一、选择题（本题共计6小题，每题3分，共计18分）1．（2020·大庆市万宝学校八年级期中）下列哪组数据能构成三角形的三边（）A ．1cm 、2cm 、3cmB ．2cm 、3cm 、4cmC ．14cm 、4cm 、9cmD ．7cm 、2cm 、4cm【答案】B2．（2020·营山县化育初级中学校八年级期中）下列图形中一定是轴对称图形的是（）A ．B ．C ．D ．【答案】A3．（2020·河北唐山市·八年级月考）下列计算错误的是（）A ．32a b ⋅＝5abB ．2a a -⋅＝3a -C ．()()936-x -x =x÷ D ．()2362a 4a -=【答案】A4．（2020·浙江杭州市·七年级其他模拟）若24(1)9xm x --+是完全平方式，则m 的值为（）A ．13B ．12±C ．11或13-D ．11-或13．【答案】D5．（2020·营山县化育初级中学校八年级期中）如图所示，在△ABC 中，∠C ＝90°，BC ＝40，AD 是∠BAC 的平分线，交BC 于点D ．若DC ∶DB ＝3∶5，则点D 到AB 的距离是（）A ．40B ．15C ．25D ．20【答案】B6．（2020·广东广州市·执信中学八年级期中）如图，已知长方形ABCD 的边长AB ＝20cm ，BC ＝16cm ，点E 在边AB 上，AE ＝6cm ，如果点P 从点B 出发在线段BC 上以2cm /s 的速度向点C 向运动，同时，点Q 在线段CD 上从点C 到点D 运动．则当时间t 为（）s 时，能够使BPE 与CQP 全等．A ．1B ．1或4C ．1或2D ．2或4【答案】B二、填空题（本题共计6小题，每题3分，共计18分）7．（2020·上海市建平中学西校七年级期中）分解因式：32327-=xxy ______．【答案】()()333+-xx y x y8．（2019·江西赣州市·八年级期末）为了创建“最美校园图书屋”，新购买了一批图书，其中科普类图书平均每本书的价格是文学类图书平均每本书价格的1.2倍．已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本，那么学校购买文学类图书平均每本书的价格是多少元？设学校购买文学类图书平均每本书的价格是x 元，根据题意列方程为____．【答案】12000120001001.2x x=+ 9．（2020·昌乐县白塔镇第一中学八年级期中）若关于x 的分式方程4333x ax x --=--有增根，则a 的值是______．【答案】－110．（2020·重庆市南川道南中学校八年级期中）如图，△ABC 的外角∠MBC 和∠NCB 的平分线BP 、CP 相交于点P ，PE ⊥BC 于E 且PE ＝3cm ，若△ABC 的周长为14cm ，S △BPC ＝7.5，则△ABC 的面积为______cm 2．【答案】611．（2020·宁津县育新中学八年级期中）如图，在△ABC 中，∠A =64°，∠ABC 与∠ACD 的平分线交于点A 1，∠A 1BC 与∠A 1CD 的平分线相交于点A 2，得∠A 2；…；∠A n -1BC 与∠A n -1CD 的平分线相交于点A n ，要使∠A n 的度数为整数，则n 的值最大为______．【答案】612．（2020·南昌市心远中学八年级期中）如图：一条船从A 处出发向正北航行，从A 望灯塔C 测得30NAC ∠=︒，当点B在射线AN 上，且BAC 为等腰三角形，则NBC ∠的度数是__________．【答案】105°或60°或150°三、（本题共计5小题，每小题6分，共计30分）13．（2020·福建泉州市·泉州七中八年级期中）分解因式：（1）2x x 30--（2）222ax8axy 8ay -+【答案】解：（1）230x x --()()65x x =-+（2）22288axaxy ay -+()22244a x xy y =-+()222a x y =-【点睛】本题考查的是利用十字乘法，提公因式，完全平方公式分解因式，掌握以上因式分解的方法是解题的关键．14．（2020·剑阁县公兴初级中学校九年级月考）先化简（21x x +－x ＋1）÷22121x x x -++，再从－1，0，1中选择合适的x 值代入求值．【答案】2221(21)11x x x x x x -+÷++-+ 222121(1)1111x x x x x x x x x x ⎡⎤++=-+⨯⎢⎥++++⎣⎦-+ 222(1)1(1)(1)1x x x x x x x x ⎡⎤-+=⨯⎢⎥+-⎣+++-⎦2(1)()1(1)(1)1x x x x +=⨯+-+ 11x =- 11x x x ≠-≠∴=，0当0x=时，原式11==1101x =--- 【点睛】本题考查分式的化简求值，其中涉及分式有意义的条件、完全平方公式、平方差公式等知识，是重要考点，难度较易，掌握相关知识是解题关键．15．（2020·马鞍山二中实验学校八年级期中）如图，已知：点P 是ABC ∆内一点．（1）求证：BPC A ∠>∠；（2）若PB 平分ABC ∠，PC 平分ACB ∠，40A ︒∠=，求P ∠的度数．【答案】（1）延长BP 交AC 于D ，如图所示：∵∠BPC 是△CDP 的一个外角，∠1是△ABD 的一个外角，∴∠BPC ＞∠1，∠1＞∠A ，∴∠BPC ＞∠A ；（2）在△ABC 中，∵∠A =40°，∴∠ABC +∠ACB =180°﹣∠A =180°﹣40°=140°，∵PB 平分∠ABC ，PC 平分∠ACB ，∴∠PBC =12∠ABC ，∠PCB =12∠ACB ，在△PBC 中，∠P =180°﹣（∠PBC +∠PCB ）=180°﹣（12∠ABC +12∠ACB ）=180°﹣12（∠ABC+∠ACB）=180°﹣12×140°=110°．【点睛】此题主要考查了三角形的外角性质、三角形内角和定理、三角形的角平分线定义；熟练掌握三角形的外角性质和三角形内角和定理是解决问题的关键．16．（2020·江苏淮安市·八年级期中）如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：（请用直尺保留作图痕迹）．（1）画出格点△ABC（顶点均在格点上）关于直线DE对称的△A1B1C1；（2）△ABC的面积是；（3）在DE上画出点Q，使△QAB的周长最小．【答案】解：（1）如图所示，△A1B1C1即为所求；（2）S△ABC＝2×3−12×1×3−12×1×2−12×1×2＝52．故答案为：5 2．（3）如图所示，点Q即为所求；【点睛】本题主要考查了利用轴对称作图，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．17．（2020·武威第十九中学八年级月考）下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．解：设x2－4x=y原式=（y+2）（y+6）+4 （第一步）= y2+8y+16 （第二步）=（y+4）2（第三步）=（x2－4x+4）2（第四步）回答下列问题：（1）该同学第二步到第三步运用了因式分解的_______．A．提取公因式B．平方差公式C．完全平方公式（2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”），若不彻底，请直接写出因式分解的最后结果_________．（3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．【答案】解：（1）该同学第二步到第三步运用了因式分解的完全平方公式，故选：C；（2）∵x2－4x+4=（x-2)2 ，∴该同学因式分解的结果不彻底，最后结果为（x-2)4 ，故答案为：不彻底，（x-2)4 ；（3）设x2－2x=y，则:原式=y(y+2)+1=y2+2y+1=(y+1)2=( x2－2x+1)2=(x﹣1)4．【点睛】本题考查利用换元法和公式法进行因式分解，熟记完全平方公式，熟练掌握因式分解的各种方法是解答的关键．四、（本题共计3小题，每小题8分，共计24分）18．（2020·全国八年级期中）如图所示，△ABC中，AB=BC．DE⊥AB于点E．DF⊥BC于点D，交AC于F．．若∠AFD=155°，求∠EDF的度数；．若点F是AC的中点，求证：∠CFD=12∠B．【答案】． ∵∠AFD=155°．∴∠DFC=25°．∵DF⊥BC．DE⊥AB．∴∠FDC =∠AED =90°．在Rt △EDC 中，∴∠C =90°．25°=65°．∵AB =BC ．∴∠C =∠A =65°．∴∠EDF =360°．65°．155°．90°=50°．．连接BF ．∵AB =BC ，且点F 是AC 的中点，∴BF ⊥AC ．12ABFCBF ABC ∠=∠=∠．∴∠CFD +∠BFD =90°．∠CBF +∠BFD =90°．∴∠CFD =∠CBF ．∴12CFDABC ∠=∠． 19．（2020·重庆西南大学银翔实验中学八年级月考）西南大学银翔实验中学初2022级举行“迎篮而上，求进不止”的篮球比赛，在某商场购买甲、乙两种不同篮球，购买甲种篮球共花费3000元，购买乙种篮球共花费2100元，购买甲种篮球数量是购买乙种篮球数量的2倍．且购买一个乙种篮球比购买一个甲种篮球多花60元；（1）求购买一个甲种篮球、一个乙种篮球各需多少元？（2）活动结束以后，学校决定再次购买甲、乙两种篮球共50个．恰逢该商场对两种篮球的售价进行调整，甲种篮球售价比第一次购买时提高了10%，乙种篮球售价比第一次购买时降低了10%．如果此次购买甲、乙两种篮球的总费用不超过8730元，那么这所学校最多可购买多少个乙种篮球？【答案】解：（1）设购买一个甲种篮球需x 元，则购买一个乙种篮球需()60x +元，根据题意可得：30002100260x x =⨯+，解得：150x =，经检验得150x =是分式方程的解，∴60210x +=，答：购买一个甲种篮球需150元，则购买一个乙种篮球需210元；（2）调整之后的价格为：甲种篮球()150110165⨯+%=（元），乙种篮球()210110189⨯-%=（元），设购买m 个乙种篮球，则购买()50m -个甲种篮球，根据题意可得：()165501898730m m -+≤，解得：20m ≤，∴这所学校最多可购买20个乙种篮球．【点睛】本题考查分式方程的应用、不等式的实际应用，理解题意并列出方程和不等式是解题的关键．20．（2020·昌乐县白塔镇第一中学八年级期中）如图1，在△ABC 中，90ACB ∠=︒，AC =BC ，直线MN 经过点C ，AD MN ⊥，垂足为点D ，BE MN ⊥，垂足为点E ．（1）请说明：①ADC CEB △≌△，②DE AD BE =+；（2）当直线MN 绕着点C 旋转到如图2所示的位置时，猜想线段DE ，AD ，BE 之间有怎样的数量关系？并说明理由．【答案】解：（1）①AD MN ⊥，BE MN ⊥，∴∠=∠=︒，ADC CEB90∴∠+∠=︒，DAC ACD90∠=︒，ACB90∴∠+∠=︒-︒=︒，ACD BCE1809090∴∠=∠；DAC ECB△中，在ADC和CEB=，∠=∠，AC CBADC CEB∠=∠，DAC ECB()∴△≌△；ADC CEBAAS△≌△，②由①得ADC CEB=，DC EB∴=，AD CE=+，DE CD CE∴=+；DE AD BE=-，（2）DE AD BE△≌△，由（1）同理可得：ADC CEB∴=，CD BE=，AD CEDE CE CD，∴=-．DE AD BE【点睛】本题考查了全等三角形的判定和性质，涉及到补角和余角的性质，熟练掌握全等三角形的判定方法是解题的关键．五、（本题共计2小题，每小题9分，共计18分）21．（2020·张家口市宣化区教学研究中心八年级期末）阅读理解（发现）如果记22()1x f x x =+，并且f （1）表示当x =1时的值，则f （1）=______；()2f 表示当2x =时的值，则()2f =______；12f ⎛⎫ ⎪⎝⎭表示当12x =时的值，则12f ⎛⎫ ⎪⎝⎭=______； ()3f 表示当3x =时的值，则()3f =______；13f ⎛⎫ ⎪⎝⎭表示当13x =时的值，则13f ⎛⎫= ⎪⎝⎭______；（拓展）试计算111(2013)(2012)(2)(1)220122013f f f f f f f ⎛⎫⎛⎫⎛⎫++⋯++++⋯++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值．【答案】解：【发现】2211(1)=211=+f ； 2224(2)=512=+f ；221112()=25112⎛⎫ ⎪⎝⎭=⎛⎫+ ⎪⎝⎭f ； 2239(3)=1013=+f ；221113()=310113⎛⎫ ⎪⎝⎭=⎛⎫+ ⎪⎝⎭f 【拓展】∵22()1x f x x =+ ∴2221()11(),111()x f x x x∴1()()1,f x f x += ∴111(2013)(2012)(2)(1)220122013f f f f f f f ⎛⎫⎛⎫⎛⎫++⋯++++⋯++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()111=2012+=201222=2012+f 【点睛】本题考查了函数值，数字变化规律，读懂题目信息，理解变化规律f 的方法并确定出1()()1f x f x+=是解题的关键． 22．（2020·广州市白云区明德中学七年级期中）如图1是一个长为2a ，宽为2b 的长方形()a b >，沿图中虚线用剪刀均匀分成四块相同小长方形，然后按图2方式拼成一个大正方形（1）你认为图2中大正方形的边长为______；小正方形（阴影部分）的边长为______．（用含a 、b 代数式表示）（2）仔细观察图2，利用图2中存在的面积关系，直接写出下列三个代数式．2()a b -，2()a b +，4ab 之间的等量关系．（3）利用（2）中得出的结论解决下面的问题．已知7a b +=，6ab =，求代数式()a b -的值．【答案】解：（1）图2中大正方形的边长为（a ＋b ）；小正方形（阴影部分）的边长为（a −b ），故填：()a b +，()a b -；（2）三个代数式之间的等量关系是：（a ＋b ）2＝（a −b ）2＋4ab ；（3）（a −b ）2＝（a ＋b ）2−4ab ＝72－4×6＝25，∴a −b ＝5．【点睛】本题主要考查公式变形能力，如何准确地确定三个代数式之间的等量关系是解题的关键．六、（本题共计1小题，每小题12分，共计12分）23．（2020·阳泉市第三中学校八年级期中）问题情境：在自习课上，小雪拿来了如下一道题目（原问题）和合作学习小组的同学们交流，如图①，△ACB 和△∠CDE 均为等腰三角形．CA =CB ，CD =CE ，∠ACB =∠DCE ．点A 、D 、E 在同一条直线上，连接BE ．求证：∠CDE =∠BCE +∠CBE ．问题发现：小华说：我做过一道类似的题目：如图②，△ACB 和△CDE 均为等边三角形，其他条件不变，求∠AEB 的度数．（1）请聪明的你完成小雪的题目要求并直接写出小华的题目要求．拓展研究：（2）如图③，△ACB 和△DCE 均为等腰直角三角形，∠ACB =∠DCE =90°，点A 、D 、E 在同一条直线上，CF 为△DCE 中DE 边上的高，连接BE ．请求∠AEB 的度数及线段CF 、AE 、BE 之间的数量关系，并说明理由．【答案】（1）小雪的题目：证明：ACB DCE ∠=∠ACD BCE ∠∠∴=在ADC 和DCE 中，CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩()ADC BEC SAS ∴≅△△CAD CBE ∴∠=∠又ACD BCE ∠=∠,CDE CAD ACD ∠=∠+∠CDE CBE BCE ∴∠=∠+∠；小华的题目：解：ACB DCE ∠=∠ACD BCE ∠∠∴=在ADC 和DCE 中，CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩()ADC BEC SAS ∴≅△△ADC BEC ∠∠∴= CDE 为等边三角形60CDE CED ∴∠=∠=︒ 又点A 、D 、E 在同一条直线上120ADC BEC ∴∠=∠=︒60AEB BEC CED ∴∠=∠-∠=︒（2）∠AEB =90︒；2AE BE CF =+；理由如下：△ACB 和△DCE 均为等腰直角三角形，,,9045AC BC CD CE ACB DCE CDE CED ∴==∠=∠=︒∠=∠=︒，,ACB DCB DCE DCB ∴∠-∠=∠-∠即ACD BCE ∠=∠在ADC 和DCE 中，CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩()ADC BEC SAS ∴≅△△,BE AD BEC ADC ∴=∠=∠,点A 、D 、E 在同一直线上∴∠=︒-︒=︒ADC18045135∴∠=︒BEC135∴∠=∠-∠=︒-︒=︒AEB BEC CED1354590，∠=︒=⊥DCE CD CE CF DE90,∴==CF DF EF∴=+=DE DF EF CF2∴=+=+．AE AD DE BE CF2【点睛】本题考查了全等三角形的判定及性质、等腰三角形的性质、等边三角形的性质，熟练掌握性质定理是解题的关键．。

2020年高中生物专题检测试卷(专题2 细胞工程)新人教版选修3

专题检测试卷(专题2)(时间：90分钟满分：100分)一、选择题(本题包括25小题，每小题2分，共50分，在每小题给出的4个选项中，只有1项符合题目要求) 1．(2018·济南调研)如图是通过植物细胞工程技术获得紫杉醇的途径，下列叙述正确的是( )A．该途径依据的原理是植物细胞具有全能性B．过程①需控制好培养基中植物激素的比例C．经过程①细胞的形态和结构未发生变化D．过程③需使用固体培养基，有利于细胞增殖答案 B解析细胞全能性以细胞发育成个体为标志，而图中并没有形成完整植物体，A项错误；过程①是脱分化，而决定植物脱分化和再分化的关键因素是培养基中植物激素的种类和比例，因此该过程需控制好培养基中植物激素的比例，B项正确；过程①是脱分化，经该过程细胞的形态和结构发生了变化，成为高度液泡化的薄壁细胞，C项错误；过程③需使用液体培养基，有利于细胞增殖，D项错误。

2．在下列选项中，需要采用植物组织培养技术的是( )①利用秋水仙素处理萌发的种子或幼苗，获得多倍体植株②获取大量的脱毒苗③利用基因工程培育抗棉铃虫的植株④单倍体育种⑤无子西瓜的快速大量繁殖A．①②③ B．③④⑤C．①②④⑤ D．②③④⑤答案 D解析培育多倍体利用的原理是秋水仙素抑制纺锤体的形成，导致染色体数目加倍，不需要采用植物组织培养技术；获取大量脱毒苗以及快速大量繁殖无子西瓜必须采用植物组织培养技术；基因工程育种以及单倍体育种过程中，受体细胞及花药培养均采用植物组织培养技术。

3．制造人工种子的原理是在组织培养得到的“胚状体”的最外面用一层有机膜包裹，并在薄膜以内放入一些营养物质，如图所示。

据此判断下列说法不正确的是( )A．“胚状体”最外面的一层有机膜和里面的营养物质分别具有种皮和胚乳的功能B．“胚状体”来源于离体的植物体细胞，其形成过程中要经过的生理过程大体上是脱分化和再分化过程C．从保证人工种子正常的生命力及生态系统物质循环上来看，其外部薄膜应具有全透性和能被微生物降解的特点D．在人工种子萌发的过程中“胚状体”细胞吸收营养液中的物质用于生长等生命活动答案 C解析从保证人工种子正常的生命力上来看，其外部薄膜应具有半透性，可以透气和透水，但是不能让薄膜以内的营养物质出来。

专题二能力提升检测卷(测)-2023年高考化学一轮复习讲练测(新教材新高考)(解析版)

专题二能力提升检测卷（本卷共20小题，满分100分，考试用时75分钟）可能用到的相对原子质量：H1Li7B11C12N14O16Na23Mg24Al 27S32Cl35.5K39Ca40Cr52Mn55Fe56Ni59Cu64La139第I卷（选择题共50分）一、选择题：本题共10个小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．在同温同压下，相同体积的甲、乙两种气体的质量比是17∶14。

若乙气体是CO，则甲气体可能是()A．H2S B．HClC．NH3D．Cl2【答案】A【解析】同温同压下，体积之比等于物质的量之比，同体积的甲、乙两种气体物质的量相同，质量比是17∶14，根据m＝nM可知，甲与乙的摩尔质量之比为17∶14，若乙气体是CO，则M(甲)∶28g·mol－1＝17∶14，故M(甲)＝34g·mol－1，各选项中只有H2S符合，故选A。

2．同温同压下，A容器中盛有H2，B容器中盛有NH3，若使它们所含的原子数相等，则两个容器的容积之比是()A．2∶1B．1∶5C．2∶3D．5∶1【答案】A【解析】假设二者物质的量分别为x mol和y mol，则H2含2x mol原子，NH3含4y mol原子，有2x＝4y，x∶y＝2∶1，同温同压下体积比也为2∶1。

3．设N A为阿伏加德罗常数的值。

下列说法正确的是()A．1L0.1mol·L－1NaClO溶液中含有ClO－的数目为0.1N AB．将1mol NH3完全溶于水，所得溶液中N(NH3·H2O)＋N(NH＋4)＝N AC．1L0.1mol·L－1NaHSO4溶液中含有的阳离子数目为0.1N AD．将1mol CH3COONa溶于稀醋酸中使溶液呈中性，溶液中含CH3COO－数目为N A 【答案】D【解析】1L0.1mol·L－1NaClO溶液中，ClO－水解，因此含有ClO－的数目小于0.1N A，故A错误；氨气溶于水是可逆反应，因此所得溶液中N(NH3)＋N(NH3·H2O)＋N(NH＋4)＝N A，故B错误；1L0.1mol·L－1NaHSO4溶液中，NaHSO4电离出钠离子和氢离子，因此含有的阳离子数目大于0.1N A，故C错误；将1mol CH3COONa溶于稀醋酸中使溶液呈中性，根据电荷守恒和溶液呈中性得到溶液中含CH3COO－数目为N A，故D正确。

阶段检测卷二元素化合物(解析版)(2)

专题突破卷02 元素化合物（考试时间：75分钟试卷满分：100分）一、选择题（本题共15小题，每小题3分，共45分。

每小题只有一项是符合题目要求的）1．(2023·上海静安二模)自然界与人类活动对硫的循环均能产生影响。

下列说法错误的是()A．火山口温度过高，附近的单质硫会被O2直接氧化为SO3B．大气中的SO2会形成酸雨，最终以H2SO4的形式进入地面或海洋C．工业排放的SO2尾气可与CaO和O2反应生成CaSO4D．常温下，浓H2SO4能使铁片钝化是由于其具有强氧化性【答案】A【解析】单质硫与O2反应只能变为SO2，SO2和O2在催化剂、加热条件下发生可逆反应生成SO3，故A错误；大气中的SO2会形成酸雨，二氧化硫和水反应生成亚硫酸，亚硫酸被氧气氧化为硫酸，因此最终以H2SO4的形式进入地面或海洋，故B正确；工业排放的SO2尾气可与CaO和O2反应生成CaSO4，因此常用氧化钙处理工业排放的SO2尾气，故C正确；浓硫酸具有强氧化性，因此常温下，浓H2SO4能使铁片钝化，故D正确。

2．明末科学家宋应星出版的《天工开物》中记载了有关“五金”的内容：“……黄金美者，其值去黑铁(生铁)一万六千倍，然使釜、鬵(xín，一种炊具)、斤(这里指菜刀、镰刀、锄头等)、斧不呈效于日用之间……贸迁有无，……”，下列解释正确的是()A．明代使用的釜、鬵一类的炊具都属于青铜合金B．添加了铬、镍的不锈钢菜刀和农具使用后即使不保养，也不会生锈C．金属的另一个用途就是铸成钱币作为贸易交往中的流通手段D．黑铁在空气中发生的腐蚀主要是化学腐蚀【答案】C【解析】明代使用的釜、鬵一类的炊具都属于铁合金，故A错误；不锈钢制作就是在普通钢中添加铬、镍等元素改变了钢铁内部结构，不锈钢不容易生锈，家里用的农具是铁合金，如果没及时洗干净后晾干，铁能与氧气、水同时接触，容易发生电化学腐蚀，容易生锈，故B错误；金属可以用来铸成钱币作为贸易交往中的流通手段，故C正确；生铁的腐蚀主要是析氢腐蚀和吸氧腐蚀，属于电化学腐蚀，故D错误。

河北省鸡泽一中2022届高三物理专题检测试题(二)(含解析)

D、只要动摩擦因素足够大，即可满足F1cosθ≤μF1sinθ，不管M多大，M都不会滑动；故D错误；
故选A．
【点评】本题关键是明确物体的受力情况，然后根据平衡条件列式分析，选项D涉及摩擦自锁现象，不难．
8.如图所示，倾斜的木板上有一静止的物块，在保证物块不相对木板滑动的情况下，现以过木板下端点O的水平轴为转轴，使木板在竖直面内顺时针缓慢旋转一个小角度．在此过程中下面说法正确的是
2.如图所示，两根轻弹簧a、b的上端固定在竖直墙壁上，下端连接在小球上．当小球静止，弹簧a、b与竖直方向的夹角分别为和．已知a、b的劲度系数分别为、，，则a、b两弹簧的伸长量之比为（）
A. B. C. D.
【答案】B
【解析】
【详解】作出小球的受力分析图如图所示：
根据平衡条件得：，故a弹簧弹力，b弹簧的弹力，根据胡克定理，得，则伸长量之比为，故B项正确，ACD三项错误．
Ff＝FN2＝
A．mgtanθ，与结论不相符，选项A错误；
B．，与结论相符，选项B正确；
C．0，与结论不相符，选项C错误；
D．，与结论不相符，选项D错误；
故选B。
7. 如图所示，质量均为M的A、B两滑块放在粗糙水平面上，两轻杆等长，杆与滑块、杆与杆间均用光滑铰链连接，在两杆铰合处悬挂一质量为m的重物C，整个装置处于静止状态，设杆与水平面间的夹角为θ．下列说法正确的是（）
解：A、将C的重力按照作用效果分解，如图所示：
根据平行四边形定则，有：
故m一定时，θ越大，轻杆受力越小，故A正确；
B、对ABC整体分析可知，对地压力为：FN=（2M+m）g；与θ无关；故B错误；
C、对A分析，受重力、杆的推力、支持力和向右的静摩擦力，根据平衡条件，有：

七年级上册数学举一反三系列(人教版)专题12 期末达标检测卷(二)(人教版)(解析版)

2019-2020学年七年级数学上学期期末达标检测卷（二）参考答案与试题解析一．选择题（共10小题，满分30分，每小题3分）1．（3分）（2018秋•徽县期末）1()3--的相反数是( ) A ．3 B ．3- C ．13 D ．13- 【分析】直接利用互为相反数的定义得出答案．【答案】解：11()33--=的相反数是：13-．故选：D ．【点睛】此题主要考查了相反数，正确把握相关定义是解题关键．2．（3分）（2018秋•大连期末）根据等式的基本性质，下列结论正确的是( )A ．若x y a a =，则x y =B ．若x y =，则x y a a= C ．若x a y a +=-，则x y =D ．若x y =，则ax by =【分析】根据等式的性质解答．【答案】解：A 、等式的两边同时乘以a 得到：x y =，故本选项符合题意．B 、当0a =时，该结论不成立，故本选项不符合题意．C 、等式的两边应该同时加上a 或者减去a ，等式x y =不成立，故本选项不符合题意．D 、等式的两边应该同时乘以a 或b ，故本选项不符合题意．故选：A ．【点睛】考查了等式的性质．性质1、等式两边加同一个数（或式子）结果仍得等式；性质2、等式两边乘同一个数或除以一个不为零的数，结果仍得等式．3．（3分）（2018秋•三门峡期末）下列式子计算正确的个数有( )①224a a a +=；②22321xy xy -=；③32ab ab ab -=；④32(2)(3)17---=-．A ．1个B ．2个C ．3个D ．0个【分析】根据合并同类项的法则和有理数的混合运算进行计算即可．【答案】解：①2222a a a +=，故①错误；②22232xy xy xy -=，故②错误；③32ab ab ab -=，故③正确；④32(2)(3)17---=-，故④正确，故选：B ．【点睛】本题考查了合并同类项的法则和有理数的混合运算，掌握运算法则是解题的关键．4．（3分）（2018秋•三门峡期末）已知72018n x y +与232019m x y +-是同类项，则2(2)m n -的值是( )A ．4048B ．16C ．4048-D ．5【分析】根据同类项的定义，所含字母相同且相同字母的指数也相同的项是同类项，注意同类项与字母的顺序无关，与系数无关．【答案】解：72018n x y +Q 与232019m x y +-是同类项，723n m ∴+=+，24m n ∴-=，22(2)416m n ∴-==．故选：B ．【点睛】本题考查同类项的定义，同类项定义中的两个“相同”：所含字母相同；相同字母的指数相同，是易混点，还有注意同类项定义中隐含的两个“无关”：①与字母的顺序无关；②与系数无关．5．（3分）（2019春•南岗区期末）下列说法错误的是( )A ．单项式235x y 的系数是35B ．单项式223a b 的次数是4C ．多项式31a -的常数项是1D ．多项式243x -是二次二项式【分析】利用单项式系数、次数定义，多项式项与次数定义判断即可．【答案】解：A 、单项式235x y 的系数是35，不符合题意； B 、单项式223a b 的次数是4，不符合题意；C 、多项式31a -的常数项是1-，符合题意；D 、多项式243x -是二次二项式，不符合题意，故选：C ．【点睛】此题考查了多项式，以及单项式，熟练掌握各自的性质是解本题的关键．6．（3分）（2018秋•三门峡期末）一个几何体的表面展开图如图所示，则这个几何体是( )A．三棱柱B．三棱锥C．四棱柱D．四棱锥【分析】根据四棱锥的侧面展开图得出答案．【答案】解：如图所示：这个几何体是四棱锥．故选：D．【点睛】此题主要考查了几何体的展开图，熟记常见立体图形的平面展开图的特征是解决此类问题的关键．7．（3分）（2018秋•三门峡期末）在如图所示的2018年1月的月历表中，任意框出表中竖列上的三个相邻的数，这三个数的和不可能是()A．27B．51C．65D．72【分析】设第一个数为x，则第二个数为7x+．列出三个数的和的方程，再根据选项解x+，第三个数为14出x，看是否存在．【答案】解：设第一个数为x，则第二个数为7x+x+，第三个数为14故三个数的和为714321x x x x++++=+当17x=时，32172x+=；当10x=时，32151x+=；当2x=时，32127x+=．故任意圈出一竖列上相邻的三个数的和不可能是65．故选：C．【点睛】此题主要考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．8．（3分）（2018秋•鄞州区期末）如图，从4点钟开始，过了40分钟后，分钟与时针所夹角的度数是( )A．90︒B．100︒C．110︒D．120︒【分析】4点时，分针与时针相差四大格，即120︒，根据分针每分钟转6︒，时针每分钟转0.5︒，则40分钟后它们的夹角为406430400.5⨯︒-⨯︒-⨯︒．【答案】解：4点40分钟时，钟表的时针与分针形成的夹角的度数406430400.5100=⨯︒-⨯︒-⨯︒=︒．故选：B．【点睛】本题考查了钟面角：钟面被分成12大格，每大格30︒；分针每分钟转6︒，时针每分钟转0.5︒．9．（3分）（2019秋•莱州市期末）有一个商店把某件商品按进价加20%作为定价，可是总卖不出去，后来老板按定价减价20%以192元出售，很快就卖掉了，这次生意的盈亏情况为()A．赚8元B．不亏不赚C．亏8元D．亏48元【分析】设进价为x元，根据进价的(120%)-，等于192，列方程求解即可．+乘以(120%)【答案】解：设进价为x元，由题意得：x+-=(120%)(120%)192∴⨯=x1.20.8192∴=x200-=（元)2001928故选：C．【点睛】本题考查了列一元一次方程在经济问题中的应用，明确进价、定价及售价之间的数量关系，是解题的关键．10．（3分）（2018秋•思明区校级期末）如图，数轴上A、B、C三点所表示的数分别是a、6、c．已知8AB=，mx x-+=的一个解，则m的值为()+=，且c是关于x的方程4160a cA．4-B．2C．4D．6【分析】根据题意，可以分别求得a、c的值，然后根据c是关于x的方程4160-+=的一个解，从而mx x可以求得m的值．【答案】解：由已知可得，8b=，AB=，668a ∴-=，得2a =-，0a c +=Q ，20c ∴-+=，得2c =，c Q 是关于x 的方程4160mx x -+=的一个解，242160m ∴-⨯+=，得4m =-，故选：A ．【点睛】本题考查实数与数轴、一元一次方程的解，解答本题的关键是明确题意，求出m 的值．二．填空题（共6小题，满分18分，每小题3分）11．（3分）（2018秋•建邺区校级期末）如图，一副三角板如图示摆放，α∠与β∠的度数之间的关系应为 90αβ∠+∠=︒ ．【分析】根据平角定义可得1809090αβ∠+∠=︒-︒=︒．【答案】解：1809090αβ∠+∠=︒-︒=︒故答案为：90αβ∠+∠=︒【点睛】此题主要考查了平角，余角，如果两个角的和等于90︒（直角）12．（3分）（2019秋•临潼区期末）若多项式28(1)58(x m xy y xy m ++-+-是常数）中不含xy 项，则m 的值为 2- ．【分析】根据合并同类项法则把原式合并同类项，根据题意列出方程，解方程得到答案．【答案】解：28(1)58x m xy y xy ++-+-28(2)58x m xy y =++--由题意得，20m +=，解得，2m =-故答案为：2-．【点睛】本题考查的是合并同类项，合并同类项法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变．13．（3分）（2019秋•滕州市期末）如图，四个有理数在数轴上的对应点分别是M 、N 、P 、Q ，若点M ，Q 表示的有理数互为相反数，则图中表示绝对值最小的数的点是 N ．【分析】首项根据点M ，Q 表示的有理数互为相反数，可得点M ，Q 表示的有理数的绝对值相等，所以点M ，Q 的中点即是原点；然后根据图示，可得点N 和点M 之间的距离大于点P 和点Q 之间的距离，所以点N 离原点最近，所以图中表示绝对值最小的数的点是N ，据此解答即可．【答案】解：因为点M ，Q 表示的有理数互为相反数，所以点M ，Q 的中点即是原点；因为点N 和点M 之间的距离大于点P 和点Q 之间的距离，所以点N 离原点最近，所以图中表示绝对值最小的数的点是N ．故答案为：N ．【点睛】（1）此题主要考查了有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．（2）此题还考查了在数轴上表示数的方法，以及数轴的特征：一般来说，当数轴方向朝右时，右边的数总比左边的数大，要熟练掌握．（3）此题还考查了绝对值的含义和应用，要熟练掌握，解答此题的关键是要明确：①当a 是正有理数时，a 的绝对值是它本身a ；②当a 是负有理数时，a 的绝对值是它的相反数a -；③当a 是零时，a 的绝对值是零．（4）此题还考查了相反数的含义以及求法，要熟练掌握，解答此题的关键是要明确：互为相反数的两个数的绝对值相等，且它们的和等于0． 14．（3分）（2019秋•沂源县校级期末）方程423x m x +=-与方程662x -=-的解相同，则m = 21- ．【分析】先解方程662x -=-得，6x =-，把6x =-代入方程423x m x +=-即可求得m 的值．【答案】解：根据方程662x -=-得6x =-；将6x =-代入程：423x m x +=-，得：3643m -+=--，解得：21m=-．【点睛】本题含有一个未知的系数．根据已知条件求未知系数的方法叫待定系数法，在以后的学习中，常用此法求函数解析式．15．（3分）（2018秋•松滋市期末）如图，OA的方向是北偏东21︒，OB的方向是北偏西40︒，若AOB AOC∠=∠，则OC的方向是北偏东82︒．【分析】先根据角的和差得到AOB∠的度数，再根据角的和差得∠的度数，根据AOC AOB∠=∠得到AOC到OC的方向．【答案】解：OAQ的方向是北偏东21︒，OB的方向是北偏西40︒，∴∠=︒+︒=︒，AOB214061Q，AOC AOB∠=∠AOC∴∠=︒，61︒+︒=︒，612182故OC的方向是北偏东82︒．故答案为：北偏东82︒．【点睛】考查了方位角，方位角是表示方向的角；以正北，正南方向为基准，来描述物体所处的方向．16．（3分）（2018秋•三门峡期末）2018年元月初，我国中东部地区普降大雪，某武警部队战士在两个地方进行救援工作，甲处有130名武警部队战士，乙处有70名武警部队战士．现在又调来200名武警部队战士支援，要使甲处的人数比乙处人数的2倍多10人，应往甲、乙两处各调去多少名武警部队战士？设应往甲处调去x名武警部队战士．根据题意，列出关于x的方程是．【分析】设应往甲处调去x名武警部队战士，则设应往乙处调去(200)x-名武警部队战士，根据调配后甲处的人数比乙处人数的2倍多10人，即可得出关于x的一元一次方程，此题得解．【答案】解：设应往甲处调去x名武警部队战士，则设应往乙处调去(200)x-名武警部队战士，依题意，得：1302[70(200)]10x x +=+-+．故答案为：1302[70(200)]10x x +=+-+．【点睛】本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键．三．解答题（共6小题，满分52分）17．（8分）（2018秋•三门峡期末）计算题（1）(45)(9)(3)-÷-⨯-（2）33412|4|(2)4-⨯+-÷-．【分析】（1）先算除法，再算乘法；（2）先算乘方和绝对值，再算乘除，最后算加法．【答案】解：（1）原式5(3)=⨯-15=-；（2）原式1864164=-⨯+÷ 24=-+2=．【点睛】此题考查有理数的混合运算，掌握运算顺序、符号的判定与计算方法是解决问题的关键．18．（8分）（2018秋•天长市期末）先化简，再求值：2223[23(2)]x y x y xy x y xy ----，其中12x =-，2y =．【分析】去小括号，去中括号，合并同类项，最后代入求出即可．【答案】解：2223[23(2)]x y x y xy x y xy ----2223[263]x y x y xy x y xy =--+-2223263x y x y xy x y xy =-+-+227x y xy =-+ 当12x =-，2y =时，原式2112()27()222=-⨯-⨯+⨯-⨯ 8=-．【点睛】本题考查了整式的化简求值和有理数的混合运算的应用，主要考查学生的化简能力和计算能力．19．（8分）（2018秋•柯桥区期末）解下列方程（1）43(2)x x+-=（2）4131136x x--=-．【分析】（1）方程去括号，移项合并，把x系数化为1，即可求出解；（2）方程去分母，去括号，移项合并，把x系数化为1，即可求出解．【答案】解：（1）去括号得：436x x+-=，移项合并得：22x=，解得：1x=；（2）去分母得：82631x x-=-+，移项合并得：119x=，解得：911x=．【点睛】此题考查了解一元一次方程，解方程去分母时注意各项都乘以各分母的最小公倍数．20．（8分）（2018秋•河北区期末）如图，已知线段AB和CD的公共部分1134BD AB CD==，线段AB、CD的中点E、F之间距离是10cm，求AB，CD的长．【分析】先设BD xcm=，由题意得3AB xcm=，4CD xcm=，6AC xcm=，再根据中点的定义，用含x的式子表示出AE和CF，再根据 2.5EF AC AE CF x=--=，且E、F之间距离是10cm，所以2.510x=，解方程求得x的值，即可求AB，CD的长．【答案】解：设BD xcm=，则3AB xcm=，4CD xcm=，6AC xcm=．Q点E、点F分别为AB、CD的中点，11.52AE AB xcm∴==，122CF CD xcm==．6 1.52 2.5EF AC AE CF x x x xcm∴=--=--=．10EF cm=Q， 2.510x∴=，解得：4x=．12AB cm∴=，16CD cm=．【点睛】本题主要考查了两点间的距离和中点的定义，注意运用数形结合思想和方程思想．21．（10分）（2019秋•海陵区校级期末）已知：如图，ON平分AOC∠，OM平分BOC∠，90AOB∠=︒；（1）40AOC∠=︒，求MON∠的大小；（2）当锐角AOC∠的度数发生改变时，MON∠的大小是否发生改变，并说明理由．【分析】（1）求得130BOC ∠=︒，然后求得1202NOC AOC ∠=∠=︒，1652MOC BOC ∠=∠=︒，根据MON MOC NOC ∠=∠-∠即可求出MON ∠的度数．（2）结合图形，根据角的和差，以及角平分线的定义，找到MON ∠与AOB ∠的关系，即可求出MON ∠的度数．【答案】解：（1）90AOB ∠=︒Q ，40AOC ∠=︒，130BOC ∴∠=︒，ON Q 平分AOC ∠，OM 平分BOC ∠，1202NOC AOC ∴∠=∠=︒，1652MOC BOC ∠=∠=︒， 652045MON MOC NOC ∴∠=∠-∠=︒-︒=︒，即45MON ∠=︒；（2）不发生改变，理由：OM Q 平分BOC ∠，ON 平分AOC ∠，12MOC BOC ∴∠=∠，12NOC AOC ∠=∠， 1()2MON MOC NOC BOC AOC ∴∠=∠-∠=∠-∠ 1()2AOB AOC AOC =∠+∠-∠ 12AOB =∠ 45=︒．所以不发生改变．【点睛】本题考查了角的计算，属于基础题，此类问题，注意结合图形，运用角的和差和角平分线的定义求解．22．（10分）（2018秋•三门峡期末）根据国家发改委实施“阶梯电价”的有关文件要求，某市结合地方实际，决定从2015年5月1日起对居民生活用电试行“阶梯电价”收费，具体收费标准见下表．若2015年5月份，该市居民甲用电100千瓦时，交电费60元．（1）上表中，a = 0.6 ，若居民乙用电200千瓦时，交电费元．（2）若某用户某月用电量超过300千瓦时，设用电量为x 千瓦时，请你用含x 的代数式表示应交的电费．（3）试行“阶梯电价”收费以后，该市一户居民月用电多少千瓦时时，其当月的平均电价每千瓦时不超过0.62元？【分析】（1）根据100150<结合应交电费60元即可得出关于a 的一元一次方程，解之即可得出a 值；再由150200300<<，结合应交电费1500.60.65=⨯+⨯超出150千瓦时的部分即可求出结论；（2）根据应交电费1500.6(300150)0.650.9=⨯+-⨯+⨯超出300千瓦时的部分，即可得出结论；（3）设该居民用电x 千瓦时，其当月的平均电价每千瓦时为0.62元，分x 在第二档及第三档考虑，根据总电费=均价⨯数量即可得出关于x 的一元一次方程，解之即可得出x 值，结合实际即可得出结论．【答案】解：（1）100150<Q ，10060a ∴=，0.6a ∴=．若居民乙用电200千瓦时，应交电费1500.6(200150)0.65122.5⨯+-⨯=（元)．故答案为：0.6；122.5．（2）当300x >时，应交的电费1500.6(300150)0.650.9(300)0.982.5x x ⨯+-⨯+-=-．（3）设该居民用电x 千瓦时，其当月的平均电价每千瓦时为0.62元，当该居民用电处于第二档时，900.65(150)0.62x x +-=，解得：250x =；当该居民用电处于第三档时，0.982.50.62x x -=，解得：294.6300x ≈<（舍去）．综上所述该居民用电不超过250千瓦时，其当月的平均电价每千瓦时不超过0.62元．【点睛】本题考查了一元一次方程的应用以及列代数式，解题的关键是：（1）根据数量关系列式计算；（2）根据数量关系列出代数式；（3）根据总电费=均价⨯数量列出关于x的一元一次方程．。

2022届高考地理模拟训练2热力环流含答案解析

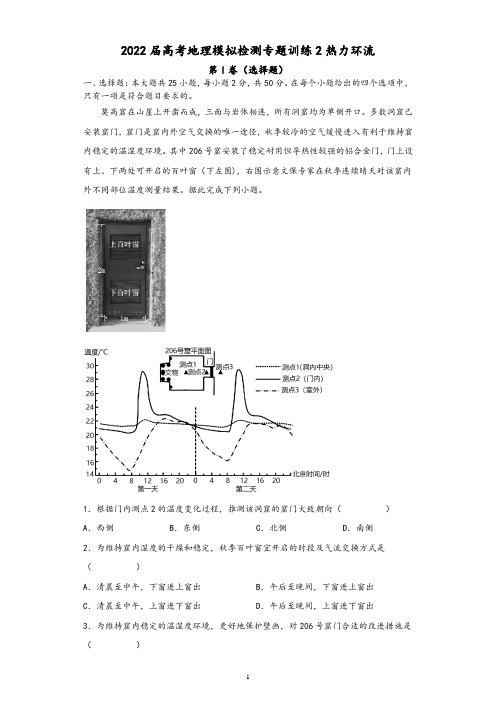
2022届高考地理模拟检测专题训练2热力环流第I卷（选择题）一、选择题：本大题共25小题，每小题2分，共50分。

在每个小题给出的四个选项中，只有一项是符合题目要求的。

莫高窟在山崖上开凿而成，三面与岩体相连，所有洞窟均为单侧开口。

多数洞窟已安装窟门，窟门是窟内外空气交换的唯一途径，秋季较冷的空气缓慢进入有利于维持窟内稳定的温湿度环境。

其中206号窟安装了稳定耐用但导热性较强的铝合金门，门上设有上、下两处可开启的百叶窗（下左图)，右图示意文保专家在秋季连续晴天对该窟内外不同部位温度测量结果。

据此完成下列小题。

1．根据门内测点2的温度变化过程，推测该洞窟的窟门大致朝向（）A．西侧B．东侧C．北侧D．南侧2．为维持窟内湿度的干燥和稳定，秋季百叶窗宜开启的时段及气流交换方式是（）A．清晨至中午，下窗进上窗出B．午后至晚间，下窗进上窗出C．清晨至中午，上窗进下窗出D．午后至晚间，上窗进下窗出3．为维持窟内稳定的温湿度环境，更好地保护壁画，对206号窟门合适的改进措施是（）A．换成导热更好的板材B．扩大门上百叶窗面积C．将窟门外面涂成浅色D．换成透明的厚玻璃门华西秋雨是我国西部地区秋季多雨的特殊天气现象，主要影响四川、重庆、贵州、宁夏南部、甘肃东部和南部、陕西南部及湖南西部、湖北西部等地。

如图为部分地区华西秋雨的日变化示意图。

据此完成问题。

4．夜雨率高是华西秋雨的一个重要特点，其主要影响因素是（）A．地形B．夏季风C．纬度位置D．海陆位置5．夜雨对农业生产的影响有（）A．缩短日照时间B．加大昼夜温差C．抑制光合作用D．利于害虫繁殖洞穴滴水衔接了洞穴外部环境和内部沉积物，能够反映出洞穴内外物质迁移和能量交换。

围岩指隧道或洞穴周围一定范围内，对洞身的稳定有影响的岩（土）体。

不同季节，洞穴内外通风模式有所不同。

下图示意广西某洞穴（有竖井与外界相通）的洞穴外大气二氧化碳、洞穴内二氧化碳、洞穴内滴水水温的季节变化。

据此完成下面小题。

初中语文八上专项测试卷二(句子)及答案

专题测试卷一字词时间: 50分钟满分: 60分一、病句的辨析与修改(19分)1．下列句子中没有语病的一项是(3分)( )A．改革开放以来，我县工业产品的数量和质量都有显著提高。

B．晋梅中学的《雪花》校刊里有很多散文、诗歌和优秀习作。

C．博物馆展出了刚出土的几千年前的文物。

D．我的故乡是湖北省黄梅县人。

2．下列各句中没有语病的一项是(3分)( )A．习近平指出，“一带一路”倡议顺应时代潮流，适应发展规律，符合各国人民的利益，具有广阔前景。

B．“中华文化湖南行”以“弘扬中华优秀传统文化，展示伟人故里锦绣湖南”为主题，举办了文化讲坛、书画精品联展等。

C．“十三·五”期间，根据总体工作部署，我国将对近1 000万左右贫困人口实施异地扶贫搬迁。

D．一个热爱读书的人，既然不能拥有舒适的书房、清净的环境，也会始终保持一份纯洁的读书情感。

3．下列句子中没有语病的一项是(3分)( )A．班级图书角的书籍资源能否共享，是班级图书角良好运作的关键。

B．“感动中国”展示的是一个国家的精神脊梁，彰显的是一个民族。

C．在“相约油菜花节，分享成长之美”活动期间，家长和学生共同参加了学校组织的开放周启动仪式。

D．国家以立法的形式把9月3日确立为中国人民抗日战争胜利纪念日，树立了“铭记历史、缅怀先烈、珍爱和平、开创未来”的坚定意志。

4．下列句子中没有语病的一项是(3分)( )A．博物馆里，参观者衣衫不整、高声喧哗、在展厅内吃东西、乱丢垃圾和不文明行为，对其他参观者和展品都是一种不尊重的表现。

B．一些亏损企业在接受有关部门审查时，发现了这些企业亏损的主要原因是管理不善。

C．所谓“先诊断后结算”，是指患者在门诊诊疗时，先缴纳押金，统一待本次所有诊疗结束后再去结账。

D．一篇文章如果字迹潦草，那么即使内容很不错，也是要不得的。

5．下列句子中没有语病的一项是(3分)( )A．在遭受强烈地震后，尼泊尔面临着饮用水、食品、帐篷等物资短缺，基础设施损坏严重，救援工作很难开展。

高考语文复习古诗歌专题检测二

古诗歌专题检测（二）1．阅读下面这首唐诗,完成(1)～(2)题。

(9分)贾客词刘驾贾客灯下起,犹言发已迟。

高山有疾路,暗行终不疑。

寇盗伏其路,猛兽来相追。

金玉四散去,空囊委路歧。

扬州有大宅,白骨无地归。

少妇当此日,对镜弄花枝。

(1)下列对诗歌有关内容的理解和赏析,不正确的一项是(3分)( )A．人评刘驾最能“以诗鸣于时”,诗开篇以同情笔意再现贾客灯下起身赶路,表现出经商艰辛。

B．贾客故事里寇盗可谓凶残,侧面反映出晚唐社会动乱、经济凋敝,以及百姓朝不保夕的命运。

C．“终不疑”语谓贾客未料夜行会身入死地,一如既往地走捷径,为悲惨的结局埋下了伏笔。

D．扬州是唐时繁华都会,也是商贾集散地,诗末点明住地扬州有深意,可使悲剧更具普遍意义。

解析：选B B项,“以及百姓朝不保夕的命运”错误,理解诗歌内容,应为“以及商人及其亲人的悲惨命运”。

(2)结合全诗,赏析“少妇当此日,对镜弄花枝”场景较为丰富的艺术效果。

(6分)答：参考答案：末尾巧写“少妇当此日”,让少妇上场而话分两头,少妇的红颜对镜和贾客的白骨无归,形成强烈对比,一乐一悲,而倍增悲情,再现了贾客及其妻子的悲惨命运。

捕捉少妇不知悲剧已然发生而对镜打扮的细节,如此鲜活的形象暗示了晚唐社会动乱所带来的民生凋敝。

[白话诗歌]2．阅读下面这首唐诗,完成(1)～(2)题。

(9分)江楼晚眺景物鲜奇吟玩成篇寄水部张员外白居易澹烟疏雨间斜阳,江色鲜明海气凉。

蜃①散云收破楼阁,虹残水照断桥梁。

风翻白浪花千片,雁点青天字一行。

好著丹青图画取,题诗寄与水曹郎。

[注] ①蜃：大蛤蜊。

江海边或沙漠中,因空气冷热骤变,光线折射,而把远处的景物显示到空中或地面上,古人误以为是蜃吐气而成,称海市蜃楼。

(1)下列对这首诗的理解和赏析,不正确的一项是(3分)( )A．首句从阳光写起,描摹斜阳余晖透过淡烟疏雨的间隙射到水面的场景,清新可人。

B．江面经雨水一洗,在夕阳的照耀之下愈发新鲜明净,风从水面阵阵袭来,给人凉爽之感。

专题44 2021年山东聊城市中考语文一轮复习检测卷(二)(解析版)

2021年山东聊城市中考语文一轮复习检测卷（二）一、字词书写1．根据拼音写汉字。

踏着春的脚步，迎着（hé xù）的春风，徜徉在美丽的江北水城，被周围的桃红柳绿深深吸引，俗话说：红花虽好，需要绿叶扶持，红花争奇斗艳，绿叶更是锦上添花，搭配在一起，令人赏心悦目，（xīn kuàng shén yí）！二、选择题2．填入下面语段横线处的句子，语序最恰当的一项是（）文化影响人的思维方式和行为习惯，调节人与世界的关系。

在一个文化厚实的社会里，；；。

这样，人方能实现从“小我”向“大我”的转变，成为一个有文化、有教养的人。

①人懂得尊重自然——他不掠夺，因为不掠夺所以有永续的生命②人懂得尊重自己——他不苟且，因为不苟且所以有品味③人懂得尊重别人——他不霸道，因为不霸道所以有道德A．②①③B．③①②C．③②①D．②③①三、名著阅读3．下面是三部名著的片段，根据你的积累，按要求答题。

（1）节选中的“A”指的是：（_________）（2）写出作品②的名称《___________》。

（3）唐僧写下“贬书”的原因：______________________________。

四、语言表达4．依照下面画线句子进行仿写，使之构成一组语意连贯的排比句。

陪伴是最真情的告白：根与土相拥，孱弱的生命充满力量；星与月相随，黑暗的夜空告别孤寂；__________________，________________。

陪伴是平淡而厚重的情憾，请珍借伴我们成长的点点滴滴。

五、句子默写5．按要求填空。

①它没有婆娑的姿态，______________________________。

（茅盾《白杨礼赞》）②谁见幽人独往来，________________________。

（苏轼《卜算子·黄州定慧院寓居作》）③__________________，受降城外月如霜。

（李益《夜上受降城闻笛》）④__________________，弓如霹雳弦惊。

2020年中考地理二轮复习专题训练卷二【地球的自转】附答案详析

2020年中考地理二轮复习专题训练卷二【地球的自转】1.地球绕着地轴旋转，叫做地球的自转。

地球的自转周期是（）A.24小时B.7天C.30天D.365天2.如果我们按地球自转方向转动地球仪（如图所示），最先从我们视线中消失的是（）A.①B.②C.③D.④3.2010年感动中国人物翟墨，从山东日照起航，历时两年零七个月，途经三大洋、五大洲，成为中国无动力帆船环球般海第一人。

读图完成下列两题。

（1）颁奖辞说“…他眺望先辈的方向，直挂去帆，从西方出发，从东方归航…”。

下列关于他的行程，说法正确的是（）A.依次经过太平洋—印度洋—大西洋—太平洋B.经过了南美洲南端的好望角C.航行方向与地球自转方向相同D.经马六甲海峡进入印度洋（2）“翟墨桅杆上高昂的五星红旗，有力的告诉世人，中国人拥抱海洋的勇气、豪情与胸怀”。

当翟墨于2009年8月返航时，五星红旗飘向的是（）A.西北B.东南C.东北D.西南4.仪是地球的模型，观察图所示地球仪，完成下题。

（1）地球仪上B点所在的大洋是（）A.大西洋B.太平洋C.印度洋D.北冰洋（2）将图示地球仪按地球自转方向转动，最早从我们视线中消失的是（）A.A点B.B点C.C点D.D点5.“地球一小时活动”于2012年3月31日晚8：30拉开帷幕，全球有143个国家的城市在当地晚8：30~9：30顺次参与了熄灯接力活动。

关于这以活动正确的是（）A.线路顺次经过大洋洲、亚洲、欧洲、美洲、非洲B.熄灯顺序自东向西，与地球自转方向一致C.亚洲国家比美洲国家更早迎来“熄灯活动”D.“地球一小时活动”进行时，各国会同时熄灯6.下面是小军绘制的地球自转方向图，正确的是（）A. B. C. D.7.读材料：2018男子足球世界杯于6月14日一7月15日在俄罗斯举行，回答下面小题。

（1）2018俄罗斯世界杯揭幕战于莫斯科当地时间6月14日18时进行，我国大部分球迷则是6月14日23时左右收看，造成两地时间差异的主要原因是（）A.纬度差异B.经度差异C.海陆位置差异D.昼夜长短差异（2）2018俄罗斯世界杯期间，下列地理现象最可信的是（）A.云南傣族人民正忙于准备泼水节庆典活动B.太阳直射点位于北半球并且将一直向北运动C.是乘船游览挪威峡湾，观看午夜太阳的最佳时期D.在相同的太阳辐射条件下，纬度相同的地方，陆地气温高于海洋8.读图，完成以下问题。

2023年安徽省阜阳市小升初数学严选思维应用题专项训练卷二(含答案及精讲)

2023年安徽省阜阳市小升初数学严选思维应用题专项训练卷二(含答案及精讲)学校:________ 班级:________ 姓名:________ 考号:________一、思维应用题(50题，每题2分)1.铺一条路，原计划每天铺3.2千米，15天铺完．实际每天比原计划多铺25%，实际多少天铺完这条路？2.甲、乙两地相距330千米，一辆汽车从甲地开往乙地，去的时候用了6小时，沿原路返回时少用了1小时，返回时的速度是多少？3.铺一条长5200米的通讯光缆，已经铺了14天，每天铺150米．剩下的要在20天内铺完，剩下的平均每天要铺多少米？4.养鸡场养了213只小鸡，养的大鸡的只数是小鸡的2倍，养鸡场一共养了多少只鸡？5.施工队准备铺一条长60米、宽3米的人行道．（1）人行道的面积是多少平方米？（2）有两种方案，一种是用边长3分米的方砖，每块3元，一种是用边长5分米的方砖，每块4元，用哪种方砖铺便宜些？6.王老师买了5个足球和3个篮球共花了505元，已知每个足球68元，那么每个篮球多少元？(列方程)7.在一次爱心捐款活动中，希望小学的四年级共捐款260元，五年级捐的款是四年级的2倍，六年级捐的款比四、五年级的总数少115元，六年级捐款多少元？8.一块长方形的土地，长和宽的比是5：3，长比宽多24米，这块土地的面积是多少平方米？9.某车间共有171名工人，如果把男工的1/8和女工的6人调走，剩下的男、女工人数正好相等，求车间原有男工多少人？（列方程解）10.甲、乙两列火车分别从相距396千米的A、B两地同时出发，相向而行，经过1.5小时相遇，已知甲车速度是乙车的1.2倍，甲、乙车每小时各行多少千米？（用方程解答）11.一个工厂有两个生产车间，甲车间人数占两个车间总人数的60%，如果从甲车间调24人去乙车间，乙车间人数则占两个车间总数的55%．两个车间共有多少人？12.食堂买来一桶油，连桶带油是104千克，用了一半油后连桶带油是54千克，油和桶各多少千克？13.一辆车从甲地开往乙地，上午行了200千米，下午行了250千米，还剩1/10没行，甲乙两地相距多少千米？14.某工厂有77个工人，每个工人平均每天可以加工甲种零件5个，或乙种零件4个，或丙种零件3个，已知3个甲种零件、1个乙种零件和9个丙种零件恰好配成一套．问应安排生产甲、乙、丙三种零件各多少人才能使生产的三种零件恰好配套？15.一块长方形菜地长598厘米，宽305厘米，给这块菜地围上篱笆，大约需要多少米的篱笆？这块菜地的面积大约是多少平方米？16.红光小学组织师生去秋游，老师28人，学生456人，每辆旅游车有40个座位，要保证每人都有座位，需要准备几辆旅游车？17.西湖公园有一个圆型喷水池，周长是31.4米，在喷水池的周围铺一条2.5米宽的路，这条路的面积是多少？18.机床厂四月份计划生产机床240台，结果提前6天完成，实际平均每天生产机床多少台？19.食堂买来大米180袋，9月份吃了总量的1/9，10月份吃的比剩下袋数的1/8还多2袋，如果剩下的每月平均吃23袋，还能吃几个月？20.植树节同学们去植树，植的树死了18棵，成活率是98%。

2023年高中数学【指数函数的定义、解析式、定义域和值域】专题练习卷二

2023年高中数学【指数函数的定义、解析式、定义域和值域】专题练习卷二考试总分：188 分考试时间： 120 分钟学校：__________ 班级：__________ 姓名：__________ 考号：__________注意事项：1．答题前填写好自己的姓名、班级、考号等信息; 2．请将答案正确填写在答题卡上;卷I （选择题）一、选择题（本题共计 11 小题，每题 3 分，共计33分）1. 指数函数在上的最大值与最小值的和为，则( )A.B.C.或D.2. 已知集合，，则 A.B.C.D.3. 令，，，则三个数，，的大小顺序是 A.B.C.D.4. 设集合，，则 A.B.C.y =b ⋅a x [b,2]6a =12−32−32A ={x |y =(x −1)}log 2B ={y |y =+1,x ∈A}2x A ∩B =()φ(1,3)(3,+∞)(1,+∞)a =60.7b =0.76c =6log 0.7a b c ()b <c <ab <a <cc <a <bc <b <aS ={y |y =−2,x ∈R}e x T ={x |−4≤x ≤1}S ∪T =()[−4,+∞)(−2,+∞)[−4,1](−2,1]D.5. 已知，则A.B.C.D.6. 函数是指数函数，则的值为（）A.B.C.或D.不确定7. 定义在上的函数满足，当时，，则 A.B.C.D.8. 设，若仅有一个常数使得对于任意的，都有满足方程，这时的取值为（）A.B.C.D.9. 函数是指数函数，则有（）A.或B.C.(−2,1]a =0.2,b =,c =log 220.20.20.3()a <b <ca <c <bc <a <bb <c <ay =(−3a +3)a 2a x a 1212R f(x)f(−x)=−f(x)x <0f(x)=(13)x f()=(12)3–√33–√−3–√9a >1c y ∈[a,2a]x ∈[a,]a 2x +y =c log a log a a +c 3456y =(−5a +5)a 2a x a =1a =4a =1a =4a ≠1D.，且10. 已知集合，，则 A.B.C.D.11. 设，若仅有一个常数使得对于任意的，都有满足方程，则的取值集合为（）A.B.C.D.二、多选题（本题共计 3 小题，每题 3 分，共计9分）12. 若函数，且是指数函数，则下列说法正确的是（）A.＝B.＝C.D.＝E.＝13. 下列命题中的真命题是( )A.，B.，C.，D.，a >0a ≠1M ={x |x <1}N={x |>1}2x M ∩N =()∅{x |x <0}{x |x <1}{x |0<x <1}a >1c x ∈[a,]a 2y ∈[1+ 2−,2−a]log a a 3=c a x a y a {4}{,2}32{2}{}32(a >0a ≠1)a 8f(0)−3a 4f(2)16∀x ∈R ≥0x 2∀x ∈R >02x−1∃x ∈R lgx <1∃x ∈R sin x +cos x =2(x)=(a −3)⋅(a >0114. 若函数，且）是指数函数，则下列说法正确的是（）A.B.C.D.卷II （非选择题）三、填空题（本题共计 12 小题，每题 3 分，共计36分）15. 集合为函数的值域，集合为函数的值域，则________．16. 函数＝，的值域为________．17. 函数的定义域是，且最大值与最小值的差为，则________．18. 函数的值域是________．19. 函数的定义域是________；值域是________．20. 已知指数函数且的图象过点，则________．21. 已知函数是指数函数，且当时，，则实数的取值范围是________.22. 已知的值域为________．23. 函数的定义域是________．24. 函数的值域为________．f(x)=(a −3)⋅(a >012a x a ≠1a =8f (0)=−3f ()=2122–√a =4A y =(x ≠0)2x −1x B y =(−1(x ∈R)13)x A ∩B =y (12)x (x ≥0)y =(a >1)a x [−1,1]1a =y =(x ∈R)1−2x −−−−−√y =1−(12)x −−−−−−−√y =(a >0a x a ≠1)(2,9)a =y =(a −1)x x <0y >1a f(x)=−1e x +1e x y =(−12)3x−118−−−−−−−−−−√f(x)=(12)x √{x |<2011}⊆(−∞,a)2x25. 若集合，则整数的最小值为________．26. 若函数的图象与轴有公共点，则的取值范围是________．四、解答题（本题共计 11 小题，每题 10 分，共计110分）27. 已知幂函数，且在上单调递增．（1）求实数的值；（2）若，求实数的取值范围． 28. 漳州市某研学基地，因地制宜划出一片区域，打造成“生态水果特色区”．经调研发现：某水果树的单株产量（单位：千克）与施用肥料（单位：千克）满足如下关系：，且单株施用肥料及其它成本总投入为元．已知这种水果的市场售价大约为元/千克，且销路畅通供不应求．记该水果树的单株利润为（单位：元）．求函数的解析式；当施用肥料为多少千克时，该水果树的单株利润最大？最大利润是多少？29. 已知指数函数的图象经过点，且函数的图象与的图象关于轴对称．求函数的解析式；若，求的取值范围．30. 函数的图像恒过定点,且点在指数函数的图像上，则 ________. 31. 设的定义域是，且对任意不为零的实数都满足．已知当时（1）求当时，的解析式（2）解不等式． 32. 已知命题，；命题：函数在区间上为减函数．若命题为真命题，求实数的取值范围；若命题"或"为真命题，且“且”为假命题，求实数的取值范围．33. 已知函数的图象经过点，其中且．求的值；求函数的值域．34. 一工厂计划生产某种当地政府控制产量的特殊产品，月固定成本为万元，设此工厂一个月内生{x |<2011}⊆(−∞,a)2x a y =(−m 12)|1−x|x m f(x)=(−m −1)m 2x 2m−2(0,+∞)m f(3−)>f()2t+12t t W x W (x)= 2(+17),0≤x ≤2x 250−,2<x ≤58x −120x +1010f(x)(1)f(x)(2)f (x)P (3,8)g(x)f (x)y (1)g(x)(2)g(2−3x +1)>g(+2x −5)x 2x 2x f (x)=(x −1)+4(a >0,a ≠1)log a A A g(x)g(3)=f(x)(−∞,0)∪(0,+∞)f(x)x f(−x)=−f(x)x >0f(x)=x 1−2xx <0f(x)f(x)<−x 3p :∀x ∈R a −2x −1≤0x 2q y =(x +3)log a (0,+∞)(1)p a (2)¬p q p q a f(x)=(x ≥0)a x−1(2,)12a >0a ≠1(1)a (2)y =f(x)(x ≥0)1产该特殊产品万件并全部销售完．根据当地政府要求产量满足，每生产万件需要再投入万元，每万件的销售收入为(万元)，且每生产万件产品政府给予补助(万元).（注：月利润月销售收入月政府补助月总成本）.写出月利润(万元)关于月产量(万件)的函数解析式；求该工厂在生产这种特殊产品中所获得的月利润最大值(万元)及此时的月生产量(万件). 35. 已知函数，为常数且，的图象经过，.试求，的值；若不等式在时恒成立，求实数的取值范围． 36. 已知是定义在上的奇函数，且时，.求函数的解析式；画出函数的图象，并写出函数单调递增区间及值域．37. 已知函数，（1）讨论函数的奇偶性；（2）证明：．x x 1≤x ≤3x 3x 15−13x 211+2ln x x=+−(1)f(x)x (2)f(x)=b ⋅(a a x b a >0a ≠1)A(1,8)B(3,32)(1)a b (2)(+(−m ≥01a )x 1b )x x ∈(−∞,1]m y =f(x)R x <0f(x)=+23x (1)f(x)(2)y =f(x)y =f(x)f(x)=(+)x 1−12x 12f(x)>0参考答案与试题解析2023年高中数学【指数函数的定义、解析式、定义域和值域】专题练习卷二一、选择题（本题共计 11 小题，每题 3 分，共计33分）1.【答案】此题暂无答案【考点】指数函数单调性的应用指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答2.【答案】此题暂无答案【考点】交集及其运算指数函数的定义、解析式、定义域和值域对数函数的定义域【解析】此题暂无解析【解答】此题暂无解答3.【答案】此题暂无答案【考点】对数值大小的比较指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答4.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域并集及其运算【解析】此题暂无解析【解答】此题暂无解答5.【答案】此题暂无答案【考点】对数值大小的比较指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答6.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答7.【答案】此题暂无答案【考点】函数奇偶性的性质指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答8.【答案】此题暂无答案【考点】指、对数不等式的解法指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答9.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答10.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域交集及其运算【解析】此题暂无解析【解答】此题暂无解答11.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答二、多选题（本题共计 3 小题，每题 3 分，共计9分）12.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答13.【答案】此题暂无答案【考点】两角和与差的正弦公式命题的真假判断与应用正弦函数的定义域和值域对数函数的值域与最值指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答14.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答三、填空题（本题共计 12 小题，每题 3 分，共计36分）15.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答16.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答17.【答案】此题暂无答案【考点】指数函数单调性的应用指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答18.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答19.【答案】此题暂无答案【考点】函数的定义域及其求法函数的值域及其求法指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答20.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答21.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答22.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答23.【答案】此题暂无答案指数函数单调性的应用指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答24.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答25.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答26.【答案】此题暂无答案函数恒成立问题指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答四、解答题（本题共计 11 小题，每题 10 分，共计110分）27.【答案】此题暂无答案【考点】幂函数的概念、解析式、定义域、值域幂函数的性质【解析】此题暂无解析【解答】此题暂无解答28.【答案】此题暂无答案【考点】函数解析式的求解及常用方法函数模型的选择与应用二次函数在闭区间上的最值基本不等式在最值问题中的应用【解析】此题暂无解析29.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域指数函数单调性的应用【解析】此题暂无解析【解答】此题暂无解答30.【答案】此题暂无答案【考点】对数函数的图象与性质对数的运算性质指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答31.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域函数奇偶性的性质【解答】此题暂无解答32.【答案】此题暂无答案【考点】命题的真假判断与应用逻辑联结词“或”“且”“非”已知函数的单调性求参数问题【解析】此题暂无解析【解答】此题暂无解答33.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答34.【答案】此题暂无答案【考点】利用导数研究函数的最值函数模型的选择与应用函数最值的应用函数解析式的求解及常用方法【解析】此题暂无解析【解答】此题暂无解答35.【答案】此题暂无答案【考点】函数恒成立问题指数函数的定义、解析式、定义域和值域【解析】此题暂无解析【解答】此题暂无解答36.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域函数奇偶性的性质函数的单调性及单调区间分段函数的解析式求法及其图象的作法【解析】此题暂无解析【解答】此题暂无解答37.【答案】此题暂无答案【考点】指数函数的定义、解析式、定义域和值域函数奇偶性的判断函数奇偶性的性质【解析】此题暂无解析【解答】此题暂无解答。

专题2 细胞是生命活动的基本单位(滚动提升卷)-备战2020年中考生物专题滚动双测卷(解析版)

专题2 细胞是生命活动的基本单位滚动提升卷班级___________ 姓名___________ 学号____________ 分数____________（考试时间：90分钟试卷满分：100分）一、选择题：本题共25个小题，每小题2分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（滚动考查生物的特征）下列属于生物的是（）A．机器人B．电脑病毒C．钟乳石D．生石花【答案】D【解析】机器人、电脑病毒、钟乳石，都不具有生物的特征，不属于生物，A、B、C不符合题意。

生石花具有生物的特征，属于生物，D符合题意。

2.（滚动考查生物的特征）关于生物特征的说法，正确的是（）A．“蜻蜓点水”体现的是生物能排出废物B．“红豆生南国，春来发几枝”体现的是生物能生长C．“种瓜得瓜，种豆得豆”体现的是生物有变异的特性D．“螳螂捕蝉，黄雀在后”体现的是生物能进行呼吸【答案】B【解析】“蜻蜓点水”是蜻蜓在产卵，体现的是生物能繁殖，A错误；“红豆生南国，春来发几枝”体现的是生长和发育现象，B正确；“种瓜得瓜，种豆得豆”体现的是生物有遗传的特性，C 错误；“螳螂捕蝉黄雀在后”体现的是生物的生活需要营养，D错误。

3.（滚动考查生物与环境的关系）“春色满园关不住，一枝红杏出墙来”，诗句中影响该现象主要的非生物因素是（）A．阳光B．空气C．温度D．水分【答案】A【解析】春天气温回升，“满园春色关不住，一枝红杏出墙来”的生态因素主要是温度，产生这一现象的非生物因素主要是非生物因素阳光对生物的影响，A正确。

4.（滚动考查生物的特征）下面是明明同学在复习《生物学》时所作的笔记，其中诗文或谚语与所蕴含的生物学知识不对应的是A．龙生龙，凤生凤，老鼠的孩子会打洞——生物的遗传现象B．几处早莺争暖树，谁家新燕啄春泥——鸟的繁殖行为C．人间四月芳非尽，山寺桃花始盛开——光对生物的影响D．大鱼吃小鱼，小鱼吃虾米——生物间的捕食关系【答案】C【解析】“龙生龙，凤生凤，老鼠的孩子会打洞”表示了生物之间的相似性，这是生物的遗传现象，A正确；在生殖季节，动物都有各自的繁殖方式，鸟类的生殖行为：如占巢、求偶、交配、孵卵、哺育等一系列行为，“几处早莺争暖树，谁家新燕啄春泥”反映了燕子的筑巢行为，筑好巢再育雏，是鸟的繁殖行为，B正确；“人间四月芳菲尽，山寺桃花始盛开”，表明环境影响生物的生长开花等，海拔每升高1千米气温下降6℃左右，因此山上的温度比山下低，山上的桃花比山下的开的晚。