基于matlab的拥塞概率的仿真
matlab 通信仿真案例

matlab 通信仿真案例Matlab是一种强大的工程仿真软件,可以用于各种领域的仿真案例,包括通信系统。
通信系统仿真是Matlab的一个常见应用领域,可以涉及到数字通信、无线通信、信号处理等方面。
下面我将从多个角度介绍几个通信仿真案例。
数字调制仿真是通信系统仿真的一个重要方面。
在Matlab中,你可以使用数字调制技术来模拟各种调制方案,比如QPSK、16-QAM、OFDM等。
你可以创建一个仿真模型,包括信道模型、噪声模型等,来评估不同调制方案在不同信噪比下的性能。
另一个常见的通信系统仿真案例是无线信道建模。
在Matlab中,你可以使用射线追踪技术或者其他无线信道建模工具,来模拟不同类型的无线信道,比如室内信道、室外信道等。
通过仿真,你可以评估不同信道条件下无线通信系统的性能表现。
此外,Matlab还可以用于设计和仿真滤波器和均衡器。
你可以使用Matlab的信号处理工具箱来设计各种数字滤波器和均衡器,并通过仿真来评估它们在通信系统中的性能。
另一个重要的通信系统仿真案例是误码率性能评估。
在Matlab 中,你可以通过模拟传输过程中的比特错误来评估系统的误码率性能。
你可以使用各种编码和调制技术,以及不同的信道条件,来评估系统在不同情况下的误码率表现。
最后,Matlab还可以用于设计和仿真通信系统中的自适应算法,比如自适应均衡、自适应调制解调等。
通过仿真,你可以评估这些自适应算法在不同信道条件下的性能表现。
总之,Matlab是一个非常强大的工程仿真工具,可以用于各种通信系统的仿真案例,包括数字调制、无线信道建模、滤波器设计、误码率性能评估以及自适应算法设计等。
希望这些信息能够对你有所帮助。
matlab 通信仿真案例

matlab 通信仿真案例
在MATLAB中,通信仿真是一个常见的应用领域,可以用于模拟
和分析数字通信系统的性能。
下面我将从多个角度介绍几个常见的
通信仿真案例。
1. OFDM系统仿真,OFDM(正交频分复用)是一种常见的多载
波调制技术,用于高速数据传输。
你可以使用MATLAB来建立一个基
本的OFDM系统仿真模型,包括信道估计、均衡和解调等模块。
通过
仿真可以分析系统在不同信噪比下的误码率性能,优化系统参数以
及算法设计。
2. 无线通信系统仿真,你可以使用MATLAB建立一个简单的无
线通信系统仿真模型,包括传输信道建模、调制解调、信道编码、
多天线技术等。
通过仿真可以评估系统的覆盖范围、传输速率、抗
干扰能力等性能指标。
3. MIMO系统仿真,MIMO(多输入多输出)技术在无线通信中
得到了广泛应用。
你可以使用MATLAB建立一个MIMO系统仿真模型,包括空间多路复用、信道估计、预编码等。
通过仿真可以分析系统
的信道容量、波束赋形技术对系统性能的影响等。
4. LTE系统仿真,LTE(长期演进)是目前移动通信领域的主流技术之一。
你可以使用MATLAB建立一个LTE系统仿真模型,包括物理层信号处理、上下行链路传输、信道编码解码等。
通过仿真可以评估系统的覆盖范围、传输速率、干扰抑制能力等性能指标。
以上是一些常见的通信仿真案例,通过MATLAB你可以方便地建立仿真模型,分析系统性能,并优化系统设计。
希望这些案例能够帮助到你。
博弈仿真matlab

博弈仿真matlab引言博弈仿真是一种有助于理解和探索博弈理论的工具。
在博弈理论中,我们通过模拟不同策略下的决策和结果来分析博弈的结果。
Matlab是一款功能强大的数值计算软件,它提供了一些有助于进行博弈仿真的工具和函数。
本文将介绍如何使用Matlab进行博弈仿真,并给出一个实例来说明。
博弈理论简介博弈理论是研究决策制定者之间相互影响的一种数学分析方法。
博弈的参与者被称为玩家,他们根据自己的利益和目标来做出决策。
博弈理论主要研究玩家的策略选择和决策结果之间的关系。
常见的博弈模型包括零和博弈、非零和博弈、合作博弈等。
在零和博弈中,玩家之间的利益是互相对立的。
一方的收益就是另一方的损失。
在非零和博弈中,玩家之间的利益可以是互相独立的,也可以是互相关联的。
合作博弈则是指玩家之间通过合作互利来达到最优决策的一种博弈形式。
Matlab中的博弈仿真工具Matlab中有几个有助于进行博弈仿真的函数和工具包。
其中最常用的是Game Theory Toolbox。
该工具包提供了一些常见的博弈模型和算法,可以帮助我们进行博弈仿真和分析。
Game Theory Toolbox的安装要使用Game Theory Toolbox,首先需要将其安装到Matlab中。
安装过程如下:1.打开Matlab软件。
$ matlab2.在命令窗口中输入以下命令,下载Game TheoryToolbox。
>> addpath('path_to_toolbox')其中,path_to_toolbox是Game Theory Toolbox 的安装路径。
3.安装完成后,可以通过以下命令检查是否安装成功。
>> ver('games')Game Theory Toolbox的功能Game Theory Toolbox提供了许多有用的函数和工具,以进行博弈模型的建立、计算博弈结果和分析策略等。
MATLAB通信仿真要点

MATLAB通信仿真要点MATLAB通信仿真是指使用MATLAB软件进行通信系统的建模、仿真和分析。
在通信领域,仿真是非常重要的工具,它可以帮助工程师们验证设计和算法,评估性能以及优化系统。
下面是进行MATLAB通信仿真时需要注意的关键要点。
1.选择合适的仿真模型:通信系统包括多个组件,例如调制、编码、传输信道、解调等。
在进行仿真之前,需要选择合适的模型来表示这些组件。
根据系统的需求,可以选择不同的模型,例如理想模型、接近实际系统的模型或者经验模型。
2.信号处理:在通信系统中,信号处理是一个核心环节。
MATLAB提供了丰富的信号处理工具箱,可以用于数字信号的分析和处理。
可以使用这些工具对通信信号进行滤波、修正、去噪等操作,以便获得更好的性能。
3. 比特错误率(BER)分析:通信系统的一个重要指标是比特错误率(Bit Error Rate,BER),即接收端误码率。
MATLAB提供了各种用于BER分析的工具,例如误码率曲线的绘制、误码率性能分析等。
可以使用这些工具来评估系统在不同条件下的性能,并进行优化。
4.信道建模:通信系统中的信道是一个关键因素,它会影响信号的传输和接收质量。
MATLAB提供了许多信道建模工具,可以用于模拟各种信道,如高斯信道、瑞利信道、多径衰落信道等。
通过对信道的建模,可以评估系统的性能,并进行通道估计和等化技术的研究。
5.参数配置和优化:通信系统中有许多参数需要配置和优化,如编码方式、调制方式、信道编码方式、解调方式等。
MATLAB提供了优化工具,可以帮助寻找最佳的参数配置,以实现最好的系统性能。
6.多用户仿真:在无线通信系统中,多用户交互会导致干扰。
MATLAB 提供了多用户仿真工具,可以对多个用户在同一信道中的交互进行建模和仿真,并评估系统的吞吐量、容量等性能。
7.分析和可视化:MATLAB具有强大的数据分析和可视化功能,可以帮助分析仿真结果。
通过使用MATLAB的数据分析工具,可以得到关键的性能指标,并比较不同方案之间的优劣。
概率论问题MATLAB仿真求解程序

clc; clear; close all; a=10; b=3; p=0.55; S=0; N=10000; m=6; %甲的赌本 %乙的赌本 %甲赢的概率 % 计数设置为0 % 模拟次数 %设定随机数状态值(1 2 3 4 5 6 ),改变这个值可以进行不同的实验
%针与线相交则记数
运行结果
Pi_m_mean=mean(Pi_m)%显示 N 次迭代之后的圆周率 pi 均值
P_mean =0.318250000000000 Pi_m_mean =3.142648986529731
赌徒输光问题
两个赌徒甲、乙两人将进行一系列赌博。在每一局中甲获胜的概率为 p , 而乙获胜的概率为 q ( p + q = 1 )。在每一局后,失败者都要支付一元线给 胜利者。在开始时甲拥有赌本 a 元,而乙拥有赌本 b 元,两个赌徒直到甲 输光或乙输光为止。求甲输光的概率。
MATLAB实现Buffon问题仿真求解程序
程序1பைடு நூலகம்
clear all; L=1; d=2; m=0; n=10000; for k=1:n x=unifrnd(0,d/2); p=unifrnd(0,pi); if x<=L*sin(p)/2 m=m+1; else end end p=vpa(m/n,4) %针的长度; %平行线间的距离(d>L); %统计满足针与线相交条件的次数并赋初值; %投针试验次数 %迭代次数 %随机产生数的长度,即投针之后针中点与平行线的距离 %随机产生的针与线相交的角度 %针与线相交的条件 %针与线相交则记数
P =0.0676 Po =0.0656
Binomial(二项分布)的使用
matlab通信系统仿真课程设计

matlab通信系统仿真课程设计
MATLAB通信系统仿真课程设计是一个涉及到通信系统原理和MATLAB编程的设计项目。
在这个课程设计中,学生需要通过理论学习和实践操作,掌握通信系统的基本原理和MATLAB的使用技巧,最终完成一个通信系统的仿真模型。
以下是一个可能的课程设计流程和内容:
1. 引言和背景知识:介绍通信系统的基本原理和相关的数学知识,包括信号传输、调制解调、信道编码等概念。
2. MATLAB基础知识:介绍MATLAB的基本语法和常用函数,包括矩阵操作、图形绘制、信号处理等。
3. 信号传输模型:学生需要根据通信系统的基本原理,设计一个简单的信号传输模型。
这个模型可以包括信号的生成、调制、传输和解调等过程。
4. 信道模型:学生需要根据通信系统的信道特性,设计一个适当的信道模型。
这个模型可以包括信道的噪声、衰落等特性。
5. 信号检测和解码:学生需要设计一个信号检测和解码的算法,以实现对传输信号的恢复和解码。
6. 性能评估和优化:学生可以通过改变信道模型、调制方式、编码方式等参数,来评估系统的性能,并根据评估结果进行优化。
7. 结果分析和报告撰写:学生需要分析仿真结果并撰写一个综合性的报告,包括系统设计和实验结果等内容。
在这个课程设计中,学生需要结合理论学习和实践操作,掌握通信系统的基本原理和MATLAB的使用技巧。
通过完成这个设计项目,学生可以加深对通信系统的理解,并提升MATLAB编程和仿真分析的能力。
matlab博弈仿真模拟方法

MATLAB(Matrix Laboratory)是一种用于数学计算、可视化和编程的高级技术计算环境,MATLAB在工程、科学和经济领域广泛应用。
其中,博弈论是MATLAB中常见的研究领域之一,通过MATLAB可以进行博弈论相关仿真模拟研究,这种方法在解决博弈论问题上具有很大的优势。
本文将介绍在MATLAB中进行博弈仿真模拟的方法。
一、博弈论基础博弈论是一种研究策略和决策的数学模型,包括博弈参与者、策略选择和利益最大化问题。
在博弈论中,常见的博弈模型包括合作博弈、非合作博弈、零和博弈等,其中零和博弈是博弈论中经常讨论的一种情况。
二、MATLAB中的博弈仿真模拟方法1. 准备工作在进行MATLAB中的博弈仿真模拟前,首先需要进行准备工作包括安装MATLAB软件、了解博弈论基础知识、准备博弈模型等。
2. 编写博弈模型在MATLAB中,可以使用代码编写博弈模型,以进行博弈仿真模拟。
编写博弈模型时,可以结合博弈论的数学模型,确定博弈参与者、策略选择和收益函数等。
3. 进行仿真模拟通过编写的博弈模型,可以在MATLAB中进行仿真模拟,观察博弈参与者在不同策略选择下的收益情况。
在仿真模拟过程中,可以设定不同的参数、条件,以观察不同情况下的博弈结果。
4. 分析结果在进行博弈仿真模拟后,需要对结果进行分析,包括对参与者收益的评估、策略选择的优劣比较、不同条件下的博弈结果对比等。
通过分析结果,可以得出对博弈模型的一些结论和观察。
三、博弈仿真模拟的应用案例在实际应用中,博弈仿真模拟方法广泛应用于经济学、管理学、政治学等领域。
在市场竞争中,企业可以使用博弈仿真模拟方法,分析不同定价策略下的市场竞争结果;在决策问题中,政府可以使用博弈仿真模拟方法,评估不同决策方案的结果。
这些应用案例都可以通过MATLAB中的博弈仿真模拟方法得到有效的研究和分析。
四、博弈仿真模拟的局限性和展望在使用MATLAB进行博弈仿真模拟时,也存在一些局限性,例如博弈模型的简化、参数设定的主观性等。
MATLAB2psk通信系统仿真报告

MATLAB2psk通信系统仿真报告自查报告。
标题,MATLAB 2psk通信系统仿真报告。
在进行MATLAB 2psk通信系统仿真报告的过程中,我对整个仿
真过程进行了仔细的自查和总结,以下是我的自查报告:
1. 仿真参数设置,在进行仿真之前,我对MATLAB的2psk通信
系统的参数进行了详细的设置,包括载波频率、符号周期、信噪比
等参数的设置。
在自查过程中,我确认了这些参数的设置是否符合
实际情况,并对其进行了适当的调整和修正。
2. 信道模型选择,在仿真过程中,我选择了合适的信道模型进
行仿真。
在自查过程中,我检查了所选信道模型的准确性和适用性,并对其进行了充分的验证和测试。
3. 误码率分析,在仿真报告中,我对2psk通信系统的误码率
进行了详细的分析和计算。
在自查过程中,我确认了误码率的计算
方法是否正确,并对仿真结果进行了充分的验证和比对。
4. 性能评估,在仿真报告中,我对2psk通信系统的性能进行了全面的评估。
在自查过程中,我确认了性能评估指标的选择是否合理,并对性能评估结果进行了充分的分析和总结。
5. 结论和展望,在仿真报告中,我对2psk通信系统的仿真结果进行了详细的总结和展望。
在自查过程中,我确认了结论的科学性和可靠性,并对未来工作进行了充分的展望和规划。
通过以上的自查过程,我对MATLAB 2psk通信系统的仿真报告进行了全面的检查和总结,保证了报告的科学性和可靠性。
在未来的工作中,我将继续努力,不断提高仿真报告的质量和水平。
MATLAB2psk通信系统仿真报告

MATLAB2psk通信系统仿真报告自查报告。
标题: MATLAB 2psk通信系统仿真报告。
在本次仿真报告中,我使用MATLAB对2psk通信系统进行了仿
真分析。
在整个仿真过程中,我对系统的性能进行了评估,并对结
果进行了分析。
在此过程中,我发现了一些错误和改进的空间,下
面是我对本次仿真报告的自查总结:
1. 参数设置,在仿真过程中,我可能忽略了一些关键参数的设置,导致了结果的偏差。
下次在进行仿真前,我会仔细检查所有参
数的设置,确保其准确性和完整性。
2. 代码实现,在编写MATLAB代码时,我可能存在一些错误或
不规范的地方,导致了程序的运行出现了问题。
下次在编写代码时,我会更加细致地审查和测试,以确保代码的正确性和稳定性。
3. 结果分析,在对仿真结果进行分析时,我可能存在了一些主
观性的评价,导致了对结果的理解出现了偏差。
下次在进行结果分
析时,我会更加客观地进行评价,确保对结果的理解和解释是准确
和全面的。
4. 改进空间,在本次仿真过程中,我发现了一些可以改进的空间,比如系统性能的优化和参数的调整等。
下次我会根据本次仿真
的经验和教训,对系统进行更加全面和深入的改进,以提高系统的
性能和稳定性。
总的来说,通过本次自查报告,我对本次仿真过程中存在的问
题和不足有了更加清晰的认识,也对下次的工作有了更加明确的改
进方向。
我会认真总结本次经验,不断提高自己的仿真能力和水平,以更好地完成今后的工作任务。
基于MATLAB的通信系统仿真研究

基于MATLAB的通信系统仿真研究一、本文概述随着信息技术的飞速发展,通信系统在人们的生活和工作中扮演着越来越重要的角色。
为了深入理解和优化这些系统的性能,基于MATLAB 的通信系统仿真研究显得尤为重要。
MATLAB作为一种功能强大的数值计算环境和编程语言,其内置的通信工具箱为通信系统仿真提供了丰富的函数库和算法支持。
本文旨在探讨基于MATLAB的通信系统仿真的原理、方法及其应用,以期通过仿真研究,对通信系统的性能进行预测、分析和优化。
本文将简要介绍MATLAB及其在通信系统仿真中的应用,阐述其相较于其他仿真工具的独特优势。
接着,本文将详细介绍基于MATLAB的通信系统仿真流程,包括系统建模、信号生成、信道模拟、误码性能分析等环节。
在此基础上,本文将探讨几种典型的通信系统,如数字基带传输系统、数字频带传输系统以及无线通信系统的仿真实现方法。
本文还将通过实际案例,展示如何利用MATLAB进行通信系统仿真研究。
这些案例将涵盖从简单的数字通信系统到复杂的无线通信网络的各个方面,旨在展示MATLAB在通信系统仿真中的广泛应用和实用性。
本文将对基于MATLAB的通信系统仿真研究进行总结和展望,分析当前研究的不足之处,并提出未来可能的研究方向。
通过本文的研究,读者可以更加深入地理解通信系统的原理和实现方法,为通信技术的进一步发展提供有力支持。
二、MATLAB基础与通信系统仿真概述MATLAB,全称Matrix Laboratory,是一款由美国MathWorks公司出品的商业数学软件,广泛应用于算法开发、数据可视化、数据分析以及数值计算等众多领域。
MATLAB以矩阵运算为基础,集成了大量的数学函数库和工具箱,用户只需通过简单的编程即可实现复杂的数学运算和算法设计。
特别值得一提的是,MATLAB拥有丰富的工具箱,如信号处理工具箱、通信工具箱等,这些工具箱为通信系统仿真提供了强大的支持。
通信系统仿真是一种通过数学模型和计算机技术来模拟实际通信系统的过程。
基于matlab ofdm通信系统仿真代码

基于matlab ofdm通信系统仿真代码
OFDM通信系统仿真模拟是以正交频分复用技术(OFDM)作为主要的信号传输技术,在实现对无线信号的检测、编码、调制、叠加噤等功
能时可以通过Matlab等软件来进行模拟仿真。
仿真工作首先建立OFDM系统的信号模型,OFDM的原理是通过将
一个OFDM信号分成多个相互正交的子载波,并在每个子载波上实现移相、移幅调制,从而在信道上传输多路符号。
由于子载波之间相互正交,故可以实现多路数据同时传输,从而提高数据传输率和传输容量。
仿真建模过程中,首先根据要求确定可用的OFDM子载波数目以
及子载波的调制方式。
然后设定数据信道的配置,选择需要用到的信
道编码,这些元素将影响OFDM系统的信噪比和数据传输率。
最后定义
噪声接收,模拟噪声叠加,并实现对接收端信号的处理,存储等步骤。
通过上述步骤,系统建模工作就完成了。
之后可以使用Matlab
对模型进行仿真,看看OFDM系统表现如何。
仿真结果可以以图像的形
式显示出来,从而更好地理解传输的性能,从而有利于调整系统参数,提高系统的效率和可靠性。
【个人总结系列-1】概率特性仿真实验与程序-Matlab仿真-随机数生成-负指数分布-k阶爱尔兰分布-超指数分布

概率特性仿真实验与程序-Matlab 仿真-随机数生成-负指数分布-k 阶爱尔兰分布-超指数分布使用Java 中的SecureRandom .nextDouble()生成一个0~1之间的随机浮点数,然后使用反函数法生成一个符合指数分布的随机变量(反函数求得为λ)1ln(R x --=)。
指数分布的参数λ为getExpRandomValue 函数中的参数lambda 。
生成一个指数分布的随机变量的代码如下,后面都将基于该函数生成一组负指数分布、K 阶爱尔兰分布、2阶超指数分布随机变量,然后将生成的随机数通过matlab 程序进行仿真,对随机数的分布特性进行验证。
生成一组参数为lambda (λ)的负指数分布的随机变量通过下面的函数生成一组λ参数为lambda 的随机变量,其中size 表示随机变量的个数。
通过该函数生成之后,可以将这些随机值保存在文件中,以备分析和验证,比如保存在exp.txt 文件中,供下面介绍的matlab 程序分析。
通过genExp (1000000, 0.2)生成1000000个参数为0.2的随机变量,然后保存到exp.txt 中,然后使用下面的matlab 程序对这些随机数的性质进行验证,如果这些随机数符合λ=0.2的负指数分布,则其均值应为1/λ,即1/0.2=5,其方差应为1/λ2=1/(0.2*0.2)=25。
然后对这些随机数的概率分布进行统计分析,以长度为1的区间为统计单位,统计各区间内随机数出现的频数,求出在各区间的概率,绘制图形,与参数为λ的真实负指数分布曲线进行对比。
下图为matlab 代码如下图所示,均值为4.996423,约等于5,方差为24.96761,约等于25,与实际情况相符。
此外,通过matlab统计的概率密度函数曲线与真实曲线基本重合(其中在0-1之间没有重合的原因是,实际情况是在0-1之间有无数个点,而matlab统计时以1为一个区间进行统计,只生成了一个统计项,而这无数个点的概率全部加到1点处,因此两条线没有重合,而且1点处的值远大于实际值,如果统计单位划分越细,0-1之间的拟合度更高),表明生成的随机数符合负指数分布。
基于MATLAB通信系统的设计仿真

基于MATLAB通信系统的设计仿真概述:通信系统是实现信息传输的关键技术,其中设计和仿真是通信系统的重要环节。
本文将介绍如何基于MATLAB进行通信系统的设计和仿真,并以调制和解调为例进行说明。
通信系统的设计和仿真步骤:1.确定系统需求:首先确定通信系统的需求,包括传输速率、距离、信噪比等参数。
2.选择调制方式:根据系统需求和传输介质的特性,选择合适的调制方式,如BPSK、QPSK、16-QAM等。
3.生成基带信号:根据调制方式和传输要求,使用MATLAB生成相应的基带信号。
4.添加调制信号:将基带信号进行调制,生成调制信号,如使用频率调制、相位调制等技术。
5.添加噪声:为了模拟真实通信环境,需要在调制信号中加入噪声信号,可以使用MATLAB提供的噪声函数。
6.解调信号:使用相应的解调技术对接收到的信号进行解调,恢复原始基带信号。
7.评估系统性能:比较解调后的基带信号与原始信号,评估系统的性能,如误码率、误符号率等。
调制与解调的MATLAB实例:以BPSK调制为例,假设系统需求为传输速率2Mbps,信噪比为20dB。
1.生成基带信号:```matlabfs = 10e6; % 采样率N=1000;%生成1000个符号bits = randi([0 1],1,N); % 生成随机的二进制信号Ts = 1/fs; % 采样周期t=0:Ts:(N-1)*Ts;%时间序列baseband_signal = bits.*2-1; % 将0或1转换为-1或1```2.添加调制信号:```matlabfc = 1e6; % 载波频率modulated_signal = baseband_signal .* cos(2*pi*fc*t); % 调制信号```3.添加噪声:```matlabEbNo=10^(20/10);%信噪比,20dB转为线性值N0=1/(2*EbNo);%噪声功率,信噪比为能量比noise = sqrt(N0/2) * randn(size(t)); % 产生高斯白噪声received_signal = modulated_signal + noise; % 加噪声```4.解调信号:```matlabdemodulated_signal = received_signal .* cos(2*pi*fc*t); % 解调信号```5.评估系统性能:```matlabest_baseband_signal = sum(demodulated_signal) > 0; % 判断信号正负,得到解调后的二进制信号error_bits = sum(bits ~= est_baseband_signal); % 计算误码个数BER = error_bits / N; % 误码率```通过调整系统参数,可以进行更详细的仿真和性能评估。
Matlab在交通仿真中的应用技巧

Matlab在交通仿真中的应用技巧引言近年来,交通拥堵问题日益严重,给人们的生活和经济发展带来了很大的困扰。
为了解决交通拥堵问题,提高交通效率,交通仿真成为了一种重要的工具。
而Matlab作为一种强大的数学计算软件,可以提供丰富的工具和函数,为交通仿真提供了很大的帮助。
本文将介绍一些Matlab在交通仿真中的应用技巧,包括交通流模型、交通信号灯优化、路网设计和交通预测等方面。
1. 交通流模型交通流模型是交通仿真的基础,它用于描述交通流的行为和变化。
在Matlab中,我们可以利用各种数学模型来建立和模拟交通流。
常用的交通流模型包括微观模型和宏观模型。
微观模型主要用于个体车辆行为的建模,宏观模型主要用于整个交通网络的流量分布和拥堵状况的模拟。
在建立交通流模型时,我们需要收集大量的交通数据,包括车辆的速度、密度和流量等信息。
利用Matlab的数据处理功能,我们可以轻松地对这些数据进行分析和建模。
例如,可以使用Matlab的数据统计函数来计算交通流的平均速度和流量,进而推导出交通流的密度和流量之间的关系。
2. 交通信号灯优化交通信号灯是调控交通流的重要手段。
合理地优化交通信号灯的配时方案,可以有效减少交通拥堵和减少人们的出行时间。
在Matlab中,我们可以利用优化算法来优化交通信号灯的配时方案。
常用的优化算法有遗传算法、粒子群算法等。
首先,我们需要建立交通信号灯的仿真模型,模拟交通信号灯的开关过程和车辆的行驶。
然后,利用Matlab的优化函数,设置优化目标和约束条件,进行信号灯配时方案的优化。
最后,通过仿真实验,评估不同配时方案的性能,选择最优的配时方案。
3. 路网设计路网设计是交通规划和交通工程中的重要环节。
合理地设计路网,可以提高交通的通行能力和效率。
在Matlab中,我们可以利用图论算法和网络流模型来进行路网设计。
首先,我们需要建立路网的拓扑结构,即道路和交叉口之间的连接关系。
然后,利用图论算法,计算路网的最短路径和最小生成树等信息。
匹配滤波检测概率matlab仿真

匹配滤波检测概率matlab仿真
匹配滤波(Matched Filter)是一种常见的信号处理技术,用
于检测和定位特定信号在噪声背景中的存在。
在MATLAB中进行匹配
滤波检测概率的仿真可以通过以下步骤实现:
1. 生成信号和噪声模型,首先,你需要定义你要检测的信号模
型以及噪声模型。
这可能涉及到信号的波特性、频率特征等,以及
噪声的统计特性。
2. 生成匹配滤波器,根据你的信号模型,设计匹配滤波器。
在MATLAB中,你可以使用fir1函数设计滤波器,也可以使用
designfilt函数设计滤波器。
3. 生成接收信号,利用你的信号模型和噪声模型,生成接收信号。
这个接收信号是信号和噪声的叠加。
4. 进行匹配滤波处理,利用生成的匹配滤波器,对接收信号进
行滤波处理。
在MATLAB中,你可以使用filter函数进行滤波处理。
5. 计算检测概率,根据滤波后的信号,你可以利用统计方法计
算检测概率。
这可能涉及到信噪比的计算、阈值的选择等。
6. 仿真结果分析,最后,对仿真结果进行分析,包括检测概率的性能评估、信噪比对检测性能的影响等。
在进行MATLAB仿真时,需要注意信号模型、滤波器设计、信号生成和性能评估等多个方面。
通过综合考虑这些因素,你可以完成匹配滤波检测概率的仿真,并得到全面的结果。
希望这个回答能够帮助到你。
基于matlab的各种简单的概率分布的仿真图

1.泊松分布曲线:
2.二项分布曲线:
由泊松定理得,服从二项分布的
随机变量,当取值合适时近似服
从泊松分布,所以二项分布曲线
与泊松分布曲线相似。
3.均匀分布曲线:
4.正态分布曲线:
5.指数分布曲线:
均匀分布的概率密度函数只在某一区间有值,区间外为0;而分布函数在此区间内为线性,区间左边为0,右边为1。
正态分布概率密度函数关于x=u (u为均值)对称,并且在x=u
处取得最大值。
由指数分布的概率密度函数和分布函数可以看出,两者的曲线变化趋势是相反的。
基于matlab的拥塞概率的仿真
基于M/M/C/∞模型拥塞概率的仿真一、M/M/C/∞模型的建立Erlang B 公式将丢失呼叫清除系统的服务等级(GOS )定义为任意一个用户遇到呼叫拥塞的概率。
.Erlang B 模型基于以下假定:1) 呼叫请求无记忆,即所有用户,包括拥塞用户可以在任何时间请求分配一个信道。
2) 在所有信道都被占用之前,任何空闲信道都能用来服务一个呼叫。
3) 用户占用一个信道间隔(称为服务时间)的概率是指数分布。
指数分布中较长时间的呼叫发生的概率较小。
4) 在中继资源中可用信道是有限的。
5) 业务请求是Poisson 过程,即呼叫间隔时间是指数分布的。
6) 呼叫请求到达时间间隔彼此独立。
7) 忙信道数等于服务中的用户数,拥塞概率为:0!!C r k C k A C P A k =⎛⎫ ⎪⎝⎭⎡⎤⎣⎦∑阻塞= 其中,C 是中继信道数,A 是中继系统的负荷。
Erlang B 公式表示的中继系统称为M/M/C/∞排队系统。
第一个M 表示呼叫到达是非记忆Poisson 过程,第二个M 表示用户服务时间指数分布,C 表示可用中继信道数,∞表示对同时服务用户数没有严格限制。
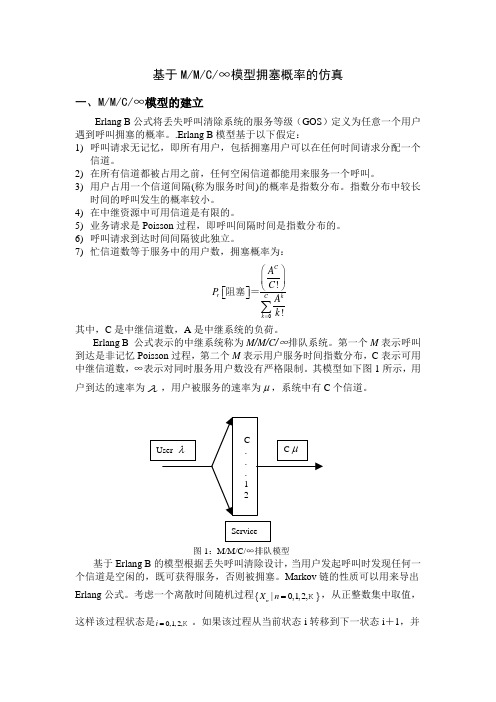
其模型如下图1所示,用户到达的速率为λ,用户被服务的速率为μ,系统中有C 个信道。
图1:M/M/C/∞排队模型基于Erlang B 的模型根据丢失呼叫清除设计,当用户发起呼叫时发现任何一个信道是空闲的,既可获得服务,否则被拥塞。
Markov 链的性质可以用来导出Erlang 公式。
考虑一个离散时间随机过程{}|0,1,2,n X n =K ,从正整数集中取值,这样该过程状态是0,1,2,i =K 。
如果该过程从当前状态i 转移到下一状态i +1,并只依赖状态i 而与前面状态无关,则该过程称为Markov 链。
利用离散时间Markov 链,我们可以在持定业务条件下,在分离观察点观察业务情况。
一个实际中继系统的运作在时间上是连续的,但可以在小时间间隔δ内分析,δ是一个很小的正数。
基于Matlab的排队问题仿真

90
武 汉 工 业 学 院 学 报
2007年
队等待时间 d ( n)的估计值 d ( n) 。Q ( n)和 d ( n)的
计算公式
∫ Q ( n)
= Q ( n)
=1
T
Q ( t) d t
T0
n
∑ d ( n) = d ( n) =
i
D /n
i =1
其 中 , D i ———第 i 个 顾 客 排 队 等 待 时 间 ;
系统进入待机状态后 ,会被任意的事件 (顾客 到达队列或顾客离开队列 )中断待机 ,而进入处理 事件的子程序中 (如图 4,图 5 所示 ) 。处理顾客到 达队列事件和处理顾客离开队列事件不会同时进 行 ,所以只有当某一事件完成后再次返回到系统中 ,
2期
高静涛 , 史百战 : 基于 M atlab的排队问题仿真
QU EU E PROBLEM S MI ULAT ION BASED ON MATLAB
GAO J ing2tao, SH I B a i2zhan (M echatronic Technology Research Institute, Lanzhou J iaotong University, Lanzhou 730070, China) Ab s tra c t: The purpose of queue p roblem sim ulation is to seek the best disposition between the service objects and setting, and ensure that the system has the best service efficiency and the most reasonable disposition. This article has discussed the basic essentials of queue p roblem , and brought forward a series of solutions formulas. Through the simulation of these form ulas by M atlab, customer ’s demand m ay be analyzed for assisting p lanners, thus servicing establishm ents which conform to the existing condition is established. Ke y wo rd s: M atlab; queue p roblem; sim ulation
【个人总结系列-1】概率特性仿真实验与程序-Matlab仿真-随机数生成-负指数分布-k阶爱尔兰分布-超指数分布

概率特性仿真实验与程序-Matlab 仿真-随机数生成-负指数分布-k 阶爱尔兰分布-超指数分布使用Java 中的SecureRandom .nextDouble()生成一个0~1之间的随机浮点数,然后使用反函数法生成一个符合指数分布的随机变量(反函数求得为λ)1ln(R x --=)。
指数分布的参数λ为getExpRandomValue 函数中的参数lambda 。
生成一个指数分布的随机变量的代码如下,后面都将基于该函数生成一组负指数分布、K 阶爱尔兰分布、2阶超指数分布随机变量,然后将生成的随机数通过matlab 程序进行仿真,对随机数的分布特性进行验证。
生成一组参数为lambda (λ)的负指数分布的随机变量通过下面的函数生成一组λ参数为lambda 的随机变量,其中size 表示随机变量的个数。
通过该函数生成之后,可以将这些随机值保存在文件中,以备分析和验证,比如保存在exp.txt 文件中,供下面介绍的matlab 程序分析。
通过genExp (1000000, 0.2)生成1000000个参数为0.2的随机变量,然后保存到exp.txt 中,然后使用下面的matlab 程序对这些随机数的性质进行验证,如果这些随机数符合λ=0.2的负指数分布,则其均值应为1/λ,即1/0.2=5,其方差应为1/λ2=1/(0.2*0.2)=25。
然后对这些随机数的概率分布进行统计分析,以长度为1的区间为统计单位,统计各区间内随机数出现的频数,求出在各区间的概率,绘制图形,与参数为λ的真实负指数分布曲线进行对比。
下图为matlab 代码如下图所示,均值为4.996423,约等于5,方差为24.96761,约等于25,与实际情况相符。
此外,通过matlab统计的概率密度函数曲线与真实曲线基本重合(其中在0-1之间没有重合的原因是,实际情况是在0-1之间有无数个点,而matlab统计时以1为一个区间进行统计,只生成了一个统计项,而这无数个点的概率全部加到1点处,因此两条线没有重合,而且1点处的值远大于实际值,如果统计单位划分越细,0-1之间的拟合度更高),表明生成的随机数符合负指数分布。
MATLAB-QPSK在AWGN信道下的仿真

QPSK 在AWGN 信道下的仿真实验一、基本原理简介 在数字相位调制中,M 个信号波形可表示为(t )= Re r g (t )e j 2皿m -1)/M e j 2n f c t=g (t )cos —(m - 1)cos 2 兀 ft - g (t )sin — (m - 1)sin 2 兀 ft Mc M c (m=1,2,…,M ,0 < t < T )式中,g(t)是信号脉冲形状,6m = 2兀(m-1)/M(m=1,2,…,M)是载波的M 个可能的 相位,用于传送发送信息。
这些信号波形具有相等的能量,即8 = f T s 2(t )dt = — f T g 2(t )dt = —80m 20 2g 而且这些信号波形可以表示为两个标准正交信号波形 f (t )和f (t )的线性星座图合,即(t ) + s f (t ),式中s (t ) = s f 8 2兀/ 八.8 . 2兀/ 八 f cos (m - 1),t i f sin (m -1)2 M 2 M 其中当M=4时就是本文要讨论的4PSK(QPSK),QPSK 的载波相位有四种取值,每种取值代表 两比特的信号。
随着信号的改变,幅度恒定的载波信号的相位在四种取值间跳变。
这四个相 位的取值为间隔相等的值,比如,0,兀/2,兀,3兀/2,每一个相位值对应于唯一的一对消息 比特。
有一种变形,称为冗/4-QPSK 是通过在每一个符号间隔的载波相位中引入附加的 九/4相移来使符号同步变得容易些。
QPSK 信号可以表示为:…2兀 = g (t )c0s 2兀ft + M (m - 1) 且二维向量s m S m 1, s m 2」 m 1 1 m 2 2 (m=1,2,…,M)8 g—g (t )cos 2 兀 ft 为 8 gf 2(t )= 一 —g (t )sin2 兀 sm式中ES 为单位符号的信号能量,即0 < t < T S 时间内的信号能量;3°为载波角频率, T s 为符号持续时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于M/M/C/∞模型拥塞概率的仿真一、M/M/C/∞模型的建立Erlang B 公式将丢失呼叫清除系统的服务等级(GOS )定义为任意一个用户遇到呼叫拥塞的概率。
.Erlang B 模型基于以下假定:1) 呼叫请求无记忆,即所有用户,包括拥塞用户可以在任何时间请求分配一个信道。
2) 在所有信道都被占用之前,任何空闲信道都能用来服务一个呼叫。
3) 用户占用一个信道间隔(称为服务时间)的概率是指数分布。
指数分布中较长时间的呼叫发生的概率较小。
4) 在中继资源中可用信道是有限的。
5) 业务请求是Poisson 过程,即呼叫间隔时间是指数分布的。
6) 呼叫请求到达时间间隔彼此独立。
7) 忙信道数等于服务中的用户数,拥塞概率为:!!C r kC k A C P Ak =⎛⎫ ⎪⎝⎭⎡⎤⎣⎦∑阻塞= 其中,C 是中继信道数,A 是中继系统的负荷。
Erlang B 公式表示的中继系统称为M/M/C/∞排队系统。
第一个M 表示呼叫到达是非记忆Poisson 过程,第二个M 表示用户服务时间指数分布,C 表示可用中继信道数,∞表示对同时服务用户数没有严格限制。
其模型如下图1所示,用户到达的速率为λ,用户被服务的速率为μ,系统中有C 个信道。
C (12)图1:M/M/C/∞排队模型基于Erlang B 的模型根据丢失呼叫清除设计,当用户发起呼叫时发现任何一个信道是空闲的,既可获得服务,否则被拥塞。
Markov 链的性质可以用来导出Erlang 公式。
考虑一个离散时间随机过程{}|0,1,2,n X n = ,从正整数集中取值,这样该过程状态是0,1,2,i = 。
如果该过程从当前状态i 转移到下一状态i +1,并C μServiceUser λ只依赖状态i 而与前面状态无关,则该过程称为Markov 链。
利用离散时间Markov 链,我们可以在持定业务条件下,在分离观察点观察业务情况。
一个实际中继系统的运作在时间上是连续的,但可以在小时间间隔δ内分析,δ是一个很小的正数。
如k N 是k δ时间内系统中的呼叫(占用信道)数目,k N 可以表示为:()k N N k δ=其中,N 是一个离散随机过程,表示在离散时间上被占用信道的数量。
转移概率,i j P 为:{},1|i j r k k P P N j N i +===让0δ→,可得:()1P λδοδ∞=-+ ()11ii P i λδμδοδ=--+≥(),10i i P i λδοδ+=+≥(),11i i P i λδοδ-=+≥(),,1,1i j P j i j i j i οδ=≠≠+≠-Markov 链的状态转移图由图2表示。
12C…μδλδ-1μδ2μδC λδλδλδμδ3μδλδ--1μδλδ21--μδλδC --1 …图2:Erlang B 中用Markov 链状态图表示的转移概率图2中具有C 个信道的中继系统可表示为一个Markov 链。
在该Markov 链状态图中,假定系统中0个信道被占用,即无用户。
在一个小的时间间隔后,系统继续保持0信道占用的概率为λδ-1。
从占用0信道变为占用1信道的概率为λδ。
另一方面,从占用一个信道变成占用0信道的概率为μδ。
类似的,系统保持为占用1信道状态的概率为μδλδ--1。
所有从一个状态转出的概率和为1。
在一段长时间后,系统到达平稳状态,具有n 信道占用。
在平稳状态,占用n 信道的概率与占用n-1信道的概率相等,并且是转移概率λδ的倍数。
这样在平稳状态条件下,n n P n P μδλδ=-1, C n ≤10=∑=Cn nP对不同的n 值可得:μδλδn P P n n =-1, C n ,,3,2,1 =μλn P P n n =-1μλ01P P =利用不同n 值对上面的方程式求值:!10n P P nn ⎪⎪⎭⎫ ⎝⎛=μλ 且∑==⎪⎭⎫⎝⎛=Ci i n nP n P P 10-1!λμ可得C 中继信道拥塞率为:∑=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛=Cn nCC n C P 0!1!1μλμλ总负荷μλλ/==H A 。
代入方程式拥塞率为:∑==Cn n CC n AC AP 0!1!1即为Erlang B 公式。
二、M/M/C 模型的仿真此仿真是在MATLAB (R2009b )的平台下进行的。
利用MATLAB 仿真呼叫接入信道过程,得出在不同呼叫速率下的拥塞率,然后用画出仿真得到的拥塞率数据和ErlangB 公式理论拥塞率曲线进行对比。
仿真步骤如下:1)业务请求是Poisson 分布,即到达间隔时间是指数分布。
程序设计产生以λ为均值的指数分布的随机数,作为一个服务的顾客到达间隔。
2)顾客服务时间是指数分布。
程序设计产生以μ为均值的指数分布的随机数,作为一个顾客的服务时间。
3)以0为起点,由顾客的到达间隔可以求出到达时刻arrive,从而进一步求出顾客离开时刻leave。
4)检查是否有空闲信道,若有则接入并占用信道,若无则拥塞5)统计总共被拥塞掉的顾客数,并除以到达的顾客数,即为拥塞率。
6)增大呼叫到达率,转至步骤1)三、仿真结果仿真参数:信道数为20,平均服务时间为20分钟,用户数为2000,总共进行了1000次仿真,呼叫到达率lamda从0开始每次增加0.01。
拥塞概率曲线和理论拥塞概率曲线如下图所示:图3:呼叫过程拥塞概率曲线四、结果分析从图3中可以看出,仿真曲线和理论曲线整体趋势基本吻合。
所以所建立的模型是正确的。
同时随着用户到达率λ的增加,而用户的服务率不变和信道的总数不变的情况下,呼叫的拥塞率逐渐增加,并且逐渐趋于平稳。
附程序%M/M/C模型的呼叫过程阻塞概率的仿真clcN = 2000; %用户数H = 30; %平均服务时间为30分,平均服务时间lamda = 0; %泊松到达过程的参数,到达速率mu = 1/H; %指数分布的参数C = 30; %信道数for i = 1 : 1 : C %channel记录接入的呼叫的离开时间leave(i) = 0;end%%%%%%%%%%%%%%%以话务量为变量进行呼叫过程阻塞概率的仿真%%%%%%%%%%%%%%%%%%%%%%LOSS(1) = 0;for k = 1:N;lamda = lamda+0.01;for i = 1 : 1: Cleave(i) = 0;endn=0; %被阻塞的用户数%产生服从Poisson到达过程的用户到达时间U1 = rand(N,1); %产生N个均匀分布的随机数temp = 0;for i = 1:1:Narrive(i) = temp - log(U1(i))/lamda;temp = arrive(i);end%产生服从指数分布的用户服务时间U2 = rand(N,1);for i = 1:1:Nservice(i) = -log(U2(i))/mu;end%产生用户离开时间for i = 1:1:Ndepart(i) = arrive(i)+service(i);end%计算阻塞概率for i = 1 : 1 : Nflag = 0; %标志信道是否被阻塞for j = 1 : 1 : Cif leave(j) < arrive(i) % 若果第i个用户到达的时间小于某一个用户在j个信道中离开的时间,则说明该信道空闲,可接入第i个用户。
leave(j) = depart(i);%则此时第j个信道中用户的离开时间记为depart(i)。
flag = 1;break;endendif flag == 0 % 阻塞n = n + 1;endendLOSS(k) = n / N;endlamda_temp = 0.01 : 0.01 : N*0.01;A = lamda_temp * H;%呼叫强度*保持时间=业务量plot(A,LOSS,'g');%绘制呼损率的图形hold on;%计算阻塞概率的理论值A = lamda_temp * H;for j = 1 : length(A)sum=0.0;for i=1:1:Ctemp = (A(j)^i) /factorial(i);sum = sum + temp;endPr(j) = (A(j)^C) / (factorial(C) * sum);%呼损率公式endplot(A, Pr, 'r');title('呼叫过程拥塞概率的仿真结果')xlabel('话务量(Elangs)')ylabel('拥塞概率')legend('仿真曲线','理论曲线')grid on。
