(完整版)Matlab概率论与数理统计
MATLAB语言及应用概率统计

第7章概率和数理统计1概率:又称或然率、机会率、机率(几率)或可能性,是概率论的基本概念。
概率是对随机事件发生的可能性的度量,一般以一个在0到1之间的实数表示一个事件发生的可能性大小。
越接近1,该事件更可能发生;越接近0,则该事件更不可能发生。
人们常说某人有百分之多少的把握能通过这次考试,某件事发生的可能性是多少,这都是概率的实例。
数理统计是伴随着概率论的发展而发展起来的一个数学分支,研究如何有效的收集、整理和分析受随机因素影响的数据,并对所考虑的问题作出推断或预测,为采取某种决策和行动提供依据或建议.2在MATLAB中,提供了专门的统计工具箱Staticstics,该工具箱有几百个专用求解概率和数理统计问题的函数。
7.1 随机数的产生7.2 随机变量的概率密度计算7.3 随机变量的累积概率值(分布函数值)7.4 随机变量的逆累积分布函数7.5 随机变量的数字特征7.6 统计作图3真正的随机数是使用物理现象产生的:比如掷钱币、骰子、转轮、使用电子元件的噪音、核裂变等等。
这样的随机数发生器叫做物理性随机数发生器,它们的缺点是技术要求比较高。
在实际应用中往往使用伪随机数就足够了。
这些数列是“似乎”随机的数,实际上它们是通过一个固定的、可以重复的计算方法产生的。
计算机或计算器产生的随机数有很长的周期性。
它们不真正地随机,因为它们实际上是可以计算出来的,但是它们具有类似于随机数的统计特征。
这样的发生器叫做伪随机数发生器。
在真正关键性的应用中,比如在密码学中,人们一般使用真正的随机数。
57.1 随机数的产生二项分布的随机数据的产生正态分布的随机数据的产生常见分布的随机数产生通用函数求各分布的随机数据67n = 6、p = 0.5时的二项分布以及正态近似二项分布,即重复n 次的伯努利试验,n 个独立的是/非试验中成功的次数的离散概率分布,其中每次试验的成功概率为p 。
二项分布的随机数据的产生•命令参数为N,P的二项随机数据•函数binornd•格式R = binornd(N, P)N、P为二项分布的两个参数,返回服从参数为N、P的二项分布的随机数。
第8章 matlab 概率论与数理统计问题的求解

8.1.3 概率问题的求解
图4-9
• 例:
>> b=1; p1=raylcdf(0.2,b); p2=raylcdf(2,b); P1=p2-p1 P1 = 0.8449
>> p1=raylcdf(1,b); P2=1-p1 P2 = 0.6065
• 例:
>> syms x y; f=x^2+x*y/3; >> P=int(int(f,x,0,1/2),y,0,1/2) P= 5/192 >> syms x y; f=x^2+x*y/3; P=int(int(f,x,0,1),y,0,2) P= 1
8.1.2.3
பைடு நூலகம்
分布
• 例:
>> x=[-0.5:.02:5]‘; %x=[-eps:-0.02:-0.5,0:0.02:5]; x=sort(x’);替代 >> y1=[]; y2=[]; a1=[1,1,2,1,3]; lam1=[1,0.5,1,2,1]; >> for i=1:length(a1) y1=[y1,gampdf(x,a1(i),lam1(i))]; y2=[y2,gamcdf(x,a1(i),lam1(i))]; end >> plot(x,y1), figure; plot(x,y2)
8.1.2.2 正态分布
正态分布的概率密度函数为:
• 例:
>> x=[-5:.02:5]'; y1=[]; y2=[]; >> mu1=[-1,0,0,0,1]; sig1=[1,0.1,1,10,1]; sig1=sqrt(sig1); >> for i=1:length(mu1) y1=[y1,normpdf(x,mu1(i),sig1(i))]; y2=[y2,normcdf(x,mu1(i),sig1(i))]; end >> plot(x,y1), figure; plot(x,y2)
数理统计的MATLAB求解

2019/3/2
8
3.1 随机变量及其分布
p2=binopdf(x,100,0.5);plot(x,p2,'*r');title('概率分布图')
2019/3/2
9
3.1 随机变量及其分布
例3.2设X~N(2,0.25) (1) 求概率P{1<X<2.5}; (2)绘制分布函数图象和分布密度图象; (3)画出区间[1.5,1.9]上的分布密度曲线下方区域。 程序:(1)p=normcdf(2.5,2,0.5)- normcdf(1,2,0.5) p = 0.8186 (2) x=0:0.1:4;px=normpdf(x,2,0.5); fx= normcdf(x,2,0.5); plot(x,px,'+b');hold on; plot(x,fx,'*r');legend('正态分布函数','正态分布密度'); (3) specs=[1.5,1.9]; pp=normspec(specs,2,0.5)
2019/3/2
10
3.1 随机变量及其分布
0.8 0.7
Probability Between Limits is 0.26209
0.6
0.5
Density
0.4
0.3
0.2
0.1
0
0
0.5
1
1.5
2 Critical Value
2.5
3
3.5
4
2019/3/2
11
3.2 随机变量函数的分布
2019/3/2
2
常见分布的随机数产生
2019/3/2
概率论与数理统计MATLAB上机实验报告

《概率论与数理统计》MATLAB上机实验实验报告一、实验目的1、熟悉matlab的操作。
了解用matlab解决概率相关问题的方法。
2、增强动手能力,通过完成实验内容增强自己动手能力。
二、实验内容1、列出常见分布的概率密度及分布函数的命令,并操作。
概率密度函数分布函数(累积分布函数) 正态分布normpdf(x,mu,sigma) cd f(‘Normal’,x, mu,sigma);均匀分布(连续)unifpdf(x,a,b) cdf(‘Uniform’,x,a,b);均匀分布(离散)unidpdf(x,n) cdf(‘Discrete Uniform’,x,n);指数分布exppdf(x,a) cdf(‘Exponential’,x,a);几何分布geopdf(x,p) cdf(‘Geometric’,x,p);二项分布binopdf(x,n,p) cdf(‘Binomial’,x,n,p);泊松分布poisspdf(x,n) cdf(‘Poisson’,x,n);2、掷硬币150次,其中正面出现的概率为0.5,这150次中正面出现的次数记为X(1) 试计算X=45的概率和X≤45 的概率;(2) 绘制分布函数图形和概率分布律图形。
答:(1)P(x=45)=pd =3.0945e-07P(x<=45)=cd =5.2943e-07(2)3、用Matlab软件生成服从二项分布的随机数,并验证泊松定理。
用matlab依次生成(n=300,p=0.5),(n=3000,p=0.05),(n=30000,p=0.005)的二项分布随机数,以及参数λ=150的泊松分布,并作出图线如下。
由此可以见得,随着n的增大,二项分布与泊松分布的概率密度函数几乎重合。
因此当n足够大时,可以认为泊松分布与二项分布一致。
4、 设22221),(y x e y x f +−=π是一个二维随机变量的联合概率密度函数,画出这一函数的联合概率密度图像。
概率与数理统计matlab实验报告1

p =
0.2909
(2).
>> p=[nchoosek(3,1)*nchoosek(9,3)*nchoosek(6,3)]/[nchoosek(12,4)*nchoosek(8,4)]
p =
0.1455
二.1.
>> p=1-0.98^200-nchoosek(200,1)*0.02*0.98^199
p =
0.9106
2.
>> p=normcdf(22,20,1.5)-normcdf(19,20,1.5)
p =
0.6563
三.1.
>> x=-10:0.01:10;
y1=normpdf(x,2,9);y2=normpdf(x,4,9);y3=normpdf(x,6,9);
plot(x,y1,x,y2,x,y3)
实
验
操
作
步
骤
(2)
.>> y=-10:0.01:10;
>> x1=normpdf(y,0,1);x2=normpdf(y,0,4);x3=normpdf(y,0,9);
>> plot(x1,y,x2,y,x3,y)
实
验
结
果
熟练掌握matlab的使用方法。
13-14-2电子信息工程实验报告1
姓名魏丰Βιβλιοθήκη 学号20120506305
班级
1203
实
概率论与数理统计的matlab实验

第35卷第20期2019年10月甘肃科技Gansu Science and TechnologyVol.35 N〇.20Oct. 2019概率论与数理统计的MATLAB实验*周后卿(邵阳学院理学院,湖南邵阳422000)摘要:《概率论与数理统计》作为理工科类一门基础文化课程,在培养应用技术型人才目标中具有非常重要的地位。
它有 自己独特的概念和计算方法,与其他学科联系紧密,同时又向基础学科、工科学科渗透,相互融合发展成为边缘学科。
本文 结合概率论与数理统计的教学实践,探讨如何利用数学实验辅助教学。
主要利用MATLAB、EXCEL、SPSS等软件,通过概 率论与数理统计课程的某些具体实例,展示了 MATLAB、EXCEL、SPSS等在课程教学中,对提高学生学习热情和提升学生 解决实际问题能力方面所发挥的作用。
关键词:概率论与数理统计;实验教学;软件中图分类号:G642概率论与数理统计是研究随机现象及其统计 规律的一门学科,它是根据大量同类随机现象的统 计规律,对随机现象出现某一结果的可能性作出一 种客观的科学判断,对这种出现的可能性大小做出 数量上的描述。
比较这些可能性的大小、研究它们 之间的联系,从而形成一整套数学理论和方法。
它 的基本概念和方法如:概率、独立性、数学期望、方 差、相关性、大数定律、中心极限定理、矩估计、极大 似然估计原理等等无不蕴含着独特的数学思想方 法。
由于它具有思维的灵活性、应用的广泛性,其理 论与方法常被人们应用于经济、管理、农业、工业和 科学技术中,涉及生产、生活的方方面面。
由于概率论与数理统计的教学内容较多,课时 有限,因而在传统教学观念中,存在这样一个误区:让学生记住公式,套用公式来计算。
但概率论与数 理统计概念繁多,理论抽象,计算繁琐,要记下也不 是一件容易的事。
这种死记硬背的教学模式导致学 生上课感觉枯燥无味,对概念理解不透彻,对其中的 思想方法难以掌握,面对实际问题时无从下手,难以 培养学生对概率知识和统计思想的应用能力M。
概率论与数理统计的MATLAB实现讲稿

第9章 概率论与数理统计的MATLAB 实现MATLAB 总包提供了一些进行数据统计分析的函数,但不完整。
利用MATLAB 统计工具箱,可以进行基本概率和数理统计分析,以及进行比较复杂的多元统计分析。
本章主要针对大学本科的概率统计课程介绍工具箱的部分功能。
9.1 随机变量及其分布利用统计工具箱提供的函数,可以比较方便地计算随机变量的分布律(概率密度函数)和分布函数。
9.1.1 离散型随机变量及其分布律如果随机变量全部可能取到的不相同的值是有限个或可列个无限多个,则称为离散型随机变量。
MATLAB 提供的计算常见离散型随机变量分布律的函数及调用格式: 函数调用格式(对应的分布) 分布律y=binopdf(x,n,p)(二项分布) )()1(),|(),,1,0(x I p p x n p n x f n xn x --⎪⎪⎭⎫ ⎝⎛=y=geopdf(x,p)(几何分布) xp p p x f )1()|(-= ),1,0( =xy=hygepdf(x,M,K,n)(超几何分布) ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛=n M x n K M x K n K M x f ),,|(y=poisspdf(x,lambda)(泊松分布) λλλ-=e x x f x !)|(),1,0( =x y=unidpdf(x,n)(离散均匀分布) NN x f 1)|(=9.1.2 连续型随机变量及其概率密度对于随机变量X 的分布函数)(x F ,如果存在非负函数)(x f ,使对于任意实数x 有⎰∞-=x dt t f x F )()(则称X 为连续型随机变量,其中函数)(x f 称为X 的概率密度函数。
MA TLAB 提供的计算常见连续型随机变量分布概率密度函数的函数及调用格式:函数调用格式(对应的分布) 概率密度函数y=betapdf(x,a,b)(β分布) )10()1(),(1),|(11<<-=--x x x b a B b a x f b ay=chi2pdf(x,v)(卡方分布) )2(2)|(2212v exv x f v x v Γ=--)0(≥xy=exppdf(x,mu)(指数分布) μμμxe xf -=1)|()0(≥xy=fpdf(x,v1,v2)(F 分布) 2211222121212121111)2()2()2(),|(v v v v v x v x vv v v v v v v x f +-⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛ΓΓ+Γ= y=gampdf(x,a,b)(伽马分布) b xa a e x ab b a x f --Γ=1)(1),|()0(≥xy=normpdf(x,mu,sigma)(正态分布) 22)(21),|(σμπσσμ--=x ex fy=lognpdf(x,mu,sigma)(对数正态分布) 22)(ln 21),|(σμπσσμ--=x ex x fy=raylpdf(x,b)(瑞利分布) 222)|(b x e b x b x f -=y=tpdf(x,v)(学生氏t 分布) 2121)2()21()|(+-⎪⎪⎭⎫ ⎝⎛+Γ+Γ=v v x v v v v x f πy=unifpdf(x,a,b)(连续均匀分布) )(1),|(],[x I ab b a x f b a -=y=weibpdf(x,a,b)(威布尔分布) )(),|(),0(1x I eabx b a x f bax b ∞--= 比如,用normpdf 函数计算正态概率密度函数值。
MATLAB教程第八章 概率和数理统计

t0 t0
某人到此办事,若等待时间超过15分钟,他就离 去。设此人一个月要去该处10次,试求: (1)恰好有两次有两次离去的概率; (4)离去的次数占多数的概率。
解:首先求任一次离去的概率,
解: p1=Hygepdf(1,500,50,10) p1 = 0.3913 p2=Hygepdf(0,500,50,10)+Hygepdf(1,500,50,10) p2 = 0.7365 p3=1-Hygepdf(0,500,50,10) p3 = 0.6548
例5:计算指数密度函数值
解: y=exppdf(5,1:5) y= 0.0067 0.0410 0.0630 0.0716 0.0736 y=exppdf(1:5,1:5) y= 0.3679 0.1839 0.1226 0.0920 0.0736
分布
例1 :某单位有内线电话300部,假设任意一时刻每部电话打外线电
话的概率为0.01,求在某一时刻恰有4部电话打外线的概率。在某一时 刻打外线电话的最可能部数是多少?
解:设X表示某一时刻该单位打外线电话的电话部数, 则X的统计规律可用二项分布来描述,X~B(300,0.01)。 记A=“某一时刻恰有4部电话打外线”,则所求概率为 p=p(A)=p(X=4)。 p=binopdf(4,300,0.01) p = 0.1689 计算某一时刻打外线电话的最可能部数 y=binopdf([0:300],300,0.01); [pp,m]=max(y) pp = 0.2252 m= 4
概率与分位数的关系 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 2.1171 2.5 p=0.9
Matlab在《概率论与数理统计》教学中的应用

Matlab在《概率论与数理统计》教学中的应用【摘要】摘要:本文探讨了Matlab在《概率论与数理统计》教学中的应用。
在介绍了研究背景、目的和意义。
在分别阐述了Matlab在概率论教学中的基本概念应用、在数理统计教学中的数据分析应用、在概率论与数理统计教学中的模拟实验设计、在教学案例分析中的应用以及在编程训练中的应用。
结论部分总结了Matlab在教学中的重要性,并展望了未来研究方向。
本文旨在为教师和学生提供更有效的教学和学习工具,以提高教学效果和学习成果。
Matlab在概率论与数理统计教学中的应用将在未来持续发展,并为该领域的研究和实践提供更多可能性。
【关键词】Matlab, 概率论, 数理统计, 教学, 应用, 模拟实验, 数据分析, 编程训练, 教学案例分析, 重要性, 研究方向, 总结1. 引言1.1 研究背景研究背景部分将重点介绍Matlab在概率论与数理统计教学中的应用现状和意义。
通过Matlab软件,学生可以直观地展示概率分布的图像、计算统计量、进行数据拟合和模拟实验等操作。
Matlab的使用不仅提高了教学效果,也使学生在处理大量数据和复杂问题时更加得心应手。
在现代社会,数据分析已经成为一项必不可少的技能。
运用Matlab软件进行概率论与数理统计教学的实践意义愈发重要。
本文将进一步探讨Matlab在概率论与数理统计教学中的具体应用,以期能够为教学改革和学生能力培养提供参考和借鉴。
1.2 目的引言概率论与数理统计是现代数学中非常重要的一门学科,它不仅是其他学科的基础,而且在各个领域都有着广泛的应用。
而在教学中,如何让学生更加直观地理解和应用这些概念,是一个很重要的问题。
本文旨在探讨Matlab在《概率论与数理统计》教学中的应用,通过应用Matlab软件,可以更好地帮助学生理解难点,提高学习的效率和趣味性,从而提高教学质量。
1.3 意义在《概率论与数理统计》教学中,Matlab的应用具有重要的意义。
MATLAB数理统计
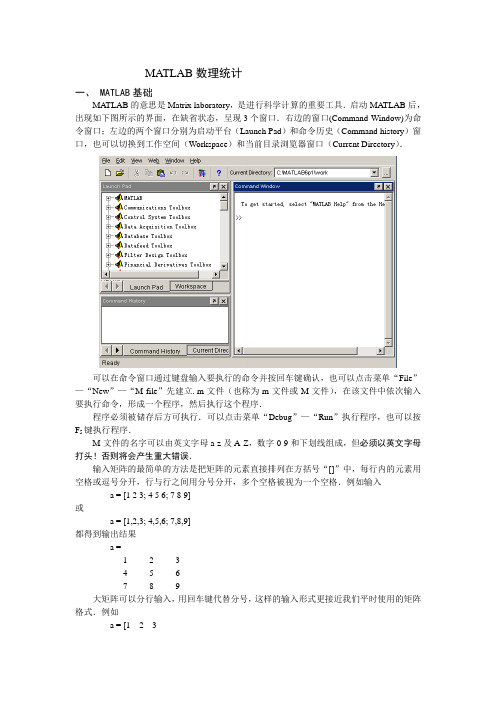
MA TLAB数理统计一、 MATLAB基础MA TLAB的意思是Matrix laboratory,是进行科学计算的重要工具.启动MA TLAB后,出现如下图所示的界面,在缺省状态,呈现3个窗口.右边的窗口(Command Window)为命令窗口;左边的两个窗口分别为启动平台(Launch Pad)和命令历史(Command history)窗口,也可以切换到工作空间(Workspace)和当前目录浏览器窗口(Current Directory).可以在命令窗口通过键盘输入要执行的命令并按回车键确认,也可以点击菜单“File”—“New”—“M-file”先建立.m文件(也称为m-文件或M-文件),在该文件中依次输入要执行命令,形成一个程序,然后执行这个程序.程序必须被储存后方可执行.可以点击菜单“Debug”—“Run”执行程序,也可以按F5键执行程序.M-文件的名字可以由英文字母a-z及A-Z,数字0-9和下划线组成,但必须以英文字母打头!否则将会产生重大错误.输入矩阵的最简单的方法是把矩阵的元素直接排列在方括号“[]”中,每行内的元素用空格或逗号分开,行与行之间用分号分开,多个空格被视为一个空格.例如输入a = [1 2 3; 4 5 6; 7 8 9]或a = [1,2,3; 4,5,6; 7,8,9]都得到输出结果a =1 2 34 5 67 8 9大矩阵可以分行输入,用回车键代替分号,这样的输入形式更接近我们平时使用的矩阵格式.例如a = [1 2 34 5 67 8 9]可以先将一个矩阵输入到Excel工作表,即先建立数据文件.然后打开“file”—“Import Data”菜单,即启动导入数据导航,按提示打开Excel工作表,将数据导入到MA TLAB的工作空间中去.矩阵也称为数组.只有一行或一列的数组称为一维数组,有多个行和多个列的数组称为二维数组.一维数组x的第i个元素记为x(i),二维数组a的第i行第j 列的元素记为a(i,j).MA TLAB采用双精度储存变量和数值计算,但能以多种格式输出数据.例如x = [4/3 1.2345e–6]则在几种常见的的格式下,输出结果分别为format short1.3333 0.0000format short e1.3333e+000 1.2345e–006format short g1.3333 1.2345e–006format long1.33333333333333 0.00000123450000format long e1.333333333333333e+000 1.234500000000000e–006format long g1.33333333333333 1.2345e–006format rat4/3 1/810045应当先执行格式命令,然后再输出数据.MA TLAB的缺省格式为format short.要显示一个变量的内容,只需在命令窗口或程序中键入该变量的名字.例如在命令窗口依次执行a=1/3 ,format long,a这三个命令,结果如下:>> a=1/3a =0.3333>> format long>> aa =0.33333333333333若最大的元素大于1000或小于0.001,则显示short或long格式时会加上一个比例.在命令后加上分号“;”,则屏幕上不会立即显示出结果,这在运算大的数据量时十分有用,如下命令产生100*100的魔方矩阵,但并不在屏幕上显示.A = magic(100);如果一个命令很长,想另起一行接着输入命令,须要在末尾加上“...”,如: s = 1 – 1/2 + 1/3 – 1/4 + 1/5 – 1/6 + 1/7 ...–1/8 + 1/9 – 1/10 + 1/11 – 1/12;可用who或whos来察看当前工作空间中有哪些变量.若要从工作空间中删除所有的变量,用clear也可以根据需要一次删除若干个变量,例如要从工作空间中删除x1,x2两个变量,用clear x1 x2你可以将工作间保存为一个二进制的.mat文件,以备以后调用.命令save june10将工作空间保存到文件june10.mat.也可只保存工作间中的部分变量值,例如要保存变量x,y,z到文件june10.mat,使用命令save june10 x y z重载时只需输入load june10要想将变量a更名为b,可使用命令b=a;clear aMA TLAB支持矩阵的加法、减法、乘法、转置、求逆等各种运算.命令a' 和inv(a)分别计算矩阵a的转置矩阵和逆矩阵.MA TLAB的算数运算符为:+ 加- 减* 乘^ 幂/ 左除\ 右除对于两个标量a, b来说,a/b=b\a=a÷b,而对于两个矩阵a, b来说,a/b=a*inv(b)b\a=inv(b)*a两个同维数组相加减,等于其对应元素相加减.一个数组与一个标量相加减,则等于数组的各元素分别与这个常数相加减.用符号“. / ”表示两个数组的除法.若x, y是同维数组,则x ./ y表示x的元素分别除以y的对应元素得到的数组.z=x ./ y即z(i, j)=x(i, j)/y(i, j).x ./ y 与y .\ x 相等,都表示x除以y,但运算是在对应元素间进行的,与矩阵的除法是不同的.矩阵的乘方用“^”符号表示,a^p的意思是a的p次方.数组的乘方用“.^”符号表示.若x=[x1, x2, …, xn], y=[y1, y2, …, yn]是同维数组,则z = x .^ y=[x1^y1, x2^y2, …, xn^yn]若c是一个标量,则z = x .^ c=[x1^c, x2^c, …, xn^c]可以使用help命令寻求帮助.例如,键入help clear即可获得clear命令的帮助信息.类似地可以得到其他命令/函数的帮助信息.二、分布函数及数字特征的计算MA TLAB提供了计算常见分布的分布函数和分位数的函数,见表11.4和表11.5.表11.4 概率分布函数y=F(x)的计算表11.5 上侧α分位数x 的计算1. 函数mean() 语法:m=mean(x)若x 是单个向量(可以是行向量,也可以是列向量),则返回结果m 是x 的均值,若x 是矩阵,则返回结果m 是行向量,它包含x 的每列数据的均值.即若 111212122212k kn n nk x x x x x x x x x x ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦则12[,,,]k m x x x = ,其中11nj iji x xn==∑(1,2,,)j k = .2. 函数var()语法:y=var(x)若x 是单个向量(可以是行向量,也可以是列向量),则返回结果y 是x 的方差,若x 是矩阵,则返回结果y 是行向量,它包含x 的每列数据的方差.V ar(x)运用n-1进行标准化处理,其中n 为数据的长度.若要运用n 进行标准化,可使用var(x,1)格式. 3. 函数std() 语法:y=std(x)std(x)=sqrt(var(x)),返回样本x 的标准差.4. 函数cov() 语法:C=cov(x)计算协方差矩阵.若x 是单个向量(可以是行向量,也可以是列向量),则返回结果C 是x 的方差,若x 是矩阵,则返回各列数据的协方差构成的协方差矩阵.cov(x)运用n-1进行标准化处理. 5. 函数corrcoef() 语法:R=corrcoef(x)返回一个相关系数矩阵R .矩阵R 的元素R(i, j)与对应的协方差矩阵C=cov(x)的元素C(i, j)的关系为(,)R i j =使用MA TLAB进行参数估计,与使用Excel进行参数估计的方法相似。
MATLAB第7章 概率论与数理统计

P{(X,Y)=(xi, yi)}= P{X=xi,Y= yi}=pij, i,j=1,2,..., 为二维离散型随机变量(X,Y)的联合分布律,也称(X,Y)的概率分布。
7.2.5二维随机变量及概率分布
7.6方差分析
在实际中,一种结果往往会受到几种不同因素的影响,如一种产品的 质量可能会受到设备性能和操作人员技能等方面的影响;不同的营销方 式对同一产品的销售量可能产生不同的效果;某一地区居民的消费水平 可能与人均收入、商品价格及广告力度等因素有关;化学合成过程可能 会受到温度、时间和材料成分的影响;农作物产量可能会受到气候、肥 料、品种及土质等因素的影响;等等。方差分析(analysis of variance, 简 写ANOVA)就是对由不同因素变化时所产生的结果进行统计特性的差异分 析,以检验各种因素对所研究对象的某一特性的影响程度,是假设检验 方法的一种多元推广。
基于一维分析方法并通过相关数学运算可以方便地实现二维或多维随 机变量及概率的分析。 【例7-21】 已知二维连续随机变量(X,Y)的联合密度函数为
f (x, y) cex2y,x 0, y 0
试求: 1) 确定常数c; 2)计算概率P{2X+Y≤1}; 3) 求(X,Y)的联合分布函数。
7.2.6随机变量函数的分布
7.5假设检验
假设检验是指先对总体分布中的参数或对总体分布做出某种 假设, 从总体中随机抽取一个样本来检验假设是否接受或拒绝。总 体假设检验分为两类:参数假设检验和总体分布假设检验。总体 假设通常设立原假设H0(或零假设,null hypothesis)和备择假设 H1(或对立假设,alternative hypothesis)。由于要从随机抽取的 一个子样本来检验总体假设是否接受或拒绝,因此可能犯两类错 误:第一类错误为拒绝真,第二类错误是接受假。
-Matlab在概率统计中的应用

第8章 Matlab在概率统计中的应用概率论与数理统计是研究和应用随机现象统计规律性的一门数学科学.其应用十分广泛,几乎遍及所有科学领域、工农业生产和国民经济各部门。
本章将利用Matlab来解决概率统计学中的概率分布、数字特征、参数估计以及假设检验等问题.8.1 数据分析8。
1。
1 几种均值在给定的一组数据中,要进行各种均值的计算,在Matlab中可由以下函数实现。
mean 算术平均值函数。
对于向量X,mean (X)得到它的元素的算术平均值;对于矩阵,mean (X)得到X各列元素的算术平均值,返回一个行向量。
nanmean 求忽略NaN的随机变量的算术平均值。
geomean 求随机变量的几何平均值。
harmmean 求随机变量的和谐平均值。
trimmean 求随机变量的调和平均值.8.1.2 数据比较在给定的一组数据中,还常要对它们进行最大、最小、中值的查找或对它们排序等操作。
Mtalab中也有这样的功能函数。
max 求随机变量的最大值元素。
nanmax 求随机变量的忽略NaN的最大值元素。
min 求随机变量的最小值元素.nanmin 求随机变量的忽略NaN的最小值元素。
median 求随机变量的中值.nanmedian 求随机变量的忽略NaN的中值。
mad 求随机变量的绝对差分平均值。
sort 对随机变量由小到大排序.sortrows 对随机矩阵按首行进行排序。
range 求随机变量的值的范围,即最大值与最小值的差(极差)。
8.1.3 累和与累积求向量或矩阵的元素累和或累积运算是比较常用的两类运算,在Matlab中可由以下函数实现。
sum 若X为向量,sum (X)为X中各元素之和,返回一个数值;若X为矩阵,sum (X)为X中各列元素之和,返回一个行向量.nansum 忽略NaN求向量或矩阵元素的累和。
cumsum 求当前元素与所有前面位置的元素和。
返回与X同维的向量或矩阵。
cumtrapz 梯形累和函数。
MATLAB在概率论和数理统计中的应用论文
MATLAB 在概率论和数理统计中的应用一、 引言概率论与数理统计作为现代数学的重要分支,在自然科学、社会科学和工程技术等领域都具有极为广泛的应用。
概率论和数理统计是研究随机现象的客观规律并付诸应用的数学学科。
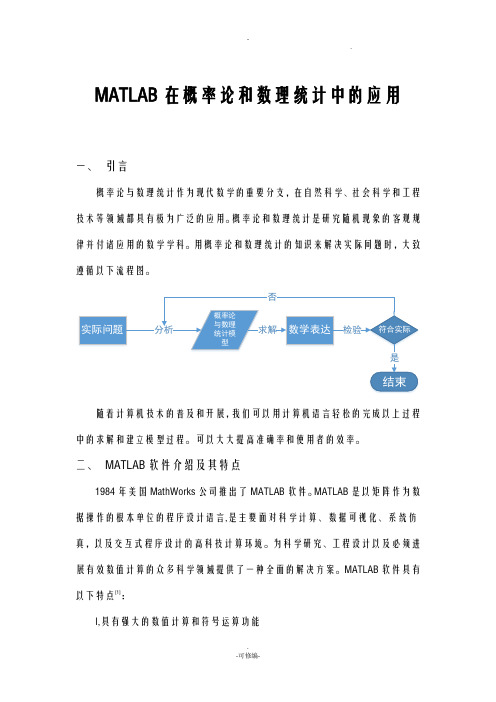
用概率论和数理统计的知识来解决实际问题时,大致遵循以下流程图。
实际问题数学表达概率论与数理统计模型符合实际结束分析求解 检验是否随着计算机技术的普及和开展,我们可以用计算机语言轻松的完成以上过程中的求解和建立模型过程。
可以大大提高准确率和使用者的效率。
二、 MATLAB 软件介绍及其特点1984年美国MathWorks 公司推出了MATLAB 软件。
MATLAB 是以矩阵作为数据操作的根本单位的程序设计语言,是主要面对科学计算、数据可视化、系统仿真,以及交互式程序设计的高科技计算环境。
为科学研究、工程设计以及必须进展有效数值计算的众多科学领域提供了一种全面的解决方案。
MATLAB 软件具有以下特点[1]:I,具有强大的数值计算和符号运算功能II,操作界面简单,编程语言自然III,具有先进的数据可视化功能IV,具有强大的开放性和可扩展性总之,MATLAB是工程师和科研者使用最广泛的软件之一。
三、MATLAB中关于概率统计的命令和函数MATLAB中的Statistics Toolbox提供了丰富的关于概率统计的命令和函数,用于解决概率论和数理统计中的常见问题。
下表将列举常用的概率统计中的命令和函数。
利用上述函数产生一个44矩阵的标准正态随机数,MATLAB代码如下:>> R=normrnd(0,1,4,4)R =-0.8095 -0.7549 -0.2414 -0.0301 -2.9443 1.3703 0.3192 -0.16491.4384 -1.7115 0.3129 0.62770.3252 -0.1022 -0.8649 1.0933 产生的随机数可以在工作窗口查看。
假设要想求参数为=1=2=2=3μσμσ,;,的正态分布的期望和方差,那么相应的MATLAB 的代码为: >> clear >> a=[1 2]; >> b=[2 3];>> [m v]=normstat(a,b) m =1 2 v =4 9在MATLAB 的统计工具箱中提供了一个演示程序disttool ,可以直观的演示常见分布的分布函数和概率密度函数。
概率论matlab实验报告

概率论与数理统计matlab上机实验报告班级:学号:姓名:指导老师:实验一常见分布的概率密度、分布函数生成[实验目的]1. 会利用MATLAB软件计算离散型随机变量的概率,连续型随机变量概率密度值。
2.会利用MATLAB软件计算分布函数值,或计算形如事件{X≤x}的概率。
3.会求上α分位点以及分布函数的反函数值。
[实验要求]1.掌握常见分布的分布律和概率密度的产生命令,如binopdf,normpdf2. 掌握常见分布的分布函数命令,如binocdf,normcdf3. 掌握常见分布的分布函数反函数命令,如binoinv,norminv[实验内容]常见分布的概率密度、分布函数生成,自设参数1、X~B(20,0.4)(1)P{恰好发生8次}=P{X=8}(2)P{至多发生8次}=P{X<=8}(1)binopdf(8,20,0.4)ans =0.1797(2)binocdf(8,20,0.4)ans =0.59562、X~P(2)求P{X=4}poisspdf(4,2)ans =0.09023、X~U[3,8](1)X=5的概率密度(2)P{X<=6}(1) unifpdf(5,3,8)ans =0.2000(2) unifcdf(6,3,8)ans =0.60004、X~exp(3)(1)X=0,1,2,3,4,5,6,7,8时的概率密度(2)P{X<=8}注意:exp(3)与教材中参数不同,倒数关系(1)exppdf(0:8,3)ans =Columns 1 through 30.3333 0.2388 0.1711Columns 4 through 60.1226 0.0879 0.0630Columns 7 through 90.0451 0.0323 0.0232(2) expcdf(8,3)ans =0.93055、X~N(8,9)(1)X=3,4,5,6,7,8,9时的概率密度值(2) X=3,4,5,6,7,8,9时的分布函数值(3)若P{X<=x}=0.625,求x(4)求标准正态分布的上0.025分位数(1)normpdf(3:9,8,3)ans =Columns 1 through 30.0332 0.0547 0.0807 Columns 4 through 60.1065 0.1258 0.1330 Column 70.1258(2)normcdf(3:9,8,3)ans =Columns 1 through 30.0478 0.0912 0.1587 Columns 4 through 60.2525 0.3694 0.5000 Column 70.6306(3)norminv(0.625,8,3)ans =8.9559(4)norminv(0.975,0,1)ans =1.96006、X~t(3)(1)X=-3,-2,-1,0,1,2,3时的概率密度值(2)X=-3,-2,-1,0,1,2,3时的分布函数值(3)若P{X<=x}=0.625,求x(4)求t分布的上0.025分位数(1)tpdf(-3:3,3)ans =Columns 1 through 30.0230 0.0675 0.2067 Columns 4 through 60.3676 0.2067 0.0675 Column 70.0230(2)tcdf(-3:3,3)ans =Columns 1 through 30.0288 0.0697 0.1955 Columns 4 through 60.5000 0.8045 0.9303 Column 70.9712(3)tinv(0.625,3)ans =0.3492(4)tinv(0.975,3)ans =3.18247、X~卡方(4)(1)X=0,1,2,3,4,5,6时的概率密度值(2) X=0,1,2,3,4,5,6时的分布函数值(3)若P{X<=x}=0.625,求x(4)求卡方分布的上0.025分位数(1)chi2pdf(0:6,4)ans =Columns 1 through 30 0.1516 0.1839 Columns 4 through 60.1673 0.1353 0.1026 Column 70.0747(2)chi2cdf(0:6,4)ans =Columns 1 through 30 0.0902 0.2642 Columns 4 through 60.4422 0.5940 0.7127 Column 70.8009(3)chi2inv(0.625,4)ans =4.2361(4)chi2inv(0.975,4)ans =11.14338、X~F(4,9)(1)X=0,1,2,3,4,5,6时的概率密度值(2) X=0,1,2,3,4,5,6时的分布函数值(3)若P{X<=x}=0.625,求x(4)求F分布的上0.025分位数(1)fpdf(0:6,4,9)ans =Columns 1 through 30 0.4479 0.1566 Columns 4 through 60.0595 0.0255 0.0122 Column 70.0063(2)fcdf(0:6,4,9)ans =Columns 1 through 30 0.5442 0.8218Columns 4 through 60.9211 0.9609 0.9788Column 70.9877(3)finv(0.625,4,9)ans =1.1994(4)finv(0.975,4,9)ans =4.7181实验二概率作图[实验目的]1.熟练掌握MATLAB软件的关于概率分布作图的基本操作2.会进行常用的概率密度函数和分布函数的作图3.会画出分布律图形[实验要求]1.掌握MATLAB画图命令plot2.掌握常见分布的概率密度图像和分布函数图像的画法[实验内容]任选四种分布,自设参数(已画八种分布图像,可熟悉各分布特点)1、X~B(20,0.4)代码:x=0:20;y=binopdf(x,20,0.4)plot(x,y,'.')结果:2、X~exp(3)概率密度图像代码:x=0:0.01:15;y=exppdf(x,3)plot(x,y)结果:分布函数代码:x=-1:0.01:15;y=expcdf(x,3)plot(x,y)结果:3、X~P(4)概率密度图形代码:x=0:10;y=poisspdf(x,4)plot(x,y,'.')结果:分布函数图形代码:x=0:0.01:10; y=poisscdf(x,4) plot(x,y)结果:4、X~U(3,8)概率密度图形代码:x=0:0.01:10;y=unifpdf(x,3,8)plot(x,y,'.')结果:分布函数图形代码:x=0:0.01:10;y=unifcdf(x,3,8) plot(x,y)结果:5、X~N(4,9)概率密度图形代码:x=-10:0.01:18;y=normpdf(x,4,3); plot(x,y)结果:分布函数图形代码:x=-10:0.01:18;y=normcdf(x,4,3); plot(x,y)结果:同一坐标系,均值是4,标准差分别为1,2,3的正态分布概率密度图形代码:x=-5:0.01:15;y1=normpdf(x,4,1);y2=normpdf(x,4,2);y3=normpdf(x,4,3);plot(x,y1,x,y2,x,y3)结果:6、X~t(3)概率密度图形代码:x=-10:0.01:10;y=tpdf(x,3);plot(x,y)结果:分布函数图形代码:x=-10:0.01:10; y=tcdf(x,3); plot(x,y)结果:7、X~卡方(4)概率密度图形代码:x=0:0.01:15;y=chi2pdf(x,4);plot(x,y)结果:分布函数图形代码:x=0:0.01:15; y=chi2cdf(x,4); plot(x,y)结果:8、X~F(4,9)概率密度图形代码:x=0:0.001:10;y=fpdf(x,4,9);plot(x,y)结果:分布函数图形代码:x=0:0.001:10; y=fcdf(x,4,9); plot(x,y)结果:实验三数字特征[实验目的]1 加深对数学期望,方差的理解2理解数学期望,方差的意义,以及具体的应用3 加深对协方差,相关系数的理解4 了解协方差,相关系数的具体的应用[实验要求]1 概率与频率的理论知识,MATLAB软件2 协方差,相关系数的理论知识,MATLAB命令cov,corrcoef [实验内容]P101-11代码:exp=[];price=[-200 100];exp(1)=expcdf(1,4)exp(2)=1-exp(1)Ey=exp*price'结果:exp =0.2212exp =0.2212 0.7788Ey =33.6402即平均获利为Ey=e^(-1/4)*300-200=33.6402p101-13代码:Syms x yfxy=(x+y)/3;Ex=int(int(fxy*x,y,0,1),x,0,2)Ey=int(int(fxy*y,y,0,1),x,0,2)Exy=int(int(fxy*x*y,y,0,1),x,0,2)E=int(int(fxy*(x^2+y^2),y,0,1),x,0,2)结果:Ex =Ey =5/9Exy =2/3E =13/6>>P102-22代码:Syms x yfxy=1;Ex=int(int(fxy*x,y,-x,x),x,0,1) Ey=int(int(fxy*y,y,-x,x),x,0,1)Ex2=int(int(fxy*x^2,y,-x,x),x,0,1) Ey2=int(int(fxy*y^2,y,-x,x),x,0,1) Dx=Ex2-Ex^2Dy=Ey2-Ey^2结果:Ex =Ey =Ex2 =1/2Ey2 =1/6Dx =1/18Dy =1/6>>P103-26代码:Syms x yfxy=2-x-y;Ex=int(int(fxy*x,y,0,1),x,0,1);Ey=int(int(fxy*y,y,0,1),x,0,1);Ex2=int(int(fxy*x^2,y,0,1),x,0,1);Ey2=int(int(fxy*y^2,y,0,1),x,0,1);Dx=Ex2-Ex^2;Dy=Ey2-Ey^2;Exy=int(int(fxy*x*y,y,0,1),x,0,1);Covxy=Exy-Ex*Eyrxy=Covxy/(sqrt(Dx)*sqrt(Dy))D=4*Dx+Dy结果:Covxy =-1/144rxy =-1/11D =55/144实验四统计中的样本数字特征实验五两个正态总体均值差,方差比的区间估计[实验目的]1掌握两个正态总体均值差,方差比的区间估计方法2会用MATLAB求两个正态总体均值差,方差比的区间估计[实验要求]两个正态总体的区间估计理论知识[实验内容]P175-27代码:x1=[0.143 0.142 0.143 0.137]x2=[0.140 0.142 0.136 0.138 0.140] x=mean(x1)y=mean(x2)s1=var(x1)s2=var(x2)s=sqrt((3*s1+4*s2)/7)t=tinv(0.975,7)d1=(x-y)-t*s*sqrt(1/4+1/5)d2=(x-y)+t*s*sqrt(1/4+1/5)结果:s =0.0026t =2.3646d1 =-0.0020d2 =0.0061即置信区间为(-0.0020,0.0061)P175-28代码:u=norminv(0.975,0,1)s=sqrt(0.035^2/100+0.038^2/100)d1=(1.71-1.67)-u*sd2=(1.71-1.67)+u*s结果:u =1.9600s =0.0052d1 =0.0299d2 =0.0501>>即置信区间为(0.0299,0.0501)P175-30代码:f1=finv(0.975,9,9)f2=finv(0.025,9,9)f3=finv(0.95,9,9)f4=finv(0.05,9,9)s12=0.5419s22=0.6065d1=s12/s22/f1d2=s12/s22/f2d3=s12/s22/f3d4=s12/s22/f4结果:d1 =0.2219d2 =3.5972d3 =0.2811d4 =2.8403>>即置信区间为(0.2219,3.5972),置信下界为0.2811,置信上界为2.8403实验五假设检验[实验目的]1 会用MATLAB进行单个正态总体均值及方差的假设检验2 会用MATLAB进行两个正态总体均值差及方差比的假设检验[实验要求]熟悉MATLAB进行假设检验的基本命令与操作[实验内容]P198-2原假设H0:平均尺寸mu=32.25;H1:平均尺寸mu<>32.25方差已知,用ztest代码:x=[32.56,29.66,31.64,30.00,31.87,31.03][h,sig,ci,zval]=ztest(x,32.25,1.1,0.05)[h,sig,ci,zval]=ztest(x,32.25,1.1,0.01)(注:h是返回的一个布尔值,h=0,接受原假设,h=1,拒绝原假设;sig表示假设成立的概率;ci为均值的1-a的置信区间;zval为Z统计量的值)结果:h =1sig =0.0124ci =30.2465 32.0068zval =-2.5014h =sig =0.0124ci =29.9699 32.2834zval =-2.5014即a=0.05时,拒绝原假设H0;a=0.01时,接受原假设H0p198-3原假设H0:总体均值mu=4.55;H1:总体均值mu<>4.55方差未知,用ttest代码:x=[4.42,4.38,4.28,4.40,4.42,4.35,4.37,4.52,4.47,4.56][h,sig,ci,tval]=ttest(x,4.55,0.05)结果:h =1sig =6.3801e-004ci =4.3581 4.4759tval =tstat: -5.1083df: 9sd: 0.0823h=1,即拒绝原假设H0p198-10是否认为是同一分布需要分别检验总体均值和方差是否相等原假设H0:mu1-mu2=0;H1:mu1-mu2<>0代码:x=[15.0,14.5,15.2,15.5,14.8,15.1,15.2,14.8]y=[15.2,15.0,14.8,15.2,15.1,15.0,14.8,15.1,14.8][h,sig,ci]=ttest2(x,y,0.05)结果:h =sig =0.9172ci =-0.2396 0.2646h=0,即接受原假设H0,mu1-mu2=0,两分布的均值相等;验证方差相等的matlab方法没有找到可采用以下语句整体检验两个分布是否相同,检验两个样本是否具有相同的连续分布[ h ,sig, ksstat]=kstest2(x,y,0.05)原假设H0:两个样本具有相同连续分布H1:两个样本分布不相同代码:x=[15.0,14.5,15.2,15.5,14.8,15.1,15.2,14.8]y=[15.2,15.0,14.8,15.2,15.1,15.0,14.8,15.1,14.8][ h ,sig, ksstat]=kstest2(x,y,0.05)结果:h =sig =0.9998ksstat =0.1528>>h=0,即接受原假设H0,两个样本有相同的连续分布。
Matlab在《概率论与数理统计》教学中的应用

Matlab在《概率论与数理统计》教学中的应用概率论与数理统计是数学系本科生的一门重要课程,也是各个理工科专业的基础课程之一。
它主要研究随机现象的规律性和数理统计的应用。
在这门课程中,学生需要掌握一些概率论和数理统计的基本概念、定理和方法,同时需要熟练掌握各种概率分布的性质和应用、随机变量和随机过程的概念、数理统计的各种抽样分布以及参数估计、假设检验等内容。
为了更好地帮助学生理解和掌握这些知识,教师可以借助Matlab这一强大的数学计算软件进行教学。
Matlab是一种被广泛应用于科学和工程领域的高级技术计算软件,其功能强大,操作简便,可用于数据处理、分析、绘图以及复杂算法的实现等。
在概率论与数理统计的教学中,利用Matlab可以方便地进行概率论和数理统计的相关计算、模拟和可视化,使得抽象的数学理论更加具体直观,提高学生对概率论与数理统计知识的理解和掌握。
下面将介绍Matlab在《概率论与数理统计》教学中的应用。
一、概率论的基本概念和方法1.1 概率分布的可视化在概率论的教学中,学生需要学习各种概率分布的性质、密度函数和分布函数的特点,以及随机变量的数学期望、方差等特征。
利用Matlab,可以方便地绘制各种概率分布的概率密度函数和分布函数图像,比如正态分布、均匀分布、指数分布、泊松分布等。
通过可视化的方式,学生可以直观地感受不同概率分布的特点和规律,加深对概率分布的理解和记忆。
1.2 随机变量的模拟和统计量的计算在概率论的教学中,学生需要了解随机变量的概念、性质,以及随机变量的分布、统计量等。
利用Matlab,可以方便地生成服从某种概率分布的随机变量序列,并进行统计量的计算,比如样本均值、样本方差等。
通过实际的随机变量模拟和统计量计算,学生可以更好地理解随机变量的特性和统计量的含义,提高对概率论知识的掌握。
二、数理统计的基本方法和应用2.1 参数估计和假设检验在数理统计的教学中,学生需要学习参数估计的方法、假设检验的原理和步骤,以及不同统计量的分布。
Matlab在《概率论与数理统计》教学中的应用

Matlab在《概率论与数理统计》教学中的应用1. 引言1.1 研究背景概率论与数理统计作为现代科学研究的基础,广泛应用于物理、生物、经济、工程等各个领域。
在教学中,传统的概率论与数理统计教学往往通过纸笔计算和手工绘图进行,这样的方式在一定程度上限制了学生对概念的理解和实际应用能力的培养。
而引入Matlab这样的数学计算软件,可以极大地提高教学效率,使学生更直观地理解抽象的数学概念,提高他们的学习兴趣和动手能力。
通过将Matlab与概率论与数理统计相结合,可以更好地展示概率分布、统计分析、随机模拟等概念,加深学生对这些内容的理解和掌握。
研究Matlab在概率论与数理统计教学中的应用具有重要意义。
本文将探讨Matlab在概率论与数理统计教学中的具体应用,分析其在教学中的优势和未来发展方向。
1.2 研究意义概率论与数理统计作为数学学科中重要的分支,旨在研究事件的发生规律以及数据的分布特征,对现代科学、技术和社会管理等领域都具有重要的应用价值。
在教学中,采用Matlab作为工具可以加深学生对概率与统计理论的理解,提高他们的计算和分析能力,培养他们解决实际问题的能力。
通过引入Matlab,学生可以更加直观地掌握数学模型的建立和计算方法,提高他们对概率与统计学习的兴趣和积极性,进一步激发他们学习的潜力。
Matlab在教学中的应用也有助于培养学生的动手能力和实际解决问题的能力,提高他们的实践能力和创新思维。
教师可以结合具体案例,引导学生运用Matlab工具分析问题,并进行模拟实验和数据处理,使学生在实践中不断探索、思考和总结,从而提高他们的学习效果和实际应用能力。
Matlab在概率论与数理统计教学中的应用具有重要的意义和价值。
2. 正文2.1 Matlab在概率论教学中的基本概念应用Matlab可以用来计算概率。
通过编写简单的代码,可以计算各种随机事件发生的概率,例如掷硬币、抛骰子等。
这样的实践可以帮助学生深入理解概率的概念,同时提高他们的计算能力。
(完整版)Matlab概率论与数理统计

(完整版)Matlab概率论与数理统计Matlab 概率论与数理统计⼀、matlab基本操作1.画图【例01.01】简单画图hold off;x=0:0.1:2*pi;y=sin(x);plot(x,y,'-r');x1=0:0.1:pi/2;y1=sin(x1);hold on;fill([x1, pi/2],[y1,1/2],'b');【例01.02】填充,⼆维均匀随机数hold off;x=[0,60];y0=[0,0];y60=[60,60];x1=[0,30];y1=x1+30;x2=[30,60];y2=x2-30;xv=[0 0 30 60 60 30 0];yv=[0 30 60 60 30 0 0];fill(xv,yv,'b');hold on;plot(x,y0,'r',y0,x,'r',x,y60,'r',y60,x,'r');plot(x1,y1,'r',x2,y2,'r');yr=unifrnd (0,60,2,100);plot(yr(1,:),yr(2,:),'m.')axis('on');axis('square');axis([-20 80 -20 80 ]);2. 排列组合C=nchoosek(n,k):kn C C =,例nchoosek(5,2)=10, nchoosek(6,3)=20.prod(n1:n2):从n1到n2的连乘【例01.03】⾄少有两个⼈⽣⽇相同的概率公式计算nn nn NNn N N N N n N N N C n p )1()1(1)!(!1!1+--?-=--=-=365364(3651)365364365111365365365365rs rs rs ?-+-+=-=-?rs=[20,25,30,35,40,45,50]; %每班的⼈数 p1=ones(1,length(rs)); p2=ones(1,length(rs));% ⽤连乘公式计算for i=1:length(rs)p1(i)=prod(365-rs(i)+1:365)/365^rs(i); end% ⽤公式计算(改进) for i=1:length(rs)for k=365-rs(i)+1:365p2(i)=p2(i)*(k/365);end ;end% ⽤公式计算(取对数) for i=1:length(rs)⼆、随机数的⽣成3.均匀分布随机数rand(m,n); 产⽣m⾏n列的(0,1)均匀分布的随机数rand(n); 产⽣n⾏n列的(0,1)均匀分布的随机数【练习】⽣成(a,b)上的均匀分布4.正态分布随机数randn(m,n); 产⽣m⾏n列的标准正态分布的随机数【练习】⽣成N(nu,sigma.^2)上的正态分布5.其它分布随机数三、⼀维随机变量的概率分布1. 离散型随机变量的分布率(1) 0-1分布 (2) 均匀分布(3) ⼆项分布:binopdf(x,n,p),若~(,)X B n p ,则{}(1)k k n kn P X k C p p -==-,x=0:9;n=9;p=0.3; y= binopdf(x,n,p); plot(x,y,'b-',x,y,'r*')y=[ 0.0404, 0.1556, 0.2668, 0.2668, 0.1715, 0.0735, 0.0210, 0.0039, 0.0004, 0.0000 ]‘当n 较⼤时⼆项分布近似为正态分布 x=0:100;n=100;p=0.3; y= binopdf(x,n,p); plot(x,y,'b-',x,y,'r*')(4)泊松分布:piosspdf(x, lambda),若~()Xπλ,则{}! k eP X kkλλ-==x=0:9; lambda =3;y= poisspdf (x,lambda);plot(x,y,'b-',x,y,'r*')y=[ 0.0498, 0.1494, 0.2240, 0.2240, 0.1680, 0.1008, 0.0504, 0.0216, 0.0081, 0.0027 ] (5)⼏何分布:geopdf (x,p),则1 {}(1)kP X k p p-==-(6)超⼏何分布:hygepdf(x,N,M,n),则{}k n kM N MnNC CP X kC--==x=0:9;p=0.3y= geopdf(x,p);plot(x,y,'b-',x,y,'r*')y=[ 0.3000, 0.2100, 0.1470, 0.1029, 0.0720, 0.0504, 0.0353, 0.0247, 0.0173, 0.0121 ]x=0:10;N=20;M=8;n=4;y= hygepdf(x,N,M,n);plot(x,y,'b-',x,y,'r*')y=[ 0.1022, 0.3633, 0.3814, 0.1387, 0.0144, 0, 0, 0, 0, 0, 0 ]2.概率密度函数(1)均匀分布:unifpdf(x,a,b),1()a x bf x b a≤≤=-其它a=0;b=1;x=a:0.1:b;y= unifpdf (x,a,b);(2)正态分布:normpdf(x,mu,sigma),221()2()2xf x eµσπσ--=x=-10:0.1:12;mu=1;sigma=4;y= normpdf(x,mu,sigma);rn=10000;z= normrnd (mu,sigma,1,rn); %产⽣10000个正态分布的随机数d=0.5;a=-10:d:12;b=(hist(z,a)/rn)/d;%以a为横轴,求出10000个正态分布的随机数的频率plot(x,y,'b-',a,b,'r.')(3)指数分布:exppdf(x,mu),11()xe a x bf xθθ-≤≤=?其它x=0:0.1:10;mu=1/2;y= exppdf(x,mu);plot(x,y,'b-',x,y,'r*')(4)2χ分布:chi2pdf(x,n),12221(;)2(2)00n xnx e xf x n nx--≥=Γ<hold onx=0:0.1:30;n=4;y= chi2pdf(x,n);plot(x,y,'b');%blue n=6;y= chi2pdf(x,n);plot(x,y,'r');%redn=8;y= chi2pdf(x,n);plot(x,y,'c');%cyan n=10;y= chi2pdf(x,n);plot(x,y,'k');%black legend('n=4', 'n=6', 'n=8', 'n=10');(5)t分布:tpdf(x,n),22((1)2)(;)1(2)n xf x nnn nπ-Γ+=+?Γ?hold onx=-10:0.1:10;n=2;y= tpdf(x,n);plot(x,y,'b');%blue n=6;y= tpdf(x,n);plot(x,y,'r');%redn=10;y= tpdf(x,n);plot(x,y,'c');%cyann=20;y= tpdf(x,n);plot(x,y,'k');%black legend('n=2', 'n=6', 'n=10', 'n=20');(6)F分布:fpdf(x,n1,n2),112122212112121222(()2)10(;,)(2)(2)00n n nnn n n nx x xf x n n n n n nx+--Γ++≥=?ΓΓ<hold onx=0:0.1:10;n1=2; n2=6;y= fpdf(x,n1,n2);plot(x,y,'b');%bluen1=6; n2=10;y= fpdf(x,n1,n2);plot(x,y,'r');%redn1=10; n2=6;y= fpdf(x,n1,n2);plot(x,y,'c');%cyann1=10; n2=10;y= fpdf(x,n1,n2);plot(x,y,'k');%blacklegend(' n1=2; n2=6', ' n1=6; n2=10', ' n1=10; n2=6', ' n1=10; n2=10');3.分布函数(){}F x P X x=≤【例03.01】求正态分布的累积概率值设2~(3,2)X N,求{25},{410},{2},{3}P X P X P X P X<<-<<>>,p1=normcdf(5,3,2)- normcdf(2,3,2)=0.5328p1=normcdf(1,0,1)- normcdf(-0.5,0,1) =0.5328p2=normcdf(10,3,2)- normcdf(-4,3,2)=0.9995p3=1-(normcdf(2,3,2)- normcdf(-2,3,2))=0.6977p4=1-normcdf(3,3,2)=0.5004. 逆分布函数,临界值(){}y F x P X x ==≤,1()x F y -=,x 称之为临界值【例03.02】求标准正态分布的累积概率值y=0:0.01:1;x=norminv(y,0,1);【例03.03】求2(9)χ分布的累积概率值hold offy=[0.025,0.975]; x=chi2inv(y,9); n=9;x0=0:0.1:30;y0=chi2pdf(x0,n); plot(x0,y0,'r');x1=0:0.1:x(1);y1=chi2pdf(x1,n); x2=x(2):0.1:30;y2=chi2pdf(x2,n); hold onfill([x1, x(1)],[y1,0],'b'); fill([x(2),x2],[0,y2],'b');函数名调⽤形式注释sort sort(x),sort(A) 排序,x 是向量,A 是矩阵,按各列排序 sortrows sortrows(A) A 是矩阵,按各⾏排序 mean mean(x) 向量x 的样本均值 var var(x) 向量x 的样本⽅差 std std(x) 向量x 的样本标准差 median median(x) 向量x 的样本中位数 geomean geomean(x) 向量x 的样本⼏何平均值 harmmean harmmean(x) 向量x 的样本调和平均值 rangerange(x)向量x 的样本最⼤值与最⼩值的差【练习1.1】⼆项分布、泊松分布、正态分布(1)对10,0.2n p ==⼆项分布,画出(,)b n p 的分布律点和折线;(2)对np λ=,画出泊松分布()πλ的分布律点和折线;(3)对2,(1)np np p µσ==-,画出正态分布2(,)N µσ的密度函数曲线;(4)调整,n p ,观察折线与曲线的变化趋势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab 概率论与数理统计、matlab 基本操作 1. 画图【例01.01】简单画图hold off; x=0:0.1:2*pi; y=sin (x);plot(x,y, '-r'); x1=0:0.1:pi/2; y1=s in( x1); hold on;fill([x1, pi/2],[y1,1/2],'b');【例01.02】填充,二维均匀随机数hold off ;x=[0,60];y0=[0,0];y60=[60,60]; x1=[0,30];y1=x1+30; x2=[30,60];y2=x2-30;plot(x,y0, 'r' ,y0,x, plot(x1,y1, 'r' ,x2,y2, yr=u nifrnd (0,60,2,100);plot(yr(1,:),yr(2,:), axis( 'on'); axis( 'square' ); axis([-20 80 -20 80 ]);xv=[0 0 30 60 60 30 0];yv=[0 30 60 60 30 0 0]; fill(xv,yv, 'b');hold on ;'r' ,x,y60, 'r' ,y60,x,'r')'r');'m.')2. 排列组合kC=nchoosek(n,k) : CC n ,例 nchoosek(5,2)=10, nchoosek(6,3)=20.prod(n1:n2):从 n1 至U n2 的连乘【例01.03】至少有两个人生日相同的概率365 364|||(365 rs 1)rs365365 364 365 rs 1 365 365365rs=[20,25,30,35,40,45,50]; %每班的人数p1= on es(1,le ngth(rs)); p2=on es(1,le ngth(rs));%用连乘公式计算for i=1:le ngth(rs) p1(i)=prod(365-rs(i)+1:365)/365A rs(i); end%用公式计算(改进) for i=1:le ngth(rs)for k=365-rs(i)+1:365p2(i)=p2(i)*(k/365); end ; end%用公式计算(取对数) for i=1:le ngth(rs)p1(i)=exp(sum(log(365-rs(i)+1:365))-rs(i)*log(365)); end公式计算P 1n!C NN nN!1 (N n)!1N nN (N 1) (N n 1)、随机数的生成3. 均匀分布随机数rand(m,n);产生m行n列的(0,1)均匀分布的随机数rand(n);产生n行n列的(0,1)均匀分布的随机数【练习】生成(a,b)上的均匀分布4. 正态分布随机数randn(m,n); 产生m行n列的标准正态分布的随机数【练习】生成N(nu,sigma42)上的正态分布5. 其它分布随机数三、一维随机变量的概率分布1. 离散型随机变量的分布率(1) 0-1分布(2) 均匀分布_ k k n k(3) 二项分布:binopdf(x,n,p),若X ~ B(n, p),则P{X k} C n p (1 p),x=0:9 ;n=9;p=0.3;y= bin opdf(x ,n, p);plot(x,y,'b-',x,y,'r*')y=[ 0.0404, 0.1556, 0.2668, 0.2668, 0.1715, 0.0735, 0.0210, 0.0039, 0.0004, 0.0000 ]当n较大时二项分布近似为正态分布x=0:100; n=100;p=0.3;y= bin opdf(x ,n, p);plot(x,y,'b-',x,y,'r*')ke⑷泊松分布:piosspdf(x, lambda),若X ~ (),贝U P{ X k}k!x=0:9; lambda = 3;y= poisspdf (x,lambda);plot(x,y,'b-',x,y,'r*')y=[ 0.0498, 0.1494, 0.2240, 0.2240, 0.1680, 0.1008, 0.0504, 0.0216, 0.0081,0.0027]k 1⑸几何分布:geopdf (x, p),贝U P{X k} p(1 p)x=0:9;p=0.3y= geopdf(x,p);plot(x,y,'b-',x,y,'r*')y=[ 0.3000, 0.2100, 0.1470, 0.1029, 0.0720, 0.0504, 0.0353, 0.0247, 0.0173, 0.0121 ] x=0:10;N=20;M=8; n=4;y= hygepdf(x,N,M, n); plot(x,y,'b-',x,y,'r*')y=[ 0.1022, 0.3633, 0.3814, 0.1387, 0.0144, 0, 0, 0, 0, 0, 0 ]2. 概率密度函数(1)均匀分布:unifpdf(x,a,b) , f (x)其它a=0;b=1;x=a:0.1:b; y= uni fpdf (x,a,b);1 2 厂(x )2 ■厂ex=-10:0.1:12;mu=1;sigma=4;y= no rmpdf(x,mu,sigma);rn=10000;z= normrnd (mu,sigma,1,rn); % 产生 10000 个正态分布的随机数 d=0.5;a=-10:d:12;b=(hist(z,a)/rn)/d;%以a 为横轴,求出10000个正态分布的随机数的频率(6)超几何分布:hygepdf(x,N,M,n),则 P{Xk}C k nM CNC N(2)正态分布:normpdf(x,mu,sigma) , f (x)plot(x,y,'b-',a,b,'r.')1 _x⑶指数分布:exppdf(x,mu), f (x)其它x=0:0.1:10;mu=1/2;■ t京■I_ey= exppdf(x,mu); plot(x,y,'b-',x,y,'r*')1n i F⑷2分布:chi2pdf(x,n) , f (x; n) 2n ^( n 2) % e x 0hold onx=0:0.1:30;n=4;y= chi2pdf(x, n);plot(x,y,'b');%blue n=6;y= chi2pdf(x, n);plot(x,y,'r');%red n=8;y=chi2pdf(x ,n );plot(x,y,'c');%cya n n=10;y= chi2pdf(x, n);plot(x,y,'k');%black lege nd(' n=4', 'n=6', 'n=8', 'n=10');n 1((n 1) 2) x2 2⑸t 分布:tpdf(x,n) , f (x; n) ------------------ 1 -J n (n. 2) nhold onx=-10:0.1:10;n=2;y= tpdf(x, n);plot(x,y,'b');%bluen=6;y= tpdf(x, n);plot(x,y,'r');%redn=10;y= tpdf(x ,n );plot(x,y,'c');%cya nn=20;y= tpdf(x, n);plot(x,y,'k');%black lege nd(' n=2', 'n=6', 'n=10', 'n=20');((m山m 门2n2) 2)小2% 2 1 5 % 2(n2 2) n2n2x 0(6) F 分布:fpdf(x,n1,n2) , f (x; n「n2) (E 2)0 x 0hold onx=0:0.1:10;n1=2; n2=6;y= fpdf(x, n1, n2);plot(x,y,'b');%bluen1=6; n2=10;y= fpdf(x, n1, n2);plot(x,y,'r');%red n1=10; n2=6;y= fpdf(x, n1, n2);plot(x,y,'c');%cyann1=10; n2=10;y= fpdf(x, n1,n 2);plot(x,y,'k');%black legend(' n仁2; n2=6', ' n1= 6; n2=10', ' n仁10;n2=6', ' n仁10; n2=10');3.分布函数F(x) P{X x}【例03.01】求正态分布的累积概率值设X ~ N(3,22),求 P{2 X 5}, P{ 4 X 10}, P{ X 2}, P{X 3},14.逆分布函数,临界值y F(x) P{X x} , x F (y) , x称之为临界值【例03.02】求标准正态分布的累积概率值y=0:0.01:1;x=normin v(y,0,1);【例03.03】求2(9)分布的累积概率值hold offy=[0.025,0.975];x=ch i2in v(y,9);n=9;x0=0:0.1:30;y0=chi2pdf(x0, n); plot(x0,y0, 'r'); x1=0:0.1:x(1);y1=chi2pdf(x1, n);x2=x(2):0.1:30;y2=chi2pdf(x2 ,n);hold onfill([x1, x(1)],[y1,0], 'b');fill([x(2),x2],[0,y2], 'b');【练习1.1】二项分布、泊松分布、正态分布(1)对n 10, p 0.2二项分布,画出b(n,p)的分布律点和折线;(2)对np,画出泊松分布()的分布律点和折线;(3)对np, 2叩(1 p),画出正态分布N( , 2)的密度函数曲线;(4)调整n, p,观察折线与曲线的变化趋势。
