8.1 由Fourier变换到小波变换
Fourier变换-Gabor变换-Wigner分布-小波变换实例分析doc资料

F o u r i e r变换-G a b o r 变换-W i g n e r分布-小波变换实例分析1、分别用短时Fourier ,Gabor 变换分析下列信号,要求提供程序,图形结果并对它们的结果进行对比分析。
采样频率FS=1920HZ ,采样长度N=512.()(10.2sin(215))cos(2300.5sin(215))sin(2120)x t t t t t ππππ=+++ Matlab 程序如下:fs=1920;%采样频率N=512; %采样长度t=0:1/fs:(N-1)/fs; %时间序列x1=(1+0.2*sin(2*pi*15*t)).*(cos(2*pi*30*t)+0.5*sin(2*pi*15*t))+sin(2*pi*120*t);%信号 figure(1)plot(t,x1);%画想(t )的图像y1=fft(x1,N); %对信号进行快速Fourier 变换 mag1=abs(y1);%求变换后的幅值 k=0:N-1; f1=k*fs/N; figure(2) grid onstem(f1,mag1);%绘制N 点DFI 的幅频特性图 xlabel('f1'); ylabel('幅值’);axis([0,256,0,2*max(abs(y1))]);%x,y 的范围 grid on figure(3)h=window(321,'hamming'); sig=x1;tfrstft(sig',1:512,512,h);%短时Fourier 变换 xlabel('时间(秒)'); ylabel('频率(Hz)'); figure(4) q=16;h=window(211,'gauss'); h=h/norm(h);tfrgabor(x1',128,q,h);%Gabor 变换 xlabel('时间(秒)'); ylabel('频率(Hz)');1.1信号的图形图1-1 信号时域波形图1.2信号N点的DFI幅频特性图图1-2 信号的幅频特性图对信号进行分析,信号共有5个频率分别是0HZ,15HZ,30HZ,45HZ,120HZ,用火柴棍状表示出来。
FOUrier变换和小波变换一般形式一线调频小波变换和多普勒小波变换

1引言传统的Fourier分析适合于平稳信号处理,使用的是一种全局的变换。
它无法表达信号的时频局域性质,而这种性质恰好是非平稳信号本质特征。
为了分析和处理非平稳信号,人们基于时频分析提出短时Fourier变换和小波变换。
短时Fourier变换是一种加窗Fourier变换,使用固定大小的时频网格,时频网格在时频平面上的变化只限于时间平移和频率平移,因此只适用于分析具有固定不变带宽的非平稳信号。
小波变换的时频分析网格的变化除了时间平移外,还有时间和频率轴比例尺度的改变,使用长宽大小不一的长方形时频分析网格,因而只适用于分析具有固定比例带宽(恒Q)的非平稳信号。
然而,在实际应用中遇到的常常只是具有近似等宽或近似等Q的分析带宽的信号。
这类信号的分析需要使用形状比矩形更复杂的时频网格。
除了上面所述的时间平移、频率平移和时频拉伸外,还应考虑矩形网格的斜方向的拉伸与旋转变化。
线调频小波变换使用的时频分析网格除了时移、频移、尺度变化以外,最主要的是包含了时频网格在时频平面上的放置以及在倾斜方向上的尺度变化(拉伸)。
由于使用各种长方形和各种平行四边形的时频网格,所以线调频小波变换可以分析具有非固定不变带宽和非固定比例带宽(非恒Q)的非平稳信号。
线调频小波基包含了Fourier变换基函数、短时Fourier变换基函数及小波变换基函数,因而三种变换都是线调频小波变换特例。
在信号的线性变换中,基函数的选取至关重要。
为了有效地刻画信号的特征,将基函数取成与待分析信号的性态相类似的信号。
然而,无论Fourier变换、短时Fourier变换、小波变换还是线调频小波变换,均适合于处理频率成分随时间作线性变化的信号,而当信号的频率成分随时间作非线性变化时上述的变换就不适应。
多普勒小波变换采用经伸缩、时移和频移的加窗多普勒信号作为基函数,以逼近信号中的非线性时变结构成分。
由于多普勒小波函数涵盖了Fourier变换的基函、短时Fourier变换基函数、小波变换基函数和线调频小波变换的基函数,因而多普勒小波变换包含了前面所论及的四种变换,能Fourier变换和小波变换一般形式—线调频小波变换和多普勒小波变换胡国胜1,2陈一天2任震11(华南理工大学电力学院,广州510640)2(广东省科技干部学院,广州510640)E-mail:hugs-2000@摘要Fourier变换、窗口Fourier变换与小波变换在许多领域得到广泛的应用。
第8章-基于LabVIEW的小波变换实现

在1986年,Meyer在创造性地构造出具有一定衰减性的光 滑函数,其二进伸缩和平移:
j,k (x)
j
2 2
(2 j
x k) |
j,k Z
周鹏 安徽工程大学电气工程学院
8.1.2 从傅里叶变换到小波变换 1. 傅里叶变换 2.短时傅里叶变换 3.小波变换
小波变换(Wavelet Transform)的概念是1984年法国 物理学家J.Morlet在分析处理地球物理勘探资料时提出来的。 小波变换的数学基础是19世纪的傅里叶变换,其后理论物理 学家A.Grossman采用平移和伸缩不变性建立了小波变换的 理论体系。1985年法国数学家Y.Meyer第一个构造出具有衰 减性的光滑小波。1988年比利时数学家I.Daubechies证明了 紧支撑正交标准小波基的存在性,使得离散小波分析成为可 能,1989年S.Mallat提出了多分辨率分析概念,统一了在此 之前的各种构造小波的方法,特别是提出了二进小波变换的 快速算法,使得小波变换完全走向实用性。
周鹏 安徽工程大学电气工程学院
8.3.2小波去噪算法的LabVIEW实现
小波去噪的基本思想是根据噪声与信号在各尺度(频带) 上的小波谱具有不同表现这一特点,将各尺度上由噪声产生 的小波谱分量,特别是将那些噪声小波谱占主导地位的尺度 上的噪声小波谱分量去掉,则保留下来的就是原信号的小波 谱,此过程为小波的重构或还原。然后再利用小波变换重构 算法,重构出原信号。由此可知小波去噪的关键是如何滤去 由噪声产生的小波谱分量。
傅里叶变换和小波变换简介

小波应用
通常来讲, 离散小波变换 (DWT)用于信号编码,而连续小 波变换 (CWT)用于信号分析。所以,DWT通常用于工程和计算机 科学而CWT经常用于科学研究。 小波变换现在被大量不同的应用领域采纳,经常取代了傅里 叶变换的位置。很多物理学的领域经历了这个范式的转变,包括 分子动力学,从头计算(ab initio calculations),天文物理学,密度 矩阵局部化,地震地质物理学,光学,湍流,和量子力学。其他 经历了这种变化的学科有图像处理,血压,心率和心电图分析, DNA分析,蛋白质分析,气象学,通用信号处理,语言识别,计 算变换一样,小波变换可以用 于原始数据(例如图像),然后将变换后的数据编码,得到有效的压 缩。JPEG 2000 是采用小波的图像标准。
它与Fourier变换、窗口Fourier变换(Gabor变换)相比,这是一个时间和频率的局域变 换,因而能有效的从信号中提取信息,通过伸缩和平移等运算功能对函数或信
号进行多尺度细化分析(Multiscale Analysis),解决了Fourier变换不能解决的 许多困难问题,从而小波变化被誉为“数学显微镜”,它是调和分析发展史上里 程碑式的进展。
傅立叶,1768年生于法国
2
傅氏变换简介
傅立叶变换历史: 1822年,法国数学家傅里叶(J.Fourier,1768-1830) 在研究热传导理论时发表了“热的分析理论”,提出并证 明了将周期函数展开为正弦级数的原理,奠定了傅里叶级数的理论基础 。 泊松(Poisson)、高斯(Guass)等人把这一成果应用到电学中去,得到广 泛应用。 19世纪末,人们制造出用于工程实际的电容器。 进入20世纪以后,谐振电路、滤波器、正弦振荡器等一系列具体问题的 解决为正弦函数与傅里叶分析的进一步应用开辟了广阔的前景。 在通信与控制系统的理论研究和工程实际应用中,傅里叶变换法具有很 多的优点。 “FFT”快速傅里叶变换为傅里叶分析法赋予了新的生命力。
傅里叶变换及小波分析

傅里叶变换及小波分析傅里叶变换 (Fourier transform) 和小波分析 (wavelet analysis) 是信号处理中经常使用的两种数学工具。
它们都可以用于将一个时间域的信号转换为频域的表示,从而帮助分析信号的频谱特性和频域处理。
傅里叶变换是一种将一个信号或者函数表示为基本频率成分的叠加形式的方法。
它基于一个假设,即任何一个周期信号可以看作是一系列正弦和余弦函数的加权和。
傅里叶变换将一个定义在时间域中的信号分解为一系列复数频率分量,每个频率分量都表示了信号中特定频率的振幅和相位信息。
这种频域的表示使得我们可以分析信号的频谱特性,包括频率成分的强度和相互之间的关系。
小波分析则是一种将信号分解为一系列多尺度基函数的方法。
与傅里叶变换只考虑特定频率的正弦和余弦函数不同,小波分析使用的基函数包含了时间和频率的局部化特性。
在小波分析中,一组称为小波基函数的窄带信号被用来分析信号。
这些小波基函数具有在时间和频域上局部化的特性,这意味着它们能够捕捉信号中短时的频率变化。
因此,小波分析可以提供更丰富的频谱信息,包括信号的时间定位和频率局部化特性。
傅里叶变换和小波分析在信号处理中有着广泛的应用。
傅里叶变换广泛应用于频域滤波、频谱分析和谱估计等领域。
通过将信号从时间域转换到频域,我们可以分析信号的频率成分和频谱特性,从而实现滤波和频谱修复等处理。
小波分析则广泛应用于信号压缩、边缘检测和图像处理等领域。
小波分析具有时间和频率局部化的特性,因此在一些需要考虑信号中的短时频率变化的应用中具有优势。
除此之外,傅里叶变换和小波分析也可以相互补充。
在一些情况下,我们可以使用傅里叶变换来获取信号的大致频谱特性,然后使用小波分析来进行进一步的细节和局部化分析。
例如,在音频信号的处理中,可以使用傅里叶变换来了解音频信号的整体频谱,然后使用小波分析来定位和分析特定频率范围内的细节和局部化特征。
总之,傅里叶变换和小波分析是信号处理中常用的数学工具。
小波变换发展史

小波变换发展史传统的信号理论,是建立在Fourier分析基础上的,而Fourier变换作为一种全局性的变化,其有一定的局限性。
在实际应用中人们开始对Fourier变换进行各种改进,小波分析由此产生了。
小波分析是一种新兴的数学分支,它是泛函数、Fourier分析、调和分析、数值分析的最完美的结晶;在应用领域,特别是在信号处理、图像处理、语音处理以及众多非线性科学领域,它被认为是继Fourier分析之后的又一有效的时频分析方法。
小波变换与Fourier变换相比,是一个时间和频域的局域变换因而能有效地从信号中提取信息,通过伸缩和平移等运算功能对函数或信号进行多尺(Multiscale Analysis),解决了Fourier变换不能解决的许多困难问题。
1.从傅立叶分析到小波分析1807年,法国学者Fourier指出任何周期函数都可以用一系列正弦波来表示,开创了傅立分析。
傅立叶分析揭示了时域与频域之间内在的联系,反映了“整个”时间范围内信号的“全部”频谱成分,是研究信号的周期现象不可缺少的工具。
建立在傅立叶分析基础上的采样定理和FFT技术奠定了现代数字化技术的理论基础。
尽管傅立叶变换具有很强的频域局域化能力,但是它明显的缺点,那就是无法反映非平稳信号在局部区域的频域特征及其对应关系,即FT在时域没有任何分辨率,无法确定信号奇异性的位置。
为了研究信号在局部时间范围内的频谱特征,1946年,Gabor提出了短时傅立叶变换(Short Time Fourier Transform,STFT),但是STFT的窗口宽度是固定的(和频率无关),这使得它无法同时兼顾信号的低频和高频特征,在分析时变信号时也有一定的局限性。
另外,STFT的窗口函数或核函数不能提供一组离散正交基,所以给数值计算带来了不便,这也是导致STFT 没有得到广泛应用的重要原因。
从傅立叶分析演变而来的小波分析的优点恰恰可以弥补傅立叶变换中存在的不足之处。
小波变换详解

基于小波变换的人脸识别近年来,小波变换在科技界备受重视,不仅形成了一个新的数学分支,而且被广泛地应用于模式识别、信号处理、语音识别与合成、图像处理、计算机视觉等工程技术领域。
小波变换具有良好的时频域局部化特性,且其可通过对高频成分采取逐步精细的时域取样步长,从而达到聚焦对象任意细节的目的,这一特性被称为小波变换的“变聚焦”特性,小波变换也因此被人们冠以“数学显微镜”的美誉。
具体到人脸识别方面,小波变换能够将人脸图像分解成具有不同分辨率、频率特征以及不同方向特性的一系列子带信号,从而更好地实现不同分辨率的人脸图像特征提取。
4.1 小波变换的研究背景法国数学家傅立叶于1807年提出了著名的傅立叶变换,第一次引入“频率”的概念。
傅立叶变换用信号的频谱特性来研究和表示信号的时频特性,通过将复杂的时间信号转换到频率域中,使很多在时域中模糊不清的问题,在频域中一目了然。
在早期的信号处理领域,傅立叶变换具有重要的影响和地位。
定义信号(t)f 为在(-∞,+∞)内绝对可积的一个连续函数,则(t)f 的傅立叶变换定义如下:()()dt e t f F t j ωω-⎰∞-∞+= (4-1) 傅立叶变换的逆变换为:()()ωωπωd e F t f t j ⎰+∞∞-=21 (4-2)从上面两个式子可以看出,式(4-1)通过无限的时间量来实现对单个频率的频谱计算,该式表明()F ω这一频域过程的任一频率的值都是由整个时间域上的量所决定的。
可见,式(4-1)和(4-2)只是同一能量信号的两种不同表现形式。
尽管傅立叶变换可以关联信号的时频特征,从而分别从时域和频域对信号进行分析,但却无法将两者有效地结合起来,因此傅立叶变换在信号的局部化分析方面存在严重不足。
但在许多实际应用中,如地震信号分析、核医学图像信号分析等,研究者们往往需要了解某个局部时段上出现了哪个频率,或是某个频率出现在哪个时段上,即信号的时频局部化特征,傅立叶变换对于此类分析无能为力。
模态分析与综合技术第8章 测量信号后处理

第8章 信号处理
8.5 小波变换
1 小波
Haar小波是一种构造形式极为简单的小波, 是Haar于1910年提出来的。
Haar小波函数定义为:
1
1 0 t 1/ 2
(t) 1 1/ 2 t 1
0 其它
0 1/2 1
-1
第8章 信号处理
8.5 小波变换
1 小波 这里给出另一个著名的小波──墨西哥帽状 小波(Mexican Hat Wavelet),其时域表达式为:
由于矩形窗的作用,使截断后信号的频谱出 现所谓的“皱波现象”。
第8章 信号处理
8.3 泄露和窗函数
由上述分析可知,泄漏是由于对无限长信 号的突然截断造成的。因此,自然想到,如果 能改变这种突然截断方式,泄漏会得到改善。 改善方案:
对于周期信号采用整周期采样(矩形 窗);
选择异于矩形窗的适当窗函数,对所取 样本函数进行不等权处理,便是一种有效的措 施。
8.4 小波变换概述
小波分析在理论与应用上得到不断补充 与拓展,现在已经和正在被广泛应用于众多 的科学技术领域:
信号分析与处理方面的信号的分解与重 构、去噪、滤波等;*****
图像分析与处理方面的图像压缩、去污 染、CT成像、彩色复印等;****
机械状态监测与故障诊断;音乐、语音识 别与合成;雷达、电子对抗;量子场论与量 子力学;地震勘探数据处理;边缘检测;机 器视觉、纹理识别;数字电ห้องสมุดไป่ตู้;流体湍流; 天体识别。
第8章 信号处理
8.2 信号离散化
fs
1 t
称为采样频率或采样速率。
s
2fs
2
t
称为采样圆频率。
离散后的数字信号如图所示:
小波分析

小波学习总结小波分析理论和方法是从傅立叶分析分析演变而来的。
傅立叶分析揭示了时域与频域之间内在的联系,反应了信号在“整个”时间范围内的“全部”频谱成分,是研究周期现象不可缺少的工具。
傅立叶变换虽然有很强的频域局域化能力,但并不具有时间局域化能力,而后一点,对于很多信号处理工作而言,特别是对于涉及非平稳信号处理的任务而言,是至关重要的。
小波变换以牺牲部分频域定位性能来取得时-频局部性的折衷,其不仅能提供较精确的时域定位,也能提供较精确的频域定位。
我们所面对的真实物理信号,更多的表现出非平稳的特性,而小波变换恰恰是处理非平稳信号的有力工具。
从Fourier变换到小波变换,目的是要找到一组时频局域化特性都良好的正交基,即小波基它的伸缩和平移将形成一系列灵活窗,最终满足时频分析要求。
由Fourier变换、STFT和小波分析的基函数及相应的时间-频率窗可知,Fourier分析的基函数在时域上具有全局性,没有任何时间分辨特性,但在频域上是完全局部化的;短时Fourier 变换的基函数对信号进行等带宽分解,时频带宽恒定;小波分析的基函数由小波基伸缩而成,其时频窗宽度随信号自适应变化,高频时窗自动变窄,低频时窗自动变宽。
小波变换的基本思想是用一组小波函数或者基函数表示一个函数或者信号,例如图像信号。
其核心就是对图像对应的像素值或者叫做图像位置的系数进行均值和差值的操作计算,产生新的由像素值的平均值和细节系数表示的图像,进一步去除一些微不足道的细节系数,从而提高小波图像的编码效率,达到取得较好的图像压缩率的目的。
小波分析中常用的三个基本概念是:连续小波变换、离散小波变换和小波重构。
(1)连续小波变换傅立叶分析是把一个信号分解成各种不同频率的正弦波,因此正弦波是傅立叶变换的基函数。
同样,小波分析是把一个信号分解成将原始小波经过移位和缩放之后的一系列小波,因此小波同样可以用作表示一些函数的基函数。
可以说,凡是能够用傅立叶分析的函数都可以用小波分析,因此小波变换也可以理解为用经过缩放和平移的一系列函数代替傅立叶变换的正弦波。
小波变换
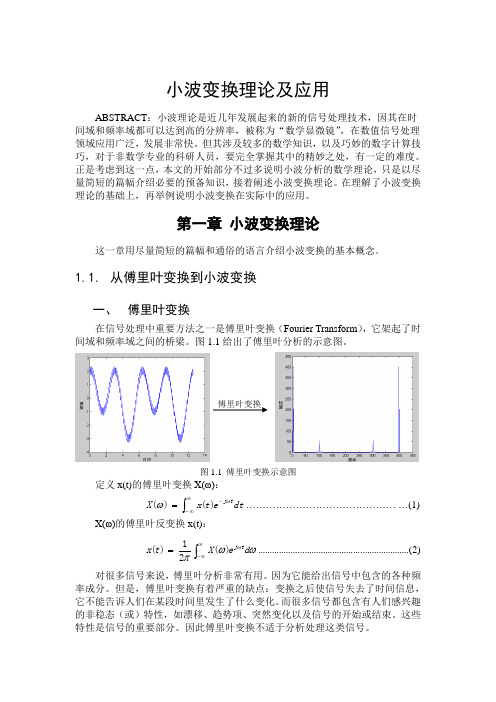
小波变换理论及应用ABSTRACT :小波理论是近几年发展起来的新的信号处理技术,因其在时间域和频率域都可以达到高的分辨率,被称为“数学显微镜”,在数值信号处理领域应用广泛,发展非常快。
但其涉及较多的数学知识,以及巧妙的数字计算技巧,对于非数学专业的科研人员,要完全掌握其中的精妙之处,有一定的难度。
正是考虑到这一点,本文的开始部分不过多说明小波分析的数学理论,只是以尽量简短的篇幅介绍必要的预备知识,接着阐述小波变换理论。
在理解了小波变换理论的基础上,再举例说明小波变换在实际中的应用。
第一章 小波变换理论这一章用尽量简短的篇幅和通俗的语言介绍小波变换的基本概念。
1.1. 从傅里叶变换到小波变换一、 傅里叶变换在信号处理中重要方法之一是傅里叶变换(Fourier Transform ),它架起了时间域和频率域之间的桥梁。
图1.1给出了傅里叶分析的示意图。
图1.1 傅里叶变换示意图 定义x(t)的傅里叶变换X(ω):⎰∞∞--=dt e t x X t j ωω)()(............................................. (1)X(ω)的傅里叶反变换x(t):⎰∞∞-=ωωπωd e X t x t j )(21)( (2)对很多信号来说,傅里叶分析非常有用。
因为它能给出信号中包含的各种频率成分。
但是,傅里叶变换有着严重的缺点:变换之后使信号失去了时间信息,它不能告诉人们在某段时间里发生了什么变化。
而很多信号都包含有人们感兴趣的非稳态(或)特性,如漂移、趋势项、突然变化以及信号的开始或结束。
这些特性是信号的重要部分。
因此傅里叶变换不适于分析处理这类信号。
傅里叶变换二、短时傅里叶变换为了克服傅里叶变换的缺点,D.Gabor(1946)提出了短时傅里叶变换(Short Time Fourier Transform), 又称为盖博(Gabor)变换或者加窗傅里叶变换(Windowed Fourier Transform)。
小波变换的Fourier实现方法

小波变换的Fourier实现方法作者:张建锋王雯露来源:《科技视界》2013年第25期【摘要】小波变换是被广泛应用到许多科研领域的有效频率分析工具。
小波变换有两种实现方式:直接逐点内积法和快速小波算法(Mallat算法和小波包算法)。
逐点计算方法需要的运行时间较长,在处理数据量较大时效率很低;而快速小波算法只是针对正交小波的离散小波变换,具有局限性。
利用卷积定理和Fourier变换的相似性定理,可以将时域的小波变换内积变换到频域的内积形式,从而可以利用Fourier变换的快速Fourier算法来实现小波变换。
本文利用随机产生的10000个数据,分别用直接逐点内积算法和Fourier算法计算序列的小波变换。
运行结果表明, Fourier算法能够明显缩短小波变换的计算时间,大大提高了运算的效率。
【关键词】小波变换;卷积定理;相似性定理20世纪80年代中期,法国地质物理学家Morlet提出了小波变换[1]。
在其后的近20多年里,小波变换理论得到了丰富和发展并逐渐成熟。
作为Fourier变换的发展,小波变换既保留了Fourier变换的优点,又弥补了Fourier变换无法有效分析非稳定信号的不足。
如今,小波分析已经广泛的应用到了很多领域,如图像处理、生物、物理、水文水资源和地球物理等。
小波变换计算有两种算法:1)利用积分公式,逐点直接进行数值积分;2)快速小波变换方法,即 Mallat算法和小波包算法[2],但是它们只针对正交小波的离散小波变换[3]。
方法1)计算运行时间较长,效率很低;而方法2)只能适应正交小波变换,具有局限性。
在这里,希望找出一种既能适应正交小波和非正交小波,又能比直接逐点变换算法效率更高的算法。
1 时域小波变换与Fourier变换相似,连续小波变换利用的内积的大小来度量信号和分析方程(小波)的相似性:连续小波变换的结果反应在图上就是一个等值线图,频率(或者尺度)为y轴,能量为z 轴,时间为x轴。
HAAR小波变换

PD om
PD om
er ww
er ww
F-XChange View !
Click to buy NOW
w.docu-track.c
8.1.2 小波概念
F-XChange View !
Click to buy NOW
w.docu-track.c
小波是定义在有限间隔而且其平均值为 零的一种函数。
小波函数在时域和频域中都应该具有某种程度 的平滑度(smoothness)和集中性 (concentration)
可以使用消失矩(vanishing moments)来描述,
用N表示小波的消失矩的数目。
例如,Daubechies小波简写成dbN, db1,
db2, ……,db9,从Daubechies小波波形来
它的地位相当于快速傅立叶变换在经典傅立叶 分析中的地位。
PD om
PD om
er ww
er ww
F-XChange View !
Click to buy NOW
w.docu-track.c
F-XChange View !
Click to buy NOW
w.docu-track.c
Inrid Daubechies,Ronald Coifman和Victor Wickerhauser等著名科学家把这个小波理论引 入到工程应用方面做出了极其重要的贡献。
PD om
PD om
er ww
er ww
F-XChange View !
Click to buy NOW
w.docu-track.c
选择
F-XChange View !
Click to buy NOW
小波变换与小波变换编码原理

成。 (3)
为另一大类:有限宽度,其它地方为 0。由 正脉冲 ,负脉冲 及 零 组
这一类可分为三个不同尺度,以 表示尺度,有
。
时,4 个正脉冲,4 个负脉冲,在
中,没有“零”,且
;
时,2 个正脉冲,2 个负脉冲,在
中,有 4 个“零”,且
;
3
时,1 个正脉冲,1 个负脉冲,在
中,有 6 个“零”,且
据量;这些上层信息仅是低频分量,附加上去便于分析而已。
2. 拉普拉斯金字塔[8] 继续上小节的内容,但从金字塔的上层向下考虑。如果有了上一层 ,能否反推下一
层 呢?答案是否定的,因为 中不含“细节”,想反推必须补充细节。要补充的细节就
是拉普拉斯金字塔的某一层。
定义“放大算子”
,它对 进行内插放大,得到放大的图 ,即
在介绍小波变换之前,我们先来学习几个与多分辨率分析相关的变换。
3.1.1 Haar 变换
Haar 变换是“紧支、二进、正则、归一小波变换”的一个实例。Haar 变换的基函数(族)
1
图 3.1 Haar 变换的基函数 hk (x) , k = 0 ~ 7
从图 3.1 可以发现:
(1)除
外,基函数的波形都是矩形脉冲对,即均呈
。
(4)同一尺度下的基函数有平移; 表示平移的位置(平移量)。
尺度越大时,平移步长也大,以二进制方式增长。以 为单位步长,
时,具有 4
步长的平移量,即每当 增加 1 时, x 的平移量为 ;
时,具有 2 步长的平移量,即
每当 增加 1 时,x 的平移量为 ,此时
区间。
。两种情形下的平移量都正好覆盖
(5)“基函数”的高度则从 起,尺度以二进制每“缩小”一档,即宽度除以 2,高度则
小波变换教程

小波变换教程小波变换教程一、序言欢迎来到这个小波变换的入门教程。
小波变换是一个相对较新的概念(大概十年的样子),但是有关于它的文章和书籍却不少。
这其中大部分都是由搞数学的人写给其他搞数学的人看的,不过,仍然有大部分搞数学的家伙不知道其他同行们讨论的是什么(我的一个数学教授就承认过)。
换言之,大多数介绍小波变换的文献对那些小波新手们来说用处不大(仅仅为个人观点)。
当我刚开始学习小波变换的时候,曾经为了弄明白这个神奇的领域到底说的是什么困扰了好多天,因为在这个领域的入门书籍少之又少。
为此我决定为那些小波新手们写这个入门级的教程。
我自己当然也是一个新手,也有很多理论性的细节没有弄清楚。
不过,考虑到其工程应用性,我觉得没有必要弄清楚所有的理论细节。
在这篇教程中,我将试图给出一些小波理论的基本原理。
我不会给出这些原理和相关公式的证明,因为我假定预期的读者在读这个教程时并不需要知道这些。
不过,感兴趣的读者可以直接去索引(所列的书籍)中获取更为深入的信息。
在这篇文档中,我假定你没有任何相关知识背景。
如果你有,请忽略以下的信息,因为都是一些很琐碎的东西。
如果你发现教程中有任何不一致或错误的信息,请联系我。
我将乐于看到关于教程的任何评论。
二、变换什么首先,我们为什么需要(对信号做)变换,到底什么是变换?原始信号中有一些信息是很难获取的,为了获得更多的信息,我们就需要对原始信号进行数学变换。
在接下来的教程中,我将时域内的信号视为原始信号,经过数学变换后的信号视为处理信号。
可用的变换有很多种,其中傅立叶变换可能是最受欢迎的一种。
实际中很多原始信号都是时域内的信号,也就是说不管信号是如何测得的,它总是一个以时间为变量的函数。
换言之,当我们画信号图的时候,横轴代表时间(独立变量),纵轴代表信号幅度(非独立变量)。
当我们画信号的时域图时,我们得到了信号的时幅表示。
对大多数信号处理应用来说,这种表示经常不是最好的表示。
在很多时候,大量特殊的信息是隐藏在信号的频率分量中的。
chap8_频域变换

压缩率为:3.3:1 压缩率为:2.24:1 压缩率为:1.7:1
另一幅图像效果
Fourier变换的压缩原理
压缩率为:16.1:1 压缩率为:10.77:1 压缩率为:8.1:1
返回
8.2 快速Fourier变换(FFT)
一、快速Fourier变换的推导
µ 令:wNx = exp(− j 2πµx ) N
则 :F ( µ ) =
N / 2 −1
1 N
∑
x =0
N −1
µ f ( x)wNx
2 2 N / 2−1 2 µ = 1 [ ∑ f (2 x)wNµx + f (2 x + 1) wN ( 2 x +1) ] ∑ 2 N x =0 N x =1 1 1 M −1 1 M −1 µx µ µ M ∆ N [ ∑ f (2 x)wM + f (2 x + 1) wMx wN ] ∑ 2 2 M x =0 M x =1 1 µ (分成奇数项和偶数项之和) = [ Fe ( µ ) + wN Fo ( µ )] 2
第八章 图像的频域变换
问题的提出: 我们人类视觉所感受到的是在空间 域和时间域的信号。但是,往往许多问 题在频域中讨论时,有其非常方便分析 的一面。
8.1 二维离散Fourier变换
Fourier变换有两个好处:
1)可以得出信号在各个频率点上的强度。 2)可以将卷积运算化为乘积运算。
8.1
正变换:
0≤µ ≤M
8.2 快速Fourier变换(FFT)
1 µ F ( µ + M ) = Fe ( µ + M ) + wN + M Fo ( µ + M ) 2 1 µ = Fe ( µ ) + wN + M Fo ( µ ) 2
小波30道题

1. 从Fourier 变换到小波变换的三个阶段: *)信号加窗;**)基加窗;***)小波基;⑴ Fourier 变换是一个强有力的数学工具,它具有重要的物理意义,即信号()f x 的Fourier 变换()()⎰+∞∞-ω-=ωx x f F x d e i表示信号的频谱。
正是Fourier 变换的这种重要的物理意义,决定了Fourier 变换在信号分析和信号处理中的独特地位,特别是作为平稳信号分析的最重要的工具。
但是,在实际应用中,所遇到的信号大多数并不是平稳的。
所以,随着应用范围的逐步扩大和理论分析的不断深入,Fourier 变换的局限性就渐渐展示出来了:首先,从理论上说,为了由Fourier 变换研究一个时域信号()f x 的频谱特性,必须获得信号在时域中的全部信息,以致于包括将来的信息;其次,Fourier 变换对信号的局部畸变没有标定和度量能力。
但是,在许多实际应用中,畸变正是我们所关心的信号在局部范围内的特征;再次,Fourier 变换不能反映信号在局部时间范围内和局部频带上的谱信息分析,或称为局部化时-频分析,而这正是许多实际应用最感兴趣的问题之一;最后,因为一个信号的频率与它的周期长度成反比,因而要给进行分析的一个灵活多变的时间和频率的“窗口”,使其在“中心频率(或称为平均频率、主频)”高的地方,时间窗自动变窄,而在“中心频率”低的地方,时间窗应自动变宽。
⑵ 时间加窗:Gabor 在1946年的论文中,为了提取信号的局部信息,这包括时间和频率两方面的局部信息,引入了一个时间局部化的“窗口函数”()g t b -,其中参数b 用于平行移动窗口,以便于覆盖整个时域。
Gabor 变换继承了Fourier 变换所具有的“信号频谱”这样的物理解释,同时,它克服了Fourier 变换只能反映信号的整体特征而对信号的局部特征没有任何分析能力的缺陷,大大地改进了Fourier 变换的分析能力,为信号处理提供了一种新的分析和处理工具,即信号的时-频分析。
小波分析方法

小波应用 一维小波分解ca1,cd1
14
一维小波分解ca3,cd3,cd2,cd1
15
一维小波分解 S=a1+d1
16
一维小波分解 S=a3+d3+d2+d1
17
二维小波分解
18
二维小波分解与重建
19
基于小波的奇异性分析
20
小波去噪(1)
21
小波去噪(2)
22
基于小波的图像融合
8 小波分析方法
8.1 小波分析与傅里叶变换的比较 8.2 小波应用
8.1 小波分析与付里叶变换的比较
傅里叶变换
我不知道风 是 在 哪 一 个方 向吹——
我 是 在 梦 中, 在 梦 的 轻 波里 依洄。
我不知道风 是 在 哪 一 个方 向吹——
我 是 在 梦 中, 她 的 温 存 ,我 的迷醉 。
可以得到小波序列:
a,b (t )
1 ( t b )( a , b R , a 0 ) aa
离散化,小波序列为
j,k (t ) 2 j / 2 ( 2 j t k )( j , k Z )
任意的函数 f (t ) L2 ( R )的连续小波为
W f ( a , b ) f , a ,b
29
IR-MMW fusion技术
30
小波融合技术在图像无线通讯中的应用
31
我不知道风 是 在 哪 一 个方 向吹——
我 是 在 梦 中, 甜 美 是 梦 里的 光辉。
我不知道风 是 在 哪 一 个方 向吹——
我 是 在 梦 中, 她 的 负 心 ,我 的伤悲 。
我不知道风 是 在 哪 一 个方 向吹——
从傅里叶Fourier变换到伽柏Gabor变换再到小波Wavelet变换

从傅里叶(Fourier)变换到伽柏(Gabor)变换再到小波(Wavelet)变换本文是边学习边总结和摘抄各参考文献内容而成的,是一篇综述性入门文档,重点在于梳理傅里叶变换到伽柏变换再到小波变换的前因后果,对于一些概念但求多而全,所以可能会有些理解的不准确,后续计划分别再展开学习研究。
通过本文可以了解到:1)傅里叶变换的缺点;2)Gabor变换的概念及优缺点;3)什么是小波;4)小波变换的概念及优点。
一、前言首先,我必须说一下,在此之前,虽然我听说过小波变换(具体是前几年听一位博士毕业答辩里提到了小波降噪)但就再也没什么了,虽然近一年来零零散散地在接触语音信号处理过程中用过短时傅里叶变换(Short Time FourierTransform, STFT),但也就如此了,之于Gabor变换听都没有听过。
这些天看稀疏基,其实也就是看各种变换了,前面看了离散余弦变换(Discrete CosineTransform, DCT)、离散正弦变换(Discrete Sine Transform, DST)、离散W变换(DiscreteW Transform, DWT)、离散哈特莱变换(Discrete Hartley Transform, DHT),总体来说理解个表皮还是比较容易的,于是打算继续学习,随便挑了一个Curvelet基打算学习一下,搜了一下资料才发现不能从这个开始学习,必须Gabor、Wavelet、Ridgelet、Curvelet、Wedgelet、Bandelet、Beamlet、Contourlet 等慢慢开始学起,我知道我又陷入了一片沼泽,但或许是一片幸福的沼泽,一个做信号处理的人对这些是应该有一个基本的概念级了解的。
这让我回忆起了几年前,我对移动通信一样,作为一名电子信息专业的大学生,居然不知道什么是TD-SCDMA,居然分不清GPS和GPRS,这一直是让我感觉很耻辱的一件事情,于是我开始看书、上网查资料,经过一段时间的努力,终于把基本的概念搞明白了,比如GSM、GPRS、EDGE、CDMA1x、CDMA2000、TD- SCDMA、WCDMA、HSPA、LTE、WiMax、wifi、Bluetooth、Zigbee、802.11、802.15.4、802.16、WLAN、WPAN、WMAN等等,感觉自己虽非身处移动通信行业,但毕竟学的这个专业,终于算是对各概念混个脸熟了。
小波变换的发展简史

小波变换的发展简史从时频分析方法发展的角度出发(对比每种方法的优缺点),简述了小波变换的发展历史。
小波变换的概念是由法国从事石油信号处理的工程师J.Morlet在1974年首先提出的,通过物理的直观和信号处理的实际需要经验的建立了反演公式,当时未能得到数学家的认可。
幸运的是,1986年著名数学家Y.Meyer偶然构造出一个真正的小波基,并与S.Mallat合作建立了构造小波基的同一方法枣多尺度分析之后,小波分析才开始蓬勃发展起来。
与Fourier变换、窗口Fourier变换相比,它是一个时间和频率的局域变换,因而能有效的从信号中提取信息,通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析,解决了Fourier变换不能解决的许多困难问题,从而小波变化被誉为“数学显微镜”,它是调和分析发展史上里程碑式的进展,势必取代傅立叶分析的位置。
1.小波分析的3个特点:小波变换,既具有频率分析的性质,又能表示发生的时间。
有利于分析确定时间发生的现象。
(傅里叶变换只具有频率分析的性质)小波变换的多分辨度的变换,有利于各分辨度不同特征的提取(图象压缩,边缘抽取,噪声过滤等)小波变换比快速Fourier变换还要快一个数量级。
信号长度为M 时,Fourier变换(左)和小波变换(右)计算复杂性分别如下公式:2. 小波基表示发生的时间和频率:傅里叶变换(Fourier)基小波基时间采样基“时频局域性” 图解:Fourier变换的基(上)小波变换基(中)和时间采样基(下)的比较4.信号的时频分析:信号时频分析的重要性:时间和频率是描述信号的两个最重要的物理量。
信号的时域和频域之间具有紧密的联系。
信号时频分析的主要方法:3. 傅里叶变换(一)傅里叶变换伟大贡献及其局限性:傅立叶变换的理论是人类数学发展史上的一个里程碑,从1807年开始,直到1966年整整用了一个半世纪多才发展成熟,她在各个领域产生了深刻的影响得到了广泛的应用,推动了人类文明的发展。
Fourier变换和Gabor变换与小波变换的比较研究

第28卷第1期2005年2月鞍山科技大学学报Journal of Anshan University of Science and Technology Vol.28No.1Feb.,2005Fourier 变换和Gabor 变换与小波变换的比较研究贾朱植1,董立文2,董 勃3,谢元旦2(1.鞍山科技大学高等职业技术学院,辽宁鞍山 114044;2.鞍山科技大学计算机科学与工程学院,辽宁鞍山 114044;3.鞍钢新轧钢股份有股公司,辽宁鞍山 114042)摘 要:对Fourier 变换、G abor 变换和小波变换进行比较。
从Fourier 变换的定义出发,进行分析阐述,指出了Fourier 变换不具有局部化分析的功能以及时频完全分离的缺点;通过对G abor 变换的核函数进行时频两域分析,说明了它品质因数是不恒定的以及它的一些缺陷;最后对小波变换的核函数进行分析,论述了小波变换具有品质因数恒定和多分辨率分析等优点。
关键词:Fourier 变换;G abor 变换;小波变换中图分类号:O174122;O17716 文献标识码:A 文章编号:167224410(2005)0120012205 Fourier 分析方法(Fourier ,1807)提供了一种把时域信号转换到频域进行分析的途径,但它只考虑时域和频域之间的一对一映射关系,是一种时频完全分离的分析方法[1]。
这种方法用于分析平稳信号,在分析非平稳信号时就有些力不从心了。
针对Fourier 变换不能局部化分析,G abor 于1946年引入了G abor 变换,又称短时Fourier 变换(Short time Fourier tranform );它在一定程度上解决了Fourier 变换的时频分离的不足。
但是,G abor 变换在待分析信号上加一个窗口函数,改变了原信号的性质,并且它本身仍然存在一些缺陷难以克服。
小波变换(Wavelet transform )理论是继Fourier 分析之后的一个突破性进展[2],它给许多相关领域提供了一种强有力的分析工具。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 小波变换及其在图像处理中的应用参考书目[1] R.C. Gonzalez and R. E.Woods, Digital Image Processing (Second edition) (中译本: 阮秋琦等译, 数字图像处理(第二版),电子工业出版社,2003) [2] S.Mallat, A Wavelet Tour of Signal Processing,1999.(中译本:杨力华等译, 信号处理的小波导引,机械工业出版社,2002[3] M. Vetterli and J. Kovacevic, Wavelets and Subband Coding, Pritice-Hall,NJ. 1995.[4] 杨福生, 小波变换的工程分析与应用, 科学出版社, 2000.8.1 从Fourier 变换到小波变换一、 引言● J.Worlet (法 地质学家)和A.Grossmann (物理学家) (1984)在处理地质数据时引入了小波的概念 ● Y.Meyer (法 数学家)(1986)构造了具有一定衰减特 性的光滑函数ψ,其二进伸缩平移系)2(2)(2,k t t jk j j -=ψψ构成)(2R L 的规范正交基。
著有专著《小波和算子》 ● S.Mallat (1987)提出多分辨率分析,给出了信号分 解和重构算法(Mallat )算法。
● I.Daubechies (1990)在波士顿近郊的专题学术会议 上10次演讲(Ten Lecture on Wavelets ,1990) 应用领域:信号分析与重构;图像处理(数据压缩编 码,边缘检测,去噪声, 数据融合); 语音信号处理; 地质勘测数据处理; 物理学、天文学; 数值分析等。
小波前16种方法或算法,其中信号处理有4种: (1) Time-frequency atoms in speech signal processing(D. Gabor, 1946)(2) Subband coding (A.Croisier and D.Esteban, 1976) (3) Pyramid coding (P.J.Burt and E.H.Adelson, 1982) (4) Zero-crossings (D.Marr, 1980)● 记号:)(R L 2: 平方可积函数组成的集合)()(R L x f 2∈∞<⎰∞∞-dx x f 2)(内积: 若 )()(R L x f 2∈, )()(R L x g 2∈则 ⎰∞∞-*=〉〈dx x g x f x g x f )()()(),(〉〈==⎰∞∞-)(),()()(x f x f dx x f x f 221〉〈=)(),()(x f x f x f● 信号)(x f 的线性展开(P.251))()(x x f i ii ϕα∑=, V x f ∈)(, V 是函数空间如果展开集)}({x i ϕ是linearly independent ,且对任何 V x f ∈)(, 均存在}{i α, 使 )()(x x f i ii ϕα∑=则称)}({x i ϕ构成V 的一个基(1) 标准正交基(Orthonormal basis)如果 ⎩⎨⎧≠===〉〈j i ji j i j i ,,,01δϕϕ则)}({x i ϕ构成V 的标准正交基, 这时〉〈=)(),(x x f i i ϕα(2) 双正交(Bi-orthogonal )如果基函数)}({x i ϕ不是标准正交的, 但)}({x i ϕ和其对偶)}(~{x iϕ满足 j i j i δϕϕ=〉〈~,则基函数和其对偶是双正交的, 这时〉〈=)(~),(x x f ii ϕα (3) Redundant or Overcomplete展开集)}({x i ϕ不是linearly independent , 它不 是V 的一个基, 这时, 展开函数及其对偶是 redundant or overcomplete 。
● 窗函数 时间窗函数r (t )⎰∞∞-=dt t r t t r t 22*)()(12122*)()()(1⎥⎦⎤⎢⎣⎡-=∆⎰∞∞-dtt r t t t r r (0*=t ,3s r =∆ )频率窗函数R (ω) ⎰∞∞-=ωωωωωd R R 22*)()(12122*)()()(1⎥⎦⎤⎢⎣⎡-=∆⎰∞∞-ωωωωωd R R R (0*=ω , ∞=∆R )Heisenberg uncertainty principle21≥∆⋅∆R r二、由Fourier 变换到小波变 1. Fourier 变换设)()(R L x f 1∈, 其Fourier 变换定义为dx e x f fx i ⎰∞∞--=ωω)()(ˆ若)()(ˆR L f 1∈ω, 则ωωπωd e fx f x i ⎰∞∞-=)(ˆ)(21 ● 缺点2. 加窗Fourier 变换(Gabor, 1946) (短时Fourier 变换STFT )〉〈=-=⎰∞∞--u x i f g f dx e u x g x f u G ,,)()(),(ωωω)(,u x g eg xi u -=ωωωωπωd e u x g u G x f xi f)(),()(-=⎰∞∞-21)(u x g -:窗函数(高斯函数))(x f : 被分析的信号,随着u 的变化,)(u x g - 所确定的窗口在时间轴(x 轴)上移动, ),(u G f ω反映了)(x f 在时刻u , 角频率为ω的信号成分的相对含量)(ˆ)()()(),(ωωωωfdx ex f dxdue u x g xf du u G xi x i f ==-=⎰⎰⎰⎰∞∞---∞∞-∞∞-∞∞-3. 时─频窗口时域: 中心为 0u , 窗宽为u σ2 频域: 中心为ω0, 频宽为ωσ2 在时─频二维相空间中,时─频窗口为],[],[0000ωωσωσωσσ+-⨯+-u u u u● 固定分辨率 (ωσσ,u 与时─频平面的位置无关)● Heisenberg uncertainty principle21≥⋅ωσσu● STFT 的缺点: 4. 小波变换定义1:设函数)()(R L x 2∈ψ, 满足允许条件∞<=⎰∞∞-ωωωψψd c 2)(ˆ则称)(x ψ为允许小波(admissible wavelet )或母小波, 按平移伸缩方式可以生成一组小波基函数)}({,x u s ψ)()(,s u x sx u s -=ψψ1 +∈∈R s R u ,)()(s u x su x s -=-ψψ1定义2:函数)()(R L x f 2∈的连续小波变换为〉〈=-⋅=⎰∞∞-)(),()()(),(,x x f dx s ux s x f u s W u s f ψψ1duds sx u s Wc x f u s f21)(),()(,ψψ⎰⎰∞∞-∞=● 由允许条件可知 000===)(ˆ)(ˆψωψω (带通滤波) ⎰∞∞-=0dx x )(ψ (小波)设 )()(x x s s -=-ψψ),()()()()(u s W dxu x x f dx x u x f f f ss s =-=-=*⎰⎰∞∞-∞∞---ψψψ(带通滤波))(1)(s xsx s ψψ=, )(ˆ)(ˆωψωψs s s = ● 时-频窗口例: )07.0()07.0(5cos 5.010cos )(++-++=t t t t t f δδππ二、 小波级数 连续小波 )()(,s u x sx u s -=ψψ1二进小波将S 离散化Z j s j∈=,21则 ))(()(,u x x jjuj -=222ψψ 将u 离散化 ,Z k k u j∈=,2则 )()(,k x x jj kj -=222ψψ 小波级数:如果ψ~是小波ψ的对偶,m k l j m l k j δδψψ=〉〈,,~, (双正交)则)()(R L x f 2∈可以展开为小波级数∑∑∈∈==Zk j k j k j Zk j k j k j x d x C x f ,,,,,,)(~)()(ψψ式中 〉〈=)(~),(,,x x f C k j k j ψ〉〈=)(),(,,x x f d k j k j ψ若ψψ=~, m k l j m l k j δδψψ=〉〈,,, (正交)则 )()(,,,x Cx f k j Zk j kj ψ∑∈=〉〈=)(),(,,x x f C k j k j ψ。
