初中数学试题编制技术评价卷_4
初中数学教师专业测评试卷

一、选择题(每题2分,共20分)1. 下列哪个选项不属于初中数学课程标准的基本理念?()A. 培养学生的数学思维和解决问题的能力B. 培养学生的数学素养和审美情趣C. 强调学生的自主学习和合作探究D. 重视学生的基础知识与基本技能2. 下列哪个说法是错误的?()A. 数学教学应以学生为主体,教师为主导B. 数学教学应注重培养学生的创新精神和实践能力C. 数学教学应以教材为本,教师应灵活运用教材D. 数学教学应只注重学生的基础知识与基本技能3. 下列哪个方法不属于启发式教学方法?()A. 问题引导法B. 案例分析法C. 讨论法D. 重复讲解法4. 下列哪个说法是正确的?()A. 数学教学应以课堂讲授为主,学生自主探索为辅B. 数学教学应以学生自主探索为主,课堂讲授为辅C. 数学教学应以课堂讲授为主,学生自主探索为主D. 数学教学应以学生自主探索为主,课堂讲授为主5. 下列哪个教学评价方法是错误的?()A. 形成性评价B. 总结性评价C. 定量评价D. 定性评价6. 下列哪个说法是错误的?()A. 数学教学应注重培养学生的逻辑思维能力B. 数学教学应注重培养学生的抽象思维能力C. 数学教学应注重培养学生的空间想象力D. 数学教学应注重培养学生的实际操作能力7. 下列哪个说法是正确的?()A. 数学教学应以教师讲授为主,学生被动接受B. 数学教学应以学生主动探究为主,教师辅助引导C. 数学教学应以教师讲授为主,学生自主探索为主D. 数学教学应以学生自主探索为主,教师被动接受8. 下列哪个说法是错误的?()A. 数学教学应注重培养学生的创新精神和实践能力B. 数学教学应注重培养学生的合作精神和团队意识C. 数学教学应注重培养学生的审美情趣和道德品质D. 数学教学应注重培养学生的竞争意识和胜利欲望9. 下列哪个教学评价方法是错误的?()A. 过程性评价B. 总结性评价C. 定量评价D. 定性评价10. 下列哪个说法是正确的?()A. 数学教学应以课堂讲授为主,学生自主探索为辅B. 数学教学应以学生主动探究为主,教师辅助引导C. 数学教学应以教师讲授为主,学生自主探索为主D. 数学教学应以学生自主探索为主,教师被动接受二、填空题(每题2分,共20分)1. 数学课程标准的基本理念包括:()、()、()。
初中数学八年级下学期素质技能测试四

初中数学八年级下学期素质技能测试四时间:120分钟 满分:150分姓名 分数一、选择题(每小题只有一个正确答案,共10个小题,满分50分)1、一次函数的图象与直线y= -x+1平行,且过点(8,2),此一次函数的解析式为( )。
A 、y=2x-14 B 、y=-x-6 C 、y=-x+10 D 、y=4x2、如果直线y =2x +m 与两坐标轴围成的三角形面积等于m ,则m 的值是( )。
A 、±3B 、3C 、±4D 、4 3、如图,已知点A (—1,0)和点B(1,2),在坐标上确定点P ,使 △ABP 为直角三角形,则满足这样的点P 的条件有( )个。
A 、2B 、4C 、6D 、7(第3题图)4、若0414=----xxx m 无解,则m 的值是( )。
A 、-2B 、2C 、3D 、-35、如果三角形的面积为5cm 2,则下图中表示三角形的一边a 与这边上的高h 的函数关系的图象是( )。
6、如图,函数2k y x =()0≠k 的图象是下图的( )。
A B CD7、一游泳池注满水,现按一定速度将水排尽,然后进行清洗,再按相同速度注满清水,使用一段时间后, 又按相同的速度将水排尽,则游泳池的存水量h (米2)随时间t (小时)变化的大致图像是( )。
A B C D8、小刘为了迎战2010年亚运会刻苦进行110米栏训练,教练对他的10次训练成绩进行统计分析,若要判断他的成绩是否稳定,则教练需要知道小刘这10次成绩的 ( ) 。
A .平均数B .中位数C .众数D .方差11题 9、如图是三个反比例函数312,,k k ky y y x x x===,在x 轴上方的图像,由此观察得到k l 、k 2、k 3的大小关系为( )。
(A ) k 1>k 2>k 3 (B ) k 3>k 1>k 2(C ) k 2>k 3>k 1 (D ) k 3>k 2>k 110、如图:AB ∥EF ∥CD ,AC ∥PQ ∥BD ,则图中最多有( )个平行四边形。
初中数学教师技能考试试卷(含解答)

初中数学教师技能考试试卷(含解答)第一部分:选择题(共40分)1. 下列哪个数是无理数?- A. 2- B. -1/2- C. √5- D. 3/4正确答案:C2. 三角形的内角和是多少度?- A. 90度- B. 180度- C. 360度- D. 540度正确答案:B3. 以下哪个图形不是正多边形?- A. 正方形- B. 正三角形- C. 正五边形- D. 正六边形正确答案:D4. 以下哪个数是一个完全平方数?- A. 18- B. 25- C. 33- D. 42正确答案:B5. 一个长方形的长是5cm,宽是3cm,它的面积是多少平方厘米?- A. 8- B. 10- C. 15- D. 16正确答案:C...第二部分:解答题(共60分)1. 请计算以下等式的解:2x + 5 = 15。
解答:将等式两边减去5,得到2x = 10。
再将等式两边除以2,得到x = 5。
所以方程的解是x = 5。
2. 请画出一个正方形,并标注出它的边长、对角线等重要特征。
解答:(插入正方形示意图)3. 请计算以下等式的解:3(x + 2) = 15。
解答:首先将等式左边进行分配律展开,得到3x + 6 = 15。
然后将等式两边减去6,得到3x = 9。
最后将等式两边除以3,得到x = 3。
所以方程的解是x = 3。
...第三部分:应用题(共40分)1. 某商店举办打折促销活动,商品原价为100元,现在打8折出售。
请计算打折后的价格是多少元?解答:打8折相当于原价乘以0.8,所以打折后的价格是100元 × 0.8 = 80元。
2. 一辆汽车以每小时60公里的速度行驶,行驶了3小时,请计算汽车行驶的总路程是多少公里?解答:汽车以每小时60公里的速度行驶3小时,所以总路程是60公里/小时 × 3小时 = 180公里。
...第四部分:解析题(共60分)1. 请解析以下数列的规律:2, 4, 6, 8, ...解答:这是一个等差数列,公差为2,首项为2。
初中数学编制试卷及答案

一、选择题(每题2分,共20分)1. 下列各数中,不是有理数的是()A. 2.5B. -1/3C. √2D. 1/22. 已知a=3,b=-2,则a-b的值是()A. 1B. -1C. 5D. -53. 若x^2-5x+6=0,则x的值为()A. 2,3B. 1,4C. 1,2D. 2,44. 在△ABC中,∠A=45°,∠B=60°,则∠C的度数是()A. 75°B. 120°C. 135°D. 150°5. 下列函数中,是反比例函数的是()A. y=x^2B. y=2xC. y=1/xD. y=3x+26. 已知x+y=5,xy=3,则x^2+y^2的值为()A. 16B. 14C. 13D. 127. 在等腰三角形ABC中,AB=AC,若∠B=50°,则∠A的度数是()A. 40°B. 50°C. 60°D. 70°8. 已知等差数列{an}的首项为2,公差为3,则第10项an的值为()A. 27B. 30C. 33D. 369. 下列图形中,不是平行四边形的是()A. 矩形B. 菱形C. 等腰梯形D. 等腰三角形10. 已知二次函数y=ax^2+bx+c的图象开口向上,且a>0,则下列结论正确的是()A. b>0B. b<0C. c>0D. c<0二、填空题(每题2分,共20分)11. 若x^2-4x+3=0,则x的值为__________。
12. 在△ABC中,∠A=70°,∠B=45°,则∠C的度数是__________。
13. 若函数y=3x+2是反比例函数,则x的值为__________。
14. 在等腰三角形ABC中,AB=AC,若底边BC的长度为6,则腰AB的长度为__________。
15. 已知等差数列{an}的首项为1,公差为2,则第5项an的值为__________。
初中数学职称试题及答案

初中数学职称试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是正确的?A. 2x + 3y = 5B. 3x - 2y = 6C. 4x + 5y = 10D. 5x + 6y = 11答案:B2. 一个数的平方是9,这个数是多少?A. 3B. -3C. 3或-3D. 9答案:C3. 计算以下表达式的结果:(2x + 3)(2x - 3) = ?A. 4x^2 - 6x + 9B. 4x^2 - 6x - 9C. 4x^2 + 6x + 9D. 4x^2 - 9答案:D4. 一个直角三角形的两条直角边长分别为3和4,斜边长是多少?A. 5B. 6C. 7D. 8答案:A5. 以下哪个分数是最简形式?A. 6/8B. 8/12C. 9/15D. 10/20答案:A6. 一个圆的半径是5厘米,它的面积是多少?A. 25π cm^2B. 50π cm^2C. 75π cm^2D. 100π cm^2答案:B7. 以下哪个方程的解是x = 2?A. x + 2 = 4B. x - 2 = 4C. x * 2 = 4D. x / 2 = 4答案:A8. 一个数的立方是8,这个数是多少?A. 2B. -2C. 2或-2D. 4答案:A9. 以下哪个选项是不等式3x - 7 < 5的解?A. x < 4B. x > 4C. x < 6D. x > 6答案:A10. 计算以下表达式的结果:(3x^2 - 2x + 1) / (x - 1) = ?A. 3x + 1B. 3x - 1C. 3x + 2D. 3x - 2答案:A二、填空题(每题2分,共20分)1. 一个数的相反数是-5,这个数是________。
答案:52. 一个数的绝对值是7,这个数可能是________或________。
答案:7或-73. 一个等腰三角形的底边长为6,两腰长为5,周长是________。
九年级评估试卷数学【含答案】

九年级评估试卷数学【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若一个正方形的边长为a,则它的对角线长为()。
A. a/2B. a√2C. 2aD. a√32. 下列函数中,奇函数是()。
A. y = x^2B. y = x^3C. y = |x|D. y = sin(x)3. 已知一组数据2, 3, 5, 7, 11,它的众数是()。
A. 2B. 3C. 5D. 74. 若一个等差数列的首项为2,公差为3,则第10项是()。
A. 29B. 30C. 31D. 325. 在直角坐标系中,点P(2, -3)关于y轴的对称点是()。
A. (-2, -3)B. (2, 3)C. (-2, 3)D. (3, -2)二、判断题(每题1分,共5分)6. 任何两个奇数之和都是偶数。
()7. 二次函数y = ax^2 + bx + c的图像一定是抛物线。
()8. 若一组数据的平均数为10,则这组数据中至少有一个数不小于10。
()9. 在三角形中,大边对大角,小边对小角。
()10. 任何有理数都可以表示为分数的形式。
()三、填空题(每题1分,共5分)11. 平方差公式:a^2 b^2 = ()。
12. 若sin(α) = 1/2,则α是()度。
13. 若一组数据为1, 3, 5, 7, 9,则它的中位数是()。
14. 若一个等差数列的第3项是7,第7项是19,则它的公差是()。
15. 在直角坐标系中,点A(3, 4)到原点的距离是()。
四、简答题(每题2分,共10分)16. 简述等差数列的定义。
17. 什么是二次函数的顶点?18. 解释概率的意义。
19. 什么是三角形的内心?20. 什么是平面直角坐标系?五、应用题(每题2分,共10分)21. 一个长方体的长、宽、高分别是8cm、6cm、4cm,求它的体积。
22. 已知一个等差数列的首项为3,公差为2,求前10项的和。
23. 解方程:2x 5 = 3(x + 1)。
初三数学试卷评估卷及答案

一、选择题(每题3分,共30分)1. 下列数中,是正数的是()A. -3B. 0C. 3D. -52. 已知函数f(x) = 2x - 1,则f(3)的值为()A. 5B. 4C. 3D. 23. 下列方程中,解为x=2的是()A. 2x + 3 = 7B. 3x - 4 = 5C. 4x + 5 = 11D. 5x - 6 = 94. 若a、b是方程x^2 - 5x + 6 = 0的两个根,则a + b的值为()A. 5B. 6C. 7D. 85. 在直角坐标系中,点A(2,3),点B(-3,4),则AB线段的长度为()A. 5B. 6C. 7D. 86. 下列图形中,是轴对称图形的是()A. 正方形B. 等边三角形C. 等腰梯形D. 平行四边形7. 若等差数列的前三项分别为a、b、c,且a + c = 10,b = 5,则该等差数列的公差为()A. 2B. 3C. 4D. 58. 下列不等式中,恒成立的是()A. 2x + 3 > x - 4B. 3x - 5 < 2x + 1C. 4x + 2 ≥ 3x - 1D. 5x - 3 ≤ 2x + 29. 下列函数中,在定义域内单调递增的是()A. y = 2x + 3B. y = -3x + 5C. y = x^2 - 2x + 1D. y = -x^2 + 2x - 110. 在△ABC中,∠A = 45°,∠B = 60°,则∠C的度数为()A. 75°B. 80°C. 85°D. 90°二、填空题(每题5分,共25分)11. 若x^2 - 4x + 3 = 0,则x的值为______。
12. 已知函数y = 3x - 2,当x=2时,y的值为______。
13. 等差数列的前三项分别为2,5,8,则该等差数列的公差为______。
14. 若等比数列的前三项分别为1,3,9,则该等比数列的公比为______。
初中数学教学评估试卷

一、选择题(每题3分,共30分)1. 下列哪个选项不是实数的分类?A. 有理数B. 无理数C. 整数D. 分数2. 已知方程 2x - 5 = 0,解得 x = ________。
3. 在直角坐标系中,点A(-2,3)关于原点的对称点是 ________。
4. 一个长方形的长是10厘米,宽是6厘米,那么它的周长是 ________厘米。
5. 下列哪个函数是单调递增函数?A. y = -2x + 3B. y = 2x - 5C. y = x^2D. y = 3/x6. 已知圆的半径是5厘米,那么它的直径是 ________厘米。
7. 下列哪个三角形是等边三角形?A. 三个角都是60°的三角形B. 三个边都相等的三角形C. 三个高都相等的三角形D. 三个中线都相等的三角形8. 下列哪个不是勾股数?A. 3, 4, 5B. 5, 12, 13C. 6, 8, 10D. 7, 24, 259. 在一次函数 y = kx + b 中,k和b分别表示 ________。
10. 下列哪个不是代数式的特征?A. 含有字母B. 有运算符号C. 只能有一个未知数D. 可以表示数量关系二、填空题(每题5分,共20分)11. 已知等差数列的第一项是2,公差是3,那么第10项是 ________。
12. 一个等腰三角形的底边长是8厘米,腰长是10厘米,那么它的面积是________平方厘米。
13. 下列方程的解是 x = ________。
14. 一个正方形的边长是6厘米,那么它的对角线长是 ________厘米。
15. 下列不等式成立的是 ________。
三、解答题(每题10分,共30分)16. 解下列方程组:$$\begin{cases}2x + 3y = 8 \\x - y = 2\end{cases}$$17. 一个长方形的长比宽多3厘米,面积是48平方厘米,求这个长方形的长和宽。
18. 一个圆的半径增加了20%,求这个圆的面积增加了多少百分比。
九年级数学评估试卷【含答案】

九年级数学评估试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若一个正方形的边长为a,则它的对角线长为()A. a/2B. a√2C. 2aD. a²2. 下列函数中,哪一个不是正比例函数?()A. y = 3xB. y = x/2C. y = 5D. y = 4x 13. 在直角坐标系中,点(3, -4)位于()A. 第一象限B. 第二象限C. 第三象限D. 第四象限4. 若一个等腰三角形的底边长为10cm,腰长为13cm,则该三角形的周长为()A. 26cmB. 32cmC. 36cmD. 40cm5. 下列哪一个数是无理数?()A. √9B. √16C. √3D. √1二、判断题(每题1分,共5分)6. 任何两个等边三角形的面积一定相等。
()7. 一元二次方程ax² + bx + c = 0的解可以用公式x = -b ± √(b² 4ac) / 2a求得。
()8. 对角线互相垂直的四边形一定是菱形。
()9. 两个负数相乘的结果一定是正数。
()10. 在一次函数y = kx + b中,当k > 0时,函数图像随着x的增大而减小。
()三、填空题(每题1分,共5分)11. 若一个圆的半径为r,则该圆的直径为______。
12. 若一个长方形的长为l,宽为w,则该长方形的对角线长为______。
13. 若一个等差数列的首项为a1,公差为d,第n项为an,则an = ______。
14. 若一个等比数列的首项为b1,公比为q,第n项为bn,则bn = ______。
15. 若一个三角形的两边长分别为3cm和4cm,且这两边的夹角为90°,则该三角形的第三边长为______。
四、简答题(每题2分,共10分)16. 请简述勾股定理的内容。
17. 请解释无理数的概念。
18. 请说明等差数列和等比数列的定义。
19. 请简述一次函数图像的性质。
八年级数学(上)评价性试题(4)(含答案)-
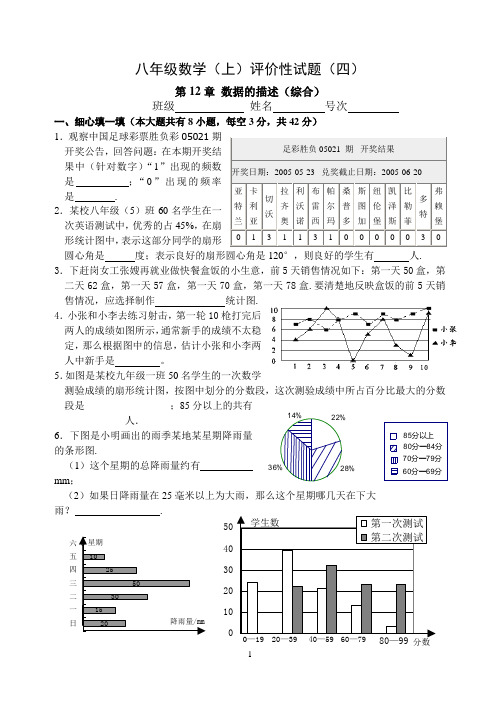
60分—69分70分—79分80分—84分85分以上22%28%36%14%01020304050分数第一次测试第二次测试0—1920—3940—5960—7980—99学生数八年级数学(上)评价性试题(四)第12章 数据的描述(综合)班级 姓名 号次一、细心填一填(本大题共有8小题,每空3分,共42分) 1.观察中国足球彩票胜负彩05021期开奖公告,回答问题:在本期开奖结果中(针对数字)“1”出现的频数是 ;“0”出现的频率是 . 2.某校八年级(5)班60名学生在一次英语测试中,优秀的占45%,在扇形统计图中,表示这部分同学的扇形圆心角是 度;表示良好的扇形圆心角是120°,则良好的学生有 人. 3.下赶岗女工张嫂再就业做快餐盒饭的小生意,前5天销售情况如下:第一天50盒,第二天62盒,第一天57盒,第一天70盒,第一天78盒.要清楚地反映盒饭的前5天销售情况,应选择制作 统计图. 4.小张和小李去练习射击,第一轮10枪打完后两人的成绩如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小张和小李两人中新手是 。
5.如图是某校九年级一班50名学生的一次数学测验成绩的扇形统计图,按图中划分的分数段,这次测验成绩中所占百分比最大的分数段是_________________;85分以上的共有____________人.6.下图是小明画出的雨季某地某星期降雨量的条形图.(1)这个星期的总降雨量约有 mm ;(2)如果日降雨量在25毫米以上为大雨,那么这个星期哪几天在下大雨? .足彩胜负 05021 期 开奖结果 开奖日期:2005-05-23 兑奖截止日期:2005-06-20 亚特兰 卡利亚 切 沃 拉齐奥 利沃诺 布雷西 帕尔玛 桑普多 斯图加 纽伦堡 凯泽斯 比勒菲 多特弗赖堡0 1 3 1 1 3 1 0 0 0 0 0 3 0 2015305025100日一二三四五六降雨量/mm星期2718101696.25一二三四五六行业种类一、钢铁及新材料业二、轿车等机械制造业三、烟草及食品业四、光电子信息业五、石化业六、环保业百分比(%)7.有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况.请你根据条形图提供的信息,回答下列问题(把答案填在题中横线上); (1)两次测试最低分在第 次测试中;(2)第 次测试较容易; 8.一组数据经整理后分成四组,第一、二、三小组的频率分别为0.1,0.3,,0.4,第一小组的频数是5,那么第四小组的频率是 ,这组数据共有 个. 二、精心选一选(本大题共8小题,每题3分,共24分) 9.下列各数中可以用来表示频率的是( )(A )-0.1 (B )1.2 (C )0.4 (D )34 10.扇形统计图中扇形占圆的30%,则此时扇形所对的圆心角为( )(A )120° (B )108° (C )90° (D )60° 组号 1 2 3 4 5 6 7 8 频数1114121313x1210(A )12 (B )13 (C )14 (D )1512.甲校女生占全校总人数的50%,乙校男生占全校总人数的50%,比较两校女生人数( )(A) 甲校多于乙校; (B) 甲校与乙校一样多 (C) 甲校多于乙校; (D) 不确定13.下图是某地区用水量与人口数情况统计图.日平均用水量为400万吨的那一年,人口数大约是( )(A )180万 (B )200万 (C )300万 (D )400万14.已知一组数据63、65、67、69、66、64、66、64、 65、68,在64.5~66.5之间的数据出现的频率是( ) (A) 0.4 (B) 0.5(C) 5 (D) 4 15.2005年第一季度,钢铁及新材料、轿车等机械制造、烟草及食品、光电子信息、石化、环保等十大行业的快速发展,带动了武汉市国民经济的快速增长。
初中数学创编试题及答案

初中数学创编试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是无理数?A. 0.5B. √2C. 0.33333D. -2答案:B2. 一个数的相反数是-3,那么这个数是:A. 3B. -3C. 0D. 9答案:A3. 一个数的绝对值是5,那么这个数可能是:A. 5或-5B. 5或0C. -5或0D. 5或-5或0答案:A4. 以下哪个选项表示的是一次函数?A. y = 2x + 3B. y = x^2 + 1C. y = 1/xD. y = x^3 - 2答案:A5. 一个圆的直径是10厘米,那么它的半径是:A. 5厘米B. 10厘米C. 20厘米D. 15厘米答案:A6. 如果一个三角形的两个内角分别是40°和60°,那么第三个内角是:A. 80°B. 90°C. 70°D. 100°答案:B7. 一个数的立方根是2,那么这个数是:A. 2B. 8C. -2D. -8答案:B8. 下列哪个选项是方程的解?A. x + 3 = 5B. x - 3 = 5C. x * 3 = 5D. x / 3 = 5答案:A9. 一个数的平方是25,那么这个数可能是:A. 5B. -5C. 5或-5D. 0答案:C10. 一个数的1/3与它的2倍相等,这个数是:A. 3B. 1/3C. 1/6D. 0答案:B二、填空题(每题4分,共20分)1. 一个数的平方是36,这个数是______。
答案:±62. 如果一个数的1/4加上2等于3,那么这个数是______。
答案:43. 一个数的3倍减去5等于10,这个数是______。
答案:54. 一个数的2/3是8,这个数是______。
答案:125. 一个数的立方是27,这个数是______。
答案:3三、解答题(每题10分,共50分)1. 已知一个数的2倍加上3等于11,求这个数。
答案:设这个数为x,则2x + 3 = 11。
初三数学学科评估试卷

一、选择题(每题4分,共40分)1. 下列各数中,绝对值最小的是()A. -2B. -1C. 0D. 12. 若a=3,b=-4,则|a-b|的值为()A. 7B. -7C. 1D. -13. 已知方程x-2=0,则x的值为()A. 2B. -2C. 0D. 无法确定4. 在直角坐标系中,点P(2,3)关于x轴的对称点的坐标是()A.(2,-3)B.(-2,3)C.(2,-3)D.(-2,-3)5. 若a、b、c成等差数列,且a+b+c=18,则b的值为()A. 6B. 9C. 12D. 156. 下列函数中,是反比例函数的是()A. y=x+1B. y=2xC. y=3/xD. y=x^27. 已知一次函数y=kx+b,若k<0,则函数图象()A. 在一、二象限B. 在一、三象限C. 在二、三象限D. 在一、四象限8. 若a、b、c、d为等比数列,且a+b+c+d=20,则b的值为()A. 5B. 10C. 15D. 209. 下列各式中,正确的是()A. (a+b)^2 = a^2 + 2ab + b^2B. (a-b)^2 = a^2 - 2ab + b^2C. (a+b)^2 = a^2 - 2ab + b^2D. (a-b)^2 = a^2 + 2ab - b^210. 若a、b、c、d成等差数列,且a+c=10,b+d=18,则ac+bd的值为()A. 50B. 100C. 150D. 200二、填空题(每题5分,共50分)11. 若a=3,b=-4,则a+b的值为______。
12. 在直角坐标系中,点A(-2,3)关于y轴的对称点的坐标是______。
13. 若a、b、c成等差数列,且a+b+c=18,则b+c的值为______。
14. 下列函数中,是二次函数的是______。
15. 若a、b、c、d成等比数列,且a+b+c+d=20,则bc+ad的值为______。
16. 若a、b、c、d成等差数列,且a+c=10,b+d=18,则ac+bd的值为______。
初二数学学科评估试卷

一、选择题(每题2分,共20分)1. 下列数中,有理数是()A. √2B. √3C. √5D. √92. 若a、b是相反数,且|a| > |b|,则下列不等式中正确的是()A. a > bB. a < bC. a = bD. a和b相等或互为相反数3. 已知三角形ABC的三个内角分别为A、B、C,若∠A = 40°,∠B = 70°,则∠C的度数是()A. 50°B. 60°C. 70°D. 80°4. 在平面直角坐标系中,点P的坐标为(2,-3),点Q关于y轴的对称点Q'的坐标是()A. (-2,3)B. (-2,-3)C. (2,3)D. (2,-3)5. 下列函数中,是二次函数的是()A. y = 2x + 3B. y = x^2 + 2x + 1C. y = x^3 + 3x^2 + 2x + 1D. y = 2x^2 - 3x + 46. 已知一次函数y = kx + b的图象经过点(-2,3),且k < 0,则下列结论正确的是()A. k = 2,b = -1B. k = -2,b = 3C. k = -1,b = 2D. k = 1,b = -37. 在等腰三角形ABC中,AB = AC,若∠BAC = 50°,则∠ABC的度数是()A. 40°B. 50°C. 60°D. 70°8. 若等边三角形的三边长分别为a、b、c,则下列等式中正确的是()A. a = b + cB. b = c + aC. c = a + bD. a = b = c9. 下列各式中,不是分式的是()A. 2/xB. x/3C. x^2/3D. 3x/210. 若x = -1是方程2x^2 - 3x + 2 = 0的解,则x + 1的值是()A. -1B. 0C. 1D. 2二、填空题(每题2分,共20分)11. 有理数-5的绝对值是______。
七年级数学学业评价测试卷

一、选择题(每题2分,共20分)1. 下列各数中,绝对值最小的是()A. -3B. 2C. 0D. -22. 若a > b,那么下列不等式中正确的是()A. a + 2 > b + 2B. a - 2 < b - 2C. a - 2 > b + 2D. a + 2 < b - 23. 已知等腰三角形ABC中,AB=AC,若BC=6,则底边AD的长度是()A. 3B. 4C. 5D. 64. 下列函数中,有最小值的是()A. y = x^2B. y = -x^2C. y = x^2 + 1D. y = -x^2 + 15. 在直角坐标系中,点P(2, -3)关于x轴的对称点坐标是()A. (2, 3)B. (-2, -3)C. (-2, 3)D. (2, -3)6. 若一个长方体的长、宽、高分别为a、b、c,则其体积V为()A. V = abcB. V = ab + ac + bcC. V = (a + b + c)^2D. V = a^2 + b^2 + c^27. 在△ABC中,若∠A = 60°,∠B = 45°,则∠C的度数是()A. 75°B. 105°C. 120°D. 135°8. 下列数中,既是质数又是合数的是()A. 17B. 18C. 19D. 209. 已知一次函数y = kx + b的图象经过点(2, 3),且k > 0,则下列结论正确的是()A. b > 0B. b < 0C. b = 0D. 无法确定10. 下列方程中,x=2是它的解的是()A. 2x + 3 = 7B. 2x - 3 = 7C. 2x + 3 = 5D. 2x - 3 = 5二、填空题(每题2分,共20分)11. 已知a = -5,b = 3,则a - b = ________。
12. 若m^2 = 9,则m = ________。
数学职称初中试题及答案

数学职称初中试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 计算下列表达式的结果:\[ 3x^2 - 2x + 1 = 0 \]A. 1B. 2C. 3D. 4答案:C3. 一个圆的半径是5厘米,那么它的周长是多少?A. 10π厘米B. 15π厘米C. 20π厘米D. 25π厘米答案:C4. 如果一个数的平方是16,那么这个数是多少?A. 4B. -4C. 4或-4D. 以上都不是答案:C5. 下列哪个分数是最简分数?A. \(\frac{6}{8}\)B. \(\frac{5}{10}\)C. \(\frac{3}{9}\)D. \(\frac{7}{8}\)答案:D6. 一个长方体的长、宽、高分别是2cm、3cm和4cm,那么它的体积是多少?A. 12cm³B. 24cm³C. 26cm³D. 28cm³答案:B7. 一个等腰三角形的底边长为6cm,两腰长为5cm,那么它的周长是多少?A. 16cmB. 17cmC. 18cmD. 19cm答案:C8. 一个数的绝对值是5,那么这个数是多少?A. 5B. -5C. 5或-5D. 09. 计算下列表达式的结果:\[ 2^3 + 3^2 \]A. 11B. 12C. 13D. 14答案:C10. 下列哪个选项是不等式 \(x + 3 > 5\) 的解?A. x > 2B. x < 2C. x = 2D. x ≤ 2答案:A二、填空题(每题2分,共20分)11. 一个数的相反数是-7,那么这个数是________。
答案:712. 一个数的倒数是\(\frac{1}{4}\),那么这个数是________。
答案:413. 一个等边三角形的边长是8cm,那么它的高是________。
答案:\(\frac{8\sqrt{3}}{2}\)cm14. 一个数的平方根是3,那么这个数是________。
数学学科评估试卷初中

一、选择题(每题2分,共20分)1. 下列各数中,无理数是()A. √4B. 3.14C. √25D. √22. 若x² + 4x + 4 = 0,则x的值为()A. -2B. 2C. -1D. 13. 在直角坐标系中,点A(2,3)关于y轴的对称点为()A.(-2,3)B.(2,-3)C.(-2,-3)D.(2,3)4. 下列等式中,正确的是()A. a² + b² = (a + b)²B. a² - b² = (a + b)²C. a² - b² = (a - b)²D. a² + b² = (a - b)²5. 若a、b、c是等差数列的前三项,且a + b + c = 12,则b的值为()A. 3B. 4C. 5D. 66. 在等腰三角形ABC中,AB = AC,∠BAC = 40°,则∠ABC的度数为()A. 40°B. 50°C. 70°D. 80°7. 下列函数中,是反比例函数的是()A. y = 2x + 3B. y = 3/xC. y = x²D. y = 2x³8. 若a、b、c是等比数列的前三项,且abc = 27,则b的值为()A. 3B. 9C. 27D. 819. 在梯形ABCD中,AD || BC,AD = 5cm,BC = 10cm,AB = CD = 4cm,则梯形的高为()A. 2cmB. 3cmC. 4cmD. 5cm10. 若等差数列{an}的公差d = 2,且a₁ + a₄ + a₇ = 36,则a₃的值为()A. 10B. 12C. 14D. 16二、填空题(每题2分,共20分)11. 已知方程2x² - 5x + 2 = 0,则x的值为______。
初中数学学科评估试卷答案

一、选择题(每题2分,共20分)1. 下列数中,是负数的是()A. -2B. 0C. 3D. 5答案:A解析:负数是小于零的数,所以选A。
2. 一个长方形的长是6厘米,宽是4厘米,它的周长是多少厘米?()A. 16厘米B. 20厘米C. 24厘米D. 30厘米答案:C解析:长方形的周长是长和宽的两倍之和,所以周长是(6+4)×2=24厘米。
3. 下列方程中,x的值是3的是()A. 2x+1=7B. 3x-2=7C. 4x+3=13D. 5x-4=13答案:B解析:将x=3代入每个方程,发现只有B选项的方程成立,所以选B。
4. 下列图形中,是正方体的是()A. 长方体B. 正方形C. 圆形D. 三角形答案:A解析:正方体是一种特殊的长方体,所以选A。
5. 下列数中,是偶数的是()A. 3B. 5C. 6D. 8答案:C解析:偶数是能被2整除的数,所以选C。
二、填空题(每题2分,共20分)6. 2的平方根是______。
答案:±√2解析:一个数的平方根是指乘以自身等于这个数的数,2的平方根是±√2。
7. 下列分数中,最简分数是______。
答案:3/4解析:最简分数是指分子和分母没有公因数的分数,3和4没有公因数,所以3/4是最简分数。
8. 一个圆的半径是5厘米,它的周长是多少厘米?答案:31.4厘米解析:圆的周长公式是C=2πr,其中r是半径,π约等于3.14,所以周长是2×3.14×5=31.4厘米。
9. 下列图形中,是轴对称图形的是______。
答案:正方形解析:轴对称图形是指存在一条直线,将图形分成两部分,两部分关于这条直线对称,正方形满足这个条件,所以选正方形。
10. 下列方程中,x的值是-2的是______。
答案:x+4=2解析:将x=-2代入方程x+4=2,发现方程成立,所以选x+4=2。
三、解答题(每题10分,共30分)11. 某班有男生30人,女生40人,求男生和女生人数的比例。
数学评价测试卷初三苏教

一、选择题(每题4分,共40分)1. 下列各数中,有理数是()A. √-4B. πC. 2.5D. 0.1010010001……2. 已知a、b是实数,且a + b = 0,则下列选项中正确的是()A. a = bB. a = -bC. ab > 0D. ab < 03. 如果一个等腰三角形的底边长为10cm,腰长为8cm,那么这个三角形的周长是()A. 26cmB. 24cmC. 28cmD. 30cm4. 下列函数中,y是x的一次函数的是()A. y = 2x + 3B. y = 3x^2 + 2C. y = 4x + 5√xD. y = 5x - 3/x5. 已知二次方程x^2 - 4x + 3 = 0,则该方程的解为()A. x = 1, x = 3B. x = 2, x = 2C. x = 1, x = 1D. x = 3, x = 36. 在平面直角坐标系中,点A(2,3)关于原点的对称点是()A.(-2,-3)B.(2,-3)C.(-2,3)D.(3,-2)7. 下列图形中,不是轴对称图形的是()A. 正方形B. 等边三角形C. 长方形D. 平行四边形8. 如果一个正方形的边长为a,那么它的对角线长是()A. √2aB. 2aC. a√2D. a/√29. 在直角三角形ABC中,∠A = 90°,AB = 3cm,BC = 4cm,那么AC的长度是()A. 5cmB. 7cmC. 6cmD. 8cm10. 下列各式中,正确的是()A. 5^0 = 0B. (-2)^3 = -8C. 0^1 = 1D. (-3)^2 = -9二、填空题(每题5分,共25分)11. 有理数a的相反数是______。
12. 已知等腰三角形底边长为8cm,腰长为6cm,那么底角是______度。
13. 一次函数y = 3x - 2的图象经过______点。
14. 二次函数y = -x^2 + 4x + 3的图象开口______,顶点坐标是______。
初中数学评职称的试卷

1. 下列关于函数的定义中,正确的是()A. 函数是数学中的一个基本概念,是指两个非空数集之间的映射关系B. 函数是一种特殊的映射,它要求每个元素在定义域中都有唯一的像C. 函数是一种有序对,由定义域和值域组成D. 函数是数学中的一个运算,它将定义域中的元素映射到值域中的元素2. 下列关于一元二次方程的解法中,错误的是()A. 直接开平法B. 配方法C. 因式分解法D. 换元法3. 在直角坐标系中,点A(3,4)关于x轴的对称点坐标是()A.(3,-4)B.(-3,4)C.(3,-4)D.(-3,-4)4. 下列关于三角函数的定义中,正确的是()A. 正弦函数表示直角三角形中,直角边与斜边的比值B. 余弦函数表示直角三角形中,邻边与斜边的比值C. 正切函数表示直角三角形中,对边与邻边的比值D. 正割函数表示直角三角形中,对边与斜边的比值5. 下列关于不等式的性质中,错误的是()A. 不等式的两边同时乘以同一个正数,不等号的方向不变B. 不等式的两边同时乘以同一个负数,不等号的方向不变C. 不等式的两边同时加上或减去同一个数,不等号的方向不变D. 不等式的两边同时除以同一个正数,不等号的方向不变6. 若函数f(x) = x^2 - 3x + 2,则f(2) = ________。
7. 已知等差数列{an}的公差为d,若a1 = 2,a5 = 12,则d = ________。
8. 在直角坐标系中,点P(2,3)到直线y = -2x + 5的距离为 ________。
9. 若sinα = 1/2,则cosα = ________。
10. 若a、b、c是等边三角形的边长,则a^2 + b^2 + c^2 = ________。
三、解答题(每题20分,共80分)11. (1)已知函数f(x) = 2x - 3,求f(-1)。
(2)若函数g(x) = 3x^2 - 2x + 1在x = 2时的值最小,求g(2)。
浙江地区初中数学学科素质评估卷附答案

浙江地区初中数学学科素质评估卷学科 初中数学 教师姓名 得分 满分:150分 时间:120分钟卷Ⅰ一、选择题:(本题共10小题,每小题4分,满分40分) 1.下列各组数中,互为相反数的是( ) A 、2与21 B 、21)(-与1 C 、-1与2)1(- D 、2与|-2| 2.下列计算,正确的是( )A 、22(a 54232)b a b = B 、222)(ba b a -=-C 、y x yx y x +=++22 D 、y x y x -+()()=y x -3.如图是由5个大小相同的正方体摆成的立方体图形,它的左视图...是( )(A) (B) (C) (D)4.某青年排球队12名队员的年龄情况如下:则这个队队员年龄的众数和中位数是 ( )A 、19,20B 、19,19C 、19,20.5D 、20,195.二次函数211y ax x =-+的图像与222y x =-图像的形状、开口方向相同,只是位置不同,则二次函数1y 的顶点坐标是(*) A 、 (19,48--) B 、(19,48-) C 、(19,48) D 、 (19,48-) 6.如图,有一施工工地上有三根直径为1m 的水泥管道两两相切地叠放在一起,则其最高点到地面的距离为( ) B 、1+ 2 2 C 、1+ 3 2 D 、1+ 32A 、2 图,点B 在圆锥母线VA 上,且VB =13VA ,过点B 作平7.如ACDBA′PD C BS 1,原圆锥的侧面积为S ,则下列判断中正确的是( ) A 、113S S =B 、114S S =C 、116S S =D 、119S S = 8. 右边给出的是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,请你运用方程思想来研究,发现这三个数的和不可能是( ) A 、 69B 、54C 、27D 、409.如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC 相似的是 ( )10. 如图,已知正方形ABCD 的边长为2,如果将线段 BD 绕着点B 旋转后,点D 落在CB 的延长线上的D′ 处,那么tan ∠BAD′等于 ( ) A 、1B 、2C 、22D 、22 卷Ⅱ二、填空题:(本题共6小题,每小题5分,满分30分) 11.2-的倒数是 ;12.若x 1、x 2是方程x 2+3x +2=0的两个根,那么x 12+x 22的值等于 _________. 13.如图,若CD 是RtΔABC 斜边上的高,AD =3,CD =4,则BC =__________ .14. 如图, //AB DC , 要使四边形ABCD ,还需补充一个条件是 .15.在边长为2的菱形ABCD 中,∠B =45°,AE 为BC 边上的高,将△ABE 沿AE 所在直线翻折后得△AB 'E ,那么△AB 'E 与四边形AECD 重叠部分的面积是 .16.已知矩形ABCD 的长AB =4,宽AD =3,按如图放置在直线AP上,然后不滑动地转动,当它转动一周时(A →A ′),顶点A 所经过的路线长等于 .日 一 二 三 四 五 六1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31D 'DCB AC三、解答题:17.(8分)分解因式:3256x x x ++。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学试题编制技术评价卷
总要求:
1.所编试题须表述简洁、准确,无歧义,不超“标”;
2.所编试题必须附上详细解答过程;
3.所编试题不能与陈题完全相同,一定要有自己的创新内容.
一、(20分)阅读下列时事材料,请你根据材料中的情形编制选择题和填空题各一道.
1.要求:①材料中出现了的数据可直接使用,但不能更改,没有出现的数据,可根据事实情况自行设定;
②选择题的选择项要有一定的思维干扰性、迷惑性;
③两题中必须要有一道是统计题.
2.材料:(来自腾讯网)江西省特大洪灾致千万人受灾、14人死亡、9人失踪.
(1)2010年6月17日以来的特大洪灾致使江西省1061万人受灾,140余万群众被迫紧急转移,目前已造成14人死亡,9人失踪,经济损失接近300亿元.
(2)6月18日上午8时,江西省黎川县遭受特大暴雨袭击,短时间内引起山洪暴发,造成严重洪涝灾害,受灾人口23万余人,重灾3万人,被洪水围困群众1.8万人,紧急转移群众4.5万人.全县倒塌房屋8000间,其中居民1300户共7000间,因灾死亡牲畜4000头,农作物受灾1.46万公顷,绝收4000公顷.
(3)据水文部门监测,6月21日4时12分,抚河廖家湾水文站出现洪峰,洪峰流量8050立方米/秒,超过1952年建站以来最大流量1590立方米/秒;21日晚,抚河中下游10万亩圩堤唱凯堤突发决口,威胁十多万人口和交通要道.令国人揪心、世人瞩目.
此前,江西省部分县城被淹.村庄被围,民众被困;交通中断,通信中断.供电中断;水库垮坝.圩堤决口.险情迭出;赣江全线超警戒.信江水位超历史.抚河流量破记录.
(4)此后,一方有难八方救援, 洪灾无情人有情,连日来,社会各界高度关注灾情,纷纷慷慨相助,奉献爱心.截至6月29日16时,江西省民政厅救灾捐赠接收办公室共接收捐款3002.317万元;交通、通信、供电也随之恢复,灾区外父母亲或亲人,经常打电话及发手机短信询问灾区内的亲人情况,……
编题1.
2010年江西省发生了特大洪灾,洪灾无情人有情,在此期间,社会各界高度关注灾情,纷纷慷慨相助,奉献爱心.从6月18日至6月29日16时,江西省民政厅救灾捐赠接收办公室共接收捐款3002.317万元,其中3002.317万元这个数字(保留四位有效数字)用科学记数表示为( D).
A.3.002×103元
B. 30.02×103元
C.3.00231×103元
D. 3.002×107元
编题2.
本次洪水进入某城市区,但不是非常严重.张某几年前大学毕业后到本市工作,他家乡的父母亲及亲人都非常担心,经常打电话及发手机短信询问情况,如图是小张从6月18日到23日每天收到短信条数的折线统计图,则他这6天中每天收到短信条数的中位数是65 条.
二、(15分)如图是某单位的两种护栏的实物图,它是用圆钢管和扁钢筋(即图中圈)材料焊接而成的.请你在两实物图中选一种建立几何模型编制一道中档难度的几何应用题,相关数据请自行设定.
编题3.
例如:如图是某单位的透空护栏的示意图,它是用外径为3cm的圆钢管与外圆直径为15cm的扁钢筋做的圆圈焊接而成的,若要做长为3.63米的护栏(高度统一为2米).
试问:需要圆钢管的总长度是多少?用扁钢筋做成圆圈有多少个?
示意图:
解:设圆圈x 个.由题意得: 15x+(x+1)×3=363, x=20(个). 圆钢管总长度:(x+1)×2=21×2=42(米). 答:(略)
三.(15分)、请你将试题“如图,在△ABC 中,AD 平分∠BAC ,BD=CD ,求证:AB=AC ”改
编成动态题. 要求:题中条件“AD 平分∠BAC ,BD=CD ”保留不变,而结论必须还是探讨AB 与 AC 的数量关系.
编题4.
如图,在△ABC 中,AD 平分∠BAC ,BD=CD ,且点D 是射线AD 上的一动点,那么: (1).当D 点在BC 上时,求证:AB=AC;
(2).当D 点不在BC 上时,(1)中的结论还成立吗?若你认为成立请说明理由,若你认为不成立,请举一反例说明之. 解:(1)如图1,过D 作DE ⊥AB 于E ,DF ⊥AC 于F ,易证△BDE ≌△CDF , ∴∠B=∠C,AB=AC
(2)不一定成立,当点D 在△ABC 的内部时,(如图2)AB=AC 成立,理由与(1)类似;当点D 在△ABC 的外部时(如图3)AB=AC 不一定成立.如:当连接BC 和11B C 时,结论成立,当连接B 1C 或C 1B 时, 结论就不成立.
四、(25分)请你编制一道以二次函数为主线的综合性试题.
要求:①抛物线必须沿下图中的射线AB 的方向平移; ②题中要涉及到求二次函数解析式、抛物线的对称性或顶点问题以及二次函数与一元二次方程的关系等内容; ③要体现分类讨论思想;
④若学生做难度系数在0.3左右,即大概相当于中考卷第24题位置的难度.
四. 编题5
如图,在平面直角坐标系中,已知A (-2,0),B (1,3),设经过A 、O
(0,0)两点且顶点C 在直线AB 上的抛物线为m , (1)求直线AB 和抛物线m 的解析式; (2)若将抛物线m 沿射线AB 方向平移(顶点C 始终在AB 上),设移动后的抛物线与x 轴在右的交点为D ,
①在上述移动过程中,当顶点C 在水平方向上移动3个单位时,A
与D 之间的距离是多少?
②当顶点在水平方向移动a 个单位时,请用含a 的代数式表示AD 的长. 解:(1)设直线AB 的解析式为y=kx+b ,
则:023k b k b =-+⎧⎨
=+⎩,1
2
k b =⎧⎨=⎩
∴AB 的解析式为y=x+2.
由于抛物线m 经过A 、O 两点,则抛物线的对称轴为x=-1,顶点在直线AB 上. ∴y=-1+2=1,
∴顶点为(-1,1).
设抛物线的解析式为2(1)1y a x =++ 当x=0,y=0时, 20(01)1a =++,a=-1, ∴2(1)1y x =-++(或22y x x =--).
(2)①根据题意,顶点在水平方向上向右平移了3个单位,顶点的横坐标为-1+3=2,纵坐标为x+2=2+2=4, 抛物线移动后的抛物线为2(2)4y x =--+, 当y=0时,1x =0,2x =4,
则点D 的坐标为(4,0), AD=4-(-2)=6.
②当顶点在水平方向向右移动了a 个单位时,顶点为(a-1,a+1), 则平移后的抛物线为2
(1)1y x a a =--+++, 当y=0时,2
(1)1x a a -+=+,
1x a =-
D (1a -0),
∴AD=1a -(-2)=1a .
五、(25分)
给你一块含30°的三角板和一只量角器(画半圆代替)或用一副三角板,请你设计合适的操作情景,编制一道既有实践操作又有探究分析的一道“压轴题”或综合题,并要求解答时需运用数形结合、分类讨论等思想方法.
在Rt △ABC 中,∠ACB=90°,AB=4,D 为AB 的中点,将一直角△DEF 纸片平放在△ACB 所在的平面上,且使直角顶点重合于点D (C 始终在△DEF 内部),设纸片的两直角边分别与AC 、BC 相交于M 、N. (1)当∠A=∠NDB=45°时,四边形MDNC 的面积 为 ;
(2)当∠A=45°,∠NDB ≠45°时,四边形MDNC 的面积是否与(1)相同?说明理由; (3)当∠A=∠NDB=30°时,四边形MDNC 的面积为 ;
(4)当∠A=30°,∠NDB ≠30°时,四边形MDNC 的面积是否发生变化?若不发生变化(即与(3)相同),说明理由,若发生变化,设四边形MDNC 的面积为S ,BN 为x ,求S 与x 之间的关系.
解:(1)如图1, 2;
(2)相同.如图2,易证:△MDC ≌△NDC , 1
2222
BDC CMDN S S ==
⨯⨯= 四边形
(3)如图3,1MDNC S DM DN === 矩形
(4)发生变化,
当∠A=30°,∠BDN ≠30°时,如图4,过D 分别作DP ⊥AC 于P ,DR ⊥BC 于R ,
∵∠PDR=∠FDE=90°,
∴∠PDM=∠NDR ,△DPM ∽△DRN ,
1RN DR PM DP ==
∴,RN=1-x ,,
11
)1
22S x =--=.。
