初三中考数学专项练习 频数与频率
备战中考数学基础必练(浙教版)频数与频率(含解析)

2019备战中考数学基础必练(浙教版)-频数与频率(含解析)一、单选题1.某校有500名学生参加外语口语考试,考试成绩在70分~85分之间的有120人,则这个分数段的频率是()A.0.2B.0.12C.0.24D.0.252.某校七年级三班有50位学生,他们来上学有的步行,有的骑车,还有的乘车,根据表中已知信息可得()A.a=18,d=24%B.a=18,d=40%C.a=12,c=24%D.a=12,c=40%3.嘉嘉将100个数据分成①﹣⑧组,如下表所示,则第⑤组的频率为()A.11B.12C.0.11D.0.124.抛一枚普通硬币10次,其中4次出现正面,则出现正面的频率为()A.2.5B.1.6C.0.6D.0.45.对某班40同学的一次数学成绩进行统计,适当分组后80~90分这个分数段的划记人数为“”,那么此班在这个分数段的人数占全班人数的百分比是()A.20%B.40%C.8%D.25%6.掷一枚质地均匀的硬币50次,硬币落地后,出现正面朝上的次数为20次,则正面朝上的频率为()A. B. C. D.17.给定一组数据如下,14,14,14,16,16,17,17,17,20,20,20,20,20,25,数17出现的频数与频率分别为()A.3和B.17和C.3和D.均不对8.有40个数据,共分成6组,第1~4组的频数分别为10,5,7,6,第5组的频率是0.1,则第6组的频数是()A.8B.28C.32D.409.有一个样本有100个数据,落在某一组内的频率是0.3,那么落在这一组内的频数是()A.50B.30C.15D.310.在频数分布表中,各小组的频数之和()A.小于数据总数B.等于数据总数C.大于数据总数D.不能确定二、填空题11.某班把学生分成5个学习小组,前4个小组的频率分别是0.04、0.04、0.16、0.34,第三个小组的频数是8,则第5小组的频率是________。
初三中考一轮复习频数与频率 题型分类 含答案(全面 非常好)

教学主题教学目标重要知识点1.2.3.易错点教学过程一、选择题1. 某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如下表所示:用电量(度)120 140 160 180 200户数 2 3 6 7 2则这20户家庭该月用电量的众数和中位数分别是【】A.180,160 B.160,180 C.160,160 D.180,180【答案】A。
2. 为调查某校2000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱体育节目的学生共有【】(A)300名(B)400名(C)500名(D)600名【答案】B。
3.数据5,7,5,8,6,13,5的中位数是【】A.5 B.6 C.7 D.8【答案】B。
4、数据8、8、6、5、6、1、6的众数是【】A.1 B.5 C. 6 D.8【答案】C。
5. 体育课上,某班两名同学分别进行5次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较这两名学生成绩的【】A.平均数B.频数分布C.中位数D.方差【答案】D。
6. 某校羽毛球训练队共有8名队员,他们的年龄(单位:岁)分別为:12,13,13,14,12,13,15,13,则他们年龄的众数为【】A.12 B.13 C .14 D.15【答案】B。
7. 下列数据3,2,3,4,5,2,2的中位数是【】A.5 B.4 C.3 D.2【答案】C。
8. 某校学生来自甲、乙、丙三个地区,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自甲地区的为180人,则下列说法不正确的是【】A.扇形甲的圆心角是72°B.学生的总人数是900人C.丙地区的人数比乙地区的人数多180人D.甲地区的人数比丙地区的人数少180人【答案】D。
9. 某同学对甲、乙、丙、丁四个市场二月份每天的白菜价格进行调查,计算后发现这个月四个市场的价格平均值相同、方差分别为2222====S8.5S 2.5S10.1S7.4,,,.二月份白菜价格最乙丁甲丙稳定的市场是【】A.甲B.乙C.丙D.丁【答案】B。
初三数学频率频数练习题

初三数学频率频数练习题1. 某班级有30个学生,他们的数学考试成绩如下:80、70、65、85、90、78、80、75、82、88、90、78、80、75、85、88、75、82、80、88、75、80、85、88、78、75、85、80、82、75。
根据以上数据,回答以下问题:问题1:数学考试的最高分是多少?问题2:数学考试的最低分是多少?问题3:请列举出数学考试的分数频数分布表。
问题4:请写出数学考试的分数频率分布表。
解答:问题1:数学考试的最高分是90。
问题2:数学考试的最低分是65。
问题3:数学考试的分数频数分布表如下:分数频数65 170 175 678 380 682 385 588 490 2问题4:数学考试的分数频率分布表如下:分数频数频率65 1 0.03370 1 0.03375 6 0.20078 3 0.10080 6 0.20082 3 0.10085 5 0.16788 4 0.13390 2 0.067以上是对某班级数学考试成绩的频率和频数进行整理和统计的练习题。
通过统计分析,我们可以清楚地了解到某个数值在数据集中出现的次数,以及该数值所占的频率。
频数表可以帮助我们直观地了解到各个分数的分布情况,而频率表则更加全面地反映了各个分数出现的比例。
对于初三学生而言,掌握频数和频率的统计概念非常重要。
通过这些练习题的实践,可以帮助学生提高数据分析能力、数学思维能力和抽象思维能力,为他们将来的学习和生活奠定良好的数学基础。
希望以上练习题对你的数学学习有所帮助,加油!。
初三频率练习题

初三频率练习题1. 问题描述请解答以下问题:1) 如果一个事件发生的频率是每周三次,请计算这个事件在一个月内发生的次数。
2) 如果一个班级有60个学生,其中40%的学生每天都锻炼身体,请计算有多少个学生每天都锻炼身体。
3) 如果一种商品的销售量占据市场总销售量的20%,而该市场总销售量是每年100万台,请计算该商品每年的销售量。
2. 频率计算1) 事件每周发生3次,一个月约为4周,则这个事件在一个月内发生的次数为:3次/周 × 4周/月 = 12次/月。
所以,这个事件在一个月内发生的次数为12次。
2) 班级有60个学生,其中40%的学生每天都锻炼身体,计算每天锻炼身体的学生人数:40% × 60 = 0.4 × 60 = 24个学生。
所以,有24个学生每天都锻炼身体。
3) 商品销售量占据市场总销售量的20%,市场总销售量为100万台,计算该商品每年的销售量:20% × 100万 = 0.2 × 100万 = 200,000台。
所以,该商品每年的销售量为200,000台。
3. 总结通过解答以上问题,我们得到了以下结果:1) 一个事件在一个月内发生12次。
2) 一个班级中有24个学生每天都锻炼身体。
3) 一种商品每年的销售量为200,000台。
这些练习题的目的是帮助学生熟悉频率的计算方法。
通过运用百分数、乘法和除法的知识,我们可以准确地计算出事件发生的次数、学生锻炼身体的人数以及商品的销售量。
这些计算对于日常生活和实际问题的解决都非常重要。
希望同学们通过这些练习题能够提高自己的计算能力和应用能力,为将来的学习和工作打下坚实的基础。
中考数学全国各地试题分类汇编 频数与频率
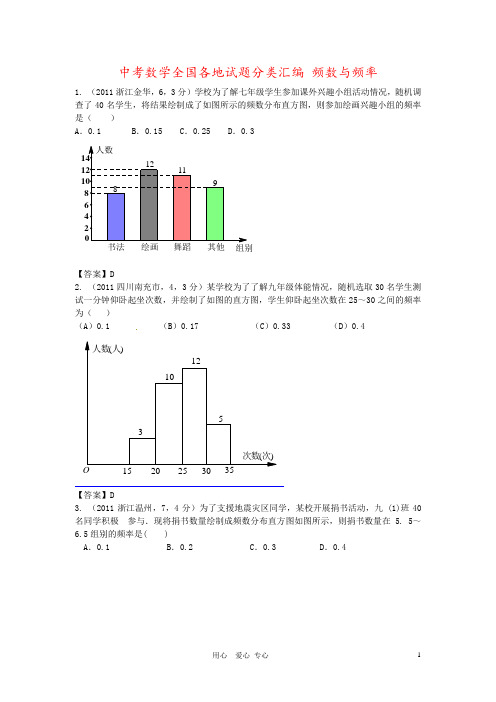
中考数学全国各地试题分类汇编 频数与频率1. (2011浙江金华,6,3分)学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )A .0.1B .0.15C .0.25D .0.3【答案】D2. (2011四川南充市,4,3分)某学校为了了解九年级体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在25~30之间的频率为( )(A )0.1 (B )0.17 (C )0.33 (D )0.4 次数(次)人数(人)35512103O【答案】D3. (2011浙江温州,7,4分)为了支援地震灾区同学,某校开展捐书活动,九 (1)班40名同学积极 参与.现将捐书数量绘制成频数分布直方图如图所示,则捐书数量在 5. 5~6.5组别的频率是( )A .0.1B .0.2C .0.3D .0.4组别人数01412108 12 11 9【答案】B4. (2011浙江丽水,6,3分)学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )A .0.1B .0.15C .0.25D .0.3【答案】D5. (2011四川内江,13,5分)“Welcome to Senior High School .”(欢迎进入高中),在这段句子的所有英文字母中,字母o 出现的频率是 . 【答案】156. (2011广东东莞,18,7分)李老师为了解班里学生的作息时间,调查班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每 组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:(1)此次调查的总体是什么?组别人数01412108 12 11 9(2)补全频数分布直方图;(3)该班学生上学路上花费时间在30分钟以上(含30分钟)的人数占全班人数的百分比是多少?【解】(1)此次调查的总体是:班上50名学生上学路上花费的时间的全体.(2)补全图形,如图所示:(3)该班学生上学路上花费时间在30分钟以上的人数有5人,总人数有50,5÷50=0.1=10%答:该班学生上学路上花费时间在30分钟以上的人数占全班人数的百分之10.7. (2011广东广州市,22,12分)某中学九年级(3)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图(图6),根据图中信息回答下列问题:(1)求a 的值;(2)用列举法求以下事件的概率:从上网时间在6~10小时的5名学生中随机选取2人,其中至少1人的上网时间在8~10小时.图6【答案】频数(学生人数)6 a25 3 2(1)a=50―6―25―3―2=14(2)设上网时间为6~8小时的三个学生为A1,A2,A3,上网时间为8~10个小时的2名学生为B1,B2,则共有A1A2,A1A3,A1B1,A1B2,A2A3,A2B1,A2B2A3B1,A3B2B1B210种可能,其中至少1人上网时间在8~10小时的共有7种可能,故P(至少1人的上网时间在8~10小时)=0.78. (2011广东汕头,18,7分)李老师为了解班里学生的作息时间,调查班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:(1)此次调查的总体是什么?(2)补全频数分布直方图;(3)该班学生上学路上花费时间在30分钟以上(含30分钟)的人数占全班人数的百分比是多少?【解】(1)此次调查的总体是:班上50名学生上学路上花费的时间的全体.(2)补全图形,如图所示:(3)该班学生上学路上花费时间在30分钟以上的人数有5人,总人数有50,5÷50=0.1=10%答:该班学生上学路上花费时间在30分钟以上的人数占全班人数的百分之10.9. (2011 浙江湖州,21,8) 班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生的发言次数进行了统计,并绘制成如下频数分布折线图(图1) .(1) 请根据图1,回答下列问题:①这个班共有名学生,发言次数是5次的男生有人、女生有人;②男、女生发言次数的中位数分别是次和次.(2) 通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2所示.求第二天发言次数增加3次的学生人数和全班增加的发言总次数.【答案】解:(1)①40;2;5 ②4;5.(2)发言次数增加3次的学生人数为:40(120%30%40%)4()⨯---=人.全班增加的发言总次数为40%40130%4024316241252⨯⨯+⨯⨯+⨯=++=(次).10. (2011浙江义乌,20,8分)为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A :50分;B :49-45分;C :44-40分;D :39-30分;E :29-0分)统计如下:根据上面提供的信息,回答下列问题:(1)在统计表中,a 的值为 ▲ ,b 的值为 ▲ ,并将统计图补充完整(温馨提示:作图时分数段 人数(人) 频率 A 48 0.2 B a 0.25 C 84 0.35 D 36 b E 12 0.05 学业考试体育成绩(分数段)统计图12243648607284人数分数段学业考试体育成绩(分数段)统计表别忘了用0.5毫米及以上的黑色签字笔涂黑);(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数. ”请问:甲同学的体育成绩应在什么分数段内? ▲ (填相应分数段的字母)(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名?【答案】解:(1) 60 , 0.15 (图略)(2) C(3)0.8×10440=8352(名)答:该市九年级考生中体育成绩为优秀的学生人数约有8352名.11. (2011山东聊城,19,8分)今年“世界水日”的主题是“城市用水:应对都市化挑战”.为了解城市居民用水量的情况,小亮随机抽查了阳光小区50户居民去年每户每月的用水量,将得到的数据整理并绘制了这50户居民去年每月总用水量的折线图和频数、频率分布表如下:注:x 表示50户居民月总用水量(m3)(1)表中的a =________;d =___________. (2)这50户居民每月总用水量超过550m3的月份占全年月份的百分率是多少(精确到1%)?(3)请根据折线统计图提供的数据,估计该小区去年每户居民平均月用水量是多少? 【答案】(1)3,61;(2)这50户居民月总用水量超过550m3的月份有5个,占全年月份的百分率为(5÷12)×100%=42%(3)(378+641+456+543+550+667+693+600+574+526+423)÷50÷12=109m312. (2011广东省,18,7分)李老师为了解班里学生的作息时间,调查班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每 组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:(1)此次调查的总体是什么?(2)补全频数分布直方图;(3)该班学生上学路上花费时间在30分钟以上(含30分钟)的人数占全班人数的百分比是多少? 组 别 频 数 频 率350<x≤400 1112 400<x≤450 1 112 450<x≤500 2 16 500<x≤550 a b550<x≤600 c d 600<x≤650 1 112 650<x≤700 2 16【解】(1)此次调查的总体是:班上50名学生上学路上花费的时间的全体.(2)补全图形,如图所示:(3)该班学生上学路上花费时间在30分钟以上的人数有5人,总人数有50,5÷50=0.1=10%答:该班学生上学路上花费时间在30分钟以上的人数占全班人数的百分之10.13. (2011山东临沂,20,6分)某中学为了解学生的课外阅读情况.就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了尚不完整的频数分布表:类别频数(人数)频率文学m 0.42艺术22 0.11科普 66 n其他28合计 1下面是自首届以来各届动漫产品成交金额统计图表(部分未完成):(1)表中m=_________,n=__________;(2)在这次抽样调查中,最喜爱阅读哪类读物的学生最多? 最喜爱阅读哪类读物的学生最少?(3)根据以上调查,试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人? 【解】(1)84,0.33;…………………………………………………………………(2分)(2)喜爱阅读文学类的学生最多(84人),喜爱阅读艺术类的学生最少(22人);…………………………………………………………………(4分)(3)1200×0.33=396(人).………………………………………………………(6分)14. (2011浙江省,20,8分)据媒体报道:某市四月份空气质量优良,高举全国榜首,青春中学九年级课外兴趣小组据此提出了“今年究竟能有多少天空气质量达到优良”的问题,他们高举国家环保总局所公布的空气质量级别表(见表1)以及市环保监测站提供的资料,从中随机抽取了今年1-4月份中30天空气综合污染指数,统计数据如下:表I:空气质量级别表空气污染指数0~50 51~100 101~150 151~200 201~250 251~300 大于300空气质量级别Ⅰ级(优)Ⅱ级(良)Ⅲ1(轻微污染)Ⅲ2(轻度污染)Ⅳ1(中度污染)Ⅳ2(中度重污染)Ⅴ(重度污染)空气综合污染指数30,32,40,42,45,45,77,83,85,87,90,113,127,153,16738,45,48,53,57,64,66,77,92,98,130,184,201,235,243请根据空气质量级别表和抽查的空气综合污染指数,解答以下问题:(1) 填写频率分布表中未完成的空格;分组频数统计频数频率0~50 0.3051~100 12 0.40101~150151~200 3 0.10201~250 3 0.10合计30 30 1.00(2) 写出统计数据中的中位数、众数;(3)请根据抽样数据,估计该市今年(按360天计算)空气质量是优良(包括Ⅰ、Ⅱ级)的天数.【答案】(1)分组频数统计频数频率0~50 9 0.3051~100 12 0.40101~150 3 0.10151~200 3 0.10201~250 3 0.10合计30 30 1.00(2) 中位数是 80 、众数是 45 。
中考数学试卷频数题及答案

一、选择题(每题3分,共30分)1. 下列数据中,频数为4的是:A. 1, 2, 2, 3, 3, 3, 4B. 1, 2, 3, 3, 4, 4, 4C. 1, 1, 2, 2, 3, 3, 3D. 1, 1, 1, 2, 2, 3, 3答案:D解析:频数是指一组数据中某个数值出现的次数。
在选项D中,数值1出现了3次,频数为4。
2. 下列关于频数的说法正确的是:A. 频数一定大于等于0B. 频数可以大于数据组中的最大值C. 频数是表示数据集中数据分布情况的一个指标D. 频数与数据组中的最小值有关答案:A解析:频数是指一组数据中某个数值出现的次数,它一定大于等于0。
选项B、C、D的说法都不准确。
3. 下列数据中,众数是3的是:A. 1, 2, 3, 3, 3, 4, 4B. 1, 2, 3, 4, 4, 5, 5C. 1, 2, 3, 3, 4, 4, 5D. 1, 2, 3, 4, 5, 5, 6答案:A解析:众数是指一组数据中出现次数最多的数值。
在选项A中,数值3出现了3次,是出现次数最多的数值,因此众数是3。
4. 下列数据中,中位数是3的是:A. 1, 2, 3, 3, 4, 5, 6B. 1, 2, 3, 4, 5, 6, 7C. 1, 2, 3, 4, 5, 6, 7, 8D. 1, 2, 3, 4, 5, 6, 7, 8, 9答案:C解析:中位数是指一组数据从小到大排列后,位于中间位置的数值。
在选项C中,数据从小到大排列后,中间位置的数值是6,因此中位数是3。
5. 下列数据中,极差是6的是:A. 1, 2, 3, 4, 5, 6B. 1, 2, 3, 4, 5, 7C. 1, 2, 3, 4, 5, 8D. 1, 2, 3, 4, 5, 9答案:B解析:极差是指一组数据中最大值与最小值之差。
在选项B中,最大值是7,最小值是1,极差为7-1=6。
二、填空题(每题4分,共16分)6. 数据组:2, 4, 4, 6, 6, 6,众数是______。
初中数学 习题:频数和频率

频数和频率学习导航 重点频率与频数的概念,频率与频数之间的关系. 难点频率与频数的计算. 易混点频率与频数的区分. 易漏点所有频率之和等于1. 易错点只看频数大小,一般无法确定获胜对象. 精华提炼1.频数、频率的概念在数据统计时每个对象出现的次数称为频数,频数与总次数的比值称为频率.说明:频率分布反映了样本数据落在各个范围数目的多少,频率分布反映了样本数据各个范围内所占的比例,它们都能反映每个对象出现的频繁程度,但也存在区别:在同一个问题中,频数反映的是对象出现频繁程度的绝对数据,所有频数之和是实验的总次数;频率反映的是对象出现频繁程度的相对数据,所有频率之和是1. 2.频数、频率之间的关系频率=频数÷数据总数,频数=频率×频率. 说明:已知频率、频数、数据总数三个量中的任意两个可以计算出第三个. 课堂练习1.下列说法正确的是( )A .频数是表示所有对象出现的次数B .频率是表示每个对象出现的次数C .所有频率之和等于1D .频数和频率都不能够反映每个对象出现的频繁程度2. 王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A 型血的人数是( ) 组别 A 型 B 型 AB 型 O 型 频率A .16人B .14人C .4人D .6人 3.某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示,根据图形所提供的样本数据,可得学生参加科技活动的频率是( )A .B .C .D .4. Lost time is never found again (岁月既往,一去不回).在这句谚语的所有英文字母中,字母“i”出现的频率是 .5.已知在一个样本中,50个数据分别落在5个组内,第一、二、三、四、五组数据的个数分别是2,8,15,20,5,则第四组的频数为 ,频率为 .6.食品安全问题已经严重影响到我们的健康.某执法部门最近就食品安全抽样调查某一家超市,从中随机抽样选取20种包装食品,并列出下表: 食品质量 优 良 合格 不合格 有害或 有毒食品数量 023n4请你根据以上信息解答下列问题: (1)这次抽样调查中,“食品质量为合格以上(含合格)”的频率为 ;(2)若这家超市经销的包装食品共有1300种,请你估计大约有多少种包装食品是“有害或有毒”的?课后训练1. 小明在选举班委时得了28票,下列说法中错误的是()A.不管小明所在班级有多少学生,所有选票中选小明的选票频率不变B.不管小明所在班级有多少学生,所有选票中选小明的选票频数不变C.小明所在班级的学生人数不少于28人D.小明的选票的频率不能大于12.某校对1200名女生的身高进行了测量,身高在~(单位:m),这一小组的频率为,则该组的人数为()A.150人B.300人C.600人D.900人3. 将100个个体的样本编成组号为①~⑧的八个组,如下表:那么第⑤组的频率为()组号①②③④⑤⑥⑦⑧频数14 11 12 13 ■■13 12 10A.14 B.l5C.D.4.将某中学八年级组的全体教师按年龄分成三组,情况如表格所示.则表中a的值应该是.第一组第二组第三组频数 6 10 a频率 b c 20%5.小红统计了她家3月份的电话通话时间,并绘制成如下的频数分布表(表中数据含最大值但不含最小值):那么小红家3月份电话通话时间不超过6min的频数是.6. 为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表(图图7-5-2.请根整理情况频数频率非常好较好70一般不好36(1)本次抽样共调查了多少学生?(2)补全统计表中所缺的数据.(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?图7-5-2频数和频率课堂练习点拨:A 、频数是表示一组数据中,符合条件的对象出现的次数.故错误;B 、频率是表示一组数据中,符合条件的对象出现的次数和总次数的比值.故错误;C 、符合频率的意义.故正确;D 、频率能够反映每个对象出现的频繁程度.故错误.故选C .点拨:本班A 型血的人数为:40×=16.故选A . 点拨:读图可知:共有(15+30+20+35)=100人,参加科技活动的频数是20.故参加科技活动的频率.故选B .点拨:由题意得,总共有25个,字母“i”出现的次数为:3次,故字母“i”出现的频率是253=. ,0,4 点拨:由题意得:第四组的频数为20,第四组的频率是20÷50=.6. 解:(1)∵这次抽样中,食品质量为合格以上(含合格)”的频数是0+2+3=5,∴频率为=; (2)1300×204=260种. 答:约有260种包装食品是“有害或有毒”的. 点拨:(1)首先求出随机抽样的20种包装食品中“食品质量为合格以上(含合格)”的数量,然后根据频率=频数÷数据总数得出结果;(2)首先求出随机抽样的20种包装食品中“有害或有毒”的频率,然后根据样本估计总体的思想,得出答案. 课后训练点拨:当全班人数变化时,所有选票中选小明的选票频率也随着变化;根据各小组频数之和等于数据总和,各小组频率之和等于1,可得B ,C ,D 都正确,A 错误.故选A .点拨:该组的人数为1200×=300(人).故选B . 点拨:第5组的频数为100-(14+11+12+13+13+12+10)=15,其频率为15:100=.故选D .点拨:∵1-20%=80%,∴(6+10)÷80%=20,∴20×20%=4.即a=4. 点拨:小红家3月份电话通话时间不超过6min 的频数是:26+12+8=46.6. 解:(1)较好的所占的比例是:360126则本次抽样共调查的人数是:70÷360120=200(人); (2)非常好的频数是:200×=42(人),一般的频数是:200-42-70-36=52(人),较好的频率是:20070=,一般的频率是:20052=,不好的频率是:20036=;(3)该校学生整理错题集情况“非常好”和“较好”的学生一共约有1500×(+)=840(人)。
初三中考一轮复习频数与频率 题型分类 含答案(全面 非常好)

教学主题教学目标重要知识点1.2.3.易错点教学过程一、选择题1. 某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如下表所示:用电量(度)120 140 160 180 200户数 2 3 6 7 2则这20户家庭该月用电量的众数和中位数分别是【】A.180,160 B.160,180 C.160,160 D.180,180【答案】A。
2. 为调查某校2000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱体育节目的学生共有【】(A)300名(B)400名(C)500名(D)600名【答案】B。
3.数据5,7,5,8,6,13,5的中位数是【】A.5 B.6 C.7 D.8【答案】B。
4、数据8、8、6、5、6、1、6的众数是【】A.1 B.5 C. 6 D.8【答案】C。
5. 体育课上,某班两名同学分别进行5次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较这两名学生成绩的【】A.平均数B.频数分布C.中位数D.方差【答案】D。
6. 某校羽毛球训练队共有8名队员,他们的年龄(单位:岁)分別为:12,13,13,14,12,13,15,13,则他们年龄的众数为【】A.12 B.13 C .14 D.15【答案】B。
7. 下列数据3,2,3,4,5,2,2的中位数是【】A.5 B.4 C.3 D.2【答案】C。
8. 某校学生来自甲、乙、丙三个地区,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自甲地区的为180人,则下列说法不正确的是【】A.扇形甲的圆心角是72°B.学生的总人数是900人C.丙地区的人数比乙地区的人数多180人D.甲地区的人数比丙地区的人数少180人【答案】D。
9. 某同学对甲、乙、丙、丁四个市场二月份每天的白菜价格进行调查,计算后发现这个月四个市场的价格平均值相同、方差分别为2222====S8.5S 2.5S10.1S7.4,,,.二月份白菜价格最乙丁甲丙稳定的市场是【】A.甲B.乙C.丙D.丁【答案】B。
新人教版九年级上册初中数学 25 频数与频率(含解析) 真题专项训练
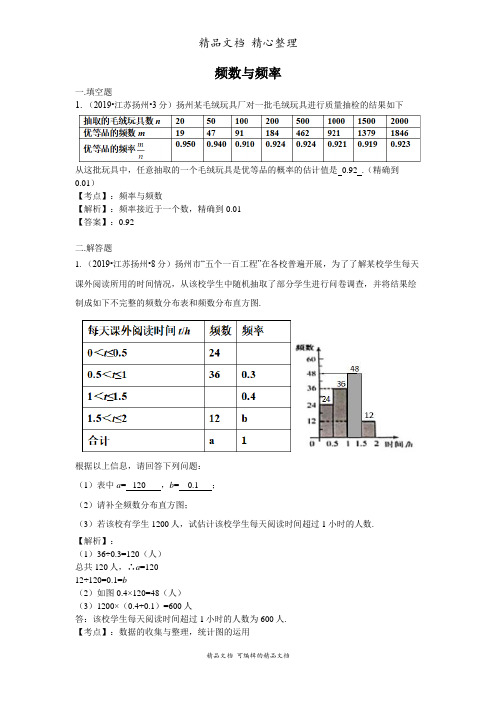
频数与频率一.填空题1. (2019•江苏扬州•3分)扬州某毛绒玩具厂对一批毛绒玩具进行质量抽检的结果如下从这批玩具中,任意抽取的一个毛绒玩具是优等品的概率的估计值是 0.92 .(精确到0.01)【考点】:频率与频数【解析】:频率接近于一个数,精确到0.01【答案】:0.92二.解答题1. (2019•江苏扬州•8分)扬州市“五个一百工程”在各校普遍开展,为了了解某校学生每天课外阅读所用的时间情况,从该校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如下不完整的频数分布表和频数分布直方图.根据以上信息,请回答下列问题:(1)表中a= 120 ,b= 0.1 ;(2)请补全频数分布直方图;(3)若该校有学生1200人,试估计该校学生每天阅读时间超过1小时的人数.【解析】:(1)36÷0.3=120(人)总共120人,∴a=12012÷120=0.1=b(2)如图 0.4×120=48(人)(3)1200×(0.4+0.1)=600人答:该校学生每天阅读时间超过1小时的人数为600人.【考点】:数据的收集与整理,统计图的运用2. (2019•广东省广州市•10分)某中学抽取了40名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.频数分布表组别时间/小时频数/人数A组0≤t<1 2B组1≤t<2 mC组2≤t<3 10D组3≤t<4 12E组4≤t<5 7F组t≥5 4请根据图表中的信息解答下列问题:(1)求频数分布表中m的值;(2)求B组,C组在扇形统计图中分别对应扇形的圆心角度数,并补全扇形统计图;(3)已知F组的学生中,只有1名男生,其余都是女生,用列举法求以下事件的概率:从F组中随机选取2名学生,恰好都是女生.【分析】(1)用抽取的40人减去其他5个组的人数即可得出m的值;(2)分别用360°乘以B组,C组的人数所占的比例即可;补全扇形统计图;(3)画出树状图,即可得出结果.【解答】解:(1)m=40﹣2﹣10﹣12﹣7﹣4=5;(2)B组的圆心角=360°×=45°,C组的圆心角=360°或=90°.补全扇形统计图如图1所示:(3)画树状图如图2:共有12个等可能的结果,恰好都是女生的结果有6个,∴恰好都是女生的概率为=.【点评】此题主要考查了列表法与树状图法,以及扇形统计图、频数分布表的应用,要熟练掌握.。
九年级数学频数与频率测试题

中学5.3 频数与频率◎测试目标1.分清频数与频率的概念.2.会根据频数分布直方图或频数分布表进行相关的计算. 一、选择题(每题7分,共28分)1.★ 某中学对200名年满16岁的男生的身高进行了测量,结果身高(单位:m )在1.68~1.70这一小组的频率为0.25,则该组的人数为( )A.60人 B.15人 C.50人 D.25人2.★ 已知样本7,8,10,14,9,7,12,11,10,8,13,10,8,11,10,9,12,9,13,11,那么这组样本数据落在8.5~11.5内的频率是( )A .0.4B .0.5C .0.6D .0.653.★ 某校为了了解学生课外阅读情况,随机调查了50名学生 各自平均每天的课外阅读时间,并绘制成条形图(如图),据此可以估计出该校所有学生平均每人每天的课外阅读时间为( )A.1小时 B.0.9小时 C.0.5小时 D.1.5小时4. ★ 某校测量了初三(1)班学生的体重(精确到1cm ),按到如下频数分布直方图,则下列说法正确的是( ) A.该班人数最多的体重段的学生数为7人 B.该班体重低于60.5的学生数为15人 C.该班体重最重段的学生数为20人 D.该班体重最重段的学生数为7人二、填空题(每题7分,共28分)5.★★ 某校抽查了50名九年级学生对手足口病三种主要传播途径的知晓情况,结果如下表:估计该校九年级600学生中,三种传播途径都知道的有 人.间/cm三种传播途径都知道的有300人.6.★ 已知在一个样本中,50个数据分别落在5个组内,第一、二、三、五组数据的个数分别为2,8,15,5,则第四组的频数和频率分别是________.7. ★ 在对100个数据进行,各小组的频数之和 ,各组数据频率和 . 8. ★ 某班的数学期中考试成绩中,最大的数据是145分,最少的是75分,,对这组数据进行整理后,确定它们的组距为7分,则这组数据可分为 组. 三、解答题(9题16分,10题12分,11题16分)9. ★★ 为了解初三6000名学生初中中考英语成绩(分数为整数)从中抽取了200名学生的英语成绩进行分析,下面是200名学生数学成绩的频率分布表:根据所给信息回答下列问题:(1)频率分布表中的数据__________a b ==,; (2)中位数落在 分数段内;(3)若成绩不低于120分的为优秀,试估计初三学生初中毕业考试英语成绩优秀的学生有 人.10.★ 为了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得到的数据整理后,画出频数分布直方图(如图),图中从左到右依次为第1、2、3、4、5组.(1)求抽取了多少名男生测量身高.(2)身高在哪个范围内的男生人数最多?(答出是第几小组即可)11.★★ 幸福中学为了了解本校中学生的身体发育状况,对八年级同龄的40名女学生的身高进行了测量,结果如下(数据均为整数,单位:厘米):167,154,159,166,169,159,162,158,159,160,164,160,157,161,158,153,158,164,158,163,158,x ,157,162,159,165,157,151,146,151,160,165,158,163,162,154,149,168,164统计人员将上述数据整理后,列出了频率分布表并画出了频数分布直方图如下:cm )根据以上信息回答下列问题:(1)频率分布表中,A、B、C、D各是多少?(2)原数据组中,x的值可能是多少?请说明理由。
青岛版数学九年级下册6.2《频数与频率》练习题

6.2 频数与频率一、选择题(共20小题;共100分)1. 下表是我国部分城市气象台对五月某一天最高温度的预报,当天预报最高温度数据的中位数是2. 频数、频率与实验总次数之间的关系是 ( )A. 频数越大,频率越大B. 总次数一定时,频数越大,频率可无限大C. 频数与总次数成正比D. 频数一定时,频率与总次数成反比3. 调查某班名同学的跳高成绩时,在收集到的数据中,不足米的数出现的频率是,则达到或超过米的数出现的频率是 ( )A. B. C. D.4. 某学校为了了解九年级学生体能情况,随机选取名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图.学生仰卧起坐次数在之间的频率为A. B. C. D.5. 绘制频数分布直方图时,计算出最大值与最小值的差为,若取组距为,则最好应分( )A. 组B. 组C. 组D. 组或组6. 在一个不透明的布袋中装有红色、白色玻璃球共个,除颜色外其他完全相同.小明通过多次摸球试验发现,摸到红色球的频率稳定在左右,则口袋中红色球可能有 ( )A. 个B. 个C. 个D. 个7. 某校为了了解九年级学生的体能情况,随机抽查了其中的名学生,测试了分钟仰卧起座的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起座次数在次之间的频率是A. B. C. D.8. 某市对名年满岁的男生的身高进行了测量,结果身高(单位: )在这一小组的频率为,则该组的人数为 ( )A. 人B. 人C. 人D. 人9. 在一个不透明的袋子里装有个黑球和若干个白球,它们除颜色外都相同.在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用如下办法:随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,记下颜色,,不断重复上述过程.小明共摸次,其中次摸到黑球.根据上述数据,小明估计口袋中白球大约有 ( )A. 个B. 个C. 个D. 个10. 将个数据分成个组,如下表:则第六组的频数为 ( )A. B. C. D.11. 大课间活动在我市各校蓬勃开展.某班大课间活动抽查了名学生每分钟跳绳次数,获得如下数据(单位:次):,,,,,,,,,,,,,,,,,,,.则跳绳次数在这一组的频率是 ( )A. B. C. D.12. 王老师对本班名学生的血型作了统计,列出如下的统计表,则本班型血的人数是组别型型型型频率A. 人B. 人C. 人D. 人13. 某校对名女生的身高进行了测量,身高在 (单位: )这一小组的频率为.,则该组的人数为 ( )A. 人B. 人C. 人D. 人14. 下列说法正确的是 ( )A. 频数越小,频率越大B. 频数大,频率也一定大C. 频数一定时,频率越小,总次数越大D. 频数很大时,频率可能超过15. 对个数据进行处理时,适当分组,各组数据个数之和与百分率之和分别等于 ( )A. ,B. ,C. ,D. ,16. 一个容量为的样本最大值为,最小值,取组距为,则可以分成 ( )A. 组B. 组C. 组D. 组17. 在样本的频数分布直方图中,有个小长方形,若中间一个小长方形的面积等于其它个小长方形面积的和的四分之一,且样本数据有个,则中间一组的频数为 ( )A. B. C. D.18. 已知一组数据,,,,,,,,,,,,,,,,,,,,那么频率为的范围是 ( )A. B. C. D.19. 为了了解某地区初三学生的身体发育情况,抽查了该地区名年龄为岁- 岁的男生体重(),得到频率分布直方图如下:根据上图可得这名学生中体重大于等于小于等于的学生人数是A. B. C. D.20. 在对某地区的一次人口抽样统计分析中,各年龄段(年龄为整数)的人数如下表所示,请根据此表回答下列问题.样本年龄在 A.B.C.D.二、填空题(共4小题;共20分)21. 对某中学同年龄的 名女学生的身高进行测量,得到一组数据,其中最大值是 ,最小值是 ,对这组数据进行整理时,打算把它们分成 组,则组距是 .22. 某班级 名学生在阶段性测试中,分数段在 分的频率为 ,则该班级在这个分数段的学生有 人.23. 已知一个县有 人参加全国初中物理竞赛,把他们的成绩分为六组,第一组到第四组的频数分别是 , , , ,第五组的频率是 ,则第六组的频率是 .24. 七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):若该小区有 户家庭,据此估计该小区月均用水量不超过 的家庭约有 户.三、解答题(共5小题;共65分)25. 某校八年级所有女生的身高统计数据如下表,请回答下列问题:(1) (2) 身高在 到 的女生有多少人?(3) 一女生的身高恰好为,哪一组包含这个身高?这一组出现的频数、频率各是多少?26. 以下问题中的数据在美国的历史上都是真实的,试对此现象进行分析:(1) 亚利桑那州历来是一个风景优美,气候宜人的地方,尤其有利于肺结核病人的疗养、康复.可是十九世纪有一位统计学家发现,在亚利桑那州死于肺结核的人数远较其他州多,患者比例普遍达到其他州的至倍.人们一度对这里优美的环境望而却步,给当地的旅游、疗养业造成了巨大的影响.(2) 上个世纪,某地的房产开发商曾对当时每户家庭人数进行过较大规模的调查,得到的结论是平均每户人.据此,在当年的住房设计中主要考虑了适宜人家庭居住的户型,结果造成了滞销,而适宜至人家庭居住的小户型和人以上的大户型却供不应求.27. 九(1)班同学为了解2011 年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:月均用水量频数户频率(1) 把上面的频数分布表和频数分布直方图补充完整;(2) 求月均用水量不超过的家庭数占被调查家庭总数的百分比;(3) 若该小区有户家庭,根据调查数据估计,该小区月均用水量超过的家庭大约有多少户?28. 我市启动了第二届“美丽港城•美在阅读”全民阅读活动.为了解市民每天的阅读时间情况,随机抽取了部分市民进行调查.根据调查结果绘制如下尚不完整的频数分布表:(1) 补全表格;(2) 将每天阅读时间不低于的市民称为“阅读爱好者”.若我市约有万人,请估计我市能称为“阅读爱好者”的市民约有多少万人?29. 5 月23,24日,兰州市九年级学生进行了中考体育测试.某校抽取了部分学生的一分钟跳绳测试成绩,将测试成绩整理后作出如右统计图.甲同学计算出前两组的频率和是,乙同学计算出第一组的频率为,丙同学计算出从左至右第二、三、四组的频数比为.结合统计图回答下列问题:(1) 这次共抽取了多少名学生的一分钟跳绳测试成绩?(2) 若跳绳次数不少于次为优秀,则这次测试成绩的优秀率是多少?(3) 如果这次测试成绩的中位数是次,那么这次测试中,成绩为次的学生至少有多少人?答案第一部分1. B2. D3. B4. D5. C6. B7. A8. A9. B 10. D11. B 12. A 13. B 14. C 15. A16. B 17. B 18. D 19. C 20. A第二部分21.22.23.24.第三部分25. (1) 这个学校八年级共有女生(人).25. (2) 身高在到的女生有(人).25. (3) 从上表可以看出,在第组,第组出现的频数是,频率为.26. (1) 由于亚利桑那州的气候、环境有利于肺结核病人的康复,所以必然会有大量外地患者前来疗养,患者比例、死亡人数的增加就不足为奇.要正确评价当地环境对肺结核患者的作用,应同时调查肺结核病人的治愈、好转率,当地居民中肺结核的发病率等.26. (2) 平均每户人并不表示大多数家庭规模为近人.开发商在关注家庭人数平均数、众数的同时应对数据作全面分析,并注重对近期准备购房对象作调查.事实上,当地媒体事后公布的数据是全部家庭中,人家庭占,人家庭占,人以上家庭占;而两年内购买新房的家庭中人家庭占,人家庭占,人以上家庭占.月均用水量频数户频率27. (1)27. (2) .即月均用水量不超过的家庭数占被调查的家庭总数的.27. (3) .所以根据调查数据统计,该小区月均用水量超过的家庭大约有户.28. (1)28. (2) (万人).答:我市能称为“阅读爱好者”的市民约有万人.29. (1) 第二组的频率为,(名),这次共抽取了名学生的一分钟跳绳测试成绩.29. (2) 第一组人数为(人),第三组人数为人,第四组人数为人.这次测试的优秀率为.29. (3) 成绩为次的学生至少有人.。
中考数学专题复习之 15 频数与频率(含解析)1 精编

15 频数与频率(含解析)一、选择题1.(3分)(2016•苏州)一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、8,则第5组的频率是()A.0.1 B.0.2 C.0.3 D.0.4【分析】根据第1~4组的频数,求出第5组的频数,即可确定出其频率.【解答】解:根据题意得:40﹣(12+10+6+8)=40﹣36=4,则第5组的频率为4÷40=0.1,故选A.【点评】此题考查了频数与频率,弄清题中的数据是解本题的关键.2.(3分)(2016•宜昌)在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其实验次数分别为10次、50次、100次,200次,其中实验相对科学的是()A.甲组B.乙组C.丙组D.丁组【考点】模拟实验.【分析】大量反复试验时,某事件发生的频率会稳定在某个常数的附近,这个常数就叫做事件概率的估计值.【解答】解:根据模拟实验的定义可知,实验相对科学的是次数最多的丁组.故选:D.【点评】考查了模拟实验,选择和抛硬币类似的条件的试验验证抛硬币实验的概率,是一种常用的模拟试验的方法.二、填空题1.(3分)(2016•南宁)如图,在4×4正方形网格中,有3个小正方形已经涂黑,若再涂黑任意一个白色的小正方形(每一个白色的小正方形被涂黑的可能性相同),使新构成的黑色部分的图形是轴对称图形的概率是.【考点】概率公式;轴对称图形.【专题】计算题.【分析】利用轴对称图形的定义由3处涂黑得到黑色部分的图形是轴对称图形,然后根据概率公式可计算出新构成的黑色部分的图形是轴对称图形的概率.【解答】解:共有13种等可能的情况,其中3处涂黑得到黑色部分的图形是轴对称图形,如图,所以涂黑任意一个白色的小正方形(每一个白色的小正方形被涂黑的可能性相同),使新构成的黑色部分的图形是轴对称图形的概率故答案为.3 133 13【点评】本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.也考查了轴对称图形.2.(3分)(2016•大连)下表是某校女子排球队队员的年龄分布则该校女子排球队队员的平均年龄是岁.【考点】加权平均数;频数与频率.【分析】根据加权平均数的计算公式列出算式,再进行计算即可.【解答】解:根据题意得:(13×1+14×1+15×7+16×3)÷12=15(岁),即该校女子排球队队员的平均年龄为15岁.故答案为:15.【点评】此题考查了加权平均数,掌握加权平均数的计算公式是本题的关键.3.(4分)(2016•成都)第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有人.【考点】扇形统计图;用样本估计总体.【分析】先求出“非常清楚”所占的百分百,再乘以该辖区的总居民,即可得出答案.【解答】解:根据题意得:9000×(1﹣30%﹣15%﹣90360×100%)=9000×30%=2700(人).答:可以估计其中对慈善法“非常清楚”的居民约有2700人.故答案为:2700.【点评】此题考查了用样本估计总体,在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.三、解答题1.(8分)(2016•泰州)某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.(1)直接写出频数分布表中a的值;(2)补全频数分布直方图;(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?【考点】频数(率)分布直方图;用样本估计总体;频数(率)分布表.【分析】(1)首先根据围棋类是14人,频率是0.28,据此即可求得总人数,然后利用18除以总人数即可求得a的值;(2)用50乘以0.20求出b的值,即可解答;(4)用总人数1500乘以喜爱围棋的学生频率即可求解.【解答】解:(1)14÷0.28=50(人),a=18÷50=0.36.(2)b=50×0.20=10,如图,(3)1500×0.28=428(人),答:若全校共有学生1500名,估计该校最喜爱围棋的学生大约有428人.【点评】本题考查了频数分布表与扇形统计图,用到的知识点是:频率=频数÷总数,用样本估计整体让整体×样本的百分比即可.2.(8分)(2016•荆州)为了弘扬荆州优秀传统文化,某中学举办了荆州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答为得分、不扣分,(1)表中m= ,n= ;(2)补全频数分布直方图;(3)全体参赛选手成绩的中位数落在第几组;(4)若得分在80分以上(含80分)的选手可获奖,记者从所有参赛选手中随机采访1人,求这名选手恰好是获奖者的概率.【考点】频数(率)分布直方图;频数(率)分布表;中位数;概率公式.【专题】统计与概率.【分析】(1)根据表格可以求得全体参赛选手的人数,从而可以求得m 的值,n 的值;(2)根据(1)中的m 的值,可以将补全频数分布直方图;(3)根据表格可以求得全体参赛选手成绩的中位数落在第几组;(4)根据表格中的数据可以求得这名选手恰好是获奖者的概率.【解答】解:(1)由表格可得,全体参赛的选手人数有:30÷0.1=300,则m=300×0.4=120,n=60÷300=0.2,故答案为:120,0.2;(2)补全的频数分布直方图如右图所示,(3)∵35+45=75,75+60=135,135+120=255,∴全体参赛选手成绩的中位数落在80≤x <90这一组;(4)由题意可得,125450.55300+=, 即这名选手恰好是获奖者的概率是0.55.【点评】本题考查频数分布直方图、频数分布表、中位数、概率公式,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.3.(6分)(2016•江西)为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查,调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图.(1)补全条形统计图.(2)若全校共有3600位学生家长,据此估计,有多少位家长最关心孩子“情感品质”方面的成长?(3)综合以上主题调查结果,结合自身现状,你更希望得到以上四个项目中哪方面的关注和指导?【考点】条形统计图;用样本估计总体.【分析】(1)用甲、乙两班学生家长共100人减去其余各项目人数可得乙组关心“情感品质”的家长人数,补全图形即可;(2)用样本中关心孩子“情感品质”方面的家长数占被调查人数的比例乘以总人数3600可得答案;(3)无确切答案,结合自身情况或条形统计图,言之有理即可.【解答】解:(1)乙组关心“情感品质”的家长有:100﹣(18+20+23+17+5+7+4)=6(人),补全条形统计图如图:(2)46100×3600=360(人). 答:估计约有360位家长最关心孩子“情感品质”方面的成长;(3)无确切答案,结合自身情况或条形统计图,言之有理即可,如:从条形统计图中,家长对“情感品质”关心不够,可适当关注与指导.【点评】本题主要考查条形统计图,条形统计图能清楚地表示出每个项目的数据,熟知各项目数据个数之和等于总数,也考查了用样本估计总体.4.(8分)(2016•百色)某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选(2)若用扇形图来描述,求分数在8≤m <9内所对应的扇形图的圆心角大小;(3)将在第一组内的两名选手记为:A 1、A 2,在第四组内的两名选手记为:B 1、B 2,从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).【考点】列表法与树状图法;频数(率)分布表;扇形统计图.【专题】统计与概率.【分析】(1)根基被调查人数为20和表格中的数据可以求得a 的值;(2)根据表格中的数据可以得到分数在8≤m <9内所对应的扇形图的圆心角大;(3)根据题意可以写出所有的可能性,从而可以得到第一组至少有1名选手被选中的概率.【解答】解:(1)由题意可得,a=20﹣2﹣7﹣2=9,即a 的值是9;(2)由题意可得,分数在8≤m <9内所对应的扇形图的圆心角为:360°×209=162°; (3)由题意可得,所有的可能性如下图所示,故第一组至少有1名选手被选中的概率是:1210=65, 即第一组至少有1名选手被选中的概率是65. 【点评】本题考查列表法与树状图法、频数分布表、扇形统计图,解题的关键是明确题意,找出所求问题需要的条件.5.(7分)(2016•深圳)深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图)根据上述统计图可得此次采访的人数为 人,m= ,n= ;(2)根据以上信息补全条形统计图;(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有 人.【考点】条形统计图;用样本估计总体;频数与频率.【分析】(1)根据频数÷频率,求得采访的人数,根据频率×总人数,求得m 的值,根据30÷200,求得n 的值;(2)根据m 的值为20,进行画图;(3)根据0.1×15000进行计算即可.【解答】解:(1)此次采访的人数为100÷0.5=200(人),m=0.1×200=20,n=30÷200=0.15;(2)如图所示;(3)高度关注东进战略的深圳市民约有0.1×15000=1500(人).【点评】本题主要考查了条形统计图以及频数与频率,解决问题的关键是掌握:频率是指每个对象出现的次数与总次数的比值(或者百分比),即频率=.解题时注意,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.6.(2016•毕节市)为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以(1)本次决赛共有名学生参加;(2)直接写出表中a=,b=;(3)请补全下面相应的频数分布直方图;(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为.【考点】频数(率)分布直方图;频数(率)分布表.【专题】探究型;统计与概率.【分析】(1)根据表格中的数据可以求得本次决赛的学生数;(2)根据(1)中决赛学生数,可以求得a、b的值;(3)根据(2)中a的值,可以将频数分布直方图补充完整;(4)根据表格中的数据可以求得本次大赛的优秀率.【解答】解:(1)由表格可得,本次决赛的学生数为:10÷0.2=50,故答案为:50;(2)a=50×0.32=16,b=14÷50=0.28,故答案为:16,0.28;(3)补全的频数分布直方图如右图所示,(4)由表格可得,决赛成绩不低于80分为优秀率为:(0.32+0.16)×100%=48%,故答案为:48%.【点评】本题考查频数分布直方图、频数分布表,解题的关键是明确题意,找出所求问题需要的条件.7.(8分)(2016•娄底)在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取利了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:根据所给信息,解答下列问题:(3)按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参赛,请估计约有多少人进入决赛?【分析】(1)用抽查的总人数乘以成绩在70≤x<80段的人数所占的百分比求出m;用成绩在80≤x<90段的频数除以总人数即可求出n;(2)根据(1)求出的m的值,直接补全频数分布直方图即可;(3)用娄底市共有的人数乘以80分以上(包括80分)所占的百分比,即可得出答案.【解答】解:(1)根据题意得:m=200×0.40=80(人),n=40÷200=0.20;故答案为:80,0.20;(2)根据(1)可得:70≤x<80的人数有80人,补图如下:(3)根据题意得:4000×(0.20+0.10)=1200(人).答:估计约有1200人进入决赛.【点评】本题考查读频数(率)分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.8.(8分)(2016•邵阳)为了解市民对全市创卫工作的满意程度,某中学教学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.请结合图中信息,解决下列问题:(1)求此次调查中接受调查的人数.(2)求此次调查中结果为非常满意的人数.(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2为进行回访,已知4为市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.【分析】(1)由满意的有20人,占40%,即可求得此次调查中接受调查的人数.(2)由(1),即可求得此次调查中结果为非常满意的人数.(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与选择的市民均来自甲区的情况,再利用概率公式即可求得答案.【解答】解:(1)∵满意的有20人,占40%,∴此次调查中接受调查的人数:20÷40%=50(人);(2)此次调查中结果为非常满意的人数为:50﹣4﹣8﹣20=18(人);(3)画树状图得:∵共有12种等可能的结果,选择的市民均来自甲区的有2种情况, ∴选择的市民均来自甲区的概率为:122=61. 【点评】此题考查了列表法或树状图法求概率以及条形与扇形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.9.(10分)(2016•益阳)在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据a= ,b= ,并将统计图补充完整;(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?【分析】(1)由统计图易得a 与b 的值,继而将统计图补充完整;(2)利用用样本估计总体的知识求解即可求得答案;(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所选两人正好都是甲班学生的情况,再利用概率公式即可求得答案.【解答】解:(1)a=1﹣0.15﹣0.35﹣0.20=0.3;∵总人数为:3÷0.15=20(人),∴b=20×0.20=4(人);故答案为:0.3,4;补全统计图得:(2)估计仰卧起坐能够一分钟完成30或30次以上的女学生有:180×(0.35+0.20)=99(人);(3)画树状图得:∵共有12种等可能的结果,所选两人正好都是甲班学生的有3种情况,∴所选两人正好都是甲班学生的概率是:312=14.【点评】此题考查了列表法或树状图法求概率以及条形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.10.(6分)(2016•金华)某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“A,B,C”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题:(1)抽取的学生中,训练后“A”等次的人数是多少?并补全统计图.(2)若学校有600名学生,请估计该校训练后成绩为“A”等次的人数.【考点】条形统计图.【分析】(1)将训练前各等级人数相加得总人数,将总人数减去训练后B、C两个等级人数可得训练后A等级人数;(2)将训练后A等级人数占总人数比例乘以总人数可得.【解答】解:(1)∵抽取的人数为21+7+2=30,∴训练后“A”等次的人数为30﹣2﹣8=20.补全统计图如图:(2)600×2030=400(人).答:估计该校九年级训练后成绩为“A”等次的人数是400.【点评】本题主要考查条形统计图,根据统计图读出训练前后各等级的人数及总人数间的关系是解题的关键,也考查了样本估计总体.11.(8分)(2016•丽水)为了帮助九年级学生做好体育考试项目的选考工作,某校统计了本县上届九年级毕业生体育考试各个项目参加的男、女生人数及平均成绩,并绘制成如图两个统计图,请结合统计图信息解决问题.(1)“掷实心球”项目男、女生总人数是“跳绳”项目男、女生总人数的2倍,求“跳绳”项目的女生人数;(2)若一个考试项目的男、女生总平均成绩不小于9分为“优秀”,试判断该县上届毕业生的考试项目中达到“优秀”的有哪些项目,并说明理由;(3)请结合统计图信息和实际情况,给该校九年级学生体育考试项目的选择提出合理化建议.【考点】条形统计图;频数(率)分布折线图.【分析】(1)先根据统计图得到“掷实心球”项目男、女生总人数,除以2可求“跳绳”项目男、女生总人数,再减去“跳绳”项目男生人数,即可得到“跳绳”项目的女生人数;(2)根据平均数公式得到该县上届毕业生的考试项目中达到“优秀”的有哪些项目即可求解;(3)根据统计图提出合理化建议,合理即可.【解答】解:(1)(400+600)÷2﹣260=1000÷2﹣260=500﹣260=240(人)答:“跳绳”项目的女生人数是240人;(2)“掷实心球”项目平均分:(400×8.7+600×9.2)÷(400+600)=(3480+5520)÷1000=9000÷1000=9(分),投篮项目平均分大于9分,其余项目平均分小于9分.故该县上届毕业生的考试项目中达到“优秀”的有投篮,掷实心球两个项目.(3)如:游泳项目考试的人数最多,可以选考游泳.【点评】本题考查的是条形统计图、频数(率)分布折线图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.12.(5分)(2016•张家界)在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:m=,n=;(2)补全条形统计图;(3)本次活动师生共捐书2000本,请估计有多少本科普类图书?【考点】条形统计图;用样本估计总体;频数(率)分布表.【分析】(1)根据频率之和为1可得n的值,再根据科普类书籍的数量和百分比求得总数,由频数之和等于总数可得m的值;(2)由(1)中m的值即可补全条形图;(3)用样本中科普类书籍的百分比乘以总数可得答案.【解答】解:(1)n=1﹣35%﹣20%﹣15%=30%,∵此次抽样的书本总数为12÷30%=40(本),∴m=40﹣12﹣14﹣6=8,故答案为:8,30%.(2)补全条形图如图:(3)2000×30%=600(本)答:估计有600本科普类图书.【点评】本题考查的是条形统计图和频数分布表,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键,熟练掌握频数之和等于总数、频率之和等于1是解题的关键.13.(6分)(2016•无锡)某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:(1)表中a=,b=;(2)请把频数分布直方图补充完整(画图后请标注相应的数据);(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?【考点】频数(率)分布直方图;用样本估计总体;频数(率)分布表.【分析】(1)直接利用已知表格中3<x≤6范围的频率求出频数a即可,再求出m的值,即可得出b的值;(2)利用(1)中所求补全条形统计图即可;(3)直接利用参加社区活动超过6次的学生所占频率乘以总人数进而求出答案.【解答】解:(1)由题意可得:a=50×0.24=12(人),∵m=50﹣10﹣12﹣16﹣6﹣2=4,∴b=450=0.08;故答案为:12,0.08;(2)如图所示:;(3)由题意可得,该校在上学期参加社区活动超过6次的学生有:1200×(1﹣0.20﹣0.24)=648(人),答:该校在上学期参加社区活动超过6次的学生有648人.【点评】此题主要考查了频数分布直方图以及利用样本估计总体,正确将条形统计图和表格中数据相联系是解题关键.14.(10分)(2016•荆门)秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,(1)在表中,a=,b=,c=;(2)补全频数直方图;(3)根据以上选取的数据,计算七年级学生的平均成绩.(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?【考点】频数(率)分布直方图;用样本估计总体;频数(率)分布表;加权平均数.【专题】统计与概率.【分析】(1)根据表格中的数据可以求得抽查的学生数,从而可以求得a、b、c的值;(2)根据(1)中c的值,可以将频数分布直方图补充完整;(3)根据平均数的定义和表格中的数据可以求得七年级学生的平均成绩;(4)根据表格中的数据可以求得“优秀”等次的学生数.【解答】解:(1)抽查的学生数:36÷0.4=90,a=9÷90=0.1,b=27÷90=0.3,c=90×0.2=18,故答案为:0.1,0.3,18;(2)补全的频数分布直方图如右图所示,(3)∵96536752785189590????=81,即七年级学生的平均成绩是81分;(4)∵800×(0.3+0.2)=800×0.5=400,即“优秀”等次的学生约有400人.【点评】本题考查频数分布直方图、用样本估计总体、加权平均数,解题的关键是明确题意,利用表格中的数据,求出所求问题的答案.15.(10分)(2016•宁夏)某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据,整理绘制出下面的条形统计图:设x表示水彩笔在使用期内需要更换的笔芯个数,y表示每支水彩笔在购买笔芯上所需要的费用(单位:元),n表示购买水彩笔的同时购买的笔芯个数.(1)若n=9,求y与x的函数关系式;(2)若要使这30支水彩笔“更换笔芯的个数不大于同时购买笔芯的个数”的频率不小于0.5,确定n的最小值;(3)假设这30支笔在购买时,每支笔同时购买9个笔芯,或每支笔同时购买10个笔芯,分别计算这30支笔在购买笔芯所需费用的平均数,以费用最省作为选择依据,判断购买一支水彩笔的同时应购买9个还是10个笔芯.【考点】一次函数的应用;频数与频率;条形统计图.【分析】(1)根据题意列出函数关系式;(2)由条形统计图得到需要更换笔芯的个数为7个对应的频数为4,8个对应的频数为6,9个对应的频数为8,即可.(3)分两种情况计算【解答】解:(1)当n=9时,y=⎩⎨⎧⨯-+⨯=⨯5)9(932793x =27(9)518(x x x ≤⎧⎨-⎩>9);(2)根据题意,“更换笔芯的个数不大于同时购买笔芯的个数”的频率不小于0.5,则“更换笔芯的个数不大于同时购买笔芯的个数”的频数大于30×0.5=15,根据统计图可得,需要更换笔芯的个数为7个对应的频数为4,8个对应的频数为6,9个对应的频数为8,因此当n=9时,“更换笔芯的个数不大于同时购买笔芯的个数”的频数=4+6+8=18>15. 因此n 的最小值为9.(3)若每支笔同时购买9个笔芯,则所需费用总和=(4+6+8)×3×9+7×(3×9+5×1)+5×(3×9+5×2)=895, 费用的平均数:1796. 若每支笔同时购买10个笔芯, 则所需费用总和=(4+6+8+7)×3×10+5×(3×10+5×1)=925,费用的平均数:1856. 因此应购买9个笔芯.【点评】此题是一次函数的应用,主要考查了一次函数的性质,统计图,解本题的关键是统计图的分析.16.(7分)(2016•泸州)为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表(1)计算出表中a 、b 的值;(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?【分析】(1)先求出抽取的总人数,再求出b 的值,进而可得出a 的值;(2)求出a 的值与总人数的比可得出结论;(3)求出喜爱新闻类人数的百分比,进而可得出结论.【解答】解:(1)∵喜欢体育的人数是90人,占总人数的20%,∴总人数=9020%=450(人). ∵娱乐人数占36%,。
中考数学专题复习之 15 频数与频率(含解析)2 精编

15 频数与频率(含解析)一、选择题1.(3分)(2016•台湾)有一个三位数8□2,□中的数字由小欣投掷的骰子决定,例如,投出点数为1,则8□2就为812.小欣打算投掷一颗骰子,骰子上标有1~6的点数,若骰子上的每个点数出现的机会相等,则三位数8□2是3的倍数的机率为何?(B)A.12B.13C.16D.310【考点】概率公式.【分析】根据3的倍数的特征,可得出所有的可能性,再用概率公式计算即可.【解答】解:投掷一颗骰子,共有6种可能的结果,当点数为2或5时,三位数8□2是3的倍数,则三位数8□2是3的倍数的机率为26=13,故选B.【点评】本题考查了概率公式,解题的关键是列出所有可能的结果,以及概率公式P(A)=nm.2.(3分)(2016•台湾)甲箱内有4颗球,颜色分别为红、黄、绿、蓝;乙箱内有3颗球,颜色分别为红、黄、黑.小赖打算同时从甲、乙两个箱子中各抽出一颗球,若同一箱中每球被抽出的机会相等,则小赖抽出的两颗球颜色相同的机率为何?()A.13B.16C.27D.712【分析】画出树状图,得出共有12种等可能的结果,颜色相同的有2种情形,即可得出结果.【解答】解:树状图如图所示:共有12种等可能的结果,颜色相同的有2种情形,故小赖抽出的两颗球颜色相同的机率=21 126;故选:B.【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比3.1.1.(3分)(2016•北京)为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断合理的是()①年用水量不超过180m3的该市居民家庭按第一档水价交费;②年用水量超过240m3的该市居民家庭按第三档水价交费;③该市居民家庭年用水量的中位数在150﹣180之间;④该市居民家庭年用水量的平均数不超过180.A.①③B.①④C.②③D.②④【分析】利用条形统计图结合中位数的定义分别分析得出答案.【解答】解:①由条形统计图可得:年用水量不超过180m3的该市居民家庭一共有(0.25+0.75+1.5+1.0+0.5)=4(万),45×100%=80%,故年用水量不超过180m3的该市居民家庭按第一档水价交费,正确;②∵年用水量超过240m3的该市居民家庭有(0.15+0.15+0.05)=0.35(万),∴0.355×100%=7%≠5%,故年用水量超过240m3的该市居民家庭按第三档水价交费,故此选项错误;③∵5万个数数据的中间是第25000和25001的平均数,∴该市居民家庭年用水量的中位数在120﹣150之间,故此选项错误;④由①得,该市居民家庭年用水量的平均数不超过180,正确,故选:B.【点评】此题主要考查了频数分布直方图以及中位数的定义,正确利用条形统计图获取正确信息是解题关键.2.3.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.二、填空题1.4分)(2016•自贡)一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机选择一条路径,则它获取食物的概率是 31 .【考点】列表法与树状图法.【分析】根据树状图判断出蚂蚁一共有多少种路可以选择,有几种可能可以获取食物即可解决问题.【解答】解:根据树状图,蚂蚁获取食物的概率是62=31.故答案为31. 【点评】本题考查树状图、概率等知识,记住概率的定义是解决问题的关键,考虑问题要全面,属于中考常考题型.2.1.1.(2016•长沙)若同时抛掷两枚质地均匀的骰子,则事件“两枚骰子朝上的点数互不相同”的概率是 56. 【考点】列表法与树状图法.【分析】画出树状图,然后根据概率公式列式计算即可得解.【解答】解:由题意作出树状图如下:一共有36种情况,“两枚骰子朝上的点数互不相同”有30种,所以,P=3036=56. 故答案为:56. 【点评】本题考查了列表法与树状图法,用到的知识点:概率=所求情况数与总情况数之比.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.三、解答题1.1.1.(10分)(2016•荆门)秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,(1)在表中,a=0.1,b=0.3,c=18;(2)补全频数直方图;(3)根据以上选取的数据,计算七年级学生的平均成绩.(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?【考点】频数(率)分布直方图;用样本估计总体;频数(率)分布表;加权平均数.【专题】统计与概率.【分析】(1)根据表格中的数据可以求得抽查的学生数,从而可以求得a、b、c的值;(2)根据(1)中c的值,可以将频数分布直方图补充完整;(3)根据平均数的定义和表格中的数据可以求得七年级学生的平均成绩;(4)根据表格中的数据可以求得“优秀”等次的学生数.【解答】解:(1)抽查的学生数:36÷0.4=90,a=9÷90=0.1,b=27÷90=0.3,c=90×0.2=18,故答案为:0.1,0.3,18;(2)补全的频数分布直方图如右图所示,(3)∵96536752785189590⨯+⨯+⨯+⨯=81,即七年级学生的平均成绩是81分;(4)∵800×(0.3+0.2)=800×0.5=400,即“优秀”等次的学生约有400人.【点评】本题考查频数分布直方图、用样本估计总体、加权平均数,解题的关键是明确题意,利用表格中的数据,求出所求问题的答案.2.1.(2016•聊城)为了让书籍开拓学生的视野,陶冶学生的情操,向阳中学开展了“五个一”课外阅读活动,为了解全校学生课外阅读情况,抽样调查了50名学生平均每天课外阅读时(2)请在给出的平面直角坐标系中画出相应的频数直方图;(3)如果该校有1500名学生,请你估计该校共有多少名学生平均每天阅读时间不少于50min?【分析】(1)根据总人数50,以及表格中的数据确定出所求数据,填写表格即可;(2)根据表格中的数据作出相应的频数直方图,如图所示;(3)由时间不少于50min的百分比,乘以1500即可得到结果.(3)根据题意得:1500×(0.28+0.12+0.04)=660(人),则该校共有660名学生平均每天阅读时间不少于50min.【点评】此题考查了频数分布直方图,用样本估计总体,以及频数分布表,弄清题中的数据是解本题的关键.1.(8分)(2016•海南)在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:请结合图表中的信息解答下列问题:(1)统计表中,a=15,b=0.3;(2)将频数分布直方图补充完整;(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为72°;(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有300株.【考点】频数(率)分布直方图;用样本估计总体;频数(率)分布表;扇形统计图.【专题】统计与概率.【分析】(1)根据题意可以求得a的值、b的值;(2)根据(1)中a的值,可以将频数分布直方图补充完整;(3)根据挂果数量在“35≤x<45”所对应的频率,可以求得挂果数量在“35≤x<45”所对应扇形的圆心角度数;(4)根据频数分布直方图可以估计挂果数量在“55≤x<65”范围的番茄的株数.【解答】解:(1)0.1612189156a=----=.180.360b==.故答案是:15,0.3;(2)补全的频数分布直方图如右图所示,(3)由题意可得,挂果数量在“35≤x<45”所对应扇形的圆心角度数为:360°×0.2=72°,故答案为:72;(4)由题意可得,挂果数量在“55≤x<65”范围的番茄有:1000×0.3=300(株),故答案为:300.【点评】本题考查频数分布直方图、用样本估计总体、扇形圆心角的度数,解题的关键是明确题意,找出所求问题需要的条件.2.1.(10分)(2016•齐齐哈尔)为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:(1)本次调查属于抽样调查,样本容量是50;(2)请补全频数分布直方图中空缺的部分;(3)求这50名学生每周课外体育活动时间的平均数;(4)估计全校学生每周课外体育活动时间不少于6小时的人数.【考点】频数(率)分布直方图;总体、个体、样本、样本容量;用样本估计总体;加权平均数.【专题】统计与概率.【分析】(1)根据题目中的信息可知本次调查为抽样调查,也可以得到样本容量;(2)根据每周课外体育活动时间在6≤x<8小时的学生人数占24%,可以求得每周课外体育活动时间在6≤x<8小时的学生人数,从而可以求得2≤x<4的学生数,从而可以将条形统计图补充完整;(3)根据条形统计图可以得到这50名学生每周课外体育活动时间的平均数;(4)根据条形统计图,可以估计全校学生每周课外体育活动时间不少于6小时的人数.【解答】解:(1)由题意可得,本次调查属于抽样调查,样本容量是50,故答案为:抽样,50;(2)由题意可得,每周课外体育活动时间在6≤x<8小时的学生有:50×24%=12(人),则每周课外体育活动时间在2≤x<4小时的学生有:50﹣5﹣22﹣12﹣3=8(人),补全的频数分布直方图如右图所示,(3)由题意可得,=5,即这50名学生每周课外体育活动时间的平均数是5;(4)由题意可得,全校学生每周课外体育活动时间不少于6小时的学生有:1000×(人),即全校学生每周课外体育活动时间不少于6小时的学生有300人.【点评】本题考查频数分布直方图、样本、总体、样本容量、用样本估计总体、加权平均数,解题的关键是明确题意,找出所求问题需要的条件.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.。
初三年级数学下学期《频数与频率》课后练习

初三年级数学下学期《频数与频率》课后练习学习是一个边学新知识边牢固的过程,对学过的知识一定要多加练习,这样才能进步,所以小编为大家整理了一份频数与频率课后练习,供大家参照。
一、选择题 (每题 5 分,共 30 分)1.一个扇形统计图中,扇形 A.B.C.D 的面积之比为2∶ 1∶ 4∶ 5,则最大扇形的圆心角为( )A.80B.100C.120D.150分组频数频率151.5~156.5~156.5~ 166.56a166.5~171.5~2.某校为了认识九年级全体男生的身体发育情况,对20名男生的身高进行了测量(测量结果均为整数,单位:厘米).将所得的数据整理后,列出频率分布表,以下表所示:则以下结论中: (1)此次抽样解析的样本是20 名学生 ;(2)频率分布表中的数据a=0.30;(3) 身高 167cm(包括 167cm) 的男生有9 人,正确的有 ( )A.(1)(2)(3)B.(1)(2)C.(1)(3)D.(2)(3)4.如图,是一个正在绘制的扇形统计图,整个圆表示某班参加体育活动的总人数,那么表示参加立定跳远训练的人数占总人数的 35%的扇形是 ( )7.如图为 2019~ 2019 年我国国内生产总值年增添率的变化情况,从图上看,以下结论中不正确的选项是( )A.2019 ~ 2019 年,国内生产总值的年增添率逐年减少B.2019 年国内生产总值的年增添率开始上升C.这 7 年中,每年的国内生产总值不断增添D.这 7 年中,每年的国内生产总值有增有减5.某校宣告了该校反响各年级学生体育达标情况的两张统计图,该校七 .八 .九三个年级共有学生800 人.甲.乙.丙三个同学看了这两张统计图后,甲说:七年级的体育达标率最高.乙说:八年级共有学生264 人 .丙说:九年级的体育达标率最高.甲.乙.丙三个同学中,说法正确的选项是( )A. 甲和乙B.乙和丙C.甲和丙D.甲和乙及丙6.长三角 16 个城市中浙江省有 7 个城市 .以下列图分别表示 2019 年这 7 个城市 GDP( 公民生产总值 ) 的总量和增添快度 .则以下对嘉兴经济的议论,错误的选项是( )A.GDP 总量列第五位B.GDP 总量高出平均值C.经济增添快度列第二位D. 经济增添快度高出平均值二、填空题 (每题 5 分,共 30 分)3.一个样本含有下面10 个数据: 52, 51, 49, 50, 47, 48,50, 51,48, 53,则最大的值是_________,最小的值是_________,若是组距为 1.5,则应分成 ________组 .5.在数据 55,66,23,33,22,65,84,87,23,24,88 中,大于等于 50 而小于等于70 的数共有 _________个6.在扇形统计图中,有两个扇形的圆心角度数之比为 3∶ 4,且较小扇形表示 24 本课本书,则较大扇形表示 ________本课本书 .10.一组数据共 50 个,分别落在 5 个小组内,第一 .二 .三.四组的数据分别为,则第五小组的频数和频率分别为________._________.11.已知样本 25,21, 23,25, 27,29, 25,28, 30,29,26, 24,25, 27,26, 22,24, 25,26, 28.若取组距为2,那么应分为 ______组,在 24.5~26.5 这一组的频数是_______.12.小亮检查本班同学的身高后,将数据绘制成以以下列图所示的频数分布直方图(每小组数据包括最小值,但不包括最大值.比方,第二小组数据x 满足: 145150,其他小组的数据近似).设班上学生身高的平均数为,则的取值范围是_______________.三、解答题 (每题 10 分,共 40 分)13.甲.乙两人在某公司做见习销售员,销售小天鹅洗衣机,他们在 1~ 8 月份的销售情况以下表所示:月份1月2月3月4月5月6月7月8月甲的销售量 (单位:台 )78676677乙的销售量 (单位:台 )56567789(1)在右边给出的坐标系中,绘制甲.乙两人这8个月的月销售量的折线图: (甲用实线 ;乙用虚线 )(2)请依照 (1)中的折线图,写出 2 条关于甲 .乙两人在这8 个月中的销售情况的信息.①② .14.为了认识学生参加体育活动的情况,学校订学生进行随机抽样检查,其中一个问题是你平均每天参加体育活动的时间是多少 ?,共有 4 个选项:A.1.5 小时以上B.1 ~ 1.5 小时C.0.51 小时D.0.5 小时以下图 1.2 是依照检查结果绘制的两幅不完满的统计图,请你依照统计图供应的信息,解答以下问题:(1)本次一共检查了多少名学生?(2)在图 1 中将选项 B 的部分补充完满;(3)若该校有3000 名学生,你估计全校可能有多少名学一生均每天参加体育活动的时间在0.5 小时以下 .图1 图215.以下列图表示的是某班同学衣服上口袋的数目:(1)从图中可否可以得出以下信息?①只有 4 个人的衣服上有 4 个口袋 ;②只有 1 个人的衣服上有8个口袋;③只有 3 个人的衣服上有 5 个口袋 ;(2)依照上图填写下面的频数分布表,并绘制频数分布直方图.口袋数目 x35x799频数记录频数16.某校为了认识九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出以下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数很多于 100 次的同学占96%,丙同学计算出从左至右第二.三.四组的频数比为4∶ 17∶15.结合统计图回答以下问题:(1)此次共抽调了多少人?(2)若跳绳次数很多于130 次为优秀,则此次测试成绩的优秀率是多少 ?四、拓展研究 (不计入总分 )17.人们常用人均教育经费来反响一个地区对教育投入的情况,我国 30 个城市 2019 年人均教育经费的统计数据以下.(单位:元 )北京 731 南宁 100长春 101重庆 102乌鲁木齐 171青岛 425深圳 584合肥 192武汉 184上海 790兰州 170呼和浩特206 广州 483 天津 440 郑州 197南京 292福州 349洛阳 127南昌 117贵阳 166吉林 76 海口 183 济南 205 昆明 234 西安 126成都 160 哈尔滨 249 石家庄 228 长沙 155 沈阳 237 (1)将以上数据进行以下分组,并填写表格:人均教育经费城市数 (频数 )(2)画出分布直方图和折线图.参照答案1.D2.B3.C4.D5.A6.B7.53 47 48.39.3210.5 0.1 11.5 8 12.13.(1)略 (2)①乙的月销售量整体上送上升趋势;②甲的月销售量整体上呈平稳态势;等等 .14.(1)解 :200 名 (2)略 (3)30005%=150 人15.(1)能获取①③ ;(2)口袋数目 x35x799频数记录频数 4761216.(1)此次共抽调150 人 ;(2)26.67%;17.(1)人均教育经费城市数 (频数 )815322(2)图略 .这个工作可让学生分组负责收集整理,登在小黑板上 ,每周一换。
中考数学专项复习《频数与频率(2)》练习(无答案)浙教版

频数与频率(02)一、选择题1.乐山大佛景区2013年5月份某周的最高气温(单位:℃)分别为:29,31,23,26,29,29,29.这组数据的极差为()A.29 B.28 C.8 D.62.一组数据1,2,2,3.下列说法正确的是( )A.众数是3 B.中位数是2 C.极差是3 D.平均数是33.为了解某射击运动员的射击成绩,从一次训练中随机抽取了了该运动员的10次射击成绩,纪录如下;8,9,8,8,10,9,10,8,9,10.这组数据的极差是()A.9 B.8.9 C.8 D.24.为了解某小区家庭垃圾袋的使用情况,小亮随机调查了该小区10户家庭一周的使用数量,结果如下(单位:个):7,9,11,8,7,14,10,8,9,7.关于这组数据,下列结论错误的是( )A.极差是7 B.众数是8 C.中位数是8。
5 D.平均数是95.为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:5102050100捐款的数额(单位:元)人数(单位:个)24531关于这15名学生所捐款的数额,下列说法正确的是( )A.众数是100 B.平均数是30 C.极差是20 D.中位数是206.王明同学随机抽查某市10个小区所得到的绿化率情况,结果如下表:20253032小区绿化率(%)小区个数2431则关于这10个小区的绿化率情况,下列说法错误的是( )A.极差是13% B.众数是25%C.中位数是25%D.平均数是26.2%7.对于一组统计数据:2,4,4,5,6,9.下列说法错误的是()A.众数是4 B.中位数是5 C.极差是7 D.平均数是58.某日福建省九地市的最高气温统计如下表:地市福州莆田泉州厦门漳州龙岩三明南平宁德最高气温(℃)292830313130303228针对这组数据,下列说法正确的是()A.众数是30 B.极差是1 C.中位数是31 D.平均数是289.已知一组数据:15,13,15,16,17,16,14,15,则这组数据的极差与众数分别是( )A.4,15 B.3,15 C.4,16 D.3,1610.我省五个旅游景区门票票价如下表所示(单位:元),关于这五个景区票价的说法中,正确的是()景区名称黄果树大瀑布织金洞玉舍森林滑雪安顺龙宫荔波小七孔票价(元) 180 120 200 130 180 A.平均数126 B.众数180 C.中位数200 D.极差7011.已知一组数据:12,5,9,5,14,下列说法不正确的是( )A.极差是5 B.中位数是9 C.众数是5 D.平均数是912.某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是()班级1班2班3班4班5班6班人数526062545862A.平均数是58 B.中位数是58 C.极差是40 D.众数是6013.有一组数据:2,5,7,2,3,3,6,下列结论错误的是()A.平均数为4 B.中位数为3 C.众数为2 D.极差是514.为了大力宣传节约用电,某小区随机抽查了10户家庭的月用电量情况,统计如下表.关于这10户家庭的月用电量说法正确的是()2530405060月用电量(度)户数12421A.中位数是40 B.众数是4 C.平均数是20.5 D.极差是315.一组数据﹣1、2、3、4的极差是()A.5 B.4 C.3 D.216.若一组数据﹣1,0,2,4,x的极差为7,则x的值是( )A.﹣3 B.6 C.7 D.6或﹣317.为了解居民用水情况,小明在某小区随机抽查了20户家庭的月用水量,结果如下表:月用水量45689(m3)户数45731则关于这20户家庭的月用水量,下列说法错误的是()A.中位数是6m3B.平均数是5。
2022年中考《频数与频率》精品专项练习 附答案

频数与频率一、选择题1. 〔2021•安徽省,第5题4分〕某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x〔单位:mm〕的数据分布如下表所示,那么棉花纤维长度的数据在8≤x<32这个范围的频率为〔〕棉花纤维长度x频数0≤x<8 18≤x<16 216≤x<24 824≤x<32 632≤x<40 3A.0.8 B.0.7 C.0.4 D.考点:频数〔率〕分布表.分析:求得在8≤x<32这个范围的频数,根据频率的计算公式即可求解.解答:解:在8≤x<32这个范围的频数是:2+8+6=16,那么在8≤x<32这个范围的频率是:.应选A.点评:此题考查了频数分布表,用到的知识点是:频率=频数÷总数.二.填空题1.(2021年四川资阳,第12题3分)某校男生、女生以及教师人数的扇形统计图如下图,假设该校师生的总人数为1500人,结合图中信息,可得该校教师人数为120人.考点:扇形统计图.分析:用学校总人数乘以教师所占的百分比,计算即可得解.解答:解:1500×〔1﹣48%﹣44%〕=1500×8%=120.故答案为:120.点评:此题考查的是扇形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.扇形统计图直接反映局部占总体的百分比大小.2.〔2021年山东泰安,第22题4分〕七〔一〕班同学为了解某小区家庭月均用水情况,随机调查了该小区局部家庭,并将调查数据整理如下表〔局部〕:月均用水量x/m30<x≤55<x≤1010<x≤1515<x≤20x>20频数/户12 20 3频率假设该小区有800户家庭,据此估计该小区月均用水量不超过10m3的家庭约有户.分析:根据=总数之间的关系求出5<x≤10的频数,再用整体×样本的百分比即可得出答案.解:根据题意得:=100〔户〕,15<x≤20的频数是0.07×100=7〔户〕,5<x≤10的频数是:100﹣12﹣20﹣7﹣3=58〔户〕,那么该小区月均用水量不超过10m3的家庭约有×800=560〔户〕;故答案为:560.点评:此题考查了用样本估计总体和频数、频率、总数之间的关系,掌握=总数和样本估计整体让整体×样本的百分比是此题的关键.三.解答题1.〔2021•毕节地区,第24题12分〕我市某校在推进新课改的过程中,开设的体育选修课有:A:篮球,B:足球,C:排球,D:羽毛球,E:乒乓球,学生可根据自己的爱好选修易门,学校李老师对某班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图〔如图〕.〔1〕请你求出该班的总人数,并补全频数分布直方图;〔2〕该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.考点:频数〔率〕分布直方图;扇形统计图;列表法与树状图法.分析:〔1〕根据C类有12人,占24%,据此即可求得总人数,然后利用总人数乘以对应的比例即可求得E类的人数;〔2〕利用列举法即可求解.解答:解:〔1〕该班总人数是:12÷24%=50〔人〕,那么E类人数是:50×10%=5〔人〕,A类人数为:50﹣〔7+12+9+5〕=17〔人〕.补全频数分布直方图如下:;〔2〕画树状图如下:,或列表如下:共有12种等可能的情况,恰好1人选修篮球,1人选修足球的有4种,那么概率是:=.点评:此题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.2.〔2021•孝感,第21题10分〕为了解中考体育科目训练情况,某县从全县九年级学生中随机抽取了局部学生进行了一次中考体育科目测试〔把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格〕,并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答以下问题:〔1〕本次抽样测试的学生人数是40;〔2〕图1中∠α的度数是54°,并把图2条形统计图补充完整;〔3〕该县九年级有学生3500名,如果全部参加这次中考体育科目测试,请估计不及格的人数为700.〔4〕测试老师想从4位同学〔分别记为E、F、G、H,其中E为小明〕中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.考点:条形统计图;用样本估计总体;扇形统计图;列表法与树状图法.分析:〔1〕用B级的人数除以所占的百分比求出总人数;〔2〕用360°乘以A级所占的百分比求出∠α的度数,再用总人数减去A、B、D级的人数,求出C级的人数,从而补全统计图;〔3〕用九年级所有得学生数乘以不及格的人数所占的百分比,求出不及格的人数;〔4〕根据题意画出树状图,再根据概率公式进行计算即可.解答:解:〔1〕本次抽样测试的学生人数是:=40〔人〕,故答案为:40;〔2〕根据题意得:360°×=54°,答:图1中∠α的度数是54°;C级的人数是:40﹣6﹣12﹣8=14〔人〕,如图:故答案为:54°;〔3〕根据题意得:3500×=700〔人〕,答:不及格的人数为700人.故答案为:700;〔4〕根据题意画树形图如下:共有12种情况,选中小明的有6种,那么P〔选中小明〕==.点评:此题考查了条形统计图和扇形统计图的综合应用,用到的知识点是用样本估计总体、频数、频率、总数之间的关系等,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.3.〔2021•四川自贡,第20题10分〕为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛〞,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,假设每正确听写出一个汉字得1分,根据测试成绩绘制出局部频数分布表和局部频数分布直方图如图表:组别成绩x分频数〔人数〕第1组25≤x<30 4第2组30≤x<35 8第3组35≤x<40 16第4组40≤x<45 a第5组45≤x<50 10请结合图表完成以下各题:〔1〕求表中a的值;〔2〕请把频数分布直方图补充完整;〔3〕假设测试成绩不低于40分为优秀,那么本次测试的优秀率是多少?〔4〕第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.考点:频数〔率〕分布直方图;频数〔率〕分布表;列表法与树状图法分析:〔1〕用总人数减去第1、2、3、5组的人数,即可求出a的值;〔2〕根据〔1〕得出的a的值,补全统计图;〔3〕用成绩不低于40分的频数乘以总数,即可得出本次测试的优秀率;〔4〕用A表示小宇B表示小强,C、D表示其他两名同学,画出树状图,再根据概率公式列式计算即可.解答:解:〔1〕表中a的值是:a=50﹣4﹣8﹣16﹣10=12;〔2〕根据题意画图如下:〔3〕本次测试的优秀率是;答:本次测试的优秀率是;〔4〕用A表示小宇B表示小强,C、D表示其他两名同学,根据题意画树状图如下:共有12种情况,小宇与小强两名男同学分在同一组的情况有2种,那么小宇与小强两名男同学分在同一组的概率是=.点评:此题考查了频数分布直方图和概率,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,概率=所求情况数与总情况数之比.4. 〔2021•湘潭,第23题〕从全校1200名学生中随机选取一局部学生进行调查,调查情况:A、上网时间≤1小时;B、1小时<上网时间≤4小时;C、4小时<上网时间≤7小时;D、上网时间>7小时.统计结果制成了如图统计图:〔第1题图〕〔1〕参加调查的学生有200人;〔2〕请将条形统计图补全;〔3〕请估计全校上网不超过7小时的学生人数.考点:条形统计图;用样本估计总体;扇形统计图分析:〔1〕用A的人数除以所占的百分比求出总人数;〔2〕用总人数减去A、B、D的人数,再画出即可;〔3〕用总人数乘以全校上网不超过7小时的学生人数所占的百分比即可.解答:解:〔1〕参加调查的学生有20÷=200〔人〕;故答案为:200;〔2〕C的人数是:200﹣20﹣80﹣40=60〔人〕,补图如下:〔3〕根据题意得:1200×=960〔人〕,答:全校上网不超过7小时的学生人数是960人.点评:此题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个工程的数据;扇形统计图直接反映局部占总体的百分比大小.5. 〔2021•益阳,第17题,8分〕某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想〞读书小组协助老师随机抽取本校的局部学生,调查他们最喜爱的图书类别〔图书分为文学类、艺体类、科普类、其他等四类〕,并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答以下问题:〔1〕求被调查的学生人数;〔2〕补全条形统计图;〔3〕该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?〔第2题图〕考点:条形统计图;用样本估计总体;扇形统计图.分析:〔1〕利用科普类的人数以及所占百分比,即可求出被调查的学生人数;〔2〕利用〔1〕中所求得出喜欢艺体类的学生数进而画出图形即可;〔3〕首先求出样本中喜爱文学类图书所占百分比,进而估计全校最喜爱文学类图书的学生数.解答:解:〔1〕被调查的学生人数为:12÷20%=60〔人〕;〔2〕喜欢艺体类的学生数为:60﹣24﹣12﹣16=8〔人〕,如下图:;〔3〕全校最喜爱文学类图书的学生约有:1200×=480〔人〕.点评:此题主要考查了条形统计图的应用以及扇形统计图应用、利用样本估计总体等知识,利用图形得出正确信息求出样本容量是解题关键.6. 〔2021•株洲,第19题,6分〕我市通过网络投票选出了一批“最有孝心的美少年〞.根据各县市区的入选结果制作出如下统计表,后来发现,统计表中前三行的所有数据都是正确的,后三行中有一个数据是错误的.请答复以下问题:〔1〕统计表中a=,b=6;〔2〕统计表后三行中哪一个数据是错误的?该数据的正确值是多少?〔3〕株洲市决定从来自炎陵县的4位“最有孝心的美少年〞中,任选两位作为市级形象代言人.A、B是炎陵县“最有孝心的美少年〞中的两位,问A、B同时入选的概率是多少?区域频数频率炎陵县 4 a茶陵县 5攸县b醴陵市8株洲县 5株洲市城区12考点:频数〔率〕分布表;列表法与树状图法.分析:〔1〕由茶陵县频数为5,频率为,求出数据总数,再用4除以数据总数求出a的值,用数据总数乘得到b的值;〔2〕根据各组频数之和等于数据总数可知各组频数正确,根据频率=频数÷数据总数可知株洲市城区对应频率错误,进而求出正确值;〔3〕设来自炎陵县的4位“最有孝心的美少年〞为A、B、C、D,根据题意列出表格,然后由表格求得所有等可能的结果与A、B同时入选的情况,再利用概率公式即可求得答案.解答:解:〔1〕∵茶陵县频数为5,频率为,∴数据总数为5÷0.125=40,∴a,b=40×0.15=6.故答案为,6;〔2〕∵4+5+6+8+5+12=40,∴各组频数正确,∵,∴株洲市城区对应频率这个数据是错误的,该数据的正确值是;〔3〕设来自炎陵县的4位“最有孝心的美少年〞为A、B、C、D,列表如下:∵共有12种等可能的结果,A、B同时入选的有2种情况,∴A、B同时入选的概率是:=.点评:此题考查读频数〔率〕分布表的能力和列表法与树状图法.同时考查了概率公式.用到的知识点:频率=频数÷总数,各组频数之和等于数据总数,概率=所求情况数与总情况数之比.7.〔2021•呼和浩特,第20题9分〕学校为了了解初三年级学生体育跳绳的训练情况,从初三年级各班随机抽取了50名学生进行了60秒跳绳的测试,并将这50名学生的测试成绩〔即60秒跳绳的个数〕从低到高分成六段记为第一到六组,最后整理成下面的频数分布直方图:请根据直方图中样本数据提供的信息解答以下问题.〔1〕跳绳次数的中位数落在哪一组?由样本数据的中位数你能推断出学校初三年级学生关于60秒跳绳成绩的一个什么结论?〔2〕假设用各组数据的组中值〔各小组的两个端点的数的平均数〕代表各组的实际数据,求这50名学生的60秒跳绳的平均成绩〔结果保存整数〕;〔3〕假设从成绩落在第一和第六组的学生中随机抽取2名学生,用列举法求抽取的2名学生恰好在同一组的概率.考点:频数〔率〕分布直方图;中位数;列表法与树状图法.分析:〔1〕根据中位数的定义先把这组数据从小到大排列,找出中间两个数的平均数,再根据中位数落在第四组估计出初三学生60秒跳绳再120个以上的人数到达一半以上;〔2〕根据平均数的计算公式进行计算即可;〔3〕先把第一组的两名学生用A、B表示,第六组的三名学生用1,2,3表示,得出所有出现的情况,再根据概率公式进行计算即可.解答:解:〔1〕∵共有50个数,中位数是第25、26个数的平均数,∴跳绳次数的中位数落在第四组;∴可以估计初三学生60秒跳绳再120个以上的人数到达一半以上;〔2〕根据题意得:〔2×70+10×90+12×110+13×130+10×150+3×170〕÷50≈121〔个〕,答:这50名学生的60秒跳绳的平均成绩是121个;〔3〕记第一组的两名学生为A、B,第六组的三名学生为1,2,3,那么从这5名学生中抽取两名学生有以下10种情况:AB,A1,A2,A3,B1,B2,B3,12,13,23,那么抽取的2名学生恰好在同一组的概率是:=;点评:此题考查了频数〔率〕分布直方图,用到的知识点是中位数、平均数、概率公式,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
频数与频率一、选择题1. (•海南,第12题3分)一个不透明的袋子中有3个分别标有3,1,﹣2的球,这些球除了所标的数字不同外其他都相同,若从袋子中随机摸出两个球,则这两个球上的两个数字之和为负数的概率是()A.B.C.D.w考点:列表法与树状图法.专题:计算题.分析:列表得出所有等可能的情况数,找出这两个球上的两个数字之和为负数的情况数,即可求出所求的概率.解答:解:列表得:3 1 ﹣23 ﹣﹣﹣(1,3)(﹣2,3)1 (3,1)﹣﹣﹣(﹣2,1)﹣2 (3,﹣2)(1,﹣2)﹣﹣﹣所有等可能的情况有6种,其中两个数字之和为负数的情况有2种,则P==.故选B点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.二、填空题1. (•黑龙江龙东,第4题3分)三张扑克牌中只有一张黑桃,三位同学依次抽取,第一位同学抽到黑桃的概率为.考点:概率公式..分析:由三张扑克牌中只有一张黑桃,直接利用概率公式求解即可求得答案.解答:解:∵三张扑克牌中只有一张黑桃,∴第一位同学抽到黑桃的概率为:.故答案为:.点评:此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.2. (•黔南州,第14题5分)在全国初中数学竞赛中,都匀市有40名同学进入复赛,把他们的成绩分为六组,第一组一第四组的人数分别为10,5,7,6,第五组的频率是0.2,则第六组的频率是0.1考点:频数与频率分析:先用数据总数乘第五组的频率得出第五组的频数,再求出第六组的频数,然后根据频率=频数÷数据总数即可求解.解答:解:∵都匀市有40名同学进入复赛,把他们的成绩分为六组,第一组一第四组的人数分别为10,5,7,6,第五组的频率是0.2,∴第五组的频数为40×0.2=8,第六组的频数为40﹣(10+5+7+6+8)=4,∴第六组的频率是4÷40=0.1.故答案为0.1.点评:本题考查了频数与频率,用到的知识点:频数=数据总数×频率,频率=频数÷数据总数,各组频数之和等于数据总数.三、解答题1. (•广西来宾,第20题8分)某校为了了解学生大课间活动的跳绳情况,随机抽取了50名学生每分钟跳绳的次数进行统计,把统计结果绘制成如表和直方图.次数70<x<90 90<x<110 110≤x<130 130≤x<150 150≤x<170人数823 16 2 1根据所给信息,回答下列问题:(1)本次调查的样本容量是50;(2)本次调查中每分钟跳绳次数达到110次以上(含110次)的共有的共有19人;(3)根据上表的数据补全直方图;(4)如果跳绳次数达到130次以上的3人中有2名女生和一名男生,学校从这3人中抽取2名学生进行经验交流,求恰好抽中一男一女的概率(要求用列表法或树状图写出分析过程).考点:频数(率)分布直方图;频数(率)分布表;列表法与树状图法.分析:(1)根据图表给出的数据可直接得出本次调查的样本容量;(2)把调查中每分钟跳绳次数达到110次以上(含110次)的人数加起来即可;(3)根据图表给出的数据可直接补全直方图;(4)根据题意画出树状图,得出抽中一男一女的情况,再根据概率公式,即可得出答案.解答:解:(1)本次调查的样本容量是:8+23+16+2+1=50;故答案为:50;(2)本次调查中每分钟跳绳次数达到110次以上(含110次)的共有的共有人数是:16+2+1=19(人);故答案为:19;(3)根据图表所给出的数据补图如下:(4)根据题意画树状图如下:共有6种情况,恰好抽中一男一女的有4种情况,则恰好抽中一男一女的概率是=.点评:此题考查了条形统计图和频数(率)分布直方图,用到的知识点是样本容量、概率公式,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.2.(年贵州安顺,第24题12分)学校举办一项小制作评比活动.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的件数是12.请你回答:(1)本次活动共有60件作品参赛;各组作品件数的众数是12件;(2)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?(3)小制作评比结束后,组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示,请用树状图或列表法求出刚好展示作品B、D的概率.考点:频数(率)分布直方图;众数;列表法与树状图法..分析:(1)直接利用频数除以频率=总数进而得出答案,再利用众的定义求出即可;(2)利用总数乘以频率=频数,进而分别求出获奖概率得出答案;(3)利用树状图列举出所有可能,进而得出答案.解答:解:(1)由题意可得出,本次活动参赛共有:12÷=12÷=60(件),各组作品件数的众数是12;故答案为:60,12;(2)∵第四组有作品:60×=18(件),第六组有作品:60×=3(件),∴第四组的获奖率为:=,第四组的获奖率为:;∵<,∴第六组的获奖率较高;(3)画树状图如下:,由树状图可知,所有等可能的结果为12种,其中刚好是(B,D)的有2种,所以刚好展示作品B、D的概率为:P==.点评:此题主要考查了频数分布直方图的应用以及众的定义以及树状图法求概率等知识,正确画出树状图是解题关键.3.(•湖北黄石,第21题8分)为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.第1题图根据以上信息,解答下列问题:(1)请补全频数分布直方图;(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?考点:频数(率)分布直方图.分析:(1)利用总人数200减去其它各组的人数即可求得第二组的人数,从而作出直方图;(2)设抽了x人,根据各层抽取的人数的比例相等,即可列方程求解;(3)利用总人数乘以一等奖的人数,据此即可判断.解答:解:(1)200﹣(35+40+70+10)=45,如下图:(2)设抽了x人,则,解得x=8;(3)依题意知获一等奖的人数为200×25%=50.则一等奖的分数线是80分.点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.4.(•浙江绍兴,第19题8分)为了解某校七,八年级学生的睡眠情况,随机抽取了该校七,八年级部分学生进行调查,已知抽取七年级与八年级的学生人数相同,利用抽样所得的数据绘制如下统计图表.组别睡眠时间xA x≤7.5B7.5≤x≤8.5C8.5≤x≤9.5D9.5≤x≤10.5E x≥10.5根据图表提供的信息,回答下列问题:(1)求统计图中的a;(2)抽取的样本中,八年级学生睡眠时间在C组的有多少人?(3)已知该校七年级学生有755人,八年级学生有785人,如果睡眠时间x(时)满足:7.5≤x≤9.5,称睡眠时间合格,试估计该校七、八年级学生中睡眠时间合格的共有多少人?考点:条形统计图;用样本估计总体;频数(率)分布表;扇形统计图.专题:计算题.分析:(1)根据扇形统计图,确定出a的值即可;(2)根据图1求出抽取的人数,乘以C占的百分比即可得到结果;(3)分别找出七八年级睡眠合格的人数,求出之和即可.解答:解:(1)根据题意得:a=1﹣(35%+25%+25%+10%)=5%;(2)根据题意得:(6+19+17+10+8)×35%=21(人),则抽取的样本中,八年级学生睡眠时间在C组的有21人;(3)根据题意得:755×+785×(25%+35%)=453+471=924(人),则该校七、八年级学生中睡眠时间合格的共有924人.点评:此题考查了条形统计图,用样本估计总体,频数(率)分布表,以及扇形统计图,弄清题中的数据是解本题的关键.5.(•江西,第20题8分)某教研机构为了解在校初中生阅读数学教科书的现状,随机抽取某部分初中学生进行了调查。
依据相关数据绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:(1)求样本容量及表格中a、b、c的值,并补全统计图;(2)若该校共有初中生2300名,请估计该校“不重视阅读教科书”的初中生人数(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?【答案】略.【考点】频数(率)分布直方图;用样本估计总体.【分析】(1)利用类别为“一般”人数与所占百分比,进而得出样本容量,进而得出a、b、c的值;(2)利用“不重视阅读数学教科书”在样本中所占比例,进而估计全校在这一类别的人数;(3)根据(1)中所求数据进而分析得出答案,再从样本抽出的随机性进而得出答案.【解答】解:(1)由题意可得出:样本容量为:57÷0.38=150(人),∴a=150×0.3=45,b=150-57-45-9=39,c=39÷150=0.26.如图所示:(2)若该校共有初中生2300名,该校“不重视阅读数学教科书”的初中人数约为:2300×0.26=598(人).(3)①根据以上所求可得出:只有30%的学生重视阅读数学教科书,有32%的学生不重视阅读数学教科书或说不清楚,可以看出大部分学生忽略了阅读数学教科书,同学们应重视阅读数学教科书,从而获取更多的数学课外知识和对相关习题、定理的深层次理解与认识.②如果要了解全省初中生阅读数学教科书的情况,应随机抽取不同的学校以及不同的年级进行抽样,进而分析.【点评】此题主要考查了频数分布直方表以及条形统计图和利用样本估计总体等知识,理论联系实际进而结合抽样调查的随机性进而得出是解题关键.6.(•宁夏,第25题8分)某花店计划下个月每天购进80只玫瑰花进行销售,若下个月按30天计算,每售出1只玫瑰花获利润5元,未售出的玫瑰花每只亏损3元.以x(0<x≤80)表示下个月内每天售出的只数,y(单位:元)表示下个月每天销售玫瑰花的利润.根据历史资料,得到同期下个月内市场销售量的频率分布直方图(每个组距包含左边的数,但不包含右边的数)如图所示:(1)求y关于x的函数关系式;(2)根据频率分布直方图,计算下个月内销售利润少于320元的天数;(3)根据历史资料,在70≤x<80这个组内的销售情况如下表:销售量/只70 72 74 75 77 79天数 1 2 3 4 3 2计算该组内平均每天销售玫瑰花的只数.考点:频数(率)分布直方图;函数关系式;加权平均数专题:图表型.分析:(1)根据利润等于售出的玫瑰花的利润与未售出的玫瑰花亏损的钱数之和列式整理即可得解;(2)列不等式求出利润小于320元时卖出的玫瑰花的只数,然后根据频率求解即可;(3)利用加权平均数的计算方法列式计算即可得解.解答:解:(1)y=5x﹣(80﹣x)×3=8x﹣240(0<x≤80);(2)根据题意,得8x﹣240<320,解得,x<70,表明玫瑰花的售出量小于70只时的利润小于320元,则50≤x<60的天数为:0.1×30=3(天),60≤x<70的天数为:0.2×30=6(天),∴利润少于320元的天数为3+6=9(天);(3)该组内平均每天销售玫瑰:75+=75(只).点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.。
