第三讲:二维图形生成算法
ch3二维图形生成技术(二次曲线)

P1
d1 = F(xp + 2, yp - 0.5) 2 2 = (xp + 2) + (yp - 0.5) = d + 2xp +3 即d 的增量为 2xp +3.
-R
2
M P2
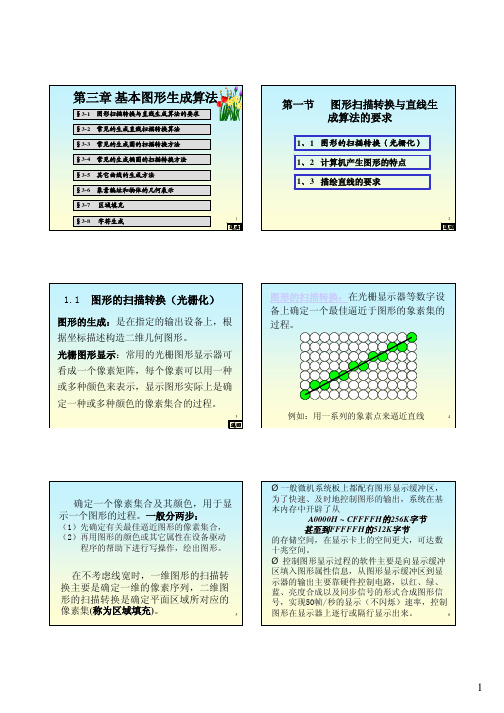
中点画圆法
若d>=0, 则P2 为下一个象素,那么再下一个象 素的判别式为: d1 = F(xp + 2, yp - 1.5) 2 2 2 = (xp + 2) + (yp - 1.5) - R = d + (2xp + 3)+(-2 yp + 2) 即d 的增量为 2 (xp - yp) +5. P1 d的初值: d0 = F(1, R-0.5) M 2 2 = 1 + (R-0.5) - R P2 = 1.25 - R
圆的等面积正多边形逼近法
当用内接正多边形逼近圆时,其面积要 小于圆的面积;而当用圆的外切正多边 形逼近圆时,其面积则要大于圆的面积。 为了使近似代替圆的正多边形和圆之间 在面积上相等,只有使该正多边形和圆 弧相交,称之为圆的等面积正多边形。
圆的等面积正多边形逼近法
步骤: 求多边形径 长,从而求 所有顶点坐 标值 由逼近误差 值,确定边 所对应的圆 心角α
程序如下(完全用整数实现): MidpointCircle(r,color) Int r, color; { int x,y,d; x = 0; y = r; d = 1-r; putpixcel(x,y,color); while( x < y) { if (d <0) { d += 2*x+3; x++; } else { d += 2*(x-y)+5; x++ ; y--; } putpixcel(x,y,color); } }
二维图形基本变换规则及应用

二维图形基本变换规则及应用(07级信息与计算科学傅强070350221)摘要利用计算机绘制的图形与我们日常见到的图片、照片是有相似之处。
除图片、照片等图形外,自然界中还存在丰富多彩的有形物体。
一般,根据图形所在空间的不同,可将图形分为:三维图形和二维图形。
图片、照片属二维图形,自然界中形形色色的物体属于三维图形。
在计算机绘图的过程中,二维图形的绘制是绘制三维图形的基础,研究计算机图形的生成必须从研究二维图形开始。
计算机绘制图形时,无论图形多么复杂,都是利用一些相应图形基元经过图形变换组成的。
在计算机绘图中,经常用到图形变换,图形变换是指图形信息经过几何变换后产生新的图形。
基本的几何变换研究物体坐标在直角坐标系内的平移、旋转和变比等规则。
本文主要介绍二维图形的一些基本变换规则及其应用关键词:直角坐标系内;平移;旋转;应用ABSTRACTUsing the computer graphics and see our daily drawings, photographs are similarities. Besides the drawings, photographs and other graphic, nature also exist rich and colorful tangible objects. In general, according to the different space, the graphics can be divided into: 3d graphics and 2d graphics. The drawings, photographs of 2d graphics, all kinds of objects in the nature belongs to 3d graphics. In computer graphics, the process of 2d graphics rendering 3d graphics drawing is the basis, research of computer graphics generation must start from the 2d graphics. Computer graphics, no matter how complex, graphics are using some corresponding graphic element composed by graphical transformation. In computer graphics, often use graphics transformation, graphics transform refers to the graphical information through after new graphics geometry transform. The basic research object coordinate geometry transform in cartesian coordinate system in translation, rotation and change rules than etc. This paper mainly introduces some basic transformation of 2d graphics and its application in the rules.Keywords: a cartesian coordinate system, Translation, Rotating, application1用户坐标到屏幕坐标的变换实际图纸上坐标系是实数域中的直角坐标系或极坐标系,统称为用户坐标系;计算机设备(如屏幕)上采用的坐标系为整数域(如屏幕一般为直角左手系),称为设备坐标系。
计算机图形学_ 二维图形变换_53 二维图形变换原理及齐次坐标_

为什么要采用齐次坐标?
在笛卡儿坐标系内,向量(x,y)是位于z=0的平面上的点 ;而向量(x,y,1)是位于z=1的等高平面上的点
对于图形来说,没有实质性的差别,但是却给后面矩阵运 算提供了可行性和方便性
假如变换前的点坐标为(x,y),变换后的点坐标为(x*,y* ),这个变换过程可以写成如下矩阵形式:
x*, y*x,
x* a1x b 1 y c1
y•M
x*, y*x
a1
y
1
b 1
c1
a2 b2 c2
上两式是完全等价的。对于向量(x,y,1),可以在几何意义 上理解为是在第三维为常数的平面上的一个二维向量。
这种用三维向量表示二维向量,或者一般而言,用一个n+1维 的向量表示一个n维向量的方法称为齐次坐标表示法
n维向量的变换是在n+1维的空间进行的,变换后的n维结果 是被反投回到感兴趣的特定的维空间内而得到的。
如n维向量(p1,p2,...,pn)表示为(hp1,hp2,...,hpn,h), 其中h称为哑坐标。 普通坐标与齐次坐标的关系为“一对多”:
变换图形就是要变换图形的几何关系,即改变顶点的坐 标;同时,保持图形的原拓扑关系不变
仿射变换(Affine Transformation或 Affine Map)是一 种二维坐标到二维坐标之间的线性变换 (1)“平直性”。即:直线经过变换之后依然是直线
(2)“平行性”。即:平行线依然是平行线,且直线上 点的位置顺序不变)
采用了齐次坐标表示法,就可以统一地把二维线形变换表示 如下式所示的规格化形式:
二维图形几何变换

⼆维图形⼏何变换⼀、基本变换1. 平移定义:将物体沿直线路径从⼀个坐标位置移到另⼀个坐标位置的重定位。
不产⽣变形⽽移动物体的刚体变换。
原始坐标位置:(x ,y ),平移距离t x 、t y ,新位置(x ′,y ′),则x ′=x +t x ,y ′=y +t y 表⽰为矩阵形式,令:→P =x y→P ′=x ′y ′→T =t x t y⼆位平移⽅程:→P ′=→P +→T2. 旋转当参考点为(0,0)定义:以某个参考点为圆⼼,将对象上的各点(x ,y )围绕圆⼼转动⼀个逆时针⾓度θ,变成新的坐标(x ′,y ′)的变换。
x ′=rcos (φ+θ)=rcos φcos θ−rsin φsin θy ′=rsin (φ+θ)=rsin φcos θ+rcos φsin θ∵x =rcos φ,y =rsin φ∴x ′=xcos θ−ysin θy ′=xsin θ+ycos θ令:→R =cos θ−sin θ−sin θcos θ写成矩阵形式:→P ′=→R ⋅→P绕任意指定的旋转位置(x r ,y r )旋转的变换⽅程1. 将坐标系原点平移到(x r ,y r )2. 在新的坐标系下做旋转变换3. 将坐标原点平移回原坐标系x ′=x r +(x −x r )cos θ−(y −y r )sin θy ′=y r +(x −x r )sin θ+(y −y r )cos θ3. 变化(缩放)Scaling定义:使对象按⽐例因⼦Sx 和Sy 放⼤或缩⼩的变换。
x ′=x ⋅S xy ′=y ⋅S y令→S =S x 00S y矩阵形式:→P ′=→S ⋅→PS x 、S y 均⼩于1,缩⼩物体尺⼨,S x 、S y 均⼤于1,放⼤物体。
S x =S y ,则保持物体相对⽐例缩放⼀致。
特殊情况当Sy =−1、Sx =1,按x 轴反射当Sy =1、Sx =−1,按y 轴反射()()()()()当Sy =−1、Sx =−1,按原点(0,0)反射⼆、变换矩阵每个基本变换均可表⽰为普通矩阵形式:→P ′=→M 1→P +→M 2平移将2×2矩阵扩充为3×3矩阵,将⼆维⼏何变换的乘法和平移项组合成单⼀矩阵表⽰平移。
计算机图形学_基本算法
应不同的设备。
12
返回
2
Ø曲线也可由直线段逼近生成 Ø解决的问题:给定直线两端点P0(x0,y0)
和P1(x1,y1),画出该直线。 主要步骤可以表示如下:
13
初值
偏差判别
移动绘图 偏差计算
终点 判断
N
Y 结束
图2-2 一般线段绘制过程的主要步骤示意图
• 偏差判别:根据当前绘图点位置与理想位置的偏差情况,确定
在不考虑线宽时,一维图形的扫描转 换主要是确定一维的像素序列,二维图 形的扫描转换是确定平面区域所对应的 像素集(称为区域填充)。
5
Ø 一般微机系统板上都配有图形显示缓冲区,
为了快速、及时地控制图形的输出,系统在基
本内存中开辟了从
A0000H ~ CFFFFH的256K字节
甚至到FFFFFH的512K字节
29
返回
因递推公式: Xi+1=Xi+1 yi+1 = kxi+1+b= k1xi+b+k∆x= yi+k∆x
所以:当 ∆x =1; yi+1 = yi+k。 即当x每递增1,y递增k(即直线斜率)
y
yi+1
DSP二维图像生成

旋转法:
将一维滤波器的H(w)以H(w)轴为旋转轴,旋转360度,从而生成H(m,n),可表示为:
H (m, n) H ( m 2 n 2 )
这种方法生成的窗口底面区是圆的;
笛卡尔生成法:
用两个一维窗口的笛卡尔(外)积来求得方形或矩形底面 区的二维窗口,可表示为:
Hc (m, n) H1(m)H2 (n)
二维图像生 成
实验原理
二维图形是指图形在二维方向上都记录信息。 他充分记录了平面上的二维空间,大大提升了信息 密度,使得在小面积上编码大数据成为可能。在二 维数字信号处理及图像处理理论中,对二维数字信 号或图像进行滤波处理时,二维滤波器的涉及通常 会采用窗口法设计递归滤波器,设计时,可采用一 维设计技术,并将其直接推广,虽然维数增加了, 但由于不用对一位滤波器的设计方法做重大修改, 从而简化了二维滤波器的设计。 在采用窗口法设计非递归滤波器的方法中,常 见的有旋转法和笛卡尔生成法。
本实验中,以余弦或者正弦函数生成一维图 像,并以y轴为旋转轴旋转360,生成二维图 形。
方法流程图
开始
定义各参数
利用循环求得x[i]值 利用旋转法定义r k = (int)(sqrt(r))
k<=39
N
y[i][j] = 0 Y
y[i][j]=x[k];
二维图像生成 结 束
pi=3.1415926; y=zeros(81,81); x=zeros(1,40); for t=0:32 for i=0:39 x(i+1)=127*(1+cos(2*pi*i/39-1-t*pi/16)); end for i=0:80 for j=0:80 y(i+1,j+1)=0; m=i; n=j; r=(m-40)*(m-40)+(n-40)*(n-40); k=ceil(sqrt(r))+1; if(k<=40 & k>=1) y(i+1,j+1)=x(k); elห้องสมุดไป่ตู้e y(i+1,j+1)=0; end end end i=0; j=0; end
第三章 二维图形的生成_直线和圆

Q
M
P=(xp,yp)
P1
当d<0,M在直线(Q点)下方,取右上方P2 ; 当d>0,M在直线(Q点)上方,取右方P1;
当d=0,选P1或P2均可,约定取P1; 能否采用增量算法呢?
2013-10-30 西安工程大学计算机图形学 17
4.1 直线段的扫描转换算法
4.1.2、中点画线法
情形1.若d0 ->M在直线上方->取P1; 此时再下一个象素的判别式为
西安工程大学计算机图形学
2013-10-30
8
4.1 直线段的扫描转换算法
4.1.1、数值微分法(DDA)
当 x 1 得
y1 y0 yi 1 yi x1 x0
即:当x方向每递增1像素,y方向递增k(即直线斜 率);每次通过上式计算出(xi , yi )取整后输出 显示器。 注意上述分析的算法仅适用于k ≤1的情形。在这 种情况下,x每增加1,y最多增加1。
2013-10-30
西安工程大学计算机图形学
9
4.1 直线段的扫描转换算法
注:当 k 1 时,必须把x,y位置互换,即利用递推 1 式 xi 1 xi y ,y每增加1,x相应增加 1 k 。 k
所以取 x2 x1 和 y2 y1 中较大者为步进方向,如下 图
当 k 1时
画线从(x0, y0)开始,d 的初值
d0=F(x0+1, y0+0.5)= a(x0 +1)+b(y0 +0.5)+c
= F(x0, y0)+a+0.5b = a+0.5b 由于只用 d 的符号作判断,为了只包含整数运算, 可以用2d 代替 d 来摆脱小数,提高效率。 即d0=2*a+b 若d0 若d<0
计算机图形学--第三讲 直线与圆生成算法

12直线生成算法圆弧绘制算法图元的概念33.1 图元的概念为其颜色值。
3.1 图元的概念3.1 图元的概念12直线生成算法圆弧绘制算法图元的概念33.2 直线生成算法曲线和各种复杂的图形均是离散成许多直线段来绘制,因而直线是二维图形生成技术的基础。
数学上的理想直线没有宽度,是由无数个点构成的集合。
对直线进行光栅化时,只能在显示器所给定的有限个像素组成的点阵中,选择能最好地逼近于该直线的一组像素,并对这些像素进行写操作。
这就是通常所说的用显示器绘制直线,即直线的扫描转换。
直线扫描转换的主要工作:快速找出像素点阵中最近的网格点3.2 直线生成算法画一条从近直线的像素序列,并填入色彩数据的过程。
这一过程也称为直线光栅化。
需要解决的问题►连续性►粗细、亮度要均匀►像素逼近待画直线►速度3.2 直线生成算法 问题1问题3.2 直线生成算法常用的直线生成算法有三种:►►►►►►3.2 直线生成算法基本思路:是用数值方法求解微分方程的一种方法,即根据长移动,由此产生连续的像素坐标3.2 直线生成算法设起点和终点坐标分别为Δx令即第3.2 直线生成算法于是有步的结果加上一个增量得到。
该算法在方向增量为3.2 直线生成算法3.2 直线生成算法下图中,用公式(表示,但显示时要用像素来表示,即采用舍入的办法得到最靠近空心圆点的像素,用这些像素(下图中的实心圆点)来表示直线。
3.2 直线生成算法void LineDDA(int{int} }3.2 直线生成算法►►想位置的偏移;►►整运算,运行效率低且取整运算不利于硬件实现基本思路:假定直线斜率P(x p,y的中点,---如果取---如果取---M与问题转换为如何判断构造判别式假设直线方程为:则由数学知识可知有下面的关系:F(F(F(所以,欲判断Q点下方,只需要把中点并检查它的符号。
构造判别式d=F(=a(当d<0取右上方当d≥0取右方P判别式的增量算法当增量为若增量为其它斜率的情况时再将算法设计:画线从d0可以用d0算法设计:例:用中点画线法12345void MidpointLine (int x { int a, b, d} /* mid PointLine */设直线的起点坐标为的情况来说明该算法。
二维图形几何变换-PPT

cos sin 0
sin cos 0
0
0 1
旋转变换
简化计算(θ很小)
1 0
x' y' 1 x y 1 1 0
0 0 1
对称变换
对称变换后得图形就是原图形关于某一轴线或原点得镜像。
Y
Y
Y
X (a)关于x轴对称
X (b)关于y轴对称
X (c)关于原点对称
对称变换
对称变换后得图形就是原图形关于某一轴线或原点得镜像。
光栅变换
任意角度得Байду номын сангаас栅旋转变换:
旋转的 象素阵列
A
1A 3
光栅网格
2
n
Gray(A)=∑ [Gray(i) × A在i上得覆盖率](Gray(x)表示某点得灰度等级)
i=1 Gray(A)=Gray(1) × A在1上得覆盖率+ Gray(2) × A在2上得覆盖率+ Gray(3) × A在3上得覆盖率
光栅变换
光栅比例变换:
n
∑ [Gray(i) × Si] Gray(A)= i=1
n
∑ Si
i=1
缩小时原图 中的相应象 素区域
(a)Sx=1/2,Xy=1/2
(b)原图
12
1
43
2
放大时原图 中的相应象 素区域
(a)Sx=1,Xy=3/2
G=(G1+G2+G3+G4)/4
G=(G1×S1 + G2×S2)/(S1 + S2)
O
x0
x
图6-9 坐标系间的变换
坐标系之间得变换
分析: y
y'
p,也即p' x'
计算机图形学第3章二维基本图(4)

二、扫描线种子填充算法实现
借助于堆栈,上述算法实现步骤如下:
1、初始化堆栈。 2、种子压入堆栈。 3、while(堆栈非空) { (1)从堆栈弹出种子象素。 (2)如果种子象素尚未填充,则:
a.求出种子区段:xleft、xright; b.填充整个区段。 c.检查相邻的上扫描线的xleft≤x≤xright区间内, 是否存在需要填充的新区段,如果存在的话, 则把每个新区段在xleft≤x≤xright范围内的最 右边的象素,作为新的种子象素依次压入堆栈。 d.检查相邻的下扫描线的xleft≤x≤xright区间内, 是否存在需要填充的新区段,如果存在的话, 则把每个新区段在 xleft≤x≤xright范围内的 最右边的象素,作为新的种子象素依次压入堆 栈。 }
扫描线种子填充算法步骤 (1)种子象素入栈。 (2)栈非空时象素出栈,否则结束。 (3)对出栈象素及左、右两边象素填充,直到遇边界XL、XR。 (4)在(XL ,XR) 内查相临的上、下两条扫描线是否为边界或已填充, 如不是,则将每区间的最右边的象素入栈。回到(2)。
练习: 用扫描线种子填充算法,写出图中顺序进栈的种子坐标及 所需最大栈空间
2、国标码 我国除了采用ASCII码外,还制定了汉字编 码的国家标准字符集:中华人民共和国国家标准 信息交换编码,代号为“GB2312-80”。该字符 集共收录常用汉字6763个,图形符号682个。 它规定所有汉字和图形符号组成一个94×94 的矩阵,在此方阵中,每一行称为“区”,用区 码来标识;每一列称为“位”,用位码来标识, 一个符号由一个区码和一个位码共同标识。 区码和位码分别需要7个二进制位,同样, 为了方便,各采用一个字节表示。所以在计算机 中,汉字(符号)国标码占用两个字节。
计算机图形学教学大纲(word文档【经典】)

XX大学《计算机图形学》教学大纲编写单位:执笔人:审核人:XX大学xx系20xx年9 月[实验要求]本课程实验要求较高,实验内容多且相关性较强,有关实验的具体要求与内容需按实验大纲执行,本大纲中不再另行说明。
第一章绪论[教学内容]计算机图形学的目标与任务;计算机图形学的内容体系;计算机图形学相关学科;计算机图形学相关领域。
[教学目标与要求]熟练掌握:计算机图形学的内容体系;计算机图形学的目标与任务;掌握:计算机图形学的应用领域;计算机图形学的相关学科;了解:计算机图形学的发展。
[重点与难点]计算机图形学的内容体系;计算机图形学的目标与任务。
[教学时数]2学时第一节计算机图形学的目标与任务一、视觉交流是计算机图形学的目标与任务二、计算机图形学的三个基本任务第二节计算机图形学的内容体系一、基础模块二、建模与表示模块三、绘制模块四、交互技术第三节计算机图形学相关学科一、图形与图像二、相关学科第四节计算机图形学的应用领域一、计算机辅助设计与制造(CAD/CAM)二、科学计算可视化三、虚拟现实四、动画第五节计算机图形学的发展一、计算机图形学的发展简史二、计算机图形学的发展趋势[复习思考题]1、图形包括哪两方面的要素?在计算机中如何表示它们?2、图形的本质是什么?3、如何看待计算机图形学的发展趋势?第二章图形系统[教学内容]Visual 图形系统概述;图形系统体系结构;图形支撑软件;图形硬件显示原理;[教学目标与要求]熟练掌握:图形系统体系结构;图形硬件显示原理掌握:图形系统基本概念和术语;了解:图形支撑软件[重点与难点]图形系统体系结构;图形硬件显示原理[教学时数]2学时第一节图形系统概述一、图形系统组成结构1.图形系统组成结构2.图形系统分类第二节图形系统体系结构一、概述二、应用程序阶段三、几何处理阶段四、光栅阶段第三节图形支撑软件一、OpenGL二、DirectX三、Java2D和Java3D第四节图形硬件显示原理一、图形显示设备及工作原理二、图形显示方式三、光栅扫描图形显示系统[复习思考题]1、从图形硬件显示原理角度,思考并分析如何显示直线?2、请你总结一下光栅显示系统的优缺点?3、在光栅显示系统中,显卡有什么作用?第三章二维图形生成[教学内容]直线生成算法;圆弧绘制算法;区域填充;字符;反走样技术;[教学目标与要求]熟练掌握:直线生成算法;区域填充;圆弧绘制算法掌握:反走样技术了解:字符编码[重点与难点]直线生成算法;区域填充;圆弧绘制算法[教学时数]8学时第一节直线生成算法一、数值微分法二、逐点比较法三、Bresenham画线法四、中点画线法第二节圆弧绘制算法一、基于光栅的整圆绘制算法二、角度离散法绘制圆弧和椭圆弧第三节区域填充一、种子填充算法二、多边形填充算法第四节字符一、字符的编码二、点阵字符三、矢量字符第五节反走样技术第六节编程实例-地图绘制一、地图绘制方法二、基于OpenGL的地图绘制[复习思考题]1、简述DDA算法、中点画线法、Bresenham画线法算法的思想?2、根据中点画圆法和Bresenham算法,绘制一条端点为(1,1)和(6,5)的直线,画出对应各像素的位置?第四章图形几何变换[教学内容]二维几何变换;三维几何变换;图形几何变换的模式;[教学目标与要求]熟练掌握:二维几何变换;三维几何变换;掌握:图形几何变换的模式;[重点与难点]二维几何变换;三维几何变换;[教学时数]6学时第一节二维几何变换一、基本变换二、二维复合变换三、二维坐标系间的变换第二节三维几何变换一、基本变换二、三维复合变换三、三维坐标系间的变换第三节图形几何变换的模式一、固定坐标系模式二、活动坐标系模式[复习思考题]1、试编写对二维点实现平移、旋转、比例变换的程序。
[课件]计算机图形学--二维几何变换PPT
![[课件]计算机图形学--二维几何变换PPT](https://img.taocdn.com/s3/m/cd1cee150b4c2e3f57276323.png)
连续旋转变换
应用于点P的两个连续旋转,得到的点P’的 坐标可计算为 P’ = R(θ2)[ R(θ1)P]= [R(θ2)R(θ1)]P 可以证明:两个连续旋转是可叠加的 R(θ2)*R(θ1)= R(θ1+θ2) 则P’的坐标可计算为 P’ = R(θ1+θ2)P
Other Transformations
大多数图形软件包中包含了平移、旋转和 缩放这些基本变换。有些软件包还提供一 些有用的其它变换,如反射(Reflection)和 错切(Shear)
2018/12/2
28
Reflection对称变换
对称变换后的图形是原图形关于某一轴线或原点 ty)P
2018/12/2 25
对于绕坐标原点的旋转变换
可简写为:P’ = R(θ)P
2018/12/2 26
对于相对于坐标原点在X和Y方向上的缩放变换
可简写为:P’ =S(sx , sy)P T、R和S分别时平移、旋转、缩放变换距阵
2018/12/2 27
2018/12/2
9
标准的旋转是当基准点在坐标 原点时,即物体绕坐标原点的 旋转。点P绕原点逆时针旋转θ, 得到P’点。则P和P’的坐标之 间的关系,如图,可如下表示 x’=rcos(θ+Ψ) =rcosθcosΨ - rsinθsinΨ y’=rsin(θ+Ψ) =rsinθcosΨ + rcosθsinΨ
P2 M 1 P1 M 2
21
齐次坐标:
是Maxwell.E.A在1946年从几何的角度提出来
的,它的基本思想是把一个n维空间的几何问 题转换到n+1维空间中去, 从形式上来说,就是用一个n+1维的向量表示 一个n维向量的方法,即n+1维向量表示n维空 间中的点。
高级CAD图形算法和计算几何

高级CAD图形算法和计算几何CAD软件是现代设计领域中不可或缺的工具,它使得设计师能够以精确的方式创建和编辑图形。
在CAD中,高级图形算法和计算几何技术扮演着至关重要的角色,帮助用户实现精确和复杂的设计。
一、高级CAD图形算法1. B样条曲线和曲面B样条曲线和曲面是CAD软件中最常用的曲线和曲面表示方法之一。
B样条曲线和曲面基于控制点和节点向量,通过插值或逼近的方式生成平滑曲线和曲面。
在CAD设计中,B样条算法可以用来绘制自由曲线和曲面,实现设计师的创意想法。
2. 实体建模实体建模是CAD软件中常用的几何建模方法之一。
通过实体建模算法,可以创建具有体积和形状的模型,例如立方体、圆柱体和球体等。
实体建模还可以进行布尔运算,例如合并、相交和剪除等操作,以实现更复杂的几何形状。
3. 三维扫描和点云处理三维扫描和点云处理技术是CAD软件中用于从现实世界获取几何数据的重要方法。
通过激光扫描等技术,可以将物理对象转换为点云数据。
然后,通过点云处理算法,可以对点云数据进行滤波、配准和重建等操作,得到准确的三维模型。
二、计算几何技术1. 二维图形变换二维图形变换是计算几何中的基本操作之一。
常见的二维图形变换包括平移、旋转、缩放和镜像等。
通过矩阵运算,可以对二维图形进行准确的变换,实现设计中的对称性、旋转和放缩等效果。
2. 直线段与多边形的相交检测在计算几何中,相交检测是常见的问题之一。
对于直线段与多边形的相交检测,可以使用射线法和线段法等算法。
相交检测可以应用于CAD软件中的碰撞检测、路径规划和拓扑分析等方面。
3. 曲线和曲面的求交和切割曲线和曲面的求交和切割是计算几何中的重要问题。
对于曲线和曲面的求交,可以使用二分法、牛顿法和追踪法等算法。
对于曲面的切割,可以使用参数化曲线和曲面的切割算法,将曲面分解为更小的曲面片段。
综上所述,高级CAD图形算法和计算几何技术在CAD软件中起着重要的作用。
它们能够实现复杂的设计需求,并提供精确和可靠的图形处理功能。
AutoCAD 二维图形生成刀具轨迹的方法(经典)

AutoCAD 二维图形生成刀具轨迹的方法数控机床是机械制造业中最重要的加工工具。
数控机床编程员将要加工的零件按照数控编程标准,编制成供数控机床执行用的数控加工程序(简称NC 程序) 。
常用的编程方法有两种:手工编程和自动编程。
手工编程枯燥、乏味,指令难记忆,遇到复杂的零件时,用手工编程要花费大量的时间,且易出错。
本文提出用ObjectARX 开发工具,在开发AutoCAD二维图形数控自动编程系统中,零件刀具轨迹信息的获取,并根据这些信息和其他参数生成刀具的运动轨迹,并直接生成加工代码。
该系统可以明显提高编程效率和编程质量,提高数控机床的利用率,降低废品率,有显著的经济效益,尤其是在复杂轮廓的编程中,更能发挥其优势。
1 零件轮廓的CAD 设计为了实现由AutoCAD 二维图形中描述零件轮廓的图形实体直接生成数控加工代码,必须从二维图形中获取数控编程所需要的主要信息———刀具轨迹,刀具轨迹信息由AutoCAD 图形数据库中描述零件轮廓的图形实体获取。
AutoCAD二维图形中有较多的内容,不仅有尺寸、剖面线、标注文本、中心线等非零件轮廓的实体;而且还有根据制图标准规定的画法(如螺纹、花键等) 画出的图形实体,这些图形实体也不能描述零件轮廓。
因此,为了从AutoCAD 图形数据库中正确地提取零件轮廓的图形实体,需在绘制图形时给描述零件轮廓的图形实体以特定的相关关联的共同性质。
可以有以下的方法:①将描述零件轮廓的图形实体放在特定的同一层; ②将描述零件轮廓的图形实体置为特定的同一颜色; ③将描述零件轮廓的图形实体指定为特定的组( Group) ; ④将描述零件轮廓的图形实体连接为一条Polyline (多线段、或称为多义线、组合线) 。
对上述方法比较的结果,采用最后一种方法更为有利,这是因为:(1) Polyline 是可以包括多个直线段和圆弧段的图形实体,这和一般数控机床所具备的直线插补和圆弧插补方法完全一致,可以方便地确定数控代码的类型;(2) Polyline 可以(用直线和圆弧) 逼近任意形状,这在零件轮廓为不规则曲线时显得十分方便,同时还可以通过控制逼近算法以调节逼近精度;(3) Polyline 中各个直线段和圆弧段是依次首尾相接的,有起点,有终点,这便于确定加工时的刀具的运动方向;(4) Polyline 虽然包含多线段和圆弧,但仍然为单一实体,便于选择拾取;(5) 通常CAD 设计结果为零件的最终尺寸,用Polyline表示零件轮廓,则毛坯及加工过程中零件的形状与尺寸通过AutoCAD 中的OFFSET、SCAL E、及STRETCH等命令方便的得到,并可由此获得加工过程中刀具的中间坐标;鉴于上述考虑,把描述零件轮廓的图形实体连接成一条多线段(可封闭也可不封闭) ,多线段的起点即就是刀具的起点,加工过程中所需的终点坐标均可由多线段各顶点的数据确定,根据这些数据即可生成数控加工代码。
二维多边形渲染算法

二维多边形渲染算法(最新版)目录1.引言2.二维多边形渲染算法的概念与分类3.常见二维多边形渲染算法3.1 扫描线算法3.2 矩形算法3.3 波形算法4.二维多边形渲染算法的应用5.发展趋势与展望6.结论正文一、引言在计算机图形学中,二维多边形渲染算法是实现图像呈现的关键技术之一。
通过对多边形进行填充和着色,可以生成各种二维图形,从而满足不同场景下的视觉需求。
本文将对二维多边形渲染算法进行详细介绍,包括算法的分类、常见算法及应用,以期为相关领域的研究者提供参考。
二、二维多边形渲染算法的概念与分类二维多边形渲染算法是指将多边形从二维空间转换到二维图像空间的过程。
根据实现方式的不同,二维多边形渲染算法可以分为以下几类:1.扫描线算法:通过扫描线技术实现多边形的渲染。
2.矩形算法:通过矩形区域实现多边形的快速填充。
3.波形算法:通过波形变换实现多边形的快速填充。
三、常见二维多边形渲染算法(1)扫描线算法扫描线算法是一种基于线条追踪的二维多边形渲染算法。
它通过计算多边形边界与扫描线的交点,实现多边形的填充和着色。
扫描线算法具有较高的渲染速度,适用于实时渲染场景。
(2)矩形算法矩形算法是一种基于矩形区域的二维多边形渲染算法。
它通过将多边形分解为若干个矩形区域,实现快速填充和着色。
矩形算法具有较高的计算效率,适用于大量多边形的渲染场景。
(3)波形算法波形算法是一种基于波形变换的二维多边形渲染算法。
它通过将多边形边界转换为波形边界,实现快速填充和着色。
波形算法具有较高的灵活性,适用于复杂多边形的渲染场景。
四、二维多边形渲染算法的应用二维多边形渲染算法广泛应用于计算机图形学、图像处理、游戏开发等领域。
例如,在计算机游戏开发中,通过使用二维多边形渲染算法,可以实现场景、角色和道具的快速呈现,提高游戏运行速度。
五、发展趋势与展望随着计算机技术的发展,二维多边形渲染算法也在不断优化和升级。
未来的发展趋势包括提高渲染速度、降低计算复杂度和提高渲染质量等方面。
二维多边形渲染算法

二维多边形渲染算法摘要:1.二维多边形渲染算法的背景和需求2.常见的二维多边形渲染算法3.二维多边形渲染算法的实现步骤4.二维多边形渲染算法的优缺点5.二维多边形渲染算法的应用领域正文:一、二维多边形渲染算法的背景和需求在计算机图形学中,渲染是指将三维场景转换成二维图像的过程。
其中,二维多边形渲染是图形学中的一个重要研究方向。
随着科技的发展,人们对于图像质量的要求越来越高,因此研究高效、精确的二维多边形渲染算法具有重要的意义。
二、常见的二维多边形渲染算法1.边积分算法边积分算法是一种基于多边形边界的渲染方法,其基本思想是将多边形划分为若干个三角形,然后对每个三角形进行渲染。
该算法的优点是计算简单,缺点是可能会产生锯齿状的图像。
2.扫描线算法扫描线算法是一种基于扫描线的渲染方法,其基本思想是将多边形沿扫描线方向切割成若干个矩形,然后对每个矩形进行渲染。
该算法的优点是能够生成平滑的图像,缺点是计算复杂度较高。
3.区域生长算法区域生长算法是一种基于区域的渲染方法,其基本思想是将多边形划分为若干个区域,然后对每个区域进行渲染。
该算法的优点是能够生成高质量的图像,缺点是需要处理复杂的区域合并和分裂问题。
三、二维多边形渲染算法的实现步骤1.建立场景图:首先,需要建立一个场景图,用于存储多边形的顶点、边和纹理信息。
2.裁剪:根据相机的位置和方向,对场景图中的多边形进行裁剪,得到可视的多边形。
3.投影:将可视的多边形投影到二维平面上,得到二维多边形。
4.渲染:根据预定的渲染算法,对二维多边形进行渲染。
四、二维多边形渲染算法的优缺点优点:能够生成高质量、平滑的图像,计算复杂度较低。
缺点:可能会产生锯齿状的图像,计算复杂度较高,处理复杂的区域合并和分裂问题。
五、二维多边形渲染算法的应用领域二维多边形渲染算法广泛应用于计算机图形学、计算机视觉、虚拟现实等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Bresenham算法
0<m<1;d=0;d=d+m;当d>1时,只保留d的小数部分作为d的新 值,x=x+1, y则根据d > 0.5来决定点亮(x+1,y)还是 (x+1,y+1)。 ?
Bresenham算法
• 令e=d-0.5。 • 则当e0时,下一象素的y坐标增加1, 而当e0时,下一象素的y坐标不变。e 的初值为-0.5。 • 从而利用e代替d,来判断下一点的取舍
基本增量算法的实现
#include<graphics.h>/*加入c图形库*/ #include<math.h>/*数学库*/ #include<conio.h>/*键盘控制*/ void Line(int x0,int y0,int x1,int y1,int value) /*从坐标(x0,y0)到(x1,y1)画颜色为value的直线*/ { int x; float dx,dy,m,y; dx=x1-x0; dy=y1-y0; m=dy/dx;/*取得斜率*/ y=y0; for(x=x0;x<=x1;x++) { putpixel(x,(int)(y+0.5),value);/*找到距理想直线最近的点,putpixel为画点 函数*/ y=y+m; /*计算下一步的y值,增幅为m*/ } }
二维图形生成算法
•二维图形生成算法
•线段的扫描变换
•基本增量算法 •中点线算法 •Bresenham画线算法
•圆与椭圆的扫描变换
线段的扫描变换
线段的扫描变换
• 象素,中心位于均衡栅格上的离散圆点 。 • 直线扫描变换算法就是获得一系列象素 的坐标,使这些象素落在所要近似的理 想直线上或位于该直线的附近。原则上 讲,象素序列应尽可能逼近理想的直线, 而且尽可能直一些。
增量初始值的计算
• 因为第一个象素是端点(x0,y0),可直接计算 d的初始值dstart,以此决定是选E还是NE。第 一个中点在(x0+1,y0 +1/2)处,有: • dstart=F(x0+1,y0+1/2)=a(x0+1)+b(y0+ 1/2)+c =ax0+by0+c+a+b/2 =F(x0,y0)+a+b/2 • 由于(x0,y0)在线上,因此F(x0,y0)=0;故 dstart=a+b/2=dy-dx/2。
基本增量算法
直线方程:y=mx+b ,0<m<1, m= △y/ △x= △y ; x=1,xi+1=xi+ 1,yi+1=yi+m
基本增量算法
• 增量算法的定义:每一步都是根据前一步进行 增量计算。这种算法通常被称作数值微分 (DDA)算法。DDA(Digital Differential Analyzer algorithm)是用数值方法解决微分方 程的一种手段 。 • 请注意如果|m|>1,则x的步进会使y的步进 超过1,此时,如果采用上述算法将会使得点 亮的象素个数太少,画出来的线没有很好的模 拟理想直线,例如:从(0,2)点到(2,100)点画线, 则会只点亮3个点来表示,光栅点太稀了。解 决办法是颠倒x与y的位置,给y以单位增量, 而x的增量为Δx=Δy/m=1/m,即取x轴和y轴中 变化最快的轴作为参考轴以保证直线被光栅化 后有足够多的象素。
对DDA的改进
为消除分数部分,将F乘上2重新定义F: F(x,y)=2(ax+by+c),使每个常量和 判断变量均乘上2,但这并不影响判断 变量d的符号,因此仍可作为中点检测 的标准。
最终结果:每一步dnew值的计算只需 做简单的加法,无需耗时的乘法。
中点线算法举例
中点线算法
• 改进:中点算法进一步把效率提高到每 步只做一个整数加法,如果再想在算法 的效率上作文章已经是不可能了。但是 DDA和中点算法严格依赖直线方程,不 能再推广。而下面讲述的Bresenham画 线算法不但能解决直线的光栅化,还能 解决圆弧、抛物线甚至自由曲线的光栅 化问题,使算法的覆盖域扩大。
圆的扫描变换
利用对称性可以 加速画圆过程; 只需计算45°弧 段,通过对称变换 可完成整圆.
圆的扫描变换(中点算法)
思路:当前显示点P=(Xp,Yp),取第 二八分圆
圆方程为x2+y2=R2 ,因此 令:F(x,y)=x2+y2 -R2
中间点M=(Xp+1,Yp-(1/2))
令: d=F(M)
判断: d=0 中点在圆上; 点亮可取E 或 SE d<0 中点在圆内; 点亮可取E d>0 中点在圆外;点亮可取SE
基本增量算法
• 考虑基本增量算法是否是最优的! 1.运算符的快速性 采用增量思想的DDA算法,每计算一个象素, 只需计算一个加法。加法已经是最快的算法 了(加减乘除开方三角函数等) 2.参数运算的快速性 DDA算法的计算中含有浮点数运算。把浮点 运算的加法变成整数加法,因为整数的加法 比浮点的加法要快很多
中点线算法
直线方程:F(x,y)=0
F(x,y)= x •dy+B •dx -y •dx
中点M=(x+1,y+1/2)
=0 M是直线一点 <0 M在直线上方 >0 M在直线下方
d=F(M)
d
=0 点亮E或者NE <0 点亮E >0是E还是NE
中点线算法
• 中点线算法的目的在于改进DDA算法,使得只采用整 形变量参加运算。 假设当前为old点,下一点为new点,则有: dold=a· (xp+1)+b· (yp+1/2)+c 如果选择的是E,M在x方向增加一个步长,那么: dnew=F(xp+2,yp+1/2)=a(xp+2)+b(yp+1/2)+c dnew=dold+a 用ΔE表示选择E后加入到d的增量,则ΔE=a=dy。 如果选择的是NE,那么M’在x方向和y方向上均需增加 一个步长,那么: dnew=F(xp+2,yp+3/2)=a(xp+2)+b(yp+3/2)+c dnew=dold+a+b 用ΔNE表示选择NE后加入到d的增量,则 ΔNE=a+b=dydx。
椭圆的扫描变换(中点算法)
思路:
方程为: F(X,Y)=b2x2+a2y2-a2b2=0
由于对称性,只考虑第一象限中的椭圆生成 •把此象限内的弧段分成两段,以法向量中两分量相等处为分界线,既斜率为-1处. •上部中点为(xp+1,yp-(1/2)),亮点选择有E和SE,取y的中值. •下部中点为(xp+(1/2),yp-1),亮点选择有S和SE,取x的中值. •判断何时从上部转入下部的条件: 法向量的两个分量是否相等. •起始点:(0,b); 终止点:(a,0)
曲线DDA算法
y=f (x) x; 可按步长逐点画出这条曲线
例如对于圆周上任意一点的坐标方程为:
x=RcosA+ x0
y=RsinA+y0 可有: dx=-(y-y0)dA dy=(x-x0)dA
(y0 , x0 ) 是曲率中心点,圆弧应 在(x,y)处起始逆时针画出。
因而 x2=x1+dx=x1-(y1-y0)dA
y2=y1+dy=y1+(x2-x0)dA
其中角度的增量dA很小,用弧度表示,A是圆弧的张角。
