云南省昆明市2018届高三第八次考前适应性训练数学(文)试题Word版含答案
云南省昆明一中2018届高三考前适应性训练数学(理)试卷及答案

云南省昆明第一中学2018届高三第八次月考理 科 数 学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}ln A x y x ==,集合{}xB y y e==,则集合A 与B 的关系是( )A . AB = B .A B ≠⊂ C .B A ≠⊂ D .A B ∈2.在复平面内,复数z 与复数103i+对应的点关于实轴对称,则z =( ) A .3i + B .3i - C .3i -+ D .3i --3.某班有50人,一次数学考试的成绩X 服从正态分布()110,100N .已知()1001100.34P x <≤=,估计该班本次考试学生数学成绩在120分以上的有( ) A .5人 B .6人 C .7人 D .8人4. ()62111x x ⎛⎫-+ ⎪⎝⎭展开式中3x 的系数为( ) A .14- B .14 C. 15 D .305.已知点F 是抛物线()2:20C x py p =>的焦点,O 为坐标原点,若以F 为圆心,FO 为半径的330x y -+=相切,则抛物线C 的方程为( )A . 22x y = B .24x y = C. 26x y = D .28x y =6.已知函数()()()2sin 0f x x ωϕω=+>的部分图像如图所示,若图中在点,A D 处()f x 取得极大值,在点,B C 处()f x 取得极小值,且四边形ABCD 的面积为32,则ω的值是( ) A .18 B .14 C. 8π D .4π7.已知函数()f x x =,函数()2g x x =-,执行如图所示的程序框图,若输入的[]3,3x ∈-,则输出m 的值为()g x 的函数值的概率为( ) A .16 B .14 C. 13 D .128.设数列{}n a 的前n 项和为n S ,若()11,,*,2n n n S S S n N n -+∈≥构成等差数列,且122,4a a =-=-,则6a =( ) A . 64- B .32- C. 16 D . 649.已知双曲线()2222:10,0x y C a b a b -=>>的左、右焦点分别为12,F F ,点A 是双曲线C 底面右顶点,点M 是双曲线C 上一点,MA 平分12F MF ∠,且12:2:1MF MF =,则双曲线的离心率为( )A .2B .3 C. 2 D .310.过正方体1111ABCD A B C D -的顶点A 的平面α与直线1AC 垂直,且平面α与平面11ABB A 的交线为直线l ,平面α与平面11ADD A 的交线为直线m ,则直线l 与直线m 所成角的大小为( )A .6π B .4π C. 3π D .2π11.已知ABC ∆的面积为6,4cos 5A =-,P 为线段BC 上一点,2BP PC =u u u r u u u r ,点P 在线段,AB AC上的投影分别为,Q R ,则PQR ∆的面积为( ) A .625 B .1225 C. 3225 D .362512.已知定义在()0,+∞上的函数()()222,6ln 4f x x m h x n x nx =-=-,其中0n >,设两曲线()y f x =与()y h x =有公共点,且在公共点处的切线相同,则mn的最大值为( ) A .163e -B .133e -C. 1332e D .2313e第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若,x y 满足约束条件3020x y x y +-≥⎧⎨-≤⎩,则函数2z x y =+的最小值为 .14.在数列{}n a 中,112a =,且()11*2n n a n N a +=∈-,设数列{}n a 的前n 项的积为n T ,则100T = .15.定义符号函数()()()()1,00,01,0x g x x x >⎧⎪==⎨⎪-<⎩,若函数()()xf xg x e =⋅,则满足不等式()()233f a a f a +<+的实数a 的取值范围是 .16.已知正方体1111ABCD A B C D -的棱长为4,点P 是1AA 的中点,点Q 是1BDC ∆内的动点,若1PQ BC ⊥,则点Q 到平面1111A B C D 的距离的范围是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在ABC ∆中,内角,,A B C 的对边分别为,,a b c ,设平面向量()()sin cos ,sin ,cos sin ,sin p A B A q B A B =+=-u r r ,且2cos p q C ⋅=u r r(Ⅰ)求C ;(Ⅱ)若c a b =+=ABC ∆中边上的高h .18.某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,部分统计数据如下表:(Ⅰ)根据以上22⨯列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?(Ⅱ)从学习成绩优秀的12名同学中,随机抽取2名同学,求抽到不使用智能手机的人数X 的分布列及数学期望.参考公式:()()()()()22=n ad bc a b c d a c b d κ-++++,其中=n a b c d +++参考数据:()0P K k ≥0.05 0,。
云南省师范大学附属中学2018届高三第八次月考文科综合试题 含答案

云南师大附中2018届高考适应性月考卷(八)文科综合参考答案一、选择题(本大题共35小题,每小题4分,共140分)【解析】1.A点位于我国东北,河流有春汛和夏汛,因汛期河水上涨,使江心洲面积减小,A正确;B点位于欧洲西部,属于温带海洋性气候,河流不会形成明显的夏汛,B错;C点位于我国东部沿海,无明显双汛期,C错;D点位于南亚恒河口附近,为热带季风气候,集中降水的季节为6~9月,此时段江心洲面积小,D错。
故选A。
2.河漫滩是河流沉积地貌,易形成于凸岸,A错;江心洲是河流携带的泥沙堆积而成,多形成于河流速度较慢的地方,D错;因上游修筑水坝,拦截泥沙,使沉积速度减慢,则江心洲面积增长速度减慢,B正确;河漫滩因季节性出露,不宜建永久建筑,C错。
故选B。
3.通过获取各主要路段交通流量的数据信息,利用计算机进行统计分析,以交通诱导图颜色呈现,利用的主要是GIS技术。
故选C。
4.GIS技术可用于城市各要素信息的整理分析并形成结果,指导生产和生活。
故选D。
5.据材料推出,12月7日,太阳直射点南移,罗斯海岸白昼逐渐变长(或已经极昼不变),A错;到达L港时,为当地上午10点,太阳应位于东偏北天空,B正确;考察船抵达罗斯海岸时是12月7日,地球公转速度逐渐加快,C错;到达L港时全球进入20日的范围不到一半,D错。
故选B。
6.新西兰的L港地处南半球西风带,盛行西北风,A错;新科考站大约位于73°S,距南极点17度,相距约1900千米,B错;新科考站位于昆仑站东北方,C正确;从L港到新站点要克服西风漂流的风浪影响,D错。
故选C。
7.黑龙江因纬度高,冬季气温低,种春小麦,A错;青海因海拔高,作物一年一熟,种植春小麦,无冬灌要求,D错;广西纬度低,气温高,无需进行冬灌,且非我国冬小麦主产区,B错;河南为我国冬小麦主产区,且冬春季低温干旱,宜实行冬灌。
故选C。
8.河南地处华北平原南部,冬灌时平均气温3~8℃,应为秋末冬初,日出东南方向,物体影子朝向西北,故选A。
(昆明市2018届高三摸底调研测试文数试卷

文科数学试卷·第1页(共8页)秘密★启用前 【考试时间:1月22日 15∶00—17∶00】昆明市2018届高三摸底调研测试文科数学本试卷满分150分,考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}(1)0M x x x =-≥,{}11N x x =-<<,则M N =A .{}10x x -<≤B .{}10x x -≤≤C .{}01x x ≤<D .{}01x x ≤≤2.2i1i=+ A .1i + B .1i -C .1i -+D .1i --3.已知向量(1,2)=-a ,(1,3)=b ,则2-=a bAB .2CD .104.设命题:N p n ∀∈,22n n ≤,则p ⌝为 A .N n ∃∈,22n n ≤ B .N n ∀∈,22n n >C .N n ∃∈,22n n >D .N n ∀∈,22n n ≥文科数学试卷·第2页(共8页)5.已知等差数列{}n a 的公差为2,且4a 是2a 与8a 的等比中项,则{}n a 的通项公式n a = A .2n - B .2nC .21n -D .21n +6.下图是1951-2016年中国年平均气温变化图. 根据上图,下列结论正确的是A .1951年以来,我国年平均气温逐年增高B .1951年以来,我国年平均气温在2016年再创新高C .2000年以来,我国年平均气温都高于19812010-年的平均值D .2000年以来,我国年平均气温的平均值高于19812010-年的平均值7.古人采取“用臼舂米”的方法脱去稻谷的外壳,获得可供食用的大米,用于舂米的“石臼”由一块正方体石料凿去一部分做成(凿去的部分可看成一个简单组合体).一个“石臼”的三视图如图所示,则凿去部分的体积为 A .63π B .72π C .79π D .99π文科数学试卷·第3页(共8页)8.定义[]x 表示不超过x 的最大整数,例如[0.6]0=,[2]2=,[3.6]3=.右面的程序框图取材于中国古代数学著作《孙子算经》.执行该程序框图,则输出a = A .9 B .16 C .23D .309.已知函数()sin f x x ω=的图象关于点2π,03⎛⎫⎪⎝⎭对称,且()f x 在π04⎡⎤⎢⎥⎣⎦,上为增函数,则ω=A .32B .3C .92D .610.在长方体1111ABCD A B C D -中,2AB AD ==,11AA =,则点B 到平面1D AC 的距离等于 ABC .1D11.若函数()221x f x x =--,对于任意的Z x ∈且(),x a ∈-∞,都有()0f x ≤恒成立,则实数a 的取值范围为 A .(],1-∞- B .(],0-∞C .(],4-∞D .(],5-∞12.过抛物线2:2(0)C y px p =>的焦点且倾斜角为锐角的直线l 与C 交于A ,B 两点,过线段AB 的中点N 且垂直于l 的直线与C 的准线交于点M ,若MN AB =,则l 的斜率为 A .13BCD .1文科数学试卷·第4页(共8页)二、填空题:本题共4小题,每小题5分,共20分。
2018年云南省高三高考适应性月考数学(文)试题Word版含答案

2018年云南省高三高考适应性月考数学(文)试题一选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.设集合(){}|ln 1A x y x ==-,集合(){}|ln 1B y y x ==-,则集合()R C A B = A. ()0,1 B. ()1,0- C. (),1-∞ D.()1,+∞ 2.在复平面内,复数12iz i=+的共轭复数对应的点位于 A. 第一象限 B. 第二象限 C. 第三象限 D.第四象限3.已知平面向量,a b满足1,1,a a b a b =⋅=+= b =4.函数()32374f x x x x =---的图象在点()()1,1f --处的切线方程为A. 210x y -+=B. 210x y --=C. 230x y ++=D.230x y +-= 5.以下三个命题中,真命题的个数有()个 ①若11a b <,则a b >;②若a b c >>,则a c b c >;③函数()1f x x x=+有最小值2 A. 0 B. 1 C. 2 D. 36.设实数,x y 满足不等式组211y xy x y ≥⎧⎪-≤⎨⎪≥⎩,则目标函数2z x y =+的最大值为A. 1B. 2C. 3D. 47.元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图1所示,即最终输出的0,x =问一开始输入的x = A.34 B. 78 C. 1516 D. 31328.在长为5的线段AB 上任取一点P ,以AP 为边长作等边三角形,为 A.45 B. 35 C. 25 D.159.要得到函数2sin cos y x x x =的图象,可将函数sin 2y x =的图象A. 向左平移3π个单位 B. 向右平移3π个单位 C. 向左平移6π个单位 D. 向右平移6π个单位10.某几何体的三视图如图2所示,则此几何体的体积为 A.43 B. 83C. 4D. 811.小晶用圆、三角形、正方形按一定规律画图,前八个图形如图3所示,则猜测第2017个图形中共含有的正方形个数为A. 670B. 672C. 335D. 33612.已知函数()()1ln ,0,0x x x f x x x e--<⎧⎪=⎨≥⎪⎩,若方程()()()210f x mf x m m +-+=⎡⎤⎣⎦有四个不等的实数根,则m 的取值范围是 A. 415m -≤<B. 1m ≤-或1m >C. 1m =-或1m >D. 1m =-或01m <<二、填空题:本大题共4小题,每小题5分,共20分. 13.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,若4cos ,,353A B a π===,则b = . 14.若P 为圆()2221x y -+=上的动点,则点P 到直线:20l x y -+=的最短距离为 .15.已知三棱锥A BCD -中,3,AB AC BD CD ====且BD CD ⊥,若点A 在平面BCD 内的投影恰好为点D ,则此三棱锥外接球的表面积为 .16.已知双曲线()222210,0x y a b a b -=>>的左、右焦点分别为12,F F ,点53,2P ⎛⎫⎪⎝⎭为双曲线上一点,若12PF F ∆的内切圆的半径为1,则双曲线的方程为 .三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程.若数列{}n a 满足111(,n nd n N d a a *+-=∈为常数),则称数列{}n a 为调和数列,现有一调和数列{}n b 满足1211,.2b b ==(1)求{}n b 的通项公式; (2)若数列2nn b c n =+,求{}n c 的前n 项和n S .18.(本题满分12分)心理健康教育老师对某班50个学生进行了心里健康测评,测评成绩满分为100分.成绩出来后,老师对每个成绩段的人数进行了统计,并得到如图4所示的频率分布直方图. (1)求a ,并从频率分布直方图中求出成绩的众数和中位数;(2)若老师从60分以下的人中选两个出来与之聊天,则这两人一个在(]40,50这一段,另一个在(]50,60这一段的概率是多少?19.(本题满分12分)如图5所示,在直角梯形ABCD 中,//,90,1,AB CD ABC CD BC ∠===点E 为AD 边上的中点,过点D 作//DF BC 交AB 于点F ,现将此直角梯形沿DF 折起,使得A FD B --为直二面角,如图乙所示. (1)求证://AB 平面CEF ;(2)若AF ,求点A 到平面CEF 的距离.已知椭圆()222210x y a b a b +=>>过点1,2⎛ ⎝⎭(1)求椭圆的标准方程;(2)已知点()4,0P ,椭圆内部是否存在一个定点,过此点的直线交椭圆于,M N 两点,且12PM PN ⋅= 恒成立,若存在,求出此点,若不存在,说明理由.21.(本题满分12分)已知函数()22.xf x e mx x =--(1)若0m =,讨论()f x 的单调性; (2)若[)0,x ∈+∞时,()12ef x >-恒成立,求m 的取值范围.请考生在第22、23两题中任选一题作答,如果多做,则按照所做的第一题计分. 22.(本题满分10分)选修4-4:极坐标与参数方程已知直角坐标系xoy 中,直线过点()1,0P ,且倾斜角α为钝角,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标.曲线C 的极坐标方程为()2212sin 3ρθ+=(1)写出直线l 的参数方程和曲线C 的直角坐标方程; (2)若56πα=,直线l 与曲线C 相交于不同的两点,M N ,求MN 的长.23.(本题满分10分)选修4-5:不等式选讲 已知函数()(), 3.f x x g x m x ==-- (1)解关于的不等式()()10g f x m +->; (2)已知()()0,,c f a c f b c ><<,求证:()()21.f a b c f c ab +<+2018年云南省高三高考适应性月考数学(文)试题参考答案第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)【解析】 1.由题意,知,∴,故,故选D .2.因为,其共轭复数为,位于第四象限,故选D . 3.由题意,,故,故选B .4.,故,即切线斜率为2,又,故易得切线方程为,故选A .5.当时,①是假命题.当时,②是假命题.函数只有当时才会有最小值,③是假命题,故真命题个数为0,故选A.6.如图1,画出可行域,显然,目标函数在点时取得最大值,最大值为4,故选D.7.即解方程,解得,故选B.8.设,则正三角形面积为,若,则,由几何概型易得知,故选C.9.,则可由的图象向左平移个单位得到,故选C.10.如图2所示,可将此几何体放入一个正方体内,则四棱锥P−ABCD即为所求,易得体积为,故选B.11.通过观察发现一个三角形等于两个圆,一个正方形等于三个三角形,即一个正方形等于六个圆.又,故应有336个正方形,故选D.12.函数的图象如图3所示,令,由图中可知,对于任意,最多有三个解,要想有四个不等的实数根,则方程必有两个不等的实数根,故,故,或.不妨设这两个根为且,则由图象可得,要想有四个不等的实数根,则或或令,即或或解得或,故选D.第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)【解析】13.∵,∴,由正弦定理得,即,故.14.最短距离为圆心到直线距离再减去半径.已知圆心为,则圆心到直线的距离为,半径为1,故最短距离为.15.∵平面,故,且知两两垂直,故可将此三棱锥放入一个长、宽、高分别为的长方体内,三棱锥的四个顶点亦为长方体的顶点,其外接球为长方体外接球.易得外接球半径为,故外接球表面积为.16.,且,故得.又,故,.又,联立化简得.又因点在双曲线上,所以,解得,故双曲线方程为.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)解:(Ⅰ)因为为调和数列,故为等差数列,又,故是以1为首项,1为公差的等差数列,…………………………(3分)故,故.…………………………(6分)(Ⅱ),…………………………(8分).………………………(12分)18.(本小题满分12分)解:(Ⅰ)由得.………………(2分)从频率分布直方图得知众数为75.…………………………(3分)40至70的频率为0.32,40至80的频率为0.68,故知中位数在70至80之间,设为,则,解得,故中位数亦为75.…………………………(6分)(Ⅱ)因为共有50个学生,故从频率分布直方图中易知(40,50]这一段有2人,(50,60]这一段有4人.通过列表可知,从这6个人中选2个人共有15种选法,从(40,50]和(50,60]这两段中各选一人共有8种选法,故由古典概型知概率为.……………………(12分)19.(本小题满分12分)(Ⅰ)证明:如图4所示,连接BD,FC交于点O,连接OE.因为BCDF为正方形,故O为BD中点.又E为AD中点,故OE为△的中位线.……………(3分),又平面CEF,∴平面CEF.…………………………(5分)(Ⅱ)解:如图5,连接FC,AC,取FD中点G,连接EG,CG.因为,易得.………………………(7分)因为原图形为直角梯形,折起后A−FD−B为直二面角,故易得平面平面.∴.又,故易得等腰△面积,而.…………………………(10分)设点A到平面CEF的距离为,∵,,即,解得.所以点A到平面CEF的距离为.…………………………(12分)20.(本小题满分12分)解:(Ⅰ)由题意知,.…………………(2分)又点在椭圆上,故椭圆标准方程为.…………………………(4分)(Ⅱ)假设存在.设点.当直线斜率存在且不为0时,设直线方程为.联立化简得.因为过椭圆内的点,故此方程必有两根.,…………………………(6分),,故得.…………………(8分)∵,故有,即,解得或,故直线方程为或.则直线恒过点或(6,0),因为此点在椭圆内部,故唯有点满足要求.…………………………(10分)当直线斜率为0时,过点的直线与椭圆的交点显然即为,,满足.当直线斜率不存在时,过点的直线与椭圆的交点M,N为,亦满足.综上,在椭圆内部存在点满足题目要求.…………………………(12分)21.(本小题满分12分)解:(Ⅰ)当时,.,令,得.易知在上单调递减,在上单调递增.…………………………(4分)(Ⅱ)恒成立,即恒成立.当时,对于任意都成立;…………………………(5分)当时,即恒成立.…………………………(6分)令,则,整理得…………………………(8分)令,注意到,,,故知在单调递增,.故知在单调递增,又.…………………………(10分)故知在(0,1)上为负,上为正.故知(0,1)上递减,上递增.故,故.…………………………(12分)22.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)直线的标准参数方程为,曲线的直角坐标方程为.…………………………………(4分)(Ⅱ)∵,∴,,∴把直线代入中,可得.∵P(1,0)在椭圆内部,所以且点M,N在点异侧,设点M,N对应的参数分别为t1,t2,则,,∴.……………………………(10分)23.(本小题满分10分)【选修4−5:不等式选讲】(Ⅰ)解:由得,∴,∴,∴不等式解集为.……………………………(5分)(Ⅱ)证明:要证,即证,只需证,只需证,只需证,只需证,只需证,又由题意知,,∴,,∴成立,故得证.………………………………(10分)。
【名师推荐】云南省昆明市2018届高三5月适应性检测数学文试题(精品解析)

云南省昆明市2018届高三5月适应性检测数学(文科)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.()A. B. C. D.【答案】C【解析】分析:求,将其分子、分母同乘以分母的共轭复数,可得,转化为两个复数相乘可得,化简可得,即。
详解:。
故选C。
点睛:求两个复数相除,可先转化为分式,分子、分母同乘以分母的共轭复数,转化为复数的乘法运算。
本题意在考查复数的运算及学生的运算能力。
2.已知集合,,则()A. B. C. D.【答案】A【解析】分析:由集合中的元素可得元素为自然数,根据可得元素只能为0,1,2.求即求两集合的公共元素,将0,1,2分别代入集合中的不等式,满足不等式的即是公共元素。
详解:。
将0,1,2分别代入集合中的不等式,可得,此不等式成立,故有0;,化简得。
此不等式成立,故有1,,化简得。
此不等式成立,故有2.故选A。
点睛:集合的运算,应先求集合中的元素,交集就是求集合的公共元素的集合。
本题考查集合的运算,数集的符号表示。
3.程大位《算法统宗》里有诗云“九百九十六斤棉,赠分八子做盘缠.次第每人多十七,要将第八数来言.务要分明依次弟,孝和休惹外人传.”意为:996斤棉花,分别赠送给8个子女做旅费,从第一个开始,以后每人依次多17斤,直到第八个孩子为止.分配时一定要等级分明,使孝顺子女的美德外传,则第八个孩子分得斤数为()A. B. C. D.【答案】D【解析】分析:根据题意可得每个孩子所得棉花的斤数构成一个等差数列,其中公差为17,项数为8,前8项和为996,应先由前n项和公式求首项,再由等差数列通项公式求第8项。
详解:根据题意可得每个孩子所得棉花的斤数构成一个等差数列,其中。
由等差数列前n项和公式可得,。
解得。
由等差数列通项公式得。
故选D。
点睛:本题考查学生的传统文化、运算能力、转化能力。
解决与等差数列有关的问题,可将条件转化为基本量,利用前n项和公式、通项公式求解。
2018届云南省昆明第一中学高三第八次月考数学(文)科试题(扫描版)

昆明一中第八期全国大联考 参考答案(文科数学)命题、审题组教师 杨昆华 李文清 孙思应 梁云虹 王在方 卢碧如 凹婷波 吕文芬 陈泳序一、选择题1. 解析:由题意,集合(0,)A =+∞,集合(0,)B =+∞,选A .2. 解析:由题意,103i 3iz ==-+,选B . 3. 解析:根据题意,由ˆ 1.20b=>,选A . 4. 解析:因为2π1cos π1sin 12cos 24223ααα⎛⎫++ ⎪-⎛⎫⎝⎭+=== ⎪⎝⎭,选C . 5. 解析:如图所示函数2z x y =-在点(1,2)C -处取得最小值,且1225z =--⨯=-,选D .6. 解析:根据正弦定理由2sin 2sin sin B A C =得22b ac =,结合2b a =可得出2c a =,所以由余弦定理得2222222441cos 244a cb a a a B ac a +-+-===,选B . 7. 解析:由题意知函数()log a f x x =,当1a >时,对数函数在()0,+∞上是增函数,且二次函数的对称轴为正数,且二次函数的图象开口向上,过坐标原点;当01a <<时,对数函数是()0,+∞上的减函数,且二次函数开口向下,过原点,综上图象可能的是A ,选A .8. 解析:由题意,令()()f x g x =,可得1x =,故当1x ≥时,()m g x =,所以3113(3)3P -==--,选C .9. 解析:设曲线()y f x =与()y h x =在公共点00(,)x y 处的切线相同,()2f x x '=,6()4h x x '=-;由题意可知0000()()()()f x h x f x h x =⎧⎨''=⎩,所以2000006ln 4624x m x x x x⎧-=-⎪⎨=-⎪⎩;由00624x x =-可得01x =或03x =-(舍去),代01x =入2006ln 4x m x x -=-可得5m =,选D .10. 解析:由题意可知,△ACB 与△APB 均为直角三角形,设点D 为AB 边的中点,则221=====AB DP DC DB DA ,所以点D 为三棱锥ABC P -的外接球的球心,故三棱锥ABC P -的外接球的半径2=R ,三棱锥ABC P -的的外接球的表面积为2π4R S =16π=,选D .11. 解析:由题意可知,将平面α平移到平面BD A 1,则直线l B A 1//,直线m D A 1//,又△BD A 1为等边三角形,可得3π1=∠D BA ,所以,直线l 与直线m 所成角的大小为π3,选C .12. 解析:设00(,)M x y ,则008x y =,以OM为直径的圆方程为22220000()()224x y x y x y +-+-=,即22000x y x x y y +--=;又因为AB 为圆22000x y x x y y +--=与圆221x y +=的公共弦,所以两圆作差可得直线AB 的方程为001x x y y +=,所以点O 到直线AB 距离为14d =≤=,当且仅当00008x y x y =⎧⎨=⎩,即00x y ⎧=⎪⎨=⎪⎩00x y ⎧=-⎪⎨=-⎪⎩d 取得最大值14,选B .二、填空题13. 解析:因为a ∥b ,所以(1)(4)23m m -+=⨯,所以5m =-或2m =,又因为a 与b 方向相反,所以5m =-. 14. 解析:因为2c =,b a =,而222a bc +=,所以23a =,21b =,所以双曲线C 的方程为22 1 3x y -=.15. 解析:据题意,四边形ABCD 为平行四边形,且432BC ⨯=,即8BC =,所以()f x 的最小正周期为8,由2π8ω=得π4ω=. 16. 解析:由()0f x =可得2266e x x x m ++=,令2266()exx x h x ++=,则2222(1)()e e x xx x x x h x ---+'==;由()0h x '>可得(1,0x ∈-,由()0h x '<可得(,1)(0,x ∈-∞-+∞,所以2266()e xx x h x ++=在(1,0)-上单调递增,在(,1)-∞-和(0,)+∞上单调递减;当1x =-时,()=(1)2e h x h -=极小值,当0x =时,()=(0)6h x h =极大值;由题意知函数()y h x =与y m =有且仅有一个交点,由函数()y h x =及y m =的图象可得(0,2e)(6,)m ∈+∞.三、解答题 (一)必考题17. 解:(1)由1n n S a =-+ 得 111n n S a ++=-+,两式相减得:11n n n n S S a a ++-=-+, 即11n n n a a a ++=-+, 即112n n a a += (1)n ≥, 所以数列{}n a 是公比为12的等比数列, 又由111a a =-+得 112a =, 所以1112nn n a a q -⎛⎫== ⎪⎝⎭; ………6分 (2)因为()()12n b f a f a =++……()n f a +12=++……()12n n n ++=,所以()1211211n b n n n n ⎛⎫===- ⎪++⎝⎭, 所以11121223n T ⎡⎛⎫⎛⎫=-+-+ ⎪ ⎪⎢⎝⎭⎝⎭⎣ (1)11n n ⎤⎛⎫+- ⎪⎥+⎝⎭⎦122111n n n ⎛⎫=-= ⎪++⎝⎭. ………12分18. 解:(1)由列联表可得()()()()()()2223042816107.87912182010n ad bc K a b c d a c b d -⨯⨯-⨯===>++++⨯⨯⨯所以能在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响. ………6分(2)根据题意,所抽取的5名同学中“学习成绩优秀”有1名同学,“学习成绩不优秀”有4名同学.………8分(3)学习成绩不优秀的4名同学分别记为A ,B ,C ,D ;“学习成绩优秀”有1名同学记为E .则再从中随机抽取3人构成的所有基本事件为:(),,A B C ,(),,A B D ,(),,A B E ,(),,A C D ,(),,A C E ,(),,A D E ,(),,B C D ,(),,B C E ,(),,B D E ,(),,C D E ,共有10种;抽取3人中恰有2名同学为“学习成绩不优秀”所含基本事件为:(),,A B E ,(),,A C E ,(),,A D E ,(),,B C E ,(),,B D E ,(),,C D E 共有6种,所求为63105P ==. ………12分19. 解:(1) 由题意,⊥AB 平面C C BB 11,⊂D B 1平面C C BB 11,可得D B AB 1⊥,又△BC B 1为等边三角形,点D 为BC 边的中点, 可得D B BC 1⊥,AB 与BC 相交于点B , 则D B 1⊥平面ABC ,⊂D B 1平面D AB 1,所以,平面D AB 1⊥平面ABC . ………6分 (2)因为△ABC 为直角三角形,2==BC AB ,所以2=∆ABC S ,由(1)可知,在直角三角形D BB 1中,0160=∠BC B ,221==BB BD , 可得31=D B ,故D B S V ABC 1⋅=∆32=,所以,三棱柱111ABC A B C -的体积为32. ………12分20. 解:(1)由已知,点(,0),(1,在椭圆1C 上,所以 221 a=,2211 1 2a b +=,解得:22a =,21b =,所以1C :221 2x y +=; 点(2,1), (4,4)-在抛物线2C 上,所以2p =,所以2C :24x y =. ………4分 (2)设2(,)4m P m (0m >),由24x y =得12y x '=, 所以切线l 的方程为:2()42m my x m -=-, ………6分设11(,)A x y ,22(,)B x y ,由222()4212m m y x m x y ⎧-=-⎪⎪⎨⎪+=⎪⎩得:4223(2)404m m x m x +-+-=,由0∆>,31222m x x m +=+得322(2)D m x m =+,代入2()42m my x m -=-得222(2)D m y m -=+,所以1D OD D y k x m ==-,所以OD l :1y x m=-, ………10分 由1x my x m =⎧⎪⎨=-⎪⎩得1y =-,所以点Q 在定直线1y =-上. ………12分21. 解:(1)因为()()2121210mx x f x mx x x x-+'=-+=>,依题意知2210mx x -+<在()0,+∞上有解. 当0m ≤时显然成立;当0m >时,由于函数221y mx x =-+的图象的对称轴104x m=>,故需且只需0∆>,即180m ->,解得18m <,故108m <<. 综上所述,实数m 的取值范围为1,8⎛⎫-∞ ⎪⎝⎭. ………5分(2)因为()11f m =-,()12f m '=,故切线L 的方程为()121y m m x -+=-, 即21y mx m =--.从而方程2ln 21mx x x mx m -+=--在()0,+∞上有且只有一解. 设()()2ln 21g x mx x x mx m =-+---, 则()g x 在()0,+∞上有且只有一个零点. 又()10g =,故函数()g x 有零点1x =.则()()()()222112111212mx m x mx x g x mx m x x x-++--'=-+-==.当12m =时,()0g x '≥,又()g x 不是常数函数,故()g x 在()0,+∞上单调递增. 所以函数()g x 有且只有一个零点1x =,满足题意. 当102m <<时,由()0g x '=,得12x m=或1x =,且112m >. 由()0g x '>,得01x <<或12x m>; 由()0g x '<,得112x m<<. 所以当x 在()0,+∞上变化时,()g x ',()g x 的变化情况如下表:根据上表知02g m ⎛⎫< ⎪⎝⎭.而函数()12ln 1g x mx x m x m ⎡⎤⎛⎫=-++++ ⎪⎢⎥⎝⎭⎣⎦.所以120g m ⎛⎫+> ⎪⎝⎭,故在1,2m ⎛⎫+∞ ⎪⎝⎭上,函数()g x 又存在一个零点,不满足题意.综上所述,12m =. ………12分(二)选考题:第22、23题中任选一题做答。
云南民族中学2018届高考适应性月考卷(八)文数-答案

b2 a2
为定值.
…………………………………………………(5 分)
(Ⅱ)解:当弦
AB
所在直线的斜率不存在时, |
AB |
2b2 a
,
∴a
2b2 a
2 | ON
|2 ,∴ | ON
| b,∴ | MN
| 2b ,
∴弦 MN 为椭圆的短轴,此时 MN // AB . ………………………………………(6 分)
由正弦定理,得 b2 ac ,
∴ a , b , c 成等比数列.
………………………………(6 分)
(Ⅱ)解:由(Ⅰ)及题设条件,得 ac 4 ,
则
cos
B
a2
c2 2ac
b2
≥
2ac ac 2ac
1 2
,当且仅当
a
c
时,等号成立.
∵
0
B
π
,∴
0
B
≤
π 3
,∴
sin
B
≤
3 2
,
∴ S△ABC
100 21
4.762
3.841
.
……………(11 分)
所以有 95%的把握认为“该校企业职工的每周平均体育运动时间与性别有关”.
19.(本小题满分 12 分)
………………………………………(12 分)
(Ⅰ)如图 3,在平面 ABC 内,过点 P 作直线 l // BC ,
∵ l 平面 A1BC , BC 平面 A1BC ,
x2
同理,联立
a
2
y2 b2
1, 得 (b2
a2k22 )x2
a2b2
0,
y k2 x,
2018届云南省昆明一中高三考前适应性训练(第八次月考)数学文(word版有答案)

2018届云南省昆明第一中学高三第八次月考文 科 数 学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}ln A x y x ==,集合{}xB y y e ==,则集合A 与集合B 的关系是( )A . AB = B .A B ≠⊂ C .B A ≠⊂ D .A B ∈2.在复平面内,复数z 与复数103i+对应的点关于实轴对称,则z =( ) A .3i + B .3i - C .3i -+ D .3i --3.设一个线性回归方程3 1.2y x ∧=+,当变量x 每增加一个单位时,则y 的变化情况正确的是( ) A .y 平均增加约1.2个单位 B .y 平均增加约3个单位 C .y 平均减少约1.2个单位 D .y 平均减少约3个单位 4. 若1sin 3α=,则2cos 24απ⎛⎫+= ⎪⎝⎭( ) A .23 B .12 C. 13D .0 5.若,x y 满足约束条件02346x y x y x y -≤⎧⎪+≤⎨⎪-≥-⎩,则函数2z x y =-的最小值为( )A . 5B .2 C. 2- D .5-6.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,若2b a =,2sin 2sin sin B A C =,则c o s B =( )A .18 B .14 C. 12D .1 7. 函数()01xy aa a =>≠且与函数()y f x =的图像关于直线y x =对称,则函数()y f x =与二次函数()21y a x x =--在同一坐标系内的图像可能是( )A .B .C. D . 8. 已知函数()f x x =,函数()2g x x =-,执行如图所示的程序框图,若输入的[]3,3x ∈-,则输出m 的值为()g x 的函数值的概率为( ) A .16 B .14 C. 13 D .129.已知定义在()0,+∞上的函数()()2,6ln 4f x x m h x x x =-=-,设两曲线()y f x =与()y h x =在公共点处的切线相同,则m 值等于( )A .3-B .1 C. 3 D .510. 已知三棱锥P ABC -中,,,4AC BC PC PB AB ⊥⊥=则三棱锥P ABC -的外接球的表面积为( )A .4πB .8π C. 12π D .16π11. 过正方体1111ABCD A BC D -的顶点A 的平面α与直线1AC 垂直,且平面α与平面11ABB A 的交线为直线l ,平面α与平面11ADD A 的交线为直线m ,则直线l 与直线m 所成角的大小为( )A .6π B .4π C. 3π D .2π 12.已知M 为函数8y x=的图像上任意一点,过M 作直线,MA MB 分别与圆221x y +=相切于,A B两点,则原点O 到直线AB 的距离的最大值为( ) A .18 B .14 D第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量()()1,2,3,4a m b m =-=-,若//a b 且方向相反,则m = .14.已知双曲线()2222:10,0x y C a b a b -=>>的渐近线方程为3y x =±,若抛物线28y x =的焦点与双曲线C 的焦点重合,则双曲线C 的方程为15. 已知函数()()2sin 03f x x πωω⎛⎫=+> ⎪⎝⎭的部分图像如图所示,若图中在点,A D 处()f x 取得极大值,在点,B C 处()f x 取得极小值,且四边形ABCD 的面积为32,则ω的值是 .16.设函数()2266xf x x x m e =++-⋅(m 为非零实数),若函数()f x 有且仅有一个零点,则m 的取值范围为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.设数列{}n a 的前n 项和为n S ,且1n n S a =-+. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若()12log f x x =,设()()()12n n b f a f a f a =+++,求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T .18.某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,询问了30名同学,得到如下的22⨯列联表:(Ⅰ)根据以上22⨯列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?(Ⅱ)从使用学习成绩优秀的12名同学中,随机抽取2名同学,求抽到不使用智能手机的人数X 的分布列及数学期望.智能手机的20名同学中,按分层抽样的方法选出5名同学,求所抽取的5名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;(Ⅲ)从问题(Ⅱ)中倍抽取的5名同学,再随机抽取3名同学,试求抽取3名同学中恰有2名同学为“学习成绩不优秀”的概率.参考公式:()()()()()22=n ad bc a b c d a c b d κ-++++,其中=n a b c d +++参考数据:19.如图,在三棱锥111ABC A B C -中,0111,,2,60A B BC A B BB A B BC BB B B C⊥⊥===∠=,点D 为边BC 的中点.(Ⅰ)证明:平面1AB D ⊥平面ABC ; (Ⅱ)求三棱柱111ABC A B C -的体积.20.已知椭圆()22122:10x y C a b a b+=>>和抛物线()22:20C x py p =>,在12,C C 上各取两个点,这四个点的坐标为()()()2,1,,,4,4⎛-⎝⎭. (Ⅰ)求12,C C 的方程;(Ⅱ)设P 是2C 在第一象限上的点,2C 在点P 处的切线l 与1C 交于,A B 两点,线段AB 的中点为D ,过原点O 的直线OD 与过点P 且垂直于x 轴的直线交于点Q ,证明:点Q 在定直线上.21. 已知函数()2ln f x mx x x =-+,(Ⅰ)若在函数()f x 的定义域内存在区间D ,使得该函数在区间D 上为减函数,求实数m 的取值范围;(Ⅱ)当102m <≤时,若曲线():C y f x =在点1x =处的切线L 与曲线C 有且只有一个公共点,求实数m 的值或取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在平面直角坐标系xoy 中,已知=曲直线11cos :sin x C y αα=+⎧⎨=⎩(α为参数)与曲线12cos :22sin x C y ββ=⎧⎨=+⎩(β为参数),且曲线1C 与2C 交于,O A 两点,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系 (Ⅰ)求曲线12,C C 的极坐标方程; (Ⅱ)直线OA 绕点O 旋转2π后,与曲线12,C C 分别交于,P Q 两点,求PQ . 23.选修4-5:不等式选讲已知函数()()3,22f x x g x x =+=-.(Ⅰ)若()()()h x f x g x =+,且()h x a ≥恒成立,求实数a 的取值范围;(Ⅱ)若()x ϕ=()x ϕ的最大值.试卷答案一、选择题1-5:ABACD 6-10:BACDD 11、12:CB二、填空题13. 5- 14.2213x y -= 15. 4π16. ()()0,26,e +∞三、解答题17. 解:(1)由1n n S a =-+ 得 111n n S a ++=-+,两式相减得:11n n n n S S a a ++-=-+, 即11n n n a a a ++=-+, 即112n n a a += ()1n ≥, 所以数列{}n a 是公比为12的等比数列,又由111a a =-+得 112a =, 所以1112nn n a a q-⎛⎫== ⎪⎝⎭;(2)因为()()()()121122nn n n b f a f a f a n +=+++=+++=,所以()1211211n b n n n n ⎛⎫==- ⎪++⎝⎭, 所以11111112221=12231+11n n T n n n n ⎛⎫⎛⎫=-+-++-=- ⎪ ⎪++⎝⎭⎝⎭. 18. 解:(1)由列联表可得()()()()()()2223042816107.87912182010n ad bc K a b c d a c b d -⨯⨯-⨯===>++++⨯⨯⨯所以能在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响.(2)根据题意,所抽取的5名同学中“学习成绩优秀”有1名同学,“学习成绩不优秀”有4名同学. (3)学习成绩不优秀的4名同学分别记为A ,B ,C ,D ;“学习成绩优秀”有1名同学记为E .则再从中随机抽取3人构成的所有基本事件为:(),,A B C ,(),,A B D ,(),,A B E ,(),,A C D ,(),,A C E ,(),,A D E ,(),,B C D ,(),,B C E ,(),,B D E ,(),,C D E ,共有10种;抽取3人中恰有2名同学为“学习成绩不优秀”所含基本事件为:(),,A B E ,(),,A C E ,(),,A D E ,(),,B C E ,(),,B D E ,(),,C D E 共有6种,所求为63105P ==. 19. 解:(1)由题意,⊥AB 平面C C BB 11,⊂D B 1平面C C BB 11,可得D B AB 1⊥,又△BC B 1为等边三角形,点D 为BC 边的中点,可得D B BC 1⊥,AB 与BC 相交于点B ,则D B 1⊥平面ABC ,⊂D B 1平面D AB 1,所以,平面D AB 1⊥平面ABC .(2)因为△ABC 为直角三角形,2==BC AB , 所以2=∆ABC S ,由(1)可知,在直角三角形D BB 1中, 0160=∠BC B ,221==BB BD , 可得31=D B ,故D B S V ABC 1⋅=∆32=,所以,三棱柱111ABC A B C -的体积为32. 20. 解:解:(1)由已知,点(,0),(1,在椭圆1C 上,所以 22 1 a =,22111 2a b+=, 解得:22a =,21b =,所以1C :22 1 2x y +=; 点(2,1), (4,4)-在抛物线2C 上,所以2p =,所以2C :24x y =.(2)设2(,)4m P m (0m >),由24x y =得12y x '=, 所以切线l 的方程为:2()42m my x m -=-, 设11(,)A x y ,22(,)B x y ,由222()4212m m y x m x y ⎧-=-⎪⎪⎨⎪+=⎪⎩得:4223(2)404m m x m x +-+-=, 由0∆>,31222m x x m +=+得322(2)D m x m =+,代入2()42m m y x m -=-得222(2)D m y m -=+,所以1D OD D y k x m ==-,所以OD l :1y x m=-, ………10分 由1x m y x m =⎧⎪⎨=-⎪⎩得1y =-,所以点Q 在定直线1y =-上. 21. 解:(1)因为()()2121210mx x f x mx x x x-+'=-+=>,依题意知2210mx x -+<在()0,+∞上有解. 当0m ≤时显然成立;当0m >时,由于函数221y mx x =-+的图象的对称轴104x m=>, 故需且只需0∆>,即180m ->,解得18m <,故108m <<.综上所述,实数m 的取值范围为1,8⎛⎫-∞ ⎪⎝⎭.(2)因为()11f m =-,()12f m '=,故切线L 的方程为()121y m m x -+=-, 即21y mx m =--.从而方程2ln 21mx x x mx m -+=--在()0,+∞上有且只有一解.设()()2ln 21g x mx x x mx m =-+---,则()g x 在()0,+∞上有且只有一个零点. 又()10g =,故函数()gx 有零点1x =.则()()()()222112111212mx m x mx x g x mx m x x x-++--'=-+-==.当12m =时,()0g x '≥,又()g x 不是常数函数,故()g x 在()0,+∞上单调递增. 所以函数()g x 有且只有一个零点1x =,满足题意.当102m <<时,由()0g x '=,得12x m =或1x =,且112m>. 由()0g x '>,得01x <<或12x m>;由()0g x '<,得112x m<<. 所以当x 在()0,+∞上变化时,()g x ',()g x 的变化情况如下表:根据上表知02g m ⎛⎫< ⎪⎝⎭.而函数()12ln 1g x mx x m x m ⎡⎤⎛⎫=-++++ ⎪⎢⎥⎝⎭⎣⎦.所以120g m ⎛⎫+> ⎪⎝⎭,故在1,2m ⎛⎫+∞⎪⎝⎭上,函数()g x 又存在一个零点,不满足题意. 综上所述,12m =. 22. 解:(1)曲线1C 是以(1,0)为圆心,1为半径的圆,其极坐标方程为2cos ρθ=, 曲线2C 是以(0,2)为圆心,2为半径的圆,其极坐标方程为4sin ρθ=. (2)由2cos 4sin θθ=得1tan2θ=,即直线OA 的斜率为12,从而sin θ=,cos θ=,由已知,设1,2P πρθ⎛⎫- ⎪⎝⎭,2,2Q πρθ⎛⎫+ ⎪⎝⎭将1,2P πρθ⎛⎫- ⎪⎝⎭代入2cos ρθ=,得12cos 2sin 2πρθθ⎛⎫=-== ⎪⎝⎭,同理,将2,2Q πρθ⎛⎫+ ⎪⎝⎭代入4sin ρθ=,得24sin 4cos 2πρθθ⎛⎫=+==⎪⎝⎭,所以,12PQ ρρ=+=+=.23. 解:(1)31, 3()3225, 3131, 1x x h x x x x x x x --<-⎧⎪=++-=-+-≤≤⎨⎪+>⎩, 所以,min ()(1)4h x h ==,只需4a ≤, 故实数a 的取值范围为(],4-∞.(2)由柯西不等式,()1x ϕ===53x =-时,等号成立,故()x ϕ的最大值为.。
【数学】云南省昆明市2018届高三教学质量检查(二统)数学(文)试题 含解析
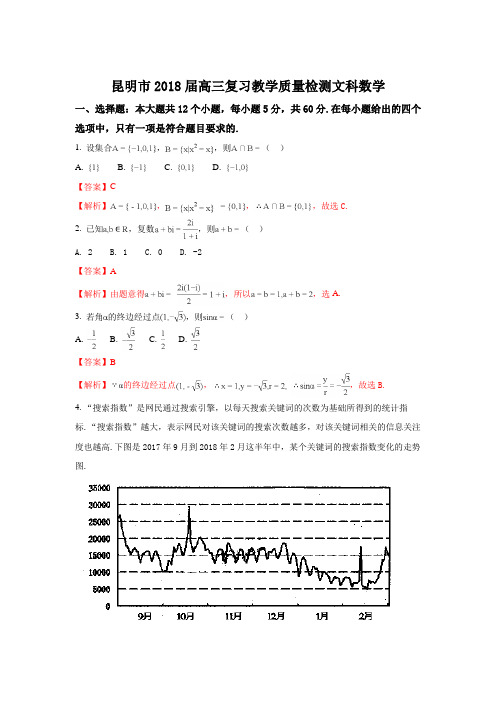
昆明市2018届高三复习教学质量检测文科数学一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合,,则()A. B. C. D.【答案】C【解析】,,,故选C.2. 已知,复数,则()A. 2B. 1C. 0D. -2【答案】A【解析】由题意得,所以,选A.3. 若角的终边经过点,则()A. B. C. D.【答案】B【解析】的终边经过点,,故选B.4. “搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.根据该走势图,下列结论正确的是()A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化B. 这半年中,网民对该关键词相关的信息关注度不断减弱C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值【答案】D5. 已知直线与圆相交于、两点,若,则实数的值等于()A. -7或-1B. 1或7C. -1或7D. -7或1【答案】C【解析】由圆的方程可知,圆心坐标,圆半径,由勾股定理可知,圆心到直线的距离为,解得或,故选C.6. 执行下面的程序框图,如果输入,,则输出的()A. 54B. 33C. 20D. 7【答案】C【解析】执行程序框图,;;,结束循环,输出,故选C.7. 一个简单几何体的三视图如图所示,其中正视图是等腰直角三角形,侧视图是边长为2的等边三角形,则该几何体的体积等于()A. B. C. D. 2【答案】D【解析】由三视图可知,该几何体是一个四棱锥,由侧视图为边长为的正三角形,结合三视图的性质可知四棱锥底面是边长为和的矩形,四棱锥的高为,故四棱锥体积为,故选D.【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力,属于难题.三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响,对简单组合体三视图问题,先看俯视图确定底面的形状,根据正视图和侧视图,确定组合体的形状.8. 若直线与函数的图像无公共点,则不等式的解集为()A. B.C. D.【答案】B【解析】与函数的图象无公共点,且,,即为,结合正切函数图象可得,,不等式的解集为,故选B.9. 设函数的最小值是1,则实数的取值范围是()A. B. C. D.【答案】B【解析】时,的最小值为要使的最小值是1,必有时,的最小值不小于,因为在上递减,所以时,,则,实数的取值范围是,故选B.10. 数列满足,则数列的前20项的和为()A. B. C. D.【答案】A11. 已知,是椭圆的两个焦点,过原点的直线交于两点,,且,则的离心率为()A. B. C. D.【答案】D【解析】,连接,由椭圆的对称性可知,是矩形,设,则,可知,由勾股定理可知,,,故选D.【方法点睛】本题主要考查双曲线的定义及离心率,属于难题.离心率的求解在圆锥曲线的考查中是一个重点也是难点,一般求离心率有以下几种情况:①直接求出,从而求出;②构造的齐次式,求出;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解.本题是利用双曲线的几何性质以及双曲线的定义根据方法①求解的.12. 已知函数,若是函数的唯一极值点,则实数的取值范围是()A. B. C. D.【答案】A【解析】由函数,可得,有唯一极值点有唯一根,无根,即与无交点,可得,由得,在上递增,由得,在上递减,,即实数的取值范围是,故选A.【方法点睛】已知函数零点(方程根)的个数,求参数取值范围的三种常用的方法:(1)直接法,直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;(2)分离参数法,先将参数分离,转化成求函数值域问题加以解决;(3)数形结合法,先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.一是转化为两个函数的图象的交点个数问题,画出两个函数的图象,其交点的个数就是函数零点的个数,二是转化为的交点个数的图象的交点个数问题 .二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 已知变量,满足,则的最小值为__________.【答案】【解析】画出表示的可行域,如图,由,可得平移直线,由图知,当直线经过点,直线在以轴上截距最小,此时最小值为,故答案为.【方法点晴】本题主要考查线性规划中利用可行域求目标函数的最值,属简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.14. 已知向量,满足,|,,则__________.【答案】【解析】,故答案为. 15. 在中,角所对的边分别是,若,,且,则的面积等于__________.【答案】【解析】因为,由正弦定理可知,,所以为等腰三角形,,,到距离,面积为,故答案为.16. 如图,等腰所在平面为,,.是的重心.平面内经过点的直线将分成两部分,把点所在的部分沿直线翻折,使点到达点(平面).若在平面内的射影恰好在翻折前的线段上,则线段的长度的取值范围是__________.【答案】【解析】因为等腰所在平面为,,.是的重心,所以可得,连接,在中,,,当与重合时最大为,此时最小,与重合)作于,此时最小为最大为,的长度的取值范围是,故答案为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知等差数列中,,.(1)求的通项公式;(2)设,求数列的前项和.【答案】(1);(2).【解析】试题分析:(1)根据等差数列中,,列出关于首项、公差的方程组,解方程组可得与的值,从而可得数列的通项公式;(2)由(1)可得,利用裂项相消法求解即可.试题解析:(1)由,得,解得.所以,数列的通项公式为.(2),所以的前项和.所以.【方法点晴】本题主要考查等差数列的通项公式,以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1);(2);(3);(4);此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.18. 在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标和,制成下图,其中“”表示甲村贫困户,“”表示乙村贫困户.若,则认定该户为“绝对贫困户”,若,则认定该户为“相对贫困户”,若,则认定该户为“低收入户”;若,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.(1)从乙村的50户中随机选出一户,求该户为“绝对贫困户”的概率;(2)从甲村所有“今年不能脱贫的非绝对贫困户”中任选2户,求选出的2户均为“低收入户”的概率;(3)试比较这100户中,甲、乙两村指标的方差的大小(只需写出结论).【答案】(1);(2);(3)甲村指标的方差大于乙村指标的方差.【解析】试题分析:(1)由图知,在乙村户中,指标的有户,根据古典概型概率公式可得结果;(2)利用列举法可得,所有可能的结果组成的基本事件有个,其中两户均为“低收入户”的事件共有个,根据古典概型概率公式可得选出的户均为“低收入户”的概率;(3) 由图可知,这户中甲村指标的方差大于乙村指标的方差..试题解析:(1)由图知,在乙村50户中,指标的有15户,所以,从乙村50户中随机选出一户,该户为“绝对贫困户”的概率为.(2)甲村“今年不能脱贫的非绝对贫困户”共有6户,其中“相对贫困户”有3户,分别记为,,.“低收入户”有3户,分别记为,,,所有可能的结果组成的基本事件有:,,,,,,,,,,,,,,.共15个,其中两户均为“低收入户”的共有3个,所以,所选2户均为“低收入户”的概率.(3)由图可知,这100户中甲村指标的方差大于乙村指标的方差.【方法点睛】本题主要考查古典概型概率公式的应用,属于难题,利用古典概型概率公式求概率时,找准基本事件个数是解题的关键,基本亊件的探求方法有 (1)枚举法:适合给定的基本事件个数较少且易一一列举出的;(2)树状图法:适合于较为复杂的问题中的基本亊件的探求.在找基本事件个数时,一定要按顺序逐个写出:先,…. ,再,…..依次….… 这样才能避免多写、漏写现象的发生.19. 如图,直三棱柱中,是的中点.(1)证明:平面;(2)若,,求点到平面的距离.【答案】(1)证明见解析;(2).【解析】试题分析:(1)连接,设与的交点为,则为的中点,连接,又是的中点,由三角形中位线定理可得,从而根据线面平行的判定定理可得平面;(2)设点到平面的距离为,因为的中点在平面上,故到平面的距离也为,三棱锥的体积,的面积,由得结果.试题解析:(1)连接,设与的交点为,则为的中点,连接,又是的中点,所以.又平面,平面,所以平面.(2)由,是的中点,所以,在直三棱柱中,,,所以,又,所以,,所以.设点到平面的距离为,因为的中点在平面上,故到平面的距离也为,三棱锥的体积,的面积,则,得,故点到平面的距离为.20. 设抛物线的焦点为,准线为.已知点在抛物线上,点在上,是边长为4的等边三角形.(1)求的值;(2)在轴上是否存在一点,当过点的直线与抛物线交于、两点时,为定值?若存在,求出点的坐标,若不存在,请说明理由.【答案】(1);(2).【解析】试题分析:(1)由题知,,则.设准线与轴交于点,则.又是边长为4的等边三角形,,所以,,从而可得结果;(2)设点,由题意知直线的斜率不为零,设直线的方程为,由得,,由韦达定理及两点间距离公式可得,同理可得,化简即可得,时为定值,此时点为定点.试题解析:(1)由题知,,则.设准线与轴交于点,则.又是边长为4的等边三角形,,所以,,即.(2)设点,由题意知直线的斜率不为零,设直线的方程为,点,,由得,,则,,.又,同理可得,则有.若为定值,则,此时点为定点.又当,时,,所以,存在点,当过点的直线与抛物线交于、两点时,为定值. 21. 函数,.(1)求函数的极值;(2)若,证明:当时,.【答案】(1)极小值;(2)证明见解析.【解析】试题分析:(1)求出,分别令求得的范围,可得函数增区间,求得的范围,可得函数的减区间,根据单调性可得函数的极值;(2)不等式等价于,由(1)得,可得,设,利用导数研究函数的单调性,根据单调性可得,进而可得结果.试题解析:(1)函数的定义域为,,由得,得,所以函数在单调递减,在上单调递增,所以函数只有极小值.(2)不等式等价于,由(1)得:.所以,,所以.令,则,当时,,所以在上为减函数,因此,,因为,所以,当时,,所以,而,所以.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.选修4-4:坐标系与参数方程22. 在平面直角坐标系中,圆的方程为,以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程是.(1)求圆的参数方程和曲线的直角坐标方程;(2)已知,是曲线与轴的两个交点,点为圆上的任意一点,证明:为定值.【答案】(1),;(2)证明见解析.【解析】试题分析:(1)由三角函数的性质可得圆的参数方程为,利用二倍角的余弦公式展开曲线的极坐标方程,利用可得曲线的直角坐标方程;(2)由(1)知,,可设,所以,化简即可的结果.试题解析:(1)圆的参数方程为,(为参数),由得:,即,所以曲线的直角坐标方程为.(2)由(1)知,,可设,所以所以为定值10.选修4-5:不等式选讲23. 已知函数.(1)解不等式;(2)若、,,,证明:.【答案】(1)或;(2)证明见解析.【解析】试题分析:(1)用分段讨论法解绝对值不等式。
(试卷+解析)2018云南师大附中适应性月考(8)-文数

一、选择题(本大题共 12 小题,每小题 5 分,共 60 分) 题号 答案 【解析】 1.由题意知:集合 A [3,3] ,集合 B (,2) ,则 A B [3,2) ,故选 D. 2.在复平面内, z 的轨迹是以 (1, 1) 为圆心,1 为半径的圆,由数形结合可知, | z | 的最小值 为 2 1 ,所以 | z |2 3 2 2 ,故选 B. 由数列 {an } 为等差数列, 设其公差为 d , 所以 (a2 a4 a6 ) (a1 a3 a5 ) 3d 3 , 即 d 1, 3. 故选 A. 1 D 2 B 3 A 4 A 5 C 6 B 7 B 8 D 9 B 10 C 11 A 12 C
5.由题意可知圆柱的高为 2,所以球心到底面的距离为 1,又由底面的半径为 1,所以圆柱的
外接球的半径为 2 ,故而圆柱的外接球的表面积为 8π ,故选 C.
π 6.由函数 f ( x) 的最大值为 4 ,则选项 A 不满足;由 ,2 为其一个对称中心,即 3 选项 D 不满足;由 f ( x1 ) f ( x2 ) 2 ,且 | x1 x2 |min 不满足;而 B 选项均满足,故选 B.
图1
内切圆的直径为 6 步,故选 B.
文科数学参考答案·第 1 页(共 9 页)
8. 到正四面体的四个顶点距离相等的截面, 如图 2 有两种情况:第一种情况,截面为边长为 1 的正三角形,共有 4 种情况;第二种情况, 截面为边长为 1 的正方形,共有 3 种情况,综
图2
上所述,所有截面的个数为 3 4 7 ,故选 D. 9.由 x,y,z 均为大于 1 的正数,令 log 2 x log 3 y log 5 z m ,则 m 0 ,且 x 2m , y 3m ,
2018届云南省西南名校联盟高考适应性月考卷文科数学试题(扫描版)

文科数学参考答案·第0页(共13页)文科数学参考答案·第1页(共13页)文科数学参考答案·第2页(共13页)文科数学参考答案·第3页(共13页)文科数学参考答案·第4页(共13页)云南师大附中2018届高考适应性月考卷(八)文科数学参考答案一、选择题(本大题共12小题,每小题5分,共60分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 DBAACBBDBCAC【解析】1.由题意知:集合[33]A =-,,集合(2)B =-∞,,则AB [32)=-,,故选D . 2.在复平面内,z 的轨迹是以(11),为圆心,1为半径的圆,由数形结合可知,||z 的最小值21,所以2||322z =-B .3.由数列{}n a 为等差数列,设其公差为d ,所以246135()()33a a a a a a d ++-++==,即1d =,故选A .4.设a 与b 的夹角为θ,由222|2|(2)()44()1168cos 13a b a b a a b b θ+=+=++=++所以1cos 2θ=-,则a 与b 的夹角为2π3,故选A .5.由题意可知圆柱的高为2,所以球心到底面的距离为1,又由底面的半径为1,所以圆柱的2,故而圆柱的外接球的表面积为8π,故选C .6.由函数()f x 的最大值为4,则选项A 不满足;由π23⎛⎫⎪⎝⎭,为其一个对称中心,即π23f ⎛⎫= ⎪⎝⎭,选项D 不满足;由12()()2f x f x ==,且12min π||2x x -=,即函数的最小正周期为π,选项C 不满足;而B 选项均满足,故选B .7.如图1,在Rt ABC △中,15CA =,8CB =,则2217AB CA CB =+, 设点I 为ABC △内切圆的圆心,设其内切圆的半径为r ,由ABC AIB BIC CIA S S S S =++△△△△,所以111222ABC S r AB r BC r CA =++=△1()2r AB BC CA ++,故而2158381517ABC S r AB BC CA ⨯===++++△,所以其 图1文科数学参考答案·第5页(共13页)内切圆的直径为6步,故选B .8.到正四面体的四个顶点距离相等的截面,如图2 有两种情况:第一种情况,截面为边长为 1的正三角形,共有4种情况;第二种情况,截面为边长为1的正方形,共有3种情况,综上所述,所有截面的个数为347+=,故选D .9.由x y z ,,均为大于1的正数,令235log log log x y z m ===,则0m >,且2m x =,3m y =,5m z =,(2)m x =,33(3)m y =,55(5)m z .又由663(2)89(3)=<=,323由10105(2)3225(5)=>=525>m y x =(0)m >在第一象限的单调性知,53z x y <B .10.由程序框图可知,当n k =时,运算前的a 值记为k a ,则程序输出的是6a ,即61a =,由程序框图可知,当输入的a 为正整数时,对任意的k ,k a 均为正整数,而61a =,则必有52a =,此时,41213254123121()33216587()2344211()30()a a a a a a a a a a a a a ⎧=⎪⎪⎧⎪⎧=⎧=⇒⎪⎨⎪⎪=⎪⎩⎪⎪=⇒⎨⎪⎪⎪⎪⎪==⇒⎨⎪⎩⎪⎪=⇒⎨⎪⎧=⎧⎪⎪⎪⎪⎪=⇒⎨⎪⎪⎪=⇒=⎨⎪⎪⎩⎪⎪⎪⎪⎪=⎪⎩⎩⎩舍,,,舍,,舍,舍, 故而,a 的可能取值为4532,,,故选C .11.如图3,设1PF m =,2PF n =,12F PF θ∠=,由题意知:22222162cos 4m n mn m n mn θ⎧++=⎪⎨+-=⎪⎩,,所以 61cos mn θ=+,又121sin sin 33tan 321cos 2F PF S mn θθθθ===+△所以π3θ=.由正弦定理可知,三角形的外接圆的直径为 图2文科数学参考答案·第6页(共13页)122ππ3sin sin 33F F ==4π3,故选A . 12.当0a ≤时,()|1|f x x =-满足题意;当03a <≤时,(2)(4)3f f -==,要满足题意需满足(1)23f a =≤,即302a <≤;当3a >时,(1)26f a =>,不合题意.综上所述,a 的取值范围是32a ≤,故选C .二、填空题(本大题共4小题,每小题5分,共20分)题号 13 14 1516 答案 4 40351111333⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,, 1【解析】13.作出不等式组313x y x y x +⎧⎪--⎨⎪⎩≥,≥,≤表示的平面区域,如图4中阴影部分所示,作出直线20x y +=,平移直线 20x y +=,当直线经过点(12)A ,时,2z x y =+取得最小 值4,所以2z x y =+的最小值为4.14.由126n n n a a a ++++=,当1n =时,则1236a a a ++=,由11a =,22a =,则33a =; 当2n =时,则2346a a a ++=,由22a =,33a =,则41a =; 当3n =时,则3456a a a ++=,由33a =,41a =,则52a =, ……观察可得,数列{}n a 是以3为周期的周期数列,且每个周期内的和为6,则数列{}n a 的前2018项的和20186726124035S =⨯++=.15.由()e e ln ||x x f x x -=++,则函数()f x 是定义在(0)(0)-∞+∞,,上的偶函数,当(0)x ∈+∞,时,令()e e x x g x -=+,所以()e e 0x x g x -'=->,即()g x 为(0)x ∈+∞,上的增图3图4文科数学参考答案·第7页(共13页)函数,又由(0)x ∈+∞,时,()()ln f x g x x =+,所以()f x 为(0)+∞,上的增函数,则不等式(31)(2)f x f -<等价于2312x -<-<,且310x -≠,解得1111333x ⎛⎫⎛⎫∈- ⎪ ⎪⎝⎭⎝⎭,,.16.设11()A x y ,,22()B x y ,,0(4)Q y ,,则切点为A 的椭圆C 的直线方程为:11143x x y y+=,切点为B 的椭圆C 的直线方程为:22143x x y y+=.由两切线均过点Q ,故而有:1012021313y y x y y x ⎧+=⎪⎪⎨⎪+=⎪⎩,,所以直线AB 的方程为013y y x +=,则直线AB 过定点(10),,所以原点到直线AB 的距离的最大值为1.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)解:(Ⅰ)由正弦定理可知:2sin cos sin 2sin 2sin()2sin cos 2cos sin A C C B A C A C A C -==+=+,所以sin 2cos sin C A C -=,因为sin 0C ≠,而(0π)A ∈,,则1cos 2A =-,所以2π3A =.…………………………………………(6分)(Ⅱ)如图5,由2b c ==ABC △是顶角为2π3的等腰三角形,则π6ABC ∠=, 所以2222π2cos63BC b c bc =+-=,即6BC =, 又2AD DC =,所以1233BD BC BA =+,则222π9||||4||4||||cos 266BD BC BA BA BC =++=, 所以26BD =.………………………………………………………………………(12分) 18.(本小题满分12分)解:(Ⅰ)2×2列联表补充如下:物理优秀 物理不优秀总计 数学优秀 40 20 60 数学不优秀152540图5文科数学参考答案·第8页(共13页)……………………………………………………………………………………(2分)(Ⅱ)由题意知:22100(40252015)8.25 6.63555456040K ⨯⨯-⨯=≈>⨯⨯⨯,所以有99%的把握认为数学与物理的学习情况有关.………………………………(6分) (Ⅲ)由题意知,数学优秀的同学为60名,数学不优秀的同学为40名. 按分层抽样抽取的5名同学中包含了3名数学优秀的同学,记为123A A A ,,, 按分层抽样抽取的5名同学中包含了2名数学不优秀的同学,记为12B B ,, 所以从这5名同学中随机选取2人的所有情况共有如下10种情况,即:12()A A ,,13()A A ,,11()A B ,,12()A B ,,23()A A ,,21()A B ,,22()A B ,,31()A B ,, 32()A B ,,12()B B ,,其中2名同学数学都优秀的情况包括:12()A A ,,13()A A ,,23()A A ,共3种情况, 所以参加该活动的2名同学数学都优秀的概率为310.………………………………(12分) 19.(本小题满分12分)(Ⅰ)证明:如图6,连接AC BD ,交于点O ,连接MO ,NO ,所以AC BD ⊥, 又AM ⊥平面ABCD ,AM BD ⊥且ACAM A =,所以BD ⊥平面ACNM ,则有MO BD ⊥,NO BD ⊥, 由1CN =,3AM =,ABCD 是边长为2的菱形,且2π3ABC ∠=, 总计 55 45 100图6文科数学参考答案·第9页(共13页)可得23MO =,2NO =,又由4MN =,即222MN MO NO =+, 所以NO MO ⊥,又MOBD O =,所以NO ⊥平面MDB ,所以平面MDB ⊥平面NDB .………………………………(6分) (Ⅱ)解:由O 为AC 的中点,则点A 到平面BMD 的距离等于点C 到平面BMD 的距离, 设点A 到平面BMD 的距离为d , 由(Ⅰ)知BD ⊥平面ACNM ,所以2A BMD B AOM D AOM B AOM V V V V ----=+=,即11233BMD AOM d S BO S ⨯⨯=⨯⨯⨯△△, 所以121233322122232AOMBMDAM AOBO S d S BD MO ⨯⨯⨯⨯⨯⨯⨯====⨯⨯⨯△△.……………………(12分) 20.(本小题满分12分)解:(Ⅰ)设圆心M 的坐标为()x y ,,则0x >.由题意知:22||1(1)x x y +-+24y x =(0)x >.………………………(4分) (Ⅱ)设AB 所在的直线的倾斜角为(0)θθ≠, 则直线AB 的方程为tan (1)y x θ=-,与抛物线的方程联立得:2222(tan )(2tan 4)tan 0x x θθθ-++=, 设A B ,的横坐标分别是12x x ,,文科数学参考答案·第10页(共13页)则有:22122222tan 4tan 14||224tan tan sin AB x x θθθθθ++=++=+==, 同理:2244||πcos sin 2CD θθ==⎛⎫± ⎪⎝⎭, 所以四边形的面积22214432322sin cos sin (2)S θθθ=⨯⨯=≥,当且仅当π4θ=或3π4θ=时,不等式取等号,所以四边形面积的最小值为32.…(12分) 21.(本小题满分12分)解:(Ⅰ)由0a b +=,则()ln f x x ax a =-+,所以1()f x a x'=-. 若0a ≤,则1()0f x a x'=->,即函数()f x 为定义域上的增函数,由(1)0f =,不合题意;若01a <<,则11()ax f x a x x -'=-=,所以()f x 为10a ⎛⎫⎪⎝⎭,上的增函数,且101a <<,由(1)0f =,不合题意;若1a >,则11()ax f x a x x -'=-=,所以()f x 为1a ⎛⎫+∞ ⎪⎝⎭,上的减函数,且11a >,由(1)0f =,不合题意;若1a =,()ln 1f x x x =-+,11()1xf x x x-'=-=,所以()f x 为(01),上的增函数,为(1)+∞, 上的减函数,所以()(1)0f x f =≤,满足题意.综上所述,满足题意的1a =.…………………………………………………………(5分)文科数学参考答案·第11页(共13页)(Ⅱ)由()0f x ≤恒成立,则0a >,又由()0f x ≤,等价于ln x ax b +≤,即等价于函数ln y x =的图象不在函数y ax b =+图象的上方,对于每一个大于零的a ,要使得a b +的值最小,需使直线y ax b =+与函数ln y x =的图象相切,此时,设切点为00(ln )x x ,且00x >, 则切线方程可以表示为0001ln ()y x x x x -=-,即001ln 1y x x x =+-, 所以001ln 1a b x x +=+-. 令1()ln 1(0)g x x x x =+->,则22111()x g x x x x-'=-+=, 所以()g x 为(01),上的减函数,为(1)+∞,上的增函数,则()(1)0g x g =≥, 所以a b +的最小值为0.………………………………………………………………(12分) 22.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)曲线C 的参数方程为:2cos sin x y θθ=⎧⎨=⎩,,π02θθ⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭其中为参数,,, 所以曲线C 的普通方程为:2214x y +=,00x y ≥,≥.又由cos x ρθ=,sin y ρθ=,所以曲线C 的极坐标方程为:2224cos 4sin ρθθ=+,π02θ⎡⎤∈⎢⎥⎣⎦,, 直线l 的极坐标方程为:4sin cos ρθθ=+.……………………………………………(5分)文科数学参考答案·第12页(共13页)(Ⅱ)如图7,由题意知:1π1π=sin sin 2626ABCD BOC AOD S S S OB OC OA OD =-⨯⨯-⨯⨯△△,由(Ⅰ)知,224731422OA ⎛⎫⎛⎫+⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭1331OB ==++2241313422OD ==⎛⎫⎛⎫+⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭,3131OC ++所以,1491()8(23)4ABCD S OB OC OA OD =⨯-⨯=10分)23.(本小题满分10分)【选修4−5:不等式选讲】 (Ⅰ)解:由()2|1||2|f x x x =-++,所以31()4[21)32x x f x x x x x ⎧⎪=-∈-⎨⎪-<-⎩,≥,,,,,,则函数()f x 的图象如图8, 则函数()f x 的最小值为3,即3m =.……………(5分) (Ⅱ)证明:由(Ⅰ)知,3a b c ++=,所以1111112226a b c a b c a b c a b c+++++⨯⨯⨯=≥, 当且仅当1a b c ===时不等式取等号,所以1113a b c++≥.…………………(10分)图8图7。
2018届昆明市高考文科数学模拟试卷及答案

2018 届昆明市高考文科数学模拟试卷及答案高中文科数学的备考,文科生们可以通过做高考文科数学模拟试题来巩固数学知识。
以下是为你的2018 届昆明市高考文科数学模拟试卷,希望能帮到你。
一、选择题1. 设集合A={x € Z|x > 2} , B={x|0 < xA.{x|2 <x<6}B.{x|0 <x<6}C.{0 , 1, 2, 3, 4, 5}D.{2 , 3, 4,5}2. =()A. - iB.iC.1D. - 13. 一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为()A.25 nB.50 nC.100 nD.200 n4. AQI(Air Quality Index ,空气质量指数)是报告每日空气质量的参数,描述了空气清洁或者污染的程度.AQI 共分六级,从一级优(0〜50),二级良(51〜100,),三级轻度污染,四级重度污染,直至无极重度污染,六级严重污染(大于300). 下面是昆明市xx 年 4 月份随机抽取的10天的AQI茎叶图,利用该样本估计昆明市2018年4 月份质量优的天数(按这个月共30天计算)为()A.3B.4C.12D.215. 已知非零向量,满足?=0, ||=3 ,且与+的夹角为,则||=()A.6B.3C.2D.36. 若tan 0 二—2,贝卩sin2 0 +cos2 0 =()A.B. —C.D.-7. 已知F1、F2为双曲线C: —=1(a>0, b>0)的左、右焦点,点P 在C的渐进线上,PF1丄x轴,若△ PF1F2为等腰直角三角形,则 C 的离心率为( )A.B.C.+1D.8. 在厶ABC中,已知AB= AC= tan / BAC- 3,贝S BC边上的高等于( )A.1B.C.D.29. 定义n!=1 x 2X 3X-X n,例如1!=1 , 2!=1 X2=2,执行右边的程序框图,若输入?=0.01,则输出的e精确到e的近似值为()A.2.69B.2.70C.2.71D.2.7210. 我国南北朝时期的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上,于 5 世纪末提出了下面的体积计算的原理(祖暅原理) :“幂势既同,贝积不容异” . “势”是几何体的高,“幂”是截面面积. 意思是,若两等高的几何体在同高处截面面积总相等,贝这两个几何体的体积相等.现有一旋转体D,它是由抛物线y=x2(x >0), 直线y=4及y轴围成的封闭图形如图1所示绕y轴旋转一周形成的几何体,利用祖暅原理,以长方体的一半为参照体(如图2所示)贝旋转体D的体积是()A.B.6 n C.8 n D.16 n11. 已知函数f(x)二,若方程f(x) - ax=O恰有两个不同的根,则实数 a 的取值范围是( )A.(0 , )B.[ , )C.( , ]D.(-汽0] U [ , +乂)12. 设F为抛物线C: y2=8x,曲线y=(k>0)与C交于点A,直线FA恰与曲线y=(k>0)相切于点A,直线FA于C的准线交于点B,贝席于( )A.B.C.D.二、填空题13. 已知实数x,y 满足,贝z=x+y 的最大值为.14. 已知函数f(x)=sin( 3 x+)( 3 >0), A、B是函数y=f(x)图象上相邻的最高点和最低点,若|AB|=2,则f(1)=.15. 已知数列{an}的前n项和为Sn,且an=4n,若不等式Sn+8》入n对任意的n € N*都成立,贝卩实数入的取值范围为.16. 若关于x的不等式a< x2 - 3x+4< b的解集恰好为[a , b], 那么b- a= .三、解答题17. 已知数列{an}满足a1=2,an+1=2an+2n+1.(I) 证明数列{}是等差数列;(II) 求数列{}的前n项和.18. 某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了 1 00名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按照[0 , 0.5) , [0.5 , 1),…,[4 , 4.5]分成9组,制成样本的频率分布直方图如图所示.(I) 求图中a的值;(II) 估计该校高一学生周末“阅读时间”的中位数;( 皿)在[1 , 1.5) , [1.5 , 2)这两组中采用分层抽样抽取7人,再从7人中随机抽取2人,求抽取的两人恰好都在一组的概率.19. 如图,已知三棱锥P- ABC BC! AC BC二AC=2 PA二PB 平面PABL平面ABC D E、F分别是AB PB PC的中点.(I )证明:PDL平面ABC;( I)若M为BC中点,且PM!平面EFD 求三棱锥P- ABC的体积.20. 已知动点M(x, y)满足:+=2, M的轨迹为曲线E.(I )求E的方程;( I)过点F(1 , 0)作直线I交曲线E于P, Q两点,交y轴于R 点,若二入1,二入2,求证:入1+入2为定值.21. 已知函数f(x)=(2x2+x)lnx - (2a+1)x2 - (a+1)x+b(a , b€R).( I )当a=1 时,求函数f(x) 的单调区间;( I)若f(x) > 0恒成立,求b - a的最小值.请考生在22、23二题中任选一题作答,如果多做,则按所做的第一题计分.[ 选修4-4:坐标系与参数方程]22. 在平面直角坐标系xOy中,曲线C的方程为(x - 2)2+y2=4 , 直线I的方程为x+y - 12=0,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.(I) 分别写出曲线C与直线I的极坐标方程;(II) 在极坐标中,极角为B ( 0€ (0 ,))的射线m与曲线C,直线I分别交于A、B两点(A异于极点0),求的最大值.[ 选修4-5 :不等式选讲]23. 已知a, b, c, m n, p都是实数,且a2+b2+c2=1, m2+n2+p2=1.( I)证明|am+bn+cp| < 1;(I)若abc z 0,证明++> 1.一、选择题1. 设集合A={x € Z|x > 2} , B={x|0 < xA.{x|2 < x<6}B.{x|0 < x<6}C.{0 , 1 , 2 , 3 , 4 , 5}D.{2 , 3 ,4 ,5}【考点】1E:交集及其运算.【分析】由A与B ,求出两集合的交集即可.【解答】解:T 集合A={x€ Z|x > 2}, B={x|0 < x<6},••• A A B={2 , 3 , 4 , 5},故选: D2. =( )A. - iB.iC.1D. - 1【考点】A5:复数代数形式的乘除运算【分析】直接由复数代数形式的乘除运算化简得答案.【解答】解:=,故选: A.3. 一个四棱柱的三视图如图所示,若该四棱柱的所有顶点都在同一球面上,则这个球的表面积为()A.25 nB.50 nC.100 nD.200 n【考点】LR:球内接多面体;LG :球的体积和表面积.【分析】由题意,四棱柱为长方体,其对角线长为=5,可得球的半径为,即可求出这个球的表面积.【解答】解:由题意,四棱柱为长方体,其对角线长为=5,二球的半径为,二这个球的表面积为=50n,故选: B.4. AQI(Air Quality Index ,空气质量指数)是报告每日空气质量的参数,描述了空气清洁或者污染的程度.AQI 共分六级,从一级优(0〜50),二级良(51〜100,),三级轻度污染,四级重度污染,直至无极重度污染,六级严重污染(大于300). 下面是昆明市xx 年 4 月份随机抽取的10天的AQI茎叶图,利用该样本估计昆明市2018年4 月份质量优的天数(按这个月共30天计算)为()A.3B.4C.12D.21【考点】BA茎叶图.【分析】通过读茎叶图求出空气质量是优的概率,从而求出30 天空气质量是优的天数即可.【解答】解:由茎叶图10天中有4天空气质量是优,即空气优的概率是p==,故30天中有x 30=12天是优,故选: C.5. 已知非零向量,满足?=0,||=3 ,且与+的夹角为,则||=( )A.6B.3C.2D.3【考点】9V:向量在几何中的应用;9S :数量积表示两个向量的夹角.【分析】利用向量的加法的平行四边形法则,判断四边形的形状,推出结果即可.【解答】解:非零向量,满足?=0,可知两个向量垂直,||=3 ,且与+的夹角为,说明以向量,为邻边,+为对角线的平行四边形是正方形,所以则||=3.故选: D.6. 若tan 0 二—2,贝卩sin2 0 +cos2 0 =()A.B. —C.D.-【考点】GI:三角函数的化简求值.【分析】利用二倍角公式、同角三角函数的基本关系,求得要求式子的值.【解答】解:sin2 0 +cos2 0 ====-,故选: D.7. 已知F1、F2为双曲线C: - =1(a>0, b>0)的左、右焦点,点P在C的渐进线上,PF1丄x轴,若△ PF1F2为等腰直角三角形,则C 的离心率为( )A.B.C.+1D.【考点】KC双曲线的简单性质.【分析】利用双曲线的简单性质,通过三角形是等腰直角三角形,列出方程求解即可.【解答】解:F1、F2为双曲线C:- =1(a>0, b>0)的左、右焦点,点P在C的渐近线上,PF1丄x轴,若△ PF1F2为等腰直角三角形,可得:,即:b=2a,可得c2 -a2=4a2,即e2=5,e>1,解得e=,则C的离心率为.故选: A.8. 在厶ABC中,已知AB= AC= tan / BAC- 3,贝S BC边上的高等于( )A.1B.C.D.2【考点】HS余弦定理的应用;HT:三角形中的几何计算【分析】求出/ BAC勺余弦函数值,然后求解BC的距离,通过求解三角形求解即可.【解答】解:在△ ABC中,已知AB= AC= tan / BAC=- 3, 可得cos/ BAC=- =-, sin / BAC=.由余弦定理可得:BC===3,设BC边上的高为h,三角形面积为:=BC?h,h==1.故选: A.9. 定义n!=1 x 2X 3X-X n,例如1!=1 , 2!=1 x2=2,执行右边的程序框图,若输入?=0.01,则输出的e精确到e的近似值为()A.2.69B.2.70C.2.71D.2.72【考点】EF:程序框图.【分析】模拟程序的运行,依次写出每次循环得到的e,n的值,当n=5时满足条件退出循环,输出e的值即可得解.【解答】解:模拟程序的运行,可得?=0.01 , e=1, n=1执行循环体, e=2, n=2不满足条件不满足条件不满足条件由于~ 0.008故选: C.10. 我国南北朝时期的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上,于 5 世纪末提出了下面的体积计算的原理( 祖暅原理) :“幂势既同,则积不容异” . “势”是几何体的高,“幂”是截面面积. 意思是,若两等高的几何体在同高处截面面积总相等,则这两个几何体的体积相等.现有一旋转体D,它是由抛物线y=x2(x >0), 直线y=4及y 轴围成的封闭图形如图1所示绕y轴旋转一周形成的几何体,利用祖暅原理,以长方体的一半为参照体(如图2所示)则旋转体D的体积是()A.B.6 n C.8 n D.16 n【考点】L5:旋转体(圆柱、圆锥、圆台).【分析】由题意,4x= n ?22,求出x= n,再求出长方体的一半的体积即可.【解答】解:由题意,4x= n ?22,二x= n,•••旋转体D的体积是=8n,故选 C.11. 已知函数f(x)=,若方程f(x) - ax=0恰有两个不同的根,则实数 a 的取值范围是( )A.(0 , )B.[ , )C.( , ]D.(-汽0] U [ , +乂)【考点】6H:利用导数研究曲线上某点切线方程;54 :根的存在性及根的个数判断.【分析】由题意,方程f(x)=ax 恰有两个不同实数根,等价于y=f(x)与y=ax有2个交点,又a表示直线y=ax的斜率,求出a的取值范围.【解答】解:•••方程f(x) - ax=0恰有两个不同实数根,二y=f(x)与y=ax有2个交点,又T a表示直线y=ax的斜率,二x>1 时,y,=,设切点为(x0 , y0), k=,二切线方程为y- yO=(x - x0),而切线过原点,二y0=1, x0=e, k=,二直线11的斜率为,又T直线12与y=x+1平行,•••直线12的斜率为,二实数a的取值范围是[,)故选: B.12. 设F为抛物线C: y2=8x,曲线y=(k>0)与C交于点A,直线FA恰与曲线y=(k>0)相切于点A,直线FA于C的准线交于点B,则等于( )A.B.C.D.【考点】K8:抛物线的简单性质.【分析】先根据抛物线的定义求出焦点坐标和准线方程,设A(x0,y0) ,根据题意可求出A(1 ,2) ,继而求出答案.【解答】解:F为抛物线C: y2=8x的焦点,贝S F(2 , 0),其准线方程为x二-2,设A(x0,y0)T y二,k=x0y0=2x0・ /…y =-,二直线AF的斜率为-二-t kAF==,. ・解得x0=1,・A(1,2),・AC=1+2=3,FD=4,・==,・=,・AB=3,・=,故选: B.二、填空题13. 已知实数x,y 满足,贝z=x+y 的最大值为3 .【考点】7C:简单线性规划.【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.【解答】解:由约束条件作出可行域如图,A(0 ,3) ,化目标函数z=x+y为y= - x+z,由图可知,当直线y=- x+z过A时,直线在y轴上的截距最大,z 有最大值为3.故答案为: 3.14. 已知函数f(x)=sin( 3 x+)( 3 >0), A B是函数y=f(x)图象上相邻的最高点和最低点,若|AB|=2,则f(1)=.【考点】HW三角函数的最值. 【分析】由图象上的两个相邻的最高点和最低点的距离为2求出3,可得函数的解析式,即可求出f(1).【解答】解:由题意可得=2,二3 =,二函数f(x)=sin(x+),•-f(1)=,故答案为:.15. 已知数列{an}的前n项和为Sn,且an=4n,若不等式Sn+8 》入n对任意的n€N*都成立,贝卩实数入的取值范围为(-汽10].【考点】8I :数列与函数的综合.【分析】先根据an=4n得到数列{an}是以4为首项,以4为公差的等差数列,再根据等差数列的求和公式得到Sn=2n+2n2原不等式转化为入w 2(n+)+2,根据基本不等式即可求出答案.【解答】解:丁数列{an}的前n项和为Sn,且an=4n,当n=1 时,a1=4,T an —an —1=4n— 4(n - 1)=4 ,二数列{an}是以4为首项,以4为公差的等差数列,Sn==2n+2n2T不等式Sn+8>^ n对任意的n€ N*都成立,二2n+2n2+8>入n对任意的n € N*都成立,即入w 2(n+)+2 ,T n+》2=4,当且仅当n=2时取等号,入w 2X4+2=10,故实数入的取值范围为(-=,10],故答案为:(-=,10].16. 若关于x 的不等式a w x2—3x+4w b 的解集恰好为[a ,b] ,那么b—a= 4 .【考点】74:一元二次不等式的解法.【分析】画出函数f(x)=x2 —3x+4的图象,可知f(x)min=1;分类讨论:a>1 时,不等式a w x2—3x+4w b 的解集分为两段区域,不符合题意;有a w 1【解答】解:画出函数f(x)=x2 - 3x+4=(x - 2)2+1的图象,可得f(x)min=f(2)=1 ,由图象可知:若a>1,则不等式a< x2 - 3x+4< b的解集分两段区域,不符合已知条件,因此a< 1,此时a< x2 - 3x+4恒成立;又T不等式a<x2 - 3x+4< b的解集为[a , b],a w 1由b2 - 3b+4二b,化为3b2 - 16b+16=0,解得b二或b=4;当b二时,由a2 - 3a+4- =0,解得a二或a=,不符合题意,舍去;二b=4,此时a=0;二b- a=4.故答案为: 4.三、解答题17. 已知数列{an}满足a1=2, an+1=2an+2n+1.(I) 证明数列{}是等差数列;(II) 求数列{}的前n项和.【考点】8H:数列递推式;8E :数列的求和.【分析】(I )根据数列的递推公式可得数列{}是首项为1,公差为 1 的等差数列,(I)由(I )可得数列{}是首项为2,公比为2的等比数列,再根据求和公式计算即可.【解答】解:(1) T a1=2, an+1=2an+2n+1二一=+1- =1,T =1,二数列{}是首项为1 ,公差为1的等差数列,(II)由(I)可得二n,=2n,•••数列{}是首项为2,公比为2的等比数列,故数列{}的前n 项和Sn==2n+1- 218. 某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了 1 00名学生进行调查,获得了每人的周末“阅读时间” (单位:小时),按照[0 , 0.5) , [0.5 , 1),…,[4 , 4.5]分成9组,制成样本的频率分布直方图如图所示.( I ) 求图中a 的值;( I ) 估计该校高一学生周末“阅读时间”的中位数;( 皿)在[1 , 1.5) , [1.5 , 2)这两组中采用分层抽样抽取7人,再从7人中随机抽取2人,求抽取的两人恰好都在一组的概率.【考点】B3:分层抽样方法;CB:古典概型及其概率计算公式.【分析】( I ) 求出高一学生周末“阅读时间”在[0 ,0.5) ,[0.5 ,1),…,[4 , 4.5]的概率,即可求图中a的值;(I)确定2< m(皿)确定基本事件的个数,即可得出结论.【解答】解:(I)由题意,高一学生周末“阅读时间”在[0,0.5) ,[0.5 ,1),…,[4 ,4.5]的概率分别为0.04 ,0.08,0.20.0.25.0.07 0.04.0.02,由 1 - (0.04+0.08+0.20+0.25+0.07+0.04+0.02)=0.5a+0.5a ,二a=0.30;(II)设该校高一学生周末“阅读时间”的中位数为m小时,因为前5组频率和为0.040.08+0.15+0.20+0.25=0.72>0.5 前4 组频率和为0.47<0.5 ,所以2< m<2.5,由0.50(m- 2)=0.5 - 0.47,得m=2.06;( 皿)在[1 , 1.5) , [1.5 , 2)这两组中的人分别有15人、20人,采用分层抽样抽取7 人分别为 3 人、 4 人再从7 人中随机抽取 2 人有=21 种抽取的两人恰好都在一组有=9 种故所求概率为.19. 如图,已知三棱锥P- ABC BC!AC BC二AC=2PA二PB 平面PABL平面ABC D E、F分别是AB PB PC的中点.(I )证明:PDL平面ABC;( I)若M为BC中点,且PM!平面EFD 求三棱锥P- ABC勺体积.【考点】LF:棱柱、棱锥、棱台的体积;LW:直线与平面垂直的判定.【分析】(I )由PA=PB D为AB中点,可得PDL AB再由面面垂直的性质可得PDL平面ABC;(n )设PM交EF于N,连接DM DN由线面垂直的性质得到PM 丄DN 由已知可得DN垂直平分PM故PD=DM求出DM进一步求得PD.即三棱锥P- ABC勺高,然后由三棱锥体积公式求得三棱锥P- ABC 的体积.【解答】(I )证明:T PA=PB D为AB中点,二PDL AB 又平面PABL平面ABC 交线为AB PD?平面PAB••• PDL平面ABC;( n )解:设PM交EF于N,连接DM DNT PML平面EFD DN平面DEF•PML DN又E , F分别是PB, PC的中点,•N为EF的中点,也是PM的中点,•DN垂直平分PM 故PD=DM又DM fe^ ABC的中位线,贝S DM==1 • PD=1.T BC L AC 则.•三棱锥P- ABC的体积20. 已知动点M(x , y)满足:+=2 , M的轨迹为曲线E.(I )求E的方程;( n )过点F(1 , 0)作直线I交曲线E于P , Q两点,交y轴于R 点,若二入1,二入2,求证:入1+入2为定值.【考点】KQ圆锥曲线的定值问题;J3 :轨迹方程.【分析】(I )由已知,可得动点N的轨迹是以C( - 1,0) , A(1 , 0)为焦点的椭圆,根据定义可得,a、c,可得曲线E的方程;(II)设P(x1 , y1) , Q(x2, y2) , R(0, y0),由二入1,,点P 在曲线E上可得…①,同理可得:…②由①②可得入1、入2是方程x2+4x+2 - 2y02=0的两个根,入1 + 入2为定值-4.【解答】解:(I )由+=2,可得点M(x, y)到定点A( - 1, 0), B(1 , 0) 的距离等于之和等于2.且AB,所以动点N的轨迹是以C(- 1, 0), A(1 , 0)为焦点的椭圆,且长轴长为2,焦距2c=2,所以,c=1, b=1, 曲线E的方程为:;(I)设P(x1 , y1) , Q(x2, y2) , R(0 , y0), 由二入1 , (x1 , y1 -y0)=入1(1 - x1 , - y1),二,T过点F(1 , 0)作直线I交曲线E于P, •••,二…①同理可得:…②由①②可得入1、入2是方程x2+4x+2 - 2y02=0的两个根,•••入1+入2为定值-4.21. 已知函数f(x)=(2x2+x)lnx - (2a+1)x2 - (a+1)x+b(a , b€R).(I)当a=1时,求函数f(x)的单调区间;(II)若f(x) > 0恒成立,求b - a的最小值.【考点】6B:利用导数研究函数的单调性;6D :利用导数研究函数的极值.【分析】(I)当a=1 时,f' (x)=(4x+1)(lnx - 1)=0,得x=e.x € (0 , e)时,f' (x)0.即可得函数f(x)的单调区间;(I)由题意得f‘ (x)=(4x+1)(lnx - a) , (x>0).可得函数f(x) 的单调增区间为(ea , ),减区间为(0 , ea)即f(x) >0恒成立,b>e2a+ea.即 b - a>e2a+ea- a,构造函数g(t)=t2+t - lnt , (t>0), g‘ (t)=.可得g(t)min=g()=.即可得b- a的最小值.【解答】解: ( I ) 当a=1 时, f(x)=(2x2+x)lnx - 3x2-2x+b(x>0).f ' (x)=(4x+1)(lnx - 1),令f' (x)=0,得x=e.x € (0 , e)时,f‘ (x)0.函数f(x)的单调增区间为(e , ),减区间为(0 , e);( I)由题意得f‘ (x)=(4x+1)(lnx - a) , (x>0).令 f ' (x)=0,得x=ea.x € (0 , ea)时,f‘ (x)0.函数f(x)的单调增区间为(ea , ),减区间为(0 , ea)f(x)min二f(ea)= - e2a - ea+b,T f(x) >0 恒成立,二f(ea)= - e2a- ea+b> 0,贝U b>e2a+ea.b- a>e2a+ea— a令ea=t, (t>0),二e2a+ea- a=t2+t - lnt ,设g(t)=t2+t - lnt , (t>0) , g‘ (t)=.当t € (0 ,)时,g,(t)0.••• g(t)在(0 ,)上递减,在(,+乂)递增.••• g(t)min=g()=.f(x) >0恒成立,b- a的最小值为.请考生在22、23 二题中任选一题作答,如果多做,则按所做的第一题计分.[ 选修4-4 :坐标系与参数方程]22. 在平面直角坐标系xOy中,曲线C的方程为(x - 2)2+y2=4 , 直线I的方程为x+y - 12=0,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.(I) 分别写出曲线C与直线I的极坐标方程;(II) 在极坐标中,极角为B ( 0€ (0 ,))的射线m与曲线C,直线I分别交于A、B两点(A异于极点0),求的最大值.【考点】Q4:简单曲线的极坐标方程;H9:余弦函数的定义域和值域.【分析】( I )利用直角坐标方程与极坐标方程的转化方法,分别写出曲线C与直线I的极坐标方程;(I)由题意|OA|=4cos 0, |OB|=,利用三角函数知识,可得结论.【解答】解:(I )曲线C的方程为(x - 2)2+y2=4,即x2+y2=4x,极坐标方程为p =4cos 0 ;直线I的方程为x+y - 12=0,极坐标方程为p cos 0 + p sin 0-12=0;(II)由题意|OA|=4cos 0, |OB|=,二==+sin(2 0 +),T0€(0 ,),二20+€(,兀),••• sin(2 0 +) € ( - 1],•••的最大值为,此时.[ 选修4-5 :不等式选讲]23. 已知a , b , c , m n , p 都是实数,且a2+b2+c2=1,m2+n2+p2=1.( I)证明|am+bn+cp| < 1;(I)若abc z 0,证明++> 1.【考点】R6:不等式的证明.【分析】利用柯西不等式即可证明结论.【解答】证明:(I)由柯西不等式,可得(a2+b2+c2)(m2+n2+p2) > (am+b n+cp)2,T a2+b2+c2=1, m2+n2+p2=1• 1 > (am+b n+cp)2,•|am+b n+cp| < 1;( I)由柯西不等式,可得++=(++)(a2+b2+c2) > (m2+n2+p2)2=1 ,• ++> 1.。
云南省昆明市2018届高三5月适应性检测数学文试题(精编含解析)

云南省昆明市2018届高三5月适应性检测数学(文科)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. ()A. B. C. D.【答案】C【解析】分析:求,将其分子、分母同乘以分母的共轭复数,可得,转化为两个复数相乘可得,化简可得,即。
详解:。
故选C。
点睛:求两个复数相除,可先转化为分式,分子、分母同乘以分母的共轭复数,转化为复数的乘法运算。
本题意在考查复数的运算及学生的运算能力。
2. 已知集合,,则=()A. B. C. D.【答案】A【解析】分析:由集合中的元素可得元素为自然数,根据可得元素只能为0,1,2.求即求两集合的公共元素,将0,1,2分别代入集合中的不等式,满足不等式的即是公共元素。
详解:。
将0,1,2分别代入集合中的不等式,可得,此不等式成立,故有0;,化简得。
此不等式成立,故有1,,化简得。
此不等式成立,故有2.故选A。
点睛:集合的运算,应先求集合中的元素,交集就是求集合的公共元素的集合。
本题考查集合的运算,数集的符号表示。
3. 程大位《算法统宗》里有诗云“九百九十六斤棉,赠分八子做盘缠.次第每人多十七,要将第八数来言.务要分明依次弟,孝和休惹外人传.”意为:996斤棉花,分别赠送给8个子女做旅费,从第一个开始,以后每人依次多17斤,直到第八个孩子为止.分配时一定要等级分明,使孝顺子女的美德外传,则第八个孩子分得斤数为()A. B. C. D.【答案】D【解析】分析:根据题意可得每个孩子所得棉花的斤数构成一个等差数列,其中公差为17,项数为8,前8项和为996,应先由前n项和公式求首项,再由等差数列通项公式求第8项。
详解:根据题意可得每个孩子所得棉花的斤数构成一个等差数列,其中。
由等差数列前n项和公式可得,。
解得。
由等差数列通项公式得。
故选D。
点睛:本题考查学生的传统文化、运算能力、转化能力。
解决与等差数列有关的问题,可将条件转化为基本量,利用前n项和公式、通项公式求解。
云南省昆明第一中学2018届高三第八次月考数学文试题

云南省昆明第一中学2018届高三第八次月考文 科 数 学 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}ln A x y x ==,集合{}xB y y e ==,则集合A 与集合B 的关系是( )A . AB = B .A B ≠⊂ C .B A ≠⊂ D .A B ∈2.在复平面内,复数z 与复数103i+对应的点关于实轴对称,则z =( ) A .3i + B .3i - C .3i -+ D .3i --3.设一个线性回归方程3 1.2y x ∧=+,当变量x 每增加一个单位时,则y 的变化情况正确的是( )A .y 平均增加约1.2个单位B .y 平均增加约3个单位C .y 平均减少约1.2个单位D .y 平均减少约3个单位4. 若1sin 3α=,则2cos 24απ⎛⎫+= ⎪⎝⎭( ) A .23 B .12 C. 13D .0 5.若,x y 满足约束条件02346x y x y x y -≤⎧⎪+≤⎨⎪-≥-⎩,则函数2z x y =-的最小值为( )A . 5B .2 C. 2- D .5-6.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,若2b a =,2sin 2sin sin B A C =,则co s B =( ) A .18 B .14 C. 12D .1 7. 函数()01xy aa a =>≠且与函数()y f x =的图像关于直线y x =对称,则函数()y f x =与二次函数()21y a x x =--在同一坐标系内的图像可能是( )A .B . C. D. 8. 已知函数()f x x =,函数()2g x x =-,执行如图所示的程序框图,若输入的[]3,3x ∈-,则输出m 的值为()g x 的函数值的概率为( )A .16 B .14 C. 13 D .129.已知定义在()0,+∞上的函数()()2,6ln 4f x x m h x x x =-=-,设两曲线()y f x =与()y h x =在公共点处的切线相同,则m 值等于( )A .3-B .1 C. 3 D .510. 已知三棱锥P ABC -中,,,4AC BC PC PB AB ⊥⊥=则三棱锥P ABC -的外接球的表面积为( )A .4πB .8π C. 12π D .16π11. 过正方体1111ABCD A BC D -的顶点A 的平面α与直线1AC 垂直,且平面α与平面11ABB A 的交线为直线l ,平面α与平面11ADD A 的交线为直线m ,则直线l 与直线m 所成角的大小为( )A .6π B .4π C. 3π D .2π 12.已知M 为函数8y x=的图像上任意一点,过M 作直线,MA MB 分别与圆221x y +=相切于,A B 两点,则原点O 到直线AB 的距离的最大值为( )A .18 B .14 C. 2 D .4第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量()()1,2,3,4a m b m =-=-,若//a b 且方向相反,则m = .14.已知双曲线()2222:10,0x y C a b a b -=>>的渐近线方程为y x =,若抛物线28y x=的焦点与双曲线C 的焦点重合,则双曲线C 的方程为 15. 已知函数()()2sin 03f x x πωω⎛⎫=+> ⎪⎝⎭的部分图像如图所示,若图中在点,A D 处()f x 取得极大值,在点,B C 处()f x 取得极小值,且四边形ABCD 的面积为32,则ω的值是 .16.设函数()2266xf x x x m e =++-⋅(m 为非零实数),若函数()f x 有且仅有一个零点,则m 的取值范围为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.设数列{}n a 的前n 项和为n S ,且1n n S a =-+.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若()12log f x x =,设()()()12n n b f a f a f a =+++,求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T .18.某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,询问了30名同学,得到如下的22⨯列联表:(Ⅰ)根据以上22⨯列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?(Ⅱ)从使用学习成绩优秀的12名同学中,随机抽取2名同学,求抽到不使用智能手机的人数X 的分布列及数学期望.智能手机的20名同学中,按分层抽样的方法选出5名同学,求所抽取的5名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;(Ⅲ)从问题(Ⅱ)中倍抽取的5名同学,再随机抽取3名同学,试求抽取3名同学中恰有2名同学为“学习成绩不优秀”的概率.参考公式:()()()()()22=n ad bc a b c d a c b d κ-++++,其中=n a b c d +++参考数据:19.如图,在三棱锥111ABC A B C -中,111,,2,60A B B C A BB B A B BC B B⊥⊥===∠=,点D 为边BC 的中点.(Ⅰ)证明:平面1AB D ⊥平面ABC ; (Ⅱ)求三棱柱111ABC A B C -的体积.20.已知椭圆()22122:10x y C a b a b+=>>和抛物线()22:20C x py p =>,在12,C C 上各取两个点,这四个点的坐标为()()()2,1,,,4,4⎛-⎝⎭. (Ⅰ)求12,C C 的方程;(Ⅱ)设P 是2C 在第一象限上的点,2C 在点P 处的切线l 与1C 交于,A B 两点,线段AB 的中点为D ,过原点O 的直线OD 与过点P 且垂直于x 轴的直线交于点Q ,证明:点Q 在定直线上.21. 已知函数()2ln f x mx x x =-+,(Ⅰ)若在函数()f x 的定义域内存在区间D ,使得该函数在区间D 上为减函数,求实数m 的取值范围; (Ⅱ)当102m <≤时,若曲线():C y f x =在点1x =处的切线L 与曲线C 有且只有一个公共点,求实数m 的值或取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在平面直角坐标系xoy 中,已知=曲直线11cos :sin x C y αα=+⎧⎨=⎩(α为参数)与曲线12cos :22sin x C y ββ=⎧⎨=+⎩(β为参数),且曲线1C 与2C 交于,O A 两点,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系(Ⅰ)求曲线12,C C 的极坐标方程; (Ⅱ)直线OA 绕点O 旋转2π后,与曲线12,C C 分别交于,P Q 两点,求PQ . 23.选修4-5:不等式选讲已知函数()()3,22f x x g x x =+=-.(Ⅰ)若()()()h x f x g x =+,且()h x a ≥恒成立,求实数a 的取值范围; (Ⅱ)若()x ϕ=()x ϕ的最大值.试卷答案一、选择题1-5:ABACD 6-10:BACDD 11、12:CB 二、填空题13. 5- 14.2213x y -= 15. 4π 16. ()()0,26,e +∞三、解答题 17. 解:(1)由1nn S a =-+ 得 111n n S a ++=-+,两式相减得:11n n n n S S a a ++-=-+, 即11n n n a a a ++=-+, 即112n n a a += ()1n ≥,所以数列{}n a 是公比为12的等比数列, 又由111a a =-+得 112a =,所以1112nn n a a q-⎛⎫== ⎪⎝⎭;(2)因为()()()()121122nn n n b f a f a f a n +=+++=+++=,所以()1211211n b n n n n ⎛⎫==- ⎪++⎝⎭, 所以11111112221=12231+11n n T n n n n ⎛⎫⎛⎫=-+-++-=- ⎪ ⎪++⎝⎭⎝⎭. 18. 解:(1)由列联表可得()()()()()()2223042816107.87912182010n ad bc K a b c d a c b d -⨯⨯-⨯===>++++⨯⨯⨯所以能在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响. (2)根据题意,所抽取的5名同学中“学习成绩优秀”有1名同学,“学习成绩不优秀”有4名同学.(3)学习成绩不优秀的4名同学分别记为A ,B ,C ,D ;“学习成绩优秀”有1名同学记为E .则再从中随机抽取3人构成的所有基本事件为:(),,A B C ,(),,A B D ,(),,A B E ,(),,A C D ,(),,A C E ,(),,A D E ,(),,B C D ,(),,B C E ,(),,B D E ,(),,C D E ,共有10种;抽取3人中恰有2名同学为“学习成绩不优秀”所含基本事件为:(),,A B E ,(),,A C E ,(),,A D E ,(),,B C E ,(),,B D E ,(),,C D E 共有6种,所求为63105P ==. 19. 解:(1)由题意,⊥AB 平面C C BB 11,⊂D B 1平面C C BB 11,可得D B AB 1⊥,又△BCB 1为等边三角形,点D 为BC 边的中点,可得D B BC 1⊥,AB 与BC 相交于点B ,则D B 1⊥平面ABC ,⊂D B 1平面D AB 1,所以,平面D AB 1⊥平面ABC .(2)因为△ABC 为直角三角形,2==BC AB , 所以2=∆ABC S ,由(1)可知,在直角三角形D BB 1中, 0160=∠BC B ,221==BB BD , 可得31=D B ,故D B S V ABC 1⋅=∆32=,所以,三棱柱111ABC A B C -的体积为32. 20. 解:解:(1)由已知,点(,0),(1,2在椭圆1C 上,所以 221 a=,22111 2a b+=, 解得:22a =,21b =,所以1C :22 1 2x y +=; 点(2,1), (4,4)-在抛物线2C 上,所以2p =,所以2C :24x y =.(2)设2(,)4m P m (0m >),由24x y =得12y x '=, 所以切线l 的方程为:2()42m my x m -=-, 设11(,)A x y ,22(,)B x y ,由222()4212m m y x m x y ⎧-=-⎪⎪⎨⎪+=⎪⎩得:4223(2)404m m x m x +-+-=, 由0∆>,31222m x x m +=+得322(2)D m x m =+,代入2()42m m y x m -=-得222(2)D m y m -=+,所以1D OD D y k x m ==-,所以OD l :1y x m=-, ………10分 由1x m y x m =⎧⎪⎨=-⎪⎩得1y =-,所以点Q 在定直线1y =-上. 21. 解:(1)因为()()2121210mx x f x mx x x x-+'=-+=>,依题意知2210mx x -+<在()0,+∞上有解. 当0m ≤时显然成立;当0m >时,由于函数221y mx x =-+的图象的对称轴104x m=>, 故需且只需0∆>,即180m ->,解得18m <,故108m <<.综上所述,实数m 的取值范围为1,8⎛⎫-∞ ⎪⎝⎭.(2)因为()11f m =-,()12f m '=,故切线L 的方程为()121y m m x -+=-, 即21y mx m =--.从而方程2ln 21mx x x mx m -+=--在()0,+∞上有且只有一解.设()()2ln 21g x mx x x mx m =-+---,则()g x 在()0,+∞上有且只有一个零点. 又()10g =,故函数()gx 有零点1x =.则()()()()222112111212mx m x mx x g x mx m x x x-++--'=-+-==.当12m =时,()0g x '≥,又()g x 不是常数函数,故()g x 在()0,+∞上单调递增. 所以函数()g x 有且只有一个零点1x =,满足题意.当102m <<时,由()0g x '=,得12x m =或1x =,且112m>. 由()0g x '>,得01x <<或12x m>; 由()0g x '<,得112x m<<. 所以当x 在()0,+∞上变化时,()g x ',()g x 的变化情况如下表:根据上表知02g m ⎛⎫< ⎪⎝⎭.而函数()12ln 1g x mx x m x m ⎡⎤⎛⎫=-++++ ⎪⎢⎥⎝⎭⎣⎦.所以120g m ⎛⎫+> ⎪⎝⎭,故在1,2m ⎛⎫+∞⎪⎝⎭上,函数()g x 又存在一个零点,不满足题意.综上所述,12m =. 22. 解:(1)曲线1C 是以(1,0)为圆心,1为半径的圆,其极坐标方程为2cos ρθ=, 曲线2C 是以(0,2)为圆心,2为半径的圆,其极坐标方程为4sin ρθ=.(2)由2c o s 4s i n θθ=得1tan 2θ=,即直线OA 的斜率为12,从而sin θ=,cos θ=,由已知,设1,2P πρθ⎛⎫- ⎪⎝⎭,2,2Q πρθ⎛⎫+⎪⎝⎭将1,2P πρθ⎛⎫- ⎪⎝⎭代入2cos ρθ=,得12cos 2sin 2πρθθ⎛⎫=-== ⎪⎝⎭, 同理,将2,2Q πρθ⎛⎫+⎪⎝⎭代入4sin ρθ=,得24sin 4cos 2πρθθ⎛⎫=+== ⎪⎝⎭,所以,12PQ ρρ=+=+=.23. 解:(1)31, 3()3225, 3131, 1x x h x x x x x x x --<-⎧⎪=++-=-+-≤≤⎨⎪+>⎩, 所以,min()(1)4h x h ==,只需4a ≤,故实数a 的取值范围为(],4-∞.(2)由柯西不等式,()1x ϕ=+≤=53x =-时,等号成立,故()x ϕ的最大值为.。
云南省昆明市2020届高三第八次考前适应性训练数学(文)试卷答案

BCB 1D云南省昆明市2020届高三第八次考前适应性训练数学(文)试卷答案一、选择题1. 解析:依题意i31e cosisin332z πππ==+=,则1i i 2z =-,选C. 2. 解析:{}{}{}3,33,0,1,2A xx x x x x =<∈=-<<∈=N N ,易知图中阴影部分对应的集合为AB ,{}0,1,2AB =,选B.3. 解析:函数()=e sin x f x x ⋅为非奇非偶函数,排除B ,C 选项;当0x =时,()00f =,所以选A.4. 解析:由已知:a 与b 共线,可得83x =-,所以b 在a 方向上的投影为:cos =a bb a b a ⋅=,, 选D.5. 解析:不超过的素数有2,3,5,7,11,13,随机选取两个不同的数基本事件为(2,3), (2,5),(2,7),(2,11),(2,13),(3,5),(3,7),(3,11),(3,13),(5,7),(5,11),(5,13),(7,11),(7,13),(11,13),其和等于的事件有(3,13)和(5,11),所以概率为215,选A . 6. 解析:因为ba-= 所以2c e a ===,选A . 7. 解析:由正弦定理得:22sin sin sin cos 2sin A B B A A +=,所以22sin (sin cos )2sin B A A A ⋅+=,即:sin 2sin B A =,所以sin 2sin b Ba A==,选D . 8. 解析:1,0i S ==;1,22S i ==;2113,3242S i =+==;3317,4482S i =+==;47115,58162S i =+==,此时输出,结合选项,选C.9.解析:设2AB =,BC 的中点为,则AD 平面1BC ,连结1B D , 则1AB D ∠是直线1AB 与平面1BC 所成角,在Rt △1ADB 中, 11315tan 5AD AB D B D ∠===,选B . 10. 解析:因为0ω>,由已知得:24πππω-≤,所以4ω≤,所以()44424x πωππωππω-∈--,,所以4423242ωπππωπππ⎧-≥⎪⎪⎨⎪-≤⎪⎩,解得732ω≤≤,选C .11. 解析:()()()=2=f x f x f x --,可推出()f x 为周期为2的函数,所以1111116=2224f f f ⎛⎫⎛⎫⎛⎫-=-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,选A. 12. 解析:有题意可知,127cos 25F BF ∠=,所以24cos 5bOBF a∠==,令5,40a t b t t ==>,(),则3c t =,所以43BDk =-,所以2222216=25D D D BD CD D D D y b y b y b b k k x x x a -+-===--,所以1225BD k =,选二、填空题13. 解析:因为()e e ln xx f x x x'=+⋅,由导数的几何意义知()1e k f '==,故曲线()e ln x f x x =⋅在点()1,0处的切线方程为()e 1y x =-.14. 解析:直线0kx y k -+=过定点()10-,, 不等式组表示的区域如图: 可知的取值范围是:117⎡⎤⎢⎥⎣⎦,.15. 解析:由()42ππθ∈,得2()2πθπ∈,,所以27cos21sin 29θθ=--=-,所以1cos 21cos 23θθ+==. 16. 解析:由题意可得,△ABD ≅△ACD ,所以AC CD ⊥,所以AD 为三棱锥A BCD -的外接球的直径,设=AB x ,则4BD x =-,所以2222(4)(4)82x x AD x x +-=+-≥=,所以三棱锥A BCD -的外接球的半径min R ,所以三棱锥A BCD -的外接球体积的最小值为三、解答题: (一)必考题:17. 解析:(1)1n =时,11a = 2n ≥时,由1123(1)2422n n n n a a a a -++++⋅⋅⋅+=…① 可得21231(1)2422n n n na a a a ---+++⋅⋅⋅+=…② ①-②,12n n a n -=,11()2n n a n -=⋅因为1a 适合11()2n n a n -=⋅,所以{}n a 的通项公式为11()2n n a n -=⋅. ………6分(2)011121111()2()()222n n n S a a a n -=++⋅⋅⋅+=⨯+⨯+⋅⋅⋅+⨯, …③1211111()2()()2222n n S n =⨯+⨯+⋅⋅⋅+⨯,…④ ③-④得01111111()()()()22222n n n S n -=++⋅⋅⋅+-⨯11()112()12212nn n S n -=-⨯-,114(2)()2n nS n -=-+⋅. ………12分 18. 解:(1)由已知,优等品的质量与尺寸的比在区间e e ,97⎛⎫⎪⎝⎭内,即()0.302,0.388y x ∈,则随机抽取的6件合格产品中,有3件为优等品记为,,a b c ,3件为非优等品记为,,d e f ,现从抽取的6件合格产品中再任选2件,基本事件为(),a b ,(),a c ,(),a d ,(),a e ,(),a f ,(),b c ,(),b d ,(),b e ,(),b f ,(),c d ,(),c e ,(),c f ,(),d e ,(),d f ,(),e f ,选中的2件均为优等品的事件为(),a b ,(),a c ,(),b c ,所求概率为15. ………6分(2)解:对b y c x =⋅(,0b c >)两边取自然对数得ln ln ln y c b x =+,令ln ,ln i i i i v x u y ==,得u b v a =⋅+,且ln a c =,根据所给统计量及最小二乘估计公式有,1222175.324.618.360.2710.542101.424.66ni i i ni i v u nvu b v nv ∧==--⨯÷====-÷-∑∑, 118.324.6612a u b v ∧∧⎛⎫=-=-⨯÷= ⎪⎝⎭,得ln 1ˆˆa c ==,故ˆe c =,所求关于的回归方程为0.5e y x =. ………12分19.(1)证明:连接CG 并延长交AB 于M ,由已知得1A G 平面ABC ,且CM AB ⊥, 所以1A G AB ,因为1CMA G G =,所以AB 平面1A MC ,所以AB 1A C ,因为四边形11A ACC 是平行四边形,且1AA AC =, 所以四边形11A ACC 是菱形, 所以11A C AC ⊥,因为1ABAC A =,所以1A C 平面1ABC ,因为1A C ⊂平面11A B C ,所以平面1ABC 平面11A B C . ………5分(2)解:由已知得1A G 平面ABC ,所以侧棱1A A与底面所成的角正切值为1tan A AG ∠=因为2AG =,所以1A G =11A A C C ==因为1A 在底面ABC 上的射影是ABC ∆的重心, 所以等边三角形ABC的边长为11BC A C ==,同理1Rt A GB ∆中,1A B =因为1A 在底面ABC 上的射影是ABC ∆的重心,所以AG BC ⊥,且1AG BC ⊥,因为1AGA G G =,所以BC ⊥平面1A AG ,所以1BC A A ⊥,因为1A A ∥1C C ,所以1C C BC ⊥,故1Rt BCC ∆中,1BC =因为2221111A C A B BC +=,所以11A BC ∆为直角三角形, 设点1B 到平面11A BC 的距离为,由111111B A B C B A BC V V --=得 1111111133A B C A BC S AG S h ∆∆⋅=⋅,所以h = 即点1B 到平面11A BC的距离为………12分20. 解:(1)由条件可知GE GF =,即点到的距离等于点到点的距离, 所以点的轨迹是以为准线,为焦点的抛物线, 其方程为:24x y =.………5分(2)设线段AB 的垂直平分线与AB 交于点M ,分别过点,A B 作11,AA l BB l ⊥⊥,垂足为11,A B ,再过点作1AC BB ⊥,垂足为,因为,PFM ABC PMF ACB ∠=∠∠=∠, 所以PFM ∆∽ABC ∆,所以FP FM ABBC=,设AF m =,BF n =(不妨设n m >),由抛物线定义得1AF AA m ==,1BF BB n ==,所以BC n m =-, 而22m n n mFM AM AF m +-=-=-=, 所以122n mFP FM AB BC n m -===-.………12分21. 解:(1)当0a =时,()ln sin f x x x =+,()0,x ∈+∞,若01x <≤,因为()1cos 0f x x x'=+>,所以()f x 在(]0,1上单调递增,又()1sin10f =>,且111sin 0e e f ⎛⎫⎛⎫=-+< ⎪ ⎪⎝⎭⎝⎭,结合零点存在性定理可知()f x 在(]0,1上有且仅有一个零点;若1x π<≤,则ln 0x >且sin 0x ≥,所以()0f x >; 若x π≥,因为ln ln 1sin x x π>>≥-,所以()0f x >;综上,()f x 在()0,+∞有且仅有一个零点. ……… 5分 (2)当1a ≥时,ax x ≥,ax x -≤-,且sin 1x ≤,故()ln 1f x x x ≤+-, 构造函数()ln 1g x x x =+-,()0,x ∈+∞,则()1xg x x-'=, 若01x <<,则()0g x '>,故()g x 在()0,1上单调递增, 若1x >,则()0g x '<,故()g x 在()1,+∞上单调递减,故()()max 10g x g ==,即()0g x ≤对任意()0,x ∈+∞恒成立,当且仅当1x =时取得等号, 当1x =时,sin 1x <,故()0f x <对任意()0,x ∈+∞恒成立. ……… 12分(二)选考题:第22、23题中任选一题做答。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
云南省昆明市2018届高三第八次考前适应性训练数学(文)试题第Ⅰ卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|31,}P x x n n N ==-∈,{|10,}Q x x x N =<∈,则集合P Q 中元素的个数为( )A .5B .4C .3D .22.设||1,||2a b ==,且向量a 与向量b 的夹角为23π,则|2|a b -=( ) A .2 B..4 D .123.设复数z 满足121zi z+=+,则z =( ) A .122i -- B .122i -+ C .122i - D .122i +4.从500件产品中随机抽取20件进行抽样,利用随机数表法抽取样本时,先将这500件产品按001,002,003,…,500进行编号,如果从随机数表的第1行第6列开始,从左往右依次选取三个数字,则选出来的第4个个体编号为( )1622 7794 3949 5443 5482 1737 9323 7887 3520 9643 8626 3491 6484 4217 5331 5724 5506 8877 0474 4767 A .435 B .482 C .173 D .2375.已知椭圆:E 22221(0)x y a b a b+=>>的左、右两个焦点和上下两个顶点都在圆M 上,则椭圆E 的离心率为( ) A.2 B.2 C.3 D.36.已知{}n a 为等比数列,若2312a a a =,且4a 与72a 的等差中项为54,则7a =( ) A .1 B .12 C .13 D .147.已知函数22,1()log ,1x a x f x x x +≤⎧=⎨>⎩,若1(())42f f =,则a =( )A .16B .15C .2D .238.已知ABC ∆是一个圆锥的底面圆的内接三角形,03,60AB ACB =∠=,母线与底面所成角的余弦值为35,则该圆锥的体积为( )A B . C .5π D .8π 9.函数tan sin |tan sin |y x x x x =+--在区间3(,)22ππ内的图象是( )10.执行如图所示的程序框图,则输出的结果是( ) A .29 B .30 C .31 D .3211.若某空间几何体的三视图如图所示,根据图中数据,可得该几何体的表面积是( )A .24+.48+ C .48+.84+12.给出定义:设'()f x 是函数()y f x =的导函数,''()f x 是函数'()f x 的导函数,若方程''()0f x =有实数解0x ,则称00(,())x f x 为函数()y f x =的“拐点”,经探究发现,任意一个三次函数32()(0)f x ax bx cx d a =+++≠都有“拐点”,且该“拐点”也是该函数的对称中心,若32()232f x x x x =-++,则1232015()()()()2016201620162016f f f f ++++=( ) A .4032 B .4030 C .2016 D .2015第Ⅱ卷二、填空题(每题5分,满分20分,将答案填在答题纸上)13.数列{}n a 是等差数列,n S 是它的前n 项和,已知315S =,9153S =,则6S = . 14.已知函数()1()a f x x a R =+∈的图象在点(1,(1))f 处的切线经过点(2,5),则a = .15.已知点P 是不等式组310301x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩,所表示的平面区域内的一个动点,点(2,1)Q -,O 为坐标原点,则||OP OQ -的最大值是 .16.已知点F 是抛物线2:4C y x =的焦点,点B 在抛物线C 上,(5,4)A ,当ABF ∆周长最小时,该三角形的面积为.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分12分)已知函数2()2cos 2f x x x =. (1)求函数()f x 的单调递增区间;(2)在ABC ∆中,,,a b c 分别是角,,A B C 的对边,1a =且()3f A =,求ABC ∆面积S 的最大值.如图,在四棱锥P ABCD -中,底面ABCD 是梯形,//AB CD ,060BAD ∠=,2AB AD =,AP BD ⊥.(1)证明:平面ABD ⊥平面PAD ;(2)若PA 与平面ABCD 所成的角为60,2,AD PA PD ==,求点C 到平面PAB 的距离.19. (本小题满分12分)对某校900名学生每周的运动时间进行调查,其中男生有540名,女生有360名,根据性别利用分层抽样的方法,从这900名学生中选取60名学生进行分析,统计数据如下表(运动时间单位:小时) 男生运动时间统计:女生运动时间统计:(1)计算,x y 的值;(2)若每周运动时间不低于6小时的同学称为“运动爱好者”,每周运动时间低于6小时的同学称为“非运动爱好者”,根据以上统计数据填写下面的22⨯列联表,能否在犯错误的概率不超过0.025的前提下认为“‘运动爱好者’ 与性别有关”?已知双曲线:E 22221x y a b-=(0,0)a b >>的一条渐近线方程为0x =,焦距为(1)求双曲线E 的方程;(2)若直线:(0)l y kx k =>与双曲线E 交于,A B 两点,且点A 在第一象限,过点A 作x 轴的垂线,交x轴于点C ,交双曲线E 于另一点1A ,连结BC 交双曲线E 于点D ,求证:1AD OA ⊥.21. (本小题满分12分) 已知函数()ln 2x m f x e x -=-.(1)若1m =,求函数()f x 的极小值; (2)设2m ≤,证明:()ln 20f x +>.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题记分.22. (本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,直线l的参数方程为x ty =-⎧⎪⎨=⎪⎩(t 为参数),当1t =时,直线l 上对应的点为A ,当1t =-时,直线l 上对应的点为B ,以O 为极点,x 轴的非负半轴为极轴建立坐标系,并在两种坐标系中取相同的长度单位,曲线C的极坐标方程为ρ=(1)分别求,A B 两点的极坐标(0,02)ρθπ>≤<; (2)设点P 为曲线C 上的动点,求PAB ∆面积的最大值.23. (本小题满分10分)选修4-5:不等式选讲 已知函数()|1|f x x =+. (1)求不等式()|4|xf x x >+;(2)若x R ∀∈,不等式()||1f x x a --≥-恒成立,求实数a 的取值范围.云南省昆明市2018届高三第八次考前适应性训练数学(文)试题参考答案一、选择题:本大题共12小题,每小题5分,共60分。
1. 解析:因为集合{}0,1,2,3,4,5,6,7,8,9Q =,所以2,5,8P Q =I ,选C .2. 解析:()222224484a b a ba ab b -=-=-⋅+=+= B . 3. 解析:由121i zz+=+得11122i i z ==---+,选A . 4. 解析:根据读取规则,依次得到的样本编号为394,435,482,173,则选出来的第4个个体编号为173,选C .5. 解析:由222b ca b c=⎧⎨=+⎩得222a c =,c e a ==A . 6. 解析:由题意知,231412a a a a a ⋅=⋅=,即42a =,且4a 与72a 的等差中项为54,所以475224a a +=⨯,即714a =.选D .7. 解析:112f a ⎛⎫=+⎪⎝⎭,当0a ≤时,1(1)3242f f f a a ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭,203a =>,不成立;当0a >,()21(1)log 142f f f a a ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭,得150a =>成立,所以15a =,选B . 8. 解析:如图,设圆锥的底面半径为r ,由正弦定理2sin AB r ACB =∠,即32sin 60r =,求得3r =,因为母线与底面所成的角的余弦值为35,所以3cos 5PAO ∠=,所以4tan 3PAO ∠=,得圆锥的高tan 3PO r PAO =⋅∠=,所以2143(3)333V ππ=⨯⨯=,选A .9. 解析:当2x ππ<≤时,()t a n s i n t a n si n 2t a ny x x x x x =++-=,当32x ππ<<时,()t a n s i n t a n si n 2s i n y x x x x x =+--=,选D .10. 解析:根据程序框图,S 是求222231log log log 342n n +++++的和,所以()21log 2S n =-+,当()21log 24S n =-+<-时,有30n >,所以31n =,此时输出132n +=,选D .11. 解析:由三视图可知,该几何体是将一个棱长为4的正方体沿着如图所示的截面ABCDEF 截去之后剩下的几何体,表面积为()(2422223324362222+⨯⎡⎤⨯+⨯+⨯+=⎢⎥⎣⎦48123+48123+ C.12. 解析:()2661f x x x '=-+,()1260f x x ''=-=得12x =,111123222842f ⎛⎫=⨯-⨯++= ⎪⎝⎭,所以()32232f x x x x =-++关于1,22⎛⎫⎪⎝⎭对称, 所以1232015201442403020162016201620162f f f f ⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+=⨯+=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,选B . 二、填空题:本大题共4小题,每小题5分,共20分。
13. 解析:因为3S ,63S S -,96S S -成等差,所以6=66S .14. 解析:切点为()1,2,()1f x x αα-'= 15. 解析:设(),P x y ,()2,1OP OQ QP x y -==-+,则(OP OQ x -=,设z =P 到定点()2,1Q -的距离,画出可行域(如图阴影部分所示),由图可知当点P 与点A 重合时,AQ 的距离最大,由130x x y =⎧⎨+-=⎩,解得12x y =⎧⎨=⎩,即()1,2A ,则z 的最大值为AQ ==,所以OP OQ -的最大值是16. 解析:过点B 作抛物线C 的准线1x =-的垂线,垂足为点1B ,因为周长AF AB BF =++1AB BB =+,所以当A ,B ,1B 三点共线时ABF ∆的周长最小,此时点B 的坐标为(4,4),ABF ∆的面积11422S =⨯⨯=. 三、解答题:解答应写出文字说明,证明过程或演算步骤。
