2018届云南省昆明市第一次市统测文科数学试卷
云南省昆明市2018年中考试数学试题(原卷版).docx

2018年昆明市初中学业水平考试数学试题卷(全卷共三个大题,共23个小题,共8页;满分120分,考试时间120分钟)一、填空题:(每小题3分,共18分。
请将答案写在相应题号后的横线上。
)1.在实数-3,0,1中,最大的数是。
2.共享单车进入昆明已两年,为市民的的低碳出行带来了方便。
据报道,昆明市共享单车投放量已达到240000辆,数字240000用科学计数法表示为。
3.如图,过直线AB上一点O作射线OC,∠BOC=29018',则AOC的度数为。
4.若13mm+=,则221mm+=5.如图,点A的坐标为(4,2)。
将点A绕坐标原点O旋转900后,再向左平移1个单位长度得到点A',则过点A'的正比例函数的解析式为。
6.如图,正六边形ABCDEF的边长为1,以点A为圆心,AB的长为半径,作扇形ABF,则图中阴影部分的面积为。
(结果保留根号和π)。
第3题图第5题图第6题图二、选择题:(每小题4分,共 32 分,在每小题给出的四个选项中,只有一个是正确的,请将正确选项的代号填在相应的括号内。
)7.下列几何体的左视图为长方形的是()A.B. C. D.8.关于x 一元二次方程x 2-x +m =0有两个不相等的实数根,则实数m 的取值范围是( )A.m <3B.m >3C.m ≤3D.m ≥39.你估算1的值( )A.在1.1和1.2之间B.在1.2和1.3之间C.在1.3和1.4之间D.在1.4和1.5之间 10.下列判断正确的是( )A.甲乙两组学生身高的平均值均为1.58,方差分别为S 2 =2.3,S 2 =1.8,则甲组学生的身高更整 齐B.为了了解某县七年级4000名学生的期中数学成绩,从中抽取100名学生的数学成绩进行调查,这个问题中样本容量为4000C.在“童心向党,阳光下成长”合唱比赛中,30个参赛队的决赛成绩如下表:D.有13名同学出生于2003年,那么在这个问题中“至少有两名同学出生在同一个月”属于必然事 件11.在∆AOC 中,OB 交AC 于点D ,量角器的摆放如图所示,则∠CDO 的度数为( ) A.900 B.950 C.1000 D.1200第11题图12.下列运算正确的是()A.(-13)2=9B.20180-38-=-1C.3a3∙2a-2 =6a(a≠0)D.18126-=13.甲乙两船从相距300km的A,B两地同时出发相向而行,甲船从A地顺流航行180km时与从B地逆流航行的乙船相遇,水流的速度为6km/h,若甲、乙两船在静水中的速度均为xkm/h,则求两船在静水中的速度可列方程为()A.18012066x x=+- B.18012066x x=-+ C.1801206x x=+ D.1801206x x=-14.如图,点A在双曲线y=kx(x>0)上,过点A作AB⊥x轴,垂足为点B。
云南省昆明市2018年中考试数学试题(原卷版)-真题卷

2018年昆明市初中学业水平考试数学试题卷(全卷共三个大题,共23个小题,共8页;满分120分,考试时间120分钟)题号第一题第一题第一题总分得分一、填空题:(每小题3分,共18分。
请将答案写在相应题号后的横线上。
)1.在实数-3,0,1中,最大的数是。
2.共享单车进入昆明已两年,为市民的的低碳出行带来了方便。
据报道,昆明市共享单车投放量已达到240000辆,数字240000用科学计数法表示为。
3.如图,过直线AB上一点O作射线OC,∠BOC=29018',则AOC的度数为。
4.若13mm+=,则221mm+=5.如图,点A的坐标为(4,2)。
将点A绕坐标原点O旋转900后,再向左平移1个单位长度得到点A',则过点A'的正比例函数的解析式为。
6.如图,正六边形ABCDEF的边长为1,以点A为圆心,AB的长为半径,作扇形ABF,则图中阴影部分的面积为。
(结果保留根号和π)。
第3题图第5题图第6题图二、选择题:(每小题4分,共 32 分,在每小题给出的四个选项中,只有一个是正确的,请将正确选项的代号填在相应的括号内。
)7.下列几何体的左视图为长方形的是()A.B. C. D.8.关于x 一元二次方程x 2-x +m =0有两个不相等的实数根,则实数m 的取值范围是( ) A.m <3B.m >3C.m ≤3D.m ≥39.是一个很奇妙的数,大量应用与艺术、建筑和统计决策等方面。
请你估算1的值( )A.在1.1和1.2之间B.在1.2和1.3之间C.在1.3和1.4之间D.在1.4和1.5之间 10.下列判断正确的是( )A.甲乙两组学生身高的平均值均为1.58,方差分别为S 2 =2.3,S 2 =1.8,则甲组学生的身高更整 齐B.为了了解某县七年级4000名学生的期中数学成绩,从中抽取100名学生的数学成绩进行调查, 这个问题中样本容量为4000C.在“童心向党,阳光下成长”合唱比赛中,30个参赛队的决赛成绩如下表:D.有13名同学出生于2003年,那么在这个问题中“至少有两名同学出生在同一个月”属于必然事 件11.在∆AOC 中,OB 交AC 于点D ,量角器的摆放如图所示,则∠CDO 的度数为( ) A.900 B.950 C.1000 D.1200第11题图12.下列运算正确的是( )A.(-13)2=9B.20180-38-=-1C.3a 3•2a -2=6a (a ≠0)D.18126-=13.甲乙两船从相距300km 的A ,B 两地同时出发相向而行,甲船从A 地顺流航行180km 时与从B 地逆流航行的乙船相遇,水流的速度为6km /h ,若甲、乙两船在静水中的速度均为xkm /h ,则求 两船在静水中的速度可列方程为( ) A.18012066x x =+- B.18012066x x =-+ C.1801206x x =+ D.1801206x x =-14.如图,点A在双曲线y=kx(x>0)上,过点A作AB⊥x轴,垂足为点B。
2018年云南省高中毕业生复习统一检测---文科数学

2018年云南省高中毕业生复习统一检测文科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2A x x =>,()(){}130B x x x =--<,则A B =( )A .∅B .{}23x x <<C .{}2x x >D .{}3x x ≥2.已知复数()()221z i i =-+,其中i 是虚数单位,则z 的模z =( )A.3 C .4 D .5 3.若x ,y 满足30,20,0.x x y x y -≤⎧⎪+-≥⎨⎪-≥⎩则2z y x =-的最大值为( )A .5B .1-C .3-D .7-4.已知,2παπ⎛⎫∈ ⎪⎝⎭,tan 2α=-,则cos α=( ) A .35- B .25-C.5-.5- 5.已知函数()2sin 6f x x π⎛⎫=- ⎪⎝⎭,则下列结论中正确的是( ) A .()y f x =的一个周期为π B .()y f x =的图像关于点,26π⎛⎫ ⎪⎝⎭对称 C. ()y f x =的图像关于直线6x π=对称 D .()y f x =在区间2,63ππ⎛⎫ ⎪⎝⎭上单调递增 6.执行下图所示的程序框图,为使输出M 的值大于9,则输入的正整数t 的最小值为( )A .2B .3 C.4 D .57.在我国古代数学名著《九章算术》中,“堑堵”指的是底面为直角三角形,且侧棱垂直于底面的三棱柱.如图,网络图中小正方形的边长为1,图中粗实线画出的是某堑堵的正视图与俯视图,则该堑堵的表面积为( )A .2+B .6 C.6+.108.在正方体1111ABCD A B C D -中,点P 是线段1BC 上任意一点,则下列结论中正确的是( )A .1AD DP ⊥B .1AP BC ⊥ C. 1AC DP ⊥D .11A P B C ⊥9.平面内到两个定点的距离之比为常数()1k k ≠的点的轨迹是阿波罗尼斯圆.已知曲线C 是平面内到两个定点()11,0F -和()21,0F 的距离之比等于常数()1a a >的阿波罗尼斯圆,则下列结论中正确的是( ) A .曲线C 关于x 轴对称 B .曲线C 关于y 轴对称C. 曲线C 关于坐标原点对称 D .曲线C 经过坐标原点10.已知函数()ln 1f x x =-,则下列结论中正确的是( )A .()()10f f f e e ⎛⎫<< ⎪⎝⎭ B .()()10f e f f e ⎛⎫<< ⎪⎝⎭C. ()()10f f e f e ⎛⎫<< ⎪⎝⎭ D .()()10f f f e e ⎛⎫<< ⎪⎝⎭11.定义:{},,min ,,.a a b a b b a b ≤⎧=⎨>⎩在区域02,0 3.x y ≤≤⎧⎨≤≤⎩内任取一点(),P x y ,则点(),P x y 满足{}min 21,11x y x y x y -++-=+-的概率为( )A .12B .16 C.18 D .11212.已知定义在R 的函数()f x 满足()()22f x f x -=--,且当2x ≥-时,()23x f x =-.若函数()f x 在区间(),1k k +()k Z ∈上有零点,则k 的值为( )A .1或6-B .0或5- C. 0或6- D .1或5-第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量()2,1a =-,()3,b m =,若向量a b +与a 垂直,则m = .14.ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c .已知cos sin b C C a=-,a =1c =,则角C = .15.设椭圆()222210x y a b a b+=>>的左右焦点分别为1F ,2F ,过焦点2F 的直线交椭圆于()11,A x y ,()22,B x y 两点.若1AF B ∆内切圆的面积为2π,且124y y -=,则该椭圆的离心率是 .16.已知函数()()2221,0,log 1,0,x x x f x x x ⎧+->⎪=⎨⎪+<⎩若()()2f f a ≤,则实数a 的取值范围是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 设数列{}n a 满足12a =,12n n n a a +-=.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设21222log log log n n b a a a =+++,求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n S .18. 某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[)40,50,[)50,60,[)60,70,[)70,80,[)80,90,[]90,100.(Ⅰ)求频率分布直方图中a 的值;(Ⅱ)求这50名问卷评分数据的中位数;(Ⅲ)从评分在[)40,60的问卷者中,随机抽取2人,求此2人评分都在[)50,60的概率.19. 如图,已知四边形ABCD 为矩形,四边形ABEF 为直角梯形,FA AB ⊥,1AD AF FE ===,2AB =,AD BE ⊥.(Ⅰ)求证:BE DE ⊥;(Ⅱ)求点F 到平面CBE 的距离.20. 已知分别过抛物线()220x py p =>上点A 、B 的两条切线交于点M ,直线AB 与x 轴不平行,线段AB 的中点为N ,抛物线的焦点为F .(Ⅰ)求证:直线MN 与y 轴平行;(Ⅱ)若点F 线段AB 上,点N 的坐标为2⎛⎫ ⎪⎪⎝⎭,求抛物线的方程.21. 设函数()()223xf x e ax a a R =-+∈. (Ⅰ)讨论()f x 的单调性;(Ⅱ)当0a >时,对于x R ∀∈,都有()5f x a ≥成立.(ⅰ)求a 的取值范围; (ⅱ)证明:()()*1111ln 123n n N n++++>+∈. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线C 的参数方程是3cos 2sin x y ϕϕ=⎧⎨=⎩(ϕ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系. (Ⅰ)求曲线C 的极坐标方程;(Ⅱ)若A ,B 分别为曲线C 上的两点,且OA OB ⊥,求证:2211OA OB +为定值.23.选修4-5:不等式选讲已知函数()121f x x x =-++.(Ⅰ)求不等式()5f x ≤的解集;(Ⅱ)若不等式()f x x m ≥-的解集为R ,求m 的取值范围.。
2018年云南省高考数学一模试卷

2018年云南省高考数学一模试卷(文科)一选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.已知集合(){}{}22|lg 1,|21xxA x y xB x -==-=<,则A B =A.{}|1x x >B. {}|0x x >C. {}|02x x <<D.{}|12x x <<2.已知复数z 满足()11z i i ⋅-=+,则z 的共轭复数的虚部为 A. 1 B. i - C. i D.-13.已知向量()()1,2,,2a b x ==-,若a b +与a b -垂直,则实数x 的值是 A. 1± B. 1 C. -1 D.-44.设,则“()0a a b -<”是“a b <”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D.既不充分也不必要条件5.已知,m n 是两条不同的直线,α是平面,则下列命题中是真命题的是 A. 若//,//m m n α,则//n α B. 若,m n αα⊥⊥,则//m n C. 若//,m m n α⊥,则//n α D. 若,m m n α⊥⊥,则//n α6.已知等比数列{}n a 为递增数列,若10,a >且()2123n n n a a a ++-=,则数列{}n a 的公比q = A. 2或12 B. 2 C. 12D.-2 7.若,2παπ⎛⎫∈ ⎪⎝⎭,且3cos 2cos 4παα⎛⎫=+ ⎪⎝⎭,则sin 2α的值为A.118 B. 118- C. 1718 D.1718-8.图1中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的,,a b i 的值分别为8,10,0,则输出的a 和i 的值分别为A. 2,5B. 2,4C. 0,4D. 0,59.函数()2x f x xe x =--的零点的个数为A.0B. 1C. 2D. 3 10.某四棱锥的三视图如图2所示,则该四棱锥的外接球的表面积为A. 3πB. 4πC. 12πD.8π11.已知函数()243,1ln ,1x x x f x x x ⎧-+-≤=⎨>⎩,若()f x a a x +≥,则a的取值范围是A. [)2,0-B. []0,1C. (]0,1D.[]2,0-12.已知P 是椭圆()2211221110x y a b a b +=>>和双曲线()2222222210,0x y a b a b -=>>的一个交点,12,F F 是椭圆和双曲线的公共焦点,123F PF π∠,则12b b 的值是 A. 3 B. 3-C.二、填空题:本大题共4小题,每小题5分,共20分).13.若实数x ,y 满足约束条件,则z=2x ﹣y 的最大值为.14.已知函数f (x )=axlnx +b (a ,b ∈R ),若f (x )的图象在x=1处的切线方程为2x ﹣y=0,则a +b= .15.设P ,Q 分别为圆x 2+y 2﹣8x +15=0和抛物线y 2=4x 上的点.则P ,Q 两点间的最小距离是 .16.已知y=f (x )是R 上的偶函数,对于任意的x ∈R ,均有f (x )=f (2﹣x ),当x ∈[0,1]时,f (x )=(x ﹣1)2,则函数g (x )=f (x )﹣log 2017|x ﹣1|的所有零点之和为 .三、解答题:本大题共5小题,共48分.解答写出文字说明、证明过程或演算过程.17.(12分)已知数列{a n}中,a n2+2a n﹣n2+2n=0(n∈N+)(Ⅰ)求数列{a n}的通项公式(Ⅱ)求数列{a n}的前n项和S n.18.(12分)某校开展“翻转合作学习法”教学实验,经过一年的实践后,对“翻转班”和“对照班”的全部220名学生的数学学习情况进行测试,按照大于或等于120分为“成绩优秀”,120分以下为“成绩一般”统计,得到如下的2×2列联表.(Ⅰ)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关;(Ⅱ)为了交流学习方法,从这次测试数学成绩优秀的学生中,用分层抽样方法抽出6名学生,再从这6名学生中抽3名出来交流学习方法,求至少抽到一名“对照班”学生交流的概率.2=:附:K(Ⅰ)求证:平面BED⊥平面PAC;(Ⅱ)求点E到平面PBC的距离.20.(12分)在圆x2+y2=9上任取一点P,过点P作x轴的垂线段PD,D为垂足,点M在线段DP上,满足=,当点P在圆上运动时,设点M的轨迹为曲线C.(Ⅰ)求曲线C的方程;(Ⅱ)若直线y=m(x+5)上存在点Q,使过点Q作曲线C的两条切线互相垂直,求实数m的取值范围.21.(12分)设函数f(x)=e2x+ae x,a∈R.(Ⅰ)当a=﹣4时,求f(x)的单调区间;(Ⅱ)若对x∈R,f(x)≥a2x恒成立,求实数a的取值范围.[选修4-4:坐标系与参数方程选讲]22.(10分)已知直线L的参数方程为(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=.(Ⅰ)直接写出直线L的极坐标方程和曲线C的普通方程;(Ⅱ)过曲线C上任意一点P作与L夹角为的直线l,设直线l与直线L的交点为A,求|PA|的最大值.[选修4-5:不等式选讲]23.已知函数f(x)=|x+a|+|x﹣2|的定义域为实数集R.(Ⅰ)当a=5时,解关于x的不等式f(x)>9;(Ⅱ)设关于x的不等式f(x)≤|x﹣4|的解集为A,B={x∈R|2x﹣1|≤3},如果A∪B=A,求实数a的取值范围.2017年云南省高考数学一模试卷(文科)参考答案与试题解析二、填空题:本大题共4小题,每小题5分,共20分).13.若实数x,y满足约束条件,则z=2x﹣y的最大值为2.【考点】简单线性规划.【分析】作出可行域,变形目标函数,平移直线找出最优解可得结论.【解答】解:作出,所对应可行域(如图△ABC),变形目标函数z=2x﹣y可得y=2x﹣z,平移直线y=2x可得当直线经过点A(1,0)时,直线的截距最小,z取最大值,代值计算可得最大值为:2.故答案为:2.【点评】本题考查简单线性规划,准确作图是解决问题的关键,属中档题.14.已知函数f(x)=axlnx+b(a,b∈R),若f(x)的图象在x=1处的切线方程为2x﹣y=0,则a+b=4.【考点】利用导数研究曲线上某点切线方程.【分析】求出函数的导数,由题意可得f(1)=2,f′(1)=2,计算即可得到所求.【解答】解:f(x)=axlnx+b的导数为f′(x)=a(1+lnx),由f(x)的图象在x=1处的切线方程为2x﹣y=0,易知f(1)=2,即b=2,f′(1)=2,即a=2,则a+b=4.故答案为:4.【点评】本题考查导数的运用:求切线的斜率,考查运算能力,正确求导和运用直线方程是解题的关键.15.设P,Q分别为圆x2+y2﹣8x+15=0和抛物线y2=4x上的点.则P,Q两点间的最小距离是2﹣1.【考点】抛物线的简单性质.【分析】由题意可得圆的圆心和半径,由二次函数可得P与圆心距离的最小值,减半径即可.【解答】解:∵圆x2+y2﹣8x+15=0可化为(x﹣4)2+y2=1,∴圆的圆心为(4,0),半径为1,设P(x0,y0)为抛物线y2=4x上的任意一点,∴y02=4x0,∴P与(4,0)的距离d==,∴由二次函数可知当x0=2时,d取最小值2,∴所求最小值为:2﹣1.故答案为:2﹣1.【点评】本题考查两点间的距离公式,涉及抛物线和圆的知识,属中档题.16.已知y=f(x)是R上的偶函数,对于任意的x∈R,均有f(x)=f(2﹣x),当x∈[0,1]时,f(x)=(x﹣1)2,则函数g(x)=f(x)﹣log2017|x﹣1|的所有零点之和为2016.【考点】函数奇偶性的性质.【分析】由题意可求得函数是一个周期函数,且周期为2,故可以研究出一个周期上的函数图象,再研究所给的区间包含了几个周期即可知道函数g(x)=f(x)﹣log2017|x﹣1|的所有零点之和.【解答】解:由题意可得函数f(x)是R上的偶函数,可得f(﹣x)=f(x),f (2﹣x)=f(x),故可得f(﹣x)=f(2﹣x),即f(x)=f(x﹣2),即函数的周期是2,y=log2017|x﹣1|在(1,+∞)上单调递增函数,当x=2018时,log2017|x﹣1|=1,∴当x>2018时,y=log2017|x﹣1|>1,此时与函数y=f(x)无交点.根据周期性,利用y=log5|x﹣1|的图象和f(x)的图象都关于直线x=1对称,则函数g(x)=f(x)﹣log2017|x﹣1|的所有零点之和为﹣2015﹣2013﹣ (3)1+3+5…+2017=2016,故答案为:2016.【点评】本题考查函数的零点,求解本题,关键是研究出函数f(x)性质.三、解答题:本大题共5小题,共48分.解答写出文字说明、证明过程或演算过程.17.(12分)(2017•云南一模)已知数列{a n}中,a n2+2a n﹣n2+2n=0(n∈N+)(Ⅰ)求数列{a n}的通项公式(Ⅱ)求数列{a n}的前n项和S n.【考点】数列递推式;数列的求和.),可得(a n﹣n)(a n﹣n+2)=0.即可【分析】(I)a n2+2a n﹣n2+2n=0(n∈N+解出.(II)利用等差数列的求和公式即可得出.),∴(a n﹣n)(a n﹣n+2)=0.【解答】解:(I)∵a n2+2a n﹣n2+2n=0(n∈N+∴a n=n,或a n=n﹣2.(II)a n=n时,S n=.a n=n﹣2时,S n==.【点评】本题考查了一元二次方程的解法、等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.18.(12分)(2017•云南一模)某校开展“翻转合作学习法”教学实验,经过一年的实践后,对“翻转班”和“对照班”的全部220名学生的数学学习情况进行测试,按照大于或等于120分为“成绩优秀”,120分以下为“成绩一般”统计,得到如下的2×2列联表.(Ⅰ)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关;(Ⅱ)为了交流学习方法,从这次测试数学成绩优秀的学生中,用分层抽样方法抽出6名学生,再从这6名学生中抽3名出来交流学习方法,求至少抽到一名“对照班”学生交流的概率.2=:附:K【分析】(Ⅰ)根据列联表中的数据计算K2,对照临界值表得出结论;(Ⅱ)求出用分层抽样方法抽出6人,对照班2人,翻转班4人,用列举法计算基本事件数,求出概率直.【解答】解:(Ⅰ)根据列联表中的数据,计算K2=≈9.167<10.828,对照临界值表知,不能在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关;(Ⅱ)这次测试数学成绩优秀的学生中,对照班有20人,翻转班有40人,用分层抽样方法抽出6人,对照班抽2人,记为A、B,翻转班抽4人记为c、d、e、f;再从这6人中抽3人,基本事件是ABc、ABd、ABe、ABf、Acd、Ace、Acf、Ade、Adf、Aef、Bcd、Bce、Bcf、Bde、Bdf、Bef、cde、cdf、cef、def共20种不同取法;至少抽到一名“对照班”学生的基本事件是ABc、ABd、ABe、ABf、Acd、Ace、Acf、Ade、Adf、Aef、Bcd、Bce、Bcf、Bde、Bdf、Bef共16种,故所求的概率为P==.【点评】本题考查了独立性检验与列举法求概率的计算问题,是基础题目.19.(12分)(2017•云南一模)如图,在四棱锥P﹣ABCD中,PC⊥平面ABCD,底面ABCD是平行四边形,AB=BC=2a,AC=2a,E的PA的中点.(Ⅰ)求证:平面BED⊥平面PAC;(Ⅱ)求点E到平面PBC的距离.【考点】点、线、面间的距离计算;平面与平面垂直的判定.【分析】(Ⅰ)设AC∩BD=O,证明AC⊥平面BED,即可证明平面BED⊥平面PAC;(Ⅱ)点E到平面PBC的距离=点O到平面PBC的距离,作OF⊥BC,垂足为F,证明OF⊥平面PBC,即可求出求点E到平面PBC的距离.【解答】(Ⅰ)证明:设AC∩BD=O,则EO∥AC,AC⊥BD,∵PC⊥平面ABCD,∴EO⊥平面ABCD,∵AC⊥平面ABCD,∴AC⊥EO,∵BD∩EO=O,∴AC⊥平面BED,∵AC⊂平面PAC,∴平面BED⊥平面PAC;(Ⅱ)解:点E到平面PBC的距离=点O到平面PBC的距离,作OF⊥BC,垂足为F,∵PC⊥平面ABCD,OF⊂平面ABCD,∴PC⊥OF,∵BC∩PC=C,∴OF⊥平面PBC∵AB=BC=2a,AC=2a,∴∠ABC=120°,∴O到BC的距离为OF=a,即点E到平面PBC的距离为a.【点评】本题考查线面垂直、平面与平面垂直的证明,考查点到平面距离的计算,考查学生分析解决问题的能力,属于中档题.20.(12分)(2017•云南一模)在圆x2+y2=9上任取一点P,过点P作x轴的垂线段PD,D为垂足,点M在线段DP上,满足=,当点P在圆上运动时,设点M的轨迹为曲线C.(Ⅰ)求曲线C的方程;(Ⅱ)若直线y=m(x+5)上存在点Q,使过点Q作曲线C的两条切线互相垂直,求实数m的取值范围.【考点】直线与椭圆的位置关系;轨迹方程.【分析】(Ⅰ)设出P(x0,y0),M(x,y),D(x0,0),由点M在线段PD 上,且满足DM=DP,M的坐标用P的坐标表示,代入圆的方程得答案;(Ⅱ)设过点Q(x0,y0)的椭圆的切线方程为y﹣y0=k(x﹣x0),由y=kx﹣kx0+y0,,整理得:(4+9k2)x2+18k(﹣kx0+y0)x+9(﹣kx0+y0)2﹣36=0,由△=324k2(﹣kx+y0)2﹣36(4+9k2)[(﹣kx0+y0)2﹣4]=0,整理得:(9﹣)k2+2kx0y0+4﹣=0.由k1k2=⇒,点Q是圆x2+y2=9与y=m(x+5)的公共点,∴O(0,0)到直线y=m(x+5)的距离d即可.【解答】解:(Ⅰ)设P(x0,y0),M(x,y),D(x0,0),∵点M在线段PD上,且满足满足=,∴x0=x,y0=y,又P在圆x2+y2=9上,∴x02+y02=9,∴x2+y2=9,曲线C的方程为:.(2)假设在直线y=m(x+5)上存在点Q(x0,y0),设过点Q(x0,y0)的椭圆的切线方程为y﹣y0=k(x﹣x0),即y=kx﹣kx0+y0.由y=kx﹣kx0+y0,,整理得:(4+9k2)x2+18k(﹣kx0+y0)x+9(﹣kx0+y0)2﹣36=0,由△=324k2(﹣kx0+y0)2﹣36(4+9k2)[(﹣kx0+y0)2﹣4]=0,整理得:(9﹣)k2+2kx0y0+4﹣=0.故过点Q(x0,y0)的椭圆的两条切线斜率k1,k2分别是:(9﹣)k2+2kx0y0+4﹣=0的两解故k1k2=⇒,∴点Q是圆x2+y2=9与y=m(x+5)的公共点,∴O(0,0)到直线y=m(x+5)的距离d即可.解得12m2≤13,即﹣,实数m的取值范围:[].【点评】本题考查了轨迹方程的求法,考查了代入法求曲线的轨迹方程,椭圆的切线问题,属于难题.21.(12分)(2017•云南一模)设函数f(x)=e2x+ae x,a∈R.(Ⅰ)当a=﹣4时,求f(x)的单调区间;(Ⅱ)若对x∈R,f(x)≥a2x恒成立,求实数a的取值范围.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.【分析】(I)当a=﹣4时,f′(x)=2e x(e x﹣2),令f′(x)=0,解得x=ln2.分别解出f′(x)>0,f′(x)<0,即可得出函数f(x)单调区间.(Ⅱ)对x∈R,f(x)≥a2x恒成立⇔e2x+ae x﹣a2x≥0,令g(x)=e2x+ae x﹣a2x,则f(x)≥a2x恒成立⇔g(x)min≥0.g′(x)=2e2x+ae x﹣a2=2 [e x﹣(﹣a)],对a分类讨论,利用导数研究函数的单调性极值与最值即可得出.【解答】解:(I)当a=﹣4时,函数f(x)=e2x﹣4e x,f′(x)=2e2x﹣4e x=2e x(e x﹣2),令f′(x)=0,解得x=ln2.当x∈(ln2,+∞)时,f′(x)>0,此时函数f(x)单调递增;当x∈(﹣∞,ln2)时,f′(x)<0,此时函数f(x)单调递减.∴函数f(x)的单调递增区间为:[ln2,+∞)时,单调递减区间为(﹣∞,ln2).(Ⅱ)对x∈R,f(x)≥a2x恒成立⇔e2x+ae x﹣a2x≥0,令g(x)=e2x+ae x﹣a2x,则f(x)≥a2x恒成立⇔g(x)min≥0.g′(x)=2e2x+ae x﹣a2=2 [e x﹣(﹣a)],①a=0时,g′(x)=2e2x>0,此时函数g(x)在R上单调递增,g(x)=e2x>0恒成立,满足条件.②a>0时,令g′(x)=0,解得x=ln,则x>ln时,g′(x)>0,此时函数g(x)在R上单调递增;x<ln时,g′(x)<0,此时函数g(x)在R上单调递减.∴当x=ln时,函数g(x)取得极小值即最小值,则g(ln)=a2(1﹣ln)≥0,解得0<a≤2e.③a<0时,令g′(x)=0,解得x=ln(﹣a),则x>ln(﹣a)时,g′(x)>0,此时函数g(x)在R上单调递增;x<ln(﹣a)时,g′(x)<0,此时函数g(x)在R上单调递减.∴当x=ln(﹣a)时,函数g(x)取得极小值即最小值,则g(ln(﹣a))=﹣a2ln(﹣a)≥0,解得﹣1≤a<0.综上可得:a的求值范围是[﹣1,2e].【点评】本题考查了利用导数研究函数的单调性极值与最值、分类讨论方法,考查了推理能力与计算能力,属于难题.[选修4-4:坐标系与参数方程选讲]22.(10分)(2017•云南一模)已知直线L的参数方程为(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=.(Ⅰ)直接写出直线L的极坐标方程和曲线C的普通方程;(Ⅱ)过曲线C上任意一点P作与L夹角为的直线l,设直线l与直线L的交点为A,求|PA|的最大值.【考点】简单曲线的极坐标方程.【分析】(Ⅰ)利用三种方程的转化方法,即可写出直线L的极坐标方程和曲线C的普通方程;(Ⅱ)曲线C上任意一点P(cosθ,2sinθ)到l的距离为d=|2cosθ+2sinθ﹣6|.则|PA|==|2sin(θ+45°)﹣6|,利用正弦函数的单调性即可得出最值.【解答】解:(Ⅰ)直线L的参数方程为(t为参数),普通方程为2x+y ﹣6=0,极坐标方程为2ρcosθ+ρsinθ﹣6=0,曲线C的极坐标方程为ρ=,即ρ2+3ρ2cos2θ=4,曲线C的普通方程为=1;(Ⅱ)曲线C上任意一点P(cosθ,2sinθ)到l的距离为d=|2cosθ+2sinθ﹣6|.则|PA|==|2sin(θ+45°)﹣6|,当sin(θ+45°)=﹣1时,|PA|取得最大值,最大值为.【点评】本题考查了参数方程化为普通方程、点到直线的距离公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.[选修4-5:不等式选讲]23.(2017•云南一模)已知函数f(x)=|x+a|+|x﹣2|的定义域为实数集R.(Ⅰ)当a=5时,解关于x的不等式f(x)>9;(Ⅱ)设关于x的不等式f(x)≤|x﹣4|的解集为A,B={x∈R|2x﹣1|≤3},如果A∪B=A,求实数a的取值范围.【考点】绝对值三角不等式;绝对值不等式的解法.【分析】(Ⅰ)当a=5,把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.(Ⅱ)由题意可得B⊆A,区间B的端点在集合A中,由此求得a的范围.【解答】解:(Ⅰ)当a=5时,关于x的不等式f(x)>9,即|x+5|+|x﹣2|>9,故有①;或②;或③.解①求得x<﹣6;解②求得x∈∅,解③求得x>3.综上可得,原不等式的解集为{x|x<﹣6,或x>3}.(Ⅱ)设关于x的不等式f(x)=|x+a|+|x﹣2|≤|x﹣4|的解集为A,B={x∈R|2x﹣1|≤3}={x|﹣1≤x≤2 },如果A∪B=A,则B⊆A,∴,即,求得﹣1≤a≤0,故实数a的范围为[﹣1,0].【点评】本题主要考查绝对值不等式的解法,集合间的包含关系,属于中档题.。
昆明市数学高三文数第一次调研测试试卷D卷

昆明市数学高三文数第一次调研测试试卷D卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共12分)1. (1分) (2018高二下·武威月考) 设集合M={-1,0,1},N={ | = },则M∩N=()A . {-1,0,1}B . {0,1}C . {1}D . {0}2. (1分)设,则A . 3B . 2C . 1D .3. (1分)已知角的终边与角β的终边关于直线y=-x对称,则sin=()A .B .C .D .4. (1分)已知P是△ABC内一点,且,则△PAB的面积与△ABC的面积之比等于()A . 1:3B . 2:3C . 1:5D . 2:55. (1分) (2016高三上·呼和浩特期中) 在等差数列{an}中,Sn为它的前n项和,若a1>0,S16>0,S17<0,则当Sn最大时,n的值为()A . 7B . 8C . 9D . 106. (1分)已知中,角A,B,C所对的边分别为a,b,c,外接圆半径是1,,且满足条件,则的面积的最大值为()A .B .C .D .7. (1分)同时满足以下三个条件的函数是()①图像过点;②在区间上单调递减③是偶函数.A .B .C .D .8. (1分) (2018高一下·阿拉善左旗期末) 已知向量, ,若 ,则实数()A . 或B . 或C .D .9. (1分) (2019高三上·赤峰月考) 已知是等比数列的前项和,若,,则数列的公比为()A . 3B . 2C . -3D . -210. (1分)已知=(cos,sin),,,若△OAB是以O为直角顶点的等腰直角三角形,则△OAB的面积等于()A . 1B .C . 2D .11. (1分)(2018·大新模拟) 函数的大致图像有可能是()A .B .C .D .12. (1分)函数的定义域是()A .B .C .D .二、填空题 (共4题;共4分)13. (1分)(2020·秦淮模拟) 在平面直角坐标系xOy中,直线l是曲线M:y=sinx(x∈[0,π])在点A 处的一条切线,且l∥OP,其中P为曲线M的最高点,l与x轴交于点B,过A作x轴的垂线,垂足为C,则________.14. (1分) (2017高一下·启东期末) 在△ABC中,已知a=6,b=5,c=4,则△ABC的面积为________.15. (1分)(2020·汨罗模拟) 2019年1月1日起新的个人所得税法开始实施,依据《中华人民共和国个人所得税法》可知纳税人实际取得工资、薪金(扣除专项、专项附加及依法确定的其他)所得不超过5000元(俗称“起征点”)的部分不征税,超出5000元部分为全月纳税所得额.新的税率表如下:2019年1月1日后个人所得税税率表全月应纳税所得额税率(%)不超过3000元的部分3超过3000元至12000元的部分10超过12000元至25000元的部分20超过25000元至35000元的部分25个人所得税专项附加扣除是指个人所得税法规定的子女教育、继续教育、大病医疗、住房贷款利息、住房租金和赡养老人等六项专项附加扣除.其中赡养老人一项指纳税人赡养60岁(含)以上父母及其他法定赡养人的赡养支出,可按照以下标准扣除:纳税人为独生子女的,按照每月2000元的标准定额扣除;纳税人为非独生子女的,由其与兄弟姐妹分摊每月2000元的扣除额度,每人分摊的额度不能超过每月1000元.某纳税人为独生子,且仅符合规定中的赡养老人的条件,如果他在2019年10月份应缴纳个人所得税款为390元,那么他当月的工资、薪金税后所得是________元.16. (1分) (2016高一下·宁波期中) 若等差数列{an}满足a7+a8+a9>0,a7+a10<0,则当n=________时,数列{an}的前n项和最大.三、解答题 (共6题;共12分)17. (2分)设数列{an}是等差数列,数列{bn}的前n项和Sn满足Sn=(bn﹣1)且a2=b1 , a5=b2(Ⅰ)求数列{an}和{bn}的通项公式;(Ⅱ)设cn=an•bn ,设Tn为{cn}的前n项和,求Tn .18. (2分)化简求值(1)已知tanα=2,求的值(2)化简:.19. (2分) (2018高一下·包头期末) 在数列中,,(1)求证:数列为等差数列;(2)若数列满足,求证: .20. (2分) (2018高二下·鸡西期末) 在中,分别是角的对边,且 . (1)求角的大小;(2)若 , ,求的面积.21. (2分) (2018高二下·赣榆期末) 已知函数,其中.(1)当时,求函数在处的切线方程;(2)若函数在定义域上有且仅有一个极值点,求实数的取值范围.22. (2分)(2017·息县模拟) 已知函数f(x)= + (1﹣a2)x2﹣ax,其中a∈R.(1)若曲线y=f(x)在点(1,f(1))处的切线方程为8x+y﹣2=0,求a的值;(2)当a≠0时,求函数f(x)(x>0)的单调区间与极值;(3)若a=1,存在实数m,使得方程f(x)=m恰好有三个不同的解,求实数m的取值范围.参考答案一、单选题 (共12题;共12分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共12分)17-1、18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、22-3、。
云南省昆明市2018届高三数学第一次摸底测试试题文.pdf

3
y
t8
2
23. 选修 4-5 :不等式选讲
已知函数 f ( x) x 2 x 3 .
(1)求不等式 f (x) 3 的解集;
(2)若不等式 f ( x) a2 6a 解集非空,求实数 a 的取值范围 .
昆明一中全国联考第一期参考答案
5
1
为 1,则 C 的方程为( )
A. x 2 y2 1
B
. x2 y2 1
C.
2
x2 y 2 1
23
x2 y2
D.
1
33
6. 用一个平面去截正方体,则截面不可能是(
)
A.等边三角形
B .直角三角形
C.
正方形
D .正六边形
x y1 7. 若 x, y 满足约束条件 x y 1 ,则目标函数 z x 2 y 的最小值为( )
A1C1, AB1 的中点 .
3
(1)证明: MN // 平面 BB1C1C ;
(2)若 CM MN ,求三棱锥 M NAC 的体积 ..
19. 某市为了解本市 2 万名学生的汉字书写水平, 在全市范围内进行了汉字听写考试, 现从
某校随机抽取了 50 名学生,将所得成绩整理后,发现其成绩全部介于
[40,100] 之间,将其
[80,100] 的人数 .
4
20. 已知中心在原点 O ,焦点在 x 轴上的椭圆 E 过点 C (0,1) ,离心率为
2
.
2
(1)求椭圆 E 的方程;
(2)直线 l 过椭圆 E 的左焦点 F ,且与椭圆 E 交于 A, B 两点,若 直线 l 的方程 .
OAB 的面积为 2 ,求 3
21. 已知函数 f ( x) ex , g (x)
云南省昆明市2018届高三数学第一次摸底测试试题文2017110201122

云南省昆明市2018届高三数学第一次摸底测试试题文第Ⅰ卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.x11.已知集合,集合,则()A{x0}B{x0x4}A Bx3A.(0,3)B.(0,3]C.(,4)D.(,4]2.若对于变量x的取值为3,4,5,6,7时,变量y对应的值依次分别为4.0,2.5,-0.5,-1,-2;若对于变量u的取值为1,2,3,4时,变量v对应的值依次分别为2,3,4,6,则变量x和y,变量u和v的相关关系是()A.变量x和y是正相关,变量u和v是正相关B.变量x和y是正相关,变量u和v是负相关C.变量x和y是负相关,变量u和v是负相关D.变量x和y是负相关,变量u和v是正相关a2i3.已知复数为纯虚数(其中是虚数单位),则的值为()i a1i11A.2 B.-2 C.D.224.如图,正方形ABCD内的图形来自宝马汽车车标的里面部分,正方形内切圆中的黑色部分和白色部分关于正方形对边中点连线成轴对称,在正方形内随机取一点,则此点取自黑色部分的概率是()11 1A .B .C .D .42845.已知双曲线C 的中心为原点,点 F ( 2,0)是双曲线C 的一个焦点,点 F 到渐近线的距离为 1,则C 的方程为()yxy222A . x 2 y 2 1B . x 2 1C.1D .223 x y2213 36.用一个平面去截正方体,则截面不可能是( ) A .等边三角形B .直角三角形C. 正方形D .正六边形1x y7.若 x , y 满足约束条件 x y1 ,则目标函数 z x 2y 的最小值为()2x y 2A .2B .1C. -2D .-18. 执行如图所示的程序框图,若输出 n 的值为 9,则判断框中可填入()A . S 45?B . S 36?C. S 45? D . S 55?9.若函数 f (x ) x ,则函数 yf (x ) log x 的零点个数是()1 2A .5个B .4个C. 3个D .2个10. 已知函数 f (x )sin(x ) sin(x )(0 ),且 f ( ) 0 ,当 取最小值时, 623以下命题中假命题是()A.函数f(x)的图象关于直线x对称12B.是函数的一个零点x f(x)62C. 函数f(x)的图象可由g(x)3sin2x的图象向左平移个单位得到3D.函数f(x)在[0,]上是增函数1211.在ABC中,B600,AC43,AC边上的高为2,则ABC的内切圆半径r()A.22B.2(21) C. 21D.2(21)12.设O为坐标原点,P是以F为焦点的抛物线y22px(p0)上任意一点,M是线段PF PM2MF OM上的点,且,则直线的斜率的最大值为()223A.B. C. D.1233第Ⅱ卷二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量a(6,k),向量b(3,1),a b与b共线,则k.14.函数f(x)x2ln x在(1,1)处的切线方程为.315.已知,,则.sin()(,)tan454216.四面体A BCD中,AB CD10,AC BD234,AD BC241,则四面体A BCD外接球的表面积为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 在等差数列{}中,公差,前5项和S,且成等比数列.a d01,3,7515a aa n(1)求数列{a}的通项公式;n(2)求()的值.a a a ak N*28263k118. 如图,在直三棱柱中,,,点分别为ABC A B C BAC900AB AC2M,N111AC AB11,1的中点.3(1)证明:MN//平面BB C C;11(2)若CM MN,求三棱锥M NAC的体积..19. 某市为了解本市2万名学生的汉字书写水平,在全市范围内进行了汉字听写考试,现从某校随机抽取了50名学生,将所得成绩整理后,发现其成绩全部介于[40,100]之间,将其成绩按如下分成六组,得到频数分布表成绩[40,50)[50,60)[60,70)[70,80)[80,90)[90,100]人数 4 10 16 10 6 4(1)在答题卡上作出这些数据的频率分布直方图;(2)估算该校50名学生成绩的平均值x和中位数(同一组中的数据用该组区间的中点值作代表);(3)以该校50名学生成绩的频率作为概率,试估计该市分数在[80,100]的人数.4220. 已知中心在原点O,焦点在x轴上的椭圆E过点C(0,1),离心率为.2(1)求椭圆E的方程;(2)直线l过椭圆E的左焦点F,且与椭圆E交于A,B两点,若OAB的面积为2,求直3线l的方程.a21. 已知函数f(x)e x,g(x)x2x,(其中a R,e为自然对数的底数,2e 2.71828……).(1)令h(x)f'(x),求h(x)的单调区间;(2)已知f(x)在x 0处取得极小值,求实数a的取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程极坐标系中,O为极点,半径为2的圆C的圆心坐标为(2,).6(1)求圆C的极坐标方程;(2)设直角坐标系的原点与极点O重合,x轴非负关轴与极轴重合,直线l的参数方程为1x t23y t82(为参数),由直线上的点向圆引切线,求线线长的最小值.t l C23.选修4-5:不等式选讲已知函数f(x)x 2x 3.(1)求不等式f(x)3的解集;(2)若不等式f(x)a26a解集非空,求实数a的取值范围.昆明一中全国联考第一期参考答案5参考答案(文科数学)命题、审题组教师 杨昆华 李文清 孙思应 梁云虹 王在方 卢碧如 凹婷波 吕文芬 陈泳序一、选择题 题号 1 2 3 4 5 6 7 8 9 10 1112答案ADBC A BBADCB A1. 解析:集合 A1, 3, B0, 4 ,所以 A I B0,3,选 A.2. 解析:由正相关和负相关的定义知道,D 正确,选 D.3. 解析:因为a 2i (a 2) (a 2)i 1 i2,所以 a 2 ,选B.4. 解析:设正方形边长为 2 ,则圆半径为 1.此时正方形面积为 2 2 4 .图中黑色部分面积为 2 .则此点取自黑色部分的概率为 2 ,选C. 4 85. 解析:设 C 的方程为: x y2 22 2 1,由已知 b 1, c 2 ,所以 a 1,所以 C 的方程为 a bx 2 y 2 1,选 A .6. 解析:因为用一个平面去截正方体,若截面为三角形,则截面三角形只能是锐角三角形,选 B .7. 解析:如图,目标函数 z 在点 A (1, 0) 处取得最小值,且 z1 ,选 B.8. 解析:模拟执行如图所示的程序框图知,该程序的功能是计算 S1 2 L 9 45 ,选A.9. 解析:如图:函数 f (x ) 与函数 g (x ) log x ,有 2 个交点,所以选D.1 263310. 解 析:f xsin xcos x 3 sinx2 23得 ,由f ( ) 0 3Z,即 3k 1,由 0 知 的最小值是 2,当 取得最小值时,kk3 33sin2f x x3.由 f3 sin 2 3 sin312 12 32可得出:函数 f (x )的图象关于直线x对称,A 为真; 12由 f3 sin 26 6 3可得出: x是函数 f (x ) 的一个零点,B 为真;6将函数 gx3 sin 2x 的图象向左平移6个单位得到3 sin 2f xx3的图象,所以C 为假;由复合函数单调性可得 f (x ) 在 0,12上是增函数,所以 D 为真,选 C. 11. 解 析 : 由1 1 S AB BC sin B 4 32 V 得 AB BC 16 , 又 由 余 弦 定 理 ABC2 2AC 2AB 2 BC 2 2AB BC cos B (AB BC )2 3AB BC ,解得 AB BC4 6 ,从而V的 周长为4( 63) .由1 () ABCA得 Sr AB BC CAABC2r2S8 32( 21)ABCAB BC CA 4( 6 3),选 B.12. 解析:由题意可得 ,0 ,设 F p 22yPy0 ,2p,当 y 00 , K0 ;当OMy,0 K .要OM求 K 的最 大 值 , 可 设 OMy 00 , 则u u u r u u u ru u u ru u u r u u ru u u ru u u ru u u ru u u r u u u r21 112y p yOMOF FM OFFPOFOP OFOP OF, 3 3 3 36p 3 3, 可 得7KOMy1 123ypyp22 yp26p 32p y2p y.当且仅当 02 2 2yp 时取得等号,选A.二、填空题13. 解析:因为 a b (3, k 1) ,且 (a b )//b ,所以3(k1)3 ,所以 k2 .14. 解析:因为1,所以切线的斜率 k3,所以切线方程为3x y2 0 . f (x ) 2xx15. 解析:由,4 2得0,4 4 ,所以 cos 1 sin 2 4,所以 cos 1 sin 24 445,所 以cos cos cos cos sin sin 4 4 4 44 4 1024 4 4 4 4410, 27 2sin 1 cos,10sin 所以 tan7 .cos16. 解析:由题意可采用割补法,考虑到四面体 A BCD 的四个面为全等的三角形,所以可在其每个面补上一个以10 , 2 34 , 2 41 为三边的三角形作为底面,分别以 x , y , z 为侧 棱长且两两垂直的三棱锥,从而可得到一个长、宽、高分别为 x , y , z 的长方体,并且x 2 y 2 100 , x 2 z 2 136 , y 2 z 2 164 . 设 球 半 径 为 R , 则 有2Rxyz200 ,所以 4R 2 200 ,得球的表面积为 200 .2222三、解答题54 5a d 15117. 解:(Ⅰ):据题意有22a 2da a 6d1113a12, 解得3 d4 ,33所以数列a的通项公式为a an1 dn; nn14433 3(Ⅱ)由(Ⅰ)得:nn ,a3 133 1n44 4所以 aa a ……2826a3k 183 (3)3 33123k43 1 3k393 1k.4 1 3 8 33 3b另解:设,则b a3 1313 nN ,nn n n nn3 144 4b所以数列b 是首项为n9 4,公比为 3的等比数列,所以数列b 的前 k 项和Tnk91 3k943 1k1 3 8.18. 解 : ( Ⅰ ) 证 明 : 连 接 A B , BC 1 , 点 M , N 分 别 为 A 1C 1 ,AB 11的中点,所以 MN 为△ A BC 的一条中位线, 11MN //BC1MN平面 B B C C , 1 1BC平面1BB C C ,1 1所以 MN // 平面 BB C C .1 1(Ⅱ)设点D,E分别为AB,A A1的中点,AA1a,则CM2a21,222248205MN1,CN,由CM MN,得CM2MN2CN2,2aa2aa4444解得a 2,又NE 平面AA1C C,NE 1,1122111VV S AMC NEM NAC N AMC33223.所以三棱锥M NAC的体积为2 3.19.解:(Ⅰ)9(Ⅱ)x 450.08550.2650.32750.2850.12950.0868.2;由已知可设中位数为60x,则0.080.20.032x 0.5;所以x 6.875,所求中位数为x 66.875.(Ⅲ)该市分数在80,100的人数64200004000,故所求人数为4000人.5020.解:(Ⅰ)设椭圆E的方程为:x y22221(a b0),a bb1c2由已知:a2a b c222得:a22,b21,所以,椭圆E的方程为:x22y21.(Ⅱ)由已知直线l过左焦点F (1,0).当直线l与x轴垂直时,2A (1,),22B (1,),此时AB2,212则21S,不满足条件.OAB22当直线l与x轴不垂直时,设直线l的方程为:y k(x 1)y k (x 1) 由 2xy 122 得 (1 2k 2 )x 2 4k 2 x 2k 22 0所以4k2xx1 221 2k,2k2 2x x1 2212k, 11 而SOFyyyy ,OAB12122 2102由已知S得OAB34 yy ,123yy(yy )4y y2 12121 2[k (x x ) 2k ]4k (x1)(x1)221212, 4k4k22(1 2k )12k2 22所以4k4k16 22(1 2k ) 1 2k92 22,则 k 4k 2 2 0 ,所以 k1, 所以直线l 的方程为: x y 1 0 或 x y 1 0 .21. 解: (Ⅰ) 因为 f (x ) e x ax1,所以 h (x ) e x a ,当 a 0 时, h (x ) 0 , h (x )的单调递增区间为,,当 a 0 时,由 h(x ) e x a 0 ,得 xln a ,xa 时, h (x ) 0 , x (ln a ,) 时, h(x ) 0 ,( , ln )所以 h (x ) 的减区间为(, ln a ) ,增区间为 (ln a,)综上可得,当 a 0 时, h (x ) 在(,) 上单调递增当 a 0 时, h (x ) 的增区间为 (ln a ,) ,减区间为(,ln a ) .(Ⅱ)由题意得 f (x ) e x ax 1, f (0) 0 ,(1)当 a 0 时, f (x ) 在(,) 上单调递增,所以当 x 0 时, f (x ) f (0)0 , 当 x0 时, f (x ) f (0) 0 ,所以 f (x ) 在 x 0 处取得极小值,符合题意. (2)当 0 a1 时, ln a 0 , 由(Ⅰ)知 f (x ) 在 (ln a,) 单调递增,所以当x(ln a,0)时,f(x)f(0)0,当x(0,)时,f(x)f(0)0,所以f(x)在x0处取得极小值,符合题意.11(3)当a1时,由(Ⅰ)知f(x)在区间(,ln a)单调递减,f(x)在区间(ln a,)单调递增,所以f(x)在x ln a处取得最小值,即f(x)f(ln a)f(0)0,所以函数f(x)在R上单调递增,所以f(x)在x0处无极值,不符合题意.(4)当a1时,ln a0,由(Ⅰ)知f(x)的减区间为(,ln a),所以当x(,0)时,f(x)f(0)0,当x(0,ln a)时,f(x)f(0)0,所以f(x)在x0处取得极大值,不符合题意,综上可知,实数a的取值范围为(,1).第22、23题中任选一题做答,如果多做,则按所做的第一题记分.22.解:(Ⅰ)设M(,)是圆上任意一点,如图,连接OC,并延长与圆C交于点A,当点M异于O,A时,连接OM、MA,直角△MOA中,OM OA cos MOA,即4cos4cos(),66当点M与O,A重合时,也满足上式,所求圆C的极坐标方程为4cos().6(Ⅱ)直线l的普通方程为3x y80,圆心C(3,1)到直线l的距离为d,3318d3r,所以直线l与圆C相离,2故切线长的最小值为32225.1223. 解:(Ⅰ)由 f (x ) x 2 x 3 3 可化为:xx 3 3 2或 x 2 x 3 3 x 2 x 3 3x 2或x 2 x 3 3 解得:x 或 2 x 2 或 x2 ,所以,不等式解集为2,.(Ⅱ)因为 f (x )x 2x 3(x 2) (x 3)5所以 5 f (x ) 5,即 f (x ) 的最小值为 5 , 要不等式 f (x ) a 2 6a 解集非空,需 f (x )a 2 6a ,min从而 a 26a 5 0 ,解得 a1或 a 5 ,所以 a的取值范围为,1U5,.13昆明一中全国联考第一期参考答案参考答案(文科数学)命题、审题组教师杨昆华李文清孙思应梁云虹王在方卢碧如凹婷波吕文芬陈泳序一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12答案 A D B C A B B A D C B A24.解析:集合A1,3,B0,4,所以A I B0,3,选A.25.解析:由正相关和负相关的定义知道,D正确,选D.26.解析:因为a 2i (a 2)(a2)i1i2,所以a 2,选B.27.解析:设正方形边长为2,则圆半径为1.此时正方形面积为224.图中黑色部分面积为2.则此点取自黑色部分的概率为2,选C.4828.解析:设C的方程为:x y22221,由已知b 1,c 2,所以a1,a b所以C的方程为x2y21,选A .yx-y=-1x+y=1329.解析:因为用一个平面去截正方体,若截面为三角形,则截面三角形22x-y=21只能是锐角三角形,选B.30.解析:如图,目标函数z在点A(1,0)处取得最小值,且z 1,选B. –5–4–3–2O–1–112345x 31.解析:模拟执行如图所示的程序框图知,该程序的功能是计算S 12L 945,选A.–2–332.解析:如图:函数f(x)与函数g(x)log x,有2个交点,所以选D.123333.解析:f x sin x cos x3sin x223得,由f()033yZ ,即3k 1,由0知的最小值是2,当k k332取得最小值时,3sin2f x x.由3–4–3–2–1O–1–21234xf3sin23sin3121232可得出:函数f(x)的图象–314关于直线 x对称,A 为真; 12由 f3 sin 2 066 3可得出: x是函数 f (x ) 的一个零点,B 为真;6将函数 g x3 sin 2x 的图象向左平移6个单位得到3 sin 2f x x3的图象,所以C 为假;由复合函数单调性可得 f (x ) 在 0,12上是增函数,所以 D 为真,选C. 34. 解 析 : 由1 1 S AB BC sin B 4 32 V 得 AB BC 16 , 又 由 余 弦 定 理 ABC2 2 AC 2AB 2 BC 2 2AB BC cos B (AB BC )2 3AB BC ,解得 AB BC4 6 ,从而V的 周长为4( 63) .由1 () ABCA得 Sr AB BC CAABC2r2S8 32( 21)ABCAB BC CA 4( 63),选 B.35. 解析:由题意可得 ,0 ,设 F p 2y2 Py, 02p,当 y, 0 00 K;当 OMy , 00 0 K.要OM求 K 的最 大 值 , 可 设OMy,则00u u u r u u u r u u u r u u u r u u r u u u r u u u r u u u r u u u r u u u r21112y p yOM OF FM OF FP OF OP OF OP OF00,33336p33,可得KOMy1123y p y p22y p0026p32p y2p y00.当且仅当22y p时取得等号,选A.02二、填空题36.解析:因为a b (3,k 1),且(a b)//b,所以3(k 1)3,所以k2.37.解析:因为1,所以切线的斜率k 3,所以切线方程为3x y20.f(x)2xx38.解析:由,42得0,44,所以cos 1sin24,所以cos 1sin24445,所以22cos cos cos cos sin sin44444410,1527 2sin 1 cos,10sin 所以 tan7 .cos39. 解析:由题意可采用割补法,考虑到四面体 A BCD 的四个面为全等的三角形,所以可在其每个面补上一个以10 , 2 34 , 2 41 为三边的三角形作为底面,分别以 x , y , z 为侧 棱长且两两垂直的三棱锥,从而可得到一个长、宽、高分别为 x , y , z 的长方体,并且x 2 y 2 100 , x 2 z 2 136 , y 2 z 2 164 . 设 球 半 径 为 R , 则 有2Rxyz 200 ,所以 4R 2 200 ,得球的表面积为 200 .2222三、解答题54 5a d 15140. 解:(Ⅰ):据题意有22a 2da a 6d1113a12, 解得3 d4 ,………4分33所以数列a的通项公式为a a n 1 d n; ………6分 nn 14 433 3(Ⅱ)由(Ⅰ)得:a313 ,nn3 1n44 4所以 aa a ……2826a3k13333 ……12343k………9分313k3931k.4138………12分333b另解:设,则b a31313n nn n N,n nn31444b所以数列b是首项为n 94,公比为3的等比数列, (9)分所以数列b的前k项和Tn k 913k9431k138.………12分1641. 解 : ( Ⅰ ) 证 明 : 连 接A B , BC 1 , 点 M , N 分 别 为 A 1C 1 , AB 11的中点,所以 MN 为△ A BC 的一条中位线, 11MN //BC1MN平面 B B C C , 1 1BC平面1BB C C ,1 1所以 MN // 平面 BB C C .………6分1 1( Ⅱ ) 设 点 D , E 分 别 为 AB , A A 1 的 中 点 , AA 1a , 则 CM 2a 21, 4820MN,CN 5,由CM MN ,得CM 2 MN 2CN 2 ,2a 2a 22a 2a 214444 解得 a 2 ,又 NE平面 AA 1C C , NE1, 111 1 22 1VVSAMCNEM NAC N AMC33 2 2 3 .所以三棱锥 M NAC 的体积为2 3. ………12分42. 解:(Ⅰ)………3分(Ⅱ)x45 0.08 55 0.2 65 0.32 75 0.2 85 0.12 95 0.08 68.2 ;………6分由已知可设中位数为 60 x ,则 0.08 0.2 0.032x 0.5; 所以x 6.875 , 所 求 中 位 数 为x 66.875. ………9分(Ⅲ)该市分数在80,100的人数64200004000,故所求人数5017为4000 人. ………12分43. 解:(Ⅰ)设椭圆 E 的方程为:xy2 222 1 (a b0) , a b1 b2 c由已知:a 2abc222得: a 22 ,b 21,所以,椭圆 E 的方程为: x 22y 21. (4)分 (Ⅱ)由已知直线l 过左焦点 F (1, 0) .当直线l 与 x 轴垂直时,2 A (1, ) ,22 B (1, ) ,此时 AB2 ,212则2 1S,不满足条件.………5分OAB22当直线l 与 x 轴不垂直时,设直线l 的方程为: y k (x1)y k x(1)由 2x2y12 得 (1 2k 2 )x 24k 2 x 2k 22 0所以4k2xx12212k,2k 22x x1 2212k,………8分11 而SOFyyyy ,OAB1212222 由已知 S得OAB4yy ,123 3yy(yy )4y y212121 2[k (x x ) 2k ]4k (x1)(x1)221212, 4k4k22(1 2k )1 2k2 22所以4k4k16 22(1 2k ) 1 2k92 22,则 k 4k 2 2 0 ,所以 k1, 所以直线l 的方程为: x y 1 0 或 x y 1 0 . ………12分44. 解: (Ⅰ) 因为 f (x ) e x ax1,所以 h (x ) e x a ,18当 a 0 时, h (x ) 0 , h (x ) 的单调递增区间为,,当 a 0 时,由 h(x ) e x a 0 ,得 xln a ,xa 时, h (x ) 0 , x (ln a ,) 时, h(x ) 0 ,( , ln )所以 h (x ) 的减区间为 (, ln a ) ,增区间为 (ln a ,)综上可得,当 a 0 时, h (x ) 在 (,) 上单调递增当 a 0 时, h (x ) 的增区间为 (ln a ,) ,减区间为 (,ln a ) . ………5分(Ⅱ)由题意得 f (x ) e x ax 1, f (0) 0 ,(1)当 a 0 时, f (x ) 在 (,) 上单调递增,所以当 x 0 时, f (x ) f (0) 0 , 当 x0 时, f (x ) f (0) 0 ,所以 f (x ) 在 x 0 处取得极小值,符合题意.(2)当 0 a 1 时, ln a 0 , 由(Ⅰ)知 f (x ) 在 (ln a ,) 单调递增,所以当 x(ln a ,0) 时, f (x ) f (0) 0 ,当 x(0,) 时, f (x ) f (0) 0 ,所以 f (x ) 在 x 0 处取得极小值,符合题意.(3)当 a 1时,由(Ⅰ)知 f (x ) 在区间 (,ln a ) 单调递减, f (x ) 在区间 (ln a ,) 单调递增,所以 f (x ) 在 x ln a 处取得最小值,即 f (x ) f (ln a ) f (0) 0 , 所以函数 f (x ) 在 R 上单调递增,所以 f (x ) 在 x 0 处无极值,不符合题意.(4)当 a 1时, ln a0 ,由(Ⅰ)知 f (x ) 的减区间为 (,ln a ) ,所以当 x(,0) 时, f (x ) f (0) 0 ,当 x (0,ln a ) 时, f (x ) f (0) 0 ,所以 f (x ) 在 x 0 处取得极大值,不符合题意,19综上可知,实数 a 的取值范围为 (,1) . ………12分第 22、23题中任选一题做答,如果多做,则按所做的第一题记分. 45. 解:(Ⅰ)设 M (,) 是圆上任意一点,如图,连接OC ,并延长与圆C 交于点 A , 当点 M 异于O , A 时,连接OM 、 MA , 直角△ MOA 中,OM OAcos MOA ,即4 cos4 cos() ,66当点 M 与O , A 重合时,也满足上式,所求圆C 的极坐标方程为4 cos() .………5分6(Ⅱ)直线l 的普通方程为 3x y 8 0 ,圆心C ( 3,1) 到直线l 的距离为 d ,3 318d3 r ,所以直线l 与圆C 相离,2故切线长的最小值为 32225 .………10分46. 解:(Ⅰ)由 f (x ) x 2 x 3 3 可化为:33 x 2x或x 2 x 3 3x 2 x 33 x 2 或x 2 x 3 3解得:x或 2 x 2 或 x2 ,所以,不等式解集为2,. ………5分(Ⅱ)因为 f (x )x 2x 3(x 2) (x 3)5所以 5 f (x ) 5,即 f (x ) 的最小值为 5 , 要不等式 f (x ) a 2 6a 解集非空,需 f (x )a 2 6a ,min从而 a 26a 5 0 ,解得 a1或 a 5 ,所以 a的取值范围为,1U5,.………10分20。
云南省昆明市2018年中考试数学试题(原卷版)【真题卷】
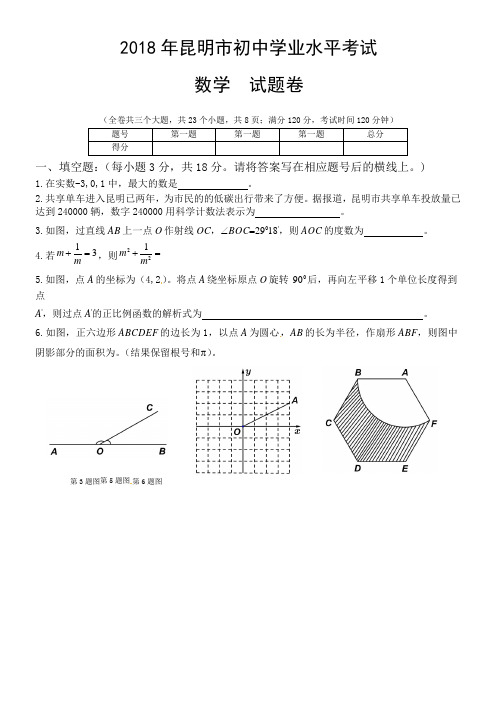
2018年昆明市初中学业水平考试数学试题卷(全卷共三个大题,共23个小题,共8页;满分120分,考试时间120分钟)题号第一题第一题第一题总分得分一、填空题:(每小题3分,共18分。
请将答案写在相应题号后的横线上。
)1.在实数-3,0,1中,最大的数是。
2.共享单车进入昆明已两年,为市民的的低碳出行带来了方便。
据报道,昆明市共享单车投放量已达到240000辆,数字240000用科学计数法表示为。
3.如图,过直线AB上一点O作射线OC,∠BOC=29018',则AOC的度数为。
4.若13mm+=,则221mm+=5.如图,点A的坐标为(4,2)。
将点A绕坐标原点O旋转900后,再向左平移1个单位长度得到点A',则过点A'的正比例函数的解析式为。
6.如图,正六边形ABCDEF的边长为1,以点A为圆心,AB的长为半径,作扇形ABF,则图中阴影部分的面积为。
(结果保留根号和π)。
第3题图第5题图第6题图二、选择题:(每小题4分,共 32 分,在每小题给出的四个选项中,只有一个是正确的,请将正确选项的代号填在相应的括号内。
)7.下列几何体的左视图为长方形的是()A.B. C. D.8.关于x 一元二次方程x 2-x +m =0有两个不相等的实数根,则实数m 的取值范围是( ) A.m <3B.m >3C.m ≤3D.m ≥39.是一个很奇妙的数,大量应用与艺术、建筑和统计决策等方面。
请你估算1的值( )A.在1.1和1.2之间B.在1.2和1.3之间C.在1.3和1.4之间D.在1.4和1.5之间 10.下列判断正确的是( )A.甲乙两组学生身高的平均值均为1.58,方差分别为S 2 =2.3,S 2 =1.8,则甲组学生的身高更整 齐B.为了了解某县七年级4000名学生的期中数学成绩,从中抽取100名学生的数学成绩进行调查, 这个问题中样本容量为4000C.在“童心向党,阳光下成长”合唱比赛中,30个参赛队的决赛成绩如下表:D.有13名同学出生于2003年,那么在这个问题中“至少有两名同学出生在同一个月”属于必然事 件11.在∆AOC 中,OB 交AC 于点D ,量角器的摆放如图所示,则∠CDO 的度数为( ) A.900 B.950 C.1000 D.1200第11题图12.下列运算正确的是( )A.(-13)2=9B.20180-38-=-1C.3a 3•2a -2=6a (a ≠0)D.18126-=13.甲乙两船从相距300km 的A ,B 两地同时出发相向而行,甲船从A 地顺流航行180km 时与从B 地逆流航行的乙船相遇,水流的速度为6km /h ,若甲、乙两船在静水中的速度均为xkm /h ,则求 两船在静水中的速度可列方程为( ) A.18012066x x =+- B.18012066x x =-+ C.1801206x x =+ D.1801206x x =-14.如图,点A在双曲线y=kx(x>0)上,过点A作AB⊥x轴,垂足为点B。
