多重循环群的Fitting子群
循环群讲义——精选推荐

§7循环群本节将讨论一类结构简单又富有代表性的特殊群――循环群.(它是一类基本而又重要的群,数学的一些分支(数论、有限域论等)和它有密切的联系.)通过对循环群的学习,可初步了解抽象代数研究问题的基本方法和格式以及论文的写作方法.本节主要内容是循环群的三大问题:存在问题/数量问题/构造问题. 先看一个简单的例子:{} ,10,10,10,1,10,10,10,32123---=G 对数的乘法作成群.特点是每个元都是固定元10的方幂.一、循环群的概念1.定义 G 称为循环群⇔群G 的每个元都是G 中某个固定元...a 的方幂⎩⎨⎧倍数--针对加法乘方--针对乘法. 记为)(a G =,a 称为G 的生成元. 即 G a G ⇔=)(是群,且⎩⎨⎧==∈∃∈∀)()(.,,加法乘法ka x a x st Z k G x k .(注意:k 与x 有关!)【一般情况下,如果没有特别声明运算是乘法或是加法,就默认是乘法形式.】2.注意:(一般情况下)生成元不唯一.a 是生成元1-⇔a 是生成元.【理由:k k a a --=)(1】3.范例【解决了循环群的存在问题.同时,将得到结论:循环群在同构意义下只有这两种!】 ①整数加群),(+Z ,)1()1(-==Z .【1±是∞阶.00)1(=⇒=±n n 】问题:还有其他生成元?(无)【设1),(1)(1)(±=⇒∈==∈⇒=k Z k n nk k k Z 】*实际上可进一步证明:)()(a G a o =⇒∞=只有两个生成元1,-a a .【课外思考题】【设)(b G =,则有111,,)(-=⇒=⇒=⇒==∈∞=or s st aa b a a b Z t s a o st t s 】 ②模n 剩余类加群),(+n Z ,])1([=n Z .问题:还有其他生成元?(有)【])1([])1([-=-=n Z n 】*实际上可进一步证明:)()(a G n a o =⇒=的生成元为r a 当且仅当1),(=n r .【习题】【若1),(=n r ,则)()()()()()(1r u r v u r v n u r vn ur a a a e a a a a a vn ur =⇒====⇒=++. 反之,r a 是生成元,1),(1|)()()()(1=⇒-⇒=⇒=⇒===-n r rk n e a a a a a G na o rk k r r .】 ◎设p 为素数,则p 阶循环群)(a G =有1-p 个生成元:12,,,-p a a a .◎设p 为素数,则模p 剩余类加群p Z 的所有非零元都是生成元.二、循环群的种类1.结构定理 设循环群)(a G =同构于⎩⎨⎧=+∞=+n a o if Z a o if Z n)(),,()(),,(. 证明 注意体会生成元a 的阶在证明过程中的用处!(1)设∞=)(a o 【作用:0=⇔=k e a k 】此时,令k a Z G k →→,:ϕ,可证ϕ是同构映射.(证略)【ϕ是映射:若h k a a =,则h k h k e aa o h k =⇒=-⇒=∞=-0)(,说明对应元唯一. 易证ϕ是满射/单射. 再证ϕ的同态性:)()()()()()(,,y x a a h k axy a y a x G y x h k h k h k ϕϕϕϕϕϕϕ+=+=+==⇒==⇒∈∀+.】 (2)设n a o =)(【作用:k n e a k|⇔=】此时,令][,:k a Z G k n →→ϕ ϕ是映射:若h k a a =,则][][|)(h k h k n e a na o h k =⇒-⇒==-,说明对应元唯一. ϕ是单射:若][][h k =,则e e a a mn h k h k n m n a o m n h k ===⇒=-⇒-=-)()(|.ϕ是满射:][)(.,,][k a st G a Z k k k n =∈∃∈∀ϕ再证ϕ的同态性: )()()()(][][)()(,,y x a a h k a xy a y a x G y x h k h k h k ϕϕϕϕϕϕϕ+=+=+==⇒==⇒∈∀+.例1:循环群)(a G =的阶为⇔n 生成元a 的阶为n .【常用结论】证法 同构必同阶.若n a o =)(,则n Z G Z a n n ==⇒≅)(.反之,设n G =,若n a o ≠)(,则 ①∞=)(a o ,则∞==⇒≅Z G Z a )(矛盾;②n k a o ≠=)(,则n k Z G Z a k k ≠==⇒≅)(也矛盾. 循环群的结构定理说明了什么?【凡是无限循环群都彼此同构;有限循环群中,同阶则同构、不同阶则不同构.】例2:n 次单位根群{}1|=∈=n n x C x U 与n Z 同构.证法1 利用结构定理. )1,,1,0(2sin 2cos 12-=+==⇔=n k n k i n k ex x i n k k n πππ )()(222i n n k i n i n k e U e e πππ=⇒=是循环群,且生成元i n e π2的阶为n ,所以n i n n Z e U ≅=)(2π.证法2 直接建立同构映射. 令][:2k e i n k →πϕ,可证ϕ是同构映射.2.意义:从同构观点看,循环群只有两类――整数加群与模n 剩余类加群.【解决了循环群的数量问题】最后,讨论循环群的构造问题.这个问题从结构定理的证明过程就可得到.三、循环群的构造[构造定理] 设循环群)(a G =,则有{}Z k a a G a o k ∈==⇒∞=|)()(;{}1,,2,1,0|)()(-===⇒=n k a a G n a o k .证明 由结构定理的证明过程即得.另证:直接证明两个集合互相包含.【由运算封闭性,右集⊆左集;反之,m a x a G x =⇒=∈∀)(.若)()(Z k a a o k ∈⇒∞=彼此互异, 此时∈=m a x 右集1;若n a o =)(,设)0(n r r kn m <≤+=,则∈==r r kn m a a a a 右集2】至此,循环群所要研究的三大问题:存在问题/数量问题/构造问题圆满得到解决.好比线性方程组解的讨论包括判定、数量、结构三大问题.当然,还可进一步把循环群和其他概念相结合,研究新的性质.比如在今后学习中可以得到:循环群是交换群;循环群的子群还是循环群;循环群的同态像还是循环群等等.四、课后思考题n or a o ∞=)(时,循环群)(a G =的生成元有哪几个?在结构定理证明中a 的阶用途是什么?◎3S 是不是循环群?◎),(+Q 不是循环群.【设)(a Q =,则210)12()(220=⇒=-⇒∈=⇒∈⇒∈≠n a n Z n na a Q a Q a a 】 ◎循环群是交换群(习题);但交换群未必是循环群.比如:{}1|=∈=n n x C x A 是循环群, ∞==1n n AU 是交换群但不是循环群. ◎循环群是少数研究清楚的群.此外,有限单群也是.【单群】没有非平凡不变子群的群.有限单群的完全分类,即找出有限单群所有的同构类,经全世界上百名的数学家约40年的共同努力,终于在1981年得到解决,这是数学史上的又一个非凡成就.有限单群分类的整个论证用了5000页以上的篇幅,散布在超过300篇文章之中,引用了很多新的群论概念和证明了大量的定理.《简爱》是一本具有多年历史的文学着作。
循环群的结构定理

循环群的结构定理
循环群的结构定理(也被称为拉格朗日定理)是群论中的一个重要结果,它描述了循环群的结构。
结构定理的陈述如下:对于任意一个有限循环群G,它的阶(元素个数)为n,则对于G的任意子群H,H的阶必定能够整除n。
换句话说,G的任意子群的阶都是n的因子。
这个定理的证明可以通过对循环群及其生成元进行推理来完成。
循环群由一个生成元生成,而生成元的阶等于整个群的阶。
对于一个子群H,可以找到一个满足生成元的幂次方等于H中的元素的最小正整数m,那么H的阶就是m的因子。
这个定理在群论中具有广泛的应用,可以用来研究循环群的子群结构、判断一个群是否循环群等。
同时,它也为我们提供了一种将问题转化为循环群的方法,在研究循环群时可以简化问题的复杂度。
需要注意的是,循环群的结构定理只适用于有限循环群,不适用于无限循环群。
对于无限循环群,其子群结构可能更加复杂。
第三章_循环群_群的结构

电子科技大学 计算机科学与工程学院
UESTC Press
循环群与其子群
证明1) 设H是循环群(g)的一个子群. 假设H={e},H自然是循环群.假设H{e},则有i0使giH, 又因为gi=(gi)1H,所以可以假定i0,说明有正指数存 在.(存在性) 设s是H中的最小正指数,即s是使gsH的最小正整数,我们 现在证明H = (gs).对于任意gmH,有 m = qs+t,0ts, 由于gqs= (gs)qH(子群H的封闭性,q个gs连乘也属于H), 所以 gt = gm(gqs)1H, (gqs存在逆元,且由于封闭性,gm,(gqs)1乘积属于H.) 由于s是使gsH的最小正整数,因此得 t = 0,gm=(gs)q. H的任意元素都是gs的幂,则H = (gs).
UESTC Press
如何构造循环群的子群?
G是n阶循环群,g是G的生成元,d|n, 如何构 造d阶循环群? 设n=d d’,群(gd’)的阶为d? (gd’)的阶为d
!
第三章 循环群、群的结构
电子科技大学 计算机科学与工程学院
UESTC Press
循环群与其子群
例3 8阶循环群G的真子群. 8的所有正因子为1,2,4,8相应的子群分别 为 {e}, {e,g4}, {e,g2,g4,g6}, G 其中{e}和G是群G的平凡子群
2)设l = n/(k,n) 由1)有(ak)l = akl = e.i 则nki,
(k , n) (k,n) n k 因为 ( (k,n) , (k,n) ) 1
n i 所以 n ( k , n) 故 ( k , n)
.由于(k,n)k,则 n (k
第三章 循环群、群的结构
近世代数课件循环群

§4 循环群
我们来阐明 H ar .事实上,一方面, 显然, ar H .另一方面,由于 G a 且 H G ,对于任意的 hH ,可设 h an ,其 中 nZ .我们取整数 q 和 s ,使得
n qr s , 0 s r . 若 s 0 ,则
§4 循环群
as anqr an (ar )q h(ar )q H , 这与 r 为 N 中的最小数矛盾.因此 s 0 ,从而,
((s, n), (t, n)) ( t , n) ((s, t), n) (s, n) (s, t)
((s, t), n)
§4 循环群
(s, n) ( t , n) (s, t)
( st , n) ([s, t] n) . (s, t)
§4 循环群
k Z ,使得 r k[s, t].所以 b ar a[s, t] . (2)假设| a | n . 由于 b H ,因此| b | | | as | ;由于 b K ,
因此| b | | | at | .也就是说, n|n,n|n,
(r, n) (s, n) (r, n) (t, n)
h an aqr (ar )q ar . 由 此 可 见 H ar . 所 以 H ar . 这 就 是 说, H 是循环群.□
§4 循环群
命 题 4.2 设 G a 是 一 个 有 限 循 环 群,| a | n , r 是任意一个整数.那么
| ar | n , (r, n)
令 s | ar | .根据命题 3.12, s | n .另一方 (r, n)
§4 循环群
面,由于 (ar )s e 且| a | n ,根据命题 3.12,
n | (rs) ,从而, n | (rs) .由于 ( n , r) 1,
循环群的性质研究

淮北师范大学2012届学士学位论文循环群的性质研究学院、专业数学科学学院数学与应用数学研究方向高等代数学生姓名潘帅学号***********指导教师姓名张波指导教师职称讲师2012年4月3日循环群的性质研究潘帅(淮北师范大学数学科学学院,淮北,235000)摘要设G是一个群,a G,如果群G中的每一个元素都能写成元素a的乘方的形式,则称G是一个循环群,循环群是近世代数中的一个重要内容,也是一类基本研究明白的群,本文主要讨论了循环群的相关性质及其应用。
文中首先介绍了群的相关基础知识,由此引出循环群的定义和它的相关性质,讨论了循环群及其元素,子群间的关系,然后利用循环群的基础理论讨论了循环群的同态、同构,并给出了循环群的自同构群是交换群的结论。
关键词:循环群,子群,同构,自同构群Study on the Properties of Cyclic GroupsPan Shuai(School of Mathematical science, Huaibei Normal University, Huaibei, 235000 )AbstractLet G be a group, a G∈. If every element can be written the form n a where ∈, then the group is a cyclic group. Cyclic groups is an important content in the n Z+algebra, also a kind of group was nearly researched understand, this subject mainly discussed the cyclic group related properties and application.The basic knowledge of relevant firstly be introduced in this subject, then drawn out the definitions of circulation and some related properties, discussed the cyclic group and its elements, even the relations between the subgroup, and used the circulation of the foundation of the theory to discuss the circulation about the homomorphism and isomorphism, lastly made us know the conclusions what automorphism group of circulation group is an exchange of group.Keywords:cyclic group, subgroup, isomorphism, automorphism group目录一、引言 (1)二、群的定义 (1)三、循环群的若干问题 (7)1、定义与性质 (7)2、循环群的性质 (8)3、循环群的判定 (9)四、循环群的同态,同构 (11)五、结论 (14)参考文献 (14)致谢 (15)一、引言当代科学技术发展的一大特点是,在几乎所有的领域,数学与计算机技术被广泛的应用。
多重循环群的一个有限定理

到 I X~ Hx I I H < a , 得 I N I I i G: i= G: 。可 G: = G: n 躅广0 i ≤ Ⅱ i : i H i = Ⅱ i : < a I Hx x I H I 。, 即 G N是 有 限群 . /
(i i )若 F t / rt i F aG是 有 限群 , G本 身 也 是 G 则 个 有 限群 .
性定理 , 只需证 明 H的每个有 限商 群是 幂零 群 即
可 , 设 H/ 是 个 有 限 群 , 引 理 知 存 在 N≤ N, 假 N 据 使 Nca 且 H/ hrH N是 有 限 群 , H 又 AG, NAG. 故
1 = I
cv的 有 名 定 理 知 G/ 是 个 剩 余 有 限 群 , 对 有 e N 故 限 群 H/ 的 每 个 非 平 凡 元 素 h 存 在 KhNAG N N, / / Nl使 h 芒 KhN,I / K / < a 记 K = , N / N: h N G 。,
K I、 , ≠ 则 nh £
()F tG F aG) i / rt i i / rt =F t F aG; ( G
可 . 取 f u ( ,( r iA ( =G, 存 在 任 EA tG) fKe ) fG) a 故
自然 的 同 构 G f Ke i G Ke i G/ 表 明 f /( r ) a / r a N,
( r i∈ { e lKe 2 … , e tf 导 出集 Ke ) K ra , ra, K ra} 诱 a 合 { e l K ra ,… , ra} 的 一 个 置 换 , K ra , e 2 Ke t上 从
而 必 有 f K) (n Ke i = n K r i ( =f r ) a e =K 即 K a 是 的一 个 特 征 子 群 , 理 为 真 . 引 证明 为 证 H 是 个 幂 零 群 , Hi c 据 r h的 幂 零 s
(完整版)循环群讲义

§7循环群本节将讨论一类结构简单又富有代表性的特殊群――循环群.(它是一类基本而又重要的群,数学的一些分支(数论、有限域论等)和它有密切的联系.)通过对循环群的学习,可初步了解抽象代数研究问题的基本方法和格式以及论文的写作方法.本节主要内容是循环群的三大问题:存在问题/数量问题/构造问题.先看一个简单的例子:{},10,10,10,1,10,10,10,32123---=G 对数的乘法作成群.特点是每个元都是固定元10的方幂.一、循环群的概念1.定义 G 称为循环群⇔群G 的每个元都是G 中某个固定元...a 的方幂⎩⎨⎧倍数--针对加法乘方--针对乘法. 记为)(a G =,a 称为G 的生成元. 即 G a G ⇔=)(是群,且⎩⎨⎧==∈∃∈∀)()(.,,加法乘法ka x a x st Z k G x k .(注意:k 与x 有关!) 【一般情况下,如果没有特别声明运算是乘法或是加法,就默认是乘法形式.】2.注意:(一般情况下)生成元不唯一.a 是生成元1-⇔a 是生成元.【理由:k k a a --=)(1】3.范例【解决了循环群的存在问题.同时,将得到结论:循环群在同构意义下只有这两种!】 ①整数加群),(+Z ,)1()1(-==Z .【1±是∞阶.00)1(=⇒=±n n 】问题:还有其他生成元?(无)【设1),(1)(1)(±=⇒∈==∈⇒=k Z k n nk k k Z 】*实际上可进一步证明:)()(a G a o =⇒∞=只有两个生成元1,-a a .【课外思考题】 【设)(b G =,则有111,,)(-=⇒=⇒=⇒==∈∞=or s st a a b a a b Zt s a o st t s 】 ②模n 剩余类加群),(+n Z ,])1([=n Z .问题:还有其他生成元?(有)【])1([])1([-=-=n Z n 】*实际上可进一步证明:)()(a G n a o =⇒=的生成元为ra 当且仅当1),(=n r .【习题】 【若1),(=n r ,则)()()()()()(1r u r v u r v n u r vn ur a a a e a a a aa vn ur =⇒====⇒=++. 反之,r a 是生成元,1),(1|)()()()(1=⇒-⇒=⇒=⇒===-n r rk n e a a a a a G n a o rk k r r .】◎设p 为素数,则p 阶循环群)(a G =有1-p 个生成元:12,,,-p a a a .◎设p 为素数,则模p 剩余类加群p Z 的所有非零元都是生成元.二、循环群的种类1.结构定理 设循环群)(a G =同构于⎩⎨⎧=+∞=+n a o if Z a o if Z n)(),,()(),,(. 证明 注意体会生成元a 的阶在证明过程中的用处! (1)设∞=)(a o 【作用:0=⇔=k e a k 】此时,令k a Z G k →→,:ϕ,可证ϕ是同构映射.(证略)【ϕ是映射:若h k a a =,则h k h k e a a o h k =⇒=-⇒=∞=-0)(,说明对应元唯一. 易证ϕ是满射/单射.再证ϕ的同态性: )()()()()()(,,y x a a h k a xy a y a x G y x h k h k h k ϕϕϕϕϕϕϕ+=+=+==⇒==⇒∈∀+.】(2)设n a o =)(【作用:k n e a k |⇔=】此时,令][,:k a Z G k n →→ϕϕ是映射:若h k a a =,则][][|)(h k h k n e a na o h k =⇒-⇒==-,说明对应元唯一. ϕ是单射:若][][h k =,则e e a a mn h k h k n m n a o m n h k ===⇒=-⇒-=-)()(|.ϕ是满射:][)(.,,][k a st G a Z k k k n =∈∃∈∀ϕ再证ϕ的同态性: )()()()(][][)()(,,y x a a h k a xy a y a x G y x h k h k h k ϕϕϕϕϕϕϕ+=+=+==⇒==⇒∈∀+.例1:循环群)(a G =的阶为⇔n 生成元a 的阶为n .【常用结论】证法 同构必同阶.若n a o =)(,则n Z G Z a n n ==⇒≅)(.反之,设n G =,若n a o ≠)(,则 ①∞=)(a o ,则∞==⇒≅Z G Z a )(矛盾;②n k a o ≠=)(,则n k Z G Z a k k ≠==⇒≅)(也矛盾. 循环群的结构定理说明了什么?【凡是无限循环群都彼此同构;有限循环群中,同阶则同构、不同阶则不同构.】例2:n 次单位根群{}1|=∈=n n x C x U 与n Z 同构. 证法1 利用结构定理. )1,,1,0(2sin 2cos 12-=+==⇔=n k n k i n k ex x i n k k n πππ )()(222i n n k i n i n k e U e e πππ=⇒=是循环群,且生成元i n e π2的阶为n ,所以n i n n Z e U ≅=)(2π.证法2 直接建立同构映射. 令][:2k e i n k →πϕ,可证ϕ是同构映射.2.意义:从同构观点看,循环群只有两类――整数加群与模n 剩余类加群.【解决了循环群的数量问题】最后,讨论循环群的构造问题.这个问题从结构定理的证明过程就可得到.三、循环群的构造[构造定理] 设循环群)(a G =,则有{}Z k a a G a o k ∈==⇒∞=|)()(;{}1,,2,1,0|)()(-===⇒=n k a a G n a o k .证明 由结构定理的证明过程即得.另证:直接证明两个集合互相包含.【由运算封闭性,右集⊆左集;反之,m a x a G x =⇒=∈∀)(.若)()(Z k a a o k ∈⇒∞=彼此互异, 此时∈=m a x 右集1;若n a o =)(,设)0(n r r kn m <≤+=,则∈==r r kn m a a a a 右集2】至此,循环群所要研究的三大问题:存在问题/数量问题/构造问题圆满得到解决.好比线性方程组解的讨论包括判定、数量、结构三大问题.当然,还可进一步把循环群和其他概念相结合,研究新的性质.比如在今后学习中可以得到:循环群是交换群;循环群的子群还是循环群;循环群的同态像还是循环群等等.四、课后思考题n or a o ∞=)(时,循环群)(a G =的生成元有哪几个?在结构定理证明中a 的阶用途是什么?◎3S 是不是循环群?◎),(+Q 不是循环群.【设)(a Q =,则210)12()(220=⇒=-⇒∈=⇒∈⇒∈≠n a n Z n na a Q a Q a a 】 ◎循环群是交换群(习题);但交换群未必是循环群.比如:{}1|=∈=n n x C x A 是循环群, ∞==1n n AU 是交换群但不是循环群.◎循环群是少数研究清楚的群.此外,有限单群也是.【单群】没有非平凡不变子群的群.有限单群的完全分类,即找出有限单群所有的同构类,经全世界上百名的数学家约40年的共同努力,终于在1981年得到解决,这是数学史上的又一个非凡成就.有限单群分类的整个论证用了5000页以上的篇幅,散布在超过300篇文章之中,引用了很多新的群论概念和证明了大量的定理.。
循环群子群讲解学习

0<r<n. 如果r≠0,那么e=a m=ang+r=angar=(an)gar=(e)gar=ar矛盾
(∵r<n); r=0m=ngn|m.
性质3 设aG且|a|=n,那么n|m a m=e. 证明 “”正是性质2.
性质10 设群G中元素a的阶是m,b的阶是n,则当ab=ba且 (m,n)=1时,|ab|=m。
证明 首先,由于|a|=m,|b|=n,ab=ba,则 (ab)mn=(am)n(bn)m=e;
其次,若有正整数s使得(ab)s=e,则 (ab) sm=(am)sbsm=bsm=e,
但|b|=n,则n|sm. 又因为(m,n)=1,所以n|s. 同理可得m|s,再根据(m,n)=1,故mn|s,从而|ab|=mn. 说明 值得注意的是:当元素a与b不满足定理中的假设条件 时,其乘积的阶会出现各种各样的情况,将无法根据a,b的阶 来作出判断。
定理2 证设明是由(1生)当成时元| a生| 成 ,的作循1环: G群。Z如,1果(ai,) 那i .么由.上如述果的,对 那么。
证明应关(1系)易当知时,,1 作是双.由射上. 述而 的对应关系易知,是双射.而
(2)当时,作1 ( ,a ,i a 由j ) 上 述1 ( a 对i j 应) 关i 系j 也易1 ( a 知i ) ,是2 双( a j 射). 而且
例5 设G={0, 1, 2}是由x3=1的三个复根组成的集合,而
G中的代数运算“○”是通常的乘法,那么< G , ○ >必为一 个乘法群。习惯上记为G3,叫做3次单位根群。这里
01,11 23,21 23.
群的融合自由积的πn-Frattini子群和πc-Frattini子群

关键词:7 r n F r a t t i n i 子群; 7 r c F r a t t i n i 子群;群的融合 自由积.
M R( 2 0 0 0 ) 主题分类:2 0 D2 5 ; 2 0 E 2 8 中图分类号:0 1 5 2 文献标识码: A
文章编号:1 0 0 3 — 3 9 9 8 ( 2 0 1 3 ) 0 1 — 1 2 3 — 0 4
元.
群 G的  ̄ n F r a t t i n i 子 群等 于其 丌 n一 非生成元 组成 的集合 定义 2 . 3 [ ] 设 G 是 群,令 = { Kc h a r GI K ≠ G, I G: Kl 是 一个 7 r 一数 ,如果 Kc h a r L c h a r G, 那么 K =L或 L=G} . 当 ≠0时,定义 7 r c F r a t ( G) =N K ∈ ; 当 = 时, 定义 7  ̄ c F r a t ( G) =G. 7 r c F r a t ( G) 称为 G 的  ̄ c F r a t t i n i 子 群. 定义 2 . 4 【 ] 设 G 是 群 ,对 任 意 的 X ∈ G, 如 果对 G 的 任意 满足 下述 性质 的子 集 :
1 2 4
数
学 物
理 学
报 பைடு நூலகம்
、 厂 0 1 . 3 3 A
定义 2 . 1 【 ] 设 G是群 , 令 Ⅳ丌= { Ⅳ Gl Ⅳ ≠G,l G: NI 是 一个 7 r 一 数, 如果 Ⅳ司 q G, 那
么 N = L或 L=G) . 当
≠0 , 定义 7  ̄ n F r a t ( G) =A N∈ J 7 v ; 当
l G: s A u ( G ) l 是一个 7 r 一 数且 G=( , s ) A u 【 , 总有 G=s A “ ( , 那么我们就称 X为 G的
第三章_循环群_群的结构

电子科技大学 计算机科学与工程学院
元素的阶及其性质
定理1 一个群G的任意元素a都能生成一个循环群,它是G的 子群.如果a是无限阶元素,则a生成无限循环群;如果a 是n阶元素,则a生成n阶循环群. 证明 设a的幂集合为S. 1)a是无限阶元素情形. 对于任意ai,ajS (i,j = 0,1,2,…),有 ai(aj)1 = aijS, 由定理2 (page 22),S是G的子群. 2)a是n阶元素情形. 对于任意ai,ajS (i,j = 0,1,2,…),有 aiaj = ai+jS, 由定理3 (page 显然无限循环群的元素都是无限阶元素. 23) ,S是G的子群. 有限循环群生成元的阶就是群的阶. 显然S是a生成的循环群.定理证毕.
这m个剩余类称为模m剩余类.记为Zm
第三章 循环群、群的结构
电子科技大学 计算机科学与工程学院
剩余类群
设 i 和 j 是两个模m的剩余类,定义剩余类的加法 如下:
i j i j(mod m)
24 6
如Z8的两个剩余类 2 和 4
第三章 循环群、群的结构
电子科技大学 计算机科学与工程学院
第三章 循环群、群的结构
电子科技大学 计算机科学与工程学院
循环群与其子群
证明2)当(g)是无限循环群时,如果n m,则gn gm,于是gms (m=0,1,2,…)两两不同,H是 无限循环群. 证明3)假设(g)是n阶循环群,设s是H中的最小正指 数,即s是使gsH的最小正整数。由于n = qs+t, 0ts,则e = gn = gqs+t, 于是 gt = (gqs)1H, s的最小性使得t = 0,所以 n = qs, H可表示为H = {e,gs,…,g(q1)s }. 当s = n时H = {e}.
群论

2.基本概念和知识点:内幂零群及有关性质。
3.问题与应用:了解内幂零群的结构。
第五节 群的初等结果
1. 主要内容:有限 群的Frattini子群、生成元、自同构群及某些特殊子群的性质、具有循环极大子群的有限 群的结构。
2.基本概念和知识点:有限 群的Frattini子群的性质、具有循环极大子群的有限 群的结构。
3.问题与应用:了解 群在 群上的作用的基本理论。
第四节关于 幂零性的Frobenius定理
1. 主要内容:介绍 幂零性的Frobenius定理。
2.基本概念和知识点:规范子群、焦点子群、 幂零群,Frobenius定理。
3.问题与应用:了解 幂零性的Frobenius定理的内容。
第五节Frobenius-群
适用对象:理科数学类一年级研究生
考核方式:考查<写一篇字数字不少于3000的课程论文、读书报告或文献综述等>。
先修课程:抽象代数学
二、课程简介
群论研究名为群的代数结构。群在抽象代数中具有基本的重要地位:许多代数结构,包括环、域和模等可以看作是在群的基础上添加新的运算和公理而形成的。群的概念在数学的许多分支都有出现,而且群论的研究方法也对抽象代数的其它分支有重要影响。群论的重要性还体现在物理学和化学的研究中,因为许多不同的物理结构,如晶体结构和氢原子结构可以用群论方法来进行建模。于是群论和相关的群表示论在物理学和化学中有大量的应用。
第二节 群在交换 群上的作用
1. 主要内容: 群在交换 群上的作用的基本理论。
2. 基本概念和知识点:Schur引理、Maschke定理的推广形式。
3.问题与应用:了解 群在交换 群上的作用的基本理论。
第三节 群在 群上的作用
抽象代数基础第一章 1.3子群 1.4循环群教案
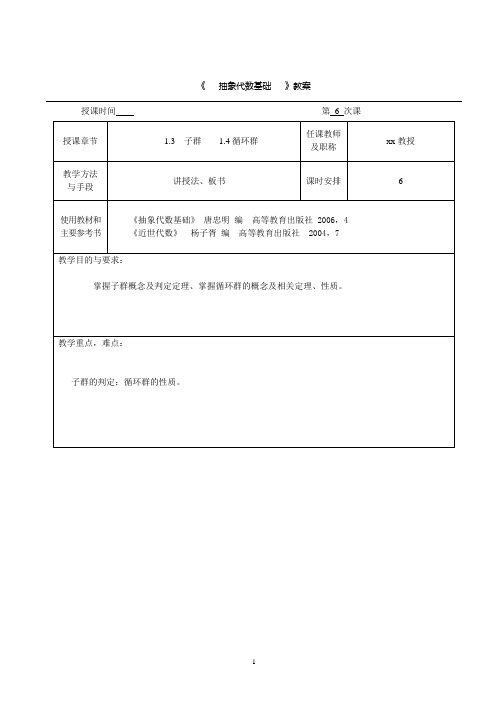
子群的判定;循环群的性质。
教学内容:
1.3子群
1、定义1 设G是一个群,H是G的一个非空子集,如果H关于G上的代数运算也构成一个群,则称H是G的子群。
显然,{e}和G是子群,称为G的平凡子群,G的不同于自身的子群称为真子群。
2、命题1 设H是群G的子群,则
1)H的单位元就是G的单位元;
2)对任意的a属于H,a在H中的逆元就是a在G中的逆元。
3、定理1 设G是一个群,H是G的一个非空子集,则H是G的子群的充分必要条件是
1)对任意的a,b属于H,都有ab属于H
2)对任意的a属于H,都有
证明:一方面,假设H是G的子群,则G上的代数运算 “. ”也是H上的代数运算,于是1)成立,从而又有 。
另一方面,G上的代数运算“. ”也是H上的代数运算,而“. ”在G上适合结合律,从而在H上也适合结合律。任取a属于G,由2)知 ,于是由1)得 ,故H中有单位元e,又由2)得 且在H中有 ,因而,H中每个元素在H中都有逆元,所以H关于G上的代数运算“. ”也构成一个群,从而H是G得一个子群。
4、命题2 设G是一个群, 是G的一族子群,则 也是G的子群。
课本P16 2群与商群
实施情况及教学效果分析
学院审核意见
学院负责人签字
年月日
5、命题3 设G是一个群,S是G的一个子集,令 是G的包含S的所有子群,则 是G的包含S的最小子群。
6、定义2 1)设G是一个群,S是G的一个子集,G的包含S的最小子群称为是G的由S生成的子群,记为<S>.
2) 设H是群G的一个子群,如果存在子集 使得 ,则称H由集合S生成,也称S是由H的一个生成元素,如果存在有限多个元素生成H,则称H是有限生成的。
群的融合自由积的两种广义Frattini子群

G =S . 即得 ∈pnF a( ' rtG).由 的任 意 性 , 结论 成立 . 接 下来 , 们将 从 p Fa ii 我 rtn 子群 是群 G的 t
= ≠ 1 如果对所有的 ≠卢, . 都有 ‰ =1, 么称 G为 子群 簇 { 的 自由积 .如 那 G}
关 定 理 ;又从 P/ Fa ii 群 是 群 的所 有 指 rtn 子 I ; t
数 为任 意素 数方 幂 P 的极 大 正 规 子群 的交 这 一
定 义 出发 , 另 一 角 度 给 出 了该 定 理 的 另 一 证 从
[ 稿 日期 ] 0 1一O 收 21 6—2 0
F a( ) = G. S Fa( )称 为 G的 pcFa ii rt G pc rt G S rtn t
果假 设所 有 的交 都 是一个 子 群 日 , 即对 任意
的 O ≠卢 O 卢 ∈F) 假设 G / (L , 都 n =H , 么 那
类似 的结 果 ,从 而推 广 了 A ai zr n和郭钦 等 人 的结 果. a
[ 键词 ] rtn 子 群 ;SFaii 群 ; 关 pnFati i pc rt 子 tn pn一非 生成 元 ;S pc一非 生成元 ; 的融合 自由积 群
[ 图分类 号 ] 12 [ 献标 志码 ] [ 章编 号 ] 6 3—8 1 (0 2 O — 0 8—0 中 05 文 A 文 17 022 1)1 02 3 17 9 2年 T n ¨ 得 到 了关 于群 的带 循 环 融合 ag
F a( rtG), 只需 要 证 明 是 G的 n一非生 成元 .
设 S是 G 的任 意 满 足 下 述 性 质 的子 集: 。是 l S l 任 意素 数 方 幂 P 且 G = < 5 。.由 G: , > 于 < 是 Ⅳ 的特 征 子群 , G, < G.因 > Ⅳ 故 >
循环群的子群的生成元

循环群的子群的生成元循环群的子群的生成元,这个名字一听就让人感觉有点儿复杂是不是?别担心,我来给你讲讲,保证你一听就明白!想象一下,群就像一个俱乐部,里面的每个成员都能和别人合作,进行一些操作。
比如加法、乘法之类的。
循环群呢,就是一个特别“团结”的俱乐部,大家的行为特别简单,都是围绕一个最重要的“领袖”成员进行的。
这个“领袖”成员就叫做生成元。
好啦,不要害怕这些专业词汇,听我慢慢解释。
你知道小时候咱们玩过那种“圈圈舞”吗?大家围着一个点转,转着转着,最后大家都跟着一个人走,不管走多远,最后都能回到起点。
这个点就相当于我们讲的“生成元”,就是唯一一个能通过重复自己,带领大家走一圈一圈的成员。
记住哦,它能决定整个群体是怎么“运转”的。
比如在加法群里,生成元就是0,大家一开始站在0的地方,然后通过加法不断走,最终每个人的步伐和位置都可以通过“0”来“生成”。
听起来是不是有点儿像魔法?那循环群的“子群”又是啥意思呢?简单来说,子群就像是循环群里的一小部分,它也遵循同样的规律,只不过它的“圈”可能比大圈小点。
这些小圈,虽然只是循环群的一部分,但每个小圈里的成员也是按照生成元的规则来运转的。
就像是一个大团体里的小分队一样,可能每个小队只有几个成员,但它们依然是在那个大团体的“大家长”——生成元的带领下活动。
你想象一下,就像一个公司里面有好多部门,每个部门都有自己的团队负责人,但大家最终还是得听总经理的。
说到这里,你是不是觉得越来越清楚了?现在我们来讲讲如何找到一个子群的生成元。
其实就像找一个线索。
假设你已经有了一个循环群,比如说一个很普通的数字群体,你可以通过对某个生成元进行反复操作,来找到所有的成员。
比如你有一个生成元g,假设你想找出一个子群,你就需要找出所有能由g反复作用得到的元素。
举个例子,假如你有个数字集合1, 2, 3, 4,生成元是1,那你不断加1得到的结果就是1, 2, 3, 4……这样一来,你就得到了一个可以构成子群的小圈。
循环群的子代数系统

循环群的子代数系统
循环群的子代数系统是一个重要的概念,它涉及到群论和代数学中的一些基本概念。
首先,循环群是一种特殊的群,其中存在一个元素a,使得群中的每一个元素都可以表示为a的幂。
也就是说,群G是循环的,如果存在一个元素a属于G,使得G={a^n|n∈Z}。
子代数系统则是指一个代数结构中的子集,该子集在所考虑的代数运算下封闭。
对于群来说,子代数系统可以看作是群的一个子集,该子集在群的乘法运算下封闭。
在循环群中,一个重要的子代数系统是循环子群。
循环子群是指由循环群的某一个元素生成的子群。
具体来说,如果a是循环群G的一个元素,那么由a生成的子群就是G的一个循环子群。
此外,循环群的另一个重要的子代数系统是正规子群。
正规子群是指一个群G的子群H,满足对于任意的$g \in G$,都有$g H = H g$。
在循环群中,如果一个子群是循环子群,那么它一定是正规子群。
总的来说,循环群的子代数系统涉及到一些重要的代数概念和结构,如循环子群和正规子群等。
这些概念和结构在群论和代数学中有广泛的应用。
群G的Л'—FITTING子群的性质

Jun l e n lJTa h r o ra 0 eces’C l g I ol e e
V 12 , o. o .6 N 4
D c.0 0 e 1
群 G的 - 砌 _
N G子群的性质
于荣格 , 江瑞侠 , 宇 高俊 ( 沧州师范学 院 数学 系 , 河北 沧州 01 1 6 0) 0
( ) G。
零的充要条件是 N ( ) J / G为 r 一幂零 。J _ 1 证 明: 因为 ( ) J一幂零群 , Q1 G是 r 故 I ( ( ) G) =
( ) N  ̄ ( ) .—Hl子群 , G是 / nG 的 r a l l 由 ( )} G ca l
( A / a G 知 I O ( ) G @ ( )从而 H G, o ( ≠ G)G @ ( ) - aG A / aG , I / A 若 ⅡG)
G / ( )设 FG  ̄ ( ) / a G , 为 ( / . G .= )m C , ( / G =N O ( )因 NO() a a N O ( )O ( )hr/ a G A / a G , N O ( ) G 从 而 a aG / aG caN O ( )G O ( )故 a aG A ,
关 键词 : — tn 子 群 ; 一可分 群 ; 一 b J Ef g r i J l 』 } 儿子群 I 中图分 类号 :1 O5 2
定 义 1 群 G的 一幂零 正 规 子群 之 积 仍 是 G 的 J一幂 f 零 正 规子 群 , 因而 G有 最 大 的 J r 一幂零 正 规子 群 , 之 为 G的 称 J一3 ̄ 子群 , 为 F ) r }t t 记 G 。
G )= )J T
. ) ( )hr/ c △ 西( )因 此 西 ( ) ( / G caN 西( ) G/ c , c G
循环群的子群

循环群的子群李样明(广东教育学院数学系,广东广州510310) 摘要:从一道习题的常见的错误的解法入手,给出循环群的子群的部分性质,得到此习题的正确解答.对《近世代数》的教学具有一定的指导意义.关键词:循环群;子群;错误中图分类号:O152.1 文献标识码:A 文章编号:100728754(2001)022*******收稿日期:2000210209作者简介:李样明(1965-),男,江西东乡人,广东教育学院数学系副教授. 在吴品三编的高等学校试用教材《近世代数》中有下面这道习题[1]:设A =(a s ),B =(a t )是循环群G =(a )的两个子群,证明:A ∩B =(a d ),此处d 是s ,t 的最小公倍数.此题常见的证明如下:Πx ∈A ∩B ,ϖm ∈Z ,使x =a m .由于a m ∈A ]s |m ;a m ∈B ]t |m ,所以d |m ,这样x =a m =a dk ∈(a d ),即A ∩B Α(a d ).另一方面,显然,(a d )ΑA ,(a d )ΑB ,故(a d )ΑA ∩B ,从而证得A ∩B =(a d ).(见杨州师院数学系《近世代数》题解(1981),P43)大部分同学及少数青年教师这样做.但仔细分析,此证明是不严密的.一般地,由a m ∈A =(a s ),我们推不出s |m 1例如在G =(a ),|a |=3时,a ∈(a 2),因为G =(a 2),但281.实际上,本题的解答较复杂.为给出一个完整的严密的证明,我们须给出循环群的一些基本性质.引理1 (循环群的结构定理)设G =(a )为循环群,则1)若a 的周期无限,则G Z +(整数加群);2)若a 的周期为n ,则G Z n (整数模n 的剩余类加群).引理2 设G =(a )为无限循环群,则a l =a s Ζl =s.引理3 设G =(a )为n 阶循环群,则a l =a s Ζn |l -s.进一步,若0Φn 1,n 2<n ,a n 1=a n 2,则n 1=n 2.(以上性质可由循环群的定义直接得出,证明较初等,故略去)引理4 设a 的阶为n ,则a l 的阶为n (l ,n ),其中(n ,l )为n ,l 的最大公约数.进而(a l )=(a (l ,n )).证明:设a l 的阶为l 1,由于(a l )n (l ,n )=a ln (l ,n )=(a n )l (n ,l )=e ,故由引理2知l 1|n (l ,n ).另一方面(a l )l 1=a ll 1=e ,故n |ll 1,从而n (l ,n )|l 1,所以l 1=n (l ,n ).第21卷 第2期广东教育学院学报2001年5月Vol.21 No.2Journal of Guangdong Education Institute May 2001由于(a l)为n(l,n)阶循环群,而a(l,n)的阶为n(n,(l,n))=n(l,n),故(a(l,n))也为n(l,n)阶循环群.又存在k1,k2使(l,n)=k1l+k2n,故a(l,n)=a k1l+k2n=(a l)k1∈(a l),从而(a(l,n))Α(a l),这样必有(a(l,n))=(a l).引理5 [(s,n),(t,n)]=([s,t],n),s,t,n为整数.证:见[2],P18,练习81上习题的证明:显然(a d)Α(a s)∩(a t),故只须证明反包含成立.Πa m∈(a s)∩(a t),则由 a m∈(a s)知a m=(a s)i=a si;(1)由 a m∈(a t)知a m=(a t)j=a tj.(2)下分两种情形讨论10 若a为无限阶的,由(1),(2),应用引理2知m=si=tj从而s|m,t|m,故d=[s,t]|m,即m=dq,即a m=a dq=(a d)q∈(a d),从而(a s)∩(a t)Α(a d),等式成立.20 设a为有限阶的,为n.设s1=(s,n),n1=n/s1,t1=(t,n),n2=n/t1.应用引理4,即有 (a s)=(a s1)={e,a s1,a2s1,…,a(n1-1)s1};(3)(a t)=(a t1)={e,a t1,a2t1,…,a(n2-1)t1}(4)又记d1=(d,n),由引理5知d1=([s,t],n)=[(s,n),(t,n)]=[s1,t1],(5)且(a d)=(a d1).(6)设a l∈(a s)∩(a t)=(a s1)∩(a t1),不妨设0≤l<n,由(3),(4),a l∈(a s1),可设a l=a s1k1,0Φk1<n1,a l∈(a t1),可设a l=a t1k2,0Φk2<n2,即有 a l=a s1k1=a t1k2,且0Φl,s1k1,t1k2<n,由引理3知 l=s1k1=t1k2,故s1|l,t1|l,即[s1,t1]|l.由(5)知d1|l,故a l∈(a d1)=(a d)这样,(a s)∩(a t)Α(a d),从而等式成立,(证毕).参考文献:[1]吴品三.近世代数[M].北京:人民教育出版社,1979.75.[2]熊全淹.初等整数论[M].武汉:湖北教育出版社,1987.Subgroups of Cyclic G roupL I Yang2ming(Dept.of Math.,Guangdong Education Institute,Guangzhou,Guangdong,510310,P.R.China)Abstract:In this paper,we give some properties of subgroups of cyclic group for the purpose of discussing an exercise in Modern A lgebra which was offen solved wrongly.It has some meaning to the teaching of Modern A lgebra.K ey w ords:cyclic group;subgroup;error21广东教育学院学报 第21卷。
Fitting子群是Abel群的有限可解群

Fitting子群是Abel群的有限可解群
刘合国
【期刊名称】《湖北大学学报(自然科学版)》
【年(卷),期】1992(14)3
【摘要】本文证明了若有限的可解SD_2—群G的Fitting子群是Abel群,则
G^(3)
【总页数】1页(P241)
【作者】刘合国
【作者单位】无
【正文语种】中文
【中图分类】O152.2
【相关文献】
1.有限群的Fitting子群对群结构的影响 [J], 聂林
2.关于有限可解群的Fitting子群的阶 [J], 肖文俊
3.极大超可解子群与有限群的超可解性 [J], 钟祥贵;廖枢华;李明华;谭春归;陈小祥
4.Sylow p-子群的非平凡子群与有限群的p-超可解性 [J], 韦华全;李娜;周宇珍
5.换位子群是不可分Abel群的有限秩可除幂零群 [J], 刘合国; 张继平; 廖军因版权原因,仅展示原文概要,查看原文内容请购买。
【doc】循环群的子群交与子群并的构造

循环群的子群交与子群并的构造第2期长沙大学1997年6JOURNALOFCHANGSHAUNIVERSITYNo.2Jun.1997.=2循环群的子群交与子群并的构造刊,宗明F2√(泰安师范专科学校.泰安271000)李振国梅门昌(内蒙河套大学,临河015000)(泰安教育学院,泰安271ooo)摘要本文络出搞环群的子群克与子群并的构造.关键词.±壁塞j群_分类号0152.1循环群是构造最简单的群.本文研究循环群的子群交与子群并的构造.引理1循环群G=妇)的子群H是循环群.若H≠{},则H=《d),其中n是H中d的最小正指数幂.当G是无限群时.H也是无限群.当G是n阶群时,m/..H是q=阶群,且H是G中唯一的g阶子群.此时H={n.,,n,……n}证明见[i]P31定理5.证完.引理2无限循环群妇)的子群《)一()甘r=士j;n阶循环群(口)的子群(口)一(d), (口)一(口)甘(r,n)=(.n),其中(r,)是r与n的最大公园数.证明1)无限群妇)的子群()=(口')甘r士s,见[13P31定理6的前半段.2)n阶群(d)的元素口的阶为一户,(d)为阶群;d(r,ml的阶也为?(口")也是户阶群;由于(,,")Ir.所以E-(口.>.从而,易得(d>=(d).3)由2)即得(>=()甘(r.,)一(.n).证完.下面均假定循环群妇)的子群H≠{}.且H一(),口是H中口的最小正指数幂.引理3循环群《口)的子群()()甘lr.证明.()(口'>,d∈(),口一()=.当(d)是无限群时,r=;当《d)是"阶群时,由上面的约定,也有r=础}总之..Ir.记r=st.口一=(口)∈《d>,从而,《)(口').证完.定理1循环群(口>的子群交《口)n(d)一(aE),其中.]是r.的最小公倍数.收稿日期:1~'97—05--31总第32期孙宗明等:循环群的子群交与子群并的构造证明先证明(d[,_0)(》n(》.根据引理3,由rl[r,j]得《d>《d,》,由5l[,,s]得《d[,_0>(口》.从而<口》<口><》n》.再证明()n(dI》(d[,_)对任意XE(d>n(>,则X=a.,由d.∈(》得,a=(d),卅=,pI由d_∈<dJ》得a= (d),Ⅲ=田.从而rIm,定理3若循环群(d》的子群并'd>U(}是(d}的子群,则(r,s)=r或s,(d}>U(吐I》>一《d>,其中(r,5)是r,5的最大公园数.证明根据引理4,(4》(dJ》或(d》<dr).根据引理3,SIR或刚S.从而得证.证完.定理4循环群(d)的子群并《d1》U<口>U……U(d》是《4>的子群,则(,I,r2……,^)等于n,……,^之一,'4r1)U'口)U……U'n)='n''_._.').证明根括}f理4与定理3,对子群的个数用数学归纳法即得.证完参考文献1焦全淹.近世代数.上捧科学技术出版社,1978.2张禾璃.近世代数基础.高等教育出版挂,1978. THESTRUCTUREOFTHESUBGR0UPlNTERSECTIONAND SUBGROUPUNIONINCYCLICGROUP3u.Zongming,1.2Zhenguo,MeiMenchang AbstractThispapergivesthestructureofthesubgroupintersectionandsubgro upU nionincyclicgroup. KeywordssubgroupintersectionSUbgroupunioncyclicgroup。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
& F := Frat G, F d F/F CU]& Abel & 1
F/F = T /F ⊕ F1/F ,
! T/F F/F & & F1/F F/F &~] & } Abel &
( T G. v
! 6 G/T ,
F/T ∼= F1/F
G/T &~] & I& } Abel & $ l = |G : F | _G@ p l,
v /& G := G/T p(F/T ), F := F/T p(F/T ), F G, " F &h G/F &hVG
q Schur-Zassenhaus ,;
8 " x# M ≤ G, G = F · M F ∩ M = 1,
F ≤ Frat G,
2
SK 2 lZ'' Fitting '
301
#
i=1
K∩N =
∞
∩
HNi
∩N
=
∞
∩
(H
N
i
∩
N
)
i=1
i=1
=
∞
∩
(H
∩
N)
·
Ni
=
H
∩
N,
i=1
H% K
=
∞
∩
HNi
= H.
i=1
. N ~]&
!i
|N| & @6
N i = 1,
3 s ∞ ∩
HNi
=
H.
(
/N &
$ Hirsch @ h(N) & J c1 N CU]& &
& b i=1
N
&!} Abel & pT x1 Z ~] &!} Abel & c1 H 7($| C rZ 0
1 rZ = V /L / V N, w H IX V , " H = HV ≤ G. w H ∩ V = H ∩ F = L,
HQL-
& _L H;V
$ H = HV ( | L 0 H bX V/L, H
$ / &+x } U := NF (L),
U
x, Lx ≤ N x = N , |N : Lx| = |N : L| = m,
; (@ 8 ` C & s, Lxs = L, xs ∈ NF (L) = N, U/N 3 U/N C~] & q F
& d L I F , =v0M; w |F : L| < ∞, 0 " |F : L| = ∞.
Keywords Polycyclic group, Fitting subgroup, Rationally irreducible subgroup, Hirsch number 1991 MR Subject Classification 20F16 Chinese Library Classification O152
W/L ≤ Z 0 ` W/L C~; x H- &
x ($|
302
Ahh
41s
; a C := CH(W/L), W/L C~; x H/C- & 6 H ≤ G ≤ F ∩ H = L,
C & H ≤ CH (W/L) = C, H/C
Abel
Dirichlet R,;%#
h(H/C) ≤ dimQ[(W/L) ⊗Z Q] − 1.
;%#
∞
∩
(N/A)i
=
∞
∩
AN i/A = 1,
i=1
i=1
;∞ ∩
AN i
=
A.
i=1
" <LBb,)wj1#996-\02k-08, e_?, g>, 1997-05-04, 1997-11-11
300
Ahh
41s
a ( " / C p% K :=
∞
∩
HNi,
H ≤ K HN = KN.
i, HN i ∩ N = (H ∩ N ) · N i,
H & Hirsch @
h(H) = h(CW ) = h(C) + h(W ) − h(C ∩ W ) = h(C) + h(W ) − h(L) ≥ h(H) + 1,
; } L C Q W , C Q W
$ ; & H = CW ( | L 0 W/L R H/L &
b H/L
& m3 H
&
# h(H) &] d 0
Abstract In this paper, we have given some properties of Fitting subgroups of polycyclic groups, which are certain refinements of Mal´cev’s well-known theorems.
CiM /1 kY&& Fitting &&sC %yW J& t~;@ ~ &
Dirichlet R,; (d [6]).
?4 1 G U]&1 kY& "1 h(H) ^R
& {h(X) | X G
&}
&] -M,; 5
` h(H) > h(Fit G),
G & & H · Fit G & Hirsch @ h(H ·
& $ L = H ∩ F H, N = NF (L) = NG(L) ∩ F NG(L), p H IX L Q N, H H F ( |
N/L 0 N/L C~]4 &U] & b Z(N/L) C~]4 &U] Abel & P
! $ 9 a Z := Z(N/L). /+x (@ r, H | rZ 0 ; / ` & r, rZ ~]
'09:
1 Segal D. Polycyclic Groups. Cambridge: Cambridge Univ Press, 1983 2 Mal´cev A I. On certain classes of infinite soluble groups. AMS Translations, 1956, 2(2): 1–21 3 Rabinson D J S. A new treatment of soluble groups with finiteness conditions on their abelian subgroups.
h(H) ≤ h(Fit G).
0 &M;N
6 g p h(H) = h(Fit G)
|H · Fit G : Fit G| = n < ∞,
x# x Hn ≤ Fit G,
h(Hn) = h(H),
Hn ≤f Fit G.
% & S&iM/1 kY&&~]| r & x F(mc
@ /6%f=& " /3A*&xd $ 9 b&@a
$ 0-
u ≤ n, Fit G xy0n%X
& Hirsch @ h(Fit Mal´cev &E
G)
≤
1 2
(n2
+
n),
q,;
3
h(G)
≤
1 2
(n2
+
n)
−
1,
*2 5 1 G C1 kY& H G &
& " h(H) ≤ h(Fit G), h(H) = h(Fit G)
! !"l! Hn ≤f Fit G / (@ n
vZT /Frat G) = Fit G/Frat G, q Fit G/Frat G s, U]&
8 5 . Fit G/Frat G = Fit (G/Frat G) C~]& G/Frat G &I~ I Abel
&r ~]& 3 G/Frat G ~]& \ -M Frat G C~]4 &U] & a
S | [1] &? <P
9 H ≤f G
H
G & @~]& &
. G xj& G & Abel &&iG/ G r~t,d&{^ o LE uo%
$ # sX &o+E [2−4]. Mal´cev &~ ,; (d [1, 2]), T $! Fit G C1 k
Y&6 G r C1 kY& S T emp Fit G & `@ K I%iM2X
; V/L R H/L & b H/L
& ms ( H
& \ H & Hirsch @
h(H) = h(HV ) = h(H) + h(V ) − h(H ∩ V ) = h(H) + h(V ) − h(L) = h(H) + h(V /L) > h(H),
h(H) &] d 0 z3 H : 7&$| C rZ 0 m3 H
& Mal´cev M
*2 1 1 N 1 kY& G & I
& H G& &
