八年级数学2月奖学金测试题
【数学】初二年奖学金考试数学考卷

【数学】初二年奖学金考试数学考卷一、选择题(每题1分,共5分)1. 已知两个数相乘,其中一个数为5,另一个数为未知数x,那么x的值为:A. 5B. 1C. 2D. 10答案:A2. 一个三角形的两边之和等于第三边,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 任意三角形答案:D3. 已知一个等差数列的前两项分别为3和5,那么这个等差数列的公差是:A. 2B. 3C. 4D. 5答案:B4. 一个圆的直径为10cm,那么这个圆的周长是:A. 10π cmB. 20cmC. 20π cmD. 50cm答案:C5. 已知一个二次函数的图像是一个开口向上的抛物线,那么这个二次函数的系数a是:A. 负数B. 正数C. 0D. 无法确定答案:B二、判断题(每题1分,共5分)1. 一个数的平方根有两个值,一个是正数,另一个是负数。
()答案:×2. 一个三角形的内角和等于180度。
()答案:√3. 一个等差数列的前三项分别为2、4、6,那么这个等差数列的公差是2。
()答案:√4. 一个圆的直径是半径的两倍。
()答案:√5. 一个二次函数的图像是一个开口向下的抛物线,那么这个二次函数的系数a是负数。
()答案:√三、填空题(每题1分,共5分)1. 三角形内角和的公式是180°。
答案:180°2. 圆的周长公式是C = πd 或C = 2πr。
答案:C = πd 或C = 2πr3. 勾股定理表达式是 a^2 + b^2 = c^2。
答案:a^2 + b^2 = c^24. 函数 f(x) = ax^2 + bx + c 的顶点坐标是 (b/2a, c b^2/4a)。
答案:(b/2a, c b^2/4a)5. 直线 l 的方程是 y = mx + b。
答案:y = mx + b四、简答题(每题2分,共10分)1. 简述三角形的内角和公式。
答案:三角形内角和的公式是180°。
二中初二上册月考试卷数学

一、选择题(每题3分,共30分)1. 下列各数中,绝对值最小的是()A. -3B. 0C. 3D. -22. 下列运算中,正确的是()A. (a+b)^2 = a^2 + 2ab + b^2 + 2abB. (a-b)^2 = a^2 - 2ab + b^2C. (a+b)^2 = a^2 - 2ab + b^2D. (a-b)^2 = a^2 + 2ab - b^23. 下列函数中,是反比例函数的是()A. y = 2x + 1B. y = x^2C. y = 1/xD. y = 3x - 24. 下列图形中,是轴对称图形的是()A. 正方形B. 长方形C. 等腰三角形D. 等边三角形5. 下列各式中,错误的是()A. a^2 = a aB. (a+b)^2 = a^2 + 2ab + b^2C. (a-b)^2 = a^2 - 2ab + b^2D. (a+b)(a-b) = a^2 - b^26. 若 a > b,则下列不等式中,正确的是()A. a^2 > b^2B. a^2 < b^2C. a > b^2D. a^2 < b7. 下列各式中,是等式的是()A. 2x + 3 = 7B. 3x - 2 < 5C. 4x = 2D. 5x + 1 ≠ 38. 下列各数中,是质数的是()A. 1B. 2C. 3D. 49. 下列各数中,是偶数的是()A. 2B. 3C. 4D. 510. 下列各数中,是正数的是()A. 0B. 1C. -1D. -2二、填空题(每题3分,共30分)11. 计算:(-3) × 4 = _______,(-2) ÷ (-1) = _______,(-5) + 3 = _______。
12. 简化下列各式:A. (a+b)^2 = _______B. (a-b)^2 = _______C. (a+b)(a-b) = _______13. 若 x + 2 = 5,则 x = _______。
【数学】初二年奖学金考试数学考卷

专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个数是质数?()A. 21B. 39C. 41D. 672. 已知一个等差数列的首项为3,公差为2,则第五项为()A. 7B. 9C. 11D. 133. 下列哪个图形是平行四边形?()A. 矩形B. 梯形C. 正方形D. 三角形4. 下列哪个单位是面积单位?()A. 米B. 平方米C. 立方米D. 千克5. 已知a=3,b=4,则a²+b²的值为()A. 7B. 12C. 25D. 9二、判断题(每题1分,共5分)1. 1的倒数是1。
()2. 0是自然数。
()3. 两条平行线之间的距离处处相等。
()4. 等腰梯形的两个底角相等。
()5. 相似三角形的面积比等于边长比的平方。
()三、填空题(每题1分,共5分)1. 已知一个正方形的边长为a,则它的面积为______。
2. 2的平方根是______。
3. 已知一个等差数列的首项为5,公差为3,则第四项为______。
4. 下列数中,______是最小的合数。
5. 一条直线的斜率为2,它在y轴上的截距为3,则该直线的方程为______。
四、简答题(每题2分,共10分)1. 简述等差数列的定义及通项公式。
2. 请写出勾股定理的内容。
3. 什么是三角形的外心?4. 请举例说明两种不同的概率求解方法。
5. 简述平行线的性质。
五、应用题(每题2分,共10分)1. 小明家离学校3公里,他以每小时4公里的速度步行去学校,需要多长时间?2. 某商店举行打折活动,原价120元的商品打8折,现价是多少?3. 一个长方形的长是10厘米,宽是6厘米,求它的面积。
4. 某班有50名学生,其中男生占60%,女生有多少人?5. 一个数加上60后乘以2,再减去30,结果为150,求这个数。
六、分析题(每题5分,共10分)1. 已知一个等差数列的前三项分别为2,5,8,求该数列的通项公式,并求出第10项的值。
初二月考试卷数学及答案

一、选择题(每题5分,共30分)1. 下列各数中,不是有理数的是()A. 3B. -5C. √2D. 0答案:C2. 下列等式中,正确的是()A. a + b = b + aB. ab = baC. a^2 = b^2D. a^3 = b^3答案:B3. 若m和n是方程2x^2 - 5x + 3 = 0的两个根,则m + n的值是()A. 5B. 3C. 2D. 1答案:A4. 已知函数f(x) = x^2 - 4x + 4,那么f(x)的图像是()A. 开口向上,顶点在x轴上B. 开口向下,顶点在x轴上C. 开口向上,顶点在y轴上D. 开口向下,顶点在y轴上答案:A5. 在直角坐标系中,点A(2, 3)关于原点对称的点是()A. (-2, -3)B. (-2, 3)C. (2, -3)D. (2, 3)答案:A二、填空题(每题5分,共25分)6. 若a和b是方程x^2 - 5x + 6 = 0的两个根,则a^2 + b^2的值是______。
答案:257. 已知函数f(x) = 3x - 2,那么f(-1)的值是______。
答案:-58. 在等差数列{an}中,a1 = 3,公差d = 2,那么a5的值是______。
答案:119. 在等比数列{bn}中,b1 = 2,公比q = 3,那么b4的值是______。
答案:16210. 若函数y = kx + b(k ≠ 0)的图像经过点(1, 3),则k的值是______。
答案:2三、解答题(每题15分,共60分)11. (15分)解下列方程:(1)2x - 5 = 3x + 1(2)5(x - 2) = 3(2x + 1)答案:(1)x = -6(2)x = -112. (15分)已知函数f(x) = 2x^2 - 3x + 1,求:(1)函数的顶点坐标(2)函数的对称轴答案:(1)顶点坐标为(3/4, -1/8)(2)对称轴为x = 3/413. (15分)已知数列{an}的通项公式为an = 2n + 1,求:(1)数列的前5项(2)数列的求和公式答案:(1)a1 = 3, a2 = 5, a3 = 7, a4 = 9, a5 = 11(2)S_n = n^2 + n14. (15分)已知函数y = kx + b(k ≠ 0)的图像经过点A(1, 2)和点B(3, 4),求:(1)函数的解析式(2)函数图像与x轴的交点坐标答案:(1)k = 1/2,b = 3/2,函数解析式为y = 1/2x + 3/2(2)交点坐标为(3, 0)。
八年级数学(下)学期 第二次月考检测测试卷含解析
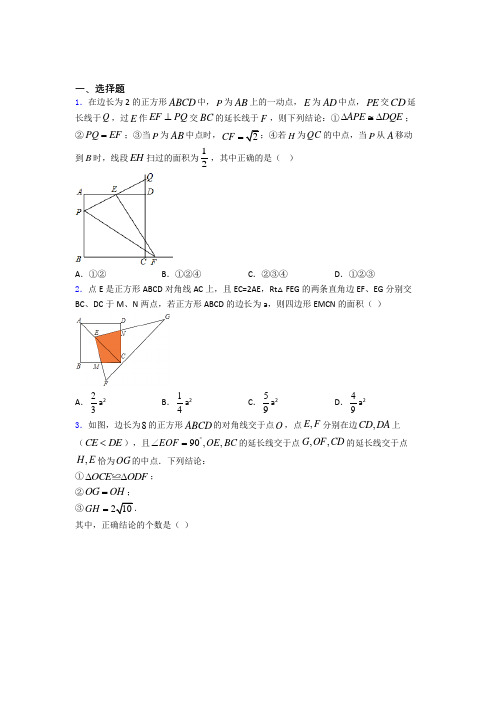
一、选择题1.在边长为2的正方形ABCD 中,P 为AB 上的一动点,E 为AD 中点,PE 交CD 延长线于Q ,过E 作EF PQ ⊥交BC 的延长线于F ,则下列结论:①APE DQE ∆≅∆;②PQ EF =;③当P 为AB 中点时,2CF =;④若H 为QC 的中点,当P 从A 移动到B 时,线段EH 扫过的面积为12,其中正确的是( )A .①②B .①②④C .②③④D .①②③2.点E 是正方形ABCD 对角线AC 上,且EC=2AE ,Rt △FEG 的两条直角边EF 、EG 分别交BC 、DC 于M 、N 两点,若正方形ABCD 的边长为a ,则四边形EMCN 的面积( )A .23a 2B .14a 2 C .59a 2 D .49a 2 3.如图,边长为8的正方形ABCD 的对角线交于点O ,点,E F 分别在边,CD DA 上 (CE DE <),且90,,EOF OE BC ︒∠=的延长线交于点 ,,G OF CD 的延长线交于点,H E 恰为OG 的中点.下列结论:①OCE ODF ∆∆≌;②OG OH =;③10GH =其中,正确结论的个数是( )A .0个B .1个C .2个D .3个4.已知点M 是平行四边形ABCD 内一点(不含边界),设12MAD MBA θθ∠=∠=,,3 MCB θ∠=,4MDC θ∠=.若110,AMB ∠=︒ 90CMD ∠=︒,60BCD ∠=︒,则( )A .142310θθθθ+--=︒B .241330θθθθ+--=︒C .142330θθθθ+--=︒D .241340θθθθ+--=︒5.如图,在矩形ABCD 中,AB =6,BC =8,E 是BC 边上一点,将矩形沿AE 折叠,点B 落在点B '处,当△B 'EC 是直角三角形时,BE 的长为( )A .2B .6C .3或6D .2或3或66.如图,正方形ABCD (四边相等、四内角相等)中,AD =5,点E 、F 是正方形ABCD 内的两点,且AE =FC =4,BE =DF =3,则EF 的平方为( )A .2B .125C .3D .47.如图的△ABC 中,AB>AC>BC,且D 为BC 上一点.现打算在AB 上找一点P ,在AC 上找一点Q,使得△APQ 与以P 、D 、Q 为顶点的三角形全等,以下是甲、乙两人的作法: 甲:连接AD,作AD 的中垂线分别交AB 、AC 于P 点、Q 点,则P 、Q 两点即为所求; 乙:过D 作与AC 平行的直线交AB 于P 点,过D 作与AB 平行的直线交AC 于Q 点,则P 、Q 两点即为所求;对于甲、乙两人的作法,下列判断何者正确( )A .两人皆正确B .两人皆错误C .甲正确,乙错误D .甲错误乙正确8.如图,45A ABC C ∠=∠=∠=︒,E 、F 分别是AB 、BC 的中点,则下列结论:①EF BD ⊥,②12EF BD =,③ADC BEF BFE ∠=∠+∠,④AD DC =,其中正确有( )A .1个B .2个C .3个D .4个9.如图,矩形ABCD 的对角线AC 、BD 交于点O ,点P 在边AD 上从点A 到点D 运动,过点P 作PE ⊥AC 于点E ,作PF ⊥BD 于点F ,已知AB=3,AD=4,随着点P 的运动,关于PE+PF 的值,下面说法正确的是( )A .先增大,后减小B .先减小,后增大C .始终等于2.4D .始终等于310.如图,△ABC 中,AB =24,BC =26,CA =14.顺次连接△ABC 各边中点,得到△A 1B 1C 1;再顺次连接△A 1B 1C 1各边中点,得到△A 2B 2C 2…如此进行下去,得到n n n A B C ,则△A 8B 8C 8的周长为( )A .1B .12C .14D .18二、填空题11.在平行四边形ABCD 中,30,23,2A AD BD ∠=︒==,则平行四边形ABCD 的面积等于_____.12.如图,ABC ∆是边长为1的等边三角形,取BC 边中点E ,作//ED AB ,//EF AC ,得到四边形EDAF ,它的周长记作1C ;取BE 中点1E ,作11//E D FB ,11//E F EF ,得到四边形111E D FF ,它的周长记作2C .照此规律作下去,则2020C =______.13.已知在矩形ABCD 中,3,3,2AB BC ==点P 在直线BC 上,点Q 在直线CD 上,且,AP PQ ⊥当AP PQ =时,AP =________________.14.如图,长方形纸片ABCD 中,AB =6 cm,BC =8 cm 点E 是BC 边上一点,连接AE 并将△AEB 沿AE 折叠, 得到△AEB′,以C ,E ,B′为顶点的三角形是直角三角形时,BE 的长为___________cm.15.菱形OBCD 在平面直角坐标系中的位置如图所示,顶点B (23,0),∠DOB =60°,点P 是对角线OC 上一个动点,E (0,-1),则EP 十BP 的最小值为__________.16.在平面直角坐标系xOy 中,点A 、B 分别在x 轴、y 轴的正半轴上运动,点M 为线段AB 的中点.点D 、E 分别在x 轴、y 轴的负半轴上运动,且DE =AB =10.以DE 为边在第三象限内作正方形DGFE ,则线段MG 长度的最大值为_____.17.如图,四边形ABCP 是边长为4的正方形,点E 在边CP 上,PE =1;作EF ∥BC ,分别交AC 、AB 于点G 、F ,M 、N 分别是AG 、BE 的中点,则MN 的长是_________.18.已知:如图,在ABC 中,AD BC ⊥,垂足为点D ,BE AC ⊥,垂足为点E ,M 为AB 边的中点,连结ME 、MD 、ED ,设4AB =,30DAC ∠=︒则EM =______;EDM 的面积为______,19.如图,有一张长方形纸片ABCD ,4AB =,3AD =.先将长方形纸片ABCD 折叠,使边AD 落在边AB 上,点D 落在点E 处,折痕为AF ;再将AEF ∆沿EF 翻折,AF 与BC 相交于点G ,则FG 的长为___________.20.如图,在平行四边形ABCD 中,53AB AD ==,,BAD ∠的平分线AE 交CD 于点E ,连接BE ,若BAD BEC ∠=∠,则平行四边形ABCD 的面积为__________.三、解答题21.如图,点E 为▱ABCD 的边AD 上的一点,连接EB 并延长,使BF =BE ,连接EC 并延长,使CG =CE ,连接FG .H 为FG 的中点,连接DH ,AF .(1)若∠BAE =70°,∠DCE =20°,求∠DEC 的度数;(2)求证:四边形AFHD 为平行四边形;(3)连接EH ,交BC 于点O ,若OC =OH ,求证:EF ⊥EG .22.如图1,在正方形ABCD 和正方形BEFG 中,点,,A B E 在同一条直线上,P 是线段DF 的中点,连接,PG PC .(1)求证:,PG PC PG PC ⊥=.简析:由Р是线段DF 的中点,//DC CF ,不妨延长GP 交DC 于点M ,从而构造出一对全等的三角形,即_______≅________.由全等三角形的性质,易证CMG 是_______三角形,进而得出结论;(2)如图2,将原问题中的正方形ABCD 和正方形BEFG 换成菱形ABCD 和菱形BEFG ,且60ABC BEF ∠=∠=︒,探究PG 与PC 的位置关系及PG PC的值,写出你的猜想并加以证明;(3)当6,2AB BE ==时,菱形ABCD 和菱形BEFG 的顶点都按逆时针排列,且60ABC BEF ∠=∠=︒.若点A B E 、、在一条直线上,如图2,则CP =________;若点A B G 、、在一条直线上,如图3,则CP =________.23.已知正方形ABCD .(1)点P 为正方形ABCD 外一点,且点P 在AB 的左侧,45APB ∠=︒.①如图(1),若点P 在DA 的延长线上时,求证:四边形APBC 为平行四边形.②如图(2),若点P 在直线AD 和BC 之间,以AP ,AD 为邻边作APQD □,连结AQ .求∠PAQ 的度数.(2)如图(3),点F 在正方形ABCD 内且满足BC=CF ,连接BF 并延长交AD 边于点E ,过点E 作EH ⊥AD 交CF 于点H ,若EH=3,FH=1,当13AE CF =时.请直接写出HC 的长________.24.如图,在正方形ABCD 中,点M 是BC 边上任意一点,请你仅用无刻度的直尺,用连线的方法,分别在图(1)、图(2)中按要求作图(保留作图痕迹,不写作法).(1)在如图(1)的AB 边上求作一点N ,连接CN ,使CN AM =;(2)在如图(2)的AD 边上求作一点Q ,连接CQ ,使CQ AM .25.如图1,已知四边形ABCD 是正方形,E 是对角线BD 上的一点,连接AE ,CE .(1)求证:AE =CE ;(2)如图2,点P 是边CD 上的一点,且PE ⊥BD 于E ,连接BP ,O 为BP 的中点,连接EO .若∠PBC =30°,求∠POE 的度数;(3)在(2)的条件下,若OE 2,求CE 的长.26.如图.正方形ABCD 的边长为4,点E 从点A 出发,以每秒1个单位长度的速度沿射线AD 运动,运动时间为t 秒(t >0),以AE 为一条边,在正方形ABCD 左侧作正方形AEFG ,连接BF .(1)当t =1时,求BF 的长度;(2)在点E 运动的过程中,求D 、F 两点之间距离的最小值;(3)连接AF 、DF ,当△ADF 是等腰三角形时,求t 的值.27.直线1234,,,,l l l l 是同一平面内的一组平行线.(1)如图1.正方形ABCD 的4个顶点都在这些平行线上,若四条直线中相邻两条之间的距离都是1,其中点A ,点C 分别在直线1l 和4l 上,求正方形的面积;(2)如图2,正方形ABCD 的4个顶点分别在四条平行线上,若四条直线中相邻两条之间的距离依次为123h h h ,,.①求证:13h h =;②设正方形ABCD 的面积为S ,求证222211 2 2 S h h h h =++.28.(解决问题)如图1,在ABC ∆中,10AB AC ==,CG AB ⊥于点G .点P 是BC 边上任意一点,过点P 作PE AB ⊥,PF AC ⊥,垂足分别为点E ,点F .(1)若3PE =,5PF =,则ABP ∆的面积是______,CG =______.(2)猜想线段PE ,PF ,CG 的数量关系,并说明理由.(3)(变式探究)如图2,在ABC ∆中,若10AB AC BC ===,点P 是ABC ∆内任意一点,且PE BC ⊥,PF AC ⊥,PG AB ⊥,垂足分别为点E ,点F ,点G ,求PE PF PG ++的值.(4)(拓展延伸)如图3,将长方形ABCD 沿EF 折叠,使点D 落在点B 上,点C 落在点C '处,点P 为折痕EF 上的任意一点,过点P 作PG BE ⊥,PH BC ⊥,垂足分别为点G ,点H .若8AD =,3CF =,直接写出PG PH +的值.29.(1)问题探究:如图①,在四边形ABCD 中,AB ∥CD ,E 是BC 的中点,AE 是∠BAD 的平分线,则线段AB ,AD ,DC 之间的等量关系为 ; (2)方法迁移:如图②,在四边形ABCD 中,AB ∥CD ,AF 与DC 的延长线交于点F ,E 是BC 的中点,AE 是∠BAF 的平分线,试探究线段AB ,AF ,CF 之间的等量关系,并证明你的结论;(3)联想拓展:如图③,AB ∥CF ,E 是BC 的中点,点D 在线段AE 上,∠EDF =∠BAE ,试探究线段AB ,DF ,CF 之间的数量关系,并证明你的结论.30.已知:如图,在ABC 中,直线PQ 垂直平分AC ,与边AB 交于点E ,连接CE ,过点C 作//CF BA 交PQ 于点F ,连接AF .(1)求证:四边形AECF 是菱形;(2)若8AC =,AE=5,则求菱形AECF 的面积.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】利用正方形的性质、全等三角形的性质、勾股定理等知识依次判断即可;【详解】解:①∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠A=∠B=90°,∵∠A=∠EDQ,∠AEP=∠QED,AE=ED,∴△AEP≌△DEQ,故①正确,②作PG⊥CD于G,EM⊥BC于M,∴∠PGQ=∠EMF=90°,∵EF⊥PQ,∴∠PEF=90°,∴∠PEN+∠NEF=90°,∵∠NPE+∠NEP=90°,∴∠NPE=∠NEF,∵PG=EM,∴△EFM≌△PQG,∴EF=PQ,故②正确,③连接QF.则QF=PF,PB2+BF2=QC2+CF2,设CF=x,则(2+x )2+12=32+x 2,∴x=1,故③错误,④当P 在A 点时,Q 与D 重合,QC 的中点H 在DC 的中点S 处,当P 运动到B 时,QC 的中点H 与D 重合,故EH 扫过的面积为△ESD 的面积=12,故④正确, 则正确的是①②④,故选B . 【点睛】本题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,难度较大.2.D解析:D【解析】【分析】根据题意过E 作EK 垂直于直线CD ,垂足为K ,再过E 作EL 垂直于直线BC ,垂足为L ,只要证明ENK ELM ∆≅∆,则可计算EKCL ENCM S S=四边形.【详解】解:根据题意过E 作EK 垂直于直线CD ,垂足为K ,再过E 作EL 垂直于直线BC ,垂足为L.四边形ABCD 为正方形∴EL=EK,EK CD EL BC ⊥⊥∴90ELM EKN ︒∠=∠=90BCD ︒∠=90KEL ︒∴∠=FEG 为直角三角形90KEM LEM KEM NEK ︒∴∠+∠=∠+∠=LEM NEK ∴∠=∠ENK ELM ∴∆≅∆2224()39EKCL ENCM S Sa a ∴===四边形 故选D.【点睛】本题主要考查正方形的性质,关键在于根据题意做辅助线. 3.C解析:C【分析】①直接利用角边角判定定理判断即可;②证明ODH OCG ∆≅∆即可;③在Rt CGH ∆中求解即可判断此答案错误.【详解】解:①∵四边形ABCD 是正方形,,AC BD 是对角线,∴OD OC =,45ODF OCE ∠=∠=︒,90DOC ∠=︒,∵90EOF ∠=︒,∴DOC DOE EOF DOE ∠-∠=∠-∠,即:EOC DOF ∠=∠,在ODF ∆和OCE ∆中,∵ODF OCE OD OC DOF COE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴ODF OCE ∆≅∆,故①正确;②∵45ODF OCE ∠=∠=︒,∴90=90=135ODF OCE ∠+︒∠+︒︒,即:ODH OCG ∠=∠,在ODH ∆和OCG ∆中,∵GOC DOH OD OC ODH OCG ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴ODH OCG ∆≅∆,∴OH OG =,故②正确;③过点O 作OM CD ⊥于点M ,∵OM CD ⊥,∴在等腰Rt OCD ∆中,118422OM CD ==⨯=, 在Rt ECG ∆和Rt EMO ∆中 ∵OME GCE OEM GEC OE GE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴4CG OM ==,由②中知:ODH OCG ∆≅∆,∴DH CG =,∴=4DH CG =,∴8412CH CD DH =+=+=,∴在Rt CGH ∆中,由勾股定理得:2222412410GH CG CH =+=+=,故③错误;综上所述:只有两个正确,故选:C .【点睛】本题主要考查正方形的性质,全等三角形的判定与性质,解题的关键是掌握正方形的四条边都相等,正方形的每条对角线平分每组对角.4.D解析:D【分析】依据平行四边形的性质以及三角形内角和定理,可得θ2-θ1=10°,θ4-θ3=30°,两式相加即可得到θ2+θ4-θ1-θ3=40°.【详解】解:∵四边形ABCD 是平行四边形,∴∠BAD=∠BCD=60°,∴∠BAM=60°-θ1,∠DCM=60°-θ3,∴△ABM 中,60°-θ1+θ2+110°=180°,即θ2-θ1=10°①,△DCM中,60°-θ3+θ4+90°=180°,即θ4-θ3=30°②,由②+①,可得(θ4-θ3)+(θ2-θ1)=40°,2413 40θθθθ∴+--=︒;故选:D.【点睛】本题主要考查了平行四边形的性质以及三角形内角和定理等知识;熟练掌握平行四边形的对角相等是解题的关键.5.C解析:C【分析】分以下两种情况求解:①当点B′落在矩形内部时,连接AC,先利用勾股定理计算出AC =10,根据折叠的性质得∠AB′E=∠B=90°,而当△B′EC为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=6,可计算出CB′=4,设BE=x,则EB′=x,CE=8﹣x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时.此时四边形ABEB′为正方形,求出BE的长即可.【详解】解:当△B′EC为直角三角形时,有两种情况:①当点B′落在矩形内部时,如图1所示.连结AC,在Rt△ABC中,AB=6,BC=8,∴AC2286+10,∵∠B沿AE折叠,使点B落在点B′处,∴∠AB′E=∠B=90°,当△B′EC为直角三角形时,得到∠EB′C=90°,∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,如图,∴EB=EB′,AB=AB′=6,∴CB′=10﹣6=4,设BE=x,则EB′=x,CE=8﹣x,在Rt△B′EC中,∵EB′2+CB′2=CE2,∴x2+42=(8﹣x)2,解得x=3,②当点B′落在AD边上时,如图2所示.此时ABEB′为正方形,∴BE=AB=6.综上所述,BE的长为3或6.故选:C.【点睛】本题考查了折叠变换的性质、直角三角形的性质、矩形的性质,正方形的判定等知识;熟练掌握折叠变换的性质,由勾股定理得出方程是解题的关键.6.A解析:A【分析】根据AB=5,AE=4,BE=3,可以确定△ABE为直角三角形,延长BE构建出直角三角形,在利用勾股定理求出EF的平方即可.【详解】∵四边形ABCD是正方形,∴AB=BC=CD=AD=5,如图,延长BE交CF于点G,∵AB=5,AE=4,BE=3,∴AE2+BE2=AB2,∴△ABE是直角三角形,同理可得△DFC是直角三角形,∵AE=FC=4,BE=DF=3,AB=CD=5,∴△ABE≌△CDF,∴∠BAE=∠DCF,∵∠ABC=∠AEB=902,∴∠CBG=∠BAE,同理可得,∠BCG=∠CDF=∠ABE,△ABE≌△BCG,∴CG=BE=3,BG=AE=4,∴EG=4-3=1,GF=4-3=1,∴EF2=EG2+GF2=1+1=2【点睛】此题考查三角形的判定,勾股定理的运用,根据已知条件构建直角三角形求值是解题的关键.7.A解析:A【分析】如图1,根据线段垂直平分线的性质得到PA=PD,QA=QD,则根据"SSS"可判断APQ≌DPQ,则可对甲进行判断;如图2,根据平行四边形的判定方法先证明四边形APDQ 为平行四边形,则根据平行四边形的性质得到PA=DQ,PD=AQ,则根据"SSS"可判断△APQ≌△DQP,则可对乙进行判断.【详解】解:如图1,∵PQ垂直平分AD,∴PA= PD,,QA= QD,∵PQ= PQ,∴△APQ≌△DPQ (SSS),所以甲正确;如图2,∵PD ∥AQ,DQ ∥AP,∴四边形APDQ为平行四达形,∴PA=DQ,,PD=AQ,∵PQ=QP,∴△APQ≌△DQP (SSS),所以乙正确;故选:A.【点睛】本题考查了作图-复杂作图,复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作,也考查了线段垂直平分线的性质、平行四边形的判定与性质和三角形全等的判定.8.C解析:C【分析】根据三角形的中位线定理“三角形的中位线平行于第三边”可得//EF AC ,12EF AC =,再由45°角可证△ABQ 为等腰直角三角形,从而可得可得AQ BQ =,进而证明AQC BQDASA ≅△△(),利用三角形的全等性质求解即可. 【详解】解:如图所示:连接AC ,延长BD 交AC 于点M ,延长AD 交BC 于Q ,延长CD 交AB 于P .45ABC C ∠=∠=︒,CP AB ∴⊥,45ABC BAD ∠=∠=︒,AQ BC ∴⊥,点D 为两条高的交点,BM ∴为AC 边上的高,即:BM AC ⊥,由中位线定理可得//EF AC ,12EF AC =, BD EF ∴⊥,故①正确;45DBQ DCA ∠+∠=︒,45DCA CAQ ∠+∠=︒,DBQ CAQ ∴∠=∠,BAD ABC ∠=∠,AQ BQ ∴=,90BQD AQC ∠=∠=︒,∴根据以上条件得AQC BQD ASA ≅△△(),BD AC ∴=,12EF AC ∴=,故②正确;45A ABC C ∠=∠=∠=︒,()18045DAC DCA BAD ABC BCD ∴∠+∠=︒-∠+∠+∠=︒,180135()180ADC DAC DCA BEF BFE ABC ∴∠=︒-∠+∠=︒=∠+∠=︒-∠,故③ ADC BEF BFE ∠=∠+∠成立;无法证明AD CD =,故④错误.综上所述:正确的是①②③,故选C .【点睛】本题考点在于三角形的中位线和三角形全等的判断及应用.解题关键是证明AQC BQD ASA ≅△△().9.C解析:C【分析】在矩形ABCD 中,由矩形边长,可得矩形面积是12,进而得134AOD ABCD S S ==矩形,由矩形对角线相等且互相平分得AO OC =,OB OD =,AC BD =,利用勾股定理可解得5AC =,则52OA OD ==,111()3222AOD AOP DOP S S S OA PE OD PF OA PE PF =+=+=+==,即可求出PE+PF 的值.【详解】解:连接PO ,如下图:∵在矩形ABCD 中,AB=3,AD=4,∴12ABCD S AB BC ==矩形,AO OC =,OB OD =,AC BD =,225AC AB +BC ,∴1112344AOD ABCD S S ==⨯=矩形, 52OA OD ==, 11115()()322222AOD AOP DOP S S S OA PE OD PF OA PE PF PE PF =+=+=+=⨯+=, ∴12 2.45PE PF +==; 故选C .【点睛】本题主要考查了矩形的性质,利用等积法间接求三角形的高线长及用勾股定理求直角三角形的斜边;利用面积法求解,是本题的解题突破点. 10.C解析:C【分析】根据三角形中位线定理求出△A 1B 1C 1的周长,根据计算总结规律,根据规律解答.【详解】根据三角形中位线定理求出△A 1B 1C 1的周长,根据计算结果总结规律,根据规律解答. 解:∵A 1、C 1分别为AB 、AC 的中点,∴A 1C 1=BC =13,同理,A 1B 1=12AC =7,B 1C 1=12AB =12, ∴△A 1B 1C 1的周长=7+12+13=32, ∴△A 1B 1C 1的周长=△ABC 的周长×12, 则△A 2B 2C 2的周长=△A 1B 1C 1的周长×12=△ABC 的周长×(12)2, …… ∴△A 8B 8C 8的周长=△ABC 的周长×(12)8=64×1256=14, 故选:C .【点睛】本题考查三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.二、填空题11.【分析】分情况讨论作出图形,通过解直角三角形得到平行四边形的底和高的长度,根据平行四边形的面积公式即可得到结论.【详解】解:过D 作DE AB ⊥于E ,在Rt ADE △中,30A ∠=︒,AD =132DE AD ∴==,332AE AD ==, 在Rt BDE △中,2BD =,22222(3)1BE BD DE ∴=-=-=,如图1,4AB ∴=,∴平行四边形ABCD 的面积4343AB DE ==⨯=,如图2,2AB =,∴平行四边形ABCD 的面积2323AB DE ==⨯=,如图3,过B 作BE AD ⊥于E ,在Rt ABE △中,设AE x =,则23DE x =-,30A ∠=︒,3BE x =, 在Rt BDE △中,2BD =, 22232()(23)x x ∴=+-, 3x ∴=,23x =(不合题意舍去),1BE ∴=,∴平行四边形ABCD 的面积12323AD BE ==⨯=,如图4,当AD BD ⊥时,平行四边形ABCD 的面积43AD BD ==,故答案为:【点睛】本题考查了平行四边形的性质,平行四边形的面积公式的运用、30度角的直角三角形的性质,根据题意作出图形是解题的关键.12.201812【分析】根据几何图形特征,先求出1C 、2C 、3C ,根据求出的结果,找出规律,从而得出2020C .【详解】∵点E 是BC 的中点,ED ∥AB ,EF ∥AC∴DE 、EF 是△ABC 的中位线∵等边△ABC 的边长为1∴AD=DE=EF=AF =12 则1C =1422⨯= 同理可求得:2C =1,3C =12发现规律:规律为依次缩小为原来的12 ∴2020C =201812故答案为:201812.【点睛】 本题考查找规律和中位线的性质,解题关键是求解出几组数据,根据求解的数据寻找规律.13【分析】 根据点P 在直线BC 上,点Q 在直线CD 上,分两种情况:1.P 、Q 点位于线段上;2.P 、Q 点位于线段的延长上,再通过三角形全等得出相应的边长,最后根据勾股即可求解.【详解】解:当P 点位于线段BC 上,Q 点位于线段CD 上时:∵四边形ABCD 是矩形,AP PQ ⊥∴∠BAP=∠CPQ ,∠APB=∠PQC∵AP PQ =∴ABP PCQ ≅∴PC=AB=32,BP=BC-PC=3-32=32 ∴AP=223322+()()=322当P 点位于线段BC 的延长线上,Q 点位于线段CD 的延长线上时:∵四边形ABCD 是矩形,AP PQ ⊥∴∠BAP=∠CPQ ,∠APB=∠PQC∵AP PQ =∴ABP PCQ ≅∴PC=AB=32,BP=BC+PC=3+32=92∴AP=223922+()()=3102故答案为:322或3102【点睛】 此题主要考查三角形全等的判定及性质、勾股定理,熟练运用判定定理和性质定理是解题的关键.14.3或6【详解】①∠B′EC=90°时,如图1,∠BEB′=90°,由翻折的性质得∠AEB=∠AEB′=12×90°=45°, ∴△ABE 是等腰直角三角形,∴BE=AB=6cm ;②∠EB′C=90°时,如图2, 由翻折的性质∠AB′E=∠B=90°,∴A 、B′、C 在同一直线上,AB′=AB ,BE=B′E ,由勾股定理得,=,∴B′C=10-6=4cm ,设BE=B′E=x ,则EC=8-x ,在Rt △B′EC 中,B′E 2+B′C 2=EC 2,即x 2+42=(8-x )2,解得x=3,即BE=3cm ,综上所述,BE 的长为3或6cm .故答案为3或6.15【分析】先根据菱形的性质可得OC 垂直平分BD ,从而可得=DP BP ,再根据两点之间线段最短可得EP BP +的最小值为DE ,然后利用等边三角形的判定与性质求出点D 的坐标,最后利用两点之间的距离公式即可得.【详解】如图,连接BP 、DP 、EP 、DE 、BD ,过点D 作DA OB ⊥于点A , (23,0)B ,OB ∴=四边形ABCD 是菱形,OC ∴垂直平分BD ,OB OD ==点P 是对角线OC 上的点,DP BP ∴=,EP BP EP DP ∴+=+,由两点之间线段最短可知,EP DP +的最小值为DE ,即EP BP +的最小值为DE , ,60OB OD DOB =∠=︒,BOD ∴是等边三角形, DA OB ⊥,12OA OB ∴==3AD ===,D ∴,又(0,1)E-,22(30)(31)19DE∴=-++=,即EP BP+的最小值为19,故答案为:19.【点睛】本题考查了菱形的性质、等边三角形的判定与性质、两点之间的距离公式等知识点,根据两点之间线段最短得出EP BP+的最小值为DE是解题关键.16.10+55【分析】取DE的中点N,连结ON、NG、OM.根据勾股定理可得55NG=.在点M与G之间总有MG≤MO+ON+NG(如图1),M、O、N、G四点共线,此时等号成立(如图2).可得线段MG的最大值.【详解】如图1,取DE的中点N,连结ON、NG、OM.∵∠AOB=90°,∴OM=12AB=5.同理ON=5.∵正方形DGFE,N为DE中点,DE=10,∴222210555NG DN DG++===.在点M与G之间总有MG≤MO+ON+NG(如图1),如图2,由于∠DNG 的大小为定值,只要∠DON=12∠DNG,且M 、N 关于点O 中心对称时,M 、O 、N 、G 四点共线,此时等号成立,∴线段MG 取最大值10+55.故答案为:10+55.【点睛】此题考查了直角三角形的性质,勾股定理,四点共线的最值问题,得出M 、O 、N 、G 四点共线,则线段MG 长度的最大是解题关键.17.5【分析】先判断四边形BCEF 的形状,再连接FM FC 、,利用正方形的性质得出AFG 是等腰直角三角形,再利用直角三角形的性质得出12MN FC =即可. 【详解】∵四边形ABCP 是边长为4的正方形,//EF BC ,∴四边形BCEF 是矩形,∵1PE =,∴3CE =,连接FM FC 、,如图所示:∵四边形ABCP 是正方形,∴=45BAC ∠ ,AFG 是等腰直角三角形,∵M 是AG 的中点,即有AM MG = ,∴FM AG ⊥,FMC 是直角三角形,又∵N 是FC 中点,12MN FC =,∵5FC ==∴ 2.5MN =,故答案为:2.5 .【点睛】本题考查了正方形的性质,矩形的判定,等腰三角形和直角三角形的性质,解题的关键在于合理作出辅助线,通过直角三角形的性质转化求解.18.2【分析】根据EM 是Rt ABE △斜边上的中线,利用直角三角形斜边上的中线等于斜边的一半即可求出EM 的长;根据已知条件推导出DME 是等边三角形,且边长为2,进一步计算即可得解.【详解】解:∵AD BC ⊥,M 为AB 边的中点,4AB =∴在Rt ABD △中,114222DM AM AB ===⨯= 同理,在Rt ABE △中,114222EM AM AB ===⨯= ∴MDA MAD ∠=∠,MEA MAE ∠=∠∵2BME MEA MAE MAE ∠=∠+∠=∠,2BMD MDA MAD MAD ∠=∠+∠=∠ ∴DME BME BMD ∠=∠-∠ 22MAE MAD =∠-∠()2MAE MAD =∠-∠2DAC =∠60=︒∵=DM EM∴DME 是等边三角形,且边长为2∴122EDM S =⨯=故答案是:2【点睛】本题考查了直角三角形斜边上的中线的性质、三角形的外角定理、角的和差以及等边三角形的判定和性质,熟练掌握相关知识点是进行推理论证的前提.19【解析】【分析】根据折叠的性质可得∠DAF=∠BAF=45°,再由矩形性质可得FC=ED=1,然后由勾股定理求出FG 即可.【详解】由折叠的性质可知,∠DAF=∠BAF=45°,∴AE=AD=3,EB=AB-AD=1,∵四边形EFCB 为矩形,∴FC=BE=1,∵AB ∥FC ,∴∠GFC=∠DAF=45°,∴GC=FC=1, ∴22112FG GC FC =+=+=,故答案为:2.【点睛】本题考查了折叠变换,矩形的性质是一种对称变换,理解折叠前后图形的大小不变,位置变化,对应边和对应角相等是解决此题的关键.20.102【分析】根据平行四边形的性质、角平分线的性质证明AD=DE=3,再根据BAD BEC ∠=∠证明BC=BE ,由此根据三角形的三线合一及勾股定理求出BF ,即可求出平行四边形的面积.【详解】过点B 作BF CD ⊥于点F ,如图所示.∵AE 是BAD ∠的平分线,∴DAE BAE ∠=∠.∵四边形ABCD 是平行四边形,∴53CD AB BC AD BAD BCE AB CD ====∠=∠,,,∥, ∴BAE DEA ∠=∠,∴DAE DEA ∠=∠,∴3DE AD ==,∴2CE CD DE =-=.∵BAD BEC ∠=∠,∴BCE BEC ∠=∠,∴BC=BE,∴112CF EF CE ===, ∴22223122BF BC CF =-=-=∴平行四边形ABCD的面积为5BF CD⋅==.故答案为:【点睛】此题考查平行四边形的性质:对边平行且相等,对角相等,等腰三角形的等角对等边的性质、三线合一的性质,勾股定理.三、解答题21.(1)50°;(2)见解析;(3)见解析【分析】(1)由平行四边形的性质和平行线的判定和性质得出答案即可;(2)由平行四边形的性质得出AD=BC,AD∥BC;证明BC是△EFG的中位线,得出BC∥FG,BC=12FG,证出AD∥FH,AD∥FH,由平行四边形的判定方法即可得出结论;(3)连接EH,CH,根据三角形的中位线定理以及平行四边形的判定和性质即可得到结论.【详解】明:(1)∵四边形ABCD是平行四边形,∴∠BAE=∠BCD=70°,AD∥BC,∵∠DCE=20°,∵AB∥CD,∴∠CDE=180°﹣∠BAE=110°,∴∠DEC=180°﹣∠DCE﹣∠CDE=50°;(2)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∠BAE=∠BCD,∵BF=BE,CG=CE,∴BC是△EFG的中位线,∴BC∥FG,BC=12 FG,∵H为FG的中点,∴FH=12 FG,∴BC∥FH,BC=FH,∴AD∥FH,AD∥FH,∴四边形AFHD是平行四边形;(3)连接EH,CH,∵CE=CG,FH=HG,∴CH=12EF,CH∥EF,∵EB=BF=12 EF,∴BE=CH,∴四边形EBHC是平行四边形,∴OB=OC,OE=OH,∵OC=OH,∴OE=OB=OC=12 BC,∴△BCE是直角三角形,∴∠FEG=90°,∴EF⊥EG.【点睛】本题考查了平行四边形的判定与性质、三角形中位线定理、等腰三角形的性质以及三角形内角和定理;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.22.(1)ΔDPM,ΔFPG;等腰直角;(2)线段PG与PC的位置关系是PG⊥PC;PG PC=3;(3)213【分析】(1)延长GP交DC于点M,由Р是线段DF的中点,//DC CF,可得∠MDP=∠GFP,DP=FP,利用ASA可证明△DPM≌△FPG;可得DM=GF,MP=GP,根据正方形的性质可得CM=CG,即可证明△CMG是等腰直角三角形,即可得答案;(2)如图,延长GP交DC于点H,利用ASA可证明△GFP≌△HDP,可得GP=HP,GF=HD,进而根据菱形的性质可证明△CHG是等腰三角形,根据等腰三角形“三线合一”的性质可得PG⊥PC,∠HCP=∠GCP,由∠ABC=60°可得∠HCG=120°,进而可得∠CGP=30°,根据含30°角的直角三角形的性质及勾股定理即可得答案;(3)利用线段的和差关系可求出图2中CG的长,由(2)可知∠CGP=30°,根据含30°角的直角三角形的性质即可求出CP的长;在图3中,延长GP到N,使GP=PN,连接DN、CN、CG,过N作NK⊥CD,交CD延长线于K,利用SAS可证明△FGP≌△DNP,可得GF=DN,∠GFP=∠NDP,根据角的和差关系可得∠CDN=120°,根据平角的定义可得∠GBC=120°,利用菱形的性质及等量代换可得DN=GB,利用SAS可证明△NDC≌△GBC,可得CN=CG,∠DCN=∠BCG,根据等腰三角形的性质可得PC⊥GN,根据角的和差关系可得∠NCG=120°,进而可得出∠CNP=30°,可得PC=12CG,根据平角的定义可得∠KDN=60°,即可得出∠KND=30°,根据含30°角的直角三角形的性质可得得出KD的长,利用勾股定理可求出KN的长,再利用勾股定理可求出CN的长,根据含30°角的直角三角形的性质即可得出PC的长.【详解】(1)如图,延长GP交DC于点M,∵Р是线段DF的中点,四边形ABCD、BEFG是正方形,点,,A B E在同一条直线上,∴//DC CF,DP=FP,CD=BC,FG=BG,在△DPM和△FPG中,MDP GFP DP FPDPM FPG ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△DPM≌△FPG,∴DM=FG,KP=GP,∴CD-DM=BC-BC,即CM=CG,∴△CMG是等腰直角三角形,∴PG⊥PC,PG=PC.故答案为:ΔDPM,ΔFPG;等腰直角(2)猜想:线段PG与PC的位置关系是PG⊥PC;PGPC3.如图,延长GP交DC于点H,∵P是线段DF的中点,∴FP=DP,∵四边形ABCD和四边形BEFG是菱形,∴CD//AB,CF//BE,CD=CB,GF=GB,∵点A B E、、在一条直线上,∴DC∥GF,∴∠GFP=∠HDP,在△GFP和△HDP中,GFP HDP FP DPGPF HPD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△GFP≌△HDP,∴GP=HP,GF=HD,∴CD-DH=CB-GB,即CG=CH,∴△CHG是等腰三角形.∴PG⊥PC,(三线合一),∠HCP=∠GCP,∵∠ABC=∠BEF=60°,∴∠HCG=120°,∴∠CGP=12(180°-120°)=30°,∴CG=2PC,∴PG=2222(2)3CG PC PC PC PC-=-=,∴PGPC=3.(3)如图2,∵AB=6,BE=2,∴CG=AB-BE=4,由(2)可知∠CGP=30°,PG⊥PC,∴PC=12CG=2,如图3,延长GP到N,使GP=PN,连接DN、CN、CG,过N作NK⊥CD,交CD延长线于K,在△DNP和△FGP中,DP FPNPD GPFPN PG=⎧⎪∠=∠⎨⎪=⎩,∴△DNP≌△FGP,∴DN=GF=BG=BE=2,∠NDP=∠GFP,∵四边形ABCD和四边形BEFG是菱形,∴CD//AB,EF//BC,∵点A、B、G在一条直线上,∴DC∥EF,∴∠CDP=∠EFP,∵∠ABC=∠BEF=60°,∴∠EFG=∠CBG=120°,∴∠NDP+CDP=∠GFP+∠EFP=∠EFG=120°,即∠NDC=120°,∴∠KDN=60°,∠KND=30°,∴KD=12DN=1,NK=223DN KD -=, ∴CK=CD+KD=7,∴CN=22CK NK +=213,在△CDN 和△CBG 中,CD BC CDN CBG ND BG =⎧⎪∠=∠⎨⎪=⎩,∴CN=CG ,∠DCN=∠BCG ,∴PC ⊥GN ,∠DCN+∠NCB=∠BCG+∠NCB=∠DCB=120°,即∠NCG=120°,∴∠CNP=12(180°-∠NCG )=30°, ∴PC=12CN=13.故答案为:2,13【点睛】本题考查正方形的性质、菱形的性质、等腰直角三角形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质及勾股定理,正确作出辅助线、熟记30°角所对的直角边等于斜边的一半的性质及全等三角形的判定定理是解题关键.23.(1)①证明见详解;②45PAQ ∠=︒,见解析;(2)5.【分析】(1)①只要证明//PB AC 即可解决问题;②如图2中,连接QC ,作DT DQ ⊥交QC 的延长线于T ,利用全等三角形的性质解决问题即可;(2)如图3中,延长EH 交BC 于点G ,设AE=x ,由题意易得AB=BC=CF=EG=3x ,然后可得CG=2x ,HG=3x-3,CH=3x-1,利用勾股定理求解即可.【详解】(1)①证明:四边形ABCD 是正方形,∴//B DP C ,45DAC ∠=︒,∴135PAC ∠=︒45APB ∠=︒,∴+180APB PAC ∠∠=︒,∴//PB AC∴四边形APBC 是平行四边形; ②四边形PADQ 是平行四边形,∴DQ//,//,AP AD PQ AD PQ BC ==,AD//B C ,∴,//PQ BC PQ BC =,∴四边形PQCB 是平行四边形,∴QC//BP ,∴45APQ DQC ∠=∠=︒,90ADC QDT ∠=∠=︒,∴DQ=DT ,45,T DQT ADQ CDT ∠=∠=︒∠=∠,AD=DC ,∴ADQ CDT ≌,∴45AQD T ∠=∠=︒,AP//DQ ,∴45PAQ DQA ∠=∠=︒;(3)CH=5,理由如下:如图3所示:延长EH 交BC 于点G ;四边形ABCD 是正方形,∴AB=BC ,90D ∠=︒, 又EH=3,FH=1,EH ⊥AD ,∴EH//CD ,∴90HGC ∠=︒设AE=x ,1,3AE CF BC CF ==,∴AB=BC=CF=EG=3x , ∴CG=2x ,HG=3x-3,CH=3x-1 在Rt HGC △中,()()22222243331CG HG CH x x x +=+-=-即,解得121,2x x ==当x=1时,AB=3(不符合题意,舍去);当x=2时,AB=6,∴CH=5.故答案为5.【点睛】本题主要考查正方形的综合问题、三角形全等及勾股定理,关键是利用已知条件及四边形的性质得到它们之间的联系,然后利用勾股定理求解线段的长即可.24.(1)见解析;(2)见解析.【分析】(1)连接BD ,BD 与AM 交于点O ,连接CO 并延长交于AB ,则CO 与AB 的交点为点。
初二月考数学试卷及答案

一、选择题(每题5分,共30分)1. 下列数中,绝对值最小的是:A. -3B. -2C. 0D. 12. 若x + y = 5,x - y = 1,则x² + y²的值为:A. 10B. 16C. 25D. 303. 在直角坐标系中,点A(2, 3)关于y轴的对称点坐标是:A. (2, -3)B. (-2, 3)C. (-2, -3)D. (2, 3)4. 若a² + b² = 25,a - b = 3,则a + b的值为:A. 4B. 6C. 8D. 105. 下列函数中,是二次函数的是:A. y = 2x + 3B. y = x² + 2x + 1C. y = 3x³ - 2D. y = x + 1/x二、填空题(每题5分,共25分)6. 若a = 2,b = -3,则a² - b²的值为______。
7. 在等腰三角形ABC中,AB = AC,∠B = 40°,则∠A的度数为______。
8. 若x² - 5x + 6 = 0,则x的值为______。
9. 已知函数y = 2x - 1,当x = 3时,y的值为______。
10. 在直角坐标系中,点P(-4, 5)到原点O的距离为______。
三、解答题(每题15分,共45分)11. 解方程:2x² - 4x - 6 = 0。
12. 已知函数y = -3x² + 4x + 1,求该函数的顶点坐标。
13. 在等边三角形ABC中,边长为6cm,求三角形的高。
四、附加题(20分)14. 已知正方体ABCD-A1B1C1D1的边长为a,求正方体的体积V。
解答:一、选择题1. C2. C3. B4. C5. B二、填空题6. 77. 80°8. 2 或 39. 510. 5√2三、解答题11. 解:2x² - 4x - 6 = 0使用求根公式得:x = [4 ± √(16 + 48)] / 4x = [4 ± √64] / 4x = [4 ± 8] / 4x₁ = 3,x₂ = -112. 解:y = -3x² + 4x + 1顶点坐标公式为(-b/2a, f(-b/2a)),其中a = -3,b = 4x = -4 / (2 -3) = 2/3y = -3(2/3)² + 4(2/3) + 1 = 1/3顶点坐标为(2/3, 1/3)13. 解:等边三角形的高可以通过勾股定理求得高= √(边长² - (边长/2)²) = √(6² - (6/2)²) = √(36 - 9) = √27 = 3√3 cm四、附加题14. 解:正方体的体积V = a³,其中a为边长V = a³ = (2√3)³ = 8 3√3 = 24√3 cm³。
八年级金试卷数学答案

一、选择题1. 答案:C。
解析:根据勾股定理,直角三角形的两条直角边的平方和等于斜边的平方,所以a² + b² = c²,代入题目中的数值得到3² + 4² = 5²,符合勾股定理,因此选C。
2. 答案:B。
解析:题目要求计算0.25 + 0.25 × 0.25,根据运算顺序,先计算乘法,得到 0.25 + 0.0625,然后计算加法,得到 0.3125,所以选B。
3. 答案:A。
解析:题目要求计算(2/3) × (4/5) ÷ (1/6),根据运算顺序,先计算乘法,得到 8/15,然后计算除法,得到8/15 × 6 = 16/5,所以选A。
4. 答案:D。
解析:题目要求判断下列命题的真假。
根据平方根的定义,正数的平方根是正数,所以命题“一个正数的平方根是负数”是假命题,因此选D。
5. 答案:B。
解析:题目要求计算下列分式的值。
将分式中的分子和分母同时乘以2,得到(2x + 2) ÷ (2x - 2),然后约分,得到(x + 1) ÷ (x - 1),所以选B。
二、填空题6. 答案:3。
解析:题目要求计算 (-2) × (-2) × (-2),根据乘法法则,负数乘以负数得到正数,所以 (-2) × (-2) × (-2) = 4 × (-2) = -8,所以填3。
7. 答案:0.4。
解析:题目要求计算(2/5) × (3/4),根据乘法法则,分子相乘,分母相乘,得到 6/20,然后约分,得到 3/10,所以填0.4。
8. 答案:8。
解析:题目要求计算(2/3) ÷ (1/2),根据除法法则,将除法转化为乘法,即(2/3) × (2/1),然后计算乘法,得到 4/3,所以填8。
9. 答案:5。
解析:题目要求计算 (3/4) - (1/2),根据减法法则,先找到两个分数的公共分母,即4,然后分别将分子相减,得到 3/4 - 2/4 = 1/4,所以填5。
【数学】初二年奖学金考试数学考卷

【数学】初二年奖学金考试数学考卷一、选择题(每题4分,共40分)1. 下列选项中,哪个数是有理数?()A. √3B. πC. 0.333…D. √12. 已知a、b是实数,且a+b=5,ab=3,则a²+b²的值为()A. 7B. 16C. 23D. 253. 下列各式中,正确的是()A. |a|=aB. |a|=±aC. |a|=aD. |a|=a²4. 已知等腰三角形的底边长为10cm,腰长为13cm,则该三角形的周长为()A. 32cmB. 42cmC. 26cmD. 31cm5. 下列函数中,哪一个是一次函数?()A. y=2x²+1B. y=x+3C. y=3x2xD. y=√x6. 有四个数,分别是一个正整数、它的平方、它的平方根和它的倒数,这四个数按照从小到大的顺序排列,排在第二位的数是()A. 正整数B. 平方根C. 平方D. 倒数7. 在直角坐标系中,点A(2,3)关于原点对称的点是()A. (2,3)B. (2,3)C. (2,3)D. (3,2)8. 下列各式中,分式有意义的是()A. 1/(x1)B. 1/√(x²1)C. 1/√(x²+1)D. 1/(x²+1)9. 下列方程中,一元二次方程的是()A. x+y=2B. x²+y²=1C. x²2x+1=0D. 2x³3x²+x=010. 已知一组数据的方差是9,那么这组数据每个数都加上3后,方差为()A. 12B. 9C. 6D. 3二、填空题(每题4分,共40分)11. 已知|a|=5,则a的值为______。
12. 已知一组数据2,3,5,7,x的平均数是5,则x的值为______。
13. 若a=3,b=2,则a²+b²的值为______。
14. 在直角坐标系中,点P(3,4)关于x轴对称的点是______。
奖学金考试试卷八年级数学

一、选择题(每题5分,共25分)1. 下列各数中,绝对值最小的是()A. -2.5B. -2C. 2D. 02. 若a=3,b=-5,则a²+b²的值为()A. 4B. 10C. 16D. 183. 在直角坐标系中,点P(2,3)关于y轴的对称点坐标是()A.(-2,3)B.(2,-3)C.(-2,-3)D.(2,3)4. 一个等腰三角形的底边长为8cm,腰长为10cm,则这个三角形的面积是()A. 40cm²B. 48cm²C. 50cm²D. 64cm²5. 下列函数中,y与x成一次函数关系的是()A. y=3x+2B. y=x²+1C. y=2x+3xD. y=5x-2x二、填空题(每题5分,共25分)6. 若x=5,则x²-2x+1的值为______。
7. 若a、b、c为等差数列,且a=2,c=8,则b的值为______。
8. 在梯形ABCD中,AD∥BC,AB=CD=5cm,BC=10cm,则梯形的高为______cm。
9. 若一个圆的半径增加了20%,则其面积增加了______%。
10. 若等边三角形的边长为a,则其周长为______。
三、解答题(每题15分,共45分)11. (解答题)已知二次函数y=ax²+bx+c(a≠0)的图象与x轴交于点A(-2,0)和B(1,0),且顶点坐标为(0,3),求该二次函数的表达式。
12. (解答题)如图,在直角坐标系中,点E(2,1),点F(4,3),求直线EF的解析式。
13. (解答题)已知等腰三角形ABC中,AB=AC,BC=8cm,AD为高,求三角形ABC的面积。
四、应用题(每题15分,共30分)14. (应用题)某商店开展促销活动,顾客购买某商品满200元即可获得100元优惠券。
小华购买了该商品300元,请问她最多可以使用几次优惠券?15. (应用题)某班级有40名学生,其中男生占60%,女生占40%。
2019-2020年八年级数学2月奖学金测试题

2019-2020年八年级数学2月奖学金测试题一、选择题:(每题3分,共30分)1.下列说法正确的是 ( )A.9的立方根是3 B.算术平方根等于它本身的数一定是1C.-2是4的平方根D.16的算术平方根是42.在,,,,0.202 002 000 2,中,无理数的个数有( ) A.6个 B.5个 C.4个 D.3个3.下列运算中,正确的是()A.B. C. D.4.对任意实数x,点P(x,-2x+3)一定不在 ( )A.第一象限 B.第二象限 C.第三象限 D.第四象限5.在直角坐标系x o y中,已知点A(0,2),B(1,3),则线段AB的长度是()A.1 B. C. D.26.已知一次函数y=kx+b的图象如图所示,则k、b的取值范围是 ( )A.k>0,b>0 B.k>0,b<0 C.k<0,b<0 D.k<0,b>07.在直线y=x+且到x轴或y轴距离为1的点有 ( )个A.1 B.2 C.3 D.48.在平面直角坐标系xOy中,点(1,-3)关于x轴对称的点的坐标为( )A.(-3,1) B.(-1,3) C.(-1,-3) D.(1,3)9.如图,在平面直角坐标系xOy中,已知AD平分∠OAB,DB⊥AB,BC//OA,点D的坐标为D(0,),点B的横坐标为1,则点C的坐标是( )A.(0,2) B.(0,+)C.(0,)D.(0,5)10.已知A、B两地相距900 m,甲、乙两人同时从A地出发,以相同速度匀速步行,20 min后到达B地,甲随后马上沿原路按原速返回,回到A地后在原地等候乙回来;乙则在B地停留10 min后也沿原路以原速返回A地,则甲、乙两人之间的距离s(m)与步行时间t(min)之间的函数关系可以用图象表示为( )二、填空题:(每题3分,共24分)11.函数y=的自变量x的取值范围为______.12.已知点P(a,b)在一次函数y=x+1的图象上,则b-a=.13.如果+(y+6)2=0,那么2x-y的立方根为_______.14.如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,∠ADB=100,则∠BAC的度数为°.15.已知等腰三角形ABC的周长为8 cm,AB=3 cm.则BC=______ _cm.16.过点(-1,-3)且与直线y=1-2x平行的直线是_______.17.已知关于x的分式方程有增根,则a=_______.18.一次函数y=-2x+b的图象与两坐标轴所围成的三角形的面积为9,则b=______.三、解答题:(共46分)19.计算:(10分)(1)(2)2222121111a a aa a a a+-+∙---+,其中.20.解方程:(10分)(1) (2)21.(8分)如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,BE、CD相交于点O. (1)若BD=CE,试说明:OB=OC,(2)若BC=10,BC边上的中线AM=12,试求AC的长.22.(8分)已知一次函数y=kx+b的图象经过点(1,5),且与正比例函数y=x的图象相交于点(2,a).求:(1)a的值;(2)k,b的值;(3)这两个函数图象与x轴所围成的三角形面积.23.(10分)如图,已知点A的坐标为(2,4),在点A处有二只蚂蚁(忽略其大小),它们同时出发,一只以每秒1个单位的速度垂直向上爬行,另一只同样以每秒1个单位的速度水平向右爬行,t秒后,它们分别到达B、C处,连接BC.若在x轴上有两点D、E,满足DB =OB,EC=OC,则(1)当t=l秒时,求BC的长度;(2)证明:无论t为何值,DE=2AC始终成立;(3)延长BC交x轴于点F,当t的取值范围是多少时,点F始终在点E的左侧?(请直接写出结果,无需书写解答过程!)。
第一学期八年级数学第二次月考试卷(含解析)

第一学期八年级数学第二次月考试卷(含解析)一、选择题1.如图,已知O 为ABC ∆三边垂直平分线的交点,且50A ∠=︒,则BOC ∠的度数为( )A .80︒B .100︒C .105︒D .120︒2.下列调查中适合采用普查的是( ) A .了解“中国达人秀第六季”节目的收视率 B .调查某学校某班学生喜欢上数学课的情况 C .调查我市市民知晓“礼让行人”交通新规的情况 D .调查我国目前“垃圾分类”推广情况3.如图,将△ABC 折叠,使点A 与BC 边中点D 重合,折痕为MN ,若AB=9,BC=6,则△DNB 的周长为( )A .12B .13C .14D .154.如图,已知∠ABC=∠DCB ,下列所给条件不能证明△ABC ≌△DCB 的是( )A .∠A=∠DB .AB=DC C .∠ACB=∠DBCD .AC=BD 5.在平面直角坐标系中,点(1,2)P 到原点的距离是( ) A .1B 3C .2D 56.如图,在△ABC 中,分别以点A ,B 为圆心,大于12AB 长为半径画弧,两弧相交于点E ,F ,连接AE ,BE ,作直线EF 交AB 于点M ,连接CM ,则下列判断不正确...的是A .AM =BMB .AE =BEC .EF ⊥ABD .AB =2CM7.在平面直角坐标系的第二象限内有一点M ,点M 到x 轴的距离为3,到y 轴的距离为4,则点M 的坐标是( ) A .(3,4)- B .(4,3)- C .(4,3)- D .()3,4- 8.点M (3,-4)关于y 轴的对称点的坐标是( )A .(3,4)B .(-3,4)C .(-3,-4)D .(-4,3)9.点P(-2,3)关于x 轴的对称点的坐标为( ) A .(2,3) B .(-2,-3) C .(2,-3) D .(-3,2) 10.已知一次函数y =kx +b 的图象经过第一、二、三象限,则b 的值可以是( )A .﹣2B .﹣1C .0D .2二、填空题11.函数1y=x 2-中,自变量x 的取值范围是 ▲ . 12.若关于x 的分式方程122x x a x x--=--有增根,则a 的值_____________. 13.3-的绝对值是 .14.已知,点(,1)A a 和点(3,)B b 关于原点O 对称,则+a b 的值为__________. 15.在△ABC 中,AB=AC ,∠BAC=100°,点D 在BC 边上,连接AD ,若△ABD 为直角三角形,则∠ADC 的度数为_____. 16.化简:|32|-=__________. 17.化简:23(3)2716--+=_____. 18.若代数式321xx -+有意义,则x 的取值范围是______________. 19.某人一天饮水1679mL ,精确到100mL 是_____.20.如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点F ,点点F 作DE ∥BC ,交AB 于点D ,交AC 于点E 。
初中数学西南师大附中八年级数学科二月月考测考试题数 学 试 题.docx

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)试题1:的绝对值是()A.5 B.C. D.试题2:下列运算正确的是()A. B.C. D.试题3:近似数0.09070的有效数字和精确度分别是()A.四个,精确到万分位 B.三个,精确到十万分位C.四个,精确到十万分位 D.三个,精确到万分位试题4:评卷人得分弧长为cm,它所对的圆心角为,则该圆的半径为()A.6 B.9C.12 D.18试题5:既是轴对称图形又是中心对称图形的是()A.梯形 B.正三角形 C.平行四边形 D.菱形试题6:甲、乙、丙三个同学排成一排拍照,则甲排在中间的概率是()A. B. C . D.试题7:右图是一个正方体的平面展开图,这个正方体是()(第7题图)试题8:在某校人才交流会上,应酬人数和招聘人数分别居前5位的行业列表如下:行业名称计算机机械营销物流贸易应聘人数(单位:人) 2 231 2 053 1 546 748 659行业名称计算机营销机械建筑化工招聘人数(单位:人) 1 210 1 030 895 763 725如果用同一行业应聘人数与招聘人数比值的大小来衡量该行业的就业情况,那么根据表中数据,对上述行业的就业情况判断正确的是()A.计算机行业好于其他行业 B.贸易行业好于化工行业C.机械行业好于营销行业 D.建筑行业好于物流行业试题9:正方形ABCD的边长为1,M是AB的中点,N是BC的中点,AN和CM相交于点O,则四边形AOCD的面积是()A. B. C.D.试题10:如图都是二次函数的图象,若b > 0,则a的值等于()A. B. C.D.1试题11:函数的自变量x的取值范围是________________.试题12:分解因式:________________.试题13:某班5名学生参加数学竞赛,成绩(单位:分)如下:80,60,100,70,90.则这5名学生的平均成绩是____________,中位数是___________.试题14:如图所示,在△ABC中,,剪去∠A后,得到四边形BCDE,则________________.试题15:在△ABC中,AB = 2,,,则∠BAC的度数为________________.试题16:右图是由边长为1个单位长度的小正方形按一定的规律拼接而成的.依此规律,第6个图案中小正方形的个数为________________.试题17:在同一坐标系中,一次函数与反比例函数的图象有交点,则常数k的取值范围是________________.试题18:某音像公司对外出租光盘的收费方法是:每张光盘出租后的前2天每天收费0.8元,以后每天收费0.5元,那么一张光盘在出租第n天后(n > 2且为整数)应收费___________元.试题19:如图,⊙M与x轴交于点A(2,0),B(8,0),与y轴相切于点C,则圆心M的坐标是________________.试题20:如图,在等腰Rt△ABC中,,分别以AB、AC为边各向外作等边△ABD,等边△ACE,CD 、BE相交于点P,连接AP,有如下四个结论:①;②;③BE⊥BD;④AP∶AE =∶.其中正确的结论是________________.试题21:计算:试题22:求不等式组的自然数解.试题23:先化简,再求值:,其中a满足.试题24:如图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路记为BC.一辆以60 km/h 匀速行驶的汽车经过公路段BC的时间是3 s,已知广告牌和公路的距离是40 m,求小华家到公路的距离(精确到1m).试题25:某公司现有甲、乙两种品牌的计算器,甲品牌计算器有A、B、C三种不同的型号,乙品牌计算器有D、E两种不同的型号,某中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器.(1) 写出所有的选购方案(利用树状图或列表方法表示);(2) 如果(1)中各种选购方案被选中的可能性相同,那么A型号计算器被选中的概率是多少?(3) 现知该中学购买甲、乙两种品牌计算器共40个(价格如图所示)恰好用了1000元人民币,其中甲品牌计算器为A型号计算器,求购买的A型号计算器有多少个?试题26:如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点处,点A落在点处.1求证:;2设AE = a,AB = b,BF = c,试猜想a、b、c之间的一种关系,并给予证明.试题27:如图,二次函数的图象与x轴相交于A、B两点,与y轴相交于点C,点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(4) 求D点的坐标;(5) 求一次函数的表达式;(6) 根据图象写出使一次函数值大于二次函数值的x的取值范围.试题28:某校七年级、八年级两年级学生参加社会实践活动,原计划租用48座客车若干辆,但还有24人无座位坐.1设原计划租用48座客车x辆,试用含x的代数式表示这两个年级学生的总人数.2现决定租用60座客车,则可比原计划租48座客车少2辆,且所租60座客车中有一辆没有坐满,但这辆车已坐的座位超过36位.请你求出该校这两个年级学生的总人数.试题29:如图,已知直线交x轴于B,交y轴于C,并与直线y = x交于点A,点P在射线OA上从点O出发沿射线OA方向以每秒1个单位长的速度运动,过P作PQ // x轴交直线于Q,以PQ为边向下作正方形PQMN,设点P 的运动时间为t秒,正方形PQMN与△AOB的重叠部分的面积为S.①当点P在线段OA上且MN在x轴上时,求点P的坐标;②求S与t的函数关系式,并求对应的t的取值范围;③当点P在线段OA上时,求S的最大值.试题1答案:A试题2答案:B试题3答案:CB试题5答案: D试题6答案: C试题7答案: D试题8答案: D试题9答案: A试题10答案: D试题11答案:试题12答案:试题13答案:80分,80分260试题15答案: 105或15试题16答案: 61试题17答案:试题18答案:试题19答案:(5,4)试题20答案: ①②③④试题21答案: 解:原式试题22答案:解:由①得:2x > – 4x > – 2由②得:∴,又∵x是自然数∴x = 0,1,2试题23答案:解:原式由得a = 1或a = 2由题意,∴a = 1∴原式试题24答案:解:连结AD、AE,并延长分别交l于B、C,则BC为视点A的盲区,且m过点A作AM⊥BC于M交E于N,则AN⊥DE,MN = 40m∵DE∥BC∴解得(米)∴小华家到公路的距离约为133米。
浙江省嘉兴市海宁市新仓中学度八年级数学2月月考试题含解析新人

浙江省嘉兴市海宁市新仓中学度八年级数学2月月考试题含解析新人浙江省嘉兴市海宁市新仓中学XXXX八年级数学二月考试试题1、选择题(此题共10题,每题3分,共30分)1题。
在下面的模式中,轴对称图形是()a .b .c .d .2。
下列组不能是三角形的边。
它是()a.1,2,3b.2,3,4 c.3,4,5 d.4,5,63。
下面的语句是命题()a。
等腰三角形是一个轴对称图形b。
画一个等于已知角度d的角。
垂直线最短吗?4.在abc和def中,BC=EF,≅c = ∠C=∠F是已知的。
添加以下条件后,不能确定△ ABC ≌def为()a . AC = DFB . ab = de c .∠a =∠d . d .∠b =∠e5。
在平面直角坐标系中,点({2,3)的象限是()a .第一象限b .第二象限c .第三象限d .第四象限226。
为了证明命题“如果a > b,a > b”是一个假命题,下列a和b的值不能用作反例()a. a = 1,b = ﹣2b.a = 0,b = ﹣1 c.a = ﹣1,B =-2 d.a = 2,b =-17。
在数轴上表示不等式系统的解集,正确的解集是()a.b.c.8。
如果a > b,则下列类型中正确的一个是()a. a-3 c。
﹣a >﹣b·﹣2a d .9。
如果比例函数y = (1-2m) x的图像通过点A(x1,y1)和B(x2,y2),当x1 y2时,则m的值范围为()A . m 0c . m10。
以下图像是()1a .b .c .d .2,在11 △ ABC中,已知∠a = 100且∠b = 60,然后∠c = 0.12。
已知等腰三角形两边的长度分别为6和5。
那么它的周长是。
13。
直角三角形的两条直角边的长度分别为6和8,斜边中线的长度为。
14。
当x时,代数表达式-3x+5不大于2。
15。
如图所示,在Rt△ABC中,16。
点a (ʋ 3,1)关于x轴对称的坐标是。
金昌市八年级下学期月考数学试卷(2月份)

金昌市八年级下学期月考数学试卷(2月份)姓名:________ 班级:________ 成绩:________一、单选题 (共8题;共16分)1. (2分)下列说法中正确的是()A . -42的平方根是±4B . 把一个数先平方再开平方得原数C . -a没有平方根D . 正数a的算术平方根是2. (2分)下列说法中,正确的是()A . 形状和大小完全相同的两个图形成中心对称;B . 成中心对称的两个图形一定重合;C . 成中心对称的两个图形的形状和大小完全重合;D . 旋转后能重合的两个图形成中心对称。
3. (2分)为了了解参加某运动会的2 000名运动员的年龄情况,从中抽查了100名运动员的年龄,就这个问题来说,下面说法正确的是()A . 2 000名运动员是总体B . 每个运动员是个体C . 100名运动员是抽取的一个样本D . 100名运动员的年龄是抽取的一个样本4. (2分) (2019九上·宁波期中) 将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为()A . ﹣或﹣12B . ﹣或2C . ﹣12或2D . ﹣或﹣125. (2分)如图,点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,OA=10,OA′=20,则五边形ABCDE的面积与五边形A′B′C′D′E′的面积的比值是()A . 2:1B . 1:2C . 4:1D . 1:46. (2分)菱形的两条对角线的长分别为6和8,则菱形的高为()A .B .C .D .7. (2分) (2016九上·无锡开学考) 如图,在▱ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF 沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有()A . 2个B . 3个C . 4个D . 5个8. (2分)如图,菱形ABCD的两条对角线相交于点O,若AC=8,BD=6,过点D作DE⊥AB,垂足为E,则DE 的长是()A . 2.4B . 4.8C . 7.2D . 10二、填空题 (共10题;共11分)9. (1分)若式子有意义,则x的取值范围是________10. (1分)若将直线y=﹣2x+1向上平移3个单位,则所得直线的表达式为________.11. (1分)若我们把十位上的数字比个位和百位上的数字都小的三位数称为凹数,如:768,645.则由1,2,3这三个数字构成的,数字不重复的三位数是“凹数”的概率是________ .12. (1分)如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C 的坐标为________.13. (2分)的算术平方根为________;3﹣2的算术平方根是________.14. (1分)分式和的最简公分母是________.15. (1分)(2017·滨海模拟) 一次函数y=(k﹣3)x+2,若y随x的增大而增大,则k的取值范围是________.16. (1分) (2016七下·老河口期中) 已知正方形ABCD的三个顶点A(﹣4,0),B(0,0),C(0,4),则第四个顶点D的坐标为________.17. (1分) (2017八下·泰州期中) 如图,正方形ABCD的边长为4cm,E为CD边的中点,,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于________cm.18. (1分)如图,在平面直角坐标系中直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线y=x-2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式是________ .三、解答题 (共8题;共37分)19. (5分)计算:.20. (5分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC和△DEF的顶点都在格点上,结合所给的平面直角坐标系解答下列问题:(1)画出△A BC向上平移4个单位长度后所得到的△A1B1C1;(2)画出△DEF绕点O按顺时针方向旋转90°后所得到的△D1E1F1;(3)△A1B1C1和△D1E1F1组成的图形是轴对称图形吗?如果是,请直接写出对称轴所在直线的解析式.21. (1分)某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为________ 人.(注:横轴上每组数据包含最小值不包含最大值)22. (5分) (2016八下·东莞期中) 已知菱形ABCD中,对角线AC和BD相交于点O,∠BAD=120°,求∠ABD 的度数.23. (5分)如图,直线OB是一次函数y=2x的图象,点A的坐标是(0,2),点C在直线OB上且△ACO为等腰三角形,求C点坐标.24. (10分) (2017八下·苏州期中) 如图,在Rt△ABC中,∠BAC=90°,AB>AC ,射线AM平分∠BAC .(1)设AM交BC于点D,作DE⊥AB于点E,DF⊥AC于点F,连接EF.有以下三种“判断”:判断1:AD垂直平分EF.判断2:EF垂直平分AD.判断3:AD与EF互相垂直平分.你同意哪个“判断”?简述理由;(2)若射线AM上有一点N到△ABC的顶点B,C的距离相等,连接NB,NC.①请指出△NBC的形状,并说明理由;②当AB=11,AC=7时,求四边形ABNC的面积.25. (1分) (2019九下·温州竞赛) 如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线,将图形分成面积相等的两部分.则将直线l向右平移3个单位后所得到直线l’的函数关系式为________.26. (5分)如图,已知在□ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG。
2022-2023学年初二下2月质量检测 (数学)(含答案)060739

2022-2023学年初二下2月质量检测 (数学)试卷考试总分:115 分 考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________一、 选择题 (本题共计 6 小题 ,每题 5 分 ,共计30分 )1. 下列汽车标志中,可以看作是中心对称图形的是 A. B. C. D.2. 若等腰三角形的顶角为,则它的底角度数为( )A.B.C.D.3. 已知,则下列不等式中正确的是( )A.B.C.D.4. 如图,点,分别是的边和边上的点,且,=,是的角平分线,则的度数为A.B.C.()70∘45∘55∘6570∘a >b −3a >−3b−>−a 3b33−a >3−ba −3>b −3D E △ABC AB AC DE//BC∠AED 64∘EC ∠DEB ∠ECB ()78∘68∘58∘D.5. 如图,在三角形中,,将此三角形绕点按顺时针方向旋转后得到三角形,若点 恰好落在线段上,,交于点,则的度数是 ( )A.B.C.D.6. 如果不等式组的解集为,那么的取值范围是( )A.B.C.D.二、 填空题 (本题共计 6 小题 ,每题 5 分 ,共计30分 )7. 已知,则________.(填、或)8. 如图,矩形的顶点、在坐标轴上,点的坐标为,现将矩形绕其右下角顶点沿轴正方向做无滑动的翻滚,点翻滚第一次到达点,翻滚到第二次时到达点,则点经过的路线与坐标轴围成图形的面积为________.9. 如图,在中,,的垂直平分线与相交于点,则的周长为________.10. 如图,直角坐标系中,的顶点都在网格点上,其中,点坐标为.(1)写出点、的坐标:48∘ABC ∠ACB =,∠B =90∘50∘C C A ′B ′B ′AB AC A ′B ′O ∠COA ′80∘70∘60∘50∘{x+5<4x−1x >m x >2m m≤2m≥2m>2m<2a <b −4−a −4−b >=<OABC A C B (2,3)OABC x A A 1A 2A △ABC AB+AC =7cm BC l AC D △ABD cm △ABC C (1,2)A B________,________、________,________(2)将先向左平移个单位长度,再向上平移个单位长度,得到,则的三个顶点坐标分别是________,________、________,________、________,________.(3)的面积为________.11. 不等式组的正整数解有________个.12. 已知在中,,,.点是线段上的一个动点,过点作的垂线交射线于点.若为等腰三角形,则的长为________.三、 解答题 (本题共计 11 小题 ,每题 5 分 ,共计55分 )13. 解不等式,并把它的解集在数轴上表示出来.14. 解不等式组:15. 如图,在中, 的平分线交于点,且.如果点是边的中点, ,求的长. 16. 如图,在中,,,,分别表示,,的对边.已知,,求;已知,,求,. 17. 已知一次函数.(1)画出函数图象;(2)说出不等式解集是________;不等式解集是________;(3)求出函数图象与坐标轴的两个交点之间的距离.18. 如图所示,的三个顶点都在边长为的小正方形组成的网格的格点上,以点为原点建立直角坐标系,回答下列问题:A()B()△ABC 21△A'B'C'A'B'C'A'()B'()C'()△ABC 1−2x <3≤2x+12△ABC ∠ABC =90∘AB =3BC =4Q AC Q AC AB P △PQB AP ≤−1x−322x−13{4x−7>5(x−1),≤3−.x 3x−22△ABC ∠ABC BE AC E DE//BC D AB AB =10cm DB Rt △ABC ∠C =90∘a b c ∠A ∠B ∠C (1)c =10b =5a (2)b =6–√∠A =60∘c a y =−2x−6−2x−6>0−2x−6<0△ABC 1O将先向上平移个单位,再向右平移个单位得到,画出,并直接写出的坐标________;将绕点顺时针旋转得到,画出;观察图形发现,是由绕点________顺时针旋转________度得到的.19. 如图,等边三角形的边长为,为边上的一点,延长至,使,连接,交于点.求证若为的中点,求的长.20. 在我市中小学标准化建设工程中,某学校计划购进一批电脑和一体机,经过市场考察得知,购进台笔记本电脑和台一体机需要万元,购进台笔记本电脑和台一体机需要万元.求每台笔记本电脑、一体机各多少万元?根据学校实际,需购进笔记本电脑和一体机共台,总费用不超过万元,但不低于万元,请你通过计算求出几种购买方案,那种方案费用最低. 21. 在平面直角坐标系中,将如图放置,为原点,在轴负半轴上,,,把绕点逆时针旋转得到,使点在线段上,反比例函数的图象经过点.求的值;过点平行于的直线与反比例函数的图象相交于点,求点的坐标. 22. 阅读理解题在平面直角坐标系中,点到直线的距离公式为:,例如,求点到直线的距离.解:由直线知:,,(1)△ABC 51△A 1B 1C 1△A 1B 1C 1A 1(2)△A 1B 1C 1(0,−1)90∘△A 2B 2C 2A 2B 2C 2(3)A 2B 2C 2△ABC ABC 2D AC AB E BE =CD DE BC P (1)DP =PE(2)D AC BP 12 3.521 2.5(1)(2)303028Rt △AOB O OA x OB =2OA =23–√△AOB O △COD B CD y =(x <0)k xC (1)k (2)C AB y =(x <0)k x M M xOy P(,)x 0y 0Ax+By+C =0(+≠0)A 2B 2d =|A +B +C |x 0y 0+A 2B2−−−−−−−√P(1,3)4x+3y−3=04x+3y−3=0A =4B =3C =−3==2|4×1+3×3−3|所以到直线的距离为:根据以上材料,解决下列问题:(1)求点到直线的距离.2(1)自变量的取值范围是________P(1,3)4x+3y−3=0d ==2|4×1+3×3−3|+4232−−−−−−√(0,0)P 13x−4y−5=0(1,0)P x+y+C =02–√C x x参考答案与试题解析2022-2023学年初二下2月质量检测 (数学)试卷一、 选择题 (本题共计 6 小题 ,每题 5 分 ,共计30分 )1.【答案】A【考点】中心对称图形【解析】根据中心对称图形的性质得出图形旋转,与原图形能够完全重合的图形是中心对称图形,分别判断得出即可.【解答】解:,旋转,与原图形能够完全重合是中心对称图形,故符合题意;,旋转,不能与原图形能够完全重合不是中心对称图形,故不符合题意;,旋转,不能与原图形能够完全重合不是中心对称图形,故不符合题意;,旋转,不能与原图形能够完全重合不是中心对称图形,故不符合题意;故选.2.【答案】B【考点】等腰三角形的性质【解析】由已知顶角为,根据等腰三角形的两底角相等的性质及三角形内角和定理,即可求出它的一个底角的值.【解答】解:∵等腰三角形的顶角为,∴它的一个底角为.故选.3.【答案】D【考点】不等式的性质【解析】看各不等式是加(减)什么数,或乘(除以)什么数得到的,再判断用不用变号.【解答】、不等式两边都乘以,不等号的方向改变,,故错误;180∘A 180∘B 180∘C 180∘D 180∘A 70∘70∘(−)÷2=180∘70∘55∘B A −3−3a <−3b A <−b、不等式两边都除以,不等号的方向改变,,故错误;、同一个数减去一个大数小于减去一个小数,,故错误;、不等式两边都减,不等号的方向不变,故正确.4.【答案】C【考点】角平分线的性质平行线的性质【解析】首先根据角平分线的定义求出的度数,然后根据平行线的性质得到的度数.【解答】解:∵=,∴==,∵是的角平分线,∴==,∵,∴=,∴=.故选.5.【答案】C【考点】旋转的性质【解析】【解答】解:∵在三角形中,=,=,∴==.由旋转的性质可知:=,∴==.又∵==,∴=,∴====.故选.6.【答案】A【考点】解一元一次不等式组B −3−<−a 3b 3BC 3−a <3−b CD 3D ∠DEC ∠ECB ∠AED 64∘∠DEB −180∘64∘116∘EC ∠DEB ∠DEC ∠CEB =∠DEB =×1212116∘58∘DE//BC ∠DEC ∠ECB ∠ECB 58∘C ABC ∠ACB 90∘∠B 50∘∠A −∠ACB−∠B 180∘40∘BC B'C ∠B ∠BB'C 50∘∠BB'C ∠A+∠ACB'+∠ACB'40∘∠ACB'10∘∠COA'∠AOB'∠OB'C +∠ACB'∠B+∠ACB'60∘C【解析】此题暂无解析【解答】解:∵解①得,解②得,∵不等式组 的解集为 ,根据大大取大的原则,∴故选.二、 填空题 (本题共计 6 小题 ,每题 5 分 ,共计30分 )7.【答案】【考点】不等式的性质【解析】根据不等式的性质求解即可.【解答】解:两边都乘以,得,两边都加,得,故答案为:.8.【答案】【考点】坐标与图形变化-旋转轨迹矩形的性质【解析】此题暂无解析【解答】此题暂无解答9.【答案】【考点】{x+5<4x−1①x >m ②k >2x >m {x+5<4x−1x >mx >2m≤2A >−1−a >−b −4−4−a >−4−b >7线段垂直平分线的性质【解析】本题考查线段垂直平分线的性质.【解答】解:的垂直平分线交于故答案为:.10.【答案】,,,,,,,,【考点】坐标与图形变化-平移【解析】(1)在第四象限,横坐标为正,纵坐标为负;的第一象限,横纵坐标均为正;(2)让三个点的横坐标减,纵坐标加即为平移后的坐标;的面积等于边长为,的长方形的面积减去个边长为,和一个边长为,的直角三角形的面积,把相关数值代入即可求解.【解答】写出点、的坐标:、将先向左平移个单位长度,再向上平移个单位长度,得到,则的三个顶点坐标分别是、、.的面积==.11.【答案】【考点】一元一次不等式组的整数解【解析】【解答】解:解方程组可得即,∵BC AC D∴BD =CD∵AB+AC =7cm∴AB+AD+BD =AB+AD+CD =AB+AC =7cm72−1430024−135A B 21(3)△ABC 3421324A B A(2,−1)B(4,3)△ABC 21△A'B'C'A'B'C'A'(0,0)B'(2,4)C'(−1,3)△ABC 3×4−2××1×3−×2×4121253{x >−1,x ≤3,−1<x ≤3正整数有.故答案为:.12.【答案】或【考点】相似三角形的性质相似三角形的判定直角三角形斜边上的中线勾股定理等腰三角形的性质【解析】(2)当为等腰三角形时,有两种情况,需要分类讨论.当点在线段上时,如题图所示.由三角形相似关系计算的长;当点在线段的延长线上时,如题图所示.利用角之间的关系,证明点为线段的中点,从而可以求出.【解答】解:在中,,,由勾股定理得:.①当点在线段上时,如图所示.∵为钝角,∴当为等腰三角形时,只可能是.∵,∴,在与中,∵,,∴.∴,即,解得:,∴;②当点在线段的延长线上时,如图所示.∵为钝角,∴当为等腰三角形时,只可能是.∵,∴,∵,,∴,∴,∴,点为线段中点,1,2,33536△PQB (I)P AB 1(△AQP ∽△ABC)AP (II)P AB 2B AP AP Rt △ABC AB =3BC =4AC =5P AB 1∠QPB △PQB PB =PQ PQ ⊥AQ ∠AQP ==∠ABC 90∘△APQ △ABC ∠AQP ==∠ABC 90∘∠A =∠A △AQP ∼△ABC =PA AC PQ BC =3−PB 5PB 4PB =43AP =AB−PB =3−=4353P AB 2∠QBP △PQB PB =BQ BP =BQ ∠BQP =∠P ∠BQP +∠AQB =90∘∠A+∠P =90∘∠AQB =∠A BQ =AB AB =BP B AP∴.综上所述,当为等腰三角形时,的长为或.故答案为:或.三、 解答题 (本题共计 11 小题 ,每题 5 分 ,共计55分 )13.【答案】解:去分母得,,去括号得,,移项、合并同类项得,,把的系数化为得,,在数轴上表示为:;【考点】解一元一次不等式在数轴上表示不等式的解集【解析】(1)先去分母,再去括号,移项、合并同类项,把的系数化为,并在数轴上表示出来即可;【解答】解:去分母得,,去括号得,,移项、合并同类项得,,把的系数化为得,,在数轴上表示为:;14.【答案】解:解不等式组: 由①式解得 .由②式解得 .在同一条数轴上表示不等式①和②的解集,如图,所以,原不等式组的解集为: .【考点】解一元一次不等式组【解析】此题暂无解析【解答】AP =2AB =2×3=6△PQB AP 5365363(x−3)≤2(2x−1)−63x−9≤4x−2−6−x ≤1x 1x ≥−1x 13(x−3)≤2(2x−1)−63x−9≤4x−2−6−x ≤1x 1x ≥−1 4x−7>5(x−1)①,≤3−②,x 3x−22x <−2x ≤245x <−2 4x−7>5(x−1)①,解:解不等式组: 由①式解得 .由②式解得 .在同一条数轴上表示不等式①和②的解集,如图,所以,原不等式组的解集为: .15.【答案】解:平分,,,,,,是的中点,,.【考点】角平分线的性质平行线的性质【解析】根据角平分线性质,平行线性质定理即可求出答案.【解答】解:平分,,,,,,是的中点,,.16.【答案】解:∵在中,,,,由得,解得.∵,,.,.由得,解得.【考点】勾股定理4x−7>5(x−1)①,≤3−②,x 3x−22x <−2x ≤245x <−2∵BE ∠ABC ∴∠ABE =∠CBE ∵DE//BC ∴∠DEB =∠CBE ∴∠ABE =∠DEB ∴BD =DE ∵D AB ∵AD =BD ∴DE =AB =×10=5cm 1212∵BE ∠ABC ∴∠ABE =∠CBE ∵DE//BC ∴∠DEB =∠CBE ∴∠ABE =∠DEB ∴BD =DE ∵D AB ∵AD =BD ∴DE =AB =×10=5cm 1212(1)Rt △ABC ∠C =90∘c =10b =5=+c 2a 2b 2=+102a 252a =53–√(2)∠A =60∘∠C =90∘∴∠B =30∘∵b =6–√∴c =26–√=+c 2a 2b 2(2=+(6–√)2a 26–√)2a =32–√含30度角的直角三角形【解析】(1)设,则,再根据勾股定理求出的值即可得出结论;(2)根据锐角三角函数的定义即可得出、的值.【解答】解:∵在中,,,,由得,解得.∵,,.,.由得,解得.17.【答案】;.,(3)∵,,∴,,∴.【考点】一次函数与一元一次不等式一次函数的图象【解析】(1)分别将、代入一次函数,求出与之相对应的、值,由此即可得出点、的坐标,连点成线即可画出函数图象;(2)根据一次函数图象与轴的上下位置关系,即可得出不等式的解集;(3)由点、的坐标即可得出、的长度,再根据勾股定理即可得出结论.(或者直接用两点间的距离公式也可求出结论)【解答】解:(1)当时,,∴一次函数与轴交点的坐标为;当时,解得:,∴一次函数与轴交点的坐标为.描点连线画出函数图象,如图所示.(2)观察图象可知:当时,一次函数的图象在轴上方;当时,一次函数的图象在轴下方.∴不等式解集是;不等式解集是.(3)∵,,∴,,∴.18.【答案】解:如图所示,即为所求,由题可得;a =4xb =3x x bc (1)Rt △ABC ∠C =90∘c =10b =5=+c 2a 2b 2=+102a 252a =53–√(2)∠A =60∘∠C =90∘∴∠B =30∘∵b =6–√∴c =26–√=+c 2a 2b 2(2=+(6–√)2a 26–√)2a =32–√x <−3x >−3x <−3x >−3B(−3,0)C(0,−6)OB =3OC =6BC ==3O +O B 2C 2−−−−−−−−−−√5–√x =0y =0y =−2x−6y x C B x B C OB OC x =0y =−2x−6=−6y =−2x−6y C (0,−6)y =−2x−6=0x =−3y =−2x−6x B (−3,0)x <−3y =−2x−6x x >−3y =−2x−6x −2x−6>0x <−3−2x−6<0x >−3B(−3,0)C(0,−6)OB =3OC =6BC ==3O +O B 2C 2−−−−−−−−−−√5–√(1)△A 1B 1C 1(−3,4)A 1如图所示,即为所求;,【考点】作图-旋转变换作图-平移变换【解析】(1)根据网格结构找出点、、平移后的对应点、、的位置,然后顺次连接即可,再根据平面直角坐标系写出点的坐标;(2)根据网格结构找出点、、绕点顺时针旋转的对应点、、的位置,然后顺次连接即可;(3)作对应点与、与的连线的垂直平分线,交点即为旋转中心,再根据图形确定出旋转角度数即可.【解答】解:如图所示,即为所求,由题可得;如图所示,即为所求;(2)△A 2B 2C 2(2,−4)90A B C A 1B 1C 1A 1A 1B 1C 1(0,−1)90∘A 2B 2C 2A A 2B B 2(1)△A 1B 1C 1(−3,4)A 1(2)△A 2B 2C 2连接,,,作这三条线段的垂直平分线,其交点即为所求的旋转中心,即为旋转角,如图所示,是由绕点顺时针旋转度得到的.19.【答案】证明:作,交于点.∴,.∵为等边三角形,∴为等边三角形,∴,∴,∴.解:若为的中点,则也是的中点,由()知,.【考点】等边三角形的性质全等三角形的判定全等三角形的性质【解析】【解答】证明:作,交于点.∴,.∵为等边三角形,∴为等边三角形,∴,(3)AA 2BB 2CC 2O ′∠CO ′C 2△A 2B 2C 2△ABC (2,−4)90(1)DF//AB BC F ∠PDF =∠E ∠PFD =∠PBE △ABC △CDF CD =DF =BE △DPF ≅△EPB DP =PE (2)D AC F BC 1FP =PB BP =0.5(1)DF//AB BC F ∠PDF =∠E ∠PFD =∠PBE △ABC △CDF CD =DF =BE∴,∴.解:若为的中点,则也是的中点,由()知,.20.【答案】解:设每台笔记本电脑万元,每台一体机万元,根据题意得:解得:答:每台笔记本电脑万元,每台一体机万元;设需购进笔记本电脑台,则购进一体机台,根据题意得:解得:,∵为正整数,∴,,.∴共有三种方案:方案一:购进笔记本电脑台,一体机台,总费用为(万元);方案二:购进笔记本电脑台,一体机台,总费用为(万元);方案三:购进笔记本电脑台,一体机台,总费用为(万元).∵,∴选择方案三最省钱,即购买电脑台,电子白板台最省钱.【考点】二元一次方程组的应用——销售问题一元一次不等式组的应用【解析】(1)先设每台电脑万元,每台一体机万元,根据购进台笔记本电脑和台一体机需要万元,购进台笔记本电脑和台一体机需要万元,列出方程组,求出,的值即可;(2)设需购进笔记本电脑台,则购进一体机台,根据需购进笔记本电脑和一体机共台,总费用不超过万元,但不低于万元,列出不等式组,求出的值,再根据每台电脑的价格和一体机的价格,算出总费用,再进行比较,即可得出最省钱的方案.【解答】解:设每台笔记本电脑万元,每台一体机万元,根据题意得:解得:答:每台笔记本电脑万元,每台一体机万元;设需购进笔记本电脑台,则购进一体机台,根据题意得:解得:,∵为正整数,∴,,.∴共有三种方案:方案一:购进笔记本电脑台,一体机台,总费用为(万元);方案二:购进笔记本电脑台,一体机台,总费用为(万元);方案三:购进笔记本电脑台,一体机台,总费用为(万元).△DPF ≅△EPB DP =PE (2)D AC F BC 1FP =PB BP =0.5(1)x y {x+2y =3.5,2x+y =2.5,{x =0.5,y =1.5,0.5 1.5(2)a (30−a){0.5a +1.5(30−a)≤30,0.5a +1.5(30−a)≥28,15≤a ≤17a a =151617151515×0.5+1.5×15=30161416×0.5+1.5×14=29171317×0.5+1.5×13=2828<29<301713x y 12 3.5212.5x y a (30−a)303028a (1)x y {x+2y =3.5,2x+y =2.5,{x =0.5,y =1.5,0.5 1.5(2)a (30−a){0.5a +1.5(30−a)≤30,0.5a +1.5(30−a)≥28,15≤a ≤17a a =151617151515×0.5+1.5×15=30161416×0.5+1.5×14=29171317×0.5+1.5×13=28∵,∴选择方案三最省钱,即购买电脑台,电子白板台最省钱.21.【答案】解:过点作垂直轴,垂足为点,∵,,,∴.∵,∴.∵,∴,,∴点坐标为,∴.设直线解析式为,∵直线过点,,∴∴,.∵,∴直线:过点,∴.联立方程组∴(舍去),,∴点坐标为.【考点】含30度角的直角三角形待定系数法求反比例函数解析式旋转的性质反比例函数与一次函数的综合待定系数法求一次函数解析式【解析】无无【解答】解:过点作垂直轴,垂足为点,28<29<301713(1)C CF x F ∠AOB =90∘AO =23–√BO =2∠ABO =60∘OB =OD ∠BOD =∠COA =60∘OC =OA =23–√OF =3–√CF =3C (−,3)3–√k =−33–√(2)AB y =kx+b AB (0,2)(−2,0)3–√{b =2,−2k +b =0,3–√k =3–√3b =2AB//CM CM y =x+3–√3b 1C(−,3)3–√=4b 1 y =x+4,3–√3y =−,33–√x =−x 13–√=−3x 23–√M (−3,1)3–√(1)C CF x F∵,,,∴.∵,∴.∵,∴,,∴点坐标为,∴.设直线解析式为,∵直线过点,,∴∴,.∵,∴直线:过点,∴.联立方程组∴(舍去),,∴点坐标为.22.【答案】;,∴,∴,∴,.【考点】一次函数图象上点的坐标特点【解析】(1)根据点到直线的距离公式即可求解;(2)根据点到直线的距离公式,列出方程即可解决问题.【解答】;,∴,∴,∴,.23.∠AOB =90∘AO =23–√BO =2∠ABO =60∘OB =OD ∠BOD =∠COA =60∘OC =OA =23–√OF =3–√CF =3C (−,3)3–√k =−33–√(2)AB y =kx+b AB (0,2)(−2,0)3–√{b =2,−2k +b =0,3–√k =3–√3b =2AB//CM CM y =x+3–√3b 1C(−,3)3–√=4b 1 y =x+4,3–√3y =−,33–√x =−x 13–√=−3x 23–√M (−3,1)3–√d ==1|3×0−4×0−5|+3242−−−−−−√=2–√|1×1+1×0+C |2–√|C +1|=2C +1=±2=−3C 1=1C 2d ==1|3×0−4×0−5|+3242−−−−−−√=2–√|1×1+1×0+C |2–√|C +1|=2C +1=±2=−3C 1=1C 2【答案】,描点、连线,画出函数图象,如图所示.观察函数图象,可找出函数性质:①函数图象关于原点中心对称;②当时,的值随值的增大而增大.或【考点】一次函数的性质一次函数的图象反比例函数的图象【解析】(1)由在分母上,即可得出自变量的取值范围是,将=代入函数关系式中即可求出值;(2)描点、连线,补充函数图象;(3)观察函数图象,随便找出两条该函数的性质即可;(4)①观察函数图象,由函数=的图象与直线=的交点的个数,可得出结论;②观察函数图象,找出当或时,函数=的图象与直线=有两个交点,此题得解.【解答】∵在分母上,∴.当=时,==.故答案为:;.描点、连线,画出函数图象,如图所示.观察函数图象,可找出函数性质:①函数图象关于原点中心对称;②当时,的值随值的增大而增大.①方程可看成函数=的图象与直线=的交点的个数,∵函数=的图象与直线=有两个交点,∴方程有个实数根.故答案为:.②观察函数图象可知,当或时,函数=的图象与直线=有两个交点.故答案为:或.x ≠0−52x >1y x t <−2t >2x x x ≠0x −2m y x+1x y 3t <−2t >2y x+1x y t x x ≠0x −2m y −2+=−1−252x ≠0−52x >1y x x+=31x y x+1x y 3y x+1x y 3x+=31x 22t <−2t >2y x+1x y t t <−2t >2。
广东省河源市田家炳实验中学2022-2023学年八年级下学期2月数学测试题(含答案解析)

广东省河源市田家炳实验中学2022-2023学年八年级下学期2月数学测试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.计算23x x ⋅的结果正确的是()A .5x B .6x C .8x D .52.下列各计算中,正确的是()A .5552b b b ⋅=B .5510x x x +=C .235m m m ⋅=D .222a b a b ⋅=3.若3×9m×27m =311,则m 的值为()A .4B .3C .5D .24.下列结果正确的是()A .()3322x x -=B .()3322x x -=-C .()2224x x -=D .()2224x x -=-5.甲型H1N1流感病毒的直径大约是0.000000081米,用科学记数法可表示为()A .8.1×10﹣9米B .8.1×10﹣8米C .81×10﹣9米D .0.81×10﹣7米6.1纳米0.000000001=米,则2.5纳米用科学记数法表示为()A .82.510-⨯米B .92.510-⨯米C .102.510-⨯米D .92510⨯米7.长方形相邻两边的长分别是3a b +与2a b -,那么这个长方形的面积是()A .22233a ab b --B .22253a ab b ++C .22253a ab b ++D .22253a ab b +-8.()()(a b a b -+=)A .22a b +B .22a b -C .222a ab b ++D .222a ab b -+9.如图,两个正方形边长分别为a 、b ,且满足a +b =10,ab =12,图中阴影部分的面积为()A .100B .32C .144D .36二、填空题10.计算:53a a a ⋅⋅=________.11.计算:()0223---=____.12.计算:(π﹣5)0=_____.13.已知3a b +=,1a b -=,则22a b -=__________.14.计算:()22x -=____.15.计算:(﹣2a )2÷a=__.16.观察下列各等式:22x x -=-22(2)(2)2x x x -+=-233(2)(24)2x x x x -++=-3244(2)(248)2x x x x x -+++=-……请你猜想:若55()A x y x y ∙+=+,则代数式A =___.三、解答题17.计算:(π﹣3.14)0+(﹣3)﹣2+2sin30°.18.计算下列各式:(1)(3x +5)(2x -3)(2)(8x 3y 3-4x 3y 2+x 2y 2)÷(-2xy )219.计算:()()()3114x x x x x-+--÷20.3113m n n y y y -+⋅=,且146m n x x x --⋅=,求m ,n 的值.21.阅读材料解决问题:当a ﹣b >0时,一定有a >b ;当a ﹣b =0时,一定有a =b ;当a ﹣b <0时,一定有a <b .(1)用“>”或“<”填空:∵(a+1)﹣(a ﹣1)0,∴(a+1)(a﹣1);(2)已知n 为自然数,P =(n+1)(n+4),Q =(n+2)(n+3),试比P 与Q 的大小;(3)已知A =654321×654324,B =654322×654323,直接写出A 与B 的大小比较结果.22.阅读下文,寻找规律:已知1x ≠,观察下列各式:()()2111x x x -+=-,()()23111x x x x -++=-,()()234111x x x x x -+++=-L(1)填空:()1x -81x =-.(2)观察上式,并猜想:①()()211nx x x x -++++=.②()()10911x x x x -++++=.(3)根据你的猜想,计算:①()()234512122222-+++++=.②2342007122222++++++= .23.(1)计算下列各式,并寻找规律:①()()211________________2-=+-=________;②()()211____________3____-=+-=________;(2)运用(1)中所发现的规,计算:2222111111112345⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭;(3)猜想222222111111111111234910n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫------ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭的结果,并写出推理过程.24.图①是一个长为2m 、宽为2n 的长方形,沿图中虚线用剪刀分成四块小长方形,然后按图②的形状拼成一个正方形.(1)请和两种不同的方法求图②中阴影部分的面积.方法1:__方法2:___(2)观察图②请你写出下列三个代数式;22(),(),m n m n +-mn 之间的等量关系;(3)根据(2)题中的等量关系,解决如下问题:①已知:3,2,a b ab -==-求2()a b +的值.②已知:21a a -=,求2a a+的值.参考答案:1.A【分析】利用同底数幂的乘法直接得到答案.【详解】解:原式=23x +=5x .故选:A .【点睛】本题考查的是同底数幂的乘法,掌握同底数幂的乘法法则是解题关键.2.C【分析】运用整式的加减或乘除规则运算.【详解】A.5552b b b ⋅=错误,应改为5510b b b ⋅=B.5510x x x +=错误,应改为5552x x x +=C.235m m m ⋅=正确D.222a b a b ⋅=错误,应改为22a b ab ⋅=所以选C【点睛】整式的乘除和加减规则要分清.3.D【详解】2312311 392733333m m m m m m ++⋅⋅=⋅⋅==∴1+2m+3m=11,解得m=2.故选D.点睛:本题考查了合并同类项,同底数幂的乘法,幂的乘方,积的乘方,理清指数的变化是解题的关键.4.C【分析】根据积的乘方的运算法则直接计算即可得出答案.【详解】解:A.()32x -=﹣8x 3,故选项A 不合题意;B.()32x -=﹣8x 3,故选项B 不合题意;C.()22x -=4x 2,正确,故选项C 符合题意;D.()22x -=4x 2,故选项D 不合题意.故选:C .【点睛】本题考查的知识点是积的乘方运算法则,掌握运算法则是解题的关键.5.B【详解】0.000000081=8.1×10﹣8米.故选B.6.B【分析】根据绝对值小于1的数可以用科学记数法表示,一般形式为10n a -⨯,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定,即可求解.【详解】解:2.5纳米0.0000000025=米92.510-=⨯米.故选:B【点睛】本题考查用科学记数法表示较小的数,熟练掌握一般形式为10n a -⨯,其中110a ≤<,n 为由原数左边起第一个不为零的数字前面的0的个数所决定是解题的关键.7.D【分析】利用长方形的面积公式和多项式乘多项式的法则,进行计算即可.【详解】解:长方形的额面积为:()()2222533a b a a ab b b -+-+=;故选D .【点睛】本题考查多项式乘多项式与几何图形的面积问题.熟练掌握多项式乘多项式法则,是解题的关键.8.B【分析】利用平方差公式计算即可.【详解】解:(a-b)(a+b)=a 2-b 2.故选B.【点睛】本题考查了平方差公式,熟记公式是解题的关键.9.B【分析】将a +b =10两边平方,利用完全平方公式展开,将ab 的值代入求出a 2+b 2的值,即为两正方形的面积之和;由两个正方形的面积减去两个直角三角形的性质即可求出阴影部分面积.【详解】解:如图所示,将a +b =10两边平方得:(a +b )2=a 2+b 2+2ab =100,将ab =12代入得:a 2+b 2+24=100,即a 2+b 2=76,则两个正方形面积之和为76;∴S 阴影=S 两正方形−S △ABD −S △BEF =a 2+b 2−12a 2−12b(a +b)=12(a 2+b 2−ab)=12×(76−12)=32,故答案为:B .【点睛】此题考查了整式的混合运算,以及化简求值,熟练掌握完全平方公式是解本题的关键.10.9a 【分析】根据同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,进行计算即可.【详解】原式5319.a a ++==故答案为:9.a .【点睛】本题考查了同底数幂的乘法,解答本题的关键是掌握同底数幂的乘法法则.11.89【分析】利用0指数幂和负整数指数幂的定义即可求解.【详解】解:原式=18199-=,故答案为:89.【点睛】本题考查了0指数幂和负整数指数幂,解题关键是牢记它们的定义,即任何非零数的零次幂等于1和()10ppx x x -=≠.12.1.【分析】根据零指数幂:a 0=1(a ≠0)求解可得.【详解】解:(π﹣5)0=1,故答案为:1.【点睛】本题考查了零指数幂的定义,掌握零指数幂定义是关键.13.3【分析】根据平方差公式即可计算求解.【详解】解:∵()()22a b a b a b -=+-,∴22313a b -=⨯=,故答案为:3.【点睛】本题主要考查了平方差公式,解题的关键在于能熟记平方差公式进行求解.14.244-+x x 【分析】利用完全平方公式求解即可.【详解】解:原式=244x x -+,故答案为:244x x -+.【点睛】本题考查了完全平方差公式,解题关键是掌握()2222a b a ab b -=-+.15.4a【分析】本题是积的乘方与同底数幂的除法的混合运算,求解时按照各自的法则运算即可.【详解】解:(﹣2a )2÷a=4a 2÷a=4a .故答案为:4a .16.432234x x y x y xy y -+-+【分析】观察一系列等式即可得到一般性规律.【详解】∵43223455()()x x y x y xy y x y x y -+-+∙+=+∴A=432234x x y x y xy y -+-+故答案为:432234x x y x y xy y -+-+.【点睛】此题考查了平方差公式,弄清题中的规律是解本题的关键.17.19.【分析】分别根据0指数幂及负整数指数幂的运算法则、特殊角的三角函数值及二次根式运算,计算出各数,再根据实数混合运算的法则进行计算即可.【详解】解:(π﹣3.14)0+(﹣3)﹣2+2sin30°=1+19﹣2+2×12=19.【点睛】本题考查的是特殊角的三角函数值以及实数的运算,熟记实数混合运算的法则是解答此题的关键.18.(1)2615x x +-;(2)124xy x -+【分析】(1)根据多项式乘以多项式的运算法则计算;(2)根据多项式除以单项式的运算法则计算.【详解】解:(1)原式=2691015x x x -+-=2615x x +-;(2)原式=()()()33223222222284444x y x y x y x y x y x y÷-÷+÷=124xy x -+【点睛】本题考查了多项式乘以多项式,多项式除以单项式,解题的关键是掌握运算法则.19.3【分析】首先根据平方差公式和多项式除以单项式把括号展开,再合并同类项即可得到结果.【详解】()()()3114x x x x x -+--÷=()2214x x ---2214x x =--+3=【点睛】此题主要考查了整式的混合运算,正确利用乘法公式是解题的关键.20.m 的值为6,n 的值为3【分析】根据同底数幂乘法法则列出两个二元一次方程建立方程组求解即可.【详解】解:∵312113m n n m n y y y y -+++⋅==,故2113m n ++=,即212m n +=,∵1436m n m n x x x x ---+⋅==,故36m n -+=,即3m n -=,则有2123m n m n +=⎧⎨-=⎩,解得63m n =⎧⎨=⎩,∴m 的值为6,n 的值为3.【点睛】本题考查了同底数幂的乘法,涉及到了二元一次方程组,解题关键是掌握同底数幂相乘,底数不变,指数相加.21.(1)>,>;(2)P <Q ;(3)A <B .【分析】(1)根据材料用作差法结合整式的加减计算即可得解;(2)结合已知,运用作差法,再运用整式的加减即可比较大小;(3)设n =654320,将A ,B 分别用含n 的代数式表示出来,再运用作差法比较即可.【详解】解:(1)∵(a+1)-(a-1)=a+1﹣a+1=2>0∴(a+1)>(a ﹣1)故答案为>,>.(2)∵P =(n+1)(n+4),Q =(n+2)(n+3),∴P-Q=(n+1)(n+4)-(n+2)(n+3)=n 2+5n+4﹣n 2﹣5n ﹣6=-2<0∴P<Q .(3)设n =654320,∴A=(n+1)(n+4)=n 2+5n+4B=(n+2)(n+3)=n 2+5n+6,∵n 2+5n+4<n 2+5n+6∴A<B .【点睛】本题考查的知识点主要是整式的加减运算,,此类题目是间接的整式加减问题,熟练掌握作差法是解题的关键.22.(1)()2345671x x x x x x x +++++++(2)①11n x +-;②111x -(3)①612-;②200821-【分析】归纳概括规律:等号左边为两个因式的乘积,第一个为()1x -,第二个为x 连续指数的和;等号的右边为两个数的差,被减数为1,减数为x 的幂,指数比等号前面第二个因式中,最大指数多1,然后将下面式子分别代入即可.【详解】(1)解: 81x -中,指数为8,故前面应该加到7x 答案为:()2345671x x x x x x x +++++++(2)解:①根据规律可得:()()211n x x x x -++++= 11n x +-②()()10911x x x x -++++= ()()()10911111111x x x x x x -++++=--=-- (3)解:①()()234512122222-+++++中,让2x =得:()()234561212222212-+++++=-②2342007122222++++++= ()()()23420071222221212+++++-+- 2008200812211-==--【点睛】本题考查了归纳概括能力,以及类比思想,准确找出规律是解题关键.23.(1)①1,12,1,12;34;②1,13,1,13;89;(2)35;(3)12n n +.【分析】(1)根据平方差公式计算即可;(2)先根据平方差公式化简,再进行约分计算即可;(3)根据(2)解题思路,先根据平方差公式化简,再进行约分计算即可.【详解】解:(1)①211131112224⎛⎫⎛⎫-=+-= ⎪⎪⎝⎭⎝⎭;②211181113393⎛⎫⎛⎫-=+-= ⎪⎝⎭⎝⎭;(2)原式11111111=11+11+11+11+22334455⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭1324354622334455=⋅⋅⋅⋅⋅⋅⋅35=;(3)原式111111=11+11+11+2233n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫--- ⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 132411122332n n n n n n -++=⋅⋅⋅⋅= .【点睛】本题是对平方差公式的考查,熟练掌握平方差公式和找到约分规律是解决本题的关键,难度适中.24.(1)(m +n )2−4mn ;(m−n )2(2)(m +n )2−4mn =(m−n )2(3)①1②±3【分析】(1)大正方形的面积减去矩形的面积即可得出阴影部分(小正方形)的面积;(2)由面积关系容易得出结论;(3)①根据(2)所得出的关系式,容易求出结果;②先求出(2a a+)2,即可得出结果.【详解】(1)方法1:(m +n )2−4mn ,方法2:(m−n )2;故答案为:(m +n )2−4mn ;(m−n )2;(2)22(),(),m n m n +-mn 之间的等量关系为:(m +n )2−4mn =(m−n )2;(3)①(a +b )2=(a−b )2+4ab =32+4×(−2)=1;②∵(a+2a)2=(a−2a)2+4×a×2a=12+8=9,∴a+2a=±3.【点睛】本题考查了完全平方公式的几何背景,正方形和矩形面积的计算;注意仔细观察图形,表示出各图形的面积是关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年八年级数学2月奖学金测试题
一、选择题:(每题3分,共30分)
1.下列说法正确的是 ( )
A.9的立方根是 3 B.算术平方根等于它本身的数一
定是1
C.-2是4的平方根D.16的算术平方根是4
2.在,,,,0.202 002 000 2,中,无理数的个数有( ) A.6个 B.5个 C.4个 D.3个
3.下列运算中,正确的是()
A.B. C. D.
4.对任意实数x,点P(x,-2x+3)一定不在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在直角坐标系x o y中,已知点A(0,2),B(1,3),则线段AB的长度是()
A.1 B. C. D.2
6.已知一次函数y=kx+b的图象如图所示,则k、b的取值范围是 ( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b<0 D.k<0,b>0
7.在直线y=x+且到x轴或y轴距离为1的点有 ( )个
A.1 B.2 C.3 D.4
8.在平面直角坐标系xOy中,点(1,-3)关于x轴对称的点的坐标为( )
A.(-3,1) B.(-1,3) C.(-1,-3) D.(1,3)
9.如图,在平面直角坐标系xOy中,已知AD平分∠OAB,DB⊥AB,BC//OA,点D的坐标为
D(0,),点B的横坐标为1,则点C的坐标是( )
A.(0,2) B.(0,+)C.(0,)D.(0,5)
10.已知A、B两地相距900 m,甲、乙两人同时从A地出发,以相同速度匀速步行,20 min
后到达B地,甲随后马上沿原路按原速返回,回到A地后在原地等候乙回来;乙则在B地
停留10 min后也沿原路以原速返回A地,则甲、乙两人之间的距离s(m)与步行时间t(min)
之间的函数关系可以用图象表示为( )
二、填空题:(每题3分,共24分)
11.函数y=的自变量x的取值范围为______.
12.已知点P(a,b)在一次函数y=x+1的图象上,则b-a=.
13.如果+(y+6)2=0,那么2x-y的立方根为_______.
14.如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
∠ADB=100,则∠BAC的度数为°.
15.已知等腰三角形ABC的周长为8 cm,AB=3 cm.则BC=______ _cm.
16.过点(-1,-3)且与直线y=1-2x平行的直线是_______.
17.已知关于x的分式方程有增根,则a=_______.
18.一次函数y=-2x+b的图象与两坐标轴所围成的三角形的面积为9,则b=______.
三、解答题:(共46分)
19.计算:(10分)
(1)
(2)
2
22
21211
11
a a a
a a a a
+-+
•-
--+
,其中.
20.解方程:(10分)
(1) (2)
21.(8分)如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,BE、CD相交于点O.
(1)若BD=CE,试说明:OB=OC,
(2)若BC=10,BC边上的中线AM=12,试求AC的长.
22.(8分)已知一次函数y=kx+b的图象经过点(1,5),且与正比例函数y=x的图象相交于点(2,a).求:
(1)a的值;
(2)k,b的值;
(3)这两个函数图象与x轴所围成的三角形面积.
23.(10分)如图,已知点A的坐标为(2,4),在点A处有二只蚂蚁(忽略其大小),它们同时出发,一只以每秒1个单位的速度垂直向上爬行,另一只同样以每秒1个单位的速度水平向右爬行,t秒后,它们分别到达B、C处,连接BC.若在x轴上有两点D、E,满足DB=OB,EC=OC,则
(1)当t=l秒时,求BC的长度;
(2)证明:无论t为何值,DE=2AC始终成立;
(3)延长BC交x轴于点F,当t的取值范围是多少时,点F始终在点E的左侧?(请直
接写出结果,无需书写解答过程!)d21559 5437 吷`)ZU%25493 6395 掕25662 643E 搾 i130489 7719 眙37911 9417 鐗。
