人教高中数学选修2-2第一章《导数及其应用》测试题B卷
人教B版选修2-2第一章导数及其应用测试题(含答案)

第一章导数及其应用测试题一、 选择题1.设 y1 x 2( ).,则 y'sin xA .2x sin x (1x 2 ) cos x2x sin x(1 x 2 ) cos xsin 2xB .sin2x2x sin x (1x 2 )2x sin x(1 x 2 )C .sin xD .sin x2.设 f ( x)ln x21 ,则 f ' (2) ( ).42C .1 D .3A .B .55553.已知 f (3)2, f ' (3)2 ,则 lim2x3 f ( x) 的值为( ).x3x 3A . 4B . 0C . 8D .不存在4.曲线 yx 3 在点( 2,8) 处的切线方程为().A . y6x 12 B . C . y8x10D . y 12x 16y2x 325.已知函数 f ( x) ax 3 bx 2cx d 的图象与 x 轴有三个不一样交点(0,0), ( x 1,0) ,(x 2 ,0) ,且 f (x) 在 x1, x 2 时获得极值,则 x 1 x 2 的值为()A . 4B . 5C . 6D .不确立6.在 R 上的可导函数 f ( x)1 x 3 1 ax2 2bx c ,当 x (0,1) 获得极大值, 当 x (1,2)32获得极小值,则 b2的取值范围是().a 1A . (1,1)B . (1,1)C .( 1,1)D . ( 1,1)422 42 27.函数 f ( x)1 e x (sin x cos x) 在区间 [0, ] 的值域为( ).22A .[1 , 1e 2 ]B . (1 , 1e 2 )C . [1, e 2 ]D . (1, e2)2 22 2aa2x 2dx ().8.积分aA.1a2 B.1a 2 C.a2 D .2 a24 29.由双曲线x 2 y 21,直线 y b, y b 围成的图形绕y 轴旋转一周所得旋转体的体a 2 b2积为()A.8ab2 B.8a2b C.4a2b D.4ab2 3 3 3 310.由抛物线y2 2x 与直线 y x 4 所围成的图形的面积是().A .1838 16D.16 B.C.3 311.设底面为等边三角形的直棱柱的体积为V ,则其表面积最小时,底面边长为().A. 3 V B.3 2V C.34V D.23V二、填空题13.曲线y x3在点 (a, a 3 )( a 0) 处的切线与 x 轴、直线 x a 所围成的三角形的面积为1,则 a _________ 。
【高中数学选修2-2:第一章-导数及其应用-单元测试题
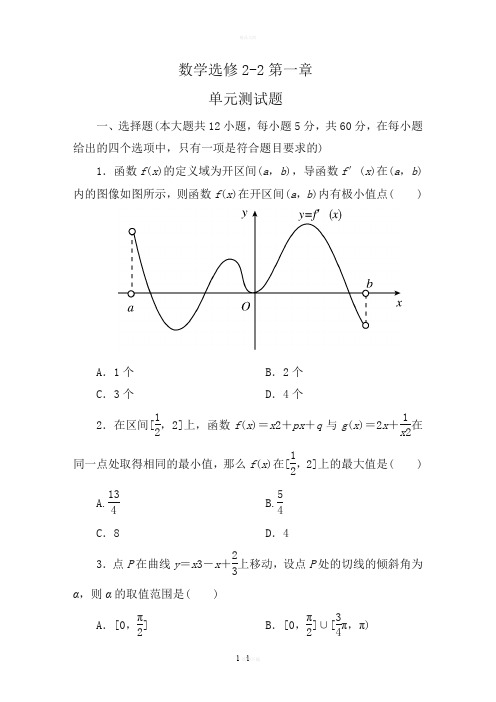
数学选修2-2第一章单元测试题一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数f (x )的定义域为开区间(a ,b ),导函数f ′(x )在(a ,b )内的图像如图所示,则函数f (x )在开区间(a ,b )内有极小值点( )A .1个B .2个C .3个D .4个2.在区间[12,2]上,函数f (x )=x 2+px +q 与g (x )=2x +1x 2在同一点处取得相同的最小值,那么f (x )在[12,2]上的最大值是( )A.134 B.54 C .8D .43.点P 在曲线y =x 3-x +23上移动,设点P 处的切线的倾斜角为α,则α的取值范围是( )A .[0,π2]B .[0,π2]∪[34π,π)C .[34π,π)D .[π2,34π]4.已知函数f (x )=12x 4-2x 3+3m ,x ∈R ,若f (x )+9≥0恒成立,则实数m 的取值范围是( )A .m ≥32B .m >32C .m ≤32D .m <325.函数f (x )=cos 2x -2cos 2x2的一个单调增区间是( )A.⎝ ⎛⎭⎪⎫π3,2π3B.⎝ ⎛⎭⎪⎫π6,π2 C.⎝⎛⎭⎪⎫0,π3 D.⎝ ⎛⎭⎪⎫-π6,π6 6.设f (x )在x =x 0处可导,且lim Δx →0f (x 0+3Δx )-f (x 0)Δx=1,则f ′(x 0)等于( )A .1B .0C .3D.137.经过原点且与曲线y =x +9x +5相切的切线方程为( ) A .x +y =0 B .x +25y =0C .x +y =0或x +25y =0D .以上皆非8.函数f (x )=x 3+ax 2+bx +c ,其中a ,b ,c 为实数,当a 2-3b <0时,f (x )是( )A .增函数B .减函数C .常数D .既不是增函数也不是减函数9.若a >2,则方程13x 3-ax 2+1=0在(0,2)上恰好有( )A .0个根B .1个根C .2个根D .3个根10.一点沿直线运动,如果由始点起经过t s 后距离为s =14t 4-53t 3+2t 2,那么速度为零的时刻是( ) A .1 s 末 B .0 s C .4 s 末D .0,1,4 s 末11.设f (x )=⎩⎪⎨⎪⎧x 2, x ∈[0,1],2-x ,x ∈(1,2],则⎠⎜⎛2f(x)d x 等于( )A .34B .45C .56D .不存在12.若函数f(x)=sin xx,且0<x 1<x 2<1,设a =sin x 1x 1,b =sin x 2x 2,则a ,b 的大小关系是( )A .a>bB .a<bC .a =bD .a 、b 的大小不能确定二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.若f(x)=13x 3-f ′(1)x 2+x +5,则f ′(1)=________.14.已知函数f(x)满足f(x)=f(π-x),且当x ∈⎝ ⎛⎭⎪⎫-π2,π2时,f(x)=x +sin x ,设a =f(1),b =f(2),c =f(3),则a 、b 、c 的大小关系是________.15.已知函数f(x)为一次函数,其图像经过点(2,4),且⎠⎜⎛01f(x)d x =3,则函数f(x)的解析式为________. 16.(2010·江苏卷)函数y =x 2(x >0)的图像在点(a k ,a 2k )处的切线与x 轴的交点的横坐标为a k +1,其中k ∈N *.若a 1=16,则a 1+a 3+a 5的值是________.三、解答题(本大题共6小题,共70分,解答应出写文字说明、证明过程或演算步骤)17.(10分)如图,直线y =kx 分抛物线y =x -x 2与x 轴所围成图形为面积相等的两部分,求k 的值.18.(12分)已知函数f(x)=x4-4x3+ax2-1在区间[0,1]上单调递增,在区间[1,2)上单调递减.(1)求a的值;(2)若点A(x0,f(x0))在函数f(x)的图像上,求证:点A关于直线x=1的对称点B也在函数f(x)的图像上.19.(12分)设x=-2与x=4是函数f(x)=x3+ax2+bx的两个极值点.(1)求常数a,b;(2)试判断x=-2,x=4是函数f(x)的极大值还是极小值,并说明理由.20.(12分)已知f(x)=ax3-6ax2+b,x∈[-1,2]的最大值为3,最小值为-29,求a,b的值.21.(12分)(2010·重庆卷)已知函数f(x)=ax3+x2+bx(其中常数a,b∈R),g(x)=f(x)+f′(x)是奇函数.(1)求f(x)的表达式;(2)讨论g(x)的单调性,并求g(x)在区间[1,2]上的最大值与最小值.22.(12分)已知函数f (x )=ln(ax +1)+1-x1+x ,x ≥0,其中a >0.(1)若f (x )在x =1处取得极值,求a 的值; (2)求f (x )的单调区间;(3)若f (x )的最小值为1,求a 的取值范围.参考答案 1.答案 A解析 设极值点依次为x 1,x 2,x 3且a <x 1<x 2<x 3<b ,则f (x )在(a ,x 1),(x 2,x 3)上递增,在(x 1,x 2),(x 3,b )上递减,因此,x 1、x 3是极大值点,只有x 2是极小值点.2.答案 D3.答案 B4.答案 A解析 因为函数f (x )=12x 4-2x 3+3m ,所以f ′(x )=2x 3-6x 2.令f ′(x )=0,得x =0或x =3,经检验知x =3是函数的一个最小值点,所以函数的最小值为f (3)=3m -272.不等式f (x )+9≥0恒成立,即f (x )≥-9恒成立,所以3m -272≥-9,解得m ≥32.5.答案 A解析 f (x )=cos 2x -cos x -1,∴f ′(x )=-2sin x ·cos x +sin x =sin x ·(1-2cos x ). 令f ′(x )>0,结合选项,选A. 6.答案 D7.答案 D 8.答案 A 9.答案 B解析 设f (x )=13x 3-ax 2+1,则f ′(x )=x 2-2ax =x (x -2a ),当x ∈(0,2)时,f ′(x )<0,f (x )在(0,2)上为减函数,又f (0)f (2)=1⎝ ⎛⎭⎪⎫83-4a +1=113-4a <0, f (x )=0在(0,2)上恰好有一个根,故选B.10.答案 D 11.答案 C解析 数形结合,如图.⎠⎜⎛02f(x)d x =⎠⎜⎛01x 2d x +⎠⎜⎛12(2-x)d x =⎪⎪⎪13x 31⎪⎪⎪+(2x -12x 2)21=13+(4-2-2+12) =56,故选C . 12.答案 A解析 f ′(x)=x cos x -sin xx2, 令g(x)=x cos x -sin x ,则g ′(x)=-x sin x +cos x -cos x =-x sin x.∵0<x<1,∴g ′(x)<0,即函数g(x)在(0,1)上是减函数,得g(x)<g(0)=0,故f ′(x)<0,函数f(x)在(0,1)上是减函数,得a>b ,故选A .13.答案 23解析 f ′(x)=x 2-2f ′(1)x +1,令x =1,得f ′(1)=23.14.答案 c<a<b解析 f(2)=f(π-2),f(3)=f(π-3),因为f ′(x)=1+cos x ≥0,故f(x)在⎝ ⎛⎭⎪⎫-π2,π2上是增函数,∵π2>π-2>1>π-3>0,∴f(π-2)>f(1)>f(π-3),即c<a<b.15.答案 f(x)=23x +83解析 设函数f(x)=ax +b(a ≠0),因为函数f(x)的图像过点(2,4),所以有b =4-2a.∴⎠⎜⎛01f(x)d x =⎠⎜⎛01 (ax +4-2a)d x =[12ax 2+(4-2a)x] |10=12a +4-2a =1.∴a =23.∴b =83.∴f(x)=23x +83.16.答案 21解析 ∵y ′=2x ,∴过点(a k ,a 2k )处的切线方程为y -a 2k =2a k (x-a k ),又该切线与x 轴的交点为(a k +1,0),所以a k +1=12a k ,即数列{a k }是等比数列,首项a 1=16,其公比q =12,∴a 3=4,a 5=1,∴a 1+a 3+a 5=21.17.解析 抛物线y =x -x 2与x 轴两交点的横坐标为x 1=0,x 2=1,所以,抛物线与x 轴所围图形面积S =⎠⎜⎛01(x -x 2)d x =⎪⎪⎪⎝ ⎛⎭⎪⎫x 22-x 3310=12-13=16. 又⎩⎪⎨⎪⎧y =x -x 2,y =kx ,由此可得抛物线y =x -x 2与y =kx 两交点的横坐标x 3=0,x 4=1-k ,所以S 2=⎠⎜⎛01-k (x -x 2-kx)d x =⎪⎪⎪⎝ ⎛⎭⎪⎫1-k 2x 2-x 331-k=16(1-k)3. 又S =16,所以(1-k)3=12,∴k =1-342.18.解析 (1)由函数f(x)=x4-4x3+ax2-1在区间[0,1]单调递增,在区间[1,2)单调递减,∴x =1时,取得极大值,∴f ′(1)=0. 又f ′(x)=4x3-12x2+2ax , ∴4-12+2a =0⇒a =4.(2)点A(x0,f(x0))关于直线x =1的对称点B 的坐标为(2-x0,f(x0)),f(2-x0)=(2-x0)4-4(2-x0)3+4(2-x0)2-1=(2-x0)2[(2-x0)-2]2-1 =x40-4x30+ax20-1=f(x0),∴A 关于直线x =1的对称点B 也在函数f(x)的图像上. 19.解析 f ′(x)=3x2+2ax +b. (1)由极值点的必要条件可知:f ′(-2)=f ′(4)=0,即⎩⎪⎨⎪⎧12-4a +b =0,48+8a +b =0,解得a =-3,b =-24.或f ′(x)=3x2+2ax +b =3(x +2)(x -4) =3x2-6x -24, 也可得a =-3,b =-24. (2)由f ′(x)=3(x +2)(x -4).当x <-2时,f ′(x)>0,当-2<x <4时,f ′(x)<0. ∴x =-2是极大值点,而当x >4时,f ′(x)>0, ∴x =4是极小值点.20.解析 a ≠0(否则f(x)=b 与题设矛盾), 由f ′(x)=3ax2-12ax =0及x ∈[-1,2],得x =0. (1)当a >0时,列表:f(x)在[0,2]上是减函数.则当x =0时,f(x)有最大值,从而b =3. 又f(-1)=-7a +3,f(2)=-16a +3,∵a >0,∴f(-1)>f(2).从而f(2)=-16a +3=-29,得a =2.(2)当a <0时,用类似的方法可判断当x =0时f(x)有最小值.当x =2时,f(x)有最大值.从而f(0)=b =-29, f(2)=-16a -29=3,得a =-2.综上,a =2,b =3或a =-2,b =-29.21.解析 (1)由题意得f ′(x )=3ax 2+2x +b .因此g (x )=f (x )+f ′(x )=ax 3+(3a +1)x 2+(b +2)x +b .因为函数g (x )是奇函数,所以g (-x )=-g (x ),即对任意实数x ,有a (-x )3+(3a +1)(-x )2+(b +2)(-x )+b =-[ax 3+(3a +1)x 2+(b +2)x +b ],从而3a +1=0,b=0,解得a =-13,b =0,因此f (x )的解析式为f (x )=-13x 3+x 2. (2)由(1)知g (x )=-13x 3+2x ,所以g ′(x )=-x 2+2. 令 g ′(x )=0,解得x 1=-2,x 2=2,则当x <-2或x >2时,g ′(x )<0,从而g (x )在区间(-∞,-2],[2,+∞)上是减函数;当-2<x <2时, g ′(x )>0,从而g (x )在[-2,2]上是增函数.由前面讨论知,g (x )在区间[1,2]上的最大值与最小值只能在x =1,2,2时取得,而g (1)=53,g (2)=423,g (2)=43.因此g (x )在区间[1,2]上的最大值为g (2)=423,最小值为g (2)=43. 22.分析 解答本题,应先正确求出函数f (x )的导数f ′(x ),再利用导数与函数的单调性、导数与极值、导数与最值等知识求解,并注意在定义域范围内求解.解析(1)f′(x)=aax+1-2(1+x)2=ax2+a-2(ax+1)(1+x)2,∵f(x)在x=1处取得极值,∴f′(1)=0,即a·12+a-2=0,解得a=1.(2)f′(x)=ax2+a-2 (ax+1)(1+x)2,∵x≥0,a>0,∴ax+1>0.①当a≥2时,在区间[0,+∞)上,f′(x)>0,∴f(x)的单调增区间为[0,+∞).②当0<a<2时,由f′(x)>0,解得x> 2-a a.由f′(x)<0,解得x< 2-a a.∴f(x)的单调减区间为(0, 2-aa),单调增区间为(2-aa,+∞).(3)当a≥2时,由(2)①知,f(x)的最小值为f(0)=1;当0<a<2,由(2)②知,f(x)在x=2-aa处取得最小值,且f(2-aa)<f(0)=1.综上可知,若f(x)的最小值为1,则a的取值范围是[2,+∞).欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。
高中数学选修22:第一章导数及其应用单元测试题.doc

数学选修 2-2 第一章单元测试题一、选择题 ( 本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数f ( x) 的定义域为开区间 ( a,b) ,导函数f′(x) 在( a,b) 内的图像如图所示,则函数 f ( x)在开区间( a,b)内有极小值点()A.1 个B.2 个C.3 个D.4 个1 12.在区间[ 2,2] 上,函数 f ( x)=x2+px+q 与g( x)=2x+x2在1同一点处取得相同的最小值,那么f(x)在[2,2]上的最大值是()C.8D.423.点P在曲线y=x3-x+3上移动,设点P处的切线的倾斜角为α,则α 的取值范围是( )ππ3A.[0 ,2 ] B.[0 ,2 ] ∪[ 4π,π)3 π 3C.[ 4π,π ) D.[ 2,4π]14.已知函数f ( x) =2x4-2x3+3m,x∈R,若f ( x) +9≥0恒成立,则实数 m的取值范围是()3 3A.m≥2 B.m>23 3C.m≤2 D.m<2x2 25.函数f ( x) =cos x-2cos 2的一个单调增区间是 ()f x 0+3 -f x 06.设f ( x) 在x=x0 处可导,且lim Δx=1,Δx→0则 f ′(x0)等于( )A.1 B.0C.3x+97.经过原点且与曲线y=x+5相切的切线方程为()A.x+y=0B.x+25y=0C.x+y= 0 或x+25y=0D.以上皆非8.函数f ( x) =x3+ax2+bx+c,其中a,b,c为实数,当a2-3b<0 时,f ( x) 是()A.增函数B.减函数C.常数D.既不是增函数也不是减函数13 29.若a>2,则方程3x -ax +1=0 在(0,2) 上恰好有 ()A.0 个根B.1 个根C.2 个根D.3 个根1 10.一点沿直线运动,如果由始点起经过t s 后距离为s=4t 4-53t 3+2t 2,那么速度为零的时刻是( )A.1 s 末B.0 sC.4 s 末D.0,1,4 s 末x2,x∈[0,1],2f(x) d x 等于 () 11.设f ( x) =则2-x,x∈ 1,2] ,0D.不存在sin x sin x1 sin x2 12.若函数 f(x) =x,且 0<x1<x2 <1,设 a=x1 ,b=x2 ,则 a,b 的大小关系是 ( )A.a>b B.a<bC.a=b D.a、b的大小不能确定二、填空题 ( 本大题共 4 小题,每小题 5 分,共 20 分.把答案填在题中横线上 )1 3 213.若 f(x) =3x -f ′(1)x +x+5,则 f ′(1) = ________.π π14.已知函数 f(x) 满足 f(x) =f( π-x) ,且当 x∈ -2,2 时,f(x) =x+sin x,设a=f(1) ,b=f(2) ,c=f(3) ,则a、b、c 的大小关系是 ________.15.已知函数f(x) 为一次函数,其图像经过点(2,4) ,且1f(x) d x=3,则函数f(x) 的解析式为________.16.(2010 ·江苏卷) 函数2y=x(x>0)的图像在点 2(a k,a k) 处的切线与x 轴的交点的横坐标为a k+1,其中k∈N*. 若a1=16,则a1+a3+a5的值是________.三、解答题 ( 本大题共 6 小题,共 70 分,解答应出写文字说明、证明过程或演算步骤 )17.(10 分) 如图,直线y=kx分抛物线y=x-x2与x轴所围成图形为面积相等的两部分,求k 的值.18.(12 分) 已知函数 f(x) =x4-4x3+ax2-1 在区间 [0,1] 上单调递增,在区间 [1,2) 上单调递减.(1)求 a 的值;(2)若点 A(x0,f(x0)) 在函数 f(x) 的图像上,求证:点 A关于直线x=1 的对称点 B 也在函数 f(x) 的图像上.19.(12 分) 设 x=- 2 与 x=4 是函数 f(x) =x3+ax2+bx 的两个极值点.(1)求常数 a,b;(2)试判断 x=- 2,x= 4 是函数 f(x) 的极大值还是极小值,并说明理由.20.(12 分) 已知 f(x) =ax3-6ax2+b,x∈[ -1,2] 的最大值为 3,最小值为- 29,求 a,b 的值.21.(12 分)(2010 ·重庆卷 ) 已知函数 f(x) =ax3+x2+ bx( 其中常数a,b∈R) ,g( x) =f ( x) +f′(x) 是奇函数.(1)求 f ( x)的表达式;(2)讨论 g( x)的单调性,并求 g( x)在区间[1,2]上的最大值与最小值.1-x22.(12 分) 已知函数f ( x) =ln( ax+1) +1+x,x≥0,其中a>0.(1)若 f ( x)在 x=1处取得极值,求 a 的值;(2)求 f ( x)的单调区间;(3)若 f ( x)的最小值为1,求 a 的取值范围.参考答案1.答案 A解析设极值点依次为 x1,x2,x3且 a<x1<x2<x3<b,则 f ( x) 在( a,x1) ,( x2,x3) 上递增,在 ( x1,x2) ,( x3,b) 上递减,因此,x1、x3是极大值点,只有x2是极小值点.2.答案 D3.答案 B4.答案 A1解析因为函数 f ( x)=2x4-2x3+3m,所以 f ′(x)=2x3-6x2.令 f ′(x)=0,得 x=0或 x=3,经检验知 x=3是函数的一个最27小值点,所以函数的最小值为 f (3)=3m-2.不等式 f ( x)+9≥0恒成27 3立,即 f ( x)≥-9恒成立,所以3m-2≥-9,解得 m≥2.5.答案 A解析 f ( x)=cos2x-cos x-1,∴f′(x)=-2sin x·cos x+sin x=sin x·(1-2cos x).令 f ′(x)>0,结合选项,选A.6. 答案 D7. 答案 D8. 答案 A9. 答案 B解析 1 3 2设 f ( x ) =3x -ax +1,则2f ′(x )=x -2ax =x ( x -2a ) ,当 x ∈(0,2) 时, f ′(x )<0,f ( x ) 在(0,2) 上为减函数,又 f (0) f (2) =8 111 3-4a +1 = 3 -4a <0,f ( x ) =0 在(0,2) 上恰好有一个根,故选 B.10. 答案 D11. 答案 C解析 数形结合,如图.2f(x) d x = 1x 2d x + 2(2 -x) d x0 11 3 11 22= 3x+ 2x -2x11 1= 3+(4 -2-2+2)5= 6,故选 C .12. 答案Af ′(x) =x cos x -sin x解析 x 2, 令 g(x) =x cos x -sin x ,则g ′(x) =- x sin x +cos x -cos x =- x sin x.∵0<x<1,∴ g ′(x)<0 ,即函数 g(x) 在 (0,1) 上是减函数,得 g(x)<g(0) =0,故 f ′(x)<0 ,函数 f(x) 在(0,1) 上是减函数,得 a>b ,故选A .213. 答案 32 2解析 f ′(x) = x -2f ′(1)x + 1,令 x=1,得 f ′(1) =3.14. 答案 c<a<b解析f(2) = f( π-2) , f(3) = f( π- 3) ,因为 f ′(x) = 1+π ππcos x≥0,故f(x)在-2,2上是增函数,∵2 >π-2>1>π-3>0,∴f( π-2)>f(1)>f( π-3) ,即 c<a<b.2815.答案 f(x) =3x+3解析设函数 f(x) =ax+b(a ≠0) ,因为函数 f(x) 的图像过点(2,4) ,所以有 b=4-2a.∴1 f(x) d x= 1 (ax +4-2a) d x0 01 2 1 1=[ ax +(4 -2a)x] | 0=a+4-2a=1.2 22 8 2 8∴a=3. ∴b=3. ∴f(x) =3x+3.16. 答案21解析2 2∵y′=2x,∴过点( a k,a k)处的切线方程为y-a k=2a k( x1-a k),又该切线与 x 轴的交点为( a k+1,0),所以 a k+1=2a k,即数列{ a k}1是等比数列,首项a1=16,其公比q=2,∴ a3=4,a5=1,∴ a1+a3 +a5=21.17. 解析抛物线 y =x -x 2 与 x 轴两交点的横坐标为x 1=0,x 2=1,所以,抛物线与 x 轴所围图形面积 S = 12) d x =x 2 x 3 11 (x -x 2 -3 0=2-1 13=6.y =x -x 2,又 由此可得抛物线 y =x -x 2 与 y =kx 两交点的横y =kx ,S- 2 x 3 -坐标 x 3= , 4= - ,所以 = 1-k (x - x 2 kx) d x =1 k x - 1k -0 x 1 k 2 02313=6(1 -k) .3又 S = ,所以 (1 -k) 3=1,∴ k =1- 4.622118. 解析 (1) 由函数 f(x) =x4-4x3+ax2-1 在区间 [0,1] 单调递增,在区间 [1,2) 单调递减,∴x =1 时,取得极大值,∴ f ′(1) = 0.又 f ′(x) = 4x3-12x2+2ax ,∴4-12+2a = 0? a = 4.(2) 点 A(x0,f(x0)) 关于直线 x =1 的对称点 B 的坐标为 (2 -x0, f(x0)) ,f(2 -x0) =(2 -x0)4 -4(2 -x0)3 +4(2 -x0)2 -1= (2 -x0)2[(2 -x0) -2]2 -1= x 40-4x30+ ax20- 1=f(x0) ,∴A 关于直线 x =1 的对称点 B 也在函数 f(x) 的图像上.19.解析 f ′(x) =3x2+2ax+b.(1) 由极值点的必要条件可知:12-4a+b=0,f ′( - 2) =f ′(4) = 0,即48+8a+b=0,解得 a=- 3,b=- 24.或f ′(x) = 3x2+2ax+b=3(x +2)(x -4)=3x2-6x-24,也可得 a=- 3,b=- 24.(2) 由 f ′(x) = 3(x +2)(x -4) .当 x<- 2 时, f ′(x) > 0,当- 2<x<4 时, f ′(x) < 0. ∴x=- 2 是极大值点,而当x>4 时, f ′(x) > 0,∴x=4 是极小值点.20.解析 a≠0( 否则 f(x) =b 与题设矛盾 ) ,由f ′(x) = 3ax2-12ax=0 及 x∈[ - 1,2] ,得 x=0. (1) 当 a>0 时,列表:x ( -1,0) 0 (0,2)f ′(x) +0 -f(x) 增极大值 b 减由上表知, f(x) 在[ - 1,0] 上是增函数,f(x) 在[0,2] 上是减函数.则当 x=0 时, f(x) 有最大值,从而b=3.又f( -1) =- 7a+3,f(2) =- 16a+3,∵a>0,∴ f( -1) >f(2) .从而 f(2) =- 16a+3=- 29,得a=2.(2)当 a<0 时,用类似的方法可判断当 x=0 时 f(x) 有最小值.当x=2 时, f(x) 有最大值.从而 f(0) =b=- 29, f(2)=-16a-29=3,得a=- 2.综上, a= 2,b=3 或 a=- 2,b=- 29.21.解析 (1) 由题意得f′(x) = 3ax2+2x+b. 因此g( x) =f ( x) +f′(x)=ax3+(3 a+1) x2+( b+2) x+b.因为函数 g( x)是奇函数,所以g(-x)=- g( x),即对任意实数x,有 a(- x)3+(3 a+1)(-x)2+( b +2)( -x) +b=- [ ax3+(3 a+1) x2+( b+2) x+b] ,从而 3a+1=0,b=0,解得a=-1,b=0,因此f ( x) 的解析式为f ( x) =-x3+x2. 331(2)由(1) 知g( x) =-1x3+2x,所以g′(x) =-x2+2. 3令g′(x)=0,解得x1=-2,x2=2,则当x<-2或x> 2时,g′(x)<0,从而 g( x)在区间(-∞,-2],[ 2,+∞)上是减函数;当- 2<x< 2时,g′(x)>0 ,从而g( x) 在[ - 2, 2] 上是增函数.由前面讨论知, g( x)在区间[1,2] 上的最大值与最小值只能在x=1,2,2 时取得,而g(1)5=3,g( 2) =4 23,g(2)4=3. 因此g( x)在区间 [1,2] 上的最大值为g( 2) =4 2,最小值为3g(2)4=3.22. 分析解答本题,应先正确求出函数 f ( x)的导数f ′(x),再利用导数与函数的单调性、导数与极值、导数与最值等知识求解,并注意在定义域范围内求解.a 2 ax2+a-2解析 (1) f′(x) =ax+1-1+x 2=ax+1 1+x 2,∵f ( x)在 x=1处取得极值,2∴f ′(1)=0,即 a·1+a-2=0,解得 a=1.(2) f′(x) =ax2+a-22,ax+1 1+x∵x≥0, a>0,∴ ax+1>0.①当 a≥2时,在区间[0,+∞)上, f ′(x)>0,∴f( x)的单调增区间为[0,+∞).②当 0<a<2 时,由 f ′(x)>0,解得 x> 2-a a.由 f ′(x)<0,解得 x< 2-a a.∴f ( x)的单调减区间为(0, 2-a 2-a a ) ,单调增区间为 ( a,+∞ ) .(3) 当a≥2时,由 (2) ①知,f ( x) 的最小值为f (0) =1;当 0<a<2,由 (2) ②知,f ( x) 在x=2-aa 处取得最小值,且2-af ( a )< f (0) =1.综上可知,若 f ( x)的最小值为1,则 a 的取值范围是[2,+∞).。
(理)选修2-2第一章《导数及其应用》单元测试题
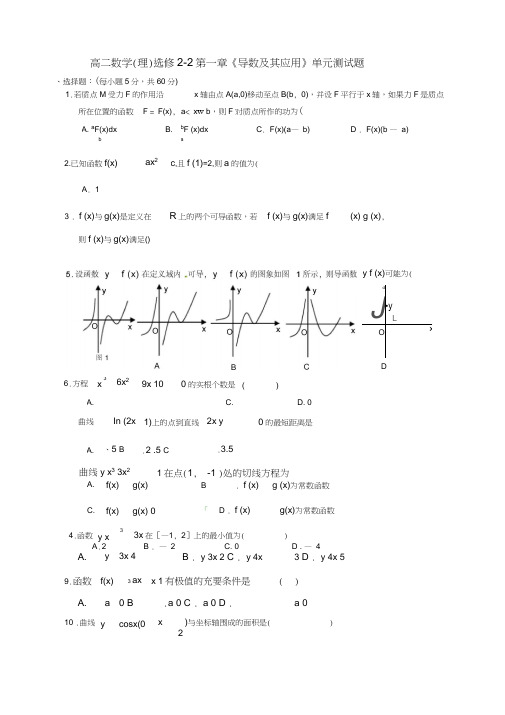
高二数学(理)选修2-2第一章《导数及其应用》单元测试题x 轴由点A(a,0)移动至点B(b , 0),并设F 平行于x 轴,如果力F 是质点则f (x)与g(x)满足()A. f(x) g(x) B . f (x) g (x)为常数函数 C. f(x)g(x) 0「 D . f (x)g(x)为常数函数4.函数 3y x3x 在[—1, 2]上的最小值为()A .2B . — 2C. 0D . — 4A.y 3x 4B . y 3x 2C . y 4x 3D . y 4x 59.函数 f(x) 3ax x 1有极值的充要条件是 ( )A.a 0 B .a 0 C . a 0 D .a 010 .曲线 ycosx(0 x)与坐标轴围成的面积是()2、选择题:(每小题5分,共60分) 1.若质点M 受力F 的作用沿所在位置的函数 F = F(x), a < x w b ,则F 对质点所作的功为( A. a F(x)dxbB.bF (x)dx aC . F(x)(a — b)D . F(x)(b — a)2.已知函数f(x)ax 2 c ,且f (1)=2,则a 的值为(A . 13 . f (x)与g(x)是定义在R 上的两个可导函数,若 f (x)与g(x)满足f(x) g (x),y f (x)可能为(dJ•y LOxA. 曲线A. 6x 2 In (2x 1)上的点到直线 C.D. 02x y0的最短距离是、5 B.2 .5 C.3.5曲线y x 3 3x 21在点(1, -1 )处的切线方程为 6.方程 9x 100的实根个数是 ()3xD5211 .由定积分的几何意义知 A. 4 B1 A.2 n B.4 1( .''1 — x — 1 2)dx =( 0 n — 2 C.~r 1 D.4 12 .若函数f(x)在R 上可导,且 A . e a f (a )>e b f (b ) B f(x)>f ' (X), .e b f (a )>e a f ( b ) a>b 时,下列不等式成立的是 ( )C . e b f (b )>e a f (a ) D. e a f (b )>e b f (a ) 二、填空题:(每小题5分,共20分) 13.已知R 上可导函数f (x )的图象如图所示,2则不等式(x2x 3)f (x ) 0的解集14. 15. 垂直于直线2x+6y + 1=0且与曲线3x 若函数f (x ) 16.设点P 是曲线y = x 3+ 3x — 5相切的直线方程是 __________ . mx 1是R 是的单调函数,则实数m 的取值范围是 ________ 一 .3x -上的任意一点,P 点处切线倾斜角为,则角的取 3 值范围是—三、解答题:(六小题,共 17 .已知函数f (x ) 在点(1 , 0 ) 70分)3 2 x ax 处相切, bx c 在 x 求 a , b , c2处取得极值,并且它的图象与直线 y 3x 3的值.(10分)18.当x 0时,证明不等式1r 2成立.(10分)19.已知函数f(x) ax3 bx2 3x在x 1处取得极值,讨论f(1)和f( 1)是函数f (x)的极大值还是极小值;(12分)320. (12 分)已知函数f(x) ax3—(a 2)x2 6x 3 ;2(1)当a 2时,求函数f(x)极小值;(2)试讨论曲线y f (x)与x轴公共点的个数121. (12 分)(2011 江西高考)设 f (x ) = -3x 3+32 (1)若f(x)在T ,+m上存在单调递增区间,求a 的取值范围;316⑵当0<a<2时,f(x)在[1,4]上的最小值为一 三,求f(x)在该区间上的最大值.22. (14 分)(2012 安阳高二检测)设函数 f(x) = x 2- mln x , h(x)= x 2-x + a.(1) 当a = 0时,f(x)>h(x)在(1 ,+s )上恒成立,求实数 m 的取值范围; (2) 当m = 2时,若函数k(x)= f(x)- h(x)在[1,3]上恰有两个不同零点,求实数^x 2 + 2ax.a 的取值范围.高二数学选修2-2第一章《导数及其应用》单元测试题参考 答案:•选择题:1. B2. A3. B4. B5. D6. C7. B8. B9. C 10. C 11.B 12.D12•填空题:13. ( , 1) ( 1,1) (3,)14. y=3x-5 15. [ ,+^) 16. [0, — )[,)32 3解Q f '(x) 3x 2 2ax b f '( 2) 3( 2)2 2a( 2) b 0 12 4a b 0•解答题:17.又f '(1) 3 2a b 3 a 1,b8又 f(x)过(1,0)点,13 a 12 b 1 c 0 c 618.证明:设f x xe 1 x -x 2,贝y 2f' x e x 1 x ,令 g(x) e x 1x,则 g'(x) e x 1当x 0时,g'x e x 10,• g(x)在 0,上单调递增,而g(0) 0,••• g x g(0)0, g(x) 0在0,上恒成立, 即 f'(x)0 在 0,恒成立.二 f (x)在 0,上单 调递增,又 f(0)0^ x 彳 10, - - e 1 xx2 0,即x 0时,2e x 1 x 1 x 2 成立.219 解:f (x) 3ax 22bx 3,依题意,f (1) f ( 1) 0,即3a 2b 3 0,解得 3a 2b 3 0.a 1,b 0 . • f (x) x 33x, f :(x) 3x 23 3(x 1)(x 1).令 f (x) 0,得x1,x 1 .若x ( , 1) (1, ),则f (x)0,故f (x)在(,1)上是增函数,f (x)在(1, )上 是增函数.若x ( 1, 1),则f (x) 0,故f(x)在(1, 1)上是减函数.所以,f( 1)2是极大 值;f(1) 2是极小值.2a 20.解:(1) f '(x) 3ax 2 3(a 2)x 6 3a(x )(x 1), f (x)极小值为 f (1)a2(2)①若a 0,则f (x) 3(x 1)2, f (x)的图像与x 轴只有一个交点;②若a 0,f (x)极大值为f(1)- 0,Q f(x)的极小值为f(Z) 0, 2 af (x)的图像与x 轴有三个交点;③若0 a 2, f (x)的图像与x 轴只有一个交点;④若a 2,则f '(x) 6(x 1)2 0, f (x)的图像与x 轴只有一个交点;⑤若a 2,由(1)知f (x)的极大值为f(2)4(- 3)230, f(x)的图像与x 轴只有一个交点;aa 44综上知,若a 0, f(x)的图像与x 轴只有一个交点;若a 0, f (x)的图像与x 轴有三个交点。
【高中数学选修2-2:第一章-导数及其应用-单元测试题
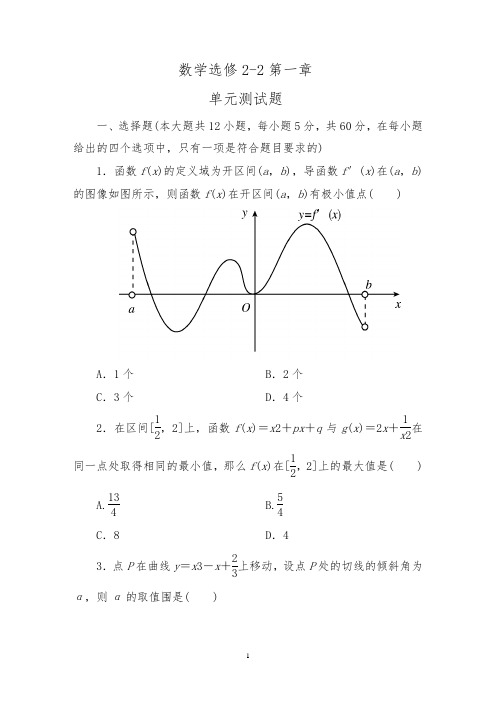
数学选修2-2第一章单元测试题一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数f (x )的定义域为开区间(a ,b ),导函数f ′(x )在(a ,b )的图像如图所示,则函数f (x )在开区间(a ,b )有极小值点( )A .1个B .2个C .3个D .4个2.在区间[12,2]上,函数f (x )=x 2+px +q 与g (x )=2x +1x 2在同一点处取得相同的最小值,那么f (x )在[12,2]上的最大值是( )A.134 B.54 C .8D .43.点P 在曲线y =x 3-x +23上移动,设点P 处的切线的倾斜角为α,则α的取值围是( )A .[0,π2]B .[0,π2]∪[34π,π)C .[34π,π)D .[π2,34π]4.已知函数f (x )=12x 4-2x 3+3m ,x ∈R ,若f (x )+9≥0恒成立,则实数m 的取值围是( )A .m ≥32B .m >32C .m ≤32D .m <325.函数f (x )=cos 2x -2cos 2x2的一个单调增区间是( )A.⎝ ⎛⎭⎪⎫π3,2π3B.⎝ ⎛⎭⎪⎫π6,π2C.⎝⎛⎭⎪⎫0,π3D.⎝ ⎛⎭⎪⎫-π6,π66.设f (x )在x =x 0处可导,且lim Δx →0f x 0+3Δx -f x 0Δx=1,则f ′(x 0)等于( )A .1B .0C .3D.137.经过原点且与曲线y =x +9x +5相切的切线方程为( )A .x +y =0B .x +25y =0C .x +y =0或x +25y =0D .以上皆非8.函数f (x )=x 3+ax 2+bx +c ,其中a ,b ,c 为实数,当a 2-3b <0时,f (x )是( )A .增函数B .减函数C .常数D .既不是增函数也不是减函数9.若a >2,则方程13x 3-ax 2+1=0在(0,2)上恰好有( )A .0个根B .1个根C .2个根D .3个根10.一点沿直线运动,如果由始点起经过t s 后距离为s =14t 4-53t 3+2t 2,那么速度为零的时刻是( ) A .1 s 末 B .0 s C .4 s 末D .0,1,4 s 末11.设f (x )=⎩⎪⎨⎪⎧x 2, x ∈[0,1],2-x ,x ∈1,2],则⎠⎜⎛2f(x)d x 等于( )A .34B .45C .56D .不存在12.若函数f(x)=sin xx,且0<x 1<x 2<1,设a =sin x 1x 1,b =sin x 2x 2,则a ,b 的大小关系是( )A .a>bB .a<bC .a =bD .a 、b 的大小不能确定二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.若f(x)=13x 3-f ′(1)x 2+x +5,则f ′(1)=________.14.已知函数f(x)满足f(x)=f(π-x),且当x ∈⎝ ⎛⎭⎪⎫-π2,π2时,f(x)=x +sin x ,设a =f(1),b =f(2),c =f(3),则a 、b 、c 的大小关系是________.15.已知函数f(x)为一次函数,其图像经过点(2,4),且⎠⎜⎛01f(x)d x =3,则函数f(x)的解析式为________. 16.(2010·卷)函数y =x 2(x >0)的图像在点(a k ,a 2k )处的切线与x 轴的交点的横坐标为a k +1,其中k ∈N *.若a 1=16,则a 1+a 3+a 5的值是________.三、解答题(本大题共6小题,共70分,解答应出写文字说明、证明过程或演算步骤)17.(10分)如图,直线y =kx 分抛物线y =x -x 2与x 轴所围成图形为面积相等的两部分,求k 的值.18.(12分)已知函数f(x)=x4-4x3+ax2-1在区间[0,1]上单调递增,在区间[1,2)上单调递减.(1)求a的值;(2)若点A(x0,f(x0))在函数f(x)的图像上,求证:点A关于直线x=1的对称点B也在函数f(x)的图像上.19.(12分)设x=-2与x=4是函数f(x)=x3+ax2+bx的两个极值点.(1)求常数a,b;(2)试判断x=-2,x=4是函数f(x)的极大值还是极小值,并说明理由.20.(12分)已知f(x)=ax3-6ax2+b,x∈[-1,2]的最大值为3,最小值为-29,求a,b的值.21.(12分)(2010·卷)已知函数f(x)=ax3+x2+bx(其中常数a,b∈R),g(x)=f(x)+f′(x)是奇函数.(1)求f(x)的表达式;(2)讨论g(x)的单调性,并求g(x)在区间[1,2]上的最大值与最小值.22.(12分)已知函数f (x )=ln(ax +1)+1-x1+x ,x ≥0,其中a >0.(1)若f (x )在x =1处取得极值,求a 的值; (2)求f (x )的单调区间;(3)若f (x )的最小值为1,求a 的取值围.参考答案 1.答案 A解析 设极值点依次为x 1,x 2,x 3且a <x 1<x 2<x 3<b ,则f (x )在(a ,x 1),(x 2,x 3)上递增,在(x 1,x 2),(x 3,b )上递减,因此,x 1、x 3是极大值点,只有x 2是极小值点.2.答案 D3.答案 B4.答案 A解析 因为函数f (x )=12x 4-2x 3+3m ,所以f ′(x )=2x 3-6x 2.令f ′(x )=0,得x =0或x =3,经检验知x =3是函数的一个最小值点,所以函数的最小值为f (3)=3m -272.不等式f (x )+9≥0恒成立,即f (x )≥-9恒成立,所以3m -272≥-9,解得m ≥32. 5.答案 A解析 f (x )=cos 2x -cos x -1,∴f ′(x )=-2sin x ·cos x +sin x =sin x ·(1-2cos x ). 令f ′(x )>0,结合选项,选A. 6.答案 D 7.答案 D 8.答案 A 9.答案 B解析 设f (x )=13x 3-ax 2+1,则f ′(x )=x 2-2ax =x (x -2a ),当x ∈(0,2)时,f ′(x )<0,f (x )在(0,2)上为减函数,又f (0)f (2)=1⎝ ⎛⎭⎪⎫83-4a +1=113-4a <0, f (x )=0在(0,2)上恰好有一个根,故选B.10.答案 D 11.答案 C解析 数形结合,如图.⎠⎜⎛02f(x)d x =⎠⎜⎛01x 2d x +⎠⎜⎛12(2-x)d x =⎪⎪⎪13x 31⎪⎪⎪+2x -12x 221=13+(4-2-2+12)=56,故选C . 12.答案 A解析 f ′(x)=x cos x -sin xx 2,令g(x)=x cos x -sin x ,则g ′(x)=-x sin x +cos x -cos x =-x sin x.∵0<x<1,∴g ′(x)<0,即函数g(x)在(0,1)上是减函数,得g(x)<g(0)=0,故f ′(x)<0,函数f(x)在(0,1)上是减函数,得a>b ,故选A .13.答案 23解析 f ′(x)=x 2-2f ′(1)x +1,令x =1,得f ′(1)=23.14.答案 c<a<b解析 f(2)=f(π-2),f(3)=f(π-3),因为f ′(x)=1+cos x ≥0,故f(x)在⎝ ⎛⎭⎪⎫-π2,π2上是增函数,∵π2>π-2>1>π-3>0,∴f(π-2)>f(1)>f(π-3),即c<a<b.15.答案 f(x)=23x +83解析 设函数f(x)=ax +b(a ≠0),因为函数f(x)的图像过点(2,4),所以有b =4-2a.∴⎠⎜⎛01f(x)d x =⎠⎜⎛01 (ax +4-2a)d x =[12ax 2+(4-2a)x] |10=12a +4-2a =1.∴a =23.∴b =83.∴f(x)=23x +83.16.答案 21解析 ∵y ′=2x ,∴过点(a k ,a 2k )处的切线方程为y -a 2k =2a k (x-a k ),又该切线与x 轴的交点为(a k +1,0),所以a k +1=12a k ,即数列{a k }是等比数列,首项a 1=16,其公比q =12,∴a 3=4,a 5=1,∴a 1+a 3+a 5=21.17.解析 抛物线y =x -x 2与x 轴两交点的横坐标为x 1=0,x 2=1,所以,抛物线与x 轴所围图形面积S =⎠⎜⎛01(x -x 2)d x =⎪⎪⎪⎝ ⎛⎭⎪⎫x 22-x 3310=12-13=16. 又⎩⎪⎨⎪⎧y =x -x 2,y =kx ,由此可得抛物线y =x -x 2与y =kx 两交点的横坐标x 3=0,x 4=1-k ,所以S 2=⎠⎜⎛01-k (x -x 2-kx)d x =⎪⎪⎪⎝⎛⎭⎪⎫1-k 2x 2-x 331-k=16(1-k)3. 又S =16,所以(1-k)3=12,∴k =1-342.18.解析 (1)由函数f(x)=x4-4x3+ax2-1在区间[0,1]单调递增,在区间[1,2)单调递减,∴x =1时,取得极大值,∴f ′(1)=0. 又f ′(x)=4x3-12x2+2ax ,∴4-12+2a =0⇒a =4.(2)点A(x0,f(x0))关于直线x =1的对称点B 的坐标为(2-x0,f(x0)),f(2-x0)=(2-x0)4-4(2-x0)3+4(2-x0)2-1 =(2-x0)2[(2-x0)-2]2-1 =x40-4x30+ax20-1=f(x0),∴A 关于直线x =1的对称点B 也在函数f(x)的图像上. 19.解析 f ′(x)=3x2+2ax +b. (1)由极值点的必要条件可知:f ′(-2)=f ′(4)=0,即⎩⎪⎨⎪⎧12-4a +b =0,48+8a +b =0,解得a =-3,b =-24.或f ′(x)=3x2+2ax +b =3(x +2)(x -4) =3x2-6x -24, 也可得a =-3,b =-24. (2)由f ′(x)=3(x +2)(x -4).当x <-2时,f ′(x)>0,当-2<x <4时,f ′(x)<0. ∴x =-2是极大值点,而当x >4时,f ′(x)>0, ∴x =4是极小值点.20.解析 a ≠0(否则f(x)=b 与题设矛盾), 由f ′(x)=3ax2-12ax =0及x ∈[-1,2],得x =0. (1)当a >0时,列表:由上表知,f(x)在[-1,0]上是增函数,f(x)在[0,2]上是减函数.则当x =0时,f(x)有最大值,从而b =3.又f(-1)=-7a +3,f(2)=-16a +3,∵a >0,∴f(-1)>f(2).从而f(2)=-16a +3=-29,得a =2.(2)当a <0时,用类似的方法可判断当x =0时f(x)有最小值. 当x =2时,f(x)有最大值.从而f(0)=b =-29, f(2)=-16a -29=3,得a =-2.综上,a =2,b =3或a =-2,b =-29.21.解析 (1)由题意得f ′(x )=3ax 2+2x +b .因此g (x )=f (x )+f ′(x )=ax 3+(3a +1)x 2+(b +2)x +b .因为函数g (x )是奇函数,所以g (-x )=-g (x ),即对任意实数x ,有a (-x )3+(3a +1)(-x )2+(b +2)(-x )+b =-[ax 3+(3a +1)x 2+(b +2)x +b ],从而3a +1=0,b=0,解得a =-13,b =0,因此f (x )的解析式为f (x )=-13x 3+x 2. (2)由(1)知g (x )=-13x 3+2x ,所以g ′(x )=-x 2+2. 令 g ′(x )=0,解得x 1=-2,x 2=2,则当x <-2或x >2时,g ′(x )<0,从而g (x )在区间(-∞,-2],[2,+∞)上是减函数;当-2<x <2时, g ′(x )>0,从而g (x )在[-2,2]上是增函数.由前面讨论知,g (x )在区间[1,2]上的最大值与最小值只能在x =1,2,2时取得,而g (1)=53,g (2)=423,g (2)=43.因此g (x )在区间[1,2]上的最大值为g(2)=423,最小值为g(2)=43.22.分析解答本题,应先正确求出函数f(x)的导数f′(x),再利用导数与函数的单调性、导数与极值、导数与最值等知识求解,并注意在定义域围求解.解析(1)f′(x)=aax+1-21+x2=ax2+a-2ax+11+x2,∵f(x)在x=1处取得极值,∴f′(1)=0,即a·12+a-2=0,解得a=1.(2)f′(x)=ax2+a-2ax+11+x2,∵x≥0,a>0,∴ax+1>0.①当a≥2时,在区间[0,+∞)上,f′(x)>0,∴f(x)的单调增区间为[0,+∞).②当0<a<2时,由f′(x)>0,解得x> 2-a a.由f′(x)<0,解得x< 2-a a.∴f(x)的单调减区间为(0, 2-aa),单调增区间为(2-aa,+∞).(3)当a≥2时,由(2)①知,f(x)的最小值为f(0)=1;当0<a<2,由(2)②知,f(x)在x=2-aa处取得最小值,且f( 2-aa)<f(0)=1.综上可知,若f(x)的最小值为1,则a的取值围是[2,+∞).。
高二数学选修2-2导数及其应用测试题(含答案)

高二数学选修2-2导数及其应用测试题一、 选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案写在答题卡上)1.设xx y sin 12-=,则='y ( ).A .x x x x x 22sin cos )1(sin 2---B .xx x x x 22sin cos )1(sin 2-+-C .x x x x sin )1(sin 22-+-D .xx x x sin )1(sin 22---2.设1ln)(2+=x x f ,则=)2('f ( ). A .54 B .52 C .51 D .53 3.已知2)3(',2)3(-==f f ,则3)(32lim3--→x x f x x 的值为( ).A .4-B .0C .8D .不存在 4.曲线3x y =在点)8,2(处的切线方程为( ).A .126-=x yB .1612-=x yC .108+=x yD .322-=x y5.已知函数d cx bx ax x f +++=23)(的图象与x 轴有三个不同交点)0,(),0,0(1x ,)0,(2x ,且)(x f 在1=x ,2=x 时取得极值,则21x x ⋅的值为( ) A .4 B .5 C .6 D .不确定 6.在R 上的可导函数c bx ax x x f +++=22131)(23,当)1,0(∈x 取得极大值,当)2,1(∈x 取得极小值,则12--a b 的取值范围是( ). A .)1,41( B .)1,21( C .)41,21(- D .)21,21(-7.函数)cos (sin 21)(x x e x f x +=在区间]2,0[π的值域为( ). A .]21,21[2πe B .)21,21(2πe C .],1[2πe D .),1(2πe8.积分=-⎰-aadx x a 22( ).A .241a π B .221a πC .2a πD .22a π9.由双曲线12222=-by a x ,直线b y b y -==,围成的图形绕y 轴旋转一周所得旋转体的体积为( )A .238ab π B .b a 238π C .b a 234π D .234ab π 10.由抛物线x y 22=与直线4-=x y 所围成的图形的面积是( ). A .18B .338C .316 D .1611.设底面为等边三角形的直棱柱的体积为V ,则其表面积最小时,底面边长为( ). A.3V B.32V C.34V D .32V 12.某人要剪一个如图所示的实心纸花瓣,纸花瓣的边界 由六段全等的正弦曲线弧)0(sin π≤≤=x x y 组成,其中 曲线的六个交点正好是一个正六边形的六个顶点,则这个 纸花瓣的面积为( ). A .2336π+ B .223312π+ C .26π+ D .22336π+第Ⅱ卷(非选择题,共90分)二、填空题(每小题4分,共16分。
【高中数学选修2-2:第一章-导数及其应用-单元测试题

数学选修2-2第一章单元测试题一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数f (x )的定义域为开区间(a ,b ),导函数f ′(x )在(a ,b )内的图像如图所示,则函数f (x )在开区间(a ,b )内有极小值点( )A .1个B .2个C .3个D .4个2.在区间[12,2]上,函数f (x )=x 2+px +q 与g (x )=2x +1x2在同一点处取得相同的最小值,那么f (x )在[12,2]上的最大值是( )A.134 B.54 C .8D .43.点P 在曲线y =x 3-x +23上移动,设点P 处的切线的倾斜角为α,则α的取值范围是( )A .[0,π2]B .[0,π2]∪[34π,π)C .[34π,π)D .[π2,34π]4.已知函数f (x )=12x 4-2x 3+3m ,x ∈R ,若f (x )+9≥0恒成立,则实数m 的取值范围是( )A .m ≥32B .m >32C .m ≤32D .m <325.函数f (x )=cos 2x -2cos 2x2的一个单调增区间是( )A.⎝ ⎛⎭⎪⎫π3,2π3B.⎝ ⎛⎭⎪⎫π6,π2C.⎝⎛⎭⎪⎫0,π3D.⎝ ⎛⎭⎪⎫-π6,π66.设f (x )在x =x 0处可导,且lim Δx→0 错误!=1,则f ′(x 0)等于( )A .1B .0C .3D.137.经过原点且与曲线y =x +9x +5相切的切线方程为( )A .x +y =0B .x +25y =0C .x +y =0或x +25y =0D .以上皆非8.函数f (x )=x 3+ax 2+bx +c ,其中a ,b ,c 为实数,当a 2-3b <0时,f (x )是( )A .增函数B .减函数C .常数D .既不是增函数也不是减函数9.若a >2,则方程13x 3-ax 2+1=0在(0,2)上恰好有( )A .0个根B .1个根C .2个根D .3个根10.一点沿直线运动,如果由始点起经过t s 后距离为s =14t 4-53t 3+2t 2,那么速度为零的时刻是( )A .1 s 末B .0 sC .4 s 末D .0,1,4 s 末11.设f (x )=错误!则错误!f(x)d x 等于( ) A .34 B .45 C .56D .不存在12.若函数f(x)=sinx x ,且0<x 1<x 2<1,设a =sinx1x1,b =sinx2x2,则a ,b 的大小关系是( ) A .a>b B .a<bC .a =bD .a 、b 的大小不能确定二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.若f(x)=13x 3-f ′(1)x 2+x +5,则f ′(1)=________.14.已知函数f(x)满足f(x)=f(π-x),且当x ∈⎝ ⎛⎭⎪⎫-π2,π2时,f(x)=x +sin x ,设a =f(1),b =f(2),c =f(3),则a 、b 、c 的大小关系是________.15.已知函数f(x)为一次函数,其图像经过点(2,4),且⎠⎛01f(x)d x =3,则函数f(x)的解析式为________.16.(2010·江苏卷)函数y =x 2(x >0)的图像在点(a k ,a 2k )处的切线与x 轴的交点的横坐标为a k +1,其中k ∈N *.若a 1=16,则a 1+a 3+a 5的值是________.三、解答题(本大题共6小题,共70分,解答应出写文字说明、证明过程或演算步骤)17.(10分)如图,直线y =kx 分抛物线y =x -x 2与x 轴所围成图形为面积相等的两部分,求k 的值.18.(12分)已知函数f(x)=x4-4x3+ax2-1在区间[0,1]上单调递增,在区间[1,2)上单调递减.(1)求a 的值;(2)若点A(x0,f(x0))在函数f(x)的图像上,求证:点A 关于直线x =1的对称点B 也在函数f(x)的图像上.19.(12分)设x =-2与x =4是函数f(x)=x3+ax2+bx 的两个极值点.(1)求常数a ,b ;(2)试判断x =-2,x =4是函数f(x)的极大值还是极小值,并说明理由.20.(12分)已知f(x)=ax3-6ax2+b ,x ∈[-1,2]的最大值为3,最小值为-29,求a ,b 的值.21.(12分)(2010·重庆卷)已知函数f(x)=ax 3+x 2+bx(其中常数a ,b ∈R ),g (x )=f (x )+f ′(x )是奇函数.(1)求f (x )的表达式;(2)讨论g (x )的单调性,并求g (x )在区间[1,2]上的最大值与最小值.22.(12分)已知函数f (x )=ln(ax +1)+1-x 1+x ,x ≥0,其中a >0.(1)若f (x )在x =1处取得极值,求a 的值; (2)求f (x )的单调区间;(3)若f (x )的最小值为1,求a 的取值范围.参考答案 1.答案 A解析 设极值点依次为x 1,x 2,x 3且a <x 1<x 2<x 3<b ,则f (x )在(a ,x 1),(x 2,x 3)上递增,在(x 1,x 2),(x 3,b )上递减,因此,x 1、x 3是极大值点,只有x 2是极小值点.2.答案 D3.答案 B4.答案 A解析 因为函数f (x )=12x 4-2x 3+3m ,所以f ′(x )=2x 3-6x 2.令f ′(x )=0,得x =0或x =3,经检验知x =3是函数的一个最小值点,所以函数的最小值为f (3)=3m -272.不等式f (x )+9≥0恒成立,即f (x )≥-9恒成立,所以3m -272≥-9,解得m ≥32.5.答案 A解析 f (x )=cos 2x -cos x -1,∴f ′(x )=-2sin x ·cos x +sin x =sin x ·(1-2cos x ). 令f ′(x )>0,结合选项,选A. 6.答案 D 7.答案 D 8.答案 A 9.答案 B解析 设f (x )=13x 3-ax 2+1,则f ′(x )=x 2-2ax =x (x -2a ),当x∈(0,2)时,f ′(x )<0,f (x )在(0,2)上为减函数,又f (0)f (2)=1⎝ ⎛⎭⎪⎫83-4a +1=113-4a <0, f (x )=0在(0,2)上恰好有一个根,故选B. 10.答案 D 11.答案 C解析 数形结合,如图.⎠⎜⎛02f(x)d x =⎠⎜⎛01x 2d x +⎠⎜⎛12(2-x)d x =⎪⎪⎪13x310错误!错误! =13+(4-2-2+12) =56,故选C . 12.答案 A解析 f ′(x)=xcosx -sinxx2,令g(x)=x cos x -sin x ,则g ′(x)=-x sin x +cos x -cos x =-x sin x.∵0<x<1,∴g ′(x)<0,即函数g(x)在(0,1)上是减函数,得g(x)<g(0)=0,故f ′(x)<0,函数f(x)在(0,1)上是减函数,得a>b ,故选A .13.答案 23解析 f ′(x)=x 2-2f ′(1)x +1,令x =1,得f ′(1)=23.14.答案 c<a<b解析 f(2)=f(π-2),f(3)=f(π-3),因为f ′(x)=1+cos x ≥0,故f(x)在⎝ ⎛⎭⎪⎫-π2,π2上是增函数,∵π2>π-2>1>π-3>0,∴f(π-2)>f(1)>f(π-3),即c<a<b.15.答案 f(x)=23x +83解析 设函数f(x)=ax +b(a ≠0),因为函数f(x)的图像过点(2,4),所以有b =4-2a.∴⎠⎛01f(x)d x =⎠⎛01 (ax +4-2a)d x =[12ax 2+(4-2a)x] |10=12a +4-2a =1. ∴a =23.∴b =83.∴f(x)=23x +83.16.答案 21解析 ∵y ′=2x ,∴过点(a k ,a 2k )处的切线方程为y -a 2k =2a k (x -a k ),又该切线与x 轴的交点为(a k +1,0),所以a k +1=12a k ,即数列{a k }是等比数列,首项a 1=16,其公比q =12,∴a 3=4,a 5=1,∴a 1+a 3+a 5=21.17.解析 抛物线y =x -x 2与x 轴两交点的横坐标为x 1=0,x 2=1,所以,抛物线与x 轴所围图形面积S =⎠⎜⎛01(x -x 2)d x =⎪⎪⎪⎝ ⎛⎭⎪⎫x22-x3310=12-13=16. 又⎩⎪⎨⎪⎧y =x -x2,y =kx ,由此可得抛物线y =x -x 2与y =kx 两交点的横坐标x 3=0,x 4=1-k ,所以S2=⎠⎛01-k (x -x 2-kx)d x =⎪⎪⎪⎝ ⎛⎭⎪⎫1-k 2x2-x331-k 0=16(1-k)3. 又S =16,所以(1-k)3=12,∴k =1-342.18.解析 (1)由函数f(x)=x4-4x3+ax2-1在区间[0,1]单调递增,在区间[1,2)单调递减,∴x =1时,取得极大值,∴f ′(1)=0. 又f ′(x)=4x3-12x2+2ax , ∴4-12+2a =0⇒a =4.(2)点A(x0,f(x0))关于直线x =1的对称点B 的坐标为(2-x0,f(x0)),f(2-x0)=(2-x0)4-4(2-x0)3+4(2-x0)2-1 =(2-x0)2[(2-x0)-2]2-1 =x40-4x30+ax20-1=f(x0),∴A 关于直线x =1的对称点B 也在函数f(x)的图像上. 19.解析 f ′(x)=3x2+2ax +b.(1)由极值点的必要条件可知:f ′(-2)=f ′(4)=0,即⎩⎪⎨⎪⎧12-4a +b =0,48+8a +b =0,解得a =-3,b =-24.或f ′(x)=3x2+2ax +b =3(x +2)(x -4) =3x2-6x -24, 也可得a =-3,b =-24. (2)由f ′(x)=3(x +2)(x -4).当x <-2时,f ′(x)>0,当-2<x <4时,f ′(x)<0. ∴x =-2是极大值点,而当x >4时,f ′(x)>0, ∴x =4是极小值点.20.解析 a ≠0(否则f(x)=b 与题设矛盾), 由f ′(x)=3ax2-12ax =0及x ∈[-1,2],得x =0. (1)当a >0时,列表:f(x)在[0,2]上是减函数.则当x =0时,f(x)有最大值,从而b =3. 又f(-1)=-7a +3,f(2)=-16a +3, ∵a >0,∴f(-1)>f(2). 从而f(2)=-16a +3=-29, 得a =2.(2)当a <0时,用类似的方法可判断当x =0时f(x)有最小值.当x =2时,f(x)有最大值.从而f(0)=b =-29, f(2)=-16a -29=3,得a =-2.综上,a =2,b =3或a =-2,b =-29.21.解析 (1)由题意得f ′(x )=3ax 2+2x +b .因此g (x )=f (x )+f ′(x )=ax 3+(3a +1)x 2+(b +2)x +b .因为函数g (x )是奇函数,所以g (-x )=-g (x ),即对任意实数x ,有a (-x )3+(3a +1)(-x )2+(b +2)(-x )+b =-[ax 3+(3a +1)x 2+(b +2)x +b ],从而3a +1=0,b =0,解得a =-13,b =0,因此f (x )的解析式为f (x )=-13x 3+x 2. (2)由(1)知g (x )=-13x 3+2x ,所以g ′(x )=-x 2+2. 令 g ′(x )=0,解得x 1=-2,x 2=2,则当x <-2或x >2时,g ′(x )<0,从而g (x )在区间(-∞,-2],[2,+∞)上是减函数;当-2<x <2时, g ′(x )>0,从而g (x )在[-2,2]上是增函数.由前面讨论知,g (x )在区间[1,2]上的最大值与最小值只能在x =1,2,2时取得,而g (1)=53,g (2)=423,g (2)=43.因此g (x )在区间[1,2]上的最大值为g (2)=423,最小值为g (2)=43. 22.分析 解答本题,应先正确求出函数f (x )的导数f ′(x ),再利用导数与函数的单调性、导数与极值、导数与最值等知识求解,并注意在定义域范围内求解.解析 (1)f ′(x )=a ax +1-错误!=错误!, ∵f (x )在x =1处取得极值,∴f′(1)=0,即a·12+a-2=0,解得a=1.(2)f′(x)=错误!,∵x≥0,a>0,∴ax+1>0.①当a≥2时,在区间[0,+∞)上,f′(x)>0,∴f(x)的单调增区间为[0,+∞).②当0<a<2时,由f′(x)>0,解得x> 2-a a.由f′(x)<0,解得x< 2-a a.∴f(x)的单调减区间为(0, 2-aa),单调增区间为(2-aa,+∞).(3)当a≥2时,由(2)①知,f(x)的最小值为f(0)=1;当0<a<2,由(2)②知,f(x)在x=2-aa处取得最小值,且f(2-aa)<f(0)=1.综上可知,若f(x)的最小值为1,则a的取值范围是[2,+∞).。
选修2-2《导数及其应用》测试题

人教B 版选修2-2《导数及其应用》测试题 姓名 得分 一.选择题:(只有一个结论正确,每小题4分,共60分) 1.曲线123-+=x x y 在点P (-1,-1)处的切线方程是 ( )A .1-=x yB .2-=x yC .x y =D .1+=x y2. 曲线f (x )= x 3+x -2在P 0点处的切线平行于直线y = 4x -1,则P 0点的坐标为 ( ) A .(1,0) B .(2,8) C .(1,0)和(-1,-4) D .(2,8)和(-1,-4)3.已知函数x x y 33-=,则它的单调递减区间是 ( ) A.)0,(-∞ B.)1,1(- C. ),0(+∞ D.)1,(--∞及),1(+∞4.已知f (x )=x ln x ,若f ′(x 0)=2,则x 0= ( ) A .e 2B .e C.ln 22D .ln 25. .设曲线11x y x +=-在点(3,2)处的切线与直线10ax y ++=垂直,则a = ( )A .2B . 2-C . 12-D.126已知函数f (x )的导函数为f ′(x ),且满足f (x )=2xf ′(1)+x 2,则f ′(1)= ( ) A .-1 B .-2 C .1 D .27. 下列求导运算正确的是 ( )xx x D e C x x B x x x A x x sin 2)cos (.log 3)3(.2ln 1)(log .11)1(.2322-='='='+='+ 8. 函数)2ln()(2--=x x x f 的单调递增区间是 ( )),和(∞+-+∞---∞2)21,1(.),2(.)21,1(.)1,(.D C B A 9. 设)()(),()(),()(,sin )(112010x f x f x f x f x f x f x x f n n '='='==+, ,)(N n ∈则=')(2005x f ( ) x D x C x B x A cos .cos .sin .sin .--10.已知函数y = f (x )在区间(a ,b )内可导,且x 0∈(a ,b ),则000()()limh f x h f x h h→+--= ( )A .f ′(x 0)B .2f ′(x 0)C .-2f ′(x 0)D .011. 设,)(,02c bx ax x f a ++=>曲线)(x f y =在点))((0,0x f x P 处切线的倾角的取值范围为]4,0[π,则P 点到曲线)(x f y =对称轴距离的取值范围为 ( )ab D ab C aB aA21,0[.]2,0[.]21,0[.]1,0[- 12.等比数列{a n }中,a 1=2,a 8=4,函数f (x )=x (x -a 1)(x -a 2)…(x -a 8),则f ′(0)= ( ) A .26B .29C .212D .215二.填空题:(每小4分,共20分)13.若过原点作曲线y =e x的切线,则切点的坐标为________,切线的斜率为________. 14.设函数f (x )=x (e x+1)+12x 2,则函数f (x )的单调增区间为________.15.函数f (x )=x 3-3x 2+1在x =________处取得极小值. 16.如果函数y=f(x)的导函数的图像如右图所示, 给出下列判断:(1) 函数y=f(x)在区间(3,5)内单调递增; (2) 函数y=f(x)在区间(-1/2,3)内单调递减;(3) 函数y=f(x)在区间(-2,2)内单调递增;(4) 当x= -1/2时,函数y=f(x)有极大值; (5) 当x=2时,函数y=f(x)有极大值;则上述判断中正确的是 .三.解答题:17.求下列函数的导数.(1)y =x 2sin x ; (2)y =log 2(2x 2+3x +1).18.设x x a x f ln 6)5()(2+-=,其中R a ∈,曲线)(x f 在点(1,f(1))处切线与y 轴交于点(0,6). (1)确定a 的值;(2)求函数)(x f 的单调区间.19.若函数xe xf x=)(在c x =处的导数值与函数值互为相反数,求c 的值.20.已知二次函数f (x )满足:①在x =1时有极值;②图象过点(0,-3),且在该点处的切线与直线2x +y =0平行. ⑴求f (x )的解析式;⑵求函数g (x )=f (x 2)的单调递增区间.21.已知函数x bx ax x f 3)(23-+=在1±=x 处取得极值。
选修2-2第一单元导数及其应用测试题含解析人教版

选修2-2第一单元导数及其应用测试题(含解析人教版)时间120分钟,满分150分.一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.曲线y =12x 2-2x 在点⎝⎛⎭⎫1,-32 处的切线的倾斜角为( ) A .-1 B .45° C .-45° D .135°[答案] D[解析] y ′=x -2,所以斜率k =1-2=-1,因此倾斜角为135°.故选D. 2.下列求导运算正确的是( ) A.⎝⎛⎭⎫x +3x ′=1+3x 2 B .(log 2x )′=1x ln2C .(3x )′=3x ·log 3eD .(x 2cos x )′=-2x sin x [答案] B[解析] ⎝⎛⎭⎫x +3x ′=1-3x2,所以A 不正确; (3x )′=3x ln3,所以C 不正确;(x 2cos x )′=2x cos x +x 2·(-sin x ),所以D 不正确;(log 2x )′=1x ln2,所以B 对.故选B. 3.如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t 时刻五角星露出水面部分的图形面积为S (t )(S (0)=0),则导函数y =S ′(t )的图像大致为( )[答案] A[解析] 由图象知,五角星露出水面的面积的变化率是增→减→增→减,其中恰露出一个角时变化不连续,故选A.4.已知f (x )=x 3+ax 2+(a +6)x +1有极大值和极小值,则a 的取值范围为( ) A .-1<a <2 B .-3<a <6 C .a <-1或a >2D .a <-3或a >6[答案] D[解析] f ′(x )=3x 2+2ax +a +6.因为f (x )既有极大值又有极小值,所以Δ>0,即4a 2-4×3×(a +6)>0,即a 2-3a -18>0,解得a >6或a <-3.故选D.5.(2014·山东理,6)直线y =4x 与曲线y =x 3在第一象限内围成的封闭图形的面积为( )A .2 2B .4 2C .2D .4[答案] D [解析] 如图所示由⎩⎪⎨⎪⎧ y =4x ,y =x 3.解得⎩⎪⎨⎪⎧ x =2,y =8,或⎩⎪⎨⎪⎧x =-2,y =-8. ∴第一象限的交点坐标为(2,8)由定积分的几何意义得S =⎠⎛02(4x -x 3)dx =(2x 2-x 44)|20=8-4=4.6.(2014·黄山模拟)已知f (x )=x ln x ,若f ′(x 0)=2,则x 0=( ) A .e 2 B .e C.ln22 D .ln2[答案] B[解析] f (x )的定义域为(0,+∞),f ′(x )=ln x +1, 由f ′(x 0)=2,得ln x 0+1=2,解得x 0=e.7.(2013·北师大附中高二期中)函数y =ln xx 的导数为( )A .y ′=1xB .y ′=ln x -1x 2C .y ′=-1x 2D .y ′=1-ln xx2[答案] D[解析] y ′=(ln x )′·x -(ln x )·x ′x 2=1-ln xx2. 8.函数f (x )=x 3-2x +3的图象在x =1处的切线与圆x 2+y 2=8的位置关系是( ) A .相切B .相交且过圆心C .相交但不过圆心D .相离[答案] C[解析] 切线方程为y -2=x -1,即x -y +1=0.圆心到直线的距离为12=22<22,所以直线与圆相交但不过圆心.故选C.9.f ′(x )是f (x )的导函数,f ′(x )的图象如图所示,则f (x )的图象可能是( )[答案] D[解析] 由图可知,当b >x >a 时,f ′(x )>0,故在[a ,b ]上,f (x )为增函数.且又由图知f ′(x )在区间[a ,b ]上先增大后减小,即曲线上每一点处切线的斜率先增大再减小,故选D.10.曲线y =e 12x 在点(4,e 2)处的切线与坐标轴所围三角形的面积为( )A.92e 2 B .4e 2 C .2e 2 D .e 2[答案] D[解析] ∵y ′=12e x2,∴在点(4,e 2)处的切线方程为y =12e 2x -e 2,令x =0得y =-e 2,令y =0得x =2, ∴围成三角形的面积为e 2.故选D.11.(2014·天门市调研)已知函数f (x )的导函数f ′(x )=a (x -b )2+c 的图象如图所示,则函数f (x )的图象可能是( )[答案] D[解析] 由导函数图象可知,当x <0时,函数f (x )递减,排除A ,B ;当0<x <x 1时,f ′(x )>0,函数f (x )递增.因此,当x =0时,f (x )取得极小值,故选D.12.(2013·泰安一中高二段测)已知函数f (x )的导函数的图象如图所示,若△ABC 为锐角三角形,则一定成立的是( )A .f (sin A )>f (cosB ) B .f (sin A )<f (cos B )C .f (sin A )>f (sin B )D .f (cos A )<f (cos B ) [答案] A[解析] 由导函数图象可知,x >0时,f ′(x )>0,即f (x )单调递增,又△ABC 为锐角三角形,则A +B >π2,即π2>A >π2-B >0,故sin A >sin(π2-B )>0,即sin A >cos B >0,故f (sin A )>f (cos B ),选A.二、填空题(本大题共4个小题,每小题4分,共16分.将正确答案填在题中横线上) 13.经过点(2,0)且与曲线y =1x 相切的直线方程为______________.[答案] x +y -2=0[解析] 设切点为⎝⎛⎭⎫x 0,1x 0,则1x 0x 0-2=-1x 20,解得x 0=1,所以切点为(1,1),斜率为-1,直线方程为x +y -2=0.14.若函数f (x )=ax 2-1x 在(0,+∞)上为增函数,则实数a 的取值范围是________.[答案] a ≥0[解析] f ′(x )=⎝⎛⎭⎫ax -1x ′=a +1x2,由题意得,a +1x 2≥0对x ∈(0,+∞)恒成立,即a ≥-1x2,x ∈(0,+∞)恒成立.∴a ≥0.15.(2014·湖北重点中学高二期中联考)已知函数f (x )=13ax 3+12ax 2-2ax +2a +1的图象经过四个象限,则实数a 的取值范围是________.[答案] (-65,-316)[解析] f ′(x )=ax 2+ax -2a =a (x -1)(x +2), 由f (x )的图象经过四个象限知,若a >0,则⎩⎪⎨⎪⎧ f (-2)>0,f (1)<0,此时无解;若a <0,则⎩⎪⎨⎪⎧f (-2)<0,f (1)>0,∴-65<a <-316,综上知,-65<a <-316.16.(2014·泉州实验中学期中)已知函数f (x )=x 3-3x ,若过点A (1,m )(m ≠-2)可作曲线y =f (x )的三条切线,则实数m 的取值范围为________.[答案] (-3,-2)[解析] f ′(x )=3x 2-3,设切点为P (x 0,y 0),则切线方程为y -(x 30-3x 0)=(3x 20-3)(x -x 0),∵切线经过点A (1,m ),∴m -(x 30-3x 0)=(3x 20-3)(1-x 0),∴m =-2x 30+3x 20-3,m ′=-6x 20+6x 0,∴当0<x 0<1时,此函数单调递增,当x 0<0或x 0>1时,此函数单调递减,当x 0=0时,m =-3,当x 0=1时,m =-2,∴当-3<m <-2时,直线y =m 与函数y =-2x 30+3x 20-3的图象有三个不同交点,从而x 0有三个不同实数根,故过点A (1,m )可作三条不同切线,∴m 的取值范围是(-3,-2).三、解答题(本大题共6个小题,共74分.解答应写出文字说明、证明过程或演算步骤) 17.(本题满分12分)设函数f (x )=ln x +ln(2-x )+ax (a >0). (1)当a =1时,求f (x )的单调区间;(2)若f (x )在(0,1]上 的最大值为12,求a 的值.[解析] 函数f (x )的定义域为(0,2), f ′(x )=1x -12-x+a ,(1)当a =1时,f ′(x )=-x 2+2x (2-x ),∴当x ∈(0,2)时,f ′(x )>0,当x ∈(2,2)时,f ′(x )<0,所以f (x )的单调递增区间为(0,2),单调递减区间为(2,2);(2)当x ∈(0,1]时,f ′(x )=2-2xx (2-x )+a >0,即f (x )在(0,1]上单调递增,故f (x )在(0,1]上的最大值为f (1)=a ,因此a =12.18.(本题满分12分)(2014·韶关市曲江一中月考)已知函数f (x )=ax 3+cx +d (a ≠0)是R 上的奇函数,当x =1时,f (x )取得极值-2.(1)求函数f (x )的解析式;(2)求函数f (x )的单调区间和极大值;(3)证明:对任意x 1、x 2∈(-1,1),不等式|f (x 1)-f (x 2)|<4恒成立. [解析] (1)∵f (x )是R 上的奇函数, ∴f (-x )=-f (x ),即-ax 3-cx +d =-ax 3-cx -d ,∴d =-d , ∴d =0(或由f (0)=0得d =0). ∴f (x )=ax 3+cx ,f ′(x )=3ax 2+c , 又当x =1时,f (x )取得极值-2,∴⎩⎪⎨⎪⎧ f (1)=-2,f ′(1)=0,即⎩⎪⎨⎪⎧ a +c =-2,3a +c =0,解得⎩⎪⎨⎪⎧a =1,c =-3. ∴f (x )=x 3-3x .(2)f ′(x )=3x 2-3=3(x +1)(x -1),令f ′(x )=0,得x =±1, 当-1<x <1时,f ′(x )<0,函数f (x )单调递减; 当x <-1或x >1时,f ′(x )>0,函数f (x )单调递增;∴函数f (x )的递增区间是(-∞,-1)和(1,+∞);递减区间为(-1,1). 因此,f (x )在x =-1处取得极大值,且极大值为f (-1)=2.(3)由(2)知,函数f (x )在区间[-1,1]上单调递减,且f (x )在区间[-1,1]上的最大值为M =f (-1)=2.最小值为m =f (1)=-2.∴对任意x 1、x 2∈(-1,1),|f (x 1)-f (x 2)|<M -m =4成立.即对任意x 1、x 2∈(-1,1),不等式|f (x 1)-f (x 2)|<4恒成立.19.(本题满分12分)求定积分⎠⎛-11f (x )d x ,其中f (x )=⎩⎪⎨⎪⎧sin x -1 (x ≤0)x 2 (x >0).[解析] ⎠⎛-11 f (x )d x =⎠⎛-10 f (x )d x +⎠⎛01f (x )d x=⎠⎛-11 (sin x -1)d x +⎠⎛01x 2d x=(-cos x -x )|0-1+13x 3|10 =cos1-2+13=cos1-53.20.(本题满分12分)已知向量a =(x 2,x +1),b =(1-x ,t ).若函数f (x )=a ·b 在区间(-1,1)上是增函数,求t 的取值范围.[解析] 依定义f (x )=x 2(1-x )+t (x +1)=-x 3+x 2+tx +t ,∴f ′(x )=-3x 2+2x +t . 若f (x )在(-1,1)上是增函数,则在(-1,1)上有f ′(x )≥0.恒成立.∵f ′(x )≥0⇔t ≥3x 2-2x ,由于g (x )=3x 2-2x 的图象是对称轴为x =13,开口向上的抛物线,故要使t ≥3x 2-2x 在区间(-1,1)上恒成立⇔t ≥g (-1),即t ≥5.而当t ≥5时,f ′(x )在(-1,1)上满足f ′(x )>0, 即f (x )在(-1,1)上是增函数. 故t 的取值范围是t ≥5.21.(本题满分12分)设函数f (x )=2x 3-3(a +1)x 2+6ax +8,其中a ∈R . (1)若f (x )在x =3处取得极值,求常数a 的值; (2)若f (x )在(-∞,0)上为增函数,求a 的取值范围. [解析] (1)f ′(x )=6x 2-6(a +1)x +6a =6(x -a )(x -1). 因f (x )在x =3处取得极值,所以f ′(3)=6(3-a )(3-1)=0,解得a =3. 经检验知当a =3时,x =3为f (x )的极值点. (2)令f ′(x )=6(x -a )(x -1)=0得x 1=a ,x 2=1.当a <0时,若x ∈(-∞,a )∪(1,+∞),则f ′(x )>0,所以f (x )在(-∞,a )和(1,+∞)上为增函数.当0≤a <1时,f (x )在(-∞,0)上为增函数.当a ≥1时,若x ∈(-∞,1)∪(a ,+∞),则f ′(x )>0,所以f (x )在(-∞,1)和(a ,+∞)上为增函数,从而f (x )在(-∞,0)上为增函数. 综上可知,当a ≥0时,f (x )在(-∞,0)上为增函数. 22.(本题满分14分)设函数f (x )=a e x +1a e x +b (a >0).(1)求f (x )在[0,+∞)内的最小值;(2)设曲线y =f (x )在点(2,f (2))处的切线方程为y =32x ,求a ,b 的值.[解析] (1)f ′(x )=a e x -1a ex ,当f ′(x )>0,即x >-ln a 时,f (x )在(-ln a ,+∞)上递增; 当f ′(x )<0,即x <-ln a 时,f (x )在(-∞,-ln a )上递减.①当0<a <1时,-ln a >0,f (x )在(0,-ln a )上递减,在(-ln a ,+∞)上递增,从而f (x )在[0,+∞)上的最小值为f (-ln a )=2+b ;②当a ≥1时,-ln a ≤0,f (x )在[0,+∞)上递增,从而f (x )在[0,+∞)上的最小值为f (0)=a +1a+b .(2)依题意f ′(2)=a e 2-1a e 2=32,解得a e 2=2或a e 2=-12(舍去).所以a =2e 2,代入原函数可得2+12+b =3,即b =12.故a =2e 2,b =12.。
高考理科数学(选修2-2) 第一章导数及其应用 本章达标测评【含答案】

第一章本章达标测评一、单选题1.一个物体的运动方程为s(t)= 1-t+t ²,其中s 的单位是米,t 的单位是秒,那么物体在4秒末的瞬时速度是 ( ) A .5米/秒 B.6米/秒 C .7米/秒 D .8米/秒 2.下列求导运算正确的是 ( ) A .B .C .(χ²cos χ)’=-2χsin χD .3.已知函数f(χ)=2In 3χ+8χ+1,则值为 ( )A.10 B .-10 C.-20 D .20 4.若,则实数a 等于 ( )A.-1B.1 C . D . 5.已知函数,χ∈R ,若f(χ)+9≥0恒成立,则实数m 的取值范围是 ( ) A .B . C.D .6.已知函数为偶函数,若曲线y=f(χ)的一条切线的斜率为,则切点的横坐标等于 ( )χχ=)'n 11(1)'e (+=x e x x 211)'1(x x x -=+xf x f oim∆-∆-→∆)1()21(l χ⎰=+2π02)cos (sin dx x a x 3-3mx x x f 332421)(+-=23≥m 23>m 23≤m 23<m x ae x e x f -+=)(23A .In 2B .21n 2C .2D . 7.已知函数是函数的导函数,则的图象大致是 ( )8.若曲线y=In (χ+a )的一条切线为y=e χ+b ,其中a ,b 为正实数,则的取值范围是 ( )A .B . C. D .[2,e)9.若函数χ在(1,+∞)上为增函数,则实数a 的取值范围是( )A.(1,+∞)B.[1,+∞)C.(-∞ ,1)D.(-∞,1] 10.若a>2,则方程在(0,2)上恰好有 ( )A .0个根B .1个根C .2个根D .3个根2xf x x x f ',cos 241)(+=)(x f )('x f 2++b ea ),22(+∞+ee [)+∞,e [)+∞,2na x x f 1221)(-=012331=+-ax x11.若函数,且0<χ₁<χ₂<1,设,,则a,b 的大小关系是( )A .a>bB .a<bC .a=bD .a 、b 的大小不能确定12.设函数f ’(χ)是函数f(χ)(χ∈ R)的导函数,若f(χ)-f( -χ)= 2χ³,且当x>0时,f ’(χ)>3χ²,则不等式f(χ)-f(χ-1)>3χ²-3χ+1的解集为 ( )A .(-∞,2)B .C .D .(2,+∞)二.填空题13.若曲线y=a χ²-1n(x+1)在点(1,b)处的切线平行于x 轴,则a=____. 14.定义1:若函数f(χ)在区间D 上可导,即f ’(χ)存在,且导函数f ’(χ)在区间D 上也可导,则称函数f(χ)在区间D 上存在二阶导数,记作f ’(χ),即f ’(χ)=[f ’(χ)]’.定义2:若函数f(χ)在区间D 上的二阶导数恒为正,即f ’(χ)>0恒成立,则称函数f(χ)在区间D 上为凹函数. 已知函数f(χ)=χ³-+1在区间D 上为凹函数,则χ的取值范围是_________ .15.要数一个圆锥形漏斗,其母线的长为20 cm ,要使体积最大,则高为____. 16.函数y=χ²(χ>0)的图象在点(,a )处的切线与χ轴的交点的横坐标为,其中k ∈N*,若a ₁=16,则a ₁+a ₃+a ₅,的值是_______三.解答题x x x f sin )(=11sin xx a =22sin x x b =),21(+∞)21,(-∞223x k a2k1+k a17.已知函数.(1)求函数在区间[1,e]上的最大值、最小值;(2)求证:在区间[1,+∞)上,函数的图象在函数的图象的下方.18.设函数=(1)讨论函数的单调性;(2)若函数在区间(-1,1)内单调递增,求k 的取值范围.19.已知函数=χIn χ,g (χ)=(-χ²+a χ-3)(a 为实数). (1)当a=5时,求函数y=g (χ)的图象在χ=1处的切线方程;(2)若关于x 的方程g(χ)=在上有两个不相等的实数根,求实数anxx x f 1221)(+=)(x f )(x f 332)(x x g =)(x f )0(≠k kx xe )(x f )(x f )(x f xe )(2xf x e ⎥⎦⎤⎢⎣⎡e e ,1的取值范围.20.设=xIn χ-a χ²+(2a-1)χ,a ∈R . (1)令g (χ)=,讨论g(χ)的单调性;(2)已知在χ=1处取得极大值,求实数a 的取值范围.21.经过多年的运作,“双十一”抢购活动已经成为整个电商行业的大型集体促销盛宴,为庆祝“双十一”网购狂欢节,某厂商决定对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量P (万件)与促销费用菇(万元)满足(其中0<χ≤a ,a 为正常数).已知生产该批产品P 万件还需投入成本( 10+2P)万元(不含促销费用),产品的销售价格定为元/件,假定厂)(x f )('x f )(x f 123+-=x p )204(p+家的生产能力完全能满足市场的销售需求.(1)将该产品的利润,y (万元)表示为关于促销费用χ(万元)的函数; (2)促销费用为多少万元时,厂家的利润最大?22.已知函数=χ³+(1-a )χ²-a(a+2)x+b ,a ,b ∈R. (1)若函数在区间(-1,1)上不单调,求a 的取值范围; (2)令,若对任意χ₁∈[-1,1],存在χ₂∈[0,2],使得f ’(χ₁) +2aχ₁=g(χ₂)成立,求a 的取值范围.第一章本章达标测评 一、选择题1.C 由题知s ’(t)= - 1+2t ’s ’(4)=7,故选C .2.DA 项,;)(x f )(x f 31619)(-=x x g 2)1(1)'11(nx x nx -=B 项,C 项,D 正确,故选D . 3.C,,故选C .4.B ,=0-(-1)+a=2,a=1,故选B .5.A,f ’(χ)=2χ³-6χ²,令,f ’(χ)=0,得χ=0或χ=3. 易知χ=3是函数的最小值点,所以函数f(χ)的最小值为f( 3)= 3m-.因为不等式f(χ)+9≥0恒成立,即f(χ)≥-9恒成立,所以3m-≥-9,解得m ≥,故选A .6.A 因为f(χ)是偶函数,所以f(χ)=f(-x ),即 ,解得a=1.所以f(χ)=,所以f ’(χ)=,设切点的横坐标为χₒ,则.设t=,则,解得t=2,即,所以χₒ=In 2,故选A .x xe x e x xe +=)'(x x x x x x sin 2cos 2)'cos 2(-=836)('+=x x f 20)1('22)1()21(0lim 2)1()21(0lim-=-∆--∆-→∆-=∆-∆-→∆f x f x f x x f x f x ⎰=+202)cos (sin πdx x a x 2020sin 2020)cos (cos sin ππππ⎰⎰+-=+xa x xds a xdx 22722723)(x ae x ae x e --+-+x e x e -+x e x e --230)0('0=--=x e x e x f )0(0>t x e 231==t t 20=x e7.A 由于f(χ)=,f ’(χ)= ,f ’(-χ)=-f ’(χ),故f ’(χ)为奇函数,其图象关于原点对称, 排除B 和D ,又当时,排除C .故选A .8.C 由题意得,设切点为(χₒ,y ₒ),则有解得b=ae-2,b>0,,,当且仅当a=1时,等号成立,故选C .9.D 由题意知f ’(χ)=。
选修2-2人教版第一章--导数与应用测试(含答案)

第一章 导数与应用姓名:__________班级:__________一、选择题1.函数)22(9323<<---=x x x x y 有 ( )A.极大值5,极小值-27;B. 极大值5,极小值-11; C .极大值5,无极小值; D .极小值-27,无极大值. 2.直线y x =与曲线y 围成的平面图形的面积是. ( )A .14 B .2 C .1 D .123.设,35,3)21,0(4)(24最小值为的最大值为≤≤>+-=x a b ax ax x f 则a 、b 值依次为 ( )A .31 , 3 B .3 , 31 C .—31, 3 D .—31, —3 4.曲线12ex y =在点2(4e ),处的切线与坐标轴所围三角形的面积为( )A.29e 2B.24e C.22e D.2e 5.若21()ln(2)2f x x b x =-++∞在(-1,+)上是减函数,则b 的取值范围是( )A. [1,)-+∞B. (1,)-+∞C. (,1]-∞-D. (,1)-∞-6.函数x x x x f cos sin cos )(23-+=上最大值等于 ( )A .274 B .278 C .2716 D .27327.函数223)(a bx ax x x f +--=在1=x 处有极值10, 则点),(b a 为 ( )A.)3,3(-B.)11,4(-C. )3,3(-或)11,4(-D.不存在8.函数1,(10)()cos ,(0)2x x f x x x π+-≤<⎧⎪=⎨≤≤⎪⎩的图象与x 轴所围成的封闭图形的面积为( )A .32 B . 1 C . 2 D .12 9.在1[,2]2x ∈上,函数2()f x x Px q =++与33()22x g x x=+在同一点取得相同的最小值,那么()f x 在1[,2]2x ∈上的最大值是( )A .134B .4C .8D .5410.函数=)(x f 12+-x x 的最大值为( )A .2-B .22-C .3-D .33- 11.函数f(x)=)(sin 2R x x x ∈-π的部分图象是 ( )A. B. C. D.12.已知函数2()f x x bx =+的图像在点(1,(1))A f 处的切线的斜率为3,数列1()f n ⎧⎫⎨⎬⎩⎭()n N *∈的前n 项和为n S ,则2009S 的值为( ) A .20072008 B .20082009 C .20092010 D .20102011 13.设c bx ax x x f +++=22131)(23,当)1,0(∈x 时取得极大值,当)2,1(∈x 时取得极小值,则12--a b 的取值范围为( )A .)4,1(B .)1,21(C .)21,41(D .)1,41(14.设定义域为R 的函数x x x f 2)(2-=,则关于x 的方程2)()(31)(23+-=x f x f x g ,能让)(x g 取极大值的x 个数为( ) A.2 B.3 C.5 D.7 二、填空题15.30|2|x dx -⎰=_____________16.已知某质点的位移s 与移动时间t 满足224t s t e-=⋅,则质点在2=t 的瞬时速度是 ;17.设函数())(0)f x ϕϕπ=+<<,若()()f x f x '+为奇函数,则ϕ=__________ 18.已知函数f (x )是以2为周期的偶函数,且当)10(log ,12)(,)1,0(2f x f x x则时-=∈的值为19.已知x x x f cos sin )(1+=,记'21()()f x f x =,'32()()f x f x =,…,)()('1x f x f n n -=)2*,(≥∈n N n ,则122009()()()444f f f πππ+++= .三、解答题20.已知()y f x =是二次函数,方程()0f x =有两相等实根,若)('x f 为)(x f 的导函数,且()22f x x '=+ (1)求()f x 的解析式.(2)求函数()y f x =与函数241y x x =--+所围成的图形的面积.21.某地建一座桥,两端的桥墩已建好,这两墩相距m 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为x 米的相邻两墩之间的桥 面工程费用为(2x 万元。
人教版选修2-2第一章导数及(含定积分)其应用测试题

人教版高二数学选修2-2第一章导数及其应用(含定积分)测试题(时间120分钟,分值150分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案写在答题卡上) 1.已知32()32f x ax x =++,若'(1)4f -=,则a 的值等于( )A .319 B .316 C .313 D .310 2、()0f x =的导数是( )A .0B .1C .不存在D .不确定3、y = ) A .23xB .213x C .12- D 4、曲线n y x =在2x =处的导数是12,则n 等于( )A .1B .2C .3D .4 5、在曲线2y x =上的切线的倾斜角为4π的点是( ) A .()0,0 B .()2,4 C .11,416⎛⎫ ⎪⎝⎭ D .11,24⎛⎫⎪⎝⎭6、关于函数762)(23+-=x x x f ,下列说法不正确的是( D )A .在区间(∞-,0)内,)(x f 为增函数B .在区间(0,2)内,)(x f 为减函数C .在区间(2,∞+)内,)(x f 为增函数D .在区间()(),02,-∞⋃+∞内,)(x f 为增函数 7、曲线3()2f x x x =+-在0p 处的切线平行于直线41y x =-,则0p 点的坐标为( )A.(1,0)B.(2,8)C.(2,8)和(1,4)--D.(1,0)和(1,4)--8、已知函数)(x f y =的图象在点M (1,f (1))处的切线方程是x y 21=+2,则(1)(1)f f '+等于( )A.1B.52C.3D.09、函数())0f x x =>的导数是( ) AB C D10.下列结论中正确的是( )A .导数为零的点一定是极值点B .如果在0x 附近的左侧0)('>x f ,右侧0)('<x f ,那么)(0x f 是极大值C .如果在0x 附近的左侧0)('>x f ,右侧0)('<x f ,那么)(0x f 是极小值D .如果在0x 附近的左侧0)('<x f ,右侧0)('>x f ,那么)(0x f 是极大值 11、积分=-⎰-a adx x a 22( ). A .241a π B .221a π C .2a π D .22a π12、由抛物线x y 22=与直线4-=x y 所围成的图形的面积是( ). A .18B .338C .316 D .16二、填空题(每小题5分,共20分)13、已知a 为实数,()()()24f x x x a =--,且()10f '-=,则a =___________. 14、函数x y x e =-上某点的切线平行于x 轴,则这点的坐标为__________. 15、在曲线323610y x x x =++-的切线中,斜率最小的切线方程是____________. 16、已知='+=)0(,cos sin )(f x x xe x f x 则__________ 三、解答题(共70分) 17、(10分)、求曲线y =在点18,4⎛⎫⎪⎝⎭处的切线方程.18、(12分)求定积分 =-+-⎰dx x x 40|)3||1(| ____________。
高中数学选修2-2第一章《导数及其应用》单元检测卷含解析

⾼中数学选修2-2第⼀章《导数及其应⽤》单元检测卷含解析选修2-2第⼀章《导数及其应⽤》单元检测题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(⾮选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题共60分)⼀、选择题(本⼤题共12个⼩题,每⼩题5分,共60分,在每⼩题给出的四个选项中,只有⼀项是符合题⽬要求的) 1.已知函数y =f (x )的图象如图,则f ′(x A )与f ′(x B )的⼤⼩关系是( )A .f ′(x A )>f ′(xB )B .f ′(x A )C .f ′(x A )=f ′(x B )D .不能确定2.任⼀作直线运动的物体,其位移s 与时间t 的关系是s =3t -t 2,则物体的初速度是()A .0B .3C .-2D .3-2t3.已知曲线y =2ax 2+1过点(a ,3),则该曲线在该点处的切线⽅程为( )A .y =-4x -1B .y =4x -1C .y =4x -11D .y =-4x +74.若点P 在曲线y =x 3-3x 2+(3-3)x +34上移动,经过点P 的切线的倾斜⾓为α,则⾓α的取值范围是( )A.0,π2B.0,π2∪2π3,πC.2π3,πD.0,2π35.函数f (x )=x 3+ax -2在区间(1,+∞)内是增函数,则实数a 的取值范围是( )A .[3,+∞) B.[-3,+∞)C .(-3,+∞) D.(-∞,-3)6.下列等式成⽴的是( )A .?ba 0d x =b -aB .?b a x d x =12C .?1-1|x |d x =2?10|x |d xD .?b a (x +1)d x =?b a x d x7.已知a >0,函数f (x )=-x 3+ax 在[1,+∞)上是单调减函数,则a 的最⼤值为( )A .1B .2C .3D .48.若函数f (x )=a sin x +13cos x 在x =π3处有最值,那么a 等于( ) A.33 B .-33 C.36 D .-369.已知?20 f (x )d x =3,则?20[f (x )+6]d x 等于( )A .9B .12C .15D .1810.设a ∈R ,若函数y =e ax +3x ,x ∈R 有⼤于零的极值点,则( )A .a >-3B .a <-3C .a >-13D .a <-1311.函数f (x )=x 1-x的单调增区间是( ) A .(-∞,1)B .(1,+∞)C .(-∞,1),(1,+∞)D .(-∞,-1),(1,+∞)12.某银⾏准备新设⼀种定期存款业务,经预测,存款量与存款利率成正⽐,⽐例系数为k (k >0),贷款的利率为4.8%,假设银⾏吸收的存款能全部放贷出去.若存款利率为x (x ∈(0,0.048)),则存款利率为多少时,银⾏可获得最⼤利益( )A .0.012B .0.024C .0.032D .0.036第Ⅱ卷(⾮选择题共90分)⼆、填空题(本⼤题共4个⼩题,每⼩题5分,共20分,把正确答案填在题中横线上)13.若f (x )=-12x 2+b ln(x +2)在(-1,+∞)上是减函数,则b 的取值范围是__________.14.设函数f (x )=ax 3-3x +1 (x ∈R),若对于x ∈[-1,1],都有f (x )≥0,则实数a 的值为________.15.如图,内接于抛物线y =1-x 2的矩形ABCD ,其中A 、B 在抛物线上运动,C 、D 在x 轴上运动,则此矩形的⾯积的最⼤值是________.16.已知函数f (x )=x 3+ax 2+bx +c ,x ∈[-2,2]表⽰过原点的曲线,且在x =±1处的切线的倾斜⾓均为34π,有以下命题:①f (x )的解析式为f (x )=x 3-4x ,x ∈[-2,2].②f (x )的极值点有且只有⼀个.③f (x )的最⼤值与最⼩值之和等于零.其中正确命题的序号为________.三、解答题(本⼤题共6个⼩题,共70分,解答应写出⽂字说明,证明过程或演算步骤)17.(本⼩题满分10分)若函数f (x )=13x 3-12ax 2+(a -1)x +1在区间(1,4)上为减函数,在区间(6,+∞)上为增函数,试求实数a 的取值范围.18.(本⼩题满分12分)已知函数f (x )=x 3+ax 2+bx +c 在x =-23与x =1时都取得极值. (1)求a ,b 的值与函数f (x )的单调区间;(2)若对x ∈[-1,2],不等式f (x )。
【高中数学选修2-2:第一章-导数及其应用-单元测试题

【高中数学选修2-2:第一章-导数及其应用-单元测试题数学选修2-2第一章单元测试题一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数f (x )的定义域为开区间(a ,b ),导函数f ′(x )在(a ,b )内的图像如图所示,则函数f (x )在开区间(a ,b )内有极小值点( )A .1个B .2个C .3个D .4个2.在区间[12,2]上,函数f (x )=x 2+px +q 与g (x )=2x +1x 2在同一点处取得相同的最小值,那么f (x )在[12,2]上的最大值是( )A.134 B.54 C .8D .43.点P 在曲线y =x 3-x +23上移动,设点P 处的切线的倾斜角为α,则α的取值范围是( )A .[0,π2]B .[0,π2]∪[34π,π)x=1的对称点B也在函数f(x)的图像上.19.(12分)设x=-2与x=4是函数f(x)=x3+ax2+bx的两个极值点.(1)求常数a,b;(2)试判断x=-2,x=4是函数f(x)的极大值还是极小值,并说明理由.20.(12分)已知f(x)=ax3-6ax2+b,x∈[-1,2]的最大值为3,最小值为-29,求a,b的值.21.(12分)(2010·重庆卷)已知函数f(x)=ax3+x2+bx(其中常数a,b∈R),g(x)=f(x)+f′(x)是奇函数.(1)求f(x)的表达式;(2)讨论g(x)的单调性,并求g(x)在区间[1,2]上的最大值与最小值.22.(12分)已知函数f(x)=ln(ax+1)+1-x1+x,x≥0,其中a>0.(1)若f(x)在x=1处取得极值,求a的值;(2)求f(x)的单调区间;(3)若f(x)的最小值为1,求a的取值范围.参考答案 1.答案 A解析 设极值点依次为x 1,x 2,x 3且a <x 1<x 2<x 3<b ,则f (x )在(a ,x 1),(x 2,x 3)上递增,在(x 1,x 2),(x 3,b )上递减,因此,x 1、x 3是极大值点,只有x 2是极小值点.2.答案 D3.答案 B4.答案 A解析 因为函数f (x )=12x 4-2x 3+3m ,所以f ′(x )=2x 3-6x 2.令f ′(x )=0,得x =0或x =3,经检验知x =3是函数的一个最小值点,所以函数的最小值为f (3)=3m -272.不等式f (x )+9≥0恒成立,即f (x )≥-9恒成立,所以3m -272≥-9,解得m ≥32.5.答案 A解析 f (x )=cos 2x -cos x -1,∴f ′(x )=-2sin x ·cos x +sin x =sin x ·(1-2cos x ). 令f ′(x )>0,结合选项,选A. 6.答案 D 7.答案 D 8.答案 A 9.答案 B解析 设f (x )=13x 3-ax 2+1,则f ′(x )=x 2-2ax =x (x -2a ),当x∈(0,2)时,f ′(x )<0,f (x )在(0,2)上为减函数,又f (0)f (2)=1⎝ ⎛⎭⎪⎫83-4a +1=113-4a <0, f (x )=0在(0,2)上恰好有一个根,故选B. 10.答案 D 11.答案 C解析 数形结合,如图.⎠⎛02f(x)d x =⎠⎛01x 2d x +⎠⎛12(2-x)d x = ⎪⎪⎪13x 310⎪⎪⎪+(2x -12x 2)21=13+(4-2-2+12) =56,故选C . 12.答案 A解析 f ′(x)=x cos x -sin xx 2,令g(x)=x cos x -sin x ,则g ′(x)=-x sin x +cos x -cos x =-x sin x.∵0<x<1,∴g ′(x)<0,即函数g(x)在(0,1)上是减函数,得g(x)<g(0)=0,故f ′(x)<0,函数f(x)在(0,1)上是减函数,得a>b ,故选A .13.答案 23解析 f ′(x)=x 2-2f ′(1)x +1,令x =1,得f ′(1)=23.14.答案 c<a<b解析 f(2)=f(π-2),f(3)=f(π-3),因为f ′(x)=1+cos x ≥0,故f(x)在⎝ ⎛⎭⎪⎫-π2,π2上是增函数,∵π2>π-2>1>π-3>0,∴f(π-2)>f(1)>f(π-3),即c<a<b.15.答案 f(x)=23x +83解析 设函数f(x)=ax +b(a ≠0),因为函数f(x)的图像过点(2,4),所以有b =4-2a.∴⎠⎛01f(x)d x =⎠⎛01 (ax +4-2a)d x=[12ax 2+(4-2a)x] |10=12a +4-2a =1.∴a =23.∴b =83.∴f(x)=23x +83.16.答案 21解析 ∵y ′=2x ,∴过点(a k ,a 2k )处的切线方程为y -a 2k =2a k (x -a k ),又该切线与x 轴的交点为(a k +1,0),所以a k +1=12a k ,即数列{a k }是等比数列,首项a 1=16,其公比q =12,∴a 3=4,a 5=1,∴a 1+a 3+a 5=21.17.解析 抛物线y =x -x 2与x 轴两交点的横坐标为x 1=0,x 2=1,所以,抛物线与x 轴所围图形面积S =⎠⎛01(x -x 2)d x =⎪⎪⎪⎝ ⎛⎭⎪⎫x 22-x 3310=12-13=16. 又⎩⎨⎧y =x -x 2,y =kx ,由此可得抛物线y =x -x 2与y =kx 两交点的横坐标x 3=0,x 4=1-k ,所以S2=⎠⎛01-k (x -x 2-kx)d x =⎪⎪⎪⎪⎝⎛⎭⎪⎪⎫1-k 2x 2-x 331-k 0=16(1-k)3. 又S =16,所以(1-k)3=12,∴k =1-342.18.解析 (1)由函数f(x)=x4-4x3+ax2-1在区间[0,1]单调递增,在区间[1,2)单调递减,∴x =1时,取得极大值,∴f ′(1)=0. 又f ′(x)=4x3-12x2+2ax , ∴4-12+2a =0⇒a =4.(2)点A(x0,f(x0))关于直线x =1的对称点B 的坐标为(2-x0,f(x0)),f(2-x0)=(2-x0)4-4(2-x0)3+4(2-x0)2-1 =(2-x0)2[(2-x0)-2]2-1 =x40-4x30+ax20-1=f(x0),∴A 关于直线x =1的对称点B 也在函数f(x)的图像上. 19.解析 f ′(x)=3x2+2ax +b. (1)由极值点的必要条件可知:f ′(-2)=f ′(4)=0,即⎩⎨⎧12-4a +b =0,48+8a +b =0,解得a =-3,b =-24.或f ′(x)=3x2+2ax +b =3(x +2)(x -4) =3x2-6x -24, 也可得a =-3,b =-24. (2)由f ′(x)=3(x +2)(x -4).当x <-2时,f ′(x)>0,当-2<x <4时,f ′(x)<0. ∴x =-2是极大值点,而当x >4时,f ′(x)>0, ∴x =4是极小值点.20.解析 a ≠0(否则f(x)=b 与题设矛盾),由f′(x)=3ax2-12ax=0及x∈[-1,2],得x=0.(1)当a>0时,列表:x (-1,0) 0 (0,2)f′(x) +0 -f(x) 增极大值b 减由上表知,f(x)在[-1,0]上是增函数,f(x)在[0,2]上是减函数.则当x=0时,f(x)有最大值,从而b=3.又f(-1)=-7a+3,f(2)=-16a+3,∵a>0,∴f(-1)>f(2).从而f(2)=-16a+3=-29,得a=2.(2)当a<0时,用类似的方法可判断当x=0时f(x)有最小值.当x=2时,f(x)有最大值.从而f(0)=b=-29, f(2)=-16a-29=3,得a=-2.综上,a=2,b=3或a=-2,b=-29.21.解析(1)由题意得f′(x)=3ax2+2x+b.因此g(x)=f(x)+f′(x)=ax3+(3a+1)x2+(b+2)x+b.因为函数g(x)是奇函数,所以g(-x )=-g (x ),即对任意实数x ,有a (-x )3+(3a +1)(-x )2+(b +2)(-x )+b =-[ax 3+(3a +1)x 2+(b +2)x +b ],从而3a +1=0,b =0,解得a =-13,b =0,因此f (x )的解析式为f (x )=-13x 3+x 2.(2)由(1)知g (x )=-13x 3+2x ,所以g ′(x )=-x 2+2.令 g ′(x )=0,解得x 1=-2,x 2=2,则当x <-2或x >2时,g ′(x )<0,从而g (x )在区间(-∞,-2],[2,+∞)上是减函数;当-2<x <2时, g ′(x )>0,从而g (x )在[-2,2]上是增函数.由前面讨论知,g (x )在区间[1,2]上的最大值与最小值只能在x =1,2,2时取得,而g (1)=53,g (2)=423,g (2)=43.因此g (x )在区间[1,2]上的最大值为g (2)=423,最小值为g (2)=43. 22.分析 解答本题,应先正确求出函数f (x )的导数f ′(x ),再利用导数与函数的单调性、导数与极值、导数与最值等知识求解,并注意在定义域范围内求解.解析 (1)f ′(x )=aax +1-2(1+x )2=ax 2+a -2(ax +1)(1+x )2, ∵f (x )在x =1处取得极值,∴f ′(1)=0,即a ·12+a -2=0,解得a =1. (2)f ′(x )=ax 2+a -2(ax +1)(1+x )2,∵x≥0,a>0,∴ax+1>0.①当a≥2时,在区间[0,+∞)上,f′(x)>0,∴f(x)的单调增区间为[0,+∞).②当0<a<2时,由f′(x)>0,解得x> 2-a a.由f′(x)<0,解得x< 2-a a.∴f(x)的单调减区间为(0, 2-aa),单调增区间为(2-aa,+∞).(3)当a≥2时,由(2)①知,f(x)的最小值为f(0)=1;当0<a<2,由(2)②知,f(x)在x=2-aa处取得最小值,且f(2-aa)<f(0)=1.综上可知,若f(x)的最小值为1,则a的取值范围是[2,+∞).。
(完整版)高中数学选修2-2第一章导数测试题

f
-13
59 =- 27<0,f(1)
=- 1<0,故函数 f(x)的图象与 x 轴仅有一个交点,且交点横坐标在
-∞,-
1 3
内,故选
A.
11.C 当 1≤x≤2 时, f′(x)≥0,则 f(2)≥f(1);
而当 0≤x≤1 时, f′(x)≤0,则 f(1)≤f(0),
从而 f(0)+f(2)≥2f(1).
sinx
|π20=1,
0
π M<N,不满足条件 M>N,则 S=M=4.
n 15.n+1
解析: f′(x)=mxm-1+a=2x+1,得 m= 2, a=1.
则
f( x)= x2+x, f
1 n
=n
1 n+ 1
11 = n- n+1,
其和为
11-12
+
12-13
+
13-
1 4
+…+
11 n-n+ 1
20.解: (1)由条件得
a×102+15001× 10- bln1= 19.2
,
a×
202+
101 50 ×
20-
bln2=
35.7
解得 a=- 1100,b=1,
则
f(
x)=-
1x020+
101 50 x-
x ln10(x≥
10).
(2)由题意知
T(x)
=f
(x)-
x=-
1x020+5510x-
16.已知函数 f(x)=12mx2+lnx-2x 在定义域内是增函数,则实数 m 的取值范围为 ________.
三、解答题 (写出必要的计算步骤,只写最后结果不得分,共 70 分)
高中数学选修2-2第1章《导数及其应用》单元测试题[1](可编辑修改word版)
](https://img.taocdn.com/s3/m/4c28ba9c804d2b160b4ec0c6.png)
25 yyO xOx选修 2-2 第一章《导数及其应用》单元测试题一、选择题:(每小题有且只有一个答案正确,每小题 5 分,共 50 分) 1. 下列结论中正确的是( )A. 导数为零的点一定是极值点B. 如果在 x 0 附近的左侧 f '(x ) > 0 ,右侧 f '(x ) < 0 ,那么 f (x 0 ) 是极大值C. 如果在 x 0 附近的左侧 f '(x ) > 0 ,右侧 f '(x ) < 0 ,那么 f (x 0 ) 是极小值D. 如果在 x 0 附近的左侧 f '(x ) < 0 ,右侧 f '(x ) > 0 ,那么 f (x 0 ) 是极大值2. 已知函数 f (x ) = ax 2 + c ,且 f '(1) =2,则 a 的值为()A .1B .C .-1D .03.f (x ) 与g (x ) 是定义在 R 上的两个可导函数,若 f (x ) 与 g (x ) 满足 f '(x ) = g '(x ) ,则 f (x ) 与 g (x ) 满足()A.f (x ) =g (x )B . f (x ) - g (x ) 为常数函数C . f (x ) = g (x ) = 0D . f (x ) + g (x ) 为常数函数4. 函数 y = x 3 - 3x 在[-1,2]上的最小值为()A .2B .-2C .0D .-45. 设函数 y =f (x ) 在定义域内可导, y = f (x ) 的图象如图 1 所示,则导函数 y = f '(x ) 可能为()图 1ABC D6.方程 x 3 - 6x 2 + 9x - 10 = 0 的实根个数是( ) A .3B .2C .1D .07. 曲线 y = ln(2x -1) 上的点到直线2x - y + 8 = 0 的最短距离是 ()A.B . 2 3C . 3D .0 8.曲线 y = cos x (0 ≤ x ≤ 2 5) 与坐标轴围成的面积是() A .4B .C .3D .229.设 p : f (x ) = e x + ln x + 2x 2 + mx + 1在(0,+∞) 内单调递增, q : m ≥ -5 ,则 p 是 q 的()A.充分不必要条件 B .必要不充分条件5 5yOxyOxyOxn 1 2 n 0-1C .充分必要条件D .既不充分也不必要条件10. 设曲线 y = xn +1(n ∈ N *) 在点(1,1)处的切线与 x 轴的交点的横坐标为 x ,则 x ⋅ x⋅ ⋅ x的值为( )1 A.B .n1 n +1nC .n +1D .1二、填空题:(每小题 5 分,共 25 分)11.若 f (x ) = e - 1 x,则lim t →0 f (1- 2t ) - f (1)t=.12. ⎰2(3x 2+ k )dx = 10,则k =;⎰83xdx =.13. 由曲线 y = x 2 + 2 与 y = 3x , x = 0 , x = 2 所围成的平面图形的面积为.14. 已 知 R 上 可 导 函 数 f (x ) 的 图 象 如 图 所 示 , 则 不 等 式(x 2 - 2x - 3) f '(x ) > 0 的 解集.15. 已知二次函数 f (x ) = ax 2 + bx + c 的导数为 f '(x ) , f '(0) > 0 ,对于任意实数 x ,有 f (x ) ≥ 0 ,则f (1) f '(0)最小值为 .三、解答题:(共 75 分) 16.(本小题满分 12 分)已知函数 f (x ) = x 3 - 3x 2 - 9x + 11(1) 写出函数 f (x ) 的递减区间;(2) 讨论函数 f (x ) 的极大值或极小值,如有试写出极值;17.(本小题满分 12 分)当 x > 0 时,证明不等式e x > 1 + x + 1x 2 成立.218.(本小题满分 12 分)已知函数 f (x ) = x 3 + ax 2 + bx + c 在 x = -2 处取得极值,并且它的图象与直线 y = -3x + 3在点( 1 , 0 ) 处相切, 求 a , b , c 的值.19.(本小题满分 12 分)如图所示,等腰三角形△ABC的底边 AB= 6 ,高CD=3,点 E 是线段 BD 上异于 B、D 的动点,点 F 在BC 边上,且EF⊥AB,现沿 EF 将△BEF折起到△PEF的位置,使PE⊥AE,记 BE=x,V(x)表示四棱锥 P-ACEF的体积。
人教高中数学选修2-2第一章《导数及其应用》测试题B卷

高中数学学习材料 (灿若寒星 精心整理制作)高中数学选修2-2第一章《导数及其应用》测试题B 卷考试时间:100分钟,满分:150分一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分)1.已知函数f (x )=ln x -f ′(-1)x 2+3x -4,则f ′(1) ( )A . -1B .-2C .8D .02.设P 为曲线C :223y x x =++上的点,且曲线C 在点P 处切线倾斜角的取值范围为04p轾犏犏臌,,则点P 横坐标的取值范围为( )A .1-1-2轾犏犏臌,B .[]-1,0C .[]0,1D .1,12轾犏犏臌3.函数f (x )=x +eln x 的单调递增区间为( )A .(0,+∞)B .(-∞,0)C .(-∞,0)和(0,+∞)D .R4.若函数f (x )=x 3-3x +a 有3个不同的零点,则实数a 的取值范围是( ).A .(-2,2)B .(-∞,-3)∪(6,+∞)C .(-3,6)D .(-∞,-1)∪(2,+∞)5. f (x )与g (x )是定义在R 上的两个可导函数,若f (x )、g (x )满足f ′(x )=g ′(x ),则 ( ) A .f (x )=g (x )B .f (x )-g (x )为常数函数C .f (x )=g (x )=0D .f (x )+g (x )为常数函数6.函数f (x )=x 3-3x +1在闭区间[-3,0]上的最大值、最小值分别是( )A .1,-1B .3,-17C .1,-17D .9,-197.已知1()sin cos f x x x =+,1()n f x +是()n f x 的导函数,即21()()f x f x ¢=,32()()f x f x ¢=,…,1()()n n f x f x +¢=,n ∈*N ,则2014()f x = ( )A .sin cos x x +B .sin cos x x -C .sin os x c x -+D .sin os x c x --8.等比数列{a n }中,a 1=2,a 8=4,f (x )=x (x -a 1)(x -a 2)…(x -a 8),f ′(x )为函数f (x )的导函数,则f ′(0)=( )A .0B .26C .29D .2129.已知点P 是曲线2ln y x x =-上的一个动点,则点P 到直线l :2y x =-的距离的最小值为( ) A .1B .2C .22D .310.设f(x)=13x 3+12a x 2+2bx +c ,当x ∈(0,1)时取得极大值,当x ∈(1,2)时取得极小值,则b -2a -1的取值范围为( ) A.(1,4) B.(12,1) C.(14,12) D.( 14,1) 二.填空题(每小题6分, 共24分)11.函数y =-23x 3+(a +1a )x 2-2x +4(a<-1)的递减区间为 .12.3239x --ò= .13.已知函数f (x )=(m -2)x 2+(m 2-4)x +m 是偶函数,函数g (x )=-x 3+2x 2+mx +5在(-∞,+∞)内单调递减,则实数m =________.14. 已知函数f (x )=-x 3+ax 2-4在x =2处取得极值,若m 、n ∈[-1,1],则f (m )+f '(n )的最小值是________. 三、解答题(共计76分)15.(本题满分12分) 设函数32()2f x x x x =-+-(x ∈R ). (Ⅰ)求曲线()y f x =在点(2,(2))f 处的切线方程; (Ⅱ)求函数()f x 在区间[]0,2上的最大值与最小值.16.(本题满分12分)设函数3221()23,0 1.3f x x ax a x b a =-+-+<< ⑴求函数()f x 的单调区间、极值.⑵若当[]1,2x a a ?+时,恒有()f x a ¢£,试确定a 的取值范围..17.(本题满分12分)某汽运集团公司生产一种品牌汽车,上年度成本价为10万元/辆,出厂价为13万元/辆,年销售量为5万辆.本年度公司为了进一步扩大市场占有量,计划降低成本,实行降价销售.设本年度成本价比上年度降低了x (0<x <1),本年度出厂价比上年度降低了0.9x .(1)若本年度年销售量比上年度增加了0.6x 倍,问x 在什么取值范围时,本年度的年利润比上年度有所增加?(2)若本年度年销售量y 关于x 的函数为y =2 011·259307()34289x x -++,则当x 为何值时,本年度年利润最大?18.(本题满分12分)已知函数()1ln ().f x ax x a R =--? (1)讨论函数()f x 在定义域内的极值点的个数;(2)若函数()f x 在1x =处取得极值,对(0,)x ∀∈+∞,()2f x bx ?恒成立, 求实数b 的取值范围.19.(本题满分14分)已知函数f (x )=ax +ln x ,其中a 为常数,设e 为自然对数的底数. (1)当a =-1时,求f (x )的最大值;(2)若f (x )在区间(0,e]上的最大值为-3,求a 的值; (3)当a =-1时,试推断方程|f (x )|=ln x x +12是否有实数解.20. (本题满分14分)已知函数.()()()21212ln 2f x ax a x x a R =-++∈(Ⅰ)若曲线()y f x =在1x =和处的3x =切线互相平行,求a 的值;(Ⅱ)求()f x 的单调区间;(Ⅲ)设,若()22g x x x =-对任意(]10,2x ∈,均存在(]10,2x ∈,使得()()12f x g x <高中数学选修2-2第一章《导数及其应用》测试题A 卷答案一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分) 1. 【答案】C【解析】∵f ′(x )=1x-2f ′(-1)x +3,f ′(-1)=-1+2f ′(-1)+3, ∴f ′(-1)=-2,∴f ′(1)=1+4+3=8.2. 【答案】 A【解析】22y x ¢=+因为切线倾斜角的范围是0,4p轾犏犏臌,所以斜率的范围是[]0,1即0221x ??∴112x-#-. 3. 【答案】 A 【解析】因为()1ef x x¢=+,由()0f x ¢>得x e >-。
人教新课标版数学高二人教数学B版选修2-2练习第一章《导数及其应用》测试

章末质量评估(一)(时间:100分钟 满分:120分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.曲线y =12x 2-2x 在点⎝ ⎛⎭⎪⎫1,-32处的切线的倾斜角为( ).A .-135°B .45°C .-45°D .135°解析 y ′=x -2,所以斜率k =1-2=-1,因此,倾斜角为135°. 答案 D2.下列求导运算正确的是( ).A.⎝ ⎛⎭⎪⎫x +3x ′=1+3x 2 B .(log 2x )′=1x ln 2 C .(3x )′=3x log 3eD .(x 2cos x )′=-2x sin x解析 ⎝ ⎛⎭⎪⎫x +3x ′=1-3x 2,所以A 不正确;(3x )′=3x ln 3,所以C 不正确;(x 2cosx )′=2x cos x +x 2·(-sin x ),所以D 不正确;(log 2x )′=1x ln 2,所以B 正确.故选B. 答案 B 3.|sin x |d x 等于( ).A .0B .1C .2D .4解析 |sin x |d x =sin x d x +(-sin x )d x =()-cos x ⎪⎪⎪π+cosx ⎪⎪⎪2ππ=1+1+1+1=4. 答案 D4.函数y =1+3x -x 3有( ).A .极小值-1,极大值1B .极小值-2,极大值3C .极小值-2,极大值2D .极小值-1,极大值3解析 y ′=-3x 2+3,令y ′=0得,x =1或x =-1, ∴f (1)=3,f (-1)=-1. 答案 D 5.函数f (x )=x 2x -1( ).A .在(0,2)上单调递减B .在(-∞,0)和(2,+∞)上单调递增C .在(0,2)上单调递增D .在(-∞,0)和(2,+∞)上单调递减 解析 f ′(x )=2x (x -1)-x 2(x -1)2=x 2-2x(x -1)2=x (x -2)(x -1)2. 令f ′(x )=0得x 1=0,x 2=2.∴x ∈(-∞,0)和(2,+∞)时,f ′(x )>0. x ∈(0,1)∪(1,2)时,f ′(x )<0. 答案 B6.函数y =x 4-4x +3在区间[-2,3]上的最小值为( ).A .72B .36C .12D .0解析y′=4x3-4,令y′=0,4x3-4=0,x=1,当x<1时,y′<0;当x>1时,y′>0得y极小值=y|x=1=0,而端点的函数值y|x=-2=27,y|x=3=72,得y min=0.答案 D7.一物体在力F(x)=3x2-2x+5(力单位:N,位移单位:m)作用力下,沿与力F(x)相同的方向由x=5 m直线运动到x=10 m处做的功是().A.925 J B.850 J C.825 J D.800 J解析W=F(x)d x=(3x2-2x+5)d x=(x3-x2+5x)⎪⎪105=(1 000-100+50)-(125-25+25)=825 (J).答案 C8.已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为().A.-1<a<2 B.-3<a<6C.a<-1或a>2 D.a<-3或a>6解析因为f(x)有极大值和极小值,所以导函数f′(x)=3x2+2ax+(a+6)有两个不等实根,所以Δ=4a2-12(a+6)>0,得a<-3或a>6.答案 D9.已知f(x)的导函数f′(x)图象如右图所示,那么f(x)的图象最有可能是图中的().解析∵x∈(-∞,-2)时,f′(x)<0,∴f(x)为减函数;同理f(x)在(-2,0)上为增函数,(0,+∞)上为减函数.答案 A10.由直线y=x,y=-x+1及x轴围成平面图形的面积为().解析画出图形,由定积分定义可知选C.答案 C11.设曲线y=x n+1(n∈N*)在(1,1)处的切线与x轴的交点的横坐标为x n,则log2 010x1+log2 010x2+…+log2 010x2 009的值为( ).A .-log 2 0102 009B .-1C .(log 2 0102 009)-1D .1解析 ∵y ′|x =1=n +1,∴切线方程为y -1=(n +1)(x -1), 令y =0,得x =1-1n +1=n n +1,即x n =nn +1.所以log 2 010x 1+log 2 010x 2+…+log 2 010x 2 009 =log 2 010(x 1·x 2·…·x 2 009)=log 2 010⎝ ⎛⎭⎪⎫12·23·…·2 0092 010=log 2 01012 010=-1. 答案 B12.由曲线y =x 2和直线x =0,x =1,y =t 2,t ∈(0,1)所围成的图形(阴影部分)的面积的最小值为 ( ) A.14 B.13 C.12D.23解析 面积为(t 2-x 2)d x + (x 2-t 2)d x=⎝ ⎛⎭⎪⎫t 2x -13x 3⎪⎪ t 0+⎝ ⎛⎭⎪⎫13x 3-t 2x ⎪⎪1t =43t 3-t 2+13, 下面求函数f (t )=43t 3-t 2+13在(0,1)上的最小值.f ′(x )=4t 2-2t ,在⎝⎛⎭⎪⎫0,12上f ′(t )<0,在⎝ ⎛⎭⎪⎫12,1上f ′(t )>0,所以f (t )=43t 3-t 2+13在⎝ ⎛⎭⎪⎫0,12上为减函数,在⎝ ⎛⎭⎪⎫12,1上为增函数,所以当t =12时,f (t )有最小值f ⎝ ⎛⎭⎪⎫12=43⎝ ⎛⎭⎪⎫123-⎝ ⎛⎭⎪⎫122+13=14.答案 A二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.若f (x )=x 3,f ′(x 0)=3,则x 0的值为________. 解析 f ′(x 0)=3x 20=3,∴x 0=±1. 答案 ±114.曲线y =ln x 在点M (e,1)处的切线的斜率是________,切线的方程为________. 解析 由于y ′=1x ,∴k =y ′|x =e =1e ,故切线的方程为y -1=1e (x -e),故y =1ex . 答案 1e x -e y =015.函数y =x 3+x 2-5x -5的单调递增区间是________. 解析 由y ′=3x 2+2x -5>0得x <-53,或x >1. 答案 ⎝ ⎛⎭⎪⎫-∞,-35,(1,+∞)16.若(x -k )d x =32,则实数k 的值为________.解析 ∫10(x -k )d x =⎝ ⎛⎭⎪⎫12x 2-k x ⎪⎪⎪10=12-k =32,∴k =-1. 答案 -1三、解答题(本大题共4小题,共40分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)设函数f (x )=2x 3-3(a +1)x 2+6ax +8,其中a ∈R .已知f (x )在x =3处取得极值. (1)求f (x )的解析式;(2)求f (x )在点A (1,16)处的切线方程. 解 (1)f ′(x )=6x 2-6(a +1)x +6a . ∵f (x )在x =3处取得极值,∴f′(3)=6×9-6(a+1)×3+6a=0,解得a=3.∴f(x)=2x3-12x2+18x+8.(2)A点在f(x)上,由(1)可知f′(x)=6x2-24x+18,f′(1)=6-24+18=0,∴切线方程为y=16.18.(10分)给定函数f(x)=x33-ax2+(a2-1)x和g(x)=x+a2x.(1)求证:f(x)总有两个极值点;(2)若f(x)和g(x)有相同的极值点,求a的值.(1)证明因为f′(x)=x2-2ax+(a2-1)=[x-(a+1)]·[x-(a-1)],令f′(x)=0,解得x1=a+1,x2=a-1.当x<a-1时,f′(x)>0;当a-1<x<a+1,f′(x)<0.所以x=a-1为f(x)的一个极大值点.同理可证x=a+1为f(x)的一个极小值点.所以f(x)总有两个极值点.(2)解因为g′(x)=1-a2x2=(x-a)(x+a)x2.令g′(x)=0,则x1=a,x2=-a.因为f(x)和g(x)有相同的极值点,且x1=a和a+1,a-1不可能相等,所以当-a=a+1时,a=-1 2;当-a=a-1时,a=1 2.经检验,当a=-12和a=12时,x1=a,x2=-a都是g(x)的极值点.19.(10分)已知函数f(x)=x3+ax2+bx+c在x=-1与x=2处都取得极值.(1)求a ,b 的值及函数f (x )的单调区间;(2)若对x ∈[-2,3],不等式f (x )+32c <c 2恒成立,求c 的取值范围. 解 (1)f ′(x )=3x 2+2ax +b ,由题意得⎩⎨⎧ f ′(-1)=0,f ′(2)=0,即⎩⎨⎧3-2a +b =0,12+4a +b =0,解得⎩⎪⎨⎪⎧a =-32,b =-6.∴f (x )=x 3-32x 2-6x +c ,f ′(x )=3x 2-3x -6. 令f ′(x )<0,解得-1<x <2; 令f ′(x )>0,解得x <-1或x >2. ∴f (x )的减区间为(-1,2),增区间为(-∞,-1),(2,+∞). (2)由(1)知,f (x )在(-∞,-1)上单调递增; 在(-1,2)上单调递减;在(2,+∞)上单调递增. ∴x ∈[-2,3]时,f (x )的最大值即为 f (-1)与f (3)中的较大者. f (-1)=72+c ,f (3)=-92+c . ∴当x =-1时,f (x )取得最大值. 要使f (x )+32c <c 2,只需c 2>f (-1)+32c , 即2c 2>7+5c ,解得c <-1或c >72. ∴c 的取值范围为(-∞,-1)∪⎝ ⎛⎭⎪⎫72,+∞.20.(10分)若函数f (x )=ax 3-bx +4,当x =2时,函数f (x )有极值-43. (1)求函数的解析式.(2)若方程f (x )=k 有3个不同的根,求实数k 的取值范围. 解 f ′(x )=3ax 2-b .(1)由题意得⎩⎪⎨⎪⎧f ′(2)=12a -b =0,f (2)=8a -2b +4=-43,解得⎩⎪⎨⎪⎧a =13,b =4,故所求函数的解析式为f (x )=13x 3-4x +4.(2)由(1)可得f ′(x )=x 2-4=(x -2)(x +2),令f ′(x )=0,得x =2或x =-2. 当x 变化时,f ′(x ),f (x )的变化情况如下表:x (-∞,-2)-2 (-2,2) 2 (2,+∞)f ′(x ) +0 -0 +f (x )283-43f (x )有极大值283,当x =2时,f (x )有极小值-43,所以函数f (x )=13x 3-4x +4的图象大致如图所示.若f (x )=k 有3个不同的根,则直线y =k 与函数f (x )的图象有3个交点,所以-43<k <283.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学选修2-2第一章《导数及其应用》测试题B 卷
考试时间:100分钟,满分:150分
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分)
1.已知函数f (x )=ln x -f ′(-1)x 2+3x -4,则f ′(1) ( )
A . -1
B .-2
C .8
D .0
2.设P 为曲线C :223y x x =++上的点,且曲线C 在点P 处切线倾斜角的取值范围为04
p 轾犏犏臌,,则点P 横坐标的取值范围为( )
A .1-1-2轾犏犏臌
, B .[]-1,0 C .[]0,1 D .1,12轾犏犏臌
3.函数f (x )=x +eln x 的单调递增区间为( ) A .(0,+∞) B .(-∞,0) C .(-∞,0)和(0,+∞) D .R
4.若函数f (x )=x 3-3x +a 有3个不同的零点,则实数a 的取值范围是( ).
A .(-2,2)
B .(-∞,-3)∪(6,+∞)
C .(-3,6)
D .(-∞,-1)∪(2,+∞)
5. f (x )与g (x )是定义在R 上的两个可导函数,若f (x )、g (x )满足f ′(x )=g ′(x ),则 ( )
A .f (x )=g (x )
B .f (x )-g (x )为常数函数
C .f (x )=g (x )=0
D .f (x )+g (x )为常数函数 6.函数f (x )=x 3-3x +1在闭区间[-3,0]上的最大值、最小值分别是( )
A .1,-1
B .3,-17
C .1,-17
D .9,-19
7.已知1()sin cos f x x x =+,1()n f x +是()n f x 的导函数,即21()()f x f x ¢=,32()()f x f x ¢=,…,1()()n n f x f x +¢=,n ∈*
N ,则2014()f x = ( ) A .sin cos x x + B .sin cos x x - C .sin os x c x -+ D .sin os x c x --
8.等比数列{a n }中,a 1=2,a 8=4,f (x )=x (x -a 1)(x -a 2)…(x -a 8),f ′(x )为函数f (x )的导函数,则f ′(0)=( )
A .0
B .26
C .29
D .212
9.已知点P 是曲线2ln y x x =-上的一个动点,则点P 到直线l :2y x =-的距离的最小值为( )
A .1
B .2
C .22
D .3。
