北京2013届西城高三二模数学文科试题及标准答案
2013北京西城高考二模数学文(含解析)

北京市西城区2013年高三二模试卷高三数学(文科) 2013.5第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.复数 i (1i)⋅-=( ). A .1i + B .1i -+C .1i -D .1i --2.已知向量(3,1)=-a ,(3,)λ=b .若a 与b 共线,则实数λ=( ). A .1- B .1C .3-D .33.给定函数:①2y x =;②2x y =;③cos y x =;④3y x =-,其中奇函数是( ). A .① B .②C .③D .④4.若双曲线221y x k+=的离心率是2,则实数k =( ).A .3B .3-C .13D .13-5.如图所示的程序框图表示求算式“235917⨯⨯⨯⨯” 之值, 则判断框内可以填入( ). A .10k ≤ B .16k ≤ C .22k ≤ D .34k ≤6.对于直线m ,n 和平面α,β,使m α⊥成立的一个充分条件是( ). A .m n ⊥,n ∥α B .m ∥β,βα⊥ C .m β⊥,n β⊥,n α⊥ D .m n ⊥,n β⊥,βα⊥7.已知函数||()e ||x f x x =+.若关于x 的方程()f x k =有两个不同的实根,则实数k 的取值范围是( ). A .(0,1) B .(1,)+∞ C .(1,0)- D .(,1)-∞-8.已知集合{1,2,3,4,5}的非空子集A 具有性质P :当a A ∈时,必有6a A -∈.则具有性质P 的集合A 的个数是( ). A .8 B .7 C .6 D .5第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9.已知直线1:310l x y -+=,2:210l x my +-=.若1l ∥2l ,则实数m =______.10.右图是甲,乙两组各6名同学身高(单位:cm )数据的茎叶图.记甲,乙两组数据的平均数依次为x 甲和x 乙, 则x 甲______x 乙. (填入:“>”,“=”,或“<”)11.在ABC △中,2BC =,7AC =,π3B =,则AB =______;ABC △的面积是______.12.设a ,b 随机取自集合{1,2,3},则直线30ax by ++=与圆221x y +=有公共点的概率是______.13.已知命题:p 函数(1)1y c x =-+在R 上单调递增;命题:q 不等式20x x c -+≤的解集是∅.若p 且q 为真命题,则实数c 的取值范围是______.14.在直角坐标系xOy 中,已知两定点(1,0)A ,(1,1)B .动点(,)P x y 满足01,0 2.OP OA OP OB ⎧≤⋅≤⎪⎨≤⋅≤⎪⎩uu u r uur uu u r uu u r 则点P 构成的区域的面积是______;点(,)Q x y x y +-构成的区域的面积是______.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知等比数列{}n a 的各项均为正数,28a =,3448a a +=. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设4log n n b a =.证明:{}n b 为等差数列,并求{}n b 的前n 项和n S .16.(本小题满分13分)如图,在直角坐标系xOy 中,角α的顶点是原点,始边与x 轴正半轴重合,终边交单位圆于点A ,且ππ,)62α∈(.将角α的终边按逆时针方向旋转π3,交单位圆于点B .记1122(,),(,)A x y B x y .(Ⅰ)若113x =,求2x ;(Ⅱ)分别过,A B 作x 轴的垂线,垂足依次为,C D .记AOC △的面积为1S ,BOD △的面积为2S .若122S S =,求角α的值.17.(本小题满分14分)-中,PA⊥底面ABCD,面ABCD为正方形,E为侧棱PD上一点,F 如图1,在四棱锥P ABCD为AB上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.(Ⅰ)求四面体PBFC的体积;(Ⅱ)证明:AE∥平面PFC;(Ⅲ)证明:平面PFC⊥平面PCD.18.(本小题满分13分)已知函数322()2(2)13f x x x a x =-+-+,其中0a >. (Ⅰ)若2a =,求曲线()y f x =在点(1,(1))f 处的切线方程;(Ⅱ)求()f x 在区间[2,3]上的最小值.19.(本小题满分14分)如图,椭圆22:1(01)y C x m m+=<<的左顶点为A ,M 是椭圆C 上异于点A 的任意一点,点P 与点A 关于点M 对称.(Ⅰ)若点P 的坐标为943(,)55,求m 的值; (Ⅱ)若椭圆C 上存在点M ,使得OP OM ⊥,求m 的取值范围.20.(本小题满分13分)已知集合1212{(,,,)|,,,n n n S x x x x x x =L L 是正整数1,2,3,,n L 的一个排列}(2)n ≥,函数1,0,()1,0.x g x x >⎧=⎨-<⎩ 对于12(,,)n n a a a S ∈…,定义:121()()(),{2,3,,}i i i i i b g a a g a a g a a i n -=-+-++-∈L L ,10b =,称i b 为i a 的满意指数.排列12,,,n b b b L 为排列12,,,n a a a L 的生成列.(Ⅰ)当6n =时,写出排列3,5,1,4,6,2的生成列;(Ⅱ)证明:若12,,,n a a a L 和12,,,n a a a '''L 为n S 中两个不同排列,则它们的生成列也不同; (Ⅲ)对于n S 中的排列12,,,n a a a L ,进行如下操作:将排列12,,,n a a a L 从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加2.北京市西城区2013年高三二模试卷高三数学(文科)参考答案及评分标准 2013.5一、选择题:本大题共8小题,每小题5分,共40分.1. A ; 2.A ; 3.D ; 4.B ; 5.C ; 6.C ; 7.B ; 8.B .二、填空题:本大题共6小题,每小题5分,共30分.9.6-; 10.>; 11.3,332; 12.59; 13.(1,)+∞; 14.2,4.注:11、14题第一空2分,第二空3分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.15.(本小题满分13分)(Ⅰ)解:设等比数列{}n a 的公比为q ,依题意 0q >. ………………1分 因为 28a =,3448a a +=,两式相除得 260q q +-=, ………………3分解得 2q =, 舍去 3q =-. ………………4分 所以 214a a q==. ………………6分 所以数列{}n a 的通项公式为 1112n n n a a q -+=⋅=. ………………7分 (Ⅱ)解:由(Ⅰ)得 41log 2n n n b a +==. ………………9分 因为 1211222n n n n b b +++-=-=, 所以数列{}n b 是首项为1,公差为12d =的等差数列. ………………11分所以 21(1)324n n n n nS nb d -+=+=. ………………13分16.(本小题满分13分)(Ⅰ)解:由三角函数定义,得 1cos x α=,2πcos()3x α=+. ………………2分因为 ππ,)62α∈(,1cos 3α=,所以 222sin 1cos 3αα=-=. ………………3分 所以 2π13126cos()cos sin 3226x αα-α-=+==. ………………5分(Ⅱ)解:依题意得 1sin y α=,2πsin()3y α=+.所以 111111cos sin sin 2224S x y ααα==⋅=, ………………7分 22211ππ12π||[cos()]sin()sin(2)223343S x y ααα==-+⋅+=-+. ……………9分依题意得2πsin 22sin(2)3αα=-+,整理得cos 20α=. ………………11分因为ππ62α<<, 所以π2π3α<<, 所以π22α=,即 π4α=. ………………13分17.(本小题满分14分)(Ⅰ)解:由左视图可得 F 为AB 的中点,所以 BFC △的面积为 11212S =⋅⋅=.………………1分因为PA ⊥平面ABCD , ………………2分 所以四面体PBFC 的体积为13P B F CB FC V S P A -∆=⋅ ………………3分 121233=⋅⋅=. ………………4分(Ⅱ)证明:取PC 中点Q ,连结EQ ,FQ . ………………5分 由正(主)视图可得 E 为PD 的中点,所以EQ ∥CD ,12EQ CD =. ………………6分又因为AF ∥CD ,12AF CD =, 所以AF ∥EQ ,AF EQ =.所以四边形AFQE 为平行四边形,所以AE ∥FQ . ………………8分因为 AE ⊄平面PFC ,FQ ⊂平面PFC ,所以 直线AE ∥平面PFC . ………………9分 (Ⅲ)证明:因为 PA ⊥平面ABCD ,所以 PA CD ⊥.因为面ABCD 为正方形,所以 AD CD ⊥.所以 CD ⊥平面PAD . ………………11分 因为 AE ⊂平面PAD ,所以 CD AE ⊥. 因为 PA AD =,E 为PD 中点,所以 AE PD ⊥.所以 AE ⊥平面PCD . ………………12分 因为 AE ∥FQ ,所以FQ ⊥平面PCD . ………………13分 因为 FQ ⊂平面PFC , 所以 平面PFC ⊥平面PCD . ………………14分 18.(本小题满分13分)(Ⅰ)解:()f x 的定义域为R , 且 2()242f x x x a '=-+-. ………………2分当2a =时,1(1)3f =-,(1)2f '=-,所以曲线()y f x =在点(1,(1))f 处的切线方程为 12(1)3y x +=--,即 6350x y +-=. ………………4分(Ⅱ)解:方程()0f x '=的判别式80a ∆=>, ………………5分令 ()0f x '=,得 1212ax =-,或2212a x =+. ………………6分()f x 和()f x '的情况如下:x 1(,)x -∞ 1x12(,)x x 2x2(,)x +∞()f x ' + 0-+ ()f x↗↘↗故()f x 的单调增区间为2(,1)2a-∞-,2(1,)2a ++∞;单调减区间为22(1,1)22a a -+. ………………9分① 当02a <≤时,22x ≤,此时()f x 在区间(2,3)上单调递增,所以()f x 在区间[2,3]上的最小值是7(2)23f a =-. ………………10分 ② 当28a <<时,1223x x <<<,此时()f x 在区间2(2,)x 上单调递减,在区间2(,3)x 上单调递增,所以()f x 在区间[2,3]上的最小值是 252()33a af x a =--. ………………12分③ 当8a ≥时,1223x x <<≤,此时()f x 在区间(2,3)上单调递减,所以()f x 在区间[2,3]上的最小值是(3)73f a =-. ………………13分 综上,当02a <≤时,()f x 在区间[2,3]上的最小值是723a -;当28a <<时,()f x 在区间[2,3]上 的最小值是5233a aa --;当8a ≥时,()f x 在区间[2,3]上的最小值是73a -.19.(本小题满分14分)(Ⅰ)解:依题意,M 是线段AP 的中点,因为(1,0)A -,943(,)55P , 所以 点M 的坐标为223(,)55. ………………2分由点M 在椭圆C 上,所以41212525m+=, ………………4分 解得 47m =. ………………6分(Ⅱ)解:设00(,)M x y ,则 2201y x m+=,且011x -<<. ① ………………7分因为M 是线段AP 的中点,所以00(21,2)P x y +. ………………8分因为 OP OM ⊥,所以 2000(21)20x x y ++=.② ………………9分由 ①,② 消去0y ,整理得 20020222x x m x +=-. ………………11分 所以0011316242(2)82m x x =+≤-++-+, ………………13分当且仅当 023x =-+时,上式等号成立.所以m 的取值范围是13(0,]24-. ………………14分 20.(本小题满分13分)(Ⅰ)解:当6n =时,排列3,5,1,4,6,2的生成列为0,1,2,1,4,3-. ………………3分 (Ⅱ)证明:设12,,,n a a a L 的生成列是12,,,n b b b L ;12,,,n a a a '''L 的生成列是与12,,,n b b b '''L . 从右往左数,设排列12,,,n a a a L 与12,,,n a a a '''L 第一个不同的项为k a 与k a ',即:n n a a '=,11n n a a --'=,L ,11k ka a ++'=,k k a a '≠. 显然 n nb b '=,11n n b b --'=,L ,11k k b b ++'=,下面证明:k k b b '≠. ………………5分 由满意指数的定义知,i a 的满意指数为排列12,,,n a a a L 中前1i -项中比i a 小的项的个数减去比i a 大 的项的个数.由于排列12,,,n a a a L 的前k 项各不相同,设这k 项中有l 项比k a 小,则有1k l --项比k a 大,从而 (1)21k b l k l l k =---=-+.同理,设排列12,,,n a a a '''L 中有l '项比k a '小,则有1k l '--项比k a '大,从而21k b l k ''=-+. 因为 12,,,k a a a L 与12,,,k a a a '''L 是k 个不同数的两个不同排列,且k k a a '≠, 所以 l l '≠, 从而 k k b b '≠.所以排列12,,,n a a a L 和12,,,n a a a '''L 的生成列也不同. ………………8分 (Ⅲ)证明:设排列12,,,n a a a L 的生成列为12,,,n b b b L ,且k a 为12,,,n a a a L 中从左至右第一个满意指数为负数的项,所以 1210,0,,0,1k k b b b b -≥≥≥≤-L . ………………9分依题意进行操作,排列12,,,n a a a L 变为排列1211,,,,,,k k k n a a a a a a -+L L ,设该排列的生成列为 12,,,n b b b '''L . ………………10分 所以 1212()()n n b b b b b b '''+++-+++L L 121121[()()()][()()()]k k k k k k k k g a a g a a g a a g a a g a a g a a --=-+-++---+-++-L L 1212[()()()]k k k k g a a g a a g a a -=--+-++-L 22k b =-≥.所以,新排列的各项满意指数之和比原排列的各项满意指数之和至少增加2.………………13分北京市西城区高三统一测试 数学(文科)选填解析一、 选择题 1.【答案】A【解析】解:()i 1i 1i -=+. 故选A .2.【答案】A【解析】解:由题可知3301λλ⋅=--=⇒=-a b . 故选A .3.【答案】D【解析】解:易判断①③为偶函数,②为非奇非偶函数,④为奇函数. 故选D .4.【答案】B【解析】解:由题可知221,a b k ==-,又因为2222212c c a b e k a a a +====-=,所以3k =-. 故选B .5.【答案】C 【解析】解:列表S 223⨯ 235⨯⨯ 2359⨯⨯⨯235917⨯⨯⨯⨯ 循环结束 k3591733输出S可知[)17,33k m ≤∈. 故选C .6.【答案】C【解析】解:由图一可知m n ⊥,n α∥,但是m α⊥不成立,故A 错; 由图二可知m β∥,βα⊥,但是m α⊥不成立,故B 错; 由图二可知m n ⊥,n β⊥,βα⊥,但是m α⊥不成立,故D 错.故选C .图一n mβα图二nmβα7.【答案】B【解析】解:易知函数||()e ||x f x x =+为偶函数, 故可了解函数正半轴()e x f x x =+图像, 求导得()e 10x f x '=+>,故函数单调递增,如图函数的最值为()1f x =. 故选B .8.【答案】B【解析】解:只需从集合{1,5},{2,4},{3}中选 取若干个集合,即可构成具有性质P 的非空子集A ,个数为3217-=. 故选B .二、 填空题 9.【答案】6-【解析】解:1212//l l k k ∴=Q ,即1263m m=-∴=-.故答案为6-.10.【答案】>【解析】解:由茎叶图可知甲的平均数151153165167170172163.36x +++++=≈甲乙的平均数150161162163164172165.36x +++++=≈乙. 故答案为>.11.【答案】3,332【解析】解:利用余弦定理得222cos 2AB BC AC B AB BC+-=⋅⋅,故3AB =,133sin 22S AB BC B =⋅⋅=. 故答案为3,332.12.【答案】59【解析】解:可知(),a b 可能的基本事件空间为()()()()()()()()(){}1,1,1,2,1,3,2,1,2,2,2,3,3,1,3,2,3,3,其中满足220031a b++≤+的有()()()()(){}1,3,2,3,3,1,3,2,3,3,y=1y=e |x|+|x|yx所以概率为59.故答案为59.13.【答案】(1,)+∞【解析】解:因为p 且q 为真,所以命题p 为真,且命题q 为真. 命题:p 函数(1)1y c x =-+在R 上单调递增,所以1c >; 命题:q 不等式20x x c -+≤的解集是∅, 所以140c ∆=-<,解得14c >. 综上所述:1c >. 故答案为(1,)+∞.14.【答案】2,4【解析】解:将已知条件化为:0102x x y ≤≤⎧⎨≤+≤⎩, 在平面xOy 上作图,其面积为2; 点(,)Q x y x y +-构成的区域等价于01202u v u +⎧≤≤⎪⎨⎪≤≤⎩, 其中u x y =+,v x y =-.在平面uOv 上, 其面积为4. 故答案为2,4.yOxvOu。
北京市西城区2013年高三二模试卷

北京市西城区2013年高三二模试卷数学(理科)(西城二模)(时间:120分钟总分:150分)第1卷(选择题共40分)一、选择题:本大题共8小题,每小题5分,共40分,在每小 题列出的四个选项中,选出符合题目要求的一项.1.已知全集},4,3,2,1,0{=U 集合,2{},3,2,1,0{==B A },4,3那么=)(B A C U( ) }1,0.{A }3,2.{B }4,1,0.{C }4,3,2,1,0.{D2.在复平面内,复数1z 的对应点是21),1,1(z Z 的对应点是),1,1(2-Z 则=21.z z ( )1.A2.B i C -. i D .3.在极坐标系中,圆心为),2,1(π且过极点的圆的方程是 ( )θρms A 2=⋅ θρsin 2-=⋅B θρcos 2.=C θρcos 2-=⋅D 4.如图所示的程序框图表示求算式“2×3×5×9×17”之值,则判断框内可以填入 ( )10.≤k A 16.≤k B 22.≤k C 34.≤k D5.设,2log ,3,233121===c b a 则 ( ) c a b A <<. c b a B <<. a b c C <<. b a c D <<.6.对于直线m , n 和平面,,βα使α⊥m 成立的一个充分条件是( )α//,.n n m A ⊥ αββ⊥,//.m B αββ⊥⊥⊥n n m C ,,. αββ⊥⊥⊥,,.n n m D7.已知正六边形ABCDEF 的边长是2,一条抛物线恰好经过该六边形的四个顶点,则抛物线的焦点到准线的距离是 ( )43.A 23.B 3.C 32.D 8.已知函数],[)(x x x f -=其中][x 表示不超过实数x 的最大整数.若关于x 的方程k kx x f +=)(有三个不同的实根,则实数k 的取值范围是 ( )]31,41()21,1.[ --A )31,41[]21,1.( --B ]1,21()41,31.[ --c )1,21[]41,31.( --D 第Ⅱ卷(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.下图是甲,乙两组各6名同学身高数据(单位:cm)的茎叶图.记甲,乙两组数据的平均数依次为,,乙甲x x则甲x 乙x (填“>” “=”或“<”)5)12.(10-x 的展开式中3x 项的系数是____.(用数字作答) 11.在△ABC 中,,3,7,2π===B AC BC 则AB= ,△ABC 的面积是12.如图,AB 是半圆0的直径,P 在AB 的延长线上,PD 与半圆0相切于点,2,4,==⊥PB PC PD AD C ,若 则CD=13.在等差数列}{n a 中,,12,5412=+=a a a 则=n a .设*),(112N n a b n n ∈-=则数列}{n b 的前n 项和=n s14.已知正数a ,b ,c 满足,,abc c b a ab b a =++=+则c 的取值范围是三、解答题:本大题共6小题,共80分,解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题共13分)如图,在直角坐标系xOy 中,角α的顶点是原点,始边与x 轴正半轴重合,终边交单位圆于点A,且⋅∈)2,6(ππα将角α的终边按逆时针方向旋转,3π交单位圆于点B .记).,(),,(2211y x B y x A(I)若,311=x 求.2x ; (Ⅱ) 分别过A ,B 作x 轴的垂线,垂足依次为C ,D .记△AOC 的面积为BOD S ∆,1的面积为⋅2s 若=1s ,22S 求角α的值.16.(本小题共13分)某超市在节日期间进行有奖促销,凡 在该超市购物满300元的顾客,将获得一次摸奖机会, 规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球, 1个白球和1个黑球.顾客不放回地每次摸出1个球,若 摸到黑球则停止摸奖,否则就要将奖盒中的球全部摸出才停止,规定摸到红球奖励10元,摸到白球或黄球奖励 5元,摸到黑球不奖励.(I)求1名顾客摸球3次停止摸奖的概率;(Ⅱ)记X 为1名顾客摸奖获得的奖金数额,求随机变量X 的分布列和数学期望.17.(本小题共14分)如图(1),四棱锥P 一ABCD 中,PD ⊥底面ABCD ,面ABCD 是直角梯形,M 为侧棱PD上一 点.该四棱锥的俯视图和侧(左)视图如图(2)所示.(I)证明:BC ⊥平面PBD.(Ⅱ)证明:AM∥平面PBC.(Ⅲ)线段CD 上是否存在点N ,使AM 与BN 所成角的余弦值为43?若存在,找到所有符合要求的点N , 并求CN 的长;若不存在,说明理由,18.(本小题共13分)如图,椭圆)10(1:22<<=+m m y x C 的左顶点为A ,M 是椭圆C 上异于点A 的任意一点,点P 与点A 关于点M 对称.(I)若点P 的坐标为),534,59(求m 的值; (Ⅱ)若椭圆C 上存在点M ,使得OP ⊥OM ,求m 的取值范围.19.(本小题共14分)已知函数x a x x x f )2(232)(23-+-=,1+其中R ∈a (I)若a=2,求曲线)(x f y =在点))1(,1(f ⋅处的切线方程;(Ⅱ)求函数)(x f 在区间[2,3]上的最大值和最小值.20.(本小题共13分)已知集合,|),,,{(121x x x x s n n =n x x ,,2 是正整数1,2,3,…,n 的一个排列),2}(≥n 函数⎩⎨⎧<->=.0,1,0,1)(x x x g 对于,),,,(21n n s a a a ∈ 定义:-+-=i i i a g a a g b ()(1),()12--++i i a a g a ,0},,,3.2{1=∈b n i 称i b 为i a 的满意指数.排列n b b b ,,,21 为排列n a a a ,,,21 的生成列,排列n a a a ,,,21 为排列n b b b ,,,21 的母列.(I)当n= 6时,写出排列3,5,1,4,6,2的生成列及排列 O ,-1,2,-3,4,3的母列; (Ⅱ)证明:若n a a a ,,,21 和n a a a ,,,21 为n s 中两个不同排列,则它们的生成列也不同;(Ⅲ)对于n s 中的排列,,,,21n a a a 定义变换.τ将排列n a a a ,,,21 从左至右第一个满意指数为负数的项调至首项,其他各项顺序不变,得到一个新的排列.证明:一定可以经过有限次变换τ将排列,,,21 a a n a 变换为各项满意指数均为非负数的排列.。
北京市西城区2013届高三第二次模拟数学文科

2013北京西城区高三二模数学文科一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 设集合{2,3,4}A =,{2,4,6}B =,若x A ∈且x B ∉,则x 等于A .2B .3 √C .4D .62. 已知命题:,cos 1p x x ∀∈≤R ,则A . :,cos 1p x x ⌝∃∈≥RB .:,cos 1p x x ⌝∀∈≥RC . :,cos 1p x x ⌝∃∈>R √D .:,cos 1p x x ⌝∀∈>R3. 设变量,x y 满足约束条件3,1,x y x y +≥⎧⎨-≥-⎩则目标函数2z y x =+的最小值为( )A .1B .2C .3D .4√4. “ln 1x >”是“1x >”的A .充分不必要条件 √B .必要不充分条件C .充要条件D .既不充分也不必要条件5. 如图,三棱柱111ABC A B C -的侧棱长和底面边长均为2,且侧棱1AA ⊥底面ABC ,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为AB. √ C. D .46. 在数列{}n a 中,11a =,1n n a a n -=+,2n ≥.为计算这个数列前10项的和,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是A .8i ≥B .9i ≥C .10i ≥ √D .11i ≥正(主)视图A BCA 1B 1C 17. 等差数列{}n a 的前n 项和为n S ,若70a >,80a <,则下列结论正确的是A .78S S <B .1516S S <C .130S > √D .150S >8. 给出函数()f x 的一条性质:“存在常数M ,使得()f x M x ≤对于定义域中的一切实数x 均成立.”则下列函数中具有这条性质的函数是 A .1y x=B .2y x =C .1y x =+D .sin y x x =二、填空题:本大题共6小题,每小题5分,共30分. 9. i 是虚数单位,i2i=+_____. 10. 函数sin cos y x x =+的最小正周期是_________,最大值是________.11. 在抛物线22y px =上,横坐标为2的点到抛物线焦点的距离为3,则p =________. 12. 圆心在x 轴上,且与直线y x =切于(1,1)点的圆的方程为________. 13. 设,,a b c 为单位向量,,a b 的夹角为60,则⋅+⋅a c b c 的最大值为________.14. 我们可以利用数列{}n a 的递推公式2,,n n n n a a n ⎧⎪=⎨⎪⎩为奇数时,为偶数时(n ∈*N )求出这个数列各项的值,使得这个数列中的每一项都是奇数.则2425a a +=_________;研究发现,该数列中的奇数都会重复出现,那么第8个5是该数列的第_____项.三、解答题:本大题共6小题,共80分. 解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分12分)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,3cos 4A =,2C A =. (Ⅰ)求cos C 的值; (Ⅱ)若24ac =,求,a c 的值.16.(本小题满分13分)在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本,这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.在选取的40名学生中,(Ⅰ)求成绩在区间[80,90)内的学生人数; (Ⅱ)从成绩大于等于80分的学生中随机选2名学生,求至少有1名学生成绩在区间[90,100]内的概率.17.(本小题满分13分)如图,已知四棱柱1111ABCD A B C D -的底面是菱形,侧棱1BB ⊥底面ABCD ,E 是侧棱1CC 的中点.(Ⅰ)求证:AC ⊥平面11BDD B ; (Ⅱ)求证://AC 平面1B DE .18.(本小题满分14分)已知椭圆2222:1(0)x y C a b a b +=>>椭圆C 上任意一点到椭圆两个焦点的距离之和为6.(Ⅰ)求椭圆C 的方程;(Ⅱ)设直线:2l y kx =-与椭圆C 交与,A B 两点,点(0,1)P ,且PA PB =,求直线l 的方程.ABDA 1B 1C 1D 1EC19.(本小题满分14分)设函数2()f x x a =-.(Ⅰ)求函数()()g x xf x =在区间[0,1]上的最小值;(Ⅱ)当0a >时,记曲线()y f x =在点11(,())P x f x (1x >l ,l 与x 轴交于点2(,0)A x ,求证:12x x >>20.(本小题满分14分)如果由数列{}n a 生成的数列{}n b 满足对任意的n ∈*N 均有1n n b b +<,其中1n n n b a a +=-,则称数列{}n a 为“Z 数列”.(Ⅰ)在数列{}n a 中,已知2n a n =-,试判断数列{}n a 是否为“Z 数列”; (Ⅱ)若数列{}n a 是“Z 数列”,10a =,n b n =-,求n a ;(Ⅲ)若数列{}n a 是“Z 数列”,设,,s t m ∈*N ,且s t <,求证:t m s m t s a a a a ++-<-.北京市西城区2010年抽样测试参考答案 高三数学试卷(文科) 2010.5一、选择题:本大题共8小题,每小题5分,共40分.题号1 2 3 4 5 6 7 8 答案B C D A B C C D二、填空题:本大题共6小题,每小题5分,共30分.9. 12i 55+ 10. 2π11. 2 12. 22(2)2x y -+=13.14. 28,640注:两空的题目,第一个空2分,第二个空3分.三、解答题:(本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.)15、解:(Ⅰ)因为3cos 4A =, 所以2cos cos 22cos 1C A A ==- …………………3分2312()148=⨯-=. …………………5分(Ⅱ)在ABC ∆中,因为3cos 4A =,所以sin A = …………………7分因为1cos 8C =,所以sin C == …………………9分 根据正弦定理sin sin a cA C=, …………………10分 所以23a c =, 又24ac =,所以4,6a c ==. …………………12分16、解:(Ⅰ)因为各组的频率之和为1,所以成绩在区间[80,90)的频率为1(0.00520.0150.0200.045)100.1-⨯+++⨯=, …………………3分所以,40名学生中成绩在区间[80,90)的学生人数为400.14⨯=(人).…………………5分(Ⅱ)设A 表示事件“在成绩大于等于80分的学生中随机选两名学生,至少有一名学生成绩在区间[90,100]内”,由已知和(Ⅰ)的结果可知成绩在区间[80,90)内的学生有4人, 记这四个人分别为,,,a b c d ,成绩在区间[90,100]内的学生有2人, …………………7分 记这两个人分别为,e f , 则选取学生的所有可能结果为:(,),(,),(,),(,),(,),(,),(,),(,),(,),a b a c a d a e a f b c b d b e b f (,),(,),(,)c d c e c f , (,),(,),(,)d e d f e f基本事件数为15, …………………9分 事件“至少一人成绩在区间[90,100]之间”的可能结果为:(,),(,),(,),(,),a e a f b e b f (,),(,),(,),(,),(,)c e c f d e d f e f ,基本事件数为9, …………………11分 所以93()155P A ==. …………………13分17、证明:(Ⅰ)因为ABCD 是菱形,所以AC BD ⊥,因为1BB ⊥底面ABCD ,所以1BB AC ⊥, …………3分 所以AC ⊥平面11BDD B . …………5分 (Ⅱ)设AC ,BD 交于点O ,取1B D 的中点F ,连接,OF EF ,则1//OF BB ,且112OF BB =,又E 是侧棱1CC 的中点,112EC CC =,11//BB CC ,11BB CC =,所以1//OF CC ,且112OF CC =, …………………7分A BDA 1B 1C 1D 1ECOF所以四边形OCEF 为平行四边形,//OC EF , …………………9分 又AC ⊄平面1B DE ,EF ⊂平面1B DE , ………………11分 所以//AC 平面1B DE . ………………13分 18、解:(Ⅰ)由已知26a =,3c a =, …………………3分 解得3a =,c =所以2223b a c =-=, …………………4分所以椭圆C 的方程为22193x y +=. …………………5分(Ⅱ)由221,932x y y kx ⎧+=⎪⎨⎪=-⎩得,22(13)1230k x kx +-+=, 直线与椭圆有两个不同的交点,所以2214412(13)0k k ∆=-+>, 解得219k >. …………………7分 设11(,)A x y ,22(,)B x y ,则1221213k x x k +=+,122313x x k =+, …………………8分 计算121222124()441313k y y k x x k k k +=+-=⋅-=-++, 所以,,A B 中点坐标为2262(,)1313k E k k -++, …………………10分 因为PA PB =,所以PE AB ⊥,1PE AB k k ⋅=-,所以2221131613k k k k --+⋅=-+, …………………12分 解得1k =±, …………………13分经检验,符合题意,所以直线l 的方程为20x y --=或20x y ++=. …………………14分 19、(Ⅰ)解:3()g x x ax =-,2()3g x x a '=-, …………………2分当0a ≤时,()g x 为R 上的增函数,所以()g x 在区间[0,1]上的最小值为(0)0g =; …………………4分 当0a >时, ()g x '的变化情况如下表:所以,函数()g x 在(,-∞,)+∞上单调递增,在(上单调递减. …………………6分1<,即03a <<时,()g x 在区间[0,1]上的最小值为g = ……………7分1≥,即3a ≥时,()g x 在区间[0,1]上的最小值为(1)1g a =-. ……8分 综上,当0a ≤时,()g x 在区间[0,1]上的最小值为(0)0g =;当03a <<时,()g x 的最小值为;当3a ≥时,()g x 的最小值为1a -.(Ⅱ)证明:曲线()y f x =在点11(,())P x f x (1x )处的切线方程为2111()2()y x a x x x --=-,令0y =,得21212x ax x +=, …………………10分所以212112a x x x x --=,因为1x >21102a x x -<,21x x <. ………11分因为1x 1122x ax ≠,所以211211222x a x ax x x +==+> …………………13分所以12x x >> …………………14分20、解:(Ⅰ)因为2n a n =-,所以221(1)21n n n b a a n n n +=-=-++=--,n ∈*N , …………………2分 所以12(1)1212n n b b n n +-=-+-++=-,所以1n n b b +<,数列{}n a 是“Z 数列”. …………………4分(Ⅱ)因为n b n =-,所以2111a a b -==-,3222a a b -==-,…,11(1)n n n a a b n ---==--, 所以1(1)12(1)2n n na a n --=-----=-(2n ≥),…………………6分 所以(1)2n n na -=-(2n ≥), 又10a =,所以(1)2n n n a -=-(n ∈*N ). …………………8分(Ⅲ)因为 111()()s m s s m s m s s s m s a a a a a a b b +++-++--=-++-=++, 111()()t m t t m t m t t t m t a a a a a a b b +++-++--=-++-=++,………………10分又,,s t m ∈*N ,且s t <,所以s i t i +<+,s i t i b b ++>,n ∈*N , 所以1122,,,s m t m s m t m s t b b b b b b +-+-+-+->>>, …………………12分所以t m t s m s a a a a ++-<-,即t m s m t s a a a a ++-<-. …………………14分。
2013北京西城区高考一模文数答案试卷

北京市西城区2013年高三一模试卷高三数学(文科)参考答案及评分标准2013.4一、选择题:本大题共8小题,每小题5分,共40分.1.B;2.A;3.D;4.B;5.C;6.C;7.A;8.B.二、填空题:本大题共6小题,每小题5分,共30分.9.0;10.74-;11.12x=-,2;12.80%;13.24;14.5,722n+.注:11、14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.15.(本小题满分13分)(Ⅰ)解:依题意,得3π()04f=,………………1分即3π3πsin cos044a+==, (3)分解得1a=. (5)分(Ⅱ)解:由(Ⅰ)得()sin cosf x x x=+.………………6分22()[()]2sing x f x x=-22(sin cos)2sinx x x=+-sin2cos2x x=+ (8)分π)4x=+.………………10分由πππ2π22π242k x k -≤+≤+,得 3ππππ88k x k -≤≤+,k ∈Z . (12)分所以 ()g x 的单调递增区间为3ππ[π,π]88k k -+,k ∈Z . (13)分16.(本小题满分14分) (Ⅰ)证明:在△ABC 中, 因为AC =,2AB =,1BC =,所以 BC AC ⊥. ………………2分 又因为 AC FB ⊥,所以 ⊥AC 平面FBC . ………………4分 (Ⅱ)解:因为⊥AC 平面FBC ,所以FC AC ⊥.因为FC CD ⊥,所以⊥FC 平面ABCD . ………………6分 在等腰梯形ABCD 中可得 1==DC CB ,所以1=FC .所以△BCD 的面积为 43=S . (7)分所以四面体FBCD的体积为:13F BCD V S FC -=⋅=. ………………9分(Ⅲ)解:线段AC 上存在点M ,且M 为AC 中点时,有EA // 平面FDM ,证明如下: ………………10分连结CE ,与DF 交于点N ,连接MN .因为 CDEF 为正方形,所以N 为CE 中点. ………………11分所以 EA //MN . ………………12分 因为 ⊂MN 平面FDM ,⊄EA 平面FDM , ………………13分所以 EA //平面FDM .所以线段AC 上存在点M ,使得EA //平面FDM 成立. ………………14分 17.(本小题满分13分)(Ⅰ)解:设“甲临时停车付费恰为6元”为事件A , ………………1分则41)12531(1)(=+-=A P . 所以甲临时停车付费恰为6元的概率是41. ………………4分(Ⅱ)解:设甲停车付费a 元,乙停车付费b 元,其中,6,14,22,30a b =. ………………6分则甲、乙二人的停车费用构成的基本事件空间为:(6,6),(6,14),(6,22),(6,30),(14,6),(14,14),(14,22),(14,30),(22,6),(22,14),(22,22), (22,30),(30,6),(30,14),(30,22),(30,30),共16种情形. ………………10分其中,(6,30),(14,22),(22,14),(30,6)这4种情形符合题意. ………………12分故“甲、乙二人停车付费之和为36元”的概率为41164P ==. (13)分18.(本小题满分13分)(Ⅰ)解:()f x 的定义域为R , 且 ()e xf x a '=+. ………………2分① 当0a =时,()e xf x =,故()f x 在R 上单调递增.从而)(x f 没有极大值,也没有极小值. ………………4分② 当0a <时,令()0f x '=,得ln()x a =-. ()f x 和()f x '的情况如下:故()f x 的单调减区间为(,ln())a -∞-;单调增区间为(ln(),)a -+∞.从而)(x f 的极小值为(ln())ln()f a a a a -=-+-;没有极大值. ………………6分(Ⅱ)解:()g x 的定义域为(0,)+∞,且11()ax g x a x x -'=-=. ………………8分③ 当0a =时,()f x 在R 上单调递增,()g x 在(0,)+∞上单调递减,不合题意. (9)分④ 当0a <时,()0g x '<,()g x 在(0,)+∞上单调递减.当10a -≤<时,ln()0a -≤,此时()f x 在(ln(),)a -+∞上单调递增,由于()g x 在(0,)+∞上单调递减,不合题意. ………………11分当1a <-时,ln()0a ->,此时()f x 在(,ln())a -∞-上单调递减,由于()f x 在(0,)+∞上单调递减,符合题意.综上,a 的取值范围是(,1)-∞-. ………………13分 19.(本小题满分14分)(Ⅰ)解:依题意,直线AB 的斜率存在,设其方程为(1)y k x =+. ………………1分将其代入22143x y +=,整理得2222(43)84120k x k x k +++-=. ………………3分设11(,)A x y ,22(,)B x y ,所以2122843k x x k -+=+. ………………4分故点G 的横坐标为21224243x x k k +-=+. 依题意,得2241434k k -=-+, ………………6分解得12k =±. ………………7分(Ⅱ)解:假设存在直线AB ,使得12S S =,显然直线AB 不能与,x y 轴垂直.由(Ⅰ)可得22243(,)4343k k G k k -++.8分因为 DG AB ⊥,所以 2223431443Dkk k k x k +⨯=---+,解得 2243D k x k -=+, 即 22(,0)43k D k -+. (10)分因为 △GFD ∽△OED , 所以 12||||S S GD OD =⇔=. ………………11分所以 2243k k -=+, (12)分整理得 2890k +=. ………………13分因为此方程无解,所以不存在直线AB ,使得 12S S =. (14)分 20.(本小题满分13分)(Ⅰ)解:当5n =时,由51(,)||i i i d A B a b ==-∑,得 (,)|12||24||12||21||53|7d A B =-+-+-+-+-=,所以 (,)7d A B =. ………………3分(Ⅱ)证明:设12(,,,)n A a a a =,12(,,,)n B b b b =,12(,,,)n C c c c =.因为 0∃>λ,使AB BC λ=,所以 0∃>λ,使得 11221122(,,)((,,)n n n n b a b a b a c b c b c b ---=---λ,,,所以 0∃>λ,使得 ()ii i i b a c b λ-=-,其中1,2,,i n =.所以i i b a -与(1,2,,)i i c b i n -=同为非负数或同为负数.………………6分所以11(,)(,)||||nni i i i i i d A B d B C a b b c ==+=-+-∑∑1(||||)ni i i i i b a c b ==-+-∑1||(,)ni i i c a d A C ==-=∑. ………………8分(Ⅲ)解法一:201(,)||i i i d A B b a ==-∑.设(1,2,,20)i i b a i -=中有(20)m m ≤项为非负数,20m -项为负数.不妨设1,2,,i m =时0i i b a -≥;1,2,,20i m m =++时,0i i b a -<.所以 201(,)||i i i d A B b a ==-∑121212201220[()()][()()]m m m m m m b b b a a a a a a b b b ++++=+++-+++++++-+++因为 (,)(,)13d I A d I B ==,所以202011(1)(1)iii i a b ==-=-∑∑, 整理得202011i ii i a b===∑∑.所以 2012121(,)||2[()]i i m m i d A B b a b b b a a a ==-=+++-+++∑.……………10分因为1212201220()()m m m b b b b b b b b b +++++=+++-+++(1320)(20)113m m ≤+--⨯=+; 又121m a a a m m +++≥⨯=,所以1212(,)2[()]m m d A B b b b a a a =+++-+++2[(13)]26m m ≤+-=.即 (,)26d A B ≤. ……………12分对于 (1,1,,1,14)A =,(14,1,1,,1)B =,有 A ,20B S ∈,且(,)(,)13d I A d I B ==,(,)26d A B =.综上,(,)d A B 的最大值为26. ……………13分解法二:首先证明如下引理:设,x y ∈R ,则有||||||x y x y +≤+. 证明:因为 ||||x x x -≤≤,||||y y y -≤≤, 所以 (||||)||||x y x y x y -+≤+≤+,即 ||||||x y x y +≤+.所以202011(,)|||(1)(1)|i i i i i i d A B b a b a ===-=-+-∑∑201(|1||1|)i i i b a =≤-+-∑202011|1||1|26i i i i a b ===-+-=∑∑. ……………11分上式等号成立的条件为1i a =,或1i b =,所以 (,)26d A B ≤. ……………12分 对于(1,1,,1,14)A =,(14,1,1,,1)B =,有 A ,20B S ∈,且(,)(,)13d I A d I B ==,(,)26d A B =.综上,(,)d A B 的最大值为26. ……………13分。
北京市西城区2013届高三第二次模拟考试文科数学试题(word版)

(A)8 (B)7
(C) 6
(D) 5
第 4 页 共 21 页
金太阳新课标资源网
金太阳新课标资源网
第Ⅱ卷(非选择题 共 110 分) 二、填空题:本大题共 6 小题,每小题 5 分, 共 30 分. 9.已知直线 l1 : x 3y 1 0 , l2 : 2x my 1 0 .若 l1 ∥ l2 , 则实数 m ______.
3
(Ⅰ)若 a 2 ,求曲线 y f (x) 在点 (1, f (1)) 处的切线 方程;
(Ⅱ)求 f (x) 在区间[2,3]上的最小值.
第 8 页 ቤተ መጻሕፍቲ ባይዱ 21 页
金太阳新课标资源网
金太阳新课标资源网
19.(本小题满分 14 分) 如图,椭圆 C : x2 y2 1 (0 m 1) 的左顶点为 A , M
14 . 在 直 角 坐 标 系 xOy 中 , 已 知 两 定 点 , A(1,0)
B(1,1) .动点
P(x,
y)
满足
0
OP OA
1,
则点
P
构成的
0 OP OB 2.
区域的面积是______;点Q(x y, x y) 构成的区
域的面积是______.
三、解答题:本大题共 6 小题,共 80 分.解答
北京市西城区 2013 届高三第二 次模拟考试文科数学试题(word 版)
金太阳新课标资源网
北京市西城区 2013 届高三第二次模拟考试
数学(文科)
第Ⅰ卷(选择题 共 40 分)
2013.5
一、选择题:本大题共 8 小题,每小题 5 分,
共 40 分.在每小题列出的四个选项中,选
第 6 页 共 21 页
北京市西城区2013届高三第二次模拟数学(文史类)
2013北京西城区高三二模数学文科一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 设集合{2,3,4}A =,{2,4,6}B =,若x A ∈且x B ∉,则x 等于A .2B .3 √C .4D .62. 已知命题:,cos 1p x x ∀∈≤R ,则A . :,cos 1p x x ⌝∃∈≥RB .:,cos 1p x x ⌝∀∈≥RC . :,cos 1p x x ⌝∃∈>R √D .:,cos 1p x x ⌝∀∈>R3. 设变量,x y 满足约束条件3,1,x y x y +≥⎧⎨-≥-⎩则目标函数2z y x =+的最小值为( )A .1B .2C .3D .4√4. “ln 1x >”是“1x >”的A .充分不必要条件 √B .必要不充分条件C .充要条件D .既不充分也不必要条件5. 如图,三棱柱111ABC A B C -的侧棱长和底面边长均为2,且侧棱1AA ⊥底面ABC ,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为AB. √ C. D .46. 在数列{}n a 中,11a =,1n n a a n -=+,2n ≥.为计算这个数列前10项的和,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是A .8i ≥B .9i ≥C .10i ≥ √D .11i ≥正(主)视图A BCA 1B 1C 17. 等差数列{}n a 的前n 项和为n S ,若70a >,80a <,则下列结论正确的是A .78S S <B .1516S S <C .130S > √D .150S >8. 给出函数()f x 的一条性质:“存在常数M ,使得()f x M x ≤对于定义域中的一切实数x 均成立.”则下列函数中具有这条性质的函数是 A .1y x=B .2y x =C .1y x =+D .sin y x x =二、填空题:本大题共6小题,每小题5分,共30分. 9. i 是虚数单位,i2i=+_____. 10. 函数sin cos y x x =+的最小正周期是_________,最大值是________.11. 在抛物线22y px =上,横坐标为2的点到抛物线焦点的距离为3,则p =________. 12. 圆心在x 轴上,且与直线y x =切于(1,1)点的圆的方程为________. 13. 设,,a b c 为单位向量,,a b 的夹角为60,则⋅+⋅a c b c 的最大值为________.14. 我们可以利用数列{}n a 的递推公式2,,n n n n a a n ⎧⎪=⎨⎪⎩为奇数时,为偶数时(n ∈*N )求出这个数列各项的值,使得这个数列中的每一项都是奇数.则2425a a +=_________;研究发现,该数列中的奇数都会重复出现,那么第8个5是该数列的第_____项.三、解答题:本大题共6小题,共80分. 解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分12分)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,3cos 4A =,2C A =. (Ⅰ)求cos C 的值; (Ⅱ)若24ac =,求,a c 的值.16.(本小题满分13分)在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本,这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.在选取的40名学生中,(Ⅰ)求成绩在区间[80,90)内的学生人数; (Ⅱ)从成绩大于等于80分的学生中随机选2名学生,求至少有1名学生成绩在区间[90,100]内的概率.17.(本小题满分13分)如图,已知四棱柱1111ABCD A B C D -的底面是菱形,侧棱1BB ⊥底面ABCD ,E 是侧棱1CC 的中点.(Ⅰ)求证:AC ⊥平面11BDD B ; (Ⅱ)求证://AC 平面1B DE .18.(本小题满分14分)已知椭圆2222:1(0)x y C a b a b +=>>椭圆C 上任意一点到椭圆两个焦点的距离之和为6.(Ⅰ)求椭圆C 的方程;(Ⅱ)设直线:2l y kx =-与椭圆C 交与,A B 两点,点(0,1)P ,且PA PB =,求直线l 的方程.ABDA 1B 1C 1D 1EC19.(本小题满分14分)设函数2()f x x a =-.(Ⅰ)求函数()()g x xf x =在区间[0,1]上的最小值;(Ⅱ)当0a >时,记曲线()y f x =在点11(,())P x f x (1x >l ,l 与x 轴交于点2(,0)A x ,求证:12x x >>20.(本小题满分14分)如果由数列{}n a 生成的数列{}n b 满足对任意的n ∈*N 均有1n n b b +<,其中1n n n b a a +=-,则称数列{}n a 为“Z 数列”.(Ⅰ)在数列{}n a 中,已知2n a n =-,试判断数列{}n a 是否为“Z 数列”; (Ⅱ)若数列{}n a 是“Z 数列”,10a =,n b n =-,求n a ;(Ⅲ)若数列{}n a 是“Z 数列”,设,,s t m ∈*N ,且s t <,求证:t m s m t s a a a a ++-<-.北京市西城区2010年抽样测试参考答案 高三数学试卷(文科) 2010.5一、选择题:本大题共8小题,每小题5分,共40分.题号 1 2 3 4 5 6 7 8 答案BCDABCCD二、填空题:本大题共6小题,每小题5分,共30分.9. 12i 55+ 10. 2π11. 2 12. 22(2)2x y -+=13.14. 28,640注:两空的题目,第一个空2分,第二个空3分.三、解答题:(本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.)15、解:(Ⅰ)因为3cos 4A =, 所以2cos cos 22cos 1C A A ==- …………………3分2312()148=⨯-=. …………………5分(Ⅱ)在ABC ∆中,因为3cos 4A =,所以sin A = …………………7分因为1cos 8C =,所以sin C == …………………9分 根据正弦定理sin sin a cA C=, …………………10分 所以23a c =, 又24ac =,所以4,6a c ==. …………………12分16、解:(Ⅰ)因为各组的频率之和为1,所以成绩在区间[80,90)的频率为1(0.00520.0150.0200.045)100.1-⨯+++⨯=, …………………3分所以,40名学生中成绩在区间[80,90)的学生人数为400.14⨯=(人).…………………5分(Ⅱ)设A 表示事件“在成绩大于等于80分的学生中随机选两名学生,至少有一名学生成绩在区间[90,100]内”,由已知和(Ⅰ)的结果可知成绩在区间[80,90)内的学生有4人, 记这四个人分别为,,,a b c d ,成绩在区间[90,100]内的学生有2人, …………………7分 记这两个人分别为,e f , 则选取学生的所有可能结果为:(,),(,),(,),(,),(,),(,),(,),(,),(,),a b a c a d a e a f b c b d b e b f (,),(,),(,)c d c e c f ,(,),(,),(,)d e d f e f基本事件数为15, …………………9分 事件“至少一人成绩在区间[90,100]之间”的可能结果为:(,),(,),(,),(,),a e a f b e b f (,),(,),(,),(,),(,)c e c f d e d f e f ,基本事件数为9, …………………11分 所以93()155P A ==. …………………13分17、证明:(Ⅰ)因为ABCD 是菱形,所以AC BD ⊥,因为1BB ⊥底面ABCD ,所以1BB AC ⊥, …………3分 所以AC ⊥平面11BDD B . …………5分 (Ⅱ)设AC ,BD 交于点O ,取1B D 的中点F ,连接,OF EF ,则1//OF BB ,且112OF BB =,又E 是侧棱1CC 的中点,112EC CC =,11//BB CC ,11BB CC =,所以1//OF CC ,且112OF CC =, …………………7分所以四边形OCEF 为平行四边形,//OC EF , …………………9分A BDA 1B 1C 1D 1ECOF又AC ⊄平面1B DE ,EF ⊂平面1B DE , ………………11分 所以//AC 平面1B DE . ………………13分 18、解:(Ⅰ)由已知26a =,3c a =, …………………3分 解得3a =,c =所以2223b a c =-=, …………………4分所以椭圆C 的方程为22193x y +=. …………………5分 (Ⅱ)由221,932x y y kx ⎧+=⎪⎨⎪=-⎩得,22(13)1230k x kx +-+=, 直线与椭圆有两个不同的交点,所以2214412(13)0k k ∆=-+>, 解得219k >. …………………7分 设11(,)A x y ,22(,)B x y ,则1221213k x x k +=+,122313x x k=+, …………………8分 计算121222124()441313k y y k x x k k k +=+-=⋅-=-++,所以,,A B 中点坐标为2262(,)1313k E k k -++, …………………10分 因为PA PB =,所以PE AB ⊥,1PE AB k k ⋅=-,所以2221131613k k k k --+⋅=-+, …………………12分 解得1k =±, …………………13分经检验,符合题意,所以直线l 的方程为20x y --=或20x y ++=. …………………14分 19、(Ⅰ)解:3()g x x ax =-,2()3g x x a '=-, …………………2分当0a ≤时,()g x 为R 上的增函数,所以()g x 在区间[0,1]上的最小值为(0)0g =; …………………4分 当0a >时, ()g x '的变化情况如下表:所以,函数()g x 在(,-∞,)+∞上单调递增,在(上单调递减. …………………6分1<,即03a <<时,()g x 在区间[0,1]上的最小值为g = ……………7分1≥,即3a ≥时,()g x 在区间[0,1]上的最小值为(1)1g a =-. ……8分 综上,当0a ≤时,()g x 在区间[0,1]上的最小值为(0)0g =;当03a <<时,()g x 的最小值为;当3a ≥时,()g x 的最小值为1a -.(Ⅱ)证明:曲线()y f x =在点11(,())P x f x (1x )处的切线方程为2111()2()y x a x x x --=-,令0y =,得21212x ax x +=, …………………10分所以212112a x x x x --=,因为1x >21102a x x -<,21x x <. ………11分因为1x 1122x ax ≠,所以211211222x a x ax x x +==+> …………………13分所以12x x >> …………………14分20、解:(Ⅰ)因为2n a n =-,所以221(1)21n n n b a a n n n +=-=-++=--,n ∈*N , …………………2分 所以12(1)1212n n b b n n +-=-+-++=-,所以1n n b b +<,数列{}n a 是“Z 数列”. …………………4分(Ⅱ)因为n b n =-,所以2111a a b -==-,3222a a b -==-,…,11(1)n n n a a b n ---==--, 所以1(1)12(1)2n n na a n --=-----=- (2n ≥),…………………6分 所以(1)2n n na -=-(2n ≥), 又10a =,所以(1)2n n n a -=-(n ∈*N ). …………………8分(Ⅲ)因为 111()()s m s s m s m s s s m s a a a a a a b b +++-++--=-++-=++ ,111()()t m t t m t m t t t m t a a a a a a b b +++-++--=-++-=++ ,………………10分又,,s t m ∈*N ,且s t <,所以s i t i +<+,s i t i b b ++>,n ∈*N ,所以1122,,,s m t m s m t m s t b b b b b b +-+-+-+->>> , …………………12分 所以t m t s m s a a a a ++-<-,即t m s m t s a a a a ++-<-. …………………14分。
北京市西城区2013一摸文科数学习题和答案

北京市西城区2013年高三一模试卷高三数学(理科) 2013.4一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知全集U=R ,集合{|02}A x x =<<,2{|10}B x x =->,那么U AB =ð(A ){|01}x x <<(B ){|01}x x <≤ (C ){|12}x x << (D ){|12}x x ≤<2.若复数i2ia +的实部与虚部相等,则实数a = (A )1- (B )1(C )2-(D )23.执行如图所示的程序框图.若输出y =角=θ(A )π6 (B )π6-(C )π3(D )π3-4.从甲、乙等5名志愿者中选出4名,分别从事A ,B ,C ,D 四项不同的工作,每人承担一项.若甲、乙二人均不能从事A 工作,则不同的工作分配方案共有(A )60种 (B )72种(C )84种(D )96种5.某正三棱柱的三视图如图所示,其中正(主)视图是边长为2的正方形,该正三棱柱的表面积是 (A)6 (B)12+(C)12+ (D)24+6.等比数列{}n a 中,10a >,则“13a a <”是“36a a <”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件7.已知函数22()log 2log ()f x x x c =-+,其中0c >.若对于任意的(0,)x ∈+∞,都有()1f x ≤,则c 的取值范围是 (A )1(0,]4(B )1[,)4+∞ (C )1(0,]8(D )1[,)8+∞8.如图,正方体1111ABCD A B C D -中,P 为底面ABCD上的动点,1PE A C ⊥于E ,且PA PE =,则点P 的轨迹是 (A )线段 (B )圆弧(C )椭圆的一部分(D )抛物线的一部分第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9.已知曲线C 的参数方程为2cos 12sin x y =⎧⎨=+⎩αα(α为参数),则曲线C 的直角坐标方程为 .10.设等差数列{}n a 的公差不为0,其前n 项和是n S .若23S S =,0k S =,则k =______.11.如图,正六边形ABCDEF 的边长为1,则AC DB ⋅=______. 12.如图,已知AB 是圆O 的直径,P 在AB 的延长线上,PC切圆O 于点C ,CD OP ⊥于D .若6CD =,10CP =, 则圆O 的半径长为______;BP =______. 13.在直角坐标系xOy 中,点B 与点(1,0)A -关于原点O 对称.点00(,)P x y 在抛物线24y x =上,且直线AP 与BP 的斜率之积等于2,则0x =______.14.记实数12,,,n x x x 中的最大数为12max{,,,}n x x x ,最小数为12min{,,,}n x x x .设△ABC的三边边长分别为,,a b c ,且a b c ≤≤,定义△ABC 的倾斜度为max{,,}min{,a b c at b c a b=⋅,}b cc a. (ⅰ)若△ABC 为等腰三角形,则t =______;(ⅱ)设1a =,则t 的取值范围是______.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数()sin cos f x x a x =-的一个零点是π4. (Ⅰ)求实数a 的值;(Ⅱ)设()()()cos g x f x f x x x =⋅-+,求()g x 的单调递增区间.16.(本小题满分13分)某班有甲、乙两个学习小组,两组的人数如下:现采用分层抽样的方法(层内采用简单随机抽样)从甲、乙两组中共抽取3名同学进行学业检测. (Ⅰ)求从甲组抽取的同学中恰有1名女同学的概率; (Ⅱ)记X 为抽取的3名同学中男同学的人数,求随机变量X的分布列和数学期望.17.(本小题满分14分)在如图所示的几何体中,面CDEF 为正方形,面ABCD 为等腰梯形,AB //CD ,BC AB 2=,60ABC ︒∠=,AC FB ⊥.(Ⅰ)求证:⊥AC 平面FBC ;(Ⅱ)求BC 与平面EAC 所成角的正弦值;(Ⅲ)线段ED 上是否存在点Q ,使平面EAC ⊥平面QBC ? 证明你的结论.18.(本小题满分13分)已知函数()ln f x ax x =-,()e 3axg x x =+,其中a ∈R .(Ⅰ)求)(x f 的极值;(Ⅱ)若存在区间M ,使)(x f 和()g x 在区间M 上具有相同的单调性,求a 的取值范围.19.(本小题满分14分)如图,椭圆22221(0)x y a b a b+=>>的左焦点为F ,过点F 的直线交椭圆于A ,B 两点.当直线AB 经过椭圆的一个顶点时,其倾斜角恰为60︒.(Ⅰ)求该椭圆的离心率; (Ⅱ)设线段AB 的中点为G ,AB 的中垂线与x 轴和y 轴分别交于,D E 两点.记△GFD 的面积为1S ,△OED (O 为原点)的面积为2S ,求12S S 的取值范围.20.(本小题满分13分)已知集合*12{|(,,,),,1,2,,}(2)n n i S X X x x x x i n n ==∈=≥N .对于12(,,,)n A a a a =,12(,,,)n nB b b b S =∈,定义1122(,,,)nnAB b a b a b a =---; 1212(,,,)(,,,)()n n a a a a a a =∈R λλλλλ;A 与B 之间的距离为1(,)||ni i i d A B a b ==-∑.(Ⅰ)当5n =时,设5(1,2,1,2,)A a =,(2,4,2,1,3)B =.若(,)7d A B =,求5a ;(Ⅱ)(ⅰ)证明:若,,n A B C S ∈,且0∃>λ,使A B B C λ=,则(,)(,)(d A B d B C d A C+=; (ⅱ)设,,n A B C S ∈,且(,)(,)(,d A B d B C d A C +=.是否一定0∃>λ,使A B B C λ=?说明理由;(Ⅲ)记(1,1,,1)n I S =∈.若A ,n B S ∈,且(,)(,)d I A d I B p ==,求(,)d A B 的最大值.北京市西城区2013年高三一模试卷高三数学(理科)参考答案及评分标准2013.4一、选择题:本大题共8小题,每小题5分,共40分.1. B ; 2.A ; 3.D ; 4.B ; 5.C ; 6.B ; 7.D ; 8.A .二、填空题:本大题共6小题,每小题5分,共30分.9.22230xy y +--=; 10.5; 11.32-12.152,5; 13.1+ 14.1,. 注:12、14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分. 15.(本小题满分13分) (Ⅰ)解:依题意,得π()04f =, ………………1分 即ππsincos 04422a -=-=, ………………3分 解得1a =. ………………5分(Ⅱ)解:由(Ⅰ)得()sin cos f x x x =-. ………………6分()()()cos g x f x f x x x =⋅-+(sin cos )(sin cos )2x x x x x =--- (7)分22(cos sin )2x x x =-+ ………………8分cos 22x x =+ ………………9分π2sin(2)6x =+. ………………10分由 πππ2π22π262k x k -≤+≤+,得 ππππ36k x k -≤≤+,k ∈Z . ………………12分所以 ()g x 的单调递增区间为ππ[π,π]36k k -+,k ∈Z . ………………13分16.(本小题满分13分)(Ⅰ)解:依题意,甲、乙两组的学生人数之比为 (35):(22)2:1++=, ……………1分所以,从甲组抽取的学生人数为2323⨯=;从乙组抽取的学生人数为1313⨯=.………2分 设“从甲组抽取的同学中恰有1名女同学”为事件A , ………………3分则 113528C C 15()C 28P A ⋅==,故从甲组抽取的同学中恰有1名女同学的概率为1528. ………………5分 (Ⅱ)解:随机变量X 的所有取值为0,1,2,3. ………………6分21522184C C 5(0)C C 28P X ⋅===⋅, 111213525221218484C C C C C 25(1)C C C C 56P X ⋅⋅⋅==+=⋅⋅, 211113235221218484C C C C C 9(2)C C C C 28P X ⋅⋅⋅==+=⋅⋅, 21322184C C 3(3)C C 56P X ⋅===⋅.……………10分所以,随机变量X的分布列为:………………11分5259350123285628564EX =⨯+⨯+⨯+⨯=. ………………13分17.(本小题满分14分) (Ⅰ)证明:因为BC AB 2=,60ABC ︒∠=,在△ABC 中,由余弦定理可得 BC AC 3=, 所以BC AC ⊥. ………………2分 又因为 AC FB ⊥,所以⊥AC 平面FBC . ………………4分(Ⅱ)解:因为⊥AC 平面FBC ,所以FC AC ⊥.因为FC CD⊥,所以⊥FC 平面ABCD. ………………5分所以,,CA CF CB 两两互相垂直,如图建立的空间直角坐标系xyz C -. (6)分在等腰梯形ABCD 中,可得 CB CD =.设1BC =,所以11(0,0,0),(0,1,0),(,,0),(,,1)2222C A BDE --.所以)1,21,23(-=,)0,0,3(=,)0,1,0(=. 设平面EAC 的法向量为=()x,y,z n ,则有0,0.CE CA ⎧⋅=⎪⎨⋅=⎪⎩n n所以10,20.x y z -+=⎨= 取1z =,得=n (0,2,1). ………………8分 设BC 与平面EAC 所成的角为θ,则||sin |cos ,|5||||CB CB CB ⋅=〈〉==θn n n , 所以BC 与平面EAC 所成角的正弦值为552. ………………9分(Ⅲ)解:线段ED 上不存在点Q ,使平面EAC ⊥平面QBC .证明如下: ………………10分假设线段ED 上存在点Q ,设 ),21,23(t Q - )10(≤≤t ,所以),21,23(t -=. 设平面QBC 的法向量为=m ),,(c b a ,则有0,0.CB CQ ⎧⋅=⎪⎨⋅=⎪⎩m m所以0,10.22b a b tc =⎧-+=⎪⎩ 取 1=c ,得=m )1,0,32(t -. ………………12分 要使平面EAC ⊥平面QBC ,只需0=⋅n m ,………………13分即 002110⨯+⨯+⨯=, 此方程无解. 所以线段ED 上不存在点Q ,使平面EAC ⊥平面QBC . ………………14分18.(本小题满分13分) (Ⅰ)解:()f x 的定义域为(0,)+∞, ………………1分且11()ax f x a x x -'=-=. ………………2分 ① 当0a ≤时,()0f x '<,故()f x 在(0,)+∞上单调递减.从而)(x f 没有极大值,也没有极小值. ………………3分② 当0a >时,令()0f x '=,得1x a=. ()f x 和()f x '的情况如下:故()f x 的单调减区间为(0,)a ;单调增区间为(,)a +∞.从而)(x f 的极小值为1()1ln f a a=+;没有极大值. ………………5分(Ⅱ)解:()g x 的定义域为R ,且 ()e 3ax g x a '=+. ………………6分③ 当0a>时,显然 ()0g x '>,从而()g x 在R 上单调递增.由(Ⅰ)得,此时()f x 在1(,)a+∞上单调递增,符合题意. ………………8分④ 当0a=时,()g x 在R 上单调递增,()f x 在(0,)+∞上单调递减,不合题意.……9分⑤ 当0a <时,令()0g x '=,得013ln()x a a=-. ()g x 和()g x '的情况如下表:当30a -≤<时,00x ≤,此时()g x 在0(,)x +∞上单调递增,由于()f x 在(0,)+∞上单调递减,不合题意. ………………11分当3a <-时,00x >,此时()g x 在0(,)x -∞上单调递减,由于()f x 在(0,)+∞上单调递减,符合题意.综上,a 的取值范围是(,3)(0,)-∞-+∞. ………………13分19.(本小题满分14分) (Ⅰ)解:依题意,当直线AB 经过椭圆的顶点(0,)b 时,其倾斜角为60︒. ………………1分设(,0)F c -,则tan 60bc︒== ………………2分 将b = 代入 222a bc =+,解得2a c =. ………………3分所以椭圆的离心率为12c e a ==. ………………4分 (Ⅱ)解:由(Ⅰ),椭圆的方程可设为2222143x y c c +=. ………………5分 设11(,)A x y ,22(,)B x y .依题意,直线AB 不能与,x y 轴垂直,故设直线AB 的方程为()y k x c =+,将其代入2223412x y c +=,整理得 222222(43)84120k x ck x k c c +++-=. (7)分则2122843ck x x k -+=+,121226(2)43cky y k x x c k +=++=+,22243(,)4343ck ck G k k -++. ………………8分 因为GD AB ⊥,所以2223431443Dckk k ck x k +⨯=---+,2243Dck x k -=+. ………………9分因为 △GFD ∽△OED ,所以2222222212222243()()||434343||()43ck ck ck S GD k k k ck S OD k ---++++==-+ (11)分222242222242(3)(3)99999()ck ck c k c k ck c k k++===+>. ………………13分所以12S S 的取值范围是(9,)+∞. ………………14分20.(本小题满分13分)(Ⅰ)解:当5n =时,由51(,)||7i i i d A B a b ==-=∑,得 5|12||24||12||21||3|7a -+-+-+-+-=,即 5|3|2a -=.由*5a ∈N ,得 51a =,或55a =. ………………3分(Ⅱ)(ⅰ)证明:设12(,,,)n A a a a =,12(,,,)n B b b b =,12(,,,)n C c c c =.因为 0∃>λ,使 AB BC λ=,所以 0∃>λ,使得 11221122(,,)((,,)n n n n b a b a b a c b c b c b ---=---λ,,,即0∃>λ,使得 ()i i i i b a c b λ-=-,其中1,2,,i n =.所以i i b a -与(1,2,,)i i c b i n -=同为非负数或同为负数. ………………5分所以 11(,)(,)||||nni i i i i i d A B d B C a b b c ==+=-+-∑∑1(||||)ni i i i i b a c b ==-+-∑1||(,)ni i i c a d A C ==-=∑. (6)分(ⅱ)解:设,,n A B C S ∈,且(,)(,)(,)d A B d B C d A C +=,此时不一定0∃>λ,使得AB BC λ=. ………………7分反例如下:取(1,1,1,,1)A =,(1,2,1,1,,1)B =,(2,2,2,1,1,,1)C ,则(,)1d A B =,(,)2d B C =,(,)3d A C =,显然(,)(,)(,)d A B d B C d A C +=. 因为(0,1,0,0,,0)AB =,(1,0,1,0,0,,0)BC =,所以不存在>0λ,使得AB BC λ=. ………………8分 (Ⅲ)解法一:因为1(,)||ni i i d A B b a ==-∑,设(1,2,,)ii b a i n -=中有()m m n ≤项为非负数,n m -项为负数.不妨设1,2,,i m=时0ii b a -≥;1,2,,i m m n =++时,0i i b a -<.所以 1(,)||ni i i d A B b a ==-∑12121212[()()][()()]m m m m n m m n b b b a a a a a a b b b ++++=+++-+++++++-+++因为 (,)(,)d I A d I B p ==,所以11(1)(1)nniii i a b ==-=-∑∑, 整理得 11nniii i a b ===∑∑.所以 12121(,)||2[()]ni i m m i d A B b a b b b a a a ==-=+++-+++∑. (10)分因为 121212()()m n m m n b b b b b b b b b +++++=+++-+++()()1p n n m p m ≤+--⨯=+;又 121m a a a m m +++≥⨯=, 所以 1212(,)2[()]m m d A B b b b a a a =+++-+++2[()]2p m m p ≤+-=.即 (,)2d A B p ≤. ……………12分 对于(1,1,,1,1)A p =+,(1,1,1,,1)B p =+,有A,nB S ∈,且(,)(,)d I A d I B p==,(,)2d A B p =.综上,(,)d A B 的最大值为2p . ……………13分 解法二:首先证明如下引理:设,x y ∈R ,则有 ||||||x y x y +≤+.证明:因为 ||||x x x -≤≤,||||y y y -≤≤,所以 (||||)||||x y x y x y -+≤+≤+,即||||||x y x y +≤+.所以 11(,)|||(1)(1)|n ni i i i i i d A B b a b a ===-=-+-∑∑1(|1||1|)ni i i b a =≤-+-∑11|1||1|2n ni i i i a b p ===-+-=∑∑. (11)分上式等号成立的条件为1ia =,或1ib =,所以 (,)2d A B p ≤. ……………12分对于(1,1,,1,1)A p =+,(1,1,1,,1)B p =+,有A,nB S ∈,且(,)(,)d I A d I B p==,(,)2.d A B pd A B的最大值为2p.……………13分综上,(,)。
数学_2013年北京市西城区高考数学一模试卷(文科)(含答案)

2013年北京市西城区高考数学一模试卷(文科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知全集U ={x ∈Z||x|<5},集合A ={−2, 1, 3, 4},B ={0, 2, 4},那么A ∩∁U B =( )A {−2, 1, 4}B {−2, 1, 3}C {0, 2}D {−2, 1, 3, 4} 2. 复数−1+i i=( )A 1+iB −1+iC −1−iD 1−i3. 执行如图所示的程序框图.若输出y =−√3,则输入角θ=( )A π6 B −π6 C π3 D −π34. 设等比数列{a n }的公比为q ,前n 项和为S n ,且a 1>0.若S 2>2a 3,则q 的取值范围是( )A (−1,0)∪(0,12) B (−12,0)∪(0,1) C (−∞,−1)∪(12,+∞) D (−∞,−12)∪(1,+∞)5. 某正三棱柱的三视图如图所示,其中正(主)视图是边长为2的正方形,该正三棱柱的表面积是( )A 6+√3B 12+√3C 12+2√3D 24+2√36. 设实数x ,y 满足条件 {x +1≥0x −y +1≥0x +y −2≤0,则y −4x 的最大值是( )A −4B −12 C 4 D 77. 已知函数f(x)=x 2+bx +c ,则“c <0”是“∃x 0∈R ,使f(x 0)<0”的( )A 充分而不必要条件B 必要而不充分条件C 充分必要条件D 既不充分也不必要条件8. 如图,正方体ABCD −A 1B 1C 1D 1中,E 是棱B 1C 1的中点,动点P 在底面ABCD 内,且PA 1=A 1E ,则点P 运动形成的图形是( ) A 线段 B 圆弧 C 椭圆的一部分 D 抛物线的一部分二、填空题:本大题共6小题,每小题5分,共30分.9. 已知向量i →=(1, 0),j →=(0, 1).若向量i →+λj →与λi →+j →垂直,则实数λ=________. 10. 已知函数f(x)={log 2x ,x >02x ,x <0,则f(14)+f(−2)=________.11. 抛物线y 2=2x 的准线方程是________;该抛物线的焦点为F ,点M(x 0, y 0)在此抛物线上,且|MF|=52,则x 0=________.12. 某厂对一批元件进行抽样检测.经统计,这批元件的长度数据 (单位:mm )全部介于93至105之间.将长度数据以2为组距分成以下6组:[93, 95),[95, 97),[97, 99),[99, 101),[101, 103),[103, 105],得到如图所示的频率分布直方图.若长度在[97, 103)内的元件为合格品,根据频率分布直方图,估计这批产品的合格率是________.13. 在△ABC 中,内角A ,B ,C 的对边边长分别为a ,b ,c ,且cosAcosB =ba =34.若c =10,则△ABC 的面积是________.14. 已知数列{a n }的各项均为正整数,其前n 项和为S n .若a n+1={a n2,a n 是偶数3a n +1,a n 是奇数且S 3=29,则a 1=________;S 3n =________.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15. 已知函数f(x)=sinx +acosx 的一个零点是3π4.(1)求实数a 的值;(2)设g(x)=[f(x)]2−2sin 2x ,求g(x)的单调递增区间.16. 在如图所示的几何体中,面CDEF 为正方形,面ABCD 为等腰梯形,AB // CD ,AC =√3,AB =2BC =2,AC ⊥FB . (Ⅰ)求证:AC ⊥平面FBC ; (Ⅱ)求四面体FBCD 的体积;(Ⅲ)线段AC 上是否存在点M ,使EA // 平面FDM ?证明你的结论.17. 某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过1小时收费6元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过4小时.(Ⅰ)若甲停车1小时以上且不超过2小时的概率为13,停车付费多于14元的概率为512,求甲停车付费恰为6元的概率;(Ⅱ)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为36元的概率.18. 已知函数f(x)=e x +ax ,g(x)=ax −lnx ,其中a ≤0. (1)求f(x)的极值;(2)若存在区间M ,使f(x)和g(x)在区间M 上具有相同的单调性,求a 的取值范围.19.如图,已知椭圆x 24+y 23=1的左焦点为F ,过点F 的直线交椭圆于A ,B 两点,线段AB 的中点为G ,AB 的中垂线与x 轴和y 轴分别交于D ,E 两点. (1)若点G 的横坐标为−14,求直线AB 的斜率;(2)记△GFD 的面积为S 1,△OED (O 为原点)的面积为S 2.试问:是否存在直线AB ,使得S 1=S 2?说明理由.20. 已知集合S n ={X|X =(x 1,x 2,…,x n ),x i ∈N ∗,i =1,2,…,n}(n ≥2).对于A =(a 1, a 2,…,a n ),B =(b 1, b 2,…,b n )∈S n ,定义AB →=(b 1−a 1,b 2−a 2,…,b n −a n );λ(a 1, a 2,…,a n )=(λa 1, λa 2,…,λa n )(λ∈R);A 与B 之间的距离为d(A,B)=∑|n i=1a i −b i |. (1)当n =5时,设A =(1, 2, 1, 2, 5),B =(2, 4, 2, 1, 3),求d(A, B);(2)证明:若A ,B ,C ∈S n ,且∃λ>0,使AB →=λBC →,则d(A, B)+d(B, C)=d(A, C); (3)记I =(1, 1,…,1)∈S 20.若A ,B ∈S 20,且d(I, A)=d(I, B)=13,求d(A, B)的最大值.2013年北京市西城区高考数学一模试卷(文科)答案1. B2. A3. D4. B5. C6. C7. A8. B9. 010. −7411. x=−12,212. 80%13. 2414. 5,7n+2215. 解:(1)∵ f(x)=sinx+acosx,且f(3π4)=0,∴ sin3π4+acos3π4=0,即√22−√2a2=0,解之得a=1.(2)由(1)得f(x)=sinx+cosx.∴ g(x)=[f(x)]2−2sin2x=(sinx+cosx)2−2sin2x=sin2x+cos2x=√2sin(2x+π4).解不等式2kπ−π2≤2x+π4≤2kπ+π2,得kπ−3π8≤x≤kπ+π8,k∈Z.∴ 函数g(x)的单调递增区间为[kπ−3π8,kπ+π8],k∈Z.16. (Ⅰ)证明:在△ABC中,∵ AC=√3,AB=2,BC=1,∴ AC2+BC2=AB2.∴ AC⊥BC.又∵ AC⊥FB,BF∩CB=B,∴ AC⊥平面FBC.(Ⅱ)∵ AC⊥平面FBC,∴ AC⊥FC.∵ CD⊥FC,∴ FC⊥平面ABCD.在Rt△ACB中,BC=12AB,∴ ∠CAB=30∘,∴ 在等腰梯形ABCD中可得∠ABD=∠CDB=∠CBD=30∘,∴ CB=DC=1,∴ FC=1.∴ △BCD的面积S=12×12×sin120∘=√34.∴ 四面体FBCD的体积为:V F−BCD=13S∗FC=√312.(Ⅲ)线段AC上存在点M,且M为AC中点时,有EA // 平面FDM,证明如下:连接CE与DF交于点N,连接MN.由CDEF为正方形,得N为CE中点.∴ EA // MN.∵ MN⊂平面FDM,EA⊄平面FDM,∴ EA // 平面FDM.所以线段AC上存在点M,使得EA // 平面FDM成立.17. (1)设“甲临时停车付费恰为6元”为事件A,则P(A)=1−(13+512)=14.所以甲临时停车付费恰为6元的概率是14.(2)设甲停车付费a元,乙停车付费b元,其中a,b=6,14,22,30.则甲、乙二人的停车费用构成的基本事件空间为:(6, 6),(6, 14),(6, 22),(6, 30),(14, 6),(14, 14),(14, 22),(14, 30),(22, 6),(22, 14),(22, 22),(22, 30),(30, 6),(30, 14),(30, 22),(30, 30),共16种情形.其中,(6, 30),(14, 22),(22, 14),(30, 6)这4种情形符合题意.故“甲、乙二人停车付费之和为36元”的概率为P=416=14.18. 解:(1)f(x)的定义域为R,且f′(x)=e x+a.①当a=0时,f(x)=e x,故f(x)在R上单调递增.从而f(x)没有极大值,也没有极小值.②当a<0时,令f′(x)=0,得x=ln(−a).f(x)和f′(x)的情况如下:从而f(x)的极小值为f(ln(−a))=−a+aln(−a);没有极大值.(2)g(x)的定义域为(0, +∞),且g′(x)=a−1x =ax−1x.③当a=0时,f(x)在R上单调递增,g(x)在(0, +∞)上单调递减,不合题意.④当a<0时,g′(x)<0,g(x)在(0, +∞)上单调递减.当−1≤a <0时,ln(−a)≤0,此时f(x)在(ln(−a),+∞)上单调递增,由于g(x)在(0, +∞)上单调递减,不合题意.当a <−1时,ln(−a)>0,此时f(x)在(−∞, ln(−a))上单调递减,由于g(x)在(0, +∞)上单调递减,符合题意.综上,a 的取值范围是(−∞, −1).19. 解:(1)依题意,直线AB 的斜率存在,设其方程为y =k(x +1). 将其代入x 24+y 23=1,整理得 (4k 2+3)x 2+8k 2x +4k 2−12=0.设A(x 1, y 1),B(x 2, y 2),所以x 1+x 2=−8k 24k 2+3. 故点G 的横坐标为x 1+x 22=−4k 24k 2+3.依题意,得−4k 24k 2+3=−14,解得k =±12.(2)假设存在直线AB ,使得 S 1=S 2,显然直线AB 不能与x ,y 轴垂直. 由(1)可得 G(−4k 24k 2+3,3k4k 2+3). 因为DG ⊥AB ,所以3k 4k 2+3−4k 24k 2+3−x D×k =−1,解得x D =−k 24k 2+3,即 D(−k 24k 2+3,0).因为△GFD ∽△OED ,所以S 1=S 2,所以|GD|=|OD|. 所以√(−k 24k 2+3−−4k 24k 2+3)2+(3k4k 2+3)2=|−k 24k 2+3|,整理得8k 2+9=0.因为此方程无解,所以不存在直线AB ,使得 S 1=S 2. 20. (1)解:当n =5时,由d(A,B)=∑|5i=1a i −b i |,得 d(A, B)=|1−2|+|2−4|+|1−2|+|2−1|+|5−3|=7,所以 d(A, B)=7. (2)证明:设A =(a 1, a 2,…,a n ),B =(b 1, b 2,…,b n ),C =(c 1, c 2,…,c n ). 因为∃λ>0,使AB →=λBC →,所以∃λ>0,使得 (b 1−a 1, b 2−a 2,…,b n −a n )=λ((c 1−b 1, c 2−b 2,…,c n −b n ), 所以∃λ>0,使得 b i −a i =λ(c i −b i ),其中i =1,2,…,n . 所以 b i −a i 与c i −b i (i =1, 2,…,n)同为非负数或同为负数.所以 d(A,B)+d(B,C)=∑|n i=1a i −b i |+∑|ni=1b i −c i |=∑(n i=1|b i −a i |+|c i −b i |)=∑|ni=1c i −a i |=d(A,C).(3) 首先证明如下引理:设x ,y ∈R ,则有|x +y|≤|x|+|y|.证明:因为−|x|≤x ≤|x|,−|y|≤y ≤|y|,所以−(|x|+|y|)≤x +y ≤|x|+|y|,即|x +y|≤|x|+|y|.所以 d(A,B)=∑|20i=1b i −a i |=∑|20i=1(b i −1)+(1−a i )| ≤∑(20i=1|b i −1|+|1−a i |)=∑|20i=1a i −1|+∑|20i=1b i −1|=26.上式等号成立的条件为a i =1,或b i =1,所以 d(A, B)≤26. 对于 A =(1, 1,…,1, 14),B =(14, 1, 1,…,1),有 A ,B ∈S 20, 且d(I, A)=d(I, B)=13,故d(A, B)=26. 综上,d(A, B)的最大值为26.。
2013北京西城二模数学(文)试题答案

北京市西城区2013年高三二模试卷高三数学(文科)参考答案及评分标准2013.5一、选择题:本大题共8小题,每小题5分,共40分.1. A ; 2.A ; 3.D ; 4.B ; 5.C ; 6.C ; 7.B ; 8.B .二、填空题:本大题共6小题,每小题5分,共30分.9.6-; 10.>; 11.3,2; 12.59; 13.(1,)+∞; 14.2,4. 注:11、14题第一空2分,第二空3分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.15.(本小题满分13分)(Ⅰ)解:设等比数列{}n a 的公比为q ,依题意 0q >. ………………1分因为 28a =,3448a a +=, 两式相除得260q q +-=, ………………3分解得2q =, 舍去3q =-. ………………4分所以214a a q==. ………………6分 所以数列{}n a 的通项公式为1112n n n a a q -+=⋅=. ………………7分(Ⅱ)解:由(Ⅰ)得 41log 2n n n b a +==. ………………9分因为 1211222n n n n b b +++-=-=, 所以数列{}n b 是首项为1,公差为12d =的等差数列. ………………11分所以21(1)324n n n n nS nb d -+=+=. ………………13分16.(本小题满分13分)(Ⅰ)解:由三角函数定义,得 1cos x =α,2cos()3x π=+α.2分因为 ,)62ππ∈(α,1cos 3=α,所以 sin ==α. ………………3分 所以211cos()cos 3226x π-=+==αα-α. ………………5分(Ⅱ)解:依题意得 1sin y =α,2sin()3y π=+α. 所以111111cos sin sin 2224S x y ==⋅=ααα, ………………7分 2221112||[cos()]sin()sin(2)223343S x y πππ==-+⋅+=-+ααα. ……………9分依题意得 2sin 22sin(2)3π=-+αα, 整理得cos 20=α. ………………11分因为 62ππ<<α, 所以 23π<<πα, 所以22π=α, 即4π=α. ………………13分17.(本小题满分14分)(Ⅰ)解:由左视图可得 F 为AB 的中点,所以 △BFC 的面积为 12121=⋅⋅=S .………………1分 因为⊥PA 平面ABCD , ………………2分 所以四面体PBFC 的体积为 PA S V BFC BFC P ⋅=∆-31………………3分 322131=⋅⋅=. ………………4分(Ⅱ)证明:取PC 中点Q ,连结EQ ,FQ . ………………5分由正(主)视图可得 E 为PD 的中点,所以EQ ∥CD ,CD EQ 21=. ………………6分又因为AF ∥CD ,CD AF 21=, 所以AF ∥EQ ,EQ AF =. 所以四边形AFQE 为平行四边形,所以AE∥FQ . ………………8分因为 ⊄AE 平面PFC ,⊂FQ 平面PFC , 所以直线AE∥平面PFC . ………………9分(Ⅲ)证明:因为 ⊥PA 平面ABCD ,所以 CD PA ⊥.因为面ABCD 为正方形,所以 CD AD ⊥. 所以⊥CD 平面PAD . ………………11分因为 ⊂AE 平面PAD ,所以 AE CD ⊥.因为 AD PA =,E 为PD 中点,所以 PD AE ⊥. 所以⊥AE 平面P. ………………12分 因为AE∥FQ,所以⊥FQ 平面P C .………………13分 因为⊂FQ 平面PFC, 所以 平面PFC ⊥平面P C D . ………………14分18.(本小题满分13分)(Ⅰ)解:()f x 的定义域为R , 且 2()242f x x x a '=-+-. ………………2分当2a =时,1(1)3f =-,(1)2f '=-, 所以曲线()y f x =在点(1,(1))f 处的切线方程为 12(1)3y x +=--, 即6350x y +-=. ………………4分(Ⅱ)解:方程()f x '=的判别式80a =>∆, ………………5分令()0f x '=,得11x =,或212x =+. ………………6分 ()f x 和()f x '的情况如下:故()f x 的单调增区间为(,1-∞,(1)+∞;单调减区间为(1.………………9分① 当02a <≤时,22x ≤,此时()f x 在区间(2,3)上单调递增, 所以()f x 在区间[2上的最小值是7(2)23f a =-. ………………10分 ② 当28a <<时,1223x x <<<,此时()f x 在区间2(2,)x 上单调递减,在区间2(,3)x 上单调递增,所以()f x 在区间[2上的最小值是25()33f x a =--. ………………12分 ③ 当8a ≥时,1223x x <<≤,此时()f x 在区间(2,3)上单调递减, 所以()f x 在区间[2上的最小值是(3)73f a =-. ………………13分综上,当02a <≤时,()f x 在区间[2,3]上的最小值是723a -;当28a <<时,()f x 在区间[2,3]上的最小值是53a -8a ≥时,()f x 在区间[2,3]上的最小值是73a -.19.(本小题满分14分)(Ⅰ)解:依题意,M 是线段AP 的中点,因为(1,0)A -,9(,55P ,所以 点M 的坐标为2(,55. ………………2分由点M 在椭圆C 上, 所以41212525m+=, ………………4分解得47m =. ………………6分 (Ⅱ)解:设00(,)M x y ,则 2201y x m+=,且011x -<<. ① ………………7分 因为 M 是线段AP 的中点, 所以00(21,2)P x y +. ………………8分因为 OP OM ⊥,所以 2000(21)20x x y ++=.② ………………9分由 ①,② 消去0y ,整理得 20020222x x m x +=-. ………………11分所以0011122(2)82m x x =+≤++-+, ………………13分 当且仅当02x =-时,上式等号成立. 所以m的取值范围是1(0,24-. ………………14分20.(本小题满分13分) (Ⅰ)解:当6n =时,排列3,5,1的生成列为0,1,2-.………………3分 (Ⅱ)证明:设12,,,n a a a 的生成列是12,,,n b b b ;12,,,n a a a ''' 的生成列是与12,,,n b b b ''' . 从右往左数,设排列12,,,n a a a 与12,,,n a a a ''' 第一个不同的项为k a 与k a ',即:n na a '=,11n n a a --'=, ,11k k a a ++'=,k k a a '≠. 显然 n nb b '=,11n n b b --'=, ,11k k b b ++'=,下面证明:k k b b '≠. ………………5分由满意指数的定义知,i a 的满意指数为排列12,,,n a a a 中前1i -项中比i a 小的项的个数减去比i a 大的项的个数.由于排列12,,,n a a a 的前k 项各不相同,设这k 项中有l 项比k a 小,则有1k l --项比k a 大,从而(1)21k b l k l l k =---=-+.同理,设排列12,,,n a a a ''' 中有l '项比k a '小,则有1k l '--项比k a '大,从而21kb l k ''=-+. 因为 12,,,k a a a 与12,,,k a a a ''' 是k 个不同数的两个不同排列,且k k a a '≠, 所以 l l '≠, 从而 k kb b '≠. 所以排列12,,,na a a 和12,,,n a a a ''' 的生成列也不同. ………………8分(Ⅲ)证明:设排列12,,,n a a a 的生成列为12,,,n b b b ,且k a 为12,,,n a a a 中从左至右第一个满意指数为负数的项,所以1210,0,,0,1k k b b b b -≥≥≥≤- . ………………9分依题意进行操作,排列12,,,n a a a 变为排列1211,,,,,,k k k n a a a a a a -+ ,设该排列的生成列为12,,,n b b b ''' . ………………10分所以 1212()()n n b b b b b b '''+++-+++ 121121[()()()][()()()]k k k k k k k k g a a g a a g a a g a a g a a g a a --=-+-++---+-++- 1212[()()()]k k k k g a a g a a g a a-=--+-++- 22k b =-≥.所以,新排列的各项满意指数之和比原排列的各项满意指数之和至少增加2.………………13分。
2013北京二模海淀 西城文科数学合集

海淀区高三年级第二学期期末练习数 学 (文科) 2013.5本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上 作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.集合{}|(1)(2)0A x x x =-+≤,B ={}0x x <,则A B = A .(,0)-∞ B .(,1]-∞ C .[1,2] D .[1,)+∞2.已知1211ln ,sin ,222a b c -===,则,,a b c 的大小关系为A.a b c <<B.a c b <<C.b a c <<D.b c a <<3.如图,在边长为a 的正方形内有不规则图形Ω. 向正方形内随机撒豆子, 若撒在图形Ω内和正方形内的豆子数分别为,m n ,则图形Ω面积的估计值为A.ma nB.na mC. 2ma nD. 2na m4.某空间几何体的三视图如右图所示,则该几何体的表面积为 A.180 B.240 C. 276 D.3005.下列函数中,为偶函数且有最小值的是 A.2()f x x x =+ B.()|ln |f x x = C.()sin f x x x = D.()e e x x f x -=+6.在四边形ABCD 中,“R λ∃∈,,AB DC AD BC λλ==”是“四边形ABCD 为平行四边 形”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件7.双曲线C 的左右焦点分别为12,F F ,且2F 恰为抛物线24y x =的焦点,设双曲线C 与该抛物线的一个交点为A ,若12AF F ∆是以1AF 为底边的等腰三角形,则双曲线C 的离心率为11D.2俯视图8.若数列{}n a 满足:存在正整数T ,对于任意正整数n 都有n T n a a +=成立,则称数列{}n a 为周期数列,周期为T . 已知数列{}n a 满足1(0)a m m =>,11, 1=1, 0 1.n n n n na a a a a +->⎧⎪⎨<≤⎪⎩,则下列结论中错误..的是 A.若45m =,则53a = B.若32a =,则m 可以取3个不同的值 C.若m ={}n a 是周期为3的数列 D.m Q ∃∈且2m ≥,使得数列{}n a 是周期数列二、填空题:本大题共6小题,每小题5分,共30分.9.复数2i___.1i=- 10.甲、乙两名运动员在8场篮球比赛中得分的数据统计如右图, 则甲乙两人发挥较为稳定的是_____.11.已知数列{}n a 是等比数列,且134a a ⋅=,48a =,则5a 的值为____. 12.直线1y x =+被圆22230x x y -+-=所截得的弦长为____.13.已知函数π()sin(2)(01)6f x x ωω=-<<的图象经过点π(,0)6,则ω=_____,()f x 在区间[0,π]上的单调递增区间为_____.14.设变量x ,y 满足约束条件10,40,1(1),y x y y k x -≥⎧⎪+-≤⎨⎪-≤-⎩其中,0R k k ∈>.(I )当1k =时,2yx 的最大值为______; (II )若2yx的最大值为1,则实数k 的取值范围是_____.三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15.(本小题满分13分)已知等差数列{}n a 的前n 项和为n S . (I) 若1101,100a S ==,求{}n a 的通项公式; (Ⅱ)若26n S n n =-,解关于n 的不等式2n n S a n +>.16.(本小题满分13分)已知点D 为ABC ∆的边BC 上一点,且2BD DC =,75,30ADB ACD ∠=∠=,AD =(I )求CD 的长; (II )求ABC ∆的面积.17.(本小题满分14分)如图1,在直角梯形ABCD 中,//AD BC ,90ADC ∠=︒,BA BC =. 把BAC ∆沿AC 折起到PAC ∆的位置,使得P 点在平面ADC 上的正投影O 恰好落在线段AC 上,如图2所示. 点,E F 分别为棱,PC CD 的中点. (I )求证:平面//OEF 平面APD ; (Ⅱ)求证:CD ⊥平面POF ;(Ⅲ) 在棱PC 上是否存在一点M ,使得M 到点,,,P O C F 四点距离相等?请说明理由.图2CDBA图118.(本小题满分13分)已知函数()ln ,()(0)af x xg x a x==->.(I )当1a =时, 若曲线()y f x =在点00(,())M x f x 处的切线与曲线()y g x =在点00(,())P x g x 处的切线平行,求实数0x 的值;(II )若(0,e]x ∀∈,都有3()()2f xg x ≥+,求实数a 的取值范围.19. (本小题满分14分)已知椭圆:C 22221(0)x y a b a b+=>>的四个顶点恰好是边长为2,一内角为60 的菱形的四个顶点.(I )求椭圆C 的方程;(II )若直线y kx =交椭圆C 于,A B 两点,且在直线:30l x y +-=上存在点P ,使得PAB ∆为等边三角形,求k 的值.20.(本小题满分13分)设A 是由m n ⨯个整数组成的m 行n 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”. (Ⅰ) 数表A 如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表(写出一种方法即可);(Ⅱ) 数表A 如表2所示,若经过任意..一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a 的值;表2(Ⅲ) 对由m n ⨯个整数组成的m 行n 列的任意一个数表A ,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由.22221212a a a a a a a a ------海淀区高三年级第二学期期末练习 数 学 (文科)参考答案及评分标准2013.5说明: 合理答案均可酌情给分,但不得超过原题分数. 一、选择题(本大题共8小题,每小题5分,共40分)二、填空题(本大题共6小题,每小题5分, 有两空的小题,第一空3分,第二空2分, 共30分)注:11题少写一个,扣两分,错写不给分 13题开闭区间都对三、解答题(本大题共6小题,共80分)15.(本小题满分13分) 解:(I )设{}n a 的公差为d因为11a =,1910101002a a S +=⨯=……………………2分 所以1101,19a a ==……………………4分 所以2d =所以 21n a n =-……………………6分(II )因为26n S n n =-当2n ≥时,21(1)6(1)n S n n -=---所以27n a n =-,2n ≥……………………9分又1n =时,11527a S ==-=-所以 27n a n =-……………………10分所以247n n S a n n +=--所以2472n n n -->,即2670n n --> 所以7n >或1n <-,所以7n >,N n ∈……………………13分16. 解:(I )因为75ADB ∠= ,所以45DAC ∠=在ACD ∆中,AD = 根据正弦定理有sin45sin30CD AD=……………………4分 所以2CD =……………………6分 (II )所以4BD =……………………7分 又在ABD ∆中,75ADB ∠= ,sin 75sin(4530)=+=……………………9分所以1sin7512ADB S AD BD ∆=⋅⋅= ……………………12分所以32ABC ABD S S ∆∆==……………………13分同理,根据根据正弦定理有sin105sin30AC AD=而 sin105sin(4560)=+= ……………………8分所以1AC =……………………10分 又4BD =,6BC =……………………11分所以1sin302ABC S AC BC ∆=⋅⋅=13分17.解:(I )因为点P 在平面ADC 上的正投影O 恰好落在线段AC 上 所以PO ⊥平面ABC ,所以PO ⊥AC …………………2分因为AB BC =,所以O 是AC 中点, …………………3分所以//OE PA …………………4分同理//OF AD又,OE OF O PA AD A ==所以平面//OEF 平面PDA …………………6分 (II )因为//OF AD ,AD CD ⊥ 所以OF CD ⊥…………………7分 又PO ⊥平面ADC ,CD ⊂平面ADC 所以PO ⊥CD …………………8分 又OF PO O =所以CD ⊥平面POF …………………10分(III)存在,事实上记点E 为M 即可 …………………11分 因为CD ⊥平面POF ,PF ⊂平面POF 所以CD PF ⊥又E 为PC 中点,所以12EF PC =…………………12分 同理,在直角三角形POC 中,12EP EC OE PC ===, …………………13分所以点E 到四个点,,,P O C F 的距离相等 …………………14分18.解:(I )当因为1a =, 211'(),()f x g x x x==…………………2分 若函数()f x 在点00(,())M x f x 处的切线与函数()g x 在点00(,())P x g x处的切线平行, 所以20011x x =,解得01x = 此时()f x 在点(1,0)M 处的切线为1y x =-()g x 在点(1,1)P - 处的切线为2y x =-所以01x =…………………4分(II )若(0,e]x ∀∈,都有3()()2f xg x ≥+ 记33()()()ln 22a F x f x g x x x =--=+-, 只要()F x 在(0,e]上的最小值大于等于0221'()a x aF x x x x-=-=…………………6分 则'(),()F x F x 随x 的变化情况如下表:…………………8分当e a ≥时,函数()F x 在(0,e)上单调递减,(e)F 为最小值所以3(e)102a F e =+-≥,得e2a ≥ 所以e a ≥…………………10分当e a <时,函数()F x 在(0,)a 上单调递减,在(,e)a 上单调递增 ,()F a 为最小值,所以3()ln 02a F a a a =+-≥,得a ≥e a ≤<………………12分 a ≤………………13分19.解:(I)因为椭圆:C 22221(0)x y a b a b+=>>的四个顶点恰好是一边长为2,一内角为60 的菱形的四个顶点,所以1a b =,椭圆C 的方程为2213x y +=………………4分(II)设11(,),A x y 则11(,),B x y --当直线AB 的斜率为0时,AB 的垂直平分线就是y 轴,y 轴与直线:30l x y +-=的交点为(0,3)P ,又因为|||3AB PO ==,所以60PAO ∠= ,所以PAB ∆是等边三角形,所以直线AB 的方程为0y =………………6分 当直线AB 的斜率存在且不为0时,设AB 的方程为y kx =所以2213x y y kx ⎧+=⎪⎨⎪=⎩,化简得22(31)3k x +=所以1||x =||AO ==8分 设AB 的垂直平分线为1y x k=-,它与直线:30l x y +-=的交点记为00(,)P x y所以31y x y x k =-+⎧⎪⎨=-⎪⎩,解得003131k x k y k ⎧=⎪⎪-⎨-⎪=⎪-⎩,则||PO =10分 因为PAB ∆为等边三角形,所以应有|||PO AO =代入得到=0k =(舍),1k =-……………13分 此时直线AB 的方程为y x =-综上,直线AB 的方程为y x =-或0y =………………14分20.解:(I )法1:42123712371237210121012101-−−−−−→−−−−−→----改变第列改变第行法2:14123712371237210121012101----−−−−−→−−−−−→--改变第列改变第列(写出一种即可)…………………3分(II) 每一列所有数之和分别为2,0,2-,0,每一行所有数之和分别为1-,1; ①如果操作第三列,则22221212a a a a a a a a----- 则第一行之和为21a -,第二行之和为52a -,210520a a -≥⎧⎨-≥⎩,解得1,2a a ==. …………………6分 ②如果操作第一行22221212a a a a a a a a -----则每一列之和分别为22a -,222a -,22a -,22a 解得1a =…………………9分 综上1a =…………………10分(III) 证明:按要求对某行(或某列)操作一次时,则该行的行和(或该列的列和) 由负整数变为正整数,都会引起该行的行和(或该列的列和)增大,从而也就使得 数阵中mn 个数之和增加,且增加的幅度大于等于1(1)2--=,但是每次操作都只 是改变数表中某行(或某列)各数的符号,而不改变其绝对值,显然,数表中mn 个数之和必然小于等于11||mnij i j a ==∑∑,可见其增加的趋势必在有限次之后终止,终止之时必然所有的行和与所有的列和均为非负整数,故结论成立…………………13分2013北京西城区高三二模数学文科一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 设集合{2,3,4}A =,{2,4,6}B =,若x A ∈且x B ∉,则x 等于A .2B .3 √C .4D .62. 已知命题:,cos 1p x x ∀∈≤R ,则A . :,cos 1p x x ⌝∃∈≥RB .:,cos 1p x x ⌝∀∈≥RC . :,cos 1p x x ⌝∃∈>R √D .:,cos 1p x x ⌝∀∈>R3. 设变量,x y 满足约束条件3,1,x y x y +≥⎧⎨-≥-⎩则目标函数2z y x =+的最小值为( )A .1B .2C .3D .4√4. “ln 1x >”是“1x >”的A .充分不必要条件 √B .必要不充分条件C .充要条件D .既不充分也不必要条件5. 如图,三棱柱111ABC A B C -的侧棱长和底面边长均为2,且侧棱1AA ⊥底面ABC ,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为AB. √ C. D .46. 在数列{}n a 中,11a =,1n n a a n -=+,2n ≥.为计算这个数列前10项的和,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是A .8i ≥B .9i ≥C .10i ≥ √D .11i ≥正(主)视图A BCA 1B 1C 17. 等差数列{}n a 的前n 项和为n S ,若70a >,80a <,则下列结论正确的是A .78S S <B .1516S S <C .130S > √D .150S >8. 给出函数()f x 的一条性质:“存在常数M ,使得()f x M x ≤对于定义域中的一切实数x 均成立.”则下列函数中具有这条性质的函数是 A .1y x=B .2y x =C .1y x =+D .sin y x x = √二、填空题:本大题共6小题,每小题5分,共30分. 9. i 是虚数单位,i2i=+_____. 10. 函数sin cos y x x =+的最小正周期是_________,最大值是________.11. 在抛物线22y px =上,横坐标为2的点到抛物线焦点的距离为3,则p =________. 12. 圆心在x 轴上,且与直线y x =切于(1,1)点的圆的方程为________. 13. 设,,a b c 为单位向量,,a b 的夹角为60,则⋅+⋅a c b c 的最大值为________.14. 我们可以利用数列{}n a 的递推公式2,,n n n n a a n ⎧⎪=⎨⎪⎩为奇数时,为偶数时(n ∈*N )求出这个数列各项的值,使得这个数列中的每一项都是奇数.则2425a a +=_________;研究发现,该数列中的奇数都会重复出现,那么第8个5是该数列的第_____项.三、解答题:本大题共6小题,共80分. 解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分12分)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,3cos 4A =,2C A =. (Ⅰ)求cos C 的值; (Ⅱ)若24ac =,求,a c 的值.16.(本小题满分13分)在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本,这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.在选取的40名学生中,(Ⅰ)求成绩在区间[80,90)内的学生人数; (Ⅱ)从成绩大于等于80分的学生中随机选2名学生,求至少有1名学生成绩在区间[90,100]内的概率.17.(本小题满分13分)如图,已知四棱柱1111ABCD A B C D -的底面是菱形,侧棱1BB ⊥底面ABCD ,E 是侧棱1CC 的中点.(Ⅰ)求证:AC ⊥平面11BDD B ; (Ⅱ)求证://AC 平面1B DE .18.(本小题满分14分)已知椭圆2222:1(0)x y C a b a b +=>>椭圆C 上任意一点到椭圆两个焦点的距离之和为6.(Ⅰ)求椭圆C 的方程;(Ⅱ)设直线:2l y kx =-与椭圆C 交与,A B 两点,点(0,1)P ,且PA PB =,求直线l 的方程.0.010.000.040.02 ABDA 1B 1C 1D 1EC19.(本小题满分14分)设函数2()f x x a =-.(Ⅰ)求函数()()g x xf x =在区间[0,1]上的最小值;(Ⅱ)当0a >时,记曲线()y f x =在点11(,())P x f x (1x >l ,l 与x 轴交于点2(,0)A x ,求证:12x x >>20.(本小题满分14分)如果由数列{}n a 生成的数列{}n b 满足对任意的n ∈*N 均有1n n b b +<,其中1n n n b a a +=-,则称数列{}n a 为“Z 数列”.(Ⅰ)在数列{}n a 中,已知2n a n =-,试判断数列{}n a 是否为“Z 数列”; (Ⅱ)若数列{}n a 是“Z 数列”,10a =,n b n =-,求n a ;(Ⅲ)若数列{}n a 是“Z 数列”,设,,s t m ∈*N ,且s t <,求证:t m s m t s a a a a ++-<-.北京市西城区2010年抽样测试参考答案 高三数学试卷(文科) 2010.5一、选择题:本大题共8小题,每小题5分,共40分.题号 1 2 3 4 5 6 7 8 答案BCDABCCD二、填空题:本大题共6小题,每小题5分,共30分.9. 12i 55+ 10. 2π11. 2 12. 22(2)2x y -+=13.14. 28,640注:两空的题目,第一个空2分,第二个空3分.三、解答题:(本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.)15、解:(Ⅰ)因为3cos 4A =, 所以2cos cos 22cos 1C A A ==- …………………3分2312()148=⨯-=. …………………5分(Ⅱ)在ABC ∆中,因为3cos 4A =,所以sin A = …………………7分因为1cos 8C =,所以sin C == …………………9分 根据正弦定理sin sin a cA C=, …………………10分 所以23a c =, 又24ac =,所以4,6a c ==. …………………12分16、解:(Ⅰ)因为各组的频率之和为1,所以成绩在区间[80,90)的频率为1(0.00520.0150.0200.045)100.1-⨯+++⨯=, …………………3分所以,40名学生中成绩在区间[80,90)的学生人数为400.14⨯=(人).…………………5分(Ⅱ)设A 表示事件“在成绩大于等于80分的学生中随机选两名学生,至少有一名学生成绩在区间[90,100]内”,由已知和(Ⅰ)的结果可知成绩在区间[80,90)内的学生有4人, 记这四个人分别为,,,a b c d ,成绩在区间[90,100]内的学生有2人, …………………7分 记这两个人分别为,e f , 则选取学生的所有可能结果为:(,),(,),(,),(,),(,),(,),(,),(,),(,),a b a c a d a e a f b c b d b e b f (,),(,),(,)c d c e c f ,(,),(,),(,)d e d f e f基本事件数为15, …………………9分 事件“至少一人成绩在区间[90,100]之间”的可能结果为:(,),(,),(,),(,),a e a f b e b f (,),(,),(,),(,),(,)c e c f d e d f e f ,基本事件数为9, …………………11分 所以93()155P A ==. …………………13分17、证明:(Ⅰ)因为ABCD 是菱形,所以AC BD ⊥,因为1BB ⊥底面ABCD ,所以1BB AC ⊥, …………3分 所以AC ⊥平面11BDD B . …………5分 (Ⅱ)设AC ,BD 交于点O ,取1B D 的中点F ,连接,OF EF ,则1//OF BB ,且112OF BB =,又E 是侧棱1CC 的中点,112EC CC =,11//BB CC ,11BB CC =,所以1//OF CC ,且112OF CC =, …………………7分所以四边形OCEF 为平行四边形,//OC EF , …………………9分A BDA 1B 1C 1D 1ECOF又AC ⊄平面1B DE ,EF ⊂平面1B DE , ………………11分 所以//AC 平面1B DE . ………………13分 18、解:(Ⅰ)由已知26a =,3c a =, …………………3分 解得3a =,c =所以2223b a c =-=, …………………4分所以椭圆C 的方程为22193x y +=. …………………5分 (Ⅱ)由221,932x y y kx ⎧+=⎪⎨⎪=-⎩得,22(13)1230k x kx +-+=, 直线与椭圆有两个不同的交点,所以2214412(13)0k k ∆=-+>, 解得219k >. …………………7分 设11(,)A x y ,22(,)B x y ,则1221213k x x k +=+,122313x x k=+, …………………8分 计算121222124()441313k y y k x x k k k +=+-=⋅-=-++,所以,,A B 中点坐标为2262(,)1313k E k k -++, …………………10分 因为PA PB =,所以PE AB ⊥,1PE AB k k ⋅=-,所以2221131613k k k k --+⋅=-+, …………………12分 解得1k =±, …………………13分经检验,符合题意,所以直线l 的方程为20x y --=或20x y ++=. …………………14分 19、(Ⅰ)解:3()g x x ax =-,2()3g x x a '=-, …………………2分当0a ≤时,()g x 为R 上的增函数,所以()g x 在区间[0,1]上的最小值为(0)0g =; …………………4分 当0a >时, ()g x '的变化情况如下表:所以,函数()g x 在(,-∞,)+∞上单调递增,在(上单调递减. …………………6分1<,即03a <<时,()g x 在区间[0,1]上的最小值为g = ……………7分1≥,即3a ≥时,()g x 在区间[0,1]上的最小值为(1)1g a =-. ……8分 综上,当0a ≤时,()g x 在区间[0,1]上的最小值为(0)0g =;当03a <<时,()g x 的最小值为;当3a ≥时,()g x 的最小值为1a -.(Ⅱ)证明:曲线()y f x =在点11(,())P x f x (1x )处的切线方程为2111()2()y x a x x x --=-,令0y =,得21212x ax x +=, …………………10分所以212112a x x x x --=,因为1x >21102a x x -<,21x x <. ………11分因为1x 1122x ax ≠,所以211211222x a x ax x x +==+> …………………13分所以12x x >> …………………14分20、解:(Ⅰ)因为2n a n =-,所以221(1)21n n n b a a n n n +=-=-++=--,n ∈*N , …………………2分 所以12(1)1212n n b b n n +-=-+-++=-,所以1n n b b +<,数列{}n a 是“Z 数列”. …………………4分(Ⅱ)因为n b n =-,所以2111a a b -==-,3222a a b -==-,…,11(1)n n n a a b n ---==--, 所以1(1)12(1)2n n na a n --=-----=- (2n ≥),…………………6分 所以(1)2n n na -=-(2n ≥), 又10a =,所以(1)2n n n a -=-(n ∈*N ). …………………8分(Ⅲ)因为 111()()s m s s m s m s s s m s a a a a a a b b +++-++--=-++-=++ ,111()()t m t t m t m t t t m t a a a a a a b b +++-++--=-++-=++ ,………………10分又,,s t m ∈*N ,且s t <,所以s i t i +<+,s i t i b b ++>,n ∈*N ,所以1122,,,s m t m s m t m s t b b b b b b +-+-+-+->>> , …………………12分 所以t m t s m s a a a a ++-<-,即t m s m t s a a a a ++-<-. …………………14分。
2013届北京市西城区高三期末数学文科试题(WORD精校版)

北京市西城区2012 — 2013学年度第一学期期末试卷高三数学(文科) 2013.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{|01}A x x =∈<<R ,{|(21)(1)0}B x x x =∈-+>R ,则A B = ( ) (A )1(0,)2(B )1(,1)2(C )1(,1)(0,)2-∞- (D )1(,1)(,1)2-∞-2.复数5i2i=+( ) (A )12i + (B )12i -+(C )12i --(D )12i -3.执行如图所示的程序框图,则输出S =( ) (A )2 (B )6 (C )15 (D )314.函数1()ln f x x x=-的零点个数为( ) (A )0 (B )1(C )2(D )35.某四棱锥的三视图如图所示,该四棱锥的体积是( ) (A )53 (B )23(C )533(D )2336.过点(2,0)M 作圆221x y +=的两条切线MA ,MB (A ,B 为切点),则MA MB ⋅=( ) (A )532(B )52(C )332(D )327.设等比数列{}n a 的公比为q ,前n 项和为n S .则“||2q =”是“627S S =”的( )(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件8.已知函数()f x 的定义域为R .若∃常数0c >,对x ∀∈R ,有()()f x c f x c +>-,则称函数()f x 具有性质P .给定下列三个函数:①()||f x x =; ②()sin f x x =; ③3()f x x x =-. 其中,具有性质P 的函数的序号是( ) (A )① (B )③(C )①②(D )②③第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9.已知向量(1,3)=a ,(,21)m m =-b .若向量a 与b 共线,则实数m =______.10.平行四边形ABCD 中,E 为CD 的中点.若在平行四边形ABCD 内部随机取一点M ,则点M 取自△ABE 内部的概率为______.11.双曲线2213645x y -=的渐近线方程为______;离心率为______.12.若函数2log ,0,()(),0x x f x g x x >⎧=⎨<⎩是奇函数,则(8)g -=______.13.已知函数π()sin()6f x x =+,其中π[,]3x a ∈-.当2a π=时,()f x 的值域是______;若()f x 的值域是1[,1]2-,则a 的取值范围是______.14.设函数2()65f x x x =-+,集合{(,)|()()0A a b f a f b =+≤,且()()0}f a f b -≥.在直角坐标系aOb 中,集合A 所表示的区域的面积为______.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分13分)在△ABC 中,内角,,A B C 的对边分别为,,a b c ,且cos2cos 0B B +=. (Ⅰ)求角B 的值;(Ⅱ)若7b =,5a c +=,求△ABC 的面积.16.(本小题满分13分)为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[4550),,第2组[5055),,第3组[5560),,第4组[6065),,第5组[6570],,得到如图所示的频率分布直方图.现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生做初检. (Ⅰ)求每组抽取的学生人数;(Ⅱ)若从6名学生中再次随机抽取2名学生进行复检,求这2名学生不在同一组的概率.17.(本小题满分14分)如图,直三棱柱111C B A ABC -中,BC AC ⊥,21===CC BC AC ,M ,N 分别为AC ,11C B 的中点. (Ⅰ)求线段MN 的长;(Ⅱ)求证:MN // 平面11A ABB ;(Ⅲ)线段1CC 上是否存在点Q ,使⊥B A 1平面MNQ ?说明理由.18.(本小题满分13分)已知函数2()xf x x b=+,其中b ∈R . (Ⅰ)若1x =-是)(x f 的一个极值点,求b 的值; (Ⅱ)求)(x f 的单调区间.19.(本小题满分14分)如图,A ,B 是椭圆22221x y a b+=(0)a b >>的两个顶点.||5AB =,直线AB 的斜率为12-. (Ⅰ)求椭圆的方程;(Ⅱ)设直线l 平行于AB ,与,x y 轴分别交于点,M N ,与椭圆相交于,C D .证明:△OCM的面积等于△ODN 的面积.20.(本小题满分13分)如图,设A 是由n n ⨯个实数组成的n 行n 列的数表,其中ij a (,1,2,3,,)i j n = 表示位于第i 行第j 列的实数,且{1,1}ij a ∈-.记(,)S n n 为所有这样的数表构成的集合.对于(,)A S n n ∈,记()i r A 为A 的第i 行各数之积,()j c A 为A 的第j 列各数之积.令11()()()n ni j i j l A r A c A ===+∑∑.(Ⅰ)对如下数表(4,4)A S ∈,求()l A 的值;(Ⅱ)证明:存在(,)A S n n ∈,使得()24l A n k =-,其中0,1,2,,k n = ; (Ⅲ)给定n 为奇数,对于所有的(,)A S n n ∈,证明:()0l A ≠.北京市西城区2012 — 2013学年度第一学期期末高三数学(文科)参考答案及评分标准2013.1一、选择题:本大题共8小题,每小题5分,共40分.1.B ; 2.A ; 3.C ; 4.B ; 5.C ; 6.D ; 7.A ; 8.B .二、填空题:本大题共6小题,每小题5分,共30分.9.1-; 10.12; 11.52y x =±,32; 12.3-; 13.1[,1]2-,[,]3ππ; 14.4π. 注:11、13题第一空2分,第二空3分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.15.(本小题满分13分)(Ⅰ)解:由已知得 22cos cos 10B B +-=, ………………2分即 (2cos 1)(cos 1)0B B -+=.解得 1cos 2B =,或cos 1B =-. ………………4分因为 0πB <<,故舍去cos 1B =-. ………………5分所以 π3B =. ………………6分(Ⅱ)解:由余弦定理得 2222cos b a c ac B =+-. ………………8分将π3B =,7b =代入上式,整理得2()37a c ac +-=. 因为 5a c +=,所以 6ac =. ………………11分所以 △ABC 的面积133sin 22S ac B ==. ………………13分16.(本小题满分13分)(Ⅰ)解:由频率分布直方图知,第3,4,5组的学生人数之比为3:2:1. …………2分所以,每组抽取的人数分别为: 第3组:3636⨯=;第4组:2626⨯=;第5组:1616⨯=. 所以从3,4,5组应依次抽取3名学生,2名学生,1名学生. ………………5分(Ⅱ)解:记第3组的3位同学为1A ,2A ,3A ;第4组的2位同学为1B ,2B ;第5组的1位同学为C . ………………6分则从6位同学中随机抽取2位同学所有可能的情形为:121311121232122231(,),(,),(,),(,),(,),(,),(,),(,),(,),(,),A A A A AB A B AC A A A B A B A C A B 3231212(,),(,),(,),(,),(,)A B A C B B B C B C ,共15种可能. ………………10分其中,111212122231323(,),(,),(,),(,),(,),(,),(,),(,),(,),A B A B A C A B A B A C A B A B A C12(,),(,)B C B C 这11种情形符合2名学生不在同一组的要求. (12)分故所求概率为1115P =. ………………13分17.(本小题满分14分)(Ⅰ)证明:连接CN .因为 111C B A ABC -是直三棱柱,所以 ⊥1CC 平面ABC , ………………1分 所以 1AC CC ⊥. ………………2分因为 BC AC ⊥, 所以 ⊥AC 平面11BCC B . ………………3分因为 1=MC ,22115CN CC C N =+=,所以 6=MN . ………………4分(Ⅱ)证明:取AB 中点D ,连接DM ,1DB . ………………5分在△ABC 中,因为 M 为AC 中点,所以BC DM //,BC DM 21=. 在矩形11B BCC 中,因为 N 为11C B 中点,所以BC N B //1,BC N B 211=.所以 N B DM 1//,N B DM 1=. 所以 四边形N MDB 1为平行四边形,所以 1//DB MN . ………………7分因为 ⊄MN 平面11A ABB ,⊂1DB 平面11A ABB , ………………8分所以 MN // 平面11A ABB . ………………9分(Ⅲ)解:线段1CC 上存在点Q ,且Q 为1CC 中点时,有⊥B A 1平面MNQ . ………11分证明如下:连接1BC .在正方形C C BB 11中易证 1BC QN ⊥.又⊥11C A 平面C C BB 11,所以 QN C A ⊥11,从而⊥NQ 平面11BC A .…………12分所以 1A B QN ⊥. ………………13分同理可得 1A B MQ ⊥,所以⊥B A 1平面MNQ .故线段1CC 上存在点Q ,使得⊥B A 1平面MNQ . ………………14分18.(本小题满分13分)(Ⅰ)解:222()()b x f x x b -'=+. (2)分依题意,令(1)0f '-=,得 1b =. ………………4分经检验,1b =时符合题意. ………………5分(Ⅱ)解:① 当0b =时,1()f x x=. 故()f x 的单调减区间为(,0)-∞,(0,)+∞;无单调增区间. ………………6分② 当0b >时,222()()b x f x x b -'=+.令()0f x '=,得1x b =,2x b =-. (8)分()f x 和()f x '的情况如下:x(,)b -∞-b -(,)b b -b(,)b +∞()f x ' -+-()f x↘↗↘故()f x 的单调减区间为(,)b -∞-,(,)b +∞;单调增区间为(,)b b -.………………11分③ 当0b <时,()f x 的定义域为{|}D x x b =∈≠±-R .因为222()0()b x f x x b -'=<+在D 上恒成立,故()f x 的单调减区间为(,)b -∞--,(,)b b ---,(,)b -+∞;无单调增区间.………………13分19.(本小题满分14分)(Ⅰ)解:依题意,得 221,2 5.b a a b ⎧=⎪⎨⎪+=⎩ (2)分解得 2a =,1b =. ………………3分所以 椭圆的方程为2214x y +=. (4)分(Ⅱ)证明:由于l //AB ,设直线l 的方程为12y x m =-+,将其代入2214x y +=,消去y , 整理得2224440x mx m -+-=. ………………6分设11(,)C x y ,22(,)D x y .所以 22122121632(1)0,2,2 2.m m x x m x x m ⎧∆=-->⎪+=⎨⎪=-⎩ ………………8分证法一:记△OCM 的面积是1S ,△ODN 的面积是2S . 由(2,0)M m ,(0,)N m , 则12S S =⇔1211|2|||||||22m y m x ⨯⨯=⨯⨯⇔12|2|||y x =. ………………10分因为 122x x m +=, 所以 11121|2||2()||2|||2y x m x m x =⨯-+=-+=, ………………13分从而12S S =. ………………14分证法二:记△OCM 的面积是1S ,△ODN 的面积是2S .则12S S =⇔||||MC ND =⇔线段,CD MN 的中点重合. ………………10分因为 122x x m +=,所以122x x m +=,1212112222y y x x m m ++=-⋅+=. 故线段CD 的中点为1(,)2m m .因为 (2,0)M m ,(0,)N m , 所以 线段MN 的中点坐标亦为1(,)2m m . ………………13分从而12S S =. ………………14分20.(本小题满分13分)(Ⅰ)解:134()()()1r A r A r A ===,2()1r A =-;124()()()1c A c A c A ===-,3()1c A =, 所以4411()()()0i ji j l A r A cA ===+=∑∑. (3)分(Ⅱ)证明:(ⅰ)对数表0A :1ij a =(,1,2,3,,)i j n = ,显然0()2l A n =.将数表0A 中的11a 由1变为1-,得到数表1A ,显然1()24l A n =-. 将数表1A 中的22a 由1变为1-,得到数表2A ,显然2()28l A n =-. 依此类推,将数表1k A -中的kk a 由1变为1-,得到数表k A . 即数表k A 满足:11221(1)kk a a a k n ====-≤≤ ,其余1ij a =. 所以 12()()()1k r A r A r A ====- ,12()()()1k c A c A c A ====- .所以 ()2[(1)()]24k l A k n k n k =-⨯+-=-,其中0,1,2,,k n = .……………7分【注:数表k A 不唯一】 (Ⅲ)证明:用反证法.假设存在(,)A S n n ∈,其中n 为奇数,使得()0l A =. 因为(){1,1}i r A ∈-,(){1,1}j c A ∈- (1,1)i n j n ≤≤≤≤,所以1()r A ,2()r A , ,()n r A ,1()c A ,2()c A , ,()n c A 这2n 个数中有n 个1,n 个1-.令1212()()()()()()n n M r A r A r A c A c A c A =⋅⋅⋅⋅⋅⋅⋅ .一方面,由于这2n 个数中有n 个1,n 个1-,从而(1)1nM =-=-. ① 另一方面,12()()()n r A r A r A ⋅⋅⋅ 表示数表中所有元素之积(记这2n 个实数之积为m );12()()()n c A c A c A ⋅⋅⋅ 也表示m , 从而21M m ==. ②①、②相互矛盾,从而不存在(,)A S n n ∈,使得()0l A =.即n 为奇数时,必有()0l A ≠. ………………13分。
北京市西城区2013年高三一模试卷数学文科(含答案)
高三数学(文科)一、选择题1.已知全集{|||5}U x x =∈<Z ,集合{2,1,3,4}A =-,{0,2,4}B =,那么U A B =ð(A ){2,1,4}- (B ) {2,1,3}-(C ){0,2}(D ){2,1,3,4}-2.复数1ii-+= (A )1i +(B )1i -+(C )1i --(D )1i -3.执行如图所示的程序框图.若输出y = 角=θ (A )π6 (B )π6-(C )π3(D )π3-4.设等比数列{}n a 的公比为q ,前n 项和为n S ,且10a >.若232S a >,则q 的取值范围是(A )1(1,0)(0,)2- (B )1(,0)(0,1)2- (C )1(,1)(,)2-∞-+∞(D )1(,)(1,)2-∞-+∞5.某正三棱柱的三视图如图所示,其中正(主) 视图是边长为2的正方形,该正三棱柱的表 面积是(A )6(B)12(C )12+(D )24+6.设实数x ,y 满足条件 10,10,20,x x y x y +≥⎧⎪-+≥⎨⎪+-≤⎩则4y x -的最大值是(A )4-(B )12-(C )4 (D )77.已知函数2()f x x bx c =++,则“0c <”是“0x ∃∈R ,使0()0f x <”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件8.如图,正方体1111ABCD A B C D -中,E 是棱11B C 的中点,动点P 在底面ABCD 内,且11PA A E =,则点P 运动形成的图形是(A )线段 (B )圆弧(C )椭圆的一部分 (D )抛物线的一部分二、填空题9.已知向量(1,0)=i ,(0,1)=j .若向量+λi j 与+λi j 垂直,则实数=λ______.10.已知函数2log ,0,()2,0,x x x f x x >⎧=⎨<⎩ 则1()(2)4f f +-=______.11.抛物线22y x =的准线方程是______;该抛物线的焦点为F ,点00(,)M x y 在此抛物线上,且52MF =,则0x =______. 12.某厂对一批元件进行抽样检测.经统计,这批元件的长度数据 (单位:mm )全部介于93至105之间.将长度数据以2为组距分成以下6组:[9395),, [9597),,[9799),,[99101),,[101103),,[103,105],得到如图所示的频率分布直方图.若长度在[97,103)内的元件为合格品,根据频率分布直 方图,估计这批产品的合格率是_____.13.在△ABC 中,内角A ,B ,C 的对边边长分别为a ,b ,c ,且cos 3cos 4A bB a ==.若10c =,则△ABC 的面积是______.14.已知数列{}n a 的各项均为正整数,其前n 项和为n S .若1, ,231, ,nn n n n a a a a a +⎧⎪=⎨⎪+⎩是偶数是奇数且329S =,则1a =______;3n S =______.三、解答题15.已知函数()sin cos f x x a x =+的一个零点是3π4. (Ⅰ)求实数a 的值;(Ⅱ)设22()[()]2sin g x f x x =-,求()g x 的单调递增区间.16.在如图所示的几何体中,面CDEF 为正方形,面ABCD 为等腰梯形,AB //CD ,AC =,22AB BC ==,AC FB ⊥.(Ⅰ)求证:⊥AC 平面FBC ; (Ⅱ)求四面体FBCD 的体积;(Ⅲ)线段AC 上是否存在点M ,使EA //平面FDM ? 证明你的结论.17.某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过1小时收费6元, 超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过4小时.(Ⅰ)若甲停车1小时以上且不超过2小时的概率为31,停车付费多于14元的概率为125,求甲 停车付费恰为6元的概率;(Ⅱ)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为36元的概率.18.已知函数()e xf x ax =+,()lng x ax x =-,其中0a ≤. (Ⅰ)求)(x f 的极值;(Ⅱ)若存在区间M ,使)(x f 和()g x 在区间M 上具有相同的单调性,求a 的取值范围.19.如图,已知椭圆22143x y +=的左焦点为F ,过点F 的直线交椭圆于,A B 两点,线段AB 的中点为G ,AB 的中垂线与x 轴和y 轴分别交于,D E 两点. (Ⅰ)若点G 的横坐标为14-,求直线AB 的斜率; (Ⅱ)记△GFD 的面积为1S ,△OED (O 为原点)的面积为2S .试问:是否存在直线AB ,使得12S S =?说明理由.一、选择题:本大题共8小题,每小题5分,共40分.1. B ; 2.A ; 3.D ; 4.B ; 5.C ; 6.C ; 7.A ; 8.B . 二、填空题:本大题共6小题,每小题5分,共30分. 9.0; 10.74-; 11.12x =-,2; 12.80%; 13.24; 14.5,722n +. 注:11、14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分. 15.(Ⅰ)解:依题意,得3π()04f =, ………………1分即 3π3πsincos 04422a +=-=, ………………3分 解得 1a =. ………………5分 (Ⅱ)解:由(Ⅰ)得 ()sin cos f x x x =+. ………………6分22()[()]2sin g x f x x =-22(sin cos )2sin x x x =+- s i n 2c o s 2xx =+ ………………8分π)4x =+. ………………10分由 πππ2π22π242k x k -≤+≤+,得 3ππππ88k x k -≤≤+,k ∈Z . ………………12分 所以 ()g x 的单调递增区间为3ππ[π,π]88k k -+,k ∈Z . ………………13分 16.(Ⅰ)证明:在△ABC 中,因为 AC =2AB =,1BC =,所以 BC AC ⊥. ………………2分 又因为 AC FB ⊥,所以 ⊥AC 平面FBC . ………………4分 (Ⅱ)解:因为⊥AC 平面FBC ,所以FC AC ⊥.因为FC CD ⊥,所以⊥FC 平面ABCD . ………………6分 在等腰梯形ABCD 中可得 1==DC CB ,所以1=FC .所以△BCD 的面积为 43=S . ………………7分所以四面体FBCD 的体积为:1312F BCD V S FC -=⋅=………………9分 (Ⅲ)解:线段AC 上存在点M ,且M 为AC 中点时,有EA // 平面FDM ,证明如下:………………10分连结CE ,与DF 交于点N ,连接MN .因为 CDEF 为正方形,所以N 为CE 中点. ………………11分 所以 EA //MN . ………………12分 因为 ⊂MN 平面FDM ,⊄EA 平面FDM , ………………13分 所以 EA //平面FDM .所以线段AC 上存在点M ,使得EA //平面FDM 成立. ………………14分 17.(Ⅰ)解:设“甲临时停车付费恰为6元”为事件A , ………………1分 则 41)12531(1)(=+-=A P . 所以甲临时停车付费恰为6元的概率是41. ………………4分 (Ⅱ)解:设甲停车付费a 元,乙停车付费b 元,其中,6,14,22,30a b =. ………………6分则甲、乙二人的停车费用构成的基本事件空间为:(6,6),(6,14),(6,22),(6,30),(14,6),(14,14),(14,22),(14,30),(22,6),(22,14),(22,22), (22,30),(30,6),(30,14),(30,22),(30,30),共16种情形. ………………10分其中,(6,30),(14,22),(22,14),(30,6)这4种情形符合题意. ………………12分 故“甲、乙二人停车付费之和为36元”的概率为41164P ==. ………………13分 18.(Ⅰ)解:()f x 的定义域为R , 且 ()e xf x a '=+. ………………2分① 当0a =时,()e xf x =,故()f x 在R 上单调递增.从而)(x f 没有极大值,也没有极小值. ………………4分② 当0a <时,令()0f x '=,得ln()x a =-.()f x 和()f x '的情况如下:故()f x 的单调减区间为(,ln())a -∞-;单调增区间为(ln(),)a -+∞.从而)(x f 的极小值为(ln())ln()f a a a a -=-+-;没有极大值. ………………6分 (Ⅱ)解:()g x 的定义域为(0,)+∞,且 11()ax g x a x x-'=-=. ………………8分 ③ 当0a =时,()f x 在R 上单调递增,()g x 在(0,)+∞上单调递减,不合题意.………………9分 ④ 当0a <时,()0g x '<,()g x 在(0,)+∞上单调递减.当10a -≤<时,ln()0a -≤,此时()f x 在(ln(),)a -+∞上单调递增,由于()g x 在(0,)+∞上单调递减,不合题意. ………………11分当1a <-时,ln()0a ->,此时()f x 在(,ln())a -∞-上单调递减,由于()f x 在(0,)+∞上单调递减,符合题意.综上,a 的取值范围是(,1)-∞-. ………………13分 19.(Ⅰ)解:依题意,直线AB 的斜率存在,设其方程为(1)y k x =+. ………………1分将其代入22143x y +=,整理得 2222(43)84120k x k x k +++-=. ………………3分 设11(,)A x y ,22(,)B x y ,所以 2122843k x x k -+=+. ………………4分故点G 的横坐标为21224243x x k k +-=+. 依题意,得2241434k k -=-+, ………………6分 解得 12k =±. ………………7分 (Ⅱ)解:假设存在直线AB ,使得 12S S =,显然直线AB 不能与,x y 轴垂直.由(Ⅰ)可得 22243(,)4343k kG k k -++. ………………8分因为 DG AB ⊥,所以 2223431443Dk k k kx k +⨯=---+, 解得 2243D k x k -=+, 即 22(,0)43k D k -+.10分因为 △GFD ∽△OED ,所以 12||||S S GD OD =⇔=. ………………11分 所以2243k k -=+, ………………12分 整理得 2890k +=. ………………13分 因为此方程无解,所以不存在直线AB ,使得 12S S =. ………………14分。
2013届北京西城区高三数学文科一模试卷及答案

2013届北京西城区高三数学文科一模试卷及答案北京市西城区2012 — 2013学年度第一学期期末试卷高三数学(文科) 2013.1第Ⅰ卷(选择题 共40分)1A )(0,C )1(1)(0,)2-∞1)(,1)222i6.过点(2,0)M 作圆221xy +=的两条切线MA ,MB (A ,B 为切点),则MA MB ⋅=( ) (A)2 (B )52 (C)2(D )3278 ①()||f x x =; ②()sin f x x =; ③3()f x xx=-.其中,具有性质P 的函数的序号是( ) (A )① (B )③(C )①② (D )②③第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9.已知向量(1,3)=a ,(,21)m m =-b .若向量a 与b 共线,则实数m =______.10.平行四边形ABCD 中,E 为CD 的中点.若在平行四边形ABCD 内部随机取一点M , 则点M 取自△ABE内部的概率为______.11.双曲线2213645x y -=的渐近线方程为______;离心率为______.12.若函数2log ,0,()(),0x x f x g x x >⎧=⎨<⎩是奇函数,则(8)g -=______.批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[4550),,第2组[5055),,第3组[5560),,第4组[6065),,第5组[6570],,得到如图所示的频率分布直方图.现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生做初检. (Ⅰ)求每组抽取的学生人数;21===CC BC AC ,M ,N 分别为AC ,11C B 的中点. (Ⅰ)求线段MN 的长; (Ⅱ)求证:MN //平面11A ABB ;(Ⅲ)线段CC上是否存在点Q,使⊥B A1平面MNQ?1说明理由.20.(本小题满分13分)如图,设A 是由n n ⨯个实数组成的n 行n 列的数表,其中a (,1,2,3,,)i j n =i j 数,且{1,1}ija∈-.记(,)S n n 为所有这样的数表构成的集合.对于(,)A S n n ∈,记()ir A 为A 的第i 行各数之积,()jc A 为A 的第j 列各数之积.令11()()()n ni ji j l A r A c A ===+∑∑.(Ⅰ)对如下数表(4,4)A S ∈,求()l A 的值;(Ⅱ)证明:存在(,)A S n n ∈,使得()24l A n k =-,其中0,1,2,,k n=;(Ⅲ)给定n 为奇数,对于所有的(,)A S n n ∈,证明:()0l A ≠.北京市西城区2012 — 2013学年度第一学期期末高三数学(文科)参考答案及评分标准2013.1一、选择题:本大题共8小题,每小题5分,共1;6注:11、13题第一空2分,第二空3分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.15.(本小题满分13分) (Ⅰ)解:由已知得22cos cos 10B B +-=, ………………2分B2b ……8分将π3B =,b =整理得2()37a c ac +-=.因为5a c +=,所以 6ac =.………………11分所以 △ABC的面积S1. C.………………6分则从6位同学中随机抽取2位同学所有可能的情形为:121311121232122231(,),(,),(,),(,),(,),(,),(,),(,),(,),(,),A A A A AB A B AC A A A B A B A C A B 3231212(,),(,),(,),(,),(,)A B A C B B B C B C ,共15种可能. ………………10分其中,((B P1 所以1AC CC ⊥. ………………2分因为BCAC ⊥, 所以⊥AC 平面11BCC B . ………………3分 因为1=MC ,CN ==所以6=MN.………………4分(Ⅱ)证明:取AB中点D,连接DM,DBB1(Ⅲ)解:线段1CC上存在点Q,且Q为1CC中点时,有⊥B A1平面MNQ.………11分证明如下:连接1BC.在正方形C CBB11中易证1BCQN⊥.又⊥11C A 平面C C BB 11,所以QNC A ⊥11,从而⊥NQ 平面11BC A .…………12分所以 1A B QN⊥.f '意. ………………5分(Ⅱ)解:① 当0b =时,1()f x x =. 故()f x 的单调减区间为(,0)-∞,(0,)+∞;无单调增区间. ………………6分② 当0b >时,222()()b x f x x b -'=+. 令()0f x '=,得1x =,2x =. ………………8分19.(本小题满分14分) (Ⅰ)解:依题意,得1,2b a ⎧=⎪=………………2分解得2a =,1b =2122 2.x x m ⎪=-⎩…8分证法一:记△OCM 的面积是1S ,△ODN 的面积是2S .由(2,0)M m ,(0,)N m , 则12S S =⇔1211|2|||||||22m y m x ⨯⨯=⨯⨯⇔12|2|||y x =. ……………|21S12所以122x x m +=,1212112222y yx x m m++=-⋅+=.故线段CD 的中点为1(,)2m m . 因为(2,0)M m ,(0,)N m ,所以 线段MN的中点坐标亦为1(,)2m m . (13)分从而12S S =.………………14分20.(本小题满分13分)(Ⅰ)解:134()()()1r A r A r A ===,2()1r A =-;124()()()1c A c A c A ===-,3()1c A =,所以4411()()()0i j i j l A r A c A ===+=∑∑.………………3分(Ⅱ)证明:(ⅰ)对数表0A :1ija=(,1,2,3,,)i j n =,显然0()2l A n =.将数表0A 中的11a 由1变为1-,得到数表1A ,显然1()24l A n =-.将数表1A 中的22a 由1变为1-,得到数表2A ,显然2()28l A n =-.依此类推,将数表1k A -中的kka 由1变为1-,得到数表kA .即数表k A 满足:11221(1)kk a a a k n ====-≤≤,其余1ij a =.所以12()()()1k r A r A r A ====-,12()()()1k c A c A c A ====-. 所以()2[(1)()]24k l A k n k n k =-⨯+-=-,其中0,1,2,,k n =.……………7分【注:数表k A 不唯一】(Ⅲ)证明:用反证法.假设存在(,)A S n n ∈,其中n 为奇数,使得()0l A =.因为(){1,1}i r A ∈-,(){1,1}j c A ∈-(1,1)i n j n ≤≤≤≤, 所以1()r A ,2()r A ,,()n r A ,1()c A ,2()c A ,,()n c A 这2n 个数中有n 个1,n 个1-.令1212()()()()()()n n M r A r A r A c A c A c A =⋅⋅⋅⋅⋅⋅⋅. 一方面,由于这2n 个数中有n 个1,n 个1-,从而(1)1n M =-=-. ①另一方面,12()()()n r A r A r A ⋅⋅⋅表示数表中所有元素之积(记这2n 个实数之积为m );12()()()n c A c A c A ⋅⋅⋅也表示m , 从而21M m==. ② ①、②相互矛盾,从而不存在(,)A S n n ∈,使得()0l A =.即n 为奇数时,必有.………………13分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市西城区2013年高三二模试卷
高三数学(文科) 2013.5
第Ⅰ卷(选择题 共40分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.复数 i (1i)⋅-=
(A )1i + (B )1i -+ (C)1i - (D )1i --
2.已知向量(=a ,)=λb .若a 与b 共线,则实数=λ
(A )1- (B)1 (C )3- (D)3
3.给定函数:①2
y x =;②2x y =;③cos y x =;④3y x =-,其中奇函数是 (A )① (B)② (C )③ (D )④
4.若双曲线2
2
1y x k +=的离心率是2,则实数k = (A )3 (B)3- (C)13 (D)13
-
5.如图所示的程序框图表示求算式“235917⨯⨯⨯⨯” 之值,
则判断框内可以填入
(A)10k ≤ (B )16k ≤
(C)22k ≤ (D)34k ≤
6.对于直线m ,n 和平面α,β,使m ⊥α成立的一个充分条件是
(A)m n ⊥,n ∥α (B )m ∥β,⊥βα
(C )m ⊥β,n ⊥β,n ⊥α (D)m n ⊥,n ⊥β,⊥βα
7.已知函数||()e ||x f x x =+.若关于x 的方程()f x k =有两个不同的实根,则实数k 的取值范围是
(A)(0,1) (B)(1,)+∞ (C )(1,0)- (D)(,1)-∞-
8.已知集合{1,2,3,4,5}的非空子集A 具有性质P :当a A ∈时,必有6a A -∈.则具有性质P 的集合A 的个数是
(A )8 (B )7 (C)6 (D)5
第Ⅱ卷(非选择题 共110分)
二、填空题:本大题共6小题,每小题5分,共30分.
9.已知直线1:310l x y -+=,2:210l x my +-=.若1l ∥2l ,则实数m =______.
10.右图是甲,乙两组各6名同学身高(单位:cm )数据 的茎叶图.记甲,乙两组数据的平均数依次为x 甲和x 乙, 则x 甲______x 乙. (填入:“>”,“=”,或“<”)
11.在△ABC 中,2BC =
,AC =,3
B π=,则AB =______;△AB
C 的面积是______. 12.设a ,b 随机取自集合{1,2,3},则直线30ax by ++=与圆221x y +=有公共点的概率是_____.
13.已知命题:p 函数(1)1y c x =-+在R 上单调递增;命题:q 不等式2
0x x c -+≤的解集是∅.若p 且q 为
真命题,则实数c 的取值范围是______. 14.在直角坐标系xOy 中,已知两定点(1,0)A ,(1,1)B .动点(,)P x y 满足01,0 2.
OP OA OP OB ⎧≤⋅≤⎪⎨≤⋅≤⎪⎩则点P 构成的区
域的面积是______;点(,)Q x y x y +-构成的区域的面积是______.
三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.
15.(本小题满分13分)
已知等比数列{}n a 的各项均为正数,28a =,3448a a +=.
(Ⅰ)求数列{}n a 的通项公式;
(Ⅱ)设4log n n b a =.证明:{}n b 为等差数列,并求{}n b 的前n 项和n S .
16.(本小题满分13分)
如图,在直角坐标系xOy 中,角α的顶点是原点,始边与x 轴正半轴重合,终边交单位圆于点A ,且,)62ππ∈(α.将角α的终边按逆时针方向旋转3π,交单位圆于点B .记),(),,(2211y x B y x A . (Ⅰ)若3
11=x ,求2x ; (Ⅱ)分别过,A B 作x 轴的垂线,垂足依次为,C D .记△AOC
的面积为1S ,△BOD 的面积为2S .若122S S =,求角α的值.
17.(本小题满分14分)
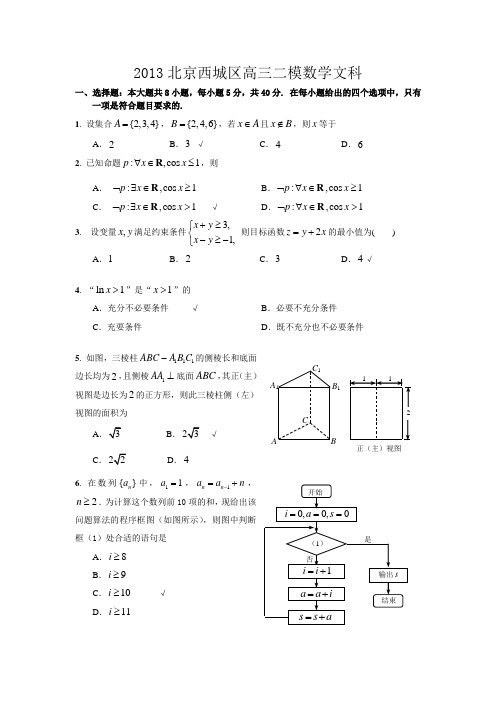
如图1,在四棱锥ABCD P -中,⊥PA 底面ABCD ,面ABCD 为正方形,E 为侧棱PD 上一点,F 为AB 上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.
(Ⅰ)求四面体PBFC 的体积;
(Ⅱ)证明:AE ∥平面PFC ;。
