2014届高三数学一轮必备“高频题型全掌握”13.直线与圆的典型题
2014高考数学理(真题讲练 规律总结 名师押题)热点专题突破:第十五讲 直线与圆

第十五讲直线与圆1.(直线方程)(2013·福建高考)设点P(x,y),则“x=2且y=-1”是“点P在直线l:x +y-1=0上”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【解析】当x=2且y=-1时,满足方程x+y-1=0, 即点P(2,-1)在直线l上.点P′(0,1)在直线l上,但不满足x=2且y=-1,∴“x=2且y=-1”是“点P(x,y)在直线l上”的充分而不必要条件.【答案】 A2.(直线与圆的位置关系)已知圆C:x2+y2-4x=0,l是过点P(3,0)的直线,则() A.l与C相交B.l与C相切C.l与C相离D.以上三个选项均有可能【解析】圆的方程可化为(x-2)2+y2=4,易知圆心为(2,0),半径为2,圆心到点P 的距离为1,所以点P在圆内.所以直线与圆相交.故选A.【答案】 A3.(弦长计算)(2013·安徽高考)直线x +2y -5+5=0被圆x 2+y 2-2x -4y =0截得的弦长为( )A .1B .2C .4D .4 6【解析】 圆的方程可化为C :(x -1)2+(y -2)2=5,其圆心为C (1,2),半径R = 5.如图所示,取弦AB 的中点P ,连接CP ,则CP ⊥AB ,圆心C 到直线AB 的距离d =|CP |=|1+4-5+5|12+22=1.在Rt △ACP 中,|AP |=R 2-d 2=2,故直线被圆截得的弦长|AB |=4.【答案】 C4.(两直线的位置关系)已知直线l 1:x -2my +3=0,直线l 2的方向向量为a =(1,2),若l 1⊥l 2,则m 的值为________.【解析】 由直线l 2的方向向量为a =(1,2),知直线l 2的斜率k 2=2,∵l 1⊥l 2,∴直线l 1的斜率存在,且k 1=12m,由k 1·k 2=-1,即12m ·2=-1,得m =-1.【答案】 -15.(圆的方程)(2013·江西高考)若圆C 经过坐标原点和点(4,0),且与直线y =1相切,则圆C 的方程是________.【解析】 因为圆的弦的垂直平分线必过圆心且圆经过点(0,0)和(4,0),所以设圆心为(2,m ).又因为圆与直线y =1相切,所以(4-2)2+(0-m )2=|1-m |,所以m 2+4=m 2-2m +1,解得m =-32,所以圆的方程为(x -2)2+⎝⎛⎭⎫y +322=254. 【答案】 (x -2)2+⎝⎛⎭⎫y +322=254(1)(2013·济南调研)设a ∈R ,则“a =1”是“直线l 1:ax +2y =0与直线l 2:x +(a +1)y +4=0平行”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件(2)过直线l 1:x -2y +3=0与直线l 2:2x +3y -8=0的交点,且到点P (0,4)距离为2的直线方程为________.【思路点拨】 (1)先求出两条直线平行的充要条件,再判断;(2)联立l 1,l 2的方程,求交点坐标,利用待定系数法求直线方程.【自主解答】 (1)若直线l 1与l 2平行,则a (a +1)-2×1=0,即a =-2或a =1, ∴a =1是直线l 1与直线l 2平行的充分不必要条件.(2)由⎩⎪⎨⎪⎧ x -2y +3=0,2x +3y -8=0,得⎩⎪⎨⎪⎧x =1,y =2.∴l 1与l 2交点为(1,2), 直线x =1显然不适合.设所求直线为y -2=k (x -1),即kx -y +2-k =0, ∵P (0,4)到直线距离为2,∴2=|-2-k |1+k 2,∴k =0或k =43.∴直线方程为y =2或4x -3y +2=0. 【答案】 (1)A (2)y =2或4x -3y +2=01.第(1)题利用两直线平行的充要条件,避免了分类讨论.第(2)题利用点斜式求直线方程,要注意判定直线的斜率是否存在.2.直线与直线的位置关系的判定方法(1)给定两条直线l 1:y =k 1x +b 1和l 2:y =k 2x +b 2,则有下列结论: l 1∥l 2⇔k 1=k 2且b 1≠b 2;l 1⊥l 2⇔k 1·k 2=-1.(2)若给定的方程是一般式,即l 1:A 1x +B 1y +C 1=0和l 2:A 2x +B 2y +C 2=0,则有下列结论:l 1∥l 2⇔A 1B 2-A 2B 1=0且B 1C 2-B 2C 1≠0或A 1C 2-A 2C 1≠0; l 1⊥l 2⇔A 1A 2+B 1B 2=0.变式训练1 (1)(2013·天津高考)已知过点P (2,2)的直线与圆(x -1)2+y 2=5相切,且与直线ax -y +1=0垂直,则a =( )A .-12B .1C .2 D.12(2)(2013·四川高考)在平面直角坐标系内,到点A (1,2),B (1,5),C (3,6),D (7,-1)的距离之和最小的点的坐标是________.【解】 (1)由题意知圆心为(1,0),由圆的切线与直线ax -y +1=0垂直,可设圆的切线方程为x +ay +c =0,由切线x +ay +c =0过点P (2,2),∴c =-2-2a ,∴|1-2-2a |1+a 2=5,解得a =2. (2)设平面上任一点M ,因为|MA |+|MC |≥|AC |,当且仅当A ,M ,C 共线时取等号,同理|MB |+|MD |≥|BD |,当且仅当B ,M ,D 共线时取等号,连接AC ,BD 交于一点M ,若|MA |+|MC |+|MB |+|MD |最小,则点M 为所求.又k AC =6-23-1=2,∴直线AC 的方程为y -2=2(x -1),即2x -y =0.①又k BD =5-(-1)1-7=-1,∴直线BD 的方程为y -5=-(x -1), 即x +y -6=0.②由①②得⎩⎪⎨⎪⎧ 2x -y =0,x +y -6=0,∴⎩⎪⎨⎪⎧x =2,y =4,∴M (2,4).【答案】 (1)C (2)(2,4)若圆C 的半径为1,圆心在第一象限,且与直线4x -3y =0和x 轴相切,则圆C 的标准方程是( )A .(x -2)2+(y -1)2=1B .(x -1)2+(y -2)2=1C .(x -1)2+(y -1)2=1D .(x -2)2+(y -2)2=1【思路点拨】 设圆心坐标,利用直线与圆相切的条件,得圆心坐标的方程,进而求待定系数,得圆C 的方程.【自主解答】 因为圆C 与x 轴相切,半径r =1,且圆心在第一象限, ∴圆心的纵坐标为1,设圆心为C (a,1)(a >0). 又直线4x -3y =0与圆C 相切,∴d =|4a -3×1|5=1,解之得a =2或a =-12(舍).故点C (2,1),则圆C 的方程为(x -2)2+(y -1)2=1. 【答案】 A1.本题抓住圆C 与x 轴相切,确定圆心纵坐标为1,减少待定参数,优化了解题过程. 2.求解圆的方程,一般利用待定系数法,即确定待定方程中的参数取值,但一定要注意圆的几何性质的灵活应用,要熟练掌握平面几何中确定圆心和半径的基本方法,如圆心在弦的中垂线上、直线和圆相切、其切点在圆上且圆心到直线的距离等于圆的半径等.变式训练2 已知圆C 过点(1,0),且圆心在x 轴的正半轴上,直线l :y =x -1被该圆所截得的弦长为22,则圆C 的标准方程为________.【解析】 设圆心坐标为(a,0)(a >0),由于圆过点(1,0),则半径r =|a -1|,圆心到直线x -y -1=0的距离为d =|a -1|2.由弦长为22可知⎝ ⎛⎭⎪⎫|a -1|22=(a -1)2-2,解得(a -1)2=4,∴a =3或a =-1(舍去). 故圆心为(3,0),半径为2,所求圆的方程为(x -3)2+y 2=4. 【答案】 (x -3)2+y 2=4在直角坐标系xOy 中,以坐标原点O 为圆心的圆与直线:x -3y =4相切.(1)求圆O 的方程;(2)若圆O 上有两点M ,N 关于直线x +2y =0对称,且|MN |=23,求直线MN 的方程;(3)圆O 与x 轴相交于A ,B 两点,圆内的动点P 使|P A |,|PO |,|PB |成等比数列,求P A →·PB →的取值范围.【思路点拨】 (1)直线与圆相切→求半径→求圆方程 (2)设MN 的方程2x -y +m =0→利用|MN |=23,求m →写MN的方程(3)利用|PO |2=|P A ||PB |建立动点P (x ,y )中变量x ,y 的等量关系,利用点与圆的位置关系求P A →·PB →的范围.【自主解答】 (1)依题意,圆O 的半径r 等于原点O 到直线x -3y =4的距离, 即r =41+3=2. 所以圆O 的方程为x 2+y 2=4.(2)由题意,可设直线MN 的方程为2x -y +m =0. 则圆心O 到直线MN 的距离d =|m |5. 由垂径分弦定理得:m 25+(3)2=22,即m =±5.所以直线MN 的方程为:2x -y +5=0或2x -y -5=0. (3)不妨设A (x 1,0),B (x 2,0),x 1<x 2.由x 2=4得A (-2,0),B (2,0). 设P (x ,y ),由|P A |,|PO |,|PB |成等比数列,得 (x +2)2+y 2·(x -2)2+y 2=x 2+y 2,即x 2-y 2=2. 因为P A →·PB →=(-2-x ,-y )·(2-x ,-y )=2(y 2-1).由于点P 在圆O 内,故⎩⎪⎨⎪⎧x 2+y 2<4,x 2-y 2=2.由此得y 2<1.所以P A →·PB →的取值范围为[-2,0).1.本题(3)在求解过程中常因忽视条件x 2-y 2=2的限制作用使所求P A →·PB →的范围变大.2.与弦长有关的问题常用几何法,即利用圆的半径r ,圆心到直线的距离d ,及半弦长l2构成直角三角形的关系来处理. 3.讨论点与圆、直线与圆及圆与圆的位置关系时,要注意数形结合,充分利用圆的几何性质寻找解题途径,减少运算量.变式训练3 (1)(2013·重庆高考)设P 是圆(x -3)2+(y +1)2=4上的动点,Q 是直线x =-3上的动点,则|PQ |的最小值为( )A .6B .4C .3D .2(2)(2013·课标全国卷Ⅱ)在平面直角坐标系xOy 中,已知圆P 在x 轴上截得线段长为22,在y 轴上截得线段长为2 3.①求圆心P 的轨迹方程; ②若P 点到直线y =x 的距离为22,求圆P 的方程.【解析】 (1)如图,圆心M (3,-1)与定直线x =-3的最短距离为|MQ |=3-(-3)=6,又圆的半径为2,故所求最短距离为6-2=4.【答案】 B【解】 (2)①设P (x ,y ),圆P 的半径为r . 由题设y 2+2=r 2,x 2+3=r 2,从而y 2+2=x 2+3. 故P 点的轨迹方程为y 2-x 2=1. ②设P (x 0,y 0).由已知得|x 0-y 0|2=22.又P 点在双曲线y 2-x 2=1上,从而得⎩⎪⎨⎪⎧|x 0-y 0|=1,y 20-x 20=1.由⎩⎪⎨⎪⎧ x 0-y 0=1,y 20-x 20=1得⎩⎪⎨⎪⎧x 0=0,y 0=-1.此时,圆P 的半径r = 3.由⎩⎪⎨⎪⎧ x 0-y 0=-1,y 20-x 20=1得⎩⎪⎨⎪⎧x 0=0,y 0=1,此时,圆P 的半径r = 3. 故圆P 的方程为x 2+(y +1)2=3或x 2+(y -1)2=3.从近两年高考看,直线与圆是高考的热点,主要涉及直线方程、圆的方程、直线与圆相切(交)的切线方程(或弦长计算).预计2014年高考仍以直线和圆的位置关系为核心,以客观题的形式进行命题.求解时应注意几何图形的性质的应用,重视数形结合的数学思想.以形助数巧求最小值已知圆C 1:(x -2)2+(y -3)2=1,圆C 2:(x -3)2+(y -4)2=9,M ,N分别是圆C 1,C 2上的动点,P 为x 轴上的动点,则|PM |+|PN |的最小值为________.【解析】 设P (x,0),C 1(2,3)关于x 轴的对称点为C 1′(2,-3),那么|PC 1|+|PC 2|=|PC 1′|+|PC 2|≥|C ′1C 2|=(2-3)2+(-3-4)2=5 2. 而|PM |=|PC 1|-1,|PN |=|PC 2|-3, ∴|PM |+|PN |=|PC 1|+|PC 2|-4≥52-4. 【答案】 52-4 【阅卷心语】易错提示 (1)弄不清圆C 外一点A 到圆上一点距离的最小值为|AC |-r ,最大值为|AC |+r ,难以将所求问题转化为求|PC 1|+|PC 2|的最小值.(2)数形结合思想意识差,难以作出C 1关于x 轴的对称点C ′1,求不出|PC 1|+|PC 2|的最小值.防范措施 (1)涉及圆的几何最值,要充分考虑圆的几何性质由形思数;(2)若两点P 1,P 2在直线l 的同侧,直线l 上的点P 到P 1与P 2的距离和最小,宜作P 1关于l 的对称点P 1′,则|P 1′P 2|为所求的最小值.1.已知点M (a ,b )在圆O :x 2+y 2=1外,则直线ax +by =1与圆O 的位置关系是________. 【解析】 由题意知点在圆外,则a 2+b 2>1,圆心到直线的距离d =1a 2+b 2<1,故直线与圆相交.【答案】 相交2.已知直线l 经过坐标原点,且与圆x 2+y 2-4x +3=0相切,切点在第四象限,则直线l 的方程为________.【解析】 由题易知,圆的方程为(x -2)2+y 2=1,圆心为(2,0),半径为1,如图,经过原点的圆的切线的倾斜角为150°,切线的斜率为tan 150°=-33,故直线l 的方程为y =-33x .【答案】 y =-33x。
2014年文数高考母题题源系列 14直线与圆的位置关系 Word版含解析]
![2014年文数高考母题题源系列 14直线与圆的位置关系 Word版含解析]](https://img.taocdn.com/s3/m/c2e1f044cf84b9d529ea7a0d.png)
【母题来源】2014全国II 卷文–12 【母题原题】设点()0,1M x ,若在圆22:+1O x y =上存在点N ,使得45OMN ∠=︒,则0x 的取值范围是( )(A )[]1,1-- (B )11,22⎡⎤-⎢⎥⎣⎦ (C )⎡⎣ (D )⎡⎢⎣⎦【命题意图】本题主要考查考查直线与圆的位置关系,考查数形结合能力和逻辑思维能力、分析问题和解决问题的能力、化归能力.【方法技巧】1.判断直线与圆的位置关系常见的有两种方法(1)代数法:――――――→判别式Δ=b 2-4ac ⎩⎪⎨⎪⎧>0⇔相交,=0⇔相切,<0⇔相离.(2)几何法:利用圆心到直线的距离d 和圆半径r 的大小关系:d<r ⇔相交,d =r ⇔相切,d>r ⇔相离.2.圆的弦长的常用求法(1)几何法:设圆的半径为r ,弦心距为d ,弦长为l ,则(l2)2=r 2-d 2(2)代数方法:运用韦达定理及弦长公式: |AB|=1+k 2|x 1-x 2|=+k 21+x 22-4x 1x 2].注意:常用几何法研究圆的弦的有关问题.求过一点的圆的切线方程时,首先要判断此点是否在圆上.然后设出切线方程,用待定系数法求解.注意斜率不存在情形.【试题拓展】求圆的的切线方程有两种情况,一是求过圆上一点()00,P x y 圆的切线方程,其方法如下:先求斜率(利用圆的切线垂直于经过切点的半径来求),再由点斜式写圆的切线方程;二是求过圆外一点()00,P x y 圆的切线方程,有两条,其方法如下:若斜率存在,可用待定系数法,再利用圆心到切线的距离等于半径列出关系式求出切线的斜率即可.【拓展一】求过圆2210x y +=上一点(2M 的圆的切线方程.1.【2014高考四川卷文第9题】设m R ∈,过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(,)P x y ,则||||PA PB +的取值范围是( )A 、B 、C 、D 、 【答案】B2.【2014高考浙江卷文第5题】已知圆02222=+-++a y x y x 截直线02=++y x 所得弦的长度为4,则实数a 的值为( )A.2-B. 4-C. 6-D.8-3.【2014高考安徽卷文第6题】过点(P 的直线l 与圆122=+y x 有公共点,则直线l的倾斜角的取值范围是( )A.]60π,( B.]30π,( C.]60[π, D.]30[π,4. 【2014高考北京卷文第7题】已知圆()()22:341C x y -+-=和两点(),0A m -,()(),00B m m >,若圆C 上存在点P ,使得90APB ∠=,则m 的最大值为( )A.7B.6C.5D.45.【黑龙江省佳木斯市第一中学2014届高三第三次调研】圆心在曲线2(0)y x x=>上,且与直线210x y ++=相切的面积最小的圆的方程为( ) A.22(1)(2)5x y -+-= B.22(2)(1)5x y -+-= C.22(1)(2)25x y -+-= D.22(2)(1)25x y -+-=6【北京市西城区2014届高三上学期期末考试数学试题】已知圆22:(1)(1)1C x y ++-=与x 轴切于A 点,与y 轴切于B 点,设劣弧»AB 的中点为M ,则过点M 的圆C 的切线方程是( )(A )2y x =+-(B )1y x =+-(C )2y x =-+ (D )1y x =+-7.【【百强校】2013-2014学年浙江省嘉兴一中高二下学期期中文科数学卷】两条平行直线和圆的位置关系定义为:若两条平行直线和圆有四个不同的公共点,则称两条平行线和圆“相交”;若两平行直线和圆没有公共点,则称两条平行线和圆“相离”;若两平行直线和圆有一个、两个或三个不同的公共点,则称两条平行线和圆“相切”.已知直线1:20l x y a -+=,22:210l x y a -++=,和圆:22240x y x ++-=相切,则实数a 的取值范围是( )A .7a >或3a <-B .a >a <C .3a -≤≤7a ≤D .7a ≥或3a ≤- 【答案】C 【解析】8.【2014高考大纲卷文第16题】直线l 1和l 2是圆222x y +=的两条切线,若l 1与l 2的交点为(1,3),则l 1与l 2的交角的正切值等于 .的圆心,且与直线10x y ++=垂直,则l 的方程是 ( ).20.20.30.30A x y B x y C x y D x y +-=-+=+-=-+=30x y -+=,故选D .考点:圆的方程,直线的垂直,直线方程.10. 【2014高考湖北卷文第17题】 已知圆1:22=+y x O 和点)0,2(-A ,若定点)2)(0,(-≠b b B 和常数λ满足:对圆O 上那个任意一点M ,都有||||MA MB λ=,则(1)=b ;(2)=λ .11.【2014高考湖南卷文第6题】若圆221:1C x y +=与圆222:680C x y x y m +--+=,则m =( ).21A .19B .9C .11D -12.【2014高考江苏卷第9题】在平面直角坐标系xoy 中,直线230x y +-=被22(2)(1)4x y -++=圆截得的弦长为 .13.【2014高考山东卷文第14题】 圆心在直线02=-y x 上的圆C 与y 轴的正半轴相切,圆C 截x 轴所得弦的长为32,则圆C 的标准方程为 .15.【2014高考全国1文第20题】已知点)2,2(P ,圆C :0822=-+y y x ,过点P 的动直线l 与圆C 交于B A ,两点,线段AB 的中点为M ,O 为坐标原点.(1)求M 的轨迹方程;(2)当OM OP =时,求l 的方程及POM ∆的面积16.【组卷网合作校特供】已知圆22:1O x y +=和点(1,4)M . (1)过点M 向圆O 引切线,求切线的方程;(2)求以点M 为圆心,且被直线28y x =-截得的弦长为8的圆M 的方程;(3)设P 为(2)中圆M 上任意一点,过点P 向圆O 引切线,切点为Q ,试探究:平面内是否存在一定点R ,使得PQPR为定值?若存在,请求出定点R 的坐标,并指出相应的定值;若不存在,请说明理由.【答案】(1):1x =或158170x y -+= (2)22(1)(4)36x y -+-=(3)存在定点R (1,4)--,此时PQ PR 为定值2或定点R 14(,)1717--,此时PQ PR 为定值617.【2013-2014学年福建省清流一中高一下学期第三阶段模块考数学试卷】已知圆22:4O x y +=和圆22:(4)1C x y +-=.(1)判断圆O和圆C的位置关系;(2)过圆C的圆心C作圆O的切线l,求切线l的方程;(3)过圆C的圆心C作动直线m交圆O于A,B两点.试问:在以AB为直径的所有圆中,M?若存在,求出圆P的方程;若不存在,请是否存在这样的圆P,使得圆P经过点(2,0)说明理由.18.【【百强校】2014届甘肃省兰州一中高考模拟四文科数学试卷】给定椭圆C :22221(0)x y a b a b +=>>,称圆心在原点O 的圆是椭圆C 的“准圆”.若椭圆C 的一个焦点为0)F ,,其短轴上的一个端点到F . (1)求椭圆C 的方程和其“准圆”方程;(2)点P 是椭圆C 的“准圆”上的动点,过点P 作椭圆的切线12l l ,交“准圆”于点M N ,.(ⅰ)当点P 为“准圆”与y 轴正半轴的交点时,求直线12l l ,的方程并证明12l l ; (ⅱ)求证:线段MN 的长为定值.考点:直线与圆及圆锥曲线的位置关系问题.。
直线与圆知识点及经典例题(含答案)

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载直线与圆知识点及经典例题(含答案)地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容圆的方程、直线和圆的位置关系【知识要点】一、圆的定义:平面内与一定点距离等于定长的点的轨迹称为圆(一)圆的标准方程这个方程叫做圆的标准方程。
说明:1、若圆心在坐标原点上,这时,则圆的方程就是。
2、圆的标准方程的两个基本要素:圆心坐标和半径;圆心和半径分别确定了圆的位置和大小,从而确定了圆,所以,只要三个量确定了且>0,圆的方程就给定了。
就是说要确定圆的方程,必须具备三个独立的条件确定,可以根据条件,利用待定系数法来解决。
(二)圆的一般方程将圆的标准方程,展开可得。
可见,任何一个圆的方程都可以写成 :问题:形如的方程的曲线是不是圆?将方程左边配方得:(1)当>0时,方程(1)与标准方程比较,方程表示以为圆心,以为半径的圆。
,(3)当<0时,方程没有实数解,因而它不表示任何图形。
圆的一般方程的定义:当>0时,方程称为圆的一般方程.圆的一般方程的特点:(1)和的系数相同,不等于零;(2)没有xy这样的二次项。
(三)直线与圆的位置关系1、直线与圆位置关系的种类(1)相离---求距离; (2)相切---求切线;(3)相交---求焦点弦长。
2、直线与圆的位置关系判断方法:几何方法主要步骤:(1)把直线方程化为一般式,利用圆的方程求出圆心和半径(2)利用点到直线的距离公式求圆心到直线的距离(3)作判断: 当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交。
代数方法主要步骤:(1)把直线方程与圆的方程联立成方程组(2)利用消元法,得到关于另一个元的一元二次方程(3)求出其Δ的值,比较Δ与0的大小:(4)当Δ<0时,直线与圆相离;当Δ=0时,直线与圆相切;当Δ>0时,直线与圆相交。
2014届高三数学理科第一轮复习单元过关( 12)-直线与圆

2014届高三数学理科第一轮复习单元过关( 12) 考查:直线与圆一、选择题:(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,有且只有一项是符合题目要求的.)1. 若直线l 与直线1y =,7x =分别交于点P 、Q ,且线段P Q 的中点坐标为(1,1)-,则直线l 的斜率为( ) A.13 B.13- C.32- D.23 2.若直线1:60l x ay ++=与2:(2)320l a x y a -++=平行,则1l 与2l 间的距离为( )B.33.如果0A C ⋅<,且0B C ⋅<,那么直线0Ax By C ++=不经过( ). A .第一象限 B .第二象限 C .第三象限 D .第四象限4.直线20ax y a -+=与圆229x y +=的位置关系是( )A .相离B .相切C .相交D .不确定5. 若函数8y ax =+与12y x b =-+的图象关于直线y x =对称,则a b +=( )A.1B.2D.46.直线1l 的斜率为2,12//l l ,直线2l 过点(1,1)-)且与y 轴交于点P ,则P 点坐标为( )A .(3,0)B .(3,0)-C .(0,3)-D .(0,3)7. 已知直线1l 与圆2220x y y ++=相切,且与直线2:3460l x y +-=平行,则直线l 1的方程是( )A .3410x y +-=B .3410x y ++=或3490x y +-=C .3490x y ++=D .3410x y +-=或3490x y ++=8.若圆222()()1x a y b b -+-=+始终平分圆22(1)(1)4x y +++=的周长,则a b 、 满足的关系是( )A .22230a a b ++-=B .222250a b a b ++++=C .22250a a b +++=D .22250a a b --+=二、填空题: (本大题共6小题,每小题5分,共30分,把答案填在答题卷中....相应横线上)9. 圆心在原点且与直线24x y +=相切的圆的方程是 .10.点(4,2)P -与圆224x y +=上任一点连线的中点的轨迹方程是___________.11.在平面直角坐标系xOy 中,已知圆224x y +=上有且只有四个点到直线1250x y c -+=的距离为1,则实数c 的取值范围是________.12.已知点(1,3),(2,1)A B --,若直线:(2)1l y k x =-+与线段AB 相交,则k 的取值范围是________.13.圆心在曲线3(0)y x x=>上,且与直线3430x y ++=相切的面积最小的圆的方程为14.已知实数x y 、满足250x y ++=,的最小值为 .二、填空题(每小题5分,共30分)9.____________________. 10.___________________. 11. ____________________.12.___________________. 13. ___________________. 14.____________________.三、解答题:本大题共4小题,解答应写出文字说明,证明过程或演算步骤15.已知直线l 与两坐标轴围成的三角形的面积为3,且经过点(3,4)A -,求直线l 的方程.16.不同两点P 、Q 的坐标分别为(,),(3,3)a b b a --,求:()Ⅰ线段P Q 的垂直平分线l 的方程;()Ⅱ圆22(2)(3)1x y -+-=关于直线l 对称的圆的方程.17.已知圆22:2440C x y x y +-+-=,是否存在斜率为1的直线l ,使以l 被圆截得的弦AB 为直径的圆过原点?若存在,求出直线l 的方程;若不存在,说明理由.18.在直角坐标系xOy 中,以O为圆心的圆与直线40x +=相切. ()Ⅰ求圆O 的方程;()Ⅱ圆O 与x 轴相交于A B 、两点,圆内的动点P 使PA PO PB、、|成等比数列,求PA PB ⋅的取值范围.2014届高三数学理科第一轮复习单元过关( 12)参考答案1解析:选B.由直线l 与直线y =1,x =7分别交于点P 、Q ,可设P (x 1,1),Q (7,y 1),再由线段PQ 的中点坐标为(1,-1),可解得:x 1=-5,y 1=-3.即直线l 上有两点P (-5,1),Q (7,-3),代入斜率公式可解得直线l 的斜率为k =1+3-5-7=-13.故选B.2 [解析]由l 1∥l 2知3=a(a -2)且2a ≠6(a -2),2a 2≠18,求得a =-1,l 1:x -y +6=0,l 2:x -y +23=0,两条平行直线l 1与l 2间的距离为d =|6-23|12+(-1)2=823.故选B. 3.C 解析:由A·C <0及B·C <0,可知A ≠0,B ≠0,又直线Ax +By +C =0过⎝⎛⎭⎫-CA ,0,⎝⎛⎭⎫0,-CB ,且-C A >0,-C B>0,∴直线不过第三象限.4[解析]直线ax -y +2a =0⇒a(x +2)-y =0,即直线恒过点(-2,0),∵点(-2,0)在圆内,所以直线与圆相交,故选C.5解析:直线y =ax +8关于y =x 对称的直线方程为x =ay +8,所以x =ay +8与y =-12x+b 为同一直线,故得⎩⎪⎨⎪⎧a =-2b =4,所以a +b =2故选B6.解析:∵点P 在y 轴上,∴设P(0,y),又∵kl 1=2,l 1∥l 2,∴kl 2=y -10-(-1)=y -1=2,∴y =3,∴P(0,3).答案:D7.D 解析:设直线l 1的方程为3x +4y +m =0.∵直线l 1与圆x 2+y 2+2y =0相切,∴|-4+m|32+42=1.∴|m -4|=5.∴m =-1或m =9.∴直线l 1的方程为3x +4y -1=0或3x +4y +9=0.8.解析 即两圆的公共弦必过(x +1)2+(y +1)2=4的圆心,两圆相减得相交弦的方程为-2(a +1)x -2(b +1)y +a 2+1=0,将圆心坐标(-1,-1)代入可得a 2+2a +2b +5=0.答案C9解析:由题意,半径R =41+22=45,所以圆的方程为x 2+y 2=165,故填x 2+y 2=165.10解析:设圆上任一点为Q(s ,t),PQ 的中点为A(x ,y),则⎩⎨⎧x =4+s 2y =-2+t2,解得⎩⎪⎨⎪⎧s =2x -4t =2y +2,将其代入圆的方程,得(2x -4)2+(2y +2)2=4,整理得(x -2)2+(y +1)2=1 11.解析 (数形结合法)由已知直线l 恒过定点P(2,1),如右图.若l 与线AB 相交,则k PA ≤k ≤k PB ,∵k PA =-2,k PB =12,∴-2≤k ≤1212.[解析] 本题考查了直线与圆的位置关系,利用数形结合可解决此题,属中档题.要使圆x 2+y 2=4上有且只有四个点到直线12x -5y +c =0的距离为1,只需满足圆心到直线的距离小于1即可.即|c|122+52<1,解|c|<13,∴-13<c<13.13.解析:设圆心(a ,3a )(a>0),则圆心到直线的距离d =|3a +12a +3|5,而d ≥15(23a ·12a +3)=3,当且仅当3a =12a ,即a =2时,取“=”,此时圆心为(2,32),半径为3,圆的方程为(x -2)2+(y -32)2=9.14.解析:x 2+y 2表示点(x ,y)到原点的距离.根据数形结合得x 2+y 2的最小值为原点到直线2x +y +5=0的距离,即d =55= 5.15.解析:设直线l 的方程是y =k(x +3)+4,它在x 轴,y 轴上的截距分别是-4k-3,3k +4,由已知,得(3k +4)(4k +3)=±6,解得k 1=-23或k 2=-83.故直线l 的方程为2x +3y -6=0或8x +3y +12=0. 16.【解析】(1)∵313P a bk b a--==--Q ,∴11l P k k =-=-Q , ∵P Q 的中点坐标为33(,)22,直线l 的方程为3x y +=.(2)设所求圆的圆心为(,)a b ,则31223322l b k a a b -⎧⨯=-⎪⎪-⎨++⎪+=⎪⎩,解得01a b =⎧⎨=⎩, ∴所求圆的圆方程为22(1)1x y +-=.17解析 假设存在斜率为1的直线l ,满足题意,则OA ⊥OB.设直线l 的方程是y =x +b ,其与圆C 的交点A ,B 的坐标分别为A(x 1,y 1),B(x 2,y 2)则y 1x 1·y 2x 2=-1,即x 1x 2+y 1y 2=0①由⎩⎪⎨⎪⎧y =x +b ,x 2+y 2-2x +4y -4=0消去y 得: 2x 2+2(b +1)x +b 2+4b -4=0, ∴x 1+x 2=-(b +1),x 1x 2=12(b 2+4b -4),②y 1y 2=(x 1+b)(x 2+b)=x 1x 2+b(x 1+x 2)+b 2=12(b 2+4b -4)-b 2-b +b 2=12(b 2+2b -4).③把②③式代入①式,得b 2+3b -4=0,解得b =1或b =-4,且b =1或b =-4都使得Δ=4(b +1)2-8(b 2+4b -4)>0成立.故存在直线l 满足题意,其方程为y =x +1或y =x -4.法二:可设直线l :0x y c -+=,经过A B 、的圆:22:244()0C x y x y x y c λ+-+-+-+=分析18.解析:(1)依题设,圆O 的半径r 等于原点O 到直线x -3y +4=0的距离,即r =41+3=2.所以圆O 的方程为x 2+y 2=4.(2)不妨设A(x 1,0),B(x 2,0),x 1<x 2.由x 2=4即得A(-2,0),B(2,0).设P(x ,y),由|PA →|,|PO →|,|PB →|成等比数列,得(x +2)2+y 2·(x -2)2+y 2=x 2+y 2,即x 2-y 2=2.PA →·PB →=(-2-x ,-y)· (2-x ,-y)=x 2-4+y 2=2(y 2-1).由于点P 在圆O 内,故⎩⎪⎨⎪⎧x 2+y 2<4x 2-y 2=2,由此得y 2<1.所以PA →·PB →的取值范围为[-2,0).。
东南大学附中2014届高考数学一轮单元复习练习直线与圆含答案

东南大学附中2014三维设计高考数学一轮单元复习精品练习:直线与圆本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.由圆x 2+y 2=4外一动点P 向该圆引两条切线PA 和PB ,若保持∠APB=60°,则点P 的轨迹方程为( )A . x 2+y 2=8B . x 2+y 2=16C . x 2+y 2=32D . x 2+y 2=64 【答案】B2.直线0Ax By +=,若从0,1,2,3,5,7这六个数字中每次取两个不同的数作为A,B 的值,则表示成不同直线的条数是( ) A .2 B .12C .22D .25【答案】C 3.由直线1y x =+上的一点向圆引切线,则切线长的最小值为( )A .1BC .D .3【答案】B4.若圆C 的半径为1,圆心在第一象限,且与直线034=-y x 和x 轴都相切,则该圆的标准方程是( )A . 1)37()3(22=-+-y x B .1)1()2(22=-+-y x C . 1)3()1(22=-+-y x D .1)1()23(22=-+-y x 【答案】B5.下列四个命题中,正确命题有( )①直线方程的一般式为Ax + By + C = 0 ②k 1·k 2 = –1为两直线垂直的充要条件③k 1 = k 2为两直线平行的必要非充分条件 ④l :A 1x + B 1y + C 1 = 0和l 2:A 2x + B 2y + C 2 = 0,(B 1≠0,B 2≠0,A 1A 2 + B 1B 2≠0),则直线l 1到l 2的角θ的正切值为21211221tan B B A A B A B A +-=θA .0个B .1个C .2个D .3个【答案】B6.圆22:420C x y x y +-+=关于直线1y x =+对称的圆的方程是( )A . 22(1)(2)5x y ++-= B . 22(4)(1)5x y ++-= C . 22(2)(3)5x y ++-= D . 22(2)(3)5x y -++=【答案】B7.若圆221x y +=与直线340x y m -+=相切,则m 的值等于( )A .5B .5-C .5或5-D .15或15- 【答案】C 8.已知两点()()7,4,5,6AB --,则线段AB 的垂直平分线的方程为( )A .56110x y ++=B .6510x y --=C .56110x y +-=D .6510x y -+=【答案】B 9.直线3x +2y= 1的倾斜角是( ) A .arctan 23B .arctan ( –23) C .π + arctan 23D .π + arctan ( –23) 【答案】D10.设圆222)5()3(r y x =+++上有且只有两点到直线234=-y x 的距离等于1,则圆的半径r 的取值范围为( ) A .561<<r B .54>r C .5654<<r D .1>r【答案】C11.圆122=+y x 上的点到直线02543=-+y x 的距离的最小值为( )A .6B .2C .3D .4【答案】D12.在平面直角坐标系xOy 中,直线3x+4y-5=0与圆2x +2y =4相交于A 、B 两点,则弦AB 的长等于( )A .B .C .D . 1【答案】C第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.若三条直线1l :032=-+y x ,2l :023=+-y x 和3l :0=+y ax 不能构成三角形,则a 的值为【答案】13a =-或2a =或3a =-14.在平面直角坐标系中,不等式组⎪⎩⎪⎨⎧≤≥+-≥+a x y x y x 040,(a 为常数)表示的平面区域的面积是9,那么a 的值为____________. 【答案】115.若方程02222=++-y x my x 表示两条直线,则m 的取值是 . 【答案】116.过原点O 作圆x 2+y 2--6x -8y +20=0的两条切线,设切点分别为P 、Q ,则线段PQ 的长为 。
【备战2014】高考数学 高频考点归类分析 直线与圆(真题为例)
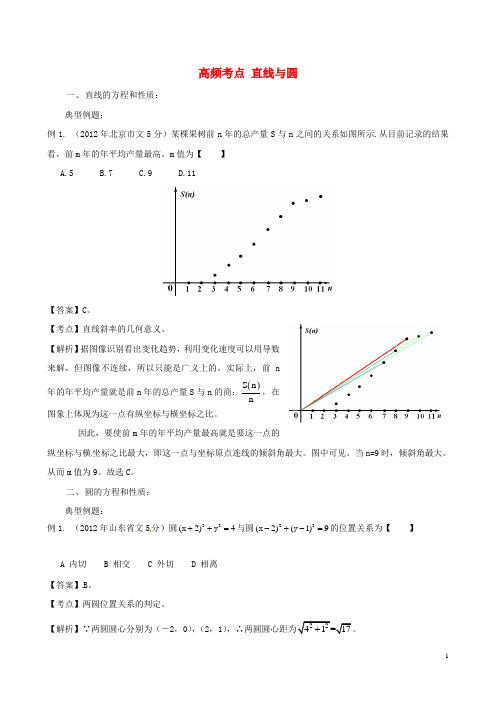
2 再由切割线定理得 BD =CD AD ,即 x 4 x =( ) ,解得 x =
2
8 3
4 4 ,故 CD = 。 3 3
▲ 。[
例 11. (2012 年北京市文 5 分)直线 y x 被圆 x 2 y 2 4 截得的弦长为
3
又已知点 P(1,1) ,则 kOP 1 。故所求直线的斜率为-1。 又所求直线过点 P(1,1) ,故由点斜式得,所求直线的方程为 y 1 x 1 ,即 x y 2 0 。 故选 A。 例 6. (2012 年福建省文 5 分)直线 x+ 3y-2=0 与圆 x +y =4 相交于 A,B 两点,则弦 AB 的长度等于 【 】 A.2 5 【答案】B。 【考点】直线与圆的位置关系。 【解析】根据圆的方程知,圆的圆心为(0,0),半径 R=2,弦心距 d= 2 3。故选 B。 例 7.(2012 年辽宁省文 5 分 )将圆 x2 y 2 2 x 4 y 1 0 平分的直线是【 ( A) x y 1 0 【答案】C。 【考点】直线和圆的方程,曲线上点的坐标与方程的关系。 【解析 】∵ x2 y2 2x 4 y 1 0 x 1 y 2 =4 ,
∴ AOB 面积的最小值为 3 。 例 13. (2012 年江苏省 5 分) 在平面直角坐标系 xOy 中, 圆 C 的方程为 x2 y 2 8x 15 0 , 若直线 y kx 2 上 至少存在一点,使得以该点为圆心,1 为半径的圆与圆 C 有公共点 ,则 k 的最大值是 ▲ . 【答案】
同上判别圆心在不在 直线 y =kx 1 上。 还可求圆心到直线 y =kx 1 的距离来判别。 例 2. (2012 年安徽省文 5 分)若直线 x y 1 0 与圆 ( x a) y 2 有公共点,则实数 a 取值范围是
常州市武进区2014届高三数学专题复习:直线与圆

4. 如 图 , 在 平 面 直 角 坐 标 系 xoy 中 , 设 三 角 形 ABC 的 顶 点 分 别 为 A(0, a), B(b,0),C(c,0) ,点 P(0, p) 在线段 AO 上的一点(异于端点),这里 a, b, c, p
均为非零实数,设直线 BP,CP 分别与边 AC ,AB 交于点 E ,F ,某同学已正确求得直线 OE 的方程为 B
(B)
(C)
(D)
2
3
5
【答案】B。
【考点】反函数。
【分析】根据题意画出图形,如图。
∵互为反函数的两个函数的图象关于 y=x 对称,
∴这两个函数的图象交于 P 点必在直线 y=x 上,且 A,B 两点
关于 y=x 对称。
∴AB⊥OP 。 ∴ 四 边 形 OAPB 的 面 积 = 1 ·AB·OP= 2
(2)设过 Q 的切线为 y y1 k1 x x1 ,
由 y x2 得 y/ 2x ,∴ k1 2x1 。
∴ y 2x1x 2x12 y1 2x1x x12 , 它 与 y c 的 交 点 为 M
x1 2
c 2 x1
, c 。
又
P
x1
2
x2
,
y1
2
y2
分别作圆 O1.圆 O2 的切线 PM、PN(M.N 分别为切点),使得 PM 2PN 试建立
适当的坐标系,并求动点 P 的轨迹方程
【答案】解:以 O1O2 的中点 O 为原点,O1O2 所在直线为 x 轴,建立如图所示
平面直角坐标系。 y
则 O1(-2,0),O2(2,0),
由已知: PM 2PN ,即PM2=2PN2,
【考点】直线与圆锥曲线的综合问题,平面向量数量积的运算。
【名师精讲】2014届高考数学一轮轻松突破复习1.8.4直线与圆、圆与圆的位置关系文

【名师精讲】2014届高考数学一轮轻松突破 1.8.4直线与圆、圆与圆的位置关系 文一、选择题1.点M(x0,y0)是圆x2+y2=a2(a >0)内不为圆心的一点,则直线x0x +y0y =a2与该圆的位置关系是( )A .相切B .相交C .相离D .相切或相交解析:由已知得x20+y20<a2,且x20+y20≠0,又∵圆心到直线的距离d =a2x20+y20>a , ∴直线与圆相离.答案:C2.设两圆C1、C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|=( )A .4B .4 2C .8D .8 2解析:依题意,可设圆心坐标为(a ,a)、半径为r ,其中r =a >0,因此圆方程是(x -a)2+(y -a)2=a2,由圆过点(4,1)得(4-a)2+(1-a)2=a2,即a2-10a +17=0,则该方程的两根分别是圆心C1,C2的横坐标,|C1C2|=2×102-4×17=8,选C.答案:C3.若a 、b 、c 是直角三角形的三边(c 为斜边),则圆x2+y2=2截直线ax +by +c =0所得的弦长等于( )A .1B .2C. 3 D .2 3答案:B4.若圆x2+y2-4x -4y -10=0上至多有三个不同点到直线l :ax +by =0的距离为22,则直线l 的斜率的取值范围是( )A .(-∞,2-3]B .[2+3,+∞)C .(-∞,2-3]∪[2+3,+∞)D .[2-3,2+3]答案: C5.直线xsin θ+ycos θ=2+sin θ与圆(x -1)2+y2=4的位置关系是( )A .相离B .相切C .相交D .以上都有可能答案:B6.已知圆x2+y2+x -6y +3=0上的两点P 、Q 关于直线kx -y +4=0对称,且OP ⊥OQ(O 为坐标原点),则直线PQ 的方程为( )A .y =-12x +32B .y =-12x +32或y =-12x +54C .y =-12x +14D .y =-12x +12或y =-12x +54解析:由P 、Q 关于直线kx -y +4=0对称知直线kx -y +4=0过已知圆的圆心(-12,3),则k =2,直线PQ 的斜率kPQ =-12. 设直线PQ 的方程为y =-12x +b ,P(x1,y1)、Q(x2,y2),则P 、Q 两点的坐标是方程组⎩⎪⎨⎪⎧ y =-12x +b x2+y2+x -6y +3=0的解,消去y 得54x2+(4-b)x +b2-6b +3=0,故x1+x2=--5, ①x1x2=-6b +5, ② 由OP ⊥OQ ⇒x1x2+y1y2=0⇒x1x2+(-12x1+b)·(-12x2+b)=0, 54x1x2-b 2(x1+x2)+b2=0, 将①,②代入得b =32或b =54. 所以直线PQ 的方程为y =-12x +32或y =-12x +54.故选B. 答案:B二、填空题7.已知圆心在x 轴上,半径为2的圆O 位于y 轴左侧,且与直线x +y =0相切,则圆O 的方程是__________.解析:设圆心为(a,0)(a <0),则|a|2=2,解得a =-2, 故圆O 的方程为(x +2)2+y2=2.答案:(x +2)2+y2=28.过原点的直线与圆x2+y2-2x -4y +4=0相交所得弦的长为2,则该直线的方程为__________.解析:设所求直线方程为y =kx ,即kx -y =0.由于直线kx -y =0被圆截得的弦长等于2,圆的半径是1,因此圆心到直线的距离等于12-22=0,即圆心位于直线kx -y =0上.于是有k -2=0,即k =2,因此所求直线方程是2x -y =0.答案:2x -y =09.若⊙O :x2+y2=5与⊙O1:(x -m)2+y2=20(m ∈R)相交于A 、B 两点,且两圆在点A 处的切线互相垂直,则线段AB 的长度是__________.解析:依题意得|OO1|=5+20=5,且△OO1A 是直角三角形,S △OO1A =12·|AB|2·|OO1|=12·|OA|·|AO1|,因此|AB|=2·|OA|·|AO1||OO1|=2×5×255=4. 答案:4三、解答题10.根据下列条件求圆的方程:(1)经过坐标原点和点P(1,1),并且圆心在直线2x +3y +1=0上;(2)已知一圆过P(4,-2),Q(-1,3)两点,且在y 轴上截得的线段长为4 3.解析:(1)显然,所求圆的圆心在OP 的垂直平分线上,OP 的垂直平分线方程为x +y -1=0.解方程组⎩⎪⎨⎪⎧ x +y -1=0,2x +3y +1=0,得圆心C 的坐标为(4,-3).又因为圆的半径r =|OC|=5,所以所求圆的方程为(x -4)2+(y +3)2=25.(2)设圆的方程为x2+y2+Dx +Ey +F =0,①将P ,Q 点的坐标分别代入①,得⎩⎪⎨⎪⎧ 4D -2E +F =-20, ②D -3E -F =10. ③令x =0,由①得y2+Ey +F =0,④由已知|y1-y2|=43,其中y1、y2是方程④的两根,所以(y1-y2)2=(y1+y2)2-4y1y2=E2-4F =48.⑤解②③⑤组成的方程组,得D =-2,E =0,F =-12,或D =-10,E =-8,F =4,故所求圆的方程为x2+y2-2x -12=0,或x2+y2-10x -8y +4=0.11.已知m ∈R ,直线-(m2+1)y =4m 和圆x2+y2-8x +4y +16=0.(1)求直线l 斜率的取值范围;(2)直线l 能否将圆C 分割成弧长的比值为12的两段圆弧?为什么? 解析:(1)直线l 的方程可化为y =m m2+1x -4m m2+1, 直线l 的斜率k =m m2+1, 因为|m|≤12(m2+1), 所以|k|=|m|m2+1≤12, 当且仅当|m|=1时等号成立.所以,斜率k 的取值范围是[-12,12]. (2)不能.由(1)知l 的方程为y =k(x -4),其中|k|≤12.圆C 的圆心为C(4,-2),半径r =2.圆心C 到直线l 的距离为d =21+k2. 由|k|≤12,得d≥45>1, 即d >r 2. 从而,若l 与圆C 相交,则圆C 截直线l 所得的弦所对的圆心角小于2π3. 所以l 不能将圆C 分割成弧长的比值为12的两段弧. 12.已知直线l :y =x +m ,m ∈R.(1)若以点M(2,0)为圆心的圆与直线l 相切于点P ,且点P 在y 轴上,求该圆的方程;(2)若直线l 关于x 轴对称的直线为l′,问直线l′与抛物线C :x2=4y 是否相切?说明理由.解析:方法一:(1)依题意,点P 的坐标为(0,m).因为MP ⊥l ,所以0-m 2-0×1=-1, 解得m =2,即点P 的坐标为(0,2). 从而圆的半径r =|MP|=-+-=22,故所求圆的方程为(x -2)2+y2=8.(2)因为直线l 的方程为y =x +m ,所以直线l′的方程为y =-x -m.由⎩⎪⎨⎪⎧ y =-x -m ,x2=4y得x2+4x +4m =0.Δ=42-4×4m=16(1-m).(1)当m =1,即Δ=0时,直线l′与抛物线C 相切;(2)当m≠1,即Δ≠0时,直线l′与抛物线C 不相切.综上,当m =1时,直线l′与抛物线C 相切;当m≠1时,直线l′与抛物线C 不相切. 方法二:(1)设所求圆的半径为r ,则圆的方程可设为(x -2)2+y2=r2.依题意,所求圆与直线l :x -y +m =0相切于点P(0,m),则⎩⎪⎨⎪⎧ 4+m2=r2,|2-0+m|2=r ,解得⎩⎨⎧ m =2,r =2 2.所以所求圆的方程为(x -2)2+y2=8.(2)同方法一.。
历年高三数学高考考点之直线与圆必会题型及答案

历年高三数学高考考点之<直线与圆>必会题型及答案体验高考1.平行于直线2x +y +1=0且与圆x 2+y 2=5相切的直线的方程是( ) A.2x +y +5=0或2x +y -5=0 B.2x +y +5=0或2x +y -5=0 C.2x -y +5=0或2x -y -5=0 D.2x -y +5=0或2x -y -5=0 答案 A解析 设所求直线方程为2x +y +c =0,依题意有|0+0+c |22+12=5,解得c =±5,所以所求直线方程为2x +y +5=0或2x +y -5=0,故选A.2.过三点A (1,3),B (4,2),C (1,-7)的圆交y 轴于M 、N 两点,则|MN |等于( ) A.26B.8C.46D.10 答案 C解析 由已知,得AB →=(3,-1),BC →=(-3,-9),则AB →·BC →=3×(-3)+(-1)×(-9)=0,所以AB →⊥BC →,即AB ⊥BC ,故过三点A ,B ,C 的圆以AC 为直径,得其方程为(x -1)2+(y +2)2=25,令x =0得(y +2)2=24,解得y 1=-2-26,y 2=-2+26,所以|MN |=|y 1-y 2|=46,选C.3.一条光线从点(-2,-3)射出,经y 轴反射后与圆(x +3)2+(y -2)2=1相切,则反射光线所在直线的斜率为( )A.-53或-35B.-32或-23C.-54或-45D.-43或-34答案 D解析 由已知,得点(-2,-3)关于y 轴的对称点为(2,-3),由入射光线与反射光线的对称性,知反射光线一定过点(2,-3).设反射光线所在直线的斜率为k , 则反射光线所在直线的方程为y +3=k (x -2), 即kx -y -2k -3=0.由反射光线与圆相切,则有d =|-3k -2-2k -3|k 2+1=1,解得k =-43或k =-34,故选D.4.已知平行直线l 1:2x +y -1=0,l 2:2x +y +1=0,则l 1,l 2的距离为______. 答案255解析 d =|1+1|22+12=255. 5.已知直线l :mx +y +3m -3=0与圆x 2+y 2=12交于A ,B 两点,过A ,B 分别做l 的垂线与x 轴交于C ,D 两点,若|AB |=23,则|CD |=________. 答案 4解析 设AB 的中点为M ,由题意知, 圆的半径R =23,|AB |=23, 所以|OM |=3,解得m =-33, 由⎩⎨⎧x -3y +6=0,x 2+y 2=12解得A (-3,3),B (0,23),则AC 的直线方程为y -3=-3(x +3),BD 的直线方程为y -23=-3x ,令y =0,解得C (-2,0),D (2,0), 所以|CD |=4.高考必会题型题型一 直线方程的求法与应用例1 (1)若点P (1,1)为圆(x -3)2+y 2=9的弦MN 的中点,则弦MN 所在直线的方程为( ) A.2x +y -3=0 B.x -2y +1=0 C.x +2y -3=0 D.2x -y -1=0答案 D解析 由题意知圆心C (3,0),k CP =-12.由k CP ·k MN =-1,得k MN =2,所以弦MN 所在直线的方程是2x -y -1=0.(2)已知△ABC 的顶点A (3,-1),AB 边上的中线所在直线方程为6x +10y -59=0,∠B 的平分线所在直线方程为x -4y +10=0,求BC 边所在直线的方程. 解 设B (4y 1-10,y 1),由AB 中点在6x +10y -59=0上,可得:6·4y 1-72+10·y 1-12-59=0,y 1=5,∴B (10,5).设A 点关于x -4y +10=0的对称点为A ′(x ′,y ′),则有⎩⎪⎨⎪⎧x ′+32-4·y ′-12+10=0,y ′+1x ′-3·14=-1⇒A ′(1,7),∵点A ′(1,7),B (10,5)在直线BC 上,∴y -57-5=x -101-10,故BC 边所在直线的方程是2x +9y -65=0. 点评 (1)两条直线平行与垂直的判定①若两条不重合的直线l 1,l 2的斜率k 1,k 2存在,则l 1∥l 2⇔k 1=k 2,l 1⊥l 2⇔k 1k 2=-1; ②判定两直线平行与垂直的关系时,如果给出的直线方程中存在字母系数,不仅要考虑斜率存在的情况,还要考虑斜率不存在的情况. (2)求直线方程的常用方法①直接法:直接选用恰当的直线方程的形式,写出结果;②待定系数法:先由直线满足的一个条件设出直线方程,使方程中含有一个待定系数,再由题给的另一条件求出待定系数.变式训练1 已知直线l 经过直线3x +4y -2=0与直线2x +y +2=0的交点P ,且垂直于直线x -2y -1=0. (1)求直线l 的方程;(2)求直线l 关于原点O 对称的直线方程.解 (1)由⎩⎪⎨⎪⎧3x +4y -2=0,2x +y +2=0解得⎩⎪⎨⎪⎧x =-2,y =2.所以点P 的坐标是(-2,2),又因为直线x -2y -1=0, 即y =12x -12的斜率为k ′=12,由直线l 与x -2y -1=0垂直可得k l =-1k ′=-2, 故直线l 的方程为:y -2=-2(x +2),即2x +y +2=0.(2)直线l 的方程2x +y +2=0在x 轴、y 轴上的截距分别是-1与-2,则直线l 关于原点对称的直线在x 轴、y 轴上的截距分别是1与2, 所求直线方程为x 1+y2=1,即2x +y -2=0.题型二 圆的方程例2 (1)如图,已知圆C 与x 轴相切于点T (1,0),与y 轴正半轴交于两点A ,B (B 在A 的上方),且|AB |=2.①圆C 的标准方程为________________.②圆C 在点B 处的切线在x 轴上的截距为________.答案 ①(x -1)2+(y -2)2=2 ②-2-1解析 ①由题意,设圆心C (1,r )(r 为圆C 的半径),则r 2=⎝ ⎛⎭⎪⎫|AB |22+12=2,解得r = 2.所以圆C 的方程为(x -1)2+(y -2)2=2.②方法一 令x =0,得y =2±1,所以点B (0,2+1).又点C (1,2),所以直线BC 的斜率为k BC =-1,所以过点B 的切线方程为y -(2+1)=x -0,即y =x +(2+1). 令y =0,得切线在x 轴上的截距为-2-1.方法二 令x =0,得y =2±1,所以点B (0,2+1).又点C (1,2),设过点B 的切线方程为y -(2+1)=kx ,即kx -y +(2+1)=0.由题意,得圆心C (1,2)到直线kx -y +(2+1)=0的距离d =|k -2+2+1|k 2+1=r =2,解得k =1.故切线方程为x -y +(2+1)=0.令y =0,得切线在x 轴上的截距为-2-1.(2)已知圆C 经过点A (2,-1),并且圆心在直线l 1:y =-2x 上,且该圆与直线l 2:y =-x +1相切. ①求圆C 的方程;②求以圆C 内一点B ⎝ ⎛⎭⎪⎫2,-52为中点的弦所在直线l 3的方程. 解 ①设圆的标准方程为(x -a )2+(y -b )2=r 2,则⎩⎪⎨⎪⎧(2-a )2+(-1-b )2=r 2,b =-2a ,|a +b -1|2=r ,解得⎩⎨⎧a =1,b =-2,r = 2.故圆C 的方程为(x -1)2+(y +2)2=2. ②由①知圆心C 的坐标为(1,-2), 则k CB =-52-(-2)2-1=-12.设直线l 3的斜率为k 3,由k 3·k CB =-1,可得k 3=2. 故直线l 3的方程为y +52=2(x -2),即4x -2y -13=0.点评 求圆的方程的两种方法(1)几何法:通过研究圆的性质、直线和圆、圆与圆的位置关系,进而求得圆的基本量和方程.(2)代数法:用待定系数法先设出圆的方程,再由条件求得各系数.变式训练2 已知圆x 2+y 2=4上一定点A (2,0),B (1,1)为圆内一点,P ,Q 为圆上的动点. (1)求线段AP 中点的轨迹方程;(2)若∠PBQ =90°,求线段PQ 中点的轨迹方程.解 (1)设AP 的中点为M (x ,y ),由中点坐标公式可知,P 点坐标为(2x -2,2y ). 因为P 点在圆x 2+y 2=4上, 所以(2x -2)2+(2y )2=4,故线段AP 中点的轨迹方程为(x -1)2+y 2=1. (2)设PQ 的中点为N (x ,y ),连接BN . 在Rt △PBQ 中,|PN |=|BN |.设O 为坐标原点,连接ON ,则ON ⊥PQ , 所以|OP |2=|ON |2+|PN |2=|ON |2+|BN |2, 所以x 2+y 2+(x -1)2+(y -1)2=4.故线段PQ 中点的轨迹方程为x 2+y 2-x -y -1=0. 题型三 直线与圆的位置关系、弦长问题例3 (1)(2015·重庆)已知直线l :x +ay -1=0(a ∈R )是圆C :x 2+y 2-4x -2y +1=0的对称轴,过点A (-4,a )作圆C 的一条切线,切点为B ,则|AB |等于( ) A.2B.42C.6D.210 答案 C解析 根据直线与圆的位置关系求解.由于直线x +ay -1=0是圆C :x 2+y 2-4x -2y +1=0的对称轴,∴圆心C (2,1)在直线x +ay -1=0上,∴2+a -1=0,∴a =-1,∴A (-4,-1). ∴|AC |2=36+4=40.又r =2,∴|AB |2=40-4=36. ∴|AB |=6.(2)已知圆C :x 2+y 2-2x +4y -4=0.①写出圆C 的标准方程,并指出圆心坐标和半径大小;②是否存在斜率为1的直线m ,使m 被圆C 截得的弦为AB ,且OA ⊥OB (O 为坐标原点).若存在,求出直线m 的方程;若不存在,请说明理由. 解 ①圆C 的标准方程为(x -1)2+(y +2)2=9, 则圆心C 的坐标为(1,-2),半径为3. ②假设存在这样的直线m , 根据题意可设直线m :y =x +b .联立直线与圆的方程⎩⎪⎨⎪⎧x 2+y 2-2x +4y -4=0,y =x +b得2x 2+2(b +1)x +b 2+4b -4=0, 因为直线与圆相交,所以Δ>0, 即b 2+6b -9<0,且满足x 1+x 2=-b -1,x 1x 2=b 2+4b -42,设A (x 1,y 1),B (x 2,y 2), 则y 1=x 1+b ,y 2=x 2+b ,由OA ⊥OB 得OA →·OB →=x 1x 2+y 1y 2=0,所以x 1x 2+(x 1+b )(x 2+b )=2x 1x 2+b (x 1+x 2)+b 2=0, 即b 2+3b -4=0得b =-4或b =1, 且均满足b 2+6b -9<0,故所求的直线m 存在,方程为y =x -4或y =x +1. 点评 研究直线与圆位置关系的方法(1)研究直线与圆的位置关系的最基本的解题方法为代数法,将几何问题代数化,利用函数与方程思想解题.(2)与弦长有关的问题常用几何法,即利用圆的半径r ,圆心到直线的距离d 及半弦长l2,构成直角三角形的三边,利用其关系来处理.变式训练3 已知以点C (t ,2t)(t ∈R ,t ≠0)为圆心的圆与x 轴交于点O ,A ,与y 轴交于点O ,B ,其中O 为原点.(1)求证:△OAB 的面积为定值;(2)设直线y =-2x +4与圆C 交于点M ,N ,若|OM |=|ON |,求圆C 的方程. (1)证明 ∵圆C 过原点O ,且|OC |2=t 2+4t2.∴圆C 的方程是(x -t )2+(y -2t )2=t 2+4t2,令x =0,得y 1=0,y 2=4t;令y =0,得x 1=0,x 2=2t ,∴S △OAB =12|OA |·|OB |=12×|4t |×|2t |=4,即△OAB 的面积为定值.(2)解 ∵|OM |=|ON |,|CM |=|CN |, ∴OC 垂直平分线段MN . ∵k MN =-2,∴k OC =12.∴2t =12t ,解得t =2或t =-2. 当t =2时,圆心C 的坐标为(2,1),|OC |=5, 此时C 到直线y =-2x +4的距离d =15<5,圆C 与直线y =-2x +4相交于两点.当t =-2时,圆心C 的坐标为(-2,-1),|OC |=5, 此时C 到直线y =-2x +4的距离d =95> 5.圆C 与直线y =-2x +4不相交, ∴t =-2不符合题意,舍去. ∴圆C 的方程为(x -2)2+(y -1)2=5.高考题型精练1.已知x ,y 满足x +2y -5=0,则(x -1)2+(y -1)2的最小值为( ) A.45B.25C.255 D.105 答案 A解析 (x -1)2+(y -1)2表示点P (x ,y )到点Q (1,1)的距离的平方.由已知可得点P 在直线l :x +2y -5=0上,所以|PQ |的最小值为点Q 到直线l 的距离,即d =|1+2×1-5|1+22=255, 所以(x -1)2+(y -1)2的最小值为d 2=45.故选A.2.“m =3”是“直线l 1:2(m +1)x +(m -3)y +7-5m =0与直线l 2:(m -3)x +2y -5=0垂直”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件答案 A解析 由l 1⊥l 2得2(m +1)(m -3)+2(m -3)=0, ∴m =3或m =-2.∴m =3是l 1⊥l 2的充分不必要条件.3.若动点A ,B 分别在直线l 1:x +y -7=0和l 2:x +y -5=0上移动,则AB 的中点M 到原点的距离的最小值为( ) A.32B.22C.33D.4 2 答案 A解析 依题意知AB 的中点M 的集合是与直线l 1:x +y -7=0和l 2:x +y -5=0的距离都相等的直线,则M 到原点的距离的最小值为原点到该直线的距离, 设点M 所在直线的方程为l :x +y +m =0, 根据平行线间的距离公式得|m +7|2=|m +5|2⇒|m +7|=|m +5|⇒m =-6,即l :x +y -6=0,根据点到直线的距离公式,得M 到原点的距离的最小值为|-6|2=3 2.4.(2016·山东)已知圆M :x 2+y 2-2ay =0(a >0)截直线x +y =0所得线段的长度是22,则圆M 与圆N :(x -1)2+(y -1)2=1的位置关系是( ) A.内切B.相交C.外切D.相离 答案 B解析 ∵圆M :x 2+(y -a )2=a 2, ∴圆心坐标为M (0,a ),半径r 1=a , 圆心M 到直线x +y =0的距离d =|a |2,由几何知识得⎝⎛⎭⎪⎫|a |22+(2)2=a 2,解得a =2. ∴M (0,2),r 1=2.又圆N 的圆心坐标N (1,1),半径r 2=1,∴|MN |=(1-0)2+(1-2)2=2,r 1+r 2=3,r 1-r 2=1.∴r 1-r 2<|MN |<r 1+r 2,∴两圆相交,故选B.5.与圆x 2+y 2=1和圆x 2+y 2-8x +7=0都相切的圆的圆心轨迹是( ) A.椭圆B.椭圆和双曲线的一支C.双曲线和一条直线(去掉几个点)D.双曲线的一支和一条直线(去掉几个点) 答案 D解析 设所求圆圆心为M (x ,y ),半径为r , 圆x 2+y 2-8x +7=0⇒(x -4)2+y 2=9,圆心设为C (4,0),由题意得当动圆与两定圆外切时, 即|MO |=r +1,|MC |=r +3,从而|MC |-|MO |=2<|OC |, 因此为双曲线的一支,当动圆与两定圆一个外切一个内切时, 必切于两定圆切点,即M 必在x 轴上, 但需去掉O ,C 及两定圆切点,因此选D.6.(2015·课标全国Ⅱ)已知三点A (1,0),B (0,3),C (2,3),则△ABC 外接圆的圆心到原点的距离为( ) A.53B.213 C.253 D.43 答案 B解析 由点B (0,3),C (2,3),得线段BC 的垂直平分线方程为x =1,① 由点A (1,0),B (0,3),得线段AB 的垂直平分线方程为y -32=33⎝⎛⎭⎪⎫x -12,②联立①②,解得△ABC 外接圆的圆心坐标为⎝ ⎛⎭⎪⎫1,233,其到原点的距离为12+⎝ ⎛⎭⎪⎫2332=213.故选B.7.(2016·山东)在[-1,1]上随机地取一个数k ,则事件“直线y =kx 与圆(x -5)2+y 2=9相交”发生的概率为________. 答案 34解析 由已知得,圆心(5,0)到直线y =kx 的距离小于半径,∴|5k |k 2+1<3,解得-34<k <34,由几何概型得P =34-⎝ ⎛⎭⎪⎫-341-(-1)=34.8.在平面直角坐标系xOy 中,圆C 的方程为x 2+y 2-8x +15=0,若直线y =kx -2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,则k 的最大值是________. 答案 43解析 圆C 的标准方程为(x -4)2+y 2=1,圆心为(4,0). 由题意知(4,0)到kx -y -2=0的距离应不大于2, 即|4k -2|k 2+1≤2.整理,得3k 2-4k ≤0.解得0≤k ≤43.故k 的最大值是43.9.在平面直角坐标系xOy 中,已知圆x 2+y 2=4上有且仅有三个点到直线12x -5y +c =0的距离为1,则实数c 的值为________. 答案 ±13解析 因为圆心到直线12x -5y +c =0的距离为|c |13,所以由题意得|c |13=1,c =±13.10.已知直线l 过点(-2,0),当直线l 与圆x 2+y 2=2x 有两个交点时,其斜率k 的取值范围是________________. 答案 (-24,24) 解析 因为已知直线过点(-2,0),那么圆的方程x 2+y 2=2x 配方为(x -1)2+y 2=1,表示的是圆心为(1,0),半径为1的圆, 设过点(-2,0)的直线的斜率为k , 则直线方程为y =k (x +2), 则点到直线距离等于圆的半径1, 有d =|k -0+2k |k 2+1=1,化简得8k 2=1, 所以k =±24, 然后可知此时有一个交点,那么当满足题意的时候, 可知斜率的取值范围是(-24,24),故答案为(-24,24). 11.已知过点A (0,1),且方向向量为a =(1,k )的直线l 与圆C :(x -2)2+(y -3)2=1相交于M ,N 两点.(1)求实数k 的取值范围;(2)若O 为坐标原点,且OM →·ON →=12,求k 的值.解 (1)∵直线l 过点A (0,1)且方向向量为a =(1,k ),∴直线l 的方程为y =kx +1. 由|2k -3+1|k 2+1<1,得4-73<k <4+73.(2)设M (x 1,y 1),N (x 2,y 2),将y =kx +1代入方程(x -2)2+(y -3)2=1,得(1+k 2)x 2-4(1+k )x +7=0,∴x 1+x 2=4(1+k )1+k 2,x 1x 2=71+k 2,∴OM →·ON →=x 1x 2+y 1y 2=(1+k 2)x 1x 2+k (x 1+x 2)+1=4k (1+k )1+k 2+8=12,∴4k (1+k )1+k 2=4,解得k =1.12.已知圆M ∶x 2+(y -2)2=1,Q 是x 轴上的动点,QA ,QB 分别切圆M 于A ,B 两点.(1)若Q (1,0),求切线QA ,QB 的方程;(2)求四边形QAMB 面积的最小值;(3)若|AB |=423,求直线MQ 的方程.解 (1)设过点Q 的圆M 的切线方程为x =my +1,则圆心M 到切线的距离为1,∴|2m +1|m 2+1=1,∴m =-43或0,∴切线QA ,QB 的方程分别为3x +4y -3=0和x =1.(2)∵MA ⊥AQ ,∴S 四边形MAQB =|MA |·|QA |=|QA | =|MQ |2-|MA |2=|MQ |2-1 ≥|MO |2-1= 3.∴四边形QAMB 面积的最小值为 3.(3)设AB 与MQ 交于点P ,则MP ⊥AB .∵MB ⊥BQ ,∴|MP |=1-⎝ ⎛⎭⎪⎫2232=13.在Rt △MBQ 中,|MB |2=|MP |·|MQ |,即1=13|MQ |,∴|MQ |=3.设Q (x ,0),则x 2+22=9,∴x =±5,∴Q (±5,0),∴直线MQ 的方程为2x +5y -25=0或2x -5y +25=0.。
2014高考数学直线与圆汇编

2014高考直线与园
1.(新课标二16.)设点M (0x ,1),若在圆O:221x y +=上存在点N ,使得∠OMN=45°,则0x 的取值范围是________.
【答案】].
1,1-[∈x ].1,1-[x .,1)M(x 1,y O 000故形外角知识,可得由圆的切线相等及三角在直线上其中和直线在坐标系中画出圆∈= 2.(重庆13)已知直线02=-+y ax 与圆心为C 的圆()()412
2=-+-a y x 相交于B A ,两点,且 ABC ∆为等边三角形,则实数=a _____.
3.(湖北).直线1l :y=x+a 和2l :y=x+b 将单位圆22:1C x y +=分成长度相等的四段弧,则22a b +=___2 _____.
4.(福建).直线:1l y kx =+与圆22:1O x y +=相交于,A B 两点,则"1"k =是“ABC ∆的面积为12
”的( A ) .A 充分而不必要条件 .B 必要而不充分条件
.C 充分必要条件 .D 既不充分又不必要条件
5.(陕西)若圆C 的半径为1,其圆心与点)0,1(关于直线x y =对称,则圆C 的标准方程为_______.
【答案】 .11-(1),1,0(∴)1,0()0,1(22=+=)的标准方程为半径为圆心为,的对称点关于点y x x y 9.
6.(江苏)在平面直角坐标系xOy 中,直线032=-+y x 被圆4)1()2(22=++-y x 截得的弦长为 ▲ .。
2014届高三数学最后一课试题拆解:直线和圆

直线和圆1. “1k =”是“直线0x y k -+=与圆221x y +=相交”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分又不必要条件【答案】A【解析】若直线0x y k -+=与圆221x y +=相交,则有圆心(0,0)到直线0x y k -+=的距1<,解得k <<,故选A.2.由直线2+=x y 上的点向圆()()22421x y -++= 引切线,则切线长的最小值为( )A .30B .31C .24D .33【解析】(1)设椭圆C 的方程为22221x y a b +=直线30x ky +-=所经过的定点是(3,0),即点F (3,0) ∵椭圆C 上的点到点F 的最大距离为8 ∴38a += 5a = ∴22216b a c =-=∴椭圆C 的方程为2212516x y +=(2)∵点(,)P m n 在椭圆C 上∴2212516m n +=,22161625m n =-[ ∴原点到直线:1l mx ny +=的距离1d ==∴直线:1l mx ny +=与圆22:1O x y +=恒相交222214()4(1)91625L r d m =-=-+∵05m ≤≤L ≤≤4.由直线2+=x y 上的点向圆()()22421x y -++= 引切线,则切线长的最小值为( )A .30B .31C .24D .33证法1:过点P 作直线l 的垂线,垂足为H .若A = 0,则直线l 的方程为C y B =-,此时点P 到直线l 的距离为0||C y B +00||||||By C C y B B +==+,可知结论是成立的. ————5分证法2:若B = 0,则直线l 的方程为Cx A =-,此时点P 到直线l 的距离为0||Cd x A =--==证法3:过点P作直线l的垂线,垂足为H.则直线PH的一个方向向量对应于直线l 的一个法向量,而直线l的一个法向量为(,)A B,又线段PH的长为d,所以,)||PHPH d A BPH→→→==或,)PH A B→=||||PQ vdv→→→∙===因为0000()()()x x A y y B Ax By Ax By-+-=+-+,而点(,)x y满足0Ax By C++=,所以0000()()Ax By Ax By Ax By C+-+=-++.因此||d=.6.已知圆C1的方程为22(2)1x y+-=,定直线l的方程为1y=-.动圆C与圆C1外切,且与直线l相切.(Ⅰ)求动圆圆心C的轨迹M的方程;(II )斜率为k 的直线l 与轨迹M 相切于第一象限的点P ,过点P 作直线l 的垂线恰好经过点A (0,6),并交轨迹M 于异于点P 的点Q ,记S 为∆POQ (O 为坐标原点)的面积,求S 的值. 解(Ⅰ)设动圆圆心C 的坐标为(,)x y ,动圆半径为R ,则1||1CC R ==+,且|1|y R += ————2分 可得|1|1y =++.由于圆C 1在直线l 的上方,所以动圆C 的圆心C 应该在直线l 的上方,所以有10y +>,2y =+,整理得28x y =,即为动圆圆心C 的轨迹M 的方程. ————5分(II )如图示,设点P 的坐标为200(,)8x x ,则切线的斜率为04x ,可得直线PQ 的斜率为04x -,所以直线PQ 的方程为20004()8x y x x x -=--.由于该直线经过点A(0,6),所以有20648x -=,得2016x =.因为点P 在第一象限,所以04x =,点P 坐标为(4,2),直线PQ 的方程为60x y +-=. —————9分由条件得1112y yx x-+?-,------------------------------------------2’即() 2210 2xy x+=动点P 的轨迹C 的方程为22121222422,1212k k x x x x k k -∴+=-=++-----------------------------12’21.已知圆C 的圆心为(,0)(3)C m m <,半径为5,圆C 与椭圆E :)0(12222>>=+b a b y a x 有一个公共点(3,1)A ,21F F 、分别是椭圆的左、右焦点.(Ⅰ)求圆C 的标准方程;(Ⅱ)若点P 的坐标为(4,4),试探究斜率为k 的直线1PF 与圆C 能否相切,若能,求出椭圆E 和直线1PF 的方程,若不能,请说明理由.∴0112442=+-k k ,解得21211==k k ,或。
高三高考数学总复习《直线与圆》题型归纳与汇总

高考数学总复习题型分类汇《直线与圆》篇经典试题大汇总目录【题型归纳】题型一倾斜角与斜率 (3)题型二直线方程 (3)题型三直线位置关系的判断 (4)题型四对称与直线恒过定点问题 (4)题型五圆的方程 (5)题型六直线、圆的综合问题 (6)【巩固训练】题型一倾斜角与斜率 (7)题型二直线方程 (8)题型三直线位置关系的判断 (9)题型四对称与直线恒过定点问题 (10)题型五圆的方程 (11)题型六直线、圆的综合问题 (12)高考数学《直线与圆》题型归纳与训练【题型归纳】题型一 倾斜角与斜率例1 直线l 310y +-=,则直线l 的倾斜角为( )A. 0150B. 0120C. 060D. 030【答案】 A【解析】由直线l 的方程为310y +-=,可得直线的斜率为33-=k ,设直线的倾斜角为[)πα,0∈,则33tan -=α,∴︒=150α. 故选:A .【易错点】基础求解问题注意不要算错【思维点拨】直线方程的基础问题(倾斜角,斜率与方程,注意倾斜角为α为2π,即斜率k 不存在的情况)应对相关知识点充分理解,熟悉熟练例2 已知三点()0,a A 、()7,3B 、()a C 9,2--在一条直线上,求实数a 的值.【答案】2=a 或92=a 【解析】597,35a k a k CB AB +=-= ∵A 、B 、C 三点在一条直线上,∴BC AB k k =,即59735a a +=-,解得2=a 或92=a .题型二 直线方程例1 经过点()1,1M 且在两坐标轴上截距相等的直线是( ).A. 2x y +=B. 1x y +=C. 1x =或1y =D. 2x y +=或x y =【答案】D【解析】若直线过原点,则直线为y x =符合题意,若直线不过原点设直线为1x y m m+=, 代入点()1,1解得2m =,直线方程整理得20x y +-=,故选D .【易错点】截距问题用截距式比较简单,但截距式1=+n y m x 中要求m ,n 均非零。
高考数学试题分项版解析专题13直线与圆文(1)

专题13 直线与圆一、选择题1. 【2014高考北京文第7题】已知圆()()22:341C x y -+-=和两点(),0A m -,()(),00B m m >,若圆上存在点,使得90APB ∠=,则的最大值为( )A. B. C. D.【答案】B考点:本小题主要考查两圆的位置关系,考查数形结合思想,考查分析问题与解决问题的能力.2. 【2015高考北京,文2】圆心为()1,1且过原点的圆的方程是( )A .()()22111x y -+-=B .()()22111x y +++=C .()()22112x y +++=D .()()22112x y -+-=【答案】D【解析】由题意可得圆的半径为r =()()22112x y -+-=,故选D. 【考点定位】圆的标准方程.【名师点晴】本题主要考查的是圆的标准方程,属于容易题.解题时一定要抓住重要字眼“过原点”,否则很容易出现错误.解本题需要掌握的知识点是圆的标准方程,即圆心(),a b ,半径为的圆的标准方程是()()222x a y b r -+-=.3.【 2014湖南文6】若圆221:1C x y +=与圆222:680C x y x y m +--+=相外切,则m =( ).21A .19B .9C .11D -【答案】C【解析】因为()()22226803425x y x y m x y m +--+=⇒-+-=-,所以250m ->25m ⇒<且圆的圆心为()3,4,根据圆与圆外切的判定(圆心距离等于半径和)可得1=+9m ⇒=,故选C.【考点定位】圆与圆之间的外切关系与判断【名师点睛】本题主要考查了圆与圆的位置关系,解决问题的关键是根据条件得到圆的半径及圆心坐标,然后根据两圆满足的几何关系进行列式计算即可.4. 【2014全国2,文12】设点()0,1M x ,若在圆22:+1O x y =上存在点,使得45OMN ∠=︒,则的取值范围是( )(A )[]1,1-- (B )11,22⎡⎤-⎢⎥⎣⎦ (C)⎡⎣ (D),22⎡-⎢⎣⎦【答案】A【考点定位】直线与圆的位置关系【名师点睛】本题考查直线与圆的位置关系,属于中档题,直线与直线设出角的求法,数形结合是快速解得本题的策略之一.5. 【2014四川,9文】设m R ∈,过定点的动直线0x my +=和过定点的动直线30mx y m --+=交于点(,)P xy ,则||||PA PB +的取值范围是()A、B、C 、D 、【答案】B【解析】试题分析:易得(0,0),(1,3)A B .设(,)P x y ,则消去得:2230x y x y +--=,所以点P 在以AB为直径的圆上,PA PB ⊥,所以222||||||10PA PB AB +==,令|10s i ||10c o sP A P θθ==,则 ||||)4PA PB πθθθ+==+.因为||0,||PA PB ≥≥,所以02πθ≤≤.sin()14πθ≤+≤||||PA PB ≤+≤选B.。
2014届高三数学一轮复习精讲精练:8.4直线与圆的位置关系

2014届高三数学一轮复习精讲精练:8.4直线与圆的位置关系|OA|=|CB|=1 ∴|PO|2=|PC|2,从而2222)4()2(-+-=+b a b a化简得实数a 、b 间满足的等量关系为: 052=-+b a . 例3.已知圆C 与两坐标轴都相切,圆心C 到直线y x=-2. 求圆C 的方程.解:设圆C 半径为r ,由已知得:22a b r a a b ⎧⎪=⎪⎪=⎨⎪+⎪=⎪⎩ ∴11a b r ==⎧⎨=⎩,或11a b r ==-⎧⎨=⎩∴圆C 方程为2222(1)(1)1,(1)(1)1x y x y -+-=+=或++.例4.如图,在平面直角坐标系x O y 中,平行于x 轴且过点A(33,2)的入射光线l 1被直线l :y =33x 反射.反射光线l 2交y 轴于B 点,圆C 过点A 且与l 1, l 2都相切.(1)求l 2所在直线的方程和圆C 的方程;(2)设P ,Q 分别是直线l 和圆C 上的动点,求PB+PQ 的最小值及此时点P 的坐标.xyO ABll解:(1)直线1:2,l y =设1232l l D D交于点,则(,).l的倾斜角为30,260l ∴的倾斜角为,23.k ∴=∴反射光线2l所在的直线方程为23(23)y x -=-. 即340x y --=.已知圆C 与1l A 切于点,设C (a,b),圆心C 在过点D 且与l 垂直的直线上,38b a ∴=+ ,又圆心C 在过点A 且与1l 垂直的直线上,33a ∴=381b a ∴=+=-,圆C 的半径r=3,故所求圆C 的方程为22(33)(1)9x y -++=.(2)设点()0,4B -关于l 的对称点0(,)B x y ',则0000432243y x y x ⎧-=⎪⎪⎨+⎪=-⎪⎩,得(23,2)B '-,固定点Q 可发现,当B P Q '、、共线时,PB PQ+最小,故PB PQ+的最小值为32213B C '-=-.此时由1332123333y x y x ⎧+-=⎪+⎪--⎨⎪=⎪⎩得31()2P . 【反馈练习】1.圆x 2+y 2-4x=0在点P(1,3)处的切线方程为320x -+=2.已知直线l 过点),(02-,当直线l 与圆xy x222=+有两个例4交点时,其斜率k 的取值范围是22-(,3.设m>0,则直线2(x+y)+1+m=0与圆x 2+y 2=m 的位置关系为相切或相离解析:圆心到直线的距离为d=21m+,圆半径为m . ∵d-r=21m +-m =21(m-2m +1)=21(m -1)2≥0,∴直线与圆的位置关系是相切或相离.4.圆(x-3)2+(y-3)2=9上到直线3x+4y-11=0的距离等于1的点有个数为35.点P 从(1,0)出发,沿单位圆122=+y x 逆时针方向运动32π弧长到达Q 点,则Q 的坐标为)23,21(-6.若圆04122=-++mx y x 与直线1-=y 相切,且其圆心在y 轴的左侧,则m 的值为347.设P 为圆122=+y x上的动点,则点P 到直线1043=--y x 的距离的最小值为 1 .8.已知平面区域00240x y x y ≥⎧⎪≥⎨⎪+-≤⎩恰好被面积最小的圆222:()()C x a y b r -+-=及其内部所覆盖.(1)试求圆C 的方程.(2)若斜率为1的直线l 与圆C 交于不同两点,.A B 满足CA CB ⊥,求直线l 的方程.解:(1)由题意知此平面区域表示的是以(0,0),(4,0),(0,2)O P Q 构成的三角形及其内部,且△OPQ 是直角三角形, 所以覆盖它的且面积最小的圆是其外接圆,故圆心是(2,1),半径是5,所以圆C 的方程是22(2)(1)5x y -+-=.(2)设直线l 的方程是:y x b =+. 因为CA CB ⊥,所以圆心C到直线l10,221011=+解得:15b=-±.所以直线l的方程是:15y x=-±.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【精选三年经典试题(数学)】2014届高三全程必备《高频题型全掌
握系列》13.直线与圆的典型题
1错误!未指定书签。
.(2013年重庆数学)已知圆()()2
2
1:231C x y -+-=,圆
()()22
2:349C x y -+-=,,M N 分别是圆12,C C 上的动点,P 为x 轴上的动点,则
PM PN +的最小值为( )
A .4
B 1
C .6-D
A
两圆的圆心和半径分别为12(2,3),(3,4)C C ,121,3r r ==。
两圆相离。
()()221:231C x y -+-=关于x 的对称圆的方程为()()22
3:231C x y -++=,圆心
3(2,3)C -,所以13PC PC =,所以动点P 到圆心32(2,3),(3,4)C C -的距离之和的最小值为
23C C ===PM PN +的最小值为
23134C C --=,选A.
2.(2013·潍坊模拟)若圆x 2+y 2=r 2
(r >0)上仅有4个点到直线x -y -2=0的距离为1,则实数r 的取值范围是
( ).
A .(2+1,+∞)
B .(2-1,2+1)
C .(0,2-1)
D .(0,2+1)
解析 计算得圆心到直线l 的距离为
22
=2>1,得
到右边草图.直线l :x -y -2=0与圆相交,l 1,l 2与l 平行,且与直线l 的距离为1,故可以看出,圆的半径应该大于圆心到直线l 2的距离2+1,故选A. 答案 A
3.(2013年辽宁数学(理))已知点
()()()30,0,0,,,.ABC ,O A b B a a ∆若为直角三角形则必有
( )
A .3
b a = B .31
b a a
=+
C .(
)3
3
10b a b a a ⎛⎫
---= ⎪⎝⎭
D .3
3
1
0b a b a a
-+--
= C
若A 为直角,则根据A 、B 纵坐标相等,所以30b a -=;若B 为直角,则利用1OB AB K K =-得31
0b a a
--
=,所以选C
4错误!未指定书签。
.(2013年高考江西卷(理))如图,半径为1的半圆O 与等边三角形ABC 夹在两平行线,12,l l 之间l //1l ,l 与半圆相交于F,G 两点,与三角形ABC 两边相交于E,D 两
点,设弧 FG 的长为(0)x x π<<,y EB BC CD =++,若l 从1l 平行移动到2
l ,则函数()y f x =的图像大致是
D
本题考查函数图象的识别和判断。
设l 与1l 的距离为t ,根据题意易知t x
-=12
cos
,即2
cos 1x
t -=。
又,332t CD BE ==332=BC 。
所以332)2cos 1(334332334+-=+=
++=x t BC CD EB y 2
cos 33432x -=,所以
易得函数图像为D。
