微积分讲义
微积分讲义1

微积分讲义1微积分讲义基础内容:函数⼀.集合1.集合的相关概念1.满⾜共同属性的对象的全体叫做集合,集合的研究对象叫元素.例:军训前学校通知:8⽉15⽇8点,⾼⼀年级学⽣到操场集合进⾏军训.试问这个通知的对象是全体的⾼⼀学⽣还是个别学⽣?每个学⽣与全体⾼⼀学⽣之间的关系?问题:世界上最⾼的⼭能不能构成⼀个集合?世界上的⾼⼭能不能构成⼀个集合?我们把研究的对象统称为“元素”,那么把⼀些元素组成的总体叫“集合”.2.元素与集合的关系有两种:属于∈,不属于?元素的特性(判断是否为集合的依据):(1)确定性:给定的集合,它的元素必须是明确的,即任何⼀个元素要么在这个集合中,要么不在这个集合中,这就是集合的确定性.(2)⽆序性:即集合中的元素是没有顺序的.(3)互异性:⼀个给定集合的元素是互不相同的,即集合中的元素是不重复出现的,这就是集合的互异性.结论:1、⼀般地,指定的某些对象的全体称为集合,标记:A,B,C,D,…集合中的每个对象叫做这个集合的元素,标记:a,b,c,d,…2、元素与集合的关系a是集合A的元素,就说a属于集合A ,记作a∈A ,a不是集合A的元素,就说a不属于集合A,记作a?A3.有限集、⽆限集、空集、单元素集N,整数集记作Z, 4.常⽤数集及其记法:⾃然数集记作N,正整数集记作*N或+有理数集记作Q,实数集记作R.注意:(1))}{ba都是单元素集a},,{((2)}0{φ的区别},{},{例1 判断以下元素的全体是否组成集合:(1)⼤于3⼩于11的偶数;()(2)我国的⼩河流; ( )(3)⾮负奇数;()(4)本校2009级新⽣;()(5)⾎压很⾼的⼈;()(6)著名的数学家;()例题2 下列各组对象不能组成集合的是( )A.⼤于6的所有整数B.⾼中数学的所有难题C.被3除余2的所有整数D.函数y=图象上所有的点练习1.下列条件能形成集合的是( )A.充分⼩的负数全体B.爱好⾜球的⼈C.中国的富翁D.某公司的全体员⼯2.下列结论中,不正确的是( )A.若a ∈N ,则-a NB.若a ∈Z ,则a 2∈ZC.若a ∈Q ,则|a |∈QD.若a ∈R ,则4、(1) -3 N ;(2) 3.14 Q ;(3) Q ;(4)0 Φ;(5) Q ;(6) R ;(7)1 N +;(8) R 。
经济数学基础(微积分)讲义全

经济数学微积分学习讲义合川电大兰冬生知识点一:5个基本函数1,常数函数,c y = (c 是常数)例如:3=y ,1-=y ,这些函数可以看成是x 隐含,例如3=y 可看成30+=x y 。
2,幂函数,αx y =(α是一个数) 形如2x y =,3x y =,5x y =是幂函数,注意:仅仅是这种形式是幂函数,其他的任何一点形式变化都不是,2x y =是幂函数,22x y =就不是幂函数,只能是下面x ,上面(指数)是一个数!以下基本函数均如此3,指数函数,x a y =,(a 是一个数) 例如:x y 2=,x y 23⋅=不是指数函数。
4,对数函数x y a log =,这里要求x 必须大于零,我们的考试常常拿来考“求定义域”这里我们只认识两个特殊的对数函数,一个是x y ln =,他是x y e log =的简写,e 是一个数,718.2=e ,和我们知道的14.3=π一样,另一个是x y lg =,他是x y 10log =的简写。
5,三角函数x y sin =,x y cos =,特别注意的是x y sin 2=,x y 2sin =,都不是三角函数。
● 这5个基本函数是我们要学习的函数的主要构成细胞。
● 例如:12sin 232+++=x x e y x ,二次函数,由幂函数,常数函数构成632-+=x x y 。
知识点二:极限1,什么是数列?数列就是按照“一定规律排列的一组数”,我们常见的是无限数列。
数学符号记为:}{n a例如:数列:1,2,4,8,16,32,……,发展规律依n 2 变化,,4,3,2,1,0=n …… 1,21,41,81,……,发展规律依n 21变化,,4,3,2,1,0=n …… 2,极限学习极限,一个非常重要的认识就是“分母越大,分数越小” 数列的极限,就是指数列的一个趋近值,(即是指一串数的趋近值)例如:1,21,31,41,……,分母由1,2,3,4,……变化,当分母无限大时,1000001,1000000001,……,最后,这个无限数列趋近于0,这里,我们简单描述这个变化,∞→n01→n分母越大,分数越小 →是趋近,∞是无穷大的意思,无穷大是指非常非常大,无法计量。
微积分讲解ppt课件

多元函数的表示 方法
多元函数可用记号 f(x1,x2,…,xn)或z=f(x,y) 表示。
多元函数的定义 域
使多元函数有意义的自 变量组合(x1,x2,…,xn) 的集合。
多元函数的值域
多元函数所有值的集合 。
20
偏导数与全微分
偏导数的定义
设函数z=f(x,y)在点(x0,y0)的某一邻域内有定义,当y固定在y0而x在x0处有增量Δx时,相应地函数有增量 f(x0+Δx,y0)-f(x0,y0)。如果Δz与Δx之比当Δx→0时的极限存在,那么此极限值称为函数z=f(x,y)在点(x0,y0)处对 x的偏导数。
22
06
微积分在实际问题中的应用
2024/1/25
23
在物理学中的应用
运动学
描述物体的位置、速度和加速度 之间的关系,通过微积分可以精 确地计算物体的运动轨迹和速度 变化。
力学
研究物体受力作用下的运动规律 ,微积分可用于求解牛顿第二定 律中的加速度和力的关系。
电磁学
分析电场和磁场的分布和变化规 律,微积分可用于求解麦克斯韦 方程组等电磁学基本方程。
2024/1/25
9
微分法则与运算技巧
微分的基本法则
包括和差微分法则、乘积 微分法则、商微分法则等 。
微分运算技巧
换元法、分部积分法、有 理化分母等,用于简化复 杂的微分运算。
隐函数与参数方程
对于无法直接求解的隐函 数和参数方程,可通过微 分法求解其导数。
微分的应用
在几何、物理、经济等领 域中的应用,如求曲线的 切线、求速度加速度、求 边际效应等。
全微分的定义
如果函数z=f(x,y)在点(x,y)的全增量Δz=f(x+Δx,y+Δy)-f(x,y)可以表示为Δz=AΔx+BΔy+o(ρ),其中A、B不依赖 于Δx, Δy而仅与x,y有关,ρ=(Δx^2+Δy^2)^0.5,则称函数z=f(x,y)在点(x,y)处可微,AΔx+BΔy称为函数 z=f(x,y)在点(x,y)处的全微分。
《微积分的基本定理》课件

物理
在物理学科中,该定理可以用来 解决各种物理量如质量、速度、 力等的积分问题,例如计算物体 的动量、动能等。
工程
在工程领域,该定理可以用来解 决各种实际问题的积分计算,例 如计算电路中的电流、求解流体 动力学中的压力分布等。
02 定理的证明
定理证明的思路
明确问题
首先,我们需要明确微积分的基本定理是关于什 么的,以及它要解决的问题是什么。
难点2
如何利用积分运算法则简化每个小部分的积 分。
关键点1
理解定积分的定义和性质,以及它们在证明 定理中的作用。
关键点2
掌握导数的定义和性质,以及它们在推导原 函数值增量中的应用。
03 定理的推论和扩 展
推论一:积分中值定理
总结词
积分中值定理是微积分中的一个重要定理,它表明在闭区间上连续的函数一定存在至少一个点,使得该函数在此 点的值为该区间上函数积分的平均值。
详细描述
积分中值定理是微积分中的一个基本定理,它表明如果一个函数在闭区间上连续,那么在这个区间内一定存在至 少一个点,使得该函数在这一点处的值等于该函数在整个区间上的平均值。这个定理在解决一些微积分问题时非 常有用,因为它可以帮助我们找到函数在某个点处的值,而不需要计算整个区间的积分。
推论二:洛必达法则
个定积分的值就是曲边梯形的面积。
应用实例二:求解不定积分
总结词
微积分的基本定理是求解不定积分的关 键工具。
VS
详细描述
不定积分是微分学的逆运算,其求解过程 需要用到微积分的基本定理。根据基本定 理,不定积分∫f(x)dx = F(x) + C,其中 F(x)是f(x)的一个原函数,C是常数。通过 基本定理,我们可以找到一个函数F(x), 使得F'(x) = f(x)。这样,我们就可以求解 不定积分了。
微积分专题讲座讲义

d dy dy 2 dy dt d y dt dx ) 公式法) ;⑷参数方程确定的函数(用导数公式: , 2 ;⑸抽象函数(正确使用导数记 dx dx dx dx dt dt
号,注意 f ( x ) 和 [ f ( x )] 的区别) ;⑹幂指函数(对数求导法) ;⑺反函数(导数公式:
2 0
f (sin x)dx ;
▲记 I n
2 0
sin n xdx 2 cos n xdx ,则有递推公式 I n
0
n 1 I n2 . n
⑤含 f , f (用分部积分) ⑥变限积分(用分部积分) 若 f ( x) 在 [ a, b] 上连续,则 ( x) 公式
x a
f (t )dt 在 [a, b] 上可导,且 x [a, b] , ( x) f ( x) .
d b d ( x) f (t )dt f ( x) ; f (t )dt f ( ( x)) ( x) ; dx x dx a d ( x) f (t )dt f ( ( x)) ( x) f ( ( x)) ( x) dx ( x ) ▲当被积函数含变量 x 时不能直接求导, 必须将变量 x 从被积函数中分离出去, 常用的方法是: 提出去或者换元.
【- 4 -】
一、一阶微分方程 一阶微分方程的一般形式是: F ( x, y, y) 0 ,解出 y :
dy f ( x, y ) ,要求掌握变量可分离的微分方程、一阶 dx
线性微分方程、.齐次微分方程、伯努利方程的解法. 求解微分方程的步骤是:判断方程的类型并用相应的方法求解. 二、可降阶的微分方程 1. y f ( x) 型的微分方程 特点:右端仅含 x .解法:积分两次. 2. y f ( x, y) 型的微分方程 特点:右端不显含未知函数 y .解法:换元,化为一阶方程求解. 步骤如下: ⑴令 y p ,则 y
微积分》第二篇第二章讲义定积分

dx
1 e4 1 x4 e 1 3e4 1 4 4 1 16
28
(4) 求定积分 2 xcos2xdx. 0
【解】
2
xcos2xdx
1
2 x(sin2x)dx
0
20
1 2
x
sin
2x
2 0
2 0
1
s
in
2
xdx
1 2
0
1 2
2 0
(c
os2
x)dx
1 2
0
1 cos2x 2
0 excosxdx 0 ex cosxdx
a
a
excosx 0 0 exsinxdx aa
1 eacosa 0 ex sinxdx a
37
即 0 excosxdx a
1 eacosa exsinx 0 0 excosxdx aa
1 eacosa 0 easina 0 excosxdx a
39
21
2 22 1
1 e2 1 4 24
【例7】求定积分 4 1 xex dx. 0
解: 原式
4
1dx
4 xexdx.
0
0
x 4
4
x
ex
dx.
0
0
4
xex
4 0
4 0
x
e
xdx
.
4 4e4 4 exdx 0
4 4e4 ex 4 5 5e4 0
25
课本P-274,题2,(1)—(4)
广义积分 f (x)dx收敛或存在. a 相反,如果极限 lim b f (x)dx不存在, b a
我们就称广义积分 f (x)dx发散或不存在. a 我们的目标:计算一些函数的广义积分
(完整word版)微积分(知识点概要).(良心出品必属精品)

微积分 (知识点概要)第一章函数、极限与连续1.1函数定义与符号1.2极限概念与运算法则1.3求极限的方法1.4函数的连续性1.1函数的定义(P1)1.若变量x、y之间存在着确定的对应关系,即当x的值给定时,唯一y值随之也就确定,则称y是x的函数,记为y=f(x)。
2.确定函数有两个要素:函数的定义域和对应关系。
例如:y=lgx2 与y =2lgx 就不是相同的函数,因为它们的定义域不同。
一旦在问题中设定函数y=f(x),记号“f”就是表示确定的对应规则,f(3)就是表示按此对应规则在x=3时所对应的函数值y等。
P6)称幂函数x k(k为常数),指数函数a x ,对数函数loga x (a为常数,a﹥0,a≠1)三角函数及反三角函数为基本初等函数。
凡由基本初等函数经有限次...加、减、乘、除及有限次复合且能用一个式子表达的函数,称为初等函数。
(1)有界性:(P5)对于函数f(x),若存在常数M、m对定义域内所有xf(x)≤M 称f(x)有上界f(x)≥m 称f(x)有下界,既有上界又有下界简称有界。
(2)奇偶性:(P3)若函数f(x)的定义域关于x=0的对称区间,又对于定义域内的任意x均有f(-x)=f(x) 则称f(x)为偶函数。
f(-x)=-f(x) 则称f(x)为奇函数。
(3)单调性:(P4)若函数f(x)在[a、b]上有定义对∀x∊[a、b]x1﹤x2时f(x1)≤f(x2) f(x) 在[a、b]上↗f(x1)≥f(x2) f(x) 在[a、b]上↘(4)周期性:(P5)若存在常数a(a≠0),使对任意x且有f(x)= f(x+a)则称f(x)为周期函数,称常数a 为f(x)的周期。
1.2极限概念与运算法则P11)当一个变量f(x)在x →a 的变化过程中变化趋势是无限地接近于一个常数b ,则称变量f(x)在x →a 的过程中极限存在。
称常数b 为它的极限,记为ax →lim f(x)=b 否则就称极限不存在。
微积分讲义chap3.3

3. Continu ous functions3.19. Defi ni tionER, E and f: E R.1. f is continuous ata E,if given >0, >0 s.t 0< x a , x E f(x) f(a) .2. f is continuous onEif f is continuous ata , a E.3.20. TheoremLet I be an open interval such that contains a poina and f : I R .Then f iscontinuous at a I iff lim f (x) f (a).x a3.21 TheoremSuppose thatE is a non empty subset oR, a E and f : E R. Then follow ing stateme nts are equivale nt:(1) f is continu ous ata.(2) If x n con verges toa and x n E , the n f(x n) f(a) as n3.22 TheoremSuppose thatE is a non empty subset oR, a E and f, g : E R . If f and g are con ti nu ous at a, the n(1) f+g and f-g are continuous ata.(2) f gg is continuous ata.(3) f is continuous at a for each real number(4) f is continuous at a provided f is well-defined.g g3.23. Defi nitionf : A R B R.g : B R C R.Define g o f : A R by (g。
《微积分》第二篇第一章讲义不定积分

二、不定积分的求法
实际上导数和不定积分是两种互逆运算。
求导数 求不定积分
互逆
求导公式 积分公式
互逆
所以类似于求初等函数的导数,求初 等函数的不定积分,也分三个方面: (1)积分的基本公式; (2)不定积分的四则运算法则; (3)不定积分与复合运算的关系.
(一)不定积分的基本公式
实际上都是由求导法则推出来的。
1 3x 2 dx 例4: 求 x 性质1 解: 1 1 3 x 2 d x 3 x d x d x 2 x x 性质2 1 21 1 11 x c 3 x 2 1 11 3 2 1 3 2 1 x x c x c 2 x 2
注意:幂函数求导数会降低幂次,求不定积分 会增加幂次。
例 4 . 1 :求 x d x 1 1 3 2 2 1 解: xd x c x x c 3 2 1
2
解:
1 1 1 2 1 x x c x c xd 1 1 2
1
求 xdx
例 4 . 2 :求 a d x ( a 为任意常数
1 (2 x ) c 3
3 2 2
(四)分部积分法
主要是用于处理被积函数是两个函数 相乘的形式的不定积分。
定理1.2(分部积分公式)
设u(x),v(x)是可微函数,则有
写成微分形式:
例5: 求 e3 2d x
x x
x x
e 3 2 d x 3 e d x 2 e d x 解:
x x
3e
x
2e c ln2e
x
2 e 3 e
x
x
定积分与微积分基本定理讲义

定积分与微积分基本定理讲义一、知识梳理1.定积分的概念如果函数f (x )在区间[a ,b ]上连续,用分点a =x 0<x 1<…<x i -1<x i <…<x n =b ,将区间[a ,b ]等分成n 个小区间,在每个小区间[x i -1,x i ]上任取一点ξi (i =1,2,…,n ),作和式∑n i =1f (ξi )Δx =∑n i =1b -a n f (ξi ),当n →∞时,上述和式无限接近某个常数,这个常数叫做函数f (x )在区间[a ,b ]上的定积分,记作ʃb a f (x )d x ,即ʃb a f (x )d x =lim n →∞∑n i =1 b -a nf (ξi ).在ʃb a f (x )d x 中,a ,b 分别叫做积分下限与积分上限,区间[a ,b ]叫做积分区间,函数f (x )叫做被积函数,x 叫做积分变量,f (x )d x 叫做被积式.2.定积分的性质(1)ʃb a kf (x )d x =k ʃb a f (x )d x (k 为常数);(2)ʃb a [f 1(x )±f 2(x )]d x =ʃb a f 1(x )d x ±ʃb a f 2(x )d x ;(3)ʃb a f (x )d x =ʃc a f (x )d x +ʃb c f (x )d x (其中a <c <b ). 3.微积分基本定理一般地,如果f (x )是区间[a ,b ]上的连续函数,且F ′(x )=f (x ),那么ʃb a f (x )d x =F (b )-F (a ),这个结论叫做微积分基本定理,又叫做牛顿—莱布尼茨公式.为了方便,常把F (b )-F (a )记作F (x )|b a ,即ʃb a f (x )d x =F (x )|b a =F (b )-F (a ).注意:1.定积分应用的常用结论当曲边梯形位于x 轴上方时,定积分的值为正;当曲边梯形位于x 轴下方时,定积分的值为负;当位于x 轴上方的曲边梯形与位于x 轴下方的曲边梯形面积相等时,定积分的值为零.2.若函数f (x )在闭区间[-a ,a ]上连续,则有(1)若f (x )为偶函数,则ʃa -a f (x )d x =2ʃa 0f (x )d x .(2)若f (x )为奇函数,则ʃa -a f (x )d x =0.题组一:思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)设函数y =f (x )在区间[a ,b ]上连续,则ʃb a f (x )d x =ʃb a f (t )d t .( )(2)若函数y =f (x )在区间[a ,b ]上连续且恒正,则ʃb a f (x )d x >0.( )(3)若ʃb a f (x )d x <0,那么由y =f (x ),x =a ,x =b 以及x 轴所围成的图形一定在x 轴下方.( )(4)曲线y =x 2与y =x 所围成图形的面积是ʃ10(x 2-x )d x .( )题组二:教材改编2.ʃe +121x -1d x =________.3.ʃ0-11-x 2d x =________. 4.[汽车以v =(3t +2)m/s 作变速直线运动时,在第1 s 至第2 s 间的1 s 内经过的位移是________ m. 题组三:易错自纠5.直线y =4x 与曲线y =x 3在第一象限内围成的封闭图形的面积为( )A .2 2B .4 2C .2D .46.若ʃT 0x 2d x =9,则常数T 的值为________.7.已知f (x )=⎩⎪⎨⎪⎧x 2,-1≤x ≤0,1,0<x ≤1,则ʃ1-1f (x )d x 的值为________. 三、典型例题题型一:定积分的计算1.定积分ʃ1-1(x 2+sin x )d x =______.2.ʃ1-1e |x |d x 的值为( )A .2B .2eC .2e -2D .2e +23.设f (x )=⎩⎪⎨⎪⎧x 2,x ∈[0,1],2-x ,x ∈(1,2],则ʃ20f (x )d x 等于( ) A.34B.45C.56 D .不存在思维升华:运用微积分基本定理求定积分时要注意以下几点:(1)对被积函数要先化简,再求积分.(2)若被积函数为分段函数的定积分,依据定积分“对区间的可加性”,先分段积分再求和.(3)对于含有绝对值符号的被积函数,要先去掉绝对值符号再求积分.题型二:定积分的几何意义命题点1:利用定积分的几何意义计算定积分典例 (1)计算:ʃ313+2x -x 2 d x =________.(2)若ʃm -2-x 2-2x d x =π4,则m =________. 命题点2:求平面图形的面积典例由曲线xy =1,直线y =x ,y =3所围成的封闭平面图形的面积为________.思维升华:(1)根据定积分的几何意义可计算定积分.(2)利用定积分求平面图形面积的四个步骤①画出草图,在直角坐标系中画出曲线或直线的大致图象;②借助图形确定出被积函数,求出交点坐标,确定积分的上、下限;③把曲边梯形的面积表示成若干个定积分的和;④计算定积分,写出答案.跟踪训练 (1)定积分ʃ309-x 2d x 的值为________. (2)如图所示,由抛物线y =-x 2+4x -3及其在点A (0,-3)和点B (3,0)处的切线所围成图形的面积为______.题型三:定积分在物理中的应用典例 一物体作变速直线运动,其v -t 曲线如图所示,则该物体在12s ~6 s 间的运动路程为____ m.思维升华:定积分在物理中的两个应用(1)变速直线运动的位移:如果变速直线运动物体的速度为v =v (t ),那么从时刻t =a 到t =b 所经过的路程s =ʃb a v (t )d t .(2)变力做功:一物体在变力F (x )的作用下,沿着与F (x )相同方向从x =a 移动到x =b 时,力F (x )所做的功是W =ʃb a F (x )d x .跟踪训练 一物体在变力F (x )=5-x 2(力单位:N ,位移单位:m)作用下,沿与F (x )成30°方向作直线运动,则由x =1运动到x =2时,F (x )做的功为( )A. 3 JB.233 JC.433J D .2 3 J答案 C 四、反馈练习1.π220sin d 2x x 等于( ) A .0 B.π4-12C.π4-14D.π2-1 2.ʃ1-1(1-x 2+x )d x 等于( )A .πB.π2 C .π+1 D .π-13.已知函数y =f (x )的图象为如图所示的折线ABC ,则ʃ1-1[(x +1)f (x )]d x 等于( )A .2B .-2C .1D .-1 5.设f (x )=⎩⎪⎨⎪⎧ x 2,x ∈[0,1],1x ,x ∈(1,e](其中e 为自然对数的底数),则ʃe 0f (x )d x 的值为( ) A.43B.54C.65D.76 6.设a =ʃ10cos x d x ,b =ʃ10sin x d x ,则下列关系式成立的是( )A .a >bB .a +b <1C .a <bD .a +b =17.定积分ʃ20|x -1|d x 等于( ) A .1 B .-1 C .0 D .28.一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度v (t )=7-3t +251+t (t 的单位:s ,v 的单位:m/s)行驶至停止,则在此期间汽车继续行驶的距离(单位:m)是( )A .1+25ln 5B .8+25ln 113C .4+25ln 5D .4+50ln 2 9.π20π2sin()d 4x x +=⎰ ________. 10.由直线x =-π3,x =π3,y =0与曲线y =cos x 所围成的封闭图形的面积为________. 11.设a >0,若曲线y =x 与直线x =a ,y =0所围成封闭图形的面积为a 2,则a =________.12.已知二次函数y =f (x )的图象如图所示,则它与x 轴所围成的面积为________.13.由曲线y =x 2和曲线y =x 围成的一个叶形图如图所示,则图中阴影部分的面积为( ) A.13B.310C.14D.1514.若S 1=ʃ21x 2d x ,S 2=ʃ211xd x ,S 3=ʃ21e x d x ,则S 1,S 2,S 3的大小关系为( ) A .S 1<S 2<S 3B .S 2<S 1<S 3C .S 2<S 3<S 1D .S 3<S 2<S 115.ʃ1-1(1-x 2+e x -1)d x =______. 16.若函数f (x )在R 上可导,f (x )=x 3+x 2f ′(1),则ʃ20f (x )d x =________.。
微积分学讲义

微积分学讲义微积分学讲义微积分学是数学的一个分支,了解这门学科的重要性和理解这门学科的要点是非常重要的。
本讲义将重点讨论一些基本概念和原理,帮助学习者更好地了解微积分的概念,并在学习中做出更快的发展。
一、定义和概念1. 定义:微积分是研究函数的变化以及该变化如何影响其及其构成成分之间的关系的学科。
2. 常用概念:直线曲线、导数和积分;微分方程和定积分等。
3. 常用公式:求导法则、椭圆公式和柯西定理等。
二、应用1. 图形的抽象表示:微积分可以帮助我们抽象表达日常面对的一些几何形状;直线曲线以及更复杂的二参数曲线可以通过微积分的函数表示出来。
2. 分析和理解复杂系统:复杂系统中的物理关系式抽象,可以通过微积分来分析理解,决策出最优控制方案。
3. 数值计算:微积分也广泛用于数值计算,如数值积分、数值微分、归纳法、概估法等。
三、实践1. 定义来自数学的变量:首先要明确变量的定义,例如定义函数y = f (x),然后通过函数解决特定问题。
2. 尝试性解决问题:对于一个微积分问题,比如求导等,要结合实际情况,尝试着动手解决问题,不同的算法可能会收效不同,甚至可能在解决一个问题的过程中发现其他的有趣概念。
3. 关注实践场景:实践中锻炼微积分的能力也是非常重要的,要联系实际,提出自己的问题,利用微积分的理论加以解答,并且灵活应对不同的实际场景。
四、方法和技巧1. 学习先学习理论基础:理论知识是最重要的,学习微积分需要先从小学一点点知识开始,了解概念,具备基本的推导能力,而不是记住公式。
2. 熟悉考试技巧:微积分中需要熟悉FAQ考试策略,对于考试中出现的新问题尽量进行抓大放小,定位问题,准备有效地解决问题。
3. 不断累积实践经验:微积分的解决问题,需要很多的实践经验,锻炼自己的处理能力,也要反复练习曾经见过的题目,以及多思考如何用微积分处理实际问题。
以上就是有关微积分的基本概念和原理的简单介绍,希望能够帮助到大家学习微积分,以及在平时的学习实践中明白微积分的应用。
微积分讲义

《微积分》讲义第一章极限一、函数极限的概念:f=A要点:⑴x 为变量;⑵A 为一常量。
二、函数极限存在的充分必要条件:f=A f=A,f=A例:判定是否存在?三、极限的四则运算法则⑴=f±g⑵=f·g⑶=……g≠0⑷k·f=k· f四、例:⑴⑵⑶⑷五、两个重要极限⑴=1 =1⑵=e =e ………型理论依据:⑴两边夹法则:若f≤g≤h,且limf=limh=A,则:limg=A⑵单调有界数列必有极限。
例题:⑴=⑵=⑶=⑷=⑸=六、无穷小量及其比较1、无穷小量定义:在某个变化过程中趋向于零的变量。
2、无穷大量定义:在某个变化过程中绝对值无限增大的变量。
3、高阶无穷小,低阶无穷小,同阶无穷小,等价无穷小。
4、定理:f=A f=A+a (a=0)七、函数的连续性1、定义:函数y=f在点处连续……在点处给自变量x一改变量x:⑴x0时,y0。
即:y=0⑵f=f⑶左连续:f=f右连续:f=f2、函数y=f在区间上连续。
3、连续函数的性质:⑴若函数f和g都有在点处连续,则:f±g、f·g、(g()≠0)在点处连续。
⑵若函数u=j在点处连续,而函数y=f在点=j()处连续,则复合函数f(j(x)) 在点处连续。
例:===4、函数的间断点:⑴可去间断点:f=A,但f不存在。
⑵跳跃间断点:f=A ,f=B,但A≠B。
⑶无穷间断点:函数在此区间上没有定义。
5、闭区间上连续函数的性质:若函数f在闭区间上连续,则:⑴f在闭区间上必有最大值和最小值。
⑵若f与f异号,则方程f=0 在内至少有一根。
例:证明方程式-4+1=0在区间内至少有一个根。
第二章一元函数微分学一、导数1、函数y=f在点处导数的定义:x y=f-f=A f'=A ……y',,。
2、函数y=f在区间上可导的定义:f',y',,。
3、基本初等函数的导数公式:⑴=0⑵=n·⑶=,=⑷=·lnɑ,=⑸=cosx,=-sinx=x,=-=secx·tanx,=-cscx·cotx⑹=-=-4、导数的运算:⑴、四则运算法则:=±=·g(x)+f(x)·=例:求下列函数的导数y=2-5+3x-7f(x)=+4cosx-siny=⑵、复合函数的求导法则:yu,uv,vw,wx yx'=''''例:y=lntanxy=lny=arcsin⑶、隐函数的求导法则:把y看成是x的复合函数,即遇到含有y的式子,先对y求导,然后y再对x求导。
微积分讲解ppt课件

3.2.1 原函数和不定积分的概念
一、案例 二、概念和公式的引出
一、案例[路程函数]
已知物体的运动方程为 s(t) t2 ,则其速度为 v(t) s(t) (t 2 ) 2t
这里速度2t是路程t2的导数,反过来,路程t2又称为速 度2t的什么函数呢?若已知物体运动的速度v(t),又如 何求物体的运动方程s(t)呢?
f xdx f x C 或 df x f x C
3.2.2 基本积分表
一、案例 二、概念和公式的引出
一、案例[幂函数的不定积分]
因为
x 1
1
x
x 1
1 是 x 的一个原函数
于是
x dx x 1 C
32微积分基本公式321原函数和不定积分的概念322基本积分表323微积分基本公式321原函数和不定积分的概念一案例二概念和公式的引出一案例路程函数已知物体的运动方程为又称为速度2t的什么函数呢
3.2 微积分基本公式
3.2.1 原函数和不定积分的概念 3.2.2 基本积分表 3.2.3 微积分基本公式
1
1
类似地, 由基本初等函数的求导公式,可以写出与之对应的不定积分公式.
二、概念和公式的引出
1.基本积分表
(1)
kdx kx C ( k 为常数)
(2) x dx x 1 C
1
1
(3)
1 x
dx
ln
x
C
(4) a xdx a x C
即两个函数和(差)的定积分等于它们定积分的和(差). 性质1可推广到有限个函数的情形.
(2) 性质2 kf xdx k f xdx k为常数
微积分ppt讲义3-3

′ − e x + e y y′ = 0 y + xy
e −y , 解得 y′ = 将x = 0代入原方程得, y x+e − e 0 + e y (0) = 0 y(0) = 0, 即x = 0时,y = 0.
x
∴ y′
x=0
ex − y = y x+e
x=0 y=0
= 1.
3
导数与微分
例 设 x 4 − xy + y 4 = 1, 求其所确定隐函数y在点 (0,1)处的切线方程 .
0 1 = C n ( x 2 )(e x )( n ) + C n ( x 2 )′(e x )( n−1) 3 ′′(e x )( n − 2) + C n ( x 2 )′′′(e x )( n− 3) +C ( x ) 2 n 2
+ L + C ( x ) (e ) n( n − 1) x 2 x = e x +2nxe + ⋅ 2e x 2 x 2 = e ( x + 2nx + n( n − 1) )
(n)
= k cos( kx + n ⋅ ) 2
n (n)
π
(cos x )
(5) (a )
x ( n)
= cos( x + n ⋅ ) 2 x n = a ⋅ ln a (a > 0)
π
(e x )( n) = e x
导数与微分
11
2、部分高阶导数的运算法则
若u = u( x ), v = v ( x )均存在n阶导数, 则
其中 ,u(0) = u, v (0) = v .
导数与微分
微积分讲义Chap 1 Completeness axiom of R

Chapter 1 The real number system1.3. Completeness axiom of R1.16 DefinitionLet R E ⊆ and φ≠E . (i).The set E is said to be bounded above if there is an R M ∈ s.t M a ≤ for allE a ∈.(ii).A number M is called an upper bound of the set E if M a ≤ for all E a ∈. (iii).A number S is called a supremum of the set E if S satisfies the followingconditions(1) if E a S a ∈∀≤,,(2) if M is an upper bound of E then M S ≤.Remark The supremum is also called the least upper bound.1.17: ExampleIf E=[0,1], prove that 1 is a supremum of E .Proof.1. ]1,0[,1=∈∀≤E a a .2. let M be an upper boundthen M a ≤ for all ]1,0[∈a])1,0[1(1∈≤⇒ M .We derive the result.1.18: RemarkIf a set has one upper bound, it has infinitely many upper boundsProof:. Let E be a subset of R .Let M a ≤ for all E a ∈.Then M is an upper bound.Let R b b ∈>,0 then M+b is also an upper bound.So, E has infinitely many upper bounds.1.19 . Theorem. Let E be a nonempty subset of R . Then the least upper bound of E is unique if it exists.Proof.Suppose that 21&s s are the least upper bounds of E.Then 21&s s are upper bounds of E .1221&s s s s ≤≤∴21s s =∴.NotationThe supremum is also called least upper bound . We use sup E to denote the supremum of nonempty set E .1.20. Theorem [Approximation property]E E R E s u p a n d ,,φ≠⊆exists. Then E a ∈>∀an is there ,0ε s.t E a E sup sup ≤<-ε.Proof:. Suppose the conclusion is false. There is an 0>ε such that.,sup E a E a ∈∀-≤ε.ε-∴E s u pis an upper bound. →←≥-⇒E E sup sup ε0>εE a ∈∃∴ s.t E a E sup sup ≤<-ε1.21. TheoremIf N E ⊆ has a supremum, then E E ∈supProof.Let supE=s.By Approximation property, there E x ∈∃0 s.t s x s ≤<-01.If s x =0 then E E ∈sup is obvious.If s x s <<-01, thenE x ∈∃1 s.t 001100x s x x s x x -≤-<⇒≤<.1. 1,0101≥-⇒∈x x N x x .2. 1)1(1,0101=--<-⇒->≥s s x x s x x s .It is a contradiction.E E ∈∴s u p● [Complete axiom of R ]Every nonempty subset E of R that is bounded above,then E has the least upper bound. .1.22 :[Archimedean Principle]N n b a R b a ∈∃⇒>∈0,,, s.t b<na.Proof:1. If b<a , then take n=1.2. If a<b , let };{b ka N k E ≤∈=.φ≠∴∈E E ,1 .⇒∈∀≤E k ab k ,E is bounded above. By Completeness of R , sup E exists.ba E EE E E >+∴∉+∴∈⇒)1(s u p 1s u p )21.1 T heorem by (sup take n=supE+11.23: Example.Let ,.......}41,21,1{=A and ,...}87,43,21{=B prove that supA=supB=1Proof.1. 1{;0}2nA n N or n =∈= 11,,0,1,2,..2n x x n ≥== . 1∴ is an upper bound.Let M be another bound..1s u p 1210=∴=≥∴A M 2. };211{N n B n ∈-= N n n ∈∀-≥,2111 1∴ is an upper bound of B.Let M be an upper bound of BTo show 1≥M .Suppose not 011>-⇒<⇒M MBy Archimedean principle, there exists N n ∈ such thatM n-<11, M n -<∃⇒121 for some N n ∈. →←>-⇒-->-=-∴M M n n n n n 212)1(1212211 M is an upper bound. 1≥∴M1s u p=∴B● [Well-Order Principle]⇒≠⊆φE N E ,E has a least element(ie.E a ∈∃ s.t E x x a ∈∀≤,)1.24. Theorem (Density of rational)Let R b a ∈, satisfy a<b , then there is a rationalnumber c s.t a<c<b.Proof:Let N n a b n∈-<,1(by Archimedean Principle). 1. If b>0, let }.;{nk b N k E ≤∈= By Archimedean Principle φ≠⇒E .By Well-Order Principle ⇒E has a least element, says 0k . .)..(1:0b nm e i E m k m <∉⇒-=∴ Let n m q =. We must show that a<q<b.q<b is obvious, now we show that a<q....11)(00b q a a q q n k n n k a b b a <<∴>∴=-=-<--=2. If b<0, then0>∃k , k is a natural number s.t b+k>0.Q c ∈∃∴ s.t a+k<c<b+kQk c Q c bk c a ∈-⇒∈<-<∴ie. There is a rational number between a & b.1.27. Definition.φ≠⊆E R E ,.1. s is called a lower bound of E if E x s x ∈∀≥,.In the case, E is called bounded below2. t is called the greatest lower bound of Eif1.E x t x ∈∀≥,,2. If M is a lower bound of E then t M ≤.3. E is bounded if E x M x ∈∀≤, for some M>0. (i.e. E is bounded above and below.)● Let E be a set of R . We define };{E x x E ∈-=-.1.28. Theoremφ≠⊆E R E ,.1. sup E exists ⇔inf (-E) existsin fact supE= -inf(-E)2. inf E exists ⇔sup (-E) existsin fact inf E= -sup (-E)Proof:1.""⇒supE exists.Now we show that –supE=inf(-E).Show that 1.-sup E is a lower bound of –E.2. if s is a lower bound of E s E sup -≤⇒-.1.E s u pis an upper bound of E E x E x E x E x ∈∀-≥-⇒∈∀≤∴,s u p ,s u pE s u p-∴ is a lower bound of –E 2. Suppose that s is a lower bound of -ESuppose not E s E s sup sup <-⇒->⇒on the other handsx E x s x -≤∴∈∀≥-, Hence, -s is a upper bound of E →←By 1.& 2, E E E sup )inf(&)inf(-=-∃-.The proof of converse is similar.Remark. The largest lower bound is also called infimum.Remark. The completeness axiom of R is equivalent to“ Every non empty, bounded below subset of R has the infimum”.1.29. Theorem.i n f i n f ,s u p s u p,,A B A B B A R B A ≤≥⇒≠⊆⊆φ if B B inf and sup exist.Hence, B A A B sup sup inf inf ≤≤≤Proof:1. suppose sup B exists.,s u p .,s u p A x B x B A B x B x ∈∀≤∴⊆∈∀≤∴A ∴ is bounded above & supB is an upper bound of ABy complete axiom of R, .sup sup &sup B A A ≤∃2. S ppose that inf B exists..,i n f ,i n f A x B x B A Bx B x ∈∀≥∴⊆∈∀≥∴A ∴ is bounded below & infB is an lower bound of A.By complete axiom of R, B A A inf inf &:inf ≥∃.Def:s u p,i n f φφ=-∞=∞1.4 Functions, countability and the algebra of sets.DefinitionLet A & B be two sets of R .A function f is a relation between A &B s.t f assigns each element x of A to aunique B y ∈DefinitionB A f →:f is called 1-1 if )()(y f x f y x ≠⇒≠Def:B A f →:f is called onto if A x B y ∈∃∈∀, s.t f (x )=yDefinition 1.34:Let E be s a set of R .1. E is said be finite if φ=E or E n f N n n →∈∃}...2,1{:&},.....3,2,1{ s.t f is 1-1 & onto.2. E is called countably infinite if E N f →∃: s.t f is 1-1 & onto.3. E is called countable if E is finite or countably infinite.4. E is called uncountable if E is not countable1.35. Theorem .The open interval (0,1) is uncountablePf:Suppose (0,1) is countable.Then there is a list for (0,1) says.....................................................................0............................................................................0.........0.........0321333231323222121312111n n n n a a a a a a a a a a a a a a a a ====Let .......0321ααα=x where {=k α10==k k αα .1f ,1if ≠=kk kk a i a kk k a ≠∴αx ∴ is not in this list →← (0,1) is uncountable 1.37. TheoremB B A ,⊆ is countable A ⇒ is countable1.38 Theoremn A A A ,......,21 are countable. },:{:1N j A x x A A E j j j N j j∈∈===∞=∈ .If j A is countable for E N j ⇒∈ is countable.。
微积分讲义_第三章-一元函数的导数和微分
3.6 导数和微分在经济学中的简单应用,由于知识体系的关联性,我们把本节放到第四章后面讲。
例11.求
的导数
【答疑编号11030311:针对该题提问】
例12.求
的导数
【答疑编号11030312:针对该题提问】
例13.求
的导数
【答疑编号11030313:针对该题提问】
例14.求
的导数
【答疑编号11030314:针对该题提问】
例15.(教材习题3.2,8题)已知 【答疑编号11030315:针对该题提问】
切线方程为 法线方程为
例8、求双曲线
处的切线的斜率,并写出在该点处的切线方程和法线方程。
【答疑编号11030108:针对该题提问】
解 由导数的几何意义, 得切线斜率为
所求切线方程为
法线方程为
六、可导与连续的关系 1.定理 凡可导函数都是连续函数. 注意:该定理的逆定理不成立,即:连续函数不一定可导。 我们有:不连续一定不可导 极限存在、连续、可导之间的关系。
2.连续函数不存在导数举例
例9、讨论函数
在x=0处的连续性与可导性。
【答疑编号11030109:针对该题提问】
解:
例10、 P115第10题
设
,α在什么条件下可使f(x)在点x=0处。
(1)连续;(2)可导。 【答疑编号11030110:针对该题提问】 解:(1)
(2)
七、小结 1.导数的实质:增量比的极限; 2.导数的几何意义:切线的斜率; 3.函数可导一定连续,但连续不一定可导;
第三章 一元函数的导数和 微分
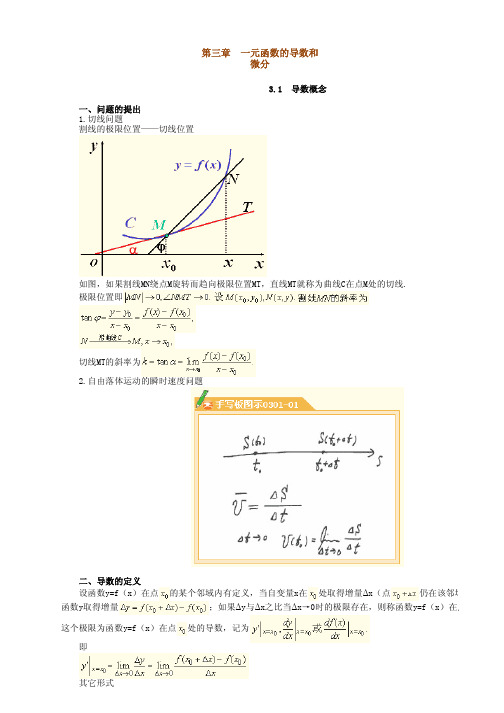
一、问题的提出 1.切线问题 割线的极限位置——切线位置
3.1 导数概念
如图,如果割线MN绕点M旋转而趋向极限位置MT,直线MT就称为曲线C在点M处的切线. 极限位置即
微积分基础知识ppt课件

.
9
2.邻域:
设 a与 是两个 , 且 实 0.数
数{x集 xa()}称为 a的 邻 点 ,域
点a叫做这邻域的中心, 叫做这邻域的半径.
a
a
a x
点 a的去心 邻的 ,域 记U 作 (a,).
U (a , ) {x0 x a }.
.
10
二、函数
1.定义 设数集 D,若存在对应法则 f ,使对 x D ,
矛盾取 . 故 N b 假 2 a设m 不xn 真 N b a 1 ! , a N b 因b 2 2 2 a a 此 ,收则x 敛当数n 3列a>a22bN的b时极xnx,限nx必n3满ba2唯2a足b一的. 不等式
.
37
两边夹准则
( 1 ) y n x n z n ( n 1 ,2 , )
n 1 1
2
.
7
具备的数学素质: ➢ 从实际问题抽象出数学模型的能力 ➢ 计算与分析的能力 ➢ 了解和使用现代数学语言和符号的能力 ➢ 使用数学软件学习和应用数学的能力
.
8
第0章 基本知识
一、基本概念
1.集合: 具有某种特定性质的对象的全体. 组成集合的事物称为该集合的元素.
aM, aM, A { a 1 ,a 2 , ,a n }
基本初等函数(幂函数,指数函数,对数函数,三角函数 和反三角函数).
.
12
几个特殊的函数举例 (1) 符号函数
1 当x0 ysgnx 0 当x0
1 当x0
y
1
o
x
-1
xsgxn x
.
13
(2) 取整函数 y=[x]
《微积分》第一篇第二章讲义(1)极限

h( x ) f ( x) , 而且有:g ( x0 ) 0 g ( x)
这时就计算: ( x0 ) h
当h( x0 ) 0时,就有lim f ( x)
x x0
1 g ( x) g ( x0 ) 此时有 lim lim x x0 f ( x) x x0 h( x) h( x0 ) 0 0. lim f x . x x0 h( x0 )
3 2、求 lim 3 x x 0
2 3、求 lim x 0 x
(二)极限的运算
1、极限的四则运算法则(P-66) 设 lim f x A, g x B,那么 lim
(1) lim( f g ) lim f lim g A B;
(2) lim( f g ) lim f lim g AB;
当自变量x本身既可以取正值,也可以 取负值的时候,就可以当x趋于无穷的定义
定义2.2’’
x
(P-61)
f x A( x ).
lim f x A 或
称为:当 x 时,f ( x)以A为极限
由定义2.2知,在例2.1中,有 1 1 或 0 x lim 0 x x x
n
2.718
(二)函数的极限
数列是一类特殊的函数,它的定义 域是正整数,对于数列已经定义了极限。 那么如果是一般的函数呢?即自变 量是连续取值的函数,它的极限又是如何 定义的?
1、x 时,函数f ( x)的极限
2、x x0时,函数f ( x)的极限
1、x 时,函数f ( x)的极限
(3) lim( Cf ) C lim f CA, 其中C是常数 f lim f A (4)若B 0, 则lim . g lim g B
《高等数学(一)微积分》讲义

5. 复合函数
给定函数链 f : D1 → f (D1) g : D → g(D) ⊂ D1
则复合函数为 f o g : D → f [g(D) ]
6. 初等函数 由基本初等函数经有限次四则运算与复合而成的由一个表达式表示的函
数。
4/69
二、 极限 (1.概念回顾 2、极限的求法,)
=
lim
x→π
1 cos x
sin x
-2 ⋅ 2(π
−
2 x)=
lim
x→π
1 -4 sin
cos x
x(π − 2x)
2
2
2
=
lim
x→π
1 -4 sin
x
⋅
cos
lxi→mπ(π −
2xx )=
1 -4
lim
x→π
−
sin −2
x =
−
1 8
2
2
2
13/69
注:使用洛必达法则必须判断所求的极限是分式型的未定式 ∞ 、 0 。 ∞0
例 5:
求 lim x→∞
x+5 x2 − 9
.
解:
lim
x→∞
x+5 x2 − 9
=
lim
x→∞
1 x
+
5 x2
1−
9 x2
=
1 lim( x→∞ x
+
5 x2
)
=
0
=
0.
lim(1 −
x→∞
9 x2
)
1
知识点:设a0 ≠ 0, b0 ≠ 0, m, n ∈ N ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考研数学强化讲义微积分§1.5常规考研题型分析常规考点一 简单极限的计算(热点)(2004)若0sin lim(cos )5xx xx b e a®-=-,则a = b= (2005)22lim sin 1x xx x=+ (2006)(1)1lim()nn n n-+= (2007)3231lim (cos sin )2x x x x x x x+++=+ (2009)cos 0x x ®(2010 ) 若011lim 1x x a e x x®轾骣÷ç犏--=÷ç÷ç犏桫臌,则a 等于 A 0 B 1 C 2 D 3 (2011)设()0()lim 13xtt f x x t ®=+,则()f x ¢=(2012)()1cos sin 4lim tan x xx x p-®=————常规考点二 无穷小、无穷大及其阶的比较(重点) (2007)当0x +®A 1-B ln(1+C1 D1-(2009)当0x ®时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价的无穷小,则A 11,6a b ==-B 11,6a b ==C 11,6a b =-=-D 11,6a b =-=(2010)设1010()ln ,(),()x f x x g x x h x e ===,则当x 充分大时有A ()()()g x h x f x <<B ()()()h x g x f x <<C ()()()f x g x h x <<D ()()()g x f x h x <<(2011)已知当0x ®时,()3sin sin3f x x x =-与k cx 是等价无穷小,则【 】 A 1,4k c == B 1,4k c ==- C 3,4k c == D 3,4k c ==- (2013)当0x ®时,用“()o x ”表示比x 高阶的无穷小,则下列式子中错误的是【 】(A) 23()()x o x o x =g ( B) 23()()()o x o x o x =g ( C ) 222()()()o x o x o x += ( D) 22()()()o x o x o x +=(2002数一)设()0f x x =在的某邻域内具有连续一阶导数,且(0)0,(0)0f f '≠≠,若()(2)(0)0af h bf h f h +-→在时是比h 高阶的无穷小,试确定a,b 的值。
(2006数二、四)试确定常数A ,B ,C 的值,使得 23(1)1()x e Bx Cx Ax o x ++=++ 其中3()o x 是当0x →时比3x 高阶的无穷小。
常规考点三 极限的计算(重点) (2000一)1402sin lim()1xx xe xxe→+++(2004)22201cos lim()sin x xx x→-(2005)011lim()1xx x e x-→+--(2006)设1sin (,),0,01arctan xy y yf x y x y xy xπ-=->>+求 (1)()lim (,)y g x f x y →+∞=(2)0lim ()x g x +→(2008)201sin limln x x x x→(2010) 求极限11ln lim 1xxx x ? 骣÷ç÷-ç÷ç÷ç桫(2011)求极限0x ®(2012)求极限222cos 40lim x xx e e x-®-(2013)当0x ®时,1cos cos2cos3x x x - 与n ax 为等价无穷小,求,n a 的值。
常规考点四 数列的极限(2006数一、二)设数列{}n x 满足110,sin (1,2,)n n x x x n π+<<==(1)证明lim n n x →∞存在,并求该极限;(2)计算11lim n x n n n x x +→∞⎛⎫ ⎪⎝⎭常规考点五 函数的连续性、间断点及其类型(重点)(2004)设函数21()2x x c f x x c xìï+ ïïï=íï>ïïïî在(,)-? 内连续,则c= (2009)函数3()sin x x f x xp -=的可去间断点的个数为A 1B 2C 3D 无穷多个 (2008)设函数()f x 在[-1,1]上连续,则0x =是函数0()()xf t dtg x x=ò的A 跳跃间断点B 可去间断点C 无穷间断点D 震荡间断点(2004)设()f x 在(,)-? 内有定义,且lim ()x f x a =,1()0()00f x g x x x ìïï¹ï=íïï=ïî,则A 0x =必是()g x 的第一类间断点B 0x =必是()g x 的第二类间断点C 0x =必是()g x 的连续点D ()g x 在点0x =处的连续性与a 的取值有关(2013) 函数1()(1)ln xx f x x x x-=+的可去间断点的个数为 【 】(A) 0 ( B) 1 ( C ) 2 ( D) 3 (2003)设1111(),[,1)sin (1)2f x x x x x p p p =+- -,试补充定义(1)f ,使得()f x 在1[,1]2上连续习题一 计算题9. 21lim[ln(1)]x x x x→∞-+10. 2201lim[()ln(1)],0x a a ax a x x→--+≠11.x ®12. 40cos(sin )cos limx x xx →-13.已知1()(),(0)(0)0.1f x g x f g x''====+且 试求011lim ()()x f x g x →⎡⎤-⎢⎥⎣⎦第二章 导数与微分§2.1 导数的概念与性质(三)内容提要导数的定义:函数在一点0x x =处的导数定义有三种形式:1. 0000()()()lim x f x x f x f x xD +D -¢=D ;2. 0000()()()limx x f x f x f x x x ®-¢=-;3. 000()()()f x A f x f x A +-ⅱ =?=导数的几何意义:1.0()f x ¢在几何上为过曲线()y f x =上点00(,())x f x 处的切线斜率;2.当0()0f x ¢¹时,01()f x -¢为过曲线()y f x =上点00(,())x f x 处的法线斜率 导数的性质:1. 可导的偶函数的导数是奇函数;2. 可导的奇函数的导数是偶函数;3. 可导的周期函数的导数仍是周期函数,且周期不变。
(四)典型例题§2.2 导数的计算(三)内容提要1、基本初等函数的导数与微分:1()x x a a a -¢= ()l n (0,1)x x a a a a a ¢=>()x x e e ¢= ()1ln x x¢=()1l o g ln a x x a¢=()s i n c o s x x ¢= ()c o s s i n x x ¢=- ()2t a n s e c x x ¢=()2cot co x c x ¢=- ()s e cs e c t a n x x x ¢= ()co cot cocx cx x ¢=- ()s i n a r c x ¢= ()a r c c o sx ¢=- ()21n 1a r c t a xx ¢=+ ()21cot 1arc x x ¢=-+ 相应的有基本初等函数微分表(略)。
2、导数与微分的四则运算法则: (1)()()()()()f x g x f x g x ¢ⅱ? ;(2) ()()()()()()()f x g x f x g x f x g x ¢ⅱ=+ (3) 2()()()()(),(()0)()()f x f xg x g x f x g x g x g x ¢骣ⅱ-÷ç? ç÷÷ç桫相应的有微分的四则运算法则。
3、复合函数的导数:设()u x j =在x 处可导,()y f u =在对应点()u x j =处可导,则复合函数[()]y f x j =在x 处可导且 dy dy du dx du dx= 4、反函数的导数:如果函数()y f x =在区间I 上单调、可导且()0f x ¢¹,则它的反函数1()x f y -= 在相应区间上可导,且有11[()]()dx f y dy f x -¢==¢。
§2.3 中值定理与泰勒公式 (三)内容提要费马定理 若()y f x =在0x x =处可导且取极值,则0()0f x '=。
罗尔定理 设()f x 在[,]a b 上连续,在(,)a b 内可导,()()f a f b =,则至少存在一点(,)a b ξ∈使得()0f ξ'=拉格朗日定理 设()f x 在[,]a b 上连续,在(,)a b 内可导,则至少存在一点(,)a b ξ∈使得()()()f b f a f b aξ-'=-柯西定理设(),()f x g x 在[,]a b 上连续,在(,)a b 内可导且()0g x '≠,则至少存在一点(,)a b ξ∈使得()()()()()()f b f a fg b g a g ξξ'-='- 泰勒定理 设()f x 在0x x =有n+1阶导数,则2()000000011()()()()()()()()()2!!n n n f x f x f x x x f x x x f x x x R x n '''=+-+-++-+L 其中()(1)1001()()(),1!n n n R x f x x x x n ξξ++=-+在与之间。
