抛物线与三角形专题练习
中考数学复习---二次函数中三角形存在性问题压轴题练习(含答案解析)

中考数学复习---二次函数中三角形存在性问题压轴题练习(含答案解析)一.相似三角形的存在性1.(2022•陕西)已知抛物线y=ax2+bx﹣4经过点A(﹣2,0),B(4,0),与y 轴的交点为C.(1)求该抛物线的函数表达式;(2)若点P是该抛物线上一点,且位于其对称轴l的右侧,过点P分别作l,x 轴的垂线,垂足分别为M,N,连接MN.若△PMN和△OBC相似,求点P的坐标.【解答】解:(1)把A(﹣2,0),B(4,0)代入y=ax2+bx﹣4得:,解得,∴抛物线的函数表达式为y=x2﹣x﹣4;(2)如图:∵y=x2﹣x﹣4=(x﹣1)2﹣,∴抛物线y=x2﹣x﹣4的对称轴是直线x=1,在y=x2﹣x﹣4中,令x=0得y=﹣4,∴C(0,﹣4),∴OB=OC=4,∴△BOC是等腰直角三角形,∵△PMN和△OBC相似,∴△PMN是等腰直角三角形,∵PM⊥直线x=1,PN⊥x轴,∴∠MPN=90°,PM=PN,设P(m,m2﹣m﹣4),∴|m﹣1|=|m2﹣m﹣4|,∴m﹣1=m2﹣m﹣4或m﹣1=﹣m2+m+4,解得m=+2或m=﹣+2或m=或m=﹣,∵点P是该抛物线上一点,且位于其对称轴直线x=1的右侧,∴P的坐标为(+2,+1)或(,1﹣).2.(2022•绵阳)如图,抛物线y=ax2+bx+c交x轴于A(﹣1,0),B两点,交y轴于点C(0,3),顶点D的横坐标为1.(1)求抛物线的解析式;(2)在y轴的负半轴上是否存在点P使∠APB+∠ACB=180°,若存在,求出点P的坐标,若不存在,请说明理由;(3)过点C作直线l与y轴垂直,与抛物线的另一个交点为E,连接AD,AE,DE,在直线l下方的抛物线上是否存在一点M,过点M作MF⊥l,垂足为F,使以M,F,E三点为顶点的三角形与△ADE相似?若存在,请求出M点的坐标,若不存在,请说明理由.【解答】解:(1)∵顶点D的横坐标为1,∴抛物线的对称轴为直线x=1,∵A(﹣1,0),∴B(3,0),∴设抛物线的解析式为:y=a(x+1)(x﹣3),将C(0,3)代入抛物线的解析式,则﹣3a=3,解得a=﹣1,∴抛物线的解析式为:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.(2)存在,P(0,﹣1),理由如下:∵∠APB+∠ACB=180°,∴∠CAP+∠CBP=180°,∴点A,C,B,P四点共圆,如图所示,由(1)知,OB=OC=3,∴∠OCB=∠OBC=45°,∴∠APC=∠ABC=45°,∴△AOP是等腰直角三角形,∴OP=OA=1,∴P(0,﹣1).(3)存在,理由如下:由(1)知抛物线的解析式为:y=﹣x2+2x+3,∴D(1,4),由抛物线的对称性可知,E(2,3),∵A(﹣1,0),∴AD=2,DE=,AE=3.∴AD2=DE2+AE2,∴△ADE是直角三角形,且∠AED=90°,DE:AE=1:3.∵点M在直线l下方的抛物线上,∴设M(t,﹣t2+2t+3),则t>2或t<0.∴EF=|t﹣2|,MF=3﹣(﹣t2+2t+3)=t2﹣2t,若△MEF与△ADE相似,则EF:MF=1:3或MF:EF=1:3,∴|t﹣2|:(t2﹣2t)=1:3或(t2﹣2t):|t﹣2|=1:3,解得t=2(舍)或t=3或﹣3或(舍)或﹣,∴M的坐标为(3,0)或(﹣3,﹣12)或(﹣,).综上,存在点M,使以M,F,E三点为顶点的三角形与△ADE相似,此时点M的坐标为(3,0)或(﹣3,﹣12)或(﹣,).3.(2022•恩施州)在平面直角坐标系中,O为坐标原点,抛物线y=﹣x2+c与y 轴交于点P(0,4).(1)直接写出抛物线的解析式.(2)如图,将抛物线y=﹣x2+c向左平移1个单位长度,记平移后的抛物线顶点为Q,平移后的抛物线与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.判断以B、C、Q三点为顶点的三角形是否为直角三角形,并说明理由.(3)直线BC与抛物线y=﹣x2+c交于M、N两点(点N在点M的右侧),请探究在x轴上是否存在点T,使得以B、N、T三点为顶点的三角形与△ABC相似,若存在,请求出点T的坐标;若不存在,请说明理由.(4)若将抛物线y=﹣x2+c进行适当的平移,当平移后的抛物线与直线BC最多只有一个公共点时,请直接写出抛物线y=﹣x2+c平移的最短距离并求出此时抛物线的顶点坐标.【解答】解:(1)∵抛物线y=﹣x2+c与y轴交于点P(0,4),∴c=4,∴抛物线的解析式为y=﹣x2+4;(2)△BCQ是直角三角形.理由如下:将抛物线y=﹣x2+4向左平移1个单位长度,得新抛物线y=﹣(x+1)2+4,∴平移后的抛物线顶点为Q(﹣1,4),令x=0,得y=﹣1+4=3,∴C(0,3),令y=0,得﹣(x+1)2+4=0,解得:x1=1,x2=﹣3,∴B(﹣3,0),A(1,0),如图1,连接BQ,CQ,PQ,∵P(0,4),Q(﹣1,4),∴PQ⊥y轴,PQ=1,∵CP=4﹣3=1,∴PQ=CP,∠CPQ=90°,∴△CPQ是等腰直角三角形,∴∠PCQ=45°,∵OB=OC=3,∠BOC=90°,∴△BOC是等腰直角三角形,∴∠BCO=45°,∴∠BCQ=180°﹣45°﹣45°=90°,∴△BCQ是直角三角形.(3)在x轴上存在点T,使得以B、N、T三点为顶点的三角形与△ABC相似.∵△ABC是锐角三角形,∠ABC=45°,∴以B、N、T三点为顶点的三角形与△ABC相似,必须∠NBT=∠ABC=45°,即点T在y轴的右侧,设T(x,0),且x>0,则BT=x+3,∵B(﹣3,0),A(1,0),C(0,3),∴∠ABC=45°,AB=4,BC=3,设直线BC的解析式为y=kx+b,则,解得:,∴直线BC的解析式为y=x+3,由,解得:,,∴M(﹣,),N(,),∴BN=×=,①当△NBT∽△CBA时,则=,∴=,解得:x=,∴T(,0);②当△NBT∽△ABC时,则=,∴=,解得:x=,∴T(,0);综上所述,点T的坐标T(,0)或(,0).(4)抛物线y=﹣x2+4的顶点为P(0,4),∵直线BC的解析式为y=x+3,∴直线BC与y轴的夹角为45°,当抛物线沿着垂直直线BC的方向平移到只有1个公共点时,平移距离最小,此时向右和向下平移距离相等,设平移后的抛物线的顶点为P′(t,4﹣t),则平移后的抛物线为y=﹣(x﹣t)2+4﹣t,由﹣(x﹣t)2+4﹣t=x+3,整理得:x2+(1﹣2t)x+t2+t﹣1=0,∵平移后的抛物线与直线BC最多只有一个公共点,∴Δ=(1﹣2t)2﹣4(t2+t﹣1)=0,解得:t=,∴平移后的抛物线的顶点为P′(,),平移的最短距离为.二.直角三角形的存在性4.(2022•广安)如图,在平面直角坐标系中,抛物线y=ax2+x+m(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,﹣4),点C 坐标为(2,0).(1)求此抛物线的函数解析式.(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)点P为该抛物线对称轴上的动点,使得△P AB为直角三角形,请求出点P 的坐标.【解答】解:(1)∵抛物线y=ax2+x+m(a≠0)的图象经过点B(0,﹣4),点C(2,0),∴,解得,∴抛物线的解析式为y=x2+x﹣4;(2)存在.理由:如图1中,设D (t ,t 2+t ﹣4),连接OD .令y =0,则x 2+x ﹣4=0,解得x =﹣4或2,∴A (﹣4,0),C (2,0),∵B (0,﹣4),∴OA =OB =4,∵S △ABD =S △AOD +S △OBD ﹣S △AOB =×4×(﹣﹣t +4)+×4×(﹣t )﹣×4×4=﹣t 2﹣4t =﹣(t +2)2+4,∵﹣1<0,∴t =﹣2时,△ABD 的面积最大,最大值为4,此时D (﹣2,﹣4); (3)如图2中,设抛物线的对称轴交x 轴于点N ,过点B 作BM ⊥抛物线的对称轴于点M .则N (﹣1.0).M (﹣1,﹣4);∵OA=OB=4,∠AOB=90°,∴∠OAB=∠OBA=45°,当∠P1AB=90°时,△ANP1是等腰直角三角形,∴AN=NP1=3,∴P1(﹣1,3),当∠ABP2=90°时,△BMP2是等腰直角三角形,可得P2(﹣1,﹣5),当∠APB=90°时,设P(﹣1,n),设AB的中点为J,连接PJ,则J(﹣2,﹣2),∴PJ=AB=2,∴12+(n+2)2=(2)2,解得n=﹣2或﹣﹣2,∴P3(﹣1,﹣2),P4(﹣1,﹣﹣2),综上所述,满足条件的点P的坐标为(﹣1,3)或(﹣1,﹣5)或(﹣1,﹣2)或(﹣1,﹣﹣2).5.(2022•辽宁)如图,抛物线y=ax2﹣3x+c与x轴交于A(﹣4,0),B两点,与y轴交于点C(0,4),点D为x轴上方抛物线上的动点,射线OD交直线AC 于点E,将射线OD绕点O逆时针旋转45°得到射线OP,OP交直线AC于点F,连接DF.(1)求抛物线的解析式;(2)当点D在第二象限且=时,求点D的坐标;(3)当△ODF为直角三角形时,请直接写出点D的坐标.【解答】解:(1)将点A(﹣4,0),C(0,4)代入y=ax2﹣3x+c,∴,解得,∴y=﹣x2﹣3x+4;(2)过点D作DG⊥AB交于G,交AC于点H,设直线AC的解析式为y=kx+b,∴,解得,∴y=x+4,设D(n,﹣n2﹣3n+4),H(n,n+4),∴DH=﹣n2﹣4n,∵DH∥OC,∴==,∵OC=4,∴DH=3,∴﹣n2﹣4n=3,解得n=﹣1或n=﹣3,∴D(﹣1,6)或(﹣3,4);(3)设F(t,t+4),当∠FDO=90°时,过点D作MN⊥y轴交于点N,过点F作FM⊥MN交于点M,∵∠DOF=45°,∴DF=DO,∵∠MDF+∠NDO=90°,∠MDF+∠MFD=90°,∴∠NDO=∠MFD,∴△MDF≌△NOD(AAS),∴DM=ON,MF=DN,∴DN+ON=﹣t,DN=ON+(﹣t﹣4),∴DN=﹣t﹣2,ON=2,∴D点纵坐标为2,∴﹣x2﹣3x+4=2,解得x=或x=,∴D点坐标为(,2)或(,2);当∠DFO=90°时,过点F作KL⊥x轴交于L点,过点D作DK⊥KL交于点K,∵∠KFD+∠LFO=90°,∠KFD+∠KDF=90°,∴∠LFO=∠KDF,∵DF=FO,∴△KDF≌△LFO(AAS),∴KD=FL,KF=LO,∴KL=t+4﹣t=4,∴D点纵坐标为4,∴﹣x2﹣3x+4=4,解得x=0或x=﹣3,∴D(0,4)或(﹣3,4);综上所述:D点坐标为(,2)或(,2)或(0,4)或(﹣3,4).三.等腰三角形的存在性6.(2022•百色)已知抛物线经过A(﹣1,0)、B(0,3)、C(3,0)三点,O 为坐标原点,抛物线交正方形OBDC的边BD于点E,点M为射线BD上一动点,连接OM,交BC于点F.(1)求抛物线的表达式;(2)求证:∠BOF=∠BDF;(3)是否存在点M,使△MDF为等腰三角形?若不存在,请说明理由;若存在,求ME的长.【解答】(1)解:设抛物线的表达式为y=ax2+bx+c,把A(﹣1,0)、B(0,3)、C(3,0)代入得:,解得,∴抛物线的表达式为:y=﹣x2+2x+3;(2)证明:∵正方形OBDC,∴∠OBC=∠DBC,BD=OB,∵BF=BF,∴△BOF≌△BDF,∴∠BOF=∠BDF;(3)解:∵抛物线交正方形OBDC的边BD于点E,∴令y=3,则3=﹣x2+2x+3,解得:x1=0,x2=2,∴E(2,3),①如图,当M在线段BD的延长线上时,∠BDF为锐角,∴∠FDM为钝角,∵△MDF为等腰三角形,∴DF=DM,∴∠M=∠DFM,∴∠BDF=∠M+∠DFM=2∠M,∵BM∥OC,∴∠M=∠MOC,由(2)得∠BOF=∠BDF,∴∠BDF+∠MOC=3∠M=90°,∴∠M=30°,在Rt△BOM中,BM=,∴ME=BM﹣BE=3﹣2;②如图,当M在线段BD上时,∠DMF为钝角,∵△MDF为等腰三角形,∴MF=DM,∴∠BDF=∠MFD,∴∠BMO=∠BDF+∠MFD=2∠BDF,由(2)得∠BOF=∠BDF,∴∠BMO=2∠BOM,∴∠BOM+∠BMO=3∠BOM=90°,∴∠BOM=30°,在Rt△BOM中,BM=,∴ME=BE﹣BM=2﹣,综上所述,ME的值为:3﹣2或2﹣.7.(2022•山西)综合与探究如图,二次函数y=﹣x2+x+4的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.点P是第一象限内二次函数图象上的一个动点,设点P的横坐标为m.过点P作直线PD⊥x轴于点D,作直线BC交PD于点E.(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式;(2)当△CEP是以PE为底边的等腰三角形时,求点P的坐标;(3)连接AC,过点P作直线l∥AC,交y轴于点F,连接DF.试探究:在点P 运动的过程中,是否存在点P,使得CE=FD,若存在,请直接写出m的值;若不存在,请说明理由.【解答】解:(1)在y=﹣x2+x+4中,令x=0得y=4,令y=0得x=8或x=﹣2,∴A(﹣2,0),B(8,0),C(0,4),设直线BC解析式为y=kx+4,将B(8,0)代入得:8k+4=0,解得k=﹣,∴直线BC解析式为y=﹣x+4;(2)过C作CG⊥PD于G,如图:设P(m,﹣m2+m+4),∴PD=﹣m2+m+4,∵∠COD=∠PDO=∠CGD=90°,∴四边形CODG是矩形,∴DG=OC=4,CG=OD=m,∴PG=PD﹣DG=﹣m2+m+4﹣4=﹣m2+m,∵CP=CE,CG⊥PD,∴GE=PG=﹣m2+m,∵∠GCE=∠OBC,∠CGE=90°=∠BOC,∴△CGE∽△BOC,∴=,即=,解得m=0(舍去)或m=4,∴P(4,6);(3)存在点P,使得CE=FD,理由如下:过C作CH⊥PD于H,如图:设P(m,﹣m2+m+4),由A(﹣2,0),C(0,4)可得直线AC解析式为y=2x+4,根据PF∥AC,设直线PF解析式为y=2x+b,将P(m,﹣m2+m+4)代入得:﹣m2+m+4=2m+b,∴b=﹣m2﹣m+4,∴直线PF解析式为y=2x﹣m2﹣m+4,令x=0得y=﹣m2﹣m+4,∴F(0,﹣m2﹣m+4),∴OF=|﹣m2﹣m+4|,同(2)可得四边形CODH是矩形,∴CH=OD,∵CE=FD,∴Rt△CHE≌Rt△DOF(HL),∴∠HCE=∠FDO,∵∠HCE=∠CBO,∴∠FDO=∠CBO,∴tan∠FDO=tan∠CBO,∴=,即=,∴﹣m2﹣m+4=m或﹣m2﹣m+4=﹣m,解得m=2﹣2或m=﹣2﹣2或m=4或m=﹣4,∵P在第一象限,∴m=2﹣2或m=4.8.(2022•东营)如图,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C.(1)求抛物线的表达式;(2)在对称轴上找一点Q,使△ACQ的周长最小,求点Q的坐标;(3)点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当△PMB是以PB为腰的等腰直角三角形时,请直接写出所有点M的坐标.【解答】解:(1)将点A(﹣1,0),点B(3,0)代入y=ax2+bx﹣3,∴,解得,∴y=x2﹣2x﹣3;(2)连接CB交对称轴于点Q,∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴为直线x=1,∵A、B关于对称轴x=1对称,∴AQ=BQ,∴AC+AQ+CQ=AC+CQ+BQ≥AC+BC,当C、B、Q三点共线时,△ACQ的周长最小,∵C(0,﹣3),B(3,0),设直线BC的解析式为y=kx+b,∴,解得,∴y=x﹣3,∴Q(1,﹣2);(3)当∠BPM=90°时,PM=PB,∴M点与A点重合,∴M(﹣1,0);当∠PBM=90°时,PB=BM,如图1,当P点在M点上方时,过点B作x轴的垂线GH,过点P作PH⊥GH 交于H,过点M作MG⊥HG交于G,∵∠PBM=90°,∴∠PBH+∠MBG=90°,∵∠PBH+∠BPH=90°,∴∠MBG=∠BPH,∵BP=BM,∴△BPH≌△MBG(AAS),∴BH=MG,PH=BG=2,设P(1,t),则M(3﹣t,﹣2),∴﹣2=(3﹣t)2﹣2(3﹣t)﹣3,解得t=2+或t=2﹣,∴M(1﹣,﹣2)或(1+,﹣2),∵M点在对称轴的左侧,∴M点坐标为(1﹣,﹣2);如图2,当P点在M点下方时,同理可得M(3+t,2),∴2=(3+t)2﹣2(3+t)﹣3,解得t=﹣2+(舍)或t=﹣2﹣,∴M(1﹣,2);综上所述:M点的坐标为(1﹣,﹣2)或(1﹣,2)或(﹣1,0).9.(2022•枣庄)如图①,已知抛物线L:y=x2+bx+c经过点A(0,3),B(1,0),过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.(1)求抛物线的关系式;(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;(3)将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE 内(包括△OAE的边界),求h的取值范围;(4)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线L:y=x2+bx+c经过点A(0,3),B(1,0),∴,解得,∴抛物线的解析式为:y=x2﹣4x+3;(2)如图,过P作PG∥y轴,交OE于点G,设P(m,m2﹣4m+3),∵OE平分∠AOB,∠AOB=90°,∴∠AOE=45°,∴△AOE是等腰直角三角形,∴AE=OA=3,∴E(3,3),∴直线OE的解析式为:y=x,∴G(m,m),∴PG=m﹣(m2﹣4m+3)=﹣m2+5m﹣3,∴S△OPE =S△OPG+S△EPG=PG•AE=×3×(﹣m2+5m﹣3)=﹣(m2﹣5m+3)=﹣(m﹣)2+,∵﹣<0,∴当m=时,△OPE面积最大,此时,P点坐标为(,﹣);(3)由y=x2﹣4x+3=(x﹣2)2﹣1,得抛物线l的对称轴为直线x=2,顶点为(2,﹣1),抛物线L向上平移h个单位长度后顶点为F(2,﹣1+h).设直线x=2交OE于点M,交AE于点N,则E(3,3),∵直线OE的解析式为:y=x,∴M(2,2),∵点F在△OAE内(包括△OAE的边界),∴2≤﹣1+h≤3,解得3≤h≤4;(4)设P(m,m2﹣4m+3),分四种情况:①当P在对称轴的左边,且在x轴下方时,如图,过P作MN⊥y轴,交y轴于M,交l于N,∴∠OMP=∠PNF=90°,∵△OPF是等腰直角三角形,∴OP=PF,∠OPF=90°,∴∠OPM+∠NPF=∠PFN+∠NPF=90°,∴∠OPM=∠PFN,∴△OMP≌△PNF(AAS),∴OM=PN,∵P(m,m2﹣4m+3),则﹣m2+4m﹣3=2﹣m,解得:m=(舍)或,∴P的坐标为(,);②当P在对称轴的左边,且在x轴上方时,同理得:2﹣m=m2﹣4m+3,解得:m1=(舍)或m2=,∴P的坐标为(,);③当P在对称轴的右边,且在x轴下方时,如图,过P作MN⊥x轴于N,过F作FM⊥MN于M,同理得△ONP≌△PMF,∴PN=FM,则﹣m2+4m﹣3=m﹣2,解得:m1=或m2=(舍);P的坐标为(,);④当P在对称轴的右边,且在x轴上方时,如图,同理得m2﹣4m+3=m﹣2,解得:m=或(舍),P的坐标为:(,);综上所述,点P的坐标是:(,)或(,)或(,)或(,).方法二:作直线DE:y=x﹣2,E(1,﹣1)是D点(2,0)绕O点顺时针旋转45°并且OD缩小倍得到,易知直线DE即为对称轴上的点绕O点顺时针旋转45°,且到O点距离缩小倍的轨迹,联立直线DE和抛物线解析式得x2﹣4x+3=x﹣2,解得x1=,x2=,同理可得x3=或x4=;综上所述,点P的坐标是:(,)或(,)或(,)或(,).10.(2023•澄城县一模)如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)、B,与y轴交于点C(0,3),直线l是抛物线的对称轴.(1)求抛物线的函数解析式;(2)在对称轴l上是否存在点M,使△MAC为等腰三角形,若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.【解答】解:(1)把点A(﹣1,0)、点C(0,3)分别代入y=﹣x2+bx+c,得.解得.故该抛物线解析式为:y=﹣x2+2x+3;(2)由(1)知,该抛物线解析式为:y=﹣x2+2x+3.则该抛物线的对称轴为直线x=﹣=1.故设M(1,m).∵A(﹣1,0)、点C(0,3),∴AC2=10,AM2=4+m2,CM2=1+(m﹣3)2.①若AC=AM时,10=4+m2,解得m=±.∴点M的坐标为(1,)或(1,﹣);②若AC=CM时,10=1+(m﹣3)2,解得m=0或m=6,∴点M的坐标为(1,0)或(1,6).当点M的坐标为(1,6)时,点A、C、M共线,∴点M的坐标为(1,0);③当AM=CM时,4+m2=1+(m﹣3)2,解得m=1,∴点M的坐标为(1,1).综上所述,符合条件的点M的坐标为(1,)或(1,﹣)或(1,0)或(1,1).11.(2023•碑林区校级一模)二次函数y=ax2+bx+2的图象交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC,设运动的时间为t秒.(1)求二次函数y=ax2+bx+2的表达式;(2)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,求此时点D的坐标.【解答】解:(1)将点(﹣1,0),B(4,0)代入y=ax2+bx+2,∴a=﹣,b=,∴y=﹣x2+x+2;(2)∵BM=5﹣2t,∴M(2t﹣1,0),设P(2t﹣1,m),∵PC2=(2t﹣1)2+(m﹣2)2,PB2=(2t﹣5)2+m2,∵PB=PC,∴(2t﹣1)2+(m﹣2)2=(2t﹣5)2+m2,∴m=4t﹣5,∴P(2t﹣1,4t﹣5),∵PC⊥PB,∴×=﹣1,∴t=1或t=2,∴M(1,0)或M(3,0),∴D(1,3)或D(3,2).12.(2023•东洲区模拟)抛物线y=ax2+bx+3经过A(﹣1,0),B(3,0)两点,与y轴正半轴交于点C.(1)求此抛物线解析式;(2)如图①,连接BC,点P为抛物线第一象限上一点,设点P的横坐标为m,△PBC的面积为S,求S与m的函数关系式,并求S最大时P点坐标;(3)如图②,连接AC,在抛物线的对称轴上是否存在点M,使△MAC为等腰三角形?若存在,请直接写出符合条件的点M的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线y=ax2+bx+3经过A(﹣1,0),B(3,0)两点,∴,解得:,∴抛物线解析式为y=﹣x2+2x+3;(2)点P作PF⊥x轴于点F,交BC于点E,设BC直线解析式为:y=kx+b,∵B(3,0),C(0,3),∴,解得,∴y=﹣x+3,由题意可知P(m,﹣m2+2m+3),E(m,﹣m+3),S=S△PBE+S△PCE,S=PE•OB=(﹣m2+2m+3+m﹣3)×3,,∵,∴当时,S有最大值,此时P点坐标为;(3)存在,M1(1,0),,,M4(1,1),①当AC=AM时,如图,设对称轴l与AB交于点E,则,∵AM2=AE2+EM2,∴,解得:,∴M点的坐标为或,②当AC=MC时,则OC为AM的垂直平分线.因此M与E重合,因此,M点的坐标为(1,0),③当AM=CM时,如图,设M点的坐标为(1,n),则AM2=22+n2=4+n2,CM2=12+(3﹣n)2,∴4+n2=12+(3﹣n)2,解得:n=1,∴M点的坐标为(1,1),综上可知,潢足条件的M点共四个,其坐标为M1(1,0),,,M4(1,1).13.(2023•三亚一模)如图,抛物线y=ax2+3x+c(a≠0)与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,8),顶点为D,连接AC,CD,DB,直线BC 与抛物线的对称轴l交于点E.(1)求抛物线的解析式和直线BC的解析式;(2)求四边形ABDC的面积;(3)P是第一象限内抛物线上的动点,连接PB,PC,当S△PBC =S△ABC时,求点P的坐标;(4)在抛物线的对称轴l上是否存在点M,使得△BEM为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线y=ax2+3x+c(a≠0)过点A(﹣2,0)和C(0,8),∴,解得,∴抛物线的解析式为y=﹣x2+3x+8.令y=0,得.解得x1=﹣2,x2=8.∴点B的坐标为(8,0).设直线BC的解析式为y=kx+b.把点B(8,0),C(0,8)分别代入y=kx+b,得,解得,∴直线BC的解析式为y=﹣x+8.(2)如图1,设抛物线的对称轴l与x轴交于点H.∵抛物线的解析式为,∴顶点D的坐标为.∴S四边形ABDC =S△AOC+S梯形OCDH+S△BDH===70.(3)∵.∴.如图2,过点P作PG⊥x轴,交x轴于点G,交BC于点F.设点.∵点F在直线BC上,∴F(t,﹣t+8).∴.∴.∴.解得t1=2,t2=6.∴点P的坐标为(2,12)或P(6,8).(4)存在.∵△BEM为等腰三角形,∴BM=EM或BE=BM或BE=EM,设M(3,m),∵B(8,0),E(3,5),∴BE==5,EM=|m﹣5|,BM==,当BM=EM时,=|m﹣5|,∴m2+25=(m﹣5)2,解得:m=0,∴M(3,0);当BE=BM时,5=,∴m2+25=50,解得:m=﹣5或m=5(舍去),∴M(3,﹣5);当BE=EM时,5=|m﹣5|,解得:m=5+5或m=5﹣5,∴M(3,5+5)或(3,5﹣5),综上所述,点M的坐标为(3,0)或(3,﹣5)或(3,5+5)或(3,5﹣5).14.(2023•南海区一模)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a >0)与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P为直线BC下方抛物线上的一动点,PM⊥BC于点M,PN∥y轴交BC 于点N.求线段PM的最大值和此时点P的坐标;(3)点E为x轴上一动点,点Q为抛物线上一动点,是否存在以CQ为斜边的等腰直角三角形CEQ?若存在,请直接写出点E的坐标;若不存在,请说明理由.【解答】解:(1)将A(﹣1,0),B(3,0)代入函数y=ax2+bx﹣3(a>0)中,得,解得,∴解析式为y=x2﹣2x﹣3,故抛物线解析式为y=x2﹣2x﹣3;(2)当x=0时,y=3,∴C(0,﹣3),∵B(3,0),∴∠OCB=∠OBC=45°,∵PN∥y轴,∴∠MNP=45°,∵PM⊥BC,∴PM=PN,则当PN最大时,PM也最大,设BC的解析式为y=mx+n,∴,解得,∴BC解析式为y=x﹣3,设P(x,x2﹣2x﹣3),N(x,x﹣3),∴PN=x﹣3﹣(x2﹣2x﹣3)=﹣(x﹣)2+,当x=时,PN最大,则PM=PN=×=,∴P(,),故PM最大值为,P点坐标为(,﹣);(3)存在,点E的坐标为(﹣5,0),(,0),(0,0),(,0).∵CEQ是以CQ为斜边的等腰直角三角形,∴设Q(x,x2﹣2x﹣3),①如图,过点E作x轴的垂线l,再分别过点C和点Q作垂线l的垂线,分别交于点M和点N,∵∠CEQ=90°,∴∠QEM+∠CEN=90°,∵∠QEM+∠MQE=90°,∴∠EQM=∠CEN,∵∠CNE=∠QME=90°,EC=EQ,∴△EMQ≌△CNE(AAS),∴CN=EM=x2﹣2x﹣3,MQ=EN=3,∴|x Q|+MQ=CN,﹣x+3=x2﹣2x﹣3,解得x=﹣2,x=3(舍去),∴OE=CM=2+3=5,E(﹣5,0),②如图,过点E作x轴的垂线l,再分别过点C和点Q作垂线l的垂线,分别交于点M和点N,同理:△EMC≌△QNE(AAS),CM=EN=x2﹣2x﹣3,NQ=EM=3,∴﹣x+x2﹣2x﹣3=3,解得x=,x=(舍去),∴OE=CM=,E(,0),③如图,点E和点O重合,点Q和点B重合,此时E(0,0),④如图,过点E作x轴的垂线l,再分别过点C和点Q作垂线l的垂线,分别交于点M和点N,同理:△EMC≌△QNE(AAS),CM=EN=x2﹣2x﹣3,NQ=EM=3,∴x+3=x2﹣2x﹣3,解得x=,x=(舍去),∴OE=CM=,E(,0),综上所述,点E的坐标为(﹣5,0),(,0),(0,0),(,0)41。
抛物线与坐标轴交点构成的三角形问题

抛物线与坐标轴交点构成的三角形问题--------思考与探索面积篇例1:已知抛物线3+2x +x -=y 2与x 轴交于A,B 两点,其中A 点位于B 点的左侧,与y 轴交于C 点,顶点为P , _________=S A O C △ _________=S BO C △ _________=S CO P △ _________=S PAB △_________=S PCB △ _________=S A CP △例:在平面直角坐标系中,有两点A (-1,0),B (3,0),如图,小敏发现所有过A ,B 两点的抛物线如果与y 轴负半轴交于点C ,M 为抛物线的顶点,那么△ACM 与△ACB 的面积比不变,请你求出这个比值。
对称篇例2、如图,一元二次方程2230x x +-=的二根12x x ,( 12x x < )是抛物线2y ax bx c =++与x 轴的两个交点B,C 的横坐标,且此抛物线过A(3,6)点.(1)求此二次函数的解析式.(2)设此抛物线的顶点为p ,对称轴与线段AC 相交于点Q ,求点P 和点Q 的坐标.(3)在X 轴上有一动点M ,当MQ+MA 取得最小值时,求点M 的坐标(4)设AC 与Y 轴交与D 点,E 点坐标为(0,1),在X 轴上找一点F ,抛物线对称轴上找一点G ,使四边形AFGE 的周长最短,并求出当四边形周长最短时的点F 、G 点坐标,并求出四边形AFGE 的周长。
形状篇1、已知抛物线c +bx +ax =y 2与x 轴正、负半轴分别交于A 、B 两点,与y 轴负半轴交于点C 。
若OA=4,OB=1,∠ACB=90°,求抛物线解析式。
2、已知:抛物线与x 轴的交点坐标为A(-1,0)和B (3,0),顶点为C,若∠ACB=90度.问1:C 点的坐标是多少?问2:在抛物线的解析式中,=-ac b 423. 若题设中的A 、B 两点的坐标未知,而已知∠ACB=90度,你能求出 =-ac b 42吗?4. 从上面的探索中我们看到解析式中的△与∠ACB 有关,那么如果△ACB 是等边三角形,则△是多少?最后, ①思因果 ; ②思规律 ; ③思多解 ; ④思变通; ⑤思归类; ⑥思错误.。
抛物线与直线形由动点生成的特殊三角形问题

抛物线与直线形(1)——由动点生成的特殊三角形问题知识纵横抛物线与直线形的结合表现形式之一是,以抛物线为载体,探讨是否存在一些点,使其能够成某些特殊三角形,有以下常见的基本形式:(1)抛物线上的点能否构成等腰三角形;(2)抛物线上的点能否构成直角三角形;(3)抛物线上的点能否构成相似三角形;解这类问题的基本思路:假设存在,数形结合,分类归纳,逐一考察。
例题求解【例1】如图,抛物线y =ax2 -5ax - 4经过.'ABC的三个顶点,已知BC // x轴,点A在x轴上,点C在y轴上,且AC =BC •(1)求抛物线的对称轴;(2)写出代B,C三点的坐标并求抛物线的解析式;(3)探究:若点P是抛物线对称轴上且在x轴下方的动点,是否存在■ PAB是等腰三角形?(龙岩市中考题)思路点拨对于(3)只需求出P点纵坐标,将问题转化为相关线段长。
解题的关键是分情况讨论并正确画图。
【例2】已知抛物线y = kx2 - 2kx _ 3k ,交x轴于A, B两点(A在B的左边),交y轴于C点,且y有最大值4.(1)求抛物线的解析式;(2)在抛物线上是否存在点P ,使PBC是直角三角形?若存在,求出P点坐标;若不存在,说明理由.(包头市中考题)思路点拨对于(2),设P点坐标为(a,b ),寻找相似三角形,建立a、b的另一关系式,解联立而得到的方程组,可求出a、b的值。
【例3】抛物线y = —l(x-i f十3与y轴交于点A,顶点为B,对称轴BC与x轴交于点4C .(1)如图1 .求点A的坐标及线段0C的长;(2 )点P在抛物线上,直线PQ // BC交x轴于点Q,连接BQ .①若含45角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一个顶点E在PQ上•求直线BQ的函数解析式;②若含30角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.S 1 2 2(2011年绍兴市中考题) 思路点拨对于(2),解题的关键是求出CQ的长。
抛物线与相似三角形专题精编

抛物线与相似三角形专题精编【例1】 如图,已知△ABC 的三个顶点坐标分别为A (-4,0)、B (1,0)、C (-2,6).(1)求经过A 、B 、C 三点的抛物线解析式;(2)设直线BC 交y 轴于点E ,连接AE ,求证:AE =CE ;(3)设抛物线与y 轴交于点D ,连接AD 交BC 于点F ,试问:以A 、B 、F 为顶点的三角形与△ABC 相似吗?点拨: 以数助形,通过计算证明.对于(3),只需证明:AB BC BF AB=.【例2】如图1,已知抛物线()20y ax bx a =+≠经过A (3,0)、B (4,4)两点. (1)求抛物线的解析式;(2)将直线OB 向下平移m 个单位长度后,得到的直线与抛物线只有一个公共点D ,求m 的值及点D 的坐标;(3)如图2,若点N 在抛物线上,且∠NBO =∠ABO ,则在(2)的条件下,求出所有满足△POD ∽△NOB 的点P 的坐标(点P 、O 、D 分别与点N 、O 、B 对应).图1 图2点拨: 对于(3),点B (4,4)、D (2,-2)的坐标隐含了什么关系?条件∠NBO =∠ABO 怎样运用?如何将△POD ∽△NOB 转化为相似三角形的基本图形?P 点的位置能否大致确定?这是解决问题的关键.归纳总结: 构造即依据问题的条件和结论给出的信息,把问题作适当的加工处理,构造与问题相关的数学模式,揭示问题的本质.例2(3)可通过几何变换,构作基本相似形,化一般为特殊,使得点P 得以定位,提高解题的境界.【例3】 如图,抛物线2y ax bx c =++的顶点坐标为(2,-1),并且与y 轴交于点C (0,3),与x 轴交于两点A 、B .(1)求抛物线的解析式;(2)设抛物线的对称轴与直线BC 交于点D ,连接AC 、AD ,求△ACD 的面积;(3)点E 是直线BC 上一动点,过点E 作y 轴的平行线EF ,与抛物线交于点F .问是否存在点E ,使得以D 、E 、F 为顶点的三角形与△BCO 相似?若存在,求出E 点的坐标;若不存在,请说明理由.点拨: 对于(3),因△BCO 是等腰直角三角形,故△DEF 也是等腰直角三角形,但相似对应关系不确定(或直角顶点不确定),应全面讨论.归纳总结: 审题的关键是在弄清字句含义的基础上,明晰数学意义,挖掘隐含条件,建立条件与结论之间的数学联系.对于例3,揭示△BOC 的形状、直线AD 与BC 的位置关系,为点的定位创造条件是解题的关键.审题的本质是从问题本身去获取从何处入手、向何方前进的信息与启示,是从问题得到“如何解这道题”的逻辑起点.“磨刀不误砍柴工”,认真审题,成也审题,败也审题.针对训练:1、如图,已知抛物线2y ax bx c =++的图象经过原点O ,交x 轴于点A ,其顶点B 的坐标为()3,3-.(1)求抛物线的解析式;(2)在抛物线上求点P ,使=2POA AOB S S △△.(3)在抛物线上是否存在点Q ,使△AQO 与△AOB 相似?如果存在,请求出Q 点的坐标;如果不存在,请说明理由.2、如图,已知二次函数()()12+48y x ax b =+的图象过点A (-4,3)、B (4,4). (1)求抛物线的解析式;(2)求证:△ACB 是直角三角形;(3)若点P 在第二象限,且是抛物线上的一动点,过点P 作PH ⊥x 轴于H ,是否存在以P 、H 、D 为顶点的三角形与△ABC 相似?若存在,求出点P 的坐标;若不存在,请说明理由.3、如图,已知抛物线的方程()()()1120C y x x m m m=-+->:与x 轴相交于点B 、C ,与y 轴相交于点E ,且点B 在点C 的左侧.(1)若抛物线1C 过点M (2,2),求实数m 的值; (2)在(1)的条件下,求△BCE 的面积;(3)在(1)条件下,在抛物线的对称轴上找一点H ,使BH +EH 最小,并求出点H 的坐标;(4)在第四象限内,抛物线1C 上是否存在点F ,使得以点B 、C 、F 为顶点的三角形与△BCE 相似?若存在,求m 的值;若不存在,请说明理由.4、如图,已知抛物线()2111444b y x b x =-++(b 是实数且b >2)与x 轴的正半轴分别交于点A 、B (点A 位于点B 的左侧),与y 轴的正半轴交于点C .(1)点B 的坐标为 ,点C 的坐标为 (用含b 的代数式表示);(2)请你探索在第一象限内是否存在点P ,使得四边形PCOB 的面积等于2b ,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO,△QOA和△QAB 中的任意两个三角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q 的坐标;如果不存在,请说明理由.本节总结:点的运动既能改变图形相关的数量关系,又能改变图形的形状及位置,从而造就相似三角形,抛物线与相似三角形的结合是抛物线上几何架构的重要表现形式.由相似三角形的性质确定动点位置,从定性到定量(点的坐标的确定),因点的运动或对应关系的不确定而进行的讨论,是解这类问题的关键.在中考综合题中,动点的运动既会影响图形相关的数量关系,又会改变图形的位置及形状,从而生成特殊三角形、特殊四边形、相似三角形,解题的关键是把图形的几何性质与点的坐标有机结合.。
2019中考数学压轴题分类复习之抛物线与三角形的综合问题
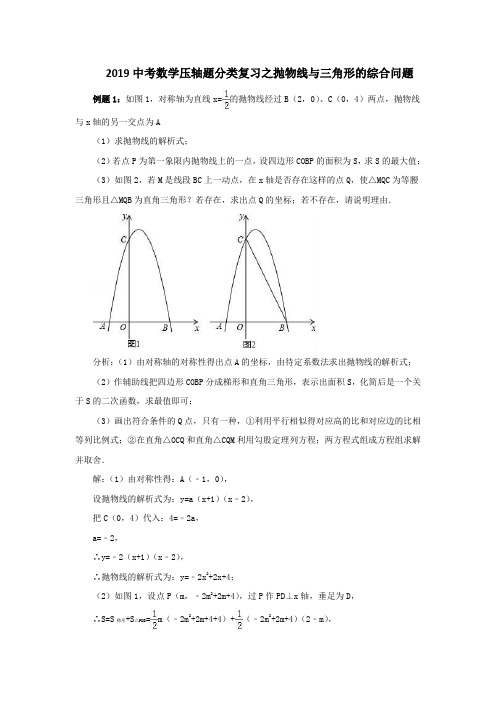
2019中考数学压轴题分类复习之抛物线与三角形的综合问题例题1:如图1,对称轴为直线x=的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A(1)求抛物线的解析式;(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.分析:(1)由对称轴的对称性得出点A的坐标,由待定系数法求出抛物线的解析式;(2)作辅助线把四边形COBP分成梯形和直角三角形,表示出面积S,化简后是一个关于S的二次函数,求最值即可;(3)画出符合条件的Q点,只有一种,①利用平行相似得对应高的比和对应边的比相等列比例式;②在直角△OCQ和直角△CQM利用勾股定理列方程;两方程式组成方程组求解并取舍.解:(1)由对称性得:A(﹣1,0),设抛物线的解析式为:y=a(x+1)(x﹣2),把C(0,4)代入:4=﹣2a,a=﹣2,∴y=﹣2(x+1)(x﹣2),∴抛物线的解析式为:y=﹣2x2+2x+4;(2)如图1,设点P(m,﹣2m2+2m+4),过P作PD⊥x轴,垂足为D,∴S=S梯形+S△PDB=m(﹣2m2+2m+4+4)+(﹣2m2+2m+4)(2﹣m),S=﹣2m2+4m+4=﹣2(m﹣1)2+6,∵﹣2<0,∴S有最大值,则S大=6;(3)如图2,存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形,理由是:设直线BC的解析式为:y=kx+b,把B(2,0)、C(0,4)代入得:,解得:,∴直线BC的解析式为:y=﹣2x+4,设M(a,﹣2a+4),过A作AE⊥BC,垂足为E,则AE的解析式为:y=x+,则直线BC与直线AE的交点E(1.4,1.2),设Q(﹣x,0)(x>0),∵AE∥QM,∴△ABE∽△QBM,∴①,由勾股定理得:x2+42=2×[a2+(﹣2a+4﹣4)2]②,由①②得:a1=4(舍),a2=,当a=时,x=,∴Q(﹣,0).同步练习:1.如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.(1)求该二次函数的解析式及点M的坐标;(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).。
专题5 抛物线与三角形、特殊四边形的综合题

1专题5 抛物线与三角形、特殊四边形的综合题1、 (2009益阳)阅读材料:如图12-1,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算三角形面积的新方法:ah S ABC 21=∆,即三角形面积等于水平宽与铅垂高乘积的一半.解答下列问题:如图12-2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结PA ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆; (3)是否存在一点P ,使S △PAB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.2、(2009烟台)如图,抛物线23y ax bx =+-与x 轴交于A B ,两点,与y轴交于C 点,且经过点(23)a -,,对称轴是直线1x =,顶点是M .(1) 求抛物线对应的函数表达式;(2) 经过C ,M 两点作直线与x 轴交于点N ,在抛物线上是否存在这样的点P ,使以点P A C N ,,,为顶点的四边形为平行四边形?若存在,请求出点P 的坐标;若不存在,请说明理由;(3) 设直线3y x =-+与y 轴的交点是D ,在线段B D 上任取一点E (不与B D ,重合),经过A B E ,,三点的圆交直线B C 于点F ,试判断A E F △的形状,并说明理由;(4) 当E 是直线3y x =-+上任意一点时,(3)中的结论是否成立?(请直接写出结论).xCOy ABD 1 123、(2009湖北荆门)一开口向上的抛物线与x 轴交于A (m -2,0),B (m +2,0)两点,记抛物线顶点为C ,且AC ⊥BC .(1)若m 为常数,求抛物线的解析式;(2)若m 为小于0的常数,那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点? (3)设抛物线交y 轴正半轴于D 点,问是否存在实数m ,使得△BOD 为等腰三角形?若存在,求出m 的值;若不存在,请说明理由.4、如图,抛物线24y ax bx a =+-经过(10)A -,、(04)C ,两点,与x 轴交于另一点B . (1)求抛物线的解析式;(2)已知点(1)D m m +,在第一象限的抛物线上,求点D 关于直线B C 对称的点的坐标; (3)在(2)的条件下,连接B D ,点P 为抛物线上一点,且45D B P ∠=°,求点P 的坐标.。
抛物线中的直角三角形(安松)

解:存在点M,使得∠ADM=90°. 理由如下: 由抛物线y=X2+2x-3,得C(0,-3), ∵CD∥x轴, ∴D的纵坐标为-3, 把y=-3代入y=X2+2x-3,得
X2+2x-3=-3, 解得:x1=-2,x2=0, ∴D的坐标为(-2,-3),
设直线AD的解析式为y1=k1x+b1,则:
k1 b1 0 2k1 b1 3
解得:
b1k1
1 -1
∴直线AD的解析式为y1=x-1.
如图,过点D作直线DM⊥直线 DA交抛物线于点M,
设直线MD的解析式为
y2=-x+b2,
把D(-2,-3)代入y2=-x+b2,得
b2=-5,
∴直线MD的解析式为y1=-x-5.
1
10 39
10
F( 1 , 39) 10 10
综上所述,.....
B
C
范例学习
例题1:如图,抛物线y =x2-2x-3与x轴交 于A(-1,0)、B(3,0),与y轴交于C(0,-3),且对称 轴为x=1.设点P为抛物线的对称轴x=1上的一动 点,求使∠PCB=90°的点P的坐标.
分析:设P(3,m),先 用两点间的距离公式表示 出PC2,PB2及BC2,程 有实数根,则存在;否则不 存在.
当PF⊥PB时,
∵点P(1,4.5)、B(4,0),
∴设直线PB的解析式为 y=-1,5x+6,
∴设直线PF的解析式为
y = 2 x + b, 3
把P(1,4.5)代入y=2/3x+b,得
b = 23,
∴根据题意6得:y
y = -x = 2x
2021年九年级中考数学复习高频考点提升练《抛物线压轴题中的三角形问题》 考题专题练习

2021年中考数学复习高频考点提升练《抛物线压轴题中的三角形问题》经典考题专题练习1.如图,在平面直角坐标系中,函数223(0)y ax ax a a=-++>的图像交x轴于点A、B,交y轴于点C,它的对称轴交x轴于点E.过点C作CD∥x轴交抛物线于点D,连接DE 并延长交y轴于点F,交抛物线于点G.直线AF交CD于点H,交抛物线于点K,连接HE、GK.(1)点E的坐标为:;(2)当△HEF 是直角三角形时,求a 的值;2.如图,二次函数y=ax 2+bx+4的图象与x轴交于点A(-1.0),B(4.0),与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E.垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.(1)求出二次函数y=ax2+bx+4和BC所在直线的表达式;(2)连接CP,CD,在移动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与△DCE相似,如果存在,求出点P的坐标,如果不存在,请说明理由.CA O EFBPDlxy3. 如图,已知抛物线y=ax2+bx+6经过两点A(﹣1,0),B(3,0),C是抛物线与y轴的点.(1)求抛物线的解析式;(2)点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,设△PBC的面积为S,求S关于m的函数表达式(指出自变量m的取值范围)和S的最大值;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N使得∠CMN=90°,且△CMN与△OBC相似,如果存在,请求出点M和点N的坐标.4. 在平面直角坐标系xOy中,把与x轴交点相同的二次函数图像称为“共根抛物线”.如图,抛物线L1:223212--=xxy的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线L2与L1是“共根抛物线”,其顶点为P.(1)若抛物线L2经过点(2,- 12),求L2对应的函数表达式;(2)当BP-CP的值最大时,求点P的坐标;(3)设点Q是抛物线L1上的一个动点,且位于其对称轴的右侧.若△DPQ与△ABC相似,求其“共根抛物线”L2的顶点P的坐标.5. 已知直线1:210=-+l y x 交y 轴于点A ,交x 轴于点B ,二次函数的图象过,A B两点,交x 轴于另一点C ,4=BC ,且对于该二次函数图象上的任意两点()111,P x y ,()222,P x y ,当125>≥x x 时,总有12>y y . (1)求二次函数的表达式;(2)若直线2:(10)=+≠l y mx n n ,求证:当2=-m 时,21l l ;(3)E 为线段BC 上不与端点重合的点,直线3:2=-+l y x q 过点C 且交直线AE 于点F ,求∆ABE 与∆CEF 面积之和的最小值.6. 如图1所示,在平面直角坐标系中,抛物线F 1:2264()515y a x =-+与x 轴交于点A (65-,0)和点B ,与y 轴交于点C .(1)求抛物线F 1的表达式;(2)如图2,将抛物线F 1先向左平移1个单位,再向下平移3个单位,得到抛物线F 2,若抛物线F 1与抛物线F 2相交于点D ,连接BD ,CD ,BC . ①求点D 的坐标;②判断△BCD 的形状,并说明理由;(3)在(2)的条件下,抛物线F 2上是否存在点P ,使得△BDP 为等腰直角三角形,若存在,求出点P 的坐标;若不存在,请说明理由.7. 如图,在平面直角坐标系xoy 中,已知直线122y x =-与x 轴交于点A ,与y 轴交于点B ,过A 、B 两点的抛物线2y ax b c =++与x 轴交于另一点()1,0C -. (1)求抛物线的解析式;(2)在抛物线上是否存在一点P ,使PAB OAB S S ∆∆=?若存在,请求出点P 的坐标,若不存在,请说明理由;8. 如图,抛物线y =ax 2+bx -6与x 轴相交于A ,B 两点,与y 轴相交于点C ,OA =2,OB =4,直线l 是抛物线的对称轴,在直线l 右侧的抛物线上有一动点D ,连接AD ,BD ,BC ,CD . (1)求抛物线的函数表达式;(2)若点D 在x 轴的下方,当△BCD 的面积是29时,求△ABD 的面积;9. 如图所示,抛物线y =ax 2+bx +c (a ≠0)与x 轴交于点A ,B 两点,与y 轴DA O CB l-11 -1 xy交于点C ,且点A 的坐标为(-2,0),点C 的坐标为(0,6),对称轴为直线x =1.点D 是抛物线上的一个动点,设点D 的横坐标为m (1<m <4),连接AC ,BC ,DC ,DB .(1)求抛物线的函数表达式;(2)当△BCD 的面积等于△AOC 的面积的34时,求m 的值;10.如图,抛物线212y x bx c =++与x 轴交于A 、B 两点(点A 在点B 左边),与y 轴交于点C .直线122y x =-经过B 、C 两点. (1)求抛物线的解析式;(2)点P 是抛物线上的一动点,过点P 且垂直于x 轴的直线与直线BC 及x 轴分别交于点D 、M .PN BC ⊥,垂足为N .设(),0M m .①点P 在抛物线上运动,若P 、D 、M 三点中恰有一点是其它两点所连线段的中点(三点重合除外).请直接写出符合条件的m 的值;②当点P 在直线BC 下方的抛物线上运动时,是否存在一点P ,使PNC △与AOC △相似.若存在,求出点P 的坐标;若不存在,请说明理由.11.已知直线y =kx ﹣2与抛物线y =x 2﹣bx +c (b ,c 为常数,b >0)的一个交点为A (﹣1,0),点M (m ,0)是x 轴正半轴上的动点.(1)当直线γ=kx ﹣2与抛物线y =x 2﹣bx +c (b ,c 为常数,b >0)的另一个交点为该抛物线的顶点E 时,求k ,b ,c 的值及抛物线顶点E 的坐标; (2)在(1)的条件下,设该抛物线与y 轴的交点为C ,若点Q 在抛物线上,且点Q 的横坐标为b ,当S △EQM 12=S △ACE 时,求m 的值; 、12. 如图所示,抛物线y =x 2﹣2x ﹣3与x 轴相交于A 、B 两点,与y 轴相交于点C ,点M 为抛物线的顶点. (1)求点C 及顶点M 的坐标.(2)若点N 是第四象限内抛物线上的一个动点,连接BN 、CN 求△BCN 面积的最大值及此时点N 的坐标.(3)直线CM 交x 轴于点E ,若点P 是线段EM 上的一个动点,是否存在以点P 、E 、O 为顶点的三角形与△ABC 相似.若存在,求出点P 的坐标;若不存在,请说明理由.13. 如图,抛物线26y ax x c =-+交x 轴于, A B 两点,交y 轴于点C .直线5y x =-+经过点,B C .(1)求抛物线的解析式;(2)抛物线的对称轴l 与直线BC 相交于点P ,连接,AC AP ,判定APC △的形状,并说明理由;14.如图,抛物线的顶点为A (h ,-1),与y 轴交于点B 1(0,)2,点F (2,1)为其对称轴上的一个定点.(1)求这条抛物线的函数解析式;(2)已知直线l 是过点C (0,-3)且垂直于y 轴的定直线,若抛物线上的任意一点P (m ,n )到直线l 的距离为d ,求证:PF =d ;(3)已知坐标平面内的点D (4,3),请在抛物线上找一点Q ,使△DFQ 的周长最小,并求此时△DFQ 周长的最小值及点Q 的坐标.15. 在平面直角坐标系xOy 中,已知抛物线y =ax 2+bx +c 与x 轴交于A (﹣1,0),B(4,0)两点,与y轴交于点C(0,﹣2).(1)求抛物线的函数表达式;(2)如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,连接BD,的最大值;记△BDE的面积为S1,△ABE的面积为S2,求S1S2(3)如图2,连接AC,BC,过点O作直线l∥BC,点P,Q分别为直线l和抛物线上的点.试探究:在第一象限是否存在这样的点P,Q,使△PQB∽△CAB.若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.。
2024陕西数学中考备考重难专题:抛物线与几何综合题特殊三角形、四边形问题课后练习【含答案】

2024陕西数学中考备考重难专题:抛物线与几何综合题特殊三角形、四边形问题考情分析年份题号题型分值抛物线的变化设问形式解题关键点201724解答题10关于y轴对称(1)求两抛物线表达式(2)求抛物线与x轴两交点坐标(3)求满足平行四边形存在的点坐标(1)轴对称性质,抛物线的对称轴,抛物线的图象,开口方向(2)两点位置(3)平行四边形的性质20212410平移(1)判断抛物线与x轴交点情况(2)写满足等腰直角三角形存在的平移过程(1)待定系数法求抛物线表达式,一元二次方程根的判别(2)抛物线图象的平移20222410中心对称(1)求与坐标轴交点坐标(2)求抛物线表达式(3)求不是菱形的平行四边形的面积(1)抛物线与坐标轴的交点问题(2)抛物线图象关于中心对称性质(3)平行四边形的性质:平行四边形的对角线互相平分例(2022陕西逆袭卷改编)如图,抛物线L:y=x2+2x-c的图象与x轴交于A,B两点(点B 在点A的左侧),与y轴交于点C(0,-3),过点A的直线与y轴交于点D,与抛物线交于点M,且tan∠BAM=1.(1)求点A,B的坐标及抛物线解析式;(2)抛物线M与抛物线L关于y轴对称,求抛物线M与y轴交点坐标;(3)若点P为抛物线L上一动点,E为直线AD上一动点,则是否存在点P,使得以点A,P,E 为顶点的三角形为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.例题图①(4)抛物线M上存在一点F,抛物线L上存在一点G,使得四边形ABFG为平行四边形,求出F,G两点坐标.例题图②探究平行四边形存在性问题的步骤:1.三定点(A、B、C),一动点(D):分别过点A、B、C作BC、AC、AB的平行线,三条平行线的交点即为所求作的点D 2.两定点(A、C),两动点(E、F):分AC为边和AC为对角线两种情况来讨论:①AC为边,平移AC,利用平行四边形的对边平行且相等确定点E、F位置②AC为对角线,取AC中点,利用平行四边形对角线互相平分来确定点E、F位置练习(2022山西逆袭复诊卷)综合与探究如图,抛物线y=38x2-94x-6与x轴交于点A,C,与y轴交于点B,点P是抛物线上任意一点,连接PB,PC,BC.练习题图(1)求点A,B,C的坐标;(2)当△PBC的面积为24时,求点P的坐标;(3)若点Q是直线x=4上一点,是否存在以点P,Q,B,C为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.练习1(2022陕西原创卷)在平面直角坐标系中,抛物线L:y=x2+bx+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,-3),抛物线L′与抛物线L关于y轴对称.练习1题图(1)求抛物线L的表达式;(2)抛物线L′的顶点为D,在x轴上是否存在一点P,使得以B、D、P为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.练习2(2022陕西黑白卷白卷)如图,抛物线y=ax2+bx+c(a≠0)与直线y=23x-2分别交x轴、y轴于点A,B,且抛物线与x轴的另一个交点为C(-1,0).(1)求抛物线的表达式;(2)点P是平面内任意一点,在抛物线对称轴上是否存在点Q,使得以A,B,P,Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.练习2题图答案典例精讲例解:(1)∵C(0,-3)∴抛物线L解析式为y=x2+2x-3,令y=0,即x2+2x-3=0,解得x=1或x=-3,∴A(1,0),B(-3,0);(2)将抛物线L化为顶点式为y=(x+1)2-4∵抛物线M与抛物线L关于y轴对称,∴抛物线M的解析式为y=(x-1)2-4令x=0,则y=-3,∴抛物线M与y轴交点坐标为(0,-3)(3)存在.在Rt△AOD中,∵tan∠BAM=tan∠OAD=ODOA=1,∴OD=OA,∠BAD=45°.如解图,分三种情况讨论:例题解题①①当AE=PE时,∠AEP=90°,∴∠EPA=∠EAP=45°,∵∠DAB=45°,∴此时点P与点B重合,∴点P 的坐标为(-3,0);②当AP =PE 时,∠EPA =90°,∴∠PEA =∠EAP =45°,∴此时点P 与点B 重合,∴点P 的坐标为(-3,0);③当AP =AE 时,∠EAP =90°,设AP 与y 轴交于点F ,则∠OFA =∠OAF =45°,∴OF =OA =1,∴点F 的坐标为(0,-1),设直线AF 的表达式为y =kx +b (k ≠0),将A (1,0),F (0,-1)代入y =kx +b 中,=k +b1=b =1=-1,∴直线AF 的表达式为y =x -1,设点P 的坐标为(x ,x 2+2x -3),∴x 2+2x -3=x -1,解得x 1=1(舍去),x 2=-2,当x =-2时,y =-2-1=-3,∴点P 的坐标为(-2,-3).综上所述,满足条件的点P 的坐标为(-3,0)或(-2,-3).(4)∵A (1,0),B (-3,0)∴AB =4∵点F 在抛物线M 上,点G 在抛物线L 上,且四边形ABFG 是平行四边形∴FG ∥AB ,FG =AB =4∵抛物线M 与抛物线L 关于y 轴对称∴两抛物线上纵坐标相同的点,横坐标关于y 轴对称∴4F G x x +=,x F =-x G分两种情况讨论,当F 、G 在x 轴上方时,即x F =-2时,x G =2当F、G在x轴下方时,即x F=2时,x G=-2将x F=-2代入抛物线M解析式y=x2-2x-3可得y F=5,x G=2,y G=5,此时F(-2,5),G(2,5)将x F=2代入抛物线M解析式y=x2-2x-3可得y F=-3,x G=-2,y G=-3,此时F(2,-3),G(-2,-3)∴综上所述,F(-2,5),G(2,5)或F(2,-3),G(-2,-3).例题解图②课堂练兵练习解:(1)在y=38x2-94x-6中,令y=0,得38x2-94x-6=0,解得x=-2或x=8,令x=0,得y=-6,∴点A(-2,0),点B(0,-6),点C(8,0);(2)当点P在直线BC下方时,如解图①,过点P作PD⊥x轴于点D,交BC于点E,设直线BC的表达式为y=kx+d(k≠0),将点B(0,-6),C(8,0)代入,得=-68+=0,解得=34=-6,∴直线BC的表达式为y=34x-6.设点P (m ,38m 2-94m -6)(0<m <8),则点E (m ,34m -6),∴PE =(34m -6)-(38m 2-94m -6)=-38m 2+3m ,∴S △PBC =12PE ·OC =12(-38m 2+3m )×8=-32m 2+12m ,当S △PBC =24时,即-32m 2+12m =24,解得m =4,此时P (4,-9);当点P 在直线BC 上方时,如解图②,由平移易求得lP 1P 2:y =34x ,联立=34=382-94-6,解得1=4+421=3+32,2=4-422=3-32,此时P 1(4+42,3+32),P 2(4-42,3-32).综上所述,点P 的坐标为(4,-9)或(4+42,3+32)或(4-42,3-32);解图①解图②练习题(3)存在.当以点P ,Q ,B ,C 为顶点的四边形是平行四边形时,分两种情况:①如解图③,当BC 作为平行四边形的一条边时,PQ ∥BC ,且PQ =BC ,∵点Q 的横坐标为4,∴|x p -4|=8,解得x p =-4或x p =12,∴P 1(-4,9),P 2(12,21);②如解图④,当BC 为平行四边形的对角线时,设对角线交于点R ,则BR =CR ,∴点R (4,-3),+2=4,点Q 在直线x =4上,∴点P 的横坐标为4,此时P 3(4,-9).综上所述,存在满足题意的点P ,点P 的坐标为(-4,9)或(12,21)或(4,-9).解图③解图④练习题课后小练练习1解:(1)分别将点B (3,0),C (0,-3)的坐标代入y =x 2+bx +c 中得9+3+=0=-3,解得=-2=-3,∴抛物线L 的表达式为y =x 2-2x -3;(2)存在.∵抛物线L ′与抛物线L 关于y 轴对称,∴抛物线L ′的表达式为y =x 2+2x -3=(x +1)2-4,∴D (-1,-4),设点P 的坐标为(m ,0),∴BD 2=(3+1)2+[0-(-4)]2=32,DP 2=(m +1)2+(0+4)2,则PB 2=(m -3)2,∵△PBD 为等腰三角形,分三种情况讨论:①当PB =BD 时,即(m -3)2=32,解得m =3+42或m =3-42,∴P 1(3+42,0),P 2(3-42,0);②当BD =PD 时,即32=(m +1)2+(0+4)2,解得m =3(舍去)或m =-5,∴P 3(-5,0);③当PB =PD 时,即(m -3)2=(m +1)2+(0+4)2,解得m =-1,∴P 4(-1,0)综上所述,点P 点坐标为(3+42,0),(3-42,0),(-5,0),(-1,0).练习2解:(1)在y =23x -2中,当x =0时,y =-2.∴B (0,-2).令y =23x -2=0,得x =3.∴A (3,0).设抛物线的表达式为y =a (x +1)(x -3),将点B(0,-2)代入,得-2=-3a,解得a=2 3 .∴抛物线的表达式为y=23(x+1)(x-3)=23x2-43x-2;(2)存在.∵A(3,0),B(0,-2),∴AB2=13.由(1)可知抛物线的对称轴为直线x=1,∴设Q(1,m),则AQ2=22+m2,BQ2=1+(m+2)2,要使以A,B,P,Q为顶点的四边形是菱形,则分三种情况讨论:①当AQ=AB,即AQ2=AB2时,四边形ABPQ为菱形,∴22+m2=13,解得m=3或m=-3,∴点Q的坐标为(1,3)或(1,-3);②当AB=BQ,即AB2=BQ2时,四边形ABQP为菱形,∴13=1+(m+2)2,解得m=23-2或m=-23-2,∴点Q的坐标为(1,23-2)或(1,-23-2),③当AQ=BQ,即AQ2=BQ2时,四边形AQBP为菱形,∴22+m2=1+(m+2)2,解得m=-1 4∴点Q的坐标为(1,-1 4 ).综上所述,点Q的坐标为(1,3)或(1,-3)或(1,23-2)或(1,-23-2)或(1,-1 4 ).。
二次函数专题—抛物线的内接特殊三角形

《二次函数》专题训练(三)——抛物线的内接特殊三角形主备:鄢自红授课:鄢自红□自学导读【学习目标】(1)掌握二次函数图象内接特殊三角形的性质,并利用性质求解析式和参数的值。
(2)通过规律的推导和运用,提高类比推理和综合解题能力。
【重、难点】规律的推导和运用【读书思考】基础知识回顾:(1)抛物线顶点坐标公式:(_____, _________),简记为___________.(2)若抛物线与x轴有两个交点A(x1,0), B(x2,0),AB=___________=________.(3)韦达定理:若ax2+bx+c=0(a≠0)有两实根x1,x2,则_________________________.□典题解析(一)抛物线与x轴两个交点和顶点确定的三角形例1.已知,二次函数y=x2+kx+1与x轴的两个交点A、B都在原点右侧,顶点为M。
当△ABM是等腰直角三角形时,(1)求k值。
(2)求判别式△.解析:先画出函数大致图象,再利用等腰三角形性质,结合直角三角形的性质求解。
问题1:例1中,如果把y=x2+kx+1换成y=ax2+bx+c,△ABM是等腰直角三角形时,△值不变吗?规律1:练习1(变式). 已知抛物线y=x2—bx (b≠0)的顶点为M,与直线y=—2两交点分别为A、B,且△ABM为等腰直角三角形,则b=_______。
问题2:前面的问题中当△ABM为等边三角形时,y=ax2+bx+c的判别式△又是多少?导学设计教学重难点与抛物线内接特殊三角形有关的定值的推导和运用.教具准备多媒体.导学流程一、导入新课,揭示目标(2分钟) 情景导入:师生对照课件解读学习目标.二、新课导学基础知识回顾:(2分钟)(课件出示题目,点学生回答)自主探究完成例1(4分钟)(学生演板)追问拓展、合作探究:(3分钟)如果把y=x2+kx+1换成y=ax2+bx+c,△ABM是等腰直角三角形时,△还是4吗?规律小结(2分钟):当y=ax2+bx+c(a≠0)与x轴交于A、B 两点,C是顶点,当△ABM为等腰直角三角形,则△=b2-4ac=4.练习1点拨:实质是把抛物线与y=0的交点变成了与y=-2的,但要注意△是方程x2-bx=-2的,而不是x2-bx=0的.自主探究问2(5分钟)1、先自主探究问题2,展示探究的结果.2、并利用探究的结论完成例2,利用例2检查学习效果。
抛物线与特殊三角形专题精编

抛物线与特殊三角形专题精编【例1】 如图,已知抛物线c bx ax y ++=2经过A (-1,0)、B (3,0)、C (0,3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P 为直线l 上的一个动点,当△P AC 的周长最小时,求点P 的坐标;(3)在直线l 上是否存在点M ,使△MAC 为等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.点拨: 对于(3),恰当设出点M 的坐标,并建立相应方程.因△MAC 的腰底不明确,故应分类讨论.归纳: 点的坐标是综合题的立足点(求解析式),又是综合题的制高点(求满足条件的点的坐标或存在性探求),求点的坐标一般历经下面两个关键步骤: (1)定位; (2)计算.【例2】 已知抛物线k kx kxy 3-22+=交x 轴于A 、B 两点(A 在B 的左边),交y 轴于C点,且y 有最大值4.(1)求抛物线的解析式;(2)在抛物线上是否存在点P ,使△PBC 是直角三角形?若存在,求出P 点坐标;若不存在,请说明理由.点拨:对于(2),设P 点坐标为(),a b ,寻找相似三角形,建立a 、b 的另一关系式,解联立而得的方程组可求出a 、b 的值.方法规律总结: 求出相应的点的坐标是解综合题的基础与关键,基本方法有: (1)计算线段长;(2)解由解析式形成的方程组; (3)运用解析式.对于例2,充分运用图形特征(如特殊三角形和特殊四边形性质、寻找全等三角形和相似三角形等)是解决问题的关键.【例3】 若1x 、2x 是关于x 的一元二次方程()200axbx c a ++=≠的两个根,则方程的两个根1x 、2x 和系数a b c 、、有如下关系:1x +2x =b a -,12cx x a⋅=.把它们称为一元二次方程根与系数关系定理.如果设二次函数()200y ax bx c a =++=≠的图象与x 轴的两个交点为()1,0A x 、()2,0B x .利用根与系数关系定理可以得到A 、B 两个交点间的距离为:AB a∆=. 参考以上定理和结论,解答下列问题: 设二次函数)0(2>++=a c bx axy 的图象与x 轴的两个交点为)0,(1x A 、)0,(2x B ,抛物线的顶点为C ,显然△ABC 为等腰三角形.(1)当△ABC 为等腰直角三角形时,求ac b 4-2的值; (2)当△ABC 为等边三角形时,求ac b 4-2的值.分析与解 作出特殊三角形的辅助线,由线段关系建立a b c 、、的等式,化简等式并求值.(1)当△ABC 为等腰直角三角形时,过C 作CD ⊥AB ,垂足为D ,则AB =2CD .∵抛物线与x 轴有两个交点,∴240b ac ∆=->.∵0a >,∴2244b ac b acAB a a--==. 又∵224444ac b b acCD a a--==, ∴224424b ac b ac a a--=⨯.∴22442b ac b ac --=, ∴()222444bac b ac --=. ∵240b ac ->,∴244b ac -=.(2)请读者完成.针对训练:1、如图,已知二次函数21:43L y x x =-+与x 轴交于A ,B 两点(点A 在点B 的左边),与y 轴交于点C .(1)写出A 、B 两点的坐标;(2)二次函数()22:430L y kx kx k k =-+≠,顶点为P .①直接写出二次函数21:43L y x x =-+与二次函数()22:430L y kx kx k k =-+≠有关图象的两条相同的性质;②是否存在实数k ,使△ABP 为等边三角形?如果存在,请求出k 的值;如不存在,请说明理由;③若直线y =8k 与抛物线L 2交于E 、F 两点,问线段EF 的长度是否会发生变化?如果不会,请求出EF 的长度;如果会,请说明理由.2、如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;(2)求经过点A、O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.3、如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON,(1)求该二次函数的关系式;(2)若点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:①证明:∠ANM=∠ONM;②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.4、抛物线2y x bx c =-++经过点A 、B 、C ,已知A (-1,0),C (0,3). (1)求抛物线的解析式;(2)如图1,P 为线段BC 上一点,过点P 作y 轴平行线,交抛物线于点D ,当△BDC 的面积最大时,求点P 的坐标;(3)如图2,抛物线顶点为E ,EF ⊥x 轴于F 点,M (m ,0)是x 轴上一动点,N 是线段EF 上一点,若∠MNC =90°,请指出实数m 的变化范围,并说明理由.本节总结: 抛物线与三角形的结合是抛物线与平面几何结合生成综合性问题的一种重要形式,这类问题以抛物线为背景,探讨是否存在一些点,使其能构成某些特殊三角形,有以下常见的形式:(1)抛物线上的点能否构成等腰三角形; (2)抛物线上的点能否构成直角三角形.这类问题把抛物线性质和平面图形性质有机结合,需综合运用待定系数法、数形结合、分类讨论等思想方法.。
专题23 二次函数抛物线与三角形的综合-2023年中考数学二轮复习核心考点拓展训练(原卷版)

专题23 二次函数抛物线与三角形的综合(原卷版)第一部分 典例剖析+针对训练类型一 二次函数与直角三角形的综合1.(2022秋•利川市期末)如图1,抛物线y =ax 2+bx ﹣3交x 轴于点A (4,0)和点B (﹣1,0),交y 轴于点C .(1)求此抛物线的解析式;(2)点P 为直线AC 下方抛物线上一动点,连接PA ,PC ,求△ACP 面积的最大值;(3)如图2直线l 为该抛物线的对称轴,在直线l 上是否存在一点M 使△BCM 为直角三角形,若存在,请求出点M 的坐标,若不存在,请说明理由.针对训练1.(2022秋•渝中区期末)抛物线y =12x 2+bx +c 与x 轴交于点A (﹣2,0)和B (4,0),与y 轴交于点C ,连接BC .点P 是线段BC 下方抛物线上的一个动点(不与点B ,C 重合),过点P 作y 轴的平行线交BC 于M ,交x 轴于N ,设点P 的横坐标为t .(1)求该抛物线的解析式;(2)用关于t 的代数式表示线段PM ,求PM 的最大值及此时点M 的坐标;(3)过点C 作CH ⊥PN 于点H ,S △BMN =9S △CHM ,①求点P 的坐标;②连接CP ,在y 轴上是否存在点Q ,使得△CPQ 为直角三角形,若存在,求出点Q 的坐标;若不存在,请说明理由.类型一 二次函数与等腰三角形的综合典例2(2021秋•重庆期末)如图,已知二次函数y=ax2+bx+3的图象交x轴于点A(1,0),B(3,0),交y轴于点C.(1)求这个二次函数的表达式;(2)点P是直线BC下方抛物线上的一动点,求△BCP面积的最大值;(3)直线x=m分别交直线BC和抛物线于点M,N,当△BMN是等腰三角形时,直接写出m的值.针对训练1.(2022秋•代县期末)综合与探究如图,抛物线y=ax2+bx+4经过A(﹣1,0),B(2,0)两点,与y轴交于点C,作直线BC.(1)求抛物线和直线BC的函数解析式.(2)D是直线BC上方抛物线上一点,求△BDC面积的最大值及此时点D的坐标.(3)在抛物线对称轴上是否存在一点P,使得以点P,B,C为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.2.(2022秋•宁陵县期中)如图,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.(1)求该抛物线的解析式;(2)在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M的坐标;若不存在,请说明理由.类型三二次函数与等腰直角三角形的综合典例3(2022秋•洛川县校级期末)已知抛物线L₁:y=﹣x2+bx+c与x轴交于A(﹣5,0),B(﹣1,0)两点.(1)求抛物线L1的表达式;(2)平移抛物线L1得到新抛物线L2,使得新抛物线L2经过原点O,且与x轴的正半轴交于点C,记新抛物线L2的顶点为P,若△OCP是等腰直角三角形,求出点P的坐标.针对训练1.(2022秋•铁西区校级期末)已知:如图,抛物线y =ax 2+bx +c (a ≠0)与坐标轴分别交于点A (0,6),B (6,0),C (﹣2,0),点P 是线段AB 上方抛物线上的一个动点.(1)求抛物线的解析式.(2)当△PAB 的面积最大时,求点P 的坐标.(3)过点P 作x 轴的垂线,交线段AB 于点D ,再过点P 作PE ∥x 轴交抛物线于点E ,连接DE ,请问是否存在点P 使△PDE 为等腰直角三角形?请直接写出点P 的坐标.第二部分 专题提优训练1.(2022秋•渝中区校级期末)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 与x 轴交于点A (﹣33,0),B (3,0),与y 轴的交点为C ,且tan ∠CAO =233.(1)求该抛物线的函数表达式;(2)点D 为AB 的中点,过点D 作AC 的平行线交y 轴于点E ,点P 为抛物线上第二象限内的一动点,连接PC ,PD ,求四边形PDEC 面积的最大值及此时点P 的坐标;(3)将该抛物线y =ax 2+bx +c 向左平移得到抛物线y ',使y '经过原点,y '与原抛物线的交点为F ,点M 为抛物线y '对称轴上的一点,若以点F ,B ,M 为顶点的三角形是直角三角形,请直接写出所有满足条件的点M 的坐标,并把求其中一个点M 的坐标的过程写出来.2.(2022秋•鞍山期末)在平面直角坐标系xOy中,抛物线C1:y=ax2+bx+c(a≠0)经过(0,2),(﹣2,2)两点.(1)若抛物线C1:y=ax2+bx+c经过(1,0),求抛物线解析式;(2)抛物线C1:y=ax2+bx+c与直线y=x+2有M,N两个交点,O为坐标原点,若△MNO是以MN为腰的等腰三角形,请直接写出a的值;(3)直线y=x+2分别与抛物线C1:y=ax2+bx+c,抛物线C2:y=﹣ax2﹣bx+c恰好有三个公共点,若其中一个公共点是另外两个公共点连接线段的中点,求a的值.3.(2022秋•前郭县期末)如图,抛物线y=ax2﹣ax﹣12a经过点C(0,4),与x轴交于A,B两点,连接AC,BC,M为线段OB上的一个动点,过点M作PM⊥x轴,交抛物线于点P,交BC于点Q.(1)直接写出a的值以及A,B的坐标:a= ,A( , ),B( , );(2)过点P作PN⊥BC,垂足为点N,设M点的坐标为M(m,0),试求PQ+2PN的最大值;(3)试探究点M在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.4.(2022•台山市校级一模)如图,抛物线y=ax2+x+6的图象与直线y=kx+b有唯一交点A(﹣1,4).(1)求抛物线和直线的解析式;(2)若抛物线与x轴的交点分别为点M、N,抛物线的对称轴上是否存在一点P,使PA+PM的值最小?如果有,请求出这个最小值,如果没有,请说明理由.(3)直线y=kx+b与x轴交于点B,点Q是x轴上一动点,请你写出使△QAB是等腰三角形的所有点Q 的横坐标.5.(2022秋•通州区期末)如图,抛物线y1=ax2﹣2x+c的图象与x轴交点为A和B,与y轴交点为D(0,3),与直线y2=﹣x﹣3交点为A和C.(1)求抛物线的解析式;(2)在直线y2=﹣x﹣3上是否存在一点M,使得△ABM是等腰直角三角形,如果存在,求出点M的坐标,如果不存在,请说明理由;(3)若点E是x轴上一个动点,把点E向下平移4个单位长度得到点F,点F向右平移4个单位长度得到点G,点G向上平移4个单位长度得到点H,若四边形EFGH与抛物线有公共点,请直接写出点E的横坐标x E的取值范围.6.(2022秋•临湘市期末)如图,抛物线y=―12x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).(1)求抛物线的表达式;(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,求出P点的坐标;如果不存在,请说明理由;(3)点F是第一象限抛物线上的一个动点,当点F运动到什么位置时,△CBF的面积最大?求出△CBF 的最大面积及此时F点的坐标.7.(2022•甘井子区校级模拟)已知抛物线y=ax2+bx+c的顶点A在x轴上.P(x1,y1),Q(x2,y2)是抛物线上两点,若x1<x2<m,则y1>y2;若x1>x2>m,则y1>y2,且当y的绝对值为1时,△APQ为等腰直角三角形(其中∠PAQ=90°).(1)求抛物线的解析式;(用含有m的式子表示)(2)当m>0,x1<m,x2>m,过点Q作QF⊥x轴,若y1•y2=1,探究∠PAO与∠AQF之间数量关系;(3)直线x=m+1(1≤m≤3)交抛物线y=ax2+bx+c于点D,将抛物线y=ax2+bx+c以直线x=m+1为对称轴向右翻折得到新抛物线,直线y=kx经过点D,交原抛物线y=ax2+bx+c的对称轴于点E,交新抛物线于另一点H,问△EAH的面积是否存在最大值或最小值,若存在,求出面积最值和m的值,若不存在,请说明理由.。
初三数学试题 抛物线与三角形面积

书山有路勤为径;学海无涯苦作舟初三数学试题抛物线与三角形面积初三数学试题抛物线与三角形面积抛物线与三角形面积抛物线与三角形面积问题涉及代数、几何知识,有一定难度。
本文通过举例来谈这类题的解法。
一、顶点在抛物线y=ax2+bx+c 的三角形面积的一般情况有:(1)、以抛物线与x 轴的两交点和抛物线的顶点为顶点的三角形,其底边的长是抛物线与x 轴两交点间的距离,高的长是抛物线顶点的纵坐标的绝对值。
其面积为:SΔ= |x1-x2|•| |= • •| |(2)、以抛物线与x 轴、y 轴的三个交点为顶点的三角形。
其底边的长是抛物线与x 轴两交点间的距离,高的长是抛物线与y 轴上的截距(原点与y 轴交点构成的线段长)的绝对值。
其面积为:SΔ= •|x1-x2|•|c|= • •|c|(3)、三角形三个顶点在抛物线其他位置时,应根据图形的具体特征,灵活运用几何和代数的有关知识。
二、 1.求内接于抛物线的三角形面积。
例1.已知抛物线的顶点C(2,),它与x 轴两交点A、B 的横坐标是方程x2-4x+3=0 的两根,求ΔABC 的面积。
解:由方程x2-4x+3=0,得x1=1, x2=3,∴ AB=|x2-x1|=|3-1|=2.∴ SΔABC= 乘以2 乘以= .例2.已知二次函数y= x2+3x+2 的图像与x 轴交于A、B 两点,与y 轴交于今天的努力是为了明天的幸福。
专题01 抛物线中的三角形面积问题-高中数学破题致胜微方法(抛物线中的面积、角度及参数范围问题)

专题01 抛物线中的三角形面积问题本内容主要研究抛物线中的面积问题.直线和抛物线相交,围成的平面图形种类很多,尤其以三角形最为常见,三角形面积的计算是重点,其他平面图形的面积可以转化为三角形面积的计算.直线和抛物线相交时联立方程,利用弦长公式,或者点线距公式,结合韦达定理解决问题.先看例题:例:已知直线l 过抛物线C 的焦点,且与C 的对称轴垂直,l 与C 交于A ,B 两点,|AB |=12,P 为C的准线上一点,则△ABP 的面积为( )A.18B.24C.36D.48解:由题意可知,|AB |是该抛物线的通径,即|AB |=2p =12,且准线上的点到AB 的距离即为焦准距,即为p =6,所以△ABP 的面积为1126362⨯⨯=. 所以本题选C整理:三角形面积(1)过x 轴上一定点H 的直线l 与抛物线交于A 、B 两点,求AOB S ∆1212AOB S OH y y ∆=- (2)过y 轴上一定点H 的直线l 与抛物线交于A 、B 两点,求AOB S ∆1212AOB S OH x x ∆=- (3)弦任意,点任意12S ∆=弦长×点线距注意:要着正确的画出图形,进而求解.再看两个例题,加深印象例:在直角坐标系xOy 中,直线l 过抛物线y 2=4x 的焦点F ,且与该抛物线相交于A ,B 两点,其中点A 在x 轴上方.若直线l 的倾斜角为60°,则△OAF 的面积为________. 解:据题意可知直线AB 方程为3(1)y x =-,与抛物线方程联立消元得243403y y --=, 解得23A y =,故11||123322AOF A S OF y =⨯=⨯⨯=△.再看一个例题:例:已知抛物线y=ax2-1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为________.解;本小题主要考查抛物线的方程及有关性质.由题意知a>0,C(0,-1),原方程变形为21 (1)x ya=+,所以1||4OCa=,即14a=,则||4ABa==,所以14122ABCS=⨯⨯=△.总结:1.根据直线和抛物线的位置关系,如果弦任意,选择公式12S∆=弦长×点线距.2.根据直线和抛物线的位置关系,如果直线过x轴上一定点H,设直线方程x my t=+,代入抛物线方程计算弦长.3.根据直线和抛物线的位置关系,如果直线过y轴上一定点H,设直线方程y kx m=+,代入抛物线方程计算弦长.练习:1. O 为坐标原点,F 为抛物线C :2y =的焦点,P 为C 上一点,若||PF =则△POF的面积为( )A.2B.C.D.42. 连接抛物线x 2=4y 的焦点F 与点M (1,0)所得的线段与抛物线交于点A ,设点O 为坐标原点,则三角形OAM 的面积为( )A.1-B.32-C.1D.32+3. 设斜率为2的直线l 过抛物线y 2=ax (a ≠0)的焦点F ,且和y 轴交于点A .若△OAF (O 为坐标原点)的面积为4,则抛物线方程为( )A.y 2=±4xB.y 2=±8xC.y 2=4xD.y 2=8x。
中考压轴大题抛物线+三角形 学生版

001如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;002如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣x2+bx+c经过点A、C,与AB交于点D.(1)求抛物线的函数解析式;(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.①求S关于m的函数表达式;②当S最大时,在抛物线y=﹣x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.003如图①,已知抛物线y=ax2+bx+c的图象经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.(1)求抛物线的解析式;(2)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.004如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.(1)求抛物线的顶点A的坐标;(2)设抛物线与y轴交于点B,与x轴交于点C,D(点C在点D的左侧),试判断△AB D的形状;005如图所示,在平面直角坐标系xOy 中,已知点A(-94,0),点C(0,3),点B 是x 轴上一点(位于点A 的右侧),以AB 为直径的圆恰好经过点C.(1)求∠ACB 的度数;(2)已知抛物线y =ax 2+bx +3经过A ,B 两点,求抛物线所对应的函数关系式;(3)线段BC 上是否存在点D ,使△BOD 为等腰三角形?若存在,则求出所有符合条件的点D 的坐标;若不存在,请说明理由.006抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(,0),且与y轴相交于点C.(1)求这条抛物线的表达式;(2)求∠ACB的度数;(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE ⊥AC,当△DCE与△AOC相似时,求点D的坐标.008如图1,已知二次函数y=ax2+x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.(1)请直接写出二次函数y=ax2+x+c的表达式;(2)判断△ABC的形状,并说明理由;(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;009如图,抛物线y=ax2+bx+2与x轴相交于A(﹣1,0),B(4,0)两点,与y轴相交于点C.(1)求抛物线的解析式;(2)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.010如图,一次函数y=﹣x﹣2 的图象与二次函数y=ax2+bx﹣4 的图象交于x 轴上一点A,与y 轴交于点B ,在x 轴上有一动点C.已知二次函数y=ax2+bx﹣4 的图象与y 轴交于点D,对称轴为直线x=n(n<0),n 是方程2x2﹣3x﹣2=0 的一个根,连接AD.(1)求二次函数的解析式.(2)试判断坐标轴上是否存在这样的点C,使得以点A、B、C 组成的三角形与△ADB 相似?若存在,试求出点C 的坐标;若不存在,请说明理由.。
抛物线与特殊三角形简单综合大题

1. (2016枣庄)如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.(1)若直线y=mx+n经过B,C两点,求抛物线和直线BC的解析式;(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求点M的坐标;(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.2. (2016新疆13分)如图,抛物线y=ax2+bx-3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=-13x+1与y轴交于点D.(1)求抛物线的解析式;(2)求证:△DBO∽△EBC;(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.1.(1)抛物线解析式为y=-x2-2x+3,直线BC的解析式为y=x+3;(2)设直线BC与对称轴x=-1的交点为M,如解图,连接AM,∵MA=MB,∴MA+MC=MB+MC=BC,∴使MA+MC最小的点M应为直线BC与对称轴x=-1的交点,把x=-1代入直线y=x+3,得y=2,∴M(-1,2);(3)设P(-1,t),∵B(-3,0),C(0,3),∴BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,①若B为直角顶点,则BC2+PB2=PC2,即18+4+t2=t2-6t+10,解得t1=-2;②若C为直角顶点,则BC2+PC2=PB2,即18+t2-6t+10=4+t2,解得t2=4;③若P 为直角顶点,则PB 2+PC 2=BC 2,即4+t 2+t 2-6t +10=18,解得t 3=3+172,t 4=3-172.综上所述,满足条件的点P 共有四个,分别为: P 1(-1,-2),P 2(-1,4),P 3(-1,3+172),P 4(-1,3-172). 2.(1)抛物线的解析式为y =x 2-2x -3(2)证明:由抛物线解析式y =x 2-2x -3=(x -1)2-4可得:E (1,-4),当x =0时,y =-13x +1=1,∴D (0,1),即OD =1,∴BD ==, 同理可得CE =2,BE =25,BC =32,在△DBO 和△EBC 中, ∵2DB DO BO EB EC BC ===∴△DBO ∽△EBC ;(3)存在,点P 的坐标为(1,-1),(1,-3+17),(1,-3-17),(1,14)或(1,-14).【解法提示】过点P 作PG ⊥y 轴于点G ,连接PC ,PB ,设抛物线对称轴与x 轴的交点为M ,设点P (1,a),则PG =1,GC =|a +3|,PM =|a |,PC 2=1+(a +3)2,PB 2=a 2+4,BC 2=18, ①当P 是等腰三角形顶点时,PC 2=PB 2,即1+(a +3)2=4+a 2,解得a =-1,∴P 1(1,-1);②当C 是等腰三角形顶点时,PC 2=CB 2,即1+(a +3)2=18, 解得a 1=-3+17,a 2=-3-17,∴P 2(1,-3+17),P 3(1,-3-17);③当B 是等腰三角形顶点时,PB 2=CB 2,即4+a 2=18,解得a 1=14,a 2=-14,∴P 4(1,14),P 5(1,-14).综上所述,存在点P ,使得△PBC 是等腰三角形,点P 的坐标分别为:P 1(1,-1),P 2(1,-3+17),P 3(1,-3-17),P 4(1,14),P 5(1,-14).。
抛物线中的等腰三角形问题

抛物线中的等腰三角形问题
在数学中,抛物线广泛被研究和探讨。
而抛物线中的等腰
三角形问题是其中一个经典的问题。
抛物线是一个二次方程的图像,具有对称性质。
而等腰三
角形是指三边长度相等的三角形。
那么,抛物线中是否存在等腰三角形呢?
答案是肯定的。
事实上,抛物线上的任何一点都可以构成
一个等腰三角形。
这是因为抛物线的性质决定了在对称位置上的两个点关于焦点的距离相等,从而满足等腰三角形的定义。
具体来说,我们可以选择抛物线上的一个点P,并且连接P 点与抛物线的焦点F。
然后,从P点向下垂直引一条垂线,与
抛物线的切线交于点Q。
这样,三角形PFQ就是一个等腰三
角形,因为PF和QF的长度相等。
值得注意的是,抛物线上的每个点都可以成为等腰三角形
的顶点,因此存在无数个等腰三角形。
抛物线中的等腰三角形问题不仅有理论上的意义,而且在
实际应用中也有一定的应用。
例如,在物体抛出运动中,抛物线的形状对于确定物体的落点和轨迹起到重要作用。
对于特定起始条件,等腰三角形在抛物线上能够提供更多的信息。
总结而言,抛物线中存在无数个等腰三角形,这是由抛物
线的对称性质所决定的。
这个问题不仅仅是数学理论上的问题,也有着实际应用中的意义。
通过研究抛物线中的等腰三角形,我们可以更深入地了解抛物线的性质和特点。
抛物线综合题——线段最大值,三角形面积最大值,直角三角形,等腰三角形,平行四边形专题

抛物线综合题突破线段,三角形面积最大值,直角三角形,等腰三角形,平行四边形专题1.如图,抛物线y=x2+bx+c与直线y=x-1交于A、B两点•点A的横坐标为-3,点B在y 轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC±x轴于C,交直线AB 于D.(1)求抛物线的解析式;(2)当m为何值时,S四边形OBDC=2S^BPD;(3)是否存在点P,使4PAD是直角三角形?若存在,求出点P的坐标;若不存在,说明理由.2.如图,已知抛物线y=-x2+bx+c与直线AB相交于A (-3, 0), B (0, 3)两点. (1)求这条抛物线的解析式; (2)设C是抛物线对称轴上的一动点,求使N CBA=90°的点C的坐标; (3)探究在抛物线上是否存在点P,使得^APB的面积等于3?若存在,求出点P的坐标;若不存在,请说明理由3.如图,已知抛物线y=x2+bx+c与直线y=-x+3交于A、B两点,点A 在y轴上,点B在x 轴上,抛物线与x轴的另一交点为C,点P在点B右边的抛物线上,PM±x轴交直线AB 于M。
(1)求抛物线解析式.(2)当PM=2BC时,求M的坐标.(3)点P运动过程中,4APM能否为等腰三角形?若能,求点P的坐标,若不能说明理由.4. △ABC在平面直角坐标系中的位置如图①所示,A点的坐标(-6,0), B点的坐标(4, 0) 点D为BC中点,点E为线段AB上一动点,连接DE经过点A,B,C三点的抛物线的解析式y=ax2+bx+8(1)求抛物线的解析式(2)如图①,将Z BDE以DE为轴翻折,点B的对称点为点G,当点G 恰好落在抛物线的对称轴上时,求G点的坐标; (3)如图②,当点E在线段AB上运动时,抛物线y=ax2+bx+8的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.5.如图①,抛物线y=ax2+bx+c与x轴相交于O、A两点直线y=-x+3与y轴交于B点,与该抛物线交于A, D两点,已知点D横坐标为-1.(1)求这条抛物线的解析式(2)如图①,在线段OA上有一动点H (不与O、A重合),过H作x轴的垂线分别交AB 于P 点,交抛物线于Q点,若x轴把4POQ分成两部分的面积之比为1:2,请求出H点的坐标;(3)如图②,在抛物线上是否存在点C,使4ABC为直角三角形?若存在,求出点C的坐标;若不存在,请说明理由图①图②备用图6.如图,抛物线y=-x2+bx+c与直线y=x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3, 5).点P是y轴右侧的抛物线上一动点,过点P作PE±x轴于点E,交CD于点F.(1)求抛物线的解析式;(2)若点P的横坐标为m (m>0),当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.(3)当点P运动到抛物线的顶点时,请在直线PE上找到一点Q,使OQ+CQ最小.并求出点Q 的坐标.7.如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于A (-1, 0)、B (3, 0)两点,直线y=x-2与x轴交于点D,与y轴交于点C.点P是x轴下方的抛物线上一动点,过点P 作PF±x轴于点F,交直线CD于点E,设点P的横坐标为m.(1)求抛物线的解析式;(2)若PE=3EF,求m的值;(3)连接PC,是否存在点P,使4PCE为等腰直角三角形?若存在,请直接写出相应的点P的横坐标m的值8.如图,抛物线y=x2+bx-3与x轴交于A、B两点(点A在点B左侧),直线l与抛物线交于A、C亮点,其中C的横坐标为2.(1)求A、C两点的坐标及直线AC的函数解析式;(2) P是线段AC上的一个动点,过点P作y轴的平行线交抛物线于点E,求4ACE面积的最大值;(3)点G是抛物线上的动点,在x轴上是否存在点F,使以A、C、F、G四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的点F的坐标;若不存在,请说明理由.9.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3, 0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连接PO、PC,并把4POC沿CO翻折,得到四边形POP’ C,那么是否存在点P,使四边形POP' C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.10.如图,抛物线y=ax2+bx与直线l交于点A (1, 5)、B (6, 0),点C是l上方的抛物线上的一动点,过C作CD±x轴于点D,交直线l于点E.连结AC、BC.(1)求抛物线的解析式;(2)设点C的横坐标为n,△ABC的面积为S,求出S的最大值;(3)在抛物线上是否存在点P,使得4PAB是直角三角形,且始终满足AB边为直角边?若存在,求出所有符合条件的P 的坐标;若不存在,简要说明理由11.在平面直角坐标系xoy中,y=ax2-2ax-3a(@<0)与x轴交于A,B两点(A在B的左侧),经过A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);5(2)点E是直线l上方的抛物线上的一点,若4ACE的面积的最大值为4,求a的值(3)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.112.已知抛物线y= - x2 - 2x+a(aW0)与y轴交于点A,顶点为M,直线y= -x - a分别与x 轴,y轴交于点B,C,并且与MA交于点N点(1)若直线BC和抛物线有两个不同交点,求a的取值范围,并用a表示交点M,A的坐标;(2)将4NAC沿着y轴翻转,若点N的对称点P恰好落在抛物线上,AP与抛物线的对称轴相交于点D,连接CD,求a的值及4PCD的面积;(3)在抛物线y=-x2-2x+a (a>0)上是否存在点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一课时 抛物线与三角形
例1 如图,已知抛物线223y x x =-++经过A (-1,0)、B (3,0)、C (0,3)三点,直线l 是抛物线的对称轴.
(1)设点P 为直线l 上的一个动点,当△PAC 的周长最小时,求点P 的坐标;
(2)在直线l 上是否存在点M ,使△MAC 为等腰三角形?若存在,求出点M 的坐标,若不存在,请说明理由.
例2 已知抛物线k kx kx y 322
-+=交x 轴于A 、B 两点(A 在B 的左边),交y 轴于C 点,且y 有最大值4.在抛物线上是否存在点P ,使△PBC 是直角三角形?若存在,求出P 点坐标,若不存在说明理由.
例3抛物线223y x x =-++经过点A (-1,0),C (0,3).
(1)如图①,P 为线段BC 上一点,过点P 作y 轴平行线交抛物线于点D ,当△BDC 的面积最大时,求点P 的坐标;
(2)如图②,抛物线顶点为E ,EF ⊥x 轴于点F ,M (m ,0)是x 轴上一动点,N 是线段EF 上一点,若∠MNC =90°,请指出实数m 的变化范围,并说明理由.
例4(2014•苏州)如图,二次函数y=a(x2﹣2mx﹣3m2)(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,﹣3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(1)用含m的代数式表示a;(2)求证:为定值;
(3)设该二次函数图象的顶点为F,探索:在x轴的负半轴上是否存在点G,连接GF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.
例5(2014•常州)在平面直角坐标系xOy中,二次函数y=﹣x2+x+2的图象与x轴交于点A,B(点
B在点A的左侧),与y轴交于点C.过动点H(0,m)作平行于x轴的直线l,直线l与二次函数y=﹣x2+x+2的图象相交于点D,E.
(1)若m>0,以DE为直径作⊙Q,当⊙Q与x轴相切时,求m的值;
(2)直线l上是否存在一点F,使得△ACF是等腰直角三角形?若存在,求m的值;若不存在,请说明理由.
例6 如图,已知234y x x =--过△ABC 的三个顶点坐标分别为A (-4,0),B (1,0),C (-2,6). (1)设直线BC 交y 轴于点E ,连接AE ,求证:AE = CE ;
(2)设抛物线与y 轴交于点D ,连接AD 交BC 于点F ,试问:以A ,B ,F 为顶点的三角形与△ABC 相似吗?
例7 (2014•漳州)已知抛物线l :y=ax 2
+bx+c (a ,b ,c 均不为0)的顶点为M ,与y 轴的交点为N ,我们称以N 为顶点,对称轴是y 轴且过点M 的抛物线为抛物线l 的衍生抛物线,直线MN 为抛物线l 的衍生直线.
(1)如图,抛物线y=x 2
﹣2x ﹣3的衍生抛物线的解析式是 _________ ,衍生直线的解析式是 _________ ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x 2
+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x 2
﹣2x ﹣3的顶点为M ,与y 轴交点为N ,将它的衍生直线MN 先绕点N 旋转到与x 轴平行,再沿y 轴向上平移1个单位得直线n ,P 是直线n 上的动点,是否存在点P ,使△POM 为直角三角形?若存在,求出所有点P 的坐标;若不存在,请说明理由.
图① 图②
例8如图①,已知抛物线23y x x =-经过A (3,0)、B (4,4)两点. (1)将直线OB 向下平移m 个单位长度后,得到的直线与抛物线只有一个公共点D ,则m =______,点D 的坐标为D (______ , _______);
(2)如图②,若点N 在抛物线上,且ABO NBO ∠=∠,则在(1)的条件下,求出所有满足POD ∆∽NOB ∆的点P 的坐标(点P 、O 、D 分别与点N 、O 、B 对应).
图① 图②
例9 (2014•钦州)如图,在平面直角坐标系中,抛物线y=﹣x 2
+bx+c 与x 轴交于A 、D 两点,与y
轴交于点B ,四边形OBCD 是矩形,点A 的坐标为(1,0),点B 的坐标为(0,4),已知点E (m ,0)是线段DO 上的动点,过点E 作PE ⊥x 轴交抛物线于点P ,交BC 于点G ,交BD 于点H . (1)当点P 在直线BC 上方时,请用含m 的代数式表示PG 的长度;
(2)在(1)的条件下,是否存在这样的点P ,使得以P 、B 、G 为顶点的三角形与△DEH 相似?若存在,求出此时m 的值;若不存在,请说明理由.。
