初二数学每日一题

合集下载

初二数学每天5道练习题

初二数学每天5道练习题每天做一些数学练习题对于初中数学学习的重要性不言而喻。

通过每日的练习，我们不仅可以巩固所学知识，还可以提高解题能力和应用技巧。

下面是一套适合初二学生的数学练习题，每天五道，希望对同学们的数学学习有所帮助。

第一天：1. 某数的十分之一是29.5，这个数是多少？2. 将一个半径为6厘米的圆切成两个相等的半圆，这两个半圆的周长之和是多少？3. 计算：[(-2)²-(-3)³]²+(3-4)×[2-(-5)]。

4. 某年级有200名学生，女生人数占总人数的30%，男生人数是多少？5. 甲乙两人同时向北走，甲每分钟走3米，乙每分钟走2米；五分钟后，甲离起点的距离是乙离起点的距离的2倍，这时，甲离起点的距离是多少米？第二天：1. 一个角的补角是210°，这个角是多少度？2. 某个正方形的边长是15厘米，这个正方形的面积是多少平方厘米？3. 计算：(x+3)²-(x-2)²，其中x=5。

4. 每个边长为9米的正方形地面上铺了一层面积为9平方米的砖，一共需要多少块砖？5. 小明拿了6个苹果，小红拿了8个苹果，小亮比小红少拿了2个苹果，那么小亮拿了几个苹果？第三天：1. 如果a:b=2:3，b:c=4:5，求a:b:c的值。

2. 一个圆的半径是5厘米，这个圆的周长是多少厘米？3. 计算：[（-2）²×(-3)³-2^5]÷(-2)²。

4. 甲车和乙车同时从A地开往B地，甲车的速度是每小时60公里，乙车的速度是甲车的一半，两车同时从A地出发，经过2个小时后乙车追上甲车，那么A地到B地之间的距离是多少公里？5. 小华比他的妹妹大了2岁，他的妹妹比小眼爱小了7岁，那么小花和小亮相比小了几岁？第四天：1. 式子[3*(-5)²+(-2)*(-3)²]的值是多少？2. 某个长方形的长是8厘米，宽是5厘米，这个长方形的周长是多少厘米？3. 解方程：2x-3=5。

初二数学上基础练习计算题

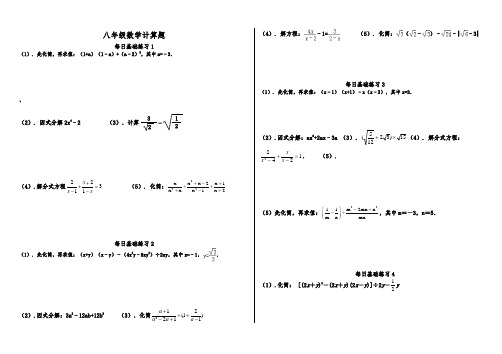
八年级数学计算题每日基础练习1（1）. 先化简，再求值：（1+a ）（1﹣a ）+（a ﹣2）2，其中a=﹣3．、（2）. 因式分解2x 4﹣2 （3）．计算3 2-12（4）.解分式方程22311x x x（5）. 化简：222x x x 2x 1x x x 1x 2+-+÷++-+每日基础练习2（1）. 先化简，再求值：（x+y ）（x ﹣y ）﹣（4x 3y ﹣8xy 3）÷2xy，其中x=﹣1，．（2）.因式分解：3a 2﹣12ab+12b 2 （3）．化简212(1)211a a a a +÷+-+- （4）. 解方程：﹣1= （5）. 化简：（﹣）﹣﹣|﹣3|每日基础练习3（1）. 先化简，再求值：（x ﹣1）（x+1）﹣x （x ﹣3），其中x=3．（2）.因式分解：ax 2+2ax ﹣3a （3）．15)32125(⨯+（4）. 解分式方程：12422=-+-x xx ．（5）.（5）先化简，再求值：2211m 2mn nm n mn -+⎛⎫-÷ ⎪⎝⎭，其中m ＝－3，n ＝5．每日基础练习4（1）.化简： [(2x ＋y )2－(2x ＋y )(2x －y )]÷2y －21y（2）.因式分解：a ab ab 442+- （3）．(827－53)· 6（4）.解方程：．（5）. 化简求值： 221m 2m 11m 2m 4++⎛⎫-÷ ⎪+-⎝⎭，其中m ＝1。

每日基础练习5（1）. 先化简，再求值：[(5x ＋2y )(3x ＋2y )＋(x ＋2y )(x －2y )]÷4x ，其中x=2，y=－3．（2）.因式分解：()()a a a 322+-+ （3）．12)323242731(⋅--（4）.解方程：．（5）.化简求值：22312x x x 1x x 2x 1-⎛⎫-÷⎪+++⎝⎭，其中x=1．每日基础练习6（1）. 化简求值：(a 2＋3)(a －2)－a (a 2－2a －2)，其中a=122- （2）因式分解：x 2－4（x －1）（3）．化简：，（5）.解方程：23112x x x x -=-+-. （4）每日基础练习7（1）. 化简：(x ―1)2+(x +3)(x ―3)+(x ―3)(x ―1)；（2）.因式分解：22)3(4)2(--+m m（3）．先化简，再求值：，其中．（4）. 方程（5）.12(75＋313－48)每日基础练习81121231548333（1）. 22)1)2)(2(+-+-x x x x －（（2）.因式分解：14-x ；（3）．先化简，再求值．，其中m=2．（4）. ）解方程：．（5）. )632)(632()232)(3(2-+-+每日基础练习9 班级姓名（1）. 化简：[(x +y )2-y (2x +y )-8x ]÷2x ．（2）. 因式分解：a a a 81721623+-（3）．先化简，再求值：（1﹣）÷，其中a=﹣2．（4）. 13321++=+x x x x （5）. 2)153()347)(347(---+每日基础练习10（1）. 化简求值：()()()()[]x xy y y x y x y x 3442323÷--+-+-,其中2=x ,31=y .（2）. 因式分解： 432244y xy y x +- （3）．)62)(2332(-+（4）.解方程：311(1)(2)x x x x -=--+ （5）. 先化简，再求值：x 23x 1x 1x 1-⎛⎫÷+- ⎪--⎝⎭，其中x 3－2．每日基础练习11（1）.化简求值：.2)3)(3()2)(3(2-=-+-+-aaaxx其中，x=1（2）.因式分解： 9a2(x-y)+4b2(y-x)（3）．计算:1)21(248-+-（4）.解方程：32211xx x+=-+（5）. 化简求值：x35x2x2x2-⎛⎫÷+-⎪--⎝⎭，其中x3-每日基础练习12（1）. 解不等式：(x+3)(x-7)+8＞(x+5)(x-1). （2）.因式分解：aaa1812223-+-（3）．）先简化，再求值：x25x32x6x3--⎛⎫÷--⎪--⎝⎭，其中x2=-（4）.解方程：2227611x x x x x-=+--（5）.⎛÷⎝每日基础练习13（1）. 先化简，再求值：2(2)(21)(21)4(1)x x x x x+++--+，其中x=（2）.因式分解： 16－24(a－b)＋9(a－b)（3）．（4）.解方程：22510x x x x -=+-（5）. 先化简，再求值：÷（x+1﹣），其中x=﹣2每日基础练习14（1）. 22))(()32(y y x y x x --+-- （2）. 因式分解：22)23()32(y x y x --+（3）．先简化，再求值：21x 2x 11x x -⎛⎫-÷ ⎪⎝⎭＋，其中x 2=．（4）.解方程： 114112=---+x x x （5）. 26)1(30--+-π每日基础练习15（1）. 解方程(3x -2)(2x -3)=(6x +5)(x -1)+15．（2）. 因式分解：2442x y x y -（3）．先化简：，再求值，其中a=．（4）. 解方程：14143=-+--x x x （5）. 11181222-⎛⎫++ ⎪⎝⎭每日基础练习16（1）. 化简求值：x （x -1）+2x （x +1）－（3x -1）（2x -5），（2）.171372222--+=--+x x x x x x 其中x =2．（3）．先化简，再求值：232224x x x x x x ⎛⎫-÷ ⎪-+-⎝⎭，其中x 取一个你喜欢的值求值（4）.分解因式：am 2﹣4an 2 （5）. )52)(103(-+ （6）.因式分解：4x 3﹣36x（7）. 22－ 3 －12 +( 3 +1) （8）. 22 －(3 －2)0+20（9）.)32)(532(+-（10）. )32)(532(+- （11）.(231⎛+ ⎝二次根式50道典型计算题1. 2484554+-+2. 2332326--3. 21418122-+- 4. 3)154276485(÷+-5.已知：的值。

八年级数学每日一题

每日一题初中数学【每日一题】（第 1 期）1、如图，∠BOC=9°，点A在OB上，且OA=1，按下列要求画图：以A为圆心，1为半径向右画弧交OC于点A1，得第1条线段AA1；再以A1为圆心，1为半径向右画弧交OB于点A2，得第2条线段A1A2；再以A2为圆心，1为半径向右画弧交OC于点A2，得第3条线段A2A3…这样画下去，直到得第n条线段，之后就不能再画出符合要求的线段了，则n=答案：n=9初中数学【每日一题】（第 2 期）2、已知：如图，△ABC是边长3cm的等边三角形，动点P、Q同时从A、B 两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当P到达点B时，P、Q两点停止运动.设点P的运动时间为t(s)，当t为时，△PBQ是直角三角形.答案：t=1秒或t=2秒初中数学【每日一题】（第 3 期）水滴石穿！3、如图，等腰△ABC中，AB=AC，∠DBC=15°，AB的垂直平分线MN交AC于点D，则∠A的度数是__°．答案：50°【解析】试题分析：设∠A=x°，根据MN为中垂线可得：∠ABD=∠A=x°，则∠ABC=(x+15)°，根据AB=AC可得：∠C=∠ABC=(x+15)°，则根据△ABC的内角和定理可得：x+x+15+x+15=180°，解得：x=50°.初中数学【每日一题】（第 4 期）锲而不舍，金石可镂！如图，在△ABC中，∠ABC与∠ACB的平分线相交于点O，过点O作DE∥BC，分别交AB、AC于点D、E，若AB=6，AC=5，则△ADE的周长是_________．答案：11【解析】试题分析：根据题意可得：△BDO和△COE是等腰三角形，OD=BD，OE=EC，则△ADE的周长=AD+DE+AE=AD+DO+OE+AE=AD+BD+AE+CE=AB+AC=6+5=11.考点：(1)、角平分线的性质；(2)、等腰三角形的性质.初中数学【每日一题】（第 5 期）小水长流，则能穿石！如图所示，三角形ABC的面积为1．AP垂直∠B的平分线BP于点P．则三角形PBC的面积是．【解析】试题分析：过点P作PE⊥BP，垂足为P，交BC于点E，由角平分线的定义可知∠ABP=∠EBP，结合BP=BP以及∠APB=∠EPB=90°即可证出△ABP≌△EBP （ASA），进而可得出AP=EP，根据三角形的面积即可得出，再根据=.故答案为：.考点：等腰三角形的判定与性质；角平分线的定义；三角形的面积；全等三角形的判定与性质．初中数学【每日一题】（第 6 期）立志不坚，终不济事！如图，△ABC是等腰直角三角形，延长BC至E使BE=BA，过点B作BD⊥AE于点D，BD与AC交于点F，连接EF．（1）求证：BF=2AD；（2）若CE=，求AC的长试题解析：（1）证明：∵△ABC是等腰直角三角形，∴AC=BC，∠FCB=∠ECA=90°，∵AC⊥BE，BD⊥AE，∴∠CBF+∠CFB=90°，∠DAF+∠AFD=90°，∵∠CFB=∠AFD，∴∠CBF=∠CAE，在△BCF与△ACE中，，∴△BCF≌△ACE，∴AE=BF，∵BE=BA，BD⊥AE，∴AD=ED，即AE=2AD，∴BF=2AD；（2）由（1）知△BCF≌△ACE，∴CF=CE=，∴在Rt△CEF中，EF==2，∵BD⊥AE，AD=ED，∴AF=FE=2，∴AC=AF+CF=2+．考点：全等三角形的判定与性质；勾股定理初中数学【每日一题】（第 7 期）已知，如图，△ABC是等边三角形，AE=CD，BQ⊥AD于Q，BE交AD于点P，求证：BP=2PQ．试题解析：∵△ABC是等边三角形，∴AB=AC，∠BAE=∠C=60°，在△ABE和△CAD中，AB=AC，∠BAE=∠C=60°，AE=CD，∴△ABE≌△CAD（SAS），∴∠1=∠2，∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°，∵BQ⊥AD，∴∠PBQ=90°﹣∠BPQ=90°﹣60°=30°，∴BP=2PQ．考点：全等三角形的判定与性质；等边三角形的性质；含30度角的直角三角形．初中数学【每日一题】（第 8 期）如图，∠MON=90°，△ABC的顶点A、B分别在OM、ON上，当A点从O点出发沿着OM向右运动时，同时点B在ON上运动，连结OC. 若AC=4，BC=3，AB=5，则OC的长度的最大值是．【解析】试题分析：取AB中点E，连接OE、CE，在直角三角形AOB中，OE=AB，利用勾股定理的逆定理可得△ACB是直角三角形，所以CE=AB，利用OE+CE≥OC，所以OC的最大值为OE+CE，即OC的最大值=AB=5．考点：勾股定理的逆定理初中数学【每日一题】（第 9 期）精诚所至，金石为开！著名画家达芬奇不仅画艺超群，同时还是一个数学家、发明家．他曾经设计过一种圆规如图所示，有两个互相垂直的滑槽（滑槽宽度忽略不计），一根没有弹性的木棒的两端A、B 能在滑槽内自由滑动，将笔插入位于木棒中点P处的小孔中，随着木棒的滑动就可以画出一个圆来．若AB=20cm，则画出的圆的半径为cm．试题解析：连接OP，∵△AOB是直角三角形，P为斜边AB的中点，∴OP=AB，∵AB=20cm，∴OP=10cm，考点：直角三角形斜边上的中线．初中数学【每日一题】（第 10 期）最可怕的是比你优秀的人还比你努力！如图，在△ABC中，AB=AC，点E为BC边上一动点（不与点B、C重合），过点E作射线EF交AC于点F，使∠AEF=∠B．（1）判断∠BAE与∠CEF的大小关系，并说明理由；（2）请你探索：当△AEF为直角三角形时，求∠AEF与∠BAE的数量关系．【解析】（1）∠BAE=∠FEC；理由如下：∵∠B+∠BAE=∠AEC，∠AEF=∠B，∴∠BAE=∠FEC；（2）如图1，当∠AFE=90°时，∵∠B+∠BAE=∠AEF+∠CEF，∠B=∠AEF=∠C，∴∠BAE=∠CEF，∵∠C+∠CEF=90°，∴∠BAE+∠AEF=90°，即∠AEF与∠BAE的数量关系是互余；如图2，当∠EAF=90°时，∵∠B+∠BAE=∠AEF+∠1，∠B=∠AEF=∠C，∴∠BAE=∠1，∵∠C+∠1+∠AEF=90°，∴2∠AEF+∠1=90°，即2∠AEF与∠BAE的数量关系是互余．【点评】此题考查了等腰三角形的性质以及外角的性质，此题难度适中，注意掌握分类讨论思想的应用．初中数学【每日一题】（第 11 期）耐心是一切聪明才智的基础！如图，△ABC的三边AB、BC、CA长分别是20、30、40，其三条角平分线将△ABC分成三个三角形，则：：等于．试题分析：由角平分线的性质可得，点O到三角形三边的距离相等，即三个三角形的AB、BC、CA的高相等，利用面积公式即可求解．过点O作OD⊥AC于D，OE⊥AB于E，OF⊥BC于F，∵O是三角形三条角平分线的交点，∴OD=OE=OF，∵AB=20，BC=30，AC=40，∴：：=2：3：4．故答案为：2：3：4．考点：角平分线的性质；三角形的面积．初中数学【每日一题】（第 12 期）如图，已知∠AOB=60°，点P在OA上，OP=8，点M、N在边OB上，PM=PN，若MN=2，则OM= ．解：过P作PC⊥MN∵PM=PN∴C为MN中点在Rt△OPC中，∠AOB=60°，∴∠OPC=30°，∴2OC=OP=8，∴OC=4则OM=OC﹣MC=4﹣1=3，初中数学【每日一题】（第 13 期）能坚持别人不能坚持的,才能拥有别人不能拥有的如图，Rt△ABC中，∠ACB=90°，CD是斜边AB上的高，角平分线AE交CD于H，EF⊥AB于F，下列结论：①∠ACD=∠B；②CH=CE=EF；③AC=AF；④CH=HD．其中正确的结论为（）A.①②④B.①②③C.②③D.①③∵∠B和∠ACD都是∠CAB的余角，∴∠ACD=∠B，故①正确；∵CD⊥AB，EF⊥AB，∴EF∥CD，∴∠AEF=∠CHE，∴∠CEH=∠CHE，∴CH=CE=EF，故②正确；∵角平分线AE交CD于H，∴∠CAE=∠BAE，∴△ACE≌△AFE（AAS），∴AC=AF，故③正确；CH=CE=EF＞HD，故④错误．故：正确答案选 B初中数学【每日一题】（第 14 期）如图，在△ABC中，AC=BC，∠C=90°，D是AB的中点，DE⊥DF，点E，F分别在AC，BC上，则DE与DF的数量关系是_______如图，连接CD．∵BC=AC，∠BCA=90°∴△ABC是等腰直角三角形∵D为AB中点∴BD=CD=AD，CD平分∠BCA，CD⊥AB∵∠A+∠ACD=∠ACD+∠FCD=90°∴∠A=∠FCD∵∠CDF+∠CDE=90°∠CDE+∠ADE=90°∴∠ADE=∠CDF，在△ADE和△CFD中∵∠A=∠FCD，AD=CD，∠ADE=∠CDF∴△ADE≌△CFD（ASA）∴DE=DF．初中数学【每日一题】（第 15 期）耐心和恒心总会得到报酬的。

初二数学每天练习题

初二数学每天练习题第一题：某超市开展了一场促销活动，一种牛奶原价每瓶15元，现在每瓶打9折，请问买10瓶需要支付的金额是多少？解答：首先，计算每瓶牛奶的打折价：15元 × 0.9 = 13.5元。

然后，计算购买10瓶牛奶所需的总金额：13.5元 × 10 = 135元。

答案：购买10瓶牛奶需要支付的金额是135元。

第二题：某班级共有60名学生，其中女生占总人数的40%，男生人数是多少？解答：首先，计算女生的人数：60 × 0.4 = 24人。

然后，计算男生的人数：60 - 24 = 36人。

答案：该班级男生的人数是36人。

第三题：一辆汽车以每小时60公里的速度行驶，行驶了3小时后还剩余多少公里未行驶？解答：首先，计算汽车行驶的总路程：60公里/小时 × 3小时 = 180公里。

然后，计算剩余未行驶的公里数：总路程 - 已行驶的公里数 = 180公里 - 180公里 = 0公里。

答案：汽车行驶了3小时后，剩余0公里未行驶。

第四题：甲乙两人的年龄之和为30岁，甲的年龄是乙的2倍，求甲和乙的年龄。

解答：设甲的年龄为x岁，则乙的年龄为2x岁。

根据题目条件，得出方程：x + 2x = 30。

合并同类项，得到3x = 30。

进行简单计算，得到x = 10。

因此，甲的年龄为10岁，乙的年龄为20岁。

答案：甲的年龄是10岁，乙的年龄是20岁。

第五题：某商品原价100元，现在打6折出售，请问打折后的价格是多少？解答：首先，计算商品的打折价：100元 × 0.6 = 60元。

答案：该商品打6折后的价格是60元。

总结：通过以上五道数学练习题，我们学习到了解决实际问题的数学运算方法。

在日常生活中，数学运算可以帮助我们解决各种实际问题，提高计算能力和分析问题的能力。

希望大家能够利用每天的练习时间，提高自己的数学水平。

八年级数学上学期每日一题1试题

第1题图 2八年级数学每日一题〔亲爱的同学们，每天练一练，越来越聪明〕班级：姓名：1. (1) 如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AE ,BF 交于点O ,∠AOF ＝90°.求证：BE ＝CF .(2) 如图2,在正方形ABCD 中,点E ,H ,F ,G 分别在边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,∠FOH ＝90°, EF ＝4.求GH 的长.(3) 点E ,H ,F ,G 分别在矩形ABCD 的边AB ,BC ,CD ,DA 上，EF ,GH 交于点O , ∠FOH ＝90°,EF ＝4. 直接写出以下两题之答案：①如图3,矩形ABCD 由2个全等的正方形组成,那么 GH=___________；②如图4,矩形ABCD 由n 个全等的正方形组成,那么 GH=___________；(用n 的代数式表示).第1题图1EDCBAO2.如图，在ABC △中，D 是BC 边上的一点，E 是AD 的中点，过点A 作BC 的平行线交BE 的延长线于F ，且AF DC =，连接CF ．(1)试说明：D 是BC 的中点；(2)假设AB ＝13，BC ＝10，AD=12,试猜想四边形ADCF 的形状，并说明理由．3.〔结果中保存π〕〔1〕操作：如图1，在线段AB 所在的直线上取一点O 〔O 点在线段外〕，将线段AB 绕点O 旋转一周，所得到的图形是个圆环〔如图2〕，此圆环的面积就是线段AB 所扫过的面积，AB=2，OA=1，那么线段AB 扫过的面积为．BA FCED〔2〕如图3，在Rt △ABC 中，∠C =90°，∠B=30°，AC=2，假设将△AB C 绕点A 旋转一周，那么边．BC ．．扫过的图形为，面积为．〔3〕假设将图3中的Rt △ABC 绕点C 旋转一周，那么边．A ．B ．扫过的图形是什么？面积为多少？4.如图，等腰梯形ABCD 中，AD ∥BC ，AB=CD ，AD=10cm ，BC=30cm ，动点P 从点A 开场沿AD 边向点D 以每秒1cm 的速度运动，同时动点Q 从点C 开场沿CB 边向点B 以每秒3cm 的速度运动，当其中一点到达端点时，另一点也随之停顿运动，设运动时间是为t 秒．〔1〕t 为何值时，四边形ABQP 是平行四边形？〔2〕四边形ABQP 能成为等腰梯形吗？假如能，求出t 的值；假如不能，请说明理由．图1图2图3B A O30CBA2OF E D CBA5.如图，四边形ABCD 中，AB=CD ，M 、N 分别是AD 、BC 的中点，延长BA 、NM 、CD 分别交于点E 、F 。

八年级上册每日一练习题

八年级上册每日一练习题一、选择题（每题3分，共30分）1. 下列关于二次根式的说法正确的是（）A. √9 = 3B. √9 = 3C. √9 = 3D. √9 = 32. 下列等式中，正确的是（）A. (a + b)² = a² + b²B. (a b)² = a² b²C. (a + b)² = a² + 2ab + b²D. (a b)² = a² 2ab + b²3. 下列关于平行四边形的性质，错误的是（）A. 对边平行且相等B. 对角相等C. 对角线互相平分D. 邻角互补4. 已知a = 3，b = 4，则a² + b²的值为（）A. 7B. 12C. 25D. 95. 下列关于圆的性质，正确的是（）A. 圆的半径等于直径的一半B. 圆的直径等于半径的两倍C. 圆的周长等于半径的两倍D. 圆的面积等于半径的平方6. 下列关于函数的说法，错误的是（）A. 函数是一种特殊的映射关系B. 函数的定义域是自变量的取值范围C. 函数的值域是因变量的取值范围D. 函数的图像是一条直线7. 下列关于概率的说法，正确的是（）A. 概率是描述事件发生可能性的数值B. 概率的取值范围是0到1C. 概率等于事件发生的次数除以总次数D. 概率等于事件不发生的次数除以总次数8. 下列关于二次函数的说法，错误的是（）A. 二次函数的图像是抛物线B. 二次函数的对称轴是x轴C. 二次函数的顶点坐标为（h，k）D. 二次函数的系数a决定了抛物线的开口方向9. 下列关于几何图形的变换，错误的是（）A. 平移变换不改变图形的形状和大小B. 旋转变换不改变图形的形状和大小C. 对称变换不改变图形的形状和大小D. 缩放变换改变图形的形状和大小10. 下列关于概率的公式，正确的是（）A. P(A∪B) = P(A) + P(B)B. P(A∪B) = P(A) P(B)C. P(A∪B) = P(A) + P(B) P(A∩B)D. P(A∪B) = P(A) P(B) + P(A∩B)二、填空题（每题3分，共30分）11. 若a² = 9，则a的值为______。

初二数学试题精选及答案

初二数学试题精选及答案一、选择题（每题3分，共30分）1. 下列哪个选项不是实数集R的子集？A. 整数集ZB. 有理数集QC. 无理数集D. 复数集C2. 如果一个三角形的两边长分别为3和4，第三边长为整数，那么第三边长可能是：A. 1B. 2C. 3D. 43. 一个数的立方根是它本身的数是：A. 0B. 1C. -1D. 以上都是4. 在直角坐标系中，点(2, -3)关于y轴的对称点的坐标是：A. (-2, -3)B. (-2, 3)C. (2, 3)D. (-2, 3)5. 一个数的绝对值是它本身，那么这个数：A. 一定是正数B. 一定是负数C. 可以是正数或0D. 可以是负数或06. 一次函数y=2x+3的图象不经过哪个象限？A. 第一象限B. 第二象限C. 第三象限D. 第四象限7. 一个数的相反数是它本身，那么这个数是：A. 正数B. 负数C. 0D. 以上都不是8. 以下哪个选项是方程2x-3=7的解？A. x=-1B. x=2C. x=5D. x=39. 一个数的平方是它本身，那么这个数是：A. 1或-1B. 0或1C. 0或-1D. 以上都不是10. 一个等腰三角形的两个底角相等，那么这个三角形的顶角可能是：A. 30°B. 45°C. 60°D. 90°二、填空题（每题3分，共30分）1. 一个数的绝对值是5，这个数可能是______。

2. 如果一个三角形的两个内角分别为30°和60°，那么第三个内角是______。

3. 一个数的立方是27，这个数是______。

4. 一个数的相反数是-8，这个数是______。

5. 一个数的平方是25，这个数是______。

6. 一次函数y=3x-2与y轴的交点坐标是______。

7. 一个等腰三角形的顶角是100°，那么它的底角是______。

8. 一个数的平方根是4，这个数是______。

初二期末每日一练习题

初二期末每日一练习题第一题：小明有一束蓝色的气球，他将气球上升5米，然后又下降3米，再上升4米，最后再下降2米。

请问气球现在高于原来位置多少米？解析：首先，小明将气球上升了5米，再下降3米，所以气球的高度是5-3=2米。

然后，小明又将气球上升了4米，再下降了2米，所以气球的高度现在是2+4-2=4米。

因此，气球现在高于原来位置3米。

第二题：小华有25个苹果，她将其中的1/5分给了小明，然后又将剩下的3/5分给了小李。

请问小明和小李各分到了多少个苹果？解析：首先，小华将25个苹果的1/5分给了小明，所以小明共分到了25*(1/5)=5个苹果。

然后，小华剩下的苹果有25-5=20个。

再将这20个苹果的3/5分给了小李，所以小李共分到了20*(3/5)=12个苹果。

因此，小明分到了5个苹果，小李分到了12个苹果。

第三题：小明去商店买了一本参考书，原价100元，现在打8折，请问小明需要支付多少钱？解析：打8折表示购买时只需要支付原价的80%，所以小明需要支付的钱数为100*80%=80元。

第四题：甲、乙、丙三人共做了一个项目，甲做了总工作量的1/4，乙做了总工作量的1/3，那么丙做了剩下的工作量的多少？解析：甲做了总工作量的1/4，乙做了总工作量的1/3，所以甲和乙两人总共做了1/4+1/3=7/12的工作量。

剩下的工作量为1-7/12=5/12，所以丙做了剩下工作量的5/12。

第五题：小华的身高是150厘米，大于她的人有50人，小于她的人有60人，请问和小华一样高的人有多少人？解析：身高大于小华的人有50人，小于小华的人有60人，所以不包括小华在内的这110人中，和小华一样高的人有110-50-60=0人。

因此，和小华一样高的人有0人。

通过以上题目的解答，我们可以练习和巩固初二期末的数学知识。

希望同学们多做类似的练习题，提高自己的数学能力。

加油！。

初二数学每日练习题

初二数学每日练习题1. 已知等差数列的首项为3，公差为4，求该等差数列的第10项。

2. 某商品原价为300元，现在打7.5折出售，求打折后的价格。

3. 若a:b=2:3，b:c=4:5，求a:b:c的比值。

4. 求解方程：2x + 5 = 17 - x。

5. 甲、乙两人共修整圆形花坛，甲每小时修整花坛的1/4，乙每小时修整花坛的1/3。

若甲、乙同时开始修整花坛，大约多少小时后两人的工作量相等？6. 已知ΔABC中的角A为45度，边AC的长度为8，边AB的长度为10，求边BC的长度。

7. 给出三个互质的正整数a、b、c，求证：a^2 + b^2 ≠ c^2。

8. 有一座高度为180米的山，山顶有一道天桥，离地面高度为150米，求这座山的斜率。

9. 甲、乙两人同时从A地出发，甲的速度为12千米/小时，乙的速度为15千米/小时。

已知AB的距离为120千米，甲、乙同时到达B地后立即返回，甲返回A地的速度为16千米/小时，乙返回A地的速度为20千米/小时。

问两人再相遇时离B地还有多远？10. 某地每小时降水量为5毫升，若一个缸的容量是500升，问需要多少时间才能将缸填满？11. 一根长10米的电线围成一个正方形，将该电线截成两段，是其中一段的长度是另外一段长度的2倍，求这两段电线的长度各是多少？12. 已知ΔABC中，BC=10，AC=15，角B的大小为45度，求∠A的角度大小。

13. 若7的3次方等于a，求a的立方根的值。

14. 设a为正整数，若a除以5余2，a除以6余3，求a。

15. 在一条长刻度尺上，A、B两点相距12厘米，C、D两点相距20厘米。

如果两点既不在同一条直线上，也不在同一条曲线上，求AC、BD两线段的距离。

16. 甲、乙、丙三人共有草地4000平方米要在一天内完成修剪，甲一小时能修剪100平方米，乙一小时能修剪120平方米，丙一小时能修剪80平方米，问还需要多少人加入团队才能在一天内完成修剪任务？17. 某商店一件商品原价为200元，现在则按照9折出售，并且再打8折，求折后价格。

八年级数学每日一题

每日一题初中数学【每日一题】（第1期）1、如图，/ B0C=9，点A在0B上，且0A=1,按下列要求画图：以A为圆心，1为半径向右画弧交0C于点A,得第1条线段AA i;再以A i为圆心，1为半径向右画弧交0B于点A2, 得第2条线段A1A2；再以A为圆心，1为半径向右画弧交0C于点A,得第3条线段心… 这样画下去，直到得第n 条线段，之后就不能再画出符合要求的线段了，则n= _______解析；由题意知；A0 - A^A^A = jfj4, - - t则ZAOA Y =20心厶］OA.= “卫具…’、:Z5OC = 9°.-.^^=18°, = 27% AA3A.B = 36= = 45°9 妝Y 90°解得n<10TH为整数，初中数学【每日一题】（第2期）2、已知：如图，△ ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB BC方向匀速移动，它们的速度都是1cm/s，当P到达点B时，P、Q两点停止运动.设点P的运动时间为t（s），当t为_____________________ 时，△ PBQ是直角三角答案：n=9形.* 匚答案：t=1秒或t=2秒解析：棍据题盍；“朮■叫硕AABC 中,AABO眈叫ZB=60° ,.'.BP= (3-t ) cm△PBQ 中* EPW-右6Q=tj若△PBQ是宜甬三角形」则ZBQR-50-1或ZBPQ=«〔1)当ZBOP^SO* 吋，理=¥»PPt = -(3-d；2解得：t=l(2)当ZBPQ-90* 吋丁BP = -BO解得：t=2二当日秒或"秒吋，APBQ是直角三角形初中数学【每日一题】(第3期)水滴石穿!3、如图，等腰△ ABC中，AB=AC / DBC=15 , AB的垂直平分线MN交AC于点D,则/ A 的度数是°.【解析】试题分析：设/ A=x°,根据MN为中垂线可得：/ ABD=/ A=x°,则/ ABC=(x+15) °，根据AB=AC可得：/ C=Z ABC=(x+15) °，则根据厶ABC的内角和定理可得：x+x+15+x+15=180 °，解得：x=50 ° .初中数学【每日一题】(第4期)锲而不舍，金石可镂！如图，在△ ABC中，/ ABC与/ ACB的平分线相交于点0,过点0作DE// BC,分别交AB AC于点D E,若AB=6, AC=5则厶ADE的周长是答案：50°答案：11【解析】试题分析：根据题意可得：△ BDO^A COE是等腰三角形，OD=BD OE=EC则厶ADE的周长=AD+DE+AE=AD+DO+OE+AE=AD+BD+AE+CE=AB+AC=6+5=11.考点：（1）、角平分线的性质；（2）、等腰三角形的性质•初中数学【每日一题】（第5期）小水长流，贝U能穿石！如图所示，三角形ABC的面积为1 . AP垂直/ B的平分线BP于点P.则三角形PBC的面积是____________________ .【解析】试题分析：过点P作PEL BP,垂足为P,交BC于点E,由角平分线的定义可知/ ABP=/ EBP 结合BP=BP以及/ APB=/ EPB=90 即可证出厶ABP^A EBP（ASA，进而可得出AP=EP根据三角形的面积即可得出，再根据— art1故答案为：-考点：等腰三角形的判定与性质；角平分线的定义；三角形的面积；全等三角形的判定与性质.初中数学【每日一题】（第6期）立志不坚，终不济事！如图，△ ABC是等腰直角三角形，延长BC至E使BE=BA过点B作BD1AE于点(1)求证：BF=2AD(2)若CE龙，求AC的长试题解析：(1)证明：•「△ ABC是等腰直角三角形,••• AC=BC/ FCB" ECA=90 ,••• ACL BE, BD L AE,•••/ CBF+Z CFB=90，/ DAF+Z AFD=90 ,vZ CFB Z AFD•••/ CBF Z CAEAC^BC^CBF=ZCAE在厶BCF与△ ACE中, ，•••△ BCF^A ACE••• AE=BFv BE=BA BD L AE,••• AD=ED 即AE=2AD••• BF=2AD(2)由(1)知厶BCF^A ACE••• CF=CE血,•••在Rt△ CEF中, EF=JH+E=2,v BD L AE, AD=ED•AF=FE=2•AC=AF+CF=2+ .考点：全等三角形的判定与性质；勾股定理初中数学【每日一题】（第7期）已知，如图，△ ABC是等边三角形，AE=CD BQLAD 于Q, BE 交AD 于点P ,初中数学【每日一题】（第8期）如图，/ MON=90 , △ ABC 的顶点 A B 分别在OM ON 上，当A 点从0点出发沿着 0M 向右运动时，同时点 B 在ON 上运动，连结 0C.若AC=4, BC=3 AB=5贝U 0C 的长度的最大【解析】30度角的直角三角形.考点：全等三角形的判定与性质；等边三角形的性质；含试题分析：取AB中点E,连接OE CE在直角三角形AOB中，OE= AB,利用勾股定理的逆定理可得△ ACB是直角三角形，所以CE= AB,利用OE+C匡OC所以OC的最大值为OE+CE即OC的最大值=AB=5考点：勾股定理的逆定理初中数学【每日一题】（第9期）精诚所至，金石为开！著名画家达芬奇不仅画艺超群，同时还是一个数学家、发明家•他曾经设计过一种圆规如图所示，有两个互相垂直的滑槽（滑槽宽度忽略不计），一根没有弹性的木棒的两端A、B 能在滑槽内自由滑动，将笔插入位于木棒中点P处的小孔中，随着木棒的滑动就可以画出一个圆来•若AB=20cm则画出的圆的半径为_______________________ cm试题解析：连接OP•••△ AOB是直角三角形，P为斜边AB的中点,丄••• OP^ AB■/ AB=20cmOP=i0cm考点：直角三角形斜边上的中线.初中数学【每日一题】（第10期）最可怕的是比你优秀的人还比你努力！如图，在△ ABC中，AB=AC点E为BC边上一动点（不与点B、C重合），过点E 作射线EF交AC于点F,使/ AEF=/ B.£C-(1)判断/ BAE与/ CEF的大小关系，并说明理由；(2)请你探索：当△ AEF为直角三角形时，求/ AEF与/ BAE的数量关系.【解析】(1)/ BAE/ FEC理由如下：•••/ B+/ BAE/ AEC / AEF=/ B，•••/ BAE/ FEC(2)如图1,当/AFE=90 时，•••/ B+/ BAE/ AEF/ CEF/ B=/ AEF=/ C,•••/ BAE/ CEF•••/ C+/ CEF=90，•••/ BAE/ AEF=90，即/ AEF与/ BAE的数量关系是互余；如图2，当/ EAF=90时，•••/ B+/ BAE/ AEF/ 1，/ B=/ AEF=/ C,•••/ BAE/ 1，vZ C+Z 1+Z AEF=90 ,••• 2Z AEF+Z 1=90°,即2Z AEF与Z BAE的数量关系是互余.A【点评】此题考查了等腰三角形的性质以及外角的性质，此题难度适中，注意掌握分类讨论思想的应用.初中数学【每日一题】（第11期）耐心是一切聪明才智的基础！如图，△ ABC的三边AB BC CA长分别是20、30、40,其三条角平分线将△ ABC分成三个三角形，则*心：*曲：鼻「削）等于试题分析：由角平分线的性质可得，点O到三角形三边的距离相等，即三个三角形的AB BC CA的高相等，禾I」用面积公式即可求解.过点O作ODL AC于D, OELAB于E，OF L BC于F，v O是三角形三条角平分线的交点，二OD=OE=OF v AB=20 BC=30 AC=4Q .•声^： $皿：'s =2: 3: 4. 故答案为：2：3：4.考点：角平分线的性质；三角形的面积.初中数学【每日一题】（第12期）如图，已知/ AOB=60，点P在0A上，OP=8点M N在边0B上，PM=PN若MN=2 贝U 0M=________________ .解：过P作PCL MN•/ PM=PN••• C为MN中点.WC = SC = = I°■在Rt△ OPC中，/ AOB=60，•••/ OPC=30，• 2OC=OP=，OC=4初中数学【每日一题】（第13期）能坚持别人不能坚持的,才能拥有别人不能拥有的如图，Rt△ ABC中，/ ACB=90 , CD是斜边AB上的高，角平分线AE交CD于H, EF丄AB于F,下列结论：①/ ACD M B;②CH=CE=EF③AC=AF④ CH=HD其中正确的结论为（）A.①②④B.①②③C.②③D.①③•••/ B和/ ACD都是/ CAB的余角，•••/ ACD M B,故①正确;v CDL AB, EF丄AB••• EF// CD，•••/ AEF=/ CHE•••/ CEH/ CHE••• CH=CE=EF故②正确；v角平分线AE交CD于H,•••/ CAE/ BAE•••△ ACE^A AFE（AAS ,••• AC=AF故③正确；CH=CE=E^HD故④错误.故：正确答案选B初中数学【每日一题】（第14期）如图，在△ ABC中, AC=BC / C=90 , D是AB的中点，DEI DF,点E, F 分别如图，连接CDv BC=AC / BCA=90•••△ ABC是等腰直角三角形v D为AB中点• BD=CD=AD CD平分/ BCA CDL AB•••/ A+Z ACD=/ ACD+Z FCD=90•••/ A=Z FCDvZ CDF Z CDE=90 Z CDE Z ADE=90•Z ADE玄CDF在厶ADE和厶CFD中vZ A=Z FCD AD=CD Z ADE Z CDF•△ADE^A CFD( ASA初中数学【每日一题】（第15期）耐心和恒心总会得到报酬的。

(完整word版)八年级寒假作业数学每日一题

C八年级数学每日练习题1、如图，在平面直角坐标系中，点A 的坐标是（－1，0），点B 的坐标是（1，0），点C 的坐标是（3，0），D 为y 轴正半轴上点，∠ODB=30°,延长DB 至E ，使BE=BD ，P 为x 轴正半轴上动点（P 在C 的右边），M 在EP 上，且∠EMA=60°,AM 交BE 于N. ⑴求证：BE=BC ； ⑵求证：∠ANB=∠EPC;⑶当P 点运动时，求BP －BN 的值.2、如图，在平面直角坐标系中，点A 与点B 的坐标分别是),0(),0,(b B a A ，且b a ,满足2232(322)0a b a b +-+++=。

点E 的坐标是(0,)(2)t t >，以AE 为边作如图所示正方形AEDC 。

DB 交（1）求点A 、点B 的坐标；（2）试用含t 的式子表示点D 和点C 的坐标；（3）当t (2)t >变化时，线段OF 的长度是否发生变化？为什么？3、如图，AD ∥BC ，∠ADC=90°，CA=CB ，CE=CD ，AC ⊥CE ，AE 交BD 于点O ，AC 交BE 于点F. （1）若∠ACD=n ︒，求∠AOB 的度数；（2）试判断BF 与EF 之间的数量关系，并说明理由.4、如图，在平面直坐标系中，点A 的坐标是（2-，0），点B 的坐标是（2，0（0，3），点D 是线段CA 延长线上一点，点E 是线段BC 上一点，DE 交x 于点F.（1）若点G 是DE 的中点，试问线段BE 和AD 有何数量关系？为什么？（2）在（1）的条件下，求△CGF 的面积.5、如图，在平面直角坐标系中，点A的坐标是（t-，0），点B的坐标是（t，0），点C的坐标是（0，t），其中0t>.点D 和点E分别是AC延长线和反向延长线上的点，CD=AE.CF⊥BD 于点F ,直线CF交x轴于点G，直线GE交DB于点M.（1）求证：GB平分∠CGM；（2）试判断∠D与∠GEC之间的数量关系，并说明你的理由；（3）若AE=12AC，则点B是MD的中点吗？为什么？6、如图，点A、B在y轴正半轴上，∠DOB=60º，点C在OD上，且OC=OA，BC=BD，点C的纵坐标是1，AB=4.（1）求点A和点B的坐标；（2）求证：AC=DC.7、如图，点A和点B分别在x轴和y轴的正半轴上，AD平分∠BAO交y轴于点D，OC⊥AB于点C，交AD于点E，过点E作EF∥AB，交OB于点F.（1）求证：OE=OD；（2）若OE=2，DF=1.8，求点B的坐标.8、如图，△ABC是等边三角形，E是BC边上一动点（不与点B、C重合），以CE 为一边在BC的另一侧作等边△CED，连结BD，AE的延长线交BD于点F，连结FC. （1）求证：AE=BD；（2）当点E在边BC上运动时（不与点B、C重合），EF DFCF+的值是否发生变化？如果不变，求出其值；如果改变，清说明理由.yx O M E D C BA9、如图，在平面角直角坐标系中，点A （0，2）、点B （-4,0），OD=3OA ，点B 与点C 关于y 轴对称，DE ⊥AB 于点E ，DM=AB.（1）求点M 的坐标；（2）求证：△AMC 是等腰直角三角形.10、如图，在平面角直角坐标系中，A （–2，0），B （0，3），C （3，0），D （0，2）.（1）求证：AB=CD 且AB ⊥CD ；（2）以A 为直角顶点在第二象限内作等腰直角三角形ABE ，过点E 作EF ⊥x 轴于点F ，求点F 的坐标；（3）若点P 为y 轴正半轴上一动点，以AP 为直角边作等腰直角三角形APQ ，∠P 运动时，OP -QR 的值是否发生变化？若不变，求出其值；若变化，请说明理由.11、如图1，在平面角直角坐标系中，点P 的坐标是（3，3），以点P 为顶点的直角∠APB 分别交y 轴正半轴和x 轴正半轴于点A 、点B.（1）当直角∠APB 绕点P 转动（保持与y 轴正半轴和x 轴正半轴相交）时，OA+OB 的值是否发生变化？说明你的理由；（2）如图2，连接OP 、AB ，若∠BAO 的平分线交OP 于点C ，CD ⊥AO 于点D ，求CD +2AB的值.12、两块等腰直角三角形纸板按如图所示方式摆放，∠BAC=∠ADE=90º，AD 、AE 分别交BC 于点M 、N.（1）请问以线段BM 、MN 和CN 为边能否构成三角形？若能构成三角形，请判断三角形的形状；若不能构成三角形，请说明理由.（2）若将三角形纸板ADE 绕点A 旋转至如图2所示位置，AE 交BC 延长线于点N ，请问以线段BM 、MN 和CN 为边能否构成三角形？为什么？图1 图213、在平面直角坐标系中，点B 的坐标是（33，），过点B 作直线a ⊥y 轴于点C ，作直线b ⊥x 轴于点A ，点P 、Q 分别是直线a 和直线b 上的点，∠POQ=45º.（1）如图1，点P 、Q 分别在线段BC 和线段AB 上，试求△BPQ 的周长；图 1 图 2（2）如图2，点P 在线段BC 的延长线上，点Q 在线段AB 的延长线上，请问线段PQ 、BQ 和BP 之间有怎样的数量关系？为什么？（3）如图3，点P 在线段BC 的反向延长线上，点Q 在线段AB 的反向延长线上，请直接写出线段PQ 、BQ 和BP 之间的数量关系：.图 314、依据（1）一组对边平行、（2）一组对边相等、（3）一组对角相等、（4）另一组对边平行、（5）另一组对边相等、（6）另一组对角相等、（7）一条对角线平分另一条对角线等条件可组成平行四边形的判定命题，请写出12个平行四边形的判定命题，并判断其真假，画图并写出证明或反例；图1A(P)图2P FE D C B A15、点P 在正方形ABCD 的边AD 所在的直线上，以BP 为对角线作正方形BEPF ，连结CE 。

初二数学天天练习题

初二数学天天练习题一、选择题1. 某数的十分之一是8，这个数是多少？A. 80B. 18C. 88D. 8002. 电影院里有100个座位，已经有68人入座了，还剩下多少个空座位？A. 32B. 68C. 100D. 1323. 若一个正方形的周长为24cm，则它的面积是多少？A. 9cm²B. 12cm²C. 36cm²D. 144cm²4. 现在是下午2点20分，再过150分钟是几点？A. 4点B. 3点C. 5点D. 6点5. 甲乙两个数相差为48，相和为100，则乙这个数是多少？A. 26B. 42C. 58D. 74二、填空题1. 一个数除以3的商是8，那么这个数是 _______。

2. 若一个数的两倍再加上6等于20，则这个数是 _______。

3. 将26分别乘以3和4，然后求这两个结果的和，得到的数是_______。

4. 甲利用650元钱换了3个苹果，单个苹果的价格是 _______。

5. 一个四边形，边长分别是5cm、7cm、6cm和8cm，它的周长是_______。

三、解答题1. 林林和丽丽把一块长方形的纸剪成两个部分，且两部分的周长相等。

如果林林剪下的部分的长是10cm，宽是8cm，丽丽剪下的部分的长是14cm，那么丽丽剪下的部分的宽是多少cm？2. 若一个数字乘以6，再加上4等于100，请你找出这个数字。

3. 一个正数比4多两倍，另一个正数比这个数少12，如果这两个数的和是44，请你找出这两个数分别是多少。

4. 一个矩形的长是6cm，宽是4cm，如图所示，每个小格子的边长都是1cm，请你计算整个矩形中格子的总数。

[图]四、解答题1. 某商店举行活动，打折销售如下：购买1件商品打9折，购买3件商品打7折。

小明准备买5件商品，请问他需要支付多少钱？2. 面积相等的两个矩形，长却不等，一个矩形的长是10cm，宽是6cm，另一个矩形的宽是4cm，长是多少？3. 原价100元的书现在打八折，请问现在的售价是多少？4. 火车站候车室的长方形地面上贴有如下规则的标示：每隔2米贴一个红色的圆圈，每隔3米贴一个蓝色的正方形，每隔4米贴一个黄色的三角形。

八年级上册数学每日一练

1．a，b，c是三角形的三边长，化简|a﹣b﹣c|﹣|b﹣c+a|+|c﹣a﹣b|后等于（）A．b+a﹣3c B．b+c﹣a C．3a+3b+3c D．a+b﹣c2．如图，把△ABC沿EF翻折，叠合后的图形如图，若∠A＝60°，∠1＝95°，则∠2的度数是（）A．15°B．20°C．25°D．35°3．如果一个多边形的内角和是外角和的5倍，那么这个多边形的边数是．4．如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E．（1）若∠B＝35°，∠E＝25°，求∠CAE的度数；（2）证明：∠BAC＝∠B+2∠E．1．如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C平分∠ACB，若∠BA'C＝122°，则∠1+∠2的度数为（）A．116°B．100°C．128°D．120°2．如图，△ABC中，∠B＝40°，∠C＝30°，点D为边BC上一点，将△ADC沿直线AD折叠后，点C落到点E处，若∠BAE＝50°，则∠DAC的度数为°．3．如图，在△ABC中，AD是BC边上的高，AE是∠BAC的平分线，若∠B＝70°，∠C ＝40°，则∠DAE的度数为．4．如图，直线AB⊥CD于点G，交EF于点H，射线GM交EF于点M，已知∠AGM：∠DGM＝2：7，∠AHF比∠DGM大10°，求∠GHM的度数．1．如图，CE是△ABC的外角∠ACD的平分线，若∠B＝30°，∠ACE＝60°，则∠A＝（）A．60°B．100°C．90°D．80°2．若一个多边形的一个内角为144°，则这个图形为正（）边形．A．十一B．十C．九D．八3．如图，大建从A点出发沿直线前进8米到达B点后向左旋转的角度为α，再沿直线前进8米，到达点C后，又向左旋转α角度，照这样走下去，第一次回到出发地点时，他共走了72米，则每次旋转的角度α为（）A．30°B．40°C．45°D．60°4．如图，点D，E，F分别是三角形ABC的边BC，AB，AC上的点，EF∥BC，∠1＝∠2，∠EDG＝90°．（1）判断线段DE与AB的位置关系，并说明理由．（2）若∠2＝60°，求∠FED的度数．1．如图，线段AB、CD相交于点O，连接AD、CB，∠DAB和∠BCD的平分线AP和CP 相交于点P，则∠P与∠D、∠B之间存在的数量关系为（）A．∠P＝2（∠B﹣∠D）B．C．D．2．如图，在四边形ABCD中，∠C＝110°，与∠BAD，∠ABC相邻的外角都是120°，则∠α的值为（）A．50°B．55°C．60°D．65°3．如图，BD＝BC，点E在BC上，且BE＝AC，DE＝AB．（1）求证：△ABC≌△EDB；（2）判断AC和BD的位置关系，并说明理由．1．如图，直线a∥直线b，Rt△ABC的直角顶点A落在直线a上，点B落在直线b上，若∠1＝18°，∠2＝32°，则∠ABC的大小为．2．若对图1中星形截去一个角，如图2，再对图2中的角A，B，E，F如法进一步截去，如图3，则图中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N＝度．3．.如图，点C、D在线段AB上，且AC＝BD，AE＝BF，AE∥BF，连接CE、DE、CF，求证CF＝DE．1．小聪利用最近学习的数学知识，给同伴出了这样一道题：假如从点A出发，沿直线走6米后向左转θ，接着沿直线前进6米后，再向左转θ……如此下去，当他第一次回到A 点时，发现自己走了72米，θ的度数为（）A．30°B．36°C．60°D．72°2．若一个正多边形的一个外角为72°，则这个正多边形的内角和为（）A．360°B．540°C．720°D．900°3．如图，AB＝BD，要使△ABC≌△DBC，还需要补充一条件：（填一个即可）．4．如图所示，已知CD＝BD，点E、F分别是CD、BD的中点，∠CAF＝∠BAE，∠B＝∠C．求证：AE＝AF．1．如图（），BE是△ABC的高．A．B．C．D．2．如图，∠B＝30°，∠CAD＝65°且AD平分∠CAE，则∠ACD等于（）A．95°B．65°C．50°D．80°3．如图，在Rt△ABC的斜边AB上截取AD＝AC，过点D作DE⊥AB交BC于E，则有（）A．DE＝DB B．DE＝CE C．CE＝BE D．CE＝BD4．如图，在四边形ABCD中，E是对角线AC上一点，连接DE，AD∥BC，AC＝AD，∠CED+∠B＝180°．△ADE与△CAB全等吗？为什么？八年级上册数学每日一练81．如图，在△ABC中，AB＝AC，点D是BC边的中点，连接AD，点P在AD上，连接BP，CP，过点D作DE⊥BP，DF⊥CP，垂足分别为EF，则下列结论：①BD＝CD；②△BDE≌△CDF；③DE＝PE；④△BCP是等腰三角形．其中正确的有．（填序号）2．如图所示，△ABC≌△AEF．在下列结论中，不正确的是（）A．∠EAB＝∠F AC B．BC＝EFC．CA平分∠BCF D．∠BAC＝∠CAF3．如图，正方形ABCD和正方形AEFG有公共点A，点B在在线段DG上．判断DG与BE的位置关系，并说明理由．八年级上册数学每日一练91．在△ABC中，D，E分别是AC、BC上的点，过点D作DF⊥AB，DG⊥BC，垂足分别是点F，G，连接DE，若DF＝DG，BE＝DE，则下面三个结论：①BF＝BG；②DE∥BF；③△ADF≌△CDG．其中正确的是（）A．①③B．②③C．①②D．①②③2．如图，在正方形OABC中，O是坐标原点，点A的坐标为（1，），则点C的坐标是（）A．（﹣，1）B．（﹣1，）C．（﹣，1）D．（﹣，﹣1）3．如图，在△AOB和△COD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝50°，（1）试说明：AC＝BD；（2）AC与BD相交于点P，求∠APB的度数．八年级上册数学每日一练101．如右图，AO、BO、CO分别平分∠BAC、∠ABC、∠ACB，OD⊥BC，△ABC的周长为12，OD＝2，则△ABC的面积为．2．如图，△ABC的三边AB、BC、CA长分别是30、40、50，∠ABC和∠ACB的角平分线交于O，则S△ABO：S△BCO：S△CAO等于（）A．1：1：1B．1：2：3C．2：3：4D．3：4：53．如图1，∠DAB＝90°，CD⊥AD于点D，点E是线段AD上的一点，若DE＝AB，DC ＝AE．（1）判断CE与BE的关系是．（2）如图2，若点E在线段DA的延长线上，过点D在AD的另一侧作CD⊥AD，并保持CD＝AE，DE＝AB，连接CB，CE，BE，试说明（1）中结论是否成立，并说明理由．1．在如图所示的3×3网格中，△ABC是格点三角形（即顶点恰好是网格线的交点），则与△ABC有一条公共边且全等（不含△ABC）的所有格点三角形的个数是（）A．4个B．3个C．2个D．1个2．如图，△ABC中，∠ABC的角平分线与∠ACB的角平分线交于点P，若点P到边BC的距离为1，△ABC的周长为12，则△ABC的面积为（）A．6B．7C．8D．93．如图，在△ABC和△DEF中，AB＝DE，∠B＝∠DEF，请你再补充一个条件，能直接运用“SAS”判定△ABC≌△DEF，则这个条件是（）A．∠ACB＝∠DEF B．BE＝CF C．AC＝DF D．∠A＝∠F4．如图，在△ABC中，D，E是BC边上的两点，AD＝AE，BE＝CD，∠1＝∠2＝110°，∠BAE＝60°，则∠BAC的度数为．5．如图，在△ABC中，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E．若DE＝1，AC ＝4，则△ADC的面积为．6．如图，已知∠1＝∠2，AC＝AE，不添加任何辅助线，再添加一个合适的条件：，使△ABC≌△ADE．（只写出一种即可）1．如图，E是△ABC的边AC的中点，过点C作CF∥AB，过点E作直线DF交AB于D，交CF于F，若AB＝9，CF＝6.5，则BD的长为．2．如图，在△ABC中，∠ACB＝90°，点D为AC边上一点，ED⊥AC，CE⊥AB，AB＝CE，若BC＝2，DE＝5，则线段AD的长为．3．如图，在△ABC中，∠ABC＝45°，过点C作CD⊥AB于点D，过点B作BM⊥AC于点M，连接MD，过点D作DN⊥MD，交BM于点N，CD与BM交于点E．下列结论：①∠ABM＝∠ACD；②DM＝DN；③∠AMD＝45°；④S△DNE＝S△ADM.其中正确结论有．（填写序号即可）4．如图所示的网格是正方形网格，图形的各个顶点均为格点，则∠P+∠Q＝度．5．如图，△ABC≌△ADE，∠B＝90°，∠C＝26°，∠DAC＝14°，则∠EAC＝．6．如图，AD是△ABC的角平分线，DF⊥AB于点F，点E，G分别是边AB，AC上的点，且DE＝DG，则∠AED+∠AGD＝度．1．如图，CA⊥AB于点A，AB＝4，AC＝2，射线BM⊥AB于点B，一动点D从点A出发以2个单位/秒的速度沿射线AB运动，E为射线BM上一动点，随着点D的运动而运动，且始终保持ED＝BC，若点D运动t秒（t＞0），△EDB与△BCA全等，则t的值为．2．如图，在正方形方格中，各正方形的顶点叫做格点，三个顶点都在格点上的三角形称为格点三角形．图中△ABC是格点三角形，请你找出方格中所有与△ABC全等，且以A为顶点的格点三角形．这样的三角形共有个（△ABC除外）．3．如图，在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC＝8，CD＝4，则四边形ABCD的面积是．4．如图，已知AE⊥AB，AF⊥AC．AE＝AB，AF＝AC，BF与CE相交于点M．求证：（1）EC＝BF；（2）EC⊥BF；（3）连接AM，求证：AM平分∠EMF．。

八年级数学每日小练习

八年级数学每日一练
1、已知 x2 16 ，则 x
2、 3 的相反数是
3 比较大小： 3 2
23
4 下列各式中，是二元一次方程的是（
）
A.
B.
C.
D.
5、若代数式 x 4 的值是 2 ，则 x 等于（）
A.2 B.
C.6 D.
八年级数学每日一练
1、 16 的平方根是
2、 x2 9 0 ，则 x
4、已知 x 1 y 32 0 ，则 x y 的平方根（
）
A. 4
B. 2
C. 2
D. 4
5、已知 3x 2 有平方根，则 x 的取值范围是（）
A. x 2 3
B. x 2 3
C. x 2 3
D. x 2 3
八年级数学每日一练
1、 9 的算术平方根是
3、已知 a 5 2 5b 1 0 ，则 a2014 a2014
4、下列运算正确的是（
）
A. a2 a3 a6 B. ab2 a2b2
C. a2 3 a5
5、计算 a a5
2a3
2
的结果为（
）
D. a2 b2 a4
A. a6 2a5
5
A.
B. 0
3
）

C.
3
5、若 a 与 1 互为相反数，则 a 1 等于（
D. 0.2
）
A. 1
B. 0
C.1
D. 2
八年级数学每日一练
1、若 3m 5,3n 2 ，则 32m3n1
2、 3 2
3、若一个角的补角是这个角的余角的 3 倍，则这个角的度数是

初二数学下册每日一练习题

初二数学下册每日一练习题今天的数学练习题是针对初二数学下册的内容，共有10道题目。

希望通过这些练习题，能够帮助大家巩固课堂上所学的知识，并提升自己的数学能力。

1. 某数的十分之一是6，这个数是多少？解析：设这个数为x，根据题意可得出方程式：x/10 = 6，两边同时乘以10得到x = 60，所以这个数为60。

2. 如果甲数的75%等于乙数的50%，而且甲数比乙数多30，求甲数和乙数各是多少？解析：设甲数为x，乙数为y，根据题意可得出方程式：x*75% = y*50%，又因为甲数比乙数多30，所以可以得到方程式 x = y + 30。

将第一个方程式化简得到x*3/4 = y/2，进一步化简得到x = 2y/3。

将这个结果代入第二个方程式中，得到2y/3 = y + 30，解方程得到y = 90，再代入第一个方程式可得到x = 120。

所以甲数为120，乙数为90。

3. 一辆汽车经过一个12米长的桥所费时间是车在公路上行驶时所费时间的2倍，这辆汽车在公路上的速度是每小时72千米，求汽车在桥上的速度。

解析：设车在公路上的速度为v，根据题意可列方程：公路上的时间 = 2 * 桥上的时间，即 12/v = 2 * 12/(v + 桥上的速度)。

已知公路上的速度为72千米/小时，代入方程式中可得：12/72 = 2 * 12/(72 + 桥上的速度)。

解方程得桥上的速度为36千米/小时。

4. AB是一条长为10cm的弦，过A点做BM垂直于AB交弧AB于点M，求AM的长度。

解析：由于BM是AB的垂线，所以ABM是一个直角三角形，根据勾股定理可得AM的平方加上BM的平方等于AB的平方。

已知AB的长度为10cm，即可列方程：AM^2 + BM^2 = AB^2。

由于AM和BM是直角三角形的两条直角边，所以BM的长度可以直接计算，即BM = AB/2 = 10/2 = 5cm。

代入方程式可得：AM^2 + 5^2 = 10^2，解方程得AM的长度为√(100-25) = √75 = 5√3 cm。

初中数学每日一题

148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
谢谢大家！
37
38
39
40
初中数学每日一题〔10〕
方法迁移——解决实验探究型问题初中数学试卷的最后压轴题，总是实验探究型问题：先在一种简单的背景下证明某个结论，然后在条件变化后，探究结论是否成立。解决问题的方法就是：将第(1)问中的方法迁移到后面 (2)和(3)的问题中。
41
42
43
44
联想与“最短〞有关的知识点：两点之间线段最短，垂线段最短，三角形两边之和大于第三边等。将相关问题转化成这样的根本数学模型即可解决问题。
20
21
22
23
24
25
26
初中数学每日一题〔6〕
分类讨论思想—探究图形个数
在几何问题中，经常会见到问:适合题意的图形有几个，对于这种探究图形个数问题，是典型的考查分类讨论思想的问题，但是能否考虑全面，关键却在于数学知识的掌握程度和运用的灵活程度。
初中数学每日一题〔7〕分类讨论思想—解决字母取值不确定性问题
每个数学结论都有其成立的条件，每一种数学方法的使用也往往有其适用范围，在我们所遇到的数学问题中，有些问题的结论不是唯一确定的，有些问题的结论在解题中不能以统一的形式进行研究，还有些问题的量是用字母表示数的形式给出的，这样字母的取值不同也会影响问题的解决。根据题目的特点和要求，分成假设干类，转化成假设干个小问题来解决，这种按不同情况分类，然后再逐一研究解决的数学思想，称之为分类讨论思想。

八年级数学每日一题共14题

P —001（1）如图1，在正方形ABCD 中，M 是BC 边（不含端点B 、C ）上任意一点,P 是BC 延长线上一点，N 是∠DCP 的平分线上一点．若∠AMN=90°，求证：AM=MN ．下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．证明：在边AB 上截取AE=MC ，连ME ．（下面请你完成余下的证明过程）（2）若将(1)中的“正方形ABCD ”改为“正三角形ABC ”（如图2）,N 是∠ACP 的平分线上一点，则当∠AMN=60°时，结论AM=MN 是否还成立？请说明理由．（3）若将（1）中的“正方形ABCD ”改为“正n 边形ABCD …X ”，请你作出猜想：当∠AMN= °时，结论AM=MN 仍然成立．（直接写出答案，不需要证明）M N P D C E B A 图1P—002 如图，点P是正方形ABCD的边CD上一点，DF⊥AP于点F，在AP的延长线上取一点G，使AF=FG，连结DG。

（1）求证：DG=DC；（2）∠CDG的平分线交AG于点H，过点B作BE⊥AG于点E，试问线段BE、DF和AH 之间有何数量关系？为什么？P—003 如图所示．∠A=90°，AB=AC，M是AC边的中点，AD⊥BM交BC于D，交BM 于E．求证：∠AMB=∠DMC．B CDP —004 问题背景某课外学习小组在一次学习研讨中，得到如下两个命题：①如图8-2-1，在正三角形ABC 中，M 、N 分别是AC 、AB 上的点，BM 与CN 相交于点O ，若∠BON= 60°，则BM = CN .②如图8-2-2，在正方形ABCD 中，M 、N 分别是CD 、AD 上的点，BM 与CN 相交于点O ，若∠BON= 90°,则BM = CN .然后运用类比的思想提出了如下的命题： ③如图8-2-3，在正五边形ABCDE 中，M 、N 分别是CD 、DE 上的点，BM 与CN 相交于点O ，若∠BON = 108°，则BM = CN .任务要求（1）请你从①、②、③三个命题中选择一个进行证明；（2）请你继续完成下面的探索：①如图8-2-4，在正n （n ≥3）边形ABCDEF …中，M 、N 分别是CD 、DE 上的点，BM 与CN 相交于点O ，问当∠BON 等于多少度时，结论BM = CN 成立？（不要求证明）②如图8-2-5，在正五边形ABCDE 中，M 、N 分别是DE 、AE 上的点，BM 与CN 相交于点O ，当∠BON = 108°时，请问结论BM = CN 是否还成立？若成立，请给予证明；若不成立，请说明理由.（1）我选 .图8-2-1 图8-2-2 图8-2-3 图8-2-4 图8-2-5P —005如图，在△ABC 中，∠A=100°，∠ABC=40°，BD 是∠ABC 的平分线，延长BD 至E ，使DE=AD.求证：BC=AB+CE.P —006如图，在平面直角坐标系中，点A 与点B 的坐标分别是),0(),0,(b B a A ，且b a ,满足2232(322)0a b a b +-+++=。

初二数学上学期每日一题12月15日

1
每日一题（12月15日）
我们知道，假分数可以化为带分数. 例如： 83=223+=2
23. 在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”. 例如：11x x -+，21
x x -这样的分式就是假分式；31x + ，221
x x + 这样的分式就是真分式 . 类似的，假分式也可以化为带分式（即：整式与真分式和的形式）. 例如：1(1)22=1111x x x x x -+-=-+++； 22111(1)1111
111x x x )x x x x x x -++-+===++----（. （1）将分式
12
x x -+化为带分式；（2）若分式211x x -+的值为整数，求x 的整数值；（3）在平面直角坐标系中（x ，y ）表示点的坐标，若2211
x y x -=+，求所有横纵坐标均为整数的点的坐标。