必修五主要公式公式挖空默写使用.doc
高中数学必修五公式整理资料讲解

精品文档高中数学必修五公式第一章 三角函数一.正弦定理:2(sin sin sin a b cR R A B C===为三角形外接圆半径)变形:2sin (sin )22sin (sin )22sin (sin )2a a R A A R b b R B B R c c R C C R ⎧==⎪⎪⎪==⎨⎪⎪==⎪⎩推论:::sin :sin :sin a b c A B C =二.余弦定理:三.三角形面积公式:111sin sin sin ,222ABC S bc A ac B ab C ∆===第二章 数列一.等差数列: 1.定义:a n+1-a n =d (常数)2.通项公式:()d n a a n •-+=11或()d m n a a m n •-+=3.求和公式:()()d n n n n a a a S n n 21211-+=+=4.重要性质(1)a a a a q p n m q p n m +=+⇒+=+ (2)m,2m,32m m m S S S S S --仍成等差数列二.等比数列:1.定义:)0(1≠=+q q a a nn 2.通项公式:q a a n n 11-•=或q a a mn m n -•=3.求和公式: )(1q ,1==na S n)(1q 11)1(11≠--=--=qq a a q q a S n n n4.重要性质(1)a a a a q p n m q p n m =⇒+=+(2)()m,2m,32q 1m m m m S S S S S --≠-仍成等比数列或为奇数三.数列求和方法总结:1.等差等比数列求和可采用求和公式(公式法).2.非等差等比数列可考虑(分组求和法) ,(错位相减法)等转化为等差或等比数列再求和, 2222222222cos 2cos 2cos a b c bc Ab ac ac B c a b ab C =+-=+-=+-222222222cos 2cos 2cos 2b c a A bca cb B aca b c C ab+-=+-=+-=精品文档若不能转化为等差或等比数列则采用(拆项相消法)求和.注意(1):若数列的通项可分成两项之和(或三项之和)则可用(分组求和法)。
高中数学必修5全部公式

高中数学必修5全部公式高中学生学习数学必修5课本内容牢记公式很重要。
那么数学必修5公式有哪些呢?下面店铺为大家整理高中数学必修5公式,希望对大家有所帮助!高中数学必修5公式高中数学提分技巧循序渐进,防止急躁由于学生年龄较小,阅历有限,为数不少的高中学生容易急躁,有的同学贪多求快,有的同学想靠几天“冲刺”一蹴而就,有的取得一点成绩便洋洋自得,遇到挫折又一蹶不振.学习是一个长期的巩固旧知识、发现新知识的积累过程,决非一朝一夕可以完成,为什么高中要上三年而不是三天!许多优秀的同学能取得好成绩,其中一个重要原因是他们的基本功扎实,他们的阅读、书写、运算技能达到了自动化或半自动化的熟练程度.学习上要学会积极归因,树立自信心,如:取得一点成绩及时体会成功,强化学习能力;遇到挫折及时调整学习方法、策略,更加努力改变挫折。
学习是一项循序渐进,长期积累的过程,要有恒心、决心,有一颗拼搏的心,要防止急躁心里,这样才能取得最后的成功。
研究学科特点,寻找最佳学习方法数学学科担负着培养学生运算能力、逻辑思维能力、空间想象能力,以及运用所学知识分析问题、解决问题的能力的重任.它的特点是具有高度的抽象性、逻辑性和广泛的适用性,对能力要求较高.学习数学一定要讲究“活”,只看书不做题不行,埋头做题不总结积累不行,对课本知识既要能钻进去,又要能跳出来,结合自身特点,寻找最佳学习方法.华罗庚先生倡导的“由薄到厚”和“由厚到薄”的学习过程就是这个道理.方法因人而异,但学习的五个环节:预习、上课、复习、作业、总结是少不了的.多交流,多反思解疑,化解分化点高中数学中易分化的地方多,这些地方一般都有方法新、难度大、灵活性强等特点.对易分化的地方要采用多次反复解疑,认真反思,总结规律,多阅读参考书等方法,多和同学交流,多向老师请教,多开展变式练习,化解分化点,以达到灵活掌握知识、运用知识的目的。
只要学习科学得法,有恒心,有信心,有拼搏心,克服急躁心里,克服“小聪明”,多交流,多反思,养成良好的学习习惯,就能顺利度过高中数学学习适应期,就能在今后的数学成绩图飞猛进。
高中必修5知识点归纳总结

必修5第一章 解三角形1.正弦定理:R CB A 2sin c sin b sin a ===,R 为三角形ABC 外接圆的半径 ⇒变形公式:⑴:C B A sin sin sin c b a ::::=⑵:C B A C B A sin c sin b sin a sin sin sin c b a ===++++ 2.余弦定理:在三角形ABC 中,有cosA 2bc -c b a 222⋅+=bc2a-c b cos 222+=⇒A B cos 2ac -c a b 222⋅+=ac 2b -c a cos 222+=⇒B 3.射影定理:B C cos c cos b a ⋅+⋅=;A C cos c cos a b ⋅+⋅=4.a 、b 、c 分别为三角形ABC 的三边,则有:①c b a 222=+,则有C=ο90 ②b a 22+>c 2, 则有C<90ο ③b a 22+<c 2, 则有C>ο90 5.三角形面积公式:B SABC sin ac 21sinC ab 21sinA bc 21⋅=⋅=⋅=∆ 第二章 数列1.等差数列:若首项是a 1,公差是d ,则()d 1-n a a 1n ⋅+= 等差数列前N 项和:()()2d 1-n n a n 2a a n 1n 1n ⋅+⋅=+=S 2.等比数列:若首项是a 1,公比是q ,则q a a 1-n 1n ⋅= 等比数列前N 项和:a n 1n ⋅=S (q=1) q -1q a -a q -1q -1a n 1n1n ⋅=⋅=)(S (q ≠1) 3.求通项公式: S S 1-n n n -a =第三章 不等式1.不等式基本性质: a-b>0⇔a>b a-b<0⇔a<b2.不等式推广性质: a>b ⇒a+c>b+c a>b 、c>0⇒ac>bc3.一元二次不等式的解法:数轴穿根法4.均值不等式:若a>0,b>0,则a+b ≥ab 2 即ab 2b a ≥+ 5.常用基本不等式:① a ²+b ²≥2ab (a 、b ∈R ) ② ab ≤2b a 22+(a 、b ∈R ) ③ ab ≤⎪⎭⎫ ⎝⎛+2b a ²(a>0,b>0) ④ 2b a 22+≥⎪⎭⎫ ⎝⎛+2b a ² (a 、b ∈R ) 6.极值定理:设x 、y 都为正数,则有 ⑴ 若x+y=s (和为定值),则当x=y 时,积xy 取得最大值4s 2⑵ xy=p (积为定值),则当x=y 时,和x+y 取得最小值p 27.柯西不等式:二维形式的柯西不等式 )()()(bd +≥+•+ac d c b a 22222 等号成立的条件: ad=bc 向量形式的柯西不等式 βαβα•≥• 等号成立:0=β或λβα=。
最新必修五主要公式(公式挖空-默写使用)

必修五主要公式1.正弦定理:________=________=________=2R ,其中R 是三角形外接圆的半径.由正弦 定理可以变形为: a ∶b ∶c =______________;2.余弦定理:a 2=_______________,b 2=________________,c 2=____________________.可以变形为:cos A =______________,cos B =______________,cos C =____________.3.S △ABC = = =4. 在三角形ABC 中,==+=A A C B A tan ;cos );sin(sin 5. 已知S n ,则a n =⎩⎪⎨⎪⎧(n =1) (n ≥2). 6.等差数列的定义:如果一个数列______________________________________,那么这个数列就叫做等差数列,这个常数叫做等差数列的________,通常用字母______表示.7.等差数列的通项公式:如果等差数列{a n }的首项为a 1,公差为d ,那么它的通项公式是_____.8.等差中项:如果________,那么A 叫做a 与b 的等差中项.9.等差数列的常用性质:(1)通项公式的推广:a n =a m +________,(n ,m ∈N *).(2)若{a n }为等差数列,且k +l =m +n ,(k ,l ,m ,n ∈N *),则__________________.10.等差数列的前n 项和公式: S n =______________=________________.11.等差数列的最值:在等差数列{a n }中,a 1>0,d <0,则S n 存在最______值;若a 1<0,d >0,则S n 存在最______值.12.等比数列的定义:如果一个数列__________________________,那么这个数列叫做等比数列,这个常数叫做等比数列的________,通常用字母______表示.13.等比数列的通项公式:设等比数列{a n }的首项为a 1,公比为q ,则它的通项a n =______.14.等比中项:若______________,那么G 叫做a 与b 的等比中项.15.等比数列的常用性质:(1)通项公式的推广:a n =a m ·____________,(n ,m ∈N *).(2)若{a n }为等比数列,且k +l =m +n ,(k ,l ,m ,n ∈N *),则__________________.16.等比数列的前n 项和公式等比数列{a n }的公比为q (q ≠0),其前n 项和为S n ,当q =1时,S n = ;当q ≠1时,S n = =17.两个实数比较大小的方法(1)作差法⎩⎪⎨⎪⎧ a -b >0⇔a b a -b =0⇔a ba -b <0⇔a b (a ,b ∈R );(2)作商法⎩⎪⎨⎪⎧ a b >1⇔a b a b =1⇔a ba b <1⇔a b(a ∈R ,b >0).18.不等式的性质 (1)传递性:a >b ,b >c ⇒a ______c .(2)同向相加性:a >b ,c >d ⇒a +c ______b +d .(3)乘法单调性:a >b ,c >0⇒ac ______bc ;a >b ,c <0⇒ac ______bc ;a >b >0,c >d >0⇒ac ______bd ;a >b >0(n ∈N *)⇒a n ______b n ;a >b >0(n ∈N *,n ≥2)⇒n a ______n b .19.不等式的一些常用性质(1)倒数性质①a >b ,ab >0⇒1a ______1b . ②a <0<b ⇒1a ______1b. ③a >b >0,0<c <d ⇒a c ______b d . ④0<a <x <b 或a <x <b <0⇒1b ______1x ______1a. 20.基本不等式ab ≤a +b 2(1)基本不等式成立的条件:____________.(2)等号成立的条件:当且仅当________时取等号.21.利用基本不等式求最值问题已知x >0,y >0,则(1)如果积xy 是定值p ,那么当且仅当__________时,x +y 有最________值是__________.(简记:积定和最小)(2)如果和x+y是定值p,那么当且仅当__________时,xy有最______值是________. (简记:和定积最大)22.根的分布23.线性规划相关概念。
高中数学必修一至五主要公式汇总(公式挖空,供学生默写使用)
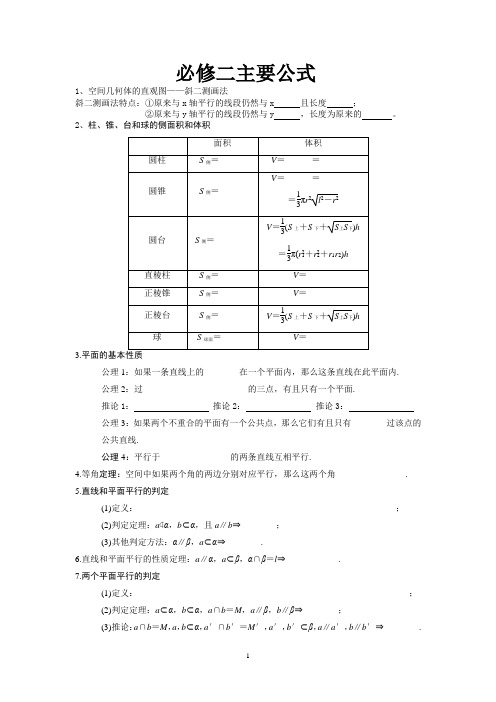
必修二主要公式1、空间几何体的直观图——斜二测画法斜二测画法特点:①原来与x轴平行的线段仍然与x 且长度;②原来与y轴平行的线段仍然与y ,长度为原来的。
2、柱、锥、台和球的侧面积和体积3.公理1:如果一条直线上的________在一个平面内,那么这条直线在此平面内.公理2:过________________________的三点,有且只有一个平面.推论1:推论2:推论3:公理3:如果两个不重合的平面有一个公共点,那么它们有且只有________过该点的公共直线.公理4:平行于________________的两条直线互相平行.4.等角定理:空间中如果两个角的两边分别对应平行,那么这两个角________________.5.直线和平面平行的判定(1)定义:___________________________________________________________;(2)判定定理:a⊄α,b⊂α,且a∥b⇒________;(3)其他判定方法:α∥β,a⊂α⇒________.6.直线和平面平行的性质定理:a∥α,a⊂β,α∩β=l⇒____________.7.两个平面平行的判定(1)定义:______________________________________________________________;(2)判定定理:a⊂α,b⊂α,a∩b=M,a∥β,b∥β⇒________;(3)推论:a∩b=M,a,b⊂α,a′∩b′=M′,a′,b′⊂β,a∥a′,b∥b′⇒________.8.两个平面平行的性质定理(1)α∥β,a⊂α⇒________;(2)α∥β,γ∩α=a,γ∩β=b⇒________.9.与垂直相关的平行的判定(1)a⊥α,b⊥α⇒________;(2)a⊥α,a⊥β⇒________.10.直线与平面垂直(1)判定直线和平面垂直的方法①利用判定定理:一条直线和一个平面内的两条________直线都垂直,则该直线和此平面垂直.②推论:如果在两条平行直线中,有一条垂直于一个平面,那么另一条直线也________这个平面.(2)直线和平面垂直的性质①直线垂直于平面,则垂直于平面内________直线.②垂直于同一个平面的两条直线________.③垂直于同一直线的两平面________.11.斜线和平面所成的角:斜线和它在平面内的射影所成的角,叫斜线和平面所成的角.12.平面与平面垂直(1)平面与平面垂直的判定方法利用判定定理:一个平面过另一个平面的____________,则这两个平面垂直.(2)平面与平面垂直的性质两平面垂直,则一个平面内垂直于________的直线垂直于另一个平面.13.直线的倾斜角与斜率(1)直线的倾斜角①定义:当直线l与x轴相交时,我们取x轴作为基准,x轴________与直线l________方向之间所成的角α叫做直线l的倾斜角.当直线l与x轴平行或重合时,规定它的倾斜角为________.②倾斜角的范围为__________.(2)直线的斜率①定义:一条直线的倾斜角α的__________叫做这条直线的斜率,斜率常用小写字母k表示,即k=________,倾斜角是90°的直线斜率不存在.②过两点的直线的斜率公式经过两点P1(x1,y1),P2(x2,y2) (x1≠x2)的直线的斜率公式为k=__________.14.15.线段的中点坐标公式若点P 1、P 2的坐标分别为(x 1,y 1)、(x 2,y 2),且线段P 1P 2的中点M 的坐标为(x ,y ),则⎩⎪⎨⎪⎧x = y = ,此公式为线段P 1P 2的中点坐标公式. 16.两条直线平行与垂直的判定(1)两条直线平行对于两条不重合的直线l 1、l 2,其斜率分别为k 1、k 2,则有l 1∥l 2⇔____________.特别地,当直线l 1、l 2的斜率都不存在时,l 1与l 2________. (2)两条直线垂直如果两条直线l 1,l 2斜率存在,设为k 1,k 2,则l 1⊥l 2⇔____________,当一条直线斜率为零,另一条直线斜率不存在时,两直线________.17.两直线相交交点:直线l 1:A 1x +B 1y +C 1=0和l 2:A 2x +B 2y +C 2=0的公共点的坐标与方程组⎩⎪⎨⎪⎧A 1x +B 1y +C 1=0A 2x +B 2y +C 2=0的解一一对应. 相交⇔方程组有__________,交点坐标就是方程组的解; 平行⇔方程组________; 重合⇔方程组有______________.18.三种距离公式(1)点A (x 1,y 1)、B (x 2,y 2)间的距离:|AB |= . (2)点P (x 0,y 0)到直线l :Ax +By +C =0的距离:d = .(3)两平行直线l 1:Ax +By +C 1=0与l 2:Ax +By +C 2=0 (C 1≠C 2)间的距离为 d =______________.19.圆的标准方程(x -a )2+(y -b )2=r 2(r >0),其中______为圆心,______为半径.20.圆的一般方程x 2+y 2+Dx +Ey +F =0表示圆的充要条件是________________,其中圆心为________________,半径r =________________.21.点与圆的位置关系点和圆的位置关系有三种.圆的标准方程(x -a )2+(y -b )2=r 2,点M (x 0,y 0)(1)点在圆上: ; (2)点在圆外: ; (3)点在圆内: .22.直线与圆的位置关系位置关系有三种:________、________、________. 判断直线与圆的位置关系常见的有两种方法: (1)代数法:――→判别式Δ=b 2-4ac⎩⎪⎨⎪⎧>0⇔相交=0⇔相切<0⇔相离(2)几何法:利用圆心到直线的距离d 和圆半径r 的大小关系:d <r ⇔相交,d =r ⇔相切,d >r ⇔相离.23.圆与圆的位置关系的判定设⊙C 1:(x -a 1)2+(y -b 1)2=r 21(r 1>0), ⊙C 2:(x -a 2)2+(y -b 2)2=r 22(r 2>0),则有: |C 1C 2|>r 1+r 2⇔⊙C 1与⊙C 2________; |C 1C 2|=r 1+r 2⇔⊙C 1与⊙C 2________; |r 1-r 2|<|C 1C 2|<r 1+r 2⇔⊙C 1与⊙C 2________; |C 1C 2|=|r 1-r 2|(r 1≠r 2)⇔⊙C 1与⊙C 2________; |C 1C 2|<|r 1-r 2|⇔⊙C 1与⊙C 2________.。
[VIP专享]高中数学必修5公式大全
![[VIP专享]高中数学必修5公式大全](https://img.taocdn.com/s3/m/5db74e1e77232f60dccca12b.png)
当 a=bsinA 或 a>b 时,B 有一解
ቤተ መጻሕፍቲ ባይዱ
当 bsinA<a≤b,则 B 有两解
int level(BinTreeNodlesevt}r*Beutsl,icnBt(rtrTuiontrcaoTetgtert,_eyapNnpetg)oy;oeN_pddinoeeodtd;fde*esreafc*ttrphsB*au{l)ti;cilrn/duh/tT;ciB/lr/tdo1eiTt;u1ea//NcnrNgoto_loiu(fdn(dtnbe*oetpivdlt{(roe(e}TbidpEititrcfrl(ero!-pbmu>tintrTvritgaey-l(>hlpbulteeie,rtrf=xdt)e,=apr{xkextta,)rt;ru{;k,kr)sd+n;tra+;u1t;ac}0txyBpieTNxv},ooidi{ndet&m*lkac)hi}nil(de)}l;s/e/ js+tr}+uj;cBf+BtoB.+Bid.r.L(;+adikTe+taanN=;t[agojB]e[tdkh=l.se+L+eA1e*+]nr.i;dfc=g(d.-[d;{aiB]1a/it;f/a.;t(dkaA[}ia[]>.kBtdB<}=a];aii.T[BLjt+;aNke.+d[Loni;-]aed-g>t)netahg,B[jt*]+h.)wBd+]{avhi;T=otilareiAedi[n(Be.i{dtm;.<Laive=etAoarngi.0[dLgie],e;jt2Ch=n(o{Sg-0ut9q1h,n/kAL])/t)/iL/[;2s1/e1AtA…aABBmf"…,.S(h+Bq"mniLT6m+irsnet8]e&mhBTen),amidn+dtn&a2Ot*acx(7o10u)n+t)0x{11*ixf=0( nT+o1)d*{ex2i_1f c(+(o!uT2/xn/-*10>tx+l2+cxh=1il;+dnx)o&2/d/h&e=tt_(pn!c:To0o//-duw>1enrw*_c2t/wchx-oi0.1ldu;xon)/)1c*t;cinx6o42.1ucleonfmtt+d/+5ap;t-a5//r7iLg9Cihs4ot8lNuet5nmof9ttdreLp4iegme.=h*ap3tMfAmBol(a[aTrTlit]ex(-;(><i2)nAlccetl[ha0i]}ise=l=ds1,0}A…Tc;[yoine2pu<-nT6ein=-yH>12tp)(]Te;v;enn[Co1-A-ti1o3m1d[u]nA)pHin-[/;in(tv-kL21]ene;]1reyais=A+)nef=[+(t-nm(k1Ta])eAT-p){y>nyA;r-p%c2eh…1iAld3e[2,1]3c,2e1oi20Vn0(u3e=bt×n4i{)n3t1a5)B0);,5b20A}{7,B(2ce[2a150,(l0)ds0cn(a20e,a)]×ie[13j1)1cnr2,a17Af2e0A4,i58g2jtB]b1u(B03}(a5r4,21[En)]06a1B;=07A51([}{0]b937S<A/3)56/HaL([06C0c,sT1b3)]uo[A.>81A0c5u,493]cBn<B0.]=taC5H[L8(0,A1De(4g]k/,Aa5>2EBef0,[)Fy,<]*4C[G)G]b[=2B1,,DHk)g+[]e>,I1AEJy,/[<(,81%C1c]-[8,a5bD1)]C>3C]B,D1<[D1]2Bd62,GFc3E>=41A,V5</1I5EdH475,Gf1231>01+0*J5,91<420G4+0e*30G241,7W1d+*787>13P031,4*9<1L74=41f=0+,515a24953>**/546,17<5+15=0g37413,2*0c5572>/4+517,5<6451*g524,0d+3>956,*5<0315f9+2,3e5W12>14P,12*<3L157g+=56,52f13053>105*693}64*1,{73+80217+9596510*77046873+1*71249264+*9503182+79012*176208590=*2092+8123169831731237*793}W2+531P352L5*0313173+s3T3125158*,21T2052=5,2…915W063…303P5,LTS Tini k1i(2i={a1b,2c,d…e…fg}S0)1,1k10in1i011k11k10n+1kk1Pn21>r+0ikm…00…11+1k0s1=0n11+n21K…ru…snkas1l ns,s=nk,nk a11a121a02K1)aru2s2kaa=2l203*:9(a1i+03/1jA2-03aB(3a131+Aa12=3B+42[…0+]3A…+a3aij1+n3inn149-+iH10-41au+jnfi84+fnm4+16a5B8n+58F1544):52=5706305306.986,2T76:0150,D811:00148110683171,F10ST6:06D413S024H515,1H12:007412101402H*1291u60+22f{f7m4*63a2+n58307*71836+21102*72306+722774*0674128+493}*()4+86*312=513219 5:13/5671(130+7822+6261+p03a1+341352+401143,41)p0=83,21a.8425,913,,p66331:121,0A1a24B13G,,CP4pJ9AD3KG21EHD12AFDaJ3GBH,EPaDHKBApGIBM3J2HEKIF1AJMCKCAEFCMFIIM
高中数学必修5公式

高中数学必修5公式
以下为高中数学必修5中常用的公式:
1. 一次函数的斜率公式:设直线y = kx + b(k≠0)与x 轴交点为A(0,b),与y轴交点为B(-b/k,0),则直线斜率为k。
公式表达式:k = (y2 - y1) / (x2 - x1)
2. 二次函数的顶点坐标公式:设二次函数为y = ax^2 + bx + c(a≠0),则函数的顶点坐标为(-b/2a,f(-
b/2a))。
公式表达式:x = -b / (2a)
3. 二次函数的判别式公式:设二次函数为y = ax^2 + bx + c(a≠0),则判别式D = b^2 - 4ac用于判断二次函数的图像与x轴的交点个数和位置。
公式表达式:D = b^2 - 4ac
4. 三角形面积公式(海伦公式):设三角形的三边长分别
为a、b、c,半周长为s,则三角形的面积S = √(s(s - a)(s - b)(s - c))。
公式表达式:S = √(s(s - a)(s - b)(s - c))
5. 等差数列的通项公式:设等差数列的首项为a1,公差为d,则第n项为an = a1 + (n - 1)d。
公式表达式:an = a1 + (n - 1)d
6. 等差数列的求和公式:设等差数列的首项为a1,末项为an,项数为n,则等差数列的和为Sn = (a1 + an) * n / 2。
公式表达式:Sn = (a1 + an) * n / 2。
必修5公式

必修51、正弦定理:在C ∆AB 中,a 、b 、c 分别为角A 、B 、C 的对边,R 为C ∆AB 的外接圆的半径,则有2sin sin sin a b cR C===A B . 2、正弦定理的变形公式:①2sin a R =A ,2sin b R =B ,2sin c R C =; ②sin 2a R A =,sin 2b R B =,sin 2c C R=;③::sin :sin :sin a b c C =A B ; ④sin sin sin sin sin sin a b c a b cC C++===A +B +A B . (正弦定理主要用来解决两类问题:1、已知两边和其中一边所对的角,求其余的量。
2、已知两角和一边,求其余的量。
)3、三角形面积公式:111sin sin sin 222C S bc ab C ac ∆AB =A ==B .4、余弦定理:在C ∆AB 中,有2222cos a b c bc =+-A ,2222cos b a c ac =+-B ,2222cos c a b ab C =+-.5、余弦定理的推论:222cos 2b c a bc +-A =,222cos 2a c b ac +-B =,222cos 2a b c C ab+-=.(余弦定理主要解决的问题:1、已知两边和夹角,求其余的量。
2、已知三边求角)6、如何判断三角形的形状:设a 、b 、c 是C ∆AB 的角A 、B 、C 的对边,则:①若222a b c +=,则90C =;②若222a b c +>,则90C <;③若222a b c +<,则90C >. 附:三角形的五个“心”; 重心:三角形三条中线交点.外心:三角形三边垂直平分线相交于一点. 内心:三角形三内角的平分线相交于一点. 垂心:三角形三边上的高相交于一点. 等差数列有以下三种方法:① ),2(1为常数d n d a a n n ≥=--②211-++=n n n a a a (2≥n ) ③b kn a n +=(k n ,为常数18、由三个数a ,A ,b 组成的等差数列可以看成最简单的等差数列,则A 称为a 与b 的等差中项.若2a cb +=,则称b 为a 与c 的等差中项. 19、若等差数列{}n a 的首项是1a ,公差是d ,则()11naa n d =+-.20、通项公式的变形:①()n m a a n m d =+-;②()11n a a n d =--;③11n a a d n -=-;④11n a a n d-=+;⑤n m a a d n m -=-.21、若{}n a 是等差数列,且m n p q +=+(m 、n 、p 、*q ∈N ),则m n p q a a a a +=+;若{}n a 是等差数列,且2n p q =+(n 、p 、*q ∈N ),则2np q a a a =+.22、等差数列的前n 项和的公式:①()12n n n a a S +=;②()112n n n S na d -=+.③12n n s a a a =+++23、等差数列的前n 项和的性质:①若项数为()*2n n ∈N ,则()21n n n S n a a +=+,且S S nd -=偶奇,1n n S aS a +=奇偶. ②若项数为()*21n n -∈N ,则()2121n n S n a -=-,且n S S a -=奇偶,1S nS n =-奇偶(其中n S na =奇,()1n S n a =-偶). 24、等比数列:1n na q a +=(注:①等比数列中不会出现值为0的项;②同号位上的值同号) 注:看数列是不是等比数列有以下四种方法:①)0,,2(1≠≥=-且为常数q n q a a n n ②112-+⋅=n n na a a (2≥n ,011≠-+n n n a a a )③n n cq a =(q c ,为非零常数).26、若等比数列{}n a 的首项是1a ,公比是q ,则11n n a a q -=.27、通项公式的变形:①n mn m a a q -=;②()11n n a a q --=;③11n na q a -=;④n m n ma q a -=. 28、若{}n a 是等比数列,且m n p q +=+(m 、n 、p 、*q ∈N ),则m n p q a a a a ⋅=⋅;若{}n a 是等比数列,且2n p q =+(n 、p 、*q ∈N ),则2np q a a a =⋅.29、等比数列{}n a 的前n 项和的公式:①()()()11111111n n n na q S a q a a q q qq =⎧⎪=-⎨-=≠⎪--⎩.②12n n s a a a =+++30、对任意的数列{n a }的前n 项和n S 与通项n a 的关系:⎩⎨⎧≥-===-)2()1(111n s s n a s a n n n②等差{n a }前n 项和n d a n d Bn An S n ⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛=+=22122③非零..常数列既可为等比数列,也可为等差数列. 附:几种常见的数列的思想方法:⑴等差数列的前n 项和为n S ,在0 d 时,有最大值. 如何确定使n S 取最大值时的n 值,有两种方法:一是求使0,01 +≥n n a a ,成立的n 值;二是由n da n d S n )2(212-+=利用二次函数的性质求n 的值. 数列通项公式、求和公式与函数对应关系如下: 数列 通项公式 对应函数等差数列(时为一次函数)等比数列(指数型函数)数列 前n 项和公式 对应函数等差数列(时为二次函数)等比数列(指数型函数)将数列的通项公式以及前n 项和看成是关于n 的函数. 例题:1、等差数列中,,则.分析:因为是等差数列,所以是关于n 的一次函数,一次函数图像是一条直线,则(n,m ),(m,n),(m+n,)三点共线,所以利用每两点形成直线斜率相等,即,得=0(图像如上) 例题:2、等差数列中,,前n 项和为,若,n 为何值时最大?分析:等差数列前n 项和可以看成关于n 的二次函数=,是抛物线=上的离散点,根据题意,,则因为欲求最大值,故其对应二次函数图像开口向下,并且对称轴为,即当时,最大。
高中数学必修五公式方法总结考前宝典

高中数学必修五公式方法总结第一章 三角函数一.正弦定理:2(sin sin sin a b cR R A B C===为三角形外接圆半径)变形:2sin (sin )22sin (sin )22sin (sin )2a a R A A R bb R B B Rc c R C C R ⎧==⎪⎪⎪==⎨⎪⎪==⎪⎩ 推论:::sin :sin :sin a b c A B C = 二.余弦定理: 三.三角形面积公式:111sin sin sin ,222ABC S bc A ac B ab C ∆=== 四、(1)两角和与差的正弦、余弦和正切公式:⑴()cos cos cos sin sin αβαβαβ-=+; ⑵()cos cos cos sin sin αβαβαβ+=-; ⑶()sin sin cos cos sin αβαβαβ-=-; ⑷()sin sin cos cos sin αβαβαβ+=+; (2)二倍角的正弦、余弦和正切公式: ⑴sin22sin cos ααα=.⑵2222cos2cos sin 2cos 112sin ααααα=-=-=- (3)、()22sin cos sin αααϕA +B =A +B +,其中tan ϕB=A第二章 数列一.等差数列: 1.定义:a n+1-a n =d (常数)2.通项公式:()d n a a n∙-+=11或()d m n a a mn∙-+=3.求和公式:()()d n n n n a a a S nn21211-+=+= 4.重要性质(1)a a a a qpnmq p n m +=+⇒+=+ (2) m,2m,32mmmS S S S S --仍成等差数列2222222222cos 2cos 2cos a b c bc A b a c ac B c a b ab C=+-=+-=+-222222222cos 2cos 2cos 2b c a A bca cb B ac a b c C ab +-=+-=+-=二.等比数列:1.定义:)0(1≠=+q q a a nn 2.通项公式:q a a n n11-∙=或q a a mn mn-∙=3.求和公式: )(1q ,1==na S n4.重要性质(1)a a a a qp n m q p n m =⇒+=+(2)()m,2m,32q 1m m m m S S S S S --≠-仍成等比数列或为奇数3.已知S n,用(S n 法)即用公式()()⎩⎨⎧≥-==-2111n S S n S a n n n五.基本不等式:(0,0)2a b ab a b +≥≥≥(当且仅当a=b 时,等号成立)(和定积最大)(积定和最小):变形变形.)2()2(;2)1(2b a ab ab b a +≤≥+ 利用基本不等式求最值应用条件:一正数 二定值三相等。
高中数学必修五实用公式.doc

2.2aeCM C=■ -CM<7高中数学必修五 正、余弦定理 知识要点:阑三角形中的边' 角的关系应(一)三角形中的角之间的关系函A+B^C=tr, un^A+B )=suiC(二)三角形中的边之间的关系窿】e+b>c, a-b<c ,直角三角形中:«a +i3= c a(三)三角形中边与角之间的关系击正弦定理1 O- 2Rmi. B.C -2AsuC上===七 =22!(破冽展I 醉色)2. sin 利 sxnB anCsinj4=-^-,sia 四=-^-,8血。
= -^-3.2R 2R 2R4. mA nnB :MC=a:b:c面积公式:= —ofrsii C = —Acsn Jl= —acsn B9 22 2余弦定理:1 / +^a -2fccGw^tA J = a a +c a -a»fWf = +4a -SifrwfC3 A a+d^-c 1 =2bcco«A.c a = 2ofrcocC.= 2«c«BJ •»»4.x=«r =/=/+£?-&;』=i2(r =/=/+/+&;5. A=9<r=/=8'M ;』是锐角od’s’+c’;日是钝角=>A 舟+<‘.J+«+C JF ■= 一22,an ---2C =co« —2, A+B . C cos --------- = aii —22,等比数列定义、公式及性质(注意类比等差)等差数列等比数列定义几何意义对等差数列,位于一条直线上.单调性与d有关,当rf>o时增;当<0时减,当时是常数列. 对正项等比数列人> "> °日g D,位于一条指数型曲线上.曲线的单调性与1有关,当»><时增;当时减.对于其它数列,炯数如' 12,部演» ,同样可以研究.中项若瓦&是,JBI州的等差中O = -----项,即2若成等比,则方叫的等比中项,即h3=ac非零三数成等比通项公式«i =,+("-胖.=<M*4前"项和公式耳=竺金=—+沁-8三类切造方循目的:",4=1败(1一/)=弦_ j [I I~法:定义(等比定理,叠加);错位减;1化简运算,消除差别,造出方程判定方法定义(证明);通项公式;前辞项和公式性质1、下标和若则a,,特别地,a»^+a»-i = 2a»若y则.%若下标成等差,则对应项也成等差若下标(项数)成等差,则对应项也成等比2、子数列A ,号一弓•母成等差思&-思压一瑶…成等比3、(子)数列和(二)等差、等比数列的定义、通项、中项、前n项和是数列的基础和重点内容,应注意:(1)通项公式与前n项和公式的灵活应用.如等差数列:a…=ai+ (nT) d=dn+ (a*) =a…,+ (n-m) d,耳=7彳^ =知心-知等.(2)公式条件,如等比数列qNl时,(3)公式的导出思想:倒序相加法、错位相减法、叠加法、迭乘法等.。
高中数学必修5公式大全

高中数学必修5公式大全1、正弦定理:在C ∆AB 中,a 、b 、c 分别为角A 、B 、C 的对边,R 为C ∆AB 的外接圆的半径,则有2sin sin sin a b cR C===A B . 2、正弦定理的变形公式:①2sin a R =A ,2sin b R =B ,2sin c R C =;②sin 2a R A =,sin 2b R B =,sin 2c C R =;③::sin :sin :sin a b c C =A B ; ④sin sin sin sin sin sin a b c a b cC C++===A +B +A B . (正弦定理主要用来解决两类问题:1、已知两边和其中一边所对的角,求其余的量。
2、已知两角和一边,求其余的量。
)⑤对于已知两边和其中一边所对的角的题型要注意解的情况。
(一解、两解、无解三中情况) 如:在三角形ABC 中,已知a 、b 、A (A 为锐角)求B 。
具体的做法是:数形结合思想 画出图:法一:把a 扰着C 点旋转,看所得轨迹以AD 有无交点:当无交点则B 无解、 当有一个交点则B 有一解、 当有两个交点则B 有两个解。
法二:是算出CD=bsinA,看a 的情况: 当a<bsinA ,则B 无解当bsinA<a ≤b,则B 有两解 当a=bsinA 或a>b 时,B 有一解注:当A 为钝角或是直角时以此类推既可。
3、三角形面积公式:111sin sin sin 222C S bc ab C ac ∆AB =A ==B . 4、余弦定理:在C ∆AB 中,有2222cos a b c bc =+-A ,2222cos b a c ac =+-B ,2222cos c a b ab C =+-.5、余弦定理的推论:222cos 2b c a bc +-A =,222cos 2a c b ac +-B =,222cos 2a b c C ab+-=.(余弦定理主要解决的问题:1、已知两边和夹角,求其余的量。
高中数学必修5常用公式及结论

每次还款
x
ab(1 b)n (1 b)n 1
元(贷款
a
元,
n
次还清,每期利率为
b
).
不等式 常用不等式:
(1) a,b R a2 b2 2ab (当且仅当 a=b 时取“=”号). (2) a,b R a b ab (当且仅当 a=b 时取“=”号).
2 (3) a3 b3 c3 3abc(a 0,b 0,c 0).
loga
f (x) loga
g(x)
g(
x)
0
f (x) g(x)
其前
n 项和公式为 sn
n(a1 an ) 2
na1
n(n 1) d 2
d 2
n2
(a1
1 d)n . 2
等比数列的通项公式 an
a1qn1
a1 qqn (n N*);来自其前 n 项的和公式为
sn
a1
(1 qn 1 q
)
,q
1
或
sn
a1 an 1 q
q
,q
1
.
na1, q 1
na1, q 1
当| x y | 最小时, | xy | 最大. 一 元 二 次 不 等 式 ax2 bx c 0(或 0) (a 0, b2 4ac 0) , 如 果 a 与
ax2 bx c 同号,则其解集在两根之外;如果 a 与 ax2 bx c 异号,则其解集
在两根之间.简言之:同号两根之外,异号两根之间.
x1 x x2 (x x1)(x x2 ) 0(x1 x2 ) ; x x1,或x x2 (x x1)(x x2) 0(x1 x2) .
含有绝对值的不等式 当 a> 0 时,有
高中数学必修五公式整理

高中数学必修五公式之马矢奏春创作声明:本文非原创,由于界面阅读感欠好而自己进行重新排版。
第一章 三角函数一.正弦定理:2(sin sin sin a b cR R A B C ===为三角形外接圆半径)变形:2sin (sin )22sin (sin )22sin (sin )2a a R A A R b b R B B R c c R C C R ⎧==⎪⎪⎪==⎨⎪⎪==⎪⎩推论:::sin :sin :sin a b c A B C = 二.余弦定理: 三.三角形面积公式:111sin sin sin ,222ABC S bc A ac B ab C ∆=== 第二章 数列 一.等差数列:1.定义:a n+1-a n =d(常数) 2.通项公式:()d n a a n •-+=11或()dm n a a m n •-+=3.求和公式:()()d n n n n a a a S n n 21211-+=+=4.重要性质(1)a a a a qp n m q p n m +=+⇒+=+(2)m,2m,32m m m S S S S S --仍成等差数列二.等比数列:1.定义:)0(1≠=+q q a a n n2.通项公式:qa a n n11-•=或qa a mn m n-•=3.求和公式:)(1q ,1==na S n4.重要性质(1)a a a a qp n m q p n m =⇒+=+(2)()m,2m,32q 1m m m m S S S S S --≠-仍成等比数列或为奇数2222222222cos 2cos 2cos a b c bc A b a c ac B c a b ab C =+-=+-=+-222222222cos 2cos 2cos 2b c a A bca cb B aca b c C ab+-=+-=+-=三.数列求和方法总结:1.等差等比数列求和可采取求和公式(公式法).2.非等差等比数列可考虑(分组求和法) ,(错位相减法)等转化为等差或等比数列再求和,若不克不及转化为等差或等比数列则采取(拆项相消法)求和.注意(1):若数列的通项可分成两项之和(或三项之和)则可用(分组求和法)。
人教A版数学必修五基础知识公式

数学必修五 基础知识公式第一章 解三角形正弦定理a sin A =b sin B =c sin C = 2R 余弦定理a 2 =b 2 +c 2 – 2bc cos A cos A = b 2 + c 2 - a 22bcb 2 = a 2 +c 2 – 2ac cos b cos B = a 2 + c 2 - b 22ac c 2 = b 2 + a 2 – 2ab cos A cos A = b 2+a 2-c 22ab三角形面积 S = 12ab sin C = 12ac sin B = 12bc sin A 三角形解的个数 0<A <π2时 b >a >b sin A 有两解 b >a = b sin A 有一解a >b 有一解a <b sin A 无解π2≤A <π 时 a >b 有一解 a ≤b 无解三角形形状(已知A 是最大角,a 是最长边)a 2<b 2 +c 2 锐角三角形a 2 =b 2 +c 2直角三角形a 2>b 2 +c 2 钝角三角形第二章 数列1.数列综述数列最大项 a n 满足⎩⎨⎧a n ≥a n +1a n ≥a n -1数列最小项 a n 满足⎩⎨⎧a n ≤a n +1a n ≤a n -1数列增减性 a n +1 – a n >0 数列为增数列 a n +1 – a n <0 数列为减数列 a n +1a n >1 数列为增数列 a n +1a n<1 数列为减数列 a n 与 S n 的关系 a n = ⎩⎨⎧S 1 (n =1)S n – S n –1 (n ≥1)2.等差数列等差数列 a n +1 – a n = d (n ≥1) a n – a n -1 = d (n ≥2)等差数列通项公式 a n = a 1 + (n –1)d a n = a m + (n –m )d等差数列前n 项和 S n =n (a 1 + a n )2 = a 1d + n (n – 1)2d = d 2n 2 + (a 1 – d 2)n = An 2 + Bn 等差数列的性质① d = a m – a n m – n = a n – a m n – m② 若 m + n = p + q , 则 a m + a n = a p + a q若 m + n = 2t , 则 a m + a n = 2a t③ 若 {a n } 中, a n = kn + q , 则 {a n } 是等差数列,公差为k 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修五主要公式
1.正弦定理:________=________=________=2R ,其中R 是三角形外接圆的半径.由正弦 定理可以变形为: a ∶b ∶c =______________;
2.余弦定理:a 2=_______________,b 2=________________,c 2=____________________.
可以变形为:cos A =______________,cos B =______________,cos C =____________.
3.S △ABC = = =
4. 在三角形ABC 中,==
+=A A C B A tan ;cos );sin(sin 5. 已知S n ,则a n =⎩⎪⎨⎪⎧
(n =1) (n ≥2). 6.等差数列的定义:如果一个数列______________________________________,那么这个数列就叫做等差数列,这个常数叫做等差数列的________,通常用字母______表示.
7.等差数列的通项公式:如果等差数列{a n }的首项为a 1,公差为d ,那么它的通项公式是_____.
8.等差中项:如果________,那么A 叫做a 与b 的等差中项.
9.等差数列的常用性质:
(1)通项公式的推广:a n =a m +________,(n ,m ∈N *).
(2)若{a n }为等差数列,且k +l =m +n ,(k ,l ,m ,n ∈N *),则__________________.
10.等差数列的前n 项和公式: S n =______________=________________.
11.等差数列的最值:在等差数列{a n }中,a 1>0,d <0,则S n 存在最______值;
若a 1<0,d >0,则S n 存在最______值.
12.等比数列的定义:如果一个数列__________________________,那么这个数列叫做等比数列,这个常数叫做等比数列的________,通常用字母______表示.
13.等比数列的通项公式:设等比数列{a n }的首项为a 1,公比为q ,则它的通项a n =______.
14.等比中项:若______________,那么G 叫做a 与b 的等比中项.
15.等比数列的常用性质:
(1)通项公式的推广:a n =a m ·____________,(n ,m ∈N *).
(2)若{a n }为等比数列,且k +l =m +n ,(k ,l ,m ,n ∈N *),则__________________.
16.等比数列的前n 项和公式
等比数列{a n }的公比为q (q ≠0),其前n 项和为S n ,
当q =1时,S n = ;
当q ≠1时,S n = =
17.两个实数比较大小的方法
(1)作差法⎩⎪⎨⎪⎧ a -b >0⇔a b a -b =0⇔a b
a -
b <0⇔a b (a ,b ∈R );
(2)作商法⎩⎪⎨⎪⎧ a b >1⇔a b a b =1⇔a b
a b <1⇔a b
(a ∈R ,b >0).
18.不等式的性质 (1)传递性:a >b ,b >c ⇒a ______c .
(2)同向相加性:a >b ,c >d ⇒a +c ______b +d .
(3)乘法单调性:
a >
b ,
c >0⇒ac ______bc ;
a >
b ,
c <0⇒ac ______bc ;
a >
b >0,
c >
d >0⇒ac ______bd ;
a >
b >0(n ∈N *)⇒a n ______b n ;
a >
b >0(n ∈N *,n ≥2)⇒n a ______n b .
19.不等式的一些常用性质
(1)倒数性质
①a >b ,ab >0⇒1a ______1b . ②a <0<b ⇒1a ______1b
. ③a >b >0,0<c <d ⇒a c ______b d . ④0<a <x <b 或a <x <b <0⇒1b ______1x ______1a
. 20.基本不等式ab ≤a +b 2
(1)基本不等式成立的条件:____________.
(2)等号成立的条件:当且仅当________时取等号.
21.利用基本不等式求最值问题
已知x >0,y >0,则
(1)如果积xy 是定值p ,那么当且仅当__________时,x +y 有最________值是__________. (简记:积定和最小)
(2)如果和x +y 是定值p ,那么当且仅当__________时,xy 有最______值是________. (简记:和定积最大)
22.根的分布
判别式
Δ=b2-4ac
Δ>0 Δ=0 Δ<0
二次函数
y=ax2+bx+c
(a>0)的图象
一元二次方程
ax2+bx+c=0 (a>0)的根有两相异实根x1,
x2(x1<x2)
有两相等实根x1=
x2=-
b
2a
没有实数根
ax2+bx+
c>0(a>0)的解集
ax2+bx+c<0
(a>0)的解集
23.线性规划相关概念
名称意义
约束条件由变量x,y组成的一次不等式
线性约束条件由x,y的________不等式(或方程)组成的不等式组目标函数欲求__________或__________的函数线性目标函数关于x,y的________解析式
可行解满足__________________的解
可行域所有__________组成的集合
最优解使目标函数取得________或__________的可行解
线性规划问题在线性约束条件下求线性目标函数的__________
或__________问题。
