山西省山大附中2013届高三数学5月月考试题 理 新人教A版 2
山大附中2014届高三5月模拟数学理含答案

O 510 15 20频率组距重量0.060.1 山西大学附中2013—2014学年高三第二学期5月下数学试题(理科)考试时间:120分钟 满分: 150分一、选择题:(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项符合题目要求) 1.已知集合{2,0,1,4}A =,集合{04,R}=<≤∈B x x x ,集合C A B =.则集合C可表示为 A .{2,0,1,4}B . {1,2,3,4}C .{1,2,4}D . {04,R}x x x <≤∈2.复数5(3)z i i i =-+(i 为虚数单位),则复数z 的共轭复数为A .2i -B .2i +C .4i -D .4i + 3. 设γβα,,为平面,n m ,为直线,则β⊥m 的一个充分条件是 A .n m n ⊥=⋂⊥,,βαβα B .γβγαγα⊥⊥=⋂,,m C .αγββα⊥⊥⊥m ,, D .αβα⊥⊥⊥m n n ,,4.阅读如下程序框图,如果输出4i =,那么空白的判断框中应填人的条件是A .?10≤SB .?12≤SC .?14≤SD .?16≤S5.220sin 2x dx π=⎰A .0B .142π-C .144π-D .12π-6.右图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本重量的中位数为A .11B .11.5C .12D .12.5 7.()9a b c ++的展开式中,432a b c 项的系数为A .126B .420C .630D .12608.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为A .23πB .3πC .29πD .169π 9.过抛物线24y x =焦点F 的直线交其于,A B 两点,O 为坐标原点.若||3AF =,则AOB ∆的面积为A 2B 2C 32D .2210.由()y f x =的图象向左平移3π个单位,再把所得图象上所有点的横坐标伸长到原来的2倍得到12sin(3)6y x π=-的图象,则()f x 为A .312sin()26x π+B .12sin(6)6x π-C .312sin()23x π+D .12sin(6)3x π+ 11.现有四个函数:①sin y x x =⋅;②cos y x x =⋅;③|cos |y x x =⋅;④2xy x =⋅的图象(部分)如下:A .①④③②B .①④②③C .④①②③D .③④②①12.定义在R 上的函数()f x 满足:()()1,(0)4,f x f x f '+>=则不等式()3x xe f x e >+(其中e 为自然对数的底数)的解集为A .()0,+∞B .()(),03,-∞+∞C .()(),00,-∞+∞D .()3,+∞二、填空题:(本大题共4小题,每小题5分,共20分)13.已知向量)1,(z x a -=,),2(z y b +=,且b a ⊥,若变量,x y 满足约束条件⎪⎩⎪⎨⎧≤+≥-≥5231y x xy x ,则z 的最大值为 . 14.正四面体ABCD 的棱长为4,E 为棱BC 的中点,过E 作其外接球的截面,则截面面积的最小值为______.15.有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行,则这一行的4张卡片所标数字之和等于10的概率为 .16.设O 是ABC ∆的三边中垂线的交点,,,a b c 分别为角,,A B C 对应的边,已知2220b b c -+=,则BC AO ⋅的范围是___________________.三、解答题: 17.(本小题满分12分)已知数列}{n a 中,51=a 且1221n n n a a -=+-(2n ≥且*n N ∈).(Ⅰ)证明:数列12n n a -⎧⎫⎨⎬⎩⎭为等差数列; (Ⅱ)求数列}{n a 的前n 项和n S .x公安部最新修订的《机动车驾驶证申领和使用规定》于2013年1月1日起正式实施,新规实施后,获取驾照要经过三个科目的考试,先考科目一(理论一),科目一过关后才能再考科目二(桩考和路考),科目二过关后还要考科目三(理论二).只有三个科目都过关后才能拿到驾驶证.某驾校现有100名新学员,第一批参加考试的20人各科目通过的参考人数 通过科目一人数通过科目二人数通过科目三人数201242(Ⅰ)估计该驾校这100名新学员有多少人一次性(不补考)获取驾驶证;(Ⅱ)第一批参加考试的20人中某一学员已经通过科目一的考试,求他能通过科目二却不能通过科目三的概率;(Ⅲ)该驾校为调动教官的工作积极性,规定若所教学员每通过一个科目的考试,则学校奖励教官100元.现从这20人中随机抽取1人,记X 为学校因为该学员而奖励教官的金额数,求X 的数学期望. 19.(本小题满分12分)如图,在四棱锥P ABCD -中,,//,,22,,PA AD AB CD CD AD AD CD AB E F ⊥⊥===分别为,PC CD 的中点,DE EC =(Ⅰ)求证:平面ABE ⊥平面BEF ;(Ⅱ)设PA a =,若平面EBD 与平面ABCD 所成锐二面角[,]43ππθ∈,求a 的取值范围. 20.(本小题满分12分)已知椭圆1C 的中心为原点O ,离心率e 2=2,其一个焦点在抛物线2:C 22y px =的准线上,若抛物线2C 与直线: 20l x y -+=相切.(Ⅰ)求该椭圆的标准方程;(Ⅱ)当点(,)Q u v 在椭圆1C 上运动时,设动点(,)P v u u v 2-+的运动轨迹为3C .若点T 满足:OT MN OM ON =+2+,其中,M N 是3C 上的点,直线OM 与ON 的斜率之积为1-2,试说明:是否存在两个定点,F F 12,使得TF TF 12+为定值?若存在,求,F F 12的坐标;若不存在,说明理由.已知函数()(1)xf x x e-=+(e 为自然对数的底数)。
山西省山大附中高三数学上学期第二次月考试题 理 新人教A版

山西大学附中2013-2014年高三下学期第二次月考数学试题(理)考试时间:120分钟 满分:150分 考查内容:高中全部一、选择题:(共12小题。
每小题5分,共60分。
在每个小题给出的四个选项中,只有一项是符合题目要求的)1.设{1,4,2}A x =,若2{1,}B x =,若B A ⊆,则x = ( ) A .0 B .-2 C .0或-2 D .0或±22.将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有 ( ) A . 10种 B .20种 C . 36种 D .52种 3.已知数据123 n x x x x ,,,,是太原市n *(3 )n n N ≥∈,个普通职工的2013年的年收入,设这n 个数据的中位数为x ,平均数为y ,方差为z ,如果再加上比尔.盖茨的2013年的年收入1n x +(约900亿元),则这1n +个数据中,下列说法正确的是( ) A .年收入平均数大大增大,中位数一定变大,方差可能不变 B .年收入平均数大大增大,中位数可能不变,方差变大 C .年收入平均数大大增大,中位数可能不变,方差也不变 D .年收入平均数可能不变,中位数可能不变,方差可能不变。
4.在各项都为正数的等比数列{}n a 中,首项为3,前3项和为21,则3a 等于 ( ) A .15 B .12 C .9 D .65.已知函数 ),()(),()(,)(12010x f x f x f x f xe x f x '='== ))(()(*1N n x f x f n n ∈'=- 则2014'(0)f =( )A .2013B .2014C .2015D .20166.设复数121,cos sin 221212i ππωω=-+=+,若12z ωω=⋅,则复数z 的虚部为( )A .12-B .12C .2-D .27.ABC ∆的三内角,,A B C 所对边的长分别为,,a b c ,设向量),(sin c a B p +=, ),sin (sin a b A C q --= .若,R ∈∃λ使,q pλ=则角C 的大小为 ( )A . 6πB . 23πC . 3πD . 2π8.过抛物线py x 22=焦点作直线l 交抛物线于,A B 两点,O 为坐标原点,则ABO ∆为( )A . 锐角三角形B . 直角三角形C . 钝角三角形D .不确定9.在ABC ∆中,120A ∠=,1AB AC ⋅=-,则BC 的最小值是 ( )A .2 C .610.已知函数()f x 在R 上满足2()2(2)88f x f x x x =--+-,则曲线()y f x =在点()1,(1)f )处切线的斜率是 ( )A .2B . 1C .3 .D . 2-11. 若实数,,,a b c d 满足222(3ln )(2)0b a a c d +-+-+=,则22()()a c b d -+-的最小值为 ( )A .2 C ..8 12.已知函数)1,0(1log )(≠>-=a a x x f a ,若1234x x x x <<<,且12()()f x f x =34()()f x f x ==,则12341111x x x x +++= ( ) A .2 B .4 C .8 D .随a 值变化二. 填空题:(本大题共4小题,每小题5分) 13.已知某几何体的三视图如图,其中正视图中半圆的直径为2,则该几何体的体积为 . 14.曲线2sin 0)y x x π=≤≤(与直线1y =围成的封闭图形的面积为 .15. 如图2,圆O :222x y π+=内的正弦曲线sin y x =与x 轴围成的区域记为M (图中阴影部分)随机往圆O 内投一个点A ,则点A 落在区域M 内的概率为 .16.已知无穷数列{}n a 具有如下性质:①1a 为正整数;②对于任意的正整数n ,当n a 为偶数时,12nn a a +=;当n a 为奇数时,112n n a a ++=.在数列{}n a 中,若当n k ≥时,1n a =,当1n k ≤<时,1n a >(2k ≥,*k N ∈),则首项1a 可取数值的个数为 (用k 表示).三.解答题:(共70分)17.(本题满分12分)已知()sin(2)cos(2)63f x x x ππ=++-.(Ⅰ)求()f x 的最大值及取得最大值时x 的值;(Ⅱ)在ABC ∆中,角A ,B ,C 的对边分别为c b a ,,若()1f C =,c =sin 2sin A B =,求ABC ∆的面积. 18.(本题满分12分)某高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周二、周三的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座。
山西省太原五中2013届高三数学5月月考试题 文 新人教A版 2

侧视图 正视图太 原 五 中2012—2013年学年度第二学期月考(5月)高 三 数 学(文)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分。
考试用时120分钟。
第Ⅰ卷(选择题 共60分)一选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四 个选项中,只有一项是符合题目要求的)1.已知集合}2,1{aA =,},{b aB =,则}21{=B A ,则=B A ( )A .}2,1,21{B .}1,21{-C .}1,21{ D .}1,1,21{-2.设()2112i iz +++=,则z =( ) A .2 B .1 C .2 D .3 3.若,2παπ⎛⎫∈ ⎪⎝⎭,1tan ,sin ()47παα⎛⎫+== ⎪⎝⎭则A .35 B .45 C .35- D .45- 4.下列命题正确的个数 ( )(1)命题“2000,13x R x x ∃∈+>”的否定是“2,13x R x x ∀∈+≤”;(2)函数22()cos sin f x ax ax =-的最小正周期为π错误!未找到引用源。
是“1a =”的必要不充分条件;(3)“22x x ax +≥在[]1,2x ∈上恒成立”⇔max min 2)()2(ax x x ≥+在[]1,2x ∈上恒成立(4)“平面向量a 与b 的夹角是钝角”的充分必要条件是“0a b ⋅<”。
A .1B .2C .3D .4执行如左下图所示的程序框图,输出的结果是56,5.则判断框内应填入的条件是( )A. 5?n ≤B.5?n <C.5?n >D.5?n ≥6. 某几何体的三视图如右上图所示,则此几何体的体积是 ( )A .20π3B .6πC .16π3D .10π3 7.当a > 0时,函数2()(2)x f x x ax e =-的图象大致是( )8.已知函数22cos sin sin 21cos 21)(22+--=x x x x x f ,则( ) A. )(x f 在83π=x 时取得最小值2,其图像关于点)0,83(π对称B. )(x f 在83π=x 时取得最小值0,其图像关于点)0,85(π对称C.)(x f 在)7,3(ππ单调递减,其图像关于直线π-=x 对称9.经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系.对某小组学生每周用于数学的学习时间x 与数学成绩y 进行数据收集如下:由表中样本数据求得回归方程为y bx a =+,则点(,)a b 与直线18100x y +=的位置关系是( )A .点在直线左侧B .点在直线右侧C .点在直线上D .无法确定10. 设x,y 满足约束条件00134x y x ya a⎧⎪≥⎪≥⎨⎪⎪+≤⎩若z =132+++x y x 的最小值为32,则a 的值( )A. 1B. 3C. 4D. 1211.三棱锥BCD A -的外接球为球O ,球O 的直径是AD ,且ABC ∆、BCD ∆都是边长为1的等边三角形,则三棱锥BCD A -的体积是( ) A .82 B . 61 C .81D .122 12. 过双曲线()0,012222>>=-b a by a x 的左焦点()0,c F -作圆222a y x =+的切线,切点为E ,延长FE 交抛物线cx y 42=于点P ,O 为原点,若()+=21,则双曲线的离心率为( )A.251+ B.231+ C.7224- D.7224+ 第Ⅱ卷(非选择题,共90分)二、填空题:(本大题共4小题,每小题5分,共20分)13. 已知c b a ,,是ABC ∆的三个内角C B A ,,对边,若,3,2==b c ,3B C A =+则=C sin .14. 已知()f x 是周期为2的奇函数,当01x <<时,()lg f x x =,设635,,,522a f b f c f ⎛⎫⎛⎫⎛⎫===⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭则,,a b c 从小到大的顺序为 .15.2a <<,则函数()2f x x =-的零点个数为 .16.在ABC ∆中,M 是线段BC 的中点,10,3==BC AM ,则=⋅AC AB .三、解答题:(本大题共6小题,共70分。
山西省山大附中2013届高三5月月考理综试题 Word版含答案.pdf

A.升高温度,反应()和()的平衡常数均减小
B.840℃后升高温度,反应()的正反应速率减小,反应()的正反应速率增大
C.900℃后,NO产率下降的主要原因是反应()平衡逆向移动
D.400℃-700℃,N2产率降低的主要原因是反应()平衡逆向移动
13、电浮选凝聚法是工业上采用的一种污水处理方法:保持污水的pH在5.0~6.0之间,通过电解生成Fe(OH)3沉淀
D.XRXrY的个体会产生四种比例相等的精子
6. 已知A、a是一对等位基因。右图①~③分别表示某种动物存在地理隔离的3个不同的种群的A基因频率的变化情
况,3个种群的初始个体数依次为26,260和2600。有关分析错误的是( )A.种群越小基因的丧失对该基因频率的影
响越大
B.②在125代时aa个体约占总数的25%
5. 几种性染色体异常果蝇的性别、育性等如图所示。有关说法正确的是
A.正常果蝇在减数第一次分裂中期的细胞内染色体组数为2个,在减数第二次分裂后期的细胞中染色体数是4条
B.引起这4种果蝇变异的原因都属于染色体变异
C.若红眼雌果蝇和红眼雄果蝇交配产生了图中一所示变异红眼后代,则是由于母本减数分裂产生异常配子所致
C、KNO3可用于制造黑火药,已知黑火药反应为S + 2KNO3 +3C=K2S + N2↑ + 3CO2↑,若有1mol KNO3被消耗,则
该反应转移电子5×6.02×1023
D、氰化钾(KCN、剧毒)可用于电镀,使镀层更细致,65g KCN晶体中,离子总数为2×6.02×1023
9、正丁烷的二氯取代产物为A(C4H8Cl2),A分子中又有一个H原子被Cl原子取代,生成的C4H7Cl3有四种同分异构
山西省吕梁学院附中2013届高三上学期第五次月考数学(理)试题 Word版含答案
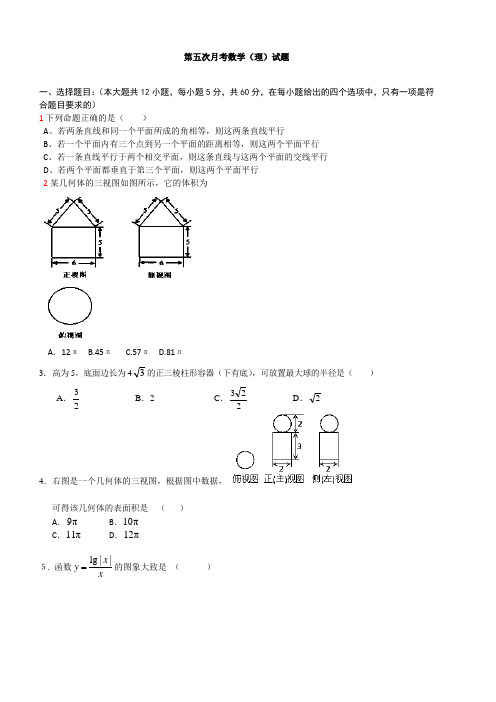
第五次月考数学(理)试题一、选择题目:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1下列命题正确的是( )A 、若两条直线和同一个平面所成的角相等,则这两条直线平行B 、若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C 、若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D 、若两个平面都垂直于第三个平面,则这两个平面平行 2某几何体的三视图如图所示,它的体积为A .12π B.45π C.57π D.81π3.高为5,底面边长为43的正三棱柱形容器(下有底),可放置最大球的半径是( )A .23 B .2 C .223 D .2 4.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是 ( ) A .9π B .10π C .11π D .12π5. 函数xx y ||lg 的图象大致是 ( )6. 已知命题p :存在(,0),23x x x ∈-∞<;命题q :ABC ∆中,若sin sin A B >,则A B >,则下列命题中为真命题的是( ) A .p 且q B .p 或(q ⌝) C .(p ⌝)且qD .p 且(q ⌝)7.已知 15152211-sin cos -==⎰N dx x M ,,则 ( )A. M N <B. M N >C. M N =D. 以上都有可能 8. 把函数sin()(0,)2y x πωϕωϕ=+><的图象向左平移3π个单位,所得的曲线的一部分如下图所示,则ωϕ、的值分别是( )A .13π, B .31π—, C .23π, D .32π—,9. 实数y x ,满足条件2,4,20,x x y x y c ≥⎧⎪+≤⎨⎪-++≥⎩目标函数3z x y =+的最小值为5,则该目标函数y x z +=3的最大值为( ) A. 10 B. 12 C. 14 D. 1510. 在等差数列{}n a 中12011a =-,其前项和为n s,若20122011120122011s s -=,则2013s =( ) A. —2012 B. —2013 C. 2012 D. 201311. 已知)2()(),1()1(+-=-=+x f x f x f x f ,方程0)(=x f 在[0,1]内有且只有一个根21=x ,则0)(=x f 在区间[]2013,0内根的个数为 ( )A.2011B.1006C.2013D.100712.设()f x 和()g x 是定义在同一区间[,]a b 上的两个函数,若对任意的[,]x a b ∈,都有|()()|1f x g x -≤,则称()f x 和()g x 在[,]a b 上是“密切函数”,[,]a b 称为“密切区间”,设 2()34f x x x =-+与()23g x x =-在[,]a b 上是“密切函数”,则它的“密切区间”可以是 ( ).A [1,4] .B [2,4] .C [3,4] .D [2,3]二、填空题:(本大题共有4个小题,每小题5分,共计20分.) 13. 已知0a >,0,2b a b >+=,则14y a b=+的最小值是_________. 14. 凸函数的性质定理为:如果函数)(x f 在区间D 上是凸函数,则对于区间D 内的任意,,21x x …,,n x 有)()()()(2121nx x x f n x f x f x f nn +⋅⋅⋅++≤+⋅⋅⋅++,已知函数x y sin =在区间),0(π上是凸函数,则ABC ∆中,C B A sin sin sin ++的最大值为 。
山西省太原五中2013届高三5月月考数学理试题(精)

太 原 五 中2012—2013年学年度第二学期月考(5月)高 三 数 学(理)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共24小题,共150分,考试时间120分钟。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内;2.选择题必须用2B 铅笔填涂;非选择题必须使用0.5毫米的黑色字迹的签字笔书写,字体工整、笔迹清楚;3.请按照题号顺序在各题的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效;4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑;5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第Ⅰ卷一、选择题:本大题共12题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合 A = {0 , 1} ,则满足条件 A B = {2 , 0 , 1 , 3}的集合 B 共有( ) A .1 个 B .2 个 C .3 个 D .4 个 2.已知复数i m z 21+=,i z 432-=若21z z 为实数,则实数m 的值为( )A .38B .23C .38- D .23-3.如图所示程序框图,其输出结果是111,则判断框中所填的条件是( )A .5≥nB .6≥nC .7≥nD .8≥n 4.已知 x ∈ R ,则 x ≥ 1是| x +1| + | x -1|= 2 | x | 的( ) A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既非充分也非必要条件 5.设数列{}n a 为等差数列,其前n 项和为n S ,已知14725899,93a a a a a a ++=++=,若对任意*n N ∈都有k n S S ≤成立,则k 的值为( ) A .22 B .21 C .20 D .196.已知点1)0,0)(,(22=+>>y x C b a b a M :是圆内任意一点,点),(y x P 是圆上任意一点,则实数1-+by ax ( )A.一定是负数B.一定等于0C.一定是正数D.可能为正数也可能为负数7.已知圆O 的半径为2,A 、B 是圆上两点,32π=∠AOB ,MN 是圆O 的一条直径,点C 在圆内且满足()()101<<-+=λλλ,则⋅的最小值为( )A .-2B .-1C .-3D .-48.已知0>ω,函数)4sin()(πω+=x x f 在区间[ππ,2]上单调递减,则实数ω的取值范围是( )A. [210219.现需编制一个八位的序号,规定如下:序号由4个数字和2个x 、1个y 、1个z 组成;2个x 不能连续出现,且y 在z 的前面;数字在1、2、4、8之间选取,可重复选取,且四个数字之积为8.则符合条件的不同的序号种数有( )A .12600B .6300C .5040D .2520 10.已知方程sin xk x=在(0,)+∞有两个不同的解,αβ(αβ<),则下面结论正确的是: A .1tan()41πααα++=- B .1tan()41πααα-+=+ C .1tan()41πβββ++=- D .1tan()41πβββ-+=+ 11.在ABC ∆中,a ,b ,c 分别是角A ,B ,C 的对边,12.已知函数)1(+=x f y 的图象关于点)0,1(-对称,且当)0,(-∞∈x 时,0)()(<'+x f x x f 成立(其中)(x f '是)(x f 的导函数),若0.30.33311(3)(3),(log 3)(log 3),(log )(log )99a fb fc f ππ=⋅=⋅=⋅,则a ,b ,c 的大小关系为( )A . a > c >bB .c>a>bC .c> b > aD . b >a> c第Ⅱ卷 二、填空题:本大题共4个小题,每小题5分。
山西大学附中2013-2014年高三下学期第一次月考数学(理)试题
山西大学附中2013-2014年高三下学期第一次月考数学(理)考试时间:120分钟 满分:150分 考查内容:高中全部 一、选择题(本大题共12小题,每小题5分,共60分.)1.已知i 为虚数单位,则1ii+的实部与虚部的乘积等于( ) A. 14 B. 14- C. 14i D. 14i -2.集合A ={}16102-+-=x x y x ,集合B ={}A x x y y ∈=,log 2,则=⋂B C A R ( )A.[]32,B.(]21,C.[]83,D.(]83, 3.已知x 与y方程∧∧∧+=a x b y 必过 ( ) A .点)2,2( B .点)0,23(C .点)2,1(D .点)4,23(4.右面的程序框图,如果输入三个实数个选项中的( )A. b c > B . c b > C. x c > D. 5.已知正项数列{}n a 中,11=a ,2=a 222112(2)n n n a a a n +-=+≥,则6a A .22 B .4 C .6.设,,a b c 是空间三条直线,,αβ则下列命题中,逆命题不正确的是( A .当c α⊥时,若c β⊥,则//αβ B .当b α⊂时,若b β⊥,则αβ⊥C .当,b a αα⊂⊄且c 是a 在α内的射影时,若b c ⊥,则a b ⊥D .当b α⊂且c α⊄时,若//c α,则//b c7.若点),(y x M 满足⎪⎩⎪⎨⎧≥≥<-+04x x y y x ,则15--x y 的取值范围是( )A.),1()3,(+∞⋃--∞B.),1[]3,(+∞⋃--∞C.)1,3(-D.]1,3[- 8.使奇函数)2cos(3)2sin()(θθ+++=x x x f 在]0,4[π-上为减函数的θ值为( )A.3π-B. 6π-C.65π D. 32π侧视图正视图9.现有4名教师参加说课比赛,共有4个备选课题,若每位选手从中有放回地随机选出一个课题进行说课,其中恰有一个课题没有被这4位选中的情况有( )种 D. 36种为AD的中点,P为边AB上一动点,则tan DPE∠的最大值为()A D.111.已知函数,log)3()(2xxxf-=实数cba,,满足),(0)()()(>>><⋅⋅abccfbfaf若实数x为方程0)(=xf的一个解,那么下列不等式中,不可能成立的是( )A.x<a B.x>b C.x<c D.x>c12.设1F、2F是双曲线22221(0,0)x ya ba b-=>>的左、右焦点,若双曲线右支上存在一点P,使22()0OPOF PF+⋅=(O为坐标原点),且122||3||PF PF=,则双曲线的离心率为( )A.32BC D.二、填空题:(本大题共4小题,每小题5分,共20分.)13.有一个几何体的三视图及其尺寸如下(单位cm),则该几何体的表面积为 .14.设(sin cos)a x x dxπ=+⎰,则二项式6(展开式中含2x项的系数是 .15.在△ABC中,a、b、c分别为、B、C的对边,三边a、b、c成等差数列,且,则cos cosA C-的值为.16.给出以下四个命题:①设2:0p a a+≠,:0q a≠,则qp是的充分不必要条件;②过点)2,1(-且在x轴和y轴上的截距相等的直线方程是01=-+yx;③若函数()y f x=与()y g x=的图像关于直线y x=对称,则函数()2y f x=与()12y g x=的图像也关于直线y x=对称;④若直线01cossin=++ααyx和直线1cos102x yα--=垂直,则角2().26k k kππαπαπ=+=+∈Z或其中正确命题的序号为.(把你认为正确的命题序号都填上)三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明,证明过程或演算步骤.)17.(本题满分12分)数列}{na的前n项和为nS,数列}{nb的前n项的和为nT,}{nb为等差数列且各项均为正数,11=a,121+=+nnSa)(*Nn∈,15321=++bbb(Ⅰ)求证:数列}{na是等比数列;(Ⅱ)若11ba+,22ba+,33ba+成等比数列,求nT.18.(本题满分12分)为了某项大型活动能够安全进行,警方从武警训练基地挑选防爆警察,从体能、射击、反应三项指标进行检测,如果这三项中至少有两项通过即可入选。
山西省山大附中2013届高三10月第二次月考 数学理试题

山西大学附中2012-2013学年第一学期高三(10月)月考数学试题(理科)一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.i 是虚数单位,=-ii25A.i 21+B.i 21--C.i 21-D.i 21+-2.设变量x ,y 满足约束条件:⎪⎩⎪⎨⎧≤--≥-≥+3213y x y x y x .则目标函数z=2x+3y 的最小值为A. 6B. 7C. 8D. 233.命题“存在R x ∈0,020≤x ”的否定是A.不存在R x ∈0, 02>x B.存在R x ∈0 02≥xC.对任意的R x ∈, 02≤xD.对任意的R x ∈, 02>x 4.设函数)0(ln 31)(>-=x x x x f 则)(x f y =A.在区间),1(),1,1(e e 内均有零点。
B.在区间),1(),1,1(e e 内均无零点。
C.在区间)1,1(e 内有零点,在区间),1(e 内无零点。
D.在区间)1,1(e 内无零点,在区间),1(e 内有零点。
5.右图是一个算法的程序框图,该算法输出的结果是A .12 B . 23 C . 34 D . 456. 在等差数列}{n a 中,已知56=a ,n S 是数列}{n a 的前n 项和,则11S =A .45B .50C .55D .607.已知函数)0,)(4sin()(>∈+=ωπωR x x x f 的最小正周期为π,为了得到函数x x g ωcos )(=的图象,只要将)(x f y =的图象A. 向左平移8π个单位长度 B. 向右平移8π个单位长度 C. 向左平移4π个单位长度 D. 向右平移4π个单位长度8已知函数⎪⎩⎪⎨⎧<-≥+=0,40,4)(22x x x x x x x f 若)()2(2a f a f >-则实数a 的取值范围是俯视图侧视图正视图A. (,1)(2,)-∞-⋃+∞B. (1,2)-C. (2,1)- D .(,2)(1,)-∞-⋃+∞ 9.设双曲线)0,0(12222>>=-b a by ax的一条渐近线与抛物线12+=x y 只有一个公共点,则双曲线的离心率为A.54 B.5 C. 210.在区间]1,1[-上随机取一个数x ,2cos x π的值介于0到21之间的概率为A. 13 B. 2π C. 12 D .23 11.已知球的直径4SC =,,A B 是该球面上的两点,AB =30ASC BSC ∠=∠=,则三棱锥S A B C -的体积为( )A.212.设抛物线x y 22=的焦点为F ,过点)0,3(M 的直线与抛物线相交于,A B 两点,与抛物线的准线相交于C ,2||=BF ,则B C F ∆与A C F ∆的面积之比ACFBCF S S ∆∆=A. 45 B .23 C .47 D .12 二.填空题:(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.) 13.有一个几何体的三视图及其尺寸如下(单位cm ),则该几何体的表面积为:_______ 14.88221083)1()1()1()2()1(-+⋅⋅⋅+-+-+=-++x a x a x a a x x ,则______6=a 。
山西省山大附中2013届高三上学期期中数学理试卷

2012~2013学年上学期期中考试 高三年级数学(理科)试卷一.选择题:本大题共12个小题,每题5分,共60分。
在每小题给出的四个选项中,有且只有一个是符合题目要求的.1. 设全集R ,若集合}1|12|{},3|2||{>-=≤-=x x B x x A ,则)(B A C R 为 ( ) A .}51|{≤<x x B .}51|{>-≤x x x 或C .}51|{>≤x x x 或D .}51|{≤≤-x x2. 命题P :若,,R b a ∈则|a|+|b|>1是|a+b|>1的充分不必要条件;命题q :不等式1|1|->-x xx x 的解集为}10|{<<x x ,则( ) A .“p 或q ” 为假命题 B.“p 且q ” 为真命题 C.“┒p 或q ” 为假命题 D.“┒p 且q ” 为真命题3.已知{}n a 为等比数列,若1064=+a a ,则9373712a a a a a a ++的值为 ( ) A. 10B.20C.60D.1004. 已知直线a 和平面,αβ,,,l a a αβαβ⋂=⊄⊄,且a 在,αβ内的射影分别为直线b 和c ,则b 和c 的位置关系是( )A.相交或平行B.相交或异面C.平行或异面D.相交﹑平行或异面5.已知,2tan =θ则)sin()2sin()cos()2sin(θπθπθπθπ-----+等于( )A.2B.-2C.0D.326.一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的体积为( ) A.()334π+ B.()34π+ C. ()238π+ D.()638π+)1,0(23≠>-=+a a a y x 的7.函数图像恒过定点A ,若点A 在直线1-=+nym x 上,且0,>n m ,则n m +3的最小值为 ( ) 高三年级数学试卷 、共4页、第1页A. 13B. 16C.2611+.D. 28. 8.若函数21()log ()2a f x x ax =-+有最小值,则实数a 的取值范围是( ) A .(0,1) B .(0,1)∪(1,2) C .(1,2 ) D .[ 2 ,+∞) 9.在△ABC 中,∠C =900,∠B =300,AC=1,M 为AB 中点,将△ACM 沿使A 、B 间的距离为2,则M 到面ABC 的距离为 ( )A..21 B. .23 C. 1. D. 2310.若函数,,cos 3sin )(R x x x x f ∈+=ωω又,0)(,2)(=-=βαf f 且||βα-的最小值为,43π则正数ω的值为( ) A.31 B. 32 C. 34 D. 23. 11.已知A 、B 、C 是平面上不共线的三点,O 是三角形ABC 的重心,动点P 满足111(2)322OP OA OB OC →→→→=++,则点P 一定为三角形的 ( )A. AB 边中线的中点B. AB 边中线的三等分点(非重心)C. 重心D. AB 边的中点 12. 已知函数⎩⎨⎧>+-≤+=0,120,1)(2x x x x x x f ,若关于x 的方程0)()(2=-x af x f 恰有5个不同的实数解,则a 的取值范围是 ( )A.(0,1)B.(0,2)C.(1,2)D.(0,3)二.填空题:本大题共4小题,每题5分,共20分13.若点P (x ,y )满足线性约束条件⎪⎩⎪⎨⎧≥≥+-≤-002303y y x y x ,点A (3,3),O 为坐标原点,则→→⋅OPOA 的最大值_________.14.如图,四边形ABCD 为菱形,四边形CEFB 为正方形,平面ABCD ⊥平面CEFB ,CE=1,∠AED=300,则异面直线BC 与AE 所成角的大小_________.15. 已知数列{}n a 满足*1331(,2)n n n a a n N n -=+-∈≥,且,51=a 若高三年级数学试卷 、共4页、第2页*1()()3n n n b a t n N =+∈且{}n b 为等差数列,则t=________。
山西省山大附中2013届高三4月月考数学理试题

山西大学附中2012-2013学年高三(4月)月考数学(理科)试卷(考试时间:120分钟)一、选择题:(每小题5分,共60分) 1.集合A={}1610-2-+=x x y x ,集合B={}A x x y y ∈=,log 2,则=⋂B C A R ( )A.[]32,B.(]21,C.[]83,D.(]83, 2的大小关系是 ( ) A. B.C.D .3.设函数na x x f )()(+=,其中,则)(x f 的展开式中4x 的系数为( )A.-360 B.360 C.-60 D.604.已知复数i z 210+=在复平面上对应点为0P ,则0P 关于直线表示是( ).A. i+1 B. i -1C. i- D.i5.在实数集R 上随机取一个数x ,事件A =“0sin ≥x ,]2,0[π∈x ”,事件B =“P (B ︱A )=( ) A C 6.已知以下三视图中有三个同时表示某一个三棱锥,则不是..该三棱锥的三视图是A .B .C .D .c b a ,,c a b <<a c b <<b a c <<c b a <<侧视正视俯视侧视正视俯视侧视正视俯视1侧视俯视7. 如下程序框图的功能是:给出以下十个数:5,9,80,43,95,73,28,17,60,36,把大于60的数找出来,则框图中的①②应分别填入的是( ) (A )1?,60+=>i i x (B )1?,60+=<i i x (C )1?,60-=>i i x (D )1?,60-=<i i x 8.已知函数)(x f 是定义在R 上的单调增函数且为奇函数,数列{}n a 是等差数列,1007>a ,则)()()()()(20132012321a f a f a f a f a f +++++ 的值( ).A.恒为正数B.恒为负数C.恒为0D.可正可负 9.如图所示是某个区域的街道示意图(每个小矩形的边表示街道),那么从A 到B 的最短线路有( )条A .100B .400C .200D .25010.如图,1F ,2F 是双曲线C :错误!未找到引用源。
山西省太原五中高三数学5月月考试题 理 新人教A版

太 原 五 中2013—2014学年度第二学期月考(5月)高 三数 学(理)第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合⎭⎬⎫⎩⎨⎧=+=14922y x xM ,⎭⎬⎫⎩⎨⎧=+=123y x y N ,则=⋂N M ( ) A 、∅ B 、{})0,2(),0,3( C 、 ]3,3[- D 、{}2,32.已知复数12,z z 在复平面内对应的点分别为(0,1),(1,3)A B -,则21zz 等于( )A .3i +B .3i -C .13i -+D .3i --3.某校在模块考试中约有1000人参加考试,其数学考试成绩ξ~N(90,a 2)(a>0,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的53,则此次数学考试成绩不低于110分的学生人数约为( ) A .600 B .400 C .300 D .2004.已知双曲线的方程为)0,0(12222>>=-b a by a x ,双曲线的一个焦点到一条渐近线的(其中c 为双曲线的半焦距长),则该双曲线的离心率为( ) A.32C.D.525. 运行如图所示的算法框图,则输出的结果S 为( ) A .1- B .1C .2-D .26. 函数()2sin()(0,0)f x x ωϕωϕπ=+>≤≤的部分图象如图所示,其 中A ,B 两点之间的距离为5,则f(x)的递增区间是( )A.[61,62]()k k k Z -+∈B. [64,61]()k k k Z --∈C. [31,32]()k k k Z -+∈ D. [34,31]()k k kZ --∈7.一个几何体的三视图如图所示,则这个几何体的体积为( )8.现有四个函数:①sin y x x =⋅;②cos y x x =⋅;③|cos |y x x =⋅;④2x y x =⋅的图象(部分)如下:则按照从左到右图象对应的函数序号安排正确的一组是( )A .①④②③B .①④③②C .④①②③D .③④②①9.在圆22(2)(2)4x y --+=内任取一点,则该点恰好在区域50303x x y x ⎧⎪⎨⎪⎩+2y -≥-2+≥≤内的概率为A .18πB .14πC .12πD .1π10在△ABC 中,D 为边BC 上一点,DC =2BD ,∠ADC=45°,若,则BD等于( )A.4.B.2+2+311.点S,A,B,C 是球O 的球面上的四个点,S,O 在平面ABC 的同侧,∠ABC=120°,AB=BC=2,平面SAC⊥平面ABC ,若三棱锥S-ABC 则该球的表面积为( ) A.18π B.16πC. 20πD. 25π 12.已知点(1,0)B ,P 是函数e x y =图象上不同于(0,1)A 的一点.有如下结论:①存在点P 使得ABP ∆是等腰三角形;②存在点P 使得ABP ∆是锐角三角形; ③存在点P 使得ABP ∆是直角三角形. 其中,正确的结论的个数为( ) A. 0 B.1 C. 2 D. 3第Ⅱ卷x 俯视图本卷包括必考题和选考题两部分。
山西省山大附中高一数学5月月考试题新人教A版

山西大学附中2013—2014学年第二学期高一5月月考数学试题 考试时间:90分钟 考试内容(三角函数、平面向量)一、选择题:(本题共12小题,每小题3分,共36分,在每小题给出的四个选项中只有一个选项符合题目要求)1.函数()2sin cos f x x x =的最小值是( ) A .1-B .2-C .2D .12.sin 45cos15cos 45sin15-oooo的值为 ( )A .3-B .12-C .12D 3 3.已知()()3,2,1,a b λ=-=-r r,向量a r 与b r 垂直,则实数λ的值为( )A .32-B .32C .23-D .234.已知ABC ∆中,,,a b c 分别为,,A B C 的对边,ο30,34,4=∠==A b a ,则B ∠等于( )A .ο30B .ο30或ο150C .ο60D .60o 或ο120 5.函数2()2sin ()1()4f x x x R π=--∈是( )A .最小正周期为π2的奇函数B .最小正周期为π的奇函数C .最小正周期为π2的偶函数D .最小正周期为π的偶函数 6.函数()sin()4f x x π=-的图像的一条对称轴是( )A .4x π=B .2x π=C .4x π=-D .2x π=-7.已知ABC ∆中,,,a b c 分别为,,A B C 的对边,cos cos a A b B =,则ABC ∆为( )A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形 8.把函数sin3y x =的图象适当变化就可以得到2(sin 3cos3)2y x x =-的图象,这个变化可以是( )A .沿x 轴方向向右平移4πB .沿x 轴方向向左平移4πC .沿x 轴方向向右平移12πD .沿x 轴方向向左平移12π9.已知O 为ABC ∆所在平面上一点,若OA OB OB OC OC OA ⋅=⋅=⋅u u u r u u u r u u u r u u u r u u u r u u u r,则O 为ABC ∆的( )A .内心B .外心C .垂心D .重心10.已知函数()3cos ,f x x x x R =-∈,若()1f x ≥,则x 的取值范围为( )A .|,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭ B .|22,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭ C .5{|,}66x k x k k Z ππππ+≤≤+∈D .5{|22,}66x k x k k Z ππππ+≤≤+∈ 11.在锐角ABC ∆中,若2C B =,则bc的范围是( )A .(0,2)B .)2,2(C .)3,2(D .)3,1(12.函数tan 42y x ππ⎛⎫=- ⎪⎝⎭的部分图象如下图所示,则()OA OB AB +⋅=u u u r u u u r u u u r ( )A .-6B .-4C .4D .6二、填空题:(本大题共4小题,每小题4分,共16分)13.若()()1,4,1,0a b ==r r,则2a b +r r 的值为14.已知βα,⎪⎭⎫⎝⎛∈ππ,43,sin(βα+)=-,53 sin ,13124=⎪⎭⎫ ⎝⎛-πβ则cos ⎪⎭⎫ ⎝⎛+4πα= _.15.在ABC ∆中,内角,,A B C 的对边分别为,,a b c ,若ABC ∆的面积222)S a b c =+-,则C = . 16.关于)42sin(3)(π+=x x f 有以下命题:①若,0)()(21==x f x f 则)(21Z k k x x ∈=-π;②)(x f 图象与)42cos(3)(π-=x x g 图象相同;③)(x f 在区间]83,87[ππ--上是减函数;④)(x f 图象关于点)0,8(π-对称。
山西省山大附中2013-2014学年高二数学5月月考试题新人教A版

山西大学附中2013-2014学年第二学期高二年级(下)5月月考数学试题(理科)时间:120分钟一.选择题:(每题有四个选项,只有一个选项是正确的,每题3分,共36分)1.记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有( )种A 480B 720C 960D 14402.某公共汽车上有10位乘客,沿途5个车站,乘客下车的可能方式有()种 A 105 B 510 C 50 D 510A3.现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这三张卡片不能是同一种颜色,且红色卡片至多一张,不同取法的总数为 A 232 B 252 C 472 D 4844.将2名教师和4名学生分成2个小组,分别安排到甲乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案由()种 A 12 B 10 C 9 D 85.现有5种不同颜色的染料,要对如图中的四个不同区域进行着色,要求有公共边的两块区域不能使用同一种颜色,则不同的着色方法的种数是( )种 A 120 B 140 C 240 D 2606.二项式41(1)n x +-(n N ∈)的展开式中,系数最大的项为A 第21n +项或22n +项B 第21n +项C 第22n + 项D 第21n +项或2n 项 7.已知甲袋中有1个黄球和2个红球,乙袋中有2个黄球和2个红球,现随机地从甲袋中取出两个球放入乙袋中,然后从乙袋中随机取出1个球,则从乙袋中取出红球的概率为 A13 B 12 C 59 D 298.从1,2,3,4,5中任意取2个不同的数,事件A=“取到的两个数之和为偶数”,事件B=“取到的两个数均为偶数”,则(|)P B A =A18 B 14 C 25 D 12 9.设0sin a xdx π=⎰,则二项式6()a x x的展开式的常数项是 A 160 B -160 C 240 D -24010.由数字0、1、2、3、4、5组成没有重复数字的6位数,其中个位数字小于十位的数字的共有( )A 210个B 300个C 464个D 600个11.将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有( )A .10种B .20种C .36种D .52种12.如果一条直线与一个平面平行,那么称此直线与平面构成一个“平行线面组”,在一个长方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“平行线面组”的个数是 A 60 B.48 C 36 D24 二.填空题(每题4分,共16分)13.在26(1)(1)ax x -+的展开式中,3x 项的系数为-16,则实数a 的值为_________14.三个人坐在一排八个座位上,若每个人的两边都要有空位,则不同的坐法总数为__________15.将5个相同的小球放到4个不同的盒子里,每个盒子里至少放一个小球,共有_____种放法16.若将函数5()f x x =表示为250125()(1)(1).......(1)f x a a x a x a x =++++++,其中0125,,.......a a a a 为实数,则3_____a =三.解答题(每题12分,共48分)17. 一个盒子里装有4张大小形状完全相同的卡片,分别标有数字2,3,4,5;另一个盒子里也装有4张大小形状完全相同的卡片,分别标有数字3,4,5,6.现从一个盒子里任取一张卡片,其上面的数记为x ,再从另一个盒子里任取一张卡片,其上面的数记为y ,记随机变量x y η=+,求η的分布列18.从5名男生和3名女生中任选3人参加奥运会火炬接力活动,若随机变量ξ表示所选3人中女生的个数,求ξ的分布列与数学期望19. 甲、乙两篮球运动员进行定点投篮练习,每人各投4个球,甲投篮命中的概率为12,乙投篮命中的概率为23, (1)求甲至多命中2个且乙命中2个的概率(2)若规定每投篮一次命中得3分,未命中得-1分,求乙所得分数Y 的概率分布和数学期望20.设袋子中装有a 个红球,b 个黄球,c 个篮球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个篮球得3分(1)当3,2,1a b c ===时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和,求ξ的分布列(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量η为取出此球所得分数,若55(),()39E D ηη==,求::a b c21.一次考试共有12道选择题,每道选择题都有4个不同的选项,其中有且只有一个是正确的,评分标准规定:每题只选一个选项,答对得5分,不答或答错得0分,某考生已确定有8道题的答案是正确的,其余题中,有两道题都可判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因为不理解题意只好乱猜,请求出该考生: (1)得60分的概率(2)所得分数X 的分布列与数学期望山西大学附中2013-2014学年第二学期高二年级(下)5月月考数学参考答案一.选择题AACAD BCBBB AB二.13. 2或3 14. 2880 15. 4 16. -10 三.17. 解:依题意,η的可能取值是5,6,7,8,9,10,11 则有P (η=5)= P (η=6)=; ;;∴η的分布列为。
山西省山大附中2013-2014年高一下5月月考数学试卷及解析AwAKwq

山西大学附中2013—2014学年第二学期高一5月月考数学试题【试卷综析】 1.试卷题型结构合理,考试内容分布基本得当。
考试内容包括二部分三角和平面向量。
2. 试题基本特点: 注重对基本知识和基本技能的考察:试题利用选择、填空、解答三种题型,考察的覆盖面广,全面考察了这一阶段学习的高中数学的基本知识和基本技能,考查了数形结合的思想方法; 注重能力考查,在知识中考能力,试题体现考虑基础的一面,但并没有降低对能力的要求,靠单纯的记忆公式就能解决的问题不多,而是将数学思想、数学素质、能力融入解题过程中。
试题通过不同的数学载体全面考查学生的基本运算能力、逻辑推理能力。
考试时间:90分钟 考试内容(三角函数、平面向量)一、选择题:(本题共12小题,每小题3分,共36分,在每小题给出的四个选项中只有一个选项符合题目要求)1.函数()2sin cos f x x x =的最小值是( )A .1-B .2-C .2D .1 【知识点】二倍角的正弦公式;三角函数的值域. 【答案解析】A 解析 :解:因为()2si n cos f x x x =sin2x ,=又∵x ∈R ,所以1sin2x 1-≤≤,故答案选A.【思路点拨】由于()2sin cos f x x x =sin2x ,=而x ∈R 故1sin2x 1-≤≤所以y min =1-. 2.sin 45cos15cos 45sin15-的值为 ( )A .B .1-C .1 D 求出值.3.已知3,2,1,a b λ=-=-,向量a 与b 垂直,则实数λ的值为( ) A .32-B .32C .23-D .23【知识点】数量积判断两个平面向量的垂直关系.【答案解析】A 解析 :解:因为向量a 与b 垂直,所以0a b ⋅=,即()()3120λ-⨯-+=, 所以32λ=-.故答案选A. 【思路点拨】根据两个向量垂直可得0a b ⋅=,再利用向量的坐标表示出两个向量的数量积,进而得到关于λ的方程并且求出λ的数值.4.已知ABC ∆中,,,a b c 分别为,,A B C 的对边,30,34,4=∠==A b a ,则B ∠等于( )A . 30B . 30或 150C .60 D .60或 120 【知识点】正弦定理.【答案解析】D 解析 b sinB=30=代入即可求得sinB 的值,进而求得B ∠.5.函数2()2sin ()1()4f x x x R =--∈是( )A .最小正周期为π2的奇函数B .最小正周期为π的奇函数 C以原函数最小正周期为22T ππ==,又因为()sin(2)sin 2f x x x -=--=,()()f x f x ∴-=-所以是奇函数, 故答案选B.【思路点拨】利用三角函数的恒等变换化简函数的解析式为sin 2x -,从而得到函数的周期性和奇偶性.6.函数()sin()4f x x π=-的图像的一条对称轴是( )A .x π=B .x π=C .x π=-D .x π=-7.已知中,分别为的对边,,则为( ) A .等腰三角形 B .直角三角形 C .等腰直角三角形 D .等腰或直角三角形 【知识点】三角形的形状判断.【答案解析】D 解析 :解:根据正弦定理,∵cos cos a A b B =, ∴sinAcosA=sinBcosB ,∴sin2A=sin2B ,∴A=B ,或2A+2B=180°即A+B=90°,所以△ABC 为等腰或直角三角形. 故答案为选D .【思路点拨】根据正弦定理把等式cos cos a A b B =的边换成角的正弦,再利用倍角公式化简整理得sin2A=sin2B ,进而推断A=B ,或A+B=90°可得结论.【典型总结】此题考查了三角形形状的判断,其中涉及正弦定理,等腰、直角三角形的判定,A .沿x 轴方向向右平移4πB .沿x 轴方向向左平移4πC .沿x 轴方向向右平移π D .沿x 轴方向向左平移12π :2(s s i n 3x s i n3x 2412y ()=()ππ=--,co s 3)x 可以12π. sin3y x =同名的三角函数,再由左加9.已知O 为ABC ∆所在平面上一点,若OA OB OB OC OC OA ⋅=⋅=⋅,则O 为ABC ∆的( ) A .内心 B .外心 C .垂心 D .重心 【知识点】向量数量积的运算性质;三角形的垂心.【答案解析】C 解析 :解:∵OA OB OB OC ⋅=⋅,0OB OC OA ()∴⋅-=OC OA AC -=,可得OB AC ⊥,因此,点O 在AC 边上的高BE 上,同理可得:O 点在BC 边上的高AF 和AB 边上的高CD 上 ∴点O 是△ABC 三条高线的交点 因此,点O 是△ABC 的垂心, OC 移项提AC ,因3sin cos ,x x x R -∈,若 A .|,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭ B .|22,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭ C .5{|,}66x k x k k Z ππππ+≤≤+∈D .5{|22,}66x k x k k Z ππππ+≤≤+∈ 【知识点】两角差的正弦公式;三角不等式.【答案解析】B 解析 :解:()s i n co s 2s i n 6f x x x x p骣琪=-=-琪桫,()1f x ≥, 即2sin 16x p 骣琪-?琪桫,1sin 62x p 骣琪-?琪桫,522666k x k p p pp p \+??,解得: 223k x k p p p p +#+,故答案选B.【思路点拨】先把原函数化简,然后转化为2sin 16x p 骣琪-?琪桫,最后解不等式即可. 11.在锐角ABC ∆中,若2C B =,则bc的范围是( ) A .(0,2) B .)2,2( C .)3,2( D .)3,1(12.函数tan 42y x ⎛⎫=-⎪⎝⎭的部分图象如下图所示,则()OA OB AB +⋅= ( )以OA OB +=(5,1)AB =(1,()OB AB ⋅==5×案为选D .【思路点拨】先利用正切OA OB +与AB 的坐标13.若()()1,4,1,0a b ==,则2a b +的值为【知识点】向量的坐标运算;向量的模. 【答案解析】5 解析 :解:()()1,4,1,0a b==,()()()21,42,03,4a b \+=+=, 22345a b \+=+=,故答案为5.【思路点拨】由已知条件用坐标表示出2a b +,然后计算出它的模即可. 14.已知βα,⎪⎭⎫⎝⎛∈ππ,43,sin(βα+)=-,53 sin ,13124=⎪⎭⎫ ⎝⎛-πβ则cos ⎪⎭⎫ ⎝⎛+4πα= _.【知识点】平方关系;两角差的余弦公式. 【答案解析】5665-解析 :解:333,,2,442p p pa pb p a b p <<<<\<+<又因为 sin(βα+)=-,53所以()4c o s ,5ab += 3244p p p b \<-<,5cos ,413p b 骣琪\-=-琪桫则()()()cos cos cos cos sin sin 4444ppp pa ab b a b b a b b 轾骣骣骣骣犏琪琪琪琪+=+--=+-++-琪琪琪琪犏桫桫桫桫臌 453125651351365骣骣琪琪=?+-?-琪琪桫桫,故答案为:5665-. 【思路点拨】先根据已知范围求出a b +,4p b -的范围,然后用a b +,4p b -表示出4pa +, 再利用两角差的余弦公式求值即可.15.在ABC ∆中,内角,,A B C 的对边分别为,,a b c ,若ABC ∆的面积222)S a b c =+-,则C = .16.关于)42sin(3)(+=x x f 有以下命题:①若,0)()(21==x f x f 则)(21Z k k x x ∈=-π;②)(x f 图象与)42cos(3)(π-=x x g 图象相同;③)(x f 在区间]3,7[ππ--上是减函数;④)(x f 图象关于点)0,(π-对称。
山西省山大附中2013届高三数学10月月考试题 理 新人教A版

山西大学附中2012~2013学年第一学期高三(10月)月考数 学 试 题(理)(考查时间:120分钟) 一.选择题(每小题5分,共60分)1. 已知全集{}{}2,|20,|220,x U R A x x x B x ==-<=-≥则()U AC B =( )A .{}|02x x <<B .{}|01x x <<C .{}|01x x <≤D .{}|02x x <≤2. 复数11i+在复平面上对应的点的坐标是( )A .(1,1) B. (1,1)- C. (1,1)-- D. (1,1)-3.老师给学生出了一道题,“试写一个程序框图,计算S =1+13+15+17+19”.发现同学们有如下几种做法,其中有一个是错误的,这个错误的做法是 ( )4.对任意x R ∈,2|2||3|4x x a a -++≥-恒成立,则a 的取值范围是( ) A.[1,5]- B.(1,5]- C.[1,5)- D.(1,5)- 5.在△ABC 中,已知D 是AB 边上一点,若CB CA CD DB AD λ+==31,2,则λ=( ) A .32B .31 C .31- D .32-6.设0<a <1,函数2()log (22)x x a f x a a =--,则使()0f x <的x 的取值范围是 A .(,0)-∞ B. (0,)+∞ C.(,log 3)a -∞ D.(log 3,)a +∞7. 已知{}n a 为等比数列,n s 是它的前n 项和。
若2312a a a ⋅=, 且4a 与72a 的等差中项为54,则5S =( )A .35 B.33 C.31 D.298.设)(x f 为偶函数,对于任意的0>x 的数,都有)2(2)2(x f x f --=+,已知4)1(=-f ,那么)3(-f 等于( )A.2B.2-C.8D.8-9.设函数()142cos 3sin 323-+θ+θ=x x x x f ,其中⎥⎦⎤⎢⎣⎡π∈θ650,,则导数()1-'f 的取值范围是( )A.]6,3[B.]34,3[+C.]6,34[-D.]34,34[+-10.双曲线)0,0(12222>>=-b a bx a y 的渐近线与抛物线12+=x y 相切,则该双曲线的离心率等于( ) A .25 B .5 C .6 D .26 11.已知函数223)(a bx ax x x f +++=在1=x 处有极值10,则)2(f 等于( ) A.11或18 B.11 C.18 D.17或18 / 12.已知正方体1111ABCD A B C D -的棱长为2, 长为2的线段MN 的一个端点M 在棱1DD 上运动, 另一端点N 在正方形ABCD 内运动, 则MN 的中点的轨迹的面积( )A .4πB .2πC .πD .2π二、填空题:(每小题5分,共20分)13.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量 为n 的样本,其频率分布直方图如图所示, 其中支出在[)60,50元的同学有30人,则n 的值为____. 14.设0(sin cos )a x x dx π=+⎰,则二项式61()a x x-展开式中含2x 项的系数是 . 15.设A B C D 、、、是半径为2的球面上的四个不同点,且满足0AB AC ⋅=,0AC AD ⋅=,0AD AB ⋅=,用123S S S 、、分别表示△ABC 、△ACD 、△ABD 的面积,则123S S S ++的最大值是 .16.给出以下四个命题:①已知命题:p 2tan ,=∈∃x R x ;命题01,:2≥+-∈∀x x R x q 则命题q p 且是真命题;②过点)2,1(-且在x 轴和y 轴上的截距相等的直线方程是01=-+y x ; ③函数()223xf x x =+-在定义域内有且只有一个零点;④若直线01cos sin =++ααy x 和直线1cos 102x y α--=垂直,则角2().26k k k ππαπαπ=+=+∈Z 或其中正确命题的序号为 .(把你认为正确的命题序号都填上)山西大学附中10月月考数学(理)答卷纸 一.选择题(每小题5分,共60分)二.填空题:(每小题5分,共20分)13.________ 14._________ _ 15. 16.____ _______ 三、解答题:(本大题共70分)17. (本小题10分)已知C B A ,,为锐角ABC ∆的三个内角,向量m (22sin ,cos sin )A A A =-+,n (1sin ,cos sin )A A A =+-,且n m ⊥.(Ⅰ)求A 的大小; (Ⅱ)求222sin cos(2)3y B B π=+-取最大值时角B 的大小.19.(本小题12分)为了某项大型活动能够安全进行,警方从武警训练基地挑选防爆警察,从体能、射击、反应三项指标进行检测,如果这三项中至少有两项通过即可入选。
山西省山大附中2014届高三数学5月月考试题 理(含解析)新人教A版

山西大学附中2013—2014学年高三第二学期5月下数学试题(理科)【试卷综析】侧重于中学数学学科的基础知识和基本技能的考查,侧重于知识交汇点的考查,对常用方法,解题技巧,解题思路全面考查,对数量关系,空间形式,数形结合,类比,推广,特殊化等都有涉及,注重通性通法,对考生数学能力提出了较高的要求,提高了区分度. 考试时间:120分钟 满分: 150分 一、选择题:(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项符合题目要求) 1.已知集合{2,0,1,4}A =,集合{04,R}=<≤∈B x x x ,集合C A B =.则集合C 可表示为A .{2,0,1,4}B . {1,2,3,4}C .{1,2,4}D . {04,R}x x x <≤∈ 【知识点】集合的概念;交集.【答案解析】C 解析:解:A 集合中包含的只有整数为0,1,2,4,而B 集合中的整数为1,2,3,4,所以C A B =为只有1,2,4的集合,所以C 正确. 【思路点拨】按集合的定义与交集的含义可以知C 集合的元素. 2.复数5(3)z i i i =-+(i 为虚数单位),则复数z 的共轭复数为 A .2i - B .2i + C .4i - D .4i + 【知识点】复数的模;复数的运算;共轭复数. 【答案解析】A 解析:解:()()3313312i i i i i i -=+∴-=+=5522z i i i z i z ∴=+=∴=+∴的共轭复数为2i -【思路点拨】先可以求出模长,再求出5i 最后z ,找出共轭复数. 3. 设γβα,,为平面,n m ,为直线,则β⊥m 的一个充分条件是 A .n m n ⊥=⋂⊥,,βαβα B .γβγαγα⊥⊥=⋂,,m C .αγββα⊥⊥⊥m ,, D .αβα⊥⊥⊥m n n ,,【知识点】线面垂直的判定与性质;面面垂直和平行的性质与判定;逻辑关系.【答案解析】D 解析:解:因为,//n m n m αα⊥⊥∴ ,//n n αβαβ⊥⊥∴,m m αβ⊥∴⊥所以αβα⊥⊥⊥m n n ,,是m β⊥的充分条件.【思路点拨】线面垂直的判定与性质;面面垂直的性质与判定找出正确的推理过程. 4.阅读如下程序框图,如果输出4i =,那么空白的判断框中应填人的条件是A .?10≤SB .?12≤SC .?14≤SD .?16≤S 【知识点】程序框图;算法.【答案解析】A 解析:解:根据算法的运算,第一次循环后2,2i S ==,第二次循环后3,8i S ==,第三次循环后4,12i S ==这时要输出i 所以应填?10≤S【思路点拨】按算法的关系可依次计算出各次的值.5.22sin 2xdx π=⎰ A .0 B .142π- C .144π- D .12π-【知识点】导数的原函数;微积分的计算.O 5 10 15 20频率组距 重量0.06 0.1 【答案解析】B 解析:解21cos sin 2x x -=:∴它的原函数可以为11sin 22x x -,220sin 2x dx π=⎰11sin 22x x - 20|π=142π- 【思路点拨】先求出函数的原函数,再利用积分计算.6.右图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本重量的中位数为 A .11 B .11.5 C .12 D .12.5 【知识点】直方图与特征数的关系;中位数的求法.【答案解析】C 解析:解:根据中位数左右两侧的面积相等,也就是概率相等所以中位数为12,第一块的面积为0.0650.3⨯=,第二块的面积为0.5所以第三块的面积为0.2,所以中位数为12时左右的面积相等. 【思路点拨】根据中位数左右两侧的面积相等,也就是概率相等所以中位数为127.()9a b c ++的展开式中,432a b c 项的系数为A .126B .420C .630D .1260 【知识点】二项式定理;二项式项的系数. 【答案解析】D 解析:解:()()99a b c a b c ++=++⎡⎤⎣⎦,展开式中432a b c 含2c ∴()7229C a b c +⋅()7a b +中展开式的43a b 项为3437C a b 432a b c ∴的系数为239776598353612603212C C ⨯⨯⨯⋅=⋅=⨯=⨯⨯.【思路点拨】可根据各字母的次数找到展开式中的对应项,然后求它的系数. 8.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为 A .23π B .3π C .29π D .169π 【知识点】三视图;锥体的体积公式.【答案解析】D 解析:解:根据三视图可知几何体为锥体,底面扇形圆心角为23π,所以底面积为1423S rl π==,锥体的高为4,所以体积为1141643339V Sh ππ==⋅⋅=.【思路点拨】根据题意求扇形的面积,求出锥体的高,代入体积公式即可.9.过抛物线24y x =焦点F 的直线交其于,A B 两点,O 为坐标原点.若||3AF =,则AOB ∆的面积为 A 22B 2C 322D .22 【知识点】直线与抛物线;三角形的面积公式. 【答案解析】C 解析:解:(32,22AF A =∴AB 的直线方程为)221y x =-,与24y x =联立可得22520x x -+=一根为12,2x x ==所以B 点的坐标为122⎛ ⎝,12111321322222AOB SOF y OF y =⋅+=⨯⨯= 【思路点拨】可将AOB ∆分解成两个三角形,AOF BOF ∆∆的和,分别求出A ,B 点的坐标,代入即可.10.由()y f x =的图象向左平移3π个单位,再把所得图象上所有点的横坐标伸长到原来的2倍得到12sin(3)6y x π=-的图象,则()f x 为 A .312sin()26x π+B .12sin(6)6x π-C .312sin()23x π+D .12sin(6)3x π+ 【知识点】图像的平移 .【答案解析】B 解析:解:可以把12sin(3)6y x π=-的图像横坐标缩短为原来的12,()2sin 322sin 666y x x ππ⎡⎤⎛⎫=-=- ⎪⎢⎥⎣⎦⎝⎭然后向右平移3π个单位,2sin 62sin 622sin 63666y x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫=--=--=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦【思路点拨】本题可以按原来平移的过程向回平移相同的单位得到.11.现有四个函数:①sin y x x =⋅;②cos y x x =⋅;③|cos |y x x =⋅;④2xy x =⋅的图象(部分)如下:则按照从左到右图象对应的函数序号安排正确的一组是A .①④③②B .①④②③C .④①②③D .③④②① 【知识点】函数的性质;函数的图像;函数的奇偶性.【答案解析】B 解析:解:由①可知函数为偶函数,所以图像为第一个,由③|cos |y x x =⋅可知0x >时0y >,0x <时0y <所以图像为最后一个,所以顺序为B 选项的顺序.【思路点拨】可以按特殊值的问题来处理,只要找出几个选项的区别就可出找出正确选项. 12.定义在R 上的函数()f x 满足:()()1,(0)4,f x f x f '+>=则不等式()3xxe f x e >+(其中e 为自然对数的底数)的解集为 A .()0,+∞ B .()(),03,-∞+∞ C .()(),00,-∞+∞ D .()3,+∞【知识点】函数的增减性与导数;导数的运算.【答案解析】A 解析:解:因为()3xxe f x e >+()30xxe f x e ⇔-->设()()3x x h x e f x e =--则()()()()()10x x x x h x e f x e f x e e f x f x '''=+-=+->⎡⎤⎣⎦所以()h x 为增函数,又因为()00h =所以()0h x >的解集为0x >.【思路点拨】可以把不等式转化成函数求定义域问题,利用导数判断函数的增减性进而可求出定义域即不等式的解集. 二、填空题:(本大题共4小题,每小题5分,共20分) 13.已知向量)1,(z x a -=,),2(z y b +=,且b a ⊥,若变量,x y 满足约束条件⎪⎩⎪⎨⎧≤+≥-≥5231y x xy x ,则z 的最大值为 . 【知识点】向量的数量积;线性规划.x x【答案解析】3解析:解:因为b a ⊥所以()202x z y z z x y -++=∴=+由可行域可知函数在()1,1点有最大值3.【思路点拨】先依据向量的运算求出目标函数Z ,再按线性规划求出最大值.14.正四面体ABCD 的棱长为4,E 为棱BC 的中点,过E 作其外接球的截面,则截面面积的最小值为______.【知识点】几何体的作图;球的半径与截面圆的半径之间的关系.【答案解析】4π解析:解:将四面体ABCD 放置于正方体中,如图所示可得正方体的外接球就是四面体ABCD 的外接球,C∵正四面体ABCD 的棱长为4,∴正方体的棱长为可得外接球半径R 满足2R=E 为棱BC 的中点,过E 作其外接球的截面,当截面到球心O 的距离最大时, 截面圆的面积达最小值,此时球心O 到截面的距离等于正方体棱长的一半,可得截面圆的半径为2=得到截面圆的面积最小值为S=2r π =4π. 故答案为:4π【思路点拨】根据题意,将四面体ABCD 放置于如图所示的正方体中,则正方体的外再利用球的截面圆性质可算出截面面积的最小值【典型总结】求解几何体的问题,一般能恢复成规则几何体的可以恢复到规则几何体中去求解.15.有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行,则这一行的4张卡片所标数字之和等于10的概率为 .【知识点】列举法;概率的定义. 【答案解析】935解析:解:从8张卡片中取出4张卡片的基本事件有4870C = 从两组1234中取4个数之和为10的情况有1234,1144,2233.取出的卡片数字为1、2、3、4时;每个数字都有两种不同的取法,则有42=16种; 取出的卡片数字为1、1、4、4时,只有1中取法; 取出的卡片数字为2、2、3、3时,只有1中取法;这8张卡片中取出4张卡片排成一行,则这一行的4张卡片所标数字之和等于10的基本事件共18个,∴从这8张卡片中取出4张卡片排成一行,则这一行的4张卡片所标数字之和等于10的概率为1897035=故答案为:935 【思路点拨】先不考虑颜色,只选数字,可得出取4个数之和为10的情况有1234,1144,2233,再考虑每种情况下不同颜色的选择方案有哪些,利用古典概型概率个数计算即可.16.设O 是ABC ∆的三边中垂线的交点,,,a b c 分别为角,,A B C 对应的边,已知2220b b c -+=,则BC AO ⋅的范围是___________________.AD ()111222AO BC AD AC AB AD AC ADAB ∴⋅=⋅-=⋅-=()2222221111112222222AC AB b c b b b -=-=--=221124b b b ⎛⎫-=-- ⎪⎝⎭222002c b b b =->∴<< 222002c b b b =->∴<<令()21124f b b ⎛⎫=-- ⎪⎝⎭所以当12b =时,有最小值14- ()()00,22f f ==所以()124f b -≤<所以BC AO ⋅的范围是1,24⎡⎫-⎪⎢⎣⎭【思路点拨】设O 是△ABC 的三边中垂线的交点,故O 是三角形外接圆的圆心如图所示,延长AO 交外接圆于D .AD 是⊙O 的直径,∴∠ACD=∠ABD=90°cos ,cos AC ABCAD BAD AD AD ∠=∠=,()111222AO BC AD AC AB AD AC ADAB∴⋅=⋅-=⋅-=()2222221111112222222AC AB b c b b b -=-=--= 221124b b b ⎛⎫-=-- ⎪⎝⎭利用二次函数求值域即可. 三、解答题: 17.(本小题满分12分)已知数列}{n a 中,51=a 且1221n n n a a -=+-(2n ≥且*n N ∈).(Ⅰ)证明:数列12n n a -⎧⎫⎨⎬⎩⎭为等差数列; (Ⅱ)求数列}{n a 的前n 项和n S .【知识点】等差数列;错位相减法. 【答案解析】(I)略(II) ()11221n n n S n n n ++=⋅+=⋅+解析:解:(Ⅰ) ∵51=a 且1221nn n a a -=+-(2n ≥且*n ∈N ).∴设12n n na b -=,则: 15122b -==1111122n n n n n n a a b b +++---=-()111212n n n a a ++=-+⎡⎤⎣⎦()1112112n n ++⎡⎤=-+⎣⎦1=,由上可知,数列12n n a -⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列.(Ⅱ)由(Ⅰ)知,()1111122n na a n --=+-⨯,即:()121n n a n =+⋅+. ∴()()()()12122132121121n nn S n n -⎡⎤=⋅++⋅+++⋅+++⋅+⎣⎦.即()1212232212n n n S n n n-=⋅+⋅++⋅++⋅+.令()1212232212n nn T n n -=⋅+⋅++⋅++⋅, ① 则()23122232212n n n T n n +=⋅+⋅++⋅++⋅. ②②-①,得()()12312222212n n n T n +=-⋅-+++++⋅12n n +=⋅.∴()11221n n n S n n n ++=⋅+=⋅+.【思路点拨】根据递推关系式可以导出等差的通项形式,列出通项公式,依据数列的特点选择特殊数列求和的方法.【典型剖解】数列问题求通项一般都向定义方向去转化,从而找出成特殊关系的数列,进而求解. 18.(本小题满分12分)公安部最新修订的《机动车驾驶证申领和使用规定》于2013年1月1日起正式实施,新规实施后,获取驾照要经过三个科目的考试,先考科目一(理论一),科目一过关后才能再考科目二(桩考和路考),科目二过关后还要考科目三(理论二).只有三个科目都过关后才能拿到(Ⅰ)估计该驾校这100名新学员有多少人一次性(不补考)获取驾驶证;(Ⅱ)第一批参加考试的20人中某一学员已经通过科目一的考试,求他能通过科目二却不能通过科目三的概率;(Ⅲ)该驾校为调动教官的工作积极性,规定若所教学员每通过一个科目的考试,则学校奖励教官100元.现从这20人中随机抽取1人,记X 为学校因为该学员而奖励教官的金额数,求X 的数学期望.【知识点】概率的定义;条件概率;分布列与数学期望. 【答案解析】(I) 10人(II)16(III)90 解析:解:(Ⅰ)由表中数据可知一次性(不补考)获取驾驶证的频率为110, 估计这100名新学员中有100×110=10人;(Ⅱ)设“通过科目一、二、三”分别为事件A ,B ,C ,则P =P (B C |A )=21126= (Ⅲ)设这个学员一次性过关的科目数为Y ,则Y 的分布列为Y 0123P25 25 110 110EY =0×25+1×25+2×110+3×110=910而X =100Y ,所以EX =100EY =100×910=90 【思路点拨】(I) 根据概率的定义求出人数 ;(II) 利用条件概率求出值(III)列出分布列,利用两个随机变量的关系求出数学期望. 19.(本小题满分12分)如图,在四棱锥P ABCD -中,,//,,22,,PA AD AB CD CD AD AD CD AB E F ⊥⊥===分别为,PC CD 的中点,DE EC = (Ⅰ)求证:平面ABE ⊥平面BEF ;(Ⅱ)设PA a =,若平面EBD 与平面ABCD 所成锐二面角[,]43ππθ∈,求a 的取值范围.【知识点】线面垂直、面面垂直的判定定理 ;二面角. 【答案解析】(I)略(II) 25215,55a ⎡⎤∈⎢⎥⎣⎦解析:解:(Ⅰ) ,//CD AB ,AD CD ⊥22===AB CD AD ,F 分别为CD 的中点,ABFD∴为矩形,BF AB ⊥ ················· 2分EF DC EC DE ⊥∴=, ,又EF AB CD AB ⊥∴,// ⊥∴=AE E EF BF , 面BEF ,⊂AE 面ABE , ∴平面ABE ⊥平面BEF(Ⅱ) EF DC EC DE ⊥∴=, ,又EF PD //,PD AB CD AB ⊥∴,//又PD AB ⊥,所以⊥AB 面PAD ,PA AB ⊥建系AB 为x 轴,AD 为y 轴,AP 为z 轴, 则)0,2,0(),0,0,1(D B ),0,0(a P ,)0,2,2(C ,)2,1,1(aE平面BCD 法向量1(0,0,1)n =,平面EBD 法向量)2,,2(2-=a a n∴]22,21[452cos 2∈+=a θ,可得]5152,552[∈a . 【思路点拨】依据题意找出面面垂直的条件证明两个面相互垂直,建立空间坐标系,利用法向量求出夹角. 20.(本小题满分12分)已知椭圆1C 的中心为原点O ,离心率e =其一个焦点在抛物线2:C 22y px =的准线上,若抛物线2C与直线: 0l x y -+=相切.(Ⅰ)求该椭圆的标准方程;(Ⅱ)当点(,)Q u v 在椭圆1C 上运动时,设动点(,)P v u u v 2-+的运动轨迹为3C .若点T 满足:OT MN OM ON =+2+,其中,M N 是3C 上的点,直线OM 与ON 的斜率之积为1-2,试说明:是否存在两个定点,F F 12,使得TF TF 12+为定值?若存在,求,F F 12的坐标;若不存在,说明理由.【知识点】椭圆的标准方程 ;直线与椭圆的位置关系 ;向量的计算.【答案解析】(I) 12422=+y x (II) 存在两个定点,F F 12,且为椭圆2216030x y +=的两个焦点,使得TF TF 12+为定值,其坐标为12(F F解析:解:(I)由22220-0y pxy py x y ⎧=⎪⇒-+=⎨+=⎪⎩,抛物线2:C 22y px =与直线: -0l x y +=相切,240p p ∴∆=-=⇒=…2分∴抛物线2C的方程为:2y =,其准线方程为:x =,离心率e =,∴c e a ==∴2222, 2a b a c ==-=, 故椭圆的标准方程为 12422=+y x ……4分 (II )设1122(,),(,)M x y N x y ,(,)P x y '',(,)T x y则2x v u y u v '=-⎧⎨'=+⎩1(2)31()3u y x v x y ⎧''=-⎪⎪⇒⎨⎪''=+⎪⎩当点(,)Q u v 在椭圆1C 上运动时,动点(,)P v u u v 2-+的运动轨迹3C 2222111[(2)]2[()]44233u v y x x y ''''∴+=⇒-++= 2 2212x y ''⇒+=3C ∴的轨迹方程为:22212x y += ………………………………………………………6分由OT MN OM ON=+2+得212111221212(,)(,)2(,)(,)(2,2),x y x x y y x y x y x x y y =--++=++ 12122,2.x x x y y y =+=+设,OM ON k k 分别为直线OM ,ON 的斜率,由题设条件知12121,2OM ON y y k k x x ⋅==-因此121220,x x y y +=…………………………………………8分因为点,M N 在椭圆22212x y +=上,所以22221122212,212x y x y +=+=, 故222222121212122(44)2(44)x y x x x x y y y y +=+++++2222112212121212(2)4(2)4(2)604(2).x y x y x x y y x x y y =+++++=++所以22260x y +=,从而可知:T 点是椭圆2216030x y +=上的点,∴存在两个定点,F F 12,且为椭圆2216030x y +=的两个焦点,使得TF TF 12+为定值,其坐标为12(F F .【思路点拨】根据题意联立方程求出几何量,列出方程,利用向量的运算建立斜率之间的关系. 21.(本题满分12分) 已知函数()(1)xf x x e-=+(e 为自然对数的底数)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山西大学附中2012-2013学年高三(5月)月考数学(理科)试卷一、选择题:(每小题5分,共60分)1.设集合2{40}A x x =->,124x B x ⎧⎫=⎨⎬⎩⎭<,则A B = ( )A .{}2x x > B. {}2x x <- C. {}22或x x x <-> D. 12x x ⎧⎫<⎨⎬⎩⎭2.如果复数ibi212+-(其中i 为虚数单位,b 为实数)的实部和虚部互为相反数,那么b =( )(A)2(B)32(C)32-(D)23.程序框图如下:如果上述程序运行的结果S 的值比2013小,若使输出的S 最大,那么判断框中应填入( )A .10k ≤B .10k ≥C .9k ≤D .9k ≥4.右图为一个空间几何体的三视图,其中俯视图是下边一个等边三角形,其内切圆的半径是1,正视图和侧视图是上边两个图形,数据如图,则此几何体的体积是( )A .3πB .23πC .3πD .43π 5.从集合{1,2,3,4,0,1,2,3,4,5}----中选出5个数组成子集,使得这5个数中的任意两数之和不等于1,则取出这样的子集的概率为( )A .5126B .55126 C.55163 D .8636.已知椭圆C :22221(0)x y a b a b+=>>的左右焦点为12,F F ,过2F的直线与圆222x y b +=相切于点A ,并与椭圆C 交与不同的两点P ,Q ,如图,若A 为线段2PF 的中点,则椭圆的离心率为( )A B C D 7. 将数(4)30012转化为十进制数为:( )A. 524B. 774C. 256D. 2608.设不等式组 1230x x y y x ≥,⎧⎪-+≥,⎨⎪≥⎩所表示的平面区域是1Ω,平面区域2Ω与1Ω关于直线0943=--y x 对称.对于1Ω中的任意一点A 与2Ω中的任意一点B,AB 的最小值等于( )A.285B.4C.125D.29.函数2ln 2(0),()21(0),x x x x f x x x ⎧-+>=⎨+≤⎩的零点个数为( )A .0B .1C .2D .310.已知函数()|sin |(0)f x x y kx k ==>的图象与直线有且仅有三个公共点,这三个公共点横坐标的最大值为α,则α等于( )A .cos α-B .αsin -C .αtan -D .αtan11.等差数列{}n a 前n 项和为n S ,已知310061006(1)2013(1)1,a a -+-=310081008(1)2013(1)1,a a -+-=-则( )A.2013100810062013,S a a =>B.2013100810062013,S a a =<C.2013100810062013,S a a =->D.2013100810062013,S a a =-< 12.已知函数2222012()ln,(),201320132013ex e e ef x a b a b e x =++- 若f()+f()++f()=503则的最小值为( )A .6B .8C .9D .12二、填空题:(每小题5分,共20分) 13. 已知53)4sin(=-x π,则x 2sin =________.14.如图,在圆O 中,O 为圆心,AB 为圆的一条弦,4=AB ,则=⋅AB AO .15. 已知1F 、2F 为双曲线C :221x y -=的左、右焦点,点P 在C 上,21PF F ∠=060,则=⋅|PF ||PF |21_______________16.在直线2-=y 上任取一点Q ,过Q 作抛物线y x 42=的切线,切点分别为A 、B ,则直线AB 恒过的点是 三、解答题:17.(本小题满分12分)ABO14图在成且已知的对边分别为角中c b a B c b a C B A ABC ,,,135sin ,,,,,,=∆等比数列. (1)求CA tan 1tan 1+的值; (2)若c a B ac +=求,12cos 的值. 18.(本小题满分12分)某市文化馆在春节期间举行高中生“蓝天海洋杯”象棋比赛,规则如下:两名选手比赛时,每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为23,且各局比赛胜负互不影响. (Ⅰ)求比赛进行4局结束,且乙比甲多得2分的概率;(Ⅱ)设ξ表示比赛停止时已比赛的局数,求随机变量ξ的分布列和数学期望.19. (本小题满分12分)如图,正三棱柱ABC -111C B A 的所有棱长都为2,)(1R CC CD ∈=λλ20.(本小题满分12分)设点(,)P x y 到直线2x =的距离与它到定点(1,0)并记点P 的轨迹为曲线C .(Ⅰ)求曲线C 的方程;(Ⅱ)设(2,0)M -,过点M 的直线l 与曲线C 相交于,E F 两点,当线段EF 的中点落在由四点1212(1,0),(1,0),(0,1),(0,1)C C B B --构成的四边形内(包括边界)时,求直线l 斜率的取值范围. 21.(本小题满分12分) 已知函数1)(2++=x bax x f 在点))1(,1(--f 的切线方程为03=++y x . (Ⅰ)求函数()f x 的解析式;(Ⅱ)设x x g ln )(=,求证:)()(x f x g ≥在),1[+∞∈x 上恒成立; (Ⅲ)已知b a <<0,求证:222ln ln b a aa b a b +>--.请考生在第22、23题中任选一题作答。
若多做,则按所做的第一题计分。
22. 已知直线1C ⎩⎨⎧=+=a t y a t x sin cos 1’(t 为参数),曲线2C ⎩⎨⎧==θθsin cos y x (θ为参数).(II)过坐标原点O 作1C 的垂线,垂足为A ,P 为OA 中点,当α变化时,求P 点轨迹的参数方程,并指出它是什么曲线.(II)在(I)的条件下,若m x f x f ≥++)5()(对一切实数x 恒成立,求实数m 的取值范围.山西大学附中 2012-2013学年高三(5月)月考数学(理科)答案 1~6 BCCBDC 7~12 BBDDBB 13.25714. 8 15. 4 16. (0,2) 17. (1)依题意,ac b =2由正弦定理及.16925sin sin sin ,135sin 2===B C A B 得 -------------------3分.51325169135sin sin sin sin sin )sin(sin cos sin cos tan 1tan 1=⨯==+=+=+C A B C A C A C C A A C A --6分 (2)由.0cos 12cos >=B B ac 知由.1312cos ,135sin ±==B B 得(舍去负值)-------------------------------8分 从而,.13cos 122===Bac b --------------------------------------------9分 由余弦定理,得.cos 22)(22B ac ac c a b --+=代入数值,得).13121(132)(132+⨯⨯-+=c a解得:.73=+c a -----------------------------------------12分18解(Ⅰ)由题意知,乙每局获胜的概率皆为21133-=.…………1分 比赛进行4局结束,且乙比甲多得2分即头两局乙胜一局,3,4局连胜,则12212114333381P C =⋅⋅⋅=. …………4分(Ⅱ)由题意知,ξ的取值为2,4,6. ………5分 则22215(2)()()339P ξ==+=…………6分12122212212120(4)()()33333381P C C ξ==+= …………7分1221216(6)()3381P C ξ=== …………9分所以随机变量ξ的分布列为ξ2 4 6P59 2081 1681………10分则520162662469818181E ξ=⨯+⨯+⨯=…………12 19.解:(Ⅰ)取BC 的中点为O ,连结AO在正三棱柱111ABC A B C -中面ABC ⊥面1CB ,ABC ∆为正三角形,所以AO BC ⊥, 故AO ⊥平面1CB .以O 为坐标原点建立如图空间直角坐标系O xyz -,――――2分则A ,1(1,2,0)B ,(1,1,0)D -,1A ,(1,0,0)B .所以1(1,3)AB =,1(1,1DA = ,(2,1,0)DB =-,因为1111230,220AB DA AB DB ⋅=+-=⋅=-=,所以111,AB DA AB DB ⊥⊥,又1DA DB D = ,所以1AB ⊥平面1A BD . ――――-6分(Ⅱ)由⑴得(1,2,0)D λ-,所以1(1,223)DA λ=- ,(2,2,0)DB λ=-,(1,2DA λ=-,设平面1A BD 的法向量1(,,)n x y z = ,平面1AA D 的法向量2(,,)n s t u =,由1110,0,n DA n DB ⎧⋅=⎪⎨⋅=⎪⎩得平面1A BD的一个法向量为1(n λ= , 同理可得平面1AA D的一个法向量21)n =-,由1212121cos ,2||||n n n n n n ⋅<>==⋅,解得14λ=,为所求.――――12分 20.解:= ………………2分整理得2212x y +=,所以曲线C 的方程为2212x y +=………………4分 (Ⅱ)显然直线l 的斜率k 存在,所以可设直线l 的方程为(2)y k x =+. 设点,E F 的坐标分别为1122(,),(,),x y x y 线段EF 的中点为G 00(,)x y ,由22(2)12y k x x y =+⎧⎪⎨+=⎪⎩ 得2222(12)8820k x k x k +++-=由2222(8)4(12)(82)0k k k ∆=-+->解得k <<.…(1) …………7分 由韦达定理得2122812k x x k-+=+,于是 1202x x x +==22412k k-+,0022(2)12k y k x k =+=+ ……………8分因为2024012k x k =-≤+,所以点G 不可能在y 轴的右边, 又直线1211,C B C B ,方程分别为1,1y x y x =+=-- 所以点G 在正方形内(包括边界)的充要条件为000011y x y x ≤+⎧⎨≥--⎩ 即22222224112122411212k k k k k k k k ⎧-≤+⎪⎪++⎨⎪≥-⎪++⎩ 亦即222210,2210.k k k k ⎧+-≤⎪⎨--≤⎪⎩ ………………10分解得k ≤≤,……………(2) 由(1)(2)知,直线l斜率的取值范围是11[,].22-………………12分 21.解:(Ⅰ)将1-=x 代入切线方程得2-=y ∴211)1(-=+-=-ab f ,化简得4-=-a b …………………………………………2分222)1(2)()1()(x xb ax x a x f +⋅+-+=' 12424)(22)1(-===-+=-'bb a b a f解得:2,2-==b a . ∴122)(2+-=x x x f . …………………………………………4分(Ⅱ)由已知得122ln 2+-≥x x x 在),1[+∞上恒成立 化简22ln )1(2-≥+x x x即022ln ln 2≥+-+x x x x 在),1[+∞上恒成立 设22ln ln )(2+-+=x x x x x h ,21ln 2)(-++='xx x x x h …………………………………………6分∵1≥x ∴21,0ln 2≥+≥xx x x ,即0)(≥'x h ∴)(x h 在),1[+∞上单调递增,0)1()(=≥h x h ∴)()(x f x g ≥在),1[+∞∈x 上恒成立 …………………………………………8分 (Ⅲ)∵b a <<0 ∴1ba>, 由(Ⅱ)知有222ln ()1b baa a->+, …………………………………………10分 整理得222ln ln b a aa b a b +>--∴当b a <<0时,222ln ln ba aa b a b +>--. …………………………………………12分 22.解:(Ⅰ)当3π=a 时,C 1的普通方程为)1(3-=x y ,C 2的普通方程为122=+y x ,联立方程组⎪⎩⎪⎨⎧=+-=1)1(322y x x y ,解得C 1与C 2的交点坐标为(1,0),)23,21(-.――――5分 (Ⅱ)C 1的普通方程为0sin cos sin =--αααy x ,A 点坐标为)cos sin ,(sin 2ααα-,故当α变化时,P 点轨迹的参数方程为21sin ,21sin cos ,2x y ααα⎧=⎪⎪⎨⎪=-⎪⎩(α为参数)P 点轨迹的普通方程为161)41(22=+-y x . 故P 点轨迹是圆心为)0,41(,半径为41的圆.――――10 23.解:(Ⅰ)由3)(≤x f 得3||≤-a x ,解得33+≤≤-x x a .又已知不等式3)(≤x f 的解集为{}51|≤≤-x x ,所以⎩⎨⎧=+-=-5313a a ,解得2=a .――――4分(Ⅱ)当2a =时,|2|)(-=x x f ,设)5()()(++=x f x f x g , 于是⎪⎩⎪⎨⎧>+≤≤--<--=++-=.2,12,23,5,3,12|3||2|)(x x x x x x x x g ――――6分所以当3-<x 时,5)(>x g ;当23≤≤-x 时,5)(=x g ; 当2x >时,5)(>x g .综上可得,()g x 的最小值为5.――――9分从而若m x f x f ≥++)5()(,即m x g ≥)(对一切实数x 恒成立, 则m 的取值范围为(-∞,5].――――10分。
