计量经济学第四版 第二章 中文答案
计量经济学精要第四版课后习题答案.doc
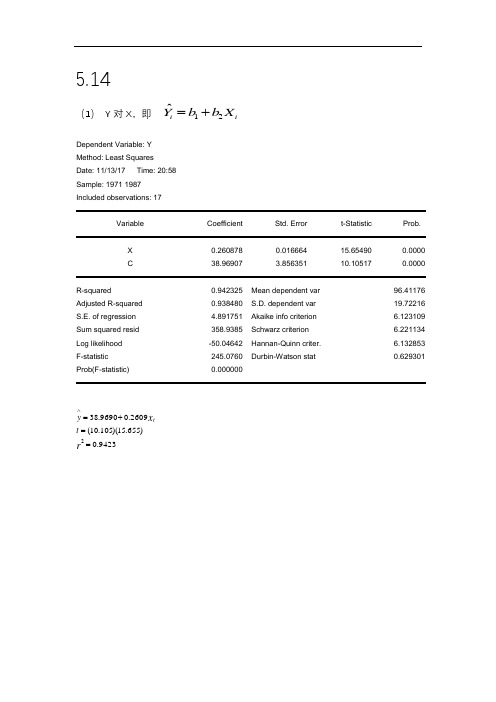
5.14(1) Y 对X ,即12ˆi iY b b X =+Dependent Variable: Y Method: Least Squares Date: 11/13/17 Time: 20:58 Sample: 1971 1987 Included observations: 17VariableCoefficient Std. Error t-Statistic Prob.X 0.260878 0.016664 15.65490 0.0000 C38.969073.85635110.10517 0.0000R-squared0.942325 Mean dependent var 96.41176 Adjusted R-squared 0.938480 S.D. dependent var 19.72216 S.E. of regression 4.891751 Akaike info criterion 6.123109 Sum squared resid 358.9385 Schwarz criterion 6.221134 Log likelihood -50.04642 Hannan-Quinn criter. 6.132853 F-statistic 245.0760 Durbin-Watson stat 0.629301Prob(F-statistic) 0.0000009423.0)655.15)(105.10(2609.09690.382==+=∧r x t y t(2)InY 对InX ,即 12ˆi iInY b b InX =+9642.0)090.20)(954.8(ln 5890.04041.1ln 2==+=∧r x t y tDependent Variable: LNY Method: Least Squares Date: 11/13/17 Time: 21:40 Sample: 1971 1987 Included observations: 17Variable Coefficient Std. Error t-Statistic Prob.C 1.404051 0.156813 8.953649 0.0000 LNX0.5889650.02931720.08981 0.0000R-squared0.964166 Mean dependent var 4.547848 Adjusted R-squared 0.961777 S.D. dependent var 0.213165 S.E. of regression 0.041675 Akaike info criterion -3.407698 Sum squared resid 0.026052 Schwarz criterion -3.309673 Log likelihood 30.96543 Hannan-Quinn criter. -3.397954 F-statistic 403.6007 Durbin-Watson stat 0.734161Prob(F-statistic)0.000000(3)InY 对X ,即 12ˆi iInY b b X =+Dependent Variable: LNY Method: Least Squares Date: 11/13/17 Time: 21:42 Sample: 1971 1987 Included observations: 17Variable Coefficient Std. Error t-Statistic Prob.C 3.931578 0.046430 84.67764 0.0000 X0.0027990.00020113.94972 0.0000R-squared0.928433 Mean dependent var 4.547848 Adjusted R-squared 0.923662 S.D. dependent var 0.213165 S.E. of regression 0.058896 Akaike info criterion -2.715956 Sum squared resid 0.052031 Schwarz criterion -2.617930 Log likelihood 25.08562 Hannan-Quinn criter. -2.706212 F-statistic 194.5946 Durbin-Watson stat 0.529132Prob(F-statistic) 0.0000009284.0)950.13)(678.84(0028.09316.3ln 2==+=∧r X t y t(4)Y 对InX ,即 12ˆi iY b b InX =+Dependent Variable: Y Method: Least Squares Date: 11/13/17 Time: 21:43 Sample: 1971 1987 Included observations: 17Variable Coefficient Std. Error t-Statistic Prob.C -192.9661 16.38000 -11.78059 0.0000 LNX54.212573.06227817.70335 0.0000R-squared0.954325 Mean dependent var 96.41176 Adjusted R-squared 0.951280 S.D. dependent var 19.72216 S.E. of regression 4.353186 Akaike info criterion 5.889824 Sum squared resid 284.2535 Schwarz criterion 5.987849 Log likelihood -48.06350 Hannan-Quinn criter. 5.899568 F-statistic 313.4086 Durbin-Watson stat 0.610822Prob(F-statistic) 0.0000009542.0)703.17)(781.11(ln 2126.549661.1922=-=+-=∧r X t Y t解:1.XY∆∆=1ˆβ斜率说明X 每变动一个单位,Y 的绝对变动量;2. E XX Y Y =∆∆=//ˆ1β斜率便是弹性系数; 3. XY Y ∆∆=/ˆ1β斜率表示X 每变动一个单位,Y 的均值的瞬时增长率; 4,. XX Y/ˆ1∆∆=β斜率表示X 的相对变化对Y 的绝对量的影响。
李子奈《计量经济学》(第4版)笔记和课后习题(含考研真题)详解

李子奈《计量经济学》(第4版)笔记和课后习题(含考研真题)详解李子奈《计量经济学》(第4版)笔记和课后习题详解第1章绪论一、计量经济学1计量经济学计量经济学,又称经济计量学,是由经济理论、统计学和数学结合而成的一门经济学的分支学科,其研究内容是分析经济现象中客观存在的数量关系。
2计量经济学模型(1)模型分类模型是对现实生活现象的描述和模拟。
根据描述和模拟办法的不同,对模型进行分类,如表1-1所示。
表1-1 模型分类(2)数理经济模型和计量经济学模型的区别①研究内容不同数理经济模型的研究内容是经济现象各因素之间的理论关系,计量经济学模型的研究内容是经济现象各因素之间的定量关系。
②描述和模拟办法不同数理经济模型的描述和模拟办法主要是确定性的数学形式,计量经济学模型的描述和模拟办法主要是随机性的数学形式。
③位置和作用不同数理经济模型可用于对研究对象的初步研究,计量经济学模型可用于对研究对象的深入研究。
3计量经济学的内容体系(1)根据所应用的数理统计方法划分广义计量经济学根据所应用的数理统计方法包括回归分析方法、投入产出分析方法、时间序列分析方法等;狭义计量经济学所应用的数理统计方法主要是回归分析方法。
需要注意的是,通常所述的计量经济学指的是狭义计量经济学。
(2)根据内容深度划分初级计量经济学的主要研究内容是计量经济学的数理统计学基础知识和经典的线性单方程计量经济学模型理论与方法;中级计量经济学的主要研究内容是用矩阵描述的经典的线性单方程计量经济学模型理论与方法、经典的线性联立方程计量经济学模型理论与方法,以及传统的应用模型;高级计量经济学的主要研究内容是非经典的、现代的计量经济学模型理论、方法与应用。
(3)根据研究目标和研究重点划分理论计量经济学的主要研究目标是计量经济学的理论与方法的介绍与研究;应用计量经济学的主要研究目标是计量经济学模型的建立与应用。
理论计量经济学的研究重点是理论与方法的数学证明与推导;应用计量经济学的研究重点是建立和应用计量模型处理实际问题。
计量经济学(第四版)习题及参考答案解析详细版

计量经济学(第四版)习题参考答案潘省初第一章 绪论试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 计量经济模型中为何要包括扰动项为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
什么是时间序列和横截面数据 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
估计量和估计值有何区别估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础略,参考教材。
请用例中的数据求北京男生平均身高的99%置信区间NS S x ==45= 用=,N-1=15个自由度查表得005.0t =,故99%置信限为x S t X 005.0± =174±×=174±也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在至厘米之间。
25个雇员的随机样本的平均周薪为130元,试问此样本是否取自一个均值为120元、标准差为10元的正态总体 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/2510/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即 此样本不是取自一个均值为120元、标准差为10元的正态总体。
计量经济学(第四版)习题及参考答案详细版

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NSS x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
计量经济学(第四版)习题及参考答案详细版

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NSS x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
计量经济学导论第四版部分课后答案中文翻译

2.10(iii) From (2.57), Var(1ˆβ) = σ2/21()n i i x x =⎛⎫- ⎪⎝⎭∑. 由提示:: 21n i i x=∑ ≥21()n i i x x =-∑, and so Var(1β ) ≤ Var(1ˆβ). A more direct way to see this is to write(一个更直接的方式看到这是编写) 21()n ii x x =-∑ = 221()n i i x n x =-∑, which is less than21n i i x=∑unless x = 0.(iv)给定的c 2i x 但随着x 的增加, 1ˆβ的方差与Var(1β )的相关性也增加.0β小时1β 的偏差也小.因此, 在均方误差的基础上不管我们选择0β还是1β 要取决于0β,x ,和n 的大小 (除了 21n i i x=∑的大小).3.7We can use Table 3.2. By definition, 2β > 0, and by assumption, Corr(x 1,x 2) < 0. Therefore, there is anegative bias in 1β : E(1β ) < 1β. This means that, on average across different random samples, the simple regression estimator underestimates the effect of the training program. It is even possible that E(1β ) is negative even though 1β > 0. 我们可以使用表3.2。
根据定义,> 0,由假设,科尔(X1,X2)<0。
因此,有一个负偏压为:E ()<。
计量经济学第2章习题参考答案

量 y 是随机变量, 解释变量 x 是非随机变量, 相关分析对资料的要求是两个变量都是随机变 量。 2. 答: 相关关系是指两个以上的变量的样本观测值序列之间表现出来的随机数学关系, 用相关 系数来衡量。 因果关系是指两个或两个以上变量在行为机制上的依赖性, 作为结果的变量是由作为原因的 变量所决定的, 原因变量的变化引起结果变量的变化。 因果关系有单向因果关系和互为因果 关系之分。 具有因果关系的变量之间一定具有数学上的相关关系。 而具有相关关系的变量之间并不一定 具有因果关系。 3. 答:主要区别:①描述的对象不同。总体回归模型描述总体中变量 y 与 x 的相互关系,而样 本回归模型描述所观测的样本中变量 y 与 x 的相互关系。 ②建立模型的不同。 总体回归模型 是依据总体全部观测资料建立的, 样本回归模型是依据样本观测资料建立的。 ③模型性质不 同。总体回归模型不是随机模型,样本回归模型是随机模型,它随着样本的改变而改变。 主要联系:样本回归模型是总体回归模型的一个估计式,之所以建立样本回归模型,目的是 用来估计总体回归模型。
1 n ∑ ui = 0 ,因为 n i =1
前者是条件期望,即针对给定的 X i 的随机干扰的期望,而后者是无条件的平均值,即针对 所有 X i 的随机干扰取平均值。
二、单项选择题 1. A 2. D 3. A 4. B 5. C 6. B 7. D 8. B 9. D 10. C 11. D 12. D 13. C
14. D 15. D 16. A 17. B
三、多项选择题 1. ACD 2. ABE 3. AC 4. BE 5. BEFH 6. DG, ABCG, G, EF 7. ABDE 8. ADE 9. ACDE
《计量经济学导论》伍德里奇-第四版-笔记和习题答案(2-8章)

inc e inc incE e inc 0 。
inc e inc
inc
2
Var e inc inc e2 。
(Ⅲ)低收入家庭支出的灵活性较低,因为低收入家庭必须首先支付衣食住行等必需品。而高收入家庭具有 较高的灵活性,部分选择更多的消费,而另一部分家庭选择更多的储蓄。这种较高的灵活性暗示高收入家庭中储 蓄的变动幅度更大。
(Ⅲ)在(Ⅱ)的方程中,如果备考课程有效,那么 1 的符号应该是什么? (Ⅳ)在(Ⅱ)的方程中, 0 该如何解释? 答: (Ⅰ)构建实验时,首先随机分配准备课程的小时数,以保证准备课程的时间与其他影响 SAT 的因素是
houri :i 1 , , n , n 表示试验中所包括的学 独立的。然后收集实验中每个学生 SAT 的数据,建立样本 sati ,
因此 GPA 0.5681 0.1022 ACT 。 此处截距没有一个很好的解释, 因为对样本而言,ACT 并不接近 0。 如果 ACT 分数提高 5 分,预期 GPA 会提高 0.1022× 5=0.511。 (Ⅱ)每次观测的拟合值和残差表如表 2-3 所示: 表 2-3
i
GPA
GPA^^源自 7.利用 Kiel and McClain(1995)有关 1988 年马萨诸塞州安德沃市的房屋出售数据,如下方程给出了房屋 价格( price )和距离一个新修垃圾焚化炉的距离( dist )之间的关系:
log price 9.40 0.312log dist n 135 , R 2 0.162
y 0 0 1 x u 0
令新的误差项为 e u 0 ,因此 E e 0 。 新的截距项为 0 0 ,斜率不变为 1 。 2.下表包含了 8 个学生的 ACT 分数和 GPA(平均成绩) 。平均成绩以四分制计算,且保留一位小数。 GPA ACT student 1 2 3 4 5 6 7 8
计量经济学第四版习题及参考答案

计量经济学第四版习题及参考答案Document number【AA80KGB-AA98YT-AAT8CB-2A6UT-A18GG】计量经济学(第四版)习题参考答案潘省初第一章 绪论试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 计量经济模型中为何要包括扰动项为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
什么是时间序列和横截面数据 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
估计量和估计值有何区别估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y 就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础略,参考教材。
请用例中的数据求北京男生平均身高的99%置信区间NSS x ==45= 用?=,N-1=15个自由度查表得005.0t =,故99%置信限为 x S t X 005.0± =174±×=174±也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在至厘米之间。
庞皓计量经济学(第四版)课后答案

第一章导论第一节什么是计量经济学计量经济学是现代经济学的重要分支。
为了深入学习计量经济学的理论与方法,有必要首先从整体上对计量经济学有一些概略性的认识,了解计量经济学的性质、基本思想、基本研究方法以及若干常用的基本概念。
一、计量经济学的产生与发展在对实际经济问题的研究中,经常需要对经济活动及其数量变动规律作定量的分析。
例如,为了研究中国经济的增长,需要分析中国国内生产总值(GDP)变动的状况? 分析有哪些主要因素会影响中国GDP的增长?分析中国的GDP与各种主要影响因素关系的性质是什么?分析各种因素对中国GDP影响的程度和具体数量规律是什么?分析所得到的数量分析结果的可靠性如何?还要分析经济增长的政策效应,或者预测中国GDP发展的趋势。
显然,对这类经济问题的定量分析,需要解决一些共性问题:提出所研究的经济问题及度量方式,确定表现研究对象的经济变量(如用GDP的变动度量经济的增长);分析对研究对象变动有影响的主要因素,选择若干作为影响因素的变量;分析各种影响因素与所研究经济现象相互关系的性质,决定相互联系的数学关系式;运用科学的数量分析方法,确定所研究的经济对象与各种影响因素间具体的数量规律;运用统计方法分析和检验所得数量结论的可靠性;运用数量研究的结果作经济分析和预测。
对社会经济问题数量规律的研究具有普遍性,计量经济学是专门研究这类问题的经济学科。
计量经济学(Econometrics)这个词是挪威经济学家、第一届诺贝尔经济学奖获得者弗瑞希(R.Frisch)在其1926年发表的《论纯经济问题》一文中,按照”生物计量学”(Biometrics)一词的结构仿造出来的。
Econometrics一词的本意是指“经济度量”,研究对经济现象和经济关系的计量方法,因此有时也译为“经济计量学”。
将Econometrics译为计量经济学,是为了强调计量经济学是一门经济学科,不仅要研究经济现象的计量方法,而且要研究经济现象发展变化的数量规律。
计量经济学(第四版)习题及参考答案详细版

计量经济学(第四版)习题参考答案潘省初第一章 绪论试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 计量经济模型中为何要包括扰动项为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
什么是时间序列和横截面数据 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
估计量和估计值有何区别估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础略,参考教材。
请用例中的数据求北京男生平均身高的99%置信区间NS S x ==45= 用=,N-1=15个自由度查表得005.0t =,故99%置信限为x S t X 005.0± =174±×=174±也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在至厘米之间。
25个雇员的随机样本的平均周薪为130元,试问此样本是否取自一个均值为120元、标准差为10元的正态总体 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/2510/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即 此样本不是取自一个均值为120元、标准差为10元的正态总体。
计量经济学(第四版)习题及参考答案解析详细版

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NS S x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
计量经济学(第四版)习习习题及参考答案详细版,DOC

欢迎共阅计量经济学(第四版)习题参考答案潘省初第一章绪论1.1试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说)(2)建立计量经济模型(3)收集数据 (4)估计参数(5)假设检验(6)预测和政策分析 1.2计量经济模型中为何要包括扰动项?这些因2.1略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间N SS x ==45=1.25 用?=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为x S t X 005.0±=174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
2.325个雇员的随机样本的平均周薪为130元,试问此样本是否取自一个均值为120元、标准差为10元的正态总体? 原假设120:0=μH备择假设120:1≠μH2.4取出16原假设:设,3.1(1)(2(3)若线性回归模型满足假设条件(1)~(4),但扰动项不服从正态分布,则尽管OLS 估计量不再是BLUE ,但仍为无偏估计量。
错只要线性回归模型满足假设条件(1)~(4),OLS 估计量就是BLUE 。
(4)最小二乘斜率系数的假设检验所依据的是t 分布,要求βˆ的抽样分布是正态分布。
对 (5)R 2=TSS/ESS 。
错R 2=ESS/TSS 。
(6)若回归模型中无截距项,则0≠∑t e 。
对(7)若原假设未被拒绝,则它为真。
错。
我们可以说的是,手头的数据不允许我们拒绝原假设。
(8)在双变量回归中,2σ的值越大,斜率系数的方差越大。
错。
因为∑=22)ˆ(tx Var σβ,只有当∑2t x 保持恒定时,上述说法才正确。
3.2设YXβˆ和XY βˆ分别表示Y 对X 和X 对Y 的OLS 回归中的斜率,证明r 3.3(((1)(2)3.4(((1) (2)3.5考虑下列双变量模型: 模型1:i i i u X Y ++=21ββ模型2:i i i u X X Y +-+=)(21αα(1)?1和?1的OLS 估计量相同吗?它们的方差相等吗? (2)?2和?2的OLS 估计量相同吗?它们的方差相等吗?(1)X Y 21ˆˆββ-=,注意到 由上述结果,可以看到,无论是两个截距的估计量还是它们的方差都不相同。
计量经济学(第四版)习题及参考答案解析详细版

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NS S x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
计量经济学第四版习题及参考答案

ncq?0孵' 1档编制存计量经济学(第四版)习题参考答案潘省初第一章绪论试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说)(2)建立计量经济模型(3)收集数据 (4)估计参数(5)假设检验(6)预测和政策分析计量经济模型中为何要包括扰动项为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因 素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
什么是时间序列和横截面数据试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民 生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人 口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面 数据的例子。
估计量和估计值有何区别 估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如「就是一个估 n 计量,F = J 。
现有一样本,共4个数,100, 104, 96, 130,则根据这个样本的数据 n第二章 计量经济分析的统计学基础略,参考教材。
请用例中的数据求北京男生平均身高的99%置信区间运用均值估计量得出的均值估计值为100 + 104 + 96 +130 =107.5 oS _5用二,N-l=15个自由度查表得%105f 故99%置信限为± Z0.0055.V =174±X = 174±也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在至厘米之间。
25个雇员的随机样本的平均周薪为130元,试问此样本是否取自一个均值为120元、标准差为10元的正态总体原假设“o:〃 = 12O备择假设”1:〃工120检验统计量查表Z0.o25 =1% 因为Z=5>Z O.025 = 1.96,故拒绝原假设,即此样本不是取自一个均值为120元、标准差为10元的正态总体。
计量经济学(第四版)习题参考答案

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析1.2 我们在计量经济模型中列出了影响因变量的解释变量,但它(它们)仅是影响因变量的主要因素,还有很多对因变量有影响的因素,它们相对而言不那么重要,因而未被包括在模型中。
为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4 估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y 就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2 NSS x ==45=1.25用=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
2.3 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/2510/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即 此样本不是取自一个均值为120元、标准差为10元的正态总体。
庞皓计量经济学 第二章 练习题及参考解答(第四版)说课讲解

国内生产总值(亿元) 48637.5 61339.9 71813.6 79715 85195.5 90564.4 100280.1 110863.1 121717.4 137422 161840.2 187318.9 219438.5 270232.3 319515.5 349081.4 413030.3 489300.6 540367.4 595244.4 643974 689052.1 743585.5
一般预算总收 入
(亿元)
地区生产总 值(亿元)
收集于网络,如有侵权请联系管理员删除
精品文档
1978 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991
1992
1993
1994 1995
1996
1997
Y 27.45 25.87 31.13 34.34 36.64 41.79 46.67 58.25 68.61 76.36 85.55 98.21 101.59 108.94
118.36
166.64
209.39 248.50
291.75
340.52
X 123.72 157.75 179.92 204.86 234.01 257.09 323.25 429.16 502.47 606.99 770.25 849.44 904.69 1089.33
1375.70
1925.91
铁路里程(万公里) 5.9 6.24 6.49 6.6 6.64 6.74 6.87 7.01 7.19 7.3 7.44 7.54 7.71 7.8 7.97 8.55 9.12 9.32 9.76 10.31 11.18 12.1 12.4
计量经济学(第四版)习题及参考答案详细版

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NSS x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
庞皓计量经济学 第二章 练习题及参考解答(第四版)
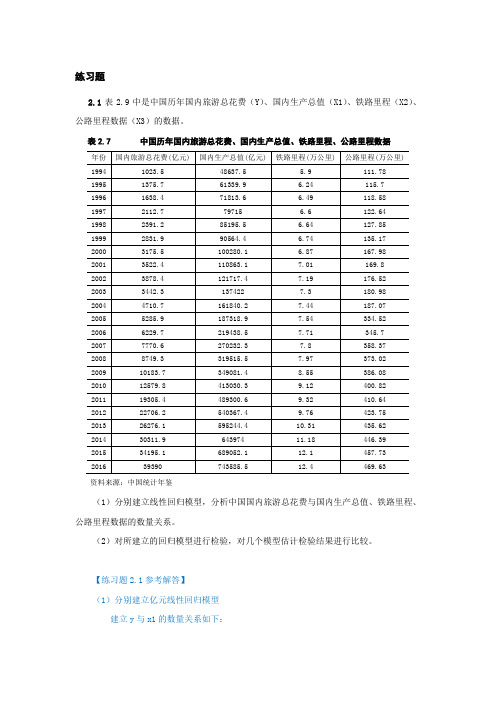
练习题2.1表2.9中是中国历年国内旅游总花费(Y)、国内生产总值(X1)、铁路里程(X2)、公路里程数据(X3)的数据。
表2.7 中国历年国内旅游总花费、国内生产总值、铁路里程、公路里程数据资料来源:中国统计年鉴(1)分别建立线性回归模型,分析中国国内旅游总花费与国内生产总值、铁路里程、公路里程数据的数量关系。
(2)对所建立的回归模型进行检验,对几个模型估计检验结果进行比较。
【练习题2.1参考解答】(1)分别建立亿元线性回归模型建立y与x1的数量关系如下:Ŷi =−3228.02+0.05X 1i建立y 与x2的数量关系如下:Ŷi =−39438.73+6165.25X 1i建立y 与x3的数量关系如下:Ŷi =−9106.17+71.64X 1i(2)对所建立的回归模型进行检验,对几个模型估计检验结果进行比较。
关于中国国内旅游总花费与国内生产总值模型,由上可知,R2=0.987,说明所建模型整体上对样本数据拟合较好。
对于回归系数的t检验:t(β1)=21.68>t0.025(21)=2.08,对斜率系数的显著性检验表明,GDP 对中国国内旅游总花费有显著影响。
同理:关于中国国内旅游总花费与铁路里程模型,由上可知,R2=0.971,说明所建模型整体上对样本数据拟合较好。
对于回归系数的t检验:t(β1)=26.50>t0.025(21)=2.08,对斜率系数的显著性检验表明,铁路里程对中国国内旅游总花费有显著影响。
关于中国国内旅游总花费与公路里程模型,由上可知,R2=0.701,说明所建模型整体上对样本数据拟合较好。
对于回归系数的t检验:t(β1)=7.02>t0.025(21)=2.08,对斜率系数的显著性检验表明,公路里程对中国国内旅游总花费有显著影响。
2.2为了研究浙江省一般预算总收入与地区生产总值的关系,由浙江省统计年鉴得到如表2.8所示的数据。
验模型的显著性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2017年,浙江省地区生产总值为52000亿元,比上年增长10%,利用计量经济模型对浙江省2017年的一般预算收入做出点预测和区间预测(3)建立浙江省一般预算收入的对数与地区生产总值对数的计量经济模型,估计模型的参数,检验模型的显著性,并解释所估计参数的经济意义。
