《点云库PCL学习教程》八叉树PPT课件
基于八叉树及KD树的混合型点云数据存储结构

基于八叉树及KD树的混合型点云数据存储结构①廖丽琼,白俊松,罗德安(北京建筑工程学院测绘工程系,北京 100044)摘 要:通过对现有点云数据存储结构进行综合分析及比较,提出了一种基于八叉树及KD树的混合型点云数据存储结构模型,文中对该模型的基本原理、实现步骤及快速索引的建立等进行了全面的论述,最后以一组实测数据为例,比较了KD树、八叉树和本文提出的混合结构三种不同数据组织方式的检索效率,证明了所提出存储结构的有效性及实用性。
关键词:海量点云;数据结构;三维激光扫描;存储结构;索引Integrated Point Cloud Storage Structure Based on Octree and KDTreeLIAO Li-Qiong, BAI Jun-Song, LUO De-An(Dept. of Surveying and Mapping, Beijing Institute of Construction Engineering and Architecture, Beijing 100044, China)Abstract: Based on analysis and comparison to existing point cloud storage structures, presents an integrated point cloud storage structure base on Octree and KDTree, describes its basic theory, work flow and index building method, at last a group of real data are employed to check and test the efficiency of Octree, KDTree and presented data structure, and the results shows that presented data structure has higher search efficiency and more suitable for point cloud data storage than the others.Key words: huge quantity of point cloud; data structure; 3D laser scanning; storage structure; index随着地面激光雷达技术的逐步成熟,以及相关仪器价格的逐步下降,越来越多的领域(如古建筑保护、施工质量检测、考古、文物数字化及建档等)开始引入该仪器,并开展了众多的应用实践,产生了良好的经济及社会效益。
PCL中八叉树理论
PCL中八叉树理论建立空间索引在点云数据处理中已被广泛的应用,常见的空间索引一般是自顶向下逐级划分空间的各种空间索引结构,比较有代表性的包括BSP树,KD树,R树,CELL树,八叉树等索引结构,其中就属KD树和八叉树在3D点云中的应用最为广泛,KD树的理论基础在上一篇推文中已经讲解,那么我们知道PCL库中已经对KD树和八叉树的数据结构的建立和索引的方法进行的实现,以方便在此基础上的其他点云的处理操作。
八叉树结构是由 Hunter 博士于1978年首次提出的一种数据模型。
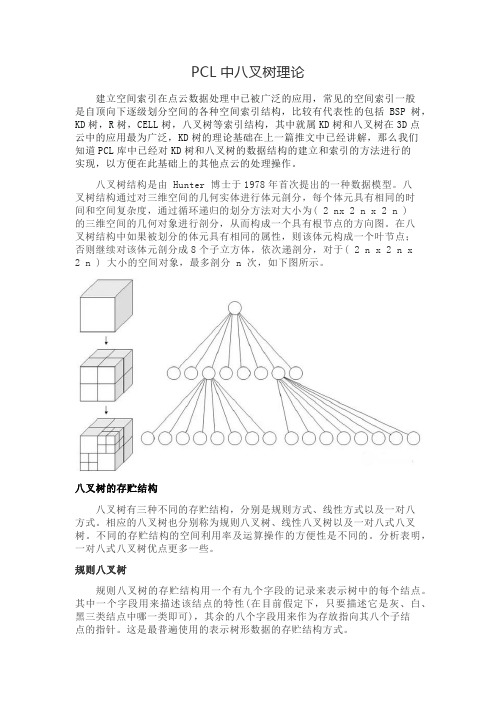
八叉树结构通过对三维空间的几何实体进行体元剖分,每个体元具有相同的时间和空间复杂度,通过循环递归的划分方法对大小为( 2 nx 2 n x 2 n )的三维空间的几何对象进行剖分,从而构成一个具有根节点的方向图。
在八叉树结构中如果被划分的体元具有相同的属性,则该体元构成一个叶节点;否则继续对该体元剖分成8个子立方体,依次递剖分,对于( 2 n x 2 n x2 n ) 大小的空间对象,最多剖分 n 次,如下图所示。
八叉树的存贮结构八叉树有三种不同的存贮结构,分别是规则方式、线性方式以及一对八方式。
相应的八叉树也分别称为规则八叉树、线性八叉树以及一对八式八叉树。
不同的存贮结构的空间利用率及运算操作的方便性是不同的。
分析表明,一对八式八叉树优点更多一些。
规则八叉树规则八叉树的存贮结构用一个有九个字段的记录来表示树中的每个结点。
其中一个字段用来描述该结点的特性(在目前假定下,只要描述它是灰、白、黑三类结点中哪一类即可),其余的八个字段用来作为存放指向其八个子结点的指针。
这是最普遍使用的表示树形数据的存贮结构方式。
规则八叉树缺陷较多,最大的问题是指针占用了大量的空间。
假定每个指针要用两个字节表示,而结点的描述用一个字节,那么存放指针要占总的存贮量的94%。
因此,这种方法虽然十分自然,容易掌握,但在存贮空间的使用率方面不很理想。
线性八叉树线性八叉树注重考虑如何提高空间利用率。
离散数学 第8章 树(祝清顺版)88页PPT文档

e6
e5
e3
e10
e9 e11
e6
e7 e8
e10
e11
离散数学
第八章 树
2007年8月20日
生成树的存在条件
定理3 任何无向连通图G 至少存在一棵生成树.
[证] 若连通图G中无回路, 则G为自身的生成树. 若G中包含回路, 则随意地删除回路上的一条边, 而
vVdeg(vi) =2m =2(n1). 另一方面, 设T有x片树叶, 可得
2(n1)= vVdeg(vi) ≥x+2(nx) 由上式解出x≥2.
离散数学
第八章 树
2007年8月20日
例题
例2 设T为6条边的树, 其顶点度为1, 2, 3. 如果T恰有3个 度为2的顶点,那么T有多少片树叶?并画出满足要求的 非同构的无向树. [解] 设T有x片树叶, 于是结点总数为
本章将对树进行详细的讨论,主要包括:
树的基本性质和生成树,
根树、有向树中的n元树、有序树和搜索树等。
离散数学
第八章 树
2007年8月20日
Discrete Mathematics
科学出版社
第1节 树
主讲:祝清顺 教授
树的概念
定义1 连通而无简单回路的无向图称为无向树, 简称树, 常用T表示树. 在树中度数为1的结点称为树叶, 度数大于1的结点称为分支结点.
e1
e4 e2 e7 e8
e6
e5 e3Fra biblioteke10
e9 e11
e1 e4 e2 e5
e3
e9
生成树T1
离散数学
第八章 树
最新-数据结构7-8-9树-PPT文档资料

本章重点:二叉树的 表示和实现
15
16 物料管理
数据结构
2、二叉树
为何要重点研究每结点最多只有两个 “叉” 的树?
二叉树的结构最简单,规律性最强; 所有树都能转为唯一对应的二叉树(可以预习6.4节)。
(1). 二叉树的定义 (2). 二叉树的性质 (3). 二叉树的存储结构
2019/4/22
2019/4/22 11
12 物料管理
数据结构
结点A的度:3 结点B的度:2 结点M的度:0
结点A的孩子:B,C,D 结点B的孩子:E,F 树的度:3 E K L A
叶子:K,L,F,G,M,I,J
结点I的双亲:D 结点L的双亲:E 结点B,C,D为兄弟 结点K,L为兄弟 J 树的深度:4
B
F
C
G H M
16
17 物料管理
数据结构
2、二叉树
(1)、二叉树的定义
是n(n≥0)个结点的有限集合,由一个根结点以及两棵互不相交的分别称 为左子树和右子树的二叉树组成。(即:空或有一个根,根有左子树、右子 树;而左右子树本身又是二叉树。)
逻辑结构: 一对二(1:2) 基本特征:① 每个结点最多只有两棵子树 (不存在度大于2的结点); ② 左子树和右子树次序不能颠倒。
3. 深度为9的二叉树中至少有
A)29 B)28 C)9
C 个结点。
D)29-1
2019/4/22
20
21 物料管理
数据结构
2、二叉树
•满二叉树: 一棵深度为k 且有2k -1个结 点的二叉树。 特点:每层都 “充满”了结 点
B
A C
L
•完全二叉树: 深度为k 的、有n个 结点的二叉树,当且 仅当其每一个结点都 与深度为k 的满二叉 树中编号从1至n的结 L 点一一对应。
《点云库PCL学习教程》八叉树PPT课件

.
3
6.1 octree概述及相关算法简介
八叉树结构是由Hunter博士于1978年首次提出的一 种数据模型。八叉树结构通过对三维空间的几何 实体进行体元剖分,每个体元具有相同的时间和 空间复杂度,通过循环递归的划分方法对大小为 2n×2n×2n的三维空间的几何对象进行剖分,从而 构成一个具有根节点的方向图。在八叉树结构中 如果被划分的体元具有相同的属性,则该体元构 成一个叶节点;否则继续对该体元剖分成8个子立 方体,依次递归剖分,对于2n×2n×2n大小的空间 对象,最多剖分n次,如图6-1所示。
octree2bufbasedatatleaft类octree2bufbase实现了同时存储管理两个八叉树于内存中如此可以非常高效地实现八叉树的建立管理等操作并且该类实现对临近树节点结构的变化探测对应到空间点云其就可以对空间曲面的动态变化进行探测在进行空间动态变化探测中非常有用例如目前基于kinect设备的体感交互应用
删除另一个缓冲区中对应八叉树的结构及其叶子节点。
void deleteCurrentBuffer()
删除当前缓冲区中对应八叉树的结构和其叶子节点。
void switchBuffers()
交换缓冲区,并重设八叉树结构。
void serializeTree(std::vector<char>& binaryTreeOut_arg, bool doXOREncoding_arg=false)
.
15
void addPointsFromInputCloud()
显示调用将点云添加到八叉树管理结构中。
void addPointFromCloud(const int pointIdx_arg, IndicesPtr indices_arg)
点云数据处理

点云数据处理ICP点云配准就是我们非常熟悉的点云处理算法之一。
实际上点云数据在形状检测和分类、立体视觉、运动恢复结构、多视图重建中都有广泛的使用。
点云的存储、压缩、渲染等问题也是研究的热点。
随着点云采集设备的普及、双目立体视觉技术、VR和AR的发展,点云数据处理技术正成为最有前景的技术之一。
PCL是三维点云数据处理领域必备的工具和基本技能,这篇博客也将粗略介绍。
三维点云数据处理方法1. 点云滤波(数据预处理)1. 点云滤波(数据预处理)点云滤波,顾名思义,就是滤掉噪声。
原始采集的点云数据往往包含大量散列点、孤立点,比如下图为滤波前后的点云效果对比。
点云滤波的主要方法有:双边滤波、高斯滤波、条件滤波、直通滤波、随机采样一致滤波、VoxelGrid滤波等,这些算法都被封装在了PCL点云库中。
2. 点云关键点我们都知道在二维图像上,有Harris、SIFT、SURF、KAZE这样的关键点提取算法,这种特征点的思想可以推广到三维空间。
从技术上来说,关键点的数量相比于原始点云或图像的数据量减小很多,与局部特征描述子结合在一起,组成关键点描述子常用来形成原始数据的表示,而且不失代表性和描述性,从而加快了后续的识别,追踪等对数据的处理了速度,故而,关键点技术成为在2D和3D 信息处理中非常关键的技术。
常见的三维点云关键点提取算法有一下几种:ISS3D、Harris3D、NARF、SIFT3D这些算法在PCL库中都有实现,其中NARF算法是博主见过用的比较多的。
3. 特征和特征描述如果要对一个三维点云进行描述,光有点云的位置是不够的,常常需要计算一些额外的参数,比如法线方向、曲率、文理特征等等。
如同图像的特征一样,我们需要使用类似的方式来描述三维点云的特征。
常用的特征描述算法有:法线和曲率计算、特征值分析、PFH、FPFH、3D Shape Context、Spin Image等。
PFH:点特征直方图描述子,FPFH:跨苏点特征直方图描述子,FPFH是PFH的简化形式。
《点云库PCL学习教程》第6章 八叉树

判断在idxX、idxY、idxZ对应的叶子节点是否存在,如果 存在返回true,否则返回false。
unsigned int getLeafCount() const
返回在该八叉树中的叶子数目。
unsigned int getBranchCount() const
返回在该八叉树中的分支数目。
void deleteTree(bool freeMemory_arg=false)
void serializeLeafs(std::vector<DataT>& dataVector_arg)
参数dataVector_arg存储八叉树中叶子节点上的数据,该 函数只串行化八叉树中的数据。
void serializeNewLeafs(std::vector<DataT>& dataVector_arg, const int minPointsPerLeaf_arg=0)
第6章 八叉树
建立空间索引在点云数据处理中已被广泛应用,常见空 间索引一般是自顶向下逐级划分空间的各种空间索引 结构,比较有代表性的包括BSP树、KD树、KDB树、R 树、R+树、CELL树、四叉树和八叉树等索引结构,而 在这些结构中KD树和八叉树在3D点云数据组织中应用 较为广泛。PCL对八叉树的数据结构建立和索引方法 进行了实现,以方便在此基础上的其他点云处理操作。 本章首先对常用的点云空间索引方法octree概念进行介 绍,然后对PCL的octree相关模块及类进行简单说明, 最后通过应用实例来展示如何对PCL中octree模块进行 灵活运用。
PCL点云库介绍

PCL点云库介绍点云库PCL模块简介1前⾔PCL(PointCloudLibrary)是在吸收了前⼈点云相关研究基础上建⽴起来的⼤型跨平台开源C++编程库,它实现了⼤量点云相关的通⽤算法和⾼效数据结构,涉及到点云获取、滤波、分割、配准、检索、特征提取、识别、追踪、曲⾯重建、可视化等。
⽀持多种操作系统平台,可在Windows、Linux、Android、MacOSX、部分嵌⼊式实时系统上运⾏。
如果说OpenCV 是2D信息获取与处理的结晶,那么PCL就在3D信息获取与处理上具有同等地位,PCL是BSD授权⽅式,可以免费进⾏商业和学术应⽤。
对于3D点云处理来说,PCL完全是⼀个的模块化的现代C++模板库。
其基于以下第三⽅库:Boost、Eigen、FLANN、VTK、CUDA、OpenNI、Qhull,实现点云相关的获取、滤波、分割、配准、检索、特征提取、识别、追踪、曲⾯重建、可视化等。
PCL利⽤OpenMP、GPU、CUDA等先进⾼性能计算技术,通过并⾏化提⾼程序实时性。
K近邻搜索操作的构架是基于FLANN(FastLibraryforApproximateNearestNeighbors)所实现的,速度也是⽬前技术中最快的。
PCL中的所有模块和算法都是通过Boost共享指针来传送数据的,因⽽避免了多次复制系统中已存在的数据的需要,从0.6版本开始,PCL就已经被移⼊到Windows,MacOS 和Linux系统,并且在Android系统也已经开始投⼊使⽤,这使得PCL的应⽤容易移植与多⽅发布。
2 PCL应⽤平台搭建机器⼈领域移动机器⼈对其⼯作环境的有效感知、辨识与认知,是其进⾏⾃主⾏为优化并可靠完成所承担任务的前提和基础。
如何实现场景中物体的有效分类与识别是移动机器⼈场景认知的核⼼问题,⽬前基于视觉图像处理技术来进⾏场景的认知是该领域的重要⽅法。
但移动机器⼈在线获取的视觉图像质量受光线变化影响较⼤,特别是在光线较暗的场景更难以应⽤,随着RGBD获取设备的⼤量推⼴,在机器⼈领域势必掀起⼀股深度信息结合2D信息的应⽤研究热潮,深度信息的引⼊能够使机器⼈更好地对环境进⾏认知、辨识,与图像信息在机器⼈领域的应⽤⼀样,需要强⼤智能软件算法⽀撑,PCL就为此⽽⽣,最重要的是PCL本⾝就是为机器⼈⽽发起的开源项⽬,PCL中不仅提供了对现有的RGBD信息的获取设备的⽀持,还提供了⾼效的分割、特征提取、识别、追踪等最新的算法,最重要的是它可以移植到android、ubuntu等主流Linux平台上,PCL⽆疑将会成为机器⼈应⽤领域⼀把瑞⼠军⼑。
点云库PCL学习教程第4章输入输出IO

4.2 PCL中I/O模块及类介绍
PCL中I/O库提供了点云文件输入输出相关的操作类, 并封装了OpenNI兼容的设备源数据获取接口,可 直接从众多感知设备获取点云图像等数据。I/O模 块利用21个类与28个函数实现了对点云的获取、 读入、存储等相关操作,其依赖于pcl_common和 pcl_octree模块以及OpenNI外部开发包。
其中,Primesense Reference Design、Microsoft Kinect和 Asus XtionPro这3种摄像头设备均进行了OpenNI兼容性 测试。选择其中任何一个设备进行点云数据采集,都 可以经OpenNI处理后转化为标准数据供上层应用使用。 如今,OpenNI已成为微软xbox360配件kinect在PC上的 开源驱动中必须安装的一个API。
点云写入到对应文件的纯虚函数接口定义,其参数意义:
file_name写入文件的文件名。 cloud需要写入的点云对象。 origin写入文件头的点云获取原点,默认为(0, 0, 0, 0)。 orientation写入文件头的点云获取方向。 binary设置写入时的类型(true为二进制,false为ASCII码,
virtual std::string getName() const = 0
返回明确的子类名字:
virtual bool isRunning() const = 0 判断是否在传输数据流:
virtual float getFramesPerSecond() const = 0 获取FPS帧率,即每秒多少帧数据。
PCL中所有的处理都是基于点云展开的,利用不同的设 备获取点云、存储点云等都是点云处理前后必须做的 流程,PCL中有自己设计的内部PCD文件格式,为此, 设计读写该格式以及与其他3D文件格式之间进行转化 的接口类都是很必要的,目前PCL内部支持对常用的 3D格式文件的打开和存储操作,以及与PCD内部格式 之间的互相转化。
PCL学习八叉树

PCL学习⼋叉树建⽴空间索引在点云数据处理中有着⼴泛的应⽤,常见的空间索引⼀般是⾃顶⽽下逐级划分空间的各种空间索引结构,⽐较有代表性的包括BSP树,KD树,KDB树,R树,四叉树,⼋叉树等索引结构,⽽这些结构中,KD树和⼋叉树使⽤⽐较⼴泛⼋叉树(Octree)是⼀种⽤于描述三维空间的状。
⼋叉树的每个节点表⽰⼀个正⽅体的体积元素,每个节点有⼋个⼦节点,这⼋个⼦节点所表⽰的体积元素加在⼀起就等于⽗节点的体积。
⼀般中⼼点作为节点的分叉中⼼。
百度百科释义:⼋叉树(Octree)的定义是:若不为空树的话,树中任⼀节点的⼦节点恰好只会有⼋个,或零个,也就是⼦节点不会有0与8以外的数⽬。
那么,这要⽤来做什么?想象⼀个⽴⽅体,我们最少可以切成多少个相同等分的⼩⽴⽅体?答案就是8个。
再想象我们有⼀个房间,房间⾥某个⾓落藏着⼀枚⾦币,我们想很快的把⾦币找出来,聪明的你会怎么做?我们可以把房间当成⼀个⽴⽅体,先切成⼋个⼩⽴⽅体,然后排除掉没有放任何东西的⼩⽴⽅体,再把有可能藏⾦币的⼩⽴⽅体继续切⼋等份….如此下去,平均在Log8(房间内的所有物品数)的时间内就可找到⾦币。
因此,⼋叉树就是⽤在3D空间中的场景管理,可以很快地知道物体在3D场景中的位置,或侦测与其它物体是否有碰撞以及是否在可视范围内。
实现⼋叉树的原理 (1). 设定最⼤递归深度。
(2). 找出场景的最⼤尺⼨,并以此尺⼨建⽴第⼀个⽴⽅体。
(3). 依序将单位元元素丢⼊能被包含且没有⼦节点的⽴⽅体。
(4). 若没达到最⼤递归深度,就进⾏细分⼋等份,再将该⽴⽅体所装的单位元元素全部分担给⼋个⼦⽴⽅体。
(5). 若发现⼦⽴⽅体所分配到的单位元元素数量不为零且跟⽗⽴⽅体是⼀样的,则该⼦⽴⽅体停⽌细分,因为跟据空间分割理论,细分的空间所得到的分配必定较少,若是⼀样数⽬,则再怎么切数⽬还是⼀样,会造成⽆穷切割的情形。
(6). 重复3,直到达到最⼤递归深度。
⼋叉树的逻辑结构如下:假设要表⽰的形体V可以放在⼀个充分⼤的正⽅体C内,C的边长为2n,形体V=C,它的⼋叉树可以⽤以下的递归⽅法来定义:⼋叉树的每个节点与C的⼀个⼦⽴⽅体对应,树根与C本⾝相对应,如果V=C,那么V的⼋叉树仅有树根,如果V≠C,则将C等分为⼋个⼦⽴⽅体,每个⼦⽴⽅体与树根的⼀个⼦节点相对应。
点云库PCL演示文稿

which is nothing else but a:
std::vector<float32> point
in C++ potential problem: everything is represented as floats (!)
Radu Bogdan RUSU
Point Cloud Library
[Motivation]
Acquisition
Data representation
Storage
PCL
Outline
1. Introduction 2. Motivation 3. Acquisition 4. Data representation 5. Storage 6. PCL
Radu Bogdan RUSU
Radu Bogdan RUSU
Point Cloud Library
[Introduction]
Motivation
Acquisition
Data representation
Storage
PCL
Introduction (2/6)
What are Point Clouds?
*
Point Cloud = a ”cloud“ (i.e., collection) of nD points (usually n = 3) p i = {xi , yi , zi } −→ P = {p 1 , p 2 , . . . , p i , . . . , p n } used to represent 3D information about the world
Point Cloud Library
《点云库PCL学习教程》PCL入门PPT课件

.
2
本章各小节目录
2.1 Windows下配置安装PCL开发环境 2.2 Linux下配置搭建PCL开发环境 2.3 其他操作系统 2.4 建立自己的PCL应用程序
.
3
2.1 Windows下配置安装PCL开发环境
.
15
2.1.2 用第三方预编译包从源码搭建开发环境
如果是除Visual Studio之外的第三方开发环境。
.
16
2.1.2 从源码搭建开发环境
从源码搭建开发环境是指读者需要自行编译链接第三方 库,然后按照2.1.2小节所介绍的编译安装PCL库。所 以在这里只介绍如何从第三方库的源码编译链接得到 第三方库,后续编译安装测试PCL与2.1.2小节一样。
.
10
将PDB解压文件复制到安装好的PCL目录下bin文件夹中, 如图2-10所示,以实现后期单步PCL源码调试,至此就 在Windows下准安装配置好PCL开发环境还需要最后一步 进行测试确保安装的正确性。
3. 测试安装是否成ake配置 文件CMakeLists.txt,如图2-11所示,其内容复制链接 /documentation/tutorials/project_inl iers.php#project-inliers中对应的代码及CMakeLists的
.
17
2.2 Linux下配置搭建PCL开发环境
对于Linux用户,搭建PCL开发环境同样有两种选择, 一是基于定期更新维护的PCL开发包,二是通过源 码编译搭建PCL开发环境,前者目前只限于Ubuntu, Debian和Fedora版本的Linux,后者需要用户自行 编译所有的第三方库,再编译PCL,对于初级用户 较困难,主要是各个库版本之间的兼容性必须选 择官方测试过的版本。
《点云库PCL学习教程》第5章 kd-tree

5.2 PCL中kd-tree模块及类介绍
PCL中kd-tree库提供了kd-tree数据结构,基于FLANN 进行快速最近邻检索。最近邻检索在匹配、特征 描述子计算、邻域特征提取中是非常基础的核心 操作。kd-tree模块利用三个类与两个函数实现了 利用kd-tree数据结构对点云的高效管理和检索, 其依赖于pcl_common模块。
纯虚函数,具体实现在其子类KdTreeFLANN中,其用来 进行r半径内的邻域搜索,参数p_q为需要查询的点, radius为需要查询的半径大小,k_indices为搜索完的邻 域点对应的索引,k_sqr_distances为搜索完的每个领 域点与查询点之间的欧式距离,max_nn为设置返回的 邻域个数上限,如果为0或者大于返回的领域个数, 其返回全部查询结果。
第5章 kd-tree
通过雷达、激光扫描、立体摄像机等三维测量设备获取 的点云数据,具有数据量大、分布不均匀等特点。作 为三维领域中一个重要的数据来源,点云数据主要是 表征目标表面的海量点集合,并不具备传统实体网格 数据的几何拓扑信息。所以点云数据处理中最为核心 的问题就是建立离散点间的拓扑关系,实现基于邻域 关系的快速查找。 本章首先对常用的点云空间索引方法kd-tree概念进行介 绍,然后对PCL的kd-tree相关模块及类进行简单说明, 最后通过应用实例来展示如何灵活应用PCL中kd-tree 模块。
图5-2 kd-tree模块中类的继承关系
类KdTree关键成员函数
KdTree(bool sorted=true)
空的构造函数
virtual void setInputCloud(const PointCloudConstPtr &cloud, const IndicesConstPtr& indices=IndicesConstPtr())
PCL中八叉树理论

PCL中八叉树理论建立空间索引在点云数据处理中已被广泛的应用,常见的空间索引一般是自顶向下逐级划分空间的各种空间索引结构,比较有代表性的包括BSP树,KD树,R树,CELL树,八叉树等索引结构,其中就属KD树和八叉树在3D点云中的应用最为广泛,KD树的理论基础在上一篇推文中已经讲解,那么我们知道PCL库中已经对KD树和八叉树的数据结构的建立和索引的方法进行的实现,以方便在此基础上的其他点云的处理操作。
八叉树结构是由 Hunter 博士于1978年首次提出的一种数据模型。
八叉树结构通过对三维空间的几何实体进行体元剖分,每个体元具有相同的时间和空间复杂度,通过循环递归的划分方法对大小为( 2 nx 2 n x 2 n )的三维空间的几何对象进行剖分,从而构成一个具有根节点的方向图。
在八叉树结构中如果被划分的体元具有相同的属性,则该体元构成一个叶节点;否则继续对该体元剖分成8个子立方体,依次递剖分,对于( 2 n x 2 n x2 n ) 大小的空间对象,最多剖分 n 次,如下图所示。
八叉树的存贮结构八叉树有三种不同的存贮结构,分别是规则方式、线性方式以及一对八方式。
相应的八叉树也分别称为规则八叉树、线性八叉树以及一对八式八叉树。
不同的存贮结构的空间利用率及运算操作的方便性是不同的。
分析表明,一对八式八叉树优点更多一些。
规则八叉树规则八叉树的存贮结构用一个有九个字段的记录来表示树中的每个结点。
其中一个字段用来描述该结点的特性(在目前假定下,只要描述它是灰、白、黑三类结点中哪一类即可),其余的八个字段用来作为存放指向其八个子结点的指针。
这是最普遍使用的表示树形数据的存贮结构方式。
规则八叉树缺陷较多,最大的问题是指针占用了大量的空间。
假定每个指针要用两个字节表示,而结点的描述用一个字节,那么存放指针要占总的存贮量的94%。
因此,这种方法虽然十分自然,容易掌握,但在存贮空间的使用率方面不很理想。
线性八叉树线性八叉树注重考虑如何提高空间利用率。
基于八叉树的点云数据的组织与可视化

基于八叉树的点云数据的组织与可视化张会霞【摘要】三维激光扫描获取了大量的点云数据,数据的组织直接影响点云数据的操作速度.采用数据库管理点云数据,对点云数据采用八叉树数据模型进行组织,建立空间索引,对点云数据进行分块提取,实现点云数据的检索以及可视化.%The three dimensional laser scanning gains the massive point cloud data,and the data organization immediate influence point cloud data operating speed. By using the database administrated point cloud data,using Octree data model to carry on the organization of the cloud data,establishing the spatial index,the point cloud data are carried on the block extraction,and realize the cloud data retrieval as well as the visualization.【期刊名称】《太原师范学院学报(自然科学版)》【年(卷),期】2011(010)003【总页数】5页(P128-132)【关键词】八叉树;点云数据;组织;可视化【作者】张会霞【作者单位】太原师范学院城市与旅游学院,山西太原030012【正文语种】中文【中图分类】TP39三维激光扫描技术(3D Laser Scanning Technology)是一种先进的全自动高精度立体扫描技术.它是一项新兴的获取空间数据的技术,同传统的测量手段相比,三维激光扫描测量技术可以连续、自动、快速地采集大量的目标物表面数据,即点云数据,并且拥有许多独特的优势[1].由于点云数据量大,把所有的点一次性的调入内存,系统运行缓慢,故需要进行合理的数据组织,建立索引.三维激光扫描获取的数据为三维目标物点云数据,由于目标物多为不规则形状,对于体状目标物数据的管理,八叉树数据模型具有独到的优势,故采用八叉树数据模型进行组织.三维激光扫描获取大量的点云数据,对点云数据采用八叉树模型进行组织,通过对点云数据层层分割,最后叶节点存储的数据量大大减少,可以加快检索速度.八叉树是一种非常直观的数据结构,具有树的深度小,遍历速度快的特点[2].八叉树分为规则八叉树和线性八叉树.规则八叉树是指直接通过八叉树结构来描述空间信息,即显性地描述节点及通过指针来表达父子关系.八叉树由中间节点组成,叶子节点保存在中间节点的子节点中.八叉树节点的数据结构要存储8个子节点的指针、父节点的指针,对于非叶子节点,还要存储下一个子节点的指针,以及该节点的属性数据,内存消耗大.线性八叉树是为了克服规则八叉树编码的不足而形成的一种高效的编码方法.这种方法只存储叶节点,包括叶节点的位置、大小、属性值.叶节点的编码称为地址码,常用的地址码是Morton码,它隐含了叶节点的位置和大小信息.比如空间目标的大小为2n×2n×2n,分辨率为1,那么任意叶节点的Morton码是一个n位数的编码[3],可以写成:八叉树的结构示意图如图1所示:点云数据由于数据量大,且都分布在目标物的外表面,在八叉树中每个节点对应一个数据块.本文对点云数据分割3次,分为4级,目的是为了分块检索数据.八叉树模型是一种中间结构,它不能直接由原始采样数据生成,只能由其他模型转换得到[4].本节由三维阵列生成八叉树模型,由于三维阵列表示的数据量大,一般情况下只作为过渡表示,把点云数据先转换成三维阵列表示,再转换成八叉树模型.对于2n×2n×2n 的三维阵列表示的目标,若某一单元的三维坐标为(I,J,K)(I,J,K=0,1,2,...,2n-1),将三维坐标转换成二进制表示有如下形式[3]:把点云数据采用八叉树模型进行分割,分割三次就产生23×23×23个三维阵列格网.确定每个点所属的三维阵列格网,也就是把点云数据归属于不同的格网中,即八叉树叶节点中.八叉树的地址码采用八进制的Morton码进行编码,通过计算每个格网的Morton码,按Morton码的大小进行排序.可根据Morton码进行分块检索.Morton码的生成算法有两种:一种是比特运算法,另一种是求余数法.比特运算法是按位操作,十进制的行号在计算机内部采用二进制的形式表示,把X、Y、Z 方向的行列号用二进制的形式II、JJ、KK表示,通过取出KK、JJ、II的二进制中的各位交叉结合,就可得到每个单元的Morton码.按位运算主要利用C语言按位操作的“或”运算,由于本文是采用C#语言进行开发,故采用第二种求Morton 码的方法求余数法进行计算.求余数法是把十进制的行列号通过求余数转换为二进制的行列号,再通过公式求出Morton码.每个点的Morton码算法如下:1)求点云数据X,Y,Z方向的最大最小点值:2)求出点云数据的外包络六面体的长L、宽W、高H:3)求出三维阵列中每个单元格的大小△X,△Y,△Z:4)求出每一个点在三维阵列中的十进制行列号l,m,k:5)将每一单元格十进制的行列号转换为二进制表示:十进制的行列号l,m,k通过求余运算,转换成二进制的行列号Ib,Jb,Kb. 6)根据二进制的行列号,计算每一点的Morton码的值.八叉树的构建在内存中进行,由于系统内存的限制,把内存结构映射到外存数据库中,并把一些信息写入外存数据库中.在数据量大时,可直接在外存数据库中进行检索,避免把所有的数据一次性的装入系统,使得系统运行缓慢.点的数据结构用C语言表示如下:struct Point数据库中点表字段设计,如表1.所对应的八叉树表字段设计,如表2.表2中Point1为叶节点的最小坐标点,Point2为叶节点的最大坐标点.code为叶节点的Morton码.采用八叉树模型组织点云数据,可以达到树的深度小,检索速度快的效果.以下代码是点云数据的八叉树模型生成算法代码,求出每个点所归属的叶节点,并把它保存在数据库中,用数据库管理点云数据,可视化时,根据需要提取出数据,加快系统运行效率.本文采用SQL Server2008管理点云数据,采用C#语言开发Map Objects组件,在Map Objects组件下进行可视化.八叉树分为四层,分割3次算法如下:1)从数据库中读出点云数据;2)求出点云数据的外包络六面体;3)求出每个点所在的十进制行列号;4)把每个十进制的行列号转换成二进制行列号;5)求出点的八叉树Morton码;6)写入数据库.关键代码如下:根据组织好的点云数据进行检索,可根据Morton码提取出点云数据,也可根据区域范围,通过八叉树索引表,确定包括那些Morton码,然后进行查询.图2是采用三维激光扫描仪获取的点云数据,本文对建筑物点云数据以文本的格式导入到SQL Server 2008数据库软件中采用八叉树数据模型进行重新组织,图3是根据Morton码提取出的点云数据,不考虑反射率,记录数71 960条,用时1 s,并在MO组件下进行可视化.实验证明,采用八叉树模型组织后的点云数据检索速度较快,适于点云数据的分块提取.本文采用八叉树组织点云数据,可实现点云数据的分块快速检索,采用MO组件进行可视化,可实现点云数据的可视化.通过编程验证,该算法效率较高.【相关文献】[1]李必军,方志祥,任娟.从激光扫描数据中进行建筑物特征提取研究[J].武汉大学(信息科学版),2003,28(1):65-70[2]惠文华,郭新成.三维 GIS中的八叉树空间索引研究[J].测绘通报,2003,1:25-27 [3]路明月,何永健.三维海量点云数据的组织与索引方法[J].地球信息科学,2008,10(2):190-194[4]李清泉,杨必胜,史文中,等.三维空间数据的实时获取、建模与可视化[M].武汉:武汉大学出版社,2003。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
4
.
5
6.2 PCL中octree模块及类介绍
PCL中octree库提供了octree数据结构,利用FLANN进 行快速邻域检索。邻域检索在匹配、特征描述子 计算、领域特征提取中是非常基础的核心操作。 octree模块利用十几个类实现了利用octree数据结 构对点云的高效管理和检索,以及相应的一些空 间处理算法,例如压缩、空间变化检测,其依赖 于pcl_common模块。
串行化输出八叉树结构到binaryTreeOut_arg向量,
doXOREncoding_arg设置输出时是否将当前缓冲区与后
台缓冲区中数据进行异或操作后再输出,异或操作是
两个八叉树结构之间差异数据的输出。
.
9
void serializeTree(std::vector<char>& binaryTreeOut_arg, std::vector<DataT>& dataVector_arg, bool doXOREncoding_arg=false)
.
3
ቤተ መጻሕፍቲ ባይዱ.1 octree概述及相关算法简介
八叉树结构是由Hunter博士于1978年首次提出的一 种数据模型。八叉树结构通过对三维空间的几何 实体进行体元剖分,每个体元具有相同的时间和 空间复杂度,通过循环递归的划分方法对大小为 2n×2n×2n的三维空间的几何对象进行剖分,从而 构成一个具有根节点的方向图。在八叉树结构中 如果被划分的体元具有相同的属性,则该体元构 成一个叶节点;否则继续对该体元剖分成8个子立 方体,依次递归剖分,对于2n×2n×2n大小的空间 对象,最多剖分n次,如图6-1所示。
第6章 八叉树
.
1
建立空间索引在点云数据处理中已被广泛应用,常见空 间索引一般是自顶向下逐级划分空间的各种空间索引 结构,比较有代表性的包括BSP树、KD树、KDB树、R 树、R+树、CELL树、四叉树和八叉树等索引结构,而 在这些结构中KD树和八叉树在3D点云数据组织中应用 较为广泛。PCL对八叉树的数据结构建立和索引方法 进行了实现,以方便在此基础上的其他点云处理操作。
返回在该八叉树中的叶子数目。
unsigned int getBranchCount() const
返回在该八叉树中的分支数目。
.
8
void deleteTree(bool freeMemory_arg=false)
删除八叉树的结构及其叶子节点。
void deletePreviousBuffer()
.
10
void deserializeTree(std::vector<char>& binaryTreeIn _arg, bool doXORDecoding_arg=false)
bool existLeaf(unsigned int idxX_arg, unsigned int idxY_arg, unsigned int idxZ_arg) const
判断在idxX、idxY、idxZ对应的叶子节点是否存在,如果 存在返回true,否则返回false。
unsigned int getLeafCount() const
.
6
octree模块中类说明
目前PCL中octree模块中目前共有16个类,以后有可能增 加。
1. class pcl::octree::Octree2BufBase<DataT, LeafT>
类Octree2BufBase实现了同时存储管理两个八叉树于内 存中,如此,可以非常高效地实现八叉树的建立管理 等操作,并且该类实现对临近树节点结构的变化探测, 对应到空间点云,其就可以对空间曲面的动态变化进 行探测,在进行空间动态变化探测中非常有用,例如 目前基于kinect设备的体感交互应用。
串行化重载函数,其中参数dataVector_arg存储八叉树中 叶子节点上的数据,其他两个参数同上。
void serializeLeafs(std::vector<DataT>& dataVector_arg)
参数dataVector_arg存储八叉树中叶子节点上的数据,该 函数只串行化八叉树中的数据。
本章首先对常用的点云空间索引方法octree概念进行介 绍,然后对PCL的octree相关模块及类进行简单说明, 最后通过应用实例来展示如何对PCL中octree模块进行 灵活运用。
.
2
本章各小节目录
6.1 octree概述及相关算法简介 6.2 PCL中octree模块及类介绍 6.3 应用实例解析
类Octree2BufBase关键成员函数:
void setMaxVoxelIndex(unsigned int maxVoxelIndex_arg)
设置在各个维度上最大的体素个数。
.
7
void setTreeDepth(unsigned int depth_arg)
设置八叉树的深度,需要在初始化八叉树时设置。
删除另一个缓冲区中对应八叉树的结构及其叶子节点。
void deleteCurrentBuffer()
删除当前缓冲区中对应八叉树的结构和其叶子节点。
void switchBuffers()
交换缓冲区,并重设八叉树结构。
void serializeTree(std::vector<char>& binaryTreeOut_arg, bool doXOREncoding_arg=false)
void serializeNewLeafs(std::vector<DataT>& dataVector_arg, const int minPointsPerLeaf_arg=0)
串行化当前缓冲区八叉树中存在但在后台缓冲区八叉树 中不存在的节点数据,其中,minPointsPerLeaf_arg为 需要串行化的节点中点的最小个数,如果点个数小于 该值则不串行化此新节点。
void add(unsigned int idxX_arg, unsigned idxY_arg, unsigned int idxZ_arg, const DataT& data_arg)
在idxX、idxY、idxZ对应的叶子节点上填充DataT的数据, 其中idxX、idxY、idxZ为在三个维度上的整型索引值。
