正弦交流电路
电工学-正弦交流电路

O
f 而对直流所呈现的容抗趋于无穷大,故
XL 与 f 的关系 可视为开路。
2.3.3 电容元件的交流电路
1. 电压电流关系 i
+
u
C
–
i
u Um sint i Im sin( t 90 )
+j •
u
I
波 形O 图
电流超前电压 90 电压与电流大小关系 电压与电流相量式
t
U XCI U jXC I
2.1 正弦电压与电流 I, U
直流电路在稳定状态下电流、电压的大
小和方向是不随时间变化的,如图所示。
正弦电压和电流是按正弦规律周期性
变化的,其波形如图示。
O u, i
t
电路图上所标的方向是指它们的参考
方向,即代表正半周的方向。
负半周时,由于的参考方向与实际方
+
向相反,所以为负值。
实
i
O i
t
际 方
第 2 章 正弦交流电路
在生产和生活中普遍应用正弦交流电,特别是三相电路应 用更为广泛。
正弦交流电路是指含有正弦电源(激励)而且电路各部分所 产生的电压和电流(响应)均按正弦规律变化的电路。
本章将介绍交流电路的一些基本概念、基本理论和基本分 析方法,为后面学习交流电机、电器及电子技术打下基础。
本章还将讨论三相交流电路和非正弦周期电压和电流。 交流电路具有用直流电路的概念无法理解和无法分析的物 理现象,因此在学习时注意建立交流的概念,以免引起错误。
•
UL
为正
时电路 中电压 电流相 量图
•
• UL UC
•
U
•
UR
•
UC
的大小和正负由
电工电子技术-第2章 正弦交流电路
•
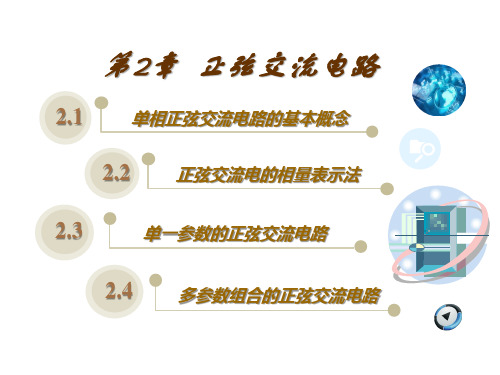
I m = 14.1∠36.9°A
其有效值相量为:I• = 10∠36.9°A
由于一个电路中各正弦量都是同频率的,所以相量只需 对应正弦量的两要素即可。即模值对应正弦量的最大值或 有效值,幅角对应正弦量的初相。
i u u、i 即时对应! R
电流、电压的瞬时值表达式
设 i Im sin t u、i 同相!
则 u ImR sin t Um sin t
u、i最大值或有效值之间符
合欧姆定律的数量关系。
Um ImR
或
U IR
•
相量关系式
•
I
U
U0
U
0 I0
RRR
相量图
U
I
(2)电阻元件上的功率关系
3
C -4
D
D 3 j4 第四象限 D 5 arctan 4
3
上式中的j 称为旋转因子,一个复数乘以j相当于在复
平面上逆时针旋转90°;除以j相当于在复平面上顺时针
旋转90°。
※数学课程中旋转因子是用i表示的,电学中为了区别 于电流而改为j。
正弦量的相量表示法
与正弦量相对应的复数形式的电压和电流称为相量。为
乘、除时用极坐标形式比较方便。
在复数运算当中,一定要根据复数所在象
限正确写出幅角的值。如:
+j
B4
A
A 3 j4 第一象限 A 553.1arctan 4 3
B 3 j4 第二象限 B 5180 arctan 4
-3 0
3
+1
3
正弦交流电

返回
上一页 下一页
(2) 平均功率(有功功率)P
i
瞬时功率在一个周期内的平均值
+
u
1T
1T
P T 0 p dt T 0 u i dt
大写 1 T 1
p
_ p
R
T
0 2 UmIm(1 cos 2ω t)dt
P
1T
UI(1 cos2ω t)dt UI
T0
O
ωt
P U I I 2R U 2 单位:瓦(W)
返 回 上一页 下一页
(3)相量的两种表示形式
相量式: U Uejψ U ψ U( cos ψ jsin ψ)
相量图: 把相量表示在复平面的图形
可不画坐标轴
I
U
(4)只有同频率的正弦量才能画在同一相量图中。
(5)相量的书写方式 • 模用最大值表示 ,则用符号:
U m 、Im
• 实际应用中,模多采用有效值,符号: U 、I
i 10 sin ( ω t 60)?A
最大值
4 2 sin (ω t 30 )A?
瞬时值
4.已知:
U 100 15V
U 100V ?负号 ? U 100 ej15 V
返回
上一页 下一页
2.3 电阻元件、电感元件与电容元件
2.3.1 电阻元件
1 电压与电流的关系
u Ri
2 电阻元件的参数
i 2π
O
ωt
T
周期 T:变化一周所需要的时间(s)
频率 f :1s 内变化的周数(Hz)
f
=
1 T
角频率ω: 正弦量 1s 内变化的弧度数
ω = 2πf
=
2π T
电工第2章 正弦交流电路

图2-2 正弦交流电波形图
2.1 正弦交流电量及基本概念
(1)最大值 又称为幅值,是正弦量的最大值,用带右下标m的大写 字母表示,如Im、Um、Em分别表示正弦电流、正弦电压、正弦电动 势的最大值。 (2)角频率ω 在单位时间内正弦量所经历的电角度,用ω表示,其单 位为弧度每秒(rad/s)。正弦交流电变化一次所需的时间,称为周期T, 其单位为秒(s),正弦量在单位时间内变化的次数,称为频率f, 其单位为赫[兹](Hz)。
图2-9 纯电阻电路
2.3 单一参数元件的正弦交流电路
(2) 有效值关系 由电流与电压的幅值关系Im= Um /R,两端同除 以 ,可得它们的有效值关系为U=IR (3) 相量关系 因为电流i和电压u均为同频率的正弦量。 相量形式为 2.电阻元件的功率 (1) 瞬时功率 在关联参考方向下,电阻元件的 瞬时功率(用小写字母p表示):
图2-4 两正弦量的同相与反相
2.1 正弦交流电量及基本概念
例2.1 已知正弦量u=220sin(314t + 30°)V, 试求正弦量的三要素、有效值及变化周期。 解:对照式(2-1),可知三要素:
2.1 正弦交流电量及基本概念
例2.2 已知正弦电压u和正弦电流i1、i2的瞬时表达式为u = 310sin(ωt -45°)V,,i2=28.2sin(ωt +45°)A,试以电压u为参考量重新写出u和 电流i1、i2的瞬时值表达式。 解:以电压u为参考量, 则电压u的表达式为 由于i1、i2与u的相位差为
2.2 正弦交流电的相量表示方法
2.2.2 正弦量的相量表示法 正弦量和相量是一一对应关系(注意:正弦量和相量不是相等
关系!)。在复平面中,例如相量可用长度为 ,与实轴正向的夹 角为ψ的矢量表示。这种表示相量的图形称为相量图。如图2-7所示
正弦交流电路定义 -回复

正弦交流电路定义-回复什么是正弦交流电路?正弦交流电路是指由正弦波形的电压或电流组成的电路系统。
正弦波形是一种周期性变化的波形,具有均匀而连续的变化特点,可以描述许多实际电源和负载所产生的电压和电流。
在正弦交流电路中,电压和电流的大小会随着时间的推移而不断变化,但其变化满足正弦函数的规律。
正弦函数是一种典型的周期函数,其图像呈现出一种重复模式,具有相同的幅值和频率。
正弦交流电路由多个元素组成,包括电源、负载以及连接电源和负载的导线。
电源可以是交流电源或直流电源,而负载可以是电阻、电感、电容或他们的组合。
在正弦交流电路中,电压和电流的变化遵循欧姆定律、基尔霍夫定律和电容、电感的特性等。
欧姆定律描述了电压、电流和电阻之间的关系,表明它们成正比关系;基尔霍夫定律描述了电流在闭合电路中的分配和电压在闭合电路中的合成;电容和电感则分别描述了电压和电流随时间的变化规律。
正弦交流电路在实际应用中具有广泛的用途。
例如,在家庭中,我们常常使用交流电路来为各种电器设备供电,如电视机、冰箱、空调等。
在工业生产中,正弦交流电路也是不可或缺的部分,被用于各种电机、照明设备、变压器、电子器件等的驱动和控制。
为了更好地分析和设计正弦交流电路,我们可以使用交流电路理论和相关工具。
交流电路理论包括复数分析法、相频特性、幅频特性、相频特性等方法和概念,可以帮助我们理解电压和电流在正弦交流电路中的行为。
此外,计算机软件也可以提供模拟和仿真工具,以帮助我们更好地理解和优化正弦交流电路的性能。
总而言之,正弦交流电路是由正弦波形的电压或电流组成的电路系统,具有周期性变化的特点。
它在日常生活和工业生产中广泛应用,通过交流电路理论和相关工具的应用,我们可以更好地分析和设计正弦交流电路。
第2章_正弦交流电路

ψ
+
90
°
- jA
- jA = 1 - 90° × r ψ = r ψ − 90°
三. 正弦量的相量表示法 相量:表示正弦量的复数。 相量:表示正弦量的复数。
相量表示方法: 相量表示方法: 设正弦量: 设正弦量: i = I msin( ω t + ψi )
大写字母上打点, 大写字母上打点,表示相量 模 =正弦量的最大值 & 最大值相量 Im = Imejψi = Im ψi 辐角= 辐角=正弦量的初相角 有效值相量
i1 i3 i2
i2 =
2 I 2 sin ( ω t + ψ 2 ), 求 i3 = i1 + i2
结论: 同频正弦量运算后仍得到同频的正弦量。 结论:●同频正弦量运算后仍得到同频的正弦量。 直接进行正弦量的运算很繁琐。 ●直接进行正弦量的运算很繁琐。 解决办法:把正弦量用相量(复数)表示, 解决办法:把正弦量用相量(复数)表示,先进行复数 运算,求出相量解, 运算,求出相量解,再根据相量解写出正弦量瞬时值表 达式。这种分析方法称为相量法。 达式。这种分析方法称为相量法 相量法。
正弦量的波形
i
Im
ψ
ωt
i = I m sin(ω t + ψ )
幅值(最大值) I m : 幅值(最大值) 角频率(弧度/ ω : 角频率(弧度/秒)
特征量: 特征量:
ψ : 初相角
2.1.1 正弦量的三要素
1. 幅度(最大值): 幅度(最大值) 最大的瞬时值,对确定的正弦量而言是一个常 最大的瞬时值, 量。最大值必须用带下标m的大写字母表示。 最大值必须用带下标m的大写字母表示。 如:Um、Im。
超前i (1)ϕ >0, u超前 , 超前 滞后u 或i滞后 滞后
电工技术-第六章正弦交流电路

❖ 例6-3-1 已知u1 3 2 sin 314t V ,u2 4 2 sin(314t 90) V , 求 u u1 u2的瞬时值表达式。
❖ 解:相量图如图6-3-2所示。 因为
U U12 U22 32 42 5 ( V )
arctan U2 arctan 4 53
❖ 综上所述,正弦交流电的交变情况主要取决 于以下三个方面: 1. 交变的快慢:用角频率反映。 2. 交变的幅度:用最大值反映。 3. 交变的起始状态:用初相位反映。
❖ 因此,把最大值、角频率、初相位称为正弦 交流电的三要素。
e Em sin(t e ) u Um sin(t u ) i Im sin(t i )
2. 最大值
交流电在一个周期内所能达到的最大瞬时值 称为最大值(又称峰值、幅值),分别用Im、 Um、Em来表示。
❖ 3. 有效值
把一交变电流i和一直流I分别通过两个阻值相同 的电阻R,如果在一个周期内,它们各自在电 阻上产生的热量彼此相等,则此直流值叫作该 交变电流的有效值。
交流电的有效值实际上就是在热效应方面同它
《电工技术》
第六章 正弦交流电
6-1 交流电的定义及正弦交流电动势的产生
❖ 1.交流电的定义
大小和时间都随时间做周期性变化的电动势、 电压和电流分别称为交变电动势、交变电压和 交变电流,统称为交流电。
(a)
(b)
(c)
图6-1-1 几个交流电的波形图
❖ 2.直流电与交流电的区别 直流电的方向不随时间而变化,交流电的大 小和方向随着时间不断变位差 两个同频率正弦交流电的相位角之差。实质上就是 它们的初相角之差。
(t 1) (t 2 ) 1 2
第3章 正弦交流电路

3.3.1 单一参数的正弦交流电路
1.纯电阻电路 (1) 电压与电流的关系
+
u iR
u
i I m sin t
_
u iR I m R sin t U m sin t
i R
对于正弦交流电路中的电阻电路(又称纯电阻 电路),一般结论为:
1)电压、电流均为同频率的正弦量。
2)电压与电流初相位相同,即两者同相。
y
i
ω
Im
i1
ωt1 φ
Im
i0
90
o
x
o
ωt1
ωt
φ
t t1 i1 I m sin(t 1)
对于一个正弦量可以找到一个与其对应的旋转矢量,反之, 一个旋转矢量也都有一个对应的正弦量。
3.2.2 复数及复数的运算 1、复数
A a jb
A r cos r sin
e j cos j sin
作相量图时要注意: 只有同频率的正弦量才 能画在一个相量图上,不 同频率的正弦量不能画在 一个相量图上。
+j
U
Φu
o
Φi
+1
I
3.3正弦交流电路的简单分析与运算
电阻元件、电感元件与电容元件都是组成 电路模型的理想元件。
所谓理想元件,就是突出元件的主要电磁 性质,而忽略其次要因素。如电阻元件具 有消耗电能的性质(电阻性),其它的电 磁性质如电感性、电容性等忽略不计。。
f = 1/T T = 1/f
i
角频率是指交流电在1s内变化的电 Im
角度。正弦量每经过一个周期T,
o
对应的角度变化了2π弧度,所以
φ
ωt
T
2f 2
正弦交流电路-详解

275.已知一正弦信号源的电压幅值为10 mV,初相位为30°,频率为1 000 Hz,则电 压瞬时值表达式为__D____。
A.u(t) 10 2 sin(314t 30)mV B. u(t) 10sin(314t 30) mV
C. u(t) 10 2 sin(2000 t 30) mV D.u(t) 10sin(2000 t 30) mV
i
初相位:
初相位等于t =0 时的相位角), O
ωt
是观察正弦波的起点。(又称相位)
初相位等于 0 的正弦量称为参考正弦量
相位差 :
如:u Umsin( ω t ψ1 ) i Imsin( ω t ψ2 )
则相位差 : ( t 1 ) ( t 2 )
ψ1 ψ2
两个同频率正旋量相位差等于初相位之差。
282.如图所示,某正弦电流波形图,其瞬时值表达式为__B____。
i 10 2 sin(314 t 90) i 10sin(314t 90) i 10sin(314t 90) i 10sin(31.4t 90)
301.正常情况下用电压表测的电压值是______;而设备名牌上的电压值是__C____。 A.最大值/最大值 B.有效值/最大值 C.有效值/有效值 D.最大值/有效值
令:XL ωL 2πfL 称为感抗
90
③相位关系 :u 超前 i 90度
ψu ψi 90
感抗的说明:
XL 2 π fL
直流:f = 0, XL =0,电感L视为短路
交流:f
XL
电感L具有通直阻交的作用
XL ω L 2 π f L 感抗XL是频率的函数
XL和I与f的关系图示:
I , XL
ωt
电工电子技术-正弦交流电路

j
•
I
dt
I( i 90)
类似地:
i(t)dt 的相量为
1
•
I
j
I
( i
)
2
五、基尔霍夫定律的相量形式
1、基尔霍夫电流定律的相量形式
在正弦交流电路中,流入任一节点的各支路电流的相量代数
流I 通过同样大小的电阻在相等的时间内产生的热量相等,
那么这个周期性变化的电流i 的有效值在数值上就等于这个
直流I。
即: T i 2 Rdt T I 2 Rdt ,
0
0
I 1 T i2dt T0
★规定:有效值──用大写字母U、I、E表示。
★交流表:其A、V指示的往往为有效值,如:220V, 380V。耐压值往往指最大值。
i
+1
求:
•
I
•
、U
,并作相量图。
பைடு நூலகம்
O
a
解:
•
I
141
.4
30
100
30
A
2
•
U
311 .1 60 220 60
V
+j
•
I
30
+1
O 60
例4:
已知
2
f
•
1000Hz,I
0.5
30A
。求i(t)
?
•
U
解: 2f 6280rad / s
i(t) 0.5 2 sin(6280 t 30)A
解:直接用三角函数进行:
u u1 u2 5sin(ωt 30) 10 sin(ωt 60)
9.33sinωt 11.16cosωt
正弦交流电路

f 1 T
2 2 f
T
小常识
* 电网频率: 中国 50 Hz 美国 、日本 60 Hz
* 有线通讯频率:300 - 5000 Hz
* 无线通讯频率: 30 kHz - 3×104 MHz
正弦波 特征量之三
-- 初相位
i 2I sin t
u u1 u2
2U1 sin t 1 2U 2 sin t 2
2U1 sin t 1 2U2 sin t 2
2U sin t 幅度、相位变化 频率不变
结论:
因角频率()不变,所以以下讨论同频率正弦波 时, 可不考虑,主要研究幅度与初相位的变化。
例 已知: i sin1000 t 30
不同频率不行。
新问题提出: 平行四边形法则可以用于相量运算,但不方便。
故引入相量的复数运算法。
相量
复数表示法 复数运算
相量的复数表示
将复数 U 放到复平面上,可如下表示:
j
bU
U
+1
U a2 b2
tg 1 b
a
a
U a jb U cos jU sin
U
b
U
a
U a jb
欧 拉
i
u
R
i 2 I sin ( t) u 2U sin ( t)
p u i Ri 2 u 2 / R
小写
p u i Ri 2 u 2 / R
iu
ωt
p
ωt
结论:
1. p 0 (耗能元件)
p 2. 随时间变化
3. p 与 u2、i2 成比例
2. 平均功率(有功功率)P:一个周期内的平均值
正弦交流电路_单一参数的正弦交流电路

iL
+
uL
L
−
u 波 形 图0
i
U•
相
t
量 图
I• 0°
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
(2)大小关系
uL L Im sin( t 90 ) U m sin( t 90 )
最大值: U m L I m 有效值: U ω L I
定义: X L L ——感抗
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
(3)相量关系 I I 0 U U 9 0 X L I 90 0 X L 90 I 0 jX L I
U jX L I j L I
u
i
0
t
第二章 正弦交流电路
2.功率 (1)瞬时功率
p ui
U m I m s in t s in t 90
(能量的吞吐)。
0
t
p
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
(3)无功功率 为了同电感的无功功率相
p u i UI sin 2t
比较,设电流 i I m s in t
u
i
为参考量,则: u U m sin( t 90 )
p uHale Waihona Puke U I sin 2 t0
t
储放 储放储放 能能 能能能能
p
0
t
u
i
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
2. 功率
平均功率(有功功率) P 1 T pdt U I I 2 R U 2
T0
R
平均功率衡量电路 中所消耗的电能, 也称有功功率。
正弦交流电路课件

电感器的感值大小与线圈的匝数、线圈的直径、 线圈的材料等因素有关。
详细描述
电感器在正弦交流电路中能够阻碍电流的变化, 使电流的变化率降低。电感器的电流和电压之间 存在相位差,相位差的大小取决于电感器的大小 。
详细描述
电感器的感值大小由亨利定律确定,即电感器的 感值与线圈中的磁场强度成正比。在正弦交流电 路中,电感器的感抗大小会随着频率的变化而变 化。
电容器
总结词
详细描述
总结词
详细描述
电容器是正弦交流电路中的另 一重要元件,用于储存电场能 量。
电容器在正弦交流电路中能够 阻碍电压的变化,使电压的变 化率降低。电容器的电流和电 压之间存在相位差,相位差的 大小取决于电容器的大小。
电容器的容值大小与电容器极 板的面积、极板之间的距离、 电介质等因素有关。
分析数据
根据实验数据,分析正弦交流 电路的基本特性和元件参数对
电路性能的影响。
仿真软件介绍与使用
软件名称
Simulink
功能特点
Simulink是MATLAB的一个附加组件,用于进行动态系统模拟和分析。它提供了丰富的库和工具,可用于构建和仿 真各种类型的电路,包括正弦交流电路。
使用方法
在Simulink中,用户可以创建电路模型,设置元件参数,选择适当的激励源和测量仪器,然后运行仿真 以观察电路的行为。分析仿真结果可以帮助用户深入理解正弦交流电路的工作原理。
谐振与频率响应
谐振
正弦交流电路中某些特定频率下的振动现象,可能导致电压或电流的异常升高 。
频率响应
表示正弦交流电路在不同频率下的性能表现,包括幅频特性和相频特性。
03
正弦交流电路的元件
电阻器
第3章正弦交流电路
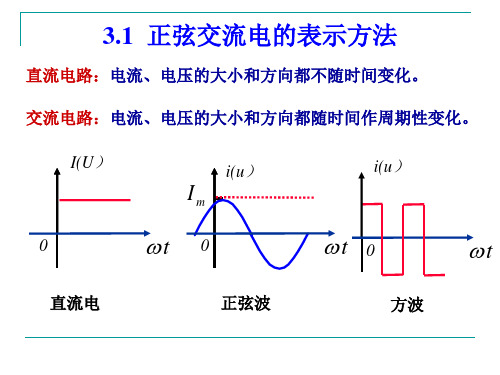
3)指数形式
A =r (cos jsin) = re j
4)极坐标形式
A=r∠
从图中可以看出,复数A的实部a、虚部b与模r构成一个直角三角形。
三者之间的关系为
r a2 b2
arctan b
个正弦量同相,如图4.2 (b)所示;
(4) 当 12 = 时,一个正弦量到达正最大值时,另一个正弦量到达
负最大值,此时称第1个正弦量与第2个正弦量反相,如图4.2 (c)所示;
(5) 当 12 = /2时,一个正弦量到达零时,另一个正弦量到达正最
大值(或负最大值),此时称第1个正弦量与第2个正弦量正交。如图4.2 (d) 所示。
U1 U1 1
U U1 U 2
U 2 U 2 2
u(t ) 2 U cos( t )
故同频正弦量相加减运算变成对 应相量的相加减运算。
i1 i2 = i3
I1 I2 I3
3.2 单一参数正弦交流电路的分析
一、纯电阻元件电路
1. 电阻元件 在正弦电路中,电流、电压虽然都是随时间变化
= 311sin(30°)= 115.5V
i= 5sin(314t 90°) = 5sin(314×0.00333 90°) = 5sin(150°)
= 2.5A
可见,当两个同频率正弦量的计时起点变化时,各自的相位将发生
变化,但其相位差不变。说明相位的大小与计时起点的选择有关,
而相位差与计时起点的选择无关。
(2)、 乘除运算——极坐标为例
若 A1= r1 1 ,若A2= r2 2
则
A 1
第4章 正弦交流电路

b
同频正弦量的乘除法运算与复数运算相同,而 且在线性电路当中,运算后的频率是不会改变的。
§4.3 电阻、电感、电容元件的交流电路
一、电阻元件的交流电路
iR 2I Rsin( t i ) uR R 2I Rsin( t i )
2U Rsin( t u )
时域下的电阻模型
由于直流电在电阻上做功大小为 I2RT ,于是根据定义有:
I RT i Rdt R Im 2 sin 2 tdt
2 2 0 0
T
T
即: I 2 RT RIm 2
T
0
1 cos 2t RTIm 2 dt 2 2
得
Im I 0.707 Im 2
结果说明正弦电流的有效值等于最大值的0.707倍。同理, 正弦电压的有效值为:
U 1 U 1 u1 U 2 U 2 u 2
b
U b U b ub
k 1
则对应于 u1 (t ) u2 (t ) ub (t ) uk (t )
有
U1 U 2 U b U k
k 1
b
同理设 i1 (t ) 2 I 1 sin( t i 1 ) i 2 (t ) 2 I 2 sin( t i 2 ) i b (t ) 2 I b sin( t ib )
复数A的实部a1及虚部a2与模a及辐角θ的关系为:
a1 a cos
其中
a2 a sin
a2 arctg a1
a
2 a1
2 a2
1.复数的表示形式:
根据上式关系式及欧拉公式
+j a2 O
第四章: 正弦交流电路

= 2U sin (t+90)
i
【小结】电感两端电压和电流关系:
O
ωt
① 两者频率相同;
90
② 电压超前电流90,即相位差为:
= u i 90
③ 大小关系:U=I·L=I· XL ; XL为感抗;
20
i(t)= 2I sin t
u(t)= 2IL sin (t+90)
2. 感抗:Ω
∵ 有效值:U =I L
u
i
o
ωt
i
i
i
i
+
--
+
u uuu
-
++-
p(t)
+ p <0 + p <0
o
p >0
p >0
∵ 储存能量和释放能量交替
进行 ∴ 电感L是储能元件。
【结论】纯电感不消耗能量, 只和电源进行能量交换(能量 的吞吐)。
ωt
储能 释能 储能 释能
24
(3)无功功率Q:
用以衡量电感电路中与电源交换能量的瞬时最大值即振幅 称作~。即:
正确写出幅、角的值。如:
+j
B 4
A
A 3 j4
第一象限
4 A 5 arctan
3
-3 0 C -4
B 3 j4
第二象限
4 B 5(180 arctan )
+1
3
3
C 3 j4
第三象限
4 C 5(arctan 180)
3
D
D 3 j4
第四象限
4 D 5( arctan )
3
式中的j 称为旋转因子,复数乘以j相当于在复平面上逆
正弦交流电路

2. 平均功率(有功功率)P:一个周期内的平均值
i
P=UI
=I2R=i U2/2RI
sint
Uu =IRR
u 2U sint
P1 Tpd t1Tuidt
T0
T0
大写 1 T 2UIsin2t dt
T0
1
T
UI(1cos2t)dtUI
T0
§ 3.4 理想电感元件上的正弦稳态响应
一、电压电流关系
即:瞬时值和相量满足基尔霍夫定律,有效值不满足
I1I2I30
I1
I3
I1-I2+I3= 0
I2
U 3
U 4
U 2 U 1 U 2 U 3 U 4 U 5 U 6 0 U 1
U 5
U 6
例: i162si nt (3)0
i282si nt (6)0
求i=i1+i2
i
解: I 1 6 3 0 5 .1 9 j3 6
Im[Ime ji e jt ]
复指数函数中的一个复常数
复常数定义为正弦量的相量,记
为
Im
相量 的表示
Im 为“最大值”相量
Im Im eji Im i
I 为“有效值”相量 IIeji Ii
相量是一个复数
注意
1)相量可以代表一个正弦量,但不等于该
正弦量。
U 50ej15° 50
2
sin(
实部是余弦量 虚部是正弦量
则 I[ m Im e j( t i)] Im sitn ( i)
正弦量可以用上述形式复数函数描述
I[ m Im e j( t i)] Im sitn ( i)
正弦量可以用上述形式复数函数描述
《电工电子技术》——正弦交流电路

dt
dt
Im sin(wt 90)
1 电压与电流之间的频率关系 电容元件两端的端电压与电流是同频率的正弦电量。
2 电压与电流之间的数值关系
最大值
Im
wCU m
Um 1 /(wC )
有效值
I wCU U U 1/(wC) X c
X c 等于电压有效值与电流有效值之比,单位为欧[姆],称为容 抗。
计算过程请参考书本,相量图为:
2.3单一参数交流电路
2.3.1单一电阻元件正弦交流电路 一、单一电阻元件正弦交流电路电压与电流之间的关系
i
u
R
i u U m sin(wt u )
R
R
2U R
sin(wt
u
)
单一电阻元件正弦交流电路电压与电流之间有如下几种关系:
1 电压与电流之间的频率关系 在单一电阻电路中,通过电阻元件的电流与其两端电压是 同频率的正弦电量。
I Ie j i I i
I 为有效值
二、相量图
在复数平面上,用几何图形表示正弦量的相量的图,称为相 量图。
已知正弦电压: 相应的电压相量为
u 220 2 sin(wt 45)
U 22045
已知正弦电流: 相应的电流相量为:
i 8 2 sin(wt 30)
字母 T 表示,单位是秒(s)。正弦量在1秒时间内重复变化的
周期数称为频率,用小写字母 f 表示,单位为赫兹(Hz),如 果1秒钟内变化一个周期,频率是1Hz。周期与频率互为倒数关 系:
f 1 T
在我国,发电厂提供的交流电的频率为50Hz,其周期 T 0.02, 这一频率称为工业标准频率,也称工频。
电工基础正弦交流电

05
正弦交流电的测量与仪 器
交流电压表与电流表
交流电压表
用于测量正弦交流电压的大小,通常采用电 磁感应原理,将交流电压转换为可测量的直 流电压。
交流电流表
用于测量正弦交流电流的大小,通常采用电 磁感应原理,将交流电流转换为可测量的直
流电流。
功率表与功率因数表
要点一
功率表
用于测量正弦交流电路的功率,可以测量有功功率和无功 功率。
THANKS FOR WATCHING
感谢您的观看
谐振与滤波
谐振
正弦交流电路中的一种特殊状态,当电路的感抗与容抗相等时,电流与电压相位相同, 产生共振现象。谐振时电路的阻抗最小,电流最大,可能会引起过电流和设备损坏。
滤波
通过电路中的电容、电感等元件,将特定频率的信号滤除,实现信号处理和噪声抑制。 在正弦交流电路中,滤波器可以用于分离不同频率的信号,提高电路的稳定性和可靠性。
正弦交流电的三要素
幅值、频率和相位。幅值表示正弦波 的最大值,频率表示单位时间内波动 的次数,相位表示正弦波在某一时刻 所处的位置。
正弦交流电的特点
周期性
01
正弦交流电每秒完成一个周期的波形变化,其频率和周期成反
比。
相位差
02
两个不同频率或不同相位的正弦交流电在合成时会产生相位差。
方向性
03
正弦交流电的电压和电流方向随时间变化,但平均值保持不变。
1
变压器由两个线圈(初级和次级)和一个磁芯组 成。初级线圈输入电压,在磁芯中产生磁场,次 级线圈感应出电压。
2
变压器的工作原理基于电磁感应定律,即变化的 磁场会产生感应电动势,而感应电动势的大小与 磁通量的变化率成正比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正弦交流电路一、选择题1、电路如图T -4,若()0221160-cos ,cos t U u t U u m m ωω==,则=•R C ω( B )。
(A) 21 (B) 3 (C) 31 (D) 21图T -4 2、在R 、L 、C串联电路的总电压、电流分别为250=•U V00,=•I 01.53A5则电路的复功率为( A )VA 。
(A) 01.531250-∠=S (B) 01.531250∠=S(C) 01.531250-∠-=S (D) 1250=S2、对于正弦交流电路中电容元件,下列相量图正确的是 D 。
(A) (B) (C) (D)3、在R 、L 、C 串联正弦交流电路中,各电压的正确关系是 C(A )U=U R +U L +U C (B )222C L R U U U U ++= (C ) U = (D) ••••-+=C L R U U U U4、正弦稳态交流电路中,正确反映电感元件电压、电流相位关系的是 D 。
25、电路的相量模型如下图所示,已知时域电流i =23cos2t A ,则u 为( A )V(A )23cos2t (B )02.4cos(236.9)t - (C )3cos2t (D )322cos2t6、电路如下图所示,电源角频率1/rad s ω=,则ab 间的等效阻抗为( A )Ω (A )jj -+11 (B )j j -+12 (C )j j--12 (D )17、将正弦电压 u = 10 cos( 314t +30︒ ) V 施加于感抗 Z L = j5 Ω 的电感元件上,则通过该元件的电流 i = ( C )。
(A) 50 cos( 314t +90︒ ) A (B) 2 cos( 314t +60︒ ) A(C) 2 cos( 314t -60︒ ) AX i uL +8、在图示电路中,电源为正弦电压,电压表V 1 的读数为60 V ,V 的读数为100V ,求V 2 的读数为( B )。
V VR LV V 12(A) 20V(B) 80V(C) 40V9、正弦交流电路中,纯电容上下列表达式正确的是 C 。
(A )C j I U CC ω-=•• (B )1C CU jCI ω••=- (C )C I U C C ω= (D )C j i u C C ω1-= 10、已知()102cos 3143i t π=+A ,下式对其向量表达正确的是( A )A 。
(A )03010∠=•I (B )66.85j I +=•(C )()060sin 60cos 210j I +=•(D )06010-∠=•I11、串联交流电路中总电压为u ,电流为i ,电阻R 取用的有功功率计算式为( D )(A )P=ui (B )P=••I U (C )P=i 2R (D )P=RI 212、如图所示电路,对该电路KVL 描述正确的是( D )(A )S U ••••=-+I C1I L ωI R ω(B )S U C ••••=++I j I L ω j I R ω (C )S U C ••••=-+I j I L ω j I R ω(D )S U ••••=-+I C1 j I L ω j I R ω13、某负载的等效阻抗Z=20+j10Ω,它的等效复导纳为( B )(A )S j Y ⎪⎭⎫ ⎝⎛+=101201(B )Y=(0.04 — j0.02 )S(C )Y=(0.5 — j0.25)S (D )Y=(0.02 — j0.01)S14、在一个电阻和电感串联的正弦稳态交流电路中,下列关系式错误的是( A )。
(A )U=U R +U L (B )u=u R +u L (C )Z R =ϕcos (D )PQ arctg =ϕ 15、图示正弦交流电路,当电源电压不变,其频率升高一倍时,各电流表的读数为( B )。
(A ) A1不变,A2增大一倍,A3减少一倍 (B ) A1不变,A2减少一倍,A3增大一倍 (C ) A1不变,A2、 A3同时增大一倍 (D ) A1不变,A2、 A3同时减少一倍16、图所示正弦交流电路,三个电流表的读数分别为 ( C )17、对于正弦稳态电路,下列说法不正确的是( )。
(A)有功功率守恒; (B)复功率和视在功率均守恒;(C)无功功率守恒; (D)有功功率和无功功率均守恒。
18、对于正弦稳态的无独立电源的二端网络0N ,当端口等效复阻抗的阻抗角出现O Z 90>ϕ时,下列说法不正确的是( C )。
(A)0N 内含有受控源; (B) 0N 发出有功功率;(C)0N 吸收有功功率; (D) 0N 既不发出也不吸收有功功率。
二、填空题1、两同频率的正弦电压分别为40V 、30V ,若使其和为50V ,则这两个正弦电压的相位差为 。
2、电路如下图所示,则电源提供的功率为 25w 。
3、R 、L 、C 串联正弦交流电路发生谐振时,其特点是输入阻抗等于 ,电流与总电压的相位关系为 ,电阻电压与总电压的关系为 。
4、在某一频率时,测得某线性时不变无源电路的阻抗为Z=8+j6Ω,则此电路呈电感 性,功率因数为 0.8 。
5.RLC 串联电路如图示,其谐振频率为 106rad/s6、某正弦电压有效值为220V ,频率为50Hz , 在 t =0 时,u (0)=220V ,则该正弦电压表达式为()220245)u t t π︒=±。
7、与电流相量 )07.7j 07.7(-=IA 对应的正弦电流可写作 i =245)t A ω︒- 。
8、正弦交流电路中,感抗X L 随频率增大而 增大 。
9、复阻抗(34)Z j =+Ω,则复导纳Y=342525j - S 10、R 、L 、C 串联电路,当频率f 0= LCf π20=,感性,容性 时电路发生谐振,当f>f 0时,电路呈 性;f<f 0时,电路呈 性。
11、已知无源一端口网络,端口0260)V u t =-,)135314cos(25.00-=t i A ,则u 与i 之间的相位差为 75°感 ,网络呈性。
12、感性负载提高功率因素的常用方法是 并联电容 。
13、图T-6电路中,欲使Ω8获得最大功率,则变比=n50 。
图T-6 图T-714、图T-7所示电路中,a ,b 端的电压为 04525∠ V 。
+-+-•IV O 05∠Ω100Ω100j V j 5ab +-abU•n:1Ω8+-V o 3010∠Ωk 2015、一个周期性u 有效值的表达式为 。
16、 图T-17电路中 则有效值电流=2I 2A图T-1717.图T-18电路中U=10V ,电路吸收的功率P=12W ,则=L U 8V 。
图T-18三、计算题 1、.图示正弦交流电路,已知各电流表有效值读数均为3A , (1)计算总电流、总电压的有效值;(2) 以电阻电压为参考相量,画出各电流、电压的相量图。
答案:(1)总电流为3A ,总电压V U 2.21253=⨯= (5分) (2) 相量图(略) (5分) 2、图示电路,当外施电压U=100V 时,各支路电流的有效值相等,即I 1=I 2=I ,且电路消耗的功率为866W ,试求电路中的电阻R 、感抗X L 及容抗X C 。
⎰=T dt u T U 0214:1+-sm U •Ω101•I 2I Ω-10j Ω10•I L j ωLU •+_•U ,010V U o sm ∠=•答案:令•U=100∠00,I1=I2=I=10A (4分)R=8.66Ω,X L=5Ω,X C=10Ω(6分)3、图示电路,问C取多大值能使端口电压u与电流i同相位。
答案:Z =5+j(15-1/1000C);C=66.7微法4、求图示电路的谐振频率。
已知L I=2H,L2=1H,M=1H,C=100μf。
答案:ω=100rad/s5、图示电路,已知I1=3A,I2=6A,I3=2A,试求电源提供的功率P。
答案:令•U=U∠00,I•1=3A、I•2=﹣j6A、I•3=j2A (5分) I•=3﹣j4A (2分)P=3×I22+2×I21=93W (3分)6、图示电路中,已知 R = 30 Ω,L = 382 mH ,C = 40 μF ,电源电压 u = 2502cos 314 t V 。
求(1)电流i 电压u 1 ; (2)有功功率P 和功率因数λ;(3)画出相量图 (I ,U , 1U )。
i RLCu u 1+-+-答案:解:(1)X L X C L C ==⨯===⨯=ωω314038************806.ΩΩZ =+-=30120805022()ΩI U Z ===250505A 3040=tan =R X ϕA )1.53314cos(25 1.53 -==t i ϕ (2分)V 86.225.618)120j 30(1.535)j (1 ∠=+-∠=+=L X R I U (2分) V )86.22314cos(25.6181 +=t u(2分)(2) P I R ==⨯===2253075053106W λcos ..o(2分)(3)U UI.. .22.8653.11。
(2分)7、已知图示正弦稳态电路中,电流表A 1、A 2的指示均为有效值(10A),求电流表A 的读数。
解:令︒•∠=0RC RC U U 10j U C j I RC C ==••ω 10==••RU I RCR A j I I I R C ︒•••∠=+=+=452101010 即电流表A 的读数为A 210。
8、图示电路中,R = 80 Ω,L = 127mH ,C = 40μF ,i = 602cos(314t + 30︒) V 。
求:(1) 电路的有功功率,无功功率和功率因数 ;(2) 画出关于U,R I , L I , C I •的相量图。
解:(1)Ω=⨯⨯==-40101273143j j L j Z L ωΩ-=⨯⨯-=-=-80104314116j j C jZ C ω S j j j Y 45802801801801401801-∠=-=-++=V YI U ︒︒︒••-∠=-∠∠==1524800458023060(3分)707.045cos cos === ϕλW 144226024800cos k I U P =⨯⨯==ϕvar 144226024800sin k I U Q =⨯⨯==ϕ(6分)相 量 图:(1分)9、图示正弦交流电路,已知电路发生谐振时,A 1读数为15A ,A 读数为9A ,求A 2的读数。
解:2215912A -=10.图示正弦交流电路,已知:V 1411=U ,A 252=I ,A 153=I ,电路消耗的功率为P=1000W ,求R 1和X L1。
