控制理论作业二答案.docx
地大《现代控制理论》在线作业二[60467]
![地大《现代控制理论》在线作业二[60467]](https://img.taocdn.com/s3/m/e1976da4b307e87100f6969d.png)
地大《现代控制理论》在线作业二
一、单选题
1.保证稳定是控制系统正常工作的必要前提,对受控系统通过反馈使其极点均具有负实部,保证系统渐近稳定称为()。
A.能控性
B.能观性
C.系统镇定
D.稳定性
答案:C
2.对于能控能观的线性定常连续系统,采用静态输出反馈闭环系统的状态()。
A.能控且能观
B.能观
C.能控
D.以上三种都有可能
答案:A
3.对于同一个系统,可有()个状态空间表达式。
A.1个
B.2个
C.3个
D.无穷多个
答案:D
4.由状态空间模型导出的传递函数()。
A.惟一
B.不惟一
C.无法判断
D.皆有可能
答案:A
5.维数和受控系统维数相同的观测器为()。
A.降维观测器
B.全维观测器
C.同维观测器
D.以上均不正确
答案:B
6.根据线性二次型最优控制问题设计的最优控制系统一定是()的。
A.渐近稳定
B.稳定
C.一致稳定
D.一致渐近稳定
答案:A
7.下列语句中,正确的是()。
A.系统状态空间实现中选取状态变量是唯一的,其状态变量的个数也是唯一的
B.系统状态空间实现中选取状态变量不是唯一的,其状态变量的个数也不是唯一的。
《现代控制理论》第三版 第二章.习题答案

2-7. 证明 2-3 中,状态方程的解: 1. 即当u(t ) K (t ),x(0 ) x0时
x(t ) e At x0 e At BK , 式中K 与u(t )同维的常数矢量。
x e x0 e A( t ) BK ( )d
At 0 t
e x0 e A( t ) ( )d BK
得 1 0; 2 1.
1 0 据 1 I A P P 1 1 0 1 0
得到 P 1 0 1 ;
T
0 0 P2 0 得 到 根 据 2 I A P2 1 1
1 0 1 1 1 于是T , P2 , T 1 1 1 1 于是 T 1 0 e 1 G (T ) e AT T T T T e 1 0 e t T T e 0 K At H (T ) e dtB dt 0 0 1 et 1 0 1 0
1
e At 0 (t ) I 1 (t ) A
1 2cos 2t 2 4sin 2t
sin 2t 2cos 2t
1 1 (2) A 4 1
1 22 1 33 A t A t 2! 3! 直接法: 7 3 t 2 13 3 2 1 5 , t t t t t 2! 6 6 2 28 3 t 13 3 2 4 4 , 1 5 t t t t t 6 2! 6 e At I At
y 2 x1 x2
1 1 0 x1 K x x 2 1 0 x2 0 即 x1 y 2 1 x2 0 u1 u 1 2
现代控制理论 王金城 第二章答案

第2章习题参考答案:2-1 (1)①⎥⎦⎤⎢⎣⎡=--t t t3200e e eA , ②待定系数法122303231123213t t t t t t e e e e e e αα--------⎡⎤⎡⎤-⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦201300t At t ee (t )I (t )A e αα--⎡⎤=+=⎢⎥⎣⎦(2)①约当标准形:2220tt At t e te e e ---⎡⎤=⎢⎥⎣⎦②122111221020t t At t s e te e L (sI A )L s e -------+-⎡⎤⎡⎤⎡⎤=-==⎢⎥⎢⎥⎣⎦+⎣⎦⎣⎦(3)①约当标准形:233300000t Att t t e e e te e ----⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦②1211133320000031000300t At tt t s e e L (sI A )L s e te s e --------⎡⎤+⎡⎤⎢⎥⎢⎥⎡⎤=-=+-=⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥+⎣⎦⎣⎦(4)①21201001Att t e t ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦②222121012001Att t e I At A t .....t !⎡⎤⎢⎥⎢⎥=+++=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦2-2(1)113141I A ()()λλλλλ---==-+--1231,λλ==-313031131344111144t t tt t t e e e e e e αα----⎡⎤+⎢⎥⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎢⎥⎣⎦-⎢⎥⎣⎦330133111122441122t tt t At t t t t e e e e e (t )(t )A e e e e αα----⎡⎤+-⎢⎥=+=⎢⎥⎢⎥-+⎢⎥⎣⎦(2)1011236116I A ()()()λλλλλλλ--=-=++++123123,,λλλ=-=-=-2310223132231662211111245832139122t t t tt t t t t t t t(e e e )(t )e (t )e (e e e )(t )e (e e e )ααα-------------⎡⎤--+-⎢⎥⎡⎤-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=-=--+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥--+-⎢⎥⎣⎦⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+-+--+--+--+-+-+-+-=---------t t t tt t t t t t t t t t t t t t t t t t t t tt t t3-2-3-2-3-2-3-2-3-2-3-2--3-2-3-2-3-2 4.540.513.5162.59123 1.520.54.582.53630.50.51.542.533e e e e e e e e e e e e e e e e e e e e e e e e e e e e A 2-3 ①211012I A ()λλλλ--==+=+ 121λλ==-11010111P λ⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦ 11011P -⎡⎤=⎢⎥⎣⎦ 11101A P AP --⎡⎤==⎢⎥-⎣⎦ ②Laplace 变换法:1111112t t t At tt t s te e te e L (sI A )L s te e te -----------⎡⎤+⎡⎤⎡⎤=-==⎢⎥⎢⎥⎣⎦+--⎣⎦⎣⎦③待定系数法:1011101t t t t t(t )e e te (t )te te αα-------⎡⎤⎡⎤+⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦01Ate (t )(t )A αα=+=t t t t t t te e te tee te ------⎡⎤+⎢⎥--⎣⎦ 2-4(1)1000001010()I ⎡⎤⎢⎥Φ=≠⎢⎥⎢⎥-⎣⎦∴不满足条件; (2)10001()⎡⎤Φ=⎢⎥⎣⎦ ∴满足条件11(0)41A ⎡⎤=Φ=⎢⎥⎣⎦2-5 2211120t t (e )(t )e --⎡⎤-⎢⎥Φ=⎢⎥⎣⎦①自身性 10001()I ⎡⎤Φ==⎢⎥⎣⎦② 传递性1021102122211020221111112200(t t )(t t )(t t )(t t )(e (e (t t )(t t )(t t )e e --------⎡⎤⎡⎤---⎢⎥⎢⎥Φ-⋅Φ-=⋅=Φ-⎢⎥⎢⎥⎣⎦⎣⎦③可逆性0000122100221111112200(t t )(t t )(t t )(t t )(e )(e (t t )(t t )e e ----------⎡⎤⎡⎤--⎢⎥⎢⎥Φ-=⋅=Φ-⎢⎥⎢⎥⎣⎦⎣⎦1(t )(t )-Φ=Φ- ∴满足2-6 (1)000t A(t )⎡⎤=⎢⎥⎣⎦202000t tA()d ττ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎰,141202100080000000t t d d τττττ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦⎰⎰ 42t t 1000(t,0)82010000⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥Φ=+++⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦ ()t t t ⎡⎤++⎢⎥=⎢⎥⎢⎥⎣⎦241+0,02801Φ (2)00t te A(t )e--⎡⎤=⎢⎥⎣⎦0010010t t t e e d eeτττ----⎡⎤⎡⎤-=⎢⎥⎢⎥-⎣⎦⎣⎦⎰ 1212121010100010t e e d d e eτττττττ----⎡⎤⎡⎤⎡⎤--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎣⎦⎣⎦⎰⎰ ∴⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++++++=-- 21+00-00-021+00,2--2tt tt t e e e e )(Φ 2-7 ∵1At 1111s 1cos 2t sin 2t e L (sI A )L 44s 2sin 2t cos 2t ----⎡⎤-⎡⎤⎢⎥⎡⎤=-==⎢⎥⎣⎦⎢⎥-⎣⎦⎣⎦∴1(t )(t )(0)-Φ=x x-1-2t -t 2t t 2t t 1-2t-t 2t t2t t 12e 2e e 2e 2e 2e (t )(t )(0)-1-1-e -e e e2e e ---------⎡⎤⎡⎤-+-+⎡⎤==⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦Φ=x xt 2tt 2t t 0t 0t2tt 2t 42-2e -2e -2e -4e (t )13e -2e e -4e ----==-----⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦A =Φ2-8 e e e e ()e e e e t t t t ttt t t tt (t )(t )t -=-⎡⎤+-=-==⎢⎥+-+⎣⎦ΦΦΦ221222222 2-9 (1)AttA(t )0(t )e (0)e Bu()d τττ-+⎰x x =At 222100t 01011t 11I At A t t 010********!2⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+++=+++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦e 2t 0t 11t 01t (t )d 2110011t ττ⎡⎤-⎡⎤⎡⎤⎡⎤⎡⎤+-⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦+⎢⎥⎣⎦⎰1t x =0(2)1t 2t t 2t At 111t 2tt 2t s 12e e e e e L (sI A )L 2s 32e 2e e 2e -------------⎡⎤--⎡⎤⎡⎤=-==⎢⎥⎢⎥⎣⎦+-+-+⎣⎦⎣⎦At t A(t )0(t )e x(0)e Bu()d τττ-=+⎰x22154()2245tt t t e e x t e e ----⎡⎤+-⎢⎥=⎢⎥-+⎣⎦2-10 Att A(t )0(t )e x(0)e Bu()d τττ-=+⎰x1At 1111s 1cos 2t sin 2t e L (sI A )L 44s 2sin 2t cos 2t ----⎡⎤-⎡⎤⎢⎥⎡⎤=-==⎢⎥⎣⎦⎢⎥-⎣⎦⎣⎦∴⎥⎦⎤⎢⎣⎡+-=t t t t t 22220.52cos sin sin cos )(x 2-11 121det(I A)(3)(1),1,334λλλλλλλ--==--==-∴11P 13⎡⎤=⎢⎥⎣⎦1311P 112--⎡⎤=⎢⎥-⎣⎦ ∴t 3tt 3t Att1t3tt 3t 3e e e e 1e Pe P 23e 3e e 3e Λ-⎡⎤--+==⎢⎥--+⎣⎦∵At(t )e (0)=x x ∴()t 3t At t 3t 0.5e 3.5e (0)e (t )0.5e 4.5e ⎡⎤+==⎢⎥+⎣⎦-1x x 2-1211i c U iR idt C U idtC=+=⎰⎰则 cc i dU RC U U dt+= 1,1R m C F μ=Ω=则()()()c c i U t U t U t +=()[1]c c i U t U U =-+[1][1][1]()At tA sI A s sI A s t e e -=-∴-=+-=+∴Φ==()()()()()01()0(1)0()010010--------=+=+⎡⎤=+-⎣⎦⎰⎰tAtA t c C i t t C t t tC u t e u e Bu d e u e d e u e e τττττ()323()0(3)(0)10()0(0)10(1)()10(1)------=+-=∴=-∴=-+⎰ c c c tt t c i u e u e e u e Vu t e e e u d τττ当t=0时,()c u t 10(1e)=- 当()tt(t )(t 1)c 00t 1,u t 10e (1e)10e|10(1e )---τ--<≤=-+=-当c t 1,u (t)0>=2-13 设()12x (kt )y(kt )x (kt )y k 1t =⎧⎪⎨=+⎡⎤⎪⎣⎦⎩∴ ()()()()12221x k 1T y k 1T x (kT )x k 1T y k 2T u(kT )0.5x (kT )0.1x (kT )⎧+=+=⎡⎤⎡⎤⎪⎣⎦⎣⎦⎨+=+=--⎡⎤⎡⎤⎪⎣⎦⎣⎦⎩ ∴状态空间表达式为:()010x k 1T x(kT )u(kT )0.10.51⎡⎤⎡⎤+=+⎡⎤⎢⎥⎢⎥⎣⎦--⎣⎦⎣⎦()[]y k 1T 10x(kT )+=⎡⎤⎣⎦若初始值y(0)=1,y(T)=0逆推y(2T)+0.5y(T)+0.1y(0)=1∴y(2T)=0.9,y(3T)=0.55,y(4T)=0.635()()()()()()()()()()(0)=+-+-+-+-+-+-+-+-+-y kT δt δt T δt T δt T δt T δt T δt T δt T δt T δt T 0.920.5530.63540.627550.622760.625870.624780.625090.625012-14t 2tt 2t Att1t tt 2t 2e e e e (t )e Pe P 2e 2ee 2e ----Λ-----⎡⎤--===⎢⎥-+-+⎣⎦Φ 设x(k 1)x(k )u(k )+=+G H0.9670.148(T)0.2960.522⎡⎤==⎢⎥-⎣⎦G Φt 2t T T 0t 2t 0.017e e (t )Bdt Bdt 0.148e 2e ----⎡⎤-⎡⎤===⎢⎥⎢⎥-+⎣⎦⎣⎦⎰⎰H Φ⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦,G H 0.96710.14840.0170.29680.52190.148离散化状态方程 :()()()0.9670.1480.017k 1k u k 0.2960.5220.148⎡⎤⎡⎤+=+⎢⎥⎢⎥--⎣⎦⎣⎦x x 1z 0.5220.148(z 0.82)(z 0.669)(z 0.82)(z 0.669)(z )0.269z 0.967(z 0.82)(z 0.669)(z 0.82)(z 0.669)--⎡⎤⎢⎥----⎢⎥-=--⎢⎥⎢⎥----⎣⎦I G ()11(k)z z z --⎡⎤=-⎣⎦ΦI G∴k k 1kk k 1k k 1k k 1k 1k k 1(1)2(1)2(1)(1)2()(1)2(1)2(1)(1)2++++++⎡⎤-⋅+-⋅-+-⋅=⎢⎥-⋅+-⋅-+-⋅⎣⎦k Φ2-15(1)AT221T 1G eI AT A T 012⎡⎤==+++=⎢⎥⎣⎦2T T 00T 1t 0(t )Bdt dt 2011T ⎡⎤⎡⎤⎡⎤⎢⎥===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦⎰⎰H Φ 当T=1s 时,()()()110.5k 1k u k 011⎡⎤⎡⎤+=+⎢⎥⎢⎥⎣⎦⎣⎦x x []10(k )=y x (2)()2T 1AT 112T 1s 1T (T e )e L sI A L 20s 20e -----⎡⎤--⎡⎤⎢⎥⎡⎤==-==⎢⎥⎣⎦⎢⎥+⎣⎦⎣⎦G 22T 2tT T002t 2T 1T 111(e )(t e )2224(t )Bdt dt 211ee 22----⎡⎤⎡⎤+-⎢⎥-⎢⎥===⎢⎥⎢⎥⎢⎥-+⎣⎦⎢⎥⎣⎦⎰⎰H Φ 当T=1时,222211e 1(1e )4(k )(k )u(k )2110e e 22----⎡⎤⎡⎤⎢⎥-⎢⎥+=+⎢⎥⎢⎥⎢⎥-+⎣⎦⎢⎥⎣⎦x x 1,)()(k k x y ⎥⎦⎤⎢⎣⎡=0110 2-16 (1)211G(s )(s 1)(s 2)s 3s 2==++++ 状态空间描述为:010x u 231⎡⎤⎡⎤=+⎢⎥⎢⎥--⎣⎦⎣⎦x[]y 10=x将其离散化--------⎡⎤--==⎢⎥-+-+⎣⎦T 2TT 2T ATT 2T T 2T 2e e e e G e2e 2ee 2e T 2T t 2t T T00t 2t T 2T 11e e e e (t )dtB dt 22e 2e e e --------⎡⎤⎡⎤-++-⎢⎥===⎢⎥⎢⎥-+⎣⎦-⎣⎦⎰⎰H Φ ∴离散化状态方程为:------------⎡⎤⎡⎤-++--⎢⎥+=+⎢⎥⎢⎥-+-+⎣⎦-⎣⎦T 2T T 2TT 2T T 2TT 2T T 2T11e e 2e e e e x[(k 1)T ]x(kT )u(kT )222e 2ee 2e e e ()[]()y k T 10x k T= (2)2T T2T T T 2TT 2T 2111z e z e z e z e ()2221z e z e z e z e ---------⎡⎤--⎢⎥----=⎢⎥⎢⎥--⎢⎥----⎣⎦Z I G 1-0.20.10.20.10.10.20.10.20.2k 0.1k 0.2k 0.1k0.1k0.2k0.1k 0.2k()[()]2zz z z z e z e z e z e =2z 2z 2z z z e z e z e z e 2(e )(e )(e )(e )2(e )2(e )2(e )(e )-------------------Φ=⋅⎡⎤--⎢⎥----⎢⎥⎢⎥--⎢⎥----⎣⎦⎡⎤--=⎢⎥--⎣⎦k Z Z ZZ 111-I G2-17 k=0时,10.510.3(1)(0)u(0)u(0)010.110.4⎡⎤⎡⎤⎡⎤=+=+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦x Gx Hk=1时,(2)(1)u(1)=+x Gx H 带入(1)x 得,1.50.3u(0)0.550.2u(0)0.3u(1)(2)01.50.03u(0)0.110.04u(0)0.4u(1)++++⎡⎤==⎢⎥++++⎣⎦x 解得 u (0)=5.35 u (1) =0.51。
现代控制理论第二章答案

cos2t
e At
TeAtT 1
1 0
0 cos2t 2sin 2t
cos2t 0.5sin 2t
2sin 2t
c os 2t
sin 2t1
c os 2t
0
0 0.5
(2)
1 1
I A
2 3 0
4 1
1 1
2 3
1
1
P1 2 P2 2
1 1 T 2 2
0.25
s 0.5
3
s 1 s 3
e At
L1[(sI
A)1]
0.5et 0.5e3t
et e3t
0.25et 0.25e3t
0.5et 0.5e3t
解法四:凯莱—哈密顿定理法
(1) 特征方程:
I A
1 2 4 0
4
0 (t)
1
(t
)
1 1
1 2
1
e1t e2t
s
0
s2 1
1 0
t 1
s
t
x(t) (t)x(0) o (t )Bu( )d
1 0
t1 t 1 11 0 0
t
1
101(
)d
1 2
t
2
t
t 1
1
【习题2-10 】有离散系统如下,求x(k)
1
x(k
1)
2 1
8
1
8 1
x(k
)
1 0
2
0 u1 (k ) 1u2 (k)
(et
(et
e3t ) e3t )
141((eet tee33t t))
1 2
(et (et
控制理论作业二答案

第三章3-1 已知二阶系统闭环传递函数为 369362++=s s G B。
试求单位阶跃响应的t r , t m ,δ% , t s 的数值?解:[题意分析]这是一道典型二阶系统求性能指标的例题。
解法是把给定的闭环传递函数与二阶系统闭环传递函数标准形式进行对比,求出n ω参数,而后把n ω代入性能指标公式中求出r t ,m t ,%δ,s t 和N 的数值。
上升时间 t r 峰值时间t m 过度过程时间t s 超调量δ%3-2 设单位反馈系统的开环传递函数为试求系统的性能指标,峰值时间,超调量和调节时间。
解:[题意分析]这是一道给定了开环传递函数,求二阶系统性能指标的练习题。
在这里要抓住二阶系统闭环传递函数的标准形式与参数(ζ,n ω)的对应关系,然后确定用哪一组公式去求性能指标。
根据题目给出条件可知闭环传递函数为与二阶系统传递函数标准形式2222nn ns s ωζωω++相比较可得12,12==n n ζωω,即n ω=1,ζ=0.5。
由此可知,系统为欠阻尼状态。
故,单位阶跃响应的性能指标为3-3 如图1所示系统,假设该系统在单位阶跃响应中的超调量%δ=25%,峰值时间m t =0.5秒,试确定K 和τ的值。
K,τ与ζ,n ω的关系;δ联系起来。
由系统结构图可得闭环传递函数为 与二阶系统传递函数标准形式相比较,可得由题目给定: %25%100%21=⨯=--ζζπδe即 25.021=--ζζπe两边取自然对数可得 依据给定的峰值时间: 5.012=-=ζωπn mt (秒)所以 85.615.02=-=ζπωn (弧度/秒)故可得τ≈0.13-4 已知系统的结构图如图2所示,若)(12)(t t x ⨯= 时,试求: (1) 当τ=0时,系统的t r , t m , t s 的值。
(2) 当τ≠0时,若使δ%=20%,τ应为多大。
可得 )/(07.750秒弧度==n ω由于ss X 2)(=输出的拉氏变换为 则拉氏反变换为(2) 当τ≠0时,闭环传递函数由 %20%100%21=⨯=--ζζπδe两边取自然对数 61.12.0ln 12-==--ζζπ, 可得故 73.85.)107.746.0(2=-⨯=o τ3-5(1) 什么叫时间响应答:系统在外加作用的激励下,其输出随时间变化的函数关系叫时间响应。
《现代控制理论》第三版_.习题答案

1 0 0 3 1 0 5 2 1 52 7 1 5 2 70 125 3 5 7 5 0 0 1 1 B 2 ; 2 5 5
1 0 a1 0 0 1 0 1 0 0 1 a2 3 7 5
0 B 0 1
C (b0 a0bn ) (bn1 an1bn ) 2 1 0
3 1 a 或者 2 2 1 a1 0 a0
e At I At 1 22 1 33 A t A t 2! 3! t2 t4 t6 t3 t5 1 4 16 64 , 4 16 t 2! 4! 6! 3! 5! 3 5 2 4 6 t t t t t t 4 16 64 , 1 4 16 64 3! 5! 2! 4! 6!
0 0 1 B M 1 0 0 0 0 1 M2
1 0 B 1 M1 B1 M2
1 B1 M1 B1 B2 M2
0
0 0 1 0 C 0 0 0 1
1-5. 根据微分方程, 写状态方程, 画模 拟结构图。
1 a2 a2 2 a1 3 2 a a a 1 2 2 a0
1 a2 a1
1 a2
12 b1 b0
b3 b 2 b1 1 b0
凯莱哈密顿法: 1,2 2 j
0 (t ) 1 1 e1t 1 2(e 2 jt e 2 jt ) (t ) 1 2t 4 2 jt 2 jt e j ( e e ) 2 1
现代控制理论基础第二章习题答案

第二章 状态空间表达式的解3-2-1 试求下列矩阵A 对应的状态转移矩阵φ(t )。
(1) ⎥⎦⎤⎢⎣⎡-=2010A (2) ⎥⎦⎤⎢⎣⎡-=0410A (3) ⎥⎦⎤⎢⎣⎡--=2110A (4) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=452100010A (5)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0000100001000010A (6)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=λλλλ000100010000A 【解】:(1) (2) (3) (4)特征值为:2,1321===λλλ。
由习题3-1-7(3)得将A 阵化成约当标准型的变换阵P 为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=421211101P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-1211321201P线性变换后的系统矩阵为:(5)为结构四重根的约旦标准型。
(6)虽然特征值相同,但对应着两个约当块。
或}0100010000{])[()(1111----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=-=Φλλλλs s s s L A sI L t 3-2-2 已知系统的状态方程和初始条件 (1)用laplace 法求状态转移矩阵; (2)用化标准型法求状态转移矩阵; (3)用化有限项法求状态转移矩阵; (4)求齐次状态方程的解。
【解】:(1) (2)特征方程为: 特征值为:2,1321===λλλ。
由于112==n n ,所以1λ对应的广义特征向量的阶数为1。
求满足0)(11=-P A I λ的解1P ,得:0110000000312111=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--P P P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0011P 再根据0)(22=-P A I λ,且保证1P 、2P 线性无关,解得:对于当23=λ的特征向量,由0)(33=-P A I λ容易求得: 所以变换阵为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==110010001321P P P P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-1100100011P 线性变换后的系统矩阵为:(3)特征值为:2,1321===λλλ。
控制理论作业二答案

第三章3-1 已知二阶系统闭环传递函数为 369362++=s s G B 。
试求单位阶跃响应的t r , t m ,δ% , t s 的数值?解:[题意分析]这是一道典型二阶系统求性能指标的例题。
解法是把给定的闭环传递函数与二阶系统闭环传递函数标准形式进行对比,求出n ω参数,而后把n ω代入性能指标公式中求出r t ,m t ,%δ,s t 和N 的数值。
上升时间 t r峰值时间t m 过度过程时间t s 超调量δ%3-2 设单位反馈系统的开环传递函数为试求系统的性能指标,峰值时间,超调量和调节时间。
解:[题意分析]这是一道给定了开环传递函数,求二阶系统性能指标的练习题。
在这里要抓住二阶系统闭环传递函数的标准形式与参数(ζ,n ω)的对应关系,然后确定用哪一组公式去求性能指标。
根据题目给出条件可知闭环传递函数为与二阶系统传递函数标准形式2222nn n s s ωζωω++相比较可得12,12==n n ζωω,即n ω=1,ζ=0.5。
由此可知,系统为欠阻尼状态。
故,单位阶跃响应的性能指标为3-3 如图1所示系统,假设该系统在单位阶跃响应中的超调量%δ=25%,峰值时间m t =0.5秒,试确定K 和τK,τ与ζ,n ω的关系;%δ,m t 与ζ,nω 由系统结构图可得闭环传递函数为 与二阶系统传递函数标准形式相比较,可得由题目给定: %25%100%21=⨯=--ζζπδe即 25.021=--ζζπe两边取自然对数可得 依据给定的峰值时间: 5.012=-=ζωπn m t (秒)所以 85.615.02=-=ζπωn (弧度/秒)3-4 已知系统的结构图如图2所示,若)(12)(t t x ⨯= 时,试求:(1) 当τ=0时,系统的t r , t m , t s 的值。
(2) 当τ≠0时,若使δ%=20%,τ应为多大。
求出可得 )/(07.750秒弧度==n ω 由于ss X 2)(=输出的拉氏变换为 则拉氏反变换为(2) 当τ≠0时,闭环传递函数由 %20%100%21=⨯=--ζζπδe两边取自然对数 61.12.0ln 12-==--ζζπ, 可得故 73.85.)107.746.0(2=-⨯=o τ3-5(1) 什么叫时间响应答:系统在外加作用的激励下,其输出随时间变化的函数关系叫时间响应。
控制理论基础第二版部分习题答案

第二章2.1 求解下列微分方程2)dd2yy ddtt2+ddyy ddtt=ee4tt,初始条件yy(0)=2, yy(0)=0.解:首先对微分方程两边进行拉氏变换,得代数方程:ss2YY(ss)−ssyy(0)−yy(0)+ssyy(ss)−yy(0)=1ss−4代入初始条件yy(0)=2, yy(0)=0.ss2YY(ss)−ssyy(ss)=1ss−4+2ss+2YY(ss)=2ss+1ss(ss−4)(ss+1)YY(ss)=2ss+AA ss+BB(ss−4)+CC(ss+1)计算得到A=-0.25,B=0.05,C=0.2;YY(ss)=47ss+15(ss−4)+120(ss+1)拉氏反变换y(t)=1.75+0.05ee4tt+0.2ee−tt(t>0)3)dd2xx ddtt2+5ddxx ddtt+6xx=6,初始条件xx(0)=2,xx(0)=2.解:首先对微分方程两边进行拉氏变换,得代数方程:ss2XX(ss)−ssxx(0)−xx(0)+5ssxx(ss)−5xx(0)+6XX(ss)=6ssXX(ss)=2ss2+12ss+6ss(ss+2)(ss+3)=AA ss+BB ss+2+CC ss+3计算得到A=1,B=5,C=-4,拉氏反变换得到,x(t)=1+5ee−2tt−4ee−3tt(t>0)2.2.一阶微分方程组为4'103'20x yx y y+=−++=,已知(0)0,'(0)0,(0)5x x y===,求解(),()x t y t。
解:首先对微分方程两边进行拉氏变换,得代数方程组:4ssXX(ss)−4xx(0)+YY(ss)=10/s−XX(ss)+(3ss+2)YY(ss)=3yy(0)XX (ss )=15ss +20ss (2ss +1)(6ss +1)YY (ss )=60ss 2+10ss (2ss +1)(6ss +1)得到:XX (ss )=20ss +6.25ss +12�+−26.25ss +16�YY (ss )=10ss +12.5ss +12�+−17.5ss +16�x(t)=20+6.25ee −12�tt-26.25ee −16�tt (t>0)y(t)=10+12.5ee −12�tt-17.5ee −16�tt(t>0)2.3解:根据基尔霍夫定律写出电路方程: 如ii 1为分电流VV =(ii 1+ii 2)RR 1+LL 1dd (ii 1+ii 2)ddtt +ii 1RR 2+1CC 1�ii 1ddtt VV =(ii 1+ii 2)RR 1+LL 1dd (ii 1+ii 2)ddtt +LL 2ddii 2ddtt +1CC 2�ii 2ddttORVV =(ii 1+ii 2)RR 1+LL 1dd (ii 1+ii 2)ddtt +ii 1RR 2+1CC 1�ii 1ddttii 1RR 2+1CC 1�ii 1ddtt =LL 2ddii 2ddtt +1CC 2�ii 2ddtt如ii 1为总电流:VV =ii 1RR 1+LL 1ddii 1ddtt +LL 2ddii 2ddtt +1CC 2�ii 2ddttLL 2ddii 2ddtt+1CC 2∫ii 2ddtt )RR 2+1CC 1∫(ii 1−ii 2)ddtt2.5将滑阀节流扣流量方程Q c x ω=Q 是阀芯位移x v 和节流口压p 的函数,c 、w 分别为流量系数和滑阀面梯度,ρ为油的密度。
控制工程2习题解答

二题目:已知,则其【】A. B.C. D。
分析与提示:由拉氏变换的定义计算,可得答案:C题目:函数f(t)的拉氏变换L[f(t)]= 。
分析与提示:拉氏变换定义式。
答案:题目:函数的拉氏变换L[f(t)]= 。
分析与提示:拉氏变换定义式可得,且f(t)为基本函数.答案:题目:若,则【】A。
B.C. D。
分析与提示:拉氏变换定义式可得,即常用函数的拉氏变换对,答案:B题目:拉氏变换存在条件是,原函数f(t)必须满足条件.分析与提示:拉氏变换存在条件是,原函数f(t)必须满足狄里赫利条件。
答案:狄里赫利题目:已知,则其【】A。
B。
C。
D。
分析与提示:由拉氏变换的定义计算,这是两个基本信号的和,由拉氏变换的线性性质,其拉氏变换为两个信号拉氏变换的和。
答案:C题目:若,则)=( )。
【】A。
1 B. 4C。
∞ D. 0分析与提示:根据拉氏变换的终值定理。
即有答案:B题目:函数的拉氏变换L[f(t)]= .分析与提示:基本函数的拉氏变换为,由拉氏变换的平移性质可知。
答案:题目:若,则)=().分析与提示:根据拉氏变换的初值定理。
即有答案:1题目:函数的拉氏变换L[f(t)]= 。
分析与提示:此为基本函数,拉氏变换为。
答案:题目:拉氏反变换的求法有多种方法,其中比较简单的方法是由查拉氏变换表得出及。
分析与提示:拉氏反变换的求法有多种方法,其中比较简单的方法是由查拉氏变换表得出及部分分式展开法。
答案:部分分式展开法题目:已知,则其为多少?分析与提示:首先对F(s)进行因式分解,即解得因此答案:题目:的拉氏反变换为。
分析与提示:此为基本函数。
答案:题目:的拉氏反变换为。
分析与提示:此为基本函数.答案:题目:的拉氏反变换为。
分析与提示:此为基本函数。
答案:题目:线性系统与非线性系统的根本区别在于【】A、线性系统有外加输入,非线性系统无外加输入B、线性系统无外加输入,非线性系统有外加输入C、线性系统满足迭加原理,非线性系统不满足迭加原理D、线性系统不满足迭加原理,非线性系统满足迭加原理分析与提示:数学模型表达式是线性的系统称为线性系统,满足叠加性和均匀性.答案:C题目:对于一个线性定常系统【】A、如有多个输入,则输出是多个输入共同作用的结果B、可用拉氏变换方法得出输入与输出之间的传递函数C、每个输入所引起的输出不可分别单独计算,因多个输入之间互相影响D、可用线性微分方程式来描述E、不能在频率域中判别它的稳定性分析与提示:线性系统满足叠加性,因此A正确,B为传递函数的定义,D为线性系统的定义之一。
北理工《自动控制理论2》在线作业【标准答案】

北理工《自动控制理论2》在线作业-0001试卷总分:100 得分:100一、单选题 (共 10 道试题,共 30 分)1.基于能量的稳定性理论是由()构建的。
A.LyapunovB.KalmanC.RouthD.Nyquist答案:A2.引入状态反馈的目的是()。
A.配置系统的极点B.改变系统的能控性C.改变系统的能观性D.使得系统能观答案:A3.齐次状态方程就是指状态方程中不考虑()的作用。
A.输入B.输出C.状态D.系统答案:A4.对于单变量系统,特征方程的根就是传递函数的()。
A.零点B.极点C.拐点D.死点答案:B5.齐次状态方程的解就是系统在无外力作用下由初始条件引起的()。
A.自由运动B.强迫运动C.离心运动D.旋转运动答案:A6.线性系统的系数矩阵A如果是非奇异的,则系统存在()平衡点。
A.一个B.两个C.三个D.无穷多个答案:A7.原系统的维数是n,则全维状态观测器的维数是()。
A.2nB.nC.3nD.n-1答案:A8.能够完整的描述系统运动状态的最小个数的一组变量称为()。
A.状态变量B.状态空间C.状态方程D.输出方程答案:A9.由初始状态所引起的自由运动称为状态的()。
A.零输入响应B.零状态响应C.输入响应D.输出响应答案:A10.以状态变量为坐标轴所构成的空间,称为()。
A.状态变量B.状态空间C.状态方程D.输出方程答案:B二、多选题 (共 10 道试题,共 30 分)11.由动态方程导出可约传递函数时,表明系统是()。
A.可控不可观测B.可观测不可控C.不可控不可观测D.可控可观测答案:ABC12.经典控制理论线性系统稳定性判别方法有()。
A.代数判据B.Nquist稳定判据C.根轨迹判据D.Lyapunov稳定性理论答案:ABC13.利用Lyapunov第二法可以分析()。
A.线性系统响应的快速性B.非线性系统的稳定性C.线性时变系统稳定性D.以上均不正确答案:ABC14.任何状态不完全能控的线性定常连续系统,总可以分解成()两部分。
现代控制理论课后题答案(第二章-第六章)

1
R R2C1 1 1 1 1 x1 x2 u1 x R1 R2C1 R2C1 R2C1 1 1 1 2 x1 x2 u1 x R2C2 R2C2 R2C2 y u2 u1 x1
即:
R1 R2C1 1 R1 R2C1 x x 2 1 R2C2
x2
u
R1
R3
y
R2
图 P2.8 RL 电网络
解 采用机理分析法求状态空间表达式。由电路原理可得到如下微分方程
2 x1 x2 R3 R2 x2 L2 x
1 x1 x2 R3 u x1 L1 x / R1
y x1 x2 R3
(2) 解 采用拉氏变换法求取状态空间表达式。对微分方程 (2)在零初试条件 下取拉氏变换得:
2s 3Y ( s ) 3sY ( s ) s 2U ( s ) U ( s ) 1 2 1 s Y (s) s 1 2 2 U ( s ) 2s 3 3s s 3 3 s 2
dy1 dy , x4 2 。 dt dt
3 Kx1 B1 M1 x
2
d ( x2 x1 ) dt
对 M 2 有:
4 f (t ) B M2x
经整理得:
1
d ( x2 x 1) dx B 2 dt dt
2
状态方程为:
1 x3 x x 2 x4 B B K 3 x1 1 x3 1 x4 x M1 M1 M1 B B B 1 4 1 x3 ( 1 2 ) x4 u x M2 M2 M2 M2
1 1 R2C1 x1 R2C1 u1 x2 1 1 R C R2C2 2 2
现代控制理论第二章例题及答案
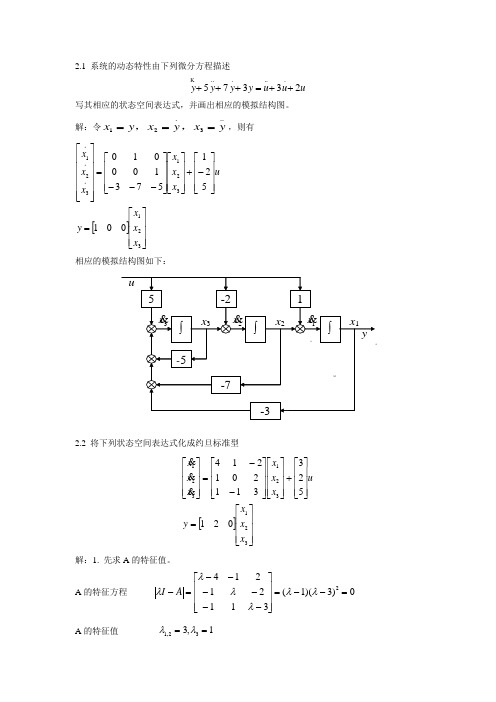
2.1 系统的动态特性由下列微分方程描述u u u y y y y 23375......++=+++写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡321321321001521573100010x x x y u x x x x x x 。
相应的模拟结构图如下:2.2 将下列状态空间表达式化成约旦标准型[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321021523311201214x x x y u x x x x x x解:1. 先求A 的特征值。
A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I A 的特征值1,332,1==λλ2. 求特征值所对应的特征向量。
当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p p 当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p p 当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p解之得 3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p p 3. 取A 的特征向量组成变换矩阵P 并求逆阵P -1,即有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=101201011P ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=-1102112101P4. 计算各矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=-1000300131012010113112012141102112101AP P⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=-3585231102112101B P[][]413101*********=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=CP5. 系统在新的状态变量下的状态空间模型为[]xy u x x ~413358~100030013~=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡= 2.3 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x(1) 画出其模拟结构图(2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W )1)(2)(3()3(2)3(2+++=+++=-s s s s s s A sI()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++---++-+++++=--)2)(1(150)3()3(2033)1)(2)(3(1)(21s s s s s s s s s s s s A sI()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++---++-+++++=--)3)(12()3()3()1)(2)(3(1210)2)(1(150)3()3(2033)1)(2)(3(1)(21s s s s s s s s s s s s s s s s s s s s B A sI[])1)(2()12()1)(2)(3(1)3)(12()3()3(100)()(1+++=+++⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++=-=-s s s s s s s s s s s B A sI C s G 2.4 已知差分方程为)(3)1(2)(2)1(3)2(k u k u k y k y k y ++=++++试将其用离散状态空间表达式表示。
现代控制理论基础第二章习题答案
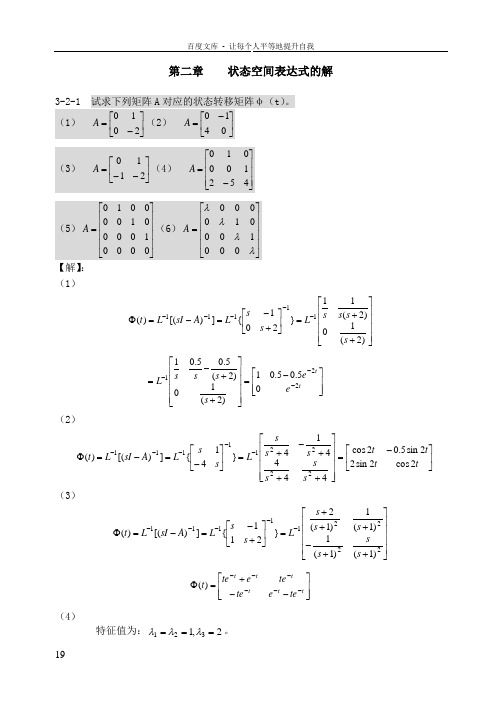
第二章 状态空间表达式的解3-2-1 试求下列矩阵A 对应的状态转移矩阵φ(t )。
(1) ⎥⎦⎤⎢⎣⎡-=2010A (2) ⎥⎦⎤⎢⎣⎡-=0410A (3) ⎥⎦⎤⎢⎣⎡--=2110A (4) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=452100010A (5)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0000100001000010A (6)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=λλλλ000100010000A 【解】:(1)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+-=-=Φ-----)2(10)2(11}201{])[()(11111s s s s L s s L A sI L t ⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-=---t t e e s s s s L 22105.05.01)2(10)2(5.05.01(2)⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⎥⎦⎤⎢⎣⎡-=-=Φ-----t tt ts s s s s sL s s L A sI L t 2cos 2sin 22sin 5.02cos 444414}41{])[()(222211111(3)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-+++=⎥⎦⎤⎢⎣⎡+-=-=Φ-----222211111)1()1(1)1(1)1(2}211{])[()(s s s s s s L s s L A sI L t ⎥⎥⎦⎤⎢⎢⎣⎡--+=Φ------t t tt tt te e te te e te t )((4)特征值为:2,1321===λλλ。
由习题3-1-7(3)得将A 阵化成约当标准型的变换阵P 为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=421211101P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-1211321201P线性变换后的系统矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==-200010011~1AP P A⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=t t t t tA e e te e e2~0000 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡===Φ-1211321200000421211101)(21~t t t ttA At e te e eP Pe e t ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--++-----++-----++--=Φt t t tt t t t t t t t t t t tt t t t t t t t tt e te e e te e e te e e te e e te e e te e e te e e te e te e t 34838424225342222322)(222222222 (5)为结构四重根的约旦标准型。
西交20春《自动控制理论》在线作业2参考答案

西交《自动控制理论》在线作业
试卷总分:100 得分:100
一、多选题(共13 道试题,共39 分)
1.相位超前校正具有以下特点()
A.系统带宽变窄,降低了系统响应的快速性
B.增益和型次未改变,稳态精度变化不大
C.加大带宽,加快了系统的响应速度,即改善系统的瞬态性能
D.增大相位裕度,提高了系统的相对稳定性
答案:BCD
2.属于代数稳定性判据的有()。
A.奈奎斯特判据
B.波德判据
C.胡尔维兹判据
D.劳斯判据
答案:CD
3.关于传递函数正确的说法有( )
A.传递函数的分母与系统的输入无关
B.传递函数分母中s的阶次不小于分子中s的阶次
C.传递函数是无量纲的
D.不同物理类型的系统,可以具有相同形式的传递函数。
现代控制理论课后作业答案程鹏王艳东

现代控制理论第一次作业1-1.由图1-1所示,可得:1311322323313112121()331()122x u x s x u x x x u x x x u x s x x x x y x x u s y x x u⎧=-⎪+=--⎧⎪⎪⎪=--=-⎪⎪⇒+⎨⎨=⎪⎪=⎪⎪=++⎩⎪⎪=++⎩ 则状态空间可表示为:()301101112000110x x uy x u--⎛⎫⎛⎫⎪ ⎪=--+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=+ 1-4.由101,111A B ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭。
11210()()1110111(1)1s s sI A s s s s ---⎛⎫Φ=-= ⎪--⎝⎭⎛⎫ ⎪-⎪= ⎪ ⎪--⎝⎭则,110[()]t Attt e e L sI A tee --⎛⎫=-= ⎪⎝⎭, ()010()()1()t ttA t t t e eBu d u d t e e τττττττττ----⎛⎫⎛⎫=⎪ ⎪-⎝⎭⎝⎭⎰⎰,()1u τ= 则,()0()(0)()1010212tAtA t t t t t t t t x t e x e Bu d e e te e te e te τττ-=+⎛⎫⎛⎫-⎛⎫=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫-= ⎪⎝⎭⎰1-5.(1)极点多项式为: 由()2rank G s =, 一阶子式公分母:2(1)s s + 二阶子式公分母:22(1)s s + 极点多项式为:22(1)s s + (2)零点多项式为:二阶子式:2222212(1)()212(1)(1)s s s s s s s s --+-++=++ 零点多项式为:1(1)()2s s -+现代控制理论第二次作业1-7.系统的状态方程为:x Ax bu =+其中,01101001n A a a a -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥---⎣⎦,001b ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦。
1101111101111011000()011**1001**111n n n n n n n n n s sI A b s s s s s s s s s s s ααααααααα----------⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥-⎢⎥⎢⎥+⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥++++⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎢⎥⎢⎥=⎢⎥++++⎢⎥⎣⎦1-8.反证法:设1121[]n rank b AbA b n n -=<,则存在一个非零向量α使得: 11111011[]00n n n bAbA b b Ab A b αααα---=+++=不防设110n α-≠,则,11111201211()n n n n A b b Ab A b αααα----=-+++两边同乘A ,则11111201211()n n n n A b Ab A b A b αααα---=-+++则可看出1n A b 能用12(,,)n b Ab A b -线性表出,以此类推,可得11+1n n n A b A b A b (,)均可由12(,,)n b Ab A b -线性表出,则:121[]n rank b AbA b n n -=≠ 与已知矛盾,假设不成立,所以有111[]n rank b AbA b n -=1-9.(1)解:010110001A ⎡⎤⎢⎥=--⎢⎥⎢⎥⎣⎦,011b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,[]121C =可控性矩阵2011110111U bAbA b -⎡⎤⎢⎥⎡⎤==-⎣⎦⎢⎥⎢⎥⎣⎦,det 0U ≠,故系统可控。
《现代控制理论》课后习题全部答案(最完整打印版)
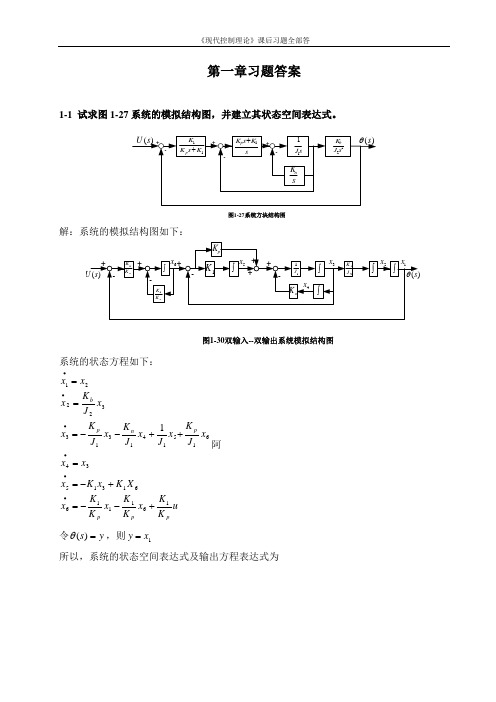
第一章习题答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙阿令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。
现代控制理论第2章答案

第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
(2) A=1141⎛⎫⎪⎝⎭解:第一种方法: 令0I A λ-=则11041λλ--=-- ,即()2140λ--=。
求解得到13λ=,21λ=- 当13λ=时,特征矢量11121p p p ⎡⎤=⎢⎥⎣⎦由 111Ap p λ=,得11112121311341p p p p ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦即112111112121343p p p p p p +=⎧⎨+=⎩,可令112p ⎡⎤=⎢⎥⎣⎦当21λ=-时,特征矢量12222p p p ⎡⎤=⎢⎥⎣⎦由222Ap p λ=,得121222221141p p p p -⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦即1222121222224p p p p p p +=-⎧⎨+=-⎩ ,可令212p ⎡⎤=⎢⎥-⎣⎦则1122T ⎡⎤=⎢⎥-⎣⎦,111241124T -⎡⎤⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦3333311111111024224422111102422t tt t tAtt t tt t e ee e e e e e e e e-----⎡⎤⎡⎤+-⎢⎥⎢⎥⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥⎢⎥⎣⎦-++⎢⎥⎢⎥⎣⎦⎣⎦第二种方法,即拉氏反变换法:1141s sI A s --⎡⎤-=⎢⎥--⎣⎦[]()()11114131s sI A s s s --⎡⎤-=⎢⎥--+⎣⎦()()()()()()()()113131413131s s s s s s s s s s -⎡⎤⎢⎥-+-+⎢⎥=⎢⎥-⎢⎥-+-+⎣⎦1111112314311111131231s s s s s s s s ⎡⎤⎛⎫⎛⎫++ ⎪ ⎪⎢⎥-+-+⎝⎭⎝⎭⎢⎥=⎢⎥⎛⎫-+⎢⎥⎪-+-+⎝⎭⎣⎦()331133111122441122t tt t At t t t t e e e e e L sI A e e e e ------⎡⎤+-⎢⎥⎡⎤=-=⎢⎥⎣⎦⎢⎥-+⎢⎥⎣⎦第三种方法,即凯莱—哈密顿定理 由第一种方法可知13λ=,21λ=-313303113131344441111114444t t t tt t t t e e e e e e e e -----⎡⎤⎡⎤+⎢⎥⎢⎥∂⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥∂-⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎢⎥⎣⎦⎣⎦3333331111101113132244014111444422t tt t At t t t t t t t t e e e e e e e e e e e e e ------⎡⎤+-⎢⎥⎡⎤⎡⎤⎛⎫⎛⎫=+++=⎢⎥ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎢⎥-+⎢⎥⎣⎦2-5 下列矩阵是否满足状态转移矩阵的条件,如果满足,试求与之对应的A 阵。
现代控制理论试卷答案3套

现代控制理论试卷 1一、(10分)判断以下结论,若是正确的,则在括号里打√,反之打×(1)用独立变量描述的系统状态向量的维数是唯一。
()(2)线性定常系统经过非奇异线性变换后,系统的能观性不变。
()(3)若一个系统是李雅普诺夫意义下稳定的,则该系统在任意平衡状态处都是稳定的。
()(4)状态反馈不改变被控系统的能控性和能观测性。
()(5)通过全维状态观测器引入状态反馈来任意配置系统的闭环极点时,要求系统必须同时能控和能观的。
()二、(12分)已知系统1001010,(0)00121x x x⎛⎫⎛⎫⎪ ⎪==⎪ ⎪⎪ ⎪⎝⎭⎝⎭,求()x t.三、(12分) 考虑由下式确定的系统:2s+2(s)=43Ws s++,求其状态空间实现的能控标准型和对角线标准型。
四、(9分)已知系统[]210020,011003x x y⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦,判定该系统是否完全能观?五、(17分) 判断下列系统的能控性、能观性;叙述李亚普诺夫稳定性的充要条件并分析下面系统的稳定性.[]xy u x x 11103211=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=六、(17分)已知子系统1∑ 111121011x x u -⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦,[]1110y x = 2∑ []22222110,01011x x u y x -⎡⎤⎡⎤=+=⎢⎥⎢⎥-⎣⎦⎣⎦求出串联后系统的状态模型和传递函数.七、(15分)确定使系统2001020240021a x x u b -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦为完全能控时,待定参数的取值范围。
八、(8分)已知非线性系统 ⎩⎨⎧--=+-=2112211sin 2x a x xx x x试求系统的平衡点,并确定出可以保证系统大范围渐近稳定的1a 的范围。
现代控制理论 试卷 1参考答案一、(10分)判断以下结论,若是正确的,则在括号里打√,反之打× (1) 用独立变量描述的系统状态向量的维数是唯一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章3-1已知二阶系统闭环传递函数为G B36。
s29s 36t r , t m ,δ% , t s 的数值?试求单位阶跃响应的解:[ 题意分析 ] 这是一道典型二阶系统求性能指标的例题。
解法是把给定的闭环传递函数与二阶系统闭环传递函数标准形式进行对比,求出n 参数,而后把n 代入性能指标公式中求出 t r, t m,% ,t s和 N 的数值。
n366(弧度 /秒)90.752 n120.66d n tg 1112 3.97(弧度/秒)241.410.72 (弧度)上升时间t rt rd 峰值时间t m 3.140.72秒0.613.97t m3.140.79秒3.97d过度过程时间 t s440.89秒(2%)t s0.756n330.70秒(5 %)t s0.756n超调量δ%% e 120.75e 0.66100% 2.8% 100%3-2设单位反馈系统的开环传递函数为G K (s)1s(s1)试求系统的性能指标,峰值时间,超调量和调节时间。
解: [ 题意分析 ] 这是一道给定了开环传递函数 , 求二阶系统性能指标的练习题。
在这里要抓住二阶系统闭环传递函数的标准形式与参数( ,n ) 的对应关系,然后确定用哪一组公式去求性能指标。
根据题目给出条件可知闭环传递函数为G B (s)Y (s) 1X (s)s2s 122与二阶系统传递函数标准形式n2 相比较可得1, 2n 1 , 即22 n sns nn =1, =。
由此可知,系统为欠阻尼状态。
故,单位阶跃响应的性能指标为t m秒3.63n 1212% e 100% 16.4%t s ( 2%)44秒0.5 18n33秒t s (5%)0.56n13-3 如图 1 所示系统,假设该系统在单位阶跃响应中的超调量% =25%,峰值时间 t m =秒,试确定 K 和τ的值。
X(s)Y(s)ks( s 1)s1图 1解: [ 题意分析 ] 这是一道由性能指标反求参数的题目,关键是找出: K, τ与, n 的关系;% , t m 与 ,n 的关系;通过, n 把 % , t m 与 K, τ联系起来。
由系统结构图可得闭环传递函数为Y (s) KKG B ( s)s(s 1) K ( s 1)s 2(1 K )s KX (s)与二阶系统传递函数标准形式相比较,可得2K ; 2 n 1 K 或2 n 1n2n12由题目给定:% e100 % 25%21即e0.25两边取自然对数可得ln 0.25 1.3863211.38630.42 1.3863 2依据给定的峰值时间:t m0.5 (秒)12n所以n 6.85(弧度/秒)0.512故可得K2n46.95 47τ≈3-4已知系统的结构图如图 2 所示,若x(t )21(t ) 时,试求:(1)当τ =0 时,系统的 t r , t m , t s的值。
(2)当τ≠ 0 时,若使δ% =20%,τ应为多大。
X(s)Y(s)0.5100s(s 2)s图 2解: [ 题意分析 ] 这是一道二阶系统综合练习题。
(1) 练习输入信号不是单位阶跃信号时,求性能指标。
关键是求出n , ,。
(2)的求法与例4- 3-3 相似。
(1)由结构图可知闭环传递函数为G B (s)Y(s)50X (s)s22s50可得n50 7.07 (弧度 / 秒)2120.14 ;tg 181.95 1.43弧度2n由于 X (s)2输出的拉氏变换为sY( s)则拉氏反变换为22s22n2n ne nty(t ) 2 1sin( d t)122 1 1.01e 0.995 sin(7t81.95 )20. 44%e1100%64%100% e 0. 99t r3.14 1.43秒20.24n17.070.99t m3.140.45 秒127.070.99nt s 332.78秒 (5%)0.147.07nt s 44秒 (2%)0.143.71n7.07(2) 当τ≠ 0时,闭环传递函数Y (s)50G B (s)s2( 2 0.5 ) s 50X (s)n507.07 (弧度 / 秒)2 n20.52(n 1)得0.5%e12由100% 20%e 120.2两边取自然对数ln 0.2 1.6112,可得1.610.461.61222(0.467.071)故o.58.73330.92 秒 (2%)t s0.46n7.073-5(1)什么叫时间响应答:系统在外加作用的激励下,其输出随时间变化的函数关系叫时间响应。
(2)时间响应由哪几部份组成?各部份的定义是什么?答:时间响应由瞬态响应和稳态响应两部分组成。
瞬态响应是系统受到外加作用后,系统从初始状态到最终稳定状态的响应过程称瞬态响应或者动态响应或称过渡过程。
稳态响应是系统受到外加作用后,时间趋于无穷大时,系统的输出状态或称稳态。
(3)系统的单位阶跃响应曲线各部分反映系统哪些方面的性能?答:时间响应由瞬态响应和稳态响应两部分组成。
瞬态响应反映系统的稳定性,相对稳定性及响应的快速性;稳态响应反映系统的准确性或稳态误差。
(4)时域瞬态响应性能指标有哪些?它们反映系统哪些方面的性能?答:延迟时间 t d;上升时间 t r;峰值时间 t m;调节时间 t s;最大超调量% .t d,t r,t m,t s 反映系统的快速性,即灵敏度,% 反映系统的相对稳定性。
3-6 设系统的特征方程式为s46s312 s211s 60试判别系统的稳定性。
解:特征方程符号相同,又不缺项,故满足稳定的必要条件。
列劳斯表判别。
s41126s36110s26136同乘6)(s14550同乘61)(s036由于第一列各数均为正数,故系统稳定。
也可将特征方程式因式分解为(s2)(s3)( s2s 1) 0根 s12,s23,1j3s3, 4均有负实部,系统稳定。
223-7 设系统的特征方程式为s32s2s 20解:列劳斯表s 31 1 2s 22s 02将特征方程式因式分解为( s 2 1)( s2) 0根为s1,2 j1, s 3 2 系统等幅振荡,所以系统临界稳定。
3-8单位反馈系统的开环传递函数为KG k (s)s(0.1s 1)(0.25s 1)试求 k 的稳定范围。
解:系统的闭环特征方程:s(0.1s 1)(0.25s 1) K 0 0.025s 3 0.35s 2 s K列劳斯表s 3 0.025 1s 2 0.35 Ks 1 0.35 0.02Ks 0K K系统稳定的充分必要条件K>0得 K<14所以保证系统稳定, K 的取值范围为 0<K<14。
3-9(1) 系统的稳定性定义是什么?答:系统受到外界扰动作用后, 其输出偏离平衡状态,当扰动消失后,间,若系统又恢复到原平衡状态,则系统是稳定的,反之系统不稳定。
(2) 系统稳定的充分和必要条件是什么?经过足够长的时答:系统的全部特征根都具有负实部,或系统传递函数的全部极点均位于半部。
[S] 平面的左(3) 误差及稳态误差的定义是什么? 答:输出端定义误差e(t) :希望输出与实际输出之差。
输入端定义误差主反馈信号之差。
稳态误差,误差函数e(t) ,当 t →∞时的误差值称为稳态误差e(t) ;输入与, 即3-10 已知单位反馈随动系统如图 3 所示。
若 K 16 , T 0.25s 。
试求:(1)典型二阶系统的特征参数和 n ;(2)暂态特性指标M p和t s ( 5 0 0 ) ;(3)欲使 M p 16 0 0 ,当 T 不变时, K 应取何值。
R( s)C ( s)Ks(Ts 1)图 3 随动系统结构图解: 由系统结构图可求出闭环系统的传递函数为Φ( s)KK / T2 s K21KTss sTT与典型二阶系统的传递函数比较2 Φ(s)n2n s2s 2 nnK , 1得T2 KT已知 K 、 T 值,由上式可得nK16 1 T8(rad / s),0.250.252 KT0. 25M p % e 121 0.25 2100% 47%于是,可100% et s33 1.5s( 5%)n0.25 8为使 M p16,由公式可求得0.5,即应使 由增大到,此时K1 1 44T40.250.25即 K 值应减小 4 倍。
3-11 控制系统框图如图4 所示。
要求系统单位阶跃响应的超调量M p9.5%,且峰值时间t p0.5s。
试确定 K 1 与的值,并计算在此情况下系统上升时间t r 和调整时间 t s (20 )。
R(s)K110 C (s) s(0.5 s1)s图 4 控制系统框图解:由图可得控制系统的闭环传递函数为:C( s)10 K1R( s) s2(110) s10K1系统的特征方程为s2(1 10 ) s 10K10。
所以10K1n2 , 2 n 1 10由题设条件:M p e12100%0.095t p120.5sn,可解得0.6 ,n 7.854,进而求得221n6.15,n K1100.8410在此情况下系统上升时间t r120.35s cos 1 ()53.100.9273radnt s (2%)40.85调整时间n3-12 设系统的特征方程式分别为1. s42s33s24s 5 02. s42s3s22s 1 03. s5s43s33s22s 2 0试用劳斯稳定判据判断系统的稳定性。
解:解题的关键是如何正确列出劳斯表,然后利用劳斯表第一列系数判断稳定性。
1.列劳斯表如下s4135s324s215s1-6s05劳斯表中第一列系数中出现负数,所以系统不稳定;又由于第一列系数的符号改变两次,1→-6 → 5,所以系统有两个根在s 平面的右半平面。
2.列劳斯表如下s4111s322s20(ε )1s1 2-2/εs01由于ε是很小的正数,ε行第一列元素就是一个绝对值很大的负数。
整个劳斯表中第一列元素符号共改变两次,所以系统有两个位于右半s 平面的根。
3.列劳斯表如下s5132s4132s300由上表可以看出,s3 行的各项全部为零。
为了求出s3 各行的元素,将s4 行的各行组成辅助方程式为A(s)= s4+3s2+2s0将辅助方程式A(s) 对 s 求导数得dA(s)4s36sds用上式中的各项系数作为s3 行的系数,并计算以下各行的系数,得劳斯表为s5132s4132s346s23/22s12/3s02从上表的第一列系数可以看出,各行符号没有改变,说明系统没有特征根在s 右半平面。
但由于辅助方程式 A(s)= s4+3s2+2=(s2+1)( s2+2)=0 可解得系统有两对共轭虚根s1,2= ± j ,s3,4= ± j2 ,因而系统处于临界稳定状态。
