哥尼斯堡七桥问题
七桥问题Seven Bridges Problem

七桥问题Seven Bridges Problem著名古典数学问题之一。
在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。
问是否可能从这四块陆地中任一块出发,恰好通过每座桥一次,再回到起点?欧勒于1736年研究并解决了此问题,他把问题归结为如下右图的“一笔画”问题,证明上述走法是不可能的。
有关图论研究的热点问题。
18世纪初普鲁士的柯尼斯堡,普雷格尔河流经此镇,奈发夫岛位于河中,共有7座桥横跨河上,把全镇连接起来。
当地居民热衷于一个难题:是否存在一条路线,可不重复地走遍七座桥。
这就是柯尼斯堡七桥问题。
L.欧拉用点表示岛和陆地,两点之间的连线表示连接它们的桥,将河流、小岛和桥简化为一个网络,把七桥问题化成判断连通网络能否一笔画的问题。
他不仅解决了此问题,且给出了连通网络可一笔画的充要条件是它们是连通的,且奇顶点(通过此点弧的条数是奇数)的个数为0或2。
当Euler在1736年访问Konigsberg, Prussia(now Kaliningrad Russia)时,他发现当地的市民正从事一项非常有趣的消遣活动。
Konigsberg城中有一条名叫Pregel的河流横经其中,这项有趣的消遣活动是在星期六作一次走过所有七座桥的散步,每座桥只能经过一次而且起点与终点必须是同一地点。
Euler把每一块陆地考虑成一个点,连接两块陆地的桥以线表示。
后来推论出此种走法是不可能的。
他的论点是这样的,除了起点以外,每一次当一个人由一座桥进入一块陆地(或点)时,他(或她)同时也由另一座桥离开此点。
所以每行经一点时,计算两座桥(或线),从起点离开的线与最后回到始点的线亦计算两座桥,因此每一个陆地与其他陆地连接的桥数必为偶数。
七桥所成之图形中,没有一点含有偶数条数,因此上述的任务无法完成.欧拉的这个考虑非常重要,也非常巧妙,它正表明了数学家处理实际问题的独特之处——把一个实际问题抽象成合适的“数学模型”。
哥尼斯堡七桥问题与图论

1736年29《哥尼斯堡的七座桥》的论文,创了数学的一个新的分支—一、哥尼斯堡七桥问题哥尼斯堡在俄罗斯境内,现称为加里宁格勒.生和培养过许多伟大人物.格尔河,横贯城中,如图1所示.流,一条称为新河,一条主流,的商业中心.区、北区、东区和南区.桥,两支流上.这一别致的桥群,图1早在18世纪,散步中走过每座桥,发点?”走遍这七座桥共有A77=7!=验,谈何容易.那么在这5040而形成了著名的图2欧拉请他帮助解决这个他似乎看到其中.经过一年的研究,29岁的并于1736年向彼得堡科哥尼斯堡的七座桥》的论文.C(岛区)、A(南区);七座桥看成这四个点、6、7七个数字表示,如图3所示.“一笔画”问题:否能一笔不.布勒格尔河模型蔡思明58遍历的路径称作欧拉路径(一个环或者一条链),如果路径闭合(一个圈),则称为欧拉回路.图论中的欧拉定理(一笔画定理)要分有向图(边有特定方向的图)与无向图(边没有特定方向的图)两种情况进行讨论.1.无向图的情况定理:连通无向图G有欧拉路径的充要条件为:G中奇度顶点(即与其相连的边数目为奇数的顶点)有0个或者2个.证明:必要性.如果图能够被一笔画成,那么对每个顶点,考虑路径中“进入”它的边数与“离开”它的边数(注意前提是无向图,所以我们不能称其为“入边”和“出边”).很显然这两个值要么相同(说明该顶点度数为偶),要么相差1(说明该顶点度数为奇).也就是说,如果欧拉路径不是回路,奇度顶点就有2个,即路径的起点和终点;如果是欧拉回路,起点与终点重合,则不存在奇度顶点.必要性得证.证明:充分性.如果图中没有奇度顶点,那么在G中随机取一个顶点v0出发,尝试构造一条回路c0.如果c0就是原路,则结束;如果不是,那么由于图是连通的,c0和图的剩余部分必然存在某公共顶点v1,从v2出发重复尝试构造回路,最终可将整张图分割为多个回路.由于两条相连的回路可以视为一条回路,所以该图必存在欧拉回路.如果图中有2个奇度顶点u和v,那么若是加一条边将u和v连接起来的话,就得到一个没有奇度顶点的连通图,由上文可知该图必存在欧拉回路,去掉这条新加的边,就是一条以u和v为起终点的欧拉路径.充分性得证.可知,哥尼斯堡七桥问题中的图有4个奇度顶点(1个度数为5,3个度数为3),所以不存在欧拉路径.2.有向图的情况定理:底图连通的有向图G有欧拉路径的充要条件为:G的所有顶点入度和出度都相等;或者只有两个顶点的入度和出度不相等,且其中一个顶点的出度与入度之差为1,另一个顶点的入度与出度之差为1.显然,可以通过与无向图情况相似的思路来证明,过程略.当时的数学界起初并未对欧拉解决七桥问题的意义有足够的认识,甚至有些人仅仅当其为一个数学游戏.图论这一数学分支诞生后并未得到很好的发展,直到200年后的1936年,匈牙利数学家科尼希出版了《有限图与无限图理论》,此为图论的第一部专著,其总结了进200年来有关图论的成果,这是图论发展的第一座里程碑.此后,图论进入发展与突破的阶段,又经过了半个多世纪的发展,现已成为数学科学的一个独立的重要分支.图论原是组合数学中的一个重要课题.我们用点表示事物,用连接点的边表示事物间的联系,便可得到图论中的图.图论为研究任何一类离散事物的关系结构提供了一种框架.图论中的理论已应用于经济学、心理学、社会学、遗传学、运筹学、逻辑学、语言学计算机科学等诸多领域.由于现代科学尤其是大型计算机的迅猛发展,使得图论大有用武之地,无论是数学、物理、化学、地理、生物等基础科学,还是信息、交通、战争、经济乃至社会科学的众多问题,都可以运用图论方法予以解决.当然,图论也是计算机科学的基础学科之一.值得一提的是,欧拉对七桥问题的研究,后演变成多面体理论,得到了著名的欧拉公式V+F=E+2,欧拉公式是拓扑学的第一个定理.哥尼斯堡的七座桥如今只剩下三座,一条新的跨河大桥已经建成,它完全跨过河心岛——内福夫岛,导游们仍向游客讲述哥尼斯堡桥的故事,有的导游甚至仍称“七桥问题”没有被解决,留给游客以遐想.虽然七座哥尼斯堡桥成了历史,但是“七桥问题”留下的“遗产”不像这些桥那样容易破坏,欧拉卓越的解答方式被永载史册.60。
哥尼斯堡七桥问题[欧拉图]
![哥尼斯堡七桥问题[欧拉图]](https://img.taocdn.com/s3/m/bc5c022cbdd126fff705cc1755270722192e59b0.png)
哥尼斯堡七桥问题[欧拉图]⼀、历史背景1736年,年仅29岁的数学家欧拉来到普鲁⼠的古城哥尼斯堡(哲学家康德的故乡,今俄罗斯加⾥宁格勒)。
普瑞格尔河正好从市中⼼流过,河中⼼有两座⼩岛,岛和两岸之间建筑有七座古桥。
欧拉发现当地居民有⼀项消遣活动,就是试图每座桥恰好⾛过⼀遍并回到原出发点,但从来没⼈成功过。
欧拉证明了这种⾛法是不可能的。
现在看来,欧拉的证明过程⾮常简单,但他对七桥问题的抽象和论证思想,开创了⼀个新的学科:图论(Graph)。
如今,⽆论是数学、物理、化学、天⽂、地理、⽣物等基础科学,还是信息、交通、经济乃⾄社会科学的众多问题,都可以应⽤图论⽅法予以解决。
图论还是计算机科学的数据结构和算法中最重要的框架(没有之⼀)。
⾸先能想到的证明⽅法是把⾛七座桥的⾛法都列出来,⼀个⼀个的试验,但七座桥的所有⾛法共⽤7\!=5040种,逐⼀试验将是很⼤的⼯作量。
欧拉作为数学家,当然没那样想。
欧拉把两座岛和河两岸抽象成顶点,每⼀座桥抽象成连接顶点的⼀条边,那么哥尼斯堡的七座桥就抽象成下⾯的图:Processing math: 100%假设每座桥都恰好⾛过⼀次,那么对于A、B、C、D四个顶点中的每⼀个顶点,需要从某条边进⼊,同时从另⼀条边离开。
进⼊和离开顶点的次数是相同的,即每个顶点有多少条进⼊的边,就有多少条出去的边,也就是说,每个顶点相连的边是成对出现的,即每个顶点的相连边的数量必须是偶数。
⽽上图中A、C、D四个顶点的相连边都是3,顶点B的相连边为5,都为奇数。
因此,这个图⽆法从⼀个顶点出发,遍历每条边各⼀次。
欧拉的证明与其说是数学证明,还不如看作是⼀个逻辑证明。
⼀个曾难住那么多⼈的问题,竟然是这样⼀个简单的出⼈意料的推理,还开创了⼀个新的学科。
欧拉⾮常巧妙的把⼀个实际问题抽象成⼀个合适的数学模型,这种研究⽅法就是我们应该掌握的数学模型⽅法。
这并不需要运⽤多么深奥的理论,但能想到这⼀点,却是解决问题的关键。
哥尼斯堡七桥问题与图论

哥尼斯堡七桥问题与图论
大家公认,图论诞生于七桥问题。
出生于瑞士的伟大数学家欧拉(Leonhard Euler,1707—1783)于1736年发表了论文《与位置几何有关的一个问题的解》,文中提出并解决了七桥问题,为图论的形成奠定了基础。
今天,图论已广泛应用在计算机学科、运筹学、控制论、信息论等学科中,成为对现实世界进行抽象的一个强有力的数学工具。
七桥问题是这样描述的:17世纪的东普鲁士有一座哥尼斯堡城(现在叫加里宁格勒,在波罗的海南岸),城中有一座岛,普雷格尔河的两条支流环绕其旁,并将整个城市分成北区、东区、南区和岛区4个区域,全城共有七座桥将4个城区连接起来,图1是这条河以及河上的两个岛和七座桥的草图。
于是,产生了一个有趣的数学难题:一个人是否能在一次步行中穿越全部的七座桥后回到起点,且每座桥只经过一次?
为了解决哥尼斯堡七桥问题,欧拉用A、B、C、D表示4个城区,用7条线表示7座桥,将哥尼斯堡七桥问题抽象为一个图模型,如图2所示,从而将哥尼斯堡七桥问题抽象为一个数学问题:求经过图中每条边一次且仅一次的回路,后来人们称之为欧拉回路。
欧拉论证了这样的回路是不存在的,并且将问题进行了一般化处理,即对于任意多的城区和任意多的桥,给出了是否存在欧拉回路的判定规则:
(1)如果通奇数桥的地方多于两个,则不存在欧拉回路;
(2)如果只有两个地方通奇数桥,可以从这两个地方之一出发,找到欧拉回路;
(3)如果没有一个地方通奇数桥,则无论从哪里出发,都能找到欧拉回路。
哥尼斯堡七桥问题给我们的启示

哥尼斯堡七桥问题给我们的启示
哥尼斯堡七桥问题是欧洲数学家欧拉在18世纪提出的一个著名的数学问题,这个问题是如何通过哥尼斯堡城市中的七座桥,每座桥只能过一次,将城市中的四块陆地分隔开来。
这个问题最终被欧拉用图论的方法解决了,也成为了现代数学和计算机科学的基础之一。
哥尼斯堡七桥问题给我们的启示是:
创新思维:欧拉在解决这个问题时,采用了新颖的图论方法,这种创新的思维方式对于解决其他问题也同样适用。
抽象思维:欧拉将哥尼斯堡城市的地图抽象成为图形,通过对图形的分析和计算,解决了这个问题。
这种抽象思维方式,对于解决其他问题也同样重要。
多角度思考:欧拉在解决这个问题时,考虑了不同的角度和方法,最终找到了解决问题的突破口。
在日常生活和工作中,也需要多角度思考问题,寻找解决问题的最佳方法。
团队协作:欧拉在研究这个问题时,与其他数学家和科学家进行了交流和合作,共同解决了这个问题。
在工作中也需要团队协作,共同解决问题,取得更好的成果。
总之,哥尼斯堡七桥问题是一个启示我们创新思维、抽象思维、多角度思考和团队协作的经典案例。
哥尼斯堡七桥问题

现在已发展成为研究连续性现象的数学分支。
拓扑学应用实例
前面所提的哥尼斯堡七桥问题、四色问题? 左手套能否在空间掉转位置后变成右手套? 一条车胎能否从里朝外的把他翻转过来? 一只有把的茶杯与救生圈更相似,还是与花瓶更相
互相衔接的两两不同的一串“弧”称为“路”。路中弧的端 点称为路的“顶点”。如果起点与终点相同称为“闭路”。 如果闭路的顶点又不相同,称为“圈”。如下所示:
路
闭路
圈
网络与一笔画问题
于是我们可以给出一笔画的理论叙述。
“一笔画”问题相当于给定一个网络。问: “有没有可能把所有的弧排成一条路”。
如果一个网络的全部弧可以排成一条路,那 么我们称这个网络为一个一笔画。
纸圈,然后只允许用一种颜色,在纸圈上的一面涂抹,最后 把整个纸圈全部抹成一种颜色,不留下任何空白。 这个纸圈应该怎样粘? 如果是纸条的首尾相粘做成的纸圈有两个面,势必要涂完一 个面再重新涂另一个面,不符合涂抹的要求。 能不能做成只有一个面、一条封闭曲线做边界的纸圈?
莫比乌斯带的发现
对于这样一个看来十分简单的问题,数百年间,曾有许多科 学家进行了认真研究,结果都没有成功。后来,德国的数学 家莫比乌斯对此发生了浓厚兴趣,他长时间专心思索、试验, 也毫无结果。
当地的市民正从事一项非常有趣的消遣活动。这项有趣的消 遣活动是在星期六作一次走过所有七座桥的散步,每座桥只 能经过一次而多人对此很感兴趣,纷纷进行试验,但在相 当长的时间里,始终未能解决。
而利用普通数学知识,每座桥均走一次,那这七座桥所有的 走法一共有5040种,而这么多情况,要一一试验,这将会是 很大的工作量。
哥尼斯堡七桥问题

你 能 画 出 来 吗 ?如 果 你 画 出 来 了 ,那 么
一 请 你 再 看 图 2能 不 能 一 笔 画 出来 ? 虽 然 你 动 了脑 筋 ,但 我 相 信 你 肯 定 不 能 一 笔 画 出来 !
为 什 么 我 的 语 气 这 么 肯 定 ?我 们 来 分 析 一 下 图2.我们 把 图2看 成 是 由 点 和 线 组
(Mobius,1790~1868)和 约翰 ·李 斯 丁 发 现 : 就 是 说 ,它 的 曲 面 只 有 一个 .关 于 莫 比乌 斯
把 一 根 纸 条 扭 转 180。后 ,两 头 再 粘 接 起 来 带 的 单 侧 性 ,同学 们 可 如 下 直 观 地 了解 ,如
做 成 的纸 带 圈 ,具 有 魔 术 般 的 性 质 .普 通 纸 果 给 莫 比乌 斯 带 着 色 ,色 笔 始 终 沿 曲 面 移
沿 河 过 桥 散 步 .渐 渐 地 ,爱 动脑 筋 的 人 们 提 出 了一 个 问题 :一个 散 步者 能否 一 次 走 遍 7
座桥 ,而 且 每 座桥 只许 通 过 一 次 ,最 后仍 回
到起 始 地 点 .这 就 是 七 桥 问题 ,一 个 著 名 的
图 1
图 2
图 论 问 题 .
果 有 偶 数 条 边 连 它 ,这 点 就 称 为 偶 点 ;如 猜 想 是 正 确 的 .欧 拉 是 这 样 解 决 问题 的 :既
果 有 奇 数 条 边 连 它 ,就 称 它 为 奇 点 .我 们 知 然 陆地 是 桥 梁 的 连 接 地 点 ,不 妨 把 图 中被 道 ,能 一 笔 画 的 图 形 只 有 两 类 :一 类 是 所 河 隔 开 的陆 地 看 成4个 点 ,7座 桥 表示 成 7条
七桥问题
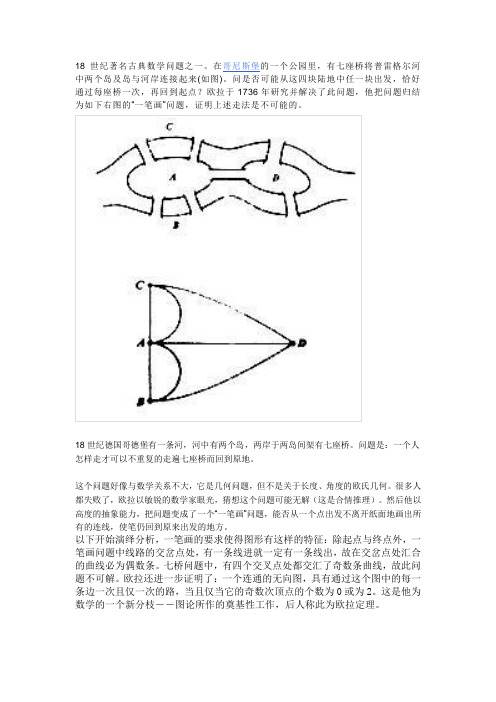
18世纪著名古典数学问题之一。
在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。
问是否可能从这四块陆地中任一块出发,恰好通过每座桥一次,再回到起点?欧拉于1736年研究并解决了此问题,他把问题归结为如下右图的“一笔画”问题,证明上述走法是不可能的。
18世纪德国哥德堡有一条河,河中有两个岛,两岸于两岛间架有七座桥。
问题是:一个人怎样走才可以不重复的走遍七座桥而回到原地。
这个问题好像与数学关系不大,它是几何问题,但不是关于长度、角度的欧氏几何。
很多人都失败了,欧拉以敏锐的数学家眼光,猜想这个问题可能无解(这是合情推理)。
然后他以高度的抽象能力,把问题变成了一个“一笔画”问题,能否从一个点出发不离开纸面地画出所有的连线,使笔仍回到原来出发的地方。
以下开始演绎分析,一笔画的要求使得图形有这样的特征:除起点与终点外,一笔画问题中线路的交岔点处,有一条线进就一定有一条线出,故在交岔点处汇合的曲线必为偶数条。
七桥问题中,有四个交叉点处都交汇了奇数条曲线,故此问题不可解。
欧拉还进一步证明了:一个连通的无向图,具有通过这个图中的每一条边一次且仅一次的路,当且仅当它的奇数次顶点的个数为0或为2。
这是他为数学的一个新分枝――图论所作的奠基性工作,后人称此为欧拉定理。
第二章 第二节 哥尼斯堡七桥问题

第二节哥尼斯堡七桥问题教学目标1.了解哥尼斯堡七桥问题的由来2.理解欧拉解决哥尼斯堡七桥问题的方法3.掌握一笔画问题的步骤教学重点掌握一笔画问题的技巧教学过程一、导入哥尼斯堡七桥问题的由来哥尼斯堡曾是东普鲁士的首府,现称加里宁格勒,在俄罗斯境内。
在第二次是世界大战时,的军警哲理入侵波兰。
后来,苏军也是从此地打进德国的。
所以哥尼斯堡是一座历史名城。
同时,在这里诞生和培养过许多伟大人物。
如著名唯心主义哲学家康德,终生没有离开此城。
在哥尼斯堡城中有一条布勒格尔河,横贯城中。
河有两条支流,一条称新河,一条叫旧河,在城中心汇合成一条主流,在合流的地方中间有一座河心岛,这是城中繁华的商业中心。
由于布勒格尔河的流过,使全城分成为四个地区:岛区、北区、东区和南区。
在布勒格尔河上,架了七座桥,其中五座将河岛与河岸连接起来,另有两座架在二支流上。
这一别致的桥群,吸引了众多的哥尼斯堡居民和游人来此河边散步或去岛上买东西。
早在18世纪,就有人提出这样的问题:“能否在一次散步中每座桥都走一次,而且只能走一次,最后又回到原来的出发点?”这个问题吸引了不少人去思考实验。
事实上,要走遍这七座桥的所有走法共有7!=5040种,要想一一验过,谈何容易。
是否在这5040中走法中存在着一条走遍七座桥而又不重复的路线呢?谁也回答不了。
因而形成了著名的“哥尼斯堡七桥问题”。
二、新授哥尼斯堡七桥问题的解决1735年,有几名大学生写信给当时正在俄国彼得堡科学院任职的天才数学家欧拉,请他帮忙解决。
欧拉并未轻视生活小题,他似乎看到其中隐藏着某种新的数学方法。
经过一年的研究,29岁的欧拉于1736年向彼得堡科学院递交了一份题为《哥尼斯堡的七座桥》的论文,圆满地解决了这一问题,同时开创了数学的一个新分支——图论。
问题的抽象——数学化欧拉是如何将这生活的趣味问题转化为数学问题的呢?又是如何证明要想一次走过这七座桥是不可能的呢?欧拉的方法十分巧妙:他用点A、B、C、D表示哥尼斯堡城的四个地区B(岛区)、C(北区)、A(东区)、D(南区);七座桥看成这四个点的连线,用f,d,a,c,b,e,g七个数字表示,如图3-1。
哥尼斯堡七桥问题与数学抽象

“抽象”是数学的武器,数学的优势 。
我们应该喜欢“抽象”,学会“抽 象”的手段。
为了让大家理解“抽象”的优势, 了解“抽象”的思想、原则、方法和作用
实践“抽象”的过程, 学会“抽象”的手段,喜欢“抽象”。
案例:“哥尼斯堡七桥问题”
一、哥尼斯堡七桥问题
C
A
B
显然要在奇结点间加重复边
如何使所加的边长度最少
归结为求奇结点间的最小
案例
一个邮递员投递信件的街道如图,图上的书 表示各段街道的千米数,他从邮局出发,走 遍各街道,最后回到邮局,走怎样的路线最 短?
3
12
4
21
哈密顿环球旅行问题: 十二面体的20个顶点代表世界上20个城市,
能否从某个城市出发在十二面体上依次经过每个 城市恰好一次最后回到出发点?
奇结点少一些好, 少到几个才能“一笔画”呢?
结论
一个点线图是“一笔画”的充分必要条件 它是连通的并且奇结点的个数为0或2。
——(一笔画原理)。 哥尼斯堡七桥问题:“不重复地走过七座桥 ”是不可能的。
欧拉在圣彼得堡科学院发表了有关的论 文,开创了“图论”的先河,也开创了“拓 扑学”的先河
中国邮递员问题
有人把拓扑学说成是“橡皮几何学”,因为橡皮膜 上的图形,随着橡皮膜的拉动,其长度、曲直、面 积等等都将发生变化。此时谈论“有多长”、“有 多大”之类的问题,是毫无意义的,人们感兴趣的 只是图形的位置关系。
不过,在橡皮几何里也有一些图形的性质保持不变 。例如:点变化后仍然是点,线变化后依旧是线, 相交的图形绝不因橡皮的拉伸和弯曲而变得不相交 。
数学方法(手段)—— 数学抽象
欧拉的第一步抽象
哥尼斯堡七桥问题

最理想的投递路线,就是该段道图是一条欧拉回路。 图(2)的投递路线如下图(3)。
含有奇点的段道图不能一笔画出,有些道路需要重复 走两次的都要添上一条弧。图(1)添弧后如图(4)。
图(3)
图(4)
• 定理1 一个能够不重复的一笔画出的连通图 中,所以的点一定都是偶点。
• 定理2 没有奇点的连通图一定能够从任意一 点开始不重复的一笔画出。
中国邮递员问题
• 中国邮递员问题(Chinese Postman Problem, CPP)是由我国管梅谷教授于1962年首先提出并
发表的 • 例如:观察下列段道图
图(1)
图(2)
从邮局出发,走遍邮区的所有街道至少
一次再回到邮局,按照什么样的路线投
递邮件才能使总的路程最短?
投递路线
一笔画
欧拉回路
3
欧拉的解法
哥尼斯堡七桥问题引起了大数学家 欧拉的兴趣。他知道,如果沿着所有可 能的路线都走一次的话,一共要走5040 次。就算是一天走一次,也需要13年多 的时间。实际上,欧拉只用了几天的时 间就解决了七桥问题。
5
欧拉的想法是:两岸的陆地与河中的小 岛,都是桥梁的连接点,它们的大小、形状均 与问题本身无关。因此,不妨把它们看作是4 个点。7座桥是7条必须经过的路线,它们的 长短、曲直,也与问题本身无关。因此,不妨 任意画7条线来表示它们。就这样,欧拉将七 桥问题抽象成了一个“一笔画”问题,从而否 定了问题的答案。
• 最优投递路线 重复的路最短 添弧的总 长度最短
• 添弧最短的条件 (1)没有重叠的添弧 (2)每一个圈上添弧的总长度不超过圈长的一
半 • 最短的一组添弧称为最优解。
6
七桥问题
哥尼斯堡七桥
哥尼斯堡七桥问题

一、哥尼斯堡七桥问题18世纪在哥尼斯堡城(今俄罗斯加里宁格勒)的普莱格尔河上有7座桥,将河中的两个岛和河岸连结,如图1所示。
城中的居民经常沿河过桥散步,于是提出了一个问题:能否一次走遍7座桥,而每座桥只许通过一次,最后仍回到起始地点。
这就是七桥问题,一个著名的图论问题。
图1这个问题看起来似乎不难,但人们始终没有能找到答案,最后问题提到了大数学家欧拉那里。
欧拉以深邃的洞察力很快证明了这样的走法不存在。
欧拉是这样解决问题的:既然陆地是桥梁的连接地点,不妨把图中被河隔开的陆地看成A、B、C、D4个点,7座桥表示成7条连接这4个点的线,如图2所示。
图2 图3于是“七桥问题”就等价于图3中所画图形的一笔画问题了。
欧拉注意到,每个点如果有进去的边就必须有出来的边,从而每个点连接的边数必须有偶数个才能完成一笔画。
图3的每个点都连接着奇数条边,因此不可能一笔画出,这就说明不存在一次走遍7座桥,而每座桥只许通过一次的走法。
欧拉对“七桥问题”的研究是图论研究的开始,同时也为拓扑学的研究提供了一个初等的例子.二、四色猜想近代三大数学难题之一。
四色猜想的提出来自英国。
1852年,毕业于伦敦大学的弗南西斯.格思里来到一家科研单位搞地图着色工作时,发现了一种有趣的现象:“看来,每幅地图都可以用四种颜色着色,使得有共同边界的国家着上不同的颜色。
”这个结论能不能从数学上加以严格证明呢?他和在大学读书的弟弟格里斯决心试一试。
兄弟二人为证明这一问题而使用的稿纸已经堆了一大叠,可是研究工作没有进展。
1852年10月23日,他的弟弟就这个问题的证明请教他的老师、著名数学家德.摩尔根,摩尔根也没有能找到解决这个问题的途径,于是写信向自己的好友、著名数学家哈密尔顿爵士请教。
哈密尔顿接到摩尔根的信后,对四色问题进行论证。
但直到1865年哈密尔顿逝世为止,问题也没有能够解决。
1872年,英国当时最著名的数学家凯利正式向伦敦数学学会提出了这个问题,于是四色猜想成了世界数学界关注的问题。
哥尼斯堡七桥问题和一笔画

哥尼斯堡七桥问题1.七桥问题在现在的地图上,你很难找到哥尼斯堡这个城市。
但是它在地理上的奇特之处使得它成为数学史上最为著名的城市之一。
这个中世纪的德国城市坐落于普雷格尔河的两岸,河的中央有两座大的岛屿,这两座岛屿通过7座桥,与河的两岸彼此连接。
后来成为附近小镇市长的数学家卡尔·戈特利布·埃勒对这些桥和岛屿十分着迷。
他一直在考虑一个问题:在所有桥都只能走一遍的前提下,如何才能把这个地方所有的桥都走遍,思考一下这个问题?放弃了吗,放弃是明智的,因为这是不可能办到的。
但是大数学家莱昂哈德·欧拉在试图解释这个数学问题时,开拓了一个新的数学领域。
卡尔曾向欧拉写信求助解决这个问题,开始欧拉认为这个问题和数学无关,所以并不是很关注,但是随着他对这个问题的深入思考,他逐渐发现了其中蕴含的重大意义。
他发现这个问题属于一个全新的几何学范畴,他称之为“位置几何”学,也就是现在著名的图论,欧拉最初的想法是,在岛屿或河岸内部行走的路线实际上并不重要,这样我们就可以把地图简化成四个区域,它们分别用一个点来表示,现在我们称之为结点。
它们之间的线代表桥,这样简化的图使我们比较容易计算每个节点的度,也就是节点之间桥的数量。
为什么度很重要呢?试想根据这个问题的规定,一旦有人想要通过一座桥到达一个岛屿,他就必须通过另一座桥离开。
也就是说进入节点和离开节点的桥必须以成对的方式出现的。
这意味着连接每个区域桥的数量一定是偶数,唯一可能的例外是在路程的起点和终点。
在这张图上所有四个节点的度很明显都为奇数,于是无论选择什么样的路线,你总会重复经过某一座桥,欧拉用这个证明发展出了一个通用的理论。
适用于存在两个或两个以上节点的图,每一个边仅经过一次的欧拉路径只可能出现在以下两种情况里:第一,当仅有两个节点为奇数度时而其它的节点都是偶数度时,这样我们就以其中一个拥有奇数度的节点作为起点,另一个作为终点;第二,当所有的节点都是偶数度时,那么欧拉路径就从同一个位置开始和结束,这被称为欧拉回路。
哥尼斯堡七桥问题探究

哥尼斯堡七桥问题探究欧拉对于《哥尼斯堡桥》一文进行了深入分析与研究,解开了“哥尼斯堡七桥问题”所蕴含的丰富数学思想。
通过对七桥问题进行研究与分析,能够让我们对于数学领域中的相关知识予以深入掌握,带给我们更为丰富的数学视角与视野。
标签:哥尼斯堡桥七桥问题欧拉数学思想一、哥尼斯堡七桥问题简述“七桥问题”出现于18世纪哥尼斯堡城。
在这个城市中有七座桥,当时居民十分热衷:一个散步者怎样将这七座桥走遍,并且每座桥都不重复。
要想符合所提出的要求,应当与以下两个条件相适应:第一,所谓的“不重复”指的是,每座桥只能走一次;第二,所谓的“走遍”指的是,每座桥都应当走到不应当被落下。
这些问题的解决是欧拉所完成的,在很多的文献资料中,都提到了欧拉对七桥问题解决的方法,实际上,在欧拉的论文《问题解决与几何位置》中,只包括以下的三幅图与两个表格。
该问题主要包括两个特征:第一,该问题全部来源于现实;第二,该问题属于新数学领域范畴,欧拉的解答所具备的创新性非常突出,对数学教育工作的开展具有至关重要的启发作用。
二、欧拉对七桥问题的解答第一步就是,对描述路线的简洁方法进行寻找。
将河流分割的陆地区域分别用A、B、C 、D表示,地点A到达地点B需要对桥a或b进行跨越,记作AB,倘若再从地点B跨越桥f到达地点D,记作ABD,字母B不仅代表首次跨越的终点,也代表第二次跨越的起点,其余地点也根据这种方法进行类推。
其发现:第一,该表示方法与跨越的桥不存在任何关联;第二,跨越n座桥的路线正好可以用n+1个字母来代表。
该问题就转变成符合条件的八个字母排列问题。
在部分区中,所连接的桥不止一座,部分字母会多次出现,所以,应当对每个字母所出现的次数进行确定。
为了对某个字母出现次数的法则进行判定,欧拉选取单独的区域A,并对多座桥进行随意设置,散步者可以利用不同的桥离开或进入A,所通过的桥数决定着字母A出现的次数,倘若桥数为奇数,表1将其规律进行了揭示,也就是桥数加1的和再除以2,就是字母A所出现的次数。
世界数学难题

世界数学难题——哥尼斯堡七桥问题18世纪时,欧洲有一个风景秀丽的小城哥尼斯堡(今俄罗斯加里宁格勒),那里的普莱格尔河上有七座桥。
将河中的两个岛和河岸连结,城中的居民经常沿河过桥散步,于是提出了一个问题:一个人怎样才能一次走遍七座桥,每座桥只走过一次,最后回到出发点?大家都试图找出问题的答案,但是谁也解决不了这个问题。
这就是哥尼斯堡七桥问题,一个著名的图论问题。
1727年在欧拉20岁的时候,被俄国请去在圣彼得堡(原列宁格勒)的科学院做研究。
他的德国朋友告诉了他这个曾经令许多人困惑的问题。
欧拉并没有跑到哥尼斯堡去走走。
他把这个难题化成了这样的问题来看:把二岸和小岛缩成一点,桥化为边,于是“七桥问题”就等价于下图中所画图形的一笔画问题了,这个图如果能够一笔画成的话,对应的“七桥问题”也就解决了。
经过研究,欧拉发现了一笔画的规律。
他认为,能一笔画的图形必须是连通图。
连通图就是指一个图形各部分总是有边相连的,这道题中的图就是连通图。
但是,不是所有的连通图都可以一笔画的。
能否一笔画是由图的奇、偶点的数目来决定的。
那么什么叫奇、偶点呢?与奇数(单数)条边相连的点叫做奇点;与偶数(双数)条边相连的点叫做偶点。
如下图中的①、④为奇点,②、③为偶点。
1.凡是由偶点组成的连通图,一定可以一笔画成。
画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
例如下图都是偶点,画的线路可以是:①→③→⑤→⑦→②→④→⑥→⑦→①2.凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。
画时必须把一个奇点为起点,另一个奇点终点。
例如下图的线路是:①→②→③→①→④3.其他情况的图都不能一笔画出。
2.哥尼斯堡七桥问题-湘教版选修4-8统筹法与图论初步教案

哥尼斯堡七桥问题-湘教版选修4-8统筹法与图论初步教案什么是哥尼斯堡七桥问题?哥尼斯堡七桥问题,又称为哥尼斯堡桥问题,是欧拉于1736年提出的一道经典问题。
该问题的问题陈述是:有一座河流将一个岛分为了两个部分,部分之间由七座桥连接。
那么,能否从该岛的一个点出发,经过每座桥恰好一次,回到出发点?这道问题是图论的一个经典问题,具有重要的理论意义和实际应用价值。
哥尼斯堡七桥问题的解法为了解决哥尼斯堡七桥问题,我们首先需要用图论的语言来描述这个问题。
在图论中,我们可以将河流和岛上的部分看成图中的点(vertex),而河上的桥则看成两个点之间的边(edge)。
这样,我们就可以将哥尼斯堡桥问题转化为在图中寻找一条路径,使得恰好经过所有边一次,并回到起点。
显然,这个问题与欧拉定理有直接关系:一个无向连通图存在欧拉回路(Eulerian circuit),当且仅当该图的每个点的度数均为偶数。
在哥尼斯堡七桥问题中,每个岛上的点的度数均为奇数,而每座桥连接的两个点的度数均为偶数。
因此,该问题无解。
为了更好地理解这个结果,我们可以继续探索欧拉定理的证明。
欧拉在证明欧拉定理时,使用了一个类似哥尼斯堡桥问题的图,即著名的“Königsberg Bridge Problem”。
在这个问题中,哥尼斯堡的四座岛上分别建有七座桥,我们可以用一个类似如下的图来描述这个问题:(2)------(1)/ | \\ / | \\(3) | (0) | \\\\ | / \\ | \\(4)------(5)---(6)在这个图中,点代表岛,边代表桥,我们需要找到一条路径,使得经过每座桥恰好一次,最终回到起点。
为了解决这个问题,我们可以使用欧拉定理的证明方法,即通过构造欧拉回路,证明该图必然存在一条符合要求的路径。
观察这个图,我们可以发现,该图无法通过欧拉回路回到起点,因为其中有两个点(0和5)的度数为奇数。
相反地,我们可以找到一条路径,使得经过每座桥恰好一次,并在终点处止步,如下图所示:(2)------(1)/ | \\ / | \\(3) | (0) | \\\\ | / \\ | \\(4) (5)---(6)这样,我们证明了哥尼斯堡桥问题无解,因为该图的每个点的度数均为奇数,不符合欧拉定理的条件。
哥尼斯堡七桥问题

七桥问题的起源
18世纪初,哥尼斯堡的居民开 始对城市中的七座桥梁产生了 浓厚的兴趣。
当时,人们开始思考是否能够 遍历这七座桥梁,每座桥只过 一次,最后回到起始点。
这个问题引起了广泛的关注和 讨论,成为了著名的哥尼斯堡 七桥问题。
02
问题描述
七座桥与哥尼斯堡城市的关系
哥尼斯堡是位于普鲁士王国的一个城市,拥有七座桥梁连接 城市的各个部分。这些桥梁是该城市的重要交通枢纽,也是 文化和历史遗产。
05
结论
哥尼斯堡七桥问题的历史地位和意义
1 2
开启图论研究先河
哥尼斯堡七桥问题被视为图论和欧拉路径研究的 起点,为后续图论学科的发展奠定了基础。
推动数学发展
该问题的解决推动了数学领域中拓扑学和几何学 的发展,对数学理论产生了深远的影响。
3
Hale Waihona Puke 激发探索精神哥尼斯堡七桥问题激发了人们对数学和图论的兴 趣,促使更多人投身于数学研究,推动数学科学 的进步。
物等,以推动数学和其他学科的共同发展。
THANKS
感谢观看
03
欧拉的研究
欧拉对七桥问题的初步探索
欧拉对七桥问题的初步探索始于对哥尼斯堡城市结构的观察。他注意到城市中的七座桥,并 思考是否可以从哥尼斯堡的一个地方开始,遍历所有的桥,每座桥只过一次,最后回到开始 的地方。
欧拉注意到,尽管哥尼斯堡的居民可能认为这是一个有趣的问题,但并没有实际的数学模型 或理论来支持或解决这个问题。
哥尼斯堡七桥问
• 引言 • 问题描述 • 欧拉的研究 • 七桥问题的扩展和影响 • 结论
01
引言
哥尼斯堡背景介绍
01
哥尼斯堡是普鲁士王国的城市, 位于普鲁士东部的奥得河畔,是 重要的交通枢纽和商业中心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一笔画
⒈凡是由偶点组成的连通图,一定可以一笔画成。画时可以把任一偶点为起 点,最后一定能以这个点为终点画完此图。 ⒉凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。画时 必须把一个奇点为起点,另一个奇点为终点。 ⒊其他情况的图都不能一笔画出。(奇点数除以二便可算出此图需几笔画 成。)
哥尼斯堡七桥问题
七桥问题
1736年29岁的欧拉向圣彼得堡科 学院递交了《哥尼斯堡的七座桥》 的论文,在解答问题的同时,开创 了数学的一个新的分支——图论与几 何拓扑,也由此展开了数学史上的 新历程。
莱昂哈德·欧拉
莱昂哈德·欧拉,瑞士数学家、自然科学家。1707年4月15日出生 于瑞士的巴塞尔,1783年9月18日于俄国圣彼得堡去世。欧拉出生 于牧师家庭,自幼受父亲的影响。13岁时入读巴塞尔大学,15岁 大学毕业,16岁获得硕士学位。欧拉是18世纪数学界最杰出的人 物之一,他不但为数学界作出贡献,更把整个数学推至物理的领 域。他是数学史上最多产的数学家,平均每年写出八百多页的论 文,还写了大量的力学、分析学、几何学、变分法等的课本, 《无穷小分析引论》、《微分学原理》、《积分学原理》等都成 为数学界中的经典著作。欧拉对数学的研究如此之广泛,因此在 许多数学的分支中也可经常见到以他的名字命名的重要常数、公 式和定理。 此外欧拉还涉及建筑学、弹道学、航海学等领域。瑞 士教育与研究国务秘书查尔斯·克莱伯曾表示:“没有欧拉的众 多科学发现,今天的我们将过着完全不一样的生活。”法国数学 家拉普拉斯则认为:读读欧拉,他是所有人的老师。 2007年,为 庆祝欧拉诞辰300周年,瑞士政府、中国科学院及中国教育部于 2007年4月23日下午在北京的中国科学院文献情报中心共同举办纪 念活动,回顾欧拉的生平、工作以及对现代生活的影响。
最终成果
1736年,在经过一年的研究之后,29岁的欧拉提交了《哥 尼斯堡七桥》的论文,圆满解决了这一问题,同时开创了 数学新一分支---图论。 在论文中,欧拉将七桥问题抽象出来,把每一块陆地考虑 成一个点,连接两块陆地的桥以线表示。并由此得到了如 图一样的几何图形。 若我们分别用A、B、C、D四个点表 示为哥尼斯堡的四个区域。这样著名的“七桥问题”便转 化为是否能够用一笔不重复的画出过此七条线的问题了。 若可以画出来,则图形中必有终点和起点,并且起点和终 点应该是同一点,由于对称性可知由B或C为起点得到的效 果是一样的,若假设以A为起点和终点,则必有一离开线 和对应的进入线,若我们定义进入A的线的条数为入度, 离开线的条数为出度,与A有关的线的条数为A的度,则A 的出度和入度是相等的,即A的度应该为偶数。即要使得 从A出发有解则A的度数应该为偶数,而实际上A的度数是5 为奇数,于是可知从A出发是无解的。同时若从B或D出发, 由于B、D的度数分别是3、3,都是奇数,即以之为起点都 是无解的
推断方法
当欧拉在1736年访问哥尼斯堡时,他发现当地的市 民正从事一项非常有趣的消遣活动。哥尼斯堡城中 有一条名叫普雷格尔河流横经其中,这项有趣的消 遣活动是在星一地 点。 欧拉把每一块陆地考虑成一个点,连接两块陆地的 桥以线表示。 后来推论出此种走法是不可能的。他的论点是这样 的,除了起点以外,每一次当一个人由一座桥进入 一块陆地(或点)时,他(或她)同时也由另一座 桥离开此点。所以每行经一点时,计算两座桥(或 线),从起点离开的线与最后回到始点的线亦计算 两座桥,因此每一个陆地与其他陆地连接的桥数必 为偶数。
七桥问题和欧拉定理
欧拉通过对七桥问题的研究,不仅圆满地回答了哥尼斯堡居民提出的问 题,而且得到并证明了更为广泛的有关一笔画的三条结论,人们通常称 之为 欧拉定理。对于一个连通图,通常把从某结点出发一笔画成所经 过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做 欧拉回路。具有欧拉回路的图叫做欧拉图。
提出时间
18世纪著名古典数学问题之一。在哥尼斯堡的一个公园 里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起 来(如图)。问是否可能从这四块陆地中任一块出发,恰 好通过每座桥一次,再回到起点?欧拉于1736年研究并 解决了此问题,他把问题归结为如右图的“一笔画”问 题,证明上述走法是不可能的。 有关图论研究的热点问题。18世纪初普鲁士的哥尼斯堡, 有一条河穿过,河上有两个小岛,有七座桥把两个岛与 河岸联系起来(如右上图)。有个人提出一个问题:一 个步行者怎样才能不重复、不遗漏地一次走完七座桥, 最后回到出发点。后来大数学家欧拉把它转化成一个几 何问题(如左图下)——一笔画问题。他不仅解决了此 问题,且给出了连通图可以一笔画的充要条件是:奇点 的数目不是0 个就是2 个(连到一点的数目如是奇数条, 就称为奇点,如果是偶数条就称为偶点,要想一笔画成, 必须中间点均是偶点,也就是有来路必有另一条去路, 奇点只可能在两端,因此任何图能一笔画成,奇点要么 没有要么在两端)
