用等效化简的方法分析电路
电路与电子电路分析:2-1 等效的概念及等效变换分析

电+
压 源
us
-
电压源
i +
uR -
外电路
u us
0
u us iRs
us Rs i
实 际
is
电
流
源
(a) i
u
+ Rs u
is Rs
R
i is u Rs
-
0
is i
电流源
外电路
(a) 对外电路等效:对外VCR曲线完全相同。
u s is Rs
is u s Rs X
7、两种实际电源模型的等效变换
•
a
a
10V
10 1A
10
b
b
例题2 求下图所示电路中的电流i。
解:利用电源的等效变换将图(a)所示电路逐步化
简为图(d)所示电路,变换过程如图(b)、 (c)所示。
2 2
2
6A
6V
2A 2
i 7
3A 2 6A
2A
2
i 7
(a)
(b)
X
解续
2
9A
2A
i
1
7
4V 1
9V
2
i
7
(c)
(d)
由图(d)可求得:i 9 4 0.5A
退出 开始
电阻电路
• 电阻电路,是指电路只由电源和电阻元件组成, 而不包含电容、电感等元件。
• 电流和电压的约束关系都是瞬时的, • 各支路某时刻的电压/电流只取决与该时刻电路
的情况,而与历史时刻无关,因此又称为无记忆 电路。 • 电阻电路各个之路上电流和电压的约束关系即 VCR只是代数方程。
第二章 电阻电路的基本分析方法与定理
用等效化简的方法分析电路

US = US1 US2 + US3
电源与等效电源参考 方向一致为+,反之为-
IS1
IS2 IS3
IS = IS1IS2 +
IS
IS3
5. 电压源并联
+ (1) + 5V_ 5V_
(2)
++ 5V_ 6V_
+ 5V_
不允许,违背KVL
6. 电流源串联
(1)
5A
5A
(2)
5A
6A
5A 不允许,违背KCL。
iS2
2)求R0;
Ro
(R1 R2 )R3 R1 R2 R3
3)得到Norton 等效电路。
例2: 用诺顿定理求 I 。
_ 4V +
1
+ 6V _
+
a
_12V
I
1
3
6
b
解:一、选择分解点
二、求最简等效电路 1. 求Isc 2. 求Ro 三、用等效电路替代后求解
4 8 最大功率传递定理
本节介绍戴维南定理的一个重要应用。 问题:电阻负载如何从电路获得最大功率?
(一)求二端网络的最简等效电路 最简:一个单回路或单节点的电路。
1. 只含电阻的电路
例 1:
3Ω
7Ω 3Ω
10Ω
6Ω
12
5Ω
例2:
20
20
a
44 b 结论:
60
60
20
60
只含电阻单口网络 等效为一个电阻
只含 电阻
22
R
2.含独立源电路
例3: + 1V _
2
3
大学电工电子技术电路的分析方法

I + _E U R0
U=E-IR0 I U
U 伏安特性
E
I E/R0
10
2.3.2 电流源
1. 理想电流源 :
定义:通过的电流与两端的电压大小无关的 理想元件。
特点 (1)元件中的电流是固定的,不会因为 外电路的不同而不同。
(2)电源两端的电压由外电路决定。
电路模型:
Ia
Is
Uab
b
11
恒流源:若理想电流源的电流恒等于常数
I3
I1
I2
R1
R2
R3 U ab
若结点电压Uab已知, 则各支路电流:
b
I1= (Uab–E1)/R1
列KCL方程: 代入
I2= (Uab–E2)/R2 I3= Uab/R3
I1+I2+I3 =0
Uab E1 Uab E2 Uab 0
R1
R2
R3
结点电压:
Uab
E1 1
R1 E2 1
R2 1
4
2.3 电源的两种模型及其等效变换 2.3.1电压源 1.理想电压源 : 定义:电压总是保持某个给定的时间函数,
与通过它的电流无关。 特点:(1)输出电 压是固定的,不会因为外电路的
不同而不同。
(2)电源中的电流由外电路决定。
5
电路模型:
Ia
Ia
+
E_
Uab
或者
E
+ _
Uab
b
b
恒压源:如果理想电压源的电压u(t)恒等于常 数U(u(t)=U),则称为恒压源。
是否能少列 一个方程?
例8
支路电流未知数少一个:
含源电路的等效化简

含源电路的等效化简
含源电路的等效化简是一种将复杂电路简化为更简单形式的方法,以便于电路分析和设计。
在等效化简过程中,通过替代电路元件、合并电路元件或建立等效电路模型,将原始电路转化为具有相同电性能但更简单的电路。
以下是含源电路等效化简的一般步骤:
1. 确定等效化简的目标:明确需要简化的电路部分以及所需的电路性能。
2. 根据电路的特性和元器件的性质应用电路定律:运用电路定律(如欧姆定律、基尔霍夫定律)分析电路中的电流、电压、电阻、功率等参数。
3. 利用等效原理简化电路元件:通过使用等效电阻、等效电容、等效电感、等效电流源、等效电压源等类型的等效元件,将一组或多组连续的电路元件简化为一个等效元件。
4. 合并电路元件:对于电路中的并联电阻、串联电阻、并联电容、串联电容等,可以根据电路性质和等效原理将它
们合并为一个等效元件。
5. 建立等效电路模型:根据等效化简的目标和电路特性,建立一个与原始电路相等效的简化电路模型。
最终,等效化简的结果是一个具有相同电路性能但更简单的电路,在电路分析和设计中更加方便和直观。
需要注意的是,等效化简是一种近似方法,可能会在某些情况下引入一定的误差,因此在实际应用中应根据具体需求和精度要求谨慎应用。
电路分析基础课件第2章 电路分析中的等效变换

v
+
Seq
-
a+
v
-b a+ v -b
n
v v v v vSeq s1 s2 s3 sn vSk k 1
2 电压源的并联
只有电压相等且极性相同时, 电压源才能并联。
ai ++ + +
i
a +
+
v vS vS
vS
b
-
-
-
v vS b- -
3 电流源的并联
iS1 iS2
例8 求:I
I1 1
解: Δ—Y 转换 2.6 10
R1
R12 R13 R12 R13 R23
100 25
4
R2
R23R13 25
2
+ 9V
R2 22
4
R3
R23R12 25
2
-
b
R14 R1 (R2 R24 ) //( R3 R34 )
R110 5 R3
ia
ia
iSn
+
iS
++
v
vv
b
-b
n
i i i iS s1 s2 sn iSk k 1
4 电流源的串联
只有电流相等且参考方向相同时,
电流源才能串联。
iS iS ... iS
i
a+
v
-b
iS
i
a+ v -b
5 电压源与电流源的串联
a i+
N
例析物理竞赛中纯电阻电路的简化和等效变换

例析物理竞赛中纯电阻电路的简化和等效变换计算一个电路的电阻,通常从欧姆定律出发,分析电路的串并联关系。
实际电路中,电阻的联接千变万化,我们需要运用各种方法,通过等效变换将复杂电路转换成简单直观的串并联电路。
本节主要介绍几种常用的计算复杂电路等效电阻的方法。
1、等势节点的断接法在一个复杂电路中,如果能找到一些完全对称的点(以两端连线为对称轴),那么可以将接在等电势节点间的导线或电阻或不含电源的支路断开(即去掉),也可以用导线或电阻或不含电源的支路将等电势节点连接起来,且不影响电路的等效性。
这种方法的关键在于找到等势点,然后分析元件间的串并联关系。
常用于由等值电阻组成的结构对称的电路。
【例题1】在图8-4甲所示的电路中,R1 = R2 = R3 = R4 = R5 = R ,试求A、B两端的等效电阻R AB。
模型分析:这是一个基本的等势缩点的事例,用到的是物理常识是:导线是等势体,用导线相连的点可以缩为一点。
将图8-4甲图中的A、D缩为一点A后,成为图8-4乙图。
3R 。
答案:R AB =8【例题2】在图8-5甲所示的电路中,R1 = 1Ω,R2 = 4Ω,R3 = 3Ω,R4 = 12Ω,R5 = 10Ω,试求A、B两端的等效电阻R AB。
模型分析:这就是所谓的桥式电路,这里先介绍简单的情形:将A、B两端接入电源,并假设R5不存在,C、D两点的电势相等。
因此,将C、D缩为一点C后,电路等效为图8-5乙对于图8-5的乙图,求R AB 是非常容易的。
事实上,只要满足21R R =43R R 的关系,该桥式电路平衡。
答案:R AB =415Ω 。
【例题3】在如图所示的有限网络中,每一小段导体的电阻均为R ,试求A 、B 两点之间的等效电阻R AB 。
【例题4】用导线连接成如图所示的框架,ABCD 是正四面体,每段导线的电阻都是1Ω。
求AB 间的总电阻。
2、电流分布法 设有电流I 从A 点流入、B 点流出,应用电流分流的思想和网络中两点间不同路径等电压的思想,(即基耳霍夫定理),建立以网络中各支路的电流为未知量的方程组,解出各支路电流与总电流I 的关系,然后经任一路径计算A 、B 两点间的电压AB U ,再由IU R ABAB =即可求出等效电阻。
电路分析基础2章等效PPT

17
四、非并非串电阻电路的等效变换
电阻非并串的两种连接形式:
1
+ i2
i1 1
i3 1
+
i3
1
+
i2
i1 1
1
+
-
-
i2
2
i3 3
Y形连接
- R12
i2 2
R31
R23
-
i3 3
Δ形连接
18
Y形连接和Δ形连接的电阻等效变换公式
Y-
G12
G1
G1G2 G2 G3
G23
G1
G2G3 G2 G3
原电路等效为电阻,阻值为
R 25
25
36
归纳总结
* 一端口电阻电路通常等效为一个电阻; * 由独立源、受控源和电阻组成的一端口
电路一般等效为一个实际电压源或实际 电流源; * 由受控源与电阻构成的一端口电路可等 效为一个电阻,该电阻可以是负电阻。
37
1、两个电阻串联
i
+
R1
u
_
R2
i
+ uR _
等效电阻
R = R1 + R2 (1)
6
证明两电阻串联的等效电路:
+ 设:端口电压 u、电流 i 的参考
方向关联,如右图所示。
u
_ 列KVL方程,有
i +
R1 _u1
+ R2 _u2
u R1i R2i (R1 R2 )i
端口电压电流的关系为欧姆定律,与一个阻值为
4 2A
+
b
解:把电流源转换为电压源,见右
电路分析基础_04用等效化简的方法分析电路

5
1.5V_
0.3A
结论
RS
+ US_
含独立 源和电 阻电路
或
RS
IS
(二) 等效化简的方法——逐步化简 例 1:求图(a)单口网络的等效电路。
将电压源与电阻的串联等效变换为电流源与电阻的并联。
将电流源与电阻的并联变换为电压源与电阻的串联等效。
例2:求 I
6_
3
+
9V
+
6V_
2
+ _ 1V
I 8
G
u
Gk
k 1
R1
R2
R
R R1R2
R1 R2
3. 理想电压源串联
+
US1__
+
US2+
US_
+
US3_
4. 理想电流源并联
US = US1 US2 + US3
电源与等效电源参考 方向一致为+,反之为-
IS1
IS2 IS3
IS = IS1IS2 +
IS
IS3
5. 电压源并联
+ (1) + 5V_ 5V_
T
i1
2
4
0.5A
1/3A
说明:。。。
T
N1
T
1'
例3: 图4-32(a)电路中,已知电容电流iC(t)=2.5e-tA,用 置换定理求i1(t)和i2(t) 。
图4-32
图4-32
解:图(a)电路中包含一个电容,它不是一个电阻电路。用 电流为iC(t)=2.5e-tA的电流源替代电容,得到图(b)所示 线性电阻电路,用叠加定理求得:
电路分析实用第2章 电路的等效变换
2.分流公式 ik Gk u Gk
n
i Gk
Gk Geq
i
k 1
u
i
G1 G2 Gn
i
i
n
Gk
Geq
k 1
第k个电阻上的分流公式为 ik Gk u Gk
n
i Gk
Gk Geq
i
两个电阻并联,分流公式为
k 1
i1
R2 R1 R2
接在n节点的两电阻乘积
Rn
三个电阻之和
2. Y - Δ 变换
R1
1
R2
2
R12
1
2
R3
R13
R23
3
R12
R1R2
R2 R3 R3
R1R3
3
R23
R1R2
R2 R3 R1
R1R3
R13
R1R2
R2 R3 R2
R1R3
电阻两两乘积之和 Rmn 下标不为 m,n的电阻
例2: 求等效电阻 Rab
U0
R2 R1 R2
US
R3 R3 R4
US
输出电压随热敏电阻值变化
根据的变化值来确定温度的值
2.5 输入电阻
从(输入)端口两端看进去 的等效电阻。
Ri
Rab
u i
例3:求输入电阻Ri。
R1 I1 I a
解:I I2 I1
U U U
+
μU
I2 +
R2 U
Ri
电阻电路的等效化简

I2、I3的端钮均断开, 分流电阻为R1+R2+R3, 根据并
联电阻分流关系, 有
所以
I
g
R1 R2 R3 Rg R1 R2 R3
I1
R1
R2
R3
IR I1 I
g
100 106 1.6 103 (500100)106
400
当量程I2=5mA时,分流电阻为R2+R3, 而R1与Rg相串联,根 据并联电阻分流关系, 有
例2.1 有一量程为100mV, 内阻为1kΩ的电压表。 如的欲电将压其表,改装成量程为U1=1V, U2=10V, U3=100V
试问应采用什么措施?
Rg
R1
R2
R3
-+ Ug
-
解: 则
U1
U2
U3
U1 Rg R1 U g Rg
图 2.2 例2.1图
R1
(U U
1 g
1)
Rg
( 100
1
103
所以,a、b两端的等效电阻
Rab=3∥(2+2) =3∥4=Ω。
电流源两端的电压 U=1×(4+Rab)=4+=5.71V。
2.4含独立源的二端网络的等效
2.4.1 含理想电压源的二端网络的等效
一、 理想电压源的串联
图2.4-1(a)所示电路是由n个理想电压源的串
联的二端网络,其端电压
n
u us1 us2 usj usn usj j 1
例2.4-1 求图2.4-4(a)所示电路中的电流I。
5Ω
5Ω
+
I
+
I
9A 5V
20
10Ω
5V
10
复杂电路化简方法【精选】

复杂电路等效转换方法(大连初二物理答疑群主:128804405,大连初三物理答疑群主:132492629)中考时,常常会遇见一些复杂的电路图,即使你欧姆定律串并联计算学得再好,如果看不懂基本就一分不得了。
再有,一些电路实物图也需要画出相应的电路原理图。
所以,将复杂电路或电路实物图转换成容易识别的电路图,是中考生必须掌握的技巧。
下面我就详细介绍一下电路等效转换法——标号法。
【第一步】找出电器串并联关系①将电路中的开关、电流表、电压表去掉,开关、电流表两端连接,电压表两端保持开路。
从电源正极向负极进发,标出标号,每过一个用电器,标号增加1,相通之处标号必须相同。
如图一。
②观察电路中的用电器之间的串并联关系,如果需要,则画出草图。
【第二步】描出回路,找到主干路(一条回路就是一条干路)③从电源正极出发,到电源负极结束,描出简单的回路图。
④将开关、电流表、电压表填补回去,画出回路。
选择元件最多的回路为主干路。
【第三步】标号⑤先给正极输出端标出标号“1”,顺着电流方向走,给主干路第一个元件前端(电流输入端)标出标号“1”;越过第一个元件,在第一个元件的末端(电流输出端)标出标号“2”,再给主干路第二个元件前端标出标号“2”;越过第二个元件,在第二个元件的末端(电流输出端)标出标号“3”,再给主干路第三个元件前端标出标号“3”,……以此类推,直至电源负极。
⑥凡是与已有标号相连的元件端,都标出相同的标号。
未有标号的元件端,则继续编号。
【第四步】画出转换电路图⑦根据原图的标号,先画出主干路,并标上相应的标号。
⑧再根据标号,画出其它的干路和支路。
【第五步】对比原电路和转换电路的元件数目⑨数出原电路元件的数目和转换电路的元件数目,防止丢失元件。
【第六步】对转换电路做适当修正⑩转换电路中,有的元件位置可能不是很合适或很美观,做适当调整。
例一:【第一步】找出电器串并联关系,并发现干路(一条回路就是一条干路)①将电路中的开关、电流表、电压表去掉,开关、电流表两端连接,电压表两端保持开路。
[电路分析]等效及等效化简
![[电路分析]等效及等效化简](https://img.taocdn.com/s3/m/c411de4a0b4e767f5acfcebc.png)
等效及等效化简
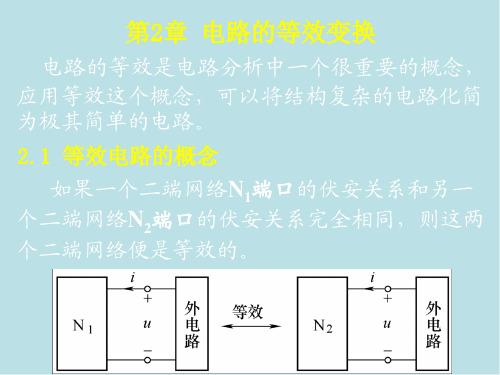
一、等效的概念
等效
在其端钮处具有相同端电压、端电流及其伏安关系( VAR )的两个网络,称为等效
( equivalence )。
相互等效的网络在由它们组成的电路中可以相互替换。
注意:等效是仅对外电路而言,而对内部电路显然是不等效的。
图 2.1-1 中, N1 和 N 1' 是等效的,是指 N1 、 N 1' 对端钮以外部分是等效的,即对 N2 而言是等效的,而对 N1 和 N 1' 内部而言是绝对不会等效的。
二、等效化简
等效化简的步骤
1 、在电路中某两个关心的节点处作分解,把电路分解成两个或多个部分;
2 、分别对各部分进行等效化简,求出其最简的等效电路;
3 、用最简的等效电路替代原电路,求出端钮处的电压或电流;
4 、若还需求电路中其他支路上的电压或电流,再回到原电路,根据已求得的端电压或端电流进行计算。
1。
最实用的5种电路分析方法

学好电路分析是后续课程的基础,可谓简单而重要,只有电路分析学好了,在后续课程中才能有良好的思路去解决问题。
电路是一门专业基础课,相对于文化基础课来说,它更侧重于解决工程实际问题,而比起专业课来讲,它则更强调物理概念和一般理论分析。
电路理论是从实际事物中抽象出来的,与实际事物既有联系又有区别的理论,因此要特别注意应用场合的条件。
电路课程具有特殊的规律,掌握了规律则学习起来就轻松多了,也容易记忆。
电路理论分析一是主要决定电路元件模型,即理想电阻元件、电感元件、电容元件,掌握了这些元件的伏安特性,则许多问题就迎刃而解。
要注意电路结构所遵循的原则即基本尔霍夫二大定律是解决电路结构问题的关键,在以上基础上应用电路中的主要原理、定理,即叠加定理、戴维南定理,对电路进行分析、计算。
为了正确、简单的分析、计算电路,对于复杂电路必须通过等效变换进行化简,这是电路理论中的首要手段,所谓等效即在不影响所需计算分析的情况下对外电路等效,这是必须牢牢掌握的。
平时要认真阅读例题。
例题是课程内容的组成部分,又是从概念到解题的中间桥梁,把定律、定理、原理以例题形式编入书中,这是电路教材的特点。
多做习题也是电路课学习的重要方面。
习题是教材中不可分割的重要部分,习题的练习,有助于加深对基本概念的理解。
习题不但要做对,更应该理解每道习题所要考察的概念,搞清为什么要出这一道题,考核了什么内容,这样学习才能学得深,学得好。
解习题是培养思考能力的一个极其重要的环节,同时也是检验自己是否真正掌握了概念的一把尺子。
区别电路模型与实际器件。
理想电路元件是从实际电路器件中科学抽象出来的假想元件。
应当注意电路元件与实际器件的联系和差别。
一般器件都可以用理想电路元件及它们的组合来模拟,但两者之间不完全等同。
例如,在频率不太高的条件下,一个线圈的数学模型就是电阻元件和电感元件的串联,而当频率较高时,线圈的绕线之间的电容效应就不容忽视,在这种情况下表征这个线圈的较精确的模型还应当包含电容元件。
(整理)端口电阻概念与例题

第2章 电阻电路的等效变换学习指导与题解一、基 本 要 求1.深刻理解两个结构不同二端网络等效的概念。
明确电路等效变换和等效化简的含义。
2.熟练掌握电阻串联、并联及并联等效化简为一个等效电阻的方法。
3.熟练掌握电压源串联和等效电流源的方法。
能正确确定等效电压源电路电流的大小和方向。
4.熟练掌握两类实际电源模型等效互换的方法。
即电压雅模型等变换为电流源模型;电流源模型等效变换为电压源模型。
能正确确定变换后电压源模型中电压和电流源电流的大小和方向。
5.掌握星形(Y )电阻网络与三角形()电阻网络等效互换的方法。
即星形连接电阻网络等效变换为三角形连接电阻网络;三角形连接电阻网络等效变换与星形连接电阻网络。
6.掌握含源线形二端网络等效化简的方法。
即将结构较复杂的含源线形二端网络等效化简为一电压源与一电阻元件串联的最简单电路,或为一电流源与一电阻并联的最简单节偶电路。
能见含源受控源线形二端网络进行等效化简。
7.掌握用等效化简的方法分析电阻电路。
8. 理解线性电路叠加性的意义。
能正确运用叠代定理来分析计算多电源线性电路中的电流和电压,包括含有受控源的电路。
9. 明确戴维南定理和诺顿定理的含义。
能正确运用戴维南定理及诺顿定理来分析电路,包括含有受控源电路。
熟练掌握求含源二端网络的戴维南等效电路和诺顿等效电路,即计算二端网络端口的开路电压oc U 、短路电流sc I 和端口内电路的等效电阻o R 的方法。
二、学 习 指 导等效变换化简电路,是电路的基本分析方法之一,是本课程重要的基本内容。
本章的教学内容可以分为如三部分: 1. 二端网络等效的概念;2. 电阻电路中等效变换和化简的基本方法;3. 含源线形二端网络包括受控源而端网络的等效化简和电路分析。
着重讨论电路等效和的等效变换的概念、电阻串、并联的等效电阻,两类电源模型的等效变换方法,遗迹含源线形而端网络的等效化简方法。
(一) 关于二端网络等效的概念 1. 二端网络等效的定义两个结构不同的二端网络,它们的端口分别外接任何相同的负载或电路时,两端口的伏安关系相等。
电源串并联实用化简方法

《大学电路/电路原理/电路分析》04--电源实用化简方法电源是指在电路中提供能量的器件,包括电压源和电流源。
在现实中电压源是很常见的,如手电筒里面的干电池,钮扣电池,蓄电池,还是发电厂里的发电机。
电压源是开路保存的,不会有能量损耗。
而电流源则很少见,因为电流源在保存时需要短路,即使是很小电阻的导线,也会造成能量耗损,所以一般在有需求的实验室才会用到电流源。
电源在电路中是充当激励的作用,并产生响应,即电压、电流。
在电路分析中,为了方便求解电路参数,需对电源进行等效变换。
本文将介绍几个实用的电源化简方法。
1独立源和受控源的区别独立源能单独发出功率,而受控源是受控于电路中某个电压或电流,有电压控制型和电流控制型。
独立源与受控源在符号上的区别是:独立源用圆形,受控源用菱形表示,如下图所示:* 甘-1 ° :~••~0)^~° °—独立蕊受控源很多学生经常分不清受控源上面标的数值是电压还是电流,其实电压源在外观上看都是引线穿过去,而电流源是不穿的。
只要把电源的类别分清了,在列写方程就不容易出错。
另外一个易错点就是很多学生认为电流源只提供电流,两端是没有电压的,这是错误的,电流源两端电压是取决外电路的结构和参数的,如在列写回路1, 2的KVL方程时,学生经常会把2A电流源两端的电压U漏掉,因为电流源只标电流,不标电压,就觉得没有电压。
当然这个题目的实际求解应该避开电流源支路,列写大回路的KVL方程,计算会更简单一些2.理想电源的等效变换理想电源是可以进行串,并联的,一般分成3种情况(1)理想电压源串联:般理想电压源是串联使用,很少进行并联,因为并联的意义不大。
理想电压源的串联可等效为一个电压源,等效过程一定要注意电压源的参考方向,如下图所示电路:—厂Qsv①-只要原电路中电压源的参考方向与等效后电压源的参考方向相同,则取“ +”, 相反则取“-”。
那么很快就可求出U s=5+6-8=3V。
电路的等效化简

i 1
(G = 1/R 称电导,单位为西门子)
今后电阻并联用“ // ”表示 例:R1 // R2
3.电阻元件的混联 (串、并联交织混合在一起)
例:求ab间的等效电阻。
Req
R1
R2
//
R3
R1
R2 R3 R2 R3
4.电阻的星形、三角形连接
(a) 星形连接(Y形)
(b) 三角形连接(形)
从星形连接变换为三角形连接
4
+ 40V -
2
+
40V-
(a)
4
2
10A
20A
4 3
+
40V-
(3)对图(b)无源二端网络的化简如下所示
5
8
10
2
10
(b)
R 5 10//(8 2) 10
I 5
8
4
2
10
2
40V+ -
40V+
-
图1
4
I
3
10Ω
(4)连接两个化简结果,有
+
40V-
I=40/(4/3+10)=60/17A
图2
is为等效电流源,当 isk与is的参考方向 相同时, isk取“+”,相反则取“- ”。
3. 理想电源之间的等效电路 与理想电压源并联的元件可去掉
a
+
US
-
+ US -
Is b a
RO
b
a + US -
b
a
+
US
-
与理想电流源串联的元件可去掉
Is
a
b
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复 杂 网 络
a u b N2
N
N1
3、单口网络: 只有两个端钮与其它电路相连接的网络,也叫 二端网络。
1)端口电压:u0 2)端口电流:i0 3)明确的单口网络:
若单口内含受控源, 则控制量和受控量 必须在同一单口内。
i0 N1 u0 b i a N1 b u u b a i N2 a N2
4、分解 的简单例子:
例 求I. 0.5 I1
2k 4.5mA
1k
I
1k
I1
1k
得:I = 1.384 mA
一、陈述 对任意含源单口网络N,都可以用一个电压源 与一个电阻相串联来等效。 R0 i i + + 等效 + 即 u N u u oc _ _ _
电压源的电压等于该网络的开路电压uoc, 这个电阻等于从此单口网络两端看进去,当网 络内部所有独立源均置零(No)时的等效电阻R0 i =0 N
4-5 几种基本电路的等效规律和公式 一、基本等效规律
1. 串联电阻的等效电路 —等效电阻 两端首尾相联
R1
R2
Rk
Rn
R
u n R Rk i k 1
2. 并联电阻的等效电路 —电导 两端首尾分别相联
G G1 G2 Gk Gn
n i G Gk u k 1
R1
R2
R
R1 R2 R R1 R2
4-4 单口网络的等效电路
1、定义:具有相同伏安关系的两个或两个以上的单口 网络,称为相互等效的网络。
N1
i O
i + u _
i
u
N2
i + u _
O
u
(1)相互等效的二端网络在电路中可以相互代 意义: 换;以简单的单口代替复杂的单口称化简; (2)只对外等效,内部并不一样。
例:图(a),已知 uS=6V,iS=2A,R1=2,R2=3。
要点: 用方便的方法 布列关于u和i的 方程; 设法消去中间 变量,得到VAR。
u [ R1 R3 (1 A) R2 ]i [us ( R1 R2 )is ]
1
例3:求图示单口
的VAR。
1
T
1 1
T T
启示: 。。。。
1
2
T
24 u i 11
4-3 置换定理
替代定理:如果网络 N由一个电阻单口网络 NR和一个 任意单口网络NL连接而成[图4-30(a)],则: 1 .如果端口电压 u 有惟一解,则可用电压为 u 的电压 源来替代单口网络NL,只要替代后的网络[图(b)]仍有惟一
T
0.5A
1/3A
5)用电流源置换掉N2,如下图; 6)由下图求i1:i1=1/9A。 说明:。。。
i1 2 4
T
T
1' N1
例3: 图4-32(a)电路中,已知电容电流iC(t)=2.5e-tA,用
置换定理求i1(t)和i2(t) 。
图4-32
图4-32
解:图(a)电路中包含一个电容,它不是一个电阻电路。用
分解方法和单口网络
——用等效化简的方法分析电路
本章的主要内容: 1、分解、等效的概念; 2、单口网络的等效化简,实际电源 的等效变换 ; 3、置换、戴维南、诺顿定理, 最大功率传递定理; 4、三端网络T形和形的等效变换。
4-1 分解方法的基本步骤
1、概述:一个复杂的电路,用前面的分析方法, 需要布列和求解多个联立方程。本章介绍的分析 的方法,是将复杂的电路进行分割,然后利用 “等效”的手段,把电路化简,以便于求解所需 的电路变量。 2、分解的概念:把复杂的电路分解为两个简单的 单口网络。
求:单口网络的伏安关系,并画出单口的等效电路。
解:在端口外加电流源i,求端口电压
u uS R1 (iS i) R2i ( R1 R2 )i uS R1iS 5 i 6 2 2 5i 10 Roi uoc
单口等效电路是电阻Ro和电压源uOC的串联, 如图(b)所示。 说明。。。
i0
a
i
i
+ Us u0 R
+ Us u u
R
b
u
us
u=Ri
u us u Ri
联立以上元件的VAR,可以求出 端口电压u0和端口电流i0。
i0
i
5、分解的步骤:
1)把给定的网络划分为两个单口网络N1和N2; 2)分别求单口网络N1和N2的VAR;
3)用N1和N2的VAR曲线的交点求得端口电压u0和 端口电流i0; 4)利用置换定理,用一个独立电压(流)源置 换其中的一个单口,如N2 ; 5)利用以前所学知识,求N1内部各变量。
1v
例2:用分解的方法求i1。
解: 1)在1-1‘分解电路,得到N1和N2; 2)求N1的VAR: 14 34
10
T
+
-
i
T
1
T
+ 2 0.5A
u
1 + 2v
i1 2 4 _
T T T
u
3
3
i
-
3)求N2的VAR;
2 2 u i 3 3
10
1' N1
1v
N2
+
-
1
T
4)联立两个VAR方程, 求出端口电流i:i=1/3A
解,则不会影响单口网络NR 内的电压和电流。
图4-30
图4-30
2.如果端口电流i有惟一解,则可用电流为i的电流源
来替代单口网络NL,只要替代后的网络[图(c)]仍有惟一解,
则不会影响单口网络NR 内的电压和电流。
替代定理的价值在于:
一旦网络中某支路电压或电流成为已知量时,则可用
一个独立源来替代该支路或单口网络NL,从而简化电路的
(4)
10v
x
10 5i1 u u 20i2 20 (i i1 )
由(1): i1 (10 u)/5
u 20i 20 (10 u) / 5
u 8 4i
方法二:外接电流源法。
N
u
i
5
10v
i1
20
u
i
(5 20)i1 20i 10 得到: u 20(i1 i)
解: U ab 100 I 10( I 50 I ) 610 I
例 2、
I1
求 ab 端钮的等效电阻。 a
1.5k 1.5k 750 I1
b
1.5k
结论
Rab = 600
1、含受控源和电阻的单口网络等效为电阻; 2、受控量支路和未知量支路保留不变换。
2、含受控源的混联电路的等效化简分析
(2)
+ 5V _
+ 6V _
6. 电流源串联
(1)
5A 5A
(2)
5A
5A 6A
不允许,违背KCL。
7. 实际电压源与实际电流源相互等效。 I RS I 重点 + +
+
U US _ U= US - RS I
IS
RS U U= RS IS - RS I
当US = RS IS; RS = RS 时,二者等效。 单口网络两种等效电路的等效变换:
u 8 4i
方法三:外接电压源法。
i
N u
5 10v 20 u i
1 1 1 ( )u 10 i 5 20 5
得到:
u 8 4i
注意:不同的方法求出的VAR是一样的,说明。。。。
Ai
R1 + us
R2
T
i +
例2:求图示单口
的VAR。
i u
-
I
T
is
i R3
-
( R1 R2 ) I R2 Ai u s u0 u0 u R3i i I i s
分析与计算。
替代定理对单口网络NL并无特殊要求,它可以是非线
性电阻单口网络和非电阻性的单口网络。
例1:求图示电路在I=2A时,20V电压源发出的功率。
解:用2A电流源替代电阻Rx和单口网络 N2
(4) I 1 (2) 2A 20V
I1 4A
P 20V (4A) 80W 产生功率 80W
电流为iC(t)=2.5e-tA的电流源替代电容,得到图(b)所示 线性电阻电路,用叠加定理求得:
10 2 i1 (t ) A 2.5e t A (2.5 1.25e t )A 22 22 10 2 i 2 (t ) A 2.5e t A (2.5 1.25e t )A 22 22
二、利用戴维南定理求最简等效电路 1. 求Uoc 2. 求Ro 三、用最简等效电路替代后求解
例5:证明戴维南等效电阻R0:
uoc R0 isc
4 - 7 诺顿定理
一、陈述
对任意含源单口网络N,可以用一个电流源与一个 电阻相并联来等效。这个电流源等于该网络的短路电 流isc,这个电阻等于从这个单口网络的端钮看进去, 当其内部所有独立源均置零时的等效电阻Ro。
3. 理想电压源串联
+ US1_ _ US2 + + US3 _ +
US = US1 US2 + US3
电源与等效电源参考 方向一致为+,反之为-
US_
4. 理想电流源并联 IS = IS1IS2 + IS3
IS1
IS2
IS3
IS
5. 电压源并联
(1)
+ 5V _
+ 5V _
