2013年高考数学试题(安徽文科卷)
2013年高考数学安徽文(word版含答案)

2013安徽高考文数解析一、选择题1.设i 是虚数单位,若复数10()3a a R i-∈-是纯虚数,则a 的值为( ) (A )3- (B )1- (C )1 (D )32.已知{}{}|10,2,1,0,1A x x B =+>=--,则()R A B =ð( )(A ){}2,1-- (B ){}2- (C ){}1,0,1-(D ){}0,13.如图所示,程序据图(算法流程图)的输出结果为( ) (A )34(B)16 (C)1112(D)25244.“(21)0x x -=”是“0x =”的( )(A)充分不必要条件 (B)必要不充分条件(C)充分必要条件 (D)既不充分也不必要条件5.若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为( ) (A)2 (B)2 (C)3 (D)9(A)1 (B )2 (C )4 (D ) 7.设n S 为等差数列{}n a 的前n 项和,8374,2S a a ==-,则9a =( ) (A )6- (B )4- (C )2- (D )28.函数()y f x =的图象如图所示,在区间[],a b 上可找到()2n n ≥个不同的数123,,,,n x x x x ,使得1212()()()n nf x f x f x x x x ===,则n 的取值范围是( ) (A){}2,3 (B){}2,3,4 (C){}3,4(D){}3,4,59.设ABC ∆的内角,,A B C 所对边的长分别为,,a b c ,若2b c a +=,3sin 5sin A B =,则角C =( )(A)3π (B)23π (C)34π (D)56π10.已知函数()32f x x ax bx c =+++有两个极值点12,x x ,且()112f x x x =<,则关于x的方程()()()2320f x af x b ++=的不同实根个数是( )(A )3(B )4 (C )5 (D )6 二、填空题11.函数1ln(1)y x=++的定义域为__________.12.若非负变量,x y 满足约束条件1,24,x y x y -≥-⎧⎨+≤⎩则x y +的最大值为________.13.若非零向量,a b 满足32a b a b ==+,则a b 与夹角的余弦值为_______.14.定义在R 上的函数()f x 满足(1)2()f x f x +=.若当01x ≤≤时,()(1)f x x x =-, 则当10x -≤≤时,()f x =_________.15.如图,正方体1111ABCD A BC D -棱长为1,P 为BC 的中点, Q 为线段1CC 上的动点,过点,,A P Q 的平面截该正方体所得的截面记为S ,则下列命题正确的是_____.(写出所有正确命题的编号)①当102CQ <<时,S 为四边形; ②当12CQ =时,S 为等腰梯形; ③当34CQ =时,S 与11C D 的交点R 满足113C R =;④当314CQ <<时,S 为六边形; ⑤当1CQ =时,S 的面积为26. 三、解答题16.(本小题满分12分)设函数()sin sin()3f x x x π=++.(1)求()f x 的最小值,并求使()f x 取得最小值的x 的集合;(2)不画图,说明函数()y f x =的图象可由sin y x =的图象经过怎样的变化得到. 17.为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中各抽取30名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如下:(1)若甲校高三年级每位学生被抽取的概率为0.05,求甲校高三年级学生总人数,并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格); (2)设甲、乙两校高三年级学生这次联考数学平均成绩分别为12,x x ,估计12x x -的值. 18.(本小题满分12分)如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60BAD ∠=.已知2,PB PD PA ===(1)证明:PC BD ⊥;(2)若E 为PA 的中点,求三菱锥P BCE -的体积.Q1A BC19.(本小题满分13分)设数列{}n a 满足12a =,248a a +=,且对任意*n N ∈,函数1212()()cos -sin n n n n n f x a a a x a x a x ++++=-++⋅⋅满足()02f π'=,(1)求数列{}n a 的通项公式;(2)若122n n n a b a ⎛⎫=+ ⎪⎝⎭,求数列{}n b 的前n 项和n S .20.(本小题满分13分)设函数()22(1)f x ax a x =-+,其中0a >,区间(){}0I x f x =>(1)求I 的长度(注:区间(),αβ的长度定义为βα-);(2)给定常数()0,1k ∈,当11k a k -≤≤+时,求I 长度的最小值.21.(本小题满分13分)已知椭圆2222:1(0)x y C a b a b+=>>的焦距为4,且过点P .数学(文科)试题参考答案一、选择题:本题考查基本知识和基本运算,每小题5分,满分50分。
2013年安徽高考数学(文科)卷及答案-推荐下载

(B)2
(B)必要不充分条件
(D)既不充分也不必要条件
(D) 4 6
2
(C) 2
(D)2
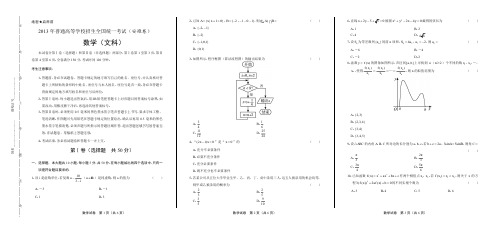
(8) 函数 y f (x) 的图像如图所示,在区间a, b上可找到 n(n 2) 个不同的数 x1, x2 ,, xn ,使得
f (x1) f (x2 ) f (xn ) ,则 n 的取值范围为
3
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置各试时类卷,管调需路控要习试在题验最到;大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资,常料要工试加况卷强下安看与全22过,22度并22工且22作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
2013年高考文科数学安徽卷
A.-6
B.-4
()
C.-2
D.2
8.函数 y f (x) 的图象如图所示,在区间[a,b] 上可找到 n( n≥2 )个不同的数 x1 , x2 ,…,
xn ,使得
f x1 = x1
f x2 x2
=…=
f xn ,则 xn
n 的取值范围为
()
A.{2,3} B. {2, 3, 4}
题
一、选择题:本大题共 10 小题,每小题 5 分,共 50 分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
无
1.设 i 是虚数单位,若复数 a 10 ( a R )是纯虚数,则 a 的值为 3i
()
A.-3
B.-1
C.1
D.3
效 数学试卷 第 1 页(共 6 页)
2.已知 A {x | x 1 0} , B {2 ,1 ,0 ,1},则 ( R A) B A.{2,1} B.{2} C. {1, 0,1} D.{0,1}
⑤当 CQ 1时,S 的面积为 6 2
数学试卷 第 4 页(共 6 页)
三、解答题:本大题共 6 小题,共 75 分.解答应写出文字说明、证明过程或演算步骤.解答 写在答题卡上的指定区域内.
16.(本小题满分 12 分) 设函数 f (x) sinx sin(x π) . 3 (1)求 f (x) 的最小值,并求使 f (x) 取得最小值的 x 的集合; (2)不画图,说明函数 y f (x) 的图象可由 y sinx 的图象经过怎样的变化得到.
14.定义在 R 上的函数 f (x) 满足 f (x+1) 2 f (x).若当 0≤x≤1 时, f (x) x(1-x) ,则当
2013年高考文科数学安徽卷试题与答案word解析版

年普通高等学校招生全国统一考试(安徽卷)数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分分,考试时间分钟。
第Ⅰ卷(选择题 共分)一、选择题:本大题共小题,每小题分,共分.在每小题给出的四个选项中,只有一项是符合题目要求的. .(安徽,文)设是虚数单位,若复数103i a --(∈)是纯虚数,则的值为( ). .- .- . .【答案】【考点】本题主要考查复数的基本运算以及基本概念,意在考查考生的运算能力。
【解析】由已知,得1010(3i)10(3i)3i (3i)(3)10a a a ++-=-=---+=--, ∵复数103ia --为纯虚数,∴-=,即=. .(安徽,文)已知={+>},={-,-,},则()∩=( )..{-,-} .{-} .{-} .{}【答案】【考点】本题主要考查集合的基本运算,意在考查考生的基本运算能力和基本概念的理解能力。
【解析】∵={>-},∴={≤-},∴()∩={-,-}..(安徽,文)如图所示,程序框图(算法流程图)的输出结果为( ).. . ..【答案】 【考点】本题主要考查程序框图的循环结构,计算输出结果,意在考查考生对循环结构的理解和计算累加的和。
【解析】开始,<,=+12,=+=; 返回,<,113244s =+=,=+=; 返回,<,31114612s =+=,=+=; 返回,<不成立,输出1112s =..(安徽,文)“(-)=”是“=”的( )..充分不必要条件 .必要不充分条件.充分必要条件 .既不充分也不必要条件【答案】【考点】本题主要考查充分必要条件的基本知识和基本概念,意在考查考生对方程的求解以及概念的识别。
【解析】由(-)=,得=12或=. 故(-)=是=的必要不充分条件. .(安徽,文)若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为( ).. . . .【答案】 【考点】本题主要考查古典概型的概率计算,意在考查考生的运算能力和对基本概念的理解。
2013年安徽高考数学试卷(含文科理科)

2013年普通高等学校招生考试(安徽卷)理科数学一、选择题1.设i 是虚数单位,z 是复数z 的共轭复数,若z ·z i +2=2z ,则z =( )(A)1+i(B)1−i(C)−1+i(D)−1−i2.如图所示,程序框图(算法流程图)的输出结果是( )(A)16(B)2524(C)34(D)11123.在下列命题中,不是公理的是( )(A)平行于同一个平面的两个平面相互平行(B)过不在同一条直线上的三点,有且只有一个平面(C)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内(D)如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线4.“a ⩽0”是“函数f (x )=|(ax −1)x |在区间(0,+∞)内单调递增”的( )(A)充分不必要条件(B)必要不充分条件(C)充分必要条件(D)既不充分也不必要条件5.某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86、94、88、92、90,五名女生的成绩分别为88、93、93、88、93.下列说法一定正确的是( )(A)这种抽样方法是一种分层抽样(B)这种抽样方法是一种系统抽样(C)这五名男生成绩的方差大于这五名女生成绩的方差(D)该班男生成绩的平均数小于该班女生成绩的平均数6.已知一元二次不等式f (x )<0的解集为{x |x <−1或x >12},则f (10x )>0的解集为( )(A){x |x <−1或x >−lg 2}(B){x |−1<x <−lg 2}(C){x |x >−lg 2}(D){x |x <−lg 2}7.在极坐标系中,圆ρ=2cos θ的垂直于极轴的两条切线方程分别为( )(A)θ=0(ρ∈R )和ρcos θ=2(B)θ=π2(ρ∈R )和ρcos θ=2(C)θ=π2(ρ∈R )和ρcos θ=1(D)θ=0(ρ∈R )和ρcos θ=18.函数y =f (x )的图象如图所示,在区间[a,b ]上可找到n (n ⩾2)个不同的数x 1,x 2,···,x n ,使得f (x 1)x 1=f (x 2)x 2=···=f (x n )x n,则n 的取值范围为( )(A){2,3}(B){2,3,4}(C){3,4}(D){3,4,5}9.在平面直角坐标系中,O 是坐标原点,两定点A ,B 满足# »OA = # »OB=# »OA ·# »OB =2,则点集{P |# »OP =λ# »OA +µ# »OB,|λ|+|µ|⩽1,λ,µ∈R }所表示的区域的面积是( )(A)2√2(B)2√3(C)4√2(D)4√310.若函数f (x )=x 3+ax 2+bx +c 有极值点x 1,x 2,且f (x 1)=x 1,则关于x 的方程3(f (x ))2+2af (x )+b =0的不同实根个数是( )(A)3(B)4(C)5(D)6二、填空题11.若(x +a3√x )8的展开式中x 4的系数为7,则实数a =.12.设△ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c .若b +c =2a ,3sin A =5sin B ,则角C =.13.已知直线y =a 交抛物线y =x 2于A ,B 两点.若该抛物线上存在点C ,使得∠ACB 为直角,则a 的取值范围为.14.如图,互不相同的点A 1,A 2,···,A n ,···和B 1,B 2,···,B n ,···分别在角O 的两条边上,所有A n B n 相互平行,且所有梯形A n B n B n +1A n +1的面积均相等.设OA n =a n .若a 1=1,a 2=2,则数列{a n }的通项公式是.O A 1A 2A 3B 1B 2B 315.如图,正方体ABCD −A 1B 1C 1D 1的棱长为1,P 为BC 中点,Q 为线段CC 1上的动点,过A 、P 、Q 的平面截该正方体所得的截面记为S ,则下列命题正确的是.(写出所有正确命题的编号)A BPQ CDA 1B 1C 1D 1••①当0<CQ <12时,S 为四边形;②当CQ =12时,S 为等腰梯形;③当CQ =34时,S 与C 1D 1交点R 满足C 1R 1=13;④当34<CQ <1时,S 为六边形;⑤当CQ =1时,S 的面积为√62.三、解答题16.已知函数f (x )=4cos ωx ·sin (ωx +π4)(ω>0)的最小正周期为π.(1)求ω的值;(2)讨论f (x )在区间[0,π2]上的单调性.17.设函数f (x )=ax −(1+a 2)x 2,其中a >0,区间I ={x |f (x)>0},(1)求I 的长度(注:区间(α,β)的长度定义为β−α);(2)给定常数k ∈(0,1),当1−k ⩽a ⩽1+k 时,求I 长度的最小值.18.设椭圆E :x 2a 2+y 21−a 2=1的焦点在x 轴上.(1)若椭圆E 的焦距为1,求椭圆E 的方程;(2)设F 1,F 2分别是椭圆E 的左、右焦点,P 为椭圆E 上第一象限内的点,直线F 2P 交y 轴于点Q ,并且F 1P ⊥F 1Q ,证明:当a 变化时,点P 在某定直线上.19.如图,圆锥顶点为P .底面圆心为O ,其母线与底面所成的角为22.5◦.AB和CD 是底面圆O 上的两条平行的弦,轴OP 与平面P CD 所成的角为60◦.(1)证明:平面P AB 与平面P CD 的交线平行于底面;(2)求cos ∠COD .O CD PB A•20.设函数f n (x )=−1+x +x 222+x 332+···+x nn2(x ∈R ,n ∈N ∗).证明:(1)对每个n ∈N ∗,存在唯一的x n ∈[23,1],满足f n (x n )=0;(2)对任意p ∈N ∗,由(1)中x n 构成的数列{x n }满足0<x n −x n +p <1n.21.某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有n 位学生,每次活动均需该系k 位学生参加(n 和k 都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系k 位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为X .(1)求该系学生甲收到李老师或张老师所发活动通知信息的概率;(2)求使P (X =m )取得最大值的整数m .2013年普通高等学校招生考试(安徽卷)文科数学一、选择题1.设i是虚数单位,若复数a−103−i(a∈R)是纯虚数,则a的值为( )(A)−3(B)−1(C)1(D)32.已知A={x|x+1>0},B={−2,−1,0,1},则(∁R A)∩B=( )(A){−2,−1}(B){−2}(C){−1,0,1}(D){0,1}3.如图所示,程序框图(算法流程图)的输出结果是( )(A)34(B)16(C)1112(D)25244.“(2x−1)x=0”是“x=0”的( )(A)充分不必要条件(B)必要不充分条件(C)充分必要条件(D)既不充分也不必要条件5.若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为( )(A)23(B)25(C)35(D)9106.直线x+2y−5+√5=0被圆x2+y2−2x−4y=0截得的弦长为( )(A)1(B)2(C)4(D)4√67.设S n为等差数列{a n}的前n项和,S8=4a3,a7=−2,则a9=( )(A)−6(B)−4(C)−2(D)28.函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n⩾2)个不同的数x1,x2,···,x n,使得f(x1)x1=f(x2)x2=···=f(x n)x n,则n的取值范围为( )(A){2,3}(B){2,3,4}(C){3,4}(D){3,4,5}9.设△ABC的内角A,B,C所对边的长分别为a,b,c,若b+c=2a,3sin A=5sin B,则角C=( )(A)π3(B)2π3(C)3π4(D)5π610.已知函数f(x)=x3+ax2+bx+c有两个极值点x1,x2,若f(x1)=x1<x2,则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数为( )(A)3(B)4(C)5(D)6二、填空题11.函数y=ln(1+1x)+√1−x2的定义域为.12.若非负变量x,y满足约束条件x−y⩾−1x+2y⩽4,则x+y的最大值为.13.若非零向量a,b满足|a|=3|b|=|a+2b|,则a与b夹角的余弦值为.14.定义在R上的函数f(x)满足f(x+1)=2f(x).若当0⩽x⩽1时,f(x)=x(1−x),则当−1⩽x⩽0时,f(x)=.15.如图,正方体ABCD−A1B1C1D1的棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是.(写出所有正确命题的编号)A BPQCDA1B1C1D1••①当0<CQ<12时,S为四边形;②当CQ=12时,S为等腰梯形;③当CQ=34时,S与C1D1交点R满足C1R1=13;④当34<CQ<1时,S为六边形;⑤当CQ=1时,S的面积为√62.三、解答题16.设函数f(x)=sin x+sin(x+π3).(1)求f(x)的最小值,并求使f(x)取得最小值的x的集合;(2)不画图,说明函数y=f(x)的图象可由y=sin x的图象经过怎样的变化得到.17.为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中各抽取30名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如图:甲乙745533253385543331006000112233586622110070022233669754428115582090(1)若甲校高三年级每位学生被抽取的概率为0.05,求甲校高三年级学生总人数,并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格);(2)设甲、乙两校高三年级学生这次联考数学平均成绩分别为¯x1,¯x2,估计¯x1−¯x2的值.18.如图,四棱锥P −ABCD 的底面ABCD 是边长为2的菱形,∠BAD =60◦.已知P B =P D =2,P A =√6.(1)证明:P C ⊥BD ;(2)若E 为P A 的中点,求三棱锥P −BCE 的体积.APEBCD19.设数列{a n }满足a 1=2,a 2+a 4=8,且对任意n ∈N ∗,函数f (x )=(a n −a n +1+a n +2)x +a n +1cos x −a n +2sin x 满足f ′(π2)=0.(1)求数列{a n }的通项公式;(2)若b n =2(a n +12a n ),求数列{b n }的前n 项和S n .20.设函数f (x )=ax −(1+a 2)x 2,其中a >0,区间I ={x |f (x )>0}.(1)求I 的长度(注:区间(α,β)的长度定义为β−α);(2)给定常数k ∈(0,1),当1−k ⩽a ⩽1+k 时,求I 长度的最小值.21.已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的焦距为4,且过点P (√2,√3).(1)求椭圆C 的方程;(2)设Q (x 0,y 0)(x 0y 0=0)为椭圆C 上一点,过点Q 作x 轴的垂线,垂足为E .取点A (0,2√2),连接AE .过点A 作AE 的垂线交x 轴于点D .点G 是点D 关于y 轴的对称点,作直线QG ,问这样作出的直线QG 是否与椭圆C 一定有唯一的公共点?并说明理由.。
2013年安徽高考数学试题及答案word版

绝密★启用前2013年普通高等学校招生全国统一考试(安徽卷)数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至4页。
全卷满分150分。
考试用时120分钟。
考生注意事项:1. 答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘帖的条形码中姓名、座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2. 答第Ⅰ卷时,每小题选出答案后,用2B铅笔把答题卡上....对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
3. 答第Ⅱ卷时,必须用0.5毫米黑色墨水签字笔在答题卡上....书写,要求字体工整、笔迹清晰。
作图题时可先用铅笔在答题卡...规定的位置绘出,确认后用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域作答,超出答题区域书写的答案无效..................,在试题卷....、草稿纸上答题无效...。
4. 考试结束,务必将试题卷和答题卡一并上交。
第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)设i是虚数单位,若复数a--(a∈R)是纯虚数,则a的值为()(A)-3 (B)-1 (C)1 (D)3(2)已知A={x|x+1>0},B={-2,-1,0,1},则(R A)∩B=()(A){-2,-1}(B){-2}(C){-2,0,1} (D){0,1}(3)如图所示,程序据图(算法流程图)的输出结果为(A)(B)(C)(D)(4)“(2x-1)x=0”是“x=0”的(A)充分不必要条件(B)必要补充分条件(C)充分必要条件(D)既不充分也不必要条件(5)若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这无人被录用的机会均等,则甲或乙被录用的概率为(A)2/3 (B)2/5(C)3/5 (D)9/10(6)直线x+2y-5+=0被圆x2+y2-2x-4y=0截得的弦长为(A)1 (B)2(C)4 (D)(7)设s n为等差数列{a n}的前n项和,s1=4a3,a2=-2,则a9=(A)6 (B)4(C)-2 (D)2(8)函数y=f(x)的图像如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…x n,使得f(x1)/x1=f(x2)/x2=…=f(x n)/x n,则n的取值范围为(A) {2,3} (B){2,3,4}(C){3,4} (D){3,4,5}(9)设△ABC的内角A,B,C所对边的长分别为a,b,c,若b+c=2a,3sinA=5sinB,则角C=(A) π/3 (B)2π/3(C)3π/4 (D)5π/6(10)已知函数f(s)=x3+ax2+bx+c有两个极致点x1,x2,若f(x1)则关于x的方程3(f(x))2+2af (x)+b=0的不同实根个数为(A)3 (B)4(C) 5 (D)6第Ⅱ卷(非选择题共100分)考生注意事项:请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效。
2013年安徽高考数学文科试卷带详解

2013年普通高等学校招生全国统一考试(安徽卷文科)一.选择题选择题:本大题共10小题.每小题5分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.设i 是虚数单位,若复数10()3i a a -∈-R 是纯虚数,则a 的值为 ( ) A.-3 B. -1 C.1 D.3【测量目标】复数的基本概念.【考查方式】根据纯虚数的定义求a .【参考答案】D【试题解析】先利用复数的运算法则将复数化为i ,x y x y +∈R ()的形式,再由纯虚数的定义求a 由纯虚数的定义,知30a -=,所以3a =.2.已知{}{}|10,2,1,0,1,A x x B =+>=--则()A B =R ð ( )A.{}2,1--B.{}2-C.{}1,0,1-D.{}0,1【测量目标】集合的基本运算(补集、交集).【考查方式】集合的表示法(描述法,列举法),求集合的补集、交集.【参考答案】A【试题解析】解不等式求出集合A ,进而得A R ð,再由集合交集的定义求解.因为集合{}|1A x x =>,所以{}|1A x x =-R ≤ð,则()A B =R ð{}{}{}|12,,012,1x x ---=-- ≤.3.如图所示,程序据图(算法流程图)的输出结果为 ( ) A.34 B.16 C.1112 D.2524第3题图【测量目标】条件语句、循环语句的程序框图.【考查方式】根据程序框图的逻辑结构求出s .【参考答案】C【试题解析】利用框图的条件结构和循环结构求解.110,2,28,0;22s n s ==<=+= 113224,48,;244n s =+=<=+=3111426,68,;4612n s =+=<=+= 628n =+=,88<不成立,输出s 的值为11.12 4.“(21)0x x -=”是“0x =”的 ( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【测量目标】充分必要条件.【考查方式】考查命题的基本关系,充分条件、必要条件的判断方法.【参考答案】B【试题解析】先解一元二次方程(21)0x x -=,再利用充分条件、必要条件的定义判断.当0x =时,显然(21)0x x -=;当(21)0x x -=时,0x =或12x =,所以“(21)0x x -=” 是“0x =”的必要不充分条件.5.若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这五人被录用的机会均等,则甲或乙被 录用的概率为 ( ) A.23 B. 25 C. 35 D.910【测量目标】随机事件与概率.【考查方式】把所求事件转化为求其对立事件,然后求出概率.【参考答案】D【试题解析】解决本题的关键是求出甲或乙被录用的可能结果种数,直接求解情况较多,可间接求解,再用古典概型求概率.由题意,从五位大学毕业生录用三人,所有不同的可能结果有(甲,乙,丙),(甲,乙,丁),(甲,乙,戊),(甲,丙,丁),(甲,丙,戊),(甲,丁,戊),(乙,丙,丁),(乙,丙,戊),(乙,丁,戊),(丙,丁,戊),共10种,其中“甲与乙均未被录取”的所有不同的可能结果只有(丙,丁,戊)这1种,故其对立事件“甲与乙被录用”的可能结果有9种,所求概率910P =.A.1B.2C.4D.【测量目标】直线与圆的相交方程、点到直线距离公式.【考查方式】把圆的一般方程化为标准方程,求出圆心和半径,然后利用勾股定理求弦长.【参考答案】C【试题解析】圆的方程可化为22:(1)(2)5C x y -+-=,其圆心为(1,2)C ,半径R =.(步骤1) 如图所示,取弦AB 的中电P ,连接CP ,则CP AB ⊥.第6题图圆心C 到直线AB的距离 1.d CP === (步骤2)Rt ACP AP 在△中,,故直线被圆截得的弦长=4AB . (步骤3)7.设nS 为等差数列{}n a 的前n 项和,83,742,S a a ==-则9a = ( ) A.-6 B. -4 C. -2 D.2【测量目标】等差数列的基本性质.【考查方式】借助等差数列前n 项的性质,计算数列的公差,进而得到9a 的值.【参考答案】A【试题解析】由等差数列的通项公式与前n 项和公式 得1883638()4()42a a S a a a +==+=. 67970.2,226a a d a a d ==-=-=+=-所以又所以公差,.8.函数()y f x =的图象如图所示,在区间[],a b 上可找到()2n n ≥个不同的数12,,,n x x x ,使得1212()()()n nf x f x f x x x x === ,则n 的取值范围为 ( ) A. {}2,3 B. {}2,3,4 C. {}3,4 D. {}3,4,5第8题图【测量目标】斜率公式、直线与曲线相交.【考查方式】考查斜率公式、直线与曲线的交点个数以及数形结合思想的应用,把1212()()()n nf x f x f x x x x === 的条件转化为曲线上点与原点的斜率相等,再转化为过原点的直线与曲线有n 个交点,考查了抽象概括能力.【参考答案】B 【试题解析】利用()f x x的几何意义,将所求转化为直线与曲线的交点个数问题并列用数形结合求解. 由题意,函数()y f x =上的任一点坐标为(,())x f x ,故()f x x 表示曲线上任一点与坐标原点连线的斜率.若()11()n nf x f x x x == ,则曲线上存在n 个点与原点连线的斜率相等,即过原点的直线与曲线()y f x =有n 个交点.如图,数形结合可得n 的取值可为2,3,4.9.设ABC △的内角A ,B ,C 所对边的长分别为,,a b c ,若2,3s i n 5s i nb c a A B +==,则角C = ( ) A. π3 B. 2π3 C. 3π4 D. 5π6【测量目标】正弦定理、余弦定理的基本运算.【考查方式】利用正弦定理、余弦定理和解三角形的基本知识,将三角形中正弦关系转化为边的关系,进而利用余弦定理求解角的大小.【参考答案】B【试题解析】利用正弦定理、余弦定理求解.3sin 5sin A B =,得35a b =,又因为2b c a += 所以57,33a b c b == (步骤1) 所以22222257()()133cos .52223b b b a bc C ab b b +-+-===-⨯⨯ (步骤2) 因为(0,π)C ∈,所以2π3C = . (步骤3) 10.已知函数32()f x x ax bx c =+++有两个极值点12,x x ,若112()f x x x =<,则关于x 的方程23(())2()0f x a f x b ++=的不同实根个数为 ( ) A. 3 B. 4 C. 5 D. 6【测量目标】函数的单调性、极值.【考查方式】利用定函数的导函数和函数图象的变化趋势,数形结合判断函数图象的交点个数进而求出实根个数.【参考答案】A【试题解析】先求给定函数的导函数,由极值点的定义及题意,得出1()f x x =或2()f x x =,再利用数形结合确定这两个方程实数根的个数.因为2()32f x x ax b '=++,函数()f x 的两个极值点为1x ,2x则1()0f x '=,2()0f x '=,所以1x ,2x 是方程2320x ax b ++=的两根 (步骤1)所以解关于x 的方程23(())2()0f x af x b ++=,得1()f x x =或2()f x x =. (步骤2)由上述可知函数()f x 在区间12(,),(,)x x -∞+∞上单调递增,在区间12(,)x x 上单调递减 (步骤3) 又112()f x x x =<,由数形结合可知1()f x x =时有两个不同实根,2()f x x =有一个实根,所以不同实根的个数为3. (步骤4)二.填空题11.函数1In(1y x =+的定义域为_____________.【测量目标】复合函数的定义域.【考查方式】根据复合函数解析式列出限制条件,根据不等式组求出定义域.【参考答案】(]0,1【试题解析】列出函数有意义的限制条件,解不等式组. 要使函数有意义,需211010x x ⎧+>⎪⎨⎪-⎩≥即2101x x x +⎧>⎪⎨⎪⎩≤即1,011x x x <->⎧⎨-⎩≤≤解得01x <≤,所以定义域为(0,1] 12.若非负数变量,x y 满足约束条件124x y x y --⎧⎨+⎩≥≤,则x y +的最大值为__________.【测量目标】二元线性规划求目标函数最值.【考查方式】结合约束条件,应用数形结合思想画出不等式组所表示的平面区域,求出线性规划目标函数的最大值.【参考答案】4【试题解析】先画出可行线,再画目标函数线过原点时的直线,向上平移,寻找满足条件的最优解,代入即可得所求.第12题图根据题目中的约束条件画出可行域,注意到,x y 非负,得可行域为如图所示的阴影部分(包括边界).作直线y x =-,并向上平移,数形结合可知,当直线过点(4,0)A 时,x y +取得最大值,最大值为4.15.如图,正方体1111ABCD A BC D -的棱长为1,P 批为BC 的中点,Q 为线段1CC 上的动点,过点,,A P Q 的平面截该正方体所得的截面记为S ,则下列命题正确的是 (写出所有正确命题的编号).第15题图①当102CQ <<时,S 为四边形;②当12CQ =时,S 为等腰梯形;③当34CQ =时,S 与11C D 的交点R满足11=3C R ;④当314CQ <<时,S 为六边形;⑤当1CQ =时,S 的面积为2【测量目标】空间立体图形截面的基本性质.【考查方式】考查了平面的基本性质、截面的画法以及各种平面图形的特征,以正方体为载体,通过几何体的截面考查了空间想象能力.【参考答案】①②③⑤【试题解析】利用平面的基本性质结合特殊四边形的判定与性质求解.① 当102CQ <<时,如图.第15题图在平面11AA D D 内,作AE PQ ,显然E 在棱1DD 上,连接EQ则S 是四边形APQE . (步骤1)② 当12CQ =时,如图.第15题图显然11PQ BC AD ,连接1D Q ,则S 是等腰梯形. (步骤2)③ 当34CQ =时,如图. 第15题图作AE PQ 交1DD 的延长线于点E ,11,,2D E AE PQ = 连接EQ 交11C D 于点R ,由于11Rt Rt RC Q RD E △△,1111::1:2C Q D E C R RD ∴==,113C R ∴=. (步骤3) ④ 当314CQ <<时,如图(3),连接RM (点M 为AE 与11A D 交点),显然S 为五边形APQRM . (步骤4)⑤ 当1CQ =时,如图. 第15题图同③可作AE PQ 交1DD 的延长线于点E ,交11A D 于点M ,显然点M 为11A D 的中点,所以S 为菱形APQM ,其面积为1122MP AQ ⨯== (步骤5)三.解答题16.(本小题满分12分)设函数π()sin sin()3f x x x =++. (Ⅰ)求()f x 的最小值,并求使()f x 取得最小值的x 的集合;(Ⅱ)不画图,说明函数()y f x =的图象可由sin y x =的图象经过怎样的变化得到.【测量目标】三角函数的图象及性质、三角恒等变换.【考查方式】把目标函数通过恒等变换转换为三角函数标准式得到结果,结合三角函数解析式,考查三角函数图象的平移伸缩变换等基础知识和基本技能.【试题解析】解:(1)ππ()sin sin cos cos sin 33f x x x x =++13sin sin sin 22x x x x x =++=ππ))66x x =+=+ . (步骤1)当πsin()16x +=-时,min ()f x =此时π3π4π2π,2π()623x k x k k +=+∴=+∈Z (步骤2)所以,()f x 的最小值为x 的集合4π|2π,3x x k k ⎧⎫=+∈⎨⎬⎩⎭Z . (步骤3)(2)sin y x =y x =; (步骤4)然后y x =向左平移π6个单位,得π())6f x x =+. (步骤5)17.(本小题满分12分)为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中各抽取30名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如下:第17题图(Ⅰ)若甲校高三年级每位学生被抽取的概率为0.05,求甲校高三年级学生总人数,并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格); (Ⅱ)设甲、乙两校高三年级学生这次联考数学平均成绩分别为12,x x ,估计12x x -的值.【测量目标】随机抽样、茎叶图.【考查方式】利用样本估计总体的思想,从茎叶图中得出数据进行平均数计算.【试题解析】解:(1)由样本数据除以所占比例得总体n ,计算样本中的及格率,利用样本估计总体设甲校高三年级学生成绩不及格人数为n .30300.056000.05n n =⇒== 255306P == (步骤1) (2)甲、乙两校平均数分别为12,x x1740504246092670922805290220843030x ++⨯++⨯++⨯++⨯++⨯== 254014503176010337010208059020693030x +++⨯++⨯++⨯++⨯+== (步骤2) 1220842069150.5303030x x ∴-=-== (步骤3)18.(本小题满分12分)如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60oBAD ∠=.已知,PB PD PA ==. (Ⅰ)证明:PC BD ⊥(Ⅱ)若E 为PA 的中点,求四棱锥P BCE -的体积.第18题图【测量目标】点、直线、平面之间的位置关系 四棱锥体积公式.【考查方式】根据线面垂直得到线线垂直;根据四棱锥体积求出体积.【试题解析】(1)证明:连接,BD AC 交于O 点第18题图PB PD = P O B D ∴⊥ (步骤1)又ABCD 是菱形 B D A C ∴⊥ (步骤2) 而AC PO O =BD ∴⊥面PACBD PC ∴⊥ (步骤3)(2) 由(1)BD PAC ⊥面011sin 453222PEC PAC S S ====△△ (步骤4) 111132322P BEC B PEC V V S PEC BO --===⨯⨯= △ (步骤5)19.(本小题满分13分)设数列{}n a 满足12a =,248a a +=,且对任意*n ∈N ,函数 1212()()cos sin n n n n n f x a a a x a x a x ++++=-++- 满足π()02f '= (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)若12()2nn n a b a =+,求数列{}n b 的前n 项和n S .【测量目标】等差数列、等比数列的基本性质.【考查方式】根据()f x 的导函数证明n a 为等差数列,然后根据首项、公差得到通项公式; 把{}n a 通项公式代入{}n b ,求出结果.【试题解析】解:(1)由12a = 248a a +=1212()()cos sin n n n n n f x a a a x a x a x ++++=-++-1212()sin cos n n n n n f x a a a a x a x ++++'=-+-- (步骤1) 121π()02n n n n f a a a a +++'=-+-=所以,122n n n a a a ++=+{}n a ∴是等差数列. (步骤2)而12a =,34a =,1d =. 2(1)11n a n n ∴=+-=+ (步骤3)(2)11112()2(1)2(1)222n n n a n nb a n n +=+=++=++ (步骤4) 11(1)2(21)221212n n n n S -++=+- 1(3)12n n n =++- 21312n n n =++- (步骤5)20.(本小题满分13分)设函数22()(1)f x ax a x =-+,其中0a >,区间{}|()0I x f x =>.(Ⅰ)求I 的长度(注:区间(),αβ的长度定义为βα-;(Ⅱ)给定常数(0,1)k ∈,当11k a k -+≤≤时,求I 长度的最小值. 【测量目标】一元二次方程、导函数.【考查方式】利用导数求函数单调区间、最值.【试题解析】解:(1)令22()(1)0f x ax a x =-+=解得10x = 221a x a =+ (步骤1) 2|01a I x x a ⎧⎫∴=<<⎨⎬+⎩⎭I ∴的长度2121a x x a -=+ (步骤2)(2)(0,1)k ∈ 则0112k a k <-+<≤≤由(1)21a I a =+ ()222101a I a -'=>+,则01a << (步骤3)故I 关于a 在()1,1k -上单挑递增,在(1,1)k +上单调递减122111(1)22k k I k k k--==+--+ (当1a k =-时) 222111(1)22k k I k k k ++==++++ (当1a k =+时) 12I I < ∴min 2122k I k k-=-+ (步骤4) 21.(本小题满分13分)【考查方式】根据焦距和点P 求出椭圆的标准方程;联立直线与椭圆方程求证公共点个数.【试题解析】解:(1)因为椭圆过点P 22231a b∴+= 且222a b c =+,2c =4. 28a ∴= 24b = 24c = ∴椭圆C 的方程是22184x y +=. (步骤1)(2)第21题图由题意,各点的坐标如上图所示 则QG 的直线方程:0000808x x y y x x --=- 化简得20000(8)80x y x x y y ---= (步骤2) 又220028x y +=所以00280x x y y +-=代入22184x y += (步骤3) 求得最后0∆=所以直线QG 与椭圆只有一个公共点. (步骤4)。
(安徽卷)2013年高考试卷(文数)

2013年普通高等学校招生全国统一考试(安徽卷)数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至4页。
全卷满分150分。
考试用时120分钟。
考生注意事项:1. 答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘帖的条形码中姓名、座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2. 答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上....对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
3. 答第Ⅱ卷时,必须用0.5毫米黑色墨水签字笔在答题卡上....书写,要求字体工整、笔迹清晰。
作图题时可先用铅笔在答题卡...规定的位置绘出,确认后用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域作答,超出答题区域书写的答案无效.............,在试题卷....、草稿纸上答.....题无效...。
4. 考试结束,务必将试题卷和答题卡一并上交。
第Ⅰ卷(选择题 共50分)一、 选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
一.选择题选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)设i 是虚数单位,若复数10()3a a R i-∈-是纯虚数,则a 的值为 ( )(A )-3(B )-1(C )1(D )3【答案】D 【解析】i a i a i a i i a i i i a i a --=+-=+-=-+-=+-+-=--)3()3(10)3(109)3(10)3)(3()3(103102,所以a =3, 故选择D【考点定位】考查纯虚数的概念,及复数的运算,属于简单题. (2)已知{}{}|10,2,1,0,1A x x B =+>=--,则()R C A B ⋂=( )(A ){}2,1--(B ){}2-(C ){}1,0,1-(D ){}0,1【答案】A【解析】A :1->x ,}1|{-≤=x x A C R ,}2,1{)(--=B A C R ,所以答案选A【考点定位】考查集合的交集和补集,属于简单题.(3)如图所示,程序据图(算法流程图)的输出结果为(A )34(B )16 (C )1112(D )2524【答案】C【解析】21210,0,2=+===s s n ; 434121,21,4=+===s s n ;12116143,43,6=+===s s n1211,8==s n ,输出所以答案选择C【考点定位】本题考查算法框图的识别,逻辑思维,属于中等难题. (4)“(21)0x x -=”是“0x =”的(A )充分不必要条件 (B )必要不充分条件(C )充分必要条件 (D )既不充分也不必要条件 【答案】B【解析】210,0)12(或==-x x x ,所以答案选择B 【考点定位】考查充分条件和必要条件,属于简单题.(5)若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这五人被录用的机会均等,则甲或乙被 录用的概率为(A )23 (B) 25 (C) 35 (D )910【答案】D【解析】总的可能性有10种,甲被录用乙没被录用的可能性3种,乙被录用甲没被录用的可能性3种,甲乙都被录用的可能性3种,所以最后的概率333110p ++== 【考点定位】考查古典概型的概念,以及对一些常见问题的分析,简单题.【解析】圆心(1,2),圆心到直线的距离d =,半径r =为4=.【考点定位】考查解析几何初步知识,直线与圆的位置关系,点到直线的距离,简单题.(7)设n S 为等差数列{}n a 的前n 项和,8374,2S a a ==-,则9a = (A )6- (B )4- (C )2- (D )2 【答案】A 【解析】188333636978()4420226a a S a a a a a a d a a d +=⇒=⇒+=∴==-=+=-【考点定位】考查等差数列通项公式和前n 项公式的应用,以及数列基本量的求解.(8) 函数()y f x =的图像如图所示,在区间[],a b 上可找到(2)n n ≥个不同的数12,,,n x x x ,使得1212()()()n nf x f x f x x x x === ,则n 的取值范围为 (A) {}2,3 (B) {}2,3,4 (C) {}3,4 (D) {}3,4,5【答案】B 【解析】1111()()0f x f x x x -=-表示11(,())x f x 到原点的斜率; 1212()()()n n f x f x f x x x x === 表示1122(,())(,())(,())n nx f x x f x x f x ,,,与原点连线的斜率,而1122(,())(,())(,())n n x f x x f x x f x ,,,在曲线图像上,故只需考虑经过原点的直线与曲线的交点有几个,很明显有3个,故选B.【考点定位】考查数学中的转化思想,对函数的图像认识.(9) 设ABC ∆的内角,,A B C 所对边的长分别为,,a b c ,若2,3s in 5s i n b c a A B+==,则角C =(A) 3π (B) 23π(C) 34π (D) 56π【答案】B【解析】B A sin 5sin 3= 由正弦定理,所以b a b a 35,53==即; 因为a c b 2=+,所以a c 37=, 212cos 222-=-+=ab c b a C ,所以32π=C ,答案选择B 【考点定位】考查正弦定理和余弦定理,属于中等难度.(10)已知函数32()f x x ax bx c =+++有两个极值点12,x x ,若112()f x x x =<,则关于x的方程23(())2()0f x a f x b ++=的不同实根个数为(A )3 (B) 4(C) 5 (D) 6【答案】A【解析】2'()32f x x ax b =++,12,x x 是方程2320x ax b ++=的两根,由23(())2()0f x af x b ++=,则又两个()f x 使得等式成立,11()x f x =,211()x x f x >=,其函数图象如下:如图则有3个交点,故选A.【考点定位】考查函数零点的概念,以及对嵌套型函数的理解.二.填空题(11)函数1ln(1)y x=++的定义域为_____________. 【答案】(]0,1【解析】2110011011x x xx x ⎧+>⇒><-⎪⎨⎪-≥⇒-≤≤⎩或,求交集之后得x 的取值范围(]0,1 【考点定位】考查函数定义域的求解,对数真数位置大于0,分母不为0,偶次根式底下大于等于0.(12)若非负数变量,x y 满足约束条件124x y x y -≥-⎧⎨+≤⎩,则x y +的最大值为__________.【答案】4【解析】由题意约束条件的图像如下:当直线经过(4,0)时,404z x y =+=+=,取得最大值.【考点定位】考查线性规划求最值的问题,要熟练掌握约束条件的图像画法,以及判断何时z 取最大.【答案】3-【解析】等式平方得:2222944a b a b a b ==++⋅则22244||||cos a a b a b θ=++⋅,即220443||cos b b θ=+⋅得1cos 3θ=-【考点定位】考查向量模长,向量数量积的运算,向量最基本的化简.(14)定义在R 上的函数()f x 满足(1)2()f x f x +=.若当01x ≤≤时。
2013年高考文科数学安徽卷-答案

2013年普通高等学校招生全国统一考试(安徽卷)数学(文科)答案解析第Ⅰ卷一、选择题 1.【答案】D【解析】21010(3i)10(3i)10(3i)(3i)(3)i 3i (3i)(3i)9i 10a a a a a a +++-=-=-=-=-+=----+-,所以3a =,故选D . 【提示】先利用复数的运算法则将复数化为i(,)x y x y +∈R 的形式,再由纯虚数的定义求a 【考点】复数的基本概念. 2.【答案】A【解析】1x >-,{|1}A x x =≤-R ð,(){1,2}A B =--R I ð,故选A . 【提示】解不等式求出集合A ,进而得A R ð,再由集合交集的定义求解. 【考点】集合的交集和补集运算. 3.【答案】C【解析】1120022n s s ===+=,,;111342244n s s ===+=,,;33111644612n s s ===+=,,; 11812n s ==,,输出,故选C . 【提示】利用框图的条件结构和循环结构求解. 【考点】条件语句、循环语句的程序框图. 4.【答案】B【解析】1(21)002x x x -==,或,故选B .【提示】先解一元二次方程(21)0x x -=,再利用充分条件、必要条件的定义判断. 【考点】充分条件和必要条件. 5.【答案】D【解析】总的可能性有10种,甲被录用乙没被录用的可能性3种,乙被录用甲没被录用的可能性3种,甲乙都被录用的可能性3种,所以最后的概率333110p ++==,故选D . 【提示】把所求事件转化为求其对立事件,然后求出概率.【考点】随机事件与概率. 6.【答案】C【解析】圆心(1,2),圆心到直线的距离d =,半径r =,所以弦长为4,故选C .【提示】把圆的一般方程化为标准方程,求出圆心和半径,然后利用勾股定理求弦长. 【考点】直线与圆的相交方程,点到直线距离公式.【考点】等差数列的基本性质. 8.【答案】B【解析】1111()()00f x f x x x -=-表示11(,())x f x 到原点的斜率;1212()()()n nf x f x f x x x x ===L 表示 1122(,()),(,())(,())n n x f x x f x x f x L ,,与原点连线的斜率,而1122(,()),(,()),(,())n n x f x x f x x f x L ,在曲线图像上,故只需考虑经过原点的直线与曲线的交点有几个,很明显有3个,故选B . 【提示】利用()f x x的几何意义,将所求转化为直线与曲线的交点个数问题并列用数形结合求解. 【考点】斜线公式,直线与曲线相交. 9.【答案】B【解析】3sin 5sin A B =Q 由正弦定理,所以5353a b a b ==即;因为2b c a +=,所以73c a =,2221cos 22a b c C ab +-==-,所以2π3C =,故选B . 【提示】利用正弦定理、余弦定理和解三角形的基本知识,将三角形中正弦关系转化为边的关系,进而利用余弦定理求解角的大小.【考点】正弦定理和余弦定理的基本运算. 10.【答案】A【解析】2()32f x x ax b '=++,12,x x 是方程2320x ax b ++=的两根,由23(())2()0f x af x b ++=,则又两个()f x 使得等式成立,11()x f x =,211()x x f x >=,其函数图象:如图则有3个交点,故选A .【提示】先求给定函数的导函数,由极值点的定义及题意,得出1()f x x =或2()f x x =,再利用数形结合确定这两个方程实数根的个数. 【考点】函数的单调性、极值.第Ⅱ卷二、填空题11.【答案】(0,1]【解析】2110011011x x x x x ⎧+>⇒><-⎪⎨⎪-≥⇒-≤≤⎩或,求交集之后得x 的取值范围(0,1].【提示】列出函数有意义的限制条件,解不等式组. 【考点】复合函数的定义域. 12.【答案】4【解析】由题意约束条件的图像如下:当直线经过(4,0)时,404z x y =+=+=, 取得最大值.【提示】先画出可行线,再画目标函数线过原点时的直线,向上平移,寻找满足条件的最优解,代入即可得所求.【考点】二元线性规划求目标函数最值. 13.【答案】13-【解析】等式平方得:2222||9||||4||4a b a b a b ==++r r r r r r g 则222||||4||4||||cos a a b a b θ=++r r r r rg ,即 2204||43||cos b b θ=+r rg ,得1cos 3θ=-.【提示】根据两个向量的夹角公式,利用向量模的转化求出两向量夹角余弦值. 【考点】向量的线性运算,平面向量的数量积.【解析】当10x -≤≤,则011x ≤+≤,故(1)(1)(11)(1)f x x x x x +=+--=-+,又(1)2()f x f x +=, 所以(1)()2x x f x +=-. 【提示】根据题意把整体代入,再根据(1)2()f x f x +=求出()f x 【考点】函数解析式. 15.【答案】①②③⑤ 【解析】(1)12CQ =,S 等腰梯形,②正确,图(1)如下;图1(2)1CQ =,S 2)如下;图2(3)34CQ =,画图(3)如下:113C R =,③正确;图3(4)314CQ <<,如图(4)是五边形,④不正确;图4(5)102CQ <<,如下图(5),是四边形,故④正确.图5【提示】利用平面的基本性质结合特殊四边形的判定与性质求解. 【考点】空间立体图形截面的基本性质. 三、解答题16.【答案】(1)ππ13()sin sin coscos sin sin sin sin 3322f x x x x x x x x x =++=+=+ππ66x x ⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭,当πsin 16x ⎛⎫+=- ⎪⎝⎭时,min ()f x = 此时π3π2π62x k +=+,4π2π,()3x k k ∴=+∈Z ,所以,()f x 的最小值为x 的集合4π2π,3x x k k ⎧⎫=+∈⎨⎬⎩⎭Z .(2)sin y x =横坐标不变,倍,得y x ;然后y x =向左平移π6个单位,得π()6f x x ⎛⎫=+ ⎪⎝⎭.【提示】把目标函数通过恒等变换转换为三角函数标准式得到结果,结合三角函数解析式,考查三角函数图象的平移伸缩变换等基础知识和基本技能. 【考点】三角函数的图象及性质,三角恒等变换.17.【答案】解:(1)设甲校高三年级学生总人数为n .由题意知,300.05n=,即600n =.样本中甲校高三年级学生数学成绩不及格人数为5.据此估计甲校高三年级此次联考数学成绩及格率为551306-=.(2)设甲、乙两校样本平均数分别为1x ',2x '.根据样本茎叶图可知,()121230()3030(75)(55814)241265(262479)(2220)92x x x x '-'='-'=-++-+--+--+-+249537729215=+--++=.因此120.5x x '-'=.故12x x -的估计值为0.5分.【提示】利用样本估计总体的思想,从茎叶图中得出数据进行平均数计算. 【考点】随机抽样,茎叶图.18.【答案】(1)连接AC ,交BD 于O 点,连接PO .因为底面ABCD 是菱形,AC BD ∴⊥,BO DO =.由PB PD =知,PO BD ⊥.再由PO AC O =I 知,BD ⊥面APC ,因此BD PC ⊥(2)因为E 是PA 的中点,所以1122P BCE C PEB C PAB B APC V V V V ----===.由2PB PD AB AD ==== 知,ABD PBD △≌△.因为60BAD ∠=︒,所以PO AO ==AC =1BO =.又PA =,222PO AO PA +=,即PO AC ⊥,故132APC S PO AC ==g △. 由(1)知,BO ⊥面APC ,因此11112232P BCE B APCAPC V V BO S --===g g g △. 【提示】根据线面垂直得到线线垂直;根据四棱锥体积求出体积. 【考点】点、直线、平面之间的位置关系,四棱锥体积公式.19.【答案】(1)由12a =,248a a +=,1212()()cos sin n n n n n f x a a a x a x a x ++++=-++-gg , 1212sin cos n n n n n f x a a a a x a x ++++'=-+-⋅-⋅(),121π02n n n n f a a a a +++⎛⎫'=-+-= ⎪⎝⎭,所以122n n n a a a ++=+{}n a ∴是等差数列.而12a =,34a =,1d =,2111n a n n ∴=+-=+g ().(2)11112212(1)222n n n a n n b a n n +⎛⎫⎛⎫=+=++=++ ⎪ ⎪⎝⎭⎝⎭,()112221212(21)11=(3)1312122n n n n n n S n n n n ++=+++-=++---.【提示】根据()f x 的导函数证明n a 为等差数列,然后根据首项、公差得到通项公式;把{}n a 通项公式代入{}n b ,求出结果.【考点】等差数列,等比数列的基本性质. 20.【答案】(1)21aa + (2)2122kk k --+【解析】(1)因为方程22100()()ax a x a -+=>有两个实根10x =,221ax a=+,故()0f x >的解集为12{|}x x x x <<,因此区间20,1a a I ⎛⎫⎪+⎝⎭=,区间长度为21a a +. (2)设2()1ad a a=+,则222()11a a d a -(+')=,令()0d a '=,得1a =.由于01k <<,当11k a -≤<时,()0d a '>, ()d a 单调递增;当11a k <≤+时,()0d a '<,()d a 单调递减.因此当11k a k -≤≤+时,()d a 的最小值必定在1a k =-或1a k =+处取得.而22123112311112<112k k k k d k k k d k k k -+(-)++(+)(-)--==(+)-+,故()1)1(d k d k -<+. 因此当1a k =-时,()d a 在区间1,]1[k k -+上取得最小值2122kk k--+. 【提示】利用导数求函数单调区间、最值. 【考点】一元二次方程,导函数.21.【答案】(1)22184x y +=(2)见解析【解析】(1)因为焦距为4,所以224a b -=.又因为椭圆C过点P ,所以22231a b+=,故28a =,24b =,从而椭圆C 的方程为22184x y +=. (2)由题意,E 点坐标为0(),0x .设0(),D D x,则0(,AE x =-u u u r,(,D AD x =-u u u r.再由AD AE ⊥知,0AE AD =u u u r u u u rg ,即080D x x +=.由于000x y ≠,故08D x x =-.因为点G 是点D 关于y 轴的对称点,所以点08,0G x ⎛⎫⎪⎝⎭.故直线QG 的斜率000028008G x Q k y x y x x =--=. 又因00()Q x y ,在C 上,所以220028x y +=④从而002QG x k y -=.故直线QG 的方程为00082x y x y x ⎛⎫=-- ⎪⎝⎭④将④代入C 方程,得22220000216640(1)6x y x x x y +-+-=.④再将④代入④,化简得220020x x x x -+=.解得0x x =,0y y =,即直线QG 与椭圆C 一定有唯一的公共点.【提示】根据焦距和点P 求出椭圆的标准方程;联立直线与椭圆方程求证公共点个数. 【考点】椭圆的标准方程及其几何性质,直线与椭圆的位置关系.。
2013年全国高考数学文科试卷安徽卷(word版)

绝密★启用前2013年普通高等学校招生全国统一考试(安徽卷)数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至4页。
全卷满分150分。
考试用时120分钟。
考生注意事项:1. 答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘帖的条形码中姓名、座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2. 答第Ⅰ卷时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
3. 答第Ⅱ卷时,必须用0.5毫米黑色墨水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
作图题时可先用铅笔在答题卡规定的位置绘出,确认后用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效。
4. 考试结束,务必将试题卷和答题卡一并上交。
第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)设i是虚数单位,若复数a--(a∈R)是纯虚数,则a的值为()(A)-3 (B)-1 (C)1 (D)3(2)已知A={x|x+1>0},B={-2,-1,0,1},则(RA)∩B=()(A){-2,-1}(B ){-2}(C){-2,0,1} (D){0,1}(3)如图所示,程序据图(算法流程图)的输出结果为(A)(B)(C)(D)(4)“(2x-1)x=0”是“x=0”的(A)充分不必要条件(B)必要补充分条件(C)充分必要条件(D)既不充分也不必要条件(5)若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这无人被录用的机会均等,则甲或乙被录用的概率为(A)2/3 (B)2/5(C)3/5 (D)9/10(6)直线x+2y-5+=0被圆x2+y2-2x-4y=0截得的弦长为(A)1 (B)2(C)4 (D)(7)设sn为等差数列{an}的前n项和,s1=4a3,a2=-2,则a9=(A)6 (B)4(C)-2 (D)2(8)函数y=f(x)的图像如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…xn,使得f(x1)/x1=f(x2)/x2=…=f(xn)/xn,则n的取值范围为(A) {2,3} (B){2,3,4}(C){3,4} (D){3,4,5}(9)设△ABC的内角A,B,C所对边的长分别为a,b,c,若b+c=2a,3sinA=5sinB,则角C=(A) π/3(B)2π/3(C)3π/4(D)5π/6(10)已知函数f(s)=x3+ax2+bx+c有两个极致点x1,x2,若f(x1)则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数为(A)3 (B)4(C) 5 (D)6第Ⅱ卷(非选择题共100分)考生注意事项:请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效。
【恒心】2013年普通高等学校招生全国统一考试(安徽卷)数学【文科】试题及名师剖析【纯word版】

绝密★启用前2013年普通高等学校招生全国统一考试(安徽卷)数学(文科)(RR(【说明】考查集合的交集和补集,属于简单题。
A.34B.16C.1112D.2524【答案】C【解析】开始,2<8,s =0+12,n =2+2=4; 返回,4<8,113244s =+=,n =4+2=6; 返回,6<8,31114612s =+=,n =6+2=8;返回,8<8不成立,输出11A .-6B .-4C .-2D .2 【答案】A【解析】由S 8=4a 3知:a 1+a 8=a 3,a 8=a 3-a 1=2d =a 7+d ,所以a 7=d =-2.所以a 9=a 7+2d =-2-4=-6.【说明】考查等差数列通项公式和前n 项公式的应用,以及数列基本量的求解。
8.函数y =f (x )的图象如图所示,在区间[a ,b ]上可找到n (n ≥2)个不同的数x 1,x 2,…,x n ,使得11f x x ()=22f x x ()=…=n nf x x (),则n 的取值范围为( ).∴C =3π.【说明】考查正弦定理和余弦定理,属于中等难度。
10.已知函数f (x )=x 3+ax 2+bx +c 有两个极值点x 1,x 2.若f (x 1)=x 1<x 2,则关于x 的方程3(f (x ))2+2af (x )+b =0的不同实根个数为( ).A .3B .4C .5D .6 【答案】A【解析】由f ′(x )=3x 2+2ax +b =0,得x=x1或x=x2,即3(f(x))2+2af(x)+b=0的根为f(x)=x1或f(x)=x2的解,由题可知f(x)的草图为:【说明】考查线性规划求最值的问题,要熟练掌握约束条件的图像画法,以及判断何时z取最大。
13.若非零向量a,b满足|a|=3|b|=|a+2b|,则a与b夹角的余弦值为__________.【答案】1 3 -【解析】∵|a|=3|b|=|a+2b|,∴|a|2=9|b|2=|a|2+4|b|2+4a·b,∴a·b=-|b|2,∴cos〈a,b〉=22||1 ||||3||3⋅-==-a b ba b b.【说明】考查向量模长,向量数量积的运算,向量最基本的化简。
2013年普通高等学校招生全国统一考试数学文试题(安徽卷)

2013年普通高等学校招生全国统一考试(安徽卷文科)[试卷总评]2013年安徽文科卷相对于2012年安徽文科卷的难度来说有所加大。
从试卷命题特点方面:(1)对主干知识(函数、数列、圆锥曲线、立体几何、三角函数、概率统计)的重点考查,尤其是函数,考了四道小题,一道大题,而且函数小题两道是以压轴题的形式出现;(2)注重能力的考查:一方面在知识的交汇处命题,如第19题;另一方面重视对数学能力和思想方法的考查,如计算能力考查(第9,13,17,21题),转化思想的考查(第8,10,20题),数形结合的考查(第6,8,10题)等等;(3)注重理论联系实际,如第17题概率统计;(4)注重对创新意识的考查,如第21题。
从试卷难度方面:选择填空跟以往的试卷一样从易到难,但在做的过程中不是那么顺畅。
第1题考查复数,难度不大;第2题考查集合的交与补以及不等式求法;第3题程序框图,简单;第4题充分必要条件,容易题;第5题古典概型,只要考生能够理解题意,基本没问题;第6题直线与圆的方程,考查圆中弦长的求法,第7题等差数列基本量的求解,简单;第11题考查函数定义域的求法,简单;第12题常规的线性规划题,难度不大;第14题,抽象函数解析式的求解,难度中等。
选择题第8,9,10题,填空题第13,15题难度加大。
第8题考查函数转化思想以及数形结合,难度很大,考生不一定能想到方法;第9题三角函数,对正弦余弦定理的考查,计算量大;第10题函数零点的考查,难度很大,不容易做好;第13题平面向量,数量积的运算,需要细心;第15题立体几何的截面问题,是考生平时学习中最不容易弄明白的地方。
大题第16题三角函数:容易,主要考查恒等变形,三角函数图像变换,考生需注意图像变换时语言的描叙;大题第17题概率统计:难度不大,对计算的要求很高,在那种高压环境下必须有个良好的心态才能做好;大题第18题立体几何:难度中等,常规性的考查了三棱锥体积的求法,在选择顶点的过程中,需要考生注意看清垂直关系;大题第19题数列:综合性强,将函数求导利用到数列求通项中,只要学生能够细心,拿下这道题还是没有问题的;大题第20题函数:题型新颖,考查考生对新问题冷静处理的能力,对区间长度的准确理解;大题第21题:难度较大,计算量大,点比较多,也容易把考生绕进去,要将这题做好,需要一定的计算基本功。
2013安徽高考文科数学真题:完整word版

(6)直线x+2y-5+ =0被圆x2+y2-2x-4y=0截得的弦长为(A)1 (B)2(C)4 (D) (7)设sn为等差数列{an}的前n项和,s1=4a3,a2=-2,则a9=(A)6 (B)4(C)-2 (D)2(8)函数y=f(x)的图像如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…xn,使得f(x1)/x1=f(x2)/x2=…=f(xn)/xn,则n的取值范围为(A) {2,3} (B){2,3,4}(C){3,4} (D){3,4,5}(9)设△ABC的内角A,B,C所对边的长分别为a,b,c,若b+c=2a,3sinA=5sinB,则角C=(A) π/3 (B)2π/3(C)3π/4 (D)5π/6(10)已知函数f(s)=x3+ax2+bx+c有两个极致点x1,x2,若f(x1)则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数为(A)3 (B)4(C) 5 (D)6第Ⅱ卷(非选择题共100分)考生注意事项:请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效。
二.填空题:本大题共5小题,每小题5分,共25分。
把答案填在答题卡的相应位置。
(11) 函数y=ln(1+1/x)+ 的定义域为_____________。
(12)若非负数变量x、y满足约束条件,则x+y的最大值为__________。
(13)若非零向量a,b满足|a|=3|b|=|a+2b|,则a与b夹角的余弦值为_______。
(14)定义在R上的函数f(x)满足f(x+1)=2f(x).若当0≤x≤1时。
f(x)=x(1-x),则当-1≤x≤0时,f(x)=________________。
(15)如图,正方体ABCD-A1B1C1D1的棱长为1,p为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的洁面记为S,则下列命题正确的是 (写出所有正确命题的编号)。
2013年安徽高考数学真题

绝密★启用前2013年普通高等学校招生全国统一考试(安徽卷)数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至4页。
全卷满分150分。
考试用时120分钟。
考生注意事项:1. 答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘帖的条形码中姓名、座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2. 答第Ⅰ卷时,每小题选出答案后,用2B铅笔把答题卡上....对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
3. 答第Ⅱ卷时,必须用0.5毫米黑色墨水签字笔在答题卡上....书写,要求字体工整、笔迹清晰。
作图题时可先用铅笔在答题卡...规定的位置绘出,确认后用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域作答,超出答题区域书写的答案无效....、草..............,在试题卷稿纸上答题无效.......。
4. 考试结束,务必将试题卷和答题卡一并上交。
第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)设i是虚数单位,若复数a--错误!未找到引用源。
(a∈R)是纯虚数,则a 的值为()(A)-3 (B)-1 (C)1 (D)3(2)已知A={x|x+1>0},B={-2,-1,0,1},则(错误!未找到引用源。
R A)∩B=()(A){-2,-1}(B){-2}(C){-2,0,1} (D){0,1}(3)如图所示,程序据图(算法流程图)的输出结果为(A)错误!未找到引用源。
(B)错误!未找到引用源。
(C)错误!未找到引用源。
(D)错误!未找到引用源。
(4)“(2x-1)x=0”是“x=0”的(A)充分不必要条件(B)必要补充分条件(C)充分必要条件(D)既不充分也不必要条件(5)若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这无人被录用的机会均等,则甲或乙被录用的概率为(A)2/3 (B)2/5(C)3/5 (D)9/10(6)直线x+2y-5+=0被圆x2+y2-2x-4y=0截得的弦长为(A )1 (B )2 (C )4 (D )(7)设s n 为等差数列{a n }的前n 项和,s 1=4a 3,a 2=-2,则a 9=(A )6 (B )4(C )-2 (D )2(8)函数y=f (x )的图像如图所示,在区间[a,b]上可找到n (n ≥2)个不同的数x 1,x 2,…x n ,使得f(x 1)/x 1=f(x 2)/x 2=…=f(x n )/x n ,则n 的取值范围为(A) {2,3} (B){2,3,4}(C){3,4} (D){3,4,5}(9)设△ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c ,若b+c=2a ,3sinA=5sinB,则角C=(A) π/3 (B)2π/3(C)3π/4 (D)5π/6(10)已知函数f (s )=x 3+ax 2+bx+c 有两个极致点x 1,x 2,若f (x 1)则关于x 的方程3(f (x ))2+2af (x )+b=0的不同实根个数为(A )3 (B)4(C) 5 (D)6第Ⅱ卷(非选择题 共100分)考生注意事项:请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效。
2013年安徽省文科数学高考试题

2013年普通高等学校夏季招生全国统一考试数学文史类(安徽卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2页,第Ⅱ卷第3至第4页.全卷满分150分,考试时间120分钟.考生注意事项:1.答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致.务必在答题卡背面规定的地方填写姓名和座位号后两位.2.答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.3.答第Ⅱ卷时,必须使用0.5毫米的黑色墨水签字笔在答题卡上....书写,要求字体工整、笔迹清晰.作图题可先用铅笔在答题卡...规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚.必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、.................草稿纸上答题无效..........4.考试结束,务必将试题卷和答题卡一并上交.第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2013安徽,文1)设i 是虚数单位,若复数103ia --(a ∈R )是纯虚数,则a 的值为( ). A .-3 B .-1 C .1 D .32.(2013安徽,文2)已知A ={x |x +1>0},B ={-2,-1,0,1},则(R A )∩B =( ). A .{-2,-1} B .{-2} C .{-1,0,1} D .{0,1}3.(2013安徽,文3)如图所示,程序框图(算法流程图)的输出结果为( ).A .34 B .16 C .1112 D .25244.(2013安徽,文4)“(2x -1)x =0”是“x =0”的( ). A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件5.(2013安徽,文5)若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为( ).A .23B .25C .35D .9106.(2013安徽,文6)直线x +2y -50被圆x 2+y 2-2x -4y =0截得的弦长为( ). A .1 B .2 C .4 D.7.(2013安徽,文7)设S n 为等差数列{a n }的前n 项和,S 8=4a 3,a 7=-2,则a 9=( ). A .-6 B .-4 C .-2 D .28.(2013安徽,文8)函数y =f (x )的图象如图所示,在区间[a ,b ]上可找到n (n ≥2)个不同的数x 1,x 2,…,x n ,使得11f x x ()=22f x x ()=…=n nf x x (),则n 的取值范围为( ).A .{2,3}B .{2,3,4}C .{3,4}D .{3,4,5} 9.(2013安徽,文9)设△ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c .若b +c =2a,3sin A =5sin B ,则角C =( ).A .π3 B .2π3 C .3π4 D .5π610.(2013安徽,文10)已知函数f (x )=x 3+ax 2+bx +c 有两个极值点x 1,x 2.若f (x 1)=x 1<x 2,则关于x 的方程3(f (x ))2+2af (x )+b =0的不同实根个数为( ).A .3B .4C .5D .6第Ⅱ卷(非选择题 共100分)考生注意事项:请用0.5毫米黑色墨水签字笔在答题卡上.....作答,在试题卷上答题.......无效....二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置. 11.(2013安徽,文11)函数1ln 1y x ⎛⎫=++ ⎪⎝⎭__________.12.(2013安徽,文12)若非负变量x ,y 满足约束条件124,x y x y -≥-⎧⎨+≤⎩则x +y 的最大值为__________.13.(2013安徽,文13)若非零向量a ,b 满足|a |=3|b |=|a +2b |,则a 与b 夹角的余弦值为__________.14.(2013安徽,文14)定义在R 上的函数f (x )满足f (x +1)=2f (x ).若当0≤x ≤1时,f (x )=x (1-x ),则当-1≤x ≤0时,f (x )=__________.15.(2013安徽,文15)如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,P 为BC 的中点,Q 为线段CC 1上的动点,过点A ,P ,Q 的平面截该正方体所得的截面记为S .则下列命题正确的是__________(写出所有正确命题的编号).①当0<CQ <12时,S 为四边形 ②当CQ =12时,S 为等腰梯形 ③当CQ =34时,S 与C 1D 1的交点R 满足C 1R =13④当34<CQ <1时,S 为六边形⑤当CQ =1时,S 的面积为2三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内.16.(2013安徽,文16)(本小题满分12分)设函数f (x )=sin x +πsin 3x ⎛⎫+⎪⎝⎭. (1)求f (x )的最小值,并求使f (x )取得最小值的x 的集合;(2)不画图,说明函数y =f (x )的图象可由y =sin x 的图象经过怎样的变化得到.17.(2013安徽,文17)(本小题满分12分)为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中各抽取30名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如下:(1)若甲校高三年级每位学生被抽取的概率为0.05,求甲校高三年级学生总人数,并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格);(2)设甲、乙两校高三年级学生这次联考数学平均成绩分别为1x ,2x ,估计12x x -值.18.(2013安徽,文18)(本小题满分12分)如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°.已知PB=PD=2,P A.(1)证明:PC⊥BD;(2)若E为P A的中点,求三棱锥P-BCE的体积.19.(2013安徽,文19)(本小题满分13分)设数列{a n}满足a1=2,a2+a4=8,且对任意n∈N*,函数f(x)=(a n-a n+1+a n+2)x+a n+1cos x-a a+2sin x满足π'02f⎛⎫=⎪⎝⎭.(1)求数列{a n}的通项公式;(2)若b n=212nn aa⎛⎫+⎪⎝⎭,求数列{b n}的前n项和S n.20.(2013安徽,文20)(本小题满分13分)设函数f(x)=ax-(1+a2)x2,其中a>0,区间I={x|f(x)>0}.(1)求I的长度(注:区间(α,β)的长度定义为β-α);(2)给定常数k∈(0,1),当1-k≤a≤1+k时,求I长度的最小值.21.(2013安徽,文21)(本小题满分13分)已知椭圆C:22221x ya b+=(a>b>0)的焦距为4,且过点P.(1)求椭圆C的方程;(2)设Q(x0,y0)(x0y0≠0)为椭圆C上一点.过点Q作x轴的垂线,垂足为E.取点A(0,,连接AE.过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG.问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.。
