地理数学方法习题

合集下载

新人教版初中数学七年级下册用坐标表示地理位置测试题及答案-精品试卷

人教版七年级下册第七章7．2.1 用坐标表示地理位置同步练习题1.如图是李明家附近区域的平面示意图，如果宠物店所在位置的坐标为(2，－4)，儿童公园所在位置的坐标为(0，－3)，则学校所在的位置是( )A．(4，－3) B．(4，3) C．(5，－1) D．(2，1)2．象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图，是一局象棋残局，已知表示棋子“马”和“车”的点的坐标分别为(4，3)，(－2，1)，则表示棋子“炮”的点的坐标为( )A．(3，2) B．(1，3) C．(0，3) D．(－3，3)3．某镇三个厂址的地理位置如下：汽车配件厂在饲料厂的正南1 000 m，酒厂在汽车配件厂的正西800 m处，若酒厂的坐标是(－800，－1 000)，则选取的坐标原点是__________．4．(探究变式)以学校所在的位置为原点，分别以向东、向北方向为x轴、y 轴正方向．若出校门向东走100米，再向北走120米记作(100，120)，小强家的位置是(－150，200)的含义是______________________________________________；出校门向南走400米，再向东走150米是小明的家，则小明家的位置应记作__ __________________________．5．如图是轰炸机机群的一个飞行队形，如果最后两架轰炸机的平面坐标分别为A(－2，1)和B(－2，－3)，那么第一架轰炸机C的平面坐标是__ ____________________．6．小兰和爸爸、妈妈到人民公园游玩，回到家后，她利用平面直角坐标系画出了公园的景区地图(如图)，可是她忘记了在图中标出原点和x轴、y轴，只知道游乐园的位置D的坐标为(2，－2)，你能帮她求出其他各景点所在位置的坐标吗？7．如图，四艘船M，N，P，Q与灯塔O的距离均为50海里，则在灯塔O 南偏西20°且与O相距50海里的船是( )A．船M B．船N C．船P D．船Q8．方格纸上有A，B两点，若以B点为原点建立平面直角坐标系，则A点坐标为(－4，3)，若以A点为原点建立平面直角坐标系，则B点坐标为( )A．(－4，－3) B．(－4，3) C．(4，－3) D．(4，3)9．如图，图书馆相对于大门的位置是_____________________，操场相对于大门的位置是______________________，车站相对于大门的位置是___________________．10. 某飞行监控中心发现某飞机从某个飞机场起飞后沿正南方向飞行100千米，然后向正西方向飞行300千米，又测得该机场的位置位于监控中心的西100千米，北300千米的地方，若以监控中心为坐标原点，以正东、正北方向为x轴、y轴的正方向，请指出该飞机现在的位置____________________．(用坐标表示)11. 如图是某市旅游景点的示意图，试建立平面直角坐标系，用坐标表示各个景点的位置．12. 如图标出了李明家附近的一些地方．(1)根据图中所建立的平面直角坐标系，写出学校、邮局的坐标；(2)某星期日早晨，李明从家里出发，沿着(－2，－1)，(－1，－2)，(1，－2)，(2，－1)，(1，－1)，(1，3)，(－1，0)，(0，－1)的路线转了一下，写出他路上经过的地方；(3)连接他在(2)中经过的地点，你能得到什么图形？答案：1. B2. B3. 饲料厂4. 出校门向西走150米，再向北走200米是小强家(150，－400)5. (2，－1)6. 解：由题意可知，是以点F为坐标原点(0，0)，射线FA为y轴的正半轴建立的平面直角坐标系，则音乐台的位置A(0，4)，湖心亭的位置B(－3，2)，望春亭的位置C(－2，－2)，牡丹园的位置E(3，3)7. C8. C9. 北偏东56°，3_km 北偏西34°，6_km 正南，4_km10. (－400，200)11. 解：答案不唯一，如：以中心广场为原点，以正东、正北方向分别为x轴、y轴的正方向建立平面直角坐标系，则钟楼(－2，4)，碑林(4，4)，古塔(－4，2)，公园(3，－3)12. 解：(1)学校(1，3)，邮局(0，－1) (2)李明家→商店→公园→汽车站→水果店→学校→游乐场→邮局(3)一艘帆船。

新编地图学教程(第二版)练习题

《新编地图学教程》（第二版）毛赞猷等编练习题一一、名词解释1.地图：是遵循一定的数学法则，将地理信息通过科学的概括综合，运用符号系统表示在一定的载体上的图形，以传递它们的数量、质量在时间和空间上的分布规律和发展变化。

2地图学：是以地图信息传输为中心，研究地图的理论、制作技术和使用方法的科学。

3水准面：当海洋静止时，自由水面与该面上各点的重力方向（铅垂线）成正交,这个面叫水准面。

4.大地水准面：在众多的水准面中，有一个与静止的平均海水面相重合，并假想其穿过大陆、岛屿形成一个闭合曲面。

5天文经度：观测点天顶子午面与格林尼治天顶子午面间的两面角。

在地球上定义为本初子午面与观测点之间的两面角。

6.天文纬度：在地球上定义为铅垂线与赤道平面间的夹角。

7.大地经度：指参考椭球面上某点的大地子午面与本初子午面间的两面角。

东经为正，西经为负。

8.大地纬度：指参考椭球面上某点的垂直线（法线）与赤道平面的夹角。

北纬为正，南纬为负。

9.地图投影：在地球椭球面和平面之间建立点与点之间函数关系的数学方法。

10.地图比例尺：地图上一直线段长度与地面相应直线水平投影长度之比。

11.主比例尺：在投影面上没有变形的点或线上的比例尺。

12.局部比例尺：在投影面上有变形处的比例尺。

13地图概括（generalization）：也称制图综合，就是采取简单扼要的手法，把空间信息中主要的、本质的数据提取后联系在一起，形成新的概念14普通地图:是用相对平衡的详细程度来表示地球表面的地貌、水系、土质植被、居民点、交通网、境界线等自然地理要素和社会人文要素一般特征的地图。

15.专题地图:是把专题现象或普通地图的某些要素在地理底图上显示的特别完备和详细，而将其余要素列于次要地位，或不予表示，从而使内容专题化的地图。

16等高线:高程相等各点连接而成的闭合曲线。

17分层设色法：它是在等高线的基础上，根据地图的用途、比例尺和区域特征，将等高线划分一些层级，并在每一层级的面积内普染不同的颜色，以色相、色调的差异表示地势高低的方法二、填空题1.地图的构成要素有：图形要素、（数学要素）、辅助要素及（补充说明）。

七年级数学用坐标表示地理位置练习题

6.2.1 用坐标表示地理位置一、选择题:(每小题3分,共15分)1.从车站向东走400米,再向北走500米到小红家;从车站向北走500米,再向西走200米到小强家,则( )A.小强家在小红家的正东B.小强家在小红家的正西C.小强家在小红家的正南D.小强家在小红家的正北2.芳芳放学从校门向东走400米,再往北走200米到家;丽丽出校门向东走200 米到家,则丽丽家在芳芳家的( )A.东南方向B.西南方向;C.东北方向D.西北方向3.由坐标平面内的三点A(1,1),B(3,-1),C(1,-3)构成的△ABC是( )A.钝角三角形B.直角三角形;C.锐角三角形D.等腰直角三角形4.已知点A(3,4),B(3,1),C(4,1),则AB与AC的大小关系是( )A.AB>ACB.AB=AC;C.AB<ACD.无法判断5.已知点A(2,2),B(2,4),O(0,0),C(2,0),那么∠BOA与∠COA的大小关系是()A.∠BOA>∠COAB.∠BOA=∠COA;C.∠BOA<∠COAD.以上三种情况都有可能二、填空题:(每小题3分,共15分)1.从小丽家出发,向南走400米,再向西走200米到公园; 从小刚家出发, 向南走200米,再向西走100米也到公园,那么小丽家在小刚家的_______方向.2.由坐标平面内的三点A(-2,-1),B(-1,-4),C(5,-2)构成的三角形是_____三角形.3.明明家在电视塔西北300米处,亮亮家在电视塔西南300米处,则明明家在亮亮家的________方向.4.在比例尺为1:20000的地图上,相距3cm的A,B两地的实际距离是________.5.一只鸽子向东飞3千米,再向北飞4千米,此时这只鸽子离原地_______千米.三、基础训练:(共10分)李明放学后向北走200米,再向西走100米,又向北走100米,然后再向西走200 米到家;张彬放学后向西走300米,再向北走300米到家. 则李明和张彬两家的位置有什么关系?四、提高训练:(共15分)如图所示,写出A,B,C,D,E这五个点的坐标,这些点在位置上有什么关系?这些点的横坐标和纵坐标之间有什么关系?五、探索发现:(共15分)在1:n(n为正整数)的地图上,如果测得两地间的距离为m, 则两地的实际距离约为mn,如果测得该地图上某地区的面积为a,那么该地区的实际面积是an吗?如果不是,那么正确结果应该是多少?请举例说明.六、能力提高:(共15分)你能想像出从你家到学校路旁的情景吗? 请按一定的比例尺画一张反映从你家到学校路边情况的地图.七、中考题与竞赛题:(共15分)有一种动物,向北走500米,再向东走500米,又向南走500米, 这时它回到了出发点,你知道这是什么动物吗?它生活在什么地方?答案:一、1.B 2.B 3.D 4.C 5.C二、1.东北 2.直角 3.正北 4.600m 5.5三、邻居四、提示:这些点在一条直线上,y+2x=2.五、解:不是an,正确结果应该是an2,以三角形为例,图上底为b,高为h,图上面积为a=12bh;实际底为bn,高为hn,实际面积为12bhn2=an2.六、略.七、企鹅,南极点.。

七年级数学下册《用坐标表示地理位置》练习题及答案(人教版)

七年级数学下册《用坐标表示地理位置》练习题及答案(人教版)一、单选题1．如图，点A位于点O的（）A．南偏东25°方向上B．东偏南65°方向上C．南偏东65°方向上D．南偏东55°方向上2．2022年第19届亚运会将在浙江杭州举行，金华将作为亚运会的分会场．以下表示金华市地理位置最合理的是（）A．距离杭州市200公里B．在浙江省C．在杭州市的西南方D．东经119.65°，北纬29.08°3．下列能够确定位置的是（）A．甲地在乙地北偏东30°的方向上B．一只风筝飞到距A地20米处C．影院座位位于一楼二排D．某市位于北纬30°，东经120°4．根据下列表述，能够确定具体位置的是（）A．北偏东25°方向B．距学校800米处C．温州大剧院音乐厅8排D．东经20°北纬30°5．在军事演习中，利用雷达跟踪某一“敌方”目标，需要确定该目标的（）A．方向B．距离C．大小D．方向与距离6．如图是北京地铁部分线路图．若车公庄坐标为（﹣3，3），崇文门站坐标为（8，﹣2），则雍和宫站的坐标为（）A ．（8，6）B ．（6，8）C ．（﹣6，﹣8）D ．（﹣8，﹣6）7．气象台为了预报台风，首先要确定台风中心的位置，则下列说法能确定台风中心位置的是（）A ．北纬128︒，东经36︒B ．距电台500海里C ．西太平洋D ．在电台的西北方向8．如图，若“帅”的位置用(1，-1)表示，“馬”的位置用(4，-1)表示，则“兵”的位置可表示为( )A ．()1,2-B ．()1,2--C ．()3,2--D ．()3,2-9．象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图，是一局象棋残局，已知表示棋子“炮”和“車”的点的坐标分别为(1,2)，(2,0)-，则表示棋子“馬”的点的坐标为（）A ．(4,2)B ．(2,4)C ．(3,2)D ．(2, 1)10．如图，矩形BCDE 的各边分别平行于x 轴或y 轴，物体甲和物体乙由点A （2，0）同时出发，沿矩形BCDE 的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2017次相遇地点的坐标是（）A．（2，0）B．（﹣1，1）C．（﹣2，1）D．（﹣1，﹣1）二、填空题11．如图，水立方所在位置表示3街与3路的十字路口，玲珑塔所在位置表示4街与7路的十字路口．如果→→→→→”表示从水立方到玲珑塔的用(3,3)表示水立方的位置，那么“(3,3)(3,4)(3,5)(3,6)(3,7)(4,7)一种路线．请你用这种形式写出一种从水立方到玲珑塔的路线，且使该路线经过鸟巢：__________．12．课间操时，小华、小军、小刚的位置如图，小军对小华说，如果我的位置用（0，﹣2）表示，小刚的位置用（2，0）表示，那么你的位置可以表示为__________．13．如图所示的棋盘放置在某个平面直角坐标系内，棋子A的坐标为（﹣2，﹣3），棋子B的坐标为（1，﹣2），那么棋子C的坐标是_____．14．如图，这是一所学校的平面示意图．已知教学楼的位置坐标为（300，0）（小正方形的边长代表100m 长）．则校门的坐标为________；图书馆的坐标为___________；实验楼的坐标为___________．15．如图，每个小方格的边长均为1，若用(1，3)→(2，3)→(3，3)→(4，3)→(4，2)→(4，1)表示由A到B的路径，请你试写出一条由A到C的路径：________________________.三、解答题16．如图，这是某城市部分简图，若宾馆、市场的位置分别用坐标（2，2）、（4，3）表示，请建立适当的平面直角坐标系，再分别写出其他各地的坐标．17．小丽和爸爸、妈妈到人民公园游玩，回到家后，她利用平面直角坐标系画出了公园的景区地图，如图所示．可是她忘记了在图中标出原点和x轴、y轴；若游乐园D的坐标为（1，-2），你能帮她先画出平面直角坐标系，并写出其他各景点的坐标吗?18．如图，这是某市部分简图，已知医院的坐标为（1，﹣2），请建立平面直角坐标系，分别写出其余各地的坐标．19．请你在下图中建立适当的直角坐标系，并写出各地点的坐标．．20．下图是某公园局部的平面示意图(每个小方格的边长为100米)．以中心广场为原点，以向东为横轴的正方向，向北为纵轴的正方向建立平面直角坐标系．(1)分别写出湖心亭、南门和东门三个地点的坐标；(2)某星期天的上午，苗苗在公园沿(－500，0)→(－200，－100)→(200，－200)→(300，300)→(0，400)的路线游玩了半天，请你写出她在路上经过的景点名称．参考答案1．C2．D3．D4．D5．D6．A7．A8．A9．A10．B→→→→→→→11．答案不唯一，如：(3,3)(4,3)(5,3)(5,4)(5,5)(5,6)(5,7)(4,7)12．(-2，-3)13．(2,1)14．（-200，0）（200，300）；（200，-200）．15．(1，3)→(2，3)→(2，4)→(3，4)(本题是开放性问题，有多种答案)16．火车站（0，0），体育场（-4，3），文化宫（-3，1），医院（-2，-2），超市（2，-3）．17．音乐台A的坐标为（−1，4），湖心亭B的坐标为（−4，2），望春亭C的坐标为（−3，−1），牡丹园E的坐标为（2，3）．18．见解析体育场（﹣1，3 ）文化宫（0，1）火车站（3，0）宾馆（5，2）市场（7，3）超市（5，﹣3）．19．以映月湖为原点，水平方向为x轴，竖直方向为y轴，建立平面直角坐标系则映月湖（0，0）；景山（5，0）；游乐园（-2，3）；碑林（7，5）；大学城（3，7）．20．(1)湖心亭(－300，200)，南门(100，－300)，东门(500，0)(2)西门→望春亭→游乐园→牡丹园→音乐台。

地理学中的数学方法

地理学中的数学方法题型：（成绩=80％卷面+20％平时）名词解释4—5′/题共20′简答计算（2选1）综合分析题：数学方法的实际应用一、名词解释：常用的统计指标（标准差、方差、均值、中位数......）相关分析、回归分析、聚类分析、主成分分析、层次分析......二、简答：1、简述相关系数的种类2、地理数据一般水平（平均值、中位数、众数......）离散程度（极差、方差、标准差......）3、数据标准化的方法4、某数学方法的一般步骤三、计算题（2选1）给出一个案例，根据所学设计怎样解决实际问题，会用什么方法、可能得到什么结果。

四、综合题地理学中数学方法的应用一、名词解释1、标准差也称为均方差，是方差的平方根。

标准差是反映一组数据离散程度最常用的一种量化形式。

标准差越高，表示实验数据越离散，也就是说越不精确；反之，标准差越低，代表实验数据越精确方差是各个数据与平均数之差的平方的平均数。

主要用于度量随机变量和均值之间的偏离程度。

方差越大，说明数据波动越大。

中位数（Median）：即一组数据按升序排序后，处于中间位置上的数据值。

如评价社会的老龄化程度时，可用中位数。

众数（Mode）：即一组数据中出现次数最多的数据值。

如生产鞋的厂商在制定各种型号鞋的生产计划时应该运用众数。

2、相关分析从狭义的角度来看，相关分析以现象之间是否相关、相关的方向和密切程度为主要研究内容，它不区别自变量与因变量；不关心关系的表现形式。

从广义的角度来看，相关分析就是研究两个或两个以上变量之间相关方向和密切程度大小以及用一定函数关系来表达现象相互关系的方法。

3、回归分析是在相关分析的基础上，具体描述因变量对自变量的线性依赖关系的形式。

即寻找能够清楚表明变量间相关关系的数学表达式，并根据这个表达式进行估计预测。

4、聚类分析是统计学中研究“物以类聚”问题的多元统计分析方法。

聚类分析是根据地理变量的属性或特征，按照其亲疏程度或相似性，在没有先验知识的情况下，采用数学方法将它们自动分类，最后得到一个能反映个体或站点之间、群体之间亲疏关系的分类系统。

现代地理学中的数学方法 (1)

r12.3
2 13
r12 r13 r23
2 23
(1 r )(1 r ) r 13 r 12 r 23 (1 r )(1 r )
2 12 2 23
（4.1.5）
r 13.2
（4.1.6）
r23.1
r23 r12 r13 (1 r )(1 r )
2 12 2 13
又如:根据甘肃省53个气象台站的多年平均数据（见教材表4.1.2），可以利用公式（4.1.1）对降水量（p）和纬度（y）之间的相关系数以及蒸发量（v）和纬度（y）之间的相关系数进行计算，结果如下
( p p)( y y )
i 1 i i 53
rpy
( p p) ( y y )
rtp
(t
i 1 12 i 1
12
i
t )( pi p )
2 2 ( p p ) i i 1 12

(ti t )
300.91 250.55 1 508.34

300 .91 0.489 5 15.83 38 .84
(2)计算结果表明，伦敦市的月平均气温（ t ）与降水量 (p) 之间呈负相关，即异向相关。
利用公式计算一级偏向关系数，如表4.1.6所示：表4.1.6
r12· 3 0.821 r13· 2 0.808 r14· 2 0.647 r14ቤተ መጻሕፍቲ ባይዱ 3 0.895
一级偏相关系数
r23· 1 -0.863 r24· 1 0.956 r24· 3 0.945 r24· 1 r34· 2 -0.875 0.371
一、两要素之间的相关分析
相关系数的计算与检验

2019春人教版数学七年级下册图片版习题课件：第七章 7.2 7.2.1 用坐标表示地理位置

解：(1)如图所示； (2)如图，点 C 即为所求； 1 1 1 (3)S△ ABC＝3× 4－ 2 × 2× 1－2 × 1× 4－2 × 3× 3＝4.5.
10. (2018· 绵阳)如图，在中国象棋的残局上建立平面直角坐标系，如果“相”和“兵”的坐标分别是(3，－1)和(－3，1)，那么“卒”的坐标为 (－2，－2) ．
11. 根据下列条件画出符合题意的示意图，并标出学校、文具超市、科技馆、文化宫的位置．文具超市：出校门向东走 150 米，向北走 50 米；科技馆：出校门向西走 500 米，再向北走 400 米，最后向西走 25 米；文化宫：出校门向南走 200 米，再向东走 200 米，最后向南走 50 米．(请选择适当的比例尺)
A
)
B．(200，150) D．(－100，－300)
7. (2018· 北京 ) 如图是老北京城一些地点的分布示意图．在图中，分别以正东、正北方向为 x 轴、y 轴的正方向建立平面直角坐标系，有如下四个结论：
①当表示天安门的点的坐标为(0， 0)，表示广安门的点的坐标为(－6，－3)时，表示左安门的点的坐标为(5，－6)； ②当表示天安门的点的坐标为(0， 0)，表示广安门的点的坐标为(－12，－6)时，表示左安门的点的坐标为(10，－12)； ③当表示天安门的点的坐标为(1， 1)，表示广安门的点的坐标为(－11，－5)时，表示左安门的点的坐标为(11，－11)； ④当表示天安门的点的坐标为(1.5，1.5)，表示广安门的点的坐标为 ( － 16.5 ，－ 7.5) 时，表示左安门的点的坐标为 (16.5，－16.5)．
上述结论中，所有正确结论的序号是( A．①②③ C．①④ B．②③④ D．①②③④

人教版七年级数学下《用坐标表示地理位置》基础练习

《用坐标表示地理位置》基础练习一、选择题（本大题共5小题，共25.0分）1．（5分）小明乘坐一艘游船出海游玩，游船上的雷达扫描探测得到的结果如图所示，每相邻两个圆之间距离是1km（小圆半径是1km），若小艇C在游船的正南方2km，则下列关于小艇A、B的位置描述，正确的是（）A．小艇A在游船的北偏东60°，且距游船3kmB．游船在的小艇A北偏东60°，且距游船3kmC．小艇B在游船的北偏西30°，且距游船2kmD．小艇B在小艇C的北偏西30°，且距游船2km2．（5分）某班级第4组第5排位置可以用数对（4，5）表示，则数对（2，3）表示的位置是（）A．第3组第2排B．第3组第1排C．第2组第3排D．第2组第2排3．（5分）已知点M（3，﹣2），N（3，﹣1），则线段MN与x轴（）A．垂直B．平行C．相交D．不垂直4．（5分）雷达二维平面定位的主要原理是：测量目标的两个信息﹣距离和角度，目标的表示方法为（m，α），其中，m表示目标与探测器的距离；α表示以正东为始边，逆时针旋转后的角度．如图，雷达探测器显示在点A，B，C处有目标出现，其中，目标A的位置表示为A（5，30°），目标C的位置表示为C（3，300°）．用这种方法表示目标B的位置，正确的是（）A．（﹣4，150°）B．（4，150°）C．（﹣2，150°）D．（2，150°）5．（5分）剧院里5排2号可以用（5，2）表示，则（7，4）表示（）A．4排7号B．2排5号C．7排4号D．5排2号二、填空题（本大题共5小题，共25.0分）6．（5分）在电影票上如果将“8排4号”记作（8，4），那么（1，5）表示．7．（5分）已知点M的坐标为（a﹣2，2a﹣3），点N的坐标为（1，5），直线MN∥x轴，则点M的横坐标为．8．（5分）对有序数对（m，n）定义“f运算”：f（m，n）＝（m+a，n﹣b），其中a、b为常数．f运算的结果也是一个有序数对，在此基础上，可对平面直角坐标系中的任意一点A（x，y）规定“F变换”：点A（x，y）在F变换下的对应点即为坐标为f（x，y）的点A′（1）当a＝0，b＝0时，f（﹣2，4）＝；（2）若点P（4，﹣4）在F变换下的对应点是它本身，则a＝，b＝．9．（5分）已知点A（5，3），AB∥y轴，且AB＝4，则B点的坐标为．10．（5分）点A与点B的纵坐标相同，横坐标不同，则直线AB与y轴的位置关系．三、解答题（本大题共5小题，共50.0分）11．（10分）结合数轴与绝对值的知识回答下列问题：数轴上表示4和1的两点之间的距离是3：而|4﹣1|＝3；表示﹣3和2两点之间的距离是5：而|﹣3﹣2|＝5；表示﹣4和﹣7两点之间的距离是3，而|﹣4﹣（﹣7）|＝3．一般地，数轴上表示数m和数n的两点之间的距离公式为|m﹣n|．（1）数轴上表示数﹣5的点与表示﹣2的点之间的距离为；（2）数轴上表示数a的点与表示﹣4的点之间的距离表示为；若数轴上a位于﹣4与2之间，求|a+4|+|a﹣2|的值；（3）如果表示数a和3的两点之间的距离是7，则可记为：|a﹣3|＝7，求a的值．12．（10分）已知，a，b满足|4a﹣b|+（a﹣4）2≤0．分别对应着数轴上的A，B 两点．（1）a＝，b＝，并在数轴上面出A、B两点；（2）若点P从点A出发，以每秒3个单位长度向x轴正半轴运动，求运动时间为多少时，点P到点A的距离是点P到点B距离的2倍；（3）数轴上还有一点C的坐标为30，若点P和点Q同时从点A和点B出发，分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动，P点到达C点后，再立刻以同样的速度返回，运动到终点A．求点P和点Q运动多少秒时，P、Q两点之间的距离为4，并求此时点Q对应的数．13．（10分）如图，三架飞机P、Q、R保持编队飞行，30秒后飞机P飞到P1的位置，飞机Q、R飞到了新位置Q1、R1．在直角坐标系中标出Q1、R1，并写出坐标．14．（10分）已知点A（﹣4，a），点B（3，a），那么过点A，B的直线与坐标轴有怎样的位置关系？15．（10分）如图，箭头图案是将坐标分别为（0，0），（0，2），（5，2），（5，3），（7，1），（5，﹣1），（5，0），（0，0）的点用线段依次连接而成的，现把图中的格点分别如下变换：（1）横坐标不变，纵坐标分别减3；（2）纵坐标不变，横坐标分别加2以上变换所得的图案与原图案相比有哪些变化？《用坐标表示地理位置》基础练习参考答案与试题解析一、选择题（本大题共5小题，共25.0分）1．（5分）小明乘坐一艘游船出海游玩，游船上的雷达扫描探测得到的结果如图所示，每相邻两个圆之间距离是1km（小圆半径是1km），若小艇C在游船的正南方2km，则下列关于小艇A、B的位置描述，正确的是（）A．小艇A在游船的北偏东60°，且距游船3kmB．游船在的小艇A北偏东60°，且距游船3kmC．小艇B在游船的北偏西30°，且距游船2kmD．小艇B在小艇C的北偏西30°，且距游船2km【分析】利用方向角的表示方法对各选项进行判断．【解答】解：小艇A在游船的北偏东30°，且距游船3km；小艇B在游船的北偏西60°，且距游船2km；游船在小艇的南偏西30°，且距游船3km；小艇B在小艇C的北偏西30°，且距游船2km．故选：D．【点评】本题考查了坐标确定位置：是熟练掌握平面内特殊位置的点的坐标特征．理解方向角的表示方法．2．（5分）某班级第4组第5排位置可以用数对（4，5）表示，则数对（2，3）表示的位置是（）A．第3组第2排B．第3组第1排C．第2组第3排D．第2组第2排【分析】依据有序数对可知，第一个数表示组数，第二个数表示排数，进而得到结果．【解答】解：某班级第4组第5排位置可以用数对（4，5）表示，则数对（2，3）表示的位置是第2组第3排，故选：C．【点评】本题主要考查了坐标确定位置，解决问题的关键是掌握坐标的概念．3．（5分）已知点M（3，﹣2），N（3，﹣1），则线段MN与x轴（）A．垂直B．平行C．相交D．不垂直【分析】根据横坐标相同即可判断；【解答】解：∵M（3，﹣2），N（3，﹣1），∴横坐标相同，∴MN⊥x轴，故选：A．【点评】本题考查坐标与图形性质，具体的是关键是熟练掌握基本知识，属于中考基础题．4．（5分）雷达二维平面定位的主要原理是：测量目标的两个信息﹣距离和角度，目标的表示方法为（m，α），其中，m表示目标与探测器的距离；α表示以正东为始边，逆时针旋转后的角度．如图，雷达探测器显示在点A，B，C处有目标出现，其中，目标A的位置表示为A（5，30°），目标C的位置表示为C（3，300°）．用这种方法表示目标B的位置，正确的是（）A．（﹣4，150°）B．（4，150°）C．（﹣2，150°）D．（2，150°）【分析】根据点A、C的位置结合其表示方法，可得出相邻同心圆的半径差为1，结合点B在第四个圆上且在150°射线上，即可表示出点B．【解答】解：∵A（5，30°），C（3，300°），∴B（4，150°）．故选：B．【点评】本题考查了坐标确定位置，根据点A、C的坐标找出点B的坐标是解题的关键．5．（5分）剧院里5排2号可以用（5，2）表示，则（7，4）表示（）A．4排7号B．2排5号C．7排4号D．5排2号【分析】第一个数表示排，第二个数表示号，将位置问题转化为有序数对．【解答】解：∵5排2号可以表示为（5，2），∴（7，4）表示7排4号．故选：C．【点评】此题主要考查了坐标确定位置，正确理解用有序数对表示位置是解题关键．二、填空题（本大题共5小题，共25.0分）6．（5分）在电影票上如果将“8排4号”记作（8，4），那么（1，5）表示1排5号．【分析】由于将“8排4号”记作（8，4），根据这个规定即可确定（1，5）表示的点．【解答】解：∵“8排4号”记作（8，4），∴（1，5）表示1排5号．故答案为：1排5号．【点评】此题主要考查了根据坐标确定点的位置，解题的关键是理解题目的规定，知道坐标与位置的对应关系．7．（5分）已知点M的坐标为（a﹣2，2a﹣3），点N的坐标为（1，5），直线MN∥x轴，则点M的横坐标为2．【分析】根据平行于x轴的直线上任意两点的纵坐标相同列出方程求出a的值，然后即可得解．【解答】解：∵直线MN∥x轴，点M的坐标为（a﹣2，2a﹣3），点N的坐标为（1，5），∴2a﹣3＝5，解得a＝4，a﹣2＝4﹣2＝2，所以，点M的横坐标为2．故答案为2．【点评】本题考查了坐标与图形性质，掌握平行于x轴的直线的上的点的坐标特征是解题的关键．8．（5分）对有序数对（m，n）定义“f运算”：f（m，n）＝（m+a，n﹣b），其中a、b为常数．f运算的结果也是一个有序数对，在此基础上，可对平面直角坐标系中的任意一点A（x，y）规定“F变换”：点A（x，y）在F变换下的对应点即为坐标为f（x，y）的点A′（1）当a＝0，b＝0时，f（﹣2，4）＝（﹣1，2）；（2）若点P（4，﹣4）在F变换下的对应点是它本身，则a＝2，b＝﹣2．【分析】（1）根据新定义运算法则解得；（2）根据新定义运算法则得到关于a、b的方程，通过解方程求得它们的值即可．【解答】解：（1）依题意得：f（﹣2，4）＝（×（﹣2）+0，×4﹣0）＝（﹣1，2）．故答案是：（﹣1，2）；（2）依题意得：f（4，﹣4）＝（×4+a，×（﹣4）+b）＝（4，﹣4）．所以×4+a＝4，×（﹣4）﹣b＝﹣4所以a＝2，b＝2．故答案是：2；2．【点评】考查了坐标与图形性质．关键是掌握对有序数对（m，n）定义“f运算”法则．9．（5分）已知点A（5，3），AB∥y轴，且AB＝4，则B点的坐标为（5，7）或（5，﹣1）．【分析】画出图形即可解决问题；【解答】解：如图，∵A（5，3），AB∥y轴，AB＝4，∴B（5，7）或B′（5，﹣1），故答案为（5，7）或（5，﹣1）【点评】本题考查坐标与图形性质，解题的关键是熟练掌握基本知识，理解题意，属于中考基础题．10．（5分）点A与点B的纵坐标相同，横坐标不同，则直线AB与y轴的位置关系垂直．【分析】由点A与点B的纵坐标相同，横坐标不同，可知直线AB与y轴的关系．【解答】解：∵点A与点B的纵坐标相同，横坐标不同，∴直线AB与y轴垂直．即直线AB与y轴的关系是垂直．故答案为：垂直【点评】本题考查坐标与图形的性质，解题的关键是明确与y轴垂直的直线上所有的点的纵坐标相等，横坐标不同．三、解答题（本大题共5小题，共50.0分）11．（10分）结合数轴与绝对值的知识回答下列问题：数轴上表示4和1的两点之间的距离是3：而|4﹣1|＝3；表示﹣3和2两点之间的距离是5：而|﹣3﹣2|＝5；表示﹣4和﹣7两点之间的距离是3，而|﹣4﹣（﹣7）|＝3．一般地，数轴上表示数m和数n的两点之间的距离公式为|m﹣n|．（1）数轴上表示数﹣5的点与表示﹣2的点之间的距离为3；（2）数轴上表示数a的点与表示﹣4的点之间的距离表示为|a+4|；若数轴上a位于﹣4与2之间，求|a+4|+|a﹣2|的值；（3）如果表示数a和3的两点之间的距离是7，则可记为：|a﹣3|＝7，求a的值．【分析】（1）根据两点间的距离公式，可得答案；（2）根据两点间的距离公式，可得答案；（3）根据绝对值的意义即可得到结论．【解答】解：（1）数轴上表示数﹣5的点与表示﹣2的点之间的距离为|﹣2﹣（﹣5）|＝3，故答案为：3；（2）数轴上表示数a的点与表示﹣4的点之间的距离表示为|a+4|，∵a位于﹣4与2之间，∴﹣4＜a＜2，∴|a+4|+|a﹣2|＝﹣a﹣4+2﹣a＝﹣2，故答案为：|a+4|；（3）∵|a﹣3|＝7，∴a﹣3＝±7，∴a＝10或﹣4．【点评】本题考查了绝对值，利用了两点间的距离公式，读懂题目信息，理解数轴上两个数之间的距离的表示方法是解题的关键．12．（10分）已知，a，b满足|4a﹣b|+（a﹣4）2≤0．分别对应着数轴上的A，B 两点．（1）a＝4，b＝16，并在数轴上面出A、B两点；（2）若点P从点A出发，以每秒3个单位长度向x轴正半轴运动，求运动时间为多少时，点P到点A的距离是点P到点B距离的2倍；（3）数轴上还有一点C的坐标为30，若点P和点Q同时从点A和点B出发，分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动，P点到达C点后，再立刻以同样的速度返回，运动到终点A．求点P和点Q运动多少秒时，P、Q两点之间的距离为4，并求此时点Q对应的数．【分析】（1）求出a、b的值即可解决问题；（2）构建方程即可解决问题；（3）分四种情形构建方程即可解决问题；【解答】解：（1）∵多项式2x3y﹣xy+16的次数为a，常数项为b，∴a＝4，b＝16，故答案为4，16．点A、B的位置如图所示．（2）设运动时间为ts．由题意：3t＝2（16﹣4﹣3t）或3t＝2（4+3t﹣16），解得t＝或8，∴运动时间为或8秒时，点P到点A的距离是点P到点B的距离的2倍；（3）设运动时间为ts．由题意：12+t﹣3t＝4或3t﹣（12+t）＝4或12+t+4+3t＝52或12+t+3t﹣4＝52，解得t＝4或8或9或11，∴点P和点Q运动4或8或9或11秒时，P，Q两点之间的距离为4．此时点Q表示的数为20，24，25，27．【点评】本题考查多项式、数轴、行程问题的应用等知识，具体的关键是学会构建方程解决问题，学会用分类讨论的思想思考问题．13．（10分）如图，三架飞机P、Q、R保持编队飞行，30秒后飞机P飞到P1的位置，飞机Q、R飞到了新位置Q1、R1．在直角坐标系中标出Q1、R1，并写出坐标．【分析】根据平移的性质以及平面直角坐标系的相关概念即可求出答案．【解答】解：由题意可知：P的坐标（﹣1，1），Q（﹣3，1），R（﹣1，﹣1）经过30秒后P1的坐标为（4，3），∴Q1的坐标（2，3），R1的坐标为（4，1）【点评】本题考查平面坐标系的概念，解题的关键是熟练运用平移的性质，本题属于基础题型．14．（10分）已知点A（﹣4，a），点B（3，a），那么过点A，B的直线与坐标轴有怎样的位置关系？【分析】根据点A（﹣4，a），点B（3，a）的纵坐标相等即可得到结论．【解答】解：∵A（﹣4，a），点B（3，a），∴过点A，B的直线平行于x轴，垂直于y轴．【点评】本题考查了坐标与图形的性质，知道平行x轴的点的特征是解题的关键．15．（10分）如图，箭头图案是将坐标分别为（0，0），（0，2），（5，2），（5，3），（7，1），（5，﹣1），（5，0），（0，0）的点用线段依次连接而成的，现把图中的格点分别如下变换：（1）横坐标不变，纵坐标分别减3；（2）纵坐标不变，横坐标分别加2以上变换所得的图案与原图案相比有哪些变化？【分析】根据平移是横坐标（纵坐标）加上（减去）相同数进行解答即可．【解答】解：因为横坐标不变，纵坐标分别减3，纵坐标不变，横坐标分别加2，属于平移，（1）横坐标不变，纵坐标分别减3，经过下列变化得到的图案，与原图案相比，形状和大小都不变，只是位置向下平移3个单位．（2）纵坐标不变，横坐标分别加2，经过下列变化得到的图案，与原图案相比，形状和大小都不变，只是位置向右平移2个单位．【点评】本题要通过题目中图形变换，使变化后得到的图案与原图案相比，形状和大小都不变，判断各选项是否属于平移问题．。

北半球的地理纬度等于该地观测北极星仰角度数的数学方法证明

北半球的地理纬度等于该地观测北极星仰角度数的数学方法证明
我们经常用北半球的地理纬度等于该地观测北极星仰角度数这一结论来解题，证明这一结论，用数学方法简洁明了。

绘图如下：
(1)设A为北半球任意一点(南半球看不到北极星)，N为北极点，那么OC为赤道平面。

北极星在ON的延长线上，OB⊥OC∴α+β=90°
(2)过A做球面切线，并与ON延长线相交于B，即AB⊥AO，θ+β=90°。

因为北极星距离地球无限远，从北极星分别射向N、A的光线平行，那么γ角即是看北极星的仰角。

α为A地的地理纬度。

因为γ=θ(内错角)，而θ+β=90°，所以γ+β=90°可得γ=α，即某地的地理纬度等于当地观测北极星仰角的度数。

XXX计量地理学课后习题

XXX计量地理学课后习题计量地理学期末第二章1.地理数据有哪几种类型，各种类型地理数据之间的区别和联系是什么？答：地理数据就是用一定的测度方式描述和衡量地理对象的有关量化指标。

按类型可分为：1）空间数据：点数据，线数据，面数据；2）属性数据：数量标志数据，品质标志数据地理数据之间的区别与联系：数据包括空间数据和属性数据，空间数据的表达可以采用栅格和矢量两种形式。

空间数据表现了地理空间实体的位置、大小、形状、方向以及几何拓扑关系。

属性数据表现了空间实体的空间属性以外的其他属性特征，属性数据主要是对空间数据的说明。

如一个城市点,它的属性数据有人口，GDP，绿化率等等描述指标。

它们有密切的关系，两者互相结合才能将一个地理试题表达清楚。

2.各种类型的地理数据的测度方法分别是什么？地理数据主要包括空间数据和属性数据：空间数据——对于空间数据的表达。

可以将其归纳为点、线、面三种几何实体以及描述它们之间空间联系的拓扑关系；属性数据——对于属性数据的表达，需求从数量标志数据和品质标志数据两方面举行描述。

其测度方法主要有：1)数量标志数据①间隔尺度（IntervalScale）数据:以有量纲的数据形式表示测度对象在某种单位（量纲）下的绝对量。

②比例尺度（Scale）数据:以无量纲的数据形式表示测度对象的相对量。

这种数据要求事先规定一个基点，然后将其它同类数据与基点数据相比较，换算为基点数据的比例。

2)品质标志数据①有序（Ordinal）数据。

当测度标准不是连续的量，而是只表示其顺序关系的数据,这种数据并不表示量的多少，而只是给出一个等级或次序。

②二元数据。

即用、1两个数据表示天文事物、天文现象或天文变乱的是非判断问题。

③名义标准（NominalScale）数据。

即用数字表示天文实体、天文要素、天文现象或天文变乱的状态类型。

3.地理数据的基本特征有哪些？1)数量化、形式化与逻辑化2 )不确定性3 )多种时空尺度4 )多维性1)来自于观测、测量部门的有关专业数据。

数学方法在地理教学中的应用

数学方法在地理教学中的应用地理是一门综合学科，渗透着自然科学思想方法和人文科学思想方法，在教学中如能充分利用其他学科的思想方法来解决或思考地理问题，将起到事半功倍的作用。

数学是自然科学的基础，它的思想方法渗透在各学科中，因此在地理教学中充分应用数学思想方法来指导学生学习可以做到老师教得轻松，学生学得愉快。

一、利用数学图解法突破教、学难点。

1、数轴法：应用数轴表示地球经度分布和时区分布，使复杂的空间思维简单化，这也是许多地理教师经常使用的方法。

如图1，数轴中点为0º，往东为东经度，往西为西经度，学生在解题时应先找出0º经线，再作其他经线排列，学生对此容易理解和掌握。

但在实际解题中，还有很多学生茫然不知所措，学生常常在180º附近的经度分布上出现错误判断。

因此我们在用数轴表示经度分布时应补充图2，数轴中点为，往东为西经度，往西为东经度，这一表示相对图1，属于逆向思维，是很多学生对180º经线东、西经分布易错之处。

将图1与图2结合起来，指导学生在解题时遇到低数字经度区就用图1解，遇到高数字经度区就用图2解。

图1180°90°W 0°90E°180°图20°90°E 180°90W°0°2、几何法：几何图形是空间思维的重要表示方法。

地理学科空间概念强，经常用平面几何来表示空间地理事物，如地球日照图、经纬网图等，因此在地理教学中，应用学生已有的几何知识求算或证明地理事物规律，既利于加深学生对知识的理解，也利于突破教学难点，起到事半功倍的作用。

如图3，为了让学生真正理解和掌握正午太阳高度角的变化规律，可借用几何方法引导学生求证（证明：正午太阳高度角 H= 90º-β，β表示所求点纬度与太阳直射点纬度差。

）平面几何在地理教学中应用很多，许多地理事物关系也可以通过几何图形形象直观地表示出来，如正午太阳高度由直射点向两侧对称递减，经常被学生忽略为向单侧递减，用图六表示（解：A为太阳，B为太阳直射点，H、Hˊ、H″太阳光线与地面的夹角即太阳高度角，由图可知，BC=BD>BE，则H>Hˊ=H″），不仅形象直观，而且这一对称变化记忆牢固。

用数学方法解决地理问题

十二种情况下用数学方法解决地理问题河北裴永刚同学们，地理学是一门综合性很强的学科，这个学科里面囊括了很多知识。

其中，很多地理知识都可以用数学方法来解决，今天我总结了初中地理学中涉及到的需要用数学方法解决的十二种情况。

希望同学们看了以后，会对你学习地理有所帮助。

1、比例尺部分的数学计算比例尺是我们初学地理接触到的内容，它表示的是地表各种地理事物缩小的程度，是地图的三要素之一，它等于图上距离与实地距离的比。

因此，比例尺是一个比值。

我们可以根据比例尺的基本公式，计算出比例尺。

也可以把比例尺公式变形从而求出图上距离和实地距离。

比例尺的原公式为：比例尺＝图上距离／实地距离，由这个基本公式可以变形出另外两个公式：图上距离＝实地距离×比例尺、实地距离＝图上距离／比例尺。

这里的计算是我们初学地理学接触到涉及数学计算的部分，比较简单，不过我们要注意单位的统一换算问题。

因为图上距离一般以“厘米”作单位，实际距离一般以“千米”作单位。

例如：（2013甘肃兰州）在比例尺为1:650000的地图上，量得兰州到白银的直线距离约为9.7厘米，则二者之间的实际直线距离大约是（）A、630千米B、630米C、63千米D、149千米实地距离＝图上距离／比例尺＝9.7÷1／650000＝6305000厘米＝63.05千米，由计算可知，答案应该为C。

2、关于经线圈中的数学计算问题关于经线纬线也是同学们初学地理遇到的问题，其中有一个问题就是关于相对的经线也就是经线圈的问题。

任何相对的两条经线都能构成一个经线圈，任何一个经线圈都能把地球分成两个相等的半球。

那么，构成经线圈的两条经线具备什么样的条件呢？因为构成经线圈的两条经线的性质是：在同一平面内，并且关于地轴对称。

所以，构成经线圈的两条经线必须具备以下两点：①经度之和为180°；②两条经线必须东西相对。

知道了经线圈所必须具备的这两点，我们就可以轻松地在已知其中一条经线情况下，找出与其相对的另一条经线。

高中地理基本不等式练习题(含答案)

高中地理基本不等式练习题(含答案)1. 以下哪个城市的平均年降水量最大？A. 北京B. 上海C. 广州D. 成都答案: C. 广州2. 下列哪个海洋的水温最高？A. 北冰洋B. 大西洋C. 太平洋D. 印度洋答案: D. 印度洋3. 在高纬度地区，以下哪个现象最可能发生？A. 首都人口多B. 气候寒冷C. 地形多样D. 降水量大答案: B. 气候寒冷4. 下列哪个国家是热带雨林气候带的代表？A. 英国B. 加拿大C. 巴西D. 俄罗斯答案: C. 巴西5. 在地理上，哪个方向是北半球的正北方向？A. 正西方向B. 正东方向C. 正南方向D. 正北方向答案: D. 正北方向6. 以下地形中，最容易形成丘陵的是？A. 平原地形B. 山地地形C. 高原地形D. 盆地地形答案: A. 平原地形7. 下列哪个气候带的地区最适宜农业?A. 热带气候带B. 寒温带C. 西风带D. 亚热带气候带答案: A. 热带气候带8. 以下哪个因素不会影响海洋的盐度？A. 降水量B. 蒸发C. 河流输入D. 海底火山喷发答案: D. 海底火山喷发9. 以下地质灾害中，属于由人类活动导致的是？A. 地震B. 泥石流C. 洪水D. 火山爆发答案: B. 泥石流10. 人口最密集的洲是？A. 亚洲B. 欧洲C. 非洲D. 北美洲答案: A. 亚洲。

地理数学方法上机实习2_

地理数学方法上机实习2（方差分析部分）上机实习目的：1. 掌握方差分析的前提条件及其检验方法2. 掌握单因素方差分析过程3. 掌握双因素方差分析过程4. 了解多因素方差分析上机练习数据1 为研究某地理要素在A,B,C,D四类地区是否相同，每地区随机采集了30个样本，样本观测值如exercise4所示。

问：该地理要素在这四个地区是否相同？如果不完全相同，进一步分析其差异性。

2 为研究某地理要素的分布是否具有垂直地带性规律，在其分布的海报高程内（400-2500m），按照等间隔采样的方法随机选择了12个高程，每高程下沿经度方向随机采集了10个样本，数据如exercise 5所示。

问：该地理要素的分布是否具有垂直地带性规律？3 某地理要素可能受到因素A,B的影响，现设计一控制试验，因素A有3个处理，因素B有4个处理，每处理下均采集了10个样本，数据如exercise 6所示。

问：因素A和B是否影响该地理要素？4 采用5种生长素处理豌豆，未处理为对照，待种子发芽后，分别每盆中移植4株，每组为6盆，每盆一个处理，试验共有4组24盆，并按组排于温室中，使同组各盆的环境条件一致。

当各盆见第一朵花时记录4株豌豆的总节间数，数据如exercise7所示，问：生长素是否影响豌豆的生长？一、方差分析的前提条件及其检验1.正态性正态性的非参数检验方法有两种：一是针对小样本的Shapiro-Wilk检验，二是针对大样本的K-S检验。

2. 独立性独立性的非参数检验方法为游程检验（Runs）。

3. 方差的同质性方差同质性的参数检验方法为Levene 检验。

二、单因素方差分析（exercise 4 and exercise 5）1. 前提条件的检验正态性检验、方差齐性、独立性检验（通常不检验独立性）Shapiro-Wilk检验结果表明：在0.05水平上，四个处理均服从正态分布。

F检验（Levene检验）结果表明：在0.05水平上，四个处理满足方差齐性。

人教版七年级下册数学用坐标表示地理位置同步练习题(含答案)

人教版七年级下册数学用坐标表示地理位置同步练习题学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，有一抛物线形拱桥，当拱顶离水面2m时，水面宽4m，当水面宽增加()4m 时，则水面应下降的高度是（）A．2m B．1m C D．)2m 2．如图是雷达屏幕在一次探测中发现的多个目标，其中对目标A的位置表述正确的是（）A．在南偏东75º方向处B．在5km处C．在南偏东15º方向5km处D．在南偏东75º方向5km处3．如图是被墨迹污染的旅游区各景点地图，隐约可见，第一景点的坐标为(0，3)，第二景点的坐标为(5，3)，景区车站坐标为(0，0)，则车站大约在（）A ．点AB ．点BC ．点CD ．点D4．下列图形中，表示南偏西60︒的射线是（）．A ．B ．C ．D ．5．如图，若炮的位置是()47，，那么卒的位置可以记作（）A ．(43)，B ．()15，C ．()34，D ．(33)，6．下列语句正确的是（）．A ．在平面直角坐标系中，(3,5)-与(5,3)-表示两个不同的点B ．平行于x 轴的直线上所有点的横坐标都相同C ．若点(,)P a b 在y 轴上，则0b =P 到x轴的距离为3D．点(3,4)7．如图所示，在平面直角坐标系中，将点A（-1，0）做如下的连续平移，A（-1，0）→A1（-1，1）→A2（2，1）→A3（2，-4）→A4（-5，-4）→A5（-5，5）…，按此规律平移下去，则A102的点坐标是（）A．(100,101)B．(101,100)C．(102,101)D．(103,102)二、填空题8．如图的方格图是某学校平面示意图，若建立适当的平面直角坐标系，花坛的位置可用坐标（3，0）表示，则教学楼的位置用坐标表示为______．9．如图，若在象棋棋盘上建立平面直角坐标系，使“兵”位于点（1，1），“炮”位于点（﹣1，2），则“马”位于点_________．10．如图，已知棋子“车”的位置表示为（﹣2，3），棋子“马”的位置表示为（1，3），则棋子“炮”的位置可表示为________．11．如图，利用平面直角坐标系画出的正方形网格中，若(12)A ，，(21)B ，，则点C 的坐标为________．12．如图，四个白色全等直角三角形与四个黑色全等三角形按如所示方式摆放成“风车”型，且黑色三角形的顶点E 、F 、G 、H 分别在白色直角三角形的斜边上，已知∠ABO ＝90°，OB ＝3，AB ＝4，若点A 、E 、D 在同一直线上，则OE 的长为______．13．对于平面直角坐标系xOy 中的点P （a ，b ），若点P 的坐标为（a +kb ，ka +b ）（其中k 为常数，且k ≠0），则称点P 为点P 的“k 属派生点”，例如：P （1，4）的“2属派生点”为P （1+2×4，2×1+4），即P ′（9，6）．若点P 在x 轴的正半轴上，点P 的“k 属派生点”为点P ′，且线段PP ′的长度为线段OP 长度的5倍，则k 的值为___．三、解答题14．在雷达探测区域，可以建立平面直角坐标系表示位置．在某次行动中，当我方两架飞机在A （-1，2）与B （3，2）位置时，可疑飞机在（-1，-3）位置，你能找到这个直角坐标系的横、纵坐标的位置吗？把它们表示出来并确定可疑飞机的位置，说说你的做法．15．如图，是一个简单的平面示意图，已知OA ＝2km ，OB ＝6km ，OC ＝BD ＝4km ，点E 为OC 的中点，回答下列问题：(1)由图可知，高铁站在小明家南偏西65°方向6km 处．请类似这种方法用方向与距离描述学校、博物馆相对于小明家的位置；(2)图中到小明家距离相同的是哪些地方？(3)若小强家在小明家北偏西60°方向2km 处，请在图中标出小强家的位置．16．下图是一零一校园内一些地点的分布示意图，在图中，分别以正东、正北方向为x 轴、y 轴的正方向建立平面直角坐标系．当表示礼堂的点的坐标为()2,0，表示第三教学楼的点的坐标为()3,2-时，图中画出平面直角坐标系，并写出田径场、图书馆和第一教学楼的坐标．参考答案：1．B【分析】以拱形桥顶为坐标原点，建立如图直角坐标系xOy ，水面宽为AB 与y 轴交于E ，水面下降后宽度为CD 与y 轴交于F ，由OE =2m ，AB =4m ，抛物线的对称轴为y 轴，可求点B （2，-2）利用待定系数法可求抛物线解析式为212y x =-，设水面下降nm ，可求D n -2-），由点D 在抛物线上，代入解析式212n =--2-解方程即可．【详解】解：以拱形桥顶为坐标原点，建立如图直角坐标系xOy ，水面宽为AB ，与y 轴交于E ，水面下降后宽度为CD ，与y 轴交于F ，∠OE =2m ，AB =4m ，抛物线的对称轴为y 轴，∠点B （2，-2）设抛物线为y =ax 2，∠抛物线过点B ，∠-2=4a ， ∠12a =-， ∠抛物线解析式为212y x =-，设水面下降nm ，∠CD =AB +()()4=4+4=∠D n -2-），∠点D 在抛物线上，∠212n =--2-，解得n =1．故选择B ．【点睛】本题考查建立平面直角坐标系，待定系数法求抛物线解析式，利用抛物线上点坐标与解析式关系求解是关键．2．D【分析】根据方向角的定义解答即可．【详解】观察图形可得，目标A在南偏东75°方向5km处，故选D．【点睛】本题考查了方向角的定义，正确理解方向角的意义是解题关键．3．B【分析】根据已知的坐标，建立平面直角坐标系即可解答．【详解】根据已知的坐标，可建立平面直角坐标系，如图，由此可得到坐标原点是B点，故选：B．【点睛】本题考查了平面直角坐标系的内容，熟练掌握点的坐标特点是解题的关键．4．D【分析】根据方位角的概念，由南向西旋转60度即可．【详解】根据方位角的概念，结合题意要求和选项，由南向西旋转60度，故选D．【点睛】考查了方向角，用方向角描述方向时，通常以正北或正南方向为角的始边，以对象所处的射线为终边，故描述方向角时，一般先叙述北或南，再叙述偏东或偏西．（注意几个方向的角平分线按日常习惯，即东北，东南，西北，西南）．5．B【分析】根据炮的位置所代表的点的横纵坐标，与卒的位置所代表的点的横纵坐标之间的数量关系确定卒的位置即可．【详解】解：∠炮的位置（4，7），观察图可知，炮的横坐标比卒大3，纵坐标比卒大2，∠卒的横坐标为：431-=，卒的纵坐标为：725-=，∠卒的位置应该表示为：（1，5），故选：B ．【点睛】此题主要考查了坐标确定位置，正确找出两点间的坐标位置关系是解题关键． 6．A【分析】根据平行与坐标轴的直线上点的坐标特点、坐标的概念、坐标轴上点的坐标特点及点到坐标轴的距离等知识点逐一判断即可得.【详解】A.在平面直角坐标系中， (−3，5) 与 (5，−3) 表示两个不同的点，此选项正确，符合题意；B.平行于 x 轴的直线上所有点的纵坐标都相同，此选项错误，不符合题意；C.若点 P (a ，b ) 在 y 轴上，则a =0 ，此选项错误，不符合题意；D.点 P (−3，4) 到 x 轴的距离为4，此选项错误，不符合题意；故选：A.【点睛】本题主要考查坐标与图形的性质，解题的关键是掌握平行与坐标轴的直线上点的坐标特点、坐标的概念、坐标轴上点的坐标特点及点到坐标轴的距离等知识点.7．C【分析】根据题意可知，点A 平移时每4次为一个周期，由102÷4=25•••2，可知点A 102的坐标与A 4n +2的点的坐标规律相同，分别求出A 2，A 6，A 10的坐标，找出规律，进而求解即可．【详解】解：由题意可知，将点A （-1，0）向上平移1个单位长度得到A 1（-1，1），再向右平移3个单位长度得到A 2（2，1），再向下平移5个单位长度得到A 3（2，-4），再向左平移7个单位长度得到A 4（-5，-4）；再向上平移9个单位长度得到A 5（-5，5）…， ∠点A 平移时每4次为一个周期．∠102÷4=25•••2，∠点A102的坐标与A4n+2的点的坐标规律相同．∠A2（2，1），A6（6，5），A10（10，9），以此类推，∠A4n+2（4n+2，4n+1），∠A102的点坐标是（102，101）．故选：C．【点睛】本题考查了规律型：点的坐标．分析题意得出点A平移时每4次为一个周期，进而得到点A102的坐标与A4n+2的点的坐标规律相同是解题的关键．8．（2，1）．【分析】根据已知点的坐标即可建立恰当的平面直角坐标系，进一步求得要求点的坐标．【详解】解：如图所示建立平面直角坐标系，则教学楼的位置是（2，1）．故答案为：（2，1）．【点睛】此题考查了平面内点的位置的确定，能够根据已知点确定平面直角坐标系．9．（4，﹣1）【分析】直接利用已知点坐标得出原点位置，再建立平面直角坐标系得出答案．【详解】解：如图所示：“马”位于点（4，﹣1）．故答案为：（4，﹣1）．【点睛】此题主要考查了坐标确定位置，正确建立平面直角坐标系是解题关键． 10．（3，2）【分析】根据“车”的位置，向下3个单位，再向左2个单位，可得坐标原点，根据“炮”在平面直角坐标系中的位置，可得答案．【详解】解：由题意可建立如图所示坐标系：则棋子“炮”的位置应记为（3，2），故答案是：（3，2）．【点睛】本题考查了坐标确定位置，利用“车”的位置建立平面直角坐标系是解题关键． 11．()3,1-【分析】根据A 、B 两点坐标找到原点坐标即可解答；【详解】解：由(12)A ，，(21)B ，，可得平面直角坐标系如下图：∠C 点坐标（3，-1），【点睛】本题考查了平面直角坐标系，掌握坐标的定义是解题关键．12．4537##8137【分析】建立平面直角坐标系，得出点A 、B 、C 、D 的坐标，利用待定系数法分别求出直线AD ，直线OC 的解析式，联立解方程组可得点E 的坐标，即可求解．【详解】解：建立平面直角坐标系如图：∠∠ABO =90°，OB =3，AB =4，△ABO ∠∠CDO ，∠OD =OB =3，CD =AB =4，∠点A (-4，-3) ，B (0，-3) ，C (3，-4) ，D (3，0)，设直线AD 的解析式为y =kx +b ，∠4330k b k b -+=-⎧⎨+=⎩，解得3797k b ⎧=⎪⎪⎨⎪=-⎪⎩， ∠直线AD 的解析式为3977y x =-，设直线OC 的解析式为y =mx ，把C(3，-4)代入，∠3m=-4，解得m=-43，∠直线OC的解析式为y=-43 x，联立397743y xy x⎧=-⎪⎪⎨⎪=-⎪⎩，解得27373637xy⎧=⎪⎪⎨⎪=-⎪⎩，∠2736 ()3737E-，，∠4537 OE=，故答案为：45 37．【点睛】本题考查全等三角形的性质，坐标与图形性质，待定系数法求函数的解析式，建立平面直角坐标系是解题的关键．13．±5【分析】先根据点P在x轴正半轴确定出点P的坐标，然后利用k表示出P'的坐标，继而表示出线段PP′的长，再根据线段PP′的长为线段OP长的5倍得到关于k的方程，解方程即可求得答案.【详解】解：设P（m，0）（m＞0），由题意：P′（m，mk），∠PP′＝5OP，∠|mk|＝5m，∠m＞0，∠|k|＝5，∠k＝±5．故答案为：±5．【点睛】本题考查了新定义下的阅读理解能力，涉及了点的坐标，绝对值的性质，两点间的距离等知识，正确理解新定义是解题的关键.14．能；可疑飞机在图中的位置见解析.【分析】根据A、B的纵坐标相等，可得AB平行于x轴，且线段AB为4个单位长度，在AB的下方两个单位画x轴，在距A点处1个单位画x轴的垂线，可得平面直角坐标系，根据点的坐标，可得可疑飞机C点的位置．【详解】解：能．如下图，可疑飞机在第三象限的C点处，在点A的正北方向距A点2个单位．【点睛】本题考查了坐标确定位置，利用平行于AB且在AB的下方一个单位画x轴，在距A点处1个单位画化x轴的垂线是解题关键．15．(1)学校在小明家北偏东45°方向2km处，博物馆在小明家南偏东50°方向4 km处(2)图中到小明家距离相同的是学校和公园和影院(3)见解析【分析】(1)由图可知，学校在小明家北偏东45°方向2km处，博物馆在小明家南偏东50方向4km处；(2)观察图形，根据OA，OE，OD的长度及图中各角度，即可得出结论．(3)作北偏西60°角，取OE = 2即可．（1）解：学校在小明家北偏东45°方向2km处，博物馆在小明家南偏东50°方向4 km处；（2）图中到小明家距离相同的是学校和公园和影院；（3）如图，点F即为小强家．【点睛】本题考查了方向角，解题的关键是熟练掌握运用方位角及确定位置需要两个元素．16．坐标系见解析；田径场的坐标为（1，5），图书馆的坐标为（-1，3），第一教学楼的坐标为（-3，-2）．【分析】根据题意建立直角坐标系，然后读出坐标即可．【详解】解：根据题意建立直角坐标系如下：则田径场的坐标为（1，5），图书馆的坐标为（-1，3），第一教学楼的坐标为（-3，-2）．【点睛】题目主要考查直角坐标系的应用，理解题意建立合适的直角坐标系是解题关键．。

地理数学方法课后作业参考答案

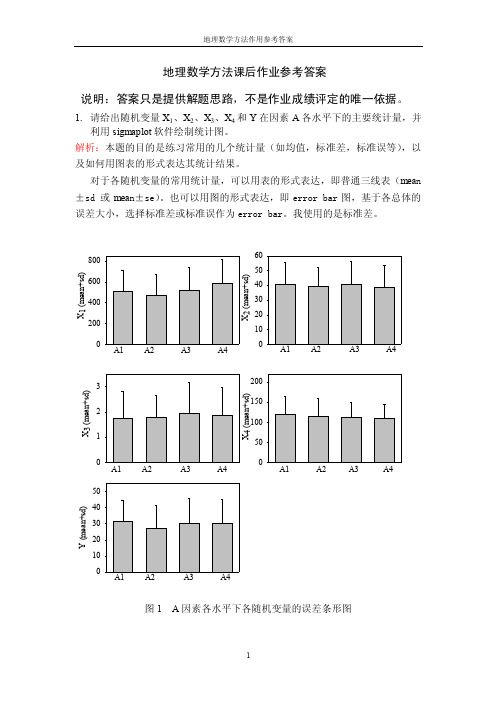
地理数学方法课后作业参考答案说明：答案只是提供解题思路，不是作业成绩评定的唯一依据。

1.请给出随机变量X1、X2、X3、X4和Y在因素A各水平下的主要统计量，并利用sigmaplot软件绘制统计图。

解析：本题的目的是练习常用的几个统计量（如均值，标准差，标准误等），以及如何用图表的形式表达其统计结果。

对于各随机变量的常用统计量，可以用表的形式表达，即普通三线表（mea n ±sd 或mea n±se）。

也可以用图的形式表达，即error bar图，基于各总体的误差大小，选择标准差或标准误作为error bar。

我使用的是标准差。

图1 A因素各水平下各随机变量的误差条形图表1A因素各水平下各随机变量的平均值和标准差因素水平XX2X3X4Y1A1 509.24(205.79) 40.86(15.00) 1.75(1.08) 119.80(44.02) 31.43(12.92) A2 472.71(201.77) 95.55(12.82) 1.79(0.90) 114.15 (44.87) 27.18(14.42) A3 518.01(218.58) 40.66(15.37) 1.95(1.21) 111.73(39.52) 30.30(15.54) A4 587.99(224.64) 38.95(14.68) 1.87(1.10) 109.59(36.62) 30.57(14.66)2.请分析因素A和B各处理下随机变量X1、X2、X3、X4和Y的均值是否存在显著性差异？请简要解释分析思路。

解析：本题的目的是联系双因素方差分析。

考察因素A和因素B是否是随机变量X1-Y的控制因子。

有两种分析思路，一是利用单因变量的双因素方差分析，分别考虑A和B因素各处理下这五个随机变量的均值是否存在显著性差异，然后进行多重比较。

二是利用多因变量的双因素方差分析，总体考虑A和B因素各处理下这五个随机变量的均值是否存在显著性差异，然后再分别对各变量进行方差分析和多重比较。

测绘学基础习题及参考答案

第一章导论习题及参考答案一、判断题（对的打“√”，错的打“×”）1.比例尺、地图投影、各种坐标系统就构成了地图的数学法则。

2.地图容纳和储存了数量巨大的信息，而作为信息的载体，只能是传统概念上的纸质地图。

3.地图的数学要素主要包括地图投影、坐标系统、比例尺、控制点、图例等。

4.实测成图法一直是测制大比例尺地图最基本的方法。

5.磁坐偏角指磁子午线与坐标纵线之间的夹角。

以坐标纵线为准，磁子午线东偏为负，西偏为正。

）6.一般情况下真方位角（A）、磁偏角（δ）、磁方位角（Am）三者之间的关系是A=Am+δ。

7.大规模的三角测量和地形图测绘，其成为近代地图学的主流。

8.城市规划、居民地布局、地籍管理等需要以小比例尺的平面地图作为基础图件。

9.实地图即为“心象地图”，虚地图即为“数字地图”。

10.方位角是由标准方向线北端或者南端开始顺时针方向到某一直线的夹角。

11.1987年国家测绘局公布：启用《1985国家高程基准》取代《黄海平均海水面》，其比《黄海平均海水面》下降29毫米。

12.目前我国各地高程控制点的绝对高程起算面是1956黄海平均海水面。

13.磁偏角只随地点的不同而不同。

14.南京紫金山最高点对连云港云台山最高点的高差为正。

15.不同地点的磁偏角是不相同的，同一地点的磁偏角是相同的。

二、名词解释1.地图2.直线定向3.真子午线4.磁子午线5.磁偏角6.子午线收敛角7.磁坐偏角 8.方位角 9.象限角 10.地图学 11.三北方向12.1956年黄海高程系三、问答题1.地图的基本特性是什么？2.我国地图学家把地图学分为哪几个分支学科组成？3.结合自己所学地图知识谈谈地图的功能有哪些？四、计算题1.已知某地的磁偏角为-5°15′，直线AB的磁方位角为134°10′，试求AB直线的真方位角。

2.已知某地的R=59°20′SE，α=？3.已知某目标方向线OA的真象限角为24°SW，OA的磁方位角为206°30′，求其真方位角和磁偏角各为多少？并分别画出草图。

地图中度数的计算与应用练习题

地图中度数的计算与应用练习题一、填空题1. 两个互为补角的角度之和为________度。

2. 地球上经度总共有________条。

3. 在地球上，东经与西经的度数值范围分别从________度到________度。

4. 1度等于________分，1分等于________秒。

5. 在地球上，纬度的范围从________度到________度。

6. 标准子午线（0度经线）通过________市。

7. 当时钟指向东边时，它的夹角是________度。

8. 地球表面上的纬线都是________大圈。

二、单项选择题1. 东经120度与西经120度相比，它们之间的夹角是：A. 0度B. 60度C. 120度D. 240度2. 地球上从南纬10度到南纬40度的范围内，共有多少纬度线：A. 30条B. 40条C. 50条D. 60条3. 两个补角为60度和120度的角，它们中较小的角是：A. 30度B. 60度C. 120度D. 150度4. 地球上通过伦敦的经线是：A. 0度经线B. 30度经线C. 60度经线D. 90度经线5. 两个相邻纬度线之间的夹角是：A. 固定不变的B. 随纬度线位置不同而变化的C. 一定是90度D. 由地球自转速度决定三、计算题1. 在地球上，东经60度与东经150度之间的夹角是多少度？2. 地球上纬度范围从赤道（0度纬度线）到北极（90度纬度线）。

某城市位于北纬40度的位置，该城市与赤道之间的夹角是多少度？3. 地球表面上通过洛杉矶（西经120度）和北京（东经116度）的经线之间的夹角是多少度？4. 经度和纬度的度数之间有何关系？请用一个数学表达式表示。

5. 美国洛杉矶（西经118度）的一个度大约等于114千米，假设从洛杉矶驾车到纽约（东经74度）的直线距离大约为3900千米，请计算从洛杉矶到纽约需要经过多少个经线。

四、应用题假设你现在位于纬度北30度、东经120度的位置，你决定参加一个全球旅行挑战赛。