必修二模块综合检测(含解析)

合集下载

人教版高中数学选择性必修第二册全册模块综合检测2(含解析)

人教版高中数学选择性必修第二册全册模块综合检测2(原卷版)(时间：120分钟，分值：150分)一、单项选择题(本题共8小题，每小题5分，共40分)1．已知函数f(x)＝e2x＋1，则f′(0)＝()A．0B．eC．2e D．e22．在等差数列{a n}中，a1＋a4＋a7＝36，a2＋a5＋a8＝33，则a3＋a6＋a9的值为() A．27B．30C．33D．363．已知a>0，b>0，a，b的等比中项为2，则a＋1b＋b＋1a的最小值为()A．3B．4 C．5D．424．函数y＝x－12x＋1在(1,0)处的切线与直线l：y＝ax垂直，则a＝() A．－3B．3C．13D．－135．已知等差数列{a n}的前n项和S n满足：S37－S23＝a，则S60＝()A．4a B．307aC．5a D．407a6．函数f(x)＝(x2＋2x)e2x的图象大致是()7．《周髀算经》有这样一个问题：从冬至日起，依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸，冬至、立春、春分日影之和为三丈一尺五寸，前九个节气日影之和为八丈五尺五寸，则芒种日影长为()A．一尺五寸B．二尺五寸C．三尺五寸D．四尺五寸8．已知函数f(x)＝x3－x和点P(1，－1)，则过点P与该函数图象相切的直线条数为() A．1B．2C．3D．4二、多项选择题(本题共4小题，每小题5分，共20分)9．已知数列{a n}的前n项和为S n，S n＝2a n－2，若存在两项a m，a n，使得a m a n＝64，则() A．数列{a n}为等差数列B．数列{a n}为等比数列C．a21＋a22＋…＋a2n＝4n－13D．m＋n为定值10．若函数e x f(x)(e＝2.7182…是自然对数的底数)在f(x)的定义域上单调递增，则称函数f(x)具有M性质．下列函数中所有具有M性质的函数为()A．f(x)＝2－x B．f(x)＝3－xC．f(x)＝x3D．f(x)＝x2＋211．设等比数列{a n}的公比为q，其前n项和为S n，前n项积为T n，并且满足条件a1>1，a6a7>1，a6－1<0，则下列结论正确的是()a7－1A．0<q<1B．a6a8>1C．S n的最大值为S7D．T n的最大值为T612．设f′(x)为函数f(x)的导函数，已知x2f′(x)＋xf(x)＝ln x，f(1)＝12，则下列结论正确的是()A．xf(x)在(1，＋∞)单调递增B．xf(x)在(0,1)单调递减C．xf(x)在(0，＋∞)上有极大值12D．xf(x)在(0，＋∞)上有极小值12三、填空题(本题共4小题，每小题5分，共20分)13.已知等差数列{a n}中，a4＝8，a8＝4，则其通项公式a n＝________.a1a9，则a n＝________，数列14.已知正项等比数列{a n}满足a1＝1，a2a6a7＝116{log2a n}的前n项和为________．15.函数f(x)＝12x2－ln x的单调递减区间是________．16.已知函数f(x)＝ln x＋mx，若函数f(x)的极小值不小于0，则实数m的取值范围为________．四、解答题(本题共6小题，共70分)17.(10分)等比数列{a n}中，已知a1＝2，a4＝16.(1)求数列{a n}的通项公式a n；(2)若a3，a5分别是等差数列{b n}的第4项和第16项，求数列{b n}的通项公式及前n项和S n.18.(12分)已知函数f(x)＝12x2－3ln x.(1)求f(x)在(1，f(1))处的切线方程；(2)试判断f(x)在区间(1，e)上有没有零点．若有，判断零点的个数．19.(12分)设数列{a n}是等差数列，其前n项和为S n，且a3＝2，S9＝54.(1)求数列{a n}的通项公式；(2)证明：1a1＋3＋1a2＋3＋1a3＋3＋…＋1a100＋3>13.20.(12分)设函数f(x)＝e x－ax－1(a∈R)．(1)若a＝2，求函数f(x)在区间[0,2]上的最大值和最小值；(2)当x≥0时，f(x)≥0，求a的取值范围．21.(12分)等差数列{a n}中，S3＝21，S6＝24，(1)求数列{a n}的前n项和公式S n；(2)求数列{|a n|}的前n项和T n.22.(12分)已知a，b∈R，设函数f(x)＝e x－ax－b x2＋1.(1)若b＝0，求f(x)的单调区间；(2)当x∈[0，＋∞)时，f(x)的最小值为0，求a＋5b的最大值．注：e＝2.71828…为自然对数的底数．人教版高中数学选择性必修第二册全册模块综合检测2(解析版)(时间：120分钟，分值：150分)一、单项选择题(本题共8小题，每小题5分，共40分)1．已知函数f (x )＝e 2x ＋1，则f ′(0)＝()A ．0B ．e C ．2e D ．e 2C解析：∵f (x )＝e 2x ＋1，∴f ′(x )＝2e 2x ＋1，∴f ′(0)＝2e.故选C ．2．在等差数列{a n }中，a 1＋a 4＋a 7＝36，a 2＋a 5＋a 8＝33，则a 3＋a 6＋a 9的值为()A ．27B ．30C ．33D ．36B解析：因为a 1＋a 4＋a 7＝3a 4＝36，所以a 4＝12.因为a 2＋a 5＋a 8＝33，所以a 5＝11.所以d＝a 5－a 4＝－1，所以a 3＋a 6＋a 9＝3a 6＝3(a 5＋d )＝30.故选B ．3．已知a >0，b >0，a ，b 的等比中项为2，则a ＋1b ＋b ＋1a 的最小值为()A ．3B ．4C ．5D ．42C解析：∵a ＋1b ＋b ＋1a ＝(a ＋b )＋a ＋b ab＝(a ＋b ＝54(a ＋b )≥54·2ab ＝5，等号成立当且仅当a ＝b ＝2，原式的最小值为5.4．函数y ＝x －12x ＋1在(1,0)处的切线与直线l ：y ＝ax 垂直，则a ＝()A ．－3B ．3C ．13D ．－13A解析：∵y ′＝3(2x ＋1)2，∴y ′|x ＝1＝13，∴函数在(1,0)处的切线的斜率是13，所以，与此切线垂直的直线的斜率是－3，∴a ＝－3.故选A ．5．已知等差数列{a n }的前n 项和S n 满足：S 37－S 23＝a ，则S 60＝()A ．4aB ．307a C ．5aD ．407aB 解析：因为S 37－S 23＝a 24＋a 25＋…＋a 37＝a 24＋a 372×14＝7(a 24＋a 37)＝a .所以S 60＝a 1＋a 602×60＝30(a 24＋a 37)＝307a .故选B ．6．函数f (x )＝(x 2＋2x )e 2x 的图象大致是()A 解析：由于f ′(x )＝2(x 2＋3x ＋1)·e 2x ，而y ＝x 2＋3x ＋1的判别式Δ＝9－4＝5>0，所以y＝x 2＋3x ＋1开口向上且有两个根x 1，x 2.不妨设x 1<x 2，所以f (x )在(－∞，x 1)，(x 2，＋∞)上递增，在(x 1，x 2)上递减．所以C ，D 选项不正确．当x <－2时，f (x )>0，所以B 选项不正确．由此得出A 选项正确．故选A ．7．《周髀算经》有这样一个问题：从冬至日起，依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸，冬至、立春、春分日影之和为三丈一尺五寸，前九个节气日影之和为八丈五尺五寸，则芒种日影长为()A ．一尺五寸B ．二尺五寸C ．三尺五寸D ．四尺五寸B解析：由题知各节气日影长依次成等差数列，设为{a n }，S n 是其前n 项和，则S 9＝9(a 1＋a 9)2＝9a 5＝85.5，所以a 5＝9.5，由题知a 1＋a 4＋a 7＝3a 4＝31.5，所以a 4＝10.5，所以公差d ＝a 5－a 4＝－1.所以a 12＝a 5＋7d ＝2.5尺．故选B ．8．已知函数f (x )＝x 3－x 和点P (1，－1)，则过点P 与该函数图象相切的直线条数为()A ．1B ．2C ．3D ．4B解析：因为f (1)＝13－1＝0，所以点P (1，－1)没有在函数的图象上．设切点坐标为(x 0，y 0)，则y 0＝x 30－x 0，则f ′(x )＝3x 2－1.由导数的几何意义可知，过切点的斜率为k ＝3x 20－1，过P (1，－1)和切点的斜率表示为k ＝y 0＋1x 0－1，－x0，3x20－1，化简可得x20(2x0－3)＝0，所以x0＝0或x0＝32.所以切点有两个，因而有两条切线方程．故选B．二、多项选择题(本题共4小题，每小题5分，共20分)9．已知数列{a n}的前n项和为S n，S n＝2a n－2，若存在两项a m，a n，使得a m a n＝64，则() A．数列{a n}为等差数列B．数列{a n}为等比数列C．a21＋a22＋…＋a2n＝4n－13D．m＋n为定值BD解析：由题意，当n＝1时，S1＝2a1－2，解得a1＝2，当n≥2时，S n－1＝2a n－1－2，所以S n－S n－1＝a n＝2a n－2－(2a n－1－2)＝2a n－2a n－1，所以a na n－1＝2，数列{a n}是以a1＝2为首项，q＝2为公比的等比数列，a n＝2n，故选项A错误，选项B正确；数列{a2n}是以a21＝4为首项，q1＝4为公比的等比数列，所以a21＋a22＋…＋a2n＝a21(1－q n1)1－q1＝4×(1－4n)1－4＝4n＋1－43，故选项C 错误；a m a n＝2m2n＝2m＋n＝64＝26，所以m＋n＝6为定值，故选项D正确．故选BD．10．若函数e x f(x)(e＝2.7182…是自然对数的底数)在f(x)的定义域上单调递增，则称函数f(x)具有M性质．下列函数中所有具有M性质的函数为()A．f(x)＝2－x B．f(x)＝3－xC．f(x)＝x3D．f(x)＝x2＋2AD解析：对于选项A，f(x)＝2－x，则g(x)＝e x f(x)＝e x·2－x为实数集上的增函数；对于选项B，f(x)＝3－x，则g(x)＝e x f(x)＝e x·3－x为实数集上的减函数；对于选项C，f(x)＝x3，则g(x)＝e x f(x)＝e x·x3，g′(x)＝e x·x3＋3e x·x2＝e x(x3＋3x2)＝e x·x2(x＋3)，当x＜－3时，g′(x)＜0，∴g(x)＝e x f(x)在定义域R上先减后增；对于选项D，f(x)＝x2＋2，则g(x)＝e x f(x)＝e x(x2＋2)，g′(x)＝e x(x2＋2)＋2x e x＝e x(x2＋2x＋2)＞0在实数集R上恒成立，∴g(x)＝e x f(x)在定义域R上是增函数．故选AD．11．设等比数列{a n}的公比为q，其前n项和为S n，前n项积为T n，并且满足条件a1>1，a6a7>1，a6－1a7－1<0，则下列结论正确的是()A．0<q<1B．a6a8>1C．S n的最大值为S7D．T n的最大值为T6AD 解析：易知q >0，若q >1，则a 6>1，a 7>1，与a 6－1a 7－1>0矛盾，故0<q <1.所以0<a 7<1.所以a 6a 8＝a 27<1.因为a 7>0，a 8>0，所以S n 的最大值一定不为S 7.因为0<a 7<1，a 6>1，所以T n 的最大值为T 6，故选AD ．12．设f ′(x )为函数f (x )的导函数，已知x 2f ′(x )＋xf (x )＝ln x ，f (1)＝12，则下列结论正确的是()A ．xf (x )在(1，＋∞)单调递增B ．xf (x )在(0,1)单调递减C ．xf (x )在(0，＋∞)上有极大值12D ．xf (x )在(0，＋∞)上有极小值12ABD解析：由x 2f ′(x )＋xf (x )＝ln x 得x ＞0，则xf ′(x )＋f (x )＝ln x x ，由[xf (x )]′＝ln xx .设g (x )＝xf (x )，即g ′(x )＝ln xx>0得x ＞1.由g ′(x )＜0得0＜x ＜1，即xf (x )在(1，＋∞)单调递增，在(0,1)单调递减，即当x ＝1时，函数g (x )＝xf (x )取得极小值g (1)＝f (1)＝12.故选ABD ．三、填空题(本题共4小题，每小题5分，共20分)13.已知等差数列{a n }中，a 4＝8，a 8＝4，则其通项公式a n ＝________.12－n 解析：∵等差数列{a n }中，a 4＝8，a 8＝4，4＝a 1＋3d ＝8，8＝a 1＋7d ＝4，解得a 1＝11，d ＝－1，∴a n ＝11＋(n －1)×(－1)＝12－n .14.已知正项等比数列{a n }满足a 1＝1，a 2a 6a 7＝116a 1a 9，则a n ＝________，数列{log 2a n }的前n 项和为________．2－n ＋1－n (n －1)2解析：由a 1＝1，a 2a 6a 7＝1161a 9得a 5＝a 1q 4＝116，q ＝12，a n －1＝2－n＋1.而log 2a n ＝－n ＋1，所以{log 2a n }的前n 项和为－n (n －1)2.15.函数f (x )＝12x 2－ln x 的单调递减区间是________．(0,1]解析：f (x )＝12x 2－ln x ，则f ′(x )＝x －1x ＝x 2－1x ＝(x ＋1)(x －1)x≤0，故0<x ≤1.16.已知函数f (x )＝ln x ＋mx，若函数f (x )的极小值不小于0，则实数m 的取值范围为________．1e，＋∞解析：由f (x )＝ln x ＋m x 得f ′(x )＝1x －m x 2＝x －mx2，定义域为(0，＋∞)．当m ≤0时，f ′(x )>0，函数y ＝f (x )单调递增，函数无极值；当m >0时，令f ′(x )＝0⇒x ＝m ，当x ∈(0，m )时，f ′(x )<0，函数y ＝f (x )单调递减；当x ∈(m ，＋∞)时，f ′(x )>0，函数y ＝f (x )单调递增．所以当x ＝m 时，函数y ＝f (x )取极小值，且为f (m )＝ln m ＋1.依题意有ln m ＋1≥0⇒m ≥1e ，因此，实数m 的取值范围是1e ，＋∞四、解答题(本题共6小题，共70分)17.(10分)等比数列{a n }中，已知a 1＝2，a 4＝16.(1)求数列{a n }的通项公式a n ；(2)若a 3，a 5分别是等差数列{b n }的第4项和第16项，求数列{b n }的通项公式及前n 项和S n .解：(1)设{a n }的公比为q ，由已知得16＝2q 3，解得q ＝2，所以a n ＝2n .(2)由(1)得a 3＝8，a 5＝32，则b 4＝8，b 16＝32.设{b n }的公差为d b 1＋3d ＝8，b 1＋15d ＝32，b 1＝2，d ＝2.从而b n ＝2＋2(n －1)＝2n .所以数列{b n }的前n 项和S n ＝(2＋2n )n2＝n 2＋n .18.(12分)已知函数f (x )＝12x 2－3ln x .(1)求f (x )在(1，f (1))处的切线方程；(2)试判断f (x )在区间(1，e)上有没有零点．若有，判断零点的个数．解：(1)由已知得f ′(x )＝x －3x ，有f ′(1)＝－2，f (1)＝12，∴在(1，f (1))处的切线方程为y －12＝－2(x －1)，化简得4x ＋2y －5＝0.(2)由(1)知f ′(x )＝(x －3)(x ＋3)x ，因为x >0，令f ′(x )＝0，得x ＝ 3.所以当x ∈(0，3)时，有f ′(x )<0，则(0，3)是函数f (x )的单调递减区间；当x ∈(3，＋∞)时，有f ′(x )>0，则(3，＋∞)是函数f (x )的单调递增区间；当x ∈(1，e)时，函数f (x )在(1，3)上单调递减，在(3，e)上单调递增．又因为f (1)＝12，f (e)＝12e 2－3>0，f (3)＝32(1－ln 3)<0，所以f (x )在区间(1，e)上有两个零点.19.(12分)设数列{a n }是等差数列，其前n 项和为S n ，且a 3＝2，S 9＝54.(1)求数列{a n }的通项公式；(2)证明：1a 1＋3＋1a 2＋3＋1a 3＋3＋…＋1a 100＋3>13.(1)解：设数列{a n }的公差为d ，∵S 9＝9a 5＝54，∴a 5＝6，∴d ＝a 5－a 35－3＝2，∴a n ＝a 3＋(n －3)d ＝2n －4.(2)证明：∵1a n ＋3＝12n －1>22n －1＋2n ＋1＝2n ＋1－2n －1，∴1a 1＋3＋1a 2＋3＋1a 3＋3＋…＋1a 100＋3>(3－1)＋(5－3)＋…＋(201－199)＝201－1>14－1＝13，∴1a 1＋3＋1a 2＋3＋1a 3＋3＋…＋1a 100＋3>13.20.(12分)设函数f (x )＝e x －ax －1(a ∈R )．(1)若a ＝2，求函数f (x )在区间[0,2]上的最大值和最小值；(2)当x ≥0时，f (x )≥0，求a 的取值范围．解：(1)f (x )＝e x －2x －1，取f ′(x )＝e x －2＝0，即x ＝ln 2，函数在[0，ln 2]上单调递减，在(ln 2,2]上单调递增，且f (0)＝0，f (2)＝e 2－5，f (ln 2)＝1－2ln 2，故函数的最大值为f (2)＝e 2－5，最小值为f (ln 2)＝1－2ln 2.(2)f (x )＝e x －ax －1，f ′(x )＝e x －a ，f (0)＝0.当a ≤0时，f ′(x )＝e x －a >0，函数单调递增，故f (x )≥f (0)＝0，成立；当a >0时，f ′(x )＝e x －a ＝0，即x ＝ln a ，故函数在(0，ln a )上单调递减，在(ln a ，＋∞)上单调递增，故f (ln a )<f (0)＝0，不成立．综上所述，a 的取值范围为(－∞，0].21.(12分)等差数列{a n }中，S 3＝21，S 6＝24，(1)求数列{a n }的前n 项和公式S n ；(2)求数列{|a n |}的前n 项和T n .解：(1)设{a n }首项为a 1，公差为d ，由S 3＝21，S 6＝24，a 1＋3×22d ＝21，a 1＋6×52d ＝24，1＝9，＝－2.∴S n ＝n ×9＋n (n －1)2×(－2)＝－n 2＋10n .(2)由(1)知，a n ＝9＋(n －1)×(－2)＝－2n ＋11，由a n ≥0得－2n ＋11≥0，即n ≤112.当n ≤5时，T n ＝|a 1|＋|a 2|＋…＋|a n |＝a 1＋a 2＋…＋a n ＝S n ＝－n 2＋10n ；当n ≥6时，T n ＝|a 1|＋…＋|a 5|＋|a 6|＋…＋|a n |＝(a 1＋a 2＋…＋a 5)－(a 6＋…＋a n )＝S 5－(S n －S 5)＝n 2－10n ＋50.综上，T nn 2＋10n (n ≤5)，2－10n ＋50(n ≥6).22.(12分)已知a ，b ∈R ，设函数f (x )＝e x －ax －b x 2＋1.(1)若b ＝0，求f (x )的单调区间；(2)当x ∈[0，＋∞)时，f (x )的最小值为0，求a ＋5b 的最大值．注：e ＝2.71828…为自然对数的底数．解：(1)f (x )＝e x －ax ，f ′(x )＝e x －a ，当a ≤0时，f ′(x )＝e x －a ≥0恒成立，函数单调递增；当a >0时，f ′(x )＝e x －a ＝0，x ＝ln a ，当x ∈(－∞，ln a )时，f ′(x )<0，函数单调递减；当x ∈(ln a ，＋∞)时，f ′(x )>0，函数单调递增．综上所述，a ≤0时，f (x )在R 上单调递增；a >0时，f (x )在(－∞，ln a )上单调递减，在(ln a ，＋∞)上单调递增．(2)f (x )＝e x－ax －bx 2＋1≥0在x ∈[0，＋∞)上恒成立，＝e －12a －52b ≥0，故a ＋5b ≤2e ，现在证明存在a ，b ，a ＋5b ＝2e ，使f (x )的最小值为0.取a ＝3e 4，b ＝5e 4(此时可使f 0)，f ′(x )＝e x －a －bx x 2＋1，f ″(x )＝e x －b (x 2＋1)x 2＋1，b ＝5e 4<1，故当x ∈[0，＋∞)时，(x 2＋1)x 2＋1≥1，e x ≥1，故f ″(x )≥0，f ′(x )在[0，＋∞)上单调递增，f 0，故f (x )在0f (x )min ＝0.综上所述，a ＋5b 的最大值为2 e.。

高中数学模块综合检测2(含解析)新人教A版选择性必修第二册-新人教A版高二选择性必修第二册数学试题

模块综合检测(二)(满分：150分时间：120分钟)一、单项选择题(本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知f (x )＝ln x 2x ，则lim Δx →0f ⎝ ⎛⎭⎪⎫12－f ⎝ ⎛⎭⎪⎫12＋Δx Δx ＝( ) A ．－2－ln 2B ．－2＋ln 2C ．2－ln 2D ．2＋ln 2A [由题意，函数f (x )＝ln x 2x ，则f ′(x )＝1x ·2x －(2x )′ln x (2x )2＝2x －12⎝ ⎛⎭⎪⎫1－12ln x 2x ，则lim Δx →0f ⎝ ⎛⎭⎪⎫12－f ⎝ ⎛⎭⎪⎫12＋Δx Δx ＝－f ′⎝ ⎛⎭⎪⎫12＝－2＋ln 22×12＝－2－ln 2，故选A.] 2．等比数列{a n }是递减数列，前n 项的积为T n ，若T 13＝4T 9，则a 8a 15＝( )A ．±2B ．±4C ．2D ．4C [∵T 13＝4T 9，∴a 1a 2…a 9a 10a 11a 12a 13＝4a 1a 2…a 9，∴a 10a 11a 12a 13＝4.又∵a 10·a 13＝a 11·a 12＝a 8·a 15，∴(a 8·a 15)2＝4，∴a 8a 15＝±2.又∵{a n }为递减数列，∴q >0，∴a 8a 15＝2.]3．已知公差不为0的等差数列{a n }的前23项的和等于前8项的和．若a 8＋a k ＝0，则k ＝( )A ．22B ．23C ．24D ．25C [等差数列的前n 项和S n 可看做关于n 的二次函数(图象过原点)．由S 23＝S 8，得S n 的图象关于n ＝312对称，所以S 15＝S 16，即a 16＝0，所以a 8＋a 24＝2a 16＝0，所以k ＝24.]4．已知函数f (x )＝(x ＋a )e x 的图象在x ＝1和x ＝－1处的切线相互垂直，则a ＝( )A ．－1B ．0C ．1D ．2A [因为f ′(x )＝(x ＋a ＋1)e x ，所以f ′(1)＝(a ＋2)e ，f ′(－1)＝a e －1＝a e ，由题意有f (1)f ′(－1)＝－1，所以a ＝－1，选A.]5．设S n 是公差不为0的等差数列{a n }的前n 项和，S 3＝a 22，且S 1，S 2，S 4成等比数列，则a 10＝( )A ．15B ．19C ．21D ．30B [由S 3＝a 22得3a 2＝a 22，故a 2＝0或a 2＝3.由S 1，S 2，S 4成等比数列可得S 22＝S 1·S 4，又S 1＝a 2－d ，S 2＝2a 2－d ，S 4＝4a 2＋2d ，故(2a 2－d )2＝(a 2－d )(4a 2＋2d )，化简得3d 2＝2a 2d ，又d ≠0，∴a 2＝3，d ＝2，a 1＝1，∴a n ＝1＋2(n －1)＝2n －1，∴a 10＝19.]6．若函数f (x )＝ax －ln x 的图象上存在与直线x ＋2y －4＝0垂直的切线，则实数a 的取值X 围是( )A ．(－2，＋∞)B ．⎝ ⎛⎭⎪⎫12，＋∞ C ．⎝ ⎛⎭⎪⎫－12，＋∞ D ．(2，＋∞)D [因为函数f (x )＝ax －ln x 的图象上存在与直线x ＋2y －4＝0垂直的切线，所以函数f (x )＝ax －ln x 的图象上存在斜率为2的切线，故k ＝f ′(x )＝a －1x ＝2有解，所以a ＝2＋1x ，x ＞0有解，因为y ＝2＋1x ，x ＞0的值域为(2，＋∞)．所以a ∈(2，＋∞)．]7．已知等差数列{}a n 的前n 项为S n ，且a 1＋a 5＝－14，S 9＝－27，则使得S n 取最小值时的n 为( )A ．1B ．6C ．7D ．6或7B [由等差数列{a n }的性质，可得a 1＋a 5＝2a 3＝－14⇒a 3＝－7，又S 9＝9(a 1＋a 9)2＝－27⇒a 1＋a 9＝－6⇒a 5＝－3，所以d ＝a 5－a 35－3＝2，所以数列{a n }的通项公式为a n ＝a 3＋(n －3)d ＝－7＋(n －3)×2＝2n －13，令a n ≤0⇒2n －13≤0，解得n ≤132，所以数列的前6项为负数，从第7项开始为正数，所以使得S n 取最小值时的n 为6，故选B.]8．若方底无盖水箱的容积为256，则最省材料时，它的高为( )A ．4B ．6C ．4.5D ．8A [设底面边长为x ，高为h ，则V (x )＝x 2·h ＝256，∴h ＝256x 2.∴S (x )＝x 2＋4xh ＝x 2＋4x ·256x 2＝x 2＋4×256x ，∴S ′(x )＝2x －4×256x 2. 令S ′(x )＝0，解得x ＝8，∴当x ＝8时，S (x )取得最小值．∴h ＝25682＝4.]二、多项选择题(本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分)9．设数列{}a n 是等差数列，S n 是其前n 项和，a 1＞0，且S 6＝S 9，则( )A ．d <0B ．a 8＝0C ．S 5＞S 6D ．S 7或S 8为S n 的最大值ABD [根据题意可得a 7＋a 8＋a 9＝0⇒3a 8＝0⇒a 8＝0，∵数列{}a n 是等差数列，a 1＞0，∴公差d <0，所以数列{}a n 是单调递减数列，对于A 、B ，d <0，a 8＝0，显然成立；对于C ，由a 6>0，则S 5<S 6，故C 不正确；对于D ，由a 8＝0，则S 7＝S 8，又数列为递减数列，则S 7或S 8为S n 的最大值，故D 正确．故选ABD.]10．如图是y ＝f (x )导数的图象，对于下列四个判断，其中正确的判断是( )A ．f (x )在(－2，－1)上是增函数B ．当x ＝－1时，f (x )取得极小值C ．f (x )在(－1，2)上是增函数，在(2，4)上是减函数D ．当x ＝3时，f (x )取得极小值BC [根据图象知当x ∈(－2，－1)，x ∈(2，4)时，f ′(x )＜0，函数单调递减；当x ∈(－1，2)，x ∈(4，＋∞)时，f ′(x )＞0，函数单调递增．故A 错误；故当x ＝－1时，f (x )取得极小值，B 正确；C 正确；当x ＝3时，f (x )不是取得极小值，D 错误．故选BC.]11．已知等比数列{}a n 的公比q ＝－23，等差数列{}b n 的首项b 1＝12，若a 9>b 9且a 10>b 10，则以下结论正确的有( )A ．a 9a 10<0B ．a 9>a 10C ．b 10>0D ．b 9>b 10AD [∵等比数列{}a n 的公比q ＝－23，∴a 9和a 10异号，∴a 9a 10<0 ，故A 正确；但不能确定a 9和a 10的大小关系，故B 不正确；∵a 9和a 10异号，且a 9>b 9且a 10>b 10，∴b 9和b 10中至少有一个数是负数，又∵b 1＝12>0 ，∴d <0，∴b 9>b 10 ，故D 正确，∴b 10一定是负数，即b 10<0 ，故C 不正确. 故选AD.]12．已知函数f (x )＝x ln x ，若0＜x 1＜x 2，则下列结论正确的是( )A ．x 2f (x 1)＜x 1f (x 2)B ．x 1＋f (x 1)＜x 2＋f (x 2)C ．f (x 1)－f (x 2)x 1－x 2＜0 D ．当ln x ＞－1时，x 1f (x 1)＋x 2f (x 2)＞2x 2f (x 1)AD [设g (x )＝f (x )x ＝ln x ，函数单调递增，则g (x 2)＞g (x 1)，即f (x 2)x 2＞f (x 1)x 1，∴x 1f (x 2)＞x 2f (x 1)，A 正确；设h (x )＝f (x )＋x ∴h ′(x )＝ln x ＋2不是恒大于零，B 错误；f (x )＝x ln x ，∴f ′(x )＝ln x ＋1不是恒小于零，C 错误；ln x ＞－1，故f ′(x )＝ln x ＋1＞0，函数单调递增．故(x 2－x 1)(f (x 2)－f (x 1))＝x 1f (x 1)＋x 2f (x 2)－x 2f (x 1)－x 1f (x 2)＞0，即x 1f (x 1)＋x 2f (x 2)＞x 2f (x 1)＋x 1f (x 2)．f (x 2)x 2＝ln x 2＞f (x 1)x 1＝ln x 1，∴x 1f (x 2)＞x 2f (x 1)，即x 1f (x 1)＋x 2f (x 2)＞2x 2f (x 1)，D 正确．故选AD.]三、填空题(本题共4小题，每小题5分，共20分．把答案填在题中的横线上)13．数列{a n }的前n 项和为S n ，若a n ＋1＝11－a n(n ∈N *)，a 1＝2，则S 50＝________. 25[因为a n ＋1＝11－a n (n ∈N *)，a 1＝2，所以a 2＝11－a 1＝－1，a 3＝11－a 2＝12，a 4＝11－a 3＝2，∴数列{a n }是以3为周期的周期数列，且前三项和S 3＝2－1＋12＝32， ∴S 50＝16S 3＋2－1＝25.]14．将边长为1 m 的正三角形薄铁皮，沿一条平行于某边的直线剪成两块，其中一块是梯形，记s ＝(梯形的周长)2梯形的面积，则s 的最小值是________． 3233[设AD ＝x (0<x <1)，则DE ＝AD ＝x ，∴梯形的周长为x＋2(1－x )＋1＝3－x .又S △ADE ＝34x 2，∴梯形的面积为34－34x 2，∴s ＝433×x 2－6x ＋91－x 2(0<x <1)，则s ′＝－833×(3x －1)(x －3)(1－x 2)2. 令s ′＝0，解得x ＝13.当x ∈⎝ ⎛⎭⎪⎫0，13时，s ′<0，s 为减函数；当x ∈⎝ ⎛⎭⎪⎫13，1时，s ′>0，s 为增函数．故当x ＝13时，s 取得极小值，也是最小值，此时s 的最小值为3233.]15．设公比为q (q >0)的等比数列{a n }的前n 项和为S n .若S 2＝3a 2＋2，S 4＝3a 4＋2，则q ＝________.32[由S 2＝3a 2＋2，S 4＝3a 4＋2相减可得a 3＋a 4＝3a 4－3a 2，同除以a 2可得2q 2－q －3＝0，解得q ＝32或q ＝－1.因为q >0，所以q ＝32.]16．已知函数f (x )是定义在R 上的偶函数，当x ＞0时，xf ′(x )＞f (x )，若f (2)＝0，则2f (3)________3f (2)(填“＞”“＜”)不等式x ·f (x )＞0的解集为________．(本题第一空2分，第二空3分)＞ (－2，0)∪(2，＋∞)[由题意，令g (x )＝f (x )x ，∵x ＞0时，g ′(x )＝xf ′(x )－f (x )x 2＞0.∴g (x )在(0，＋∞)单调递增，∵f (x )x 在(0，＋∞)上单调递增，∴f (3)3＞f (2)2即2f (3)＞3f (2)．又∵f (－x )＝f (x )，∴g (－x )＝－g (x )，则g (x )是奇函数，且g (x )在(－∞，0)上递增，又g (2)＝f (2)2＝0，∴当0＜x ＜2时，g (x )＜0，当x ＞2时，g (x )＞0；根据函数的奇偶性，可得当－2＜x ＜0时，g (x )＞0，当x ＜－2时，g (x )＜0. ∴不等式x ·f (x )＞0的解集为{x |－2＜x ＜0或x ＞2}．]四、解答题(本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．(本小题满分10分)在等差数列{}a n 中，已知a 1＝1，a 3＝－5.(1)求数列{}a n 的通项公式；(2)若数列{}a n 的前k 项和S k ＝－25，求k 的值．[解](1)由题意，设等差数列{}a n 的公差为d ，则a n ＝a 1＋()n －1d ，因为a 1＝1，a 3＝－5，可得1＋2d ＝－5，解得d ＝－3，所以数列{}a n 的通项公式为a n ＝1＋()n －1×()－3＝4－3n .(2)由(1)可知a n ＝4－3n ，所以S n ＝n [1＋(4－3n )]2＝－32n 2＋52n ，又由S k ＝－25，可得－32k 2＋52k ＝－25，即3k 2－5k －50＝0，解得k ＝5或k ＝－103，又因为k ∈N *，所以k ＝5.18．(本小题满分12分)已知函数f (x )＝a ln x ＋12x 2.(1)求f (x )的单调区间；(2)函数g (x )＝23x 3－16(x ＞0)，求证：a ＝1时f (x )的图象不在g (x )的图象的上方．[解](1)f ′(x )＝a x ＋x (x ＞0)，若a ≥0，则f ′(x )＞0，f (x )在 (0，＋∞)上单调递增；若a ＜0，令f ′(x )＝0，解得x ＝±－a ，由f ′(x )＝(x －－a )(x ＋－a )x ＞0，得x ＞－a ，由f ′(x )＜0，得0＜x ＜－a .从而f (x )的单调递增区间为(－a ，＋∞)，单调递减区间为(0，－a )． (2)证明：令φ(x )＝f (x )－g (x )，当a ＝1时，φ(x )＝ln x ＋12x 2－23x 3＋16(x ＞0)，则φ′(x )＝1x ＋x －2x 2＝1＋x 2－2x 3x ＝(1－x )(2x 2＋x ＋1)x. 令φ′(x )＝0，解得x ＝1.当0＜x ＜1时，φ′(x )＞0，φ(x )单调递增；当x ＞1时，φ′(x )＜0，φ(x )单调递减．∴当x ＝1时，φ(x )取得最大值φ(1)＝12－23＋16＝0，∴φ(x )≤0，即f (x )≤g (x )．故a ＝1时f (x )的图象不在g (x )的图象的上方．19．(本小题满分12分)已知数列{}a n 的前n 项和为S n ，且2S n ＝3a n －1.(1)求数列{}a n 的通项公式；(2)若数列{}b n 满足b n ＝log 3a n ＋1，求数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1b n b n ＋1的前n 项和T n .[解](1)由2S n ＝3a n －1()n ∈N ＋得，2S n －1＝3a n －1－1()n ≥2.两式相减并整理得，a n ＝3a n －1()n ≥2.令n ＝1，由2S n ＝3a n －1()n ∈N ＋得，a 1＝1.故{}a n 是以1为首项，公比为3的等比数列，因此a n ＝3n －1()n ∈N ＋.(2)由b n ＝log 3a n ＋1，结合a n ＝3n －1得，b n ＝n .则1b n b n ＋1＝1n ()n ＋1＝1n －1n ＋1 故T n ＝1b 1b 2＋1b 2b 3＋…＋1b n b n ＋1＝⎝ ⎛⎭⎪⎫1－12＋⎝ ⎛⎭⎪⎫12－13＋…＋1n －1n ＋1＝n n ＋1. 20．(本小题满分12分)某旅游景点预计2019年1月份起前x 个月的旅游人数的和p (x )(单位：万人)与x 的关系近似地满足p (x )＝12x (x ＋1)(39－2x )(x ∈N *，且x ≤12)．已知第x 个月的人均消费额q (x )(单位：元)与x 的近似关系是q (x )＝⎩⎪⎨⎪⎧ 35－2x (x ∈N *，且1≤x ≤6)，160x (x ∈N *，且7≤x ≤12).(1)写出2019年第x 个月的旅游人数f (x )(单位：万人)与x 的函数关系式；(2)问2019年第几个月旅游消费总额最大？最大月旅游消费总额为多少元？[解](1)当x ＝1时，f (1)＝p (1)＝37，当2≤x ≤12，且x ∈N *时，f (x )＝p (x )－p (x －1)＝12x (x ＋1)(39－2x )－12(x －1)x (41－2x )＝－3x 2＋40x ，验证x ＝1也满足此式，所以f (x )＝－3x 2＋40x (x ∈N *，且1≤x ≤12)．(2)第x 个月旅游消费总额(单位：万元)为g (x )＝⎩⎨⎧ (－3x 2＋40x )(35－2x )(x ∈N *，且1≤x ≤6)，(－3x 2＋40x )·160x (x ∈N *，且7≤x ≤12)，即g (x )＝⎩⎪⎨⎪⎧6x 3－185x 2＋1 400x (x ∈N *，且1≤x ≤6)，－480x ＋6 400(x ∈N *，且7≤x ≤12). (i)当1≤x ≤6，且x ∈N *时，g ′(x )＝18x 2－370x ＋1 400，令g ′(x )＝0，解得x ＝5或x ＝1409(舍去)．当1≤x ＜5时，g ′(x )＞0，当5＜x ≤6时，g ′(x )＜0，∴当x ＝5时，g (x )max ＝g (5)＝3 125.(ii)当7≤x ≤12，且x ∈N *时，g (x )＝－480x ＋6 400是减函数，∴当x ＝7时，g (x )max ＝g (7)＝3 040.综上，2019年5月份的旅游消费总额最大，最大旅游消费总额为3 125万元．21．(本小题满分12分)已知数列{a n }的通项公式为a n ＝3n －1，在等差数列{b n }中，b n >0，且b 1＋b 2＋b 3＝15，又a 1＋b 1，a 2＋b 2，a 3＋b 3成等比数列．(1)求数列{a n b n }的通项公式；(2)求数列{a n b n }的前n 项和T n .[解](1)∵a n ＝3n －1，∴a 1＝1，a 2＝3，a 3＝9.∵在等差数列{b n }中，b 1＋b 2＋b 3＝15，∴3b 2＝15，则b 2＝5.设等差数列{b n }的公差为d ，又a 1＋b 1，a 2＋b 2，a 3＋b 3成等比数列，∴(1＋5－d )(9＋5＋d )＝64，解得d ＝－10或d ＝2.∵b n >0，∴d ＝－10应舍去，∴d ＝2，∴b 1＝3，∴b n ＝2n ＋1.故a n b n＝(2n＋1)·3n－1.(2)由(1)知T n＝3×1＋5×3＋7×32＋…＋(2n－1)3n－2＋(2n＋1)3n－1，①3T n＝3×3＋5×32＋7×33＋…＋(2n－1)3n－1＋(2n＋1)3n，②①－②，得－2T n＝3×1＋2×3＋2×32＋2×33＋…＋2×3n－1－(2n＋1)×3n ＝3＋2×(3＋32＋33＋…＋3n－1)－(2n＋1)×3n＝3＋2×3－3n1－3－(2n＋1)×3n＝3n－(2n＋1)×3n＝－2n·3n.∴T n＝n·3n.22．(本小题满分12分)设函数f (x)＝x3－6x＋5，x∈R.(1)求f (x)的极值点；(2)若关于x的方程f (x)＝a有3个不同实根，某某数a的取值X围；(3)已知当x∈(1，＋∞)时，f (x)≥k(x－1)恒成立，某某数k的取值X围．[解](1)f ′(x)＝3(x2－2)，令f ′(x)＝0，得x1＝－2，x2＝ 2.当x∈(－∞，－2)∪(2，＋∞)时，f ′(x)＞0，当x∈(－2，2) 时，f ′(x)＜0，因此x1＝－2，x2＝2分别为f (x)的极大值点、极小值点．(2)由(1)的分析可知y＝f (x)图象的大致形状及走向如图所示．要使直线y＝a 与y＝f (x)的图象有3个不同交点需5－42＝f (2)＜a＜f (－2)＝5＋4 2.则方程f (x)＝a有3个不同实根时，所某某数a的取值X围为(5－42，5＋42)．(3)法一：f (x)≥k(x－1)，即(x－1)(x2＋x－5)≥k(x－1)，因为x＞1，所以k≤x2＋x－5在(1，＋∞)上恒成立，令g(x)＝x2＋x－5，由二次函数的性质得g(x)在(1，＋∞)上是增函数，所以g(x)＞g(1)＝－3，所以所求k的取值X围是为(－∞，－3]．法二：直线y＝k(x－1)过定点(1，0)且f (1)＝0，曲线f (x)在点(1，0)处切线斜率f ′(1)＝－3，由(2)中图知要使x∈(1，＋∞)时，f (x)≥k(x－1)恒成立需k≤－3.故实数k的取值X围为(－∞，－3]．。

2024_2025学年新教材高中英语模块综合检测2含解析牛津译林版必修第二册

模块综合检测(二)Ⅰ.阅读理解(共15小题；每小题2.5分，满分37.5分)AClass 501Shy children need our help to get over their fears.In this class，we'll cover the basics—the origins of shyness，strategies (策略) for getting over the kind of shyness your child experiences，social skills you can teach in your home，and tips for working with teachers to help your child perform well at school.Where：Karman Executive Center，Bellevue，WashingtonWhen：From 7：00 p．m.to 9：30 p．m.，on Fridays in MayFee：$75.00Class 502This is a special class for children designed to teach communication skills all of us need，but shy people are afraid to use.We'll cover everything from how to start conversations with strangers to ways of keeping you calm when you do.You'll learn what makes some people more popular than others and what you can do to feel more like you fit in.Where：Karman Executive Center，Bellevue，WashingtonWhen：From 6：30 p．m.to 8：30 p．m.，on Tuesdays in MayFee：$68.00Class 503While a person's IQ is thought to be relatively fixed，our EQ is believed to develop over the course of a lifetime.Why not give your child a head start? Explore what EQ is all about.We'll review five of the basic qualities which are believed to make up EQ.We'll discuss ways to identify (确认) your child's emotional strengths and weaknesses and what you can do to improve their emotional development.Where：Karman Executive Center，Bellevue，WashingtonWhen：From 6：30 p．m.to 9：30 p．m.，on Wednesday，May 8thFee：$59.00Class 504Do you find yourself searching for something to say when you meet someone new in your work? Then why not join us in learning the secret of successful conversation? In this funfilled evening，we will simplify and practise the art of conversation to make yourself and others at home.Where：North Campus，Bellevue，WashingtonWhen：From 6：30 p．m.to 9：30 p．m.，on Thursday，May 23rdFee：$49.00【语篇解读】本文是一则广告。

2025版新教材高中英语模块综合质量检测二新人教版必修第二册

模块综合质量检测(二)第Ⅰ卷选择题第一部分听力(共两节，满分30分)第一节(共5小题；每小题1.5分，满分7.5分)听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1．When will the weather turn to be sunny?A．This afternoon. B．Tomorrow morning. C．Tomorrow afternoon.2．On which day will the woman hold her birthday party?A．Friday. B．Saturday. C．Sunday.3．What are the speakers talking about?A．Who designed the cup. B．Where the cup was made. C．How the woman got the cup.4．What's the probable relationship between the speakers?A．Neighbors. B．Friends. C．Couple.5．What place does the man like best?A．Mont Saint Michel. B．Pyramids of Giza. C．Bagan City.其次节(共15小题；每小题1.5分，满分22.5分)听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6、7题。

6．How many people visited the Temple with the woman?A．One. B．Two. C．Three.7．How did the woman learn about the Temple?A．From the Internet. B．From the locals. C．From the guide.听第7段材料，回答第8、9题。

人教版高中数学选择性必修第二册全册模块综合检测1(含解析)

人教版高中数学选择性必修第二册全册模块综合检测1(原卷版)(时间：120分钟，分值：150分)一、单项选择题(本题共8小题，每小题5分，共40分)1．数列{a n}满足a n＋1＝3a n＋1，a1＝1，则此数列的第3项是()A．13B．10C．7D．42．{a n}为等差数列，且a7－2a4＝－1，a3＝0，则公差d＝()A．－2B．－12D．2C．123．已知函数f(x)＝3x2＋2，则f′(5)＝()A．15B．30C．32D．774．设等比数列{a n}满足a1＋a2＝－1，a1－a3＝－3，则S6＝()A．－63B．－21C．21D．635．函数f(x)＝xx2＋1的单调递增区间是()A．(－∞，－1)B．(－1,1)C．(1，＋∞)D．(－∞，－1)和(1，＋∞)6．数列{a n}满足a1＝1，log2a n＋1＝log2a n＋1(n∈N*)，它的前n项和为S n，则满足S n>1025的最小n值是()A．9B．10C．11D．127．函数f(x)＝ln xx＋1的图象大致是()8．函数f (x )＝ln x ＋ax 有小于1的极值点，则实数a 的取值范围是()A ．(0,1)B ．(－∞，－1)C ．(－1,0)D ．(－∞，－1)∪(0，＋∞)二、多项选择题(本题共4小题，每小题5分，共20分)9．过点P (2，－6)作曲线f (x )＝x 3－3x 的切线，则切线方程可能是()A ．3x ＋y ＝0B ．24x －y －54＝0C ．9x －y －24＝0D ．12x －y －24＝010．记S n 为等差数列{a n }的前n 项和．若a 1＋3a 5＝S 7，则以下结论一定正确的是()A ．a 4＝0B ．S n 的最大值为S 3C ．S 1＝S 6D ．|a 3|<|a 5|11．在数列{a n }中，若a 2n －a 2n －1＝p (n ≥2，n ∈N *，p 为常数)，则{a n }称为“等方差数列”．下列对“等方差数列”的判断，其中正确的为()A ．若{a n }是等方差数列，则{a 2n }是等差数列B ．若{a n }是等方差数列，则{a 2n }是等方差数列C ．{(－1)n }是等方差数列D ．若{a n }是等方差数列，则{a kn }(k ∈N *，k 为常数)也是等方差数列12．设f (x )＝x a ·cos x ，x ∈π6，π3的最大值为M ，则()A ．当a ＝－1时，M <3B ．当a ＝2时，M <33C ．当a ＝1时，M >32D ．当a ＝3时，M <12三、填空题(本题共4小题，每小题5分，共20分)13.已知等差数列{a n }的前n 项和为S n ，a 1＝9，S 99－S 55＝－4，则a n ＝________.14.设函数f (x )＝x 3＋ax 2，若曲线y ＝f (x )在点P (1，f (1))处的切线方程为x ＋y ＝0，则实数a ＝________.15.已知等差数列{a n }的前n 项和为S n ＝pn 2－2n ＋q (p ，q ∈R ，n ∈N *)，则q ＝______；若a 1与a 5的等差中项为8，则p ＋q ＝________.16.设a ，b ∈R ，若x ≥0时恒有0≤x 4－x 3＋ax ＋b ≤(x 2－1)2，则ab 等于________．四、解答题(本题共6小题，共70分)17.(10分)在等差数列{a n}中，已知a1＋a2＋a3＝21，a1a2a3＝231.(1)求该数列中a2的值；(2)求该数列的通项公式a n.18.(12分)(1)求曲线y＝1x在点(－1，－1)处的切线方程；(2)求经过点(4,0)且与曲线y＝1x相切的直线方程．19.(12分)设f(x)＝a ln x＋12x－32x＋1，曲线y＝f(x)在点(1，f(1))处取得极值．(1)求a的值；(2)求函数f(x)的单调区间和极值．20.(12分)设数列{a n}满足：a1＝1，且2a n＝a n＋1＋a n－1(n≥2)，a3＋a4＝12.(1)求{a n}的通项公式；(2)n项和．21.(12分)已知数列{a n}的前n项和为S n，a1＝1，a2＝13，a na n＋1＝2a n＋1(n∈N*且n≥2)．(1)(2)n项和T n.22.(12分)已知a∈R，函数f(x)＝(－x2＋ax)e x(x∈R)．(1)当a＝2时，求函数f(x)的单调区间；(2)若函数f(x)在(－1,1)上单调递增，求a的取值范围．人教版高中数学选择性必修第二册全册模块综合检测1(解析版)(时间：120分钟，分值：150分)一、单项选择题(本题共8小题，每小题5分，共40分)1．数列{a n }满足a n ＋1＝3a n ＋1，a 1＝1，则此数列的第3项是()A ．13B ．10C ．7D ．4A解析：因为a n ＋1＝3a n ＋1，a 1＝1，所以a 2＝3a 1＋1＝3×1＋1＝4，所以a 3＝3a 2＋1＝3×4＋1＝13.故选A ．2．{a n }为等差数列，且a 7－2a 4＝－1，a 3＝0，则公差d ＝()A ．－2B ．－12C ．12D ．2B解析：∵a 7－2a 4＝－1，∴a 3＋4d －2(a 3＋d )＝－1，∴4d －2d ＝－1，∴d ＝－12.3．已知函数f (x )＝3x 2＋2，则f ′(5)＝()A ．15B ．30C ．32D ．77B解析：依题意f ′(x )＝6x ，所以f ′(5)＝30.故选B ．4．设等比数列{a n }满足a 1＋a 2＝－1，a 1－a 3＝－3，则S 6＝()A ．－63B ．－21C ．21D ．63B解析：设数列{a n }的公比为q ，∵a 1＋a 2＝－1，a 1－a 3＝－3，1＋a 1q ＝－1，1－a 1q 2＝－3，1＝1，＝－2，∴S 6＝a 1(1－q 6)1－q ＝1－643＝－21.故选B ．5．函数f (x )＝xx 2＋1的单调递增区间是()A ．(－∞，－1)B ．(－1,1)C ．(1，＋∞)D ．(－∞，－1)和(1，＋∞)B解析：f (x )的定义域为R ，且f ′(x )＝x 2＋1－2x ·x (x 2＋1)2＝1－x 2(x 2＋1)2＝(1＋x )(1－x )(x 2＋1)2，所以当－1<x <1时，f ′(x )>0，f (x )单调递增，所以f (x )的单调递增区间为(－1,1)．故选B ．6．数列{a n }满足a 1＝1，log 2a n ＋1＝log 2a n ＋1(n ∈N *)，它的前n 项和为S n ，则满足S n >1025的最小n 值是()A ．9B ．10C ．11D ．12C 解析：数列{log 2a n }是以0为首项，公差为1的等差数列，log 2a n ＝0＋(n －1)×1＝n －1，a n＝2n －1，Sn＝1＋2＋22＋23＋…＋2n －1＝1－2n1－2＝2n －1>1025，2n >1026.因为210＝1024,211＝2048，所以，最小n 值是11.选C ．7．函数f (x )＝ln xx ＋1的图象大致是()C解析：由f (x )＝ln xx ＋1，得f ′(x )＝1＋1x －ln x(x ＋1)2(x >0)．令g (x )＝1＋1x－ln x ，则g ′(x )＝－1x 2－1x ＝－1＋x x 2<0，所以g (x )在(0，＋∞)上单调递减．又g (e)＝1e >0，g (e 2)＝1＋1e 2－ln e 2＝1e 2－1<0，所以存在x 0∈(e ，e 2)，使得g (x 0)＝0，所以当x ∈(0，x 0)时，g (x )＞0，f ′(x )＞0；当x ∈(x 0，＋∞)时，g (x )＜0，f ′(x )＜0.所以f (x )在(0，x 0)上单调递增，在(x 0，＋∞)上单调递减．故选C ．8．函数f (x )＝ln x ＋ax 有小于1的极值点，则实数a 的取值范围是()A ．(0,1)B ．(－∞，－1)C ．(－1,0)D ．(－∞，－1)∪(0，＋∞)B解析：因为f(x)＝ln x＋ax，所以函数定义域为{x|x>0}．由f′(x)＝1x＋a＝0，得a≠0，x＝－1a.又函数f(x)＝ln x＋ax有小于1的极值点，所以－1a<1且a<0，所以a<－1.故选B．二、多项选择题(本题共4小题，每小题5分，共20分)9．过点P(2，－6)作曲线f(x)＝x3－3x的切线，则切线方程可能是()A．3x＋y＝0B．24x－y－54＝0C．9x－y－24＝0D．12x－y－24＝0AB解析：∵y′＝3x2－3.设曲线的切点为(x0，y0)，则k＝3x20－3，y0＝x30－3x0.∴切线方程为y－(x30－3x0)＝(3x20－3)(x－x0)．又切线经过点P(2，－6)，则－6－(x30－3x0)＝(3x20－3)(2－x0)，解得x0＝0或x0＝3，∴切点为(0,0)时，切线方程为3x＋y＝0；切点为(3,18)时，切线方程为24x－y－54＝0.10．记S n为等差数列{a n}的前n项和．若a1＋3a5＝S7，则以下结论一定正确的是() A．a4＝0B．S n的最大值为S3C．S1＝S6D．|a3|<|a5|AC解析：设等差数列{a n}的公差为d，则a1＋3(a1＋4d)＝7a1＋21d，解得a1＝－3d，所以a n＝a1＋(n－1)d＝(n－4)d，所以a4＝0，故A正确；因为S6－S1＝5a4＝0，所以S1＝S6，故C正确；由于无法确定d的正负，故S3可能为最大值，也可能为最小值，故B不正确；因为a3＋a5＝2a4＝0，所以a3＝－a5，即|a3|＝|a5|，故D不正确．故选AC．11．在数列{a n}中，若a2n－a2n－1＝p(n≥2，n∈N*，p为常数)，则{a n}称为“等方差数列”．下列对“等方差数列”的判断，其中正确的为()A．若{a n}是等方差数列，则{a2n}是等差数列B．若{a n}是等方差数列，则{a2n}是等方差数列C．{(－1)n}是等方差数列D．若{a n}是等方差数列，则{a kn}(k∈N*，k为常数)也是等方差数列ACD解析：对于A，{a n}是等方差数列，可得a2n－a2n－1＝p(n≥2，n∈N*，p为常数)，即有{a2n}是首项为a21，公差为d的等差数列，故正确；对于B，例如：数列{n}是等方差数列，但是数列{n}不是等方差数列，所以B不正确；对于C，数列{(－1)n}中，a2n－a2n－1＝[(－1)n]2－[(－1)n－1]2＝0(n≥2，n∈N)，所以数列{(－1)n}是等方差数列，故C正确；对于D,数列{a n}中的项列举出来是：a1，a2，…，a k…，a2k，…，数列{a kn}中的项列举出来是：a k，a2k，a3k，….∵a2kn＋k－a2kn＋k－1＝a2kn＋k－1－a2kn＋k－2＝…＝a2kn＋1－a2kn＝p，∴a2kn＋k－a2kn＝(a2kn＋k－a2kn＋k－1)＋(a2kn＋k－1－a2kn＋k－2)＋…＋(a2kn＋1－a2kn)＝kp，∴a2k(n＋1)－a2kn＝kp,所以，数列{a kn}是等方差数列，故D 正确．故选ACD．12．设f(x)＝x a·cos x，x∈π6，π3的最大值为M，则()A．当a＝－1时，M<3B．当a＝2时，M<33C．当a＝1时，M>32D．当a＝3时，M<12AB解析：对于选项A，当a＝－1时，f(x)＝cos xx在区间π6，π3上递减，所以M＝cosπ6π6＝33π<3，故选项A正确．对于选项B，当a＝2时，f(x)＝x2·cos x，则f′(x)＝x cos x(2－xtanx)>0，∴f(x)在区间π6，π3上递增，即M＝π218<33，故选项B正确．对于选项C，当a＝1时，x<tan x恒成立，所以f(x)＝x cos x<tan x cos x＝sin x≤32，所以M<32，故选项C 错误．对于选项D，当a＝3时，f(x)＝x3·cos x，则f′(x)＝x2cos x(3－xtan x)>0，∴f(x)在区间π6，π3上递增，∴M＝12·>12，故选项D错误．故选AB．三、填空题(本题共4小题，每小题5分，共20分)13.已知等差数列{a n}的前n项和为S n，a1＝9，S99－S55＝－4，则a n＝________.－2n＋11解析：设公差为d，因为S99－S55＝－4，所以4d－2d＝－4，即d＝－2.所以a n＝a1＋(n－1)d＝9－2(n－1)＝－2n＋11.14.设函数f(x)＝x3＋ax2，若曲线y＝f(x)在点P(1，f(1))处的切线方程为x＋y＝0，则实数a＝________.－2解析：因为点P(1，f(1))在该切线上，所以f(1)＝－1，则f(1)＝1＋a＝－1，解得a＝－2.15.已知等差数列{a n}的前n项和为S n＝pn2－2n＋q(p，q∈R，n∈N*)，则q＝______；若a1与a5的等差中项为8，则p＋q＝________.02解析：由等差数列的性质可得q＝0.又a1与a5的等差中项为8，所以a1＋a5＝16，即S5＝(a1＋a5)×52＝40，所以25p－10＝40，解得p＝2，即p＋q＝2＋0＝2.16.设a ，b ∈R ，若x ≥0时恒有0≤x 4－x 3＋ax ＋b ≤(x 2－1)2，则ab 等于________．－1解析：验证发现，当x ＝1时，将1代入不等式有0≤a ＋b ≤0，所以a ＋b ＝0，当x ＝0时，可得0≤b ≤1，结合a ＋b ＝0可得－1≤a ≤0.令f (x )＝x 4－x 3＋ax ＋b ，即f (1)＝a ＋b ＝0.又f ′(x )＝4x 3－3x 2＋a ，f ′′(x )＝12x 2－6x ，令f ′′(x )＞0，可得x ＞12，则f ′(x )＝4x 3－3x 2＋a 在0，12上递减，在12，＋∞上递增．又－1≤a ≤0，所以f ′(0)＝a ＜0，f ′(1)＝1＋a ≥0.又x ≥0时恒有0≤x 4－x 3＋ax ＋b ，结合f (1)＝a ＋b ＝0知，1必为函数f (x )＝x 4－x 3＋ax ＋b 的极小值点，也是最小值点．故有f ′(1)＝1＋a ＝0，由此得a ＝－1，b ＝1.所以ab ＝－1.四、解答题(本题共6小题，共70分)17.(10分)在等差数列{a n }中，已知a 1＋a 2＋a 3＝21，a 1a 2a 3＝231.(1)求该数列中a 2的值；(2)求该数列的通项公式a n .解：(1)由等差数列性质得a 1＋a 2＋a 3＝3a 2＝21，∴a 2＝7.(2)设等差数列公差为d ，∴a 1a 2a 3＝(a 2－d )a 2·(a 2＋d )＝7(7－d )(7＋d )＝7(49－d 2)＝231.解得d ＝±4，∴a n ＝a 2＋(n －2)d ，即a n ＝4n －1或a n ＝－4n ＋15.18.(12分)(1)求曲线y ＝1x在点(－1，－1)处的切线方程；(2)求经过点(4,0)且与曲线y ＝1x 相切的直线方程．解：∵y ＝1x ，∴y ′＝－1x2.(1)当x ＝－1时，得在点(－1，－1)处的切线的斜率为－1，∴切线方程为y ＋1＝－(x ＋1)，即x ＋y ＋2＝0.(2)设切点为x 0，1x 0，则切线的斜率为－1x 20，∴切线方程为y －1x 0＝－1x 20(x －x 0)，∵切线过点(4,0)，∴－1x 0＝－1x 20(4－x 0)，解得x 0＝2，∴所求切线方程为y －12＝－14(x －2)，即x ＋4y －4＝0.19.(12分)设f (x )＝a ln x ＋12x －32x ＋1，曲线y ＝f (x )在点(1，f (1))处取得极值．(1)求a 的值；(2)求函数f (x )的单调区间和极值．解：(1)因为f (x )＝a ln x ＋12x －32x ＋1，所以f ′(x )＝a x －12x 2－32.由f ′(1)＝0，可得a －2＝0，解得a ＝2.(2)由(1)可知，f (x )＝2ln x ＋12x －32x ＋1，f ′(x )＝－(3x －1)(x －1)2x 2.令f ′(x )＝0，解得x 1＝13，x 2＝1，又因为函数f (x )定义域为(0，＋∞)，所以f (x )(1，＋∞)故f (x )的极大值为f (1)＝0，f (x )的极小值为2－2ln 3.20.(12分)设数列{a n }满足：a 1＝1，且2a n ＝a n ＋1＋a n －1(n ≥2)，a 3＋a 4＝12.(1)求{a n }的通项公式；(2)n 项和．解：(1)由2a n ＝a n ＋1＋a n －1(n ≥2)可知数列{a n }是等差数列，设公差为d ，因为a 1＝1，所以a 3＋a 4＝a 1＋2d ＋a 1＋3d ＝12，解得d ＝2，所以{a n }的通项公式为a n ＝2n －1(n ∈N *)．(2)由(1)知1a n a n ＋2＝1(2n －1)(2n ＋3)＝n 项和S n …＋＋13－12n ＋1－＝13－n ＋1(2n ＋1)(2n ＋3).21.(12分)已知数列{a n }的前n 项和为S n ，a 1＝1，a 2＝13，a na n ＋1＝2a n ＋1(n ∈N *且n ≥2)．(1)(2)n 项和T n .(1)证明：因为a na n ＋1＝2a n ＋1，所以a n ＝a n ＋1＋2a n a n ＋1，即a n －a n ＋1＝2a n a n ＋1，等式两边同时除以a n a n ＋1，得1a n ＋1－1a n＝2(n ≥2)，且1a 2－1a 1＝2，1，公差为2的等差数列．(2)解：由(1)得1a n ＝2n －1，3na n ＝(2n －1)3n ，则T n ＝1×3＋3×32＋…＋(2n －1)3n ①，3T n ＝1×32＋…＋(2n －3)3n ＋(2n －1)3n ＋1②，①－②得－2T n ＝3＋2(32＋…＋3n )－(2n －1)3n ＋1＝3＋2×9×(1－3n －1)1－3－(2n －1)3n ＋1＝2(1－n )3n ＋1－6，故T n ＝(n －1)3n ＋1＋3.22.(12分)已知a ∈R ，函数f (x )＝(－x 2＋ax )e x (x ∈R )．(1)当a ＝2时，求函数f (x )的单调区间；(2)若函数f (x )在(－1,1)上单调递增，求a 的取值范围．解：(1)a ＝2时，f (x )＝(－x 2＋2x )·e x 的导数为f ′(x )＝e x (2－x 2)．由f′(x)＞0，解得－2<x<2，由f′(x)＜0，解得x＜－2或x> 2.即有函数f(x)的单调递减区间为(－∞，－2)，(2，＋∞)，单调递增区间为(－2，2)．(2)函数f(x)＝(－x2＋ax)·e x的导数为f′(x)＝e x[a－x2＋(a－2)x]．由函数f(x)在(－1,1)上单调递增，则有f′(x)≥0在(－1,1)上恒成立，即为a－x2＋(a－2)x≥0，即有x2－(a－2)x－a≤0，则有1＋(a－2)－a≤0且1－(a－2)－a≤0，解得a≥3 2，则a的取值范围为3 2，＋。

必修二模块综合检测(含解析)

模块综合检测一、选择题(每小题2分，共50分)1．(2010·高考)下列叙述正确的是( )A．DNA是蛋白质合成的直接模板B．每种氨基酸仅由一种密码子编码C．DNA复制就是基因表达的过程D．DNA是主要的遗传物质解析：DNA是蛋白质合成的间接模板，直接模板是mRNA；有的氨基酸可以由几种密码子编码；DNA复制是基因的传递过程，而转录和翻译才是基因的表达过程；绝大多数生物以DNA 为遗传物质，所以DNA是主要的遗传物质。

答案：D2．(2012·高考)下列关于遗传实验和遗传规律的叙述，正确的是( )A．非等位基因之间自由组合，不存在相互作用B．杂合子与纯合子基因组成不同，性状表现也不同C．孟德尔巧妙设计的测交方法只能用于检测F1的基因型D．F2的3∶1性状分离比一定依赖于雌雄配子的随机结合解析：配子形成过程中，非同源染色体上的非等位基因之间自由组合，若两对基因控制一对相对性状，则非等位基因之间可存在相互作用；杂合子和显性纯合子的基因组成不同，但都表现出显性性状；测交实验可以用于检测F1的基因型，也可用于判定F1在形成配子时遗传因子的行为；F2出现3∶1的性状分离比依赖于多种条件，如一对相对性状由一对等位基因控制、雌雄配子随机结合、所有胚胎成活率相等、群体数量足够多等。

答案：D3．下列不属于基因和染色体行为存在平行关系证据的是( )A．基因有完整性和独立性，但染色体的结构会发生变化，从染色体转变成染色质B．在体细胞中，基因和染色体都是成对存在的C．成对的基因和同源染色体都是一个来自父方，一个来自母方D．在减数分裂过程中，非等位基因与非同源染色体都会发生自由组合解析：染色体和染色质的关系是同一物质在不同细胞时期的不同形态，都具有完整性和独立性。

答案：A4. 马与驴杂交所得的骡子一般都不能产生正常的生殖细胞，这是因为( )A．骡子的基因发生了重组B．骡子的染色体结构发生了变异C．骡子的染色体数目不稳定D．骡子的染色体联会紊乱解析：马的体细胞有64条染色体，驴的体细胞有62条染色体，马和驴杂交的后代——骡子的体细胞有63条染色体。

第02讲必修2模块综合检测题含解析精品

必修2模块综合检测题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．直线x ＝tan 60°的倾斜角是( ) A ．90° B ．60° C ．30°D ．不存在2．给出下列四个命题：①垂直于同一直线的两条直线互相平行； ②垂直于同一平面的两个平面互相平行；③若直线l 1，l 2与同一平面所成的角相等，则l 1，l 2互相平行； ④若直线l 1，l 2是异面直线，则与l 1，l 2都相交的两条直线是异面直线．其中假命题的个数是( ) A ．1B ．2C ．3D ．43．方程y ＝ax ＋1a表示的直线可能是( )4．若l 、m 、n 是互不相同的空间直线，α、β是不重合的平面，则下列命题中为真命题的是( )A ．若α∥β，l ⊂α，n ⊂β，则l ∥nB ．若α⊥β，l ⊂α，则l ⊥βC ．若l ⊥n ，m ⊥n ，则l ∥mD ．若l ⊥α，l ∥β，则α⊥β5．已知三棱锥S —ABC 的各顶点都在一个半径为r 的球面上，球心O 在AB 上，SO ⊥底面ABC ，AC ＝2r ，则球的体积与三棱锥体积之比是( )A ．πB ．2πC ．3πD ．4π6．如图，在正方体ABCD －A 1B 1C 1D 1中，E 、F 、G 、H 分别为AA 1、AB 、BB 1、B 1C 1的中点，则异面直线EF 与GH 所成的角等于( )A ．45°B ．60°C ．90°D ．120°7．直线x －2y ＋1＝0关于直线x ＝1对称的直线方程是( ) A ．x ＋2y －1＝0 B ．2x ＋y －1＝0 C ．2x ＋y －3＝0D ．x ＋2y －3＝08．以等腰直角三角形ABC 斜边BC 上的高AD 为折痕，将△ABC 折成二面角C －AD －B 为多大时，在折成的图形中，△ABC 为等边三角形．( )A ．90°B ．60°C ．45°D ．30°9．经过点M (1,1)且在两坐标轴上截距相等的直线是( ) A ．x ＋y ＝2B ．x ＋y ＝1C ．x ＝1或y ＝1D ．x ＋y ＝2或x ＝y10．若圆x 2＋y 2－2x －4y ＝0的圆心到直线x －y ＋a ＝0的距离为22，则a 的值为( ) A ．－2或2 B ．12或32C ．2或0D ．－2或011．直线3x ＋y －23＝0截圆x 2＋y 2＝4得的劣弧所对的圆心角是( ) A ．30°B ．45°C ．60°D ．90°12．在平面直角坐标系中，与点A (1,2)距离为1，且与点B (3,1)的距离为2的直线共有( )A ．1条B ．2条C ．3条D ．4条第Ⅱ卷(非选择题共90分)二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．一个三棱锥S －ABC 的三条侧棱SA 、SB 、SC 两两互相垂直，且长度分别为1，6，3，已知该三棱锥的四个顶点都在同一个球面上，则这个球的表面积为.14．圆x 2＋y 2＋x －6y ＋3＝0上两点P 、Q 关于直线kx －y ＋4＝0对称，则k ＝________． 15．如图，某几何体的三视图，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则该几何体的体积为________．16．已知圆C：x2＋y2－4x－6y＋8＝0，若圆C和坐标轴的交点间线段恰为圆C′直径，则圆C′的标准方程为__________________．三、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)17．(本小题满分10分)已知△ABC三边所在直线方程为AB：3x＋4y＋12＝0，BC：4x －3y＋16＝0，CA：2x＋y－2＝0．求AC边上的高所在的直线方程．18．(本小题满分12分)求经过点P(6，－4)且被定圆O：x2＋y2＝20截得的弦长为62的直线AB的方程．19．(本小题满分12分) 如图所示，在四棱锥P －ABCD 中，底面ABCD 为正方形，E 为侧棱PC 的中点，求证P A ∥平面EDB ．20．(本小题满分12分)如图所示，在四棱柱(侧棱垂直于底面的四棱柱)ABCD －A 1B 1C 1D 1中，已知DC ＝DD 1＝2AD ＝2AB ，AD ⊥DC ，AB ∥DC ．(1)求证D 1C ⊥AC 1；(2)设E 是DC 上一点，试确定E 的位置，使D 1E ∥平面A 1BD ，并说明理由．21．(本小题满分12分)已知M 与两定点O (0,0)、A (3,0)的距离之比为12．(1)求M 点的轨迹方程；(2)若M 的轨迹为曲线C ，求C 关于直线2x ＋y －4＝0对称的曲线C ′的方程．22．(本小题满分12分) 如图所示，四棱锥P —ABCD 的底面ABCD 是半径为R 的圆的内接四边形，其中BD 是圆的直径，∠ABD ＝60°，∠BDC ＝45°．PD 垂直底面ABCD ，PD ＝22R ，E ，F 分别是PB ，CD 上的点，且PE EB ＝DFFC，过点E 作BC 的平行线交PC 于G ．(1)求BD 与平面ABP 所成角θ的正弦值；(2)证明：△EFG 是直角三角形； (3)当PE EB ＝12时，求△EFG 的面积．必修2模块综合检测题参考答案【第1题解析】直线方程为，直线的倾斜角为.故选A【第2题解析】①忽视两直线可以相交，②可以相交、平行，③l 1、l 2可以异面、相交，④与l 1、l 2都相交的两直线可以相交，故选D ．∴SO ＝r ，又∵O 在AB 上，AB ＝2r ，AC ＝r ，∠ACB ＝90°∴BC ＝r ，∴V S －ABC ＝31×21×r ×r ×r ＝31r 3．又∵球的体积V ＝34πr 3，∴VS －ABC V ＝r31＝4π．故选D . 【第6题解析】连接A 1B ，BC 1，A 1C 1，∵E 、F 、G 、H 分别为AA 1、AB 、BB 1、B 1C 1的中点，∴EF ∥21A 1B ，GH ∥21BC 1，∴∠A 1BC 1即为异面直线EF 与GH 所成的角．又∵ABCD —A 1B 1C 1D 1是正方体 ∴A 1B ＝BC 1＝A 1C 1，∴∠A 1BC 1＝60°．故选B .【第7题解析】直线x －2y ＋1＝0与x ＝1的交点为A (1,1)，点(－1,0)关于x ＝1的对称点为B (3,0)也在所求直线上，∴所求直线方程为y －1＝－21(x －1)，即x ＋2y －3＝0．故选D 【第8题解析】关键利用折叠前后不变的垂直关系，如图所示，可知∠BDC 为二面角的平面角，设 BD ＝CD ＝a ，则可求BC ＝AB ＝AC ＝a ，故∠BDC ＝90°．故选A. 【第9题解析】设直线方程为和，再把（1,1）代入直线的方程即得直线方程，故选D.【第10题解析】圆的方程可化为(x －1)2＋(y －2)2＝5，则圆心为(1,2)．由点到直线的距离公式得d ＝2|1－2＋a|＝22，解得a ＝2或0．故选C .【第11题解析】可先求出圆心到直线的距离d ＝，由于半径为2，设圆心角为θ，则知cos 2θ＝23，∴θ＝60°．故选C.【第12题解析】满足要求的直线应为圆心分别为A 、B ，半径为1和2的两圆的公切线，而圆A 与圆B 相交，所以公切线有两条．故选B.线即为球的直径，长为4．∴球半径为2，S 球＝4πR 2＝16π．故填16π .【第16题解析】圆C ：x 2＋y 2－4x －6y ＋8＝0与x 轴没有交点，只与y 轴相交，取x ＝0，得y 2－6y ＋8＝0解得两交点分别为(0,2)和(0,4)，由此得圆C ′的圆心坐标为(0,3)，半径为1，所以标准方程为x 2＋(y －3)2＝1．故填x 2＋(y －3)2＝1 . 【第17题答案】x －2y ＋4＝0．【第17题解析】由4x －3y ＋16＝03x ＋4y ＋12＝0，解得交点B (－4,0)，∵BD ⊥AC ，∴k BD ＝－kAC 1＝21，∴AC 边上的高线BD 的方程为y ＝21(x ＋4)，即x －2y ＋4＝0．【第18题答案】x ＋y －2＝0或7x ＋17y ＋26＝0．【第18题解析】由题意知，直线AB 的斜率存在，且|AB |＝6，OA ＝2，作OC ⊥AB 于C ．在Rt △OAC 中，|OC |＝＝．设所求直线的斜率为k ，则直线的方程为y ＋4＝k (x －6)，即kx －y －6k －4＝0． ∵圆心到直线的距离为，∴1＋k2|6k ＋4|＝，即17k 2＋24k ＋7＝0，∴k ＝－1或k ＝－177．故所求直线的方程为x ＋y －2＝0或7x ＋17y ＋26＝0．【第19题答案】证明见解析【第20题答案】（1）证明见解析；（2）当E 是DC 的中点时，可使D 1E ∥平面A 1BD ．【第20题解析】(1)证明在直四棱柱ABCD －A 1B 1C 1D 1中，连接C 1D ，∵DC ＝DD 1，∴四边形DCC 1D 1是正方形，∴DC 1⊥D 1C ．又AD ⊥DC ，AD ⊥DD 1，DC ∩DD 1＝D ，∴AD ⊥平面DCC 1D 1，D 1C ⊂平面DCC 1D 1，∴AD ⊥D 1C ．∵AD ，DC 1⊂平面ADC 1，且AD ∩DC 1＝D ，∴D 1C ⊥平面ADC 1，又AC 1⊂平面ADC 1，∴D 1C ⊥AC 1．(2)解在DC 上取一点E ，连接AD 1，AE ，设AD 1∩A 1D ＝M ，BD ∩AE ＝N ，连接MN ，∵平面AD 1E ∩平面A 1BD ＝MN ，要使D 1E ∥平面A 1BD ，须使MN ∥D 1E ，又M 是AD 1的中点．∴N 是AE 的中点．又易知△ABN ≌△EDN ，∴AB ＝DE ．即E 是DC 的中点．综上所述，当E 是DC 的中点时，可使D 1E ∥平面A 1BD ．【第21题答案】（1）(x ＋1)2＋y 2＝4；（2）5192＋5122＝4．【第21题解析】 (1)设M 坐标为(x ， y )，由题意得2＋y2x2＋y2＝21，整理得(x ＋1)2＋y 2＝4．所以M 点的轨迹方程为(x ＋1)2＋y 2＝4．(2)因为曲线C ：(x ＋1)2＋y 2＝4，所以C 关于直线2x ＋y －4＝0对称的曲线C ′是与C 半径相同的圆，故只需求C ′的圆心坐标即可，设C ′的圆心坐标(x 0，y 0)．由题意得－4＝0y0，解得512．故曲线C ′的方程为5192＋5122＝4．【第22题答案】（1）1166；（2）证明见解析；（3）94R 2．在△P AB 中，P A 2＋AB 2＝PB 2，即△P AB 是以∠P AB 为直角的三角形，设点D 到面P AB 的距离为h ，由V P —ABD ＝V D —P AB 有P A ·AB ·h ＝AB ·AD ·PD ，即h ＝PA AD ·PD ＝R 2R ＝1166R ，∴sin θ＝BD h ＝1166． (2)证明 ∵EG ∥BC ，∴EB PE ＝GC PG ．而EB PE ＝FC DF ，∴GC PG ＝FC DF，∴GF ∥PD ，∴GF ⊥BC ．而BC ∥EG ，∴GF ⊥EG ，∴△EFG 是直角三角形．(3)解当EB PE ＝21时，BC EG ＝PB PE ＝31，PD GF ＝CD CF ＝32，即EG ＝31BC ＝31×2R ×sin45°＝32R ， GF ＝32PD ＝32×2R ＝32R ，∴S △EFG ＝21EG ·GF ＝21×32R ×32R ＝94R 2．。

必修二湘教版试题：模块综合测评含解析

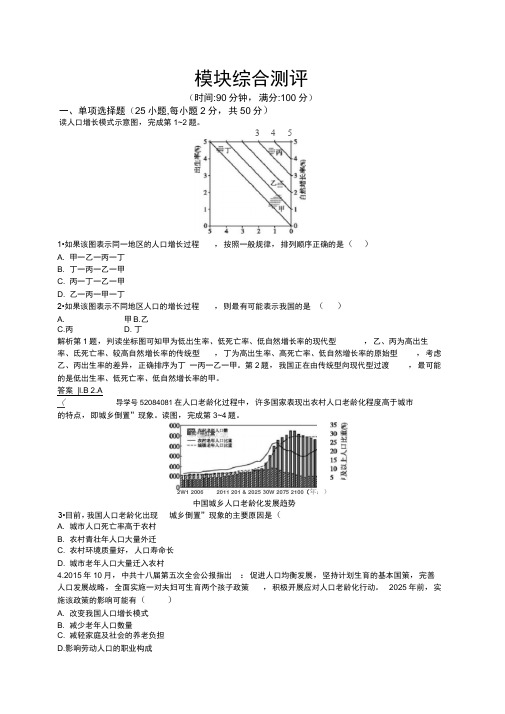
模块综合测评（时间:90分钟，满分:100分）一、单项选择题（25小题,每小题2分，共50分）读人口增长模式示意图，完成第1~2题。

3 4 51•如果该图表示同一地区的人口增长过程，按照一般规律，排列顺序正确的是（）A. 甲一乙一丙一丁B. 丁一丙一乙一甲C. 丙一丁一乙一甲D. 乙一丙一甲一丁2•如果该图表示不同地区人口的增长过程，则最有可能表示我国的是（）A. 甲B.乙C.丙D. 丁解析第1题，判读坐标图可知甲为低出生率、低死亡率、低自然增长率的现代型，乙、丙为高出生率、氐死亡率、较高自然增长率的传统型，丁为高出生率、高死亡率、低自然增长率的原始型，考虑乙、丙出生率的差异，正确排序为丁一丙一乙一甲。

第2题，我国正在由传统型向现代型过渡，最可能的是低出生率、低死亡率、低自然增长率的甲。

答案|l.B 2.A〈导学号52084081在人口老龄化过程中，许多国家表现出农村人口老龄化程度高于城市的特点，即城乡倒置”现象。

读图，完成第3~4题。

■如*平打章2W1 2006 2011 201 & 2025 30W 2075 2100（年：）中国城乡人口老龄化发展趋势3•目前，我国人口老龄化出现城乡倒置”现象的主要原因是（A. 城市人口死亡率高于农村B. 农村青壮年人口大量外迁C. 农村环境质量好，人口寿命长D. 城市老年人口大量迁入农村4.2015年10月，中共十八届第五次全会公报指出：促进人口均衡发展，坚持计划生育的基本国策，完善人口发展战略，全面实施一对夫妇可生育两个孩子政策，积极开展应对人口老龄化行动。

2025年前，实施该政策的影响可能有（）A. 改变我国人口增长模式B. 减少老年人口数量C. 减轻家庭及社会的养老负担D.影响劳动人口的职业构成解析第3题，农村青壮年人口大量外迁，使得农村老年人口比重增高，即为城市倒置”。

第4题,人口增长模式是随社会生产力水平的发展而发展，故A项错；全面放开二胎”政策，是为了减少老年人口比重减轻老龄化程度，会加重家庭负担，特别是少儿数量增加，少儿抚养比上升。

人教高中物理必修2-- 模块综合测评--(附解析答案)

模块综合测评(用时：60分钟满分：100分)一、选择题(本题共8小题，每小题6分，共48分．在每小题给出的四个选项中，1～5小题只有一项符合题目要求，6～8题有多项符合题目要求．全部选对的得6分，选对但不全的得3分，有选错的得0分)1．下列关于力和运动的说法中，正确的是( )A．物体在变力作用下不可能做直线运动B．物体做曲线运动，其所受的外力不可能是恒力C．不管外力是恒力还是变力，物体都有可能做直线运动D．不管外力是恒力还是变力，物体都有可能做匀速圆周运动【解析】物体做曲线运动的条件是合力与速度不在同一条直线上，若受到的变力和速度方向相同，则做直线运动，A错误；平抛运动是曲线运动，过程中受到的合力恒定，等于重力大小，B错误；匀速圆周运动过程中，物体受到的加速度时时刻刻指向圆心，根据牛顿第二定律可知受到的合力时时刻刻指向圆心，为变力，D错误．【答案】 C2．在飞船进入圆形轨道环绕地球飞行时，它的线速度大小( )A．等于7.9 km/sB．介于7.9 km/s和11.2 km/s之间C．小于7.9 km/sD．介于7.9 km/s和16.7 km/s之间【解析】卫星在圆形轨道上运动的速度v＝G Mr.由于r＞R，所以v＜G MR＝7.9 km/s，C正确．【答案】 C3．韩晓鹏是我国首位在冬奥会雪上项目夺冠的运动员．他在一次自由式滑雪空中技巧比赛中沿“助滑区”保持同一姿态下滑了一段距离，重力对他做功1 900 J，他克服阻力做功100 J．韩晓鹏在此过程中( )A．动能增加了1 900 JB．动能增加了2 000 JC．重力势能减小了1 900 JD．重力势能减小了2 000 J【解析】根据动能定理得韩晓鹏动能的变化ΔE＝W G＋W f＝1 900 J－100 J＝1 800 J>0，故其动能增加了1 800 J，选项A、B错误；根据重力做功与重力势能变化的关系W G＝－ΔE p，所以ΔE p＝－W G＝－1 900 J<0，故韩晓鹏的重力势能减小了1 900 J，选项C正确，。

2024_2025学年高中英语模块综合检测含解析新人教版选择性必修第二册

模块综合检测Ⅰ.阅读理解(共15小题；每小题2.5分，满分37.5分)AThe other day I found my old certificates(证书)．We had exams called O levels when we were sixteen.(They are called something different now.) It's so long ago that I'd forgotten what we'd studied.I had nine O levels when I left school and one was in cookery.I was surprised because I'm a terrible cook!——Celia My main memory is what we had to wear! I had a purple skirt with yellow lines on it, and then we had those silly hats with a purple line round them.Girls would do anything to lose their hats.Then when I was about twelve, my parents moved to the United States and I went to my new school in my favourite clothes.It was great!——AliceI had a normal(正常的)day at school, but I also had music lessons because my parents wanted me to learn the violin.So I had special classes at school before everyone else arrived.So most pupils started at eight thirty, but I had to go to school at seven o'clock for my music lessons.Then at the end of the day, I'd do sport, so often I didn't finish until five in the afternoon.That was a long day for a tenyearold.——DeanI travel a lot nowadays, and I suppose my interest in other countries began with geography and a teacher I liked called Mr.Byford.We'd learn about faraway places and strange areas.I think it made me want to visit them later in life.——Susan 【语篇解读】本文是应用文，四个人共享了各自对学生时代的回忆。

2024_2025学年高中英语模块综合检测2含解析外研版选择性必修第二册

模块综合检测(二)Ⅰ.阅读理解(共15小题；每小题2.5分，满分37.5分)AHomestay in Sydney，Australia1．Four persons wrote these passages so as to________．A．look for suitable roommatesB．search for homestay informationC．book a suitable room in SydneyD．advertise rooms for homestayD[写作意图题。

依据文章的标题“Homestay in Sydney，Australia”可知，四个人写这些文章是为了给住宿家庭做广告。

故选D。

]2．One person who lives in John's apartment________．A．can smoke in the apartmentB．can use John's washing machine to wash clothesC．has to walk a long way to get to the sports fieldD．is provided with breakfast and lunch on weekdaysD[细微环节理解题。

依据其次则广告中的“The cost is $220 per week，including breakfast and lunch on weekdays.”可知，住在John的公寓的人在工作日被供应早餐和午餐。

故选D。

]3．If Peter wants to find a homestay room near Sydney University，he should send an email to ________．A．markalarms@ optusnet .auB．mineanny@ hotmailC．cliqi9239@ hotmailD．ainsley gilkes@ yahoo .auB[细微环节理解题。

高一语文(语文版)必修2 模块综合测评 Word版含解析.docx

模块综合测评(满分:150分时间:150分钟)第Ⅰ卷阅读题甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成第1~3题。

①一场名为“ALS冰桶挑战赛”的活动正在互联网线上线下如火如荼地进行。

活动规则极为简单,挑战者要么在24小时内向美国ALS(肌肉萎缩性侧面硬化病)公益协会捐出100美元,要么往自己头上浇一桶冰水,并录下视频上传至网络,同时向自己的三个朋友发起挑战。

②关于“冰桶挑战”的起源,一个广为认可的说法是,美国一位身患ALS的波士顿大学棒球手弗雷特及其朋友们发起了这项活动。

活动的目的在于筹款,并让世人对这种被称为“渐冻人”的罕见疾病有更多的了解。

据悉,目前针对ALS没有比较好的治疗方法,患者存活期一般是2~5年。

英国物理学家斯蒂芬·霍金就是ALS病的患者。

③借助于社交网络的力量,“冰桶挑战”迅速传播。

美国《大西洋月刊》15日称,Facebook上参与这个话题的网友已达1 500万人次。

参与者包括Facebook创始人扎克伯格、微软创始人比尔·盖茨、特斯拉创始人马斯克等。

名人效应带来连锁反应。

短短两周内,ALS协会已经收到近400万美元的捐款,是2013年同期的4倍。

不过“认怂”的名人也有。

据国外媒体报道,美国总统奥巴马在被点名后,并没有选择湿身,而是选择用捐款来支持该活动。

这几天,这桶冰水已浇至中国。

在新浪微博上,“冰桶挑战”是排名第一的热门话题,短短几天,阅读量已达数亿。

小米科技董事长雷军、优酷土豆CEO古永锵、奇虎董事长周鸿祎、百度董事长李彦宏等都完成了各自挑战。

可以想象的是,国内掀起的“冰桶”热,动静也不会小。

④然而,在“冰桶”热背后,却有着两种截然不同的舆论。

一部分网友不屑于一些名人在传播公益的同时夹带“私货”,批评该活动是炒作多于公益;另一部分网友则认为,不管形式如何,只要达到目的就好。

笔者以为,单从宣传角度来看,该活动确实达到了目的,让更多人了解这一病症,唤起世人的同情心。

物理模块必修2综合检测(含详解答案)

物理模块必修2综合检测（含详解答案）限时：90分钟总分：100分一、选择题(每小题4分，共40分)1．某物体在一足够大的光滑水平面上向西运动，当它受到一个向南的恒定外力作用时，物体的运动将是()A．直线运动且是匀变速直线运动B．曲线运动但加速度方向不变、大小不变，是匀变速曲线运动C．曲线运动但加速度方向改变、大小不变，是非匀速曲线运动D．曲线运动但加速度方向和大小均改变，是非匀变速曲线运动2．某物体的运动由水平方向和竖直方向两个分运动合成，已知水平方向的运动加速度为4m/s2，竖直方向的加速度为3m/s2，则该物体实际运动的加速度大小为()A．7m/s2B．1m/s2C．5m/s2D．在1～7m/s2之间，具体大小不确定3．某人以一定的速率乘小船垂直河岸向对岸划去，在平时水流缓慢时，渡河所用时间为2分钟，某次由于降雨，河里的水流速度加快，若这个人仍以这一速率垂直渡河，则这次渡河的时间() A．比2分钟时间长B．比2分钟的时间短C．时间仍等于2分钟D．由于水速不清，故时间不能确定4．质量为m的物体随水平传送带一起匀速运动，A为传送带的终端皮带轮．如图1所示，皮带轮半径为r ，要使物体通过终端时能水平抛出，皮带轮的转速至少为( )图1A.12πg r B.gr C.gr D.gr 2π5．如图2所示，质量为m 的小球固定在长为l 的细轻杆的一端，绕细杆的另一端O 在竖直平面内做圆周运动．球转到最高点A 时，线速度的大小为gl /2，此时( )图2A ．杆受到mg /2的拉力B ．杆受到mg /2的压力C．杆受到3mg/2的拉力D．杆受到3mg/2的压力6．(2011·山东卷)甲、乙为两颗地球卫星，其中甲为地球同步卫星，乙的运行高度低于甲的运行高度，两卫星轨道均可视为圆轨道．以下判断正确的是()A．甲的周期大于乙的周期B．乙的速度大于第一宇宙速度C．甲的加速度小于乙的加速度D．甲在运行时能经过北极的正上方7．木星至少有16颗卫星，1610年1月7日伽利略用望远镜发现了其中的4颗．这4颗卫星被命名为木卫1、木卫2、木卫3和木卫4.他的这个发现对于打破“地心说”提供了重要的依据．若将木卫1、木卫2绕木星的运动看做匀速圆周运动，已知木卫2的轨道半径大于木卫1的轨道半径，则它们绕木星运行时()A．木卫2的周期大于木卫1的周期B．木卫2的线速度大于木卫1的线速度C．木卫2的角速度大于木卫1的角速度D．木卫2的向心加速度大于木卫1的向心加速度8．星球上的物体在星球表面附近绕星球做匀速圆周运动所必须具备的速度v1叫做第一宇宙速度，物体脱离星球引力所需要的最小速度v2叫做第二宇宙速度，v2与v1的关系是v2＝2v1.已知某星球的半径为r，它表面的重力加速度是地球表面重力加速度g的1/6.若不计其他星球的影响，则该星球的第一宇宙速度v1和第二宇宙速度v2分别是()A．v1＝gr，v2＝2grB．v1＝gr6，v2＝gr3C．v1＝gr6，v2＝gr3D．v1＝gr，v2＝gr 39．中国人自己制造的第一颗直播通信卫星“鑫诺二号”在西昌卫星发射中心发射成功，定点于东经92.2度的上空(拉萨和唐古拉山口即在东经92.2.度附近)，“鑫诺二号”载有22个大功率转发器，如果正常工作，可同时支持200余套标准清晰度的电视节目，它将给中国带来1 000亿元人民币的国际市场和几万人的就业机会，它还承担着“村村通”的使命，即满足中国偏远山区民众能看上电视的愿望．关于“鑫诺二号”通信卫星的说法正确的是()A．它一定定点在赤道上空B．它可以定点在拉萨或唐古拉山口附近的上空C．它绕地球运转，有可能经过北京的上空D．与“神舟六号”载人飞船相比，“鑫诺二号”的轨道半径大，环绕速度小10．有一宇宙飞船到了某行星上(该行星没有自转运动)，以速度v接近行星赤道表面匀速飞行，测出运动的周期为T，已知万有引力常量为G，则可得()A．该行星的半径为v T 2πB．该行星的平均密度为3πGT2C．无法测出该行星的质量D．该行星表面的重力加速度为2πv T二、填空题(每题5分，共20分)11．在“探究平抛运动的运动规律”的实验中，可以描绘出小球平抛运动的轨迹，实验简要步骤如下：A．让小球多次从________位置上滚下，在一张印有小方格的纸上记下小球碰到铅笔笔尖的一系列位置，如图3中的a、b、c、d所示．B．按图安装好器材，注意斜槽末端________，记下平抛初位置O点和过O点的竖直线．C．取下白纸以O为原点，以竖直线为y轴建立平面直角坐标系，用平滑曲线画出小球做平抛运动的轨迹．图3图4(1)完成上述步骤，将正确的答案填在横线上．(2)上述实验步骤的合理顺序是________．(3)已知图3中小方格的边长L＝2.5 cm，则小球平抛的初速度为v0＝________m/s，小球在b点的速率为________m/s.(取g＝10m/s2) 12．小明同学在学习了圆周运动的知识后，设计了一个课题，名称为：快速测量自行车的骑行速度．他的设想是：通过计算踏脚板转动的角速度，推算自行车的骑行速度．经过骑行，他得到如下的数据：在时间t内踏脚板转动的圈数为N，那么脚踏板转动的角速度ω＝________；要推算自行车的骑行速度，还需要测量的物理量有________；自行车骑行速度的计算公式v＝________.图513．我国在1984年4月8日成功发射了第一颗试验地球同步通信卫星，1986年2月1日又成功发射了一颗地球同步通信卫星，它们进入预定轨道后，这两颗人造卫星的运行周期之比T1∶T2＝________，轨道半径之比R1∶R2＝________，绕地球公转的角速度之比ω1∶ω2＝________.14．1969年7月21日，美国宇航员阿姆斯特朗在月球上烙下了人类第一只脚印，迈出了人类征服月球的一大步．在月球上，如果阿姆斯特朗和同伴奥尔德林用弹簧秤称量出质量为m的仪器的重力为F；而另一位宇航员科林斯驾驶指令舱，在月球表面附近飞行一周，记下时间为T，根据这些数据写出月球质量的表达式________．三、计算题(每题10分，共40分)15．(10分)水平抛出的一个石子，经过0.4 s落到地面，落地时的速度方向跟水平方向的夹角是53°，(g取10m/s2，sin53°＝0.8，cos53°＝0.6)求：(1)石子的抛出点距地面的高度；(2)石子抛出的水平初速度；(3)石子的落地点与抛出点的水平距离．16．(10分)如图6所示，一过山车在半径为R的轨道内运动，过山车的质量为M，里面人的质量为m，运动过程中人与过山车始终保持相对静止．求：(1)当过山车以多大的速度经过最高点时，人对座椅的压力大小刚好等于人的重力？此时过山车对轨道的压力为多大？(2)当过山车以6gR的速度经过最低点时，人对座椅的压力为多大？图617. (10分)如图7所示，在倾角为α＝30°的光滑斜面顶点处固定一原长l0＝0.2m的轻弹簧，弹簧另一端与放在光滑斜面体上质量m ＝2kg的物体C相连后，弹簧长度变为l1＝0.25m．当斜面连同物体C 一起绕竖直轴AB 转动时，求：图7(1)转速n ＝60 r/min 时弹簧的长度是多少？(2)转速为多少时，物体C 对斜面无压力？(g 取10m/s 2)18．(10分)2008年12月，天文学家们通过观测的数据确认了银河系中央的黑洞“人马座A *”的质量与太阳质量的倍数关系．研究发现，有一星体S2绕人马座A *做椭圆运动，其轨道半长轴为9.50×102天文单位(地球公转轨道的半径为一个天文单位)，人马座A *就处在该椭圆的一个焦点上．观测得到S2星的运行周期为15.2年．(1)若将S2星的运行轨道视为半径r ＝9.50×102天文单位的圆轨道，试估算人马座A *的质量M A 是太阳质量M S 的多少倍(结果保留一位有效数字)；(2)黑洞的第二宇宙速度极大，处于黑洞表面的粒子即使以光速运动，其具有的动能也不足以克服黑洞对它的引力束缚．由于引力的作用，黑洞表面处质量为m 的粒子具有的势能为E p ＝－G Mm R (设粒子在离黑洞无限远处的势能为零)，式中M、R分别表示黑洞的质量和半径．已知引力常量G＝6.7×10－11N·m2/kg2，光速c＝3.0×108m/s，太阳质量M S＝2.0×1030kg，太阳半径R S＝7.0×108m，不考虑相对论效应，利用上问结果，在经典力学范围内求人马座A*的半径R A与太阳半径R S之比应小于多少(结果按四舍五入保留整数)．答案与解析1.解析：由于物体后来受到的是一个向南的恒力作用，因而物体将做匀变速运动，又由于物体所受的这个力向南，与物体原来的运动方向不在一直线上，因而物体一定做曲线运动，一定要注意加速度是由物体所受的外力和质量决定的，且加速度方向总和合外力方向一致．答案：B2.解析：有的人可能会错选D，造成错误的主要原因是对两个分运动的确定性没有把握好，因为两个分运动一个水平方向另一个竖直方向，大小也都确定了，当然合运动也是一个定值，而不是一个范围，由平行四边形定则很容易可以求出合运动的加速度a＝5m/s2.若两个分运动是确定的，则合运动就一定是确定的，因而做题前，一定要看清题目，避免画蛇添足．答案：C3.解析：造成错解的主要原因是对运动的独立性没有理解透彻，认为水流加快时，船的速度增大，渡河时间减少，而实际上，船的速度增大了，但是船的位移也增大了，而船在垂直河岸的分速度大小并第 10 页共 15 页金太阳新课标资源网没有改变，河的宽度是一定的，由于渡河时间等于垂直河岸的位移与垂直河岸的渡河速度即小船速度的比值，而以上两个量都不变，故时间不变，仍为2分钟．答案：C4.解析：如果物体的速度为gr ，则在圆周最高点mg －F N ＝m v 2r ，F N ＝0，即对轨道无压力，物体做平抛运动．答案：C5.解析：假设球受杆的拉力，则T ＋mg ＝m v 2l ，T ＝－mg 2，负号说明球受杆的力应向上，故杆受球的压力大小为mg 2. 答案：B6.解析：本题考查万有引力与航天中的卫星问题，意在考查考生对天体运动规律、第一宇宙速度的理解和同步卫星的认识．对同一个中心天体而言，根据开普勒第三定律可知，卫星的轨道半径越大，周期就越长，A 正确．第一宇宙速度是环绕地球运行的最大线速度，B错．由G Mm r 2＝ma 可得轨道的半径大的天体加速度小，C 正确．同步卫星只能在赤道的正上空，不可能经过北极的正上方，D 错．答案：AC7.解析：木卫1和木卫2做匀速圆周运动所需要的向心力由万有引力提供，即G Mm r 2＝ma ＝m v 2r ＝mω2r ＝m ⎝ ⎛⎭⎪⎫2πT 2r ，解得a ＝G M r 2，v ＝ G M r ，ω＝ G M r 3，T ＝ 4π2r 3GM ；由题设条件知r 2>r 1，所以a 1>a 2，v 1>v 2，ω1>ω2，T 1<T 2，选项A 正确．金太阳新课标资源网答案：A8.解析：对于贴着星球表面的卫星mg ′＝m v 21r ，解得：v 1＝g ′r ＝gr6，又由v 2＝2v 1，可求出v 2＝ gr 3. 答案：B9.解析：“鑫诺二号”通讯卫星是同步卫星，必位于赤道上空，A 正确．由地理知识，拉萨、唐古拉山、北京均不在赤道，B 、C 错误．同步卫星T ＝24 h ，大于“神舟六号”飞船的周期，根据GMmr 2＝m 4π2T 2r ，T ＝4π2r 3GM ，知T 大，r 大，v ＝ GMr ，则v 小，D 正确．答案：AD10.解析：由T ＝2πR v 可得：R ＝v T 2π，A 正确；又GMmR 2＝m v 2R 可得：M ＝v 3T 2πG ，C 错误；由M ＝43πR 3·ρ，得：ρ＝3πGT 2，B 正确，又GMmR 2＝mg ，得：g ＝2πvT ，D 正确．答案：ABD11.解析：由表格可以看出，a 、b 、c 、d 四点水平方向之间的距离都是2个方格边长，所以它们相邻两点之间的时间间隔相等，根据Δy bc －Δy ab ＝gt 2得t ＝ Δy bc －Δy abg ＝ 2l －lg ＝l g ＝2.5×10－210s ＝0.05 s. 平抛运动的初速度等于水平方向匀速运动的速度，即 v 0＝x t ＝2l t ＝2×2.5×10－20.05m/s ＝1.0m/s ，金太阳新课标资源网b 点的竖直分速度v by ＝3l 2t ＝3×2.5×10－22×0.05m/s ＝0.75m/s ，故b 点的速率v b ＝v 20＋v 2y ＝1.25m/s.答案：(1)A.同一 B ．切线水平 (2)BAC (3)1.0 1.25 12.解析：依据角速度的定义式ω＝θt ，得ω＝2N πt ；要求自行车的骑行速度，还要知道牙盘的齿轮数m (半径r 1)、飞轮的齿轮数n (半径r 2)、自行车后轮的半径R ；由v 1＝ωr 1＝v 2＝ω2r 2，又齿轮数与轮子的半径成正比，则有ωm ＝ω2n ，且ω2＝ω后，v ＝ω后R ，联立以上各式解得v ＝m n ωR ＝2πmNnt R 或v ＝r 1r 2ωR ＝2πNr 1tr 2R .答案：2πNt 牙盘的齿轮数m 、飞轮的齿轮数n 、自行车后轮的半径R (牙盘的半径r 1、飞轮的半径r 2、自行车后轮的半径R )mn ωR 或2πmNnt R (2πNr 1r 2t R 或r 1r 2ωR )．13.解析：所有同步卫星除与质量有关的物理量不同外，其他所有物理量的大小都是相同的．答案：1∶1 1∶1 1∶114.解析：在月球表面质量为m 的物体重力近似等于万有引力．设月球的半径为R ，则由F ＝GMmR2，得R ＝GMmF ①；设指令舱的质量为m ′，指令舱靠近月球表面飞行，其轨道半径约等于月球半径，做圆周运动的向心力等于万有引力，则有GMm ′R 2＝m ′⎝ ⎛⎭⎪⎫2πT 2R ②，则由①②式得M ＝T 4F 316π4Gm 3.金太阳新课标资源网答案：T 4F 316π4Gm 315.解析：(1)由h ＝12gt 2得h ＝0.8m.(2)tan53°＝v y v 0＝gtv 0解得v 0＝3m/s.(3)x ＝v 0t ＝1.2m.答案：(1)0.8m (2)3m/s (3)1.2m16.解析：(1)在最高点时，人的重力和座椅对人的压力的合力提供向心力，根据牛顿第二定律F N ＋mg ＝m v 21R ，F N ＝mg ，解得v 1＝2gR .将过山车和人作为一个整体，向心力由整体的总重力和轨道的压力的合力提供，设此时轨道对整体的压力为F ，根据牛顿第二定律F＋(M ＋m )g ＝(M ＋m )v 21R ，解得F ＝(M ＋m )g .根据牛顿第三定律，过山车对轨道的压力为(M ＋m )g ，方向向上． (2)在最低点时，以人为研究对象 F ′－mg ＝m v ′2R ，解得F ′＝7mg .根据牛顿第三定律可知，人对座椅的压力为7mg ，方向向下．答案：(1)2gR (M ＋m )g (2)7mg 17.解析：金太阳新课标资源网图8物体在斜面上受到三个力作用：mg 、F N 和F ，如图1所示．设弹簧劲度系数为k ，物体放在斜面上平衡时F ＝mg sin30°，由胡克定律得F ＝k (l 1－l 0)，所以k (l 1－l 0)＝mg sin30°，k ＝mg sin30°/(l 1－l 0)＝200N/m.(1)设斜面体和物体C 以n ＝60 r/min ＝1 Hz 转动时弹簧的长度为l 2，此时，物体所受的力在竖直方向上平衡，即F N cos30°＋k (l 2－l 0)sin30°＝mg ，在水平方向上合力为向心力，即k (l 2－l 0)cos30°－F N sin30°＝4π2n 2ml 2cos30°，由以上两式解得L 2＝0.36m.(2)设转速为n ′时，物体对斜面无压力，此时弹簧的长度为l 3.由k (l 3－l 0)sin30°＝mg ，k (l 3－l 0)cos30°＝4π2n ′2ml 3cos30°，得l 3＝mgk sin30°＋l 0＝0.4m ，所以n ′＝k (l 3－l 0)4π2ml 3≈1.125 r/s ＝67.5 r/min.答案：(1)0.36m (2)67.5 r/min18.解析：(1)S2星绕人马座A *做圆周运动的向心力由人马座A *对S2星的万有引力提供，设S2星的质量为m S2，角速度为ω，周期为T ，则G M A m S2r2＝m S2ω2r ，金太阳新课标资源网ω＝2πT ，设地球质量为m E ，公转轨道半径为r E ，周期为T E ，则 G M S m E r 2E ＝m E (2πT E)2r E ，综合上述三式得M A M S ＝⎝ ⎛⎭⎪⎫r r E 3⎝ ⎛⎭⎪⎫T E T 2.式中T E ＝1年， r E ＝1天文单位，代入数据可得M AM S≈4×106. (2)引力对粒子作用不到的地方即为无限远，此时粒子的势能为零．“处于黑洞表面的粒子即使以光速运动，其具有的动能也不足以克服黑洞对它的引力束缚”，说明了黑洞表面处以光速运动的粒子在远离黑洞的过程中克服引力做功，粒子在到达无限远之前，其动能便减小为零，此时势能仍为负值，则其能量总和小于零．根据能量守恒定律，粒子在黑洞表面处的能量也小于零，则有12mc 2－G MmR <0，依题意可知R ＝R A ，M ＝M A ，可得R A <2GM Ac2，代入数据得R A <1.2×1010m. R AR S<17. 答案：(1)4×106R AR S<17。

2024_2025学年高中英语模块综合测评含解析新人教版必修2

模块综合测评(时间:120分钟满分:150分)第Ⅰ卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。

每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1.What does the man mean?A.She should take more exercise.B.She’d better have a few days’ rest.C.She is badly ill.2.On which day will Mr White be free?A.This Saturday.B.Next Friday.C.Next Sunday.3.Where does the conversation most probably take place?A.At a bookstore.B.At a post office.C.At a supermarket.4.How many people are mentioned in the dialogue?A.At least four.B.Only three.C.More than five.5.At which price may the man buy the chair in the end?A.$15.B.$25.C.$20.其次节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。

每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。

听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料,回答第6至8题。

6.What are the two speakers talking about?A.The building of London.B.The traffic of London.C.Travelling in Britain.7.What does the woman think of the London taxi?A.Rather slow. B fortable. C.Too expensive.8.In the woman’s opinion,what is the best way to travel in London?A.By bus.B.By underground.C.On foot.听第7段材料,回答第9至11题。

高中英语模块综合检测(含解析)新人教版必修2

模块综合检测选择题部分Ⅰ.阅读理解(共10小题；每小题2.5分，满分25分)阅读下列短文，从每题所给的A、B、C和D四个选项中，选出最佳选项。

AWhat makes you happy? Music? Money? Spending time with friends?For American young people, family time is the main source (来源) of happiness, according to a recent survey (调查) of 1,280 American young people.Most of them say it is a good relationship with their parents that makes them happy.“My mum tells me that, even if I do something silly, she's still going to love me no matter what happens.Just knowing that makes me feel very happy，” says Kristiana St.John, 17, a high school student in New York.After family, it is relationships with friends that seem to matter most.There were also many other kinds of answers given to the “What makes you happy？” question.For Chad Fiedler, 17, ha ppiness is “just waking up in the morning and looking forward to what he's going to do that day”．And for Esohe Roland, 14, it's “playing the trumpet (小号) in his school band”．So, what is happiness? Let's hear what Chinese teenagers want to say.For Bao Yiqiao, 15, Beijing, happiness comes from success brought by hard work.She felt happy when she was admitted to a top high school.She was happy when she came fifth in a recent swimming competition.For Jiang Wenyu, 17, Dalian, spending time with his family makes him happy.Whenever he feels down at school, his parents encourage him to go on.They always help him to find a way out.语篇解读：本文主要介绍的是不同的人对幸福的来源有不同的感受和理解。

2024_2025学年新教材高中英语模块检测含解析新人教版必修第二册

模块素养检测(Units 1～5)(120分钟150分)第一部分听力(共两节, 满分30分)第一节(共5小题; 每小题1. 5分, 满分7. 5分)听下面5段对话。

每段对话后有一个小题, 从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。

听完每段对话后, 你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

Text 1W: Look at these hats. Aren’t they lovely?M: ①Yes, they are lovely, but the price is not lovely.1. What is the man’s opinion about these hats?A. They are attractive but expensive.B. They are lovely and cheap.C. They aren’t attractive but cheap.答案: AText 2W: Don’t be nervous. ②They will simply measure your height and weight and then take your blood pressure.M: That doesn’t sound too bad. I think I’m ready for it.2. What will the man have?A. A blood test.B. A physical examination.C. A job interview.答案: BText 3W: ③I heard you got full marks in the math exam. Congratulations!M: Thanks! ③I’m sure you also did a good job.3. What’s the probable relationship between the speakers?A. Teacher and student.B. Classmates.C. Colleagues.答案: BText 4M: I’m afraid we’ll have to cancel the trip, G race.W: Yeah, this is much more important. ④You’ll have to go to the funeral. He was your uncle.4. Why can’t the speakers go on the trip?A. The man’s uncle died.B. The man got sick.C. The woman has to attend a meeting.答案: AText 5M: I wish I had learned English well when I was in high school.W: ⑤You always said you didn’t think English was of great importance.M: ⑤I realize I was wrong and it’s too late.W: It’s never too late to learn.5. What can we know about the man?A. He has realized the significance of English.B. He used to learn English well.C. It is too late for him to learn English now.答案: A其次节(共15小题; 每小题1. 5分, 满分22. 5分)听下面5段对话或独白。

必修二模块综合检测(含解析)

人教版高中数学选择性必修第二册 全册模块综合检测2(含解析)

高中数学 模块综合检测2(含解析)新人教A版选择性必修第二册-新人教A版高二选择性必修第二册数学试题

2024_2025学年新教材高中英语模块综合检测2含解析牛津译林版必修第二册

2025版新教材高中英语模块综合质量检测二新人教版必修第二册

人教版高中数学选择性必修第二册 全册模块综合检测1(含解析)

必修二模块综合检测(含解析)

第02讲 必修2模块综合检测题 含解析 精品

必修二湘教版试题：模块综合测评含解析

人教高中物理必修2-- 模块综合测评--(附解析答案)

2024_2025学年高中英语模块综合检测含解析新人教版选择性必修第二册

2024_2025学年高中英语模块综合检测2含解析外研版选择性必修第二册

高一语文(语文版)必修2 模块综合测评 Word版含解析.docx

物理模块必修2综合检测(含详解答案)

2024_2025学年高中英语模块综合测评含解析新人教版必修2

高中英语模块综合检测(含解析)新人教版必修2

2024_2025学年新教材高中英语模块检测含解析新人教版必修第二册

人教版高中数学选择性必修第二册全册模块综合检测2(含解析)

高中数学模块综合检测2(含解析)新人教A版选择性必修第二册-新人教A版高二选择性必修第二册数学试题

人教版高中数学选择性必修第二册全册模块综合检测1(含解析)

第02讲必修2模块综合检测题含解析精品