骰子建模

合集下载

(完整word版)3DONE三维设计色子

第一章初识三维设计第五节骰子学习目标：1，学会设计较为复杂的三维实体，增强三维立体感2，掌握布尔运算3，掌握不同的确定点方法4，掌握材质渲染命令5，培养三维空间坐标计算能力骰子，古代汉族民间娱乐用来投掷的博具。

相传是三国时魏国曹植所造。

通常作为桌上游戏的小道具，最常见的骰子是六面骰，它是一颗立方体，上面分别有一到六个孔（或数字），其相对两面之数字和必为七。

中国的骰子习惯在一点和四点涂上红色。

另外，你知道“骰子”应该怎么读么？应该读作“tóu zǐ”，而不是“shǎi zǐ”哦，你中枪了没有？一、绘制过程1，骰子的基本体就是一个正六面体，在“基本实体”中选择“六面体”，把“点”定在（0, 0, 0），长宽高都设为20，（如图1-5-1）。

图1-5-12，绘制点数1点数1，在六面体的上底面中心挖去一个半球即可。

因此，选择“基本实体”中的“球体”，“中心”定位在上底面的中心（如图1-5-2）。

在定位时，鼠标沿着上底面轻轻移动，可以感受到鼠标会被自动地“吸附”到5个特殊的点去：即上底面的4个顶点和中心点。

图1-5-2如果感受不到鼠标被自动“吸附”到中心点，那还有另外两种方法：第一，根据在开始绘制六面体时，我们设定了它的“点”是（0, 0, 0），它的高度是20，因此它上底面的中心点也就应该是（0, 0, 20），可以自行输入这个“中心”坐标。

第二，在定位时，选择不同的方式。

点击“中心”框右侧的下拉箭头，选择“两者之间”（如图1-5-3），然后依次点击位于对角线上的两个顶点（即A、C点或B、D点），选择“百分比”为“50”。

通过这样的操作就可以定位出到点A距离为AC长度50%的点，即AC的中点（如图1-5-4）。

那为什么是50%？因为上底面的中心也就是对角线的中点。

图1-5-3图1-5-4修改球的半径为“4”，确定后得到如图1-5-5。

但这并不是我们所设想的效果，我们设想的应该是凹进去一个坑，而不是凸出来。

骰子简单制作方法

骰子简单制作方法骰子是一种常见的游戏工具，它有六个面，每个面上分别有一到六个点，被广泛用于各种棋盘游戏、赌博游戏和教具。

如果你想亲手制作一个自己的骰子，那么本文将为你介绍一种简单的制作方法。

下面是详细的步骤：材料准备：- 一个方形的纸盒（如药品包装盒或饼干盒）- 海绵材料- 胶水或胶带- 颜料笔或彩色纸- 剪刀步骤一：准备纸盒并切割首先，找一个方形的纸盒作为骰子的外层。

你可以使用一个药品包装盒或没有印刷的饼干盒。

确保纸盒的四个面都是平坦的。

接下来，用剪刀将纸盒的盖子和底部完全剪掉，只保留四个侧面。

步骤二：制作骰子骨架使用剩余的纸盒四个侧面构建骰子的骨架。

将纸盒切割成类似正方形的形状，每边长度为5厘米。

然后将这些纸板拼接在一起，形成一个长方体，确保每个面都平行且垂直于相邻的面。

你可以使用胶水或胶带固定纸板，以便确保骨架的稳定性。

步骤三：填充骨架为了让骰子有合适的重量和稳定性，我们需要将骨架填充物。

这里我们可以使用海绵材料。

将海绵切割成与纸盒大小相同的小块，然后将其粘贴在骨架内部的每个面上。

确保填充物均匀分布，并使骰子的触感更加舒适。

步骤四：装饰骰子表面现在，你可以根据个人喜好和创意来装饰骰子的外观。

你可以使用彩色纸剪出不同的形状贴在骰子的每个面上，或者用颜料笔直接在骰子上绘制图案。

你可以选择用不同的颜色来代表不同的数字（例如，红色代表数字1，蓝色代表数字2，以此类推）。

步骤五：等待干燥完成装饰后，确保颜料或胶水干透。

这样可以确保骰子的外观持久耐用，并避免在使用时将颜料或胶水脱落。

制作完成后，你就可以享受用自己亲手制作的骰子玩游戏的乐趣了。

这个制作过程简单明了，不需要太多的专业工具和技能，适用于任何年龄层次的人。

当然，如果你对于骰子的外观和纸盒材质有更高要求，你可以尝试使用更高级的材料和工具来进行制作。

总的来说，制作骰子是一项有趣的手工活动，可以锻炼你的动手能力和创造力，同时也是一个很好的家庭亲子活动。

如何用简单易懂的例子解释隐马尔可夫模型教学文案

如何用简单易懂的例子解释隐马尔可夫模型如何用简单易懂的例子解释隐马尔可夫模型？ - 知乎隐马尔可夫（HMM）好讲，简单易懂不好讲。

我想说个更通俗易懂的例子。

我希望我的读者是对这个问题感兴趣的入门者，所以我会多阐述数学思想，少写公式。

霍金曾经说过，你多写一个公式，就会少一半的读者。

还是用最经典的例子，掷骰子。

假设我手里有三个不同的骰子。

第一个骰子是我们平常见的骰子（称这个骰子为D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6。

第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是1/4。

第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8。

假设我们开始掷骰子，我们先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。

然后我们掷骰子，得到一个数字，1，2，3，4，5，6，7，8中的一个。

不停的重复上述过程，我们会得到一串数字，每个数字都是1，2，3，4，5，6，7，8中的一个。

例如我们可能得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4这串数字叫做可见状态链。

但是在隐马尔可夫模型中，我们不仅仅有这么一串可见状态链，还有一串隐含状态链。

在这个例子里，这串隐含状态链就是你用的骰子的序列。

比如，隐含状态链有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率（transition probability）。

在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。

D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。

这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。

比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。

【趣味数学】骰子模型揭开概率统计之谜

骰子模型揭开概率统计之谜——抽象形象与数形思想●骰子坦然设局不公一赌场庄主正在大声吆喝：恭喜发财，骰子可爱，输1元钱，赢100块！这种吆喝还真有效果，围上赌席的赌客还真的不少.一位中学数学教师对这种赌局也产生了“兴趣”，钻上前去想看个究竟.原来，赌具是三粒骰子：赌局设计如下：如果同时出现3个6点（即下图）：则赌客可以赢得庄家的100元！如果不同时出现3个6点（下图为其一种）：则赌客输给庄家的只是1元钱！难怪有这么多人参赌的，原来输赢之比竟为1：100！这位数学教师稍微一想，差点笑了出来! 此时也正好与一个赌客回头相见：“你站在这儿干啥，还不快点押，输一赢百，天下哪有这种便宜事！”说也奇怪，赌场上还真的有赢100元的人，当然他不一定是押的3个6，也可能押的是3个5，或3个4的，总之都是输一赢百.数学教师摇了摇头，小声对那位赌客说：“假如我手中现在有216元钱，按这种赌局，在未投下骰子之前，我事先就输子116元！”那位赌客听不懂这位教师的话，回头又赌去了.这数学教师对满场的赌客感到遗憾，但又无法说服他们.回家之后，赶紧挥笔，写下这篇奇文——抛掷骰子，揭开概率统计之谜！●一掷骰子敲开概率之门投掷一枚骰子后，不论哪一面朝上，都是一个“事件”.不同的人去投掷这枚骰子，或同一个人多次投掷这枚骰子，结果会不尽相同.所以每次投掷，都是“随机事件”.投掷一枚骰子的结果，不看也知道：出现的点数必定是1，2，3，4，5，6之一，所以出现1-6点是“必然事件”.不论什么人投掷这枚骰子，决不会出现1—6以外的点.所以出现这些点都是“不可能事件”.投掷一枚骰子，有6种不同的结果，每种结果出现的可能性相同，所以又称这样的事件为“等可能事件”.投掷一枚骰子，既然是等可能事件，所以出现1—6的任何一点，可能性都是16.或者说，出现1—6的任何一点，概率都是16. 投掷一枚骰子，既然出现1—6的任何一点，概率都是16，而且这6个16之和是1，所以必然事件发生的概率是1；出现1—6以外的任何一点都不可能，所以不可能事件发生的概率是0；而随机事件是既可能发生，也可能不发生，所以随机事件发生的概率总界于0与1之间.概率学就是研究事物发生的可能性的.我们在今后的社会实践中一定会碰到大量的“事件”，通过“骰子模型”学好了概率论，掌握其基本规律，就能最大限度地避免有害事件，促成有益事件，有应对各种不同事件的强大能力.● 再掷骰子认知概率初步【例1】将骰子先后抛掷2次，计算：（1）一共有多少种不同的结果？（2）其中向上的点数之和是5的结果有多少种？（3）向上的数之和是5的概率是多少？【解析】（1）一枚骰子抛掷一次，骰子向上的点数可以是1，2，3，4，5，6.共6种不同的结果.先后抛掷两次，属于重复排列，故有2636=种不同的结果.（2）用数对(),x y 表示先后两次抛掷骰子出现的点数，那么向上的点数之和是5的情况有（1，4）；（2，3）；（3，2）；（4，1）共4种.（3）由（1）知将骰子先后抛掷2次的基本事件总数为36n =，由（2）知事件A ：其中向上的点数之和是5的事件A 的种数4m =.故向上的点数之和是5的概率是：()19m P A n ==. 【说明】本例提供了求等可能事件概率的基本方法：如果一次试验中可能出现的结果有card （I ）=n 个，其中某个特殊事件A 出现的结果有card （A ）=m 个，则事件A 发生的概率P （A ）=()1m n.公式（1）就是古典概率的基本公式.链接：一个骰子连续投2 次，点数和为4的概率是．【答案】112● 三掷骰子找到加法公式【例2】抛掷骰子一次，（1）出现2点或3点的概率是多少？（2）不出现2点或3点的概率是多少？【解析1】（1）设抛掷骰子一次，出现2点或3点的事件为A ，因为基本事件总数n =6，而事件A 的种数m =2.由公式（1）：()2163p A == （2）设抛掷骰子一次，不出现2点或3点的事件为B ，则B 有1，4，5，6共四种可能.即这时n =6，m =4. 由公式（1）：()4263p B ==.【解析2】（1）设抛掷骰子一次，出现2点的事件为A ，出现3点的事件为B ，那么：()()1,6p A p B ==故出现2点或3点的概率()()()111663p A B p A p B +=+=+=.（2）设抛掷骰子一次，不出现2点或3点的事件为C ，则()()1211.33p C p A B =-+=-=在本例中，抛掷骰子一次，出现2点与出现3点不能同时发生.这种不可能同时发生的两个事件叫做互斥事件.互斥事件适合概率的加法，即若事件A 与B 互斥，那么P （A +B ）=P （A ）+P （B ）（2）.若事件A ，B ，C ，…X 互斥，那么P （A +B +C +…+X ）=P （A ）+P （B ）+P （C ）+…+P （X ）（2′）. 抛掷骰子一次，出现2或3点与不出现2或3点也不能同时发生.所以这两个事件也是互斥事件.但抛掷骰子一次，出现2或3点与不出现2或3点又必定有一个发生.这种其中必定有一个发生的事件称为对立事件. 故若记事件A 的对立事件为A ，那么()()()13P A P A +=.互斥事件与对立事件的关系：两事件互斥时不一定对立，但两事件对立则一定互斥.也就是说：两事件互斥是它们对立的必要不充分条件.反过来，两事件对立则是它们互斥的充分不必要条件.链接：从20名男同学，10名女同学中任选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的概率为（）A ．929 B ．1029 C ．1929 D ．2029【分析】本题不属于“骰子模型”，但很容易将其改造成为“骰子模型”：投掷30枚骰子，其中有20枚出现奇数点，10枚出现偶数点.从中任取3枚既有奇数点又有偶数点的概率是多少？【解析1】（利用互斥事件）不受限制的选法有3301C 30292840606=⨯⨯⨯=种，选出的3名同学中既有男生又有女生有两种情况，1男2女的选法有122010C C 2045900⋅=⨯=种，2男1女的选法有212010C C 190101900⋅=⨯=种.这两种情况互斥，故选出的3名同学中既有男生又有女生的选法共有1900+900=2800种，其概率为280020406029P ==.选D.【解析2】（利用对立事件）不受限制的选法有3301C 30292840606=⨯⨯⨯=种，选出的3名同学中全为男生的选法有3201C 20191811406=⨯⨯⨯=种，全为女生的选法有310C 110981206=⨯⨯⨯=种.故不合条件的选法有1140+120=1260种，其概率为12609406029P ==.于是选出的3名同学中既有男生又有女生的选法，其概率为20129P P =-=，选D.● 四用骰子弄明乘法规律【例3】回到文首的问题上来，某一家赌场开出的参赌条件是：每人每次出资1元掷骰子3枚，如出现3个6点则奖100元，否则付出的1元归赌主所有.你认为这条规则公平吗？试简述理由.【解析】不妨将投出的3枚骰子编号为1，2，3.显然第1枚骰子出现6点的概率是16；在第1枚骰子出现6点的条件下，第2枚骰子出现6点的概率也是16；在1，2号骰子都出现6点的条件下，第3枚骰子再出现6点的概率还是16.根据分步计数原理，3枚骰子同时出现6点的概率是1111666216⨯⨯=.这就是说，这家赌场所设置的参赌规则1：100是不公平的，只有将规则定为1：216才算公平.事实上，一切赌场都是赢利机构，它们所制定的参赌规则都不可能公平.在本例中掷骰子3枚，每枚是否出现6点互相没有影响，这种事件就是相互独立事件. 一般地：相互独立事件A 与B 同时发生的概率是P （A ·B ）=P （A ）·P （B ）. （4）如果事件A ，B ，…X 都互相独立，那么它们同时发生的概率是P （A ·B ·…·X ）=P （A ）·P （B ）·…·P （X ）. （4′）链接：某人射击一次击中的概率是0.6，经过3次射击，此人至少有两次击中目标的概率为（）A ．81125 B.54125 C.36125 D.27125【解析】设此人在3次射击中，至少有两次击中目标的事件为A ，则A 有两种情况.一是3次全击中，其概率为33275125⎛⎫= ⎪⎝⎭；另一是3次射击恰有两次击中，这又有23C 种情况，每种情况都是2中1不中，故其概率为：2233354C 155125⎛⎫⎛⎫⋅⋅-=⎪⎪⎝⎭⎝⎭. 这两种情况互斥，根据公式2，所求概率为()275481125125125p A =+=，选A. 【说明】 1.本题虽然不是骰子模型，却很容易改造成为骰子模型：掷骰子3枚，其中至少出现2个6点的概率是多少？读者不妨解之.（参考答案：227） 2.本例的题型属于“独立重复试验”.一般地，如果在1次试验中某事件发生的概率是P ，那么在n 次独立重复试验中该事件恰好发生k 次的概率()()()15n kk kn n P k C P P -=-.● 五看骰子见到概率“期望”抛掷一枚骰子，设得到的点数为ξ，则ξ可能取的值有1，2，3，4，5，6共6种不同的结果，每种结果出现的概率都是1，写成分布列就是：这样，抛掷一枚骰子，得到点数的期望是：()1123456 3.56E ξ=+++++= ()11226n n E x p x p x p ξ=++++L L.需要说明的是：1．ξ是随机试验过程中的自变量，而P 则是ξ的函数.在本质上它与函数()y f x =中的变量x 与y 的关系是一样的.不同的是，一般地说，x 表示连续型的变量，它是不可数的；而ξ则是离散型的随机变量，它是可数的，只能在正整数范围内取值；2．写出离散型随机变量的分布列，实质上是写出某种试验过程中所有不同的试验结果及其发生的概率；3．任一离散型随机变量的分布列都具有如下的两个性质：（1）0,1,2,i P i ≥=L ；（2）121P P ++=L . 这两个性质是检测分布列是否写得正确的主要标准.4．所谓ξ的数学期望就是ξ各种取值的平均数.如果ξ的不同值出现的概率都相等，它就是简单平均数；如果ξ的不同值出现的概率不全相等，它就是加权平均数.例如：同时投掷10枚骰子，出现3个1点，4个2点，2个5点和1个6点，那么这次投掷中平均点数是多少？显然，用()11256 3.54+++=计算是不妥的，正确的算法是： ()113245261 2.7110⨯+⨯+⨯+⨯=.这里所掷相同点的次数3，4，2，1便称为权.如果利用期望公式6，那么应该先写出点数ξ的分布列. ∵()()()()34211,2,5,6p p p p ξξξξ========，故有： ξ的期望1256 2.7210101010E ξ=⨯+⨯+⨯+⨯=比较1,2两种算法，可见它们的实质是一样的.而且在多种情况下，第1种算法更为简便.因此我们说，求期望就是求平均数.【例4】掷骰子3枚，如果出现6点就能获奖，写出离散型随机变量ξ的分布列和获奖的数学期望.【解析】掷骰子3枚，随机变量ξ=0，1，2，或3.ξ=0表示3枚骰子中没有一个出现6点，∴P （ξ=0）=351256216⎛⎫= ⎪⎝⎭；ξ=1表示3枚骰子中恰有一个出现6点，∴P （ξ=1）=2131575C 66216⎛⎫⋅⋅= ⎪⎝⎭； ξ=2表示3枚骰子中恰有2个出现6点，∴P （ξ=2）=2231515C 66216⎛⎫⋅⋅= ⎪⎝⎭；ξ=3表示3枚骰子都出现6点，，∴P （ξ=3）=3116216⎛⎫= ⎪⎝⎭.ξ的数学期望是：E ξ=0×125216+1×75216+2×15216+3×1216=12.链接：甲、乙等五名奥运志愿者被随机地分到A B C D ，，，四个不同的岗位服务，每个岗位至少有一名志愿者．（Ⅰ）求甲、乙两人同时参加A 岗位服务的概率；（Ⅱ）求甲、乙两人不在同一个岗位服务的概率；（Ⅲ）设随机变量ξ为这五名志愿者中参加A 岗位服务的人数，求ξ的分布列．【解析】 5个人分配到4个岗位服务，每岗至少1人，所以必然是某一个岗位有2人，其余各岗都是1人.于是基本事件总数为2454C A 240⋅=.（Ⅰ）设“甲、乙两人同时参加A 岗位服务”的事件为A ，则其余3人只能分配到B ，C ，D 岗各1人，所以事件A 的种数为33A 6=，于是332454A 1()C A 40P A ==.即甲、乙两人同时参加A 岗位服务的概率是140．（Ⅱ）设“甲、乙两人不在同一个岗位服务的”事件为B ，则其对立事件为B ：“甲、乙两人在同一个岗位服务”.由（Ⅰ），甲、乙两人同时参加A 岗位服务的概率是140.同理，甲、乙两人同时参加B ，C ，D 岗位服务的概率也是140.这四种情况互斥，∴()114.4010p B =⨯=，所以，甲、乙两人不在同一岗位服务的概率是()1911010p B =-=.（Ⅲ）由条件，参加A 岗位服务的人数至少1人，最多2人.所以随机变量ξ=1或ξ=2.且这两类世间互相对立.设事件C ：恰有两人同时参加A 岗位服务，则事件C 的种数为2353C A 60⋅=，而基本事件总数仍为2454C A 240⋅=.∴()()60122404p C p ξ====. 而()()1311.44p p C ξ===-=于是ξ的分布列是● 六邀骰子妙释 “方差” 真谛【例5】在某次商业活动中，甲、乙2人同时获得了头彩.可是头奖名额只有一个，于当商家看到这个结果时全傻眼了.如果计算总点数，两人都是35；如果计算平均数，两人都是3.5.商家让他们重掷，却又遭到两人拒绝.亲爱的读者，你有办法解决吗？【分析】解决本例，仅用期望的知识已经不够了，必须借助方差：()()()()22211227n n D x E p x E p x E p ξξξξ=-⋅+-⋅++-⋅+L L或标准差：()8σξ=.【解析】记甲在每次投掷骰子中所获得的点数为ξ. 则ξ的期望()1122231415262 3.510E ξ=⨯+⨯+⨯+⨯+⨯+⨯=，其方差： ()()()()()()2222222211 3.52 3.53 3.51010101224 3.55 3.56 3.5 3.45101010D ξ=-⋅+-⋅+-⋅+-⋅+-⋅+-⋅=记乙在每次投掷骰子中所获得的点数为η，则η的期望()1112133435161 3.510E η=⨯+⨯+⨯+⨯+⨯+⨯=其方差： ()()()()()()2222221131 3.52 3.53 3.51010103114 3.55 3.56 3.5 1.85101010D η=-⋅+-⋅+-⋅+-⋅+-⋅+-⋅=因为乙所掷出的点数波动较小.故若两人中有且只有一人获头奖，则头奖应给乙.【说明】 1.由于期望的实质就是平均数，所以本例利用求加权平均数的方法去求期望，计算反而更为简单；2.判断期望与方差的优劣，标准是不一样的.一般的说，因为期望反映平均数，所以其值越高越好，而方差则是反映数据温带性的，所以波动越小越好.链接：甲、乙、丙三名射箭运动员在某次测试中各射箭20次，三人的测试成绩如下表：123s s s ，，分别表示甲、乙、丙三名运动员这次测试成绩的标准差，则有（）Ａ．312s s s >> Ｂ．213s s s >> Ｃ．123s s s >> Ｄ．231s s s >> 【分析】虽然是一道选择题，但数据不少，计算繁多.若处理不当，必然耗时费力.对于客观题的基本原则是尽可能多想少算.即如本题要选出正确答案，按常规须要4个步骤：（1）求期望；（2）求方差；（3）求标准差；（4）比较3个标准差的大小.以上繁复计算达10次之多.如此操作决不是命题人的本意.减少计算量的主要途径是：（1）利用求加权平均数的方法期望；（2）尽可能使用心算.【解析】 ()7891058.520x +++⨯==Q 甲()()()()222221578.588.598.5108.5 1.2520s ⎡⎤⨯-+-+-+-⎣⎦∴==()()71068948.520x +⨯++⨯==Q 乙()()()()222222678.5108.5488.598.5 1.4520s ⎡⎤⎡⎤⨯-+-+⨯-+-⎣⎦⎣⎦∴== ()()71048968.520x +⨯++⨯==Q 丙()()()()222223478.588.5688.598.5 1.0520s ⎡⎤⎡⎤⨯-+-+⨯-+-⎣⎦⎣⎦∴== 于是由222213s s s >>，得213s s s >>，选B.● 七让骰子验明“正态”真身【例6】将1枚投掷骰子1次，若出现奇数点则记0分，出现偶数点则记1分.试写出这枚骰子投掷10次后得分和的分布列.【解析】记这枚骰子投掷10次后的得分和为ξ，则ξ的可能值为0，1，2，3，4，5，6，7，8，9，10.共11种.记投掷骰子1次出现奇数点的事件为A ，那么出现偶数点的事件为A . 显然()()111,1.222p A p A ==-=由公式（5）：()()1n k k kn nP k C P P -=-得： ()010010101110C 1221024p ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭；()11011101011101C 1;221024p -⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭()21022101011452C 1;221024p -⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭()310331010111203C 1;221024p -⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭()410441010112104C 1;221024p -⎛⎫⎛⎫=-= ⎪⎪⎝⎭⎝⎭()510651010112525C 1;221024p -⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭图1 以下()()101021064;1024p p ==()()101012073;1024p p ==()()10104582;1024p p == ()()10101091;1024p p ==()()101011001024p p ==可知ξ的分布列是：ξ 012345678910P110241010244510241201024210102425210242101024120102445102410102411024我们仔细观察这张表，不难发现它除仍然符合（1）0,1,2,i P i ≥=L ；（2）121P P ++=L 外，还具有对称性，即与首末等距离的两概率之值相等. 如果再计算期望与方差，可得：()1512001090360840126012608403609010510241024E ξ=++++++++++== ()1256025160405480210021048040516025 2.510241024D ξ=++++++++++==如果在直角坐标系中画出它的图象如图1，那么我们已经可以见到正态曲线的雏形：它关于直线x =5对称，这正好与E ξ=5相吻合.（而方差或标准差则正态曲线的“高低”，“胖瘦”，这里略去.）在这个图象中，如果过折线的各个顶点依次向右画x 轴的平行线段，得到10个小矩形.显然这些矩形面积之和近似等于折线与x 轴及其两端的垂线所包围平面部分的面积.由于这些小矩形的宽度都是1，所以所有矩形面积的和为：110451111024102410241024S ⎛⎫=++++⨯= ⎪⎝⎭L .以上所分析的是n =10的情况.可以设想：当n →+∞时，这条折线的极限就是正态曲线，这与利用频率分布直方图所得到的正态曲线，在实质上是一样的.正态曲线的性质很多.但在解题中，最重要最实用的性质是如下两条：图 2图3 图4 （1）它关于直线x μ=对称.这里μ表示总体平均数，即总体中变量ξ的期望；（2）它的主要功能是利用面积来表示概率.如图2，当[],x a b ∈时，直线x a =与x b =之间所包围的平面部分的面积，就是总体在区间(),a b 内取值的概率.特别地，整条正态曲线与x轴所包夹的平面部分面积，一定是1.链接1：设随机变量ξ服从正态分布(2,9)N ,若(1)(1)P c P c ξξ>+=<-, 则 c =( )A.1B.2C.3D.4【解析】条件(1)(1)P c P c ξξ>+=<-表示如图3中两块阴影部分的面积相等，所以x c =必为正态曲线的对称轴.条件(2,9)N 说明题中总体平均数μ=2，也就是正态曲线的对称轴为x =2.（方差29s =或标准差3σ=）.故知c =2，选B.链接2：在某项测量中，测量结果ξ服从正态分布N （1，2σ）（σ>0），若ξ在（0，1）内取值的概率为0.4，则ξ在（0，2）内取值的概率为 .【解析】如图4，条件N （1，2σ）说明正态曲线的对称轴x =1，故当ξ在（0，1）内取值的概率为0.4，时ξ在（1，2）内取值的概率亦为0.4，∴ξ在（0，2）内取值的概率为0.8.链接3：已知随机变量服从正态分布()22,N σ，()40.84P ξ≤=，则()()0P ξ≤=A ．0.16 B. 0.32 C. 0.68 D. 0.84【解析】如图5，正态曲线的对称轴为x =2.图 5 图6 ∵()40.84P ξ≤=，∴()410.840.16P ξ≥=-=. 而()()2222,p p ξξ≥+=≤-即()()040.16p p ξξ≤=≥=.选A.【评注】以上3道试题，从题型看它们都不是标准正态分布（标准正态分布的条件是期望μ=0，即相应正态曲线的对称轴为y 轴）.若按常规解题，应首先通过公式()F x =φx μσ-⎛⎫ ⎪⎝⎭转化为标准正态分布.其方法是：以下的解析是方法吗？？？【解析】由()()224220.84P P P ξξξσσ-⎛⎫≤=-≤=≤=⎪⎝⎭， ()()022P P ξξ≤=-≤-22P ξσσ--⎛⎫=≤ ⎪⎝⎭ 222211P ξφφσσσσ-⎛⎫⎛⎫⎛⎫=-=-=-≤ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭0.16=. 显然这个计算将繁杂得多.链接4：设两个正态分布2111()(0)N μσσ>，和2222()(0)N μσσ>，的密度函数图像如图6所示.则有（）A ．1212,μμσσ<<B ．1212,μμσσ<>C ．1212,μμσσ><D ．1212,μμσσ>>【解析】正态分布2()(0)N μσσ>，中，x μ=表示对称轴，由图6知12120,0,μμμμ<>∴<.σ表示标准差.由正态分布公式 ()()()222,,2πx f x x μσσ--=∈-∞+∞可知，σ越大，曲线越“矮胖”；σ越小，曲线越“瘦高”，∴12σσ<.选A.。

英文骰子设计方案

英文骰子设计方案项目概述英文骰子是一种常用的游戏骰子，通常用于各种角色扮演游戏、桌游和赌博游戏中。

本文档将详细介绍英文骰子的设计方案，包括骰子的外观设计、材料选择、制造工艺以及质量控制方面的考虑。

1. 外观设计英文骰子通常采用六面体的形状，每个面上都有一个数字或一个符号表示点数。

在外观设计方面，我们需要考虑以下几个因素：•字体: 字体应该清晰易读，并且与骰子的主题相匹配。

常见的字体选择包括Sans-serif、Arial、Times New Roman等。

•数字和符号: 数字和符号应该具有辨识度，并且在不同的方向上都可以方便地辨认。

•颜色: 骰子的颜色应该鲜明且易于辨认。

通常使用饱和度较高的颜色，如红、蓝、绿等。

此外，不同点数的面可以使用不同的颜色来区分。

2. 材料选择英文骰子通常由塑料制成，因为塑料具有较低的成本、可塑性好、容易加工等优点。

然而，对于高端的骰子，也可以考虑使用其他材料，例如：•金属: 金属骰子具有更高的质感和重量感，适合用于赌场或高档游戏。

•木材: 木质骰子可以给人一种传统的感觉，并且有独特的纹理和质感。

在选择材料时，还需要考虑其可持续性和环保性。

3. 制造工艺英文骰子的制造工艺主要包括以下几个步骤：•设计: 使用计算机辅助设计（CAD）软件进行骰子的三维模型设计，并确定各个面的布局和点数。

•注塑: 使用注塑机将熔化的塑料材料注入到骰子的模具中，待塑料凝固后，取出成品。

•打磨: 对注塑出来的骰子进行打磨，去除表面的毛刺和瑕疵。

•印刷: 使用丝网印刷技术将数字和符号印刷在骰子的各个面上。

•涂漆: 使用适当的颜料或涂层对骰子进行上色，以增加鲜艳度和保护骰子表面。

•包装: 对成品骰子进行包装，并添加相应的标签或说明书。

4. 质量控制为了确保英文骰子的质量和可靠性，我们需要进行一系列的质量控制措施：•外观检查: 检查骰子的外观是否完整，颜色是否一致，字体是否清晰等。

•尺寸检测: 检测骰子的尺寸是否符合设计要求，包括边长、角度等。

骰子制作总结

骰子制作总结简介骰子是一种常见的游戏工具，用于进行投掷和计算游戏结果。

本文将总结骰子制作的基本步骤以及一些注意事项，帮助读者了解如何制作自己的骰子。

材料准备在开始制作骰子之前，需要准备以下材料： - 塑料骰子模具 - 树脂或塑料材料 - 涂料和刷子（可选） - 色彩填充物（可选）制作步骤步骤一：制作模具首先，需要制作一个骰子模具。

可以使用塑料或者硅胶等材料制作模具，确保模具能够准确地复制骰子的形状和细节。

可以通过手工雕刻或者使用3D打印等技术来制作模具。

步骤二：准备树脂材料将树脂材料按照包装上的说明准备好。

确保树脂材料的品质和比例准确无误，这对于最终的骰子质量至关重要。

步骤三：注入树脂将准备好的树脂材料缓慢地注入到模具中，确保树脂填满整个模具。

可以用手指或者刷子轻轻拍打模具，将空气泡从树脂中排出。

步骤四：等待固化根据树脂材料的说明，等待足够的时间使其固化。

通常需要等待几小时，甚至一夜。

步骤五：取出成品当树脂完全固化后，可以小心地从模具中取出骰子。

使用小刀或者刮板等工具可以更容易地取出骰子。

步骤六：涂装（可选）根据个人喜好，可以选择为骰子涂装。

使用涂料和刷子，可以为骰子添加颜色和图案，使其更加独特。

步骤七：填充色彩（可选）如果想要骰子具有多种颜色，可以在制作过程中加入色彩填充物。

将色彩填充物均匀地加入到树脂中，然后进行注入和固化的步骤。

注意事项1.在制作骰子之前，确保工作区域的通风良好，以避免有害气味和蒸汽对身体的伤害。

2.仔细阅读树脂材料的说明，并按照正确的比例混合树脂，以确保骰子的质量。

3.在注入树脂时，注意控制注入的速度以及空气泡的排出。

这将确保骰子的表面光滑，没有明显的气泡。

4.在固化过程中，不要过早地取出骰子，以免对其形状产生不良影响。

耐心等待树脂完全固化，确保骰子的质量。

5.如果选择涂装和填充色彩，注意选择耐久性好且适用于树脂材料的涂料和色彩填充物。

结论通过以上步骤和注意事项，我们可以制作出漂亮且高质量的骰子。

双骰游戏数学模型

双骰游戏数学模型
双骰游戏是一种使用两个骰子进行的游戏。

每个骰子有六个面，上面的数字分别为1到6。

在双骰游戏中，玩家投掷两个骰子，并根据骰子的点数进行赌注。

下面是一个详细的数学模型来描述双骰游戏：
1. 概率分布：
- 每个骰子的点数都是均匀分布的，即每个点数出现的概率
都是1/6。

- 两个骰子的点数之和的概率分布可以通过两个骰子点数的
所有可能组合来计算。

例如，点数之和为2的概率是1/36，因为只
有一种组合(1+1)可以得到2；点数之和为3的概率是2/36，因为有
两种组合(1+2和2+1)可以得到3；以此类推。

2. 期望值：
- 期望值是指在多次试验中某个事件发生的平均次数。

在双
骰游戏中，可以计算以下几个期望值：
- 单个骰子的点数的期望值是3.5，因为每个点数出现的
概率都是1/6，所以期望值为(1+2+3+4+5+6)/6=3.5。

- 两个骰子的点数之和的期望值是7，因为点数之和的概
率分布是对称的，所以期望值为(2+3+4+5+6+7+8+9+10+11+12)/36=7。

3. 赔率：
- 赔率是指赌注和赢得赌注的比例。

在双骰游戏中，赔率可
以根据点数之和的概率分布和赌注的设定来计算。

- 例如，如果赌注是10元，点数之和为7的概率是6/36，那么赢得赌注的概率就是6/36，赔率就是1:6。

这些是双骰游戏的数学模型的一些基本要素。

根据这些模型，可以计算出各种概率、期望值和赔率，来帮助玩家做出更明智的投注决策。

Tinkercad(123d design)实战案例讲解之家务骰子创建

2020/10/13
3.复制长方体，并将其隐藏（复制：CTRL+C、粘贴：CTRL+V）
• 首先，选中长方体，此时长方体边框线条颜色变亮，如下图所示。
2020/10/13
• 然后，复制/粘贴长方体，新的长方体位置不动（即红框中的数值为0）。如下图所示。
2020/10/13
• 隐藏刚刚复制的长方体：选中刚刚复制的长方体，然后单击“隐藏”命令即可，如下图所示。
2020/10/13
例如第三章的水杯关于tinkercad更详细的学习资料请阅读西锐三维中小学3d打印教学专用教材tinkercad实战案例讲解没有合并对象则3d打印后杯子主体和杯子把手是相互独立的即3d打印后的杯子把手是可以拿出来的
Tinkercad(123d design)实战案例讲解
之家务骰子创建
2020/10/13
2020/10/13
二、 Tinkercad 主界面
在启动 Autodesk Tinkercad 后，可以看出其界面由 APP 菜单，主工具条，网格，三维视图，导航工具条，工具包，栅格，单位，登录和帮助菜单组成。如下图所示。
2020/10/13
三、案例分析
“一个和尚挑水吃，两个和尚抬水吃，三个和尚没水吃。”这个寓言故事也告诉我们一个道理，办事如果事呢？我相信很多人也曾有过互相推扯。那么，怎么在保证和谐的基础上又能让对方愿意干活呢？此时，我们的家务骰子就有其用武之地了。本章将带大家学习创建家务骰子，创建过程中我们将重点学习布尔运算命令。如下图所示。
2020/10/13
四、操作步骤
家务骰子包含六个面，每个面上的文字分别是“刷鞋、洗马桶、买菜、做饭、拖地、倒垃圾”。当然，我们也可以自定义每个面的文字。下面将讲述如何创建家务骰子三维模型，具体的操作步骤如下：

数学综合实践教学掷一掷(3篇)

第1篇一、引言数学作为一门基础学科，其理论与实际应用密切相关。

为了提高学生的数学素养和实践能力，我国教育部门大力推广数学综合实践教学。

其中，掷一掷作为一项简单而有趣的数学活动，既能让学生在轻松愉快的氛围中感受数学的魅力，又能锻炼学生的逻辑思维和数据分析能力。

本文将从掷一掷的起源、规则、教学目标、实践过程以及教学反思等方面进行探讨。

二、掷一掷的起源与规则1. 起源掷一掷起源于古代的占卜文化，人们通过掷骰子等方式来预测未来。

随着历史的发展，掷一掷逐渐演变成一种娱乐活动，并融入了数学元素。

2. 规则（1）使用一副标准的骰子，共有六个面，分别标有1至6的点数。

（2）掷骰子时，要求骰子自由滚动，直至静止。

（3）记录掷骰子所得的点数。

（4）根据点数进行相应的数学运算或游戏。

三、教学目标1. 培养学生的数学兴趣，激发学生对数学的热爱。

2. 提高学生的逻辑思维能力，锻炼学生的数据分析能力。

3. 培养学生的团队合作精神，提高学生的沟通协作能力。

4. 帮助学生将数学知识应用于实际生活，增强学生的实践能力。

四、实践过程1. 准备工作（1）准备一副标准的骰子。

（2）制作掷一掷的规则卡片，方便学生了解游戏规则。

（3）将学生分成若干小组，每组4-6人。

2. 游戏过程（1）讲解游戏规则，让学生了解掷一掷的基本玩法。

（2）各小组轮流掷骰子，记录所得点数。

（3）根据点数进行数学运算或游戏，如计算点数之和、找出最大/最小点数等。

（4）各小组分享自己的解题思路和结果，进行讨论和交流。

3. 总结与反思（1）教师引导学生总结掷一掷的规则和数学运算方法。

（2）各小组分享自己在游戏过程中的收获和体会。

（3）教师针对学生的表现进行点评，指出优点和不足。

五、教学反思1. 激发学生兴趣，提高学习积极性掷一掷游戏具有趣味性，能够激发学生的学习兴趣，提高他们的学习积极性。

2. 培养学生的逻辑思维和数据分析能力掷一掷游戏涉及数学运算和数据分析，有助于培养学生的逻辑思维和数据分析能力。

《UG骰子画法教程》课件

骰子画法的应用场景
骰子画法适用于创建常见的零部件，如螺丝、齿轮和曲柄连杆等。
骰子画法的基本操作方法
使用UG软件提供的骰子画法工具，按照指定的参数设置进行操作。
骰子画法的高级用法
骰子画法的参数设置
通过调整骰子画法的参数设置，可以实现更加复杂的零部件绘制。
骰子画法的高级操作方法
学习更高级的骰子画法操作方法，可以应对复杂的场景和特殊的设计需求。
案例演练
1
案例：如何使用骰子画法快速创建一个螺丝
通过本案例演练，学习如何使用骰子画法快速创建螺丝零部件，并设置参数实现不同尺寸和螺纹类型。
2
案例：如何使用骰子画法快速创建一个齿轮
本案例演练将教您如何使用骰子画法在UG软件中快速创建齿轮零部件，并调整参数实现不同模数和齿数。
3
案例：如何使用骰子画法快速创建一个曲柄连杆
学习如何利用骰子画法进行曲柄连杆的快速绘制，并了解如何设置参数以适应不同的运动特征。
总结
本课程为大家详细介绍了UG软件中的骰子画法，一种快速创建常见零部件的方法。同时还介绍了骰子画法的高级用法，应对复杂的设计场景。感谢大家的学习，祝大家学有所获！
《UG骰子画法教程》PPT课件
UG骰子画法教程课件，为您详细介绍如何使用UG软件进行骰子画法操作。快速地创建常见的零部件，提高设计效率。
课程介绍
本课程将为大家详细介绍如何使用UG软件进行骰子画法操作，快速地创建一些常见的零部件。提高设计效率与工作效果。
骰子画法的基本知识
什么是骰子画法
骰子画法是UG软件中的一种零部件快速创建方法。

简单骰子制作方法

简单骰子制作方法介绍骰子作为一种常见的游戏工具，被广泛用于各种桌面游戏、赌博游戏和教育游戏中。

制作一个简单的骰子并不困难，本文将介绍一种简单的制作骰子的方法。

所需材料•盒子：可以使用小纸盒、塑料盒或者木盒作为骰子的外框。

•印刷纸：用于覆盖盒子的外表面，上面有骰子的数字。

•胶水或者双面胶：用于固定纸张和盒子。

•剪刀：用于剪裁纸张。

•尺子：用于测量纸张和盒子的尺寸。

制作步骤第一步：准备工作•使用尺子测量盒子的尺寸，确保纸张能够完全覆盖盒子的六个面。

•根据盒子的尺寸，使用剪刀将印刷纸剪裁成合适的大小。

第二步：制作纸面•在印刷纸的一侧绘制骰子的六个面，每个面上分别绘制1到6的数字。

•可以使用计算机绘图软件或者手工绘制，确保数字清晰可见。

•如果使用计算机绘图软件，可以选择合适的字体和颜色。

第三步：固定纸面•使用胶水或者双面胶将印刷纸粘贴在盒子的六个面上。

•确保纸张贴合紧密，没有皱褶或者气泡。

第四步：组装骰子•将盒子的六个侧面按照正确的顺序折叠并固定，形成一个立体的立方体结构。

•使用胶水或者双面胶固定盒子的边角。

第五步：完成骰子•检查骰子的各个面是否清晰可见，数字是否正确。

•如果有需要，可以使用尺子和剪刀修整纸张的边缘。

结论使用上述简单的步骤和材料，您可以制作一个简单的骰子。

这个自制的骰子可以用于各种桌面游戏和教育游戏中。

鼓励您根据自己的需要进行创作，例如使用不同的纸张、颜色和设计来制作更加个性化的骰子。

制作骰子不仅有助于提高手工能力，还可以增加乐趣和创造力。

希望您享受制作的过程并用这个自制的骰子玩游戏！。

categorical distribution实例

categorical distribution实例
一个实例是投掷一枚公平的六面骰子，所得到的结果可以是1、2、3、4、5或6。

在这种情况下，我们可以使用分类分布来描述每一个结果出现的概率。

假设我们想要估计每一个结果出现的概率，我们可以使用分类分布来建模。

假设我们有一个数据集，其中包含了1000次对这枚骰子的投
掷结果。

我们可以将这些投掷结果表示为一个包含1000个元
素的向量，其中每一个元素表示一次投掷的结果。

我们可以使用这个数据集来估计每一个结果出现的概率。

使用分类分布，我们可以假设每一个结果出现的概率是相等的，即每一个结果出现的概率都是1/6。

然后，通过计算在数据集
中每一个结果出现的次数，并除以总的投掷次数，我们可以得到每一个结果出现的概率估计。

例如，假设在1000次投掷中，结果1出现了150次，结果2
出现了200次，结果3出现了100次，结果4出现了250次，
结果5出现了150次，结果6出现了150次。

通过计算，我们
可以得到每一个结果出现的概率估计为1/6。

这个例子说明了如何使用分类分布来建模和估计数据集中结果的概率分布。

它在许多领域中都有广泛应用，包括自然语言处理、图像处理和机器学习等。

3D one建模课程之《骰子的制作》

设计《爱情公寓》中的20面骰子这次我们来做一个爱情公寓中的多面骰子（20面）。

教学目标：1、正多边形草图、文字草图的绘制。

2、拔模命令的使用。

3、通过镜像复制实体。

4、引导学生观察生活并将观察所得用于实践。

5、通过多面骰子角度激发学生对数学和几何的兴趣。

学情分析：本实例并不困难，设计的软件命令也不是很多，学生按老师的讲解应该可以很容易完成作品。

但是多面骰子涉及的数学几何知识对不同年龄的学生要区别对待。

高中生可以讲原理，高中以下的孩子简单了解就好。

教学重难点：1、拔模命令的使用，以及拔模角度的确定。

2、镜像复制和给每个面添加数字是需要耐心的。

教学过程：一、引入。

《爱情公寓》是现在很多学生喜欢的电视剧，可以播放一小段与多面骰子相关的电视剧片段，吸引学生的注意力，激起学生学习的兴趣。

二、展示实物。

让学生观察20面骰子的实物，了解其结构，思考使用3D ONE如何来制作。

三、请同学说一说自己想到的制作方法，老师给予点评。

四、上机操作。

教师可以讲授+个别指导的方法带领学生制作骰子模型。

制作步骤：1、绘制骰子单面的草图。

使用正多边形工具，绘制正三角形。

半径20mm。

2、拉伸，高度10mm。

3、拔模。

点击特征造型里的拔模，选择实体上面，角度-20.9度。

（这里可以联系几何中的三角函数）4、骰子单面的实体后，进行镜像复制，对称面选择侧面的斜面。

如下图。

5、同样的方法在各个方向进行镜像复制，这里需要耐心哦。

6、多次镜像后，得到20面体的外形。

7、给各个面加上数字。

为了方便，我们先将各个面进行隐藏，逐一现实各个面所在的实体。

8、先从第一个面开始加入数字。

在表面使用文字草图工具，输入数字“1”。

并通过移动和旋转调整数字的位置。

9、拉伸数字草图，高度-1，在拉伸的布尔类型里面选择减运算。

10、同样的方法，逐一显示各个面，并且按照顺序在各个面上制作数字。

11、渲染。

完成五、展示分享。

今天我们的分享方式不是平常的讲解和展示，而是使用我们自己制作的骰子来玩一盘飞行棋，大家玩起来！~~。

骰子造高楼教案

骰子造高楼教案教案标题：骰子造高楼教案目标：1. 帮助学生理解骰子的结构和功能。

2. 培养学生的团队合作和问题解决能力。

3. 提高学生的数学思维和空间想象力。

教案步骤：引入活动：1. 引导学生回忆骰子的外形和结构，并让他们思考骰子可以用来做什么。

2. 提出问题：如果给你一些骰子，你能用它们造出一个高楼吗？探究活动：3. 将学生分成小组，每组提供一定数量的骰子和一张纸板作为基地。

4. 要求学生通过组合骰子来建造一个尽可能高的塔楼，同时确保塔楼的稳定性。

5. 鼓励学生在建造过程中尝试不同的组合方式，并记录下他们的尝试和结果。

讨论和总结：6. 让每个小组展示他们建造的塔楼，并鼓励其他小组提出问题和分享建议。

7. 引导学生讨论他们在建造过程中遇到的困难和解决方法。

8. 引导学生总结他们从这个活动中学到的关于骰子结构和塔楼建造的知识。

拓展活动：9. 提出更具挑战性的问题：如果给你更多的骰子，你能建造出一个更高的塔楼吗？让学生再次尝试并记录他们的尝试和结果。

10. 鼓励学生尝试使用不同形状的骰子，如长方体、正方体等，来建造更复杂的结构。

评估：11. 观察学生在活动中的参与程度和团队合作能力。

12. 评估学生在讨论中的表达能力和对问题解决的理解。

13. 收集学生记录的尝试和结果，评估他们对骰子结构和塔楼建造的理解程度。

教案扩展：1. 可以将这个活动与数学课程结合，引导学生计算骰子的表面积和体积，以及塔楼的高度和稳定性。

2. 可以引导学生探究其他建筑结构的稳定性，如金字塔、拱桥等，并与骰子塔楼进行比较。

教案提示：1. 确保提供足够的骰子和纸板，以便学生可以自由地进行尝试和实践。

2. 鼓励学生积极参与讨论和分享自己的想法，营造积极的学习氛围。

3. 在活动结束后，及时总结学生的学习成果，并给予肯定和鼓励。

UGNX7骰子模型制作步骤

• 设计流程:
1. 新建文件dice.prt并进入建模工作环境 2. 创建长方体特征,XC,YC,ZC的高度均为16.5
过中点绘制下图所示的线段
4. 移动长方体到线段的中点-点到点(√关联)
5.删除曲线,复制特征到图层2 6. 创建圆角特征,R=1.5
7. 抽取实体面
8. 抽取曲线
案例说明：
本案例是一个简单曲面创建的典型代表.
通过这个案例的学习我们可以全面掌握运用曲线网格生成的基本方法和技巧.
案例建模所用知识点：
创建曲线网格相切曲面创建桥接曲面创建等参数曲线创建等分点
案例建模时间:
2小时
• 案例分析:
通过分析产品的用途、特性、设计参数及要求来确定产品的工艺条件，然后根据下图所示的设计流程，从整体上掌握该产品的思路与过程，培养良好的设计思路.
9. 等分上述六条曲线移至图层
10. 桥接曲线
11. 绘制如下图的直线,并投影到指定曲面上
12. 修剪片体
13. 创建点集,个数为10.
14. 绘制如下图的三条线段,长度为30以上
15. 选择上述三条曲线 ,创建投影曲线
16. 创建桥接曲线
17. 创建网格曲线;边界约束为G1
18. 抽取等参数曲线,数量为3(U方向):
36. 创建矩形阵列(旋转坐标系),直径为5,圆心在(2,0,0)
37. 创建如图曲线,并移动坐标系到如图位置:
38. 创建球特征,直径为5,圆心在(0,2,0)同时求差创建直径为9.2的圆
39. 移动坐标系到下图位置创建球特征,直径为5,圆心在(0,0,2)同时求差: 旋转阵列:
40. 移动坐标系到绝对坐标位置 41. 创建特征操作,环形阵列

Maya玛雅滚动骰子教程

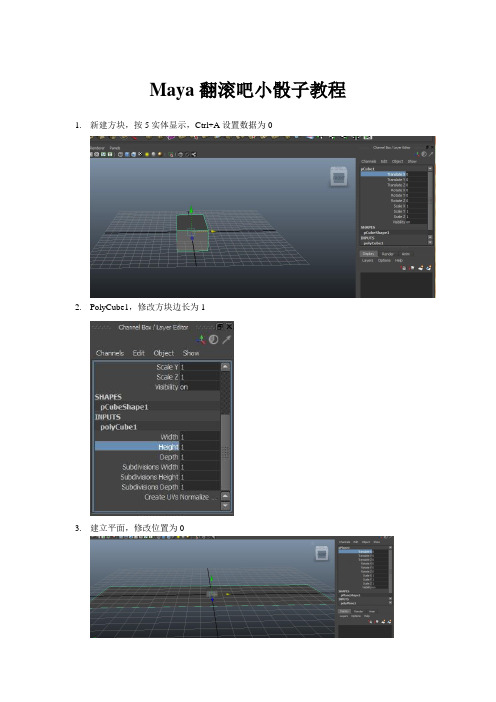
Maya翻滚吧小骰子教程1.新建方块，按5实体显示，Ctrl+A设置数据为02.PolyCube1，修改方块边长为13.建立平面，修改位置为04.方块的Y轴数据上移0.55.修改方块材质。

Window，Render，Hypershade6.选择Blinn（金属）7.双击显示的球，修改颜色8.中键拖动材质附加到方块上9.选择左上角的Polygors，选择Rendering10.选择工具栏中的Texturing，选择第一项3D Paint Tool后的小方格11.按B键左键调节画笔大小12.点击File Textures选项的Assign/Edit Textures.13.调节画布大小和格式14.Flood选项，修改颜色，点击Flood Paint将方块表面全部填充15.选择画笔形式，选择颜色，点击方块画图16.画完5面后，移开底层平面17.选择画笔模式，继续画第6面18.画完将平面移回19.选择工具栏的Window，选择UV20.UV Texture Editor可以查看6个面的图画，做修改21.修改动画帧数22.在0帧时，将Rotate Z锁定23.在100帧时，将Rotate Z改为-360，锁定24.选择右上角Insert，按V，讲中心拖动到右下角，按Insert恢复25.选择右边数据栏上的Edit，Channel Control26.选择Rotate Pivot 相关的数据，选定27.按<<Move 添加28.锁定29.方块旋转90度时将中心转移到右下角，锁定30.方块旋转180度时将中心转移到右下角，锁定31.方块旋转270度时将中心转移到右下角，锁定32.方块旋转360度时将中心转移到右下角，锁定33.选择工具栏的Window,Animation Editors,Graph Editor34.选择2-6项，按F调节视角35.按上方图标，将弧线改成折线36.下方修改帧数37.选择工具栏的Window,Animation Editors,Graph Editor。

应用骰子模型 ,探究正态分布

应用骰子模型，探究正态分布引例：将1枚投掷骰子1次，若出现奇数点则记0分，出现偶数点则记1分.试写出这枚骰子投掷10次后得分和的分布列.【解析】记这枚骰子投掷10次后的得分和为ξ，则ξ的可能值为0，1，2，3，4，5，6，7，8，9，10.共11种.记投掷骰子1次出现奇数点的事件为A ，那么出现偶数点的事件为A . 显然()()111,1.222p A p A ==-=由公式（5）：()()1n k k kn nP k C P P -=-得： ()010010101110C 1221024p ⎛⎫⎛⎫=-= ⎪⎪⎝⎭⎝⎭；()11011101011101C 1;221024p -⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭()21022101011452C 1;221024p -⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭()310331010111203C 1;221024p -⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭()410441010112104C 1;221024p -⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭()510651010112525C 1;221024p -⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭以下()()101021064;1024p p ==()()101012073;1024p p ==()()10104582;1024p p == ()()10101091;1024p p ==()()101011001024p p ==可知ξ的分布列是：我们仔细观察这张表，不难发现它除仍然符合（1）0,1,2,i P i ≥=L ；（2）121P P ++=L 外，还具有对称性，即与首末等距离的两概率之值相等. 如果再计算期望与方差，可得：()1512001090360840126012608403609010510241024E ξ=++++++++++== ()1256025160405480210021048040516025 2.510241024D ξ=++++++++++== 如果在直角坐标系中画出它的图象如图1，那么我们已经可以见到正态曲线的雏形：它关于直线x =5对称，这正好与E ξ=5相吻合.（而方差或标准差则正态曲线的“高低”，“胖瘦”，这里略去.）图1图2图3在这个图象中，如果过折线的各个顶点依次向右画x 轴的平行线段，得到10个小矩形.显然这些矩形面积之和近似等于折线与x 轴及其两端的垂线所包围平面部分的面积.由于这些小矩形的宽度都是1，所以所有矩形面积的和为：110451111024102410241024S ⎛⎫=++++⨯= ⎪⎝⎭L .以上所分析的是n =10的情况.可以设想：当n →+∞时，这条折线的极限就是正态曲线，这与利用频率分布直方图所得到的正态曲线，在实质上是一样的.正态曲线的性质很多.但在解题中，最重要最实用的性质是如下两条：（1）它关于直线x μ=对称.这里μ表示总体平均数，即总体中变量ξ的期望；（2）它的主要功能是利用面积来表示概率.如图2，当[],x a b ∈时，直线x a =与x b = 之间所包围的平面部分的面积，就是总体在区间(),a b 内取值的概率.特别地，整条正态曲线与x轴所包夹的平面部分面积，一定是1.链接1：（08·湖南卷第4题）设随机变量ξ服从正态分布(2,9)N ,若(1)(1)P c P c ξξ>+=<-, 则c = ( )A.1B.2C.3D.4 【解析】条件(1)(1)P c P c ξξ>+=<-表示如图3中两块阴影部分的面积相等，所以x c =必为正态曲线的对称轴.条件(2,9)N 说明题中总体平均数μ=2，也就是正态曲线的对称轴为x =2.（方差29s =或标准差3σ=）. 故知c =2，选B.图 4图5图6链接2：（07·全国2理14）在某项测量中，测量结果ξ服从正态分布N （1，2σ）（σ>0），若ξ在（0，1）内取值的概率为0.4，则ξ在（0，2）内取值的概率为 .【解析】如图4，条件N （1，2σ）说明正态曲线的对称轴x =1，故当ξ在（0，1）内取值的概率为0.4，时ξ在（1，2）内取值的概率亦为0.4， ∴ξ在（0，2）内取值的概率为0.8.链接3：（07·浙江卷理5）已知随机变量服从正态分布()22,N σ，()40.84P ξ≤=，则()()0P ξ≤=A ．0.16 B. 0.32 C. 0.68 D. 0.84 【解析】如图5，正态曲线的对称轴为x =2. ∵()40.84P ξ≤=，∴()410.840.16P ξ≥=-=. 而()()2222,p p ξξ≥+=≤-即()()040.16p p ξξ≤=≥=.选A.【评注】以上3道试题，从题型看它们都不是标准正态分布（标准正态分布的条件是期望μ=0，即相应正态曲线的对称轴为y 轴）.若按常规解题，应首先通过公式()F x =φx μσ-⎛⎫⎪⎝⎭转化为标准正态分布.其方法是：以下的解析是方法吗？？？【解析】由()()224220.84P P P ξξξσσ-⎛⎫≤=-≤=≤=⎪⎝⎭， ()()022P P ξξ≤=-≤-22P ξσσ--⎛⎫=≤ ⎪⎝⎭222211P ξφφσσσσ-⎛⎫⎛⎫⎛⎫=-=-=-≤ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭0.16=.显然这个计算将繁杂得多.链接4：（08·安徽卷第10题）设两个正态分布2111()(0)N μσσ>，和2222()(0)N μσσ>，的密度函数图像如图6所示.则有（）A ．1212,μμσσ<<B ．1212,μμσσ<>C ．1212,μμσσ><D ．1212,μμσσ>>【解析】正态分布2()(0)N μσσ>，中，x μ=表示对称轴，由图6知12120,0,μμμμ<>∴<.σ表示标准差.由正态分布公式()()()222,,x f x x μσ--=∈-∞+∞可知，σ越大，曲线越“矮胖”；σ越小，曲线越“瘦高”，∴12σσ<.选A.例已知：从某批材料中任取一件时，取得的这件材料强度ξ服从).18,200(2N （1）计算取得的这件材料的强度不低于180的概率．（2）如果所用的材料要求以99％的概率保证强度不低于150，问这批材料是否符合这个要求．分析：这是一个实问题，只要通过数学建模，就可以知道其本质就是一个“正态分布下求随机变量在某一范围内取值的概率”的问题；本题的第二问是一个逆向式问法，只要把握实质反向求值即可．解：（1）-=⎪⎭⎫⎝⎛-Φ-=<-=≥1181201801)180(1)180(ξξP P;8665.0)11.1()]11.1(1[1)11.1(=Φ=Φ--=-Φ（2）可以先求出：这批材料中任取一件时强度都不低于150的概率为多少，拿这个结果与99％进行比较大小，从而得出结论．;9973.0)78.2()]78.2(1[1)78.2(1182001501)150(1)150(=Φ=Φ--=-Φ-=⎪⎭⎫⎝⎛-Φ-=<-=≥ξξP P即从这批材料中任取一件时，强度保证不低于150的概率为99.73％＞99％，所以这批材料符合所提要求．说明：“不低于”的含义即在表达式中为“大于或等于”．转化“小于”后，仍须再转化为非负值的标准正态分布表达式，从而才可查表．公共汽车门的高度例若公共汽车门的高度是按照保证成年男子与车门顶部碰头的概率在1％以下设计的，如果某地成年男子的身高)36,175(~N ξ（单位：㎝），则该地公共汽车门的高度应设计为多高？分析：实际应用问题，分析可知：求的是门的最低高度，可设其为)cm (x ，使其总体在不低于x 的概率值小于1％，即：%101.0)(=<≥x P ξ，从中解出x 的范围．解：设该地公共汽车门的高度应设计高为x cm ，则根据题意可知：%1)(<≥x P ξ，由于)36,175(~N ξ，所以，;01.061751)(1)(<⎪⎭⎫⎝⎛-Φ-=<-=≥x x P x P ξξ 也即：;99.06175>⎪⎭⎫⎝⎛-Φx通过查表可知：;33.26175>-x 解得：;98.188>x即该地公共汽车门至少应设计为189cm 高．说明：逆向思维和逆向查表，体现解决问题的灵活性．关键是理解题意和找出正确的数学表达式．学生成绩的正态分布例某班有48名同学，一次考试后数学成绩服从正态分布．平均分为80，标准差为10，问从理论上讲在80分至90分之间有多少人？分析：要求80分至90分之间的人数，只要算出分数落在这个范围内的概率，然后乘以总人数即可，而计算这个概率，需要查标准正态分布表，所以应首先把这个正态总体化成标准正态总体．解：设x 表示这个班的数学成绩，则x 服从)10,80(2N 设1080-=x Z 则z 服从标准正态分布)1,0(N ．查标准正态分布表，得：5000.0)0(,8413.0)1(==ΦΦ所以，3413.05000.08413.0)0()1()10()1080901080108080()9080(=-=∅-∅=<<=-<-<-=<<z p x p x p ∴163824.163413.048≈=⨯．说明：这类问题最容易犯的错误是没有转化成标准正态分布就直接求解，一般地，我们在解决正态总体的有关问题时均要首先转化成标准正态总体．。

数学建模第一章作业(章绍辉)

y
0
0.1
0.2
0.3
0.4
0.5 x
0.6
0.7
0.8
0.9
1
3. 两个人玩双骰子游戏，一个人掷骰子，另一个人打赌掷骰子者不能掷出所需点数，输赢的规则如下：如果第一次掷出 3 或 11 点，打赌者赢；如果第一次掷出 2、7 或 12 点，打赌者输；如果第一次掷出 4,5,6,8,9 或 10 点，记住这个点数，继续掷骰子，如果不能在掷出 7 点之前再次掷出该点数，则打赌者赢. 请模拟双骰子游戏，要求写出算法和程序，估计打赌者赢的概率. 你能从理论上计算出打赌者赢的精确概率吗？请问随着试验次数的增加，这些概率收敛吗？解答（一）算法输入模拟试验的次数 n；输出打赌者赢的概率 p. 第 1 步初始化计数器 k=0；第 2 步对 i=1,2,…,n，循环进行第 3～7 步；第 3 步产生两个在 1～6 这 6 个整数中机会均等地取值的随机数，并把这两个随机数之和赋值给 x；第 4 步如果 x 是 3 或 11，那么 k 加 1，进入下一步循环；否则，做第 5 步；第 5 步如果 x 不是 2、7 和 12，那么做第 6～8 步；否则，直接进入下一步循环；第 6 步产生两个在 1～6 这 6 个整数中机会均等地取值的随机数，并把这两个随机数之和赋值给 y；第 7 步如果 y 不等于 x，也不等于 7，重复第 6 步所做的；第 8 步如果 y 等于 7，那么 k 加 1，进入下一步循环；否则，直接进入下一步循环；第 9 步计算概率 p=k./n .
第一章习题参考答案
1. 请编写绘制以下图形的 MATLAB 命令，并展示绘得的图形.
x2 2 (1) x y 1、x y 4 分别是椭圆 y 1 的内切 4

圆柱形骰子的设计调查报告

圆柱形骰子的设计调查报告根据您的要求，以下是圆柱形骰子的设计调查报告：1. 背景圆柱形骰子是一种非常有趣的骰子形状，与传统的立方形骰子形状不同。

这种骰子在外观上更加独特，设计师们可以通过不同的几何外观、纹理和颜色设计许多吸引人的骰子形态。

2. 调查目的我们的调查旨在了解公众对圆柱形骰子的看法和喜好，希望能够为相关企业提供更为准确的设计和生产建议。

3. 调查内容和方法我们通过线上问卷和线下访谈的方式对300人进行了调查。

问卷中涉及的问题有：- 您是否知道圆柱形骰子？- 您是否曾经使用过圆柱形骰子？- 您觉得哪些几何形状最适合设计圆柱形骰子？- 您更喜欢圆柱形骰子还是立方形骰子？- 您希望圆柱形骰子有哪些特殊的设计元素，例如花纹、图案、颜色等方面？此外，我们还进行了一些现场调查和观察，观察对象包括不同年龄层和性别分布的人群，以及各类棋牌和桌游爱好者。

4. 调查结果我们的调查结果显示：- 大多数受访者（80%）表示知道圆柱形骰子，但只有40%的人使用过。

- 受访者对于圆柱形骰子的几何形状偏好在环形和椭圆形之间。

另外，有一些人也提出了五角形或六角形等不同的形状建议。

- 圆柱形骰子的受欢迎程度略低于立方形骰子，但也有一定数量的受访者表示喜欢这种骰子。

- 受访者普遍认为，圆柱形骰子的设计元素可以更加多元化和创新，例如使用不同的花纹和图案，添加元素和特效等。

5. 结论通过这次调查我们可以得出以下几点结论：- 圆柱形骰子是一种相对较为新颖和独特的骰子设计形状。

- 圆柱形骰子设计的几何形状可以更灵活创新，如环形、椭圆形、五角形和六角形等。

- 圆柱形骰子可以通过更多元化和创新的设计元素，如花纹、图案、颜色等，吸引更多用户使用。

以上是我们的调查报告，希望能够对您有所帮助。