2018春八年级数学下册第一章三角形的证明4角平分线第2课时三角形内角的平分线作业课件新版北师大版

合集下载

嘉定区五中八年级数学下册第一章三角形的证明 4角平分线第2课时三角形三个内角的平分线课件新版北

求证 : P 点在∠BAC 的角平分线 B 上.
A
ND
P
M F
EC
证明 : ∵BM 是△ABC 的角平分线 , 点 P 在 BM 上 ,
且 PD⊥AB , PE⊥BC , 垂足分别为 D , E ,
∴PD = PE〔角平分线上的点到这个角的两边的距离
相等〕.
A
同理 : PE = PF. ∴PD = PE = PF.
三角形的三个内角的角平分线交于一点．这一点到三角形三边的距离相等．
结束语
同学们，你们要相信梦想是价值的源泉，相信成功的信念比成功本身更重要，相信人生有挫折没有失败，相信生命的质量来自决不妥协的信念，考试加油!奥利给~
12.2 三角形全等的判定(ASA AAS)
复习
1.什么是全等三角形？ 2.判定两个三角形全等方式有哪些?
边边边 :
三边対应相等的两个三角形全等。
边角边 :
有两边和它们夹角対应相等的两个
复习引入
1.什么样的图形是全等三角形？ 2.判定两个三角形全等要具备什么条件?
边边边 : 三边対应相等的两个三角形全等。
边角边 : 有两边和它们夹角対应
创设情景
一张教学用的三角形硬纸板不小心被撕坏了 , 如下图 , 你能制作一张与原来同样大小的新教具？能恢复三角形的原貌吗？
2
部相交于点C.
〔3〕画射线OC.射线OC即为所求.
作角平分线是最基本的尺规作图,大家一定要掌握噢!
已知 : 平角∠AOB. 求作 : 平角∠AOB的角平分线.
C
B
O
A
结论 : 作平角的平分线的方式就是过直线上一点作这条直线的垂线的方式.
二角平分线的性质实验 : OC是∠AOB的平分线 , 点P是射线OC上的

八年级数学下册第一章三角形的证明 4角平分线第1课时角平分线的性质与判定课件(新版)北师大版

垂足且 PD = PE.
求证：OP 平分∠AOB.
O
DA1 2PCEB证明：∵PD⊥OA，PE⊥OB，
DA
∴∠ODP =∠OEP = 90°.
∵ PD = PE， OP = OP，
O
∴Rt△DOP ≌ Rt△EOP（HL）.
1 2
PC
EB
∴∠1 =∠2（全等三角形对应角相等）.
∴OP 平分∠AOB.
（5）如图，∵ PE⊥AB，
C
PF⊥AC，PE = PF，
F P
∴点 P 在∠BAC 的平 D 分线上（到角两边距离相等
的点在这个角的平分线上）.
A
E
B
√
随堂演练
1. 如图，在△ABC 中，AB = AC，AD 是 ∠BAC 的角平分线，DE⊥AB，DF⊥AC，垂足分别是 E、F，则下列四个结论：
如果有一个点到角两边的距离相等，那么这个点必在这个角的平分线上．
这个命题是假命题．角平分线是角内部的一条射线，而角的外部也存在到角两边距离相等的点．
定理在一个角的内部，到角的两边距离相等的点在这个角的平分线上.
已知：如图，点 P 为∠AOB 内一
点，且 PD⊥OA，PE⊥OB，D、E 为
（1）如图，∵AD 平
C
分∠BAC，PE⊥AB，
F P
D PF⊥AC，
∴PE = PF（角平分
A
E
B 线上的点到这个角的两边
距离相等）. √
C
（2）如图，∵ PE = PF，
F P
∴ AD 平分∠BAC D （到角两边距离相等的点在
这个角的平分线上）.
A
E
B
×
（3）如图，∵ 点 P 在

北师大版八年级数学下册第一章三角形的证明基础拔高讲义(角平分线的性质和判定、角平分线模型)(含答案)

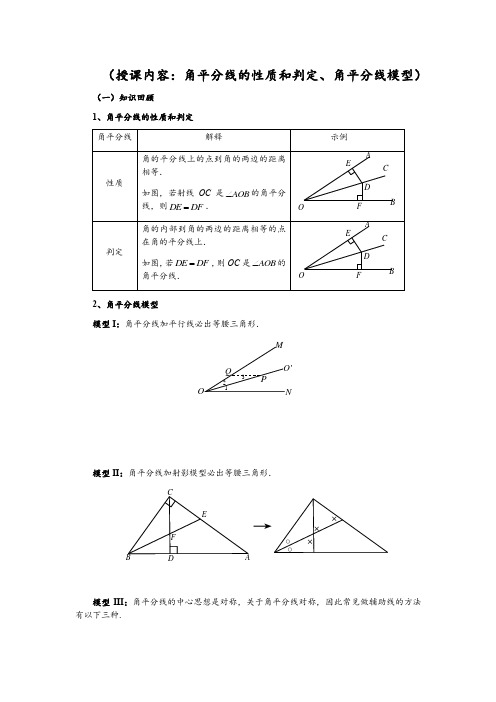
（授课内容：角平分线的性质和判定、角平分线模型）（一）知识回顾1、角平分线的性质和判定2、角平分线模型模型I ：角平分线加平行线必出等腰三角形．模型II ：角平分线加射影模型必出等腰三角形．→模型III ：角平分线的中心思想是对称，关于角平分线对称，因此常见做辅助线的方法有以下三种．FCDE××○○×M Q'O ONP123（二）例题讲解1、角平分线的性质和判定（1）如图，在ABC △中，90C ∠=︒，AD 是角平分线，DE AB ⊥，3cm DE =，5cm BD =，则BC =__________．（2）（14—15年嘉祥期末）在ABC △中，90BAC ∠=︒，3AB =，4AC =，5BC =，若点P 是ABC △的三条角平分线的交点，则点P 到边BC 的距离是_____________．【解析】（1）8cm ；（2）1（提示：过点P 作三边的垂线，利用面积进行求解）．（1）证明：三角形三个角的角平分线交于一点．（2）（14年—15年金牛区期末）如图，ABC △的外角一平分线CP 和内角平分线BP 相交于点P ，若=80BAC ∠︒，则=CAP ∠____________．【解析】（1）如图，在ABC △中，设BAC ∠、ABC ∠的平分线的交点为I ，过I 点作ID AB ⊥于D ，IE AC ⊥于E ，IF E DCBA第19题第CAE DBBEABPIF BC ⊥于F ，连接IC ．∵AI 、BI 都是角平分线， ∴ID IE =，ID IF =， ∴IE IF =，∴CI 是ACB ∠的平分线，∴三角形三个角的平分线交于一点．（2）50°（提示：过点P 向三边作垂线，证明AP 是BAC ∠的外交角平分线） 2、角平分线模型（1）如图3-1，在ABC △中，BD 、CD 分别平分ABC ∠和ACB ∠，//ED AB ，//FD AC ．如果6BC =，则DEF △的周长为__________．（2）如图3-2，ABC ∠的平分线与ACB ∠的外角平分线相交于点D ，过点D 作EF //BC ，交AB 于E ，交AC 于F ，若8cm BE =，5cm CF =，则EF =________．（3）如图3-3，ABC △的内角ABC ∠和外角ACD ∠的平分线相交于点E ，BE 交AC 于点F ，过点E 作EG//BD 交AB 于点G ，交AC 于点H ，连接AE ，有以下结论：①12BEC BAC =∠∠；②HEF CBF △≌△；③BG CH GH =+；④AEB ACE +∠∠ 90=︒，其中正确的结论有_____________（只填序号）图3-1 图3-2 图3-3【解析】（1）6；（2）3cm ；（3）①③④．H FGABC DEBAEF CDA GDFE（1）（14—15年青羊区期末）如图4-1，在ABC △中，90BAC ∠=︒，AD BC ⊥于点D ，ABC ∠的平分线BE 交AD 于F ，交AC 于E ，若3AE =，2DF =，则AD =_____________．（2）如图4-2，已知：在ABC △中，90BAC ∠=︒，AD BC ⊥于D ，BCA ∠的角平分线交AD 与F ，交AB 于E ，//FG BC 交AB 于G ．4cm AE =，12cm AB =，则BG =__________，GE =__________．图4-1 图4-2【解析】（1）5；（2）4cm ；4cm ．过E 作EH 垂直BC 交BC 于H 点，易证AEC EHC △≌△；由角度分析易知AEF AFE ∠=∠，即AE AF =，则有EH EA AF ==；又可证AGF BHE △≌△，则1248AG EB ==-=，则844BG =-=，4GE =．如图，在ABC △中，12∠=∠，2AB AC =，AD BD =．求证：DC AC ⊥．ABF EADCF E GADCFE GHABDC12ABDC12E【解析】过D 作DE AB ⊥于MON ∠，∵AD BD =，DE AB ⊥， ∴ADE BDE △≌△， ∴12AE BE AB AC ===， ∵12∠=∠，∴ADE ADC △≌△， ∴90ACD AED ∠=∠=︒，∴DC AC ⊥．如图所示，在ABC △中，90BAC ∠=︒，AB AC =，BE 平分ABC ∠，CE BE ⊥．求证：12CE BD =．【解析】延长CE 、BA 相交于F ，在BEC △和BEF △中，12BE BE BEF BEC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BEC BEF △≌△ ∴12CE EF CF ==∵BE CE ⊥，∴190F ∠=︒-∠B ACEDAEDF 123同理390F ∠=︒-∠，∴13∠=∠在ABD △和ACF △中，13AB AC BAD CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABD ACF △≌△ ∴BD CF =，∴12CE BD =．如图，在ABC △中，60ABC ∠=︒，AD 、CE 分别平分BAC ∠、ACB ∠，AD 、CE 交于O ．（1）求AOC ∠的度数；（2）求证：AC AE CD =+．【解析】（1）=120AOC ∠︒；（2）在AC 上截取AT ，使AT AE =，连接OT ，在AOE △和AOT △中，AT AEOAT OAE AO AO =⎧⎪∠=∠⎨⎪=⎩∴(SAS)AOE AOT △≌△，∴60AOT AOE ∠=∠=︒，∴60COT COD ∠=∠=︒ 在COT △和COD △中， 60COT COD OC OCOCT OCD ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴(ASA)COT COD △≌△，∴CT CD =， ∴AE CD AT CT AC +=+=．AECOAECOT已知等腰ABC △，100A ∠=︒，ABC ∠的平分线交AC 于D ．求证：BD AD BC +=．【解析】解法一：如图，在BC 上截取BE BD =，连接DE ，过D 作DF//BC ，交AB 于F ，则32∠=∠，ADF ECD ∠=∠．又∵12∠=∠，∴13∠=∠，故DF BF =．显然FBCD 是等腰梯形． ∴BF DC =，DF DC =．∵1112(180100)20222ABC ∠=∠=⨯︒-︒=︒，1(1802)802BED BDE ∠=∠=︒-∠=︒，∴180100DEC BED ∠=︒-∠=︒，∴100FAD DEC ∠=∠=︒，∴AFD EDC △≌△，AD EC =．又∵BE BD =，∴BC BD EC BD AD =+=+．解法二：如图，延长BD 到E ，使DE AD =，在BC 上截取BF BA =．∵1=2∠∠，BD 为公共边，∴BAD BFD △≌△，AD FD =，ADB FDB ∠=∠．∵1111(180100)20222ABC ∠=∠=⨯︒-︒=︒，∴180(1)180(10020)60ADB A ∠=︒-∠+∠=︒-︒+︒=︒． ∴60FDB ∠=︒，故60FDC ∠=︒，60EDC ∠=︒． ∵DF DE =，∴DFC DEC △△≌．∴E DFC ∠=∠，34∠=∠．∵2206080DFC FDB ∠=∠+∠=︒+︒=︒， ∴80E ∠=︒．∵440∠=︒，∴340∠=︒，故3480ECB ∠=∠+∠=︒．∴ECB E ∠=∠，故BC BE =． ∵BE BD DE =+，∴BC BD AD =+．解法三：如图，延长BD 到E ，使BE BC =．ABDCAD CFE1233ABDCFE124ABDCE12F延长BA 到F ，使BF BC =．连接CE 、EF 、DF ． ∵12∠=∠，BD 公共，∴BDC BDF △△≌ ． ∴BDC BDF ∠=∠，BCD BFD ∠=∠．又∵120100120BDC BAC ∠=∠+∠=︒+︒=︒，40BCD ∠=︒，∴40BFD ∠=︒．∵BE BF =，120∠=︒．∴80BEF BFE ∠=∠=︒， ∴804040DFE ∠=︒-︒=︒．而180********FAD BAD ∠=︒-∠=︒-︒=︒．∴FAD DEF ∠=∠．又FD 公共，∴FAD FED △≌△． ∴ED AD =．∴BC BE BD AD ==+．如图，ABC △中，90BAC ∠=︒，AB AC =，AD BC ⊥，垂足为D ，AE 平分BAD ∠，交BC 于点E ．在ABC △外有一点F ，使FA AE ⊥，FC BC ⊥．（1）求证：BE CF =；（2）在AB 上取一点M ，使2BM DE =，连接MC ，交AD 于点N ，连接ME ．求证：①ME BC ⊥；②DE DN =．【解析】（1）由题意得，90BAC EAF ∠=∠=︒，∴90BAE CAF CAE ∠==︒-∠，在ABE △和ACF △中， 45BAE CAF AB ACABE ACF ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ∴(ASA)ABE ACF △≌△， ∴BE CF =．（2）①作ET AB ⊥于点T ，则DE TE =， ∴22BM DE TE ==，45ABE BET ∠=∠=︒， ∴TE TB =，2BM TB =，TB TM TE ==，B AMFND C∴ME BC ⊥②由①得，ME BC ⊥，AD BC ⊥，∴AD//ME ，∴22.5MEA NAE MAE ∠=∠=∠=︒， ∴ME MA =，∴CM 平分ACB ∠，即22.5ACN DCN ∠=∠=︒，在ADE △和CDN △中， 9022.5ADE CDN AD CDDAE DCN ∠=∠=︒⎧⎪=⎨⎪∠=∠=︒⎩∴(ASA)ADE CDN △≌△ ∴DE DN =．（三）作业设计1、（1）如图1-1，ABC △的周长是22，OB ，OC 分别平分ABC ∠和ACB ∠，OD BC ⊥于D ，且3OD =，求ABC △的面积．（2）如图1-2，ABC △的B ∠、C ∠的外角平分线交于点D ．求证：AD 是BAC ∠的平分线．图1-1 图1-2【解析】（1）∵O 点为ABC △的两内角平分线的交点，∴O 点到三边距离相等． ∴ABC OAB OBC OAC S S S S =++△△△△BADCOABCDABC DF EG1()3332AB BC AC =⨯++⨯=．（2）分别过D 作DE 、DF 、DG 垂直于AB 、BC 、AC ，垂足分别为E 、F 、G ，∵BD 平分CBE ∠，DE BE ⊥，DF BC ⊥， ∴DE DF =．同理DG DF =， ∴DE DG =，∴点D 在EAG ∠平分线上， ∴AD 是BAC ∠的平分线．2、（1）如图2-1，在ABC △中，ABC ∠和ACB ∠的平分线交于点E ，过点E 作//MN BC 交AB 于M ，交AC 于N ，若9BM CN +=，则线段MN 的长为_____．（2）如图2-2，BD 平分ABC ∠，CD 平分外角ACG ∠．DE//BC 交AB 于E ，交AC 于F ．线段EF 与BE 、CF 有什么关系?图2-1 图2-2【解析】（1）9；（2）如图所示中仍有两个等腰三角形BED △、CDF △，从而DE BE =，CF DF =，又EF ED DF BE CF =-=-，故EF BE CF =-．3、如图，在四边形ABCD 中，//AD BC ，A ∠的角平分线AE 交DC 于E ，BE 是B ∠的角平分线．求证：（1）AE BE ⊥；（2）AD BC AB +=．图4GFDCA EBAB C ENMADECBADECBF【解析】（1）∵//AD BC ，∴22180EAB EBA ∠+∠=︒∴90EAB EBA ∠+∠=︒，∴AE BE ⊥．（2）在AB 上截取AF ，使AF AD =，连接EF ，在ADE △和AFE △中， DA FA DAE BAE AE AE =⎧⎪∠=∠⎨⎪=⎩∴(SAS)ADE AFE △≌△ ∴ED EF =，ADE AFE ∠=∠ ∵//AD BC ，∴180ADE C ∠+∠=︒ ∵180EFB AFE ∠+∠=︒，∴EFB C ∠=∠ 在EFB △和ECB △中， EBF EBC EFB CBE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴(AAS)EFB ECB △≌△， ∴EF EC =，∴DE CE =， ∴AD BC AF BF AB +=+=．4、如图所示，在ABC △中，3ABC C ∠=∠，12∠=∠，BE AE ⊥．求证：2AC AB BE -=．【解析】延长BE 交AC 于M ．∵AE BE ⊥，12∠=∠，ABCE12ABCE12M 354∴34∠=∠，AB AM =，BE EM =， ∴AC AB AC AM MC -=-=，2BM BE =，又∵345C ∠=∠=∠+∠，353ABC C ∠=∠+∠=∠， ∴553C C ∠+∠+∠=∠， ∴5C ∠+∠，∴MB MC =， ∴2AC AB BE -=．5、如图，ABC △中，AB AC =，108A ∠=︒，BD 平分ABC ∠交AC 于D 点．求证：BC AC CD =+．【解析】方法一：在BC 上截取E 点使BE BA =，连结DE ．∵BD 平分ABC ∠，∴ABD EBD ∠=∠．在ABD △与EBD △中∵AB EB =，ABD EBD ∠=∠，BD BD =， ∴ABD EBD △≌△，∴A DEB ∠=∠，∵108A ∠=︒，∴108DEB ∠=︒，∴72DEC ∠=︒．又∵361854ADB ∠=︒+︒=︒，∴72CDE ∠=︒，∴CDE DEC ∠=∠，∴CD CE =， ∵BC BE EC =+，∴BC AC CD =+．方法二：如图，延长CA 到F ，使CF CB =，连结BF ． ∵AB AC =，且108BAC ∠=︒， ∴36ABC C ∠=∠=︒． ∵CB CF =，∴F FBC ∠=∠．∴FAB C ABC ∠=∠+∠．∴72FAB ∠=︒．∵12ADB C ABC ∠=∠+∠，∴54ADB ∠=︒．又∵54FBD ∠=︒, ∴BF AB AC FD ===． ∴AF CD =．∴BC AC CD =+．ABCDABCDEABCDF6、如图，Rt ABC △中，90ACB ∠=︒，CD AB ⊥，垂足为D ．AF 平分CAB ∠，交CD 于点E ，交CB 于点F ．（1）求证：CE CF =．（2）将图6-1中的ADE △沿AB 向右平移到'''A D E △的位置，使点'E 落在BC 边上，其它条件不变，如图6-2所示．试猜想：'BE 与CF 有怎样的数量关系?请证明你的结论．图6-1 图6-2【解析】（1）相等（2）如图，过点E 作EG AC ⊥于G ．又∵AF 平分CAB ∠，ED AB ⊥，∴ED EG =．由平移的性质可知：''D E DE =，∴''D E GE =． ∵90ACB ∠=︒．∴90ACD DCB ∠+∠=︒，∵CD AB ⊥于D ．∴90B DCB ∠+∠=︒∴ACD B ∠=∠, 在Rt CEG △与Rt ''BE D △中，∵GCE B ∠=∠，''CGE BD E ∠=∠，''GE D E =， ∴''CEG BE D △△≌，∴'CE BE =，由（1）可知'CF BE =．图1FEDC BAE‘图2GD′A′FE DCBA。

北师大版八年级数学下册第一章三角形的证明4 第1课时角平分线的性质

应用格式：
C
∵ PD⊥OA，PE⊥OB，PD = PE，
P
∴ 点 P 在∠AOB 的平分线上. O
E
B
典例精析
例2 如图，在△ABC中，∠BAC= 60°，点 D 在 BC 上
，AD = 10，DE⊥AB，DF⊥AC，垂足分别为 E，F，且
DE = DF，求 DE 的长.
A
E F
B
D
C
解：∵ DE⊥AB，DF⊥AC，垂足分别为E，F
改变点 C 的位置，线段 CD 和 CE 还相等吗?
对此你能得出什么结论？动手证一证.
结论：角的平分线上的点到角
的两边的距离相等.
O
A D
C
CB E
结论证明
已知：如图，OC 是∠AOB 的平分线，点 P 在 OC 上，
PD⊥OA，PE⊥OB，垂足分别为 D，E.
求证：PD = PE. 证明：∵ PD⊥OA，PE⊥OB，
(1) 角的平分线；
(2) 点在该平分线上；
(3) 垂直距离.
O
定理的作用：证明线段相等.
应用格式：
DA PC
EB
∵ OP 是∠AOB 的平分线，推理的理由有三个，必须写
PD⊥OA，PE⊥OB， ∴ PD = PE
完全，不能少了任何一个.
(角平分线上的点到这个角的两边的距离相等).
典例精析
例1 如图，AM 是∠BAC 的平分线，点 P 在 AM 上，
PD⊥AB，PE⊥AC，垂足分别是 D、E，PD = 4 cm，
则 PE = ___4___cm.
B D
M P
A
EC
温馨提示：存在两条垂线段——直接应用
2 角平分线的判定

八年级数学下册第一章三角形的证明1.4角平分线教案1新版北师大版

《角平分线》线段的垂直平分线是义务教育课程标准实验教科书（北师版）《数学》八年级下册第一章第 4 节内容，本章主要是有关命题的证明及三角形的性质；本节要求了解勾股定理逆定理的证明方法结合具体例子了解逆命题的概念，会识别两个互逆命题、知道原命题成立其。

所以本节的重点是进一步掌握演绎推理的方法。

学生的知识技能基础：通过上节的学习，学生对于角平分线性质定理和逆定理均有一个很深的了解和理解，在此基础上本节主要是通过例题来巩固定理和逆定理的应用，提高学生证明推理能力。

【知识与能力目标】（1）证明与角的平分线的性质定理和判定定理相关的结论。

（2）角平分线的性质定理和判定定理的灵活运用。

【过程与方法目标】（1）进一步发展学生的推理证明意识和能力。

（2）培养学生将文字语言转化为符号语言、图形语言的能力。

（3）提高综合运用数学知识和方法解决问题的能力。

【情感态度价值观目标】①能积极参与数学学习活动，对数学有好奇心和求知欲。

②在数学活动中获得成功的体验，锻炼克服困难的意志，建立自信心。

【教学重点】①三角形三个内角的平分线的性质。

②综合运用角平分线的判定和性质定理，解决几何中的问题。

【教学难点】角平分线的性质定理和判定定理的综合应用。

教学过程第一环节：设置情境问题，搭建探究平台问题I习题1. 8的第1题作三角形的三个内角的角平分线，你发现了什么？能证明自己发现的结论一定正确吗？于是，首先证明“三角形的三个内角的角平分线交于一点”。

当然学生可能会提到折纸证明、软件演示等方式证明，但最终，教师要引导学生进行逻辑上的证明。

第二环节：展示思维过程，构建探究平台已知：如图，设△ ABC的角平分线.BM CN相交于点P,证明：P点在ZB AC的角平分线上.证明：过P点作PDL AB PF1 AC PE丄BC其中D E、F是垂足.••• BM是△ ABC的角平分线，点P在BM上，••• PD=PE角平分线上的点到这个角的两边的距离相等）.同理：PE=PF.• PD=PF.•••点P在Z BAC的平分线上（在一个角的内部，且到角两边距离相等的点，在这个角的平分线上）.•••△ABC的三条角平分线相交于点P.在证明过程中，我们除证明了三角形的三条角平分线相交于一点外，还有什么“附带”的成果呢？（PD=PE=PF,即这个交点到三角形三边的距离相等. ）于是我们得出了有关三角形的三条角平分线的结论，即定理三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等.F三边垂直平分线三条角平分线三角形锐角三角形交于三角形内一点交于三角形内一点钝角三角形交于三角形外一点直角三角形交于斜边的中点问题2如图：直线11、丨2、丨3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可选择的地址有几处？你如何发现的？要求学生思考、交流。

湘教版八年级下册数学第1章直角三角形三角形的角平分线(1)

【点拨】∵ED⊥AB，∠A＝30°，∴DE＝12AE＝3 cm. ∵BE 平分∠ABC，ED⊥AB，∠ACB＝90°，∴CE＝DE＝3 cm.
10．如图，△ABC的三边AB，AC，BC的长分别为4， 6，8，其三条角平分线将△ABC分成三个三角形，则S△OAB∶S△OAC∶S△OBC等于( )
A．2∶3∶4B．1∶1∶1 C．1∶2∶3D．4∶3∶2
1．三角形内有一点到三角形三边的距离相等，则这个点一定是三角形的( ) B
A．三条高的交点 B．三条角平分线的交点 C．三边中线的交点 D．三边垂直平分线的交点
2．如图，在△ABC中，∠ABC，∠ACB的平分线相交于O，下列结论正确的是( ) B
A．∠1>∠2 B．∠1＝∠2 C．∠1<∠2 D．不能确定∠1与∠2的大小关系
4．已知△ABC内一点M，如果点M到两边AB，BC的距离相等，那么点M( ) C
A．在AC边的高上 B．在AC边的中线上 C．在∠ABC的平分线上 D．在AC边的垂直平分线上
5．【中考·扬州】如图，在△ABC 中，按以下步骤作图： ①以点 B 为圆心，任意长为半径作弧，分别交 AB，BC 于点 D，E； ②分别以点 D，E 为圆心，大于12DE 的长为半径作弧，两弧交于点 F； ③作射线 BF 交 AC 于点 G.
第1章直角三角形
1.4 角平分线的性质第2课时三角形的角平分线
提示：点击进入习题
新知笔记
三边
答案显示
1B
2B
3A
4C
5 27
6 125° 7 B
8D
9C
10 A
11 10
12 见习题 13 见习题 14 见习题
三角形的三条内角平分线相交于一点，这一点到三角形__三__边____的距离相等．

数学八年级下册北师大版第1章 3. 第2课时三角形三边垂直平分线的性质

解：同理得∠M＝40°.
18
18
(3)你发现了怎样的规律？试证明；
解：规律是：等腰三角形一腰的垂直平分线与底边相
交所成的锐角等于顶角的一半，
证明：设∠A＝α，
则有∠B＝12(180°－α)． ∠M＝90°－12(180°－α)＝12α.
19
19
(4)将(1)中的∠A 改为钝角，(3)中的规律仍成立吗？若不成立，应怎样修改．
第一章三角形的证明
3．线段的垂直平分线
第2课时三角形三边垂直平分线的性质
1
1
2
2
学点一三角形三边垂直平分线的性质
三角形三边垂直平分线的交点到三三个个顶顶点点的距离相等．
3
3
如图，某公园的三个出口 A、B、C 构成△ABC，想要在公园内修建一个公共厕所，要求到三个出口距离都相等，则公
12
12
解：如图，连接 BD，CD. 由题意：DA＝DB＝DC， ∴∠DAB＝∠DBA，∠DBC＝∠DCB，∠DAC＝∠DCA， ∵∠AEC＝3∠BAE＝3α，∠AEC＝∠BAE＋∠ABE， ∴∠ABE＝2α， ∴∠DAB＝∠DBA＝∠DBC＝∠DCB＝α， ∴∠EAC＝12(180°－4α)＝90°－2α.
15
15
5．在△ABC 中，AB＝AC，AB 的垂直平分线交 AB 于 N，交 BC 的延长线于 M，∠A＝40°.
16
16
(1)求∠M 的度数；
解：∵∠B＝12(180°－∠A)＝70°， ∵MN 垂直平分 AB， ∴∠BNM＝90°，,∴∠M＝20°.
17
17
(2)若将∠A 的度数改为 80°，其余条件不变，再求∠M 的大小；
A．AC、BC 两边高线的交点处

八年级下册数学各章节知识梳理

八年级下册数学各章节知识梳理教学目标：经历探究、猜想过程能够运用公理和所学过的定理证明线段垂直平分线的性质定里和判定定理能够利用尺规作已知线段的垂直平分线重难点：重点是写出线段垂直平分线的性质定理的逆命题。

难点是两者的应用上的区别及各自的作用易错点：精确理解线段垂直平分线的性质定理，解题时要考虑全面，防止漏解整体分析【一】教学目标八年级是初中学习过程中的关键时期，学生根底的好坏，直接影响到将来是否能升学。

优生不多，思想不够活泼，有少数学生不上进，思维跟不上。

要在本期获得理想成绩，老师和学生都要付出努力，充分发挥学生是学习的主体，教师是教的主体作用，注重方法，培养能力。

【二】教材分析本学期教学内容共计六章：《三角形的证明》、《一元一次不等式和一元一次不等式组》、《图形的平移与旋转》、《因式分解》、《分式与分式方程》、《平行四边形》。

《三角形的证明》：本章将证明与等腰三角形和直角三角形的性质及判定有关的一些结论，证明线段垂直平分线和角平分线的有关性质，将研究直角三角形全等的判定，进一步体会证明的必要性。

《一元一次不等式和一元一次不等式组》：本章通过具体实例建立不等式，探究不等式的根本性质，了解一般不等式的解、解集、解集在数轴上的表示，一元一次不等式的解法及应用；通过具体实例渗透一元一次不等式、一元一次方程和一次函数的内在联系．最后研究一元一次不等式组的解集和应。

《图形的平移与旋转》：本章将在小学学习的根底上进一步认识平面图形的平移与旋转，探究平移，旋转的性质，认识并观赏平移，中心对称在自然界和现实生活中的应用。

《因式分解》：本章通过具体实例分析分解因式与整式的乘法之间的关系揭示分解因式的实质，最后学习分解因式的几种根本方法。

《分式与分式方程》：本章通过分数的有关性质的回忆建立了分式的概念、性质和运算法则，并在此根底上学习分式的化简求值、解分式方程及列分式方程解应用题，能解决简单的实际应用问题。

《平行四边形》：本章将研究平行四边形的性质与判定，以及三角形中位线的性质，还将探究多边形的内角和，外角和的规律；经历操作，实验等几何发觉之旅，享受证明之美。

北师大版八年级数学下册《线段的垂直平分线》三角形的证明PPT课件(第2课时)

实践探究，交流新知
解：(1)已知三角形的一条边及这条边上的高，能作出三角形，并且能作出无数多个，如图所示． (2)已知等腰三角形的底边，用尺规作出等腰三角形，这样的等腰三角形也有无数多个． (3)如果等腰三角形的底边和底边上的高都一定，这样的等腰三角形应该只有两个，它们是全等的，且分别位于已知底边的两侧，如图所示．
北师大版八年级下册第一章三角形的证明
线段的垂直平分线（第2课时）
前言
学习目标
1.会证明三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等，并解决相关的问题． 2.会用尺规作已知线段的垂直平分线，培养尺规作图的技能．
学习重点
掌握三角形三条边的垂直平分线的性质，能利用尺规作出符合条件的三角形.
(1)教材第26页随堂练习． (2)教材第26页习题1.8第1，2题.
同学们，下课！
． 39°
3．如图，在△ABC中，∠BAC是钝角． (1)画出边BC上的中线AD； (2)画出边BC上的高AH.
第1题
第2题
第3题
课堂小结，整体感知
1.课堂小结：请同学们回顾本节课所学的内容，有哪些收获？（1）三角形三条边的垂直平分线的性质（2）尺规作线段的垂直平分线、等腰三角形
2.布置作业：
学习难点
三角形三条边的垂直平分线性质的证明及应用.
创设情境，导入新课
1.问题提出：利用尺规作三角形三条边的垂直平分线，当作图完成后你发现了什么？ 2.问题探究： ①三角形三边的垂直平分线交于一点； ②这一点到三角形三个顶点的距离相等．
创设情境，导入新课
3.问题解决：如图，剪一个三角形纸片，通过折叠找出每条边的垂直平分线，观察这三条垂直平分线，上述结论是否成立？ 4.问题思考：以上结论都是通过眼睛观察得到的，那么该结论一定成立吗？我们还需运用已学过的公理和定理进行推理证明，这样，此发现才更有意义．

八年级数学下册第一章三角形的证明 2 直角三角形第2课时直角三角形全等的判定教案北师大版

八年级数学下册第一章三角形的证明2 直角三角形第2课时直角三角形全等的判定教案北师大版年级：姓名：第2课时直角三角形全等的判定【知识与技能】能够证明直角三角形全等的“HL”的判定定理，进一步理解证明的必要性【过程与方法】进一步经历用几何符号和图形描述命题的条件和结论的过程，建立初步的符号感【情感态度】进一步掌握推理证明的方法，发展演绎推理能力【教学重点】能够证明直角三角形全等的“HL”的判定定理【教学难点】进一步理解证明的必要性.一.情景导入，初步认知1.判断两个三角形全等的方法有哪几种？2.已知一条边和斜边，求作一个直角三角形.想一想，怎么画？同学们相互交流.3.有两边及其中一边的对角对应相等的两个三角形全等吗？如果其中一个角是直角呢？请证明你的结论.【教学说明】教师顺水推舟，询问能否证明：“斜边和一条直角边分别相等的两个直角三角形全等”，从而引入新课.二.思考探究，获取新知探究：“HL”定理.已知：在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，AB=A′B′，BC=B′C′．求证：Rt△ABC≌Rt△A′B′C′.证明：在Rt△ABC中，AC2=AB2一BC2(勾股定理)．又∵在Rt△ A' B' C'中，A' C' 2=A'B'2一B'C'2 (勾股定理)．∴AB=A'B'，BC=B'C'，AC=A'C'．∴Rt△ABC≌Rt△A'B'C' (SSS)．【归纳结论】斜边和一条直角边对应相等的两个直角三角形全等．（这一定理可以简单地用“斜边、直角边”或“HL”表示．)【教学说明】讲解学生的板演，借此进一步规范学生的书写和表达.分析命题的条件，既然其中一边和它所对的直角对应相等，那么可以把这两个因素总结为直角三角形的斜边对应相等，于是直角三角形有自己的全等判定定理.三.运用新知，深化理解1.见教材P20例题2.填空：如下图，Rt△ABC和Rt△DEF，∠C=∠F=90°.（1）若∠A=∠D，BC=EF，则Rt△ABC≌Rt△DEF的依据是AAS.（2）若∠A=∠D，AC=DF，则Rt△ABC≌Rt△DEF的依据是ASA.（3）若∠A=∠D，AB=DE，则Rt△ABC≌Rt△DEF的依据是AAS.（4）若AC=DF，AB=DE，则Rt△ABC≌Rt△DEF的依据是HL.（5）若AC=DF，CB=FE，则Rt△ABC≌Rt△DEF的依据是SAS.3.已知：Rt△ABC和Rt△A'B'C'，∠C=∠C'=90°，BC=B'C'，BD、B'D'分别是AC、A'C'边上的中线，且BD=B'D'. 求证：Rt△ABC≌Rt△A'B'C'．证明：在Rt△BDC和Rt△B'D'C'中，∵BD=B'D',BC=B'C',∴Rt△BDC≌Rt△B'D'C' (HL定理)．∴CD=C'D'．又∵AC=2CD，A'C'=2C'D'，∴AC=A'C'．∴在Rt△ABC和Rt△A'B'C '中，∵BC=B'C '，∠C=∠C '=90°，AC=A'C'，∴Rt△ABC≌Rt△A'B'C(SAS)．4.如图，已知∠ACB=∠BDA=90°，要使△ACB≌△BDA，还需要什么条件?把它们分别写出来，并证明.解：AC=DB.∵AC=DB,AB=BA,∴△ACB≌△BDA（HL）其他条件：CB=DA或四边形ACBD是平行四边形等.证明略.【教学说明】这是一个开放性问题，答案不唯一，需要我们灵活地运用公理和已学过的定理，观察图形，积极思考，并在独立思考的基础上，通过同学之间的交流，获得各种不同的答案．5.如图，在△ABC与△A'B'C'中，CD、C'D'分别分别是高，并且AC＝A'C'，CD=C'D'．∠ACB=∠A'C'B'．求证：△ABC≌△A'B'C'．分析：要证△ABC≌△A'B'C'，由已知中找到条件：一组边AC=A'C'，一组角∠ACB=∠A'C'B'．如果寻求∠A=∠A'，就可用ASA证明全等；也可以寻求∠B=∠B'，这样就可用AAS；还可寻求BC=B'C'，那么就可根据SAS……注意到题目中有CD、C'D'是三角形的高，CD=C'D'．观察图形，这里有三对三角形应该是全等的，且题目中具备了HL定理的条件，可证得Rt△ADC≌Rt△A'D'C'，因此证明∠A=∠A' 就可行．证明：∵CD、C'D'分别是△ABC、△A'B'C'的高(已知)，∴∠ADC=∠A'D'C'=90°．在Rt△ADC和Rt△A'D'C'中，AC=A'C'(已知)，CD=C'D' (已知)，∴Rt△ADC≌Rt△A'D'C' (HL)．∠A=∠A'，(全等三角形的对应角相等)．在△ABC和△A'B'C'中，∠A=∠A' (已证)，AC=A'C' (已知)，∠ACB=∠A'C'B' (已知)，∴△ABC≌△A'B'C' (ASA)．【教学说明】通过上述师生共同活动，学生板书推理过程之后可发动学生去纠错，教师最后再总结.四.师生互动，课堂小结直角三角形的判定方法有五种，注意“HL”仅适用于直角三角形.五.教学板书布置作业:教材“习题1.6”中第3、4、5 题.本节课我们讨论了在一般三角形中两边及其一边对角对应相等的两个三角形不一定全等．而当一边的对角是直角时，这两个三角形是全等的，从而得出判定直角三角形全等的特殊方法——HL定理，并用此定理安排了一系列具体的、开放性的问题，不仅进一步掌握了推理证明的方法，而且发展了同学们演绎推理的能力．同学们这一节课的表现很值得夸赞．。

新北师大版八年级数学下册《一章三角形的证明4.角平分线三角形中的角平分线》教案_5

三、教学过程分析
本节课设计了五个教学环节：第一环节：设置情境
温故知新；第二环节：
探究新知；第三环节：巩固练习；第四环节：随堂练习；第五环节：课时小结；
第六环节：课后作业
1：情境引入
我们曾用折纸的方法探索过角平分线上的点的性质，步骤如下：
从折纸过程中，我们可以得出 CD=CE，
即角平分线上的点到角两边的距离相等．
北师大版八年级数学
教学设计
平顶山市第五十六中学鲁刘琴
（3）用直尺和圆规画已知角的平分线及作图的依据讨论。 3.巩固练习综合利用角平分线的性质和判定、直角三角形的相关性质解决问题。进一步发展学生的推论证明能力。在学生独立完成推理过程的基础上，教师要给出书写示范例题：在 △ABC 中，∠ BAC = 60 °，点 D 在 BC 上， AD = 10 ， DE⊥ AB ，DF⊥AC ，垂足分别为 E，F，且 DE = DF，求 DE 的长 . （4）课本例题学习 4：随堂练习课本第 29 页 1、 2 题。 5：课堂小结这节课证明了角平分线的性质定理和判定定理，在有角的平分线（或证明是角的平分线）时，过角平分线上的点向两边作垂线段，利用角平分线的判定或性质则使问题迅速得到解决。 6：课后作业习题 1． 9 第 1，2，3,4 题．
O
1 2
A D
P C
E B
指导 )
我们用公理和已学过的定理证明了我们折纸过程中得出的结论．我们把它叫
做角平分线的性质定理。 (用多媒体演示 )角平分线上的点到这个角的两边的距
离相等．
（ 2）你能写出这个定理的逆命题吗 ?
我们在前面学习线段的垂直平分线时，已经历过构造其逆命题的过程，我们
可以类比着构造角平分线性质定理的逆命题．

八年级下册数学(北师版)同步课件：第一章三角形的证明 4 角平分线(2)

E B
角形的内心).
三角形一个内角和与它不相邻的两个外角的平分线交于一点, 这个的点叫做三角形的旁
心.这样的点有三个.
独立
知识的升华
作业
习题
祝你成功！
独立作业 1
1.已知:如图,∠C=900, ∠B=300,AD是Rt△ABC的角平分线. 求证:BD=2CD.
习题
A
B
DC
老师期望: 你能写出规范的证明过程.
做一做 1
几何的三种语言
定理:三角形的三条角平分线相交于一点,并且这
一点到三边的距离相等.
如图,在△ABC中,
∵BM,CN,AH分别是△ABC的三条角
A
平分线,且PD⊥AB,PE⊥BC,PF⊥AC( N D
M
已知),
PF
∴BM,CN,AH相交于一点P,且 PD=PE=PF(三角形的三条角平分线
B
相交于一点,并且这一点到三边的
1 2
个角的内部,且到角的两边距离相
P C
等的点,在这个角的平分线上).
E
老师提示:这个结论又是经常用B
来证明点在直线上(或直线经过
某一点)的根据之一.
做一做 1
亲历知识的发生和发展
剪一个三角形纸片通过折叠找出每个角的平分线.
观察这三条角平分线,你发现了什么?
结论:三角形三个角的平分线相交于一点.
请你说明OC为什么是∠AOB的平分线,并与同伴进行交流
老师提示: 作角平分线是最基本的尺规作图,这
回顾思考
角ቤተ መጻሕፍቲ ባይዱ分线的性质
定理角平分线上的点到这个角的两边距离相等.
如图, ∵OC是∠AOB的平分线,P是OC 上任意一点,PD⊥OA,PE⊥OB,垂

八年级数学下册第1章三角形的证明 1.4 角平分线第2课时三角形三条内角的平分线课件

A
D
N
F
P
M
C E
第八页，共二十二页。
想一想：点P在∠A的平分线上吗？这说明三角形的三条(sān
tiáo)角平分线有什么关系？
A
点P在∠A的平分线上.
D
N
F
P
M
B
C
E
结论：三角形的三条角平分线交于一点，并且这点(zhè diǎn)
到三边的距离相等.
第九页，共二十二页。
例1.如图,在△ABC中,已知AC=BC,
第二十二页，共二十二页。
A
B
O
P
DM
C
第十三页，共二十二页。
例3 如图，在△ABC中，点O是△ABC内一点(yī diǎn)，且点O到△ABC三
边的距离相等．若∠A＝40°，则∠BOC的度数为( )
A
A．110° B．120° C．130° D．140°
解析：由已知，O到三角形三边的距离(jùlí)
相等，所以O是内心，即三条角平分线
发现(fāxiàn)：三角形的三条角平分线相交于一点.
第四页，共二十二页。
活动2 分别过交点作三角形三边的垂线，用刻度尺量一量 (yī liànɡ)，每组垂线段，你发现了什么？
你能证明(zhèngmíng) 这个结论吗？
发现：过交点作三角形三边(sān biān)的垂线段相等.
第五页，共二十二页。
试一试
剪一个三角形纸片，通过折叠找出每个角的角平分线，观察这三条角平分线，你是否发现同样(tóngyàng)的结论？与同伴交流．
结论(jiélùn)：三角形三个角的平分线相交于一点.
怎样证明这个结论呢?
第六页，共二十二页。

北师大版八年级下册数学第一章三角形的证明第4节《角平分线》参考课件

相等的点,在这个角的平分线上.
如图, ∵PD=PE, PD⊥OA,PE⊥OB,垂足分
A D
别是D,E(已知),
O
∴点P在∠AOB的平分线上.(在一
1 2
P C
个角的内部,且到角的两边距离相
E
等的点,在这个角的平分线上).
B
老师提示:这个结论又是经常用来证明点在直线
上(或直线经过某一点)的根据之一.
例题讲析
角的两边距离相等.
∵OC是∠AOB的平分线,P是OC
上任意一点
O
,PD⊥OA,PE⊥OB,垂足分别
是D,E(已知)
∴PD=PE(角平分线上的点到
这个角的两边距离相等).
A D
1P
2
C
E B
逆定理在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上. ∵PD=PE, PD⊥OA,PE⊥OB,垂 O 足分别是D,E(已知), ∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).
任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E.
求证:PD=PE.
A D
分析:要证明PD=PE,只要
证明它们所在△OPD≌△OPE
O
1 2
P C
而△OPD≌△OPE的条件由已知易知它满足公理(AAS).
故结论可证.
E B
老师期望:你能写出规范的证明过程.
证明： ∵ OC是∠AOB的平分线 ∴ ∠1= ∠2 ∵ PD⊥OA,PE⊥OB ∴ ∠PDO= ∠PEO ∵OP=OP ∴ △OPD≌△OPE (AAS). ∴ PD=PE
BD 2 2D2E4 2cm
ACBCCD BD (44 2)cm

2018春八年级数学下册第一章三角形的证明4角平分线第2课时三角形内角的平分线作业课件新版北师大版

嘉定区五中八年级数学下册 第一章 三角形的证明 4角平分线第2课时 三角形三个内角的平分线课件新版北

八年级数学下册 第一章 三角形的证明 4角平分线第1课时 角平分线的性质与判定课件(新版)北师大版

北师大版八年级数学下册第一章三角形的证明基础拔高讲义(角平分线的性质和判定、角平分线模型)(含答案)

北师大版八年级数学下册第一章 三角形的证明4 第1课时 角平分线的性质

八年级数学下册第一章三角形的证明1.4角平分线教案1新版北师大版

湘教版八年级下册数学第1章 直角三角形 三角形的角平分线(1)

数学八年级下册北师大版第1章 3. 第2课时 三角形三边垂直平分线的性质