高三数学双基 一
高考数学复习双基统一测试试题及参考答案

高考数学复习双基统一测试试题本试卷分第I 卷(选择题)和II 卷(非选择题)两部分,满分150分,考试时间120分钟。
参考公式:如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B ) 如果事件A 、B 相互独立,那么P (A·B )=P (A )·P (B ) 如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k次的概率P n (k )=kn k k n P P C --)1(球的体积公式:334R V π=(其中R 表示球的半径) 球的表面积公式S=4πR 2(其中R 表示球的半径)第I 卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)下列四个选项中,只有一个是符合题目要求的。
.1.已知全集},,{},,{},,,,,{e b a B c b A e d c b a U ===集合,则( )∩B= ( )A .{e a ,}B .},,{d c bC .},,{e c aD .}{c2.过点P (-2,4)作圆25)1()2(:22=-+-y x C 的切线l ,直线03:=-y ax m 与直线l 平行,则a 的值是( )A .2B .58 C .512 D .43.若关于x 的不等式042≥--a x x ,对任意]1,0(∈x 恒成立,则a 的取值范围是( )A .4-≥aB .3-≥aC .03≤<-aD .3-≤a4.已知向量a =(λ,-2),b =(-3,5),且a 与b 的夹角为钝角,则λ的取值范围是( ) A .),56()56,310(+∞⋃- B .)310(∞+-C .)310,(--∞D .]310,(--∞5.如图,都不是正四面体的表面展开图的是( )A .①⑥B .④⑤C .②③D .④⑥6.已知a >b >c >0,t 是方程02=++c bx ax 的实根,则t 的取值范围是( )A .(-∞,-1)B .(-1,0)C .(0,1)D .(1,+∞)7.正方体的八个顶点中,有四个顶点恰好是正四面体的顶点,则这个正方体的表面积与正四面体的表面积之比是 ( )A .2:3B .1:2C .1:3D .3:2 8.要得到函数)42cos(π-=xy 的图象,只需将y=sin2x的图象( )A .向左平移2π B .向右平移2π C .向左平移4πD .向右平移4π 9.已知点P 在曲线323+-=x x y 上移动,若经过点P 的曲线的切线的倾斜角为α,则a 的取值范围是( )A .),43[)2,0[πππ⋃ B .),65[)2,0[πππ⋃C .),43[ππD .]43,0[π10.数列1,(1+2),(1+2+22),…,(1+2+…+2n -1),…的前n 项和等于 ( )A .2nB .2n -nC .2n+1 -n -2D .n·2n11.(理科答)甲、乙两名篮球队员轮流投篮至某人投中为止。
高三数学教学计划

高三数学教学方案高三数学教学方案高三数学教学方案1 一、数学的“双基”是指数学的根底知识、根本技能和数学思想方法。
它是数学才能培养的重要载体与有效支撑,是学生数学素养的重要组成部分,也是高考数学的考察重点,因此在复习时应注重以下几点:(一)根底复习,要“细”; 力求主次清楚,突出重点。
1、课本是一切知识的来与根底,课本中结论,定理与性质,都是学习数学非常重要的环节;因此立足课本,迅速激活已学过的各个知识点,强调课本的重要性,不放过课本的每一个角落。
2、注意所做题目使用知识点覆盖范围的变化,有意识地考虑、研究这些知识点在课本中所处的地位和互相之间的联络。
3、要重视数学概念的复习,深化体会数学概念的本质特征.如在函数的复习习过程中要重视函数概念的复习,深化体会函数的本质特征,学会函数的思维方式。
(二)对核心的知识要概括,解题的方法要概括,对每一章节、每一单元的问题解决的思维方式做一概括!在知识的复习过程中注意每一模块复习完要注意引导学生建立网络图,其目的是一方面,所学知识层次明晰,知识的逻辑关系清楚,更重要的是,这个知识构造图也表达了学生应掌握的数学思维的根本形式与方法。
将典型问题模型化,将通解通法固化在我们的解题思维中,可以有效地进步我们解决数学问题的才能,有效地进步复习的质量,也是教师进步复习效率最应该做的事情。
(三)分层教学,教学内容要有针对性。
高三数学复习,绝不能等同高一,高二阶段,平铺直叙,对每章的知识构造,在复习开始与复习完毕时都要能写出或说出各章节的知识构造与知识体系,特别要强调课本内涉及的内容与课外补充的内容,及高考考过的知识点,为此,师生要研究近三年的高考题目。
例如:“函数”一章,课本目录:集合与函数、根本初等函数、函数方程与零点。
因为函数是高考的重头戏,函数知识与函数思想地位,需让同学们下大力气掌握,扩大内容:求函数解析式,函数值域,求函数定义域,函数图像及变换,函数与不等式,函数思想的应用;重点知识重点掌握,重点训练,也是近几年高考的一个方向,而对于集合,因为高考要求降低,就适当减少课时,针对性处理数学知识点。
辽宁省大连市2024届高三上学期期末双基测试数学检测卷(有答案)

辽宁省大连市2024届高三上学期期末双基测试数学检测卷注意事项:1.请在答题纸上作答,在试卷上作答无效2.本试卷分和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第I 卷一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求1.已知集合,则( ){}*11,2,3,4,5,2x A B x ⎧⎫-==∈⎨⎬⎩⎭N A B ⋂=A.B.C.D.{}5{}2,4{}3,5{}1,3,52.设复数,则( )1i4i 1i z -=++z =A.0B.1C.2D.33.在中,若,则( )ABC 1,3AD mDB CD CA CBλ==+ λ=A. B. C. D.231313-23-4.在财务审计中,我们可以用“本•福特定律”来检验数据是否造假.本福特定律指出,在一组没有人为编造的自然生成的数据(均为正实数)中,首位非零的数字是这九个事件不是等19~可能的.具体来说,随机变量是一组没有人为编造的首位非零数字,则χ.则根据本•福特定律,首位非零数字是1与首位非零数字()1lg,1,2,,9k P k k k χ+=== 是8的概率之比约为( )(保留至整数,参考数据:).lg20.301,lg30.477==A.4B.6C.7D.85.已知曲线“表示焦点在轴上的椭圆”的一个充分非()()22:log 2024log 20241a b C x y +=y必要条件是( )A.B.0a b <<1a b<<C. D.32a b <<1b a<<6.已知函数,若存在实数满足()()[]2log ,0,2πsin ,2,104x x f x x x ⎧∈⎪=⎨⎛⎫∈ ⎪⎪⎝⎭⎩1234,,,x x x x ,且,则的值是( )()()()()1234f x f x f x f x ===1234x x x x <<<34124x x x x +⋅A.3B.6C.8D.127.设,则( )11155,2ln sin cos ,ln48844a b c ⎛⎫==+= ⎪⎝⎭A.B.a b c <<b a c<<C. D.c b a <<a c b <<8.已知函数满足下列条件:①对任意()sin πcos π(1,1,0)f x a x b x a b ωωω=+>>>恒成立;②在区间上是单调函数;③经过点()1,4xf x f ⎛⎫∀∈≤ ⎪⎝⎭R ()f x 34,77⎡⎤⎢⎥⎣⎦的任意一条直线与函数图像都有交点,则的取值范围是()()b ()y f x =ωA.B.(]280,13,9⎡⎤⋃⎢⎥⎣⎦()280,13,9⎡⎤⋃⎢⎥⎣⎦C.D.][(0,13,5⎤⋃⎦()30,1,52⎡⎤⋃⎢⎥⎣⎦二、多项选择题:(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9.在中,角的对边分别是,若,ABC ,,A B C ,,a b c cos sin a B b A c +=,则()222sin a ab c ab C =+-=A. B.tan 2C =π3A =C.D.的面积为b =ABC10.如图,在棱长为1的正方体中,分别是的中点,1111ABCD A B C D -M N P 、、1111C D C C A A 、、则()A.平面截正方体所得截面为等腰梯形1A MN B.三棱锥的体积为1D MNB -112C.异面直线与MN 1D P D.1A D BM⊥11.已知三个盒子,其中盒子内装有2个红球,1个黄球和1个白球;盒子内装,,A B C A B 有2个红球,1个白球;盒子内装有3个红球,2个黄球.若第一次先从盒子内随机抽取C A 1个球,若取出的球是红球放入盒子中;若取出的球是黄球放入盒子中;若取出的球是A B 白球放入盒子中,第二次从第一次放入盒子中任取一个球,则下列说法正确的是()C A.在第一次抽到黄球的条件下,第二次抽到红球的概率为12B.第二次抽到红球球的概率为13C.如果第二次抽到的是红球,则它来自号盒子的概率最大B D.如果将5个不同的小球放入这三个盒子内,每个盒子至少放1个,则不同的放法有150种12.已知椭圆左焦点,左顶点,经过的直线交椭圆于两点(点22:143x y E +=F C F l ,A B 在第一象限),则下列说法正确的是( )A A.若,则的斜率2AF FB=l k =B.的最小值为4AF BF +274C.以为直径的圆与圆相切AF 224x y +=D.若直线的斜率为,则,AC BC 12,k k 1294k k ⋅=-第II 卷三、填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)13.如图所示是一个样本容量为100的频率分布直方图,则由图形中的数据,可知其分60%位数为__________.14.十九世纪下半叶集合论的创立,奠定了现代数学的基础.著名的“康托三分集”是数学理性思维的构造产物,具有典型的分形特征,其操作过程如下:将闭区间均分为三段,去掉中[]0,1间的区间段,记为第一次操作:再将剩下的两个区间...分为三段,并各12,33⎛⎫ ⎪⎝⎭120,,,133⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦自去掉中间的区间段,记为第二次操作...,如此这样,每次在上一次操作的基础上,将剩下的各个区间分别均分为三段,同样各自去掉中间的区间段.操作过程不断地进行下去,以至无穷,剩下的区间集合即是“康托三分集”.若使去掉的各区间长度之和小于,则操作的次18212024数的最大值为__________.n (参考数据:)456722220.1975,0.1317,0.0878,0.05853333⎛⎫⎛⎫⎛⎫⎛⎫≈≈≈≈ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭15.已知,若点是抛物线上的任意一点,点是圆上任意()3,0A P 28y x =Q 22(2)1x y -+=一点,则最小值是__________.2||PA PQ16.如图所示,在圆锥内放入两个球,它们都与圆锥相切(即与圆锥的每条母线相切,12,O O 切点圆分别为.这两个球都与平切,切点分别为,丹德林(G.Dandelin )12,C C α12,F F 利用这个模型证明了平面与圆锥侧面的交线为椭圆,为此椭圆的两个焦点,这两个α12,F F 球也称为G.Dandelin 双球.若圆锥的母线与它的轴的夹角为,的半径分别为3012,C C 2,5,点为上的一个定点,点为椭圆上的一个动点,则从点沿圆锥表面到达M 2C P P 的路线长与线段的长之和的最小值是__________.M 1PF 四、解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)已知函数,其中,__________.()()sin 2cos2f x x xϕ=++π2ϕ<请从以下二个条件中任选一个,补充在题干的横线上,并解答下列问题:①是的一个零点;②.π12-()f x ()π03f f ⎛⎫= ⎪⎝⎭(1)求的值;ϕ(2)当时,若曲线与直线恰有一个公共点,求的取值范围.ππ,63x ⎡⎤∈-⎢⎥⎣⎦()y f x =y m =m 注:如果选择条件①和条件②分别解答,按第一个解答计分.18.(本小题满分12分)如图,多面体,四边形是矩形,梯形平面ABCDNM DBMN ,ABCD AD ∥,BC DN ⊥,为中点,.π,2ABCD CBD ∠=E AB 2,1AD BD DN BC ====(1)证明:平面;AN ∥MDE (2)求平面和平面所成角余弦值.MNC MNA 19.(本小题满分12分)已知数列满足.设.{}n a ()*111,1,N 2,n n n a n a a n a n +-⎧==∈⎨⎩为奇数为偶数21nn b a -=(1)证明:数列为等比数列,并求出的通项公式;{}2n b -{}n b (2)求数列的前项和.{}n a 2n 20.(本小题满分12分)某农场2021年在3000亩大山里投放一大批鸡苗,鸡苗成年后又自行繁育,今年为了估计山里成年鸡的数量,从山里随机捕获400只成年鸡,并给这些鸡做上标识,然后再放养到大N 山里,过一段时间后,从大山里捕获1000只成年鸡,表示捕获的有标识的成年鸡的数目.X (1)若,求的数学期望;10000N =X (2)已知捕获的1000只成年鸡中有20只有标识,试求的估计值(以使得最N ()20P X =大的的值作为的估计值).N N 21.(本小题满分12分)已知抛物线经过点,经过点的直线与抛物线交两2:2(0)G x py p =>()2,1()0,2l G ,A B 点,过两点作抛物线的切线相交于点为线段(两点除外)上一动点,,A B G ,P Q AB ,A B 直线与抛物线交两点.PQ G ,C D (1)若的的面积为,求直线方程;PABl (2)求证.PCPD CQDQ=22.(本小题满分12分)已知函数(为自然对数的底数).()ln 1x a x f x e a x +=--e (1)若,求实数的值;()0f x ≥a (2)证明:;()21sin 2ln x x xe x x->+-(3)对恒成立,求取值范围.2π,,2cos 2x x xe ax x x x ∞⎛⎫∈-+≥+- ⎪⎝⎭a 答案与评分标准数学说明:一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半:如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数,选择题和填空题不给中间分第I 卷一、单项选择题1.C2.D3.A2.D3.A4.B5.C6.A7.B8.A.7.解:,构造函数由211111ln sin cos ln 1sin ,1ln 188444b c ⎛⎫⎛⎫⎛⎫⎛⎫=+=+=++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭得,构造函数()sin ,ln 1x x x x <+<11111sin ,ln 1sin sin ,;44444a b ⎛⎫>+<<> ⎪⎝⎭()()()2211ln 1,11(1)(1)x xf x x f x x x x x =+-='-=++++在上单调递增,即,故()f x []0,1c a >c a b>>另法:1111ln ,1ln 1444x x x c ⎛⎫⎛⎫-<=++>⎪ ⎪⎝⎭⎝⎭8.方法一:由函数可知函数周期是,()sin πcos π(0)f x a x b x ωωω=+>2π2πωω=因为①对任意恒成,所以函数的一条对称轴是,()1,4x f x f ⎛⎫∀∈≤ ⎪⎝⎭R 14x =又因为在区间是单调函数,所以,()f x 34,77⎡⎤⎢⎥⎣⎦()11347114147m m ωω⎧+⨯≤⎪⎪⎨⎪++⨯≥⎪⎩所以,所以为0或1.12,m m -<≤∈Z m 当时,;当时,0m =2809ω<≤1m =285659ω≤≤由已知得,因为经过点的任意一条直线与函数图像max ()f x =()b ()y f x =,所以.b a≥因为①对任意恒成,所以.()1,4x f x f ⎛⎫∀∈≤ ⎪⎝⎭R 1πππcos sin 0444f a b ωωω'⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭所以,ππtan,1tan 144a b ωω=-≤≤由或,得或,所以或2809ω<≤285659ω≤≤ππ044ω<≤3ππ7π449ω≤≤01ω<≤2839ω≤≤方法二:()()ππ,tan ,0,,2b f x x a ωϕϕϕ⎛⎫⎛⎫=+=∈ ⎪ ⎪⎝⎭⎝⎭由①可知:,即(*)1πππ42m ωϕ⨯+=+()πππ,42m m Z ωϕ=-++∈由②可知:,()34ππ,π77x ωϕωϕωϕ⎡⎤+∈++⎢⎥⎣⎦因为函数在上是单调函数,所以34,77⎡⎤⎢⎥⎣⎦()34πππ,ππ,π,7722k k k Z ωϕωϕ⎡⎤⎡⎤++⊆-++∈⎢⎥⎢⎥⎣⎦⎣⎦将(*)带入化简可得:3724721127k k T πωπϕππωπϕπ⎧+≥-+⎪⎪⎪+≤+⎨⎪⎪≥⎪⎩2828()5528(),()907k m k m k m Z ωωω⎧≥-+-⎪⎪⎪≤--∈⎨⎪<≤⎪⎪⎩所以,下同方法一.2828560,,959ω⎛⎤⎡⎤∈⋃ ⎥⎢⎥⎝⎦⎣⎦二、多项选择题9.AC10.ACD11.AD12.BCD10.解:对于,在正方体中,连接,因为分别为中点,所以A 11,CD AB ,M N 111,CD C C ,在正方体中,,所以,又因为MN ∥1D C 1A B ∥1D C MN ∥1A B 1MA NB ==所以平面截正方体所得截面为等腰梯形,A 正确;1A MN 对于B ,错误;1111111111,3322224D MNB B D MN D MN V V BC S B--==⨯⨯=⨯⨯⨯⨯= 对于C ,因为,所以异面直线与所成角即为直线与所成角,MN∥1D C MN 1DP 1D C 1D P 设所成角为,则,C 正θ222222111132||cos 2D P D C CP D P D C θ⎛⎫+-+-===⋅确;对于,在正方体中易知平面平面,所以正D 1A D ⊥11,ABC D BM ⊂11ABC D 1,D A D BM ⊥确.11.解:记第一次抽到第红、黄、白球的事件分别为,则有123,,A A A ,对于,在第一次抽到黄球的条件下,则黄球放入盒()()()12311,24P A P A P A ===A B 子内,因此第二次抽到红球的概率为正确;21,A42P ==于B ,记第二次在第盒内抽到白球的事件分别为,而两两互,,A B C ()1,2,3i B i =123,,A A A 斥,和为,记第二次在第号盒内抽到红球的事件分别为,而Ω,,A B C ()1,2,3i C i =两两互斥,和为,错;记第123,,A A A Ω()()()112233111,,,222P C A P C A P C A B ===∣∣∣二次抽到红球的事件为,C ()()()33111111111()2242422i i i i i i i P C P AC P A P C A ==⎡⎤==⋅=⨯+⨯+⨯=⎣⎦∑∑∣若取出的球是红球放入盒子中;若取出的球是黄球放入盒子中;若取出的球是白球放入A B 盒子中,第二次从第一次放入盒子中任取一个球,C ()()()()()()()()111222121111112242,112422P A P C A P A P C A P A C P A C P C P C ⨯⨯⋅⋅======∣∣∣∣,,()()()()333311142142P A P C A P A C P C ⨯⋅===∣∣即第二次抽到的是红球,则它来自盒子的概率最大,不正确;A C 把5个不同的小球分成3组的不同分组方法数是种,22353522C C C A ⎛⎫+ ⎪⎝⎭将每一种分组方法分成的小球放在3个盒子中有种不同放法,33A 由分步乘法计数原理得不同的放法种数是种,D 正确.2233535322150C C C A A ⎛⎫+⋅= ⎪⎝⎭易知:,对于,若,显然直线的斜率存在且大于0,设()()121,0,1,0F F -A 112AF F B =1l 直线,联立椭圆方程,化简整理得()()()111221(0),,,,l y k x k A x y B x y =+>()221143y k x x y ⎧=+⎪⎨+=⎪⎩,显然,又()22224384120k x k x k +++-=221212228412Δ0,,4343k k x x x x k k -->+==++,故,整理得,由()()1111221,,1,AF x y F B x y =---=+()12121x x --=+1223x x +=-解得,又,故错误;21221221228432341243k x x k x x k x x k ⎧-+=⎪+⎪⎪+=-⎨⎪-⎪=⎪+⎩254k =0k >k A =对于,易知直线的斜率不为0,设直线,联立椭圆方B 1l()()11122:1,,,,l x my A x y B x y =-程,化简整理得,显然221143x my x y =-⎧⎪⎨+=⎪⎩()2234690m y my +--=,由点在轴的上方,显然,又12122269Δ0,,3434m y y y y m m ->+==++A x 120,0y y ><,1112,AF yBF y ====()()2221121211143439134m m AF BF m m +++=====++,故()11111111114311332744554444BF AF AF BF AF BF AF BF AF BF ⎛⎛⎫⎛⎫ +=++=++≥+= ⎪ ⎪ ⎪ ⎪ ⎝⎭⎝⎭⎝,当且仅当,即时取等,正确;11114BF AF AF BF =112AF BF =B 对于,设的中点为,则,又C ()111,,A x y AF P 111,22x y P -⎛⎫⎪⎝⎭,由椭圆定义知:,即,22AF OP ==21222AF AF +=122AF OP =-又的圆心为,半径为2,故以为直径的圆与圆内切,224x y +=()0,0O 1AF 224x y +=正确;C 方法二:12.解:易知:,对于,若,显然直线的斜率存在且大于()()121,0,1,0F F -A 112AF F B=1l0,设直线,联立椭圆方程,化简整理得()()111221,,,,l x my A x y B x y =-221143x my x y =-⎧⎪⎨+=⎪⎩,显然()2234690mx my +--=12122269Δ0,,,3434m y y y y m m ->+==++又,故,()()1111221,,1,AF x y F B x y =---=+122y y =-由,解得,又,故,A 错误;122122126349342m y y m y y m y y ⎧+=⎪+⎪-⎪=⎨+⎪=-⎪⎪⎩245m =0k>k =对于,由点在轴的上方,显然,又B A x 120,0y y ><,1112,AF y BF y ==()()2221121211143439134m m AF BF m m +++=====++,故()11111111114311332744554444BF AF AF BF AF BF AF BF AF BF ⎛⎛⎫⎛⎫ +=++=++≥+= ⎪ ⎪ ⎪ ⎪ ⎝⎭⎝⎭⎝,当且仅当,即时取等,正确;11114BF AF AF BF =112AF BF =B 对于D ,,2121212122222698124,,,34343434m m y y y y x x x x m m m m ---++==+==++++()()()212122*********934,D124822244243434AC BCy y y y m k k m x x x x x x m m -+⋅====--+-++++++⋅+++正确第II 卷三、填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)13.1414.5解:记表示第次去掉的长度,,第2次操作,去掉的线段长为,n a n 113a ∴=222,3a =第次操作,去掉的线段长度为,n 123n n na -=,则,12133212313nnn S ⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦∴==- ⎪⎝⎭-21821220310.10033202432024n n<>⎛⎫⎛⎫-⇒≈ ⎪ ⎪⎝⎭⎝⎭由的最大值为5.56220.1317,0.0878,33n⎛⎫⎛⎫≈≈∴ ⎪ ⎪⎝⎭⎝⎭15.4-解:由题意得抛物线的焦点为,准线方程为.28y x =()2,0F 2x =-又点是抛物线上一点,点是圆上任意一点,P Q 22(2)1x y -+=max ||1,PQ PF ∴=+∴.令,点的坐标为,则,22||||1PA PA PQ PF ≥+1t PF =+P (),P P x y ()233P X PF t t =-=-≥,()()()222222||338(33)83412P P P P PA x y x x t t t t ∴=-+=-+=--+-=-+,当且仅当,即22||412124441PA t t t PF t t -+∴==+-≥-=+12t t =时t =等号成立.的最小值为.2||PA PQ∴4-16.6解:在椭圆上任取一点,连接交球于点,交球于点,P VP 1O Q 2O R连接,在与中有:111112,,,,O Q O F PO PF O R 11ΔO PF 1ΔO PQ ,(为圆的半径,为圆的半径,),111O Q O F =1r 1C 2r 2C ,11190O QP O F P ∠∠== 为公共边,所以,所以,1O P 111ΔΔO PF O PQ ≅1PF PQ =设点沿圆锥表面到达的路线长为,P M PM d 则,1PM PM PF d PQ d PQ PR QR+=+≥+=当且仅当为直线与椭圆交点时取等号,P VM ,所以最小值为6,125261sin302r r QR --===四、解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)解:选条件①(1)由题设.πππsin cos 01266f ϕ⎛⎫⎛⎫⎛⎫-=-++-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以.πsin 6ϕ⎛⎫-= ⎪⎝⎭因为,所以.ππ22ϕ-<<2πππ363ϕ-<-<所以.ππ63ϕ-=-所以.π6ϕ=-(2)由(1)()π1sin 2cos2cos262f x x x x x⎛⎫=-+=+ ⎪⎝⎭.πsin 26x ⎛⎫=+ ⎪⎝⎭令ππ5π2t 666t x ⎛⎫=+- ⎪⎝⎭……所以在单调递增,在单调递减,y sint =ππ,62⎡⎤-⎢⎥⎣⎦π5π,26⎡⎤⎢⎥⎣⎦于是,当且仅当,即时,取得最大值1;ππ262x +=π6x =()f x 当且仅当,即时,取得最小值.ππ266x +=-π6x =-()f x 12-又,即时,.π5π266x +=π3x =π5π1sin 362f ⎛⎫==⎪⎝⎭所以的取值范围是.m {}11,122⎡⎫-⋃⎪⎢⎣⎭选条件②.(1)由题设.2π2πsin cos0sin cos33ϕϕ⎛⎫+=++ ⎪⎝⎭整理得.πsin 6ϕ⎛⎫-= ⎪⎝⎭以下同选条件(1).18.(本小题满分12分)证明:(1)连接线段交与于点,连接,BN DM O OE 四边形是矩形,点是线段中点, DBMN ∴O BN 点是中点,, E AB OE ∴∥AN 平面平面,OE ⊂ ,MDE AN ⊄MDE平面.AN ∴∥MDE (2),AD ∥π,,2BC CBD DA DB ∠=∴⊥平面平面,DN ⊥ ,,ABCD DA DB ⊂,,ABCD DN DA DN DB ∴⊥⊥三条直线两两互相垂直,,,DN DA DB ∴以为原点,以为轴正方向建立空间直角坐标系,D ,,DA DB DN,,x y z ()()()()0,2,2,0,0,2,2,0,0,1,2,0M N A C -设平面的法向量为,MNA ()()(),,z ,0,2,0,2,0,2m x y NM NA ===-,令,则0220,200m NA x z y m NM ⎧⋅=-=⎧⎪∴⎨⎨=⋅=⎩⎪⎩ 1x =()1,0,1m = 设平面的法向量为,MNC ()()(),,,0,2,0,1,0,2n a b c NM MC ===--,令,则,020,200n MC a c b n NM ⎧⋅=--=⎧⎪∴⎨⎨=⋅=⎩⎪⎩ 2a =()2,0,1n =- 设平面与平面所成角为,则MNC MNA θ||cos |cos ,|||||m n m n m n θ⋅=<>===平面与平面.∴MNC MNA 19.(本小题满分12分)解:(1)由题意可知:,111b a ==,()121221212212222n n n n n n b a a a a b ++--===-=-=-故,()11222,210,20n n n b b b b +-=--=-≠∴-≠ 得,1222n n b b +-=-故是以为首项,以为公比的等比数列,{}2n b -121b -=-2q =且,故1*22,n n b n --=-∈N 1*22,N n nb n -=-+∈(2)由(1)知,,即,1*22,N n n b n -=-+∈1*2122,N n n a n --=-+∈由题意知:,故,()*11,212,2n n n a n k a k N a n k +-=-⎧=∈⎨=⎩*2211,n n a a n N -=-∈故数列的前项和{}n a 2n ()()2135212462n n n S a a a a a a a a -=+++++++++ ()135212n a a a a n-=++++- ()0121222222n n n-⎡⎤=-+++++-⎣⎦ 1122322312n n n n+-=-⨯+=-++-20.(本小题满分12分)解:(1)以服从超几何分布,且,X 10000,400N M ==故.()40010004010000E X =⨯=(2)当时,;1380N <()200P X ==当时,1380N ≥()20980400400100020N NC C P X C -⋅==令,则()2010004004001000N N C C f N C -⋅=()()()()()()20980400140010001209804004001000111000140011400980N N N NC C f N N N C C C f N N N C +-+-⋅++-+-==⋅++--22139899939913781379N N N N -+⨯=--,22139899939913781379,19999N N N N N -+⨯≥--∴≤当时,;当时,138019999N ≤≤()()1f N f N ≤+20000N ≥,()()1f N f N >+所以当或20000时,最大,所以的值为19999或20000.19999N =()f N N 21.(本小题满分12分)解:(1)已知抛物线经过点,所以抛物线2:2(0)G x py p =>()2,12:4G x y =设,由题意可知直线斜率存在,设直线方程为,()()1122,,,A x y B x y AB AB 2y kx =+联立方程组,可得,242x y y kx ⎧=⎨=+⎩2480x kx --=所以,21212Δ16320,4,8k x x k x x =+>+==-所以弦长2AB x =-=,所以切线方程:,即①12y x '=AP ()11112y y x x x -=-2111124y x x x =-同理可得切线方程:②BP 2221124y x x x =-联立①和②方程组21122211241124y x x x y x x x ⎧=-⎪⎪⎨⎪=-⎪⎩解得:,所以,122,22x x x k y +===-()2,2P k -又因为点到直线距离P AB d 所以,()3221422ABPS AB d k =⨯=+=ò可得,即,所以直线方程为21k =1k =±AB 2y x =±+(2)方法一:设,设,()()()003344,,,,,Q x y C x y D x y (),,1,1PC CQ PD DQ λμλμ==≠-≠-所以,所以,()()3303032,2,x k y x x y y λ-+=--03032121k x x y y λλλλ+⎧=⎪⎪+⎨-+⎪=⎪+⎩代入抛物线方程得:,()()()2002412k x y λλλ+=+-+化简得()()22200004448480,xy kx y k λλ-+-+++=同理,()()22200004448480x y kx y k μμ-+-+++=即是方程的两根,,λμ()()22200004448480xy x kx y x k -+-+++=因为点在直线上,即,()00,Q x y AB 004480kx y -+=所以方程化为,可得,()222004480xy x k -++=0λμ+=即成立.PCPD CQDQ=方法二:设,()()()3344,,,,,Q Q Q x y C x y D x y 由题意知直线的斜率存在,设直线方程为:,PQ PQ ()()22,y m x k m k +=-≠联立方程组,可得,()2422,x y y m x k ⎧=⎪⎨+=-⎪⎩24880x mx km -++=,()23434Δ164880,4,88m km x x m x x km =-+>+==+因为,3,QPC x DQ x =-=-4,,Q PD x CQ x =-=-因为所以()()()()344320,20Q Q k x x x k x xx -->-->||||||||QPC DQ PD CQ x -=----()()()23434341422Q m k x x x k x x x x ⎡⎤=+---++⎣⎦③()()()()221448164124Q Q m k m x km m k m x km ⎡⎤⎡⎤=+-++=+-++⎣⎦⎣⎦由两条直线联立:,可得,()222y m x k y kx ⎧+=-⎨=+⎩24Q km x k m +=-+代入③可知()()22441240km PC DQ PD CQ m k m km k m +⎡⎤-=+-++=⎢⎥-+⎣⎦即成立.PCPD CQDQ=22.(本小题满分12分)解(1)方法一:,()()()ln 0,ln 10,ln 10x x x f x xe a x x e a x x +≥∴-+-≥∴-+-≥ 令,对任意恒成立,令,ln ,.10tt x x t R e at =+∈∴--…t ∈R ()1t h t e at =--当时,,与恒成立矛盾,不合题意;0a <101220a h e e a ⎛⎫=-<-< ⎪⎝⎭()0h t …当时,,与恒成立矛盾,不合题意;0a =()()111,1110t h t e h e e -=--=-=-<()0h t …当时,在上递减,在上递增,0a >()(),t h t e a h t =-'(),ln a ∞-()ln ,a ∞+的最小值为.()h t ∴()ln ln 1h a a a a =--令,则,知在上递增,在上递减,()ln 1a a a a ϕ=--()ln a a ϕ'=-()a ϕ()0,1()1,∞+,要使,当且仅当.()max ()10a ϕϕ∴==()ln 10a a a a ϕ=--…1a =综上,实数的值为1.a 方法二:,()()()ln 0,ln 10,ln 10x x x f x xe a x x e a x x +≥∴-+-≥∴-+-≥ 令,对任意恒成立,ln ,.10tt x x t e at =+∈∴--R …t ∈R 当时,,因为,所以;0t >1t e a t -≤1111t e t t t -+->=1a ≤当时,,因为,所以;0t <1t e a t -≥1111t e t t t -+-<=1a ≥当时,不等式恒成立;0t =综上,实数的值为1.a 方法三:将等价为,当时,()0f x ≥()ln 10x g x xe ax a x =---≥0a <,与恒成立矛盾,不合题意,当时,也不合题意101220a h e e a ⎛⎫=-<-< ⎪⎝⎭()0h t …0a =当时0a >,()()()()()()1111x xxx xe a x x e a x a g x x e a x x x '+-+-+=+--==令,所以在单调递增,()()(),10x x h x xe a h x x e ==+'->()h x ()0,∞+因为,()()()00,10a a h a h a ae a a e =-<=-=->所以,使得,即,即,()00,x ∞∃∈+()00h x =00x X e a =00ln ln x x a +=当,即,所以单调递减;()()000,,0x x h x '∈<()0g x '<()g x 当,即,所以单调递增,()()00,,0x x h x ∞'∈+>()0g x '>()g x 所以()()0min 000000()ln 1ln 1ln 1x g x g x x e ax a x a a x x a a a ==---=-+-=--令,()()ln 1,ln a a a a aϕϕ'=--=-当单调递增;当单调递减,()()()0,1,0,a a a ϕϕ>'∈()()()1,,0,a a a ∞ϕϕ∈+<'可知.()()10a ϕϕ≤=所以当且仅当时成立.1a =()ln 10x g x xe ax a x =---≥即时,.()0f x ≥1a =(2)方法一:证明:由(1)知,当时,,即,1a =ln 10x xe x x ---…ln 1xxe x x ++…,22ln x x e x x x x ∴++…证明:等价于证明下面证明()21sin 2ln xx xe x x->+-,()()2ln 2ln 21sin x x x x x x x ++>+--即证.222sin 0x x x -+->令.()()222sin ,212cos g x x x x g x x x-+=-'=--当时,显然单调递增,,01x <…()g x '()()π112cos112cos03g x g '=-'<-=…在上单调递减,,()g x ∴(]0,1()()122sin10g x g =->…当时,显然,即.1x >222sin 0x x x -+-…()0g x >故对一切,都有,即.()0,x ∞∈+()0g x >()()2ln 2ln 21sin x x x x x x x ++>+--故原不等式成立.()()22ln 21sin x x e x x x >+--方法二:证明:由(1)知,当时,,即,1a =ln 10x xe x x ---…ln 1xxe x x ++…22ln x x e x x x x∴++…证明:等价于证明下面证明()21sin 2ln xx xe x x->+-,()()2ln 2ln 21sin x x x x x x x ++>+--即证.222sin 0x x x -+->因为,所以.2221(1)0x x x x -+--=-≥221x x x -+≥+因为,显然.sin ,1sin x x x >≥222sin 0x x x -+-…故原不等式成立.()()22ln 21sin x x e x x x >+--(3)方法一:令,()()2cos ,sin x x g x e ax x g x e a x=--+=--'①若,当时,,1a >0x ≥()cos x g x e x =-''在单调递增,()()0,g x g x >'∴'' [)0,∞+,()()()100,1sin 1110a g g a e a a a a +=+=--+>+-'-'= 故存在唯一,使得,则当为减函数,()00,x ∞∈+()00g x '=()()00,,x x g x ∈,此时,与题意不符(舍).()()()00,00g g x g =∴<'= ()0xg x ∴<②若1a ≤(i )当,则由①可知,在单调递增,0x ≥()()cos 0,x g x e x g x =-≥'''[)0,∞+在单调递增,所以()()()010,g x g a g x ∴-≥'>'>[)0,∞+()()00g x g ≥=所以成立.22cos x xe ax x x x ≥+-(ii )当在单调递增,()()()π,0,cos ,sin ,2x x x g x e x g x e x g x ⎛⎫∈-=-=+ '⎪⎝⎭'''''''π,02⎛⎫- ⎪⎝⎭,故存在唯一,使得,()π2π01,102g g e -⎭''''⎛⎫=-=-< '⎪'⎝ 0π,02x ⎛⎫∈- ⎪⎝⎭()00g x '''=当时,在上单调递减,0π,2x x ⎛⎫∈- ⎪⎝⎭()()0,g x g x <'''''0π,2x ⎛⎫- ⎪⎝⎭当时,在上单调递增,()0,0x x ∈()()"'0,g x g x >''()0,0x ,故存在唯一,使得,()π2π00,02g g e -⎛'⎫=-='''> ⎪⎝⎭10π,2x x ⎛⎫∈- ⎪⎝⎭()10g x ''=当时,在上单调递增,1π,2x x ⎛⎫∈- ⎪⎝⎭()()0,g x g x >'''1π,2x ⎛⎫- ⎪⎝⎭当时,在上单调递减,()1,0x x ∈()()0,g x g x <'''()1,0x 在恒成立,()()π2π010,10,02g a g e a g x -⎛⎫=->-=-+>∴> ⎪⎝⎭''' π,02⎛⎫- ⎪⎝⎭在单调递增恒成立,()g x ∴π,02⎛⎫- ⎪⎝⎭()()()00,0g x g xg x ∴<=∴>时,恒成立,1a ∴≤()0xg x >综上所述,1a ≤方法二:因为,所以.22cos xxe ax x x x ≥+-()2cos 0x x e ax x --+≥当时,恒成立,所以恒成立,0x ≥2cos 0x e ax x --+≥2cos xe x ax -+≥令在上()()()2cos ,sin 11sin 10,x x x e x x x e x x x x ϕϕϕ=-+-=--≥+--≥'[)0,x ∞∈+单调递增,,所以,所以.()()00x ϕϕ≥=2cos xe x x ax -+≥≥1a ≤当时,恒成立,所以恒成立,π02x -<≤2cos 0x e ax x --+≤2cos x e x ax -+≤令,()()2cos ,sin 1x x x e x x x e x ϕϕ=-+-'-=-当时,,令,使得,0x <()cos xx e x ϕ=-''0πcos 0,,02x e x x ⎛⎤-=∃∈- ⎥⎝⎦00cos x e x =当时,在上单调递增,0π,2x x ⎛⎫∈- ⎪⎝⎭()()0,x x ϕϕ>'∴''π,02⎛⎫- ⎪⎝⎭当时,在上单调递减,()0,0x x ∈()()0,x x ϕϕ<'∴''()0,0x ,()ππ22ππ00,sin 1022e e ϕϕ--⎛⎫⎛⎫=-=---=> ⎪ ⎪⎝'⎝⎭'⎭ 恒成立,()π,0,02x x ϕ⎛⎤∴ ''∀∈->⎥⎝⎦在上单调递增减,在上单调递增,()x ϕ'π,02x ⎛⎤∈- ⎥⎝⎦()()()00,x x ϕϕϕ'≥='π,02x ⎛⎤∈- ⎥⎝⎦所以,所以,所以.综上所述.()()00x ϕϕ≤=2cos xe x x ax -+≤≤1a ≤1a ≤方法三:()2cos 0x x e ax x --+≥①当时,恒成立,即在恒成立,令0x >2cos 0x e ax x --+≥2cos x e xa x -+≤()0,∞+,()()()21sin 2cos 2cos (0),x x x e x x x e xh x x h x x x --+--+=='>令在上单调()()()()()1sin 2cos ,cos 0,x x g x x e x x x g x x e x g x =--+>'-=-∴()0,∞+递增,在上单调递增,()()()()00,0,g x g h x h x ∴>'>=∴∴()0,∞+,由洛必达法则()()0h x h ∴>()01,1h a =∴≤②当时,恒成立,即在恒成立,π02x -<<2cos 0xe ax x --+≤2cos x e x a x -+≤π,02⎛⎫- ⎪⎝⎭同方法一①,,()()cos 0,cos x x g x x e x e x=-=∴='存在唯一,使得,0π,02x ⎛⎫∈- ⎪⎝⎭()00g x '=当时,在上单调递减,0π,2x x ⎛⎫∈- ⎪⎝⎭()()()cos 0,x g x x e x g x =-<'0π,2x ⎛⎫- ⎪⎝⎭当时,在上单调递增,()0,0x x ∈()()()cos 0,x g x x e x g x =->'()0,0x ,()π2πππ00,10222g g e -⎛⎫⎛⎫=-=---< ⎪ ⎪⎝⎭⎝⎭ 在恒成立,在单调递减,()0g x ∴<π,02⎛⎫- ⎪⎝⎭()()0,h x h x <∴'∴π,02⎛⎫- ⎪⎝⎭,()()0h x h ∴>用洛必达法则.()01,1h a =∴≤③当时,恒成立,0x =()2cos 0x x e ax x --+≥综上所述,1a ≤(用洛必达法则扣1分)。
高三数学双基百分百1

2011年高考数学双基达标百分百(一)班级 姓名 座号 成绩一、填空题(每小题5分,共50分)1.y 的定义域是2.设a =⎪⎭⎫ ⎝⎛αsin ,23,⎪⎭⎫ ⎝⎛α=31,cos ,且b //a ,则锐角α=_________ 3.若不等式621<-a x 的解集为()+∞-,1,则实数a 等于4. 等比数列}{n a 中,121=+a a ,854=+a a ,则=+1110a a ____________5. 函数2()y xi x R =+∈(i 为虚数单位)与函数y a =有且仅有一个交点,则实数a =6. (理)已知直线l 的参数方程是435()325x t t R y t ⎧=+⎪⎪∈⎨⎪=-+⎪⎩,求过点(4,1)-且 与l 平行的直线m 在y 轴上的截距为(文)设变量,x y 满足约束条件:222y x x y x ≥⎧⎪+≤⎨⎪≥-⎩,则22y x z +=的最大值是7.直角坐标系xoy 内有点A (2,1),B (2,2),C (0,2),D (0,1),将四边形ABCD 绕直线1y =旋转一周,所得到几何体的体积为 .8. 两对夫妇排成一排照相,则任何一对夫妇都不相邻的概率为_____________9.有些计算机对表达式的运算处理过程实行“后缀表达式”,运算符号紧跟在运算对象的后面,按照从左到右的顺序运算,如表达式3(2)7,x *-+其运算为3,,2,,,7,,x -*+若计算机进行运算(3),,2,,,lg,x x --*那么使此表达式有意义的x 的范围为10.设]3,1[,2)(∈-=x x a x x f ,若)3()(f x f ≤对任意]3,1[∈x 都成立,则实数a 的取值范围是_________二、选择题(每小题5分,共15分)11.若{}232,a a a ∈-,则a 值等于( )(A )3; (B )1- ; (C )3或1-; (D )无解;12.甲校有3600名学生,乙校有5400名学生,丙校有1800名学生,为统计三校学生某方面的情况,计划采用分层抽样法,抽取一个样本容量为90人的样本,应在这三校分别抽取学生( )(A )30人,30人,30人; (B )30人,45人,15人;(C )20人,30人,40人; (D )30人,50人,10人;13. 2λ>是圆锥曲线12522=--+λλx y 的焦距与实数λ无关的( ) (A) 充分非必要条件; (B) 必要非充分条件;(C) 充要条件; (D) 既非充分也非必要条件;三、解答题(本大题共2题,满分35分)14.(本题满分15分)设m x f x +-=131)(. (1)求m 的值,使)(x f 为奇函数;(2)对(1)中的)(x f ,若方程1)(221+=+-c x x f 在[1,4]上有解,求c 的范围.15.(本题满分20分)已知数列{}n a 满足:11,2a =1110n n n a a a +++-=,n N *∈. (1) 写出数列的前6项的值;(2) 猜想数列{}2n a 与{}21n a -的单调性,并选择一种情形证明你的结论.2011年高考数学双基达标百分百(一)参考答案一、填空题1.[)0,+∞提示:由201110201110x xx -≥⇒≥⇒≥,所以所求定义域为[)0,+∞ 2.4πα= 提示:由平行的定义得:4,2,0,12sin sin 3123cos παπαααα=∴⎪⎭⎫ ⎝⎛∈=⇒= 3.4a =-提示:由,462<∴<+ax ax 讨论当0a >时,则有a x 4<不符合, 当0a <时,a x 4>,4,14,1-=∴-=-∴->a ax Θ 4.512提示:设公比为q ,()21354a a q a a +=+,则2,83=∴=q q ,有5122)(99211110==+=+q a a a a ;5.2a =提示:作出y =y a =的图像,可得2a =6.(理)4y =-提示:由题意得:过点(4,1)-且 与l 平行的直线m ,它们的方向向量相同。
谈高三数学复习中能力与“双基”并举的教学策略

( )由子一 代 到子 二代 , 2 只需 以( + 代 乱 ) , 以( + ) + )代 , ( “ ( 以 + ) 代 W, 。 即可 求 得 子二 代 与子 一代 的基 因 型式 比例是 一 样 的. 评 析 本 题是 概 率和 遗传 学 的交叉 综 合题 , 是跨 学科 综 合题 的典 型 代 表。 类 题 也 可 以是 学 此 科 内跨模 块 的综 合 题 , 如几 何 与代数 、 列 与不 等 数 式、 向量 与三 角综 合 题 等 , 高考 试题 中能力 考 查 是 的重 头 戏. 类题 的教 学 , 注 重联 系与 转 化 , 这 要 注 重学科 思 想 方法 , 以培 养 思维 和能 力 为落脚 点 , 应 精 选 和优 化 典 型例 题 , 不 是 漫 无 边 际地 搞 题 海 而 战术 , 则 , 但 会 增 加 学 生课 业 负 担 , 否 不 更无 法 提 高教 学效 率 . 5 析 解探 究 性开 放题 例 4 ( 0 1 江苏省 高考 附加 题 ) 整数 21 年 设 ≥ 4 P( ,)是平 面 直角 坐 标 系 x , a6 Oy 中的 点 , 其 中 a, b∈ { , , , , , 1 2 3 … )口> b . ( ) A 为满足 口 = 3 1记 一6 的点 P的个数 , A ; 求
1 灵 活 呈 现 “ 基 ”题 双
A( ) 圆 。 =【 绕 坐标原 点 沿逆 时针 x, 在 c +Y = 上 = 方 向匀速 旋转 ,2秒旋 转一 周. 1 已知时 间 t 时 , 一0
1
点 A 的坐标是( )则当 0 t 1 时, ÷, ’ ≤ ≤ 2 动点
厶 厶
辽宁省大连市2023届高三上学期期末双基测试数学试题解析版

2023年大连市高三双基测试数学注意事项:1.请在答题纸上作答,在试卷上作答无效.2.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷━.单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求.1.已知集合{}1,2,3,4,5A =,12x B x Z ⎧⎫-=∈⎨⎬⎩⎭,则A B = ()A.{}5 B.{}3,5 C.{}1,3,5 D.{}2,4【答案】C 【解析】【分析】逐一验证集合{}1,2,3,4,5A =中的元素是否也属于集合12x B x Z ⎧⎫-=∈⎨⎬⎩⎭即可.【详解】因为集合{}1,2,3,4,5A =,12x B xZ ⎧⎫-=∈⎨⎬⎩⎭可得1x =时,11012Z B -=∈⇒∈;2x =时,211222Z B -=∉⇒∉;3x =时,31132Z B -=∈⇒∈;4x =时,413422Z B -=∉⇒∉;5x =时,51252Z B -=∈⇒∈;综上,集合,A B 的公共元素为1,3,5,所以A B = {}1,3,5,故选:C.2.i 是虚数单位,若复数543i z =+,则z 的共轭复数z =()A.43i 55+ B.43i 55- C.43i 55-+ D.43i 55--【答案】A 【解析】【分析】根据复数除法运算可化简得到z ,由共轭复数定义可得结果.【详解】()()()543i 543i 43i 43i 43i 43i 555z --====-++- ,43i 55z ∴=+.故选:A.3.已知命题0:p x ∃∈R ,20010x x -+<,则p ⌝是()A.0x ∃∈R ,20010x x -+≥ B.0x ∀∈R ,20010x x -+<C.x ∀∈R ,210x x -+≥ D.x ∀∈R ,210x x -+>【答案】C 【解析】【分析】由特称命题的否定可直接得到结果.【详解】由特称命题的否定可知p 为:x ∀∈R ,20010x x -+≥.故选:C.4.开普勒(Johannes Kepler ,1571~1630),德国数学家、天文学家,他发现所有行星运行的轨道与公转周期的规律:所有行星绕太阳运动的轨道都是椭圆,且所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比都相等.已知金星与地球的公转周期之比约为2:3,地球运行轨道的半长轴为a ,则金星运行轨道的半长轴约为()A.0.66aB.0.70aC.0.76aD.0.96a【答案】C 【解析】【分析】设金星运行轨道的半长轴为1a ,金星和地球的公转周期分别为1t ,2t ,根据题意可得1123a a =,进而结合332.512 2.1>>,即可得出结果.【详解】设金星运行轨道的半长轴为1a ,金星和地球的公转周期分别为1t ,2t ,由开普勒定律得3312212a a t t =.因为1223t t =,所以33149a a =,即13a a =.因为函数3y x =在(),-∞+∞上单调递增,且12592611281000>>,且3312592612.5, 2.181000==,所以332.512 2.1>>,因此112 2.50.700.933a a a a <=<<,故选:C.5.若二项式()6210ax a x ⎛⎫+> ⎪⎝⎭的展开式中所有项的系数和为64,则展开式中的常数项为()A.10B.15C.25D.30【答案】B 【解析】【分析】根据赋值法可得系数和,进而求解1a =,由二项式展开式的通项公式即可求解常数项.【详解】令1x =,则所有的项的系数和为()6164a +=,由于0a >,所以1a =,621x x ⎛⎫+ ⎪⎝⎭展开式的通项为6263166C C r r r r rr T x x x ---+==,故当630r -=时,即2r =,此时展开式中的常数项为26C 15=,故选:B6.若ππ,42α⎛⎫∈ ⎪⎝⎭,且2π1cos cos 222αα⎛⎫++=- ⎪⎝⎭.则tan α=()A.B.2C.3D.【答案】C 【解析】【分析】根据二倍角公式以及诱导公式化简得21cos 2cos sin 2ααα-=-,进而根据齐次式以及弦切互化即可求解.【详解】由2π1cos cos 222αα⎛⎫++=-⎪⎝⎭得22221cos 2cos sin 1cos 2cos sin 2cos sin 2αααααααα--=-⇒=-+,进而得212tan 11tan 2αα-=-+,化简得:2tan 4tan 30αα-+=,所以tan 3α=或tan 1α=,由于ππ,42α⎛⎫∈ ⎪⎝⎭,所以tan 1α>,故tan 3α=,故选:C7.已知()4324ln 32ea -=,1e b =,c =,则()A.a c b<< B.c<a<b C.a b c<< D.b a c<<【答案】A 【解析】【分析】构造函数()ln xf x x=,其中0x >,利用导数分析函数()f x 的单调性,可得出()4ln 32e a f -=、()e b f =、()2c f =,比较4ln 32e -、2、e 的大小关系,结合函数()f x 在(]0,e 上的单调性可得出a 、b 、c 的大小关系.【详解】构造函数()ln x f x x =,其中0x >,则()21ln xf x x -'=,当0e x <<时,()0f x ¢>;当e x >时,()0f x '<.所以,函数()f x 的增区间为()0,e ,减区间为()e,+∞.因为()()4ln3244ln32324ln 324ln 32e e e a f ----==,()e e 1b f ==,()e log 4ln 42ln 2ln 224442c f ======,因为24ln 3242e e e 12648-⎛⎫==< ⎪⎝⎭,则4ln 32e 2e -<<,则()()()4ln 32e 2ef f f -<<,故a c b <<.故选:A.8.已知函数(),()f x g x 的定义域均为R ,且()(2)5,()(4)7f x g x g x f x +-=--=.若()y g x =的图像关于直线2x =对称,(2)4g =,则()221k f k ==∑()A.21-B.22- C.23- D.24-【答案】D 【解析】【分析】根据对称性和已知条件得到()(2)2f x f x +-=-,从而得到()()()352110f f f +++=- ,()()()462210f f f +++=- ,然后根据条件得到(2)f 的值,再由题意得到()36g =从而得到()1f 的值即可求解.【详解】因为()y g x =的图像关于直线2x =对称,所以()()22g x g x -=+,因为()(4)7g x f x --=,所以(2)(2)7g x f x +--=,即(2)7(2)g x f x +=+-,因为()(2)5f x g x +-=,所以()(2)5f x g x ++=,代入得[]()7(2)5f x f x ++-=,即()(2)2f x f x +-=-,所以()()()()35212510f f f +++=-⨯=- ,()()()()46222510f f f +++=-⨯=- .因为()(2)5f x g x +-=,所以(0)(2)5f g +=,即()01f =,所以()(2)203f f =--=-.因为()(4)7g x f x --=,所以(4)()7g x f x +-=,又因为()(2)5f x g x +-=,联立得,()()2412g x g x -++=,所以()y g x =的图像关于点()3,6中心对称,因为函数()g x 的定义域为R ,所以()36g =因为()(2)5f x g x ++=,所以()()1531f g =-=-.所以()()()()()()()()221123521462213101024()k f f f f f f f f f k =+++++++++=----=-⎡⎤⎡⎤⎣⎦⎣⎦=∑ .故选:D【点睛】含有对称轴或对称中心的问题往往条件比较隐蔽,考生需要根据已知条件进行恰当的转化,然后得到所需的一些数值或关系式从而解题.二、多项选择题:(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9.将函数()()cos 2πf x x =-图象上所有的点向左平移π6个单位长度,得到函数()g x 的图象,则()A.()g x 的最小正周期为πB.()g x 图象的一个对称中心为7π,012⎛⎫⎪⎝⎭C.()g x 的单调递减区间为()π5ππ,π36k k k ⎡⎤++∈⎢⎥⎣⎦Z D.()g x 的图象与函数πsin 26⎛⎫=-- ⎪⎝⎭y x 的图象重合【答案】ABC 【解析】【分析】根据三角函数平移变换和诱导公式可得()πcos 23g x x ⎛⎫=-+⎪⎝⎭;根据余弦型函数最小正周期可知A 错误;利用代入检验法可知B 错误;根据余弦型函数单调区间的求法可知C 正确;利用诱导公式化简()g x 解析式可得()πsin 26g x x ⎛⎫=- ⎪⎝⎭,知D 错误.【详解】由题意知:()πππcos 2πcos 2633g x f x x x ⎛⎫⎛⎫⎛⎫=+=+-=-+ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭;对于A ,()g x 的最小正周期2ππ2T ==,A 正确;对于B ,当7π12x =时,π7ππ3π23632x +=+=,此时()3πcos02g x =-=,7π,012⎛⎫∴ ⎪⎝⎭是()g x 的一个对称中心,B 正确;对于C ,令()ππ2π22π3k x k k -+≤+≤∈Z ,解得:()2ππππ36k x k k -+≤≤-+∈Z ,即()π5πππ36k x k k +≤≤+∈Z ,()g x ∴的单调递减区间为()π5ππ,π36k k k ⎡⎤++∈⎢⎥⎣⎦Z ,C正确;对于D ,()π2ππππcos 2πcos 2cos 2sin 233266g x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫=+-=-=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,()g x ∴与πsin 26⎛⎫=--⎪⎝⎭y x 图象不重合,D 错误.故选:ABC.10.下列结论正确的有()A.若随机变量()2~1,N ξσ,()40.77P ξ≤=,则()20.23P ξ≤-=B.若随机变量1~10,3X B ⎛⎫ ⎪⎝⎭,则()3119D X -=C.已知回归直线方程为10.8y bx=+ ,且4x =,50y =,则9.8b = D.已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11.若这组数据的平均数、中位数、众数依次成等差数列,则丢失数据的所有可能值的和为22【答案】AC 【解析】【分析】根据正态分布对称性知A 正确,计算()()32920D X D X +==,B 错误,将()x y代入回归直线,计算得到C 正确,讨论三种情况得到可能数据的和为12,D 错误,得到答案.【详解】对于A ,()()2410.770.23P P ξξ≤-=≥=-=,故A 正确;对于B ,()122010339D X =⨯⨯=,所以()220313209D X -=⨯=,故B 不正确;对于C ,回归直线方程经过点(),x y ,将4x =,50y =代入求得9.8b= ,故C 正确;对于D ,设丢失的数据为x ,则这组数据的平均数为317x+,众数为3,当3x ≤时,中位数为3,此时36731x ++=,解得10-;当35x <<时,中位数为x ,此时31327xx ++=,解得4x =;当5x ≥时,中位数为5,此时113073x+=+,解得18x =.所以所有可能x 的值和为1041812-++=,故D 不正确.故选AC.11.正方体1111ABCD A B C D -的棱长为1,E ,F ,G 分别为BC ,11,CC BB 的中点,则()A .直线1D D 与直线AF 垂直B.直线1A G 与平面AEF 平行C.平面AEF 截正方体所得的截面面积为98D.点1A 与点D 到平面AEF 的距离相等【答案】BCD 【解析】【分析】根据棱柱的结构特征,建立以D 为原点,以DA 、DC 、1D D 所在的直线为x 轴、y 轴、z 轴的空间直角坐标系D xyz -,利用向量法即可判断A ,根据线线平行即可判断B,根据梯形面积即可判断C,根据中点关系即可判断D.【详解】在棱长为1的正方体1111ABCD A B C D -中,建立以D 为原点,以DA 、DC 、1D D 所在的直线为x 轴、y 轴、z 轴的空间直角坐标系D xyz -,如图所示:E 、F 、G 分别为BC 、1CC 、1BB 的中点,则()0,0,0D ,()10,0,1D ,()1,0,0A ,10,1,2F ⎛⎫ ⎪⎝⎭,对于A,()10,0,1DD = ,11,1,2AF ⎛⎫=- ⎪⎝⎭,∴1102DD AF ⋅=≠ ,故A 错误;对于B :连接1AD ,1D F ,1//AD EF ,A ∴,1D ,E ,F 四点共面,由于11//A D GF ,11=A D GF ,所以四边形11A D FG 为平行四边形,故11//AG D F ,又1AG ⊂/平面AEF ,1D F ⊂平面AEF ,1//A G ∴平面AEF ,故B 正确,对于C ,连接1AD ,1FD ,1//AD EF ,∴四边形1AD FE 为平面AEF截正方体所得的截面,1AD ==2EF =,12D F AE ===,∴四边形1AD FE324=,则四边形1AD FE的面积为192248⎫⨯+⨯=⎪⎪⎭,故C 正确;对于D,连接1A D 交1AD 于点O ,故O 是1A D 的中点,且O 是线段1A D 与平面1AD FE 的交点,因此点1A 和点D 到平面AEF 的距离相等,故D 正确.故选:BCD .12.已知点F 是抛物线24y x =的焦点,AB ,CD 是经过点F 的弦且AB CD ⊥,直线AB的斜率为k ,且0k >,C ,A 两点在x 轴上方,则()A.3OC OD ⋅=-B.四边形ABCD 面积最小值为64C.1114AB CD += D.若16AF BF ⋅=,则直线CD 的斜率为【答案】ACD 【解析】【分析】由抛物线的方程可得焦点F 的坐标,设直线AB 的方程,与抛物线的方程联立,可得两根之和及两根之积,由抛物线的性质可得弦长||AB ,同理可得||CD 的值,由均值不等式可得四边形的面积的最小值,经过判断可得命题的真假.【详解】由抛物线的方程可得焦点(1F ,0),由题意可得直线AB ,CD 的斜率存在且不为0,设直线CD 的方程为:1(0)x my m =+<,设1(C x ,1)y ,2(D x ,2)y ,联立214x my y x=+⎧⎨=⎩,整理可得:2440y my --=,显然0∆>,124y y m +=,124y y =-,21212()242x x m y y m +=++=+,21212()116y y x x ==,所以12121(4)3OC OD x x y y ⋅=+=+-=-,所以A 正确;由于21244CD x x p m =++=+,1AB CDk k =-,所以将CD 中的m 换成1m -代入CD 中得2144AB m=+,()()22222411114182823222ACBDm S AB CD m m m m +⎛⎫⎛⎫=⋅=⨯+⋅=++= ⎪ ⎪ ⎪⎝⎭⎝⎭四边形,当且仅当1m =-时等号成立,所以四边形的最小面积为32,所以B 不正确;设3(A x ,3)y ,4(B x ,4)y ,若||||16AF BF ⋅=,即343434(1)(1)116x x x x x x ++=+++=,整理可得4343()116x x x x +++=,即21411126m ⎛⎫+++= ⎪⎝⎭,解得213m =,即33m =±,而直线CD 的斜率10k m =<,所以直线CD的斜率为D 正确;可得弦长()2||41CD m =+,21||41AB m ⎛⎫=+ ⎪⎝⎭,所以2221111||||4(1)4(1)4m AB CD m m +=+=++,所以C 正确;故选:ACD第Ⅱ卷三、填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)13.设向量()(),2,2,1a m b == ,且222||a b a b +=+ ,则m =_________.【答案】1-【解析】【分析】根据向量模长的坐标公式即可代入求解.【详解】由()(),2,2,1a m b == 得()2,3a b m +=+ ,根据222||a b a b +=+ 得()2222925m m ++=++,解得1m =-,故答案为:1-14.若直线3y ax =-为函数()1ln f x x x=-图像的一条切线,则a 的值是________.【答案】2【解析】【分析】根据切点求解函数()f x 的切线方程,列方程组得02000112,ln 13a x x x x +=--=-,进而可求解0x ,即可得a .【详解】设()1ln f x x x =-的切点为00(,)x y ,其中0001ln y x x =-,由()211f x x x'=+得切线的斜率为()020011k f x x x '==+,所以切线方程为:()002000111ln y x x x x x x ⎛⎫-+=+- ⎪⎝⎭,即02000112ln 1y x x x x x ⎛⎫=++-- ⎪⎝⎭,直线3y ax =-是()f x 的切线,所以2000112ln 13a x x x x ⎧+=⎪⎪⎨⎪--=-⎪⎩,记()2ln 2,g x x x =-+则()2120g x x x'=+>,所以()g x 在定义域内单调递增,而()10g =,所以方程2ln 20x x-+=的根为1x =,因此01x =,进而得200112a x x =+=,故答案为:215.已知()()12,0,,0F c F c -为椭圆2222:1x y C a b+=的两个焦点,P 为椭圆C 上一点(P 不在y 轴上),12PF F △的重心为G ,内心为M ,且12//GM F F ,则椭圆C 的离心率为___________.【答案】12##0.5【解析】【分析】根据重心坐标公式以及内切圆的半径,结合等面积法,得到,a c 的关系,即可求解离心率.【详解】设()()000,0P x y x ≠,由于G 是12PF F △的重心,由重心坐标公式可得00,33x y G ⎛⎫⎪⎝⎭,由于12//GM F F ,所以M 的纵坐标为03M y y =,由于M 是12PF F △的内心,所以12PF F △内切圆的半径为03y r =,由椭圆定义得12212,2PF PF a F F c +==,()2121210120122111223PF F MF F MF P MPF y S S S S F F y F F PF F P =++⇒⋅=++ ,()001222232y c y a c a c e =+⇒=⇒=,故答案为:1216.已知菱形ABCD 边长为6,2π3ADC ∠=,E 为对角线AC 上一点,3AE =ABD △沿BD 翻折到A BD ' 的位置,E 移动到E '且二面角A BD A '--的大小为π3,则三棱锥A BCD -'的外接球的半径为______;过E '作平面α与该外接球相交,所得截面面积的最小值为__________.【答案】①.21②.9π【解析】【分析】设AC BD O = ,证明出BD ⊥平面A CO ¢,分析可知π3AOA '∠=,以点O 为坐标原点,OC 、OB 所在直线分别为x 、y 轴,平面AOA '内过点O 且垂直于AC 的直线为z 轴建立空间直角坐标系,设三棱锥A BCD -'的外接球球心为(),,M x y z ,根据题意可得出关于x 、y 、z 的方程组,可求得球心M 的坐标,即可求出球M 的半径长,求出ME ',可求得截面圆半径的最小值,再利用圆的面积公式可求得截面圆面积的最小值.【详解】设AC BD O = ,翻折前,在菱形ABCD 中,则AC BD ⊥,即AO BD ⊥,CO BD ⊥,翻折后,则有A O BD '⊥,所以,二面角A BD A '--的平面角为π3AOA '∠=,在菱形ABCD 中,2π3ADC ∠=,则π3BAD ∠=,又因为6AB AD ==,所以,ABD △是边长为6的等边三角形,同理可知,BCD △是边长为6的等边三角形,因为A O BD '⊥,CO BD ⊥,A O CO O '⋂=,A O '、CO ⊂平面A CO ¢,BD ∴⊥平面A CO ¢,以点O 为坐标原点,OC 、OB 所在直线分别为x 、y 轴,平面AOA '内过点O 且垂直于AC 的直线为z轴建立如下图所示的空间直角坐标系,则点()0,3,0B、()C 、()0,3,0D -、339,0,22A ⎛⎫'- ⎪ ⎪⎝⎭、()E ',设三棱锥A BCD -'的外接球球心为(),,M x y z ,由MB MDMB MC MB MA ⎧='⎪=⎨⎪=⎩可得()()()(()222222222222222222333339322x y z x y z x y z x y z x y z x y z ⎧⎪+-+=+++⎪⎪⎪+-+=-++⎨⎪⎪⎛⎛⎫+-+=+++-⎪ ⎪ ⎝⎭⎪⎝⎭⎩,解得03x y z ⎧=⎪=⎨⎪=⎩,所以,三棱锥A BCD -'的球心为)M,球M的半径为MB =.ME '=,设球心M 到截面α的距离为d ,平面α截球M 的截面圆的半径为r,则d ME '≤=,3r ∴=≥=,过E '作平面α与该外接球相交,所得截面面积的最小值为2π39π⨯=.;9π.【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径;③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可;④坐标法:建立空间直角坐标系,设出外接球球心的坐标,根据球心到各顶点的距离相等建立方程组,求出球心坐标,利用空间中两点间的距离公式可求得球的半径.四、解答题:(本大题共6小题共70分,解答应写出文字说明x 证明过程或演算步骤)17.已知公差为正数的等差数列{}n a 的前n 项和为1,1n S a =,________.请从以下二个条件中任选一个,补充在题干的横线上,并解答下列问题:①248S S S 、、成等比数列,②251072a a a -=.(1)求数列{}n a 的通项公式;(2)若11n n n b a a +=,求数列{}n b 的前n 项和n T .【答案】(1)21n a n =-(2)21n nT n =+【解析】【分析】(1)先设等差数列{}n a 的公差为(0)d d >,再根据等差数列的求和公式和等比中项的性质,根据条件①②分别列出关于首项1a 与公差d 的方程,解出d 的值,即可计算出数列{}n a 的通项公式;(2)先根据第(1)题的结果计算出数列{}n b 的通项公式,再运用裂项相消法即可计算出前n 项和n T .【小问1详解】由题意,设等差数列{}n a 的公差为(0)d d >,方案一:选择条件①41121816,43442822,8S a d a S a d d d S a +=+==+⨯=+,根据248S S S 、、成等比数列得2428S S S =,代入得()()()1121462828a d d a a d +=++,又11a =,化简整理,可得220d d -=,由于0d >,所以2d =,12(1)21n a n n ∴=+-=-,*n ∈N .方案二:选择条件②由251072a a a -=,可得()()211149(6)2a d a d a d ++-+=,又11a =,解得2d =,12(1)21n a n n ∴=+-=-,*n ∈N 【小问2详解】由(1)可得111111(21)(21)22121n n n b a a n n n n +⎛⎫===- ⎪-+-+⎝⎭,则12n nT b b b =++⋅⋅⋅+1111111112323522121n n ⎛⎫⎛⎫⎛⎫=⨯-+⨯-+⋅⋅⋅+⨯- ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭111111123352121n n ⎛⎫=⨯-+-+⋅⋅⋅+- ⎪-+⎝⎭111221n ⎛⎫=⨯- ⎪+⎝⎭21nn =+.18.记ABC 内角A 、B 、C 的对边分别为a 、b 、c ,且()()()sin sin sin sin b c B C A C a +-=-.(1)求B 的值;(2)若ABC,2b =,求ABC 周长.【答案】(1)π3B =(2)6【解析】【分析】(1)利用正弦定理结合余弦定理可求得cos B 的值,结合角B 的取值范围可求得角B 的值;(2)利用三角形的面积公式可求得ac 的值,再利用余弦定理可求得a c +的值,即可求得ABC 的周长.【小问1详解】解:由()()()sin sin sin sin b c B C A C a +-=-,根据正弦定理可得()()()b c b c a c a +-=-,所以,222a c b ac +-=,由余弦定理可得2221cos 22a c b B ac +-==,()0,πB ∈ ,因此,π3B =.【小问2详解】解:因为1sin 24ABC S ac B ac === ,4ac ∴=,由余弦定理可得()()22222222cos 3124b a c ac B a c ac a c ac a c =+-=+-=+-=+-=,4a c ∴+=,因此,ABC 的周长为6a b c ++=.19.如图多面体ABCDEF ,正方形ABCD 的边长为4,AF ⊥平面ABCD ,2AF =,//AF DE ,DE AF <.(1)求证://CE 平面ABF ;(2)若二面角B CF E --的大小为α,且310cos 10α=,求DE 长.【答案】(1)证明见解析(2)1DE =【解析】【分析】(1)利用线面平行和面面平行的判定可证得平面//CDE 平面ABF ,由面面平行的性质可证得结论;(2)以A 为坐标原点建立空间直角坐标系,设()02DE t t =<<,利用二面角的向量求法可构造方程求得t 的值,即为DE 的长.【小问1详解】//AF DE ,//AB CD ,DE ⊄平面ABF ,CD ⊄平面ABF ,AF ⊂平面ABF ,AB ⊂平面ABF ,//DE ∴平面ABF ,//CD 平面ABF ,CD DE D = ,,CD DE ⊂平面CDE ,∴平面//CDE 平面ABF ,CE ⊂ 平面CDE ,//CE ∴平面ABF .【小问2详解】以A 为坐标原点,,,AB AD AF正方向为,,x y z轴,可建立如图所示空间直角坐标系,设()02DE t t =<<,则()4,0,0B ,()4,4,0C ,()0,0,2F ,()0,4,E t ,()0,4,0BC ∴= ,()4,4,2CF =-- ,()4,0,CE t =-,设平面BCF 的法向量(),,n x y z =,则404420BC n y CF n x y z ⎧⋅==⎪⎨⋅=--+=⎪⎩ ,令1x =,解得:0y =,2z =,()1,0,2n ∴= ;设平面CEF 的法向量(),,m a b c =,则442040CF m a b c CE m a tc ⎧⋅=--+=⎪⎨⋅=-+=⎪⎩,令4c =,解得:a t =,2b t =-,(),2,4m t t ∴=- ;cos cos ,10m n m n m n α⋅∴=<>==⋅ ,解得:1t =或134t =(舍),1DE =∴.20.某地区为居民集体筛查新型传染病毒,需要核酸检测,现有()*N ,2k k k ∈≥份样本,有以下两种检验方案,方案一,逐份检验,则需要检验k 次;方案二:混合检验,将k 份样本分别取样混合在一起检验一次,若检验结果为阴性,则k 份样本均为阴性,若检验结果为阳性,为了确定k 份样本的阳性样本,则对k 份本再逐一检验.逐份检验和混合检验中的每一次检验费用都是16元,且k 份样本混合检验一次需要额外收20元的材料费和服务费.假设在接受检验的样本中,每份样本是否为阳性是相互独立的,且据统计每份样本是阴性的概率为()01p p <<.(1)若()*N ,2k k k ∈≥份样本采用混合检验方案,需要检验的总次数为X ,求X 分布列及数学期望;(2)①若5,k p =>性;②若p =,采用方案二总费用的数学期望低于方案一,求k 的最大值.参考数据:ln20.7,ln3 1.1,ln7 1.9,ln10 2.3,ln11 2.4=====【答案】(1)见解析(2)①见解析,②k 的最大值为11【解析】【分析】(1)X 的可能值为1和1k +,分别求出对应的概率,再结合期望公式,即可求解,(2)①结合期望公式,求出方案二的期望,再结合作差法,即可求解.②结合期望公式,以及利用导数研究函数的单调性,即可求解.【小问1详解】X 的可能值为1和1k +,(1)k P X p ==,(1)1k P X k p =+=-,所以随机变量X 的分布列为:所以()1(1)[1]1【小问2详解】①设方案二总费用为Y ,方案一总费用为Z ,则1620Y X =+,所以方案二总费用的数学期望为:()16()2016[1]20k E Y E X k kp =+=+-+,又5k =,所以55()16[65]2080116E Y p p =-+=-+,又方案一的总费用为51680Z =⨯=,所以()55()80801168036Z E Y p p --+=--=,当p >50.451p <<,508036p <-,,所以()>Z E Y ,所以该单位选择方案二合理.②由①方案二总费用的数学期望()16()2016[1]20k E Y E X k kp =+=+-+,当p =79()1612016(e )4k k E Y k k k k -⎡⎤=+-+=+-⎢⎥⎢⎥⎣⎦,又方案一的总费用为16Z k =,令()<E Y Z 得:7916e 164kk k k -⎛⎫+-< ⎪⎝⎭,所以79e4kk ->,即79ln e ln 4k k -⎛⎫> ⎪⎝⎭,所以9ln ln 074k k -->,设9()ln ln [2,)74x f x x x =--∈+∞,所以117(),[2,)77-=-=∈+∞'x f x x x x,令()0f x '>得27x <,()0f x '<得7x >,所以()f x 在区间[2,7)上单调递增,在区间(7,)+∞上单调递减,()max ()7f x f =ln712(ln3ln2)0.10=---=>,888(8)3ln22(ln3ln2)5ln22ln3 1.30777f =---=--=->,999(9)2ln32(ln3ln2)2ln2 1.40777f =---=-=->,1010(10)ln102(ln3ln2) 1.5077f =---=->,1111(11)ln112(ln3ln2) 1.6077f =---=->,121212(12)ln122(ln3ln2)4ln2ln3 1.70777f =---=--=-<,所以k 的最大值为11.21.已知双曲线222:1x Q y a-=的离心率为,经过坐标原点O 的直线l 与双曲线Q 交于A ,B 两点,点()11,A x y 位于第一象限,()22,C x y 是双曲线Q 右支上一点,AB AC ⊥,设113,2y D x ⎛⎫- ⎪⎝⎭(1)求双曲线Q 的标准方程;(2)求证:C ,D ,B 三点共线;(3)若ABC 面积为487,求直线l 的方程.【答案】(1)2214x y -=(2)证明见解析(3)13y x =【解析】【分析】(1)根据离心率即可求解2a =,(2)利用坐标运算,结合点差法以及向量共线的坐标表示即可求解,(3)根据三角形面积公式,利用联立方程,韦达定理,代入化简即可得到关于k 的方程,【小问1详解】由双曲线222:1x Q y a -=,所以152e a ==,解得2a =,所以双曲线Q 的标准方程为2214x y -=【小问2详解】由()11,A x y 得()11,B x y --,又()22,C x y ,所以()11,OA x y =,()2121,AC x x y y =--,由OA AC ⊥得()()1211210x x x y y y -+-=①,由于()11,A x y ,()22,C x y 在双曲线上,所以222212121,144x x y y -=-=,相减得()221222121212121244y y x x x xy y y y x x -+-=+⇒=--②由①②得1211214x x x y y y =-++③,()2121111,,2,,2BC x x y y BD x y ⎛⎫=++=- ⎪⎝⎭ 由于110,0x y >>,所以()21212121111121222y y x x y y x x x x y y ++++-=+-,将③代入得()()212121112111112012224y y x x y y x x y y x y y y ⎛⎫+-+++-=⎪⎝- ⎭+=,所以//BC BD,因此C ,D ,B 三点共线【小问3详解】设直线l 的方程为()0y kx k =>,联立直线l 与双曲线的方程为:()222214414y kx k x x y =⎧⎪⇒-=⎨-=⎪⎩,故2114002k k ->⇒<<,所以212414x k =-,直线AC 的方程为()111y y x x k -=--,联立()21121111222148144014y y x x x x k x y x y k k k k x y ⎧-=--⎪⎪⎛⎫⎛⎫⎛⎫⇒-++-+-=⎨ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎪-=⎪⎩,所以()111228,04x ky x x k ++=-∆>-由于//AD y 轴,10y >,所以152AD y =,所以()()()()211111111121122281551010224444ABC x y ky x ky x ky S y x x y y k k k+++=⨯+=⨯=⨯=⨯--- ,由于11y kx =,212414x k =-代入得()()()()3232323211122224221440101010401414444174417ABC k k k kx k x k k x k k k k S k k k k k k k ⎛⎫++ ⎪+++⎝⎭-=====----+⎛⎫+- ⎪⎝⎭,令10k t k+=>,则240484257ABC t S t ==- ,化简得224351500t t --=,由于0t >,所以103t =,因此1103k k +=,解得3k =或13k =由于102k <<,所以13k =,故直线l 方程为13y x =【点睛】方法点睛:解析几何中的弦长以及面积问题以及最值是常见的类型,对于这类问题一般有两种方法:一是几何意义,特别是用曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将解析几何中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法求解.22.已知函数()()()22111ln ln ,e 22ex f x x x kx k g x x f x =++-=--,(1)若–1k ≤时,求证:函数()f x )只有一个零点;(2)对12x x ∀≠时,总有()()12122g x g x x x ->-恒成立,求k 的取值范围.【答案】(1)见解析(2)1e k ≤-【解析】【分析】(1)求导,利用导数确定函数的单调性,进而结合零点存在性定理即可求解,(2)将问题等价转化为()2g x x -在定义域内单调递增,构造函数()()2F x g x x =-,只需要证明()0F x '≥,进而分离参数,问题转化成21()=e e ln 12x x p x x x----,只()k p x ≤恒成立,利用导数求解最值即可.【小问1详解】由()21ln ln 2f x x x kx k =++-得()ln 1x f x k x x'=++,记()()()2ln 1ln ,x x h x f x k h x x x x -''==++=,则当01x <<时,()0h x '>,当1x >时,()0h x '<,因此()h x 在01x <<单调递增,在1x >单调递减,故()()11h x h k ≤=+,当1k ≤-时,10k +≤,所以()0h x ≤,因此()0f x '≤,所以()f x 在定义域()0,∞+单调递减,而()10f =,因此函数()f x )只有一个零点【小问2详解】不妨设12x x <,则由()()12122g x g x x x ->-得()()()()()12121122222g x g x x x g x x g x x <-<-⇒--,故函数()2g x x -在定义域内单调递增,记()()2F x g x x =-,则()0F x '≥,即()()()22112e 2ln 12e e 0e x x F x x k x xg x f x '''=-=-------=≥-,所以21n 2e e l 1x x k x x----≥,记21()=e e ln 12x x p x x x----,只需要()k p x ≤恒成立即可,22222ln ln 2e ()=2e x xx x x x p x x =+'+,记()()22ln ,=2e 0x q x x x x +>,()()21=41e 0x q x x x x'++>,所以()q x 在()0,∞+单调递增,()2221e 112e 0,2e 12e 10e q q -⎛⎫=>=-<-< ⎪⎝⎭,所以存在01,1x e ⎛⎫∈ ⎪⎝⎭,使得()00q x =,即022002n 0e l x x x +=,所以0200000l 11ln 2n 1e x x x x x x ==-,由于01,1x e ⎛⎫∈ ⎪⎝⎭,所以()01ln 0,1x ∈,令()e x t x x =,由于当0x >时,0,e 0x x >>,且函数,e x y x y ==均为单调递增的函数,所以()ex t x x =由020001ln 12e x x x x =得()0012ln t x t x ⎛⎫= ⎪⎝⎭,所以0012ln x x =,即0201e x x =,当00x x <<时,()0p x '<,()p x 单调递减,当0x x >时,()0p x '>,()p x 单调递增,所以()()()0002min 0000112ln 111e 122e e ex x x x x x p x p x ---==---==---,故1ek ≤-【点睛】本题主要考查利用导数研究函数的单调性、求函数的最值以及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:①分离参数()a f x ≥恒成立(()max a f x ≥即可)或()a f x ≤恒成立(()min a f x ≤即可);②数形结合(()y f x =图象在()y g x =上方即可);③分类讨论参数.。
辽宁省大连市2023届高三上学期期末双基测试数学试卷含答案

2023年大连市高三双基测试注意事项:1.请在答题纸上作答,在试卷上作答无效.2.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷一.单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求. 1.已知集合{}1,2,3,4,5A =,12x B x Z ⎧⎫-=∈⎨⎬⎩⎭,则=A B(A ){}5(B ){}3,5(C ){}1,3,5(D ){}2,42.i 是虚数单位,若复数z =543i+,则z 的共轭复数z = (A )43i 55+ (B )43i 55- (C )43i 55-+(D )43i 55-- 3.已知命题0:p x ∃∈R ,20010x x -+<,则p ⌝是(A )0x ∃∈R ,20010x x -+≥(B )x ∀∈R ,210x x -+≥(C )x ∀∈R ,210x x -+< (D )x ∀∈R ,210x x -+>4.开普勒(Johannes Kepler ,1571~1630),德国数学家、天文学家,他提出的行星运动三定律之三:如图,所有行星绕太阳 运动的轨道都是椭圆,且所有行星轨道的半长轴的三次方与它 的公转周期的二次方的比都相等.已知金星与地球的公转周期之 比约为2:3,地球运行轨道的半长轴为a ,则金星运行轨道的半长轴约为(参考数据:133 1.442≈ ) (A )0.66a (B )0.70a (C )0.76a (D )0.96a5.若二项式62(10)x x a a ⎛⎫ ⎪⎭>+⎝的展开式中所有项的系数和为64,则展开式中的常数项为(A )10 (B )15 (C )25 (D )306.tan α=(A (B )2 (C )3 (D7.已知432(4ln 32)1,,a b c e e -===,则 (A )a c b << (B )c a b << (C )a b c << (D )b a c <<8.已知函数(),()f x g x 的定义域均为R ,且()(2)5,()(4)7f x g x g x f x +-=--=.若()y g x =的图像关于直线2x =对称,(2)4g =,则221()k f k ==∑(A )21- (B )22- (C )23- (D )24-二.多项选择题:(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.) 9.将函数()cos(2)f x x π=-图像上所有的点向左平移6π个单位长度,得到函数()g x 的图像,则(A )()g x 的最小正周期为π(B )()g x 图像的一个对称中心为7,012π⎛⎫⎪⎝⎭(C )()g x 的单调递减区间为()5,36k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z(D )()g x 的图像与函数sin 26y x π⎛⎫=-- ⎪⎝⎭的图像重合10.下列正确的是( )(A )若随机变量()2~1,N ξσ,()40.77P ξ≤=,则()20.23P ξ≤-=(B )若随机变量1~10,3X B ⎛⎫ ⎪⎝⎭,则()3119D X -=(C )已知回归直线方程为ˆ10.8=+y bx,且4x =,50y =,则ˆ9.8=b (D )已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11.若这组数据的平均数、中位数、众数依次成等差数列,则丢失数据的所有可能值的和为2211. 正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F ,G 分别为BC ,CC 1,BB 1的中点,则(A )直线D 1D 与直线AF 垂直(B )直线A 1G 与平面AEF 平行(C )平面AEF 截正方体所得的截面面积为98 (D )点A 1与点D 到平面AEF 的距离相等12.已知点F 是抛物线24y x =的焦点,,AB CD 是经过点F 的弦且AB CD ⊥,直线AB 的斜率为k ,且0k >,,C A 两点在x 轴上方,则(A )3OC OD ⋅=- (B )四边形ABCD 面积最小值为64(C )111||||4AB CD += (D )若||||16AF BF ⋅=,则直线CD 的斜率为 第Ⅱ卷三.填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)13. 设向量a (,2)m =,b (2,1)=,且222+=+a b a b ,则=m .14.若直线3y ax =-为函数1()ln f x x x =-图像的一条切线,则a 的值是 . 15. 已知12(,0)(,0)F c F c -,为椭圆2222:1x yC a b+=的两个焦点,P 为椭圆C 上一点(P 不在y 轴上),12PF F ∆的重心为G ,内心为M ,且GM ∥12F F ,则椭圆C 的离心率为 .16. 已知菱形ABCD 边长为6,23ADC π∠=,E 为对角线AC 上一点,AE =ABD △沿BD 翻折到A BD '△的位置,E 移动到E '且二面角A BD A '--的大小为3π,则三棱锥A BCD '-的外接 球的半径为______;过E '作平面α与该外接球相交,所得截面面积的最小值为______.四.解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)已知公差为正数的等差数列{}n a 的前项和为n S ,11a =,_______.请从以下二个条件中任选一个,补充在题干的横线上,并解答下列问题:①2S 、4S 、8S 成等比数列,②251072a a a -=.(I)求数列{}n a 的通项公式;(II)若11n n n b a a +=,求数列{}n b 的前n 项和n T .18.(本小题满分12分)记ABC ∆内角A ,B ,C 的对边分别为a ,b ,c ,且()(sin sin )(sin sin )b c B C A C a +-=-.(I) 求B的值;(II )若ABC ∆,2b =,求ABC ∆周长.19.(本小题满分12分) 如图多面体ABCDEF ,正方形ABCD 的边长为4AF ⊥面ABCD ,2AF =,AF ∥DE ,DE <(I )求证:CE ∥平面ABF .(II )若二面角--BCF E 的大小为α,且|cos |α=DE 长.某地区为居民集体筛查新型传染病毒,需要核酸检测,现有*(,2)k k k ∈≥N 份样本,有以下两种检验方案,方案一:逐份检验,则需要检验k 次;方案二:混合检验,将k 份样本分别取样混合在一起检验一次,若检验结果为阴性,则k 份样本均为阴性,若检验结果为阳性,为了确定k 份样本的阳性样本,则对k 份本再逐一检验.逐份检验和混合检验中的每一次检验费用都是16元,且k 份样本混合检验一次需要额外收20元的材料费和服务费.假设在接受检验的样本中,每份样本是否为阳性是相互独立的,且据统计每份样本是阴性的概率为()01p p <<.(I )若()*,2k k k ∈≥N 份样本采用混合检验方案,需要检验的总次数为X ,求X分布列及数学期望;(II )①若5,k p =>案二的合理性;②若p =,采用方案二总费用的数学期望低于方案一,求k 的最大值. 参考数据:ln 20.7=,ln 3 1.1=,ln 7 1.9=,ln10 2.3=,ln11 2.4=已知双曲线Q :2221-=x y a 的离心率为2,经过坐标原点O 的直线l 与双曲线Q 交于,A B 两点,点()11,A x y 位于第一象限,()22,C x y 是双曲线Q 右支上一点,⊥AB AC ,设113,2⎛⎫- ⎪⎝⎭y D x .(I )求双曲线Q 的标准方程; (II )求证:,,C D B 三点共线; (III )若∆ABC 面积为487,求直线的l 方程.1 / 172023年大连市高三双基测试参考答案与评分标准数学说明:一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分.第Ⅰ卷一.单项选择题1.(C );2.(A );3. (B );4. (C );5. (B );6.(C );7.(A );8.(D ) 部分试题解答: 5. 答案:A解析:由题意可知当1x =时,6(1)64a +=,解得1a =,二项式621x x ⎛⎫+ ⎪⎝⎭的展开式的通项公式为()66212661C C rr r rr r r T x x x ---+⎛⎫=⋅=⋅ ⎪⎝⎭⋅, 令630r -=,解得2r =,所以展开式中的常数项为26315T C ==.故选A.2 / 176. 答案C整理,得2tan 4tan 30αα-+=,解得tan 3α=或tan 1α=.所以tan 3α=.故选C .7.解:44ln ln ln 4ln 232,,4232eea b c e e=====构造函数2ln 1ln (),'()0,x xf x f x x e x x -====,故()f x 在(0,)e +单调递增,在(,)e +∞单调递减,max1()f f e e ==,而428,232e e <<,故4()(2)32ef f <,故选A.8.解:因为()y g x =的图像关于直线2x =对称,所以()()22g x g x -=+,因为()(4)7g x f x --=,所以(2)(2)7g x f x +--=,即(2)7(2)g x f x +=+-,因为()(2)5f x g x +-=,所以()(2)5f x g x ++=,代入得[]()7(2)5f x f x ++-=,即()(2)2f x f x +-=-,所以()()()()35212510f f f +++=-⨯=-,()()()()46222510f f f +++=-⨯=-.因为()(2)5f x g x +-=,所以(0)(2)5f g +=,即()01f =,所以()(2)203f f =--=-.因为()(4)7g x f x --=,所以(4)()7g x f x +-=,又因为()(2)5f x g x +-=,联立得,()()2412g x g x -++=,所以()y g x =的图像关于点()3,6中心对称,因为函数()g x 的定义域为R ,所以()36g =,因为()(2)5f x g x ++=,所以()()1531f g =-=-.所以3 / 17()()()()()()()()221123521462213101024()k f f f f f f f f f k =+++++++++=----=-⎡⎤⎡⎤⎣⎦⎣⎦=∑K K .二.多项选择题9.(A )(B )(C );10.(A )(C );11.(B )(C )(D );12.(A )(C )(D ) 10.解:对于A ,()()2410.770.23P P ξξ≤-=≥=-=,故A 正确; 对于B ,()122010339D X =⨯⨯=,所以()220313209D X -=⨯=,故B 不正确; 对于C ,回归直线方程经过点(),x y ,将4x =,50y =代入求得9.8b =,故C 正确;对于D ,设丢失的数据为x ,则这组数据的平均数为317x+,众数为3,当3x ≤时,中位数为3,此时36731x ++=,解得10x =-;当35x <<时,中位数为x ,此时23137x x+=+,解得4x =;当5x ≥时,中位数为5,此时113073x+=+,解得18x =.所以所有可能x 的值和为1041812-++=11. 答案BCD解:∵CC 1与AF 不垂直,而DD 1∥CC 1,∴AF 与DD 1不垂直,故(A )错误;取B 1C 1的中点N ,连接A 1N ,GN ,可得平面A 1GN ∥平面AEF ,则直线A 1G ∥平面AEF ,故(B )正确;把截面AEF 补形为四边形AEFD 1,由四边形AEFD 1为等腰梯形,可得平面AEF 截正方体所得的截面面积S =98,故(C )正确;显然点A 1与点D 到平面AEFD 1的距离相等,故(D )正确.故选BCD12.【答案】ACD对于A ,由题可知,设直线CD 的方程为:1=+x my ,4 / 17联立241⎧=⎨=+⎩y x x my ,消x 得:2440--=y my ,设1122(,),(,)C x y D x y ,则124=-y y ,则221212144=⋅=y y x x 所以1212143OC OD x x y y ⋅=+=-=-,故A 正确; 对于B ,又因为2124(1)=-===+CD y y m同理:214(1)=+AB m, 222211114(1)4(1)8(2)32(1)22当且仅当时取等==⋅+⋅+=++≥=ACBD S AB CD m m m m m故B 错误;对于C ,22211114(1)4(1)4+=+=++m AB CD m m ,故C 正确; 对于D ,设直线AB 的方程为:1=+x ky ,联立241⎧=⎨=+⎩y x x my ,消x 得:2440--=y my ,设3344(,),(,)A x y B x y ,则344=-y y ,又34,,==AF BF5 / 17所以2234(1)4(1)16=+=+=AF BF k y y k,解得:23,==k k所以直线CD的斜率为D 正确. 故选:ACD .第Ⅱ卷三.填空题13.—1; 14. 2; 15.12;9π 14.解:设切点0001,ln x x x ⎛⎫-⎪⎝⎭,其中00x >,()211f x x x '=+,()020011f x x x '=+, 所以过点0001,ln x x x ⎛⎫- ⎪⎝⎭的切线方程为()002000111ln y x x x x x x ⎛⎫⎛⎫--=+- ⎪ ⎪⎝⎭⎝⎭,即020001121ln y x x x x x ⎛⎫=+--+ ⎪⎝⎭,因为切线为3y ax =-故20011a x x =+, 00231ln x x -=--+,01,2x a ∴== 15. 解:设),,(00y x P 由G 为21PF F ∆的重心得:G 的坐标为),3,3(00y x G 再由且GM ∥12F F ,所以M 点的纵坐标为3y ,在21PF F ∆中,c F F a PF PF 2,22121==+,所以21PF F ∆的面积为02121y F F S =,又因为M 为21PF F ∆的内心,所以M 点的纵坐标即为内切圆的半径,所以6 / 173)(2102211y PF F F PF S ⨯++=,所以021*******321y F F y PF F F PF =⨯++)(,即0022132221y c y c a =⨯+)(,所以c a 2=,所以椭圆C 的离心率21=e . 16.解:因为23ADC π∠=且四边形ABCD 为菱形, 所以CBD △,A BD '△均为等边三角形,取CBD △,A BD '△的重心为,M N ,过,M N作平面CBD 、平面A BD '的垂线,且垂线交于一点O , 此时O 即为三棱锥A BCD '-的外接球球心,如下图所示:记AC BD O '=,连接,CO OO ',因为二面角A BD C '--的大小为23π, 且A O BD ''⊥,CO BD '⊥,所以二面角A BD C '--的平面角为23A O C π''∠=, 因为O M O N ''=,所以cos cos MO O NO O ''∠=∠,所以3MO O NO O π''∠=∠=,又因为6BC =,所以6sin3CO A O π'''===,所以MO NO ''==所以tan33OM O M π'==,又23CM CO '==,所以OC ==三棱锥A BCD '-.当截面面积取最小值时,此时OE'⊥截面,又因为截面是个圆,设圆的半径为r,外接球的半径为R,又因为13NE A O'''==3ON OM==,所以OE'==所以3r==,所以此时截面面积为9Sπ=.四.解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)解:(I)选择①:设等差数列{}n a的公差为d,则0d>,由题意可得2428S S S=,即()()()2462828d d d+=++,2d=,因此()1121na a n d n=+-=-.选择②:设等差数列{}n a的公差为d,则0d>,由251072a a a-=得2(14)(19)(16)2d d d++-+=,解得2d=,因此()1121na a n d n=+-=-. ………………………………… 5分(II)由(I)可得()()111111212122121nn nba a n n n n+⎛⎫===-⎪-+-+⎝⎭,所以11111111112335212122121nnTn n n n⎛⎫⎛⎫=-+-++-=-=⎪ ⎪-+++⎝⎭⎝⎭.…………………… 10分18.(本小题满分12分)解:(I)由()(sin sin)()sinb c B C a c A+-=-,根据正弦定理可得()()()b c b c a c a+-=-,………………………………………………… 2分即222b ac ac=+-,222ac a c b=+-由余弦定理2222cosb ac ac B=+-,得2221cos22a c bBac+-==,…………………………………………………………………… 4分7 / 178 / 17由于0B π<<,所以3B π=.………………………………………………………………… 6分(II )因为ABC ∆,所以1sin 2ac B ==,即4ac =,………………………………………………… 8分 因为2224b a c ac =+-=,所以228a c +=,………………………………………………10分所以4a c +==,所以ABC ∆周长为6. ………………………………… 12分 19.(本小题满分12分)解:(I )因为//DE AF ,又因为DE ⊄平面ABF ,AF ⊂平面ABF ,所以//DE 平面ABF . …………………………………………………… 2分因为底面ABCD 是正方形,所以//CD AB , 又因为CD ⊄平面ABF ,AB ⊂平面ABF ,所以//CD 平面ABF . ……………………………………………………4分 因为CD ⊂平面CDE ,DE ⊂平面CDE ,CDDE D =,所以平面CDE ∥平面ABF .因为CE ⊂平面CDE ,所以CE ∥平面ABF . …………………………………………………………6分 (II )以A 为坐标原点,分别以AB ,AD ,AF 所在直线为x 轴、y 轴、z 轴,建立如图空间直角坐标系.由4AB AD AF ===得,(000)A ,,,(400)B ,,,(440)C ,,,(002)F ,,,(040)D ,,,(04)E m ,,.设平面BCF 的法向量为1111()x y z =,,n ,由已知得,(402)FB =-,,,(442)FC =,,-, 由1100.FB FC ⎧⋅=⎪⎨⋅=⎪⎩,n n 得111114204420.x z x y z -=⎧⎨+-=⎩,不妨取11x =,则1102y z ==,,从而平面BCF 的一个法向量为1(102)=,,n .………………………………………………… 8分9 / 17设平面ECF 的法向量为2222()x y z =,,n ,又(40)CE m =-,,,由2200CE FC ⎧⋅=⎪⎨⋅=⎪⎩,,n n 得22222404420.x mz x y z -+=⎧⎨+-=⎩,不妨取24z =,则222x m y m ==-,, 所以平面ECF 的一个法向量为2(24)m m =-,,n . ………………………………………………… 10分所以12|cos ||cos ,|10α=<>=n n . 化简得2417130m m -+=,解得1m =或134m =, 因为DE AF <,所以1DE =. ………………………………………………… 12分20.(本小题满分12分)解:(I )X 的可能值为1和1k +,()1k P X p ==,()11kP X k p =+=-, 所以随机变量X 的分布列为:所以11(1)1EX p k p k kp =⨯++⨯-=+-.……………………………………………3分z yx A BDEF10 / 17(II )①设方案二总费用的数学期望为E Y (),方案一总费用的数学期望为Z ,则1620Y X =+,所以方案二总费用的数学期望为:()()162016(1)20kE Y E X k kp =+=+-+,又5k =,所以()516(620)5E Y p =-+589116p =-+,又方案一的总费用的数学期望为80Z =,所以()5916(5)4Z E Y p -=-,当p >59120p <<,59110544p <-<, 所以()Z E Y >,所以该单位选择方案二合理. …………………………………………………7分②由①知方案二总费用的数学期望()()162016()120kE Y E X k kp =+=+-+,当p =时,() 16120k E Y k k k =+-+⎡⎤⎢⎥⎢⎥⎣⎦79164k k ke -⎛⎫ ⎪⎝=+⎭-,又方案一的总费用为16Z k =,令()E Y Z <得:7916164k k ke k -⎛⎫ ⎪⎭<⎝+-,所以794kke->,即79ln ln 4k ke -⎛⎫> ⎪⎝⎭,所以9ln ln 074k k -->,………9分设()[)9ln ln ,2,74x f x x x =--∈+∞,所以()[)117,2,77xf x x x x-'=-=∈+∞, 令()0f x '>得27x ≤<,()0f x '<得7x >,11 / 17所以()f x 在区间[)2,7上单调递增,在区间()7,+∞上单调递减,……………………………10分 ()()()max 7ln 712ln 3ln 20.10f x f ==---=>,()()88883ln 22ln 3ln 25ln 22ln 3 1.30777f =---=--=->, ()()99992ln 32ln 3ln 22ln 2701.477f =---=-=->,()()1010ln102ln 3ln 2 1.507710f =---=->, ()()111111ln112ln 3ln 2 1.6077f =---=->, ()()12121212ln122ln 3ln 24ln 2ln 3 1.70777f =---=--=-<, 所以k 的最大值为11. ………………………………………………………………12分 21.(本小题满分12分)(1)由题可知2=a ,解得2=a 所以双曲线Q 的标准方程为2214-=x y . ………………………………………………………2分 (II )方法一:由题可知,直线AB 、AC 斜率存在且不为0. 因为AB AC ⊥ 所以1⋅=-AB AC k k ,即1211211-⋅=--y y y x x x .12 / 17又点,A C 在双曲线Q 右支上221122221414⎧-=⎪⎪⎨⎪-=⎪⎩x y x y ,作差得:211221124()-+=-+y y x x x x y y ,则212112121114()4+-===-+-BC y y x x yk x x y y x , ……………………………………………………4分又1111131224--==--BD y y y k x x 所以=BC BD k k .又BC 、BD 有公共点,所以、、B C D 三点共线. …………………………………………6分 方法二:由题可知,直线AB 、AC 斜率存在且不为0. 因为AB AC ⊥ 所以1⋅=-AB AC k k ,即1211211-⋅=--y y y x x x .① 又因为2221212122212121BC ACy y y y y y k k x x x x x x +--⋅==+--,又因为222212121,1,44x x y y -=-= 所以22212221111444BC ACx x k k x x --+⋅=-.② 由①②得4AB BCk k =-,所以1114BC yk x =-,……………………………………………………4分13 / 171111131224--==--BD y y y k x x ,所以=BC BDk k .又BC 、BD 有公共点,所以、、B C D 三点共线. …………………………………………6分 (III )设直线AC 的方程为1111()-=--y y y x x x , 联立方程组111122()14⎧-=--⎪⎪⎨⎪-=⎪⎩y y y x x x x y ,化简得22222221111112221114()()(1)8440++-+⋅-⋅-=x x x y x x y x y y y 22111222111112222111218()8()4410⎧+⎪+⎪+=-=⎪-⎨-⎪⎪∆>⎪⎩x x y y x x y x x x x y y , 因为11215()22∆=⋅⋅+ABC S y x x , 所以22111122118(152)24∆+=⋅-⋅ABCS y x x y x y , 所以221112211110()4∆+=-ABCy x x y x y S , ………………………………………………………………8分 又221114-=x y ,所以221144-=x y14 / 172222221111111112222222222111111111111111331111422411111111221110()10()440()4(4)(4)(4)(4)40()40()4174))4(4(17∆++⋅+==--⋅--⋅-++ ==-++-=ABCy y y S y y y y y x x y x x y x x y x y x y x y x y x y x x x y x x x x y y x ……………10分令11=y k x ,则22140()48174)4(17∆+==+-ABC k k k S k,令1=+t k k ,整理得:224351500--=t t .因为0t >,所以103=t , 所以231030-+=k k ,解得:133或==k k , 又因为双曲线C 的渐近线为12=±y x ,所以13=k . 所以直线l 的方程为13=y x . ………………………………………………………………12分 方法二:直线l 的方程为=y kx ,则直线AC 的方程为11()-=--y y k x x ,联立11221()14⎧-=--⎪⎪⎨⎪-=⎪⎩y y x x k x y ,化简得221111241(1)8()4()40-+⋅+-⋅+-=x x x y x y k k k k ,15 / 17111228()40+⎧+=-⎪∴-⎨⎪∆>⎩x ky x x k 因为11215()22∆=⋅⋅+ABC S y x x , 所以11211528(42)∆=⋅⋅+-ABC S y x ky k, ()()232322111111112221210108()10)1522(4444∆++++===----=⋅⋅ABCkx k x k k x x ky x y ky k k k y k S ……………8分 联立2214=⎧⎪⎨-=⎪⎩y kxx y ,消y 得:22414x k =-, 所以()()332321222422411040()1040()1414441744()17∆++++-====---++-ABC k k k k kxk k k k kkk k k kS ………10分 令1=+t k k ,240484257∆==-ABC t S t ,整理得:224351500--=t t .因为0t >,所以103=t ,所以231030-+=k k ,解得:133或==k k , 又因为双曲线C 的渐近线为12=±y x ,所以13=k . 所以直线l 的方程为13=y x . ………………………………………………………………12分16 / 1722.(本小题满分12分)),又k ()∴f x 在(0,)+∞单调递减,又()10=f ,∴函数()f x 的只有一个零点。
高三数学双基强化训练

高三数学双基强化训练(一)一、 选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有 一项是符合题目要求的.1. 已知集合{}2,M m =,{}1,2,3N =,则“3m =”是“M N ⊆”的( ). A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件2. 已知i 是虚数单位,,a b ∈R ,3ii 1ia b ++=-,则a b +等于( ). A. 1-B. 1C. 3D. 43. 已知命题001:,cos 2p x x ∃∈R …,则p ⌝是( ). A. 001,cos 2x x ∃∈R …B. 001,cos 2x x ∃∈>R C. 1,cos 2x x ∀∈R …D. 1,cos 2x x ∀∈>R 4. 方程2log 2=+x x 的解所在的区间为( ).A .()0.5,1B .()1,1.5C .()1.5,2D .()2,2.55. 设等差数列{}n a 的前n 项和为n S ,若211a =-,592a a +=-,则当n S 取最小值时,n 等于( ). A. 9B. 8C. 7D. 66. 已知函数()1f x kx =-,其中实数k 随机选自区间[]2,2-,[]0,1x ∀∈,()0f x …的概率是( ).A.14 B.13 C.12D.34 7. 已知O 是坐标原点,点()21A -,,若点(),M x y 为平面区域212x y x y +⎧⎪⎨⎪⎩………上的一个动点,则OA OM ⋅uu r uuu r的取值范围是( ).A. []0,1B. []0,2C. []1,0-D. []1,2-8. 如图所示,正方体1111ABCD A B C D -的棱长为1, P 为BC 的中点,Q 为线段1CC 上的动点,过点A ,P ,Q 的平面截该正方体所得的截面记为S .①当102CQ <<时, S 为四边形②截面在底面上投影面积恒为定值34③存在某个位置,使得截面S 与平面1A BD 垂直 ④当34CQ =时, S 与11C D 的交点1R 满足1113C R = 其中正确命题的个数为( ). A. 1B. 2C. 3D. 4二、填空题(本大题共6小题,每小题5分,共30分) 9.已知sin cos αα-=,()0,πα∈,则tan α= .10. 若平面向量a ,b 满足1+=a b ,+a b 平行于x 轴,且()2,1=-b ,则=a .11. 已知双曲线()222210,0x y a b a b-=>>的一条渐近线垂直于直线:250l x y --=,双曲线的一个焦点在l 上,则双曲线的方程为 .12. 某几何体的三视图(单位:cm )如图所示,其中俯视图中的曲线是四分之一的圆弧,则该几何体的体积等于 cm 3,表面积等于 cm 2.13. 已知点()2,1M 及圆224x y +=,则过M点的圆的切线方程为 ,若直线正视图侧视图俯视图QD 1C 1B 1A 1DCBAP40ax y -+=与圆相交于A ,B两点,且||AB =,则a = .14.定义:如果函数()y f x =在定义域内给定区间[],a b 上存在0x ()0a x b <<,满足()()()0f b f a f x b a-=-,则称函数()y f x =是[],a b 上的“平均值函数”,0x 是它的一个均值点,例如2x y =是[]1,1-上的平均值函数,0就是它的均值点.现有函数()3f x x mx =+ 是[]1,1-上的平均值函数,则实数m 的取值范围是 .高三数学双基强化训练(二)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知i 是虚数单位,若()i 12i z =-+,则z 的虚部为( ). A .2- B .1- C .1 D .2 2.已知命题:sin p x x x ∀∈>R,,则p 的否定形式为( ). A. 00sin x x x ∃∈R,… B. 00sin x x x ∃∈<R, C. sin x x x ∀∈R,… D. sin x x x ∀∈<R, 3.已知()1,x =a 和()2,2x =+-b ,若⊥a b ,则x =( ). A. 6 B. 4 C. 2 D. 04.等比数列{}n a 的各项为正数,且564718a a a a +=,则3132310log log log a a a +++=L ( ). A. 32log 5+ B. 8 C. 10 D. 12 5.执行如图所示的程序框图,若输入10n =,则输出S =( ).A .115B .1110C .3655D .72556.随机抛掷一枚质地均匀的骰子,让正面向上的点数a ,则函数()222f x x ax =++有两个不同零点的概率为( ). A .31 B .21 C .23 D .567.将函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像向左平移π6个单位,得到函数()y f x =的图像,则下列说法正确的是( ). A .()f x 是偶函数B .()f x 周期为π2 C .()f x 图像关于π6x =对称 D .()f x 图像关于π,06⎛⎫- ⎪⎝⎭对称 8.函数()log 31a y x =+-(0a >且1a ≠)的图像恒过定点A ,若点A 在直线10mx ny ++=上,其中0m >,0n >,则11m n+的最小值为( ). A.3+.4+ D.9.某四棱锥的三视图如图所示,则最长的一条侧棱的长度是( ). A.B.C.D.10.不等式1043x y x y -+⎧⎪⎨⎪⎩………所表示的平面区域的面积为( ).A .1B .2C .3D .411.设()ln 1f x ax x =-+有三个不同的零点,则a 的取值范围是( ). A .()0,e B .()20,e C .10,e ⎛⎫⎪⎝⎭ D .210,e ⎛⎫ ⎪⎝⎭12.已知函数()2122f x x ax =+,()23ln g x a x b =+,设两曲线()y f x =与()y g x =有公共点,侧左()视图正主()视图且在该点处的切线相同,且当()0,a ∈+∞时,实数b 的最大值是( ).A .613e 6B .233e 2C .61e 6D .237e 2二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.13.已知向量OA AB ⊥u u u r u u u r ,3OA =u u u r,则OA AB ⋅=u u u r u u u r .14.已知90ABC ∠=o ,PA ⊥平面ABC ,若1PA AB BC ===,则四面体PABC 的外接球(顶点都在球面上)的表面积为_________.15.若ABC △的三个内角A ,B ,C 的对应边a ,b ,c 满足2a b c =+,则角A 的取值范围为____________.16.设实数x ,y 满足22430x y x +-+=,则222x y y +-的最大值为 .高三数学双基强化训练(三)一、 选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有 一项是符合题目要求的.1.已知集合{}{}220,0,1,2A x x x B =-=…,则A B =I ( ).A.{}0B.{}0,1C.{}0,2D.{}0,1,2 2.下列函数中,定义域是R 且为增函数的是( ).A.e xy -= B.3y x = C.ln y x = D.y x = 3.已知向量()2,4=a ,()1,1=-b ,则2-=a b ( ). A.()5,7 B.()5,9 C.()3,7 D.()3,94.如图所示的程序框图表示求算式“235917⨯⨯⨯⨯”之值,则判断框内不能填入( ).A. 17k …B. 23k …C. 28k …D. 33k …5.设{}n a 是公比为q 的等比数列,则“01q <<”是“{}n a ”为递减数列的( ). A.充分且不必要条件 B.必要且不充分条件 C.充分必要条件 D.既不充分也不必要条件6.已知函数()26log f x x x=-,在下列区间中,包含()f x 零点的区间是( ). A.()0,1 B.()1,2 C.()2,4 D.()4,+∞7.已知圆()()22:341C x y -+-=和两点(),0A m -,()(),00B m m >,若圆C 上存在点P ,使得90APB ∠=o ,则m 的最大值为( ).A.7B.6C. 5D.48.某堆雪在融化过程中,其体积V (单位:3m )与融化时间t (单位:h )近似满足函数关系:()311010V t H t ⎛⎫=- ⎪⎝⎭(H 为常数),其图像如图所示.记此堆雪从融化开始到结束的平均融化速度为()3m /h v .那么瞬时融化速度等于()3m /h v 的时刻是图中的( ). A. 1t B. 2t C. 3t D. 4tS=1,k=2开始结束S=S×kk=2k-1输出S二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中的横线上. 9.复数12i2i-+的虚部为__________. 10.设双曲线C的两个焦点为(),),一个顶点是()1,0,则C 的方程为_________.11.某三棱锥的三视图如图所示,则该三棱锥的最长棱的棱长为 .12.某市电信宽带私人用户月收费标准如下表:假定每月初可以和电信部门约定上网方案.若某用户每月上网时间为66小时,应选择__________方案最合算.侧(左)视图正(主)视图13.若x ,y 满足11010y x y x y ⎧⎪--⎨⎪+-⎩………,则z y =+的最小值为 .14.如图所示,在棱长为2的正方体1111ABCD A B C D -中,E 为BC 的中点,点P 在线段1D E 上,点P 到直线1CC 的距离的最小值为 .高三数学双基强化训练(四)二、 选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有 一项是符合题目要求的.1.集合{}|ln ,1A y y x x =∈=>R ,{}2,1,1,3B =--则下列结论正确的是( ). A . {}2,1A B =--I B . ()(),0A B =-∞R U ð C . [0,)A B =+∞UD . (){}2,1A B =--R I ð2.下列四个函数中,在区间]1,1[-上单调递增的函数是( ). A .2x y = B .x y 2=C .x y 2log =D .x y 2sin =3.若向量||a=,||b 2=,(),a b a -⊥则a ,b 的夹角是( ).A .5π12 B .π3 C .π6 D .π44.已知变量,x y 满足2025020x y x y y --⎧⎪+-⎨⎪-⎩………,则31x y u x +=+的取值范围是( ).A 1A .514,25⎡⎤⎢⎥⎣⎦ B .11,25⎡⎤--⎢⎥⎣⎦ C .15,22⎡⎤-⎢⎥⎣⎦ D .514,25⎡⎤-⎢⎥⎣⎦5.函数()2452ln =-+-f x x x x 的零点个数为( ). A .3 B .2 C .1 D .06.如图所示,在执行程序框图所示的算法时, 若输入3a ,2a ,1a ,0a 的值依次是1,3-,3,1-,则输出v 的值为( ).A .2-B .2C .8-D .87.已知奇函数(),0,(),0>⎧=⎨<⎩f x x y g x x 如果()=x f x a (0>a 且1)≠a 对应的图像如图所示,那么()=g x ( ).A.12-⎛⎫ ⎪⎝⎭xB. 12⎛⎫- ⎪⎝⎭xC. 2-xD.2-x 8.已知抛物线C :的焦点为F ,过点F 的直线l 与抛物线C 在第一、四象限分别交于A ,B 两点,||3||AF BF =,则直线倾斜角为( ). A .15oB . 30oC . 45oD.60o二、填空题(本大题共6小题,每小题5分,共30分) 9.已知复数满足(i 1)2-=z ,则z 为________.10.已知函数()()2sin ω=f x x (0>ω)的最小正周期为π,则=ω ,在()0,π内 满足0)(0=x f 的0x = .11.设数列{}n a 是由正数组成的等比数列,n S 为其前n 项和,已知151a a =,37S =,则)0(22>=p px y l z5S = .12.在边长为1的正方形ABCD 中,,E F 分别为BC 和DC 的中点,则DE BF ⋅=u u u v u u u v________.13.已知函数()3221(1)3f x x a x b x =--+,其中a ,b 为常数,任取[]0,4a ∈,[]0,3b ∈函数()f x 在R 上是增函数的概率为 .14.长方体1111D C B A ABCD -的底面是边长为a 的正方形,若在侧棱1AA 上至少存在一点E ,使得︒=∠901EB C ,则侧棱的长的最小值为 .高三数学双基强化训练(五)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知集合{}252140A x x x =-+-<,{}36B x x =∈-<<Z ,则()U A B I ð的元素的个数为( ).A. 3B. 4C. 5D. 6(2)若一个复数的实部与虚部互为相反数,则称此复数为“理想复数”.已知()i ,,i 12iaz b a b =+∈-R 为虚数单位为“理想复数”,则( ). A. 350a b += B. 350a b -= C. 50a b += D. 50a b -=(3)某学校有教师132人,职工33人,学生1485人.为了解食堂情况,拟采用分层抽样的方法从以上人员中抽取50人进行抽查,则在学生中应抽取人数为( ). A. 36人 B.45人 C.32人 D.48人(4)在数列{}n a 中,12a =-,12nn n a a +=-,则2017a 的值为 ( ).A. 20182- B. 20182C. 20172- D. 20172(5)设e 是自然对数的底,0a >且1a ≠,0b >且1b ≠,则“log 2log e a b >”是“01a b <<<”的( ).A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件(6)如图所示,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的1AA体积为( ).A.23B. 4C. 8D. (7)要得到函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图像,只需将函数sin 2y x =的图像( ). A. 向左平移6π个单位 B. 向右平移个3π单位 C. 向左平移3π个单位 D. 向右平移6π个单位(8)在如图所示的程序图中,若函数()1220log 0x x f x x x ⎧⎪=⎨>⎪⎩,,…,则输出的果是( ).A. 3-B.161 C. 41D. 4(9)设()338xf x x =+-,用二分法求方程3380xx +-=在()1,2x ∈内近似解的过程中,()10f <,()1.50f >,()1.250f <,则方程的根落在区间( ).A. ()1,1.25B. ()1.25,1.5C. ()1.5,2D. 不能确定(10)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC -为鳖臑, PA ⊥平面ABC , 2PA AB ==,4AC =,三棱锥P ABC -的四个顶点都在球O 的球面上,则球O 的表 面积为( ).A. 8πB. 12πC. 20πD. 24π(11)已知双曲线()22221024x y b b b -=<<-与x 轴交于,A B 两点,点()0,C b ,则ABC ∆面积的最大值为( ).(A )1 (B )2 (C )4 (D )8(12)已知函数()()2ln 1f x a x x =+-在区间()0,1内任取两个实数p ,q ,且p q ≠,不等式()()112f p f q p q+-+>-恒成立,则实数a 的取值范围为( ).A .(]12,30B .(],18-∞C .[)18,+∞D .(]2,18- (13)设向量()2,2=a ,b 与a 的夹角为34π且2⋅=-a b ,则b 的坐标为__________. (14)已知实数x ,y 满足条件30302x y x y y +-⎧⎪--⎨⎪⎩………,则y x 的取值范围是__________.(15)在平面直角坐标系xOy 中,过点()1,0M 的直线l 与圆225x y +=交于A ,B 两点,其中A点在第一象限,且2BM MA =u u u u r u u u r,则直线l 的方程为______________.(16)已知数列{}n a 是各项均不为零的等差数列,n S 为其前n 项和,且()2*21n n S a n -=∈N ,若不CBAP等式1122318111log n n n a a a a a a λ++++L …对任意*n ∈N 恒成立,则实数λ的最大值是 .高三数学双基强化训练(一)参考答案一、选择题二、填空题9. 1- 10. ()1,1-或()3,1- 11.221520x y -= 12. 3π ,126π+ 13. 2x =或34100x y +-=,33,4⎛⎤-- ⎥⎝⎦解析部分1. 解析 M N ⊆时,{}1,2M =或{}2,3,故“3m =”是“M N ⊆”的充分而不必要条件.故选A.2. 解析因为()()()()3i 1i 3i 12i 1i 1i 1i +++==+--+,所以1a =,2b =,所以3a b +=.故选C. 3. 解析 根据否命题是对原命题的条件和结论同时否定,以及特称命题的否定是全称命题可知选项D 正确.故选D.4. 解析 令()2log 2f x x x =+-,则()21log 11210f =+-=-<,()2221.5log 1.5 1.52log 1.50.5log 0.50f =+-=->=,所以方程2log 2x x +=的解在区间()1,1.5内.故选B.5. 解析 设等差数列{}n a 的公差为d ,则由259112a a a =-⎧⎨+=-⎩得11112122a d a d +=-⎧⎨+=-⎩,所以113a =-,2d =,所以{}n a 的前n 项和()2214749n S n n n =-=--,所以7n =时,n S 最小.故选C.6. 解析 函数()1f x kx =-的图像恒过()0,1-点,当k 在区间[]2,2-内变化时,()f x 经过的区域如图中的阴影部分所示(包括边界).当()f x 经过点()1,0时,1k =.当21k-剟时,满足对[]0,1x ∀∈,()0f x …,所以根据几何概型求概率知所求概率34P =.故选D.7. 解析 不等式组对应的可行域如图所示.由向量数量积的几何意义知当M 点坐标为()0,2时,OA OM ⋅u u u r u u u u r 取得最大值2,当M 点坐标为()1,1时,OA OM ⋅u u u r u u u u r 取得最小值1-,所以OA OM ⋅u u u r u u u u r的取值范围是[]1,2-.故选D.8. 解析 对应①,当12CQ =时,Q 为1CC 的中点.又P 为BC 的中点,所以1//PQ BC .又11//BC AD ,所以1//PQ AD ,所以截面S 过1D 点.如图a 所示.所以当102CQ <<时,截面S 与正方体表面的交点在棱1DD 上,截面S 为四边形,如图b 所示.故①正确.y=对于②,当1CQ =时,截面S 即为平面1APC E ,其中E 为11A D 中点,如图c 所示,它在底面上投影的面积34APCF S S =<Y ,故②错误. 对于③,当1CQ =时,易知1AC ⊥平面1A BD ,而1AC ⊂截面S ,所以截面S ⊥平面1A BD ,如图d 所示,故③正确. 对于④,当34CQ =时,如图e 所示,截面S 即为五边形1APQR E ,延长AP ,DC ,1R Q ,易知三条延长线交于一点T ,且1CT =,又11113C R C Q CT CQ ==,所以1113C R =.故④正确. 故选C.图aQD 1C 1B 1A 1DCBAP图bPABCDA 1B 1C 1D 1Q图cFE PABCD A 1B 1C 1Q ()D 1图dD 1C 1Q ()B 1A 1DCBAPE E R 1D 1C 1B 1A 1DCQ9. 解析把sin cos αα-=22sin 2sin cos cos 2αααα-+=,所以()2222sin 2sin cos cos 2sin cos αααααα-+=+,整理得22sin 2sin cos cos 0αααα++=①因为()0,πα∈,所以cos 0α≠,所以①两边同时除以cos α可得2tan 2tan 10αα++=,即()2tan 10α+=,所以tan 1α=-.10. 解析 由题可得()1,0+=a b 或()1,0-,又()2,1=-b ,所以()1,1=-a 或()3,1-. 11. 解析 直线l 的斜率为12,所以双曲线的一条渐近线的斜率为2-,所以2ba= ①.由双曲线的焦点在直线l 上,且焦点纵坐标为0,得5c = ②.由①②得25a =,220b =,所以双曲线方程为221520x y -=. 12. 解析 几何体的直观图如图所示.结合三视图中数据知该几何体是底面半径是3,高是4的圆锥的14,所以体积()()2311π343πcm 43V =⨯⨯⨯⨯=. 表面积()()21112π33422π35126πcm 2424S ⨯⎛⎫=⨯⨯⨯+⨯⨯+⨯⨯=+⎪⎝⎭.13. 解析 设切线方程为()12y k x -=-,即210kx y k --+=,所以2=,2244144k k k -+=+,所以34k =-,所以切线方程为34100x y +-=.经检验,当斜率不存在时,即直线2x =也是圆的切线,所以过M 点的圆的切线方程为34100x y +-=或2x =.因为AB =,圆的半径2r =,所以圆心()0,0到直线40ax y -+=的距离1d ===,所以a =.14. 解析 设0x 是函数()3f x x mx =+的均值点,所以有()()()()011111f f f x m --==+--,又()3000f x x mx =+,所以有30010x mx m +--=,此方程在()01,1x ∈-时有解.将方程参变量分离得2001m x x =---,变形得201324m x ⎛⎫=-+- ⎪⎝⎭,所以在()01,1x ∈-范围内,当012x =-时,max 34m =-,当01x =时,min 3m =-,又01x ≠,所以33,4m ⎛⎤∈-- ⎥⎝⎦.高三数学双基强化训练(二)答案部分一、选择题二、填空题13. 9 14.3π 15. 0,3π⎛⎤ ⎥⎝⎦16. 5+解析部分1.解析 ()i 12i 2i z =-+=--,所以z 的虚部为1-.故选B.2.解析 p 的否定形式为“0x ∃∈R ,00sin x x …”.故选A.3.解析 由⊥a b ,则()()=1,2,220x x x ⋅⋅+-=-=a b ,得2x =.故选C.4.解析 由{}n a 为等比数列,则1105647a a a a a a ==,得1109a a =,则()()53132310312103110log log log log log 10a a a a a a a a +++===L L .故选C.5.解析 由10n =,所以12i =时退出循环, 则2221111110++++=21411011335911S =+++=---⨯⨯⨯L L 11111151233591111⎛⎫-+-+-=⎪⎝⎭L .故选A. 6.解析 由()222f x x ax =++有两个不同零点,则2480a ->,得a >a <a 可以为2,3,4,5,6.而总的基本事件{}1,2,3,4,5,6Ω=,则56P =.故选D. 7.解析 将函数cos 23y x π⎛⎫=+⎪⎝⎭的图像向左平移6π个单位后的图像的函数为2cos 2cos 2633y x x ⎛ππ⎫π⎛⎫⎛⎫=++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则此函数非奇非偶,最小正周期为π,关于直线6x π=对称,不关于点,06π⎛⎫-⎪⎝⎭对称.故选C. 8.解析 易知点()2,1A --,又点A 在直线10mx ny ++=上,所以210m n --+=,即21m n +=,则()11112233n m m n m n m n m n ⎛⎫+=++=+++ ⎪⎝⎭…,当且仅当n =时等号成立.故选A. 9.解析 由三视图得直观如图所示为四棱锥P ABCD -,易知最长得侧棱为PC ,则222243229PC =++=,PC =故选B.10.解析 作出可行域如图所示,易知()4,5A ,()4,3B ,()2,3C ,所以12222ABC S =⨯⨯=△, 故选B.2PDCB A 32211.解析 ()ln 1f x ax x =-+有三个不同的零点,即1y ax =+与ln y x =的函数图像由三个交点,做出图像如图所示,易知1y x =-+与ln y x =在1x =的左侧图像相切,要使两函数由三个交点,则0a >,1y ax =+与ln y x =(01x <<)有一个交点,1y ax =+与ln y x =(1x >)有两个交点.当1y ax =+与ln y x =(1x >)相切时,设切点为()00,ln x x ,则有切线为()0001ln y x x x x -=-,将()0,1代入得20e x =,2e a -=,从而20e a -<<.故选D.12.解析 设公共点的横坐标为0x ,由题意得()()()()0000f x g x f x g x =⎧⎪⎨''=⎪⎩,即22000200123ln 232x ax a x b a x a x ⎧+=+⎪⎪⎨⎪+=⎪⎩① ②, 由②得0x a =,代入①式得2253ln 2a b a a =-+.令()2253ln 2a h a a a =-+,()()213ln h a a a '=-,当130e a <<时,()0h a '>,()h a 单调递增;当13e a >时,()0h a '<,()h a 单调递减,所以()1233max 3e e 2h a h ⎛⎫== ⎪⎝⎭.故选B.13.解析 由题意知()20OA AB OA OB OA OA OB OA ⋅=⋅-=⋅-=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ,得29OA OB OA ⋅==u u u r u u u r u u u r .故填9.14.解析 如图所示,将此四面体放入棱长为1得正方体中,则此四面体的外接球,即为正方体的外接球.由()222221113R =++=,则243S R =π=π.故填3π.15.解析 由余弦定理得22222213312cos 22282b c b c b c a b c A bc bc c b +⎛⎫+- ⎪+-⎛⎫⎝⎭===+- ⎪⎝⎭…,当且仅当b c =时等号成立,则03A π<….故填0,3π⎛⎤ ⎥⎝⎦. 16.解析 曲线22430x y x +-+=,即为()2221x y -+=,则此曲线表示圆心为()2,0C ,半径为1r =的圆,()2222211x y y x y +-=+--,其几何意义为圆C 上的点与点()0,1A 的距离的平方再减1.所以所求式的最大值为())221115AC r +-=-=+.故填5+.高三数学双基强化训练(三)参考答案与解析一、选择题二、填空题9. 1- 10. 221x y -= 11. 乙 13. 1解析部分1. 解析 由已知{}02A x x x=或剠,又{}0,1,2B =,所以{}0,2A B =I .故选C.2. 解析 e xy -=在R 上单调递减;ln y x =定义域为()0,+∞;y x =在(),0-∞上单调递减.故选B.PCBA 13. 解析 ()()()24,81,15,7-=--=a b .故选A.4. 解析 由程序框图的要求可模拟算法如下表:综合选项知,若33k …时,第6步还需进行123591733S =⨯⨯⨯⨯⨯⨯的运算,故判断框内不能填33k ….故选D.5. 解析 若01q <<,如12a =-,12q =,则21a =-,312a =-,414a =-,则{}n a 为递增数列,故01q <<不是{}n a 为递减数列的充分条件;若{}n a 为递减数列,如1-,2-,4-,8-,则11a =-,()20,1q =∉.故01q <<不是{}n a 为递减数列的必要条件.综上,“01q <<”是“{}n a 为递减数列”的既不充分也不必要条件.故选D. 6. 解析 解法一(图像法):由题意,函数16y x=与22log y x =的图像交点P 的横坐标,即为函数()f x 的零点.如图所示,函数16y x =在()0,+∞上单调递减,且132y x ==, 1342y x ==,函数22log y x =在()0,+∞上单调递增,且2132y x =<=, 223log 4242y x ==>=.故()2,4P x ∈.故选C.解法二:因为函数()f x 在()0,+∞上单调递减,且()220f =>,()1402f =-<,所以函数()f x 在区间()2,4上有唯一零点. 故选C. 7. 解析 设点P 的坐标为(),x y ,则P 点在以AB 为直径的圆上,即P 点的轨迹方程为()2220x y m y +=≠.如图所示,若圆()()22:341C x y -+-=上存在点P ,使得90APB ∠=o ,则圆222x y m +=与圆C 一定有公共点.此时m 的取值范围为[]4,6.故m 的最大值为6.故选B.8. 分析 本题重点考查了导数的物理意义与几何意义.解析 如图所示,曲线()y v t =与y 轴的交点为A ,与x 轴交点为B .依题意,若此堆雪从融化开始到结束的平均融化速度v 等于瞬时融化速度,则表示曲线()y v t =上的某一点处的导数值等于AB 所在直线的斜率.据图知()3AB v t k '=.故选C.9. 解析 因为()()()()12i 2i 12i 225ii 2i 2i 2i 41-----===-++-+,所以复数12i 2i -+的虚部为1-.10. 解析由题意知,c =1a =,则1b ==.又焦点在x 轴上,故双曲线C的方程为221x y -=.11. 解析 由三视图可知,原三棱锥如图所示,且PA ⊥平面ABC ,90ABC ∠=o ,2PA AC ==,所以PC =AB BC ==PB =故最长的棱长为12. 解析 由题意知,若选择甲方案.则用户上网费用固定为70元;若选择乙方案,则超时费用为0.0560618⨯⨯=元,该用户上网费用合计68元;若选择丙方案,则超时费用为0.056036108⨯⨯=元,该用户上网费用合计138元. 综上,该用户应选择乙方案.13. 解析 由题意可知,不等式组11010y x y x y ⎧⎪--⎨⎪+-⎩………所对应的平面区域为如图所示的阴影部分.且,()0,1A ,()1,0B ,()2,1C .0y z +-=过点()0,1A 时,z 有最小值为1.14. 分析 点P 到直线1CC 的距离的最小值为异面直线1ED 与1CC 的公垂线.解析 连接DE ,过点P 作DE 的垂线于点P ',连接CP ',因为平面1DD E ⊥平面ABCD ,且平面1D DE I 平面ABCD DE =,又PP DE '⊥,PP '⊂平面1DD E ,所以PP '⊥平面ABCD ,故PP CP ''⊥,又1CP CC '⊥,因此点P 到1CC 的距离为CP '.若点P 到直线1CC 的距离最小,则CP DE '⊥,此时5CP '=.因此点P 到直线1CC的距离的最小值为5.高三数学双基强化训练(四)参考答案一、选择题二、填空题10.π2 11. 31412. 1- 13.71214. 2a 解析部分1. 解析 由题意可得{}0A y y =>,则{}0A y y =R …ð.所以(){}2,1A B=--R I ð.故选D.2. 解析 因为函数2xy =在定义域R 上单调递增,所以在区间[]1,1-上单调递增.故选B.3. 解析 由()-⊥a b a ,可得()20--=g g a b a =a b a ,即2cos ,0-=g a b a b a ,解得cos ,2==b a .又[],0,π∈b a ,所以a ,b 的夹角为π4.故选D. 4. 解析 x ,y 对应的可行域如图阴影部分所示.P'PED 1DB 1A 1C 1AB()313333111x y x y y u x x x ++-+-===++++,31y x -+可看作点()1,3P -与可行域内的点的连线的斜率,由图可得31PB PA y k k x -+剟,12PB k =-,15PA k =-,所以51425u剟.故选A.5. 解析 令()245g x x x =-+,()2ln h x x =.则()f x 的零点个数即为()g x 与()h x 的交点个数.作出草图,如图所示.由图可知,交点个数为2个.故选B.6. 解析 由程序框图可知,第一次循环为:31a =,0311v =⨯+=,312i =-=;第二次循环:23a =-,()1330v =⨯+-=,211i =-=;第三次循环为:13a =,0333v =⨯+=,110i =-=;第四次循环为:01a =-,()3318v =⨯+-=,011i =-=-.此时循环结束.输出v 的值为8.故选D.7. 解析 由图可知()112f =,所以12a =,即()12xf x ⎛⎫= ⎪⎝⎭.又函数y 为奇函数,所以()()f x g x -=-,即()()g x f x =--,亦即()2x g x =-. 故选D.8. 解析 由题意作图,如图所示.由抛物线的第二定义得,AD AF =,BF BN =.由3AFBF=,x得3AD BN=.令BF k =,可得2AE k =,4AB k =,则30EBA ∠=o ,所以直线l 的倾斜角为60o.故选D.9. 解析 由题意可得()()()2i 12i 1i 1i 1i 1z +===----+,所以z ==10. 解析 由2πT ω=,又πT =,所以2ω=.则()2sin2f x x =.由()00f x =,得02sin 20x =,即()0π2k x k =∈Z .又()00,πx ∈,所以0π2x =. 11. 解析 设此数列的公比为()0q q >,由已知151a a =,得231a =所以31a =,由37S =,知33327a a a q q ++=,即2610q q --=,解得12q =,进而14a =, 所以551412311412S ⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦==-. 12. 解析 以B 点为原点,以BC 边所在直线为x 轴,以BA 边所在直线为y 轴建立平面直角坐标系,如图所示.因为正方形ABCD 的边长为1,可得()0,0B ,()1,0C ,()0,1A ,()1,1D ,1,02E ⎛⎫ ⎪⎝⎭,11,2F ⎛⎫ ⎪⎝⎭.则1111,11,12222DE BF ⎛⎫⎛⎫=--=--=- ⎪ ⎪⎝⎭⎝⎭u u u r u u u r g g . 13.解析 ()()2221f x x a x b '=--+,若函数()f x 在R 上是增函数,则对于任意x ∈R ,()0f x '…恒成立. 所以()224140a b ∆=--…,即()()110a b a b +---…,设“在()f x 在R 上是增函数”为事件A ,则事件A 对应的区域为()()(){},|110a b a b a b +---…,全部试验结果构成的区域{}(,)|04,03a b abΩ=剟剟,所以()113411337223412A S P A S Ω⨯-⨯⨯-⨯⨯===⨯. 故函数在R 上是增函数的概率为712. 14.解析 如图所示,在长方体1111ABCD A B C D -中,若190C EB ∠=o,则1C E EB ⊥,且11B C ⊥平面11ABB A ,故11B C BE ⊥,又1111C E B C C =I ,1C E ,11B C ⊂平面11B C E ,因此BE ⊥平面11B C E ,得1BE B E ⊥.在矩形11ABB A 中,由1BE B E ⊥,得11A B E AEB △∽△,即111A B AEA E AB=,设1A E =ka ,则a AE ka a =,得aAE k=,0k >.因此112a AA A E AE ka a k =+=+=…,当且仅当1k =时取“=”.故1AA 长的最小值为2a.O (高三数学双基强化训练(五)答案部分一、选择题二、填空题13. ()1,0-或()0,1- 14.[]0,2 15. 1y x =- 16. 12解析部分(1)分析 A 集合是一元二次不等式,先求解,要注意二次项系数为负数,然后求出集合A 的补集,对于集合B ,注意x ∈Z .然后求交集. 解析 因为{}{}221421504215054U A x x x A x x x x x ⎧⎫=-+>⇒=-+=⎨⎬⎩⎭剎剟ð,{}2,1,0,1,2,3,4,5B =--,故{}1,2,3,4,5A B =I .故选C.(2)分析 先进行复数的除法运算,将复数化简,再利用实部和虚部互为相反数,可求得b 的值. 解析 因为()12i 2i i 555a a a z b b +⎛⎫=+=++ ⎪⎝⎭,所以由题设中定义的心概念可得2055a a b ⎛⎫++=⎪⎝⎭,即350a b +=.故选A.(3)分析 本题是一个分层抽样方法,根据总体数和要抽取的样本数,得到每个个体被抽到的概率,利用这个概率乘以学生人数,得到学生要抽取的人数,属于基础题.解析 由题意知本题是一个分层抽样方法,根据学校有教师132人,职工33人,学生1485人,采用分层抽样的方法从以上人员中抽取50人进行抽查,则每个个体被抽到的概率是D 1B 1C 1A 1ED C BA50113233148533=++又因为学生有1485人,所以在学生中应抽取114854533⨯=,故答案为:45人.故选B.(4)分析 根据题意知12n n n a a +-=-,又12a =-,利用累加法即可求得2017a 的值.解析 因为12n n n a a +=-,所以212a a =-,2322a a =-,L ,112n n n a a --=-,以上等式相加得2n n a =-,所以201720172a =-.故选C.(5)分析 根据对数函数的性质结合充分必要条件的定义可以直接进行判断.解析 因为1a b <<<0,所以log 2log 2log e a b b >>,而反之不成立,所以必要不充分条件.故选B.(6)分析 根据题网格中的三视图可得该几何体是一个以主视图为底面的四棱柱,代入棱柱体积的公式可以得到答案.解析 由已知可得该几何体是一个以主视图为底面的四棱柱,底面面积224S =⨯=,高2h =,故体积8V Sh ==.故选C.(7)分析 图像的变换问题主要是抓住其中的一个点进行观测,本题要注意系数2 解析 因函数sin 26y x π⎛⎫=+ ⎪⎝⎭,故只需将函数sin 2y x =的图像向左平移6π个单位. 故选A.(8)分析 根据算法的程序框图,准确选择函数关系式求值. 解析 当4a =-时,()4142016f --==>,1211log 41616a f ⎛⎫=== ⎪⎝⎭,进入循环,()124log 420b f ===-<,()21224a f -=-==,输出4a 1= .故选C. (9)分析 首先要判断函数的单调性,在理解方程根和函数零点的关系.解析 方程3380xx +-=的解等价于()338xf x x =+-的零点.由于()f x 在R 上连续且单调递增,()()1.25 1.50f f ⋅<所以()f x 在()1.25,1.5内有零点且唯一,所以方程3380xx +-=的根落在区间()1.25,1.5.故选B .(10)分析 由题意可得PC 为球O 的直径,先求出PC ,即可知球O 的半径,然后可求出球的表面积.解析 由题可知,底面ABC △为直角三角形,且2ABC =π∠,则BC =,则球O 的直径2R ==,所以R =,则球O 的表面积2420S R =π=π.故选C.(11)分析 由题意双曲线与x 轴的两交点A ,B 的坐标分别为(),由面积公式结合均值不等式来求解解析由题意A ,B 两点为(),因此ABC S ==△22(4)22b b +-=…,当且仅当224b b =-,即b =号成立.故最大值为2.故选B .(12)分析 由()()2ln 1f x a x x =+-,考虑到()()()21ln 111f x a x x +=++-+⎡⎤⎣⎦,再求导数,将恒成立问题进行转化为二次不等式,结合函数的单调性求解.解析 因为()()2ln 1f x a x x =+-,所以()()()21ln 111f x a x x +=++-+⎡⎤⎣⎦,所以()()1212af x x x '+=-++,因为(),0,1p q ∈,且p q ≠,所以不等式()()112f p f q p q +-+>-恒成立()()()()11211f p f q p q +-+⇔>+-+恒成立()12f x '⇔+>恒成立,即()()212012a x x x -+><<+恒成立,整理得:()()22201a x x >+<<恒成立,因为函数()222y x =+的对称轴方程为2x =-,所以该函数在区间()0,1上单调递增,所以()22218x +<,所以18a ….故选C . (13)分析 利用向量的数量积公式求出两向量的夹角的余弦值,再利用向量模公式列出方程组,解方程组即可得解.解析 由题意得,设向量(),x y =b ,因为2⋅=-a b ,则222x y +=-,即 10x y ++=-,由向量a ,b 所成的角为34π,则cos 42⋅3π=⇒=⋅a b a b ,得221x y +=, 联立方程组,解得1x =-,0y =或0x =,1y =-,所以向量b 的坐标为()1,0=-b 或()0,1=-b .(14)分析 根据不等式组作出可行域,理解y x的几何意义是过原点的直线的斜率,然后进行求解. 解析 如图所示,可行域为三角形区域内部以及边界,目标函数y x 表示区域内任意一点与原点连线的斜率,故临界位置为过()3,0点时,斜率为0;过()1,2点时,斜率为2,故填[]0,2.(15)分析 根据直线的特殊性进行设直线为1x my =+,再将直线与方程联立求解.解析 由题意,设直线1x my =+与圆225x y +=联立,可得()221240m y my ++-=,设()11,A x y ,()22,B x y ,则122y y =-,12221m y y m +=-+,12241y y m ⋅=-+,联立解得1m =,则直线l 的方程为1y x =-.故答案为1y x =-. (16)分析 由数列为等差数列,可设出公差d ,再由()2*21n n S a n -=∈N ,可以得出第1,2项,则可求出通项公式,又用裂项法得()()111111212122121n n a a n n n n +⎛⎫==- ⎪-+-+⎝⎭,求和后结合1122318111log n n n a a a a a a λ++++L …,进行转化可得则实数λ的最大值. 解析 因为数列{}n a 是各项均不为零的等差数列,设公差为d ,又()2*21n n S a n -=∈N ,所以1n =时,211a a =,解得11a =.2n =时,232S a =,即()2331d d +=+,解得2d =或1d =-(舍去).所以()12121n a n n =+-=-.所以()()111111212122121n n a a n n n n +⎛⎫==- ⎪-+-+⎝⎭.所以12231111111111123352121n n a a a a a a n n +⎡⎤⎛⎫⎛⎫⎛⎫+++=-+-++-= ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎣⎦L L 11122121n n n ⎛⎫-= ⎪++⎝⎭.不等式1122318111log n n n a a a a a a λ++++L …,即18log 21n n n λ+…,化为:181log 21n λ+….不等式1122318111log n n n a a a a a a λ++++L …对任意*n ∈N 恒成立,所以181log 3λ…,所以311082λ⎛⎫<= ⎪⎝⎭….则实数λ的最大值是12.故答案为:12.。
高三数学双基自测参考答案

高三数学双基自测
WYS
2017.7
所以 q 为真.故②③正确.
[答案]②③
20.B [解析](∁UA)∩B={1,3,6,7}∩{1,3,5,7}={1,3,7},选 B. 21.A [解析]A={x∈Z|-1<x≤2}={0,1,2},B={x|x≥45},所以 A∩B={1,2}
22.B [解析]A={x|-1<x<5},B={x|-2<x<2},
解得:m>-3+2 2或 m<-3-2 2.
[答案] (-∞,-3-2 2)∪(-3+2 2,+∞) 11.B [解析]根据命题“若 p,则 q”的逆否命题是“若¬q,则¬p”,故选 B. 12.B [解析]因为 x2-2x-3>0,所以该不等式的解集为{x|x<-1 或 x>3}, 所以 x>4⇒x2-2x-3>0. 但 x2-2x-3>0⇒/ x>4, 所以“x>4”是“x2-2x-3>0”的充分而不必要条件. 13.C [解析]命题 p 为:若一个函数的图象关于原点对称,则它是奇函数,故选 C. 14.[答案]“若一个三角形的两条边相等,则这两条边所对的角也相等”
10. [解析]可判断函数 f(x)=x-2 1在[2,6]上递减,所以 f(x)max=f(2)=2,f(x)min=f(6)=25.
[答案] 2
2 5
2 / 38
高三数学双基自测
WYS
11.[答案]D
12.B [解析]因为 f(x)=ax2+bx 是定义在[a-1,2a]上的偶函数,
15. [解析]当 x2=3x+4 时,x=-1 或 4,当 x=-1 时,x= 3x+4不成立,即 p⇒/ q.
高三数学双基强化训练
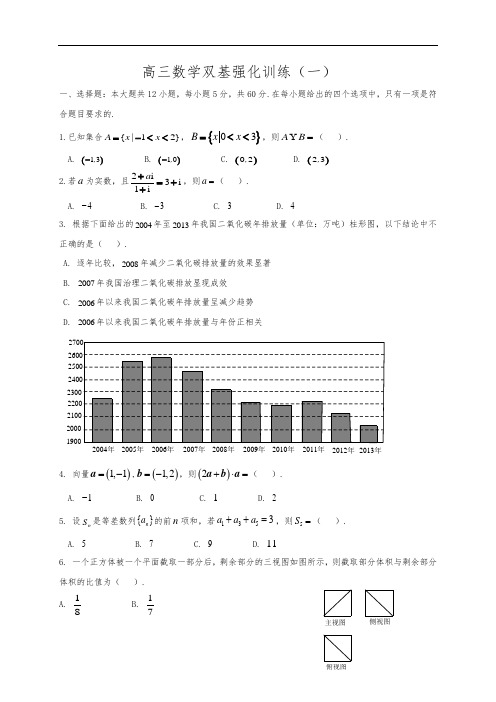
高三数学双基强化训练(一)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|12}A x x =-<<,{}03B x x =<<,则=B A Y ( ). A. ()13,- B. ()10,- C. ()02, D. ()23, 2.若a 为实数,且2i3i 1ia +=++,则a =( ). A. 4- B. 3- C. 3 D. 43. 根据下面给出的2004年至2013年我国二氧化碳年排放量(单位:万吨)柱形图,以下结论中不正确的是( ).A. 逐年比较,2008年减少二氧化碳排放量的效果显著B. 2007年我国治理二氧化碳排放显现成效C. 2006年以来我国二氧化碳年排放量呈减少趋势D. 2006年以来我国二氧化碳年排放量与年份正相关4. 向量()1,1=-a ,()1,2=-b ,则()2+⋅=a b a ( ). A. 1- B. 0 C. 1 D. 25. 设n S 是等差数列}{n a 的前n 项和,若1353a a a ++=,则5S =( ).A. 5B. 7C. 9D. 116. 一个正方体被一个平面截取一部分后,剩余部分的三视图如图所示,则截取部分体积与剩余部分体积的比值为( ). A.81 B. 712010年2012年2009年2013年2004年2006年2007年2008年2011年2005年19002000俯视图侧视图主视图C.61 D. 51 7. 已知三点()1,0A,(B,(C ,则ABC △外接圆的圆心到原点的距离为( ).A. 35B. 321C. 352D. 348. 如图所示,程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的a =( ). A. 0 B. 2 C. 4 D. 149. 已知等比数列{}n a 满足411=a,()35441a a a =-,则=2a ( ). A. 2 B. 1 C. 21 D. 8110.已知A ,B 是球O 的球面上两点,90AOB ∠=o ,C 为该球面上的动点.若三棱锥O ABC-体积的最大值为36,则球O 的表面积为( ).A. 36πB. 64πC. 144πD. 256π 11.设()ln f x x =,0a b <<,若p f =,2a b q f +⎛⎫= ⎪⎝⎭,()()12r f a f b =+⎡⎤⎣⎦,则下列关系式中正确的是( ). A. q r p =<B. q r p =>C. p r q =<D. p r q =>12. 设函数()()21ln 11f x x x =+-+,则使得()()21f x f x >-成立的x 的取值范围是( ).A. 113,⎛⎫ ⎪⎝⎭B. ()113,,⎛⎫-∞+∞ ⎪⎝⎭UC. 1133,⎛⎫- ⎪⎝⎭D. 1133,,⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭U二、填空题:本大题共4小题,每小题5分,共20分. 把答案填在题中的的横线上. 13. 已知函数()32f x ax x =-的图像过点()14,-,则a = .14. 若x ,y 满足约束条件50210210x y x y x y +-⎧⎪--⎨⎪-+⎩„…„,则y x z +=2的最大值为 .15.已知双曲线过点(4,且渐近线方程为x y 21±=,则该双曲线的标准方程 为 .16.已知曲线ln y x x =+在点()11,处的切线与曲线()221y ax a x =+++相切,则a = .高三数学双基强化训练(二)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U =R ,集合{}21P x x =„,那么U P =ð( ).A.(),1-∞-B.()1,+∞C.()1,1-D.()(),11,-∞-+∞U 2. “0,0a b厖”是“2a b+”的( ). A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 3. 已知函数()πsin 23f x x ⎛⎫=+ ⎪⎝⎭,为了得到()cos2g x x =的图像,则只要将()f x 的图像( ). A. 向左平移π12个单位长度 B. 向右平移π6个单位长度 C. 向右平移π12个单位长度D. 向左平移π6个单位长度4. 已知A ,B是单位圆上的动点,且AB ,单位圆的圆心是O ,则OA AB ⋅=u u u r u u u r( ).A.C. 32-D.325.一个正三棱柱的侧棱长和底面边长相等,体积为如图所示,左视图是一个矩形,则这个矩形的面积是( ).A .4 B.C .26.若()1e ,1x -∈,ln a x =,ln 12xb ⎛⎫= ⎪⎝⎭,ln 2xc =,则a ,b ,c 的大小关系为( ).A.c b a >>B.b c a >>C.a b c >>D.b a c >>7.设1m >,实数x ,y 满足约束条件1y x y mx x y ⎧⎪⎨⎪+⎩…„„,目标函数5z x y =+的最大值为4,则m 的值为( ).A .5B .4C .3 D. 28.若以曲线()y f x =上任意一点(),M x y 为切点作切线l ,曲线上总存在异于点M 的点(),N x y '',使得以点N 为切点作切线l '满足l l '∥,则称曲线()y f x =具有“可平行性”.已知下列曲线:①3y x x =-;②1y x x=+;③sin y x =;④()22ln y x x =-+,其中具有“可平行性”的曲线是( ).A .①②B .②③C .①②③ D.①③④ 二、填空题:本大题共6小题,每小题5分,共30分. 9.已知向量)=a ,()0,1=-b ,c (),3k =.若2-a b 与c 共线,则k =________.10.已知等差数列{}n a 的前n 项和为n S ,且26S S =,若41a =,则5a = .11.若a ,b ,c 是直角ABC △的三边的边长(c 为斜边),则圆C :224x y +=被直线l :0ax by c ++=所截得的弦长为.12.盒子中有大小相同的3只白球,2只黑球,若从中随机地摸出两只球,则两只球颜色相同的概率是__________.13.若双曲线2213x y m -=的右焦点恰好与抛物线212y x =的焦点重合,则实数m 的值为. 14. 设集合(){}222*,,S x y xy k k =+∈N „,(){}*,34,T x y x y m m =+=∈N .俯视图若满足“S T =∅I ”的k 值恰有4个,则所有符合条件的m 值构成的集合为.高三数学双基强化训练(三)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有 一项是符合题目要求的.1.设a ∈R ,若()2i i a -(i 为虚数单位)为正实数,则a = ( ) . A .2 B .1 C .0 D. 1- 2.已知{}{}{}2,3,4,5,3,4,5,2,4,5U M N ===,则( ).A.{}4M N =IB.M N U =UC.()U N M U =U ð D.()U M N N =I ð3. 下列命题中的假命题...是( ). A .3,0x x ∃∈<R B .“0>a ”是“0>a ”的充分不必要条件[C .,20xx ∀∈>R D .若q p ∧为假命题,则p ,q 均为假命题 4.在等差数列{}n a 中,21232a a +=,则3152a a +的值是( ). A .24 B. 48 C. 96 D .无法确定 5. 某程序框图如图所示,该程序运行后输出i 的值是( ). A. 63 B. 31 C. 27 D. 156.动圆M 经过双曲线2213y x -=左焦点且与直线2x =相切, 则圆心M 的轨迹方程是( ). 图1 A .24y x = B .24y x =- C .28y x = D .28y x =-7. O 是ABC △所在的平面内的一点,且满足()()20OB OC OB OC OA -⋅+-=u u u r u u u r u u u r u u u r u u u r,则ABC △的形状一定为( ).A .正三角形 B.直角三角形 C.等腰三角形 D.斜三角形8. 对,a b ∀∈R ,运算“⊕”,“⊗”定义为:()()a a b a b b a b <⎧⎪⊕=⎨⎪⎩…,()()a ab a b b a b ⎧⎪⊗=⎨<⎪⎩…,则下列各式中不恒成立的是( ). (1)a b a b a b ⊗+⊕=+ (2)a b a b a b ⊗-⊕=- (3)[][]a b a b a b ⊗⋅⊕=⋅ (4)[][]a b a b a b ⊗÷⊕=÷ A .(1),(3)B .(2),(4)C .(1),(2),(3)D .(1),(2),(3),(4)二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中的横线上.9. 某单位有200名职工,现用系统抽样法,从中抽取40名职工作样本,将全体职工随机按1~200编号,并按编号顺序平均分为40组(1~5号,6~10号,…,196~200号).若第5组抽出的号码为22,则第9组抽出的号码应是 . 10.在ABC △中,,,a b c 分别是角,,A B C 所对的边, π3A =,1a c ==,则ABC △的面积 S = ______.11. 已知实数0m ≠,函数()2,12,1x m x f x x m x +<⎧=⎨--⎩…,若()()11f m f m -=+,则m 的值为________. 12. 若向量()cos ,sin αα=a ,()cos sin ββ=,b ,且2+⋅„a b a b ,则()cos αβ-的值是 . 13.在平面直角坐标系xOy 中,直线y x b =+是曲线ln y a x =的切线,则当0a >时,实数b 的最小值是 . 14.已知集合(){},31M x y x yx =--剟,()(){},1,0,1,0N P PA A B =-,则表示M N I 的图形面积等于 .高三数学双基强化训练(四)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集U =R ,集合{}20A x x x =+…,则集合U A =ð( ). A .[]1,0-B .()1,0-C .(][),10,-∞-+∞UD .[]0,12.若复数()()2132i m m m m -+-+是纯虚数(其中i 为虚数单位),则m =( ).A.0或1B.1C.0D.1或23.若实数x ,y 满足约束条件010220x y x y x y -⎧⎪+-⎨⎪-+⎩„……,则2z x y =-的最大值为( ).A. 1- B .2 C .1D .04. 要得到函数sin y x =的图像,只需要将函数πcos 3y x ⎛⎫=-⎪⎝⎭的图像( ). A .向右平移π6个单位 B .向右平移π3个单位 C .向左平移π3个单位 D .向左平移π6个单位5. ”是“()()130x x --<”成立的 ( ). A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分也不必要条件6.若直线y kx =与圆()2221x y -+=的两个交点关于直线20x y b ++=对称,则,k b 的值分别为( ).7.已知12,F F 分别是椭圆的左,右焦点,现以2F 为圆心作一个圆恰好经过椭圆中心并且交椭圆于点,M N ,若过1F 的直线1MF 是圆2F 的切线,则椭圆的离心率为( ) .A .13-B .32-C .22D .238.设函数()f x 的定义域为D ,如果存在正实数k ,对于任意x D ∈,都有x k D +∈,且()()f x k f x +>恒成立,则称函数()f x 为D 上的“k 型增函数”,已知函数()f x 是定义在R 上的奇函数,且当0x >时,()2f x x a a =--,若()f x 为R 上的“2014型增函数”,则实数a 的取值范围是( ).A. 1007a <-B. 1007a <C. 10073a <D. 10073a <-二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中的横线上.9.投掷两颗相同的正方体骰子(骰子质地均匀,且各个面上依次标有点数1,2,3,4,5,6)一次,则两颗骰子向上点数之积等于6的概率为________. 10.在等差数列{}n a 中,912162a a =+,则数列{}n a 的前11项和11S 等于. 11.已知某几何体的三视图如图所示,则该几何体的体积为________.12.函数2ln y x x =+的图像与函数3y x b =-的图像有3个不同的交点,则实数b 的取值范围是. 13.若[)1,x ∈+∞,不等式()22410x x m m -++>恒成立,则实数m 的取值范围是_______. 14.已知函数()f x 是定义在R 上的奇函数,当0x <时,()()e 1x f x x =+,给出下列命题: ①当0x >时,()()e 1x f x x =+;②函数()f x 有2个零点;③()0f x >的解集为()()1,01,-+∞U ;④12,x x ∀∈R ,都有()()122f x f x -<. 其中正确的命题是_______.高三数学双基强化训练(五)一、 选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}2320A x x x =-+=,{}2,1,1,2B =--,则A B =I ( ).A.{}2,1--B.{}1,2-C.{}1,2D.{}2,1,1,2--2. 下列函数中,既是奇函数又在区间()0,+∞上单调递减的是( ). A.22y x =-+B.1y x=C.2xy -=D.ln y x =3. 在复平面内,复数()21+2i 对应的点位于( ).A.第一象限B.第二象限C.第三象限D.第四象限 4. 某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是( ).(锥体体积公式:13V Sh =,其中S 为底面面积,h 为高)A.3B.2D.15. 执行如图所示的程序框图,则输出s 的值为( ). A.10 B.17 C.19 D.366. 设a ,b 是实数,则“a b >”是“a a b b >”的( ). A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件7. 已知无穷数列{}n a 是等差数列,公差为d ,前n 项和为n S ,则( ). A.当首项10,0a d ><时,数列{}n a 是递减数列且n S 有最大值 B.当首项10,0a d <<时,数列{}n a 是递减数列且n S 有最小值 C.当首项10,0a d >>时,数列{}n a 是递增数列且n S 有最大值 D.当首项10,0a d <>时,数列{}n a 是递减数列且n S 有最大值8.如图a 对应于函数()f x ,则在下列给出的四个函数中,图b 对应的函数只能是( ).侧视图俯视图11222211图a 图b A. ()1y f x =+B. ()1y fx =+ C. ()1y f x =-D. ()1y f x =-二、填空题(本大题共6小题,每小题5分,共30分)9. 双曲线2214x y m -=m = ,其渐近线方程为 . 10. 不等式组0,20,30x x y x y ⎧⎪+⎨⎪-+⎩„……所表示平面区域的面积为 .11.设向量)=a ,()2,2=-b ,若()()λλ+⊥-a b a b ,则实数λ= .12. 已知函数()3269f x x x x =-+,则()f x 在闭区间[]1,5-上的最小值为 , 最大值为 . 13.已知直线:l y =,点(),P x y 是圆()2221x y -+=上的动点,则点P 到直线l 的距离的最小值为 .14. 已知函数()()π2sin 0,6f x x x ωω⎛⎫=+>∈ ⎪⎝⎭R .又()12f x =-,()20f x =且12x x - 的最小值等于π,则ω的值为 .高三数学双基强化训练(一)答案部分一、选择题二、填空题13. 2- 14. 8 15. 2214x y -= 16. 8 解析部分1. 解析 因为对于A 有{}12A x x =-<<,对于B 有{}03B x x =<< .画数轴即可得{}13A B x x =-<<U .故选A. 2. 解析 可去分母两边同乘1i +,得()()2i 1i 3i 24i a +=++=+,则4a =.故选D.3. 解析 由柱形图可以看出,我国二氧化碳排放量呈下降趋势,故年排放量与年份是负相关关系,依题意,需选不正确的.故选D.4. 解析 由向量的坐标表示方法知,22==2a a ,3⋅-a b =. 故有()22=2=+⋅+⋅a b a a a b 223=1⨯-.故选C.5. 解析 由已知1353a a a ++=,则333a =,31a =.又因为()1535552=22a a a S +⨯==35=5a .故选A.6. 解析 由三视图得,在正方体1111ABCD A B C D -中,截取四面体111A A B D -,如图所示,设正方体棱长为a ,则11133111326AA B D V a a =⨯=﹣, 故剩余几何体体积为3331566a a a -=,所以截取部分体积与剩余部分体积的比值为15.故选D.7. 解析 因为圆心在直线BC 的垂直平分线1x =上,设圆心()1Db ,,由DA DB =,得b =3b =. A 1所以圆心到原点的距离3d ==.故选B. 8. 解析 根据程序框图可知,在执行程序过程中,a ,b 的值依次为14a =,18b =;14a =,4b =;10a =,4b =;6a =,4b =;2a =,4b =;2a =,2b =.到此有2a b ==,程序运行结束,输出a 的值为2.故选B . 9.解析 由等比数列的性质得2354a a a =,即()24441a a =-,则42a = .所以有3418a q a ==,所以2q =.故2112a a q == .故选C. 10. 解析 根据题意作图,如图所示.当点C 位于垂直于面AOB 的直径端点时, 三棱锥O ABC -的体积最大,则可设球O 的半径为R , 此时21132OABC C AOB V V R ==⨯⨯﹣﹣31366R R ==, 故6R =,则球O 的表面积为24π144πS R ==.故选C .11.解析1ln 2p fab ===;+ln 22a b a b q f +⎛⎫== ⎪⎝⎭;()()11ln 22r f a f b ab =+=⎡⎤⎣⎦. 因为()ln f x x =是增函数, 所以2a b f f +⎛⎫>⎪⎝⎭,所以q p r >=.故选C.12.解析 由题意知()()f x f x -=,即()f x 为偶函数.2a b+>当0x …时,因为()()221211xf x x x '=+++,所以()f x 在[)0+∞,上是增函数.由偶函数的性质,可得()f x 在(),0-∞上为减函数,且关于y 轴对称. 所以使()()21f x f x >-成立的条件是21x x >-,解得113x << .故选A.13.解析 由题意知()124f a -=-+=,故2a =-.14.分析 本题可作出可行域求解,也可以把不等式看成等号,求出三个顶点,代入目标函数计算可快速取出最值.解析 解法一:画出满足不等式组的可行域,如图中阴影部分所示. 联立21050x y x y -+=⎧⎨+-=⎩,解得32x y =⎧⎨=⎩,即()3,2A .目标函数2z x y =+变形为2y x z =-+,由图可知,当直线2y x z =-+经过点A 时,z 取得最大值. max 2328z =+⨯=.解法二:三个顶点分别为()3,2A ,()2,3B ,()1,1C . 分别代入2z x y =+,可得当3x =,2y =时,max 8z =.评注 线性规划问题是近年考试的热点,关键体现不等式及不等式组在实际中的应用,对于不含参数的问题可代入顶点值求解,也可以画出可行域来求解.15.解析 根据题意知,双曲线的渐近线方程为12y x =±,可设双曲线的方程为224x y m -=,把点(4 代入得1m =.所以双曲线的方程为2214xy -=.16.解析 根据题意,曲线ln y x x =+在点()11,处的切线斜率为2,故切线方程为21y x =-,与()221y axa x =+++联立,得220ax ax ++=,显然0a ≠,所以由判别式28a a ∆=-=0,得8a =.评注 由导数的意义求函数问题是基本的研究方法,函数问题首先要考虑定义域的范围,含有参数一般要对参数进行分类讨论.高三数学双基强化训练(二)答案部分一、 选择题二、 填空题10.1- 11.2513.6 14.{}21,22,23,24,25解析部分1.解析{}11P x x =-剟,所以()(),11,U P =-∞-+∞U ð.故选D.2.解析0,02a ba b+⇒厖?;若2a b+有意义的,a b 同号或0ab =,结合02a b+…可得0,0a b 厖.综上,0,0a b厖是2a b+.故选C. 3.解析因为()πcos 2sin 22g x x x ⎛⎫==+⎪⎝⎭πππsin 212312x f x ⎡⎤⎛⎫⎛⎫=++=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,所以将函数()f x 的图像向左平移π12个单位得到()g x 的图像.故选A. 4.解析 解法一: ()2OA AB OA OB OA OA OB OA ⋅=⋅-=⋅-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r,又AB =u u u r ,1OA OB ==u u u r u u u r ,得2221cos 22OA OB AB AOB OA OB+-∠==-⋅u u u r u u u r u u u r u u u r u u u r,所以2π3AOB ∠=, 因此1cos ,2OA OB OA OB OA OB ⋅=⋅=-u u u r u u u r u u u r u u u r u u u r u u u r ,因此32OA AB ⋅=-u u u r u u u r . 故选C.解法二: 如图所示,取AB 的中点C ,连接OC ,则OC AB ⊥,1OA =,AC =,所以π6OAB ∠=, 则()3cos π122OA AB OA AB OAB ⎛⋅=⋅-∠=-=- ⎝⎭u u u r u u u r u u u r u u u r .5.解析 这个正三棱柱的直观图如图所示,设1AB BC CA AA a ====,过A 作AD BC ⊥交BC 于D ,过1A 作BD 1C 1B 1A 1DC BA1111A D B C ⊥交11B C 于1D 点,连接1DD,则2AD a =. 31124V Sh BC AD AA a ==⋅⋅==2a =. 所以S左视图111=2A D DA S AD AA =⋅==矩形故选B.6.解析因为()1e ,1x -∈,所以ln 0a x =<,ln 112xb ⎛⎫=> ⎪⎝⎭,()ln 20,1x c =∈,则b c a >>.故选B.评注 解决这类比较大小的问题常常借助于中间量来进行比较,常用的中间量是“0”和“1”. 7.解析由实数,x y 满足的约束条件知,可行域如图所示.5z x y =+在点B 处取最大值,且1,11m B m m ⎛⎫ ⎪++⎝⎭,代入15411mz m m =+=++,得3m =. 故选C.8.解析 ①()231,1y'=x f x '-=-有两个相等实根,因此曲线3y x x =-不具有“可平行性”;②211y'x =-,()f x a '=()(),1a ∈-∞总有两个不同的实根与之对应,因此曲线1y x x=+是具有“可平行性”的曲线;③cos y'x =,则cos x a =[]()1,1a ∈-至少有两个不同的实根与之对应,因此曲线sin y x =是具有“可平行性”的曲线; ④124y'=x+x-,当()4f x '=时,只有一个实根2x =,因此曲线()22ln x x -+不具1有“可平行性”.综上,②③是具有“可平行性”的曲线.故选B.评注 本题将“可平行性”这一抽象的概念转化为曲线对应函数的导函数是否存在2个不同的零点的问题,使解答变得易于操作.9.解析)2=-a b ,又()2//-c a b ,所以3k =k =10.解析因为26S S =,故34560a a a a +++=,又数列{}n a 为等差数列,所以3645a a a a +=+ 所以450a a +=,由41a =,得51a =-.11.解析 由题意知圆心C 到直线l 的距离为d =1=.又2r =,所以l 被圆C 截得的弦长为2=12.解析设3只白球分别为1a ,2a ,3a ,2只黑球分别为1b ,2b .若摸出两只球,颜色相同的有:()12,a a ;()13,a a ;()23,a a ;()12,b b 共4种情况.从这5只球中任意摸出2只的情形有()()()()()()121311122321,,,,,,,,,,,a a a a a b a b a a a b ()()()()22313212,,,,,,,a b a b a b b b 共有10种情况,则摸出的两只球颜色相同的概率是25. 评注 使用枚举法师时,应按照“查字典”的方法一一列举,这样可保证不重不漏. 13.解析因为抛物线212y x =的焦点坐标为()3,0,所以39m +=,得6m =.14.解析依题意,若满足“S T =∅I ”的k 值恰有4个,则455m<…,且m *∈Ν, 故21,22,23,24,25.m =故符合条件的m 值构成的集合为{}21,22,23,24,25.高三数学双基强化训练(三)答案部分一、 选择题:二、 填空题9.42 11.34-12.1 13.1- 14.4π3+ 解析部分1. 解析 ()()22i i 2i 1i a a a -=--()21i 2a a =-+,由已知()2i i a -为正实数,可得2a -10=且20a >,解得1a =(1-舍去).故选B.2. 解析 因为{}3,4,5,M ={}2,4,5,N =所以{}2,3,4,5M N U ==U ,故B 正确;M N =I {}45,,故A 错;(){}3,4,5U N M U =≠U ð,故C 错;(){}2U M N N =≠Ið,故D 错.故选B.3. 解析 1∃-∈R ,使得()31=10,--<A 为真命题;00,a a >⇒>但0a >不一定得到0a >,所以“a 0>”是“0a >”的充分不必要条件,所以B 为真命题;当x ∈R 时,函数2xy =的值域为()0,,+∞所以C 为真命题;若p q ∧为假命题,则有p 假q 真、p 真q 假、p 假q 假三种情况,所以D 为假命题. 故选D.4. 解析 在等差数列{}n a 中,2127232a a a +==,所以7=16a ,()3157772+=2483=48a a a d a d a -++=.故选B.5.解析 0,1,150S i ==<→1,3,350S i ==<→2,7,750S i ==<→5,15,1550S i ==<→26,31,3150S i ==<→677,63,6350S i ==>→输出63i =.故选A.6.解析 双曲线2213y x -=的左焦点为()2,0-,由已知,动圆经过点()2,0-,且与直线2x =相切,所以圆心M 到定点()2,0-的距离与到定直线2x =的距离相等,其轨迹满足抛物线的定义,轨迹方程为22y px =-,又因为22p=,所以圆心M 的轨迹方程为28y x =-.故选D. 7.解析 因为()()2OB OC OB OC OA -⋅+-u u u r u u u r u u u r u u u r u u u r ()()CB OB OA OC OA ⎡⎤=⋅-+-⎣⎦u u u r u u u r u u u r u u u r u u u r= CB ⋅u u u r ()AB AC +u u u r u u u r 0=,即()()0AB AC AB AC -⋅+=u u u r u u u r u u u r u u u r,得22AB AC =u u u r u u u r ,故AB AC =,即ABC △为等腰三角形.故选C.8.解析 根据定义可知运算“⊕”是求出,a b 中较小的数,运算“⊗”是求出,a b 中较大的数.根据加法、乘法运算均有交换律知(1),(3)成立,而(2),(4)不能确定.故选B. 9.解析 由题意,平均分成40组,每组相同位置的编号组成一个公差为5的等差数列.设此数列为{}n a ,故()11n a a n d =+-且522a =,得12a =,则()*53n a n n =-∈N ,所以942a =. 因此第9组抽出的数为42. 10. 解析 由正弦定理得sin sin a c A C =,sin3=1sin C ,解得sin C =12.又因为2π0,3C ⎛⎫∈ ⎪⎝⎭,所以π6C =,ππ2B A C =--=,所以ABC △为直角三角形,所以ABC S △=1122ac =1⨯=11.解析 由已知0,m ≠则当0m >时,有11,m -<1+1m >,所以()1f m -=()21+m m -,()()1+=1+2f m m m --,又因为()1+f m =()1f m -,所以()()21+=1+2m m m m ---,解得3=02m -<(舍去);当0m <时,有11m ->,11m +<,所以()()112f m m m -=---,()()1+=21+f m m m +,所以()12m m ---=()21+m m +,解得34m =-.综上所述,m 的值为34-.12.解析 由已知得1,1==a b ,所以cos ,cos ,1⋅=⋅=a b a b a b a b „.因为2+⋅a b a b „,所以()()224+⋅„a b a b ,即()222+24+⋅⋅a b a b a b „,所以()22+24⋅⋅a b a b „,即()()12+10⋅-⋅a b a b ….又由20+>g …a b a b 可得0⋅a b …,所以10⋅-a b …,即1⋅a b …,因此=1⋅a b .又()cos cos sin sin cos αβαβαβ⋅+=-a b =,所以()cos 1.αβ-=13. 解析 设切点为()00,x y ,由已知得01x x ay'x===,即1ax =,0a x =. 因为切点()00,x y 分别在直线y x b =+与曲线ln y a x =上,所以有000ln +y a x y x b =⎧⎨=⎩,将0x a =代入上式,并消去0y ,可得ln b a a a =-,所以1ln +1ln b'a a a a=⋅-=,令0b'=,得1a =,当01a <<时,0b'<,函数ln b a a a =-在()0,1上单调递减,当1a >时,0b'>,函数ln b a a a =-在()1,+∞上单调递增,所以1a =为函数ln b a a a =-的极小值点,所以min ln111b =-=-.即实数b 的最小值为1-.14. 解析 设(),P x y ,则PA =PB =因为PA ,所以222PA PB …,所以有()22+1x y +()2221x y ⎡⎤-+⎣⎦…,化简得226+10x y x +-„, 即()223+8x y -„,则()()2231,38x y x M N x y x y ⎧⎫--⎧⎪⎪⎪=⎨⎨⎬-+⎪⎪⎪⎩⎩⎭I 剟„,其表示的平面区域如图阴影部分所示.设直线10x y --=与圆分别交于,E F 两点,过圆心G 作EF 的垂线,垂足为H ,连接GF ,GE .则圆心G 到EF 的距离GH == GF r ==EF ==π3FGH ∠=,所以2π3EGF ∠=. =S S S -阴弓形半圆=()EGF EGF S S S --△半圆扇形=22111π222r r EF GH α-+⋅=(21π2⋅-(212π23⨯⨯12+⨯4π3=+高三数学双基强化训练(四)答案部分一、选择题二、填空题9. 1910. 132 11.32 12.5ln 2,24⎛⎫+ ⎪⎝⎭13.⎝⎭14.③④ 解析部分1.解析因为集合{}20A x x x =+…,即(][),10,A =-∞-+∞U ,所以()1,0U A =-ð.故选B. 2.解析由已知可得()210320m m m m ⎧-=⎪⎨-+≠⎪⎩,解得120,1m m ==(舍),所以0m =.故选C.3.解析满足不等式组的平面区域如图阴影部分所示,当平面区域内的点取A 时,可使目标函数2z x y =-取得最大值.由2200x y x y -+=⎧⎨-=⎩,得22x y =⎧⎨=⎩,即()2,2A .所以max 2222z =⨯-=.故选B.4.解析因为ππsin cos cos 22y x x x ⎛⎫⎛⎫==-=-⎪ ⎪⎝⎭⎝⎭ππcos 36x ⎛⎫=-- ⎪⎝⎭.所以要得到sin y x =的图像,需要把πcos 3y x ⎛⎫=-⎪⎝⎭的图像向右平移π6个单位后得到.故选A. 5.解析设不等式12x -<的解集为A ,则()1,3A =-,设不等式()()130x x --<的解集为B .则()1,3B =.因为B A ⊂≠,所以“12x -<”是“()()130x x --<”成立的必要不充分条件.故选B.6.解析依题意y kx =与直线20x y b ++=互相垂直,且20x y b ++=的斜率为2-, 所以()21k ⋅-=-,12k =.因为直线y kx =与圆的两交点关于直线20x y b ++=对称, 所以圆心()2,0在直线20x y b ++=上,即2200b ⨯++=,得4b =-.故选A.7.解析依题意画图如下.由已知,在12Rt MF F △中,122F F c =,2MF c =,所以1MF =.由椭圆定义,知122MF MF a +=2c a +=,所以e =1c a ==.故选A.8. 分析 由于a 的正负导致函数图像形态不同,所以需依据a 的正负进行分类讨论解析若()f x 为R 上的“2014型增函数”,则()()2014f x f x +>在R 上恒成立.因为()f x 是R 上奇函数,所以其图像关于原点对称,又知0x >时()2f x x a a =--,所以①当0>a 时,()f x 的图像如图3所示.要使()()2014f x f x +>在R 上恒成立,须满足()f x 向左平移的距离大于6a ,即20146a >,所以100703a <<.②当0a <时,()f x 的图像如图4所示.由图可知,()f x 向左平移后的图像总在()f x 图像的上方.即()()2014f x f x +>恒成立.③当0a =时,()f x 的解析式为()()f x x x =∈R ,所以()()2014f x f x +>恒成立.综上所述,实数a 的取值范围是10073a <.故选C. 评注 本题应用数形结合的思想直观地呈现出解题思路,降低了思维的难度.9.解析由题意,基本事件数为66=36⨯.其中点数之积等于6的情况有16,61,23,32⨯⨯⨯⨯共4种.所以41369P ==. 10.解析因为9121=+62a a ,所以912212a a =+,所以6121212a a a +=+,故612a =. 116111112132S a ==⨯=.11.解析满足题图中三视图的几何体P ABC -如图所示,其中平面PBC ⊥平面ABC ,且PA BC ⊥.过P 作PD BC ⊥于点D ,则AD BC ⊥.所以由三视图可得3,21 3.1PD BC BD DC AD ==+=+==.所以13V S =底.PD 1132BC AD PD =⨯⨯⨯⨯113313322=⨯⨯⨯⨯=12.解析因为2ln y x x =+与3y x b =-有3个不同交点⇔2ln 3b x x x =--+有3个不同零点.令()2ln 3f x x x x =--+,则()123f x x x '=--+=2231x x x -+-()()211x x x--=-. ()f x ',()f x 的变化情况如下表.)11135ln ln 224224f ⎛⎫=--+=+ ⎪⎝⎭,()11ln132f =--+=.又2ln 3b x x x =--+有3个不同零点,所以b 的取值范围为5ln 2,24⎛⎫+⎪⎝⎭. 13.解析()()()222410241x x x x m m m m -++>⇔->-+()2m m ⇔->122x x⎛⎫-+⎪⎝⎭. 令2xt =,因为[)1,x ∈+∞,所以2t …. 若使()21m m t t ⎛⎫->-+ ⎪⎝⎭()2t …恒成立,需满足 DCBAP()2max1m m t t ⎡⎤⎛⎫->-+ ⎪⎢⎥⎝⎭⎣⎦,函数1t t ⎛⎫-+ ⎪⎝⎭在[)2,+∞上是单调递减的,所以max115222t t ⎡⎤⎛⎫⎛⎫-+=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.即252m m ->-, 解这个一元二次不等式得m的取值范围是122⎛⎝⎭. 评注 本题分离了参数与变量,变更主元,通过求函数的最值得出参数取值范围,这种变更主元的思想在解题中起到了重要的作用. 14.解析因为0x <时,()()e1xf x x =+,当0x >时,0x -<,所以()()e 1x f x x --=-+.又因为()f x 是R 上的奇函数,所以()()()e 1xf x f x x -=--=-.故①错误;由()()e1xf x x =+()0x <,得()()e 2x f x x '=+,令()0f x '=,得2x =-.当(),2x ∈-∞-时,()0f x '<,()f x 单调递减; 当()2,0x ∈-时,()0f x '>,()f x 单调递增.()22e f --=-为(),0-∞上的极小值.当x →-∞时,()0f x '→,()0f x →,且()f x 是R 上奇函数,()00f =,其图像关于原点对称,根据以上分析可得()f x 的图像如图6所示.由图像可得函数()f x 有3个零点.故②错误()()()e 1 00 0e 1 0x x x x f x x x x -⎧->⎪==⎨⎪+<⎩,令()0f x =,得11x =-,20x =,31x =.由图像可得()0f x >的解集为()()1,01,-+∞U .故③正确;因为()f x 的图像夹在1y =-与1y =两条直线之间,且图像与1y =-,1y =无交点. 所以12,x x ∀∈R ,都有()()122f x f x -<.故④正确. 综上所述,正确的命题为③④.评注 本题在画函数图像时,先后用到了求导、极限化与对称性的思想方法,在判断命题正误时用到了数形结合的思想,这些思想的运用为解题铺平了道路.高三数学双基强化训练(五)参考答案一、选择题9. 1 ,12y x =±10. 3211. 12. 16- ,20114.12解析部分1. 解析 集合{}1,2A =,所以{}1,2A B =I .故选C.2. 解析 对于A ,22y x =-+是偶函数,对于C ,2xy -=在R 上是减函数;对于D ,ln y x =是非奇非偶函数.故选B.3. 解析 ()212i 14i 434i +=+-=-+,故对应的点位于第二象限.故选B. 4. 解析 根据俯视图定底,侧视图定高可得三棱锥的底面积122S =⨯=h =以113V ==.故选D. 5. 解析 0,2,2102,3,3105,5,510S k S k S k ==<→==<→==<→10,S =9,91019,17,1710k S k =<→==>→输出. 19S =.故选C.6. 解析 令()f x x x =,则()22,0,0x x f x x x ⎧⎪=⎨-<⎪⎩….所以()f x 在R 上单调递增,所以a b a a b b >⇔>,即“a b >”是“a a b b >”成立的充要条件.故选C.7. 解析 对于无穷的等差数列{}n a ,当0d >时,是递增数列,当0d <时,是递减数列,故排除D ;当10a >,0d <时,n S 有最大值,故A 正确;当10a <,0d <时,n S 无最小值,故B 不正确;当10a >,0d >时,n S 无最大值,故C 不正确.故选A.8. 解析 观察图b 与图a ,可知将图a 中的图像作出其关于y 轴对称的部分,可得()f x -的图像,再将()f x -的图像向右平移一个单位,可得()()11f x f x --=-⎡⎤⎣⎦的图像,即为图b.故选C.9. 解析 由双曲线的方程得24a =,2b m =.因为c e a ==,所以2254c a =,所以22254a b a +=,即4544m +=,所以1m =,所以双曲线的渐近线方程为12y x =±. 10. 解析 不等式组所表示的平面区域如图所示阴影部分.联立2030x y x y +=⎧⎨-+=⎩,解得()1,2A -,联立030x x y =⎧⎨-+=⎩,解得()0,3B ,所以11331222AOB A S OB x ==⨯⨯=△.11. 解析 由()()λλ+⊥-a b a b ,得()()0λλ+⋅-=a b a b ,即2220λ-=a b ,故222λ=a b ,且2=a ,=b 248λ=,解得λ=12. 解析 ()()()23129313f x x x x x '=-+=--[]()1,5x ∈-,所以在区间()1,3内,()0f x '<,()f x 单调递减,在区间()1,1-和()3,5内,()0f x '>,()f x 单调递增,所以()f x 在区间[]1,5-的最大值为()(){}1,5f f 的较大者,最小值为()(){}1,3f f -的最小者.经计算比较得()()max 520f x f ==,()()min 116f x f =-=-.13. 解析 圆心()2,0到直线0l y -=的距离2d ==,所以点P 到直线l 的距离的最小值等于1d r -=.14. 解析 因为()12f x =-为()f x 的最小值,所以1x x =是()f x 的一条对称轴.因为()20f x =,所以()2,0x 是()f x 的一个对称中心.又因为12x x -的最小值为π,所以相邻的对称轴与对称中心的距离为π.所以=π4T ,4πT =,所以2π12T ω==.。
高三数学双基强化训练

高三数学双基强化训练(一)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有 一项是符合题目要求的. 1.sin 240o的值为( ).A .2 B .12 C .12- D .2- 2.已知双曲线C :22214x y b-=经过点()4,3,则双曲线C 的离心率为( ).A .12B C .2 D .23.执行如图所示的程序框图,则输出的z 的值是( ).A .21B .32C .34D .644.已知命题p :x ∀∈R ,20x >,命题q :,αβ∃∈R ,使()tan αβ+=tan α+tan β,则下列命题为真命题的是( ).A .p q ∧B .()p q ∨⌝C .()p q ⌝∧D .()p q ∧⌝ 5.设集合{}22A x a x a =-<<+,{}2450B x x x =--<,若A B ⊆,则实数a 的取值范围为( ).A .[]1,3B .()1,3C .[]3,1--D .()3,1-- 6.已知数列{}n a 满足13a =,且143n n a a +=+()*n ∈N ,则数列{}na 的通项公式为( ).A .2121n -+ B .2121n -- C .221n +D .221n-7.已知函数()223f x x x =-++,若在区间[]4,4-上任取一个实数0x ,则使()00f x …成立的概率为( ). A .425B .12C .23D .18.设函数()3233f x x ax bx =++有两个极值点1x ,2x ,且[]11,0x ∈-,[]21,2x ∈,则点(),a b 在aOb 平面上所构成区域的面积为( ).A .14B .12C .34D .1二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中的横线上. 9.已知i 为虚数单位,复数1iiz -=,则z = . 10.已知向量(),1x =a ,()2,y =b ,若()1,1+=-a b ,则x y += .11.某种型号的汽车紧急刹车后滑行的距离y km 与刹车时的速度x km /h 的关系可以 用2y ax =来描述,已知这种型号的汽车在速度为60km/h 时,紧急刹车后滑行的距离 为b km .一辆这种型号的汽车紧急刹车后滑行的距离为3b km ,则这辆车的行驶速度12.若x ,y 满足11010y x y x y ⎧⎪--⎨⎪+-⎩………,则z x =的最小值为 .13. 一个几何体的三视图如图所示,图中直角三角形的直角边长均为1,则该几何体体积 为 .14.设点()0,1M x ,若在圆O :221x y +=上存在点N ,使得45OMN ∠=o,则0x 的取值范围是 .高三数学双基强化训练(二)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.若集合{}{}211,|0A x x x B x x x =+=+=+<,则A B =I ( ). A. ()1,0- B.[)1,0- C. (]1,0- D . []1,0- 2.复数z 满足1(1)i z z -=+,则z 的值是( ).A . 1i + B.1i - C.i D.i -3.双曲线221kx y -=的一条渐近线与直线210x y ++=垂直,则此双曲线的离心率是( ).C. 4.51(1)2x +的展开式中2x 的系数为( ). A.5 B.52 C.54 D.585.m ,n 是不同的直线,,αβ是不重合的平面,下列说法正确的是( ). A .若//,,m n αβαβ⊂⊂,则//m n B .若,,//,//m n m n αββ⊂,则//αβC .,m n 是异面直线,若//,//,//,//m m n n αβαβ,则//αβ D. 若//,//m αβα,则//m β6.过点()2,3的直线 l 与圆 22:430C x y x +++=交于,A B 两点,当弦AB 取最大值时,直线l 的方程为( ).A .3460x y -+= B.3460x y --= C. 4380x y -+= D. 438 0x y +-= 7.已知函数2sin (0)y x ωω=>的图像与直线2y =-的相邻的两个公共点之间的距离为2π3,则ω的值为( ). A .13 B.32 C. 3 D.238.某三棱锥的三视图如图所示,则该三棱锥的表面积是( ).A. 2B. 4+C. 2+D. 59. 从1,2,3,4,5这5个数中中任取3个不同的数,其中,这3数构成一组勾股数的概率为( ). A.15 B . 310 C . 110 D . 3510.阅读如图所示的程序框图,运行相应的程序,则输出的结果为( ). A .2 B .1 C .0 D .1-11.在ABC △中,,,a b c 分别是角,A B C ,的对边,且2cos 22A b c c+=,则ABC △是( ).A.直角三角形B.等腰三角形或直角三角形 C .正三角形 D .等腰直角三角形12.已知函数3()23f x x x =-.若过点(1,)P t 存在3条直线与曲线()y f x =相切,则t 的取值范围为 ( ).A.()3-∞-,B. ()3,1--C.()1-+∞,D. ()0,1二、填空题:本大题共四小题,每小题5分,共20分,把答案填在题中的横线上. 13.函数()y f x =的反函数为2log y x =,则(1)f -=________.俯视图侧(左)视图正(主)视图14.设,x y 满足约束条件:1227y x y x y +⎧⎪⎨⎪+⎩………,则z x y =+的最大值_______.15.已知(1,1),,OA OB =-=-=+u u u r u u u ra ab a b .若OAB △是以O 为直角顶点的等腰直角三角形,则OAB △的面积是_______.16.椭圆()222210x y a b a b +=>>的右焦点(),0F c 关于直线by x c=的对称点Q 在椭圆上,则椭圆的离心率是_______.高三数学双基强化训练(三)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2A x x =<,{}320B x x =->,则( ). A .32A B x x ⎧⎫=<⎨⎬⎩⎭I B .A B =∅I C .32A B x x ⎧⎫=<⎨⎬⎩⎭U D .A B =R U 2.为评估一种农作物的种植效果,选了n 块地作试验田.这n 块地的亩产量(单位:kg )分别为12n x x x ⋯,,,,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( ). A .12n x x x ⋯,,,的平均数 B .12n x x x ⋯,,,的标准差 C .12n x x x ⋯,,,的最大值 D .12n x x x ⋯,,,的中位数 3.下列各式的运算结果为纯虚数的是( ).A .()2i 1i + B .()2i 1i - C .()21i + D .()i 1i +4.如图所示,正方形ABCD 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( ). A.14 B. π8 C. 12 D. π45.已知F 是双曲线22:13y C x -=的右焦点,P 是C 上一点,且PF 与x 轴垂直,点A 的坐标是()1,3,则APF △的面积为( ). A .13 B .12 C .23 D .326.如图所示,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 不平行的是( ).7.设x ,y 满足约束条件3310x y x y y +⎧⎪-⎨⎪⎩………,则z x y =+的最大值为( ). A .0B .1C .2D .38.函数sin 21cos xy x=-的部分图像大致为( ).9.已知函数()()ln ln 2f x x x =+-,则( ).A.()f x 在()0,2上单调递增B.()f x 在()0,2上单调递减C.()y f x =的图像关于直线1x =对称D.()y f x =的图像关于点()1,0对称10如图所示的程序框图是为了求出满足321000n n ->的最小偶数n ,).B.AM NQBA.M NQ BA C.AM QNBD.BANQMA.1000?A >和1n n =+B.1000?A >和2n n =+C.1000?A …和1n n =+D.1000?A …和2n n =+11.ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知()sin sin sin cos 0B A C C +-=,2a =,c =则C =( ). A .π12B .π6C .π4D .π312.设A ,B 是椭圆22:13x y C m+=长轴的两个端点,若C 上存在点M 满足120AMB ∠=o ,则m 的取值范围是( ).A.(][)0,19,+∞UB.([)9,+∞UC.(][)0,14,+∞UD.([)4,+∞U二、填空题:本题共4小题,每小题5分,共20分.13.已知向量()1,2=-a ,(),1m =b .若向量+a b 与a 垂直.则m = . 14.曲线21y x x=+在点()1,2处的切线方程为 . 15.已知π0,2α⎛⎫∈ ⎪⎝⎭,tan 2α=,则πcos 4α⎛⎫-= ⎪⎝⎭ . 16.已知三棱锥S ABC -的所有顶点都在球O 的球面上,SC 是球O 的直径,若平面SCA ⊥平面SCB ,SA AC =,SB BC =,三棱锥S ABC -的体积为9,则球O 的表面积为 .高三数学双基强化训练(四)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}1M x x =<,{}2,x N y y x M ==∈,则集合()M N R I ð等于( ).A.[)1,1,2⎛⎤-∞+∞ ⎥⎝⎦UB.1,12⎛⎫ ⎪⎝⎭C.1,2⎛⎤-∞ ⎥⎝⎦D.[)1,+∞2.已知复数()4i1i b z b +=∈-R 的实部为1-,则复数z b -在复平面上对应的点在( ).A.第一象限B.第二象限C.第三象限D.第四象限3.下列说法中正确的是( )A.若分类变量X 和Y 的随机变量2K 的观测值k 越大,则“X 与Y 相关”的可信程度越小B.对于自变量x 和因变量y ,当x 取值一定时,y 的取值具有一定的随机性,x ,y 之间的这种非确定关系叫做函数关系C.相关系数2r 越接近1,表明两个随机变量线性相关性越弱D.若分类变量X 与Y 的随机变量2K 的观测值k 越小,则两个分类变量有关系的把握性越小 4.如图所示是2016年某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字.这些数据的中位数是,去掉一个最低分和一个最高分后所剩数据的平均数是( ). A.86.5,86.7B.88;86.7C.88;86.8D.86.5;86.85.在如图所示的知识结构图中:“求简单函数的导数”的“上位”要素有( ).A.1个B.2个C.3个D.4个6.下面四个推理,不属于演绎推理的是( ).A.因为函数()sin y x x =∈R 的值域为[]1,1-,21x -∈R ,所以()()sin 21y x x =-∈R 的值域也为[]1,1-B.昆虫都是6条腿,竹节虫是昆虫,所以竹节虫有6条腿C.在平面中,对于三条不同的直线a ,b ,c ,若a b ∥,b c ∥,则a c ∥,将此结论放到空间中也是如此D.如果一个人在墙上写字的位置与他的视线平行,那么,墙上字迹离地的高度大约是他的身高,凶手在墙上写字的位置与他的视线平行,福尔摩斯量得墙壁上的字迹距离地面六尺多,于是,他得出了凶手身高六尺多的结论7.如图所示,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED ,则sin CED ∠=( ).8989454987EDCBA8.已知()f x 满足对x ∀∈R ,()()0f x f x -+=,且0x …时,()e x f x m =+(m 为常数),则()ln5f -的值为( ). A.4B.4-C.6D.6-9.若实数数列:1-,1a ,2a ,3a ,81-成等比数列,则圆锥曲线2221y x a +=的离心率是( ). A.1310.四棱锥P ABCD -的三视图如下图所示,四棱锥P ABCD -的五个顶点都在一个球面上,E ,F 分别是棱AB ,CD 的中点,直线EF被球面所截得的线段长为 ). A.12πB.24πC.36πD.48π22340x xy y z -+-=,则当11.设正实数x ,y ,z 满足xy z取得最大值时,212x y z +-的最大值为( ).A.0B.1C.94D.312.已知,a b 是实数,1和1-是函数()32f x x ax bx =++的两个极值点,设()()()h x f f x c =-,其中()2,2c ∈-,函数()y h x =的零点个数为( ).A.8B.11C.10D.9二、填空题:本大题共4小题,每小题5分,共20分.13.有三张卡片,分别写有1和2,1和3,2和3,甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 .14.已知ABC △的外接圆的半径为8,且sin :sin :sin 2:3:4A B C =,则ABC △的面积为 . 15.已知O 为三角形ABC 的外心,2AB a =,2AC a=,120BAC ∠=︒,若AO xAB y AC =+u u u r u u u r u u u r ,则36x y+的最小值为 .16.设函数3,eln ,e x x x y a x x 2⎧-+<=⎨⎩…的图象上存在两点P ,Q ,使得POQ △是以O为直角顶点的直角三角a形(其中O 为坐标原点),且斜边的中点恰好在y 轴上,则实数a 的取值范围是 .高三数学双基强化训练(五)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知命题:,221xp x x ∀∈>+R ,则p ⌝( ).A.,221xx x ∀∈+R … B. ,221xx x ∀∈<+R C. ,221xx x ∃∈+R … D.,221xx x ∃∈>+R 2.已知集合103x A x x ⎧+⎫=∈⎨⎬-⎩⎭Z…,{}2|1,B y y x x A ==+∈,则集合B 的含有元素1的子集个数为( ).A. 5B. 4C. 3D. 23.若,x y 满足3040x y x y x -⎧⎪+⎨⎪⎩………,则3x y +的最大值为( ).A. 0B. 2C. 4D. 6 4.复数()2i 3i =-( ).A.13i 5- B. 13i 5+ C. 3i 5+ D.3i5-5.已知定义在区间[]3,3-上的函数()2x f x m =+满足()26f =,在[]3,3-上随机取一个实数x ,则使得()f x 的值不小于4的概率为( ). A.56 B. 12 C. 13 D.166.执行右图所示的程序框图,如果输出a 的值大于2017,那么判断框内的条件是( ). A. 9?k >B. 9?k …C. 10?k <D.11?k …7.在等差数列{}n a 中,已知37,a a 是函数()243f x x x =-+的两个零点,则{}n a 的前9项和等于( ).A. 18-B. 9C. 18D.368.函数()133,1log ,1x x f x x x ⎧⎪=⎨>⎪⎩…,则()1y f x =-的图像是( ).9.曲线()()22110x y x +-=…上的点到直线10x y --=的距离的最大值为a ,最小值为b ,则a b -的值是( ).A.B. 2C.1+1 10. 如图所示,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则此几何体的表面积为( ).A. 42+B.62+C. 10D. 1211.设12,F F 是椭圆()2221024x y b b+=<<的左、右焦点,过1F 的直线l 交椭圆于A,B 两点,若22AF BF +的最大值为5,则椭圆的离心率为( ).A.12B. 2C.12D.212.已知函数()()2e 31xf x a x a x =--+,若函数()f x 在区间()0,ln3上有极值,则实数a 的取值范围是( ).A.D.A.1,2⎛⎫-∞-⎪⎝⎭ B. (),1-∞- C. 11,2⎛⎫-- ⎪⎝⎭D. ()(),20,1-∞-U二、填空题:本大题共4小题,每小题5分,共20分.13.已知向量()()2,0,1,2==a b ,若λ-a b 与()1,2=-c 垂直,则实数λ的值为 . 14.若1sin 33απ⎛⎫-=⎪⎝⎭,则cos 23απ⎛⎫+= ⎪⎝⎭.15.,则该三棱锥外接球的直径为 . 16.数列{}n a 的前n 项和为21n S n n =++,()()()*12nn n b a n =--∈N ,则数列{}n b 的前50项的和为 .高三数学双基强化训练(一)答案部分 一、选择题二、填空题9. 10. 3- 11. 12. 113.1614. []1,1- 解析部分1. 解析 ()sin 240sin 18060sin 602=+=-=-o ooo.故选D.2. 解析 由题可得216914b-=,解得23b =,所以2227c a b =+=,所以2c e a ==.故选C.3. 解析 1x =,2y =,220z =<−−→是2x =,2y =,420z =<−−→是2x =,4y =,820z =<−−→是4x =,8y =,3220z =>−−→否输出32z =.故选B.4. 解析 因为x ∈R 时,20x …,所以命题p 是假命题;当tan 0α=或tan 0β=时,都有()tan tan tan αβαβ+=+,所以命题q 是真命题,所以()p q ⌝∧是真命题.故选C.5. 解析 由题可得{}15B x x =-<< ,若A B ⊆,则有2125a a --⎧⎨+⎩……,解得13a剟.故选A.6. 解析 因为143n n a a +=+,所以()1141n n a a ++=+.又因为114a +=,所以{}1n a +是以4为首项,4为公比的等比数列,所以1214442n n n n a -+=⨯==,所以221n n a =-.故选D.7. 解析 令()0f x …,即2230x x -++…,解得13x -剟,所以当[]01,3x ∈-时,()00f x …,所以根据几何概型知成立的概率()()311442P --==--. 故选B.8. 解析 由()3233f x x ax bx =++可得()2363f x x ax b '=++.因为()f x 有两个极值点1x ,2x ,所以()0f x '=有两个根1x ,2x ,且[]11,0x ∈-,[]21,2x ∈,又因为()f x '的图像开口向上,所以有()()()()10001020f f f f '-⎧⎪'⎪⎨'⎪⎪'⎩…………,即2102144a b b a b a b -⎧⎪⎪⎨+-⎪⎪+-⎩…………,对应的可行域如图阴影部分所示,所以点(),a b 在平面aOb 上所构成区域的面积111111121121222222S =⨯-⨯⨯-⨯⨯-⨯⨯=.故选D.49. 解析 221i i i 1i i iz --===--,所以z 10. 解析 ()()2,11,1x y +=++=-a b ,所以2111x y +=⎧⎨+=-⎩,解得12x y =-⎧⎨=-⎩,所以3x y +=-.11. 解析 由题意可得3600b a =,所以33360010800b a a =⨯=,所以这辆车的行驶速度/h x ==.12. 解析 画出不等式组所表示的可行域,如图中所示的阴影部分.联立11y x y x =-⎧⎨=-+⎩,得()1,0B .由z x =+,得y x z =+.由图可知,当y x =+经过点()1,0B 时,z 取得最小值,min 1z =.13. 解析 由三视图可知该几何体是底面为直角三角形,高为1的倒置的三棱锥,将其放入正方体中如图所示,所以111111326V ⎛⎫=⨯⨯⨯⨯= ⎪⎝⎭.14. 解析 解法一:如图所示,在圆O 上任取一点N ,连接ON ,在OMN △中, 由正弦定理得sin sin ON OM OMN ONM =∠∠,即sin sin ON ONM OM ONM OMN∠==∠∠.又因为111CA3π0,4ONM ⎛⎫∠∈ ⎪⎝⎭,所以(]sin 0,1ONM ∠∈,故(OM ∈,即212x +…,得011x -剟,所以0x 的取值范围是[]1,1-.解法二:过点M 作圆O 的切线,切点为Q ,连接OQ ,如图所示,则)45,90OMQ ⎡∠∈⎣oo,所以sin sin 452OMQ ∠=o …又在Rt OMQ △中,1sin OQ OMQ OM OM ∠==,所以12OM …,即OM …11x -剟,即0x 的取值范围是[]1,1-.评注 对于存在性问题,可利用转化思想,将其转化为最值求解.高三数学双基强化训练(二)答案部分一、选择题二、填空题13.1214. 5 15. 2 16. 2解析部分1. 解析 集合{}1A x x =-…,{}10B x x =-<<<,()1,0A B =-I .故选A. 2. 解析 由()11i z z -=+,得()1i 1i z -=+,即1ii 1iz +==-. 故选C.3. 解析 双曲线221kx y -=的渐近线方程为y =.若双曲线的一条渐近线与直线210x y ++=垂直,()21-=-,所以14k =,故双曲线方程为2214x y -=,此双曲线的离心率c e a ==.故选A. 4.解析 由15511C C 22rrr r r r T x x +⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,令2r =,得2x 项的系数为22515C 22⎛⎫= ⎪⎝⎭.故选B. 5. 解析 对于选项A :若//αβ,m α⊂,n β⊂, 则m n =∅I ,但不一定//m n ,m 与n 也可能异面;对于选项B :若,m n α⊂,//m β,//n β,不一定推出//αβ, 如果前提附加m n O =I ,则//αβ;对于选项D :若//αβ,//m α,则//m β或m β⊂,因此选项D 错误.故选C. 6. 解析 依题意,当弦AB 取最大值时,直线l 过圆心()2,0C -,则直线l 的斜率34k =,方程为()324y x =+,即3460x y -+=.故选A. 7. 解析 依题意,函数()2sin 0y x ωω=>的周期2π3T =,即2π2π3ω=,得3ω=.故选C.8. 解析 据三棱锥的三视图,还原几何体P ABC -,且PA ⊥平面ABC ,底面ABC △为等腰三角形,12222ABC S =⨯⨯=△,1122PAB PAC S S ==⨯=△△,122PBC S =⨯=△22PAB PAC ABC PBC S S S S +++=++=△△△△.故选C.9. 解析 从1,2,3,4,5中任取3个不同的数,有如下10种情况:{}1,2,3,{}1,2,4,{}1,2,5,{}1,3,4,{}1,3,5,{}1,4,5,{}2,3,4,{}2,3,5,{}2,4,5,{}3,4,5.其中,这3数构成一组勾股数,则{}3,4,5满足条件.因此,这3个数构成一组勾股数的概率为110.故选C. 10. 解析 依题意,当6i =时输出S 的值.则π3π4π5πcoscos πcos cos cos 02222S =++++=.故选C. 11. 解析 由21cos cos 222A b c A c ++==,即11cos b A c +=+,得cos b A c=. 解法一(正弦定理):由正弦定理,得sin cos sin BA C=,所以()sin sin cos sin πB C A A C ==-+=⎡⎤⎣⎦()sin sin cos cos sin A C A C A C +=+,因此sin cos 0A C =,得cos 0C =,π2C =. 所以ABC △是直角三角形.故选A.解法二(余弦定理):由余弦定理,得2222b b c a c bc+-=,整理得222c a b =+,所以ABC △为直角三角形.故选A. 12. 解析 设函数()323f x x x =-上任意一点()()00,x f x ,在点()()00,x f x 处的切线方程为()()()000y f x f x x x '-=-, 即()()()3200002363y x x x x x --=--.2111P CB A若过点()1,t ,则()()()()32320000002363146 3 t x x x x x x =-+--=-+-*依题意,方程()*有三个不等实根.令()32463g x x x =-+-,()()212121210g x x x x x '=-+=--=,得10x =,21x =.当()(),0,1,x ∈-∞+∞时,()0g x '<,函数()g x 在()(),0,1,-∞+∞上单调递减; 当()0,1x ∈时,()0g x '>,函数()g x 在()0,1上单调递增. 因此()g x 的极小值为()03g =-,极大值为()11g =-. 若()t g x =有三个不等实根,则31t -<<-.故选B.13. 解析 由()f x 的反函数为2log y x =,得()2xf x =,则()11122f --==. 14. 解析 不等式组表示的区域,如图所示. 当直线z x y =+过点()2,3A 时,z 取得最大值5.15. 解析 依题意,OA OB =u u u r u u u r ,且OA OB ⊥u u u r u u u r ,得0⋅=⎧⎪⎨=⎪⎩a b a b ,12OAB S OA OB =u u u r u u u r △,又2OA OB =====u u u r u u u r ,所以12222OAB S =⨯⨯=△. 16. 解析 设椭圆的左焦点为()1,0F c -,依题意1OF OQ OF ==.又点O 为12F F 的中点,所以112OQ FF =, 则1QFF △为直角三角形,得1FQ FQ ⊥u u u r u u u r.又直线:bl y x c=垂直于FQ ,故1//FQ l , 所以直线1F Q 的斜率为bc,可得直角顶点()0,Q b ,且π4FQO ∠=,故b c =.所以椭圆的离心率2c e a ===.高三数学双基强化训练(三)答案部分一、选择题 二、填空题13. 7 14. 1y x =+15.1016. 36π 解析部分1. 解析 由320x ->得32x <,所以{}33222A B x x x x x x ⎧⎫⎧⎫=<<=<⎨⎬⎨⎬⎩⎭⎩⎭I I .故选A. 2. 解析 刻画评估这种农作物亩产量稳定程度的指标是标准差.故选B. 3. 解析 因为2(1i)2i +=为纯虚数.故选C.4. 解析 不妨设正方形边长为a ,由图形的对称性可知,太极图中黑白部分面积相等,即各占圆面积的一半.由几何概型概率的计算公式得,所求概率为221228a a ⎛⎫⨯π⨯ ⎪π⎝⎭=.故选B.5. 解析 由2224c a b =+=,得2c =,所以()2,0F ,将2x =代入2213y x -=,得3y =±,所以3PF =,又A 的坐标是(1,3),故APF △的面积为()1332122⨯⨯-=.故选D. 6. 解析 由选项B ,//AB MQ ,则直线//AB 平面MNQ ;由选项C ,//AB MQ ,则直线//AB 平面MNQ ;由选项D ,//AB NQ ,则直线//AB 平面MNQ .故选项A 不满足.故选A.7.解析 如图所示,目标函数z x y =+经过(3,0)A 时最大,故max 303z =+=.故选D.8.解析 由题意知,函数sin 21cos xy x=-为奇函数,故排除B ;当x =π时,0y =,排除D ;当1x =时,sin 201cos1y =>-,排除A.故选C.9. 解析 由题意知,(2)ln(2)ln ()f x x x f x -=-+=,所以()f x 的图像关于直线1x = 对称,选项C 正确,选项D 错误,又()112(1)(02)2(2)x f x x x x x x -'=-=<<--,在(0,1)上单调递增,在[)1,2上单调递减,选项A ,B 错误.故选C.10.解析 由题意选择321000nn->,则判定框内填1000?A …,由因为选择的n 为偶数,所以矩形框内填2n n =+.故选D.11.解析 由题意sin()sin (sin cos )0A C A C C ++-=得sin cos cos sin sin sin sin cos 0A C A C A C A C ++-=,即sin (sin cos )sin 04C A A C A π⎛⎫+=+= ⎪⎝⎭,所以34A π=. 由正弦定理sin sin a c A C =,得23sin sin 4C=π,即1sin 2C =,得6C π=.故选B. 12.解析 因为在C 上存在点M ,满足120AMB ∠=o,所以()max 120AMB ∠o ….当点M 位于短轴端点时,AMB ∠取得最大值.① 当03m <<时,如图1所示,有120AMB ∠o …,则60,30AMO MAO∠∠o o 厔,所以x()21tan 33m MAO ∠=…,解得01m <…;图1 图2② 当3m >时,如图2示,有120AMB ∠o …,则60,30AMO MAO∠∠o o 厔,所以()2tan 33mMAO ∠=…,解得9m …. 综上可得,的取值范围是(][)0,19,+∞U .故选A.评注:先研究“椭圆()222210x y a b a b+=>>,,A B 是长轴两端点,M 位于短轴端点时,AMB ∠最大”这一结论.图3 如图3所示,因为AMB MBx MAx∠=∠-∠,所以tan tan tan 1tan tan 1MB MA MB MAk k MBx MAxAMB MBx MAx k k -∠-∠∠==+∠⋅∠+⋅.设()0MA k t t =>,因为22MB MAa k k b⋅=-(中点弦的一个结论),所以2222222222tan 1a a b b tt ab t t AMB a c c ba --+∠==---…(当且仅当222a t b =,即a t b =时等号成立,此时M 位于短轴端点处).13.解析 由题得()1,3m +=-a b ,因为+a b 与a ()0+⋅=a b a ,所以(1)230m --+⨯=,解得7m =.14.解析 设()y f x =,则()212f x x x'=-,所以()1211f '=-=,所以曲线在(1,2)处的切线方程为21(1)y x -=⨯-,即1y x =+.15. 解析 由tan 2,sin 2cos ααα==得.又22sin cos 1αα+=, 所以21cos 5α= .因为0,2απ⎛⎫∈ ⎪⎝⎭,所以cos 5α=,sin 5α=. 所以cos cos cos sin sin 444αααπππ⎛⎫-=+ ⎪⎝⎭525210=+⨯=. 16. 解析 取SC 的中点O ,即球心.联结OA ,OB , 因为SA AC =,SB BC =,所以,OA SC OB SC ⊥⊥.因为平面SAC ⊥平面SBC ,OA ⊂平面SAC ,平面SAC I 平面SBC SC =,所以OA ⊥平面SBC . 设OA r =,3111123323A SBC SBC V S OA r r r r -=⨯⨯=⨯⨯⨯⨯=△9=,解得3r =,所以球的表面积为2436r π=π.高三数学双基强化训练(四)答案部分一、选择题二、填空题13. 1和3 15. 16. 10e+1⎛⎤ ⎥⎝⎦,解析部分1.解析 {}11M x x =-<<,122N y y ⎧⎫=-<<⎨⎬⎩⎭,则1,12M N ⎛⎫=- ⎪⎝⎭I ,()[)1,1,2M N ⎛⎤=-∞-+∞ ⎥⎝⎦R I U ð.故选A.2.解析 ()()4i 1444i 1i i 1i 222b b b z b +-+==++=+-,由实部位1-,得6b =,则75i z b -=-+,则在复平面对应的点位于第二象限.故选B.3.解析 若分类变量X 和Y 的随机变量2K 的观测值k 越大,则“X 与Y 相关”的可信程度越大,所以A 错误;对于自变量x 和因变量y ,当x 取值一定时,y 的取值具有一定的随机性,x ,y 之间的这种非确定关系叫做相关关系,所以B 错误;相关系数2r 越接近1,表明两个随机变量线性相关性越强,所以C 错误;若分类变量X 与Y 的随机变量2K 的观测值k 越小,则两个分类变量有关系的把握性越小,所以D 正确.故选D.4.解析 由茎叶图知,中位数为88,去掉一个最低分和一个最高分后,所剩数据的平均数为848588888986.85++++=.故选C.5.解析 由题图知“上位”要素有3个.故选C.6.解析 C 选项为类比推理.故选C.7.解析 由题图知,DE =CE =1CD =,由余弦定理得222cos2DE CE DC CED DE CE +-∠==⋅⋅,则sin 10CED ∠=.故选B.8.解析 x ∀∈R ,()()0f x f x -+=,即()()f x f x -=-,所以()f x 为奇函数,则()00e 0f m =+=,得1m =-.()()()ln5ln5ln5e14f f -=-=--=-,故选B.9.解析 由题知2281a =,且20a <,得29a =-,则圆锥曲线的方程为2219y x -=,则=1e =故选D. 10.解析 由三视图作出四棱锥的直观图,如图所示,知此几何体可以放在棱长为a 的正方体中,则()2223R a =,得2R =.由直线EF与球心的距离2a d ==得=即226R =,则2412S R =π=π.故选A.11.解析 由题意知22431x y xy xy z z +-=…,当且仅当2x y =时等号成立,所以1xy z 1?.当1xyz=11,即2x y =,xy z =时,221244x y z x x +-=-,令()244f x x x =-,()2334484x f x x x x-'=-+=,当02x <<时,()0f x '>,()f x 单调递增;当2x >时,()0f x '<,()f x 单调递减.所以()()max 21f x f ==.故选B.12.解析 ()232f x x ax b '=++,由题意,1和1-是方程2320x ax b ++=的两根,所以有()2113a +-=-,()113b ⨯-=,得0,3a b ==-,所以()33f x x x =-,如图所示,由于()2,2c ∈-,则()f t c =有三个根,设其为123,,t t t (123t t t <<),有121t -<<,211t -<<,312t <<.再由()1f x t =,()2f x t =,()3f x t =分别有三个根,则共有9个根,即()()()h x f f x c =-的零点个数为9.故选D.13.解析 由丙的诉述,丙的卡片为1和2或1和3,当丙的卡片为1和2时,则乙的卡片为2和3,d F OD PCBAE甲的卡片为1和3,满足题意.当丙的卡片为1和3时,易知不满足题意.故填1和3.14.解析 由正弦定理知a :b :c =sin A :sin B :sin C =2:3:4.由余弦定理知2222223427cos 22348b c a A bc +-+-===⨯⨯,则sin A =,a =,b =,c =,12S ==. 15.解析 由题意知,222214222AO AB xAB y AB AC a x y AB a ⋅=+⋅=-==u u u r u u u r u u u r u u u r u u u r u u u r ①222241222AO AC xAB AC y AC x y AC a a⋅=⋅+=-+==u u u r u u u r u u u r u u u r u u u r u u ur ②联立①②,解得22132624x ay a ⎧=+⎪⎨⎪=+⎩,则2213+6=26x y a a ++…当且仅当2212a a =时等号成立.故填16.解析 假设曲线()y f x =上存在两点,P Q 满足题设要求,则,P Q 只能在y 轴两侧. 不妨设()(),P t f t ()0t >,则()32,Q t tt -+,因为POQ △是以O 为直角顶点的直角三角形,所以0OP OQ ⋅=u u u r u u u r,即()()2320t f t t t -++= ①若此方程有解,则存在满足题设要求的两点,P Q ;若此方程无解,则不存在满足题设要求的两点,P Q .若0e t <<,则()32f t t t =-+,将其代入①式得()()232320t t ttt -+-++=,即4210t t -+=,而此方程无解,因此e t …,此时()ln f t a t =,代入①式整理得()11ln t t a=+,令()()()1ln e h x x x x =+…,则()1ln 10h x x x'=++>,所以()h x 在[)e +∞,上单调递增,()()e =e+1h t h >,所以对于10e 1a <+…,此方程总有解,即方程①总有解.故填10e+1⎛⎤ ⎥⎝⎦,.高三数学双基强化训练(五)答案部分一、选择题二、填空题 13. 23- 14.79- 15. 16. 49解析部分1.解析 命题:,221x p x x ∀∈>+R ,则命题:,221xp x x ⌝∃∈+R ….故选C.2.解析 由{}{}13,1,0,1,2A x x x =-<∈=-Z …, 得{}1,2,5B =,则集合B 的含有元素1的子集有{}1,{}1,2,{}1,5,{}1,2,5,共4种.故选B.3.解析 画出可行域如图所示.设3z x y =+,得3y z x =-,平移直线3y z x =-.由图可知,当直线3y z x =-经过点B 时,直线3y z x =-的截距最大.由304x y x y -=⎧⎨+=⎩=,得()1,3B ,此时z 最大, 3136z =⨯+=,所以3x y +的最大值为6.故选D.4.解析 复数()()()()213i 2213ii 3i 13i 13i 13i 5--===-++-.故选A. 5.解析 由已知,()2226f m =+=,得2m =.要使得()f x 的值不小于4,则()24x f x m =+…,得1x …,又[]3,3x ∈-,所以[]1,3x ∈.故()f x 的值不小于4的概率为()31213363P -===--.故选C.6.解析 模拟程序框图的运行过程.已知1,1k a ==,满足循环条件,执行循环体, 6a =,3k =; 满足循环条件,执行循环体, 33a =,5k =; 满足循环条件,执行循环体, 170a =,7k =; 满足循环条件,执行循环体, 857a =,9k =; 满足循环条件,执行循环体, 4294a =,11k =;由题意,此时应该不满足循环条件.退出循环.输出4294a =. 由此可根据选项知判断框内的条件为10?k <.故选C.7.解析 已知37,a a 是函数()243f x x x =-+的两个零点,所以374a a +=.又数列{}n a 为等差数列,所以{}n a 的前9项和()()19379991822a a a a S ++===.故选C. 8.解析 由已知,得()()1133,01log 1,0x x f x x x -⎧⎪-=⎨-<⎪⎩….当0x =时, 3y =.故排除选项A,D;可得()()13ln 3,011,01ln 3x x f x x x -⎧-⎪'-=⎨<⎪-⎩…,则函数()1f x -在()0,+∞上单调递减, 在(),0-∞上单调递增.故选C.9.解析 曲线()()22110x y x +-=…表示以()0,1为圆心,以1为半径的左半圆.因为圆心到直线10x y --=的距离d ==所以圆上的点到直线10x y --=的最大距离1a =,最小距离为()0,0到直线10x y --=的距离,即2b ==,则11a b -==.故选C.10.解析 如图所示,还原该几何体为四棱锥A BCDE -,将四棱锥A BCDE -放入一个棱长为2的正方体内,可知AB AC ===,3AE AD ==.则此几何体的表面积21112222226222⨯+⨯+⨯⨯=+.故选B.11.解析 由题意,得22112248AB AF BF AF BF AF BF a ++=+++==,若22AF BF +的最大值为5,则AB 的最小值为3.可知当AB 过点1F 且垂直x 轴时AB 最小,为22b a,即223b a =,得23b =.又1c ==,所以离心率12c e a ==.故选A. 12.解析 已知()()2e 31xf x a x a x =--+.令()()()e 231xf x a x ag x '=--+=.由函数()f x 在区间()0,ln3上有极值,等价于在()g x 在区间()0,ln3上单调且有零点,则()()0ln30g g <,即()()3132ln3310a a a a -----<,可得210a +<,解得12a <-.此时()e 20xg x a '=-<,所以()g x 在区间()0,ln3上单调递减,所以a 的取值范围是1,2⎛⎫-∞-⎪⎝⎭.故选A.13.解析 因为λ-a b 与c 垂直,所以()0λ-⋅=a b c ,即()()()2,01,21,2230λλ-⋅-=--=⎡⎤⎣⎦,解得23λ=-.故填23-.14.解析 由ππ1sin sin cos 32663αααπ⎡π⎤⎛⎫⎛⎫⎛⎫-=-+=+=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 得22π17cos 22cos 1213639ααπ⎛⎫⎛⎫⎛⎫+=+-=⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故填79-.15.解析 ,则可知它一定可以放在棱长为1的正方体内,则该三棱锥的外接球即为此正方体的外接球, 故该三棱锥外接球的直径即为正方体的体对角线,故填16.解析 由题知, 113a S ==,且21n S n n =++,()2211111n S n n n n -=-+-+=-+,以上两式相减,得()*122,n n n a S S n n n -=-=∈N …, 则()11321b =-⨯-=-,()()()*1222,nn b n n n =--∈N …, 所以5012501249698S b b b =+++=-+-+-+=L L ()121234474849-+-+-++-+=L ()12244949-+-+=.故填49.。
高三数学双基强化训练

高三数学双基强化训练(一)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}220A x x x =-…,{}22,B y y x x x A ==-∈,则A B =U ( ). A.[]02, B.[]12-, C.(]2-∞, D.[)0+∞, 2.如果复数()3i2ib z b -=∈+R 的实部和虚部相等,则z =( ). A.32 B.22 C.3 D.23.在一次跳伞训练中,甲、乙两位学员各跳一次.设命题p 是“甲降落在指定范围”,q 是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为( ). A.()() p q ⌝∨⌝ B.()p q ∨⌝ C.()()p q ⌝∧⌝ D.p q ∨4.已知{}n a 是公差为12的等差数列,n S 为{}n a 的前n 项和.若2a ,6a ,14a 成等比数列,则5S =( ). A.352 B.35 C.252D.25 5.以正方形的一条边的两个端点为焦点,且过另外两个顶点的椭圆与双曲线的离心率之积为( ). A.22B.1C.2D.2 6.如图是秦九韶算法的一个程序框图,则输出的S 为( ). A.()()1030020a x a x a a x +++的值 B.()()302100a x a x a a x +++的值C.()()001230a x a x a a x +++的值 D.()()20310a x a x a a x +++的值7.中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器——商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x 为( ). A.1.2 B.1.6 C.1.8 D.2.48.已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>><⎪⎝⎭的图像的相邻两对称中心的距离为π,且()π2f x f x ⎛⎫+=- ⎪⎝⎭,则函数π4y f x ⎛⎫=- ⎪⎝⎭是( ).A.奇函数且在0x =处取得最小值B.偶函数且在0x =处取得最小值C.奇函数且在0x =处取得最大值D.偶函数且在0x =处取得最大值9.已知函数()22,0lg ,0x x x f x x x ⎧+⎪=⎨>⎪⎩„,则函数()()11g x f x =--的零点个数为( ).A.1B.2C.3D.410.已知O ,A ,B 三地在同一水平面内,A 地在O 地正东方向2 km 处,B 地在O 地正北方向2 km 处,某测绘队员在A ,B 之间的直线公路上任选一点G 作为测绘点,用测绘仪进行测绘,O 地为一磁场,km 的范围内会测绘仪等电子仪器形成干扰,使测量结果不准确,则该测绘队员能够得到准确数据的概率是( ).A.12-B.2C.1D.1211.已知函数())20162016log 20162xx f x x -=+-+,则关于x 的不等式()()314f x f x ++>的解集为( ).A.14⎛⎫-+∞ ⎪⎝⎭,B.14⎛⎫-∞- ⎪⎝⎭, C.()0+∞,D.()0-∞, 12.已知函数()322339f x x ax a x a =--+.若14a >,且当[]1,4x a ∈时,()12f x a '„恒成立,则a 的取值范围为( ). A.14,45⎛⎤⎥⎝⎦ B.1,14⎛⎤ ⎥⎝⎦ C.1,13⎡⎤-⎢⎥⎣⎦ D.40,5⎡⎤⎢⎥⎣⎦二、填空题:本大题共4小题,每小题5分,共20分.13.已知函数()y f x =的图像在点()()22M f ,处的切线方程是4y x =+,则()()22f f +'= .14.设2a b +=, 0b >, 则12a a b+的最小值为 . 15.已知圆229C x y +=:,直线110l x y --=:与22100l x y +-=:的交点设为P 点,过点P 向圆C 作两条切线m ,n 分别与圆相切于A ,B 两点,则ABP S =△ .16.设数列{}()1,n a n n ∈N …满足12a =,26a =,且()()2112n n n n a a a a +++---=,若[]x 表示不超过x 的最大整数,则122017201720172017a a a ⎡⎤+++=⎢⎥⎣⎦L .高三数学双基强化训练(二)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.在复平面内表示复数()i 12i -的点位于( ).A.第一象限B.第二象限C.第三象限D.第四象限 2.对任意等比数列{}n a ,下列说法一定正确的是( ). A. 139,,a a a 成等比数列 B. 236,,a a a 成等比数列 C. 248,,a a a 成等比数列 D. 369,,a a a 成等比数列3.下列函数中,最小正周期为π且图像关于原点对称的函数是( ). A. πcos 22y x ⎛⎫=+⎪⎝⎭ B.πsin 22y x ⎛⎫=+ ⎪⎝⎭C.sin 2cos 2y x x =+D.sin cos y x x =+4.已知向量()()(),3,1,4,2,1k ===a b c ,且()23-⊥a b c ,则实数k =( ). A. 92-B. 0C. 3D. 152 5.执行如图所示的程序框图,若输出k 的值为6,则判断框内可填入的条件是( ). A .12s >B. 35s > C. 710s > D.45s >6.已知命题:p 对x ∀∈R ,总有20x>;:q “1x >”是“2x >”的充分不必要条件. 则下列命题为真命题的是( ).A. p q ∧B. p q ⌝∧⌝C. p q ⌝∧D. p q ∧⌝ 7.某几何体的三视图如图所示,则该几何体的表面积为( ).A. 54B. 60C. 66D. 728.设12,F F 分别为双曲线()222210,0x y a b a b-=>>的左、右焦点,双曲线上存在一点P使得是否k=k-1k k =9,s =1结束开始s=s ∙k k+1俯视图左视图正视图3254121293,4PF PF b PF PF ab +=⋅=,则该双曲线的离心率为( ). A.43 B. 53 C. 94 D. 3 9. 如图所示,在矩形ABCD 中,点A 在x 轴上,点B 的坐标为()1,0,且点C 与点D 在函数()1,011,02x x f x x x +⎧⎪=⎨-+<⎪⎩…的图像上.若在矩形ABCD 内随机取一点,则此点取自阴影部分的概率等于( ).A .16B .14C .38D .1210. 在ABC △中,π4B =,则sin sin AC ⋅的最大值是( ).A.14 B .34C.2 D.24+11.已知点()2,3A -在抛物线C :22y px =的准线上,过点A 的直线与C 在第一象限相切于点B ,记C 的焦点为F ,则直线BF 的斜率为( ). A .12 B .23 C .34 D .4312.设函数()()e21xf x x ax a =--+,其中1a <,若存在唯一的整数0x 使得()00f x <,则a 的取值范围是( ). A.3,12e ⎡⎫-⎪⎢⎣⎭ B.33,2e 4⎡⎫-⎪⎢⎣⎭ C.33,2e 4⎡⎫⎪⎢⎣⎭ D.3,12e ⎡⎫⎪⎢⎣⎭二、填空题:本大题共四小题,每小题5分,共20分.把答案填在题中的横线上.13.设全集{}{}{}110,1,2,3,5,8,1,3,5,7,9U n n A B =∈==N 剟,则()U A B =I ð______. 14.函数())2log 2f x x =的最小值为_________.15.设点()0,1M x ,若在圆O :221x y +=上存在点N ,使得30OMN ∠=o ,则0x 的取值范围是 .16.如图所示,在正方体1111ABCD A B C D -中,点E 是边BC 的中点.点P 在直线1BD (除B ,1D 两点)上运动的过程中,平面DEP 可能经过的该正方体的顶点是(写出满足条件的所有顶点).高三数学双基强化训练(三)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.若集合{}52A x x =-<<,{}33B x x =-<<,则A B =I ( ).A. {}32x x -<< B. {}52x x -<< C. {}33x x -<< D. {}53x x -<< 2.圆心为()1,1且过原点的圆的方程是( ).A.()()22111x y -+-= B.()()22111x y +++= C.()()22112x y +++= D.()()22112x y -+-= 3.下列函数中为偶函数的是( ). A.2sin y xx = B.2cos y x x = C.ln y x = D.2x y -=4.如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( ).A.310 B. 15 C. 110 D. 1205.执行如图所示的程序框图,输出的k 值为( ).A.3B.4C.5D.6 6.设a ,b 是非零向量,“g a b =a b ”是“//a b ”的( ). A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( ). A.128. 设实数a ,b ,t 满足1sin a b t +==,若t 确定,则( ). A . 2b 唯一确定 B . 22a a +唯一确定C .sin 2b唯一确定 D . 2a a +唯一确定二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中的横线上. 9.复数()i 1i +的实部为 .10.32-, 123,2log 5三个数中最大数的是 .11.在ABC △中,3a =,b =2π3A ∠=,B ∠= . 12.如图所示,ABC △及其内部的点组成的集合记为D ,(),P x y 为D 中任意一点,则23z x y =+的最大值为 .13. 已知F 是双曲线C :2218y x -=的右焦点,P 是C左支上一点,(A , 当APF △周长最小时,该三角形的面积为 .14.高三年级267位学生参加期末考试,某班37位学生的语文成绩,数学成绩与总成绩在全年级中俯视图侧(左)视图正(主)视图的排名情况如下图所示,甲、乙、丙为该班三位学生.从这次考试成绩看,①在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是 ; ②在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是 .高三数学双基强化训练(四)一、 选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知全集{}1,2,3,4,5,6U =,集合{}2,3,5M =,{}4,5N =,则集合()U M N U ð中元素的个数是( ). A .0个 B .1个 C .2个 D .3个2.41i=-( ). A. 1C. 2D. 3.设124a =,21log 4b =,213c ⎛⎫= ⎪⎝⎭,则a ,b ,c 的大小关系是( ).A. a c b >>B. a b c >>C. b a c >>D. c a b >>总成绩年级名次267总成绩年级名次4. 已知ABC △是等腰直角三角形,D 是斜边BC 的中点,2AB=,则()AB AC AD +⋅u u r u u ru u r=( ). A .2 B..4 D5. 若某几何体的三视图如图所示,则此几何体的直观图是( ).A .B .C .D .6.水厂监控某一地区居民用水情况,该地区A ,B ,C ,D 四个小区在8:0012:00:时用水总量Q 与时间t 的函数关系如图所示,在这四个小区中,单位时间内用水量逐步增加的是( ).俯视图侧视图正视图7. 已知函数()y f x =()x ∈R 是偶函数,其部分图像如图所示, 则在区间()2,0-上与函数()f x 的单调性相同的是( ).A.21y x =-+ B.cos y x =C. e ,0e ,0x x x y x -⎧⎪=⎨<⎪⎩… D.2log y x =8. 已知四面体A BCD -满足下列条件:(1)有一个面是边长为1的等边三角形;(2)有两个面是等腰直角三角形.21Oyx那么四面体A BCD -的体积的取值集合是( ).A .12,212⎧⎪⎨⎪⎪⎩⎭B .13,612⎧⎪⎨⎪⎪⎩⎭C .232121224⎨⎪⎪⎩⎭ D.122,61224⎧⎪⎨⎪⎪⎩⎭ 二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中的横线上.9. 已知函数()2,1,1x x f x x x ⎧=⎨->⎩…,若()2f x =,则.10. 执行下面的程序框图,如果输入的5n =,那么输出的S 的值为______.11. 某工厂对一批产品进行了抽样检测.如图所示是根据抽样检测后的产品净重(单位:克) 数据绘制的频率分布直方图,其中产品净重的范围是[]96,106,样本数据分组为[)96,98,[)98,100,[)100,102,[)102,104,[]104,106,已知样本中产品净重小于100克的个数是36,则样本中[98,104)的产品的个数是_____________.12. 数列{}n a 中,如果132n n a a +=-()*n ∈N ,且112a =,那么数列{}n a 的前5项的和5S 的值为 .=x13. 已知圆()()22115x y ++-=经过椭圆:C 22221x y a b+=()0a b >>的右焦点F 和上顶点B ,则椭圆C 的离心率为_______.14. 点P 到曲线C 上所有点距离中的最小值称为点P 到曲线C 的距离. 已知点()2,0P ,若点P 到曲线C①2230x y -=;②22(1)(3x y ++-=;③225945x y +=;④22y x =. 符合题意的正确序号是 (写出所有正确的序号).高三数学双基强化训练(五)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知()()i 1i a b +-=,其中i 为虚数单位,则实数,a b 的值分别为( ). A. 1,1a b =-= B. 1,2a b =-= C.1,1a b == D.1,2a b ==2.如果命题:120p x y -+-=,命题()():120q x y --=,那么命题p 是命题q 的( ). A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件3.要得到函数πcos 23y x ⎛⎫=- ⎪⎝⎭的图像只需将cos2y x =的图像( ). A.向右平移π3个单位长度 B.向左平移π3个单位长度 C.向右平移π6个单位长度 D.向左平移π6个单位长度4.某程序框图如图所示,程序运行后,输出s 的结果是( ).A.143B.120C.99D.805.过点()1,2C -的直线与圆226210x y x y +-++=交于,A B 两点,则AB 的最小值是( ).A.5B.4D.6.函数()22,01ln ,0x x x f x x x ⎧+=⎨-+>⎩„的零点个数为 ( ).A.4B. 3C.2D.17.已知函数()y f x =是在闭区间[]0,2上单调递增的偶函数,设()()()2,0,1a f b f c f =-==-,则( ).A. b c a <<B.a b c << C. a c b << D. c b a << 8. 在R 上定义运算()1a b a b ⊗=-.若不等式()()1x y x y +⊗-<对于任意实数x 恒成立,则实数y 的取值范围是( ).A.()0,2B.()1,1-C.31,22⎛⎫-⎪⎝⎭ D. 13,22⎛⎫- ⎪⎝⎭二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中的横线上. 9.已知集合{}{}22560,280A x x x B x x x =-+==+-=,则A B =U ___________.10.若变量x y ,满足约束条件33023010x y x y x y +-⎧⎪--⎨⎪-+⎩…„…,则z x y =+的最大值为____________.11.若双曲线()222210,0x y a b a b -=>>与抛物线223y bx =有一个交点为(,则此双曲线的离心率为___________.12. 在ABC △中,,,a b c 分别为角,,A B C 的对边,若cos cos b c B C =,且21cos ,32A b ==,则a 的值为___________.13.在ABC △中,2BD CD =u u u r u u u r ,若AD AB AC λμ=+u u u r u u u r u u u r,则4λμ-=___________.14. 在正方体1111ABCD A B C D -中,点Q 是1CC 的中点,点F 是侧面11BCC B 内的动点且1A F ∥平面1AD Q ,则1A F 与平面11BCC B 所成角的正切值的取值范围为 .高三数学双基强化训练(一)答案部分一、选择题二、填空题13. 7 14.34 15. 1922516. 2016解析部分1.解析 易得集合A 为[]02,,集合B 为y 的值域[]10-,,则[]12A B =-U ,.故选B.QABCDA 1B 1C 1D 12.解析 令3ii 2ib a a -=++,展开3i 3i b a a -=+,解得3a =,39b a =-=-,故3z =.故选A. 3.解析 已知命题p 是“甲降落在指定范围”,则命题p ⌝是“甲没有降落在指定范围”;同理,命题q ⌝是“乙没有降落在指定范围”,则“至少有一位学员没有降落在指定范围”可表示为()()p q ⌝∨⌝.故选A.4.解析 因为{}n a 是公差为12的等差数列,n S 为{}n a 的前n 项和,2614a a a ,,成等比数列,所以2111111513222a a a ⎛⎫⎛⎫⎛⎫+⨯=++⨯ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,解得132a =, 所以535412552222S ⨯=⨯+⨯=.故选C. 5.解析 以正方形的一条边的两个端点为焦点,且过另外两个顶点的椭圆的离心率为1e ==,双曲线的离心率为2e ==,故他们的积为1.故选B. 6.解析 32303,2,k S a k S a a x ==−−→==+−−→是是()123001,k S a a a x x ==++−−→是()()01023000,k S a a x a a x x ==+++−−→否输出.故选C.7.解析 由三视图知,商鞅铜方升由一圆柱和一长方体组合而成.由题意得()215.43112.62x x ⎛⎫-⨯⨯+π⋅= ⎪⎝⎭,解得 1.6x =.故选B.8.解析 因为()f x 的图象的相邻两对称中心的距离为π,所以2T=π,22T ωπ=π=,所以1ω=.所以()()sin f x A x ϕ=+. 由()π2f x f x ⎛⎫+=- ⎪⎝⎭,得()πsin sin 2A x A x ϕϕ⎛⎫++=-+ ⎪⎝⎭, 所以π22x x k ϕϕ++=-++π或()π22x x k k ϕϕ++=π--++π,∈Z . 又π2ϕ<,令0k =,得π4ϕ=.所以()πsin 4f x A x ⎛⎫=+ ⎪⎝⎭.则πππsin cos ,0444y f x A x A x A ⎛⎫⎛⎫=-=-+=>⎪ ⎪⎝⎭⎝⎭.故选D.9.解析 ()()()()()()2242,11211,1011lg 11,1lg 11,10x x x x x x g x f x x x x x ⎧⎧-+-+---⎪⎪=--==⎨⎨--<--->⎪⎪⎩⎩…„,所以当1x …时,函数()g x 有1个零点,当1x <时,函数()g x 有两个零点,所以函数的零点共有3个.故选C.10.解析 由题意,AOB △是直角三角形,2OA OB ==,所以AB =O 的东北方向范围为14个圆,与AB 相交于C D ,两点,作OE AB ⊥,则OE =2CD =,所以该测绘队员能够得到准确数据的概率是112-=-.故选A.11.解析 令())20162016log 2016x x g x x -=+-,原不等式()()314f x f x ++>等价于()()310g x g x ++>,注意到()()g x g x =--, 即()g x 为奇函数,分析()g x 的解析式可知,()g x 在定义域内单调递增, 则()()131314g x g x x x x +>-⇒+>-⇒>-. 12.解析 ()22369f x x ax a '=--的图象是一条开口向上的抛物线,关于x a =对称. 若114a <„,则()f x '在[]14a ,上是增函数,从而()f x '在[]14a ,上的最小值是()21369f a a '=--,最大值是()2415f a a '=.由()12f x a '„,得221236912a x ax a a ---剟,于是有()2136912f a a a '=---…,且()241512f a a a '=„.由()112f a '-…得113a -剟,由()412f a a '„得405a 剟.所以14,45a ⎛⎤∈ ⎥⎝⎦. 若1a >,则()21212f a a a '=>.故当[]14x a ∈,时()12f x a '„不恒成立. 所以使()[]()1214f x a x a '∈,„恒成立的a 的取值范围是14,45⎛⎤⎥⎝⎦. 13.解析 由函数在某点的导数等于函数在该点的切线的斜率可知()21f '=,又点M 必在切线上,代入切线方程4y x =+,可得()26f =,所以有()()227f f '+=. 14.解析111124444a a a ab b a b a b a b ++=+=±++±+….(当且仅当2a b =时等号成立),最小值为34(此时2a =-,4b =) 15.解析 由圆229C x y +=:,得圆心()00O ,,半径3r =;直线1l 和2l 的交点坐标为()3,4P , 切线长4PA PB ==,PA OA ⊥,3OA OB r ===;设AB 与OP 的交点为M , 则AB OP ⊥,POB PBM △∽△,得165PM =,125BM =, 所以2425AB BM ==,1162419225525ABP S =⨯⨯=△. 16.解析 由已知得{}1n n a a -+是以4为首项,2为公差的等差数列,所以122n n a a n -=++.利用累加可得()1112n a a n n n -=+++,()()()()112112n a n n n n n +=+++=++. 从而2n a n n =+.1220161220162017201720171112017a a a a a a ⎡⎤⎛⎫⎛⎫+++=+++⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦L L . 又1220161111111111122320162017223a a a +++=+++=-+-++⨯⨯⨯L L L 1111201620172017-=-, 则122016111120172017120162017a a a ⎡⎤⎛⎫⎡⎤⎛⎫+++=-=⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭⎣⎦L .高三数学双基强化训练(二)答案部分一、选择题二、填空题13. {}7,9 14. 14-15. ⎡⎣ 16.11,,A B D解析部分1. 解析 由()2i 12i i 2i 2i -=-=+,复数对应的点在第一象限.故选A.2. 解析 因为{}n a 是等比数列,所以()()*10n na q q n a +=≠∈N , 则369,,a a a 成等比数列. 故选D. 3. 解析 对于选项A :πcos 2sin 22y x x ⎛⎫=+=- ⎪⎝⎭, 函数的最小正周期为π且图像关于原点对称; 对于选项B :πsin 2cos 22y x x ⎛⎫=+= ⎪⎝⎭, 函数的最小正周期为π且图像关于y 轴对称; 对于选项C:πsin 2cos224y x x x ⎛⎫=+=+ ⎪⎝⎭,函数的最小正周期为π,但其图像不关于原点对称; 对于选项D:πsin cos 4y x x x ⎛⎫=+=+ ⎪⎝⎭,函数的最小正周期为2π,且图像不关于原点对称.故选A.4. 解析 由()23-⊥a b c ,且(),3k =a ,()1,4=b ,()2,1c =, 得()22360k --=,解得3k =.故选C.5. 解析 程序框图的执行过程如下:1,9s k ==;9,810s k ==;988,710910s k =⨯==;877,610810s k =⨯==,循环结束. 故可填入的条件为710s >.故选C.6. 解析 p 是真命题,q 为假命题,故p ⌝为假命题,q ⌝为真命题. 从而p q ∧为假,p q ⌝∧⌝为假,p q ⌝∧为假,p q ∧⌝为真.故选D.7. 解析 该几何体的直观图如图所示,易知该几何体的表面积是由两个直角三角形,两个直角梯形和一个矩形组成的.则其表面积()()25525411343535602222S +⨯+⨯=⨯⨯+⨯⨯+++⨯=.故选B.8. 解析 设1PF m =,2PF n =,依题意不妨设0m n >>.于是3294m n b m n a mn ab ⎧⎪+=⎪-=⎨⎪⎪=⎩,所以9432m n m nmn +-=⋅⋅,得3m n =或13m n =-(舍). 所以a n =,43b n =,53c n =,故53c e a ==.故选B. 9. 解析 依题意,()1,2C ,()2,2D -,326ABCD S =⨯=矩形,133122S =⨯⨯=阴影,则点取阴影部分的概率等于312=64.故选B.10. 解析 在ABC △中,π4B =,则3π4AC +=,因此3πsin sin sin sin sin 422A C A A A A A ⎛⎫⎛⎫⋅=⋅-=+= ⎪ ⎪ ⎪⎝⎭⎝⎭)2sin cos sin A A A +=11cos2π1sin 222242A A A ⎤-⎫⎛⎫+=-+=⎥⎪ ⎪⎝⎭⎝⎭⎣⎦1πsin 2244A ⎛⎫-+ ⎪⎝⎭3π04A <<.当ππ242A -=,即3π8A =时,sin sin A C ⋅取得最大值24+.故选D.11. 解析 依题意,抛物线()220y px p =>的准线方程为2x =-,2543所以22p-=-,得4p =,因此抛物线的方程为28y x =. 设过点()2,3A -的直线方程为()32y k x -=+,联立直线方程与抛物线方程,得()2328y k x y x⎧-=+⎪⎨=⎪⎩, 消x 建立关于y 的一元二次方程得2328y y k ⎛⎫-=+ ⎪⎝⎭,即2816240ky y k -++=,()64416240k k ∆=-+=,得22320k k +-=,解得12k =或2-(舍). 因此直线与抛物线相切于点()8,8B ,则直线BF 的斜率43k =.故选D. 12.解析 设()()e21xg x x =-,()h x ax a =-,可转化成存在唯一的整数0x ,使得()()g x h x <. 因为()()'e21xg x x =+,所以当12x <-时,()'0g x <,()g x 在1,2⎛⎫-∞- ⎪⎝⎭上单调递减;当12x >-时,()'0g x >,()g x 在1,2⎛⎫-+∞ ⎪⎝⎭上单调递增. 因为当0x =时,()01g =-,()01h a =->-,所以()()00g h <. 又因为存在唯一的整数0x ,使得()()g x h x <,所以()()()()1111g h g h ⎧⎪⎨--⎪⎩……,即e 032ea ⎧⎪⎨--⎪⎩……,解得32e a ….又因为1a <,所以312ea <„.故选D .y=e x13. 解析 {}4,6,7,9,10U A =ð,(){}{}{}4,6,7,9,101,3,5,7,97,9U A B ==I I ð. 14. 解析 ()()2log 2f x x =+=()221log 22log 2x x += ()222log log x x +.令2log t x =∈R ,则2,y t t t =+∈R ,函数的最小值为14-.因此函数的最小值为14-.15. 解析 解法一:依题意,若圆22:1O x y +=上存在点N ,使得30OMN ∠=o,如图所示.因为OMN OMN '∠∠„,所以30OMN '∠o …,因此1sin 2ON OMN OM ''∠=…,即112OM …, 得2OM „,故2014x +„,解得0x .所以0x的取值范围是⎡⎣.解法二:在OMN △中,由30OMN ∠=o,据正弦定理得sin 30sin ON OMONM=∠o, 即sin 2sin sin 30ONMOM ONM ∠==∠o. 又()0,150ONM ∠∈o o,所以02OM <„,2,解得0x所以的取值范围是⎡⎣.16. 解析 依题意,平面DEP 可能经过正方体的顶点是1A ,1B ,D .因为平面1A DE 与直线1BD 相交,平面1B DE 与直线1BD 相交.且1//BD 平面1C DE.高三数学双基强化训练(三)答案部分一、选择题二、填空题9. 1 10. 2log 5 11.π412. 7 13. 乙;数学 解析部分1. 解析 依题意,得{}32A B x x =-<<I .故选A.2. 解析 由已知可得圆心为()1,1,所以圆的方程为()()22112x y -+-=. 故选D.3. 解析 函数2sin y x x =为奇函数,2cos y x x =为偶函数,ln y x =与2x y -=为非奇非偶函数.故选B.4. 解析 从1,2,3,4,5中任取3个不同的数构成一组勾股数,只有1种情形,即这3个数为3,4,5.从5个不同的数中任取3个不同的数有10种情形,分别是1,2,3;1,2,4;1,2,5;1,3,4;1,3,5;1,4,5;2,3,4;2,3,5;2,4,5; 3,4,5.因此,3个数构成一组勾股数的概率是110.故选C. 5. 解析 执行程序框图,13322a =⨯=,1k =,3124a =<−−→否 313224a =⨯=,2k =,3144a =<−−→否313428a =⨯=,3k =,3184a =<−−→否3138216a =⨯=,4k =,31164a =<−−→是输出4k =.故选B.6. 解析 因为cos ,⋅=a b a b a b ,所以若⋅=a b a b ,则cos ,1=a b ,即,0=a b ,因此//a b .反之,若//a b ,并不一定推出⋅=a b a b ,而是⋅=a b a b ,原因在于:若//a b ,则,0=a b 或π,而当,=πa b 时,=-g a b a b ,所以“⋅=a b a b ”是“//a b ”的充分不必要条件.故选A.7. 解析 利用特殊的几何体——正方体,还原几何体.如图所示,四棱锥1C ABCD -为三视图所故选C.8. 解析 由,,a b t ∈R ,满足1sin a b t +==,得222121t a a a =+=++,若t 确定,则22a a +唯一确定.故选B.9. 解析 ()2i 1i i i 1i +=+=-+ ,其实部为1-.10. 解析 3128-=,123=2log 52>,故1322log 532->>,所以最大的数是2log 5.11. 解析 在ABC △中,由正弦定理知sin sin a b A B =sin B=,所以sin 2B =, 又由题可得π0,3B ⎛⎫∈ ⎪⎝⎭,得π4B =. 12. 解析 依题意,23z x y =+在点()2,1A 处取得最大值7.13. 解析 如图所示,APF C AP PF AF =++△,由已知AF 为定值,当APF △周长最小时,则PA PF +最小.根据双曲线的定义知,2PF PF a '=+(F '为双曲线的左焦点),得2PA PF PA PF a '+=++.若PA PF +最小,则PA PF '+最小,即A ,P ,F '三点共线.D 1D B 1A 1C 1ABC又(A ,()3,0F '-,则AF k '=,AF '所在的直线方程为)3y x =+,联立方程)22318y x y x ⎧=+⎪⎨-=⎪⎩,消去y 建立关于x 的一元二次方程得29140x x ++=, 解得12x =-,27x =-.据题意2P x =-,P y =116622APF AF F PF F S S S ''=-=⨯⨯⨯⨯=△△△14. 解析 从图像的直观分析,判断结论.①从图像知,在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是乙; ②从图像知,在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是数学.高三数学双基强化训练(四)答案部分一、选择题二、填空题9. 1 10. 14 11. 90 12. 252-13.1014. ①②④ 解析部分1. 解析 由题意可得{}2,3,4,5M N =U ,又因为{}1,2,3,4,5,6U =,所以(){}1,6U M N =U ð.故集合()U M N U ð中元素的个数是2个.故选C.2. 解析441i 1i ===--故选D. 3. 解析由1242a ===,2221log log 224b -===-,21139c ⎛⎫== ⎪⎝⎭,可得b c a <<.故选A.4. 解析 由ABC △为等腰直角三角形,且点D 是斜边BC 的中点可得2AB AC AD +=u u u r u u u r u u u r,又由题可求得AD =()2224AB AC AD AD AD +==⨯=u u u r u u u r u u u r u u u r u u u rg .故选C.5. 解析 由正视图是正方形,可排除A 选项;由侧视图中虚线是从左上角到右下角,可排除C ,D 两个选项.故选B.6. 分析 单位时间内的用水量,即为函数()Q t 的斜率,亦即函数()Q t 的导函数.解析 对于选项A ,()Q t '为一常数;对于选项B ,()Q t '单调递增,符合题意;对于选项C ,()Q t '单调递减;对于选项D ,()Q t '先增大后减小.故选B.7. 解析 因为函数()f x 是偶函数,且在()0,2上单调递增,所以()f x 在()2,0-上单调递减.画出2log y x =的草图,如图所示.由图可知,2log y x =在()2,0-上单调递减.故选D.8. 分析 在四面体A BCD -中,先确定其中一个面为等边三角形,如BCD △为等边三角形,再对棱的垂直情况进行讨论.不妨将棱分为两类,一类是,,AB AC AD ,为侧棱;一类是,,BC BD CD ,为底面的棱,则根据题意可以有:①侧棱互相垂直;②一条侧棱与底面垂直;③不同的侧棱与不同的底面的棱垂直,然后分别根据条件求出体积即可.解析 在四面体A BCD -中,令BCD △是边长为1的等边三角形.①若,,AB AC AD 两两垂直,如图(a )所示,点A 为“墙角”,可求出==AB AC AD ,ABC △,ACD △,ABD △均为等腰直角三角形,符合条件(2),此时A BCD D ABC V V --==11133222224ABC S AD ⎛=⨯⨯⨯⨯= ⎝⎭g △.排除A ,B . ②若AB BD ⊥,AB BC ⊥,即AB ⊥平面BCD ,如图(b )所示,则1AB =,AC AD ==ABC △,ABD △均为等腰直角三角形,符合条件(2),此时A BCD V -=11111332BCD S AB ⎛=⨯⨯⨯= ⎝⎭g △.排除D .故选C .图(a ) 图(b ) 图(c )评注 对于第3种情况,可假设AB BC ⊥,如图(c )所示,则1AB =,AC =1AD =时,可有AD CD ⊥,ABC △,ACD △均为等腰直角三角形,符合条件(2),取AC 中点O ,连接,OB OD ,由题可得,OB AC OD AC ⊥⊥,所以AC ⊥平面BOD ,且可求出2OB OD ==,又因为1BD =,所以222OB OD BD +=,即OB OD ⊥,所以112224OBD S =⨯=△,所以13A BCD A BOD C BOD BOD V V V S OA ---=+=+g △1133BOD BOD S OC S AC ==g g △△1134⨯=12.9. 解析 当22x =时,得1x =,满足1x …;当2x -=时,得2x =-,与1x >矛盾,故舍去,所以1x =.10. 解析 由程序框图可知,第一次循环为:055S =+=,514n =-=,42<−−→否第二次循环:549S =+=,413n =-=,32<−−→否第三次循环:9312S =+=,312n =-=,22<−−→否 第四次循环为:12214S =+=,211n =-=,12<−−→是 此时循环结束,输出S 的值为14.11. 解析 由直方图可知,小于100克的频率为()0.050.120.3+⨯=,所以样本的总个数为ABCDABCDBCDA361200.3=个,则样本中[)98,104的产品个数为()1200.10.150.125290⨯++⨯=个. 12. 解析 由132n n a a +=-,得132n n a a +-=-,所以数列{}n a 是首项为12,公差为32-的等差数列,则()531132555252222S a a d ⎡⎤⎛⎫==⨯+=⨯+⨯-=-⎪⎢⎥⎝⎭⎣⎦. 13. 解析 依题意,令0y =得()2115x ++=,即1x =或3x =-,所以椭圆右焦点为()1,0F ,令0x =得()2115y -+=,即3y =或1-,所以椭圆上顶点为()0,3B ,因此1c =,3b =,a =,椭圆离心率10c e a ===.14. 解析 对于①,将2230x y -=0y -=0y +=,即曲线C 表示两条相交直线,因此点()2,0P 到曲线2230x y -=的距离d ==对于②,点()2,0P 到曲线()(2213x y ++-=的距离d ==,满足题意,故②正确;对于③,设曲线225945x y +=上任意一点Q 的坐标为(),x y ,其中33x-剟,则()222224552449x PQ x y x x -=-+=-++=24992x ⎛⎫- ⎪⎝⎭,所以当3x =时,2PQ 最小,即min 1PQ =,不满足题意,故舍去.对于④,设曲线22y x =上任意一点M 的坐标为2,2y y ⎛⎫⎪⎝⎭,则()2222202y PM y ⎛⎫=-+-= ⎪⎝⎭ 2442222424133442y y y y y y ⎛⎫++-=-+=-+ ⎪⎝⎭…,当且仅当22y =时取“=”,因此PM ,故④正确.综上所述,符合题意的正确序号是①②④.高三数学双基强化训练(五)答案部分一、选择题:二、填空题:9.{}4,2,3- 10. 9 11. 3 12. 613.6- 14.2,⎡⎣解析部分1.解析 ()()()i 1i +1+1i a a a b +-=-=,所以101a a b -=⎧⎨+=⎩,解得12a b =⎧⎨=⎩.故选D.2.解析 命题:120p x y -+-=,即10x -=且20y -=,即1x =且2y =. 命题()():120q x y --=,即10x -=或20y -=,即1x =或2y =. 由于p q ⇒,而q p ⇒/,所以p 是q 的充分不必要条件.故选A.3.解析 因为ππcos 2cos 236y x x ⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,根据函数图像平移左加右减的规律,只需将cos 2y x =的图像向右平移π6个单位长度.故选C.4.解析 该程序框图的模拟分析如下表所示.由上表,输出s 的值为()3211035211202+⨯++⋅⋅⋅+==. 故选B.5.解析 将圆的方程226210x y x y +-++=化为标准方程为()()22319x y -++=,则圆心()3,1O -,所以3OC =<,所以点C 在圆O 内.设圆心O 到AB 的距离为d,则AB =当过点C 的直线与OC 垂直时,d 有最大值,此时AB 有最小值,所以4AB ==.故选C.6.解析 解法一(图像法):函数()f x 的图像如图所示.观察图像可得函数()f x 的零点个数为3.故选B.解法二:若220x x +=,则0x =或2-,符合条件;若1ln 0x -+=,则e x =,符合条件,所以()f x 有3个零点.故选B.7.解析 因为偶函数对称区间的单调性相反,所以函数()y f x =在[]2,0-上单调递减,又因为210-<-<,所以()()()210f f f ->->,即a c b >>.故选A.8.解析 由定义的新运算可得()()()()1x y x y x y x y +⊗-=+-+,所以()()11x y x y +-+<,整理得2210x x y y -+++-<.因为此不等式对实数x 恒成立,所以()()2214110y y ∆=-⨯-+-<.解得3122y -<<,即y 的取值范围为31,22⎛⎫- ⎪⎝⎭.故选C. 9.解析 由题可得{}2,3A =,{}4,2B =-,所以{}4,2,3A B =-U .10.解析 画出不等式组表示的平面区域如图所示,当直线z x y =+过点A 时,z 有最大值,联立方程10230x y x y -+=⎧⎨--=⎩,解得45x y =⎧⎨=⎩,即()4,5A ,所以max 9z =.11.解析将(代入抛物线方程中,得2233b =⨯,解得1b =,所以双曲线为2221x y a -=,再将点(代入双曲线方程中,得a =2c ==,所以c e a ==. 12.解析 用正弦定理将cos cos b c B C =中边的关系转化为角的关系,得sin sin cos cos B CB C=,即tan tan B C =.又因为(),0,πB C ∈,所以B C =,12b c ==.由余弦定理可得2221111212cos 2442236a b c bc A =+-=+-⨯⨯⨯=,所以6a =.13.解析 如图所示,由2BD CD =u u u r u u u r得点D 是BC 延长线上一点,且BC CD =,所以()12AC AB AD =+u u u r u u u r u u u r ,所以2AD AC AB =-u u u r u u u r u u u r.又因为AD AB AC λμ=+u u u r u u u r u u u r ,所以1,2λμ=-=,所以41426λμ-=-⨯-=-.14.解析 设平面1AD Q 与直线BC 交于点P ,则可证得点P 为BC 的中点,连接,AP QP ,取1BB 的中点E ,11B C 的中点G ,连接11,,A E A G EG ,如图所示.易证QP EG ∥,又因为QP ⊂平面1AD Q ,EG ⊄平面1AD Q ,所以EG ∥平面1AD Q .同理1A G ∥平面1AD Q .又因为1AG EG G =I ,所以平面1A GE ∥平面1AD Q .由已知1A F ∥平面1AD Q ,所以1A F ⊂平面1A GE .设1A F 与平面11BCC B 所成的角为θ,因为11A B ⊥平面11BCC B ,所以111tan A B B Fθ=.当点F 与E 或G 重合时,1B F最大,1=0DC31 tan θ有最小值,此时1111tan 212A B B F θ===;当点F 为EG 中点,即1B F EG ⊥时,1B F 最小,tan θ有最大值,此时111tan A B B F θ===所以tan θ的取值范围是2,⎡⎣.PGED 1C 1B 1A 1D CB A Q。
2021年高三数学上学期第一次双基检测试卷 文(含解析)

2021年高三数学上学期第一次双基检测试卷文(含解析)一、选择题(共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={x|x2﹣2x≤0},B={x|﹣1<x<1},则A∩B=()A.∅B. {x|﹣1<x≤0}C.{x|0≤x<1} D. R2.复数(i是虚数单位)在复平面上对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是()A. r2<r4<0<r3<r1B. r4<r2<0<r1<r3C. r4<r2<0<r3<r1D. r2<r4<0<r1<r34.有以下四个命题p1:∃x∈(﹣∞,0),4<5,p2:在锐角三角形ABC中,若tanA>tanB,则A>B;p3:∃x∈R,cosx0≥1;p4:∀x∈R,x2﹣x+1>0其中假命题是()A. p1B. p2C. p3D. p45.已知向量=(λ,1),向量=(2,1+λ),且与﹣垂直,则λ的值为()A. 0 B. 0或3 C.﹣3或0 D. 46.已知双曲线﹣=1的一条渐近线与直线l:2x+y+2=0垂直,则此双曲线的离心率是()A.B.C.D. 47.设x,y满足,则z=x+2y的最小值等于()A.﹣3 B. 3 C. 6 D. 128.等比数列{a n}的前n项和为S n,且a1+a3=,S4=,则S n()A.B.C.D. 2n﹣39.已知棱长为四面体ABCD的各顶点在同一个球面上,则该球的体积为()A.πB.πC.πD.3π10.执行如图所示的程序框图,若输出y=2,则输出的x的取值范围是()A. [6,23] B.(12,25] C.(14,26] D. [25,52]11.一个组合体的三视图如图所示,则该几何体的体积为()A. 16 B. 20 C.D.12.已知函数f(x)=|2x﹣2|,若m≠n,且f(m)=f(n),则m+n的取值范围是()A.(1,+∞)B.(2,+∞)C.(﹣∞,1)D.(﹣∞,2)二、填空题(共4小题,每小题5分,满分20分)13.曲线y=x+在点(1,2)处的切线方程为.14.已知数列{a n}满足a1=2,a n+1=a n+n(n∈N*),则a n的最小值是.15.已知函数f(x)=Asin(x+φ)(A>0,|φ|<),当x=π时,f(x)取最大值,则f (x)在[﹣π,0]上的单调增区间是.16.已知抛物线y2=2x,过焦点F的直线与抛物线交于A,B两点,过A,B分别作y轴的垂线,垂足分别为C,D,则|AC|+|BD|的最小值为.三、解答题(共6小题。
高三数学下学期第一次3月双基测试试题 文含解析 试题

2021届高三数学下学期第一次〔3月〕双基测试试题文〔含解析〕一、选择题〔本大题一一共12小题,一共分〕A={0,1,2,3,4},B={-1,0,1,2},那么A∩B=〔〕A. B. 1,C. D. 0,1,2,3,【答案】B【解析】【分析】根据集合的交集的概念得到结果.【详解】∵A={0,1,2,3,4},B={-1,0,1,2};∴A∩B={0,1,2}.应选:B.【点睛】这个题目考察了集合的交集的概念和运算,属于根底题.2.i〔1+i〕=〔〕A. B. C. D.【答案】A【解析】【分析】根据复数的乘法运算得到结果.【详解】根据复数的乘法运算得到:原式i〔1+i〕=i-1.应选:A.【点睛】这个题目考察了复数的乘法运算,题目简单根底.n与平面α,β,假设n⊂α,那么“n⊥β〞是“α⊥β〞的〔〕A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】A【解析】【分析】根据课本的面面垂直的断定得到假设“n⊥β,n⊂α,那么“α⊥β〞,假设n⊂α,α⊥β,那么n不一定垂直β,进而得到答案.【详解】假设“n⊥β,n⊂α,那么“α⊥β〞,假设n⊂α,α⊥β,那么n不一定垂直β,也可能平行,故n⊥β〞是“α⊥β〞的充分不必要条件应选:A.【点睛】这个题目考察了充分不必要条件的判断,判断充要条件的方法是:①假设p⇒q为真命题且q⇒p为假命题,那么命题p是命题q的充分不必要条件;②假设p⇒q为假命题且q⇒p为真命题,那么命题p是命题q的必要不充分条件;③假设p⇒q为真命题且q⇒p为真命题,那么命题p是命题q的充要条件;④假设p⇒q为假命题且q⇒p为假命题,那么命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分〞的原那么,判断命题p与命题q的关系.的最小正周期是〔〕A. B. C. D.【答案】B【解析】【分析】根据三角函数的周期公式得到结果.【详解】根据三角函数的周期公式的求法,得到:函数,∵ω=2,∴T=π.应选:B.【点睛】这个题目考察了三角函数的周期公式的应用,题目比拟简单.存在周期性,其最小正周期为T=.5.某高中的一次测验中,甲、乙两个班级的九科平均分的雷达图如下图,以下判断错误的选项是〔〕A. 乙班的理科综合成绩强于甲班B. 甲班的文科综合成绩强于乙班C. 两班的英语平均分分差最大D. 两班的语文平均分分差最小【答案】D【解析】【分析】先对图象数据进展处理,再逐一进展判断即可得到结果.【详解】由甲、乙两个班级的九科平均分的雷达图可得:乙班的理科综合成绩强于甲班,即选项正确,甲班的文科综合成绩强于乙班,即选项正确,两班的英语平均分分差最大,即选项正确,两班地理平均分分差最小,即选项错误,应选D.【点睛】此题考察了对图象数据的处理才能,意在考察灵敏应用所学知识解答问题的才能,属于中档题.6.2,b,8是等比数列,那么实数b=〔〕A. 6B. 4C.D. 4或者【答案】D【解析】【分析】根据等比数列的性质的得到,进而得到结果.【详解】∵2,b,8成等比数列,根据等比数列的性质得到:∴b=±4.应选:D.【点睛】这个题目考察了等比数列的性质的应用,题目比拟简单根底.y=〔x∈R〕的值域为〔〕A. B. C. D.【答案】C【解析】【分析】根据指数函数的性质以及反比例函数的图像的性质得到结果.【详解】因为2x>0,所以由2x+1>1,再由反比例图象的性质得到:0<<1.应选:C.【点睛】这个题目考察了函数值域的求法,以及指数函数的性质的应用题目比拟根底. 8.△ABC的内角A、B、C所对边分别为a、b、c,且满足atanA=bcosC+ccosB,那么∠A=〔〕A. B. C. D.【答案】A【解析】【分析】利用正弦定理以及两角和的正弦公式、诱导公式可得结果.【详解】,,由,根据正弦定理:可得,所以,那么,应选A.【点睛】此题考察正弦定理和三角形的内角和定理以及两角和的正弦公式的运用,考察运算才能,属于根底题. 正弦定理是解三角形的有力工具,其常见用法有以下三种:〔1〕知道两边和一边的对角,求另一边的对角〔一定要注意讨论钝角与锐角〕;〔2〕知道两角与一个角的对边,求另一个角的对边;〔3〕证明化简过程中边角互化;〔4〕求三角形外接圆半径.a、b满足a+b=ab,那么ab的最小值为〔〕A. 1B.C. 2D. 4【答案】D【解析】【分析】根据a+b≥2,当且仅当a=b=2时取等号,代入计算即可求出ab的最小值.【详解】∵ab=a+b≥2,≥2,∴ab≥4,当且仅当a=b=2时取等号,故ab的最小值为4,应选:D.【点睛】此题考察了根本不等式的应用,属于根底题.在利用根本不等式求最值时,要特别注意“拆、拼、凑〞等技巧,使其满足根本不等式中“正〞(即条件要求中字母为正数)、“定〞(不等式的另一边必须为定值)、“等〞(等号获得的条件)的条件才能应用,否那么会出现错误.y2=2x的焦点为F,点P在抛物线上,且|PF|=2,过点P作抛物线准线的垂线交准线于点Q,那么|FQ|=〔〕A. 1B. 2C.D.【答案】B【解析】【分析】不妨设点P在x轴的上方,设P〔x1,y1〕,根据抛物线的性质可得x1=,即可求出点P的坐标,那么可求出点Q的坐标,根据两点间的间隔公式可求出.【详解】不妨设点P在x轴的上方,设P〔x1,y1〕,∵|PF|=2,∴x1+=2,∴x1=∴y1=,∴Q〔-,〕,∵F〔,0〕,∴|FQ|==2,应选:B.【点睛】此题考察了直线和抛物线的位置关系,抛物线的性质,两点间的间隔公式,属于根底题.一般和抛物线有关的小题,很多时可以应用结论来处理的;平时练习时应多注意抛物线的结论的总结和应用,尤其和焦半径联络的题目,一般都和定义有关,实现点点距和点线距的转化.11.我国古代数学名著?九章算术?中有如下问题:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺.问积几何〞,羡除是一个五面体,其中三个面是梯形,另两个面是三角形,一个羡除的三视图如图粗线所示,其中小正方形网格的边长为1,那么该羡除的外表中,三个梯形的面积之和为〔〕A. 40B. 43C. 46D. 47 【答案】C【解析】【分析】画出几何体的直观图,利用三视图所给数据,结合梯形的面积公式,分别求解梯形的面积即可.【详解】由三视图可知,该几何体的直现图如图五面体,其中平面平面,,底面梯形是等腰梯形,高为3 ,梯形的高为4 ,等腰梯形的高为,三个梯形的面积之和为,应选C.【点睛】此题考察空间几何体的三视图,求解外表积,属于中档题.三视图问题是考察学生空间想象才能最常见题型,也是高考热点.观察三视图并将其“翻译〞成直观图是解题的关键,不但要注意三视图的三要素“齐,长对正,宽相等〞,还要特别注意实线与虚线以及一样图形的不同位置对几何体直观图的影响.x=0是函数f〔x〕=x4-ax3+1的极小值点,那么实数a的取值集合为〔〕A. B. C. D.【答案】B【解析】【分析】根据求导公式和法那么求出f′〔x〕,由条件转化为:x=0是方程f′〔x〕=0的实根,通过导函数的符号,求解a的范围.【详解】由题意f〔x〕=x4-ax3+1得f′〔x〕=4x3-3ax2,∵x=0是函数f〔x〕的极小值点,∴x=0是方程f′〔x〕=0的实根,x<0时,4x3-3ax2≤0,可得a≥0,x>0时,4x3-3ax2≥0,可得a≤0,可得a=0.∴实数a的取值集合为{0}.应选:B.【点睛】此题考察了利用导数研究函数的极值问题,考察了转化思想和分析问题才能,属于中档题.极值点即导函数的零点,但是必须是变号零点,即在零点两侧正负相反;极值即将极值点代入原函数获得的函数值,注意分清楚这些概念,再者对函数求导后假如出现二次,那么极值点就是导函数的两个根,可以结合韦达定理应用解答。
高三双基数学试卷

考试时间:120分钟满分:100分一、选择题(每题5分,共30分)1. 已知函数$f(x)=ax^2+bx+c$,若$a\neq0$,且$f(1)=0$,$f(-1)=0$,$f(2)=4$,则下列选项中正确的是()。
A. $a=1$,$b=0$,$c=0$B. $a=1$,$b=-2$,$c=0$C. $a=2$,$b=-4$,$c=4$D. $a=2$,$b=0$,$c=4$2. 在等差数列$\{a_n\}$中,$a_1=3$,$a_4=13$,则公差$d$的值为()。
A. 2B. 3C. 4D. 53. 若$|x-1|+|x+2|=5$,则$x$的取值范围是()。
A. $-3\leq x\leq 2$B. $-2\leq x\leq 1$C. $-1\leq x\leq 3$D. $-3\leq x\leq -1$4. 若等比数列$\{a_n\}$中,$a_1=2$,$a_4=16$,则公比$q$的值为()。
A. 2B. 4C. 8D. 165. 若复数$z=a+bi$(其中$a$,$b$是实数),若$|z|=1$,则下列选项中正确的是()。
A. $a^2+b^2=1$B. $a^2-b^2=1$C. $a^2+b^2=-1$D. $a^2-b^2=-1$二、填空题(每题5分,共20分)6. 已知函数$f(x)=2x^3-3x^2+4x-1$,则$f'(1)=______$。
7. 在等差数列$\{a_n\}$中,$a_1=1$,$a_5=21$,则$a_{10}=______$。
8. 若$|x-2|+|x+3|=5$,则$x$的取值范围是______。
9. 若复数$z=a+bi$(其中$a$,$b$是实数),若$|z|=1$,则下列选项中正确的是______。
三、解答题(每题10分,共40分)10. 已知函数$f(x)=x^3-3x^2+4x-1$,求$f(x)$的极值。
11. 已知等差数列$\{a_n\}$中,$a_1=3$,公差$d=2$,求$\lim_{n\rightarrow\infty}\frac{a_1+a_2+\cdots+a_n}{n}$。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学双基 一
1.已知集合),1(+∞-=M ,集合{}0)2(|≤+=x x x N ,则N M ⋂= A .]2,0[ B . ),0(+∞ C . ]0,1(- D . )0,1(-
2.已知a ,b 是实数,则“⎩⎨
⎧>>3
2
b a ”是“5>+b a ” A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件 3.若某程序框图如图所示,则该程序运行后输出 的值是
A .4
B .5
C .6
D .7 4.已知直线l ,m 和平面α, 则下列命题正确的 A .若l ∥m ,m ⊂α,则l ∥α B .若l ∥α,m ⊂α,则l ∥m C .若l ⊥m ,l ⊥α,则m ∥α D .若l ⊥α,m ⊂α,则l ⊥m 5.已知是虚数单位,复数
i
i
+3= A .i 103101+ B .i 103101+- C .i 8
3
81+- D .i 8381--
6.函数y =sin (2x +π
4
)的图象可由函数y =sin 2x 的图象
A .向左平移π8个单位长度而得到
B .向右平移π8个单位长度而得到
C .向左平移π4个单位长度而得到
D .向右平移
π
4
个单位长度而得到
7.已知a 、b 均为单位向量,)2()2(b a b a -⋅+=2
3
3-
,a 与b 的夹角为 A .30° B .45° C .135° D .150°
n =12, i =1
n =3n +1
开 始 n 是奇数?
输出i 结 束 是 否 n = n =5?
是 否
n 2
i =i +1 (第3题图)
8.在递增等比数列{a n }中,4,2342=-=a a a ,则公比q = A .-1 B .1 C .2 D .2
1
9.若实数x ,y 满足不等式组⎪⎩
⎪
⎨⎧≤≥+≥+-3005x y x y x 则2x +4y 的最小值是
A .6
B .4
C .-2
D .-6 10.某学校三个社团的人员分布如下表(每名同学只参加一个社团):
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从社团成员中抽取30人,结果合唱社被抽出12人,则这三个社团人数共有_____. 11.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知C =3
π
,b=3, 若△ABC 的面积为
2
3
3 ,则c= . 12.如图,F 1,F 2是双曲线
C :22
221x y a b
-=(a >0,b >
0)的左、右焦点,过F 1的直线与C 的左、右两支分别交于A ,B 两点.若 | AB | : | BF 2 | : | AF 2 | =3 : 4 : 5,则双曲线的离心率为 .
合唱社 粤曲社 武术社 高一 45 30 a 高二
15
10
20
x
y O
A B
F 1
F 2
(第12题图)
一、选择题:CABDA AACD
二、填空题:
10、150 11、7 12、13。
