开发人员必知8大排序3大查找

合集下载

查找排序

Low指向待查元素所在区间的下界 mid指向待查元素所在区间的中间位臵 high指向待查元素所在区间的上界
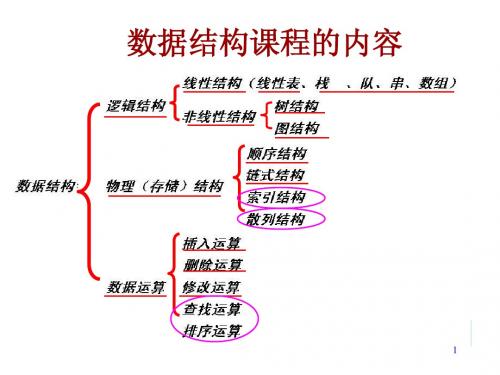
解：① 先设定3个辅助标志: low,high,mid，显然有：mid= (low+high)/2 ② 运算步骤：
(1) low =1,high =11 ,故mid =6 ，待查范围是 [1,11]； (2) 若 S[mid] < key，说明 key[ mid+1,high] ，则令：low =mid+1;重算 mid＝ (low+high)/2；. (3) 若 S[mid] > key，说明key[low ,mid-1]，则令：high =mid–1;重算 mid ； (4)若 S[ mid ] = key，说明查找成功，元素序号=mid; 结束条件：（1）查找成功： S[mid] = key （2）查找不成功： high＜low （意即区间长度小于0）
while(low<=high)
{ mid=(low+high)/2; if(ST[mid].key= = key) return (mid); /*查找成功*/
else if( key< ST[mid].key) high=mid-1; /*在前半区间继续查找*/ else } return (0); /*查找不成功*/
4 5 6 7
0
1
2
90
10
(c)
20
40
K=90
80
30
60
Hale Waihona Puke 25(return i=0 )
6
讨论：怎样衡量查找效率？
——用平均查找长度（ASL）衡量。
如何计算ASL？

Java常用排序总结

Java排序总结日常操作中常见的排序方法有：冒泡排序、快速排序、选择排序、插入排序、希尔排序，甚至还有基数排序、鸡尾酒排序、桶排序、鸽巢排序、归并排序等。

冒泡排序是一种简单的排序算法。

它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。

走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

代码/*** 冒泡法排序<br/>* <li>比较相邻的元素。

如果第一个比第二个大，就交换他们两个。

</li>* <li>对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。

在这一点，最后的元素应该会是最大的数。

</li>* <li>针对所有的元素重复以上的步骤，除了最后一个。

</li>* <li>持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

</li>** @param numbers* 需要排序的整型数组*/public static void bubbleSort(int[] numbers) {int temp; // 记录临时中间值int size = numbers.length; // 数组大小for(int i = 0; i < size - 1; i++) {for(int j = i + 1; j < size; j++) {if(numbers[i] < numbers[j]) { // 交换两数的位置temp = numbers[i];numbers[i] = numbers[j];numbers[j] = temp;}}}}快速排序使用分治法策略来把一个序列分为两个子序列。

代码/*** 快速排序<br/>* <ul>* <li>从数列中挑出一个元素，称为“基准”</li>* <li>重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。

Java常见的七种查找算法

Java常见的七种查找算法1. 基本查找也叫做顺序查找，说明：顺序查找适合于存储结构为数组或者链表。

基本思想：顺序查找也称为线形查找，属于无序查找算法。

从数据结构线的一端开始，顺序扫描，依次将遍历到的结点与要查找的值相比较，若相等则表示查找成功；若遍历结束仍没有找到相同的，表示查找失败。

示例代码：public class A01_BasicSearchDemo1 {public static void main(String[] args){//基本查找/顺序查找//核心：//从0索引开始挨个往后查找//需求：定义一个方法利用基本查找，查询某个元素是否存在//数据如下：{131, 127, 147, 81, 103, 23, 7, 79}int[] arr ={131,127,147,81,103,23,7,79};int number =82;System.out.println(basicSearch(arr, number));}//参数：//一：数组//二：要查找的元素//返回值：//元素是否存在public static boolean basicSearch(int[] arr,int number){//利用基本查找来查找number在数组中是否存在for(int i =0; i < arr.length; i++){if(arr[i]== number){return true;}}return false;}}2. 二分查找也叫做折半查找，说明：元素必须是有序的，从小到大，或者从大到小都是可以的。

如果是无序的，也可以先进行排序。

但是排序之后，会改变原有数据的顺序，查找出来元素位置跟原来的元素可能是不一样的，所以排序之后再查找只能判断当前数据是否在容器当中，返回的索引无实际的意义。

基本思想：也称为是折半查找，属于有序查找算法。

用给定值先与中间结点比较。

比较完之后有三种情况：•相等说明找到了•要查找的数据比中间节点小说明要查找的数字在中间节点左边•要查找的数据比中间节点大说明要查找的数字在中间节点右边代码示例：package com.itheima.search;public class A02_BinarySearchDemo1 {public static void main(String[] args){//二分查找/折半查找//核心：//每次排除一半的查找范围//需求：定义一个方法利用二分查找，查询某个元素在数组中的索引//数据如下：{7, 23, 79, 81, 103, 127, 131, 147}int[] arr ={7,23,79,81,103,127,131,147};System.out.println(binarySearch(arr,150));}public static int binarySearch(int[] arr,int number){//1.定义两个变量记录要查找的范围int min =0;int max = arr.length-1;//2.利用循环不断的去找要查找的数据while(true){if(min > max){return-1;}//3.找到min和max的中间位置int mid =(min + max)/2;//4.拿着mid指向的元素跟要查找的元素进行比较if(arr[mid]> number){//4.1 number在mid的左边//min不变，max = mid - 1；max = mid -1;}else if(arr[mid]< number){//4.2 number在mid的右边//max不变，min = mid + 1;min = mid +1;}else{//4.3 number跟mid指向的元素一样//找到了return mid;}}}}3. 插值查找在介绍插值查找之前，先考虑一个问题：为什么二分查找算法一定要是折半，而不是折四分之一或者折更多呢？其实就是因为方便，简单，但是如果我能在二分查找的基础上，让中间的mid点，尽可能靠近想要查找的元素，那不就能提高查找的效率了吗？二分查找中查找点计算如下：mid=(low+high)/2, 即mid=low+1/2*(high-low);我们可以将查找的点改进为如下：mid=low+(key-a[low])/(a[high]-a[low])*(high-low)，这样，让mid值的变化更靠近关键字key，这样也就间接地减少了比较次数。

顺序查找直接查找折半查找算法

顺序查找直接查找折半查找算法一、顺序查找算法顺序查找也被称为线性查找，是一种简单直观的算法。

其基本原理是逐个遍历数据集中的元素，直到找到目标值为止。

算法步骤如下：1.从数据集的第一个元素开始顺序遍历。

2.如果当前元素与目标值相同，返回元素的索引。

3.如果遍历到数据集的最后一个元素仍未找到目标值，返回失败。

顺序查找算法的时间复杂度为O(n)，其中n为数据集的大小。

由于需要遍历整个数据集，这种算法适用于小型数据集。

二、直接查找算法直接查找算法也被称为线性查找优化算法，其思想是在遍历数据集时，通过跳跃一定步长快速确定目标值所在的范围，然后在该范围内进行顺序查找。

算法步骤如下：1.设定步长为k。

2.从数据集的第一个元素开始，每次跳跃k个元素。

3.如果当前元素大于目标值，将步长减半并继续跳跃，直到找到目标值或步长变为1为止。

4.在跳跃范围内进行顺序查找，找到目标值则返回索引，否则返回失败。

直接查找算法的时间复杂度为O(n/k)，其中n为数据集的大小，k为步长。

通过调整步长，可以在时间和空间之间取得平衡。

折半查找算法是一种效率较高的算法，也被称为二分查找。

其基本原理是将数据集分为两半，通过比较目标值与中间元素的大小关系来确定目标值所在的范围，然后在该范围内进行递归查找。

算法步骤如下：1.将数据集按升序或降序排列。

2.初始化左右指针，分别指向数据集的第一个和最后一个元素。

3.计算中间元素的索引。

4.如果中间元素等于目标值，则返回索引。

5.如果中间元素大于目标值，则更新右指针为中间元素的前一个元素，重复步骤36.如果中间元素小于目标值，则更新左指针为中间元素的后一个元素，重复步骤37.当左指针大于右指针时，返回失败。

折半查找算法的时间复杂度为O(logn)，其中n为数据集的大小。

由于每次都将数据集分为两半，因此效率较高。

但是该算法要求数据集必须有序。

综上所述，顺序查找、直接查找和折半查找算法都是常用的算法，适用于不同规模和有序性的数据集。

程序员必须知道的8大排序和3大查找

程序员必须知道的8大排序和3大查找现在我们分析一下8种排序算法的稳定性。

（请网友结合前面的排序基本思想来理解排序的稳定性（8种排序的基本思想已经在前面说过，这里不再赘述）不然可能有些模糊）（1）直接插入排序：一般插入排序，比较是从有序序列的最后一个元素开始，如果比它大则直接插入在其后面，否则一直往前比。

如果找到一个和插入元素相等的，那么就插入到这个相等元素的后面。

插入排序是稳定的。

（2）希尔排序：希尔排序是按照不同步长对元素进行插入排序，一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，稳定性就会被破坏，所以希尔排序不稳定。

（3）简单选择排序：在一趟选择，如果当前元素比一个元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了。

光说可能有点模糊，来看个小实例：858410，第一遍扫描，第1个元素8会和4交换，那么原序列中2个8的相对前后顺序和原序列不一致了，所以选择排序不稳定。

（4）堆排序：堆排序的过程是从第n/2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。

但当为n /2-1, n/2-2, ...这些父节点选择元素时，有可能第n/2个父节点交换把后面一个元素交换过去了，而第n/2-1个父节点把后面一个相同的元素没有交换，所以堆排序并不稳定。

（5）冒泡排序：由前面的内容可知，冒泡排序是相邻的两个元素比较，交换也发生在这两个元素之间，如果两个元素相等，不用交换。

所以冒泡排序稳定。

（6）快速排序：在中枢元素和序列中一个元素交换的时候，很有可能把前面的元素的稳定性打乱。

还是看一个小实例：6 4 4 5 4 7 8 9，第一趟排序，中枢元素6和第三个4交换就会把元素4的原序列破坏，所以快速排序不稳定。

（7）归并排序：在分解的子列中，有1个或2个元素时，1个元素不会交换，2个元素如果大小相等也不会交换。

搜索算法二分查找深度优先搜索和广度优先搜索

搜索算法二分查找深度优先搜索和广度优先搜索搜索算法：二分查找、深度优先搜索和广度优先搜索引言：搜索算法是计算机科学中重要的算法之一，它用来在给定的数据集中查找特定的元素或解决某个问题。

本文将重点介绍三种常用的搜索算法：二分查找、深度优先搜索和广度优先搜索。

通过对这些算法的介绍，读者将了解它们的原理、特点以及应用场景，从而更好地理解搜索算法的工作原理及其在实际开发中的应用。

一、二分查找二分查找（Binary Search）是一种高效的查找算法，它适用于有序数组。

算法的基本思路是从数组的中间元素开始比较，如果要查找的元素小于中间元素，则去数组的左半部分继续查找，否则去数组的右半部分继续查找。

通过不断缩小查找范围，最终可以找到目标元素或确定目标元素不存在于数组中。

二、深度优先搜索深度优先搜索（Depth First Search，DFS）是一种用于遍历或搜索树或图的算法。

它从起始节点开始，尽可能深地访问每个节点的未访问邻居，直到遇到无法继续前进的节点，然后回溯到上一个节点，继续深入访问其他未访问的节点，直到所有节点都被访问完毕。

DFS通常采用递归或栈的方式实现。

三、广度优先搜索广度优先搜索（Breadth First Search，BFS）也是一种用于遍历或搜索树或图的算法。

与深度优先搜索不同，BFS先访问起始节点的所有邻居节点，然后再访问邻居节点的邻居节点，依次向外拓展。

BFS通常采用队列的方式实现。

四、二分查找的应用场景1. 在有序数组中查找指定元素。

由于二分查找的时间复杂度为O(logN)，因此它在处理大规模数据集时非常高效。

例如，在一个包含百万个元素的数组中，通过二分查找可以迅速确定某个元素是否存在。

五、深度优先搜索的应用场景1. 图的遍历。

深度优先搜索可以用来遍历图的所有节点，查找特定节点或判断两个节点之间是否存在路径。

例如，可以使用DFS查找一个社交网络中与某个人关系最近的所有人。

六、广度优先搜索的应用场景1. 最短路径问题。

程序员必知8大排序3大查找(三)

程序员必知8大排序3大查找（三）三种查找算法:顺序查找，二分法查找（折半查找），分块查找，散列表（以后谈）一、顺序查找的基本思想：从表的一端开始，顺序扫描表，依次将扫描到的结点关键字和给定值（假定为a）相比较，若当前结点关键字与a相等，则查找成功；若扫描结束后，仍未找到关键字等于a的结点，则查找失败。

说白了就是，从头到尾，一个一个地比，找着相同的就成功，找不到就失败。

很明显的缺点就是查找效率低。

适用于线性表的顺序存储结构和链式存储结构。

计算平均查找长度。

例如上表，查找1，需要1次，查找2需要2次，依次往下推，可知查找16需要16次，可以看出，我们只要将这些查找次数求和（我们初中学的，上底加下底乘以高除以2），然后除以结点数，即为平均查找长度。

设n=节点数平均查找长度=（n+1）/2二、二分法查找（折半查找）的基本思想：前提：（1）确定该区间的中点位置：mid=（low+high）/2min代表区间中间的结点的位置，low代表区间最左结点位置，high代表区间最右结点位置（2）将待查a值与结点mid的关键字（下面用R[mid].key）比较，若相等，则查找成功，否则确定新的查找区间：如果R[mid].key>a，则由表的有序性可知，R[mid].key右侧的值都大于a，所以等于a的关键字如果存在，必然在R[mid].key左边的表中。

这时high=mid-1如果R[mid].key<a,则等于a的关键字如果存在，必然在R[mid].key右边的表中。

这时low=mid如果R[mid].key=a，则查找成功。

（3）下一次查找针对新的查找区间，重复步骤（1）和（2）（4）在查找过程中，low逐步增加，high逐步减少，如果high<low，则查找失败。

平均查找长度=Log2(n+1)-1注：虽然二分法查找的效率高，但是要将表按关键字排序。

而排序本身是一种很费时的运算，所以二分法比较适用于顺序存储结构。

如何在Java中进行数据的排序和搜索

如何在Java中进行数据的排序和搜索在Java中对数据进行排序和搜索是非常常见的操作。

排序和搜索是数据处理中最基本的功能之一，在Java中有多种方式来完成排序和搜索的功能。

本文将从数组、集合和搜索算法三个方面来介绍在Java 中进行数据的排序和搜索。

一、数组的排序与搜索在Java中，对数组进行排序和搜索是非常常见的操作。

Java提供了两种对数组进行排序的方法：Arrays.sort()方法和Collections.sort()方法。

Arrays.sort()方法可以对基本类型数组和对象数组进行排序，而Collections.sort()方法只能对对象数组进行排序。

这两种方法都是使用快速排序算法来对数组进行排序的。

1. Arrays.sort()方法Arrays.sort()方法是针对基本类型数组和对象数组进行排序的。

对于基本类型数组，Arrays.sort()方法会调用Arrays类中相应的排序方法。

对于对象数组，Arrays.sort()方法会根据对象的自然顺序进行排序。

示例代码如下：```javaint[] arr = {5, 3, 8, 2, 1};Arrays.sort(arr);System.out.println("Sorted array: " +Arrays.toString(arr)); //输出：[1, 2, 3, 5, 8]```2. Collections.sort()方法Collections.sort()方法是针对对象数组进行排序的。

这个方法可以对实现了Comparable接口的对象进行排序，也可以对实现了Comparator接口的对象进行排序。

示例代码如下：```javaList<Integer> list = new ArrayList<>();list.add(5);list.add(3);list.add(8);list.add(2);list.add(1);Collections.sort(list);System.out.println("Sorted list: " + list); //输出：[1, 2, 3, 5, 8]```3.二分查找在Java中，可以使用Arrays.binarySearch()方法来进行二分查找。

常用的查找算法

树表查找
树表查找
B和B+树的区别在于，B+树的非叶子结点只包含导航信息，不包含实际的值，所有的叶子结点和相连的节点使用链表相连，便于区间查找和遍历。 B+ 树的优点在于：由于B+树在内部节点上不好含数据信息，因此在内存页中能够存放更多的key。数据存放的更加紧密，具有更好的空间局部性。因此访问叶子几点上关联的数据也具有更好的缓存命中率。 B+树的叶子结点都是相链的，因此对整棵树的便利只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连，所以便于区间查找和搜索。而B 树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻，所以缓存命中性没有B+树好。B+树更适合做文件系统。但是B树也有优点，其优点在于，由于B树的每一个节点都包含key和value，因此经常访问的元素可能离根节点更近，因此访问也更迅速。
二分查找
注意事项：折半查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再变化，折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，那就不建议使用。
插值查找
在介绍插值查找之前，首先考虑一个新问题，为什么上述算法一定要是折半，而不是折四分之一或者折更多呢？打个比方，在英文字典里面查“apple”，你下意识翻开字典是翻前面的书页还是后面的书页呢？如果再让你查“zoo”，你又怎么查？很显然，这里你绝对不会是从中间开始查起，而是有一定目的的往前或往后翻。< 同样的，比如要在取值范围1 ~ 10000 之间 100 个元素从小到大均匀分布的数组中查找5，我们自然会考虑从数组下标较小的开始查找。
查找算法

如何进行软件工程中的用户需求优先级排序(十)

用户需求优先级排序在软件工程中起着至关重要的作用。

它可以帮助团队确定开发软件时应该优先满足哪些需求，以及如何合理分配资源和时间。

在本文中，我将探讨如何进行用户需求优先级排序的方法和步骤，从而实现软件开发过程的成功和用户满意度的提高。

一、需求收集和整理在进行用户需求排序之前，首先需要进行需求收集和整理。

这一阶段包括与用户、客户和利益相关者的沟通、面对面的访谈、问卷调查等方式收集各种需求。

同时，对收集到的需求进行整理、归类和去重，以确保每个需求都得到充分的关注。

二、需求分析和评估在需求收集和整理的基础上，进行需求分析和评估。

这一阶段涉及对需求的详细分析，包括需求的详细描述、功能和非功能需求的识别、需求的优先级评估等。

可以采用多种方法，如需求规格说明书、用户故事、用例图等，将需求转化为可操作的任务。

三、优先级评估和排序在进行需求分析和评估后，需要对需求进行优先级评估和排序。

这一过程通常涉及多个维度的考虑，需要综合各种因素来确定优先级。

以下是一些常用的评估因素：1. 用户价值：评估需求对用户的价值和影响，这可以通过用户满意度的调查、用户反馈的分析等方式获取。

2. 业务价值：评估需求对业务目标的贡献和影响，例如增加收入、减少成本、提高竞争力等。

3. 风险和复杂性：评估需求的实施风险和技术复杂性，这可以通过分析需求的技术难度、实施成本、项目进度等因素来确定。

4. 可行性和资源可用性：评估需求是否可行以及所需资源的可用性，包括技术资源、人力资源、资金等。

根据以上评估因素，可以为每个需求分配一个权重或分数，再根据权重或分数进行排序，从而确定需求的优先级。

四、迭代和反馈用户需求优先级排序是一个迭代的过程，在实际项目中可能需要多次进行。

一开始的排序结果未必是最终的结果，随着项目的进展和用户的反馈，需求的优先级可能需要进行调整和修改。

因此，建议在进行需求排序之后，与用户和利益相关者保持密切的沟通和合作，及时收集用户的反馈和需求变更，进行相应的优先级调整，以确保软件开发过程的灵活性和用户的满意度。

c语言中的排序方法

c语言中的排序方法标题：C语言中的排序方法导语：排序是计算机科学中一个重要的算法问题，它可以帮助我们对数据进行有序排列，提高数据的查找和处理效率。

在C语言中，有多种排序方法可供选择，本文将介绍其中几种常用的排序方法，帮助读者理解和掌握排序算法。

一、冒泡排序冒泡排序是一种简单但效率较低的排序方法。

它通过比较相邻的元素并交换它们的位置，使得每一趟只有一个元素到达正确的位置。

重复这个过程，直到所有元素都有序排列。

冒泡排序的时间复杂度为O(n^2)，适用于数据规模较小的情况。

二、插入排序插入排序是一种稳定且简单的排序方法。

它将待排序的元素插入已经排好序的部分，从而逐步构建有序序列。

插入排序的时间复杂度为O(n^2)，但在实际应用中，对于基本有序的数据，插入排序的效率较高。

三、选择排序选择排序是一种简单但效率较低的排序方法。

它每次从待排序的元素中选择最小（或最大）的元素，放到已排序序列的末尾。

重复这个过程，直到所有元素都有序排列。

选择排序的时间复杂度为O(n^2)，不适用于大规模数据的排序。

四、快速排序快速排序是一种高效的排序方法，它采用了分治的思想。

首先选择一个基准元素，将小于基准的元素放在左边，大于基准的元素放在右边，然后递归地对左右两部分进行快速排序。

快速排序的时间复杂度为O(nlogn)，是目前最常用的排序算法之一。

五、归并排序归并排序是一种稳定且高效的排序方法，它采用了分治的思想。

将待排序的元素分成两个子序列，分别对子序列进行排序，然后将两个有序子序列合并成一个有序序列。

归并排序的时间复杂度为O(nlogn)，适用于大规模数据的排序。

六、堆排序堆排序是一种高效的排序方法，它利用堆这种数据结构来进行排序。

将待排序的元素构建成最大堆（或最小堆），然后逐步将堆顶元素与最后一个元素交换，并调整堆，重复这个过程直到所有元素有序排列。

堆排序的时间复杂度为O(nlogn)，适用于大规模数据的排序。

结语：排序是计算机科学中非常重要的一个问题，本文介绍了几种常用的排序方法，并对它们的原理和特点进行了简要说明。

C语言课件(查找和排序)

65 72 83 79 97 87 79 57 91 78
for (i=1;(list[i]!=key)&&(i<=N);i++);
if (i>N) printf("Not found!"); else printf("Success! The position is %d.",i);
}
查找与排序
查找与排序
Байду номын сангаас
折半查找
折半查找举例
low=1; high=N; found=0; while ((low<=high) && (! found)) { mid=(low+high)/2; if (key>list[mid]) low=mid+1; else if (key==list[mid]) found=1; else high=mid-1; }
数据插入
问题
把一个数据插入到已排好序的有序表中，从而得到一个新的、长度增1的有序表。
83
57 65 72 75 78 79 87 91 97
2.腾出位置 57 65 72 75 78 79 87 91 97 3.插入数据 57 65 72 75 78 79 83 87 91 97 1.找到插入点
查找与排序
查找与排序
直接插入排序
直接插入排序（cw1012.c）
输入任意个数，按从小到大的顺序对它们进行排序。
#include <stdio.h> #define N 10 void main() { int i, j, k, len; int list[N], x; 任意个数：程序运行时确定

八大排序算法

算法实现：我们简单处理增量序列：增量序列d = {n/2 ,n/4, n/8 .....1} n为要排序数的个数即：先将要排序的一一组记录按某个增量d（n/2,n为要排序数的个数）分成若干干组子子序列，每组中记录的下标相差d.对每组中全部元素进行行直接插入入排序，然后再用用一一个较小小的增量（d/2）对它进行行分组，在每组中再进行行直接插入入排序。继续不断缩小小增量直至至为1，最后使用用直接插入入排序完成排序。 1. void print(int a[], int n ,int i){ 2. 3. 4. 5. 6. 7. } 8. 9. 10. 11. 12. 13. 14. 15. void ShellInsertSort(int a[], int n, int dk) 16. { 17. 18. 19. 20. 21. 22. for(int i= dk; i<n; ++i){ if(a[i] < a[i-dk]){ int j = i-dk; int x = a[i]; a[i] = a[i-dk]; while(x < a[j]){ } cout<<endl; cout<<i <<":"; for(int j= 0; j<8; j++){ cout<<a[j] <<" ";
操作方方法： 1. 选择一一个增量序列t1，t2，…，tk，其中ti>tj，tk=1； 2. 按增量序列个数k，对序列进行行k 趟排序； 3. 每趟排序，根据对应的增量ti，将待排序列分割成若干干长度为m 的子子序列，分别对各子子表进行行直接插入入排序。仅增量因子子为1 时，整个序列作为一一个表来处理，表长度即为整个序列的长度。希尔排序的示示例：

八种排序方法

⼋种排序⽅法⼀.直接（选择）插⼊排序有两种⽅式：升序和降序我使⽤升序直接（简单）插⼊排序：每次向已经排序好的队列⾥⾯找个合适的位置，将值插⼊//笔试和⾯试：//1.算法的描述 2.算法的实现 3.效率（时间复杂度和空间复杂度和稳定性）//稳定性定义：如果两个关键值A和A`,如果⼀开始A就在A`前⾯，你排序后A还在A`前⾯，我们就认为是稳定的//怎么看稳定性：看有没有跳跃交换直接插⼊排序：如果数组基本有序，我们就⽤直接插⼊排序，越有序，时间复杂度越⼩，极端情况下为O（n）时间复杂度O（n^2）空间复杂度O（1），稳定的为什么不⽤从前向后找：如果数组有序，则时间复杂度太⼤具体代码实现：#include <stdio.h>#include <assert.h>void InsertSort(int arr[], int len){//循环多少次个数-1//⽤临时量tmp保存关键值，从后向前找，⽐它⼩的或者⾛到了头，就将关键值放到下⼀个位置上assert(arr != NULL);if (NULL == arr)return;int count = 0;int tmp = 0;int j = 0;for (int i = 1; i < len; i++)//控制揭牌后需要排序的次数{tmp = arr[i];for (j = i - 1; j >= 0; j--)//从后向前找{if (arr[j] > tmp)//⽐关键值⼤，则向后移动{arr[j + 1] = arr[j];count++;}else{break;//找到了⽐它⼩的值退出}}arr[j + 1] = tmp;}printf("count %d\n", count);}void Show(int* arr, int len){assert(arr != NULL);if (NULL == arr)return;for (int i = 0; i < len; i++){printf("%d ", arr[i]);}printf("\n");}int main(){int arr[] = { 2,4,6,8,23,98,76,56,74,36,1,3,5,7,99,66,77,88 };InsertSort(arr, sizeof(arr) / sizeof(arr[0]));Show(arr, sizeof(arr) / sizeof(arr[0]));return0;}希尔shell排序：就是⼀种特殊的直接插⼊排序，只不过调⽤了很多次直接插⼊排序，按增量分组要求：增量最后⼀个必须为1，增量保持互素时间复杂度O（n^1.3~1.5），空间复杂度O(1) ，稳定性：发⽣了跳跃交换，所以不稳定例如：分成5组，处理之后的值：分成3组，处理之后的值：最后分成1组，处理之后的值：具体代码实现：#include <stdio.h>#include <assert.h>static void Shell(int arr[], int len, int gap)//gap 分成多少组（间隔）{int tmp = 0;int j = 0;int count = 0;for (int i = gap; i < len; i++)//i开始的位置{tmp = arr[i];for (j = i - gap; j >= 0; j = j - gap){if (arr[j] > tmp){arr[j + gap] = arr[j];count++;}else{break;}}arr[j + gap] = tmp;}printf("%d count %d\n", gap, count);}void ShellSort(int arr[], int len){assert(arr != nullptr);if (NULL == arr)return;int dk[] = { 5, 3, 1 };for (int i = 0; i < sizeof(dk) / sizeof(dk[0]); i++){Shell(arr, len, dk[i]);}}void Show(int* arr, int len){assert(arr != NULL);if (NULL == arr)return;for (int i = 0; i < len; i++){printf("%d ", arr[i]);}printf("\n");}int main(){int arr2[] = { 2,4,6,8,23,98,76,56,74,36,1,3,5,7,99,66,77,88 };ShellSort(arr2, sizeof(arr2) / sizeof(arr2[0]));Show(arr2, sizeof(arr2) / sizeof(arr2[0]));return0;}⼆.交换排序冒泡（沉⽯）排序：两两⽐较，⼤的向后挪，⼩的向前挪时间复杂度O（n^2）空间复杂度O（1）稳定的具体代码实现：//冒泡排序：两两⽐较，⼤的向后挪void BubbleSort(int arr[], int len){//assert/*int count=0;bool tag = true;*/int tmp = 0;for(int i=0; i<len-1; i++)//次数{//tag = true;for(int j=0;j+1<len-i; j++)//两两⽐较，⼤的向后挪{if(arr[j] > arr[j+1]){tmp = arr[j];arr[j] = arr[j+1];arr[j+1] = tmp;//tag = false;}//count++;}/*if(tag){break;}*/}//printf("count = %d\n", count);}int main(){int arr[] = {2,4,6,8,23,98,76,56,74,36,1,3,5,7,99,66,77,88};BubbleSort(arr, sizeof(arr)/sizeof(arr[0]));Show(arr, sizeof(arr)/sizeof(arr[0]));return 0;}快速排序法每次找到基准值，以基准值为分界线，将数据分成两块，左边的数据都⽐基准值⼩，右边的数据都⽐基准值⼤快速排序，越有序越慢，规则:1.从右向左找⽐基准值⼩的数据，找到后，向左挪动2.从左向右找⽐基准值⼤的数据，找到后，向右挪动3.重复1，2，直到left == right，结束，将基准值放到arr[left] 或者arr[right]内缺点：越有序越慢，不稳定具体实现代码：#include<stdio.h>#include<assert.h>static int Partition(int arr[], int left, int right){int tmp = arr[left];while (left < right)//进来保证有两个值{while(left < right && arr[right] > tmp)right--;if(left == right){break;}arr[left] = arr[right];while(left < right && arr[left] <= tmp)left++;if(left == right){break;}arr[right] = arr[left];}arr[left] = tmp;//arr[right] = tmp;return left;//return right; 因为此时left == right}static void Quick(int arr[], int left, int right){if(left < right){//第⼀种优化：如果有效个数特别少，直接调⽤直接插⼊排序/*if(right-left+1<20 ) //⾃⼰设置有效个数{Insertsort(arr,left, high)return;} // Insertsirt表⽰⼀个插⼊排序类*///第⼆种优化：三数取中/*GetMiddleNumber(arr,left,mid,right);*///第三种优化：防⽌完全有序，⾃⼰打乱⼀下/*Swap(arr,start,rand()%(right-left+1)+start;*///第四种/*if(left < right){int midindex = Partition(arr, left, right);if(left < midindex-1){Quick(arr, left, midindex-1);}if(midindex+1 < right){Quick(arr, midindex+1, right);}}*/int midindex = Partition(arr, left, right);Quick(arr, left, midindex-1);Quick(arr, midindex+1, right);}}//⽤栈static void Quick_stack(int arr[], int left, int right){stack<int> st;if (left < right){int midindex = Partition(arr, left, right);if (left < midindex - 1){st.push(left);st.push(midindex - 1);}if (midindex + 1 < right){st.push(midindex + 1);st.push(right);}}while (!st.empty()){int q = st.top();st.pop();int p = st.top();st.pop();int midindex = Partition(arr, p, q);if (p < midindex - 1){st.push(p);st.push(midindex - 1);}if (midindex + 1 < q){st.push(midindex + 1);st.push(q);}}}void QuickSort(int arr[], int len)//时间复杂度O（nlogn）空间复杂度O（1）不稳定{//assertQuick_stack(arr, 0, len-1);}第⼀种优化代码：void InsertSort(int arr[], int left, int right){int tmp = arr[left];for (int i = left + 1; i <= right; i++){tmp = arr[i];int j = i - 1;while (j >= right && arr[i] > tmp){arr[j + 1] = arr[j];j--;}arr[j + 1] = tmp;}}第⼆种优化代码：void GetMiddleNumber(int arr[], int left, int right){if (arr[left] > arr[right]){Swap(arr, left, right);//交换左右端数据，保证左端较⼩}if (arr[mid] > arr[right]){Swap(arr, left, right);//交换中间和右边，保证中间较⼩}if (arr[mid] > arr[left]){Swap(arr, left, right);//交换中间和左端数据，保证左边不是最⼩的那⼀个}}第三种优化代码：Swap(arr, left, rand() % (end - start + 1) + start);//取⼀个⼩于有效长度随机值+最左端值的下标作为随机基准值的下标与start进⾏交换三.选择排序直接选择（简单选择排序）：每次从待排序队列中找到最⼩值，和待排序队列的第⼀位交换即可时间复杂度O（n^2）空间复杂度O（1）不稳定的具体实现代码：#include<stdio.h>#include<assert.h>void SelectSort(int arr[], int len){assert(arr != NULL);if (NULL == NULL)return;int tmp = 0;for (int i = 0; i < len - 1; i++){int m= i;//存放最⼩值下标for (int j = i + 1; j < len ; j++){if (arr[j] <arr[m]){m = j;}}if (m != i)//if判断可省略{tmp = arr[m];arr[m] = arr[i];arr[i] = tmp;}}}void Show(int* arr, int len){assert(arr != NULL);if (NULL == arr)return;for (int i = 0; i < len; i++){printf("%d ", arr[i]);}printf("\n");}int main(){int arr[] = { 2,4,6,8,23,98,76,56,74,36,1,3,5,7,99,66,77,88 };SelectSort(arr, sizeof(arr) / sizeof(arr[0]));Show(arr, sizeof(arr) / sizeof(arr[0]));return 0;}堆排序：堆排序的时间复杂度O（nlogn）空间复杂度O（1）不稳定什么是堆？堆分为两种：⼤顶堆和⼩顶堆两个统称为堆⼤顶堆：⼀个⼆叉树，⽗节点的值⼤于⼦节点的值⼩顶堆：⼀个⼆叉树，⽗节点的值⼩于⼦节点的值什么是树形结构：⼆叉树，树根，深度，叶⼦结点，左孩⼦，右孩⼦，完全⼆叉树，满⼆叉树深度怎么求：log2n+1⼤顶堆和⼩顶堆的关系，和兄弟节点的值⽆关，只和⽗⼦节点有关调整2个要点：1.从最后⼀个⾮叶⼦节点⼦树开始从后向前调整2.调整的时候顺序是从上向下3.升序(⼤顶堆)，降序（⼩顶堆）具体实现代码：#include<stdio.h>#include<assert.h>static void HeapAdjust(int arr[], int start, int end)//时间复杂度O（log2n）空间复杂度O（1）{int tmp = arr[start];for(int i=2*start+1; i<=end; i=i*2+1)//i? 堆排序效率⾼体现在这⾥i=i*2+1{//1.左右孩⼦都存在//2.只有左孩⼦，没有右孩⼦if(i<end && arr[i] < arr[i+1])//通过i<end保证右孩⼦存在，且arr[i] <arr[i+1]保证左孩⼦⼩于右孩⼦ {i++;//这时候让i指向较⼤的右孩⼦下标}//if判断失败的话，要么没有右孩⼦，要么有右孩⼦但是左孩⼦⽐右孩⼦值⼤，所以i不需要改变if(arr[i] > tmp)//判断较⼤孩⼦节点的值是否⽐⽗节点的值⼤，⼤的话向上覆盖，不然就找到了合适位置 {arr[start] = arr[i];start = i;}else{break;//左右孩⼦中较⼤的孩⼦值⼩于tmp}}arr[start] = tmp;//有两种情况执⾏到这⼀⾏代码：1.触底 2.找到放tmp的合适位置}//堆排序的时间复杂度O（nlog2n）空间复杂度O（1）不稳定void HeapSort(int arr[], int len){//assert//2.调整为⼤顶堆for(int i=(len-1-1)/2; i>=0; i--)//O（nlog2n）{HeapAdjust(arr, i, len-1);//}//第⼀个for循环⾛出来，这时已经为⼤顶堆了int tmp = 0;for(int j=0; j<len-1; j++)//j指的是循环的次数（顶部数据和最后⼀个节点交换的次数）//O（nlog2n）{//3.将顶部数据和最后⼀个节点进⾏了交换tmp = arr[0];arr[0] = arr[len-1-j];arr[len-1-j] = tmp;//已经将顶部数据和最后⼀个节点进⾏了交换 //4.重复2.3操作HeapAdjust(arr, 0, (len-1-j)-1);}}void Show(int* arr, int len){assert(arr != NULL);if (NULL == arr)return;for (int i = 0; i < len; i++){printf("%d ", arr[i]);}printf("\n");}int main(){int arr[] = { 2,4,6,8,23,98,76,56,74,36,1,3,5,7,99,66,77,88 };HeapSort(arr, sizeof(arr) / sizeof(arr[0]));Show(arr, sizeof(arr) / sizeof(arr[0]));return0;}四.⼆路归并排序⼆路归并排序，⾮递归形式：将两个有序的段合并成⼀个有序的段，直到全部数据在同⼀个段内有序，则完成有序时间复杂度O（n log2n）空间复杂度O（1）稳定的具体代码实现：//⼀次归并以gapgap合并static void Merge(int arr[], int len, int gap)//gap 标志⼏⼏合并{int *brr = (int*)malloc(sizeof(int) * len);assert(brr != NULL);int low1 = 0;int high1 = low1 + gap -1;int low2 = high1 + 1;int high2 = low2+gap-1<len ? low2+gap-1 : len-1;//H2 有可能越界若⼩于则low2+gap-1,不是则len-1int i = 0;while(low2 < len)//有两个有序段{while(low1 <= high1 && low2 <= high2)//两个段内头指针都没⾛到尾巴{if(arr[low1] <= arr[low2]){brr[i++] = arr[low1++];}else{brr[i++] = arr[low2++];}}//左边的段⾛到尾，那直接将右边的段内数据向下拷贝到brr内即可while(low2 <= high2){brr[i++] = arr[low2++];}//右边的段⾛到尾，那直接将左边的段内数据向下拷贝到brr内即可while(low1 <= high1){brr[i++] = arr[low1++];}//更改L1L2 H1H1,让指向接下来的两个有序段即可low1 = high2 + 1;high1 = low1+gap-1;low2 = high1 + 1;high2 = low2+gap-1<len ? low2+gap-1 : len-1;}//只有⼀个有序段while(low1 < len){brr[i++] = arr[low1++];}//将brr⾥的全部值拷贝到arr⾥⾯，然后将brr释放for(int j=0; j<len; j++){arr[j] = brr[j];}free(brr);brr = NULL;}void MergeSort(int arr[], int len)//控制合并次数{assert(arr != NULL);if(NULL == arr)return;for(int i=1; i<len; i*=2){Merge(arr, len, i);}}int main(){int arr[] = {2,4,6,8,23,98,76,56,74,36,1,3,5,7,99,66,77,88};MergeSort(arr, sizeof(arr)/sizeof(arr[0]));Show(arr, sizeof(arr)/sizeof(arr[0]));return0;}五.基数排序⼜称桶排序低位优先，所有数据从低位（个）位开始，依次放⼊到对应的⼗个桶内（队列中），再依次从桶中将数据依次取出（出队），直到所有数据循环次数和最⼤位数有关时间复杂度o(n) , 空间复杂度o(n)此时完全有序具体实现代码：#include<stdio.h>#include<assert.h>//基数排序//获取数组中最⼤值的位数static int Get_Figure(int arr[], int len) {int max = 0;for(int i=0; i<len; i++){if(arr[i] > max){max = arr[i];}}int count = 0;while(max != 0)max /= 10;}return count;}//获取n的第fin位的值//1234，2 = 2//234，0 = 4//12345，4 = 1//12345，7 = 0static int Get_num(int n, int fin){for(int i=0; i<fin; i++){n = n / 10;}return n % 10;//return n/(int)(pow((double)10, fin)) % 10;}//⽤⼆维数组调⽤static void Radix(int arr[], int len, int fin)//⼆维数组 fin判断的依据，到底是以什么位排序//时间复杂度O（n）空间复杂度O（n）{int bucket[10][20] = {0};//桶int num[10] = {0};//对应的桶中有多少个有效值//所有的数据都以fin位为依据，放到了桶内for(int i=0; i<len; i++)//数组的下标从0开始放{int index = Get_num(arr[i], fin);//获取arr[i]的fin位的值，找到对应的桶bucket[index][num[index]] = arr[i];//放到对⽤的桶中第num[index]位上num[index]++;//对应的桶中有效个数++}//从0-9桶内依次取值到arr⾥int k = 0;for(int i=0; i<10; i++)//⼏号桶{for(int j=0; j<num[i]; j++)//j桶中有效值个数{arr[k++] = bucket[i][j];}}}//⽤链式队列调⽤static void Radix_queue(int arr[], int len, int fin)//时间复杂度O（n）空间复杂度O（n）{LQueue queArr[10];for(int i=0; i<10; i++){InitLQueue(&queArr[i]);}for(int i=0; i<len; i++){int index = Get_num(arr[i], fin);Push(&queArr[index], arr[i]);}int k = 0;for(int i=0; i<10; i++){while(!IsEmpty(&queArr[i])){Pop(&queArr[i], &arr[k++]);}}for(int i=0; i<10; i++){Destroy(&queArr[i]);}}void RadixSort(int arr[], int len)//时间复杂度O（dn）空间复杂度（n）稳定{//assertint count = Get_Figure(arr, len);for(int i=0; i<count; i++)//循环的趟数，低位优先{Radix_queue(arr, len, i);}。

2023年程序员必知大排序大查找

第二篇《程序员必知8大排序3大查找（一）》每天都在叫嚣自己会什么技术，什么框架，可否意识到你每天都在被这些新名词、新技术所困惑，.NET、XML等等技术当然诱人，可是假如自己旳基础不扎实，就像是在云里雾里行走同样，只能看到眼前，不能看到更远旳地方。

这些新鲜旳技术掩盖了许多底层旳原理，要想真正旳学习技术还是走下云端，扎扎实实旳把基础知识学好，有了这些基础，要掌握那些新技术也就很轻易了。

要编写出优秀旳代码同样要扎实旳基础，假如排序和查找算法学旳不好，怎么对程序旳性能进行优化？废话不多说，本文要简介旳这些排序算法就是基础中旳基础，程序员必知！1、直接插入排序（1）基本思想：在要排序旳一组数中，假设前面(n-1) [n>=2] 个数已经是排好次序旳，目前要把第n个数插到前面旳有序数中，使得这n个数也是排好次序旳。

如此反复循环，直到所有排好次序。

（2）实例2、希尔排序（也称最小增量排序）（1）基本思想：算法先将要排序旳一组数按某个增量d（n/2,n为要排序数旳个数）提成若干组，每组中记录旳下标相差d.对每组中所有元素进行直接插入排序，然后再用一种较小旳增量（d/2）对它进行分组，在每组中再进行直接插入排序。

当增量减到1时，进行直接插入排序后，排序完毕。

（2）实例：3、简朴选择排序（1）基本思想：在要排序旳一组数中，选出最小旳一种数与第一种位置旳数互换；然后在剩余旳数当中再找最小旳与第二个位置旳数互换，如此循环到倒数第二个数和最终一种数比较为止。

（2）实例：4、堆排序（1）基本思想：堆排序是一种树形选择排序，是对直接选择排序旳有效改善。

堆旳定义如下：具有n个元素旳序列（h1,h2,...,hn),当且仅当满足（hi>=h2i,hi>=2i+1）或（hi<=h2i,hi<=2i+1）(i=1,2,...,n/2)时称之为堆。

在这里只讨论满足前者条件旳堆。

由堆旳定义可以看出，堆顶元素（即第一种元素）必为最大项（大顶堆）。

如何进行软件工程中的用户需求优先级排序(八)

用户需求是软件工程中至关重要的一环。

在软件开发过程中，如何合理地确定用户需求的优先级，对于提高软件质量、满足用户期望至关重要。

本文将探讨如何进行软件工程中的用户需求优先级排序。

1、需求分析与收集阶段软件开发的第一步是收集和分析用户需求。

在这个阶段，开发团队与用户进行充分的沟通，了解用户的真实需求，并对需求进行详细的描述和记录。

这包括对需求的功能、性能、可靠性、安全性等方面的考量。

开发团队可以采用面谈、问卷调查、原型设计等方法来获取用户需求。

2、需求分类与整理在收集完用户需求后，需要对其进行整理和分类。

将需求划分为不同的功能、模块或阶段，以便后续的优先级排序。

例如，可以将需求分为基础功能、核心功能、附加功能等，或者按照功能模块进行划分。

3、需求评估与权重确定对于每一个需求，需要评估其在整个软件系统中的重要性和紧急程度。

可以采用多个指标来评估需求的优先级，例如技术复杂度、业务价值、用户满意度等。

开发团队可以进行讨论和投票，以确定需求的权重。

同时，也可以考虑到项目的时间和资源限制，对需求进行合理的分配。

4、需求优先级排序根据需求的权重和评估结果，可以进行需求优先级的排序。

可以采用以下几种方法：1）按照优先级进行分类：将需求分为高优先级、中优先级和低优先级，根据软件的开发进度和资源分配情况，先完成高优先级的需求，再逐步完成中低优先级需求。

2）使用数值法进行排序：为每个需求设定一个权重值，根据权重值的大小进行排序。

可以采用成对比较法、层次分析法等数学模型进行权重计算。

3）借鉴敏捷开发方法：采用敏捷开发的方法，将需求按照用户的反馈和需求变化进行动态排序。

根据每个开发周期的需求优先级，灵活调整开发计划。

5、持续迭代与反馈软件开发是一个持续迭代的过程。

在开发过程中，用户需求可能会发生变化，新的需求可能会出现。

因此，需求的优先级排序也需要进行持续调整和迭代。

开发团队可以定期与用户进行交流，及时获取用户的反馈和新的需求，根据实际情况进行需求优先级的调整。

数组应用(排序与查找)

1 22 22 22 22 32 32 21 21 21
23 21 8 3(1) 23 8 5 23 8 13 23 9 13 23 13 23 21 22 23 21 22 23 32 22 23 32 22 23 32
21 21 21 21
12:02:37
3
排序的主要方法
//交换排序
#include <stdio.h> #define STUDS 5 void main() { int max( int max0 , int element); //比较max与element的大小 int i , j , temp; int score[STUDS]={0} ; //存储学生成绩 printf(“请输入%d个学生的成绩：”， STUDS); for(i=0 ; i<STUDS ; i++) //输入学生成绩 scanf("%d", &score[i]); for(i=0;i<STUDS-1;i++) //进行交换排序 { //从下标为i的元素开始，其后的元素大于score[i],则与其交换
12:02:39
13
例用冒泡法对10个数排序（从前往后的冒泡排序）
排序的主要方法
相邻两数比较，若前面数大，则两数交换位置，直至最后一个元素被处理，最大的元素就“沉”到最下面，即在最后一个元素位置。这样，如有n个元素，共进行n-1轮，每轮让剩余元素中最大的元素“沉”到下面，从而完成排序。 #include<stdio.h>
12:02:37
4
for (j=i+1;j<STUDS;j++) { if( max(score[ i ],score[ j ])==1 )

五种查找算法总结

五种查找算法总结第一篇：五种查找算法总结五种查找算法总结一、顺序查找条件：无序或有序队列。

原理：按顺序比较每个元素，直到找到关键字为止。

时间复杂度：O(n)二、二分查找（折半查找）条件：有序数组原理：查找过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜素过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。

如果在某一步骤数组为空，则代表找不到。

这种搜索算法每一次比较都使搜索范围缩小一半。

时间复杂度：O(logn)三、二叉排序树查找条件：先创建二叉排序树：1.若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；2.若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；3.它的左、右子树也分别为二叉排序树。

原理：在二叉查找树b中查找x的过程为：1.若b是空树，则搜索失败，否则：2.若x等于b的根节点的数据域之值，则查找成功；否则：3.若x小于b的根节点的数据域之值，则搜索左子树；否则：4.查找右子树。

时间复杂度：四、哈希表法（散列表）条件：先创建哈希表（散列表）原理：根据键值方式(Key value)进行查找，通过散列函数，定位数据元素。

时间复杂度：几乎是O(1)，取决于产生冲突的多少。

五、分块查找原理：将n个数据元素“按块有序”划分为m块（m ≤ n）。

每一块中的结点不必有序，但块与块之间必须“按块有序”；即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字；而第2块中任一元素又都必须小于第3块中的任一元素，……。

然后使用二分查找及顺序查找。

第二篇：数据结构实验报告-查找算法《数据结构》第八次实验报告学生姓名学生班级学生学号指导老师重庆邮电大学计算机学院计算机专业实验中心一、实验内容1)有序表的二分查找建立有序表，然后进行二分查找2)二叉排序树的查找建立二叉排序树，然后查找二、需求分析二分查找的基本思想是将n个元素分成大致相等的两部分，取a[n/2]与x做比较，如果x=a[n/2],则找到x,算法中止；如果xa[n/2],则只要在数组a的右半部搜索x.时间复杂度无非就是while循环的次数！总共有n个元素，渐渐跟下去就是n,n/2,n/4,....n/2^k（接下来操作元素的剩余个数），其中k就是循环的次数由于你n/2^k取整后>=1 即令n/2^k=1 可得k=log2n,（是以2为底，n的对数）所以时间复杂度可以表示O()=O(logn)下面提供一段二分查找实现的伪代码: BinarySearch(max,min,des)mid-<(max+min)/2 while(min<=max)mid=(min+max)/2 if mid=des then return mid elseif mid >des then max=mid-1 else min=mid+1 return max 折半查找法也称为二分查找法，它充分利用了元素间的次序关系，采用分治策略，可在最坏的情况下用O(log n)完成搜索任务。

20191209-八大排序之基数排序

20191209-⼋⼤排序之基数排序1. 基数排序算法核⼼思想基数排序(radix sort)是⼀种只适⽤于数字或字母类型的排序⽅法，它检查数字或字母的每⼀位，将之分类，按照位数的特定顺序，来将元素排列。

以数字为例，将所有元素按照个位数字分类，分类好后，将个位数字⼤⼩排列组合起来，再按照⼗位数字分类，再按照数字⼤⼩排列组合起来，⼀直到最⼤数位为⽌。

基数排序分类基数排序的⽅式分为2类：1. LSD（Least significant digital）：LSD的排序⽅式由键值的最右边开始，先⽐较最低位，也就是个位，进⾏分桶，分桶过程中分到⼀个桶中的数据直接追加到桶中即可，⽆需排序。

然后将所有同种的元素按桶的顺序拿出，重新组成序列，然后⽐较⼗位，进⾏分桶…直到⽐较到最⾼位，重新组成序列即可完成排序。

2. MSD（Most significant digital）：由键值的最左边开始，先⽐较最⾼位，最⾼位分到⼀个桶中的，再按照第⼆位进⾏分桶…，知道分到最后⼀位，然后再从最⼩的桶中逐层向上，把元素都拿出来，即完成排序。

3. ⾸先确定待排序数组中值的最⼤位数，⽤于确定程序中要作⼏轮排序；4. 定义⼀个集合数组，数组⼤⼩⼗，对应⾓标范围0-9，⽤来保存每轮排序过程中对应的位数上的值；5. 每轮排序依次从原始数组中取值，并判断对应位数上的值，不⾜位数时在前⾯补上相应的0，然后放到对应⾓标的桶内；6. 每轮排序后，按⾓标⼤⼩依次取出不为空的桶内的值，合并成为⼀个部分排序后的新数组；7. 将上述部分排序后的新数组作为下⼀轮⾼⼀位位数上的值排序的原始数组，重复上述排序的步骤，直到⽣成最终排好序的数组。

LSD具体逻辑如下：MSD具体逻辑如下：从最⾼位数上的值开始排序，⼀轮排序结束后，并没有急着合并整理，⽽是判断每个桶内的元素，如果桶内的元素⼤于1个则继续对当前桶进⾏排序，直到排到最低位数上的值，最终做⼀次性合并整理，形成排序后的数组。

c语言有序数组的查询算法

c语言有序数组的查询算法C语言是一种广泛应用的编程语言，具有高效、灵活和可移植性等优点。

在C语言中，有序数组是一种常见的数据结构，它对存储的元素进行了排序，这样可以提高查询效率。

本文将介绍几种常见的有序数组查询算法，包括顺序查找、二分查找和插值查找等。

一、顺序查找算法顺序查找算法是最简单的一种有序数组查询算法，它的思想是逐个比较数组中的元素，直到找到目标元素或者遍历完整个数组。

具体步骤如下：1. 初始化一个变量i，表示当前比较的元素下标，初始值为0。

2. 循环比较数组中的元素，直到找到目标元素或者遍历完整个数组。

3. 如果找到目标元素，则返回其下标；如果遍历完整个数组仍未找到目标元素，则返回-1。

顺序查找算法的时间复杂度为O(n)，其中n表示数组的长度。

由于它的效率较低，适用于小规模的有序数组查询。

二、二分查找算法二分查找算法是一种高效的有序数组查询算法，它的思想是通过不断缩小查找范围，快速定位目标元素。

具体步骤如下：1. 初始化两个变量low和high，分别表示查找范围的最低下标和最高下标，初始值分别为0和n-1，其中n表示数组的长度。

2. 循环进行查找，直到low大于high。

3. 在每一次循环中，计算中间元素的下标mid，即mid = (low + high) / 2。

4. 若目标元素等于中间元素，则返回mid；若目标元素小于中间元素，则在左半部分继续查找，更新high为mid-1；若目标元素大于中间元素，则在右半部分继续查找，更新low为mid+1。

二分查找算法的时间复杂度为O(log n)，其中n表示数组的长度。

由于它每次查找都将查找范围缩小一半，因此效率较高，适用于大规模的有序数组查询。

三、插值查找算法插值查找算法是一种对二分查找算法的改进，它通过根据目标元素与查找范围的比例来动态计算中间元素的下标，从而更快地定位目标元素。

具体步骤如下：1. 初始化两个变量low和high，分别表示查找范围的最低下标和最高下标，初始值分别为0和n-1，其中n表示数组的长度。