钢结构第二版第三章答案
钢结构第三章

第三章习题参考答案注意:①要求学生尽量图示;②若无特别说明,焊缝计算长度可不考虑起弧、落弧的影响。
③题中“(考虑荷载分项系数后)”的意思为荷载设计值,时刻提醒学生别忘了结构可靠度理论。
3.1 解:①对接焊缝:3125010208.318550012w t w N MPa f MPa l t σ⨯===>=⨯,不满足要求,改用斜对接焊缝,取切割斜度为1.5:l ,即5.1tan =θ、o 56=θ。
②围角焊缝、双拼接板:设盖板宽2460b mm =,注意拼接板截面面积必须验算:2246050012t ⨯≥⨯,取28t mm =(常用的板厚以偶数居多)。
角焊缝的焊脚尺寸h f 应根据板件厚度确定:由于此处的焊缝在板件边缘施焊,且拼接盖板厚度t 2=8mm>6mm ,t 2< t 1,则()()max 21~281~26~7f h t mm mm =-=-=min 5f h mm ===取角焊缝的焊脚尺寸h f =6mm ,角焊缝的强度设计值2/160mm N f wf =,则()f e w f e w f f h l h f b h f N -=-422β代入数据,注意围焊缝只有一个起弧点和一个落弧点,有()31250102 1.221600.7646041600.766l ⨯-⨯⨯⨯⨯⨯=⨯⨯⨯⨯-解、取整得 l =195mm上、下各一块拼接板的长度为 2l 10219510400mm L =+=⨯+= 最后选定的上、下拼接板的尺寸为2—460×8×400。
3.2 解:注意仅腹板在此拼接、翼缘在此无拼接,即翼缘处无焊缝、当然也无需验算,但截面依然是工字形的,不少同学仅按腹板矩形截面计算是完全错误的。
焊缝处1026.375M kN m =⋅、172.5V kN =3394112801032(2808)1000 2.979101212x I mm =⨯⨯-⨯-⨯=⨯ 63x S 280165085008250 3.27610mm =⨯⨯+⨯⨯=⨯ 63x1S 28016508 2.27610mm =⨯⨯=⨯最大剪应力为:3622max9172.510 3.2761023.7N/mm 125N/mm 2.979108w x v x VS f I t τ⨯⨯⨯===<=⨯⨯ 上翼缘和腹板交接处“l ”点的正应力:621191026.37510500172.3N/mm 2.97910x My I σ⨯⨯===⨯ 剪应力:362119172.510 2.2761016.5N/mm 2.979108x x VS I t τ⨯⨯⨯===⨯⨯ 由于“1”点同时受有较大的正应力和剪应力(无需单独验算),故应验算折算应力:22174.7/ 1.1185204/N mm N mm =<⨯=均满足要求。
钢结构连接习题及答案

第三章钢结构连接习题及答案(总10页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第三章 钢结构的连接习题参考答案1. 已知A3F 钢板截面mm mm 20500⨯用对接直焊缝拼接,采用手工焊焊条E43型,用引弧板,按Ⅲ级焊缝质量检验,试求焊缝所能承受的最大轴心拉力设计值。
解:查附表得:2518mm N f w t =则钢板的最大承载力为:KN f bt N w t w 185010185205003=⨯⨯⨯==- 2.焊接工字形截面梁,设一道拼接的对接焊缝,拼接处作用荷载设计值:弯矩mm KN M ⋅=1122,剪力KN V 374=,钢材为Q235B ,焊条为E43型,半自动焊,Ⅲ级检验标准,试验算该焊缝的强度。
解:查附表得:2518mm N f w t =,2512mm N f w v =。
截面的几何特性计算如下:惯性矩:44233102682065071428014280121210008121mm I x ⨯=⎥⎦⎤⎢⎣⎡⨯⨯+⨯⨯⨯+⨯⨯=翼缘面积矩:41198744050714280mm S x =⨯⨯=则翼缘顶最大正应力为:2243185215021026820610281011222mm N f mm N .h I M w t x =<=⨯⨯⨯⨯=⋅=σ 满足要求。
腹板高度中部最大剪应力:2243125075281026820625008500198744010374mm N f mm N .t I VS w vw x x =<=⨯⨯⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯==τ满足要求。
上翼缘和腹板交接处的正应力:2120805075002150507500mm N ..=⨯=⨯σ=σ上翼缘和腹板交接处的剪应力:243116434810268206198744010374mmN .t I VS w x x =⨯⨯⨯⨯==τ 折算应力:2222212152031100606434320803mm N .f .mm N ...w t =<=⨯+=τ+σ满足要求。
第三章 钢结构的连接课后习题答案

第三章 钢结构的连接3.1 试设计双角钢与节点板的角焊缝连接(图3.80)。
钢材为Q235B ,焊条为E43型,手工焊,轴心力N=1000KN (设计值),分别采用三面围焊和两面侧焊进行设计。
解:(1)三面围焊 2160/w f f N mm = 123α=213α= 确定焊脚尺寸: ,max min 1.2 1.21012f h t mm ≤=⨯=, ,min min 1.5 1.512 5.2f h t mm ≥==, 8f h mm = 内力分配:30.7 1.2220.78125160273280273.28w f f f N h b f N KN β=⋅⋅⋅=⨯⨯⨯⨯⨯==∑3221273.281000196.69232N N N KN α=-=⨯-= 3112273.281000530.03232N N N KN α=-=⨯-= 焊缝长度计算:11530.032960.720.78160w w f fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 1296830460608480wf l mm h mm '=+=≤=⨯=,取310mm 。
22196.691100.720.78160w w f f N l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 2110811860608480wf l mm h mm '=+=≤=⨯=,取120mm 。
(2)两面侧焊确定焊脚尺寸:同上,取18f h mm =, 26f h mm = 内力分配:22110003333N N KN α==⨯=, 11210006673N N KN α==⨯= 焊缝长度计算: 116673720.720.78160w w f f N l mm h f ≥==⋅⨯⨯⨯∑,则实际焊缝长度为:mm h mm l f w48086060388283721=⨯=<=⨯+=',取390mm 。
(完整版)钢结构课后习题第三章

(完整版)钢结构课后习题第三章第三章部分习题参考答案3.8 已知A3F 钢板截⾯mm mm 20500?⽤对接直焊缝拼接,采⽤⼿⼯焊焊条E43型,⽤引弧板,按Ⅲ级焊缝质量检验,试求焊缝所能承受的最⼤轴⼼拉⼒设计值。
解:焊缝质量等级为Ⅱ级,抗拉的强度设计值20.85182.75/w f f f N mm == 采⽤引弧板,故焊缝长度500w l b mm ==承受的最⼤轴⼼拉⼒设计值3500*20*182.75*101827.5N btf kN -===3.9 焊接⼯字形截⾯梁,在腹板上设⼀道拼接的对接焊缝(如图3-66),拼接处作⽤荷载设计值:弯矩M=1122kN ·mm ,剪⼒V=374kN ,钢材为Q235B ,焊条为E43型,半⾃动焊,三级检验标准,试验算该焊缝的强度。
解:(1)焊缝截⾯的⼏何特性惯性矩3341(28102.827.2100)26820612x I cm =-= ⼀块翼缘板对x 轴的⾯积矩3128 1.4(507)2234.4X S cm =??+=半个截⾯对x 轴的⾯积矩31500.8253234.4X X S S cm =+??=(2)焊缝强度验算焊缝下端的剪应⼒33214374102234.41038.9/268206108x x w VS N mm I t τ===?? 焊缝下端的拉应62max4112210500209/0.852********x M h N mm f I σ??=?==>? 所以,该焊缝不满⾜强度要求(建议将焊缝等级质量提为⼆级)则 max σ2209/N mm =<215f =2/N mm下端点处的折算应2222max 3219.6/ 1.1236.5/N mm f N mm στ+=<=且焊缝中点处剪应⼒33224374103234.41056.3/125/268206108w x v x w VS N mm f N mm I t τ===<=??3.10 试设计如图3-67所⽰双⾓钢和节点板间的⾓焊缝连接。
钢结构基础第三章课后习题答案
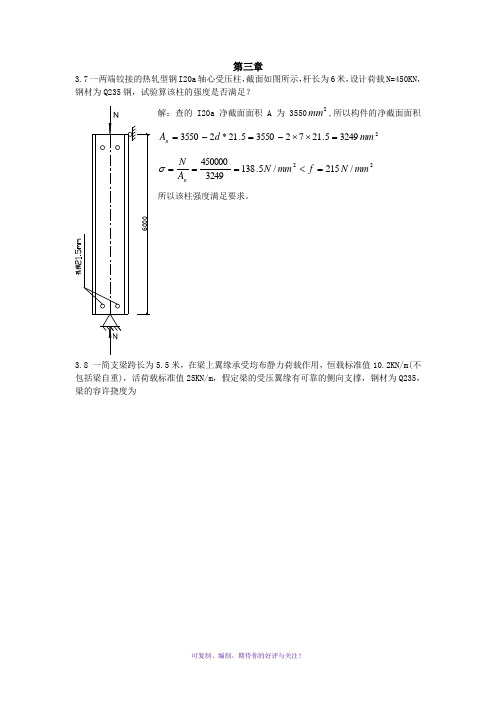
第三章3.7一两端铰接的热轧型钢I20a 轴心受压柱,截面如图所示,杆长为6米,设计荷载N=450KN ,钢材为Q235钢,试验算该柱的强度是否满足?解:查的I20a 净截面面积A 为35502mm ,所以构件的净截面面积232495.217235505.21*23550mm d A n =⨯⨯-=-=22/215/5.1383249450000mm N f mm N A N n =<===σ 所以该柱强度满足要求。
3.8 一简支梁跨长为5.5米,在梁上翼缘承受均布静力荷载作用,恒载标准值10.2KN/m(不包括梁自重),活荷载标准值25KN/m ,假定梁的受压翼缘有可靠的侧向支撑,钢材为Q235,梁的容许挠度为l/250,试选择最经济的工字型及H 型钢梁截面,并进行比较。
解:如上图示,为钢梁的受力图荷载设计值m KN q /24.47254.12.102.1=⨯+⨯= 跨中最大弯矩KNm ql M 63.1785.524.47818122=⨯⨯==f w M x x ≤=γσmax 所以3561091.7)21505.1/(1063.178mm fM w x x ⨯=⨯⨯=≥γ 查型钢表选择I36a ,质量为59.9kg/m,Wx 为8750003mm ,所以钢梁自重引起的恒载标注值m KN /58702.010008.99.59=÷⨯=,可见对强度影响很小,验算挠度即可:荷载标准值m KN q k /79.35252.1058702.0=++=挠度mm EI l q x k 13.1310576.11006.2384105.579.3553845851244=⨯⨯⨯⨯⨯⨯⨯==ω<[l/250]=22mm I36a 满足挠度要求。
查型钢表选择HN400x200x8x13,质量为66kg/m,Wx 为11900003mm钢梁自重引起的恒载标注值m KN /6468.010008.966=÷⨯=,可见对强度影响很小,验算挠度即可:荷载标准值m KN q k /85.35252.106468.0=++=挠度mm EI l q x k 7.810237001006.2384105.585.3553845451244=⨯⨯⨯⨯⨯⨯⨯==ω<[l/250]=22mm HN400x200x8x13满足挠度要求。
钢结构基础第三章课后习题答案

一两端铰接的热轧型钢I20a 轴心受压柱,截面如图所示,杆长为6米,设计荷载N=450KN ,钢材为Q235钢,试验算该柱的强度是否满足?解:查的I20a 净截面面积A 为35502mm ,所以构件的净截面面积232495.217235505.21*23550mm d A n =⨯⨯-=-=22/215/5.1383249450000mm N f mm N A N n =<===σ 所以该柱强度满足要求。
一简支梁跨长为米,在梁上翼缘承受均布静力荷载作用,恒载标准值m(不包括梁自重),活荷载标准值25KN/m ,假定梁的受压翼缘有可靠的侧向支撑,钢材为Q235,梁的容许挠度为l/250,试选择最经济的工字型及H 型钢梁截面,并进行比较。
解:如上图示,为钢梁的受力图荷载设计值m KN q /24.47254.12.102.1=⨯+⨯= 跨中最大弯矩KNm ql M 63.1785.524.47818122=⨯⨯== f w M x x ≤=γσmax 所以3561091.7)21505.1/(1063.178mm fM w x x ⨯=⨯⨯=≥γ查型钢表选择I36a ,质量为m,Wx 为8750003mm ,所以钢梁自重引起的恒载标注值m KN /58702.010008.99.59=÷⨯=,可见对强度影响很小,验算挠度即可:荷载标准值m KN q k /79.35252.1058702.0=++= 挠度mm EI l q x k 13.1310576.11006.2384105.579.3553845851244=⨯⨯⨯⨯⨯⨯⨯==ω<[l/250]=22mm I36a 满足挠度要求。
查型钢表选择HN400x200x8x13,质量为66kg/m,Wx 为11900003mm钢梁自重引起的恒载标注值m KN /6468.010008.966=÷⨯=,可见对强度影响很小,验算挠度即可:荷载标准值m KN q k /85.35252.106468.0=++= 挠度mm EI l q x k 7.810237001006.2384105.585.3553845451244=⨯⨯⨯⨯⨯⨯⨯==ω<[l/250]=22mm HN400x200x8x13满足挠度要求。
第三章钢结构连接习题及答案

第三章 钢结构的连接习题参考答案1. 已知A3F 钢板截面mm mm 20500⨯用对接直焊缝拼接,采用手工焊焊条E43型,用引弧板,按Ⅲ级焊缝质量检验,试求焊缝所能承受的最大轴心拉力设计值。
解:查附表1.2得:2518mm N f w t =则钢板的最大承载力为:KNf bt N w t w 185010185205003=⨯⨯⨯==-2.焊接工字形截面梁,设一道拼接的对接焊缝,拼接处作用荷载设计值:弯矩mm KN M ⋅=1122,剪力KN V 374=,钢材为Q235B ,焊条为E43型,半自动焊,Ⅲ级检验标准,试验算该焊缝的强度。
解:查附表1.2得:2518mm N f w t =,2512mm N f w v =。
截面的几何特性计算如下:惯性矩:44233102682065071428014280121210008121mm I x ⨯=⎥⎦⎤⎢⎣⎡⨯⨯+⨯⨯⨯+⨯⨯=翼缘面积矩:41198744050714280mm S x =⨯⨯=则翼缘顶最大正应力为:2243185215021026820610281011222mm N f mm N .h I M w tx =<=⨯⨯⨯⨯=⋅=σ 满足要求。
腹板高度中部最大剪应力:2243125075281026820625008500198744010374mm N f mm N .t I VS w vw x x =<=⨯⨯⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯==τ满足要求。
上翼缘和腹板交接处的正应力:2120805075002150507500mm N ..=⨯=⨯σ=σ上翼缘和腹板交接处的剪应力:243116434810268206198744010374mmN .t I VS w x x =⨯⨯⨯⨯==τ 折算应力:2222212152031100606434320803mm N .f .mm N ...w t =<=⨯+=τ+σ 满足要求。
钢结构原理习题答案第三章-7页word资料

3.1. 试设计双角角钢与节点板的角焊缝连接(如下图)。
钢材为Q235-B ,焊条为E43型,手工焊,作用着轴心力1000KN (设计值),分别采用三面围焊和两面侧焊进行设计。
解: 角焊缝强度设计值:焊缝内力分配系数为:321=α(肢背),311=α(肢尖) 最大焊缝厚度:肢背:mm 9~8)2~1(10h max f =-=, 肢尖及角钢端部:f max h 1.21012mm =⨯= 最小焊缝厚度: (1).若采用三面围焊:正面角焊缝的长度等于相连角钢肢的宽度,即mm b l w 1253==,所有焊缝厚度均取为6mm ,则正面角焊缝所能承受的内力3N 为:1w1we f N 564200l 66425.8mm 2h f 20.76160=+=+=⨯⨯⨯,取43cm 。
2w2w e f N 230800l 66177.7mm 2h f 20.76160=+=+=⨯⨯⨯,取18cm 。
(2).若采用两面侧焊,肢背焊缝厚度为8mm ,肢尖焊缝厚度为6mm 。
1w1we f N 667000l 1616388.2mm 2h f 20.78160=+=+=⨯⨯⨯,取40cm 。
2w2w e f N 333000l 1212259.8mm 2h f 20.76160=+=+=⨯⨯⨯,取26cm 。
1f 1w 1f h 60l h 8<<,2f 2w 2f h 60l h 8<<,即肢背和肢尖焊缝均满足最大焊缝长度和最小焊缝长度的构造要求。
3.2. 试求图3.81所示连接的最大荷载。
钢材为Q235-B ,焊条为E43型,手工焊,角焊缝焊脚尺寸1h 8mm =,1e 30mm =。
解: 图3.81中几段焊缝组成的围焊共同承受剪力V=F 和扭矩T=F*(e1+e2)的作用。
由题知角焊缝的焊脚尺寸8f h mm = 1e 30cm = 计算截面的重心位置为 则220546159e mm =-=计算中由于实际焊缝长度略大于图示长度,不再扣除水平焊缝的端部缺陷 焊缝的极惯性矩:324322441210.70.85020.70.820.5252018312120.520.70.820.520.70.820.5( 4.6)0.70.850 4.62129.5122201832129.522312.5()(3015.9)45.945.9X y P x y y Tx pI cm I cm I I I cm T F e e F FT r F I τ=⨯⨯⨯+⨯⨯⨯⨯≈=⨯⨯⨯⨯+⨯⨯⨯⨯-+⨯⨯⨯≈=+=+==+=⨯+=⨯⨯==2442442510 5.141022312.51045.915.910 3.271022312.510x Typ F T r F F I τ--⨯⨯≈⨯⨯⨯⨯⨯==≈⨯⨯轴心力V=F 在A 点产生的应力 则A 点处: 160/w f f N mm F <=→=239.1KN 所以最大设计荷载为239.1KN3.3. 试设计如图所示牛腿与柱的连接角焊缝①②③。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章
图为一两端铰接的焊接工字形等截面钢梁,钢材为Q235。
梁上作用有两个集中荷载P =300 kN (设计值),集中力沿梁跨度方向的支承长度为100mm 。
试对此梁进行强度验算并指明计算位置。
解:首先计算梁的截面模量,计算出梁在荷载作用下的弯矩和剪力,然后按照规定的计算公式
度、局部承压强度和折算应力强度等。
(1)计算截面模量
324x 1
88002280104041255342933mm 12
I =
⨯⨯+⨯⨯⨯=
33
4
y 11
210280800836620800mm 1212I =⨯⨯⨯+⨯⨯=3x1280104041131200mm S =⨯⨯=
3x2400
113120040081771200mm 2
S =+⨯⨯
= (2)验算截面强度
梁上剪力和弯矩图分布如图所示,由此确定危险点。
①弯曲正应力
B 、
C 两点间梁段弯矩最大
()128010213.51310
b t -==>,不考虑截面发展塑性 6x max x nx 60010410
196MPa 215MPa 11255342933
M f W σγ⨯⨯===<=⨯
②剪应力
A 、
B 两点间梁段和
C 、
D 两点间的梁段上的剪力最大
3x2max
v x w 30010177120052.9MPa 125MPa 12553429338
VS f I t τ⨯⨯===<=⨯ ③局部承压
在集中力作用B 、C 两点处没有加劲肋,应验算局部承压应力。
x y R 52100510150mm l a h h =++=+⨯=
3
c z w 130010250MPa>215MPa 1508
F
f l t ψσ⨯⨯====⨯
④折算应力
B 左截面、
C 右截面处同时存在较大的弯矩、剪力和局部压应力,应计算腹板与翼缘交界处的折算应力。
局部承压验算已不满足,此处不必验算折算应力。
一焊接工字形截面简支梁,跨中承受集中荷载P=1500kN (不包含自重),钢材为Q235,梁的跨度及几何尺寸如图所示。
试按强度要求确定梁截面。
解:①内力计算
梁的支座反力(未计主梁自重): 1.21500
900kN 2
R ⨯== 跨中最大弯矩:max 1.2150083600kN m 44
PL M ⨯⨯===⋅ ②初选截面
梁所需要的净截面抵抗矩为:6
33x nx x 36001015946843.85mm 15946.8cm 1.05215
M W f γ⨯===≈⨯
梁的高度在净空上无限制,按刚度要求,工作平台主梁的容许挠度为l /400,则梁容许的最小高度为:(参照均布荷载作用)
min 8000
533.3mm 1515
l h ≥
==
按经验公式,可得梁的经济高度:e 3030146.2cm h ===
参照以上数据,考虑到梁截面高度大一些,更有利于增加刚度,初选梁的腹板高度h w =150cm 。
腹板厚度按抗剪强度:max w v 1.2 1.2900000
5.76mm 1500125
w V t h f ⨯≥
==⨯
考虑局部稳定和构造因素: 1.11cm w t === 取腹板t=14mm 。
根据近似公式计算所需翼缘板面积:2w w x w 15946.8 1.4150
71.31cm 61506
t h W bt h ⨯=
-=-= 翼缘板宽:b =(1/~1/6)h =250~600mm ,取b=420mm 。
翼缘板厚:t =7131/420=,取t=16mm 。
翼缘外伸宽度:b 1=(420-14)/2=203mm 。
1203
12.71316
b t ==<=
③截面验算
截面的实际几何性质:
2w w 2150 1.4242 1.6344.4cm A h t bt =+=⨯+⨯⨯=
2
3
2
34112()1221150 1.61.4150242 1.61165964cm 122x w w w I t h bt h t ⎡⎤=++⎢⎥
⎣⎦+⎛⎫=
⨯⨯+⨯⨯= ⎪⎝⎭
3x 116596412812.8cm 91
W ==
3115004201685093760mm 2S ⎛⎫
=⨯⨯+= ⎪⎝⎭
321500150042016815001420843760mm 22S ⎛⎫
=⨯⨯++⨯⨯= ⎪⎝⎭
主梁自重估算:
单位长度梁的质量为:×100×7850×10-6
×=m
式中为考虑腹板加劲肋等附加构造用钢使自重增大的系数,则梁的自重为:g =m ×=m
由梁自重产生的跨中最大弯矩:22max 11
3.18 1.2830.5kN m 88
M ql =
=⨯⨯⨯=⋅ 由梁自重产生的支座剪力:11
3.18 1.2815.3kN 22
V ql ==⨯⨯⨯=
跨中最大弯矩:max 300030.53030.5kN m M =+=⋅
弯曲应力:622
x 3
x nx 3030.510225N/mm 215N/mm 1.0512812.810M f W σγ⨯===>=⨯⨯ 225215
100% 4.7%5%215
-⨯=<,所选截面符合要求,截面尺寸如图所示。
(也可重新选较大截面再进行验算) 支座处最大剪应力:
()3
max
v x w 90015.31020843760116.9MPa 125MPa 1165964000014
VS f I t τ+⨯⨯===<=⨯ 次梁处放置支承加劲肋,不需验算腹板的局部压应力。
跨中左侧和右侧截面处的弯矩和剪应力均最大,故需验算腹板与翼缘交界处的折算应力: 跨中截面腹板边缘正应力:
62x 4
nx 3030.510750194.9N/mm 116596410
M W σ⨯⨯===⨯ 跨中截面腹板边缘剪应力:
()3
max
x w 90015.310509376028.6MPa 1165964000014
VS I t τ+⨯⨯===⨯
跨中截面腹板边缘折算应力:
22z 201.1N/mm 1.1 1.1215236.5N/mm f σ===<=⨯=
某两端铰接的拉弯构件,截面为I45a 轧制工字形钢,钢材为Q235。
作用力如图所示,截面无削弱,要求确定构件所能承受的最大轴线拉力。
解:由附表查得I45a 型钢的截面特性:243
x x 102cm 32240cm 1430cm A I W ===,,
翼缘平均厚度18mm>16mm ,钢材的强度设计值f =205N/mm 2。
根据强度条件有:
x 23
n x nx 0.25200020510210 1.05143010M N P P A W γ⨯+=+<⨯⨯⨯ 解得P <,所以该压弯构件所能承受的最大轴线拉力为 KN (设计值)。
求如图所示T 形截面的形心、惯性矩、截面抵抗矩系数。
V
解:相对翼缘外边缘的x ′- x ′轴,翼缘:2
f 200102000mm A =⨯=,f 5mm y =-;腹板:2
w 240102400mm A =⨯=,f 130mm y =-,则截面形心到翼缘外边缘的距离:
f w w 1f w 200052400130
73.2mm 20002400A y A y y A A +-⨯-⨯=
==-++
则22401073.2176.8mm y =+-= ()()2
3x 2
341200102001073.2512
11024024010176.812028582123mm 12I =
⨯⨯+⨯⨯-+⨯⨯+⨯⨯-=
()334
y 2
3411
10200240106686667mm 1212
11024024010176.812028582123mm 12
I =⨯⨯+⨯⨯=+⨯⨯+⨯⨯-=
3x x1128582123390466mm 73.2I W y ===
3x x 2228582123161664mm 176.8
I W y ===
2。
