三类液面高度的变化问题

合集下载

浮力液面升降问题的类型及解题技巧

液面升降问题的分析冰浮于液面的问题是生活中的常见问题,在各类试卷中经常出现,但由于这类问题的现象不太明显,观察需要的时间较长,不为一般的学生所重视.即使一部分学生有意识地去进行观察,出会现因为问题类型比较多,而结论只有“升”和“降”两种,常常出现而把现象和条件的对应关系混淆的现象，导致认识的偏差。

为了更深刻地理解引起液面“升”、“降”的原因，准确把握条件和现象之间的关系。

可以将各类问题进行分类处理，从最基本的漂浮在液面上的冰熔化成水后液面的升降问题为基点，逐步展开思考形成系统的认识。

更重要的是可以通过这些问题的讨论和思考，把许多有关物体浮沉及液面变化问题连成一个整体。

一、液面升降的主要类型有：类型一：纯冰浸于液体，熔化后判断液面升降1、纯冰在纯水中熔化；2、纯冰在盐水〔或其它密度比水大的液体〕中熔化；3、纯冰在密度比水小的液体中熔化；类型二：冰块中含有其它杂质，冰块熔化后判断水面升降。

1、含有木块〔或其它密度比水小的固体〕的冰块在纯水中熔化；2、含有石块〔或其它密度比水大的固体〕的冰块在纯水中熔化；3、含有煤油〔或其它密度比水小的液体〕的冰块在纯水中熔化；类型三：冰块中含有一定质量的气体，冰块熔化后判断水面升降。

类型四：容器中的固态物质投入水中后判断液面升降1、固态物质的密度小于水的密度2、固态物质的密度等于水的密度3、固态物质的密度大于水的密度二、解题关键：液面上升也好、下降也好，关键在于我们比较的问题是什么，确立好问题就知道如何下手。

实际上我们要比较的是冰熔化前〔或物体投放前〕在液体中排开液体的体积和冰熔化成水后的体积〔或物体投放后液体体积〕的大小关系：假设前体积大于后体积，液面下降；假设前体积等于后体积，液面不变；假设前体积小于后体积，液面上升。

三、判断方法1、比较体积变化法：比较的是冰熔化前〔或物体投放前〕在液体中排开液体的体积和冰熔化成水后的体积〔或物体投放后液体体积〕的大小关系：假设前体积大于后体积，液面下降；假设前体积等于后体积，液面不变；假设前体积小于后体积，液面上升。

三类液面高度的变化问题

当物体上表面相对于原液面上移
ｈａ — ｈ２一ｈｌ＝＝＝２ｃｍ，
据 ③ 式知液面高度下降了
Ｓ物ｈａ
△ 隆一
一
Ｓ底一Ｓ物
６０ｃｍ × ２ｃｍ８０ｃｍ一６０ｃｍ
故物体Ａ此时浸入水中的深度为
ｈ一物一ｈａ一 △ 降一２ｃｍ，
《数理天地》初中版
· 物理中的思想和方法 ·
物理中的思想和方法
２Ｏｌ１年第９期
鸯面离鹰陶蜜他问题
王伦宇（湖北省广水市城郊入液体（１）将物体浸入柱形容器的液体中，若物体排开液体的体积为排，容器的横截面积为Ｓ底，则物体浸入前后液面高度的变化量为
（２）浸入柱形容器中的柱形物体高出液面，当容器中放出液体放后，液面高度下降了
一
．
⑤
例２如图４所示，正方体木块Ａ漂浮在水面上，不可伸长的悬绳刚好处于松弛状态，已知绳子能承受的最大拉力为２Ｎ，木块重Ｇ未一５Ｎ，木块的边长为１０ｃｍ，长方体容器的底面积为６００ｃｍ，若打开阀
的垂线，与小明、小华的速度图线相交，再从交点作ｔ轴的垂
图１
线，垂足即为小明、小华通过路程１０５ｍ、１００ｍ
所用的时间ｔ明、ｔ华．可看出ｔ明＜ｔ华，即小明先

液面升降问题2

液面升降问题 2液面升降问题分析液面升降的主要类型有:一、纯冰漂浮在不同液体中熔化后液面的升降情况:1、纯冰在纯水中熔化;(液面高度不变)2、纯冰在盐水(或其它密度比水大的液体)中熔化;(液面高度上升)3、纯冰在密度比水小的液体中熔化;(液面高度下降)二、含有固体杂质的冰漂浮在水中熔化后的液面升降情况:4、含有木块(或其它密度比水小的固体)的冰块在纯水中熔化;(液面高度不变)5、含有石块(或其它密度比水大的固体)的冰块在纯水中熔化;(液面高度下降)三、含有液体杂质的冰漂浮在水中熔化后的液面升降情况:6、含有煤油(或其它密度比水小的液体)的冰块在纯水中熔化;(液面高度上升)7、含有盐水(或其它密度比水大的液体)的冰块在纯水中熔化;(液面高度下降)四、含有气体的冰漂浮在水中熔化后的液面升降情况:8、一块冰漂浮在容器的水面上，冰块中含有一定质量的气体(空气、氢气、二氧化碳)，当冰完全熔化后，容器中的水面如何变化,(液面高度不变)例1:有一块冰浮在容器的水面上，当冰块完全熔化后，水面高度将怎样变化, 解析:冰块熔化前排开水的体积(即图中斜线部分)为:V,F/ρg,G/ρg,m/ρ(?漂浮时F,G) 排浮水冰水冰水浮冰冰块化成的水的体积为:V,m/ρ,m/ρ(?冰化成水后质量不变m= m) 水水冰水冰水所以液面高度不变推论:纯水水面上浮有纯冰.当冰熔化时液面将不变。

当冰熔化时，水对容器底的压强不变。

例2:若一冰块在水中，冰块与容器底部相接触并相互间有压力，则当冰块完全熔化后，容器内的水面将怎样变化,解析:冰块没有漂浮在水面上，冰块所受浮力小于冰块所受重力，所以熔化前F,G ，浮冰而F=G = ρg V，即ρg V,G，故得V,G/(ρg) 浮排水排水排冰排冰水熔化为水的体积V=m/ρ= m/ρ= G/(ρg) 水水水冰水冰水所以V,V，即熔化后水面要上升。

排水333例3:有一块冰漂浮在一杯浓盐水中(冰的密度是0(9×10千克,米;浓盐水的密度是1(1×10千3克,米)(如果冰块全部熔化后，则 ( )A(液面不变 B(液面上升 C(液面下降 D(无法判断解析:冰块熔化前，在盐水中处于漂浮状态(则有F=G，即浮ρg V=mg V=m/ρ........(1) 盐排冰排冰盐冰块熔化后，排开液体的体积等于冰熔化成水的体积，即V’=V= m/ρ(?冰化成水后质量不变m= m, m/ρ,m/ρ)……..(2) 排水水水冰水水水冰水比较冰块熔化前与冰块熔化后排开液体的体积可得m= m, ρ<ρ 。

中考物理复习《浮力液面高度变化量计算方法与技巧》

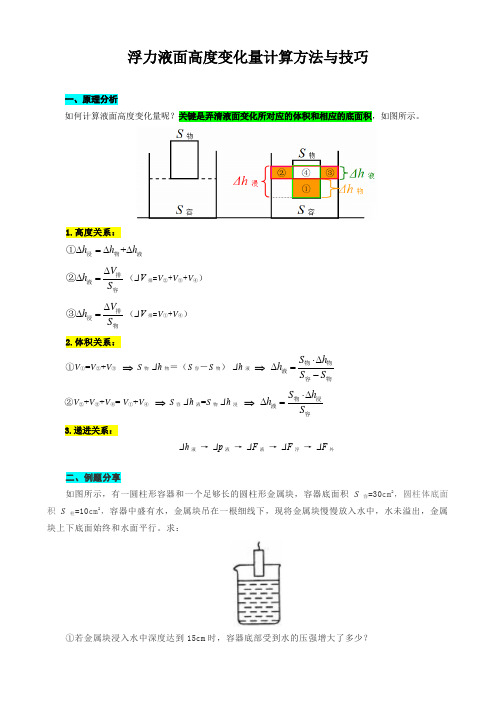
浮力液面高度变化量计算方法与技巧一、原理分析如何计算液面高度变化量呢？关键是弄清液面变化所对应的体积和相应的底面积，如图所示。

1.高度关系：+h h h ∆=∆∆浸物液①V h S ∆∆=排液容②（ΔV 排=V ②+V ③+V ④）V h S ∆∆=排浸物③（ΔV 排=V ①+V ④）2.体积关系：①V ①=V ②+V ③ ⇒ S 物·Δh 物＝（S 容－S 物）·Δh 液 ⇒ S h h S S ⋅∆∆=-物物液物容②V ②+V ③+V ④= V ①+V ④ ⇒ S 容·Δh 液=S 物·Δh 浸 ⇒ S h h S ⋅∆∆=浸物液容3.递进关系：Δh 液 → Δp 液 → ΔF 液 → ΔF 浮 → ΔF 外二、例题分享如图所示，有一圆柱形容器和一个足够长的圆柱形金属块，容器底面积S 容=30cm 2，圆柱体底面积S柱=10cm 2，容器中盛有水，金属块吊在一根细线下，现将金属块慢慢放入水中，水未溢出，金属块上下底面始终和水面平行。

求：①若金属块浸入水中深度达到15cm 时，容器底部受到水的压强增大了多少？②若绳子从金属块底部刚好接触到水面时开始向下放下15cm时，容器底部受到水的压强增了多少？1.第1小问分析过程：要求水对容器底部增加的压强，也就是求水位增加的高度。

如何求水位增加的高度呢？思维过程如下：当圆柱体浸入水中15cm时，实际上是一个动态过程，圆柱体一边下降，水位一边上升，圆柱体下降的深度加上水位上升的高度刚好为15cm。

由此可见，如何将动态变化过程转化为静态过程才是解题关键。

多数同学可能有这样的思维过程：假设原来水位不变，我们把圆柱体浸入水中后排开的水用容器接到，然后将排开的水再倒回容器中。

这个时候有两种思考：（1）倒入圆柱体两边的空白处，这样水位上升的高度，Δh=V排/(S容－S柱)。

显然，圆柱体浸入水中的深度就是15cm+Δh，跟题意矛盾。

液面高度变化求法解析

Vol .5() No .3Mar .2021此i f教学参考习题研究液面高度变化求法解析石玉东(河北省献县商林中学河北沧州062250)文章编号：1〇〇2-218X (2021)03-0051-03 中图分类号：G 632.4 文献标识码：B摘要：对常见的液面高度变化问题进行分类，并对每类情况进行了详尽的解析；通过分析第1类物体上下移动型，总结出了求液面高度变化量的计算公式，并用此公式解决了第2和第3类问题；前3类都是物体浸入液体体积即V #变而液体总体积V 液总不变的问题，第4类是V *不变改变的问题，第5类是V *和V **都改变的问题。

关键词：液体；浮力；液面升降；体积浮力和液体压强是初中物理考查的重点和难点，解答此类题目的关键在于正确求出液面高度的变化量A A 。

那么，求解A A 有何规律可循呢？下面对相关问题分类进行说明。

_、物体上下移动型题目1物体放在柱形容器液体中，当物体在液体中向上、向下移动时，求液面高度的变化A A 。

解法1观察推导法观察物体浸人液体中的体积即^#变化时，液面实际的升降情况，弄清的变化量A V#与容器中的哪部分体积相等，进而求出A /i 。

解法2假定分离法将物体在液面处分为上、下两部分，假定这两部分在液面处分离，并使其中一部分上升或下降，弄清M 升'#，所以M j3容厶'V "排S 容。

原液面现液面图4图假定分离法：物体下移前，如图4所示，假定原液面上部分不动，下部分沉底。

物体下移后，如图5所示，假定现液面上部分不动，下部分沉底，设原液面上升的体积（图5中灰色部分）为A /^=f。

〇容排=A V ^ = S容A /i 升A V 升，比较图4和图5容易看出AV 排=AV 升=S 容A/i 升，所以A/i 升=。

V#的变化量与容器中的哪部分体积相等，进而求出M 。

原液面现液面 AK ,，A /i #AK »J /j 飞八/ _ ——、H I—A"3-3- - _ ±2：•AK 轉，—:,TAK #图1图2图31.物体下移观察推导法：如图2所示，物体向下移动，V #变 2.物体上移观察推导法：如图7所示，物体向上移动，V 排变小，液面下降。

液面升降问题知多少

（上接第６页）
（Ｊ若物体漂浮或悬浮。Ｐｆ一ｆｌ【
若冰化成水，则液体增加的体积就是这部分
水的体积
＇＝卫生：盟盟：也，＾
。
如果物体从冰上被放人液体中，物体漂浮或悬
浮，则此时液面不变。冰融化成水，会引起液面升高。因此，此情况液面上升。（Ｊ若物体漂浮或悬浮。Ｐ二印
圈４
所以
ＰｇＡＧＶｌ
ＰｇＶＧ
所以
＾＝排
且
一
圈２
Ｐｇ
所以．＾＋Ｖｆ — 一＋ —盟伸Ｖ排Ｉ＜ — ～＝
ＰｇＰｇ
所以此时排开水的总体积为
所以液面下降
二、冰漂浮在液面上．冰融化后液面的升降
所以此时排开水的总体积为
Ｖ＋ＶＬ＿Ｌ：Ｖ：＋
ＰｌｇＰ｝ｇｆＩｆｌｊｆ
所以液面高度不变。（）若把放入水中．口下沉三
如『．会有以下关系军４ｌ
图１
又因为
所以所以
Ｆｐｇ＝Ｖ摊
：且
， ’
Ｐ
Ｐ
ＰｇＰ斗ｇｃ
，＇
如果ＰＩＩＩｆ
，则且
＞直。即Ｖ＞
如果物体从冰上被放人液体中．物体漂浮或悬
ＰｇＰＩｆｇＩ
说明液面要上升；

液面升降Δh问题

甲乙丙40 h /cm50 60 F /N20 30 0 4 2610 8 1070 液面升降问题△h 的大小指液面高度的变化量，它是浮力问题与液体压强综合计算题的结合点。

液面升降的高度Δh 根据产生的原因大致可分为三类：一、液体的体积不增减，仅仅由于V 排变化而引起的液面升降Δh 的问题。

二、V 排可能发生变化，由于增减液体而导致的△ h 变化三、V 排和液体的质量都变化从而导致的△ h 变化例题1：如图所示，底面积为S b 的圆柱形容器内盛有适量的水，另一底面积为S ａ的圆柱体A 有部分体积浸在水中，当圆柱体A 相对于容器下降高度为h 时，水没有溢出，圆柱体A 也未全部没入水中，物体A 所受水的浮力增加了。

例题2：如图甲所示，圆柱形平底容器置于水平桌面上，其底面积为500cm 2。

在容器内放入一个底面积为200cm 2、高为20cm 的圆柱形物块，物块底部的中心通过一段细线与容器底部相连。

向容器内缓慢注入某种液体直至将其注满，如图乙所示。

已知在注入液体的过程中细线对物块的拉力F 随液体深度h 的变化关系图像如图丙所示。

若将细线剪断，当物块静止时，液体对容器底部的压强为 Pa 。

（g =10N/kg ）例题3：如图甲所示，装有部分水的试管竖直漂浮在容器内的水面上，试管内水面与容器底部的距离为h ，试管壁粗细均匀、厚度不计；现将一物块完全浸没在该试管水中，发现试管内水面与容器底部的距离恰好仍为h ，如图乙所示，若试管横截面积与容器横截面积之比为1:5，则下列说法正确的是( ) A ．放入的物块密度为5×103kg/m 3 B ．放入的物块密度为1.25×103kg/m 3 C ．放入的物块密度为2.25×103kg/m 3 D ．小试管与容器内水面变化的高度相等专项训练（一）1.如图9甲所示，A B 、两个实心正方体所受重力分别为A B G G 、，它们的密度分别为A B ρρ、，它们的边长分别为A B h h 、．若将它们放在水平地面上，对地面产生的压强分别为A B p p 、．若将它们放入柱状容器的水中（水未溢出），物体静止后，如图9乙所示，A 物体有1/3的体积露出水面，B 物体静止在水中，容器底部受到的压力比未放入两物体时增加1F ；若将B 物体取出轻压在A 物体上（水未溢出），待物体静止后．容器底部受到水的压力比未放入两物体时增加2F ．若已知2A B p p =，甲乙1 1.52N F =，g 取10N/kg ．则下列说法正确的是（）A ．:3:1AB h h =B ．200Pa A B p p -=C ．0.04m B h =D ．211.52N A B G G F F +==；2．一个竖直放置在水平桌面上的圆柱形容器，内装某种液体。

北京中考浮力题之液面升降Δh解析及相关练习教师用

浮力中关于液面升降的例题解析△h 的大小指液面高度的变化量，它是浮力问题与液体压强综合计算题的结合点。

对于它的分析求解是初中物理计算题的难点和重点。

液面升降的高度Δh 根据产生的原因可以分为三类：但实际变化远远不止于此!其中由于V 排变化引起的液面升降Δh 的问题是基本题型，也是中考要重点考察的内容，为了使同学们正确分析此类问题，找出解决问题的关键，现将其核心知识及几种△h 产生情况的分析方法阐述如下：一、液体的体积不增减，仅仅由于V 排变化而引起的液面升降Δh 的问题。

【例1】如图1所示，容器的B 为粗细均匀的圆柱状，且横截面积S 容=200cm2。

物体A 为横截面积为S A=30cm2，高度为的h A 的圆柱体。

将物体A 放入液体中，物体A 浸入的深度为h 1，液体上升的高度为△h ，则液面上升的高度△h 等于什么？ 2、公式推导：△ h=V 排/S 容。

----(1)又根据物体排开液体的体积等于浸入的物体的体积即：V 排=V 浸入，物体A 为圆柱体，故有：S 容△ h = S A h 1 h= S A h 1/S 容。

----(2)3、此式适用的条件是：V 水不变，而只有V 排的变化，且容器必须是柱状的。

此式的实质是：被物体排开的液体的体积V 排，分布于容器整个截面积(S 容)上，使液面变化△ h 。

如下图3。

思考：如图4所示的柱形容器，横截面积S 容，物体为横截面积为S A ，高度为的h A 的圆柱体。

将物体放入液体中，物体浸入的深度为h 1，液体上升的高度为△h ，图1AB图2甲乙则液面上升的高度△h等于什么？二、V排可能发生变化，由于增减液体而导致的△ h变化1、产生原因：物体均自由漂浮在液面上，液体密度不变，所以V排不变。

当向容器内注入同种液体使其体积增加了△ V，所以这种△ h的由来是因为容器内液体体积增加而导致的。

2、公式△ h=△ V液/S容。

-----(2)三、V排和液体的质量都变化从而导致的△ h变化1、产生的原因：分析比较图7可知容器中液体增加了△ V液，物体浸入液体的体积同时也增加了△ V排。

(完整版)浮力液面升降问题的类型及解题技巧

为了更深刻地理解引起液面“升”、“降”的原因，准确把握条件和现象之间的关系。

可以将各类问题进行分类处理，从最基本的漂浮在液面上的冰熔化成水后液面的升降问题为基点，逐步展开思考形成系统的认识。

更重要的是可以通过这些问题的讨论和思考，把许多有关物体浮沉及液面变化问题连成一个整体。

一、液面升降的主要类型有：类型一：纯冰浸于液体，熔化后判断液面升降1、纯冰在纯水中熔化；2、纯冰在盐水（或其它密度比水大的液体）中熔化；3、纯冰在密度比水小的液体中熔化；类型二：冰块中含有其它杂质，冰块熔化后判断水面升降。

1、含有木块（或其它密度比水小的固体）的冰块在纯水中熔化；2、含有石块（或其它密度比水大的固体）的冰块在纯水中熔化；3、含有煤油（或其它密度比水小的液体）的冰块在纯水中熔化；类型三：冰块中含有一定质量的气体，冰块熔化后判断水面升降。

实际上我们要比较的是冰熔化前（或物体投放前）在液体中排开液体的体积和冰熔化成水后的体积（或物体投放后液体体积）的大小关系：若前体积大于后体积，液面下降；若前体积等于后体积，液面不变；若前体积小于后体积，液面上升。

三、判断方法1、比较体积变化法：比较的是冰熔化前（或物体投放前）在液体中排开液体的体积和冰熔化成水后的体积（或物体投放后液体体积）的大小关系：若前体积大于后体积，液面下降；若前体积等于后体积，液面不变；若前体积小于后体积，液面上升。

中考复习专题之液面升降问题

中考复习专题之液面升降问题一、液面升降现象的各类和变化规律：A、纯冰在纯水中熔化——不变B、纯冰在盐水（或其它密度比水大的液体）中熔化——升高C、纯冰在密度比水小的液体中熔化——降低D、含有木块（或其它密度比水小的固体）的冰块在纯水中熔化——不变E、含有石块（或其它密度比水大的固体）的冰块在纯水中熔化——降低F、含有煤油（或其它密度比水小的液体）的冰块在纯水中熔化——升高。

（煤油最后露出水面的部分在水面散开，从而增加了液面的高度。

）二、解题思路：1．传统的常规解法，即比较变化前后两个排开液体体积的大小关系。

例1：有一块冰浮在容器的水面上，当冰块完全熔化后，水面高度将怎样变化？解：冰块熔化前排开水的体积为：V排＝F浮/ρ水g＝G冰/ρ水g＝m 冰/ρ水∵漂浮时F浮＝G冰冰块化成的水的体积为：V＝m水/ρ水＝m 冰/ρ水∵冰化成水后质量不变，所以液面高度不变（相当于冰块化成的水刚好填补满了排开的部分）例2：有一块冰中含有小石块，浮在容器的水面上，当冰块完全熔化后，水面高度怎样变化？解：熔化前排开水体积为：V排＝F浮/ρ水g＝G总/ρ水g＝（G冰＋G石）/ρ水g＝（m冰＋m石）/ρ水①熔化后的体积为冰化成的水的体积加上沉在容器底的石块的体积，即：V＝V水＋V石＝m水/ρ水＋m石/ρ石＝m冰/ρ水＋m石/ρ石②比较①②式，∵ρ石>ρ水，∴V<V排，所以液面下降。

例3：有一块冰中含有液态的煤油，浮在容器内的水面上，当冰块完全熔化后，液面将怎样变化？解：熔化前排开水体积为：V排＝F浮/ρ水g＝G总/ρ水g＝（G冰＋G油）/ρ水g＝（m冰＋m油）/ρ水①熔化后的体积为V＝V水＋V油＝m水/ρ水＋m油/ρ油＝m冰/ρ水＋m 油/ρ油②比较①②式，∵ρ油<ρ水，∴V>V排，所以液面上升。

2．全新的巧解思路：①因为此类题中容器的形状不影响最后的结论，因此可以把容器假想为柱体。

②柱体内装液体时，容器底所受到的总压力F总等于容器内所有物体受到的总重力，即：F总＝G总。

浮力专题：液面变化及其解题技巧(很全面、很详尽)

学习好资料欢迎下载液面升降问题的分析各种情况都包含，配有详图2018年2月11日对于液体中的物体由于某种变化而引起的液面升降问题的形式出现，本文介绍一种简便快捷的判断方法——“状态法”．（一）、状态法：就是对液体变化前、后的物体所处的状态进行比较来判断液面的上升、下将、不变的方法．（二）、状态法迅速判断液面升降方法：①若变化前后液体中的物体都处于漂浮、悬浮状态，而无沉体出现，则液面不变；②若液体中的物体，在变化前无沉体，而变化后有沉体出现，则液面下降；③若液体中的物体，在变化前有沉体，而变化后无沉体出现，则液面升高;说明：变化前后液体中物体的总质量保持不变；容器中液体的密度不变．（三）、证明设液体中的物体的总重为G，变化前后在液体中所受的总浮力分别为Ｆ浮、Ｆ浮′．若变化前后均无沉体出现，由浮沉条件知①Ｆ浮′＝Ｆ浮＝Ｇ，ρ液ｇＶ排′＝ρ液ｇＶ排，则Ｖ排′＝Ｖ排，液面不变．②若变化前无沉体，变化后有沉体，由浮沉条件知Ｆ浮＝Ｇ，Ｆ浮′＜Ｇ，则Ｆ浮′＜Ｆ浮，即Ｖ排′＜Ｖ排，故液面下降．③若变化前有沉体，变化后无沉体，由浮沉条件知Ｆ浮＜Ｇ，Ｆ浮′＝Ｇ，则Ｆ浮′＞Ｆ浮，即Ｖ排′＞Ｖ排，故液面上升．一、液面升降的主要类型有：类型Ⅰ：纯冰浸于液体，熔化后判断液面升降①、纯冰在纯水中熔化；②、纯冰在盐水（或其它密度比水大的液体）中熔化；③、纯冰在密度比水小的液体中熔化；类型Ⅱ：冰块中含有其它杂质，冰块熔化后判断水面升降。

①、含有木块（或其它密度比水小的固体）的冰块在纯水中熔化；②、含有石块（或其它密度比水大的固体）的冰块在纯水中熔化；③、含有煤油（或其它密度比水小的液体）的冰块在纯水中熔化；类型Ⅲ：冰块中含有一定质量的气体，冰块熔化后判断水面升降。

类型Ⅳ：容器中的固态物质投入水中后判断液面升降①、固态物质的密度小于水的密度②、固态物质的密度等于水的密度③、固态物质的密度大于水的密度二、解题关键：无论液面上升或者下降，关键在比较的问题是什么，确立好问题就知道如何下手。

浮力液面升降问题的类型及解题技巧

为了更深刻地理解引起液面“升”、“降”的原因，准确把握条件和现象之间的关系。

可以将各类问题进行分类处理，从最基本的漂浮在液面上的冰熔化成水后液面的升降问题为基点，逐步展开思考形成系统的认识。

更重要的是可以通过这些问题的讨论和思考，把许多有关物体浮沉及液面变化问题连成一个整体。

对于液体中的物体由于某种变化而引起的液面升降问题的形式出现，本文介绍一种简便快捷的判断方法——“状态法”．（一）、什么叫状态法所谓“状态法”，就是对变化前后液体中的物体所处的状态进行比较来判断液面的升降．（二）、如何用“状态法”速断液面升降若变化前后液体中的物体都处于漂浮、悬浮状态，而无沉体出现，则液面不变；若液体中的物体，在变化前无沉体，而变化后有沉体出现，则液面下降；若液体中的物体，在变化前有沉体，而变化后无沉体出现，则液面升高．说明：变化前后液体中物体的总质量保持不变；容器中液体的密度不变．（三）、证明设液体中的物体的总重为G ，变化前后在液体中所受的总浮力分别为Ｆ浮、Ｆ浮′．若变化前后均无沉体出现，由浮沉条件知Ｆ浮′＝Ｆ浮＝Ｇ，ρ液ｇＶ排′＝ρ液ｇＶ排，则Ｖ排′＝Ｖ排，液面不变．若变化前无沉体，变化后有沉体，由浮沉条件知Ｆ浮＝Ｇ，Ｆ浮′＜Ｇ，则Ｆ浮′＜Ｆ浮，即Ｖ排′＜Ｖ排，故液面下降．若变化前有沉体，变化后无沉体，由浮沉条件知Ｆ浮＜Ｇ，Ｆ浮′＝Ｇ，则Ｆ浮′＞Ｆ浮，即Ｖ排′＞Ｖ排，故液面上升．一、液面升降的主要类型有：类型一：纯冰浸于液体，熔化后判断液面升降1、纯冰在纯水中熔化；2、纯冰在盐水（或其它密度比水大的液体）中熔化；3、纯冰在密度比水小的液体中熔化；类型二：冰块中含有其它杂质，冰块熔化后判断水面升降。

总复习浮力液面高度变化专题(定稿)闫

V排
Δh
F浮
G
A
h1 h2
ΔP
ΔF压
甲
乙
情景一：V排变化导致液面高度变化
A
Δh液升 Δh物降
A
甲

乙
液面上升的高度Δh液升与Δh物降的关系？ S物Δh物降=（S容-S物）Δh液升
情景一：V排变化导致液面高度变化
A
Δh液降 Δh物升
A
甲
乙
液面下降高度Δh液降与Δh物升的关系？
S物Δh物升=（S容-S物）Δh液降
若注入液体的过程中细线对物块的拉力F随液体深度h的变化关系图像如图丙所示。请问：能从图像中得到什么信息？
（1）
（2）
F浮=G物
h=30cm
h’=35cm F拉=8N
（4）
（ 5）
H=60cm
（3）
绳恰好拉直
恰好浸没
例3．如图10甲所示，圆柱形平底容器置于水平桌面上，其底面积为500cm2。在容器内放入一个底面积为 200cm2、高为20cm的圆柱形物块，物块底部的中心通过一段细线与容器底部相连。向容器内缓慢注入某种液体直至将其注满，如图10乙所示。已知在注入液体的过程中细线对物块的拉力F随液体深度h的变化关系图像如图10丙所示。若将细线剪断，当物块静止时，液体对容器底部的压强为 Pa。（g=10N/kg）
S容=500cm2
S物= 200cm2、h物= 20cm
h=30cm h’=35cm h容=60cm Δh
（1）
（2）
刚好F浮=G物 F浮=G物
（3）
（4）
（5）绳恰好直 F拉=0N F浮=G物
（6）恰好浸没 F浮不变 F拉=8N

液面高度变化问题

液面高度变化问题力学压轴题之液面变化问题。

纵观11年各区一模，在23题这个位置上，出现频率最高的就是液面变化问题了，例如：海淀一模，东城一模，西城一模，怀柔一模，通州一模，都涉猎到了液面变化量问题。

大家都公认液面变化有三难：1.很难判断何时是环形体积何时是整个体积；2.液面在变，浮力也在变，究竟有何联系；3.如何分析变化的物理过程。

为了帮助大家解决这些困惑，现以2011年海淀一模为例，为大家介绍下具体方法：(2011年海淀一模第23题)圆柱形平底容器置于水平桌面上，其底面积为500cm2。

在容器内放入一个底面积为200cm2、高为20cm 的圆柱形物块，物块底部的中心通过一段细线与容器底部相连。

向容器内缓慢注入某种液体直至将其注满，如图10乙所示。

已知在注入液体的过程中细线对物块的拉力F随液体深度h的变化关系图像如图10丙所示。

若将细线剪断，当物块静止时，液体对容器底部的压强为：Pa.（g=10N/kg）这是典型的液面变化问题，此题包括了上面所说的三个难点，解决了这三个问题，此题即可迎刃而解，我们来逐一攻破:物理过程分析：分析物理变化过程主要是对整个过程进行受力分析，根据受力的特点确定所在状态，此题可分为三个过程：过程一：甲图刚注入液体时，浮力由小变大，慢慢等于重力，此过程绳子慢慢伸长，当重力等于浮力时，绳子刚好被拉直且拉力为0，处于临界状态，此时液体深为30cm。

过程二：当液体深由30cm到35cm时，液面继续上升，物快浸入液体中的体积越来越大，浮力慢慢变大，到35cm时，物快刚好完全浸没，拉力达到最大，此时有G物+F=F浮过程三：继续注入液体，液面升高，但物快所受浮力不变，拉力不变。

液面在变浮力也在变：此题当液体深度从0到35cm过程中，液面高度在变，浮力也在变，尤其是30cm到35cm时更能看出其特点：液面变化5cm拉力变化8N，也就是浮力变化了8N。

所以可以根据浮力的变化量关系列等式ΔF浮=ρ液gΔV排，可以求出ρ液=0.8×103kg/立方米环形体积还是整个体积要想求液体对容器底部的压强，我们必须求剪断细线后液面下降的高度，这时很多同学都在犹豫，使用环形面算体积呢，还是用整个面积算体积呢？我们知道剪断细线之后物块露出液面的体积为ΔV露，应该等于整个液面下降的体积，所以应该是整个面积来求，ΔV露=ΔhS，Δh=2cm,最后液面高度为58cm,由P=ρ液gh=4640pa。

(名师整理)最新物理中考专题复习《液面高度变化问题剖析》精品教案

液面高度变化问题剖析一、考点突破灵活利用力学知识，解决液面高度变化问题。

二、重难点提示灵活利用力学知识，解决液面高度变化问题。

浮冰问题：（＞＞＞盐水水冰酒精）1.漂浮在容器内盐水面上的纯冰块，当冰块熔化后，液面上升。

（盐水）水2.漂浮在容器内水面上的纯冰块、夹有木块的冰块或夹有气泡的冰块，当冰块熔化后，容器内液面不变。

（）木水3.漂浮在容器内水面上的夹有铁块的冰块，当冰块熔化后，液面下降。

4漂浮在容器内盐水面上的纯冰块，当冰块熔化后，液面上升。

（）盐水水浮冰问题：（＞＞＞盐水水冰酒精）例题1将一块冰放在水中，静止。

冰熔化后，水面____________（选填“上升”“下降”“高度不变”）；如果冰块里有一个气泡，则冰熔化后，水面____________；如果冰块里有一块木块，则冰熔化后，水面____________；如果冰块里有一小石块，则冰熔化后，水面____________（以上各空均选填“上升”“下降”“高度不变”）思路分析：（1）对纯冰块而言，根据上题的解题方法，同样可得m g V g冰水排冰块排开水的体积冰熔化成水后的体积V V，则液面不变。

水排V m/排冰V m/水冰水水（2）对夹有木块的冰而言，冰熔化成水后，木块仍将漂浮于水面。

此时应比较冰变成水后的体积V与木块漂浮于水面时排开水的体积水V排之和（即V V），跟夹有木块的冰排开的水的体积V。

水排排结论：①若V V水②若V V水③若V V水排排排V，则液面不变；排V，则液面上升；排V，则液面下降。

排设木块的质量为m，纯冰块的质量为m，夹有木块的冰浮在水面上有木冰m g m g V g夹有木块的冰排开水的体积V （m m）/排冰木水冰变成水后的体积仍为V m/水冰水冰熔化成水后，木块仍浮于水面，设其排开水的体积为V，则排m g V g木水排所以V排m/木水显然V V水排m/冰水m/木水(m冰m)/水水V排根据上述结论①知，液面不变。

【重要提示】将木块换成密度小于的其他物块，此结论仍成立。

2020年中考物理二轮复习小专题-液面升降问题

液面变化液面高度变化是中考物理的常见形式，也是中考物理的难点，直接影响学生的得分率。

解决这类问题时，要求学生能画图分析，灵活运用相关的知识，不能生搬硬套，死记结论，或者仅限于比较繁琐的传统解法，应掌握解题方法和解题过程，培养学生独立思考分析问题的能力。

1、水面浮冰（1）纯冰浸于液体：①、纯冰浮于纯水上，熔化后液面无变化。

②、纯冰浮于盐水上（液体密度大于水的密度时），冰熔化后液面上升。

③、纯冰浮于液体上（液体密度小于水的密度时），冰熔化后液面下降。

（2）冰中含有杂质，漂浮在纯水上时：①、含有木块（杂质密度小于等于水的密度），冰熔化后液面不变。

②、含有石块（杂质密度大于水的密度时），冰熔化后液面下降。

③、含有煤油（或其它密度比水小的液体），冰熔化后液面上升。

（3）冰块中含有一定质量的气体时：①、冰块中含有气体（空气、氢气、二氧化碳），当冰完全熔化后气体挥发，容器中的水面下降。

②、若漂浮在水面上的冰块中有一气泡，冰块里的气泡的质量可以忽略不计，冰熔化后水面保持不变。

（4）容器中的固态物质投入水中后判断液面升降：①、固态物质的密度小于水的密度时，物体投入水中后水面高度无变化②、固态物质的密度等于水的密度时，物体投入水中后水面高度无变化。

③、固态物质的密度大于水的密度时，物体投入水中后水面高度下降。

2、柱形容器液面升降V物S（2）当物体漂浮在液面上时：Δh＝G ρ液gS (3)物体向下（向上）运动h 时，Δh＝S 1hS 2−S 1如图3所示，有一横截面积为S 1、重为G 圆柱形容器；一个足够长的直柱形金属块，其横截面积为S 2，容器中盛有密度为ρ，深度为h 、体积为V 的液体；金属块吊在一根细线下，现将金属块慢慢浸入液体中深为h ，液面上升h ∆，金属块始终没有浸没于液体中。

（一）求在金属块浸入液体前：（1）液体对容器底部的压强p 1；gh p ρ=1；（2）液体对容器底部的压力F 1；液G ghS S p F ===ρ11；（3）容器对水平地面的压力F 2；G G G S p F ＋＋液==12；（4）容器对水平地面的压强p 2；SG G p ＋液=2。

2023年中考物理复习《液面高度、压强的变化》

液面高度、压强的变化一、冰块漂在水中，熔化后液面高度怎么变？液体对底部压强怎么变？冰熔化为水后，质量是不变的，由于ρ水＞ρ冰，由m V ρ=，质量没变的情况下，密度变大，则熔化后体积会变小，有多小呢？可能会出现三种情况：所以，解决此类题目的关键就是在比较V 排和熔化后水的体积V 水！哪个式子里面含有V 排呢？阿基米德原理：F 浮=ρ液gV 排，因为冰漂浮，所以F 浮=G 冰即 F 浮=G 冰=ρ液gV 排（这里ρ液即ρ水）哪个式子里面含有V 水呢？冰熔化成水，质量不改变：G 冰=G 水=m 水g =ρ水gV 水所以得：ρ液gV 排=ρ水gV 水所以：V 排= V 水，即冰熔化刚刚好把那个坑填满，所以液面高度不变由液体压强公式：p =ρgh （ρ始终为ρ水，h 不变）所以液体对底部压强不变可不可以先看液体对底部压强p 怎么变？然后再根据液体压强公式p =ρgh ，推出液面高度h 怎么变？首先液体对底部产生压强是因为液体对容器底部有压力产生的，根据压强公式F p S=，因为底部受力面积是不变的，若能判断出液体对底部压力怎么变，若F 变大，则p 也变大；若F 不变，则p 不变；若F 变小，则p 也变小。

把冰拎出来，会有这样一个坑，坑的体积不就是V 排！ V 排冰 ①熔化后水的体积V 水＞V 排，则液面高度会升高（最终液面是相平的，比起原来的会升高）水 ②熔化后水的体积V 水＝V 排，则液面高度不变水 ③熔化后水的体积V 水＜V 排，则液面高度会升高（最终液面是相平的，比起原来的会降低）水综上，得F 支=F 支′，容器底部对液体的支持力没变，故液体对容器底的压力也不变，又因为受力面积没变，所以液体对底部压强p 不变。

由液体压强公式p =ρgh ，ρ始终为ρ水，故液面高度也不变。

二、冰块漂在盐水中，熔化后液面高度怎么变？液体对底部压强怎么变？依然是比较V 排和熔化后水的体积V 水哪个式子里面含有V 排呢？阿基米德原理：F 浮=ρ液gV 排，因为冰漂浮，所以F 浮=G 冰即 F 浮=G 冰=ρ液gV 排（这里ρ液即ρ盐水）哪个式子里面含有V 水呢？冰熔化成水，质量不改变：G 冰=G 水=m 水g =ρ水gV 水所以得：ρ盐水gV 排=ρ水gV 水即 ρ盐水V 排=ρ水V 水因为 ρ盐水＞ρ水所以：V 排＜ V 水由液体压强公式：p =ρgh （ρ始终为ρ水，h 不变）所以液体对底部压强不变冰 F 支 F 压（水对容器）液体对容器底部的压力，容器是受力对象，以容器是受力对象不好分析，我们分析它的反作用力，即容器对液体的支持力，它们是大小相等的，所以选择液体，即水作为受力对象，分析熔化前容器底部对水的支持力F 支和熔化后容器底部对水的支持力F 支′。

【初中物理】初中物理液面升降问题处理技巧

【初中物理】初中物理液面升降问题处理技巧浮力这部分内容是初中物理中比较难的一部分，特别是一些特殊题型解法让学生感觉很头疼。

对于这类题型，需要认真的总结归纳，弄清楚题目所涉及的知识之间的相互关联，掌握分析该类题型的方法和技巧，再辅之以相当数量的练习，这样才能达到牢固掌握和举一反三的目的。

下面就浮力中的液面升降问题的处理方法，简单阐述一下。

液面升降的主要类型有：1、冰在水中熔化；2、冰在盐水（或其他密度比水大的液体）中熔化；3、含有木块（或其他密度比水小的固体）的冰在水中熔化；4、含有石块（或其他密度比水大的固体）的冰在水中熔化；5、含有煤油（或其他密度比水小的液体）的冰在水中熔化。

以上类型，一般的问题都是判断冰完全熔化后，容器中液面的高度变化情况。

对于类型1，漂浮在水中的冰块完全熔化后，水面高度如何变化的问题，介绍一下常规方法。

如图，漂浮在水面上的冰块对应的V排为图中红色斜线部分体积。

首先要明确的是，如果冰熔化都得到水的体积V水=V排，则容器中液面高度不变，若V水>V排，则液面高度上升，若V水<</SPAN>V排，则液面高度降低。

因此，此题关键是判断V水与V排的关系。

V水是冰熔化后得到水的体积，而冰熔化过程中质量不变，根据这个特点，冰熔化后得到水的重力等于冰的重力，即；而V排是与冰的浮力直接相关的，由于冰漂浮在水中，所以浮力等于冰的重力，即，综合两个方程，得到，则V水=V排，从而得到容器中液面高度不变。

用类似的方法，可以分析别的类型。

例如类型3，包含有木块的冰漂浮在水中，当冰完全熔化之后，木块漂浮，判断容器中液面高度的变化，如图：如果我们用V排来表示冰和木块整体漂浮是对应的排开水的体积，用V水表示冰完全熔化后得到水的体积，用V木排表示冰熔化后木块漂浮时木块排开液体的体积，那么，液面高度的变化需要判断的是V排与V水+V木排的大小关系，若两者相等，液面高低不变，若前者大于后者，则液面降低，反之，液面升高，判断方法依然是利用浮力和重力的关系，推导公式就可以得到。

三类液面高度的变化问题

浮力液面升降问题的类型及解题技巧

三类液面高度的变化问题

液面升降问题2

中考物理复习《浮力液面高度变化量计算方法与技巧》

液面高度变化求法解析

液面升降问题知多少

液面升降Δh问题

北京中考浮力题之液面升降Δh解析及相关练习 教师用

(完整版)浮力液面升降问题的类型及解题技巧

中考复习专题之液面升降问题

浮力专题：液面变化及其解题技巧(很全面、很详尽)

浮力液面升降问题的类型及解题技巧

总复习浮力液面高度变化专题(定稿)闫

液面高度变化问题

(名师整理)最新物理中考专题复习《液面高度变化问题剖析》精品教案

2020年中考物理二轮复习小专题-液面升降问题

2023年中考物理复习《液面高度、压强的变化》

【初中物理】初中物理液面升降问题处理技巧

北京中考浮力题之液面升降Δh解析及相关练习教师用