二次函数y=ax2(a≠0)与y=ax2+c(a≠0)的图象与性质—知识讲解

合集下载

九年级数学二次函数y=ax2bxc(a≠0)的图像与性质(知识讲解2)Word版含解析

专题2.13 二次函数y=ax2+bx+c(a≠0)的图像与性质（知识讲解2）-2021-2022学年九年级数学下册基础知识专项讲练（北师大版）专题2．13 二次函数y=ax²+bx+c(a≠0)的图像与性质（知识讲解2）类型六、两个二次函数图像的综合判断1．已知二次函数y ＝ax 2与y ＝﹣2x 2+c ．（1）随着系数a 和c 的变化，分别说出这两个二次函数图象的变与不变；（2）若这两个函数图象的形状相同，则a ＝；若抛物线y ＝ax 2沿y 轴向下平移2个单位就能与y ＝﹣2x 2+c 的图象完全重合，则c ＝；（3）二次函数y ＝﹣2x 2+c 中x 、y 的几组对应值如表：表中m 、n 、p 的大小关系为（用“＜”连接）．2．如图，抛物线F ：2y ax bx c =++的顶点为P ，抛物线：与y 轴交于点A ，与直线OP 交于点B ．过点P 作PD ⊥x 轴于点D ，平移抛物线F 使其经过点A 、D 得到抛物线F ′：2y a x b x c '''=++，抛物线F ′与x 轴的另一个交点为C ．（1）当a = 1，b =－2，c = 3时，求点C 的坐标(直接写出答案)；（2）若a 、b 、c 满足了22b ac =，⊥求b ：b ′的值；⊥探究四边形OABC 的形状，并说明理由．类型七、根据二次函数图象判断式的符号3．如图，二次函数2y ax bx c =++的图象开口向上，图象经过点()1,2-和()1,0，且与y 轴相交于负半轴．第()1问：给出四个结论：①0a >；②0b >；③0c >；④0a b c ++=．写出其中正确结论的序号（答对得3分，少选、错选均不得分）第 ()2问：给出四个结论：⊥abc ＜0；⊥2a +b ＞0；⊥a +c =1；⊥a ＞1．写出其中正确结论的序号．4．抛物线()20y ax bx c a =++≠的图象如图所示：（1）判断a ，b ，c ，24b ac -的符号；（2）当OA OB =时，求a ，b ，c 满足的关系．5．已知抛物线2y ax bx c =++，如图所示，直线1x =-是其对称轴，()1确定a ，b ，c ，24b ac =-的符号；()2求证：0a b c -+>；()3当x 取何值时，0y >，当x 取何值时0y <．类型八、根据抛物线上的对称点求对称轴6．已知二次函数y=ax2+bx 的图象过点（6，0），（﹣2，8）．（1）求二次函数的关系式；（2）写出它的对称轴和顶点坐标．7．已知二次函数2y x bx c =-++，函数值y 与自变量x 之间的部分对应值如表：（1）写出二次函数图象的对称轴．（2）求二次函数的表达式．（3）当41x -<<-时，写出函数值y 的取值范围．8．已知二次函数y ＝ax 2﹣2ax ．（1）二次函数图象的对称轴是直线x ＝；（2）当0≤x ≤3时，y 的最大值与最小值的差为4，求该二次函数的表达式；（3）若a ＜0，对于二次函数图象上的两点P （x 1，y 1），Q （x 2，y 2），当t ≤x 1≤t +1，x 2≥3时，均满足y 1≥y 2，请结合函数图象，直接写出t 的取值范围．9．如图，已知抛物线2142y x x =--+与x 轴交于点A 、B （点A 在点B 的左侧），与y 轴交于C.（1）求点A 、B 、C 的坐标；（2）若点E 与点C 关于抛物线的对称轴对称，求梯形AOCE 的面积.类型九、二次函数y=ax2 +bx+c (a≠0)的最值10．如图在平面直角坐标系中，一次函数y kx b =+的图像经过点()0,4A -、()2,0B 交反比例函数m y x=()0x >的图像于点()3,C a ，点P 在反比例函数的图像上，横坐标为n ()03n <<，//PQ y 轴交直线AB 于点Q ，D 是y 轴上任意一点，连接PD 、QD ．（1）求一次函数和反比例函数的表达式；（2）求DPQ 面积的最大值．11．已知二次函数y ＝ax 2+bx ﹣3的图象经过点（1，﹣4）和（﹣1，0）．（1）求这个二次函数的表达式；（2）x 在什么范围内，y 随x 增大而减小？该函数有最大值还是有最小值？求出这个最值．12．已知二次函数的图象经过三点（1,0)()3,0-，30,2⎛⎫- ⎪⎝⎭ (1)求二次函数的解析式；(2)求抛物线的顶点坐标，对称轴以及抛物线与坐标轴的交点；(3)当x 为何值时，函数有最大值或最小值？最大值或最小值是多少？类型十、二次函数y=ax2 +bx+c (a≠0)图象中的将军饮马问题13．如图，抛物线y ＝﹣x 2+bx+c （a≠0）与x 轴交于A （1，0），B （﹣4，0）两点．（1）求该抛物线的解析式；（2）设（1）中的抛物线交y 轴于C 点，在该抛物线的对称轴上求出Q 点的坐标使得⊥QAC 的周长最小．14．如图，抛物线y ＝﹣x 2+bx+c （a≠0）与x 轴交于A （1，0），B （﹣4，0）两点．（1）求该抛物线的解析式；（2）设（1）中的抛物线交y 轴于C 点，在该抛物线的对称轴上求出Q 点的坐标使得⊥QAC 的周长最小．15．如图，在平面直角坐标系中，抛物线l 1：y ＝x 2+bx+c 过点C(0，﹣3)，且与抛物线l 2：y ＝﹣12x 2﹣32x+2的一个交点为A ，已知点A 的横坐标为2．点P 、Q 分别是抛物线l 1、抛物线l 2上的动点．（1）求抛物线l 1对应的函数表达式；（2）若点P 在点Q 下方，且PQ⊥y 轴，求PQ 长度的最大值；（3）若以点A 、C 、P 、Q 为顶点的四边形为平行四边形，直接写出点P 的坐标．16．如图，抛物线212y x bx c =++与直线132y x =+分别相交于A 、B 两点，其中点A 在y 轴上，且此抛物线与x 轴的一个交点为()3,0C -．（1）求抛物线的解析式（2）在抛物线对称轴l 上找一点M ，使MBC ∆的周长最小，请求出这个周长的最小值．类型十一、二次函数图象的平移17．已知：抛物线y ＝﹣x 2+bx +c 经过点B （﹣1，0）和点C （2，3）．（1）求此抛物线的表达式；（2）如果此抛物线沿y 轴平移一次后过点（﹣2，1），试确定这次平移的方向和距离．18．已知抛物线212y x bx c =-++经过点（1，0），（0，32）．（1）求该抛物线的函数表达式；（2）抛物线212y x bx c =-++可以由抛物线212y x =-怎样平移得到？请写出一种平移的方法．19．已知二次函数y ＝x 2－4x ＋3．（1）直接写出函数图象的顶点坐标、与x 轴交点的坐标；（2）将图象先向左平移2个单位，再向下平移2个单位，得到新的函数图象，直接写出平移后的图象与y 轴交点的坐标．类型十二、二次函数综合20．如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点三点0(1)A ，,(50)B ，,4(0)C ，．（1）求抛物线的解析式和对称轴；（2）P 是抛物线对称轴上的一点，求满足PA PC +的值为最小的点P 坐标（请在图1中探索）；（3）在第四象限的抛物线上是否存在点E ，使四边形OEBF 是以OB 为对角线且面积为12的平行四边形？若存在，请求出点E 坐标，若不存在请说明理由.（请在图2中探索） 21．已知抛物线23y ax bx =++过()30A -,，()10B ,两点，交y 轴于点C ．（1）求该抛物线的表达式．（2）设P 是该抛物线上的动点，当PAB 的面积等于ABC 的面积时，求P 点的坐标．22．已知m,n是方程x2－6x+5=0的两个实数根，且m<n，抛物线y=－x2+bx+c的图象经过点A(m,0)、B(0,n)．(1)求这个抛物线的解析式；(2)设（1）中抛物线与x轴的另一交点为C,抛物线的顶点为D，试求出点C、D的坐标和⊥BCD的面积；(3)P是线段OC上的一点，过点P作PH⊥x轴，与抛物线交于H点，若直线BC把⊥PCH 分成面积之比为2：3的两部分，请求出P点的坐标．23．如图，抛物线y＝x2﹣2x﹣3与x轴交于A，B两点，与y轴交于点D，抛物线的顶点为C．（1）求A，B，C，D的坐标；（2）求四边形ABCD的面积．参考答案：1．（1）二次函数y＝ax2的图象随着a的变化，开口大小和开口方向都会变化，但是对称轴、顶点坐标不会改变；二次函数y＝﹣2x2+c的图象随着c的变化，开口大小和开口方向都没有改变，对称轴也没有改变，但是，顶点坐标会发生改变；（2）±2，﹣2；（3）p＜m＜n 【分析】(1)根据二次函数的性质即可得到结论；(2)由函数图象的形状相同得到a=±2，根据上加下减的平移规律即可求得函数y =ax2-2，根据完全重合，得到c =-2．(3)由二次函数的解析式得到开口方向和对称轴，然后根据点到对称轴的距离即可判断．【详解】解：（1）二次函数y＝ax2的图象随着a的变化，开口大小和开口方向都会变化，但是对称轴、顶点坐标不会改变；二次函数y＝﹣2x2+c的图象随着c的变化，开口大小和开口方向都没有改变，对称轴也没有改变，但是，顶点坐标会发生改变；（2）⊥函数y＝ax2与函数y＝﹣2x2+c的形状相同，⊥a＝±2，⊥抛物线y＝ax2沿y轴向下平移2个单位得到y＝ax2﹣2，与y＝﹣2x2+c的图象完全重合，⊥c＝﹣2，故答案为：±2，﹣2．（3）由函数y＝﹣2x2+c可知，抛物线开口向下，对称轴为y轴，⊥1﹣0＜0﹣（﹣2）＜5﹣0，⊥p＜m＜n，故答案为：p＜m＜n．【点睛】本题考查了二次函数的性质，二次函数图象与几何变换，二次函数图象上点的坐标特征，熟知图形平移不变性的性质是解答此题的关键．2．（1）C（3，0）；（2）⊥2：3；⊥矩形，理由见解析【分析】（1）由于抛物线F′由抛物线F平移所得，开口方向和开口大小都无变化，因此a＝a′＝1；由于两条抛物线都与y轴交于A点，那么c＝c′＝3．然后可根据抛物线F的坐标求出其顶点坐标，即可得出D点的坐标，然后将D的坐标代入抛物线F′中，即可求出抛物线F′的解析式，进而可求出C点的坐标．（2）⊥与（1）的方法类似，在求出D的坐标后，将D的坐标代入抛物线F′中，即可得出关于b，b′的关系式即可得出b，b′的比例关系．⊥探究四边形OABC的形状，无非是平行四边形，菱形，矩形这几种．那么首先要证的是四边形OABC 是个平行四边形，已知了OA //BC ，只需看A ，B 的纵坐标是否相等，即OA 是否与BC 的长相等．根据抛物线F 的解析式可求出P 点的坐标，然后用待定系数法可求出OP 所在直线的解析式．进而可求出抛物线F 与直线OP 的交点B 的坐标，然后判断B 的纵坐标是否与A 点相同，如果相同，则四边形OABC 是矩形（⊥AOC ＝90°），如果B ，A 点的纵坐标不相等，那么四边形AOCB 是个直角梯形．【详解】解：（1） ⊥a = 1，b =－2，c = 3⊥223y x x =-+=()212x -+⊥P （1，2）⊥过点P 作PD ⊥x 轴于点D ，⊥D （1，0）由于抛物线F ′由抛物线F 平移所得，开口方向和开口大小都无变化，因此a ＝a ′＝1；由于两条抛物线都与y 轴交于A 点，那么c ＝c ′＝3．⊥抛物线F ′：23y x b x '=++，代入D （1，0）得0=1+b ’+3解得b ’=-4⊥243y x x =-+=()()13x x --⊥点C 的坐标为（3，0）；（2）⊥抛物线2y ax bx c =++，令x =0，则y =c ，⊥A 点坐标（0，c ）．⊥22b ac =， ⊥244224442ac b ac ac ac c a a a --===， ⊥点P 的坐标为（2b a -，2c ）． ⊥PD ⊥x 轴于D ，⊥点D 的坐标为（2b a -，0）．根据题意，得a =a ′，c = c ′，⊥抛物线F ′的解析式为2'y ax b x c =++．又⊥抛物线F ′经过点D （2b a-，0），⊥220()42b b a b c a a'=⨯+-+． ⊥2024b bb ac '=-+．又⊥22b ac =，⊥2032b bb '=-．⊥b :b ′=23．⊥由⊥得，抛物线F ′为232y ax bx c =++．令y =0，则2302ax bx c ++=． ⊥12,2b b x x a a=-=-． ⊥点D 的横坐标为2b a- ⊥点C 的坐标为（ba -，0）．设直线OP 的解析式为y kx =．⊥点P 的坐标为（,22b c a -）， ⊥22c b k a =-， ⊥22222ac ac b b k b b b =-=-=-=-， ⊥2b y x =-． ⊥点B 是抛物线F 与直线OP 的交点， ⊥22b ax bxc x ++=-． ⊥12,2b b x x a a=-=-． ⊥点P 的横坐标为2b a-， ⊥点B 的横坐标为ba -．把b x a =-代入2b y x =-，得22()222b b b ac y c a a a=--===． ⊥点B 的坐标为(,)b c a-． ⊥BC //OA ，AB //OC ．（或BC //OA ，BC =OA ），⊥四边形OABC 是平行四边形．又⊥⊥AOC =90°，⊥四边形OABC 是矩形．【点睛】本题着重考查了待定系数法求二次函数的性质、函数的平移变换、探究矩形的构成情况等重要知识点．3．（1）正确的序号为⊥⊥；（2）正确的序号为⊥⊥⊥．【分析】（1）根据抛物线开口向上对⊥进行判断；根据抛物线对称轴x=-2b a在y 轴右侧对⊥进行判断；根据抛物线与y 轴的交点在x 轴下方对⊥进行判断；根据x=1时，y=0对⊥进行判断；（2）有（1）得到a>0，b<0，c<0，则可对⊥进行判断；根据0<-2b a<1可对⊥进行判断；把点(-1,2)和(1,0)代入解析式得a ﹣b +c =2，a +b +c =0,整理有a+c=1，则可对⊥进行判断；根据a=1-c ，c<0可对⊥进行判断．【详解】（1）⊥由抛物线的开口方向向上可推出a ＞0，正确；⊥因为对称轴在y 轴右侧，对称轴为x =2b a-＞0．又⊥a ＞0，⊥b ＜0，错误；⊥由抛物线与y 轴的交点在y 轴的负半轴上，⊥c ＜0，错误；⊥由图象可知：当x =1时y =0，⊥a +b +c =0，正确．故（1）中，正确结论的序号是⊥⊥．（2）⊥⊥a ＞0，b ＜0，c ＜0，⊥abc ＞0，错误；⊥由图象可知：对称轴x =2b a -＞0且对称轴x =2b a -＜1，⊥2a +b ＞0，正确； ⊥由图象可知：当x =﹣1时y =2，⊥a ﹣b +c =2，当x =1时y =0，⊥a +b +c =0；a ﹣b +c =2与a +b +c =0相加得2a +2c =2，解得：a +c =1，正确；⊥⊥a +c =1，移项得：a =1﹣c ．又⊥c ＜0，⊥a ＞1，正确．故（2）中，正确结论的序号是⊥⊥⊥．【点睛】二次函数y =ax 2+bx +c 系数符号的确定：（1）a 由抛物线开口方向确定：开口方向向上，则a ＞0；否则a ＜0．（2）b 由对称轴和a 的符号确定：由对称轴公式x =2b a-判断符号．（3）c 由抛物线与y 轴的交点确定：交点在y 轴正半轴，则c ＞0；否则c ＜0．（4）b 2﹣4ac 由抛物线与x 轴交点的个数确定：2个交点，b 2﹣4ac ＞0；1个交点，b 2﹣4ac =0；没有交点，b 2﹣4ac ＜0．4．（1）240b ac ->；（2）10ac b -+=．【分析】（1）根据图形，开口向下得a ＜0，x =0时可得c ＞0，由对称轴可得b ＞0，与x 轴有两个不同交点可得b 2﹣4ac ＞0；（2）由于B 点坐标可以表示为：（0，c ），|OA |=|OB |，可知A （﹣c ，0）即可进行求解．【详解】（1）由图象可知，抛物线开口向下，可得：a ＜0；x =0时，y =c ＞0；⊥对称轴x =02b a->，a ＜0，⊥b ＞0；图象与x 轴有两个不同交点可得b 2﹣4ac ＞0；（2）当|OA |=|OB |时，即A 点坐标为（﹣c ，0），代入抛物线方程得y =ac 2﹣bc +c 两边同时除以c 得：ac ﹣b +1=0．【点睛】本题考查了二次函数图象与系数的关系，难度一般，关键在已知条件下表示出A 点的坐标代入抛物线方程．5．（1）0a <，0b <，0c >，240b ac =->；（2）详见解析；（3）当31x -<<时，0y >；当3x <-或1x >时，0y <．【分析】（1）根据开口方向确定a 的符号，根据对称轴的位置确定b 的符号，根据抛物线与y 轴的交点确定c 的符号，根据抛物线与x 轴交点的个数确定b 2-4ac 的符号；（2）根据图象和x=-1的函数值确定a -b+c 与0的关系；（3）抛物线在x 轴上方时y ＞0；抛物线在x 轴下方时y ＜0．【详解】()1∵抛物线开口向下，∴0a <，∵对称轴12b x a=-=-， ∴0b <，∵抛物线与y 轴的交点在x 轴的上方，∴0c >，∵抛物线与x 轴有两个交点，∴240b ac =->；()2证明：∵抛物线的顶点在x 轴上方，对称轴为1x =-，∴当1x =-时，0y a b c =-+>；()3根据图象可知，当31x -<<时，0y >；当3x <-或1x >时，0y <．【点睛】本题考查了二次函数图象与系数的关系，解题的关键是熟练的掌握二次函数图象与系数的关系.6．（1）y=12x2﹣3x ；（2）对称轴为直线x=3、顶点坐标为（3，﹣92）．【分析】（1）根据图像过点（6，0），（﹣2，8）列方程组求出a 、b 的值即可，（2）把解析式配方后即可确定对称轴和顶点坐标．【详解】（1）⊥y=ax 2+bx 的图象过点（6，0），（﹣2，8）．⊥3660428a b a b +=⎧⎨-=⎩，解得：123a b ⎧=⎪⎨⎪=-⎩ ， ⊥二次函数解析式为y=12x 2﹣3x ；（2）⊥y=12x 2﹣3x=12（x ﹣3）2﹣92， ⊥抛物线的对称轴为直线x=3、顶点坐标为（3，﹣92）．【点睛】本题考查了待定系数法求二次函数的解析式、二次函数的三种形式．将二次函数的一般解析式转化为顶点式时，可采用了“配方法”．灵活运用二次函数的三种形式是解题关键. 7．（1）x=2；（2）242y x x =---；（3）22y -<≤【分析】（1）二次函数是轴对称图形，而（-4，-2），（0，-2）关于对称轴对此，利用中点坐标公式可求，（2）求二次函数解析式2y x bx c =-++，可知b,c 待定，但（-4，-2），（0，-2）只能取一点，取两点坐标（-1，1），（0，-2）代入解之即可，（3）由于对称轴与x 轴交点横坐标，在41x -<<-，说明x=-4与x=-1取值不是最大值，为此x=-4与x=-1对应的函数值的最小值与x=-2时函数值即可．【详解】解：（1）⊥二次函数是轴对称图形，4x =-、0x =时的函数值相等，都是2-，对称轴是（-4，-2），（0，-2）两点连结的中垂线，⊥此函数图象的对称轴为直线4022x -+==-；（2）由点（-1，1），（0，-2）在抛物线上将()1,1-，()0,2-代入2y x bx c =-++，得：112b c c --+=⎧⎨=-⎩，解得：42b c =-⎧⎨=-⎩， ⊥二次函数的表达式为：242y x x =---；（3）⊥()224222y x x x =---=-++，⊥当2x =-时，y 取得最大值2，由表可知当4x =-时=2y -，当=1x -时1y =，⊥当41x -<<-时，22y -<≤．【点睛】本题考查利用列表求对称轴表示式，二次函数解析式，函数值范围，关键利用数形结合思想，掌握二次函数的性质，函数值的求法，抛物线最值．8．（1）1；（2）y ＝x 2﹣2x 或y ＝﹣x 2+2x ；（3）﹣1≤t ≤2【分析】（1）由对称轴是直线x ＝2b a -，可求解；（2）分a ＞0或a ＜0两种情况讨论，求出y 的最大值和最小值，即可求解；（3）利用函数图象的性质可求解．【详解】解：（1）由题意可得：对称轴是直线x ＝22a a--＝1，故答案为：1；（2）当a ＞0时，⊥对称轴为x ＝1，当x ＝1时，y 有最小值为﹣a ，当x ＝3时，y 有最大值为3a ，⊥3a ﹣（﹣a ）＝4．⊥a ＝1，⊥二次函数的表达式为：y ＝x 2﹣2x ；当a ＜0时，同理可得y 有最大值为﹣a ； y 有最小值为3a ，⊥﹣a ﹣3a ＝4，⊥a ＝﹣1，⊥二次函数的表达式为：y ＝﹣x 2+2x ；综上所述，二次函数的表达式为y ＝x 2﹣2x 或y ＝﹣x 2+2x ；（3）⊥a ＜0，对称轴为x ＝1，⊥x ≤1时，y 随x 的增大而增大，x ＞1时，y 随x 的增大而减小，x ＝﹣1和x ＝3时的函数值相等，⊥t ≤x 1≤t +1，x 2≥3时，均满足y 1≥y 2，⊥t ≥﹣1，t +1≤3，⊥﹣1≤t ≤2．【点睛】本题考查了二次函数的性质，二次函数图象上点的坐标特征等知识点的综合应用，能利用分类思想解决问题是本题的关键．9．（1）A （-4,0），B （2,0），C,0,4）；（2）12【分析】（1）在抛物线的解析式中，令x=0可以求出点C 的坐标，令y=0可以求出A 、B 点的坐标；（2）先求出E 点坐标，然后求出OA ，OC ，CE 的长计算面积即可.【详解】解：（1）当y=0时，212x --x+4=0，解得x 1=－4，x 2=2， ⊥A （－4，0），B （2，0），当x=0时，y=4，⊥C （0，4）；（2）y=212x -﹣x+4=12-（x+1）2+92， ⊥抛物线y=212x -﹣x+4的对称轴是直线x=－1， ⊥E 的坐标为（－2，4），则OA=4，OC=4，CE=2，S 梯形AOCE =(24)4122+⨯= 【点睛】本题是对二次函数的基础考查，熟练掌握二次函数与x 轴，y 轴交点坐标的求解及梯形面积知识是解决本题的关键.10．（1）624,y x y x=-=；（2）4. 【分析】（1）利用点()0,4A -、()2,0B 求解一次函数的解析式，再求C 的坐标，再求反比例函数解析式；（2）设6,,P n n ⎛⎫ ⎪⎝⎭则(),24,Q n n -再表示PQ 的长度，列出三角形面积与n 的函数关系式，利用函数的性质可得答案．【详解】解：（1）设直线AB 为,y kx b =+把点()0,4A -、()2,0B 代入解析式得：420b k b =-⎧⎨+=⎩解得：24k b =⎧⎨=-⎩∴ 直线AB 为24,y x =-把()3,C a 代入得：2342,a =⨯-=()3,2,C ∴把()3,2C 代入：,m y x= 236m ∴=⨯=，6,y x∴= （2）设6,,P n n ⎛⎫ ⎪⎝⎭//PQ y 轴，则(),24,Q n n - 由0＜n ＜3，()666242424,PQ n n n n n n∴=--=-+=-+ 16242DPQ S n n n ⎛⎫∴=-+ ⎪⎝⎭()222314,n n n =-++=--+即当1n =时， 4.DPQ S ∴=最大【点睛】本题考查的是利用待定系数法求解一次函数与反比例函数的解析式，以及利用二次函数的性质求解面积的最值，掌握以上知识是解题的关键．11．（1）y ＝x 2﹣2x ﹣3；（2）当x ＜1时，y 随x 增大而减小，该函数有最小值，最小值为﹣4．【分析】（1）将（1，﹣4）和（﹣1，0）代入解析式中，即可求出结论；（2）将二次函数的表达式转化为顶点式，然后根据二次函数的图象及性质即可求出结论．【详解】（1）根据题意得3430a b a b +-=-⎧⎨--=⎩，解得12a b =⎧⎨=-⎩，所以抛物线解析式为y ＝x 2﹣2x ﹣3；（2）∵y ＝（x ﹣1）2﹣4，∴抛物线的对称轴为直线x ＝1，顶点坐标为（1，﹣4），∵a ＞0，∴当x ＜1时，y 随x 增大而减小，该函数有最小值，最小值为﹣4．【点睛】此题考查的是二次函数的综合大题，掌握利用待定系数法求二次函数解析式、二次函数的图象及性质是解决此题的关键．12．(1)21322y x x =+-；(2)顶点()1,2--，对称轴=1x -，交点：()()31,0,3,0,0,2⎛⎫-- ⎪⎝⎭；(3)=1x -时函数有最小值为2-．【分析】（1）抛物线的点过（1,0)3,0，可以设抛物线的解析式为y=a(x -1)(x+3)，把点30,2⎛⎫- ⎪⎝⎭代入解得a 即可；（2）由配方法，得出抛物线解析式的顶点式，可得顶点坐标，对称轴以及抛物线与坐标轴的交点；（3）由抛物线的开口向上，可得函数有最小值，顶点坐标的纵坐标是函数的最小值．【详解】(1)设抛物线解析式为y=a(x -1)(x+3)，将30,2⎛⎫- ⎪⎝⎭代入，解得12a =，所以抛物线解析式为21322y x x =+-，故答案为：21322y x x =+-；（2）抛物线解析式为21322y x x =+-，配方可得，()221123=1222y x x x =+-+-（）， ⊥顶点()1,2-- ，对称轴=1x -，由（1）知，交点：()()31,0,3,0,0,2⎛⎫-- ⎪⎝⎭，故答案为：顶点()1,2--，对称轴=1x -，交点：()()31,0,3,0,0,2⎛⎫-- ⎪⎝⎭； (3)由（2）可知，函数解析式为()21122y x =+-，开口向上，函数有最小值，当=1x - 时函数有最小值为2-，故答案为：=1x -时函数有最小值为2-．【点睛】本题考查了二次函数的解析式求法，二次函数的性质，熟练掌握二次函数的性质是解题的关键．13．（1）y ＝﹣x 2﹣3x+4（2）Q （﹣32，52）【分析】（1）函数的表达式为：y ＝﹣（x ﹣1）（x+4），即可求解；（2）点B 为点A 关于函数对称轴的对称点，连接BC 交函数对称轴与点Q ，则点Q 为所求，即可求解．【详解】解：（1）函数的表达式为：y ＝﹣（x ﹣1）（x+4）＝﹣x 2﹣3x+4；（2）抛物线的对称轴为：x ＝﹣32，点B 为点A 关于函数对称轴的对称点，连接BC 交函数对称轴与点Q ，则点Q 为所求，点C（0，4），将点B、C坐标代入一次函数表达式：y＝kx+m得：404k mm-+=⎧⎨=⎩，解得：14km=⎧⎨=⎩，故直线BC的表达式为：y＝x+4，当x＝﹣32时，y＝52，则点Q（﹣32，52）．【点睛】本题考查了利用待定系数法求二次函数解析式，周长最小本质上考查抛物线的对称轴上求出Q点的坐标使得QA+QC最短，点B为点A关于函数对称轴的对称点，连接BC 交函数对称轴与点Q，原理是是两点之间线段最短14．（1）y＝﹣x2﹣3x+4（2）Q（﹣32，52）【分析】（1）函数的表达式为：y＝﹣（x﹣1）（x+4），即可求解；（2）点B为点A关于函数对称轴的对称点，连接BC交函数对称轴与点Q，则点Q为所求，即可求解．【详解】解：（1）函数的表达式为：y＝﹣（x﹣1）（x+4）＝﹣x2﹣3x+4；（2）抛物线的对称轴为：x＝﹣32，点B为点A关于函数对称轴的对称点，连接BC交函数对称轴与点Q，则点Q为所求，点C（0，4），将点B、C坐标代入一次函数表达式：y＝kx+m得：404k mm-+=⎧⎨=⎩，解得：14km=⎧⎨=⎩，故直线BC的表达式为：y＝x+4，当x＝﹣32时，y＝52，则点Q（﹣32，52）．【点睛】本题考查了利用待定系数法求二次函数解析式，周长最小本质上考查抛物线的对称轴上求出Q点的坐标使得QA+QC最短，点B为点A关于函数对称轴的对称点，连接BC 交函数对称轴与点Q，原理是是两点之间线段最短15．（1）y＝x2﹣2x﹣3；（2）12124；（3）(﹣1，0)或(3，0)或(43-，139)或(﹣3，12)【分析】（1）将x＝2代入y＝﹣12x2﹣32x+2，从而得出点A的坐标，再将A（2，﹣3），C（0，﹣3）代入y＝x2+bx+c，解得b与c的值，即可求得抛物线l1对应的函数表达式；（2）设点P的坐标为（m，m2﹣2m﹣3），则可得点Q的坐标为（m，﹣12m2﹣32m+2），从而PQ等于点Q的纵坐标减去点P的纵坐标，利用二次函数的性质求解即可；（3）设点P的坐标为（n，n2﹣2n﹣3），分两类情况：第一种情况：AC为平行四边形的一条边；第二种情况：AC为平行四边形的一条对角线．分别根据平行四边形的性质及点在抛物线上，得出关于n的方程，解得n的值，则点P的坐标可得．【详解】解：（1）将x＝2代入y＝﹣12x2﹣32x+2，得y＝﹣3，⊥点A的坐标为（2，﹣3）．将A（2，﹣3），C（0，﹣3）代入y＝x2+bx+c，得23=2+23b cc⎧-+⎨-=⎩，解得23bc=-⎧⎨=-⎩，⊥抛物线l1对应的函数表达式为y＝x2﹣2x﹣3；（2）⊥点P、Q分别是抛物线l1、抛物线l2上的动点．⊥设点P的坐标为（m，m2﹣2m﹣3），⊥点P在点Q下方，PQ⊥y轴，⊥点Q的坐标为（m，﹣12m2﹣32m+2），⊥PQ＝﹣12m2﹣32m+2﹣（m2﹣2m﹣3），＝﹣32m2+12m+5，⊥当m＝﹣112=3622⎛⎫⨯-⎪⎝⎭时，PQ长度有最大值，最大值为：﹣23126⎛⎫⨯ ⎪⎝⎭+1126⨯+5＝12124；⊥PQ长度的最大值为121 24；（3）设点P的坐标为（n，n2﹣2n﹣3），第一种情况：AC为平行四边形的一条边．AC=2⊥当点Q在点P右侧时，点Q的坐标为（n+2，﹣12（n+2）2﹣32（n+2）+2），将Q的坐标代入y＝﹣12x2﹣32x+2，，得n2﹣2n﹣3＝﹣12（n+2）2﹣32（n+2）+2，解得，n＝0或n＝﹣1．⊥n＝0时，点P与点C重合，不符合题意，舍去，⊥n＝﹣1，⊥点P的坐标为（﹣1，0）；⊥当点Q在点P左侧时，点Q的坐标为（n﹣2，﹣12（n﹣2）2﹣32（n﹣2）+2），将Q的坐标代入y＝﹣12x2﹣32x+2，得n2﹣2n﹣3＝﹣12（n﹣2）2﹣32（n﹣2）+2，解得n＝3或n＝﹣43．⊥此时点P的坐标为（3，0）或（﹣43，139）；第二种情况：AC为平行四边形的一条对角线．Q点的纵坐标y Q，n2-2n-3-(-3)=-3-y Q，y Q=-n2+2n-3，点Q的坐标为（2﹣n，﹣n2+2n﹣3），将Q的坐标代入y＝﹣12x2﹣32x+2，得﹣n2+2n﹣3＝﹣12（2﹣n）2﹣32（2﹣n）+2，解得，n＝0或n＝﹣3．⊥n＝0时，点P与点C重合，不符合题意，舍去，⊥n＝﹣3，⊥点P的坐标为（﹣3，12）．综上所述，点P的坐标为(﹣1，0)或(3，0)或(43，139)或(﹣3，12)．【点睛】本题考查抛物线解析式，平行y轴线段的最值，平行四边形的性质，掌握抛物线解析式，平行y轴线段的最值，平行四边形的性质，利用平形四边形的性质构造方程是解题关键．16．（1）215322y x x =++；（2【分析】（1）利用132y x =+的解析式求解A 的坐标，把()0,3A ，()3,0C -代入212y x bx c =++，利用待定系数法列方程组，解方程组可得答案；（2）联立两个函数解析式，求解B 的坐标，线段BC 的长度，如图，要使MBC 的周长最小，则MB MC +最小，设二次函数215322y x x =++与x 轴的另一交点为D ，抛物线的对称轴为：552,1222x =-=-⨯ 点()2,0D -，连接,BD 交对称轴于,M MD MC =，此时，MB MC MB MD BD +=+=最小，再利用勾股定理求解BD =【详解】.解：（1）抛物线212y x bx c =++与直线132y x =+交于y 轴上一点A ，令0,x = 则3,y =∴ 点()0,3A 把()0,3A ，()3,0C -代入212y x bx c =++得： 39302c b c =⎧⎪⎨-+=⎪⎩，解得：523b c ⎧=⎪⎨⎪=⎩， ∴抛物线的解析式是215322y x x =++；（2）将直线132y x =+与二次函数215322y x x =++联立得方程组： 213215322y x y x x ⎧=+⎪⎪⎨⎪=++⎪⎩ 215133,222x x x ∴++=+ 240,x x ∴-=解得：0x =或4x =-，04,,31x x y y ==-⎧⎧∴⎨⎨==⎩⎩()0,3A ，()4,1B ∴-BC ∴=如图，要使MBC 的周长最小，则MB MC +最小，设二次函数215322y x x=++与x 轴的另一交点为D ，抛物线的对称轴为：552,1222x =-=-⨯ ()3,0C - ∴ 点()2,0D -，连接,BD 交对称轴于,MMD MC ∴=，此时，MB MC MB MD BD +=+=最小，此时：BD ==MBC ∴【点睛】本题考查的是利用待定系数法求解二次函数的解析式，二次函数的性质，利用轴对称的性质求解三角形的周长的最小值，掌握以上知识是解题的关键．17．（1）y =﹣x 2+2x +3；（2）需将抛物线向上平移4个单位【分析】（1）把点B 和点C 的坐标代入函数解析式解方程组即可；（2）求出原抛物线上x ＝－2时，y 的值为－5，则抛物线上点（－2，－5）平移后的对应点为（－2，－1），根据纵坐标的变化可得平移的方向和平移的距离．【详解】解：（1）把B （﹣1，0）和点C （2，3）代入y ＝﹣x 2＋bx ＋c得10423b c b c --+=⎧⎨-++=⎩，解得23b c =⎧⎨=⎩，所以抛物线解析式为y ＝﹣x 2＋2x +3；（2）把x ＝﹣2代入y ＝﹣x 2＋2x +3得y ＝﹣4﹣4＋3＝﹣5，点（﹣2，﹣5）向上平移4个单位得到点（﹣2，﹣1），所以需将抛物线向上平移4个单位．【点睛】本题主要考查待定系数法求二次函数的解析式及抛物线的平移，熟练掌握待定系数法求二次函数的解析式是解题的关键．18．（1）213y 22x x =--+；（2）先向左平移1单位，再向上平移2个单位【分析】（1）把已知点的坐标代入抛物线解析式求出b 与c 的值即可；（2）先将抛物线的一般式转化为顶点式，然后指出满足题意的平移方法即可．【详解】解：（1）把()1,0，30,2⎛⎫ ⎪⎝⎭代入抛物线解析式得： 10232b c c ⎧-++=⎪⎪⎨⎪=⎪⎩，解得：132b c =-⎧⎪⎨=⎪⎩，则抛物线解析式为213y 22x x =--+；（2）抛物线解析式为22131y (1)2222x x x =--+=-++，抛物线213y 22x x =--+可以由抛物线212y x =-先向左平移1单位，再向上平移2个单位．【点睛】本题考查了二次函数图象与几何变换，二次函数的性质，二次函数图象上点的坐标特征，以及待定系数法求二次函数解析式，熟练掌握二次函数性质是解本题的关键． 19．（1）顶点坐标为()2,1-，与x 轴的交点坐标为()1,0，()3,0；（2）()0,3-．【分析】（1）根据配方法，可得顶点式解析式，根据函数值为零，可得相应自变量的值；（2）根据图象向左平移加，向右平移减，向上平移加，向下平移减，可得平移后的解析式，根据自变量与函数值的关系，可得答案．【详解】解：（1）()22x 4321y x x =--＝－＋，顶点坐标为()2,1-，当0y =时，2430x x -+=，解得1x =或3x =，即图象与x 轴的交点坐标为()1,0，()3,0；（2）图象先向左平移2个单位，再向下平移2个单位，得()2,2212y x =-+--，化简得23y x =-，当0x =时，3y =-，即平移后的图象与y 轴交点的坐标()0,3-．【点睛】本题考查了二次函数的性质，利用配方法得出顶点坐标，利用图象向左平移加，向右平移减，向上平移加，向下平移减得出平移后的解析式是解题关键．20．（1）2545442y x x -+＝，函数的对称轴为：3x ＝；（2）点8(3)5P ，；（3）存在，点E 的坐标为12(2,)5-或12,)5(4-．【分析】1（）根据点AB 、的坐标可设二次函数表达式为：()()()21565y a x x a x x +--＝﹣＝，由C 点坐标即可求解；2（）连接B C 、交对称轴于点P ，此时PA PC +的值为最小，即可求解； 3（）512E E OEBF S OB y y ⨯⨯四边形＝＝＝，则125E y ＝，将该坐标代入二次函数表达式即可求解．【详解】解：1（）根据点0(1)A ，,(50)B ，的坐标设二次函数表达式为：()()()21565y a x x a x x +--＝﹣＝，⊥抛物线经过点4(0)C ，，则54a ＝，解得：45a ＝，抛物线的表达式为：()()2224416465345555245y x x x x x --+--+＝=＝，函数的对称轴为：3x ＝； 2（）连接B C 、交对称轴于点P ，此时PA PC +的值为最小，设BC 的解析式为：y kx b +＝，将点B C 、的坐标代入一次函数表达式：y kx b +＝得：05,4k b b =+⎧⎨=⎩解得：4,54k b ⎧=-⎪⎨⎪=⎩ 直线BC 的表达式为：4y x 45=-+，当3x ＝时，85y ＝，故点835P （，）； 3（）存在，理由：四边形OEBF 是以OB 为对角线且面积为12的平行四边形，则512E E OEBF S OB y y ⨯⨯四边形＝＝＝，点E 在第四象限，故：则125E y ＝-，将该坐标代入二次函数表达式得：()24126555y x x -+＝＝-，解得：2x ＝或4，故点E 的坐标为122,5（-）或12,5（4-）．【点睛】本题考查二次函数综合运用，涉及到一次函数、平行四边形性质、图形的面积计算等，其中2（），求线段和的最小值，采取用的是点的对称性求解，这也是此类题目的一般解法．21．（1）y=-x 2-2x +3；（2）P 坐标为（-，-3）或（-1-3）．【分析】（1）把A与B坐标代入求出a与b的值，即可确定出表达式；（2）根据已知三角形面积相等求出P的坐标即可．【详解】解：（1）把A与B坐标代入得：9330a ba b c-+=⎧⎨++=⎩，解得：12ab=-⎧⎨=-⎩，则该抛物线的表达式为y=-x2-2x+3；（2）由抛物线解析式得：C（0，3），⊥⊥ABC面积为12×3×4=6，⊥⊥P AB面积为6，即12×|Py|×4=6，即Py=3或-3，当P y=3时，可得3=-x2-2x+3，解得：x=-2或x=0（舍去），此时P坐标为（-2，3）；当y P=-3时，可得-3=-x2-2x+3，解得：x=-此时P坐标为（-，-3）或（-1-3）．【点睛】本题考查了待定系数法求二次函数解析式，以及二次函数图象上点的坐标特征，熟练掌握待定系数法是解本题的关键．22．(1)、y=－x2－4x+5；(2)、15；(3)、(－,0)或(－,0).【详解】试题分析：(1)、首先求出方程的解得出点A和点B的坐标，然后利用待定系数法求出函数解析式；(2)、根据二次函数的解析式得出点C的坐标和顶点坐标，过D作x轴的垂线交x轴于M，从而求出⊥DMC、梯形MDBO和⊥BOC的面积，然后得出面积；(3)、设P点的坐标为（a,0），得出直线BC的方程，则PH与直线BC的交点坐标为(a，a+5)，PH与抛物线的交点坐标为H(a,－a2－4a+5)，然后根据EH=EP和EH=EP两种情况分别求出点P的坐标.试题解析：(1)、解方程x2－6x+5=0，得x1=5,x2=1.由m<n，m=1,n=5,。

关于二次函数的图像与性质的数学教案(9篇)

关于二次函数的图像与性质的数学教案（9篇）二次函数的图像与性质的数学教案篇1【学问与技能】1.会用描点法画函数y=ax2(a＞0)的图象，并依据图象熟悉、理解和把握其性质.2.体会数形结合的转化，能用y=ax2(a＞0)的图象和性质解决简洁的实际问题.【过程与方法】经受探究二次函数y=ax2(a＞0)图象的作法和性质的过程，获得利用图象讨论函数的阅历，培育观看、思索、归纳的良好思维习惯.【情感态度】通过动手画图，同学之间沟通争论，到达对二次函数y=ax2(a＞0)图象和性质的真正理解，从而产生对数学的兴趣，调动学生的积极性.【教学重点】1.会画y=ax2(a＞0)的图象.2.理解，把握图象的性质.【教学难点】二次函数图象及性质探究过程和方法的体会教学过程.一、情境导入，初步熟悉问题 1 请同学们回忆一下一次函数的图象、反比例函数的图象的特征是什么?二次函数图象是什么外形呢?问题2 如何用描点法画一个函数图象呢?【教学说明】①略；②列表、描点、连线.二、思索探究，猎取新知探究1 画二次函数y=ax2(a＞0)的图象.画二次函数y=ax2的图象.【教学说明】①要求同学们人人动手，按“列表、描点、连线”的步骤画图y=x2的图象，同学们画好后相互沟通、展现，表扬画得比拟标准的同学.②从列表和描点中，体会图象关于y轴对称的特征.③强调画抛物线的三个误区.误区一:用直线连结，而非光滑的曲线连结，不符合函数的变化规律和进展趋势.误区二：并非对称点，存在漏点现象，导致抛物线变形。

误区三:无视自变量的取值范围，抛物线要求用平滑曲线连点的同时，还需要向两旁无限延长，而并非到某些点停顿.二次函数的图像与性质的数学教案篇2一学习目标1、把握二次函数的图象及性质；2、会用二次函数的图象与性质解决问题；学习重点：二次函数的性质；学习难点：二次函数的性质与图像的应用；二学问点回忆：函数的性质函数函数图象a0a0性质三典型例题：例 1：已知是二次函数，求m的值例 2：（1）已知函数在区间上为增函数，求a的范围；（2）知函数的单调区间是，求a；例 3：求二次函数在区间[0，3]上的最大值和最小值；变式：（1）已知在[t，t+1]上的最小值为g(t)，求g(t)的表达式。

初中数学_二次函数y=ax2(a≠0)的图像和性质教学设计学情分析教材分析课后反思

初中数学教学设计课题：22.1.2 二次函数y=ax2的图象和性质教学过程设计教学环节师生行为设计意图课前准备师：播放关于抛物线的欣赏图片生：欣赏图片使学生二次函数的图像有一个大概的感知，激发学生的学习兴趣.冬藏师：幻灯片出示忆一忆1.正比例函数y=kx(k≠0)的图像是一条经过的一条。

2.当时，正比例函数y=kx(k≠0)的图像经过原点和一、三象限。

此时y随x的增大而当时，正比例函数y=kx(k≠0)的图像经过原点和二、四象限。

此时y随x的增大而说出你的结论：3.比较正比例函数xyxyxy3,31,===的函数图像说出你的结论：生：根据题目作答复习旧知，了解探究函数图像与性质的一般方法，为类比探究y=ax2的图象和性质埋下伏笔。

春耕师：出示问题画出二次函数2222,21,xyxyxy==-=的图像生：在教师准备好的坐标纸上作图。

通过做图感知二次函数是一条抛物线，为后续进行二次函数y=ax2的图象和性质打下基础。

春耕师：与学生一起用描点法画出二次函数y=x2的图像。

师生共同探究二次函数的图像的画法，体会数形结合的数学思想。

从数到形，通过数来判断，通过形来验证。

师：先让学生判断所给出的x的取值特点，再观察计算得出的y的取值，判断对应点与y轴的关系。

先在平面直角坐标系中描出各点，再让学生观察各点与y轴的关系，猜测二次函数y=x2的图像特点春耕函数y=ax2(k≠0)的图像的几个基本知识点1.抛物线的定义2.对称轴的描述3.顶点的定义通过几个基本概念的介绍使学生深化对抛物线的理解夏耘探究一函数y=ax2(k≠0)的图像与系数a的符号的关系以函数y=x2与y= - x2为例1.开口方向出现了怎样的变化？2.函数值y随自变量的变化情况呢？对称轴左侧对称轴右侧生：学生讨论小组合作完成在动画的演示下帮助学生完成对二次函数a的符号与函数图像的探究夏耘与学生一起梳理刚才得出的结论a的符号抛物线的开口方向及时梳理系统内化知识.夏耘探究二：函数y=ax 2(k≠0)的图像与系数|a|的关系学生小组合作讨论解决。

九年级数学二次函数y=ax2bxc(a≠0)的图像与性质(知识讲解1)Word版含解析

专题2.12 二次函数y=ax2+bx+c(a≠0)的图像与性质（知识讲解1）-2021-2022学年九年级数学下册基础知识专项讲练（北师大版）专题2.12 二次函数y=ax²+bx+c(a≠0)的图象与性质（知识讲解1）【学习目标】1．会用描点法画二次函数2(0)y ax bx c a =++≠的图象；会用配方法将二次函数2y ax bx c =++的解析式写成2()y a x h k =-+的形式；2．通过图象能熟练地掌握二次函数2y ax bx c =++的性质；3．经历探索2y ax bx c =++与2()y a x h k =-+的图象及性质紧密联系的过程，能运用二次函数的图象和性质解决简单的实际问题，深刻理解数学建模思想以及数形结合的思想．【要点梳理】要点一、二次函数2(0)y ax bx c a =++≠与2(1)(0)y a x t k a =-+≠之间的相互关系 1．顶点式化成一般式从函数解析式2()y a x h k =-+我们可以直接得到抛物线的顶点(h ，k)，所以我们称2()y a x h k =-+为顶点式，将顶点式2()y a x h k =-+去括号，合并同类项就可化成一般式2y ax bx c =++． 2．一般式化成顶点式 22222()()()22b b b b y ax bx c a x x c a x x c a a a a ⎡⎤=++=++=++-+⎢⎥⎣⎦224()24b ac b a x a a-=++．对照2()y a x h k =-+，可知2b h a =-，244ac b k a-=．∴抛物线2y ax bx c =++的对称轴是直线2b x a =-，顶点坐标是24(,)24b ac b a a--．特别说明：1．抛物线2y ax bx c =++的对称轴是直线2b x a =-，顶点坐标是24(,)24b ac b a a--，可以当作公式加以记忆和运用．2．求抛物线2y ax bx c =++的对称轴和顶点坐标通常用三种方法：配方法、公式法、代入法，这三种方法都有各自的优缺点，应根据实际灵活选择和运用．要点二、二次函数2(0)y ax bx c a =++≠的图象的画法 1．一般方法：列表、描点、连线； 2．简易画法：五点定形法．其步骤为：（1）先根据函数解析式，求出顶点坐标和对称轴，在直角坐标系中描出顶点M ，并用虚线画出对称轴．（2）求抛物线2y ax bx c =++与坐标轴的交点，当抛物线与x 轴有两个交点时，描出这两个交点A 、B 及抛物线与y 轴的交点C ，再找到点C 关于对称轴的对称点D ，将A 、B 、C 、D 及M 这五个点按从左到右的顺序用平滑曲线连结起来．特别说明：当抛物线与x 轴只有一个交点或无交点时，描出抛物线与y 轴的交点C 及对称点D ，由C 、M 、D 三点可粗略地画出二次函数图象的草图；如果需要画出比较精确的图象，可再描出一对对称点A 、B ，然后顺次用平滑曲线连结五点，画出二次函数的图象，要点三、二次函数2(0)y ax bx c a =++≠的图象与性质 1．二次函数2(0)y ax bx c a =++≠图象与性质2．二次函数2(0)y ax bx c a =++≠图象的特征与a 、b 、c 及b2-4ac 的符号之间的关系要点四、求二次函数2(0)y ax bx c a =++≠的最大（小）值的方法如果自变量的取值范围是全体实数，那么函数在顶点处取得最大（或最小）值，即当2b x a =-时，244ac b y a-=．特别说明：如果自变量的取值范围是x1≤x≤x2，那么首先要看2ba-是否在自变量的取值范围x1≤x≤x2内，若在此范围内，则当2b x a =-时，244ac b y a-=，若不在此范围内，则需要考虑函数在x1≤x≤x2范围内的增减性，如果在此范围内，y 随x 的增大而增大，则当x ＝x2时，22y bx c ++；当x ＝x1时，211y ax bx c =++，如果在此范围内，y 随x 的增大而减小，则当x ＝x1时，2max 11y ax bx c =++；当x ＝x2时，2min 22y ax bx c =++，如果在此范围内，y 值有增有减，则需考察x ＝x1，x ＝x2，2bx a=-时y 值的情况．特别说明：【典型例题】类型一、二次函数2(0)y ax bx c a =++≠化为顶点式1．已知抛物线2y x bx c =-++经过点A （3，0），B （﹣1，0）．（1）求抛物线的解析式；（2）求抛物线的顶点坐标．举一反三：【变式1】2．用配方法把二次函数y=12x 2–4x+5化为y=a(x+m)2+k 的形式，再指出该函数图象的开口方向、对称轴和顶点坐标．【变式2】3．已知二次函数2y x 4x 3=-+．()1用配方法将其化为2y a(x h)k =-+的形式；()2在所给的平面直角坐标系xOy 中，画出它的图象．【变式3】4．已知二次函数y ＝﹣2x 2+bx +c 的图象经过点A （0，4）和B （1，﹣2）．（1）求此抛物线的解析式；（2）求此抛物线的对称轴和顶点坐标；（3）设抛物线的顶点为C ，试求∴CAO 的面积．类型二、画二次函数2(0)y ax bx c a =++≠的图象5．已知：二次函数243y x x =++ （1）求出该函数图象的顶点坐标；（2）在所提供的网格中画出该函数的草图．举一反三：【变式1】6．已知二次函数y =﹣x 2+4x ．（1）写出二次函数y =﹣x 2+4x 图象的对称轴；（2）在给定的平面直角坐标系中，画出这个函数的图象（列表、描点、连线）；（3）根据图象，写出当y ＜0时，x 的取值范围．【变式2】7．已知二次函数y ＝12x 2﹣x ﹣32．（1）在平面直角坐标系内，画出该二次函数的图象；（2）根据图象写出：①当x 时，y ＞0； ②当0＜x ＜4时，y 的取值范围为．【变式3】8．已知抛物线22232(0)y ax ax a a =--+≠．（1）求这条抛物线的对称轴；（2）若该抛物线的顶点在x 轴上，求其解析式；（3）设点()1,P m y ，()23,Q y 在抛物线上，若12y y <，求m 的取值范围．类型三、二次函数2(0)y ax bx c a =++≠的性质9．把抛物线21:23C y x x =++先向右平移4个单位长度，再向下平移5个单位长度得到抛物线2C ．（1）直接写出抛物线2C 的函数关系式；（2）动点(),6P a -能否在拋物线2C 上？请说明理由；（3）若点()()12,,,A m y B n y 都在抛物线2C 上，且0m n <<，比较12,y y 的大小，并说明理由．举一反三：【变式1】10．在平面直角坐标系xOy 中，关于x 的二次函数2y x px q +=+的图象过点(1,0)-，(2,0)．（1）求这个二次函数的表达式；（2）求当21x -≤≤时，y 的最大值与最小值的差；（3）一次函数(2)2y m x m =-+-的图象与二次函数2y x px q +=+的图象交点的横坐标分别是a 和b ，且3a b <<，求m 的取值范围．【变式2】11．如图，已知抛物线y=x 2-2x -3与x 轴交于A 、B 两点．（1）当0＜x ＜3时，求y 的取值范围；（2）点P 为抛物线上一点，若S △PAB =10，求出此时点P 的坐标．【变式3】12．已知抛物线2y ax bx c =++，如图所示，直线1x =-是其对称轴，()1确定a ，b ，c ，24b ac =-的符号；()2求证：0a b c -+>；()3当x 取何值时，0y >，当x 取何值时0y <．类型四、二次函数的图象及各项的系数13．如图，抛物线y＝﹣x2+(m﹣1)x+m与y轴交于点(0，3)．（1）m的值为________；（2）当x满足________时，y的值随x值的增大而减小；（3）当x满足________时，抛物线在x轴上方；（4）当x满足0≤x≤4时，y的取值范围是________．举一反三：【变式1】14．已知二次函数y=ax2+bx+c的图象如图所示，给出下列结论：∴abc＞0；∴a﹣b+c＜0；∴2a+b﹣c＜0；∴4a+2b+c＞0，∴若点（﹣23，y1）和（73，y2）在该图象上，则y1＞y2．其中正确的结论是_____（填入正确结论的序号）类型五、一次函数、二次函数图象的综合判断15．如图，已知直线y=-2x+m与抛物线y=ax2+bx+c相交于A，B两点，且点A（1，4）为抛物线的顶点，点B在x轴上．（1）求m 的值；（2）求抛物线的解析式；（3）若点P 是x 轴上一点，当∴ABP 为直角三角形时直接写出点P 的坐标．举一反三：【变式1】16．已知二次函数()2229y mx m x m =++++．()1如果二次函数的图象与x 轴有两个交点，求m 的取值范围；()2如图，二次函数的图象过，点()4,0A ，与y 轴交于点B ，直线AB 与这个二次函数图象的对称轴交于点P ，求点P 的坐标．【变式2】17．如图所示，已知直线y=12-x 与抛物线y=2164x -+交于A 、B 两点，点C 是抛物线的顶点．(1)求出点A 、B 的坐标； (2)求出∴ABC 的面积；(3)在AB 段的抛物线上是否存在一点P ，使得∴ABP 的面积最大？若存在，请求出点P 的坐标；若不存在，请说明理由．参考答案：1．（1）2y x 2x 3=-++（2）（1，4）【详解】解：（1）∴抛物线2y x bx c =-++经过点A （3，0），B （－1，0）， ∴抛物线的解析式为；()()y x 3x 1=--+，即2y x 2x 3=-++，（2）∴抛物线的解析式为()22y x 2x 3x 14=-++=--+， ∴抛物线的顶点坐标为：（1，4）．（1）根据抛物线2y x bx c =-++经过点A （3，0），B （﹣1，0），直接由交点式得出抛物线的解析式．（2）将抛物线的解析式化为顶点式，即可得出答案．2．抛物线的开口向上，对称轴是直线x ＝4，顶点坐标是(4，－3)．【分析】用配方法把一般式化为顶点式，根据二次函数的性质解答即可．【详解】解：∵y ＝12x 2－4x ＋5＝12(x －4)2－3，∴抛物线的开口向上，对称轴是直线x ＝4，顶点坐标是(4，－3)．【点睛】本题考查的是二次函数的三种形式，正确利用配方法把一般式化为顶点式是解题的关键．3．（1）2(x 2)1--；（2）见解析.【分析】（1）利用配方法把二次函数解析式化成顶点式即可；（2）利用描点法画出二次函数图象即可．【详解】解：()21y x 4x 3=-+=222x 4x 223-+-+ =2(x 2)1--()22y (x 2)1=--，∴顶点坐标为()2,1-，对称轴方程为x 2=．函数二次函数2y x 4x 3=-+的开口向上，顶点坐标为()2,1-，与x 轴的交点为()3,0，()1,0， ∴其图象为：故答案为（1）2(x 2)1--；（2）见解析.【点睛】本题考查二次函数的配方法，用描点法画二次函数的图象，掌握配方法是解题的关键．4．（1）y ＝﹣2x 2﹣4x +4；（2）对称轴为直线x ＝﹣1，顶点坐标为（﹣1，6）；（3）∴CAO 的面积为2．【分析】（1）利用待定系数法把A （0，4）和B （1，﹣2）代入y ＝﹣2x 2+bx +c 中，可以解得b ，c 的值，从而求得函数关系式即可；（2）利用配方法求出图象的对称轴和顶点坐标；（3）由（2）可得顶点C 的坐标，再根据三角形的面积公式即可求出△CAO 的面积．【详解】解：（1）把A （0，4）和B （1，﹣2）代入y ＝﹣2x 2+bx +c ，得：24212c b c =⎧⎨-⨯++=-⎩，解得：44b c =-⎧⎨=⎩，所以此抛物线的解析式为y ＝﹣2x 2﹣4x +4；（2）∴y ＝﹣2x 2﹣4x +4 ＝﹣2（x 2+2x ）+4 ＝﹣2[（x +1）2﹣1]+4 ＝﹣2（x +1）2+6，∴此抛物线的对称轴为直线x ＝﹣1，顶点坐标为（﹣1，6）；（3）由（2）知：顶点C （﹣1，6）， ∴点A （0，4），∴OA ＝4， ∴S △CAO ＝12OA •|xc |＝12×4×1＝2，即△CAO 的面积为2．故答案为（1）y ＝﹣2x 2﹣4x +4；（2）对称轴为直线x ＝﹣1，顶点坐标为（﹣1，6）；（3）△CAO 的面积为2．【点睛】本题考查了用待定系数法求二次函数的解析式，二次函数解析式的三种形式，二次函数的性质以及三角形的面积，难度适中．正确求出函数的解析式是解题的关键． 5．（1） (－2，－1)；（2）见解析【分析】（1）将二次函数化为顶点式即可得出顶点坐标；（2）利用五点法画二次函数的图象即可．【详解】（1）243y x x =++化为顶点式为2(2)1y x =+- 则该函数图象的顶点坐标为(2,1)--；（2）先求出自变量x 在4,3,2,1,0----处的函数值，再列出表格当4x =-和0x =时，3y =当3x =-和=1x -时，2(1)4(1)30y =-+⨯-+= 当2x =-时，1y =- 列出表格如下：由此画出该函数的草图如下：【点睛】本题考查了二次函数的顶点式、画二次函数的图象，掌握函数图象的画法是解题关键．6．（1）对称轴是过点（2，4）且平行于y轴的直线x=2；（2）见解析；（3）x＜0或x＞4．【详解】试题分析：（1）把一般式化成顶点式即可求得；（2）首先列表求出图象上点的坐标，进而描点连线画出图象即可．（3）根据图象从而得出y＜0时，x的取值范围．试题解析：（1）∴y=-x2+4x=-（x-2）2+4，∴对称轴是过点（2，4）且平行于y轴的直线x=2；（2）列表得：描点，连线．（3）由图象可知，当y＜0时，x的取值范围是x＜0或x＞4．7．（1）见解析；（2）①x＜﹣1或x＞3；②﹣2≤y＜52．【分析】（1）先把解析式配成顶点式得到抛物线的顶点坐标为（1，2）；再分别求出抛物线与坐标轴的交点坐标，然后利用描点法画二次函数图象；（2）∴利用函数图象写出抛物线在x轴上方所对应的自变量的范围即可；∴先确定x＝4时，y＝52，然后利用函数图象写出当0＜x＜4时对应的函数值的范围．【详解】解：（1）∴y＝12（x﹣1）2﹣2，∴抛物线的对称轴为直线x＝1，顶点坐标为（1，2）；当x＝0时，y＝12x2﹣x﹣32＝﹣32，则抛物线与y轴交点坐标为（0，﹣32）当y ＝0时，12 x 2﹣x ﹣32＝0，解得x 1＝﹣1，x 2＝3，抛物线与x 轴的交点坐标为（﹣1，0）、（3，0），如图，（2）∴当x ＜﹣1或x ＞3时，y ＞0； ∴当0＜x ＜4时，﹣2≤y ＜52；故答案为x ＜﹣1或x ＞3；﹣2≤y ＜52．【点睛】本题考查了抛物线与x 轴的交点：把求二次函数y ＝ax 2+bx +c （a ，b ，c 是常数，a ≠0）与x 轴的交点坐标问题转化解关于x 的一元二次方程即可求得交点横坐标．也考查了二次函数的性质．8．（1）1x =；（2）233322y x x =-+或221y x x =-+-；（3）当a ＞0时，13m -<<；当a ＜0时，1m <-或3m >．【分析】（1）将二次函数化为顶点式，即可得到对称轴；（2）根据（1）中的顶点式，得到顶点坐标，令顶点纵坐标等于0，解一元二次方程，即可得到a 的值，进而得到其解析式；（3）根据抛物线的对称性求得点Q 关于对称轴的对称点，再结合二次函数的图象与性质，即可得到m 的取值范围．【详解】（1）∴22232y ax ax a =--+， ∴22(1)32y a x a a =---+， ∴其对称轴为：1x =．（2）由（1）知抛物线的顶点坐标为：2(1,23)a a --，∴抛物线顶点在x 轴上， ∴2230a a --=，解得：32a =或1a =-，当32a =时，其解析式为：233322y x x =-+，当1a =-时，其解析式为：221y x x =-+-，综上，二次函数解析式为：233322y x x =-+或221y x x =-+-．（3）由（1）知，抛物线的对称轴为1x =， ∴()23,Q y 关于1x =的对称点为2(1,)y -，当a ＞0时，若12y y <，则-1＜m ＜3；当a ＜0时，若12y y <，则m ＜-1或m ＞3.【点睛】本题考查了二次函数对称轴，解析式的计算，以及根据二次函数的图象性质求不等式的取值范围，熟知相关计算是解题的关键．9．（1）2(3)3y x =--；（2）不在，见解析；（3）12y y >，见解析【分析】（1）先求出抛物线1C 的顶点坐标，再根据向右平移横坐标加，向下平移纵坐标减求出平移后的抛物线的顶点坐标即可；（2）根据抛物线2C 的顶点的纵坐标为3-，即可判断点()6P a -，不在拋物线2C 上；（3）根据抛物线2C 的增减性质即可解答．【详解】（1）抛物线221:23(1)2C y x x x =++=++，∴抛物线1C 的顶点坐标为(﹣1，2)，根据题意，抛物线2C 的顶点坐标为(-1+4，2-5)，即(3，﹣3)， ∴抛物线2C 的函数关系式为：2(3)3y x =--；（2）动点P 不在抛物线2C 上．理由如下：∴抛物线2C 的顶点为()3,3-，开口向上， ∴抛物线2C 的最低点的纵坐标为3-． ∴63P y =-<-，∴动点P 不在抛物线2C 上；（3）12y y >．理由如下：由（1）知抛物线2C 的对称轴是3x =，且开口向上， ∴在对称轴左侧y 随x 的增大而减小． ∴点()()12,,,A m y B n y 都在抛物线2C 上，且03m n <<<， ∴12y y >．【点睛】本题考查了二次函数图象与几何变换，二次函数图象上点的坐标特征，熟练掌握平移的规律“左加右减，上加下减”以及熟练掌握二次函数的性质是解题的关键． 10．（1）2y x x 2=--；（2）254；（3）1m <．【分析】（1）利用待定系数法将点(1,0)-，(2,0)代入解析式中解方程组即可；（2）根据（1）中函数关系式得到对称轴12x =，从而知在21x -≤≤中，当x=-2时，y 有最大值，当12x =时，y 有最小值，求之相减即可；（3）根据两函数相交可得出x 与m 的函数关系式，根据有两个交点可得出∆>0，根据根与系数的关系可得出a ，b 的值，然后根据3a b <<，整理得出m 的取值范围．【详解】解：（1）∴2y x px q +=+的图象过点(1,0)-，(2,0)，∴10420p q p q -+=⎧⎨++=⎩解得12p q =-⎧⎨=-⎩ ∴2y x x 2=--（2）由（1）得，二次函数对称轴为12x =∴当21x -≤≤时，y 的最大值为(-2)2-(-2)-2=4,y 的最小值为21192224⎛⎫--=- ⎪⎝⎭ ∴y 的最大值与最小值的差为925444⎛⎫--= ⎪⎝⎭；（3）由题意及（1）得()2222y m x my x x ⎧=-+-⎨=--⎩整理得()()2340x m x m ----=即()(1)40x x m +--=⎡⎤⎣⎦∴一次函数(2)2y m x m =-+-的图象与二次函数2y x px q +=+的图象交点的横坐标分别是a 和b ，∴()()23440m m ∆=-+-> 化简得210250m m -+> 即()250m -> 解得m≠5∴a ，b 为方程()(1)40x x m +--=⎡⎤⎣⎦的两个解又∴3a b << ∴a=-1，b=4-m 即4-m>3 ∴m<1综上所述，m 的取值范围为1m <．【点睛】本题考查了利用待定系数法求二次函数解析式，二次函数图象的性质，根与系数的关系等知识．解题的关键是熟记二次函数图象的性质． 11．(1) ﹣4≤y ＜0;(2) P 点坐标为（﹣2，5）或（4，5）【详解】分析：(1)、首先将抛物线配成顶点式，然后根据x 的取值范围，从而得出y 的取值范围；(2)、根据题意得出AB 的长度，然后根据面积求出点P 的纵坐标，根据抛物线的解析式求出点P 的坐标．详解：（1）∴抛物线的解析式为y=x 2﹣2x ﹣3，∴y=x 2﹣2x ﹣3=（x ﹣1）2﹣4， ∴顶点坐标为（1，﹣4），由图可得当0＜x ＜3时，﹣4≤y ＜0．（2）当y=0时，x 2﹣2x ﹣3=0，解得：x 1=-1 x 2=3 ∴A （﹣1，0）、B （3，0）， ∴AB=4．设P （x ，y ），则S △PAB =AB•|y|=2|y|=10， ∴|y|=5， ∴y=±5． ∴当y=5时，x 2﹣2x ﹣3=5，解得：x 1=﹣2，x 2=4，此时P 点坐标为（﹣2，5）或（4，5）； ∴当y=﹣5时，x 2﹣2x ﹣3=﹣5，方程无解；综上所述，P 点坐标为（﹣2，5）或（4，5）．点睛：本题主要考查的是二次函数的性质，属于基础题型．求函数值取值范围时，一定要注意自变量的取值范围是否是在对称轴的一边．12．（1）0a <，0b <，0c >，240b ac =->；（2）详见解析；（3）当31x -<<时，0y >；当3x <-或1x >时，0y <．【分析】（1）根据开口方向确定a 的符号，根据对称轴的位置确定b 的符号，根据抛物线与y 轴的交点确定c 的符号，根据抛物线与x 轴交点的个数确定b 2-4ac 的符号；（2）根据图象和x=-1的函数值确定a -b+c 与0的关系；（3）抛物线在x 轴上方时y ＞0；抛物线在x 轴下方时y ＜0．【详解】()1∵抛物线开口向下， ∴0a <， ∵对称轴12bx a=-=-， ∴0b <，∵抛物线与y 轴的交点在x 轴的上方， ∴0c >，∵抛物线与x 轴有两个交点， ∴240b ac =->；()2证明：∵抛物线的顶点在x 轴上方，对称轴为1x =-，∴当1x =-时，0y a b c =-+>；()3根据图象可知，当31x -<<时，0y >；当3x <-或1x >时，0y <．【点睛】本题考查了二次函数图象与系数的关系，解题的关键是熟练的掌握二次函数图象与系数的关系.13．（1）3；（2）x ＞1；（3）-1＜x ＜3；（4）-5≤y ≤4 【分析】根据函数的图象和性质即可求解．【详解】解：（1）将（0，3）代入y ＝﹣x 2+（m ﹣1）x +m 得，3＝m ，故答案为3；（2）m ＝3时，抛物线的表达式为y ＝﹣x 2+2x +3，函数的对称轴为直线x ＝2ba-＝1， ∴﹣1＜0，故抛物线开口向下，当x ＞1时，y 的值随x 值的增大而减小，故答案为x ＞1；（3）令y ＝﹣x 2+2x +3，解得x ＝﹣1或3，从图象看，当﹣1＜x ＜3时，抛物线在x 轴上方；故答案为﹣1＜x ＜3；（4）当x ＝0时，y ＝3；当x ＝4时，y ＝﹣x 2+2x +3＝﹣5，而抛物线的顶点坐标为（1，4），故当x 满足0≤x ≤4时，y 的取值范围是﹣5≤y ≤4，故答案为﹣5≤y ≤4．【点睛】本题主要考查二次函数的图像与性质及系数的关系，熟练掌握二次函数的图像与性质及系数的关系是解题的关键． 14．∴∴∴【详解】解：∴抛物线开口向下， ∴a ＜0，∴对称轴在y 轴右边， ∴b ＞0，∴抛物线与y 轴的交点在x 轴的上方， ∴c ＞0，∴abc ＜0，故∴错误；∴二次函数y =ax 2+bx +c 图象可知，当x =﹣1时，y ＜0，∴a ﹣b +c ＜0，故∴正确；∴二次函数图象的对称轴是直线x =1，c ＞0， ∴2b a-=1， ∴2a +b =0，∴2a +b ＜c ，∴2a +b ﹣c ＜0，故∴正确；∴二次函数y =ax 2+bx +c 图象可知，当x =2时，y ＞0，∴4a +2b +c ＞0，故∴正确；∴二次函数图象的对称轴是直线x =1，∴抛物线上x =23-时的点与当x =83时的点对称， ∴x ＞1，y 随x 的增大而减小，∴y 1＜y 2，故∴错误；故答案为∴∴∴．【点睛】本题考查了二次函数的图象与系数的关系，要熟练掌握，解答此题的关键是要明确：∴二次项系数a 决定抛物线的开口方向和大小：当a ＞0时，抛物线向上开口；当a ＜0时，抛物线向下开口；∴一次项系数b 和二次项系数a 共同决定对称轴的位置：当a 与b 同号时（即ab ＞0），对称轴在y 轴左；当a 与b 异号时（即ab ＜0），对称轴在y 轴右．（简称：左同右异）∴常数项c 决定抛物线与y 轴交点．抛物线与y 轴交于（0，c ）．15．（1）m ＝6；（2）y ＝﹣x 2+2x +3；（3）点P 的坐标为（7，0）或（1，0）．【分析】（1）将点A 坐标代入y=-2x+m ，即可求解；（2）y=-2x+6，令y=0，则x=3，故点B （3，0），则二次函数表达式为：y=a （x -1）2+4，将点B 的坐标代入上式，即可求解；（3）分∴BAP=90°、∴AP （P′）B=90°两种情况，求解即可．【详解】解：（1）将点A 坐标代入y ＝﹣2x+m 得：4＝﹣2+m ，解得：m ＝6；（2）y ＝﹣2x+6，令y ＝0，则x ＝3，故点B （3，0），则二次函数表达式为：y ＝a （x ﹣1）2+4，将点B 的坐标代入上式得：0＝a （3﹣1）2+4，解得：a ＝﹣1，故抛物线的表达式为：y ＝﹣（x ﹣1）2+4＝﹣x 2+2x+3；（3）∴当∴BAP ＝90°时，直线AB 的表达式为：y ＝﹣2x+6，则直线PB 的表达式中的k 值为12，设直线PB 的表达式为：y ＝12x+b ，将点A 的坐标代入上式得：4＝12×1+b ，解得：b ＝72，即直线PB 的表达式为：y ＝12x+72，当y ＝0时，x ＝﹣7，即点P （7，0）；∴当∴AP （P′）B ＝90°时，点P′（1，0）；故点P 的坐标为（7，0）或（1，0）．【点睛】本题考查的是二次函数综合运用，涉及到一次函数的基本知识，要注意类讨论，避免遗漏，本题较为简单．16．（1）45m <且0m ≠；（2）P 点坐标为()1,6．【分析】解：（1）根据题意得0m ≠且()24(2)490m m m =+-⋅+>；（2）先求二次函数的解析式，再求抛物线的对称轴，用待定系数法求直线AB 的解析式，再求AB 与对称轴的交点P.【详解】解：()1根据题意得0m ≠且()24(2)490m m m =+-⋅+>，所以45m <且0m ≠； ()2把()4,0A 代入()2229y mx m x m =++++得()168290m m m ++++=，解得1m =-，所以抛物线解析式为2228(1)9y x x x =-++=--+，所以抛物线的对称轴为直线1x =，当0x =时，2288y x x =-++=，则()0,8B ，设直线AB 的解析式为y kx b =+，把()4,0A ，()0,8B 代入得{408k b b +==，解得{28k b =-=，所以直线AB 的解析式为28y x =-+，当1x =时，286y x =-+=，所以P 点坐标为()1,6．【点睛】本题考核知识点：二次函数与一次函数. 解题关键点：理解二次函数图象的交点问题.17．(1)点A 、B 的坐标分别为：(6，﹣3)，(﹣4，2)；(2)30；(3)当a ＝1时，∴ABP 的面积最大，此时点P 的坐标为(1，234)．【分析】（1）由直线1y x 2=-与抛物线21y x 64=-+交于A 、B 两点，可得方程211x x 624-=-+，解方程即可求得点A 、B 的坐标；（2）首先由点C 是抛物线的顶点，即可求得点C 的坐标，又由S △ABC =S △OBC +S △OAC 即可求得答案；（3）首先过点P 作PD∴OC ，交AB 于D ，然后设21P a,a 64⎛⎫-+ ⎪⎝⎭，即可求得点D 的坐标，可得PD 的长，又由S △ABP =S △BDP +S △ADP ，根据二次函数求最值的方法，即可求得答案．【详解】解：(1)∴直线1y x 2=-与抛物线21y x 64=-+交于A 、B 两点， ∴211x x 624-=-+，解得：x ＝6或x ＝﹣4，当x ＝6时，y ＝﹣3，当x ＝﹣4时，y ＝2，∴点A 、B 的坐标分别为：(6，﹣3)，(﹣4，2)；(2)∴点C 是抛物线的顶点．∴点C 的坐标为(0，6)，∴S △ABC ＝S △OBC +S △OAC ＝12×6×4+12×6×6＝30；(3)存在．过点P 作PD∴OC ，交AB 于D ，设P(a ，﹣14a 2+6)，则D(a ，﹣12a)， ∴PD ＝﹣14a 2+6+12a ， ∴S △ABP ＝S △BDP +S △ADP ＝12×(﹣14a 2+6+12a)×(a+4)+12×(﹣14a 2+6+12a)×(6﹣a)＝25125(a 1)44--+ (﹣4＜a ＜6)， ∴当a ＝1时，∴ABP 的面积最大，此时点P 的坐标为(1，234)．【点睛】此题考查了二次函数与一次函数的交点问题，三角形面积的求解以及二次函数的最值问题等知识．此题综合性很强，难度较大，解题的关键是方程思想与数形结合思想的应用．。

关于二次函数的知识点总结

关于二次函数的知识点总结导语：二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。

下面是由小编整理的关于二次函数的知识点总结。

欢迎阅读！1、二次函数及其图像二次函数(quadraticfunction)是指未知数的最高次数为二次的多项式函数。

二次函数可以表示为f(x)=ax^2bxc(a不为0)。

其图像是一条主轴平行于y轴的抛物线。

一般的，自变量x和因变量y之间存在如下关系：一般式y=ax∧2；bxc(a≠0,a、b、c为常数)，顶点坐标为(-b/2a，-(4ac-b∧2)/4a)；顶点式y=a(xm)∧2k(a≠0,a、m、k为常数)或y=a(x-h)∧2k(a≠0,a、h、k为常数)，顶点坐标为(-m，k)对称轴为x=-m，顶点的位置特征和图像的开口方向与函数y=ax∧2的图像相同，有时题目会指出让你用*法把一般式化成顶点式；交点式y=a(x-x1)(x-x2)[仅限于与x轴有交点A(x1，0)和B(x2，0)的抛物线]；重要概念：a，b，c为常数，a≠0，且a决定函数的开口方向，a>0时，开口方向向上，a<0时，开口方向向下。

a的绝对值还可以决定开口大小,a的绝对值越大开口就越小,a的绝对值越小开口就越大。

牛顿*值公式(已知三点求函数解析式)y=(y3(x-x1)(x-x2))/((x3-x1)(x3-x2)(y2(x-x1)(x-x3))/((x2-x1)(x2-x3)(y1(x-x2)(x-x3))/((x1-x2)(x1-x3)。

由此可引导出交点式的系数a=y1/(x1*x2)(y1为截距)求根公式二次函数表达式的右边通常为二次三项式。

x是自变量，y是x的二次函数x1,x2=[-b±(√(b^2-4ac))]/2a(即一元二次方程求根公式)求根的方法还有因式分解法和*法在平面直角坐标系中作出二次函数y=2x的平方的图像，可以看出，二次函数的图像是一条永无止境的抛物线。

《y=ax2的图象和性质》示范教学方案

第二十一章二次函数与反比例函数21.2二次函数的图象和性质第1课时二次函数y=ax²的图象和性质一、教学目标1.正确理解抛物线的有关概念；2.会用描点法画出二次函数y＝ax²的图象，概括出图象的特点；3.掌握形如y＝ax²的二次函数图象的性质，并会应用；4.通过动手操作、合作交流，积累数学活动经验，培养动手能力和观察能力．二、教学重点及难点重点：1.正确理解抛物线的有关概念；2.会用描点法画出二次函数y＝ax²的图象，概括出图象的特点；难点：掌握形如y＝ax²的二次函数图象的性质，并会应用.三、教学用具多媒体教室四、相关资料《描点法画y=ax²的一般步骤》动画、《二次函数y=ax2的图象和性质（一）》微课、《二次函数y=ax2的图象和性质（二）》微课五、教学过程【情景引入】我们都见过篮球运动员投篮，你知道篮球从出手到落入篮圈内的路线是什么图形吗？它是如何画出来的？我们把篮球从出手到落入篮圈内的曲线叫抛物线，你还能举出一些抛物线的例子吗？【合作探究】将学生划分成多个小组，小组内同学进行合作探究.探究一：二次函数y=ax²的图象.1.画出二次函数y=x2的图象.解:(1)列表中自变量x可以是任意实数,列表表示几组对应值.(3)连线:用平滑的曲线顺次连接各点,得到函数y=x²的图象,如图所示.此图片是动画缩略图，本动画为《描点法画y=ax²的一般步骤》知识探究，通过交互式动画的方式，运用了本资源，可以吸引学生的学习兴趣，适用于描点法画y=ax²的一般步骤的教学.若需使用，请插入【数学探究】描点法画y=ax²的一般步骤.2.观察二次函数y=x2的图象,思考下列问题:(1)二次函数y=x2的图象是什么形状？(2)图象是轴对称图形吗？如果是,它的对称轴是什么？(3)图象有最低点吗？如果有,最低点的坐标是什么？总结：函数y=x2的图象是一条关于y轴(x=0)对称的曲线,这条曲线叫做抛物线.实际上二次函数的图象都是抛物线.二次函数y=x2的图象可以简称为抛物线y=x2.由图象可以看出,抛物线y=x2开口向上;y轴是抛物线y=x2的对称轴；抛物线y=x2与它的对称轴的交点(0,0)叫做抛物线的顶点,它是抛物线y=x2的最低点.实际上每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线的顶点,顶点是抛物线的最低点或最高点.本图片是微课的首页截图，本微课资源针对《二次函数y=ax2的图象和性质（一）》进行讲解，并结合具体例题，提高知识的应用能力，有利于启发教师教学或学生预习或复习使用.若需使用，请插入微课【知识点解析】二次函数y=ax2的图象和性质（一）.探究二：二次函数y=ax2的性质.在同一平面直角坐标系中，画出下列函数的图象：①y＝12x2；②y＝2x2；③y＝－12x2；④y＝－2x2.根据图象回答下列问题：(1)这些函数的图象都是轴对称图形吗？如果是，对称轴是什么？(2)图象有最高点或最低点吗？如果有，最高点或最低点的坐标是什么？解：列表：描点、连线，函数图象如图所示．(1)这四个函数的图象都是轴对称图形，对称轴都是y 轴；(2)函数y ＝2x 2和y ＝12x 2的图象有最低点，函数y ＝－12x 2和y ＝－2x 2的图象有最高点，这些最低点和最高点的坐标都是(0，0)．总结：一般地,抛物线y =ax 2的对称轴是y 轴,顶点是原点.当a >0时,抛物线y =ax 2的开口向上,顶点是抛物线的最低点,当a 越大时,抛物线的开口越小；当a <0时,抛物线y =ax 2的开口向下,顶点是抛物线的最高点,当a 越大时,抛物线的开口越大. 从二次函数y =ax 2的图象可以看出:如果a >0,当x <0时,y 随x 的增大而减小,当x >0时,y 随x 的增大而增大; 如果a <0,当x <0时,y 随x 的增大而增大,当x >0时,y 随x 的增大而减小. 设计意图：设置问题让学生在教师的带领下通过合作探究等方法总结出二次函数y =ax ²的图像与性质，在探究的过程中，学生掌握了难点知识，并且加深了对重要知识点的理解与记忆.本图片是微课的首页截图，本微课资源针对《二次函数y =ax 2的图象和性质（二）》进行讲解，并结合具体例题，提高知识的应用能力，有利于启发教师教学或学生预习或复习使用.若需使用，请插入微课【知识点解析】二次函数y =ax 2的图象和性质（二）. 【新知应用】1.当ab >0时，抛物线y ＝ax 2与直线y ＝ax ＋b 在同一直角坐标系中的图象大致是( ).解析：根据a 、b 的符号来确定．当a >0时，抛物线y ＝ax ²的开口向上．∵ab >0，∴b >0.∴直线y ＝ax ＋b 过第一、二、三象限．当a <0时，抛物线y ＝ax ²的开口向下．∵ab >0，∴b <0.∴直线y ＝ax ＋b 过第二、三、四象限．故选D.2.如图，四个二次函数图象中，分别对应：①y ＝ax 2；②y ＝bx 2；③y ＝cx 2；④y ＝dx 2，则a 、b 、c 、d 的大小关系为( ).A ．a >b >c >dB ．a >b >d >cC ．b >a >c >dD ．b >a >d >c解析：抛物线y ＝ax 2的开口大小由|a |确定，|a |越大，抛物线的开口越小；|a |越小，抛物线的开口越大．故选A.3.已知二次函数y ＝ax 2(a ≠0)与直线y ＝2x －3相交于点A (1，b )，求： (1)a ，b 的值；(2)函数y ＝ax 2的图象的顶点M 的坐标及直线与抛物线的另一个交点B 的坐标； (3)△AMB 的面积．解：：(1)∵点A (1，b )是直线y ＝2x －3与二次函数y ＝ax 2的图象的交点，∴点A 的坐标满足二次函数和直线的关系式，∴⎩⎪⎨⎪⎧b ＝a ×12，b ＝2×1－3，∴⎩⎪⎨⎪⎧a ＝－1，b ＝－1； (2)由(1)知二次函数为y ＝－x 2，顶点M (即坐标原点)的坐标为(0，0)．由－x 2＝2x －3，解得x 1＝1，x 2＝－3，∴y 1＝－1，y 2＝－9，∴直线与二次函数的另一个交点B 的坐标为(－3，－9)；(3)如图所示，作AC ⊥x 轴，BD ⊥x 轴，垂足分别为C 、D ，根据点的坐标的意义，可知MD ＝3，MC ＝1，CD ＝1＋3＝4，BD ＝9，AC ＝1，∴S △AMB ＝S 梯形ABDC －S △ACM －S △BDM ＝12×(1＋9)×4－12×1×1－12×3×9＝6.设计意图：促进学生在练习的过程中熟练掌握二次函数y =ax ²的基本性质解决问题的方法. 【随堂检测】1.作出函数y ＝－x 2的图象，观察图象，并利用图象回答下列问题：(1)在y 轴左侧图象上任取两点A (x 1，y 1)，B (x 2，y 2)，使x 2<x 1<0，试比较y 1与y 2的大小； (2)在y 轴右侧图象上任取两点C (x 3，y 3)，D (x 4，y 4)，使x 3＞x 4＞0，试比较y 3与y 4的大小．解：(1)图象如图所示，由图象可知y 1＞y 2； (2)由图象可知y 3<y 4.2.已知函数y ＝(1－n )xn 2＋n －4是关于x 的二次函数，当n 为何值时，抛物线有最低点？并求出这个最低点的坐标．这时当x 为何值时，y 随x 的增大而增大？解：∵函数y ＝(1－n )xn 2＋n －4是关于x 的二次函数，∴⎩⎪⎨⎪⎧n 2＋n －4＝2，1－n ≠0.解得n ＝2或n＝－3.∵抛物线有最低点，∴1－n >0，即n <1.∴n ＝－3.∴当x >0时，y 随x 的增大而增大．3.当m 为何值时，函数y ＝mxm 2－m 的图象是开口向下的抛物线？当x 为何值时，y 随x 的增大而增大？这个函数有最大值还是最小值？这个值是多少？解：由题意，得m 应满足⎩⎪⎨⎪⎧m <0，m 2－m ＝2，解得m ＝－1.当x <0时，y 随x 的增大而增大．这个函数有最大值，最大值是0.4. 如图，是一座抛物线形拱桥的示意图，在正常水位时，水面AB 的宽为20m ，如果水位上升3m ，水面CD 的宽为10m .(1)建立如图所示的坐标系，求此抛物线的函数表达式；(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地，已知甲地距此桥280km(桥长忽略不计)．货车正以每小时40km 的速度开往乙地，当行驶了1h 时，忽然接到紧急通知：前方连降暴雨，造成水位以每小时0.25m 的速度持续上涨(货车接到通知时，水位在CD 处，当水位涨到桥拱最高点O 时，禁止车辆通行)．问：如果货车按原来速度行驶，能否安全通过此桥？若能，请说明理由；若不能，要使货车安全通过此桥，速度应超过每小时多少千米？解：(1)设抛物线的函数表达式为y ＝ax 2(a ≠0)，拱桥最高点O 到水面CD 的距离为h m ，则D (5，－h )，B (10，－h －3)．∴⎩⎪⎨⎪⎧25a ＝－h ，100a ＝－h －3，解得⎩⎪⎨⎪⎧a ＝－125，h ＝1.∴抛物线的函数表达式为y ＝－125x 2；(2)水位由CD 处涨到最高点O 的时间为h ÷0.25＝1÷0.25＝4(h )，货车按原来速度行驶的路程为40×1＋40×4＝200<280，∴货车按原来速度行驶不能安全通过此桥．设货车速度提高到x km/h ，即当4x ＋40×1＝280时，x ＝60.∴要使货车安全通过此桥，货车的速度应超过60km/h.设计意图：针对本节课学习的内容进行巩固，让学生在练习的过程中熟练掌握本节内容的重难点.六、课堂小结本节课主要学习了哪些知识?1.二次函数y=ax²的图象是什么样子？它的特点是什么？二次函数y=ax²的图象是抛物线，它的对称轴是y轴,顶点是原点.2.二次函数y=ax²的性质是什么？当a>0时,抛物线y=ax2的开口向上,顶点是抛物线的最低点,当a越大时,抛物线的开口越小；当a<0时,抛物线y=ax2的开口向下,顶点是抛物线的最高点,当a越大时,抛物线的开口越大.从二次函数y=ax2的图象可以看出:如果a>0,当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大;如果a<0,当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.设计意图：通过问题的设置将本节课所学的知识点进行集中的梳理，归纳总结出本节课的重点知识.七、板书设计第1课时二次函数y=ax²的图象和性质1.二次函数y=ax²的图象是什么样子？它的特点是什么？二次函数y=ax²的图象是抛物线，它的对称轴是y轴,顶点是原点.2.二次函数y=ax²的性质是什么？当a>0时,抛物线y=ax2的开口向上,顶点是抛物线的最低点,当a越大时,抛物线的开口越小；当a<0时,抛物线y=ax2的开口向下,顶点是抛物线的最高点,当a越大时,抛物线的开口越大.从二次函数y=ax2的图象可以看出:如果a>0,当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大;如果a<0,当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.。

人教版数学九年级上学期课时练习-二次函数y=ax2(a≠0)的图象与性质(知识讲解)(人教版)

专题22.3 二次函数（巩固篇）（专项练习）一、单选题知识点一、二次函数的判断1．下列实际问题中，可以看作二次函数模型的有（）①正常情况下，一个人在运动时所能承受的每分钟心跳的最高次数b 与这个人的年龄a 之间的关系为b ＝0.8（220－a ）；①圆锥的高为h ，它的体积V 与底面半径r 之间的关系为V ＝13πr 2h （h 为定值）；①物体自由下落时，下落高度h 与下落时间t 之间的关系为h ＝12gt 2（g 为定值）； ①导线的电阻为R ，当导线中有电流通过时，单位时间所产生的热量Q 与电流I 之间的关系为Q ＝RI 2（R 为定值）.A ．1个B ．2个C ．3个D ．4个2．关于函数y=（500﹣10x ）（40+x ），下列说法不正确的是（） A ．y 是x 的二次函数 B ．二次项系数是﹣10 C ．一次项是100D ．常数项是200003．下列函数关系中，是二次函数的是（）A ．在弹性限度内，弹簧的长度y 与所挂物体质量x 之间的关系B ．当距离一定时，火车行驶的时间t 与速度v 之间的关系C ．等边三角形的周长c 与边长a 之间的关系D ．圆心角为120°的扇形面积S 与半径R 之间的关系 4．下列各式中，y 是x 的二次函数的是（） A ．y=a 2x +bx+c B ．x 2+y -2=0C ．y 2-ax=-2D ．2x -y 2+1=0知识点二、二次函数的参数5．若函数y ＝（a ﹣1）x 2+2x +a 2﹣1是二次函数，则（） A ．a ≠1B ．a ≠﹣1C ．a ＝1D ．a ＝±16．当函数21(1)23a y a x x +=-++ 是二次函数时，a 的取值为（）A ．1a =B ．1a =±C ．1a ≠D ．1a =-7．若y=（m ＋1）265m m x --是二次函数，则m= （）A ．－1B ．7C ．－1或7D ．以上都不对8．下列结论正确的是（） A ．y=ax 2是二次函数B ．二次函数自变量的取值范围是所有实数C ．二次方程是二次函数的特例D ．二次函数的取值范围是非零实数知识点三、二次函数的解析式9．用一根长60cm 的铁丝围成一个矩形，那么矩形的面积2()y cm 与它的一边长()x cm 之间的函数关系式为（）A ．230(030)y x x x =-<<B ．230(030)y x x x =-+<C ．230(030)y x x x =-+<<D ．230(030)y x x x =-+<10．某商店从厂家以每件21元的价格购进一批商品，该商店可以自行定价．若每件商品售为x 元，则可卖出（350-10x ）件商品，那么商品所赚钱y 元与售价x 元的函数关系为（）A ．2105607350y x x =--+B ．2105607350y x x =-++C ．210350y x x =-+D ．2103507350y x x =-+-11．下列函数关系中，可以看做二次函数y=ax 2+bx+c （a≠0）模型的是（） A ．在一定距离内，汽车行驶的速度与行驶的时间的关系 B ．正方形周长与边长之间的关系 C ．正方形面积和正方形边长之间的关系 D ．圆的周长与半径之间的关系12．某商店从厂家一每件21元的价格购进一批商品，该商店可以自行定价．若每件商品售为x 元，则可卖出（350-10x ）件商品，那商品所赚钱y 元与售价x 元的函数关系为（）A ．y ＝-10 x 2-560x+7350B ．y ＝-10 x 2+560x -7350C ．y ＝-10 x 2+350xD ．y ＝-10 x 2+350x -7350二、填空题知识点一、二次函数的判断13．二次函数21212y x x =-+ 中，二次项系数为____，一次项是____，常数项是___ 14．下列函数中：①y=－x 2；①y=2x ；①y=22+x 2－x 3；①m=3－t －t 2是二次函数的是______(其中x 、t 为自变量).15．下列各式：()()()()2222212;2;;;12;2(1)2;2122y x y x y y y x x y x y x x x x x=+====-+=-+=+--；其中y 是x 的二次函数的有________（只填序号）16．二次函数y ＝3x 2+5的二次项系数是_____，一次项系数是_____．知识点二、二次函数的参数17．定义：由a ，b 构造的二次函数()2y ax a b x b =+++叫做一次函数y ＝ax ＋b 的“滋生函数”，一次函数y ＝ax ＋b 叫做二次函数()2y ax a b x b =+++的“本源函数”（a ，b 为常数，且0a ≠）．若一次函数y ＝ax ＋b 的“滋生函数”是231y ax x a =-++，那么二次函数231y ax x a =-++的“本源函数”是______．18．如果函数2(1)2m m y m x -=++是二次函数，那么m =____．19．当m____________________________时，函数22(23)(2)y m m x m x m =--+-+是二次函数．20．点(),1m 是二次函数221y x x =--图像上一点，则236m m -的值为__________知识点三、二次函数的解析式21．图（1）是一个水平摆放的小正方体木块，图（2）、（3）是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，则第n 个叠放的图形中，小正方体木块总数m 与n 的解析式是______．22．如图，正方形ABCD 的边长是10cm ，E 是AB 上一点，F 是AD 延长线上的一点，BE DF =．四边形AEGF 是矩形，矩形AEGF 的面积()2cm y 与BE 的长cm x ()010x <≤的函数关系是______．23．将二次函数245y x x =-+化成2()y a x h k =-+的形式为__________． 24．二次函数()()y 412x x 3=-+-的一般形式2y ax bx c =++是________．三、解答题25．已知函数y ＝(m 2－m )x 2＋(m －1)x ＋2－2m . (1)若这个函数是二次函数，求m 的取值范围． (2)若这个函数是一次函数，求m 的值． (3)这个函数可能是正比例函数吗？为什么？26．已知函数()229123y k x kx =-++是关于x 的二次函数，求不等式141123k k -+≥-的解集．27．某农科所研究出一种新型的花生摘果设备，一期研发成本为每台6万元，该摘果机的销售量y (台)与售价x (万元/台)之间存在函数关系：24y x =-+．（1）设这种摘果机一期销售的利润为1W (万元)，问一期销售时，在抢占市场份额(提示：销量尽可能大)的前提下利润达到32万元，此时售价为多少？（2）由于环保局要求该机器必须增加除尘设备，科研所投入了7万元研究经费，使得环保达标且机器的研发成本每台降低了1万元，若科研所的销售战略保持不变，请问在二期销售中利润达到63万元时，该机器单台的售价为多少？参考答案1．C解：形如y=ax2+bx+c（a、b、c是常数且a≠0）的函数是二次函数，由二次函数的定义可得①①①是二次函数，故选C．2．C【分析】先化简，整理成一般式，然后对每个选项判断即可.解：①y=（500﹣10x）（40+x）=-10x2+100x+20000，①y是x的二次函数，二次项系数是-10，一次项系数是100，常数项是20000，①A、B、D正确，C错误.故选C.【点拨】本题考查了二次函数的一般形式，一般地，形如y=ax2+bx+c（a，b，c为常数，a≠0）的函数叫做二次函数，其中a是二次项系数，b是一次项系数，c是常数项，据此求解即可.3．D【分析】根据各选项的意思，列出个选项的函数表达式，再根据二次函数定义的条件判定则可．解：A、y=mx+b，当m≠0时（m是常数），是一次函数，错误；B、t=sv，当s≠0时，是反比例函数，错误；C、C=3a，是正比例函数，错误；D、S=13πR2，是二次函数，正确．故选D．【点拨】本题考查二次函数的定义．4．B解：利用二次函数的定义，可知：A.y=a2x+bx+c，应说明a≠0，故此选项错误；B.x2+y-2=0可变为y=2x+2，是二次函数，故此选项正确；C.y2-ax=-2不是二次函数，故此选项错误；D.x2-y2+1=0不是二次函数，故此选项错误；故选B．5．A 【分析】利用二次函数定义进行解答即可．解：由题意得：a ﹣1≠0，解得：a ≠1，故选：A ．【点拨】本题主要考查了二次函数的定义，准确计算是解题的关键． 6．D 【分析】根据二次函数的定义去列式求解计算即可．解：①函数21(1)23ay a x x +=-++ 是二次函数，①a -1≠0，2a 1+=2， ①a≠1，21a =， ①1a =-，故选D ．【点拨】本题考查了二次函数的定义，熟记二次函数的定义并灵活列式计算是解题的关键．7．B 【分析】令x 的指数为2，系数不为0，列出方程与不等式解答即可．解：由题意得：m 2-6m -5=2；且m+1≠0；解得m=7或-1；m≠-1， ①m=7，故选：B ．【点拨】利用二次函数的定义，二次函数中自变量的指数是2；二次项的系数不为0． 8．B 【分析】根据二次函数的定义和自变量的取值范围，逐一判断解答问题．解：A 、应强调a 是常数，a≠0，错误；B、二次函数解析式是整式，自变量可以取全体实数，正确；C、二次方程不是二次函数，更不是二次函数的特例，错误；D、二次函数的自变量取值有可能是零，如y=x2，当x=0时，y=0，错误．故选B．【点拨】本题考查二次函数的定义和自变量的取值范围,解题关键是熟练掌握定义．9．C【分析】由矩形另一边长为周长的一半减去已知边长求得另一边的长，进一步根据矩形的面积等于相邻两边长的积列出关系式即可．解：由题意得：矩形的另一边长=60÷2-x=30-x，矩形的面积y（cm2）与它的一边长x（cm）之间的函数关系式为y=x（30-x）=-x2+30x （0＜x＜30）．故选：C．【点拨】此题考查根据实际问题列二次函数关系式，掌握矩形的边长与所给周长与另一边长的关系是解题的关键．10．B【分析】商品所赚钱=每件的利润×卖出件数，把相关数值代入即可求解．解：每件的利润为（x-21），①y=（x-21）（350-10x）=-10x2+560x-7350．故选B．【点拨】本题考查了根据实际问题列二次函数关系式，解决本题的关键是找到总利润的等量关系，注意先求出每件商品的利润．11．C【分析】利用二次函数的性质：一般地，把形如y=ax2+bx+c（其中a、b、c是长常数，a≠0，b，c可以为0）的函数叫做二次函数．逐一分析解答即可．解：A、在一定距离内，汽车行驶的速度与行驶的时间的关系是一种反比例关系，不能看作二次函数y=ax2+bx+c模型；B 、正方形周长与边长之间的关系属于一次函数，不能看作二次函数y=ax 2+bx+c模型；C 、正方形面积和正方形边长之间的关系，可以看做二次函数y=ax 2+bx+c 模型；D 、圆的周长与半径之间的关系属于一次函数，不能看作二次函数y=ax 2+bx+c 模型．故选C ．【点拨】本题考查了二次函数的性质，建立二次函数的模型要从解析式，数值的变化和图象几个方面分析．12．B解：根据商品的单价利润×销售的件数=总利润，即可得y=（x -21）（350－10x ）=－10x 2＋560x －7350，故选B.13．12-2x , 1【分析】函数化简为一般形式：y=ax 2+bx+c （a ，b ，c 是常数且a≠0）．在一般形式中ax 2叫二次项，bx 叫一次项，c 是常数项．其中a ，b ，c 分别叫二次项系数，一次项系数，常数项．解：①y=ax 2+bx+c （a ，b ，c 是常数且a≠0）．在一般形式中ax 2叫二次项，bx 叫一次项，c 是常数项．其中a ，b ，c 分别叫二次项系数，一次项系数，常数项①21212y x x =-+ 中，二次项系数为12，一次项是-2x ，常数项是1.故答案是：12; -2x;1.【点拨】考查了二次函数的定义，二次函数的一般形式：y=ax 2+bx+c （a ，b ，c 是常数且a≠0）．在一般形式中ax 2叫二次项，bx 叫一次项，c 是常数项．其中a ，b ，c 分别叫二次项系数，一次项系数，常数项．14．①① 【分析】一般地，如果y ＝ax 2＋bx ＋c (a ，b ，c 是常数，a ≠0)，那么y 叫做x 的二次函数．根据二次函数的定义条件判定则可．解：①y ＝－x 2，二次项系数为－1，是二次函数；①y ＝2x ，是一次函数；①y ＝22＋x 2－x 3，含自变量的三次方，不是二次函数；①m ＝3－t －t 2，是二次函数. 故填①①．【点拨】本题考查二次函数的定义．一般地，如果y ＝ax 2＋bx ＋c (a ，b ，c 是常数，a ≠0)，那么y 叫做x 的二次函数．判断一个函数是二次函数需要注意三点： (1)经整理后，函数表达式是含自变量的整式； (2)自变量的最高次数为2；(3)二次项系数不为0，尤其是含有字母系数的函数，应特别注意，二次项系数a 是否为0．15．①①① 【分析】根据二次函数的定义与一般形式即可求解．解：y 是x 的二次函数的有①，①，①．故答案是：①，①，①．【点拨】本题考查了二次函数的定义，一般形式是y=ax 2+bx+c （a≠0，且a ，b ，c 是常数，x 是未知数）．16． 3 0 【分析】根据二次函数的定义解答即可．解：二次函数y ＝3x 2+5的二次项系数是3，一次项系数是0．故答案是：3；0．【点拨】考查二次函数的定义，是基础题，熟记概念是解题的关键，要注意没有一次项，所以一次项系数看做是0．17．2-1y x =﹣【分析】由“滋生函数”和“本源函数”的定义，运用待定系数法求出函数231y ax x a =-++的本源函数．解：由题意得3=++1=a b a b ⎧⎨⎩﹣解得=2=1a b ⎧⎨⎩﹣﹣①函数231y ax x a =-++的本源函数是2-1y x =﹣．故答案为：2-1y x =﹣．【点拨】本题考查新定义运算下的一次函数和二次函数的应用，解题关键是充分理解新定义“本源函数”．18．2．【分析】直接利用二次函数的定义得出m 的值．解：①函数2(1)2m m y m x -=++是二次函数，①m 2−m ＝2，（m−2）（m ＋1）＝0，解得：m 1＝2，m 2＝−1，①m ＋1≠0，①m≠−1，故m ＝2．故答案为：2．【点拨】此题主要考查了二次函数的定义，正确得出m 的方程是解题关键．19．不等于1-和3【分析】我们一般把形如2y ax bx c =++(a b c 、、为常数)的函数称之为二次函数，其中二次项系数不能为0，据此进一步求解即可.解：根据二次函数的定义可得：2230m m --≠，即：()()130m m +-≠，①1m ≠-，且3m ≠，即当m 不等于1-和3时，原函数为二次函数，故答案为：不等于1-和3.【点拨】本题主要考查了二次函数的定义的运用，熟练掌握相关概念是解题关键. 20．6【分析】把点(),1m 代入221y x x =--即可求得22m m -值，将236m m -变形()232m m -，代入即可．解：①点(),1m 是二次函数221y x x =--图像上，①2121m m =--则222m m -=．①()223632326m m m m -=-=⨯=故答案为：6．【点拨】本题考查了二次函数图象上点的坐标特征，根据点坐标求待定系数是解题的关键．21．m =2n 2−n【分析】图（1）中只有一层，有（4×0＋1）一个正方形，图（2）中有两层，在图（1）的基础上增加了一层，第二层有（4×1＋1）个．图（3）中有三层，在图（2）的基础长增加了一层，第三层有（4×2＋1），依此类推出第n 层正方形的个数，即可推出当有n 层时总的正方形个数．解：经分析，可知：第一层的正方形个数为（4×0＋1），第二层的正方形个数为（4×1＋1），第三层的正方形个数为（4×2＋1），……第n 层的个数为：[4×（n −1）＋1]，第n 个叠放的图形中，小正方体木块总数m 为：1＋（4×1＋1）＋（4×2＋1）＋…＋[4×（n −2）＋1]＋[4×（n −1）＋1]＝1＋4×1＋1＋4×2＋1＋…＋4×（n −2）＋1＋4×（n −1）＋1＝n ＋4（1＋2＋3＋…＋n −2＋n −1）＝n ＋4()()1112n n +--⨯ ＝n ＋2n （n −1）＝2n 2−n ．即：m =2n 2−n ．故答案为：m =2n 2−n【点拨】本题解题关键是根据图形的变换总结规律，由图形变换得规律：每次都比上一次增加一层，增加第n 层时小正方形共增加了4（n −1）＋1个，将n 层的小正方形个数相加即可得到总的小正方形个数．22．2100y x =-+##2100y x =-【分析】由已知图形可以分析得到矩形AEGF 的长AF 为(10)x +cm ，宽AE 为(10)x -cm ，由面积公式即可计算得到正确答案．解：①正方形ABCD 的边长是10cm ，且BE DF =①矩形AEGF 的长AF 的长为(10)x +cm ，宽AE 的长为(10)x -cm①矩形AEGF 的面积为：()()21010=100y AF AE x x x ==+--+故答案为：2100y x =-+【点拨】本题考查变量之间的关系，由矩形面积推导二次函数关系式等知识点．数形结合列式计算是解此类题的关键．23．22()1y x =-+【分析】利用配方法整理即可得解．解：222454()4121y x x x x x =-+=-++=-+，所以22()1y x =-+．故答案为22()1y x =-+．【点拨】本题考查了二次函数的解析式有三种形式：(1)一般式：2(y ax bx c =++0,a a b c ≠、、为常数)； (2)顶点式：2()y a x h k =-+；(3)交点式(与x 轴)：12()()y a x x x x =--．24．2y 8x 20x 12=-++【分析】直接利用乘法运算法则化成一般式．解：y ＝−4（1＋2x ）（x−3）＝−8x 2＋20x ＋12，故答案为y ＝−8x 2＋20x ＋12．【点拨】此题考查二次函数的解析式的三种形式，熟练掌握这几种形式是解题的关键．25．(1). m ≠0且m ≠1.(2). m ＝0.(3). 不可能试题分析：（1）根据二次函数的二次项系数不等于0，可得答案；（2）根据二次函数的二次项系数等于0，常数项不等于0，是一次函数，可得答案；（3）根据二次函数的二次项系数等于0，常数项等于0，可得正比例函数．解：(1)①这个函数是二次函数，①m 2－m ≠0，①m (m －1)≠0，①m ≠0且m ≠1.(2)①这个函数是一次函数，①①m ＝0.(3)不可能．①当m ＝0时，y ＝－x ＋2，①不可能是正比例函数．26．15k ≤且13k ≠-．【分析】首先利用二次函数的定义得出k 不能取的值，进而解不等式得出答案.解：∵函数()229123y k x kx =-++是关于x 的二次函数，∴2910k -≠，解得：13k ≠±， 141123k k -+≥- ()()312416k k -≥+-，解得：15k ≤，故不等式141123k k -+≥-的解集为：15k ≤且13k ≠-．【点拨】此题主要考查了二次函数的定义以及解不等式，正确解不等式是解题关键. 27．（1）在抢占市场份额的前提下利润要达到32万元，此时售价为8万元/台；（2）要使二期利润达到63万元，销售价应该为10万元/台．【分析】（1）先根据等量关系式：总利润=（售价-成本）⨯销售量，列出函数关系式，再将132W =代入函数关系式得出方程求解即得；（2）先根据等量关系式：总利润=（售价-新成本）⨯销售量-7，列出函数关系式，再将263W =代入函数关系式得出方程求解即得．解：（1）根据题意列出函数关系式如下：21(6)(6)(24)(15)81W x y x x x =-⋅=--+=--+当132W =时，2(15)8132x --+=，解得18x =，222x =．①要抢占市场份额①8x =．答：在抢占市场份额的前提下利润要达到32万元，此时售价为8万元/台．（2）降低成本之后，每台的成本为5万元，每台利润为(5)x -万元，销售量24y x =-+．依据题意得22(5)(24)729127W x x x x =--+-=-+-，当263W =时，22912763x x -+-=，解得110x =，219x =．①要继续保持扩大销售量的战略①10x =答：要使二期利润达到63万元，销售价应该为10万元/台．【点拨】本题考查函数解析式及解一元二次方程，解题关键是正确找出等量关系式：总利润=（售价-成本）⨯销售量．。

九年级数学第二章二次函数y=ax2(a≠0)的图象与性质

二次函数y=ax2(a≠0)的图象与性质【学习目标】1．经历探索二次函数y=ax2和y=ax2＋c的图象的作法和性质的过程，进一步获得将表格、表达式、图象三者联系起来的经验．2．会作出y=ax2和y=ax2＋c的图象，并能比较它们与y=x2的异同，理解a与c对二次函数图象的影响．3．能说出y=ax2＋c与y=ax2图象的开口方向、对称轴和顶点坐标．4．体会二次函数是某些实际问题的数学模型．5.掌握二次函数y=ax2(a≠0)与y=ax2+c (a≠0)的图象之间的关系.【要点梳理】要点一、二次函数y=ax2（a≠0）的图象与性质1.二次函数y=ax2(a≠0)的图象二次函数y=ax2的图象（如图），是一条关于y轴对称的曲线，这样的曲线叫做抛物线.抛物线y=ax2（a≠0）的对称轴是y轴，它的顶点是坐标原点.当a＞ 0时，抛物线的开口向上，顶点是它的最低点；当a＜0时，抛物线的开口向下，顶点是它的最高点.2.二次函数y=ax2(a≠0)的图象的画法——描点法描点法画图的基本步骤：列表、描点、连线.（1）列表：选择自变量取值范围内的一些适当的x的值，求出相应的y值，填入表中.（自变量x 的值写在第一行，其值从左到右，从小到大.）（2）描点：以表中每对x和y的值为坐标，在坐标平面内准确描出相应的点.一般地，点取的越多，图象就越准确.（3）连线：按照自变量的值由小到大的顺序，把所描的点用平滑的曲线连结起来.要点进阶：（1）用描点法画二次函数y=ax2（a≠0）的图象时，应在顶点的左、右两侧对称地选取自变量x的值，然后计算出对应的y值.（2）二次函数y=ax 2(a≠0)的图象，是轴对称图形，对称轴是y 轴．y=ax 2(a≠0)是最简单的二次函数.（3）画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点. 3.二次函数y=ax 2(a ≠0)的图象的性质二次函数y=ax 2（a≠0）的图象的性质，见下表：函数图象开口方向顶点坐标对称轴函数变化最大（小）值y=ax 2a ＞0向上（0，0） y 轴 x ＞0时，y 随x 增大而增大； x ＜0时，y 随x 增大而减小.当x=0时，y 最小=0y=ax 2a ＜0向下（0，0） y 轴 x ＞0时，y 随x 增大而减小； x ＜0时，y 随x 增大而增大.当x=0时，y 最大=0要点进阶：顶点决定抛物线的位置.几个不同的二次函数，如果二次项系数a 相同，那么抛物线的开口方向、开口大小完全相同，只是顶点的位置不同. │a │相同，抛物线的开口大小、形状相同.│a │越大，开口越小，图象两边越靠近y 轴，│a │越小，开口越大，图象两边越靠近x 轴. 要点二、二次函数y=ax 2+c(a ≠0)的图象与性质 1.二次函数y=ax 2+c(a ≠0)的图象（1）0a >j xOy()20y ax c c =+>cjyxOc()20y ax c c =+<（2）0a <2.二次函数y=ax 2+c(a ≠0)的图象的性质关于二次函数2(0)y ax c a =+≠的性质，主要从抛物线的开口方向、顶点、对称轴、函数值的增减性以及函数的最大值或最小值等方面来研究．下面结合图象，将其性质列表归纳如下：函数2(0,0)y ax c a c =+>> 2(0,0)y ax c a c =+<>图象开口方向向上向下顶点坐标 (0，c) (0，c) 对称轴y 轴y 轴函数变化当0x >时，y 随x 的增大而增大；当0x <时，y 随x 的增大而减小.当0x >时，y 随x 的增大而减小；当0x <时，y 随x 的增大而增大.最大（小）值当0x =时，y c =最小值当0x =时，y c =最大值3.二次函数()20y axa =≠与()20y ax c a =+≠之间的关系j yxOc()20y ax c c =+>j y xOc()20y ax c c =+<()20y ax a =≠的图象向上（c ＞0）【或向下（c ＜0）】平移│c │个单位得到()20y ax c a =+≠的图象. 要点进阶：抛物线2(0)y ax c a =+≠的对称轴是y 轴，顶点坐标是(0，c)，与抛物线2(0)y ax a =≠的形状相同．函数2(0)y ax c a =+≠的图象是由函数2(0)y ax a =≠的图象向上（或向下）平移||c 个单位得到的，顶点坐标为(0，c)．抛物线y ＝ax 2(a ≠0)的对称轴、最值与顶点密不可分，其对称轴即为过顶点且与x 轴垂直的一条直线，其顶点横坐标x ＝0，抛物线平移不改变抛物线的形状，即a 的值不变，只是位置发生变化而已．【典型例题】类型一、二次函数y=ax 2（a ≠0）的图象与性质例1．已知a≠0，在同一直角坐标系中，函数y=ax 与y=ax 2的图象有可能是（）A ．B ．C ．D ．举一反三：【变式】在同一平面直角坐标系中，一次函数y ax c =+与二次函数2y ax c =+的图象大致为（）．例2.根据下列条件求a 的取值范围：(1)函数y ＝(a-2)x 2，当x ＞0时，y 随x 的增大而减小，当x ＜0时，y 随x 的增大而增大； (2)函数y ＝(3a-2)x 2有最大值； (3)抛物线y ＝(a+2)x 2与抛物线212y x =-的形状相同； (4)函数2a ay ax +=的图象是开口向上的抛物线．举一反三：【变式】二次函数y ＝mx 22-m 有最高点，则m ＝___________．例3. 二次函数223y x =的图象如图所示，点A 0位于坐标原点，点A 1，A 2，A 3，…，A 2013在y 轴的正半轴上，点B 1，B 2，B 3，…，B 2013在二次函数223y x =位于第一象限的图象上，若△A 0B 1A 1，△A 1B 2A 2，△A 2B 3A 3，…，△A 2012B 2013A 2013都为等边三角形，求△A 2012B 2013A 2013的边长．类型二、二次函数y=ax 2+c(a ≠0)的图象与性质例4.关于二次函数y=2x 2+3，下列说法中正确的是（）A. 它的开口方向是向下；B. 当x ＜﹣1时，y 随x 的增大而减小；C. 它的对称轴是x=2；D. 当x=0时，y 有最大值是3.举一反三：【变式】如图所示，抛物线2(0)y ax c a =+<交x 轴于G 、F ，交y 轴于点D ，在x 轴上方的抛物线上有两点B 、E ，它们关于y 轴对称，点G 、B 在y 轴左侧，BA ⊥OG 于点A ，BC ⊥OD 于点C ．四边形OABC 与四边形ODEF 的面积分别为6和10，则△ABG 与△BCD 的面积之和为________．例5.有一个抛物线形的拱形隧道，隧道的最大高度为6m ，跨度为8m ，把它放在如图所示的平面直角坐标系中．（1）求这条抛物线所对应的函数关系式；（2）若要在隧道壁上点P （如图）安装一盏照明灯，灯离地面高4.5m ．求灯与点B 的距离．【巩固练习】一、选择题1.若抛物线210(2)m y m x-=+的开口向下，则m 的值为( )．A ．3B ．-3C ．23D ．23-2.抛物线24y x =--的顶点坐标，对称轴分别是( )． A ．(2，0)，直线x ＝-4 B ．(-2，0)，直线x ＝4 C ．(1，3)，直线x ＝0 D ．(0，-4)，直线x ＝03.两条抛物线2y x =与2y x =-在同一坐标系内，下列说法中不正确的是（）A ．顶点相同B ．对称轴相同C ．开口方向相反D ．都有最小值4.关于213y x =，2y x =，23y x =的图像，下列说法中不正确的是（） A ．顶点相同 B ．对称轴相同 C ．图像形状相同 D ．最低点相同5．在同一直角坐标系中，函数y=kx 2﹣k 和y=kx+k （k ≠0）的图象大致是（）.A. B. C. D.6.图中是一个横断面为抛物线形状的拱桥，当水面在l 处时，拱顶(拱桥洞的最高点)离水面2 m ，水面宽4 m ．如图所示建立平面直角坐标系，则抛物线的解析式是( )．A ．22y x =- B ．22y x = C ．212y x =-D ．212y x =二、填空题7.抛物线23y x =-的开口，对称轴是，顶点坐标是．8.将抛物线2y x =-向上平移5个单位后，得到的抛物线的解析式是____ ____．9.已知(x 1，y 1)，(x 2，y 2)是抛物线2y ax =(a ≠0)上的两点．当210x x <<时，21y y <，则a 的取值范围是________．10. 对于二次函数y=ax 2，已知当x 由1增加到2时，函数值减少4，则常数a 的值是．11.抛物线2y ax c =+与23y x =的形状相同，其顶点坐标为（0，1），则其解析式为．12．如图，⊙O 的半径为2，1C 是函数212y x =的图象，2C 是函数212y x =-的图象，则阴影部分的面积是 .三、解答题13．如图是一个横断面为抛物线形状的拱桥，当水面宽4米时，拱顶（拱桥洞的最高点）离水面2米，水面下降1米时，水面的宽度为多少米？14.已知直线1y x =+与x 轴交于点A ，抛物线22y x =-的顶点平移后与点A 重合．(1)求平移后的抛物线C 的解析式；(2)若点B(1x ，1y )，C(2x ，2y )在抛物线C 上，且1212x x -<<，试比较1y ，2y 的大小．15. 已知正方形周长为Ccm ，面积为S cm 2．（1）求S 和C 之间的函数关系式，并画出图象；（2）根据图象，求出S=1 cm 2时，正方形的周长；（3）根据图象，求出C 取何值时，S ≥4 cm 2．。

二次函数辅导讲义（学生版）

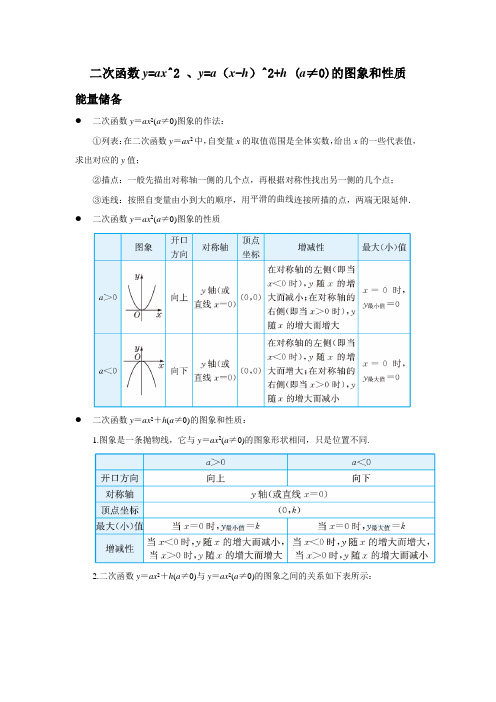
⼆次函数辅导讲义（学⽣版）⼆次函数辅导讲义⼀、基础知识讲解+中考考点、例题分析考点1：⼆次函数的图象和性质⼀、考点讲解：1．⼆次函数的定义：形如（a≠0，a，b，c为常数）的函数为⼆次函数．2．⼆次函数的图象及性质：⑴⼆次函数y=ax2 (a≠0）；当a＞0时，抛物线开⼝向上，顶点是最低点；当a＜0时，抛物线开⼝向下，顶点是最⾼点；a越⼩，抛物线开⼝越⼤．y=a(x－h)2＋k的对称轴是x=h，顶点坐标是（h，k）。

⑵⼆次函数，顶点为（－，），对称轴x=－；当a＞0时，抛物线开⼝向上，图象有最低点，且x＞－，y随x的增⼤⽽增⼤，x＜－，y随x的增⼤⽽减⼩；当a＜0时，抛物线开⼝向下，图象有最⾼点，且x＞－，y随x的增⼤⽽减⼩，x＜－，y随x的增⼤⽽增⼤．解题⼩诀窍：⼆次函数上两点坐标为（），（），即两点纵坐标相等，则其对称轴为直线。

3．图象的平移：⼆次函数y=ax2 与y=－ax2 的图像关于x轴对称。

平移的简记⼝诀是“上加下减，左加右减”。

⼀、经典考题剖析：【考题1】在平⾯直⾓坐标系内，如果将抛物线向右平移2个单位，向下平移3个单位，平移后⼆次函数的关系式是（）Ａ．Ｂ．Ｃ．Ｄ．2．⼆次函数的图象上有两点(3，－8)和(－5，－8)，则此拋物线的对称轴是（）A． B. C. D.4．已知⼆次函数(a≠0）与⼀次函数y=kx+m(k≠0）的图象相交于点A（－2，4）,B(8，2)，如图1－2－7所⽰，能使y1＞y2成⽴的x取值范围是_______5．已知直线y=x 与⼆次函数y=ax 2 －2x －1的图象的⼀个交点 M 的横标为1，则a 的值为（）A 、2B 、1C 、3D 、 46．已知反⽐例函数y= x k 的图象在每个象限内y 随x 的增⼤⽽增⼤，则⼆次函数y=2kx 2 －x+k 2的图象⼤致为图1－2－3中的（）7、读材料：当抛物线的解析式中含有字母系数时，随着系数中的字母取值的不同，抛物线的顶点坐标也将发⽣变化．例如：由抛物线①，有y=②，所以抛物线的顶点坐标为（m ，2m －1），即③④。

二次函数y=ax^2(a≠0)与y=ax^2+c(a≠0)的图象与性质(基础)

要点一、二次函数的概念1.二次函数的概念一般地，形如_____________________（a≠0，a, b, c为常数）的函数是二次函数.若b=0，则y=ax2+c；若c=0，则y=ax2+bx；若b=c=0，则y=ax2.以上三种形式都是二次函数的特殊形式，而y=ax2+bx+c（a≠0）是二次函数的一般式.二次函数由特殊到一般，可分为以下几种形式：①（a≠0）；②（a≠0）；③（a≠0）；④（a≠0），其中；⑤（a≠0）.要点诠释：如果y=ax2+bx+c(a,b,c是常数，a≠0)，那么y叫做x的二次函数．这里，当a=0时就不是二次函数了，但b、c可分别为零，也可以同时都为零．a 的绝对值越大，抛物线的开口越________.2.二次函数解析式的表示方法1. 一般式：（，，为常数，）；2. 顶点式：（，，为常数，）；3. 两根式：（，，是抛物线与轴两交点的横坐标）（或称交点式）.要点诠释：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与轴有交点，即时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.要点二、二次函数y=ax 2（a ≠0）的图象及性质 1.二次函数y=ax 2(a ≠0)的图象用描点法画出二次函数y=ax 2（a≠0）的图象，如图，它是一条关于y 轴对称的曲线，这样的曲线叫做抛物线.因为抛物线y=x 2关于y 轴对称，所以y 轴是这条抛物线的对称轴，对称轴与抛物线的交点是抛物线的顶点，从图上看，抛物线y=x 2的顶点是图象的最低点。

因为抛物线y=x 2有最低点，所以函数y=x 2有最小值，它的最小值就是最低点的纵坐标.2.二次函数y=ax 2(a ≠0)的图象的画法用描点法画二次函数y=ax 2（a≠0）的图象时，应在顶点的左、右两侧对称地选取自变量x 的值，然后计算出对应的y 值，这样的对应值选取越密集，描出的图象越准确.2y ax bx c =++a b c 0a ≠2()y a x h k =-+a h k 0a ≠12()()y a x x x x =--0a ≠1x 2x x x 240b ac -≥a>0 a<01.二次函数y=ax2+c(a≠0)的图象（1）（2）2.二次函数y=ax2+c(a≠0)的图象的性质关于二次函数的性质，主要从抛物线的开口方向、顶点、对称轴、函数值的增减性以及函数的最大值或最小值等方面来研究．下面结合图象，将其性质列表归纳如下：函数a>a<2(0)y ax c a=+≠2(0,0)y ax c a c=+>>2(0,0)y ax c a c=+<>j jjj1．（2016•松江区一模）下列函数中，属于二次函数的是（） A ．y=2x +1 B ．y=（x ﹣1）2﹣x 2C ．y=2x 2﹣7D ．【思路点拨】根据一次函数、反比例函数、二次函数的定义判断各选项即可得出答案．举一反三：【变式】如果函数232(3)1m m y m x mx -+=-++是二次函数，求m 的值．类型二、二次函数y=ax 2（a ≠0）的图象及性质2．函数y ＝x 2的图象对称轴左侧上有两点A(a ，15)，B(b ，)，则a-b_______0(填“＞”、“＜”或“＝”号)．举一反三：【变式1】二次函数与的形状相同，开口大小一样，开口方向相反，则．【变式2】（2015•山西模拟）抛物线y=﹣x 2不具有的性质是（）． A.开口向上 B. 对称轴是y 轴 C. 在对称轴的左侧，y 随x 的增大而增大 D. 最高点是原点类型三、二次函数y=ax 2+c(a ≠0)的图象及性质3．求下列抛物线的解析式：142y ax =22y x =-a =（1）与抛物线形状相同，开口方向相反，顶点坐标是（0，-5）的抛物线；（2）顶点为（0，1），经过点（3，-2）并且关于y 轴对称的抛物线．4．在同一直角坐标系中，画出和的图象，并根据图象(如图所示)回答下列问题．(1)抛物线向________平移________个单位得到抛物线；(2)抛物线，开口方向是________，对称轴为________，顶点坐标为________；(3)抛物线，当x________时，随x 的增大而减小；当x________时，函数y 有最________值，其最________值是________．【巩固练习】一、选择题2132y x =-+2y x =-21y x =-+21y x =-+2y x =-21y x =-+21y x =-+1．下列函数中是二次函数的有（）.①y=x+；②y=3（x ﹣1）2+2；③y=（x+3）2﹣2x 2；④y=+x ．A ．4个B ．3个 C.2个 D ．1个2．（2016•当涂县三模）函数y=﹣x 2+1的图象大致为（）A ．B ．C ．D ．3．把抛物线向上平移1个单位，所得到抛物线的函数表达式为( )． A ． B ． C ． D ．4．一台机器原价60万元，如果每年的折旧率是x ，两年后这台机器的价格为y 万元，则y 与x 之间的函数关系式为( )．A ．y ＝60(1-x)2B ．y ＝60(1-x)C ．y ＝60-x 2D ．y ＝60(1+x)2 5．在同一坐标系中，作出，，的图象，它们的共同点是（）． A ．关于y 轴对称，抛物线的开口向上 B ．关于y 轴对称，抛物线的开口向下 C ．关于y 轴对称，抛物线的顶点都是原点 D ．关于原点对称，抛物线的顶点都是原点 6．汽车的刹车距离y (m)与开始刹车时的速度x(m/s)之间满足二次函数，若汽车某次的刹车距离为5 m ，则开始刹车时的速度为( )． A ．40 m/s B ．20m/s C ．10 m/s D ．5 m/s二、填空题7．已知抛物线的解析式为y ＝-3x 2，它的开口向________，对称轴为________，顶点坐标是________，当x ＞0时，y 随x 的增大而________． 8．（2016春•潜江校级期中）若函数y=（a ﹣5）x是二次函数，则a= ．9．已知抛物线y ＝x 2上有一点A ，A 点的横坐标是-1，过点A 作AB ∥x 轴，交抛物线于另一点B ，2y x =21y x =+2(1)y x =+21y x =-2(1)y x =-22y x =22y x =-212y x =21(0)20y x x =>则△AOB 的面积为________． 10．函数，、的图象大致如图所示，则图中从里向外的三条抛物线对应的函数关系式是_____________________．第10题第12题11．（2015•巴中模拟）对于二次函数y=ax 2，已知当x 由1增加到2时，函数值减少4，则常数a 的值是___________．12．如图所示，用一段长30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD ，设AB 的边长为x 米，则菜园的面积y(单位：米2)与x(单位：米)的函数关系式为______________________(不要求写自变量的取值范围)．三、解答题 13．已知是二次函数，且当x ＞0时，y 随x 的增大而增大．(1)求m 的值； (2)画出函数的图象．14. 几位同学聚会，每两个人之间握手一次，试写出握手的总数m 与参加聚会的人数n 之间的函数关系式．2y x =212y x =23y x =2(2)m my m x+=+。

《二次函数——二次函数的图象与性质》数学教学PPT课件(9篇)

在函数y＝x2的图象上，则y1，y2，y3之间的大小
y3>y2>y1
关系为___________．
导引：因为a>1，所以0<a－1<a<a＋1, 所以这三个点
都在函数y＝x2的图象的对称轴的右侧．根据
“当x>0时，y随x的增大而增大”的性质，可得
y3>y2>y1.
（来自《点拨》）
知2－讲
总结
当所比较的点都在抛物线的对称轴的同一侧时，
y值都随x值的增大而增大
D．当x<0时，函数y＝x2，y的值随x值的增大的变化情况与当x>0
时，函数y＝－x2，y的值随x值的增大的变化情况相同
（来自《典中点》）
知2－练
4 如图，一次函数y1＝kx＋b的图象与二次函数y2＝
x2的图象交于A(－1，1)和B(2，4)两点，则当y1<y2时，x的取
值范围是( D )
1
(1，2
), 可知, 其中有两点在第一象限, 一
点在第四象限, 排除B,
1
C；在第一象限内,
y1的对应
2
点(1, 2)在上, y3的对应点(1， )在下, 排除A.
知1－练
1 关于二次函数y＝3x2的图象，下列说法错误的是( C )
A．它是一条抛物线
B．它的开口向上，且关于y轴对称
C．它的顶点是抛物线的最高点
可直接利用函数的增减性进行大小比较．
（来自《点拨》）
知2－练
1 已知点(x1，y1)，(x2，y2)是二次函数y＝－x2的图象
上的两点，当x1<x2<0时，y1与y2的大小关系为
y1＜y2
________．

九年级数学下册第五章二次函数的图象与性质二次函数y=ax2(a≠0)的图像和性质课件新版苏科版

当x=0 时,y最小值=0 当x=0 时,y 最大值=0
要点解读:
知2－讲
①判断二次函数的增减性的技巧:从抛物线的对称轴分开,自左
向右看,“上坡路”就是y随x的增大而增大,“下坡路”就是y
随x 的增大而减小.
②在二次函数y=ax(2a≠0)中,a的正负性决定开口方向, |a|决定开
口的大小．|a|越大,抛物线开口越小,反之,|a|越小,抛物线开口
的值要在坐标原点(0,0)的左右两边对称选取,
③连线时,按照自变量由小到大(或由大到小)的顺序,并且用光滑
的曲线顺次连接,初始点和末端点处要注意适当“向外延伸”,
切忌用线段连接或漏点、跨点连接
注意:
知1－讲
(1)由表格可知,在画y= 12x2的图像时,我们可以先描出
(03)连线:按自变量由小到大(或由大到小)的顺序,依次用平滑的曲线连接各点.
知1－讲
2. 抛物线二次函数y=ax2的图像是一条抛物线,抛物线的顶点在原点、对称轴是y 轴. 当a＞ 0 时,抛物线的开口向上,顶点是抛物线的最低点；当a＜ 0 时,抛物线的开口向下,顶点是抛物线的最高点.
特别提醒:
知2－讲
解:由抛物线的开口方向,知a＞0,b＞0,c＜0,d＜0,由抛物线的开口大小,知|a|＞|b|,|c|＞|d|,因此a＞b,c＜d. ∴ a＞ b＞d＞c.
知2－讲
巧题妙解: 如图5.2-3,当x=1 时,四个函数值分别等于二次项系数, ∴ 直线 x=1 与四条抛物线的交点从上到下依次为
第5章二次函数
5.2 二次函数的图像和性质
5.2.1 二次函数y=ax2(a≠0)的图像和性质
1 课时讲解二次函数y=ax2 的图像的画法

北京市第四中学九年级数学上册同步学案 01《二次函数y=ax^2(a≠0)与y=ax^2 c(a≠0)的图象与性质》

《二次函数》专题第一讲：二次函数y=ax 2 (a ≠0)与y=ax 2+c(a ≠0)的图象与性质北京四中梁威一、最简单的二次函数2y ax =1．画出二次函数2y x =的图象——画图步骤？如何列表？解：在2y x =中，自变量x 为任意实数．列表如下：描点，用平滑曲线顺次连接各点．1．画出二次函数2y x =的图象：2．归纳二次函数2y x =的图象性质：形状、大小和位置．（1）这条曲线叫做抛物线2y x =．一般地，二次函数2y ax bx c =++的图象叫做抛物线2y ax bx c =++．（2）开口方向：_________．（3）对称轴：____________________；对称轴方程：0x =．思考如何进行证明？（x ，y ）和（－x ，y ）都在同一条抛物线上．（4）顶点：抛物线2y x =与其对称轴的交点（0，0），即原点．顶点是抛物线的最_____点；即当0x =时，y 取________值．（5）图象位于第________象限．形：在y 轴左侧，抛物线呈________趋势；在y 轴右侧，抛物线呈________趋势．数：当0x <时，y 随x 的增大而________；当0x >时，y 随x 的增大而________．探究：分别在同一平面直角坐标系中，画出下列两组函数： (1) 212y x =,22y x =,2y x =; (2) 2y x =-,212y x =-,22y x =-的图象，并考虑这些抛物线有什么共同点和不同点．3．归纳二次函数2y ax =的图象及其性质：一般地，抛物线2y ax =的对称轴是______轴，顶点是________．（1）当0a >时，抛物线的开口________，顶点（0，0）是抛物线的最低点．抛物线位于第________象限．在y 轴左侧，抛物线呈________趋势；在y 轴右侧，抛物线呈________趋势．当0x =时，y 最小=________．当0x >时，y 随x 增大而________；当0x <时，y 随x 增大而________．a 越大，抛物线的开口越________；（2）当0a <时，抛物线的开口_______，顶点（0，0）是抛物线的最______点．当0x =时，y 最大=______．当0x >时，y 随x 增大而________；当0x <时，y 随x 增大而________．抛物线位于第________象限．在y 轴左侧，抛物线呈________趋势；在y 轴右侧，抛物线呈________趋势．a 越大，抛物线的开口越________．（3）a 大，抛物线的开口越________； a 越小，抛物线的开口越________．二、二次函数2y ax c =+的图象和性质在同一平面直角坐标系中，画出21y x =+，21y x =-的图象．解：列表利用平移变换，描点画图，得到21y x =+和21y x =-的图象．把抛物线2y x =向上平移1个单位，就得到抛物线21y x =+；把抛物线向下平移1个单位，就得到抛物线21y x =-．1．二次函数2y ax c =+的图象是抛物线，其性质是：（1）当0a >时，开口方向、对称轴、增减性与2y ax =相同，不同的是顶点坐标为（____，____），当0x =时，y 最小=________．（2）当0a <时，开口方向、对称轴、增减性与2y ax =相同，不同的是顶点坐标为（____，____），当0x =时，y 最大=________．2．抛物线2y ax =与2y ax c =±有何联系？（1）抛物线2y ax =与2y ax c =±的形状完全_______，只是在坐标系中的_______不同．（2）抛物线2y ax =向_______平移_______个单位长度得到抛物线2y ax c =+；抛物线2y ax =向_______平移_______个单位长度得到抛物线 2y ax c =-；练习：1.(1)二次函数2y ax =与22y x =-的形状相同，开口大小一样，开口方向相反，则a = ．(2)不计算比较大小：函数2y x =的图象左侧上有两点A （a ，15），B （b ，0.5），则a b ．2.(1)抛物线225y x =--的开口方向，对称轴是，顶点坐标是．(2)抛物线2y ax c =+与23y x =的形状相同，其顶点坐标为（0，1），则其解析式为．(3)抛物线2172y x =-+向平移个单位后，得到抛物线2132y x =-- 3.在同一平面直角坐标系中，一次函数y ax c =+与二次函数2y ax c =+的图象大致为（）．x y OxyOA ．B ．x y Oxy OC ．D ．。

22.1.2二次函数y=ax2的图像和性质教案

1.注重个体差异，针对不同学生的理解程度，进行有针对性的讲解和指导。
2.增加课堂互动，鼓励学生提问和发表观点，提高他们的课堂参与度。
3.丰富教学手段，运用多媒体、实物演示等手段，让学生更直观地理解二次函数的性质。
4.加强课后辅导，关注学生对知识点的掌握情况，及时解答他们的疑问。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解二次函数y=ax2的基本概念。二次函数是形如y=ax2的函数，其中a为常数，且a≠0。它是描述物体抛物线运动、图形变换等方面的重要数学工具。
2.案例分析：接下来，我们来看一个具体的案例。这个案例展示了二次函数y=ax2在抛物线运动中的应用，以及它如何帮助我们解决问题。
3.掌握二次函数y=ax2的增减性，会判断给定区间内函数的增减情况；
4.掌握二次函数y=ax2的最大（小）值及其取值情况。
二、核心素养目标
（1）通过探究二次函数y=ax2的图像和性质，培养学生的直观想象和逻辑推理能力；
（2）使学生能够运用数学语言表达二次函数的性质，提高学生的数学表达能力；
（3）培养学生运用二次函数解决实际问题的能力，增强数学应用意识；
4.学生小组讨论环节，大家围绕二次函数在实际生活中的应用展开了热烈的讨论。但在分享成果时，我发现有些小组的成果过于表面，没有深入挖掘二次函数的性质。为此，我将在接下来的教学中，加强引导，让学生更好地运用所学知识解决实际问题。
结回顾环节，学生对本节课的知识点有了更深入的理解，但仍有个别学生对二次函数的增减性和最值掌握不够牢固。在今后的教学中，我会加强这些知识点的巩固。
（4）通过小组合作学习，培养学生的团队协作能力和交流沟通能力；
（5）引导学生发现二次函数图像与性质之间的关系，提高学生的数据分析能力。

华东师大版九年级数学下册26.2.3二次函数的图像与性质(二) 课件

解：因为当x＝2时，二次函数y＝a(x－h)2有最大值，
所以函数图象的开口向下，对称轴是直线x＝2，
所以当x＞2时，y随x的增大而减小．
10．[2021·衡阳期末]在函数y＝2(x＋1)2的图象上有三
点A(1，y1)，B(－3，y2)，C(－2，y3)，则y1，y2，
y3的大小关系是( A )
A．y1＝y2＞y3
象左右平移|h| 个单位得到.抛物线y=a(x-h)²的顶点是
（h,0）,对称轴是x=h.
方法点拨
平移规律：左加右减，横变纵不变.
1. “ 左加 ” 表示当 h ＜ 0 时，函数 y=a(x － h)2 可变形为
y=a(x+|h|)2 ，其图象可以由函数 y=ax2 的图象向左平移|h|
点坐标为(h，0)，函数最大值为0，因为当2≤x≤5时，与其对应
的函数值y的最大值为－1，所以h不能取2～5(含2与5)之间的
数．当h<2时，函数在x＝2处取最大值－1，把(2，－1)代入y
＝－(x－h)2，解得h＝1或h＝3(不合题意，舍去)；当h>5时，
函数在x＝5处取最大值－1，把(5，－1)代入y＝－(x－h)2，解
得h＝6或h＝4(不合题意，舍去)．综上可知，h的值为1或6.
【答案】 B
12．如图，抛物线y＝a(x＋1)2的顶点为A，与y轴的负半轴交于
点B，且OB＝OA.
(1)求抛物线对应的函数表达式；
解：由题意得A(－1，0)．
因为OB＝OA，所以B(0，－1)．
将B(0，－1)的坐标代入y＝a(x＋1)2，得a＝－1，
左
________个单位得到．
2-2. 抛物线y=2(x－4)2的顶点坐标为________；对称

人教版九年级数学讲义二次函数的图像与性质(含解析)

第5讲二次函数的图象与性质知识定位讲解用时：2分钟A、适用范围：人教版初三，基础一般B、知识点概述：本讲义主要用于人教版初三新课，本节课我们主要学习二次函数的图象与性质，本节课的重点是掌握二次函数的平移法则，能够结合二次函数图象和性质判断a、b、c的之间的关系，而难点在于二次函数的图象和性质的综合考查，需要学生能够根据二次函数的图象与性质正确分析并解决问题。

希望同学们能够认真学习并掌握，为后面二次函数的应用打好基础。

知识梳理讲解用时：25分钟二次函数的图象（1）二次函数y=ax2（a≠0）的图象的画法：①列表：先取原点（0，0），然后以原点为中心对称地选取x值，求出函数值，列表；①描点：在平面直角坐标系中描出表中的各点；①连线：用平滑的曲线按顺序连接各点；①在画抛物线时，取的点越密集，描出的图象就越精确，但取点多计算量就大，故一般在顶点的两侧各取三四个点即可，连线成图象时，要按自变量从小到大（或从大到小）的顺序用平滑的曲线连接起来，画抛物线y=ax2（a≠0）的图象时，还可以根据它的对称性，先用描点法描出抛物线的一侧，再利用对称性画另一侧。

x…-223--112-0121232…2y x= (4)491140141494…（2）二次函数y=ax2+bx+c（a≠0）的图象二次函数y=ax2+bx+c（a≠0）的图象看作由二次函数y=ax2的图象向右或向左平移|ab2|个单位，再向上或向下平移|abac442-|个单位得到的。

12341234xyxyOO1212----图1图2向上（）或向下（）平移个单位向上（）或向下（）平移个单位向左（）或向右（）平移个单位向左（）或向右（）平移个单位课堂精讲精练【例题1】抛物线212y x =向左平移8个单位，再向下平移9个单位，所得的抛物线的解析式是___________________。

【答案】218232y x x =++【解析】本题考查了二次函数平移规则，根据二次函数的平移法则，“上加下减，左加右减”，可知平移后的函数解析式为()21892y x =+-，整理即为218232y x x =++讲解用时：2分钟解题思路：牢记平移法则即可。

二次函数y=ax2+c(a≠0)的图象与性质优秀教案

教学设计§2.3二次函数的图象与性质（二）——北师大版九（下）教材分析:本节内容是北师大版九年级下册第二章《二次函数的图象与性质（二）》的第三节,对发展学生的推理能力有好处。

本节创设了丰富的现实情景，使学生充分体会二次函数的性质在解决问题中的作用，认识显示世界中蕴涵着丰富的数学信息。

知识与技能目1、使学生能利用描点法正确作出函数y＝ax2 ＋c 的图象。

2、理解并掌握二次函数y＝ax2 ＋c 的图像性质及它与函数y ＝ax2 的关系。

3经历操作、研究、归纳和总结二次函数y ＝ax ＋c 的图像性质及它与函数y＝ax2 的关系，让学生进一步体尝试去发现二次函数的图象特征；体会其性质；渗透由特殊到一般的辩证唯物主义观点和数形结合的数学思想，培养观察能力和分析问题、解决问题的能力。

情感、态度与价值观1、培养学生探索、观察、发现的良好品质以及克服困难的毅力，并学会归纳总结自己的结论，体会成功的喜悦，加强继续学习的兴趣。

2、通过细心画图，培养学生严谨细致的学习态度。

教学重点：会用描点法画出二次函数y ＝ax 2＋b 的图象，理解二次函数y＝ax2 ＋b 的性质，理解函数y＝ax2 ＋b 与函数y＝ax2 的相互关系是教学重点。

.教学难点：正确理解二次函数y ＝ax2＋c 的性质，理解抛物线y ＝ax ＋ c 与抛物线y ＝ax 2的关系是教学的难点。

教学方法与教学手段：1、情境探究、师生互动。

2、自主探索、分层推进。

3、动态演示、直观形象。

教学设计思想：1、课堂组织策略：创设贴近学生生活、生动有趣的问题情境，开展有效的数学活动，组织学生主动参与、勤于动手、积极思考，使他们在自主探究与合作交流的过程中，学会二次函数性质的应用。

2、学生学习策略：明确学习目标，了解所需掌握的知识，在教师的组织、引导、点拨下主动地从事观察、实验、猜测、验证与交流等数学活动，从而真正有效地理解和掌握知识。

教学用具与教学设备：投影仪、多煤体。

知识卡片-二次函数y=ax^2 、y=a(x-h)^2+k (a≠0)的图象和性质

二次函数y=ax^2 、y=a（x-h）^2+h (a≠0)的图象和性质能量储备●二次函数y＝ax2(a≠0)图象的作法：①列表：在二次函数y＝ax2中，自变量x的取值范围是全体实数，给出x的一些代表值，求出对应的y值；②描点：一般先描出对称轴一侧的几个点，再根据对称性找出另一侧的几个点；③连线：按照自变量由小到大的顺序，用平滑的曲线连接所描的点，两端无限延伸．●二次函数y＝ax2(a≠0)图象的性质●二次函数y＝ax2＋h(a≠0)的图象和性质：1.图象是一条抛物线，它与y＝ax2(a≠0)的图象形状相同，只是位置不同.2.二次函数y＝ax2＋h(a≠0)与y＝ax2(a≠0)的图象之间的关系如下表所示：●二次函数y＝a(x－h)2的图象和性质二次函数y＝a(x－h)2(a≠0)的图象是一条抛物线，它的对称轴是平行于y轴或与y轴重合的直线x＝h，顶点坐标是(h，0)，它与y＝ax2(a≠0)的图象形状相同，位置不同，y＝a(x－h)2(a≠0)的图象是由y＝ax2(a≠0)的图象向右（或左）平移|h|个单位长度得到的．二次函数y＝a(x－h)2(a≠0)与y＝ax2(a≠0)的图象之间的关系如下表所示：●二次函数y＝a(x－h)2＋h的图象和性质1.二次函数y＝a(x－h)2＋h(a≠0)的图象是一条抛物线，它的对称轴是直线x＝h，顶点坐标为(h，h)，是由抛物线y＝ax2(a≠0)向右(或左)平移|h|个单位长度，再向上(或下)平移|h|个单位长度得到的．由y＝ax2(a≠0)的图象到y＝a(x－h)2＋h(a≠0)的图象具体的平移操作如图所示．2.二次函数y＝a(x－h)2＋h(a≠0)的图象和性质：通关宝典★基础方法点方法点1：对于二次函数y ＝a (x －h )2(a ≠0)图象上的两点A (x 1，y 1)，B (x 2，y 2)，当a >0时，若|x 1－h |<|x 2－h |，则y 1<y 2；当a <0时，若|x 1－h |<|x 2－h |，则y 1>y 2；而对任何a ≠0，若|x 1－h |＝|x 2－h |，则y 1＝y 2.例1：在同一平面直角坐标系中，画出函数y ＝－12x 2与y ＝－12(x －1)2的图象，并根据图象回答下列问题：(1)抛物线y ＝－12(x －1)2可以看成将抛物线y ＝－12x 2做怎样的平移得到的？(2)函数y ＝－12(x －1)2的图象的对称轴是________；当x ________时，曲线自左向右上升；除顶点外，抛物线上的点都在________．(3)函数y ＝－12(x －1)2，当x ______时，y 随x 的增大而减小；当x ______时，y 有最大值，最大值是________．解：先列表：然后描点、连线，得函数y ＝－12x 2与y ＝－12(x －1)2的图象，如图所示．(1)抛物线y ＝－12(x －1)2可以看成是将抛物线y ＝－12x 2向右平移1个单位长度得到的．(2)函数y ＝－12(x －1)2的图象的对称轴是直线x ＝1；当x ＜1时，曲线自左向右上升；除顶点外，抛物线上的点都在x 轴的下方．(3)函数y ＝－12(x －1)2，当x ＞1时，y 随x 的增大而减小；当x ＝1时，y 有最大值，最大值是0．,方法点二：抛物线y ＝ax 2(a ≠0)可以通过平移规律“左加右减自变量，上加下减常数项”得到抛物线y ＝a (x －h )2＋h (a ≠0)．例2 已知抛物线y ＝a (x －h )2＋h 是由抛物线y ＝－12x 2先向上平移2个单位长度，再向右平移1个单位长度得到的．(1)求出a ，h ，h 的值．(2)在同一平面直角坐标系中，画出y ＝a (x －h )2＋h 与y ＝－12x 2的图象．(3)观察y ＝a (x －h )2＋h 的图象，当x ________时，y 随x 的增大而增大；当x ________时，函数y 有最________值，最________值是y ________.(4)观察y ＝a (x －h )2＋h 的图象，你能说出对于一切x 的值，函数值y 的取值范围吗？解：(1)∵将抛物线y ＝－12x 2先向上平移2个单位长度，再向右平移1个单位长度得到的抛物线是y ＝－12(x －1)2＋2，∴a ＝－12，h ＝1，h ＝2.(2)函数y ＝－12(x －1)2＋2与y ＝－12x 2的图象如图22-1-5所示．(3)观察y ＝a (x －h )2＋h 的图象，当x ＜1时，y 随x 的增大而增大；当x ＝1时，函数y 有最大值，最大值是y ＝2．(4)由y ＝a (x －h )2＋h 的图象知，对于一切x 的值，总有y ≤2.,★★易混易误点易混易误点1:二次函数图象左右平移时易混淆例3：如何平移二次函数y ＝－13(x ＋1)2－3的图象得到二次函数y ＝－13x 2＋2的图象？解：将二次函数y ＝－13(x ＋1)2－3的图象向右平移1个单位长度，再向上平移5个单位长度，就得到二次函数y ＝－13x 2＋2的图象．,分析：二次函数图象的平移可以依据其相应顶点的平移来判断，其中左右平移要记清“左加右减”，防止弄反方向导致错误．因此研究抛物线的平移问题，关键是要准确求出抛物线的顶点坐标，进而研究其顶点位置的变化．本题易错认为是把二次函数的图象向左平移．蓄势待发考前攻略● 考查二次函数y ＝ax 2，y ＝ax 2＋c 的图象与性质，主要从开口方向、顶点坐标、对称轴、增减性等方面研究．常见题型为选择题，一般为中、低档题．● 考查求二次函数图象的顶点坐标、对称轴及开口方向，中考题常以选择题、填空题的形式出现，难度不大．完胜关卡。