蓉城名校联盟2017-2018学年度下期高中2017级期中联考文科数学试卷
蓉城名校联盟2018级高三第三次联考文科数学试卷及答案

数学(文科)
第1页 共6页
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效! 数学(文科) 第 2 页 共 6 页
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
数学(文科)
教育大数据运营事业部绘制
第3页 共6页
更多试卷微信搜:试卷答案公众号 座位号
$ [01] [02] [03] [04] [05] [06] [07] [08] [09] [10] [11] [12] [13] [14] [15]
为_______.
x 1,x 0
15.已知函数
f
(x)
x2
2x ,x
,若 0
f
( x1 )
f
(x2 ) ,且 x1
x2 ,则 |
x1
x2
| 的最大
值为_______.
高中 2018 级文科数学试题 第 2 页 (共 4 页)
16.已知等比数列{an} 的前 n 项和 Sn 满足 Sn 2n1 m ,数列{bn} 满足bn log2 an ,其中
图示规范填涂;非选择题必须使用 0.5
事 毫米的黑色墨迹签字笔作答。 3.必须在题目所指示的答题区域内作答,超出答题区域的答案无效,在草稿纸、
项
试题卷上答题无效。
4.保持答题卡清洁、完整,严禁折叠,严禁使用涂改液和修正带。
蓉城名校联盟2017~2018学年度(下)高中2017级期末联考(含答案)

蓉城名校联盟2017~2018学年度(下)高中2017级期末联考生物(考试时间共90分钟,满分100分)命题人:鲁海荣周定辉试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)扫描查看成绩分析报告注意事项:1.答题前,考生务必在答题卡上将自己的学校、姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚,考生考试条码由监考老师粘贴在答题卡上的“条码粘贴处”。
2.选择题使用2B铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
第I卷选择题(共60分)一、选择题:本大题有40个小题,每题只有一个正确答案,每题1.5分,共60分。
1.下列关于细胞周期的叙述中,正确的是A.细胞周期是指连续分裂的细胞从分裂开始到分裂结束为止B.利用药物抑制DNA合成,细胞将停留在分裂期C.分裂间期能进行DNA分子的复制、转录和翻译D.不同生物减数分裂的细胞周期持续时间不同2.豌豆体细胞内有7对染色体,在根尖细胞分裂中期A.细胞中有28条染色单体B.细胞中有7个四分体C.细胞中有28个双链DNA分子D.有4个染色体组3.下列关于“观察洋葱根尖分生组织细胞有丝分裂”的叙述,正确的是A.制片流程为:解离→染色→漂洗→制片B.制片之前要通过漂洗洗去碱性染料,便于显微镜下观察C.视野中不同细胞的染色体数目可能不相等D.观察中期细胞可清晰地看到染色体,随后染色体着丝点分裂4.下列关于细胞分化的叙述,正确的是A.细胞分化是指分裂的细胞在形态和结构上的变化B.哺乳动物的造血干细胞是未经分化的细胞C.分化的细胞可形成不同的组织和器官D.高度分化的细胞都能恢复到分化前的状态5.下列关于细胞衰老与凋亡的叙述,错误的是A.刚出生的婴儿体内有衰老细胞B.凋亡细胞中含有与凋亡有关的蛋白质C.衰老细胞的表面积与体积的比值减少D.细胞凋亡有利于人体维持内部环境的稳定6.下列关于细胞癌变的叙述,错误的是A.癌变前后,细胞的形态结构发生显著变化B.细胞癌变是多个基因发生突变的累积效应C.吸烟可诱发人体细胞产生原癌基因和抑癌基因D.经常压抑自己的情绪会增加癌症发生的可能性7.下列关于自交、杂交、测交的叙述中,错误的是A.纯合子的自交后代是纯合子,杂合子的自交后代是杂合子B.通过杂交可将两个或多个品种的优良性状集中在一起C.通过测交能够测定F1代产生配子的种类和比例D.测交和自交都可以用来判断显性豌豆的基因型8.科学研究过程一般包括发现问题、提出假设、验证假设、得出结论等。
【全国校级联考word版】四川省蓉城名校联盟高中2017-2018学年高一4月联考语文试题

汇聚名校名师,奉献精品资源,打造不一样的教育!1 蓉城名校联盟2017--2018学年度(下)高中2017级期中联考语文考试时间共150分钟,满分150分注意事项:1.答题前,考生务必在答题卡上将自己的学校、姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚,考生考试条码由监考老师粘贴在答题卡上的“条码粘贴处”。
2.选择题使用2B 铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案:非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
一、现代文阅读(35分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1--3题。
香草美人----中国文人的妾妇心理张秀敏①虽说王逸在其《楚辞章句·离骚序》中对“香草美人”进行了解析,但是对于“香草美人”的理解是众说纷纭。
闻一多先生只用一句“男人说女人话”对“香草美人”进行了简单明了的解释,虽然这种说法不十分精确贴切,但从一定程度上说明了这种艺术手法所具有的特点。
令人疑惑的是,在中国古代文学中,这种男人说女人话的现象并不只是个人行为,却是极为常见的,“香草美人”作为一种独特的比兴手法,继屈原之后备受文人喜爱。
许多文人都进入屈原香草美人的话语系统,以女性的角度来进行诗词创作。
②先秦文学中屈原的“香草美人”意象便以盛装的女性盼望男性的欢爱来隐喻对君王恩遇的期待,其核心便是弃妇衍生的闺怨情结。
在《离骚》中“借男女以喻君臣”:“既替余以蕙纕兮,又申之以揽茝”、“众女嫉余以娥眉兮,谣诼谓余以善淫”。
在这里屈原自比为女子,因为佩戴香草而加罪,众多女流嫉妒自己美丽的双眉,而对自己造谣中伤。
这些诗句,都是以女性口吻所作,即“男人说女人话”,从女子心理角度出发,自喻为女子,来抒发作者自己内心的苦闷与无奈。
③周乐诗曾列举屈原、宋玉、曹植、辛弃疾诗词中男人说女人话的许多例子,关于辛弃疾,他说:“即以豪放风格见长的辛弃疾也有如许忸怩的词章:‘长门事,准拟佳期误,娥眉曾有人妒’(《摸鱼儿》)”。
2018~2019学年度上期高中2017级期末联考文科数学答案

一、选择题:本题共 12 小题,每小题 5 分,共 60 分。 1 D 2 C 3 B 4 A 5 B 6 A 7 C 8 A 9 C 10 D 11 D 12 A
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。 13.12 14. ,1 3, 15. 3 5 16.9
------------11 分 ------------12 分
1 4 3 VB PAD 3 4 3 3 VP ADM
21. (12 分) 解: (1)设 C 的方程为 y mx 则 8 2m
2
2 3 3
-------------------1 分 -------------------2 分 ------------------3 分 ------------------4 分 ------------------5 分
---------------8 分
ˆ 所以 b
ˆ 4 0.03 50 2.5 . a
y 0.03x 2.5 . 故 y 关于 x 的线性回归方程为
ˆ 0.03 300 2.5 11.5 . (2) 由(1)得:当 x 300 时, y
所以植被覆盖面积为 300 公顷时,下降的气温大约是 11.5 ℃.---------------10 分 18. (12 分) 解: (1)方程 m 2 x 1 m y m 4 0 可化为
CD AD ------------1 分 又平面 PAD 平面 ABCD ------------4 分 CD 平面 PAD 又 CD 平面 PCD ------------6 分 平面 PCD 平面 PAD 1 (2) VP ADM VM PAD VB PAD ------------9 分 2 S PAD 3 4 3 4
蓉城名校联盟2017~2018学年度(下)高中2017级期中联考语文答案

【解析】判断过于绝对,原文为“可能会成为知识传播的新途径”;并且“该到了耳朵唱 主角的时代了”只是毕飞宇的一家之言。 8.【答案】AD
【解析】B 材料一不只关注了毕飞宇这一个体事件,同时第二段也从面上谈到了音频知识 付费领域的争论,所以与材料二的角度并不是完全不同。C“阅读比听书更好”的分析有误, 原文中“这两种方式很难说哪一种更好”;E“找到了用武之地”的分析有误,原文为“更有 用武之地”。 9.【答案示例】
2017-2018年四川省蓉城名校联盟高一上学期期中数学试卷带答案

2017-2018学年四川省蓉城名校联盟高一(上)期中数学试卷一、选择题(本大题共12小题,每小题5分,共60分;在每小题给出的四个选项中,只有一项是正确的)1.(5.00分)已知集合A={x|0<x<},B={x|1≤x<2},则A∪B=()A.{x|x≤0}B.{x|x≥2}C.{x|1≤x<}D.{x|0<x<2}2.(5.00分)下列四组函数中的f(x),g(x),表示同一个函数的是()A.f(x)=1,g(x)=x0B.f(x)=x﹣1,g(x)=﹣1C.f(x)=x2,g(x)=()4D.3.(5.00分)下列函数中,既是偶函数又在区间(0,+∞)上单调递增的函数是()A.y=log2(x+1)B.y=|x|+1 C.y=﹣x2+1 D.y=2﹣|x|4.(5.00分)若,b=log24.1,c=20.8,则a,b,c的大小关系为()A.a<b<c B.b<a<c C.a<c<b D.c<a<b5.(5.00分)函数f(x)=﹣|x﹣2|+e x的零点所在的区间是()A.(﹣1,0)B.(0,1) C.(1,2) D.(2,3)6.(5.00分)函数f(x)=(x∈R)的值域是()A.(0,1) B.(0,1]C.[0,1) D.[0,1]7.(5.00分)函数y=a x﹣a(a>0,a≠1)的图象可能是()A.B. C.D.8.(5.00分)已知,若f(﹣a)+f(1)=0,则实数a的值等于()A.﹣3或﹣1 B.﹣3 C.3或1 D.39.(5.00分)已知是R上的增函数,那么a的取值范围是()A.(1,+∞)B.(0,+∞)C.(1,2]D.(0,2]10.(5.00分)已知f(x)=,当时,则实数m的取值范围是()A.(﹣1,0)∪(0,1)B.(﹣∞,﹣1)∪(1,+∞)C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(0,1)11.(5.00分)设奇函数f(x)在[﹣3,3]上是增函数,f(﹣3)=﹣1,当a∈[﹣3,3]时,f(x)≤t2﹣2at+1对所有的x∈[﹣3,3]恒成立,则t的取值范围是()A.t≥6或t≤﹣6 B.t≥6或t≤﹣6或t=0C.t>6或t<﹣6 D.t>6或t<﹣6或t=012.(5.00分)定义在R上的函数f(x)满足f(﹣x)﹣f(x)=0,且f(x+2)=f(x),当x∈[0,1]时,f(x)=3x若方程ax﹣f(x)=0(a>0)恰有四个不相等的实数根,则实数a的取值范围是()A.()B.(] C. D.二、填空题(本大题共4小题,每小题5分,共20分)13.(5.00分)函数f(x)=+log0.5(7﹣x)的定义域是.14.(5.00分)若{1,a,ab}={0,a2,a+2b},则a2017+b2017的值为.15.(5.00分)已知f(+1)=x﹣1,则f(x)=.16.(5.00分)若函数f(x)=log a(2x2+x)(a>0,a≠1)在区间恒有f (x)>0,则f(x)的单调递增区间是.三、解答题(本大题共6个小题,共70分;解答应写出文字说明、证明过程或演算步骤)17.(10.00分)集合A={x|﹣1≤x<3},B={x|2x﹣4≥x﹣2}(1)求A∩B:(2)若集合C={x|2x+a>0}.满足B∪C=C.求实数a的取值范围.18.(12.00分)求值:(1)(2).19.(12.00分)设f(x)是定义在R上的偶函数,当0≤x≤2时,y=x,当x>2时,y=f(x)的图象是顶点为P(3,4),且过点A(2,2)的抛物线的一部分.(1)求函数f(x)在(2,+∞)上的解析式;(2)在直角坐标系中直接画出函数f(x)的图象;(3)写出函数f(x)的值域及单调增区间.20.(12.00分)我县有甲,乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.(1)设在甲家租一张球台开展活动x小时的收费为f(x)元(15≤x≤40),在乙家租一张球台开展活动x小时的收费为g(x)元(15≤x≤40).试求f(x)和g(x);(2)问:小张选择哪家比较合算?为什么?21.(12.00分)已知幂函数在(0,+∞)上单调递增.(1)求m的值并写出f(x)的解析式;(2)试判断是否存在a>0,使函数g(x)=(2a﹣1)x﹣a•f(x)+1在[﹣1,2]上的值域为,若存在,求出a的值;若不存在,请说明理由.22.(12.00分)对于函数f(x),若在定义域内存在实数x,满足f(﹣x)=﹣f (x),则称f(x)为“局部奇函数”.(1)已知f(x)=ax2+2x﹣8a(a≠0),试判断f(x)是否为“局部奇函数”?并说明理由;(2)若f(x)=2x+2m是定义在区间[﹣1,1]上的“局部奇函数”,求实数m的取值范围;(3)若f(x)=4x﹣m•2x+1+m2﹣9为定义域R上的“局部奇函数”,求实数m的取值范围.2017-2018学年四川省蓉城名校联盟高一(上)期中数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分;在每小题给出的四个选项中,只有一项是正确的)1.(5.00分)已知集合A={x|0<x<},B={x|1≤x<2},则A∪B=()A.{x|x≤0}B.{x|x≥2}C.{x|1≤x<}D.{x|0<x<2}【解答】解:集合A={x|0<x<},B={x|1≤x<2},所以A∪B={x|0<x<}∪{x|1≤x<2}={x|0<x<2},故选:D.2.(5.00分)下列四组函数中的f(x),g(x),表示同一个函数的是()A.f(x)=1,g(x)=x0B.f(x)=x﹣1,g(x)=﹣1C.f(x)=x2,g(x)=()4D.【解答】解:对于A,函数f(x)=1(x∈R),与g(x)=x0=1(x≠0)的定义域不同,不是同一函数;对于B,函数f(x)=x﹣1(x∈R),与g(x)=﹣1=x﹣1(x≠0)的定义域不同,不是同一函数;对于C,函数f(x)=x2(x∈R),与g(x)==x2(x≥0)的定义域不同,不是同一函数;对于D,函数f(x)=|x|=(x∈R),与g(x)=(x∈R)的定义域相同,对应关系也相同,是同一函数.故选:D.3.(5.00分)下列函数中,既是偶函数又在区间(0,+∞)上单调递增的函数是()A.y=log2(x+1)B.y=|x|+1 C.y=﹣x2+1 D.y=2﹣|x|【解答】解:A.y=log2(x+1)是增函数,但在定义域上为非奇非偶函数,不满足条件,B.y=|x|+1是偶函数又在区间(0,+∞)上单调递增,满足条件.C.y=﹣x2+1,是偶函数,在区间(0,+∞)上单调递减,不满足条件,D.y=2﹣|x|是偶函数,在区间(0,+∞)上单调递减,不满足条件,故选:B.4.(5.00分)若,b=log 24.1,c=20.8,则a,b,c的大小关系为()A.a<b<c B.b<a<c C.a<c<b D.c<a<b【解答】解:∵a=<0,b=log24.1>2,c=20.8∈(1,2).∴a<c<b.故选:C.5.(5.00分)函数f(x)=﹣|x﹣2|+e x的零点所在的区间是()A.(﹣1,0)B.(0,1) C.(1,2) D.(2,3)【解答】解:∵函数f(x)=﹣|x﹣2|+e x,∴f(0)=﹣2+1=﹣1<0,f(1)=e﹣1>0,∴f(0)f(1)<0.根据函数零点的判定定理可得函数(x)=﹣|x﹣2|+e x的零点所在的区间是(0,1),故选:B.6.(5.00分)函数f(x)=(x∈R)的值域是()A.(0,1) B.(0,1]C.[0,1) D.[0,1]【解答】解:函数f(x)===1∵,∴函数f(x)=(x∈R)的值域为(0,1),故选:A.7.(5.00分)函数y=a x﹣a(a>0,a≠1)的图象可能是()A.B. C.D.【解答】解:由于当x=1时,y=0,即函数y=a x﹣a 的图象过点(1,0),故排除A、B、D.故选:C.8.(5.00分)已知,若f(﹣a)+f(1)=0,则实数a的值等于()A.﹣3或﹣1 B.﹣3 C.3或1 D.3【解答】解:∵,f(﹣a)+f(1)=0,∴f(1)=2×1=2,∴f(﹣a)=﹣2,当﹣a>0时,f(﹣a)=﹣2a=﹣2,解得a=1,不成立;当﹣a≤0时,f(﹣a)=﹣a+1=﹣2,解得a=3.综上,实数a的值等于3.故选:D.9.(5.00分)已知是R上的增函数,那么a的取值范围是()A.(1,+∞)B.(0,+∞)C.(1,2]D.(0,2]【解答】解:∵是R上的增函数,∴,解得:a∈(1,2],故选:C.10.(5.00分)已知f(x)=,当时,则实数m的取值范围是()A.(﹣1,0)∪(0,1)B.(﹣∞,﹣1)∪(1,+∞)C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(0,1)【解答】解:由已知中函数f(x)=,可得:f(﹣x)=﹣f(x)恒成立,即函数f(x)为奇函数,则可化为mf(m)<0,当m>0时,由log3m<0得:m∈(0,1),当m<0时,由得:m∈(﹣1,0),综上:m∈(﹣1,0)∪(0,1),故选:A.11.(5.00分)设奇函数f(x)在[﹣3,3]上是增函数,f(﹣3)=﹣1,当a∈[﹣3,3]时,f(x)≤t2﹣2at+1对所有的x∈[﹣3,3]恒成立,则t的取值范围是()A.t≥6或t≤﹣6 B.t≥6或t≤﹣6或t=0C.t>6或t<﹣6 D.t>6或t<﹣6或t=0【解答】解:根据题意,f(x)是奇函数且f(﹣3)=﹣1,则f(3)=1,又由f(x)在[﹣3,3]上是增函数,则f(x)在[﹣3,3]上最大值为f(3)=1,若当a∈[﹣3,3]时,f(x)≤t2﹣2at+1对所有的x∈[﹣3,3]恒成立,则有1≤t2﹣2at+1对于a∈[﹣3,3]恒成立,即t2﹣2at≥0对于a∈[﹣3,3]恒成立,当t=0时显然成立当t≠0时,则t2﹣2at≥0成立,又a∈[﹣3,3]令g(a)=2at﹣t2,a∈[﹣3,3]当t>0时,g(a)是减函数,故令g(3)≥0,解得t≥6当t<0时,g(a)是增函数,故令g(﹣3)≥0,解得t≤﹣6综上知,t≥6或t≤﹣6或t=0;故选:B.12.(5.00分)定义在R上的函数f(x)满足f(﹣x)﹣f(x)=0,且f(x+2)=f(x),当x∈[0,1]时,f(x)=3x若方程ax﹣f(x)=0(a>0)恰有四个不相等的实数根,则实数a的取值范围是()A.()B.(] C. D.【解答】解:若方程ax﹣f(x)=0(a>0)恰有4个不相等的实数根,等价于函数f(x)与y=ax的图象有4个不同的交点,由f(x+2)=f(x),得函数的周期为2,且为偶函数,故函数f(x)的图象如图所示:,结合图象,<a<1,故选:A.二、填空题(本大题共4小题,每小题5分,共20分)13.(5.00分)函数f(x)=+log 0.5(7﹣x)的定义域是[3,7).【解答】解:由,得3≤x<7.∴函数f(x)=+log0.5(7﹣x)的定义域是[3,7),故答案为:[3,7).14.(5.00分)若{1,a,ab}={0,a2,a+2b},则a2017+b2017的值为﹣1.【解答】解:∵{1,a,ab}={0,a2,a+2b},∴b=0,a2=1≠a,即a=﹣1,故a2017+b2017=﹣1,故答案为:﹣115.(5.00分)已知f(+1)=x﹣1,则f(x)=x2﹣2x,(x≥1).【解答】解:由题意,设+1)=t,(t≥1)则x=(t﹣1)2那么f(t)=(t﹣1)2﹣1=t2﹣2t∴f(x)=x2﹣2x,(x≥1)故答案为:x2﹣2x,(x≥1)16.(5.00分)若函数f(x)=log a(2x2+x)(a>0,a≠1)在区间恒有f(x)>0,则f(x)的单调递增区间是.【解答】解:函数f(x)=log a(2x2+x)(a>0,a≠1)在区间恒有f(x)>0,由于x∈,得2x2+x∈(0,1),又在区间恒有f(x)>0,故有a ∈(0,1)对复合函数的形式进行,结合复合函数的单调性的判断规则知,函数的单调递增区间为(﹣∞,﹣)故应填(﹣∞,﹣)三、解答题(本大题共6个小题,共70分;解答应写出文字说明、证明过程或演算步骤)17.(10.00分)集合A={x|﹣1≤x<3},B={x|2x﹣4≥x﹣2}(1)求A∩B:(2)若集合C={x|2x+a>0}.满足B∪C=C.求实数a的取值范围.【解答】解:(1)∵集合A={x|﹣1≤x<3},B={x|2x﹣4≥x﹣2}={x|x≥2},∴A∩B={x|2≤x<3}.(2)∵集合C={x|2x+a>0}={x|x>﹣},B={x|2x﹣4≥x﹣2}={x|x≥2},满足B∪C=C.∴B⊆C,∴﹣≤2,解得a≥﹣4.∴实数a的取值范围是[﹣4,+∞).18.(12.00分)求值:(1)(2).【解答】解:(1)原式=﹣1++=﹣1++=.(2)原式=+3+﹣=2+3+1﹣=.19.(12.00分)设f(x)是定义在R上的偶函数,当0≤x≤2时,y=x,当x>2时,y=f(x)的图象是顶点为P(3,4),且过点A(2,2)的抛物线的一部分.(1)求函数f(x)在(2,+∞)上的解析式;(2)在直角坐标系中直接画出函数f(x)的图象;(3)写出函数f(x)的值域及单调增区间.【解答】解:(1)∵当x>2时,y=f(x)的图象是顶点在p(3,4),且过点A (2,2)的抛物线的一部分,可设y=a(x﹣3)2+4,再把点A(2,2)代入,可得2=a+4,求得a=﹣2,∴y=﹣2(x﹣3)2+4(x>2).∴由于函数f(x)在R上是偶函数,它的图象关于y轴对称,故函数的解析式为f(x)=.(2)函数f(x)的图象如图所示:(3)由图象可得,函数f(x)的值域为(﹣∞,4],单调增区间为(﹣∞,﹣3],[0,3].20.(12.00分)我县有甲,乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.(1)设在甲家租一张球台开展活动x小时的收费为f(x)元(15≤x≤40),在乙家租一张球台开展活动x小时的收费为g(x)元(15≤x≤40).试求f(x)和g(x);(2)问:小张选择哪家比较合算?为什么?【解答】解:(1)f(x)=5x,(15≤x≤40)(3分)(6分)(2)由f(x)=g(x)得或即x=18或x=10(舍)当15≤x<18时,f(x)﹣g(x)=5x﹣90<0,∴f(x)<g(x)即选甲家当x=18时,f(x)=g(x)即选甲家也可以选乙家当18<x≤30时,f(x)﹣g(x)=5x﹣90>0,∴f(x)>g(x)即选乙家.(8分)当30<x≤40时,f(x)﹣g(x)=5x﹣(2x+30)=3x﹣30>0,∴f(x)>g(x)即选乙家.(10分)综上所述:当15≤x<18时,选甲家;当x=18时,选甲家也可以选乙家;当18<x≤40时,选乙家.(12分)21.(12.00分)已知幂函数在(0,+∞)上单调递增.(1)求m的值并写出f(x)的解析式;(2)试判断是否存在a>0,使函数g(x)=(2a﹣1)x﹣a•f(x)+1在[﹣1,2]上的值域为,若存在,求出a的值;若不存在,请说明理由.【解答】解:(1)∵f(x)是幂函数,∴m2﹣2m+1=1,解得:m=0或m=2,而f(x)在(0,+∞)递增,故m=0,故f(x)=x2;(2)由(1)g(x)=(2a﹣1)x﹣ax2+1,=﹣a(x﹣)2+,①当∈[﹣1,2],即a∈[,+∞)时,=,a=2,g(﹣1)=﹣4,g(2)=﹣1;②当∈(2,+∞)时,解得﹣<a<0,∵a>0,∴这样的a不存在.③当∈(﹣∞,﹣1),即a∈(0,)时,g(﹣1)=,g(2)=﹣4,解之得,这样的a不存在.综①②③得,a=2.即当a=2时,结论成立.22.(12.00分)对于函数f(x),若在定义域内存在实数x,满足f(﹣x)=﹣f (x),则称f(x)为“局部奇函数”.(1)已知f(x)=ax2+2x﹣8a(a≠0),试判断f(x)是否为“局部奇函数”?并说明理由;(2)若f(x)=2x+2m是定义在区间[﹣1,1]上的“局部奇函数”,求实数m的取值范围;(3)若f(x)=4x﹣m•2x+1+m2﹣9为定义域R上的“局部奇函数”,求实数m的取值范围.【解答】解:(1)f(﹣x)+f(x)=0,则2ax2﹣16a=0得到有解,所以f(x)为局部奇函数.…(4分)(2)由题可知2﹣x+2x+4m=0有解,﹣,…(6分)设,,所以,所以.…8分(3)若f(x)为局部奇函数,则f(﹣x)+f(x)=0有解,得4x﹣m•2x+1+m2﹣9+4﹣x﹣m•2﹣x+1+m2﹣9=0,令2x+2﹣x=t≥2,从而F(t)=t2﹣2mt+2m2﹣20=0在[2,+∞)有解.…(10分)①F(2)≤0,即﹣2≤m≤4;②,即,综上,…(12分)。
四川省成都市2017-2018学年高一下学期期中考试数学试题Word版含答案 (2)

四川省成都市2017-2018学年下学期期中考试高一数学试题一、选择题(本大题共12小题,每小题5分,共60分)1.sin15cos15的值是A .12B 3C .14D 3 2.不等式23520x x +->的解集为 A.1(3,)2- B. 1(,3)2- C. 1(,3)(,)2-∞-⋃+∞ D. 1(,)(3,)2-∞-⋃+∞ 3.已知n S 为等差数列{}n a 的前n 项和,若4910a a +=,则12S 等于A .30B .45C .60D .1204.已知3sin()25πα-=,则cos()πα+的值为 A .45 B .45- C .35 D .35- 5.若0,0a b c d >><<则一定有 A.a b c d > B. a b c d < C. a b d c > D. a b d c< 6.在ABC ∆中, 2cos a b C =,则这个三角形一定是A. 等腰三角形B. 直角三角形C. 等腰直角三角形D. 等腰或直角三角形7.如图,要测出山坡上石油钻井的井架BC 的高,从山脚A 测得60AC m =,塔顶B 的仰角45,塔底C 的仰角15,则井架的高BC 为A .202mB .302mC .203mD .303m8.已知,(0,)x y ∈+∞,且满足1112x y+=,那么4x y +的最小值为 A.3232+322+ D. 429.已知{}n a 是等比数列,且5371,422a a a =+=,则9a = A .2± B .8 C .18 D .2 10.已知sin 2cos αα-=tan 2α= A. 34 B. 34- C. 43 D. 43- 11.在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,且BC 边上的高为2a ,则c b b c +最大值为A .2 BC..412.给出以下三个结论:①若数列{}n a 的前n 项和为*31()n n S n N =+∈,则其通项公式为123n n a -=⋅;②已知a b >,一元二次不等式220ax x b ++≥对于一切实数x 恒成立,又存在0x R ∈,使2020ax x b ++=成立,则22a b a b +-的最小值为 ③若正实数y x ,满足xy y x 442=++,且不等式03422)2(2≥-+++xy a a y x 恒成立,则实数a 的取值范围是),25[]3,(+∞--∞ . 其中正确的个数为A .0B .1C .2D .3二、填空题(本大题共4小题,每小题5分,共20分)13. 在ABC ∆中,,,a b c 分别是角,,A B C 的对边,,且3,c 1a ==,3B π=,则b 的值为 ; 14.数列{}n a 中,1121,2n n n a a a a +==+,则其通项公式n a = ;15.已知304πα<<,且3sin()45πα-=,则cos2α= ; 16.函数()f x 是定义在R 上的不恒为零的函数,对于任意实数,x y 满足:(2)2,()()()f f xy xf y yf x ==+,(2)(2n n n f a n =∈*)N ,*(2)()n n f b n N n =∈ 考查下列结论:①(1)1f = ;②()f x 为奇函数;③数列{}n a 为等差数列;④数列{}n b 为等比数列.以上结论正确的是 .三、解答题(本大题共6小题,共70分)17. (10分)已知不等式20ax x c ++>的解集为{}|13x x <<.(1)求,a c 的值;(2)若不等式2240ax x c ++>的解集为A ,不等式30ax cm +<的解集为B ,且A B ⊆,求实数m 的取值范围.18.(10分)已知A B C 、、为ABC ∆的三内角,且其对边分别为a b c 、、,若1cos cos sin sin 2B C B C -=. (1)求A ;(2)若a =4b c +=,求ABC ∆的面积.19.(12分)已知等差数列{}n a 的前n 项和为n S ,且满足4724,63S S ==.(1)求数列{}n a 的通项公式;(2)若2n a n b =,求数列{}n b 的前n 项和n T .20.(12分)已知向量2(3sin ,1),(cos ,cos )444x x x m n ==,若()f x m n =⋅,(1)求()f x 递增区间;(2)ABC ∆中,角,,A B C 的对边分别是,,a b c ,且(2)cos cos a c B b C -=,求()f A 的取值范围.21.(12分)设数列{}n a 的前n 项和为1,1n S a =,且对任意正整数n ,满足1220n n a S ++-=.(1)求数列{}n a 的通项公式;(2)设n n b na =,求数列{}n b 的前n 项和n T .22.(14分)已知数列{},{}n n a b 满足:1,n n a b += 1(1)(1)n n n n b b a a +=-+,且11,a b 是函数2()16163f x x x =-+的零点11()a b <. (1)求112,,a b b ;(2)设11n n c b =-,求证:数列{}n c 是等差数列,并求数列{}n b 的通项公式; (3)设1223341n n n S a a a a a a a a +=++++,不等式4n n aS b <恒成立时,求实数a 的取值范围.四川省成都市2017-2018学年高一下学期期中考试数学试题参考答案一、选择题1~5 CBCDD 6~10ABCDA 11~12 CC二、填空题13;14.21n +;15.2425-;16.②③④ 三、解答题 17.解:(1)由题意:1 和3是方程20ax x c ++=的两根,且0a <,.....1分 所以,011313a a c a ⎧⎪<⎪⎪+=-⎨⎪⎪⨯=⎪⎩............. 3分;解得1434a c ⎧=-⎪⎪⎨⎪=-⎪⎩;............. 5分 (2)由(1)得13,44a c =-=-,所以2240ax x c ++>即为212304x x -+->, 解得,26x <<,∴{}|26A x x =<<,又30ax cm +<,即为0x m +>解得x m >-,∴{}|B x x m =>-........8分 ∵A B ⊂,∴2m -≤,即2m ≥-,∴m 的取值范围是[)2,-+∞...............10分18.解:(1)∵1cos cos sin sin 2B C B C -=,∴1cos()2B C +=, 又∵0B C π<+<,∴3B C π+=. ........................3分 ∵A B C π++=,∴23A π=....................5分 (2)由余弦定理2222cos a b c bc A =+-⋅,得222()22cos3b c bc bc π=+--⋅,即1121622()2bc bc =--⋅-, ∴4bc =, ................................8分∴11sin 422ABC S bc A ∆=⋅=⋅=. ...............10分 19.解:(1)因为{}n a 为等差数列,所以4171434242767632S a d S a d ⨯⎧=+=⎪⎪⎨⨯⎪=+=⎪⎩ , 解得132a d =⎧⎨=⎩ ,21n a n ∴=+ ; ......................5分 (2)212224n a n n nb +===⋅ , ..........................7分128(41)2(444)3n nn T -∴=+++= . ..........................10分 20.解:(1)()f x m n =⋅2cos cos 444x x x +1cos 222x x +=+1sin()262x π=++, ..........................3分 由22,2262x k k k Z πππππ-≤+≤+∈得:4244,33k x k k Z ππππ-≤≤+∈, ()f x ∴的递增区间为42[4,4],33k k k Z ππππ-+∈ ..................6分 (2)(2)cos cos a c B b C -=,由正弦定理得(2sin sin )cos sin cos A C B B C -=, 2sin cos sin cos sin cos A B C B B C ∴-=,2sin cos sin()A B B C ∴=+,,sin()sin 0A B C B C A π++=∴+=≠,1cos 2B ∴=..............8分 0B π<<,2,033B A ππ∴=∴<<,6262A πππ∴<+<,1sin()(,1)262A π+∈, 又1()sin()262x f x π=++,1()sin()262A f A π∴=++, 故函数()f A 的取值范围是3(1,)2 ..........................12分 21. 解:(1)1220n n a S ++-=,∴ 当2n ≥时,1220n n a S -+-=,....1分 两式相减得11220n n n n a a S S +--+-=,1220,n n n a a a +-+=112n n a a +∴=;.3分 又当1n =时,212112202a S a a +-=⇒=,即11()2n n a a n N +=∈+.......4分 {}n a ∴是以首项11a =,公比12q =的等比数列, ∴ 数列{}n a 的通项公式为112n n a -⎛⎫= ⎪⎝⎭.......................6分(2)由(1)知,12n n n n b na -==,...................7分 则22123112222n n n n n T ---=+++++,① 23111231222222n n n n n T --=+++++,②.................8分 ①-②得211111122222n n n n T -=++++-,...........................10分1(1)1122(1)2(2)1222212n n n n n n n n -=-=--=-+- ,....................11分 所以,数列{}n b 的前n 项和为114(2)2n n T n -=-+ ...................12分 22. 解:由2161630x x -+=解得:1213,44x x ==,1113,44a b ∴==………1分 由11,(1)(1)n n n n n n b a b b a a ++==-+得11(2)2n n n n n b b b b b +==--…………2分 将134b =代入得245b = ……………………………………………………3分 (2)因为11112n n b b +-=--,所以12111111n n n n b b b b +-==---- ………………4分 即11n n c c +=-,又111143114c b ===--- ∴ 数列{}n c 是以4-为首项,1-为公差的等差数列. ………………5分 4(1)(1)3n c n n ∴=-+-⨯-=-- ……………………………………6分 由11n n c b =-得1121133n n n b c n n +=+=-=++ ……………………………7分 (3)由题意及(2)知:113n n a b n =-=+……………………………………8分 12233411114556(3)(4)11111111()()()()4556673411444(4)n n n S a a a a a a a a n n n n n n n +∴=++++=+++⨯⨯++=-+-+-++-++=-=++………………………9分 (法一)由22(1)(36)84043(3)(4)n n an n a n a n aS b n n n n +-+---=-=<++++恒成立 即2(1)(36)80a n a n -+--<恒成立,…………………………………10分 设2()(1)(36)8f n a n a n =-+--①当1a =时,()380f n n =--<恒成立②当1a >时,由二次函数的性质2()(1)(36)80f n a n a n =-+--<不可能恒成立 ③当1a <时,由于3631(1)02(1)21a a a --=--<-- 所以2()(1)(36)8f n a n a n =-+--在[)1,+∞上单调递减 由2(1)(1)(36)84150f a n a n a =-+--=-<得154a < 1a ∴<,4n n aS b <恒成立综上所述:所求a 的取值范围是(,1]-∞...........................14分版权所有:高考资源网()。
四川省蓉城名校2017-2018学年高二数学上学期期中试题 文

蓉城名校2017-2018学年高二数学上学期期中试题 文考试时间共120分钟,满分150分试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)注意事项:1.答题前,考生务必在答题卡上将自己的姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚,考生考试条码由监考老师粘贴在答题卡上的“条码粘贴处”。
2.选择题使用2B 铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
第Ⅰ卷 选择题(共60分)一、选择题:本大题共有12小题,每小题5分,共60分。
在每小题给出的四个选项中, 有且只有一项是符合题目要求的。
1.已知直线1:310l x y +-=与直线2:0l mx y -=平行,则实数m 的取值是A .13 B .13- C .3 D .3-2.双曲线22149x y -=的渐近线方程是 A .3y 2x =± B .2y 3x =± C .9y 4x =± D .4y 9x =± 3.下列选项中,说法错误的...是 A .命题“若0232=+-x x ,则1=x ”的逆否命题为: “若1x ≠,则232x x -+≠0”B .“1x =”是“2320x x -+=”的充分不必要条件C .命题p :2,0x R x x ∃∈-≤, 则⌝p :2,0∀∉->x R x x D .若∨p q 为假命题,则,p q 均为假命题4.圆()224+9x y -=和圆()22325x y +-=的位置关系是 A .内切 B .相交 C .外切 D .外离5,焦点是)0,4(-、)0,4(,则双曲线的标准方程为 A .221412x y -= B .221124x y -= C .221106x y -= D .221610x y -= 6.到两定点)3,0(1-F 和)3,0(2F 的距离之和为6的点M 的轨迹是A .椭圆B .圆C .线段D .双曲线7.己知命题“R x ∈∃,使02)1(22≤+-+x a x ”是假命题,则实数a 的取值范围是 A .(,3)(5,+)-∞-∞ B .()3,1- C .(3,5)-D .(][),35,+-∞-∞ 8.已知双曲线方程为2214y x -=,过(1,0)P 的直线l 与双曲线只有一个公共点, 则l 的条数共有A .4条B .3条C .2条D .1条9.若直线(2)3=-+y k x 与曲线=y 有两个公共点,则实数k 的取值范围是 A .5(0,)12 B .13[,]34 C .5(,)12+∞ D .53(,]12410.椭圆221169x y +=上一点P 到直线110x y ++=的距离最大值为A .. C . D 11.设P 是椭圆2212516x y +=上一动点,F 是椭圆的左焦点,椭圆外一点()64,M , 则PF PM +的最大值为A .15B .16C D12.如图,已知双曲线1C :22221(0,0)x y a b a b-=>>,椭圆2C 以双曲线的焦点为顶点,以 双曲线的顶点为焦点,双曲线1C 的一条渐近线与以椭圆2C 的长轴为直径的圆交于A ,B 两点,与椭圆2C 交于C ,D 两点,且34CD AB ,则双曲线1C 的离心率为A . 5B .17C D .7142y x ,第Ⅱ卷 非选择题(共90分)二、填空题:本大题共4小题,每小题5分,共20分。
蓉城名校联盟高中2017级高三第一次联考文科数学参考答案及评分标准

∴
A
0,
π 2
且 sin A 2 5 5
-------------2 分
又 a b ,a 2 5 ,b 5 3
sin A sin B
2
sin B b sin A 3
a
2
又b<a B < A B π 3
-------------4 分 ------------6 分
----------10 分
a < 0 a > 0 时 gx有一个零点
0 a < e e < a 0 时 gx无零点
a e a e 时 gx有一个零点
a > e a < e 时 gx有两个零点
综上: a < e 时 gx有两个零点
(二)选考题:共 10 分。
22.(10 分)
(1)
C1
的普通方程为
x2 16
y2 9
1
C2 的直角坐标方程为 x y 8 0
(2) MN 4 cos 3sin 8 2
5cos 8 3 3 2
2
22
MN 的最小值为 3 2 2
23.(10 分)
2x 11, x 3
(1)当 a 2 时 f x 5, 3 x 2
2x 1, x 2
f x 0 的解集为{ x | 11 x 1 }
2
2
(2) f x 2 x a x 3 8
xa x3 a3
--------9 分 --------10 分
当 ln x 1> 0 时 eln x 1 < aln x 1 ex aln x 1> ex eln x 1 0
2017-2018学年成都市“六校联考”第三期期中数学(文科)试题

成都市“六校联考”2017-2018学年第三学期期中试题数 学(文)(全卷满分:150分 完成时间:120分钟)注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积A .πB .π2C .π3D .π42.已知点A ()2,1-和B ⎪⎪⎭⎫ ⎝⎛0,33在直线()001:≠=--a y ax l 的两侧,则直线l 倾斜角的取值范围是A .⎪⎭⎫⎝⎛3,4ππ B .⎪⎭⎫ ⎝⎛65,32ππ C .⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛πππ,433,0 D .⎪⎭⎫ ⎝⎛32,3ππ 3.若l 、m 、n 是互不相同的空间直线,α、β是不重合的平面,则下列结论正确的是A .//,,l n αβαβ⊂⊂⇒//l nB .,l αβα⊥⊂⇒l β⊥C .,l n m n ⊥⊥⇒//l mD .,//l l αβ⊥⇒βα⊥ 4. 对任意的实数k ,直线y =kx +1与圆222x y +=的位置关系一定是A .相离B .相切C .相交但直线不过圆心D .相交且直线过圆心5.点A ,B ,C ,D 均在同一球面上,且AB ,AC ,AD 两两垂直,且AB =1,AC =2,AD =3,则该球的表面积为 A .7π B .14π C .72π D .7143π 6.已知圆22:(2)(1)3C x y -++=,从点(1,3)P --发出的光线,经x 轴反射后恰好经过圆心C ,则入射光线的斜率为A .43-B .23-C .43D .234 3 2 2 正视图 侧视图俯视图7.设变量x ,y 满足约束条件00220x x y x y ≥⎧⎪-≥⎨⎪--≤⎩则z =3x -2y 的最大值为A .4B . 2C .0D .68.若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为A .120B .150C .180D .240 9.已知点P (x ,y )是直线kx +y +4=0(k >0)上一动点,PA ,PB 是圆C :x 2+y 2-2y =0的两条切线,A ,B 为切点,若四边形PACB 的最小面积是2,则k 的值为A .4B .3C .2D .210.如图所示,在棱长为2的正四面体A BCD -中,E 是棱AD 的中点,若P 是棱AC 上一动点,则BP PE +的最小值为A .3B .7C .13+D .511.若直线b x y +=与曲线224690(3)x x y y y -+-+=≤有公共点,则b 的取值范围是A .]221,1[+-B .]221,221[+-C .[122,3]-D .]3,21[-12.如图,正方体ABCD ﹣A 1B 1C 1D 1的棱长为1,线段B 1D 1上有两个动点E 、F ,且EF = 12.则下列结论中正确的个数.....为 ①AC ⊥BE ; ②EF ∥平面ABCD ; ③三棱锥A ﹣BEF 的体积为定值; ④AEF ∆的面积与BEF ∆的面积相等,A .4B .3C .2D .1(10题图) (12题图)第II 卷(非选择题)二、填空题:本大题共4小题,每小题5分,共20分。
【精品】2017-2018学年四川省蓉城名校联盟高二(上)期中数学试卷(文科)

第 5 页(共 22 页)
【点评】 本题考查双曲线的简单性质,涉及渐近线的求解,属基础题.
3.(5 分)下列选项中,说法错误的是(
)
A.命题 “若 x2﹣3x+2=0,则 x=1”的逆否命题为: “若 x≠ 1,则 x2﹣ 3x+2≠0”
B.“ x=1是”“2x﹣3x+2=0”的充分不必要条件 C.命题 p:? x∈R,x2﹣x≤0,则 ?p:? x?R,x2﹣x>0 D.若 p∨ q 为假命题,则 p,q 均为假命题
的方程.
20.(12 分)已知椭圆 C:
过点(0,﹣3),且离心率为 .
( 1)求椭圆 C 的方程;
第 3 页(共 22 页)
( 2)若直线 l 与椭圆 C 交于不同的两点 A、 B,当线段 AB 的中点为 M( 4, 2) 时,求直线 l 的方程.
21.( 12 分)设圆
的圆心为 C,
是圆内一定点, Q 为
题 q:方程
表示双曲线.
( 1)若 a=1,且 p∧q 为真,求实数 m 的取值范围; ( 2)若 q 是 p 的充分不必要条件,求实数 a 的取值范围. 19.( 12 分)已知圆 C 经过点 A(5,2),B(3,2)且圆心在直线 x﹣y+1=0 上. ( 1)求圆 C 的方程; ( 2)过点 P( 3, 1)作直线 l 与圆 C 相交于 M, N 两点,且 | MN| =6,求直线 l
于基础题.
2.(5 分)双曲线
=﹣ 1 的渐近线方程是(
)
A.y=± x
B.y=± x
C.y=± x
D.y=± x
【分析】 化方程为标准方程,可得 a,b,代入 y=
可得渐近线方程.
蓉城名校联盟2017~2018学年度(下)高中2017级入学考试数学答案
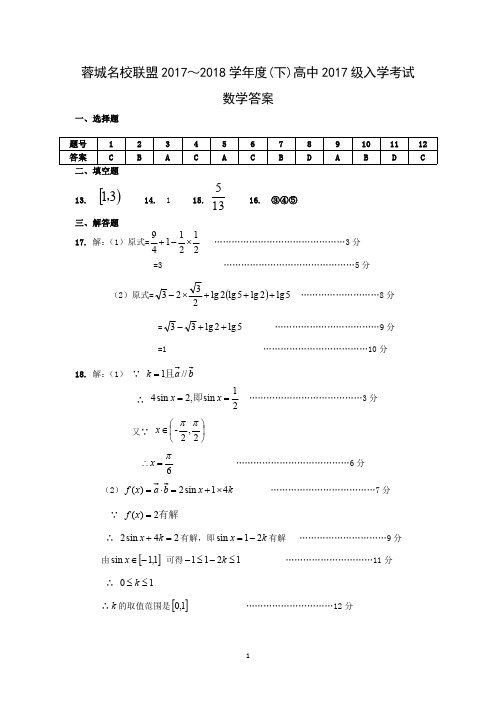
………………………………9 分 ………………………………10 分
1 2
…………………………………3 分
, 2 2
…………………………………6 分 ………………………………7 分
x
6
(2) f ( x ) a b 2 sin x 1 4k ∵ f ( x ) 2有解
………………………………2 分
20 lg 20000 lg 2 lg 10 4 …………………………4 分 0.001 ………………………………5 分 0.301 4 4.3 lg
因此,这是一次约为里氏 4.3 级的地震. (2)由 M lg A lg A0 可得 ……………………………6 分
蓉城名校联盟 2017~2018 学年度(下)高中 2017 级入学考试 数学答案
一、选择题 题号 答案 1 C 2 B 3 A 4 C 5 A 6 C 7 B 8 D 9 A 10 B 11 D 12 C
二、填空题 13.
1, 3
14.
1
15.
5 13
16.
③④⑤
三、解答题 17. 解: (1)原式=
∴ f ( x1 ) f ( x2 ) 0 即 f ( x1 ) f ( x2 ) ……………………………11 分 ∴ 函数 f ( x ) 在定义域上是增函数.……………………………12 分
当x (2) ∵ x ∴
5 , . 12 12
2x
2 , . ……………………………………9 分 6 3 3
3 ,……………………………………10 分 12
∴ f ( x ) max f
四川省蓉城名校联盟2017-2018学年高二上学期12月月考文科数学试题

蓉城名校联盟2018~2019学年度上期高中2017级期末联考文科数学考试时间共120分钟,满分150分注意事项:1.答题前,考生务必在答题卡上将自己的学校、姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚,考生考试条码由监考老师粘贴在答题卡上的“条码粘贴处”。
2.选择题使用2B铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项只有一项是符合题目要求的。
1.已知命题:,,则命题的否定为A. ,B. ,C. ,D. ,【答案】D【解析】【分析】直接利用特称命题的否定是全称命题写出结果即可.【详解】因为特称命题的否定是全称命题,所以,命题:,则¬p为:,.故选:D.【点睛】本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.2.总体由编号为,,…,,的个个体组成,现从中抽取一个容量为的样本,请以随机数表第行第列开始,向右读取,则选出来的第个个体的编号为70 29 17 12 13 40 33 12 38 26 13 89 51 0356 62 18 37 35 96 83 50 87 75 97 12 55 93A. B. C. D.【解析】【分析】根据随机数表,依次进行选择即可得到结论.【详解】从随机数表第行第列开始由左到右依次选取两个数字中小于30的编号依次为29,17,12,13,26,03,则第5个个体的编号为26.故选:C.【点睛】本题主要考查简单随机抽样的应用,正确理解随机数法是解决本题的关键,比较基础.3.已知甲:或,乙:,则甲是乙的A. 充要条件B. 必要不充分条件C. 充分不必要条件D. 既不充分也不必要条件【答案】B【解析】【分析】根据充分条件和必要条件的定义即可得到结论.【详解】“或”推不出““能推出“或”,必要性具备,∴甲是乙的必要不充分条件故选:B【点睛】本题主要考查充分条件和必要条件的判断,注意“或”是或命题,一真俱真,属于基础题.4.已知直线的方程为,直线的方程为,则的充要条件是A. 或B.C. D. 或【答案】A【解析】直接由两直线垂直的系数间的关系列式求解m的值.【详解】∵直线的方程为,直线的方程为,∴l1⊥l2的充要条件是即m(2m﹣2)=0,解得:m=0或m=1.故选:A.【点睛】本题考查直线的一般式方程与直线的垂直关系,若两直线A1x+B1y+C1=0与A2x+B2y+C2=0垂直,则A1A2+B1B2=0,是基础题.5.在正方体中,点分别是棱的中点,则异面直线与所成角为A. B.C. D.【答案】B【解析】【分析】根据MN∥,可知∠即为异面直线与所成的角,解之即可.【详解】∵点分别是棱的中点,∴为平行四边形,∴MN∥∴∠即为异面直线与所成的角,在等边三角形中,易知:∠∴异面直线与所成角为60°故选:B【点睛】本题考查的知识点是异面直线及其所成的角,其中通过平移构造出两条异面直线所成的角是解答本题的关键.6.执行如图所示的程序框图,若输入的值为,则输出的值为A. B. C. D.【答案】A【解析】【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量T的值,模拟程序的运行过程,可得答案.【详解】执行程序框图,有,,不满足条件返回,,不满足条件返回,,不满足条件返回,,满足条件退出循环,输出,故选:A【点睛】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.7.甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,,分别表示甲乙两名运动员这项测试成绩的平均数,s1,s2分别表示甲乙两名运动员这项测试成绩的标准差,则有()A. B.C. D.【答案】B【解析】【分析】根据茎叶图看出两组数据,先求出两组数据的平均数,再求出两组数据的方差,比较两组数据的方差的大小就可以得到两组数据的标准差的大小.【详解】由茎叶图可看出甲的平均数是,乙的平均数是,∴两组数据的平均数相等.甲的方差是(36+1+0+0+1+36),乙的方差是(49+4+0+0+4+49).∴甲的标准差小于乙的标准差,故选:B.【点睛】本题考查两组数据的平均数和方差的意义,是一个基础题,解题时注意平均数是反映数据的平均水平,而标准差反映波动的大小,波动越小数据越稳定.8.某市进行了一次法律常识竞赛,满分分,共有人参赛,得分全在内,经统计,得到如下的频率分布直方图,若得分在的有人,则A.B.C.D.【答案】A【解析】【分析】由频率分布直方图的性质能求出a的值,进而可得值.【详解】由频率分布直方图的性质得:(a+0.010+0.020+0.030+0.035)×10=1,解得:a=0.005∵有人参赛,得分在的有人,∴解得:N=600故选:A【点睛】本题主要考查了频率、频数的计算问题,也考查了数形结合的数学思想,是基础题目.9.以下命题为真命题的个数为①若命题的否命题是真命题,则命题的逆命题是真命题②若,则或③若为真命题,为真命题,则是真命题④若,,则的取值范围是A. B. C. D.【答案】C【解析】【分析】由逆否命题同真同假可知①②正确,根据复合命题真值表可知③错误,把不等式有解问题转化为函数的最值问题可判④正确.【详解】①根据命题的否命题与命题的逆命题互为逆否命题,同真同假,故①正确;②命题的逆否命题为:若a=2且b=3,则a+b=5,显然正确,故原命题正确,故②正确;③若为真命题,为真命题,则p为假命题,q为真命题,是假命题,故③错误;④,,则的最大值大于零即可,易知在上单调递增,所以>0,即,故④正确.故选:C.【点睛】本题考查命题真假的判断.其中②的判断是本题难点,转化为其逆否命题是关键,属于基础题.10.在棱长为2的正方体中,点为底面的中心,在正方体内随机取一点,则点到点的距离大于1的概率为()A. B. C. D.【答案】D【解析】本题考查几何概型,空间几何体的体积,空间想象能力.到点的距离不大于1的点在以点为球心,1为半径的半球内;其体积为正方体体积为则在正方体内随机取一点,则点到点的距离大于1的概率为故选B11.若椭圆与双曲线的离心率之积等于,则称这组椭圆和双曲线为孪生曲线.已知曲线:与双曲线是孪生曲线,且曲线与曲线的焦点相同,则曲线的渐近线方程为A. B. C. D.【答案】D【解析】【分析】由孪生曲线定义可知双曲线的基本量,从而得到其渐近线方程.【详解】曲线:的离心率为,又曲线:与双曲线是孪生曲线,∴双曲线的离心率为由曲线与曲线的焦点相同可知:双曲线的焦点位于y轴上,且半焦距为4∴双曲线的实半轴长为,短半轴长为,∴曲线的渐近线方程为:【点睛】本题以“孪生曲线”为背景,考查了椭圆与双曲线的简单几何性质,属于中档题.12.已知⊙的方程是,,,若在⊙上存在点,使,则实数的取值范围是A. B.C. D.【答案】A【解析】【分析】在⊙上存在点,使转化为以AB为直径的圆与⊙有公共点的问题,列不等式求解即可.【详解】根据直径对的圆周角为90°,结合题意可得以AB为直径的圆和圆有交点,即两个圆相交或相切.而以AB为直径的圆的方程为,两个圆的圆心距为,故|m﹣|≤≤|m+|,求得≤m≤,故选:A.【点睛】本题主要考查圆和圆的位置关系,体现了等价转化的数学思想,属于中档题.二、填空题:本题共4小题,每小题5分,共20分。
四川省蓉城名校联盟高中2017-2018学年高一4月联考

四川省蓉城名校联盟高中2017-2018学年高一4月联考注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2. 回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3. 回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4. 考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷本卷共30小题。
每小题2分,共60分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
下图是“某国人口自然增长率随时间变化示意图”,读图完成1-3题。
1. 关于该国人口变化的叙述,正确的是A. ①时期对应的人口增长模式为现代型B. ②时期人口总数大于③时期C. 发达国家人口增长模式特点与④时期完全相同D. 人口总数依次是③>④>⑤2. 目前世界各国人口增长模式与②④时期符合的一组国家是A. 日本、中国B. 中国、法国C. 尼日利亚、德国D. 新加坡、日本3. 该国不同时期面临的人口问题是A. ①时期人口老龄化日趋严重,老龄人口增多B. ②时期青壮年劳动力过剩,就业压力过重C. ③时期人口素质偏低,教育压力过大D. ④时期城市人口比重过高,与经济发展不相适应根据统计,中国近几十年来人口总数在不断攀升。
1980年总人口数量约9.87亿人,1990年约11.43亿人,2000年约12.67亿人,2010年约13.41亿人,人口专家预测中国未来人口数量还会不断上涨。
据此完成第4题。
4. 与我国1990-2010人口增长率变化过程相符的是下图为简易人口迁移示意图。
据此完成5-6题。
5. 若该图表示近年来世界人口流动的主要方向,则下列表述正确的是A. 甲地人口出现负增长,劳动力不足B. 乙地工资待遇较低C. 人口迁移方向从非洲迁往西亚D. 乙地人口增长过快6. 下列现象属于人口迁移的是A. 新疆游牧民的迁徙生活B. 国庆节期间去三亚旅游C. 暑假到外地打工,勤工俭学D. 高中毕业后到外省上大学生态城市建设是促进城市可持续发展的必然选择。
四川省成都2017-2018届高考模拟数学文科试题(一)含答案

2018届高考模拟考试试题(一)数学(文科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}1,3,0122≤==≤-+=x y y N x x x M x ,则集合{}N x M x x ∉∈且,为A.(]0,3B.[]4,3-C.[)4,0-D.[]4,0-2.已知向量()1,1AB = ,()2,3AC =,则下列向量中与BC 垂直的是A.()3,6a =B.()8,6b =-C.()6,8c =D.()6,3d =-3.在四面体S ABC -中,2,==⊥BC AB BC AB 2===SB SC SA ,则该四面体外接球的表面积是A.π34B.π316C.π310D.π384.已知ααππαα2cos 2sin ),,2(,53sin 则且∈=的值等于A.23B.43C.—23D.—435.某几何体的三视图如图所示,则此几何体的体积为A .3B .38C .6226++D .226+6.下列命题中正确的是A.若a ,b ,c 是等差数列,则log 2a ,log 2b ,log 2c 是等比数列B.若a ,b ,c 是等比数列,则log 2a ,log 2b ,log 2c 是等差数列C.若a ,b ,c 是等差数列,则2a,2b,2c是等比数列D.若a ,b ,c 是等比数列,则2a,2b,2c是等差数列7.为了有效管理学生迟到问题,某校专对各班迟到现象制定了相应的等级标准,其中D 级标准为“连续10天,每天迟到不超过7人”,根据过去10天1、2、3、4班的迟到数据,一定符合D 级标准的是A .1班:总体平均值为3,中位数为4B .2班:总体平均值为1,总体方差大于0C ..3班:中位数为2,众数为3D .4班:总体平均值为2,总体方差为38.若将函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移ϕ个单位,所得图象关于y 轴对称,则ϕ的最小正值是A.512πB.3πC.23πD.56π-9.执行如图所示的程序框图,若输入1m =,3n =,输出的 1.75x =,则空白判断框内应填的条件为A .1m n -<B .0.5m n -<C .0.2m n -<D .0.1m n -<10.若a >0,b >0,且函数f (x )=4x 3-ax 2-2bx -2在x =1处有极值,则ab 的最大值是A.2B.3C.6D.911.设函数f (x )=(x -a )2+(ln x 2-2a )2,其中x >0,a ∈R ,存在x 0使得f (x 0)≤b 成立,则实数b 的最小值为A.15B.25C.45D.112已知定义在R 的函数()f x 是偶函数,且满足()()[]2202f x f x +=-,在,上的解析式为()21,011,12x x f x x x ⎧-≤<=⎨-≤≤⎩,过点()3,0-作斜率为k 的直线l ,若直线l 与函数()f x 的图象至少有4个公共点,则实数k 的取值范围是A.11,33⎛⎫- ⎪⎝⎭B.1,63⎛-- ⎝C.1,63⎛-+ ⎝D.163⎛⎫- ⎪⎝⎭第Ⅱ卷(共90分)本卷包括必考题和选考题两部分.第(13)~(21)题为必考题,每个试题考生都必须作答.第(22)~(23)题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.16.13.已知点()()()()2,2,1,2,2,1,1,1D C B A ---,则向量AB 在CD 方向上的投影为________.14.已知底面边长为,侧棱长为S ABCD -内接于球1O .若球2O 在球1O 内且与平面ABCD 相切,则球2O 的直径的最大值为.15.已知)(x f 是定义域为R 的偶函数,当0≤x 时,x x x f 2)(2+=,那么,不等式3)(<x f 的解集是.16()()3F x f x =-的所有零点依次记为123123,,,,...n n x x x x x x x x <<<< ,则1231222n n x x x x x -+++++= __________.三、解答题(本大题共6小题,共7017.已知平面向量a =(3,-1),b (1)证明:a ⊥b ;(2)若存在不同时为零的实数k 和t ,使c =a +(t 2-3)b ,d =-k a +t b ,且c ⊥d ,试求函数关系式k =f (t ).18.为了了解某学校高三年级学生的数学成绩,从中抽取n 名学生的数学成绩(百分制)作为样本,按成绩分成5组:[5060),,[6070),,[7080),,[8090),,[90100],,频率分布直方图如图所示.成绩落在[7080),中的人数为20.(Ⅰ)求a 和n 的值;(Ⅱ)根据样本估计总体的思想,估计该校高三年级学生数学成绩的平均数x 和中位数m ;(Ⅲ)成绩在80分以上(含80分)为优秀,样本中成绩落在[5080),中的男、女生人数比为1:2,成绩落在[80100],中的男、女生人数比为3:2,完成22⨯列联表,并判断是否有95%的把握认为数学成绩优秀与性别有关.参考公式和数据:22()()()()()n ad bc K a b c d a c b d -=++++.20()P K k ≥0.500.050.0250.0050k 0.4553.8415.0247.879男生女生合计优秀不优秀合计19.如图,在直三棱柱ABC -A 1B 1C 1中,平面A 1BC 丄侧面A 1ABB 1,且AA 1=AB =2.(1)求证:AB 丄BC ;(2)若直线AC 与面A 1BC 所成的角为,求四棱锥A 1-BB 1C 1C 的体积.20.已知椭圆C :22221x y a b +=(0a b >>)的左右焦点分别为1F ,2F ,离心率为12,点A 在椭圆C 上,1||2AF =,1260F AF ∠=︒,过2F 与坐标轴不垂直的直线l 与椭圆C 交于P ,Q 两点,N 为P ,Q 的中点.(Ⅰ)求椭圆C 的方程;(Ⅱ)已知点1(0,8M ,且MN PQ ⊥,求直线MN 所在的直线方程.21.(本小题满分12分)已知函数()()22ln f x x x a x a R =-+∈.(1)当2a =时,求函数()f x 在()()1,1f 处的切线方程;(2)当0a >时,若函数()f x 有两个极值点()1212,x x x x <,不等式()12f x mx ≥恒成立,求实数m 取值范围.请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.22.(本题满分10分)选修4—4:坐标与参数方程在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系,圆C 的极坐标方程为ρ=22cos l =t ,=-1+22t (t 为参数),直线l 和圆C 交于A ,B 两点,P 是圆C 上不同于A ,B 的任意一点.(1)求圆心的极坐标;(2)求△PAB 面积的最大值.23.(本题满分10分)选修4-5:不等式选讲已知函数()ln(|21||23|)f x x x =+--.(1)求不等死()0f x ≤的解集;(2)当m 取何值时,()f x m <恒成立.成都龙泉中学2018届高考模拟考试试题(一)数学(文科)参考答案1—5DDBCB6—10CDABD 11—12CB13.13.51114.815.)3,3(-16.445π17.(1)证明∵a ·b =3×12-1×32=0,∴a ⊥b .(2)解∵c =a +(t 2-3)b ,d =-k a +t b ,且c ⊥d ,∴c ·d =[a +(t 2-3)b ]·(-k a +t b )=-k a 2+t (t 2-3)b 2+[t -k (t 2-3)]a ·b =0.又a 2=|a |2=4,b 2=|b |2=1,a ·b =0,∴c ·d =-4k +t 3-3t =0,∴k =f (t )=t 3-3t 4(t ≠0).18.解析:(Ⅰ)由题意可得101(0.0050.010.0150.02)10a =-+++⨯,∴0.05a =,∴2040100.05n ==⨯.(Ⅱ)由题意,各组的频率分别为0.05,0.2,0.5,0.15,0.1,∴550.05650.2750.5850.15950.175.5x =⨯+⨯+⨯+⨯+⨯=.设中位数为m ,则(70)0.050.5(0.050.2)m -⨯=-+,∴75m =.(Ⅲ)由题意,优秀的男生为6人,女生为4人,不优秀的男生为10人,女生为20人,22⨯列联表男生女生合计优秀6410不优秀102030合计162440由表可得2240(620410) 2.222 3.84116241030K ⨯⨯-⨯=≈<⨯⨯⨯,∴没有95%的把握认为数学成绩优秀与性别有关.19.解:(1)取A 1B 的中点为D ,连接AD,面面,,面(2)∠ACD 即AC 与面A 1BC 所成线面角,等于;直角△ABC 中A 1A =AB =2,D 为AB 的中点,∵,【解析】本题主要考查的是线面垂直的性质以及棱锥体积的计算,意在考查考生的逻辑推理能力和运算求解能力.(1)根据线面垂直的判定定理证明,然后根据线面垂直的性质证得;(2)由(1)可得∠ACD 即AC 与面A 1BC 所成线面角,解三角形求得根据棱锥的体积公式即可得到答案.20.解:(Ⅰ)由12e =,得2a c =,因为1||2AF =,2||22AF a =-,由余弦定理得22121212||||2||||cos ||AF AF AF AF A F F +-⋅=,解得1c =,2a =,∴2223b a c =-=,∴椭圆C 的方程为22143x y +=.(Ⅱ)因为直线PQ 的斜率存在,设直线方程为(1)y k x =-,11(,)P x y ,22(,)Q x y ,联立22(1),1,43y k x x y =-⎧⎪⎨+=⎪⎩整理得2222(34)84120k x k x k +-+-=,由韦达定理知2122834k x x k+=+,121226()234ky y k x x k k -+=+-=+,此时243(,)k k N -++,又1(0,M ,则222221324348344320MN kk k k k k k k ++++==--+,∵MN PQ ⊥,∴1MN k k =-,得到12k =或32.则2MN k =-或23MN k =-,MN 的直线方程为16810x y +-=或162430x y +-=.21.解:(1)当时,;,则,所以切线方程为,即为.…4分(2)令,则当时,,函数在上单调递增,无极值点;当且,即时,由,得当变化时,与的变化情况如下表:00单调递增极大值单调递减极小值单调递增当时,函数有两个极值点,则,.由可得..令.因为,所以,,即在递减,即有,所以实数的取值范围为.22.解(1)圆C 的普通方程为x 2+y 2-2x +2y =0,即(x -1)2+(y +1)2=2.所以圆心坐标为(1,-1)(2)直线l 的普通方程:22x -y -1=0,圆心到直线l 的距离d =|22+1-1|3=223,所以|AB |=22-89=2103,点P 到直线AB 距离的最大值为r +d=2+223=523,S max =12×2103×523=1059.23.解:(1)由()0f x ≤有:ln(|21||23|)ln1x x +--≤,所以0|21||23|1x x <+--≤,即12021231x x x ⎧-⎪⎨⎪<--+-⎩≤,≤或1322021231x x x ⎧-<<⎪⎨⎪<++-⎩,≤或32021231x x x ⎧⎪⎨⎪<+-+⎩≥≤,解得不等式的解集为1324x x ⎧⎫<⎨⎩⎭≤.(2)由()f x m <恒成立得max ()f x m <即可.由(1)0|21||23|x x <+--得函数()f x 的定义域为1⎛⎫+∞ ⎪⎝⎭,所以有13ln(42)22()3ln 42x x f x x ⎧⎛⎫-<< ⎪⎪⎪⎝⎭=⎨⎛⎫⎪ ⎪⎪⎝⎭⎩,≥,所以max ()ln 4f x =,即ln 4m >.。
四川省蓉城名校2017-2018学年高一第一学期期中数学试卷

蓉城名校2017-2018学年高一数学上学期期中试题考试时间共120分钟,满分150分试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)注意事项:1.答题前,考生务必在答题卡上将自己的姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚,考生考试条码由监考老师粘贴在答题卡上的“条码粘贴处”。
2.选择题使用2B 铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
第Ⅰ卷 选择题(共60分)一、选择题(本大题共12小题,每小题5分,共60分;在每小题给出的四个选项中,只有一项是正确的)1.已知集合{|0{|12},A x x B x x A B =<=≤<=则A .{}0x x ≤B .{}02x x << C.{0x x ≤≤D .{}2x x ≥2.下列四组函数中的(),()f x g x ,表示同一个函数的是A .f (x )=1,g (x )=x 0B .f (x )=x -1,g (x )=xx 2-1C .f (x )=x 2,g (x )=(x )4D .⎩⎨⎧<-≥==)0()0)(|,|)(x x x x x g x x f (3.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是A .2log (1)y x =+B .21y x =-+C .1y x =+D .2xy -=4,2log 4.1b =,0.82c =,则,,a b c 的大小关系为 A .a b c << B .b a c << C .a c b << D .c a b <<5.函数()2xf x e x -=-+的零点所在的一个区间是A .1,0-()B .0,1()C .1,2()D .2,3()6.函数f (x )=1xxe e+()x R ∈的值域是 A .()0,1B .(]0,1C .[)0,1D .[]0,17.函数y =a x–a ( a >0,a ≠1)的图象可能是A .B .C .D . 8.已知20()10x x f x x x >⎧=⎨+≤⎩,,,若()(1)0f a f -+=,则实数a 的值等于A .3-或1-B .3-C .3或1D .39R 上的增函数,那么a 的取值范围是A .(1,+∞)B .(0,+∞)C .(1,2 ]D .(0,2 ]10.已知313log 0log ((0))x x x x f x >⎧⎪⎨-<⎪=⎩,,,当()()0f m f m m -->时,则实数m 的取值范围是 A .()()1,00,1- B .()(),11,-∞-+∞C .()()1,01,-+∞D .()(),10,1-∞-11.设奇函数()x f 在[3,3]-上是增函数,(3)1f -=-,当[3,3]a ∈-时,()122+-≤at t x f 对所有的[3,3]x ∈-恒成立,则t 的取值范围是A .66t t ≥≤-或B .660t t t ≥≤-=或或C .66t t ><-或D .660t t t ><-=或或12.定义在R 上的函数()f x 满足()()0f x f x --=,且(2)()f x f x +=,当[]0,1x ∈ 时,()3f x x =若方程()0ax f x -=(0a >)恰有四个不相等的实数根,则实数a的取值范围是 A .3(,1)5B .3(,1]5C .3[,1)5D .3[,1]5第Ⅱ卷 非选择题(共90分)二、填空题(本大题共4小题,每小题5分,共20分) 13.函数0.5()log (7)f x x -的定义域是 .14.若{}{}21,,0,,2a ab a a b =+,则20172017ab +的值为 . 15.1)1,()f x f x =-=已知则 .16.若函数2()log (2)a f x x x =+()0,1a a >≠在区间102⎛⎫ ⎪⎝⎭,内恒有()0f x >,则()f x的单调递增区间为 .。
