蓉城名校联盟2017—2018学年度(下)高中2017级入学考试数学试题(含详细参考答案)
蓉城名校联盟2017~2018学年度(下)高中2017级期末联考(含答案)

蓉城名校联盟2017~2018学年度(下)高中2017级期末联考生物(考试时间共90分钟,满分100分)命题人:鲁海荣周定辉试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)扫描查看成绩分析报告注意事项:1.答题前,考生务必在答题卡上将自己的学校、姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚,考生考试条码由监考老师粘贴在答题卡上的“条码粘贴处”。
2.选择题使用2B铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
第I卷选择题(共60分)一、选择题:本大题有40个小题,每题只有一个正确答案,每题1.5分,共60分。
1.下列关于细胞周期的叙述中,正确的是A.细胞周期是指连续分裂的细胞从分裂开始到分裂结束为止B.利用药物抑制DNA合成,细胞将停留在分裂期C.分裂间期能进行DNA分子的复制、转录和翻译D.不同生物减数分裂的细胞周期持续时间不同2.豌豆体细胞内有7对染色体,在根尖细胞分裂中期A.细胞中有28条染色单体B.细胞中有7个四分体C.细胞中有28个双链DNA分子D.有4个染色体组3.下列关于“观察洋葱根尖分生组织细胞有丝分裂”的叙述,正确的是A.制片流程为:解离→染色→漂洗→制片B.制片之前要通过漂洗洗去碱性染料,便于显微镜下观察C.视野中不同细胞的染色体数目可能不相等D.观察中期细胞可清晰地看到染色体,随后染色体着丝点分裂4.下列关于细胞分化的叙述,正确的是A.细胞分化是指分裂的细胞在形态和结构上的变化B.哺乳动物的造血干细胞是未经分化的细胞C.分化的细胞可形成不同的组织和器官D.高度分化的细胞都能恢复到分化前的状态5.下列关于细胞衰老与凋亡的叙述,错误的是A.刚出生的婴儿体内有衰老细胞B.凋亡细胞中含有与凋亡有关的蛋白质C.衰老细胞的表面积与体积的比值减少D.细胞凋亡有利于人体维持内部环境的稳定6.下列关于细胞癌变的叙述,错误的是A.癌变前后,细胞的形态结构发生显著变化B.细胞癌变是多个基因发生突变的累积效应C.吸烟可诱发人体细胞产生原癌基因和抑癌基因D.经常压抑自己的情绪会增加癌症发生的可能性7.下列关于自交、杂交、测交的叙述中,错误的是A.纯合子的自交后代是纯合子,杂合子的自交后代是杂合子B.通过杂交可将两个或多个品种的优良性状集中在一起C.通过测交能够测定F1代产生配子的种类和比例D.测交和自交都可以用来判断显性豌豆的基因型8.科学研究过程一般包括发现问题、提出假设、验证假设、得出结论等。
四川省蓉城名校联盟2017-2018学年度高二上期期末联考理科数学试卷(word版)

四川省蓉城名校联盟2017-2018学年度上期高2016级期末联考数学试卷第Ⅰ卷 选择题(共60分)一.选择题:(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的)。
1. 设命题,则为2:,2n p n N n ∀∈≤p ⌝A.B.C.D. 2,2nn N n >∀∈2,2n n N n ∃∈≤2,2n n N n >∃∈2,2nn N n =∃∈2.某学校高中部学生中,高一年级有700人,高二年级有500人,高三年级有300人,为了了解该校高中学生的健康状况,用分层抽样的方法从高中学生中抽取一个容量为的样本,已知从高n 三年级学生中抽取15人,则为n A.40B.55C. 65D.753.某人在打靶中,连续射击两次,事件“至少有一次中靶”的对立事件是A.两次都不中靶B.只有一次中靶C.至多有一次中靶D.两次都中靶4.“”是方程“表示椭圆”的52m -<<22152x y m m +=-+A.必要不充分条件 B.充分不必要条件 C.既不充分也不必要条件 D.充要条件5.已知命题;命题:若,则,下列命题为真命题的是2:0,1p x R x x ∈++>∀q a b <22a b <A.B. C. D. p q ∧p q ∧⌝p q ⌝∨p q⌝∨⌝6.已知双曲线-=1 (a >0,b >0)的离心率为,则双曲线的渐进线方程为:C x 2a 2y 2b 243C A. B.C. D. 43y x =±34y x =±y x =y x =7.过点且在两坐标轴上截距的绝对值相等的直线的条数为(2,1)A -A.2 B.3C.4D.无法确定8.右图是把二进制的数111111(2)化成十进制数的一个程序框图,则判断框内应填入的条件是A .i≤4B .i≤5C .i >5D .i >49.已知集合表示的平面区域为,若在区域内任取一点,则点240(,)00x y x y x y x y +-≤⎧⎧⎫⎪⎪⎪+≥⎨⎨⎬⎪⎪⎪-≥⎩⎩⎭ΩΩ(,)P x y 的坐标满足不等式的概率为P 221x y +≤A.B.C.D.316π16π32π364π10.点是抛物线上的点,点是圆关于直线对称的曲M 22y x =N 221:(1)(3)1C x y +++=10x y ++=线上的点,则的最小值是C MN1-1-1-1-11.过双曲线右焦点作一条直线,当直线斜率为1时,直线与双曲线左、右22221(0)5a a x ya -=>-F 两支各有一个交点;当直线斜率为2时,直线与双曲线右支有两个不同交点,则的取值范围为a A. B.C. D.2)12.设为椭圆上一点,点关于原点的对称点为,为椭圆的右焦点,且A 22221(0)x y a b b a +=>>A B F ,若,已知椭圆离心率为,则的取值范围为0AF BF =g ,123ABF ππ⎡⎤∠∈⎢⎥⎣⎦e 1eA. B.C.D.⎛ ⎝(第Ⅱ卷 非选择题二、填空题(本大题共4小题,每小题5分,共20分)13. 抛掷一枚质地均匀的骰子,向上的点数不小于3的概率的是________.14.甲乙两名运动员在某项测试中的6次成绩的茎叶图如右图所示,甲乙的平均数都等于乙的众数,则成绩较为稳定(方差较小)的那位运动员成绩的方差为_______.15.已知动点分别与两点连线的斜率乘积为,则动点的轨迹方程为P (2,0),(2,0)A B -34-P ________________.16.在平面直角坐标系中,双曲线的右支与焦点为的抛物线xOy 22221(0,0)x y a bb a -=>>F交于、,若,则=_______.20)2(x py p =>A B AF BF t OF +=t 三、解答题(本大题共6小题,共70分;解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)现从A 、B 、C 、D 、E 五人中选取三人参加一个重要会议,五人中每个人被选中的机会均相等,求:(1)A 和B 都被选中的概率;(2)A 和B 至少有一个被选中的概率。
蓉城名校联盟2017-2018学年度高一下学期期末联考理科数学试题及答案

15.若圆 C 满足如下条件:①圆心在直线 x 3 y 0 上;②与 y 轴相切;③被直线 x y 0 截得的弦长为 2 7 ,则圆 C 的方程为 .
16.在边长为 2 的正方体 ABCD ABC D 中,点 P 为 CD 与 DC 的交点,若 PDBC 四点在同一球面上,则球的体积为 D' A' B' C' .
19. (12 分)已知圆 C: x y 2 x 4 y 4 0 内有一点 P 1,1 , AB 为过点 P 且倾斜
B. 45 B.6
C. 120 C. 10
D. 135 D.4
2. 等比数列{an}的各项均为正数, 且 a5 a6 2 , 则 log 2 a2 log 2 a3 log 2 a8 log 2 a9 3.两直线 l 1: x (1 m) y 2 0 与 l 2 : 2mx y 3 0 互相垂直,则实数 m 的值为
2 1 B. C. 2 D. 2或1 3 3 2 2 2 2 4.圆 ( x 2) ( y 2) 16 与圆 ( x 2) ( y 1) 4 的位置关系为
A. A.内切 B. 外切 C.相交 D.相离 5. 已知 ABC 的内角 A、 B、 C 的对边分别为 a, b, c , 若 a 2 , c 2 3 , cosA 且 b c ,则 b A. 3 B. 2 C. 2 2 D. 2 或 4
C 的值为 2
3 4 10 10
B. D.
1 3 3 10 10
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分) 13.已知集合 A {x | x 1} , B {x | x 2 x 0} ,则 A B
蓉城名校联盟高中2017级高三第一次联考文科数学参考答案及评分标准

∴
A
0,
π 2
且 sin A 2 5 5
-------------2 分
又 a b ,a 2 5 ,b 5 3
sin A sin B
2
sin B b sin A 3
a
2
又b<a B < A B π 3
-------------4 分 ------------6 分
----------10 分
a < 0 a > 0 时 gx有一个零点
0 a < e e < a 0 时 gx无零点
a e a e 时 gx有一个零点
a > e a < e 时 gx有两个零点
综上: a < e 时 gx有两个零点
(二)选考题:共 10 分。
22.(10 分)
(1)
C1
的普通方程为
x2 16
y2 9
1
C2 的直角坐标方程为 x y 8 0
(2) MN 4 cos 3sin 8 2
5cos 8 3 3 2
2
22
MN 的最小值为 3 2 2
23.(10 分)
2x 11, x 3
(1)当 a 2 时 f x 5, 3 x 2
2x 1, x 2
f x 0 的解集为{ x | 11 x 1 }
2
2
(2) f x 2 x a x 3 8
xa x3 a3
--------9 分 --------10 分
当 ln x 1> 0 时 eln x 1 < aln x 1 ex aln x 1> ex eln x 1 0
蓉城名校联盟2018级高三第一次联考理科数学含答案

高中 2018 级理科数学试题 第 1 页 (共 4 页)蓉城名校联盟 2018 级高三第一次联考理科数学注意事项:1.答题前,考生务必在答题卡上将自己的学校、姓名、班级、准考证号用 0.5 毫米黑色签字笔填写清楚,考生考试条形码由监考老师粘贴在答题卡上的“条形码粘贴处”。
2.选择题使用2B 铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用 0.5 毫米黑色签字笔在答题卡的对应区域内作答, 超出答题区域答题的答案无效; 在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
一、选择 题: 本题共 12 小题, 每小题 5 分,共 60 分。
在每小题给出的四个选项中 ,只有一项是符合题目要求的。
1. 已知全集为实数集R , 集合A ={x |0≤ x ≤4}, B = {x |x 2−8x + 15 > 0} , 则()R A B I C =A. [4,5]B. [0,3]C. [3 , 4]D. (3,4)2. 已知复数21i z =−, 则 |z| = A. 1 B.D. 23. 命题 p :“π(0,),sin tan 2x x x ∀∈<”的否定¬p 为 A.π(0,),sin tan 2x x x ∀∈≥ B. π(0,),sin tan 2x x x ∀∈> C. 000π(0,),sin tan 2x x x ∃∈≥ D. 000π(0,),sin tan 2x x x ∃∉≥ 4. 已知等差数列{a n }的前n 项和为S n ,a 3 , a 1 是方程x 2− 8x −13 = 0的两根,则S 9 =A. 36B. 40C. 72D. 805. 已知3e 1π1tan()4dx x α+=−⎰,则2sin cos cos sin αααα+=− A. −4 B. 4 C. 5 D. −56. 已知随机变量 X 服从二项分布 B (4, p ), 其期望 E (X ) =3, 随机变量 Y 服从正态分布 N (l , 2) , 若 P (Y >0) = p , 则 P (0< Y < 2) =A. 23B. 34C. 14D. 12 7. “1(0,)3m ∈”是“函数(31)4,1(),1m x m x f x mx x −+<⎧=⎨−≥⎩ 是定义在R 上的减函 数”的 A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件高中 2018 级理科数学试题 第 2 页 (共 4 页)8. 美国在今年对华为实行了禁令,为了突围实现技术自主,华为某分公司抽调了含甲、 乙的 5 个工程师到华为总部的 4 个不同的技术部门参与研发, 要求每个工程师只能去一个部门,每个部门至少去一个工程师,且甲乙两人不能去同一个部门,则不同的安排方式一共有 ( )种A. 96B. 120C. 180D. 2169. ()|lg |f x x =, 若()()f a f b = 且 a <b , 则不等式log log (21)0a b x x +−>的解集为A. (1,+∞)B. (0,1)C.(12,+∞)D.( 12,1) 10. 已知二项式1(3)nx x −的展开式中所有项的系数和为512, (),[0,]r n f r C r n =∈且r ∈N , 则函数f (r )取最大值时 r 的取值为A. 4B. 5C. 4 或 5D. 611. 已知函数||()e cos x f x x =+, 设10.32(0.3),(2),(log 0.2)a f b f c f −−===,则A. c <b <aB. c <a <bC. b <a <cD. b <c <a12. 已知函数 f (x ) 的定义域为 R , 且对任意x ∈R 都满足f (I+ x )=f (l −x ) , 当 x ≤1 时,ln ,01()e ,0x x x f x x <≤⎧=⎨≤⎩(其中 e 为自然对数的底数),若 函 数 ()||2g x m x =−与 y = f (x ) 的图像恰有两个交点, 则实数 m 的取值范围是A. m ≤0 或 m = eB. 0<m ≤32C. 32<m <e D. m >e 二、填空 题: 本题共 4 小题, 每小题 5 分, 共 20 分。
蓉城名校联盟2017级高三第二联考理科数学试题Word版

蓉城名校联盟2017级高三第二次联考理科数学注意事项:1.答题前,考生务必在答题卡上将自己的学校、姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚,考生考试条形码由监考老师粘贴在答题卡上的“条形码粘贴处”。
2.选择题使用2B 铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效:在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}1,13,4A =-,, 集合{}2430B x x x =-+>,则A I B=A. {-1,4}B. {-1,1,4}C. {-1,3,4}D. (-∞,1) U (3,+∞)2.已知复数z =,则z =A. 1B.C.2D.3 3.已知实数0<a<b ,则下列说法正确的是 A. c c a b > B. ac 2<bc 2 C. ln a < ln b D. 11()()22a b < 4.已知命题p: x <2m+1,q: x 2-5x +6<0,且p 是q 的必要不充分条件,则实数m 的取值范围为 A. m>12 B. m≥12 C. m>1 D. m≥1 5.若数列{}n a 为等差数列,且满足5383a a a +=+,S n 为数列{}n a 的前n 项和,则S 11=A.27B.33C.39D.446.已知α,β是空间中两个不同的平面,m ,n 是空间中两条不同的直线,则下列说法 正确的是A.若m α⊂,n β⊂,且α⊥β,则m ⊥nB.若m α⊂,n α⊂,且m βP ,n βP ,则αβPC.若m ⊥β,n βP ,且α⊥β,则m ⊥nD.若m ⊥α,n P β,且αβP ,则m ⊥n7.已知抛物线y 2 = 20x 的焦点与双曲线22221(0,0)x y a b a b-=>>的一个焦点重合,且抛物线的准线被双曲线截得的线段长为92,那么该双曲线的离心率为 A. 54 B. 53 C. 52 D. 58.如图,在△ABC 中,13AN AC =u u u r u u u r , P 是BN 上的一点,若23mAC AP AB =-u u u r u u u r u u u r ,则实数m 的值为 A. 13 B. 19C.1D.2 9. 已知实数a >0,b >1满足a +b =5,则211a b +-的最小值为 A. 3+22 B. 3+42 C. 322+ D. 342+ 10.已知集合A= {}1,2,3,4,5,6的所有三个元素的子集记为B 1,B 2,B 3,…B n , n N *∈记b i 为集合B i 中的最大元素,则b 1+b 2+b 3+…+b n =A.45B.105C.150D.21011.关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请全校m 名同学每人随机写下一个都小于1的正实数对(x ,y);再统计两数能与1构成钝角三角形三边的数对(x ,y)的个数a;最后再根据统计数a 估计π的值,那么可以估计π的值约为 A.4a m B. 2a m + C. 2a m m + D. 42a m m + 12. 已知(2sin ,cos ),(3,2cos )2222x x x x a b ωωωω==r r ,函数()f x a b =⋅r r 在区间4[0,]3π上恰有3个极值点,则正实数ω的取值范围为 A. 85[,)52 B. 75(,]42 C. 57[,)34 D. 7(,2]4 二、填空题:本题共4小题,每小题5分,共20分。
蓉城名校联盟2017~2018学年度(下)高中2017级入学考试数学答案
………………………………9 分 ………………………………10 分
1 2
…………………………………3 分
, 2 2
…………………………………6 分 ………………………………7 分
x
6
(2) f ( x ) a b 2 sin x 1 4k ∵ f ( x ) 2有解
………………………………2 分
20 lg 20000 lg 2 lg 10 4 …………………………4 分 0.001 ………………………………5 分 0.301 4 4.3 lg
因此,这是一次约为里氏 4.3 级的地震. (2)由 M lg A lg A0 可得 ……………………………6 分
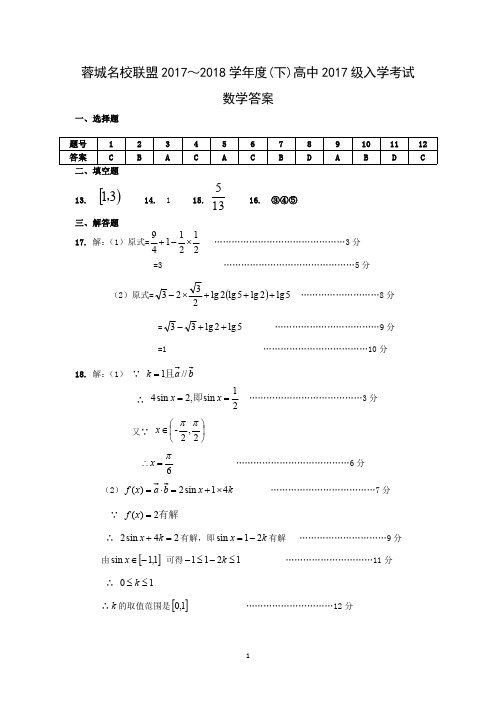
蓉城名校联盟 2017~2018 学年度(下)高中 2017 级入学考试 数学答案
一、选择题 题号 答案 1 C 2 B 3 A 4 C 5 A 6 C 7 B 8 D 9 A 10 B 11 D 12 C
二、填空题 13.
1, 3
14.
1
15.
5 13
16.
③④⑤
三、解答题 17. 解: (1)原式=
∴ f ( x1 ) f ( x2 ) 0 即 f ( x1 ) f ( x2 ) ……………………………11 分 ∴ 函数 f ( x ) 在定义域上是增函数.……………………………12 分
当x (2) ∵ x ∴
5 , . 12 12
2x
2 , . ……………………………………9 分 6 3 3
3 ,……………………………………10 分 12
∴ f ( x ) max f
四川省蓉城名校联盟高2017级高二上期12月月考文科数学试题(解析版)

蓉城名校联盟2018~2019学年度上期高中2017级期末联考文科数学考试时间共120分钟,满分150分注意事项:1.答题前,考生务必在答题卡上将自己的学校、姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚,考生考试条码由监考老师粘贴在答题卡上的“条码粘贴处”。
2.选择题使用2B铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项只有一项是符合题目要求的。
1.已知命题:,,则命题的否定为A. ,B. ,C. ,D. ,【答案】D【解析】【分析】直接利用特称命题的否定是全称命题写出结果即可.【详解】因为特称命题的否定是全称命题,所以,命题:,则¬p为:,.故选:D.【点睛】本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.2.总体由编号为,,…,,的个个体组成,现从中抽取一个容量为的样本,请以随机数表第行第列开始,向右读取,则选出来的第个个体的编号为70 29 17 12 13 40 33 12 38 26 13 89 51 0356 62 18 37 35 96 83 50 87 75 97 12 55 93A. B. C. D.【答案】C【解析】【分析】根据随机数表,依次进行选择即可得到结论.【详解】从随机数表第行第列开始由左到右依次选取两个数字中小于30的编号依次为29,17,12,13,26,03,则第5个个体的编号为26.故选:C.【点睛】本题主要考查简单随机抽样的应用,正确理解随机数法是解决本题的关键,比较基础.3.已知甲:或,乙:,则甲是乙的A. 充要条件B. 必要不充分条件C. 充分不必要条件D. 既不充分也不必要条件【答案】B【解析】【分析】根据充分条件和必要条件的定义即可得到结论.【详解】“或”推不出““能推出“或”,必要性具备,∴甲是乙的必要不充分条件故选:B【点睛】本题主要考查充分条件和必要条件的判断,注意“或”是或命题,一真俱真,属于基础题.4.已知直线的方程为,直线的方程为,则的充要条件是A. 或B.C. D. 或【答案】A【解析】【分析】直接由两直线垂直的系数间的关系列式求解m的值.【详解】∵直线的方程为,直线的方程为,∴l1⊥l2的充要条件是即m(2m﹣2)=0,解得:m=0或m=1.故选:A.【点睛】本题考查直线的一般式方程与直线的垂直关系,若两直线A1x+B1y+C1=0与A2x+B2y+C2=0垂直,则A1A2+B1B2=0,是基础题.5.在正方体中,点分别是棱的中点,则异面直线与所成角为A. B.C. D.【答案】B【解析】【分析】根据MN∥,可知∠即为异面直线与所成的角,解之即可.【详解】∵点分别是棱的中点,∴为平行四边形,∴MN∥∴∠即为异面直线与所成的角,在等边三角形中,易知:∠∴异面直线与所成角为60°故选:B【点睛】本题考查的知识点是异面直线及其所成的角,其中通过平移构造出两条异面直线所成的角是解答本题的关键.6.执行如图所示的程序框图,若输入的值为,则输出的值为A. B. C. D.【答案】A【解析】【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量T的值,模拟程序的运行过程,可得答案.【详解】执行程序框图,有,,不满足条件返回,,不满足条件返回,,不满足条件返回,,满足条件退出循环,输出,故选:A【点睛】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.7.甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,,分别表示甲乙两名运动员这项测试成绩的平均数,s1,s2分别表示甲乙两名运动员这项测试成绩的标准差,则有()A. B.C. D.【答案】B【解析】【分析】根据茎叶图看出两组数据,先求出两组数据的平均数,再求出两组数据的方差,比较两组数据的方差的大小就可以得到两组数据的标准差的大小.【详解】由茎叶图可看出甲的平均数是,乙的平均数是,∴两组数据的平均数相等.甲的方差是(36+1+0+0+1+36),乙的方差是(49+4+0+0+4+49).∴甲的标准差小于乙的标准差,故选:B.【点睛】本题考查两组数据的平均数和方差的意义,是一个基础题,解题时注意平均数是反映数据的平均水平,而标准差反映波动的大小,波动越小数据越稳定.8.某市进行了一次法律常识竞赛,满分分,共有人参赛,得分全在内,经统计,得到如下的频率分布直方图,若得分在的有人,则A.B.C.D.【答案】A【解析】【分析】由频率分布直方图的性质能求出a的值,进而可得值.【详解】由频率分布直方图的性质得:(a+0.010+0.020+0.030+0.035)×10=1,解得:a=0.005∵有人参赛,得分在的有人,∴解得:N=600故选:A【点睛】本题主要考查了频率、频数的计算问题,也考查了数形结合的数学思想,是基础题目.9.以下命题为真命题的个数为①若命题的否命题是真命题,则命题的逆命题是真命题②若,则或③若为真命题,为真命题,则是真命题④若,,则的取值范围是A. B. C. D.【答案】C【解析】【分析】由逆否命题同真同假可知①②正确,根据复合命题真值表可知③错误,把不等式有解问题转化为函数的最值问题可判④正确.【详解】①根据命题的否命题与命题的逆命题互为逆否命题,同真同假,故①正确;②命题的逆否命题为:若a=2且b=3,则a+b=5,显然正确,故原命题正确,故②正确;③若为真命题,为真命题,则p为假命题,q为真命题,是假命题,故③错误;④,,则的最大值大于零即可,易知在上单调递增,所以>0,即,故④正确.故选:C.【点睛】本题考查命题真假的判断.其中②的判断是本题难点,转化为其逆否命题是关键,属于基础题.10.在棱长为2的正方体ABCD-A 1B1C1D1中,点O为底面ABCD的中心,在正方体ABCD-A1B1C1D1内随机取一点P,则点P到点O的距离大于1的概率为( )A. B. C. 1- D. 1-【答案】D【解析】【分析】本题是几何概型问题,欲求点P与点O距离大于1的概率,先由与点O距离等于1的点的轨迹是一个半球面,求出其体积,再根据几何概型概率公式结合正方体的体积易得结果.【详解】本题是几何概型问题,与点O距离等于1的点的轨迹是一个半球面,其体积为:V1“点P与点O距离大于1的概率”事件对应的区域体积为23,则点P与点O距离大于1的概率是.故选:D.【点睛】解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,求与面积有关的几何概型问题关鍵是计算问题的总面积以及事件的面积;几何概型问题还有以下几点容易造成失分,在备考时要高度关注:(1)不能正确判断事件是古典概型还是几何概型导致错误;(2)基本事件对应的区域测度把握不准导致错误;(3)利用几何概型的概率公式时, 忽视验证事件是否等可能性导致错误.11.若椭圆与双曲线的离心率之积等于,则称这组椭圆和双曲线为孪生曲线.已知曲线:与双曲线是孪生曲线,且曲线与曲线的焦点相同,则曲线的渐近线方程为A. B. C. D.【解析】【分析】由孪生曲线定义可知双曲线的基本量,从而得到其渐近线方程.【详解】曲线:的离心率为,又曲线:与双曲线是孪生曲线,∴双曲线的离心率为由曲线与曲线的焦点相同可知:双曲线的焦点位于y轴上,且半焦距为4∴双曲线的实半轴长为,短半轴长为,∴曲线的渐近线方程为:【点睛】本题以“孪生曲线”为背景,考查了椭圆与双曲线的简单几何性质,属于中档题.12.已知⊙的方程是,,,若在⊙上存在点,使,则实数的取值范围是A. B.C. D.【答案】A【解析】【分析】在⊙上存在点,使转化为以AB为直径的圆与⊙有公共点的问题,列不等式求解即可.【详解】根据直径对的圆周角为90°,结合题意可得以AB为直径的圆和圆有交点,即两个圆相交或相切.而以AB为直径的圆的方程为,两个圆的圆心距为,故|m﹣|≤≤|m+|,求得≤m≤,故选:A.【点睛】本题主要考查圆和圆的位置关系,体现了等价转化的数学思想,属于中档题.二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
………………………………9 分 ………………………………10 分
1 2
…………………………………3 分
, 2 2
…………………………………6 分 ………………………………7 分
x
6
(2) f ( x ) a b 2 sin x 1 4k ∵ f ( x ) 2有解
∴ f ( x1 ) f ( x2 ) 0 即 f ( x1 ) f ( x2 ) ……………………………11 分 ∴ 函数 f ( x ) 在定义域上是增函数.……………………………12 分
∴ 2 sin x 4k 2 有解,即 sin x 1 2k 有解 由 sin x 1,1 可得 1 1 2k 1 ∴ 0 k 1 ∴ k 的取值范围是 0,1
…………………………9 分
…………………………11 分
…………………………12 分
1
19. 解: (1) M lg 20 lg 0.001
M lg
A A 10 M A A0 10 M . ……………………………8 分 A0 A0
7 5
当 M=7 时,地震的最大振幅为 A1 A0 10 ; …………………………9 分 当 M=5 时,地震的最大振幅为 A2 A0 10 . …………………………10 分 所以,两次地震的最大振幅之比为
………………………………2 分
20 lg 20000 lg 2 lg 10 4 …………………………4 分 0.001 ………………………………5 分 0.301 4 4.3 lg
因此,这是一次约为里氏 4.3 级的地震. (2)由 M lg A lg A0 可得 ……………………………6 分
蓉城名校联盟 2017~2018 学年度(下)高中 2017 级入学考试 数学答案
一、选择题 题号 答案 1 C 2 B 3 A 4 C 5 A 6 C 7 B 8 D 9 A 10 B 11 D 12 C
二、填空题 13.
1, 3
14.
1
15.
5 13
16.
③④⑤
三、解答题 17. 解: (1)原式=
9 1 1 1 4 2 2
=3
………………………………………3 分 ………………………………………5 分
(2)原式= 3 2
3 lg 2lg 5 lg 2 lg 5 2
………………………8 分
= 3 3 lg 2 lg 5 =1 18. 解: (1) ∵ k 1且a // b ∴ 4 sin x 2, 即 sin x 又∵ x -
A1 A0 10 7 10 2 100 …………………………11 分 5 A2 A0 10
答:7 级地震的最大振幅大约是 5 级地震的最大振幅的 100 倍. 20. 解: (1)∵A>0, ∴根据函数图象知 A=2. 又周期 T 满足 ∴ ……………………12 分 …………………………………1 分
f ( x) min f 2 . ……………………………………12 分 3
2
21. 解: (1)法一:若存在实数 a 使 f ( x ) 为奇函数, 则 f ( x) f ( x) a ∴ 2a ∴ a
3 3 a x 0 3 1 3 1
x1
3 3 x1 1 3 3 x2 1 3 3 x1 3 x2 x2 = 3 x2 1 3 x1 1 3 1 3 x1 1
……………9 分
由 x1 x2 , 可得 3 ∴
x2
3 x1 0
3 x2 1 0,3 x1 1 0,3 x1 3 x2 0 ……………………………10 分
法二:若存在实数 a 使 f ( x ) 为奇函数,易知函数定义域为 R.
3 3 0 解得 a . ………………………………1 分 3 1 2 3 3 3 3 3 x 0 当 a 时, f ( x ) f ( x ) x 2 2 3 1 2 3 1 3 ∴ 存在实数 a 使 f ( x ) 为奇函数. ………………………………5 分 2
T 2 . 2 3 6 2 . 解得 2.
……………………………………3 分
T
2
时,2 sin( 2 ) 2. 6 6 ∴ 2k , k Z . ……………………………………5 分 6 ∵ , ∴ . ……………………………………6 分 2 6 ∴ f ( x ) 2 sin( 2 x ). ……………………………………7 分 6
当x (2) ∵ x ∴
5 , . 12 12
2x
2 , . ……………………………………9 分 6 3 3
3 ,……………………………………10 分 12
∴ f ( x ) max f
由 f ( 0) a
0
(2) 函数 f ( x ) 在定义域上是增函数. 证明:任取 x1 , x2 R 且 x1 x2 , 则
……………………………6 分 ……………………………7 分
f ( x1 ) f ( x2 ) a
3 3 3 3 a x2 x1 x2 3 1 3 1 3 1 3 1
x
……………………1 分
3 3 3 3 33 3(3 x 1) x 3 3 x 1 3 x 1 3x 1 3 1
……………………………… ………………4 分
3 . 2
∴ 当实数 a
3 时, f ( x ) 为奇函数. ……………………………………5 分 2
