立体几何专题复习1
立体几何专题复习(自己精心整理)

专题一证明平行垂直问题题型一证明平行关系(1)如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B 1C1的中点.求证:MN∥平面A1BD.(2)在正方体AC1中,M,N,E,F分别是A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN∥平面EFDB.思考题1 (1)如图所示,平面PAD⊥平面ABCD,ABCD为正方形,△PAD 是直角三角形,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点,求证:平面EFG∥平面PBC.(2)如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=22,M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.求证:PQ∥平面BCD.题型二证明垂直关系(微专题)微专题1:证明线线垂直(1)已知空间四边形OABC中,M为BC中点,N为AC中点,P为OA中点,Q为OB中点,若AB=OC.求证:PM⊥QN.(2)(2019·山西太原检测)如图,直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,E,F分别是CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点,求证:DF⊥AE.微专题2:证明线面垂直(3)在正方体ABCD-A1B1C1D1中,求证:BD1⊥平面ACB1.(4)(2019·河南六市一模)在如图所示的几何体中,ABC-A1B1C1为三棱柱,且AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,∠ADC=60°.若AA1=AC,求证:AC1⊥平面A1B1CD.微专题3:证明面面垂直(5)已知正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点,求证:平面DEA⊥平面A1FD1.(6)如图,四边形ABCD 为正方形,PD ⊥平面ABCD ,PD ∥QA ,QA =AB =12PD ,求证:平面PQC⊥平面DCQ.思考题2 (1)(2019·北京东城区模拟)如图,在四棱锥P -ABCD 中,底面ABCD 是正方形,侧棱PD⊥底面ABCD ,PD =DC ,E 是PC 的中点,作EF⊥B P 交BP 于点F ,求证:PB⊥平面EFD.(2)(2019·济南质检)如图,在三棱锥P -ABC 中,AB =AC ,D 为BC 的中点,PO ⊥平面ABC ,垂足O 落在线段AD 上.已知BC =8,PO =4,AO =3,OD =2.①证明:AP⊥BC;②若点M 是线段AP 上一点,且AM =3,试证明平面AMC⊥平面BMC.题型三 探究性问题在四棱锥P -ABCD 中,PD ⊥底面ABCD ,底面ABCD 为正方形,PD =DC ,E ,F 分别是AB ,PB 的中点.(1)求证:EF⊥CD;(2)在平面PAD 内是否存在一点G ,使GF⊥平面PCB.若存在,确定G 点的位置;若不存在,试说明理由.思考题3 (2019·山西长治二模)如图所示,四棱锥P -ABCD 的底面是边长为1的正方形,PA ⊥CD ,PA =1,PD =2,E 为PD 上一点,PE =2ED.(1)求证:PA⊥平面ABCD ;(2)在侧棱PC 上是否存在一点F ,使得BF∥平面AEC ?若存在,指出F 点的位置,并证明;若不存在,说明理由.专题二 求解异面直线所成角和线面角问题题型一 异面直线所成的角(1)在棱长为2的正方体ABCD -A 1B 1C 1D 1中,O 是底面ABCD 的中心,E ,F 分别是CC 1,AD 的中点,则异面直线OE 和FD 1所成的角的余弦值等于________.(2)(2019·安徽知名示范高中联合质检)若在三棱柱ABC-A1B1C1中,∠A1AC=∠BAC=60°,平面A1ACC1⊥平面ABC,AA1=AC=AB,则异面直线AC1与A1B所成角的余弦值为思考题1 (2019·湖南雅礼中学期末)如图1,在矩形ABCD中,AB=2,BC=1,E是DC 的中点;如图2,将△DAE沿AE折起,使折后平面DAE⊥平面ABCE,则异面直线AE和BD所成角的余弦值为________.题型二定义法求线面角(1)(2019·山东荷泽期末)在斜三棱柱ABC-A1B1C1中,侧棱AA1⊥平面AB1C1,且△AB1C1为等边三角形,B1C1=2AA1=2,则直线AB与平面B1C1CB所成角的正切值为( )A.32B.22C.64D.62(2)如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )A.[33,1] B.[63,1] C.[63,223] D.[223,1]思考题2 (1)(2019·河北石家庄一模)如图所示,在三棱柱ABC-A1B1 C1中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则BB1与平面AB1C1所成的角的大小为________.(2)把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为( )A.90° B.60° C.45° D.30°题型三向量法求线面角(1)(2019·河南郑州月考)如图,已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PA=PD=5,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是________.(2)如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=2,CF=3.若直线FO与平面BED所成的角为45°,则AE=________.思考题3 (1)正四棱锥S-ABCD中,O为顶点S在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC所成的角是________.(2)(2019·河南百校联盟联考)已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )A.34B.134C.3913D.393(1)(2019·太原模拟一)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA⊥BD.①求证:PB=PD;②若E,F分别为PC,AB的中点,EF⊥平面PCD,求直线PB与平面PCD所成角的大小.(2)(2019·湖南长郡中学选拔考试)如图,在直三棱柱ABC-A1B1C1中,BA=BC=5,AC=8,D为线段AC的中点.①求证:BD⊥A1D;②若直线A1D与平面BC1D所成角的正弦值为45,求AA1的长.思考题 4 (2019·石家庄质检二)如图,三棱柱ABC-A 1B1C1中,侧面BB1C1C为∠CBB1=60°的菱形,AB=AC1.(1)证明:平面AB1C⊥平面BB1C1C;(2)若AB⊥B1C,直线AB与平面BB1C1C所成的角为30°,求直线AB1与平面A1B1C所成角的正弦值.专题三求解二面角问题题型一定义法求二面角(1)(2019·台州一模)在边长为a的等边三角形ABC中,AD⊥BC于点D,沿AD折成二面角B-AD-C,若此时BC=12a,则二面角B-AD-C的大小为________.(2)如图,二面角α-l-β的大小是60°,线段AB⊂α,B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是(3)已知三棱锥P-ABC的所有顶点都在表面积为16π的球O的球面上,AC为球O的直径.当三棱锥P-ABC的体积最大时,设二面角P-AB-C的大小为θ,则sinθ=( )A.23B.53C.63D.73思考题1 (1)如图,在矩形ABCD中,AB=2,AD=3,点E为AD的中点,现分别沿BE,CE将△ABE,△DCE翻折,使得点A,D重合于F,此时二面角E-BC-F的余弦值为( )A.721B.74C.32D.34(2)如图,设AB为圆锥PO的底面直径,PA为母线,点C在底面圆周上,若PA=AB=2,AC=BC,则二面角P-AC-B的正切值是________.题型二向量法求二面角(1)已知点E,F分别在正方体ABCD-A1B1C1D1的棱BB1,CC1上,且B1E=2EB,CF=2FC1,则面AEF与面ABC所成的锐二面角的正切值为________.(2)(2019·河南安阳)二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=217,则该二面角的大小为( ) A.150°B.45° C.60° D.120°思考题2 (1)设平面α的一个法向量为n1=(1,2,-2),平面β的一个法向量为n2=(-2,-4,k),若α和β所成的锐二面角的余弦值为23,则k=________.(2)(2019·辽宁丹东模拟)如图,正方形A1BCD折成直二面角A-BD-C,则二面角A-CD-B的余弦值是________.(3)(2019·广东中山模拟)在矩形ABCD中,已知AB=2,AD=22,M,N分别为AD和BC的中点,沿MN把平面ABNM折起,若折起后|AC|=6,则二面角A-MN-C的大小为( ) A.30° B.45° C.60° D.90°(2019·惠州二次调研)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥PB,PC=2.(1)求证:平面PAB⊥平面ABCD;(2)若PA=PB,求二面角A-PC-D的余弦值.思考题3 (2019·河北五一名校联考)在斜三棱柱(侧棱不垂直于底面)ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,底面△ABC是边长为2的正三角形,A1A=A1C,A1A⊥A1C.(1)求证:A1C1⊥B1C;(2)求二面角B1-A1C-C1的正弦值.题型三空间角的综合问题(2019·唐山五校联考)如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD,E是PB的中点.(1)求证:平面EAC⊥平面PBC;(2)若二面角P-AC-E的余弦值为63,求直线PA与平面EAC所成角的正弦值.思考题 4 (2019·江南十校素质检测)如图,在以A,B,C,D,E,F为顶点的五面体中,平面CDEF⊥平面ABCD,FC=FB,四边形ABCD为平行四边形,且∠BCD=45°.(1)求证:CD⊥BF;(2)若AB=2EF=2,BC=2,直线BF与平面ABCD所成角为45°,求平面ADE与平面BCF 所成锐二面角的余弦值.专题四综合问题题型一空间的距离(1)(2019·江西九江期末)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD为正方形,E为CD的中点,F为PA的中点,且PA=AB=2.则点P到平面BEF的距离为( )A.55B.255C.214D.42121(2)已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E,F分别是AB,AD的中点,求点B到平面GEF的距离.思考题1 (1)(2019·黑龙江哈尔滨期末)三棱柱ABC-A1B1C1底面为正三角形,侧棱与底面垂直,若AB=2,AA1=1,则点A到平面A1BC的距离为( )A.34B.32C.334D.32.(2017·课标全国Ⅰ,理)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.(2)(2019·湖南长沙一模)正方体ABCD-A1B1C1D1的棱长为1,E,F分别为BB1,CD的中点,求点F到平面A1D1E的距离.题型二探究性问题(2019·湖南重点校联考)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=22,BC=42,PA=2.(1)求证:AB⊥PC;(2)在线段PD上,是否存在一点M,使得二面角M-AC-D的大小为45°,如果存在,求BM与平面MAC所成角的正弦值,如果不存在,请说明理由.思考题2 (2019·西安八校联考)已知几何体ABCC1B1N的直观图如图所示,CB⊥底面ABB1N,且ABB1N为直角梯形,侧面BB1C1C为矩形,AN=AB=BC=4,BB1=8,∠NAB=∠ABB1=90°.(1)连接B1C,若M为AB的中点,在线段CB上是否存在一点P,使得MP∥平面CNB1?若存在,求出BP的长;若不存在,请说明理由.(2)求二面角C-NB1-C1的余弦值.题型三翻折问题(2019·安徽合肥调研性检测)平面四边形ABCD中,∠DAB=π2,AD=AB,△BCD为等边三角形.现将△ABD沿BD翻折得到四面体P-BCD,点E,F,G,H分别为PB,PD,CD,CB的中点.(1)求证:四边形EFGH为矩形;(2)当平面PBD⊥平面CBD时,求直线BG与平面PBC所成角的正弦值.思考题3 如图,在直角梯形ABCP中,∠A=∠B=90°,AB=BC=3,AP=6,CD⊥AP于D,现将△PCD沿线段CD折成60°的二面角P-CD-A,设E,F,G分别是PD,PC,BC的中点.(1)求证:PA∥平面EFG;(2)若M为线段CD上的动点,求直线MF与平面EFG所成角的最大角,并确定成最大角时点M在什么位置?高考题呈现1.(2014·全国Ⅱ)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设AP=1,AD=3,三棱锥P-ABD的体积V=34,求A到平面PBC的距离.2.(2016·北京)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD= 5.(1)求证:PD⊥平面PAB;(2)求直线PB与平面PCD所成角的正弦值;(3)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求AMAP的值;若不存在,说明理由.3.(2018·浙江)如图,已知多面体ABC-A1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.(1)证明:AB1⊥平面A1B1C1;(2)求直线AC1与平面ABB1所成的角的正弦值.4.(2016·课标全国Ⅲ)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面PAB;(2)求直线AN与平面PMN所成角的正弦值.5.(2018·课标全国Ⅰ)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.6.(2016·课标全国Ⅰ,理)如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.(1)证明:平面ABEF⊥平面EFDC;(2)求二面角E-BC-A的余弦值.7.(2017·课标全国Ⅰ,理)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.8.(2018·课标全国Ⅱ,理)如图,在三棱锥P-ABC中,AB=BC=22,PA =PB =PC =AC =4,O 为AC 的中点.(1)证明:PO⊥平面ABC ;(2)若点M 在棱BC 上,且二面角M -PA -C 为30°,求PC 与平面PAM 所成角的正弦值.9.(2018·北京,理)如图,在三棱柱ABC -A 1B 1C 1中,CC 1⊥平面ABC ,D ,E ,F ,G 分别为AA 1,AC ,A 1C 1,BB 1的中点,AB =BC =5,AC =AA 1=2.(1)求证:AC⊥平面BEF ; (2)求二面角B -CD -C 1的余弦值; (3)证明:直线FG 与平面BCD 相交.10.(2017·北京,理)如图,在四棱锥P -ABCD 中,底面ABCD 为正方形,平面PAD⊥平面ABCD ,点M 在线段PB 上,PD ∥平面MAC ,PA =PD =6,AB =4.(1)求证:M 为PB 的中点; (2)求二面角B -PD -A 的大小;(3)求直线MC 与平面BDP 所成角的正弦值.。
高三理科数学立体几何复习专题
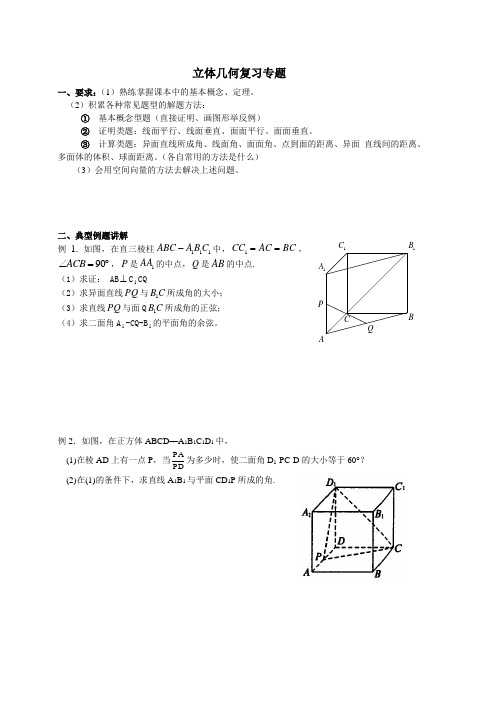
立体几何复习专题一、要求:(1)熟练掌握课本中的基本概念、定理。
(2)积累各种常见题型的解题方法:① 基本概念型题(直接证明、画图形举反例)② 证明类题:线面平行、线面垂直、面面平行、面面垂直。
③ 计算类题:异面直线所成角、线面角、面面角、点到面的距离、异面 直线间的距离、多面体的体积、球面距离。
(各自常用的方法是什么)(3)会用空间向量的方法去解决上述问题。
二、典型例题讲解例1. 如图,在直三棱柱111ABC A B C -中,1CC AC BC ==,90ACB ∠=︒,P 是1AA 的中点,Q 是AB 的中点.(1)求证: AB ⊥C 1CQ(2)求异面直线PQ 与1B C 所成角的大小; (3)求直线PQ 与面Q 1B C 所成角的正弦; (4)求二面角A 1-CQ-B 1的平面角的余弦。
例2.如图,在正方体ABCD —A 1B 1C 1D 1中, (1)在棱AD 上有一点P ,当P DP A为多少时,使二面角D 1-PC-D 的大小等于60°? (2)在(1)的条件下,求直线A 1B 1与平面CD 1P 所成的角.ABC1A 1B 1C PQ例3.如图,将长AA′=33,宽AA 1=3的矩形沿长的三等分线处折叠成一个三棱柱,如图所示:(1) 求平面APQ 与底面ABC 所成二面角的正切值; (2) 求三棱锥A 1—APQ 的体积.例4.如图,矩形ABCD 与ADQP 所在平面垂直,将矩形ADQP 沿PD 对折,使得翻折后点Q 落在BC 上,设AB=1,PA=h ,AD=y.(1)试求y 关于h 的函数解析式;(2)当y 取最小值时,指出点Q 的位置,并求出此时AD 与平面PDQ 所成的角; (3)在条件(2)下,求三棱锥P —ADQ 内切球的半径.三、巩固练习1、如图,已知面ABC ⊥面BCD ,AB ⊥BC ,BC ⊥CD ,且AB=BC=CD ,设AD 与面AB C 所成角为α,AB 与面ACD 所成角为β,则α与β的大小关系为(A )α<β (B )α=β (C )α>β (D )无法确定 2、下列各图是正方体或正四面体,P ,Q ,R ,S 分别是所在棱的中点,这四个点中不共面...的一个图是PP PPQ Q QQRRR R SSS SPPPPQQQQ RRRR SS SSPPPPQQQQ R RRR SSS S PPPPQQQQRRRR SSS S(A ) (B ) (C ) (D )3、在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,P ,Q 是对角线A 1C 上的点,且PQ =2a,则三棱锥P -BDQ 的体积为(A )3363a (B )3183a (C )3243a (D )无法确定 4、已知球的内接三棱锥的三条侧棱两两垂直,长度分别为3cm ,2cm 和3cm ,则此球的体积为(A )33312cm π (B )33316cm π (C )3316cm π (D )3332cm π5、如图,在一根长11cm ,外圆周长6cm 的圆柱形柱体外表面,用一根细铁丝缠绕,组成10个螺旋,如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为(A ) 61cm (B )157cm (C )1021cm (D )1037cm6、设a 、b 是两条不同的直线,α、β是两个不同的平面,则下列四个命题:① 若b a ⊥,α⊥a ,α⊄b ,则α//b ;②若α//a , βα⊥,则β⊥a ; ③若β⊥a ,βα⊥,则α//a 或α⊂a ;④若b a ⊥,α⊥a ,β⊥b ,则βα⊥ 其中正确命题的个数为 ( )A .0B .1C .2D .37、正三棱锥ABC S —的侧棱长和底面边长相等,如果E 、F 分别为SC ,AB 的中点,那么异面直线EF 与SA 所成角为( ) A .090 B .060 C .045 D .030 8.右图是正方体的平面展开图,在这个正方体中: ①BM 与DE 平行; ②CN 与BE 是异面直线; ③CN 与BM 成60°角 ④DM 与BN 垂直以上四个命题中,正确的是 ( )A B C A BCAB CA BCP P P P A .①②③ B .②④ C .②③④ D .③④9.将棱长为1的正方体木块切削成一个体积最大的球,则该球的体积为( )A .π23 B .π32 C .6π D .34π 10.正方体ABCD -A 1B 1C 1D 1中,E 是BC 的中点,则A 1C 与DE 所成的角的余弦为( )A .1515 B .1510 C .630 D .1010 11.有3个命题(1)底面是正三角形,其余各个面都是等腰三角形的棱锥是三棱锥; (2)各个侧面都是等腰三角形的四棱锥是正四棱锥;(3)底面是正三角形,相邻两侧面所成的二面角都相等的三棱锥是正三棱锥。
高考数学立体几何专题复习(含答案)
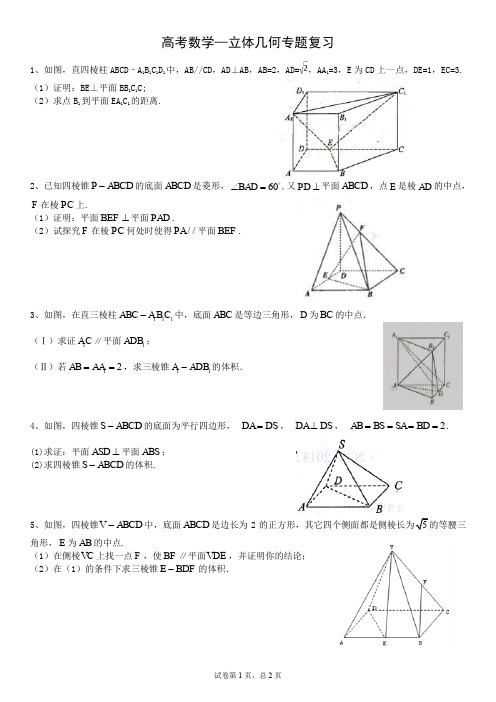
的中点.
(Ⅰ)证明: PA / / 平面 EDB ; (Ⅱ)求三棱锥 A BDP 的体积.
试卷第 2 页,总 2 页
参考答案
1、【答案】(1)详见解析;(2) . 试题分析(:1)过 B 作 CD 的垂线交 CD 于 F,则
6、如图所示,在直三棱柱 ABC-A1B1C1 中,AC=3,BC=4,AB=5,AA1=4,点 D 是 AB 的中点. (1)求证:AC1∥平面 CDB1; (2)求异面直线 AC1 与 B1C 所成角的余弦值.
7、如图所示,在三棱锥 A BOC 中,OA 底面 BOC ,OAB OAC 300 , AB AC 2 , BC 2 ,
高考数学—立体几何专题复习
1、如图,直四棱柱 ABCD–A1B1C1D1 中,AB//CD,AD⊥AB,AB=2,AD= ,AA1=3,E 为 CD 上一点,DE=1,EC=3. (1)证明:BE⊥平面 BB1C1C; (2)求点 B1 到平面 EA1C1 的距离.
2、已知四棱锥 P ABCD 的底面 ABCD 是菱形, BAD 60 ,又 PD 平面 ABCD ,点 E 是棱 AD 的中点, F 在棱 PC 上. (1)证明:平面 BEF 平面 PAD . (2)试探究 F 在棱 PC 何处时使得 PA / / 平面 BEF .
答案第 1 页,总 6 页
试题解析:
(1)证明:
PD EB
平面ABCD 平面ABCD
PD
EB
,
又底面 ABCD 是 A 60 的菱形,且点 E 是棱 AD 的中点,所以 EB AD ,
立体几何综合复习——空间角(完整版)

立体几何专题复习-----空间角的求法(一)异面直线所成的角:定义:已知两条异面直线,a b ,经过空间任一点O 作直线//,//a a b b '',,a b ''所成的角的大小与点O 的选择无关,把,a b ''所成的锐角(或直角)叫异面直线,a b 所成的角(或夹角).为了简便,点O 通常取在异面直线的一条上理解说明:(1)平移法:即根据定义,以“运动”的观点,用“平移转化”的方法,使之成为相交直线所成的角。
(2)异面直线所成的角的范围:]2,0(π(3)异面直线垂直:如果两条异面直线所成的角是直角,则叫两条异面直线垂直.两条异面直线,a b 垂直,记作a b ⊥. (4)求异面直线所成的角的方法:法1:通过平移,在一条直线上找一点,过该点做另一直线的平行线;法2;找出与一条直线平行且与另一条相交的直线,那么这两条相交直线所成的角即为所求(5).向量法: CDAB CD AB →→=.cos θ(二)直线和平面所成的角1.线面角的定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角2、记作:θ;3、范围:[0,2π]; 当一条直线垂直于平面时,所成的角θ=2π,即直线与平面垂直;1.二面角的平面角:(1)过二面角的棱上的一点O 分别在两个半平面内作棱的两条垂线,OA OB ,则AOB ∠叫做二面角lαβ--的平面角(2)一个平面垂直于二面角l αβ--的棱l ,且与两半平面交线分别为,,OA OB O 为垂足,则AOB ∠也是l αβ--的平面角说明:(1)二面角的平面角范围是[0,180];(2)二面角的平面角为直角时,则称为直二面角,组成直二面角的两个平面互相垂直 (3)二面角的平面角的特点:1)角的顶点在棱上 ;2)角的两边分别在两个面内 ;3)角的边都要垂直于二面角的棱。
2、作二面角的平面角的常用方法:①、点P 在棱上——作垂直于棱的直线(如图1) ;②、点P 在一个半平面——三垂线定理法;(如图2) ③、点P 在二面角内——垂面法。
上海立体几何配套复习题(一)

专题01空间点、直线、平面之间的位置关系综合题专练一、单选题1.(2021·上海市松江二中高二月考)已知直线a ,b 及平面 α,有下列命题:①//a b a b αα⊥⎧⇒⎨⊥⎩;②//a b a b αα⊥⎧⇒⊥⎨⎩;③//////a b a b αα⎧⇒⎨⎩;④//a b a b αα⎧⇒⊥⎨⊥⎩.则其中正确命题的个数为()A .0个B .1个C .2个D .4个2.(2021·上海杨浦·复旦附中高二期中)如图是正方体的平面展开图,在这个正方体中,①BM 与ED 平行;②CN 与BE 是异面直线;③CN 与BM 成60°;④DM 与BN 垂直.以上四个命题中,正确命题的序号是()A .①②③B .②④C .③④D .②③④3.(2021·长宁区·上海市延安中学高二期中)已知正方体1111ABCD A B C D -,P 为1CC 中点,对于下列两个命题:(1)过点P 有且只有一条直线与直线AB ,11A D 都相交;(2)过点P 有且只有一条直线与直线AB ,11A D 都成45°角.则以下判断正确的是()A .(1)为真命题;(2)为真命题B .(1)为真命题;(2)为假命题C .(1)为假命题;(2)为真命题D .(1)为假命题;(2)为假命题4.(2021·上海普陀·曹杨二中高二月考)下列图形中,一定可以确定一个平面的是()A .四边形B .空间三点C .两两相交且交点均不相同的四条直线D .交于同一点的三条直线5.(2021·上海市大同中学)已知a 和b 是成80 角的两条直面直线,则过空间一点且与a b 、都成50 角的直线共有()A .2条B .3条C .4条D .无数条6.(2021·上海市杨浦高级中学高二期末)已知直线a 、b 是两条不重合的直线,α、β是两个不重合的平面,则下列命题正确的是()A .若a α⊥,a β⊥,则//αβB .若//a α,//b β,//αβ,则//a bC .若a b ⊥r r ,b α⊥,//a β,则//αβD .若//αβ,a 与α所成角和b 与β所成角相等,则//a b7.(2021·上海市洋泾中学高二月考)关于直线l 、m 及平面α、β,下列命题中正确的是()A .若//l α,m αβ= ,则//l mB .若l α⊥,//m α,则l m ⊥C .若//l α,//m α,则//l mD .若//l α,m l ⊥,则m α⊥8.(2021·上海市建平中学高二月考)ABC 的三边长分别3、4、5,P 为ABC 所在平面外一点,令集合Q ={P P 为ABC 所在平面外一点,且到三边所在直线的距离都是3},则集合Q 的子集个数为()A .2B .4C .8D .169.(2021·上海市亭林中学高二期中)设直线,a b 与平面α所成的角相等,则直线,a b 的位置关系为()A .平行B .平行或异面C .平行或相交D .平行、相交或异面10.(2021·上海市进才中学高二期中)已知平面l αβ= ,B ,C l ∈,A α∈,且A l ∉,D β∈,且D l ∉,则下列叙述错误的是()A .直线AD 与BC 是异面直线B .直线CD 在α上的射影可能与AB 平行C .过AD 有且只有一个平面与BC 平行D .过AD 有且只有一个平面与BC 垂直二、填空题11.(2021·上海奉贤区·高二期末)在《九章算术》中定义“底面为直角三角形而有一侧棱垂直于底面的三棱锥为鳖臑”.如图,在鳖臑ABCD 中,侧棱AB ⊥底面BCD ,1AB =,2BC =,1CD =,则异面直线AC 与BD 所成角的大小为______.12.(2021·上海市建平中学高二期中)已知圆锥的轴截面PAB 是等边三角形,C 为底面弧AB 的中点,D 为母线PB 的中点,则异面直线PA 和CD 所成角的大小为________13.(2021·上海静安·高二期末)如图,三棱锥P -ABC 中,PA ⊥底面ABC ,底面ABC 是边长为2的正三角形,且23PA =,若M 是BC 的中点,则异面直线PM 与AC 所成角的大小是__________(结果用反三角函数值表示)14.(2021·上海市复兴高级中学)四面体ABCD 中,2AB CD ==,4AC AD BC BD ====,则异面直线AB 与CD 的距离为________15.(2021·上海普陀区·曹杨二中高二期末)已知空间四边形ABCD ,2AB CD ==,且AB 与CD 所成的角为3π,设E 、F 分别是BC 、AD 的中点,则EF 的长度为______.16.(2021·徐汇区·上海中学高二月考)下列判断中:①三点确定一个平面;②一条直线和一点确定一个平面;③两条直线确定一个平面;④三角形和梯形一定是平面图形;⑤四边形一定是平面图形;⑥六边形一定是平面图形;⑦两两相交的三条直线确定一个平面.其中正确的是___________.17.(2021·上海市中国中学高二月考)一个正方体的展开图如图所示,B 、C 、D 为原正方体的顶点,A 为原正方体一条棱的中点,在原来的正方体中,直线CD 与AB 所成角的余弦值为______.18.(2021·上海市洋泾中学高二月考)如图,1111ABCD A B C D -是棱长为1的正方体,一个质点从A 出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i 段与第2i +所在直线必须是异面直线(其中i 是正整数),质点走完的第99段与第1段所在的直线所成的角是___________.19.(2021·上海徐汇区·位育中学)在棱长为2的正方体1111ABCD A B C D -中,M N 、分别是111A B CC 、的中点,用过D M N 、、三点的平面截正方体,则截面图像的周长为__________20.(2021·上海市建平中学高二月考)已知异面直线,a b 所成角为3π,过空间一点P 有且仅有2条直线与,a b 所成角都是θ,则θ的取值范围是___________.三、解答题21.(2021·上海市松江二中高二月考)在正四棱柱1111ABCD A B C D -中,AB =2,过1A 、1C 、B 三点的平面截去正四棱柱的一个角后,得到如图所示的几何体111ABCD A C D -,且这个几何体的体积为203,点P ,Q 分别是1A D 和AC 的中点.(1)求异面直线1D P 与1C Q 所成角的大小;(2)求直线C 1D 与平面11A C B 所成角的大小.(用反三角函数表示)22.(2021·上海市西南位育中学高二期中)长方体1111ABCD A B C D -中,11,2AB AA AD ===,点E 是棱BC 的中点.(1)求异面直线1BB 与1D E 所成角的大小;(2)求点A 到平面1A DE 的距离.23.(2021·上海杨浦·复旦附中高二期中)已知正方体1111ABCD A B C D -的棱长为2,若M ,N 分別是111,CC A D 的中点,作出过M ,N ,B 三点的截面,并求出这截面的周长.24.(2021·上海市奉贤区奉城高级中学高二期中)如图所示,在长方体1111ABCD A B C D -中,1AB =,2BC =,15CC =,M 为棱1CC 上一点.(1)若132C M =,求异面直线1A M 和11CD 所成角的正切值;(2)若11C M =.试证明:BM ⊥平面11A B M .25.(2021·宝山区·上海交大附中高二期中)如图,正四棱柱1111ABCD A B C D -的底面是边长为2的正方形,侧棱长为1.(1)求直线1A C 与直线1AD 所成角的余弦值;(2)求二面角11D A C A --平面角大小的余弦值;(3)在直线1A C 上是否存在一个动点P ,使得P 在平面1D AC 的投影恰好为1D AC 的重心,若存在,求线段PC 的长度,若不存在,说明理由.26.(2021·上海市大同中学)如图,在四棱锥P ABCD -中,PA ⊥面ABCD ,2,7AB BC AD CD ====,3,120,PA ABC G =∠=︒为线段PC 上的点.(1)证明:BD ⊥平面PAC ;(2)若G 是PC 的中点,求DG 与平面PAC 所成的角的正切值;(3)在(2)的条件下求异面直线BG 与PD 所成角的余弦值.27.(2021·上海市大同中学)已知长方体ABCD﹣A1B1C1D1中,M,N分别为AA1和AB的中点.求证:(1)D1,M,N,C四点共面;(2)D1M、DA、CN三线共点.28.(2021·上海市中国中学高二月考)已知空间四边形SABC各边及对角线的长都是1.(1)求边SA、BC的距离;(2)求异面直线SB与AC所成角大小.29.(2021·上海市建平中学高二月考)如图,已在正四棱锥P ABCD -,4PA =,底面边长为4,Q 为PB 的中点.(1)求作平面QAD 与正四棱锥P ABCD -的截面;(2)求二面角Q AD B --的大小.30.(2021·上海徐汇区·位育中学)如图所示,在直三棱柱111ABC A B C -中,底面是等腰直角三角形,90ACB ∠= ,12CA CB CC ===.点1D D ,分别是棱11AC A C ,的中点.(1)求证:11、、、D B B D 四点共面;(2)求直线1BC 与平面11DBB D 所成角的大小.。
中考专题1——立体图形中的最短路径问题

中考复习专题1——立体几何中的最短路径问题姓名:(蚂蚁沿阶梯、正方体、长方体、圆柱、圆锥外侧面吃食问题)1、台阶问题如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A 和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?2、圆柱问题有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?变式1:有一圆柱形油罐,已知油罐底面圆周长是12m,高AB是5m,要从点A处开始绕油罐一周建造梯子,正好到达A点的正上方B处,问梯子最短有多长?变式2:桌上有一个圆柱形玻璃杯(无盖),高为12厘米,底面周长18厘米,在杯口内壁离杯口3厘米的A处有一滴蜜糖,一只小虫从桌上爬至杯子外壁,当它正好爬至蜜糖相对方向离桌面3厘米的B处时,突然发现了蜜糖。
问小虫至少爬多少厘米才能到达蜜糖所在的位置。
ABABcABD C D 1C 1①421AC 1=√42+32=√25;②A B B 1CA 1C 1412AC 1=√62+12=√37;A B 1D 1D A 1C 1③412AC 1=√52+22=√29 .3、正方体问题 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B的最短距离是( ). (A )3 (B ) 5 (C )2 (D )14、长方体问题 如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C 1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?分析:展开图如图所示,372925<<路线①即为所求。
小结:长、宽、高中,较短的两条边的和作为一条直角边,最长的边作为另一条直角边, 斜边长即为最短路线长。
5、圆锥问题 如图,已知O 为圆锥的顶点,MN 为圆锥底面的直径,一只蜗牛从M 点出发,绕圆锥侧面爬行到N 点时,所爬过的最短路线的痕迹(虚线)在侧面展开图中的位置是( ).A BABA’ABCABC211AB A 1B 1D CD 1C 124ACB D练习:1、现要在如图所示的圆柱体侧面A 点与B 点之间缠一条金丝带(金丝带的宽度忽略不计),圆柱体高为6cm ,底面圆周长为16cm ,则所缠金丝带长度的最小值为 。
高考数学(文)《立体几何》专题复习

(2)两个平面垂直的判定和性质
✓ 考法5 线面垂直的判定与性质
1.证明直线 与平面垂直 的方法
2.线面垂直 的性质与线 线垂直
(1)判定定理(常用方法): 一条直线与一个平面内的两条相交直线都垂直,则该直线
与此平面垂直.判定定理中的两条相交直线必须保证“在平面 内相交”这一条件. (2)性质: ①应用面面垂直的性质(常用方法):若两平面垂直,则在一 个平面内垂直于交线的直线必垂直于另一个平面,是证明线 面垂直的主要方法; ②(客观题常用)若两条平行直线中的一条垂直于一个平面, 则另一条也垂直于这个平面.
64
65
✓ 考法4 面面平行的判定与性质
1.证明平面 与平面平行 的常用方法 2.空间平行关系 之间的转化
66
✓ 考法3 面面平行的判定与性质
1.证明平面 与平面平行 的常用方法
这是立体几何中证明平行关系常用的思路,三 种平行关系的转化可结合下图记忆
2.空间平行关系 之间的转化
67
68
600分基础 考点&考法
定义 判定方法
2.等角定理
判定定理 反证法 两条异面直线所成的角
✓ 考法2 异面直线所成的角
常考形式
直接求 求其三角函数值
常用方法
作角
正弦值 余弦值 正切值
证明 求值 取舍
55
56
57
58
600分基础 考点&考法
➢ 考点46 线面、面面平行的判定与性质 ✓ 考法3 线面平行的判定与性质 ✓ 考法4 面面平行的判定与性质
1.计算有关 线段的长
2.外接球、内切 球的计算问题
观察几何体的特征 利用一些常用定理与公式 (如正弦定理、余弦定理、勾股定理、 三角函数公式等) 结合题目的已知条件求解
立体几何复习专题及答案-高中数学

立体几何复习专题姓名: 班级:考点一、空间中的平行关系1.如图,在三棱锥P ABC -中,02,3,90PA PB AB BC ABC ====∠=,平面PAB ⊥平面ABC ,D 、E 分别为AB 、AC 的中点. (1)求证:DE //平面PBC ; (2)求证:AB PE ⊥;(3)求三棱锥B PEC -的体积.2. 如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,PCD △为等边三角形,平面PAC ⊥平面PCD ,PA CD ⊥,2CD =,3AD =,(Ⅰ)设G H ,分别为PB AC ,的中点,求证:GH ∥平面PAD ; (Ⅱ)求证:PA ⊥平面PCD ;3.如图,七面体ABCDEF 的底面是凸四边形ABCD ,其中2AB AD ==,120BAD ∠=︒,AC ,BD 垂直相交于点O ,2OC OA =,棱AE ,CF 均垂直于底面ABCD .(1)证明:直线DE 与平面BCF 不.平行;4.(2014新课标Ⅱ)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ;(Ⅱ)设二面角D AE C --为60°,AP =1,AD =3,求三棱锥E ACD -的体积.考点二、空间中的垂直关系5.如图,在四面体ABCD 中,E ,F 分别是线段AD ,BD 的中点,90ABD BCD ∠=∠=,2EC =,2AB BD ==,直线EC 与平面ABC 所成的角等于30.(1)证明:平面EFC ⊥平面BCD ;6.已知某几何体的直观图和三视图如下图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)求证:BN ⊥平面11C B N ;(2)设M 为AB 中点,在C B 边上求一点P ,使//MP 平面1C NB ,求CBPP 的值.7.(2016全国I )如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF为正方形,2AF FD =,90AFD ∠=,且二面角D AF E --与二面角C BE F --都是60.(I )证明:平面ABEF⊥平面EFDC ;(II )求二面角E BC A --的余弦值.考点三、折叠问题和探究性问题中的位置关系8.如图 1,在直角梯形ABCD 中, //,AB CD AB AD ⊥,且112AB AD CD ===.现以AD 为一边向外作正方形ADEF ,然后沿边AD 将正方形ADEF 翻折,使ADEF 平面与平面ABCD 垂直, M 为ED 的中点,如图 2.(1)求证: //AM 平面BEC ;(2)求证: BC ⊥平面BDE ; .9.如图,在边长为4的正方形ABCD 中,点E,F 分别是AB,BC 的中点,点M 在AD 上,且14AM AD =,将AED,DCF 分别沿DE,DF 折叠,使A,C 点重合于点P ,如图所示2.()1试判断PB 与平面MEF的位置关系,并给出证明;()2求二面角M EF D --的余弦值.10.如图所示,直角梯形ABCD 中,//AD BC ,AD AB ⊥,22AB BC AD ===,四边形EDCF 为矩形,3CF =,平面EDCF ⊥平面ABCD . (1)求证:DF //平面ABE ;(2)求平面ABE 与平面EFB 所成锐二面角的余弦值. (3)在线段DF 上是否存在点P ,使得直线BP 与平面ABE 所成角的正弦值为34,若存在,求出线段BP 的长,若不存在,请说明理由.11.如图1,在边长为4的正方形ABCD中,E是AD的中点,F是CD的中点,现-.将三角形DEF沿EF翻折成如图2所示的五棱锥P ABCFE(1)求证:AC//平面PEF;(2)若平面PEF⊥平面ABCFE,求直线PB与平面PAE所成角的正弦值.12.(2011•浙江)如图,在三棱锥P﹣ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2(1)证明:AP⊥BC;(2)在线段AP上是否存在点M,使得二面角A﹣MC﹣β为直二面角?若存在,求出AM的长;若不存在,请说明理由.13.如图,在直三棱柱111ABC A B C -中,底面ABC 为等边三角形,122CC AC ==.(Ⅰ)求三棱锥11C CB A -的体积;(Ⅱ)在线段1BB 上寻找一点F ,使得1CF AC ⊥,请说明作法和理由.考点四、知空间角求空间角问题14.(2014天津)如图四棱锥P ABCD -的底面ABCD 是平行四边形,2BA BD ==2AD =,5PA PD ==E ,F 分别是棱AD ,PC 的中点.(Ⅰ)证明: EF ∥平面PAB ; (Ⅱ)若二面角P AD B --为60°, (ⅰ)证明:平面PBC ⊥平面ABCD(ⅱ)求直线EF 与平面PBC 所成角的正弦值. PCDBF15.四棱锥P ABCD -中,底面ABCD 为矩形,PA ABCD ⊥平面,E 为PD 的中点.(1)证明://E PB A C 平面;(2)设13AP AD ==,,三棱锥P ABD -的体积34V =,求二面角D -AE -C 的大小16.如图,四棱锥P ABCD -中, PA ⊥底面ABCD ,底面ABCD 是直角梯形,90ADC ∠=︒, //AD BC , AB AC ⊥, 2AB AC ==,点E 在AD 上,且2AE ED =.(Ⅰ)已知点F 在BC 上,且2=CF FB ,求证:平面PEF ⊥平面PAC ;(Ⅱ)当二面角--A PB E 的余弦值为多少时,直线PC 与平面PAB 所成的角为45︒?立体几何专题参考答案1. (1)证明:∵在△ABC 中,D 、E 分别为AB 、AC 的中点,∴DE ∥BC . ∵DE ⊄平面PBC 且BC ⊂平面PBC ,∴DE ∥平面PBC . (2)证明:连接PD .∵PA =PB ,D 为AB 的中点,∴PD ⊥AB .∵DE ∥BC ,BC ⊥AB ,∴DE ⊥AB .又∵PD 、DE 是平面PDE 内的相交直线, ∴AB ⊥平面PDE .∵PE ⊂平面PDE ,∴AB ⊥PE .(3)解:∵PD ⊥AB ,平面PAB ⊥平面ABC ,平面PAB ∩平面ABC =AB ,∴PD ⊥平面ABC ,可得PD 是三棱锥P -BEC 的高. 又∵33,2BECPD S==,1332B PEC P BEC BEC V V S PD --∆∴==⨯=. 2.(I )见解析;(II )见解析;(III )33. (I )证明:连接BD ,易知AC BD H ⋂=,BH DH =,又由BG PG =,故GHPD ,又因为GH ⊄平面PAD ,PD ⊂平面PAD , 所以GH ∥平面PAD .(II )证明:取棱PC 的中点N ,连接DN ,依题意,得DN PC ⊥, 又因为平面PAC ⊥平面PCD ,平面PAC平面PCD PC =,所以DN ⊥平面PAC ,又PA ⊂平面PAC ,故DN PA ⊥, 又已知PA CD ⊥,CD DN D =,所以PA ⊥平面PCD . 3.(1)见解析;(2)23535本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
立体几何专题复习(自己精心整理)

专题一证明平行垂直问题题型一证明平行关系(1)如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD。
(2)在正方体AC1中,M,N,E,F分别是A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN∥平面EFDB.思考题1(1)如图所示,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点,求证:平面EFG∥平面PBC.(2)如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=22,M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.求证:PQ∥平面BCD。
题型二证明垂直关系(微专题)微专题1:证明线线垂直(1)已知空间四边形OABC中,M为BC中点,N为AC中点,P为OA中点,Q为OB中点,若AB=OC。
求证:PM⊥QN.(2)(2019·山西太原检测)如图,直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,E,F分别是CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点,求证:DF⊥AE。
微专题2:证明线面垂直(3)在正方体ABCD-A1B1C1D1中,求证:BD1⊥平面ACB1.(4)(2019·河南六市一模)在如图所示的几何体中,ABC-A1B1C1为三棱柱,且AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,∠ADC=60°.若AA1=AC,求证:AC1⊥平面A1B1CD。
微专题3:证明面面垂直(5)已知正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点,求证:平面DEA⊥平面A1FD1.(6)如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=错误!PD,求证:平面PQC⊥平面DCQ。
思考题2(1)(2019·北京东城区模拟)如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥BP交BP于点F,求证:PB⊥平面EFD。
立体几何复习专题---- 线线夹角

立体几何复习专题--空间角之线线角一、基础知识1.定义: 直线a 、b 是异面直线,经过空间一交o ,分别a ΄//a ,b ΄//b ,相交直线a ΄b ΄所成的锐角(或直角)叫做异面直线夹角。
2.范围: ⎥⎦⎤⎝⎛∈2,0πθ3.方法: 平移法、(1)平移法:在图中选一个恰当的点(通常是线段端点或中点)作a 、b 的平行线,构造一个三角形,并解三角形求角。
步骤:①根据定义,通过平移,找到异面直线所成的角θ;②解含有θ的三角形,求出角θ的大小.(常用到余弦定理)余弦定理: abcb a 2cos 222-+=θ (计算结果可能是其补角)(2) 补形法:把空间图形补成正方体、平行六面体、长方体等几何体,以便发现异面直线间的关系(3)三线角公式 用于求线面角和线线角.斜线和平面内的直线与斜线的射影所成角的余弦之积等于斜线和平面内的直线所成角的余弦 即:θθθc o s c o s c o s 21=若 OA 为平面的一条斜线,O 为斜足,OB 为OA 在面α内的射影,OC 为面α内的一条直线,其中θ为OA 与OC 所成的角,θ1为OA 与OB 所成的角,即线面角,θ2为OB 与OC 所成的角,那么 cos θ=cos θ1·cos θ2 (同学们可自己证明),它揭示了斜线和平面所成的角是这条斜线和这个平面内的直线所成的一切角中最小的角(常称为最小角定理)【典型例题】【例1】在正方体1111ABCD A BC D -中,下列几种说法正确的是 ( ) A 、11AC AD ⊥ B 、11D C AB ⊥ C 、1AC 与DC 成45角 D 、11AC 与θcba B αOAC1BC 成60角答案:D 。
解析:A 1C 1与AD 成45°,D 1C 1与AB 平行,AC 1与DC 所成角的正切为22。
【例2】(1)如图,在正方体1111ABCD A B C D -中,E,FG,H 分别为1AA ,AB ,1BB ,11B C 的中点,则异面直线EF 与GH 所成的角等于 (2)如图,正四棱柱1111ABCD A B C D -中,12AA AB =,则异面直线1A B 与1AD 所成角的余弦值为(3) 如图,在直三棱柱ABC -A 1B 1C 1中,∠BCA= 90,点D 1、F 1分别是A 1B 1和A 1C 1的中点,若BC=CA=CC 1,求BD 1与AF 1所成的角的余弦值_________。
高中数学高考复习专题《立体几何》微专题1 空间中的距离

1.典型例题
题型一、点到直线的距离
例 1 已知正方体 ABCD-A1B1C1D1 的棱长为 2,E 为棱 A1B1 的中点,F 为棱 C1D1 的中点,
则 BF=
,点 A 到直线 BE 的距离为
.
【答案】3,45 5
【解析】如图 2 所示,连结 B1F,在△BB1F 中可得 BF=3.作 AH⊥BE 于 H,连结 AE,
E
A
F
B
图4
D
C
E O
A
F
B
图5
【答案】(1)2
2;(2)2
1111;(3)2
11. 11
【解析】如图 5 所示,连结 AC 交 BD 于 O.
(1)可证 OC⊥BD,OC⊥PC,又 OC=2 2,∴异面直线 PC、BD 间的距离为
2 2.
(2)法一 可证 BD∥平面 PEF,∴点 O 到平面 PEF 的距离等于点 B 到平面 PEF 的距
(4)两条异面直线间的距离
和两条异面直线分别垂直相交的直线,叫两条异面直线的公垂线;公垂线上夹在两异
面直线间的线段的长度,叫两异面直线间的距离.
如图 1 所示,AA1 与 BC 为异面直线.易知 AB⊥AA1,AB⊥BC,因此异面直线 AA1 与 BC 间的距离为 1.
(5)直线和平面的距离
一条直线和一个平面平行,这条直线上任意一点到这个平面的距离,叫做这条直线和这
D1
C1
A1
B1
D
C
A (2)点到平面的距离
B 图1
从平面外一点引平面的垂线,这个点和垂足间的距离,叫做这个点到这个平面的距离.
如图 1 所示,易知 AA1⊥平面 A1C1,因此点 A 到平面 A1C1 的距离为 1. (3)两条平行直线间的距离
高中数学《立体几何》专题复习 (1)

高中数学《立体几何》专题复习一1.(2018·安徽东至二中段测)将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括()A.一个圆台、两个圆锥B.两个圆台、一个圆柱C.两个圆台、一个圆锥D.一个圆柱、两个圆锥答案 D解析把等腰梯形分割成两个直角三角形和一个矩形,由旋转体的定义可知所得几何体包括一个圆柱、两个圆锥.故选D.2.以下关于几何体的三视图的论述中,正确的是()A.正方体的三视图是三个全等的正方形B.球的三视图是三个全等的圆C.水平放置的正四面体的三视图都是正三角形D.水平放置的圆台的俯视图是一个圆答案 B解析画几何体的三视图要考虑视角,但对于球无论选择怎样的视角,其三视图总是三个全等的圆.3.如图所示,几何体的正视图与侧视图都正确的是()答案 B解析侧视时,看到一个矩形且不能有实对角线,故A,D排除.而正视时,有半个平面是没有的,所以应该有一条实对角线,且其对角线位置应为B中所示,故选B.4.一个几何体的三视图如图,则组成该几何体的简单几何体为()A.圆柱和圆锥B.正方体和圆锥C.四棱柱和圆锥D.正方体和球答案 C5.(2018·沧州七校联考)三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB 的长为()A.16 3 B.38C.4 2 D.211答案 C解析由已知中的三视图可得SC⊥平面ABC,且底面△ABC为等腰三角形.在△ABC中,AC=4,AC边上的高为23,所以BC=4.在Rt△SBC中,由SC=4,可得SB=4 2. 6.(2017·衡水中学调研卷)已知一个四棱锥的高为3,其底面用斜二侧画法所画的水平放置的直观图是一个边长为1的正方形,则此四棱锥的体积为()A.2 2 B.6 2C.1 D. 2答案 A解析因为底面用斜二侧画法所画的水平放置的直观图是一个边长为1的正方形,所以在直角坐标系中,底面是边长为1和3的平行四边形,且平行四边形的一条对角线垂直于平行四边形的短边,此对角线的长为22,所以该四棱锥的体积为V=13×22×1×3=2 2.7.(2018·四川泸州模拟)一个正四棱锥的所有棱长均为2,其俯视图如图所示,则该正四棱锥的正视图的面积为()A. 2B. 3C.2 D.4答案 A解析由题意知,正视图是底边长为2,腰长为3的等腰三角形,其面积为12×2×(3)2-1= 2.8.(2018·湖南郴州模拟)一只蚂蚁从正方体ABCD-A1B1C1D1的顶点A出发,经正方体的表面,按最短路线爬行到顶点C1的位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是()A.①②B.③④C.①③D.②④答案 D解析由点A经正方体的表面,按最短路线爬行到达顶点C1的位置,共有6种路线(对应6种不同的展开方式),若把平面ABB1A1和平面BCC1B1展到同一个平面内,连接AC1,则AC1是最短路线,且AC1会经过BB1的中点,此时对应的正视图为②;若把平面ABCD和平面CDD1C1展到同一个平面内,连接AC1,则AC1是最短路线,且AC1会经过CD的中点,此时对应的正视图为④.而其他几种展开方式对应的正视图在题中没有出现.故选D.9.某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是()答案 D解析依题意,此几何体为组合体,若上、下两个几何体均为圆柱,则俯视图为A;若上边的几何体为正四棱柱,下边几何体为圆柱,则俯视图为B;若上边的几何体为底面为等腰直角三角形的直三棱柱,下边的几何体为正四棱柱时,俯视图为C;若俯视图为D,则正视图中还有一条虚线,故该几何体的俯视图不可能是D,故选D.10.(2018·江西上馓质检)点M,N分别是正方体ABCD-A1B1C1D1的棱A1B1,A1D1的中点,用过平面AMN和平面DNC1的两个截面截去正方体的两个角后得到的几何体如图,则该几何体的正(主)视图,侧(左)视图、俯视图依次为()A.①②③B.②③④C.①③④D.②④③答案 B解析由直视图可知,该几何体的正(主)视图、侧(左)视图、俯视图依次为②③④,故选B. 11.(2018·四川宜宾期中)某几何体的三视图如图所示,则该几何体最长棱的长度为()A.4 B.3 2C.2 2 D.2 3答案 D解析由三视图可知,该几何体为如图所示的四棱锥P-ABCD,由图可知其中最长棱为PC,因为PB2=PA2+AB2=22+22=8,所以PC2=PB2+BC2=8+22=12,则PC=23,故选D.12.(2018·北京东城区期末)在空间直角坐标系O-xyz中,一个四面体的顶点坐标分别为(0,0,2),(2,2,0),(0,2,0),(2,2,2).画该四面体三视图中的正视图时,以xOz平面为投影面,则得到的正视图可以为()答案 A解析设S(2,2,2),A(2,2,0),B(0,2,0),C(0,0,2),则此四面体S-ABC如图①所示,在xOz平面的投影如图②所示.其中S′是S在xOz平面的投影,A′是A在xOz平面的投影,O是B在xOz平面的投影,SB 在xOz平面的投影是S′O,并且是实线,CA在xOz平面的投影是CA′,且是虚线,如图③. 13.(2018·江西宜春模拟)某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大为()A.2 2 B.4C.2 3 D.2 6答案 C解析由三视图知该几何体为棱锥S-ABD,其中SC⊥平面ABCD,将其放在正方体中,如图所示.四面体S-ABD的四个面中△SBD的面积最大,三角形SBD是边长为22的等边三角形,所以此四面体的四个面中面积最大为34×8=2 3.故选C.14.(2018·江苏张家港一模)若将一个圆锥侧面沿一条母线剪开,其展开图是半径为2 cm的半圆,则该圆锥的高为________cm.答案 3解析设圆锥的底面圆半径为r cm,则2πr=2π,解得r=1 cm,∴h=22-1= 3 cm. 15.(2018·成都二诊)已知正四面体的俯视图如图所示,其中四边形ABCD是边长为2的正方形,则这个四面体的正视图的面积为________.答案2 2解析由俯视图可得,原正四面体AMNC可视作是如图所示的正方体的一内接几何体,则该正方体的棱长为2,正四面体的正视图为三角形,其面积为12×2×22=2 2.16.(2018·上海长宁区、嘉定区质检)如图,已知正三棱柱的底面边长为2,高为5,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为________.答案13解析将正三棱柱ABC-A1B1C1沿侧棱AA1展开,再拼接一次,如图所示,在展开图中,最短距离是六个矩形形成的大矩形对角线的长度,也即为三棱柱的侧面上所求距离的最小值.由已知求得矩形的长等于6×2=12,宽等于5,由勾股定理得d=122+52=13.17.某几何体的正(主)视图和侧(左)视图如图1,它的俯视图的直观图是矩形O1A1B1C1如图2,其中O1A1=6,O1C1=2,则该几何体的侧面积为________.答案96解析由俯视图的直观图可得y轴与C1B1交于D1点,O1D1=22,故OD=42,俯视图是边长为6的菱形,则该几何体是直四棱柱,侧棱长为4,则侧面积为6×4×4=96. 1.(课本习题改编)如图为一个几何体的三视图,则该几何体是()A.四棱柱B.三棱柱C.长方体D.三棱锥答案 B解析由几何体的三视图可知,该几何体的直观图如图所示,即为一个平放的三棱柱.2.(2018·山东泰安模拟)某三棱锥的三视图如图所示,其侧视图为直角三角形,则该三棱锥最长的棱长等于()A.4 2 B.34C.41 D.5 2答案 C解析根据几何体的三视图,得该几何体是底面为直角三角形,有两个侧面垂直于底面,高为5的三棱锥,最长的棱长等于25+16=41,故选C.3.(2018·安徽毛坦厂中学月考)已知一个几何体的三视图如图所示,则这个几何体的直观图是()答案 C解析A项中的几何体,正视图不符,侧视图也不符,俯视图中没有虚线;B项中的几何体,俯视图中不出现虚线;C项中的几何体符合三个视图;D项中的几何体,正视图不符.故选C.4.(2017·山东德州质检)如图是正方体截去阴影部分所得的几何体,则该几何体的侧视图是()答案 C解析此几何体的侧视图是从左边往右边看,故其侧视图应选C.5.(2017·广东汕头中学摸底)如图是一正方体被过棱的中点M,N,顶点A及过N,顶点D,C1的两个截面截去两角后所得的几何体,该几何体的正视图是()答案 B6.(2017·贵州七校联考)如图所示,四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)()A.①②⑥B.①②③C.④⑤⑥D.③④⑤答案 B解析正视图应该是边长为3和4的矩形,其对角线左下到右上是实线,左上到右下是虚线,因此正视图是①;侧视图应该是边长为5和4的矩形,其对角线左上到右下是实线,左下到右上是虚线,因此侧视图是②;俯视图应该是边长为3和5的矩形,其对角线左上到右下是实线,左下到右上是虚线,因此俯视图是③,故选B.7.(2014·课标全国Ⅰ)如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱答案 B解析由题知,该几何体的三视图为一个三角形,两个四边形,经分析可知该几何体为三棱柱,故选B.8.用一个平行于水平面的平面去截球,得到如图所示的几何体,则它的俯视图是()答案 B解析D项为主视图或者侧视图,俯视图中显然应有一个被遮挡的圆,所以内圆是虚线,故选B.9.底面水平放置的正三棱柱的所有棱长均为2,当其正(主)视图有最大面积时,其侧(左)视图的面积为()A.2 3 B.3C. 3 D.4答案 A解析当正视图面积最大时,侧视图是一个矩形,一个边长为2,另一边长是三棱柱底面三角形的高为3,故侧视图面积为2 3.10.(2015·北京,文)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A.1 B. 2C. 3 D.2答案 C解析将三视图还原成几何体的直观图,如图,由三视图可知,底面ABCD是边长为1的正方形,SB⊥底面ABCD,SB=AB=1,由勾股定理可得SA=SC=2,SD=SB2+DB2=1+2=3,故四棱锥中最长棱的棱长为 3.故选C. 11.(2017·南昌模拟)若一几何体的正视图与侧视图均为边长为1的正方形,则下列图形一定不是该几何体的俯视图的是()答案 D解析 若该几何体的俯视图为选项D ,则其正视图为长方形,不符合题意,故选D. 12.某几何体的正视图与侧视图如图所示,若该几何体的体积为13,则该几何体的俯视图可以是( )答案 D解析 通过分析正视图和侧视图,结合该几何体的体积为13,可知该几何体的底面积应为1,因为符合底面积为1的选项仅有D 选项,故该几何体为一个四棱锥,其俯视图为D. 13.(2018·兰州诊断考试)某几何体的三视图如图所示,且该几何体的体积是3,则正视图中x 的值是( )A .2 B.92 C.32 D .3答案 D解析 由三视图知,该几何体是四棱锥,底面是一个直角梯形,底面积S =12×(1+2)×2=3,高h =x ,所以其体积V =13Sh =13×3x =3,解得x =3,故选D.14.某几何体的三视图如图所示,则该几何体中,最大侧面的面积为( )A.12B.22C.52D.62答案 C解析 由三视图知,该几何体的直观图如图所示.平面AED ⊥平面BCDE ,四棱锥A -BCDE 的高为1.四边形BCDE 是边长为1的正方形,则S △AED =12×1×1=12,S △ABC =S △ABE =12×1×2=22,S △ACD =12×1×5=52,故选C.15.(2017·山东师大附中月考)如图是各棱长均为2的正三棱柱ABC -A 1B 1C 1的直观图,则此三棱柱侧视图的面积为________. 答案 2 3解析 依题意,得此三棱柱的侧视图是边长分别为2,3的矩形BB 1D 1D ,故其面积是2 3.16.(2017·北京西城区期末)已知一个正三棱柱的所有棱长均相等,其侧(左)视图如图所示,那么此三棱柱正(主)视图的面积为________. 答案 2 3解析 由正三棱柱三视图还原直观图可得正(主)视图是一个矩形,其中一边的长是侧(左)视图中三角形的高,另一边是棱长.因为侧(左)视图中三角形的边长为2,所以高为3,所以正视图的面积为2 3.17.用小立方块搭一个几何体,使它的正视图和俯视图如图所示,则它最多需要______个小立方块.答案14解析本题考查了三视图的有关知识.需要小立方块最多则:第一层最多6个,第二层最多5个,第三层最多3个,故最多用14个.18.(2017·湖南株洲质检)已知底面为正方形的四棱锥,其一条侧棱垂直于底面,那么该四棱锥的三视图可能是下列各图中的()答案 C解析通过对以下四个四棱锥的三视图对照可知,只有选项C是符合要求.。
立体几何复习专题(空间角)

专题:空间角一、基础梳理1.两条异面直线所成的角(1)异面直线所成的角的范围:(0,]2π。
(2)异面直线垂直:如果两条异面直线所成的角是直角,则叫两条异面直线垂直。
两条异面直线,a b 垂直,记作a b ⊥。
(3)求异面直线所成的角的方法:(1)通过平移,在一条直线上(或空间)找一点,过该点作另一(或两条)直线的平行线; (2)找出与一条直线平行且与另一条相交的直线,那么这两条相交直线所成的角即为所求。
平移技巧有:平行四边形对边平移、三角形中位线平移、补形平移技巧等。
1:三棱柱111B A O OAB -,平面11O OBB ⊥平面OAB ,90,601=∠=∠AOB OB O ,且12,OB OO ==OA =B A 1与1AO 所成角的余弦。
2.直线和平面所成的角(简称“线面角”) (1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角。
一直线垂直于平面,所成的角是直角;一直线平行于平面或在平面内,所成角为0︒角。
直线和平面所成角范围:[0,2π]。
(2)最小角定理:斜线和平面所成角是这条斜线和平面内 经过斜足的直线所成的一切角中最小的角。
(3)公式:已知平面α的斜线a 与α内一直线b 相交成θ角, 且a 与α相交成ϕ1角,a 在α上的射影c 与b 相交成ϕ2角, 则有θϕϕcos cos cos 21= 。
由(3)中的公式同样可以得到:平面的斜线和它在平面 内的射影所成角,是这条斜线和这个平面内的任一条直 线所成角中最小的角。
AB O 1A1B1O考点二:直线和平面所成的角例2. 如图,在三棱柱ABC A B C '''-中,四 边形A ABB ''是菱形,四边形BCC B ''是矩形,C B AB ''⊥,02,4,60C B AB ABB '''==∠=, 求AC '与平面BCC B ''所成角的正切。
高三《立体几何》专题复习

高三《立体几何》专题复习一、常用知识点回顾1、三视图。
正侧一样高,正俯一样长,侧府一样宽,看不到的线画虚线。
2、常用公式与结论。
(1)圆柱、圆锥、圆台的侧面展开图及侧面积公式;(2)空间几何体的表面积与体积公式;(3)全品高考复习方案(听课手册)105页的常用结论3、两条异面直线所成的角;直线与平面所成的角。
4、证明两条直线平行的常用方法;直线与平面平行的判定与性质;面面平行的判定与性质。
5、证明两条直线垂直的常用方法;直线与平面垂直的判定与性质;两个平面垂直的判定与性质。
二、题型训练题型一:三视图的运用,求几何体的体积、表面积例1、如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()(A)18+(B)54+(C)90(D)81【练习1】某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()C.3D.2【练习2】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A.90πB.63πC.42πD.36π【练习3】如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )(A )20π(B )24π(C )28π(D )32π例2、在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( )(A )4π (B )9π2 (C )6π (D )32π3变式1:在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=5,则V的最大值是变式2:在封闭的长方体ABCD-A1B1C1D1内有一个体积为V的球.若AB=BC=6,AA1=3,则V的最大值是变式3:(1)长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为(2)体积为8的正方体的顶点都在同一球面上,则该球面的表面积为变式4:【练习1】已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A. B.12π C. D.10π【练习3】已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30°,若SAB的面积为8,则该圆锥的体积为_______题型二:平行问题例1、如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(I)证明MN∥平面PAB; (II)求四面体N-BCM的体积.【练习1】如图,四棱锥P-ABCD中,侧面PADAD,为等边三角形且垂直于底面ABCD,AB=BC=12∠BAD=∠ABC=90°。
专题01 空间几何体专题复习

本重点包括柱、锥、台、球的概念、性质、表面积与体积,直观图与三视图,这些是立体几何的基础,也是研究空间问题的基本载体,所以是高考考查的热点。
知识框架1、空间几何体的结构2、空间几何体的三视图和直观图3、空间几何体的表面积和体积一、考查形式与特点1、本章内容多以客观题出现,考查基本知识,对空间几何体的特征与性质的理解,三视图和直观图,几何体表面积与体积的计算等。
三视图考查特点:一是给出空间图形,选择其三视图;二是已知其中两种三视图,画出另外一种视图;三是三视图与面积体积计算结合在一起考查。
2、球体在近几年的高考中出现频率较高,特别是棱柱、棱锥中球的内切、外接问题,在复习时更要注意多练习相关的题目。
对球中的体积、表面积、球面距离等问题也要进行重点掌握。
3、培养与发展考生的空间想象能力、推理证明能力、运用图形语言进行交流的能力。
考查空间想象能力及空间模型的构造能力。
二、方法策略1、“化整为零”是本章的基本思想。
将一个复杂的几何体分割成若干个常见的熟悉的几何体,或者把几个简单的几何体组合成一个新的几何体,目的在于化繁为简,寻求解题的捷径。
立体几何和平面几何有着密切的联系,空间图形的局部性往往可以透过平面图形的性质去研究,利用截面可以把锥体中的元素关系转化为三角形中的元素关系。
2、“以直代曲”的思想方法即通过空间图形的展开将立体几何问题转化为平面几何问题,曲面问题转化为平面问题,如在推导圆柱、圆锥、圆台的侧面积公式时,就是将其侧面展开,转化为长方形、扇形、圆环来解决。
3、三视图之间的投影规律为:正、俯视图――长对正;正、侧视图――高平齐;俯、侧视图――宽相等。
三视图是新增内容,是高考考查重点,它能极大培养学生的空间想象能力与感知能力,熟悉常见简单几何体三视图在数量上的关系,善于将三视图中的数量关系与原几何体的数量关系联系起来,进行相关的计算。
4、球的表面积与体积的计算的关键是求出球的半径,然后再利用表面积公式及体积公式求解.球的表面积与体积问题常置于多面体的组合体中,解答时要充分利用切、接点正确作出过球心截面,从而使空间问题转化为平面问题,再利用球的半径与多面体的元素的关系求解.特别要注意的题型是球与长方体、正方体的组合体.5、解决问题的重要手段:截、展、拆、拼(1)“截”是指截面,平行于柱、锥、台底面的截面,旋转体的轴截面是帮助我们解题的有力“工具”。
高中数学 立体几何专题复习

图2侧视图俯视图正视图4x33x4DCBA侧视图正视图立体几何专题(一)一、三视图考点透视:①能想象空间几何体的三视图,并判断(选择题) ②通过三视图计算空间几何体的体积或表面积③解答题中也可能以三视图为载体考查证明题和计算题④旋转体(圆柱、圆锥、圆台或其组合体)的三视图有两个视图一样。
⑤基本几何体的画法,如:三棱柱(侧视图)、挡住的注意画虚线。
1. 一空间几何体的三视图如图2所示, 该几何体的 体积为85123π+,则正视图中x 的值为 A. 5 B . 4 C. 3 D . 22. 一个正方体截去两个角后所得几何体的正视图(又称主视图)、 侧视图(又称左视图)如右图所示,则其俯视图为c3.如图4,已知一个锥体的正视图(也称主视图),左视图(也称侧视图)和俯视图均为直角三角形, 且面积分别为3,4,6,则该锥体的体积是 4 .4. 如图1-3,某几何体的正视图(主视图)是平行四边形, 侧视图(左视图)和俯视图都是矩形,则该几何体的体积 为A .63B .93C .123D .1835、已知某几何体的直观图(图1)与它的三视图(图2), 其中俯视图为正三角形,其它两个视图是矩形.已知D 是正视图 左视图俯视图图4_3 _3 这个几何体的棱11C A 上的中点。
(Ⅰ)求出该几何体的体积;(Ⅱ)求证:直线11//BC AB D 平面; (Ⅲ)求证:直线11B D AA D ⊥平面.二、直观图掌握直观图的斜二测画法:①平行于两坐标轴的平行关系保持不变;②平行于y 轴的长度为原来的一半,x 轴不变;③新坐标轴夹角为45°。
6、如图,梯形A 1B 1C 1D 1是一平面图形ABCD 的直观图(斜二测),若A 1D 1∥O 1y 1,A 1B 1∥C 1D 1,A 1B 1=2,C 1D 1=3,A 1D 1=1,则梯形ABCD 的面积是( ) A .10 B .5 C .5 2D .102三、表面积和体积不要求记忆,但要会使用公式。
高三立体几何专题复习

高考立体几何专题复习一.考试要求:〔1〕掌握平面的根本性质,会用斜二测的画法画水平放置的平面图形的直观图,能够画出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想象它们的位置关系。
〔2〕了解空两条直线的位置关系,掌握两条直线平行与垂直的判定定理和性质定理,掌握两条直线所成的角和距离的概念〔对于异面直线的距离,只要求会计算已给出公垂线时的距离〕。
〔3〕了解空间直线和平面的位置关系,掌握直线和平面平行的判定定理和性质定理,理解直线和平面垂直的判定定理和性质定理,掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念,了解三垂线定理及其逆定理。
〔4〕了解平面与平面的位置关系,掌握两个平面平行的判定定理和性质定理。
掌握二面角、二面角的平面角、两个平面间的距离的概念,掌握两个平面垂直的判定定理和性质定理。
〔5〕会用反证法证明简单的问题。
〔6〕了解多面体的概念,了解凸多面体的概念。
〔7〕了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图。
〔8〕了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图。
〔9〕了解正多面体的概念,了解多面体的欧拉公式。
〔10〕了解球的概念,掌握球的性质,掌握球的外表积、体积公式。
二.复习目标:1.在掌握直线与平面的位置关系(包括直线与直线、直线与平面、平面与平面间的位置关系)的根底上,研究有关平行和垂直的的判定依据(定义、公理和定理)、判定方法及有关性质的应用;在有关问题的解决过程中,进一步了解和掌握相关公理、定理的容和功能,并探索立体几何中论证问题的规律;在有关问题的分析与解决的过程中提高逻辑思维能力、空间想象能力及化归和转化的数学思想的应用.2.在掌握空间角(两条异面直线所成的角,平面的斜线与平面所成的角及二面角)概念的根底上,掌握它们的求法(其根本方法是分别作出这些角,并将它们置于*个三角形通过计算求出它们的大小);在解决有关空间角的问题的过程中,进一步稳固关于直线和平面的平行垂直的性质与判定的应用,掌握作平行线(面)和垂直线(面)的技能;通过有关空间角的问题的解决,进一步提高学生的空间想象能力、逻辑推理能力及运算能力.3.通过复习,使学生更好地掌握多面体与旋转体的有关概念、性质,并能够灵活运用到解题过程中.通过教学使学生掌握根本的立体几何解题方法和常用解题技巧,开掘不同问题之间的在联系,提高解题能力.4.在学生解答问题的过程中,注意培养他们的语言表述能力和"说话要有根据〞的逻辑思维的习惯、提高思维品质.使学生掌握化归思想,特别是将立体几何问题转化为平面几何问题的思想意识和方法,并提高空间想象能力、推理能力和计算能力.5.使学生更好地理解多面体与旋转体的体积及其计算方法,能够熟练地使用分割与补形求体积,提高空间想象能力、推理能力和计算能力.三.教学过程:〔Ⅰ〕根底知识详析高考立体几何试题一般共有4道(选择、填空题1--2道, 解答题1道), 共计总分20分左右,考察的知识点在20个以. 选择填空题考核立几中的计算型问题, 而解答题着重考察立几中的逻辑推理型问题, 当然, 二者均应以正确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着"多一点思考,少一点计算〞的开展.从历年的考题变化看, 以多面体和旋转体为载体的线面位置关系的论证,角与距离的探常考常新的热门话题.1.有关平行与垂直(线线、线面及面面)的问题,是在解决立体几何问题的过程中,大量的、反复遇到的,而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的容,因此在主体几何的总复习中,首先应从解决"平行与垂直〞的有关问题着手,通过较为根本问题,熟悉公理、定理的容和功能,通过对问题的分析与概括,掌握立体几何中解决问题的规律——充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想,以提高逻辑思维能力和空间想象能力.2.判定两个平面平行的方法:〔1〕根据定义——证明两平面没有公共点;〔2〕判定定理——证明一个平面的两条相交直线都平行于另一个平面;〔3〕证明两平面同垂直于一条直线。
立体几何专题复习

立体几何专题复习例1:如图1,在棱长均为4的三棱柱ABC-A1B1C1中,若平面ABC⊥平面BCC1B1,∠B1BC=60°,求三棱锥B1-ABC的体积.【解答】设BC的中点为D,连结AD.则在△ABC中∵AB=AC且D为BC的中点∴AD⊥BC∵平面ABC⊥平面B1C1CB,其交线为BC,AD⊂平面ABC,∴AD⊥平面B1C1CB在△ABC中,由AB=AC=BC=4得AD=2 3.在△B1BC中,∵B1B=BC=4,∠B1BC=60°图1∴△B1BC是等边三角形∴S△B1BC=34×42=43,而三棱锥B1-ABC的体积等于三棱锥A-B1BC的体积,即VB1-ABC=VA-B1BC=13×S△B1BC·AD=13×43×23=8.【点评】锥体的体积求解的关键是求高,本题利用面面垂直的性质定理,通过作交线的垂线,得到线面垂直,从而找到高所在直线.例2:如图2,在边长为6 cm的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.求多面体E-AFNM的体积.图2【解答】 ∵⎭⎬⎫AB ⊥BE AB ⊥BF ⇒AB ⊥平面BEF 且AB =6,BE =BF =3∴V A -BEF =9, 又V E -AFNM V E -ABF =S 四边形AFNM S △ABF=34∴V E -AFNM =274. 【点评】 本题中求多面体E -AFNM 的体积,采取的是比例法,由于E 点到平面ABF 的高不易求出,故采取等体积转化,先求出整个三棱锥的体积,再通过同高可以将体积转化为面积之比.如图3,四棱锥P -ABCD 中,PA ⊥平面ABCD ,底面ABCD 为直角梯形且AB ∥CD ,∠BAD =90°,PA=AD =DC =2,AB =4.(1)求证:BC ⊥PC ;(2)四面体A -PBC 的体积.【解答】 (1)证明:作CE ⊥AB 于点E ,则AE =EB =CE =2,BC =22,连结AC ,则AC =22,故∠ACB =90°,即AC ⊥CB .又PA ⊥平面ABCD ,故PA ⊥BC∴BC ⊥平面PAC 又PC ⊂面PAC ,因此BC ⊥PC . 图3(2)过A 作AM ⊥PC ,由(1)易得BC ⊥平面PAC ,故BC ⊥AM ,所以AM ⊥PBC ,因此线段AM 的长为点A 到平面PBC 的距离.在Rt △PAC 中,PC =23,AM =263,即点A 到平面PBC 的距离为263. 在△PBC 中,PC =23,BC =22,PB =25,由余弦定理得cos ∠PBC =PB 2+BC 2-PC 22PB ·BC =105,∴sin∠PBC=155,∴S△PBC=12PB·BC·sin∠PBC=26,∴V A-PBC=13S△PBC·AM=83.即AC⊥CB.又PA⊥平面ABCD,故PA⊥BC,∴BC⊥平面PAC又PC⊂面PAC,因此BC⊥PC.(2)过A作AM⊥PC,由(1)易得BC⊥平面PAC,故BC⊥AM,所以AM⊥PBC,因此线段AM的长为点A到平面PBC的距离.在Rt△PAC中,PC=23,AM=263,即点A到平面PBC的距离为263.在△PBC中,PC=23,BC=22,PB=25,由余弦定理得cos∠PBC=PB2+BC2-PC22PB·BC=105,∴sin∠PBC=155,∴S△PBC=12PB·BC·sin∠PBC=26,∴V A-PBC=13S△PBC·AM=83.规律总结1:1.空间几何体的表面积和体积的研究策略研究空间几何体的结构→计算相关边长→代入公式计算.2.空间几何体的结构的研究策略运用转化的思想,将空间几何体的问题转化为平面问题,如几何体的外接球或内切球问题;转化为多边形与圆的外接或内切问题.3.组合体体积的求解组合体的体积求解无论是分割还是补形,关键是有利于求出几何体的高,即找到线面垂直.例3:已知m,n,l是直线,α、β是平面,下列命题中,正确命题的序号是________.①若l垂直于α内两条直线,则l⊥α;②若l平行于α,则α内有无数条直线与l平行;③若m∥β,m⊂α,n⊂β,则m∥n;④若m⊥α,m⊥β,则α∥β.【答案】②④【解析】①中只有当两条直线相交时l⊥α才恒成立,故①不正确;若l ∥α,则过l任作平面β与α相交,则交线必与l平行,由于β的任意性,故②正确;③中只有当n是α与β的交线时结论才恒成立,故③不正确,④正确。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学第二轮复习专题——立体几何专题复习1、如图,已知面ABC ⊥面BCD ,AB ⊥BC ,BC ⊥CD ,且AB=BC=CD ,设AD 与面AB C 所成角为α,AB与面ACD 所成角为β,则α与β的大小关系为(A )α<β (B )α=β (C )α>β (D )无法确定2、下列各图是正方体或正四面体,P ,Q ,R ,S 分别是所在棱的中点,这四个点中不共面...的一个图是PR SSQ RPQQSSPPQSS(A ) (B ) (C ) (D )3、在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,P ,Q 是对角线A 1C 上的点,且PQ =2a,则三棱锥P -BDQ 的体积为(A )3363a (B )3183a (C )3243a (D )无法确定 4、已知球的内接三棱锥的三条侧棱两两垂直,长度分别为3cm ,2cm 和3cm ,则此球的体积为(A )33312cm π (B )33316cm π (C )3316cm π (D )3332cm π5、如图,在一根长11cm ,外圆周长6cm 的圆柱形柱体外表面,用一根细铁丝缠绕,组成10个螺旋,如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为(A ) 61cm (B )157cm (C )1021cm (D )1037cm6、设a 、b 是两条不同的直线,α、β是两个不同的平面,则下列四个命题:① 若b a ⊥,α⊥a ,α⊄b ,则α//b ;②若α//a , βα⊥,则β⊥a ; ③若β⊥a ,βα⊥,则α//a 或α⊂a ;④若b a ⊥,α⊥a ,β⊥b ,则βα⊥ 其中正确命题的个数为 ( )A .0B .1C .2D .37、正三棱锥ABC S —的侧棱长和底面边长相等,如果E 、F 分别为SC,AB 的中点,那么异面直线EF 与SA 所成角为 ( ) A .090 B .060 C .045 D .030 8.右图是正方体的平面展开图,在这个正方体中: ①BM 与DE 平行; ②CN 与BE 是异面直线; ③CN 与BM 成60°角 ④DM 与BN 垂直以上四个命题中,正确的是 ( ) A .①②③ B .②④ C .②③④D .③④9.将棱长为1的正方体木块切削成一个体积最大的球,则该球的体积为( )A .π23B .π32 C .6π D .34π 10.正方体ABCD -A 1B 1C 1D 1中,E 是BC 的中点,则A 1C 与DE 所成的角的余弦为( )A .1515B .1510 C .630 D .1010 11.有3个命题(1)底面是正三角形,其余各个面都是等腰三角形的棱锥是三棱锥; (2)各个侧面都是等腰三角形的四棱锥是正四棱锥;(3)底面是正三角形,相邻两侧面所成的二面角都相等的三棱锥是正三棱锥。
其中假命题的个数是 ( ) A .0B .1C .2D .312、一个水平放置的平面图形的斜二测直观图是一个底角为45,腰和上底边均为1的等腰梯形,则这个平面图形的面积是 ( )A.2221+B. 22+C. 21+D. 221+ 13、在空间四边形ABCD 各边上分别取E 、F 、G 、H 四点,如果EF 和GH 能相交于点P ,那么(A )点P 必在直线AC 上 (B )点P 必在直线BD 上 (C )点P 必在平面ABC 内 (D )点P 必在平面上ABC 外14、设长方体的三条棱长分别为a ,b ,c ,若长方体所有棱的长度之和为24,一条对角线长度为5,体积为2,则=++cb a 111 (A )411 (B )114 (C )211 (D )112 15、若三棱锥A-BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等,则动点P 的轨迹与ABC 组成图形可能是:( )(A ) (B )(C ) (D )16、已知异面直线a 、b 成6︒0角,过空间一点p ,与a 、b 也都成6︒0角的直线,可以作( )A .1条B .2条C .3条D .4条 17.若a ,b ,l 是两两异面的直线,a 与b 所成的角是3π,l 与a 、l 与b 所成的角都是α, 则α的取值范围是A .[65,6ππ] B .[2,3ππ] C .[65,3ππ] D .[2,6ππ] 18、对于平面M 与平面N, 有下列条件: ①M 、N 都垂直于平面Q; ②M 、N 都平行于平面Q; ③ M 内不共线的三点到N 的距离相等; ④ l , M 内的两条直线, 且l // M, m // N; ⑤ l , m 是异面直线,且l // M, m // M; l // N, m // N, 则可判定平面M 与平面N 平行的条件的个数A .1B .2C .3D .419.如图,直三棱柱ABC -A 1B 1C 1的体积为V ,点P 、Q 分别在侧棱AA 1和CC 1上,AP=C 1Q ,则四棱锥B-APQC 的体积为(A )2V (B )3V (C )4V (D )5VACPQA 1B 1C 1ABA 1B 1C 1ACDE F20.棱长为a 的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为(A )33a (B )43a (C )63a (D )123a21.如图,在斜三棱柱A 1B 1C 1-ABC 中,∠BAC =900,BC 1⊥AC ,则C 1在底面ABC 上的射影H 必在 (A )直线AB 上 (B )直线BC 上 (C )直线AC 上 (D )△ABC 内部 22.如图所示,在多面体ABCDEF 中,已知ABCD 是边长为3的正方形,EF ∥AB ,EF =23,EF 与面AC 的距离为2,则该多面体的体积为 (A )29 (B )5 (C )6 (D )215 23.(天津卷6)如图,在棱长为2的正方体1111D C B A ABCD -中,O 是底面ABCD 的中心,E 、F 分别是1CC 、AD 的 中点。
那么异面直线OE 和1FD 所成的角的余弦值等于(A)510 (B)515 (C)54 (D)3224.(天津卷10)如图,在长方体1111D C B A ABCD -中,3,4,61===AA AD AB ,分别过BC 、11D A 的两个平行截面将长方体分成三部分, 其体积分别记为111DFD AEA V V -=,C F C B E B V V 11113==。
若1:4:1::321=V V V ,则截面11EFD A 的面积为 (A)104(B)38 (C)134 (D)1625.北纬45圈上有甲、乙两地,它们分别在东经50与东经140,则甲、乙两地的球面距离是(地球半径为R ) A .12R πB .13R πC .14R πDR 26.(福建卷16)如图1,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器。
当这个正六棱柱容器的底面边长为 时,其容积最大。
27、已知∠ACB=90º,S 为平面ABC 外一点,且∠SCA=∠SCB=60º,则直线SC 和平面ABC 所成的角为 .28、点A 是二面角α-l -β内一点,AB ⊥α于B ,AC ⊥β于C ,设AB=3,AC=2,∠BAC=60︒,则点A 到棱l 的距离是 . 29.由图(1)有关系''''PA B PAB S PA PB S PA PB ⋅=⋅ ,则由图(2)有关系'''P A B C P ABCV V --= 。
ABDEPAA A(1)(2)30.如图,在四棱锥P-ABCD中,E为CD上的动点,四边形ABCD为时,体积V P-AEB恒为定值(写上你认为正确的一个答案即可).31.在棱长为a的正方体ABCD—A1B1C1D1, E、F分别为BC与A1D1的中点,(1)求直线A1C与DE所成的角;(2)求直线AD与平面B1EDF所成的角;(3)求面B1EDF 与面ABCD所成的角。
在三棱锥S—ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=23,M、N分别为AB、SB的中点.(Ⅰ)证明:AC⊥SB;(Ⅱ)求二面角N—CM—B的大小;(Ⅲ)求点B到平面CMN的距离.32.如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F。
(1)证明PA//平面EDB;(2)证明PB⊥平面EFD;(3)求二面角C—PB—D的大小。
,(1)求点D 到AB 所在直线的距离. (2)求二面角A 1-BD -B 1的度数. 答案ADADADCDCADDAAB16、满分12分。
如图,以C 为原点建立空间直角坐标系O xyz -。
(I )解:依题意得B ()0 ,1 ,0,N ()1 ,0 ,1,∴()()()3011001222=-+-+-=(II )解:依题意得1A ()2 ,0 ,1,B ()0 ,1 ,0,C ()0 ,0 ,0,1B ()2 ,1 ,0。
∴()2 ,1 ,11-=BA ,()2 ,1 ,01=CB 。
⋅1BA 31=CB 。
6=,5= ∴ <cos ⋅1BA 301011=>CB (III )证明:依题意得1C ()2 ,0 ,0,M⎪⎭⎫⎝⎛2 ,21 ,21,=A 1()2 ,1 ,1--,=C 1⎪⎭⎫⎝⎛0 ,21 ,21 , ∴ ⋅A 1=C 1002121=++-,∴⊥ 1A C 1 ——12分17、本小题考查直线与平面平行,直线与平面垂直,二面角等基础知识,考查空间想象能力和推理论证能力,满分12分。
方法一:(1)证明:连结AC ,AC 交BD 于O ,连结EO 。
∵底面ABCD 是正方形,∴点O 是AC 的中点 在PAC ∆中,而⊂EO 平面 所以,PA // (2)证明:∵PD ⊥底面∵PD=DC ∴PC DE ⊥同样由PD ⊥底面ABCD ,得PD ⊥BC 。
∵底面ABCD 是正方形,有DC ⊥BC ,∴BC ⊥平面PDC 。
而⊂DE 平面PDC ,∴DE BC ⊥。
② 由①和②推得⊥DE 平面PBC 。
而⊂PB 平面PBC ,∴PB DE ⊥又PB EF ⊥且E EF DE = ,所以PB ⊥平面EFD 。
(3)解:由(2)知,DF PB ⊥,故EFD ∠是二面角C —PB —D 的平面角。
由(2)知,DB PD EF DE ⊥⊥,。
设正方形ABCD 的边长为a ,则a BD a DC PD 2,===a BD PD PB 322=+=, a DC PD PC 222=+=a PC DE 2221==。
