[推荐学习]2019年高考数学一轮复习课时分层训练40简单几何体的结构及其三视图和直观图理北师大版

合集下载

2019年高考数学一轮复习课时分层训练40简单几何体的结构及其三视图和直观图理北师大版

课时分层训练(四十) 简单几何体构造及其三视图与直观图A组根底达标一、选择题1．用任意一个平面截一个几何体，各个截面都是圆面，那么这个几何体一定是( )A．圆柱B．圆锥C．球体D．圆柱、圆锥、球体组合体C[截面是任意且都是圆面，那么该几何体为球体．]2．以下说法正确是( )A．棱柱两个底面是全等正多边形B．平行于棱柱侧棱截面是矩形C．{直棱柱}⊆{正棱柱}D．{正四面体}⊆{正三棱锥}D[因为选项A中两个底面全等，但不一定是正多边形；选项B 中一般棱柱不能保证侧棱与底面垂直，即截面是平行四边形，但不一定是矩形；选项C中{正棱柱}⊆{直棱柱}，故A、B、C都错；选项D中，正四面体是各条棱均相等正三棱锥，故正确．] 3．(2021·河北石家庄质检)一个三棱锥主视图与俯视图如图718所示，那么该三棱锥左视图可能为( )图718A B C DD[由题图可知，该几何体为如下图三棱锥，其中平面ACD⊥平面BCD，所以该三棱锥左视图可能为选项D.]4．(2021·东北三省四市模拟(一))如图719，某几何体三视图如下图，那么该几何体各条棱中最长棱与最短棱长度之与为( )【导学号：79140221】图719A．6 B．42C．25＋2 D．26＋2D[由三视图知，该几何体是底面腰长为2等腰直角三角形、长为4侧棱垂直于底面(垂足为腰与底边交点)三棱锥，所以该三棱锥最长棱棱长为42＋(22)2＝26，最短棱棱长为2，所以该几何体中最长棱与最短棱长度之与为26＋2，应选D.]5．我国古代数学家刘徽在学术研究中，不迷信古人，坚持实事求是．他对?九章算术?中“开立圆术〞给出公式产生质疑，为了证实自己猜想，他引入了一种新几何体“牟合方盖〞：如图7110以正方体相邻两个侧面为底做两次内切圆柱切割，然后剔除外部，剩下内核局部．如果“牟合方盖〞主视图与左视图都是圆，那么其俯视图形状为( )图7110 B[由题意得在正方体内做两次内切圆柱切割，得到几何体直观图如下图，由图易得其俯视图为B，应选B.]二、填空题6．(2021·福建龙岩联考)一水平放置平面四边形OABC，用斜二测画法画出它直观图O′A′B′C′如图7111所示，此直观图恰好是一个边长为1正方形，那么原平面四边形OABC面积为________．图71112 2 [因为直观图面积是原图形面积24倍，且直观图面积为1，所以原图形面积为2 2.]7．正方体棱长为1，其俯视图是一个面积为1正方形，左视图是一个面积为2矩形，那么该正方体主视图面积等于________．2 [由题意知此正方体主视图与左视图是一样，主视图面积与左视图面积相等为 2.]8．如图7112所示，在正方体ABCDA1B1C1D1中，点P是上底面A1B1C1D1内一动点，那么三棱锥PABC主视图与左视图面积比值为________.【导学号：79140222】图71121 [三棱锥PABC主视图与左视图为底边与高均相等三角形，故它们面积相等，面积比值为1.]三、解答题9．某几何体三视图如图7113所示．图7113(1)判断该几何体是什么几何体？(2)画出该几何体直观图．[解] (1)该几何体是一个正方体切掉两个14圆柱后几何体． (2)直观图如下图．10．如图7114，在四棱锥P ABCD 中，底面为正方形，PC 与底面ABCD 垂直，如图7115为该四棱锥主视图与左视图，它们是腰长为6 cm 全等等腰直角三角形．图7114 图7115(1)根据图中所给主视图、左视图，画出相应俯视图，并求出该俯视图面积；(2)求PA .[解] (1)该四棱锥俯视图为(内含对角线)边长为6 cm 正方形，如图，其面积为36 cm 2.(2)由左视图可求得PD ＝PC 2＋CD 2＝62＋62＝6 2.由主视图可知AD ＝6，且AD ⊥PD ，所以在Rt△APD 中，PA ＝PD 2＋AD 2＝(62)2＋62＝6 3 cm.B 组能力提升11．(2021·贵州适应性考试)如图7116，在正方体ABCD A 1B 1C 1D 1中，点P 是线段A 1C 1上动点，那么三棱锥PBCD俯视图与主视图面积之比最大值为( )图7116A．1 B．2C. 3 D．2D[设正方体棱长为1，那么由题意得三棱锥主视图面积S主视图＝12×1×1＝12，而三棱锥俯视图面积最大值为S俯视图＝S四边形ABCD＝1×1＝1，所以三棱锥PBCD俯视图与主视图面积之比最大值为S俯视图S主视图＝2，应选D.]12．正四棱锥VABCD中，底面面积为16，一条侧棱长为211，那么该棱锥高为________.【导学号：79140223】6 [如图，取正方形ABCD中心O，连接VO，AO，那么VO就是正四棱锥VABCD高．因为底面面积为16，所以AO＝2 2.因为一条侧棱长为211.所以VO＝VA2－AO2＝44－8＝6.所以正四棱锥VABCD高为6.]13．正三棱锥VABC主视图、左视图与俯视图如图7117所示．图7117(1)画出该三棱锥直观图；(2)求出左视图面积．[解] (1)直观图如下图．(2)根据三视图间关系可得BC ＝23， ∴左视图中VA ＝42－⎝ ⎛⎭⎪⎪⎫23×32×232＝23，∴S △VBC ＝12×23×23＝6.。

2019版高考数学一轮复习训练：基础与考点过关第八章立体几何初步

1. 公理 1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内．
公理 2：如果两个平面有一个公共点，那么它们还有其他公共点，这些公共点的集合是经过这个公共点的一条直线．
公理 3：经过不在同一条直线上的三点，有且只有一个平面．推论 1：经过一条直线和这条直线外的一点，有且只有一个平面．推论 2：经过两条相交直线，有且只有一个平面．推论 3：经过两条平行直线，有且只有一个平面． 2. 空间两条直线的位置关系
2
所以 GH∥BC，且 GH＝ BC，
所以四边形 BCHG为平行四边形． (2) 解： C，D，F，E 四点共面．理由如下：由
1 BE∥FA， BE＝ 2FA，点 G为 FA 的中点知，
BE∥ FG， BE＝ FG，所以四边形 BEFG为平行四边形，所以 EF∥BG. 由 (1) 知 BG∥CH， BG＝ CH，所以 EF∥CH，所以 EF 与 CH共面．又 D∈FH，所以 C， D， F， E 四点共面．
1 ∥FA， BE＝ 2FA，点 G， H 分别为 FA， FD的中点．
(1) 求证：四边形 BCHG是平行四边形． (2) C ， D， F，E 四点是否共面？为什么？
1 (1) 证明：因为点 G， H 分别为 FA， FD的中点，所以 GH∥AD， GH＝2AD.又 BC∥AD， BC
1 ＝ AD，
(1) 判定定理：过平面内一点与平面外一点的直线，和这个平面内不经过该点的直线是异面直线．
(2) 符号表示：若 l ? α， A?α ， B∈ α ， B?l ，则直线 AB 与 l 是异面直线．
5. 异面直线所成的角
(1) 定义：设 a，b 是异面直线，经过空间任意一点 O，作直线 a′∥ a， b′∥ b，我们

浙江专版2019版高考数学一轮复习学案：第七章立体几何+Word版含答案

第七章立体几何第一节空间几何体的结构特征及三视图与直观图1．简单几何体(1)多面体的结构特征2．直观图(1)画法：常用斜二测画法．(2)规则：①原图形中x轴、y轴、z轴两两垂直，直观图中，x′轴、y′轴的夹角为45°(或135°)，z′轴与x′轴和y′轴所在平面垂直．②原图形中平行于坐标轴的线段，直观图中仍平行于坐标轴．平行于x轴和z轴的线段在直观图中保持原长度不变，平行于y轴的线段长度在直观图中变为原来的一半．3．三视图(1)几何体的三视图包括正视图、侧视图、俯视图，分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线．(2)三视图的画法①基本要求：长对正，高平齐，宽相等．②画法规则：正侧一样高，正俯一样长，侧俯一样宽；看不到的线画虚线．[小题体验]1．若一个三棱柱的三视图如图所示，其俯视图为正三角形，则这个三棱柱的高和底面边长分别为( )A．2,2 3 B．22，2C．4,2 D．2,4解析：选D 由三视图可知，正三棱柱的高为2，底面正三角形的高为23，故底面边长为4，故选D.2．(教材习题改编)如图，长方体ABCDA′B′C′D′被截去一部分，其中EH∥A′D′，则剩下的几何体是________，截去的几何体是______．答案：五棱柱三棱柱1．台体可以看成是由锥体截得的，易忽视截面与底面平行且侧棱延长后必交于一点．2．空间几何体不同放置时其三视图不一定相同．3．对于简单组合体，若相邻两物体的表面相交，表面的交线是它们的分界线，在三视图中，易忽视实虚线的画法．[小题纠偏]1.如图，能推断这个几何体可能是三棱台的是( )A．A1B1＝2，AB＝3，B1C1＝3，BC＝4B ．A 1B 1＝1, AB ＝2，B 1C 1＝32，BC ＝3，A 1C 1＝2，AC ＝3C ．A 1B 1＝1，AB ＝2，B 1C 1＝32，BC ＝3，A 1C 1＝2，AC ＝4D ．AB ＝A 1B 1，BC ＝B 1C 1，CA ＝C 1A 1解析：选C 根据棱台是由棱锥截成的，可知A 1B 1AB ＝B 1C 1BC ＝A 1C 1AC，故A ，B 不正确，C 正确；D 项中满足这个条件的是一个三棱柱，不是三棱台，故D 不正确．2．用一个平行于水平面的平面去截球，得到如图所示的几何体，则它的俯视图是( )解析：选B 俯视图中显然应有一个被遮挡的圆，所以内圆是虚线，故选B. 3．(教材习题改编)利用斜二测画法得到的 ①三角形的直观图一定是三角形； ②正方形的直观图一定是菱形； ③等腰梯形的直观图可以是平行四边形； ④菱形的直观图一定是菱形．以上结论正确的个数是________．解析：由斜二测画法的规则可知①正确；②错误，是一般的平行四边形；③错误，等腰梯形的直观图不可能是平行四边形；而菱形的直观图也不一定是菱形，④也错误．答案：1考点一空间几何体的结构特征基础送分型考点——自主练透[题组练透]1．用任意一个平面截一个几何体，各个截面都是圆面，则这个几何体一定是( ) A ．圆柱 B ．圆锥C ．球体D ．圆柱、圆锥、球体的组合体解析：选C 截面是任意的且都是圆面，则该几何体为球体． 2．给出下列几个命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；②底面为正多边形，且有相邻两个侧面与底面垂直的棱柱是正棱柱；③棱台的上、下底面可以不相似，但侧棱长一定相等．其中正确命题的个数是( )A．0 B．1C．2 D．3解析：选B ①不一定，只有这两点的连线平行于轴时才是母线；②正确；③错误，棱台的上、下底面是相似且对应边平行的多边形，各侧棱延长线交于一点，但是侧棱长不一定相等．3．给出下列命题：①棱柱的侧棱都相等，侧面都是全等的平行四边形；②若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直；③在四棱柱中，若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱；④存在每个面都是直角三角形的四面体．其中正确命题的序号是________．解析：①不正确，根据棱柱的定义，棱柱的各个侧面都是平行四边形，但不一定全等；②正确，若三棱锥的三条侧棱两两垂直，则三个侧面构成的三个平面的二面角都是直二面角；③正确，因为两个过相对侧棱的截面的交线平行于侧棱，又垂直于底面；④正确，如图，正方体ABCDA1B1C1D1中的三棱锥C1ABC，四个面都是直角三角形．答案：②③④[谨记通法]解决与空间几何体结构特征有关问题的3个技巧(1)把握几何体的结构特征，要多观察实物，提高空间想象能力；(2)紧扣结构特征是判断的关键，熟悉空间几何体的结构特征，依据条件构建几何模型；(3)通过反例对结构特征进行辨析．考点二空间几何体的三视图重点保分型考点——师生共研[典例引领]1．(2018·东北四市联考)如图，在正方体ABCDA1B1C1D1中，P是线段CD的中点，则三棱锥PA1B1A的侧视图为( )解析：选D 如图，画出原正方体的侧视图，显然对于三棱锥PA1B1A，B(C)点均消失了，其余各点均在，从而其侧视图为D.2．(2018·杭州模拟)已知三棱锥的正视图与俯视图如图所示，俯视图是边长为2的正三角形，那么该三棱锥的侧视图可能为( )解析：选B 由正视图可看出长为2的侧棱垂直于底面，侧视图为直角三角形，直角边长为2，另一直角边为底边三角形的高 3.故侧视图可能为B.[由题悟法]1．已知几何体，识别三视图的技巧已知几何体画三视图时，可先找出各个顶点在投影面上的投影，然后再确定线在投影面上的实虚．2．已知三视图，判断几何体的技巧(1)对柱、锥、台、球的三视图要熟悉．(2)明确三视图的形成原理，并能结合空间想象将三视图还原为直观图．(3)遵循“长对正、高平齐、宽相等”的原则．[提醒] 对于简单组合体的三视图，应注意它们的交线的位置，区分好实线和虚线的不同．[即时应用]1．(2018·沈阳教学质量监测)“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体．它由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好似两个扣合(牟合)在一起的方形伞(方盖)．其直观图如图，图中四边形是为体现其直观性所作的辅助线．当其正视图和侧视图完全相同时，它的俯视图可能是( )解析：选B 根据直观图以及图中的辅助四边形分析可知，当正视图和侧视图完全相同时，俯视图为B ，故选B.2．一个几何体的三视图如图所示，则该几何体的直观图可以是( )解析：选D 由俯视图是圆环可排除A 、B 、C ，进一步将已知三视图还原为几何体，可得选项D.考点三空间几何体的直观图重点保分型考点——师生共研[典例引领](2018·杭州模拟)在等腰梯形ABCD 中，上底CD ＝1，腰AD ＝CB ＝2，下底AB ＝3，以下底所在直线为x 轴，则由斜二测画法画出的直观图A ′B ′C ′D ′的面积为________．解析：画出等腰梯形ABCD 的实际图形及直观图A ′B ′C ′D ′如图所示，因为OE ＝22－12＝1，所以O ′E ′＝12，E ′F ′＝24.所以直观图A ′B ′C ′D ′的面积为S ′＝12×(1＋3)×24＝22.答案：22[由题悟法]原图与直观图中的“三变”与“三不变”(1)“三变”⎩⎪⎨⎪⎧坐标轴的夹角改变与y 轴平行的线段的长度改变减半图形改变(2)“三不变”⎩⎪⎨⎪⎧平行性不变与x 轴平行的线段长度不变相对位置不变[即时应用]如图，矩形O ′A ′B ′C ′是水平放置的一个平面图形的直观图，其中O ′A ′＝6 cm ，O ′C ′＝2 cm ，则原图形是( )A ．正方形B ．矩形C ．菱形D ．一般的平行四边形解析：选C 如图，在原图形OABC 中，应有OD ＝2O ′D ′＝2×22＝4 2 cm ，CD ＝C ′D ′＝2 cm.∴OC ＝OD 2＋CD 2＝22＋22＝6 cm ，∴OA ＝OC ，故四边形OABC 是菱形．一抓基础，多练小题做到眼疾手快1．某几何体的正视图和侧视图完全相同，均如图所示，则该几何体的俯视图一定不可能是( )解析：选D 几何体的正视图和侧视图完全一样，则几何体从正面看和侧面看的长度相等，只有等边三角形不可能．2．下列说法正确的是( )A．棱柱的两个底面是全等的正多边形B．平行于棱柱侧棱的截面是矩形C．{直棱柱}⊆{正棱柱}D．{正四面体}⊆{正三棱锥}解析：选D 因为选项A中两个底面全等，但不一定是正多边形；选项B中一般的棱柱不能保证侧棱与底面垂直，即截面是平行四边形，但不一定是矩形；选项C中{正棱柱}⊆{直棱柱}，故A、B、C都错；选项D中，正四面体是各条棱均相等的正三棱锥，故正确．3．某几何体的三视图如图所示，那么这个几何体是( )A．三棱锥B．四棱锥C．四棱台D．三棱台解析：选A 因为正视图和侧视图都为三角形，可知几何体为锥体，又因为俯视图为三角形，故该几何体为三棱锥．4.在如图所示的直观图中，四边形O′A′B′C′为菱形且边长为2 cm，则在直角坐标系xOy中，四边形ABCO的形状为________，面积为________cm2.解析：由斜二测画法的特点知该平面图形是一个长为4 cm，宽为2 cm的矩形，所以四边形ABCO的面积为8 cm2.答案：矩形85.已知某几何体的三视图如图所示，正视图和侧视图都是矩形，俯视图是正方形，在该几何体上任意选择4个顶点，以这4个点为顶点的几何体的形状给出下列命题：①矩形；②有三个面为直角三角形，有一个面为等腰三角形的四面体；③两个面都是等腰直角三角形的四面体．其中正确命题的序号是________．解析：由三视图可知，该几何体是正四棱柱，作出其直观图，ABCDA1B1C1D1，如图，当选择的4个点是B1，B，C，C1时，可知①正确；当选择的4个点是B，A，B1，C时，可知②正确；易知③不正确．答案：①②二保高考，全练题型做到高考达标1．(2018·台州模拟)一个简单几何体的正视图、俯视图如图所示，则其侧视图不可能为( )A．正方形B．圆C．等腰三角形D．直角梯形解析：选D 该几何体是一个长方体时，其中一个侧面为正方形，A可能；该几何体是一个横放的圆柱时，B可能；该几何体是横放的三棱柱时，C可能，只有D不可能．2．如图所示是水平放置三角形的直观图，点D是△ABC的BC边中点，AB，BC分别与y′轴、x′轴平行，则三条线段AB，AD，AC中( )A．最长的是AB，最短的是ACB．最长的是AC，最短的是ABC．最长的是AB，最短的是ADD．最长的是AC，最短的是AD解析：选B 由条件知，原平面图形中AB⊥BC，从而AB＜AD＜AC.3．(2018·沈阳教学质量监测)如图，网格纸的各小格都是正方形，粗实线画出的是一个凸多面体的三视图(两个矩形，一个直角三角形)，则这个几何体可能为( )A．三棱台B．三棱柱C．四棱柱D．四棱锥解析：选B 根据三视图的法则：长对正，高平齐，宽相等，可得几何体如图所示，这是一个三棱柱．4.(2018·温州第八高中质检)如图，水平放置的三棱柱的侧棱长和底边长均为2，且侧棱AA1⊥平面A1B1C1，正视图是边长为2的正方形，该三棱柱的侧视图面积为( )A．4 B．2 3C．2 2 D. 3解析：选B 由题可得，该几何体的侧视图是一个长方形，其底边长是底面正三角形的高3，高为2，所以侧视图的面积为S＝2 3.5．已知四棱锥PABCD的三视图如图所示，则四棱锥PABCD的四个侧面中面积最大的是( )A ．3B ．2 5C ．6D ．8解析：选C 四棱锥如图所示，取AD 的中点N ，BC 的中点M ，连接PM ，PN ，则PM ＝3，PN ＝5，S △PAD ＝12×4×5＝25，S △PAB ＝S △PDC ＝12×2×3＝3， S △PBC ＝12×4×3＝6.所以四个侧面中面积最大的是6.6.(2018·台州模拟)如图所示，在正方体ABCD A1B 1C 1D 1中，点E 为棱BB 1的中点，若用过点A ，E ，C 1的平面截去该正方体的上半部分，则剩余几何体的侧视图为( )解析：选C 取DD 1的中点F ，连接AF ，FC 1，则过点A ，E ，C 1的平面即为面AEC 1F ，所以剩余几何体的侧视图为选项C.7．设有以下四个命题：①底面是平行四边形的四棱柱是平行六面体； ②底面是矩形的平行六面体是长方体； ③直四棱柱是直平行六面体； ④棱台的相对侧棱延长后必交于一点．其中真命题的序号是________．解析：命题①符合平行六面体的定义，故命题①是正确的；底面是矩形的平行六面体的侧棱可能与底面不垂直，故命题②是错误的；因为直四棱柱的底面不一定是平行四边形，故命题③是错误的；命题④由棱台的定义知是正确的．答案：①④8．一个圆台上、下底面的半径分别为3 cm 和8 cm ，若两底面圆心的连线长为12 cm ，则这个圆台的母线长为________cm.解析：如图，过点A 作AC ⊥OB ，交OB 于点C . 在Rt △ABC 中，AC ＝12 cm ，BC ＝8－3＝5 (cm)． ∴AB ＝122＋52＝13(cm)．答案：139．已知正三角形ABC 的边长为2，那么△ABC 的直观图△A ′B ′C ′的面积为________．解析：如图，图①、图②所示的分别是实际图形和直观图．从图②可知，A ′B ′＝AB ＝2，O ′C ′＝12OC ＝32， C ′D ′＝O ′C ′sin 45°＝32×22＝64. 所以S △A ′B ′C ′＝12A ′B ′·C ′D ′＝12×2×64＝64.答案：6410．已知正三棱锥V ABC 的正视图、侧视图和俯视图如图所示．(1)画出该三棱锥的直观图； (2)求出侧视图的面积．解：(1)直观图如图所示．(2)根据三视图间的关系可得BC ＝23，∴侧视图中VA ＝42－⎝ ⎛⎭⎪⎫23×32×232＝23，∴S △VBC ＝12×23×23＝6.三上台阶，自主选做志在冲刺名校1．用若干块相同的小正方体搭成一个几何体，该几何体的三视图如图所示，则搭成该几何体需要的小正方体的块数是( )A ．8B ．7C ．6D ．5解析：选C 画出直观图，共六块．2．(2018·湖南东部六校联考)某三棱锥的三视图如图所示，该三棱锥的四个面的面积中，最大的面积是( )A ．4 3B ．8 3C ．47D ．8解析：选C 设该三棱锥为P ABC ，其中PA ⊥平面ABC ，PA ＝4，则由三视图可知△ABC 是边长为4的等边三角形，故PB ＝PC ＝42，所以S △ABC ＝12×4×23＝43，S △PAB ＝S △PAC ＝12×4×4＝8，S △PBC ＝12×4×22－22＝47，故四个面中面积最大的为S △PBC ＝47，选C.3.如图，在四棱锥P ABCD 中，底面为正方形，PC 与底面ABCD 垂直，下图为该四棱锥的正视图和侧视图，它们是腰长为6 cm 的全等的等腰直角三角形．(1)根据图中所给的正视图、侧视图，画出相应的俯视图，并求出该俯视图的面积；(2)求PA.解：(1)该四棱锥的俯视图为(内含对角线)边长为6 cm的正方形，如图，其面积为36 cm2.(2)由侧视图可求得PD＝PC2＋CD2＝62＋62＝6 2.由正视图可知AD＝6，且AD⊥PD，所以在Rt△APD中，PA ＝PD2＋AD2＝22＋62＝6 3 cm.第二节空间几何体的表面积与体积1．圆柱、圆锥、圆台的侧面展开图及侧面积公式2．空间几何体的表面积与体积公式[小题体验]1．如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( )A ．20πB ．24πC ．28πD ．32π解析：选C 由三视图知该几何体是圆锥与圆柱的组合体，设圆柱底面圆半径为r ，周长为c ，圆锥母线长为l ，圆柱高为h .由图得r ＝2，c ＝2πr ＝4π，h ＝4，由勾股定理得：l ＝22＋32＝4，S 表＝πr 2＋ch ＋12cl ＝4π＋16π＋8π＝28π.2．(教材习题改编)某几何体的三视图如图所示，则该几何体的体积为________．解析：由三视图可知，该几何体是一个直三棱柱，其底面为侧视图，该侧视图是底边为2，高为3的三角形，正视图的长为三棱柱的高，故h ＝3，所以该几何体的体积V ＝S ·h ＝⎝ ⎛⎭⎪⎫12×2×3×3＝3 3. 答案：3 33．若球O 的表面积为4π，则该球的体积为________．解析：由题可得，设该球的半径为r ，则其表面积为S ＝4πr 2＝4π，解得r ＝1.所以其体积为V ＝43πr 3＝43π.答案：43π1．求组合体的表面积时，组合体的衔接部分的面积问题易出错．2．由三视图计算几何体的表面积与体积时，由于几何体的还原不准确及几何体的结构特征认识不准易导致失误．3．易混侧面积与表面积的概念． [小题纠偏]1．(教材习题改编)圆柱的底面直径与高都等于球的直径，则球的体积与圆柱体积之比为________，球的表面积与圆柱的侧面积之比为________．答案：2∶3 1∶12．若某几何体的三视图如图所示，则此几何体的表面积是________．解析：由三视图可知，该几何体由一个正四棱柱和一个棱台组成，其表面积S ＝3×4×2＋2×2×2＋4×22×2＋4×6＋12×(2＋6)×2×2＝72＋16 2.答案：72＋16 2考点一空间几何体的表面积基础送分型考点——自主练透[题组练透]1.某几何体的三视图如图所示，则该几何体的表面积等于( )A ．8＋2 2B ．11＋2 2C ．14＋2 2D ．15解析：选 B 由三视图知，该几何体是一个直四棱柱，上、下底面为直角梯形，如图所示．直角梯形斜腰长为12＋12＝2，所以底面周长为4＋2，侧面积为2×(4＋2)＝8＋22，两底面的面积和为2×12×1×(1＋2)＝3，所以该几何体的表面积为8＋22＋3＝11＋2 2.2．(2018·浙江新高考联盟高三期初联考)如图是某四棱锥的三视图，则该几何体的表面积等于( )A ．34＋6 5B ．44＋12 5C ．34＋6 3D ．32＋6 5解析：选A 由三视图知几何体底面是一个长为6，宽为2的矩形，高为4的四棱锥，所以该几何体的表面积为12×6×25＋12×6×4＋2×12×2×5＋6×2＝34＋65，故选A.3．如图，网格纸上小正方形的边长为1，粗线是一个棱锥的三视图，则该棱锥的表面积为( )A ．6＋42＋2 3B ．8＋4 2C ．6＋6 2D ．6＋22＋4 3解析：选A 由三视图可知该棱锥为如图所示的四棱锥P ABCD ，S △PAB＝S △PAD ＝S △PDC ＝12×2×2＝2，S △PBC ＝12×22×22×sin 60°＝23，S 四边形ABCD ＝22×2＝42，故该棱锥的表面积为6＋42＋2 3.[谨记通法]几何体的表面积的求法(1)求表面积问题的思路是将立体几何问题转化为平面问题，即空间图形平面化，这是解决立体几何的主要出发点．(2)求不规则几何体的表面积时，通常将所给几何体分割成基本的柱、锥、台体，先求这些柱、锥、台体的表面积，再通过求和或作差求得几何体的表面积．注意衔接部分的处理．考点二空间几何体的体积重点保分型考点——师生共研[典例引领]1．(2018·金华高三期末考试)某几何体的三视图如图所示，则该几何体的体积为( )A.223 B.233C.423D.433解析：选D 由三视图可知该几何体是一个以俯视图为底面的四棱锥，其直观图如图所示．底面ABCD 的面积为2×2＝4，高PO ＝3，故该几何体的体积V ＝13×4×3＝433.2．(2018·宁波十校联考)某几何体的三视图如图所示，则该几何体的体积等于________，表面积等于________．解析：如图，由三视图可知该几何体是底面半径为2，高为3的圆柱的一半，故该几何体的体积为12×π×22×3＝6π，表面积为2×12×π×22＋4×3＋π×2×3＝10π＋12.答案：6π 12＋10π[由题悟法]有关几何体体积的类型及解题策略[即时应用]1．(2018·西安质检)某几何体的三视图如图所示，该几何体的体积为( )A.43 B ．52 C.73 D ．3解析：选A 根据几何体的三视图，得该几何体是下部为直三棱柱，上部为三棱锥的组合体，如图所示．则该几何体的体积是V 几何体＝V 三棱柱＋V 三棱锥＝12×2×1×1＋13×12×2×1×1＝43.2．(2018·杭州高级中学模拟)一个几何体的三视图如图所示，则该几何体的体积为( )A ．1B ．32 C.12D.34解析：选C 由题可得，该几何体是一个四棱锥，底面是上下底边分别为1和2，高为1的直角梯形，又四棱锥的高为1.所以该几何体的体积为V ＝13×12×(1＋2)×1×1＝12.3.(2018·温州高三一模)如图，一个简单几何体的三视图的正视图与侧视图都是边长为1的正三角形，其俯视图的轮廓为正方形，则该几何体的体积为________，表面积为________．解析：如图，还原三视图为正四棱锥，易得正四棱锥的高为32，底面积为1，体积V ＝13×1×32＝36；易得正四棱锥侧面的高为⎝ ⎛⎭⎪⎫322＋⎝ ⎛⎭⎪⎫122＝1，所以表面积S ＝4×12×1×1＋1＝3. 答案：363 考点三与球有关的切、接问题题点多变型考点——多角探明 [锁定考向]与球相关的切、接问题是高考命题的热点，也是考生的难点、易失分点，命题角度多变．常见的命题角度有： (1)球与柱体的切、接问题；(2)球与锥体的切、接问题．[题点全练]角度一：球与柱体的切、接问题1．已知直三棱柱ABC A 1B 1C 1的6个顶点都在球O 的球面上，若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，则球O 的半径为( )A.3172B ．210 C.132D ．310解析：选C 如图，由球心作平面ABC 的垂线，则垂足为BC 的中点M .又AM ＝12BC ＝52，OM ＝12AA 1＝6，所以球O 的半径R ＝OA ＝⎝ ⎛⎭⎪⎫522＋62＝132.2.如图，已知球O 是棱长为1的正方体ABCD A 1B 1C 1D 1的内切球，则平面ACD1截球O 的截面面积为( )A.66π B.π3C.π6D.33π 解析：选C 平面ACD 1截球O 的截面为△ACD 1的内切圆．因为正方体的棱长为1，所以AC ＝CD 1＝AD 1＝2，所以内切圆的半径r ＝22×tan 30°＝66，所以S ＝πr 2＝π×16＝16π.角度二：球与锥体的切、接问题3．(2018·绍兴质检)四棱锥P ABCD 的底面ABCD 是边长为6的正方形，且PA ＝PB ＝PC ＝PD ，若一个半径为1的球与此四棱锥所有面都相切，则该四棱锥的高是( )A ．6B ．5C.92D.94解析：选D 过点P 作PH ⊥平面ABCD 于点H .由题知，四棱锥P ABCD 是正四棱锥，内切球的球心O 应在四棱锥的高PH 上．过正四棱锥的高作组合体的轴截面如图，其中PE ，PF 是斜高，M 为球面与侧面的一个切点．设PH ＝h ，易知Rt △PMO ∽Rt △PHF ，所以OM FH ＝PO PF ，即13＝h －1h 2＋32，解得h ＝94.4．(2017·全国卷Ⅰ)已知三棱锥S ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径．若平面SCA ⊥平面SCB ，SA ＝AC ，SB ＝BC ，三棱锥S ABC 的体积为9，则球O 的表面积为________．解析：如图，连接AO ，OB ，∵SC 为球O 的直径， ∴点O 为SC 的中点， ∵SA ＝AC ，SB ＝BC ， ∴AO ⊥SC ，BO ⊥SC ，∵平面SCA ⊥平面SCB ，平面SCA ∩平面SCB ＝SC ， ∴AO ⊥平面SCB ，设球O 的半径为R ，则OA ＝OB ＝R ，SC ＝2R . ∴V S ABC ＝V A SBC ＝13×S △SBC ×AO＝13×⎝ ⎛⎭⎪⎫12×SC ×OB ×AO ，即9＝13×⎝ ⎛⎭⎪⎫12×2R ×R ×R ，解得 R ＝3，∴球O 的表面积为S ＝4πR 2＝4π×32＝36π. 答案：36π[通法在握]解决与球有关的切、接问题，其通法是作截面，将空间几何问题转化为平面几何问题求解，其解题的思维流程是：[演练冲关]1．一个六棱柱的底面是正六边形，侧棱垂直于底面，所有棱的长都为1，顶点都在同一个球面上，则该球的体积为( )A ．20πB.205π3C ．5πD.55π6解析：选D 由题意知六棱柱的底面正六边形的外接圆半径r ＝1，其高h ＝1，∴球半径为R ＝r 2＋⎝ ⎛⎭⎪⎫h 22＝1＋14＝52，∴该球的体积V ＝43πR 3＝43×⎝ ⎛⎭⎪⎫523π＝55π6. 2．(2018·镇海期中)一个棱长为6的正四面体纸盒内放一个正方体，若正方体可以在纸盒内任意转动，则正方体体积的最大值为________．解析：由题可得，要使正方体可以在纸盒内任意转动，则只需该正方体在正四面体的内接球内即可．因为正四面体的棱长为6，所以其底面正三角形的高为33，正四面体的高为26，则该正四面体的内球的半径为62，设该正方体的边长为a ，要满足条件，则3a ≤6，即a ≤ 2.所以正方体的最大体积为V ＝a 3≤2 2.答案：2 2一抓基础，多练小题做到眼疾手快1．(2018·浙江名校联考)“某几何体的三视图完全相同”是“该几何体为球”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件解析：选B 由题可得，球的三个视图都是圆，所以三视图完全相同；三视图完全相同的几何体除了球，还有正方体，所以是必要不充分条件．2．(2018·长兴中学适应性测试)一个几何体的三视图如图所示，则该几何体的体积为( )A ．64B ．72C ．80D ．112解析：选C 由题可得，该几何体是一个棱长为4的正方体与一个底面是边长为4的正方形，高为3的四棱锥的组合体，所以其体积为V ＝43＋13×42×3＝80.3．如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是28π3，则它的表面积是( )A ．17πB ．18πC ．20πD ．28π解析：选A 由几何体的三视图可知，该几何体是一个球体去掉上半球的14，得到的几何体如图．设球的半径为R ，则43πR 3－18×43πR 3＝283π，解得R ＝2.因此它的表面积为78×4πR 2＋34πR 2＝17π.故选A.4．(2018·嘉兴模拟)如图是一个几何体的三视图，若它的体积是33，则a ＝________，该几何体的表面积为________．解析：由题可得，该几何体是一个水平放置的三棱柱，其底面是一个底边长为2、高为a 的等腰三角形，高为3.因为其体积为33，所以V ＝12×2a ×3＝3a ＝33，解得a ＝ 3.所以该几何体的表面积为S ＝2×12×2×3＋2×3×3＝23＋18.答案： 3 23＋185．(2018·丽水模拟)若三棱锥P ABC 的最长的棱PA ＝2，且各面均为直角三角形，则此三棱锥的外接球的体积是________，表面积是________．解析：如图，根据题意，可把该三棱锥补成长方体，则该三棱锥的外接球即该长方体的外接球，易得外接球的半径R ＝12PA ＝1，所以该三棱锥的外接球的体积V ＝43×π×13＝43π，表面积S ＝4πR 2＝4π.答案：43π 4π二保高考，全练题型做到高考达标1．圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为( )A ．7B ．6C ．5D ．3解析：选A 设圆台较小底面半径为r ，则另一底面半径为3r .由S ＝π(r ＋3r )·3＝84π，解得r ＝7.2．一个六棱锥的体积为23，其底面是边长为2的正六边形，侧棱长都相等，则该六棱锥的侧面积为( )A ．6B ．8C ．12D ．24解析：选C 由题意可知该六棱锥为正六棱锥，正六棱锥的高为h ，侧面的斜高为h ′. 由题意，得13×6×34×22×h ＝23，∴h ＝1， ∴斜高h ′＝12＋32＝2，∴S 侧＝6×12×2×2＝12.故选C.3．(2018·温州十校联考)已知某个几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的体积是( )A ．4 B.163 C ．8D.323解析：选 B 由题可得，该几何体是一个底面为长方形的四棱锥，所以其体积为V ＝13×4×2×2＝163.4．(2018·兰州实战考试)一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个等腰直角三角形，则该几何体外接球的体积为( )A.32π B.32C ．3πD ．3解析：选A 由题意得，该几何体为四棱锥，且该四棱锥的外接球即为棱长为1的正方体的外接球，其半径为32，故体积为43π⎝ ⎛⎭⎪⎫323＝32π，故选A. 5．(2018·宁波十校联考)如图，某多面体的三视图中正视图、侧视图和俯视图的外轮廓分别为直角三角形、直角梯形和直角三角形，则该多面体的各条棱中，最长的棱的长度为( )A ．2 2 B.10 C ．2 3D.13解析：选C 由题可得，该几何体是水平放置的四棱锥，其底面是一个直角梯形．所以其最长的棱的长度为22＋22＋22＝2 3.6．(2018·衢州调研)已知某几何体的三视图如图所示，则此几何体的体积是________；表面积是________．。

2019版高考数学一轮复习第七章立体几何分层限时跟踪练(7).doc

非常考案通用版2019版高考数学一轮复习第七章立体几何分层限时跟踪练(7)一、选择题1．一个几何体的三视图如图7212所示，其中俯视图与侧视图均为半径是2的圆，则这个几何体的体积是( )图7212A ．16 πB ．14 πC ．12 πD ．8 π【解析】由三视图可知，该几何体为一个球切去四分之一个球后剩余部分，由于球的半径为2，所以这个几何体体积为34×43π×23＝8π.【答案】 D2．(2015·北京高考)某三棱锥的三视图如图7213所示，则该三棱锥的表面积是( )图7213A ．2＋ 5B ．4＋ 5C ．2＋2 5D ．5【解析】作出三棱锥的示意图如图，在△ABC 中，作AB 边上的高CD ，连接SD .在三棱锥S ABC 中，SC ⊥底面ABC ，SC ＝1，底面三角形ABC 是等腰三角形，AC ＝BC ，AB 边上的高CD ＝2，AD ＝BD ＝1，斜高SD ＝5，AC ＝BC ＝ 5.∴S表＝S △ABC ＋S △SAC ＋S △SBC ＋S △SAB ＝12×2×2＋12×1×5＋12×1×5＋12×2×5＝2＋2 5.【答案】 C3．(2015·全国卷Ⅱ)一个正方体被一个平面截去一部分后，剩余部分的三视图如图7214，则截去部分体积与剩余部分体积的比值为( )图7214A.18B.17C.16D.15【解析】由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分，如图所示，截去部分是一个三棱锥．设正方体的棱长为1，则三棱锥的体积为V1＝13×12×1×1×1＝16，剩余部分的体积V2＝13－16＝56.所以V1V2＝1656＝15，故选D.【答案】 D4．(2015·安徽高考)一个四面体的三视图如图7215所示，则该四面体的表面积是( )图7215A．1＋ 3 B．2＋ 3C．1＋2 2 D．2 2【解析】根据三视图还原几何体如图所示，其中侧面ABD ⊥底面BCD ，另两侧面ABC 、ACD 为等边三角形，则S 表面积＝2×12×2×1＋2×34×(2)2＝2＋ 3. 【答案】 B5．正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为( )A. 81π4 B ．16π C ．9π D.27π4【解析】如图所示，设球半径为R ，底面中心为O ′且球心为O ，∵正四棱锥P ABCD 中AB ＝2，∴AO ′＝ 2. ∵PO ′＝4， ∴在Rt △AOO ′中，AO 2＝AO ′2＋OO ′2，∴R 2＝(2)2＋(4－R )2，解得R ＝94，∴该球的表面积为4πR 2＝4π×⎝ ⎛⎭⎪⎫942＝81π4，故选A. 【答案】 A 二、填空题6．如图7216，正方体ABCD A 1B 1C 1D 1的棱长为1，E ，F 分别为线段AA 1，B 1C 上的点，则三棱锥D 1EDF 的体积为．图7216【解析】 VD 1EDF ＝VF DD 1E ＝13 ·AB ＝13×12×1×1×1＝16.【答案】 167．设甲、乙两个圆柱的底面积分别为S 1，S 2，体积分别为V 1，V 2，若它们的侧面积相等，且S 1S 2＝94，则V 1V 2的值是．【解析】设甲、乙两圆柱的底面半径分别为r 1，r 2，母线长分别为l 1，l 2，则由S 1S 2＝94得r 1r 2＝32.又两圆柱侧面积相等，即2πr 1l 1＝2πr 2l 2，则l 1l 2＝r 2r 1＝23，所以V 1V 2＝S 1l 1S 2l 2＝94×23＝32. 【答案】 328．已知一个棱长为2的正方体，被一个平面截后所得几何体的三视图如图7217所示，则该几何体的体积是．图7217【解析】根据三视图，画出其直观图，几何体由正方体切割而成，即正方体截去一个棱台．如图所示．其中正方体棱长为2，AF ＝AE ＝1，故所求几何体体积为V ＝23－13×2×12×1×1＋12×2×2＋12×1×1×12×2×2＝173. 【答案】173三、解答题9．(2015·荥阳月考)已知球的两平行截面的面积分别为5π和8π，它位于球心的同一侧，且相距为1，求这个球的体积．【解】如图，设以r 1为半径的截面面积为5π，圆心为O 1，以r 2为半径的截面面积为8π，圆心为O 2，O 1O 2＝1，球的半径为R ，设OO 2＝x ，可得下列关系式：r 22＝R 2－x 2，πr 22＝π(R 2－x 2)＝8π，r 21＝R 2－(x ＋1)2，πr 21＝π[R 2－(x ＋1)2]＝5π，∴R 2－x 2＝8，R 2－(x ＋1)2＝5，解得R ＝3，∴球的体积为V ＝43πR 3＝43π×33＝36π.10．(2015·全国卷Ⅱ)如图7218，长方体ABCD A 1B 1C 1D 1中，AB ＝16，BC ＝10，AA 1＝8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E ＝D 1F ＝4.过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形．图7218(1)在图中画出这个正方形(不必说明画法和理由)； (2)求平面α把该长方体分成的两部分体积的比值．【解】 (1)交线围成的正方形EHGF 如图所示．(2)如图，作EM ⊥AB ，垂足为M ，则AM ＝A 1E ＝4，EB 1＝12，EM ＝AA 1＝8. 因为四边形EHGF 为正方形，所以EH ＝EF ＝BC ＝10. 于是MH ＝EH 2－EM 2＝6，AH ＝10，HB ＝6. 故S 四边形A 1EHA ＝12×(4＋10)×8＝56，S 四边形EB 1BH ＝12×(12＋6)×8＝72.因为长方体被平面α分成两个高为10的直棱柱，所以其体积的比值为97⎝ ⎛⎭⎪⎫79也正确. [能力练]扫盲区提素能1．(2015·山东高考)在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3 B.4π3 C.5π3D ．2π【解析】过点C 作CE 垂直AD 所在直线于点E ，梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径，线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径，ED 为高的圆锥，如图所示，该几何体的体积为V ＝V 圆柱－V 圆锥＝π·AB 2·BC －13·π·CE 2·DE ＝π×12×2－13π×12×1＝5π3，选C. 【答案】 C2．如图7219，直三棱柱ABC A 1B 1C 1的六个顶点都在半径为1的半球面上，AB ＝AC ，侧面BCC 1B 1是半球底面圆的内接正方形，则侧面ABB 1A 1的面积为( )图7219A ．2B ．1 C. 2 D.22【解析】由题意知，球心在侧面BCC 1B 1的中心O 上，BC 为截面圆的直径，∴∠BAC ＝90°，△ABC 的外接圆圆心N 是BC 的中点，同理△A 1B 1C 1的外心M 是B 1C 1的中点．设正方形BCC 1B 1的边长为x ，在Rt △OMC 1中，OM ＝x 2，MC 1＝x 2，OC 1＝R ＝1(R 为球的半径)，∴⎝ ⎛⎭⎪⎫x 22＋⎝ ⎛⎭⎪⎫x 22＝1，即x ＝2，则AB ＝AC ＝1，∴S 矩形ABB 1A 1＝2×1＝ 2.【答案】 C3．圆锥的全面积为15 π cm 2，侧面展开图的圆心角为60°，则该圆锥的体积为cm 3.【解析】设底面圆的半径为r ，母线长为a ，则侧面积为12×(2πr )a ＝πra .由题意得⎩⎪⎨⎪⎧πra ＋πr 2＝15π，πra ＝16πa 2，解得⎩⎪⎨⎪⎧r 2＝157，a 2＝36×157，故圆锥的高h ＝a 2－r 2＝53，所以体积V ＝13πr 2h ＝13π×157×53＝2537π(cm 3)．【答案】2573π 4．已知正四面体的俯视图如图7220所示，其中四边形ABCD 是边长为2的正方形，则这个正四面体的表面积为，体积为．图7220【解析】由题意知正四面体的直观图E ACF 补成正方体如图所示．由正方体棱长为2，知正四面体的棱长为22，正四面体表面积为34×(22)2×4＝8 3.点E 到平面ACF 的距离为222－⎝⎛⎭⎪⎫32×22×232＝433. 正四面体的体积为13×433×34×(22)2＝83.【答案】 8 3835．如图7221所示，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且△ADE ，△BCF 均为正三角形，EF ∥AB ，EF ＝2，求该多面体的体积．图7221【解】如图所示，分别过A ，B 作EF 的垂线，垂足分别为G ，H ，连接DG ，CH ，则原几何体分割为两个三棱锥和一个直三棱柱，∵三棱锥高为12，直三棱柱高为1，AG ＝12－⎝ ⎛⎭⎪⎫122＝32，取AD 中点M ，则MG ＝22，∴S △AGD ＝12×1×22＝24，∴V ＝24×1＋2×13×24×12＝23. 6．如图7222，已知平行四边形ABCD 中，BC ＝2，BD ⊥CD ，四边形ADEF 为正方形，平面ADEF ⊥平面ABCD ，G ，H 分别是DF ，BE 的中点．记CD ＝x ，V (x )表示四棱锥F ABCD 的体积．图7222(1)求V (x )的表达式； (2)求V (x )的最大值．【解】 (1)∵平面ADEF ⊥平面ABCD ，交线为AD 且FA ⊥AD ，∴FA ⊥平面ABCD . ∵BD ⊥CD ，BC ＝2，CD ＝x ， ∴FA ＝2，BD ＝4－x 2(0＜x ＜2)， ∴S ▱ABCD ＝CD ·BD ＝x 4－x 2，∴V (x )＝13S ▱ABCD ·FA ＝23x 4－x 2(0＜x ＜2)．(2)V (x )＝23x 4－x 2＝23－x 4＋4x 2＝23－x 2－22＋4.∵0＜x ＜2，∴0＜x 2＜4，∴当x 2＝2，即x ＝2时，V (x )取得最大值，且V (x )max ＝43.。

高三一轮复习立体几何教案,习题,答案

第七章立体几何第一节空间几何体的结构特征及三视图和直观图2019考纲考题考情1．空间几何体的结构特征2．空间几何体的三视图(1)三视图的形成与名称空间几何体的三视图是用平行投影得到的，这种投影下与投影面平行的平面图形留下的影子与平面图形的形状和大小是完全相同的，三视图包括正视图、侧视图、俯视图。

(2)三视图的画法①在画三视图时，重叠的线只画一条，挡住的线要画成虚线。

②三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线。

3．空间几何体的直观图空间几何体的直观图常用斜二测画法来画，基本规则是：(1)原图形中x轴、y轴、z轴两两垂直，直观图中，x′轴、y′轴的夹角为45°(或135°)，z′轴与x′轴、y′轴所在平面垂直。

(2)原图形中平行于坐标轴的线段，直观图中还是平行于坐标轴的线段。

平行于x轴和z轴的线段长度在直观图中保持不变，平行于y轴的线段长度在直观图中变为原来的一半。

1．台体可以看成是由锥体截得的，易忽视截面与底面平行且侧棱延长后必交于一点。

2．三视图的基本要求(1)长对正，高平齐，宽相等。

(2)在绘制三视图时，分界线和可见轮廓线都用实线画出，被遮挡的部分的轮廓线用虚线表示出来，即“眼见为实、不见为虚”。

在三视图的判断与识别中要特别注意其中的虚线。

3．斜二测画法中的“三变”与“三不变”“三变”⎩⎪⎨⎪⎧ 坐标轴的夹角改变，与y 轴平行的线段的长度变为原来的一半，图形改变。

“三不变”⎩⎪⎨⎪⎧平行性不改变，与x ，z 轴平行的线段的长度不改变，相对位置不改变。

一、走进教材1．(必修2P 8A 组T 1(1)改编)在如图所示的几何体中，是棱柱的为________。

(填写所有正确的序号)答案 ③⑤2．(必修2P 15练习T 1改编)已知如图所示的几何体，其俯视图正确的是()解析由俯视图定义易知选项C符合题意。

故选C。

答案 C二、走近高考3．(2018·全国卷Ⅰ)某圆柱的高为2，底面周长为16，其三视图如图所示。

全国通用近年高考数学一轮复习第七章立体几何初步课时作业三十九7.1空间几何体的结构及其三视图和直观

（全国通用版）2019版高考数学一轮复习第七章立体几何初步课时分层作业三十九7.1 空间几何体的结构及其三视图和直观图文编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（全国通用版）2019版高考数学一轮复习第七章立体几何初步课时分层作业三十九7.1 空间几何体的结构及其三视图和直观图文）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（全国通用版）2019版高考数学一轮复习第七章立体几何初步课时分层作业三十九7.1 空间几何体的结构及其三视图和直观图文的全部内容。

课时分层作业三十九空间几何体的结构及其三视图和直观图一、选择题(每小题5分,共25分）1.由平面六边形沿某一方向平移形成的空间几何体是 ( ）A.六棱锥B。

六棱台C.六棱柱D.非棱柱、棱锥、棱台的一个几何体【解析】选C。

平面六边形沿某一方向平移形成的空间几何体符合棱柱的定义.2.水平放置的△ABC的直观图如图，其中B′O′=C′O′=1,A′O′=，那么原△ABC是一个（)A。

等边三角形B。

直角三角形C。

三边中只有两边相等的等腰三角形D.三边互不相等的三角形【解析】选A。

AO=2A′O′=2×=，在Rt△AOB中，AB==2，同理AC=2,所以BC是等边三角形.3。

一个简单几何体的正视图、侧视图分别为如图所示的矩形、正方形,则其俯视图不可能为( )A.矩形B。

直角三角形C。

椭圆 D.等腰三角形【解析】选D。

依题意，题中的几何体的俯视图的长为3、宽为2，因此结合题中选项知,其俯视图不可能是等腰三角形。

【变式备选】下列结论正确的是( )A.各个面都是三角形的几何体是三棱锥B.以三角形的一条边所在直线为旋转轴,其余两边绕旋转轴旋转形成的曲面所围成的几何体叫圆锥C。

(浙江版)2019年高考数学一轮复习(讲+练+测)：专题8.1空间几何体的结构及其三视图和直观图(练)

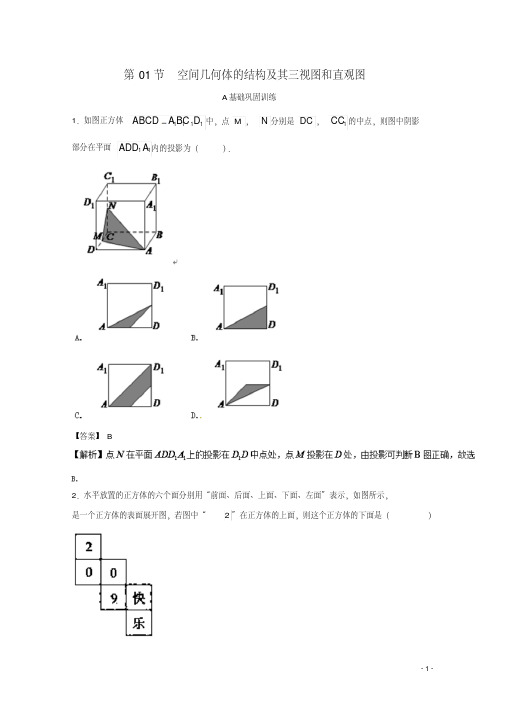
第01节空间几何体的结构及其三视图和直观图A 基础巩固训练1．如图正方体1111ABCD A BC D 中，点M ，N 分别是DC ，1CC 的中点，则图中阴影部分在平面11ADD A 内的投影为（）．【答案】B2．水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面”表示，如图所示，是一个正方体的表面展开图，若图中“2”在正方体的上面，则这个正方体的下面是（）A. 0B. 9C. 快D. 乐【答案】B3．若一个圆锥的侧面展开图是面积为的半圆面，则该圆锥的母线与轴所成的角为( )A. B. C. D.【答案】A【解析】设圆锥的母线长为，底面半径为，圆锥的侧面展开图是面积为的半圆面，，即，又圆锥的侧面积公式，，解得，即，则，即圆锥的母线与圆锥的轴所成角的大小为，故选 A.4．下列几何体各自的三视图中，有且仅有两个视图相同的是（）A. ①②B. ①③C. ①④D. ②④【答案】D5.已知正三角形ABC的边长为a，那么△ABC的平面直观图△A′B′C′的面积为________．【答案】6 16a2【解析】如图①②所示的实际图形和直观图．由斜二测画法可知，A′B′＝AB＝a，O′C′＝12OC＝34a，在图②中作C′D′⊥A′B′于D′，则C′D′＝22O′C′＝68a.∴S△A′B′C′＝12A′B′·C′D′＝12×a×68a＝616a2.B能力提升训练1.【2018届安徽省屯溪第一中学高三第二次月考】一个四面体的顶点在空间直角坐标系中的坐标分别是,,，，则该四面体的正视图的面积不可能为（）A. B. C. D.【答案】B【解析】一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是：（1，0，1），（1，1，0），（0，1，1），（0，0，0），几何体的直观图如图，是以正方体的顶点为顶点的一个正四面体，其正视图的最大投影面是在x-O-y 或x-O-z 或y-O-z 面上，投影面是边长为1的正方形，∴正视图的最大面积为1，∴不可能为,故选B.2.【海南省嘉积中学高三下学期测试】已知正六棱柱的底面边长和侧棱长相等，体积为3123cm ．其三视图中的俯视图（如右图所示），则其左视图的面积是（）A ．243cmB ．223cm C ．28cmD ．24cm【答案】A3.【山东省日照市高三3月第一次模拟考试】三棱柱的侧棱与底面垂直，且底面是边长为2的等边三角形，其正（主）视图（如图所示）的面积为8，则侧（左）视图的面积为（）A.8B.4C.43D.3【答案】C【解析】由图可知该几何体是直三棱柱,直三棱柱的棱长为4,底面等边三角形的高为3，所以其左视图的面积为43.故选C.4. 【2018届河南省中原名校高三第三次联考】把边长为2的正方形ABCD沿对角线BD折起，连结AC，得到三棱锥C ABD，其正视图、俯视图均为全等的等腰三角形（如图所示），则其侧视图的面积为（）A.32B.12C. 1D.22【答案】C【解析】如图：∵正视图、俯视图均为全等的等腰直角三角形，5．【2017年福建省数学基地校高三复习试卷】如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的几条棱中，最长的棱的长度为（）(A)62 (B)42 (C) 6 (D)4【答案】C【解析】如图所示原几何体为三棱锥D ABC ，其中4,42,25AB BC AC DB DC ，24246DA，故最长的棱的长度为6DA ，选CC 思维扩展训练1.【2017届辽宁省大连市第八中学高三春季模拟】棱长为a 的正方体内有一个棱长为x 的正四面体，且该正四面体可以在正方体内任意转动，则x 的最大值为（）A. 12a B.32a C.36a D.63a【答案】D2．【2018届贵州省贵阳市第一中学高三上月考一】如图是某几何体的三视图，则该几何体的各个棱长中，最长的棱的长度为（）A. B. C. D.【答案】C【解析】几何体ABCD为图1中粗线所表示的图形，最长棱是AC，，故选C．3.【2018届广西桂林市柳州市高三综合模拟金卷（1）】已知直三棱柱的6个顶点都在球的球面上,若,,则球的半径为（）A. B. C. D.【答案】C4.【2017届陕西省西安市西北工业大学附属中学高三下第八次模拟】已知正方体1111ABCDA BC D 的棱长为2，其表面上的动点T 到底面ABCD 的中心O 的距离为2，则线段TO 的中点的轨迹长度为（）A.B.2 C.3 D.4【答案】B【解析】动点T 的轨迹是以O 为球心，以2为半径的球面，球面与平面11AACC 的交点轨迹是以AC 中点'O 为圆心，以1为半径的半圆，对应OT 中点'T 的轨迹是以12为半径的半圆，长度为11122l ，由于球面同时与面11AA BB 、面11BBCC 、面11CC DD 都相交，交'T 的轨迹长度为422，故选 B.5.【皖北协作区高三年级联考】空间中任意放置的棱长为2的正四面体ABCD .下列命题正确的是_________.（写出所有正确的命题的编号）①正四面体ABCD 的主视图面积可能是2；②正四面体ABCD 的主视图面积可能是362；③正四面体ABCD 的主视图面积可能是3；④正四面体ABCD的主视图面积可能是 2⑤正四面体ABCD的主视图面积可能是4.【答案】①②③④【解析】对于四面体ABCD，如下图：将正四面体放入正方体中，如上右图，光线垂直于正方体正对我们的面时，主视图是正方形，其面积为222，并且此时主视图面积最大，故④正确，⑤不正确.。

2019年高考数学一轮复习课时分层训练44简单几何体的表面积与体积理北师大版

课时分层训练(四十四) 简单几何体外表积与体积A 组根底达标一、选择题1．(2021·北京高考)某三棱锥三视图如图759所示，那么该三棱锥体积为( )图759A ．60B ．30C ．20D ．10D [由三视图画出如下图三棱锥P ACD ，过点P 作PB ⊥平面ACD 于点B ，连接BA ，BD ，BC ，根据三视图可知底面ABCD 是矩形，AD ＝5，CD ＝3，PB ＝4，所以V 三棱锥P ACD ＝13×12×3×5×4＝10. 应选D.]2．(2021·全国卷Ⅱ)如图7510是由圆柱与圆锥组合而成几何体三视图，那么该几何体外表积为( )图7510A ．20πB ．24πC ．28πD ．32π C [由三视图可知圆柱底面直径为4，母线长(高)为4，所以圆柱侧面积为2π×2×4＝16π，底面积为π·22＝4π；圆锥底面直径为4，高为23，所以圆锥母线长为(23)2＋22S ＝16π＋4π＋8π＝28π.]3．(2021·全国卷Ⅲ)如图7511，网格纸上小正方形边长为1，粗实线画出是某多面体三视图，那么该多面体外表积为( )图7511A ．18＋36 5B ．54＋185C ．90D ．81B [由三视图可知该几何体是底面为正方形斜四棱柱，其中有两个侧面为矩形，另两个侧面为平行四边形，那么外表积为(3×3＋3×6＋3×35)×2＝54＋18 5.应选B.]4．某几何体三视图如图7512所示，且该几何体体积是3，那么主视图中x 值是( )图7512A ．2B ．92 C.32 D ．3D [由三视图知，该几何体是四棱锥，底面是直角梯形，且S底＝12×(1＋2)×2＝3，所以V ＝13x ·3＝3，解得x ＝3.]5．(2021·石家庄质检)某几何体三视图如图7513所示，那么该几何体体积是( )【导学号：79140241】图7513A ．16B ．20C ．52D ．60B [由三视图得该几何体直观图如下图，其中四边形ABCD 为邻边长分别为2,4长方形，四边形CDEF 为上底为2、下底为6、高为3等腰梯形，所以该几何体可以看作是由两个底面为直角边长分别为3,4直角三角形，高为2三棱锥与一个底面为直角边长分别为3,4直角三角形，高为2三棱柱组成，那么该几何体体积为2×13×12×3×4×2＋12×3×4×2＝20，应选B.] 二、填空题6．一个六棱锥体积为23，其底面是边长为2正六边形，侧棱长都相等，那么该六棱锥侧面积为________．12 [设正六棱锥高为h ，棱锥斜高为h ′.由题意，得13×6×12×2×3×h ＝23，∴h ＝1， ∴斜高h ′＝12＋(3)2＝2， ∴S 侧＝6×12×2×2＝12.] 7．(2021·江苏高考)如图7514，在圆柱O 1O 2内有一个球O ，该球与圆柱上、下底面及母线均相切，记圆柱O 1O 2体积为V 1，球O 体积为V 2，那么V 1V 2值是________．图751432[设球O 半径为R ， ∵球O 与圆柱O 1O 2上、下底面及母线均相切，∴圆柱O 1O 2高为2R ，底面半径为R .∴V 1V 2＝πR 2·2R 43πR 3＝32.] 8．(2021·天津高考)一个正方体所有顶点在一个球面上，假设这个正方体外表积为18，那么这个球体积为________．92π [设正方体棱长为a ，那么6a 2＝18，∴a ＝ 3. 设球半径为R ，那么由题意知2R ＝a 2＋a 2＋a 2＝3，∴R ＝32. 故球体积V ＝43πR 3＝43π×⎝ ⎛⎭⎪⎪⎫323＝92π.] 三、解答题9.如图7515，在三棱锥D ABC 中，BC ⊥AD ，BC ＝2，AD ＝6，AB ＋BD ＝AC ＋CD ＝10，求三棱锥D ABC 体积最大值.【导学号：79140242】图7515[解] 由题意知，线段AB ＋BD 与线段AC ＋CD 长度是定值，∵棱AD 与棱BC 相互垂直，设d 为AD 到BC 距离，那么V D ABC ＝AD ·BC ×d ×12×13＝2d ，当d 最大时，V D ABC 体积最大．∵AB ＋BD ＝AC ＋CD ＝10，∴当AB ＝BD ＝AC ＝CD ＝5时，d 有最大值42－1＝15.此时V ＝215.10.如图7516，长方体ABCD A 1B 1C 1D 1中，AB ＝16，BC ＝10，AA 1＝8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E ＝D 1FE ，F 平面α与此长方体面相交，交线围成一个正方形．图7516(1)在图中画出这个正方形(不必说明画法与理由)；(2)求平面α把该长方体分成两局部体积比值．[解] (1)交线围成正方形EHGF 如下图．(2)如图，作EM ⊥AB ，垂足为M ，那么AM ＝A 1E ＝4，EB 1＝12，EM ＝AA 1＝8.因为四边形EHGF 为正方形，所以EH ＝EF ＝BC ＝10. 于是MH ＝EH 2－EM 2＝6，AH ＝10，HB ＝6.故S 四边形A 1EHA ＝12×(4＋10)×8＝56，S 四边形EB 1BH ＝12×(12＋6)×8＝72. 因为长方体被平面α分成两个高为10直棱柱，所以其体积比值为97⎝ ⎛⎭⎪⎪⎫79也正确.] B 组能力提升11．(2021·东北三省四市模拟(一))点A ，B ，C ，D 在同一个球球面上，AB ＝BC ＝1，∠ABC ＝120°.假设四面体ABCD 体积最大值为34，那么这个球外表积为( ) A.500π81B ．4π C.25π9 D ．100π9D [因为AB ＝BC ＝1，∠ABC ＝120°，所以由正弦定理知△ABC 外接圆半径r ＝12×AB sin 30°＝1，S △ABC ＝12AB ×BC sin 120°＝34.设外接圆圆心为Q ，那么当DQ 与平面ABC 垂直时，四面体ABCD 体积最大，所以13S △ABC ×DQ ＝34，所以DQO ，半径为R ，那么在Rt△AQO 中，OA 2＝AQ 2＋OQ 2，即R 2＝12＋(3－R )2，解得R ＝53，所以球外表积S ＝4πR 2＝100π9，应选D.] 12．H 是球O 直径AB 上一点，AH ∶HB ＝1∶2，AB ⊥平面α，H 为垂足，α截球O 所得截面面积为π，那么球O 外表积为________.【导学号：79140243】92π [如图，设球O 半径为R ，那么由AH ∶HB ＝1∶2得 HA ＝13·2R ＝23R ， ∴OH ＝R 3. ∵截面面积为π＝π·(HM )2，∴HM ＝1.在Rt△HMO 中，OM 2＝OH 2＋HM 2，∴R 2＝19R 2＋HM 2＝19R 2＋1， ∴R ＝324， ∴S 球＝4πR 2＝4π·⎝ ⎛⎭⎪⎪⎫3242＝92π.]13．四面体ABCD 及其三视图如图7517所示，平行于棱AD ，BC 平面分别交四面体棱AB ，BD ，DC ，CA 于点E ，F ，G ，H .图7517(1)求四面体ABCD 体积；(2)证明：四边形EFGH 是矩形．[解] (1)由该四面体三视图可知，BD ⊥DC ，BD ⊥AD ，AD ⊥DC ，BD ＝DC ＝2，AD ＝1，∴AD ⊥平面BDC ，∴四面体ABCD 体积V ＝13×12×2×2×1＝23. (2)证明：∵BC ∥平面EFGH ，平面EFGH ∩平面BDC ＝FG ，平面EFGH ∩平面ABC ＝EH ，∴BC ∥FG ，BC ∥EH ，∴FG ∥EH .同理EF ∥AD ，HG ∥AD ，∴EF ∥HG ，∴四边形EFGH 是平行四边形．又∵AD ⊥平面BDC ，∴AD ⊥BC ，∴EF ⊥FG .∴四边形EFGH 是矩形．。

高考数学一轮复习课时分层训练36 简单几何体的结构、三视图和直观图文北师大版

课时分层训练(三十六) 简单几何体的结构、三视图和直观图A组基础达标(建议用时：30分钟)一、选择题1．关于简单几何体的结构特征，下列说法不正确的是( )A．棱柱的侧棱长都相等B．棱锥的侧棱长都相等C．三棱台的上、下底面是相似三角形D．有的棱台的侧棱长都相等B[根据棱锥的结构特征知，棱锥的侧棱长不一定都相等．]2．(2018·石家庄模拟)等腰三角形ABC的直观图是( ) 【导学号：00090229】图719A．①②B．②③C．②④D．③④D[由直观图画法可知，当∠x′O′y′＝45°时，等腰三角形的直观图是④；当∠x′O′y′＝135°时，等腰三角形的直观图是③；综上，等腰三角形ABC的直观图可能是③④.]3．(2017·云南玉溪一中月考)将长方体截去一个四棱锥后得到的几何体如图7110所示，则该几何体的左视图为( )图7110A B C DD [易知左视图的投影面为矩形．又AF 的投影线为虚线， ∴该几何体的左视图为选项D ．]4．(2018·东莞模拟)下列三视图所对应的直观图是()图7111C [由题意可知，几何体的直观图下部是长方体，上部是圆柱，并且高相等，应选C ．] 5．(2015·全国卷Ⅱ)一个正方体被一个平面截去一部分后，剩余部分的三视图如图7112，则截去部分体积与剩余部分体积的比值为()图7112A ．18 B ．17 C ．16D ．15D [由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分，如图所示，截去部分是一个三棱锥．设正方体的棱长为1，则三棱锥的体积为V 1＝13×12×1×1×1＝16，剩余部分的体积V 2＝13－16＝56.所以V 1V 2＝1656＝15，故选D ．]二、填空题6．(2017·福建龙岩联考)一水平放置的平面四边形OABC ，用斜二测画法画出它的直观图O ′A ′B ′C ′如图7113所示，此直观图恰好是一个边长为1的正方形，则原平面四边形OABC 的面积为________．图71132 2 [因为直观图的面积是原图形面积的24倍，且直观图的面积为1，所以原图形的面积为2 2.]7．如图7114所示，在正方体ABCD A 1B 1C 1D 1中，点P 是上底面A 1B 1C 1D 1内一动点，则三棱锥P ABC 的主视图与左视图的面积的比值为________．图71141 [三棱锥P ABC 的主视图与左视图为底边和高均相等的三角形，故它们的面积相等，面积比值为1.]8．某三棱锥的三视图如图7115所示，则该三棱锥最长棱的棱长为________. 【导学号：00090230】图71152 2 [由题中三视图可知，三棱锥的直观图如图所示，其中PA⊥平面ABC ，M 为AC 的中点，且BM ⊥AC ，故该三棱锥的最长棱为PC ．在Rt △PAC 中，PC ＝PA 2＋AC 2＝22＋22＝2 2.]三、解答题9．某几何体的三视图如图7116所示．图7116(1)判断该几何体是什么几何体？ (2)画出该几何体的直观图．[解] (1)该几何体是一个正方体切掉两个14圆柱后的几何体．(2)直观图如图所示．10．如图7117①，在四棱锥P ABCD 中，底面为正方形，PC 与底面ABCD 垂直，如图7117②为该四棱锥的主视图和左视图，它们是腰长为6 cm 的全等的等腰直角三角形．图7117①图7117①(1)根据图中所给的主视图、左视图，画出相应的俯视图，并求出该俯视图的面积； (2)求PA ．【导学号：00090231】[解] (1)该四棱锥的俯视图为(内含对角线)边长为6 cm 的正方形，如图，其面积为36 cm 2.(2)由左视图可求得PD ＝PC 2＋CD 2＝62＋62＝6 2. 由主视图可知AD ＝6，且AD ⊥PD ，所以在Rt△APD中，PA＝PD2＋AD2＝22＋62＝6 3 cm.B组能力提升(建议用时：15分钟)1．在如图7118所示的空间直角坐标系Oxyz中，一个四面体的顶点坐标分别是(0,0,2)，(2,2,0)，(1,2,1)，(2,2,2)，给出编号①②③④的四个图，则该四面体的主视图和俯视图分别为( )图7118A．①和②B．③和①C．④和③D．④和②D[如图，在坐标系中标出已知的四个点，根据三视图的画图规则判断三棱锥的主视图为④，俯视图为②.]2．(2017·长郡中学质检)如图7119是一个几何体的三视图，则该几何体任意两个顶点间距离的最大值是( )图7119A．4 B．5C．3 2 D．3 3D[由三视图作出几何体的直观图(如图所示)，计算可知AF最长，且AF＝BF2＋AB2＝3 3.]3．(2018·长春模拟)三棱锥SABC及其三视图中的主视图和左视图如图7120所示，则棱SB的长为________．【导学号：00090232】图712042[由已知中的三视图可得SC⊥平面ABC，且底面△ABC为等腰三角形，在△ABC中AC＝4，AC边上的高为23，故BC＝4，在Rt△SBC中，由SC＝4，可得SB＝4 2.]。

2019年高考数学一轮复习课时分层训练36简单几何体的结构三视图和直观图文北师大版2018040936

课时分层训练(三十六) 简单几何体的结构、三视图和直观图A组基础达标(建议用时：30分钟)一、选择题1．关于简单几何体的结构特征，下列说法不正确的是( )A．棱柱的侧棱长都相等B．棱锥的侧棱长都相等C．三棱台的上、下底面是相似三角形D．有的棱台的侧棱长都相等B[根据棱锥的结构特征知，棱锥的侧棱长不一定都相等．]2．(2018·石家庄模拟)等腰三角形ABC的直观图是( ) 【导学号：00090229】图719A．①②B．②③C．②④D．③④D[由直观图画法可知，当∠x′O′y′＝45°时，等腰三角形的直观图是④；当∠x′O′y′＝135°时，等腰三角形的直观图是③；综上，等腰三角形ABC的直观图可能是③④.]3．(2017·云南玉溪一中月考)将长方体截去一个四棱锥后得到的几何体如图7110所示，则该几何体的左视图为( )图7110A B C DD[易知左视图的投影面为矩形．又AF的投影线为虚线，∴该几何体的左视图为选项D．]4．(2018·东莞模拟)下列三视图所对应的直观图是( )图7111C[由题意可知，几何体的直观图下部是长方体，上部是圆柱，并且高相等，应选C．] 5．(2015·全国卷Ⅱ)一个正方体被一个平面截去一部分后，剩余部分的三视图如图7112，则截去部分体积与剩余部分体积的比值为( )图7112A．18B．17C．16D．15D[由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分，如图所示，截去部分是一个三棱锥．设正方体的棱长为1，则三棱锥的体积为V1＝13×12×1×1×1＝16，剩余部分的体积V2＝13－16＝56.所以V1V2＝1656＝15，故选D．]二、填空题6．(2017·福建龙岩联考)一水平放置的平面四边形OABC，用斜二测画法画出它的直观图O′A′B′C′如图7113所示，此直观图恰好是一个边长为1的正方形，则原平面四边形OABC的面积为________．图71132 2 [因为直观图的面积是原图形面积的24倍，且直观图的面积为1，所以原图形的面积为2 2.]7．如图7114所示，在正方体ABCDA1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥PABC的主视图与左视图的面积的比值为________．图71141 [三棱锥PABC的主视图与左视图为底边和高均相等的三角形，故它们的面积相等，面积比值为1.]8．某三棱锥的三视图如图7115所示，则该三棱锥最长棱的棱长为________. 【导学号：00090230】图71152 2 [由题中三视图可知，三棱锥的直观图如图所示，其中PA⊥平面ABC，M为AC的中点，且BM⊥AC，故该三棱锥的最长棱为PC．在Rt△PAC中，PC＝PA2＋AC2＝22＋22＝2 2.]三、解答题9．某几何体的三视图如图7116所示．图7116(1)判断该几何体是什么几何体？ (2)画出该几何体的直观图．[解] (1)该几何体是一个正方体切掉两个14圆柱后的几何体．(2)直观图如图所示．10．如图7117①，在四棱锥P ABCD 中，底面为正方形，PC 与底面ABCD 垂直，如图7117②为该四棱锥的主视图和左视图，它们是腰长为6 cm 的全等的等腰直角三角形．图7117①图7117①(1)根据图中所给的主视图、左视图，画出相应的俯视图，并求出该俯视图的面积； (2)求PA ．【导学号：00090231】[解] (1)该四棱锥的俯视图为(内含对角线)边长为6 cm 的正方形，如图，其面积为36 cm 2.(2)由左视图可求得PD ＝PC 2＋CD 2＝62＋62＝6 2. 由主视图可知AD ＝6，且AD ⊥PD ，所以在Rt△APD中，PA＝PD2＋AD2＝622＋62＝6 3 cm.B组能力提升(建议用时：15分钟)1．在如图7118所示的空间直角坐标系Oxyz中，一个四面体的顶点坐标分别是(0,0,2)，(2,2,0)，(1,2,1)，(2,2,2)，给出编号①②③④的四个图，则该四面体的主视图和俯视图分别为( )图7118A．①和②B．③和①C．④和③D．④和②D[如图，在坐标系中标出已知的四个点，根据三视图的画图规则判断三棱锥的主视图为④，俯视图为②.]2．(2017·长郡中学质检)如图7119是一个几何体的三视图，则该几何体任意两个顶点间距离的最大值是( )图7119A．4 B．5C．3 2 D．3 3D[由三视图作出几何体的直观图(如图所示)，计算可知AF最长，且AF＝BF2＋AB2＝3 3.]3．(2018·长春模拟)三棱锥SABC及其三视图中的主视图和左视图如图7120所示，则棱SB的长为________．【导学号：00090232】图712042[由已知中的三视图可得SC⊥平面ABC，且底面△ABC为等腰三角形，在△ABC中AC＝4，AC边上的高为23，故BC＝4，在Rt△SBC中，由SC＝4，可得SB＝4 2.]。

2019高三数学一轮复习试题：空间几何体的结构精品教育.doc

高三数学一轮复习试题：空间几何体的结构
导读：高考，比的不是智商高低，比的是谁的耐心好，经过一轮、二轮、三轮复习的摧残还能有几个小伙伴说自己屹立不倒的?今天查字典数学网小编末宝就给大家带来了高考数学一轮复习的同步练习，快来看看吧。

3.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为( )
【答案】：D
【解析】：通过正视图及俯视图可看出该几何体为半个圆锥和一个三棱锥组合在一起，故侧视图为D。

4.一个几何体的三视图如图所示，正视图和侧视图都是等边三角形，且该几何体的四个点在空间直坐标系O-xyz中的坐标分别是(0,0,0)，(2,0,0)，(2,2,0)，(0,2,0)，则第五个顶点的坐标可能为( )
6.如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是( )
A.三棱锥
B.三棱柱
C.四棱锥
D.四棱柱
【答案】：B
【解析】：由题知，该几何体的三视图为一个三角形，两
个四边形，经分析可知该几何体为三棱柱，故选B。

更多数学复习资讯，尽在查字典数学网。

末宝带你游数学：
高三数学一轮复习试题：简单的线性规划问题
高三数学一轮复习试题：数学归纳法
高三数学一轮复习试题：一元二次不等式及其解法。