实验六：matlab古典密码与破译

合集下载

古典密码实验报告

实验报告一、实验室名称：SimpleSPC信息安全云实验系统二、实验项目名称：古典密码——置换密码三、实验学时：1学时四、实验原理：1) 算法原理a) 置换密码算法是不改变明文字符，而是按照某一规则重新排列消息中的比特或字符顺序，才而实现明文信息的加密。

将明文中的字母按照给定的顺序安排在一个矩阵中，然后用根据密钥提供的顺序重新组合矩阵中的字母，从而形成密文。

其解密过程是根据密钥的字母数作为列数，将密文按照列、行的顺序写出，再根据密钥给出的矩阵置换产生新的矩阵，从而恢复明文。

b) 置换密码（Permutation Cipher），又称换位密码。

算法实施时，明文的字母保持相同，但顺序会被打乱。

置换只不过是一个简单的换位，每个置换都可以用一个置换矩阵Ek来表示。

每个置换都有一个与之对应的逆置换Dk。

置换密码的特点是仅有一个发送方和接受方知道的加密置换（用于加密）及对应的逆置换（用于解密）。

它是对明文L长字母组中的字母位置进行重新排列，而每个字母本身并不改变。

c) 设n为一固定整数，P、C和K分别为明文空间、密文空间和密钥空间。

明/密文是长度为n的字符序列，分别记为X（x1,x2，…,xn）属于P和Y(y1,y2,…,yn)属于C ，K是定义在{1,2,…,n}的所有置换组成的集合。

对任何一个密钥（即一个置换），定义置换如下：加密置换为：解密置换为：上式中，是的逆置换，密钥空间K的大小为n！2) 算法参数置换密码算法主要有c、m、k、n四个参数。

c为密文，m是明文，k为密钥，n为模数。

3) 算法流程算法流程。

如图所示五、实验目的：1）学习置换密码的原理2）学习置换密码的算法实现六、实验内容：1.在虚拟机上运行置换密码.exe可执行文件，根据提示输入明文和密钥，同时检查输出的解密后的结果是否与明文一致。

2.学习掌握置换密码的原理，并根据明文和密钥计算出对应的加密文，并与程序输出的结果进行比对，掌握其加密解密的过程。

古典密码实验报告

哈尔滨工程大学实验报告实验名称：古典密码算法班级：学号：姓名：实验时间：2014年4月成绩：指导教师：实验室名称：哈尔滨工程大学实验室与资产管理处制一、实验名称古典密码算法二、实验目的通过编程实现经典的代替密码算法和置换密码，包括移位密码、维吉尼亚密码、周期置换密码、列置换密码，加深对代替技术的了解，为现代分组密码实验奠定基础。

三、实验环境（实验所使用的器件、仪器设备名称及规格）运行Windows 或Linux 操作系统的PC 机，具有gcc(Linux)、VC（Windows）等C 语言编译环境。

四、实验任务及其要求（1）根据实验原理部分对移位密码的介绍，自己创建明文信息，并选择一个密钥，编写移位密码的实现程序，实现加密和解密操作。

（2）根据实验原理部分对维吉尼亚密码的介绍，自己创建明文信息，并选择一个密钥，编写维吉尼亚密码的实现程序，实现加密和解密操作。

（3）根据实验原理部分对周期置换密码的介绍，自己创建明文信息，并选择一个密钥，编写周期置换密码的实现程序，实现加密和解密操作。

（4）根据实验原理部分对列置换密码的介绍，自己创建明文信息，并选择一个密钥，编写列置换密码的实现程序，实现加密和解密操作。

五、实验设计（包括原理图、真值表、分析及简化过程、卡诺图、源代码等）1．移位密码移位密码（Shift Cipher）是一种典型的单表替代密码，也称为加法密码。

移位密码的加密方法就是将明文中的每个字母用其在字母表后面的第k 个字母替代，它的加密过程可以表示为： c = (m + k) mod n其中，m 为明文字母在字母表中的位置数；n 为字母表中的字母总数；k 为密钥；c 为密文字母在字母表中对应的位置数。

相应的，移位密码的解密过程可以表示为：m = (c - k) mod n移位密码的一个典型代表就是凯撒密码（Ceaser Cipher），它是k=3 时的移位密码。

使用英文字母表的撒密码的加（解）密可以表示为：m = (c + 3) mod 26 m = (c - 3) mod 26，例如，明文：attacks at nine am密钥：3加密：将明文分组对每一个密文字母，依英文字母表，用其右的第 3 个字母代替密文：dwwdfnv dw qlqh dp另外，使用凯撒密码加密后的密文“dwwdfnvdwilyhsp”，其明文为“attacks at five pm”。

现代密码学——古典密码算法(实验报告)

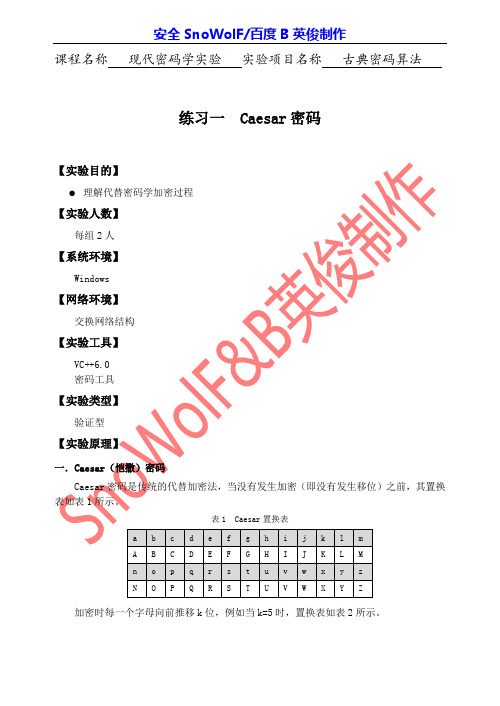
安全SnoWolF/百度B英俊制作课程名称现代密码学实验实验项目名称古典密码算法练习一 Caesar密码加密时每一个字母向前推移k位，例如当k=5时，置换表如表2所示。

表2 Caesar置换表于是对于明文：datasecurityhasevolvedrapidly经过加密后就可以得到密文：IFYFXJHZWNYDMFXJATQAJIWFUNIQD若令26个字母分别对应整数0～25，如表3所示。

表3 Caesar置换表则Caesar加密变换实际上是：c=(m+k)mod26其中m是明文对应的数据，c是与明文对应的密文数据，k是加密用的参数，也称为密钥。

很容易得到相应的Caesar解密变换是：m=D(c)=(c–k)mod26例如明文：datasecurity对应的数据序列：301901842201781924当k=5时经过加密变换得到密文序列：852452397252213243对应的密文为：IFYFXJHZWNYD【实验步骤】本练习主机A、B为一组，C、D为一组，E、F为一组。

首先使用“快照X”恢复Windows系统环境。

一．手动完成Caesar密码(1) 在实验原理部分我们已经了解了Caesar密码的基本原理，那么请同学们写出当密钥k=3时，对应明文：data security has evolved rapidly的密文： GDWD VHFXULWB KDV HYROYHG UDSLGOB 。

(2) 进入实验平台，单击工具栏中的“密码工具”按钮，启动密码工具，在向导区点击“Caesar密码”。

在明文输入区输入明文：data security has evolved rapidly。

将密钥k调节到3，查看相应的密文，并与你手动加密的密文进行比较。

请根据密钥验证密文与明文对应关系是否正确。

二．Caesar加密(1) 进入“加密解密”｜“Caesar密码”视图，在明文输入区输入明文（明文应为英文），单击“加密”按钮进行加密。

密码锁编程 matlab程序

一、背景介绍密码锁是一种常见的安全设备，通过输入密码来开启或关闭设备。

密码锁编程是指使用计算机编程语言对密码锁进行控制和设置。

MATLAB是一种功能强大的编程语言和工程软件，可以用来实现密码锁的编程。

二、密码锁编程的基本原理1. 密码输入与验证：用户通过键盘输入密码，程序接收并验证密码的正确性。

2. 开锁与关锁：当密码输入正确时，程序可以通过控制电子锁实现开锁操作；密码错误时，程序可以记录错误次数并进行报警。

3. 程序界面设计：可以通过MATLAB的图形界面设计工具创建用户友好的交互界面，提供输入密码和显示结果的功能。

三、密码锁编程的具体步骤1. 设置密码：首先需要设定一个初始密码，并将其储存在程序中。

2. 用户输入：程序需要接收用户输入的密码。

3. 验证密码：程序对用户输入的密码进行验证，判断是否与设定的初始密码一致。

4. 开锁与关锁：如果密码验证通过，程序可以通过控制电子锁实现开锁操作；如果密码错误，程序可以进行相应的处理。

5. 界面设计：通过MATLAB的图形界面设计工具创建交互界面，包括输入密码框、确认按钮和显示结果的部分。

四、密码锁编程的技术要点1. 数据处理：程序需要对用户输入的密码进行适当的加密和比对，确保密码的安全性。

2. 控制操作：程序需要调用相应的接口函数，实现对电子锁的控制和操作。

3. 用户交互：程序需要设计良好的用户界面，让用户能够方便地进行密码输入和了解操作结果。

五、密码锁编程的应用领域1. 家用密码锁：可以用MATLAB编程实现智能门锁、保险柜等设备的密码管理。

2. 商用密码锁：可以将MATLAB编程应用在银行保险柜、企业办公室等需要高安全性的场合。

3. 教育科研：密码锁编程也可以作为MATLAB编程教学和科研实验的一个具体应用案例。

六、密码锁编程的未来发展随着科技的不断发展和智能化水平的提高，密码锁编程也将在更广泛的领域得到应用。

随着物联网和大数据技术的兴起，密码锁编程还可以与其他领域的技术进行深度融合，实现更加智能、安全的密码管理系统。

密码与破译

明文字母表密文字母表 ABCDEFGHIJKLMNOPQRSTUVWXYZ CONSTRUABDEFGHIJKLMPQVWXYZ
在设计密钥时，也可在明文字母表中选择一个特定字母，然后从该特定字母开始写密钥单词将密钥单词隐藏于其中。例如，对于上例，选取特定字母 k，则可得：明文字母表密文字母表 ABCDEFGHIJKLMNOPQRSTUVWXYZ KLMPQVWXYZCONSTRUABDEFGHIJ
1 2 3 4 5 6 7 8 9 10 11 12 13
1 20 , , 17 3
Y
25
19 , 24
24 24
N
14
O
15
P
Q
R
18
S
19
T
20
U
21
V
22
W X
23 24
Z
0
16 17
Hill2 加密举例

2 1
A
1
1 3 (m o d 2 6 ) 3 (m o d 2 6 ) 0
1
2 (m o d 2 6 ) 1
B A
(m o d 2 6 )
3 9 0
2 (m o d 2 6 ) 1
1 0
8 9
敌方截获破译
明文（信息）
解密器
密文
接收方
古典密码
替代密码移位密码代数密码
随着计算机与网络技术的迅猛发展，大量各具特色的密码体系不断涌现。离散数学、数论、计算复杂性、混沌、……，许多相当高深的数学知识都被用上，逐步形成了（并仍在迅速发展的）具有广泛应用面的现代密码学。

matlab实验四古典密码与破译

8 .6 .9 .5 6 . 9 . 5 . 10 (1) 设 A 5 .8 .4 .9 10 . 6 . 11 . 10
Z 26
中的整数对应：
，验证矩阵 A 能否作为 Hill4 密码体制的加密矩阵．用框
图画出你的验算过程，并编写相应的计算机程序。 (*)(2) 设明文为 HILL CRYPTOGRAPHIC SYSTEM IS TRADJITIONAL．利用上面的表值与加密矩阵给此明文加密，并将得到的密文解密．画出加密与解密过程的框图并编写相应的计算机程序。 5. 设已知一份密文为 Hill2 密码体系，其中出现频数最高的双字母是 RH 和 NI，而在明文语言中，出现频数最高的双字母为 TH 和 HE．由这些信息按表 5 给出的表值能得到什么样的加密矩阵?
1 A 0 2 4
，求其在模 27 意义下的明文．
编辑说明： 1、 Hill2 密码的解密过程，即为上一题中加密过程的逆过程。 2、将自己的名字的拼音作为 Hill2 密文进行解密，在输入要解密的密文文字(全部为大写字母或空格)时，若密文文字总个数为奇数，则需在最后一个密文字母后面加一个 “哑字母”或“空格” (在下面的程序中是加与最后一个密文字母相同的字母)。程序：模 27 意义下的解密程序 m=27;enmat=[1 2;0 4];demat=[1 13;0 7];ZERO=64;c=[];en=[]; astr=input('输入要解密的密文文字(全部为大写字母或空格)：') while any(double(astr)>90 | double(astr)<65& double(astr)~=32) astr=input('输入错误，应该全部为大写字母或空格：') end an=double(astr);lh=length(an); if mod(length(an), 2)==1 an=[an, an(length(an))]; end an=an-ZERO; for i=1:length(an) if an(i)==-32 an(i)=0; end end c=reshape(an, 2, length(an)/2); dn=mod(demat*c, m); en=reshape(dn,1,length(an)); en=en+ZERO; for i=1:length(en) if en(i)==64 en(i)=32; end end en=en(1:lh); char(en)

古典密码与matlab

在长篇文章中，英文字母和字母组合出现的频率有一定的统计规律

容易被破译
10

任选一篇普通的英文文章。统计每个英文字母在文章中出现的次数。计算出每个字母出现的次数在总的字母个数中所占的百分比。再换几篇文章做同样的统计，比较统计的结果。统计每一种双字母组合出现的次数在总次数中所占的百分比，从中选出出现频率最高的双字母组合。

字母 A B C D E F G H
表值字母
I
J K L M
1 2
3
4 5 6
7
8
9 10 11 12 13
N O P Q R S T U V W X Y Z 表值 14 15 16 17 18 19 20 21 22 23 24 25 0 13
例子：想好一个英文单词：red 将密文三个字母为一组分成3组，第1、2、 3组分别用密钥17、4、3 进行加法密码的解密

16

依次比较上下两行中处于同一列的字母，统计出上下两个字母相同的列在被统计的列的总数中所占百分比。
观察对不同的n,这些百分数的变化情况。是否对某个n,这个百分比显著上升？这说明什么问题？
17

由一个同学选定一篇稍长一些的文章，选定一个密钥字，用维吉尼亚密码加密。将所得的译文交给另外的同学去破译所用的密钥字的长度。

31
有关的MATLAB 命令（double）

double: 如果是字符型的，则给出每一个字符的 ASCII码。语法： double(X) 例子： X=double(‘a’) Returns X=
97
32

数学建模实验报告古典密码与破译

古典密码与破译一、实验目的及意义本实验主要涉及代数，利用模运算意义下的矩阵乘法、求逆矩阵、线性无关、线性空间与线性变换等概念和运算，学习古典密码体制的加密、解密和破译过程．二、实验内容1.Hill2加密；2.Hill2解密。

三、实验步骤1. 开启软件平台——MA TLAB，开启MA TLAB编辑窗口；2. 根据加密解密算法步骤编写M文件1.保存文件并运行；2.观察运行结果(数值或图形)；3.根据观察到的结果和体会写出实验报告。

四、实验要求与任务根据实验内容和步骤，完成以下实验，要求写出实验报告。

1. 实际问题(甲) 的修正：按照甲方与乙方的约定，他们之间的密文通信采用Hill2 密码，密钥为二阶矩阵1204A⎛⎫= ⎪⎝⎭且汉语拼音的26 个字母以及空格(字母A~Z 的表值为1~26，空格的表值为0）与0～26 之间的整数建立一一对应的关系，称之为字母的表值，试修正表1、表2 以及附录中的程序，以给出模27 意义下矩阵可逆的判别方法和具体求法．2. 若将你姓名的拼音作为明文，例如：赵本山(ZHAO BEN SHAN，含空格)，密钥等参见练习1，求其在模27 意义下的Hill2密文．3. 若将你姓名的拼音作为Hill2密文，例如：赵本山(ZHAO BEN SHAN，含空格)，密钥等参见练习1，求其在模27 意义下的明文．五. 程序代码及运行结果（经调试后正确的源程序）1.实际问题(甲) 的修正：按照甲方与乙方的约定，他们之间的密文通信采用Hill2 密码，密钥为二阶矩阵1204A⎛⎫= ⎪⎝⎭且汉语拼音的26 个字母以及空格(字wilyes11收集博客(与学习无关)：/u/1810231802母A~Z 的表值为1~26，空格的表值为0）与0～26 之间的整数建立一一对应的关系，称之为字母的表值，试修正表1、表2 以及附录中的程序，以给出模27 意义下矩阵可逆的判别方法和具体求法．表1 明文字母的表值①求模27倒数表(prog1_MOD27.m)程序代码：m=27;for a=1:mfor i=1:mif mod(a*i,m)==1fprintf('%d 的模%d倒数是: %d\n',a,m,i);break;end;end;end运行结果：1 的模27倒数是: 12 的模27倒数是: 144 的模27倒数是: 75 的模27倒数是: 117 的模27倒数是: 48 的模27倒数是: 1710 的模27倒数是: 1911 的模27倒数是: 513 的模27倒数是: 2514 的模27倒数是: 216 的模27倒数是: 2217 的模27倒数是: 819 的模27倒数是: 1020 的模27倒数是: 2322 的模27倒数是: 1623 的模27倒数是: 2025 的模27倒数是: 1326 的模27倒数是: 26②判断二阶矩阵在模27意义下是否可逆，可逆则求其逆(prog1.m)程序代码：m=27;aa=input('输入一个2×2的矩阵，格式:[a11 a12;a21 a22]:')while size(aa)~=[2 2]aa=input('输入一个2×2的矩阵，格式:[a11 a12;a21 a22]:')enda=det(aa);bb=aa;if gcd(m,a)~=1disp(' 该矩阵不可逆')elsefor i=1:mif mod(a*i,m)==1antaa=i;break;endendastar=[aa(2,2) -aa(1,2);-aa(2,1) aa(1,1)];invaa=mod(antaa*astar,m);disp(['原矩阵是:',mat2str(aa),',它的逆矩阵(mod',num2str(m),')是:',mat2str(invaa)]) end运行结果：输入一个2×2的矩阵，格式:[a11 a12;a21 a22]:[1 2;0 4]aa =1 20 4原矩阵是:[1 2;0 4],它的逆矩阵(mod27)是:[1 13;0 7]2.若将你姓名的拼音作为明文，例如：赵本山(ZHAO BEN SHAN，含空格)，密钥等参见练习1，求其在模27 意义下的Hill2密文．程序代码：(prog2.m)m=27;enmat=[1 2;0 4];demat=[1 13;0 7];ZERO=64;c=[];en=[];fprintf('本组成员的姓名为吴亚山李杰赵传来,拼音为:\n')fprintf('WU YA SHAN LI JIE ZHAO CHUAN LAI\n')fprintf('以[1 2;0 4]为密钥对此拼音串加密\n')astr=['WU YA SHAN LI JIE ZHAO CHUAN LAI'];an=double(astr);if mod(length(an),2)==1an=[an,an(length(an))];endan=an-ZERO;for i=1:length(an)if an(i)==-32an(i)=0;endendc=reshape(an,2,length(an)/2);dn=mod(enmat*c,m);en=reshape(dn,1,length(an));en=en+ZERO;for i=1:length(en)if en(i)==64en(i)=32;endenden=en(1: length(an));disp(['密文是:',char(en)])运行结果：本组成员的姓名为吴亚山李杰赵传来,拼音为:WU YA SHAN LI JIE ZHAO CHUAN LAI以[1 2;0 4]为密钥对此拼音串加密密文是:KCWSA HEBBXUI AIE OEDFFLWCBBXUSI3.若将你姓名的拼音作为Hill2密文，例如：赵本山(ZHAO BEN SHAN，含空格)，密钥等参见练习1，求其在模27 意义下的明文．程序代码：(prog3.m)m=27;enmat=[1 2;0 4];demat=[1 13;0 7];ZERO=64;c=[];en=[];fprintf('本组成员的姓名为吴亚山李杰赵传来,拼音密文为:\n')fprintf('KCWSA HEBBXUI AIE OEDFFLWCBBXUSI\n')fprintf('以[1 13;0 7]为密钥对此拼音串密文解密\n')astr=['KCWSA HEBBXUI AIE OEDFFLWCBBXUSI'];an=double(astr);if mod(length(an),2)==1an=[an,an(length(an))];endan=an-ZERO;for i=1:length(an)if an(i)==-32an(i)=0;endendc=reshape(an,2,length(an)/2);dn=mod(demat*c,m);en=reshape(dn,1,length(an));en=en+ZERO;for i=1:length(en)if en(i)==64en(i)=32;endenden=en(1: length(an));disp(['明文是:',char(en)])运行结果：本组成员的姓名为吴亚山李杰赵传来,拼音密文为:KCWSA HEBBXUI AIE OEDFFLWCBBXUSI以[1 13;0 7]为密钥对此拼音串密文解密明文是:WU YA SHAN LI JIE ZHAO CHUAN LAI六．实验总结本实验主要涉及代数，利用模运算意义下的矩阵乘法、求逆矩阵、线性无关、线性空间与线性变换等概念和运算，学习古典密码体制的加密、解密和破译过程．实验中解决了如下问题：求模27倒数表；判断二阶矩阵在模27意义下是否可逆，可逆则求其逆；求明文字符串在模27意义下的Hill2密文；求密文字符串在模27意义下的Hill2密文。

古典密码学实验

一、实验背景与目的通过实现简单的古典密码算法，理解密码学的相关概念如明文（plaintext）、密文（ciphertext）、加密密钥(encryption key)、解密密钥（decryption key）、加密算法(encryption algorithm)、解密算法(decryption algorithm)等。

二、实验环境Visual C++6.0三、实验内容(1)用C\C++语言实现仿射变换（Affine）加/解密算法；2）(2)用C\C++语言实现统计26个英文字母出现的频率的程序；(3)利用仿射变换加/解密程序对一段较长的英文文章进行加密，再利用统计软件对明文和密文中字母出现的频率进行统计并作对比，观察有什么规律。

其中a, b为密钥，25,0≤≤ba，且gcd(a, 26)=1实验要求：加/解密程序对任意满足条件的a、b都能够处理。

仿射变换：加密：()26mod,bammEcba+==解密：()()26mod1,bcacDmba-==-四、实验原理一个仿射变换对应于一个矩阵和一个向量的乘法，而仿射变换的复合对应于普通的矩阵乘法，只要加入一个额外的行到矩阵的底下，这一行全部是0除了最右边是一个1，而列向量的底下要加上一个1。

仿射变换原理在基于MQ问题的多变元公钥密码中,公钥一般是方程组,但是这种没有处理的方程组很容易受到插值法的攻击,例如:首先在q元有限域上选取个变量以及个变量。

构造方程组:这里面公钥信息方程组就是:其中是明文信息,而则是密文。

可以看出这样的公钥信息很容易受到插值法的攻击,下面使用仿射将明文信息进行隐藏。

先选取一个可逆矩阵,然后进行以下变换:其中是一个可逆矩阵,这样变化以后就可以将转化成以为变量的方程组.在加密解密程序中，需要对明文进行仿射变换，但是要对大小写做判断，并且处理空格，逗号，等特殊符号。

五、实验结果分析如图为统计26个英文字母在文章中的概率如图为加密解密算法密文如下六、实验心得在第一次的密码学上机实验中，我见到并学到了一系列的密码学知识，同时也掌握了如何用不同的方法生成全排序。

MATLAB全部实验及答案

2）A*B和A.*B
3）A^3和A.^3
4）[A，B]和[A（[1，3]，：）；B^2]
2、设有矩阵A和B，A=[1 2 3 4 5；6 7 8 9 10；11 12 13 14 15；16 17 18 19 20；21 22 23 24 25]，B=[3 0 16；17 -6 9；0 23 -4；9 7 0；4 13 11]
使用Windows的“开始”菜单。
运行MATLAB系统的启动程序matlab.exe。
利用桌面上的快捷方式。
MATLAB主窗口
命令窗口(Command Window)
当前目录窗口(Current Directory)
工作空间窗口(Workspace)
命令历史窗口(Command History)
2、下列符号中哪些是MATLAB的合法变量名？用给变量赋值的方法在机器上验证你的答案（3vars、global、help、My_exp、sin、X+Y、_input、E-4、AbCd、AB_C_。）
6、利用MATLAB提供的rand函数和圆整函数随机生成4Ｘ3整数矩阵A，进行如下操作
1）A各列元素的平均值和中值
平均值
>> A_mean=mean(A)
A_mean =
0.5000 0.7500 0.7500
中值
>> A_median=median(A)
A_median =
0.5000 1.0000 1.0000
整数类型的运算函数
创建逻辑类型数据的函数
MATLAB的逻辑运算
MATLAB的关系运算
格式化字符
三、主要仪器及耗材
计算机
四、实验内容和步骤
1、已知A=[12 34 -4；34 7 87；3 65 7]，B=[1 3 -1；2 0 3；3 -2 7]，求下列表达式的值：

古典密码算法

古典密码算法实验⼀古典密码算法古典密码算法曾经被⼴泛应⽤，⼤都⽐较简单，使⽤⼿⼯和机械操作来实现加密和解密。

它的主要对象是⽂字信息，利⽤密码算法实现⽂字信息的加密和解密。

古典密码学可以分为代替密码（也叫做移位密码）和置换密码（也叫做换位密码）两种，其中代替密码典型的有Caesar密码，数乘密码和仿射变换等，置换密码有单表置换和多表置换等。

⼀、实验⽬的1.理解代替密码学加密过程2.理解置换密码学加密过程⼆、实验环境Windows，交换⽹络结构，每组2⼈，VC++6.0，密码⼯具三、实验原理1.Caesar（恺撒）密码Caesar密码是传统的代替加密法，当没有发⽣加密（即没有发⽣移位）之前，其置换表如1-1所⽰。

加密时每⼀个字母向前推移k位，例如当k=5时，置换表如1-2所⽰。

于是对于明⽂：data security has evolved rapidly经过加密后就可以得到密⽂：IFYF XJHZWNYD MFX JATQAJI WFUNIQD若令26个字母分别对应整数0～25，如表1-3所⽰。

则Caesar加密变换实际上是：c=(m+k)mod26其中m是明⽂对应的数据，c是与明⽂对应的密⽂数据，k是加密⽤的参数，也称为密钥。

很容易得到相应的Caesar解密变换是：m=D(c)=(c–k)mod26例如明⽂：data security对应的数据序列：301901842201781924当k=5时经过加密变换得到密⽂序列：852452397252213243对应的密⽂为：I F Y F X J H Z W N Y D2.单表置换密码单表置换密码也是⼀种传统的代替密码算法，在算法中维护着⼀个置换表，这个置换表记录了明⽂和密⽂的对照关系。

当没有发⽣加密（即没有发⽣置换）之前，其置换表如1-4所⽰。

在单表置换算法中，密钥是由⼀组英⽂字符和空格组成的，称之为密钥词组，例如当输⼊密钥词组：I LOVE MY COUNTRY 后，对应的置换表如表1-5所⽰。

古典加密的破解方法

古典加密的破解方法
首先，凯撒密码是一种简单的替换密码，通过将字母按照一个
固定的偏移量进行移动来加密消息。

对于凯撒密码，最简单的破解
方法是通过暴力破解，即尝试所有可能的偏移量来解密消息。

现代
计算机可以很快地完成这一过程，因此凯撒密码在现代已经不再安全。

其次，替换密码是指用一个字母替换另一个字母来加密消息，
这种加密方法可以通过频率分析来破解。

频率分析是指统计加密文
本中每个字母出现的频率，然后将其与明文中字母的频率进行比较。

通过比较频率，可以推断出替换的规律，从而破解替换密码。

另外，重组密码是一种将明文中的字母重新排列来加密消息的
方法，这种加密方法可以通过暴力破解或者利用语言学特征来破解。

暴力破解是指尝试所有可能的排列组合来解密消息，而利用语言学
特征则是通过分析语言中字母和字母组合的规律来破解密码。

除了上述方法，还可以利用一些现代密码学的技术来破解古典
加密，比如使用计算机来进行穷举搜索、使用机器学习算法来破解
密码等。

总的来说，古典加密的破解方法主要包括暴力破解、频率
分析、语言学特征分析以及现代密码学技术的应用。

随着计算机和密码学的发展，古典加密的安全性已经大大降低，因此在实际使用中应当选择更加安全的现代加密方法。

古典密码与破译

现在，我们说明式(3)中确定的P0就是明文P。事实上，由式(3)，式(2)和式(1)，我们得到 P0 a (E b) a((aP b) b) aaP P (mod M)，由于0 P < M，0 P0 < M，所以，由上式得到P0 = P。

A 1 N B 2 O C 3 P D 4 Q E 5 R F 6 S G 7 T H 8 U I 9 V J W K X L Y M Z
10 11 12 13
14 15 16 17 18 19 20 21 22 23 24 25 0
（2）选择一个二阶可逆正整数方阵A，称为Hill2密码的加密矩阵，它是这个加密体制的密钥（只有通信双方掌握）。
3、主要函数文件的实现
（1）对于任意一个矩阵A，它是否能成为一个加密密码？

function flag=ifinv(A,m) detA=det(A); if gcd(m,detA)==1 flag=1 else flag=0 end
（2）如何求A在模m下的逆矩阵根据高等代数可得其求解公式为
例1 设符号a，b，，y，z分别与整数0，1，，24， 25对应，使用仿射加密方法，取M = 26，a = 1，b = 3，a = 1，对明文P中的每一个符号用这一方法加密： E P 3 (mod 26)。这就是所谓的“恺撒密码”。在古罗马时代，恺撒大帝在传送军事命令时，把每个英文字母用它后面的第三个字母代替，即按表2的替换方式： P a b c d e f g h i j k l m
加密方法
单表密码有密钥，但字母的频率不变（凯撒密码，福尔摩斯密码）多表密码不同位置字母加密对应数不同（维吉尼亚密码）多字符单边代换密码（希尔密码）现代密码体制密文序列模仿随机序列

322-古典密码与破译

322-古典密码与破译实验六古典密码与破译一、问题背景和实验目的保密通讯在军事、政治、经济斗争和竞争中的重要性是不言而喻的(在斗争或竞争中，一方要将信息传递给己方的接收者，同时又要防止其他人(特别明文) 经过加密，是敌方) 知道信息的内容(他采用的一种方式是:将原来的信息(称为变成密文之后发送出去，使敌方即使得到密文也读不懂，而合法的接收者收到密文之后却可以按照预先约定好的方法加以解密，再翻译成明文(而敌方却要千方百计从密文破译出明文来(一方如何编制密码使之不易被破译，另一方则要找到其弱点加以破译，这就构成了密码学的主要内容(从密码学的发展来看，密码可分为古典密码 (即以字符为基本加密单元的密码)，以及现代密码(即以信息块为基本加密单元的密码)(这里我们将介绍古典密码的加密和破译原理(本实验主要涉及代数，利用模运算意义下的矩阵乘法、求逆矩阵、线性无关、线性空间与线性变换等概念和运算，学习古典密码体制的加密、解密和破译过程(二、相关函数(命令)及简介1(input('一些提示语句'):由键盘输入表达式(注:a=input('')，对不同的变量类型 a，输入时要注意相应的格式，若 a 为字符则要加' '，若a 为矩阵则要加[ ]等(2(length(a):给出数组 a 的长度(3(mod(m, n):求 m 被 n 整除后的余数(4(det(a):求矩阵 a 的行列式(5(inv(a):求矩阵 a 的逆矩阵(6(reshape(a, m, n):将矩阵 a 重排成 m*n 的矩阵(例如:a=1:10; b=reshape(a, 2, 5)b= 1 3 5 7 92 4 6 8 107(double('字符'):将'字符'内的字符转化成 ASCII 码(8(char(a):将 a 的每个数值转化为字符(例如:c=double('love')c = 108 111 118 101char(c)ans = love9([m, n]=size(a):求矩阵a的维数.10(gcd(m, n):求m, n的最大公约数(11(fprintf(fid, format, A, ...):以指定格式将数据写入文件，若无参数fid，则输出到屏幕(,,三、实验内容1.Hill 密码的两个实际问题: 2实际问题(甲):甲方收到与之有秘密通信往来的乙方的一个密文信息，密文内容:W K V A C P E A O C I X G W I Z U R O Q W A B A L O H D K C E A F C L W WC V L E M I M C C按照甲方与乙方的约定，他们之间的密文通信采用 Hill 密码，密钥为二阶矩阵212,,且汉语拼音的 26 个字母与 0,25 之间的整数建立一一对应的关系，称之为A,,,03,,字母的表值，具体的表值见表 1(问这段密文的原文是什么?表1明文字母的表值A B C D E F G H I J K L M1 2 3 4 5 6 7 8 9 10 11 12 13N O P Q R S T U V W X Y Z14 15 16 17 18 19 20 21 22 23 24 25 0实际问题(乙):甲方截获了一段密文:M O F A X J E A B A U C R S X J L U Y H Q A T C Z H W B C S C P 经分析这段密文是用 Hill 密码编译的，且这段密文的字母 U C R S 依次代表字母T A C 2O，问能否破译这段密文的内容?2. Hill 密码的数学模型 2一般的加密过程是这样的:明文加密器密文普通信道解密器明文 ,,,,,其中的“ 普通信道解密器”这个环节容易被敌方截获并加以分析( ,,在这个过程中，运用的数学手段是矩阵运算，加密过程的具体步骤如下:1) 根据明文字母的表值，将明文信息用数字表示，设明文信息只需要 26 个拼音大写字母 A—Z(也可以不止 26 个，如还有小写字母、数字、标点符号等)，通信双方给出这 26 个字母表值(见表 1)(A2) 选择一个二阶可逆整数方阵，称为 Hill 密码的加密矩阵，它是这个加密体制2的“密钥”(是加密的关键，仅通信双方掌握)(问题(甲)已给出了这个二阶矩阵(3) 将明文字母依次逐对分组(Hill 密码的加密矩阵为二阶矩阵，则明文字母每 2 个2一组(可以推广至 Hilln 密码，则每 n 个明文字母为一组)(若最后一组仅有一个字母，则补充一个没有实际意义的哑字母，这样使每一组都由 2 个明文字母组成(查出每个明文字母的表值，构成一个二维列向量 ( ,,,,A,A4) 乘以，得一新的 2 维列向量，由的两个分量反查字母表值得到, 的两个字母即为密文字母(以上 4 步即为 Hill 密码的加密过程( 2解密过程，即为上述过程的逆过程(12,,例:明文为HDSDSXX (“华东师大数学系”的拼音缩写)，，求这段明文A,,,03,,的Hill密文( 2解:将明文相邻文母每 2 个分为一组:,,HD SD SX XX (1) 最后一个字母 X 为哑字母，无实际意义(查表1得到每对字母的表值，并构造 2 维列向量:8191924,,,,,,,, (2) ,,,,,,,,, , , ,,,,,,,,442424,,,,,,,,将上述 4 个向量左乘矩阵A，得到 4 个 2 维列向量:16276772,,,,,,,, (3) ,,,,,,,,, , , ,,,,,,,,12127272,,,,,,,,作模 26 运算(每个元素都加减 26 的整数倍，使其化为 0,25 之间的一个整数)得到:1616271,,,,,,,, (mod26),(mod26),,,,,,,,,,,12121212,,,,,,,,67157220,,,,,,,, (mod26),(mod26),,,,,,,,,,72207220,,,,,,,,反查表 1 得到每对表值对应的字母为:PL AL OT TT (4)(“华东师大数学系”的拼音缩写) 的密文( 这就得到了“HDSDSXX”要将这段密文解密，只要将上述加密过程逆转回去，即将密文按同样方式分组，查它们的表值即得:1611520,,,,,,,, (5) ,,,,,,,,, , , ,,,,,,,,12122020,,,,,,,,(5) 是前面的 (3) 经模26运算的结果(但如何由 (5) 中的向量求得(2) 中的向量呢? 这是在模运算意义下，如何解方程组:A,,, (6)det()0A,的问题(一个一般的 n 阶方阵可逆的充要条件为 (但在模 26 意义下矩阵可Zm,,0,1,2,,1逆与一般的矩阵可逆有所不同(记整数集合，m 为一正整数，模m ,,m可逆定义如下:A定义1:对于一个元素属于集合的 n 阶方阵，若存在一个元素属于集合的ZZmmB方阵，使得ABBAEm,,(mod),,1ABA称为模 m 可逆，为的模 m 逆矩阵，记为( BAm,(mod)Em(mod)的意义是，每一个元素减去 m 的整数倍后，可以化成单位矩阵(例如: ,,2752,, (mod26),E,,2653,,abm,1(mod)定义2:对的一个整数，若存在的一个整数，使得，称为bbZZaamm ,1的模倒数或乘法逆，记作( bam,(mod)m可以证明，如果与无公共素数因子，则有唯一的模倒数(素数是指除了 1 与amam,1自身外，不能被其他非零整数整除的正整数)，反之亦然(例如，. 利用这39(mod26),点，可以证明下述命题:det()A命题:元素属于的方阵A模可逆的充要条件是，和没有公共素数因子，Zmmmdet()A即和互素( m显然，所选加密矩阵必须符合该命题的条件(问题(甲)所选择的明文字母共 26 个，，26 的素数因子为 2 和 13，所以上的m,26Z26ac,,det()(mod)AmAA方阵可逆的充要条件为不能被 2 和 13 整除(设，若满A,,,bd,,足命题的条件，不难验证:db,,,,,11 Aadbc()(mod26),,,,ca,,,,1()(mod26)adbc,()(mod26)adbc,其中是的倒数(显然，是中的数( Z()adbc,26中有模 26 倒数的整数及其倒数可见表 2( Z26表2 模 26 倒数表a1 3 5 7 9 11 15 17 19 21 23 25-1 1 9 21 15 3 19 7 23 11 5 17 25 a表2 可用下列程序求得:m=26;for a=1:mfor i=1:mif mod(a*i, m)==1fprintf('The INVERSE (mod %d) of number: %d is: %d\n', m, a, i) end; end; end注意:附录1给出的 Matlab 程序，可以用于判断一个2 阶方阵在模 26 意义下是否可逆，并在可逆的前提下求出其逆矩阵(读者可结合下列演算的实例加以验证(,1利用表 1 可以演算出的如下: A(mod26),,32,,,,,11 A(mod26)3(mod26),,,01,,32,,, ,9(mod26),,01,,2718,,, ,(mod26),,09,,18,, ,,(mod26)B,,09,,于是，可以简单地计算得到:16112197,,,,,,,, BB*,*,,,,,,,,,,,1210812108,,,,,,,,1517520180,,,,,,,, BB*,*,,,,,,,,,,2018020180,,,,,,,,再进行模 26 运算后得到:8191924,,,,,,,, ,,,,,,,,,,,442424,,,,,,,,即得到明文:HD SD SX X(X)(用 Matlab 编程进行加密算法的程序参见附录 2(而用 Matlab 编写的相应的解密算法程序参见附录 3(表 3 问题 (甲) 的解序号分组密文密文表值明文表值分组明文1 W 23 7 GK 11 21 U2 V 22 4 DA 1 9 I3 C 3 1 AP 16 14 N4 E5 13 MA 1 9 I5 O 15 13 MC 3 1 A6 I 9 19 SX 24 8 H7 G 7 9 IW 23 25 Y8 I 9 9 IZ 0 0 Z,,9 U 21 9 IR 18 6 F10 O 15 21 U Q 17 23 W11 W 23 5 EA 1 9 I12 B 2 10 JA 1 9 I13 L 12 2 B O 15 5 E14 H 8 14 ND 4 10 J15 K 11 9 IC 3 1 A16 E 5 13 MA 1 9 I17 F 6 4 DC 3 1 A18 L 12 14 N W 23 25 Y19 W 23 21 UC 3 1 A20 V 22 14 N L 12 4 D21 E 5 5 E M 13 13 M22 I 9 9 IM 13 13 M23 C 3 1 AC 3 1 A于是，实际问题(甲)的解为:GU DIAN MI MA SHI YI ZI FU WEI JI BEN JIA MI DAN YUAN DE MI MA即为:“古典密码是以字符为基本加密单元的密码”( 以下来解实际问题(乙)(实际问题 (乙) 属于破译问题(前面的加密与解密过程类似于在二维向量空间进行线性变换与其逆变换，每个明文向量是一个上的二维向量，乘以加密矩阵后，仍为上ZZmmA的一个二维向量(由于加密矩阵为可逆矩阵，所以，如果知道了两个线性无关的二维,1AA明文向量与其对应的密文向量，就可以求出它的加密矩阵及( 问题 (乙) 的密文中只出现一些字母，当然它可以是汉语拼音，或英文字母或其他语m,26言的字母(所以可猜测秘密信息是由 26 个字母组成，设(通常由破译部门通过大量的统计分析与语言分析确定表值(假如，所确定的表值为表 1，已知,,,UTRC,,,,,,,, ,,,,,,,,,,,,CASO,,,,,,,,注:前的为密文，后的为明文( "","",按照表1，UT2120,,,,,,,, ,,,,,,,,,A111,,,,,,,,CA31,,,,,,,,RC183,,,,,,,, ,,,,,,,,,A222,,,,,,,,SO1915,,,,,,,,2118在模 26 意义下，，它有模 26 倒数，所,,,,,det(,)(mod26)345(mod26)712319以，在模 26 意义下线性无关，类似地，也可以验证，,,,det(,)11(mod26),,,,,,121212线性无关(TTTTT,1,1TPXC,记，则，记，其中( PC,,(,),(,),,,,PACPAC,,,()XA,()1212 TTTPE以下在模 26 意义下对进行一系列初等行变换将变成单位矩阵，则相(|)PCT,1TCX应的将变成，即( ()A10117,,,,,,11T经过以上的一系列推导，可得 AA,,(),,,,,17909,,,,相应的 Matlab 程序参见附录 4.利用与实际问题(甲)同样的解密方法，可以求得，这段密文的明文是:| HE | WI LL | VI SI T| A | CO LL EG E | T HI S | A FT ER NO ON | 分析这段文字，如果依竖线所划分成的词汇，则这段密文可理解为如下一段文字:''He will visit a college this afternoon''(这样，可以认为破译成功(四、自己动手1. 实际问题 (甲) 的修正:按照甲方与乙方的约定，他们之间的密文通信采用Hill212,,密码，密钥为二阶矩阵且汉语拼音的 26 个字母以及空格(字母 A~Z 的表值A,,,04,,为 1~26，空格的表值为 0)与 0,26 之间的整数建立一一对应的关系，称之为字母的表值，试修正表 1、表 2 以及附录中的程序，以给出模 27 意义下矩阵可逆的判别方法和具体求法(2. 若将你姓名的拼音作为明文，例如:赵本山 (ZHAO BEN SHAN，含空格)，密钥等参见练习 1，求其在模 27 意义下的Hill密文( 23. 若将你姓名的拼音作为Hill密文，例如:赵本山 (ZHAO BEN SHAN，含空格)，2,,,密钥等参见练习 1，求其在模 27 意义下的明文(4. 利用所介绍的Hill密码体制的原理，根据给定的 26 个英文字母的乱序表值(见2表4)，设计与建立 Hill密码体制的加密、解密与破译框图并建立必要的计算机程序(设4英文 26 个字母以下面的乱序表与中的整数对应: Z26表4A B C D E F G H I J K L M5 23 2 20 10 15 8 4 18 25 0 16 13N O P Q R S T U V W X Y Z7 3 1 19 6 12 24 21 17 14 22 11 9869569510(1) 设，验证矩阵A能否作为 Hill密码体制的加密矩阵(用框图A,45849106114画出你的验算过程，并编写相应的计算机程序((2) 设明文为HILL CRYPTOGRAPHIC SYSTEM IS TRADJITIONAL(利用上面的表值与加密矩阵给此明文加密，并将得到的密文解密(画出加密与解密过程的框图并编写相应的计算机程序(5. 设已知一份密文为 Hill 密码体系，其中出现频数最高的双字母是 RH和NI，2而在明文语言中，出现频数最高的双字母为 TH 和 HE(由这些信息按表 5 给出的表值能得到什么样的加密矩阵?A B C D E F G H I J K L M0 1 2 3 4 5 6 7 8 9 10 11 12N O P Q R S T U V W X Y Z13 14 15 16 17 18 19 20 21 22 23 24 256. 找出元素属于的所有可能的 Hill 密码加密矩阵(若截获了如下一段密文Z226UTCQCVFOYQUVMGMGULFOLEYHDUHOPEASWXTIFBAMWT且已知它是根据表 1 按 Hill 密码体制加密的，你能否将其解密? 2五、附录附录 1:判断一个 2 阶方阵是否模 26 意义下可逆;若可逆，求出模 26 意义下的逆矩阵(m=26;aa=input('输入一个2×2的矩阵，格式:[a11 a12;a21 a22]: ')while size(aa)~=[2 2]aa=input('输入一个2×2的矩阵，格式:[a11 a12;a21 a22]: ')enda=det(aa);bb=aa;if gcd(m, a)~=1disp('该矩阵不可逆'),,,elsefor i=1:mif mod(a*i, m)==1antaa=i;endendastar=[aa(2,2) -aa(1,2);-aa(2,1) aa(1,1)];invaa=mod(antaa*astar,m);: ', mat2str(invaa)]) disp(['原矩阵是:', mat2str(aa), '，它的逆矩阵(mod', num2str(m), ') 是end注:(1) 实际应用中，当二阶密钥矩阵(可逆)为已知时，就不要每次再输入矩阵了(例12,,如:模 26 意义下的二阶密钥矩阵为，则可直接输入:enmat=[1, 2;0, 3]; 以取A,,,03,,代第 3,7 行(18,,(2) 附录 2 中的 demat=[1, 8;0, 9] 即实为本程序的结果，读者也可将demat=,,09,,附录 1 归并到附录 2、附录 3 中，以使附录 2、附录 3 保持独立( (3) 注意附录 2、附录 3 中当字符串的长度不是偶数时的处理方法( (4) 特别注意当m,27时，应如何适当地修改附录 2、附录 3，才能完成对空格的正确处理(12,,附录2:模 26 意义下，密钥(加密)为矩阵时，对任意输入的大写字母A,,,03,,串的加密程序(m=26;enmat=[1 2;0 3];demat=[1 8;0 9];ZERO=64;c=[];e1=[];astr=input('输入要加密的明文文字(全部为大写字母):') whileany(double(astr)>90 | double(astr)<65)astr=input('输入错误，应该全部为大写字母:')enda1=double(astr);lh=length(a1); if mod(length(a1), 2)==1a1=[a1, a1(length(a1))]; enda1=a1-ZERO;for i=1:length(a1)if a1(i)==26a1(i)=0;endendc=reshape(a1, 2, length(a1)/2); d1=mod(enmat*c, m);e1=reshape(d1, length(a1), 1);,,,e1=e1';e1=e1+ZERO;for i=1:length(e1)if e1(i)==64e1(i)=90;endende1=e1(1:lh);char(e1)18,,附录 3:模 26 意义下，密钥(解密)为矩阵时，对任意输入的大写字A,,,09,,母串的解密程序(m=26;enmat=[1 2;0 3];demat=[1 8;0 9];ZERO=64;c=[];e1=[];astr=input('输入要解密的密文文字(全部为大写字母):') whileany(double(astr)>90 | double(astr)<65)astr=input('输入错误，应该全部为大写字母:') enda1=double(astr);lh=length(a1); if mod(length(a1), 2)==1a1=[a1, a1(length(a1))]; enda1=a1-ZERO;for i=1:length(a1)if a1(i)==26a1(i)=0;endendc=reshape(a1, 2, length(a1)/2);d1=mod(demat*c, m);e1=reshape(d1, length(a1), 1); e1=e1';e1=e1+ZERO;for i=1:length(e1)if e1(i)==64e1(i)=90;endende1=e1(1:lh);char(e1)TTTPE附录 4:在模 26 意义下对进行一系列初等行变换将变成单位矩阵过(|)PC程的 Matlab 程序.m=26;zero=64;p=input('输入要解密的密文文字(全部为大写字母):'),,,while any(double(astr)>90 | double(astr)<65)p=input('输入要解密的密文文字(全部为大写字母):')endp=double(p)-zero;p=reshape(p, 2, 2); c=input('输入相应的明文文字(全部为大写字母):')while any(double(astr)>90 | double(astr)<65)input('输入相应的明文文字(全部为大写字母):')endc=double(c)-zero;c=reshape(c, 2, 2); pc=[p', c'];if pc(1, 1)==0;emp=pc(1, :);pc(1, :)=pc(2, :);pc(2, :)=temp; endfor i=1:(m-1)if mod(pc(1, 1)*i, m)==1ant=i;endendpc(1, :)=mod(pc(1, :).*ant, m);pc(2, :)=mod(pc(2, :)-pc(1, :).*pc(2, 1), m); for i=1:(m-1)if mod(pc(2, 2)*i, m)==1ant=i;endendpc(2, :)=mod(pc(2, :).*ant, m);pc(1, :)=mod(pc(1, :)-pc(2, :).*pc(1, 2), m); a=[pc(:, 3), pc(:, 4)]; a=a',,,。

matlab实验内容答案解析

实验报告说明:matlab课程实验需撰写8个实验报告,每个实验报告内容写每次实验内容中标号呈黑体大号字显示的题目。

第一次实验内容实验_ MATLAB运算基础一、实验目的1. 熟悉启动和退出MATLAB的方法。

2. 熟悉MATLAB命令窗口的组成。

3•掌握建立矩阵的方法。

4•掌握MATLAB各种表达式的书写规则以及常用函数的使用。

二、实验内容1•先求下列表达式的值,然后显示MATLAB工作空间的使用情况并保存全部变量。

(1) Zl =2 sin85。

1 + e22-0.45,0.3“ _ -0.3d提示：利用冒号表达式生成a向量，求各点的函数值时用点乘运算。

t20</<1(4)Z4=$—11</<2 ，其中t = 0 : 0.5 : 2.52<t<3提示:用逻辑表达式求分段函数值。

2 •已知_12 34 -4_i 3 -rA =34 7 87,B = 2 0 33 65 73-2 7求下列表达式的值：(1) A+6二B和A-B+I(其中I为单位矩阵)。

(2) A*B和A.*B o(3) A^3 和A\3。

(4) A/B和B\A。

(5 ) [A , B]和[A([l f3],；)；B A2]。

3•设有矩阵A和B_12345・~301667891017-69A =1112131415,B =023-41617181920970212223242541311(1) 求它们的乘积C。

2 将矩阵C的右下角3x2子矩阵赋给D(3) 查看MATLAB I作空间使用情况。

4.完成下列操作：(1) 求［100,999］之间能被21整除的数的个数。

提示:先利用冒号表达式,再利用find和length函数。

(2) 建立一个字符串向量,删除其中的大写字母。

提示：利用find函数和空矩阵。

第二次实验内容实验三选择结构程序设计一、实验目的1. 掌握建立和执行M文件的方法。

2. 掌握利用if语句实现选择结构的方法。

实验六：matlab古典密码与破译

古典密码实验报告

古典密码实验报告

现代密码学——古典密码算法(实验报告)

密码锁编程 matlab程序

密码与破译

matlab实验四 古典密码与破译

古典密码与matlab

数学建模实验报告古典密码与破译

古典密码学实验

MATLAB全部实验及答案

古典密码算法

古典加密的破解方法

古典密码与破译

322-古典密码与破译

matlab实验内容答案解析

matlab实验四古典密码与破译