基于位移的概率极限状态设计
道亨送电线路三维设计平台使用培训ppt模板

三维设计模块中能进行导线连接设置,方便进行进出线档、 交叉换相档的设计。
三维模块中,能进行严密的三维电气校核。测量任意两个 物体的空间距离以及导地线对地垂直距离。
三维模块中,切换工况可显示当时的导地线、绝缘子串偏 摆。
由于二维、三维设计时同步更新,设计完成时,二维部分 可以直接当提交的设计成果。
提供基础作用力接口数据,供基础程序调用。
输出司令图
支持主杆接头钢圈连接计算
支持横担桁架计算
道亨荷载计算系统可计 算各类自立式铁塔、钢管 杆、水泥杆(包括分歧塔、 多回路塔)电线荷载和塔 身风荷载,并输出荷载图, 以便电气专业提供给结构 专业使用。
铁塔荷载除能计算挂 点受力之外,还可以计算 塔身及基础受力。
水泥杆设计:《道亨水泥杆设计系统》
荷载计算:《道亨荷载计算软件》
简单积木式的快速建模 支持超过10个高度的长短腿
操作方便,数据应有尽有
向导式菜单,操作一目了然
交互编辑功能强大
可输出铁塔司令图 亦可与道亨铁塔绘图系列产品无缝连接
可使用WPS表格输出xls格式计算书
支持复杂单杆计算
特点三、地质条件设置灵活多样,不同接腿的地质条 件可以不一样。
特点四、多种基础形式同时优选,便于比较分析选择。
特点五、采用道亨专业出图程序输出施工图,调整图 块、输出施工图一气呵成。
适用于各种不同土质的钢管杆基础。包含:普通钢管 杆基础设计、钢管杆桩基础设计。
适用于小电压等级、地质条件较好地区的水泥杆基础 的设计。专业解决水泥杆基础计算及结构优化。
多跳线情况,考虑了跳线对跳线串的作用力,更加贴近真 实情况。
支持硬跳线计算
2.《道亨大跨越方案选择计算模块》
能力谱设计方法的若干问题

地点
Erzinci, Turky Kailali, India Northridge, USA Kobe, Japan Sahalin, Russian
中国 丽江 中国 伽师 中国 包头 Kane, Iran 中国 张北 Izmit, Turky 中国 集集 Gujilat, India
震级 6.8 6.2 6.7 7.2 7.6 7.0 6.9 6.4 7.1 6.2 7.4 7.3 7.7
违规、不符合抗震、偷工减料 同土耳其,地表位错
未经抗震设计、施工质量低劣
back
PBD方法的基本概念
• 含义
– 以预定的结构性态目标为依据的抗震设计方法
• 几个名词
– 性态目标——在不同地震水准下结构应达到的性能水准 – 性能水准——某地震水准下结构的最大破坏程度 – 地震水准——同一地区按重现期不同划分的地震强度 – 性能指标——描述性能水准的物理量指标
FEMA 273 & 274. 1998 6. B. Gupta, S. K. Kunnath. Adaptive spectra-based pushover procedure for seismic evaluation of structure,
Earthquake spectra. 2000. 16(2). 367-392 7. R. S. Lawson, V. Vance and Helmut Krawinkler. Nonlinear static push-over analysis-why, when, and how? 5th
基于能量的设计方法 energy-based design
按延性系数的设计方法
能力谱—需求谱设计方法
直接基于位移的设计方法
静力弹塑性分析(Pushover分析)两种方法剖析
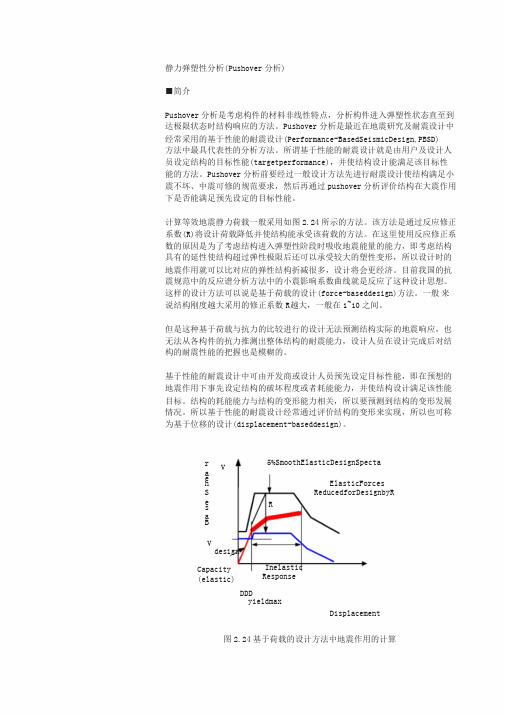
静力弹塑性分析(Pushover分析)■简介Pushover分析是考虑构件的材料非线性特点,分析构件进入弹塑性状态直至到达极限状态时结构响应的方法。
Pushover分析是最近在地震研究及耐震设计中经常采用的基于性能的耐震设计(Performance-BasedSeismicDesign,PBSD)方法中最具代表性的分析方法。
所谓基于性能的耐震设计就是由用户及设计人员设定结构的目标性能(targetperformance),并使结构设计能满足该目标性能的方法。
Pushover分析前要经过一般设计方法先进行耐震设计使结构满足小震不坏、中震可修的规范要求,然后再通过pushover分析评价结构在大震作用下是否能满足预先设定的目标性能。
计算等效地震静力荷载一般采用如图2.24所示的方法。
该方法是通过反应修正系数(R)将设计荷载降低并使结构能承受该荷载的方法。
在这里使用反应修正系数的原因是为了考虑结构进入弹塑性阶段时吸收地震能量的能力,即考虑结构具有的延性使结构超过弹性极限后还可以承受较大的塑性变形,所以设计时的地震作用就可以比对应的弹性结构折减很多,设计将会更经济。
目前我国的抗震规范中的反应谱分析方法中的小震影响系数曲线就是反应了这种设计思想。
这样的设计方法可以说是基于荷载的设计(force-baseddesign)方法。
一般来说结构刚度越大采用的修正系数R越大,一般在1~10之间。
但是这种基于荷载与抗力的比较进行的设计无法预测结构实际的地震响应,也无法从各构件的抗力推测出整体结构的耐震能力,设计人员在设计完成后对结构的耐震性能的把握也是模糊的。
基于性能的耐震设计中可由开发商或设计人员预先设定目标性能,即在预想的地震作用下事先设定结构的破坏程度或者耗能能力,并使结构设计满足该性能目标。
结构的耗能能力与结构的变形能力相关,所以要预测到结构的变形发展情况。
所以基于性能的耐震设计经常通过评价结构的变形来实现,所以也可称为基于位移的设计(displacement-baseddesign)。
基础隔震结构基于位移的设计方法

震结 构基 于位移 的设 计应 将 隔震层 的位 移作 为 控 制指 标 . 本文取 隔震 层的 水平 最 大 反应 位 移△ _作 为基 础 隔震结构 的位 移指标 , 则相 应 的设 计准则 为
度体系, 先假定一个台理 的位移模式 , 将原体系转
收稿 日期 : ∞1 l 一 8 2 一 O 1
维普资讯
第1 卷 第 1 期
2O O 2越 1月
广 州大学 学报 ( 自然科 学 版)
J U ̄A FG A G i 】 】 rY №l工l c O ] LO U N Z ̄U IⅡv殂Sr ( ta s妇噼 & I I l
vo . N01 11 . J . 湖 2 锄
全 . 地震作 用 下 , 在 隔震 结 构 的位 移 主 要 集 中在 隔 震层 , 因此 , 隔震 层 位 移 的验 算 是 隔震 结构 设 计 对 的关键 内容 . 文将 直接基 于位 移 的设计方 法 引入 本 到 隔震 结构 的设计 中 , 出 隔震结 构基 于位 移设 计 提 的位 移指标 和 设 计准 则 , 建立 了设 计位 移 反应 谱 , 给 出了设计 步 骤和 实例 .
箍筋进 行设 计 , 使其 具有 相应 的变形 能力 .
2 基 础 隔震结构 基 于位 移设 计 应 考 虑 的问题
2 1 基础厢震结构基于位移设计的 目标位移 隔震结构设计 的关键是隔震层的设计 , 隔震结
构 减震性 能的好 坏取决 于 隔震层 的设 计 , 隔震结构
在 地震作 用下位 移反 应 主要 集 中在 隔震层 . 由于隔
文章编号 d6 1 29 2 ̄ )13 50 7. 2 (o 2o.0 - . 4 (7 5
基础 隔震结构基于 位移的设 计方法
【国家自然科学基金】_基于位移的抗震设计_基金支持热词逐年推荐_【万方软件创新助手】_20140801

科研热词 钢筋混凝土桥墩 位移反应谱 基于性能的抗震设计 基于位移 地震响应 非线性动力分析 隔震 阻尼比 铅芯橡胶支座 能力谱法 目标位移 时程分析 损伤指数 振型叠加 抗震分析 抗震 弹塑性位移 屈曲约束支撑 层间位移角 层间位移 基于位移的抗震设计 地震危险性 地震区划 半刚性连接 位移需求 黏滞阻尼器 非迭代方法 非线性黏滞阻尼器 非线性黏滞流体阻尼器 非线性 非弹性位移谱 静力非线性 静力弹塑性分析 隧道工程 附加改进肘型斜撑阻尼器 阻尼比修正系数 钢骨混凝土剪力墙结构 钢筋混凝土框架 钢筋混凝土剪力墙 钢框架-钢筋混凝土核心筒混合结构 钢-混组合框架 钢-混凝土组合结构 重力坝 适用性 连续梁桥 近场地震 轴压比 设计承载力 规范反应谱 装配式连续板桥 能力谱 耗能
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
结构超强 结构优化 组合梁 简化抗震分析 等效阻尼比 等效阻尼 等效单自由度系统 等效侧向刚度 等延性弹塑性反应谱 等位移准则 等价输入干扰 空间变异性 离散性 直接基于位移设计方法 理想弹塑性 混凝土拱桥 消能减震 消能体系 水工结构 正规化累积耗能参数 模态pushover分析 概率极限状态 桩基工程 桥梁设计 桥梁工程 桥 框架柱 极限目标位移 有限元法 有限元 有效截面抗弯刚度 方钢管混凝土柱 斜拉桥 接触单元 损伤指标 拱桥 拉、压剪屈服 抗震设计 抗震性能 抗滑稳定评价 性能设计 性能目标 性能水准 性能指标 性能抗震设计 性态抗震设计 循环塑性 强度折减系数 强度折减因子 弹塑性结构 弹塑性反应谱 弹塑性位移反应谱 延性 差动
浅析关于桥梁抗震设计规范反应谱若干问题

市政桥梁154 2015年20期浅析关于桥梁抗震设计规范反应谱若干问题张秋生齐齐哈尔博恩公路勘察设计有限责任公司,黑龙江齐齐哈尔 161000摘要:反应谱法在桥梁抗震设计中是有一定应用价值的,虽然目前大多数抗震设计规程都指出对大跨度桥梁进行抗震设计应采用动态时程分析法,但是有必要研究反应谱法的优点及不足,以确保桥梁工程在地震过程中有足够的抗震能力和合理的结构安全度。
关键词:桥梁;抗震设计规范;反应谱;修正系数中图分类号:tion wa 文献标识码:A 文章编号:1671-5810(2015)20-0154-021 反应谱法基本概念人类在与地震的斗争中发展了各种抗震分析方法,分为确定性方法和概率性方法两大类。
静力法、反应谱法和时程分析法均属于确定性方法,随机振动、虚拟激励法属于概率性方法。
通常所说的结构地震反应分析,就是建立结构地震振动方程,然后通过求解振动方程得到结构地震反应(位移、内力等的过程。
在结构抗震理论发展中,静力法、反应谱法和动力时程分析法三个阶段的形成和发展是人类对自然规律认识的不断深入与完善的过程。
反应谱理论考虑了结构物的动力特性,而且简单正确地反映了地震动的特性,因此得到了广泛认可和应用。
2 中国建筑抗震设计规范中国的《建筑抗震设计规范(GB50011-2001 )》(中国人民共和国建设部等,2001)以地震影响系数a的形式给出设计谱,地震影响系数由设计基本地震加速度、设计地震分组、场地类别以及阻尼比确定。
设计反应谱曲线包括4段:直线上升段、平台段、曲线下降段和直线下降段。
特征周期Tg 根据场地类别和设计地震分组查表确定。
阻尼比的影响通过参数η1、γ、η2考虑。
由于大多数工程中阻尼比都取为0.05,所以在下面的反应谱比较中,阻尼比均取为0.05。
2.1 上升段:2.2 水平段:2.3 曲线下降段:2.4 直线下降段:与上一版抗震设计规范GB711-89相比,GB50011-2001反应谱周期范围由3s扩展到了6s,增加了直线下降段。
【国家自然科学基金】_验算点法_基金支持热词逐年推荐_【万方软件创新助手】_20140801

推荐指数 1 1 1 1 1
2014年 序号 1 2 3 4 5 6
2014年 科研热词 锈蚀模型 耐久性 碳纤维加固 可靠度指标 变异系数 rc桥梁 推荐指数 1 1 1 1 1 1
推荐指数 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
2011年 科研热词 推荐指数 验算点法 4 可靠指标 2 可靠性 2 可靠度 2 频率 1 非正交多项式 1 随机梁式结构 1 锚杆挡土墙 1 递推随机有限元方法 1 边坡工程 1 自适应协方差矩阵进化策略 1 统一强度理论 1 结构 1 空间变异性 1 爆炸 1 波动范围 1 沿空留巷 1 概率分析 1 概率分布 1 标准值 1 有限单元法 1 支护结构 1 地质成因 1 土坡 1 围岩稳定性准则 1 响应面法 1 可靠度分析 1 jc法 1
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号1 2 3 4 5
科研热词 概率极限状态 抗震设计 基于位移 可靠度 分项系数
推荐指数 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10
科研热词 验算点法 随机性 随机场 边坡稳定性 边坡工程 空间变异性 极值理论 敏感性分析 坑蚀 可靠性
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
科研热词 验算点法 频遇值 钢绞线 钢筋混凝土短柱 钢拉杆 目标可靠度 混凝土 桥梁工程 材料分项系数 最小二乘法 时变可靠度 抗力分项系数 抗力 大型跨海桥梁 基础结构 可靠指标 受弯承载力 准永久值 一次二阶矩法 frp筋
极限状态设计法简介

极限状态设计法简介顾迪民一, 定义①极限状态设计法以相应于结构和构件各种功能要求的极限状态,如承载能力的极限状态和正常使用的极限状态等为依据的设计方法。
结构和构件应满足这些极限状态的限制。
② 许用应力设计法在规定的使用载荷(标准值)作用下,按线性弹性理论算得的结构或构件中的应力(计算应力)应不大于规范规定的材料许用应力。
材料的许用应力由材料的平均极限抗力(屈服点、临界应力和疲劳强度)除以安全系数而得,安全系数可由经验确定。
③ 概率设计法以概率理论为基础确定的结构或构件的失效概率)P (f 或可靠概率)1P P )(P (f s s =+来定量地度量结构或构件的可靠性。
用此法设计的各类结构或构件具有大体相同的可靠度。
④ 概率极限状态设计法在概率设计法基础上,进一步建立结构可靠性指标与极限状态方程之间的数学关系。
在设计表达式中采用载荷分项系数,这些分项系数也是根据各载荷变量的统计特征在概率分析的基础上经优选确定的。
载荷分项系数的确定有三种水平:其一为部分系数由概率分析确定,部分系数用经验确定,也称半概率极限状态设计法;其二为所有系数均由概率分析确定,但其概率分布曲线一列用正态分布曲线代替,故称近似概率极限状态设计法;其三为全概率极限状态设计法,是发展趋向.二, 近似概率极限状态设计法1, 极限状态承载能力极限状态------静强度,动力强度和稳定等计算.正常使用极限状态------静,动变形(刚性)和耐久性(疲劳)的计算.2, 结构可靠度包括结构安全性,适用性和耐久性.其定义为:在规定时间(寿命)内,规定条件下,完成预定功能的概率. 3, 极限状态方程0),,(321=⋅⋅⋅⋅⋅⋅⋅=n X X X X g Z式中Xi 是影响结构可靠度的变量。
在结构设计中可归纳为二个基本变量R (抗力)和S (载荷效应—内力)。
0),(=-==S R S R g ZR = S ,极限状态;R < S , 失效;R > S ,有效(可靠)。
概率极限状态设计法

优化设计
通过概率分析和计算,可以更加 精确地确定结构的优化设计方案, 提高结构性能和经济效益。
局限性
计算量大
概率极限状态设计法需要进行大量的概率分 析和计算,对计算资源和计算能力要求较高 ,增加了设计成本和时间。
数据要求高
该方法需要大量的数据支持,包括材料性能、载荷 、环境条件等数据,数据获取和处理难度较大。
确定载荷和载荷组合
载荷
分析结构所承受的外部载荷,如重力 、风载、地震等,以及内部载荷,如 压力、温度等。
载荷组合
根据工程实际情况,确定载荷的组合 方式,如同时作用、顺序作用等,以 考虑各种载荷对结构的影响。
确定结构极限状态
极限状态
定义结构的极限状态,如承载能力、稳定性、疲劳寿命等,以确定结构的失效准则。
应用范围有限
概率极限状态设计法主要适用于大型复杂结 构的可靠性设计和优化,对于小型简单结构 可能并不适用。
未来发展方向
智能化发展
未来可以通过引入人工智能和机器学习技术,提高概率极限状态 设计法的智能化水平,简化设计过程,提高设计效率。
多学科交叉融合
未来可以将概率极限状态设计法与其他学科领域进行交叉融合,如 结构健康监测、新材料等,拓展其应用范围和领域。
建筑结构优化设计
通过概率极限状态设计法,可以对建筑结构进行优化设计,提高建筑的性能和效率,降低 建筑的建设成本和维护成本。
建筑结构耐久性评估
利用概率极限状态设计法可以对建筑结构的耐久性进行评估,预测建筑在使用过程中的性 能变化和损伤程度,提前采取措施进行维修和加固。
机械工程中的应用
机械零部件的可靠性评估
未来展望
随着科技的不断发展,概率极限状态设计法将进一步发展, 考虑更多的不确定性因素和复杂环境条件,提高结构或系 统的可靠性和安全性。
混凝土结构按近似概率的极限状态设计法

通过蒙特卡洛模拟计算结构的可靠性。
混凝土结构极限状态设计的步骤
1
确定设计参数和设计概要
明确设计参数和要求,制定设计方案。
分析构件的极限状态
2
使用相关方法计算结构极限状态的可
靠性。
3
校核设计条件
检查设计条件是否满足要求,如变形
优化设计
4
约束、荷载承受能力等。
通过调整结构参数和设计方案以提高 可靠性。
混凝土结构极限状态设计的理论基础
强度理论
基于材料的强度和荷载的概率分布。如极限状态设计(LRFD)。
可靠性理论
在设计中考虑不确定性。如概率有限元法。
常用的极限状态设计方法
1
最不利条件设计法
按预先设定的最不利条件计算结构的
寿命设计法
2
极限状态。
考虑结构在使用寿命内可能遭受的荷
载和环境作用。
3
概率有限元法
混凝土结构按近似概率的 极限状态设计法
在混凝土结构设计中,了解极限状态设计法是非常重要的。本演示将介绍概 率设计与确定性设计的区别,以及混凝土结构极限状态设计的常用方法和步 骤。
确定性设计 vs. 概率设计
1 确定性设计
以固定参数进行设计,忽略随机性。可靠性较低。
ቤተ መጻሕፍቲ ባይዱ2 概率设计
考虑参数的统计分布,通过概率计算设计可靠性。可靠性更高。
混凝土结构按近似概率的极限状态设计 法的应用
工程实例
演示具体工程案例,展示按近似概率的极限状态 设计法可以如何应用于混凝土结构设计。
成功案例
分享成功实施该设计方法的案例,如高层建筑、 桥梁等。
总结与展望
1 极限状态设计法的优势
2 未来发展方向
极限状态设计法

极限状态设计法极限状态设计法是一种在工程设计中广泛应用的方法,它的目标是确保结构在极端条件下的安全性和可靠性。
本文将介绍极限状态设计法的基本原理、应用范围以及在实际工程中的重要性。
极限状态设计法是一种基于概率理论的设计方法,它考虑了结构在极端负荷情况下的破坏机制和失效概率。
通过对结构的荷载、材料性能和几何形状等因素进行全面的分析和计算,可以确定结构在设计寿命内的安全性。
极限状态设计法的应用范围非常广泛,涵盖了建筑、桥梁、航空航天、核工程等各个领域。
在建筑领域,极限状态设计法可以用于确定建筑物在地震、风灾等极端自然灾害下的安全性。
在桥梁设计中,极限状态设计法可以用于确定桥梁在超载、冰雪等极端条件下的承载能力。
在航空航天领域,极限状态设计法可以用于确定飞机在起飞、降落等关键阶段的结构安全性。
极限状态设计法在实际工程中的重要性不言而喻。
通过采用这种设计方法,可以有效地降低结构的失效风险,提高结构的安全性和可靠性。
同时,极限状态设计法还可以帮助工程师优化结构设计,减少材料和成本的浪费。
在进行极限状态设计时,需要考虑多种因素。
首先是荷载的确定,包括静态荷载、动态荷载和温度荷载等。
其次是材料的性能参数,如强度、刚度和韧性等。
此外,还需要考虑结构的几何形状和连接方式等因素。
为了实现极限状态设计的目标,工程师通常会采用一系列的分析方法和计算工具。
其中包括有限元分析、可靠性分析和统计学方法等。
通过这些方法的综合应用,可以对结构的安全性进行全面的评估和验证。
极限状态设计法是一种重要的工程设计方法,它可以确保结构在极端条件下的安全性和可靠性。
在实际工程中,合理应用极限状态设计法可以提高工程项目的质量和可持续发展能力。
因此,工程师们应该深入了解和掌握这一设计方法,并在实践中加以应用。
Pushover分析(同济大学翁大根)

基本安全指标 建筑性能水平
小震
地震地面运动
中震
小震
可用 (Operational)
立即居住 (Immediate Occupation)
生命安全 (Life Safety)
√
大震 大震
中震
√ √
√
注:基本安全指标如上表所示,是达到3-C(生命安全水准)及5-E(结构稳定水准)的双水准性能指标。
非线性静力分析(1)
速评估方法。
从形式上看,这是一种将静力弹塑性分析与反应谱相结
合、进行图解的快捷计算方法,它的结果具有直观、信息
丰富的特点。
非线性静力分析(3)
(Nonlinear Static Procedure)
Pushover方法是90年代以后出现的基于位移的抗震设计
(Displacement-Based Seismic Design)和基于性能(功能) 的抗震设计(Performance-Based Seismic Design, PBSD) 方法得于实现的重要工具。
退化;或者是某一构件(或一组构件)的侧向变形达到某一数值时, 导致结构失去重力承载能力。
11、精确模拟整体的强度退化。如果结构在第10步达到了侧向变形极
限,便停止加载,此时会有一个或者一组构件已经无法继续承担大部分或 所有的荷载,即其强度已明显退化,然后这根(批)构件的刚度会减少, 或者消失。从第3步开始再建立新的能力曲线。建立尽可能多的 Pushover曲线,可以更充分地表现强度丧失的全过程。图8.2中以三条不 同的能力曲线为例子表现这个过程。
(Nonlinear Static Procedure)
Pushover方法从本质上说是一种静力分析方法,对结构
基于位移的混凝土框架结构抗震设计方法探究

三水准设 防要求 , 本工程采用性能 的设计方法 。
9 基 础分 析
8 . 1 多遇地 震作 用 下满足 的 内容
在多遇地震作用下 结构 完好 , 无 损伤 , 不 经过 修理 即 可继续 使用 。
第4 0卷 第 6期 2 0 1 4年 2 月 文章编号 : 1 0 0 9 — 6 8 2 5 ( 2 0 1 4 ) 0 6 . 0 0 4 9 . 0 3
山 西 建 筑
S HAN XI ARC HI T EC T UR E
Vo 1 . 4 0 N o . 6
8 . 4 设 防地震 作 用下 弹塑性 层 间位移 角
最大楼层位移 角 , 在 , y向分别为 1 / 1 0 8 , 1 / 1 2 4 , 计算满足不
对结 构支撑屋面的大柱进行设 防地震 弹性 承载力验算 , 并按 此进
J C C A D的计算结果表 明, 在正 常适 用极 限状 态下荷载效应 的 行配 筋设 计。确认 结构在更高性 能点时 的承载能力 。3 ) 不屈 服 、 标准组合下 , 柱最大竖 向力值 为 5 7 0 0 k N左右 , 基 础单桩 承载 力 弹性设计 的内力调 整和组 合原 则 : a . 不考虑 强 柱弱 梁 、 强 剪 弱弯 特征值为 5 0 0 k N, 布置 1 2根桩 , 承载力能满足要求。
8 . 3 罕遇 地震 作 用下 满足 的 内容
结构 整体满足规范所要求 的大震不倒 的变形 限值 1 / 5 0 。
所的合理先进 的首选型式 。
2 ) 大于 1 2 m梁采 用 中震 不屈 服验算 , 对 支撑 屋面 大柱采 用 中震 弹性验算 , 使结构 的关键构件得 到安全保证很有 必要 。 3 ) 本工程达 到预期性 能 目标 , 设计满足规范要求 。
第3章_极限状态设计法

的荷载效应的总和;
R — 表示结构构件抗力。
2. 结构状态
根据S、R的取值不同,Z值可能出现三种情况(图
3-1):
3.1.4 极限状态方程
Z = R-S >0 时, 结构处于可靠状态;
Z = R-S =0 时, 结构处于极限状态;
Z = R-S <0 时, 结构处于失效状态。
图3-1 极限状态方程取值示意图
3.1.3 结构功能的极限状态
能完成预定的各项功能时,结构处于有效状态;反 之,则处于失效状态,有效状态和失效状态的分界,称 为极限状态,是结构开始失效的标志。极限状态可分为 二类。
1.承载能力极限状态 结构或构件达到最大承载能力或者达到不适于继续 承载的变形状态,称为承载能力极限状态。超过承载能 力极限状态后,结构或构件就不能满足安全性的要求。
(4)β与失效概率Pf的对应关系
3. 目标可靠指标
《建筑结构可靠度设计统一标准》根据结构的安全等 级和破坏类型,规定了按承载能力极限状态设计时的目 标可靠指标[β],见表3-3。β ≥ [β]
结构和结构构件的破坏类型分为延性破坏和脆性破坏 两类。延性破坏有明显的预兆,可及时采取补救措施, 所以目标可靠指标可定得稍低些。脆性破坏常常是突发 性破坏,破坏前没有明显的预兆,所以目标可靠指标就 应该定得高一些。
3. 建筑结构的功能要求
(2)适用性 结构在正常使用过程中应具有良好的 工作性。例如,不产生影响使用的过大变形或振幅, 不发生足以让使用者不安的过宽的裂缝等。
(3)耐久性 结构在正常维护条件下应有足够的耐 久性,完好使用到设计规定的年限,即设计使用年限。 例如,混凝土不发生严重风化、腐蚀、脱落,钢筋不 发生锈蚀等。
(3-24)
属于结构工程设计方法的有

属于结构工程设计方法的有结构工程设计方法是指在工程结构设计过程中所采用的系统化的、科学化的设计思路和方法论。
它是基于力学和结构力学原理,并融合了材料力学、实验力学、计算力学等多学科知识的综合性设计方法。
下面将会详细介绍几种常用的结构工程设计方法。
1. 传统结构设计方法传统的结构设计方法通常基于经验和试错的方法。
设计师在设计结构时,先根据经验和实践选择适当的材料,并确定结构的形状和尺寸。
然后,通过简化的数学模型和手工计算,对结构进行分析,根据结果对结构进行修改和优化。
2. 强度设计方法强度设计方法是指根据结构的承载能力和使用要求,通过力学原理和计算方法对结构的强度进行设计。
常用的强度设计方法包括极限状态设计法(ULS)和工作状态设计法(SLS)。
极限状态设计法是基于结构在极限荷载下失效的形式来设计结构,其中包括强度极限状态和位移极限状态。
工作状态设计法是指根据结构在正常使用情况下的变形和挠度要求,通过对结构进行轴心力、弯矩和剪力等参数的计算,来设计结构的尺寸和形状。
3. 塑性设计方法塑性设计方法是一种针对金属结构的设计方法,它基于材料的塑性变形能力进行设计。
它通常用于钢结构和铝合金结构的设计。
塑性设计方法中,结构的设计考虑了结构的全塑性行为,并使用合理的载荷组合来确定塑性变形的位移、弯曲和压缩等。
塑性设计方法的优点是可以提高结构的使用强度和破坏韧性,但需要注意结构的可靠性和可控性。
4. 极限状态设计方法极限状态设计方法是一种结构设计方法,它通过对结构在荷载作用下产生破坏的概率进行评估,确定结构的尺寸和形状。
极限状态设计方法是基于概率论和可靠性理论,并考虑了结构的荷载、材料性能和结构参数的不确定性。
通过统计分析和可靠性评估,确定结构在特定荷载下破坏的概率,并根据安全指标和可靠性指标进行设计。
总结起来,结构工程设计方法包括传统设计方法、强度设计方法、塑性设计方法和极限状态设计方法。
它们是结构工程设计的基础和核心,通过科学的方法对结构进行优化和合理化设计,以实现结构的经济性和安全性。
概率极限状态设计方法

概率极限状态设计方法概念:以概率为基础的极限状态设计方法,简称为概率极限状态设计法,1功能函数、极限状态方程结构构件完成预定功能的工作状态可以用作用效应S 和结构抗力R 的关系来描述,这种表达式称为结构功能函数,用Z 来表示当时,结构能够完成预定的功能,处于可靠状态;当时,结构不能完成预定的功能,处于失效状态;当时,即,结构处于极限状态。
,称为极限状态方程。
2结构可靠度、失效概率及可靠指标结构在规定的时间内,在规定的条件下完成预定功能的概率,称为结构的可靠度4结构的安全等级建筑结构设计时,应根据结构破坏可能产生的后果(危及人的生命、造成经济损失、产生社会影响等)的严重性,采用不同的安全等级。
建筑结构的安全等级划分见表 3.3 。
5目标可靠指标当有关变量的概率分布类型及参数已知时,就可按上述β值计算公式求得现有的各种结构构件的可靠指标。
《统一标准》以我国长期工程经验的结构可靠度水平为校准点,考虑了各种荷载效应组合情况,选择若干有代表性的构件进行了大量的计算分析,规定结构构件承载能力极限状态的可靠指标,称为目标可靠指标β。
结构构件属延性破坏时,目标可靠指标β取为 3.2 ;结构构件属脆性破坏时,目标可靠指标β取为 3.7 。
表3.3 建筑结构的安全等级对应于直接作用按随时间的变异分类,结构上的荷载可分为三类:( 1 )永久荷载,如结构自重、土压力、预应力等;( 2 )可变荷载,如楼面活荷载、屋面活荷载、积灰荷载、吊车荷载、风荷载和雪荷载等;( 3 )偶然荷载,如爆炸力、撞击力等。
荷载代表值是指设计中用以验算极限状态所采用的荷载量值。
建筑结构设计时,对不同荷载应采用不同的代表值。
永久荷载采用标准值作为代表值;可变荷载应根据设计要求采用标准值、组合值或准永久值作为代表值;偶然荷载应按建筑结构使用的特点确定其代表值。
6 荷载标准值荷载标准值是《荷载规范》规定的荷载基本代表值,为设计基准期内最大荷载统计分布的特征值(如均值、众值、中值或某个分位值)(如均值、众值、中值或某个分位值)。
概率极限状态设计法

概率极限状态设计法
概率极限状态设计法(Probabilistic limit state design,简称PLS)是一种基于概率理论的结构设计方法。
该方法以结构的极限状态作为设计依据,综合考虑结构的材料特性、载荷情况及其变化、结构的几何形态等因素,以保证结构在其使用寿命期间不会出现失效或崩塌的风险。
PLS方法通过建立结构的可靠性模型,将结构的可靠度表达为一个概率值,即结构在使用寿命期间失效的概率。
在设计过程中,通过限定结构的可靠度指标,如失效概率或安全系数等,来保证结构的安全性。
PLS方法的优点是能够综合考虑结构的不确定性因素,如材料强度、载荷变化等,从而更加准确地预测结构的可靠度和安全性。
同时,该方法还能够灵活地进行结构优化设计,以满足设计要求和经济性要求。
不过,PLS方法也存在一些限制。
例如,该方法需要较为精确的概率统计数据,如材料强度的概率分布等,且依赖于结构的可靠性模型选取和参数确定的准确性。
同时,该方法也需要较高的计算复杂度,对于大型结构的分析和设计较为困难。
总之,PLS方法是一种基于概率理论的结构设计方法,能够综合考虑结构的不确定性因素,以保证结构在使用寿命期间的安全性。
该方法
具有一定的优点和限制,需要在实际应用中进行权衡和选择。
第三章 按近似概率论理论的极限状态设计法_实用设计表达式

n
…3-27
式中,f1 ––– 为可变荷载的频遇值系数。
第 三 章
第三章 结构设计方法
• 荷载的准永久组合 Sl:
Sl SGk qi SQik
i 1 n
…3-26a
式中,qi ––– 第i个可变荷载的准永久值系数
可变荷载的准永久值 qi 可变荷载标准值
具体计算见 [例3-1] P44
解:基本效应组合(可变荷载控制)
1 S ( M ) ( G g k Q qk )l 2 8 1 (1.2 3 1.4 6) 62 54kN m 8
第 三 章
第三章 结构设计方法
基本效应组合(永久荷载控制)
1 S ( M ) ( G g k Q qk )l 2 8
fs ––– 钢材强度设计值。
是由钢材强度的标准值fsk除以材料分项
系数(s >1.0)求得。
fsk是由数理统计且具有95%保证率的材料 强度。
• 结构构件的抗力应根据截面的受力状态不同 用相应的计算模型确定。
第 三 章
第三章 结构设计方法
返回
3.3.3 正常使用极限状态设计表达式
1.荷载效应组合的代表值 • 结构或构件超过正常使用极限状态时所造成
第 三 章
第三章 结构设计方法
2.多个荷载时,应考虑内力组合设计值 (1)基本组合:(按承载能力极限状态设计时) 对由可变荷载效应控制的组合,按下式计算
S G cG Gk Q1cQ1Q1k Qi cQi ci Qik γ
i 2
n
…3-24
对由永久荷载效应控制的组合,按下式计算
ci ––– 第i个可变荷载的组合系数
关于桥梁抗震设计规范反应谱若干问题_韦晓

第27卷第2期同济大学学报Vol.27.No.2 1999年4月JOUR NAL OF T ONGJI UNIVER SIT Y A p r.1999关于桥梁抗震设计规范反应谱若干问题韦晓袁万城王志强范立础(同济大学桥梁工程系,上海,200092)摘要从桥梁抗震设计反应谱分析与设计角度出发,讨论了当前我国《桥梁抗震设计规范》制订中关于反应谱曲线和反应谱组合方法等几个需要解决的问题.关键词规范反应谱;长周期;阻尼比;振型组合;多级抗震设防分类号U422Some Problems on Aseismic Desi g n Code Res p onseS p ectrum for Brid g esW ei Xiao Yuan W anchen g W an g Zhi q ian g Fan L ichu(D ep artment of Bridge En gin eerin g,Tongji Un ivers it y,Shanghai,200092)Abstract In this p a p er,based on demand of aseism ic res p onse s p ectrum anal y sis and desi g n,som e ex istin g p roblems in aseismic design code for br idge structur es,such as long period response spectrum value and technique for response spectrum combination,are pointed out and the possible solution m ethods to them ar e also proposed.Keywords Code response spectrum;Long period;Damping ratio;Combination method of vibration mode;Multilevel aseism ic protection在结构抗震理论发展中,静力、反应谱和动力分析方法3个阶段的形成和发展是人类对自然规律认识的一个不断深入与完善的过程.1942年M.A.Biot明确提出了从强震记录中计算反应谱的概念,1953年Housner等人对此加以实现,并在随后的加州抗震设计规范中首先采用了将反应谱理论作为抗震设计方法,以取代过去的静力系数法.由于反应谱理论不仅简单正确地反映了地震动的特性而且同时考虑了结构物的动力特性,因而迅速在世界范围内得到了广泛的承认.50年代后期,这一抗震理论已基本取代了静力系数法,从而奠定了反应谱理论在抗震设计中的主导地位.使用反应谱方法进行桥梁结构的抗震分析首先需要解决两个问题:一是合理的地震动反应谱输入;二是恰当的反应谱组合方法.本文目的就是从这两个问题出发来讨论我国现行《公路工程抗震设计规范》(JTJ004—89)(以下简称部规)桥梁抗震部分中的几个需要解决的问题,并给出了可以进一步研究的一点建议,供目前正在制定的《桥梁抗震设计规范》前期研究工作参考.1长周期反应谱取值长周期反应谱问题是当前地震工程研究的一个热点问题.其主要原因就是基于长周期结构的历史震害,以及与随着我国经济建设发展,高耸结构和大跨度桥梁建设的飞速发展迫切需要解决长周期反应谱取值问题有关,而目前规范反应谱又不能涵盖长周期结构抗震的需要.同济大学土木工程防灾国家重点实验室完成的国内20多座大桥抗震分析,从第一阶自振周期来看[1]:主跨1385m的江阴长江公路大桥收稿日期:1998-04-15第一作者:男,1968年生,博士生225Fig .1Response spectrum of displacementaccording to code Fig .2Enveloping displacement response curve of Humen Bridge west tower in longitude direction response1)同济大学桥梁工程系.徐浦大桥主桥动力特性分析研究报告之三:徐浦大桥主桥自振特性测定.1997是19.6s (前七阶振动周期均在5s 以上);主跨为888m 的虎门大桥是11s ;主跨602m 的杨浦大桥是12.8s .规范反应谱截止周期是5s ,因而不能满足大跨度桥梁抗震反应谱分析的要求.为此,现行部规反应谱长周期部分有两个问题需要解决:①长周期反应谱取值规定一个下平台值不尽合理;②反应谱截止周期应当适当延长.规范反应谱的一个显著特点是其具有统计特征.部规加速度反应谱是国家地震局工程力学研究所根据900多条国内外强震记录,按5%阻尼比得到的加速度反应谱,并考虑安全经济因素后的统计结果.规范规定长周期采用定值0.3αmax ,是个值得探讨的问题.实际强震记录计算表明,反应谱长周期段衰减很快.事实上,《建筑抗震设计规范》(GBJ11—89)的送审稿曾建议取消3s 以后0.2αmax ,因为这样将导致位移反应谱是一上升曲线(如图1).加速度反应谱以一定值加以表示,显然与实际情况不符,因为T →∞时,结构位移反应谱与地面最大位移一致.根据加速度反应谱与位移反应谱近似关系S a =ω2S d ,则加速度反应谱长周期部分应符合1/T 2衰减规律.南浦大桥抗震计算表明[1],按规范反应谱谱值和对规范谱长周期用1/T 2衰减规律修正这两种情况进行抗震分析,桥墩弯距结果会相差1.5倍,设计上无法接受.因此没有必要定义0.3这一下限值,应当还物理规律之本来面目.下一步问题是应当如何确定长周期反应谱?目前解决问题的途径有2个:①大量布设宽频带加速度仪;②采用地震学和工程地震学相结合方法,利用现有记录反演长周期成分.现有绝大多数记录是从当初的模拟记录强震仪得到的,在0.125Hz 以下频率段成分可信度很低,这是仪器本身的问题;另外原因是数字化处理和校正过程中许多长周期分量连同低频噪声一并滤掉.大量布设宽频带强震仪是一个获得丰富低频成分反应谱的理想方法.第二种方法是根据强震地面运动理论模拟面波对长周期分量的影响[2],利用地震仪记录结果,对长周期部分进行反演.因为理论研究表明面波对强震地面运动中长周期分量有不可忽视的作用,在一定条件下,面波可能成为控制地面运动长周期的主要震相.图1规范位移反应谱图2虎门大桥西塔主跨纵向位移反应包络图2规范反应谱阻尼修正不同阻尼影响反应谱取值有两个方面内容:①不同阻尼影响规范反应谱曲线形状;②桥梁各振型阻尼比影响反应谱取值.目前国内的抗震设计规范设计反应谱几乎都以5%的临界阻尼比为依据(核电站抗震设计规范除外),这对普通钢筋混凝土桥梁是适宜的.但大跨度桥梁结构不同振型频率阻尼比往往小于5%.从同济大学对3座200多米的斜拉桥实测结果的资料来看[3],各阶振型的阻尼比在1%~10%之间变化.最近对主跨590m 的上海徐浦大桥实测结果表明1),低阶振型阻尼比甚至会小于1.0%,因而对于不同振型应使用不同阻尼比.从强震记录不同阻尼比反应谱计算对比看[4],阻尼比不仅影响反应谱的形状,而且对反应谱不同周期段的影响程度是不一样的,但总的趋势是阻尼对长周期部分反应谱的影响小,对高频部分影响大.阻尼比取值或者不同振型阻尼比取值的不同会直接影响到地震反应的预测结果[1],如图2所示.而且随着结构控制技术、减震耗能措施的大量推广应用,结构中不同构件之间的阻尼比会有很大的变化.第2期韦晓等:关于桥梁抗震设计规范反应谱若干问题226同济大学学报第27卷1)Eurocode 8.Stru ctures in seismic re g ion s -desi g n .Part2:Brid g es .Drafts ,A p ril ,1993胡聿贤先生是我国最早考虑对加速度反应谱进行阻尼修正的学者.他在60年代根据单自由度体系平稳随机反应分析和对强震记录的反应谱统计提出了一个修正公式[5]:βT ,ξ=1316.6ξ+0.160.8T αβT ,ξ=0.05,αξ=0.05-ξ0.156+3.38ξ(1)从式(1)可以看出,他采用了T =0.8s 和ξ=0.05为基准点进行反应谱阻尼修正.现行欧洲桥梁抗震设计规范1)给出了反应谱阻尼修正公式η=7/2+ξ≥0.7(2)其中ξ是以百分比形式表示.显然式(2)是以5%阻尼比反应谱作为基准.日本桥梁抗震设计规范[6]是最早采用反应谱阻尼修正的国家规范.规范采用阻尼修正系数对反应谱值进行修正,它与振型阻尼系数h 1有关,C D =1.5/40h i +1+0.5(3)h i 与振型衰减系数h j 有关,规范给出相应计算公式并根据不同的结构情况给出h j 的具体值.上面给出的第一种修正方法侧重于地震动特性影响的描述,后二者则侧重于结构的动力特性修正.由于不同阻尼比的取值对反应谱短周期部分谱值影响较大,因而对量大面广的短周期桥梁结构的地震反应预测精度会有较大影响,我国新的桥规应对反应谱值进行不同阻尼比的谱值修正.3规范反应谱取值跳跃问题这个问题有两个方面需要解决:①场地类型不同产生的取值跳跃问题;②烈度不同影响取值的跳跃问题.目前抗震设防仍根据烈度进行设防,而烈度是以整数形式表达.烈度取整数形式是有其特殊背景的.现行部规的基础是基于1980年的全国第二代烈度区划图,它与1990年的第三代全国烈度区划图有很大的不同.第二代区划图制定采用的是确定性的地震危险性分析方法,是基于未来100年某一地方可能发生的最大地震烈度.地震危险性分析确定烈度大小基于两个原则:①历史上在某一地区发生过的最大地震今后仍可能发生;②某一断层构造上发生过的最大地震,今后仍可以在此断层或性质相似的断层构造上发生,即所谓的历史地震重演和构造类比原则,基于这两个原则直接进行确定性的烈度区划.第三代区划图作了改进,采用了综合概率的地震危险性分析方法,按各潜在震源计算对某一场地的烈度贡献,给出了未来50年内超越概率10%的烈度大小.对于一个具体场地第三代区划图分析结果并不一定是一整数形式,取整的原则是采用7下8上的原则.照此,同样是7度区,其烈度会在6.8~7.7度之间变化.两个地区一个是7.8度,另一个是7.7度的情况,一个就要进行8度抗震设防,而另一个则进行7度抗震设防,结果是2个设防地面加速度会有一倍之差,因而采用烈度的方法必然会产生这种不合理结果.抗震规范对于这种烈度跳跃变化应如何处理?取消烈度的概念,是一条解决问题的途径.目前第四代全国烈度区划图正在制定,将给出加速度峰值的区划图,新的规范应考虑与之衔接.不同场地加速度反应谱取值跳跃是另一突出的问题.部规采用地基允许承载力[σ0]来进行场地类别划分,当两个场地实测结果为129kPa 和130kPa ,从数值上没有本质区别,但根据规范,两个场地土类别是Ⅳ类和Ⅲ类,从而会使选取的加速度反应谱在某一周期段有明显的区别.部规在附录中给出了采用剪切波速、质量密度和分层厚度评定场地指数的方法来确定反应谱.该方法符合选用场地评定物理指标的发展趋势,可以避免场地分类分界的矛盾.但笔者认为用剪切波速仍有很大局限性,不同场地和不同土类的剪切波速离散性较大,另外桥梁大多建在江河岸边,这种场地上剪切波速现场测试也有一定的困难.笔者认为如能借助静力触探方法得到的各土层测试结果,建立相应综合评定公式,是值得推荐的方法.4位移反应谱目前的抗震设计方法实质上是基于强度的设计方法,结构设计先通过折减弹性力来确定结构的设计强度水平,并利用结构的延性能力来弥补结构强度的不足,仅仅通过一个强度水平破坏指标并不能有效227第2期韦晓等:关于桥梁抗震设计规范反应谱若干问题地控制结构期望的破坏方式.桥梁结构不同于建筑结构,后者由于内部高次超静定,一个部位的缺陷可以由其它途径来弥补.前者往往是静定或低次静定,单个构件或部件之间的破坏就会影响整个桥梁的功能,它对地震位移十分敏感,地震位移计算不当,如低估地震位移,相邻结构(如城市立交)由于预留间距不足就会发生冲击破坏;活动支座处座长设置不足会引起落梁和桥跨损坏.近几年来,国外学者发展一种新的抗震设计方法———基于位移的设计方法[7].它以地震时结构的反应位移作为设计依据,因为对于特定的破坏水准可以通过结构目标极限应变来标定,以应变作为破坏水准,同时可以适用于不同的破坏状态,因而结构中受力水平可以通过位移来反算求解.该方法物理概念清楚,符合结构设计的发展要求,因此有必要发展我国桥梁抗震设计基于位移的设计方法,规范同时应当给出位移反应谱曲线.5反应谱振型组合方法振型组合方法是反应谱理论的另一重要问题,是影响桥梁地震反应预测精度的关键因素.目前各国抗震规范采用的组合方法主要是基于平稳随机振动理论的SRSS,CQC和DSC法等一致激励振型组合方法.最普遍的SRSS法,对于频率分离较好的平面结构的抗震计算有良好的精度,为大多数国家的抗震设计规范所采用,如我国现行部规,美国的AASHT O规范,欧洲的Eurocode8规范.该方法对于中小桥梁的地震反应计算有较高精度,但对于频率密集的空间结构由于忽略了各振型间的耦合影响,通常会过高或过低地估计结构的地震反应.CQC法是80年代初W ilson等人基于随机过程导出的比例阻尼线性多自由度体系振型组合规则,较好地考虑了密集频率时的振型相关性,克服了SRSS法的不足.欧洲规范和日本规范采用了这种振型组合方法作为对SRSS法的补充.DSC法是用振型相关系数考虑振型间耦合项影响,所采用的振型相关系数是基于地面运动白噪声过程假定而得出的,为新西兰桥梁抗震规范所采用.CQC法理论基础是随机振动理论,它必须符合地震动是宽带过程和平稳随机过程的假定.大跨度桥梁振动周期相对地面运动持时相对较长,阻尼比较小,结构地震反应在地面运动持时内过渡到弱平稳态有很大困难,因而对地震反应主要贡献的振型多数处于非平稳态,现有各种反应谱组合方法要准确估计各个振型之间的相关性有困难.最近文献[8]基于一致虚拟激励原理提出了新的一种振型组合方法HOC (harm onic-or iented com bination),它可以提高大跨度桥梁一致激励反应谱方法的预测精度.但笔者认为一定意义上该方法是一种算法,而且与其它方法比较的参考标准是时程分析结果,时程分析结果很大程度上取决于输入地震动时程的频谱成分,对其适用性有待进一步研究.正在制定的桥梁抗震规范有意将其适用范围扩大到大跨度桥梁结构,由于不同振型组合方法会导致不同的地震反应预测精度,所以应当明确不同情况下采用不同振型组合方法的指导性条款.另外当前反应谱组合方法主要是基于单分量地震动作用下的振型组合问题,从大跨度桥梁抗震分析角度来看,发展不同地震动分量作用下和多点激励下的地震反应振型组合,并应用到我国规范中去尚有待进一步探究. 6采用多级抗震设计反应谱多级抗震设防思想是在核电站抗震设计规范中首先提出来的.核电站抗震设计要求满足安全运行地震(OBE)和安全停堆地震(SSE)两级设计地震动.前者保证核电站在一般情况下不停止运行,后者在特殊情况下不产生核扩散事故.后来被逐渐推广到了另外一些重大工程中.由于其先进的抗震设防思想,很快被建筑、桥梁等结构专业规范所采纳.我国现行建筑抗震设计规范已经采用了“小震不坏、中震可修、大震不倒”的多级抗震设防思想,运用两种大小的地震动进行抗震设计.美国桥梁抗震设计规范和日本桥梁抗震设计规范也采用了这种抗震设防思想,并规定了相应阶段的设计分析方法.我国现行部规没有明确体现这一先进的抗震设计思想,虽然采用了综合影响系数C z来体现桥梁在遭受基本烈度时的非线性影响,但工程师应用起来概念含糊,设计上不能保证大震不倒的要求,仍然是一阶段的抗震设计.采用多级抗震设防要确定多级设防的超越概率以及相应的设计反应谱.我国第三代烈度区划图是一个超越概率的烈度区划,即50年超越概率10%,这针对量大面广的一般桥梁结构是合理的.大跨度桥梁228同济大学学报第27卷一般都以100年作为设计使用寿命,因而应当对应100年超越概率的反应谱作为地震输入.根据结构重要性确定相应的设计使用寿命和超越概率,显然应在多级抗震设防中加以考虑.在有些国家抗震规范中已考虑这一原则,如美国ATC3规范对一般工业或民用建筑设防水准是50年超越概率10%,对陆海空三军重要房屋抗震设计指南规定设防标准是100年超越概率10%.正在制定的我国第四代烈度区划图给出的是地震动参数区划图.由于区划图是针对量大面广的建(构)筑物,因而对大跨度桥梁桥规制定中仍然应当规定进行桥址的地震危险性分析.但桥规应当从经济安全角度出发规范地震危险性分析的超越概率水准,使得地震部门进行危险性分析时有章可循,有利于大跨度桥梁的多级抗震设防分析与设计的实现.7结论通过上述讨论分析,可以归纳几点结论与建议:(1)规范应体现多级抗震设防的设计思想.抗震设防标准是桥梁抗震设计规范的重要组成部分,它直接影响到桥梁建设安全和经济两方面内容.显然过高估计设防标准有利于桥梁安全,但不符合我国国情;为了经济而不合理地降低或过低估计设防标准,我们已经为之付出了惨重的代价.采用基于概率的多级抗震设计方法有利于与桥梁结构可靠度设计方法相衔接.(2)改进当前规范中反应谱抗震分析的不足.反应谱分析方法是目前结构抗震设计的主流方法.由于桥梁结构自身的特殊性,现行规范有关桥梁抗震设计反应谱分析中存在的上述几个主要问题应尽快加以解决,并反映到我国目前正在制定的《桥梁抗震设计规范》之中,以满足我国大规模的桥梁建设事业的需要.(3)采用基于位移与能力的设计方法.当前基于弹性反应谱法的抗震设计存在很大的不确定性,基于位移设计方法和能力设计方法相结合的方法是桥梁抗震设计的发展趋势.位移设计方法以结构位移为设计依据,可以充分考虑结构不同的破坏极限状态.能力设计就是通过主要抗侧力体系构件应用恰当的设计和构造细部设计来作为强震下的延性耗能机构,其它构件依据耗能机构的延性确定的强度进行设计,以保证结构在地震作用下能按设计人员的要求位置进行耗能,起到控制结构的目的.因而在桥梁初步设计阶段可以用反应谱理论为主,而细部构件设计以能力设计方法为主的桥梁抗震设计思想是规范发展的趋势,这样可以克服弹性反应谱设计方法的不足.参考文献1范立础.桥梁抗震.上海:同济大学出版社,19972章在墉,王彬,李文艺.地震动长周期特性研究的现状及方法.见:文集编委会主编.地震工程研究文集.北京:地震出版社, 1992.457~4633李国豪主编.桥梁结构稳定与振动.第2版.北京:中国铁道工业出版社,19974谢礼立,周雍年,胡成祥,等.地震动反应谱长周期特性.地震工程与工程振动,1990(1):1~195胡聿贤.地震工程学.北京:地震出版社,19886日本道路协会.道路桥示文书.同解说,v耐震设计编.东京都:丸善株式会社,19967Priestle y M J N,S eib le F,Calvi G M.Seismic desi g n and retrof it of brid g es.New Y ork:J ohn W ile y&Sons,19968王淑波.大型桥梁抗震设计反应谱理论及应用研究:[学位论文].上海:同济大学桥梁工程系,1997。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第29卷第1期2009年2月 地 震 工 程 与 工 程 振 动JOURNAL OF E ARTHQUAKE E NGI N EER I N G AND E NGI N EER I N G V I B RATI O N Vol .29No .1 Feb .2009 收稿日期:2008-08-16; 修稿日期:2008-11-06 基金项目:国家自然科学基金项目(90815002);广东省自然科学基金项目(8451064101000293) 作者简介:张海燕(1978-),女,讲师,博士,主要从事结构工程研究1E 2mail:zhy116107@ 文章编号:1000-1301(2009)01-0083-06基于位移的概率极限状态设计张海燕1,3,易伟建2(11亚热带建筑科学国家重点实验室华南理工大学,广东广州510640;21湖南大学土木工程学院,湖南长沙410082;31华南理工大学土木工程系,广东广州510640)摘 要:尽管近年来国内外学者提出了多种基于位移的抗震设计方法,但采用的与位移相关的反应谱大多是平均谱,设计过程可以看作是确定性的。
基于位移的抗震设计应该建立在可靠度理论基础之上。
利用作者在概率延性需求谱方面已有的研究成果和可靠度分析方法———验算点法,本文提出了根据基于位移的目标可靠指标直接进行结构设计的方法,并给出了设计流程图。
为便于工程应用,在进行了大量分析计算之后,本文建议了基于位移的概率极限状态分项系数设计表达式,并确定了其中的分项系数。
最后,本文对一8层框架结构采用建议的分项系数设计表达式进行了设计,并对有待于进一步研究的问题进行了简要分析。
关键词:基于位移;抗震设计;可靠度;概率极限状态;分项系数中图分类号:P315.95 文献标志码:AD ispl acem en t 2ba sed probab ilisti c li m it st a te desi gnZHANG Haiyan 1,3,YIW eijian 2(11State Key laborat ory of Subtr op ical A rchitecture Science,South China University of Technol ogy,Guangzhou 510640,China;21College of Civil Engineering,Hunan University,Changsha 410082,China;31Depart m ent of Civil Engineering,South China University of Technol ogy,Guangzhou 510640,China )Abstract:Recently many dis p lace ment 2based seis m ic design methods have been p r oposed by researchers .I n most of these methods the average dis p lace ment 2related s pectra are adop ted,and the design p r ocedure can be considered deter m inate .D is p lace ment 2based seis m ic design should be based on the reliability theory .U tilizing the authors ’re 2search results on p r obabilistic ductility de mand s pectru m and the reliability analysis method,such as checking point method,the direct p r obabilistic design p r ocedure and the fl owchart t o reach the dis p lace ment 2based target reliability index are p resented .By a large a mount of computati on and analysis,a p racticable partial coefficient design exp res 2si on based on p r obabilistic li m it states design is p r oposed,and a gr oup of op ti m al partial coefficients are obtained .I n the end,an eight 2st ory structure is designed by using the p r oposed partial coefficient design exp ressi on,and the deficiency of this method is indicated .Key words:dis p lace ment 2based;seis m ic design;reliability;p r obabilistic li m it state;partial coefficient引言基于性能的抗震设计是近年来地震工程界的热点课题之一[1-3]。
基于位移的抗震设计是实现基于性能的抗震设计的重要途径。
与传统的基于力的抗震设计相比,在基于位移的抗震设计中,位移不仅是初步设计完成之后的一个验算指标,同时还是控制着整个设计过程的关键参数。
目前基于位移的抗震设计主要有两种思路:一种是根据指定的性能水平得到结构的整体位移需求之后,获得结构的层间位移需求和梁柱等构件的变形需求,再根据构件的变形与截面曲率延性、配箍率、相对受压区高度或轴压比等的关系进行截面设计[3],该思路目前急需解决的问题是如何确定结构的整体位移与构件变形以及构件变形与纵向配筋、配箍率、轴压比等的关系;另一种是先由结构的整体位移需求计算结构的整体屈服强度需求,再采用现有的基于力的方法进一步设计[4]。
由于强度和弹性刚度是设计人员所熟悉的两个设计参数,且传统设计方法经过几十年的研究已经日臻完善,故作者认为将基于位移的整体结构设计与基于力的构件设计结合起来是现阶段比较可行的一种设计方案,本文所采用的也正是这种研究思路。
本文首先对几种基于位移的确定性抗震设计方法进行了介绍,然后提出了基于位移的概率极限状态设计方法,并推导了分项系数设计表达式。
图1 等强度位移反应谱Fig .1 Constant 2strength dis p lace ment res ponse s pectra 1 基于位移的确定性设计方法 在基于力的抗震设计中,弹性加速度反应谱扮演着重要的角色,在基于位移的抗震设计中,与位移或位移延性有关的谱,如高阻尼弹性位移反应谱、非弹性位移反应谱、延性需求谱等也同样重要。
近年来国内外学者提出了多种基于位移的抗震设计方法,如替代结构法[5]、非弹性反应谱法[4]、能力谱方法[6,7]等。
这些方法在基本设计步骤上有相似之处:首先根据性能要求,确定设计位移D m ,并估计屈服位移D y 或延性系数μ,然后根据与位移有关的谱确定满足设计位移的结构周期T 与屈服强度需求F y ,再根据周期和屈服强度需求并利用现有基于力的方法进一步设计。
而它们的一个重要不同之处在于所采用的与位移有关的谱不同:替代结构法采用的是高阻尼弹性位移反应谱;非弹性反应谱法采用的是在已有的R (强度折减系数)-μ-T 关系基础上建立的等延性位移反应谱(D -T 格式);能力谱法则是采用等延性的谱加速度-谱位移格式(ADRS 格式)的需求曲线。
此外,本文作者[8]还提出了另一种可用于抗震设计的位移反应谱,即等强度位移反应谱(如图1所示),与等延性位移反应谱相比它能更清楚地反映结构的屈服强度与最大位移需求之间的关系。
在图1中,参数η称为屈服水平系数,其定义为:η=F ym ・PG A (1)式中,m 为单自由度体系的质量,PG A 是地面峰值加速度。
由于实际工程中许多结构都可以简化或通过pushover 分析方法等效成单自由度体系,故目前对基于位移的抗震设计研究多停留在单自由度体系上。
对多自由度结构,当按照上述任一方法获得了等效单自由度体系的屈服强度需求F y 之后,根据多自由度结构与单自由度体系的等效关系,将其转换为多自由度结构的基底剪力,然后分配到每一楼层、每一构件等。
在上述几种基于位移的抗震设计方法中,与位移相关的设计谱都是平均谱,设计过程可以看作是确定性的;而地震作用具有很大的随机性,结构本身也是随机的,基于位移的抗震设计应该建立在可靠度理论基础之上。
2 基于位移的概率设计方法基于概率可靠度理论进行结构设计,主要有两方面的工作要完成:(1)确定目标可靠度。
基于性能的抗震设计的一个重要思想就是“多级抗震设防”,而每级抗震设防目标的可靠度可能有所不同,例如“小震不坏”的可靠度与“大震不倒”可能不一样。
当结构很重要或业主有要求时,还可适当提高设防目标或设防目标的可靠度。
受某些因素限制,本文不打算考察目标可靠度的取值。
有研究表明大震作用下钢筋混凝土框架结构薄弱层的层间位移可靠指标在1.7~2.1的范围内[11],在本文48地 震 工 程 与 工 程 振 动 第29卷中目标可靠指标均假定为1.8。
(2)根据目标可靠度,对结构或构件进行设计。
这主要有两种方法:一是根据目标可靠度,直接采用可靠度分析方法如验算点法进行计算;二是采用基于概率的极限状态设计法,推导分项系数设计表达式。
2.1 根据目标可靠度直接设计结构基于位移的结构极限状态方程为:D m -D cr =0(2)式中,随机变量D m 、D cr 分别为最大位移反应和期望性能水平的界限位移。
界限位移D cr 通常认为服从对数正态分布[12],其统计参数要根据试验数据、震害经验确定,在此不对其进行研究,而采用假定值。
最大位移反应D m 通常也认为服从对数正态分布[8],这样剩下的问题就只有D m 的统计参数的确定。
结构最大位移反应的随机性与结构质量、基本周期、屈服强度以及地震动等的随机性有关。
由于在设计过程中,通常要先估计结构构件的基本尺寸及材料强度等级,而它们的随机性一般相对较小,故本文仅把结构参数中的屈服强度F y 作为随机变量,而把结构基本周期和质量作为确定性变量。
地震动的随机性可通过地震动三要素的随机性来体现,而地震动幅值特性和频谱特性的随机性可由屈服水平系数η和等η概率延性需求谱(即μ的条件概率分布)分别加以考虑[8],地震动持时特性的随机性在此不予考虑。
