江苏省昆山市兵希中学中考数学 第40课时 与圆有关的位置关系课件 苏科版
合集下载
高中数学223圆与圆的位置关系课件苏教版必修
本题所求圆与已知圆半径差为 1，而两个圆心的纵 坐标之差的绝对值大于 3，故内切是不可能的，但解题中不考虑内 切情况是不严密的．
汇报结束
谢谢大家! 请各位批评指正
法二 由法一得直线 AB 为 4x＋3y－10＝0， C1 到直线 AB 的距离为 d＝|20＋155－10|＝5， 而圆 C1 的半径为 r＝5 2. 由圆的性质可知 AB＝2 r2－d2＝2 50－25＝10. 法三 圆 C1 的圆心为(5,5)，r1＝5 2， 圆 C2 的圆心为(－3，－1)，r2＝5 2， ∴C1C2＝ 5＋32＋5＋12＝10. ∴四边形 AC1BC2 是正方形． ∴AB＝C1C2＝10.
解析 本题主要考查两圆的位置关系，两圆有公共点时，它 们只能是内切、外切或相交，因此圆心距 d 满足|r2－r1|≤d≤r1＋ r2，即|6－ m|≤5≤ m＋6，从而 1≤ m≤11,1≤m≤121.
答案 1≤m≤121
题型二 两圆的相交弦问题与公切线问题 【例 2】 已知圆 C1：x2＋y2－10x－10y＝0 和圆 C2：x2＋y2＋ 6x＋2y－40＝0 相交于 A、B 两点，求弦 AB 的长． [思路探索] 本题主要考查两圆的相交弦问题，关键要寻找关 于弦 AB 的相关量．由于两圆方程已知，可先求 A、B 的坐标，再 求弦长；也可转化为直线 AB 与圆 C1 或圆 C2 的相交问题．
误区警示 忽视相切的含义 【示例】 求半径为 4，且与圆 x2＋y2－4x－2y－4＝0 和直线 y＝0 都相切的圆的方程． [错解] 由题意，知所求圆与直线 y＝0 相切且半径为 4，可设 圆心坐标为 O1(a,4)， 则圆的方程为(x－a)2＋(y－4)2＝16. 圆 x2＋y2－4x－2y－4＝0 的标准方程为(x－2)2＋(y－1)2＝32， 则圆心为 O2(2,1)，半径为 3. 若两圆相切，则|O1O2|＝3＋4＝7， 所以 a－22＋4－12＝7， 解得 a＝2±2 10.
2020届苏科版中考数学一轮复习：与圆有关的位置关系
初三数学与圆有关的位置关系专题复习知 识 梳 理一、点和圆的位置关系d<r ⇔点P 在⊙O 内； d=r ⇔点P 在⊙O 上； d>r ⇔点P 在⊙O 外。
二、直线与圆的位置关系（1）相交：两个公共点，割线＜====＞d<r ； （2）相切：唯一公共点，切线＜====＞ d=r ； （3）相离：没有公共点，相离＜====＞ d>r 。
切线的判定：经过半径的外端并且垂直于这条半径的直线。
切线的性质：圆的切线垂直于经过切点的半径。
切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。
圆内接四边形性质（四点共圆的判定条件）圆内接四边形对角互补、外交等于内对角。
三角形的内切圆：与三角形的各边都相切的圆；内心：三角形的三条内角平分线的交点。
三、圆和圆的位置关系1、相离：相离分为外离：d>R+r 和内含：d<R-r （R>r ）。
2、相切：相切分为外切：d=R+r 和内切：d=R-r （R>r ）。
3、相交：R-r<d<R+r （R≥r ）。
4、两圆相切、相交的性质：如果两圆相切，那么切点一定在连心线上，它们是轴对称图形，对称轴是两圆的连心学员姓名 年 级 初三 上课时间辅导科目 数学学科教师课 题 与圆有关的位置关系线；相交的两个圆的连心线垂直平分两圆的公共弦。
热 身 训 练1．若⊙O 的半径为4cm ，点A 到圆心O 的距离为3cm ，那么点A 与⊙O 的位置关系是( A )A ．点A 在圆内B ．点A 在圆上 C.点A 在圆外 D ．不能确定2．已知⊙O 的半径为5,弦AB 的弦心距为3,则AB 的长是 83．已知直角三角形的两直角边长分别为5和12，则它的外接圆半径R =___6.5___， 内切圆半径r =___2___．4．⊙O 的半径为6，⊙O 的一条弦AB 为63，以3为半径的同心圆与直线AB 的位置关系是 相切 ．5．MN 是半径为1的⊙O 的直径，点A 在⊙O 上，∠AMN =30°，B 为AN 弧的中点，点P 是直径MN 上一个动点，则求PA+PB 的最小值。
九年级数学上册-与圆有关的位置关系复习课件-苏科版
4.8为半径的圆与线段AB的位置关系 是___相__切______;
设⊙O的半径为r,那 当么 _0_＜__r_＜__4_._8_或__r_＞_ 8时,
⊙O与线段AB没交点; 当___4_._8_＜_r_≤_6_____时, ⊙O与线段AB有两个交点; 当 r__=_4_._8_或___6_＜__r_≤_8 时,
圆心到直线的距离等于 圆的半径,那么此直线是 圆的切线
判定 过半径的外端且垂直于
定理 半径的直线是圆的切线
(二〕切线的性质
假设0A⊥CD于A,
且OA=d=r． 那么CD是⊙Ｏ
交点Ａ不明确： 作OA⊥CD于A,证OA=r
的切线
即可
假设0A是⊙O的半径， 交点Ａ明确：
且0A⊥CD 那么CD是⊙Ｏ
连OA,证OA⊥CD即可
回忆“与圆有关的位置关系〞中相关的概念，性质与判定．
２．思想方法：
数形结合，类比，分类讨论，方程思想．
面积法，代数法．
第二十五页，编辑于星期五：十三点 三十八分。
结束 语
• 谢谢同学们的配合！
• 三十八分。
I D
第二十三页，编辑于星期五：十三点 三十八分。
2、破残的圆形轮片上，弦AB的垂直平分线交AB 于C，交弦AB于D. (1)求作此残片所在的圆(不写作法，保存作图痕迹)； (2)假设AB＝24cm，CD＝8cm，求(1)中所作圆的半径.
第二十四页，编辑于星期五：十三点 三十八分。
课时小结
１．知识：
2．⊙O和⊙P的半径分别为5和2，OP＝3，那么⊙O和⊙P的位置 关系
是〔 D 〕
A、外离 B、外切
C、相交
D、内切
3.两圆相切,圆心距为10cm,其中一个圆的半径为6cm,那么另一个圆的半径
设⊙O的半径为r,那 当么 _0_＜__r_＜__4_._8_或__r_＞_ 8时,
⊙O与线段AB没交点; 当___4_._8_＜_r_≤_6_____时, ⊙O与线段AB有两个交点; 当 r__=_4_._8_或___6_＜__r_≤_8 时,
圆心到直线的距离等于 圆的半径,那么此直线是 圆的切线
判定 过半径的外端且垂直于
定理 半径的直线是圆的切线
(二〕切线的性质
假设0A⊥CD于A,
且OA=d=r． 那么CD是⊙Ｏ
交点Ａ不明确： 作OA⊥CD于A,证OA=r
的切线
即可
假设0A是⊙O的半径， 交点Ａ明确：
且0A⊥CD 那么CD是⊙Ｏ
连OA,证OA⊥CD即可
回忆“与圆有关的位置关系〞中相关的概念，性质与判定．
２．思想方法：
数形结合，类比，分类讨论，方程思想．
面积法，代数法．
第二十五页，编辑于星期五：十三点 三十八分。
结束 语
• 谢谢同学们的配合！
• 三十八分。
I D
第二十三页，编辑于星期五：十三点 三十八分。
2、破残的圆形轮片上，弦AB的垂直平分线交AB 于C，交弦AB于D. (1)求作此残片所在的圆(不写作法，保存作图痕迹)； (2)假设AB＝24cm，CD＝8cm，求(1)中所作圆的半径.
第二十四页，编辑于星期五：十三点 三十八分。
课时小结
１．知识：
2．⊙O和⊙P的半径分别为5和2，OP＝3，那么⊙O和⊙P的位置 关系
是〔 D 〕
A、外离 B、外切
C、相交
D、内切
3.两圆相切,圆心距为10cm,其中一个圆的半径为6cm,那么另一个圆的半径
初中数学中考知识点考点学习课件PPT之 与圆有关的位置关系知识点学习PPT
又 ， ， ， ，即 .又 是 的半径， 为 的切线．
图（2）
方法二:如图（3），连接 , .
图（3）
是 的直径， .在 中，∵点 是 的中点，
， . ， . ， ， ，即 .又 是 的半径， 为 的切线．
（3） 如图（3）， 的外接圆为 ，过点 作 的切线，过点 作该切线的垂线，交 于另一点 ，垂足为 ，连接 .
一图串考法
考法 切线的性质（8年5考）
1.[2022河南,20] 为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环 与水平地面相切于点 ,推杆 与铅垂线 的夹角为 ,点 , , , , 在同一平面内.当推杆 与铁环 相切于点 时,手上的力量通过切点 传递到铁环上,会有较好的启动效果.
,点 在射线 上 切半圆 于点
证明:连接 . , .又 , , , . 切半圆 于点 , .又 且 , 平分 , , .
4.[2017河南,18] 如图，在 中， ，以 为直径的 交 边于点 ，过点 作 ，与过点 的切线交于点 ，连接 .
图（4）
命题角度 与切线有关的证明与计算
例1 在 中， .
（1） 如图（1）， 的平分线交 于点 ,以点 为圆心， 的长为半径画圆．
图（1）
① 求证： 是 的切线；
证明：如图（1），过点 作 于点 .
图（1）
， .又 平分 ， , 是 的切线.
特立探究设正 边形的边长为 ，外接圆半径为R.则：正六边形： ；正方形： ；正三角形： .
一题串考点
已知在 中，点 为 的中点.
（1） 如图（1），连接 ，若 ， ，以点 为圆心， 为半径画圆.
图（2）
方法二:如图（3），连接 , .
图（3）
是 的直径， .在 中，∵点 是 的中点，
， . ， . ， ， ，即 .又 是 的半径， 为 的切线．
（3） 如图（3）， 的外接圆为 ，过点 作 的切线，过点 作该切线的垂线，交 于另一点 ，垂足为 ，连接 .
一图串考法
考法 切线的性质（8年5考）
1.[2022河南,20] 为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环 与水平地面相切于点 ,推杆 与铅垂线 的夹角为 ,点 , , , , 在同一平面内.当推杆 与铁环 相切于点 时,手上的力量通过切点 传递到铁环上,会有较好的启动效果.
,点 在射线 上 切半圆 于点
证明:连接 . , .又 , , , . 切半圆 于点 , .又 且 , 平分 , , .
4.[2017河南,18] 如图，在 中， ，以 为直径的 交 边于点 ，过点 作 ，与过点 的切线交于点 ，连接 .
图（4）
命题角度 与切线有关的证明与计算
例1 在 中， .
（1） 如图（1）， 的平分线交 于点 ,以点 为圆心， 的长为半径画圆．
图（1）
① 求证： 是 的切线；
证明：如图（1），过点 作 于点 .
图（1）
， .又 平分 ， , 是 的切线.
特立探究设正 边形的边长为 ，外接圆半径为R.则：正六边形： ；正方形： ；正三角形： .
一题串考点
已知在 中，点 为 的中点.
（1） 如图（1），连接 ，若 ， ，以点 为圆心， 为半径画圆.
【数学课件】苏科版九年级数学上课件：圆与圆的位置关系4
相离 相切
外离 内含 外切
内切
没有公共点 有惟一公共点
关 系
相交 有两个公共点
活动二
两圆之间的位置关系除了根据两圆的 交点个数判定外，还有别的方法吗？
设两圆的圆心距为d ，两圆的半径分别 为R、r。
r
R
d
外离
d﹥ R+r
rd
内含
d﹤ R-r
R
rR
O1 d
o2
外切 d= R+r
rR O1d o2
这个惟一的公共点叫切点
切点
相交:两个圆有两个公共点 时,叫做这两个圆相交.
内切:两个圆有惟一公共点, 并且除了这个公共点外,一 个圆上的点都在另一个圆 的内部时,叫做这两个圆内 切. 这个惟一的公共点叫切点
特例
内含:两圆无公共点,并且一个圆上的点都 在另一个圆的内部时,叫两圆内含.
圆 与 圆 的 位 置
四、典型例题
例1 已知⊙O1、⊙O2 的半径为r1、r2,圆
心距d=5,r1=2. （1）若⊙O1与⊙O2外切，求r2； （2）若r2=7，⊙O1与⊙O2有怎样的位置关 系？ （3）若r2=4，⊙O1与⊙O2有怎样的位置关 系？
五、拓展与提高
已知⊙O1与⊙O2的半径分别为R,r(R>r), 圆心距为d。若关于x的一元二次方程x2－ 2(d－R)x+r2=0有两个相等的实数根，试判 定⊙O1与⊙O2的位置关系。
六、归纳总结
圆与圆的位置关系
位置关系 图形 交点个数 d与R、r的关系
相 外离 离 内含
相交
相 外切 切 内切
d＞R+r
0
d＜R-r (R＞r)
2
R-r ＜d＜R+r(R≥r)
初中数学苏科版九年级上册直线与圆的三种位置关系
B
d=2.4c m
2、当r满足_r_=__2_.4__c_m____ 时，
⊙C与直线AB相切．
5
3、当r满足__r_＞___2_.4__c_m__时，
⊙C与直线AB相交．
4
D
C
A
3
小结：
判定直线 与圆的位置关系的方法有__两__种： （1）根据定义，由___直_线__与__圆__的__公_共__点___的 个数来判断； （2）根据性质，_____圆__心__到__直_线__的__距__离__d_ ____与_半__径__r_____的关系来判断。
.O
r d .A .B
H.
.O
d r .D
.
2
C
l 相切
d .Or
.E . N .F
Q.
3
相交
相离
1、直线与圆相离 <=> d>r
想一想
你当能直根线据与d圆与r
2、直线与圆相切 <=> d=r 的相大离小、关相系切确、
3、直线与圆相交 <=> d<r
定相直交线时与，圆d的与 位r有置何关关系系吗？?
BC=4cm，以C为圆心，r为半径的圆
与AB有怎样的位置关系？为什么？
分析 （1）r=2cm；（2）r=2.4cm (3)r=3cm。
B
2.4cm
解根：据过直C线作与C圆D⊥的A位B置，关垂系足的为数D。量
特征，必须在用Rt圆△心AB到C直中线，的距离d与
半径r的大小进行比较；
AB=
2
2=
2
4
关键=是5（确c定m）圆心C到直线AB的距 离d，根这据个三距角离形是面什积么公呢式？有怎么求这
d=2.4c m
2、当r满足_r_=__2_.4__c_m____ 时，
⊙C与直线AB相切．
5
3、当r满足__r_＞___2_.4__c_m__时，
⊙C与直线AB相交．
4
D
C
A
3
小结：
判定直线 与圆的位置关系的方法有__两__种： （1）根据定义，由___直_线__与__圆__的__公_共__点___的 个数来判断； （2）根据性质，_____圆__心__到__直_线__的__距__离__d_ ____与_半__径__r_____的关系来判断。
.O
r d .A .B
H.
.O
d r .D
.
2
C
l 相切
d .Or
.E . N .F
Q.
3
相交
相离
1、直线与圆相离 <=> d>r
想一想
你当能直根线据与d圆与r
2、直线与圆相切 <=> d=r 的相大离小、关相系切确、
3、直线与圆相交 <=> d<r
定相直交线时与，圆d的与 位r有置何关关系系吗？?
BC=4cm，以C为圆心，r为半径的圆
与AB有怎样的位置关系？为什么？
分析 （1）r=2cm；（2）r=2.4cm (3)r=3cm。
B
2.4cm
解根：据过直C线作与C圆D⊥的A位B置，关垂系足的为数D。量
特征，必须在用Rt圆△心AB到C直中线，的距离d与
半径r的大小进行比较；
AB=
2
2=
2
4
关键=是5（确c定m）圆心C到直线AB的距 离d，根这据个三距角离形是面什积么公呢式？有怎么求这
2.5直线与圆的位置关系(2)-苏科版九年级数学上册课件
•
┌
例2.PA、PB是⊙O的切线，切点分别为A、B， C是⊙O上一点，若∠APB=40°，求∠ACB的度数.
注：1、独立思考； 2、学生代表交流； 3、独立完成解答过程， 同伴互查互纠；
P 40°
A
1
2 O? C B
总结切线性质的用法:
找切点,连半径,得垂直。
AB是⊙O的直径，弦AD平分∠BAC，过点D的切线交 AC于点E.请判断DE与AC有怎样的位置关系？为什么？
AC=BC；请判断直线AB与⊙O的位置关系，并说
明理由.(书P73/第7题）
要求：1、独立思考，并解答；
2、同伴互查互纠；
3、学生代表交流；
•
A
━ ━
•O
•┓ •
CB
2.在Rt⊿ABC中,∠B=90°,∠A的平分线交BC
于D,以D为圆心,DB的长为半径作⊙D,
求证:AC是⊙D的切线
A
要求：1、学生回顾； 2、学生代表交流；
（三）应用切线的判定解决问题：
1、如图，AB是⊙O的直径，∠B=45°AB=AC， 判断AC与⊙O的位置关系，并说明理由
1. 要求1、独立思考； 2、学生代表交流； 3、教师给出规范解答；
B
45°
O
┐
A
45°
C
2.△ABC内接于⊙O，AB是⊙O的直径， ∠1=∠B，判断直线AD与⊙O的位置关系， 并说明理由.（书P67/例2）
d •E
┌
B
r D
C
1、比较：
第3题与第4题添加辅助线有何不同之处？
2、归纳：
证明圆的切线时，根据不同情况如何添辅助线？
要求：1、独立思考； 2、学生代表交流；
（一）已知，如图直线l与⊙O相切于点A.半径OA
┌
例2.PA、PB是⊙O的切线，切点分别为A、B， C是⊙O上一点，若∠APB=40°，求∠ACB的度数.
注：1、独立思考； 2、学生代表交流； 3、独立完成解答过程， 同伴互查互纠；
P 40°
A
1
2 O? C B
总结切线性质的用法:
找切点,连半径,得垂直。
AB是⊙O的直径，弦AD平分∠BAC，过点D的切线交 AC于点E.请判断DE与AC有怎样的位置关系？为什么？
AC=BC；请判断直线AB与⊙O的位置关系，并说
明理由.(书P73/第7题）
要求：1、独立思考，并解答；
2、同伴互查互纠；
3、学生代表交流；
•
A
━ ━
•O
•┓ •
CB
2.在Rt⊿ABC中,∠B=90°,∠A的平分线交BC
于D,以D为圆心,DB的长为半径作⊙D,
求证:AC是⊙D的切线
A
要求：1、学生回顾； 2、学生代表交流；
（三）应用切线的判定解决问题：
1、如图，AB是⊙O的直径，∠B=45°AB=AC， 判断AC与⊙O的位置关系，并说明理由
1. 要求1、独立思考； 2、学生代表交流； 3、教师给出规范解答；
B
45°
O
┐
A
45°
C
2.△ABC内接于⊙O，AB是⊙O的直径， ∠1=∠B，判断直线AD与⊙O的位置关系， 并说明理由.（书P67/例2）
d •E
┌
B
r D
C
1、比较：
第3题与第4题添加辅助线有何不同之处？
2、归纳：
证明圆的切线时，根据不同情况如何添辅助线？
要求：1、独立思考； 2、学生代表交流；
（一）已知，如图直线l与⊙O相切于点A.半径OA
中考数学第40课时与圆有关的位置关系课件苏科版
B
F
0
CD
A
◆巩固练习 能力自测P158页1、2
CP
◆解题指导
例2、如图所示，AB是⊙O直径，OD⊥弦BC于点F， 且交⊙O于点E，若∠AEC=∠ODB． （1）判断直线BD和⊙O的位置关系，并给出证明； （2）当AB=10，BC=8时，求BD的长．
◆解题指导
例3、如图所示， ⊙O1与⊙O2外切于点P，O1O2的延 长线交⊙O2于点A，AB切⊙O1于点B，交⊙O2于点C， BE是⊙O1的直径，过点B作BF⊥O1P，垂足为F，延长 BF交PE于点G。 ● （1）求证：3PB2=PG PE 3 （2）若PF=2 ，tanA= 4 ,求O1O2的长
02
（3）两圆相交
. · r R
01 02
R- r<d<R+r （R≥r）
R
. · r 01 02
（4）两圆内切
d = R- r (R>r)
（5）两圆内含
0≤d<R- r （R>r)
两圆按公共点个数可 如何分类？
外离 内含
没
有相
公 共
离
点
外切 内切 相交
一
个
公相
共 点
切
两
个
公
相
共 点
交
三、圆和圆的位置关系：
（3）连结圆心和圆外一点
二、直线与圆的位置关系：
M E
D K G
.O H
NF
如图,四边形DEFG外切于⊙O,切点分别为M、N、H、K 试证明:EF+DG=ED+GF
结论：圆的外切四边形的对边之和相等。
二、直线与圆的位置关系：
直角三角形的内切圆半径
苏科版九年级数学上册2.5 直线与圆的位置关系(二)课件
1
DC
变式 △ABC内接
于⊙O，AB是⊙O的弦，
B
∠CAD=∠ABC，判断直
O
线AD与⊙O的位置关系，A 12
E
并说明理由.
DC
证明一条直线是圆的切线时:
直线与圆有交点时，连接交点与圆心，证垂直.
探索交流
如图,直线CD与⊙O相切于点A,直径AB与直线CD 有怎样的位置关系?说说你的理由.
ቤተ መጻሕፍቲ ባይዱ
直径AB垂直于直线CD.
(1)以点C为圆心作圆,当半径为多
长时,AB与⊙C相切? A
解:(1)过点C作CD⊥AB于D.
D
∵AB=8cm,AC=4cm.
┐
C
B
∴ BC= 82-42=4 3 4×4 3
CD= 4 =2 3
因此,当半径长为 2 3 cm时,AB与⊙C相切.
练习
• 1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
6、“教学的艺术不在于传授本领，而在于激励、唤醒、鼓舞”。2021年11月下午7时23分21.11.819:23November 8, 2021
• 7、“教师必须懂得什么该讲，什么该留着不讲，不该讲的东西就好比是学生思维的器，马上使学生在思维中出现问题。”“观 察是思考和识记之母。”2021年11月8日星期一7时23分3秒19:23:038 November 2021
(2)以点C为圆心,分别以2cm,4cm
为半径作两个圆,这两个圆与AB分 A
别有怎样的位置关系?
D
解:(2)由(1)可知,圆心到AB
┐
的距离d= 2 3cm,所以
C
B
当r=2cm时,d>r,AB与⊙C相离; 当r=4cm时,d<r,AB与⊙C相交.
九年级数学上册 圆与圆的位置关系课件 苏科版
径为5，另一个圆的半径为
.
6．已知⊙O1与⊙O2的半径分别为 R,r(R>r),圆心距为d,且两圆相交,
试判定关于x的一元二次方程
x2－2（d－R）x+r2=0根的情况.
7、如图，王大伯家房屋后有一块长12m,宽8m的 矩形空地，他在以长边BC为直径的半圆内种菜. 他家养的一只羊平时拴在A处的一棵树上，拴羊 的绳长为3m. 问羊是否能吃到菜？为什么？
2.两圆半径分别为10 cm和R,圆心距为13cm， 若这两圆相切，则R的值是___ .
3．半径为5cm的⊙O外一点P，则以点P为 圆心且与⊙O相切的⊙P能画______个．
4.两圆半径之比为3：5，当两圆内切时， 圆心距为4 cm，则两圆外切时圆心距的 长为____．
5．两圆内切，圆心距为3，一个圆的半
D
C
O
A
B
8两两相切地堆放在一
起，则其最高点到地面的距离
是
.
9. ⊙O2和⊙O1相交于点A、B，它们 的半径分别为2和2 ，公共弦AB长为
2，若圆心O1、O2在AB的同侧，
则∠O1AO2=_____.
A
O1
O2
B
10、如图，在△ABC中，∠C＝90°，AC＝8， AB＝10，点P在AC上，AP＝2，若⊙O的圆心 在线段BP上，且⊙O与AB、AC都相切，则⊙O 的半径是多少？
圆与
系
圆
关
的
置位
点与圆的位置关系
直线与圆的位置关系
圆与圆的位置关系
认真观察观察结果
外离:两圆没有公共点,并且一个圆上的点
都在另一个圆的外部时,叫两圆外离.
切点
外切:两圆有惟一公共点,并且除了公共点
江苏省昆山市兵希中学九年级数学上册 5.3 圆周角课件(2) 苏科版
知识回顾
我们学习过哪些与圆有关的角？ 它们之间有什么关系？
C
O B A E
D
A
1、如图，BC为⊙O的直径，它所 对的圆周角是多少度？为什么？ 2、如图，圆周角∠A=90°，弦BC 经过圆心吗？为什么？
B
O
C
A
B
O
C
结论得出
圆周角定理的推论：
1、直径或半圆所对的圆周角是直角. 2、900的圆周角所对的弦是直径.
C O E
A
B
D
例题讲解
如图，△ABC的顶点都在⊙O上，AD是△ABC的 高，AE是⊙O的直径.△ABE与△ACD相似吗？为什 么？
A
O
B
E
D
C
例题讲解
如图， A、B、E、C四点都在⊙O上，AD是 △ABC的高，∠CAD=∠EAB, AE是⊙O的直径吗？ 为什么？
A B O E C
D
1.利用三角尺可以画出圆的直径，为什么？ 你能用这种方法确定一个圆形工件的圆.如图，点A、B、C、D在圆上，AB=8, BC=6, AC=10,CD=4.则AD= .
D
C
A
B
2.如图，AB是⊙O的直径，CD是⊙O的弦，AB=6, ∠DCB=30°，则弦BD= 。
例题讲解
如图，AB是⊙O的直径，弦CD与AB相交于点E， ∠ACD=60°，∠ADC=50°,求∠CEB的度数.
2、如图，AB、CD是⊙O的直径，弦CE∥AB. 弧BD与弧BE相等吗？为什么？
A C
O D B E
3.如图，△ABC的3个顶点都在⊙O上，直径AD=4， ∠ABC=∠DAC，求AC的长。
我们学习过哪些与圆有关的角？ 它们之间有什么关系？
C
O B A E
D
A
1、如图，BC为⊙O的直径，它所 对的圆周角是多少度？为什么？ 2、如图，圆周角∠A=90°，弦BC 经过圆心吗？为什么？
B
O
C
A
B
O
C
结论得出
圆周角定理的推论：
1、直径或半圆所对的圆周角是直角. 2、900的圆周角所对的弦是直径.
C O E
A
B
D
例题讲解
如图，△ABC的顶点都在⊙O上，AD是△ABC的 高，AE是⊙O的直径.△ABE与△ACD相似吗？为什 么？
A
O
B
E
D
C
例题讲解
如图， A、B、E、C四点都在⊙O上，AD是 △ABC的高，∠CAD=∠EAB, AE是⊙O的直径吗？ 为什么？
A B O E C
D
1.利用三角尺可以画出圆的直径，为什么？ 你能用这种方法确定一个圆形工件的圆.如图，点A、B、C、D在圆上，AB=8, BC=6, AC=10,CD=4.则AD= .
D
C
A
B
2.如图，AB是⊙O的直径，CD是⊙O的弦，AB=6, ∠DCB=30°，则弦BD= 。
例题讲解
如图，AB是⊙O的直径，弦CD与AB相交于点E， ∠ACD=60°，∠ADC=50°,求∠CEB的度数.
2、如图，AB、CD是⊙O的直径，弦CE∥AB. 弧BD与弧BE相等吗？为什么？
A C
O D B E
3.如图，△ABC的3个顶点都在⊙O上，直径AD=4， ∠ABC=∠DAC，求AC的长。
江苏省昆山市锦溪中学九年级数学上册 5.1圆(1)教案 苏
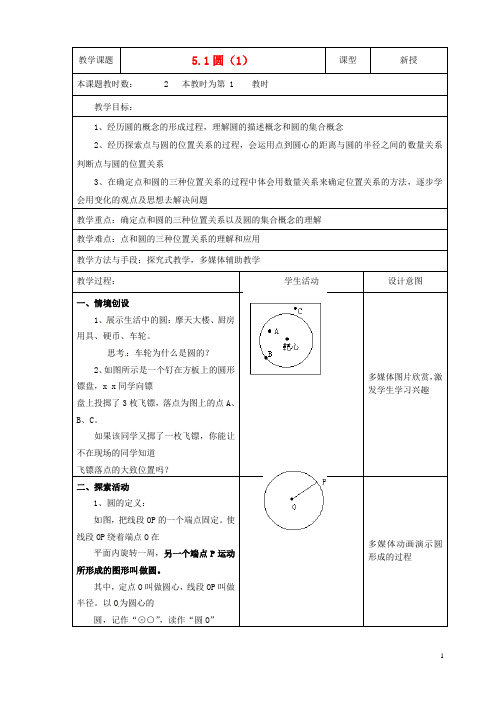
教学课题 5.1圆（1）课型新授本课题教时数： 2 本教时为第 1 教时教学目标：1、经历圆的概念的形成过程，理解圆的描述概念和圆的集合概念2、经历探索点与圆的位置关系的过程，会运用点到圆心的距离与圆的半径之间的数量关系判断点与圆的位置关系3、在确定点和圆的三种位置关系的过程中体会用数量关系来确定位置关系的方法，逐步学会用变化的观点及思想去解决问题教学重点：确定点和圆的三种位置关系以及圆的集合概念的理解教学难点：点和圆的三种位置关系的理解和应用教学方法与手段：探究式教学，多媒体辅助教学教学过程：学生活动设计意图一、情境创设1、展示生活中的圆：摩天大楼、厨房用具、硬币、车轮。
思考：车轮为什么是圆的？2、如图所示是一个钉在方板上的圆形镖盘，x x同学向镖盘上投掷了3枚飞镖，落点为图上的点A、B、C。
如果该同学又掷了一枚飞镖，你能让不在现场的同学知道飞镖落点的大致位置吗？多媒体图片欣赏，激发学生学习兴趣二、探索活动1、圆的定义：如图，把线段OP的一个端点固定。
使线段OP绕着端点O在平面内旋转一周，另一个端点P运动所形成的图形叫做圆。
其中，定点O叫做圆心，线段OP叫做半径。
以O为圆心的圆，记作“⊙○”，读作“圆O”多媒体动画演示圆形成的过程2、画圆：确定一个圆的两个要素是_______和________，以定点A为圆心作圆，能作______个圆；以定长r为半径作圆，能作______个圆；以定点A为圆心、定长r为半径作圆，能且只能作_______个圆。
3、圆的集合定义考虑情境创设中的B点位置，给出以下定义：平面上到定点的距离等于定长的点的集合叫做圆。
4、点和圆的位置关系为什么不在现场的同学听了xx同学的描述，能知道飞镖的大致落点呢？——点和圆的三种位置关系。
你能用数量关系来刻画点和圆的这几种位置关系吗？若⊙O的半径为r，点P到圆心O的距离为d，那么：点P在圆内 d ＜ r点P在圆上 d = r点P在圆外 d ＞ r三、例题教学例1. 如图已知矩形ABCD的边AB=3厘米，AD=4厘米（1）以点A为圆心，3厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？（2）以点A为圆心，4厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？（3）以点A为圆心，5厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？例2. 2005年9月11日，第十五号台风“卡努”登陆浙江，A市接到台风警报时，台风中心位于A 市正南方向125km的B处，正以15km/h的速度沿BC方向移动。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（2）若PF= 3
2
，tanA= 3
4
,求O1O2的长
E
G
01 F
P
A
02
C B
◆解题指导
例4、如图所示， ⊙0的半径OD经过弦AB（不是直径）
的中点C，过AB的延长线上一点P作⊙0的切线PE，E为
切点，PE∥OD；延长直径AG交PE于点H；直线DG交OE于
点F，交PE于点K
（1）求证：四边形OCPE是矩形
◆考点链接 一、点和圆的位置关系
点与圆的位置关系有三种：点在圆内、点在圆上、点在圆外．
设⊙O 的半径为r，点P到圆心的距离OP=d，则有：
点P在⊙O内
d＜r
dp
r
点P在⊙O上
d=r
d
r
p
点P在⊙O外
d＞r
Pd r
二、直线与圆的位置关系：
图形
直线与圆的 位置关系
公共点的个数
圆心到直线的距离 d 与半径 r 的关系
D AP
O
B
C
C
A
OP B
D
二、直线与圆的位置关系：
B
7、割线定理：
∵PAB、PCD是⊙O的两条割线
A
O
∴ PA.·PB=PC·PD
P C
D
8、切割线定理：
∵PT是⊙O的切线，PAB是⊙O的割线 T
∴ PT2 =PA·PB
O
P
A
B
三、圆和圆的位置关系：
r
R
· · 01 d
02
r
R
· · 01
02
┓
E
C
二、直线与圆的位置关系： 5、弦切角定理: 弦切角等于它所夹的弧对的圆周角
∵AB是⊙O的切线， AC是⊙O的弦
∴ ∠BAC= ∠ADC
Ｃ
D
Ｏ
ＡＢ
二、直线与圆的位置关系： 6、相交弦定理
∵弦AB、CD相交于点P ∴ PA·PB=PC·PD
相交弦定理的推论
∵AB是直径，AB⊥CD于点P ∴ PC2=PD2 =PA·PB
（3）连结圆心和圆外一点
二、直线与圆的位置关系：
M E
D K G
.O H
NF
如图,四边形DEFG外切于⊙O,切点分别为M、N、H、K 试证明:EF+DG=ED+GF
结论：圆的外切四边形的对边之和相等。
二、直线与圆的位置关系：
直角三角形的内切圆半径
已知:如图,⊙O是Rt△ABC的内切圆,∠C是直
角,三边长分别是a,b,c.
A
0 B
CP
◆解题指导
例2、如图所示，AB是⊙O直径，OD⊥弦BC于点F，且 交⊙O于点E，若∠AEC=∠ODB． （1）判断直线BD和⊙O的位置关系，并给出证明； （2）当AB=10，BC=8时，求BD的长．
◆解题指导
例3、如图所示， ⊙O1与⊙O2外切于点P，O1O2的延长线 交⊙O2于点A，AB切⊙O1于点B，交⊙O2于点C，BE是⊙O1 的直径，过点B作BF⊥O1P，垂足为F，延长BF交PE于点G。 （1）求证：PB2=PG ● PE
A
求⊙O的半径r.
r abc. 2
直角三角形的外接圆半径
D
O
●
┗
F
┓
B
EC
R c 2
二、直线与圆的位置关系：
三角形的内切圆半径
已知:如图,△ABC的面积为S,三边长分别为a,b,c. 求内切圆⊙O的半径r.
S 1 ra b c.
2
A
D
F
O
●
r 2S . B abc
（1）两圆外离 d > R+r （2）两圆外切
d = R+r
rR
· · 01
02
（3）两圆相交
. · r R
01 02
R- r<d<R+r （R≥r）
R
. · r 01 02
（4）两圆内切
d = R- r (R>r)
（5）两圆内含
0≤d<R- r （R>r)
两圆按公共点个数可 如何分类？
外离 内含
公共点的名称
．Ｏ r d┐ l
相离
0
d>r
直线名称
．ｏ
．O
d .┐r l
A
.
B
r ┐d .
lC
相切 相交
1
2
d=r 切点 切线
d<r 交点 割线
二、直线与圆的位置关系：
1、切线的判定定理 经过半径的外端并且垂直于这条半径的直线是圆的切线.
∵OA是半径， 直线CD⊥OA
∴直线CD是⊙O的切线
●O
2、切线的性质定理
二、直线与圆的位置关系：
4、切线长定理：
从圆外一点引圆的两条切线，它们的切线长相等，圆 心和这一点的连线平分两条切线的夹角。
B
。
P
O
A
∵PA、PB分别切⊙O于A、B ∴PA = PB ∠OPA=∠OPB
反思：在解决有关圆的切线长的问题时，往往需要 我们构建基本图形。
A
。
O
P
B
（1）分别连结圆心和切点 （2）连结两切点
C
圆的切线垂直于过切点的半径.
A
D
∵CD是⊙O的切线, ∴CD⊥OA
二、直线与圆的位置关系： 3.证明一条直线是圆的切线思路和添辅助线的方法
（1）直线与圆有交点时，“连半径，证垂直”； （2）直线与圆交点没给出时，“作垂直，证半径”.
遇到切线连半径，切点不明作垂线，有时半径变直径。
注：已知直线和圆相切时： 常连接切点与圆心。
没
有相
公 共
离
点
外切 内切 相交
一
个
公
相
共 点
切
两
个
公ห้องสมุดไป่ตู้
相
共 点
交
三、圆和圆的位置关系：
如果两个圆相切，那么切点一定在连心线上。
外切
内切
三、圆和圆的位置关系：
相交两圆的连心线垂直平分公共弦
A
O1
O2
B
◆考点热身 1、能力自测P155页1、2、3、4、5
◆解题指导
例1、如图所示，AB是⊙O的直径，PA切⊙0于点A，OP 交⊙O于点C，连接BC，若∠P=30°，求∠B的度数
（2）求证：HK=HG
KH
E
（3）若EF=2，FO=1，求KE的长
G B
F
0
CD
A
◆巩固练习 能力自测P158页1、2