17周作业纸
科学第17周作业---声音、呼吸与消化复习 (1)

14四上科学第17周作业---声音、呼吸与消化复习您的姓名: [填空题] *_________________________________您的班级: [单选题] *○四(1)班○四(2)班○四(3)班○四(4)班○四(5)班○四(6)班○四(7)班○四(8)班1. 声音是由物体振动引起的,物体振动停止后发声不会停止 [判断题] *对错(正确答案)答案解析:声音由物体振动引起的,物体振动停止后发声也会停止2. 我们拍球时,虽然能听见声音,但是看不见球面或地面的振动,因此拍球发声时不振动。
[判断题] *对错(正确答案)答案解析:它们发声了轻微振动,只是这种振动我们不容易看到,就像我们拍击桌面一样3. 只要我们对物体用力,物体就能发出声音。
[判断题] *对错(正确答案)答案解析:按压桌面就不会发出声音4. 使橡皮筋发出声音只能拉直拨动。
[判断题] *对错(正确答案)5. 弯曲钢尺是可以使钢尺发声的方法之一。
[判断题] *对错(正确答案)6. 陨石撞击月球,我们能听到响声。
[判断题] *对错(正确答案)7. 将振动的音叉放入水槽内的水中,我们用耳朵贴在水槽边可以听到音叉振动的声音,其传播路径是 [单选题] *音叉-水-水槽-人耳(正确答案)音叉-人耳音叉-空气-人耳8. 我们改变电视机的音量时,改变的是声音的强弱。
[判断题] *对(正确答案)错9. 用不同的力敲击同一个音叉,声音的高低会发生变化。
[判断题] *对错(正确答案)答案解析:用不同的力去敲击同一个音叉,声音的强弱会发生变化。
10. 用力拨动钢尺,发出的声音强,是因为钢尺的振动幅度大。
[判断题] *对(正确答案)错11. 声音的强弱可以用音量来描述。
[判断题] *对(正确答案)错12. 用力拍打篮球,篮球发出的声音越强,这是因为篮球的振动幅度越大。
[判断题] *对(正确答案)错13. 敲击小鼓的鼓面时,纸屏上吊着的泡沫塑料小球会被弹起。
6-16网课数学A作业纸(8.7一8.13)

8月7号初三数学作业纸(A )班级 姓名 学号 家长签名:课题:解直角三角形(1) 一、选择题:1.在Rt △ABC 中,∠C =900,a 、b 、c 分别为∠A 、∠B 、∠C 对式错误的是 ( ) .a csin .b ccos .b a tan .a b tan A A B B C B D A ====2.根据下列所给的条件解直角三角形,结果不能确定的是 ( ) (1)已知一直角边和一锐角;(2)已知两锐角;(3)已知两直角边;(4)已知斜边和一锐角;(5)已知一直角边和斜边.A .(2)(3)B .(2)(4)C .(2)D .(2)(4)(5) 3.等腰三角形的底角为30°,底边长为2 3,则腰长为 ( )A .4B .2 3C .2D .2 24. 在Rt △ABC 中,∠C =90°,∠B =35°,AB =7,则BC 的长为 ( )A. 7sin35°B. 035cos 7C. 7cos35°D. 7tan35° 5.将如图所示三角板的直角顶点放置在直线AB 上的点O 处,使斜边CD ∥AB ,则∠α的正弦值为 ( ) A.12 B.32 C.22D .1二、填空题:6.在△ABC 中,∠C =90°,若sinA=0.314,则cosB= .7.在△ABC 中,∠C =90°,a=1,c=2,则∠B= ,b= . 8.在△ABC 中,∠C =90°,∠A =30°,a=5,则b= .9.(2018•孝感),在Rt △ABC 中,∠C =90°,AB =10,AC =8,则sin A = . 10.半径为10cm ,弧长为12π的扇形围成圆锥(接缝忽略不计),那么圆锥的母线与圆锥高的夹角的余弦值是 .11.(2018•无锡)已知△ABC 中,AB =10,AC =2,∠B =30°,则△ABC 的面积等于 .. 12.(2018•北京)如图所示的网格是正方形网格,∠BAC ∠DAE .(填“>”,“=”或“<”)第5题图 第12题图B CA三、解答题:11.在Rt △ABC 中,∠C=90°:(1)已知a=4,b=8,求c . (2)已知b=10,∠B=60°,求a ,c .12.在ABC 中,∠A 、∠B 都是锐角,且sinA=21,tanB=3,AB=10,求各角度数及各边长.13.(2019•盐城)如图,在△ABC 中,BC =+,∠C =45°,AB =AC ,求AC 的长.14.已知:如图在等腰△ABC 中,AB=AC=13,BC=10,求sinA 的值.8月8号初三数学作业纸(A )班级 姓名 学号 家长签名:课题:解直角三角形(2) 一、选择题:1.在△ABC 中,若tanA=33,sinB=21,你认为最确切的判断是 ( ) A.△ABC 是等腰三角形 B.△ABC 是等腰直角三角形 C.△ABC 是直角三角形 D.△ABC 是一般锐角三角形2.半径为R 的圆内接正三角形的高是 ( ) A .23R B. 2RC. RD. R 23 3.已知正十边形的半径为R ,则它的边长a 10等于 ( ) A. 2Rcos180B. 2Rsin180C. Rsin180D. Rcos1804.(2018•贵阳)如图,A 、B 、C 是小正方形的顶点,且每个小正方形的边长为1,则tan ∠BAC 的值为( ) A .B .1C .D .二、填空题:5.如果一个正八边形的半径为2,那么它的面积为 .(结果保留根号形式)6.已知正六边形的面积为33cm 2,则它的外接圆的半径为 cm.三、解答题:7.如图,在△ABC 中,∠ACB =90°,BC =3,AC =4,CD ⊥AB ,垂足为D ,求sin ∠ACD 和tan ∠BCD 的值.8.(2019•淮安)如图,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH 沿CH折叠,点B落在矩形内点P处,连接AP,求tan∠HAP的值.9.四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=23,AD=2,求四边形ABCD 的面积.10.如图,根据图中数据完成填空,再按要求答题:sin2A1+sin2B1=;sin2A2+sin2B2=;sin2A3+sin2B3= .(1)观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B=.(2)如图④,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,利用三角函数的定义和勾股定理,证明你的猜想.(3)已知:∠A+∠B=90°,且sinA=,求sinB.8月9号初三数学作业纸(A )班级 姓名 学号 家长签名:课题:锐角三角形的简单应用(1) 一、填空题1.如图,为了测量电线杆的高度AB ,在离电线杆15米的C 处,用1.2米高的测角仪CD 测得电线杆顶端B 的仰角a =30°,则电线杆AB 的高度为________.第1题 第2题 第3题2.有人说,数学家就是不用爬树或把树砍倒就能够知道树高的人.小敏想知道校园内一棵大树的高,他测得CB=10米,∠ACB=60°,则树高AB 为3.如图所示,小明在家里楼顶上的点A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A 处看电梯楼顶部点B 处的仰角为60°,在点A 处看这栋电梯楼底部点C 处的俯角为45°,两栋楼之间的距离为30m ,则电梯楼的高BC 为____ __ 二、解答题:4.如图 ,在某建筑物AC 上,挂着“多彩淮安”的宣传条幅BC ,小明站在点F 处,看条幅顶端B ,测的仰角为︒30,再往条幅方向前行20米到达点E 处,,看到条幅顶端B ,测的仰角为︒60,求宣传条幅BC 的长.ABC5.如图,小方在五月一日假期中到郊外放风筝,风筝飞到C 处时的线长为20米,此时小方正好站在A 处,并测得∠CBD=60°,牵引底端B 离地面1.5米,求此时风筝离地面的高度(结果精确到1米,参考数据:2 1.41≈,3 1.73≈)6.如图,在大楼AB 的正前方有一斜坡CD ,CD =4米,坡角∠DCE =30°,小红在斜坡下的点C 处测得楼顶B 的仰角为60°,在斜坡上的点D 处测得楼顶B 的仰角为45°,其中点A ,C ,E 在同一直线上. (1)求斜坡CD 的高度DE ;(2)求大楼AB 的高度.(结果保留根号)7.如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜度由45°降为30°,已知原滑滑板AB 的长为5米,点D 、B 、C 在同一水平地面上. 求:(1)改善后滑滑板会加长多少?(精确到0.01)(2)若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?说明理由 .(参考数据:2 1.414,3 1.732,6 2.449=== )8月10号初三数学作业纸(A)班级姓名学号家长签名:课题:锐角三角形的简单应用(2)一、选择题1.每周一学校都要举行庄严的升国旗仪式,让我们感受到了国旗的神圣.某同学站在离旗杆12米远的地方,当国旗升起到旗杆顶时,他测得视线的仰角为45°,若这位同学的目高1.6米,则旗杆的高度约为()A.12米 B.10.4米 C.13.6米 D.24米2.一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要()A.米2B.米2C.(4+)米2D.(4+4tanθ)米2第2题图第3题图第4题图第5题图3.(2019•苏州)如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18m的地面上,若测角仪的高度是1.5m.测得教学楼的顶部A处的仰角为30°.则教学楼的高度是()A.55.5m B.54m C.19.5m D.18m二、填空题4.已知跷跷板长3m,当跷跷板的一端碰到地面时,另一端离地面1.5m.求此时跷跷板与地面的夹角为____cm2.5.将一副三角尺按如图所示叠放在一起,若AB=14 cm,则阴影部分的面积是____cm2.三、解答题6.如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:8秒后船向岸边移动了多少米?7. (2019•徐州)如图,无人机于空中A处测得某建筑顶部B处的仰角为45°,测得该建筑底部C处的俯角为17°.若无人机的飞行高度AD为62m,求该建筑的高度BC.(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)8. 如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角45°,测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约为多少m?(精确到0.1m)。
七年级数学作业纸

1.1生活数学班级: 姓名: 训练时间: 成绩:预习题训练: 1. 展示一些常见的汽车图标:德国宝马德国别克美国福特德国奥迪通用雪佛来韩国现代从中寻找熟悉的图形,感受丰富的图形世界(韩国现代)新授训练:1、根据算式中的数的变化,填写运算符号:10 30 20 20 60 15=300 20 20 4=280 20 4=14 4=102、如图1.2-3,用几根火柴拼成的两把椅子和一张方桌,请移动期中的3根火柴,将方桌挪到椅子中间。
3、池塘里的睡莲的面积每天增长一倍,9天可长满整个池塘,那么需要天睡莲长满半个池塘。
1.2活动 思考班级: 姓名: 训练时间: 成绩: 预习题训练:1、由火柴棒拼出一列图形,每个图形由几个正方形组成,通过观察发现:(1)组成4个正方形的火柴棒根数是 ;(2)组成5个正方形的火柴棒根数是 ;(3)组成100个正方形的火柴棒根数是 ;(4)组成n 个正方形的火柴棒根数是 。
答:(1)13根;(2)16根;(3)301根;(4)(3n+1)根。
2、抛一枚均匀的硬币,正面向上与向下的可能性均为50%,连投九次都是正面朝上,则第十次出现正面朝上的可能性是 。
新授训练:1、如图1.2-4,由若干根火柴棒拼成小金鱼的图形:(1)拼一个金鱼需要 根火柴;(2)拼三个金鱼需要 根火柴;(3)拼n 个金鱼需要 根火柴;6、我国股市交易中每买、卖一次需交千分之七点五的各种费用,某投资者每股10元的价格买入扬农股份的股票1000股,当股票涨到12元一股时全部售出,那么投资者实际盈利多少元?7、一个由3个大人和4个小孩组成的家庭去某地旅游。
甲旅行社的收费标准是:如果买4张全票,则其余人按半价优惠;乙旅行社的收费标准是:家庭旅游算团体票,按原价的43优惠。
这两家旅行社的原价均为每人100元。
这个家庭选择哪家旅行社所花的费用少?当小孩数是5时,这个家庭选择哪家旅行社所花的费用少?比较随着小孩数的增加,哪家旅行社收费更优惠?班级: 姓名: 训练时间: 成绩: 预习题训练:1. 指出下列数那些是正数那些是负数,并指出它们的特点.5.3-,21,211-,4,0,5.2,+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,0.05正数:负数:新授训练 在下列数-56,+1,6.7,-14,0,722, -5 ,25% 中,属于整数的有 ( )2、把下列各数分别填入相应的集合里。
4-9文通中学八年级数学作业纸
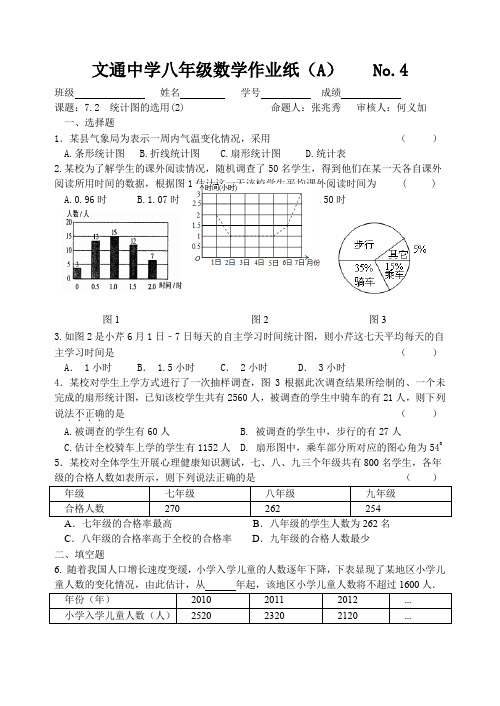
文通中学八年级数学作业纸(A ) No.4班级 姓名 学号 成绩 课题:7.2 统计图的选用(2) 命题人:张兆秀 审核人:何义加 一、选择题1.某县气象局为表示一周内气温变化情况,采用 ( ) A.条形统计图 B.折线统计图 C.扇形统计图 D.统计表2.某校为了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,根据图1估计这一天该校学生平均课外阅读时间为 ( ) A.0.96时 B.1.07时 C.1.15时 D.1.50时3.如图2是小芹6月1日﹣7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是 ( ) A . 1小时 B . 1.5小时 C . 2小时 D . 3小时4.某校对学生上学方式进行了一次抽样调查,图3根据此次调查结果所绘制的、一个未完成的扇形统计图,已知该校学生共有2560人,被调查的学生中骑车的有21人,则下列说法不正确...的是 ( ) A.被调查的学生有60人 B. 被调查的学生中,步行的有27人 C.估计全校骑车上学的学生有1152人 D. 扇形图中,乘车部分所对应的图心角为5405.某校对全体学生开展心理健康知识测试,七、八、九三个年级共有800名学生,各年级的合格人数如表所示,则下列说法正确的是 ( )A .七年级的合格率最高B .八年级的学生人数为262名C .八年级的合格率高于全校的合格率D .九年级的合格人数最少 二、填空题6. 随着我国人口增长速度变缓,小学入学儿童的人数逐年下降,下表显现了某地区小学儿图1图2图37. 《中华人民共和国个人所得税法》规定,公民全月工资,薪金所得不超过800元的部分不必纳税,超过800元的部分为全月应纳税所得额,此项税款按下表分段累进计算某人三、解答题8.为了了解某市120000名初中学生的视力情况,某校数学兴趣小组调查、收集了相关数据,并进行了整理分析.(1)小明在眼镜店调查了1000名初中学生的视力,小刚在邻居中调查了20名初中学生的视力,他们的抽样是否合理?并说明理由.(2)该校数学兴趣小组从该市七、八、九年级各随机抽取了1000名学生进行调查,整理他们的视力情况数据,得到如下的折线统计图.请你根据抽样调查的结果,估计该市120000名初中学生视力不良的人数是多少?9. 某校根据课程设置要求,开设了数学类拓展性课程,为了解学生最喜欢的课程内容,随机抽取了部分学生进行问卷调查(每人必须且只选其中一项),并将统计结果绘制成如下统计图(不完整).请根据图中信息回答问题:(1)求m,n的值。
二年级数学暑假作业打印版每天10道计算5道应用题共40天

7月7日-8日一.计算题二.应用题1.爸爸、妈妈和我分别掰了9个玉米,小弟弟掰了6个。
问我们全家一共掰了多少个玉米?2.小兔种了5行萝卜,每行9个。
送给邻居兔奶奶15个,还剩多少个?3.王师傅做了80个面包,第一次卖了17个,第二次卖了25个,还剩多少个?4.妈妈买了15个苹果,买的橘子比苹果少6个,问一共买了多少个水果?5.动物园有熊猫4只,有猴子是熊猫的3倍。
问一共有熊猫和猴子多少只?6.图书馆有90本书。
一年级借走20本,二年级借走17本。
问图书馆还有多少本书?7.二.一班有女生15人,男生比女生多11人,问二.一班有学生多少人?8.小汽车每辆能坐4人,大客车能坐25人,有3辆小汽车和1辆大客车。
问一共能坐多少人?9.商店里有4盒皮球,每盒6个,卖出20个,还剩多少个?10.小明有6套画片,每套3张,有买来4张,问现在有多少张?---------------------------------------------------------------------------------------7月9日-10日一.脱式计算24+12÷6 35-63÷7 5×8-39 (23+49)÷8 48-18÷3(52-45)×6 23+5×8 2×6+37 90-3×9 8×7-347×5+18 32÷4+2572÷(24-16) (34+47)÷9 56-2×675+15-36 60+40÷850-(30+12) (21-18)×8 45÷(3×3)二.应用题1.学校买回3盒乒乓球,每盒8个,平均发给二年级4个班,每个班分得几个乒乓球?2.小熊捡了9个玉米,小猴检的是小熊的4倍,他们一共捡了多少个玉米?3.食品店有85听可乐,上午卖了46听,下午卖了30听,还剩多少听?4.操场上原有16个同学,又来了14个。
数学作业纸B5打印版

数学作业纸B5打印版今天,我要向大家介绍一款实用的数学作业纸——B5打印版。
这款作业纸不仅适合学生在家庭中完成数学作业,也适用于课堂上的数学练习。
让我们来了解一下B5打印版数学作业纸的特点。
这款作业纸采用了标准的B5纸张大小,方便学生使用和携带。
页面布局简洁明了,方便学生阅读和理解题目。
作业纸还包含了各种类型的数学题目,包括加减乘除、分数、小数、图形等,可以全面地帮助学生巩固数学知识。
除了常规的数学题目外,B5打印版数学作业纸还增加了一些特别的设计。
比如,在每页的底部,都设置了一个小小的“提示”板块,包含了该页题目的解答方法和注意事项。
这个设计非常实用,可以帮助学生更好地理解题目,提高解题的正确率。
另外,B5打印版数学作业纸还注重题目的多样性和趣味性。
在题目设计中,不仅有常规的计算题和应用题,还有不少有趣的数学游戏和智力题。
这些题目可以激发学生的学习兴趣,让他们在轻松愉快的氛围中完成数学作业。
B5打印版数学作业纸是一款非常实用的学习工具。
它不仅包含了各种类型的数学题目,还增加了提示板块和趣味题目,可以帮助学生更好地理解数学知识,提高解题能力。
如果大家正在寻找一款高质量的数学作业纸,那么B5打印版绝对是一个不错的选择。
本试卷为"幼小衔接数学试卷",主要针对幼儿园大班的小朋友进行数学知识的测试,帮助他们更好地适应小学的数学学习。
本试卷包含20道题目,涵盖了数与运算、图形与空间、逻辑与推理等数学基础知识,旨在帮助小朋友们建立正确的数学观念,提高他们的数学素养。
本部分包含10道题目,主要测试学生对数的基本概念、数的比较、数的加减法等基本运算的掌握情况。
本部分包含5道题目,主要测试学生对图形的基本认知、空间概念的理解和运用能力。
本部分包含5道题目,主要测试学生的逻辑推理能力,包括对问题的分析、判断和推理能力。
内容丰富:本试卷涵盖了幼儿园数学教育的多个方面,有助于全面了解学生的数学学习情况。
初二数学暑假作业

(1)求证:四边形 EADB 是菱形;(2)连接 EC,当∠BAC=60°,BC= 2 3 时,求△ECB 的面积.
作匀速运动,到达点 D 停止,则△APM 的面积 y 与点 P 经过的路程 x 之间的函数关系的图象大致是
(
)
A
B
C
D
二.填空题:
9.如图,正方形 ABCD 的面积是 2,E,F,P 分别是 AB,BC,AC 上的动点,PE+PF 的最小值等于
.
3
10.如图,E 为矩形纸片 ABCD 的 BC 边上一点,将纸片沿 AE 向上折叠,使点 B 落在 DC 边上的 F 点处.
1.作业 4《一元二次方程》; 2.作业 5《一元二次方程》; 3.作业 6《二次函数》;
1.作业 7《二次函数》; 2.作业 8《二次函数》; 3.作业 9《二次函数》; 4.(246 班必做) 作业 10《二次函数综合》; 1.(246 班必做) 作业 11《二次函数综合》; 2.作业 12 综合练习 3.作业 13 综合练习 4.作业 14 综合练习 1.作业 15 综合练习 2.(246 班必做) 作业 16《几何综合》; 3.(246 班必做) 作业 17《几何综合》; 4.(246 班必做) 作业 18《几何综合》;
折痕交 AD 于点 E,交 BC 于点 F,连接 BE,则△ABE 的周长为
.
13.在△ABC 中,AB>AC,AD 平分∠BAC,CD⊥AD,E 是 BC 的中点,若 AB=12,AC=10,则 DE=
.
14.如图,菱形 ABCD 中, BAD 120 ,CF⊥AD 于点 E,且 BC=CF,连接 BF 交对角线 AC 于点 M,
蒙氏数学作业纸5答案

蒙氏数学作业纸5答案蒙氏数学作业纸5答案【篇一:蒙氏托二班六月份第一周作业纸】txt>一,生活教育:1.鼓励宝宝口渴时主动饮水2.鼓励宝宝尝试自己剥开蛋壳3.鼓励宝宝尝试自己穿脱袜子二,教学活动一.活动名称:儿歌《脚丫丫穿衣服》目标:乐于自己穿袜子,学会念儿歌脚丫丫操脚尖翘一翘,脚跟摇一摇,翘一翘,摇一摇,小脚小脚跳一跳。
二.活动名称:捏《雨花石》目标:培养幼儿手指协调性三.活动名称:歌曲《小龙人》目标:让宝宝感受歌曲的快乐小龙人我头上有犄角,我身后有尾巴,谁也不知道,我有多少秘密。
我头上有犄角,我身后有尾巴,谁也不知道,我有多少秘密。
我是一条小青龙,我有多少小秘密,我是一条小青龙,我有多少小秘密,我有许多的秘密,就不告诉你,就不告诉你,就不告诉你。
四.活动名称:蒙氏操作《解鞋带》目标:让宝宝练习解鞋带,培养宝宝的生活自理能力和自我服务意识五.活动名称:体能游戏《帮老奶奶运水果》目标:通过宝宝钻的动作,培养宝宝身体灵活性六.活动名称:音乐律动《手指歌》目标:帮助宝宝拇指、食指及小指的分化,增加手指灵活性【篇二:蒙氏数学】利说:1、幼儿的敏感期。
1--2.5岁的幼儿已经有了大小、多少、轻重、长短等数量经验。
而5--6岁的幼儿已经有数学的概念化。
如数、量、空间等的概念。
2、丰富的感官经验是数学学习的一个基础。
如眼睛、耳朵、鼻子、手等就有看、听、嗅、味、触等感官经验。
3、蒙氏数学的核心是提供丰富的材料,通过操作学习。
4、学习成果的爆发性。
“业精于勤荒于嬉”要有耐心,要给孩子充足的时间,通过前期的积累,就能达到一定程度的爆发。
皮亚杰说:1、孩子早期的数学学习是离不开操作的。
它分为动作水平、表象水平和抽象水平三个阶段。
2、知识习得建立在经验之上。
班图拉的亲历学习。
二、操作材料教师具备教师用书;孩子是学具、操作册、作业纸。
对作业纸的发放也是很与学问的。
可以整本发,也可以是撕下来有目的的发放。
对操作材料上的图形要先让幼儿感知再让幼儿辨别。
初中英语书面作业设计样例(九年级)第17-19周

:选自《知识与能力训练》根底版
拓展性
作业
〔选做〕
1.
:学生听录音填空,在提升听力技巧的同时,增进文化知识。
:英语B本
2.
:学生谈论相关话题,在真实语境中运用语言知识。
:英语B本
单元名称
Unit8
Surprise endings
:选自《知识与能力训练》根底版
拓展性
作业
〔选做〕
:学生根据思维导图写一篇观影报告报告,了解报告写作结构,锻炼写作水平。
:选自《知识与能力》提高版
单元名称
Unit8
Surprise endings
课题
综合练习1
节次
第七课时
作业类型
作业内容
设计和题目
根底性
作业
〔必做〕
1.
:学生通过朗读对话,了解表达反对意见的常用语句,提升学生在真实情境中使用语言的能力。
:英语B本
2. English Book B P. 99
:学生根据讨论结果,写一篇短文介绍海报中的故事,提升写作能力。
:英语B本
单元名称
Unit8
Surprise endings
课题
综合练习2
节次
第八课时
作业类型
作业内容
设计和题目
根底性
作业
〔必做〕
1.Read and remember all the words and phrases in Unit 8.
:学生写出单词的不同形式,了解单词词性和词形的变化,拓宽词汇量,了解构词法,提升词汇学习策略。
:选自《知识与能力训练》根底版
高等数学作业纸山东交通学院

第六章 微分方程第一节 微分方程的基本概念一. 单项选择题1. 下列各式中不是常微分方程的为 .A. ()()y P x y Q x '+=B. 2y y y '''+=C. 20ax bx c ++=D. d d 0x y y x += 2. 函数yC x =-(C 为任意常数)是微分方程1xy y '''-=的 .A. 通解B. 特解C. 是解,但既不是通解也不是特解D. 不是解 3. 微分方程0y y ''+=的通解是y = .A. 1sin C xB. 1cos C xC. 1sin cos C x x +D. 12sin cos C x C x + 4. 已知某微分方程的通解为()212e x y C C x =+且满足01x y==,00x y ='=,则有 .A. 2e x y =B. 2e x y x =C. ()212e x y x =-D. 22e x y =二. 计算题验证函数1y x =-是微分方程0y y x '+-=的解.第二节 可分离变量的微分方程一. 填空题1. 微分方程0xy y '+=满足初始条件12x y ==的特解为 .2. 微分方程ex yy -'=的通解为 .3. 微分方程d 2d 0x y y x +=满足初始条件21x y ==的特解为 .二. 计算题1. 求微分方程d 0xy x y =满足初始条件1e x y ==的特解.2. 求微分方程0d d sin cos =+rr θθθ的通解.3. 22d d y x xyxy +=,e 2e ==x y .第三节 一阶线性微分方程一. 填空题1. 方程()()y P x yQ x '+=的通解为 .2. 微分方程()d d 0x y x x y ++=的通解为 .3. 微分方程1=+'y y x 满足初始条件10x y ==的特解为 .二. 单项选择题1. 方程()d d 0x y y y x +-=的通解为 .A. e x yy C = B. e y x y C = C. 2e y xy Cx = D. 2ey xy Cx -=2. 设()y x 满足微分方程2cos tan y x y x '+=,且π40x y ==. 则0x y== .A. π4B. π4- C. 1- D. 1三. 计算题1. 求微分方程sin cos e xy y x -'+=的通解.2. 已知曲线经过点()1,1,它的切线在纵轴上的截距等于切点的横坐标,求该曲线的方程.3. 若连续函数()f x 满足()()202d xf x f t t x +=⎰,求()f x .第五节 二阶常系数齐次线性微分方程一. 填空题1. 函数12cos ,sin y x y x ωω==是线性 (填相关或无关),若12(),()y x y x 是方程()()0y P x y Q x y '''++=的两个特解,此时方程的通解为 .2. 设12,y y 是方程0y py qy '''++=的两个解,且满足1212e ,e x x y y y y -+=-=,则方程的通解为 ;常数p = ,q = .3. 微分方程0y y ''-=的通解为 .4. 微分方程250y y y '''-+=的通解为 .5. 以12e (sin cos )x y C x C x =+为通解的二阶常系数齐次线性微分方程为 .二.计算题1. 求方程20y y y '''-+=满足条件()()04,02y y '==-的特解.2. 设函数()y y x =满足条件()()43002,04y y y y y '''++=⎧⎨'==-⎩ ,求广义积分0()d y x x +∞⎰.第六节 二阶常系数非齐次线性微分方程一. 单项选择题1. 已知1y x =是方程y y x ''+=的一个解,2e 2x y =是方程e xy y ''+=的一个解,则方程e x y y x ''+=+的通解为y = .A.e 2xx + B.12cos sin C x C x +C.12cos sin C x C x x ++D.12e cos sin 2xC x C x x +++2. 微分方程e xy y ''-=的一个特解应具有形式 . A. ()e xax b + B. e x ax C. ()2e xax b x+ D. e x a二.求下列微分方程的通解或给定初始条件下的特解1. ()()542e 01,01xy y y y y '''⎧-+=⎪⎨'==⎪⎩.2. xx y y y e 22=+'-''.第七章 空间解析几何与向量代数第一节 向量及其线性运算一. 填空题1. 点0(4,5,3)P -到y 轴的距离为 ;到yOz 面的距离为 ;到原点的距离为 .2. 点(,,)a b c 关于yOz 面的对称点是 ;与(,,)a b c -关于 面对称;关于原点的对称点是 .3. 点M 的向径与x 轴成45角,与y 轴成60角,长度为6,若在z 轴上的坐标是负值, 则点M 的坐标为 .4. 与向量(6,7,6)a =-平行的单位向量为 .5. 向量AB 在,,x y z 轴上的投影依次为4,4,7-,它的终点坐标为(2,1,7)B -,则起点坐标为 .二. 单项选择题1. ()()0,3,4,2,1,2a b ==-,则Pr a j b = . A.3 B.13-C.1-D.1 2. 下列各组角可以作为某向量的方向角的是 . A .90,150,60αβγ===B .45,135,60αβγ===C .60αβγ===D .60,120,150αβγ===三. 解答题1. 已知两点()1M 和()23,0,2M .计算向量12M M 的模,方向余弦和方向角.2. 已知三个力123F i j k =++,2234F i j k =-+-,3345F i j k =-+作用于同一点,求合力F 的大小及方向余弦.3. 设向量()()()()1,5,3,6,4,2,0,5,7,20,27,35,a b c d ==--=-=--求常数,,x y z ,使得向量,,xa yb zc 及d 可以构成封闭的折线.第二节 数量积 向量积一. 填空题1. 向量()()3,1,2,1,2,1a b =--=-, 则()23a b -⋅= , 2a b ⨯= . 2. a b ⇔⊥ ;a b ⇔∥ .3. 已知点()()()2,4,,3,7,5,,10,9A n B C m 三点共线,则m = ,n = .二. 单项选择题已知4,2a b ==且42a b ⋅=,则a b ⨯= .A B ...2 三. 计算题1. 已知()()()2,3,1,1,1,3,1,2,0a b c =-=-=-,求()a b c ⨯⋅.2. 求向量()4,3,4a =-在向量()2,2,1b =上的投影.3. 已知12(1,1,2),(3,3,1)M M -和3(3,1,3)M ,求与1223M M M M ,同时垂直的单位向量.4. 求以()3,0,2,(5,2,1),(0,1,3)A B C -为顶点的三角形的面积.5. 已知3,26,72a b a b ==⨯=,求a b ⋅.第三节 曲面及其方程一. 填空题1. xOy 面上双曲线224936x y -=分别绕x 轴与y 轴旋转一周所得旋转曲面的方程依 次为 与 .2. 曲面2221x y z --=是由O x y 面上的曲线221x y -=绕x 轴旋转一周所得,或由 面上曲线 绕 轴旋转一周所得.3.z =表示的曲面为 .4.222x y R +=表示的曲面为 .二. 选择题将下列曲面的方程与曲面的形状进行搭配:A. 222()x a y a -+=;B. 222z x y =+及2262z x y =--所围成的图形;C. 22z x =-;D. 22x y z +=及2y x =与1z =所围成的图形.三. 计算题1.设一动点与两定点()1,2,3A 和()2,1,4B -等距离,求该动点的轨迹方程.2. 一动点M到平面10x-=的距离等于它到x轴的距离的两倍,求点M的轨迹方程.3. 说明下列旋转曲面是怎样形成的:(1)2221499x y z++=;(2) .22214yx z-+=第四节 空间曲线及其方程一. 填空题1. 母线平行于y 轴且经过曲线2222222160x y z x z y ++=⎧⎨+-=⎩的柱面方程为 . 2. 曲线22291x y z x z ++=⎧⎨+=⎩在xOy 面的投影曲线方程为 .二. 单项选择题1. 曲线2221:1645230x y z x z ⎧+-=⎪Γ⎨⎪-+=⎩关于xOy 面的投影柱面方程是 . A. 2220241160x y x +--= B. 22441270y z z +--= C. 22220241160x y x R z +--=⎧⎨=⎩ D. 224412700y z z x +--=⎧⎨=⎩2. 球面2222x y z R ++=与平面x z a +=的交线在xOy 面的投影曲线方程是 .A. 2222()a z y z R -++=B. 2222()x y a x R ++-=C. 2222()0a z y z R z -++=⎧⎨=⎩D. 2222()0a x x y R z -++=⎧⎨=⎩ 三. 解答题1. 求通过曲线2222222160x y z x y z ++=⎧⎨-+=⎩,且母线分别平行于x 轴及y 轴的柱面方程.2. 把空间曲线方程2216236x y x z +=⎧⎨+=⎩化为参数方程.3.将曲线的一般方程2224x y z y x++=⎧⎨=⎩化为参数方程.4. 求两个椭圆抛物面222z x y =+与2262z x y =--所围成的立体在xOy 坐标面的投影区域.第五节 平面及其方程一.填空题1. 若平面经过点()000,,x y z 且垂直于向量(),,A B C ,则该平面方程为.2. 平行于xOz 面且经过点()2,5,3-的平面方程为 .3. 经过x 轴和点()3,1,2--的平面方程为 .4. 点()2,1,1到平面10x y z +-+=的距离为 .二. 单项选择题1.两平行平面23490x y z -++=与234150x y z -+-=的距离为 .A . 629B .2429 CD提示:两平行平面的距离为平面上任一点到另一平面的距离.2. 平面260x y z -+-=与平面250x y z ++-=的夹角为 .A.π3B.2π3 C.π4 D. 3π4三. 解答题1. 求平行于x 轴且经过两点()4,0,2-和()5,1,7的平面方程.2. 若平面过点()1,0,1-且平行于向量()2,1,1a =和()1,1,0b =-,求该平面方程.3. 确定k 的值,使平面290x ky z +--=在y 轴上的截距为3-.4. 求平面2250x y z -++=与各坐标面夹角的余弦.第六节 空间直线及其方程一. 填空题1.直线102340x y z x y z +++=⎧⎨-++=⎩的对称式方程为 .2.直线300x y z x y z ++=⎧⎨--=⎩与平面10x y z --+=的夹角为 .3.直线326040x y z x y z D -+-=⎧⎨+-+=⎩与z 轴相交,则D = . 二. 单项选择题1.两直线1158:121x y z L --+==-与26:23x y L y z -=⎧⎨+=⎩的夹角为 . A .π6 B .π4 C .π3 D .π22.过点()2,0,3-且与直线247035210x y z x y z -+-=⎧⎨+-+=⎩垂直的平面方程是 .A .16(2)14(0)11(3)0x y z --+-++=B. (2)2(0)4(3)0x y z ---++=C .3(2)5(0)2(3)0x y z -+--+=D.16(2)14(0)11(3)0x y z -++++-=3.设直线3210:21030x y z L x y z +++=⎧⎨--+=⎩及平面:4220x y z ∏-+-=,则直线L .A .平行于∏B .在∏上C .垂直于∏D .与∏斜交三. 解答题1.求过点(3,2,5)-且与平面430x z --=和2510x y z ---=平行的直线方程.2.求直线1010x y zx y z+--=⎧⎨-++=⎩在平面0x y z++=上的投影直线方程.3.求过直线1:L4020x yy+-=⎧⎨-=⎩且平行于直线221:211x y zL+-==的平面方程.4. 求直线2223038180x y zx y z+-+=⎧⎨++-=⎩与直线533903210x y zx y z-+-=⎧⎨-+-=⎩的夹角.第八章 多元函数微分法及其应用第一节 多元函数的基本概念一. 填空题1. 点集{}22(,)14D x y x y =≤+≤是 (开/闭)集,是 (有/无)界集,边界曲线为 及 .2. 设函数1ln()z x y =+,则其定义域为 . 3. 设224(,)xy f x y x y=+,则(,)f tx ty = . 4. 设2(,e )y f x y x y +=,则(,)f x y = . 5. 101lim(1)x x y xy →→+= . 6. 判断函数1sin ,0(,)0,0x y y f x y y ⎧≠⎪=⎨⎪=⎩的连续性:在(0,0) 点 ;在(1,0) 点 .(填连续或不连续) 二. 单项选择题1. 若0lim (,)y kx x f x y A =→=对任何k 都成立,则必有 . A .(),f x y 在()0,0处连续 B .(),f x y 在()0,0处偏导数存在C .00lim (,)x y f x y A →→=D .00lim (,)x y f x y →→不一定存在 2. 设函数22,(,)(0,0)(,)0,(,)(0,0)xy x y x yf x y x y ⎧≠⎪+=⎨⎪=⎩,则 . A .极限00lim (,)x y f x y →→存在,但(),f x y 在点()0,0处不连续B .极限00lim (,)x y f x y →→存在,且(),f x y 在点()0,0处连续 C .极限00lim (,)x y f x y →→不存在,故(),f x y 在点()0,0处不连续 D .极限00lim (,)x y f x y →→不存在,但(),f x y 在点()0,0处连续三. 计算题 1. 2201sin()cos lim x y xy xy x x y x →→+-2. 302220()x y x y →→+3. 证明极限22400lim x y xy x y→→+不存在. (选做题)第二节 偏导数 第三节 全微分一. 填空题1. 设(,)z f x y =在点()0,1处偏导数存在,则用定义式表达为(0,1)x f = ;(0,1)y f = .2.函数(,)z f x y =在D 内(,)(,)xy yx f x y f x y =的充分条件为二阶偏导数(,)xy f x y 与(,)yx f x y .3. 若函数(,)z f x y =在点(,)x y 可微,则d z = .4. 设()221ln(1)arctan y z x y x +=++,则(1,0)zx ∂=∂ . 5. 设()23sin z x y =,则d z = .二. 单项选择题1. 函数(,)z f x y =在点00(,)x y 偏导数存在是(,)f x y 在该点连续的 . A .充分非必要条件 B .必要非充分条件 C .充分必要条件 D .既非充分也非必要条件2. 若0000(,)(,)0x y z x y z x y ==,则(,)z f x y =在点00(,)x y . A .连续且可微 B .连续但不一定可微 C .可微但不一定连续 D .不一定可微也不一定连续3. 考虑二元函数的下面4条性质:①(,)f x y 在点00(,)x y 处连续; ②(,)f x y 在点00(,)x y 处的两个偏导数连续; ③(,)f x y 在点00(,)x y 处可微; ④(,)f x y 在点00(,)x y 处的两个偏导数存在. 若用“P Q ⇒”表示可由性质P 推出性质Q ,则有 . A .②⇒③⇒① B .③⇒②⇒① C .③⇒④⇒① D .③⇒①⇒④三. 计算题1.设z =(1,2),,d z zz x y∂∂∂∂.2. 设2(1)x yz xy +=+,求11x y z x==∂∂.3. 设2sin(),0(,),0x y xy f x y xy x xy ⎧≠⎪=⎨⎪=⎩,求(0,1)x f .第四节 多元复合函数的求导法则一. 填空题1. 若(,)z f x u =,而(,)u x y ϕ=,则zx∂=∂ ,z y ∂=∂ . 2. 设22e ln()xy z x y =++,则zx∂=∂ ,z y ∂=∂ . 3. 设22()y z f x y =-,其中()f u 为可导函数,则zx∂=∂ . 二. 计算题1. 设()()z x y x y ϕψ=++-,其中,ϕψ具有二阶连续的导数,求2222z zx y∂∂-∂∂.2. 设(32,42)z f u v u v =+-,其中(,)f x y 可微,求,,d z zz u v∂∂∂∂.3. 设()22,z f xy x y =-,f 具有二阶连续的偏导数,求22,z z y y ∂∂∂∂.4. 设(,,),e yz f u x y u x ==,其中f 具有二阶连续的偏导数,求2zx y∂∂∂.第五节 隐函数的求导公式一. 填空题1. 设(,)z x y 为由方程22ln()0xz xyz xyz -+=确定的函数,则zx∂=∂ . 2. 设方程2210x y +-=确定了一个隐函数()y f x =,则22d d x yx== .3. 设(,)u u x y =,(,)v v x y =是由方程组cos cosv x u u v x u u ⎧=⎪⎪⎨⎪=⎪⎩所确定的隐函数,则ux ∂=∂ .二. 单项选择题1. 设(,)0x az y bz ϕ--=,则z zab x y∂∂+=∂∂ . A .a B .b C .1- D .1 2. 设e e e zyxz x y =+,则zy∂=∂ . A .e e (1)e y x z y z ++ B .e e (1)e x y z x z +- C .e e (1)e y x z y z -- D .e e (1)e x y z x z ++三. 计算题1. 设333z xyz a -=,求,z zx y∂∂∂∂.2. 方程xyz +=(,)z z x y =,求z 在点(1,0,1)-处的全微分.3. 设(),()y y x z z x ==是由方程组()(,,)0z xf x y F x y z =+⎧⎨=⎩所确定的隐函数,其中f 具有一阶连续的导数, F 具有一阶连续的偏导数,求d d z x.第六节 多元函数微分学的几何应用一. 填空题1. 曲面221z x y =+-在点(2,1,4)M 处法向量为 .2. 曲线2226x y z x y z ⎧++=⎨++=⎩在点 处的切向量平行向量(1,0,1)-.3. 曲面e 23zz xy -+=在点()1,2,0处的切平面方程为 .二. 单项选择题1. 已知曲面224z x y =--上点P 处的切平面平行于平面2210x y z ++-=,则点P 的坐标为 .A .(1,1,2)-B .(1,1,2)-C .(1,1,2)D .(1,1,2)-- 2. 曲面222426x y z -+=在点(2,2,3)处法线方程为 .A .223143x y z ---==-- B .223143x y z ---==- C .223143x y z ---==-- D .223143x y z ---== 3. 在曲线23,,x t y t z t ==-=的所有切线中,与平面24x y z ++=平行的切线的条数 为 .A .只有一条B .只有二条C .至少有三条D .不存在三.计算题1. 求曲线e cos ,e sin ,e tttx t y t z ===在0t =时的法平面与切线方程.2. 求曲面ln xz y z=+在点(1,1,1)M 处的法线与切平面方程.3. 求曲面22z x y =+上与平面240x y z +-=平行的切平面方程.第七节 方向导数与梯度一. 填空题1. 函数(ln u x =+在点(1,0,1)A 处沿A 指向点(3,2,2)B -的方向导数为.2. 函数()222ln u x y z =++在点(1,2,2)M -处的梯度grad M u = .二. 计算题1. 设22(,)2f x y x xy y =-+,求在点(2,3)处的方向导数fl∂∂的最大值.2. 求函数u =在点(1,2,2)M -沿曲线24,2,2x t y t z t===-在此点的切线方向的方向导数.第八节 多元函数的极值及其求法一. 填空题选择题1. 设函数(,)z f x y =在点00(,)x y 具有偏导数,则(,)z f x y =在点00(,)x y 具有极值的 必要条件为 .2. 设函数(,)z f x y =在点00(,)x y 处可微,且0000(,)(,)0x y f x y f x y ==,则函数z 在00(,)x y 处 .A .必有极值,可能是极大,也可能是极小B .可能有极值,也可能无极值C .必有极大值D .必有极小值三.解答题1. 求函数44(,)()f x y x y x y =+-+的极值.2. 在椭球面222221x y z ++=上求一点,使函数222(,,)f x y z x y z =++在该点沿方向(1,1,0)l =-的方向导数最大.第九章 重积分第一节 二重积分的概念与性质一. 填空题1. 二重积分的定义是对 区域上的 函数而说的,当和式极限 (填极限表达式)存在时,二重积分存在.2. 设曲顶柱体的顶部曲面函数(,),(,)0z f x y f x y =≥,它的底部区域为D ,则曲顶柱 体的体积用二重积分表示为 .3. 设{}22(,)1D x y x y =+≤,则d Dσ=⎰⎰ .4. 由二重积分的几何意义知,Dσ= ,(22:4,0D x y y ≤≤+);Dσ= ,(22:1D x y ≤+). 二. 单项选择题设[]31ln()d ,DI x y σ=+⎰⎰32()d ,DI x y σ=+⎰⎰[]33sin()d ,DI x y σ=+⎰⎰其中D 由10,0,1,2x y x y x y ==+=+=围成,则123,,I I I 之间的大小顺序为 .A. 321I I I >>B. 123I I I >>C. 231I I I >>D. 213I I I >>三. 解答题估计DI =:01,02D x y ≤≤≤≤.第二节 二重积分的计算(1)一. 填空题1. 设:1D x y +≤,则(123)d d Dx y x y +-=⎰⎰ .2. 设220d (,)d x xI x f x y y =⎰⎰,改变积分次序,则I = .3. 设平面薄片所占的闭区域D 是由直线2,x y y x +==和x 轴所围成,面密度22(,)x y x y μ=+,则该薄片的质量用二重积分表示为 ,值等于 .二. 单项选择题1. 设D 是以(0,0)O ,(1,0)A ,(1,2)B ,(0,1)C 为顶点的梯形所围成的闭区域,则(,)d Df x y σ⎰⎰化成二次积分是 .A.1101d (,)d xx f x y y +⎰⎰B.1201d (,)d x x f x y y +⎰⎰C.11210011d (,)d d (,)d y y f x y x y f x y x -+⎰⎰⎰⎰ D.112101d (,)d d (,)d y y f x y x y f x y x -+⎰⎰⎰⎰2. 设10()d f x x a =⎰,{}(,)01,01D x y x y ≤≤≤≤=则()()d d Df x f y x y =⎰⎰ .A. aB. 2a C.212a D. 0 三. 计算题1. 计算(32)d Dx y σ+⎰⎰,其中D 是由两坐标轴及直线2x y +=所围成的平面闭区域.2. 计算22d dDxx yy⎰⎰,其中D是由直线2,x y x==与曲线1xy=所围成的闭区域.3.计算Dσ⎰⎰,其中D是由抛物线2y x=及直线y x=所围成的闭区域.4. 计算32211d sin dxx y y-⎰⎰.第二节 二重积分的计算(2)一. 填空题1. 利用极坐标计算二重积分的转换公式为:(,)d d Df x y x y =⎰⎰ .2. 由圆曲线222x y y +=围成的积分区域D 用极坐标型的不等式表示为 .3. 化20d xx f y ⎰⎰为极坐标形式的二次积分为 .二. 单项选择题1. 设区域{}222(,),0,0D x y x y a a y ≤≥=+>,则22()d d =D xy x y +⎰⎰ .A.π300d d aθρρ⎰⎰ B. π200d d aθρρ⎰⎰ C. π32π02d d aθρρ-⎰⎰ D. π22π02d d aθρρ-⎰⎰2. 二次积分πcos 20d (cos ,sin )d f θθρθρθρρ⎰⎰可以转化成 .A. 10d (,)d y f x y x ⎰B. 100d (,)d y f x y x ⎰C.110d (,)d x f x y y ⎰⎰D. 10d (,)d x f x y y ⎰三. 计算题1. 计算d d Dxy x y ⎰⎰,其中D 是由圆周222x y a +=所围成的闭区域.2. 计算arctand Dyxσ⎰⎰,其中D 是由圆周22224,1x y x y +=+=及直线0y y x ==,所围成的第一象限内的闭区域. 3.计算Dσ,其中D 是圆环形闭区域{}22(,)14x y x y ≤≤+.4. 设一薄片所占的区域D 是由曲线222,(0),x y x y ≥+=直线y x =以及x 轴所围成,面密度为μ=,求该薄片的质量.第四节 重积分的应用一. 填空题1. 光滑曲面(,)z f x y =在平面xOy 上的投影区域为xy D ,那么该曲面的面积可用二重积分表示为 .2. 设有一平面薄片占有xOy 面上的闭区域D ,面密度为(,)x y μ,则该薄片的质量用二重积分表示为 ;该薄片的质心坐标用二重积分表示为x = ,y = ;该薄片关于坐标轴的转动惯量用二重积分表示为x I = ,y I = . 3. 曲面228z x y =--与22z x y =+所围立体的体积用二重积分可表示为 , 化为极坐标下的二次积分为 ,其值等于 .二. 单项选择题在第一卦限中,由曲面221z x y =--和平面y x =,y =及0z =所围立体的体积可表示成二次积分 . A.π12300d (1)d θρρρ-⎰⎰ B. π123π04d (1)d θρρρ-⎰⎰C.π1240d (1)d θρρρ-⎰⎰ D. π122π03d (1)d θρρρ-⎰⎰三. 计算题1. 计算以xOy 面上的圆周22x y x +=围成的闭区域D 为底,以曲面z =的曲顶柱体的体积.2. 求球面2222x y z a ++=含在柱面22(0)x y ax a +=>内部的那部分面积.3. 均匀薄片的面密度为常数1,所占闭区域D 由抛物线292y x =与直线2x =所围成, 求转动惯量x I 和y I .第十章 曲线积分与曲面积分第一节 对弧长的曲线积分一. 填空题1. 设空间曲线Γ在(,,)x y z 处的线密度为(,,)x y z μ,则曲线质量m = ,曲线对x 轴的转动惯量为x I = .2. 设平面曲线L 为下半圆周y =则曲线积分22()d Lx y s +⎰= .3. 设平面曲线弧L 的方程为()x y ψ=,c y d ≤≤,则曲线积分(,)d Lf x y s =⎰ .(写出计算公式)设平面曲线弧L 的参数方程为(),()x t y t ϕψ==,t αβ≤≤,则曲线积分(,)d Lf x y s =⎰ .(写出计算公式)设平面曲线弧L 的极坐标方程:()ρρθ=,αθβ≤≤,则曲线积分(,)d Lf x y s =⎰.(写出计算公式)二. 单项选择题1. 设L 为0x x =,302y ≤≤,则4d L s =⎰ .A .40xB .4C .06xD .6 2. 设L 为连接(0,0),(1,0),(0,1)O A B 的三角形围线,则曲线积分()d Lx y s +⎰= .A .1+.1 D .0三. 计算题1. 计算d L x s ⎰,其中L 是抛物线2y x =上介于0x =与1x =之间的一段弧.2. ()d x y z s Γ--⎰其中Γ是点(1,0,2)A 与点(3,2,1)B 之间的直线段.3. 22()d L x y s +⎰,其中L 为圆周222x y x +=.第二节 对坐标的曲线积分一. 填空题1. xOy 面内,一质点沿曲线从A 点移动到B 点,在移动的过程中,质点受到的力(,)F x y =(,)(,)P x y i Q x y j +时,则变力所作的功为W = , 若设d (d ,d )r x y =,则功也可记为向量形式W = .2. 若L :()()x t y t ϕψ=⎧⎨=⎩,t α=对应L 的始点,t β=对应L 的终点则(,)d (,)d LP x y x Q x y y βα+=⎰⎰d t .3. 设弧AB 是22y x =由(8,4)A 到(2,2)B -的一段弧,则d d ABy x x y +=⎰(表示为x 的定积分)= (表示为y 的定积分).二. 单项选择题设L 为11y x =--由(0,0)到(2,0)的折线段,则()d ()d Ly x x x y y -++=⎰ .A .1-B .0C .2-D .1三. 计算题1. 计算2d d (31)d x x y y z y z Γ++--⎰,其中Γ为由点(2,3,4)A 到(1,1,1)B 的一段直线.2.2222()d ()d Lx y x x y y -++⎰,其中L 为由点(0,0)A 沿抛物线2y x =到(2,4)B 的一段弧.3. xOy 面内,有一质点在变力(,)F x y =2()2x xy x i j ++作用下,沿222:L x y R +=顺时针方向从(0,)R 运动到(,0)R ,求变力所作的功W .第三节 格林公式及其应用一. 填空题1. 设函数(,),(,)P x y Q x y 在 上具有 ,则有格林公式 ,其中L 是 .2. 若G 为单连通区域,(,),(,)P x y Q x y 在G 内有一阶连续的偏导数,则d d L P x Q y +⎰在G 内与路径无关的充要条件为 ,或 ,或 . 3. 设(,),(,)P x y Q x y 在单连通区域G 内有一阶连续的偏导数且P Qy x∂∂=∂∂,则 (1,2)(0,0)(,)d (,)d P x y x Q x y y +⎰= .(化为定积分). 4. 设d (,)(2)d (2)d u x y x y x x y y =+++,则(,)u x y = .二. 单项选择题1. 设分段光滑正向闭曲线L 围成的平面区域的面积为σ,则在下列曲线积分中, ①d Ly x -⎰② (e )d x Ly x +⎰ ③1d d 2Ly x x y -⎰结果等于σ的个数是 .A .0B .1C .2D .3 2.22d d Lxy x x y y -⎰= ,其中L 为正向圆周222x y R +=(0)R >.A .4π2RB .4πRC .4π2R - D .0三. 计算题1. 计算(cos23)d (e )d y Lx y x x y --+⎰,其中L 是以(1,1),(3,1),(3,5)A B C 为顶点的三角形的正向边界曲线.2. 计算22d d Lxy y x y x -⎰,其中L 为圆周224x y +=,按顺时针方向.3.22()d (sin )d Lx y x x y y --+⎰,其中L 是圆周y =(0,0)到(1,1)的一段弧.第四节 对面积的曲面积分一. 填空题1. 分片光滑的有界曲面∑,曲面上任一点(,,)x y z 的面密度为(,,)x y z μ,则曲面的质量为m = ,对z 轴的转动惯量z I = .2. 设曲面∑:(,)x x y z =的面积为S ,∑在yOz 面投影为yz D ,则d S ∑⎰⎰= .3. 设积分曲面∑关于yOz 面对称,∑在yOz 面前方的部分为1∑,则 当 时,(,,)d 0f x y z S ∑=⎰⎰;当 时,1(,,)d 2(,,)d f x y z S f x y z S ∑∑=⎰⎰⎰⎰.二. 单项选择题∑为球面2222,(0)x y z R R ++=>,则曲面积分222()d x y z S ∑++⎰⎰= .A .4πR B .42πR C .44πR D . 46πR三. 计算题1. 4(2)d 3x y z S ∑++⎰⎰,∑是平面1234x y z++=在第一卦限的部分.2. 222()d x y z S ∑++⎰⎰,∑是锥面z =1z =所围成立体的表面.3. 计算2d x S ∑⎰⎰,其中∑为圆柱面221xy +=在02z ≤≤的部分.第十一章 无穷级数第一节 无穷级数的概念与基本性质一. 填空题1. 当 时(q 满足的条件),等比级数0,0nn aq a ∞=≠∑收敛,且收敛于 . 2. 若级数1nn u∞=∑收敛,则级数1(0.01)nn u∞=+∑ (填收敛或发散).3. 级数112n n ∞=∑ (填收敛或发散). 4. 若级数1nn u∞=∑收敛于S ,则级数11n n u∞+=∑收敛于 .二. 判断下列级数的收敛性,若收敛求其和1. 11(21)(21)n n n ∞=-+∑. 2. 1n ∞=∑.3. 11123n n n ∞=⎛⎫+ ⎪⎝⎭∑. 4. 1111nn n ∞=⎛⎫+ ⎪⎝⎭∑.第二节 正项级数及其审敛法一. 填空题1. p -级数11p n n ∞=∑(0p >)当 时收敛,当 时发散(填p 的范围). 2. 比较审敛法极限形式判定正项级数敛散性:1n n u ∞=∑和1n n v ∞=∑均为正项级数,且limnn nu l v →∞=,若0l <<+∞, ; 若0l =, ; 若l =+∞, . 3. 用比值审敛法判定正项级数1n n u ∞=∑收敛性时,如果()1lim,0n n nu u ρρ+→∞≤≤=∞+,则当 时,级数收敛;当 时,级数发散.二. 判别以下级数的敛散性1. 2112n n ∞=+∑ . 2. 12!n n n n n ∞=∑.3. 21sin π33nn nn ∞=∑. 4.11πtan2n n n ∞+=∑.第三节 交错级数和任意项级数一. 填空题1. 若交错级数11(1)n n n u ∞-=-∑满足条件(1) ,(2) ,则级数收敛. 2. 若级数1nn u∞=∑绝对收敛,则级数1nn u∞=∑必定 ,级数1nn u∞=∑必定 ; 若级数1nn u∞=∑条件收敛,则级数1nn u∞=∑ 必定 ,级数1nn u∞=∑必定 (填写收敛或者发散).二. 单项选择题1. 下列级数绝对收敛的是 .A. 11(1)nn n ∞=-∑ B.31arctan n n n ∞=∑ C.11sin n n n ∞=∑D. 1(1)nn ∞=-∑2. 下列级数条件收敛的是 .A. 1(1)1nn n n ∞=-+∑B.1(1)n ∞=-∑1(1)n n ∞=-∑ D. 211(1)n n n ∞=-∑3. 设10(1,2)n a n n<=≤,则下列级数中肯定收敛的是 . A.1nn a∞=∑ B.1(1)nn n a ∞=-∑C.1n ∞=21(1)n nn a ∞=-∑ 4. 设,,1,2,22n n n nn n a a a a p q n +-===,则下列命题正确的是 .A. 若1nn a∞=∑条件收敛,则1nn p∞=∑和1nn q∞=∑都收敛B.若1nn a∞=∑绝对收敛,则1nn p∞=∑和1nn q∞=∑都收敛 C.若1nn a∞=∑条件收敛,则1nn p∞=∑和1nn q∞=∑的敛散性都不定 D.若1nn a∞=∑绝对收敛,则1nn p∞=∑和1nn q∞=∑的敛散性都不定三. 判断以下级数的敛散性,若收敛,判断是绝对收敛还是条件收敛1. 21sin n nn ∞=∑.2. 11(1)n n ∞-=-∑.3. 212(1)!n n n n ∞=-∑.第四节 幂级数一.填空题1. 设幂级数1nn n a x∞=∑在4x =-发散,在3x =收敛,则级数1(5)nn n a ∞=-∑ ,12nn n a ∞=∑ (填收敛或发散).2. 幂级数1nnn a x∞=∑的收敛半径计算公式为: .3. 幂级数12nn n x ∞=∑的收敛半径为 ,收敛区间为 .二. 单项选择题1. 设幂级数nn n a x∞=∑在2x =处收敛,则该级数在1x =-处必定 .A. 发散B. 条件收敛C. 绝对收敛D. 敛散性不能确定2. 当44x -<≤时,幂级数14nnn x n ∞=⋅∑的和函数为 . A. ln(4)x -- B.4ln(4)x -- C. ln 14x ⎛⎫-- ⎪⎝⎭ D. ln 14x ⎛⎫+ ⎪⎝⎭三. 求下列幂级数的收敛域 1. 1!21nn n xn ∞=+∑.2. 1nn ∞=.3. 2111(1)21n n n x n +∞-=-+∑.4. 求幂级数11n n nx∞-=∑的收敛域及和函数.。
2022-2023学年第一学期北师大版九年级数学第十七周周末综合作业题(附答案)

2022-2023学年第一学期北师大版九年级数学第十七周周末综合作业题(附答案)一.选择题1.如图,点A、B、C在⊙O上,∠ABO=30°,∠ACO=45°,则∠BOC等于()A.60°B.90°C.150°D.160°2.关于抛物线y=x2﹣2x﹣1,下列说法中错误的是()A.开口方向向上B.对称轴是直线x=1C.当x>1时,y随x的增大而减小D.顶点坐标为(1,﹣2)3.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是()A.sin A=B.cos A=C.tan A=D.cos B=4.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=2,则⊙O的半径为()A.4B.6C.8D.125.如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为πcm2,则扇形圆心角的度数为()A.120°B.140°C.150°D.160°6.抛物线y=ax2+bx+c的对称轴为直线x=﹣1,图象过(1,0)点,部分图象如图所示,下列判断中:其中正确的个数是()①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(﹣2.5,y1),(﹣0.5,y2)均在抛物线上,则y1>y2;⑤5a﹣2b+c<0.A.2个B.3个C.4个D.5个7.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为()A.1个B.2个C.3个D.4个8.如图,以点P为圆心,以为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为()A.(4,)B.(4,2)C.(4,4)D.(2,)9.如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为()A.cm B.(2+π)cm C.cm D.3cm二.填空题10.如图,是半圆,点O为圆心,C、D两点在上,且AD∥OC,连接BC、BD.若=65°,则∠ABD的度数为.11.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD 等于海里.12.如图,平行四边形ABCD的一边AB在x轴上,长为5,且∠DAB=60°,反比例函数y=和y=分别经过点C,D,则AD=.13.有三张正面分别写有数字﹣1,1,2的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片随机抽一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率为.14.《孙子算经》是我国古代重要的数学著作,成书于约一千五百年前,其中有道歌谣算题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问杆长几何?”歌谣的意思是:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五,同时立一根一尺五的小标杆,它的影长五寸(提示:仗和尺是古代的长度单位,1丈=10尺,1尺=10寸),可以求出竹竿的长为尺.15.如图是某几何体的三视图及相关数据,则该几何体的侧面积是.16.如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升飞机从A地出发,垂直上升900米到达C处,在C处观察B地的俯角为30°,则A,B两地之间的距离为.17.若函数y=16x与y=的图象有一个交点是,则另一个交点坐标是.18.一艘货轮由西向东航行,在A处测得灯塔P在它的北偏东60°方向,继续航行到达B 处,测得灯塔P在正南方向10海里的C处是港口,点A、B、C在一条直线上,则这艘货轮由A处到B处航行的路程为海里(结果保留根号).19.如图,已知AM为⊙O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交⊙O于点D、E,∠BMD=40°,则∠EOM=.20.已知边长为6cm的等边三角形ABC,以AB为直径画半圆(如图),则阴影部分的面积是(结果保留π)21.如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处.……按此规律运动到点A2020处,则点A2020与点A0间的距离是.22.如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若∠ADB=100°,则∠ACB的度数为.三.解答题23.计算题:(1)计算:sin45°+cos230°•tan60°﹣tan45°;(2)已知α是锐角,2sin(α﹣15°)=,求﹣|cosα﹣tan|的值.24.在一次数学兴趣小组活动中,阳光和乐观两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则阳光获胜,反之则乐观获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;(2)游戏对双方公平吗?请说明理由.25.如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,点C坐标为(﹣1,0),点A坐标为(0,2).一次函数y=kx+b的图象经过点B、C,反比例函数y =的图象经过点B.(1)求一次函数和反比例函数的关系式;(2)直接写出当x<0时,kx+b﹣<0的解集;(3)在x轴上找一点M,使得AM+BM的值最小,直接写出点M的坐标和AM+BM的最小值.26.如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.(1)求斜坡AB的水平宽度BC;(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF =3.5m 时,求点D 离地面的高.(结果保留根号)27.汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x (元)与每月租出的车辆数(y )有如下关系:x (元)3000 3200 3500 4000 y (辆) 100 96 90 80(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求按照表格呈现的规律,每月租出的车辆数y (辆)与每辆车的月租金x (元)之间的关系式.(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x (x ≥3000)的代数式填表:租出的车辆数(辆)未租出的车辆数(辆) 租出每辆车的月收益(元) 所有未租出的车辆每月的维护费(元)(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请说明理由.28.如图,点M 在函数y =(x >0)的图象上,过点M 分别作x 轴和y 轴的平行线交函数y =(x >0)的图象于点B ,C .(1)若点M 的坐标为(1,3),求B ,C 两点的坐标;(2)若点M 是y =(x >0)的图象上任意一点,求△BMC 的面积.29.为了身体健康,越来越多的人喜欢上了行走健身,为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡AB =260米,坡度为1:;将斜坡AB 的高度AE 降低AC =30米后,斜坡AB 改造为斜坡CD ,其坡度为1:4.求斜坡CD的长.(结果保留根号)30.某校组织代表队参加市“与经典同行”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分).A组:75≤x<80;B组:80≤x<85;C组:85≤x <90;D组:90≤x<95;E组:95≤x<100,并绘制如下两幅不完整的统计图:请根据图中信息,解答下列问题:(1)参加初赛的选手共有名,请补全频数分布直方图;(2)扇形统计图中,E组人数占参赛选手的百分比是多少?它对应的圆心角是多少度?(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中两名女生的概率.31.某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元,设矩形一边长为x,面积为S平方米.(1)求S与x之间的函数关系式,并写出自变量x的取值范围;(2)设计费能可以达到30000元吗?为什么?(3)当x是多少米时,设计费最多?最多是多少元?32.如图,一次函数y=kx+b与反比例函数y=(x>0)交于A(2,4),B(a,1)两点,与x轴、y轴分别交于点C,D.(1)求一次函数和反比例函数的表达式;(2)求证:AD=BC.33.如图,AB是⊙O的直径,C是⊙O上一点,D是的中点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F.(1)求证:AE是⊙O的切线;(2)若DH=9,sin C=,求直径AB的长.34.如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.(1)求抛物线的表达式;(2)如图1,若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求此时E点的坐标;(3)如图2,在x轴上是否存在一点D使得△ACD为等腰三角形?若存在,请求出所有符合条件的点D的坐标;若不存在,请说明理由.35.如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F,(1)求证:CF=BF;(2)若CD=12,AC=16,求⊙O的半径和CE的长.36.某宾馆有30个房间供游客住宿,当每个房间的房价为每天160元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于260元.设每个房间的房价每天增加x元(x为10的整数倍).(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;(2)设宾馆一天的利润为w元,求w与x的函数关系式;(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?37.如图,已知抛物线与x轴交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).(1)求抛物线的解析式;(2)设抛物线顶点为D,求四边形AEDB的面积;(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由.38.如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.(1)说明:AP是⊙O的切线;(2)若OC=CP,AB=6,求CD的长.39.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,BC =+1.斜边AB、DC相交于点O.(1)求CO的长;(2)若把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),这时AB与CD1相交于点O1,此时,求:CO1的长;(3)若把三角板D1CE1绕着点C顺时针再旋转15°得△D2CE2(如图丙),这时AB与CD2相交于点O2,此时,求:CO2的长.40.如图,抛物线y=﹣x2+bx+c交x轴于A,B两点,交y轴于点C,直线y=﹣x+2经过点B,C.(1)求抛物线的解析式;(2)点P是直线BC上方抛物线上一动点,设点P的横坐标为m.求△PBC面积最大值和此时m的值;(3)Q是抛物线上一点,若∠ABC=∠CBQ,直线BQ与y轴交于点M,请直接写出M 的坐标.参考答案一.选择题1.解:过A作⊙O的直径,交⊙O于D;在△OAB中,OA=OB,则∠BOD=∠ABO+∠OAB=2×30°=60°,同理可得:∠COD=∠ACO+∠OAC=2×45°=90°,故∠BOC=∠BOD+∠COD=150°.故选:C.2.解:抛物线y=x2﹣2x﹣1,∵a=1>0,∴开口方向向上,故选项A不合题意;对称轴是直线x=﹣=﹣=1,故选项B不合题意;当x>1时,y随x的增大而增大,故选项C符合题意;y=x2﹣2x﹣1=(x﹣1)2﹣2,顶点坐标为(1,﹣2),故选项D不合题意.故选:C.3.解:∵∠ACB=90°,CD⊥AB,∴∠A+∠DCA=90°,∠DCA+∠BCD=90°,∴∠A=∠BCD,∴sin A=sin∠BCD=,故选:A.4.解:∵圆心角∠AOC与圆周角∠B所对的弧都为,且∠B=60°,∴∠AOC=2∠B=120°,又OA=OC,∴∠OAC=∠OCA=30°,∵OP⊥AC,∴∠APO=90°,在Rt△AOP中,OP=2,∠OAC=30°,∴OA=2OP=4,则圆O的半径4.故选:A.5.解:∵OB=10cm,AB=20cm,∴OA=OB+AB=30cm,设扇形圆心角的度数为α,∵纸面面积为πcm2,∴﹣=π,∴α=150°,故选:C.6.解:①由图象开口向上,则a>0,故b>0,∵c<0,∴abc<0,故①错误.②∵抛物线与x轴有两个交点,∴b2﹣4ac>0,故②正确.③∵抛物线与x轴的一个交点是(1,0),对称轴是直线x=﹣1,∴抛物线与x轴的另一个交点是(﹣3,0),∴9a﹣3b+c=0,故③正确.④∵点(﹣0.5,y2)在抛物线上,对称轴为直线x=﹣1,∴(﹣1.5,y2)也在抛物线上,∵﹣1.5>﹣2.5,且(﹣1.5,y2),(﹣2.5,y1)都在对称轴的左侧,∴y1>y2,故④正确.⑤∵抛物线对称轴x=﹣1,经过(1,0),∴﹣=﹣1,a+b+c=0,∴b=2a,c=﹣3a,∴5a﹣2b+c=5a﹣4a﹣3a=﹣2a<0,∴⑤正确.故正确的判断是②③④⑤共4个.故选:C.7.解:∵抛物线开口向下,∴a<0,而抛物线的对称轴为直线x=﹣=1,即b=﹣2a,∴3a+b=3a﹣2a=a<0,所以①正确;∵2≤c≤3,把x=﹣1,y=0代入y=ax2+bx+c,得a﹣b+c=0,∴c=﹣3a,∴2≤﹣3a≤3,∴﹣1≤a≤﹣,所以②正确;∵抛物线的顶点坐标(1,n),∴x=1时,二次函数值有最大值n,∴a+b+c≥am2+bm+c,即a+b≥am2+bm,所以③正确;∵抛物线的顶点坐标(1,n),∴抛物线y=ax2+bx+c与直线y=n﹣1有两个交点,∴关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根,所以④正确.故选:D.8.解:过点P作PC⊥AB于点C;即点C为AB的中点,又点A的坐标为(2,0),点B的坐标为(6,0),故点C(4,0)在Rt△P AC中,P A=,AC=2,即有PC=4,即P(4,4).故选:C.9.解:∵△ABC是等边三角形,∴∠ACB=60°,∴∠AC(A)=120°,点B两次翻动划过的弧长相等,则点B经过的路径长=2×=π(cm).故选:C.二.填空题10.解:∵是半圆,即AB是直径,∴∠ADB=90°,又∵AD∥OC,∴OC⊥BD,∴=65°,∴=180°﹣65°﹣65°=50°,∴∠ABD=.故答案为:25°.11.解:根据题意可知∠CAD=30°,∠CBD=60°,∵∠CBD=∠CAD+∠ACB,∴∠CAD=30°=∠ACB,∴AB=BC=20海里,在Rt△CBD中,∠BDC=90°,∠DBC=60°,sin∠DBC=,∴sin60°=,∴CD=20×sin60°=20×=10海里,故答案为:10.12.解:设点C(x,),则点D(﹣x,),∴CD=x﹣(﹣x)=x,∵四边形ABCD是平行四边形,∴CD=AB=5,∴x=5,解得x=2,∴D(﹣3,),作DE⊥AB于E,则DE=,∵∠DAB=60°,∴AD===2,故答案为2.13.解:画树状图图得:∵共有6种等可能的结果,点(a,b)在第二象限的有2种情况,∴点(a,b)在第二象限的概率为:=.故答案为:.14.解:设竹竿的长度为x尺,∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,∴=,解得x=45(尺).故答案为:45.15.解:根据图形可知圆锥的高为6,母线长为8,则底面半径为2,圆锥侧面积公式=底面周长×母线长×,圆锥侧面积=×π×2×2×8=16π.故答案为:16π.16.解:由题意知∠BAC=90°,∠ABC=30°,AC=900米,∵tan∠ABC=,∴AB===900(米),故答案为:900米.17.解:∵两函数图象关于原点对称,∴两函数图象交点关于原点对称,∴的对称点为(﹣,﹣4).故答案为(﹣,﹣4).18.解:根据题意得:PC=10海里,∠PBC=90°﹣45°=45°,∠P AC=90°﹣60°=30°,在直角三角形APC中,∵∠P AC=30°,∠C=90°,∴AC=PC=10(海里),在直角三角形BPC中,∵∠PBC=45°,∠C=90°,∴BC=PC=10海里,∴AB=AC=BC=(10﹣10)(海里);故答案为:(10﹣10).19.解:连接EM,∵AB=AC,∠BAM=∠CAM,∴AM⊥BC,∵AM为⊙O的直径,∴∠ADM=∠AEM=90°,∴∠AME=∠AMD=90°﹣∠BMD=50°∴∠EAM=40°,∴∠EOM=2∠EAM=80°,故答案为:80°.20.解:如图,根据等边三角形和圆的对称性,阴影部分的面积就是扇形OMN的面积,由题意得,扇形OMN的半径为3cm,圆心角的度数为60°,S阴影部分=S扇形OMN==,故答案为:.21.解:如图,∵⊙O的半径=2,由题意得,A0A1=4,A0A2=2,A0A3=2,A0A4=2,A0A5=2,A0A6=0,A0A7=4,…∵2020÷6=336…4,∴按此规律运动到点A2020处,A2020与A4重合,∴A0A2020=A0A4=2.22.解:如图:连接OA,OB,∵四边形AOBD是圆内接四边形,∴∠AOB+∠D=180°,∵∠ADB=100°,∴∠AOB=80°,∴∠ACB=40°.故答案为:40°.三.解答题23.解:(1)原式==1+﹣1=;(2)∵2sin(α﹣15°)=,∴,∴α﹣15°=45°,∴α=60°,∴原式=====1﹣24.解:(1)根据题意列表如下:6789 39101112410111213511121314可见,两数和共有12种等可能结果;(2)游戏对双方公平,理由如下:∵两数和共有12种等可能的情况,其中和小于12的情况有6种,∴阳光获胜的概率为=,∴乐观获胜的概率是,∵=,∴游戏对双方公平.25.解:(1)过点B作BF⊥x轴于点F,∵点C坐标为(﹣1,0),点A坐标为(0,2).∴OA=2,OC=1,∵∠BCA=90°,∴∠BCF+∠ACO=90°,又∵∠CAO+∠ACO=90°,∴∠BCF=∠CAO,在△AOC和△CFB中∴△AOC≌△CFB(AAS),∴FC=OA=2,BF=OC=1,∴点B的坐标为(﹣3,1),将点B的坐标代入反比例函数解析式可得:1=,解得:k=﹣3,故可得反比例函数解析式为y=﹣;将点B、C的坐标代入一次函数解析式可得:,解得:.故可得一次函数解析式为y=﹣x﹣.(2)结合点B的坐标及图象,可得当x<0时,kx+b﹣<0的解集为:﹣3<x<0;(3)作点A关于x轴的对称点A′,连接B A′与x轴的交点即为点M,∵A(0,2),∴A′(0,﹣2),设直线BA′的解析式为y=ax+b,将点A′及点B的坐标代入可得:,解得:.故直线BA′的解析式为y=﹣x﹣2,令y=0,可得﹣x﹣2=0,解得:x=﹣2,故点M的坐标为(﹣2,0),AM+BM=BM+MA′=BA′==3.综上可得:点M的坐标为(﹣2,0),AM+BM的最小值为3.26.解:(1)∵坡度为i=1:2,AC=4m,∴BC=4×2=8m.(2)作DS⊥BC,垂足为S,且与AB相交于H.∵∠DGH=∠BSH,∠DHG=∠BHS,∴∠GDH=∠SBH,∴=,∵DG=EF=2m,∴GH=1m,∴DH==m,BH=BF+FH=3.5+(2.5﹣1)=5m,设HS=xm,则BS=2xm,∴x2+(2x)2=52,∴x=m∴DS=+=2m.27.解:(1)由表格数据可知y与x是一次函数关系,设其解析式为y=kx+b.由题:,解之得:,∴y与x间的函数关系是y=﹣x+160.(2)如下表:租出的车辆数﹣x+160未租出的车辆数x﹣60租出的车每辆的月收益x﹣150所有未租出的车辆每月的维护费x﹣3000(3)设租赁公司获得的月收益为W元,依题意可得:W=(﹣x+160)(x﹣150)﹣(x﹣3000)=(﹣x2+163x﹣24000)﹣(x﹣3000)=﹣x2+162x﹣21000=﹣(x﹣4050)2+307050当x=4050时,Wmax=307050,即:当每辆车的月租金为4050元时,公司获得最大月收益307050元.故答案为:﹣x+160,x﹣60,x﹣150,x﹣3000.28.解:(1)∵点M的坐标为(1,3),MC⊥x轴,MB⊥y轴,且B,C在函数的图象上,∴当x=1时,y=1,∴点C的坐标为(1,1)∴当y=3时,,∴点B的坐标为;(2)设点M的坐标为(a,b)∵点M在函数的图象上,∴ab=3∵点B,C在函数的图象上,∴点C的坐标为,B点坐标为∴,,∴S△BMC=•BM•MC=••=•=.29.解:在Rt△ABE中,∵,∴∠ABE=30°,∵AB=260,∴,∵AC=30,∴CE=130﹣30=100,在Rt△CDE中,∵tan D=1:4,∴,∴,∴(米),答:斜坡CD的长是米.30.解:(1)参加初赛的选手共有:8÷20%=40(人),B组有:40×25%=10(人),频数分布直方图补充如下:故答案为:40;(2)E组人数占参赛选手的百分比是:×100%=15%;E组对应的圆心角度数是:360°×15%=54°;(3)根据题意画树状图如下:由上图可以看出,所有可能出现的结果有l2种,这些结果出现的可能性相等,选中两名女生的结果有2种,则选中两名女生的概率是==.31.解:(1)矩形的一边长为x米,周长为16米.另一边长为(8﹣x)米,∴S=x(8﹣x)=﹣x2+8x,其中0<x<8;(2)能.理由是:∵设计费为每平方米2000元,∴当设计费为30000元时,面积为:30000÷2000=15(平方米)即﹣x2+8x=15,解得x1=3,x2=5;∴设计费能达到30000元;(3)∵S=﹣x2+8x=﹣(x﹣4)2+16,∴当x=4时,S最大值=16,∴16×2000=32000.∴当x是4米时,矩形的最大面积为16平方米,设计费最多,最多是32000元.32.解:(1)将A(2,4)代入,得m=8,∴反比例函数的表达式为∴又B(a,1)在反比例函数的图象上,∴,解得,a=8∴B(8,1)将A(2,4),B(8,1)代入y=kx+b中,得,解得:∴一次函数的表达式为.(2)由(1)可知,一次函数的表达式为当x=0时,y=5;当y=0时,x=10;∴C(10,0),D(0,5),如图,过点A作y轴的垂线与y轴交于点E,过B作x轴的垂线与x轴交于点F,∴E(0,4),F(8,0),∴AE=2,DE=1,BF=1,CF=2∴在Rt△ADE中,由勾股定理得:在Rt△BCF中,由勾股定理得:∴AD=BC.33.证明:(1)连接OC,∵D是的中点,∴∠AOD=∠COD∵OA=OC,∴OE⊥AC,即∠AFE=90°,∴∠E+∠EAF=90°∵∠AOE=2∠C,∠CAE=2∠C,∴∠CAE=∠AOE∴∠E+∠AOE=90°,∴∠EAO=90°∴AE是⊙O的切线(2)∵∠C=∠B∵OD=OB,∴∠B=∠ODB,∴∠ODB=∠C∴,∴由勾股定理得:∵∠C=∠FDH,∠DFH=∠CFD∴△DFH∽△CFD∴∴∴设OA=OD=x,∴∵AF2+OF2=OA2∴,解得:x=10∴OA=10∴直径AB的长为20.34.解:(1)将点A(1,0),B(﹣3,0)代入y=ax2+bx+3,得,,解得,,∴抛物线表达式为y=﹣x2﹣2x+3;(2)如图1,过点E作EF⊥x轴于点F,设E(a,﹣a2﹣2a+3)(﹣3<a<0),∴EF=﹣a2﹣2a+3,BF=a+3,OF=﹣a,∴===,∴当时,S四边形BOCE最大,且最大值为;当时,,此时,点E坐标为;(3)如图2,连接AC,①当CA=CD时,此时CO为底边的垂直平分线,满足条件的点D1,与点A关于y轴对称,点D1坐标为(﹣1,0);②当AD=AC时,在Rt△ACO中,∵OA=1,OC=3,由勾股定理得,AC==,以点A为圆心,AC的长为半径作弧,交x轴于两点D2,D3,即为满足条件的点,此时它们的坐标分别为,;③当DA=DC时,线段AC的垂直平分线与x轴的交点D4,即为满足条件的点,设垂直AC的垂直平分线交y轴于点P,过AC中点Q,∵∠AOC=∠BOC=∠PQC=∠PQA=90°,∠D4PO=∠CPQ,∴∠ACO=∠OD4P,∴△D4AQ∽△CAO,∴=,即=,∴D4A=5,∴OD4=D4A﹣OA=4,∴点D4的坐标为(﹣4,0);综上所述,存在符合条件的点D,其坐标为D1(﹣1,0)或或或D4(﹣4,0).35.解:(1)证明:∵AB是⊙O的直径,∴∠ACB=90°,又∵CE⊥AB,∴∠CEB=90°,∴∠2=90°﹣∠ABC=∠A,又∵C是弧BD的中点,∴∠1=∠A,∴∠1=∠2,∴CF=BF;(2)∵C是弧BD的中点,∴=,∴BC=CD=12,又∵在Rt△ABC中,AC=16,∴由勾股定理可得:AB=20,∴⊙O的半径为10,∵S△ABC=AC•BC=AB•CE,∴CE==9.6.36.解:(1)y=30﹣x(0≤x≤100,且x是10的整数倍);(2)w=(30﹣x)(160+x﹣20)=﹣x2+16x+4200;(3)w=﹣x2+16x+4200=﹣(x﹣80)2+4840∴当x=80时,w最大为10600.当x=80时,y=30﹣x=22.答:一天订住22个房间时,宾馆每天利润最大,最大利润是4840元.37.解:(1)∵抛物线与y轴交于点(0,3),∴设抛物线解析式为y=ax2+bx+3(a≠0)根据题意,得,解得.∴抛物线的解析式为y=﹣x2+2x+3;(2)如图,设该抛物线对称轴是DF,连接DE、BD.过点B作BG⊥DF于点G.由顶点坐标公式得顶点坐标为D(1,4)设对称轴与x轴的交点为F∴四边形ABDE的面积=S△ABO+S梯形BOFD+S△DFE=AO•BO+(BO+DF)•OF+EF•DF=×1×3+×(3+4)×1+×2×4=9;(3)相似,如图,BD=;∴BE=DE=∴BD2+BE2=20,DE2=20即:BD2+BE2=DE2,所以△BDE是直角三角形∴∠AOB=∠DBE=90°,且,∴△AOB∽△DBE.38.(1)证明:连接AO,AC(如图).∵BC是⊙O的直径,∴∠BAC=∠CAD=90°.∵E是CD的中点,∴CE=DE=AE.∴∠ECA=∠EAC.∵OA=OC,∴∠OAC=∠OCA.∵CD是⊙O的切线,∴CD⊥OC.∴∠ECA+∠OCA=90°.∴∠EAC+∠OAC=90°.∴OA⊥AP.∵A是⊙O上一点,∴AP是⊙O的切线;(2)解:由(1)知OA⊥AP.在Rt△OAP中,∵∠OAP=90°,OC=CP=OA,即OP=2OA,∴sin P=.∴∠P=30°.∴∠AOP=60°.∵OC=OA,∴∠ACO=60°.在Rt△BAC中,∵∠BAC=90°,AB=6,∠ACO=60°,∴.又∵在Rt△ACD中,∠CAD=90°,∠ACD=90°﹣∠ACO=30°,∴CD====4.39.解:(1)过点O作OH⊥BC于点H.在Rt△OHB中,∠HOB=90°﹣∠B=45°=∠B∴OH=HB.∵在Rt△DCE中,∠DCE=90°﹣∠D=60°∴在Rt△OHC中,∠COH=90°﹣∠OCH=90°﹣60°=30°∴OC=2CH.又∵OH=CH•tan∠OCH=,∴HB=OH=.又∵CH+HB=CB,∴CH+=.∴CH=1.∴CO=2CH=2;(2)∵∠BCE1=15°∴∠O1CB=60°﹣15°=45°=∠B.∴∠CO1B=180°﹣(45°+45°)=90°∴CO1=BC•sin∠B==;(3)从甲图到丙图的过程中,由于旋转角均为15°,且在乙图中CO1⊥AB,所以CO2与CO在这个旋转过程中关于直线CO1成轴对称.所以CO2=CO=2.40.解:(1)针对于直线y=﹣x+2,令x=0,则y=2,∴C(0,2),令y=0,则﹣x+2=0,∴x=4,∴B(4,0),∵抛物线y=﹣x2+bx+c过点B,点C,∴,∴,∴抛物线的解析式为y=﹣x2+x+2;(2)如图1,过点P作PD∥y轴交直线BC于D,∵点P的横坐标为m,∴P(m,﹣m2+m+2),D(m,﹣m+2),∴PD=﹣m2+m+2﹣(﹣m+2)=﹣m2+4m,∴S△PBC=PD(x B﹣x C)=(﹣m2+4m)×4=﹣2(m﹣2)2+8,当m=2时,S△PBC最大,其值为8.(3)如图2,过点C作CN⊥BM于N,∴∠MNC=90°=∠BOC,∵∠ABC=∠CBQ,∴CN=OC=2,∵∠CMN=∠BMO,∠CNM=∠BOM=90°,∴△MNC∽△MOB,∴,∴,∴OM=2MN,∴CM=OM﹣OC=2MN﹣2,在Rt△CNM中,根据勾股定理得,MN2+CN2=CM2,∴MN2+4=(2MN﹣2)2,∴MN=0(舍)或MN=,∴OM=2MN=,∴M(0,),当点Q与点A重合时,点M和点O重合,此时M(0,0),即点M的坐标为(0,0)或(0,).。
蒙氏数学作业纸69页答案

蒙氏数学作业纸69页答案1、19.对于实数a、b、c,“a>b”是“ac2(c平方)>bc2(c平方) ; ”的()[单选题] * A.充分不必要条件B.必要不充分条件(正确答案)C.充要条件D.既不充分也不必要条件2、43、长度分别为3cm,5cm,7cm,9cm的四根木棒,能搭成(首尾连结)三角形的个数为[单选题] *A.1B.2C.3(正确答案)D.43、下列语句中,描述集合的是()[单选题] *A、比1大很多的实数全体B、比2大很多的实数全体C、不超过5的整数全体(正确答案)D、数轴上位于原点附近的点的全体4、直线2x-y=1的斜率为()[单选题] *A、1B、2(正确答案)C、3D、45、32、在、、、、、3.14这六个数中, 无理数的个数有()[单选题] *A) 1 个;B) 2 个; (正确答案)C) 3 个;D) 4 个.6、花粉的质量很小,一粒某种植物花粉的质量约为000037毫克,已知1克=1000毫克,那么000037毫克可用科学记数法表示为[单选题] *A. 7×10??克B. 7×10??克C. 37×10??克D. 7×10??克(正确答案)7、6.方程x2=3x的根是()[单选题] *A、x = 3B、x = 0C、x1 =-3, x2 =0D、x1 =3, x2 = 0(正确答案)8、12.下列方程中,是一元二次方程的为()[单选题] *A. x2+3xy=4B. x+y=5C. x2=6(正确答案)D. 2x+3=09、48.如图,M是AG的中点,B是AG上一点.分别以AB、BG为边,作正方形ABCD和正方形BGFE,连接MD和MF.设AB=a,BG=b,且a+b=10,ab=8,则图中阴影部分的面积为()[单选题] *A.46B.59(正确答案)C.64D.8110、从3点到6点,分针旋转了多少度?[单选题] *90°960°-1080°(正确答案)-90°11、17. 的计算结果为()[单选题] *A.-7B.7(正确答案)C.49D.1412、8.(2020·课标Ⅱ)已知集合U={-2,-1,0,1,2,3},A={-1,0,1},B={1,2},则?U(A∪B)=( ) [单选题] *A.{-2,3}(正确答案)B.{-2,2,3}C.{-2,-1,0,3}D.{-2,-1,0,2,3}13、50.式子(2+1)(22+1)(24+1)(28+1)…(21024+1)+1化简的结果为()[单选题] *A.21024B.21024+1C.22048(正确答案)D.22048+114、下列说法正确的是[单选题] *A.一个数前面加上“-”号,这个数就是负数B.零既不是正数也不是负数(正确答案)C.零既是正数也是负数D.若a是正数,则-a不一定是负数15、8. 下列事件中,不可能发生的事件是(? ? ).[单选题] *A.明天气温为30℃B.学校新调进一位女教师C.大伟身长丈八(正确答案)D.打开电视机,就看到广告16、10.如图,点O在直线AE上,OC平分∠AOE,∠DOB是直角.若∠1=25°,那么∠AOB的度数是()[单选题] *A.65°B.25°(正确答案)C.90°D.115°17、30、等腰三角形ABC中,AB=2BC,且BC=12,则△ABC的周长为( ). [单选题]A. 48B. 60(正确答案)C. 48或60D. 3618、41.若m2﹣n2=5,则(m+n)2(m﹣n)2的值是()[单选题] * A.25(正确答案)B.5C.10D.1519、-330°是第()象限角?[单选题] *第一象限(正确答案)第二象限第三象限第四象限20、15.下列数中,是无理数的为()[单选题] *A.-3.14C.√3(正确答案)D.021、若3x+4y-5=0,则8?·16?的值是( ) [单选题] *A. 64B. 8C. 16D. 32(正确答案)22、设函数在闭区间[0,1]上连续,在开区间(0,1)上可导,且(x)>0 则()[单选题] *A、f(0)<0B、f(0)<1C、f(1)>f(0)D、f(1)<f(0)(正确答案)23、46.若a+b=7,ab=10,则a2+b2的值为()[单选题] *A.17B.29(正确答案)C.2524、25.{菱形}∩{矩形}应()[单选题] *A.{正方形}(正确答案)B.{矩形}C.{平行四边形}D.{菱形}25、6.若一个正比例函数的图象经过点(2,-3),则这个图象一定也经过点( ) [单选题]*A.(-3,2)B.( 3/2,-1)C.(2/3,-1)(正确答案)D.( -2/3,1)26、15.一次社会调查中,某小组了解到某种品牌的薯片包装上注明净含量为,则下列同类产品中净含量不符合标准的是()[单选题] *A 56gB .60gC.64gD.68g(正确答案)27、计算(a2)3的结果是[单选题] *A. a?B. a?(正确答案)C. a?D. 3a228、9、横坐标为3的点一定在()[单选题] *A.与x轴平行,且与x轴的距离为3的直线上B.与y轴平行,且与y轴的距离为3的直线上C.与x轴正半轴相交,与y轴平行,且与y轴的距离为3的直线上(正确答案)D.与y轴正半轴相交,与x轴平行,且与x轴的距离为3的直线上29、6.已知集合A={0,1,2},则集合B={(x,y)|x≥y,x∈A,y∈A}中元素的个数是( ) [单选题] *A.1B.3C.6(正确答案)D.930、40.若x+y=2,xy=﹣1,则(1﹣2x)(1﹣2y)的值是()[单选题] *A.﹣7(正确答案)B.﹣3 C.1 D.9。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第17周周末作业姓名()学号()
一、看拼音写词语。
yǔzhòu fēi chuán zāi hài dào yǐnɡbìxū biã yǒu dònɡ tiān
( )( )( )( )( )
dà qì wǎn chãnɡshì qinɡ jūn jiàn wãn lùpiāo fú yóu xì
( )( )( )( )( )( ) 二、选择正确的音节填在()里。
bēn bân zhōng zhòng mòmãi juãjiào
1、嫦(cháng)娥(ã)奔()月是个神话故事。
同学们在操场上奔()跑。
2、祖国永远在我们心中()。
小鸟被猎(liâ)人打中()了。
3、河水没()过小腿(tuǐ),我没()有办法过河。
4、我觉()得我该(gāi)上床睡(shuì)觉()了。
三、给下面的句子填上标点符号。
1、这道题真难□该怎么做呢□
2、我有一位好妈妈□她很疼我□
3、我们的祖国多么广大□
4、南极真的特别冷吗□
5、妹妹多想有一个漂亮的布娃娃□
四、把下面的词语连成句子,再加上标点。
1、活动课间丰富多彩真是
2、吹得小草头春风探(tàn)出了
五、在括号里填上合适的词语。
一圈圈()一条()一片片()一把把()
一只()一座()一首()一个()
()的图画()的人们()的校园()的树苗
六、按课文内容填空。
1、有时候我很(),有时候我很暴躁。
我做过()好事,灌溉(),()()人们()。
我也做过许多坏事,淹没(),冲毁(),给人们带来()。
人们想出()管住我,让我()好事,()坏事。
2、青蛙妈妈带着小青蛙()岸上。
她()一颗石子,()河里,河水被激起一圈圈()。
波纹碰到(),又一圈圈地荡回来。
七、词语接龙。
化——()——()——()——()岸——()——()——()——()
八、阅读短文,回答问题。
(一)
平常我在池子里睡觉,在小溪里散步,在江河里奔跑,在海洋里跳舞,唱歌,开大会。
1、将正确的答案的序号,填在横线上。
A、水缓缓流淌。
B、水波涛汹涌、奔腾呼啸。
C、水平静的时候。
D、水奔涌向前。
这里的“睡觉”指__ __;“散步”指___ _;“奔跑”指__ __;“跳舞”“唱歌”“开大会”指__ ____。
(二)
一片一片的黄叶从树上落下来。
有的落到水里,小鱼游过去,藏在底下,把它当(dàng)作伞。
有的落在岸边,蚂蚁爬上去,来回跑着,把它当作运动场。
1、“一片一片”指:A.一片 B.两片 C.很多片。
(在正确的答案上面画“√”。
)
2、这段话中描)写的动物有:、。
写它们的动作的词语、、、。
3、这段话中“它”指,小鱼和蚂蚁分别把它当作和。
4、用“————”画出比喻(yù)句
九、看图写话。
图上的动物是谁?它真是医生吗?它
要去给谁“看病”?结果怎样?结合图意,
编个有意思的故事。
