第九章 组合变形
材料力学09组合变形_1斜弯曲_土

解: 梁为斜弯曲 作弯矩图 可见危险截面位于固定 端处,其上铅垂弯矩、 水平弯矩分别为
Mz 1.5 kN m
M y 2 kN m
1.5 kN m Mz
2 kN m
My
x x
9
抗弯截面系数
Wz
bh2 6
46875 mm3
Wy
hb2 6
31250
mm3
1.5 kN m
第九章 组合变形
第一节 引 言
主要任务: 解决组合变形杆件的强度问题 基本假设: 在线弹性、小变形条件下,假设组合变形中的每一
种基本变形彼此独立、互不影响。 基本方法: 叠加法,即将组合变形分解为几种基本变形,分别
计算每种基本变形的内力、应力;然后进行叠加, 确定构件的危险截面、危险点以及危险点的应力状 态;最终建立组合变形杆件的强度条件。
解: 大梁为斜弯曲 当小车行至梁跨度中点时,
梁的最大弯矩最大。
将 F 沿 y、z 主轴分解,有
Fy F cos 29 kN
Fz F sin 7.76 kN
作弯矩图, 可见跨中截面为危 x
险截面,其上铅垂弯矩、水平 M z
Mz
弯矩分别为 x
Mz Fy l / 4 29 kN m
max
M max Wz
Fl 4 43.3 MPa Wz
可见,载荷虽然只偏离了铅垂线 15°,但最大正应力却为原来的 3.5 倍。因此,当截面的 Wz 和 Wy 相差较大时,应尽量避免斜弯 曲。
8
[例2] 图示矩形截面梁,已知 l = 1m,b = 50 mm,h = 75 mm。试 求梁中最大正应力及其作用点位置。若截面改为直径 d = 65 mm 的 圆形,再求其最大正应力。
组合变形

32.2 MPa t
40.2 MPa c
※立柱不满足强度要求
例3:图示矩形截面钢杆,用应变片测得上下表面的 轴向正应变分别为a=1×10-3,b=0.4×10-3,材料的 弹性模量E=210GPa.(1)试绘制横截面上的正应力 分布图;(2)求拉力P及偏心距。 a P P a 25 b 5
S
F
M
a
C
y
1
F
1
Mz Wz
例1 工字梁两端简支,载 荷P=60KN ,若材料 的[σ]=160MPa,试选 择工字钢型号
解:1.分解载荷
Py P s in 2 0 .5 2 K N P Pz P c o s 5 6 .3 8 K N
弯曲(xoy平面) 弯曲(xoz平面)
5 6 .3 8 kN m
C
z
E
例5:短柱的形心为矩形,尺寸为bh,试确定截 面核心 若中性轴与AB边重合: z 中性轴在坐标轴的截距:
A
b B
D a h/6 h C
i
yP
2 z
2 z
ay
h 2
, az
ya y
IZ A
i
2 z
yP
,a z
bh
3
i
2 y
zP
2
12 2 bh 12 h
11.6
A
3
FN
M max WZ
0.2 0.3
FN A
(5.83 5.83) 11.66 MPa
350 10 0.2
2 3
8.75
350 50 6 0.2 0.3
最新9组合变形汇总

例9-5:图示Z形截面杆,在自由端作用一集中力F,该杆的变 形设有四种答案:
(A)平面弯曲变形; (B)斜弯曲变形; (C)弯扭组合变形; (D)压弯组合变形。
F
F
例9-6:具有切槽的正方形木杆,受力如 图。求:
(1)m-m截面上的最大拉应力σt 和最 大压应力σc;
(2)此σt是截面削弱前的σt值的几倍?
大小有关,而与外力的大小无关;②一般情况下,I y I z 中性轴不与外力作用平面垂直;③对于圆形、正方形和正
多边形,通过形心的轴都是形心主轴,Iy Iz,
此时梁不会发生斜弯曲。
〈四〉强度校核:
对矩形截面,可以直接断定截面的 LmaxYmax必发生在
' '' 具有相同符号的截面角点处。
max
y
zP z iy2
0
根据该方程式可知中性轴是不过形心的直线。
现令:应力零线N-N,它在y、z轴上的截距分别为 a y a z 分别将
ay,0 0, az 代入 k 表达式得:
ay
iZ 2 yP
aZ
iy2 zP
由ay、az就可把应力零线的位置确定下来,应力零线就是该 截面的中性轴。上式表明ay、az 均与yp 、 zp符号相反,所以中性 轴与偏心压力分别在坐标原点的两侧,以中性轴为界,一侧受
曲。
思考题
正方形,圆形,当外力作用线通过截面形心时,为平面弯曲还 是斜弯曲?
目录
§9-3 拉伸(压缩)与弯曲的组合变形
例1:一折杆由两根圆杆焊接而成,已知 圆杆直径d=100mm,试求圆杆的最大拉应力σt 和最大压应力 σc 。
解: X A 3 kN
YA 4 kN
任 意 横 截 面 x上 的 内 力 :
《材料力学组合变形》课件

拉伸与压缩组合变形的分析方法
01
02
03
弹性分析方法
基于弹性力学的基本原理 ,通过求解弹性方程来分 析杆件内部的应力和应变 分布。
塑性分析方法
在材料进入塑性阶段后, 采用塑性力学的基本理论 来分析杆件的承载能力和 变形行为。
材料力学在组合变形中的应用实例
01
02
03
04
桥梁工程
桥梁的受力分析、桥墩的稳定 性分析等。
建筑结构
高层建筑、大跨度结构的受力 分析、抗震设计等。
机械工程
机械零件的强度、刚度和稳定 性分析,如轴、轴承、齿轮等
。
航空航天
飞机和航天器的结构分析、材 料选择和制造工艺等。
材料力学在组合变形中的发展趋势
特点
剪切与扭转组合变形具有复杂性和多样性,其变形行为受到多种因素的影响,如 材料的性质、杆件的长度和截面尺寸、剪切和扭转的相对大小等。
剪切与扭转组合变形的分析方法
1 2 3
工程近似法
在分析剪切与扭转组合变形时,通常采用工程近 似法,通过简化模型和假设来计算杆件的应力和 变形。
有限元法
有限元法是一种数值分析方法,可以模拟杆件在 剪切与扭转组合变形中的真实行为,提供更精确 的结果。
弯曲组合变形的分析方法
叠加法
刚度矩阵法
叠加法是分析弯曲组合变形的基本方 法之一。该方法基于线性弹性力学理 论,认为各种基本变形的应力、应变 分量可以分别计算,然后按照线性叠 加原理得到最终的应力、应变分布。
刚度矩阵法是通过建立物体内任意一 点的应力、应变与外力之间的关系, 来求解复杂变形问题的一种方法。对 于弯曲组合变形,可以通过构建系统 的刚度矩阵来求解。
9.组合变形

2 y
2 z
设挠度 的方向与Y轴间的夹角 ,则:
z Iz tg tg y Iy
讨论:由上式可看出:要使得 必须:I z I y 即,只 有在 I z I y 的条件下,才是平面弯曲, 否则是斜弯 曲。
思考题
正方形,圆形,当外力作用线通过截面形心时,为平面弯曲还 是斜弯曲?
总目录
本章要点
(1)斜弯曲 (2)偏心压缩 (3)弯扭组合变形
重要概念
组合变形、斜弯曲、偏心压缩、弯扭组合
§9-1 概述
*工程中几种常见的组合变形:
斜弯曲 —————斜屋架上的檩条 拉弯组合 ————冻结管 偏心压缩 ————设有吊车的厂房柱子 弯扭组合变形——机床中靠齿轮传递的轴
由于组合变形是几种基本变形相互组合的结果, 因此,在进行组合变形下的强度和刚度计算时,只 需分别计算形成这种组合变形的几种基本变形下的 应力和变形,然后进行叠加即可得到组合变形下的 应力和变形。 计算组合变形强度问题的步骤如下:
可得中性轴的方程式为:
yP y z P z 1 2 2 0 iz iy
根据该方程式可知中性轴是不过形心的直线。
现令:应力零线N-N,它在y、z轴上的截距分别为 a y a z 分别将 a y ,0 0, az 代入 k 表达式得:
iZ 2 ay yP
aZ
2 1 2 2 1 2 2 3 3 1 2
将C式代入上式,简化整理后可得:
W 3
2
2 n
代入<a><b>式即可得:
1 W
M W 0.75Tn2
材料力学斜弯曲

y
中性轴
Fl
另一条类似。
四、挠度的方向
z F wy
l
x
y
w φ β wz
F
Fl 3 sin 自由端 wy 3EI z
方向
Fl 3 cos wz 3EI y
t an
wy wz
Iy Iz
t an
结论
挠度
中性轴
t an
一、概念
z
Fy
φ
F
Fz
外力:作用线不与形心主 惯性轴重合; 内力: 弯矩矢不与形心主 惯性轴重合(可分解成两 y 个形心主惯性轴方向的弯 矩); 变形:挠曲线不与载荷线 共面。
斜弯曲
F1
平面弯曲
F2
二、正应力强度条件
例:分析图示斜弯曲变形
z
z
y φ
y
F
A
F φ
B
l
z
y
1.分类:
平面弯曲(绕 y 轴) + 平面弯曲(绕 z 轴)
图中力F是否使梁产生平面弯曲?
F
z y
F
F
z z y
y
弯曲中心的意义
非对称截面梁平面弯曲的条件: 1.外力平行于形心主惯性平面 保证 Iyz=0
(推导弯曲正应力时要求满足Iyz=0)
F
M
2.外力作用线通过弯曲中心 保证 不扭转
图中力F使梁产生平面弯曲, 同时还产生扭转。
A
y
C
z
§9.3 拉(压)弯组合
A
D1
t max
D2
M y max M z max t max 单向应力状态 W c max Wz y
第九章 组合变形
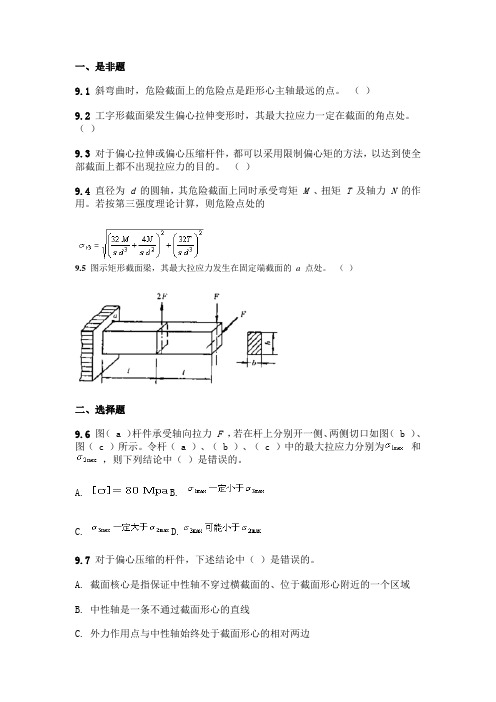
一、是非题9.1 斜弯曲时,危险截面上的危险点是距形心主轴最远的点。
()9.2 工字形截面梁发生偏心拉伸变形时,其最大拉应力一定在截面的角点处。
()9.3 对于偏心拉伸或偏心压缩杆件,都可以采用限制偏心矩的方法,以达到使全部截面上都不出现拉应力的目的。
()9.4 直径为d 的圆轴,其危险截面上同时承受弯矩M 、扭矩T 及轴力N 的作用。
若按第三强度理论计算,则危险点处的9.5 图示矩形截面梁,其最大拉应力发生在固定端截面的a 点处。
()二、选择题9.6 图( a )杆件承受轴向拉力F ,若在杆上分别开一侧、两侧切口如图( b )、图( c )所示。
令杆( a )、( b )、( c )中的最大拉应力分别为和,则下列结论中()是错误的。
A. B.C. D.9.7 对于偏心压缩的杆件,下述结论中()是错误的。
A. 截面核心是指保证中性轴不穿过横截面的、位于截面形心附近的一个区域B. 中性轴是一条不通过截面形心的直线C. 外力作用点与中性轴始终处于截面形心的相对两边D. 截面核心与截面的形状、尺寸及载荷大小有关三. 计算题9.8材料为灰铸铁HT 15-33的压力机框架如图所示。
许用拉应力为,许用压应力为,试校核该框架立柱的强度。
9.9图示皮带轮传动轴,传递功率N =7kW ,转速n =200 r/min 。
皮带轮重量Q =1.8 kN 。
左端齿轮上啮合力与齿轮节圆切线的夹角(压力角)为。
轴的材料为A5钢,其许用应力。
试分别在忽略和考虑皮带轮重量的两种情况下,按第三强度理论估算轴的直径。
答案9.1 × 9.2 √ 9.3 × 9.4 √ 9.5 √ 9.6 C 9.7 D9.8解:9.9解:。
材料力学 第九章组合变形杆件强度计算

cos sin y0 + z0 = 0 Iz Iy
—— 中性轴方程(过截面形心的直线) 中性轴方程(过截面形心的直线)
b 中性轴 α
cos sin y0 + z0 = 0 Iz Iy
z
d
设中性轴与水平对称轴 z 的夹角为 ,则: 的夹角为α,
y0 tan α = z0
I z sin I y cos
=9.57mm
§9-3 拉伸(压缩)与弯曲的组合 拉伸(压缩)
当杆受轴向力F和横向力 共同作用时 当杆受轴向力 和横向力q共同作用时,杆将产 和横向力 共同作用时, 生拉伸(压缩)和弯曲组合变形. 生拉伸(压缩)和弯曲组合变形. q F
A B
F
对于弯曲刚度EI较大的杆, 对于弯曲刚度 较大的杆,由横向力引起的弯 较大的杆 曲变形与截面尺寸相比很小,因此, 曲变形与截面尺寸相比很小,因此,由轴向力在弯 曲变形上引起的附加弯矩可以忽略不计. 曲变形上引起的附加弯矩可以忽略不计. 附加弯矩可以忽略不计 q F F A B w x FA q FS M=FAx-qx2/2-Fw F A M w FN x 附加弯矩 FA
第九章 组合变形杆件 的强度计算
作者:黄孟生
§ 9 -1 概 述
构件发生两种或两种以上基本变形的组合, 构件发生两种或两种以上基本变形的组合,若几种变 形所对应的应力(或变形)属于同一数量级. 形所对应的应力(或变形)属于同一数量级.则构 件的变形称为组合变形. 组合变形.
组合变形的实例: 组合变形的实例
F
y
=
Iz = tan Iy
斜弯曲时, 注:① 当 Iy≠Iz 时,则α≠ .斜弯曲时,中性轴与外力作用
线不垂直. 线不垂直. ② 当Iy = Iz 时,则α= 只发生平面弯曲,而不发生斜 .只发生平面弯曲, 弯曲. 弯曲.
组合变形

MT WT
在杆的根部a处取一单元体分析
y 0, x B , x T
计算主应力
1 B B 2 2 ( ) T 2 3 2
2 0
第三、第四强度理论
r 3 4
2 B 2 T
2 2 r4 B 3 T
即最大安全载荷为 790N。
r3
M 2 T2 W
(0.2Q ) 2 (0.18Q ) 2 6 80 10 0.033 32 Q 790N
例8-5 某齿轮轴,n=265r/min、NK=10kW、D1=396mm, D2=168mm, =20o , d=50mm,[]= 50MPa。校核轴的强度。
C max
N M max c A Wz
例8-1 悬臂吊车,横梁由 25 a 号工字钢制成,l=4m,电葫芦重 Q1=4kN,起重量Q2=20kN, =30º , []=100MPa,试校核强度。
(1)外力计算
取横梁AB为研究对象,受力如 图b所示。
梁 上载荷为 P =Q1+Q2 = 24kN, 斜杆的拉力S 可分解为XB和YB
f
f f
2 y
2 z
如悬臂梁自由端挠度等于P的分量 平面内挠度的几何叠加。
py , pz
在各自弯曲
pl 3 fy cos 3 EI z 3 EI z pz l 3 pl 3 fz sin 3 EI y 3 EI y
pyl 3
故自由端的总挠度:
f
f f
2 y
2 z
总挠度 f 的方向线与y轴之间的夹角 可由下式求得
如图b所示。
(2)作内力图
建筑力学与结构——组合变形

一、应力 将力F沿y轴和z轴分解为两个分量Fy和Fz,得:
这两个分量分别引起沿铅垂面和水平面的平面弯曲。求距 自由端为x的截面上任意点K的正应力,该点的坐标为z和y。
课题2 斜弯曲变形的应力和强度计算
在前面曾经指出,对于横截面具有对称轴的梁,当外力作用在纵向 对称平面内时,梁的轴线在变形后将变成为一条位于纵向对称面内的平 面曲线。这种变形形式称为平面弯曲。
但当外力不作用在纵向对称平面内时,如下图所示。实验及理论研 究表明,此时梁的挠曲线并不在梁的纵向对称平面内,即不属于平面弯 曲,这种弯曲称为斜弯曲。
σmax发生在D1点,最小正应力σmin发生在D2点,且ymax = |ymin|, Zmax=|Zmin|,σmax=|σmin| ,因此
若材料的抗拉与抗压强度相同,其强度条件就可以写为:
对于不易确定危险点的截面,例如边界没有棱角而呈 弧线的截面,如下图左所示,则需要研究应力的分布规律, 确定中性轴位置。为此,将斜弯曲正应力表达式改写为
在作强度计算时,须先确定危险截面,然后在危险截面上确定危险 点。对斜弯曲来说,与平面弯曲一样,通常也是由最大正应力控制。所 以对如上图右所示的悬臂梁来说,危险截面显然在固定端,因为该处弯 矩Mz和My的绝对值达到最大。至于要确定该截面上的危险点的位置,则 对于工程中常用的具有凸角而又有两条对称轴的截面,如矩形、工字形 等,根据对变形的判断,可知最大正应力
由上式可见,中性轴是一条通过横截面形心的直线。设它 与z轴的夹角为α, 如下图所示,则有
组合变形

1 b
断裂破坏仅与最大正应力有关。适用于脆性材料的二向或
2最大正应变理论(第二强度理论) :
由于
1 1 [ 1 ( 2 3 )] E
1 b
当最大正应变等于强度极限对应的正应变时,断裂破坏。
b
b
E
1 ( 2 3 ) b
m
x
m m
Pz
z Py y
m
z
P
P
y
Py P sin Pz P cos
矩形截面梁,作用集中力P与Z轴成角,确定m—m截面的应力
m
m
Mz
z
Mz My
m
z
My
m
M
y
y
Py P sin Pz P cos M yz Iy
Mzy Iz
M y Pz x Px cos M cos M z Py x Px sin M sin
z y cos sin 0 Iy Iz
过形心的斜直线
最大、最小正应力,a、b两点。
斜弯曲时中性轴斜率与弯矩作用面的关系
z y cos sin 0 中性轴方程 Iy Iz z Iy tan tan y Iz
z
y
中性轴
当 I y I z 时, 说明载荷作用面与中性层不垂直 当 Iy Iz 时
1 3 2
对应第四强度理论
1 1 2 2 2 3 2 3 1 2 3 2
复杂应力状态危险点单元体的强度条件:
ri [ ]
ri
组合变形

第九章 组合变形授课学时:8学时主要内容:拉弯、斜弯曲和弯扭组合变形的强度和变形的校核和计算。
§9–1 概 述1.定义在复杂外载荷作用下,构件的变形会包含几种简单变形,当几种变形所对应的应力属同一量级时,不能忽略之,这类构件的变形称为组合变形。
2.组合变形形式两个平面弯曲的组合;拉伸或压缩与弯曲的组合;扭转与弯曲。
3.组合变形的研究方法 —— 叠加原理 对于线弹性状态的构件,将其组合变形分解为基本变形,考虑在每一种基本变形下的应力和变形,然后进行叠加。
4.解题步骤外力分析:外力向形心简化并沿主惯性轴分解内力分析:求出每个外力分量对应的内力方程和内力图,确定危险面。
应力分析:画危险面应力分布图,叠加,建立危险点的强度条件。
§9–2拉(压)弯组合例 起重机的最大吊重kN P 12=,[]2/100m kN =σ。
试为横梁AB 选择适用的工字钢。
解:(1)受力分析由0=∑AM得kN T y 18=,kN T T y x 245.12==(2)作AB 的弯矩图和剪力图,确定C(3)确定工字钢型号按弯曲强度确定工字钢的抗弯截面系数[]363120101001012cm MW =⨯⨯=≥σ查表取3141cm W =的16号工字钢,其横截面积为21.26cm 。
在C 左侧的下边缘压应力最大,需要进行校核。
+=MPaMPa W M A N 1003.94101411012104.2610246343max max <=⨯⨯+⨯⨯=+=--σ固所选工字钢为合适。
§9–3斜弯曲1.斜弯曲概念:梁的横向力不与横截面对称轴或形心主惯性轴重合,这时杆件将在形心主惯性平面内发生弯曲,变形后的轴线与外力不在同一纵向平面内,2.解题方法1)分解:将外载沿横截面的两个形心主轴分解,于是得到两个正交的平面弯曲。
2)叠加:对两个平面弯曲进行研究;然后将计算结果叠加起来。
例 矩形截面悬臂梁,求根部的最大应力和梁端部的位移。
009-第九章-强度理论与组合变形

F
F=100kN
Z
0.32m
0.32m
Fs
100kN
X
100kN M
32kNm
X
第11页,共85页。
7K 100
88.6 11.4
I z 2370 104 mm4
Wz 237 103 mm3
Iz
/
S
z
max
17.2cm
解:1、画内力图
11
2、最大正应力校核
max
3、最大切应力理论(第三强度理论)
强度条件: 1 3
4、最大形状改变比能理论: (第四强度理论;均方根理论;歪形能理论;畸形能理论)
强度条件:
1
2
(1 2 )2
( 2
3 )2
( 3
1)2
22
第22页,共85页。
三、结论: xd ( ; r )
r1 1 r 2 1 ( 2 3 )
9
第9页,共85页。
强度理论的应用——
x
max
min
x
2
( x )2
2
xy 2
1
3
xy
r3 x2 4 xy2
r4 x2 3 xy2
使用条件:屈服破坏, 2 0 。
10
第10页,共85页。
例:如图所示工字型截面梁,已知〔σ〕=180MPa〔τ 〕 =100MPa
29
第29页,共85页。
§8—5 斜弯曲
一、斜弯曲的概念
梁上的外力都垂直于轴线,外力的作用面不在梁的纵向对称面 内,变形后梁的轴线不在外力的作用平面内由直线变为曲线(梁上的 外力都垂直于轴线且过弯曲中心,但不与形心主轴重合或平行)。
09组合变形_2弯拉弯压_少课时_机

危险点的最大拉应力
m
t max
M
Wz
FN A
A
l
m
t max
cmax
B
F
t max
M
Wz
FN A
5. 根据危险点的应力状态,建立 强度条件
危险点为单向拉伸应力状态,故得 弯曲与拉伸组合变形的强度条件
m
t max
cmax m
A
l
tmax
M Wz
FN A
≤
t
m
t max
式中, M、FN 分别为危险截面上的弯矩、轴力。
强度计算
Fy
Fx
P
对于塑性材料,弯压组合变形的强度条件为
max
M Wz
FN A
≤[ ]
在确定工字钢型号时,可先不考虑轴力的影响,得
W
M
≥
10 103 N m 0.1103 m3 100 cm3
z [ ] 100 106 Pa
W ≥ 100 cm3 z
查型钢表,初选 No 14 工字钢,其
Wz 102 cm3
A 21.5 cm2
再代入强度条件进行校核
M
max Wz
FN A
10103 N 102 106
m m3
26103 N 21.5104 m2
110106 Pa 110 MPa [ ] 100 MPa
强度条件不符合要求
重选 No 16 工字钢,其
Wz 141 cm3
B
F
二、弯曲与压缩组合
类似可得,弯曲与压缩组合变形 的强度条件
对于塑性材料:
max
M Wz
FN A
≤
对于脆性材料:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
FN
69.28kN x
M
(c) a
B
x
30kN m
第九章 组合变形 【例9-2】如图 9-4a所示的钻床,其圆形截面立柱为铸铁所制, 许用拉应力=35MPa,受到的工作压力P=20kN,试确定钻床立 柱的直径。 解:(1)内力分析,求得
400 d P P
FN P 20kN M 0.4 P 8kN m
第九章 组合变形 【例 9-1】如图 9-3 所示的钢制托架,横梁 AD 为圆形截面梁直径 d=200mm,在D端受到作用力F=30kN,a=3m,b=1m, 梁材料的许 用应力[σ]=160MPa,不计梁的自重,试校核梁AD强度。 解:(1)梁AD受力简图如图所示, 列平衡方程
a D C F B
R
第九章 组合变形 危险点处于单向应力状态。危险 点的最终应力为两种基本变形产 生的正应力的代数和。
a A
O
Fx
x
b
Fy
l y
F
max N M
N
Fcos A
M
Flsin Wz
FN
F cos
x M
(b) a
B
x
min N M
Flsinα
(c)
第九章 组合变形
9.2 扭转与弯曲组合变形
一、弯扭组合强度计算
F
由力的平移定理,将 力 F 向杆 AB 的右端截 面形心B平移,得到 一作用于B处的横向 力和作用于横截面的 力偶。
y d B A z l a C x
F A B T
Fa
第九章 组合变形 作杆AB的扭矩图和弯矩图,可判断出A截面为杆的危险截 面。 T Fa, M Fl
M
A
30
0
A
(F ) 0
3FC sin30 0 4 F 0
解得 FC 80kN
将 Fc 分解成轴向力和垂直力, 并作梁AD的轴力图和弯矩图
A
F Ax 30 0
C
D
F Ay
FC
F
第九章 组合变形
a
由内力图可知梁的危险点在C 截面下 边缘点
A
30
0
D C F
FN M max max A W 4 FN 32M max 2 d d 3 4 69.28 103 32 30 103 2 π 0.2 π 0.23 40.40MPa
M 2 T 2 r3 Wz
M 2 0.75T 2 r4 Wz
第九章 组合变形 【例 9-3】如图 9-6a 所示,钢制传动轴传递的功率 P = 5kW ,转速 n=300 r/min ,皮带轮 A 的直径为 D=200mm ,皮带张力 FT=2Ft ,轴 材料的许用应力 []=80MPa ,传动轴的直径为 50mm ,试按第三强 度理论校核轴的强度。
32 M
选取立柱直径d=135mm,综合轴向拉力和弯矩对立柱进行校核:
FN M 4 FN 32M 所 以 d=135mm 能 够 满 足 t max 钻床立柱的强度要求。 A W d 2 d 3 4 20 103 32 8 103 34.52MP a t 2 3 π 0.135 π 0.135
第九章 组合变形
对于抗拉和抗压强度不相等的材料,要分别按 最大拉应力和最大压应力进行强度计算,其强 度条件为:
FN M max t max t A Wz FN M max c max c A Wz
(9-1)
对于抗拉和抗压强度相同的材料,则按截面最 大应力进行强度计算即可。
基于CAXA和VRP的船用喷油泵的拆装仿真设计
第九章 组合变形
第九章 组合变形
组合变形:弯曲、扭转、剪切与轴向拉压,是杆件变形的 四种基本形式,许多杆件的变形或者属于变形的基本形式 ,或者属于两种或两种以上的基本变形形式的组合,即所 谓组合变形。
第九章 组合变形
组合变形的应力计算方法:叠加原理。 条件:材料小变形且服从胡克定律的条件。
F A B
A
Fa
K1
从图可知,上下边 缘点为危险点。
K2
T x
M
Fa
K1
x
A
K2
Fl
因为危险点,存在最大扭转切应力和 弯曲正应力 T M σ Wp Wz
K1
对危险点取单元体,可发现其处于平面应力状态,因此按 照强度理论来建立强度条件。 对于塑性材料制成的圆轴,可采用第三强度理论和第四强 度理论。
第三强度理论校核:
2 2 M 2 T 2 32 477.45 159.15 41MPa σ 3 Wz π 0.05
σ r3
所以该传动轴满足强度条件。
因此该立柱产生轴向拉 伸和弯曲的组合变形。
M
FN
400
P
第九章 组合变形 (2)强度计算 先考虑弯曲应力来选取立柱直径:
400
t max
d 3
M 32M t 3 W d
3 32 8 10 3 132.5mm 6 π 35 10
M
P
FN
t
第九章 组合变形
二、偏心拉伸(压缩)
e
F
F M y
e ——偏心距
若偏心力F作用点在杆的对称轴上——
FN F M Fe
t max
c max
FN M t A Wz
FN M c A Wz
第九章 组合变形
F F 二、偏心拉伸(压缩) e M y z
Me
F
第九章 组合变形 解得:
T x
2M e 2 159.15 Ft 1591.5N 3 D 200 10 F FT Ft 3Ft 4774.5N
159.15N m
M
x
477.45N m
作轴的扭矩图和弯矩图,截面B有最大扭矩和最大弯矩。
Tmax 159.15kN m, M max 477.45kN m
ey
F
ez
Mz
F
My
y z
e ——偏心距
若偏心力F作用点不在杆的任 一对称轴上,需将弯距分解 以截面对称轴为惯性轴的两 个弯矩: FN M y M z t max t A Wy Wz
c max FN M y M z c A W y Wz
解:(1)受力分析,将皮带轮上 的力向轴线简化,得到轴的计算简 图如图所示。轴所受的扭力偶矩为 P M e 9549 n 5 9549 159.15N m 300 由平衡方程 D D FT Ft Ft M e 2 2
D
C
B
A
Me
200
Ft
100
FT
Me
杆件在几个载荷共同作用下产生的应力和变形, 等同于 每个载荷单独作用 下产生的应力和变形的 总和 。根据叠加后的应力,选择合适的强度条件 进行强度计算。
第九章 组合变形
9.1 轴向拉(压)和弯曲组合变形的强度计算
一、弯拉(压)组合 如果作用在杆件的载荷除了轴向拉(压)力,还有垂直于 线的横向力,杆将产生轴向拉(压)与弯曲的组合变形 。或是外力作用线虽然平行于杆的轴线,但不通过截面形 心,也是发生弯曲与轴向拉(压)的组合,称为弯拉(压 )组合。 P
