中考数学压轴题解题策略3梯形的存在性问题解题策略
中考数学压轴题解题方法铅锤法等

中考数学压轴题解题方法铅锤法等全文共2篇示例,供读者参考一、学会运用数形结合思想数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系,寻求代数问题的解决方法(以形助数),或利用数量关系来研究几何图形的性质,解决几何问题(以数助形)的一种数学思想。
数形结合思想使数量关系和几何图形巧妙地结合起来,使问题得以解决。
纵观近几年全国各地的中考压轴题,绝大部分都是与平面直角坐标系有关。
其特点是通过建立点与数即坐标之间的对应关系,一方面可用代数方法研究几何图形的性质,另一方面又可借助几何直观,得到某些代数问题的解答。
二、学会运用函数与方程思想从分析问题的数量关系入手,适当设定未知数,把所研究的数学问题中已知量和未知量之间的数量关系,转化为方程或方程组的数学模型,从而使问题得到解决的思维方法,这就是方程思想。
用方程思想解题的关键是利用已知条件或公式、定理中的已知结论构造方程(组)。
这种思想在代数、几何及生活实际中有着广泛的应用。
直线与抛物线是初中数学中的两类重要函数,即一次函数与二次函数所表示的图形。
因此,无论是求其解析式还是研究其性质,都离不开函数与方程的思想。
例如函数解析式的确定,往往需要根据已知条件列方程或方程组并解之而得。
三、学会运用分类讨论的思想分类讨论思想可用来检测学生思维的准确性与严密性,常常通过条件的多变性或结论的不确定性来进行考察。
有些问题,如果不注意对各种情况分类讨论,就有可能造成错解或漏解,纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
在解答某些数学问题时,有时会遇到多种情况,需要对各种情况加以分类,并逐类求解,然后综合得解,这就是分类讨论法。
分类讨论是一种逻辑方法,是一种重要的数学思想,同时也是一种重要的解题策略,它体现了化整为零、积零为整的思想与归类整理的方法。
分类的原则:(1)分类中的每一部分是相互独立的;(2)一次分类按一个标准;(3)分类讨论应逐级进行.正确的分类必须是周全的,既不重复、也不遗漏。
中考数学压轴题解题技巧方法

中考数学压轴题解题技巧方法压轴题这类题目一般分数多,难度大,考验综合能力强,在考试中是能够拉开成绩的题目,也是很多同学重点钻研项目。
下面是为大家整理的关于中考数学压轴题解题技巧,希望对您有所帮助!中考数学压轴题经典之作解法中考数学压轴题经典解法一:学会大体上把复杂图形拆解变成一些基本图形与几何相关的压轴题一直是中考热门考查对象,此类问题所给出的图形都较为复杂,甚至需要添加一些辅助线才能顺利解决问题。
中考数学压轴题脍炙人口解法二:不要忘了十分相似这个活宝压轴题具体会考什么?没有进入考场看到习题试卷那一刻,谁都不知道,加上压轴题牵涉到的涉入知识点较多。
如果我们刻意急著靠猜题、押题等这种方式去应付压轴题的学习,很可能会让考生输的很惨。
况且面对压轴题就毫无办法了吗?不要去猜题押题,但我们可以去研究题型,发现知识点和解题方法之间辨认出的联系,如相似就是一个极其热门的考点。
中考数学压轴题算术经典解法三:解决动态问题,要学会动中找静动态问题一直是中考数学热点,也是化学分析压轴题最喜欢定量分析题型之一。
解决此类问题,一定要认真观察点阵在运动变化过程中,图形的位置、大小、方向怎么变?往哪变?更要发现什么量是没变,学会动中找静。
中考数学压轴题实操1、基本知识不丢半分在不断加强中考数学的备考中强化知识网络的梳理,并熟练掌握中考考纲要求的知识点。
“首先要梳理知识网络,思路清晰善用。
其次要掌握数学考纲,对考试心中有谱。
掌握今年中考数学的考纲,用考纲来统领知识初稿,掌握好必要的基础知识和过好基本的解题技巧,根据考纲和自己的实际情况来侧重复习。
2、运用数形结合价值观中考数学压轴题解题技巧之一就是数形结合思想,是指从几何直观的角度,利用几何图形的几何体性质研究数量关系,寻求李群问题的解决方法,或利用数量关系来研究几何图形的性质,解决几何问题的一种数学思想。
纵观近几年我市各地的中考压轴题,绝大部分都是与平面直角坐标系有关的,其特点是通过建立点与数即坐标间的对应关系,一方面可用代数方法研究几何图形的,另一方面又可借助几何准确,得到某些代数问题的解答。
(完整版)梯形存在性问题

(完整版)梯形存在性问题梯形是一种四边形,其中有两边是平行的。
然而,梯形的存在性问题引起了人们的关注。
本文旨在探讨梯形存在性问题,并提供解答。
梯形的定义首先,让我们回顾一下梯形的定义。
根据几何学的基本原理,梯形是一种四边形,其中有两边是平行的。
这两条平行边被称为梯形的底边和顶边。
其他两条非平行边被称为梯形的腰。
梯形的内角之和等于360度。
梯形存在性问题的关键是确定一个四边形是否满足这个定义。
梯形存在性问题的讨论梯形存在性问题是一个有趣而复杂的讨论话题。
在研究中,人们提出了不同的观点和证明,以探讨梯形的存在性。
一种常见的观点是,无法通过给定的四边形的边长和角度来判断该四边形是否为梯形。
因为给定的边长和角度可能存在多种排列方式,能够形成不同的四边形,有的属于梯形,而有的则不是。
另一种观点认为,如果能够找到一种排列方式,使得四边形的两条边平行,并且满足其他梯形的定义条件,那么这个四边形就是梯形。
但是,这种观点也存在争议,因为存在无法找到这样一种排列方式的情况。
解答鉴于梯形存在性问题的复杂性和争议性,目前还没有确定的解答。
不同的数学家和几何学家持有不同的观点和证明。
然而,作为学术界的一员,我们应该持开放态度,并尊重不同的观点和研究成果。
我们可以通过进一步研究和讨论,为解决梯形存在性问题做出更多的贡献。
总结梯形存在性问题是一个复杂而有趣的讨论话题。
在探讨这个问题时,我们需要了解梯形的定义,并认识到不同的观点和证明。
尽管目前还没有确定的解答,但我们可以通过持开放态度和进一步研究,为解决梯形存在性问题做出贡献。
注:本文所述观点仅代表个人理解,不作为法律或学术证据。
中考数学压轴题函数梯形问题精选解析

2013中考数学压轴题函数梯形问题精选解析(一)例1已知平面直角坐标系xOy中,抛物线y=ax2-(a+1)x与直线y=kx的一个公共点为A(4,8).(1)求此抛物线和直线的解析式;(2)若点P在线段OA上,过点P作y轴的平行线交(1)中抛物线于点Q,求线段PQ 长度的最大值;(3)记(1)中抛物线的顶点为M,点N在此抛物线上,若四边形AOMN恰好是梯形,求点N的坐标及梯形AOMN的面积.备用图解析(1)抛物线的解析式为y=x2-2x,直线的解析式为y=2x.(2)如图1,当P为OA的中点时,PQ的长度取得最大值为4.(3)如图2,如果四边形AOMN是梯形,那么点N的坐标为(3,3),梯形AOMN的面积为9.图1 图2例 2已知二次函数的图象经过A(2,0)、C(0,12) 两点,且对称轴为直线x=4,设顶点为点P,与x轴的另一交点为点B.(1)求二次函数的解析式及顶点P的坐标;(2)如图1,在直线 y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由;(3)如图2,点M是线段OP上的一个动点(O、P两点除外),以每秒2个单位长度的速度由点P向点O 运动,过点M作直线MN//x轴,交PB于点N.将△PMN沿直线MN对折,得到△P 1MN . 在动点M 的运动过程中,设△P 1MN 与梯形OMNB 的重叠部分的面积为S ,运动时间为t 秒,求S 关于t 的函数关系式.图1 图2解析(1)设抛物线的解析式为2(4)y a x k =-+,代入A (2,0)、C (0,12) 两点,得40,1612.a k a k +=⎧⎨+=⎩ 解得1,4.a k =⎧⎨=-⎩ 所以二次函数的解析式为22(4)4812y x x x =--=-+,顶点P 的坐标为(4,-4).(2)由2812(2)(6)y x x x x =-+=--,知点B 的坐标为(6,0).假设在等腰梯形OPBD ,那么DP =OB =6.设点D 的坐标为(x ,2x ). 由两点间的距离公式,得22(4)(24)36x x -++=.解得25x =或x =-2. 如图3,当x =-2时,四边形ODPB 是平行四边形.所以,当点D 的坐标为(52,54)时,四边形OPBD 为等腰梯形.图3 图4 图5(3)设△PMN 与△POB 的高分别为PH 、PG .在Rt △PMH 中,PM =,PH MH t ==.所以'24P G t =-.在Rt △PNH 中,PH t =,1122NH PH t ==.所以32MN t =. ① 如图4,当0<t ≤2时,重叠部分的面积等于△PMN 的面积.此时2133224S t t t =⨯⋅=. ②如图5,当2<t <4时,重叠部分是梯形,面积等于△PMN 的面积减去△P ′DC 的面积.由于2''P DC PMN S P G S PH ⎛⎫= ⎪⎝⎭△△,所以222'2433(24)44P DC t S t t t -⎛⎫=⨯=- ⎪⎝⎭△. 此时222339(24)1212444S t t t t =--=-+-.考点伸展第(2)题最好的解题策略就是拿起尺、规画图:方法一,按照对角线相等画圆.以P 为圆心,OB 长为半径画圆,与直线y =2x 有两个交点,一个是等腰梯形的顶点,一个是平行四边形的顶点.方法二,按照对边相等画圆.以B 为圆心,OP 长为半径画圆,与直线y =2x 有两个交点,一个是等腰梯形的顶点,一个是平行四边形的顶点.。
中考数学复习指导:中考数学梯形存在性问题压轴题解析
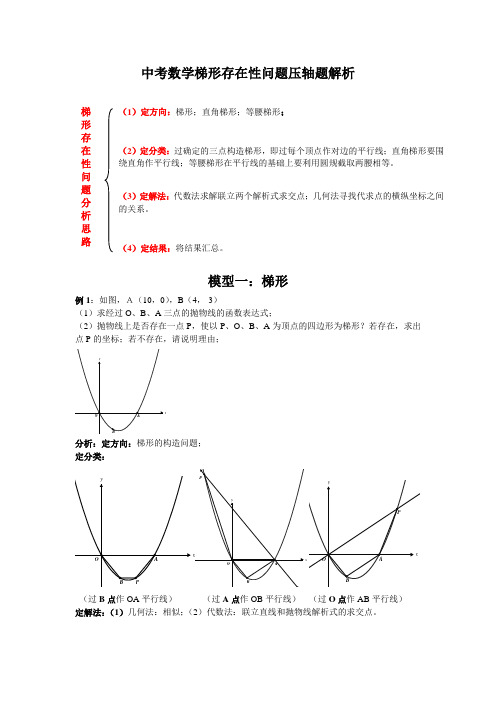
中考数学梯形存在性问题压轴题解析模型一:梯形例1:如图,A(10,0),B (4,-3)(1)求经过O 、B 、A 三点的抛物线的函数表达式;(2)抛物线上是否存在一点P ,使以P 、O 、B 、A 为顶点的四边形为梯形?若存在,求出梯形存在性问题分析思路定结果:三种情况汇总; 解法1: (1)x x y 45812-=情形一:B P ∥OA;四边形OBPA 为梯形。
B 、P 关于对称轴对称得:P (6,-3) 情形二:B A ∥OP;四边形OBAP 为梯形。
易证:△POC ∽△BADOC ADPC BD = OCPC 63=;PC OC 2= 则设P (2a ,a )a a a 2454812⋅-⋅=7),(021==a a 舍去P (14,7)情形三:PA ∥OB;四边形OBAP 为梯形。
易证:△PA C ∽△BODAC ODPC BD = AC PC 43=;PC AC 34= 则设P (b 34,b )3445)34(812b b b ⋅-⋅=12),(021==b b 舍去P (-6,12)综上所述:P (6,-3)、(14,7)、(-6,12解法2:情形三:PA ∥OB;四边形OBAP 为梯形。
直线OB 的解析式:x y 43-= 所以设PA 解析式:b x y +-=43直线PA 经过A (10,0)21543+-=x y⎪⎪⎩⎪⎪⎨⎧+-=-=2154345812x y x x y ⎩⎨⎧=-=126y x )(102舍去=x P (-6,12)练习1:已知),2(),,1(n B m A -是反比例函数xy 32=图象上的两个点. (1)求A 点和B 点坐标;(2)若点(10)C -,,则在反比例函数ky x=图象上是否存在点D ,使得以A B C D ,,,四点为顶点的四边形为梯形?若存在,求出点D 的坐标;若不存在,请说明理由.分析:(过A 点作BC 的平行线:图1) (过C 点作AB 的平行线:图2、图3)答案:6D ⎛ ⎝⎭或(1D或(2D -. 点睛:为什么不过B 点作AC 的平行线呢?因为这条平行线与双曲线没有交点。
中考数学压轴题预测,压轴题解题策略,解题技巧,专项训练完整版

最新中考数学压轴题展望,压轴题解题策略,解题技巧,专项训练数学综压轴题是为观察考生综合运用知识的能力而设计的,集中表现知识的综合性和方法的综合性,多半为函数型综合题和几何型综合题。
函数型综合题:是给定直角坐标系和几何图形,先求函数的分析式,再进行图形的研究,求点的坐标或研究图形的某些性质。
求已知函数的分析式主要方法是待定系数法,重点是求点的坐标,而求点的坐标基本方法是几何法(图形法)和代数法(分析法)。
几何型综合题:是先给定几何图形,依据已知条件进行计算,而后有动点(或动线段)运动,对应产生线段、面积等的变化,求对应的(未知)函数的分析式,求函数的自变量的取值范围,最后依据所求的函数关系进行研究研究。
一般有:在什么条件以下图形是等腰三角形、直角三角形,四边形是平行四边形、菱形、梯形等,或研究两个三角形知足什么条件相像等,或研究线段之间的数目、地点关系等,或研究面积之间知足必定关系时求x的值等,或直线(圆)与圆的相切时求自变量的值等。
求未知函数分析式的重点是列出包括自变量和因变量之间的等量关系(即列出含有x、y的方程),变形写成y=f(x)的形式。
找等量关系的门路在初中主要有益用勾股定理、平行线截得比率线段、三角形相像、面积相等方法。
求函数的自变量的取值范围主假如找寻图形的特别地点(极端地点)和依据分析式求解。
而最后的研究问题变化多端,但少不了对图形的剖析和研究,用几何和代数的方法求出x的值。
解中考压轴题技术:中考压轴题大多是以坐标系为桥梁,运用数形联合思想,经过成立点与数即坐标之间的对应关系,一方面可用代数方法研究几何图形的性质,另一方面又可借助几何直观,获得某些代数问题的解答。
重点是掌握几种常用的数学思想方法。
一是运用函数与方程思想。
以直线或抛物线知识为载体,列(解)方程或方程组求其分析式、研究其性质。
二是运用分类议论的思想。
对问题的条件或结论的多变性进行观察和研究。
三是运用转变的数学的思想。
浅析中考数学压轴题的发展趋势及解题策略

图3科研浅析中考数学压轴题⑨发展趋势及解题策略O昆明市第三中学李加禄中考数学压轴题的知识覆盖面广、关系复杂、思路难觅、解法灵活,综合性强,既考查基础知识和基本技能,又考察数学思想方法和数学能力。
难度较大,是中考的夺分题。
因此,如何提高解综合题的能力是广大师生在应考复习中关注的一个现实问题。
一、从一道压轴题谈中考压轴题的发展趋势例1.(07年昆明市中考题)如图,在直角坐标系中,点A的坐标为(一2,0),连结OA,将线段O A绕原点0顺时针旋转1200,得到线段O B.(1)求点B的坐标;(2)求经过A、0、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点c,使A BO C的周长最/b?若存在,求出点c的坐标;若不存在,请说明理由;(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么A PA B是否有最大面积?若有,求出此时P点的坐标及A PA B的最大面积;若没有,请说明理由。
(注意:本题中的结果均保留根号)y●●●_.r j。
A O1工解:(略)分析:该题用到的知识点有:旋转的性质;勾股定理;列方程或方程组用待定系数法确定一次甬数或二次函数的解析式;利用对称性和二次函数求最值;面积的存在性问题等。
通过分析本题以及近年来全国各地的中考试题,可以发现数学压轴题呈现以下发展趋势:1.以坐标系为桥梁,运用数形结合思想。
通过建立点与数即坐标之间的对应关系,一方面应用代数法研究几何图形的性质,另一面借助几何直观,得到某些代数问题的解答。
2.以直线或抛物线知识为载体,运用函数与方程思想。
直线与抛物线是初中数学中的两类重要函数,即一次函数与二次函数所表示的图形。
因此,无论是求其解析式还是研究其性质,都离不开函数与方程的思想。
例如函数解析式的确定,往往需要根据已知条件列方程或方程组并解之而得。
3.利用条件或结论的开放性,运用分类讨论的思想。
开放题是中考题多样化和时代发展要求的产物。
单一的题型和测试目标限制了学生应用知识解决实际问题的能力,不利于激发学生的创造性。
中考数学梯形压轴题解决策略

中考数学梯形压轴题解决策略作者:谢激强来源:《读天下》2020年第24期摘;要:数学作为初中阶段的主要课程,直接决定学生中考整体质量,受到广大师生的青睐。
梯形压轴题作为数学试卷的重难点,也是令大部分学生头痛的所在。
文中结合中考数学梯形压轴题特点,探讨如何做好这类题型的解答,提高解题质量与效率。
关键词:中考数学;梯形压轴题;解题思路中考数学试题命制中梯形压轴题较为常见,通常会和几何图形、函数图像等内容结合起来,也有形式为动点的,全面考查学生综合运用能力。
这就造成部分学生遇到这类题目后束手无策,白白失去大量分数。
文中全面分析如何解决数学梯形压轴题。
一、中考数学梯形压轴题的分析(一)梯形压轴题特点中考数学压轴题不是简单考查独立知识点的掌握程度,也不是如何运用某种解题思想与方法,而是对学生数学综合能力素养的考查,涉及非常多的数学知识点,全面运用各类数学思想方法,因此中考數学梯形压轴题特点:考查基础知识与技能的掌握;数学知识灵活运用能力;数学思维能力;数学研究能力的考查。
中考数学试卷上压轴题分数较大,想要取得好的数学成绩,绝对不能忽略压轴题。
数学教师已经意识到这点,中考数学复习时有意无意的加大压轴题的训练力度,但受到传统教育思想影响,师生都习惯题海战术,造成复习效果不理想。
要想提高中考数学压轴题的复习质量,需要总结压轴题的特点,采取针对性的复制策略,提高数学梯形压轴题的解题效率。
(二)压轴题解题思路梯形或等腰梯形问题解决时,要按照相应顺序进行:首先做好分类,分析时利用题目给出的已知条件,根据题意情况进行分类;其次画图,将符合题意的情况画出相应的图;最后完成计算,解决每一个画出图形的单位问题,解题时明白每种情况的都是相互独立的。
如果题干中给出一个三角形,解题时要从图形上找到第四个点,与三角形共同围成梯形,这时通过三角形定点做出对边平行线,移动这条平行线就能得到它与三角形的交点,这些交点与三角形其他顶点共同构成梯形,结合同位角、内错角等列出相应的方程;如果要解决一个等腰三角形,解题思路由梯形转为等腰梯形,根据“等腰梯形两边相等”,利用代数法或几何法证明两边相等即可。
浅谈中考数学压轴题的发展趋势及解题策略

浅谈中考数学压轴题的发展趋势及解题策略1. 引言1.1 中考数学压轴题的重要性中考数学压轴题作为中考数学考试中的重要组成部分,承载着选拔优秀学生、检验学生数学综合能力的重要任务。
其重要性主要体现在以下几个方面:一、检验学生对知识的掌握程度。
中考数学压轴题通常涵盖了整个学期所学的知识点,要求学生在解题时能够综合运用知识,考察学生是否真正掌握了各个知识点。
二、考察学生的逻辑思维能力。
中考数学压轴题往往具有一定的难度和复杂性,要求学生能够运用逻辑推理和分析问题的能力来解题,从而培养学生的逻辑思维能力。
三、培养学生的解决问题的能力。
中考数学压轴题常常是一些较为综合性的问题,需要学生具备较强的解决问题的能力,包括分析问题、提出解决方案和合理推断的能力。
四、激励学生学习数学的兴趣。
通过解决中考数学压轴题,学生可以感受到数学的魅力和趣味,从而激发学习数学的兴趣,促使他们更加努力地钻研数学知识。
中考数学压轴题在中考数学考试中具有举足轻重的地位,对学生的学习和成长起着至关重要的作用。
在备考中,学生应当重视中考数学压轴题的练习和掌握,以确保在考试中取得理想的成绩。
1.2 中考数学压轴题的历史演变中考数学压轴题的历史演变源远流长,可以追溯到我国古代科举制度时期。
在科举考试中,对于数学能力的考察也是不可或缺的部分。
随着时间的推移,数学考题的形式和内容也在不断变化和发展。
从过去几十年的中考数学压轴题历年真题来看,最初的数学考题更加注重基础知识和题型的应用。
简单的计算题、几何题和代数题等都是考生必须掌握的内容。
随着教育教学理念的更新和数学教育的发展,中考数学压轴题的内容逐渐趋向于注重思维能力和综合运用能力的考察。
在解题时需要考生灵活应用所学知识,进行逻辑推理和综合分析,而不仅仅是死记硬背基础知识。
随着科技的发展和教育改革的深化,中考数学压轴题也逐渐倾向于注重学生的实际运用能力和创新思维。
涉及到实际问题的数学模型、数学证明题等成为中考数学压轴题中的重要内容。
中考数学存在性问题的解题策略

中考数学存在性问题的解题策略摘要:现今不仅是高考对考生很重要,更多的家长认为走进一所好的高中就有一只脚踏进了名牌大学的校门。
“存在性”问题是中考试题中最容易丢分的题型,本文简要分析中考数学存在性问题的解题策略。
关键词:存在性问题解题分析一、“存在性”问题“存在性”问题是指判断满足某种条件的某种事物是否存在的问题。
应对这种问题要求学生的知识覆盖面广,综合分析能力强,对整个知识的结构体系熟悉,解题的方法要灵活。
常见的解此类题的思路为:假设其存在→根据存在性推理论证→得出结论→是否与假设相符合→结论存在(看是否违背公理和定理),根据此思路具体做出判断,我们知道“存在性”问题的结论有两种可能,所以开放性强,我们需要假设存在后对其进行推理或者计算,所以对学生的基本能力要求较高,并且具备较强的探索性。
二、举例分析现在我们就以举例的方式来解析。
(2)首先分析其与x轴有两个交点,x1,x2的倒数和为2/3,根据这个可以得出一个式子。
那么我们知道此二次函数与x轴交点的横坐标就是一元二次方程的根。
那么此题就很容易得出答案了。
例2:已知x1、x2是一元二次方程ax²+bx+c=0(a≠0,c≠0)的两个实数根,且x1/x2=m/n(m≠0,n≠0)(1)试用m和n表示b²/ac的式子;(2)是否存在实数m和n,满足x1/x2=m/n,使b²/ac=6/5成立?若存在,求出m和n的值;若不存在,说明理由。
分析:这个题目存在两个可能性:即存在和不存在。
那么对于此类问题我们一般假设其存在(当然你也可以假设不存在,这样假设不好证明),然后根据已知的条件和有关的性质推理,求解;最后根据推理的过程得出结论。
若其与已知条件相符合,那么就说明假设存在,结论成立。
若地已知条件不相符合就说明结论不成立。
此题通过韦达定理得a、b、c、m、n的关系式,然后在假设已知的条件成立,写出关于m、n为根的一元二次方程。
梯形解题方法与技巧

梯形解题方法与技巧梯形是一种常见的几何形状,对于解题来说,掌握梯形的特性和解题方法是非常重要的。
以下是一些梯形解题的方法和技巧:梯形的定义和特性梯形是一个四边形,其中两边是平行线段,而另外两边则不平行。
梯形的特性包括:1. 梯形有两对对边分别平行。
2. 相邻两边的夹角总和为180度。
3. 梯形的对角线长度相等。
4. 梯形的高是连接两条平行边的线段的垂直距离。
计算梯形的面积梯形的面积可以用以下公式计算:$$ A = \frac{a+b}{2} \times h $$其中,$A$ 表示梯形的面积,$a$ 和 $b$ 分别表示上底和下底的长度,$h$ 表示梯形的高。
梯形解题的常见方法在解梯形相关问题时,可以使用以下方法:1. 计算面积:根据梯形的面积公式计算梯形的面积。
这是解决梯形问题的常用方法。
2. 寻找已知条件:在题目中寻找已知条件,如底边长度、高、面积等,然后利用这些已知条件解题。
3. 应用梯形的性质:利用梯形的特性解决问题,比如利用梯形的对角线相等的性质进行推导。
4. 利用相似三角形:当梯形的两条平行边和某条边平行时,可以利用相似三角形的性质解题。
示例问题以下是一些关于梯形的示例问题,用于演示解题方法:示例问题 1已知一个梯形的底边长度为8 cm,顶边长度为4 cm,高为6 cm,求梯形的面积。
解题思路:根据梯形的面积公式,代入已知的底边长度、顶边长度和高,计算得到梯形的面积:$$ A = \frac{8+4}{2} \times 6 = 36 \text{ cm}^2 $$因此,这个梯形的面积为36平方厘米。
示例问题 2已知一个梯形的顶边长度是底边长度的一半,梯形的高为10 cm,求梯形的面积。
解题思路:根据已知条件可得顶边长度为底边长度的一半,即 $b =\frac{a}{2}$。
代入梯形的面积公式,得到:$$ A = \frac{a+\frac{a}{2}}{2} \times 10 = \frac{3a}{4} \times 10 = \frac{3}{4}a \times 10 = \frac{30}{4}a = \frac{15}{2}a $$因此,这个梯形的面积为 $\frac{15}{2}a$。
2020届上海市中考数学压轴题解题策略:梯形的存在性问题(加精)

中考数学压轴题解题策略梯形的存在性问题解题策略专题攻略解梯形的存在性问题一般分三步:第一步分类,第二步画图,第三步计算.一般是已知三角形的三个顶点,在某个图象上求第四个点,使得四个点围成梯形.过三角形的每个顶点画对边的平行线,这条直线与图象的交点就是要探寻的梯形的顶点.因为梯形有一组对边平行,因此根据同位角或内错角,一定可以构造一组相等的角,然后根据相似比列方程,可以使得解题简便.例题解析例❶如图1-1,四边形ABCD是直角梯形,AD//BC,∠B=90°,AD=24cm,BC=28cm.点P从点A 出发以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达终点时,另一个点也随之停止运动.从运动开始,经过多长时间,四边形PQCD成为平行四边形?成为等腰梯形?图1-1【解析】这道题目中蕴含了一个经典的判断题:一组对边平行,另一组对边相等的四边形是平行四边形吗?回答是否定的.可能是平行四边形,也可能是等腰梯形,区别在于另一组对边是否平行.如图1-2,如果四边形PQCD是平行四边形,那么PD=QC.所以24-t=3t.解得t=6.如图1-3,如果四边形PQCD是等腰梯形,作PM⊥BC,DN⊥B C,垂足分别为M、N,那么QM=CN.所以t-(28-3t)=4.解得t=8.图1-2 图1-3例❷如图2-1,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动;同时点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.当点P 到达点A时停止运动,点Q也随之停止.伴随着P、Q的运动,DE保持垂直平分PQ,DE交BC于点E.设P、Q运动的时间是t秒(t>0),在运动的过程中,四边形QBED能否成为直角梯形?若能,求出t的值;若不能,请说明理由.图2-1【解析】在四边形QBED中,∠B是确定的锐角,∠QDE是直角.如果要成为梯形,存在DE//QB和DQ//EB两种情况.站在梯形的外部看梯形,问题就迎刃而解.如图2-2,当DE//QB时,∠DQB=90°,此时△AQP是直角三角形.如图2-3,当DQ//EB时,四边形DECP是矩形,△AQP是直角三角形.这样就转化为解Rt△AQP了.已知AP=3t-,AQ=t,3cos5A=.如图2-2,335AQ tAP t==-时,解得98t=.如图2-3,335AP tAQ t-==时,解得158t=.解题时,只需要画出图2-4和图2-5这样的示意图就好了.图2-2 图2-3 图2-4 图2-5例❸如图,已知A、B是双曲线2yx=上的两个点,A、B的横坐标分别为2和-1,BC⊥x轴,垂足为C.在双曲线上是否存在点D,使得以A、B、C、D为顶点的四边形是梯形?如果存在,求出点D的坐标;如果不存在,请说明理由.图3-1【解析】△ABC是确定的,过每个顶点画对边的平行线,与双曲线的交点就是要求的点D.已知A(2,1),B(-1,-2),C(-1,0).设2(,)D xx.①如图3-2,过点A作BC的平行线,不存在点D.②如图3-3,当BD//AC时,∠ACE=∠DBF,所以AE DFCE BF=.解方程22131xx+=+,得x=-1或x=6.此时1(6,)3D.③如图3-4,当CD//AB时,∠ABN=∠DCM,所以AN DMBN CM=.解方程2313xx=+,得x=1或x=-2.此时D(1,2)或(-2,-1).图3-2图3-3 图3-4从上面的解题过程我们可以感受到:画图可以快速找到目标,计算可以准确定位.根据等角的正切值相等列方程比较简便.在图3-4中,解方程还达到了“一石二鸟”的目的.例❹如图4-1,已知抛物线233384y x x =--与x 轴的交点为A 、D (A 在D 的右侧),与y 轴的交点为C ,设点C 关于抛物线对称轴的对称点为B ,在抛物线上是否存在点P ,使得以A 、B 、C 、P 为顶点的四边形为梯形?若存在,求出点P 的坐标;若不存在,请说明理由.图4-1【解析】过△ABC 的三个顶点分别画对边的平行线,与抛物线的交点就是点P .易知A (4, 0),D (-2, 0),C (0,-3),B (2,-3).设P 233(,3)84x x x --. ①如图4-2,当AP //BC 时,点P 就是点D ,此时P (-2, 0).②如图4-3,当CP //BA 时,作PE ⊥BC ,AF ⊥BC ,垂足分别为E 、F .根据PE AF CE BF=,得233(3)(3)3842x x x ----=.解得x =6.此时P (6, 6). ③如图4-4,假设BP //AC ,那么BG AF PG CF=.所以233(3)(3)38424x x x ----=-. 解得x =2.此时点P 与点B 重合,梯形不存在.图4-2 图4-3 图4-4例❺ 如图5-1,把两个全等的Rt △AOB 和Rt △COD 分别置于平面直角坐标系中,使直角边OB 、OD 在x 轴上.已知点A (1,2).抛物线y =ax 2+bx +c 经过O 、A 、C 三点.(1)求该抛物线的函数解析式;(2)点P 为线段OC 上的一个动点,过点P 作y 轴的平行线交抛物线于点M ,交x 轴于点N ,问是否存在这样的点P ,使得四边形ABPM 为等腰梯形?若存在,求出此时点P 的坐标;若不存在,请说明理由.图5-1【解析】在等腰梯形中,构造辅助线常见的方法,就是把等腰梯形分割为一个矩形和两个全等的直角三角形.如图5-2,图5-3,在坐标平面内,如果梯形的两底与坐标轴平行,一般根据BE=FC列方程.在图5-2中,x A-x B=x C-x D;在图5-3中,y B-y A=y D-y C.(1)抛物线的解析式为23722y x x=-+.(2)如图5-4,如果梯形ABPM是等腰梯形,那么AM′=BP′,因此y A-y M′=y P′-y B.直线OC的解析式为12y x=,设点P的坐标为1(,)2x x,那么237(,)22M x x x-+.解方程23712()222x x x--+=,得123x=,22x=.x=2的几何意义是P与C重合,此时梯形不存在.所以21(,)33P.事实上,我们事先并不知道点M(或点P)的准确位置在哪里?甚至不知道点M(或点P)在AB的右侧还是左侧?但这不影响我们解题,先假设,再列方程,然后根据方程的解验证位置.图5-2 图5-3 图5-4例❻如图6-1,在矩形ABCD中,AB=3,BC=4,动点P从点D出发沿DA向终点A运动,同时动点Q从点A出发沿对角线AC向终点C运动.过点P作PE//DC,交AC于点E,动点P、Q的运动速度都是每秒1个单位长度,当点P运动到点A时,P、Q两点同时停止运动,设运动时间为x秒,当x为何值时,四边形PQBE为梯形?图6-1【解析】按照四边形PQBE的对边平行,分两种情况讨论:①当PE//QB时,由于PE//AB,所以QB//AB,因此Q、A重合,此时四边形PQBE是矩形,不是梯形(如图6-2).②如图6-3,当PQ//BE时,△APQ∽△CBE,由AP CBAQ CE=,得4454xx x-=.解得45x=.图6-2 图6-3。
初三冲刺——梯形存在性讨论

A B C M 1 M 2梯形是相对限制较少的一类四边形,要使得一个四边形是梯形,只需要有其中一组对边平行,另一组对边不平行即可。
因此,在此类问题中,要么对点有较高的限制(在某一直线上),要么对梯形形状有较高要求(等腰或直角)、综合利用各个条件,才能求出最后的结果【例1】 知识内容: 梯形的限制较少,因此估计出现的情况就会有特别多,在处理时需要想清所有估计情况,再进行讨论处理。
有一种比较常见的情况是:若已知三点AB C,另一点M 在某固定直线上,形成的四边形A BCM 为梯形,则会有两种情况:①A M//BC ;②C M//AB ,如图所示、【例2】 解题思路:(1) 依照题目条件,求出已知3个点的坐标; (2) 分情况进行讨论; (3) 对估计的各种情况,求出已知边所在直线的方程; (4) 依照直线方程,求得与其平行的直线的方程,再解出待求点的坐标;(5) 依照题目实际情况,验证所有估计点是否满足要求并作答。
注:若两条直线平行,则这两条直线的斜率相等。
【例1】 在平面直角坐标系中(如图),已知抛物线与x 轴交于点A(-1,0)和点B,与y 轴交于点C (0,-2)、(1)求该抛物线的表达式,并写出其对称轴;(2)点E 为该抛物线的对称轴与x 轴的交点,点F 在对称轴上,四边形ACEF 为梯形,求点F的坐标;(3)点D为该抛物线的顶点,设点P (t, 0),且t〉3,假如△BDP 和△CDP 的面积相等,求t 的值。
【解析】解:(1)将A 、C 代入抛物线解析式,ﻩ解得抛物线解析式为:、 对称轴为:直线、 ﻩ(2)E 点为(1,0),分情况讨论:①AC //EF ﻩ直线AC的解析式为。
例题解析梯形的存在性问题 知识结构知识精讲 模块一:一般梯形的存在性问题知识概述 梯形的存在性问题 一般梯形的存在性问题 特殊梯形的存在性问题ﻩﻩ∴直线EF的解析式为、ﻩﻩ∴与对称轴的交点为(1,0),与E点重合(舍)。
梯形问题的解题策路与方法

梯形问题的解题策路与方法解决梯形问题经常要根据条件添加辅助线,把梯形问题转化为较简单的三角形或平行四边形问题解决,使一些分散的条件适当集中,再进行解答。
一、延长两腰延长梯形的两腰,使它们交于一点,可得到两个相似三角形。
例1如图,在梯形ABCD 中,BC AD //,BC EF //,梯形AEFD 的面积与梯形EBCF的面积相等。
求证:2222EF BC AD =+。
分析:条件是两个梯形的面积相等,而结论是三线段长的平方关系,如果延长两腰交于一点,就可得到三个相似的三角形,再利用相似三角形的面积比与相似比的关系变形就可得出结论。
证明:延长BA 、CD 使它们相交于O 点,∵EF AD //, ∴2⎪⎭⎫ ⎝⎛=EF AD S S OEF OAD ∆∆ 222EF AD EF S S S OEF OAD OEF -=-∆∆∆∴O AD D EF AEFD S S S ∆∆-=梯形OEF S EF AD EF ∆⋅-=222。
同理,OEF AEFD S EF EF BC S ∆⋅-=222梯形∵EBCF AEFD S S 梯形梯形=故得2222EF BC AD EF -=-∴2222EF BC AD =+评注:面积与线段的平方关系可借助相似三角形来解决。
此题添加辅助线后得到若干个相似三角形,把条件都集中在三角形中,有助于问题的解决。
二、平移对角钱平移对角钱,一般是过小底的一个端点作一条对角线的平行线,与另一底的延长线相交,得到一个平行四边形和三角形,把梯形问题转化为平行四边形和三角形问题解决。
在解题中,平移一条对角线后得到一个直角三角形,并且所有条件在聚集在这个三角形中,使问题易于解决。
三、作梯形的高从梯形小底的两端向大底引垂线,可以得到一个矩形和两个直角三角形。
例 3 如图,梯形ABCD 中,BC AD //,AC 、BD 为对角线,求证:AD BC CD AB BD AC ⋅++=+22222分析:由结论联想到勾股定理,因此,分别过A 、D 作BC 的垂线,垂足为E 、F ,得到AEC Rt ∆和DFB Rt ∆,分别用勾段定理,然后化简就可得到结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学压轴题解题策略
梯形的存在性问题解题策略
专题攻略
解梯形的存在性问题一般分三步:
第一步分类,第二步画图,第三步计算.
一般是已知三角形的三个顶点,在某个图象上求第四个点,使得四个点围成梯形.过三角形的每个顶点画对边的平行线,这条直线与图象的交点就是要探寻的梯形的顶点.因为梯形有一组对边平行,因此根据同位角或内错角,一定可以构造一组相等的角,然后根据相似比列方程,可以使得解题简便.
例题解析
例❶如图1-1,四边形ABCD是直角梯形,AD//BC,∠B=90°,AD=24cm,BC=28cm.点P从点A出发以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达终点时,另一个点也随之停止运动.从运动开始,经过多长时间,四边形PQCD成为平行四边形?成为等腰梯形?
图1-1
【解析】这道题目中蕴含了一个经典的判断题:一组对边平行,另一组对边相等的四边形是平行四边形吗?回答是否定的.
可能是平行四边形,也可能是等腰梯形,区别在于另一组对边是否平行.
如图1-2,如果四边形PQCD是平行四边形,那么PD=QC.
所以24-t=3t.解得t=6.
如图1-3,如果四边形PQCD是等腰梯形,作PM⊥BC,DN⊥B C,垂足分别为M、N,那么QM=CN.所以t-(28-3t)=4.解得t=8.
图1-2 图1-3
例❷如图2-1,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动;同时点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.当点P到达点A时停止运动,点Q也随之停止.伴随着P、Q的运动,DE保持垂直平分PQ,DE交BC于点E.设P、Q运动的时间是t秒(t>0),在运动的过程中,四边形QBED能否成为直角梯形?若能,求出t的值;若不能,请说明理由.
图2-1
【解析】在四边形QBED中,∠B是确定的锐角,∠QDE是直角.如果要成为梯形,存在DE//QB和DQ//EB两种情况.
站在梯形的外部看梯形,问题就迎刃而解.
如图2-2,当DE//QB时,∠DQB=90°,此时△AQP是直角三角形.
如图2-3,当DQ//EB时,四边形DECP是矩形,△AQP是直角三角形.
这样就转化为解Rt△AQP了.已知AP=3t-,AQ=t,
3 cos
5
A=.
如图2-2,
3
35
AQ t
AP t
==
-
时,解得
9
8
t=.如图2-3,
33
5
AP t
AQ t
-
==时,解得
15
8
t=.
解题时,只需要画出图2-4和图2-5这样的示意图就好了.
图2-2 图2-3 图2-4 图2-5
例❸如图,已知A、B是双曲线
2
y
x
=上的两个点,A、B的横坐标分别为2和-1,BC
⊥x轴,垂足为C.在双曲线上是否存在点D,使得以A、B、C、D为顶点的四边形是梯形?如果存在,求出点D的坐标;如果不存在,请说明理由.
图3-1
【解析】△ABC是确定的,过每个顶点画对边的平行线,与双曲线的交点就是要求的点
D.已知A(2,1),B(-1,-2),C(-1,0).设
2 (,)
D x
x
.
①如图3-2,过点A作BC的平行线,不存在点D.
②如图3-3,当BD//AC时,∠ACE=∠DBF,所以AE DF CE BF
=.
解方程
2
2
1
31
x
x
+
=
+
,得x=-1或x=6.此时
1
(6,)
3
D.
③如图3-4,当CD//AB时,∠ABN=∠DCM,所以
AN DM
BN CM
=.
解方程
2
3
13
x
x
=
+
,得x=1或x=-2.此时D(1,2)或(-2,-1).
图3-2 图3-3 图3-4 从上面的解题过程我们可以感受到:画图可以快速找到目标,计算可以准确定位.根据等角的正切值相等列方程比较简便.在图3-4中,解方程还达到了“一石二鸟”的目的.例❹如图4-1,已知抛物线2
33
3
84
y x x
=--与x轴的交点为A、D(A在D的右侧),与y轴的交点为C,设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由.
图4-1
【解析】过△ABC的三个顶点分别画对边的平行线,与抛物线的交点就是点P.
易知A(4, 0),D(-2, 0),C(0,-3),B(2,-3).设P2
33
(,3)
84
x x x
--.
①如图4-2,当AP//BC时,点P就是点D,此时P(-2, 0).
②如图4-3,当CP//BA时,作PE⊥BC,AF⊥BC,垂足分别为E、F.
根据
PE AF
CE BF
=,得
2
33
(3)(3)
3
84
2
x x
x
----
=.解得x=6.此时P(6, 6).
③如图4-4,假设BP//AC,那么
BG AF
PG CF
=.所以
2
33
(3)(3)
3
84
24
x x
x
----
=
-
.解得x=2.此时点P与点B重合,梯形不存在.
图4-2 图4-3 图4-4
例❺ 如图5-1,把两个全等的Rt △AOB 和Rt △COD 分别置于平面直角坐标系中,使直角边OB 、OD 在x 轴上.已知点A (1,2).抛物线y =ax 2
+bx +c 经过O 、A 、C 三点.
(1)求该抛物线的函数解析式;
(2)点P 为线段OC 上的一个动点,过点P 作y 轴的平行线交抛物线于点M ,交x 轴于点N ,问是否存在这样的点P ,使得四边形ABPM 为等腰梯形?若存在,求出此时点P 的坐标;若不存在,请说明理由.
图5-1
【解析】在等腰梯形中,构造辅助线常见的方法,就是把等腰梯形分割为一个矩形和两个全等的直角三角形.如图5-2,图5-3,在坐标平面内,如果梯形的两底与坐标轴平行,一般根据BE =FC 列方程.在图5-2中,x A -x B =x C -x D ;在图5-3中,y B -y A =y D -y C .
(1)抛物线的解析式为23722y x x =-+. (2)如图5-4,如果梯形ABPM 是等腰梯形,那么AM ′=BP ′,因此y A -y M ′=y P ′-y B . 直线OC 的解析式为12y x =,设点P 的坐标为1(,)2x x ,那么237(,)22
M x x x -+. 解方程23712()222x x x --+=,得123
x =,22x =. x =2的几何意义是P 与C 重合,此时梯形不存在.所以21(,)33
P . 事实上,我们事先并不知道点M (或点P )的准确位置在哪里?甚至不知道点M (或点P )在AB 的右侧还是左侧?但这不影响我们解题,先假设,再列方程,然后根据方程的解验证位置.
图5-2 图5-3 图5-4
例❻ 如图6-1,在矩形ABCD 中,AB =3,BC =4,动点P 从点D 出发沿DA 向终点A 运
动,同时动点Q从点A出发沿对角线AC向终点C运动.过点P作PE//DC,交AC于点E,动点P、Q的运动速度都是每秒1个单位长度,当点P运动到点A时,P、Q两点同时停止运动,设运动时间为x秒,当x为何值时,四边形PQBE为梯形?
图6-1
【解析】按照四边形PQBE的对边平行,分两种情况讨论:
①当PE//QB时,由于PE//AB,所以QB//AB,因此Q、A重合,此时四边形PQBE是矩形,不是梯形(如图6-2).
②如图6-3,当PQ//BE时,△APQ∽△CBE,由AP CB
AQ CE
=
,得44
5
4
x
x x
-
=.解得
4
5
x=.
图6-2 图6-3。
