平面直角坐标系下的动点问题专题复习
(完整版)初一平面直角坐标系动点问题(经典难题)

(2)在y轴上是否存在一点P,连接PA,PB,使 = ,
若存在这样一点,求出点P的坐标,若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)给出下列结论: 的值不变, 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
5.观察下列有序数对:(3,﹣1)(﹣5, )(7,﹣ )(﹣9, )…根据你发现的规律,第100个有序数对是.
6、观察下列有规律的点的坐标:
依此规律,A11的坐标为,A12的坐标为.
7、以0为原点,正东,正北方向为x轴,y轴正方向建立平面直角坐标系,一个机器人从原点O点出发,向正东方向走3米到达A1点,再向正北方向走6米到达A2,再向正西方向走9米到达A3,再向正南方向走12米到达A4,再向正东方向走15米到达A5,按此规律走下去,当机器人走到A6时,A6的坐标是.
平面直角坐标系动点问题
(一)找规律
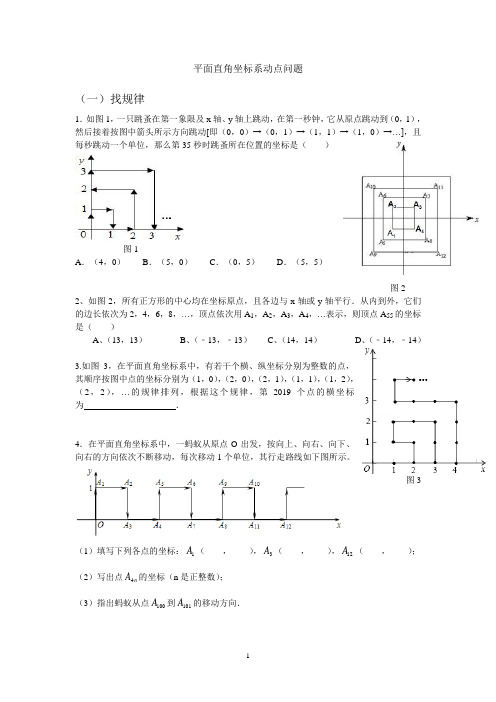
1.如图1,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )
图1
A.(4,0)B.(5,0)C.(0,5)D.(5,5)
(1)汽车行驶到什么位置时离A村最近?写出此点的坐标.
(2)汽车行驶到什么位置时离B村最近?写出此点的坐标.
(3)请在图中画出汽车行驶到什么位置时,距离两村的和最短?
4.如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
七年级平面直角坐标系动点规律问题(经典难题)
平面直角坐标系动点问题(一)找规律1.如图1,一只跳蚤在第一象限及x 轴、y 轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )图1A .(4,0)B .(5,0)C .(0,5)D .(5,5)图22、如图2,所有正方形的中心均在坐标原点,且各边与x 轴或y 轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A 1,A 2,A 3,A 4,…表示,则顶点A 55的坐标是( ) A 、(13,13) B 、(﹣13,﹣13) C 、(14,14) D 、(﹣14,﹣14)3.如图3,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2019个点的横坐标为 .4.在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如下图所示。
图3(1)填写下列各点的坐标:1A (____,____),3A (____,____),12A (____,____); (2)写出点n A 4的坐标(n 是正整数); (3)指出蚂蚁从点100A 到101A 的移动方向.5.观察下列有序数对:(3,﹣1)(﹣5,)(7,﹣)(﹣9,)…根据你发现的规律,第100个有序数对是 .6、观察下列有规律的点的坐标:依此规律,A 11的坐标为 ,A 12的坐标为 .7、以0为原点,正东,正北方向为x 轴,y 轴正方向建立平面直角坐标系,一个机器人从原点O 点出发,向正东方向走3米到达A 1点,再向正北方向走6米到达A 2,再向正西方向走9米到达A 3,再向正南方向走12米到达A 4,再向正东方向走15米到达A 5,按此规律走下去,当机器人走到A 6时,A 6的坐标是 .8、如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2019次,点P 依次落在点201921,,,P P P 的位置,则点2019P 的横坐标为 .9、如图,在平面直角坐标系上有个点P (1,0),点P 第1次向上跳动1个单位至点P 1(1,1),紧接着第2次向左跳动2个单位至点P 2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P 第100次跳动至点P 100的坐标是 .点P 第2019次跳动至点P 2019的坐标是 .图4 图5 10、如图5,已知A l (1,0),A 2(1,1),A 3(﹣1,1),A 4(﹣1,﹣1),A 5(2,﹣1),….则点A 2019的坐标为 .1PAOyxP1. 如图,一个粒子在第一象限内及x 、y 轴上运动,在第一分钟内它从原点运动到()1,0,而后它接着按图所示在x 轴、y 轴平行的方向上来回运动,且每分钟移动1个长度单位,那么,在1989分钟后这个粒子所处的位置是( ).A .()35,44B .()36,45C .()37,45D .()44,352. 如果将点P 绕定点M 旋转180︒后与点Q 重合,那么称点P 与点Q 关于点M 对称,定点M 叫做对称中心,此时,点M 是线段PQ 的中点,如图,在直角坐标系中,ABO △的顶点A 、B 、O 的坐标分别为()1,0、()0,1、()0,0,点1P ,2P ,3P ,…中相邻两点都关于ABO △的一个顶点对称,点1P 与点2P 关于点A 对称,点2P 与点3P 关于点B 对称,点3P 与点4P 关于点O 对称,点4P 与点5P 关于点A 对称,点5P 与点6P 关于点B 对称,点6P 与点7P 关于点O 对称,…对称中心分别是A ,B ,O ,A ,B ,O ,…且这些对称中心依次循环,已知1P 的坐标是()1,1.试写出点2P 、7P 、100P 的坐标.3. 如图,在平面直角坐标系中,四边形各顶点的坐标分别为:()0,0A ,()7,0B ,()9,5C ,()2,7D .(1)求此四边形的面积.(2)在坐标轴上,你能否找到一点P ,使50PBC S =△?若能,求出P 点坐标;若不能,请说明理由.4. 如图①,已知OABC 是一个长方形,其中顶点A 、B 的坐标分别为()0,a 和()9,a ,点E在AB 上,且13AE AB =,点F 在OC 上,且13OF OC =.点G 在OA 上,且使GEC △的面积为20,GFB △的面积为16,试求a 的值.图②5. 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如()1,0,()2,0,()2,1,()1,1,()1,2,()2,2……根据这个规律,第2019个点的横坐标为_______.6. 在平面直角坐标系xOy 中,我们把横、纵坐标都是整数的点叫做整点.已知点()0,4A ,点B 是x 轴正半轴上的整点,记AOB △内部(不包括边界)的整点个数为m ,当3m =时,点B 的横坐标的所有可能值是_______;当点B 的横坐标为4n (n 为正整数)时,m =________(用含n 的代数式表示).7. 如图,把自然数按图的次序排在直角坐标系中,每个自然数都对应着一个坐标.如1的对应点是原点()0,0,3的对应点是()1,1,16的对应点是()1,2-,那么2019的对应点的坐标是_______.8.如图,长方形BCDE 的各边分别平行于x 轴或y 轴,物体甲和物体乙由点()2,0A 同时出发,沿长方形BCDE 的边作环绕运动,物体甲按逆时针方向以每秒1个单位长度的速度匀速运动,物体乙按顺时针方向以每秒2个单位长度的速度匀速运动,求两个物体开始运动后的第2019次相遇地点的坐标.9. 在平面直角坐标系中,如图①,将线段AB 平移至线段CD ,连接AC 、BD . (1)直接写出图中相等的线段、平行的线段; (2)已知()3,0A -、()2,2B --,点C 在y 轴的正半轴上.点D 在第一象限内,且5ACD S =△,求点C 、D 的坐标;(3)如图②,在平面直角坐标系中,已知一定点,()1,0M ,两个动点(),21E a a +、(),23F b b -+,请你探索是否存在以两个动点E 、F 为端点的线段EF 平行于线段OM 且等于线段OM .若存在,求以点O 、M 、E 、F 为顶点的四边形的面积,若不存在,请说明理由.图②10 . 如图,AOCD 是放置在平面直角坐标系内的梯形,其中O 是坐标原点.点A 、C 、D 的坐标分别为()0,8,()5,0,()3,8,若点P 在梯形内,且PAD POC S S =△△,PAO PCD S S =△△,求P 点的坐标.11. 操作与研究(1)对数轴上的点P 进行如下操作:先把点P 表示的数乘以13,再把所得数对应的点向右平移1个单位,得到点P 的对应点'P B .点A ,B 在数轴上,对线段AB 上的每个点进行上述操作后得到线段''A B ,其中点A ,B 的对应点分别为'A ,'B .如图①,若点A 表示的数是3-,则点'A 表示的数是______;若点'B 表示的数是2,则点表示的数是______;已知线段AB 上的点E 经过上述操作后得到的对应点'E 与点E 重合,则点E 表示的数是_________.(2)如图②,在平面直角坐标系xOy 中,对正方形ABCD 及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一个实数a ,将得到的点先向右平移m 个单位,再向上平移n 个单位()0,0m n >>,得到正方形''''A B C D 及其内部的点,其中点A ,B 的对应点分别为'A ,'B .已知正方形ABCD 内部的一个点F 经过上述操作后得到的对应点'F 与点F 重合,求点F 的坐标.图①A B'-1-2-3-412340图②(二)几何综合问题1、已知点A 的坐标是(3,0)、AB=5,(1)当点B 在X 轴上时、求点B 的坐标、(2)当AB//y 轴时、求点B 的坐标2、如图,已知A 、B 两村庄的坐标分别为(2,2)、(7,4),一辆汽车在x 轴上行驶,从原点O 出发.(1)汽车行驶到什么位置时离A 村最近?写出此点的坐标. (2)汽车行驶到什么位置时离B 村最近?写出此点的坐标. (3)请在图中画出汽车行驶到什么位置时,距离两村的和最短?4.如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1)求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形D C 3-1BA O x y PDCBAOx y (2)在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S ∆=ABDC S 四边形,若存在这样一点,求出点P 的坐标,若不存在,试说明理由.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时(不与B ,D 重合)给出下列结论:①DCP BOP CPO ∠+∠∠的值不变,②DCP CPOBOP∠+∠∠的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.5.已知:在平面直角坐标系中,四边形ABCD 是长方形, ∠A =∠B =∠C =∠D =90°,AB ∥CD ,AB =CD =8cm ,AD =BC =6cm ,D 点与原点重合,坐标为(0,0). (1)写出点B 的坐标.(2)动点P 从点A 出发以每秒3个单位长度的速度向终点B 匀速运动, 动点Q 从点C 出发以每秒4个单位长度的速度沿射线CD 方向匀速运动,若P ,Q 两点同时出发,设运动时间为t 秒,当t 为何值时,PQ ∥BC ?(3)在Q 的运动过程中,当Q 运动到什么位置时,使△ADQ 的面积为9? 求出此时Q 点的坐标.6.如图在平面直角坐标系中,A(a,0),B(b,0),(﹣1,2).且|2a+b+1|+=0.(1)求a、b的值;(2)①在y轴的正半轴上存在一点M,使S△COM=S△ABC,求点M的坐标.②在坐标轴的其他位置是否存在点M,使S△COM=S△ABC仍成立?若存在,请直接写出符合条件的点M的坐标.7.如图,在下面的直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b 满足关系式.(1)求a,b的值;(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.8.在平面直角坐标系中,点A(a,b)是第四象限内一点,AB⊥y轴于B,且B(0,b)是y轴负半轴上一点,b2=16,S△AOB=12.(1)求点A和点B的坐标;(2)如图1,点D为线段OA(端点除外)上某一点,过点D作AO垂线交x轴于E,交直线AB于F,∠EOD、∠AFD的平分线相交于N,求∠ONF的度数.(3)如图2,点D为线段OA(端点除外)上某一点,当点D在线段上运动时,过点D作直线EF交x轴正半轴于E,交直线AB于F,∠EOD,∠AFD的平分线相交于点N.若记∠ODF=α,请用α的式子表示∠ONF的大小,并说明理由.。
七年级期中平面直角坐标系动点问题专项练习

平面直角坐标系动点问题
1、已知点A 的坐标是(3,0)、AB=5,(1)当点B 在X 轴上时、求点B 的坐标、(2)当AB//y 轴时、求点B 的坐标
2、如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次,点P 依次落在点
1232008P P P P ,,,
,的位置,则点2008P 的横坐标为?
3、如图6-7,已知A 、B 两村庄的坐标分别为(2,2)、(7,4),一辆汽车在x 轴上行驶,从原点O 出发.
(1)汽车行驶到什么位置时离A 村最近?写出此点的坐标. (2)汽车行驶到什么位置时离B 村最近?写出此点的坐标. (3)请在图中画出汽车行驶到什么位置时,距离两村的和最短?
4.如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .
(1)求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形
(2)在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S =ABDC S 四边形, 若存在这样一点,求出点P 的坐标,若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)
给出下列结论:①
DCP BOP
CPO
∠+∠
∠
的值不变,②
DCP CPO
BOP
∠+∠
∠
的值不变,其中有且只
有一个是正确的,请你找出这个结论并求其值.。
初一-平面直角坐标系动点问题(经典难题)

初一-平面直角坐标系动点问题(经典难题)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN平面直角坐标系动点问题(一)找规律1.如图1,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是()图1A.(4,0) B.(5,0) C.(0,5) D.(5,5)图2 2、如图2,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是()A、(13,13)B、(﹣13,﹣13)C、(14,14)D、(﹣14,﹣14)3.如图3,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2015个点的横坐标为.4.在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如下图所示。
图3(1)填写下列各点的坐标:1A (____,____),3A (____,____),12A (____,____);(2)写出点n A 4的坐标(n 是正整数); (3)指出蚂蚁从点100A 到101A 的移动方向.5.观察下列有序数对:(3,﹣1)(﹣5,)(7,﹣)(﹣9,)…根据你发现的规律,第100个有序数对是 . 6、观察下列有规律的点的坐标:依此规律,A 11的坐标为 ,A 12的坐标为 .7、以0为原点,正东,正北方向为x 轴,y 轴正方向建立平面直角坐标系,一个机器人从原点O 点出发,向正东方向走3米到达A 1点,再向正北方向走6米到达A 2,再向正西方向走9米到达A 3,再向正南方向走12米到达A 4,再向正东方向走15米到达A 5,按此规律走下去,当机器人走到A 6时,A 6的坐标是 .8、如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次,点P 依次落在点1232008P P P P ,,,,的位置,则点2008P的横坐标为 .9、如图,在平面直角坐标系上有个点P (1,0),点P 第1次向上跳动1个单位至点P 1(1,1),紧接着第2次向左跳动2个单位至点P 2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P 第100次跳动至点P 100的坐标是 .点P 第2009次跳动至点P 2009的坐标是 .图4 图510、如图5,已知A l (1,0),A 2(1,1),A 3(﹣1,1),A 4(﹣1,﹣1),A 5(2,﹣1),….则点A 2007的坐标为 .1PAOy xP(二)几何综合问题1、已知点A的坐标是(3,0)、AB=5,(1)当点B在X轴上时、求点B的坐标、(2)当AB//y轴时、求点B的坐标2、如图,已知A、B两村庄的坐标分别为(2,2)、(7,4),一辆汽车在x 轴上行驶,从原点O出发.(1)汽车行驶到什么位置时离A村最近?写出此点的坐标.(2)汽车行驶到什么位置时离B村最近?写出此点的坐标.(3)请在图中画出汽车行驶到什么位置时,距离两村的和最短?4.如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.(1)求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形(2)在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S ∆=ABDC S 四边形,若存在这样一点,求出点P 的坐标,若不存在,试说明理由.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时(不与B ,D 重合)给出下列结论:①DCP BOPCPO∠+∠∠②DCP CPOBOP∠+∠∠你找出这个结论并求其值.5.已知:在平面直角坐标系中,四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0).(1)写出点B的坐标.(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动, 动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t秒,当t为何值时,PQ∥BC(3)在Q的运动过程中,当Q运动到什么位置时,使△ADQ的面积为9求出此时Q点的坐标.6.如图在平面直角坐标系中,A(a,0),B(b,0),(﹣1,2).且|2a+b+1|+=0.(1)求a、b的值;(2)①在y轴的正半轴上存在一点M,使S△COM=S△ABC,求点M的坐标.②在坐标轴的其他位置是否存在点M,使S△COM=S△ABC仍成立?若存在,请直接写出符合条件的点M的坐标.7.如图,在下面的直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b满足关系式.(1)求a,b的值;(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.8.在平面直角坐标系中,点A(a,b)是第四象限内一点,AB⊥y轴于B,且B(0,b)是y轴负半轴上一点,b2=16,S△AOB=12.(1)求点A和点B的坐标;(2)如图1,点D为线段OA(端点除外)上某一点,过点D作AO垂线交x轴于E,交直线AB于F,∠EOD、∠AFD的平分线相交于N,求∠ONF的度数.(3)如图2,点D为线段OA(端点除外)上某一点,当点D在线段上运动时,过点D作直线EF交x轴正半轴于E,交直线AB于F,∠EOD,∠AFD的平分线相交于点N.若记∠ODF=α,请用α的式子表示∠ONF的大小,并说明理由.。
七年级数学下册 专题训练:平面直角坐标系中点的规律探究(精选30题)(解析版)

七年级下册数学《第七章平面直角坐标系》专题:平面直角坐标系中点的规律探究一、选择题(共10题)1.(2022秋•定远县期中)如图,在平面直角坐标系中,点A(﹣1,0),点A第1次向上跳动1个单位至点A1(﹣1,1),紧接着第2次向右跳动2个单位至点A2(1,1),第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…依此规律跳动下去,点A第2022次跳动至点A2022的坐标是()A.(505,1009)B.(﹣506,1010)C.(﹣506,1011)D.(506,1011)【分析】设第n次跳动至点A n,根据部分点A n坐标的变化找出变化规律“A4n(﹣n﹣1,2n),A4n+1(﹣n﹣1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数)”,依此规律结合2022=505×4+2即可得出点A2022的坐标.【解答】解:设第n次跳动至点A n,观察,发现:A(﹣1,0),A1(﹣1,1),A2(1,1),A3(1,2),A4(﹣2,2),A5(﹣2,3),A6(2,3),A7(2,4),A8(﹣3,4),A9(﹣3,5),…,∴A4n(﹣n﹣1,2n),A4n+1(﹣n﹣1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数).∵2022=505×4+2,∴A2022(506,1011).故选:D.【点评】本题考查了规律型中点的坐标,根据部分点A n坐标的变化找出变化规律是解题的关键.2.(2022秋•古田县期中)在平面直角坐标系中,设一质点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去.设P n(x n,y n),n=1,2,3…,则x1+x2+…+x2017的值为()A.2016B.2017C.﹣2016D.2015【分析】根据给定的平移规律,可得x1=1,x2=﹣1,x3=﹣1,x4=3,进一步可得x1+x2+x3+x4=1+(﹣1)+(﹣1)+3=2,同理可得x5+x6+x7+x8=3+(﹣3)+(﹣3)+5=2,再根据2017÷4=504...1,进一步计算即可.【解答】解:根据题意,可得x1=1,x2=﹣1,x3=﹣1,x4=3,∴x1+x2+x3+x4=1+(﹣1)+(﹣1)+3=2,同理可得x5+x6+x7+x8=3+(﹣3)+(﹣3)+5=2,∵2017÷4=504...1,∴x2017=2×504+1=1009,∴x1+x2+…+x2017=504×2+1009=2017,故选:B.【点评】本题考查了坐标与平移,找出点坐标之间的规律是解题的关键.3.(2022秋•李沧区期末)如图,在平面直角坐标系中,A1(1,﹣2),A2(2,0),A3(3,2),A4(4,0),…根据这个规律,点A2023的坐标是()A.(2022,0)B.(2023,0)C.(2023,2)D.(2023,﹣2)【分析】由图形得出点的横坐标依次是1、2、3、4、…、n,纵坐标依次是﹣2、0、2、0、﹣2、0、2、…,四个一循环,继而求得答案.【解答】解:观察图形可知,点的横坐标依次是1、2、3、4、…、n,纵坐标依次是﹣2、0、2、0、﹣2、0、2、…,四个一循环,2023÷4=505……3,所以点A2023坐标是(2023,2).故选:C.【点评】本题考查了规律型:点的坐标,学生的观察图形的能力和理解能力,解题的关键是根据图形得出规律.4.(2021春•浉河区期末)如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(﹣2,2),第四次向右跳动5个单位至点A4(3,2),…,以此规律跳动下去,点A第2021次跳动至点A2021的坐标是()A.(﹣1009,1009)B.(﹣1010,1010)C.(﹣1011,1011)D.(﹣1012,1012)【分析】根据点的坐标、坐标的平移寻找规律即可求解.【解答】解:因为A1(﹣1,1),A2(2,1),A3(﹣2,2),A4(3,2),A5(﹣3,3),A6(4,3),A7(﹣4,4),A8(5,4),…A2n﹣1(﹣n,n),A2n(n+1,n)(n为正整数),所以2n﹣1=2021,n=1011,所以A2020(﹣1011,1011),故选:C.【点评】本题考查了点的坐标、坐标的平移,解决本题的关键是寻找点的变化规律.5.(2021秋•九江期末)如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙都从点A(2,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2022次相遇点的坐标是()A.(2,0)B.(﹣1,1)C.(﹣2,0)D.(﹣1,﹣1)【分析】根据两个物体运动速度和矩形周长,得到两个物体的相遇时间间隔,进而得到两个点相遇的位置规律.【解答】解:由已知,矩形周长为12,∵甲、乙速度分别为1单位/秒,2单位/秒,则两个物体每次相遇时间间隔为121+2=4秒,则两个物体相遇点依次为(﹣1,1)、(﹣1,﹣1)、(2,0),∵2022=3×673…3,∴第2022次两个物体相遇位置为(2,0),故选:A.【点评】本题为平面直角坐标系内的动点坐标规律探究题,解答关键是找到两个物体相遇的位置的变化规律.6.(2022春•启东市期中)如图,在平面直角坐标系xOy中,点A坐标是(1,1).若记点A坐标为(a1,a2),则一个点从点A出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8)…,每个点的横纵坐标都是整数,按此规律一直运动下去,则a2020+a2021+a2022的值为()A.2021B.2022C.1011D.1012【分析】观察已知点的坐标可得,所有数列奇数个都是从1开始逐渐递增的,且都等于所在的个数加上1再除以2,则a2021=1011,偶数列等于所在的个数除以4,能够整除的,结果的相反数就是所求出的数,不能整除的,等于结果的整数部分加1,且符号为正,进而可得结果.【解答】解:由直角坐标系可知A(1,1),B(2,﹣1),C(3,2),D(4,﹣2),……,即a1=1,a2=1,a3=2,a4=﹣1,a5=3,a6=2,a7=4,a8=﹣2,……,所有数列奇数个都是从1开始逐渐递增的,且都等于所在的个数加上1再除以2,则a2021=1011,偶数列等于所在的个数除以4,能够整除的,结果的相反数就是所求出的数,不能整除的,等于结果的整数部分加1,且符号为正,∴a2021=﹣505,2023÷4=505……3,∴a2022=506,故a2020+a2021+a2022=1012,故选:D.【点评】本题主要考查了规律型:点的坐标,探索数字与字母规律是解题关键.7.(2022•浉河区校级开学)如图,在平面直角坐标系中,A1(2,0),B1(0,1),A1B1的中点为C1;A2(0,3),B2(﹣2,0),A2B2的中点为C2;A3(﹣4,0),B3(0,﹣3),A3B3的中点为C3;A4(0,﹣5),B4(4,0),A4B4的中点为C4;…;按此做法进行下去,则点C2022的坐标为()A.(﹣1012,−20232)B.(﹣1011,20232)C.(﹣1011,−20232)D.(﹣1012,−20212)【分析】根据题意得点∁n的位置按4次一周期的规律循环出现,可求得点C2022在第二象限,从而可求得该题结果.【解答】解:由题意可得,点∁n的位置按4次一周期的规律循环出现,∵2022÷4=505……2,∴点C2022在第二象限,∵位于第二象限内的点C2的坐标为(﹣1,32),点C6的坐标为(﹣3,72),点C10的坐标为(﹣5,112),……∴点∁n的坐标为(−2,r12),∴当n=2022时,−2=−20222=−1011,r12=2022+12=20232,∴点C2022的坐标为(﹣1011,20232),故选:B.【点评】此题考查了点的坐标方面规律性问题的解决能力,关键是能根据题意确定出该点的出现规律.8.(2022春•冷水滩区校级期中)如图,已知A1(1,2)A2(2,2)A3(3,0)A4(4,﹣2)A5(5,﹣2)A6(6,0)……,按这样的规律,则点A2021的坐标为()A.(2021,2)B.(2020,2)C.(2021,﹣2)D.2020,﹣2)【分析】观察发现,每6个点形成一个循环,再根据点A6的坐标及2021÷6所得的整数及余数,可计算出点A2021的横坐标,再根据余数对比第一组的相应位置的数可得其纵坐标.【解答】解:观察发现,每6个点形成一个循环,∵A6(6,0),∴OA6=6,∵2021÷6=336…5,∴点A2021的位于第337个循环组的第5个,∴点A2021的横坐标为6×336+5=2021,其纵坐标为:﹣2,∴点A2021的坐标为(2021,﹣2).故选:C.【点评】本题考查了平面直角坐标系中的点的规律问题,发现题中的规律并正确计算出点A2021所处的循环组是解题的关键.9.(2022春•宣化区期末)如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒2个单位长度,则第2022秒时,点P的坐标是()A.(2021,0)B.(2021,﹣1)C.(2022,1)D.(2022,0)【分析】根据图象可得移动4次图象完成一个循环,从而可得出点A2015的坐标.【解答】解:半径为1个单位长度的半圆的周长为:12×2×1=,∵点P从原点O出发,沿这条曲线向右运动,速度为每秒2个单位长度,∴点P1秒走12个半圆,当点P从原点O出发,沿这条曲线向右运动,运动时间为1秒时,点P的坐标为(1,1),当点P从原点O出发,沿这条曲线向右运动,运动时间为2秒时,点P的坐标为(2,0),当点P从原点O出发,沿这条曲线向右运动,运动时间为3秒时,点P的坐标为(3,﹣1),当点P从原点O出发,沿这条曲线向右运动,运动时间为4秒时,点P的坐标为(4,0),当点P从原点O出发,沿这条曲线向右运动,运动时间为5秒时,点P的坐标为(5,1),当点P从原点O出发,沿这条曲线向右运动,运动时间为6秒时,点P的坐标为(6,0),…,∵2022÷4=505余2,∴P的坐标是(2022,0),故选:D.【点评】此题考查了点的规律变化,解答本题的关键是仔细观察图象,得到点的变化规律,解决问题.10.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,﹣1)…根据这个规律探索可得,第100个点的坐标()A.(14,0)B.(14,﹣1)C.(14,1)D.(14,2)【分析】观察图形可知,横坐标相等的点的个数与横坐标相同,根据求和公式求出第100个点的横坐标以及在这一横坐标中的所有点中的序数,再根据横坐标是奇数时从上向下排列,横坐标是偶数时从下向上排列,然后解答即可.【解答】解:由图可知,横坐标是1的点共有1个,横坐标是2的点共有2个,横坐标是3的点共有3个,横坐标是4的点共有4个,…,横坐标是n的点共有n个,1+2+3+…+n=or1)2,当n=13时,13×(13+1)2=91,当n=14时,14×(14+1)2=105,所以,第100个点的横坐标是14,∵100﹣91=9,∴第100个点是横坐标为14的点中的第9个点,∵第142=7个点的纵坐标是0,∴第9个点的纵坐标是2,∴第100个点的坐标是(14,2).故选:D.【点评】本题是对点的变化规律的考查,观察得到横坐标相等的点的个数与横坐标相同是解题的关键,还要注意横坐标为奇数和偶数时的排列顺序不同.二、填空题(共10题)11.(2022春•东洲区期末)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(﹣1,1),第2次接着运动到点(﹣2,0),第3次接着运动到点(﹣3,2),…,按这样的运动规律,经过第2022次运动后,动点P的坐标是.A.(2022,0)B.(﹣2022,0)C.(﹣2022,1)D.(﹣2022,2)【分析】观察图形可知:每4次运动为一个循环,并且每一个循环向左运动4个单位,用2022÷4可判断出第2022次运动时,点P在第几个循环第几次运动中,进一步即可计算出坐标.【解答】解:动点P的运动规律可以看作每运动四次为一个循环,每个循环向左运动4个单位,∵2022÷4=505……2,∴第2022次运动时,点P在第506次循环的第2次运动上,∴横坐标为﹣(505×4+2)=﹣2022,纵坐标为0,∴此时P(﹣2022,0).故答案为:(﹣2022,0).【点评】本题考查规律型:点坐标,解答时注意探究点的运动规律,又要注意动点的坐标的象限符号.12.(2022秋•肃州区校级期末)如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…则点A2022的坐标是.【分析】根据题意可以发现规律:A4n(﹣n,n),A4n+1(n+1,n),A4n+2(n+1,﹣n ﹣1),A4n+3(﹣n﹣1,﹣n﹣1),根据规律求解即可.【解答】解:根据题意可以发现规律:A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),A6(2,﹣2),A7(﹣2,﹣2),A8(﹣2,2),…,∴A4n(﹣n,n),A4n+1(n+1,n),A4n+2(n+1,﹣n﹣1),A4n+3(﹣n﹣1,﹣n﹣1),∵2022=4×505+2,∴点A2022的坐标为(506,﹣506),故答案为:(506,﹣506).【点评】本题主要考查规律性:点的坐标,读懂题意,找出点的坐标规律是解答此题的关键.13.(2021秋•同安区期末)如图,点A(0,1),点A1(2,0),点A2(3,2),点A3(5,1)…,按照这样的规律下去,点A2021的坐标为.【分析】观察图形得到奇数点的规律为,A1(2,0),A3(5,1),A5(8,2),…,A2n﹣1(3n﹣1,n﹣1),由2021是奇数,且2021=2n﹣1,则可求A2n﹣1(3032,1010).【解答】解:观察图形可得,A1(2,0),A3(5,1),A5(8,2),…,A2n﹣1(3n﹣1,n﹣1),A2(3,2),A4(6,3),A6(9,4),…,A2n(3n,n+1),∵2021是奇数,且2021=2n﹣1,∴n=1011,(3032,1010),∴A2n﹣1故答案为(3032,1010).【点评】本题考查点的坐标规律;熟练掌握平面内点的坐标,能够根据图形的变化得到点的坐标规律是解题的关键.14.(2022•嘉峪关一模)如图,平面直角坐标系xOy内,动点P按图中箭头所示方向依次运动,第1次从点(0,1)运动到点(1,0),第二次运动到点(2,﹣2),第3次运动到点(3,0),……按这样的运动规律,动点P第2022次运动到的点的坐标是.【分析】根据图形分析点P的运动规律:第n次运动到的点的横坐标为n,纵坐标每四次为一个循环,即可得到答案.【解答】解:∵第1次运动到点(1,0),第二次运动到点(2,﹣2),第3次运动到点(3,0),…,∴第n次运动到的点的横坐标为n,纵坐标每四次一个循环,从第一次运动到的纵坐标开始,分别为0、﹣2、0、1、…,∵2022÷4=505⋯2,∴动点P第2022次运动到的点的坐标是(2022,﹣2),故答案为:(2022,﹣2).【点评】此题考查了图形坐标的规律,正确理解图形运动坐标变化规律,得到点P的坐标是解题的关键.15.(2022秋•涡阳县校级月考)如图,一动点在第一象限内及x轴,y轴上运动,第一分钟,它从原点运动到(1,0),第二分钟,从(1,0)运动到(1,1),而后它接着按图中箭头所示在与x轴,y轴平行的方向来回运动,每分钟运动1个单位长度.第30分钟,动点所在的位置的坐标是.【分析】根据移动次数与点的坐标的所呈现的规律进行计算即可.【解答】解:根据移动的方向,距离所呈现的规律可得,当移动到点(1,0)时,对应的移动次数为1次,当移动到点(2,0)时,对应的移动次数为4+2×2=8次,当移动到点(3,0)时,对应的移动次数为8+1=9次,当移动到点(4,0)时,对应的移动次数为9+3×2+1+4×2=24次,当移动到点(5,0)时,对应的移动次数为24+1=25次,所以移动30次,所对应的点的坐标为(5,5),故答案为:(5,5).【点评】本题考查点的坐标,发现移动次数与点的坐标所呈现的规律是正确解答的关键.16.(2022•绥化三模)如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长度,点P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,﹣1),P5(﹣1,﹣1),P6(﹣1,2),…,根据这个规律,点P2022的坐标为.【分析】根据各个点的位置关系,可得出下标为4的倍数的点在第四象限,被4除余1的点在第三象限的角平分线上,被4除余2的点在第二象限,被4除余3的点在第一象限的角平分线上,点P2022的在第三象限,且横纵坐标的绝对值=2022÷4的商,纵坐标是2022÷4的商+1,再根据第三项象限内点的符号得出答案即可.【解答】解:∵2022÷4=505…2,∴点P2022在第二象限,∵P6(﹣1,2),P10(﹣2,3),P14(﹣3,4),…,6÷4=1…2,10÷4=2…2,14÷2=3..2,…,∴P2022(﹣505,506).故答案为:(﹣505,506).【点评】本题考查了规律型:点的坐标,是一个阅读理解,猜想规律的题目,解答此题的关键是首先确定点所在的大致位置,所在正方形,然后就可以进一步推得点的坐标.17.(2022秋•杏花岭区校级期中)在平面直角坐标系xOy中,对于点P(x,y),我们把点P1(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,⋯,A n,若点A1的坐标为(3,1),则点A2022的坐标为.【分析】根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2022除以4,根据商和余数的情况确定点A2022的坐标即可.【解答】解:∵A1的坐标为(3,1),∴A2(0,4),A3(﹣3,1),A4(0,﹣2),A5(3,1),…,依此类推,每4个点为一个循环组依次循环,∵2022÷4=505余2,∴点A2022的坐标与A2的坐标相同,为(0,4);故答案为:(0,4).【点评】此题考查点的坐标规律,读懂题目信息,理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键.18.(2022春•长安区校级期中)如图1,弹性小球从点P(0,3)出发,沿图中所示方向运动,每当小球碰到长方形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到长方形的边时,记为点P1,第2次碰到长方形的边时,记为点P2,…,第n次碰到长方形的边时,记为点P n,则点P3的坐标是;点P2022的坐标是.【分析】根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2022除以6,根据商和余数的情况确定所对应的点的坐标即可.【解答】解:如图,根据图形知点P3的坐标是(8,3),根据图形可以得到:每6次反弹为一个循环组依次循环,经过6次反弹后动点回到出发点(0,3),∵2022÷6=337,当点P第2021次碰到矩形的边时为第337个循环组的第6次反弹,点P的坐标为(0,3),故答案为:(8,3),(0,3).【点评】本题考查了矩形的性质、点的坐标的规律;作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.19.(2022春•五华区校级期中)如图,在直角坐标系中,长方形OABC的长为2,宽为1,将长方形OABC沿x轴翻转1次,点A落在A1处,翻转2次,点A落在A2处,翻转3次,点A落在A3处(点A3与点A2重合),翻转4次,点A落在A4处,以此类推…,若翻转2022次,点A落在A2022处,则A2022的坐标为.【分析】探究规律,利用规律解决问题即可.【解答】解:由题意A1(3,2),A2(A3)(5,0),A4(6,1),•••,发现4次一个循环,∵2022÷4=505.....2,∴A2022的纵坐标与A2相同,横坐标=505×6+5=3035,∴A2022(3035,0),故答案为:(3035,0).【点评】本题考查坐标与图形的变化﹣对称,规律型问题,解题的关键是学会探究规律的方法,属于中考填空题中的压轴题.20.(2022春•江岸区校级月考)如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点.其顺序按图中“→”方向依次排列:(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→…根据这个规律,第87个点的坐标为,第2022个点的坐标为.【分析】观察图形可知,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,并且右下角的点的横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当右下角的点横坐标是偶数时,以横坐标为1,纵坐标为右下角横坐标的偶数减1的点结束,根据此规律解答即可.【解答】解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,并且右下角的点的横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当右下角的点的横坐标是偶数时,以横坐标为1,纵坐标为右下角横坐标的偶数减1的点结束.例如:右下角的点的横坐标为1,共有1个,1=12,右下角的点的横坐标为2时,共有4个,4=22,右下角的点的横坐标为3时,共有9个,9=32,右下角的点的横坐标为4时,共有16个,16=42,......,右下角的点的横坐标为9时,共有92=81个,9是奇数,以横坐标为9,纵坐标为0的点结束,故第87个点的坐标为(10,5),右下角的点的横坐标为n时,共有n2个,∵452=2025,45是奇数,∴第2025个点是(45,0),∴第2020个点的坐标为(45,3)故答案为:(10,5),(45,3).【点评】本题考查了点的坐标的规律变化,观察出点的个数按照平方数的规律变化是解题的关键.三、解答题(共10题)21.(2022秋•无为市月考)在平面直角坐标系中,一个动点A从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次只移动1个单位长度,其行走路线如图所示.(1)填写下列各点的坐标:A4,A6,A12,A14.(2)按此规律移动,n为正整数,则点A4n的坐标为,点A4n+2的坐标为.(3)动点A从点A2022到点A2023的移动方向是.(填“向上”、“向右”或“向下”)【分析】(1)根据点的坐标变化即可填写各点的坐标;(2)根据(1)发现规律即可写出点A4n的坐标(n为正整数);(3)根据(2)发现的规律,每四个点一个循环,进而可得蜗牛从点A2020到点A2021的移动方向.【解答】解:(1)根据点的坐标变化可知:各点的坐标为:A4(2,0),A6(3,1),A12(6,0),A14(7,1);故答案为:(2,0),(3,1),(6,0),(7,1);(2)根据(1)发现:点A4n的坐标(n为正整数)为(2n,0);点A4n+2的坐标为(2n+1,1);故答案为:(2n,0),(2n+1,1);(3)因为每四个点一个循环,所以2023÷4=505…3.所以从点A2022到点A2023的移动方向是向下.故答案为:向下.【点评】本题考查了规律型﹣点的坐标,解决本题的关键是根据点的坐标变化发现规律,总结规律,运用规律.22.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0)…(1)填写下列各点的坐标:P9(、),P12(、),P15(、)(2)写出点P3n的坐标(n是正整数);(3)点P60的坐标是(、);(4)指出动点从点P210到点P211的移动方向.【分析】由题意可以知道,动点运动的速度是每次运动一个单位长度,(0,1)→(1,1)→(1,0)→(1,﹣1)……通过观察找到有规律的特殊点,如P3、P6、P9、P12,发现其中规律是脚标是3的倍数的点,依次排列在x轴上,且相距1个单位,明确这个规律即可解决以上所有问题.【解答】解:(1)由动点运动方向与长度可得P3(1,0),P6(2,0),可以发现脚标是3的倍数的点,依次排列在x轴上,且相距1个单位,即动点运动三次与横轴相交,故答案为P9(3,0),P12(4、0),P15(5、0).(2)由(1)可归纳总结点P3n的坐标为P3n(n,0),(n是正整数);(3)根据(2),∵60=3×20,∴点P60的横坐标是20故点P60的坐标是(20、0)故答案为(20、0).(4)∵210=3×70,符合(2)中的规律∴点P210在x轴上,又由图象规律可以发现当动点在x轴上时,偶数点向上运动,奇数点向下运动,而点P210是在x轴上的偶数点所以动点从点P210到点P211的移动方向应该是向上.【点评】本题是一个阅读理解,猜想规律的题目,解答此题的关键是首先确定动点移动的数字与方向上的规律,然后再进一步按规律解决要求的点的位置.23.(2021秋•长丰县期末)如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2、4、6、8、…,顶点依次用A1、A2、A3、A4、…表示.(1)请直接写出A5、A6、A7、A8的坐标;(2)根据规律,求出A2022的坐标.【分析】(1)看图观察即可直接写出答案;(2)根据正方形的性质找出部分A n点的坐标,根据坐标的变化找出变化规律“A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n 为自然数)”,依此即可得出结论.【解答】解:(1)A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2);(2)观察发现:A1(﹣1,﹣1),A2(﹣1,1),A3(1,1),A4(1,﹣1),A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2),A9(﹣3,﹣3),…,∴A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数),∵2022=505×4+2,∴A2022(﹣506,506).【点评】本题考查了规律型:点的坐标,解题的关键是找出变化规律“A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数)”.本题属于基础题,难度不大,解决该题型题目时,根据点的坐标的变化找出变化规律是关键.24.一个质点在第一象限及x轴、y轴移动,在第一秒时,它从原点移动到(0,1),然后按着下列左图中箭头所示方向移动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动1个单位.(1)该质点移动到(1,1)的时间为秒,移动到(2,2)的时间为秒,移动到(3,3)的时间为秒,…,移动到(n,n)的时间为秒.(2)该质点移动到(7,4)的时间为秒.【分析】(1)根据图形可得出质点移动到(1,1),(2,2),(3,3)的时间,根据规律可得出质点移动(n,n)的时间;(2)现有(1)的结论得出(7,7)的时间,再加上3即可得出移动到(7,4)的时间.【解答】解:(1)由图可知移动到(1,1)的时间为2秒,移动到(2,2)的时间为6秒,移动到(3,3)的时间为12秒,根据变化规律可得移动到(n,n)的时间为n(n+1),故答案为:2,6,12,n(n+1);(2)由(1)可得移动到(7,7)的时间为7×8=56,56+3=59,∴移动到(7,4)的时间为59秒,故答案为59.【点评】本题主要考查点的坐标的变化规律,关键是要能找到质点移动到(n,n)的时间的规律.25.(2022•马鞍山一模)如图,某小区绿化区的护栏是由两种大小不等的正方形间隔排列组成,将护栏的图案放在平面直角坐标系中.已知小正方形的边长为1,A1的坐标为(2,2),A2的坐标为(5,2).(1)A3的坐标为,A n的坐标为用含n的代数式表示;(2)若护栏长为2020,则需要小正方形个,大正方形个.【分析】(1)根据已知条件与图形可知,大正方形的对角线长为2,由此可得规律:A1,A 2,A 3,…,A n 各点的纵坐标均为2,横坐标依次大3,由此便可得结果;(2)先求出一个小正方形与一个大正方形所构成的护栏长度,再计算2020米包含多少这样的长度,进而便可求出结果.【解答】解:(1)∵A 1的坐标为(2,2)、A 2的坐标为(5,2),∴A 1,A 2,A 3,…,A n 各点的纵坐标均为2,∵小正方形的边长为1,∴A 1,A 2,A 3,…,A n 各点的横坐标依次大3,∴A 3(5+3,2),A n (2+3+3+⋅⋅⋅+3︸(K1)个3,2),即A 3(8,2),A n (3n ﹣1,2),故答案为(8,2);(3n ﹣1,2);(2)∵2020÷3=673…1,∴需要小正方形674个,大正方形673个.【点评】本题是点的坐标的规律题,首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.26.如图,在直角坐标系中,第一次将△OAB 变换成△OA 1B 1,第二次将△OA 1B 1变成△OA 2B 2,第三次将△OA 2B 2变成△OA 3B 3,已知A (1,5),A 1(2,5),A 2(4,5),A 3(8,5);B (2,0),B 1(4,0),B 2(8,0),B 3(16,0).(1)观察每次变换前后三角形有何变化,找出规律.按此规律将△OA 3B 3变成△OA 4B 4,则A 4的坐标是,B 4的坐标是.(2)若按第(1)题中找到的规律将△OAB 进行n 次变换,得到△OA n B n ,比较每次变换中三角形顶点的坐标有何变化,找出规律,推测A n 的坐标是,B n 的坐标是.【分析】(1)对于A 1,A 2,A n 坐标找规律可将其写成竖列,比较从而发现A n 的横坐标为2n ,而纵坐标都是5,同理B 1,B 2,B n 也一样找规律.(2)根据第一问得出的A 4的坐标和B 4的坐标,再此基础上总结规律即可知A n 的坐标是(2n ,5),B n 的坐标是(2n +1,0).【解答】解:(1)因为A(1,5),A1(2,5),A2(4,5),A3(8,5)…纵坐标不变为5,同时横坐标都和2有关,为2n,那么A4(16,5);因为B(2,0),B1(4,0),B2(8,0),B3(16,0)…纵坐标不变,为0,同时横坐标都和2有关为2n+1,那么B的坐标为B4(32,0);故答案为:(16,5),(32,0);(2)由上题第一问规律可知A n的纵坐标总为5,横坐标为2n,B n的纵坐标总为0,横坐标为2n+1,∴A n的坐标是(2n,5),B n的坐标是(2n+1,0).故答案为:(2n,5),(2n+1,0).【点评】本题考查了学生观察图形及总结规律的能力,涉及的知识点为:平行于x轴的直线上所有点纵坐标相等,x轴上所有点的纵坐标为0.27.小明在学习了平面直角坐标系后,突发奇想,画出了这样的图形(如图),他把图形与x轴正半轴的交点依次记作A1(1,0),A2(5,0),…A n,图形与y轴正半轴的交点依次记作B1(0,2),B2(0,6),…B n,图形与x轴负半轴的交点依次记作C1(﹣3,0),C2(﹣7,0),…∁n,图形与y轴负半轴的交点依次记作D1(0,﹣4),D2(0,﹣8),…D n,发现其中包含了一定的数学规律.请根据你发现的规律完成下列题目:(1)请分别写出下列点的坐标:A3,B3,C3,D3;(2)请分别写出下列点的坐标:A n,B n,∁n,D n;(3)请求出四边形A5B5C5D5的面积.【分析】(1)根据点的坐标规律解答即可;(2)根据点的坐标规律解答即可;(3)根据四边形A5B5C5D5的面积=△5B5+△5B5+△5B5+△5B5计算即可.【解答】解:(1)A3(9,0),B3(0,10),C3(﹣11,0),D3(0,﹣12).(2)A n(4n﹣3,0),B n(0,4n﹣2),∁n(﹣4n+1,0),D n(0,﹣4n).(3)∵A5(17,0),B5(0,18),C5(﹣19,0),D5(0,﹣20).∴四边形A5B5C5D5的面积=△5B5+△5B5+△5B5+△5B5=12×17×18+12×18×19+12×19×20+12×20×17=684.故答案为:A3(9,0),B3(0,10),C3(﹣11,0),D3(0,﹣12).A n(4n﹣3,0),B n(0,4n﹣2),∁n(﹣4n+1,0),D n(0,﹣4n).【点评】此题考查点的坐标,关键是根据图形得出点的坐标的规律进行分析.28.(2021春•自贡期末)综合与实践问题背景:(1)已知A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出这几个点,并分别找到线段AB和CD中点P1、P2,然后写出它们的坐标,则P1,P2.探究发现:(2)结合上述计算结果,你能发现若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为.拓展应用:(3)利用上述规律解决下列问题:已知三点E(﹣1,2),F(3,1),G(1,4),第四个点H(x,y)与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.【分析】(1)根据坐标的确定方法直接描点,:分别读出各点的纵横坐标,即可得到各中点的坐标;(2)根据(1)中的坐标与中点坐标找到规律;(3)利用(2)中的规律进行分类讨论即可答题.【解答】解:(1)如图:A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出它们如下:线段AB和CD中点P1、P2的坐标分别为(2,2)、(﹣1,﹣2)故答案为:(2,2)、(﹣1,﹣2).(2)若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为(1+22,1+22).故答案为:(1+22,1+22).(3)∵E(﹣1,2),F(3,1),G(1,4),∴EF、FG、EG的中点分别为:(1,32)、(2,52)、(0,3)∴①HG过EF中点(1,32)时,r12=1,r42=32解得:x=1,y=﹣1,故H(1,﹣1);②EH过FG中点(2,52)时,−1+2=2,2+2=52解得:x=5,y=3,故H(5,3);③FH过EG的中点(0,3)时,3+2=0,1+2=3解得:x=﹣3,y=5,故H(﹣3,5).∴点H的坐标为:(1,﹣1),(5,3),(﹣3,5).【点评】本题考查了坐标与图形性质.通过此题,要熟记平面直角坐标系中线段中点的横坐标为对应线段的两个端点的横坐标的平均数,中点的纵坐标为对应线段的两个端点的纵坐标的平均数.29.(2022•包河区二模)如图,在平面直角坐标系中,点A1的坐标为(1,0)、点A2的坐标为(2,0)、点A3的坐标为(3,0)、…,过点A1、A2、A3、…分别作x轴垂线,交直线y=x于点B1、B2、B3、…,△OA1B1覆盖的整点(横、纵坐标均为整数的点)的个数记为P1,面积的值记为S1;△OA2B2覆盖的整点的个数记为P2,面积的值记为S2;△OA3B3覆盖的整点的个数记为P3,面积的值记为S3;…(1)由题意可知:P1=3、S1=12;P2=6、S2=2;P3=10、S3=92;则P4=、S4=;(2)P7﹣S7=;。
七年级平面直角坐标系动点问题专项练习
平面直角坐标系动点问题1、已知点A 的坐标是(3,0)、AB=5,(1)当点B 在X AB OAP x P 1232008P P P P,,,,2008P x ABDC S 四边形PAB S ∆ABDC S 四边形DCP BOP CPO ∠+∠∠DCP CPO BOP ∠+∠∠20b -=OHC ACEOEC ∠+∠∠035=-+-b a (1)求长方形ABCD 的面积.(2)如图2,长方形ABCD 以每秒1个单位长度的速度向右平移,同时点E 从原点O 出发沿x 轴以每秒2 个单位长度的速度向右运动,设运动时间为t 秒.①当t=4时,直接写出三角形OAC 的面积为 ;② 若AC ∥ED ,求t 的值;(3)在平面直角坐标系中,对于点()P x y ,,我们把点(11)P y x '-++,叫做点P 的伴随点,已知点1A 的伴随点为2A ,点2A 的伴随点为3A ,点3A 的伴随点为4A ,…,这样依次得到点1A ,2A ,3A ,…,n A .①若点1A 的坐标为(3,1),则点3A 的坐标为 ,点2014A 的坐标为 ;②若点1A 的坐标为(a ,b ),对于任意的正整数n ,点n A 均在x 轴上方,则a ,b 应满足的条件为 .探究案【例1】如图,在平面直角坐标中,A (0,1),B (2,0),C (2,).(1)求△ABC 的面积;(2)如果在第二象限内有一点P (a ,),试用a 的式子表示四边形ABOP 的面积;(3)在(2)的条件下,是否存在这样的点P ,使四边形ABOP 的面积与△ABC 的面积相等?若存在,求出点P 的坐标,若不存在,请说明理由.【例2】在平面直角坐标系中,已知A (-3,0),B (-2,-2),将线段AB 平移至线段CD ,连AC 、BD .(1)如图1,直接写出图中相等的线段,平行的线段;(2)如图2,若线段AB 移动到CD ,C 、D 两点恰好都在坐标轴上,求C 、D 的坐标;(3)若点C 在y 轴的正半轴上,点D 在第一象限内,且S △ACD =5,求C 、D 的坐标;(4)在y 轴上是否存在一点P ,使线段AB 平移至线段PQ 时,由A 、B 、P 、Q 构成的四边形是平行四边形面积为10,若存在,求出P 、Q 的坐标,若不存在,说明理由;【例3】如图,△ABC 的三个顶点位置分别是A (1,0),B (-2,3),C (-3,0).(1)求△ABC 的面积;(2)若把△ABC 向下平移2个单位长度,再向右平移3个单位长度,得到△A B C ''',请你在图中画出△A B C ''';(3)若点A 、C 的位置不变,当点P 在y 轴上什么位置时,使2ACP ABCS S =V V ; (4)若点B 、C 的位置不变,当点Q 在x 轴上什么位置时,使2BCQ ABCS S =V V . 【例4】如图1,在平面直角坐标系中,A (a ,0),C (b ,2),且满足2(2)20a b ++-=,过C作CB ⊥x 轴于B .(1)求三角形ABC 的面积; (2)若过B 作BD ∥AC 交y 轴于D ,且AE ,DE 分别平分∠CAB ,∠ODB ,如图2,求∠AED 的度数;(3)在y 轴上是否存在点P ,使得三角形ABC 和三角形ACP 的面积相等,若存在,求出P 点坐标;若不存在,请说明理由.训练案1、如图,在平面直角坐标系中,四边形ABCD 各顶点的坐标分别是A (0,0),B (7,0),C (9,5),D (2,7)(1)在坐标系中,画出此四边形;(2)求此四边形的面积;(3)在坐标轴上,你能否找一个点P ,使S △PBC =50,若能,求出P 点坐标,若不能,说明理由.2、如图,A 点坐标为(-2, 0), B 点坐标为(0, -3).(1)作图,将△ABO 沿x 轴正方向平移4个单位, 得到△DEF , 延长ED 交y 轴于C 点, 过O 点作OG ⊥CE , 垂足为G ;(2) 在(1)的条件下, 求证: ∠COG =∠EDF ;(3)求运动过程中线段AB 扫过的图形的面积.3、在平面直角坐标系中,点B (0,4),C (-5,4),点A 是x 轴负半轴上一点,S 四边形AOBC =24.(1)线段BC 的长为 ,点A 的坐标为 ; (2)如图1,EA 平分∠CAO ,DA 平分∠CAH ,CF ⊥AE点F ,试给出∠ECF 与∠DAH 之间满足的数量关系式,并说明理由;(3)若点P 是在直线CB 与直线AO 之间的一点,连接BP 、OP ,BN 平分CBP ∠,ON 平分AOP ∠,BN 交ON 于N ,请依题意画出图形,给出BPO ∠与BNO ∠之间满足的数量关系式,并说明理由.4、在平面直角坐标系中,OA =4,OC =8,四边形ABCO 是平行四边形.(1)求点B 的坐标及的面积ABCO S 四边形;(2)若点P 从点C 以2单位长度/秒的速度沿CO 方向移动,同时点Q 从点O 以1单位长度/秒的速度沿OA 方向移动,设移动的时间为t 秒,△AQB 与△BPC 的面积分别记为AQB S ∆,BPC S ∆,是否存在某个时间,使AQB S ∆=3OQBPS 四边形,若存在,求出t 的值,若不存在,试说明理由;(3)在(2)的条件下,四边形QBPO 的面积是否发生变化,若不变,求出并证明你的结论,若变化,求出变化的范围.5、如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D 连结AC ,BD .(1)求点C ,D 的坐标及四边形ABDC 的面积S 四边形ABDC ;(2)在y 轴上是否存在一点P ,连结PA ,PB ,使S △PAB =S △PDB ,若存在这样一点,求出点P 点坐标,若不存在,试说明理由;(3)若点Q 自O 点以个单位/s 的速度在线段AB 上移动,运动到B 点就停止,设移动的时间为t 秒,(1)是否是否存在一个时刻,使得梯形CDQB 的面积是四边形ABCD 面积的三分之一?(4)是否是否存在一个时刻,使得梯形CDQB 的面积等于△ACO 面积的二分之一?6、在直角坐标系中,△ABC 的顶点A (—2,0),B (2,4),C (5,0).(1)求△ABC 的面积(2)点D 为y 负半轴上一动点,连BD 交x 轴于E ,是否存在点D 使得ADE BCE S S ∆∆=?若存在,请求出点D 的坐标;若不存在,请说明理由.A yxO C B A(-2,0)B(0,-3)y x 0(3)点F (5,n )是第一象限内一点,,连BF ,CF ,G 是x 轴上一点,若△ABG 的面积等于四边形ABDC 的面积,则点G 的坐标为 (用含n 的式子表示)2016年初中数学组卷 一.选择题(共8小题)1.(2016春?北流市校级期中)已知点P (0,a )在y 轴的负半轴上,则点Q (﹣a 2﹣1,﹣a+1)在( )A .第一象限B .第二象限C .第三象限D .第四象限2.(2016春?邵阳县校级月考)已知点P (x ,y )的坐标满足|x|=3,=2,且xy <0,则点P 的坐标是( )A .(3,﹣2)B .(﹣3,2)C .(3,﹣4)D .(﹣3,4)3.(2015?重庆)在平面直角坐标系中,若点P 的坐标为(﹣3,2),则点P 所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限4.(2015?台湾)已知直线L 的方程式为x=3,直线M 的方程式为y=﹣2,判断下列何者为直线L 、直线M 画在坐标平面上的图形?( ) A . B . C . D .5.(2015?安顺)点P (﹣2,﹣3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )A .(﹣3,0)B .(﹣1,6)C .(﹣3,﹣6)D .(﹣1,0)6.(2015?钦州)在平面直角坐标系中,将点A (x ,y )向左平移5个单位长度,再向上平移3个单位长度后与点B (﹣3,2)重合,则点A 的坐标是( )A .(2,5)B .(﹣8,5)C .(﹣8,﹣1)D .(2,﹣1)7.(2015春?鄂州校级期中)如图,一个粒子在第一象限和x ,y 轴的正半轴上运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x 轴、y 轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…)且每秒运动一个单位长度,那么2010秒时,这个粒子所处位置为( )A .(14,44)B .(15,44)C .(44,14)D .(44,15)8.(2015?宝应县校级模拟)点P (m+3,m ﹣1)在x 轴上,则点P 的坐标为( )A .(0,﹣2)B .(2,0)C .(4,0)D .(0,﹣4)二.填空题(共8小题)9.(2015?青岛)如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别变为原来的,那么点A 的对应点A′的坐标是 .10.(2015?曲靖二模)如图所示,在平面直角坐标系中,一动点从原点O 出发,按向上,向右,向下,向右的方向不断移动,每移动一个单位,得到点A 1(0,1)、A 2(1,1)、A 3(1,0)、A 4(2,0),…,那么点A 2015的坐标为 .11.(2014春?洛龙区校级期中)已知点O (0,0),B (1,2),点A 在坐标轴上,且S △OAB =2,则满足条件的点A 的坐标为 .12.(2014春?信州区校级期中)已知AB ∥x 轴,且AB=3,若点A 的坐标是(﹣1,2),则B 点的坐标是 .F A O C Byx13.(2014春?朝阳区校级期中)已知:点A(0,5),B(0,2),在坐标轴上找点C,使△ABC的面积为5,则点C的坐标是.14.(2014秋?靖江市校级期中)在平面直角坐标系中,若点M(﹣2,6)与点N(x,6)之间的距离是3,则x的值是.15.(2014春?江岸区期中)在平面直角坐标系中,一个长方形的三个顶点坐标分别为(﹣1,﹣1),(﹣1,1),(5,﹣1),则第四个顶点的坐标是.16.(2014春?鼓楼区校级期中)已知A(2,﹣6),B(2,﹣4),那么线段AB=.三.解答题(共14小题)17.(2015?赣州校级模拟)在如图所示的平面直角坐标系中描出下面各点:A(0,3);B(1,﹣3);C(3,﹣5);D(﹣3,﹣5);E(3,5);F(5,7);G(5,0).(1)将点C向x轴的负方向平移6个单位,它与点重合.(2)连接CE,则直线CE与y轴是什么关系?(3)顺次连接D、E、G、C、D得到四边形DEGC,求四边形DEGC的面积.18.(2015春?伊春校级期末)(1)在坐标平面内画出点P(2,3).(2)分别作出点P关于x轴、y轴的对称点P1,P2,并写出P1,P2的坐标.19.(2015秋?兴平市期末)若x,y为实数,且满足|x﹣3|+=0.(1)如果实数x,y对应为平面直角坐标系上的点A(x,y),则点A在第几象限?(2)求()2015的值?20.(2015春?平南县期末)在平面直角坐标系中,点A(a,3﹣2a)在第一象限.(1)若点A到x轴的距离与到y轴的距离相等,求a的值;(2)若点A到x轴的距离小于到y轴的距离,求a的取值范围.21.(2015秋?双柏县期末)如图,A、B两点的坐标分别是(2,﹣3)、(﹣4,﹣3).(1)请你确定P(4,3)的位置;(2)请你写出点Q的坐标.22.(2015秋?沭阳县校级期末)如图,已知A(﹣2,3)、B(4,3)、C(﹣1,﹣3)(1)求点C到x轴的距离;(2)求△ABC的面积;(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.23.(2015春?博兴县期末)在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0),B (5,0),C(3,3),D(2,4).(1)求线段AB的长;(2)求四边形ABCD的面积.24.(2015春?丹江口市期末)(1)已知两点A(﹣3,m),B(n,4),若AB∥x轴,求m的值,并确定n的范围;(2)若点(5﹣a,a﹣3)在第一、三象限的角平分线上,求a的值.25.(2015秋?埇桥区期末)已知点A(m+2,3)和点B(m﹣1,2m﹣4),且AB∥x轴.(1)求m的值;(2)求AB的长.26.(2015春?建昌县期末)已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B 在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动).(1)写出B点的坐标();(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.27.(2015春?文安县期末)如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A、B的坐标:A(,)、B(,)(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).(3)△ABC的面积为.28.(2015春?北京校级期中)我们规定以下三种变换:(1)f(a,b)=(﹣a,b).如:f(1,3)=(﹣1,3);(2)g(a,b)=(b,a).如:g(1,3)=(3,1);(3)h(a,b)=(﹣a,﹣b).如:h(1,3)=(﹣1,﹣3).按照以上变换有:f(g(2,﹣3))=f(﹣3,2)=(3,2),求f(h(5,﹣3))的值.29.(2015春?繁昌县期中)已知点A(1+2a,4a﹣5),且点A到两坐标轴的距离相等,求点A的坐标.30.(2015秋?务川县校级期中)平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4)B(2,4)C(3,﹣1).(1)试在平面直角坐标系中,标出A、B、C三点;(2)求△ABC的面积.(3)若△DEF与△ABC关于x轴对称,写出D、E、F的坐标.参考答案一.选择题(共8小题)1.B;2.D;3.B;4.B;5.A;6.D;7.A;8.C;二.填空题(共8小题)9.(2,3);10.(1007,0);11.(2,0)或(-2,0)或(0,4)或(0,-4); 12.(-4,2)或(2,2);13.(,0)或(-,0);14.1或-5;15.(5,1);16.2;三.解答题(共14小题)17.D;(-3,-5);18.;19.;20.;21.;22.;23.;24.;25.;26.(4,6);27.2;-1; 4;3;0;0;2;4;-1; 3;5;28.;29.;30.;。
七年级平面直角坐标系动点问题专项练习
平面直角坐标系动点问题1、已知点A 的坐标是(3,0)、AB=5,(1)当点B 在X 轴上时、求点B 的坐标、(2)当AB OAP x P 1232008P P P P ,,,,2008P xABDC S 四边形PAB S ∆ABDCS 四边形DCP BOP CPO ∠+∠∠DCP CPOBOP∠+∠∠20b -=OHC ACEOEC∠+∠∠035=-+-b a (1)求长方形ABCD 的面积.(2)如图2,长方形ABCD 以每秒1个单位长度的速度向右平移,同时点E 从原点O 出发沿x 轴以每秒2 个单位长度的速度向右运动,设运动时间为t 秒. ①当t=4时,直接写出三角形OAC 的面积为 ; ② 若AC ∥ED ,求t 的值;(3)在平面直角坐标系中,对于点()P x y ,,我们把点(11)P y x '-++,叫做点P 的伴随点,图6-724题图2 24题图1已知点1A 的伴随点为2A ,点2A 的伴随点为3A ,点3A 的伴随点为4A ,…,这样依次得到点1A ,2A ,3A ,…,n A .①若点1A 的坐标为(3,1),则点3A 的坐标为 ,点2014A 的坐标为 ; ②若点1A 的坐标为(a ,b ),对于任意的正整数n ,点n A 均在x 轴上方,则a ,b 应满足的条件为 .探究案【例1】如图,在平面直角坐标中,A (0,1),B (2,0),C (2,). (1)求△ABC 的面积;(2)如果在第二象限内有一点P (a ,),试用a 的式子表示四边形ABOP 的面积;(3)在(2)的条件下,是否存在这样的点P ,使四边形ABOP 的面积与△ABC 的面积相等?若存在,求出点P 的坐标,若不存在,请说明理由.【例2】在平面直角坐标系中,已知A (-3,0),B (-2,-2),将线段AB 平移至线段CD ,连AC 、BD .(1)如图1,直接写出图中相等的线段,平行的线段;(2)如图2,若线段AB 移动到CD ,C 、D 两点恰好都在坐标轴上,求C 、D 的坐标;(3)若点C 在y 轴的正半轴上,点D 在第一象限内,且S △ACD =5,求C 、D 的坐标;(4)在y 轴上是否存在一点P ,使线段AB 平移至线段PQ 时,由A 、B 、P 、Q 构成的四边形是平行四边形面积为10,若存在,求出P 、Q 的坐标,若不存在,说明理由;【例3】如图,△ABC 的三个顶点位置分别是A (1,0),B (-2,3),C (-3,0). (1)求△ABC 的面积;(2)若把△ABC 向下平移2个单位长度,再向右平移3个单位长度,得到△A B C ''',请你在图中画出△A B C ''';(3)若点A 、C 的位置不变,当点P 在y 轴上什么位置时,使2ACP ABC S S =V V ;(4)若点B 、C 的位置不变,当点Q 在x 轴上什么位置时,使2BCQ ABC S S =V V .【例4】如图1,在平面直角坐标系中,A (a ,0),C (b ,2),且满足2(2)0a +=,过C 作CB ⊥x 轴于B .(1)求三角形ABC 的面积;(2)若过B 作BD ∥AC 交y 轴于D ,且AE ,DE 分别平分∠CAB ,∠ODB ,如图2,求∠AED 的度数;(3)在y 轴上是否存在点P ,使得三角形ABC 和三角形ACP 的面积相等,若存在,求出P 点坐标;若不存在,请说明理由.训练案1、如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别是A(0,0),B(7,0),C(9,5),D(2,7)(1)在坐标系中,画出此四边形;(2)求此四边形的面积;(3)在坐标轴上,你能否找一个点P,使S△PBC=50,若能,求出P点坐标,若不能,说明理由.2、如图,A点坐标为(-2, 0),B点坐标为(0,-3).(1)作图,将△ABO沿x轴正方向平移4个单位,得到△DEF,延长ED交y轴于C点,过O点作OG⊥CE,垂足为G;(2) 在(1)的条件下,求证: ∠COG=∠EDF;(3)求运动过程中线段AB扫过的图形的面积.3、在平面直角坐标系中,点B (0,4),C (-5,4),点A 是x 轴负半轴上一点,S 四边形AOBC =24.(1)线段BC 的长为 ,点A 的坐标为 ;(2)如图1,EA 平分∠CAO ,DA 平分∠CAH ,CF⊥AE 点F ,试给出∠ECF 与∠DAH 之间满足的数量关系式,并说明理由;(3)若点P 是在直线CB 与直线AO 之间的一点,连接BP 、OP ,BN 平分CBP ∠,ON 平分AOP ∠,BN 交ON 于N ,请依题意画出图形,给出BPO ∠与BNO ∠之间满足的数量关系式,并说明理由.4、在平面直角坐标系中,OA =4,OC =8,四边形ABCO 是平行四边形.(1)求点B 的坐标及的面积ABCO S 四边形;(2)若点P 从点C 以2单位长度/秒的速度沿CO 方向移动,同时点Q 从点O 以1单位长度/秒的速度沿OA 方向移动,设移动的时间为t 秒,△AQB 与△BPC 的面积分别记为AQB S ∆,BPC S ∆,是否存在某个时间,使AQB S ∆=3OQBPS 四边形,若存在,求出t 的值,若不存在,试说明理由;(3)在(2)的条件下,四边形QBPO 的面积是否发生变化,若不变,求出并证明你的结论,若变化,求出变化的范围.5、如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D 连结AC ,BD .(1)求点C ,D 的坐标及四边形ABDC 的面积S 四边形ABDC ;(2)在y 轴上是否存在一点P ,连结PA ,PB ,使S △PAB =S △PDB ,若存在这样一点,求出点P 点坐标,若不存在,试说明理由;(3)若点Q 自O 点以个单位/s 的速度在线段AB 上移动,运动到B 点就停止,设移动的时间为t 秒,(1)是否是否存在一个时刻,使得梯形CDQB 的面积是四边形ABCD 面积的三分之一?(4)是否是否存在一个时刻,使得梯形CDQB 的面积等于△ACO 面积的二分之一?6、在直角坐标系中,△ABC 的顶点A (—2,0),B (2,4),C (5,0). (1)求△ABC 的面积(2)点D 为y 负半轴上一动点,连BD 交x 轴于E ,是否存在点D 使得ADE BCE S S ∆∆=?若存在,请求出点D 的坐标;若不存在,请说明理由.(3)点F(5,n)是第一象限内一点,,连BF,CF,G是x轴上一点,若△ABG的面积等于四边形ABDC的面积,则点G的坐标为(用含n的式子表示)2016年初中数学组卷一.选择题(共8小题)1.(2016春?北流市校级期中)已知点P(0,a)在y轴的负半轴上,则点Q(﹣a2﹣1,﹣a+1)在()A.第一象限 B.第二象限 C.第三象限 D.第四象限2.(2016春?邵阳县校级月考)已知点P(x,y)的坐标满足|x|=3,=2,且xy<0,则点P 的坐标是()A.(3,﹣2)B.(﹣3,2)C.(3,﹣4)D.(﹣3,4)3.(2015?重庆)在平面直角坐标系中,若点P的坐标为(﹣3,2),则点P所在的象限是()A.第一象限 B.第二象限 C.第三象限 D.第四象限4.(2015?台湾)已知直线L的方程式为x=3,直线M的方程式为y=﹣2,判断下列何者为直线L、直线M画在坐标平面上的图形?()A. B. C. D.5.(2015?安顺)点P(﹣2,﹣3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为()A.(﹣3,0)B.(﹣1,6)C.(﹣3,﹣6)D.(﹣1,0)6.(2015?钦州)在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(﹣3,2)重合,则点A的坐标是()A.(2,5)B.(﹣8,5)C.(﹣8,﹣1)D.(2,﹣1)7.(2015春?鄂州校级期中)如图,一个粒子在第一象限和x,y轴的正半轴上运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…)且每秒运动一个单位长度,那么2010秒时,这个粒子所处位置为()A.(14,44)B.(15,44)C.(44,14)D.(44,15)8.(2015?宝应县校级模拟)点P(m+3,m﹣1)在x轴上,则点P的坐标为()A.(0,﹣2)B.(2,0)C.(4,0)D.(0,﹣4)二.填空题(共8小题)9.(2015?青岛)如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别变为原来的,那么点A的对应点A′的坐标是.10.(2015?曲靖二模)如图所示,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0),…,那么点A2015的坐标为.11.(2014春?洛龙区校级期中)已知点O(0,0),B(1,2),点A在坐标轴上,且S△OAB=2,则满足条件的点A的坐标为.12.(2014春?信州区校级期中)已知AB∥x轴,且AB=3,若点A的坐标是(﹣1,2),则B 点的坐标是.13.(2014春?朝阳区校级期中)已知:点A(0,5),B(0,2),在坐标轴上找点C,使△ABC 的面积为5,则点C的坐标是.14.(2014秋?靖江市校级期中)在平面直角坐标系中,若点M(﹣2,6)与点N(x,6)之间的距离是3,则x的值是.15.(2014春?江岸区期中)在平面直角坐标系中,一个长方形的三个顶点坐标分别为(﹣1,﹣1),(﹣1,1),(5,﹣1),则第四个顶点的坐标是.16.(2014春?鼓楼区校级期中)已知A(2,﹣6),B(2,﹣4),那么线段AB= .三.解答题(共14小题)17.(2015?赣州校级模拟)在如图所示的平面直角坐标系中描出下面各点:A(0,3);B(1,﹣3);C(3,﹣5);D(﹣3,﹣5);E(3,5);F(5,7);G(5,0).(1)将点C向x轴的负方向平移6个单位,它与点重合.(2)连接CE,则直线CE与y轴是什么关系?(3)顺次连接D、E、G、C、D得到四边形DEGC,求四边形DEGC的面积.18.(2015春?伊春校级期末)(1)在坐标平面内画出点P(2,3).(2)分别作出点P关于x轴、y轴的对称点P1,P2,并写出P1,P2的坐标.19.(2015秋?兴平市期末)若x,y为实数,且满足|x﹣3|+=0.(1)如果实数x,y对应为平面直角坐标系上的点A(x,y),则点A在第几象限?(2)求()2015的值?20.(2015春?平南县期末)在平面直角坐标系中,点A(a,3﹣2a)在第一象限.(1)若点A到x轴的距离与到y轴的距离相等,求a的值;(2)若点A到x轴的距离小于到y轴的距离,求a的取值范围.21.(2015秋?双柏县期末)如图,A、B两点的坐标分别是(2,﹣3)、(﹣4,﹣3).(1)请你确定P(4,3)的位置;(2)请你写出点Q的坐标.22.(2015秋?沭阳县校级期末)如图,已知A(﹣2,3)、B(4,3)、C(﹣1,﹣3)(1)求点C到x轴的距离;(2)求△ABC的面积;(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.23.(2015春?博兴县期末)在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0),B(5,0),C(3,3),D(2,4).(1)求线段AB的长;(2)求四边形ABCD的面积.24.(2015春?丹江口市期末)(1)已知两点A(﹣3,m),B(n,4),若AB∥x轴,求m的值,并确定n的范围;(2)若点(5﹣a,a﹣3)在第一、三象限的角平分线上,求a的值.25.(2015秋?埇桥区期末)已知点A(m+2,3)和点B(m﹣1,2m﹣4),且AB∥x轴.(1)求m的值;(2)求AB的长.26.(2015春?建昌县期末)已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动).(1)写出B点的坐标();(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.27.(2015春?文安县期末)如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A、B的坐标:A(,)、B(,)(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).(3)△ABC的面积为.28.(2015春?北京校级期中)我们规定以下三种变换:(1)f(a,b)=(﹣a,b).如:f(1,3)=(﹣1,3);(2)g(a,b)=(b,a).如:g(1,3)=(3,1);(3)h(a,b)=(﹣a,﹣b).如:h(1,3)=(﹣1,﹣3).按照以上变换有:f(g(2,﹣3))=f(﹣3,2)=(3,2),求f(h(5,﹣3))的值.29.(2015春?繁昌县期中)已知点A(1+2a,4a﹣5),且点A到两坐标轴的距离相等,求点A的坐标.30.(2015秋?务川县校级期中)平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4)B(2,4)C(3,﹣1).(1)试在平面直角坐标系中,标出A、B、C三点;(2)求△ABC的面积.(3)若△DEF与△ABC关于x轴对称,写出D、E、F的坐标.2016年04月05日44的初中数学组卷参考答案一.选择题(共8小题)1.B;2.D;3.B;4.B;5.A;6.D;7.A;8.C;二.填空题(共8小题)9.(2,3); 10.(1007,0); 11.(2,0)或(-2,0)或(0,4)或(0,-4);12.(-4,2)或(2,2); 13.(,0)或(-,0);14.1或-5;15.(5,1);16.2;三.解答题(共14小题)17.D;(-3,-5); 18.;19.;20.;21.;22.;23.;24.;25.;26.(4,6);27.2; -1;4; 3; 0; 0; 2; 4; -1;3; 5; 28.;29.;30.;。
平面直角坐标系动点问题综合专题
教案纸科目名称数学审批意见:课 题平面直角坐标系中动点综合类专题学生姓名任课教师 学生年级 初一授 课 日 期 授 课 形 式□AA □AB教学目的:1、深刻理解平面直角坐标系的应用 2、掌握一般型动点问题的分类讨论思维及方法教学重点:动点问题分类讨论思想教学难点:动点问题分类讨论思想1、已知点A 的坐标是(3,0)、AB=5,(1)当点B 在X 轴上时、求点B 的坐标、(2)当AB//y 轴时、求点B 的坐标2、如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次,点P 依次落在点1232008P P P P ,,,,的位置,则点2008P 的横坐标为?L L1PAOyxPDC 3-1BA Oxy3、如图6-7,已知A 、B 两村庄的坐标分别为(2,2)、(7,4),一辆汽车在x 轴上行驶,从原点O 出发.(1)汽车行驶到什么位置时离A 村最近?写出此点的坐标. (2)汽车行驶到什么位置时离B 村最近?写出此点的坐标.(3)在x 轴上存在一点C(10,0),当汽车行驶到P 点时,三角形AOP 与三角形BPC 的面积相等,求出P 点坐标及面积?4.如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD . (1)求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形(2)在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S =ABDC S 四边形, 若存在这样一点,求出点P 的坐标,若不存在,试说明理由.8642-2-5510BA图6-7PDCBAOx y (3)在y 轴上是否存在一点P ,连结PA ,PB ,使S △PAB =S △PDB ,若存在这样一点,求出点P 点坐标,若不存在,试说明理由;(4)若点Q 自O 点以0.5个单位/s 的速度在线段AB 上移动,运动到B 点就停止,设移动的时间为t 秒,是否是否存在一个时刻,使得梯形CDQB 的面积是四边形ABCD 面积的三分之一?QDC3-1B A oxy(5)是否是否存在一个时刻,使得梯形CDQB 的面积等于△ACO 面积的二分之一?(6)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时(不与B ,D 重合)给出下列结论:①DCP BOP CPO ∠+∠∠的值不变,②DCP CPOBOP∠+∠∠的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.DC 3-1BA oxy5、如图,在平面直角坐标系中,已知点A (-5,0),B (5,0),D (2,7), (1)求C 点的坐标; (2)动点P 从B 点出发以每秒1个单位的速度沿BA 方向运动,同时动点Q 从C 点出发也以每秒1个单位的速度沿y 轴正半轴方向运动(当P 点运动到A 点时,两点都停止运动)。
完整版)初一平面直角坐标系动点问题(经典难题)

完整版)初一平面直角坐标系动点问题(经典难题)一)找规律1.如图1,一只跳蚤在第一象限及x轴、y轴上跳动。
在第一秒钟,它从原点跳动到(0,1),然后按照箭头所示方向跳动(即(0,0)→(0,1)→(1,1)→(1,0)→…),每秒跳动一个单位。
那么第35秒时跳蚤所在位置的坐标是(4,1),因此答案为A。
2.如图2,所有正方形的中心都在坐标原点,且各边与x轴或y轴平行。
从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示。
顶点A55的坐标是(54,54),因此答案为A。
3.如图3,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列。
根据这个规律,第2015个点的横坐标为1,因此答案为A。
4.在平面直角坐标系中,一只蚂蚁从原点O出发,按照向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图3所示。
1)填写下列各点的坐标:A1(0,1),A3(2,1),A12(6,﹣2);2)点A4n的坐标为(2n,﹣2n+1);3)蚂蚁从点A100到A101的移动方向为向上。
5.观察下列有序数对:(3,﹣1),(﹣5,0),(7,﹣1),(﹣9,0),…根据你发现的规律,第100个有序数对是(195,﹣1)。
6.观察下列有规律的点的坐标:A1(1,0),A2(2,1),A3(4,0),A4(8,1),…依照规律,A11的坐标为(1024,1),A12的坐标为(2048,0)。
7.以原点为起点,正东,正北方向为x轴,y轴正方向建立平面直角坐标系。
一个机器人从原点O点出发,向正东方向走3米到达A1点,再向正北方向走6米到达A2,再向正西方向走9米到达A3,再向XXX方向走12米到达A4,再向正东方向走15米到达A5,按此规律走下去,当机器人走到A6时,A6的坐标是(﹣3,﹣3)。
初一年级平面直角坐标系动点问题(经典难题)

平面直角坐标系动点问题(一)找规律1. 如图1,一只跳蚤在第一象限及x 轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1), 然后接着按图中箭头所示方向跳动[即(0, 0)T( 0, 1)^( 1, 1)T( 1 , 0)T…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( ) 7*A.( 4, 0) B . (5, 0) C . (0, 5) D . (5, 5)图2 2、如图2,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2, 4, 6, 8,…,顶点依次用A1, A2, A B,A4,…表示,则顶点A55的坐标是3. 如图3,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1, 0),( 2, 0),(2,1),( 1 ,1),( 1 , 2),(2 , 2),…的规律排列,根据这个规律,第2015个点的横坐标为 .4. 在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如下图所示。
A (13, 13)B (—13,—13)C (14, 14)A,__A3D、(—14, —14)图3(1 )填写下列各点的坐标:Ai ( _____ , ____ ), A3 ( ______ , ____ ), A2 ( ______ , ___ );(2)写出点A4n的坐标(n是正整数);(3)指出蚂蚁从点Aoo到Aoi的移动方向.5、观察下列有序数对:(3, - 1) (- 5,寺)(7,-寺)(-9,壬)…根据你发现的规律,第100个有序数对是_______ .6、观察下列有规律的点的坐标:Ai (b 1) 扣Q “ 4) A. (4, 2) 去6 7) A s临-->3 A*(7, 10) A3 (S s4).......................... ,依此规律,A ii的坐标为_______________ , A i2的坐标为_______________ .7、以0为原点,正东,正北方向为x轴,y轴正方向建立平面直角坐标系,一个机器人从原点O点出发,向正东方向走3米到达A1点,再向正北方向走6米到达A2,再向正西方向走9米到达A3,再向正南方向走12米到达A4,再向正东方向走15米到达A5,按此规律走下去,当机器人走到A6时,A6的坐标是_______________.8、如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2008次,点P依次落在点9、如图,在平面直角坐标系上有个点P (1, 0),点P第1次向上跳动1个单位至点Pi ( 1, 1),紧接着第2次向左跳动2个单位至点(-1, 1),第3次向上跳动1个单位,第向右跳动3个单位,第5次又向上跳动1 单位,第6次向左跳动4个单位,…,依规律跳动下去,点P第100次跳动至点Pi oo的坐标是P24次个此___________________________________________________________ .点P第2009次跳动至点F2QQ9的坐标是_____________ .-3 ^2~7 2 3 t图4 图510、如图5,已知A( 1,0),A2( 1,1),A3 (- 1, 1), A4 (- 1,—1), A s (2,—1),….则点A2007的坐标为______________(二)几何综合问题1、已知点A的坐标是(3, 0)、AB=5,( 1)当点B在X轴上时、求点B的坐标、(2)当AB//y轴时、求点B的坐标2、如图,已知A、B两村庄的坐标分别为(2, 2)、( 7, 4), 一辆汽车在X轴上行驶,从原点O出发.(1)汽车行驶到什么位置时离A村最近?写出此点的坐标.(2)汽车行驶到什么位置时离B村最近?写出此点的坐标.(3 )请在图中画出汽车行驶到什么位置时,距离两村的和最短?8 164B2A» 1 | 1 11111111-512115111114. 如图,在平面直角坐标系中,点A, B的坐标分别为(一1 , 0) , ( 3, 0),现同时将点A, B分别向上平移2个单位,再向右平移1个单位,分别得到点A B的对应点C, D,连接AC, BD CD(1) 求点C, D的坐标及四边形ABDC勺面积绻边形ABDC⑵在y轴上是否存在一点P,连接PA, PB,使S PAB =S四边形ABDC ,若存在这样一点,求出点P的坐标,若不存在,试说明理由.⑶点P是线段BD上的一个动点,连接PC PO当点P在DCP BOP DCP 给出下列结论:①的值不变,②BD上移动时(不与CPO的值不变,B, D重合)CPO BOP有一个是正确的,请你找出这个结论并求其值.其中有且只5. 已知:在平面直角坐标系中,四边形ABCD是长方形,/ A=Z B=Z C=/ D=90°, AB// CDAB=CD=8cm, AD=BC=6cm D点与原点重合,坐标为(0,0).(1)写出点B的坐标.(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t秒,当t为何值时,PQ/ BC?(3)在Q的运动过程中,当Q运动到什么位置时,使厶ADC的面积为9?求出此时Q点的坐6.如图在平面直角坐标系中, A (a, 0), B ( b, 0),( Y P—>BAX0(D) W --------- CQ7: X1, 2).且|2a+b+1|+ Q时乱-4=0.(1) 求a、b 的值;(2) ①在y轴的正半轴上存在一点②在坐标轴的其他位置是否存在点M使“C^&ABC仍成立?若存在,请直接写出符M,使S AABC,求点M的坐标.合条件的点M的坐标.7.如图,在下面的直角坐标系中,已知 A (0, a), B ( b, 0), C(b, 4)三点,其中a, b满足关系式(1 )求a,b的值;(2)如果在第二象限内有一点P(m式子表示四边形ABOP勺面积;(3)在(2)的条件下,是否存在点的面积与厶ABC的面积相等?若存在, 若不存在,请说明理由.&在平面直角坐标系中,点 A ( a, b)是第四象限内一点,AB丄y轴于B,且B (0, b)是2y轴负半轴上一点,b =16, S^AOE=12.(1)求点A和点B的坐标;(2)如图1,点D为线段0A (端点除外)上某一点,过点D作A0垂线交x轴于E,交直线AB于F,/ EOD Z AFD的平分线相交于N,求/ ONF的度数.(3)如图2,点D为线段0A(端点除外)上某一点,当点D在线段上运动时,过点D作直线EF交x轴正半轴于E,交直线AB于F, / EOD /AFD的平分线相交于点N若记/ ODF a, 请用a的式子表示/ ONF的大小,并说明理由.。
初一平面直角坐标系动点问题经典难题

平面直角坐标系动点问题(一)找规律1.如图1,一只跳蚤在第一象限及x 轴、y 轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( ) 图1A .(4,0)B .(5,0)C .(0,5)D .(5,5)图22、如图2,所有正方形的中心均在坐标原点,且各边与x 轴或y 轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A 1,A 2,A 3,A 4,…表示,则顶点A 55的坐标是( ) A 、(13,13) B 、(﹣13,﹣13) C 、(14,14) D 、(﹣14,﹣14)3.如图3,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2015个点的横坐标为 .4.在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如下图所示。
图3 (1)填写下列各点的坐标:1A (____,____),3A (____,____),12A (____,____); (2)写出点n A 4的坐标(n 是正整数); (3)指出蚂蚁从点100A 到101A 的移动方向.5.观察下列有序数对:(3,﹣1)(﹣5,)(7,﹣)(﹣9,)…根据你发现的规律,第100个有序数对是 .6、观察下列有规律的点的坐标:依此规律,A 11的坐标为 ,A 12的坐标为 .7、以0为原点,正东,正北方向为x 轴,y 轴正方向建立平面直角坐标系,一个机器人从原点O 点出发,向正东方向走3米到达A 1点,再向正北方向走6米到达A 2,再向正西方向走9米到达A 3,再向正南方向走12米到达A 4,再向正东方向走15米到达A 5,按此规D C y DCyDC3-1BA O xy律走下去,当机器人走到A 6时,A 6的坐标是 .8、如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次,点P 依次落在点1232008P P P P ,,,,的位置,则点2008P 的横坐标为 .9、如图,在平面直角坐标系上有个点P (1,0),点P 第1次向上跳动1个单位至点P 1(1,1),紧接着第2次向左跳动2个单位至点P 2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P 第100次跳动至点P 100的坐标是 .点P 第2009次跳动至点P 2009的坐标是 . 图 4 图5 A 310、如图5,已知A l (1,0),A 2(1,1),(﹣1,1),A 4(﹣1,﹣1),A 5(2,﹣1),….则点A 2007的坐标为 .(二)几何综合问题1、已知点A 的坐标是(3,0)、AB=5,(1)当点B 在X 轴上时、求点B 的坐标、(2)当AB//y 轴时、求点B 的坐标2、如图,已知A 、B 两村庄的坐标分别为(2,2)、(7,4),一辆汽车在x 轴上行驶,从原点O 出发.(1)汽车行驶到什么位置时离A 村最近?写出此点的坐标. (2)汽车行驶到什么位置时离B 村最近?写出此点的坐标. (3)请在图中画出汽车行驶到什么位置时,距离两村的和最短?4.如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1)求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形 (2)在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S =ABDC S 四边形,若存在这样一点,求出点P 的坐标,若不存在,试说明理由. (3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在PBD上移动时(不与B,D重合)给出下列结论:①DCP BOPCPO∠+∠∠的值不变,②DCP CPOBOP∠+∠∠的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.5.已知:在平面直角坐标系中,四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0).(1)写出点B的坐标.(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动, 动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t秒,当t为何值时,PQ∥BC?(3)在Q的运动过程中,当Q运动到什么位置时,使△ADQ的面积为9? 求出此时Q点的坐标.6.如图在平面直角坐标系中,A(a,0),B(b,0),(﹣1,2).且|2a+b+1|+=0.(1)求a、b的值;(2)①在y轴的正半轴上存在一点M,使S△COM=S△ABC,求点M的坐标.②在坐标轴的其他位置是否存在点M,使S△COM=S△ABC仍成立?若存在,请直接写出符合条件的点M的坐标.7.如图,在下面的直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b满足关系式.(1)求a,b的值;(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.8.在平面直角坐标系中,点A(a,b)是第四象限内一点,AB⊥y轴于B,且B(0,b)是y轴负半轴上一点,b2=16,S△AOB=12.(1)求点A和点B的坐标;(2)如图1,点D为线段OA(端点除外)上某一点,过点D作AO垂线交x轴于E,交直线AB于F,∠EOD、∠AFD的平分线相交于N,求∠ONF的度数.(3)如图2,点D为线段OA(端点除外)上某一点,当点D在线段上运动时,过点D作直线EF交x轴正半轴于E,交直线AB于F,∠EOD,∠AFD的平分线相交于点N.若记∠ODF=α,请用α的式子表示∠ONF的大小,并说明理由.。
人教版八年级上册数学期末动点问题压轴题专题训练(含解析)

人教版八年级上册数学期末动点问题压轴题专题训练(1)当时,点C 的坐标为 .(2)动点A 在运动的过程中,试判断发生变化,请说明理由.(3)当时,在坐标平面内是否存在一点若存在,请直接写出点P 的坐标;若不存在,请说明理由.(1)如图1,当点在边上时.①求证:;②求证:;(2)如图2,当点在边的延长线上时,其他条件不变,请写出2a =3a =D BC ABD ACE ≌△△BC DC CE =+D BC(1)请直接写出点A 和点B 的坐标;(2)请判断的形状并说明理由;(3)下列结论:①四边形为定值.请选择一个正确的结论并说明理由.(1)求证:;(2)求的面积;(3)点M ,N 分别是线段,上的动点,连接,求的最小值.DEF OEDF OEF DFE ∠+∠CD CE =CDE BC BD MN 12MN DN +(1)求出点的坐标.(2)求证:.(3)数学活动小组进行深入探究后发现变,你同意这个说法吗?请说明理由B OD BC =(1)如图①,请找出图中与相等的角,并说明理由;(2)如图②,交轴于点,过点作轴于点,求证:平分;(3)如图③,若,点在轴正半轴移动,且,取,连交轴OAB ∠BC x M C CD x ⊥,2D AM CD =AD BAC ∠()3,0A B y OB OA >()0,3P CP x边三角形,使其与点在直线的两侧,与直线相交于点(点与点A 不重合),连接.(1)如图,当时,①求证:;②在点A 运动的过程中,的度数是否会发生改变?如果会请说明理由,如果不会请求出的度数;(2)在点A 运动的过程中,试探究线段,,之间的数量关系.11.在平面直角坐标系中,点在轴的正半轴上,点在第一象限,,.(1)如图1,求证:是等边三角形;(2)如图1,若点M 为y 轴正半轴上一动点,以为边作等边三角形,连接并延长交轴于点,求证:;(3)如图2,若,,点为的中点,连接、交于,请问、与之间有何数量关系,并证明你的结论.12.在平面直角坐标系中,点A 为y 轴正半轴上一点,点B 为x 轴上一动点,连接ABD C AB DC l E E EB 120BAC ∠<︒ABE ACE =∠∠DCB ∠DCB ∠EA EB ED A y B OB AB =150BOP ∠=︒OAB BM BMN NA x P 2AP AO =BC BO ⊥BC BO =D CO AC DB E AE BE CE,以为腰作等腰,.(1)如图1,点B 在x 轴负半轴上,点C 的坐标是,直接写出点A 和点B 的坐标;(2)如图2,点B 在x 轴负半轴上,交x 轴于点D ,若平分.且点C 的纵坐标是,求线段的长;(3)如图3,点B 在x 轴正半轴上,以为边在左侧作等边,连接,,若,且,求的面积.13.等腰直角中,,,,点、分别是轴,轴上两个动点,直角边交轴于点,斜边交轴于点.(1)如图1,已知点的横坐标为,直接写出点的坐标;(2)如图2,若点为轴上的固定点,且,当点在轴正半轴运动时,分别以、为直角边在第一、二象限作等腰直角和等腰直角,连接交轴于点,问当点在轴的正半轴上运动时,的长度是否变化?若变化请说明理由;若不变化,请求出的长度.14.在平面直角坐标系中,点为坐标原点,点、分别位于轴和轴AB AB Rt ABC △90BAC ∠=︒(2,2)-AC BD ABC ∠3-BD BC BC BCE EO CO 60COE ∠=︒8CO =AOC ABC 90BAC ∠=︒AB AC =ABC C ∠=∠B A x y AC x D BC y E C 2-A A x ()6,0A -B y OB AB BOD ABC CD y P B y BP BP O ()6,0B -()0,6A x y上,连接,交轴于点.(1)求点的坐标;(2)动点从出发以个单位/秒的速度沿轴向终点运动,连接,将线段绕着点逆时针旋转后得到线段,与为对应点.连接、,为的面积,用含的式子表示;(3)在()的条件下,连接,过点作于,交轴于,交于,若,求点的坐标.15.如图①,在中,,现有一动点,从点出发,沿着三角形的边运动,回到点停止,速度为,设运动时间为秒.(1)如图①,当的面积等于面积的一半时,求的值:(2)如图②,点在边上,点在边上,在的边上,若另外有一个动点与点同时从点出发,沿着边运动,回到点停止.在两点运动过程中的某一时刻,以为顶点的三角形恰好与全等,求点的运动速度.16.如图,在平面直角坐标系中,,点在轴正半轴上,.AB CA AB ⊥x C C P B 2x C AP AP A 90︒AQ P Q PQ CQ S PCQ △t S 2BQ A AH BQ ⊥G x H PQ AC M :2:1APM AQM S S = H Rt ABC △90,12cm,16cm,20cm B AB BC AC ∠=︒===P A AB BC CA →→A 2cm /s t ABP ABC t D BC 4cm CD =E AC 5cm,,3cm CE ED BC ED =⊥=ABC Q P A AC CB BA →→A ,,A P Q EDC △Q ()0,9A B x 45OAB ∠=︒(1)求出点坐标;(2)动点从点出发,以每秒个单位长度的速度沿轴正半轴运动,同时点从点出发,以相同速度沿轴向左运动,连接,过点作交直线于点,连接,设点的运动时间为,请用含的式子表示的面积;(3)在(2)的条件下,直线与直线交于点,当时,求点坐标.17.已知中,,过点的直线交轴于,其中是方程组的解,(1)求的值(2)动点从点出发,沿线段以每秒1个单位的速度运动,运动时间为秒;请用含的式子表示线段的长度;并直接写出此时的取值范围;(3)在(2)的条件下,当为何值时,直线与直线互相垂直.18.在平面直角坐标系中,O 为坐标原点,直线交x 轴的正半轴于点A ,交y 轴的B P O 1y Q B x PQ O OG PQ ⊥AB G PG P t t OPG PQ AB H 72OPG S =△H AOB OA OB a ==A AM x (),0M b ,a b 3830a b a b +=⎧⎨+=⎩,a b P A AO t t OP t t BP AM AB(1)如图1求的长;(2)如图2动点E 在第二象限,点E 的坐标为,连接,,请写出面积s 与t 的关系;(3)在(2)的条件下,如图3点F 在第一象限,连接、、,,连接,当,求的值.OD (,)t m DE OE ODE FE FD FA 30ADF ∠=FE FA =EB 12,4EBO ODA ODA EFA EOB ∠=∠∠+∠=∠t m +参考答案:1.(1)(2)动点A 在运动的过程中,的值不变,(3)或或【分析】本题考查全等三角形判定及性质.(1)根据题意过点C 作轴于点,证明出,利用全等性质即可得到本题答案;(2)由(1)得,利用全等性质及点坐标表示线段长即可得到本题答案;(3)根据题意分3种情况讨论P 点位置,利用全等三角形性质及判定即可得到本题答案.【详解】(1)解:如下图,过点C 作轴于点E ,则,,∵是等腰直角三角形,∴,∴,∴.在和中,∴(AAS ),∵,∴,∴,∴;(2)解:动点A 在运动的过程中,的值不变.理由如下:(2,3)-+c d (4,)1-(3,2)--(2,1)-CE y ⊥E ACE BAO ≌ACE BAO ≌CE y ⊥CEA AOB ∠=∠ABC ,90AC BA BAC =∠︒=90ACE CAE BAO CAE ∠+∠=︒=∠+∠ACE BAO ∠=∠ACE △BAO CEA AOB ACE BAOAC BA ∠=∠⎧⎪∠=∠⎨⎪=⎩ACE BAO ≌(0,1),(0,2)B A -12BO AE AO CE ====,123OE =+=2,3C -()+c d由(1)知,,∵,,∴,∴,∴,又∵点C 的坐标为,∴,即的值不变;(3)解:存在一点P ,使与全等,符合条件的点P 的坐标是或或,分为三种情况讨论:①如下图,过点P 作轴于点E ,则,∴,∴,在和中,,∴(AAS ),∴,∴,即点P 的坐标是,②如下图,过点C 作轴于点M ,过点P 作轴于点E ,ACE BAO ≌(0,1)B (0,)A a -1,BO AE AO CE a ====1OE a =+(,1)C a a --(,)c d 11c d a a +=--=-+c d PAB ABC (4,)1-(3,2)--(2,1)-PE x ⊥90PBA AOB PEB ∠=∠=∠=︒90,90EPB PBE PBE ABO ∠+∠=︒∠+∠=︒EPB ABO ∠=∠PEB △BOA △EPB OBA PEB BOA PB BA ∠=∠⎧⎪∠=∠⎨⎪=⎩PEB BOA △≌△1,3PE BO EB AO ====314OE =+=(4,)1-CM x ⊥PE x ⊥则.∵,∴,∴,∴,∴,在和中,,∴(AAS ),∴.∵,∴,即点P 的坐标是;③如下图,过点P 作轴于点E ,则.∵,∴,∴,90CMB PEB ∠=∠=︒CAB PAB △≌△45,PBA CBA BC BP ∠=∠=︒=90CBP ∠=︒90,90MCB CBM CBM PBE ∠+∠=︒∠+∠=︒MCB PBE ∠=∠CMB BEP △MCB EBP CMB BEP BC PB ∠=∠⎧⎪∠=∠⎨⎪=⎩CMB BEP △≌△,PE BM CM BE ==3,4),10C B -((,)2,413PE OE BE BO ==-=-=(3,2)--PE x ⊥90BEP BOA ∠=∠=︒CAB PBA △≌△,90AB BP CAB ABP =∠=∠=︒90,90ABO PBE PBE BPE ∠+∠=︒∠+∠=︒∴.在和中,,∴(AAS ),∴,∴,即点P 的坐标是,综上所述,符合条件的点P 的坐标是或或.2.(1)①见解析;②见解析;(2),见解析【分析】本题主要考查了等边三角形,全等三角形.(1)①根据等边三角形的性质得出,,,根据得出,从而说明三角形全等;②根据全等的性质得出,然后根据即得;(2)根据等边三角形的性质得出,,,根据得出,从而说明,根据全等的性质得出,然后根据即得.【详解】(1)证明:①∵和是等边三角形,∴,,.∴,∴.在和中,,∴;②∵,ABO BPE ∠=∠BOA △PEB △ABO BPE BOA PEB BA PB ∠=∠⎧⎪∠=∠⎨⎪=⎩BOA PEB △≌△1,3PE BO BE OA ====312OE BE BO =-=-=(2,1)-(4,)1-(3,2)--(2,1)-BC CD CE +=AB AC =AD AE =60BAC DAE ∠=∠=︒BAC DAC DAE DAC ∠-∠=∠-∠BAD EAC ∠=∠BD CE =BC BD CD =+AB AC =AD AE =60BAC DAE ∠=∠=︒BAC DAC DAE DAC ∠+∠=∠+∠BAD EAC ∠=∠ABD ACE ≌△△BD CE =+=BC CD BD ABC ADE V 60BAC DAE ∠=∠=︒AB BC AC ==AD DE AE ==BAC DAC DAE DAC ∠-∠=∠-∠BAD CAE ∠=∠ABD △ACE △AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩()SAS ABD ACE △≌△ABD ACE ≌△△∵,,∴,∴是等腰直角三角形,即∵点D 是线段中点,∴,,(0,6)A (6,0)B 6O A O B ==AOB ∠AB OD AB ⊥12OD AD AB ==∠∵,,∴在中,∵在(1)中已求出根据翻折可知:、∴N 点关于的对称点H 在根据对称性有:∴,∴是等边三角形,∵N 点关于的对称点是点H ,3BD =30CBD ∠=︒DG Rt BDG △12DG BD =CE CD =11BDC BKC △BE BK DBC KBC ∠=∠60BDK DBC KBC ∠=∠+∠=︒BDK BE NH如图,,即:,在中,PNC DNC∠=∠24PNC αβ∠==2αβ=MCN DCM DCN x β∠=∠+∠=+MCN △180MCN DCN NMC ∠+∠+∠=2180x βαα+++=︒3180x βα++=︒解得:,.II.当点在线段上时,如图,,,即:,在中,,,即:联立得:,解得:,此时:,不合题意舍去;III .当点在线段上时,如图,,52550x βα=︒⎧⎪=︒⎨⎪=︒⎩∴5DCM ∠=︒N PD 180PNC DNC ∠+∠=︒∴24180αβ+=︒290αβ+=︒∴MCN DCM DCN x β∠=∠+∠=+ CMN PCN MCN CMN x βα∠=∠+∠=++∴4180PCN NDC x βαβ∠+∠=+++=︒5180x βα++=︒2602905180x x ααββα+=︒⎧⎪+=︒⎨⎪++=︒⎩11.2526.2537.5x βα=︒⎧⎪=︒⎨⎪=︒⎩11.2526.5PCN DCN ∠=︒<∠=︒N DM PNC DNC ∠=∠【详解】(1)解:过点B 作轴于点D ,∵,∴,∵轴,∴,∵,∴,∴,在和中,,∴,∴,∵,∴;(2)解:∵,∴,∴,∵轴,∴,∴,∴,在和中,BD y ⊥()()6,0,0,3A C -6,3OA OC ==BD y ⊥90BCD CBD ∠+∠=︒90ACB ∠=︒90BCD ACO ∠+∠=︒ACO CBD ∠=∠ACO △CBD △90AOC CDB ACO CBDAC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩≌ACO CBD 6,3OA CD OC BD ====()0,3C ()3,3B -90ACB ∠=︒90BCF ∠=︒90CBF F ∠+∠=︒BE y ∥90AEF ∠=︒90CAD F ∠+∠=︒CAD CBF ∠=∠CAD CBF V∴,∴,∵,∴∴.【点睛】本题主要考查了三角形综合,折叠的性质,全等三角形的判定和性质,角平分线的性质,解题的关键是掌握全等三角形的判定方法,全等三角形对应边相等,对应角相等;折叠前后对应角相等;角平分线上的点到两边距离相等.7.(1)(2)见解析(3)的度数总是保持不变,理由见解析【分析】本题考查了全等三角形的性质与判定,等腰三角形的性质,坐标与图形;(1)根据等腰三角形的性质解答即可;(2)根据等式的性质得出,进而利用证明与全等,进而解答即可;(3)根据全等三角形的性质得出,进而利用平角的定义解答即可.【详解】(1)解:如图所示,过作轴于,()Rt Rt HL EFO EFN ≌FN FO =(),0F t FO t=-2FG HG t +=-()2,0-COD ∠BAC OAD ∠=∠SAS BAC OAD AOD ABO ∠=∠A AE x ⊥E),点C 是的中点,,D 作轴于点F ,,,4=AB 114222AB ==⨯=DF x ⊥90DFO =︒90FDO DOF +∠=︒),的坐标为,关于x 轴的对称点,则的坐标为,交x 轴于点,则为定值,此时的周长最小.作轴于点Q ,114222AB '==⨯=M '()0,2M '''M ''M AM ''P PAM C AM AP ''=+ AM 'PAM '△()4,4A -AQ y ⊥对于(3),作轴,先证明,可得,再得出,进而得出,根据等腰直角三角形的性质和判定即可得出答案.【详解】(1).理由:,;(2)证明:如图②中,延长交的延长线于点..∵,,,.,即.垂直平分,平分.(3)的长度不变,.理由:如图③中,过点作轴于点...CH y ⊥≌CHB BOA △△,3===CH BO BH OA 3==OA OP ==OB PH CH OAB OBC ∠=∠90,90OAB OBA OBC OBA ∠+∠=∠+∠=︒︒ OAB OBC ∴∠=∠AB CD T ,90,90,AD CD ADT T BAM BCT BAM ⊥∴∠=∴∠+∠=∴∠=∠︒︒ BC BA ===90CB T A B M ∠∠︒()CBT ABM ASA ∴≌△△CT AM ∴=2,2AM CD CT CD =∴= CD DT =,AD CT AD ⊥∴ CT ,AC AT AD ∴=∴BAC ∠OQ 3OQ =C CH y ⊥H 90,90CHB BOA HBC HCB ∴∠=∠=∴∠+∠=︒︒90,90,ABC OBA HBC HCB OBA ∠=∴∠+∠=︒︒∴∠=∠..,..,.【点睛】本题主要考查了全等三角形的性质和判定,同角的余角相等,线段垂直平分线的性质,等腰直角三角形的性质和判定等,构造辅助线是解题的关键.10.(1)①见解析;②不变,(2)或【分析】(1)①根据垂直平分线的性质得出,再由等边对等角及各角之间的数量关系求解即可;②设与交于点M ,根据等边三角形的性质及各角之间的关系得出,即可求解;(2)分两种情况进行分析:当时,当时,分别利用全等三角形的判定和性质及等边三角形的判定和性质分析求解即可.【详解】(1)证明:①点A 、E 在线段的垂直平分线l 上,∴,∴,∴,即;②在点A 运动的过程中,的度数不变,理由如下:如图,设与交于点M ,(),CB AB CHB BOA AAS =∴ ≌△△,3∴===CH BO BH OA ()()3,0,0,3,3A P OA OP ∴== ,BH OP OB PH CH ∴=∴==90,45CHP CPH OPQ ∠=∴∠=∠=︒︒ 90,45∠=∴∠=︒=︒∠ POQ OQP OPQ 3OQ OP ∴==30DCB ∠=︒ED EB EA =+EB ED EA=+AC AB EC EB ==,AB CD 260ECB ∠=︒120BAC ∠<︒120BAC ∠>︒BC ,AC AB EC EB ==,ABC ACB EBC ECB ∠∠∠∠==ABC EBC ACB EBC ∠∠∠∠-=-ABE ACE ∠∠=DCB ∠AB CD∵是等边三角形,∴ ,∴,∴,∴,∴,∴,∵,∴,即;(2)当时,在上截取,连接,∵,∴,由(1)得直线,,∴,∴是等边三角形,∴ ,∴,即,ABD ,60AB AD BAD ∠==︒AD AC =ADC ACE ∠∠=,ABE ADC EBC ECB ∠∠∠∠==,180,180AMD EMB BED ABE EMB BAD ADC AMD ∠∠∠∠∠∠∠∠==︒--=︒--60BED BAD ∠∠==︒,EBC ECB BED EBC ECB ∠∠∠∠∠+==260ECB ∠=︒30DCB ∠=︒120BAC ∠<︒ED EF EA =AF ED DF EF =+ED DF EA =+l BC ⊥30DCB ∠=︒903060AED ∠=︒-︒=︒AEF 60,EAF BAD AE AF ∠∠==︒=–EAF BAF BAD BAF ∠∠∠∠=-BAE DAF ∠∠=∴,∴,∵,∴;当时,如图所示在上截取,连接,∵,∴,由(1)得直线,,,∴,∴F 是等边三角形,∴,∴,∴,∴,∴,∵,∴;综上可得:或.【点睛】题目主要考查线段垂直平分线的性质,全等三角形的判定和性质,等边三角形的判定和性质等,理解题意,作出相应辅助线是解题关键,同时注意进行分类讨论.11.(1)见解析(2)见解析(3),证明见解析【分析】(1)根据有一个角是的等腰三角形是等边三角形可得结论;(SAS)BAE DAF ≌ EB DF =ED DF EA =+ED EB EA =+120BAC ∠>︒EB EF EA =AF EB BF EF =+EB BF EA =+l BC ⊥30DCB ∠=︒BE BC =903060AEB AEC ∠∠==︒-︒=︒AE 60,EAF BAD AE AF ∠∠==︒=–EAF DAF BAD DAF ∠∠∠∠-=EAD BAF ∠∠=(SAS)BAF DAE ≌ BF ED =EB BF EA =+EB ED EA =+ED EB EA =+EB ED EA =+AE BE CE =+60︒(2)根据证明,得,由8字形可得,最后由含角的直角三角形的性质可得结论;(3)如图2,在上截取,先证,方法是根据题意得到三角形为等边三角形,三角形为等腰直角三角形,确定出度数,根据,且,得到度数,进而确定出为,再由,得到,再由,且夹角,利用得到三角形与三角形全等,利用全等三角形的对应边相等得到,得到三角形为等边三角形,得到,由,等量代换即可得证.【详解】(1)解:证明:,,,,是等边三角形;(2)证明:由(1)知:是等边三角形,,是等边三角形,,,,,,,,,,,,SAS MBO NBA ≌OMB ANB ∠∠=60FAM FBN ∠∠==︒30︒AC AG CE =60AEB ∠=︒ABO BOC ABD ∠AB BC =150ABC ∠=︒BAE ∠AEB ∠60︒AG CE =AE CG =AB CB =BAC BCA ∠=∠SAS BCG BAE BG BE =BEG BE EG =AE EG AG =+150BOP ∠=︒ 90AOP ︒=∠60AOB ∴∠=︒OB AB = OAB ∴ OAB 60ABO ∴∠=︒BMN BM BN ∴=60MBN ∠=︒MBO NBA ∴∠=∠AB OB = (SAS)MBO NBA ∴△≌△OMB ANB ∴∠=∠AFM BFN ∠=∠ 60FAM FBN ∴∠=∠=︒60OAP FAM ∠=∠=︒ 90AOP ︒=∠30APO ∴∠=︒;(3),理由如下:如图2,在上截取,连接,,即,,,,为的中点,平分,即,,,,,,,在和中,,,,为等边三角形,,.【点睛】本题是三角形综合题,考查了等腰直角三角形的性质和判定,等边三角形的性质和判定,全等三角形的判定和性质,以及含角的直角三角形的性质,添加辅助线.12.(1),2AP AO ∴=AE BE CE =+AC AG EC =BG AG EG CE EG +=+AE CG =BC BO ⊥ BC BO =90OBC ∴∠=︒D CO BD ∴OBC ∠45CBD OBD ∠=∠=︒60ABO ∠=︒ 105ABD ∴∠=︒150ABC ∠=︒AB OB BC == 15BAC BCA ∴∠=∠=︒154560AEB ∴∠=︒+︒=︒ABE CBG AB CB BAE BCG AE CG =⎧⎪∠=∠⎨⎪=⎩(SAS)ABE CBG ∴△≌△BG BE ∴=BEG ∴△BE EG ∴=AE AG EG CE BE ∴=+=+30︒()02A ,()40B -,∴,∵∴,∵,∴,,90ADC BOA ∠=︒=∠90CAD BAO ABO ∠+∠=︒=∠CAD ABO ∠=∠(2,2)C -2CD =2OD =∴,,∴,;(2)解:如图2,作轴,交轴于,交的延长线于,∴,∵平分,∴,,,∴,∴,∵,∴,∵,∴,∴,∵,,∴,∴,∴的长为6;(3)解:∵为等边三角形,∴,,如图3,在上截取,使,连接,2AO CD ==4BO AD AO OD ==+=()02A ,()40B -,CM x ⊥x N BA M 90BNM BNC ∠=︒=∠BD ABC ∠MBN CBN ∠=∠BN BN =90BNM BNC ∠=︒=∠()ASA MBN CBN ≌3MN CN ==∥CM AO ACM CAO ∠=∠90CAO BAO ABD BAO ∠+∠=︒=∠+∠CAO ABD ∠=∠ACM ABD ∠=∠AC AB =90MAC DAB ∠=︒=∠()ASA ACM ABD ≌6BD CM CN MN ==+=BD BCE BE CE =60BEC EBC ECB ∠=∠=∠=︒OC OF OF OE =EF∴是等边三角形,∴,∴∵,∴,∴,OEF OE EF =60OEF ∠=︒=∠OEF BEF BEC ∠-∠=∠-∠OE EF =BEO CEF ∠=∠()SAS BEO CEF ≌OBE FCE ∠=∠13.(1)(2)【分析】(1)如图①,过作 轴于, 证明可得从而可得答案;(2)如图①,过点作 轴于点.证明 ,可得 ,再证明,从而可得: .【详解】(1)解: 如图①,过作 轴于,∴,∵,∴,∴,∵,∴.∴,,∴,∴,故答案为 : .(2)的长度不变,理由如下:如图②, 过点作 轴于点.()0,23BP =C CF y ⊥F ,ACF BAO ≌CF AO =C CE y ⊥E CBE BAO ≌,6CE BO BE AO ===CPE DPB ≌3BP EP ==C CF y ⊥F 90,90CFA AOB ACF CAF ∠=∠=︒∠+∠=︒90BAC ∠=︒90CAF OAB ∠+∠=︒ACF OAB ∠=∠AC AB =()AAS ACF BAO ≌CF AO =2c x =- 2CF AO ==()0,2A ()0,2BP C CE y ⊥E∵ ,∴∵∴ .∵90ABC ∠=︒90CBE ABO ∠+∠=︒90BAO ABO ∠+∠=︒CBE BAO ∠=∠90CEB AOB ∠=∠=∵,∴,在和中,90BAC PAQ ∠=∠=︒BAP CAQ ∠=∠BAP △CAQ AB AQ =⎧∴四边形为正方形,∴,过作于点,∵AOCN 6OA CN OC ===T TL CN ⊥L AH BQ⊥AOH TLQ ≌∴,解得;②当点在上,点∴,解得;3AP DE cm AQ EC ===,352x =103x =cm/s P AB 5AP EC cm AQ ==,532x =65x =cm/s∴点P 的路程为∴点P 的路程为3AP ED AQ EC ===,AB +1216205AQ =++-=4543x =5AP EC cm AQ ==,AB +1216203AQ =++-=4345x =从出发,以每小时从出发,以相同速度沿,①当在线段上时,P O Q B OQ ∴=AP =t P AO,等腰,,设,,为的一个外角,RO PO ∴=∴POR 45R BAO ∴∠=∠=︒QPO α∠=45RPQ α∴∠=︒-QON BOG α∠==∠ABO ∠ OBG,,,,90HTA ∴∠=︒45HAT OAB ∠=∠=︒45HAT AHT ∴∠=∠=︒HT AT ∴=由(1)知,,则,∵直线与直线互相垂直,∴,()1.0M -1OM =BP AM 90MNB ∠=︒。
七年级平面直角坐标系动点规律问题(经典难题)(可编辑修改word版)

于 △ ABO 的一个顶点对称,点 P1 与点 P2 关于点 A 对称,点 P2 与点 P3 关于点 B 对称,点 P3 与点 P4 关于点 O 对称,点 P4 与点 P5 关于点 A 对称,点 P5 与点 P6 关于点 B 对称,点 P6 与 点 P7 关于点 O 对称,…对称中心分别是 A , B , O , A , B , O ,…且这些对称中心依次
律走下去,当机器人走到 A6 时,A6 的坐标是
.
8、如图,将边长为 1 的正三角形 OAP 沿 x 轴正方向连续翻转 2019 次,点 P 依次落在点
P1, P2 ,, P2019 的位置,则点 P2019 的横坐标为
.
y
P
AO
P1
x
9、如图,在平面直角坐标系上有个点 P(1,0),点 P 第 1 次向上跳动 1 个单位至点
3.如图 3,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,
其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),
(1,2),(2,2),…的规律排列,根据这个规律,第 2019 个点的横坐
标为
.
4.在平面直角坐标系中,一蚂蚁从原点 O 出发,按向上、向右、向下、向右的方向依次 不断移动,每次移动 1 个单位,其行走路线如下图所示。
C.(0,5)
D.(5,5)
图2 2、如图 2,所有正方形的中心均在坐标原点,且各边与 x 轴或 y 轴平行.从内到外,它们 的边长依次为 2,4,6,8,…,顶点依次用 A1,A2,A3,A4,…表示,则顶点 A55 的坐 标是( )
平面直角坐标系中的动点问题初一

平面直角坐标系中的动点问题初一
在平面直角坐标系中,动点问题涉及到描述物体运动轨迹和位置变化的问题。
一般情况下,我们使用x轴和y轴来表示平面直角坐标系。
在动点问题中,通常我们需要给出动点的起始位置和速度等运动参数,然后根据问题要求来分析动点的运动轨迹。
举例来说,如果一个物体的起始位置在坐标原点(0,0),它以每秒1单位的速度沿着x轴正方向运动,那么可以通过速度×时间的公式来计算物体在t秒后的位置,即(x,y) = (1t, 0)。
还有一些常见的动点问题,比如:
1. 若动点A在t时刻的位置为(x,y),那么在t+1时刻的位置是多少?
2. 若动点A在t=0时刻的位置为(0, 0),它以每秒2单位的速度沿着x轴正方向运动,那么在t秒后的位置是多少?
3. 若动点A在t=0时刻的位置为(0, 2),它以每秒3单位的速度沿着y轴负方向运动,那么在t秒后的位置是多少?
这些问题的解答需要根据给定的运动参数和问题要求来确定物体的位置变化。
在解答过程中,我们可以运用坐标系中的几何概念和运动学知识来分析和计算。
希望以上内容对你有所帮助!。
平面直角坐标系动点问题的解题技巧

平面直角坐标系动点问题的解题技巧在学习数学的过程中,平面直角坐标系动点问题是不可避免的一部分。
解决这类问题需要掌握一些基本的技巧和方法。
本文将从几个方面介绍平面直角坐标系动点问题的解题技巧。
1. 确定直角坐标系和参照系在解决平面直角坐标系动点问题之前,首先需要确定直角坐标系和参照系。
直角坐标系是用来描述物体运动的空间坐标系,而参照系则是用来描述物体运动的时间坐标系。
在确定坐标系和参照系后,我们就可以把物体的位置、速度和加速度等物理量表示为坐标和时间的函数。
2. 建立物理模型建立物理模型是解决平面直角坐标系动点问题的关键。
在建立物理模型时,需要考虑物体的运动状态、受力情况和物体的基本性质。
我们可以通过建立动力学模型和几何模型来描述物体的运动状态,并利用这些模型来计算物体的位置、速度和加速度等物理量。
3. 使用向量加减法在解决平面直角坐标系动点问题时,向量加减法是非常重要的。
通过使用向量加减法,我们可以将物体的运动状态表示为一个向量,从而方便计算物体的位置、速度和加速度等物理量。
此外,在使用向量加减法时,我们还需要注意向量的大小和方向,以便准确表示物体的运动状态。
4. 利用微积分知识微积分是解决平面直角坐标系动点问题的重要工具。
通过利用微积分知识,我们可以求解物体的速度和加速度,进而计算出物体的位置。
在利用微积分求解问题时,我们需要注意函数的导数和积分等基本概念,以便正确求解问题。
5. 应用三角函数知识三角函数知识也是解决平面直角坐标系动点问题的必备知识之一。
在解决平面直角坐标系动点问题时,我们经常需要涉及到角度和三角函数的计算。
因此,掌握三角函数知识是非常必要的。
总之,解决平面直角坐标系动点问题需要掌握一些基本的技巧和方法。
通过正确使用直角坐标系和参照系、建立物理模型、使用向量加减法、利用微积分知识以及应用三角函数知识等方法,我们可以有效地解决平面直角坐标系动点问题,提高数学解题能力。
平面直角坐标系下的动点问题专题复习

如图,OABC 是一张放在平面直角坐标系中的矩形纸片,O 为原点,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,OA 、OC 是方程1092xx -=的两个根(OA >OC ),在AB 边上取一点D ,将纸片沿CD 翻折,使点B 恰好落在OA 边上的点E 处. (1)求OA 、OC 的长; (2)求D 、E 两点的坐标;(3)若线段CE 上有一动点P 自C 点沿CE 方向向E 点匀速运动(点P 运动到点E 后停止运动),运动的速度为每秒1个单位长度,设运动的时间为t 秒,过P 点作ED 的平行线交CD 于点M .是否存在这样的t 值,使以C 、E 、M 为顶点的三角形为等腰三角形?若存在,请直接写出t 值及相应的时刻点M 的坐标;若不存在,请说明理由.如图1,OABC 是一张放在平面直角坐标系中的矩形纸片,O 为原点,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,5OA =,4OC =.(1)在OC 边上取一点D ,将纸片沿AD 翻折,使点O 落在BC 边上的点E 处,求D E ,两点的坐标;(2)如图2,若AE 上有一动点P (不与A E ,重合)自A 点沿AE 方向向E 点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t 秒(05t <<),过P 点作ED 的平行线交AD 于点M ,过点M 作AE 的平行线交DE 于点N .求四边形PMNE 的面积S 与时间t 之间的函数关系式;当t 取何值时,S 有最大值?最大值是多少?(3)在(2)的条件下,当t 为何值时,以A M E ,,为顶点的三角形为等腰三角形,并求出相应的时刻点M 的坐标.如图,点A 在Y 轴上,点B 在X 轴上,且OA=OB=1,经过原点O 的直线L 交线段AB 于点C ,过C 作OC 的垂线,与直线X=1相交于点P ,现将直线L 绕O 点旋转,使交点C 从A 向B 运动,但C 点必须在第一象限内,并记AC 的长为t ,分析此图后,对下列问题作出探究: (1)当△AOC 和△BCP 全等时,求出t 的值。
七年级平面直角坐标系动点规律问题(经典难题)

平面直角坐标系动点问题(一)找纪律1.如图1,一只跳蚤在第一象限及x轴.y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示偏向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤地点地位的坐标是()图1A.(4,0)B.(5,0)C.(0,5)D.(5,5)图2 2.如图2,所有正方形的中间均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,极点依次用A1,A2,A3,A4,…暗示,则极点A55的坐标是()A.(13,13)B.(﹣13,﹣13)C.(14,14)D.(﹣14,﹣14)3.如图3,在平面直角坐标系中,有若干个横.纵坐标分离为整数的点,其次序按图中点的坐标分离为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的纪律分列,依据这个纪律,第2019个点的横坐标为.4.在平面直角坐标系中,一蚂蚁从原点O动身,按向上.向右.向下.向右的偏向依次不竭移动,每次移动1个单位,其行走路线如下图所示. 图3(1)填写下列各点的坐标:1A (____,____),3A (____,____),12A (____,____);(2)写出点n A 4的坐标(n 是正整数);(3)指出蚂蚁从点100A 到101A 的移动偏向.5.不雅察下列有序数对:(3,﹣1)(﹣5,)(7,﹣)(﹣9,)…依据你发明的纪律,第100个有序数对是.6.不雅察下列有纪律的点的坐标:依此纪律,A 11的坐标为,A 12的坐标为.7、以0为原点,正东,正南偏向为x 轴,y 轴正偏向树立平面直角坐标系,一个机械人从原点O 点动身,向正东偏向走3米到达A 1点,再向正南偏向走6米到达A 2,再向正西偏向走9米到达A 3,再向正南偏向走12米到达A 4,再向正东偏向走15米到达A 5,按此纪律走下去,当机械人走到A 6时,A 6的坐标是.8.如图,将边长为1的正三角形OAP 沿x 轴正偏向持续翻转2019次,点P 依次落在点201921,,,P P P 的地位,则点2019P 的横坐标为 .9.如图,在平面直角坐标系上有个点P (1,0),点P 第1次向上跳动1个单位至点P 1(1,1),紧接着第2次向左跳动2个单位至点P 2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此纪律跳动下去,点P 第100次跳动至点P 100的坐标是.点P 第2019次跳动至点P 2019的坐标是. 图4 图510.如图5,已知A l (1,0),A 2(1,1),A 3(﹣1,1),A 4(﹣1,﹣1),A 5(2,﹣1),….则点A 2019的坐标为.1. 如图,一个粒子在第一象限内及x .y 轴上活动,在第一分钟内它从原点活动到()1,0,尔后它接着按图所示在x 轴.y 轴平行的偏向上往返活动,且每分钟移动1个长度单位,那么,在1989分钟后这个粒子所处的地位是( ).A .()35,44B .()36,45C .()37,45D .()44,352. 假如将点P 绕定点M 扭转180︒后与点Q 重合,那么称点P 与点Q 关于点M 对称,定点M 叫做对称中间,此时,点M 是线段PQ 的中点,如图,在直角坐标系中,ABO △的极点A .B .O 的坐标分离为()1,0.()0,1.()0,0,点1P ,2P ,3P ,…中相邻两点都关于ABO △的一个极点对称,点1P 与点2P 关于点A 对称,点2P 与点3P 关于点B 对称,点3P 与点4P 关于点O 对称,点4P 与点5P 关于点A 对称,点5P 与点6P 关于点B 对称,点6P 与点7P 关于点O 对称,…对称中间分离是A ,B ,O ,A ,B ,O ,…且这些对称中间依次轮回,已知1P 的坐标是 1P A O yxP()1,1.试写出点2P .7P .100P 的坐标.3. 如图,在平面直角坐标系中,四边形各极点的坐标分离为:()0,0A ,()7,0B ,()9,5C ,()2,7D .(1)求此四边形的面积.(2)在坐标轴上,你可否找到一点P ,使50PBC S =△?若能,求出P 点坐标;若不克不及,请解释来由.4. 如图①,已知OABC 是一个长方形,个中极点A .B 的坐标分离为()0,a 和()9,a ,点E 在AB 上,且13AE AB =,点F 在OC 上,且13OF OC =.点G 在OA 上,且使GEC △的面积为20,GFB △的面积为16,试求a 的值.5. 如图,在平面直角坐标系中,有若干个横坐标分离为整数的点,其次序按图中“→”偏向分列,如()1,0,()2,0,()2,1,()1,1,()1,2,()2,2……依据这个纪律,第2019个点的横坐标为_______.6. 在平面直角坐标系xOy 中,我们把横.纵坐标都是整数的点叫做整点.已知点()0,4A ,点B 是x 轴正半轴上的整点,记AOB △内部(不包含鸿沟)的整点个数为m ,当3m =时,点B 的横坐标的所有可能值是_______;当点B 的横坐标为4n (n 为正整数)时,m =________(用含n 的代数式暗示).7. 如图,把天然数按图的次序排在直角坐标系中,每个天然数都对应着一个坐标.如1的对应点是原点()0,0,3的对应点是()1,1,16的对应点是()1,2-,那么2019的对应点的坐标是_______.8.如图,长方形BCDE 的各边分离平行于x 轴或y 轴,物体甲和物体乙由点()2,0A 同时动身,沿长方形BCDE 的边作围绕活动,物体甲按逆时针偏向以每秒1个单位长度的速度匀速活动,物体乙按顺时针偏向以每秒2个单位长度的速度匀速活动,求两个物体开端活动后的第2019次相遇地点的坐标.9. 在平面直角坐标系中,如图①,将线段AB 平移至线段CD ,衔接AC .BD .(1)直接写出图中相等的线段.平行的线段;(2)已知()3,0A -.()2,2B --,点C 在y 轴的正半轴上.点D 在第一象限内,且5ACD S =△,求点C .D 的坐标;(3)如图②,在平面直角坐标系中,已知必定点,()1,0M ,两个动点(),21E a a +.(),23F b b -+,请你摸索是否消失以两个动点E .F 为端点的线段EF 平行于线段OM 且等于线段OM .若消失,求以点O .M .E .F 为极点的四边形的面积,若不消失,请解释来由. 10 . 如图,AOCD 是放置在平面直角坐标系内的梯形,个中O 是坐标原点.点A .C .D 的坐标分离为()0,8,()5,0,()3,8,若点P 在梯形内,且PAD POC S S =△△,PAO PCD S S =△△,求P 点的坐标.11. 操纵与研讨(1)对数轴上的点P 进行如下操纵:先把点P 暗示的数乘以13,再把所得数对应的点向右平移1个单位,得到点P 的对应点'P B . 点A ,B 在数轴上,对线段AB 上的每个点进行上述操纵后得到线段''A B ,个中点A ,B 的对应点分离为'A ,'B .如图①,若点A 暗示的数是3-,则点'A 暗示的数是______;若点'B 暗示的数是2,则点暗示的数是______;已知线段AB 上的点E 经由上述操纵后得到的对应点'E 与点E 重合,则点E 暗示的数是_________.(2)如图②,在平面直角坐标系xOy 中,对正方形ABCD 及其内部的每个点进行如下操纵:把每个点的横.纵坐标都乘以统一个实数a ,将得到的点先向右平移m 个单位,再向上平移n 个单位()0,0m n >>,得到正方形''''A B C D 及其内部的点,个中点A ,B 的对应点分离为'A ,'B .已知正方形ABCD 内部的一个点F 经由上述操纵后得到的对应点'F 与点F 重合,求点F 的坐标.(二)几何分解问题1.已知点A 的坐标是(3,0).AB=5,(1)当点B 在X 轴上时.求点B 的坐标.(2)当AB//y 轴时.求点B 的坐标2.如图,已知A .B 两村庄的坐标分离为(2,2).(7,4),一辆汽车在x 轴上行驶,从原点O 动身.(1)汽车行驶到什么地位时离A 村比来?写出此点的坐标.(2)汽车行驶到什么地位时离B 村比来?写出此点的坐标.(3)请在图中画出汽车行驶到什么地位时,距离两村的和最短?4.如图,在平面直角坐标系中,点A,B 的坐标分离为(-1,0),(3,0),现同时将点A,B 分离向上平移2个单位,再向右平移1个单位,分离得到点A,B 的对应点C,D,衔接AC,BD,CD .(1)求点C,D 的坐标及四边形ABDCABDC S 四边形(2)在y 轴上是否消失一点P,衔接PA,PB,PAB S ∆=ABDC S 四边形,若消失如许一点,求出点P 的坐标,若不消失,试解释来由.(3)点P 是线段BD 上的一个动点,衔接PC,PO,当点P 在BD 上移动时(不与B,D 重合)给出下列结论:①DCP BOP CPO ∠+∠∠的值不变,②DCP CPOBOP ∠+∠∠的值不变,个是准确的,请你找出这个结论并求其值.5.已知:在平面直角坐标系中,四边形ABCD 是长方形, ∠A =∠B =∠C =∠D =90°,AB ∥CD ,AB =CD =8cm ,AD =BC =6cm ,D 点与原点重合,坐标为(0,0).(1)写出点B 的坐标.(2)动点P 从点A 动身以每秒3个单位长度的速度向终点B 匀速活动, 动点Q 从点C 动身以每秒4个单位长度的速度沿射线CD 偏向匀速活动,若P ,Q 两点同时动身,设活动时光为t 秒,当t 为何值时,PQ∥BC?(3)在Q的活动进程中,当Q活动到什么地位时,使△ADQ的面积为9? 求出此时Q点的坐标.6.如图在平面直角坐标系中,A(a,0),B(b,0),(﹣1,2).且|2a+b+1|+=0.(1)求a.b的值;(2)①在y轴的正半轴上消失一点M,使S△COM=S△ABC,求点M的坐标.②在坐标轴的其他地位是否消失点M,使S△COM=S△ABC仍成立?若消失,请直接写出相符前提的点M的坐标.7.如图,鄙人面的直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,个中a,b知足关系式.(1)求a,b的值;(2)假如在第二象限内有一点P(m,),请用含m的式子暗示四边形ABOP的面积;(3)在(2)的前提下,是否消失点P,使四边形ABOP的面积与△ABC的面积相等?若消失,求出点P的坐标;若不消失,请解释来由.8.在平面直角坐标系中,点A(a,b)是第四象限内一点,AB⊥y轴于B,且B(0,b)是y轴负半轴上一点,b2=16,S△AOB=12.(1)求点A和点B的坐标;(2)如图1,点D为线段OA(端点除外)上某一点,过点D作AO 垂线交x轴于E,交直线AB于F,∠EOD.∠AFD的等分线订交于N,求∠ONF的度数.(3)如图2,点D为线段OA(端点除外)上某一点,当点D在线段上活动时,过点D作直线EF交x轴正半轴于E,交直线AB于F,∠EOD,∠AFD的等分线订交于点N.若记∠ODF=α,请用α的式子暗示∠ONF的大小,并解释来由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图,OABC 是一张放在平面直角坐标系中的矩形纸片,O 为原点,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,OA 、OC 是方程
10
92x
x -=
的两个根(OA >OC ),在AB 边上取一点D ,将纸片沿CD 翻折,使点B 恰好落在OA 边上的点E 处. (1)求OA 、OC 的长; (2)求D 、E 两点的坐标;
(3)若线段CE 上有一动点P 自C 点沿CE 方向向E 点匀速运动(点P 运动到点E 后停止运动),运动的速度为每秒1个单位长度,设运动的时间为t 秒,过P 点作ED 的平行线交CD 于点M .是否存在这样的t 值,使以C 、E 、M 为顶点的三角形为等腰三角形?若存在,请直接写出t 值及相应的时刻点M 的坐标;若不存在,请说明理由.
如图1,OABC 是一张放在平面直角坐标系中的矩形纸片,O 为原点,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,5OA =,4OC =.
(1)在OC 边上取一点D ,将纸片沿AD 翻折,使点O 落在BC 边上的点E 处,求D E ,两点的坐标;
(2)如图2,若AE 上有一动点P (不与A E ,重合)自A 点沿AE 方向向E 点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t 秒(05t <<),过P 点作ED 的平行线交AD 于点M ,过点M 作AE 的平行线交DE 于点N .求四边形PMNE 的面积S 与时间t 之间的函数关系式;当t 取何值时,S 有最大值?最大值是多少?
(3)在(2)的条件下,当t 为何值时,以A M E ,,为顶点的三角形为等腰三角形,并求出相应的时刻点M 的坐标.
y B
C O
A
D
E
y B
C O
A
D
E P
M
N
如图,点A 在Y 轴上,点B 在X 轴上,且OA=OB=1,经过原点O 的直线L 交线段AB 于点C ,过C 作OC 的垂线,与直线X=1相交于点P ,现将直线L 绕O 点旋转,使交点C 从A 向B 运动,但C 点必须在第一象限内,并记AC 的长为t ,分析此图后,对下列问题作出探究: (1)当△AOC 和△BCP 全等时,求出t 的值。
(2)通过动手测量线段OC 和CP 的长来判断它们之间的 大小关系?并证明你得到的结论。
(3)①设点P 的坐标为(1,b ),试写出b 关于t 的函数
关系式和变量t 的取值范围。
②求出当△PBC 为等腰三角形时点P 的坐标。
2、 ( 湖北天门)如图①,在平面直角坐标系中,A 点坐标为(3,0),B 点坐标为(0,4).动 点M 从点O 出发,沿OA 方向以每秒1个单位长度的速度向终点A 运动;同时,动点N 从点A 出发沿AB 方向以每秒3
5个单位长度的速度向终点B 运动.设运动了x 秒.
(1)点N 的坐标为(________________,________________);(用含x 的代数式表示) (2)当x 为何值时,△AMN 为等腰三角形?
(3)如图②,连结ON 得△OMN ,△OMN 可能为正三角形吗?若不能,点M 的运动速度不变, 试改变点N 的运动速度,使△OMN 为正三角形,并求出点N 的运动速度和此时x 的值.
(1)依题意可知,折痕AD 是四边形OAED 的对称轴, ∴在Rt ABE △中,5AE AO ==,4AB =.
3BE ∴=.2CE ∴=.
E ∴点坐标为(2,4)
. 在Rt DCE △中,2
2
2
DC CE DE +=, 又
DE OD =.
222(4)2OD OD ∴-+= . 解得:5
2
CD =
.
图
D ∴点坐标为502⎛⎫
⎪
⎝⎭,
(2)如图①
PM ED ∥,APM AED ∴
△∽△. PM AP ED AE
∴=
,又知AP t =,5
2ED =,5AE = 5522
t t
PM ∴=⨯=, 又5PE t =-.
而显然四边形PMNE 为矩形.
215(5)222PMNE t S PM PE t t t ∴==⨯-=-+矩形2
1525
228
PMNE S t ⎛⎫∴=--+
⎪⎝⎭四边形,又5
052
<
< ∴当52t =
时,PMNE S 矩形有最大值258
. (3)(i )若以AE 为等腰三角形的底,则ME MA =(如图①) 在Rt AED △中,ME MA =,PM AE ⊥,P ∴为AE 的中点,
15
22
t AP AE ∴===.
又PM ED ∥,M ∴为AD 的中点.
过点M 作MF OA ⊥,垂足为F ,则MF 是OAD △的中位线,
1524MF OD ∴==,15
22OF OA ==,
∴当52t =
时,5052⎛⎫
<< ⎪⎝⎭
,AME △为等腰三角形.
此时M 点坐标为5524⎛⎫ ⎪⎝⎭
,.
(
ii )若以AE 为等腰三角形的腰,则5AM
AE ==(如图②) 在Rt
AOD △中,AD === 过点M 作MF OA ⊥,垂足为F .
PM ED ∥,APM AED ∴
△∽△. AP
AM
AE AD
∴
=. 55
5
AM AE t AP AD ⨯∴====
,12PM t ∴=
=.
MF MP ∴==5
OF OA AF OA AP =-=-=
-
∴当t =
(05<<),此时M 点坐标为(5-
.
综合(i )(ii )可知,5
2
t =
或t =A M E ,,为顶点的三角形为等腰三角形,相应M
点的坐标
为5524⎛⎫ ⎪⎝⎭
,
或(5-.
如图,将OA = 6,AB = 4的矩形OABC 放置在平面直角坐标系中,动点M 、N 以每秒1个单位的速度分别从点A 、C 同时出发,其中点M 沿AO 向终点O 运动,点N 沿CB 向终点B 运动,当两个动点运动了t 秒时,过点N 作NP ⊥BC ,交OB 于点P ,连接MP .
(1)点B 的坐标为 ;用含t 的式子表示点P 的坐标为 ;(3分)
(2)记△OMP 的面积为S ,求S 与t 的函数关系式(0 < t < 6);并求t 为何值时,S 有最大值?(4分) (3)试探究:当S 有最大值时,在y 轴上是否存在点T ,使直线MT 把△ONC 分割成三角形和四边形两部分,且三角形的面积是△ONC 面积的
1
3
?若存在,求出点T 的坐标;若不存在,请说明理由.(3分)
(2010•福建省莆田市)如图1,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在
x
(备用图)
轴的正半轴上,OA =1,OC =2,点D 在边OC 上且54
OD =
. (1)求直线AC 的解析式;
(2)在y 轴上是否存在点P ,直线PD 与矩形对角线AC 交于点M ,使得DMC △为等腰三角形?若存在,直接写出....
所有符合条件的点P 的坐标;若不存在,请说明理由. (3)抛物线2
y x =-经过怎样平移,才能使得平移后的抛物线过点D 和点E (点E 在y 轴正半轴上),且ODE △沿DE 折叠后点O 落在边AB 上O ′处?
( 2010•鸡西)如图,矩形OABC 在平面直角坐标系中,若OA 、OC 的长满足
(
223
OA OC -+-. ⑴求B 、C 两点的坐标. ⑵把△ABC 沿AC 对折,点B 落
在点B ′处,线段AB ′与x 轴交于点D,求直线BB ′的解析式.
⑶在直线BB ′上是否存在点P,使△ADP 为直角三角形?若存在,请直接写出 P 点坐标;若不存在,请说明理由.
(2010•攀枝花)22.(12分)如图,在矩形ABCD 中,AB =6,AD =23,点P 是边BC 上的动点(点P 不与
B 、
C 重合),过点P 作直线PQ ∥B
D ,交CD 边于点Q ,再把△CPQ 沿着直线PQ 对折,点C 的对应点是点R .设CP =x ,△PQR 与矩形ABCD 重叠部分的面积为y . (1)求∠CPQ 的度数;
(2)当x 取何值时,点R 落在矩形ABCD 的边AB 上?
(3)当R 在矩形ABCD 外部时,求y 与x 的函数关系式及此时函数值y 的取值范围.
第25题
B ′
B
A
y C
D
O
A
B
C D
Q
P
D
A
E
R
F
B C
P Q。
