插值与拟合习题课
其他例题和练习(拟合与插值)

function f=nihehanshu(x,xdata) f=x(1)*exp(xdata)+x(2)*xdata.^2+x(3)*xdata.^3 保存为文件 nihehanshu.m
例4 已知观测数据点如表所示
x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 y 3.1 3.27 3.81 4.5 5.18 6 7.05 8.56 9.69 11.25 13.17 求三个参数 a, b, c的值, 使得曲线 f(x)=aex+bx2+cx3 与 已知数据点在最小二乘意义上充分接近. 编写下面的程序调用拟合函数.
2. 已知观测数据点如表所示 x 1.6 2.7 1.3 4.1 3.6 2.3 y 17.7 49 13.1 189.4 110.8 34.5
0.6
4
4.9
409.1
3
65
2.4
36.9
求a, b, c的值, 使得曲线 f(x)=aex+bsin x+c lnx 与已知数据 点在最小二乘意义上充分接近.
插值问题
已知 n+1个节点 ( x j , y j ) ( j 0,1, n, 其中 x j
互不相同, 不妨设 a x0 x1 xn b ) ,
求任一插值点
x ( x j )
*
处的插值 y * . 节点可视为由 y g (x) 产生, g 表达式复杂, 甚至无表达式
x=0:0.1:1 y=[-0.447,1.978,3.28,6.16,7.08,7.34,7.66,9.56,9.48,9.3,11.2] plot(x,y,'k.','markersize',25) axis([0 1.3 -2 16]) p3=polyfit(x,y,3) p6=polyfit(x,y,6) t=0:0.1:1.2 s=polyval(p3,t) s1=polyval(p6,t) hold on plot(t,s,'r-','linewidth',2) plot(t,s,'b--','linewidth',2) grid
插值和拟合参考答案

插值和拟合实验目的:了解数值分析建模的方法,掌握用Matlab进行曲线拟合的方法,理解用插值法建模的思想,运用Matlab一些命令及编程实现插值建模。
实验要求:理解曲线拟合和插值方法的思想,熟悉Matlab相关的命令,完成相应的练习,并将操作过程、程序及结果记录下来。
实验内容:一、插值1.插值的基本思想·已知有n +1个节点(xj,yj),j = 0,1,…, n,其中xj互不相同,节点(xj, yj)可看成由某个函数y= f (x)产生;·构造一个相对简单的函数y=P(x);·使P通过全部节点,即P (xk) = yk,k=0,1,…, n ;·用P (x)作为函数f ( x )的近似。
2.用MA TLAB作一维插值计算yi=interp1(x,y,xi,'method')注:yi—xi处的插值结果;x,y—插值节点;xi—被插值点;method—插值方法(‘nearest’:最邻近插值;‘linear’:线性插值;‘spline’:三次样条插值;‘cubic’:立方插值;缺省时:线性插值)。
注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
练习1:机床加工问题机翼断面下的轮廓线上的数据如下表:x 0 3 5 7 9 11 12 13 14 15y 0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6 用程控铣床加工机翼断面的下轮廓线时每一刀只能沿x方向和y方向走非常小的一步。
表3-1给出了下轮廓线上的部分数据但工艺要求铣床沿x方向每次只能移动0.1单位.这时需求出当x坐标每改变0.1单位时的y坐标。
试完成加工所需的数据,画出曲线.步骤1:用x0,y0两向量表示插值节点;步骤2:被插值点x=0:0.1:15; y=interp1(x0,y0,x,'spline');步骤3:plot(x0,y0,'k+',x,y,'r')grid on>> x0=[0 3 5 7 9 11 12 13 14 15 ];>> y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6 ];>> x=0:0.1:15;y=interp1(x0,y0,x,'spline');plot(x0,y0,'k+',x,y,'r')grid on0510150.511.522.53.用MA TLAB 作网格节点数据的插值(二维) z=interp2(x0,y0,z0,x,y,’method’) 注:z —被插点值的函数值;x0,y0,z0—插值节点;x ,y —被插值点;method —插值方法(‘nearest’ :最邻近插值;‘linear’ :双线性插值; ‘cubic’ :双三次插值;缺省时:双线性插值)。
练习2--插值与拟合

用MATLAB作网格节点数据的插值
z=interp2(x0,y0,z0,x,y,’method’)
被插值点 的函数值
插值 节点
被插值点
插值方法
‘nearest’ 最邻近插值; ‘linear’ 双线性插值; ‘cubic’ 双三次插值;
缺省时 双线性插值. 要求x0,y0单调;x,y可取为矩阵,或x 取行向量,y取为列向量,x,y的值分别不能超 出x0,y0的范围.
用MATLAB作非线性最小二乘拟合
Matlab的提供了两个求非线性最小二乘拟合的函数: lsqcurvefit和lsqnonlin。两个命令都要先建立M-文件fun.m, 在其中定义函数f(x),但两者定义f(x)的方式是不同的,可参 考例题. 1. lsqcurvefit 已知数据点: xdata=(xdata1,xdata2,…,xdatan), ydata=(ydata1,ydata2,…,ydatan) lsqcurvefit用以求含参量x(向量)的向量值函数
F(x,xdata)=(F(x,xdata1),…,F(x,xdatan))T
中的参变量x(向量),使得
n 2
( F ( x, xdata ) ydata )
i 1 i i
最小
输入格式为: (1) x = lsqcurvefit (‘fun’,x0,xdata,ydata); (2) x =lsqcurvefit (‘fun’,x0,xdata,ydata,options); (3) x = lsqcurvefit (‘fun’,x0,xdata,ydata,options,’grad’); (4) [x, options] = lsqcurvefit (‘fun’,x0,xdata,ydata,…); (5) [x, options,funval] = lsqcurvefit (‘fun’,x0,xdata,ydata,…); (6) [x, options,funval, Jacob] = lsqcurvefit (‘fun’,x0,xdata,ydata,…); 说明:x = lsqcurvefit (‘fun’,x0,xdata,ydata,options); fun是一个事先建立的 定义函数F(x,xdata) 的 M-文件, 自变量为x和 xdata 选项见无 迭代初值 已知数据点 约束优化
学号_姓名_专业_插值拟合练习题
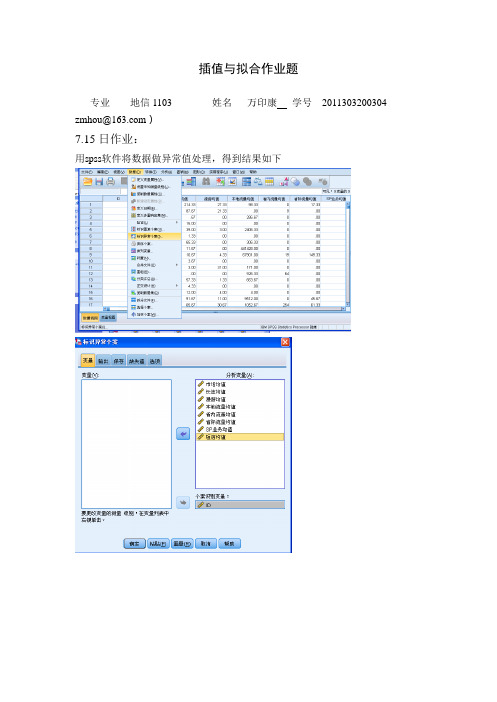
插值与拟合作业题专业____地信1103______ 姓名___万印康学号__2011303200304__ zmhou@)7.15日作业:用spss软件将数据做异常值处理,得到结果如下异常个案原因列表原因:1案例ID 原因变量变量影响变量值变量范数4352 4352 省内流量均值.801 196237 918.64 3439 3439 省际流量均值.872 109954.00 630.3612 2333 2333 省际流量均值.897 78112.00 630.3612 1294 1294 长途均值.937 2112.00 96.2106 619 619 省际流量均值.915 66558.00 630.3612 130 130 漫游均值.925 607.67 18.3570 3611 3611 短信均值.976 1081 100.07 2506 2506 省际流量均值.843 60101.67 630.3612 2180 2180 短信均值.975 1043 100.07 1470 1470 短信均值.964 1029 100.07 2391 2391 短信均值.976 1029 100.07 2453 2453 漫游均值.675 472.33 18.3570 2125 2125 漫游均值.907 548.00 18.3570 1147 1147 短信均值.947 980 100.07 154 154 省内流量均值.891 79672 918.64 1850 1850 短信均值.961 954 100.07 2512 2512 短信均值.973 959 100.07 1936 1936 本地流量均值.899 1110435.33 30279.9692 4322 4322 短信均值.933 922 100.07 2992 2992 短信均值.931 921 100.07 2371 2371 短信均值.914 903 100.07 995 995 短信均值.848 864 100.07 259 259 短信均值.964 916 100.07 3657 3657 短信均值.902 881 100.07 2527 2527 本地流量均值.873 1040059.00 30279.9692 1370 1370 短信均值.900 855 100.07 472 472 短信均值.924 862 100.073252 3252 短信均值.936 863 100.074017 4017 省内流量均值.663 60975 918.642337 2337 短信均值.938 852 100.071611 1611 短信均值.884 824 100.073656 3656 短信均值.958 855 100.07940 940 短信均值.716 747 100.071836 1836 短信均值.821 785 100.07820 820 漫游均值.503 46.00 3.67382735 2735 短信均值.951 835 100.071887 1887 短信均值.751 746 100.074148 4148 短信均值.859 790 100.07葡萄酒样品检验同样可以利用相同方法进行异常值检测。
数学建模插值与拟合实验题

数学建模插值与拟合实验题
1.处理2021年大学生数学建模竞赛a题:“中国人口增长预测”附件中的数据,得
到以下几个问题的拟合结果,并绘制图形
(1)将1994~2022岁婴儿的性别比设为2022,预测性别比例为2022~2022。
(2)生育率随年龄的变化而变化,试以生育年龄为自变量,生育率为因变量,对各
年的育龄妇女生育率进行拟合;
(3)根据时间分布分析城镇、城镇的生育率,以时间为自变量,以生育率为因变量,拟合城镇、城镇的生育率,并将生育率从2022预测到2022。
(4)将某年的城镇化水平pu(t)定义为当年的城镇人口数与总人口数之
Karmeshu(1992)发现,自20世纪50年代以来,随着经济发展水平的提高,发达国
家城市人口的增长速度一直快于农村地区。
但是,随着城市化水平的提高,达到100%,速度将会放缓。
城市化水平的增长曲线粗略地表现为“S”型Logistic曲线〔4〕,对中国
人口1%的调查数据进行了曲线拟合,从附录2中给出了2001~2022的数据,得到了曲线,并绘制了城市化水平从2001到2050的曲线。
2.处理2021年大学生数学建模竞赛a题:“城市表层土壤重金属污染分析”附件中
的数据,完成下列问题
(1)以城区采样点为插值节点,绘制城区地形图和等高线图;(2)绘制城区8种
重金属浓度的空间分布图。
并指出最高和最低浓度点的位置。
插值的方法可用三次插值、kriging插值、shepard插值等。
工具可用matlab,也可
用surfer软件实现。
拟合与插值专题ppt课件

一种是插值法,数据假定是正确的,要求以某种方法描述数 据点之间所发生的情况。
另一种方法是曲线拟合或回归。人们设法找出某条光滑曲线, 它最佳地拟合数据,但不必要经过任何数据点。
本专题的主要目的是:了解插值和拟合的基本内容; 掌握用Matlab求解插值与拟合问题的基本命令。
cj 103 4.54 4.99 5.35 5.65 5.90 6.10 6.26 6.39 6.50 6.59
该问题即解最优化问题:
min 1 F (a,b, k)
2
1 2
10
[a be0.02kt j
j 1
c j ]2
解法1. 用命令lsqcurvefit
F(x,tdata)= (a be0.02kt1 ,, a be0.02kt10 )T ,x=(a,b,k)
ydata=(ydata1,ydata2,…,ydatan) lsqcurvefit用以求含参量x(向量)的向量值函数
F(x,xdata)=(F(x,xdata1),…,F(x,xdatan))T
中的参变量x(向量),使得
1
2
n i 1
( F ( x,
xdatai )
2
ydatai )
最小
输入格式: (1) x = lsqcurvefit (‘fun’,x0,xdata,ydata); (2) x =lsqcurvefit (‘fun’,x0,xdata,ydata,lb, ub);
1)编写M-文件 curvefun1.m
function f=curvefun1(x,tdata)
f=x(1)+x(2)*exp(-0.02*x(3)*tdata)
数学建模插值与拟合课件
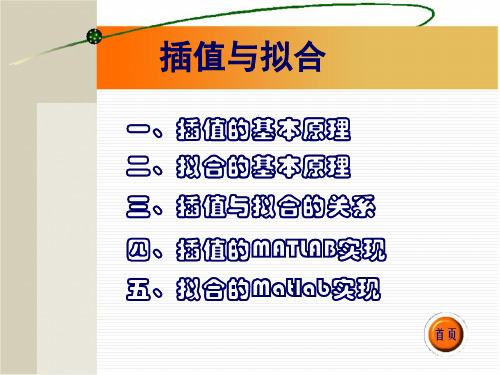
设函数 y f (x) 在 n 1个相异点 x0 , x1, x2 , , xn 上的值为 y 0 , y1, y2 , , yn ,要求一个次数≤n 的代数多
项式
Pn (x) a0 a1x a2 x 2 an x n
使在节点 xi 上成立 Pn (xi ) yi (i 0,1,2, , n) ,称此为 n 次代数插值问题,Pn (x) 称为插值多项式。可以证明 n
如果不要求近似函数通过所有数据点, 而是要求它能较好地反映数据变化规律的近 似函数的方法称为数据拟合。(必须有函数 表达式)
近似函数不一定(曲线或曲面)通过所 有的数据点。
三、插值与拟合的区别和联系
1、联系 都是根据实际中一组已知数据来构造一个能够 反映数据变化规律的近似函数的方法。 2、区别 插值问题不一定得到近似函数的表达形式,仅 通过插值方法找到未知点对应的值。数据拟合 要求得到一个具体的近似函数的表达式。
图所示,当n 增大时,pn x在两端会发出激烈
的振荡,这就是所谓龙格现象。
龙格现象
2
y=1/(1+x2) y=p4(x) y=p10(x) 1.5
1
0.5
0
-0.5
-5 -4 -3 -2 -1
0
1
2
3
4
5
x
To MATLAB lch(larg1)
分段插值的概念
所谓分段插值,就是将被插值函数逐段 多项式化。一般来说,分段插值方法的处理 过程分两步,先将所考察的区间作一分划
y1
lj(x)
当n =2 时,有三点二次(抛物线)插值多项式:
P2
(x)
(x (x0
x1)(x x2 ) x1)(x0 x2 )
第4、5讲 插值与拟合 作业参考答案

第四、五讲作业题参考答案一、填空题1、拉格朗日插值基函数在节点上的取值是( 0或1 )。
2、当1,1,2x =-,时()034f x =-,,,则()f x 的二次插值多项式为 (2527633x x +- )。
3、由下列数据所确定的唯一插值多项式的次数为( 2次 )。
4、根据插值的定义,函数()x f x e -=在[0,1]上的近似一次多项式1()P x =( 1(1)1e x --+ ),误差估计为( 18 )。
5、在做曲线拟合时,对于拟合函数x y ax b =+,引入变量变换y =( 1y),x =(1x)来线性化数据点后,做线性拟合y a bx =+。
6、在做曲线拟合时,对于拟合函数Ax y Ce =,引入变量变换( ln()Y y = )、X x =和B C e =来线性化数据点后,做线性拟合Y AX B =+。
7、设3()1f x x x =+-,则差商[0,1,2,3]f =( 1 )。
8、在做曲线拟合时,对于拟合函数()A f x Cx =,可使用变量变换(ln Y y =)(ln X x = )和B C e =来线性化数据点后,做线性拟合Y AX B =+。
9、设(1)1,(0)0,(1)1,(2)5,()f f f f f x -====则的三次牛顿插值多项式为( 321166x x x +-),其误差估计式为(4()(1)(1)(2),(1,2)24f x x x x ξξ+--∈-) 10、三次样条插值函数()S x 满足:()S x 在区间[,]a b 内二阶连续可导,(),,0,1,2,,,k k k k S x y x y k n ==(已知)且满足()S x 在每一个子区间1[,]k k x x +上是( 三次多项式 )。
11、1()[a,b]()f x L x =函数在上的一次(线性)插值函数(公式)( ()()x b x af a f b a b b a--+-- ),1()R x =( 1()()(),2f x a x b a b ξξ''--≤≤ )。
数学建模案例与方法教学课件第5章插值法与拟合方法

5.1 城市供水量的预测问题
图5-3 三种插值函数曲线
5.1 城市供水量的预测问题
3. 用2000—2006年每年1月份城市的总用水量预测
由表5-2可得到7个 插值节点(x i,y i), 其中,xi=i,i=1,2,…,7, 其散点图如图5-4所示。 用三次样条插值法求得 的f(8)=4 378.139 0×104 t即为所求的 2007年1月份总用水量 的估计值,表5-3
5.1 城市供水量的预测问题
5.1.2 用插值法预测2007年1月份城市的总用水量
预测2007年1月份城市的用水量有三种 办法:一是用2006年的日用水量进行预测, 二是用2000—2006年每年1月份的日用水量 进行预测,三是用2000—2006年每年1月份
5.1 城市供水量的预测问题
1. 用2006年的日用水量进行预测
图5-4 2000—2006年每年1月份 城市的总用水量散点图
5.1 城市供水量的预测问题
5.1 城市供水量的预测问题
5.1.3 用数据拟合方法预测2007年1月份城市的总用水量 1. 用2006年每天的日用水量进行预测
由图5-1可知,这些点并不是简单地成线性或二次关系, 而是具有很强的聚集性。我们试图用几个多项式进行拟合。 用 MATLAB工具箱得到的拟合结果见表5-4。
5.2.1 曲线拟合
【实例】 气象部门观测到一天中某些时刻t的温度T变化数据见 表5-6。试描绘出温度变化曲线。
5.2 MATLAB与拟合、插值
曲线拟合就是计算出两组数据之间的一 种函数关系,由此可描绘其变化曲线及估计
曲线拟合有多种方式,下面是一元函数 采用最小二乘法对给定数据进行多项式曲线
5.2 MATLAB与拟合、插值
数值分析—插值拟合复习题

第 1 章插值
§1. 填空
(1). 设 Pk(xk,yk) , k=1,2,…,5 为函数 y=x2-3x+1 上的 5 个互异的点,过 P1,…,P5 且次数不超过 4 次的插值多项式是 ______ 。 y=x2-3x+1 (2). 设 x0, x1, x3 是区间[a, b]上的互异节点,f(x)在[a, b]上具有各阶导 数,过该组节点的 2 次插值多项式的余项为: ______ . R2(x)=
令 x=xi+1/2+s(h/2) 上式化简为
kn。lk(x)是关于互异节点 x0, x1,…, xn 的 Lagrange 插值基函数 证明:由插值唯一性定理知。 (9). (a10f)设 p(x)是任意首次项系数为 1 的 n+1 次多项式,lk(x)是关于 互异节点 x0, x1,…, xn, 的 Lagrange 插值基函数 证明 p( x ) p( x k )l k ( x ) w n1 ( x )
(1). 设 x=3.214, y=3.213, 欲计算 u= x 算式 u= . u=
y , 请给出一个精度较高的
选择填空 (6). 计算 f=( 2 -1)6 , 取 2 =1.4 , 利用下列算式,那个得到的结果 最好?(C) (A)
x y x y
(2). 设 y=f (x1,x2) 若 x1,x2,的近似值分别为 x1*, x2*,令 y*=f(x1*,x2*)作为 y 的近似值,其绝对误差限的估计式为: | |f(x1*, x 2*) |x1-x*1|+ | f(x1*,x2*)|x2-x*2| (3). 要使 20 的近似值的相对误差限 0.1%, 应至少取 _______ 位有 效数字?
数据插值与曲线拟合习题

数据插值与曲线拟合习题(1) 已知下列表值试用线性与二次Lagrange 插值多项式分别计算当x =1.25时y 的值。
习题解答:一、(1)线性Lagrange 插值多项式 根据计算公式:得出该插值结果为:4.5。
(2)二次Lagrange 插值多项式 根据计算公式:得出该插值结果为:4.125. 二、输入命令:X=[1 2 4 7 9 12 13 15 17];211121221()x x x x P x y y x x x x --=+--020*******010*********()()()()()()()()()()()()()x x x x x x x x x x x x P x y y y x x x x x x x x x x x x ------=++------Y=[1.5 3.9 6.6 11.7 15.6 18.8 19.6 20.6 21.1];plot(X,Y,'*-');下面是显示f与x的散点图:不难看出图形近似为一条直线,因此猜测用一次多项式来拟合,输入命令:P=polyfit(X,Y,1)P =1.2918 1.7840下面绘出的是拟合曲线和散点图对比图形:可以看出拟合效果并不理想。
根据表格数据,我们用二次曲线来拟合,输入命令:P=polyfit(X,Y,2)P =-0.0592 2.3265 -0.9803得到拟合函数为:P(x)=-0.0592.*x.^2+2.3265.*x-0.9803;对比图形如下:可以看出拟合效果有明显改善,拟合曲线与散点图基本上是吻合的,因此f与x的关系式为f==-0.0592.*x.^2+2.3265.*x-0.9803;可见曲线拟合本身就是一个猜测的过程,通常是不地修正拟合函数,使拟合效果达到满意的程度。
插值与拟合例题

1 山区地貌:在某山区测得一些地点的高程如下表:(平面区域1200<=x<=4000,1200<=y<=3600),试作出该山区的地貌图和等高线图,并对几种插值方法进行比较。
3600 3200 2800 2400 2000 1600 1200 14801500 1550 1510 1430 1300 1200 980 15001550 1600 1550 1600 1600 1600 1550 15001200 1100 1550 1600 1550 1380 1070 15001200 1100 1350 1450 1200 1150 1010 1390 1500 1500 1400 900 1100 1060 950 1320 1450 1420 1400 1300 700 900 850 1130 1250 1280 1230 1040 900 500 700Y/x1200 1600 2000 2400 2800 3200 3600 40002 用给定的多项式,如y=x3-6x2+5x-3,产生一组数据(xi,yi,i=1,2,…,n),再在yi上添加随机干扰(可用rand产生(0,1)均匀分布随机数,或用rands产生N(0,1)分布随机数),然后用xi 和添加了随机干扰的yi作的3次多项式拟合,与原系数比较。
如果作2或4次多项式拟合,结果如何?3 用电压V=10伏的电池给电容器充电,电容器上t时刻的电压为,其中V0是电容器的初始电压,是充电常数。
试由下面一组t,V数据确定V0,。
2用给定的多项式,如y=x3-6x2+5x-3,产生一组数据(xi,yi,i=1,2,…,n),再在yi上添加随机干扰(可用rand产生(0,1)均匀分布随机数,或用rands产生N(0,1)分布随机数),然后用xi和添加了随机干扰的yi作的3次多项式拟合,与原系数比较。
分别作1、2、4、6次多项式拟合,比较结果,体会欠拟合、过拟合现象。
lesson9插值与数据拟合建模(2)

(2)三次样条函数的定义
设[a,b] 的一个划分:a=x0<x1, x2 , ..., xn= b, 函数f ( x )各节点的值分别为:
f ( xi )=yi (i=1,2,...,n) 如果三次样条函数:
3
满足: S ( xi )=yi (i=1,2,...,n)
B:弹性细梁受集中载荷作用形成的挠度曲 线,在小挠度的情况下,恰好表示为三 次样条函数,集中载荷的作用点,恰好 就是三次样条函数的节点。
(1)二次样条的定义
设[a,b] 的一个划分:a=x0<x1, x2 , ..., xn= b, 函数f ( x )各节点的值分别为:
f ( xi )=yi (i=1,2,...,n) 如果二次样条函数:
8、检验
以不同的时间为起点得到的一天总用水量相差多少
一个物理定理
由托里查里(Torricelli)定律知,从水箱中 流出水的最大速度与水位高的平方成正比.对 于所给的数据,其水位的最大高度为35.5E, 最小高度为27E,因此对两个高度的最大流速 比为 35.5 / 27 ,这个数字已很接近l,所以 可以假定水位对流速没有影响.类似地,还假 设大气情况、温
长度单位:E(=30.24cm) 容积单位:G(=3.785L(升))
某些镇的用水管理机构需估计公众的用水速度(单 位是G/h)和每天总用水量的数据.许多地方没有测量 流入或流出水箱流量的设备,而只能测量水箱中的水 位(误差不超过5%).当水箱水位低于某最低水位L时, 水泵抽水,灌入水箱,直至水位达到最高水位H为止。 但这也无法测量水泵的流量,因此在水泵启动时不易 建立水箱中水位和水泵工作时用水量之间关系。水泵 一天灌水1~2次,每次约2h。试估计在任意时刻(包括 水泵灌水期间)t流出水箱的流量f(t),并估计一天的总 用水量。
插值与拟合习题课

插值与拟合习题课一、已知sin x 在30,45,60的值分别为1,,222,分别用一次插值和二次插值求sin 50的近似值,并估计截断误差.解:一次插值时,取靠近50的两个角度45,60作节点,将角度化为弧度为5,,1843πππ,此时有()134224334x x L x ππππππ--=+--55sin 50sin 0.7600801818L ππ⎛⎫=≈= ⎪⎝⎭由截断误差公式()()()()()()()101...1!n n n f R x x x x x x x n ξ+=---+有()()()101"()2f R x x x x x ξ=--代入值即得5155()sin 0.006595161823184183R ππππππ⎛⎫⎛⎫⎛⎫≤---= ⎪⎪⎪⎝⎭⎝⎭⎝⎭二次插值时,取012,,643x x x πππ===,此时有2143()2646346433634x x L x ππππππ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭=++⎛⎫⎛⎫------ ⎪⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭55sin 50sin ()0.7654341818L ππ∴=≈=+其截断误差为351555()cos 183!618618418315550.767382103!186184183R ππππππππππππππ-⎛⎫⎛⎫⎛⎫≤---- ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫≤---=⨯ ⎪⎪⎪⎝⎭⎝⎭⎝⎭()二、设2()[,]f x C a b ∈且()()0f a f b ==,求证:21max ()()max ()8a xb a x b f x b a f x ≤≤≤≤''≤-证:以a ,b 为插值节点进行线性插值,有1()()()()()(,)2!f f x L x x a x b a b ξξ''-=--∈因为1()()()0x b x aL x f a f b a b b a--=+=--,有进而1max ()max ()max ()()2a x b a x ba xb f x f x x a x b ≤≤≤≤≤≤''≤⋅--21()max ()8a xb b a f x ≤≤''=- 因为函数()()x a x b --在1()2x a b =+处取最大值。
插值与拟合专题

2、用MATLAB解插值计算 2.1 一维插值函数
yi=interp1(x,y,xi,'method')
xi处的插 值结果 插值节点 被插值点 插值方法
‘nearest’ :最邻近插值 ‘linear’ : 线性插值; ‘spline’ : 三次样条插值; ‘cubic’ : 立方插值。 缺省时: 分段线性插值。
1.1.2 分段插值法
• 图中看到,随着节点的增加,Lagrange插值函数次 数越高,插值函数在两端容易产生龙格现象,为了 改进高次插值的缺陷,就产生了分段插值。 • 分段插值基本思想:将被插函数逐段多项式化。 • 处理过程:将区间[a,b ]划分: x0 xn b a • 在每个子段 [ xi , xi 1 ]上构造低次多项式,然后将其拼 接在一起作为整个区间[a,b ]上的插值函数,这样构 造出的插值函数称为分段多项式,改进了多项式插 值整体性太强的缺点,可以进行局部调整而不会影 响整体。
第二片(上三角形区域):(x, y)满足 y j1 y j y (x x i ) y i x i 1 x i 插值函数为: f ( x, y) f1 (f 4 f1 )( y y j ) (f 3 f 4 )( x x i )
注意:(x, y)当然应该是在插值节点所形成的矩形区 域内。显然,分片线性插值函数是连续的;
x x1 x 2 基函数为 l0 ( x) x x 1 2 2 x 0 1 x x0 x 1 l1 ( x) x 1 x1 x0 2 1
x0 1, y0 0.95 ; x1 2, y1 0.82
线性插值函数为
L1 ( x) y0l0 ( x) y1l1 ( x) 0.95(2 x) 0.82( x 1) 0.13x 1.08
数值分析---2插值与拟合习题课

插值与拟合习题课一、已知sin x 在30,45,60的值分别为1,,222,分别用一次插值和二次插值求sin 50的近似值,并估计截断误差.解:一次插值时,取靠近50 的两个角度45,60作节点,将角度化为弧度为5,,1843πππ,此时有()134224334x x L x ππππππ--=+--55sin 50sin 0.7600801818L ππ⎛⎫=≈=⎪⎝⎭由截断误差公式()()()()()()()101...1!n n n f R x x x x x x xn ξ+=---+ 有()()()101"()2f R x x x x x ξ=--代入值即得5155()sin 0.006595161823184183R ππππππ⎛⎫⎛⎫⎛⎫≤---= ⎪⎪⎪⎝⎭⎝⎭⎝⎭二次插值时,取012,,643x x x πππ===,此时有214363()22646346433634x x x x L x ππππππππππππ⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭=++⎛⎫⎛⎫⎛⎫⎛⎫------ ⎪⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭55sin 50sin ()0.7654341818L ππ∴=≈=+其截断误差为351555()cos 183!618618418315550.767382103!186184183R ππππππππππππππ-⎛⎫⎛⎫⎛⎫≤---- ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫≤---=⨯ ⎪⎪⎪⎝⎭⎝⎭⎝⎭()二、设2()[,]f x C a b ∈且()()0f a f b ==,求证:21max ()()max ()8a xb a x b f x b a f x ≤≤≤≤''≤-证:以a ,b 为插值节点进行线性插值,有1()()()()()(,)2!f f x L x x a x b a b ξξ''-=--∈因为1()()()0x b x aL x f a f b a b b a--=+=--,有进而1max ()max ()max ()()2a x b a x ba xb f x f x x a x b ≤≤≤≤≤≤''≤⋅--21()max ()8a xb b a f x ≤≤''=- 因为函数()()x a x b --在1()2x a b =+处取最大值。
其他例题和练习(拟合与插值)讲义共46页文档

31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
25、学习是劳动,是充满思想的劳动。—命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、已知sin x 在30,45,60
的值分别为1,
,222
,分
别用一次插值和二次插值求sin 50
的近似值,并估计截断误差.
解:一次插值时,取靠近50 的两个角度45,60 作节
点,将角度化为弧度为5,,1843πππ
,此时有
(
)1324334
x L x π
ππ-
=
+
--
155sin 50sin 0.7600801818L ππ⎛⎫
=≈= ⎪⎝⎭
由截断误差公式
()()()()()()()101...1!
n n n f R x x x x x x x n ξ+=---+
有()
()()101"()2f R x x x x x ξ=-- 代入值即得
15155()sin 0.006595161823184183R ππππππ⎛⎫⎛⎫⎛⎫≤---= ⎪⎪⎪⎝⎭⎝⎭⎝⎭
二次插值时,取012,,6
4
3x x x π
π
π
=
=
=
,此时有
21436364()222646346433634x x x x x x L x ππππππππππππππππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛
⎫⎛⎫------ ⎪⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭
=++⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫------ ⎪⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭
55sin 50sin ()0.7654341818
L ππ
∴=≈=
+
其截断误差为
351555()cos 183!618618418315550.767382103!186184183R ππππππππππππππ-⎛⎫⎛⎫⎛⎫
≤---- ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫≤---=⨯ ⎪⎪⎪⎝⎭⎝⎭⎝⎭
()
二、设2
()[,]f x C a b ∈且()()0f a f b ==,求证:
21
max ()()max ()8
a x
b a x b f x b a f x ≤≤≤≤''≤- 证:以a ,b 为插值节点进行线性插值,有
1()
()()()()
(,)2!
f f x L x x a x b a b ξξ''-=--∈
因为1()()()0x b x a
L x f a f b a b b a
--=
+=--,有
进而
1
max ()max ()max ()()2a x b a x b
a x
b f x f x x a x b ≤≤≤≤≤≤''≤⋅-- 21
()max ()8
a x
b b a f x ≤≤''=-
因为函数()()x a x b --在1
()2x a b =+处取最大值。
三、给出概率积分2
2
()x
x f x dx
e
-
=⎰的数表
用二次插值计算
(1) 当x =0.472时,积分值等于多少? (2) 当x 为何值时积分值为0.5? 解:(1)选最接近0.472的前三个节点 x 0=0.46,x 1=0.47,x 2=0.48有二次插值
0212201010210120122021()()()()()()()
()()()()()()()()()
x x x x x x x x l x f x f x x x x x x x x x x x x x f x x x x x ----=+------+--
带入数值,有2(0.472)0.495552928l =
2(0.472)(0.472)0.495552928f l ≈=
故有当x =0.472时,积分值等于0.495552928 (2)原函数连续单调,可用反插值法计算。
将x 看成y 的函数,即()x y ϕ=,用二次插值计算。
选距函数值在0.5最近的三个节点 0y =0.4937452,1y =0.5027498,
2y =0.5116683
及对应的自变量值为
0x =0.47,1x =0.48,2x =0.49,有
0212201
010210120122021()()()()
()()()()()()()()()
y y y y y y y y l y x x y y y y y y y y y y y y x y y y y ----=+------+--
有
2(0.5)0.47692924x l ≈=
故当0.476929624x ≈时,积分值等于0.5。
