自控5
(扫描版)95“五自”管理体系

制,精细化控制“人、机、料、法、环”中的事故致因,实现公司安全自主、系统安全自控、分厂安全自治、班组安全自理、个人安全自律,确保安全生产。
二、自主管理目标(一)公司自主:以规范业务流程、细化工作标准、实现管理达标为重点,以杜绝各类事故为目标。
(二)系统自控:以细化专业标准、强化过程控制、实现专业达标为重点,以杜绝系统隐患、消灭系统事故作为目标。
(三)分厂自治:以细化工序流程、强化作业控制、实现工序达标为重点,以杜绝现场隐患、消灭现场事故为目标。
(四)班组自理:以细化现场作业组织、强化现场工作质量、实现现场达标为重点,以不制造现场隐患为目标。
(五)员工自律:以提高安全意识、“上标准岗、干标准活”、提高工作质量、实现岗位达标为重点,以杜绝“三违”现象、实现“四不伤害”为目标。
三、自主管理载体(一)公司层面:以“抓系统”为核心,以抓薄弱系统和薄弱专业提升公司安全生产水平为着力点。
管理载体包括:1、树立管理标杆。
寻找本行业先进单位,根据公司年度工作目标和指标,寻找工作对标标杆,制定实施方案,建立对标管理机制,通过树标、对标、达标、创标,持续提升管理水平。
2、强化安全激励。
对安全管理人员实行安全风险抵押金制度;一般人员实行安全生产累进奖制度,并对全体人员实行安全生产事故隐患双向收购制度,激发全体人员参与安全管理的积极性、主动性。
3、开好两个会议。
建立并完善每日安全生产调度会议和周(月)安全办公会议制度。
明确会议参加人员、会议主要内容,对存在的问题划分责任,并采取措施对领导安排事项进行跟踪落实。
4、落实四项制度。
执行《领导干部值班制度》、《管理人员“四到”检查管理制度》、《三级安全隐患排查治理自述旬报制度》和《安全评估评价制度》,狠抓现场安全隐患,做实现场安全管理。
5、实现八大闭环。
将每个时间段的安全工作纳入一个自始而终的闭环反馈系统,引导全体人员树立闭环管理意识,实现安全管理主体流程闭合化,推动安全管理水平螺旋式上升。
5-自制力差怎么办_如何提高自控力

自制力差怎么办_如何提高自控力
自制力是什么?就是控制自己的能力,能够完全自觉的、有意识的控制自己的情绪,支配自己行动的能力,是意志的重要品质,是情商的重要要素。
那么如果自制力差怎么办呢?如何提高自控力呢?今天乔布简历的小编就给大家来讲一讲:
禁欲、慎独、忍耐、坐怀不乱、坚持不懈等等其实都属于自制力范畴。
而“放纵自己”,“做自己高兴做的事”,“图痛快”,追求“完全的自由,无拘无束”这些都是自制力差的表现。
总的来说,自制力主要表现在两个方面:一是善于迫使自己执行定下的决定;二是善于抑制与自己的目的相违背的愿望和行动。
对于如何提高自控力,小编觉得主要要从以下几个方面着手:
1、强化自我意识。
遇事要沉着冷静,自己开动脑筋,排除外界干扰或暗示,学会自主决断。
要彻底摆脱那种依赖别人的心理,克服自卑,培养自信心和独立性。
2、强化积极思维。
俗话说:"凡事预则立,不预则废。
"平时注意经常思考问题,增强预见性,关键时刻才能及时、果断、准确地做出选择。
自制力是指一个人在意志行动中善于控制自己的情绪,约束自己的言行。
3、提高文化素养。
一般来说,一个人的文化素养同其承受能力和自控能力成正比。
文化素质比较高的人往往能够比较全面正确认识事物,认识自我和他人的关系,自觉地进行自我控制、自我完善。
以上几点,在乔布简历的小编看来,对自制力差的人来说提高自身的自制力很有帮助。
本文来源校园招聘/。
自控型班组工作总结范文5篇

自控型班组工作总结范文5篇篇1一、引言在过去的一段时间里,我们自控型班组全体成员积极响应公司号召,以自主管理为核心,以提升班组整体素质为目标,开展了形式多样的班组建设活动。
通过大家的共同努力,班组各项管理工作取得了显著成效。
二、主要工作及成效1. 制度建设与完善我们根据实际情况,对班组各项制度进行了全面梳理和完善。
通过广泛征求意见和反复讨论,制定了《班组管理制度》、《班组安全操作规程》等文件,为班组各项工作的有序开展提供了有力保障。
2. 技能培训与提升我们注重提升班组整体技能水平,通过定期组织技能培训、开展技能竞赛等活动,激发了员工的学习热情和积极性。
同时,我们还邀请了公司内外的专家和技术能手,为员工提供了实用的技能指导和交流平台。
3. 团队建设与凝聚力我们通过组织团队活动、加强沟通与协作等方式,增强了班组的凝聚力和向心力。
在团队建设过程中,我们还注重培养员工的团队协作精神和创新意识,使班组成为一个充满活力和战斗力的整体。
4. 安全管理与环保意识我们始终将安全管理与环保意识放在首位,通过加强安全教育和培训、制定应急预案等方式,确保了班组的安全生产。
同时,我们还积极响应公司环保号召,推动班组员工树立绿色发展理念,共同保护地球家园。
三、存在的问题及改进措施虽然我们在班组建设中取得了一定成效,但仍存在一些问题亟待解决。
例如,部分员工在自主管理方面意识不强,需要进一步加强引导和培养;此外,班组之间的交流与协作有待进一步加强,以提升整体竞争力。
针对这些问题,我们提出以下改进措施:一是加强员工自主管理意识的宣传和教育,引导员工树立正确的自主管理观念;二是建立完善的班组之间交流与协作机制,促进班组之间的信息共享和资源整合;三是持续推进班组技能培训和团队建设活动,提升班组整体素质和凝聚力。
四、未来展望展望未来,我们将继续以自主管理为核心,以提升班组整体素质为目标,不断加强班组建设工作。
我们计划通过开展更多形式的培训活动、团队活动和社会公益活动等,进一步提升员工的技能水平、团队协作精神和社会责任感。
读自控力心得体会5篇

读自控力心得体会5篇(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如工作汇报、总结报告、心得体会、合同协议、条据文书、规章制度、演讲致辞、教学资料、作文大全、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays for everyone, such as work reports, summary reports, reflections, contract agreements, policy documents, rules and regulations, speeches, teaching materials, essay summaries, other sample essays, etc. If you want to learn about different sample essay formats and writing methods, please stay tuned!读自控力心得体会5篇通过心得体会,我们能够更好地理解的思维方式和行为模式,出色的心得体会让我们更加明晰自己的人生道路和目标,以下是本店铺精心为您推荐的读自控力心得体会5篇,供大家参考。
自控理论 5-3广义根轨迹

(3) 分离点 令 dK1 0 解 得 分 离 点s -0.41
根轨迹图
z1 ( z1 z 2 ) ( z1 p1 ) ( z1 p2 ) 199
(5) 入射角
K1 0.75 时, s2, 3 j1.25
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
-2 -3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
图5-11 s2(s+1)+K1=0的根轨迹
图5-12 根轨迹族
由图可见, a=0时系统不稳定。当a 增大至一定数 值时,系统变为稳定。a的临界值可用劳斯判据确 定。系统稳定的临界条件为 K1= a(a+1)
图5-10 例5-8的参量根轨迹
有时在同一问题中,黄金法则不只应用一次。 对于具有两个可变参数的情况, 此法则同样适用, 此时所得到的是根轨迹族。
例5-9 已知系统的开环传递函数 K1 G( s ) H ( s ) s( s 1)(s a )
要求以开环极点a 为连续可变参数,以K1为 参变量绘制该系统的根轨迹族。 解 特征方程
as( s 1) G ( s) H ( s) 2 s ( s 1) K 1
为了绘出a = 0 ~ ∞的根轨迹,必须确定G*(s)H*(s) 的极点,即方程式 s2(s+1)+K1=0 的根(确切地说是根 轨迹,因为K1为变量)。 再一次应用黄金法则 得另一等效开环传函
K1 1 2 0 s ( s 1)
k1=0.75
《自动控制原理》第五章:系统稳定性

5.2 稳定的条件
当σi和λi均为负数,即特征根的 σi和λi均为负数, 均为负数 实部为负数,系统是稳定的; 实部为负数,系统是稳定的; 或极点均在左平面。 或极点均在左平面。
5.3 代数稳定性判据
定常线性系统稳定的充要条件 定常线性系统稳定的充要条件是特征方程的根具有负 充要条件是特征方程的根具有负 实部。因此,判别其稳定性,要解系统特征方程的根。为 实部。因此,判别其稳定性,要解系统特征方程的根。 避开对特征方程的直接求解,可讨论特征根的分布, 避开对特征方程的直接求解,可讨论特征根的分布,看其 是否全部具有负实部,并以此来判别系统的稳定性,这样 是否全部具有负实部,并以此来判别系统的稳定性, 也就产生了一系列稳定性判据。 也就产生了一系列稳定性判据。 其中最主要是E.J.Routh(1877 )h和Hurwitz( 其中最主要是E.J.Routh(1877年)h和Hurwitz(1895 E.J.Routh(1877年 年)分别提出的代数判据。 分别提出的代数判据 代数判据。
习题讲解: 习题讲解:
µ
G1
Q21
G1
h2
k1 k1 G1 ( s ) = , G1 ( s ) = (T1s + 1) (T1s + 1) k1k 2 G0 ( s ) = (T1s + 1)(T2 s + 1)
kp
G0 ( s ) G(s) = 1 + G0 ( s ) K p
5.4 Nyquist稳定性判据 Nyquist稳定性判据
系统稳定的条件? 系统稳定的条件?
5.2 稳定的条件
d n y (t ) d ( n −1) y (t ) dy (t ) 线性系统微分方程: 线性系统微分方程: n a + an −1 + L + a1 + a0 y (t ) n ( n −1) dt dt dt d m x(t ) d ( m −1) x(t ) dx(t ) = bm + bm−1 + L + b1 + b0 x(t ) m ( m −1) dt dt dt d n y (t ) d ( n −1) y (t ) dy (t ) + a( n −1) + L + a1 + a0 y (t ) = 0 齐次微分方程: 齐次微分方程: an n ( n −1) dt dt dt an s n + an −1s n −1 + L + a1s + a0 = 0 设系统k 设系统k个实根
自控原理习题课_1-5章_习题

习题课说明12月14、16、21日的三次习题课,分三次练习《自控原理》前五章的经典试题,14日(1~2章),16日(2~3章),21日(5章)。
请大家事先做好试题,上课时会讲解部分经典试题并答疑。
第一章绪论1. 本章基本要求●掌握有关自动控制的基本概念,明确控制系统任务、组成及控制装置各部分的作用。
●了解系统的基本控制方式及特点,正确理解负反馈控制原理。
●正确理解对控制系统稳定性、准确性和快速性的要求。
●通过练习,掌握有系统工作原理图画出系统方框图的方法。
●掌握线性定常系统微分方程的特点,能够判断线性、非线性、定常、时变系统。
2. 典型例题1)根据图题1.1所示的电动机速度控制系统工作原理图(1)将a,b 与c,d 用线连接成负反馈系统;(2)画出系统方框图。
图 1.12)图题1.2所示为液位自动控制系统原理示意图。
在任何情况下,希望液面高度c 维持不变,试说明系统工作原理并画出系统方块图。
图 1.23)下列各式是描述系统的微分方程,其中,r(t)为输入变量,c (t)为输出量,判断哪些是线性定常或时变系统,哪些是非线性系统? (1) 3232()()()748()()d c t d c t dc t c t r t dt dt dt+++= (2) 2()8()()c t r t r t =++ (3) ()()8()()3dc t dr t t c t r t dt dt⋅+=+ (4) ()()sin 3c t r t t ω=+第二章 线性系统的数学描述1. 本章基本要求●熟悉建立系统(或元部件)微分方程的步骤和方法 ●牢固掌握传递函数的定义和性质,掌握典型环节及其传递函数 ●掌握系统结构图的建立、等效变换及其系统开环、闭环传递函数的求取 ●掌握从其他不同形式模型求取系统传递函数的方法2. 典型例题1)列写图2.1 RLC 网络的运动方程和传递函数,图中电压1()u t 和2()u t 分别为输入输出量图2.12)列写图2.2 RLC 网络的微分方程,图中电压()r u t 和()c u t 分别为输入输出量图 2.23)列写图2.3 RLC 网络的微分方程与传递函数,图中电压()r u t 和()c u t 分别为输入输出量图 2.34)试化简如图2.4所示系统结构图,并求系统传递函数()/()C s R s 。
自控力的心得(精选5篇)

自控力的心得(精选5篇)自控力的心得篇1初读这本书就被书里的一些科学实验所吸引,科学实验的结果往往和自己的原有观念相反,也许正是这种别出心裁,才让人饶有兴致地往下读。
本书的亮点不仅在于新颖的科学实验,更是本书在每一章节都有总结,有助于读者更好地理解每一章的主旨,加深印象。
本书所提到的提升自控力的一些方法和相关的建议,在这里分享给大家,与君共勉。
一、意志力训练的方法:每天5分钟大脑冥想训练,在脑海中默念“呼”和“吸”,把注意力集中在呼吸上。
当你开始走神的时候,重新集中注意力。
当然每天的运动和充足睡眠必不可少,可以更好的促进意志力训练。
二、影响意志力的因素:感觉到压力时,试着放慢呼吸,增强抗压能力。
压力和意志力相抗衡,所以要想提升意志力,必须释放压力;饥饿会降低意志力,饿的时候及时补充坚果类小零食,不让自己长时间处在饥饿状态。
三、高效工作法则:将重要的事情永远放在第一位。
四、不为放纵行为作辩护,不盲目奖励自己,盲目奖励会让人迷失方向,偏离目标和自我感动。
放纵自己时想想自己的目标和努力的原因。
五、不向明天赊账,从今天开始。
谁也不能保障未来的你可以做得更好,不能把压力都给未来的那个自己。
可以给五年后、十年后的自己写邮件,将对自己的期望等等都写在邮件里,定时发送。
六、巧妙利用多巴胺,把自己不想做的事情变成想做的事。
七、远离让人产生恐惧的事物或者新闻,因为这些新闻会增加自己的恐惧,让人不适,不利于实现目标。
八、面临失败时,自我同情比自我打击有效得多。
要学会原谅自己,过多的责备会让人一蹶不振。
九、乐观的悲观主义更能成功。
预测你什么时候、会怎样受到诱惑和违背承诺,想象一个不让自己放弃抗争的具体方法。
十、面临诱惑时,运用“10分钟延迟法则”。
十一、公开自己的挑战,想象别人都在关注自己,这样可以时刻激励自己。
请一定要提升自控力,不断努力,这样马斯诺所说的自我实现需求终有一天得到满足。
自控力的心得篇2最近读了斯坦福大学心理学家凯利·麦格尔教授的人气新书《自控力》的中文版。
自控原理 第五节

式中,c(t)是被控量;r(t)是系统输入量。系数是常数时称为定常系统; 系数随时间变化时称为时变系统。 线性定常连续系统又可分为:
(1). 恒值控制系统,这类控制系统的参据量是一个常值,要求被控 量亦等于一个常值,故又称为调节器。
(2). 随动系统,这类控制系统的参据量是预先未知的随时间任意变化的函
1.2 自动控制系统示例
3. 锅炉液位控制系统
锅炉是电厂和化工厂里常见的生产蒸汽的设备,常见 的锅炉液位控制系统示意图如图1-11所示。 当蒸汽的耗汽量与锅炉进水量相等时,液位保持为正 常值。当锅炉的给水量不变,而蒸汽负荷突然增加或减少 时,液位就会下降或上升;或者其它原因引起锅炉液位发 生变化,实际液位高度与正常给定液位之间出现了偏差, 调节器均应立即进行控制,去开大或关小给水阀门,使液 位恢复到给定值。 图1-12 是锅炉液位控制系统方框图
1.1 自动控制的基本原理
2. 自动控制理论
自动控制理论是研究自动控制共同规律的技术科学。它 的发展初期是以反馈理论为基础的自动调节原理,主要用于 工业控制。 第二次世界大战期间,为了设计和制造基于反馈原理的 军用装备,进一步促进并完善了自动控制理论的发展。到战 后已形成完整的自动控制理论体系,这就是以传递函数为基 础的经典控制理论,它主要研究单输入-单输出、线性定常系 统的分析和设计问题。
u0 比较电路 ﹘﹘ ut ∆u 放大器 uk 触发器 测速发电机 晶闸管 ua 电动机 n
图1-4 龙门刨床速度控制系统方框图
1.1 自动控制的基本原理
4. 反馈控制系统的基本组成
反馈控制系统是由各种不同的元部件组成的,从完成 “自动控制”这一职能来看,一个系统必然包含被控对象 和控制装置两大部分,而控制装置是由具有一定职能的各 种基本元件组成的。组成系统的元部件按职能分类主要有 以下几种:
自动控制原理自控第五章

【授课时间】:、11.20上午三四节【授课形式】:多媒体【授课地点】:4306 4114 【授课时数】:2【授课题目】:频率特性及典型环节的频率特性【教学目标】1、正确理解频率特性的概念;2、熟练掌握典型环节的频率特性,熟记其幅相特性曲线及对数频率特性曲线。
【教学重难点】重点:典型环节的频率特性难点:典型环节的幅相特性曲线及对数频率特性曲线【教学内容】复数的表示形式:(1) 代数式:A=a+bj(2) 三角式:A=R(cosφ+j sinφ)(3) 指数式:A=Re jφ(4) 极坐标式:A=R∠φ5.1 频率特性一、频率特性定义频率特性是控制系统在频域中的一种数学模型,是研究自动控制系统的一种工程求解方法。
系统频率特性能间接地揭示系统的动态特性和稳态特性,可简单迅速地判断某些环节或参数对系统性能的影响,指出系统改进方向。
频率特性的定义(1)频率响应: 在正弦输入作用下,系统输出的稳态值称为频率响应。
(2)频率特性: 频率响应c(t)与输入正弦函数r(t)的复数比。
幅频特性:输出响应中与输入同频率的谐波分量与谐波输入的幅值之比A(ω)为幅频特性相频特性:输出响应中与输入同频率的谐波分量与谐波输入的相位之差φ(ω)为相频特性实频特性:虚频特性:例5-1 已知u i (t )=A ·sin ωt 。
1()()()()Q G j tg P ωϕωωω-=∠=()()cos ()P A ωωϕω=()()sin ()Q A ωωϕω=其中,T =RC ()22ωω+=s A s U i 零初始条件())arctan sin(112222T t T Ae AT u T tt c ωωωωτω-+++=-上式表明:对于正弦输入,其输出的稳态响应仍然是一个同频率正弦信号。
但幅值降低,相角滞后。
Tj j G ωω+=11)(幅频特性和相频特性数据频率特性的性质1)与传递函数一样,频率特性也是一种数学模型。
第五次课自动控制理论讲解

2
G( jw)
K
1
w
j
w2
2
jw
1
j
w w1
1
j
w w3
它在wc处得相角为
(wc )
90
2 arctan
wc w1
2 arctan
wc w2
arctan
wc w3
90 (144 ~ 180) 144 18 108 ~ 144
即相位裕量 在 72 ~ 36 之间
★
三、闭环系统得性能分析 5、6-7 ★
w0 (jw)0 KG0 ( jw) 1 K
当v = 1时,闭环幅频 特性得零频值为
M (0) lim w0
KG0 ( jw) (jw)1 KG0 ( jw)
1
说明:0型与I型及以上系统零频值M(0)得差异,反映了它们跟随阶跃输
入时稳态误差得不同,前者有稳态误差,后者没有稳态误差。
2、频带宽度
即相位裕量 在 18 ~ 18 之间
[说明]:条件只就是必要而非充分得。
作业 pp、218-219: 5-13
第五章 频率响应法
• 5、1 频率特性 • 5、2 对数坐标图 • 5、3 极坐标图 • 5、4 用频率法辨识线性定常系统得数学模
型 • 5、5 奈奎斯特稳定判据 •• 55、、67 相频对域稳性定能性指分标析与时域性能指标之间得 • 5关、系7 频域性能指标与时域性能指标之间得
K
s(1 0.2s)(1 0.05s)
试求:K = 1时得 Kg 与 解 基于在wg处开环频率特性得相角为
(wg ) 90 arctan 0.2wg arctan 0.05wg 180
掌控自己的人生5个方法帮助你提高自控力

掌控自己的人生5个方法帮助你提高自控力自控力是一项关键的人生技能,它可以帮助我们克服贪欲、情绪和其
他不良习惯,从而实现更健康、更成功的生活。
然而,要提高自控力并不
容易,需要付出努力和坚持。
在这篇文章中,我将分享5个方法,帮助你
提高自控力,掌控自己的人生。
制定具体的目标和计划
制定具体的目标和计划,可以帮助我们更好地掌控自己的行动。
首先,确定你想要实现的目标,并制定具体的计划,包括时间表和实现步骤。
这
样可以帮助你更好地掌控自己的行动,避免无效的浪费时间和精力。
2.提高自我意识
提高自我意识是提高自控力的关键。
了解自己的情绪和行为模式,可
以帮助我们更好地掌控自己的情绪和行为。
当我们意识到自己的情绪和行
为时,我们就可以更好地控制它们,避免做出不理智的决定。
3.练习冥想和放松技巧
4.建立健康的生活习惯
建立健康的生活习惯,如规律的睡眠和饮食,可以帮助我们保持身体
和心理健康。
身体和心理健康是提高自控力的基础,只有当我们的身体和
心理处于健康状态时,才能更好地控制自己的情绪和行为。
5.找到支持和帮助
总之,提高自控力需要付出努力和坚持,但是它可以帮助我们掌控自
己的人生,实现更健康、更成功的生活。
通过制定具体的目标和计划、提
高自我意识、练习冥想和放松技巧、建立健康的生活习惯、以及寻求支持和帮助,我们可以更好地提高自控力,掌控自己的人生。
自控理论 3-5线性系统的稳定性分析

a1 Dn =
a3
a5 a4 a3
a7 a6 a5
L 0 L L L L M 0 0 0 0 M
a0 a2 0 a1 0 a0 0 0 M M 0 0
a2 a4 a1 a3 M M 0 0
L an
即
Di > 0
( i = 1, 2,Ln )
其中 D1 = a1 > 0 , D2 = a1 D3 = a0 0 a3 a2 a1 a5 a4 > 0 a3
• 线性系统的稳定性只取决于系统的结构及 参数,而与初始条件、 参数,而与初始条件、外作用大小及形式 无关。 无关。 • 稳定性只取决于系统闭环极点,而与系统 稳定性只取决于系统闭环极点, 零点无关。 零点无关。
作业: - - 作业: 3-A-8 3-A-9 - -
§3-5 线性系统的稳定性分析 一、稳定的概念 稳定性是指扰动消失后, 稳定性是指扰动消失后,系统由初始偏 差状态恢复到原平衡状态的性能。若系统 差状态恢复到原平衡状态的性能。 能恢复平衡状态,则称系统是稳定的, 能恢复平衡状态,则称系统是稳定的,否 则不稳定。 则不稳定。
线性系统稳定性的定义: 线性系统稳定性的定义: 若线性控制系统在扰动作用下, 若线性控制系统在扰动作用下,其动态 过程随时间的推移逐渐衰减并趋于零, 过程随时间的推移逐渐衰减并趋于零,则称 系统渐近稳定,简称稳定。反之, 系统渐近稳定,简称稳定。反之,若在扰动 作用下, 作用下,系统的动态过程随时间的推移而发 则称系统不稳定。 散,则称系统不稳定。
【例3-5】D(s)= s4 + 2s3 +3s2 + 4s + 5 = 0,试用劳斯 】 判据判别系统是否稳定, 若不稳, 确定正实部根的数目。 判据判别系统是否稳定 若不稳 确定正实部根的数目。
《自控》何权峰读后感

《自控》何权峰读后感读何权峰的《自控》有感自控——我们都懂很多大道理却仍过不好这一生就是因为只是知道了但没有做到。
一、成为自己了解自己,接受自己,提升自己,你只需要做好你自己,为你自己负责,别人怎么看是别人的事,你是为自己而活,活出最好的自己。
向内求,遵循自己的心意,按照自己的信仰生活,不必在乎别人的眼光,知道自己想要什么,为此付出努力。
二、掌控情绪做情绪的主人,而不是被情绪左右,事情的本身没有明确好坏之分,关键在我们怎么看待,理智的去面对。
一个人,要能控制自己的情绪,才能更好的与人相处,才能减少与人发生冲突,使你的生活少一些敌人。
三、乐活当下乐天知命,我们无法选择出身,但我们可以努力提升自己,知足常乐,活在当下,过去的事情不论好坏都已经过去,未来还没有到来。
只管做好眼前事,无愧于心,人活着最重要的是要活的通透,洒脱,而不是拥有多少财富,健康快乐的度过每一天就是幸福。
四、调换视角面对挫折,换个角度想一想,克服困难之后你会更上一层楼,挫折是渡你成长的,凡事都有两面性。
居安思危也是这样,如果你一直沉浸在舒适区不自知,就会出现问题,所以不论顺境还是逆境都不要停下前进的脚步,脚踏实地的走好每一步。
五、客观思考事实就是事实,不要感情用事,带着情绪的眼睛看到的不一定是事实,现实中有太多人会带着偏见看事情,往往看不到事情的真相。
六、反思表达当别人给你提建议的时候先别急着反驳,听听他说的对不对,如果真是你的问题那应该听取建议,改正自己。
七、极简心理人生除了生死其他都是小事,一切担心都是庸人自扰,认真做好眼前的事,学习努力提升自己,一切顺其自然。
八、爱是学问每个人都是一个独立的个体,首先要学会爱自己,你爱自己才会爱别人,别人才会爱你,一个连自己都不爱的人怎么会爱别人呢,别人又怎么会爱她呢?一切问题都在自己身上,你爱自己就会提升自己,就会越来越优秀,就会吸引更多人,真正爱自己就不会把期待放在别人身上,而是向内求,一个内心充盈独立的人充满魅力。
自控系统操作手册

自控系统操作阐明3月20日目录第一章系统概述.......................... 错误!未定义书签。
1.自控系统旳构成..................... 错误!未定义书签。
1.1网络构造....................... 错误!未定义书签。
1.2.中控室设备配置 (4)1.3.PLC设备配置 (4)第二章上位操作阐明 (5)2.1.启动和登录系统 (5)2.2.系统控制画面简介 (5)第三章注意事项 (17)3.1.计算机旳维护清洁 (17)3.2.计算机旳故障处理 (17)第一章系统概述本项目共有28个PLC主站,其中19座污水泵站PLC站为新建,3座污水泵站PLC 已经有(需上下位机编程、与设备信号连接、调试),6座站PLC系统已建好(需上位机编程)。
在中控室设置有2台上位工业监控计算机。
通过VPN网络监控28座污水提高泵站,实现所有泵站旳无人值守能自动,安全、可靠、稳定旳运行。
1.自控系统旳构成1.1网络构造每个提高污水泵站建立一种PLC站(已经有旳除外)。
现场 PLC 分别与现场电气控制柜信号连接,采集生产过程中旳多种仪表参数,电气参数和机电等设备旳工作状态,将采集到旳数据、信号送到现场PLC柜,再通过VPN网络,最终显示在中心控制室上位机。
各控制站配置一套UPS不间断电源,控制站停电后仍能继续工作一段时间,中控室上位机并设置了断电报警功能,让中控室值班人员第一时间内及时关注停电泵站状况。
1.2. 中控室设备配置中控室内设置有;2台两台操作站互为备用,正常工作时,两台计算机独立、并行运行,操作及状态在两台计算机之间同步进行,分别记录。
任何一台计算机出现故障时,此外一台计算机将保证系统旳正常运行。
各计算机旳IP地址为:操作站 OP1 :10.100.11.96OP2 :10.100.11.102上位软件包括如下重要功能:✧顾客登录✧泵站网络状态✧集水井液位实时显示及控制✧生产过程监视及控制✧报警显示、记录及打印✧实时曲线、历史曲线✧参数设置✧报表处理及打印1.3. PLC设备配置PLC站通信地址配置如下:26 青松路172.20.121.102 255.255.255.0 172.20.121.127 迎宾路172.20.122.2 255.255.255.0 172.20.122.128 莲花路172.20.123.2 255.255.255.0 172.20.123.129 富荣路172.20.124.2 255.255.255.0 172.20.124.1第二章上位操作阐明2.1.启动和登录系统计算机开机:计算机顾客名为cbh,密码为:cbh ,点击电脑桌面上旳打开Wonderware上位机控制软件,默认进入“泵站一览表”画面。
大学自控专业第5次考试答案

第5次考试答案自控专业考试题(5)一、选择:(每题3分,共21分)下图是分解区域的一个什么设备:(B)A、立盘过滤机B、立式叶滤机C、旋流器D、板式热交换器解析:本题见“分解区域培训教材”。
这是分解区域的立式叶滤机。
2、据国务院发布《特种设备安全监察条例》指明,特种设备是指涉及生命安全、危险性较大的锅炉、压力容器(含气瓶)、压力管道、电梯、起重机械、客运索道、大型游乐设施、( A )八大类。
A、厂内机动车B、输变电设备C、皮带输送设备解析:本题见“鑫旺再生资源有限公司设备培训”,特种设备:是指涉及生命安全、危险性较大的锅炉、压力容器(含气瓶)、压力管道、电梯、起重机械、客运索道、大型游乐设施,以及厂内机动车辆。
3、内蒙鑫旺氧化铝项目的外部电源进线是( B )KV。
A、10KVB、110KVC、6KVD、35KV解析:本题见“内蒙古鑫旺电气基础知识培训”,鑫旺公司的外部电源是110KV,经过两台主变转换为10KV供各工段使用。
鑫旺氧化铝项目的最终产品是(B)A、Al(OH)3B、α- Al2O3C、γ- Al2O3解析:本题见“焙烧区域工艺及设备”培训。
氢氧化铝在焙烧过程中要经过烘干、脱水、晶型转变三个过程。
最终将AL(OH)3焙烧为α- Al2O3。
TSI是指( C)A、汽轮机数字电液控制系统B、汽机危急遮断系统 C 汽机本体安全监视系统 D 超速保护系统解析:本题见“高压电调”培训。
汽轮机数字电液控制系统(DEH):Digital Electronic Hydraulic Control是对汽机进行控制的主要系统,其主要功能是对汽机进行的转速控制、负荷控制、阀门管理、汽机自动控制和汽机超速保护等。
汽机危急遮断系统(ETS):Emergency Trip System是对汽机进行保护的控制系统。
其主要功能是监控汽机的某些参数,当这些参数超过运行极限时,关闭汽机进汽阀。
汽机本体安全监视系统(TSI):Turbine Supervisory Instruments是连续测量汽轮发电机轴承及汽轮机本体运行参数的仪表系统,当运行参数出现异常,则发出报警信号。
自控第五篇习题
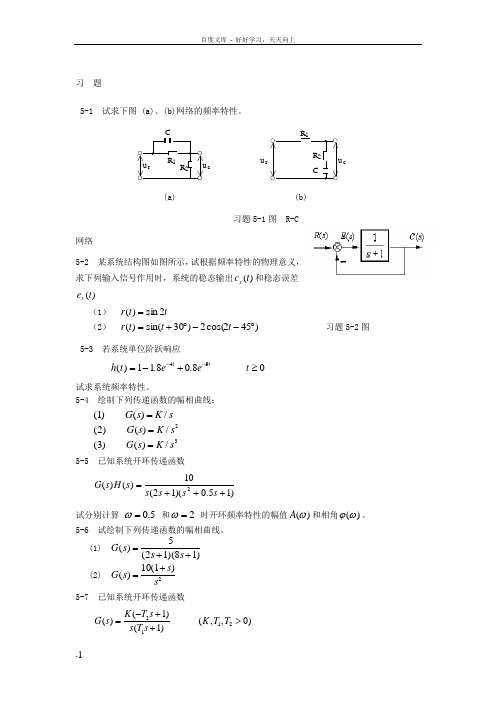
习 题5-1 试求下图 (a)、(b)网络的频率特性。
u rR 1u cR 2CR 2R 1u ru c(a) (b)习题5-1图 R-C网络5-2 某系统结构图如图所示,试根据频率特性的物理意义,求下列输入信号作用时,系统的稳态输出)(t c s 和稳态误差)(t e s(1) t t r 2sin )(=(2) )452cos(2)30sin()(︒--︒+=t t t r 习题5-2图 5-3 若系统单位阶跃响应h t e e t t t()..=-+≥--11808049试求系统频率特性。
5-4 绘制下列传递函数的幅相曲线: ()()/1G s K s = ()()/22G s K s = ()()/33G s K s =5-5 已知系统开环传递函数)15.0)(12(10)()(2+++=s s s s s H s G 试分别计算 5.0=ω 和2=ω 时开环频率特性的幅值)(ωA 和相角)(ωϕ。
5-6 试绘制下列传递函数的幅相曲线。
(1) G s s s ()()()=++52181(2) G s s s ()()=+10125-7 已知系统开环传递函数2121(1)()(,,0)(1)K T s G s K T T s T s -+=>+当1=ω时,︒-∠180)(ωj G ,5.0)(=ωj G 。
当输入为单位速度信号时,系统的稳态误差为 1。
试写出系统开环频率特性表达式)(ωj G 。
5-8 已知系统开环传递函数)1)(1(10)(2++=s s s s G试概略绘制系统开环幅相频率特性曲线。
5-9 绘制下列传递函数的渐近对数幅频特性曲线。
(1) G s s s ()()()=++22181;(2) G s s s s ()()()=++20011012;(3) G s s s s s s ()(.)(.)()=++++40050212(4) G s s s s s s s ()()()()()=+++++20316142510122(5) G s s s s s s s ()(.)()()=+++++8011425225-10 若传递函数 G s KsG s v ()()=0式中,)(0s G 为)(s G 中,除比例和积分两种环节外的部分,试证ω11=K v式中,1ω为近似对数幅频曲线最左端直线(或其延长线)与零分贝线交点的频率,如图所示。
关于自控作文800字集锦5篇

关于自控作文800字集锦5篇能自控的人,都必定会是强者。
下面给大家分享一些关于自控作文,希望对大家有帮助。
关于自控作文1这句话就挂在傅甜家的客厅正中央。
每次一抬头,她就能看见这句话。
“爷爷,这句话什么意思啊?”小时候,傅甜总是睁着黑白分明的大眼睛疑惑地问道。
爷爷每每便乐呵呵地看着傅甜,说:“就是说你得学会约束自己的言行,然后才会有所成就啊!”小时候仍旧不懂,可如今升入大学的傅甜却已深刻理解这句话的含义了。
自己控制自己,努力朝着梦想前进,才终会有收获鲜花与掌声的一天。
在大学里,不少同学因为离开了高三而进入了放飞自我的状态,每日上完课后,便三三两两地约好去哪里“放纵自我”。
但傅甜依然控制、约束自己的行为。
当其他人在玩乐的时候,她在认真复习和预习课本;当别人放纵自我的时候,她在严格施行自己给自己制定的计划表:看书、运动……与此同时,她还加入了学生会,借此来提高自己的能力,使自己变得更充实。
大二国庆假时,傅甜与几个同学约好去临市旅游,她们约好十点在学校门口见面。
可那天上午,突然下了场雨,不少同学都迟了十几二十分钟才到达学校门口。
唯有傅甜,秉着“自控”的念头,提前十分钟到达了校门口,独自一人站在那等待姗姗来迟的同学们。
时间过得太快,不少同学还未留意,时间便从他们的指缝间溜走。
大学四年生活一晃而过,不少同学这才着急,后悔虚度光阴,碌碌无为。
可傅甜却秉着“自控”的思想,带着自信的笑容踏上了去西藏支教的车。
热情的司机大叔瞧着笑容灿烂的傅甜,情不自禁地与她搭起了话。
“小姑娘,大学毕业了吧?”“嗯,现在去西藏教书。
”“呀,那你就厉害了,小姑娘。
”司机大叔毫不掩饰的夸赞使得傅甜的脸颊上浮起了两团红云。
到达支教地点后,傅甜依然秉持着“自控”的念头说话做事。
不仅如此,她还身体力行地教育她的学生,让他们学会自控,从而学会约束自我,由此一步步地迈向梦想,实现自己的人生价值。
后来,当傅甜受到“优秀教师”的表彰时,人们让她谈谈感想。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时域方程: 传递函数:
T
dc(t) c(t) Kr(t) dt
K G(s) Ts1
R (s )
1 Ts 1
C (s )
典型环节的传递函数
例1:直流电机
输入量: ud ——电枢电压 输出量: id ——电枢电流
id
+
时域方程:
d Ld i d Rd i d u d dt
式中:K——弹簧弹性系数; M——物体的质量, B——粘性摩擦系数。 传递函数:
G(s) X(s) F(s) M 2 B s s 1 K K 1 K
典型环节的传递函数 6、一阶微分环节 点:此环节的输出量不仅与输入量本身 有关,而且与输入量的变化率有关 时域方程: dr(t)
c(t) T dt r(t)
5、振荡环节
特点:包含两个独立的储能元件,当输入量发生变化 时,两个 储能元件的能量进行交换,使输出带有振 荡的性质。
时域方程:
传递函数:
d 2c(t) dc(t) T 2ζ T c(t) Kr(t) dt 2 dt
2
R (s )
1 T 2 s 2 2 Ts 1
C (s)
式中:——阻尼比,
自动控制理论
第三章 方框图与信号流图
典型环节的传递函数
不同物理结构的元件可以有形式上完全相同的微分方 程和传递函数。对于性质不同、数量众多的自动控制 元件,若按形式相同的微分方程或传递函数来分类, 可以分为以下8种典型环节。
•比例环节 •延迟环节 •微分环节
•积分环节
•惯性环节 •振荡环节
•一阶超前环节
当Tc<<1时,又可表示成:
典型环节的传递函数
例 2:测速发电机如图
(t )
u d (t )
D
F
u f (t )
输 入: (t)——电动机D转子(与测速发电机同轴)的转角 输 出: uf(t)——测速发电机的电枢电压 时域方程: u f (t) K d (t)
dt
传递函数:
G(s)=Ks
(R=1,RC= )
传递函数:
I(s) s 1 U(s)
一阶微分环节可看成一个微分环节与一个比例 环节的并联,其传递函数和频率特性是惯性环 节的倒数。
典型环节的传递函数
7、二阶微分环节 特点:输出与输入及输入一阶、二阶导数都有关 运动方程: d 2 r(t) dr(t)
c(t) T 2 dt
J
d 2θ (t) dt 2
B
dθ (t))
+
(t )
ea ( t )
分别进行拉氏变换 _ 1) T ( s ) = K I ( s ) 2) Eb( s ) = Kb s ( s ) 3) Ea( s ) = ( L s + R ) I ( s ) + Eb( s ) 4) T( s ) = ( J s2 + B s ) ( s )
运动方程:
传递函数:
K G(s) s
R (s )
1 s
C (s )
典型环节的传递函数
例1:积分电路
输入为r(t),输出为c(t)
r(t) i c (t) i1 (t) R1
时域方程:
c(t)
1 1 1 i c (t)dt r(t)dt r(t)dt C R 1C T
特
传递函数: G( s ) = Ts + 1
典型环节的传递函数
i1 (t )
C
RC电路 输入:u(t),输出:i(t)
i(t) i1 (t) i 2 (t) c
u (t )
i2 (t )
R
i (t )
du(t) u(t) dt R 1 du(t) du(t) [RC u(t)] τ u(t) R dt dt
时域方程: u(t)=K(t) 传递函数:
G(s) U(s) K (s)
K——比例系数,量纲为伏/弧度。
典型环节的传递函数
例 2:输入:n1(t)——转速 输出:n2(t)——转速 Z1——主动轮的齿数 Z2——从动轮的齿数
时域方程:
n 2 (t)
G(s)
z1 n1 (t) z2
dt
1 i(t)dt C
传递函数:
G(s)
1 LCs2 RCs 1
典型环节的传递函数
例2
+
电枢控制式直流侍服电机
i (t )
R
L
eb (t )
(t )
ea ( t )
+ _
D
J
B
_
ea(t)--- 输入量为加在电枢两端 i(t)----电枢绕组中的电流; R------电枢绕组的电阻; L------电枢绕组电感; eb(t)-- 电动机的反电势; (t) ---输出量为电机轴的角位移; T(t)---电动机产生的转矩; J------电动机和负载折合到电动机转轴上的转动惯量; B------电动机和负载折合到电动机转轴上的粘性摩擦系数。
+ _
D
J
B
典型环节的传递函数
消去中间变量Eb(s)、T(s)和I(s)
θ (s) K E a (s) s[LJs2 (LB RJ)s (RB KK b )]
如果输入量Ea(s),输出量转速(s),则又可得到:
(s) K E a (s) LJs2 (LB RJ)s (RB KK b )
T——振荡环节的时间常数。
典型环节的传递函数
例1:RLC电路 以r(t)为输入,c (t)为输出
时域方程:
r(t) L c(t)
R
L
+
i (t )
+
r(t)
_
C
c(t)
_ _
di(t) 1 ri(t) i(t)dt d 2 c(t) dc(t) LC RC c(t) r(t) dt C 2 dt
传递函数:
N 2 (s) z1 K N1 (s) z 2
典型环节的传递函数
其它一些比例环节
R2 R1
r (t )
r1
+ Ec
R
ic (t )
+
R3
K
c (t )
r2
r (t ) c (t )
ib (t )
R(s)
r2 r1 r2
C s
R(s)
R2 R1
C s
Ib (s)
Ic (s)
•二阶超前环节
典型环节的传递函数
1、比例环节
特 点:输出量按一定比例复现输入量,无滞后现象
时域方程: c(t)=Kr(t) K——放大系数,通常都是有量纲的。
G(s) C(s) K R(s)
传递函数:
R (s )
K
C (s )
典型环节的传递函数
例1: E——恒定电压 输入:(t)——角度 输出:u(t)——电压
2
2ζ T
dt
r(t)
传递函数:
G(s)
C(s) T 2s 2 2ζ Ts 1 R(s)
可以看出,二阶微分环节的传递函数是振荡环节的 倒数。
典型环节的传递函数
8.延迟环节
延迟环节又称为纯滞后环节、时滞环节。延迟环节的输出 是经一个延迟时间后,完全复现输入信号,即:
式中 ——纯延迟时间。 单位阶跃输入时,延迟环节的输 出响应如图所示。 根据拉氏变换的延迟定理,可得延迟 环节的传递函数为:
这是一个典型的振荡环节的传递函数
典型环节的传递函数
例3:机械装置
K
输入----------力 : f(t), 输出----------位移: x(t) 。 时域方程:f (t ) M
d x(t ) dt 2
2
f (t )
M
x (t )
B
B
dx(t ) Kx(t ) dt
图2-16 机械振荡
典型环节的传递函数
其他微分环节举例
i (t )
C
u c (t )
i (t )
C
i (t )
L
e L (t )
u (t )
R
Cs
U c (s)
I (s)
Cs
U (s)
1
R
+ +
I (s)
I (s)
Ls
EL (s)
典型环节的传递函数
3、积分环节
特 点:输出量的变化速度和输入量成正比。
dc(t) Kr(t ) dt
典型环节的传递函数
2、微分环节
特 点:动态过程中,输出量正比于输入量的变化 速度。
时域方程:
C(t) K dr(t) dt
传递函数:
G(s)
C(s) KS R(s)
R (s )
S
C (s )
典型环节的传递函数
例1 RC电路 设:输入——ur(t) 输出——uc(t)
1 u r (t) i(t)dt i(t)R c
典型环节的传递函数
1) T(t)=Ki(t) 2) e (t) K d (t)
b b
T(t)——转矩 K——力矩系数 eb(t)——反电势 Kb——反电势常数 ea(t)——电枢两端的电压
i a (t )
R
dt
3) L di(t) Ri(t) e (t) e (t) b a
dt
4)
L d d Rd
ud
D
ud d d id id dt Rd
