湖南师大附中星城实验中学2013—2014学年度第二学期八年级期中考试含答案
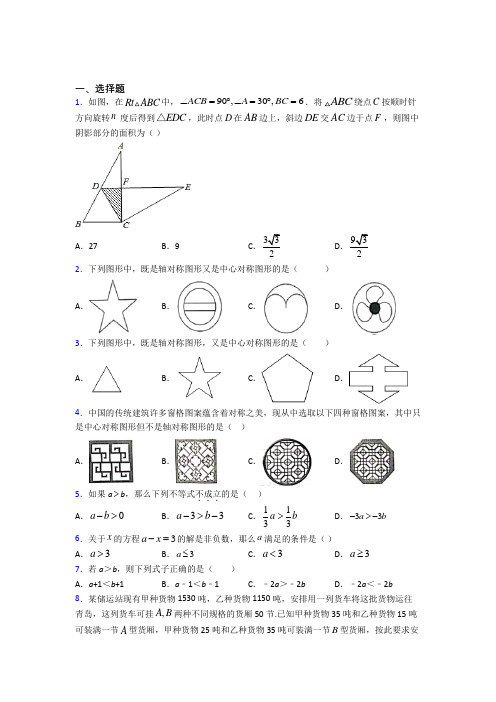
湖南省师大附中2013-2014学年高一下学期期中考试 物理A卷

物理(A卷)时量:90分钟满分:150得分:______________第Ⅰ卷(文理倾向都做)一、单项选择题(本题12小题,每小题4分,共48分。
在各选项中只有一个选项是正确的,请将答案写在答卷上。
)1.下列叙述符合史实的是()A.开普勒对天体的运行做了多年的研究,最终提出了万有引力定律B.第谷和开普勒通过大量的天文观测和数据分析完善了“地心说”C.牛顿发现了行星的运动规律D.第一次通过实验比较准确地测出万有引力常量的科学家是卡文迪许2.根据开普勒行星运动规律推出的下列结论中,哪个是错误的()A.行星绕太阳沿椭圆轨道运转时,各点的速度大小相等B.开普勒行星运动规律也适用于卫星绕行星的运动C.不同人造地球卫星在不同轨道上运动时,轨道半长轴的三次方与公转周期的二次方的比值都相等D.同一人造地球卫星在不同轨道上运动时,轨道半长轴的三次方与公转周期的二次方的比值都相等3.做平抛运动的物体,每秒的速度增量总是()A.大小相等,方向相同B.大小不等,方向不同C.大小相等,方向不同D.大小不等,方向相同4.下列说法不正确的是()A.曲线运动一定是变速运动B.曲线运动中物体所受的合外力一定不等于零C.物体做曲线运动时,其合外力与速度一定不在同一条直线上D.曲线运动中物体受的合外力不可能为恒力5.关于功的概念,以下说法正确的是()A.力是矢量,位移是矢量,所以功也是矢量B.功有正、负之分,若某个力对物体做负功,表明这个力对该物体的运动起阻碍作用C.若某一个力对物体不做功,说明该物体一定没有位移D.合力的功等于各分力做的功的矢量和6.如图所示,x 轴在水平地面内,y 轴沿竖直方向.图中画出了y 轴上沿x 轴正方向抛出的三个小球abc 的运动轨迹,其中b 和c 从同一点抛出,不计空气阻力,则 ( ) A .a 的飞行时间比b 长 B .b 的飞行时间比c 长C .a 的初速度最大D .c 的末速度比b 大7.长为L 的轻杆一端固定一个小球,小球以杆的另一端为圆心在竖直面内做圆周运动,则下列说法正确的是( ) A.B.若小球过最高点的速度不为零,则杆对小球的弹力一定为拉力C.小球过最低点时,杆对小球的弹力可能为支持力D.小球过最底点时,一定处于超重状态8.如图所示,质量为m 的物体,在与水平方向成θ角的拉力F 作用下,沿水平面做匀速直线运动,物体与地面间动摩擦因数为μ.当物体的位移为x 时,拉力F 做的功为( ) A .Fx B .θcos FxC .x mg F )sin cos (θμθ-D .θμsin mg9.如图所示,是在同一轨道平面上的三颗不同的人造地球卫星,关于各物理量的关系,下列说法正确的是( ) A .根据gr v =,可知C B A v v v <<B .根据万有引力定律可知,所受的万有引力C B A F F F >> C .角速度C B A ωωω>>D .向心加速度C B A a a a <<10.下列关于地球同步卫星的说法中正确的是 ( )A .它的周期与地球自转同步,但高度和速度可以选择,高度越大,速度越小B .运行速度小于7.9 km/sC .我们国家发射的同步通讯卫星定点在北京上空D .它绕地球运行的角速度比月球绕地球运行的角速度小 11.下列关于万有引力定律及其表达式221r m m GF =的说法中正确的是( ) A .万有引力定律是卡文迪许发现的,适用于自然界中任何两个物体; B .当r 趋近于0时,万有引力趋于无穷大;C .两物体受到的相互引力总是大小相等,与两物体的质量是否相等无关;D .万有引力就是重力12.如图所示的皮带传动装置中,轮B和C同轴,A、B、C分别是三个轮边缘的质点,且其半径R A=R C=2R B,则三质点的向心加速度之比a A:a B:a C等于()A.1:2:4 B.2:1:2C.4:2:1 D.4:1:4二、填空题(每空3分,共18分)13.滑雪运动员以20m/s的速度从一平台水平飞出,落地点与飞出点的高度差3.2m。
31星城实验中学初二语文期中考试试卷含答案

湖南师大附中星城实验学校2018年-2019学年度第二学期期中考试八年级语文试卷一、语言积累与运用(共26分)1.下列加点字的注音及词语书写完全正确的一项是( )(2分)A.猝然(cù)要塞(sài) 不逊(xùn) 正襟危坐B.吹嘘(xū) 绯红(fěi)诘责(jié) 诚惶诚恐C.悄然(qiāo)翘首(qiáo)愚钝(dùn)摧枯拉朽D.畸形(qí ) 酒肆(sì)督战(dū)眼花瞭乱2.下列加点的词语使用有误的一项是( )2分A.他平时投机钻营,最会见风使舵,一看到有人得势,便对其颔首低眉,一副奴才嘴脸。
B.据全国文明城市评比问卷调查显示:在各种不文明的行为中,市民对不遵守交通法则、乱闯红灯的行为深恶痛疾。
C省博给我这样一个机会让我和这些文化名流一起担任理事我感到诚惶诚恐。
D.在雏鹰学习经验交流会上,优秀毕业生曾子容满怀激情地演讲着那扣扬顿挫的声音紧紧抓住了听众的心。
3.下列句子没有语病的一项是()2分A“一带一路猫绘了一幅和平特互利共赢的新思路,是东方智慧的中国方案B校运会那天我校共有大约800色左右师生运动员参加了体育项目的比赛。
C为了防止酒驾这类事件不再发生,交警部门采取了强有力的措施。
D.在阅读文学名著的过程中,我明白了许多做人的道理,感悟了人生的真谛。
4.下列句子排序最恰当的一项是( )(2分)①真正的友情储蓄,是不可以单向支取的。
②友情,是人生一笔受益匪浅的储蓄。
③自任何带功利性的友情儲蓄,不仅得不到利息,而且连本钱都会丧失殆尽。
④而是要通过彼此的积累加重其分量这储蓄,是患难中的倾囊相助,是迷途上的逆耳忠言,是跌倒时一把真诚的搀扶,是痛苦时抹去泪水的一缕春风。
A.①④②⑤③B.②⑤①④③C.②③①⑤④D.②①⑤④③5.下列表述不正确的一项是( )(2分)A.《朝花夕拾》是鲁迅先生的一部小说集,其中的名篇有《从百草园到三味书屋》、《父亲的病》、《无常》等,本学期我们学习了其中的《藤野先生》。
【湘教版】八年级数学下期中试卷(及答案)

② 是等边三角形;
③ ;
④ .
其中正确的是______________(填写序号)
三、解答题
21.如图,平面直角坐标系的原点在边长为1个单位长度的小正方形组成的网格的格点上, 为格点三角形(三角形的顶点在网格的格点上)
(1)直接写出下列点的坐标: (______,______), (______,______), (______,______).
1.B
解析:B
【分析】
根据中心对称图形的概念对各选项分析判断即可得解.
【详解】
解:A、不是中心对称图形,故本选项不符合题意;
B、是中心对称图形,故本选项符合题意;
C、不是中心对称图形,故本选项不符合题意;
D、不是中心对称图形,故本选项不符合题意.
故选:B.
【点睛】
本题考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
14.在平面直角坐标系xoy中,已知点A(2,3),若将OA绕原点O逆时针旋转90°得到OA′,则点A′的坐标是____________.
15.某次知识竞赛共有 题,答对一题得 分,答错或不答扣 分,小华得分要超过 分,他至少要答对__________题
16.如图,直线y=ax+b和y=kx+2与x铀分别交于点A(﹣2,0),点B(2.8,0).则 的解集为_____.
(1)完成下列步骤,画出函数y=|x|的图像;
①列表、填空:
x
…
﹣2
﹣1
0
1
2
…
y
…
1
0
2
…
②描点,
③连线
(2)观察函数图像,写出该函数图像的一条性质.
【湘教版】八年级数学下期中试题含答案(1)

一、选择题1.下列命题中真命题的是( )A .42=±B .点A(2,1)与B(-2,-1)关于原点对称C .64的立方根是±4D .若a<b ,则ac<bc2.下列图形中,既是中心对称图形,又是轴对称图形的是( )A .B .C .D . 3.怀化是一个多民族聚居的地区,民俗文化丰富多彩.下面是几幅具有浓厚民族特色的图案,其中既是轴对称图形又是中心对称图形的是( ) A . B .C .D .4.下列图形中,既是轴对称图形又是中心对称图形的是( ) A . B . C . D . 5.三角形的两边长分别是4和11,第三边长为34m +,则m 的取值范围在数轴上表示正确的是( )A .B .C .D .6.如果关于x 的不等式组2243(2)x m x x -⎧≥⎪⎨⎪-≤-⎩的解集为x≥1,且关于x 的方程(1)23m x x --=-有非负整数解,则所有符合条件的整数m 的值有( )个. A .2个 B .3个 C .4个 D .5个7.若a >b ,则下列式子正确的是( )A .a +1<b +1B .a ﹣1<b ﹣1C .﹣2a >﹣2bD .﹣2a <﹣2b 8.已知a 、b 为有理数,且a<0,b>0,a >b ,则( ).A .a<-b<b<-aB .-b<a<b<-aC .-a<b<-b<aD .-b<b<-a<a 9.等腰三角形的一个角为40︒,则其底角的度数为( ). A .40︒ B .70︒ C .40︒或70︒ D .50︒或70︒ 10.如图所示,O 为直线AB 上一点,OC 平分∠AOE ,∠DOE =90°,则①∠AOD 与∠BOE 互为余角;②OD 平分∠COA ;③若∠BOE =56°40',则∠COE =61°40';④∠BOE =2∠COD .结论正确的个数为( )A .4B .3C .2D .111.如图,一棵高5米的树AB 被强台风吹斜,与地面BC 形成60︒夹角,之后又被超强台风在点D 处吹断,点A 恰好落在BC 边上的点E 处,若2BE =,则BD 的长是( )A .2B .3C .218D .247 12.如图,等腰ABC 中,10AB AC ==,12BC =,点D 是底边BC 的中点,以A 、C 为圆心,大于12AC 的长度为半径分别画圆弧相交于两点E 、F ,若直线EF 上有一个动点P ,则线段PC PD +的最小值为( )A .6B .8C .10D .12二、填空题13.如图,把正方形铁片OABC 置于平面直角坐标系中,顶点A 的坐标为(3,0),点()1,2P 在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置,…,则正方形铁片连续旋转2019次后,则点P 的坐标为_________.14.已知:如图,在AOB ∆中,9034AOB AO cm BO cm ︒∠===,,,将AOB ∆绕顶点O ,按顺时针方向旋转得到11A OB ∆,线段1OB 与边AB 相交于点D ,则线段1B D 最大值为=________cm15.关于x 的不等式组3222553x x x m +⎧+⎪⎪⎨+⎪<+⎪⎩有且只有4个整数解,则常数m 的取值范围是_____.16.不等式组2x a x >⎧⎨>⎩的解为2x >,则a 的取值范围是______. 17.关于x 的不等式132x a x -≤⎧⎨-<⎩有5个整数解,则a 的取值范围是______. 18.如图,已知△ABC 的周长是18,OB 、OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D ,且OD =1,△ABC 的面积是_____.19.已知C ,D 两点在线段AB 的垂直平分线上,且∠ACB =50°,∠ADB =86°,则∠CAD 的度数是_____.20.等腰三角形一腰上的高与另一腰的夹角为40︒,则这个等腰三角形的底角度数为____________.三、解答题21.如图,是由边长为1的小正方形组成的76⨯的网格,ABC ∆的顶点都在格点上,请仅用无刻度的直尺作图.(1)作ABC ∆的角平分线BD ;(2)在网格中确定一个格点P ,作45ABP ∠=︒.22.在如图所示的平面直角坐标系中,有ABC(1)将ABC 向x 轴负半轴方向平移4个单位得到111A B C △,画出图形并写出点1A 的坐标.(2)以原点O 为旋转中心,将ABC 顺时针旋转90︒后得到222A B C △,画出图形并写出点2A 的坐标.(3)222A B C △可以看作是由111A B C △先向右平移4个单位,然后以原点O 为旋转中心,顺时针旋转90︒得到的.除此之外,222A B C △还可以由111A B C △,经过旋转变换得到,请在图中找出旋转中心.23.在近期“抗疫”期间,某药店销售A 、B 两种型号的口罩,已知销售80只A 型和45只B 型的利润为21元,销售40只A 型和60只B 型的利润为18元.(1)求每只A 型口罩和B 型口罩的销售利润;(2)该药店计划一次购进两种型号的口罩共2000只,其中B 型口罩的进货量不少于A 型口罩的进货量且不超过它的3倍,则该药店购进A 型、B 型口罩各多少只,才能使销售总利润最大?24.在平面直角坐标系中,一次函数y kx b =+(k ,b 是常数,且0k ≠)的图象经过点(2,1)和(1,7)-.(1)求该函数的表达式;(2)若点(5,3)P a a -在该函数的图象上,求点P 的坐标;(3)当311y -<<时,求x 的取值范围.25.如图,在四边形ABCD 中,90B ∠=︒,AC 平分BAD ∠,DE AC ⊥,AB AE =.(1)求证:AC AD =.(2)若BC CD ⊥,试判断ACD △的形状,并说明理由.26.如图,在△ABC 中,AB =AC ,DE 垂直平分AB ,垂足为D ,与AC 交于点E ,连接BE . (1)若∠A =42°,求∠EBC 的度数;(2)若AB =10,△BEC 的周长为16,求△ABC 的周长.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】根据算术平方根、点关于原点对称、立方根以及不等式的性质进行判断即可.【详解】解:A42,故原选项是假命题,不符合题意;B. 点A(2,1)与B(-2,-1)关于原点对称,是真命题,故此选项是真命题,符合题意;C.64的立方根是4,故原选项是假命题,不符合题意;D.当c≤0时ac≥bc,故原选项是假命题,不符合题意;故选B【点睛】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.2.C解析:C【分析】根据中心对称图形的定义:旋转180度之后与自身重合称为中心对称,轴对称是折叠后能够与自身完全重合称为轴对称,根据定义去解题.【详解】解:A、是中心对称图形,不是轴对称图形,故本选项错误;B、不是中心对称图形,是轴对称图形,故本选项错误;C、既是中心对称图形又是轴对称图形,故本选项正确;D、不是中心对称图形,是轴对称图形,故本选项错误.故选:C.【点睛】本题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.3.C解析:C【分析】直接利用轴对称图形和中心对称图形的概念求解.【详解】A、是轴对称图形,不是中心对称图形,故此选项错误;B、是轴对称图形,不是中心对称图形,故此选项错误;C、既是中心对称图形也是轴对称图形,故此选项正确;D、是轴对称图形,但不是中心对称图形,故此选项错误.故选C.【点睛】此题主要考查了中心对称与轴对称的概念:轴对称的关键是寻找对称轴,两边图象折叠后可重合,中心对称是要寻找对称中心,旋转180°后与原图重合.4.B解析:B【分析】观察四个选项中的图形,根据轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合;找出既是轴对称图形又是中心对称图形的那个即可得出结论.【详解】A是中心对称图形;B既是轴对称图形又是中心对称图形;C是轴对称图形;D不是轴对称图形,是中心对称图形.故选:B.【点睛】此题考查中心对称图形以及轴对称图形,牢记轴对称及中心对称图形的特点是解题的关键.5.A解析:A【分析】已知两边的长,第三边应该大于任意两边的差,而小于任意两边的和,列不等式进行求解后再进行判断即可.【详解】解:根据三角形的三边关系,得11-4<3+4m <11+4,解得1<m <3.故选:A .【点睛】此类求三角形第三边的范围的题,实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.6.A解析:A【分析】表示出不等式组的解集,由已知解集确定出m 的范围,表示出方程的解,由方程的解为非负整数,确定出整数m 的值即可.【详解】解:不等式组整理得:41≥+⎧⎨≥⎩x m x , ∵不等式组的解集为x ≥1,∴m +4≤1,即m ≤-3,方程去分母得:m -1+x =3x -6, 解得:5+2=m x , ∵方程有非负整数解,∴50m +≥,且5+m 能被2整除,∴-53m ≤≤-,∴当m=-5时,符合题意,当m=-3时,符合题意,则符合条件的整数m 的值有2个,故选:A .【点睛】本题考查一元一次不等式组的整数解,熟练掌握不等式组的解法是解本题的关键. 7.D解析:D【分析】根据不等式的性质逐一判断,判断出式子正确的是哪个即可.【详解】解:∵a >b ,∴a +1>b +1,∴选项A 不符合题意;∵a >b ,∴a ﹣1>b ﹣1,∴选项B 不符合题意;∵a >b ,∴﹣2a <﹣2b ,∴选项C 不符合题意;∵a >b ,∴﹣2a <﹣2b ,∴选项D 符合题意.故选:D .【点睛】本题考查了不等式的性质,要熟练掌握,特别要注意在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于0,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.8.A解析:A【分析】根据绝对值和不等式的性质,经计算,即可得到答案.【详解】∵a<0,b>0∴0a ->,0b -< ∴a a =-,b b =,a a <-,b b >- ∵a b >∴a b ->∴a b <-∴a b b a <-<<-故选:A .【点睛】本题考查了绝对值和不等式的知识;解题的关键是熟练掌握不等式和绝对值的性质,从而完成求解.9.C解析:C【分析】结合题意,根据等腰三角形、三角形内角和的性质计算,即可得到答案.【详解】当40︒角为等腰三角形顶角时,其底角的度数为18040702;当40︒角为等腰三角形底角时,其底角的度数为40︒;故选:C .【点睛】 本题考查了等腰三角形、三角形内角和的性质;解题的关键是熟练掌握等腰三角形的性质,从而完成求解.10.B解析:B【分析】由平角的定义与90DOE ∠=︒,即可求得AOD ∠与∠BOE 互为余角;又由角平分线的定义,可得22AOE COE AOC ∠=∠=∠,即可求得2BOE COD ∠=∠,若5640BOE ∠=︒',则6140COE ∠=︒'.【详解】解:90DOE ∠=︒,90COD COE ∴∠+∠=︒,90EOB DOA ∴∠+∠=︒,故①正确; OC 平分AOE ∠,22AOE COE AOC ∴∠=∠=∠;1801802BOE AOE COE ∴∠=︒-∠=︒-∠,90COD COE ∠=︒-∠,2BOE COD ∴∠=∠,90AOD BOE ∠=︒-∠,故②不正确,④正确;若5640BOE ∠=︒',180AOE BOE ∠+∠=︒,11(180)(1805640)614022COE BOE ∴∠=︒-∠=︒-︒'=︒'. 故③正确;∴①③④正确.故答案为:B .【点睛】此题考查了平角的定义与角平分线的定义.题目中要注意各角之间的关系,解题时要仔细识图.11.C解析:C【分析】过点D 作DM ⊥BC ,设BD=x ,然后根据题意和含30°的直角三角形性质分别表示出BM ,EM ,DE 的长,结合勾股定理列方程求解.【详解】解:过点D 作DM ⊥BC ,设BD=x ,由题意可得:AB=5,AD=DE=5-x∵∠ABC=60°,DM ⊥BC ,∴在Rt △BDM 中,∠BDM=30° ∴1122BM BD x ==,则122ME BE BM x =-=-∴2222BD BM DE ME -=-,222211()(5)(2)22x x x x -=---解得:218x =,即BD=218米 故选:C .【点睛】本题考查含30°的直角三角形性质和勾股定理解直角三角形,正确理解题意掌握相关性质定理列方程求解是关键.12.B解析:B【分析】由作法知EF 是AC 的垂直平分线,可得AP=CP ,线段PC PD +的最小就是PA+PD ,当A 、P 、D 三点共线时最短,由点D 是底边BC 的中点,可BD=CD =6,由AB=AC ,可得AD BC ⊥,在Rt △ABD 中,由勾股定理得:22AB BD 8-即可.【详解】解:连结PA ,由作法知EF 是AC 的垂直平分线,∴AP=CP ,∴PC+PD=PA+PD ,线段PC PD +的最小就是PA+PD ,当A 、P 、D 三点共线时最短,∵点D 是底边BC 的中点,∴BD=CD=11BC=12=622⨯, ∵AB=AC ,∴AD BC ⊥,在Rt △ABD 中,由勾股定理得:22221068AB BD --=,(PC+PD )最小=(PA+PD )最小=AD=8.故选择:B .【点睛】本题考查垂直平分线的性质,等腰三角形的三线合一性质,勾股定理,掌握垂直平分线的性质,等腰三角形的三线合一性质,勾股定理,关键是利用垂直平分线将PC转化为PA,找到P、A、D三点共线时最短.二、填空题13.(60581)【分析】首先求出P1~P5的坐标探究规律后利用规律解决问题【详解】解:第一次P1(52)第二次P2(81)第三次P3(101)第四次P4(132)第五次P5(172)…发现点P的位置4解析:(6058,1)【分析】首先求出P1~P5的坐标,探究规律后,利用规律解决问题.【详解】解:第一次P1(5,2),第二次P2(8,1),第三次P3(10,1),第四次P4(13,2),第五次P5(17,2),…发现点P的位置4次一个循环,∵2019÷4=504…3,P2019的纵坐标与P3相同为1,横坐标为12×504+10=6058,∴P2019(6058,1),故答案为(6058,1).【点睛】本题考查坐标与图形的变化、规律型:点的坐标等知识,解题的关键是学会从特殊到一般的探究规律的方法,属于中考常考题型.14.【分析】根据已知条件由勾股定理可得AB=5当时OD最小由等积法可得代入数据可得即可求出线段最大值【详解】在中∴AB=∵∴OD最小时最大当时OD最小即OD为的高∴即解得:∴线段最大值为:=cm故答案为解析:85【分析】根据已知条件由勾股定理可得AB=5,当1B O AB ⊥时,OD 最小,由等积法可得AO OB AB OD =,代入数据可得125OD =,即可求出线段1B D 最大值. 【详解】 在Rt AOB 中,34AO cm BO cm ==,,∴5=,∵11B D B O OD =-,14B O BO cm ==,∴OD 最小时,1B D 最大,当1B O AB ⊥时,OD 最小,即OD 为AOB 的高,∴AO OB AB OD =,即345OD ⨯=, 解得:125OD =, ∴线段1B D 最大值为:1245-=85cm , 故答案为:85. 【点睛】 本题主要考查了勾股定理,线段的最值问题,根据图形分析线段取得最值的情况是解题的关键.15.【分析】首先利用不等式的基本性质解不等式组再从不等式的解集中找出适合条件的整数解再确定字母的取值范围即可【详解】解:解①得:解②得:∴不等式组的解集为:∵不等式组只有4个整数解即不等式组只有4个整数 解析:423m -<≤- 【分析】首先利用不等式的基本性质解不等式组,再从不等式的解集中找出适合条件的整数解,再确定字母的取值范围即可.【详解】解:3222553x x x m +⎧+⎪⎪⎨+⎪<+⎪⎩①② 解①得:1x ≥-,解②得:3102m x +<, ∴不等式组的解集为:31012m x +-≤<, ∵不等式组只有4个整数解,即不等式组只有4个整数解为﹣1、0、1、2, 则有310232m +<≤, 解得:423m -<≤-, 故答案为:423m -<≤-【点睛】本题考查不等式组的解法及整数解的确定.解不等式要用到不等式的性质:(1)不等式的两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式的两边乘(或除以)同一个负数,不等号的方向改变.16.【分析】根据不等式组的公共解集即可确定a 的取值范围【详解】由不等式组的解为可得故答案为:【点睛】本题主要考查了不等式组的解法关键是熟练掌握不等式组解集的确定:同大取大;同小取小;大小小大中间找;大大 解析:2a ≤【分析】根据不等式组的公共解集即可确定a 的取值范围.【详解】由不等式组2x a x >⎧⎨>⎩的解为2x >, 可得2a ≤.故答案为:2a ≤.【点睛】本题主要考查了不等式组的解法,关键是熟练掌握不等式组解集的确定:同大取大;同小取小;大小小大中间找;大大小小找不到.17.【分析】首先解每个不等式两个不等式的解集的公共部分就是不等式组的解集确定整数解据此即可写出a 的范围【详解】解:解不等式①得;解不等式②得:则不等式的解集为∵不等式有5个整数解∴一定是01234∴即故 解析:12a ≤<【分析】首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,确定整数解,据此即可写出a 的范围.【详解】解:132x a x -≤⎧⎨-<⎩①②, 解不等式①得,4x ≤;解不等式②得:2x a >-,则不等式的解集为24a x -<≤,∵不等式132x a x -≤⎧⎨-<⎩有5个整数解, ∴一定是0,1,2,3,4.∴120a ,即12a ≤<,故答案为:12a ≤<.【点睛】此题考查的是一元一次不等式组的解法,根据x 的取值范围,得出x 的整数解,然后代入方程即可解出a 的值.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.18.9【分析】过点O 作OE ⊥AB 于EOF ⊥AC 与F 连接OA 根据角平分线的性质求出OEOF 根据三角形面积公式计算得到答案【详解】解:过点O 作OE ⊥AB 于EOF ⊥AC 于F 连接OA ∵OB 平分∠ABCOD ⊥BC解析:9【分析】过点O 作OE ⊥AB 于E ,OF ⊥AC 与F ,连接OA ,根据角平分线的性质求出OE 、OF ,根据三角形面积公式计算,得到答案.【详解】解:过点O 作OE ⊥AB 于E ,OF ⊥AC 于F ,连接OA ,∵OB 平分∠ABC ,OD ⊥BC ,OE ⊥AB ,∴OE =OD =1,同理可知,OF =OD =1,∴△ABC 的面积=△OAB 的面积+△OAC 的面积+△OBC 的面积, =12×AB ×OE +12×AC ×OF +12×BC ×OD , =12×18×1, =9,故答案为:9.【点睛】本题主要考查了角平分线的性质,准确计算是解题的关键.19.18°或112°【分析】分点C与点D在线段AB两侧点C与点D在线段AB同侧两种情况根据线段垂直平分线的性质等腰三角形的性质解答【详解】解:如图∵CD两点在线段AB的中垂线上∴CA=CBDA=DB∵C解析:18°或112°【分析】分点C与点D在线段AB两侧、点C与点D在线段AB同侧两种情况,根据线段垂直平分线的性质、等腰三角形的性质解答.【详解】解:如图,∵C、D两点在线段AB的中垂线上,∴CA=CB,DA=DB,∵CD⊥AB,∴∠ACD=12∠ACB=12×50°=25°,∠ADC=12∠ADB=12×86°=43°,当点C与点D在线段AB两侧时,∠CAD=180°﹣∠ACD﹣∠ADC=180°﹣25°﹣43°=112°,当点C与点D′在线段AB同侧时,∠CAD′=∠AD′C﹣∠ACD′=43°﹣25°=18°,故答案为:18°或112°.【点睛】本题考查的是线段垂直平分线的性质、等腰三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.20.65°或25°【分析】在等腰△ABC中AB=ACBD为腰AC上的高∠ABD=40°讨论:当BD在△ABC内部时如图1先计算出∠BAD=50°再根据等腰三角形的性质和三角形内角和计算;当BD在△ABC解析:65°或25°【分析】在等腰△ABC中,AB=AC,BD为腰AC上的高,∠ABD=40°,讨论:当BD在△ABC内部时,如图1,先计算出∠BAD=50°,再根据等腰三角形的性质和三角形内角和计算;当BD 在△ABC外部时,如图2,先计算出∠BAD=50°,再根据等腰三角形的性质和三角形外角性质计算.【详解】解:在等腰△ABC中,AB=AC,BD为腰AC上的高,∠ABD=40°,当BD在△ABC内部时,如图1,∵BD为高,∴∠ADB=90°,∴∠BAD=90°﹣40°=50°,∵AB=AC,∴∠ABC=∠ACB=1(180°﹣50°)=65°;2当BD在△ABC外部时,如图2,∵BD为高,∴∠ADB=90°,∴∠BAD=90°﹣40°=50°,∵AB=AC,∴∠ABC=∠ACB,而∠BAD=∠ABC+∠ACB,∠BAD=25°,∴∠ACB=12综上所述,这个等腰三角形底角的度数为65°或25°.故答案为:65°或25°.【点睛】本题考查了等腰三角形的性质、三角形的内角和定理以及三角形的外角性质,正确分类、熟练掌握上述知识是解题的关键.三、解答题21.(1)见解析;(2)见解析【分析】(1)由勾股定理得AB=224+3=5,可得AB=BC=5,取AC中点D,连结BD,根据等腰三角形三线合一性质,BD平分∠ABC;(2)构造三角形ABP是等腰直角三角形,根据网格先确定AP=AB=5,由AB是横3竖4的网格,绕点A逆时针旋转90°即为AP,连结BP,可得∠ABP=45°.【详解】解:(1)由勾股定理得AB=224+3=5,BC=5,∴AB=BC=5,∴取AC中点D,连结BD,∴根据等腰三角形三线合一性质,BD平分∠ABC,如图1,BD即为所作.(2)构造三角形ABP是等腰直角三角形,根据网格先确定AP=AB=5,由AB是横3竖4的网格,绕点A逆时针旋转90°即为AP,连结BP,∴△ABP为等腰直角三角形,∴∠ABP=45°,即为所作.如图2,ABP【点睛】本题考查角平分线,45°角的作图问题,掌握勾股定理,等腰三角形的判定与性质,等腰直角三角形的判定与性质,图形旋转的性质是解题关键.22.(1)见解析,(-1,3);(2)见解析,(3,-3);(3)点P (-2,-2)【分析】(1)找出点A、B、C向左平移4个单位的对应的点A1、B1、C1的位置,然后顺次连接即可得到△A1B1C1;(2)利用网格特点,找出点A、B、C以原点O为旋转中心,顺时针旋转90°后的对应的点A2、B2、C2的位置,然后顺次连接即可得到△A2B2C2;(3)根据垂径定理,垂直平分弦的直线经过圆心,任意连接两个对应点,再作出对应点连线的垂直平分线,交点就是旋转中心.【详解】解:(1)图形如图,点A1的坐标是(-1,3);(2)图形如图,点A2的坐标是(3,-3);(3)连接A1A2,B1B2,并分别作A1A2,B1B2的垂直平分线,相交于点P,所以,点P(-2,-2)就是所求的旋转中心.【点睛】本题考查了旋转变换与平移变换作图,找出对应点的位置是作图的关键,对应点的连线的垂直平分线过旋转中心是找旋转中心常用的方法,需要熟练掌握.23.(1)每只A型口罩销售利润为0.15元,每只B型口罩销售利润为0.2元;(2)药店购进A型口罩500只、B型口罩1500只,才能使销售总利润最大.【分析】(1)设每只A型口罩销售利润为a元,每只B型口罩销售利润为b元,根据“销售80只A 型和45只B型的利润为21元,销售40只A型和60只B型的利润为180元”列方程组解答即可;(2)根据题意即可得出y关于x的函数关系式;再根据题意列不等式得出x的取值范围,再结合一次函数的性质解答即可.【详解】解:(1)设每只A 型口罩销售利润为a 元,每只B 型口罩销售利润为b 元,根据题意得:804521406018a b a b +=⎧⎨+=⎩, 解得0.150.2a b =⎧⎨=⎩, 答:每只A 型口罩销售利润为0.15元,每只B 型口罩销售利润为0.2元;(2)设购进A 型口罩x 只,这2000只口罩的销售总利润为y 元.根据题意得,y=0.15x+0.2(2000-x ),即y=-0.05x+400;根据题意得,200020003x x x x-≥⎧⎨-≤⎩,解得500≤x≤1000, ∴y=-0.05x+400(500≤x≤1000);∵k=-0.05<0;∴y 随x 的增大而减小,∵x 为正整数,∴当x=500时,y 取最大值,则2000-x=1500,即药店购进A 型口罩500只、B 型口罩1500只,才能使销售总利润最大.【点睛】本题主要考查了一次函数的应用,二元一次方程组及一元一次不等式的应用,解题的关键是根据一次函数x 值的增大而确定y 值的增减情况.24.(1)25y x =-+;(2)(2,9)P -;(3)34x -<<.【分析】(1)利用待定系数即可求得函数的表达式;(2)将(5,3)P a a -代入函数解析式,求得a 的值后即可求得P 的坐标;(3)根据y 的取值范围,可得x 的不等式,求解即可.【详解】解:(1)一次函数y kx b =+过(2,1)和(-1,7),∴127k b k b =+⎧⎨=-+⎩, 解得:25k b =-⎧⎨=⎩, ∴25y x =-+;(2)由(1)可知:25y x =-+,将(5,3)P a a -代入25y x =-+,∴32(5)5a a =--+,解得3a =,即39,52a a =-=-,∴(2,9)P -;(3)∵25y x =-+,当311y -<<时,则32511x -<-+<,解得:34x -<<,∴x 的取值范围:34x -<<.【点睛】本题考查待定系数法求一次函数解析式,一次函数与一元一次不等式.解题时注意:直线上任意一点的坐标都满足函数关系式y=kx+b .25.(1)见解析;(2)等边三角形,理由见解析【分析】(1)根据题意可证ABC AED ≌△△,继而得出结论; (2)根据BC CD ⊥,可知90BCD B ∠=∠=︒,即可判断//AB CD ,进而可证AD CD AC ==,从而得出结论;【详解】(1)证明:∵90B ∠=︒,DE AC ⊥,∴90B AED ∠=∠=︒,∵AC 平分BAD ∠,∴BAC EAD ∠=∠,在ABC 和AED 中,∵ABC AED AB AE BAC EAD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ABC AED ASA ≌△△,∴AC AD =;(2)解:ACD △是等边三角形,理由如下:∵BC CD ⊥,∴90BCD B ∠=∠=︒,∴//AB CD ,∴BAC ACD DAC ∠=∠=∠,∴AD CD AC ==,∴ACD △是等边三角形;【点睛】本题考查了全等三角形的性质与判定、平行线的性质与判定、等边三角形的判定,熟练掌握知识点是解题的关键;26.(1)27°;(2)26【分析】(1)根据等腰三角形的性质和三角形内角和定理求出∠ABC 的度数,根据线段的垂直平分线的性质求出∠EBA 的度数,计算即可;(2)根据线段的垂直平分线的性质和三角形的周长公式求出AC +BC +AB =16+5+5=26,计算即可.【详解】(1)∵AB=AC,∠A=42︒,∴∠ABC=∠C=69︒.∵DE是AB的垂直平分线,∴EA=EB,∴∠EBA=∠A=42︒,∴∠EBC=27︒;(2)∵DE是AB的垂直平分线,AB=10∴EB=AE,△BEC的周长=EB+BC+EC=EA+BC+EC=AC+BC=16,则△ABC的周长=AB+BC+AC=26.【点睛】本题考查的是线段的垂直平分线的性质和等腰三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.。
【湘教版】八年级数学下期中模拟试卷(及答案)

一、选择题1.如图,在ABC 中,D 是BC 边上的中点,连结AD ,把ABD △沿AD 翻折,得到AB D ',连接CB ',若2BD CB '==,3AD =,则AB C '的面积为( )A .332B .23C .3D .22.下列命题是真命题的是( )A .三角形的三条高线相交于三角形内一点B .一组对边平行,另一组对边相等的四边形是平行四边形C .对于所有自然数n ,237n n -+的值都是质数D .三角形一条边的两个顶点到这条边上的中线所在直线的距离相等3.当2a <时,化简3(2)a a -的结果是( )A .(2)a a a -B .(2)a a a --C .(2)a a a -D .(2)a a a -- 4.如图为实数a ,b 在数轴上的位置,则222()()()b a a b +---=( )A .-aB .bC .0D .a-b5.已知y 443x x -+-,则x y 的值为( ). A .43 B .43- C .34D .34- 6.3 ) A 15B . 18C 13D . 1.57.平行四边形一边的长是12cm ,则这个平行四边形的两条对角线长可以是( ) A .4cm 或6cm B .6cm 或10cm C .12cm 或12cm D .12cm 或14cm 8.如图,以平行四边形ABCD 的边AB 、BC 、CD 、DA 为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E 、F 、G 、H ,顺次连结这四个点,得四边形EFGH ,当()090ADC αα∠=︒<<︒时,有以下结论:①180GCF α∠=︒-;②90HAE α∠=︒+;③HE HG =;④ EH GH ⊥;⑤四边形EFGH 是平行四边形.则结论正确的是( )A .①③④B .②③⑤C .①③④⑤D .②③④⑤ 9.如图,在矩形纸片ABCD 中,BC a =,将矩形纸片翻折,使点C 恰好落在对角线交点O 处,折痕为BE ,点E 在边CD 上,则CE 的长为( )A .12aB .25aC .32aD .33a 10.如图,△ABC 中,∠BAC=90°,AB=8,将△ABC 沿直线BC 向右平移,得到△EDF ,连接AD ,若四边形ACFD 为菱形,EC=4,则平移的距离为( )A .4B .5C .6D .811.如图,在Rt ABC ∆中,90,45,2B BCA AC ︒︒∠=∠==,点D 在BC 边上,将ABD ∆沿直线AD 翻折,点B 恰好落在AC 边上的点E 处,若点P 是直线AD 上的动点,连接,PE PC ,则PEC ∆的周长的最小值为( )A .22-B .2C .21+D .1 12.如图,在ABC 中,13,17,AB AC AD BC ==⊥,垂足为D ,M 为AD 上任一点,则22MC MB -等于( )A .93B .30C .120D .无法确定二、填空题13.已知菱形的面积为962cm ,两条对角线之比为3∶4,则菱形的周长为__________. 14.如图,在四边形ABCD 中,AC a =,BD b =,且AC BD ⊥顺次连接四边形ABCD 各边的中点,得到四边形1111D C B A ,再顺次连接四边形1111D C B A 各边中点,得到四边形2222A B C D …如此进行下去,得到四边形n n n n A B C D ,下列结论正确的有__________.①四边形2222A B C D 是矩形;②四边形4444A B C D 是菱形;③四边形5555A B C D 的周长是4a b +.15.()235328+--=__________.16.计算:22)=___________.17.273=_____18.如图,在Rt ABC ∆中,90A ∠=︒,ABC ∠的平分线BD 交AC 于点D ,DE 是BC 的垂直平分线,点E 是垂足.若2DC =,1AD =,则BE 的长为__________.19.如图,A 点坐标为(3,0),C 点坐标为(0,1),将OAC 沿AC 翻折得ACP △,则P 点坐标为_________.20.如图AD=4,CD=3,∠ADC=90°,AB=13,BC=12,则图形ABCD 的面积=______________.三、解答题21.如图,已知点E 是ABCD 的边CD 延长线上的一点;连接AE ,BD ,且//AE BD ;过点E 作EF BC ⊥,交BC 的延长线于点F ,连接DF ;求证:DF DE =22.如图,点A ,B ,C ,D 在同一条直线上,点E ,F 分别在直线AD 的两侧,且AC BD =,EBC FCB ∠=∠,BE CF =.求证:四边形AFDE 是平行四边形;23.计算:20116(2019)|527|32π-⎛⎫⨯+---- ⎪⎝⎭. 24.解方程组和计算(1)计算:①(6﹣215) ×3﹣612; ②4(3+7)0+12×8﹣(1﹣2)2 (2)解方程组:①43522x y y x +=⎧⎨=-⎩; ②3414233x y x y -=⎧⎨-=⎩. 25.如图,在ABC 中,90ACB ∠=︒,5AB =,3BC =,点P 从点A 出发,以每秒2个单位长度的速度沿折线A C B A ---运动.设点P 的运动时间为t 秒()0t >. (1)求AC 的长及斜边AB 上的高.(2)当点P 在CB 上时,①CP 的长为______________(用含t 的代数式表示).②若点P 在BAC ∠的角平分线上,则t 的值为______________.(3)在整个运动过程中,直接写出BCP 是等腰三角形时t 的值.26.如图,A (-1,0),C (1,4),点B 在x 轴上,且BC =5.(1)求点B 的坐标;(2)求△ABC 的面积.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】证明AD ∥CB′,推出S △ACB′=S △CDB′即可解决问题.【详解】∵D 是BC 的中点,∴BD DC =,由翻折的性质可知ADB ADB '∠=∠,DB DB '=,∴2BD CB '==,∴2CD DB CB ''===,∴CDB '是等边三角形, ∴60CDB DCB ''∠=∠=︒,120BDB '∠=︒, ∴120ADB ADB '∠=∠=︒, ∴60ADC CDB '∠=∠=︒, ∴ADC DCB '∠=∠, ∴//AD CB ',∴22ACB CDB S S ''===△△ 故选:C .【点睛】本题考查了折叠的性质,等边三角形的判定和性质,三角形的面积等知识,解题的关键是学会用转化的思想思考问题.2.D解析:D【分析】根据钝角三角形的高的交点在三角形外部可对A 进行判断;根据平行四边形的判定对B 进行判断;取n=6可对C 进行判断;根据三角形全等的知识可对D 进行判断.【详解】解:A 、钝角三角形的三条高线相交于三角形外一点,所以A 选项错误;B 、一组对边平行,另一组对边也平行的四边形是平行四边形,所以B 选项错误;C 、当n=6时,n 2-3n+7=25,25不是质数,所以C 选项错误;D 、通过证明三角形全等,可以证明三角形一条边的两个顶点到这条边上的中线所在直线的距离相等,所以D 选项准确.故选:D .【点睛】本题考查了命题:判断事物的语句叫命题;正确的命题称为真命题;错误的命题称为假命题.也考查了平行四边形的判定及全等三角形的判定和性质.3.B解析:B【分析】根据二次根式的性质即可化简.【详解】解:∵2a <∴a 20-<∴-故选:B .【点睛】此题主要考查二次根式的化简,解题的关键是熟练掌握二次根式的性质.4.C解析:C【分析】由数轴可得a 、b 和a-b 的正负,再由二次根式性质去根号、合并同类项即可.【详解】根据实数a 、b 在数轴上的位置得知:-1<a <0<b <1,∴a-b <0,则原式=b-a-(b-a )=b-a-b+a=0.故选:C .【点睛】考查了数轴及二次根式的化简,解题关键是由数轴得出a 、b 和a-b 的正负情况. 5.A解析:A【分析】由二次根式有意义的条件可得出x 的值,即可得出y 的值,计算出x y 的值即可. 【详解】因为3y =,4040x x -≥⎧∴⎨-≥⎩, ∴x =4,∴y =3, ∴43x y =.故选:A.【点睛】本题主要考查二次根式有意义的条件,熟记二次根式有意义的条件是解题关键.6.C解析:C【分析】先根据二次根式的性质化简各项,再根据同类二次根式的定义逐项判断即得答案.【详解】解:A、15与3不是同类二次根式,故本选项不符合题意;B、1832=,所以18与3不是同类二次根式,故本选项不符合题意;C、11333=,所以13与3是同类二次根式,故本选项符合题意;D、61.5=,所以 1.5与3不是同类二次根式,故本选项不符合题意;故选:C.【点睛】本题考查了二次根式的性质和同类二次根式的定义,属于基础题型,熟练掌握上述知识是解题的关键.7.D解析:D【分析】由四边形ABCD是平行四边形,可得OA=12AC,OB=12BD,然后利用三角形三边关系分析求解即可求得答案.【详解】解:∵四边形ABCD是平行四边形,∴OA=12AC,OB=12BD,A、∵AC=4cm,BD=6cm,∴OA=2cm,OB=3cm,∴OA+OB=5cm<12cm,不能组成三角形,故不符合;B、∵AC=6cm,BD=10cm,∴OA=3cm,OB=5cm,∴OA+OB=8cm<12cm,不能组成三角形,故不符合;C 、∵AC=12cm ,BD=12cm ,∴OA=6cm ,OB=6cm ,∴OA+OB=12cm=12cm ,不能组成三角形,故不符合;D 、∵AC=12cm ,BD=14cm ,∴OA=6cm ,OB=7cm ,∴OA+OB=13cm >12cm ,能组成三角形,故符合;故选D .【点睛】此题考查了平行四边形的性质以及三角形的三边关系.注意掌握平行四边形的对角线互相平分.8.D解析:D【分析】根据平行四边形性质得出∠ABC=∠ADC=α,∠BAD=∠BCD ,AB=CD ,AD=BC ,AD ∥BC ,AB ∥CD ,根据等腰直角三角形得出BE=AE=CG=DG ,AH=DH=BF=CF ,∠ABE=∠EAB=∠FBC=∠FCB=∠GCD=∠GDC=∠HAD=∠EDA=45°,求出∠HAE=∠HDG=∠FCG=∠FBE=90°+α,证△FBE ≌△HAE ≌△HDG ≌△FCG ,推出∠BFE=∠GFC ,EF=EH=HG=GF ,求出∠EFG=90°,根据正方形性质得出即可.【详解】解:∵四边形ABCD 是平行四边形,∴∠ABC=∠ADC=α,∠BAD=∠BCD ,AB=CD ,AD=BC ,AD ∥BC ,AB ∥CD ,∵平行四边形ABCD 的边AB 、BC 、CD 、DA 为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E 、F 、G 、H ,∴BE=AE=CG=DG ,AH=DH=BF=CF ,∠ABE=∠EAB=∠FBC=∠FCB=∠GCD=∠GDC=∠HAD=∠EDA=45°,∵AB ∥CD ,∴∠BAD=∠BCD=180°-α,∴∠EAH=360°-45°-45°-(180°-α)=90°+α,∠GCF=360°-45°-45°-(180°-α)=90°+α, ∴①错误;②正确;∠HDG=45°+45°+α=90°+α,∠FBE=45°+45°+α=90°+α,∴∠HAE=∠HDG=∠FCG=∠FBE ,在△FBE 、△HAE 、△HDG 、△FCG 中,BF AH DH CF FBE HAE HDG FCG BE AE DG CG ===⎧⎪∠=∠=∠=∠⎨⎪===⎩,∴△FBE ≌△HAE ≌△HDG ≌△FCG (SAS ),∴∠BFE=∠GFC ,EF=EH=HG=GF ,③正确;∴四边形EFGH 是菱形,∵∠BFC=90°=∠BFE+∠EFC=∠GFC+∠CFE ,∴∠EFG=90°,∴四边形EFGH 是正方形,⑤正确;∴EH ⊥GH ,④正确;故选:D .【点睛】本题考查了等腰直角三角形,全等三角形的性质和判定,正方形的判定,平行四边形的性质,菱形的判定的应用,主要考查学生的推理能力.9.D解析:D【分析】首先证明△OBC 是等边三角形,在Rt △EBC 中求出CE 即可解决问题;【详解】解:∵四边形ABCD 是矩形,∴OB=OC ,∠BCD=90°,由翻折不变性可知:BC=BO ,∴BC=OB=OC ,∴△OBC 是等边三角形,∴∠OBC=60°,∴∠EBC=∠EBO=30°,∴BE=2CE根据勾股定理得:333a , 故选:D .【点睛】本题考查翻折变换,等边三角形的判定和性质等知识,解题的关键是证明△OBC 是等边三角形. 10.C解析:C【分析】根据平移的性质可得8,,AB DE AC DF BC EF ====,设AC DF CF AD x ====,求得BC=4x +,再由勾股定理理出方程求解即可.【详解】解:由平移的性质可得:8,,AB DE AC DF BC EF ====又∵四边形ACFD 是菱形∴设AC DF CF AD x ====又∵4EC =∴4BC EF CF CE x ==+=+又∵∠90BAC ︒=∴222AB AC BC +=∴2228(4)x x +=+解得,6x =即6AD DF CF AC ====故平移的距离为:6AD =故选:C .【点睛】本题主要考查了平移的性质,熟练掌握平移的基本性质是解答此题的关键.11.B解析:B【分析】连接BP ,根据已知条件求出AB=BC=1,由翻折得:BD=DE ,∠BDA=∠EDA ,AE=AB=1,1,证明△BDP ≌△EDP ,推出BP=EP ,当点P 与点D 重合时,即可求出PEC ∆的周长的最小值.【详解】连接BP ,在Rt ABC ∆中,90,45B BCA ︒∠=∠=︒,∴∠BAC=45BCA ∠=︒,AB=BC ,∴22222AB AC ===,∴AB=BC=1,由翻折得:BD=DE ,∠BDA=∠EDA ,AE=AB=1,∴1,在△BDP 和△EDP 中, BD ED BDP EDP DP DP =⎧⎪∠=∠⎨⎪=⎩,∴△BDP ≌△EDP ,∴BP=EP ,∴当点P 与点D 重合时,PE+PC=PB+PC=BC 的值最小,此时PEC ∆的周长最小, PEC ∆的周长的最小值为1故选:B ..【点睛】此题考查翻折的性质,勾股定理,全等三角形的判定及性质,解题的关键是根据翻折的性质证得△BDP ≌△EDP ,由此推出当点P 与点D 重合时PEC ∆的周长最小,合情推理科学论证.12.C解析:C【分析】由,AD BC ⊥结合勾股定理可得:2222,AC AB DC BD -=-2222MC MB DC BD -=-,再把已知线段的长度代入计算即可得到答案.【详解】解:,AD BC ⊥222222,,AB AD BD AC AD DC ∴=+=+22222222,AC AB AD DC AD BD DC BD ∴-=+--=-1713AC AB ==,,22221713304120DC BD ∴-=-=⨯=,,AD BC ⊥222222,,MC MD DC BM BD DM ∴=+=+22222222120.MC MB MD DC DM BD DC BD ∴-=+--=-=故选:.C【点睛】本题考查的是勾股定理的应用,掌握利用勾股定理解决问题是解题的关键.二、填空题13.40【分析】依题意已知菱形的面积以及对角线之比首先根据面积公式求出菱形的对角线长然后利用勾股定理求出菱形的边长【详解】解:设两条对角线长分别为3x 和4x 由题意可得:解得:x=±4(负值舍去)∴对角线解析:40cm【分析】依题意,已知菱形的面积以及对角线之比,首先根据面积公式求出菱形的对角线长,然后利用勾股定理求出菱形的边长.【详解】解:设两条对角线长分别为3x 和4x ,由题意可得:134962x x =,解得:x=±4(负值舍去) ∴对角线长分别为12cm 、16cm ,又∵菱形的对角线互相垂直平分,根据勾股定理可得菱形的边长,则菱形的周长为40cm .故答案为:40cm .【点睛】此题主要考查菱形的性质和菱形的面积公式,综合利用了勾股定理.14.②③【分析】利用三角形的中位线的性质证明四边形是矩形四边形是菱形四边形是矩形四边形是菱形从而可得到规律序号n 是奇数时四边形是矩形当序号n 是偶数时四边形是菱形再探究n 是奇数时四边形的周长即可解决问题【 解析:②③【分析】利用三角形的中位线的性质证明四边形1111D C B A 是矩形,四边形2222A B C D 是菱形,四边形3333A B C D 是矩形,四边形4444A B C D 是菱形,从而可得到规律,序号n 是奇数时四边形是矩形,当序号n 是偶数时四边形是菱形,再探究n 是奇数时四边形的周长即可解决问题.【详解】解: 1111,,,A B C D 分别是,,,AB BC CD DA 的中点,1111111111//,,//,,22A B AC A B AC C D AC C D AC ∴== 11//,A D BD 11111111//,,A B C D A B C D ∴=∴ 四边形1111D C B A 是平行四边形,,AC BD ⊥ 11//,A B AC 11//,A D BD 1111,A B A D ∴⊥∴ 四边形1111D C B A 是矩形,1111,AC B D ∴=如图,2222,,,A B C D 分别是11111111,,,A B B C C D D A 的中点,∴ 2211221111,,22A B AC A D B D == 四边形2222A B C D 是平行四边形, 2222,A B A D ∴=∴ 四边形2222A B C D 是菱形,故①不符合题意,2222,A C B D ∴⊥同理可得:四边形3333A B C D 是矩形,四边形4444A B C D 是菱形,故②符合题意,······总结规律:四边形n n n n A B C D , 当序号n 是奇数时四边形是矩形,当序号n 是偶数时四边形是菱形,111111111111,,2222A B C D AC a A D B C BD b ====== ∴ 四边形1111D C B A 的周长为,a b +如图, 四边形1111D C B A 是矩形,四边形2222A B C D 是菱形,2222,,,A B C D 分别是11111111,,,A B B C C D D A 的中点,222222112211,,,A C B D A C A D B D A B ∴⊥==由中位线的性质同理可得:33332233332211111111,,22242224A DBC BD a a D C A B A C b b ===⨯====⨯= 所以四边形3333A B C D 的周长为()1,2a b + 由规律可得:四边形5555A B C D 是矩形, 同理可得:四边形5555A B C D 的周长是()11.224a b a b +⨯+=故③符合题意.故答案为②③.【点睛】本题考查三角形的中位线的性质,中点四边形,菱形的判定与性质,矩形的判定与性质,解题的关键是学会从特殊到一般,探究规律,利用规律解决问题.15.7-【分析】首先利用绝对值的性质和二次根式算术平方根立方根的性质化简然后再计算加减即可【详解】解:【点睛】此题主要考查了实数运算关键是掌握绝对值的性质和二次根式的性质解析:【分析】首先利用绝对值的性质和二次根式、算术平方根、立方根的性质化简,然后再计算加减即可.【详解】3()--=322=32+2=7【点睛】此题主要考查了实数运算,关键是掌握绝对值的性质和二次根式的性质.16.2【分析】根据二次根式的性质化简即可【详解】2故答案为:2【点睛】此题考查二次根式的性质掌握二次根式的性质:是解答此题的关键解析:2【分析】根据二次根式的性质化简即可.【详解】2=2,故答案为:2【点睛】==,是解答此题的关键.此题考查二次根式的性质.掌握二次根式的性质:2a a17.【分析】先将化为再合并同类二次根式即可【详解】解:=故答案为【点睛】此题考查了二次根式的加减法把化为是解答此题的关键解析:【分析】化为【详解】==.故答案为【点睛】化为18.【分析】根据是的垂直平分线得到BD=CDBE=CE推出∠DBC=∠C根据BD平分推出∠ABD=∠CBD=∠C求出∠C=得到DE=1利用勾股定理求出CE即可得到BE【详解】∵是的垂直平分线∴BD=CD【分析】根据DE是BC的垂直平分线,得到BD=CD,BE=CE,推出∠DBC=∠C,根据BD平分ABC∠,推出∠ABD=∠CBD=∠C,求出∠C=30,得到DE=1,利用勾股定理求出CE即可得到BE.【详解】∵DE是BC的垂直平分线,∴BD=CD,BE=CE,∴∠DBC=∠C,∵BD平分ABC∠,∴∠ABD=∠CBD,∴∠ABD=∠CBD=∠C,∵∠ABD+∠CBD+∠C=90︒,∴∠C=30,∵2DC=,∴DE=1,∴=,【点睛】此题考查线段垂直平分线的性质,角平分线的性质,直角三角形30度角的性质,勾股定理,熟记线段垂直平分线的性质及角平分线的性质是解题的关键.19.【分析】在Rt△COA中根据OA=和OC=1根据勾股定理可得AC=2得到根据翻折性质可得继而可得在Rt△PAG中根据所对直角边等于斜边的一半可以求出AG的长利用勾股定理可求出PG的长从而得到P点坐标解析:32⎫⎪⎪⎝⎭【分析】在Rt △COA 中,根据OA=3和OC=1,根据勾股定理可得AC=2,得到30CAO ∠=︒,根据翻折性质可得CAO PAC ∠=∠,继而可得60PAO ∠=︒,30GPA ∠=︒,在Rt △PAG 中,根据30所对直角边等于斜边的一半可以求出AG 的长,利用勾股定理可求出PG 的长,从而得到P 点坐标.【详解】如下图,过点P 作PG x ⊥轴于点G ,∵3,OC=1,∴22+2OA OC =,∴12OC AC =, ∴30CAO ∠=︒, ∵△AOC 沿AC 翻折得到△APC ,∴CAO PAC ∠=∠,∴=60PAO ∠︒,=30GPA ∠︒,3,∴132AG AP ==,2232PG PA GA =-=, ∴333 ∴点P 的坐标为3322⎛⎫ ⎪ ⎪⎝⎭,, 故答案为:332⎫⎪⎪⎝⎭,. 【点睛】本题考查折叠的性质、含30︒角的直角三角形及勾股定理,熟练掌握含30︒角的直角三角形及勾股定理是解题的关键.20.24【分析】连接AC 在中根据勾股定理求得AC 的长度利用勾股定理逆定理可得为直角三角形根据即可求解【详解】解:连接AC 在中∴∵∴∴为直角三角形∴故答案为:24【点睛】本题考查勾股定理及其逆定理掌握勾股 解析:24【分析】连接AC ,在Rt ACD △中根据勾股定理求得AC 的长度,利用勾股定理逆定理可得ABC 为直角三角形,根据ABCD ABC ACD S SS =-即可求解.【详解】解:连接AC , ,在Rt ACD △中,90ADC ∠=︒,4=AD ,3CD =, ∴225AC AD CD =+=,∵13AB =,12BC =,∴222AC BC AB +=,∴ABC 为直角三角形,90ACB ∠=︒, ∴112422ABCD ABC ACD S S S AC BC AD CD =-=⋅-⋅=, 故答案为:24.【点睛】本题考查勾股定理及其逆定理,掌握勾股定理的内容是解题的关键.三、解答题21.见解析【分析】根据平行四边形的性质可得AB CD =,//AB CD ,然后结合题意利用两组对边分别平行的四边形是平行四边形可判定四边形ABDE 是平行四边形,然后利用平行四边形的性质和直角三角形斜边中线等于斜边一半证明求解.【详解】证明:∵四边形ABCD 是平行四边形,∴AB CD =,//AB CD ,又∵//AE BD∴四边形ABDE 是平行四边形;∴AB DE =,即CD DE =;又EF BC ⊥于点F ;∴∠EFC=90°∴在Rt CEF △中,点D 是斜边CE 的中点∴DF DE =.【点睛】本题考查平行四边形的性质和判定以及直角三角形斜边中线等于斜边的一半,掌握相关性质定理正确推理论证是解题关键.22.见解析【分析】证明△ABE ≌△DCF ,得到AE=DF ,∠EAB=∠FDC ,推出AE ∥DF ,即可证明结论.【详解】解:∵AC=BD ,即AB+BC=CD+CB ,∴AB=CD ,∵∠EBC=∠FCB ,∴∠ABE=∠DCF ,在△ABE 和△DCF 中,AB CD ABE DCF BE CF =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△DCF (SAS ),∴AE=DF ,∠EAB=∠FDC ,∴AE ∥DF ,∴四边形AFDE 是平行四边形.【点睛】本题考查了全等三角形的判定和性质,平行四边形的判定,解题的关键是根据全等得到对应角和对应边相等.23.2.【分析】实数的混合运算,注意先算乘方,然后算乘除,最后算加减,有小括号先算小括号里面的.【详解】解:2016(2019)|52π-⎛⎫--- ⎪⎝⎭=61|543⨯+---154=+-2=-【点睛】本题考查实数的混合运算、二次根式的性质和负整数指数幂的运算等知识,掌握运算顺序和计算法则正确计算是解题关键.24.(1)①-②;(2)①111015x y ⎧=⎪⎪⎨⎪=⎪⎩;②3019x y =⎧⎨=⎩【分析】(1)①直接利用二次根式的混合运算法则化简,进而计算得出答案;②直接利用负整数指数幂的性质以及二次根式的混合运算法则分别化简得出答案;(2)①直接利用代入消元法解方程得出答案;②直接利用加减消元法解方程得出答案.【详解】解:(1)①原式62=⨯==-,故答案为:-②原式=4+(122⨯+-=4+2-故答案为:;(2)解①方程组:435(1)22(2)+=⎧⎨=-⎩x yy x,把(2)代入(1)中得:4x+3(2x﹣2)=5,解得:x=11 10,把x=1110代入(2)得y=15,所以方程组的解为:111015xy⎧=⎪⎪⎨⎪=⎪⎩,故答案为111015xy⎧=⎪⎪⎨⎪=⎪⎩;解②方程组:3414(1) 233(2)-=⎧⎨-=⎩x yx y,(1)×2﹣(2)×3得:-8y+9y=28﹣9,解得y=19,把y=19代入(2)中得:2x﹣57=3,解得x=30,所以方程组的解为:3019 xy=⎧⎨=⎩.故答案为:3019 xy=⎧⎨=⎩.【点睛】本题考查了二次根式的四则运算及二元一次方程组的解法,属于基础题,计算过程中细心即可.25.(1)125;(2)①24t -;②83;(3)t 的值为0.5或4.75或5或5.3. 【分析】(1)直接利用勾股定理即可求得AC 的长,再利用等面积法即可求得斜边AB 上的高; (2)①CP 的长度等于运动的路程减去AC 的长度,②过点P '作P 'D ⊥AB ,证明Rt △AC P '≌Rt △AD P '得出AD=AC=4,分别表示各线段,在Rt △BD P '利用勾股定理即可求得t 的值;(3)由图可知,当△BCP 是等腰三角形时,点P 必在线段AC 或线段AB 上,①当点P 在线段AC 上时,此时△BCP 是等腰直角三角形,②当点P 在线段AB 上时,又分三种情况:BC=BP ;PC=BC ;PC=PB ,分别求得点P 运动的路程,再除以速度即可得出答案.【详解】解:(1)∵90C ∠=︒,5AB =,3BC =,∴在Rt ABC ∆中, 2222534AC AB BC =-=-=.∴AC 的长为4.设斜边AB 上的高为h .∵1122AB h AC BC ⨯⨯=⨯⨯, ∴1153422h ⨯⨯=⨯⨯, ∴125h =. ∴斜边AB 上的高为125. (2)已知点P 从点A 出发,以每秒2个单位长度的速度沿折线A-C-B-A 运动, ①当点P 在CB 上时,点P 运动的长度为:AC+CP=2t ,∵AC=4,∴CP=2t-AC=2t-4.故答案为:2t-4.②当点P '在∠BAC 的角平分线上时,过点P '作P 'D ⊥AB ,如图:∵A P '平分∠BAC ,P 'C ⊥AC ,P 'D ⊥AB ,∴P 'D=P 'C=2t-4,∵BC=3,∴B P '=3-(2t-4)=7-2t ,在Rt △AC P '和Rt △AD P '中,AP AP P D P C ''''=⎧⎨=⎩, ∴Rt △AC P '≌Rt △AD P '(HL ),∴AD=AC=4,又∵AB=5,∴BD=1,在Rt △BD P '中,由勾股定理得:2221(24)(72)t t +-=- 解得:83t =, 故答案为:83; (3)由图可知,当△BCP 是等腰三角形时,点P 必在线段AC 或线段AB 上,①当点P 在线段AC 上时,此时△BCP 是等腰直角三角形,∴此时CP=BC=3,∴AP=AC-CP=4-3=1,∴2t=1,∴t=0.5;②当点P 在线段AB 上时,若BC=BP ,则点P 运动的长度为:AC+BC+BP=4+3+3=10,∴2t=10,∴t=5;若PC=BC ,如图2,过点C 作CH ⊥AB 于点H ,则BP=2BH ,在△ABC 中,∠ACB=90°,AB=5,BC=3,AC=4,∴AB•CH=AC•BC ,∴5CH=4×3,∴125CH =, 在Rt △BCH 中,由勾股定理得:22123() 1.85BH =-=, ∴BP=3.6, ∴点P 运动的长度为:AC+BC+BP=4+3+3.6=10.6,∴2t=10.6,∴t=5.3;若PC=PB ,如图3所示,过点P 作PQ ⊥BC 于点Q ,则30.52BQ CQ BC ==⨯=,∠PQB=90°, ∴∠ACB=∠PQB=90°,∴PQ ∥AC ,∴PQ 为△ABC 的中位线,∴PQ=0.5×AC=0.5×4=2, 在Rt △BPQ 中,由勾股定理得:223()2 2.52BP =+=, 点P 运动的长度为:AC+BC+BP=4+3+2.5=9.5,∴2t=9.5,∴t=4.75.综上,t 的值为0.5或4.75或5或5.3.【点睛】本题考查勾股定理,HL 定理,等腰三角形的性质和判定.掌握等面积法和分类讨论思想是解题关键.26.(1)B (4,0)或B (-2,0);(2)10或2【分析】(1)过点C 作CD ⊥x 轴,垂足为D ,根据勾股定理可求出BD=3,求出B 点坐标; (2)根据三角形面积公式计算即可.【详解】解:(1)如图,过点C 作CD ⊥x 轴,垂足为D ,可知D 点坐标为(1,0),∵BC=5,CD=4,∴22543-=,当B 点在点D 右侧时,B 点坐标是(4,0),当B 点在点D 左侧时,B 点坐标是(-2,0);(2)当B 点在点D 右侧时,S △ABC =12AB CD ⨯⨯, =1542⨯⨯,=10;当B 点在点D 左侧时,S △ABC =112AB CD ⨯⨯, =1142⨯⨯, =2.【点睛】此题主要考查了勾股定理、利用坐标求线段长、根据坐标轴上线段长求坐标以及利用坐标求三角形的面积,正确的掌握坐标与线段长的关系是解题关键.。
湖南省下学期初中八年级期中考试数学试卷(含答案解析)

湖南省下学期初中八年级期中考试数学试卷总分:120分 时量:120分钟一.选择题(本大题共12个小题,每小题3分,共36分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列方程是一元二次方程的是( )A. (1)(2)1x x -+=B .810x -=C .2210x x += D .223250x xy y --=2.小明骑车去学校,骑了一会后车子出了故障,修了一会,然后继续骑车去学校.如果用横坐标表示时间 t ,纵坐标表示路程 s ,下列各图能较好地反映 s 与 t 之间函数关系的是( )3.一次函数(32)1y m x m =++-(m 为常数)的图像经过原点,则m 的值为( ) A .0 B.1 C.23- D.-2 4.一元二次方程2(1)9x -=的解为( )A.4B.-2C.4或-2D.3或-3 5.一元二次方程2810x x --=配方后可变形为( )A. 15)4(2=-x B.17)4(2=-x C.17)4(2=+x D. 15)4(2=+x 6.一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,然后再按演讲内容占50%、演讲能力占40% 、演讲效果占10%的比例计算选手的综合成绩.某选手的演讲内容、演讲能力、演讲效果成绩依次为85,95,95,则该选手的综合成绩为 ( ) A.92 B.88 C.90 D.95 7.数据5,2,3,5,5,1,3的众数和中位数分别是( )A.5,4B.3,5C.5,5D.5,38.为了比较甲、乙两种水稻秧苗是否出苗整齐,每种秧苗各取10株分别量出每株长度,发现两组秧苗的平均长度一样,甲、乙方差分别是3.9和15.8,则下列说法正确的是( )A .甲秧苗出苗更整齐B .乙秧苗出苗更整齐C .甲、乙出苗一样整齐D .无法确定9.已知一次函数2y mx n =+-的图像如图所示,则m 、n 的取值范围是( )A.m >0,n <2B. m >0,n >2C. m <0,n <2D. m <0,n >210.某商品原售价289元,经过连续两次降价后售价为256元,设平均每次降价的百分率为x ,则下面所列方程中正确的是( )A. ()22891256x -= B. ()22561289x -= C. 289(1-2x )=256 D. 256(1-2x )=28911.如图,一次函数y kx b =+的图象与坐标轴的交点坐标分别为A (0,2),B (-3,0),下列说法:(1)y 随x 的增大而减小;(2)2b =;(3)关于x 的方程0kx b +=的解为2x =;(4)关于x 的不等式<0kx b +的解集<-3x .其中说法正确的有( )个A. 1B.2C. 3D.0 12.如图所示,函数x y =1和34312+=x y 的图象相交于(-1,1),(2,2)两点.当21y y >时,x 的取值范围是( )A.2x >B.12x -<<C.1x <-D.12x x <->或二.填空题(本大题共6个小题,每小题3分,把答案填在答卷的横线上) 13.一元二次方程22x x =的解是 .14.在函数3y x =-中,自变量x 的取值范围是 .15.一次函数26y x =-的图像与两坐标轴围成的三角形的面积是 .16.若关于x 的一元二次方程22(1)10kx k x k +++-=有实数根,则k 的取值范围是 .17. 已知一元二次方程2430x x --=的两根为,m n ,则22m mn n -+= . 18.已知一次函数y kx b =+的自变量x 满足13x -≤≤时,函数值y 满足71y -≤≤,则该一次函数解析式为 .三.解答题:(本大题共8小题,共66分,解答应写出文字说明、证明过程或演算步骤) 19.(共8分)解方程:(1)2120x x +-= (2)241)2)(12(x x x -=+- 20.(共6分)已知关于x 的一元二次方程222100x x a ++-=一个根为2,求a 的值及方程的另一根.21. (共6分)如图,已知直线l 经过点A (-1,0)与点B (2,3)求直线l 对应函数的解析式.22.(共9分)我国是世界上严重缺水的国家之一,某校为了组织“节约用水从我做起”活动,随机调查了本校120名同学家庭月人均用水量和节水措施情况,如图1、图2是根据调查结果做出的统计图的一部分.请根据信息解答下列问题:(1)图1中淘米水浇花所在的扇形的圆心角度数为;(2)补全图2;(3)求120名同学家庭月人均用水量的中位数和众数;(4)如果全校学生家庭总人数为3000人,根据这120名同学家庭月人均用水量,估计全校学生家庭月用水总量是多少吨?图1图223.(共8分)如图,某中学准备在校园里利用围墙的一段,其余三面用围栏,围成一个矩形花园ABCD(围墙MN最长可利用25m).现计划用50m长的围栏,请你设计一种围法,使矩形花园的面积为300m2.24.(共9分)长沙市某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元,相关资料表明:甲、乙两种树苗的成活率分别为85%和90%, (1)若购买这两种树苗共用去21000元,求甲、乙两种树苗各购买多少株? (2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?(3)在(2)的条件下,应如何选购树苗,使购买的树苗的总费用最低?并求出最低总费用. 25.(共10分)使得函数值为零的自变量的值称为函数的零点。
湖南初二初中数学期中考试带答案解析

湖南初二初中数学期中考试班级:___________ 姓名:___________ 分数:___________一、选择题1.下列各有理式中,分式有(),,,,A.1个B.2个C.3个D.4个2.如图,在△中,点是延长线上一点=40°,=120°,则等于()A.60°B.70°C.80°D.90°3.下面四个图形中,线段BE是△ABC的高的图是()4.下列计算正确的是( )A.2-2= -4B.2-2= 4C.2-2=D.2-2=5.在下列长度的各组线段中,能组成三角形的是()A.1,2,4B.1,4,9C.3,4,5D.4,5,9 6.如图,在△中,=36°是边上的高,则的度数是()A.18°B.24°C.30°D.36°7.下列命题不是真命题的是()A.两直线平行同位角相等B.对顶角相等C.若,则D.若,则8.已知在△ABC中有两个角的大小分别为40°和70°,则这个三角形是A.直角三角形B.等边三角形C.钝角三角形D.等腰三角形9.解分式方程,去分母后所得的方程是()A.B.C.D.10.校运动会上,初二(3)班啦啦队买了两种价格的雪糕,其中甲种雪糕共花费40元,乙种雪糕共花费30元,甲种雪糕比乙种雪糕多20根.乙种雪糕价格是甲种雪糕价格的1.5倍,若设甲种雪糕的价格为元,根据题意可列方程为()A.B.C.D.二、填空题1.写出“两直线平行,内错角相等.”的逆命题2.当x=时,分式无意义。
3.分式,,的最简公分母为。
4.某红外线遥控器发出的红外线波长为0.000 000 94 m,用科学记数法表示这个数是。
5.计算:=。
6.等边三角形是轴对称图形,它有___ ___条对称轴。
7.分式方程的根为8.在△ABC中,,则9.如图,△ABC中边AB的垂直平分线分别交BC、AB于点D、E, AE=3cm,△ADC•的周长为9cm,则△ABC的周长是____ ___10.若解分式方程产生增根,则____ ___三、计算题1.(4分)计算:2.(4分)计算:3.(4分)先约分,再求值其中四、解答题1.(4分)解方程:2.(5分)等腰三角形的两边长分别为7和3,求这个等腰三角形的周长3.(5分)已知:如图∠EAC是△ABC的外角,AD平分∠EAC,且AD∥BC,求证:AB=AC4.(7分)同一条高速公路沿途有三座城市A、B、C,C市在A市与B市之间,A、C两市的距离为540千米,B、C两市的距离为600千米.现有甲、乙两辆汽车同时分别从A、B两市出发驶向C市,已知甲车比乙车的速度慢10千米/时,结果两辆车同时到达C市.求两车的速度.5.(7分)已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD :∠DAB=1﹕2,求∠B的度数.湖南初二初中数学期中考试答案及解析一、选择题1.下列各有理式中,分式有(),,,,A.1个B.2个C.3个D.4个【答案】B【解析】判断分式的根据是看分母中是否含有字母,如果含有字母则是分式,如果不含字母则不是分式因此是分式。
2013-2014学年八年级(下)期中数学试卷参考答案与试题解析

2013-2014学年八年级(下)期中数学试卷参考答案与试题解析一、精心选一选.(每小题给出的4个选项中只有一个符合题意,请将答案填入答案卡)1.(3分)代数式中,分式有()解:分式有,+b2.(3分)使分式有意义的x的值是()B.;B.(=+,此选项错误;=﹣4.(3分)(2010•桂林)若反比例函数的图象经过点(﹣3,2),则k的值为()5.(3分)(2010•宁德)反比例函数y=(x>0)的图象如图所示,随着x值的增大,y值(),当6.(3分)已知反比例函数,下列结论不正确的是()的图象上,故本选项正确;y=y=BC===.,,2 ))9.(3分)如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为()AB===10AE=BE=×10.(3分)(2005•长沙)已知长方形的面积为10,则它的长y与宽x之间的关系用图象大致可表示为图中B.,y=二、细心填一填(本大题共5个小题,共15分.请将正确答案填写在相应的位置)11.(3分)(2013•吉安模拟)化简的结果是a+b.12.(3分)(2010•温州)当x=5时,分式的值等于2.解:由题意得13.(3分)(2010•长沙)已知反比例函数的图象如图,则m的取值范围是m<1.,当14.(3分)如图所示,以Rt△ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=12,则S3=16.15.(3分)观察给定的分式…猜想并探究规律,那么第7个分式是,第n个分式是(﹣1)n﹣1.•个分式为三、专心解一解.(本大题共10个小题,共55分..请认真读题,冷静思考.解答题应写出文字说明、理由过程或演算步骤.)16.(6分)(2012•湛江模拟)计算:+2﹣1.=3+﹣17.(5分)计算:(3x2yz﹣1)2•(2x﹣1y﹣2)3(结果写成含正整数指数幂的形式).18.(6分)先化简再求值:(﹣)÷+2x,其中x=﹣2.•+2x19.(4分)三角形的三边长分别为3,4,5,求这个三角形的面积.×20.(5分)已知一个反比例函数的图象经过点(2,﹣6).(1)求这个函数的解析式;(2)当y=﹣4时,求自变量x的值.y=,;21.(5分)我国是一个水资源贫乏的国家,节约用水,人人有责.为提高水资源的利用率,某住宅小区安装了循环用水装置,现在每天比原来少用水10吨.经测算,原来400吨水的使用时间现在只需240吨水就可以了,求这个小区现在每天用水多少吨?=,22.(6分)已知:如图,AB=3,AC=4,AB⊥AC,BD=12,CD=13.(1)求BC的长度;(2)线段BC与线段BD的位置关系是什么?说明理由.BC=23.(6分)如图,长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点B与点D重合,折痕为EF,求AE的长.24.(5分)在甲村至乙村的公路有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险而需要暂时封锁?请通过计算进行说明.AB BCAB CD=25.(7分)如图,已知反比例函数的图象经过点C(﹣3,8),一次函数的图象过点C且与x轴、y轴分别交于点A、B,若OA=3,且AB=BC.(1)求反比例函数的解析式;(2)求AC和OB的长.)根据题意,反比例函数的图象经过点(∴反比例函数的解析式(.。
湖南初二初中数学期中考试带答案解析

湖南初二初中数学期中考试班级:___________ 姓名:___________ 分数:___________一、选择题1.在,-0.1010010001……,,,,,中,无理数的个数是()A.1个B.2个C.3个D.4个2.和数轴上的点一一对应的是()A.整数B.有理数C.无理数D.实数3.化简的结果为()A.1B.-1C.-5D.-74.已知点P(3,-2)与点Q关于y轴对称,则点Q的坐标为()A.(-3,2)B.(-3,-2)C.(3,2)D.(3,-2)5.一次函数的图象经过第_____________________象限()A.一、二、三B.一、二、四C.一、三、四D.二、三、四6.已知(2,a)和(1,b)在一次函数的图象上,则()A.a>b B.a<b C.a = b D.无法判断7.已知一次函数的草图如右所示,则下列结论正确的是()A.k>0,b>0B.k>0,b<0C.k<0,b>0D.k<0,b<08.如下图所示,一辆客车从甲站驶往乙站,中途休息了一段时间.如果用横轴表示时间t,纵轴表示客车行驶的路程s,那么下列四个图中较好地反映了s 与 t之间的函数关系的是()9.把直线向下平移5个单位,得到的直线所对应的函数解析式为()A.B.C.D.10.一次函数与,在同一平面直角坐标系的图象是 ( )二、填空题1.0.64的平方根是_____,的立方根是_______________。
2.的相反数是________________,绝对值是_________________。
3.直线中,随的增大而减小,则的取值范围是_____________。
4.比较大小:_____(填“>”、“<”或“=”)。
5.若实数有意义,则=__________________________。
6.某种储蓄的月利率为0.5﹪,现存入1000元,则本息和y (元)与所存月数x 之间的函数关系式是_____________。
湖南初二初中数学期中考试带答案解析

湖南初二初中数学期中考试班级:___________ 姓名:___________ 分数:___________一、选择题1.当时,分式无意义 ( )A.0B.1C.-1D.-22.若某三角形的两边长分别为3和4,则下列长度的线段能作为其第三边的是()A.1B.5C.7D.93.将一副常规的三角尺按如图方式放置,则图中∠AOB的度数为()A.75°B.95°C.105°D.120°4.下列计算正确的是()A.x+x=2x2B.C.D.(2x)2=2x25.在等腰三角形ABC中,它的两边长分别为8cm和3cm,则它的周长为()A.19cm B.19cm或14cm C.11cm D.10c6.2011年3月11日,里氏9.0级的日本大地震导致当天地球的自转时间较少了0.000 001 6秒,将0.000 001 6用科学记数法表示为()A.B.C.D.7.若把分式中的和都扩大倍,那么分式的值()A.扩大倍B.不变C.缩小倍D.缩小倍8.对于下列各组条件,不能判定△≌△的一组是()A.∠A=∠A′,∠B=∠B′,AB=A′B′B.∠A=∠A′,AB=A′B′,AC=A′C′C.∠A=∠A′,AB=A′B′,BC=B′C′D.AB=A′B′,AC=A′C′,BC=B′C′9.如图,BD、CD分别是△ABC的两个外角∠CBE、∠BCF•的平分线,若,则∠D的度数是()A. 40°B. 50°C. 65°D. 55°10.观察下图及图形所对应的算式,根据你发现的规律计算1+8+16+24+……+8n(n是正整数)的结果为 ( ▲ )A.B.C.D.二、填空题1.如果分式的值为0,则x的值应为________。
2.计算:=____________3.如图,在△ABC中,AB=AC,,则∠BCD=_____度.4.把命题“对顶角相等”改写成“如果…那么…”的形式_______________________________.5.化简= .6.如图所示,在△ABC中,AB =" 5,BC" = 7,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为________7.关于x的方程产生增根,则常数m的值等于_____________.8.如图,△ABC中,AB=AC,D为AB上一点,且AD=DC=BC,则∠A为_____度9.如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,已知∠ADE=40°,则∠DBC= °.三、解答题1.计算:2.解分式方程:3.如图,在△ABC和△CDE中,AB//CD,AB=CE,AC=CD.求证:∠B="∠E."4.先化简,再求值:,其中x=3.5.某校学生利用双休时间去距学校10km的炎帝故里参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.6.如图,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC.(1)求证:△ABE≌△ACD;(2)求证:△ADE是等边三角形.7.如图,在等边三角形ABC中,顶点A,C处各有一只蚂蚁,它们同时出发,分别以同样的速度由A向B和由C向A爬行,经过t秒后,它们分别到达D,E处,请问两只蚂蚁在爬行过程中,(1)CD与BE有何数量关系,为什么?(2)DC与BE相交所成的∠BFC的大小是否发生变化?若有变化,请说明理由;若没有变化,求出∠BFC的大小。
长沙名校初二数学期中考试卷(8套)

0.026、0.015、0.032.则射击成绩最稳定的选手是
(填“甲”、“乙”、“丙”中的一个).
15.若一个菱形的两条对角线的长分别为 6 和 8,则这个菱形的面积为
.
16.一根竹子高 10 尺,折断后竹子顶端落在离竹子底端 3 尺处.折断处离地面的高度是
.
17.如图所示,在矩形 ABCD 中,DE⊥AC 于 E,∠ADE:∠EDC=3:2,则∠BDE 的度数是
(2)若
,
为平行四边形; ,
,求
的度数。
24.(8分)如图,四边形
中, // ,
,
中点,射线 交 的延长线于点 ,连接 。
,点 为 的
(1)求证:四边形
Байду номын сангаас
(2)若
,
是菱形。 ,求 BF的长。
4
25.(8分)某电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,已知某户居 民每月应交电费 (元)与用电量 (度)的函数图象是一条折线(如图),根据图象解下列问题:
第 1页(共 6页)
A. 6
32
B.
5
18
C.
5
24
D.
5
9.如图,平行四边形 ABCD 中,AE 平分∠BAD,若 CE=3cm,AB=4cm,则平行四边形 ABCD
的周长是( )
A.23cm
B.22cm
C.21cm
D.20cm
10.已知直线
y
x
3
与
y
2x
2
的交点的坐标为
-
5,- 8 ,则方程组
与 轴相交于点 ,与 轴相交于点 .
(1)求
的面积;
(2)过 点作直线 与 轴相交于点 ,若
湖南师大附中星城实验中学2013—2014学年度第二学期八年级期中考试含答案 (3)

精品1湖南师大附中星城实验中学2013—2014学年度第二学期期中考试八年级数学(闭卷:试题卷和答题卷一体)时量:100分钟 分值:120分命题人: 审题人:一、选择题(3分×10=30分)1.当3a =时,在实数范围内无意义的式子是(C )A aB 1a -C 52a -D 2a 2.分别以下列四组数为一个三角形的边长:(1)3,4,5;(2)5,12,13;(3)8,15,17;(4)4,5,6.其中能构成直角三角形的有(B ) A .4组 B .3组 C .2组 D .1组3.已知平行四边形ABCD 中,200A C ∠+∠=,则B ∠的度数是(C ) A .100 B .160 C .80 D .604.如图,平行四边形ABCD 的对角线AC 、BD 相交于点O ,下列结论不正确的是(D ) A .DC ∥AB B .OA =OC C .AD =BC D .DB 平分∠ADC 5.下列命题中,真命题是(B )A .对角线相等的四边形是矩形B .对角线互相平分的四边形是平行四边形C .对角线互相垂直的四边形是菱形D .对角线互相垂直平分的四边形是正方形 6.矩形两条对角线的夹角为60,一条较短边长为5cm ,则其对角线长为(B ) A .5cm B .10cm C .15cm D .53cm7.小王计划用100元钱买乒乓球,所购买球的个数W (个)与单价n (元)的关系式100W n=中(A ) A .100是常量,W ,n 是变量 B .100,W 是常量,n 是变量 C .100,n 是常量,W 是变量 D .无法确定 8.下列函数:①3y x =-;②3y x =-;③232y x =;④13xy =+.其中是一次函数的是(D )A .①②B .①③C .②③D .①④ 9.已知一次函数23y x =-经过哪几个象限(B )A .一、二、三B .一、三、四C .一、二、四D .二、三、四 10.方程10x +=得解就是函数1y x =+的图像与(A )精品1yx第13题43215432O 1A .x 轴交点的横坐标 B .y 轴交点的横坐标 C .y 轴交点的纵坐标 D .以上都不对 二、填空题(3分×8=24分) 11.计算:182÷= 3 .12.已知250x y -++=,则x y += -3 。
2湖南师大附中 星城实验中学初二下英语期中考试卷

湖南师大附中星城实验学校2018-2019学年度第二学期期中考测试卷时量:100分钟分值:120分命题人:审题人:Ⅱ.知识运用(共两节,满分20分)第一节语法填空(共10小题,满分10分)从A、B、C三个选项中选择最佳答案填空。
21.—What’s ________ matter? —I have ________stomachache.A./; aB. the; aC. the; an22.Don’t put off_________ to see the dentist when you have a toothache.A. goingB. to goC.go23.It's important _________ us _________ English well.A. for; learningB. for; to learnC. of; to learn24.—_______ I have a look at your new watch? —Yes, you can.A. WillB. CouldC. Must25.—What were you doing________ others were reading in the classroom.—I was sweeping the floor.A.whileB. afterC. until26.—I have too much housework to do at home.—_______ you ask your husband for help?A. Why don’tB. Why notC. How about27. There are ______ rules here and there.A. too muchB. much tooC. too many28.The girl _____ with two cats in the yard when the earthquake(地震) happened.A. was playingB. is playingC. were playing29. —Would you like to drink tea or coffee?—_______. I like milk.A.BothB. EitherC. Neither30.—How does Mr Smith usually go to work?—He _____ there to lose weight.A. used to walkB. is used to walkC. is used to walking第二节词语填空(共10小题,每小题1分,满分10分)通读下面的短文,掌握其大意,然后从各题所给的A、B、C三个选项中选出最佳答案。
湖南省长沙市湖南师大附中星城实验中学2023-2024学年八年级下学期第一次月考数学试题(含解析)

湖南师大附中星城实验学校2023-2024学年第二学期八年级第一次作业检测数学试题时量∶120分钟 分值∶120分一. 选择题(每小题3分,共30分)1.使式子有意义的x 的取值范围是( )A .B .C .D .2.下列各组数中以a ,b ,c 为边的三角形不是直角三角形的是( )A .,,B .,,C .,,D .,,3.下列式子中,属于最简二次根式的是( )ABCD4.在平行四边形中,的值可以是( )A .B .C .D .5.如图,A ,B 两点被池塘隔开,在外选一点C ,连接,,并分别找出它们的中点D ,E , 现测得, 则长为( )A .B .C .D .6.菱形在平面直角坐标系中的位置如图所示,点的坐标是,点的纵坐标是,则点的坐标是( )2x >2x ≥2x <2x ≤4a =5b =6c =5a =12b =13c =6a =8b =10c =3a =4b =5c =ABCD :::A B C D ∠∠∠∠1:2:3:41:2:2:11:1:2:22:1:2:1AB AC BC 40m DE =AB 20m 40m 60m 80m OBCA C ()8,0A 2BA .B .C .D .7.如图,矩形的对角线相交于点,,若矩形对角线长为4,则线段的长度为( )A .B .4C .D .38.如图,在平行四边形中,平分,则平行四边形的周长是( )A .14B .16C .18D .209.如图,长方形的顶点A ,B 在数轴上,点A 表示-1,,.若以点A 为圆心,对角线长为半径作弧,交数轴正半轴于点M ,则点M 所表示的数为( )ABCD10.已知得( )A.B .C .D .二. 填空题(每小题3分,共18分)()4,2()4,2-()2,6-()2,6ABCD AC BD 、O 60AOB ∠=︒AD ABCD DE 23ADC BE CE ∠==,,ABCD ABCD 3AB =1AD =AC 11210a -<<2a -2a -2a 2a11=12.若,则.13.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为,则正方形的面积之和为 .14.中,,则 .15.如图,菱形中,对角线、相交于点O ,E 为边中点,菱形的周长为28,则的长等于 .16.如图, 在中,,点为斜边上的一个动点, 过分别作于点, 作于点,连接,则线段的最小值为三. 解答题(共72分)17.计算∶18.19.先化简,再求值∶,其中()230a ++=()2023a b+=16cm A B C D ,,,2cm ABCD Y 240A C ∠+∠=︒B ∠=ABCD AC BD AD ABCD OE Rt ABC △9034BAC AB AC ∠=︒==,,P BC P PE AB ⊥E PF AC ⊥F EF EF ()101152π-⎛⎫-++- ⎪⎝⎭))2111+++-21211x x x x -+⎛⎫-÷ ⎪⎝⎭1x =20.如图,在四边形中,,,,,(1)求的长;(2)求证:.21.如图, 四边形是矩形, 把矩形沿对角线折叠, 点落在点处,与相交于点.(1)求证∶(2)若求的面积.22.为了缓解望城区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图). 从侧面 D 点测得显示牌顶端C 点的仰角,测得显示牌底端B 点的仰角 .(1)已知立杆高度是,求路况显示牌的高度(即求的长度, 结果保留根号).(2)已知路况显示牌最高点C 距离地面9米(即米),求立杆高度(结果保留根号).23.已知:如图,在平行四边形中,M ,N 分别是,的中点,,连接交于点O .ABCD AC BC ⊥4AB =BC =1CD =AD =AC AD CD ⊥ABCD AC B E CE AD O AO CO=30∠= ,OCD AB AOC 60ADC ∠=︒45ADB ∠=︒AB 4m BC 9AC =AB ABCD AD BC 90AND ∠=︒CM DN(1)求证:;(2)若,求的大小;(3)过点C 作 于点E , 交于点P , 若 ,求的长.24.已知:点A 的坐标为,点B 的坐标为,以为斜边做等腰,点C 在第一象限内,(1)如图1, 求的长;(2)如图1,如果点A ,B ,O ,E 恰好是平行四边形的四个顶点, 求点 E 的坐标;(3)如图 2, 求平行四边形 顶点D 的坐标.25.我们不妨约定:对角线互相垂直的凸四边形叫做“理正四边形”.(1)①在“平行四边形,矩形,菱形”中,一定是“理正四边形”的有 ;②在凸四边形中,且则该四边形 “理正四边形”.(填“是”或“不是”或“有可能是”)(2)如图1,四边形是面积为1的“理正四边形”,且求的值;(3)如图2,在平面直角坐标系中第一象限内有动点E ,且四边形是“理正四边形”(点A 在x 轴负半轴上,点B 在y 轴负半轴上,点C 在x 轴正半轴上,点D 在 y 轴正半轴上),在并且, 求的取值范围.ABN AMN ≌40CNM ∠=︒MND ∠CE MN ⊥DN 2,12PE =∠=∠CE ()0,8()6,0-AB Rt ABC △AB ABCD ABCD AB AD =,CB CD ≠ABCD 3-=AC BD :AC BD 12,OE ≤≤ABCD 3EA EB EC ED ====:AC BD参考答案与解析1.B【分析】本题考查了二次根式有意义的条件;根据二次根式有意义,被开方数非负列式求解即可.有意义可得,解得:,故选:B .2.A【分析】本题考查了勾股定理的逆定理;根据勾股定理的逆定理,验证两条较小边的平方和是否等于最大边的平方,如果有这种关系,这个三角形就是直角三角形.【详解】解:A.∵,∴以a ,b ,c 为边的三角形不是直角三角形,符合题意;B.∵,∴以a ,b ,c 为边的三角形是直角三角形,符合题意;C.∵,∴以a ,b ,c 为边的三角形是直角三角形,符合题意;D.∵,∴以a ,b ,c 为边的三角形是直角三角形,符合题意;故选:A .3.C【分析】20x -≥2x ≥222456+≠22251213+=2226810+=222345+=本题考查最简二次根式,涉及二次根式性质等知识,根据二次根式性质将选项中的二次根式化简,再利用最简二次根式定义逐项判断即可得到答案,熟练掌握最简二次根式定义是解决问题的关键.为最简二次根式,故选:C.4.D【分析】本题考查了平行四边形的性质;根据平行四边形对角相等的性质可知满足即可.【详解】解:∵四边形是平行四边形,∴,∴的值可以是,故选:D.5.D【分析】本题考查了三角形中位线定理;根据题意可知是的中位线,然后由三角形的中位线平行于第三边且等于第三边的一半计算即可.【详解】解:∵点D,E分别是,的中点,∴是的中位线,∴,故选:D.6.B【分析】连接AB交OC于点D,由菱形OACB中,根据菱形的性质可得OD=CD=4,BD=AD=2,由此即可求得点B的坐标.【详解】∵连接AB交OC于点D,===,A CB D∠=∠∠=∠ABCD,A CB D∠=∠∠=∠:::A B C D∠∠∠∠2:1:2:1DE ABCAC BCDE ABC280mAB DE==∵四边形ABCD 是菱形,∴AB ⊥OC ,OD =CD ,AD =BD ,∵点C 的坐标是(8,0),点A 的纵坐标是2,∴OC =8,BD =AD =2,∴OD =4,∴点B 的坐标为:(4,-2).故选B .【点睛】本题考查了菱形的性质与点与坐标的关系.熟练运用菱形的性质是解决问题的关键,解题时注意数形结合思想的应用.7.C【分析】本题考查矩形中求线段长,涉及矩形性质、等边三角形的判定与性质、含的直角三角形性质及勾股定理等知识,由矩形性质得到,,结合等边三角形的判定与性质确定,从而利用含的直角三角形性质求出相应边长,再由勾股定理求解即可得到答案,熟练掌握矩形性质、等边三角形的判定与性质、含的直角三角形性质及勾股定理是解决问题的关键.【详解】解:在矩形中,,,矩形的对角线相交于点,,,是等边三角形,则,在中,,则,矩形对角线长为4,,30︒AC BD =90BAD ∠=︒60ABO ∠=︒30︒30︒ABCD AC BD =90BAD ∠=︒ ABCD AC BD 、O OA OD ∴=60AOB ∠=︒ AOB ∴ 60ABO ∠=︒Rt △ABD 60ABO ∠=︒30ADB ∠=︒ 122AB BD ∴==在中,由勾股定理可得,故选:C .8.B【分析】本题主要考查了平行四边形的性质,等角对等边,角平分线的定义,先由平行四边形的性质和角平分线的定义证明,得到,再求出,即可根据平行四边形周长公式求出答案.【详解】解:∵四边形是平行四边形,∴,∴,∵平分,∴,∴,∴,又∵,∴平行四边形的周长,故选:B .9.A【分析】先利用勾股定理求出,根据,求出,由此即可解决问题.【详解】解:∵四边形是矩形,∴,∵,∴∵,∴,∴点M.故选A .【点睛】本题考查实数与数轴、勾股定理等知识,解题的关键是灵活应用勾股定理求出的长.Rt △ABD AD ===CED CED ∠=∠3CE CD ==5CB CE BE =+=ABCD AD BC BC AD AB CD ==∥,,ADE CED ∠=∠DE ADC ∠ADE CDE ∠=∠CED CED ∠=∠3CE CD ==5CB CE BE =+=ABCD 535316AB BC CD AD =+++=+++=AC AC AM =OM ABCD 90ABC ∠=︒3,1AB AD BC ===AC ==1AM AC OA ===1OM AM OA =-=-1,AC AM10.B【分析】首先将两个根式的被开方数化为完全平方式,再根据a 的取值范围,判断出底数的符号,然后根据二次根式的意义化简.【详解】解∵,;∵,∴,,.故选:B .【点睛】本题主要考查了二次根式的化简,能够熟练运用完全平方公式对被开方数进行变形是解答本题的关键.11.【分析】根据二次根式的性质计算.【详解】解:原式故答案为:【点睛】本题主要考查了二次根式的化简.注意最简二次根式的条件是:①被开方数的因数是整数,因式是整式;②被开方数中不含能开得尽方的因数因式.上述两个条件同时具备(缺一不可)的二次根式叫最简二次根式.12.2222222211111142,42a a a a a a a a a a a a ⎛⎫⎛⎫⎛⎫⎛⎫-+=++=++-=-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭10a -<<10a a +<2110a a a a--=>=11a a a a =--+-2a=-=1-【分析】根据得到,,求得,代入计算即可.【详解】∵,∴,,∴,,∴,∴,故答案为:.【点睛】本题考查了算术平方根的非负性,绝对值的非负性,有理数的乘方,熟练掌握运算法则,灵活运用整体思想是解题的关键.13.256【分析】根据勾股定理知,以两条直角边为边作出的两个正方形面积和等于以斜边为边的正方形面积.【详解】解:如图,由勾股定理可知,正方形A 与B 的面积和等于正方形M 的面积.正方形C 与D 的面积和等于正方形N 的面积.并且正方形M 与N 的面积和等于最大的正方形的面积.因此的面积之和是为最大正方形的面积 ,故答案为:256.【点睛】本题考查了勾股定理的意义及应用,熟练掌握勾股定理是解题的关键.14.##60度【分析】由平行四边形的性质得出,.再结合即可求解.【详解】解:∵四边形为平行四边形,∴,.()230a +30a +=20b -=1a b +=-()230a +=30a +=20b -=3a =-2b =1a b +=-()()2023202311a b =+=--1-A B C D 、、、216256==2cm 60︒A C ∠=∠180A B ∠+∠=︒240A C ∠+∠=︒ABCD A C ∠=∠180A B ∠+∠=︒∵,∴,∴.故答案为:.【点睛】本题考查平行四边形的性质.掌握平行四边形的对角相等,邻角互补是解题关键.15.3.5【分析】根据菱形性质得出,,根据直角三角形斜边中线等于斜边一半得出.【详解】解:∵四边形为菱形,∴,,∴,∵E 为边中点,∴.故答案为:3.5【点睛】本题主要考查了菱形的性质,直角三角形斜边中线等于斜边一半,解题关键是熟练掌握菱形的性质和直角三角形的性质.16.【分析】本题考查动点最值问题—点线模型,涉及矩形的判定与性质、点到直线距离的最小值、勾股定理及等面积法求线段长等知识,先由矩形的判定与性质,将线段的最小值转化为线段的最小值,再由点到直线距离中垂线段最短,过作,如图所示,再利用勾股定理求出长,最后利用等面积法求解即可得到答案,熟练掌握矩形判定与性质、点到直线距离最值是解决问题的关键.【详解】解:连接,如图所示:240A C ∠+∠=︒120A ∠=︒18012060B ∠=︒-︒=︒60︒AC BD ⊥12874AB BC CD AD ====⨯=1 3.52OE AD ==ABCD AC BD ⊥12874AB BC CD AD ====⨯=90AOD ∠=︒AD 1 3.52OE AD ==125EF AP A ⊥AP BC BC AP在中,,,,四边形是矩形,,点为斜边上的一个动点,线段的最小值为线段的最小值,由点到直线的距离中垂线段最短,过作,如图所示:在中,,则由勾股定理可得,由等面积法可得,即,解得,故答案为:.17.【分析】本题考查了零次幂,负整数指数幂,绝对值,二次根式的性质;先根据零次幂,负整数指数幂,绝对值,二次根式的性质化简,再计算即可.【详解】解:原式.18.【分析】此题考查了二次根式的混合运算,根据二次根式的性质化简,完全平方公式和平方差公式计算即可,熟练掌握运算法则是解题的关键.【详解】解:原式,RtABC △90BAC ∠=︒PE AB ⊥PF AC ⊥∴AEPF EF AP ∴= P BC ∴EF AP P BC A ⊥AP BC Rt ABC △9034BAC AB AC ∠=︒==,,5BC ===∴1122ABC S AB AC BC AP =⋅=⋅△345AP ⨯=125AP =125101258=+--10=-1-(21)31=-+++-,.19.【分析】本题考查分式的化简求值,涉及因式分解、分式混合运算、代数式求值及二次根式混合运算等知识,先利用分式化简求值,再将代入运用二次根式混合运算求值即可得到答案,熟练掌握分式化简求值是解决问题的关键.【详解】解:,当时,原式.20.(1)2;(2)见解析.【分析】(1)在中运用勾股定理计算即可;(2)在中,运用勾股定理逆定理证明即可.【详解】(1)解:在中,,(2)在中,,,,331=---1=11x -1x =21211x x x x -+⎛⎫-÷ ⎪⎝⎭()211x x x x x -⎛⎫=-÷ ⎪⎝⎭()211x x x x -=⨯-11x =-1x ====Rt ACB ADC △AC BC⊥Q 90ACB ∴∠=︒Rt ACB 4AB =BC =2AC ∴==ADC △1CD = AD =2AC =【点睛】本题考查了勾股定理和勾股定理的逆定理;熟练掌握用勾股定理求直角三角形边长,用勾股定理逆定理证明直角三角形或垂直是解题的关键.21.(1)证明见解析【分析】本题考查了矩形的性质以及翻折变换的性质、等腰三角形的判定与性质、含的直角三角形性质、勾股定理等知识, 熟记矩形的各种性质以及三角形的面积公式是解题的关键.(1) 由矩形的性质和折叠的性质证明,再由等腰三角形的判定与性质即可得到;(2)由含的直角三角形性质及勾股定理得到,的长, 再由三角形面积公式计算即可得到答案.【详解】(1)证明:四边形是矩形,,,又由折叠可知,,;(2)解:在中,,,又22214AD CD ∴+=+=2224AC ==222AD CD AC ∴+=90ADC ∴∠=︒AD CD∴⊥30︒DAC ECA ∠=∠AO CO =30︒AO CO ABCD AD BC ∴∥DAC BCA ∴∠=∠BCA ECA ∠=∠DAC ECA ∴∠=∠AO CO ∴=Rt COD 90,30D OCD ∠=︒∠=︒12OD OC ∴=AB CD ==在中,由勾股定理可得,解得,,22.(1)路况显示牌的高度为(2)立杆高度为【分析】本题主要考查了含直角三角形的性质,勾股定理,二次根式的化简;(1)先根据等腰直角三角形的判定和性质求出,然后根据含直角三角形的性质求出,再利用勾股定理求出,进而可得答案;(2)利用勾股定理构建方程求出,再根据等腰直角三角形的判定和性质可得的高度.【详解】(1)解:∵,,∴,∵,∴,∴,∴,∴,答:路况显示牌的高度为;(2)解:由(1)知,∵,∴,∴,∵,,∴,Rt COD 22212OC OC ⎛⎫=-⎪⎝⎭2OC=2AO OC ∴==11·222AOC S AO CD ∴==⨯=△()m4AB 30︒AD 30︒CD AC AD AB 90BAD ∠=︒45ADB ∠=︒4m AD AB ==60ADC ∠=︒30ACD ∠=︒28m CD AD ==AC ===()4m BC AC AB =-=-()m 4-2CD AD =222CD AD AC =+22249AD AD =+AD =90BAD ∠=︒45ADB ∠=︒AB AD ==答:立杆高度为.23.(1)见解析(2)(3)【分析】(1)由四边形是平行四边形,可得,,求出,,利用证得;(2)首先证明四边形是平行四边形,再利用直角三角形的性质求出,可得平行四边形是菱形,然后根据菱形的性质可得答案;(3)证明,可求出,然后由含角的直角三角形的性质求出,再证明,进而可求得的长.【详解】(1)证明:∵四边形是平行四边形,∴,,∴,∵M 、N 分别是的中点,∴,又∵,∴;(2)证明:∵四边形是平行四边形,∴,,∵M 、N 分别是的中点,∴,∴四边形是平行四边形,∵M 是的中点,,∴,∵平行四边形是菱形,∴;(3)解:由(2)得,∴,,AB 20MND ∠=︒3CE =ABCD AD BC =AD BC ∥MAN BNA ∠=∠AM BN =SAS ABN AMN ≌CDMN NM MD =CDMN 12MND DNC ∠=∠=∠=∠230MND DNC ∠=∠=∠=︒30︒PN PC PN =CE ABCD AD BC =AD BC ∥MAN BNA ∠=∠AD BC 、AM BN =AN AN =()SAS ABN AMN ≌ABCD AD BC ∥AD BC =AD BC 、=MD NC CDMN AD 90AND ∠=︒NM AM MD ==CDMN 1202MND CNM ∠=∠=︒NM MD =AD BC∥1MND ∠=∠1DNC ∠=∠∵,∴,∵,即,∴,∴,∴,∵,∴,∴.【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定、菱形的判定与性质、等腰三角形的判定与性质、含角的直角三角形的性质,熟练掌握相关判定定理和性质定理是解题的关键.24.(1)(2)点 E 的坐标为或或(3)点D 的坐标为或或【分析】(1)根据点A 、B 的坐标可得,,然后利用勾股定理计算的长即可;(2)设,分情况讨论:①当为对角线时,②当为对角线时,③当为对角线时,分别根据对角线交点的坐标列方程求解即可;(3)作轴于M ,轴于N ,交y 轴于F ,证明,四边形是正方形,求出,然后分情况讨论:①当为对角线时,②当为对角线时,③当为对角线时,分别根据对角线交点的坐标列方程求解即可.【详解】(1)解:∵,,∴,,∴在中,;(2)解:由题意得,,12∠=∠12MND DNC ∠=∠=∠=∠CE MN ⊥90CEN ∠=︒290MND DNC ∠+∠+∠=︒230MND DNC ∠=∠=∠=︒22PN PE ==2DNC ∠=∠2PC PN ==3CE PE PC =+=30︒10AB =()6,8()6,8--()6,8-()7,7-()7,9()5,7--8OA =6OB =AB (),E a b OA OB AB CM x ⊥CN y ⊥BC ()AAS ACN BCM ≌NOMC ()1,1C AB AC BC ()0,8A ()6,0B -8OA =6OB =Rt OAB10AB ==()0,8A ()6,0B -设,分情况讨论:①当为对角线时,则:,,解得:,,∴;②当为对角线时,则:,,解得:,,∴;③当为对角线时,则:,,解得:,,∴;综上,点 E 的坐标为或或;(3)解:如图,作轴于M ,轴于N ,交y 轴于F ,则,∵,∴,四边形是矩形,∵,∴,又∵,(),E a b OA 602a -=822b =6a =8b =()6,8E OB 622a -=802b +=6a =-8b =-()6,8E --AB 622a -=822b =6a =-8b =()6,8E -()6,8()6,8--()6,8-CM x ⊥CN y ⊥BC 90CNA CMB ∠=∠=︒90NOM ∠=︒90NCM NCB BCM ∠=∠+∠=︒NOMC 90ACB ACN NCB ∠=∠+∠=︒ACN BCM ∠=∠AC BC =∴,∴,,∴矩形是正方形,∴,∵,,∴,∴,∴,∴,设,①当为对角线时,则:,,解得:,,∴;②当为对角线时,则:,,解得:,,∴;③当为对角线时,则:,,解得:,,∴;综上,点D 的坐标为或或.【点睛】本题考查了坐标与图形性质,勾股定理,平行四边形的性质,矩形的判定和性质,正方形的判定和性质,全等三角形的判定和性质,正确分类讨论是解题的关键.25.(1)菱形;不是()AAS ACN BCM ≌CN CM =AN BM =NOMC NO OM =8AO AN NO =+=6BM BO OM OM =-=+68OM OM ++=1OM =1OM NO ==()1,1C (),D m n AB 6122m -+=8122n +=7m =-7n =()7,7D -AC 1622m -=8122n +=7m =9n =()7,9D BC 6122m -+=1822n +=5m =-7n =-()5,7D --()7,7-()7,9()5,7--【分析】本题考查了平行四边形的新定义问题,涉及到垂直平分线的性质和判定,矩形的性质和判定,勾股定理,不等式的性质等知识点,灵活掌握不等式的性质,合理的进行变形是解题的关键.(1)①根据平行四边形,矩形,菱形的性质判断即可;②四边形是“理正四边形”,利用垂直平分线的性质和判定可得,与题目条件矛盾,即可得出结论.(2)利用分割法求四边形的面积,得,又,利用完全平方的变形,可求出,联立为关于,的二元一次方程组,进而可求出,的值,再求比值即可.(3)过E 作于M ,于N ,设,由勾股定理可求出,进而可得,求出,的表达式,再求出,再由,可得,则,运用不等式的性质先求出,再求出,变形可得,再分别求出当和时的范围,运用不等式组的知识,可求得.【详解】(1)解:因为菱形的对角线互相垂直,所以菱形是“理正四边形”,而平行四边形、矩形的对角线不一定垂直,所以不一定是“理正四边形”;若四边形是“理正四边形”,则,,,是的垂直平分线,,AC BD <ABCD CB CD =CB CD ≠ABCD 2BD AC ⋅=3-=AC BD AC BD +AC BD AC BD EM BD ⊥EN AC ⊥,ME ON m OM NE n ====22194m BD +=22194n AC +=222222221118441144m BD n AC m BD n AC ⎧+++=⎪⎪⎨⎪+=+⎪⎩2BD 2AC 222299AC n BD m-=-222m n OE +=2214m n ≤+≤204m <<222598m n m +≤-≤+2222225899m AC m m BD m ++≤≤--222214171199AC m BD m -+≤≤-+--24=m 2=0m 22AC BD 2251295AC BD <<AC BD ①②ABCD AC BD ⊥AB AD = OB OD ∴=∴AC BD CB CD ∴=又四边形不是“理正四边形”.故答案为:菱形,不是.(2)四边形是面积为1的“理正四边形”,,,,,,联立解得(3)如图,过E 作于M ,于N ,,,,四边形是矩形,,CB CD ≠ ∴ABCD ABCD ()111112222ABD BCD ABCD S S S BD AO BD OC BD AO OC BD AC ∴=+=⋅+⋅=⋅+=⋅= 四边形2BD AC ∴⋅=3AC BD -= ()()222434217AC BD AC BD AC BD ∴+=-+⋅=+⨯=AC BD ∴+=3AC BD AC BD ⎧+=⎪⎨-=⎪⎩AC BD ⎧=⎪⎪⎨⎪=⎪⎩:AC BD =∴EM BD ⊥EN AC ⊥ EM BD ⊥EN AC ⊥90MON OME ONE ∴∠=∠=∠=︒∴OMEN,设,,在中,,,在中,,,,整理得,解得:,,在中,,,,,E 是第一象限内的动点,,,,,,,,,OM NE ME ON ∴==,ME ON m OM NE n ====3EA EB EC ED ==== ∴Rt DME △222ME MD DE +=22194m BD ∴+=Rt NEC 222NE NC CE +=22194n AC ∴+=222222221118441144m BD n AC m BD n AC ⎧+++=⎪⎪∴⎨⎪+=+⎪⎩22222222+=7244=44BD AC m n BD AC n m ⎧--⎨--⎩2222364364AC n BD m ⎧=-⎨=-⎩22222236493649AC n n BD m m --∴==--Rt MEO 222ME MO OE +=222m n OE ∴+=12,OE ≤≤ 214OE ∴≤≤2214m n ∴≤+≤ 0,0m n ∴>>204m ∴<<290m ∴->2214m n ≤+≤ 2221n 4m m -≤≤-22241m n m ∴-≤-≤-222598m n m ∴+≤-≤+, ,,,,当时,,当时,,,【点睛】本题考查了平行四边形的新定义问题,涉及到等腰三角形的性质和判定,垂直平分线的性质和判定,矩形的性质和判定,勾股定理,不等式的性质等知识点,灵活掌握不等式的性质,合理的进行变形是解题的关键.222222598999m n m m m m +-+∴≤≤---2222225899m AC m m BD m ++∴≤≤--()()22222291491799m m AC m BD m --+--+∴≤≤--222214171199AC m BD m ∴-+≤≤-+--204m <<∴24=m 2291255AC BD <2=0m 225899AC BD <<2251295AC BD ∴<<AC BD <。
湖南师大附中2013-2014学年上学期化学期中考试(含答案)

湖南师大附中2013-2014学年上学期期中考试高二化学试卷一、选择题:(本大题含16个小题,每小题3分,共48分.每小题只有一个选项符合题意)1.(3分)某化学反应在较低温度下自发,较高温度下非自发.有关该反应的下列说法正确的是()A.△H>0,△S>0 B.△H>0,△S<0 C.△H<0,△S>0 D.△H<0,△S<0A.υ(A)=2 mol/(L•min)B.υ(B)=0.3 mol/(L•s)C.υ(C)=0.8 mol/(L•s)D.υ(D)=1 mol/(L•s)A.水的离子积变大、pH变小、呈酸性B.水的离子积变大、pH变小、呈中性C.水的离子积变小、pH变大、呈碱性D.水的离子积不变、pH不变、呈中性A.A l2(SO4)3B.N a3PO4C.C H3COOH D.N aHSO45.(3分)下列有关滴定操作的顺序正确的是()①检查滴定管是否漏水②用蒸馏水洗涤玻璃仪器③用标准溶液润洗盛标准溶液的滴定管,用待测液润洗盛待测液的滴定管④装标准溶液和待测液并调整液面(记录初读数)⑤取一定体积的待测液于锥形瓶中A.①③②④⑤⑥B.①②③④⑤⑥C.②③①④⑤⑥D.④⑤①②③⑥6.(3分)(2014•海珠区模拟)已知在298K时下述反应的有关数据:C(s)+O2(g)═CO(g)△H1=﹣110.5kJ•mol﹣1C(s)+O2(g)═CO2(g)△H2=﹣393.5kJ•mol﹣1A.+283.5kJ•mol﹣1B.+172.5kJ•mol﹣1C.﹣172.5kJ•mol﹣1D.﹣504kJ•mol﹣1 7.(3分)已知某可逆反应m A(g)+n B(g)⇌p C(g)△H,在密闭容器中进行,如图表示在不同反应时间t 时温度T和压强P与反应物B在混合气体中的百分含量B%的关系曲线.由曲线分析,下列判断正确的是()A .T1<T2,P1>P2,m+n >p,△H<0 B.T1>T2,P1<P2,m+n>p,△H>0 C.T1<T2,P1>P2,m+n<p,△H<0 D.T1>T2,P1<P2,m+n<p,△H>0A.化学反应速率v B.水的离子积常数K wC.化学平衡常数K D.醋酸的电离平衡常数K a9.(3分)一定量的盐酸跟过量的镁粉反应时,为了适当减缓反应速度,但不影响生成氢气的总量,可向盐酸中加入适量的()①NaOH固体②H2O③铜屑④CH3COONa固体A.①②B.②③④C.②③⑤D.②④10.(3分)在已经处于化学平衡状态的体系中,如果下列量发生变化,其中一定能表明化学平衡移动的是()A.反应混合物的浓度B.反应体系的压强C.正、逆反应的速率D.反应物的转化率11.(3分)在体积和温度不变的密闭容器中充入a mol X和足量Y,发生反应:2X(g)+Y A.平衡正向移动B.X的转化率不变C.Y的转化率增大D.X的转化率减小12.(3分)相同体积、相同pH的某一元强酸溶液①和某一元弱酸溶液②分别与足量的锌粉A.B.C.D.13.(3分)常温下,一定体积pH=2的二元弱酸H2R溶液与一定体积pH=12的NaOH溶液14.(3分)含等物质的量NaOH的溶液分别用pH为2和3的CH3COOH溶液中和,设消15.(3分)若溶液中由水电离产生的c(OH﹣)=1×10﹣14mol•L﹣1,满足此条件的溶液中一定可以大量共存的离子组是()16.(3分)在一定温度下,在氢氧化钙的悬浊液中,存在氢氧化钙固体与其电离出的离子间溶解结晶平衡:Ca(OH)2(s)⇌Ca2+(aq)+2OHˉ(aq),向此种悬浊液中加入少量的氧化钙粉末,充分反应后恢复到原温度.下列叙述正确的是()二、填空题、(本大题含5个小题,共42分)17.(8分)在体积为1L的容器中,进行如下化学反应:CO2(g)+H2(g)⇌CO(g)+H2O (g),△H=Q kJ•mol﹣1(1)该反应的化学平衡常数表达式为K=(2)该反应为反应(选填吸热、放热).(3)某温度下,若平衡浓度符合c(CO2)•c(H2)=c(CO)•c(H2O),试判断此时的温度为℃,若该温度下以1mol CO2和3mol H2为反应物,达到平衡时的反应热是kJ.18.(8分)由甲、乙两人组成的实验小组,在同样的实验条件下,用同样的实验仪器和方法步骤进行两组中和热测定的实验,实验试剂及其用量如表所示._______、-----.(2)实验测得的温度是①的起始温度13.0℃、终了温度19.8℃;②的起始温度13.0℃、终了温度19.3℃.则△H1和△H2的大小关系是,导致这种差异的主要原因是.19.(8分)现有S2﹣、NH4+、Al3+、Na+、SO42﹣、AlO2﹣、Fe3+、HCO3﹣、Cl﹣等离子,请按要求填空:(1)在水溶液中,该离子水解呈碱性的是﹣.(2)在水溶液中,该离子水解呈酸性的是.(3)既能在酸性较强溶液里、又能在碱性较强的溶液里大量存在的离子有.(4)既不能在酸性较强溶液里、又不能在碱性较强的溶液里大量存在的离子有﹣.20.(10分)(1)25℃时,pH=12的KOH溶液和pH=12的K2CO3溶液中,由水电离出的C (OH﹣)之比是.(2)已知常温下0.1mol•L﹣1 CH3COONa溶液PH约为8①用离子方程式表示CH3COONa溶液PH为8的原因:﹣;②溶液中:C(OH﹣)=;C(Na+)=.(3)实验室在配制FeCl3的溶液时,常将FeCl3固体先溶于中,然后再用蒸馏水稀释到所需的浓度,以抑制其水解,否则得到的是浑浊的溶液.21.(8分)已知Zn2+与碱反应可生成白色沉淀,碱过量,白色沉淀溶解生成Zn(OH)42﹣.如图是向含Zn2+的溶液中逐滴加入氢氧化钠溶液的变化过程示意图,横坐标为溶液的pH,纵坐标为Zn2+离子或Zn(OH)42﹣离子物质的量浓度的对数值.回答下列问题.(1)往ZnCl2溶液中加入足量的氢氧化钠溶液,反应的离子方程式可表示为:.(2)从图中数据计算可得Zn(OH)2的溶度积(K sp)═.(3)某废液中含Zn2+离子,为提取Zn2+离子可以控制溶液中pH值的范围是.(4)已知往ZnCl2溶液中加入硝酸铅或醋酸铅溶液可以制得PbCl2白色晶体,25℃时,PbCl2固体在盐酸中的溶解度如下:根据表数据分析和推测,下列说法中有一项是错误的,这一项是A.随着盐酸浓度的增大,PbCl2固体的溶解度先变小后又变大B.PbCl2固体在0.50mol•L﹣1盐酸中的溶解度小于在纯水中的溶解度C.PbCl2能与浓盐酸发生某种化学反应D.PbCl2固体不可能溶解于饱和食盐水中.三、计算题、(本大题含2个小题,共10分)22.(4分)25℃时,若体积为V a、pH=a的某一元强酸与体积V b、pH=b的某一元强碱混合,恰好中和,且已知V a<V b和a=0.5b,求a的取值范围.23.(6分)在恒温恒容的密闭容器中,x mol A气体和y mol B气体,发生如下反应:2A(g)+3B(g)⇌2C(g)+D(g),平衡时混合气体总的物质的量为4mol,容器内的压强变为原来的0.8倍,A的转化率为50%.求平衡混合气体中C的体积分数.答案1--5:D B B A B 6--10:B B C D D11--16:D C A D B A(1)17、(2)吸热(3)830 3/4Q18、(1)环形玻璃搅拌棒量筒△H1<△H2(2)NH3•H2O是弱电解质,存在电离平衡,电离过程是吸热程19、(1)S2﹣、AlO2﹣、HCO3﹣(2)NH4+、Al3+、Fe3+((3)Na+、SO42﹣、Cl﹣(4)HCO3﹣20、(1)1:1010(2)①CH3COO﹣+H2O⇌CH3COOH+OH﹣②C(H+)+C(CH3COOH)C(CH3COOH)+C(CH3COO ﹣)((3)较浓的盐酸21、(1)Zn++4OH﹣=Zn(OH)42﹣(2) 10﹣17(3) PH为8﹣12之间(4) D解答:解:两溶液混合后溶液恰好为中性,则:V a•c(H+)b=V b•c(OH﹣)a,===10(a+b﹣14)<1,所以(a+b﹣14)<0,而a=0.5b,即3a<14,a<,又pH=b=2a>7,a>,所以<a<,答:a的取值范围为:<a<.解答:解:恒温恒容的密闭容器中,x mol A气体和y mol B气体,2A(g)+3B(g)⇌2C(g)+D(g)起始量(mol)x y 0 0变化量(mol)0.5x 0.75x 0.5x 0.25x平衡量(mol)x﹣0.5x y﹣0.75x 0.5x 0.25x平衡时混合气体总的物质的量为:4=x﹣0.5x+y﹣0.75x+0.5x+0.25x,容器内的压强变为原来的0.8倍,气体物质的量为原来的0.8倍,4=(x+y)×0.8 x=2,y=3;平衡混合气体中C的体积分数=×100%=25%,答:平衡混合气体中C的体积分数25%.。
湖南师大附中星城实验学校2020—2021学年八年级下学期期中考试语文试题

湖南师大附中星城实验学校2020—2021 学年度第二学期八年级下册语文期中测试(闭卷)分值:120分时量:150分钟一、积累与运用(共20 分)1. 选出下列词语字音字形完全正确的一顶是()(2分)A. 犹豫两栖(qī)龟裂(jūn)草长莺飞B. 农谚(yàn)骨骼(gé)粗糙(zāo)消声匿迹C. 海棠翩然山麓海枯石烂D. 沼泽(zhāo)雾霾追朔天衣无缝2.下列句子中加点成语使用有误的一项是()(2分)A.出了三峡,江面宽阔,眼前豁然开朗....。
B.这次的演出,集合杰出的艺人同台亮相,其精彩程度令人叹为观止....。
C.老师的声音戛然而止....,而同学们还沉醉在老师美妙的故事中。
D.小伙伴们在花园里玩提迷藏的游戏,不一会儿,大家都销声匿迹....了。
3.下列句子没有语彩的一句是()(2 分)A. 能否真正保护好著作权,关键在于全面树立公众的著作权保护意识。
B.科技发明和人力资本会推动知识和技术密集型产业以及国家经济的健康。
C.本届金砖国家领导人会晤期间,以“文明相容、民心相通”为主题的金砖国家文化节已经在厦门正式启动。
D. 我们应该刻苦学习,否则不刻苦学习,就跟不上时代的步伐。
4.下列句子语序排列正确的一项是()(2 分)①如果浪费个人时间,蹉跎年华,虚掷生命,是个人的损失。
②而浪费国家和民族的时间,造成历史倒退,则是亿万人民的损失。
③因此赢得时间,接受挑战,为民造福,没有不能创造的奇迹。
④最大的浪费是时间的浪费。
⑤时间孕育机遇,机遇来自时间。
A ⑤②①③④ B.④①②⑤③ C.①②③⑤④ D.④②①⑤③5.下列关于传统文化及文学常识的表述正确的一项是()(2分)A.小林见邻居刘爷爷手提重物,步履蹒跚,忙上前去帮忙,说:“刘爷爷,我来鼎力相助!”B.《诗经》是我国最早的一部诗歌总集,也是我国诗歌浪漫主义传统的源头,共305篇,又称“诗三百”。
C.我国传统二十四节气歌中的"秋处露秋寒霜降"一句,依次对应的节气为:立秋、处暑、寒露、秋分、小寒、霜降。
师大附中八年级下学期期中考试物理考试卷(带答案与解析)解答解析、考点详解.doc

师大附中八年级下学期期中考试物理考试卷(带答案与解析)的正确答案、解答解析、考点详解姓名:_____________ 年级:____________ 学号:______________1.【题文】改革开放30年来,照相机、摄像机已经进入了普通家庭,它们的镜头相当于一个透镜,拍摄时所成的像是倒立、缩小的(选填“虚”、“实”)像. 【答案】凸实【解析】照相机、摄像机已经进入了普通家庭,它们的镜头相当于一个凸透镜,拍摄时所成的像是倒立、缩小的实像.2.【题文】古代入用冰磨制成凸透镜取火,这是利用了凸透镜对光线的_______作用。
【答案】会聚【解析】古代入用冰磨制成凸透镜取火,这是利用了凸透镜对光线的会聚作用。
3.【题文】在探究凸透镜成像规律时,已知凸透镜的焦距是8厘米,那么当蜡烛距凸透镜的距离为18厘米时,可以在光屏上得到一个倒立____的_______像 【答案】缩小实像【解析】凸透镜的焦距是8厘米,当蜡烛距凸透镜的距离为18厘米时,是照相机的成像情况,所以是倒立缩小的实像。
4.【题文】力的三要素是:力的______、和________。
【答案】大小方向作用点【解析】力的三要素是:力的大小、方向和作用点。
5.【题文】重力是由于地球的吸引而使物体受到的力,它的方向总是_______. 【答案】竖直向下【解析】分析:地球上的物体所受重力的方向总是竖直向下.解:由于地球的吸引而使物体受到重力作用,物体所受重力的方向总是竖直向下的. 故答案为:竖直向下.6.【题文】穿旱冰鞋的小孩用手推墙会感到墙也在推他,使他后退。
这表明物体间力的作用_______ 用力弯锯条,锯条变弯了,这说明力可以使物体发生________ 【答案】相互的形变【解析】穿旱冰鞋的小孩用手推墙会感到墙也在推他,使他后退。
这表明物体间力的作用相互的;用力弯锯条,锯条变弯了,这说明力可以使物体发生形变。
7.【题文】把一只盛满水的杯子放在桌面的纸条上,尽快地抽动纸条,这时会看到杯子静止不动,这是由于杯子具有__________ 【答案】惯性【解析】把一只盛满水的杯子放在桌面的纸条上,尽快地抽动纸条,这时会看到杯子静止不动,这是由于杯子具有惯性。
【湘教版】八年级数学下期中第一次模拟试题附答案(2)
一、选择题1.如图,在Rt ABC 中,90,30,6ACB A BC ∠=︒∠=︒=.将ABC 绕点C 按顺时针方向旋转n 度后得到EDC △,此时点D 在AB 边上,斜边DE 交AC 边于点F ,则图中阴影部分的面积为( )A .27B .9C .33D .93 2.下列图形中,既是轴对称图形又是中心对称图形的是( ) A . B . C . D . 3.下列图形中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D . 4.中国的传统建筑许多窗格图案蕴含着对称之美,现从中选取以下四种窗格图案,其中只是中心对称图形但不是轴对称图形的是( )A .B .C .D . 5.如果a >b ,那么下列不等式不成立...的是( ) A .0a b -> B .33a b ->- C .1133a b > D .33a b ->-6.关于x 的方程3a x -=的解是非负数,那么a 满足的条件是( )A .3a >B .3a ≤C .3a <D .3a ≥ 7.若a >b ,则下列式子正确的是( ) A .a +1<b +1 B .a ﹣1<b ﹣1 C .﹣2a >﹣2b D .﹣2a <﹣2b 8.某储运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物运往青岛,这列货车可挂,A B 两种不同规格的货厢50节.已知甲种货物35吨和乙种货物15吨可装满一节A 型货厢,甲种货物25吨和乙种货物35吨可装满一节B 型货厢,按此要求安排,A B 两种货厢的节数,有几种运输方案( )A .1种B .2种C .3种D .4种9.下列说法中,不正确的有( )①不在角的平分线上的点到这个角的两边的距离不相等;②三角形两内角的平分线的交点到各边的距离相等;③到三角形三边距离相等的点有1个④线段中垂线上的点到线段两端点的距离相等,⑤到三角形三个顶点距离相等的点有1个A .0个B .1个C .2个D .3个10.已知等腰三角形的两边长分别为a ,b ,且a ,b 满足3a -+|b ﹣4|=0,则此等腰三角形的周长为( )A .7B .10C .11D .10或11 11.如图,在ABC ∆中,AB AC =,120BAC ∠=︒,AD 是ABC ∆的中线,且6AD =,AE 是BAD ∠的角平分线,//DF AB 交AE 的延长线于点F ,则DF 的长为( )A .3B .4C .5D .612.若以Rt ABC △的一边为边画一个等腰三角形,使它的第三个顶点也在Rt ABC △的其他边上,则这样的等腰三角形最多能画出( )A .3个B .5个C .6个D .7个二、填空题13.已知点P 的坐标为(a ,b )(a >0),点Q 的坐标为(c ,2),且|a ﹣c|+8b -=0,将线段PQ 向右平移a 个单位长度,其扫过的面积为24,那么a+b+c 的值为_____. 14.如图,三角形DEF 是由三角形ABC 通过平移得到,且点B ,E ,C ,F 在同一条直线上,若14BF =,4EC =,则BE 的长度是______.15.一个三角形的三条高的长都是整数,若其中两条高的长分别为4和12,则第三条高的长为_____.16.如图,数轴上所表示关于x 的不等式组的解集是__________.17.如图,直线y kx b =+交坐标轴于,A B 两点,则不等式0kx b +>的解是__________.18.如图,在ABC 与ADE 中,90BAC DAE ∠=∠=︒,AB AC =,AD AE =,点C ,D ,E 在同一条直线上,连接BD ,BE ,则ACE DBC ∠+∠=______.19.如图,在第1个1A BC 中,30B ∠=︒,1A B CB =;在边1A B 上任取一点D ,延长1CA 到2A ,使121A A A D =,得到第2个12A A D ;在边2A D 上任取一点E ,延长12A A 到3A ,使232A A A E =,得到第3个23A A E △,按此做法继续下去,则第n 个三角形中以n A 为顶点的内角度数是________.20.如图,在ABC 中,,45,,AB AC BAC AD BE =∠=︒是ABC 的高,点Р是直线AD 上一动点,当PC PE +最小时,则BPC ∠为______度.三、解答题21.在边长为1的小正方形网格中,AOB 的顶点均在格点上.(1)B 点关于直线1y =对称的点的坐标为___________;(2)将AOB 向左平移3个单位长度,再向上平移2个单位长度得到111AO B ,请画出111AO B ;(3)在(2)的条件下,AOB 边AB 上有一点P 的坐标为(),a b ,则平移后对应点1P 的坐标为___________.22.在平面直角坐标系中,O 为原点,点A (2,0),点B (0,2),把△ABO 绕点B 逆时针旋转,得△A ′BO ′,点A ,O 旋转后的对应点为A ′,O ′.记旋转角为α.(1)如图①,当点O ′落在边AB 上时,求点O ′的坐标;(2)如图②,当α=60°时,求AA ′的长及点A ′的坐标.23.设一次函数()11y m x =-,()21y n x =+(m ,n 是常数,且m≠0,m≠n ,n>0) (1)当m=3,n=2时,①求函数y 1,y 2图象的交点坐标.②若y 1>y 2,求自变量x 的取值范围.(2)在0<x<1的范围内,有且只有部分函数值满足y 1>y 2,求证:m+n<0.24.为发展校园足球运动,某城区四校决定联合购买一批足球运动装备.市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)求每套队服和每个足球的价格是多少元;(2)若城区四校联合购买100套队服和()10a a >个足球,请用含a 的式子分别表示出到甲商场和乙商场购买装备所花费用;(3)在(2)的条件下,计算a 为何值时,两家商场所花费用相同;(4)在(3)的条件下,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?(直接写出方案)25.如图.在△ABC 中,∠C =90 °,∠A =30°.(1)用直尺和圆规作AB 的垂直平分线,分别交AB 、AC 于D 、E ,交BC 的延长线于F ,连接EB .(不写作法,保留作图痕迹)(2)求证:EB 平分∠ABC .(3)求证:AE =EF .26.如图,在ABC 中,D 为BC 上一点,BD CD =,AD AC ⊥于点A ,30BAD ∠=︒.(1)求证:12AC AB =; (2)当4AB =,3AD =时,求ABD S .【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】由旋转的性质,易得BC=DC=6,由在Rt △ABC 中,∠ACB=90°,∠A=30°,即可求得∠B=60°,即可判定△DBC 是等边三角形,易得△DFC 是含30°角的直角三角形,则可求得DF 与FC 的长,继而求得阴影部分的面积.【详解】解:∵将△ABC 绕点C 按顺时针方向旋转n 度后得到△EDC ,∴BC=DC ,∵在Rt △ABC 中,∠ACB=90°,∠A=30°,∴∠B=90°-∠A=60°,∴△DBC 是等边三角形,∴∠DCB=60°,∴∠DCA=90°-∠DCB=90°-60°=30°,∵BC=6,∴DC=6,∵∠FDC=∠B=60°,∴∠DFC=90°, ∴132DF DC ==, ∴FC =∴S阴影=S △DFC =11322DF FC ⋅=⨯⨯=, 故选:D .【点睛】本题考查了旋转的性质、等边三角形的判定与性质、含30°角的直角三角形的性质以及勾股定理,此题综合性较强,难度适中,注意掌握旋转前后图形的对应关系,注意数形结合思想的应用.2.B解析:B【分析】根据轴对称图形与中心对称图形的概念求解.【详解】解:A 、是轴对称图形,不是中心对称图形,故此选项错误;B 、是轴对称图形,也是中心对称图形,故此选项正确;C 、是轴对称图形,不是中心对称图形,故此选项错误;D 、既不是轴对称图形,也不是中心对称图形,故此选项错误;故选:B .【点睛】此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合. 3.D解析:D【分析】根据轴对称图形与中心对称图形的概念求解.【详解】A 、是轴对称图形,不是中心对称图形,故此选项不符合题意;B 、是轴对称图形,不是中心对称图形,故此选项不符合题意;C 、是轴对称图形,不是中心对称图形,故此选项不符合题意;D 、是轴对称图形,是中心对称图形,故此选项符合题意;故选:D .【点睛】此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合. 4.A解析:A【分析】本题根据中心对称图形和轴对称图形的定义可直接得出结果.【详解】A 选项属于中心对称图形但不是轴对称图形,故正确;B 选项既属于中心对称图形也属于轴对称图形,故不正确;C 选项既属于中心对称图形也属于轴对称图形,故不正确;D 选项既属于中心对称图形也属于轴对称图形,故不正确.故选:A .【点睛】本题考查了中心对称图形和轴对称图形的定义,属于基础题,熟练掌握中心对称图形和轴对称图形的定义是解题的关键.5.D解析:D【分析】根据不等式的基本性质逐项判断即可得.【详解】A 、0a b ->,成立;B 、不等式的两边同减去3,不改变不等号的方向,即33a b ->-,成立;C 、不等式的两边同乘以正数13,不改变不等号的方向,即1133a b >,成立;D 、不等式的两边同乘以负数3-,改变不等号的方向,即33a b -<-,不成立; 故选:D .【点睛】本题考查了不等式的基本性质,熟练掌握不等式的基本性质是解题关键.6.D解析:D【分析】求出方程的解,根据已知得出a-3≥0,求出即可.【详解】解:解方程a-x=3得:x=a-3,∵方程的解是非负数,∴a-3≥0,解得:a≥3,故选:D .【点睛】本题考查了一元一次方程的解,解一元一次不等式,解一元一次方程的应用,关键是得出一个关于a 的不等式.7.D解析:D【分析】根据不等式的性质逐一判断,判断出式子正确的是哪个即可.【详解】解:∵a >b ,∴a +1>b +1,∴选项A 不符合题意;∵a >b ,∴a ﹣1>b ﹣1,∴选项B 不符合题意;∵a >b ,∴﹣2a <﹣2b ,∴选项C 不符合题意;∵a >b ,∴﹣2a <﹣2b ,∴选项D 符合题意.故选:D .【点睛】本题考查了不等式的性质,要熟练掌握,特别要注意在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于0,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.8.C解析:C【分析】设用A 型货厢x 节,B 型货厢()50x -节,根据题意列不等式组求解,求出x 的范围,看有几种方案.【详解】解:设用A 型货厢x 节,B 型货厢()50x -节,根据题意列式:()()35255015301535501150x x x x ⎧+-≥⎪⎨+-≥⎪⎩,解得2830x ≤≤, 因为x 只能取整数,所以x 可以取28,29,30,对应的()50x -是22,21,20,有三种方案.故选:C .【点睛】本题考查一元一次不等式组的应用,解题的关键是根据题意列出不等式组求解,需要注意结果要符合实际情况.9.C解析:C【分析】根据角平分线的性质和线段垂直平分线的性质逐一进行判断即可.【详解】①根据角平分线的判定可知①正确;②根据角平分线的性质可知②正确;③缺乏前提条件:在三角形内部,若不限制条件,到三角形三边距离相等的点有4个,故③错误;④根据垂直平分线的性质可知④正确;⑤缺乏前提条件:在平面内,若不在平面内到三角形三个顶点距离相等的点有无数个,故⑤错误,∴错误的有2个,故选:C .【点睛】本题主要考查角平分线的性质和判定及垂直平分线的性质,掌握角平分线的性质和垂直平分线的性质是解题的关键.10.D解析:D【分析】先根据非负数的性质列式求出a 、b 的值,再分4是腰长与底边两种情况讨论求解.【详解】解:根据题意得,a-3=0,b-4=0,解得a=3,b=4,①4是腰长时,三角形的三边分别为4、4、3,∵4+4>3,∴能组成三角形,4+4+3=11,②4是底边时,三角形的三边分别为3、3、4,能组成三角形,周长=3+3+4=10,所以,三角形的周长为11或10.故选:D.【点睛】本题考查了等腰三角形的性质,绝对值非负数,偶次方非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0求出a、b的值是解题的关键,难点在于要分情况讨论并且利用三角形的三边关系进行判断.11.D解析:D【分析】根据等腰三角形三线合一的性质可得AD⊥BC,∠BAD=∠CAD,求出∠DAE=∠EAB=30°,根据平行线的性质求出∠F=∠BAE=30°,从而得到∠DAE=∠F,根据等角对等边求出AD=DF,即可求解.【详解】∵AB= AC,AD是△ABC的中线,∴AD⊥BC,∠BAD=∠CAD=12∠BAC=12×120°= 60°,∵AE是∠BAD的角平分线,∴∠DAE=∠EAB=12∠BAD=1260°= 30°,∵DF// AB∴∠F=∠BAE= 30°,∴∠DAE=∠F= 30°,∴AD= DF=6;故答案为:D.【点睛】本题考查的是直角三角形的性质,等腰三角形的性质,平行线的性质,掌握等腰三角形的性质是解题的关键.12.D解析:D【分析】先以Rt△ABC三个顶点分别为圆心,再以每个顶点所在的较短边为半径画弧,即可确定等腰三角形的第三个顶点,也可以作三边的垂直平分线确定等腰三角形的第三个顶点.【详解】解:如图1,以B为圆心,BC长为半径画弧,交AB于点D,连接CD,则△BCD是等腰三角形;如图2,以A为圆心,AC长为半径画弧,交AB于点D,连接CD,则△ACD是等腰三角形;如图3,作AB的垂直平分线,交AC于点D,连接BD,则△BCD是等腰三角形;如图4,以C为圆心,BC长为半径画弧,交AC于点D,交AB于点F,连接BD,CF 则△BCD、△BCF是等腰三角形;如图5,作BC的垂直平分线,交AB于点D,连接CD,则△BCD是等腰三角形;如图6,作AC的垂直平分线,交AB于点D,连接CD,△ACD是等腰三角形,∴符合题意的等腰三角形最多能画7个,故选:D.【点睛】本题考查等腰三角形的判定的应用,通过作垂直平分线或者画弧的方法确定相等的边是解题关键.二、填空题13.16【分析】利用非负数的性质可求出b的值a=c进而可得PQ的长再根据平移的性质和平行四边形的面积公式即可求出a进一步即可求出答案【详解】解:∵|a﹣c|+=0又∵|a﹣c|≥0≥0∴a﹣c=0b﹣8解析:16【分析】利用非负数的性质可求出b的值,a=c,进而可得PQ的长,再根据平移的性质和平行四边形的面积公式即可求出a,进一步即可求出答案.【详解】b-0,解:∵|a﹣8b-,又∵|a﹣c|≥08∴a﹣c=0,b﹣8=0,∴a=c,b=8,∴P(a,8),Q(a,2),∴PQ=6,∵线段PQ向右平移a个单位长度,其扫过的面积为24,a⨯=,解得a=4,∴624∴a=c=4,∴a+b+c =4+8+4=16.故答案为:16.【点睛】本题考查了非负数的性质、图形与坐标以及平移的性质等知识,正确理解题意、熟练掌握上述知识是解题的关键.14.5【分析】根据平移的性质得BE =CF 再利用BE +EC +CF =BF 得到BE +4+BE =14然后解方程即可【详解】∵三角形DEF 是由三角形ABC 通过平移得到∴BE =CF ∵BE +EC +CF =BF ∴BE +4解析:5【分析】根据平移的性质得BE =CF ,再利用BE +EC +CF =BF 得到BE +4+BE =14,然后解方程即可.【详解】∵三角形DEF 是由三角形ABC 通过平移得到,∴BE =CF ,∵BE +EC +CF =BF ,∴BE +4+BE =14,∴BE =5.故答案为5.【点睛】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.15.5或4【分析】先设长度为412的高分别是ab 边上的边c 上的高为h △ABC 的面积是S 根据三角形面积公式可求结合三角形三边的不等关系可得关于h 的不等式组解即可【详解】解:设长度为412的高分别是ab 边上解析:5或4.【分析】先设长度为4、12的高分别是a ,b 边上的,边c 上的高为h ,△ABC 的面积是S ,根据三角形面积公式,可求222,,412S S S a b c h===,结合三角形三边的不等关系,可得关于h 的不等式组,解即可.【详解】解:设长度为4、12的高分别是a ,b 边上的,边c 上的高为h ,△ABC 的面积是S ,那么 222,,412S S S a b c h===, 又∵a-b <c <a+b ,∴2222412412S S S S c -<<+, 即2233S S S h <<, 解得3<h <6,∴h=4或h=5,故答案为:5或4.【点睛】本题考查了三角形面积、三角形三边之间的关系、解不等式组.求出整数值后,能根据三边关系列出不等式组是解题关键.16.【分析】数轴的某一段上面表示解集的线的条数与不等式的个数一样那么这段就是不等式组的解集实心圆点包括该点空心圆圈不包括该点>向右<向左两个不等式的公共部分就是不等式组的解集【详解】解:由图示可看出从- 解析:12x -<≤【分析】数轴的某一段上面,表示解集的线的条数,与不等式的个数一样,那么这段就是不等式组的解集.实心圆点包括该点,空心圆圈不包括该点,>向右<向左.两个不等式的公共部分就是不等式组的解集.【详解】解:由图示可看出,从-1出发向右画出的折线且表示-1的点是空心圆,表示x>-1;从2出发向左画出的折线且表示2的点是实心圆,表示x≤2,不等式组的解集是指它们的公共部分.所以这个不等式组的解集是:12x -<≤.故答案为:12x -<≤.【点睛】本题考查在数轴上表示不等式组的解集.不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.17.【分析】看在x 轴上方的函数图象所对应的自变量的取值即可【详解】由图象可以看出x 轴上方的函数图象所对应自变量的取值为故不等式的解集是故答案为:【点睛】本题考查了一次函数与一元一次不等式的关系:从函数的 解析:2x >-【分析】看在x 轴上方的函数图象所对应的自变量的取值即可.【详解】由图象可以看出,x 轴上方的函数图象所对应自变量的取值为2x >-,故不等式0kx b +>的解集是2x >-.故答案为:2x >-.【点睛】本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b 的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y=kx+b 在x 轴上(或下)方部分所有的点的横坐标所构成的集合.18.45°【分析】由等腰直角三角形的性质可得∠ABC=45°根据SAS 可证△ABD ≌△ACE 可得∠ACE=∠ABD 即∠ACE+∠DBC=∠ABD+∠DBC=∠ABC=45°【详解】解:∵∠BAC=90°解析:45°【分析】由等腰直角三角形的性质可得∠ABC=45°,根据“SAS”可证△ABD ≌△ACE ,可得∠ACE=∠ABD ,即∠ACE+∠DBC=∠ABD+∠DBC=∠ABC=45°.【详解】解:∵∠BAC=90°,AB=AC ,∴∠ABC=45°,∵∠BAC=∠DAE ,∴∠BAD=∠CAE ,且AB=AC ,AD=AE ,∴△ABD ≌△ACE (SAS ),∴∠ACE=∠ABD ,∴∠ACE+∠DBC=∠ABD+∠DBC=∠ABC=45°,故答案为:45°【点睛】本题考查了全等三角形的判定与性质,等腰直角三角形的性质,熟练运用全等三角形的判定解决问题是本题的关键.19.【分析】先根据等腰三角形的性质求出∠BA1C 的度数再根据三角形外角的性质及等腰三角形的性质分别求出∠DA2A1∠EA3A2及∠FA4A3的度数找出规律即可得出第n 个三角形中以An 为顶点的底角度数【详 解析:11752n -⎛⎫⨯︒ ⎪⎝⎭【分析】先根据等腰三角形的性质求出∠BA 1C 的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠DA 2A 1,∠EA 3A 2及∠FA 4A 3的度数,找出规律即可得出第n 个三角形中以A n 为顶点的底角度数.【详解】解:∵在△CBA 1中,∠B=30°,A 1B=CB , ∴∠BA 1C=1802B ︒-∠=75°,∵A1A2=A1D,∠BA1C是△A1A2D的外角,∴∠DA2A1=12∠BA1C=12×75°;同理可得,∠EA3A2=(12)2×75°,∠FA4A3=(12)3×75°,∴第n个三角形中以A n为顶点的底角度数是(12)n-1×75°.故答案为:(12)n-1×75°.【点睛】本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠DA2A1,∠EA3A2及∠FA4A3的度数,找出规律是解答此题的关键.20.【分析】连接PC只要证明PB=PC即可推出PC+PE=PB+PE可得PBE共线时PC+PE的值最小最小值为BE的长度从而结合等腰三角形的性质求解【详解】解:如图连接PC∵AB=ACAD⊥BC∴BD=解析:135【分析】连接PC,只要证明PB=PC,即可推出PC+PE=PB+PE,可得P、B、E共线时,PC+PE的值最小,最小值为BE的长度,从而结合等腰三角形的性质求解.【详解】解:如图,连接PC,∵AB=AC,AD⊥BC,∴BD=CD,∴PB=PC,∴PC+PE=PB+PE,又∵BE⊥AC∴P、B、E共线时,PC+PE的值最小为BE的长,∵AB=AC,∠BAC=45°,BE⊥AC∴∠ABC=∠ACB=67.5°,∠ABE=45°∴∠PBC=∠PCB=67.5°-45°=22.5°∴∠BPC=180°-22.5°×2=135°故答案为:135.【点睛】本题考查轴对称-最短路线问题,等腰三角形的性质、线段的垂直平分线的性质等知识,解题的关键是灵活运用所学知识解决问题.三、解答题21.(1)(3,0);(2)见详解;(3)(a−3,b+2)【分析】(1)根据坐标系可得B点坐标,再根据关于直线y=1轴对称即可得到答案;(2)首先确定A、B、C三点平移后的对应点位置,然后再连接即可;(3)根据点平移后横坐标−3,纵坐标+2,进而即可得到答案.【详解】解:(1)∵点B的坐标为(3,2),∴B点关于直线1y 对称的点的坐标为(3,0),故答案为:(3,0);(2)如图所示:(3)P的坐标为(a,b)平移后对应点P1的坐标为(a−3,b+2).故答案为:(a−3,b+2).【点睛】此题主要考查了作图−−平移变换以及轴对称,关键是几何图形都可看做是由点组成,我们在画一个图形的平移图形时,也就是确定一些特殊点的对应点.22.(1)点O′2,22);(2)AA′=2,点A′的坐标为(3,3【分析】(1)根据点A(2,0),点B(0,2),可得△ABO是等腰直角三角形,当点O′落在边AB上时,α=45°,可得点O′的横坐标为12AB2,纵坐标为22,即可得答案;(2)根据勾股定理得AB,由旋转性质可得∠A′BA=60°,A′B=AB,继而得出AA′和点A′的坐标.【详解】解:(1)如图①,∵点A(2,0),点B(0,2),∴OA =OB =2,△ABO 是等腰直角三角形,∴AB =22, 当点O′落在边AB 上时,α=45°,∴点O′的横坐标为22O ′B =2,纵坐标为2﹣2, ∴点O′的坐标为(2,2﹣2);(2)如图②,当α=60°时,∴∠ABA′=60°,AB =A′B ,∴△ABA′为等边三角形,∴AA′=A′B =AB =22,连接OA′,在△OBA′和△OAA′中,OB OA OA OA A A A B '''=⎧='⎪⎨⎪=⎩, ∴△OBA′≌△OAA′(SSS ),∴∠BOA′=∠AOA′,∠BA′O =∠AA′O ,∴直线OA′的函数解析式为y =x ,∴OA′⊥AB ,∴OA′26,∴点A′的坐标为3,3.【点睛】本题主要考查旋转的性质及全等三角形的性质与判定、等边三角形的性质,等腰三角形的性质,熟练掌握旋转的性质是解题的关键.23.(1)①(5,12);②x>5;(2)见解析.【分析】(1)①将m=3、n=2代入两个一次函数,然后联立解二元一次方程组即可;②根据题意列不等式求解即可;(2)先确定两函数与y 轴的交点坐标以及所多顶点,然后再根据x 的取值范围即可解答.【详解】解:(1)当m=3,n=2时,133y x =-,222y x =+①联立3322y x y x =-⎧⎨=+⎩,解得512x y =⎧⎨=⎩∴交点坐标为(5,12);②y 1>y 2则3322x x >-+解得x>5;(2)∵()11y m x =-与y 轴交点为(0,m -),1y 过定点(1,0),()21y n x =+与y 轴交点为(0,n ),同时2y 过定点(-1,0),∵在0<x<1的范围内,有且只有部分函数值满足y 1>y 2∴根据图像得到m ->n 即m+n<0.【点睛】本题属于一次函数的综合题,主要考查了一次函数的性质、解二元一次方程组、解不等式,考查知识点较多,灵活应用相关知识成为解答本题的关键.24.(1)150元;100元;(2)甲商场()10014000a + ,乙商场()8015000a +元;(3)50a =;(4)当50a =时,两家花费一样;当1050a <<时,到甲处购买更合算;当50a 时,到乙处购买更合算【分析】(1)设每个足球的定价是x 元,则每套队服是()50x +元,根据“两套队服与三个足球的费用相等”得出等量关系,列出一元一次方程,求解即可;(2)根据甲商场和乙商场的方案列出式子即可;(3)令100140008015000,a a ++=解方程即可;(4)列出不等式分别求解即可.【详解】解:(1)设每个足球的定价是x 元,则每套队服是()50x +元.根据题意得()2503x x +=解得100,50150x x +==. 答:每套队服150元,每个足球100元.(2)到甲商场购买所花的费用为:()1001001501001001400010a a ⎛⎫⨯+-=+ ⎪⎝⎭元; 到乙商场购买所花的费用为:()100150+100808015000a a ⨯⨯%=+元;(3)由100140008015000,a a ++=得:50a =,所以:当50a =时,两家花费一样。
2湖南师大附中星城实验学校初二英语期中考试卷及答案

湖南师大附中星城实验学校八年级第一学期期中测试英语试题卷分值:120分时量:90分钟命题人:刘佳审题人:刘苹21 Look at my new smart phone.Wow, it’s so cool! When ________ you ________ it?A. do; buyB. did; buyC. did; bought22. _______ bad day! It’s raining hard. We have to stay at home.A. What aB. HowC. What23. ______do you stay up late?Never. I always go to bed early.A. How longB. How oftenC. How much24. ________ Mr. Zhang is poor,________ he is always happy..A. Although; /B. Although; butC. But; although25. I think Peter is as ________ as Helen.A. hard-workingB. more hard-workingC. the most hard-working26. The game show is really boring. I can’t ________ it?A. standB. likeC. mind27. The Changjiang River is ________ river in China.A. longB. longerC. the longest28. Tom is similar ________ his mother, and he is different his fatherA. as; fromB. to; fromC. from; to29. My two cousins decide ________ on a vacation together,A. GoingB. to goC. go30. Thanks for telling me about your life at school.__________.A.You are welcomeB. Of courseC. Have a good day第二节词语填空通读下面的短文,掌握其大意,然后从各题所给的A、B、C三个选项中选出最佳答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
湖南师大附中星城实验中学2013—2014学年度第二学期期中考试
八年级数学(闭卷:试题卷和答题卷一体)
时量:100分钟 分值:120分
命题人: 审题人:
一、选择题(3分×10=30分)
1.当3a =时,在实数范围内无意义的式子是(C )
A
B
C
D
2.分别以下列四组数为一个三角形的边长:(1)3,4,5;(2)5,12,13;(3)8,15,17;(4)4,5,6.其中能构成直角三角形的有(B ) A .4组 B .3组 C .2组 D .1组
3.已知平行四边形ABCD 中,200A C ∠+∠=,则B ∠的度数是(C ) A .100 B .160 C .
80 D .
60
4.如图,平行四边形ABCD 的对角线AC 、BD 相交于点O ,下列结论不正确的是(D ) A .DC ∥AB B .OA =OC C .AD =BC D .DB 平分∠ADC 5.下列命题中,真命题是(B )
A .对角线相等的四边形是矩形
B .对角线互相平分的四边形是平行四边形
C .对角线互相垂直的四边形是菱形
D .对角线互相垂直平分的四边形是正方形 6.矩形两条对角线的夹角为60,一条较短边长为5cm ,则其对角线长为(B ) A .5cm B .10cm C .15cm D
.cm
7.小王计划用100元钱买乒乓球,所购买球的个数W (个)与单价n (元)的关系式
100
W n
=
中(A ) A .100是常量,W ,n 是变量 B .100,W 是常量,n 是变量 C .100,n 是常量,W 是变量 D .无法确定 8.下列函数:①3y x =-;②3y x =-;③232y x =
;④13
x
y =+.其中是一次函数的是(D )
A .①②
B .①③
C .②③
D .①④ 9.已知一次函数23y x =-经过哪几个象限(B )
A .一、二、三
B .一、三、四
C .一、二、四
D .二、三、四 10.方程10x +=得解就是函数1y x =+的图像与(A )
2
第13题
A .
x 轴交点的横坐标
B .y 轴交点的横坐标
C .y 轴交点的纵坐标
D .以上都不对
二、填空题(3分×8=24分) 11÷
= 3 .
1250y ++=,则x y += -3 。
13.如图,在平面直角坐标系中有两点()40,
A 和()
03,B ,则这两点之间的距离为 5 . 14.在ΔABC 中,点D 、E 分别是边AB 、AC 的中点,已知DE =6,则BC = 12 . 15.菱形的面积是24 cm 2,一对角线长为6cm ,则另一对角线长为 8cm . 16.函数36y x =-,当函数值18y =时,自变量x 的值是 8 . 17.若()2
1m y m x =
-是正比例函数,则m 的值为 -1 .
18.函数65y x
=-+的图像是由直线6
y x =-向 上 平移 5 个单位长度得到的. 三、解答题 19.计算(8分)
(1
)35
)+
(2((
)
(
2
121++----解:原式
=
2
15+-- 解:原式
41++--
=215--
3+ =13--20.(6分)有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度与芦苇的长度分别是多少?
21.(6分)如图,在平行四边形ABCD 中,点E 、F 分别在
BC 、AD 上,且DF BE =.
求证:四边形AECF 是平行四边形.
B
D
()2
2215112
113
1213解:据题意,设水池深为尺,则芦苇长为尺, 由勾股定理得: 解得:= =答:水深尺,芦苇长尺.
x x x x x x ++=+∴+证明:四边形是平行四边形,
//, //
, 即 四边形是平行四边形.
ABCD AD BC AD BC AF CE DF BE
AD DF BC BE AF CE AECF ∴=∴=∴-=-=∴
3
22.(6分)甲、乙两车从A 城出发前往B 城.在整个行程中,汽车离开A 城的距离y 与时刻t 的对应关系如图所示.(1)A ,B 两城相距多远?(2)哪辆车先出发?哪辆车先到B 城? (3)甲、乙两车的平均速度分别是多少?
23.(6分)已知y 与x +3成正比,当x =2时,y =-5,求y 与x 之间的函数关系式.
()()3302552313解:与成正比,
可设(,),
当时,,
解得:, 函数解析式为 .
y x y k x k x y k k y x +=+≠==-∴-=+=-∴=--
24.(6分)已知一次函数的图像过点(3,5)和(-4,-9),求这个一次函数的解析式.
25.(8分)某市推出电脑上网包月制,每月收取费用用y (元)与上网时间x (小时)的函数关系式如图所示,其中AB 是线段,且BC 是射线. (1)写出y 与x 之间的函数关系式及自变量的取值范围. (2)若小王6月份上网25小时,他应付多少元的上网费用?7月份上网50小时又应付多少元呢?
(3)若小王8月份上网费用为100元,则他在该月份的上网时间是多少?
354935492121解:设一次函数解析式为 , 因为 的图象过点(,)与(,),所以,
.,
解得 . 所以这个一次函数的解析式为 .
y kx b y kx b k b k b k b y x =+=+--⎧+=⎨-+=-⎩⎧=⎨=-⎩=-40030220302254050250208010040100100220600, ;解:(1) , . () 当 时, 元; 当 时,= 元.
(3)因为,所以当 时,
, 解得: .答:(2)若小王6月份上网25小时,他应付40元的上网费用;7月份上网5小时应付80元. (3)若小王8月x y x x x y x y y x x h ⎧≤≤=⎨
->⎩====⨯->==-=00份上网费用为1元,则他在该月份的上网时间是60.
h
4
26.(10分)如图,正方形ABCD 的对角线交于点O ,点O 又是正方形111A B C O 的一个顶点,而且这两个正方形的边长相等.试证明:无论正方形111A B C O 绕点O 怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的
1
4
.
27.(10分)如图,在平面直角坐标系中,A 点的坐标为(4,0),点P 是直线1
42
y x =-+ 在第一象限上的一点,O 是原点.
(1)设P 点的坐标为(x ,y ),ΔO
P A 的面积为S ,试求S 关于x 的函数关系式,并
直接写出自变量x 的取值范围.
(2)是否存在点P ,使PO=PA ?若存在,请求出P 点的坐标;若不存在,请说明理由.
解:(1)过P 点作PD x ⊥轴于D . ∵ P 点在直线
1
42
y x =-
+上第一象限内的一点,且坐标为(x ,y )∴ 11
4422
PD y x x ==-
+=-+. ∵ A 点的坐标为(4,0), ∴ OA =4, ∴ ΔOPA 的面积为
111
44808222
(),()S OA PD x x x =
⋅=⨯⨯-+=-+<< (2)假设存在这样的点P ,过点P 作PD x ⊥轴于D .当OP =AP 时,
则122OD AD OA ==
=,∴ 1
2432
PD =-⨯+=, ∴ 在第一象限存在一个点P (2,3),使OP =AP .。
