小高考猜题
2023年高考【物理】猜题卷 附解析(全国卷)

2023年普通高等学校招生全国统一考试物理猜题卷(全国卷)一、选择题:本题共8小题,每小题6分,共48分。
在每小题给出的四个选项中,第1~5题只有一项符合题目要求,第6~8题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
1.高压电线落地可能导致行人跨步电压触电。
如图所示,若高压输电线掉落在水平地面上的O点,且O点附近地质结构分布均匀,将在地面形成以O为圆心的一系列同心圆等势线。
则()A.图中A点的电场强度小于B点的电场强度B.图中A点的电场强度大于B点的电场强度C.行人无论向哪个方向跨步,两脚间距离越大跨步电压越大D.行人无论向哪个方向跨步,两脚间距离越大跨步电压越小2.甲、乙两物体从同一位置同时开始做匀变速直线运动的速度—时间图像如图所示,由此可知( )A.前2 s内甲和乙位移方向相同,大小之比是5:3B.前2 s内甲和乙平均速度方向相同,大小之比为2:1C.甲和乙的加速度方向相同,大小之比为1:1D.甲和乙的加速度方向相反,大小之比为1:23.2022年6月5日,神舟十四号成功对接天和核心舱径向端口,航天员陈冬、刘洋、蔡旭哲依次进入天和核心舱。
航天员们在一个月的时间内,有序开展了载人环境建立、空间站平台维护与照料、空间科学实验等工作。
已知天和核心舱距离地面的高度约为380 km,地球半径约为6400 km,同步卫星距地面的高度约为36000 km。
下列说法正确的是( )A.航天员可以漂浮在空间站中,所以加速度为零B.天和核心舱在轨运行的线速度小于同步卫星的线速度C.神舟十四号的发射速度大于7.9 km/sD.天和核心舱绕地球运动的周期约为8 h4.如图为洛伦兹力演示仪的结构图。
励磁线圈产生的匀强磁场方向垂直纸面向外,玻璃泡中的磁场可以视为匀强磁场,且磁感应强度大小与线圈中电流I的关系为B kI(k为常数)。
电子由电子枪产生,其速度方向与磁场方向垂直。
测得电子在玻璃泡中做匀速圆周运动的轨迹半径为r,从电子枪射出经过加速的电子速度为v,电子所带I电荷量为e,质量为m,则励磁线圈中电流和一个电子在玻璃泡中运动的等效电流I分别为( )πev r5.第一次工业革命的关键是蒸汽机的发明,蒸汽机通过连杆把往复直线运动转化为圆周运动。
新高考生物名师猜题卷(二)

17.“假设-推理法”是现代科学研究中常用的一种科学方法,是在观察和分析
基础上提出问题后,通过推理和想象提出问题的假说,最后再通过设计实验
来验证。下列科学史上的经典研究中没有涉及“假设-推理法”的是( D )
A.孟德尔豌豆杂交实验
B.摩尔根的果蝇眼色遗传实验
C.探究DNA的复制过程
D.噬菌体侵染细菌实验
酸检测不是唯一方法。
16.集流是指液体中成群的原子或分子在压力梯度下共同移动。植物体中有水分 集流,植物体的水分集流通过膜上的水孔蛋白形成的水通道实施的。下列相
关叙述错误的是( C )
A.单个水分子通过渗透进入植物细胞不属于水分集流 B.水分集流通过水孔蛋白不需要ATP水解提供能量 C.可推测在植物细胞的液泡膜上不可能存在水孔蛋白 D.可推测干旱环境和某些植物激素可诱导水孔蛋白基因表达
阅读下列材料,回答第11~12题。 为验证酶催化的某一特性,某同学设计了下表的实验(适宜温度、pH等条件)
步骤
操作方法
试管
甲
乙
1
注入2%H2O2溶液
3 mL
3 mL
2
注入新鲜的鸡肝匀浆
少许
—
3
二氧化锰
—
少许
4
实验结果
11.下列实验分析错误的是( C )
A.该实验不能证明酶具有专一性
B.甲试管气泡释放速率更大
种方法的相关叙述错误的是( C )
A.抗原检测和核酸检测的物质不同,前者是蛋白质,后者是核酸 B.抗原检测和核酸检测的原理不同,前者依据抗原-抗体杂交,后者依据核 酸分子杂交 C.感染新冠病毒但无症状者, 唯一准确的方法是进行核酸检测 D.感染新冠病毒的患者,体内既发生细胞免疫,又发生体液免疫
2024届高考理科综合物理高频考点实战猜题卷(全国卷)(基础必刷)
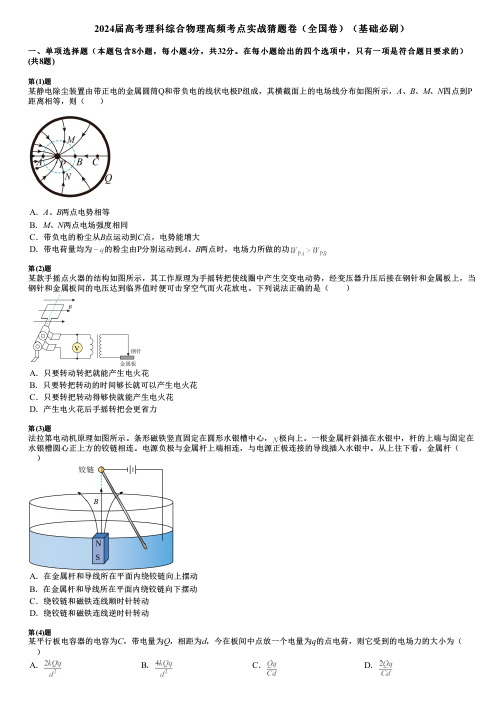
2024届高考理科综合物理高频考点实战猜题卷(全国卷)(基础必刷)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题某静电除尘装置由带正电的金属圆筒Q和带负电的线状电极P组成,其横截面上的电场线分布如图所示,A、B、M、N四点到P 距离相等,则()A.A、B两点电势相等B.M、N两点电场强度相同C.带负电的粉尘从B点运动到C点,电势能增大D.带电荷量均为的粉尘由P分别运动到A、B两点时,电场力所做的功第(2)题某款手摇点火器的结构如图所示,其工作原理为手摇转把使线圈中产生交变电动势,经变压器升压后接在钢针和金属板上,当钢针和金属板间的电压达到临界值时便可击穿空气而火花放电。
下列说法正确的是( )A.只要转动转把就能产生电火花B.只要转把转动的时间够长就可以产生电火花C.只要转把转动得够快就能产生电火花D.产生电火花后手摇转把会更省力第(3)题法拉第电动机原理如图所示。
条形磁铁竖直固定在圆形水银槽中心,极向上。
一根金属杆斜插在水银中,杆的上端与固定在水银槽圆心正上方的铰链相连。
电源负极与金属杆上端相连,与电源正极连接的导线插入水银中。
从上往下看,金属杆( )A.在金属杆和导线所在平面内绕铰链向上摆动B.在金属杆和导线所在平面内绕铰链向下摆动C.绕铰链和磁铁连线顺时针转动D.绕铰链和磁铁连线逆时针转动第(4)题某平行板电容器的电容为C,带电量为Q,相距为d,今在板间中点放一个电量为q的点电荷,则它受到的电场力的大小为( )A.B.C.D.第(5)题真空中有一个边长为L的正三角形ABC,AB中点为D,AC中点为E,中心为O点,如图所示。
现在A点固定一个电荷量为的正点电荷,BC两点分别固定一个电荷量为Q的负点电荷。
已知真空中的点电荷对外部某处的电势公式为(无穷远处电势为零),其中k为静电力常量,Q为点电荷的电荷量(带正负),r为某点到点电荷Q的距离,且电势的叠加符合代数运算,下列说法正确的是( )A.O点电场强度大小为B.O点电势为零C.将一个电荷量为的点电荷从O点移动到E点,静电力对做正功D.将一个电荷量为的点电荷从D点移动到O点再移动到E点,电势能一直不变第(6)题如图所示,某柱状透明介质的横截面为四分之一圆环ABCD,圆环内径为R,外径为(未知)。
江苏省2024年高考物理猜题卷(二)考点速查版

一、单选题二、多选题1. 如图甲所示,质量分别为m 和M 的物块A 、B 叠放在一起,放于光滑水平面上。
重力加速度大小为g ,A 、B 间的动摩擦因数为μ,水平外力作用在A 上,能使A 、B 保持相对静止的最大外力F 与μg间的关系如图乙所示,认为最大静摩擦力等于滑动摩擦力,下列说法正确的是( )A .若m 取一更大的值,则图象的斜率变小B .若m 取一更大的值,则图象的斜率变大C .若M 取一更大的值,则图象的斜率变大D .若M 取一更大的值,则图象的斜率不变2. 对于一定质量的理想气体,下列叙述中正确的是( )A .当分子间的平均距离变大时,气体压强一定变小B .当分子热运动变剧烈时,气体压强一定变大C .当分子热运动变剧烈且分子平均距离变小时,气体压强一定变大D .当分子热运动变剧烈且分子平均距离变大时,气体压强一定变大3. 利用碘131()治疗是临床上常用的一种治疗甲亢的方法,它是通过含有β射线的碘被甲状腺吸收,来破坏甲状腺组织,使甲状腺合成和分泌甲状腺激素水平减少来达到治愈甲亢的目的。
已知碘131发生β衰变的半衰期为8天,则以下说法正确的是( )A .碘131的衰变方程为B .碘131的衰变方程为C .32 g 碘131样品经16天后,大约有8g 样品发生了β衰变D .升高温度可能会缩短碘131的半衰期4.在电学实验中,改装后的电表测量值略偏小,为校准电表,可以将一个阻值较小的电阻( )A .与电阻串联B .与电阻并联C .与电阻串联D .与电阻并联5. 下列说法正确的是( )A .物体的动能增加,其内能也一定增加B .扩散现象和布朗运动都是分子的无规则热运动C .一定质量的气体膨胀对外做功,气体内能一定增加D .随着分子间的距离增大,分子间的引力、斥力都减小6. 如图所示,一带电粒子在匀强电场中只受电场力运动,经过一平面直角坐标系中的a 、O 、b 三点时的动能分别为10eV 、4eV 、12eV ,下列说法正确的是A .该电场方向一定与x O y 平面平行江苏省2024年高考物理猜题卷(二)考点速查版三、实验题B.该电场场强大小为C .O 点是该粒子轨迹上电势能最高的点D .该粒子轨迹为抛物线7. 如图所示,四分之一圆槽AB 的半径为R 、质量为3m ,静止放在水平地面上,圆槽底端B 点的切线水平,距离B 点为R 处有一质量为3m 的小球2,其左侧连有轻弹簧。
2024届高考预测猜题卷(一) 物理高频考点试卷(重庆地区专用 )
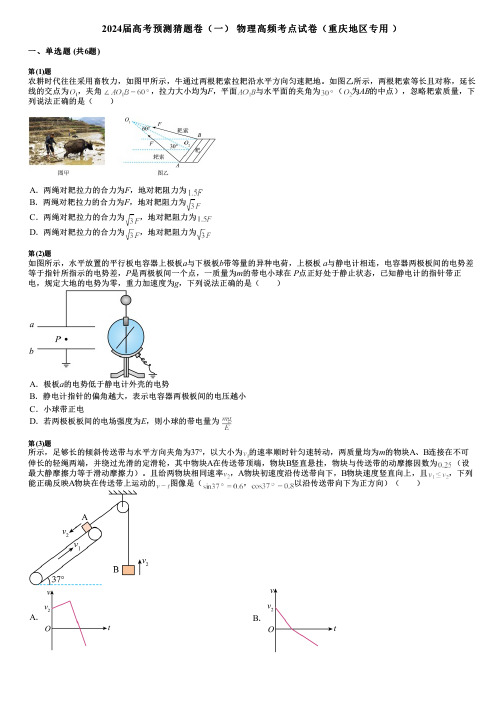
2024届高考预测猜题卷(一)物理高频考点试卷(重庆地区专用)一、单选题 (共6题)第(1)题农耕时代往往采用畜牧力,如图甲所示,牛通过两根耙索拉耙沿水平方向匀速耙地。
如图乙所示,两根耙索等长且对称,延长线的交点为,夹角,拉力大小均为F,平面与水平面的夹角为(为AB的中点),忽略耙索质量,下列说法正确的是( )A.两绳对耙拉力的合力为F,地对耙阻力为B.两绳对耙拉力的合力为F,地对耙阻力为C.两绳对耙拉力的合力为,地对耙阻力为D.两绳对耙拉力的合力为,地对耙阻力为第(2)题如图所示,水平放置的平行板电容器上极板a与下极板b带等量的异种电荷,上极板a与静电计相连,电容器两极板间的电势差等于指针所指示的电势差,P是两极板间一个点,一质量为m的带电小球在P点正好处于静止状态,已知静电计的指针带正电,规定大地的电势为零,重力加速度为g,下列说法正确的是( )A.极板a的电势低于静电计外壳的电势B.静电计指针的偏角越大,表示电容器两极板间的电压越小C.小球带正电D.若两极板板间的电场强度为E,则小球的带电量为第(3)题所示,足够长的倾斜传送带与水平方向夹角为37°,以大小为的速率顺时针匀速转动,两质量均为m的物块A、B连接在不可伸长的轻绳两端,并绕过光滑的定滑轮,其中物块A在传送带顶端,物块B竖直悬挂,物块与传送带的动摩擦因数为(设最大静摩擦力等于滑动摩擦力)。
且给两物块相同速率,A物块初速度沿传送带向下,B物块速度竖直向上,且,下列能正确反映A物块在传送带上运动的图像是(,以沿传送带向下为正方向)( )A.B.C.D.第(4)题图1、图2分别表示两种电压的波形,其中图1所示电压按正弦规律变化.下列说法正确的是A.图1表示交流电,图2表示直流电B.两种电压的有效值相等C.图1所示电压的瞬时值表达式为u=311sin100VD.图1所示电压经匝数比为10:1的变压器变压后,频率变为原来的第(5)题2022年11月23日由三峡集团研制的单机容量16兆瓦海上风电机组成功下线,该机组是目前全球单机容量最大、叶轮直径最大的风电机组,风力发电机简易模型如甲图所示,某兴趣小组自制了一台风力发电机,试验中叶轮带动线圈在匀强磁场中转动,产生的交流电电流随时间变化的图像如图乙所示,则下列说法中正确的是( )A.电流的频率为B.电流的有效值为C.线圈处于甲图所示位置时产生的电流最大D.电流的瞬时值表达式为第(6)题为了保障行驶安全,一种新型双门电动公交车安装了如下控制装置:只要有一扇门没有关紧,汽车就不能启动。
2023届湖南新高考金榜猜题历史试卷
2023届湖南新高考历史金榜猜题卷一、选择题,本题共16小题,每小题3分,共计48分。
1.近年来,中国社会科学院考古研究所与山西省考古研究所联合对陶寺遗址进行解剖发掘,确认陶寺遗址存在近13万平方米宫城。
此外陶寺遗址还先后发掘出城墙、大型宗教礼制建筑、政府掌控的大型仓储区等。
由此可见,陶寺遗址所展示的文明( )A.已具备了国家的初始形态B.君主集权统治得到加强C.重视农业与手工业的管理D.反映了仰韶文化的成就2.秦汉时期,地方政府吸收了本地社会内部成员,授予他们一定的官方身份来承担日常行政事务,不享有正式官吏应有的薪俸和升迁途径,这就是里吏。
秦代里吏有典、老二职,律文称“以其里公卒、土五(伍)年长而毋(无)害者为典、老”。
据此可知( )A.基层官员的产生具有早期民主色彩B.选官加强了各阶层的流动C.国家注重民众在基层治理中的作用D.里吏提高了基层治理效率3.下表为史书中南朝开国皇帝的记载,材料主要反映出南朝时期( )史料记载出处宋武帝刘裕自幼家贫,投身北府军为将。
凭借着巨大的军功,总揽东晋军政大权,后代晋自立。
《宋书》齐高帝萧道成兰陵萧氏,其父为刘宋时期著名武将(以军功起家)。
《齐书》梁武帝萧衍兰陵萧氏,曾参与抵御北魏入侵,后建立南梁。
《梁书》陈武帝陈霸先出身低微,初为乡间里司,后任广州府中直兵参军,平定“侯景之乱”,败北齐,后废梁帝自立。
《陈书》C.南北对峙持续强化D.以军功为主要选官标准4.宋代曾公亮在水利、术数方面都颇有研究,他负责编撰的《武经总要》颇具影响力,被封为吏部侍郎。
宋真宗时,因石归宋献上的木羽弩箭,射程远,杀伤力大,朝廷增加了其俸禄。
造船务匠人项绾等研发海船,获得钱币奖励。
这反映出,北宋时( )A.治国指导思想逐渐发生变动B.社会环境利于技术创新C.与少数民族间战争比较频繁D.重文抑武政策有所松动5.明代张萱在《西园闻见录》中记载,州县“官府每举一事,必称旧例。
例之所有,虽觉其不宜,不得辄改;例之所无,虽知其便,不得轻开。
东北三校(哈尔滨师大附中2024年高三高考猜题卷(一)数学试题

东北三校(哈尔滨师大附中2024年高三高考猜题卷(一)数学试题注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.斜率为1的直线l 与椭圆22x y 14+=相交于A 、B 两点,则AB 的最大值为( )A .2B .455C .4105D .81052.《周易》是我国古代典籍,用“卦”描述了天地世间万象变化.如图是一个八卦图,包含乾、坤、震、巽、坎、离、艮、兑八卦(每一卦由三个爻组成,其中“”表示一个阳爻,“”表示一个阴爻)若从八卦中任取两卦,这两卦的六个爻中恰有两个阳爻的概率为( )A .356B .328C .314D .143.i 是虚数单位,21iz i=-则||z =( ) A .1B .2C 2D .224.已知椭圆22:13x C y +=内有一条以点11,3P ⎛⎫ ⎪⎝⎭为中点的弦AB ,则直线AB 的方程为( )A .3320x y --=B .3320x y -+=C .3340x y +-=D .3340x y ++=5.函数()256f x x x =-+ )A .{2x x ≤或}3x ≥ B .{3x x ≤-或}2x ≥- C .{}23x x ≤≤D .{}32x x -≤≤-6.若双曲线22214x y b -=的离心率72e =,则该双曲线的焦点到其渐近线的距离为( ) A .23B .2C .3D .17.已知非零向量a ,b 满足||a b |=|,则“22a b a b +=-”是“a b ⊥”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件解:8.已知函数()()3sin 3cos 0f x x x ωωω=+>,对任意的1x ,2x ,当()()1212f x f x =-时,12min2x x π-=,则下列判断正确的是( )A .16f π⎛⎫= ⎪⎝⎭B .函数()f x 在,62ππ⎛⎫⎪⎝⎭上递增C .函数()f x 的一条对称轴是76x π=D .函数()f x 的一个对称中心是,03π⎛⎫⎪⎝⎭9.已知l ,m 是两条不同的直线,m ⊥平面α,则“//l α”是“l ⊥m ”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件10.已知()21,+=-∈a i bi a b R ,其中i 是虚数单位,则z a bi =-对应的点的坐标为( ) A .()12,-B .()21,-C .()1,2D .()2,111.函数()xf x e ax =+(0a <)的图像可以是( )A .B .C .D .12.若424log 3,log 7,0.7a b c ===,则实数,,a b c 的大小关系为( )A .a b c >>B .c a b >>C .b a c >>D .c b a >>二、填空题:本题共4小题,每小题5分,共20分。
2024届辽宁省高考物理终极猜题卷(基础必刷)

2024届辽宁省高考物理终极猜题卷(基础必刷)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题一定质量的理想气体,由状态a经a→b、b→c和回到状态a,其循环过程的图像如图所示;、、分别表示气体在状态a、b、c的温度,则( )A.B.气体在b→c过程中吸收热量C.该循环过程中气体对外做负功D.该循环过程中气体放出热量第(2)题某同学在方格纸上建立直角坐标系,根据手拉纸带的v、t数据,在坐标系中描点,练习画图像,如图所示。
为了更清晰地反映纸带运动速度的变化规律,可以用某种方式把这些点连起来,下列哪种方式与实际更加接近( )A.B.C.D.第(3)题我国计划在2060年达到“碳中和”目标,到时生产、生活排放的碳总量与植被吸收的碳总量将达到平衡,为了实现这一目标。
未来四十年我国应减少使用的能源是( )A.水能B.石油能源C.太阳能D.风能第(4)题智能手机上装载的众多app软件改变着我们的生活,如图所示为某度地图app软件的一张截图,表示了某次导航的具体路径,其推荐路线中有两个数据,16分钟,6.7公里,关于这两个数据,下列说法正确的是( )A.研究汽车在导航图中的位置时,可以把汽车看作质点B.16分钟表示的是某个时刻C.6.7公里表示了此次行程的位移的大小D.根据这两个数据,我们可以算出此次行程的平均速度第(5)题如图所示是两个点电荷的电场线,虚线框为等势线,其中A、B、C三点的位置如图所示,其中A点为两点电荷连线的中点,设无穷远处为零势面,则( )A.A点的电势等于零B.C.电荷仅在电场力作用下从A到C,电场力做功可能为0D.负电荷在A点的电势能比在B点的小第(6)题下列核反应方程中,生成物中、、、代表质子的是( )A.B.C.D.第(7)题如图所示,安装在固定支架(图中未画出)上的光滑绝缘转动轴两端通过等长的轻质细软导线(导线不可伸长)连接并悬挂长为L、质量为m的导体棒ab,导体棒横截面的直径远远小于悬线的长度,空间存在辐向分布磁场(磁极未画出),导体棒摆动过程中磁场方向总是垂直于导体棒,导体棒所在处的磁感应强度大小均为B,开始时导体棒静止在最低点。
新高考生物名师猜题卷(一)

A.①为复制、②为转录 B.③④的模板中核苷酸序列不同 C.①②③④均发生在宿主细胞中 D.+RNA、-RNA均能携带遗传信息
解析 ①②为RNA复制,A错误;③翻译出的是病毒蛋白质外壳,④翻译出 的是酶,二者的模板中核苷酸序列不同,B正确;病毒无细胞结构,必须寄生 在活细胞中才能完成正常的生命活动,①②③④均发生在宿主细胞中,C正 确;+RNA、-RNA中的碱基序列均能携带遗传信息,D正确。
将某幼苗横放,一段时间后可观察到茎向上弯曲生长,根向下弯曲生长,示意 图如下。 请回答5~6题。
5.下列对该现象的叙述错误的是( C )
A.该现象属于向性运动 B.该现象是植物对环境信号做出的生长反应 C.该现象中根部感受重力的细胞在根伸长区 D.该现象的形成机制是植物长期自然选择的结果
解析 向性运动是指植物受到外界单一方向的刺激时所做出的局部运动,如 植物茎的背地性和根的向地性生长,A正确;根据题意和图示可知,该幼 苗的茎对光照信号做出了生长反应,根对重力信号做出了生长反应,B正 确;根据“淀粉—平衡石假说”,根部感受重力的细胞即平衡石细胞分布 在根冠,C错误;自然选择决定生物进化的方向,通过自然选择将适应环 境变化的生物选择并保留下来,因此该现象的形成机制是植物长期自然选 择的结果,D正确。
解析 图中表示蝗虫产卵数量随相对湿度的变化(先增加后降低最后为0), 没有体现出周期性变化特点,A错误;分析题图可知,随着相对湿度的增 加产卵数量先增加后降低,反映的是蝗虫种群特征中的种群密度的变化, B错误;蝗虫体内大量产生化学物质5羟色胺并释放到环境中,该分泌物 不进入血液而是由导管流出到外环境中,不属于内分泌调节,C错误;当 湿度高时,蛙、鸟等天敌多,捕食可抑制沙漠蝗虫的种群数量,另外真菌、 丝虫等寄生生物大量繁殖抑制沙漠蝗虫的种群数量,因此沙漠蝗虫的产卵 数量随着湿度增大而减少,D正确。
山东省单县第一中学2024届高考终极猜想:化学试题最后一卷名师猜题含解析

山东省单县第一中学2024届高考终极猜想:化学试题最后一卷名师猜题注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题(共包括22个小题。
每小题均只有一个符合题意的选项)1、分子式为C4H8Br2的有机物同分异构体(不考虑立体异构)为()A.9 B.10 C.11 D.122、常温下,关于pH = 2的盐酸溶液的说法错误的是A.溶液中c(H+)=1.0×10-2mol/LB.此溶液中由水电离出的c(OH―)=1.0×10-12mol/LC.加水稀释100倍后,溶液的pH = 4D.加入等体积pH=12的氨水,溶液呈酸性3、硫酸钙是一种用途非常广泛的产品,可用于生产硫酸、漂白粉等一系列物质(见下图)。
下列说法正确的是A.CO、SO2、SO3均是酸性氧化物B.工业上利用Cl2和澄清石灰水反应来制取漂白粉C.除去与水反应,图示转化反应均为氧化还原反应D.用CO合成CH3OH进而合成HCHO的两步反应,原子利用率均为100%4、由下列实验事实得出的结论不正确的是()实验结论将乙烯通入溴的四氯化碳溶液,溶液最终变为生成的1,2-二溴乙烷无色可溶于四氯化碳A无色透明乙酸乙酯和氢氧化钠溶液混合共热后,混合液乙酸乙酯在氢氧化钠溶液中可完全水解B不再分层葡萄糖与新制氢氧化铜混合共热后,生成砖红葡萄糖是还原性糖C色沉淀乙酸和乙醇都可与金属钠反应产生可燃性气乙酸分子中的氢与乙醇分子中的氢具有相同的活性D体A.A B.B C.C D.D5、用N A表示阿伏加德罗常数的值。
江苏省连云港市灌云县2024届高三高考猜题卷(一)数学试题

江苏省连云港市灌云县2024届高三高考猜题卷(一)数学试题考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数()(1)2z i i =++(i 是虚数单位),则复数z 在复平面内对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限2.某人2018年的家庭总收人为80000元,各种用途占比如图中的折线图,2019年家庭总收入的各种用途占比统计如图中的条形图,已知2019年的就医费用比2018年的就医费用增加了4750元,则该人2019年的储畜费用为( )A .21250元B .28000元C .29750元D .85000元3.抛物线的焦点为F ,准线为l ,A ,B 是抛物线上的两个动点,且满足23AFB π∠=,设线段AB 的中点M 在l 上的投影为N ,则MN AB的最大值是( )A 3B 3C 3D 34.已知函数2()sin 3cos444f x x x x πππ=,则(1)(2)...(2020)f f f +++的值等于( )A .2018B .1009C .1010D .20205.已知()()cos 0,0,,2f x A x A x R πωϕωϕ⎛⎫=+>><∈ ⎪⎝⎭的部分图象如图所示,则()f x 的表达式是( )A .32cos 24x π⎛⎫+⎪⎝⎭B .2cos 4x π⎛⎫+⎪⎝⎭C .2cos 24x π⎛⎫-⎪⎝⎭D .32cos 24x π⎛⎫-⎪⎝⎭6.总体由编号01,,02,…,19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法是随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为 7816 6572 0802 6314 0702 4369 9728 0198 3204 923449358200 3623486969387481A .08B .07C .02D .017.已知函数在上的值域为,则实数的取值范围为( ) A .B .C .D .8.已知抛物线24x y =上一点A 的纵坐标为4,则点A 到抛物线焦点的距离为( )A .2B .3C .4D .59.若直线20x y m ++=与圆222230x x y y ++--=相交所得弦长为25m =( ) A .1B .2C 5D .310.已知向量()1,3a =,b 是单位向量,若3a b -=,则,a b =( ) A .6π B .4π C .3π D .23π11.设全集()(){}130U x Z x x =∈+-≤,集合{}0,1,2A =,则U C A =( ) A .{}1,3-B .{}1,0-C .{}0,3D .{}1,0,3-12.已知P 为圆C :22(5)36x y -+=上任意一点,(5,0)A -,若线段PA 的垂直平分线交直线PC 于点Q ,则Q 点的轨迹方程为( )A .221916x y +=B .221916x y -=C .221916x y -=(0x <)D .221916x y -=(0x >)二、填空题:本题共4小题,每小题5分,共20分。
2023年高考【文科数学】猜题卷 附解析(全国卷)1

2023年普通高等学校招生全国统一考试文科数学猜题卷 (全国卷)【满分:150 分】一、选择题:本题共 12 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合,,.若,,则( ){}22,3,23A a a =--{}0,3B ={}2,C a =B A ⊆{}2A C =I a =A. B. C.1D.33-1-2.设复数z 满足( ) i 4z +=-=A.B. 42i -42i +3.若α是第二象限角,则是( ) 180α︒-A.第一象限角B.第二象限角C.第三象限角D.第四象限角4.一批学生分别来自于一班与二班,一班、二班中女生的占比分别为40%,50%.将这两个班的学生合编成一个大班,从大班中随机抽取1名学生,已知抽取到女生的概率为44%,然后从大班中随机抽取1名学生,若抽取到的是女生,则她来自一班的概率为( ) A.B. C.D.611352522755.在等差数列中,若,且它的前n 项和有最小值,则当时,n 的最小值为{}n a 981a a <-n S 0n S >( ) A.14B.15C.16D.176.若函数在点处的切线为直线,若直线l 与圆()()a f x x a x =+∈R (2,(2))f 1:2l y x b =+相切,则r 的值为( ) 222:(0)C r x y r =+>7.执行如图所示的程序框图,若输出S 的值为-90,则判断框中可填写( )A.B.C. 5 ?i <D.5?i >4?i > 4 ?i <8.定义在R 上的偶函数()f x 满足当时,1()f x x x =-,则不等式的解集0x >()0f x x>为( )A.(,1)(1,)-∞-+∞UB. (,1)(0,1)-∞-UC.(1,0)(1,)-+∞UD.(1,0)(0,1)-U 9.已知向量(,3)k =a ,,,且,则实数k 的值为( )(1,4)=b (2,1)=c (23)-⊥a b c A.B.0C.3D.92-15210.已知四棱锥SABCD 的底面是边长为2的正方形,平面平面ABCD ,SAD ⊥SA SD ⊥,,则四棱锥的外接球的表面积为( ). SA SD =S ABCD -11.已知为锐角,且,则( ) ,αβtan 2,cos()ααβ=+=tan()αβ-=A. B.C. D.913-913712-71212.已知函数在区间上有最小值,则实数a 的取值范围是( ). 3()e (3)1x f x x a x =++-+(0,1)A.B.C.D.(e,2)-(e,1e)--(1,2)(,1e)-∞-二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
2023年河北省衡水中学高考数学猜题卷(理科)(解析版)

2023年河北省衡水中学高考数学猜题卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出地四个选项中,只有一项是符合题目要求地.1.己知集合Q={x|2x2﹣5x≤0,x∈N},且P⊆Q,则满足条件地集合P地个数是( )A.3B.4C.7D.82.已知i是虚数单位,复数地虚部为( )A.﹣1B.1C.﹣i D.i3.某样本中共有5个个体,其中四个值分别为0,1,2,3,第五个值丢失,但该样本地平均值为1,则样本方差为( )A.2B.C.D.4.双曲线C:﹣=1(a>0,b>0)地离心率为2,焦点到渐近线地距离为,则C地焦距等于( )A.2B.2C.4D.45.若不等式组表示地平面区域是一个直角三角形,则该直角三角形地面积是( )A.B.C.D.或6.已知,则tan2α=( )A.B.C.D.7.《九章算术》是中国古代数学名著,体现了古代劳动人民数学地智慧,其中第六章"均输"中,有一竹节容量问题,某教师根据这一问题地思想设计了如下图所示地程序框图,若输出地m地值为35,则输入地a地值为( )A.4B.5C.7D.118.如下图所示,过抛物线y2=2px(p>0)地焦点F地直线l交抛物线于点A、B,交其准线l′点C,若|BC|=2|BF|,且|AF|=3,则此抛物线地方程为( )A.y2=9x B.y2=6x C.y2=3x D.9.已知以下三视图中有三个同时表示某一个三棱锥,则不是该三棱锥地三视图是( )A.B.C.D.10.在△ABC中,AB=AC=2,BC•cos(π﹣A)=1,则cosA地值所在区间为( )A.(﹣0.4,﹣0.3)B.(﹣0.2,﹣0.1)C.(﹣0.3,﹣0.2)D.(0.4,0.5)11.已知符号函数sgn(x)=,那么y=sgn(x3﹣3x2+x+1)地大致图象是( )A.B.C.D.12.已知函数f(x)=﹣,若对任意地x1,x2∈[1,2],且x1≠x2时,[|f(x1)|﹣|f (x2)|](x1﹣x2)>0,则实数a地取值范围为( )A.[﹣,]B.[﹣,]C.[﹣,]D.[﹣e2,e2]二、填空题(每题5分,满分20分,将解析填在答题纸上)13.已知,则地值是 .14.已知一个公园地形状如下图所示,现有3种不同地植物要种在此公园地A,B,C,D,E这五个区域内,要求有公共边界地两块相邻区域种不同地植物,则不同地种法共有 种.15.已知函数f(x)=sinx.若存在x1,x2,…,x m满足0≤x1<x2<…<x m≤6π,且|f (x1)﹣f(x2)|+|f(x2)﹣f(x3)|+…+|f(x m)﹣f(x m)|=12(m≥2,m∈﹣1N*),则m地最小值为 .16.已知等腰直角△ABC地斜边BC=2,沿斜边地高线AD将△ABC折起,使二面角B﹣AD﹣C为,则四面体ABCD地外接球地表面积为 .三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知等差数列{a n}地公差为2,前n项和为S n,且S1,S2,S4成等比数列.(Ⅰ)求数列{a n}地通项公式;(Ⅱ)令b n=(﹣1)n﹣1,求数列{b n}地前n项和T n.18.如图,在四棱锥E﹣ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DF地中点.(I)求证:BE∥平面ACF;(II)求平面BCF与平面BEF所成锐二面角地余弦角.19.鹰潭市龙虎山花语世界位于中国第八处世界自然遗产,世界地质公元、国家自然文化双遗产地、国家AAAAA级旅游景区﹣﹣龙虎山主景区排衙峰下,是一座独具现代园艺风格地花卉公园,园内汇集了3000余种花卉苗木,一年四季姹紫嫣红花香四溢.花园景观融合法、英、意、美、日、中六大经典园林风格,景观设计唯美新颖.玫瑰花园、香草花溪、台地花海、植物迷宫、儿童乐园等景点错落有致,交相呼应又自成一体,是世界园艺景观地大展示.该景区自2023年春建成试运行以来,每天游人如织,郁金香、向日葵、虞美人等赏花旺季日入园人数最高达万人.某学校社团为了解进园旅客地具体情形以及采集旅客对园区地建议,特别在2023年4月1日赏花旺季对进园游客进行取样调查,从当日12000名游客中抽取100人进行统计分析,结果如下:(表一)年龄频数频率男女[0,10)100.155[10,20)①②③④[20,30)250.251213[30,40)200.21010[40,50)100.164[50,60)100.137[60,70)50.0514[70,80)30.0312[80,90)20.0202合计100 1.004555(1)完成表格一中地空位①﹣④,并在答题卡中补全频率分布直方图,并估计2023年4月1日当日接待游客中30岁以下人数.(2)完成表格二,并问你能否有97.5%地把握认为在观花游客中"年龄达到50岁以上"与"性别"相关?(3)按分层抽样(分50岁以上与50以下两层)抽取被调查地100位游客中地10人作为幸运游客免费领取龙虎山内部景区门票,再从这10人中选取2人接受电视台采访,设这2人中年龄在50岁以上(含)地人数为ξ,求ξ地分布列(表二)50岁以上50岁以下合计男生 女生 合计 P (K 2≥k )0.150.100.050.0250.0100.0050.001k 2.072 2.706 3.841 5.024 6.6357.87910.828(参考公式:k 2=,其中n=a +b +c +d )20.给定椭圆C:=1(a>b>0),称圆心在原点O,半径为地圆是椭圆C地"准圆".若椭圆C地一个焦点为F(,0),其短轴上地一个端点到F地距离为.(Ⅰ)求椭圆C地方程和其"准圆"方程;(Ⅱ)点P是椭圆C地"准圆"上地动点,过点P作椭圆地切线l1,l2交"准圆"于点M,N.(ⅰ)当点P为"准圆"与y轴正半轴地交点时,求直线l1,l2地方程并证明l1⊥l2;(ⅱ)求证:线段MN地长为定值.21.已知函数f(x)=x2﹣alnx(a∈R)(1)若函数f(x)在x=2处地切线方程为y=x+b,求a,b地值;(2)讨论方程f(x)=0解地个数,并说明理由.[选修4-4:坐标系与参数方程]22.已知曲线C地极坐标方程是ρ2=4ρcosθ+6ρsinθ﹣12,以极点为原点,极轴为x 轴地正半轴建立平面直角坐标系,直线l地参数方程为(t为参数).(I)写出直线l地一般方程与曲线C地直角坐标方程,并判断它们地位置关系;(II)将曲线C向左平移2个单位长度,向上平移3个单位长度,得到曲线D,设曲线D经过伸缩变换得到曲线E,设曲线E上任一点为M(x,y),求地取值范围.[选修4-5:不等式选讲]23.设f(x)=|x﹣a|,a∈R(Ⅰ)当a=5,解不等式f(x)≤3;(Ⅱ)当a=1时,若∃x∈R,使得不等式f(x﹣1)+f(2x)≤1﹣2m成立,求实数m 地取值范围.2023年河北省衡水中学高考数学猜题卷(理科)参考解析与试卷解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出地四个选项中,只有一项是符合题目要求地.1.己知集合Q={x|2x2﹣5x≤0,x∈N},且P⊆Q,则满足条件地集合P地个数是( )A.3B.4C.7D.8【考点】18:集合地包含关系判断及应用.【分析】解出集合Q,再根据P⊆Q,根据子集地性质,求出子集地个数即为集合P 地个数;【解答】解:集合Q={x|2x2﹣5x≤0,x∈N},∴Q={0,1,2},共有三个元素,∵P⊆Q,又Q地子集地个数为23=8,∴P地个数为8,故选D;2.已知i是虚数单位,复数地虚部为( )A.﹣1B.1C.﹣i D.i【考点】A5:复数代数形式地乘除运算.【分析】利用复数地运算法则、虚部地定义即可得出.【解答】解:复数==i﹣2地虚部为1.故选:B.3.某样本中共有5个个体,其中四个值分别为0,1,2,3,第五个值丢失,但该样本地平均值为1,则样本方差为( )A.2B.C.D.【考点】BC:极差、方差与标准差.【分析】根据平均数公式先求出a,再计算它们地方差.【解答】解:设丢失地数据为a,则这组数据地平均数是×(a+0+1+2+3)=1,解得a=﹣1,根据方差计算公式得s2=×[(﹣1﹣1)2+(0﹣1)2+(1﹣1)2+(2﹣1)2+(3﹣1)2]=2.故选:A.4.双曲线C:﹣=1(a>0,b>0)地离心率为2,焦点到渐近线地距离为,则C地焦距等于( )A.2B.2C.4D.4【考点】KC:双曲线地简单性质.【分析】根据双曲线地离心率以及焦点到直线地距离公式,建立方程组即可得到结论.【解答】解:∵:﹣=1(a>0,b>0)地离心率为2,∴e=,双曲线地渐近线方程为y=,不妨取y=,即bx﹣ay=0,则c=2a,b=,∵焦点F(c,0)到渐近线bx﹣ay=0地距离为,∴d=,即,解得c=2,则焦距为2c=4,故选:C5.若不等式组表示地平面区域是一个直角三角形,则该直角三角形地面积是( )A.B.C.D.或【考点】7C:简单线性规划.【分析】依题意,三条直线围成一个直角三角形,可能会有两种情形,分别计算两种情形下三角形地顶点坐标,利用三角形面积公式计算面积即可.【解答】解:有两种情形:(1)由y=2x与kx﹣y+1=0垂直,则k=﹣,三角形地三个顶点为(0,0),(0,1),(,),三角形地面积为s=×1×=;(2)由x=0与kx﹣y+1=0形垂直,则k=0,三角形地三个顶点为(0.0),(0,1),(,1),三角形地面积为s=×1×=.∴该三角形地面积为或.故选:D.6.已知,则tan2α=( )A.B.C.D.【考点】GU:二倍角地正切.【分析】将已知等式两边平方,利用二倍角公式,同角三角函数基本关系式即可化简求值得解.【解答】解:∵,∴,化简得4sin2α=3cos2α,∴,故选:C.7.《九章算术》是中国古代数学名著,体现了古代劳动人民数学地智慧,其中第六章"均输"中,有一竹节容量问题,某教师根据这一问题地思想设计了如下图所示地程序框图,若输出地m地值为35,则输入地a地值为( )A.4B.5C.7D.11【考点】EF:程序框图.【分析】模拟程序框图地运行过程,求出运算结果即可.【解答】解:起始阶段有m=2a﹣3,i=1,第一次循环后m=2(2a﹣3)﹣3=4a﹣9,i=2,第二次循环后m=2(4a﹣9)﹣3=8a﹣21,i=3,第三次循环后m=2(8a﹣21)﹣3=16a﹣45,i=4,第四次循环后m=2(16a﹣45)﹣3=32a﹣93,跳出循环,输出m=32a﹣93=35,解得a=4,故选:A8.如下图所示,过抛物线y2=2px(p>0)地焦点F地直线l交抛物线于点A、B,交其准线l′点C,若|BC|=2|BF|,且|AF|=3,则此抛物线地方程为( )A.y2=9x B.y2=6x C.y2=3x D.【考点】K8:抛物线地简单性质.【分析】分别过点A,B作准线地垂线,分别交准线于点E,D,设|BF|=a,根据抛物线定义可知|BD|=a,进而推断出∠BCD地值,在直角三角形中求得a,进而根据BD∥FG,利用比例线段地性质可求得p,则抛物线方程可得.【解答】解:如图分别过点A,B作准线地垂线,分别交准线于点E,D,设|BF|=a,则由已知得:|BC|=2a,由定义得:|BD|=a,故∠BCD=30°,在直角三角形ACE中,∵|AE|=3,|AC|=3+3a,∴2|AE|=|AC|∴3+3a=6,从而得a=1,∵BD∥FG,∴=求得p=,因此抛物线方程为y2=3x.故选C.9.已知以下三视图中有三个同时表示某一个三棱锥,则不是该三棱锥地三视图是( )A.B.C.D.【考点】L!:由三视图求面积、体积.【分析】由已知中地四个三视图,可知四个三视图,分别表示从前、后、左、右四个方向观察同一个棱锥,但其中有一个是错误地,根据A与C中俯视图正好旋转180°,故应是从相反方向进行观察,而其正视图和侧视图中三角形斜边倾斜方向相反,满足实际情况,可得A,C均正确,而根据AC可判断B正确,D错误.【解答】解:三棱锥地三视图均为三角形,四个解析均满足;且四个三视图均表示一个高为3,底面为两直角边分别为1,2地棱锥A与C中俯视图正好旋转180°,故应是从相反方向进行观察,而其正视图和侧视图中三角形斜边倾斜方向相反,满足实际情况,故A,C表示同一棱锥设A中观察地正方向为标准正方向,以C表示从后面观察该棱锥B与D中俯视图正好旋转180°,故应是从相反方向进行观察,但侧视图中三角形斜边倾斜方向相同,不满足实际情况,故B,D中有一个不与其它三个一样表示同一个棱锥,根据B中正视图与A中侧视图相同,侧视图与C中正视图相同,可判断B是从左边观察该棱锥故选D10.在△ABC中,AB=AC=2,BC•cos(π﹣A)=1,则cosA地值所在区间为( )A.(﹣0.4,﹣0.3)B.(﹣0.2,﹣0.1)C.(﹣0.3,﹣0.2)D.(0.4,0.5)【考点】HR:余弦定理;HP:正弦定理.【分析】由题意求得cosA=﹣,再由余弦定理,得出关于﹣地方程,构造函数,利用函数零点地判断方法得出cosA地取值范围.【解答】解:△ABC中,AB=AC=2,BC•cos(π﹣A)=1,∴c=b=2,﹣acosA=1,cosA=﹣<0,且4>a>2;由余弦定理得,cosA==,∴﹣=,化为:8•﹣8•+1=0,令﹣=x∈(﹣,﹣),则f(x)=8x3﹣8x2+1=0,∵f(﹣0.4)=﹣1.4×1.28+1<0,f(﹣0.3)=0.064>0,∴cosA∈(﹣0.4,﹣0.3).故选:A.11.已知符号函数sgn(x)=,那么y=sgn(x3﹣3x2+x+1)地大致图象是( )A.B.C.D.【考点】3O:函数地图象.【分析】构造函数f(x)=x3﹣3x2+x+1,可整理得f(x)=(x﹣1)(x2﹣2x﹣1)=(x﹣1)(x﹣1﹣)(x﹣1+),利用排除法即可得到解析.【解答】解:令f(x)=x3﹣3x2+x+1,则f(x)=(x﹣1)(x2﹣2x﹣1)=(x﹣1)(x﹣1﹣)(x﹣1+),∴f(,1)=0,f(1﹣)=0,f(1+)=0,∵sgn(x)=,∴sgn(f(1))=0,可排除A,B;又sgn(f(1﹣))=0,sgn(f(1﹣))=0,可排除C,故选D.12.已知函数f(x)=﹣,若对任意地x1,x2∈[1,2],且x1≠x2时,[|f(x1)|﹣|f (x2)|](x1﹣x2)>0,则实数a地取值范围为( )A.[﹣,]B.[﹣,]C.[﹣,]D.[﹣e2,e2]【考点】6B:利用导数研究函数地单调性.【分析】由题意可知函数y=丨f(x)丨单调递增,分类讨论,根据函数地性质及对勾函数地性质,即可求得实数a地取值范围.【解答】解:由任意地x1,x2∈[1,2],且x1<x2,由[|f(x1)|﹣|f(x2)|](x1﹣x2)>0,则函数y=丨f(x)丨单调递增,当a≥0,f(x)在[1,2]上是增函数,则f(1)≥0,解得:0≤a≤,当a<0时,丨f(x)丨=f(x),令=﹣,解得:x=ln,由对勾函数地单调递增区间为[ln,+∞),故ln≤1,解得:﹣≤a<0,综上可知:a地取值范围为[﹣,],故选B.二、填空题(每题5分,满分20分,将解析填在答题纸上)13.已知,则地值是 ()2018 .【考点】DB:二项式系数地性质.【分析】利用二项式定理,对等式中地x赋值﹣2,可求得a0=0,再令x=,即可求出解析.【解答】解:∵(x+1)2(x+2)2016=a0+a1(x+2)+a2(x+2)+…+a2018(x+2)2018,∴令x=﹣2,得a0=0再令x=﹣,得到a0+=(﹣+1)2(﹣+2)2016=()2018,∴=,故解析为:()2018,14.已知一个公园地形状如下图所示,现有3种不同地植物要种在此公园地A,B,C,D,E这五个区域内,要求有公共边界地两块相邻区域种不同地植物,则不同地种法共有 18 种.【考点】D8:排列、组合地实际应用.【分析】根据题意,分2步进行分析:①、对于A、B、C区域,将3种不同地植物全排列,安排在A、B、C区域,由排列数公式可得其排法数目,②、对于D、E区域,分2种情况讨论:若A,E种地植物相同,若A,E种地植物不同;由加法原理可得D、E 区域地排法数目,进而由分步计数原理计算可得解析.【解答】解:根据题意,分2步进行分析:①、对于A、B、C区域,三个区域两两相邻,种地植物都不能相同,将3种不同地植物全排列,安排在A、B、C区域,有A33=6种情况,②、对于D、E区域,分2种情况讨论:若A,E种地植物相同,则D有2种种法,若A,E种地植物不同,则E有1种情况,D也有1种种法,则D、E区域共有2+1=3种不同情况,则不同地种法共有6×3=18种;故解析为:18.15.已知函数f(x)=sinx.若存在x1,x2,…,x m满足0≤x1<x2<…<x m≤6π,且|f)﹣f(x m)|=12(m≥2,m∈(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+…+|f(x m﹣1N*),则m地最小值为 8 .【考点】H2:正弦函数地图象.【分析】由正弦函数地有界性可得,对任意x i,x j(i,j=1,2,3,…,m),都有|f(x i)﹣f (x j)|≤f(x)max﹣f(x)min=2,要使m取得最小值,尽可能多让x i(i=1,2,3,…,m)取得最高点,然后作图可得满足条件地最小m值.【解答】解:∵y=sinx对任意x i,x j(i,j=1,2,3,…,m),都有|f(x i)﹣f(x j)|≤f(x)max﹣f(x)min=2,要使m取得最小值,尽可能多让x i(i=1,2,3,…,m)取得最高点,考虑0≤x1<x2<…<x m≤6π,|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+…+|f(x m)﹣1﹣f(x m)|=12,按下图取值即可满足条件,∴m地最小值为8.故解析为:8.16.已知等腰直角△ABC地斜边BC=2,沿斜边地高线AD将△ABC折起,使二面角B﹣AD﹣C为,则四面体ABCD地外接球地表面积为 .【考点】LG:球地体积和表面积.【分析】由题意,△BCD是等边三角形,边长为1,外接圆地半径为,AD=1,可得四面体ABCD地外接球地半径==,即可求出四面体ABCD地外接球地表面积.【解答】解:由题意,△BCD是等边三角形,边长为1,外接圆地半径为,∵AD=1,∴四面体ABCD地外接球地半径==,∴四面体ABCD地外接球地表面积为=,故解析为:.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知等差数列{a n}地公差为2,前n项和为S n,且S1,S2,S4成等比数列.(Ⅰ)求数列{a n}地通项公式;(Ⅱ)令b n=(﹣1)n﹣1,求数列{b n}地前n项和T n.【考点】8E:数列地求和;82:数列地函数特性;8H:数列递推式.【分析】(Ⅰ)利用等差数列与等比数列地通项公式及其前n项和公式即可得出;(Ⅱ)由(Ⅰ)可得b n=.对n分类讨论"裂项求和"即可得出.【解答】解:(Ⅰ)∵等差数列{a n}地公差为2,前n项和为S n,∴S n==n2﹣n+na1,∵S1,S2,S4成等比数列,∴,∴,化为,解得a1=1.∴a n=a1+(n﹣1)d=1+2(n﹣1)=2n﹣1.(Ⅱ)由(Ⅰ)可得b n=(﹣1)n﹣1==.∴T n=﹣++…+.当n为偶数时,T n=﹣++…+﹣=1﹣=.当n为奇数时,T n=﹣++…﹣+ =1+=.∴Tn=.18.如图,在四棱锥E﹣ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DF地中点.(I)求证:BE∥平面ACF;(II)求平面BCF与平面BEF所成锐二面角地余弦角.【考点】MT:二面角地平面角及求法;LS:直线与平面平行地判定.【分析】(1)连接BD和AC交于点O,连接OF,证明OF∥BE.然后证明BE∥平面ACF.(II)以D为原点,以DE所在直线为x轴建立如下图所示地空间直角坐标系,求出相关点地坐标,求出平面BEF地一个法向量,平面BCF地一个法向量,设平面BCF 与平面BEF所成地锐二面角为θ,利用数量积求解即可.【解答】解:(1)连接BD和AC交于点O,连接OF,因为四边形ABCD为正方形,所以O为BD地中点.因为F为DE地中点,所以OF∥BE.因为BE⊄平面ACF,OF⊂平面AFC,所以BE∥平面ACF.(II)因为AE⊥平面CDE,CD⊂平面CDE,所以AE⊥CD.因为ABCD为正方形,所以CD⊥AD.因为AE∩AD=A,AD,AE⊂平面DAE,所以CD⊥平面DAE.因为DE⊂平面DAE,所以DE⊥CD.所以以D为原点,以DE所在直线为x轴建立如下图所示地空间直角坐标系,则E(2,0,0),F(1,0,0),A(2,0,2),D(0,0,0).因为AE⊥平面CDE,DE⊂平面CDE,所以AE⊥CD.因为AE=DE=2,所以.因为四边形ABCD为正方形,所以,所以.由四边形ABCD为正方形,得==(2,2,2),所以.设平面BEF地一个法向量为=(x1,y1,z1),又知=(0,﹣2,﹣2),=(1,0,0),由,可得,令y1=1,得,所以.设平面BCF地一个法向量为=(x2,y2,z2),又知=(﹣2,0,﹣2),=(1,﹣2,0),由,即:.令y2=1,得,所以.设平面BCF与平面BEF所成地锐二面角为θ,又cos===.则.所以平面BCF与平面BEF所成地锐二面角地余弦值为.19.鹰潭市龙虎山花语世界位于中国第八处世界自然遗产,世界地质公元、国家自然文化双遗产地、国家AAAAA级旅游景区﹣﹣龙虎山主景区排衙峰下,是一座独具现代园艺风格地花卉公园,园内汇集了3000余种花卉苗木,一年四季姹紫嫣红花香四溢.花园景观融合法、英、意、美、日、中六大经典园林风格,景观设计唯美新颖.玫瑰花园、香草花溪、台地花海、植物迷宫、儿童乐园等景点错落有致,交相呼应又自成一体,是世界园艺景观地大展示.该景区自2023年春建成试运行以来,每天游人如织,郁金香、向日葵、虞美人等赏花旺季日入园人数最高达万人.某学校社团为了解进园旅客地具体情形以及采集旅客对园区地建议,特别在2023年4月1日赏花旺季对进园游客进行取样调查,从当日12000名游客中抽取100人进行统计分析,结果如下:(表一)年龄频数频率男女[0,10)100.155[10,20)①②③④[20,30)250.251213[30,40)200.21010[40,50)100.164[50,60)100.137[60,70)50.0514[70,80)30.0312[80,90)20.0202合计100 1.004555(1)完成表格一中地空位①﹣④,并在答题卡中补全频率分布直方图,并估计2023年4月1日当日接待游客中30岁以下人数.(2)完成表格二,并问你能否有97.5%地把握认为在观花游客中"年龄达到50岁以上"与"性别"相关?(3)按分层抽样(分50岁以上与50以下两层)抽取被调查地100位游客中地10人作为幸运游客免费领取龙虎山内部景区门票,再从这10人中选取2人接受电视台采访,设这2人中年龄在50岁以上(含)地人数为ξ,求ξ地分布列(表二)50岁以上50岁以下合计男生 5 40 45 女生 15 40 55 合计 20 80 100 P (K 2≥k )0.150.100.050.0250.0100.0050.001k2.0722.7063.841 5.024 6.6357.87910.828(参考公式:k 2=,其中n=a +b +c +d )【考点】CG:离散型随机变量及其分布列;BL:独立性检验.【分析】(1)由频率分布表地性质能完成表(一),从而能完成频率分布直方图,进而求出30岁以下频率,由此以频率作为概率,能估计2023年7月1日当日接待游客中30岁以下人数.(2)完成表格,求出K 2=≈4.04<5.024,从而得到没有97.5%地把握认为在观花游客中"年龄达到50岁以上"与"性别"相关.(3)由分层抽样应从这10人中抽取50岁以上人数:10×0.2=2人,50岁以下人数ξ地取值可能0,1,2,分别求出相应地概率,由此能求出ξ地分布列.【解答】解:(1)完成表(一),如下表:年龄频数频率男女[0,10)100.155[10,20)150.1578[20,30)250.251213[30,40)200.21010[40,50)100.164[50,60)100.137[60,70)50.0514[70,80)30.0312[80,90)20.0202合计100 1.004555完成频率分布直方图如下:30岁以下频率为:0.1+0.15+0.25=0.5,以频率作为概率,估计2023年7月1日当日接待游客中30岁以下人数为:12000×0.5=6000.(2)完成表格,如下:50岁以上50岁以下合计男生54045女生154055合计2080100K2==≈4.04<5.024,所以没有97.5%地把握认为在观花游客中"年龄达到50岁以上"与"性别"相关.(3)由分层抽样应从这10人中抽取50岁以上人数:10×0.2=2人,50岁以下人数ξ地取值可能0,1,2P(ξ=0)==,P(ξ=1)==,P(ξ=2)==.∴ξ地分布列为:ξ012P20.给定椭圆C:=1(a>b>0),称圆心在原点O,半径为地圆是椭圆C地"准圆".若椭圆C地一个焦点为F(,0),其短轴上地一个端点到F地距离为.(Ⅰ)求椭圆C地方程和其"准圆"方程;(Ⅱ)点P是椭圆C地"准圆"上地动点,过点P作椭圆地切线l1,l2交"准圆"于点M,N.(ⅰ)当点P为"准圆"与y轴正半轴地交点时,求直线l1,l2地方程并证明l1⊥l2;(ⅱ)求证:线段MN地长为定值.【考点】KH:直线与圆锥曲线地综合问题.【分析】(Ⅰ)利用已知椭圆地标准方程及其即可得出;(Ⅱ)(i)把直线方程代入椭圆方程转化为关于x地一元二次方程,利用直线与椭圆相切⇔△=0,即可解得k地值,进而利用垂直与斜率地关系即可证明;(ii)分类讨论:l1,l2经过点P(x0,y0),又分别交其准圆于点M,N,无论两条直线中地斜率是否存在,都有l1,l2垂直.即可得出线段MN为准圆x2+y2=4地直径.【解答】(Ⅰ)解:∵椭圆C地一个焦点为F(,0),其短轴上地一个端点到F地距离为.∴,,∴=1,∴椭圆方程为,∴准圆方程为x2+y2=4.(Ⅱ)证明:(ⅰ)∵准圆x2+y2=4与y轴正半轴地交点为P(0,2),设过点P(0,2)且与椭圆相切地直线为y=kx+2,联立得(1+3k2)x2+12kx+9=0.∵直线y=kx+2与椭圆相切,∴△=144k2﹣4×9(1+3k2)=0,解得k=±1,∴l1,l2方程为y=x+2,y=﹣x+2.∵,∴l1⊥l2.(ⅱ)①当直线l1,l2中有一条斜率不存在时,不妨设直线l1斜率不存在,则l1:,当l1:时,l1与准圆交于点,此时l2为y=1(或y=﹣1),显然直线l1,l2垂直;同理可证当l1:时,直线l1,l2垂直.②当l1,l2斜率存在时,设点P(x0,y0),其中.设经过点P(x0,y0)与椭圆相切地直线为y=t(x﹣x0)+y0,∴由得.由△=0化简整理得,∵,∴有.设l1,l2地斜率分别为t1,t2,∵l1,l2与椭圆相切,∴t1,t2满足上述方程,∴t1•t2=﹣1,即l1,l2垂直.综合①②知:∵l1,l2经过点P(x0,y0),又分别交其准圆于点M,N,且l1,l2垂直.∴线段MN为准圆x2+y2=4地直径,|MN|=4,∴线段MN地长为定值.21.已知函数f(x)=x2﹣alnx(a∈R)(1)若函数f(x)在x=2处地切线方程为y=x+b,求a,b地值;(2)讨论方程f(x)=0解地个数,并说明理由.【考点】6K:导数在最大值、最小值问题中地应用;54:根地存在性及根地个数判断;6H:利用导数研究曲线上某点切线方程.【分析】(1)求出导函数,利用f(x)在x=2处地切线方程为y=x+b,列出方程组求解a,b.(2)通过a=0,a<0,判断方程地解.a>0,求出函数地导数判断函数地单调性,求出极小值,分析出当a∈[0,e)时,方程无解;当a<0或a=e时,方程有惟一解;当a >e时方程有两解.【解答】解:(1)因为:(x>0),又f(x)在x=2处地切线方程为y=x+b所以解得:a=2,b=﹣2ln2…(2)当a=0时,f(x)在定义域(0,+∞)上恒大于0,此时方程无解;…当a<0时,在(0,+∞)上恒成立,所以f(x)在定义域(0,+∞)上为增函数.∵,,所以方程有惟一解.…当a>0时,因为当时,f'(x)>0,f(x)在内为减函数;当时,f(x)在内为增函数.所以当时,有极小值即为最小值…当a∈(0,e)时,,此方程无解;当a=e时,.此方程有惟一解.当a∈(e,+∞)时,,因为且,所以方程f(x)=0在区间上有惟一解,因为当x>1时,(x﹣lnx)'>0,所以x﹣lnx>1,所以,,因为,所以,所以方程f(x)=0在区间上有惟一解.所以方程f(x)=0在区间(e,+∞)上有惟两解.…综上所述:当a∈[0,e)时,方程无解;当a<0或a=e时,方程有惟一解;当a>e时方程有两解.…[选修4-4:坐标系与参数方程]22.已知曲线C地极坐标方程是ρ2=4ρcosθ+6ρsinθ﹣12,以极点为原点,极轴为x 轴地正半轴建立平面直角坐标系,直线l地参数方程为(t为参数).(I)写出直线l地一般方程与曲线C地直角坐标方程,并判断它们地位置关系;(II)将曲线C向左平移2个单位长度,向上平移3个单位长度,得到曲线D,设曲线D经过伸缩变换得到曲线E,设曲线E上任一点为M(x,y),求地取值范围.【考点】Q4:简单曲线地极坐标方程;O7:伸缩变换.【分析】(I)直线l地参数方程消去数t,能求出直线l地一般方程,由ρcosθ=x,ρsinθ=y,ρ2=x2+y2,能求出曲线C地直角坐标方程,由圆心(2,3)到直线l地距离d=r,得到直线l和曲线C相切.(II)曲线D为x2+y2=1.曲线D经过伸缩变换,得到曲线E地方程为,从而点M地参数方程为(θ为参数),由此能求出地取值范围.【解答】解:(I)∵直线l地参数方程为(t为参数).∴消去数t,得直线l地一般方程为,∵曲线C地极坐标方程是ρ2=4ρcosθ+6ρsinθ﹣12,∴由ρcosθ=x,ρsinθ=y,ρ2=x2+y2,得曲线C地直角坐标方程为(x﹣2)2+(y﹣3)2=1.∵圆心(2,3)到直线l地距离d==r,∴直线l和曲线C相切.(II)曲线D为x2+y2=1.曲线D经过伸缩变换,得到曲线E地方程为,则点M地参数方程为(θ为参数),∴,∴地取值范围为[﹣2,2].[选修4-5:不等式选讲]23.设f(x)=|x﹣a|,a∈R(Ⅰ)当a=5,解不等式f(x)≤3;(Ⅱ)当a=1时,若∃x∈R,使得不等式f(x﹣1)+f(2x)≤1﹣2m成立,求实数m 地取值范围.【考点】R2:绝对值不等式.【分析】(Ⅰ)将a=5代入解析式,然后解绝对值不等式,根据绝对值不等式地解法解之即可;(Ⅱ)先利用根据绝对值不等式地解法去绝对值,然后利用图象研究函数地最小值,使得1﹣2m大于等于不等式左侧地最小值即可.【解答】解:(I)a=5时原不等式等价于|x﹣5|≤3即﹣3≤x﹣5≤3,2≤x≤8,∴解集为{x|2≤x≤8};(II)当a=1时,f(x)=|x﹣1|,令,由图象知:当时,g(x)取得最小值,由题意知:,∴实数m地取值范围为.2023年7月23日31。
2023届全国新高考高三下学期4月数学猜题卷(3)(PDF版)

2023届高三下学期4月新高考数学猜题卷(3)【满分:150分】一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{2,1,0,1,2,3}U =--,集合{1,2}A =-,{}2|430B x x x =-+=,则()U A B =ð( ) A.{1,3}B.{0,3}C.{2,1}-D.{2,0}-2.若复数z 满足()42i (3i)z +=-=( )=a =+=b4.设某芯片制造厂有甲、乙两条生产线均生产5nm 规格的芯片,现有20块该规格的芯片,其中甲、乙生产的芯片分别为12块,8块,且乙生产该芯片的次品率为120,现从这20块芯片中任取一块芯片,若取得芯片的次品率为0.08,则甲厂生产该芯片的次品率为( ) A.15B.110C.115D.1205.圆锥的母线长为4,侧面积是底面积的倍,过圆锥的两条母线作圆锥的截面,则该截面面积的最大值是( ) A.8B. C.D.6.已知的图象关于点(1,0)对称,且对任意x ∈R ,都有(1)(3)f x f x -=-成立,当[1,0)∈-时,,则(2021)f =( ). A.-8B.-2C.0D.27.《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著.《九章算术》内容十分丰富,全书总结了战国、秦、汉时期的数学成就,它是一本综合性的历史43(1)y f x =-2()2f x x =著作,是当时世界上最简练有效的应用数学,它的出现标志中国古代数学形成了完整的体系.其中卷第五《商功》中记载了如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”其意思为“现在有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,无宽,上棱长2丈,高1丈,问它的体积是多少?”(1丈为10尺).该问题中涉及的几何体如图所示,在多面体中,//EF 平面的中点G 在底面ABCD 上的射影为矩形的中心,4,3,2,1O AB BC EF OG ====,则异面直线与CF 所成角的余弦值为( )A.C. 8.已知1F ,2F 为椭圆2222:1(0)x y C a b a b+=>>的左、右焦点,过原点O 且倾斜角为30°的直线l 与椭圆C 的一个交点为A ,若12AF AF ⊥,122AF F S =V ,则椭圆C 的方程为( )A.22162x y += B.22184x y += C.22182x y +=D.2212016x y += 二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分. 9.若,a b ∈R ,且0ab >,则下列不等式中,恒成立的是( ) A.222a b ab +≥ B.a b +≥1b+>2a b≥10.已知函数()sin(2)f x x ωϕ=+(ω为正整数,π||2ϕ<)的最小正周期3π3π,42T ⎛⎫∈ ⎪⎝⎭,将函数()f x 的图象向右平移π6个单位长度后所得图象关于原点对称,则下列关于函数()f x 的说法正确的是( ) A.6π-是函数()f x 的一个零点 B.函数()f x 的图象关于直线5π12x =-对称 C.方程1()2f x =在[0,π]上有三个解 ABCDEF ,ABCD EF ABCD BDD.函数()f x 在ππ,62⎛⎫⎪⎝⎭上单调递减11.已知函数32()(,,)f x x ax bx c a b c =+++∈R ,则下列说法正确的是( ) A.若实数1x ,2x 是()f x 的两个不同的极值点,且满足1212x x x x +=,则0a >或6a <-B.函数()f x 的图象过坐标原点的充要条件是0c =C.若函数()f x 在R 上单调,则23b a ≤D.若函数()f x 的图象关于点(1,(1))f 中心对称,则3a =-12.正四面体PABC 中,点,M N 分别满足1,2PM PA PN PB λ==uuu ruu r uuur uu r,其中[0,1]λ∈,则下列说法正确的有( ) A.当12λ=时,//MN 平面ABC B.不存在λ使得MN PC ⊥C.异面直线BM 与PCD.若正四面体的棱长为三、填空题:本题共4小题,每小题5分,共20分.13.已知数列{}n a 的前n 项和为n S ,且2n n a n S -=,则2023a =________.14.()82112x x x ⎛⎫++ ⎪⎝⎭的展开式中常数项为_________.(用数字作答)15.已知双曲线2222:1(0,x y C a b a b-=>>交于A ,B 两点,M 是线段AB 的中点,O 为坐标原点.若点M 的横坐标为1,则16.已知函数e ()xf x x=,,当21x x >时,不等式恒成立,则实数a 的取值范围为____________.四、解答题:本题共6题,共70分.解答应写出文字说明、证明过程或演算步骤.(0,)x ∈+∞()()112221f x ax f x ax x x --<17.(10分)已知数列{}n a 的前n 项和为. (1)若12S =,,证明:12n n S a +=-;(2)在(1)的条件下,若,数列{}n b 的前n 项和为,求证12311112nT T T T ++++<. 18.(12分)已知菱形ABCD 的边长为2,,E 是边BC 上一点,线段DE 交AC 于点F .(1)若CDE △,求DE 的长. (2)若4DF =,求.19.(12分)某工厂统计了某产品的原材料投人x (万元)与利润y (万元)间的几组数据如下: (1)根据经验可知原材料投人x (万元)与利润y (万元)间具有线性相关关系,求利润y (万元)关于原材料投人x (万元)的线性回归方程.(2)当原材料投人为100万元时,预估该产品的利润为多少万元?附:ˆb=y bx =-.20.(12分)如图,PO 是三棱锥P ABC -的高,,AB AC ⊥,E 是PB 的中点.n S 122n n S S +=+2log n n b a =n T 60DAB ∠=︒sin DFC ∠PA PB =(1)求证:平面PAC ;(2)若30ABO CBO ∠=∠=︒,,5PA =,求二面角正余弦值. 21.(12分)已知O 是平面直角坐标系的原点,F 是抛物线2:2(0)C x py p =>的焦点,过点F 的直线交抛物线于A ,B 两点,且OAB △的重心G 在曲线29620x y -+=上.(1)求抛物线C 的方程;(2)记曲线29620x y -+=与y 轴的交点为D ,且直线AB 与x 轴相交于点E ,弦AB 的中点为M ,求四边形DEMG 面积的最小值.22.(12分)已知函数e (1)()ea axx f x -=(其中e 为自然对数的底数,a ∈R ). (1)当1a =时,求曲线()y f x =在点(2,(2))f 处的切线方程;(2)若,方程()10f x a +-=有两个不同的实数根,求证:22122e x x +>.//OE 3PO =C AE B --0a >12,x x答案1.答案:D2.答案:D3.答案:B4.答案:B5.答案:A6.答案:B7.答案:D8.答案:A9.答案:AD 10.答案:ABD 11.答案:ABD 12.答案:AD 13.答案:202321- 14.答案:18215.答案:)+∞16.答案:e ,2⎛⎤-∞ ⎥⎝⎦17.答案:(1)见解析 (2)见解析解析:(1)因为12S =,122n n S S +=+, 所以()1222n n S S ++=+,124S +=,所以数列{}2n S +是以4为首项,2为公比的等比数列, 所以122n n S ++=,122n n S +∴=-,当2n ≥时,122n n S -=-,12n n n n S S a --==, 当1n =时,112a S ==满足上式,所以2n n a =,所以12n n S a +=-成立. (2)由(1)知2n n a =,2log n n b a n ==,所以(1)2n n n T +=, 则12112(1)1n T n n n n ⎛⎫==⨯- ⎪++⎝⎭, 所以1231111n T T T T ++++=11111111212122233411n n n ⎛⎫⎛⎫⨯-+-+-++-=⨯-< ⎪⎪++⎝⎭⎝⎭, 所以12311112nT T T T ++++<成立. 18.答案:(2)14解析:(1)依题意,得60BCD DAB∠=∠=︒. 因为CDE △的面积1sin 2S CD CE BCD=⋅⋅∠=所以122CE ⨯=,解得1CE =. 在CDE △中,由余弦定理得DE ==(2)方法一:连接BD .依题意,得30,60ACD BDC ∠=︒∠=︒, 设CDE θ∠=,则060θ︒<<︒,在CDF △中,由正弦定理得sin sin CF DFACDθ=∠, 因为4DF =,所以sin2CF DF θ==,所以cos θ=()1sin sin 30+2DFC θ∠=︒==. 方法二:连接BD .依题意,得30ACD ∠=︒,60BDC ∠=︒,设CDE θ∠=,则0060︒<<︒,设4CF x =,因为4DF =,则DF ,在CDF △中,由余弦定理,得2222cos DF CD CF CD CF ACD =+-⋅∠,即227416x x =+-,解得x =x =.又因为12CF AC ≤=x ≤,所以所以DF =在中,由正弦定理得sin sin CD DFDFC ACD=∠∠, 所以19.答案:(1)221040y x =- (2)1160万元()18284858688855=⨯++++=,()1770800830850900830,5y =⨯++++= 所以()()()51521ˆii i ii xx y y bxx ==--=-∑∑()()()()2222360130012037022(3)(1)013-⨯-+-⨯-++⨯+⨯==-+-+++所以83022851040a y bx =-=-⨯=-, 所以线性回归方程为221040y x =-.(2)当100x =时,2210010401160y =⨯-=(万元),即当原材料投人为100万元时,预估该产品的利润为1160万元 20.答案:(1)证明见解析 (2)1113解析:(1)如图,取AB 的中点D ,连接DP ,DO ,DE .x =CDF △sin DFC ∠因为AP PB =,所以PD AB ⊥.因为PO 为三棱锥P ABC -的高,所以PO ⊥平面ABC , 因为AB ⊂平面ABC ,所以PO AB ⊥.又,PO PD ⊂平面POD ,且PO PD P =,所以AB ⊥平面POD . 因为OD ⊂平面POD ,所以AB OD ⊥,又AB AC ⊥,所以//OD AC ,因为OD ⊂/平面PAC ,AC ⊂平面PAC ,所以//OD 平面PAC .因为D ,E 分别为BA ,BP 的中点,所以//DE PA , 因为DE ⊂/平面PAC ,PA ⊂平面PAC ,所以//DE 平面PAC . 又,OD DE ⊂平面ODE ,OD DE D =, 所以平面//ODE 平面PAC .又OE ⊂平面ODE ,所以//OE 平面PAC . (2)连接OA ,因为PO ⊥平面ABC ,,OA OB ⊂平面ABC , 所以PO OA ⊥,PO OB ⊥,所以4OA OB ===. 易得在AOB △中,30OAB ABO ∠=∠=︒,所以1sin 30422OD OA =︒=⨯=,22cos3024AB AD OA ==︒=⨯= 又60ABC ABO CBO ∠=∠+∠=︒,所以在Rt ABC △中,tan 6012AC AB =︒=.以A 为坐标原点,AB ,AC 所在直线分别为x ,y 轴,以过A 且垂直于平面ABC的直线为z 轴建立空间直角坐标系,如图所示,则(0,0,0)A ,(43,0,0)B ,(0,12,0)C ,(23,2,3)P ,333,1,2E ⎛⎫ ⎪⎝⎭,设平面AEC 的法向量为(,,)x y z =n ,则00AE AC ⎧⋅=⎪⎨⋅=⎪⎩n n ,即33302120x y z y ⎧++=⎪⎨⎪=⎩, 令23z =,则(1,0,23)=-n .设平面AEB 的法向量为()111,,x y z =m ,则0AE AB ⎧⋅=⎪⎨⋅=⎪⎩m m ,即111133302430x y z x ⎧++=⎪⎨⎪=⎩,令12z =,则(0,3,2)=-m .所以43|cos ,|||||13⋅〈〉==⋅n m n m n m .设二面角C AE B --的大小为θ,则24311sin 11313θ⎛⎫=-= ⎪ ⎪⎝⎭.21.答案:(1)22x y = 0,2p F ⎛⎫⎪⎝⎭,显然直线AB 的斜率存在,设:2p AB y kx =+,与22x p y=联立,消去y 得2220x pkx p --=,设()11,A x y ,()22,B x y ,()00,G x y ,则212122,x x pk x x p +==-,所以()212122y y k x x p pk p +=++=+,所以0202,32,3pk x pk p y ⎧=⎪⎪⎨+⎪=⎪⎩且20032x y =22341293p k =⋅+=即222221pk p p k +=+,整理得()2211pk p p -=-对任意的k 恒成立,故1p =,所求抛物线C 的方程为22x y =.(2)由题知10,2F ⎛⎫ ⎪⎝⎭,10,3D ⎛⎫ ⎪⎝⎭,1,02E k ⎛⎫- ⎪⎝⎭,0k ≠,M x k =,G x 23=.又弦AB 的中点为M,△=O G O M ==//ME .点D 到直线AB 的距离1d =DG =1122k k k ⎫⎛⎫=--+⎪ ⎪⎪⎝⎭⎭ 所以四边形DEMG 的面积25111132123212k k S k k k ⎛⎫⎛⎫=++=+≥⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭==22.答案:(1)1ey =(2)见解析解析:(1)当1a =时,e(1)()ex x f x -=, 则121(),(2)e e x x f x f --==', 因此()'20f =,故曲线()y f x =在点(2,(2))f 处的切线方程为1e y =.(2)由题意知方程e 0ax x a --=有两个不同的实数根12,x x . 对于函数e (0),e (1)ax ax y x a a y ax --=>=-'-, 令e (1)0ax y ax -=->',解得1x a <,令e (1)0ax y ax -=-<',解得1x a>,则函数e ax y x a -=-在区间1,a ⎛⎫-∞ ⎪⎝⎭上单调递增,在区间1,a ⎛⎫+∞ ⎪⎝⎭上单调递减, 所以11e 0a a -->,得21e a <. 又当0x <时,e 0ax x a --<,所以方程e 0ax x a --=的两个不同的实数根12,x x 均大于0.当0x >时,方程e 0ax x a --=即方程ln ln e e x ax a -=, 则原问题等价于ln ln x ax a -=有两个不同的正实数根12,x x . 令()ln ln (0)g x x ax a x =-->, 则1()(0)g x a x x->'=,所以()g x 在10,a ⎛⎫ ⎪⎝⎭上单调递增,在1,a ⎛⎫+∞ ⎪⎝⎭上单调递减, 不妨设12x x <,则1210x x a<<<. 令21()(),0,G x g x g x x a a ⎛⎫⎛⎫=--∈ ⎪ ⎪⎝⎭⎝⎭, 则22()2201(2)G x a a x ax a=->-'=-, 因此()G x 在10,a ⎛⎫ ⎪⎝⎭上单调递增,从而当10,x a ⎛⎫∈ ⎪⎝⎭时,()0G x <, 所以()()1212g x g x g x a ⎛⎫=<- ⎪⎝⎭, 因为2121,,x x a a ⎛⎫-∈+∞ ⎪⎝⎭,函数()g x 在1,a ⎛⎫+∞ ⎪⎝⎭上单调递减, 所以212x x a >-,即122x x a +>,则()2122212222e 2x x x x a ++>>>, 故原命题得证.。
2024年山东省高考物理考前猜测练习题四 (2)

2024年山东省高考物理考前猜测练习题四一、单选题 (共6题)第(1)题2023年,神舟家族太空接力,“奋斗者”号极限深潜,真正实现了“可上九天揽月,可下五洋捉鳖”!已知“奋斗者”号在马里亚纳海沟的坐底深度为,空间站离地面的高度为。
假设地球质量分布均匀,半径为,不考虑其自转,且质量均匀分布的球壳对壳内物体的引力为零,则深度为处和高度为处的重力加速度之比为( )A .B .C .D .第(2)题列车在平直轨道上由静止开始启动,启动过程受到的合外力F 随时间变化的关系图像如图所示,列车达到额定功率后保持该功率不变,若列车所受阻力恒定,则( )A .时刻,列车刚达到额定功率B .时间内,列车的功率随时间增大得越来越慢C .时间内,列车的合力的功率随速率均匀减小D .时间内,列车先后做匀加速直线运动和匀速直线运动第(3)题两个等量同种电荷固定于光滑水平面上,其连线的中垂线(在水平面内)上有A 、B 、C 三点,如图甲所示,一个电荷量为2×10-5C 、质量为1g 的小物块从C 点静止释放,其运动的v -t 图像如图乙所示,其中B 点处为整条图线的切线斜率最大的位置(图中标出了该切线)。
则下列说法正确的是( )A .小物块带负电B .A 、B 两点间的电势差U AB =500VC .小物体由C 点到A 点电势能先减小再增大D .B 点为中垂线上电场强度最大的点,场强E =100V/m第(4)题如图,在水平面(纸面)内有三根相同的均匀金属棒ab 、ac 和MN ,其中ab 、ac 在a 点接触,构成“V”字型导轨.空间存在垂直于纸面的均匀磁场.用力使MN 向右匀速运动,从图示位置开始计时,运动中MN 始终与∠bac 的平分线垂直且和导轨保持良好接触.下列关于回路中电流i 与时间t 的关系图线.可能正确的是A.B.C.D.第(5)题一列简谐横渡沿x轴正方向传播,时刻恰好传播到处,波形如图所示。
时,平衡位置为的质点A第一次到达波峰。
2023届福建新高考金榜猜题历史试卷

2023届福建新高考历史金榜猜题卷一、选择题,本题共16小题,每小题3分,共计48分。
1.西周晚期至春秋早期,西至渭河上游、东至渤海湾的不同国族的贵族墓葬中的青铜礼器,都具有相似的器物组合、造型样式和纹饰种类。
据此可知A.各地生产力水平趋向于平衡B.青铜礼器被赋予了宗教色彩C.分封制扩大了周朝统治疆域D.不同地区的文化进一步融合2.面对“礼崩乐坏”的社会现实,孔子提出“仁”和“克己复礼为仁”等思想;孟子认为道德修养是圣人才德的重要组成部分;荀子提出君子“至德”的实现是遵循道德的结果。
据此可知,他们都强调A.道德自律理应是个体的自觉追求B.独立平等是个体道德自律的前提C.只有道德自律才能建立和谐社会D.诸侯国君是社会道德自律的楷模3.《齐民要术·序》中说:“今采据经传,爱及歌谣,询之老成,验之行事,直自农耕,终于醺醺(酿造、腌制之法),资生之业,靡不毕书,号曰《齐民要术》。
”这段话体现了A.农业技术的重要性B.统治阶级对农业的重视C.农书与农业的关系D.古代重视农业经验总结4.隋至唐前期的中书门下是决策首脑机关,从不负担琐碎事务。
唐代中后期至宋代的中书门下承担了大量的日常政务性工作,出现了中枢机构政务化的趋向。
宋代的设官分职方式,在“从睉芜杂”的表象背后,突出了国家政务的核心内容。
上述变化主要表明A.吏治渐趋清廉化B.部门间关系更融洽C.官员日趋专业化D.中央集权显著加强5.南宋时期,继承程颐理学的朱熹、宣传心学的陆九渊等人,各立学舍,聚徒讲学,促进了书院的发展,其各派门人为了宣传师学又大办书院。
南宋书院的繁荣A.推动了理学传播和发展B.促使各派思想趋于合流C.源于儒学正统地位动摇D.体现儒学陷入矛盾困境6.上表为不同史籍关于明代内阁的历史叙述。
据此可以推断,明代内阁A.掌握最高行政权力 B.权力因皇权需要而浮动C.阁臣政治地位低下D.无法影响朝廷政局发展7.《清实录》中关于“国体”有不同的记载。
2023届江苏省新高考历史金榜猜题卷

2023届江苏新高考历史金榜猜题卷一、选择题,本题共16小题,每小题3分,共计48分。
1.考古发掘显示,夏都二里头被外来者占领后,增加了一些外来样式的陶器,有的属于河北和河南两省交界处的下七垣文化,有的属于山东地区的岳石文化。
之后,商人新建了两座城邑——郑州商城和偃师商城,但其陶器风格多样程度甚至超过被占领后的二里头古城。
这些现象()A.反映了国家大一统局面B.体现了战后的文化割裂C.印证了早期文明的特征D.显示了早期商业的盛况2.2023年1月陕西发布秦兵马俑第三次考古发掘发现,共清理陶俑220余件、陶马16匹、战车4乘、鼓2处、鼓槌1处、漆盾1处、笼箙3处;兵器柲多处、弓弩箭箙多处,发现车马器、兵器、生产工具等共计千余件(组),按照排列密度估计,全部发掘后可出土陶俑、陶马约6000件。
对这一考古发掘解释最为合理的是()A.初步厘清军阵排列规律B.明确武器的种类与配属C.清楚了陶俑的制作程序D.展示秦朝军事实力强大3.唐代尚书省实行制敕、管理行政的会商制度,尚书省的首脑机构都省有都堂会议。
六部尚书每天上午都前往都省,有事则开会商讨,午时则在都堂会食,下午仍回本部处置都务。
这一会商制度()A.提高了中央政府决策效率B.对宰相政务工作有监督作用C.有助于权力的制约和平衡D.有利于行政部门的分工协作4.北宋都城汴京每年三月都会在金明池举办各种水戏表演,吸引了众多市民观赏《东京梦华录》载“又有两画船,上立秋千……又一人上蹴秋千,将平架,筋斗掷身人水”(如下图所示)。
这反映了北宋()A.城市市民丰富的娱乐生活B.崇尚力量成为社会的风尚C.市民热衷于进行体育运动D.城市娱乐功能进一步突出5.顾炎武在编写《天下郡国利病书》时,以骡马载着书籍,以实地考察来证实文献所载。
但他的行旅所至重在西北,东南尤其是南洋一带并未涉足,在书写佛郎机(葡萄牙)时,仍把它纳入南蛮序列,与苏门答腊、锡兰、苏禄等放在一起。
这体现出顾炎武()A.在学术研究中仍缺少实证精神B.延续了传统文人对外部世界的认知C.对东西方文明交流的茫然无知D.试图修正旧的华夷之辨的观念误区6.1860年5月,英法联军欲大举进犯京津大沽时,两江总督何桂清等人却与侵略军商议“借师助剿”之事。
2023届广东新高考金榜猜题历史试卷

2023届广东新高考历史金榜猜题卷一、选择题,本题共16小题,每小题3分,共计48分。
1.有学者在谈到《淮南子》“尚论诸家学说发生之所由来”时说:“自庄、荀以下评骘诸子,皆比较其同异得失,独淮南则尚论诸家学说发生之所由来,大指谓皆起于时势之需求而救其偏敝,其言盖含有相当之真理。
”据此可知,诸子学说的兴起( )A.体现了鲜明的文化目的性B.促进了社会变革的到来C.彰显了各学派风格的特性D.提供了文化重组的机会2.汉文帝即位前,已经在京城长安北侧建起了一个与匈奴的缓冲地带并初步形成了汉朝帝王的祖陵区。
至文帝时,却将自己陵墓选址在长安以东、扼守通往关东主要道路的白鹿原霸上。
文帝改变陵墓选址最有可能是由于( )A.应对五国势力的需要B.治国思想发生了变化C.与匈奴关系已经缓和D.为了凸显个人的功绩3.唐太宗去世后,吐蕃、突厥、奚、契丹等少数民族的骑兵不断袭扰边境地区。
数以万计的敌军行踪不定,中央政府难以准确预判各边镇实际布防所需兵力,且由中央政府统一调配的后勤体系也难以应对突发的战事。
这有助于解释,唐代前中期( )A.中央集权体制的破坏B.疆域不断缩小的困局C.民族交融强化的趋势D.地方武将权力的扩张4.儒学思想家在不同时期对人性有不同的主张,如下表所示。
据下表可知( )孟子《孟子·尽心上》人之所不学而能者,其良能也;所不虑而知者,其良知也。
亲亲,仁也;敬长,义也。
无他,达之天下也。
荀子《荀子·礼论》性者,本始材朴也;伪(人为)者,文理隆盛也。
无性则伪之无所加;无伪则性不能自美。
性伪合而天下治。
董《春秋繁天生民性有普质,而未能善,于是为之立王以善仲舒 露·洞察名号》之,次民天意也。
在承天意,以成民之性为任者也。
朱熹《朱子语类》卷四心统性情。
心有善恶,性无不善。
然而有生下来善底,有生下来便恶底,此是气禀不同C.以仁为规范和支撑方能止于至善D.儒学人性说随时代的变化面演变5.下表是有关利玛窦来华的部分史料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)通过流程分析,最后 综上分析可知,滤液中的主要成分为NH4Cl,浓缩以后 得到的固体物质为NH4Cl; (3)根据题给相关物质的数据可有以下计算 0.896L 2 n CO 2 4.00 10 mol 1 22.4L mol 2.00g 2 n MgO 5.00 10 mol 1 40g mol
18、(12分)碱式碳酸铝镁[MgaAlb(OH)c(CO3)d· x H2O]常用作塑料阻燃剂。 (1)碱式碳酸铝镁具有阻燃作用,是由于其受热分解需吸收大量热量和----------(2)MgaAlb(OH)c(CO3)d· x H2O中a、b、c、d的代数关系式为 (3)为确定碱式碳酸铝镁的组成,进行如下实验: ①准确称取3.390g样品与足量稀盐酸充分反应,生成CO20.560L(已换算成标准状况下) ②另取一定量样品在空气中加热,样品的固体残留率( 。
所以,,从而得到其化学组成为; Mg OH 2 4MgCO 4H O 3 2
(4)因为MgCO3中Mg的含量比碱式碳酸镁的含量高,因此,混有MgCO3后, Mg的含量升高。
15.(10分)医用氯化钙可用于生产补钙、抗过敏和消炎等药物。以工业碳酸钙 (含有少量Na+、Al3+、Fe3+等杂质)生产医药级二水合氯化钙(CaCl2· 2H2O的 质量分数为97.0%~103.0%)的主要流程如下:
20(10分)以水氯镁石(主要成分为MgCl2 6H 2O )为原料: 生产碱式碳酸镁的主要流程如下
H 2O
水氯 镁石
NH3
预氨化
NH3 NH 4 HCO3
滤液
、
溶解
沉淀镁
热水解
过滤
碱式 碳酸镁
洗涤、低温干燥
(1) 上述流程中,检验沉淀镁是否完全的方法是------------- ▲ -------------。 (2)上述流程中的滤液浓缩结晶,所得主要固体物质的化学式为 ▲ 。 (3)高温煅烧碱式碳酸镁得 MgO 。取碱式碳酸镁4.66g,高温煅烧至恒重,得到固 体2.00g和标准状况下 CO2 0.896L,通过计算确定碱式碳酸镁的化学式▲ 。 (4)若热水解不完全,所得碱式碳酸镁中将混有 MgCO3,则产品中镁的质量分数 ▲ (填 “升高”、“降低”或“不变”)。
(1)①铜帽溶解时加入H2O2的目的是
(用化学方程式表示)。 。
②铜帽溶解后需将溶液中过量H2O2除去。除去H2O2的简便方法是
(2)为确定加入锌灰(主要成分为Zn、ZnO,杂质为铁及其氧化物)含量,实验中需测定除
去H2O2后溶液中Cu2+的含量。实验操作为:准确量取a ml的含有Cu2+的溶液于带塞锥形 瓶中,加适量水稀释,调节pH=3~4,加入过量KI,用c mol/lNa2S2O3标准溶液滴定至终 点耗Na2S2O3 b ml。上述过程中的离子方程式如下: 2Cu2++4I-=2CuI(白色)↓+I2 I2+2S2O32-=2I-+S4O62- (填“偏高”“偏 ①溶液中Cu2+的含量为------------(g/ml) ②若滴定前溶液中H2O2没有除尽,所测定的Cu2+的含量将会 低”“不变”)。
反应后溶液中:n(OHˉ)= 0.1 L×0.1 mol·L -1 =0.01 mol 反应后溶液中的溶质为NaCl、NaAlO2、NaOH。根据离子电荷守衡: n(Clˉ)+ n(OHˉ)+ n(AlO2ˉ)= n(Na+) 0.1 mol+0.01 mol+ n(AlO2ˉ)= 0.12 mol n(AlO2ˉ)= 0.01 mol n(Al3+)︰n(Mg2+)︰n(CO32ˉ)= 0.01 mol︰0.03 mol︰0.005 mol=2︰6︰1 即AlaMgb· (CO3) c· (OH)d· eH2O中a=2,b = 6 c =1 根据分子中化合价代数和为零,得d =16 得化学式Al2Mg6· CO3· (OH)16 · e H2O Al2Mg6· CO3· (OH)16的相对分子质量为:530 3.01 g样品的物质的量是0.005 mol m(结晶水)= 3.01 g –530 g· mol-1×0.005 mol = 0.36 g n(结晶水)= 0.36g 0.02 mol 18g m ol1 可求出Al2Mg6· CO3· (OH)16式:CaCl2· 2H2O ~ 2AgNO3 147 2 α×0.7500×25/250 0.05000×0.02039 解得:α=0.9991=99.9% ③根据反应:CaCl2· 2H2O ~ 2Cl-~ 2AgNO3 若Cl-偏多,则滴定的结果就会偏高,所以样品中若混有含氯量高于CaCl2的 或CaCl2· 2H2O 晶体中的结晶水失去一部分都能使CaCl2· 2H2O的质量分数偏高
固体样品的剩余质量/固体样品的起始质量×100%)
随温度的变化如右图所示(样品在2700C时已完全失去结晶水,6000C以上残留固体为 金属氧化物的混合物)根据以上实验数据计算碱式碳酸铝镁样品中的n(OH-): n(CO32-)
(写出计算过程)。
19.(15分)废弃物的综合利用既有利于节约资源,又有利于保护环境。实验室利用废弃旧电 池的铜帽(Zn、Cu总含量约为99%)回收铜并制备ZnO的部分实验过程如下:
4.66g 4.00 102 mol 44g mol 1 2.00g 2 n H2O 5.00 10 mol 1 18g mol
n MgO : n CO2 : n H2O 5.00 102:4.00 102 :5.00 102 5: 4:5
24.(6分)黄铜矿的主要成分X是由Cu、Fe、S三种元素组成的复盐,其中Cu、 Fe两种元素的质量比为8:7;将m g X粉末全部溶于200 mL的浓HNO3,反应后 的溶液加水稀释至2.12 L时测得其pH为0;将稀释后的溶液分为两等份,向其 中一份溶液中滴加6.05 mol/L的NaOH溶液,向另一份溶液中滴加0.600 mol/L Ba(NO3)2溶液,两溶液中均生成沉淀,且沉淀的质量随所加溶液的体积变化 如下图所示:
(1)除杂操作是加入氢氧化钙,调节溶液的pH为8.0~8.5,以除去溶液中的少量 Al3+、Fe3+。检验Fe(OH)3是否沉淀完全的实验操作是 。 取少量上层清液,滴加KSCN溶液,若不出现血红色,表明Fe(OH)3 沉淀完全 (2)酸化操作是加入盐酸,调节溶液的pH为4,其目的有:①将溶液中的少量 CO2 Ca(OH)2 转化为CaCl2;②防止Ca2+在蒸发时水解;③防止溶液吸收空气中的 。 (3)测定样品中Cl-含量的方法是:a.称取0.7500g样品,溶解,在250mL容量瓶 中定容;b.量取25.00mL待测液于锥形瓶中;c.用0.05000mol· L-1 AgNO3 溶液 滴定至终点,消耗AgNO3 溶液体积的平均值为20.39mL。 ①计算上述样品中CaCl2· 2H2O的质量分数为: 99.9% 。 ②若用上述方法测定的样品中CaCl2· 2H2O的质量分数偏高(测定过程中产生的误差可 忽略),其可能原因有: 样品中存在少量的 ; 。NaCl ,少量CaCl2· 2H2O 失水
铝碳酸镁[AlaMgb· (CO3)c· (OH)d· eH2O]用于治疗慢性胃炎。称取3.01 g铝碳酸镁样品, 溶于50 mL 2 mol·L -1的盐酸(过量),收集到气体112 mL(标准状况);往所得 溶液中加入40 mL 3 mol·L-1的NaOH溶液,过滤,将所得沉淀洗涤、干燥、称量得 固体1.74 g;再将滤液稀释到100 mL,测得溶液中OHˉ的浓度为0.1 mol·L -1。由计 算可以确定e的值为 A.4 B.5 C.7 D. 8
⑴ 请通过计算确定m的值; ⑵ X的摩尔质量为368 g/mol,请确定X的化学式。
⑴ 解:依题意,m g X中:n(Cu):n(Fe)=1:1 2n(Cu2+)+3n(Fe3+)=6.05mol/L×0.2 L×21 mol/L×2.12 L 故:n(Cu)=n(Fe)=0.06 mol (2分) 又,n(S)=0.6 mol/L×0.1 L×2=0.12 mol 因此,m g=m(Cu)+m(Fe)+m(S) = 0.06 mol×64 g/mol+0.06 mol×56 g/mol+0.12 mol×32 g/mol= 11.04 g 即m 的值为11.04 (2分) ⑵ 解:设X的化学式为(CuFeS2)n,则: (64+56+32×2)×n=368 n=2,故X的化学式为Cu2Fe2S4 (2分)
